Solution for Problem Set 19-20
|
|
|
- Bruce Potter
- 5 years ago
- Views:
Transcription
1
2 Solution for Problem Set 19-0 compiled by Dan Grin and Nate Bode) April 16, 009 A 19.4 Ion Acoustic Waves [by Xinkai Wu 00] a) The derivation of these equations is trivial, so we omit it here. b) Write the proton density as n = n 0 +δn and substitute it into the equations of part a), keeping only terms linear in δn, u, and Φ. We find δn t + n u 0 z = 0 1) u t = e Φ m p z ) Φ z = e ɛ 0 δn n 0e k B T e Φ ). 3) Plugging the plane-wave solution where δn, u, and Φ are all of the form exp[ikz ωt)] into the above linearized equations, we find iωδn + n 0 iku = 0 4) iωu = e ikφ 5) m p k Φ = e δn n ) 0e Φ. 6) ɛ 0 k B T e For the above algebraic equation to possess a solution, the determinant of its coefficient matrix must vanish, which gives ω k n 0e ) + n 0e k = 0. 7) ɛ 0 k B T e ɛ 0 m p Solving this yields the dispersion relation ) 1/ ) with λ D = ɛ0k BT e n 0e and ωpp = n0e 1/. ɛ 0m p ω = ω pp 1 + 1/k λ D) 1/, 8) 1
3 For long-wavelength, kλ D << 1, one finds which agrees with eq. 0.36). ) 1/ kb T e ω ω pp kλ D = k, 9) m p 19.6 Dispersion and Faraday rotation of pulsar pulses [by Alexei Dvoretskii 000] a) The pulses are limited in time, so they must be composed of a range of frequencies. Such a wave packet will propagate at the group velocity. For high frequencies, v g = dω ) dk = c 1 ω p ω c 1 ω p ω. 10) The difference in propagation time is given by [ 1 t = dx v g ω H ) 1 ]. v g ω L ) Simplifying and assuming ω H ω L ω p and constant, we get t = L c Using n = m 3 we get ω p = 10 4 s 1, so indeed ω p ω L ω H. The distance to the pulsar is then L m. b) Consider the Faraday rotation and ω p ω L dχ dx = ω pω c ω c. The overall rotation angle is then given by χ = 1 ω ω c pω c dx. χ t = e ω p B m ω p dx = e nb = e m ndx m < B >. 11) From here the interstellar magnetic field can be estimated to be < B > G.
4 B 19.5 Ion Acoustic Solitons [by Keith Matthews 005] a) You ll note that the u coefficient k B T e /m p ) 1/ is the characteristic velocity of the system, so let s name it v c. Also define α k B T e /e. Then u = v c ɛu 1 + ɛ u +...) Φ = αɛφ 1 + ɛ Φ +...). 1) For an arbitrary field ψ, ψ t = α 1/ ψ ɛ λ D + 3/ ψ ω pp ɛ τ ψ z = ω pp 1/ ψ ɛ. 13) λ D i) From the continuity eqn at leading order ɛ 3/ we find n 1 + u 1 = 0, 14) and at ɛ 5/ order we have u + n 1u 1 ) = 0. 15) ii) To leading order ɛ 3/ the equation of motion produces However eα m pv c = 1 so we have u 1 eα Φ 1 m p v c = 0. We note that λ D ω p p = v c so to ɛ 5/ we have u 1 Φ 1 = 0. 16) u + u 1 τ + 1 u 1 ) = Φ.η 17) iii) en0λd αɛ 0 = 1 so at order ɛ and ɛ Poisson s eqn gives n 1 = Φ 1 18) Φ 1 = 1 n Φ 1 Φ 1 ). 19) 3
5 iv) From Eqs. 14), 16) and 18) we find Taking n 1 = u 1 = Φ 1. 0) of Eq. 19) and invoking Eq. 0) gives 3 n 1 3 = 1 n Φ 1 n 1 ) We find that we can take care of the n 17) and again invoking Eq. 0). Φ n Φ = n 1 τ + 3 Substituting Eq. ) into 1) gives us 3 n 1 3 = 1 n 1 τ + n 1 ). 1) term by adding Eqs. 15) and n 1 ). ) ) n 1. 3) which is just what the doctor ordered. Since n 1 = u 1 = Φ 1 any of the three can solve this KdV equation Exploration of Modes in CMA Diagram [by Kip Thorne 005] a) EM waves in a cold unmagnetized plasma can only propagate when their frequency exceeds the plasma frequency ω p, as can be seen from their dispersion relation ω = ωp + c k. Thus ω = ω p represents a cut-off. There is no turn-on. The unmagnetized condition places us on the x-axis, and the lower limit of the frequency places us to the left of unity. These waves correspond to the diagram in the lower left corner with the modification that with no magnetic field the distinction between X and O dissolves, and R and L modes have the same phase velocity, so the are represented by the same circle. b) Denote REM: Right hand polarized electromagnetic waves LEM: Left hand polarized electromagnetic waves RW: Right hand polarized Whistler waves LW: Left hand polarized Whistler waves. From Fig we can deduce the following relation between V φ = c n and ω. As we move from the lower left to the upper right on the CMA diagram, ω decreases with B and n fixed. So we sequentially encounter ) ) LEM LW LEM) RW ). REM RW 4
6 Figure 1: phase velocity vs. frequency for parallel propagating modes The boundaries corresponding to ɛ L = 0 and ɛ R = 0 are specified in the diagram and correspond to the mode changes above. c) Denote: O: ordinary mode XL: extraordinary lower mode XH: extraordinary hybrid mode XU: extraordinary upper mode. From Fig we can extract the following relation between the phase velocity and the frequency. As ω decreases with B and n fixed, we observe the following pattern ) ) XL XH XH) XL). O O The boundary for these regions are described by ɛ 1 = 0, ɛ 3 = 0, ɛ 1 = 0 respectively. Combined with the previous result b), we obtain the pattern shown in the CMA diagram. On the upper right in CMA one can see that RW becomes XL as we move from parallel to perpendicular mode and LW ceases to exist at some θ < π/. Similar phenomena can be read off from the CMA diagram. C 5
7 Figure : phase velocity vs. frequency for perpendicular propagating modes 19.8 Reflection of Short Waves by the Ionosphere [by Keith Matthews 005] The brute force approach: For adiabatic spatial variations in the index of refraction, Fermat s principle chooses rays of extremal time. This gives simple differential equations Eq. 6.4)) which we express as r component: θ component: d r ds + dñ/dr ñ ) [ dr ) ] ds 1 = 0 ñ dθ ds = C a constant. 4) We choose polar coordinates because, as we shall see, the maximum range is of the order of the radius of the earth r e. s parametrizes the path length. We are told that the electron density is exponential in altitude: n e = n 0 e y/y0. where y is the altitude r r e. From the values given in the problem: y 0 = 1.71 km and n 0 = 10 7 /m 3. From Eq ): ñ = 1 ωpe ω which we write as ñ 1 ηn e where η e m eɛ 0ω. ηn 0 = and r e = km.) Note that ñ = 1 y 0 ñ 1). I define ψ 0 at the point of transmission as the angle between the vertical 6
8 and the outgoing ray. As a result the initial conditions are cos ψ 0 = ) dr ds ) 0, and because sin ψ 0 = r 0 dθ ds ) 0, C = ñ 0 r 0 sin ψ 0. r 0 = r e and I set θ 0 = 0. Numerically integrate with s as the independent variable until rs f ) = r e. I used Mathematica.) The results give r and θ as a function of s, so you have to calculate the range R = r e θs f ). By searching around I found the maximum range to be 6677 km for ψ 0 = 90 deg. It is vital that this ray does not pass through the maximum altitude of y max = 00 km. I found that y top = 5.7 km. 0.1 Two-fluid Equation of Motion [by Xinkai Wu 00] We ll first write things in components and in the end convert back to vector/tensor notation. The Vlasov equation reads f s t + f vj s x j + f aj s = 0. 5) vj We ll make use of the following definitions n s = f s dv v n s u i s = f s v i dv v Ps ik = m s f s v i u i s)v k u k s)dv v = m s f s v i v k dv v m s n s u i s uk s. 6) Multiplying the Vlasov eq. by v k, integrating over velocity space, using integration by parts at various places and the fact that aj v = 0, also using the explicit j expression Eq. 0.3) for the acceleration due to external EM field, we get n s u k s) t + ) P jk s x j m + n su j su k s n sq s E k + u s B) k ) = 0. 7) m s Now using the continuity equation, n s t = x j n su j s), 8) one immediately sees that Eq. 7) reduces to Eq. 0.11) after converting to vector notation. D 7
9 0.4 Landau Contour Deduced Using Laplace Transforms [by Xinkai Wu 000] a) This part is nothing but a definition of Laplace transformation. b) The z-dependence is e ikz, giving / z ik. Also integration by parts gives 0 dte pt F s1 / t = F s1 v, 0) + p 0 dte pt F s1 v, t) 9) Noticing the above facts, we get by Laplace transforming the Vlasov equation: 0 = F s1 v, 0) + p F s1 v, p) + vik F s1 v, p) + q s /m s )F s0ẽp) 30) where s = p, e. Laplace transforming E = ρ/ɛ 0 gives us a second equation: ikẽp) = s q s /ɛ 0 ) dv[f s0 v)/p + F s1 v, p)] = s q s /ɛ 0 ) dv F s1 v, p). 31) Where to get the last equality we ve used the fact that the unperturbed charge density is zero, i.e. the contribution from F s0 v) vanishes. Combining these two equations we easily get Eq. 0.41). c) Setting ip = ω, and plugging Eq. 0.41) into Eq. 0.4), we immediately get Eq. 0.6) without that overall minus sign. E 0.5 Ion Acoustic Dispersion Relation [by Xinkai Wu 000] Recall the definitions of Debye length and plasma frequency for species s: ) ne 1/ ω ps = ɛ 0 m s ) 1/ ɛ0 k B T s λ Ds = ne, 3) and the Maxwellian distribution is ) 1/ ms F s v) = n exp [ m sv ]. 33) πk B T s k B T s 8
10 Now consider the integral For ωr k >> k BT s m s going to use for I p. For ωr k I s ω r k ) P F sv) dv. 34) v ω r /k, I s nk ω see eq. 1.37)), and this is the formula we are r << k BT s m s, I s nms k BT s as can be easily seen by ignoring the ω r /k in the denominator in the integral), and this is the formula we ll use for I e. In our problem, the total F v) is given by F = F e + me m p F p, and thus the total Iω r /k) is given by I = I e + me m p I p. Now that we have the explicit approximate) expressions for F and I, substitution into Eqs. 0.34) and 0.35) yields the desired expressions for ω r and ω i, after approximating F e ω r /k) as n me πk BT e ) 1/ in the numerator of 0.35), which is justified by our assumption ωr k << k BT e m e ). 0.8 Range of Unstable Wave Numbers [by Jeff Atwell] For instability, we need a ζ with ζ i > 0 such that k = Zζ) is real and positive. The corresponding ω = kζ specifies the mode. ζ with ζ i > 0 correspond to points in the interior of the closed curve in the Z plane see Fig. 0.4). So the intersection of the positive Z r axis and the interior of the closed curve gives the range of wave numbers that we are looking for. The shape of this closed curve depends on the distribution function F v). We are told our distribution function has two maxima, v 1 and v, and one minimum, v min. This means that the closed curve in the Z plane crosses the Z r axis three times, twice moving downward, and once moving upward. The curve in Fig. 0.4 happens to be an example of this situation.) Suppose v 1 < v. Then in the case of the closed curve shown in Fig 0.4, we may write the range of wave numbers which have at least one unstable mode as Zv ) < k < Zv min ) where Z is evaluated using Eq. 0.47)). For different shapes of the closed curve i.e. for different combinations of Zv 1 ), Zv min ), and Zv ) being positive and negative) the wave number range will be a bit different, but similar. The steps in going from Eq. 0.47) to Eq. 0.49) work for maxima of F v), in addition to minima. This means that in the case shown in Fig. 0.4 we can instead write the minimum wave number with an unstable mode as for example. e kmin = Zv ) = m e ɛ 0 + [F v) F v )] v v ) dv, 9
11 Solution for Problem Set 19-0 compiled by Dan Grin and Nate Bode) April 16, 009 A 19.4 Ion Acoustic Waves [by Xinkai Wu 00] a) The derivation of these equations is trivial, so we omit it here. b) Write the proton density as n = n 0 +δn and substitute it into the equations of part a), keeping only terms linear in δn, u, and Φ. We find δn t + n u 0 z = 0 1) u t = e Φ m p z ) Φ z = e ɛ 0 δn n 0e k B T e Φ ). 3) Plugging the plane-wave solution where δn, u, and Φ are all of the form exp[ikz ωt)] into the above linearized equations, we find iωδn + n 0 iku = 0 4) iωu = e ikφ 5) m p k Φ = e δn n ) 0e Φ. 6) ɛ 0 k B T e For the above algebraic equation to possess a solution, the determinant of its coefficient matrix must vanish, which gives ω k n 0e ) + n 0e k = 0. 7) ɛ 0 k B T e ɛ 0 m p Solving this yields the dispersion relation ) 1/ ) with λ D = ɛ0k BT e n 0e and ωpp = n0e 1/. ɛ 0m p ω = ω pp 1 + 1/k λ D) 1/, 8) 1
12 For long-wavelength, kλ D << 1, one finds which agrees with eq. 0.36). ) 1/ kb T e ω ω pp kλ D = k, 9) m p 19.6 Dispersion and Faraday rotation of pulsar pulses [by Alexei Dvoretskii 000] a) The pulses are limited in time, so they must be composed of a range of frequencies. Such a wave packet will propagate at the group velocity. For high frequencies, v g = dω ) dk = c 1 ω p ω c 1 ω p ω. 10) The difference in propagation time is given by [ 1 t = dx v g ω H ) 1 ]. v g ω L ) Simplifying and assuming ω H ω L ω p and constant, we get t = L c Using n = m 3 we get ω p = 10 4 s 1, so indeed ω p ω L ω H. The distance to the pulsar is then L m. b) Consider the Faraday rotation and ω p ω L dχ dx = ω pω c ω c. The overall rotation angle is then given by χ = 1 ω ω c pω c dx. χ t = e ω p B m ω p dx = e nb = e m ndx m < B >. 11) From here the interstellar magnetic field can be estimated to be < B > G.
13 B 19.5 Ion Acoustic Solitons [by Keith Matthews 005] a) You ll note that the u coefficient k B T e /m p ) 1/ is the characteristic velocity of the system, so let s name it v c. Also define α k B T e /e. Then u = v c ɛu 1 + ɛ u +...) Φ = αɛφ 1 + ɛ Φ +...). 1) For an arbitrary field ψ, ψ t = α 1/ ψ ɛ λ D + 3/ ψ ω pp ɛ τ ψ z = ω pp 1/ ψ ɛ. 13) λ D i) From the continuity eqn at leading order ɛ 3/ we find n 1 + u 1 = 0, 14) and at ɛ 5/ order we have u + n 1u 1 ) = 0. 15) ii) To leading order ɛ 3/ the equation of motion produces However eα m pv c = 1 so we have u 1 eα Φ 1 m p v c = 0. We note that λ D ω p p = v c so to ɛ 5/ we have u 1 Φ 1 = 0. 16) u + u 1 τ + 1 u 1 ) = Φ.η 17) iii) en0λd αɛ 0 = 1 so at order ɛ and ɛ Poisson s eqn gives n 1 = Φ 1 18) Φ 1 = 1 n Φ 1 Φ 1 ). 19) 3
14 iv) From Eqs. 14), 16) and 18) we find Taking n 1 = u 1 = Φ 1. 0) of Eq. 19) and invoking Eq. 0) gives 3 n 1 3 = 1 n Φ 1 n 1 ) We find that we can take care of the n 17) and again invoking Eq. 0). Φ n Φ = n 1 τ + 3 Substituting Eq. ) into 1) gives us 3 n 1 3 = 1 n 1 τ + n 1 ). 1) term by adding Eqs. 15) and n 1 ). ) ) n 1. 3) which is just what the doctor ordered. Since n 1 = u 1 = Φ 1 any of the three can solve this KdV equation Exploration of Modes in CMA Diagram [by Kip Thorne 005] a) EM waves in a cold unmagnetized plasma can only propagate when their frequency exceeds the plasma frequency ω p, as can be seen from their dispersion relation ω = ωp + c k. Thus ω = ω p represents a cut-off. There is no turn-on. The unmagnetized condition places us on the x-axis, and the lower limit of the frequency places us to the left of unity. These waves correspond to the diagram in the lower left corner with the modification that with no magnetic field the distinction between X and O dissolves, and R and L modes have the same phase velocity, so the are represented by the same circle. b) Denote REM: Right hand polarized electromagnetic waves LEM: Left hand polarized electromagnetic waves RW: Right hand polarized Whistler waves LW: Left hand polarized Whistler waves. From Fig we can deduce the following relation between V φ = c n and ω. As we move from the lower left to the upper right on the CMA diagram, ω decreases with B and n fixed. So we sequentially encounter ) ) LEM LW LEM) RW ). REM RW 4
15 Figure 1: phase velocity vs. frequency for parallel propagating modes The boundaries corresponding to ɛ L = 0 and ɛ R = 0 are specified in the diagram and correspond to the mode changes above. c) Denote: O: ordinary mode XL: extraordinary lower mode XH: extraordinary hybrid mode XU: extraordinary upper mode. From Fig we can extract the following relation between the phase velocity and the frequency. As ω decreases with B and n fixed, we observe the following pattern ) ) XL XH XH) XL). O O The boundary for these regions are described by ɛ 1 = 0, ɛ 3 = 0, ɛ 1 = 0 respectively. Combined with the previous result b), we obtain the pattern shown in the CMA diagram. On the upper right in CMA one can see that RW becomes XL as we move from parallel to perpendicular mode and LW ceases to exist at some θ < π/. Similar phenomena can be read off from the CMA diagram. C 5
16 Figure : phase velocity vs. frequency for perpendicular propagating modes 19.8 Reflection of Short Waves by the Ionosphere [by Keith Matthews 005] The brute force approach: For adiabatic spatial variations in the index of refraction, Fermat s principle chooses rays of extremal time. This gives simple differential equations Eq. 6.4)) which we express as r component: θ component: d r ds + dñ/dr ñ ) [ dr ) ] ds 1 = 0 ñ dθ ds = C a constant. 4) We choose polar coordinates because, as we shall see, the maximum range is of the order of the radius of the earth r e. s parametrizes the path length. We are told that the electron density is exponential in altitude: n e = n 0 e y/y0. where y is the altitude r r e. From the values given in the problem: y 0 = 1.71 km and n 0 = 10 7 /m 3. From Eq ): ñ = 1 ωpe ω which we write as ñ 1 ηn e where η e m eɛ 0ω. ηn 0 = and r e = km.) Note that ñ = 1 y 0 ñ 1). I define ψ 0 at the point of transmission as the angle between the vertical 6
17 and the outgoing ray. As a result the initial conditions are cos ψ 0 = ) dr ds ) 0, and because sin ψ 0 = r 0 dθ ds ) 0, C = ñ 0 r 0 sin ψ 0. r 0 = r e and I set θ 0 = 0. Numerically integrate with s as the independent variable until rs f ) = r e. I used Mathematica.) The results give r and θ as a function of s, so you have to calculate the range R = r e θs f ). By searching around I found the maximum range to be 6677 km for ψ 0 = 90 deg. It is vital that this ray does not pass through the maximum altitude of y max = 00 km. I found that y top = 5.7 km. 0.1 Two-fluid Equation of Motion [by Xinkai Wu 00] We ll first write things in components and in the end convert back to vector/tensor notation. The Vlasov equation reads f s t + f vj s x j + f aj s = 0. 5) vj We ll make use of the following definitions n s = f s dv v n s u i s = f s v i dv v Ps ik = m s f s v i u i s)v k u k s)dv v = m s f s v i v k dv v m s n s u i s uk s. 6) Multiplying the Vlasov eq. by v k, integrating over velocity space, using integration by parts at various places and the fact that aj v = 0, also using the explicit j expression Eq. 0.3) for the acceleration due to external EM field, we get n s u k s) t + ) P jk s x j m + n su j su k s n sq s E k + u s B) k ) = 0. 7) m s Now using the continuity equation, n s t = x j n su j s), 8) one immediately sees that Eq. 7) reduces to Eq. 0.11) after converting to vector notation. D 7
18 0.4 Landau Contour Deduced Using Laplace Transforms [by Xinkai Wu 000] a) This part is nothing but a definition of Laplace transformation. b) The z-dependence is e ikz, giving / z ik. Also integration by parts gives 0 dte pt F s1 / t = F s1 v, 0) + p 0 dte pt F s1 v, t) 9) Noticing the above facts, we get by Laplace transforming the Vlasov equation: 0 = F s1 v, 0) + p F s1 v, p) + vik F s1 v, p) + q s /m s )F s0ẽp) 30) where s = p, e. Laplace transforming E = ρ/ɛ 0 gives us a second equation: ikẽp) = s q s /ɛ 0 ) dv[f s0 v)/p + F s1 v, p)] = s q s /ɛ 0 ) dv F s1 v, p). 31) Where to get the last equality we ve used the fact that the unperturbed charge density is zero, i.e. the contribution from F s0 v) vanishes. Combining these two equations we easily get Eq. 0.41). c) Setting ip = ω, and plugging Eq. 0.41) into Eq. 0.4), we immediately get Eq. 0.6) without that overall minus sign. E 0.5 Ion Acoustic Dispersion Relation [by Xinkai Wu 000] Recall the definitions of Debye length and plasma frequency for species s: ) ne 1/ ω ps = ɛ 0 m s ) 1/ ɛ0 k B T s λ Ds = ne, 3) and the Maxwellian distribution is ) 1/ ms F s v) = n exp [ m sv ]. 33) πk B T s k B T s 8
19 Now consider the integral For ωr k >> k BT s m s going to use for I p. For ωr k I s ω r k ) P F sv) dv. 34) v ω r /k, I s nk ω see eq. 1.37)), and this is the formula we are r << k BT s m s, I s nms k BT s as can be easily seen by ignoring the ω r /k in the denominator in the integral), and this is the formula we ll use for I e. In our problem, the total F v) is given by F = F e + me m p F p, and thus the total Iω r /k) is given by I = I e + me m p I p. Now that we have the explicit approximate) expressions for F and I, substitution into Eqs. 0.34) and 0.35) yields the desired expressions for ω r and ω i, after approximating F e ω r /k) as n me πk BT e ) 1/ in the numerator of 0.35), which is justified by our assumption ωr k << k BT e m e ). 0.8 Range of Unstable Wave Numbers [by Jeff Atwell] For instability, we need a ζ with ζ i > 0 such that k = Zζ) is real and positive. The corresponding ω = kζ specifies the mode. ζ with ζ i > 0 correspond to points in the interior of the closed curve in the Z plane see Fig. 0.4). So the intersection of the positive Z r axis and the interior of the closed curve gives the range of wave numbers that we are looking for. The shape of this closed curve depends on the distribution function F v). We are told our distribution function has two maxima, v 1 and v, and one minimum, v min. This means that the closed curve in the Z plane crosses the Z r axis three times, twice moving downward, and once moving upward. The curve in Fig. 0.4 happens to be an example of this situation.) Suppose v 1 < v. Then in the case of the closed curve shown in Fig 0.4, we may write the range of wave numbers which have at least one unstable mode as Zv ) < k < Zv min ) where Z is evaluated using Eq. 0.47)). For different shapes of the closed curve i.e. for different combinations of Zv 1 ), Zv min ), and Zv ) being positive and negative) the wave number range will be a bit different, but similar. The steps in going from Eq. 0.47) to Eq. 0.49) work for maxima of F v), in addition to minima. This means that in the case shown in Fig. 0.4 we can instead write the minimum wave number with an unstable mode as for example. e kmin = Zv ) = m e ɛ 0 + [F v) F v )] v v ) dv, 9
Waves in plasma. Denis Gialis
 Waves in plasma Denis Gialis This is a short introduction on waves in a non-relativistic plasma. We will consider a plasma of electrons and protons which is fully ionized, nonrelativistic and homogeneous.
Waves in plasma Denis Gialis This is a short introduction on waves in a non-relativistic plasma. We will consider a plasma of electrons and protons which is fully ionized, nonrelativistic and homogeneous.
Chapter 9 WAVES IN COLD MAGNETIZED PLASMA. 9.1 Introduction. 9.2 The Wave Equation
 Chapter 9 WAVES IN COLD MAGNETIZED PLASMA 9.1 Introduction For this treatment, we will regard the plasma as a cold magnetofluid with an associated dielectric constant. We then derive a wave equation using
Chapter 9 WAVES IN COLD MAGNETIZED PLASMA 9.1 Introduction For this treatment, we will regard the plasma as a cold magnetofluid with an associated dielectric constant. We then derive a wave equation using
Waves in plasmas. S.M.Lea
 Waves in plasmas S.M.Lea 17 1 Plasma as an example of a dispersive medium We shall now discuss the propagation of electromagnetic waves through a hydrogen plasm an electrically neutral fluid of protons
Waves in plasmas S.M.Lea 17 1 Plasma as an example of a dispersive medium We shall now discuss the propagation of electromagnetic waves through a hydrogen plasm an electrically neutral fluid of protons
Waves in Cold Plasmas: Two-Fluid Formalism
 Contents 1 Waves in Cold Plasmas: Two-Fluid Formalism 1 1.1 Overview...................................... 1 1. Dielectric Tensor, Wave Equation, and General Dispersion Relation..... 3 1.3 Two-Fluid Formalism...............................
Contents 1 Waves in Cold Plasmas: Two-Fluid Formalism 1 1.1 Overview...................................... 1 1. Dielectric Tensor, Wave Equation, and General Dispersion Relation..... 3 1.3 Two-Fluid Formalism...............................
Fundamentals of wave kinetic theory
 Fundamentals of wave kinetic theory Introduction to the subject Perturbation theory of electrostatic fluctuations Landau damping - mathematics Physics of Landau damping Unmagnetized plasma waves The plasma
Fundamentals of wave kinetic theory Introduction to the subject Perturbation theory of electrostatic fluctuations Landau damping - mathematics Physics of Landau damping Unmagnetized plasma waves The plasma
Cold plasma waves. Waves in non-magnetized plasma Cold plasma dispersion equation Cold plasma wave modes
 Cold plasma waves Waves in non-magnetized plasma Cold plasma dispersion equation Cold plasma wave modes EM wave propagation through and interaction with plasmas belong to central issues of plasma physics.
Cold plasma waves Waves in non-magnetized plasma Cold plasma dispersion equation Cold plasma wave modes EM wave propagation through and interaction with plasmas belong to central issues of plasma physics.
Plasma Processes. m v = ee. (2)
 Plasma Processes In the preceding few lectures, we ve focused on specific microphysical processes. In doing so, we have ignored the effect of other matter. In fact, we ve implicitly or explicitly assumed
Plasma Processes In the preceding few lectures, we ve focused on specific microphysical processes. In doing so, we have ignored the effect of other matter. In fact, we ve implicitly or explicitly assumed
= qe cos(kz ωt). ω sin(αt) This is further averaged over the distribution of initial ( ) α + ω. = 2m k P g(α) sin(αt) g(α) = g(0) + αg (0) + α2 2 g +
 6 Landau Damping 61 Physical Picture of Landau Damping Consider a 1-dimensional electrostatic (longitudinal) wave with k E in the absence of magnetic field Taking v = ẑv and E = ẑe cos(kz ωt), the singleparticle
6 Landau Damping 61 Physical Picture of Landau Damping Consider a 1-dimensional electrostatic (longitudinal) wave with k E in the absence of magnetic field Taking v = ẑv and E = ẑe cos(kz ωt), the singleparticle
Heating and current drive: Radio Frequency
 Heating and current drive: Radio Frequency Dr Ben Dudson Department of Physics, University of York Heslington, York YO10 5DD, UK 13 th February 2012 Dr Ben Dudson Magnetic Confinement Fusion (1 of 26)
Heating and current drive: Radio Frequency Dr Ben Dudson Department of Physics, University of York Heslington, York YO10 5DD, UK 13 th February 2012 Dr Ben Dudson Magnetic Confinement Fusion (1 of 26)
Lectures on basic plasma physics: Kinetic approach
 Lectures on basic plasma physics: Kinetic approach Department of applied physics, Aalto University April 30, 2014 Motivation Layout 1 Motivation 2 Boltzmann equation (a nasty bastard) 3 Vlasov equation
Lectures on basic plasma physics: Kinetic approach Department of applied physics, Aalto University April 30, 2014 Motivation Layout 1 Motivation 2 Boltzmann equation (a nasty bastard) 3 Vlasov equation
Superposition of electromagnetic waves
 Superposition of electromagnetic waves February 9, So far we have looked at properties of monochromatic plane waves. A more complete picture is found by looking at superpositions of many frequencies. Many
Superposition of electromagnetic waves February 9, So far we have looked at properties of monochromatic plane waves. A more complete picture is found by looking at superpositions of many frequencies. Many
Let s consider nonrelativistic electrons. A given electron follows Newton s law. m v = ee. (2)
 Plasma Processes Initial questions: We see all objects through a medium, which could be interplanetary, interstellar, or intergalactic. How does this medium affect photons? What information can we obtain?
Plasma Processes Initial questions: We see all objects through a medium, which could be interplanetary, interstellar, or intergalactic. How does this medium affect photons? What information can we obtain?
Plasma waves in the fluid picture I
 Plasma waves in the fluid picture I Langmuir oscillations and waves Ion-acoustic waves Debye length Ordinary electromagnetic waves General wave equation General dispersion equation Dielectric response
Plasma waves in the fluid picture I Langmuir oscillations and waves Ion-acoustic waves Debye length Ordinary electromagnetic waves General wave equation General dispersion equation Dielectric response
AST 553. Plasma Waves and Instabilities. Course Outline. (Dated: December 4, 2018)
 AST 553. Plasma Waves and Instabilities Course Outline (Dated: December 4, 2018) I. INTRODUCTION Basic concepts Waves in plasmas as EM field oscillations Maxwell s equations, Gauss s laws as initial conditions
AST 553. Plasma Waves and Instabilities Course Outline (Dated: December 4, 2018) I. INTRODUCTION Basic concepts Waves in plasmas as EM field oscillations Maxwell s equations, Gauss s laws as initial conditions
Solution for Problem Set 21
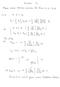 Solution for Problem Set 21 (compiled by Nate Bode April 24, 2009 A 21.1 Non-resonant Particle Energy in Wave [by Keith Matthews adapted from Chris Hirata] The rate of change of the non-resonant electron
Solution for Problem Set 21 (compiled by Nate Bode April 24, 2009 A 21.1 Non-resonant Particle Energy in Wave [by Keith Matthews adapted from Chris Hirata] The rate of change of the non-resonant electron
MEMORANDUM-4. n id (n 2 + n2 S) 0 n n 0. Det[ɛ(ω, k)]=0 gives the Dispersion relation for waves in a cold magnetized plasma: ω 2 pα ω 2 cα ω2, ω 2
![MEMORANDUM-4. n id (n 2 + n2 S) 0 n n 0. Det[ɛ(ω, k)]=0 gives the Dispersion relation for waves in a cold magnetized plasma: ω 2 pα ω 2 cα ω2, ω 2 MEMORANDUM-4. n id (n 2 + n2 S) 0 n n 0. Det[ɛ(ω, k)]=0 gives the Dispersion relation for waves in a cold magnetized plasma: ω 2 pα ω 2 cα ω2, ω 2](/thumbs/88/116941429.jpg) Fundamental dispersion relation MEMORANDUM-4 n S) id n n id n + n S) 0 } n n 0 {{ n P } ɛω,k) E x E y E z = 0 Det[ɛω, k)]=0 gives the Dispersion relation for waves in a cold magnetized plasma: n P ) [
Fundamental dispersion relation MEMORANDUM-4 n S) id n n id n + n S) 0 } n n 0 {{ n P } ɛω,k) E x E y E z = 0 Det[ɛω, k)]=0 gives the Dispersion relation for waves in a cold magnetized plasma: n P ) [
Wave propagation in an inhomogeneous plasma
 DRAFT Wave propagation in an inhomogeneous plasma Felix I. Parra Rudolf Peierls Centre for Theoretical Physics, University of Oxford, Oxford OX NP, UK This version is of 7 February 208. Introduction In
DRAFT Wave propagation in an inhomogeneous plasma Felix I. Parra Rudolf Peierls Centre for Theoretical Physics, University of Oxford, Oxford OX NP, UK This version is of 7 February 208. Introduction In
Scattering of ECRF waves by edge density fluctuations and blobs
 PSFC/JA-14-7 Scattering of ECRF waves by edge density fluctuations and blobs A. K. Ram and K. Hizanidis a June 2014 Plasma Science and Fusion Center, Massachusetts Institute of Technology Cambridge, MA
PSFC/JA-14-7 Scattering of ECRF waves by edge density fluctuations and blobs A. K. Ram and K. Hizanidis a June 2014 Plasma Science and Fusion Center, Massachusetts Institute of Technology Cambridge, MA
Gravitational radiation
 Lecture 28: Gravitational radiation Gravitational radiation Reading: Ohanian and Ruffini, Gravitation and Spacetime, 2nd ed., Ch. 5. Gravitational equations in empty space The linearized field equations
Lecture 28: Gravitational radiation Gravitational radiation Reading: Ohanian and Ruffini, Gravitation and Spacetime, 2nd ed., Ch. 5. Gravitational equations in empty space The linearized field equations
Space Physics. ELEC-E4520 (5 cr) Teacher: Esa Kallio Assistant: Markku Alho and Riku Järvinen. Aalto University School of Electrical Engineering
 Space Physics ELEC-E4520 (5 cr) Teacher: Esa Kallio Assistant: Markku Alho and Riku Järvinen Aalto University School of Electrical Engineering The 6 th week: topics Last week: Examples of waves MHD: Examples
Space Physics ELEC-E4520 (5 cr) Teacher: Esa Kallio Assistant: Markku Alho and Riku Järvinen Aalto University School of Electrical Engineering The 6 th week: topics Last week: Examples of waves MHD: Examples
Vlasov-Maxwell Equations and Cold Plasma Waves
 Astronomy 53 Spring 016) uening Bai Mar.,, 016 Vlasov-Maxwell Equations and Cold Plasma Waves The Vlasov-Maxwell equations Consider a plasma as a collection of N charged particles, each particle i has
Astronomy 53 Spring 016) uening Bai Mar.,, 016 Vlasov-Maxwell Equations and Cold Plasma Waves The Vlasov-Maxwell equations Consider a plasma as a collection of N charged particles, each particle i has
Electrodynamics I Final Exam - Part A - Closed Book KSU 2005/12/12 Electro Dynamic
 Electrodynamics I Final Exam - Part A - Closed Book KSU 2005/12/12 Name Electro Dynamic Instructions: Use SI units. Short answers! No derivations here, just state your responses clearly. 1. (2) Write an
Electrodynamics I Final Exam - Part A - Closed Book KSU 2005/12/12 Name Electro Dynamic Instructions: Use SI units. Short answers! No derivations here, just state your responses clearly. 1. (2) Write an
Introduction. Chapter Plasma: definitions
 Chapter 1 Introduction 1.1 Plasma: definitions A plasma is a quasi-neutral gas of charged and neutral particles which exhibits collective behaviour. An equivalent, alternative definition: A plasma is a
Chapter 1 Introduction 1.1 Plasma: definitions A plasma is a quasi-neutral gas of charged and neutral particles which exhibits collective behaviour. An equivalent, alternative definition: A plasma is a
Kinetic Theory of Warm Plasmas
 Contents 22 Kinetic Theory of Warm Plasmas 1 22.1 Overview...................................... 1 22.2 Basic Concepts of Kinetic Theory and its Relationship to Two-Fluid Theory 3 22.2.1 Distribution Function
Contents 22 Kinetic Theory of Warm Plasmas 1 22.1 Overview...................................... 1 22.2 Basic Concepts of Kinetic Theory and its Relationship to Two-Fluid Theory 3 22.2.1 Distribution Function
Vlasov simulations of wave-particle interactions and turbulence in magnetized plasma
 Vlasov simulations of wave-particle interactions and turbulence in magnetized plasma IRF-U, Uppsala, 16 November 2016 Bengt Eliasson ABP Group, Physics Department, SUPA Strathclyde University, UK Collaborators:
Vlasov simulations of wave-particle interactions and turbulence in magnetized plasma IRF-U, Uppsala, 16 November 2016 Bengt Eliasson ABP Group, Physics Department, SUPA Strathclyde University, UK Collaborators:
kg meter ii) Note the dimensions of ρ τ are kg 2 velocity 2 meter = 1 sec 2 We will interpret this velocity in upcoming slides.
 II. Generalizing the 1-dimensional wave equation First generalize the notation. i) "q" has meant transverse deflection of the string. Replace q Ψ, where Ψ may indicate other properties of the medium that
II. Generalizing the 1-dimensional wave equation First generalize the notation. i) "q" has meant transverse deflection of the string. Replace q Ψ, where Ψ may indicate other properties of the medium that
Thermal Energy at the Nanoscale Homework Solution - Week 3
 Thermal Energy at the Nanoscale Homework Solution - Week 3 Spring 3. Graphene ZA mode specific heat (a) The cutoff wavevector K Q is found by equating the number of states in k-space within a circle of
Thermal Energy at the Nanoscale Homework Solution - Week 3 Spring 3. Graphene ZA mode specific heat (a) The cutoff wavevector K Q is found by equating the number of states in k-space within a circle of
arxiv: v2 [nlin.ps] 14 Aug 2016
![arxiv: v2 [nlin.ps] 14 Aug 2016 arxiv: v2 [nlin.ps] 14 Aug 2016](/thumbs/74/70318692.jpg) arxiv:1605.05726v2 [nlin.ps] 14 Aug 2016 Stability of ion acoustic nonlinear waves and solitons in magnetized plasmas Piotr Goldstein and Eryk Infeld Theoretical Physics Division, National Centre for Nuclear
arxiv:1605.05726v2 [nlin.ps] 14 Aug 2016 Stability of ion acoustic nonlinear waves and solitons in magnetized plasmas Piotr Goldstein and Eryk Infeld Theoretical Physics Division, National Centre for Nuclear
Problem Set 10 Solutions
 Massachusetts Institute of Technology Department of Physics Physics 87 Fall 25 Problem Set 1 Solutions Problem 1: EM Waves in a Plasma a Transverse electromagnetic waves have, by definition, E = Taking
Massachusetts Institute of Technology Department of Physics Physics 87 Fall 25 Problem Set 1 Solutions Problem 1: EM Waves in a Plasma a Transverse electromagnetic waves have, by definition, E = Taking
Magnetospheric Physics - Final Exam - Solutions 05/07/2008
 Magnetospheric Physics - Final Exam - Solutions 5/7/8. Dipole magnetic field a Assume the magnetic field of the Earth to be dipolar. Consider a flux tube with a small quadratic cross section in the equatorial
Magnetospheric Physics - Final Exam - Solutions 5/7/8. Dipole magnetic field a Assume the magnetic field of the Earth to be dipolar. Consider a flux tube with a small quadratic cross section in the equatorial
13.1 Ion Acoustic Soliton and Shock Wave
 13 Nonlinear Waves In linear theory, the wave amplitude is assumed to be sufficiently small to ignore contributions of terms of second order and higher (ie, nonlinear terms) in wave amplitude In such a
13 Nonlinear Waves In linear theory, the wave amplitude is assumed to be sufficiently small to ignore contributions of terms of second order and higher (ie, nonlinear terms) in wave amplitude In such a
Lecture10: Plasma Physics 1. APPH E6101x Columbia University
 Lecture10: Plasma Physics 1 APPH E6101x Columbia University Last Lecture - Conservation principles in magnetized plasma frozen-in and conservation of particles/flux tubes) - Alfvén waves without plasma
Lecture10: Plasma Physics 1 APPH E6101x Columbia University Last Lecture - Conservation principles in magnetized plasma frozen-in and conservation of particles/flux tubes) - Alfvén waves without plasma
WaFu Notes Discussions around the cold plasma model
 WaFu Notes Discussions around the cold plasma model Lise-Marie Imbert-Gérard Summer 7 These notes correspond - more or less - to the presentation I gave at the WaFu summer school on July 6th, 7 in Paris.
WaFu Notes Discussions around the cold plasma model Lise-Marie Imbert-Gérard Summer 7 These notes correspond - more or less - to the presentation I gave at the WaFu summer school on July 6th, 7 in Paris.
Derivation of the General Propagation Equation
 Derivation of the General Propagation Equation Phys 477/577: Ultrafast and Nonlinear Optics, F. Ö. Ilday, Bilkent University February 25, 26 1 1 Derivation of the Wave Equation from Maxwell s Equations
Derivation of the General Propagation Equation Phys 477/577: Ultrafast and Nonlinear Optics, F. Ö. Ilday, Bilkent University February 25, 26 1 1 Derivation of the Wave Equation from Maxwell s Equations
Electromagnetic waves in magnetized plasma The dispersion relation
 Electromagnetic waves in magnetized plasma The dispersion relation Bruno Després (LJLL-UPMC) Electromagnetic waves in magnetized plasma The dispersion relation p. 1 / 32 Vlasov-Maxwell Vectors are in bold.
Electromagnetic waves in magnetized plasma The dispersion relation Bruno Després (LJLL-UPMC) Electromagnetic waves in magnetized plasma The dispersion relation p. 1 / 32 Vlasov-Maxwell Vectors are in bold.
Plasma Physics Prof. V. K. Tripathi Department of Physics Indian Institute of Technology, Delhi
 Plasma Physics Prof. V. K. Tripathi Department of Physics Indian Institute of Technology, Delhi Lecture No. # 09 Electromagnetic Wave Propagation Inhomogeneous Plasma (Refer Slide Time: 00:33) Today, I
Plasma Physics Prof. V. K. Tripathi Department of Physics Indian Institute of Technology, Delhi Lecture No. # 09 Electromagnetic Wave Propagation Inhomogeneous Plasma (Refer Slide Time: 00:33) Today, I
Propagation of EM Waves in material media
 Propagation of EM Waves in material media S.M.Lea 09 Wave propagation As usual, we start with Maxwell s equations with no free charges: D =0 B =0 E = B t H = D t + j If we now assume that each field has
Propagation of EM Waves in material media S.M.Lea 09 Wave propagation As usual, we start with Maxwell s equations with no free charges: D =0 B =0 E = B t H = D t + j If we now assume that each field has
PHYS 110B - HW #5 Fall 2005, Solutions by David Pace Equations referenced equations are from Griffiths Problem statements are paraphrased
 PHYS 0B - HW #5 Fall 005, Solutions by David Pace Equations referenced equations are from Griffiths Problem statements are paraphrased [.] Imagine a prism made of lucite (n.5) whose cross-section is a
PHYS 0B - HW #5 Fall 005, Solutions by David Pace Equations referenced equations are from Griffiths Problem statements are paraphrased [.] Imagine a prism made of lucite (n.5) whose cross-section is a
Summer College on Plasma Physics. 30 July - 24 August, The particle-in-cell simulation method: Concept and limitations
 1856-30 2007 Summer College on Plasma Physics 30 July - 24 August, 2007 The particle-in-cell M. E. Dieckmann Institut fuer Theoretische Physik IV, Ruhr-Universitaet, Bochum, Germany The particle-in-cell
1856-30 2007 Summer College on Plasma Physics 30 July - 24 August, 2007 The particle-in-cell M. E. Dieckmann Institut fuer Theoretische Physik IV, Ruhr-Universitaet, Bochum, Germany The particle-in-cell
9 The conservation theorems: Lecture 23
 9 The conservation theorems: Lecture 23 9.1 Energy Conservation (a) For energy to be conserved we expect that the total energy density (energy per volume ) u tot to obey a conservation law t u tot + i
9 The conservation theorems: Lecture 23 9.1 Energy Conservation (a) For energy to be conserved we expect that the total energy density (energy per volume ) u tot to obey a conservation law t u tot + i
Lecture notes 5: Diffraction
 Lecture notes 5: Diffraction Let us now consider how light reacts to being confined to a given aperture. The resolution of an aperture is restricted due to the wave nature of light: as light passes through
Lecture notes 5: Diffraction Let us now consider how light reacts to being confined to a given aperture. The resolution of an aperture is restricted due to the wave nature of light: as light passes through
Light in Matter (Hecht Ch. 3)
 Phys 531 Lecture 3 9 September 2004 Light in Matter (Hecht Ch. 3) Last time, talked about light in vacuum: Maxwell equations wave equation Light = EM wave 1 Today: What happens inside material? typical
Phys 531 Lecture 3 9 September 2004 Light in Matter (Hecht Ch. 3) Last time, talked about light in vacuum: Maxwell equations wave equation Light = EM wave 1 Today: What happens inside material? typical
The Euler Equation of Gas-Dynamics
 The Euler Equation of Gas-Dynamics A. Mignone October 24, 217 In this lecture we study some properties of the Euler equations of gasdynamics, + (u) = ( ) u + u u + p = a p + u p + γp u = where, p and u
The Euler Equation of Gas-Dynamics A. Mignone October 24, 217 In this lecture we study some properties of the Euler equations of gasdynamics, + (u) = ( ) u + u u + p = a p + u p + γp u = where, p and u
Fourier transforms, Generalised functions and Greens functions
 Fourier transforms, Generalised functions and Greens functions T. Johnson 2015-01-23 Electromagnetic Processes In Dispersive Media, Lecture 2 - T. Johnson 1 Motivation A big part of this course concerns
Fourier transforms, Generalised functions and Greens functions T. Johnson 2015-01-23 Electromagnetic Processes In Dispersive Media, Lecture 2 - T. Johnson 1 Motivation A big part of this course concerns
u xx + u yy = 0. (5.1)
 Chapter 5 Laplace Equation The following equation is called Laplace equation in two independent variables x, y: The non-homogeneous problem u xx + u yy =. (5.1) u xx + u yy = F, (5.) where F is a function
Chapter 5 Laplace Equation The following equation is called Laplace equation in two independent variables x, y: The non-homogeneous problem u xx + u yy =. (5.1) u xx + u yy = F, (5.) where F is a function
WAVE PACKETS & SUPERPOSITION
 1 WAVE PACKETS & SUPERPOSITION Reading: Main 9. PH41 Fourier notes 1 x k Non dispersive wave equation x ψ (x,t) = 1 v t ψ (x,t) So far, we know that this equation results from application of Newton s law
1 WAVE PACKETS & SUPERPOSITION Reading: Main 9. PH41 Fourier notes 1 x k Non dispersive wave equation x ψ (x,t) = 1 v t ψ (x,t) So far, we know that this equation results from application of Newton s law
Energy-Conserving Numerical Simulations of Electron Holes in Two-Species Plasmas
 Energy-Conserving Numerical Simulations of Electron Holes in Two-Species Plasmas Yingda Cheng Andrew J. Christlieb Xinghui Zhong March 18, 2014 Abstract In this paper, we apply our recently developed energy-conserving
Energy-Conserving Numerical Simulations of Electron Holes in Two-Species Plasmas Yingda Cheng Andrew J. Christlieb Xinghui Zhong March 18, 2014 Abstract In this paper, we apply our recently developed energy-conserving
Wave Phenomena Physics 15c. Lecture 17 EM Waves in Matter
 Wave Phenomena Physics 15c Lecture 17 EM Waves in Matter What We Did Last Time Reviewed reflection and refraction Total internal reflection is more subtle than it looks Imaginary waves extend a few beyond
Wave Phenomena Physics 15c Lecture 17 EM Waves in Matter What We Did Last Time Reviewed reflection and refraction Total internal reflection is more subtle than it looks Imaginary waves extend a few beyond
Plasmas as fluids. S.M.Lea. January 2007
 Plasmas as fluids S.M.Lea January 2007 So far we have considered a plasma as a set of non intereacting particles, each following its own path in the electric and magnetic fields. Now we want to consider
Plasmas as fluids S.M.Lea January 2007 So far we have considered a plasma as a set of non intereacting particles, each following its own path in the electric and magnetic fields. Now we want to consider
Influence of Generalized (r, q) Distribution Function on Electrostatic Waves
 Commun. Theor. Phys. (Beijing, China) 45 (2006) pp. 550 554 c International Academic Publishers Vol. 45, No. 3, March 15, 2006 Influence of Generalized (r, q) istribution Function on Electrostatic Waves
Commun. Theor. Phys. (Beijing, China) 45 (2006) pp. 550 554 c International Academic Publishers Vol. 45, No. 3, March 15, 2006 Influence of Generalized (r, q) istribution Function on Electrostatic Waves
from which follow by application of chain rule relations y = y (4) ˆL z = i h by constructing θ , find also ˆL x ˆL y and
 9 Scattering Theory II 9.1 Partial wave analysis Expand ψ in spherical harmonics Y lm (θ, φ), derive 1D differential equations for expansion coefficients. Spherical coordinates: x = r sin θ cos φ (1) y
9 Scattering Theory II 9.1 Partial wave analysis Expand ψ in spherical harmonics Y lm (θ, φ), derive 1D differential equations for expansion coefficients. Spherical coordinates: x = r sin θ cos φ (1) y
The hitch in all of this is figuring out the two principal angles and which principal stress goes with which principal angle.
 Mohr s Circle The stress basic transformation equations that we developed allowed us to determine the stresses acting on an element regardless of its orientation as long as we know the basic stresses σx,
Mohr s Circle The stress basic transformation equations that we developed allowed us to determine the stresses acting on an element regardless of its orientation as long as we know the basic stresses σx,
Pulsars and Radio Wave Propagation: Probes of the ISM Wednesday, March 2, 2010
 Pulsars and Radio Wave Propagation: Probes of the ISM Wednesday, March 2, 2010 CONTENTS: 1 Introduction 2 Dispersion Measures A Radio Wave Propagation in a Plasma B Pulse Arrival Times 3 Rotation Measures
Pulsars and Radio Wave Propagation: Probes of the ISM Wednesday, March 2, 2010 CONTENTS: 1 Introduction 2 Dispersion Measures A Radio Wave Propagation in a Plasma B Pulse Arrival Times 3 Rotation Measures
Liouville Equation. q s = H p s
 Liouville Equation In this section we will build a bridge from Classical Mechanics to Statistical Physics. The bridge is Liouville equation. We start with the Hamiltonian formalism of the Classical Mechanics,
Liouville Equation In this section we will build a bridge from Classical Mechanics to Statistical Physics. The bridge is Liouville equation. We start with the Hamiltonian formalism of the Classical Mechanics,
Nonlinear electrostatic structures in unmagnetized pair-ion (fullerene) plasmas
 Nonlinear electrostatic structures in unmagnetized pair-ion (fullerene) plasmas S. Mahmood Theoretical Plasma Physics Division, PINSTECH Islamabad Collaborators: H. Saleem National Center for Physics,
Nonlinear electrostatic structures in unmagnetized pair-ion (fullerene) plasmas S. Mahmood Theoretical Plasma Physics Division, PINSTECH Islamabad Collaborators: H. Saleem National Center for Physics,
PH575 Spring Lecture #26 & 27 Phonons: Kittel Ch. 4 & 5
 PH575 Spring 2009 Lecture #26 & 27 Phonons: Kittel Ch. 4 & 5 PH575 Spring 2009 POP QUIZ Phonons are: A. Fermions B. Bosons C. Lattice vibrations D. Light/matter interactions PH575 Spring 2009 POP QUIZ
PH575 Spring 2009 Lecture #26 & 27 Phonons: Kittel Ch. 4 & 5 PH575 Spring 2009 POP QUIZ Phonons are: A. Fermions B. Bosons C. Lattice vibrations D. Light/matter interactions PH575 Spring 2009 POP QUIZ
Classical electric dipole radiation
 B Classical electric dipole radiation In Chapter a classical model was used to describe the scattering of X-rays by electrons. The equation relating the strength of the radiated to incident X-ray electric
B Classical electric dipole radiation In Chapter a classical model was used to describe the scattering of X-rays by electrons. The equation relating the strength of the radiated to incident X-ray electric
Chapter 3. Head-on collision of ion acoustic solitary waves in electron-positron-ion plasma with superthermal electrons and positrons.
 Chapter 3 Head-on collision of ion acoustic solitary waves in electron-positron-ion plasma with superthermal electrons and positrons. 73 3.1 Introduction The study of linear and nonlinear wave propagation
Chapter 3 Head-on collision of ion acoustic solitary waves in electron-positron-ion plasma with superthermal electrons and positrons. 73 3.1 Introduction The study of linear and nonlinear wave propagation
ELECTROMAGNETISM SUMMARY
 Review of E and B ELECTROMAGNETISM SUMMARY (Rees Chapters 2 and 3) The electric field E is a vector function. E q o q If we place a second test charged q o in the electric field of the charge q, the two
Review of E and B ELECTROMAGNETISM SUMMARY (Rees Chapters 2 and 3) The electric field E is a vector function. E q o q If we place a second test charged q o in the electric field of the charge q, the two
Solutions: Homework 7
 Solutions: Homework 7 Ex. 7.1: Frustrated Total Internal Reflection a) Consider light propagating from a prism, with refraction index n, into air, with refraction index 1. We fix the angle of incidence
Solutions: Homework 7 Ex. 7.1: Frustrated Total Internal Reflection a) Consider light propagating from a prism, with refraction index n, into air, with refraction index 1. We fix the angle of incidence
qb 3 B ( B) r 3 e r = 3 B r e r B = B/ r e r = 3 B ER 3 E r 4
 Magnetospheric Physics - Homework solution, /8/14 18 Gradient and curvature drift (a) A single proton has a parallel and perpendicular energy of 1 kev. Compute (B B) /B 3 and determine the instantaneous
Magnetospheric Physics - Homework solution, /8/14 18 Gradient and curvature drift (a) A single proton has a parallel and perpendicular energy of 1 kev. Compute (B B) /B 3 and determine the instantaneous
RF cavities (Lecture 25)
 RF cavities (Lecture 25 February 2, 2016 319/441 Lecture outline A good conductor has a property to guide and trap electromagnetic field in a confined region. In this lecture we will consider an example
RF cavities (Lecture 25 February 2, 2016 319/441 Lecture outline A good conductor has a property to guide and trap electromagnetic field in a confined region. In this lecture we will consider an example
Electromagneic Waves in a non- Maxwellian Dusty Plasma
 Electromagneic Waves in a non- Maxwellian Dusty Plasma Nazish Rubab PhD student, KF University Graz IWF-OEAW Graz 26 January, 2011 Layout Dusty Plasma Non-Maxwellian Plasma Kinetic Alfven Waves Instability
Electromagneic Waves in a non- Maxwellian Dusty Plasma Nazish Rubab PhD student, KF University Graz IWF-OEAW Graz 26 January, 2011 Layout Dusty Plasma Non-Maxwellian Plasma Kinetic Alfven Waves Instability
THE CONVECTION DIFFUSION EQUATION
 3 THE CONVECTION DIFFUSION EQUATION We next consider the convection diffusion equation ɛ 2 u + w u = f, (3.) where ɛ>. This equation arises in numerous models of flows and other physical phenomena. The
3 THE CONVECTION DIFFUSION EQUATION We next consider the convection diffusion equation ɛ 2 u + w u = f, (3.) where ɛ>. This equation arises in numerous models of flows and other physical phenomena. The
Assignment 8. [η j, η k ] = J jk
![Assignment 8. [η j, η k ] = J jk Assignment 8. [η j, η k ] = J jk](/thumbs/76/73228750.jpg) Assignment 8 Goldstein 9.8 Prove directly that the transformation is canonical and find a generating function. Q 1 = q 1, P 1 = p 1 p Q = p, P = q 1 q We can establish that the transformation is canonical
Assignment 8 Goldstein 9.8 Prove directly that the transformation is canonical and find a generating function. Q 1 = q 1, P 1 = p 1 p Q = p, P = q 1 q We can establish that the transformation is canonical
PLASMA ASTROPHYSICS. ElisaBete M. de Gouveia Dal Pino IAG-USP. NOTES: (references therein)
 PLASMA ASTROPHYSICS ElisaBete M. de Gouveia Dal Pino IAG-USP NOTES:http://www.astro.iag.usp.br/~dalpino (references therein) ICTP-SAIFR, October 7-18, 2013 Contents What is plasma? Why plasmas in astrophysics?
PLASMA ASTROPHYSICS ElisaBete M. de Gouveia Dal Pino IAG-USP NOTES:http://www.astro.iag.usp.br/~dalpino (references therein) ICTP-SAIFR, October 7-18, 2013 Contents What is plasma? Why plasmas in astrophysics?
12A Reflection & Transmission (Normal Incidence)
 12A Reflection & Transmission (Normal Incidence) Topics: Reflection and transmission, boundary conditions, complex exponentials. Summary: Students begin by expressing in exponential notation the boundary
12A Reflection & Transmission (Normal Incidence) Topics: Reflection and transmission, boundary conditions, complex exponentials. Summary: Students begin by expressing in exponential notation the boundary
Electromagnetic Wave Propagation Lecture 13: Oblique incidence II
 Electromagnetic Wave Propagation Lecture 13: Oblique incidence II Daniel Sjöberg Department of Electrical and Information Technology October 2016 Outline 1 Surface plasmons 2 Snel s law in negative-index
Electromagnetic Wave Propagation Lecture 13: Oblique incidence II Daniel Sjöberg Department of Electrical and Information Technology October 2016 Outline 1 Surface plasmons 2 Snel s law in negative-index
Two ion species studies in LAPD * Ion-ion Hybrid Alfvén Wave Resonator
 Two ion species studies in LAPD * Ion-ion Hybrid Alfvén Wave Resonator G. J. Morales, S. T. Vincena, J. E. Maggs and W. A. Farmer UCLA Experiments performed at the Basic Plasma Science Facility (BaPSF)
Two ion species studies in LAPD * Ion-ion Hybrid Alfvén Wave Resonator G. J. Morales, S. T. Vincena, J. E. Maggs and W. A. Farmer UCLA Experiments performed at the Basic Plasma Science Facility (BaPSF)
Lecture 3: Asymptotic Methods for the Reduced Wave Equation
 Lecture 3: Asymptotic Methods for the Reduced Wave Equation Joseph B. Keller 1 The Reduced Wave Equation Let v (t,) satisfy the wave equation v 1 2 v c 2 = 0, (1) (X) t2 where c(x) is the propagation speed
Lecture 3: Asymptotic Methods for the Reduced Wave Equation Joseph B. Keller 1 The Reduced Wave Equation Let v (t,) satisfy the wave equation v 1 2 v c 2 = 0, (1) (X) t2 where c(x) is the propagation speed
Introduction to Plasma Physics
 Mitglied der Helmholtz-Gemeinschaft Introduction to Plasma Physics CERN School on Plasma Wave Acceleration 24-29 November 2014 Paul Gibbon Outline Lecture 1: Introduction Definitions and Concepts Lecture
Mitglied der Helmholtz-Gemeinschaft Introduction to Plasma Physics CERN School on Plasma Wave Acceleration 24-29 November 2014 Paul Gibbon Outline Lecture 1: Introduction Definitions and Concepts Lecture
Review of Fundamental Equations Supplementary notes on Section 1.2 and 1.3
 Review of Fundamental Equations Supplementary notes on Section. and.3 Introduction of the velocity potential: irrotational motion: ω = u = identity in the vector analysis: ϕ u = ϕ Basic conservation principles:
Review of Fundamental Equations Supplementary notes on Section. and.3 Introduction of the velocity potential: irrotational motion: ω = u = identity in the vector analysis: ϕ u = ϕ Basic conservation principles:
Dispersion relations, stability and linearization
 Dispersion relations, stability and linearization 1 Dispersion relations Suppose that u(x, t) is a function with domain { < x 0}, and it satisfies a linear, constant coefficient partial differential
Dispersion relations, stability and linearization 1 Dispersion relations Suppose that u(x, t) is a function with domain { < x 0}, and it satisfies a linear, constant coefficient partial differential
Landau Damping Simulation Models
 Landau Damping Simulation Models Hua-sheng XIE (u) huashengxie@gmail.com) Department of Physics, Institute for Fusion Theory and Simulation, Zhejiang University, Hangzhou 310027, P.R.China Oct. 9, 2013
Landau Damping Simulation Models Hua-sheng XIE (u) huashengxie@gmail.com) Department of Physics, Institute for Fusion Theory and Simulation, Zhejiang University, Hangzhou 310027, P.R.China Oct. 9, 2013
Electromagnetic optics!
 1 EM theory Electromagnetic optics! EM waves Monochromatic light 2 Electromagnetic optics! Electromagnetic theory of light Electromagnetic waves in dielectric media Monochromatic light References: Fundamentals
1 EM theory Electromagnetic optics! EM waves Monochromatic light 2 Electromagnetic optics! Electromagnetic theory of light Electromagnetic waves in dielectric media Monochromatic light References: Fundamentals
12. Nonlinear optics I
 1. Nonlinear optics I What are nonlinear-optical effects and why do they occur? Maxwell's equations in a medium Nonlinear-optical media Second-harmonic generation Conservation laws for photons ("Phasematching")
1. Nonlinear optics I What are nonlinear-optical effects and why do they occur? Maxwell's equations in a medium Nonlinear-optical media Second-harmonic generation Conservation laws for photons ("Phasematching")
Relation between Periodic Soliton Resonance and Instability
 Proceedings of Institute of Mathematics of NAS of Ukraine 004 Vol. 50 Part 1 486 49 Relation between Periodic Soliton Resonance and Instability Masayoshi TAJIRI Graduate School of Engineering Osaka Prefecture
Proceedings of Institute of Mathematics of NAS of Ukraine 004 Vol. 50 Part 1 486 49 Relation between Periodic Soliton Resonance and Instability Masayoshi TAJIRI Graduate School of Engineering Osaka Prefecture
Electromagnetic Modeling and Simulation
 Electromagnetic Modeling and Simulation Erin Bela and Erik Hortsch Department of Mathematics Research Experiences for Undergraduates April 7, 2011 Bela and Hortsch (OSU) EM REU 2010 1 / 45 Maxwell s Equations
Electromagnetic Modeling and Simulation Erin Bela and Erik Hortsch Department of Mathematics Research Experiences for Undergraduates April 7, 2011 Bela and Hortsch (OSU) EM REU 2010 1 / 45 Maxwell s Equations
Kinetic Theory of Warm Plasmas
 Contents 22 Kinetic Theory of Warm Plasmas 1 22.1 Overview...................................... 1 22.2 Basic Concepts of Kinetic Theory and its Relationship to Two-FluidTheory 3 22.2.1 Distribution Function
Contents 22 Kinetic Theory of Warm Plasmas 1 22.1 Overview...................................... 1 22.2 Basic Concepts of Kinetic Theory and its Relationship to Two-FluidTheory 3 22.2.1 Distribution Function
Summary of various integrals
 ummary of various integrals Here s an arbitrary compilation of information about integrals Moisés made on a cold ecember night. 1 General things o not mix scalars and vectors! In particular ome integrals
ummary of various integrals Here s an arbitrary compilation of information about integrals Moisés made on a cold ecember night. 1 General things o not mix scalars and vectors! In particular ome integrals
Collisionless Shocks and the Earth s Bow Shock
 Collisionless Shocks and the Earth s Bow Shock Jean-Luc Thiffeault AST 381 Gas Dynamics 17 November 1994 1 Introduction The mean free path for particle collisions in the solar wind at the boundary of the
Collisionless Shocks and the Earth s Bow Shock Jean-Luc Thiffeault AST 381 Gas Dynamics 17 November 1994 1 Introduction The mean free path for particle collisions in the solar wind at the boundary of the
Kinetic, Fluid & MHD Theories
 Lecture 2 Kinetic, Fluid & MHD Theories The Vlasov equations are introduced as a starting point for both kinetic theory and fluid theory in a plasma. The equations of fluid theory are derived by taking
Lecture 2 Kinetic, Fluid & MHD Theories The Vlasov equations are introduced as a starting point for both kinetic theory and fluid theory in a plasma. The equations of fluid theory are derived by taking
Dr. A A Mamun Professor of Physics Jahangirnagar University Dhaka, Bangladesh
 SOLITARY AND SHOCK WAVES IN DUSTY PLASMAS Dr. A A Mamun Professor of Physics Jahangirnagar University Dhaka, Bangladesh OUTLINE Introduction Static Dust: DIA Waves DIA Solitary Waves DIA Shock Waves Mobile
SOLITARY AND SHOCK WAVES IN DUSTY PLASMAS Dr. A A Mamun Professor of Physics Jahangirnagar University Dhaka, Bangladesh OUTLINE Introduction Static Dust: DIA Waves DIA Solitary Waves DIA Shock Waves Mobile
The ideal Maxwellian plasma
 The ideal Maxwellian plasma Dr. L. Conde Departamento de Física Aplicada. E.T.S. Ingenieros Aeronáuticos Universidad Politécnica de Madrid Plasmas are,... The plasma state of matter may be defined as a
The ideal Maxwellian plasma Dr. L. Conde Departamento de Física Aplicada. E.T.S. Ingenieros Aeronáuticos Universidad Politécnica de Madrid Plasmas are,... The plasma state of matter may be defined as a
A Propagating Wave Packet The Group Velocity
 Lecture 7 A Propagating Wave Packet The Group Velocity Phys 375 Overview and Motivation: Last time we looked at a solution to the Schrödinger equation (SE) with an initial condition (,) that corresponds
Lecture 7 A Propagating Wave Packet The Group Velocity Phys 375 Overview and Motivation: Last time we looked at a solution to the Schrödinger equation (SE) with an initial condition (,) that corresponds
Massachusetts Institute of Technology Physics 8.03 Practice Final Exam 3
 Massachusetts Institute of Technology Physics 8.03 Practice Final Exam 3 Instructions Please write your solutions in the white booklets. We will not grade anything written on the exam copy. This exam is
Massachusetts Institute of Technology Physics 8.03 Practice Final Exam 3 Instructions Please write your solutions in the white booklets. We will not grade anything written on the exam copy. This exam is
Classwork IV The Wave Equation in 3D
 Electromagnetism II 20th February 2012 Classwork IV The Wave Equation in 3D So far, we have resolved the components of Maxwell s equations to be able to determine wave solutions. Here, we practise using
Electromagnetism II 20th February 2012 Classwork IV The Wave Equation in 3D So far, we have resolved the components of Maxwell s equations to be able to determine wave solutions. Here, we practise using
1 Assignment 1: Nonlinear dynamics (due September
 Assignment : Nonlinear dynamics (due September 4, 28). Consider the ordinary differential equation du/dt = cos(u). Sketch the equilibria and indicate by arrows the increase or decrease of the solutions.
Assignment : Nonlinear dynamics (due September 4, 28). Consider the ordinary differential equation du/dt = cos(u). Sketch the equilibria and indicate by arrows the increase or decrease of the solutions.
Physics Sep Example A Spin System
 Physics 30 7-Sep-004 4- Example A Spin System In the last lecture, we discussed the binomial distribution. Now, I would like to add a little physical content by considering a spin system. Actually this
Physics 30 7-Sep-004 4- Example A Spin System In the last lecture, we discussed the binomial distribution. Now, I would like to add a little physical content by considering a spin system. Actually this
ELECTROMAGNETIC WAVES
 Physics 4D ELECTROMAGNETIC WAVE Hans P. Paar 26 January 2006 i Chapter 1 Vector Calculus 1.1 Introduction Vector calculus is a branch of mathematics that allows differentiation and integration of (scalar)
Physics 4D ELECTROMAGNETIC WAVE Hans P. Paar 26 January 2006 i Chapter 1 Vector Calculus 1.1 Introduction Vector calculus is a branch of mathematics that allows differentiation and integration of (scalar)
Part VIII. Interaction with Solids
 I with Part VIII I with Solids 214 / 273 vs. long pulse is I with Traditional i physics (ICF ns lasers): heating and creation of long scale-length plasmas Laser reflected at critical density surface Fast
I with Part VIII I with Solids 214 / 273 vs. long pulse is I with Traditional i physics (ICF ns lasers): heating and creation of long scale-length plasmas Laser reflected at critical density surface Fast
Lectures on basic plasma physics: Introduction
 Lectures on basic plasma physics: Introduction Department of applied physics, Aalto University Compiled: January 13, 2016 Definition of a plasma Layout 1 Definition of a plasma 2 Basic plasma parameters
Lectures on basic plasma physics: Introduction Department of applied physics, Aalto University Compiled: January 13, 2016 Definition of a plasma Layout 1 Definition of a plasma 2 Basic plasma parameters
PHYSICS Computational Plasma Physics
 PHYSICS 78 - Computational Plasma Physics INSTRUCTOR Dr. Earl Scime (escime@wvu.edu) 93-34, ext. 1437 Office hours: MW :30 3:30 and whenever door is open Rm 18 & 05 Hodges Hall Class: MWF 1:30-:0 Rm 334
PHYSICS 78 - Computational Plasma Physics INSTRUCTOR Dr. Earl Scime (escime@wvu.edu) 93-34, ext. 1437 Office hours: MW :30 3:30 and whenever door is open Rm 18 & 05 Hodges Hall Class: MWF 1:30-:0 Rm 334
Magnetohydrodynamic waves in a plasma
 Department of Physics Seminar 1b Magnetohydrodynamic waves in a plasma Author: Janez Kokalj Advisor: prof. dr. Tomaž Gyergyek Petelinje, April 2016 Abstract Plasma can sustain different wave phenomena.
Department of Physics Seminar 1b Magnetohydrodynamic waves in a plasma Author: Janez Kokalj Advisor: prof. dr. Tomaž Gyergyek Petelinje, April 2016 Abstract Plasma can sustain different wave phenomena.
Problem set 3. Electromagnetic waves
 Second Year Electromagnetism Michaelmas Term 2017 Caroline Terquem Problem set 3 Electromagnetic waves Problem 1: Poynting vector and resistance heating This problem is not about waves but is useful to
Second Year Electromagnetism Michaelmas Term 2017 Caroline Terquem Problem set 3 Electromagnetic waves Problem 1: Poynting vector and resistance heating This problem is not about waves but is useful to
where the last equality follows from the divergence theorem. Now since we did this for an arbitrary volume τ, it must hold locally:
 8 Electrodynamics Read: Boas Ch. 6, particularly sec. 10 and 11. 8.1 Maxwell equations Some of you may have seen Maxwell s equations on t-shirts or encountered them briefly in electromagnetism courses.
8 Electrodynamics Read: Boas Ch. 6, particularly sec. 10 and 11. 8.1 Maxwell equations Some of you may have seen Maxwell s equations on t-shirts or encountered them briefly in electromagnetism courses.
Math 211, Fall 2014, Carleton College
 A. Let v (, 2, ) (1,, ) 1, 2, and w (,, 3) (1,, ) 1,, 3. Then n v w 6, 3, 2 is perpendicular to the plane, with length 7. Thus n/ n 6/7, 3/7, 2/7 is a unit vector perpendicular to the plane. [The negation
A. Let v (, 2, ) (1,, ) 1, 2, and w (,, 3) (1,, ) 1,, 3. Then n v w 6, 3, 2 is perpendicular to the plane, with length 7. Thus n/ n 6/7, 3/7, 2/7 is a unit vector perpendicular to the plane. [The negation
Electromagnetic waves in free space
 Waveguide notes 018 Electromagnetic waves in free space We start with Maxwell s equations for an LIH medum in the case that the source terms are both zero. = =0 =0 = = Take the curl of Faraday s law, then
Waveguide notes 018 Electromagnetic waves in free space We start with Maxwell s equations for an LIH medum in the case that the source terms are both zero. = =0 =0 = = Take the curl of Faraday s law, then
Phase Synchronization
 Phase Synchronization Lecture by: Zhibin Guo Notes by: Xiang Fan May 10, 2016 1 Introduction For any mode or fluctuation, we always have where S(x, t) is phase. If a mode amplitude satisfies ϕ k = ϕ k
Phase Synchronization Lecture by: Zhibin Guo Notes by: Xiang Fan May 10, 2016 1 Introduction For any mode or fluctuation, we always have where S(x, t) is phase. If a mode amplitude satisfies ϕ k = ϕ k
Physics Dec Time Independent Solutions of the Diffusion Equation
 Physics 301 10-Dec-2004 33-1 Time Independent Solutions of the Diffusion Equation In some cases we ll be interested in the time independent solution of the diffusion equation Why would be interested in
Physics 301 10-Dec-2004 33-1 Time Independent Solutions of the Diffusion Equation In some cases we ll be interested in the time independent solution of the diffusion equation Why would be interested in
