Outline. Calculus for the Life Sciences. Falling Cat 1. Introduction. Lecture Notes Differential Equations and Integr
|
|
|
- Barnaby Ray
- 5 years ago
- Views:
Transcription
1 Calculus for the Life Sciences Joseph M. Mahaffy, Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego State University San Diego, CA jmahaffy Fall 016 (1/58) Outline Examples 5 Modeling 6 Lecture Notes s and Integr (/58) 1 Begin the study of antiderivatives or integrals Previously, studied differential equations that vary linearly with the unknown function (dependent variable) Malthusian growth Radioactive decay Newton s law of cooling Contamination of a lake Time varying (the independent variable) terms entering the equation require other techniques Objects under the influence of gravity Time varying buildup of contaminants in an animal (3/58) The cat has evolved to be a stealthy animal with quick reflexes and extremely good jumping ability Members of the cat family are considered the best mammalian predators on this planet, occupying a very wide range of niches Many of the smaller cats have adapted to hunting in trees (or perhaps larger cats have adapted to ground hunting) Cats evolved a very flexible spine, which aids in their ability to spring for prey, absorb shock from their lightning fast strikes, and rapidly rotate their bodies in mid air With their very sensitive inner ear for balance, which is combined with quick reflexes and a flexible spine, a cat that falls is capable of righting itself very rapidly, insuring that it lands on the ground feet first Lecture Notes s and Integr (4/58)
2 3 - Scientific Studies This property of falling feet first has been admired by humans for many years There was a study in the Annals of Improbable Research (1998) on the number of times a particular cat ended up on its feet when dropped from several different heights There was a scientific study of cats falling out of New York apartments, where paradoxically the cats falling from the highest apartments actually fared better than ones falling from an intermediate height [1] Jared M. Diamond (1988), Why cats have nine lives, Nature 33, pp (5/58) To the left is the dynamics of a cat falling from an inverted position and ending on its feet It has been shown that a cat can react sufficiently fast that this inversion process (which itself has been the subject of detailed studies) can happen in about 0.3 seconds With this information, determine the minimum height from which a cat can be dropped to insure that it lands on its feet Lecture Notes s and Integr (6/58) 4 5 Model for the The physics of the cat rotating during a fall is a moderately complex study Our problem is to find if the cat has sufficient time to right itself Use Mass times acceleration is equal to the sum of all the forces acting on the object Since the cat is falling only a short distance at a fairly low velocity, it is safe to assume that the only force acting on the cat is gravity Model for the Equation for ma = mg m is the mass of the cat a is the acceleration of the cat mg is the force of gravity (assuming up is positive) g is a constant (g = 979 cm/sec at a latitude like San Diego when you add centripetal acceleration to the standard value given for g, which is cm/sec ) (7/58) Lecture Notes s and Integr (8/58)
3 6 7 Recall that acceleration is the derivative of the velocity Velocity is the derivative of position Let h(t) be the height (or position) of the cat at any time t The equation above implies that the height of a cat is governed by the differential equation d h = g This is a second order linear differential equation (9/58) (cont) The height of the cat is found by solving this differential equation with two initial conditions Since the cat is simply falling, assume that the initial velocity starts from rest, so is zero v(0) = h (0) = 0 Let ground level be a height of zero, so the cat begins at some height above ground level, h(0) = h 0 > 0 The problem reduces to solving this initial value problem and finding what values h 0 of produce a solution such that h(0.3) > 0 Lecture Notes s and Integr (10/58) 8 Solution - Acceleration is the derivative of velocity, so find the velocity at any time Thus, solve the first order differential equation v (t) = g with v(0) = 0 What velocity function v(t), which upon differentiation produces g, a constant? We need an antiderivative of a constant The derivative of a straight line produces a constant A straight line with a slope of g is v(t) = gt+c 9 Solution (cont) - : The velocity satisfies v(t) = gt+c Notice that the antiderivative produces an arbitrary constant, since the derivative of any constant is zero The initial conditions find the arbitrary constant The velocity for any time is v(0) = c = 0 v(t) = gt (11/58) Lecture Notes s and Integr (1/58)
4 10 11 Solution - : The velocity is the derivative of the height Find an antiderivative of velocity to determine the height of the cat Solve the initial value problem h (t) = v(t) = gt with h(0) = h 0 We must find an antiderivative of gt Recall that a quadratic function has a linear derivative The general solution of this initial value problem is h(t) = gt +c c arbitrary (13/58) Solution (cont) - : The initial condition gives h(0) = h 0 = c The height of the cat any time t satisfies h(t) = gt +h 0 With g = 979 cm/sec, the equation for height in centimeters is h(t) = h t Evaluate this at t = 0.3 sec and obtain h(0.3) = h (0.3) = h cm Thus, the cat must be higher than 44.1 cm for it to have sufficient time to right itself before hitting the ground (This is about 1.5 feet) Lecture Notes s and Integr (14/58) Examples 1 There is a special class of differential equations where the derivative of the unknown function depends only on a time varying function f(t) (no dependence on y) These differential equations satisfy dy = f(t) The solution to this differential equation is an antiderivative of the function f(t) The antiderivative is also known as the integral The solution of the time varying differential equation is written y(t) = f(t) (15/58) A function F(t) is an antiderivative of f(t) if F (t) = f(t) From the formula for the derivative of t n+1, we see that d (tn+1 ) = (n+1)t n The antiderivative satisfies (n+1) t n = t n+1 The integral formula for t n can be written t n = tn+1 n+1 +C Note that the integral formula has an arbitrary constant C Lecture Notes s and Integr (16/58)
5 Examples Examples 3 The integral of a constant is a linear function k = kt+c Other e kt = ekt k +C = ln t +C t cos(kt) = sin(kt) +C k sin(kt) = cos(kt) +C k (17/58) Let F(t) and G(t) be antiderivatives of f(t) and g(t) and constants k and C Additive Property: (f(t)+g(t)) = f(t)+ Scalar Property: kf(t) = k g(t) = F(t)+G(t)+C f(t) = kf(t)+c Lecture Notes s and Integr (18/58) Integral Example 1 Example 1: Consider the integral (x 3 e 5x + x ) dx Examples (x 3 e 5x + x ) ( ) ( ) x 4 e 5x dx = + x dx 4 5 ( ) = x4 + e 5x x 1 + +C 5 1 = x4 + e 5x 5 x +C Integral Example Example : Consider the integral ( 4sin(x) 3 ) dx x Examples ( 4sin(x) 3 ) ( ) cos(x) dx = 4 3ln(x)+C x = cos(x) 3ln(x)+C (19/58) Lecture Notes s and Integr (0/58)
6 Integral Example 3 Example 3: Consider the integral (3x 4e x) dx Examples Integral Example 4 Example 4: Consider the integral ( sin(3x) 4x 3 ) dx Examples (3x 4e x) x 3) dx = 3( 4( e x )+C 3 = x 3 +4e x +C ( sin(3x) 4x ) ( ) cos(3x) 3 dx = 3 4 = 3 cos(3x) 4x +C = 3 cos(3x)+ x +C x 3 dx (1/58) Lecture Notes s and Integr (/58) Integral Example 5 Examples Integral Example 6 Examples Example 5: Consider the integral ( 3 cos ( t ( 3 cos ( t ) ) 1 t ) 1 t ) = 3( sin ( t 1 = 6 sin ( t )) 1 ln(t)+c ) 1 ln(t)+c Example 6: Consider the integral ( 6 t e t 3) ( ( 6t 1/ e 3) t = 6 t 3/ 3 ) et 3t+C = 4t 3/ 1 et 3t+C (3/58) Lecture Notes s and Integr (4/58)
7 Example 1 DE Example 1: Initial Value Problem Examples dy = 4t e t, y(0) = 10 Example DE Example : Initial Value Problem dy Examples = t sin(t), y(0) = 3 y(t) = (4t e t ) = t + 1 e t +C y(t) = (t sin(t)) = t +cos(t)+c y(0) = 1 +C = 10 so C = 19 y(0) = 1+C = 3 so C = y(t) = t + 1 e t + 19 (5/58) y(t) = t +cos(t)+ Lecture Notes s and Integr (6/58) Example 3 DE Example 3: Initial Value Problem dy Examples = 4 y, y(0) = 5 Rewrite y = (y ), so this linear differential equation Make substitution z(t) = y(t), so z(0) = 5 = 3 dz = z, with z(0) = 3 z(t) = 3e t = y(t) or y(t) = +3e t Example 4 DE Example 4: Initial Value Problem y(t) = dy = 4 t, y(1) = Examples ( ) 4 = 4ln(t)+C t y(1) = 4ln(1)+C = so C = y(t) = 4ln(t)+ (7/58) Lecture Notes s and Integr (8/58)
8 Examples 1 : A ball is thrown vertically with gravity (g = 3 ft/sec ) being the only force acting on the ball (air resistence is ignored) Assume that the ball begins at ground level, h(0) = 0 ft, and is given an initial upward velocity of 64 ft/sec (about 44 mph) Determine the height of the ball, h(t), at any time t 0, and when the ball hits the ground Find the maximum height of the ball and the velocity with which it hits the ground Graph the solution for all time up until the ball hits the ground Examples with the mass of the ball, m, acceleration of the ball, a, and force of gravity, mg, satisfies ma = mg or a = g = 3 Acceleration is the derivative of velocity, so a = dv = 3 Thus, v(t) = 3 = 3t+C The initial velocity is v(0) = 64 ft/sec, so v(0) = C = 64 or v(t) = 64 3t (9/58) Lecture Notes s and Integr (30/58) Examples 3 Solution (cont): Velocity Equation satisfies v(t) = 64 3t Velocity is the derivative of position or height, h(t) Thus, v(t) = dh = 64 3t h(t) = (64 gt) = 64t 16t +C 1 The initial height is h(0) = C 1 = 0 ft, so h(t) = 64t 16t Examples 4 Solution (cont): Height Equation is h(t) = 64t 16t = 16t(t 4) The ball hits the ground at t = 4 sec with v(4) = 64 3(4) = 64 ft/sec At the maximum height, the velocity is zero v(t) = 64 3t = 0 or t = sec The maximum height is h() = 64() 16(4) = 64 ft (31/58) Lecture Notes s and Integr (3/58)
9 Examples 5 Modeling 1 Graph of Height of the Ball h(t) (ft) Height of Ball t (sec) (33/58) - Fish in the Great Lakes Region Fishing is an important recreational activity around the Great Lakes Since the mid-1970s, the Michigan Department of Health has been issuing warnings about eating the fish from the Great Lakes The greatest concern is the buildup of PCBs in fatty tissues PCBs are linked to cancer PCBs have estrogen effects that might disrupt development PCBs have declined 90% since 1975 Lecture Notes s and Integr (34/58) Modeling Modeling 3 - Mercury in the Great Lakes Region Mercury (Hg) is concentrated in the tissues of the fish Mercury, a heavy metal, is a dangerous neurotoxin that is very difficult to remove from the body It concentrates in the tissues of fish, particularly large predatory fish such as Northern Pike, Lake Trout, Bass, and Walleye The primary sources of mercury in the Great Lakes region Runoff of different minerals that are mined Incinerators that burn waste, especially batteries Most batteries no longer contain mercury Bacteria converts mercury into the highly soluble methyl mercury Enters fish by simply passing over their gills Larger fish consume small fish and concentrate mercury (35/58) - Mercury and Health Higher levels of Hg in fish may cause children problems in their developing neural system Mercury in the diet may lead to impaired development of the nervous system and learning disorders There is a warning that young children and pregnant women should limit their consumption to less than one fish per month and avoid the larger, fattier, predatory fishes with some fish caught in certain areas to be avoided all together The fat problem is for the PCBs, not the Hg Others are recommended to limit their consumption to less than one fish a week and avoid eating the larger fish, such as Lake Trout over inches Lecture Notes s and Integr (36/58)
10 Modeling 4 Modeling Modeling 1 - Mercury Buildup in Fish So why do fish build up the dangerous levels of Hg in their tissues? Hg is not easily removed from the system, so when ingested it tends to remain in the body The best way to remove heavy metals is the use of chelating agents Mathematically, this build up is seen as the integral of the ingested Hg over the lifetime of the fish Thus, older and larger fish should have more Hg than the younger fish (37/58) Modeling - Model Weight of a Fish Classic model for growth of a fish (length) is the von Bertalanffy equation The record Lake Trout in Michigan is 7.9 kg (14 cm in length) Assume that the weight of a Lake Trout satisfies the differential equation: dw = 0.015(5 w) with w(0) = 0 This is a Linear with the solution: w(t) = 5 5e 0.015t It takes 5.5 years to reach kg, about 15 years to reach 5 kg, with a limiting level of 5 kg for Lake Trout Lecture Notes s and Integr (38/58) Modeling Modeling Modeling Modeling 3 Graph for Weight of Lake Trout Weight (kg) Weight of Lake Trout Age (yr) (39/58) Modeling - Model for Mercury in a Fish Assume fish eat food roughly proportional to its weight Let H(t) be the amount of Hg (in mg) in a growing Lake Trout Assume the concentration of Hg in a fish s food is constant (though in fact, the larger fish will eat more heavily contaminated, larger fish) The rate of Hg added to the tissues of a fish satisfies the differential equation with k = 0.03 mg/yr: dh = k( 5 5e 0.015t) with H(0) = 0 Lecture Notes s and Integr (40/58)
11 Modeling Modeling 4 Model for : The differential equation is dh = k( 5 5e 0.015t) with H(0) = 0 The right hand side of the differential equation is a function of t only, so solution is found by integrating: Taking antiderivatives: H(t) = k (5 5e 0.015t ) H(t) = 5k ) (t e 0.015t C Modeling Modeling 5 Model for : The solution is ) H(t) = 5k (t e 0.015t C The initial condition gives H(0) = 0, so H(0) = 5k ( C) or C = 00 3 With k = 0.03, the solution becomes H(t) = 0.5(3t+00e 0.015t 00) mg of Hg (41/58) Lecture Notes s and Integr (4/58) Modeling Modeling 6 Modeling Modeling 7 Graph for Mercury in Lake Trout Amount of Mercury (mg) Mercury in Lake Trout Age (yr) Model for : Model gives the amount of Hg in a trout The amount of mercury in an aging Lake Trout increases as it eats more prey containing mercury It is more important to know what the concentration of mercury in the flesh of the Lake Trout that is eaten The concentration of mercury increases in a Lake Trout as it ages It is clear why the Michigan Department of Health advises against eating larger fish (43/58) Lecture Notes s and Integr (44/58)
12 Modeling Modeling 8 1 Concentration of Mercury in Lake Trout The concentration of Hg is measured in µg (of mercury) per gram (of fish) c(t) = H(t) w(t) Concentration of Hg (µ g/g) Concentration of Hg in Lake Trout Age Lecture (yr) Notes s and Integration (45/58) : For many years, lead (Pb) was an additive to paint used to reduce molds and improve adhesion The federal govenment required leaded paint be used in low income housing until the late 1960s As leaded paint is shed or removed, lead enters dust in homes, reaching levels of 0.5% by weight of lead Lead-laden dust is particularly problematic in the development of small children They are exposed to lead from the dust ingested by normal hand-to-mouth play activities (crawling followed by thumb-sucking or playing with toys and sucking on them) Lecture Notes s and Integr (46/58) 3 : Neural Effects The highest exposure to lead is relatively short, but it is a critical time in neural development The heavy metals do not leave the body and are often not discovered until after the child enters school at age 5 and is found to have neurological difficulties The long term effects of lead in a child can be severe Learning disabilities, decreased growth, hyperactivity, impaired hearing, and even brain damage Concentrations as low as 10 µg/dl in the blood results in developmental toxicity (EPA limit dropped to 5 µg/dl in 01) Nerve conduction slows at 0 µg/dl in the blood Vitamin D metabolism and hemoglobin synthesis is impaired at 40 µg/dl in the blood (47/58) Modeling Multiple pharmacokinetic models have been developed Create a model of lead exposure based on a child s activity level Assume that the majority of the lead enters through the ingestion of contaminated dirt The amount of lead ingested depends on the hand-to-mouth activity of the child This activity usually increases from birth to age years, then rapidly declines as other forms of activity replace the hand-to-mouth activities Lecture Notes s and Integr (48/58)
13 4 5 Modeling Activity in a Small Girl Assume that the hand-to-mouth activity of a small girl in the age 0-4 months satisfies the differential equation da = 0.0(1 a) with a(0) = 0 a(t) is the activity time in hours per day, and t is the age in months Solve this differential equation Graph the solution Determine the activity level in hours per day at age 4 months (49/58) Solution for Model of Activity in a Small Girl The differential equation is written: da = 0.0(a 1) with a(0) = 0 The differential equation describing the activity of a child, a(t), is very similar to our study of Newton s law of cooling Make the substitution, z(t) = a(t) 1, with z (t) = a (t), so dz = 0.0z with z(0) = a(0) 1 = 1 The solution is z(t) = 1e 0.0t = a(t) 1 or a(t) = 1(1 e 0.0t ) Lecture Notes s and Integr (50/58) 6 7 Graph of Baby Activity: Note that Activity (a(t) in hrs) a(4) = 1(1 e 0.48 ) = 4.57 hr Hours of Activity Age (months) (51/58) Lead Accumulation in the Child The lead will enter the girl s body proportional to her activity time a(t) = 1(1 e 0.0t ) Bioavailable lead is typically 0.1% of household dust by weight Assume the total amount of lead (P(t)) in her body satisfies the differential equation: dp(t) = ka(t) with P(0) = 0 a(t) is the activity time and k = 00 µg-day/hour of play/month Find the solution P(t) and graph this solution Lecture Notes s and Integr (5/58)
14 8 Lead Accumulation in the Child The model satisfies P(0) = 0 with dp = 00(1(1 e 0.0t )) = 400(1 e 0.0t ) The right hand side of this differential equation only depends on t Integration of this differential equation gives the solution Integration is representative of the accumulation or sum of the past lead acquired through the playing activity Obtain the solution from P(t) = 400 (1 e 0.0t ) 9 Lead Accumulation in the Child P(t) = 400 (1 e 0.0t ) ( ) = e 0.0t ) = 400 (t e 0.0t 0.0 +C = 400 ( t+50e 0.0t +C ) (53/58) Lecture Notes s and Integr (54/58) Graph of Lead Build Up in a Child Lead Accumulation in the Child The inititial condition is ( ) P(0) = 0 = e 0.0(0) +C It follows that C = 50 and the solution is P(t) = 400 ( t+50e 0.0t 50 ), where P(t) is measured in µg accumulated by t months Quantity of Lead in Body (µ g) Lead Content of Child (55/58) Age (months) Lecture Notes s and Integr (56/58)
15 1 13 Concentration of Lead in the Child: The solution above gives the amount of lead in the girl, P(t) = 400 ( t+50e 0.0t 50 ), but it is the concentration that matters Assume that this lead is uniformly distributed throughout the body Find the lead level measured from blood samples at ages one and two Typical measurements are in terms of µg/dl Note that 10 dl of blood weighs about 1 kg, and a girl at age one (1 months) weighs 10 kg, while she weighs about 1 kg at age (4 months) (57/58) Concentration of Lead: From the solution P(t) P(1) = 400 ( 1+50e ) = 3195 µg, Since the girl weighs 10 kg, the concentration is given by c(1) = 3195 µg 10 kg = µg/dl This value is clearly dangerous to neural development A calculation for a girl at age two or 4 months gives P(4) = 400 ( 4+50e ) = 11,854 µg Since the girl weighs 1 kg, the concentration is given by c(4) = This level is considered deadly 11,854 µg 1 kg = µg/dl Lecture Notes s and Integr (58/58)
Math Elementary Differential Equations
 Math 337 - Elementary Differential Equations Joseph M. Mahaffy, jmahaffy@sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego State
Math 337 - Elementary Differential Equations Joseph M. Mahaffy, jmahaffy@sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego State
Outline. Calculus for the Life Sciences. What is a Differential Equation? Introduction. Lecture Notes Introduction to Differential Equa
 Outline Calculus for the Life Sciences Lecture Notes to Differential Equations Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu 1 Department of Mathematics and Statistics Dynamical Systems Group Computational
Outline Calculus for the Life Sciences Lecture Notes to Differential Equations Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu 1 Department of Mathematics and Statistics Dynamical Systems Group Computational
Outline. Calculus for the Life Sciences. Malthusian Growth Model. Introduction. Lecture Notes Separable Differential Equations
 Calculus for the Life Sciences Lecture Notes Outline 1 Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center
Calculus for the Life Sciences Lecture Notes Outline 1 Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center
Outline. Formic Acid
 Outline Calculus for the Life Sciences Lecture Notes and Functions Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu 1 2 Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences
Outline Calculus for the Life Sciences Lecture Notes and Functions Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu 1 2 Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences
Calculus for the Life Sciences
 Calculus for the Life Sciences Lecture Notes and Functions Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center
Calculus for the Life Sciences Lecture Notes and Functions Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center
Math 308 Exam I Practice Problems
 Math 308 Exam I Practice Problems This review should not be used as your sole source of preparation for the exam. You should also re-work all examples given in lecture and all suggested homework problems..
Math 308 Exam I Practice Problems This review should not be used as your sole source of preparation for the exam. You should also re-work all examples given in lecture and all suggested homework problems..
Calculus for the Life Sciences
 Calculus for the Life Sciences Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego State University
Calculus for the Life Sciences Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego State University
Calculus for the Life Sciences
 Improved Calculus for the Life Sciences ntial Equations Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center
Improved Calculus for the Life Sciences ntial Equations Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center
Math 308 Exam I Practice Problems
 Math 308 Exam I Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture and all suggested homework problems..
Math 308 Exam I Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture and all suggested homework problems..
Antiderivatives. Definition A function, F, is said to be an antiderivative of a function, f, on an interval, I, if. F x f x for all x I.
 Antiderivatives Definition A function, F, is said to be an antiderivative of a function, f, on an interval, I, if F x f x for all x I. Theorem If F is an antiderivative of f on I, then every function of
Antiderivatives Definition A function, F, is said to be an antiderivative of a function, f, on an interval, I, if F x f x for all x I. Theorem If F is an antiderivative of f on I, then every function of
APPLICATIONS OF DIFFERENTIATION
 4 APPLICATIONS OF DIFFERENTIATION APPLICATIONS OF DIFFERENTIATION 4.9 Antiderivatives In this section, we will learn about: Antiderivatives and how they are useful in solving certain scientific problems.
4 APPLICATIONS OF DIFFERENTIATION APPLICATIONS OF DIFFERENTIATION 4.9 Antiderivatives In this section, we will learn about: Antiderivatives and how they are useful in solving certain scientific problems.
Solutions to Homework 1, Introduction to Differential Equations, 3450: , Dr. Montero, Spring y(x) = ce 2x + e x
 Solutions to Homewor 1, Introduction to Differential Equations, 3450:335-003, Dr. Montero, Spring 2009 problem 2. The problem says that the function yx = ce 2x + e x solves the ODE y + 2y = e x, and ass
Solutions to Homewor 1, Introduction to Differential Equations, 3450:335-003, Dr. Montero, Spring 2009 problem 2. The problem says that the function yx = ce 2x + e x solves the ODE y + 2y = e x, and ass
Outline Calculus for the Life Sciences II. Pollution in a Lake 1. Introduction. Lecture Notes Numerical Methods for Differential Equations
 Improved Improved Outline Calculus for the Life Sciences II tial Equations Joseph M. Mahaffy, mahaffy@math.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences
Improved Improved Outline Calculus for the Life Sciences II tial Equations Joseph M. Mahaffy, mahaffy@math.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences
Basic Differential Equations
 Unit #15 - Differential Equations Some problems and solutions selected or adapted from Hughes-Hallett Calculus. Basic Differential Equations 1. Show that y = x + sin(x) π satisfies the initial value problem
Unit #15 - Differential Equations Some problems and solutions selected or adapted from Hughes-Hallett Calculus. Basic Differential Equations 1. Show that y = x + sin(x) π satisfies the initial value problem
MATH 135 Calculus 1 Solutions/Answers for Exam 3 Practice Problems November 18, 2016
 MATH 35 Calculus Solutions/Answers for Exam 3 Practice Problems November 8, 206 I. Find the indicated derivative(s) and simplify. (A) ( y = ln(x) x 7 4 ) x Solution: By the product rule and the derivative
MATH 35 Calculus Solutions/Answers for Exam 3 Practice Problems November 8, 206 I. Find the indicated derivative(s) and simplify. (A) ( y = ln(x) x 7 4 ) x Solution: By the product rule and the derivative
Differential Equation (DE): An equation relating an unknown function and one or more of its derivatives.
 Lexicon Differential Equation (DE): An equation relating an unknown function and one or more of its derivatives. Ordinary Differential Equation (ODE): A differential equation that contains only ordinary
Lexicon Differential Equation (DE): An equation relating an unknown function and one or more of its derivatives. Ordinary Differential Equation (ODE): A differential equation that contains only ordinary
What will you learn?
 Section 2.2 Basic Differentiation Rules & Rates of Change Calc What will you learn? Find the derivative using the Constant Rule Find the derivative using the Power Rule Find the derivative using the Constant
Section 2.2 Basic Differentiation Rules & Rates of Change Calc What will you learn? Find the derivative using the Constant Rule Find the derivative using the Power Rule Find the derivative using the Constant
A. 1 B. 2 C. 4.5 D. 7 E. 8
 Calculus & Advanced Topics Spring 2011 1. The derivative of x 2 cos(x) is 2x sin(x) x 2 sin(x) 2x cos(x) x 2 sin(x) 2x sin(x) 2x cos(x) 2. 1 2 4.5 7 8 3. 0 1 6/5 3/2 undefined 4. Find the derivative of
Calculus & Advanced Topics Spring 2011 1. The derivative of x 2 cos(x) is 2x sin(x) x 2 sin(x) 2x cos(x) x 2 sin(x) 2x sin(x) 2x cos(x) 2. 1 2 4.5 7 8 3. 0 1 6/5 3/2 undefined 4. Find the derivative of
Calculus for the Life Sciences
 Calculus for the Life Sciences Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego State University
Calculus for the Life Sciences Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego State University
Chapter 2 Notes, Kohler & Johnson 2e
 Contents 2 First Order Differential Equations 2 2.1 First Order Equations - Existence and Uniqueness Theorems......... 2 2.2 Linear First Order Differential Equations.................... 5 2.2.1 First
Contents 2 First Order Differential Equations 2 2.1 First Order Equations - Existence and Uniqueness Theorems......... 2 2.2 Linear First Order Differential Equations.................... 5 2.2.1 First
Outline. Calculus for the Life Sciences. Crow Predation on Whelks. Introduction. Lecture Notes Optimization. Joseph M. Mahaffy,
 Calculus for the Life Sciences Lecture Notes Optimization Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center
Calculus for the Life Sciences Lecture Notes Optimization Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center
Lecture Notes in Mathematics. Arkansas Tech University Department of Mathematics
 Lecture Notes in Mathematics Arkansas Tech University Department of Mathematics Introductory Notes in Ordinary Differential Equations for Physical Sciences and Engineering Marcel B. Finan c All Rights
Lecture Notes in Mathematics Arkansas Tech University Department of Mathematics Introductory Notes in Ordinary Differential Equations for Physical Sciences and Engineering Marcel B. Finan c All Rights
CHAPTER 1. First-Order Differential Equations and Their Applications. 1.1 Introduction to Ordinary Differential Equations
 CHAPTER 1 First-Order Differential Equations and Their Applications 1.1 Introduction to Ordinary Differential Equations Differential equations are found in many areas of mathematics, science, and engineering.
CHAPTER 1 First-Order Differential Equations and Their Applications 1.1 Introduction to Ordinary Differential Equations Differential equations are found in many areas of mathematics, science, and engineering.
1. The accumulated net change function or area-so-far function
 Name: Section: Names of collaborators: Main Points: 1. The accumulated net change function ( area-so-far function) 2. Connection to antiderivative functions: the Fundamental Theorem of Calculus 3. Evaluating
Name: Section: Names of collaborators: Main Points: 1. The accumulated net change function ( area-so-far function) 2. Connection to antiderivative functions: the Fundamental Theorem of Calculus 3. Evaluating
Differential Equations
 Chapter 7 Differential Equations 7. An Introduction to Differential Equations Motivating Questions In this section, we strive to understand the ideas generated by the following important questions: What
Chapter 7 Differential Equations 7. An Introduction to Differential Equations Motivating Questions In this section, we strive to understand the ideas generated by the following important questions: What
Differential Equations & Separation of Variables
 Differential Equations & Separation of Variables SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should reference Chapter 8. of the recommended textbook (or the equivalent
Differential Equations & Separation of Variables SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should reference Chapter 8. of the recommended textbook (or the equivalent
Applications of the definite integral to rates, velocities and densities
 Chapter 4 Applications of the definite integral to rates, velocities and densities 4.1 Two cars, labeled 1 and 2 start side by side and accelerate from rest. Figure 4.1 shows a graph of their velocity
Chapter 4 Applications of the definite integral to rates, velocities and densities 4.1 Two cars, labeled 1 and 2 start side by side and accelerate from rest. Figure 4.1 shows a graph of their velocity
APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS
 APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS PROBLEM SET #1 Related Rates ***Calculators Allowed*** 1. An oil tanker spills oil that spreads in a circular pattern whose radius increases at the rate of
APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS PROBLEM SET #1 Related Rates ***Calculators Allowed*** 1. An oil tanker spills oil that spreads in a circular pattern whose radius increases at the rate of
Lecture Notes for Math 251: ODE and PDE. Lecture 6: 2.3 Modeling With First Order Equations
 Lecture Notes for Math 251: ODE and PDE. Lecture 6: 2.3 Modeling With First Order Equations Shawn D. Ryan Spring 2012 1 Modeling With First Order Equations Last Time: We solved separable ODEs and now we
Lecture Notes for Math 251: ODE and PDE. Lecture 6: 2.3 Modeling With First Order Equations Shawn D. Ryan Spring 2012 1 Modeling With First Order Equations Last Time: We solved separable ODEs and now we
First Order ODEs (cont). Modeling with First Order ODEs
 First Order ODEs (cont). Modeling with First Order ODEs September 11 15, 2017 Bernoulli s ODEs Yuliya Gorb Definition A first order ODE is called a Bernoulli s equation iff it is written in the form y
First Order ODEs (cont). Modeling with First Order ODEs September 11 15, 2017 Bernoulli s ODEs Yuliya Gorb Definition A first order ODE is called a Bernoulli s equation iff it is written in the form y
1 Antiderivatives graphically and numerically
 Math B - Calculus by Hughes-Hallett, et al. Chapter 6 - Constructing antiderivatives Prepared by Jason Gaddis Antiderivatives graphically and numerically Definition.. The antiderivative of a function f
Math B - Calculus by Hughes-Hallett, et al. Chapter 6 - Constructing antiderivatives Prepared by Jason Gaddis Antiderivatives graphically and numerically Definition.. The antiderivative of a function f
Laplace Transform Problems
 AP Calculus BC Name: Laplace Transformation Day 3 2 January 206 Laplace Transform Problems Example problems using the Laplace Transform.. Solve the differential equation y! y = e t, with the initial value
AP Calculus BC Name: Laplace Transformation Day 3 2 January 206 Laplace Transform Problems Example problems using the Laplace Transform.. Solve the differential equation y! y = e t, with the initial value
Antiderivatives and Indefinite Integrals
 Antiderivatives and Indefinite Integrals MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After completing this lesson we will be able to use the definition
Antiderivatives and Indefinite Integrals MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After completing this lesson we will be able to use the definition
Chapter 2 Differentiation. 2.1 Tangent Lines and Their Slopes. Calculus: A Complete Course, 8e Chapter 2: Differentiation
 Chapter 2 Differentiation 2.1 Tangent Lines and Their Slopes 1) Find the slope of the tangent line to the curve y = 4x x 2 at the point (-1, 0). A) -1 2 C) 6 D) 2 1 E) -2 2) Find the equation of the tangent
Chapter 2 Differentiation 2.1 Tangent Lines and Their Slopes 1) Find the slope of the tangent line to the curve y = 4x x 2 at the point (-1, 0). A) -1 2 C) 6 D) 2 1 E) -2 2) Find the equation of the tangent
The Princeton Review AP Calculus BC Practice Test 2
 0 The Princeton Review AP Calculus BC Practice Test CALCULUS BC SECTION I, Part A Time 55 Minutes Number of questions 8 A CALCULATOR MAY NOT BE USED ON THIS PART OF THE EXAMINATION Directions: Solve each
0 The Princeton Review AP Calculus BC Practice Test CALCULUS BC SECTION I, Part A Time 55 Minutes Number of questions 8 A CALCULATOR MAY NOT BE USED ON THIS PART OF THE EXAMINATION Directions: Solve each
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. D) u = - x15 cos (x15) + C
 AP Calculus AB Exam Review Differential Equations and Mathematical Modelling MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the general solution
AP Calculus AB Exam Review Differential Equations and Mathematical Modelling MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the general solution
Unit #1 - Transformation of Functions, Exponentials and Logarithms
 Unit #1 - Transformation of Functions, Exponentials and Logarithms Some problems and solutions selected or adapted from Hughes-Hallett Calculus. Note: This unit, being review of pre-calculus has substantially
Unit #1 - Transformation of Functions, Exponentials and Logarithms Some problems and solutions selected or adapted from Hughes-Hallett Calculus. Note: This unit, being review of pre-calculus has substantially
Unit #9 - Definite Integral Properties, Fundamental Theorem of Calculus
 Unit #9 - Definite Integral Properties, Fundamental Theorem of Calculus Definite Integrals in Modeling Some problems and solutions selected or adapted from Hughes-Hallett Calculus.. The rate at which the
Unit #9 - Definite Integral Properties, Fundamental Theorem of Calculus Definite Integrals in Modeling Some problems and solutions selected or adapted from Hughes-Hallett Calculus.. The rate at which the
CHAPTER 2 Differentiation
 CHAPTER Differentiation Section. The Derivative and the Slope of a Graph............. 9 Section. Some Rules for Differentiation.................. 56 Section. Rates of Change: Velocit and Marginals.............
CHAPTER Differentiation Section. The Derivative and the Slope of a Graph............. 9 Section. Some Rules for Differentiation.................. 56 Section. Rates of Change: Velocit and Marginals.............
9. (1 pt) Chap2/2 3.pg DO NOT USE THE DEFINITION OF DERIVATIVES!! If. find f (x).
 math0spring0-6 WeBWorK assignment number 3 is due : 03/04/0 at 0:00pm MST some kind of mistake Usually you can attempt a problem as many times as you want before the due date However, if you are help Don
math0spring0-6 WeBWorK assignment number 3 is due : 03/04/0 at 0:00pm MST some kind of mistake Usually you can attempt a problem as many times as you want before the due date However, if you are help Don
Motivation and Goals. Modelling with ODEs. Continuous Processes. Ordinary Differential Equations. dy = dt
 Motivation and Goals Modelling with ODEs 24.10.01 Motivation: Ordinary Differential Equations (ODEs) are very important in all branches of Science and Engineering ODEs form the basis for the simulation
Motivation and Goals Modelling with ODEs 24.10.01 Motivation: Ordinary Differential Equations (ODEs) are very important in all branches of Science and Engineering ODEs form the basis for the simulation
5.3 Interpretations of the Definite Integral Student Notes
 5. Interpretations of the Definite Integral Student Notes The Total Change Theorem: The integral of a rate of change is the total change: a b F This theorem is used in many applications. xdx Fb Fa Example
5. Interpretations of the Definite Integral Student Notes The Total Change Theorem: The integral of a rate of change is the total change: a b F This theorem is used in many applications. xdx Fb Fa Example
Displacement and Total Distance Traveled
 Displacement and Total Distance Traveled We have gone over these concepts before. Displacement: This is the distance a particle has moved within a certain time - To find this you simply subtract its position
Displacement and Total Distance Traveled We have gone over these concepts before. Displacement: This is the distance a particle has moved within a certain time - To find this you simply subtract its position
Review for the Final Exam
 Calculus Lia Vas. Integrals. Evaluate the following integrals. (a) ( x 4 x 2 ) dx (b) (2 3 x + x2 4 ) dx (c) (3x + 5) 6 dx (d) x 2 dx x 3 + (e) x 9x 2 dx (f) x dx x 2 (g) xe x2 + dx (h) 2 3x+ dx (i) x
Calculus Lia Vas. Integrals. Evaluate the following integrals. (a) ( x 4 x 2 ) dx (b) (2 3 x + x2 4 ) dx (c) (3x + 5) 6 dx (d) x 2 dx x 3 + (e) x 9x 2 dx (f) x dx x 2 (g) xe x2 + dx (h) 2 3x+ dx (i) x
Example (#1) Example (#1) Example (#2) Example (#2) dv dt
 1. Become familiar with a definition of and terminology involved with differential equations Calculus - Santowski. Solve differential equations with and without initial conditions 3. Apply differential
1. Become familiar with a definition of and terminology involved with differential equations Calculus - Santowski. Solve differential equations with and without initial conditions 3. Apply differential
Section 1.3 Integration
 Section 1.3 Integration Key terms: Integral Constant of integration Fundamental theorem of calculus First order DE One parameter family of solutions General solution Initial value problem Particular solution
Section 1.3 Integration Key terms: Integral Constant of integration Fundamental theorem of calculus First order DE One parameter family of solutions General solution Initial value problem Particular solution
Motion Along a Straight Line
 Chapter 2 Motion Along a Straight Line PowerPoint Lectures for University Physics, Twelfth Edition Hugh D. Young and Roger A. Freedman Lectures by James Pazun Copyright 2008 Pearson Education Inc., publishing
Chapter 2 Motion Along a Straight Line PowerPoint Lectures for University Physics, Twelfth Edition Hugh D. Young and Roger A. Freedman Lectures by James Pazun Copyright 2008 Pearson Education Inc., publishing
Average rates of change May be used to estimate the derivative at a point
 Derivatives Big Ideas Rule of Four: Numerically, Graphically, Analytically, and Verbally Average rate of Change: Difference Quotient: y x f( a+ h) f( a) f( a) f( a h) f( a+ h) f( a h) h h h Average rates
Derivatives Big Ideas Rule of Four: Numerically, Graphically, Analytically, and Verbally Average rate of Change: Difference Quotient: y x f( a+ h) f( a) f( a) f( a h) f( a+ h) f( a h) h h h Average rates
Physics 101 Discussion Week 3 Explanation (2011)
 Physics 101 Discussion Week 3 Explanation (2011) D3-1. Velocity and Acceleration A. 1: average velocity. Q1. What is the definition of the average velocity v? Let r(t) be the total displacement vector
Physics 101 Discussion Week 3 Explanation (2011) D3-1. Velocity and Acceleration A. 1: average velocity. Q1. What is the definition of the average velocity v? Let r(t) be the total displacement vector
Math 106 Answers to Exam 3a Fall 2015
 Math 6 Answers to Exam 3a Fall 5.. Consider the curve given parametrically by x(t) = cos(t), y(t) = (t 3 ) 3, for t from π to π. (a) (6 points) Find all the points (x, y) where the graph has either a vertical
Math 6 Answers to Exam 3a Fall 5.. Consider the curve given parametrically by x(t) = cos(t), y(t) = (t 3 ) 3, for t from π to π. (a) (6 points) Find all the points (x, y) where the graph has either a vertical
Solutions x. Figure 1: g(x) x g(t)dt ; x 0,
 MATH Quiz 4 Spring 8 Solutions. (5 points) Express ln() in terms of ln() and ln(3). ln() = ln( 3) = ln( ) + ln(3) = ln() + ln(3). (5 points) If g(x) is pictured in Figure and..5..5 3 4 5 6 x Figure : g(x)
MATH Quiz 4 Spring 8 Solutions. (5 points) Express ln() in terms of ln() and ln(3). ln() = ln( 3) = ln( ) + ln(3) = ln() + ln(3). (5 points) If g(x) is pictured in Figure and..5..5 3 4 5 6 x Figure : g(x)
Practice Questions From Calculus II. 0. State the following calculus rules (these are many of the key rules from Test 1 topics).
 Math 132. Practice Questions From Calculus II I. Topics Covered in Test I 0. State the following calculus rules (these are many of the key rules from Test 1 topics). (Trapezoidal Rule) b a f(x) dx (Fundamental
Math 132. Practice Questions From Calculus II I. Topics Covered in Test I 0. State the following calculus rules (these are many of the key rules from Test 1 topics). (Trapezoidal Rule) b a f(x) dx (Fundamental
QUESTION 1: Find the derivatives of the following functions. DO NOT TRY TO SIMPLIFY.
 QUESTION 1: Find the derivatives of the following functions. DO NOT TRY TO SIMPLIFY. (a) f(x) =tan(1/x) (b) f(x) =sin(e x ) (c) f(x) =(1+cos(x)) 1/3 (d) f(x) = ln x x +1 QUESTION 2: Using only the definition
QUESTION 1: Find the derivatives of the following functions. DO NOT TRY TO SIMPLIFY. (a) f(x) =tan(1/x) (b) f(x) =sin(e x ) (c) f(x) =(1+cos(x)) 1/3 (d) f(x) = ln x x +1 QUESTION 2: Using only the definition
(a) (x 2) dx (d) (x +1) 2 dx. (e) x 1/2 dx. (h) 1. (3/x) dx. Solution: (a) sin(x) dx. (b) 2 cos(x) dx =4sinx π/4. (c) (x 2) dx = ( x 2 /2 2x ) 3
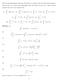 () Use the Fundamental Theorem of Calculus to compute each of the following integrals. The last few are a little more challenging, and will require special care. Some of these integrals may not eist. Eplain
() Use the Fundamental Theorem of Calculus to compute each of the following integrals. The last few are a little more challenging, and will require special care. Some of these integrals may not eist. Eplain
Fall 2016 Math 2B Suggested Homework Problems Solutions
 Fall 016 Math B Suggested Homework Problems Solutions Antiderivatives Exercise : For all x ], + [, the most general antiderivative of f is given by : ( x ( x F(x = + x + C = 1 x x + x + C. Exercise 4 :
Fall 016 Math B Suggested Homework Problems Solutions Antiderivatives Exercise : For all x ], + [, the most general antiderivative of f is given by : ( x ( x F(x = + x + C = 1 x x + x + C. Exercise 4 :
Math , Spring 2010: Exam 2 Solutions 1. #1.) /5 #2.) /15 #3.) /20 #4.) /10 #5.) /10 #6.) /20 #7.) /20 Total: /100
 Math 231.04, Spring 2010: Exam 2 Solutions 1 NAME: Math 231.04 Exam 2 Solutions #1.) /5 #2.) /15 #3.) /20 #4.) /10 #5.) /10 #6.) /20 #7.) /20 Total: /100 Instructions: There are 5 pages and a total of
Math 231.04, Spring 2010: Exam 2 Solutions 1 NAME: Math 231.04 Exam 2 Solutions #1.) /5 #2.) /15 #3.) /20 #4.) /10 #5.) /10 #6.) /20 #7.) /20 Total: /100 Instructions: There are 5 pages and a total of
Math 308, Sections 301, 302, Summer 2008 Lecture 5. 06/6/2008
 Math 308, Sections 301, 302, Summer 2008 Lecture 5. 06/6/2008 Chapter 3. Mathematical methods and numerical methods involving first order equations. Section 3.3 Heating and cooling of buildings. Our goal
Math 308, Sections 301, 302, Summer 2008 Lecture 5. 06/6/2008 Chapter 3. Mathematical methods and numerical methods involving first order equations. Section 3.3 Heating and cooling of buildings. Our goal
Use separation of variables to solve the following differential equations with given initial conditions. y 1 1 y ). y(y 1) = 1
 Chapter 11 Differential Equations 11.1 Use separation of variables to solve the following differential equations with given initial conditions. (a) = 2ty, y(0) = 10 (b) = y(1 y), y(0) = 0.5, (Hint: 1 y(y
Chapter 11 Differential Equations 11.1 Use separation of variables to solve the following differential equations with given initial conditions. (a) = 2ty, y(0) = 10 (b) = y(1 y), y(0) = 0.5, (Hint: 1 y(y
Antiderivatives. DEFINITION: A function F is called an antiderivative of f on an (open) interval I if F (x) = f(x) for all x in I EXAMPLES:
 Antiderivatives 00 Kiryl Tsishchanka DEFINITION: A function F is called an antiderivative of f on an (open) interval I if F (x) = f(x) for all x in I EXAMPLES:. If f(x) = x, then F(x) = 3 x3, since ( )
Antiderivatives 00 Kiryl Tsishchanka DEFINITION: A function F is called an antiderivative of f on an (open) interval I if F (x) = f(x) for all x in I EXAMPLES:. If f(x) = x, then F(x) = 3 x3, since ( )
Review Exercises for Chapter 2
 Review Eercises for Chapter 367 Review Eercises for Chapter. f 1 1 f f f lim lim 1 1 1 1 lim 1 1 1 1 lim 1 1 lim lim 1 1 1 1 1 1 1 1 1 4. 8. f f f f lim lim lim lim lim f 4, 1 4, if < if (a) Nonremovable
Review Eercises for Chapter 367 Review Eercises for Chapter. f 1 1 f f f lim lim 1 1 1 1 lim 1 1 1 1 lim 1 1 lim lim 1 1 1 1 1 1 1 1 1 4. 8. f f f f lim lim lim lim lim f 4, 1 4, if < if (a) Nonremovable
Math Exam 02 Review
 Math 10350 Exam 02 Review 1. A differentiable function g(t) is such that g(2) = 2, g (2) = 1, g (2) = 1/2. (a) If p(t) = g(t)e t2 find p (2) and p (2). (Ans: p (2) = 7e 4 ; p (2) = 28.5e 4 ) (b) If f(t)
Math 10350 Exam 02 Review 1. A differentiable function g(t) is such that g(2) = 2, g (2) = 1, g (2) = 1/2. (a) If p(t) = g(t)e t2 find p (2) and p (2). (Ans: p (2) = 7e 4 ; p (2) = 28.5e 4 ) (b) If f(t)
Please read for extra test points: Thanks for reviewing the notes you are indeed a true scholar!
 Please read for extra test points: Thanks for reviewing the notes you are indeed a true scholar! See me any time B4 school tomorrow and mention to me that you have reviewed your integration notes and you
Please read for extra test points: Thanks for reviewing the notes you are indeed a true scholar! See me any time B4 school tomorrow and mention to me that you have reviewed your integration notes and you
Objective One Scientific Method
 Objective One Scientific Method Planet Mean Distance from Sun (millions of km) The First Five Planets from the Sun Orbital Period of Revolution (Earth time) Period of Rotation (Earth time) Equatorial Diameter
Objective One Scientific Method Planet Mean Distance from Sun (millions of km) The First Five Planets from the Sun Orbital Period of Revolution (Earth time) Period of Rotation (Earth time) Equatorial Diameter
AdvAlg6.4GraphingQuadratics.notebook. March 07, Newton s Formula h(t) = 1 gt 2 + v o t + h o 2. time. initial upward velocity
 Notes Lesson 6 4 Applications of Quadratic Functions Newton s Formula h(t) = 1 gt 2 + v o t + h o 2 Height of object time Constant (accel. due to gravity) *32 ft/sec 2 *9.8 m/sec 2 **MEMORIZE THESE** initial
Notes Lesson 6 4 Applications of Quadratic Functions Newton s Formula h(t) = 1 gt 2 + v o t + h o 2 Height of object time Constant (accel. due to gravity) *32 ft/sec 2 *9.8 m/sec 2 **MEMORIZE THESE** initial
MA 125 CALCULUS I SPRING 2007 April 27, 2007 FINAL EXAM. Name (Print last name first):... Student ID Number (last four digits):...
 CALCULUS I, FINAL EXAM 1 MA 125 CALCULUS I SPRING 2007 April 27, 2007 FINAL EXAM Name (Print last name first):............................................. Student ID Number (last four digits):........................
CALCULUS I, FINAL EXAM 1 MA 125 CALCULUS I SPRING 2007 April 27, 2007 FINAL EXAM Name (Print last name first):............................................. Student ID Number (last four digits):........................
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Chapter Practice Test Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the general solution to the eact differential equation. ) dy dt =
Chapter Practice Test Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the general solution to the eact differential equation. ) dy dt =
WeBWorK demonstration assignment
 WeBWorK demonstration assignment The main purpose of this WeBWorK set is to familiarize yourself with WeBWorK. Here are some hints on how to use WeBWorK effectively: After first logging into WeBWorK change
WeBWorK demonstration assignment The main purpose of this WeBWorK set is to familiarize yourself with WeBWorK. Here are some hints on how to use WeBWorK effectively: After first logging into WeBWorK change
Review for the Final Exam
 Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
Ordinary Differential Equations: Worked Examples with Solutions. Edray Herber Goins Talitha Michal Washington
 Ordinary Differential Equations: Worked Examples with Solutions Edray Herber Goins Talitha Michal Washington July 31, 2016 2 Contents I First Order Differential Equations 5 1 What is a Differential Equation?
Ordinary Differential Equations: Worked Examples with Solutions Edray Herber Goins Talitha Michal Washington July 31, 2016 2 Contents I First Order Differential Equations 5 1 What is a Differential Equation?
Calculus for the Life Sciences
 Calculus for the Life Sciences Integration Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego State
Calculus for the Life Sciences Integration Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego State
Goals: To develop skills needed to find the appropriate differential equations to use as mathematical models.
 Unit #16 : Differential Equations Goals: To develop skills needed to find the appropriate differential equations to use as mathematical models. Differential Equation Modelling - 1 Differential Equation
Unit #16 : Differential Equations Goals: To develop skills needed to find the appropriate differential equations to use as mathematical models. Differential Equation Modelling - 1 Differential Equation
Basic Theory of Differential Equations
 page 104 104 CHAPTER 1 First-Order Differential Equations 16. The following initial-value problem arises in the analysis of a cable suspended between two fixed points y = 1 a 1 + (y ) 2, y(0) = a, y (0)
page 104 104 CHAPTER 1 First-Order Differential Equations 16. The following initial-value problem arises in the analysis of a cable suspended between two fixed points y = 1 a 1 + (y ) 2, y(0) = a, y (0)
MATH 122A FINAL EXAM STUDY GUIDE (Spring 2014)
 MATH A FINAL EXAM STUDY GUIDE (Spring 0) The final eam for spring 0 will have a multiple choice format. This will allow us to offer the final eam as late in the course as possible, giving more in-class
MATH A FINAL EXAM STUDY GUIDE (Spring 0) The final eam for spring 0 will have a multiple choice format. This will allow us to offer the final eam as late in the course as possible, giving more in-class
Chapter. Integration. 1. Antidifferentiation: The Indefinite Integral. 2. Integration by Substitution. 3. Introduction to Differential Equations
 Integration Chapter. Antidifferentiation: The Indefinite Integral 2. Integration by Substitution 3. Introduction to Differential Equations 4. Integration by Parts Chapter Summary and Review Problems Antidifferentiation:
Integration Chapter. Antidifferentiation: The Indefinite Integral 2. Integration by Substitution 3. Introduction to Differential Equations 4. Integration by Parts Chapter Summary and Review Problems Antidifferentiation:
3.8 Exponential Growth and Decay
 3.8 Exponential Growth and Decay Suppose the rate of change of y with respect to t is proportional to y itself. So there is some constant k such that dy dt = ky The only solution to this equation is an
3.8 Exponential Growth and Decay Suppose the rate of change of y with respect to t is proportional to y itself. So there is some constant k such that dy dt = ky The only solution to this equation is an
The acceleration of gravity is constant (near the surface of the earth). So, for falling objects:
 1. Become familiar with a definition of and terminology involved with differential equations Calculus - Santowski. Solve differential equations with and without initial conditions 3. Apply differential
1. Become familiar with a definition of and terminology involved with differential equations Calculus - Santowski. Solve differential equations with and without initial conditions 3. Apply differential
2 If ax + bx + c = 0, then x = b) What are the x-intercepts of the graph or the real roots of f(x)? Round to 4 decimal places.
 Quadratic Formula - Key Background: So far in this course we have solved quadratic equations by the square root method and the factoring method. Each of these methods has its strengths and limitations.
Quadratic Formula - Key Background: So far in this course we have solved quadratic equations by the square root method and the factoring method. Each of these methods has its strengths and limitations.
Mathematics Sample Questions
 Mathematics Sample Questions Directions for questions 1 15 For each of the questions below, choose the best answer from the four choices given. You may use the paper you received as scratch paper. 1. If
Mathematics Sample Questions Directions for questions 1 15 For each of the questions below, choose the best answer from the four choices given. You may use the paper you received as scratch paper. 1. If
Question Instructions Read today's Notes and Learning Goals
 111 Basic: Optimization I (6105689) Question 1 2 3 4 5 6 7 8 9 10 11 12 13 Instructions Read today's Notes and Learning Goals 1. Question Details MinMax Graph 1 [3173669] An object is launched straight
111 Basic: Optimization I (6105689) Question 1 2 3 4 5 6 7 8 9 10 11 12 13 Instructions Read today's Notes and Learning Goals 1. Question Details MinMax Graph 1 [3173669] An object is launched straight
Math 307 E - Summer 2011 Pactice Mid-Term Exam June 18, Total 60
 Math 307 E - Summer 011 Pactice Mid-Term Exam June 18, 011 Name: Student number: 1 10 10 3 10 4 10 5 10 6 10 Total 60 Complete all questions. You may use a scientific calculator during this examination.
Math 307 E - Summer 011 Pactice Mid-Term Exam June 18, 011 Name: Student number: 1 10 10 3 10 4 10 5 10 6 10 Total 60 Complete all questions. You may use a scientific calculator during this examination.
Section , #5. Let Q be the amount of salt in oz in the tank. The scenario can be modeled by a differential equation.
 Section.3.5.3, #5. Let Q be the amount of salt in oz in the tank. The scenario can be modeled by a differential equation dq = 1 4 (1 + sin(t) ) + Q, Q(0) = 50. (1) 100 (a) The differential equation given
Section.3.5.3, #5. Let Q be the amount of salt in oz in the tank. The scenario can be modeled by a differential equation dq = 1 4 (1 + sin(t) ) + Q, Q(0) = 50. (1) 100 (a) The differential equation given
ODE Math 3331 (Summer 2014) June 16, 2014
 Page 1 of 12 Please go to the next page... Sample Midterm 1 ODE Math 3331 (Summer 2014) June 16, 2014 50 points 1. Find the solution of the following initial-value problem 1. Solution (S.O.V) dt = ty2,
Page 1 of 12 Please go to the next page... Sample Midterm 1 ODE Math 3331 (Summer 2014) June 16, 2014 50 points 1. Find the solution of the following initial-value problem 1. Solution (S.O.V) dt = ty2,
Graded and supplementary homework, Math 2584, Section 4, Fall 2017
 Graded and supplementary homework, Math 2584, Section 4, Fall 2017 (AB 1) (a) Is y = cos(2x) a solution to the differential equation d2 y + 4y = 0? dx2 (b) Is y = e 2x a solution to the differential equation
Graded and supplementary homework, Math 2584, Section 4, Fall 2017 (AB 1) (a) Is y = cos(2x) a solution to the differential equation d2 y + 4y = 0? dx2 (b) Is y = e 2x a solution to the differential equation
MATH 18.01, FALL PROBLEM SET #5 SOLUTIONS (PART II)
 MATH 8, FALL 7 - PROBLEM SET #5 SOLUTIONS (PART II (Oct ; Antiderivatives; + + 3 7 points Recall that in pset 3A, you showed that (d/dx tanh x x Here, tanh (x denotes the inverse to the hyperbolic tangent
MATH 8, FALL 7 - PROBLEM SET #5 SOLUTIONS (PART II (Oct ; Antiderivatives; + + 3 7 points Recall that in pset 3A, you showed that (d/dx tanh x x Here, tanh (x denotes the inverse to the hyperbolic tangent
AP Calculus AB Unit 6 Packet Antiderivatives. Antiderivatives
 Antiderivatives Name In mathematics, we use the inverse operation to undo a process. Let s imagine undoing following everyday processes. Process Locking your car Going to sleep Taking out your calculator
Antiderivatives Name In mathematics, we use the inverse operation to undo a process. Let s imagine undoing following everyday processes. Process Locking your car Going to sleep Taking out your calculator
Position, Velocity, Acceleration
 191 CHAPTER 7 Position, Velocity, Acceleration When we talk of acceleration we think of how quickly the velocity is changing. For example, when a stone is dropped its acceleration (due to gravity) is approximately
191 CHAPTER 7 Position, Velocity, Acceleration When we talk of acceleration we think of how quickly the velocity is changing. For example, when a stone is dropped its acceleration (due to gravity) is approximately
Students! (1) with calculator. (2) No calculator
 Students! (1) with calculator Let R be the region bounded by the graphs of y = sin(π x) and y = x 3 4x, as shown in the figure above. (a) Find the area of R. (b) The horizontal line y = splits the region
Students! (1) with calculator Let R be the region bounded by the graphs of y = sin(π x) and y = x 3 4x, as shown in the figure above. (a) Find the area of R. (b) The horizontal line y = splits the region
Lecture 7 - Separable Equations
 Lecture 7 - Separable Equations Separable equations is a very special type of differential equations where you can separate the terms involving only y on one side of the equation and terms involving only
Lecture 7 - Separable Equations Separable equations is a very special type of differential equations where you can separate the terms involving only y on one side of the equation and terms involving only
Boyce/DiPrima/Meade 11 th ed, Ch 1.1: Basic Mathematical Models; Direction Fields
 Boyce/DiPrima/Meade 11 th ed, Ch 1.1: Basic Mathematical Models; Direction Fields Elementary Differential Equations and Boundary Value Problems, 11 th edition, by William E. Boyce, Richard C. DiPrima,
Boyce/DiPrima/Meade 11 th ed, Ch 1.1: Basic Mathematical Models; Direction Fields Elementary Differential Equations and Boundary Value Problems, 11 th edition, by William E. Boyce, Richard C. DiPrima,
Assignment # 3, Math 370, Fall 2018 SOLUTIONS:
 Assignment # 3, Math 370, Fall 2018 SOLUTIONS: Problem 1: Solve the equations: (a) y (1 + x)e x y 2 = xy, (i) y(0) = 1, (ii) y(0) = 0. On what intervals are the solution of the IVP defined? (b) 2y + y
Assignment # 3, Math 370, Fall 2018 SOLUTIONS: Problem 1: Solve the equations: (a) y (1 + x)e x y 2 = xy, (i) y(0) = 1, (ii) y(0) = 0. On what intervals are the solution of the IVP defined? (b) 2y + y
Chapter1. Ordinary Differential Equations
 Chapter1. Ordinary Differential Equations In the sciences and engineering, mathematical models are developed to aid in the understanding of physical phenomena. These models often yield an equation that
Chapter1. Ordinary Differential Equations In the sciences and engineering, mathematical models are developed to aid in the understanding of physical phenomena. These models often yield an equation that
MAT 210 TEST 2 REVIEW (Ch 12 and 13)
 Class: Date: MAT 0 TEST REVIEW (Ch and ) Multiple Choice Identify the choice that best completes the statement or answers the question.. The population P is currently 0,000 and growing at a rate of 7,000
Class: Date: MAT 0 TEST REVIEW (Ch and ) Multiple Choice Identify the choice that best completes the statement or answers the question.. The population P is currently 0,000 and growing at a rate of 7,000
Lesson 6 MA Nick Egbert
 Overview In this lesson we start our stu of differential equations. We start by considering only exponential growth and decay, and in the next lesson we will extend this idea to the general method of separation
Overview In this lesson we start our stu of differential equations. We start by considering only exponential growth and decay, and in the next lesson we will extend this idea to the general method of separation
PHYS1100 Practice problem set, Chapter 2: 6, 10, 13, 17, 22, 24, 25, 34, 42, 50, 55, 65, 71, 82
 PHYS00 Practice problem set, Chapter : 6, 0, 3, 7,, 4, 5, 34, 4, 50, 55, 65, 7, 8.6. Model: We will consider Larry to be a particle. Solve: Since Larry s speed is constant, we can use the following equation
PHYS00 Practice problem set, Chapter : 6, 0, 3, 7,, 4, 5, 34, 4, 50, 55, 65, 7, 8.6. Model: We will consider Larry to be a particle. Solve: Since Larry s speed is constant, we can use the following equation
SCIE1000 Theory and Practice in Science Final Examination, Semester One 2011
 1. Researchers propose two models for estimating the weight of accumulated flammable material in a forest, where weight is measured in appropriate units and t is the number of years since the most recent
1. Researchers propose two models for estimating the weight of accumulated flammable material in a forest, where weight is measured in appropriate units and t is the number of years since the most recent
Chapter 2 Solutions. = 16.1 m/s. = 11.5 m/s m. 180 km = ( ) h. = 2.5 m/s. = 3.3 m/s
 Chapter Solutions *.1 (a) v.30 m/s v x 57.5 m 9.0 m 3.00 s 16.1 m/s (c) v x 57.5 m 0 m 5.00 s 11.5 m/s. (a) Displacement (8.50 10 4 m/h) 35.0 60.0 h + 130 103 m x (49.6 + 130) 10 3 m 180 km Average velocity
Chapter Solutions *.1 (a) v.30 m/s v x 57.5 m 9.0 m 3.00 s 16.1 m/s (c) v x 57.5 m 0 m 5.00 s 11.5 m/s. (a) Displacement (8.50 10 4 m/h) 35.0 60.0 h + 130 103 m x (49.6 + 130) 10 3 m 180 km Average velocity
AP Calculus AB Semester 1 Practice Final
 Class: Date: AP Calculus AB Semester 1 Practice Final Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the limit (if it exists). lim x x + 4 x a. 6
Class: Date: AP Calculus AB Semester 1 Practice Final Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the limit (if it exists). lim x x + 4 x a. 6
PHY2020 Fall 2011, Test 1
 PHY2020 Fall 2011, Test 1 I understand that the University of Florida expects its students to be honest in all their academic work. I agree to adhere to this commitment to academic honesty and understand
PHY2020 Fall 2011, Test 1 I understand that the University of Florida expects its students to be honest in all their academic work. I agree to adhere to this commitment to academic honesty and understand
XXIX Applications of Differential Equations
 MATHEMATICS 01-BNK-05 Advanced Calculus Martin Huard Winter 015 1. Suppose that the rate at which a population of size yt at time t changes is proportional to the amount present. This gives rise to the
MATHEMATICS 01-BNK-05 Advanced Calculus Martin Huard Winter 015 1. Suppose that the rate at which a population of size yt at time t changes is proportional to the amount present. This gives rise to the
