Queens School Physics Department
|
|
|
- Randell Harrison
- 5 years ago
- Views:
Transcription
1 Queens School Physics Deprtment S Bridging Workbook Nme:
2 Chpter : Rerrnging equtions The first step in lerning to mnipulte n eqution is your bility to see how it is done once nd then repet the process gin nd gin until it becomes second nture to you. In order to show the process once I will be using letters rther thn physicl concepts. You cn rerrnge n eqution bc with b s the subject b c or c s the subject c b ny of these three symbols b, c, cn be itself summtion, subtrction, multipliction, division, or combintion of ll. So, when you see more complicted eqution, try to identify its three individul prts, b, c before you strt rerrnging it. Worked exmples v v Eqution First Rerrngement Second Rerrngement f v f T T f f v u f u f v f v f T u f THINK! s you cn see from the third worked exmple, not ll rerrngements re useful. In fct, for the lens eqution only the second rerrngement cn be useful in problems. So, in order to improve your criticl thinking nd know which rerrngement is the most useful in every sitution, you must prctise with s mny equtions s you cn.
3 NOW TRY THIS! From now on the multipliction sign will not be shown, so written s bc bc Fill in the blnk spces with your own exmples. will be simply Eqution First Rerrngement Second Rerrngement (Power of lens) P f f v (Mgnifiction of lens) m u v u c (refrctive index) n v c v Q (current) I (electric potentil) (power) t E P t E V Q (power) P VI (conductnce) (resistnce) (resistnce) G V R I R G I V (power) P I R (power) (stress) V P R F F (strin) x l x l (Young s modulus) E (conductnce) G L (resistnce) R L (resistivity) 3
4 (phse ngle) (displcement) ft y sin f t sin (Young s interference) (quntum energy) E hf (electron wvelength) h mv L x d f h 4
5 5 Chpter : Rtios. Mnipulting rtios These re the most useful wys of mnipulting rtios. They will help you when you rerrnge equtions. First: C B D D C B Second: C D B D C B Third: D D C B B D C B Fourth: D D C B B D C B nd finlly, this is how you simplify complex frction: c b d d c b THINK! It is lwys useful to convert complex frction into simple one, using the form bove, before you try nything else. If b or d re missing, substitute them with number. NOW TRY THIS! Here re some exmples to do: [6] 3 4
6 Molecules of DN hve been stretched using opticl tweezers. Using the following dt find the cross sectionl re of DN strnd, if the Young s modulus of DN is 0 8 P nd lod of 4 x 0-0 N results in 0% strin. [] Here is how you strt: mnipulte the eqution until you hve on the left-hnd side nd only t this point substitute ll the symbols for their equivlent numbers. E E F (ns: x0-7 m ) 6
7 . How to convert sentences into rtios Hve look t these problems nd try to solve them. Problem nn hs 800 pples in bskets. Ech bsket holds 6 pples. How mny bskets does she hve? (ns: 50 bskets) Problem The electric current through wire is 3 (3 Coulombs per second). Ech electron hs chrge of.6 x 0-9 C. How mny electrons pss through the wire per second? (ns:.88 x 0 9 electrons) Problem 3 swimming pool is 7 m long. trnsverse wve of 3 m wvelength is creted. How mny complete oscilltions re creted if the wve fills the pool? (ns: 9 wves) THINK! Did you find problem more difficult to do? If yes, think bout this: ll the problems follow the sme logicl sequence. Bskets (in problem ) correspond to electrons (in problem ) nd wvelengths (in problem 3). pples (in problem ) correspond to chrge (in problem ) nd length (in problem 3). Here is nother set of problems: 7
8 Problem 4 John hs 47 pers in bskets. How mny bskets does he need for 4 pers? (ns: bskets) Problem 5 The weight of 50.0 kg person on the moon is 80.0N. How much would 7.0 kg person weigh on the moon? (ns: 5 N) Problem 6 When stereo sound informtion is trnsmitted through cble, 3 bits re sent every.7μs. Clculte how mny bits you cn send during seconds ( s = x 0 6 μs) (ns:.8 x 0 6 bits) THINK! Did you find problem 6 more difficult to do? If yes, think bout this: ll the problems follow the sme logicl sequence. Bskets (in problem 4) correspond to weight (in problem 5) nd bits (in problem 6). Pers (in problem 4) correspond to mss (in problem 5) nd time (in problem 6). FOLLOW THIS! You cn solve ll the bove problems nd mny more using the method below: STEP. Write two sentences, one exctly below the other, tht describe the reltionship between the two vribles. Mke sure you hve the sme vrible on ech side. Use the letter x for the unknown vrible. e.g. 8 bits in byte 300 bits in x byte 8
9 STEP. Convert the two sentences into rtio e.g x STEP 3. Use the properties of rtios to help you rerrnge nd solve the problem e.g. 8x 300 x x 400 NOW TRY THIS! Convert the degrees to rdins nd the rdins to degrees using rtios: e.g. 80 degrees in π rdins x degrees in y rdins Degrees Rdins 4 6 9
10 Chpter 3: How to use nd convert prefixes Mthemticl Prefixes [] Prefix Symbol Nme Multiplier femto f qudrillionth 0-5 pico p trillionth 0 - nno n billionth 0-9 micro µ millionth 0-6 milli m thousndth 0-3 centi c hundredth 0 - deci d tenth 0 - dek d ten 0 hecto h hundred 0 kilo k thousnd 0 3 meg M million 0 6 gig G billion 0 9 ter T trillion 0 pet P qudrillion 0 5 When you re given vrible with prefix you must convert it into its numericl equivlent in stndrd form before you use it in n eqution. FOLLOW THIS! lwys strt by replcing the prefix symbol with its equivlent multiplier. For exmple: 0.6 μ = 0.6 x km = 3 x 0 3 m 0 ns = 0 x 0-9 s DO NOT get tempted to follow this further (for exmple: 0.6 x 0-6 =.6 x 0-7 nd lso 0 x 0-9 s = 0-8 s) unless you re bsolutely confident tht you will do it correctly. It is lwys sfer to stop t the first step (0 x 0-9 s) nd type it like this into your clcultor. NOW TRY THIS!.4 kw = 0 μc = 4 cm = 340 MW = 46 pf = 0.03 m = 5 Gbytes = 43 kω = 0.03 MN = 0
11 Chpter 4: How to solve lengthy problem Problems in physics cn pper to be difficult t first sight. However, once you nlyse the problem in well-defined steps you should be ble to solve it without ny difficulty. The steps you need to follow re:. Identify the vribles you re given nd the ones you re sked to find. Convert ll units given to SI units 3. Give different symbol to ech vrible; try to stick to the well known symbols. To simplify, write the vlues for ech symbol (m=600) but don t worry bout writing the units t this stge. 4. Recognise which eqution/s to use. You do this by looking t wht vribles re vilble to you nd wht vribles you re sked to find. This is criticl stge; experience is the most importnt fctor here. This is why you need to prctise gin nd gin... This is lso why you need to KNOW LL YOUR EQUTIONS VERY WELL! 5. Find the logicl sequence for using these equtions in order to rech the desirble outcome. gin, experience is very importnt here! 6. Write the finl nswer nd dd the correct units. EXMPLE cr of mss 600 kg is trvelling t 0 ms -. When the brkes re pplied, it comes to rest in 0.0 km. Wht is the verge force exerted by the brkes? [3] (Note: there re mny wys to solve this problem nd in shorter method will be introduced.) STEP. mss= 600 kg initil velocity = 0 m s - finl velocity = 0 m s - stopping distnce = 0.0 km force =? STEP. re they ll in SI units? No. So... stopping distnce = 0.0 km = 0.0 x 0 3 m = 0 m STEP 3. m 600 u v s F?
12 STEP 4. E W (Chnge in energy = work done) W Fs (Work done = force x distnce in the direction of the force) EK mv (Kinetic energy = 0.5 x mss x velocity x velocity) STEP 5. Find the initil kinetic energy: E K mu Find the finl kinetic energy: E K mv Find the chnge in kinetic energy: E E K E K Equlise the chnge in kinetic energy with the work done nd rerrnge to find the force: E W E Fs F E s F F 3000 STEP 6. The finl nswer is F 3000N The negtive sign shows tht the force is in opposite direction to the velocity, i.e. it is the frictionl force tht stops the cr. NOW TRY THIS! girl diving from 5 m pltform wishes to know how fst she enters the wter. She is in the ir for.75 s nd dives from rest (with n initil speed of zero). Wht cn you tell her bout her entry speed? (g = 9.8 m s - ) [7] REMEMBER! Follow ll steps! Do not try to rush through! STEP.
13 STEP. STEP 3. STEP 4. STEP 5. STEP 6. 3
14 Chpter 5: How to recognise hidden mthemticl menings in sentences This chpter gives you first tste of the hidden mthemticl menings in sentences nd words. dd your own s you progress in the course. SENTENCE Chrge per unit time Metres per second per second Resistnce per unit length the product of voltge nd current The sum of powers of the lenses MTHEMTICL MENING Chrge divided by time Metres divided by second squred Resistnce divided by length Multiply voltge with current dd ll powers of lenses 4
15 Chpter 6: Logrithms 6. Definition of logrithms The use of logrithms sounds relly scry but once you lern the bsics you will be ble to mnipulte equtions with logrithms with no problem. This is the most importnt eqution tht summrises the ide behind ll logrithms: [4] x y log y x nd here re few exmples: 3 8 log 8 3 (you red: the logrithm of 8 to the bse is 3) log (red: the log of 000 to the bse 0 is 3) NOW TRY THIS! log log log log log log log Properties of logrithms ll the reltionships below re true, regrdless of the vlue of the bse. [5] log 0 log 5
16 log ( p q) log p log q log p q log p log q r log ( x ) rlog x 6.3 The two most fmous logrithms In physics the two most useful logrithms re: the Common logrithms which use bse 0 nd the Nturl logrithms which use the irrtionl number e (e=.78883) s the bse. To void complicting the equtions, the symbol for Common logrithms is log x nd the symbol for Nturl logrithms is ln x 0 log x insted of 6.4 How to solve problems with logrithms There re mny res of physics where you will encounter logrithms: sound levels, noise limittion on mximum bits per smple, rdioctive decy, dischrge of cpcitor etc. The importnt thing is to know wht to do in ll cses. When you re sked to mnipulte logrithmic eqution remember to USE the definition of logrithm s prt of the mnipultion process. For instnce, if you wnt to solve the eqution below with V totl s the subject you follow these steps: b log V V totl b totl b ( ) Vtotl Vnoise Vnoise V noise NOW TRY THIS!. Solve the sme eqution, but with V noise s the subject: 6
17 . The number of decibels d is given by the eqution d 0log 0 I I ) Rerrnge this eqution with I s the subject (the first step hs been done for you): I d d 0log0 log I 0 0 I I b) Now, rerrnge this eqution with I s the subject: 3. sound tht is on the threshold of udible intensity is 0 - W m - (like hering pin drop). This is tken s the bseline intensity I. pinful sound (like jet tking off) hs n intensity of bout 0 W m -. Wht is the sound level of the jet in db? [8]. The decibel formul is given in question bove. (ns: 30 db) 7
18 Chpter 7: Grphs 7. Types of grphs Grphs re VERY importnt in physics becuse they show ptterns between vribles. stright line grph tht strts from the (0,0) point is the best proof tht two vribles re directly proportionl. Stright line grph You should know from your mths tht the generl eqution for stright line is y x b cuts the y-xis., where is the grdient of the grph nd b is the point tht the line y b x You must lso know from your mths the eqution for hyperbol, prbol, n ellipse etc. Mke your own tble including ll the grph shpes you know nd their functions. Mke sure you include the logrithmic nd exponentil functions. Function Grph Exmple in physics y x b 8
19 7. How to choose the right grph for plotting lthough the bove list is importnt, when it comes to finding reltionship between two vribles the only grph tht cn show this very clerly is the stright line grph. EXMPLE Let s sy tht you wnt to prove the reltionship between the kinetic energy of n object nd its velocity. You plot velocity on the x-xis nd kinetic energy on the y-xis. You will get 9
20 curve which s you now is prbol (since the kinetic energy is directly proportionl to the squre of the velocity). Now let s sy you do nother experiment tht, unknown to you, lso follows the sme pttern. You will lso get curve when you plot the grph. Will you be ble to recognise tht this is prbol? Wht if it is curve tht is very close to prbol but not quite? Wht cn you do to be sure tht you hve crcked the reltionship? Think gin bout the exmple bove. If insted of plotting kinetic energy ginst velocity you plot kinetic energy ginst velocity squred wht will you get? You will get stright line through zero! Moreover, you will be certin tht the reltionship is tht: the kinetic energy is directly proportionl to the velocity squred. So wht hve we lerned so fr? LWYS IM T PLOTTING TWO VRIBLES THT WILL GIVE YOU STRIGHT LINE! Here re some exmples: To prove tht resistnce R is inversely proportionl to cross sectionl re, plot R ginst. This should give you stright line. To prove tht the squre of the period T of pendulum is directly proportionl to its length l plot either T ginst l or T ginst l NOW TRY THIS!. The pendulum eqution is: T l g ) Wht vribles should you plot ginst ech other in order to prove tht the period of the pendulum does not depend on its mss? Wht will the shpe of this grph be? b) Wht vribles should you plot ginst ech other to prove tht the period depends on the grvittionl field strength s shown by the eqution? 0
21 . The universl grvittionl lw is given by the eqution: F G mm r ) Wht vribles should you plot ginst ech other in order to prove tht the ttrctive force is directly proportionl to both msses of the objects? b) Wht vribles should you plot ginst ech other in order to prove tht the ttrctive force is inversely proportionl to the distnce squred between the objects? 7.3The significnce of the grdient During your course you will be sked to decide which grphs to plot in order to show reltionship or to clculte physicl constnt. We hve lredy noted how importnt it is to im t plotting grph tht will end up being stright line. This gives you definite nswer bout the reltionship between the two vribles. But there is more to it. The grdient of this line will give you informtion bout constnt in your experiment. EXMPLE Let s sy tht you wnt to mesure the grvittionl field strength of Erth with pendulum. T ginst l. The You vry the length nd mesure the period. You then decide to plot grph will be stright line. Wht will its grdient be? To find this, compre the pendulum eqution with the stright line eqution s shown below: T 4 l g y x b
22 I hope you cn see tht y corresponds to to zero, nd corresponds to 4 g grdient from your grph you will know the vlue of clculte g from this s: T, x corresponds to l, b corresponds. This tells you tht once you mesure the 4 g nd you will then be ble to grdient 4 4 g g grdient NOW TRY THIS! Try to find the grdient in ll the situtions listed below. The first three hve been done for you. Eqution Plot y ginst x grdient Constnt V x xis: current grdient R R R (for fixed resistor) I y xis: voltge V x xis: voltge R R grdient (for fixed resistor) I y xis: current R x xis: force l grdient y xis: extension E l E E grdient R L R L F x l mv Fs (stopping distncevelocity reltionship) xd L (double slit interference) xd L (double slit interference) x xis: L y xis: R x xis: y xis: R x xis: v y xis: s x xis: d y xis: x x xis: L y xis: x grdient (Young s modulus) (resistivity) grdient grdient F grdient grdient (resistivity) (fricition) (wvelength) (wvelength)
23 prt from its use s explined bove, the grdient in ll lines (curved or stright) corresponds to the derivtive of the function you plot. This is why if you plot time on the x- xis nd displcement on the y-xis the grdient corresponds to the velocity of the object. If the line is curved the grdient does not sty the sme, which mens tht it is equl to the instntneous velocity of the object. For the sme reson if you plot time on the x-xis nd velocity on the y-xis the grdient corresponds to the ccelertion of the object. If the line is curved the grdient does not sty the sme, which mens tht it is equl to the instntneous ccelertion of the object. 7.4The significnce of the re under grph The re between grph of y = f(x) nd the x-xis is equl to the definite integrl of the function. This formul gives positive result for grph bove the x-xis, nd negtive result for grph below the x-xis. [9] This is why the re under velocity-time grph is equl to the distnce covered by the object. If the grph is stright line then the re under cn be clculted very precisely s the re of tringle or trpezium etc. If the line is curve, the re is often estimted to good precision before it cn give you some useful informtion. You will use this ide more t level so for the moment we will leve it t this stge. 3
Scientific notation is a way of expressing really big numbers or really small numbers.
 Scientific Nottion (Stndrd form) Scientific nottion is wy of expressing relly big numbers or relly smll numbers. It is most often used in scientific clcultions where the nlysis must be very precise. Scientific
Scientific Nottion (Stndrd form) Scientific nottion is wy of expressing relly big numbers or relly smll numbers. It is most often used in scientific clcultions where the nlysis must be very precise. Scientific
GCSE to AS Physics: Why Physics:
 GSE to S Physics: Why Physics: The modern world is built on n understnding o physics. From Frdy s discoeries which led to the lrge scle production o electricity we he deeloped computers, telecommunictions,
GSE to S Physics: Why Physics: The modern world is built on n understnding o physics. From Frdy s discoeries which led to the lrge scle production o electricity we he deeloped computers, telecommunictions,
SUMMER KNOWHOW STUDY AND LEARNING CENTRE
 SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
Higher Checklist (Unit 3) Higher Checklist (Unit 3) Vectors
 Vectors Skill Achieved? Know tht sclr is quntity tht hs only size (no direction) Identify rel-life exmples of sclrs such s, temperture, mss, distnce, time, speed, energy nd electric chrge Know tht vector
Vectors Skill Achieved? Know tht sclr is quntity tht hs only size (no direction) Identify rel-life exmples of sclrs such s, temperture, mss, distnce, time, speed, energy nd electric chrge Know tht vector
DIRECT CURRENT CIRCUITS
 DRECT CURRENT CUTS ELECTRC POWER Consider the circuit shown in the Figure where bttery is connected to resistor R. A positive chrge dq will gin potentil energy s it moves from point to point b through
DRECT CURRENT CUTS ELECTRC POWER Consider the circuit shown in the Figure where bttery is connected to resistor R. A positive chrge dq will gin potentil energy s it moves from point to point b through
Improper Integrals, and Differential Equations
 Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Math 8 Winter 2015 Applications of Integration
 Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
Week 10: Line Integrals
 Week 10: Line Integrls Introduction In this finl week we return to prmetrised curves nd consider integrtion long such curves. We lredy sw this in Week 2 when we integrted long curve to find its length.
Week 10: Line Integrls Introduction In this finl week we return to prmetrised curves nd consider integrtion long such curves. We lredy sw this in Week 2 when we integrted long curve to find its length.
Chapter 0. What is the Lebesgue integral about?
 Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
Chapter 1: Fundamentals
 Chpter 1: Fundmentls 1.1 Rel Numbers Types of Rel Numbers: Nturl Numbers: {1, 2, 3,...}; These re the counting numbers. Integers: {... 3, 2, 1, 0, 1, 2, 3,...}; These re ll the nturl numbers, their negtives,
Chpter 1: Fundmentls 1.1 Rel Numbers Types of Rel Numbers: Nturl Numbers: {1, 2, 3,...}; These re the counting numbers. Integers: {... 3, 2, 1, 0, 1, 2, 3,...}; These re ll the nturl numbers, their negtives,
PART 1 MULTIPLE CHOICE Circle the appropriate response to each of the questions below. Each question has a value of 1 point.
 PART MULTIPLE CHOICE Circle the pproprite response to ech of the questions below. Ech question hs vlue of point.. If in sequence the second level difference is constnt, thn the sequence is:. rithmetic
PART MULTIPLE CHOICE Circle the pproprite response to ech of the questions below. Ech question hs vlue of point.. If in sequence the second level difference is constnt, thn the sequence is:. rithmetic
GRADE 4. Division WORKSHEETS
 GRADE Division WORKSHEETS Division division is shring nd grouping Division cn men shring or grouping. There re cndies shred mong kids. How mny re in ech shre? = 3 There re 6 pples nd go into ech bsket.
GRADE Division WORKSHEETS Division division is shring nd grouping Division cn men shring or grouping. There re cndies shred mong kids. How mny re in ech shre? = 3 There re 6 pples nd go into ech bsket.
ARITHMETIC OPERATIONS. The real numbers have the following properties: a b c ab ac
 REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
Unit #9 : Definite Integral Properties; Fundamental Theorem of Calculus
 Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
UNIT 1 FUNCTIONS AND THEIR INVERSES Lesson 1.4: Logarithmic Functions as Inverses Instruction
 Lesson : Logrithmic Functions s Inverses Prerequisite Skills This lesson requires the use of the following skills: determining the dependent nd independent vribles in n exponentil function bsed on dt from
Lesson : Logrithmic Functions s Inverses Prerequisite Skills This lesson requires the use of the following skills: determining the dependent nd independent vribles in n exponentil function bsed on dt from
MATHEMATICAL TECHNIQUES FOR A- LEVEL PHYSICS
 Name:. MTHEMTICL TECHNIQUES FOR - LEVEL PHYSICS (TO CCOMPNY THE DVNCING PHYSICS COURSE) Mr Green, Mrs Wynne, Mr Clark, Mr Harris Kesgrave High School (Based on a version by Maria Pavlidou, Cleeve school)
Name:. MTHEMTICL TECHNIQUES FOR - LEVEL PHYSICS (TO CCOMPNY THE DVNCING PHYSICS COURSE) Mr Green, Mrs Wynne, Mr Clark, Mr Harris Kesgrave High School (Based on a version by Maria Pavlidou, Cleeve school)
and that at t = 0 the object is at position 5. Find the position of the object at t = 2.
 7.2 The Fundmentl Theorem of Clculus 49 re mny, mny problems tht pper much different on the surfce but tht turn out to be the sme s these problems, in the sense tht when we try to pproimte solutions we
7.2 The Fundmentl Theorem of Clculus 49 re mny, mny problems tht pper much different on the surfce but tht turn out to be the sme s these problems, in the sense tht when we try to pproimte solutions we
Bridging the gap: GCSE AS Level
 Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
A sequence is a list of numbers in a specific order. A series is a sum of the terms of a sequence.
 Core Module Revision Sheet The C exm is hour 30 minutes long nd is in two sections. Section A (36 mrks) 8 0 short questions worth no more thn 5 mrks ech. Section B (36 mrks) 3 questions worth mrks ech.
Core Module Revision Sheet The C exm is hour 30 minutes long nd is in two sections. Section A (36 mrks) 8 0 short questions worth no more thn 5 mrks ech. Section B (36 mrks) 3 questions worth mrks ech.
Section 4.8. D v(t j 1 ) t. (4.8.1) j=1
 Difference Equtions to Differentil Equtions Section.8 Distnce, Position, nd the Length of Curves Although we motivted the definition of the definite integrl with the notion of re, there re mny pplictions
Difference Equtions to Differentil Equtions Section.8 Distnce, Position, nd the Length of Curves Although we motivted the definition of the definite integrl with the notion of re, there re mny pplictions
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 5 NOVEMBER 2014
 SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 5 NOVEMBER 014 Mrk Scheme: Ech prt of Question 1 is worth four mrks which re wrded solely for the correct nswer.
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 5 NOVEMBER 014 Mrk Scheme: Ech prt of Question 1 is worth four mrks which re wrded solely for the correct nswer.
Math 113 Exam 1-Review
 Mth 113 Exm 1-Review September 26, 2016 Exm 1 covers 6.1-7.3 in the textbook. It is dvisble to lso review the mteril from 5.3 nd 5.5 s this will be helpful in solving some of the problems. 6.1 Are Between
Mth 113 Exm 1-Review September 26, 2016 Exm 1 covers 6.1-7.3 in the textbook. It is dvisble to lso review the mteril from 5.3 nd 5.5 s this will be helpful in solving some of the problems. 6.1 Are Between
Chapters 4 & 5 Integrals & Applications
 Contents Chpters 4 & 5 Integrls & Applictions Motivtion to Chpters 4 & 5 2 Chpter 4 3 Ares nd Distnces 3. VIDEO - Ares Under Functions............................................ 3.2 VIDEO - Applictions
Contents Chpters 4 & 5 Integrls & Applictions Motivtion to Chpters 4 & 5 2 Chpter 4 3 Ares nd Distnces 3. VIDEO - Ares Under Functions............................................ 3.2 VIDEO - Applictions
Kinematics equations, some numbers
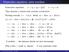 Kinemtics equtions, some numbers Kinemtics equtions: x = x 0 + v 0 t + 1 2 t2, v = v 0 + t. They describe motion with constnt ccelertion. Brking exmple, = 1m/s. Initil: x 0 = 10m, v 0 = 10m/s. x(t=1s)
Kinemtics equtions, some numbers Kinemtics equtions: x = x 0 + v 0 t + 1 2 t2, v = v 0 + t. They describe motion with constnt ccelertion. Brking exmple, = 1m/s. Initil: x 0 = 10m, v 0 = 10m/s. x(t=1s)
4.4 Areas, Integrals and Antiderivatives
 . res, integrls nd ntiderivtives 333. Ares, Integrls nd Antiderivtives This section explores properties of functions defined s res nd exmines some connections mong res, integrls nd ntiderivtives. In order
. res, integrls nd ntiderivtives 333. Ares, Integrls nd Antiderivtives This section explores properties of functions defined s res nd exmines some connections mong res, integrls nd ntiderivtives. In order
Exponentials - Grade 10 [CAPS] *
![Exponentials - Grade 10 [CAPS] * Exponentials - Grade 10 [CAPS] *](/thumbs/88/115984632.jpg) OpenStx-CNX module: m859 Exponentils - Grde 0 [CAPS] * Free High School Science Texts Project Bsed on Exponentils by Rory Adms Free High School Science Texts Project Mrk Horner Hether Willims This work
OpenStx-CNX module: m859 Exponentils - Grde 0 [CAPS] * Free High School Science Texts Project Bsed on Exponentils by Rory Adms Free High School Science Texts Project Mrk Horner Hether Willims This work
The Wave Equation I. MA 436 Kurt Bryan
 1 Introduction The Wve Eqution I MA 436 Kurt Bryn Consider string stretching long the x xis, of indeterminte (or even infinite!) length. We wnt to derive n eqution which models the motion of the string
1 Introduction The Wve Eqution I MA 436 Kurt Bryn Consider string stretching long the x xis, of indeterminte (or even infinite!) length. We wnt to derive n eqution which models the motion of the string
Improper Integrals. Type I Improper Integrals How do we evaluate an integral such as
 Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Summer Work package for IB and A level prospective physics students.
 Summer Work package for IB and A level prospective physics students. Task 1. Read the first 3 sections of Mathematical techniques for A level physics (rearranging equations, ratios and prefixes). (This
Summer Work package for IB and A level prospective physics students. Task 1. Read the first 3 sections of Mathematical techniques for A level physics (rearranging equations, ratios and prefixes). (This
Student Session Topic: Particle Motion
 Student Session Topic: Prticle Motion Prticle motion nd similr problems re on the AP Clculus exms lmost every yer. The prticle my be prticle, person, cr, etc. The position, velocity or ccelertion my be
Student Session Topic: Prticle Motion Prticle motion nd similr problems re on the AP Clculus exms lmost every yer. The prticle my be prticle, person, cr, etc. The position, velocity or ccelertion my be
20 MATHEMATICS POLYNOMIALS
 0 MATHEMATICS POLYNOMIALS.1 Introduction In Clss IX, you hve studied polynomils in one vrible nd their degrees. Recll tht if p(x) is polynomil in x, the highest power of x in p(x) is clled the degree of
0 MATHEMATICS POLYNOMIALS.1 Introduction In Clss IX, you hve studied polynomils in one vrible nd their degrees. Recll tht if p(x) is polynomil in x, the highest power of x in p(x) is clled the degree of
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER /2019
 ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS MATH00030 SEMESTER 208/209 DR. ANTHONY BROWN 7.. Introduction to Integrtion. 7. Integrl Clculus As ws the cse with the chpter on differentil
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS MATH00030 SEMESTER 208/209 DR. ANTHONY BROWN 7.. Introduction to Integrtion. 7. Integrl Clculus As ws the cse with the chpter on differentil
Operations with Polynomials
 38 Chpter P Prerequisites P.4 Opertions with Polynomils Wht you should lern: How to identify the leding coefficients nd degrees of polynomils How to dd nd subtrct polynomils How to multiply polynomils
38 Chpter P Prerequisites P.4 Opertions with Polynomils Wht you should lern: How to identify the leding coefficients nd degrees of polynomils How to dd nd subtrct polynomils How to multiply polynomils
7.2 The Definite Integral
 7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
Pre-Session Review. Part 1: Basic Algebra; Linear Functions and Graphs
 Pre-Session Review Prt 1: Bsic Algebr; Liner Functions nd Grphs A. Generl Review nd Introduction to Algebr Hierrchy of Arithmetic Opertions Opertions in ny expression re performed in the following order:
Pre-Session Review Prt 1: Bsic Algebr; Liner Functions nd Grphs A. Generl Review nd Introduction to Algebr Hierrchy of Arithmetic Opertions Opertions in ny expression re performed in the following order:
Summer Work Packet for MPH Math Classes
 Summer Work Pcket for MPH Mth Clsses Students going into Pre-clculus AC Sept. 018 Nme: This pcket is designed to help students sty current with their mth skills. Ech mth clss expects certin level of number
Summer Work Pcket for MPH Mth Clsses Students going into Pre-clculus AC Sept. 018 Nme: This pcket is designed to help students sty current with their mth skills. Ech mth clss expects certin level of number
Main topics for the Second Midterm
 Min topics for the Second Midterm The Midterm will cover Sections 5.4-5.9, Sections 6.1-6.3, nd Sections 7.1-7.7 (essentilly ll of the mteril covered in clss from the First Midterm). Be sure to know the
Min topics for the Second Midterm The Midterm will cover Sections 5.4-5.9, Sections 6.1-6.3, nd Sections 7.1-7.7 (essentilly ll of the mteril covered in clss from the First Midterm). Be sure to know the
n f(x i ) x. i=1 In section 4.2, we defined the definite integral of f from x = a to x = b as n f(x i ) x; f(x) dx = lim i=1
 The Fundmentl Theorem of Clculus As we continue to study the re problem, let s think bck to wht we know bout computing res of regions enclosed by curves. If we wnt to find the re of the region below the
The Fundmentl Theorem of Clculus As we continue to study the re problem, let s think bck to wht we know bout computing res of regions enclosed by curves. If we wnt to find the re of the region below the
Indefinite Integral. Chapter Integration - reverse of differentiation
 Chpter Indefinite Integrl Most of the mthemticl opertions hve inverse opertions. The inverse opertion of differentition is clled integrtion. For exmple, describing process t the given moment knowing the
Chpter Indefinite Integrl Most of the mthemticl opertions hve inverse opertions. The inverse opertion of differentition is clled integrtion. For exmple, describing process t the given moment knowing the
IMPORTANT. Read these directions carefully:
 Physics 208: Electricity nd Mgnetism Finl Exm, Secs. 506 510. 7 My. 2004 Instructor: Dr. George R. Welch, 415 Engineering-Physics, 845-7737 Print your nme netly: Lst nme: First nme: Sign your nme: Plese
Physics 208: Electricity nd Mgnetism Finl Exm, Secs. 506 510. 7 My. 2004 Instructor: Dr. George R. Welch, 415 Engineering-Physics, 845-7737 Print your nme netly: Lst nme: First nme: Sign your nme: Plese
a < a+ x < a+2 x < < a+n x = b, n A i n f(x i ) x. i=1 i=1
 Mth 33 Volume Stewrt 5.2 Geometry of integrls. In this section, we will lern how to compute volumes using integrls defined by slice nlysis. First, we recll from Clculus I how to compute res. Given the
Mth 33 Volume Stewrt 5.2 Geometry of integrls. In this section, we will lern how to compute volumes using integrls defined by slice nlysis. First, we recll from Clculus I how to compute res. Given the
13.4 Work done by Constant Forces
 13.4 Work done by Constnt Forces We will begin our discussion of the concept of work by nlyzing the motion of n object in one dimension cted on by constnt forces. Let s consider the following exmple: push
13.4 Work done by Constnt Forces We will begin our discussion of the concept of work by nlyzing the motion of n object in one dimension cted on by constnt forces. Let s consider the following exmple: push
The area under the graph of f and above the x-axis between a and b is denoted by. f(x) dx. π O
 1 Section 5. The Definite Integrl Suppose tht function f is continuous nd positive over n intervl [, ]. y = f(x) x The re under the grph of f nd ove the x-xis etween nd is denoted y f(x) dx nd clled the
1 Section 5. The Definite Integrl Suppose tht function f is continuous nd positive over n intervl [, ]. y = f(x) x The re under the grph of f nd ove the x-xis etween nd is denoted y f(x) dx nd clled the
PHYS Summer Professor Caillault Homework Solutions. Chapter 2
 PHYS 1111 - Summer 2007 - Professor Cillult Homework Solutions Chpter 2 5. Picture the Problem: The runner moves long the ovl trck. Strtegy: The distnce is the totl length of trvel, nd the displcement
PHYS 1111 - Summer 2007 - Professor Cillult Homework Solutions Chpter 2 5. Picture the Problem: The runner moves long the ovl trck. Strtegy: The distnce is the totl length of trvel, nd the displcement
1 Probability Density Functions
 Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Section 5.1 #7, 10, 16, 21, 25; Section 5.2 #8, 9, 15, 20, 27, 30; Section 5.3 #4, 6, 9, 13, 16, 28, 31; Section 5.4 #7, 18, 21, 23, 25, 29, 40
 Mth B Prof. Audrey Terrs HW # Solutions by Alex Eustis Due Tuesdy, Oct. 9 Section 5. #7,, 6,, 5; Section 5. #8, 9, 5,, 7, 3; Section 5.3 #4, 6, 9, 3, 6, 8, 3; Section 5.4 #7, 8,, 3, 5, 9, 4 5..7 Since
Mth B Prof. Audrey Terrs HW # Solutions by Alex Eustis Due Tuesdy, Oct. 9 Section 5. #7,, 6,, 5; Section 5. #8, 9, 5,, 7, 3; Section 5.3 #4, 6, 9, 3, 6, 8, 3; Section 5.4 #7, 8,, 3, 5, 9, 4 5..7 Since
Before we can begin Ch. 3 on Radicals, we need to be familiar with perfect squares, cubes, etc. Try and do as many as you can without a calculator!!!
 Nme: Algebr II Honors Pre-Chpter Homework Before we cn begin Ch on Rdicls, we need to be fmilir with perfect squres, cubes, etc Try nd do s mny s you cn without clcultor!!! n The nth root of n n Be ble
Nme: Algebr II Honors Pre-Chpter Homework Before we cn begin Ch on Rdicls, we need to be fmilir with perfect squres, cubes, etc Try nd do s mny s you cn without clcultor!!! n The nth root of n n Be ble
Preparation for A Level Wadebridge School
 Preprtion for A Level Mths @ Wdebridge School Bridging the gp between GCSE nd A Level Nme: CONTENTS Chpter Removing brckets pge Chpter Liner equtions Chpter Simultneous equtions 6 Chpter Fctorising 7 Chpter
Preprtion for A Level Mths @ Wdebridge School Bridging the gp between GCSE nd A Level Nme: CONTENTS Chpter Removing brckets pge Chpter Liner equtions Chpter Simultneous equtions 6 Chpter Fctorising 7 Chpter
How can we approximate the area of a region in the plane? What is an interpretation of the area under the graph of a velocity function?
 Mth 125 Summry Here re some thoughts I ws hving while considering wht to put on the first midterm. The core of your studying should be the ssigned homework problems: mke sure you relly understnd those
Mth 125 Summry Here re some thoughts I ws hving while considering wht to put on the first midterm. The core of your studying should be the ssigned homework problems: mke sure you relly understnd those
In-Class Problems 2 and 3: Projectile Motion Solutions. In-Class Problem 2: Throwing a Stone Down a Hill
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Deprtment of Physics Physics 8T Fll Term 4 In-Clss Problems nd 3: Projectile Motion Solutions We would like ech group to pply the problem solving strtegy with the
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Deprtment of Physics Physics 8T Fll Term 4 In-Clss Problems nd 3: Projectile Motion Solutions We would like ech group to pply the problem solving strtegy with the
1 Which of the following summarises the change in wave characteristics on going from infra-red to ultraviolet in the electromagnetic spectrum?
 Which of the following summrises the chnge in wve chrcteristics on going from infr-red to ultrviolet in the electromgnetic spectrum? frequency speed (in vcuum) decreses decreses decreses remins constnt
Which of the following summrises the chnge in wve chrcteristics on going from infr-red to ultrviolet in the electromgnetic spectrum? frequency speed (in vcuum) decreses decreses decreses remins constnt
f(x) dx, If one of these two conditions is not met, we call the integral improper. Our usual definition for the value for the definite integral
 Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Goals: Determine how to calculate the area described by a function. Define the definite integral. Explore the relationship between the definite
 Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Lecture 1: Introduction to integration theory and bounded variation
 Lecture 1: Introduction to integrtion theory nd bounded vrition Wht is this course bout? Integrtion theory. The first question you might hve is why there is nything you need to lern bout integrtion. You
Lecture 1: Introduction to integrtion theory nd bounded vrition Wht is this course bout? Integrtion theory. The first question you might hve is why there is nything you need to lern bout integrtion. You
Review of basic calculus
 Review of bsic clculus This brief review reclls some of the most importnt concepts, definitions, nd theorems from bsic clculus. It is not intended to tech bsic clculus from scrtch. If ny of the items below
Review of bsic clculus This brief review reclls some of the most importnt concepts, definitions, nd theorems from bsic clculus. It is not intended to tech bsic clculus from scrtch. If ny of the items below
Chapter 1: Logarithmic functions and indices
 Chpter : Logrithmic functions nd indices. You cn simplify epressions y using rules of indices m n m n m n m n ( m ) n mn m m m m n m m n Emple Simplify these epressions: 5 r r c 4 4 d 6 5 e ( ) f ( ) 4
Chpter : Logrithmic functions nd indices. You cn simplify epressions y using rules of indices m n m n m n m n ( m ) n mn m m m m n m m n Emple Simplify these epressions: 5 r r c 4 4 d 6 5 e ( ) f ( ) 4
Logarithms. Logarithm is another word for an index or power. POWER. 2 is the power to which the base 10 must be raised to give 100.
 Logrithms. Logrithm is nother word for n inde or power. THIS IS A POWER STATEMENT BASE POWER FOR EXAMPLE : We lred know tht; = NUMBER 10² = 100 This is the POWER Sttement OR 2 is the power to which the
Logrithms. Logrithm is nother word for n inde or power. THIS IS A POWER STATEMENT BASE POWER FOR EXAMPLE : We lred know tht; = NUMBER 10² = 100 This is the POWER Sttement OR 2 is the power to which the
approaches as n becomes larger and larger. Since e > 1, the graph of the natural exponential function is as below
 . Eponentil nd rithmic functions.1 Eponentil Functions A function of the form f() =, > 0, 1 is clled n eponentil function. Its domin is the set of ll rel f ( 1) numbers. For n eponentil function f we hve.
. Eponentil nd rithmic functions.1 Eponentil Functions A function of the form f() =, > 0, 1 is clled n eponentil function. Its domin is the set of ll rel f ( 1) numbers. For n eponentil function f we hve.
Jim Lambers MAT 169 Fall Semester Lecture 4 Notes
 Jim Lmbers MAT 169 Fll Semester 2009-10 Lecture 4 Notes These notes correspond to Section 8.2 in the text. Series Wht is Series? An infinte series, usully referred to simply s series, is n sum of ll of
Jim Lmbers MAT 169 Fll Semester 2009-10 Lecture 4 Notes These notes correspond to Section 8.2 in the text. Series Wht is Series? An infinte series, usully referred to simply s series, is n sum of ll of
A. Limits - L Hopital s Rule ( ) How to find it: Try and find limits by traditional methods (plugging in). If you get 0 0 or!!, apply C.! 1 6 C.
 A. Limits - L Hopitl s Rule Wht you re finding: L Hopitl s Rule is used to find limits of the form f ( x) lim where lim f x x! c g x ( ) = or lim f ( x) = limg( x) = ". ( ) x! c limg( x) = 0 x! c x! c
A. Limits - L Hopitl s Rule Wht you re finding: L Hopitl s Rule is used to find limits of the form f ( x) lim where lim f x x! c g x ( ) = or lim f ( x) = limg( x) = ". ( ) x! c limg( x) = 0 x! c x! c
Sample Problems for the Final of Math 121, Fall, 2005
 Smple Problems for the Finl of Mth, Fll, 5 The following is collection of vrious types of smple problems covering sections.8,.,.5, nd.8 6.5 of the text which constitute only prt of the common Mth Finl.
Smple Problems for the Finl of Mth, Fll, 5 The following is collection of vrious types of smple problems covering sections.8,.,.5, nd.8 6.5 of the text which constitute only prt of the common Mth Finl.
CHM Physical Chemistry I Chapter 1 - Supplementary Material
 CHM 3410 - Physicl Chemistry I Chpter 1 - Supplementry Mteril For review of some bsic concepts in mth, see Atkins "Mthemticl Bckground 1 (pp 59-6), nd "Mthemticl Bckground " (pp 109-111). 1. Derivtion
CHM 3410 - Physicl Chemistry I Chpter 1 - Supplementry Mteril For review of some bsic concepts in mth, see Atkins "Mthemticl Bckground 1 (pp 59-6), nd "Mthemticl Bckground " (pp 109-111). 1. Derivtion
Infinite Geometric Series
 Infinite Geometric Series Finite Geometric Series ( finite SUM) Let 0 < r < 1, nd let n be positive integer. Consider the finite sum It turns out there is simple lgebric expression tht is equivlent to
Infinite Geometric Series Finite Geometric Series ( finite SUM) Let 0 < r < 1, nd let n be positive integer. Consider the finite sum It turns out there is simple lgebric expression tht is equivlent to
Main topics for the First Midterm
 Min topics for the First Midterm The Midterm will cover Section 1.8, Chpters 2-3, Sections 4.1-4.8, nd Sections 5.1-5.3 (essentilly ll of the mteril covered in clss). Be sure to know the results of the
Min topics for the First Midterm The Midterm will cover Section 1.8, Chpters 2-3, Sections 4.1-4.8, nd Sections 5.1-5.3 (essentilly ll of the mteril covered in clss). Be sure to know the results of the
NUMERICAL INTEGRATION. The inverse process to differentiation in calculus is integration. Mathematically, integration is represented by.
 NUMERICAL INTEGRATION 1 Introduction The inverse process to differentition in clculus is integrtion. Mthemticlly, integrtion is represented by f(x) dx which stnds for the integrl of the function f(x) with
NUMERICAL INTEGRATION 1 Introduction The inverse process to differentition in clculus is integrtion. Mthemticlly, integrtion is represented by f(x) dx which stnds for the integrl of the function f(x) with
Density of Energy Stored in the Electric Field
 Density of Energy Stored in the Electric Field Deprtment of Physics, Cornell University c Tomás A. Aris October 14, 01 Figure 1: Digrm of Crtesin vortices from René Descrtes Principi philosophie, published
Density of Energy Stored in the Electric Field Deprtment of Physics, Cornell University c Tomás A. Aris October 14, 01 Figure 1: Digrm of Crtesin vortices from René Descrtes Principi philosophie, published
The Fundamental Theorem of Calculus, Particle Motion, and Average Value
 The Fundmentl Theorem of Clculus, Prticle Motion, nd Averge Vlue b Three Things to Alwys Keep In Mind: (1) v( dt p( b) p( ), where v( represents the velocity nd p( represents the position. b (2) v ( dt
The Fundmentl Theorem of Clculus, Prticle Motion, nd Averge Vlue b Three Things to Alwys Keep In Mind: (1) v( dt p( b) p( ), where v( represents the velocity nd p( represents the position. b (2) v ( dt
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
different methods (left endpoint, right endpoint, midpoint, trapezoid, Simpson s).
 Mth 1A with Professor Stnkov Worksheet, Discussion #41; Wednesdy, 12/6/217 GSI nme: Roy Zho Problems 1. Write the integrl 3 dx s limit of Riemnn sums. Write it using 2 intervls using the 1 x different
Mth 1A with Professor Stnkov Worksheet, Discussion #41; Wednesdy, 12/6/217 GSI nme: Roy Zho Problems 1. Write the integrl 3 dx s limit of Riemnn sums. Write it using 2 intervls using the 1 x different
MAT187H1F Lec0101 Burbulla
 Chpter 6 Lecture Notes Review nd Two New Sections Sprint 17 Net Distnce nd Totl Distnce Trvelled Suppose s is the position of prticle t time t for t [, b]. Then v dt = s (t) dt = s(b) s(). s(b) s() is
Chpter 6 Lecture Notes Review nd Two New Sections Sprint 17 Net Distnce nd Totl Distnce Trvelled Suppose s is the position of prticle t time t for t [, b]. Then v dt = s (t) dt = s(b) s(). s(b) s() is
AP Calculus Multiple Choice: BC Edition Solutions
 AP Clculus Multiple Choice: BC Edition Solutions J. Slon Mrch 8, 04 ) 0 dx ( x) is A) B) C) D) E) Divergent This function inside the integrl hs verticl symptotes t x =, nd the integrl bounds contin this
AP Clculus Multiple Choice: BC Edition Solutions J. Slon Mrch 8, 04 ) 0 dx ( x) is A) B) C) D) E) Divergent This function inside the integrl hs verticl symptotes t x =, nd the integrl bounds contin this
10. AREAS BETWEEN CURVES
 . AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
. AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
1 The Riemann Integral
 The Riemnn Integrl. An exmple leding to the notion of integrl (res) We know how to find (i.e. define) the re of rectngle (bse height), tringle ( (sum of res of tringles). But how do we find/define n re
The Riemnn Integrl. An exmple leding to the notion of integrl (res) We know how to find (i.e. define) the re of rectngle (bse height), tringle ( (sum of res of tringles). But how do we find/define n re
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
#6A&B Magnetic Field Mapping
 #6A& Mgnetic Field Mpping Gol y performing this lb experiment, you will: 1. use mgnetic field mesurement technique bsed on Frdy s Lw (see the previous experiment),. study the mgnetic fields generted by
#6A& Mgnetic Field Mpping Gol y performing this lb experiment, you will: 1. use mgnetic field mesurement technique bsed on Frdy s Lw (see the previous experiment),. study the mgnetic fields generted by
I1 = I2 I1 = I2 + I3 I1 + I2 = I3 + I4 I 3
 2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
Mathematics of Motion II Projectiles
 Chmp+ Fll 2001 Dn Stump 1 Mthemtics of Motion II Projectiles Tble of vribles t time v velocity, v 0 initil velocity ccelertion D distnce x position coordinte, x 0 initil position x horizontl coordinte
Chmp+ Fll 2001 Dn Stump 1 Mthemtics of Motion II Projectiles Tble of vribles t time v velocity, v 0 initil velocity ccelertion D distnce x position coordinte, x 0 initil position x horizontl coordinte
Section 6: Area, Volume, and Average Value
 Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Higher Maths. Self Check Booklet. visit for a wealth of free online maths resources at all levels from S1 to S6
 Higher Mths Self Check Booklet visit www.ntionl5mths.co.uk for welth of free online mths resources t ll levels from S to S6 How To Use This Booklet You could use this booklet on your own, but it my be
Higher Mths Self Check Booklet visit www.ntionl5mths.co.uk for welth of free online mths resources t ll levels from S to S6 How To Use This Booklet You could use this booklet on your own, but it my be
ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 1 - Thurs 28th Sept 17 Review of trigonometry and basic calculus
 ES 111 Mthemticl Methods in the Erth Sciences Lecture Outline 1 - Thurs 28th Sept 17 Review of trigonometry nd bsic clculus Trigonometry When is it useful? Everywhere! Anything involving coordinte systems
ES 111 Mthemticl Methods in the Erth Sciences Lecture Outline 1 - Thurs 28th Sept 17 Review of trigonometry nd bsic clculus Trigonometry When is it useful? Everywhere! Anything involving coordinte systems
Year 12 Mathematics Extension 2 HSC Trial Examination 2014
 Yer Mthemtics Etension HSC Tril Emintion 04 Generl Instructions. Reding time 5 minutes Working time hours Write using blck or blue pen. Blck pen is preferred. Bord-pproved clcultors my be used A tble of
Yer Mthemtics Etension HSC Tril Emintion 04 Generl Instructions. Reding time 5 minutes Working time hours Write using blck or blue pen. Blck pen is preferred. Bord-pproved clcultors my be used A tble of
Math 113 Exam 2 Practice
 Mth 3 Exm Prctice Februry 8, 03 Exm will cover 7.4, 7.5, 7.7, 7.8, 8.-3 nd 8.5. Plese note tht integrtion skills lerned in erlier sections will still be needed for the mteril in 7.5, 7.8 nd chpter 8. This
Mth 3 Exm Prctice Februry 8, 03 Exm will cover 7.4, 7.5, 7.7, 7.8, 8.-3 nd 8.5. Plese note tht integrtion skills lerned in erlier sections will still be needed for the mteril in 7.5, 7.8 nd chpter 8. This
Exponentials & Logarithms Unit 8
 U n i t 8 AdvF Dte: Nme: Eponentils & Logrithms Unit 8 Tenttive TEST dte Big ide/lerning Gols This unit begins with the review of eponent lws, solving eponentil equtions (by mtching bses method nd tril
U n i t 8 AdvF Dte: Nme: Eponentils & Logrithms Unit 8 Tenttive TEST dte Big ide/lerning Gols This unit begins with the review of eponent lws, solving eponentil equtions (by mtching bses method nd tril
Handout: Natural deduction for first order logic
 MATH 457 Introduction to Mthemticl Logic Spring 2016 Dr Json Rute Hndout: Nturl deduction for first order logic We will extend our nturl deduction rules for sententil logic to first order logic These notes
MATH 457 Introduction to Mthemticl Logic Spring 2016 Dr Json Rute Hndout: Nturl deduction for first order logic We will extend our nturl deduction rules for sententil logic to first order logic These notes
MATH 115 FINAL EXAM. April 25, 2005
 MATH 115 FINAL EXAM April 25, 2005 NAME: Solution Key INSTRUCTOR: SECTION NO: 1. Do not open this exm until you re told to begin. 2. This exm hs 9 pges including this cover. There re 9 questions. 3. Do
MATH 115 FINAL EXAM April 25, 2005 NAME: Solution Key INSTRUCTOR: SECTION NO: 1. Do not open this exm until you re told to begin. 2. This exm hs 9 pges including this cover. There re 9 questions. 3. Do
Edexcel GCE Core Mathematics (C2) Required Knowledge Information Sheet. Daniel Hammocks
 Edexcel GCE Core Mthemtics (C) Required Knowledge Informtion Sheet C Formule Given in Mthemticl Formule nd Sttisticl Tles Booklet Cosine Rule o = + c c cosine (A) Binomil Series o ( + ) n = n + n 1 n 1
Edexcel GCE Core Mthemtics (C) Required Knowledge Informtion Sheet C Formule Given in Mthemticl Formule nd Sttisticl Tles Booklet Cosine Rule o = + c c cosine (A) Binomil Series o ( + ) n = n + n 1 n 1
Definition of Continuity: The function f(x) is continuous at x = a if f(a) exists and lim
 Mth 9 Course Summry/Study Guide Fll, 2005 [1] Limits Definition of Limit: We sy tht L is the limit of f(x) s x pproches if f(x) gets closer nd closer to L s x gets closer nd closer to. We write lim f(x)
Mth 9 Course Summry/Study Guide Fll, 2005 [1] Limits Definition of Limit: We sy tht L is the limit of f(x) s x pproches if f(x) gets closer nd closer to L s x gets closer nd closer to. We write lim f(x)
Name Solutions to Test 3 November 8, 2017
 Nme Solutions to Test 3 November 8, 07 This test consists of three prts. Plese note tht in prts II nd III, you cn skip one question of those offered. Some possibly useful formuls cn be found below. Brrier
Nme Solutions to Test 3 November 8, 07 This test consists of three prts. Plese note tht in prts II nd III, you cn skip one question of those offered. Some possibly useful formuls cn be found below. Brrier
Conservation Law. Chapter Goal. 5.2 Theory
 Chpter 5 Conservtion Lw 5.1 Gol Our long term gol is to understnd how mny mthemticl models re derived. We study how certin quntity chnges with time in given region (sptil domin). We first derive the very
Chpter 5 Conservtion Lw 5.1 Gol Our long term gol is to understnd how mny mthemticl models re derived. We study how certin quntity chnges with time in given region (sptil domin). We first derive the very
AQA Further Pure 2. Hyperbolic Functions. Section 2: The inverse hyperbolic functions
 Hperbolic Functions Section : The inverse hperbolic functions Notes nd Emples These notes contin subsections on The inverse hperbolic functions Integrtion using the inverse hperbolic functions Logrithmic
Hperbolic Functions Section : The inverse hperbolic functions Notes nd Emples These notes contin subsections on The inverse hperbolic functions Integrtion using the inverse hperbolic functions Logrithmic
Recitation 3: More Applications of the Derivative
 Mth 1c TA: Pdric Brtlett Recittion 3: More Applictions of the Derivtive Week 3 Cltech 2012 1 Rndom Question Question 1 A grph consists of the following: A set V of vertices. A set E of edges where ech
Mth 1c TA: Pdric Brtlett Recittion 3: More Applictions of the Derivtive Week 3 Cltech 2012 1 Rndom Question Question 1 A grph consists of the following: A set V of vertices. A set E of edges where ech
Equations and Inequalities
 Equtions nd Inequlities Equtions nd Inequlities Curriculum Redy ACMNA: 4, 5, 6, 7, 40 www.mthletics.com Equtions EQUATIONS & Inequlities & INEQUALITIES Sometimes just writing vribles or pronumerls in
Equtions nd Inequlities Equtions nd Inequlities Curriculum Redy ACMNA: 4, 5, 6, 7, 40 www.mthletics.com Equtions EQUATIONS & Inequlities & INEQUALITIES Sometimes just writing vribles or pronumerls in
Z b. f(x)dx. Yet in the above two cases we know what f(x) is. Sometimes, engineers want to calculate an area by computing I, but...
 Chpter 7 Numericl Methods 7. Introduction In mny cses the integrl f(x)dx cn be found by finding function F (x) such tht F 0 (x) =f(x), nd using f(x)dx = F (b) F () which is known s the nlyticl (exct) solution.
Chpter 7 Numericl Methods 7. Introduction In mny cses the integrl f(x)dx cn be found by finding function F (x) such tht F 0 (x) =f(x), nd using f(x)dx = F (b) F () which is known s the nlyticl (exct) solution.
The Fundamental Theorem of Calculus
 The Fundmentl Theorem of Clculus Professor Richrd Blecksmith richrd@mth.niu.edu Dept. of Mthemticl Sciences Northern Illinois University http://mth.niu.edu/ richrd/mth229. The Definite Integrl We define
The Fundmentl Theorem of Clculus Professor Richrd Blecksmith richrd@mth.niu.edu Dept. of Mthemticl Sciences Northern Illinois University http://mth.niu.edu/ richrd/mth229. The Definite Integrl We define
AB Calculus Review Sheet
 AB Clculus Review Sheet Legend: A Preclculus, B Limits, C Differentil Clculus, D Applictions of Differentil Clculus, E Integrl Clculus, F Applictions of Integrl Clculus, G Prticle Motion nd Rtes This is
AB Clculus Review Sheet Legend: A Preclculus, B Limits, C Differentil Clculus, D Applictions of Differentil Clculus, E Integrl Clculus, F Applictions of Integrl Clculus, G Prticle Motion nd Rtes This is
( ) as a fraction. Determine location of the highest
 AB Clculus Exm Review Sheet - Solutions A. Preclculus Type prolems A1 A2 A3 A4 A5 A6 A7 This is wht you think of doing Find the zeros of f ( x). Set function equl to 0. Fctor or use qudrtic eqution if
AB Clculus Exm Review Sheet - Solutions A. Preclculus Type prolems A1 A2 A3 A4 A5 A6 A7 This is wht you think of doing Find the zeros of f ( x). Set function equl to 0. Fctor or use qudrtic eqution if
38 Riemann sums and existence of the definite integral.
 38 Riemnn sums nd existence of the definite integrl. In the clcultion of the re of the region X bounded by the grph of g(x) = x 2, the x-xis nd 0 x b, two sums ppered: ( n (k 1) 2) b 3 n 3 re(x) ( n These
38 Riemnn sums nd existence of the definite integrl. In the clcultion of the re of the region X bounded by the grph of g(x) = x 2, the x-xis nd 0 x b, two sums ppered: ( n (k 1) 2) b 3 n 3 re(x) ( n These
Physics 201 Lab 3: Measurement of Earth s local gravitational field I Data Acquisition and Preliminary Analysis Dr. Timothy C. Black Summer I, 2018
 Physics 201 Lb 3: Mesurement of Erth s locl grvittionl field I Dt Acquisition nd Preliminry Anlysis Dr. Timothy C. Blck Summer I, 2018 Theoreticl Discussion Grvity is one of the four known fundmentl forces.
Physics 201 Lb 3: Mesurement of Erth s locl grvittionl field I Dt Acquisition nd Preliminry Anlysis Dr. Timothy C. Blck Summer I, 2018 Theoreticl Discussion Grvity is one of the four known fundmentl forces.
