Mañé s Conjecture from the control viewpoint
|
|
|
- Mervin Johnson
- 5 years ago
- Views:
Transcription
1 Mañé s Conjecture from the control viewpoint Université de Nice - Sophia Antipolis
2 Setting Let M be a smooth compact manifold of dimension n 2 be fixed. Let H : T M R be a Hamiltonian of class C k, with k 2, satisfying the following properties: (H1) Superlinear growth: For every K 0, there is C (K) R such that H(x, p) K p + C (K) (x, p) T M. (H2) Uniform convexity: For every (x, p) T M, 2 H p 2 (x, p) is positive definite.
3 Critical value of H Definition We call critical value of H the constant c = c[h] defined as { { ( )} } c[h] := H x, du(x). inf u C 1 (M;R) max x M In other terms, c[h] is the infimum of numbers c R such that there is a C 1 function u : M R satisfying H ( x, du(x) ) c x M.
4 Critical value of H Definition We call critical value of H the constant c = c[h] defined as { { ( )} } c[h] := H x, du(x). inf u C 1 (M;R) max x M In other terms, c[h] is the infimum of numbers c R such that there is a C 1 function u : M R satisfying Note that min x M H ( x, du(x) ) c x M. {H(x, 0)} c[h] max {H(x, 0)}. x M
5 Critical subsolutions of H Definition We call critical subsolution any Lipschitz function u : M R such that H ( x, du(x) ) c[h] for a.e. x M.
6 Critical subsolutions of H Definition We call critical subsolution any Lipschitz function u : M R such that H ( x, du(x) ) c[h] for a.e. x M. Let L : TM R be the Tonelli Lagrangian associated with H by Legendre-Fenchel duality, that is { } L(x, v) := max p v H(x, p) (x, v) TM. p Tx M
7 Critical subsolutions of H Definition We call critical subsolution any Lipschitz function u : M R such that H ( x, du(x) ) c[h] for a.e. x M. Let L : TM R be the Tonelli Lagrangian associated with H by Legendre-Fenchel duality, that is { } L(x, v) := max p v H(x, p) (x, v) TM. p Tx M A Lipschitz function u : M R is a critical subsolution if and only if u ( γ(b) ) u ( γ(a) ) b for every Lipschitz curve γ : [a, b] M. a L ( γ(t), γ(t) ) ds + c (b a),
8 The Fathi-Siconolfi-Bernard Theorem Theorem (Fathi-Siconolfi, 2004; Bernard, 2007) The set SS 1 (H) (resp. SS 1,1 (H)) of critical subsolutions of class C 1 (resp. C 1,1 ) is nonempty.
9 The Fathi-Siconolfi-Bernard Theorem Theorem (Fathi-Siconolfi, 2004; Bernard, 2007) The set SS 1 (H) (resp. SS 1,1 (H)) of critical subsolutions of class C 1 (resp. C 1,1 ) is nonempty. As a consequence, the set of x M such that u critical subsolution of class C 1 = H ( x, du(x) ) = c[h] is nonempty.
10 Projected Aubry set and Aubry set Definition and Proposition The projected Aubry set of H defined as A(H) = { x M H ( x, du(x) ) = c[h], u SS 1 (H) }, is compact and nonempty.
11 Projected Aubry set and Aubry set Definition and Proposition The projected Aubry set of H defined as A(H) = { x M H ( x, du(x) ) = c[h], u SS 1 (H) }, is compact and nonempty. Any critical subsolution u is C 1 at any point of A(H) and satisfies H ( x, du(x) ) = c[h], x A(H).
12 Projected Aubry set and Aubry set Definition and Proposition The projected Aubry set of H defined as A(H) = { x M H ( x, du(x) ) = c[h], u SS 1 (H) }, is compact and nonempty. Any critical subsolution u is C 1 at any point of A(H) and satisfies H ( x, du(x) ) = c[h], x A(H). For every x A(H), the differential of a critical subsolution at x does not depend on u.
13 Projected Aubry set and Aubry set Definition and Proposition The projected Aubry set of H defined as A(H) = { x M H ( x, du(x) ) = c[h], u SS 1 (H) }, is compact and nonempty. Any critical subsolution u is C 1 at any point of A(H) and satisfies H ( x, du(x) ) = c[h], x A(H). For every x A(H), the differential of a critical subsolution at x does not depend on u. The Aubry set of H defined by A(H) := {( x, du(x) ) x A(H), u crit. subsol. } T M is compact, invariant by φ H t, and is a Lipschitz graph over A(H).
14 Back to the critical value Proposition The critical value of H satisfies { c[h] = min u C 1 (M;R) max x M { H ( x, du(x) )} }. Proposition The critical value of H satisfies { 1 c[h] = inf T T 0 L ( γ(t), γ(t) ) } dt, where the infimum is taken over the Lipschitz curves γ : [0, T ] M such that γ(0) = γ(t ).
15 Examples Let V : M R be a potential of class C 2 and H : T M R be the Hamiltonian defined by H(x, p) = 1 2 p 2 + V (x) (x, p) T M. Then c[h] = max M V and { } Ã(H) = (x, 0) V (x) = max V. M Let X be a smooth vector field on M and L : TM R defined by L X (x, v) = 1 v X (x) 2 (x, 2 v) TM. Then c[h] = 0 and the projected Aubry set always contains the set of recurrent points of the flow of X.
16 The Mañé Conjecture Conjecture (Mañé, 96) For every Tonelli Hamiltonian H : T M R of class C k (with k 2), there is a residual subset (i.e., a countable intersection of open and dense subsets) G of C k (M) such that, for every V G, the Aubry set of the Hamiltonian H V := H + V is either an equilibrium point or a periodic orbit.
17 The Mañé Conjecture Conjecture (Mañé, 96) For every Tonelli Hamiltonian H : T M R of class C k (with k 2), there is a residual subset (i.e., a countable intersection of open and dense subsets) G of C k (M) such that, for every V G, the Aubry set of the Hamiltonian H V := H + V is either an equilibrium point or a periodic orbit. Strategy of proof: Density result. Stability result.
18 Mañé s density Conjecture Proposition (Contreras-Iturriaga, 1999) Let H : T M R be a Hamiltonian of class C k (with k 3) whose Aubry set is an equilibrium point (resp. a periodic orbit). Then, there is a smooth potential V : M R, with V C k as small as desired, such that the Aubry set of H V is a hyperbolic equilibrium (resp. a hyperbolic periodic orbit).
19 Mañé s density Conjecture Proposition (Contreras-Iturriaga, 1999) Let H : T M R be a Hamiltonian of class C k (with k 3) whose Aubry set is an equilibrium point (resp. a periodic orbit). Then, there is a smooth potential V : M R, with V C k as small as desired, such that the Aubry set of H V is a hyperbolic equilibrium (resp. a hyperbolic periodic orbit). Conjecture (Mañé s density conjecture) For every Tonelli Hamiltonian H : T M R of class C k (with k 2) there exists a dense set D in C k (M) such that, for every V D, the Aubry set of the Hamiltonian H V is either an equilibrium point or a periodic orbit.
20 The C 1 closing Lemma Theorem (Pugh, 1967) Let M be a smooth compact manifold. Suppose that some vector field X has a nontrivial recurrent trajectory through x M and suppose that U is a neighborhood of X in the C 1 topology. Then there exists Y U such that Y has a closed orbit through x.
21 The C 1 closing Lemma Theorem (Pugh, 1967) Let M be a smooth compact manifold. Suppose that some vector field X has a nontrivial recurrent trajectory through x M and suppose that U is a neighborhood of X in the C 1 topology. Then there exists Y U such that Y has a closed orbit through x. Theorem (Pugh-Robinson, 1983) Let (N, ω) be a symplectic manifold of dimension 2n 2 and H : N R be a given Hamiltonian of class C 2. Let X be the Hamiltonian vector field associated with H and φ H the Hamiltonian flow. Suppose that X has a nontrivial recurrent trajectory through x N and that U is a neighborhood of X in the C 1 topology. Then there exists Y U such that Y is a Hamiltonian vector field and Y has a closed orbit through x.
22 Strategy of proof Given a Tonelli Hamiltonian, we need to find: a potential V : M R small, a periodic orbit γ : [0, T ] M (γ(0) = γ(t )), a Lipschitz function v : M R, in such a way that the following properties are satisfied: H V ( x, dv(x) ) 0 for a.e. x M, T 0 L V ( γ(t), γ(t) ) dt = 0.
23 Strategy of proof Given a Tonelli Hamiltonian, we need to find: a potential V : M R small, a periodic orbit γ : [0, T ] M (γ(0) = γ(t )), a Lipschitz function v : M R, in such a way that the following properties are satisfied: H V ( x, dv(x) ) 0 for a.e. x M, ( c[hv ] 0) T 0 L V ( γ(t), γ(t) ) dt = 0.
24 Strategy of proof Given a Tonelli Hamiltonian, we need to find: a potential V : M R small, a periodic orbit γ : [0, T ] M (γ(0) = γ(t )), a Lipschitz function v : M R, in such a way that the following properties are satisfied: H V ( x, dv(x) ) 0 for a.e. x M, ( c[hv ] 0) T 0 L V ( γ(t), γ(t) ) dt = 0. ( c[hv ] 0)
25 A connecting problem Let be given two solutions ( xi, p i ) : [0, τ] R n R n i = 1, 2, of the Hamiltonian system { ẋ(t) = p H ( x(t), p(t) ) ṗ(t) = x H ( x(t), p(t) ).
26 A connecting problem Let be given two solutions ( xi, p i ) : [0, τ] R n R n i = 1, 2, of the Hamiltonian system { ẋ(t) = p H ( x(t), p(t) ) ṗ(t) = x H ( x(t), p(t) ). Question Can I add a potential V to the Hamiltonian H in such a way that the solution of the new Hamiltonian system { ẋ(t) = p H ( x(t), p(t) ) ṗ(t) = x H ( x(t), p(t) ) V (x(t)), starting at ( x 1 (0), p 1 (0) ) satisfies ( x(τ), p(τ) ) = ( x2 (τ), p 2 (τ) )?
27 Picture x 1 ( ) x 2 ( )
28 Picture x 1 ( ) x 2 ( ) Supp (V )
29 Control approach Study the mapping where E : L 1 ([0, τ]; R n ) R n R n u ( x u (τ), p u (τ) ) ( xu, p u ) : [0, τ] R n R n is the solution of { ẋ(t) = p H ( x(t), p(t) ) starting at ( x 1 (0), p 1 (0) ). ṗ(t) = x H ( x(t), p(t) ) u(t), u = 0
30 Exercise x 0 u = 0 u = 0 x τ Exercise Given x, u : [0, τ] R n as above, does there exists a function V : R n R whose the support is included in the dashed blue square above and such that V (x(t)) = u(t) t [0, τ]?
31 Exercise (solution) There is a necessary condition τ 0 ẋ(t), u(t) dt = 0.
32 Exercise (solution) There is a necessary condition As a matter of fact, τ 0 τ ẋ(t), u(t) dt = 0 ẋ(t), u(t) dt = 0. τ 0 ẋ(t), V (x(t)) dt = V (x τ ) V (x 0 ) = 0.
33 Exercise (solution) There is a necessary condition As a matter of fact, τ 0 τ ẋ(t), u(t) dt = 0 ẋ(t), u(t) dt = 0. τ 0 ẋ(t), V (x(t)) dt = V (x τ ) V (x 0 ) = 0. Proposition If the above necessary condition is satisfied, then there is V : R n R satisfying the desired properties such that V C 1 K r u.
34 Exercise (solution) If x(t) = (t, 0), that is x 0 r x τ
35 Exercise (solution) If x(t) = (t, 0), that is x 0 r x τ then we set V (t, y) := φ ( y /r ) [ t n 1 u 1 (s) ds + yi 0 i=1 0 ] u i+1 (t + s) ds, for every (t, y), with φ : [0, ) [0, 1] satisfying φ(s) = 1 s [0, 1/3] and φ(s) = 0 s 2/3.
36 Closing Aubry sets in C 1 topology Theorem (Figalli-R, 2010) Let H : T M R be a Tonelli Hamiltonian of class C k with k 4, and fix ɛ > 0. Then there exists a potential V : M R of class C k 2, with V C 1 < ɛ, such that c[h V ] = c[h] and the Aubry set of H V is either an (hyperbolic) equilibrium point or a (hyperbolic) periodic orbit.
37 Closing Aubry sets in C 1 topology Theorem (Figalli-R, 2010) Let H : T M R be a Tonelli Hamiltonian of class C k with k 4, and fix ɛ > 0. Then there exists a potential V : M R of class C k 2, with V C 1 < ɛ, such that c[h V ] = c[h] and the Aubry set of H V is either an (hyperbolic) equilibrium point or a (hyperbolic) periodic orbit. The above result is not satisfactory. The property having an Aubry set which is an hyperbolic closed orbit is not stable under C 1 perturbations.
38 Toward a proof of Mañé s Conjecture in C 2 topology Theorem (Figalli-R, 2010) Assume that dim M 3. Let H : T M R be a Tonelli Hamiltonian of class C k with k 4, and fix ɛ > 0. Assume that there are a recurrent point x A(H), a critical viscosity subsolution u : M R, and an open neighborhood V of O +( x ) such that u is at least C k+1 on V. Then there exists a potential V : M R of class C k 1, with V C 2 < ɛ, such that c[h V ] = c[h] and the Aubry set of H V is either an (hyperbolic) equilibrium point or a (hyperbolic) periodic orbit.
39 Application to Mañé s Lagrangians Recall that given X a C k -vector field on M with k 2, the Mañé Lagrangian L X : TM R associated to X is defined by L X (x, v) := 1 v X (x) 2 2 x (x, v) TM, while the Mañé Hamiltonian H X : TM R is given by H X (x, p) = 1 p p, X (x) (x, p) T M. x Corollary (Figalli-R, 2010) Let X be a vector field on M of class C k with k 2. Then for every ɛ > 0 there is a potential V : M R of class C k, with V C 2 < ɛ, such that the Aubry set of H X + V is either an equilibrium point or a periodic orbit.
40 Discussion Theorem (Bernard, 2007) Assume that the Aubry set is exactly one hyperbolic periodic orbit, then any critical solution is smooth in a neighborhood of A(H). As a consequence, there is a smooth critical subsolution.
41 Discussion Theorem (Bernard, 2007) Assume that the Aubry set is exactly one hyperbolic periodic orbit, then any critical solution is smooth in a neighborhood of A(H). As a consequence, there is a smooth critical subsolution. Conjecture (Regularity Conjecture for critical subsolutions) For every Tonelli Hamiltonian H : T M R of class C there is a set D C (M) which is dense in C 2 (M) (with respect to the C 2 topology) such that the following holds: For every V D, there is a smooth critical subsolution.
42 Thank you for your attention!!
Generic Aubry sets on surfaces
 Université de Nice - Sophia Antipolis & Institut Universitaire de France Nanjing University (June 10th, 2013) Setting Let M be a smooth compact manifold of dimension n 2 be fixed. Let H : T M R be a Hamiltonian
Université de Nice - Sophia Antipolis & Institut Universitaire de France Nanjing University (June 10th, 2013) Setting Let M be a smooth compact manifold of dimension n 2 be fixed. Let H : T M R be a Hamiltonian
Geometric control and dynamical systems
 Université de Nice - Sophia Antipolis & Institut Universitaire de France 9th AIMS International Conference on Dynamical Systems, Differential Equations and Applications Control of an inverted pendulum
Université de Nice - Sophia Antipolis & Institut Universitaire de France 9th AIMS International Conference on Dynamical Systems, Differential Equations and Applications Control of an inverted pendulum
On the Hausdorff Dimension of the Mather Quotient
 On the Hausdorff Dimension of the Mather Quotient Albert Fathi, Alessio Figalli, Ludovic Rifford February 29, 2008 Abstract Under appropriate assumptions on the dimension of the ambient manifold and the
On the Hausdorff Dimension of the Mather Quotient Albert Fathi, Alessio Figalli, Ludovic Rifford February 29, 2008 Abstract Under appropriate assumptions on the dimension of the ambient manifold and the
Regularity of solutions to Hamilton-Jacobi equations for Tonelli Hamiltonians
 Regularity of solutions to Hamilton-Jacobi equations for Tonelli Hamiltonians Université Nice Sophia Antipolis & Institut Universitaire de France Nonlinear Analysis and Optimization Royal Society, London,
Regularity of solutions to Hamilton-Jacobi equations for Tonelli Hamiltonians Université Nice Sophia Antipolis & Institut Universitaire de France Nonlinear Analysis and Optimization Royal Society, London,
Closing Aubry sets II
 Closing Aubry sets II A. Figalli L. Rifford July 1, 1 Abstract Given a Tonelli Hamiltonian H : T M R of class C k, with k 4, we prove the following results: 1 Assume there is a critical viscosity subsolution
Closing Aubry sets II A. Figalli L. Rifford July 1, 1 Abstract Given a Tonelli Hamiltonian H : T M R of class C k, with k 4, we prove the following results: 1 Assume there is a critical viscosity subsolution
A Kupka-Smale Theorem for Hamiltonian systems. systems from Mañé s viewpoint, a control approach. Ludovic Rifford PICOF 12
 A Kupka-Smale Theorem for Hamiltonian systems from Mañé s viewpoint, a control approach Université de Nice - Sophia Antipolis & Institut Universitaire de France PICOF 12 The Kupka-Smale Theorem for vector
A Kupka-Smale Theorem for Hamiltonian systems from Mañé s viewpoint, a control approach Université de Nice - Sophia Antipolis & Institut Universitaire de France PICOF 12 The Kupka-Smale Theorem for vector
MATHER THEORY, WEAK KAM, AND VISCOSITY SOLUTIONS OF HAMILTON-JACOBI PDE S
 MATHER THEORY, WEAK KAM, AND VISCOSITY SOLUTIONS OF HAMILTON-JACOBI PDE S VADIM YU. KALOSHIN 1. Motivation Consider a C 2 smooth Hamiltonian H : T n R n R, where T n is the standard n-dimensional torus
MATHER THEORY, WEAK KAM, AND VISCOSITY SOLUTIONS OF HAMILTON-JACOBI PDE S VADIM YU. KALOSHIN 1. Motivation Consider a C 2 smooth Hamiltonian H : T n R n R, where T n is the standard n-dimensional torus
A generic property of families of Lagrangian systems
 Annals of Mathematics, 167 (2008), 1099 1108 A generic property of families of Lagrangian systems By Patrick Bernard and Gonzalo Contreras * Abstract We prove that a generic Lagrangian has finitely many
Annals of Mathematics, 167 (2008), 1099 1108 A generic property of families of Lagrangian systems By Patrick Bernard and Gonzalo Contreras * Abstract We prove that a generic Lagrangian has finitely many
Lecture 3. Topology of the set of singularities of a solution of the Hamilton-Jacobi Equation
 Lecture 3. Topology of the set of singularities of a solution of the Hamilton-Jacobi Equation Albert Fathi Padova, 14 February 2018 We will present results which are a joint work with Piermarco Cannarsa
Lecture 3. Topology of the set of singularities of a solution of the Hamilton-Jacobi Equation Albert Fathi Padova, 14 February 2018 We will present results which are a joint work with Piermarco Cannarsa
Generic hyperbolicity of Aubry sets on surfaces
 Generic hyperbolicity of Aubry sets on surfaces G. Contreras A. Figalli L. Rifford May 26, 214 Abstract Given a Tonelli Hamiltonian of class C 2 on the cotangent bundle of a compact surface, we show that
Generic hyperbolicity of Aubry sets on surfaces G. Contreras A. Figalli L. Rifford May 26, 214 Abstract Given a Tonelli Hamiltonian of class C 2 on the cotangent bundle of a compact surface, we show that
Green bundles : a dynamical study
 Green bundles : a dynamical study Marie-Claude Arnaud December 2007 1 CONTENT 1) Hamiltonian and Lagrangian formalism 2) Lipschitz Lagrangian submanifolds, images of such manifolds and minimization properties
Green bundles : a dynamical study Marie-Claude Arnaud December 2007 1 CONTENT 1) Hamiltonian and Lagrangian formalism 2) Lipschitz Lagrangian submanifolds, images of such manifolds and minimization properties
Local semiconvexity of Kantorovich potentials on non-compact manifolds
 Local semiconvexity of Kantorovich potentials on non-compact manifolds Alessio Figalli, Nicola Gigli Abstract We prove that any Kantorovich potential for the cost function c = d / on a Riemannian manifold
Local semiconvexity of Kantorovich potentials on non-compact manifolds Alessio Figalli, Nicola Gigli Abstract We prove that any Kantorovich potential for the cost function c = d / on a Riemannian manifold
VISCOSITY SOLUTIONS OF HAMILTON-JACOBI EQUATIONS, AND ASYMPTOTICS FOR HAMILTONIAN SYSTEMS
 VISCOSITY SOLUTIONS OF HAMILTON-JACOBI EQUATIONS, AND ASYMPTOTICS FOR HAMILTONIAN SYSTEMS DIOGO AGUIAR GOMES U.C. Berkeley - CA, US and I.S.T. - Lisbon, Portugal email:dgomes@math.ist.utl.pt Abstract.
VISCOSITY SOLUTIONS OF HAMILTON-JACOBI EQUATIONS, AND ASYMPTOTICS FOR HAMILTONIAN SYSTEMS DIOGO AGUIAR GOMES U.C. Berkeley - CA, US and I.S.T. - Lisbon, Portugal email:dgomes@math.ist.utl.pt Abstract.
WEAK KAM THEORETIC ASPECTS FOR NONREGULAR COMMUTING HAMILTONIANS
 WEAK KAM THEORETIC ASPECTS FOR NONREGULAR COMMUTING HAMILTONIANS ANDREA DAVINI AND MAXIME ZAVIDOVIQUE Abstract. In this paper we introduce the notion of commutation for a pair of continuous and convex
WEAK KAM THEORETIC ASPECTS FOR NONREGULAR COMMUTING HAMILTONIANS ANDREA DAVINI AND MAXIME ZAVIDOVIQUE Abstract. In this paper we introduce the notion of commutation for a pair of continuous and convex
Topology of the set of singularities of a solution of the Hamilton-Jacobi Equation
 Topology of the set of singularities of a solution of the Hamilton-Jacobi Equation Albert Fathi IAS Princeton March 15, 2016 In this lecture, a singularity for a locally Lipschitz real valued function
Topology of the set of singularities of a solution of the Hamilton-Jacobi Equation Albert Fathi IAS Princeton March 15, 2016 In this lecture, a singularity for a locally Lipschitz real valued function
A few words about the MTW tensor
 A few words about the Ma-Trudinger-Wang tensor Université Nice - Sophia Antipolis & Institut Universitaire de France Salah Baouendi Memorial Conference (Tunis, March 2014) The Ma-Trudinger-Wang tensor
A few words about the Ma-Trudinger-Wang tensor Université Nice - Sophia Antipolis & Institut Universitaire de France Salah Baouendi Memorial Conference (Tunis, March 2014) The Ma-Trudinger-Wang tensor
LECTURE NOTES ON MATHER S THEORY FOR LAGRANGIAN SYSTEMS
 LECTURE NOTES ON MATHER S THEORY FOR LAGRANGIAN SYSTEMS ALFONSO SORRENTINO Abstract. These notes are based on a series of lectures that the author gave at the CIMPA Research School Hamiltonian and Lagrangian
LECTURE NOTES ON MATHER S THEORY FOR LAGRANGIAN SYSTEMS ALFONSO SORRENTINO Abstract. These notes are based on a series of lectures that the author gave at the CIMPA Research School Hamiltonian and Lagrangian
Periodic Orbits of Weakly Exact Magnetic Flows
 Nonl. Analysis and Differential Equations, Vol. 1, 213, no. 2, 93-1 HIKARI Ltd, www.m-hikari.com Periodic Orbits of Weakly Exact Magnetic Flows Osvaldo Osuna Instituto de Física y Matemáticas, Universidad
Nonl. Analysis and Differential Equations, Vol. 1, 213, no. 2, 93-1 HIKARI Ltd, www.m-hikari.com Periodic Orbits of Weakly Exact Magnetic Flows Osvaldo Osuna Instituto de Física y Matemáticas, Universidad
Hyperbolic periodic orbits and Mather sets in certain symmetric cases
 Hyperbolic periodic orbits and Mather sets in certain symmetric cases M.-. ARNAUD July 12, 2006 Abstract We consider a Lagrangian function L : T M R which is superlinear and convex in the fibers and has
Hyperbolic periodic orbits and Mather sets in certain symmetric cases M.-. ARNAUD July 12, 2006 Abstract We consider a Lagrangian function L : T M R which is superlinear and convex in the fibers and has
Optimal transportation on non-compact manifolds
 Optimal transportation on non-compact manifolds Albert Fathi, Alessio Figalli 07 November 2007 Abstract In this work, we show how to obtain for non-compact manifolds the results that have already been
Optimal transportation on non-compact manifolds Albert Fathi, Alessio Figalli 07 November 2007 Abstract In this work, we show how to obtain for non-compact manifolds the results that have already been
Journal of Differential Equations
 J. Differential Equations 25 211) 2389 241 Contents lists available at ScienceDirect Journal of Differential Equations www.elsevier.com/locate/jde A particular minimization property implies C -integrability
J. Differential Equations 25 211) 2389 241 Contents lists available at ScienceDirect Journal of Differential Equations www.elsevier.com/locate/jde A particular minimization property implies C -integrability
Geometry of generating function and Lagrangian spectral invariants
 Geometry of generating function and Lagrangian spectral invariants Yong-Geun Oh IBS Center for Geometry and Physics & POSTECH & University of Wisconsin-Madsion Paris, Alanfest, July 18, 2012 Yong-Geun
Geometry of generating function and Lagrangian spectral invariants Yong-Geun Oh IBS Center for Geometry and Physics & POSTECH & University of Wisconsin-Madsion Paris, Alanfest, July 18, 2012 Yong-Geun
CAUCHY PROBLEMS FOR STATIONARY HAMILTON JACOBI EQUATIONS UNDER MILD REGULARITY ASSUMPTIONS. Olga Bernardi and Franco Cardin.
 JOURNAL OF GEOMETRIC MECHANICS doi:10.3934/jgm.2009.1.271 c American Institute of Mathematical Sciences Volume 1, Number 3, September 2009 pp. 271 294 CAUCHY PROBLEMS FOR STATIONARY HAMILTON JACOBI EQUATIONS
JOURNAL OF GEOMETRIC MECHANICS doi:10.3934/jgm.2009.1.271 c American Institute of Mathematical Sciences Volume 1, Number 3, September 2009 pp. 271 294 CAUCHY PROBLEMS FOR STATIONARY HAMILTON JACOBI EQUATIONS
Chain recurrence, chain transitivity, Lyapunov functions and rigidity of Lagrangian submanifolds of optical hypersurfaces
 arxiv:1510.04491v1 [math.ds] 15 Oct 2015 Chain recurrence, chain transitivity, Lyapunov functions and rigidity of Lagrangian submanifolds of optical hypersurfaces Alberto Abbondandolo 1 Olga Bernardi 2
arxiv:1510.04491v1 [math.ds] 15 Oct 2015 Chain recurrence, chain transitivity, Lyapunov functions and rigidity of Lagrangian submanifolds of optical hypersurfaces Alberto Abbondandolo 1 Olga Bernardi 2
HAMILTONIAN ELLIPTIC DYNAMICS ON SYMPLECTIC 4-MANIFOLDS
 HAMILTONIAN ELLIPTIC DYNAMICS ON SYMPLECTIC 4-MANIFOLDS MÁRIO BESSA AND JOÃO LOPES DIAS Abstract. We consider C 2 Hamiltonian functions on compact 4-dimensional symplectic manifolds to study elliptic dynamics
HAMILTONIAN ELLIPTIC DYNAMICS ON SYMPLECTIC 4-MANIFOLDS MÁRIO BESSA AND JOÃO LOPES DIAS Abstract. We consider C 2 Hamiltonian functions on compact 4-dimensional symplectic manifolds to study elliptic dynamics
Duality and dynamics in Hamilton-Jacobi theory for fully convex problems of control
 Duality and dynamics in Hamilton-Jacobi theory for fully convex problems of control RTyrrell Rockafellar and Peter R Wolenski Abstract This paper describes some recent results in Hamilton- Jacobi theory
Duality and dynamics in Hamilton-Jacobi theory for fully convex problems of control RTyrrell Rockafellar and Peter R Wolenski Abstract This paper describes some recent results in Hamilton- Jacobi theory
arxiv: v1 [math.ds] 2 Nov 2010
![arxiv: v1 [math.ds] 2 Nov 2010 arxiv: v1 [math.ds] 2 Nov 2010](/thumbs/94/121306739.jpg) LECTURE NOTES ON MATHER S THEORY FOR LAGRANGIAN SYSTEMS ALFONSO SORRENTINO arxiv:111.59v1 [math.ds] 2 Nov 21 Contents 1. Introduction 1 2. Tonelli Lagrangians and Hamiltonians on compact manifolds 3 3.
LECTURE NOTES ON MATHER S THEORY FOR LAGRANGIAN SYSTEMS ALFONSO SORRENTINO arxiv:111.59v1 [math.ds] 2 Nov 21 Contents 1. Introduction 1 2. Tonelli Lagrangians and Hamiltonians on compact manifolds 3 3.
Transport Continuity Property
 On Riemannian manifolds satisfying the Transport Continuity Property Université de Nice - Sophia Antipolis (Joint work with A. Figalli and C. Villani) I. Statement of the problem Optimal transport on Riemannian
On Riemannian manifolds satisfying the Transport Continuity Property Université de Nice - Sophia Antipolis (Joint work with A. Figalli and C. Villani) I. Statement of the problem Optimal transport on Riemannian
THE PALAIS-SMALE CONDITION ON CONTACT TYPE ENERGY LEVELS FOR CONVEX LAGRANGIAN SYSTEMS
 THE PALAIS-SMALE CONDITION ON CONTACT TYPE ENERGY LEVELS FOR CONVEX LAGRANGIAN SYSTEMS Gonzalo Contreras Comunicación Técnica No I-3-1/25-4-23 (MB/CIMAT) THE PALAIS-SMALE CONDITION AND MAÑÉ S CRITICAL
THE PALAIS-SMALE CONDITION ON CONTACT TYPE ENERGY LEVELS FOR CONVEX LAGRANGIAN SYSTEMS Gonzalo Contreras Comunicación Técnica No I-3-1/25-4-23 (MB/CIMAT) THE PALAIS-SMALE CONDITION AND MAÑÉ S CRITICAL
(x k ) sequence in F, lim x k = x x F. If F : R n R is a function, level sets and sublevel sets of F are any sets of the form (respectively);
 STABILITY OF EQUILIBRIA AND LIAPUNOV FUNCTIONS. By topological properties in general we mean qualitative geometric properties (of subsets of R n or of functions in R n ), that is, those that don t depend
STABILITY OF EQUILIBRIA AND LIAPUNOV FUNCTIONS. By topological properties in general we mean qualitative geometric properties (of subsets of R n or of functions in R n ), that is, those that don t depend
Variational Analysis and Tame Optimization
 Variational Analysis and Tame Optimization Aris Daniilidis http://mat.uab.cat/~arisd Universitat Autònoma de Barcelona April 15 17, 2010 PLAN OF THE TALK Nonsmooth analysis Genericity of pathological situations
Variational Analysis and Tame Optimization Aris Daniilidis http://mat.uab.cat/~arisd Universitat Autònoma de Barcelona April 15 17, 2010 PLAN OF THE TALK Nonsmooth analysis Genericity of pathological situations
Weak KAM pairs and Monge-Kantorovich duality
 Advanced Studies in Pure Mathematics 47-2, 2007 Asymptotic Analysis and Singularities pp. 397 420 Weak KAM pairs and Monge-Kantorovich duality Abstract. Patrick Bernard and Boris Buffoni The dynamics of
Advanced Studies in Pure Mathematics 47-2, 2007 Asymptotic Analysis and Singularities pp. 397 420 Weak KAM pairs and Monge-Kantorovich duality Abstract. Patrick Bernard and Boris Buffoni The dynamics of
An introduction to Birkhoff normal form
 An introduction to Birkhoff normal form Dario Bambusi Dipartimento di Matematica, Universitá di Milano via Saldini 50, 0133 Milano (Italy) 19.11.14 1 Introduction The aim of this note is to present an
An introduction to Birkhoff normal form Dario Bambusi Dipartimento di Matematica, Universitá di Milano via Saldini 50, 0133 Milano (Italy) 19.11.14 1 Introduction The aim of this note is to present an
Essential hyperbolicity versus homoclinic bifurcations. Global dynamics beyond uniform hyperbolicity, Beijing 2009 Sylvain Crovisier - Enrique Pujals
 Essential hyperbolicity versus homoclinic bifurcations Global dynamics beyond uniform hyperbolicity, Beijing 2009 Sylvain Crovisier - Enrique Pujals Generic dynamics Consider: M: compact boundaryless manifold,
Essential hyperbolicity versus homoclinic bifurcations Global dynamics beyond uniform hyperbolicity, Beijing 2009 Sylvain Crovisier - Enrique Pujals Generic dynamics Consider: M: compact boundaryless manifold,
Franks Lemma for C 2 Mane Perturbations of Riemannian Metrics and Applications to Persistence
 Franks Lemma for C Mane Perturbations of Riemannian Metrics and Applications to Persistence A Lazrag, Ludovic Rifford, Rafael Ruggiero To cite this version: A Lazrag, Ludovic Rifford, Rafael Ruggiero.
Franks Lemma for C Mane Perturbations of Riemannian Metrics and Applications to Persistence A Lazrag, Ludovic Rifford, Rafael Ruggiero To cite this version: A Lazrag, Ludovic Rifford, Rafael Ruggiero.
On the number of Mather measures of Lagrangian systems
 On the number of Mather measures of Lagrangian systems Patrick Bernard November 2009 Patrick Bernard 1 CEREMADE, CNRS Pl. du Maréchal de Lattre de Tassigny 75775 Paris Cedex 16 France patrick.bernard@ceremade.dauphine.fr
On the number of Mather measures of Lagrangian systems Patrick Bernard November 2009 Patrick Bernard 1 CEREMADE, CNRS Pl. du Maréchal de Lattre de Tassigny 75775 Paris Cedex 16 France patrick.bernard@ceremade.dauphine.fr
Invariant measures of Hamiltonian systems with prescribed asymptotic Maslov index
 Invariant measures of Hamiltonian systems with prescribed asymptotic Maslov index Alberto Abbondandolo and Alessio Figalli September 29, 27 Dedicated to Vladimir Igorevich Arnold Abstract We study the
Invariant measures of Hamiltonian systems with prescribed asymptotic Maslov index Alberto Abbondandolo and Alessio Figalli September 29, 27 Dedicated to Vladimir Igorevich Arnold Abstract We study the
HAMILTON-JACOBI THEORY AND PARAMETRIC ANALYSIS IN FULLY CONVEX PROBLEMS OF OPTIMAL CONTROL. R. T. Rockafellar 1
 HAMILTON-JACOBI THEORY AND PARAMETRIC ANALYSIS IN FULLY CONVEX PROBLEMS OF OPTIMAL CONTROL R. T. Rockafellar 1 Department of Mathematics, Box 354350 University of Washington, Seattle, WA 98195-4350 rtr@math.washington.edu
HAMILTON-JACOBI THEORY AND PARAMETRIC ANALYSIS IN FULLY CONVEX PROBLEMS OF OPTIMAL CONTROL R. T. Rockafellar 1 Department of Mathematics, Box 354350 University of Washington, Seattle, WA 98195-4350 rtr@math.washington.edu
REGULARITY THEORY FOR HAMILTON-JACOBI EQUATIONS
 REGULARITY THEORY FOR HAMILTON-JACOBI EQUATIONS DIOGO AGUIAR GOMES Abstract. The objective of this paper is to discuss the regularity of viscosity solutions of time independent Hamilton-Jacobi Equations.
REGULARITY THEORY FOR HAMILTON-JACOBI EQUATIONS DIOGO AGUIAR GOMES Abstract. The objective of this paper is to discuss the regularity of viscosity solutions of time independent Hamilton-Jacobi Equations.
Weak KAM Theorem in Lagrangian Dynamics Preliminary Version Number 10. Albert FATHI
 Weak KAM Theorem in Lagrangian Dynamics Preliminary Version Number 10 Albert FATHI Lyon, Version 15 June 2008 ii Contents Preface vii Introduction ix 0.1 The Hamilton-Jacobi Method............ xi 1 Convex
Weak KAM Theorem in Lagrangian Dynamics Preliminary Version Number 10 Albert FATHI Lyon, Version 15 June 2008 ii Contents Preface vii Introduction ix 0.1 The Hamilton-Jacobi Method............ xi 1 Convex
A strong form of Arnold diffusion for two and a half degrees of freedom
 A strong form of Arnold diffusion for two and a half degrees of freedom arxiv:1212.1150v1 [math.ds] 5 Dec 2012 V. Kaloshin, K. Zhang February 7, 2014 Abstract In the present paper we prove a strong form
A strong form of Arnold diffusion for two and a half degrees of freedom arxiv:1212.1150v1 [math.ds] 5 Dec 2012 V. Kaloshin, K. Zhang February 7, 2014 Abstract In the present paper we prove a strong form
1 )(y 0) {1}. Thus, the total count of points in (F 1 (y)) is equal to deg y0
 1. Classification of 1-manifolds Theorem 1.1. Let M be a connected 1 manifold. Then M is diffeomorphic either to [0, 1], [0, 1), (0, 1), or S 1. We know that none of these four manifolds are not diffeomorphic
1. Classification of 1-manifolds Theorem 1.1. Let M be a connected 1 manifold. Then M is diffeomorphic either to [0, 1], [0, 1), (0, 1), or S 1. We know that none of these four manifolds are not diffeomorphic
LECTURE 15: COMPLETENESS AND CONVEXITY
 LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
Differential Games II. Marc Quincampoix Université de Bretagne Occidentale ( Brest-France) SADCO, London, September 2011
 Differential Games II Marc Quincampoix Université de Bretagne Occidentale ( Brest-France) SADCO, London, September 2011 Contents 1. I Introduction: A Pursuit Game and Isaacs Theory 2. II Strategies 3.
Differential Games II Marc Quincampoix Université de Bretagne Occidentale ( Brest-France) SADCO, London, September 2011 Contents 1. I Introduction: A Pursuit Game and Isaacs Theory 2. II Strategies 3.
Entropy of C 1 -diffeomorphisms without dominated splitting
 Entropy of C 1 -diffeomorphisms without dominated splitting Jérôme Buzzi (CNRS & Université Paris-Sud) joint with S. CROVISIER and T. FISHER June 15, 2017 Beyond Uniform Hyperbolicity - Provo, UT Outline
Entropy of C 1 -diffeomorphisms without dominated splitting Jérôme Buzzi (CNRS & Université Paris-Sud) joint with S. CROVISIER and T. FISHER June 15, 2017 Beyond Uniform Hyperbolicity - Provo, UT Outline
Notes on symplectic geometry and group actions
 Notes on symplectic geometry and group actions Peter Hochs November 5, 2013 Contents 1 Example of Hamiltonian mechanics 1 2 Proper actions and Hausdorff quotients 4 3 N particles in R 3 7 4 Commuting actions
Notes on symplectic geometry and group actions Peter Hochs November 5, 2013 Contents 1 Example of Hamiltonian mechanics 1 2 Proper actions and Hausdorff quotients 4 3 N particles in R 3 7 4 Commuting actions
The Monge problem on non-compact manifolds
 The Monge problem on non-compact manifolds Alessio Figalli Scuola Normale Superiore Pisa Abstract In this paper we prove the existence of an optimal transport map on non-compact manifolds for a large class
The Monge problem on non-compact manifolds Alessio Figalli Scuola Normale Superiore Pisa Abstract In this paper we prove the existence of an optimal transport map on non-compact manifolds for a large class
STABILITY OF PLANAR NONLINEAR SWITCHED SYSTEMS
 LABORATOIRE INORMATIQUE, SINAUX ET SYSTÈMES DE SOPHIA ANTIPOLIS UMR 6070 STABILITY O PLANAR NONLINEAR SWITCHED SYSTEMS Ugo Boscain, régoire Charlot Projet TOpModel Rapport de recherche ISRN I3S/RR 2004-07
LABORATOIRE INORMATIQUE, SINAUX ET SYSTÈMES DE SOPHIA ANTIPOLIS UMR 6070 STABILITY O PLANAR NONLINEAR SWITCHED SYSTEMS Ugo Boscain, régoire Charlot Projet TOpModel Rapport de recherche ISRN I3S/RR 2004-07
The Geometry of Hyperbolic Manifolds via the Curve Complex
 The Geometry of Hyperbolic Manifolds via the Curve Complex Talk by Ken Bromberg August 22, 2007 One of the goals of this course has been to demonstrate how the combinatorics of the curve complex relate
The Geometry of Hyperbolic Manifolds via the Curve Complex Talk by Ken Bromberg August 22, 2007 One of the goals of this course has been to demonstrate how the combinatorics of the curve complex relate
IV Canonical relations for other geometrical constructions
 IV Canonical relations for other geometrical constructions IV.1. Introduction In this chapter we will further exploit the concept of canonical relation and show how it can be used to create center sets,
IV Canonical relations for other geometrical constructions IV.1. Introduction In this chapter we will further exploit the concept of canonical relation and show how it can be used to create center sets,
Vadim Kaloshin & Maria Saprykina
 An Example of a Nearly Integrable Hamiltonian System with a Trajectory Dense in a Set of Maximal Hausdorff Dimension Vadim Kaloshin & Maria Saprykina Communications in Mathematical Physics ISSN 1-3616
An Example of a Nearly Integrable Hamiltonian System with a Trajectory Dense in a Set of Maximal Hausdorff Dimension Vadim Kaloshin & Maria Saprykina Communications in Mathematical Physics ISSN 1-3616
Thuong Nguyen. SADCO Internal Review Metting
 Asymptotic behavior of singularly perturbed control system: non-periodic setting Thuong Nguyen (Joint work with A. Siconolfi) SADCO Internal Review Metting Rome, Nov 10-12, 2014 Thuong Nguyen (Roma Sapienza)
Asymptotic behavior of singularly perturbed control system: non-periodic setting Thuong Nguyen (Joint work with A. Siconolfi) SADCO Internal Review Metting Rome, Nov 10-12, 2014 Thuong Nguyen (Roma Sapienza)
PARTIAL REGULARITY OF BRENIER SOLUTIONS OF THE MONGE-AMPÈRE EQUATION
 PARTIAL REGULARITY OF BRENIER SOLUTIONS OF THE MONGE-AMPÈRE EQUATION ALESSIO FIGALLI AND YOUNG-HEON KIM Abstract. Given Ω, Λ R n two bounded open sets, and f and g two probability densities concentrated
PARTIAL REGULARITY OF BRENIER SOLUTIONS OF THE MONGE-AMPÈRE EQUATION ALESSIO FIGALLI AND YOUNG-HEON KIM Abstract. Given Ω, Λ R n two bounded open sets, and f and g two probability densities concentrated
Aubry Mather Theory from a Topological Viewpoint
 Aubry Mather Theory from a Topological Viewpoint III. Applications to Hamiltonian instability Marian Gidea,2 Northeastern Illinois University, Chicago 2 Institute for Advanced Study, Princeton WORKSHOP
Aubry Mather Theory from a Topological Viewpoint III. Applications to Hamiltonian instability Marian Gidea,2 Northeastern Illinois University, Chicago 2 Institute for Advanced Study, Princeton WORKSHOP
arxiv: v1 [math.ds] 1 May 2016
![arxiv: v1 [math.ds] 1 May 2016 arxiv: v1 [math.ds] 1 May 2016](/thumbs/71/65571911.jpg) LECTURE NOTES ON CLOSED ORBITS FOR TWISTED AUTONOMOUS TONELLI LAGRANGIAN FLOWS GABRIELE BENEDETTI arxiv:165.258v1 [math.ds] 1 May 216 Abstract. These notes were prepared in occasion of a mini-course given
LECTURE NOTES ON CLOSED ORBITS FOR TWISTED AUTONOMOUS TONELLI LAGRANGIAN FLOWS GABRIELE BENEDETTI arxiv:165.258v1 [math.ds] 1 May 216 Abstract. These notes were prepared in occasion of a mini-course given
DIFFERENTIAL GEOMETRY, LECTURE 16-17, JULY 14-17
 DIFFERENTIAL GEOMETRY, LECTURE 16-17, JULY 14-17 6. Geodesics A parametrized line γ : [a, b] R n in R n is straight (and the parametrization is uniform) if the vector γ (t) does not depend on t. Thus,
DIFFERENTIAL GEOMETRY, LECTURE 16-17, JULY 14-17 6. Geodesics A parametrized line γ : [a, b] R n in R n is straight (and the parametrization is uniform) if the vector γ (t) does not depend on t. Thus,
Half of Final Exam Name: Practice Problems October 28, 2014
 Math 54. Treibergs Half of Final Exam Name: Practice Problems October 28, 24 Half of the final will be over material since the last midterm exam, such as the practice problems given here. The other half
Math 54. Treibergs Half of Final Exam Name: Practice Problems October 28, 24 Half of the final will be over material since the last midterm exam, such as the practice problems given here. The other half
A Tourist s Guide to The General Topology of Dynamical Systems
 A Tourist s Guide to The General Topology of Dynamical Systems Graduate Studies in Mathematics, V. 1, American Mathematical Society Providence, R.I. Ethan Akin Mathematics Department The City College 137
A Tourist s Guide to The General Topology of Dynamical Systems Graduate Studies in Mathematics, V. 1, American Mathematical Society Providence, R.I. Ethan Akin Mathematics Department The City College 137
Tonelli Full-Regularity in the Calculus of Variations and Optimal Control
 Tonelli Full-Regularity in the Calculus of Variations and Optimal Control Delfim F. M. Torres delfim@mat.ua.pt Department of Mathematics University of Aveiro 3810 193 Aveiro, Portugal http://www.mat.ua.pt/delfim
Tonelli Full-Regularity in the Calculus of Variations and Optimal Control Delfim F. M. Torres delfim@mat.ua.pt Department of Mathematics University of Aveiro 3810 193 Aveiro, Portugal http://www.mat.ua.pt/delfim
NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY. (τ + arg z) + 1
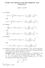 NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY JOHN M. ALONGI p.11 Replace ρ(t, z) = ρ(t, z) = p.11 Replace sin 2 z e τ ] 2 (τ + arg z) + 1 1 + z (e τ dτ. sin 2 (τ + arg z) + 1 z 2 z e τ ] 2 1 + z (e τ dτ.
NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY JOHN M. ALONGI p.11 Replace ρ(t, z) = ρ(t, z) = p.11 Replace sin 2 z e τ ] 2 (τ + arg z) + 1 1 + z (e τ dτ. sin 2 (τ + arg z) + 1 z 2 z e τ ] 2 1 + z (e τ dτ.
ON JOHN MATHER S SEMINAL CONTRIBUTIONS IN HAMILTONIAN DYNAMICS
 ON JOHN MATHER S SEMINAL CONTRIBUTIONS IN HAMILTONIAN DYNAMICS ALFONSO SORRENTINO To the memory of John N. Mather, a remarkable man and mathematician. (1942 2017) John N. Mather was undoubtedly one of
ON JOHN MATHER S SEMINAL CONTRIBUTIONS IN HAMILTONIAN DYNAMICS ALFONSO SORRENTINO To the memory of John N. Mather, a remarkable man and mathematician. (1942 2017) John N. Mather was undoubtedly one of
g 2 (x) (1/3)M 1 = (1/3)(2/3)M.
 COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
Equilibria with a nontrivial nodal set and the dynamics of parabolic equations on symmetric domains
 Equilibria with a nontrivial nodal set and the dynamics of parabolic equations on symmetric domains J. Földes Department of Mathematics, Univerité Libre de Bruxelles 1050 Brussels, Belgium P. Poláčik School
Equilibria with a nontrivial nodal set and the dynamics of parabolic equations on symmetric domains J. Földes Department of Mathematics, Univerité Libre de Bruxelles 1050 Brussels, Belgium P. Poláčik School
Weak convergence and large deviation theory
 First Prev Next Go To Go Back Full Screen Close Quit 1 Weak convergence and large deviation theory Large deviation principle Convergence in distribution The Bryc-Varadhan theorem Tightness and Prohorov
First Prev Next Go To Go Back Full Screen Close Quit 1 Weak convergence and large deviation theory Large deviation principle Convergence in distribution The Bryc-Varadhan theorem Tightness and Prohorov
Robustly transitive diffeomorphisms
 Robustly transitive diffeomorphisms Todd Fisher tfisher@math.byu.edu Department of Mathematics, Brigham Young University Summer School, Chengdu, China 2009 Dynamical systems The setting for a dynamical
Robustly transitive diffeomorphisms Todd Fisher tfisher@math.byu.edu Department of Mathematics, Brigham Young University Summer School, Chengdu, China 2009 Dynamical systems The setting for a dynamical
Nonlinear Control. Nonlinear Control Lecture # 3 Stability of Equilibrium Points
 Nonlinear Control Lecture # 3 Stability of Equilibrium Points The Invariance Principle Definitions Let x(t) be a solution of ẋ = f(x) A point p is a positive limit point of x(t) if there is a sequence
Nonlinear Control Lecture # 3 Stability of Equilibrium Points The Invariance Principle Definitions Let x(t) be a solution of ẋ = f(x) A point p is a positive limit point of x(t) if there is a sequence
An introduction to the Aubry-Mather theory
 São Paulo Journal of Mathematical Sciences 4, 1 (2010), 17 63 An introduction to the Aubry-Mather theory Andrey Biryuk and Diogo A. Gomes Departamento de Matemática and Center for Mathematical Analysis,
São Paulo Journal of Mathematical Sciences 4, 1 (2010), 17 63 An introduction to the Aubry-Mather theory Andrey Biryuk and Diogo A. Gomes Departamento de Matemática and Center for Mathematical Analysis,
The quasi-periodic Frenkel-Kontorova model
 The quasi-periodic Frenkel-Kontorova model Philippe Thieullen (Bordeaux) joint work with E. Garibaldi (Campinas) et S. Petite (Amiens) Korean-French Conference in Mathematics Pohang, August 24-28,2015
The quasi-periodic Frenkel-Kontorova model Philippe Thieullen (Bordeaux) joint work with E. Garibaldi (Campinas) et S. Petite (Amiens) Korean-French Conference in Mathematics Pohang, August 24-28,2015
Topological degree and invariance of domain theorems
 Topological degree and invariance of domain theorems Cristina Ana-Maria Anghel Geometry and PDE s Workshop Timisoara West University 24 th May 2013 The invariance of domain theorem, appeared at the beginning
Topological degree and invariance of domain theorems Cristina Ana-Maria Anghel Geometry and PDE s Workshop Timisoara West University 24 th May 2013 The invariance of domain theorem, appeared at the beginning
Symbolic extensions for partially hyperbolic diffeomorphisms
 for partially hyperbolic diffeomorphisms Todd Fisher tfisher@math.byu.edu Department of Mathematics Brigham Young University Workshop on Partial Hyperbolicity Entropy Topological entropy measures the exponential
for partially hyperbolic diffeomorphisms Todd Fisher tfisher@math.byu.edu Department of Mathematics Brigham Young University Workshop on Partial Hyperbolicity Entropy Topological entropy measures the exponential
Neighboring feasible trajectories in infinite dimension
 Neighboring feasible trajectories in infinite dimension Marco Mazzola Université Pierre et Marie Curie (Paris 6) H. Frankowska and E. M. Marchini Control of State Constrained Dynamical Systems Padova,
Neighboring feasible trajectories in infinite dimension Marco Mazzola Université Pierre et Marie Curie (Paris 6) H. Frankowska and E. M. Marchini Control of State Constrained Dynamical Systems Padova,
MIN-MAX REPRESENTATIONS OF VISCOSITY SOLUTIONS OF HAMILTON-JACOBI EQUATIONS AND APPLICATIONS IN RARE-EVENT SIMULATION
 MIN-MAX REPRESENTATIONS OF VISCOSITY SOLUTIONS OF HAMILTON-JACOBI EQUATIONS AND APPLICATIONS IN RARE-EVENT SIMULATION BOUALEM DJEHICHE, HENRIK HULT, AND PIERRE NYQUIST Abstract. In this paper a duality
MIN-MAX REPRESENTATIONS OF VISCOSITY SOLUTIONS OF HAMILTON-JACOBI EQUATIONS AND APPLICATIONS IN RARE-EVENT SIMULATION BOUALEM DJEHICHE, HENRIK HULT, AND PIERRE NYQUIST Abstract. In this paper a duality
Deterministic Dynamic Programming
 Deterministic Dynamic Programming 1 Value Function Consider the following optimal control problem in Mayer s form: V (t 0, x 0 ) = inf u U J(t 1, x(t 1 )) (1) subject to ẋ(t) = f(t, x(t), u(t)), x(t 0
Deterministic Dynamic Programming 1 Value Function Consider the following optimal control problem in Mayer s form: V (t 0, x 0 ) = inf u U J(t 1, x(t 1 )) (1) subject to ẋ(t) = f(t, x(t), u(t)), x(t 0
The optimal partial transport problem
 The optimal partial transport problem Alessio Figalli Abstract Given two densities f and g, we consider the problem of transporting a fraction m [0, min{ f L 1, g L 1}] of the mass of f onto g minimizing
The optimal partial transport problem Alessio Figalli Abstract Given two densities f and g, we consider the problem of transporting a fraction m [0, min{ f L 1, g L 1}] of the mass of f onto g minimizing
Def. A topological space X is disconnected if it admits a non-trivial splitting: (We ll abbreviate disjoint union of two subsets A and B meaning A B =
 CONNECTEDNESS-Notes Def. A topological space X is disconnected if it admits a non-trivial splitting: X = A B, A B =, A, B open in X, and non-empty. (We ll abbreviate disjoint union of two subsets A and
CONNECTEDNESS-Notes Def. A topological space X is disconnected if it admits a non-trivial splitting: X = A B, A B =, A, B open in X, and non-empty. (We ll abbreviate disjoint union of two subsets A and
Recent Trends in Differential Inclusions
 Recent Trends in Alberto Bressan Department of Mathematics, Penn State University (Aveiro, June 2016) (Aveiro, June 2016) 1 / Two main topics ẋ F (x) differential inclusions with upper semicontinuous,
Recent Trends in Alberto Bressan Department of Mathematics, Penn State University (Aveiro, June 2016) (Aveiro, June 2016) 1 / Two main topics ẋ F (x) differential inclusions with upper semicontinuous,
ẋ = f(x, y), ẏ = g(x, y), (x, y) D, can only have periodic solutions if (f,g) changes sign in D or if (f,g)=0in D.
 4 Periodic Solutions We have shown that in the case of an autonomous equation the periodic solutions correspond with closed orbits in phase-space. Autonomous two-dimensional systems with phase-space R
4 Periodic Solutions We have shown that in the case of an autonomous equation the periodic solutions correspond with closed orbits in phase-space. Autonomous two-dimensional systems with phase-space R
Dynamic and Stochastic Brenier Transport via Hopf-Lax formulae on Was
 Dynamic and Stochastic Brenier Transport via Hopf-Lax formulae on Wasserstein Space With many discussions with Yann Brenier and Wilfrid Gangbo Brenierfest, IHP, January 9-13, 2017 ain points of the
Dynamic and Stochastic Brenier Transport via Hopf-Lax formulae on Wasserstein Space With many discussions with Yann Brenier and Wilfrid Gangbo Brenierfest, IHP, January 9-13, 2017 ain points of the
1.4 The Jacobian of a map
 1.4 The Jacobian of a map Derivative of a differentiable map Let F : M n N m be a differentiable map between two C 1 manifolds. Given a point p M we define the derivative of F at p by df p df (p) : T p
1.4 The Jacobian of a map Derivative of a differentiable map Let F : M n N m be a differentiable map between two C 1 manifolds. Given a point p M we define the derivative of F at p by df p df (p) : T p
The Minimum Speed for a Blocking Problem on the Half Plane
 The Minimum Speed for a Blocking Problem on the Half Plane Alberto Bressan and Tao Wang Department of Mathematics, Penn State University University Park, Pa 16802, USA e-mails: bressan@mathpsuedu, wang
The Minimum Speed for a Blocking Problem on the Half Plane Alberto Bressan and Tao Wang Department of Mathematics, Penn State University University Park, Pa 16802, USA e-mails: bressan@mathpsuedu, wang
1 Lyapunov theory of stability
 M.Kawski, APM 581 Diff Equns Intro to Lyapunov theory. November 15, 29 1 1 Lyapunov theory of stability Introduction. Lyapunov s second (or direct) method provides tools for studying (asymptotic) stability
M.Kawski, APM 581 Diff Equns Intro to Lyapunov theory. November 15, 29 1 1 Lyapunov theory of stability Introduction. Lyapunov s second (or direct) method provides tools for studying (asymptotic) stability
TOPOLOGY TAKE-HOME CLAY SHONKWILER
 TOPOLOGY TAKE-HOME CLAY SHONKWILER 1. The Discrete Topology Let Y = {0, 1} have the discrete topology. Show that for any topological space X the following are equivalent. (a) X has the discrete topology.
TOPOLOGY TAKE-HOME CLAY SHONKWILER 1. The Discrete Topology Let Y = {0, 1} have the discrete topology. Show that for any topological space X the following are equivalent. (a) X has the discrete topology.
The Monge problem for supercritical Mañé potentials on compact manifolds
 Advances in Mathematics 27 (26) 691 76 www.elsevier.com/locate/aim The Monge problem for supercritical Mañé potentials on compact manifolds Patrick Bernard a,, Boris Buffoni b a Institut Fourier, Grenoble,
Advances in Mathematics 27 (26) 691 76 www.elsevier.com/locate/aim The Monge problem for supercritical Mañé potentials on compact manifolds Patrick Bernard a,, Boris Buffoni b a Institut Fourier, Grenoble,
Introduction to Continuous Dynamical Systems
 Lecture Notes on Introduction to Continuous Dynamical Systems Fall, 2012 Lee, Keonhee Department of Mathematics Chungnam National Univeristy - 1 - Chap 0. Introduction What is a dynamical system? A dynamical
Lecture Notes on Introduction to Continuous Dynamical Systems Fall, 2012 Lee, Keonhee Department of Mathematics Chungnam National Univeristy - 1 - Chap 0. Introduction What is a dynamical system? A dynamical
A FRANKS LEMMA FOR CONVEX PLANAR BILLIARDS
 A FRANKS LEMMA FOR CONVEX PLANAR BILLIARDS DANIEL VISSCHER Abstract Let γ be an orbit of the billiard flow on a convex planar billiard table; then the perpendicular part of the derivative of the billiard
A FRANKS LEMMA FOR CONVEX PLANAR BILLIARDS DANIEL VISSCHER Abstract Let γ be an orbit of the billiard flow on a convex planar billiard table; then the perpendicular part of the derivative of the billiard
History (Minimal Dynamics Theorem, Meeks-Perez-Ros 2005, CMC Dynamics Theorem, Meeks-Tinaglia 2008) Giuseppe Tinaglia
 History (Minimal Dynamics Theorem, Meeks-Perez-Ros 2005, CMC Dynamics Theorem, Meeks-Tinaglia 2008) Briefly stated, these Dynamics Theorems deal with describing all of the periodic or repeated geometric
History (Minimal Dynamics Theorem, Meeks-Perez-Ros 2005, CMC Dynamics Theorem, Meeks-Tinaglia 2008) Briefly stated, these Dynamics Theorems deal with describing all of the periodic or repeated geometric
FOURTH ORDER CONSERVATIVE TWIST SYSTEMS: SIMPLE CLOSED CHARACTERISTICS
 FOURTH ORDER CONSERVATIVE TWIST SYSTEMS: SIMPLE CLOSED CHARACTERISTICS J.B. VAN DEN BERG AND R.C.A.M. VANDERVORST ABSTRACT. On the energy manifolds of fourth order conservative systems closed characteristics
FOURTH ORDER CONSERVATIVE TWIST SYSTEMS: SIMPLE CLOSED CHARACTERISTICS J.B. VAN DEN BERG AND R.C.A.M. VANDERVORST ABSTRACT. On the energy manifolds of fourth order conservative systems closed characteristics
LINEAR-CONVEX CONTROL AND DUALITY
 1 LINEAR-CONVEX CONTROL AND DUALITY R.T. Rockafellar Department of Mathematics, University of Washington Seattle, WA 98195-4350, USA Email: rtr@math.washington.edu R. Goebel 3518 NE 42 St., Seattle, WA
1 LINEAR-CONVEX CONTROL AND DUALITY R.T. Rockafellar Department of Mathematics, University of Washington Seattle, WA 98195-4350, USA Email: rtr@math.washington.edu R. Goebel 3518 NE 42 St., Seattle, WA
Lagrangian Manifolds, Viscosity Solutions and Maslov Index
 Journal of Convex Analysis Volume 9 (2002), No. 1, 185 224 Lagrangian Manifolds, Viscosity Solutions and Maslov Index D. McCaffrey University of Sheffield, Dept. of Automatic Control and Systems Engineering,
Journal of Convex Analysis Volume 9 (2002), No. 1, 185 224 Lagrangian Manifolds, Viscosity Solutions and Maslov Index D. McCaffrey University of Sheffield, Dept. of Automatic Control and Systems Engineering,
HJ equations. Reachability analysis. Optimal control problems
 HJ equations. Reachability analysis. Optimal control problems Hasnaa Zidani 1 1 ENSTA Paris-Tech & INRIA-Saclay Graz, 8-11 September 2014 H. Zidani (ENSTA & Inria) HJ equations. Reachability analysis -
HJ equations. Reachability analysis. Optimal control problems Hasnaa Zidani 1 1 ENSTA Paris-Tech & INRIA-Saclay Graz, 8-11 September 2014 H. Zidani (ENSTA & Inria) HJ equations. Reachability analysis -
BACKGROUND IN SYMPLECTIC GEOMETRY
 BACKGROUND IN SYMPLECTIC GEOMETRY NILAY KUMAR Today I want to introduce some of the symplectic structure underlying classical mechanics. The key idea is actually quite old and in its various formulations
BACKGROUND IN SYMPLECTIC GEOMETRY NILAY KUMAR Today I want to introduce some of the symplectic structure underlying classical mechanics. The key idea is actually quite old and in its various formulations
Hamilton-Jacobi theory for optimal control problems on stratified domains
 Louisiana State University LSU Digital Commons LSU Doctoral Dissertations Graduate School 2010 Hamilton-Jacobi theory for optimal control problems on stratified domains Richard Charles Barnard Louisiana
Louisiana State University LSU Digital Commons LSU Doctoral Dissertations Graduate School 2010 Hamilton-Jacobi theory for optimal control problems on stratified domains Richard Charles Barnard Louisiana
Hyperbolic Dynamics. Todd Fisher. Department of Mathematics University of Maryland, College Park. Hyperbolic Dynamics p.
 Hyperbolic Dynamics p. 1/36 Hyperbolic Dynamics Todd Fisher tfisher@math.umd.edu Department of Mathematics University of Maryland, College Park Hyperbolic Dynamics p. 2/36 What is a dynamical system? Phase
Hyperbolic Dynamics p. 1/36 Hyperbolic Dynamics Todd Fisher tfisher@math.umd.edu Department of Mathematics University of Maryland, College Park Hyperbolic Dynamics p. 2/36 What is a dynamical system? Phase
Action minimizing properties and distances on the group of Hamiltonian diffeomorphisms
 Action minimizing properties and distances on the group of Hamiltonian diffeomorphisms Alfonso Sorrentino Claude Viterbo 2 CEREMADE, UMR du CNRS 7534 Université Paris-Dauphine 75775 Paris Cedex 6, France
Action minimizing properties and distances on the group of Hamiltonian diffeomorphisms Alfonso Sorrentino Claude Viterbo 2 CEREMADE, UMR du CNRS 7534 Université Paris-Dauphine 75775 Paris Cedex 6, France
LECTURE 10: THE ATIYAH-GUILLEMIN-STERNBERG CONVEXITY THEOREM
 LECTURE 10: THE ATIYAH-GUILLEMIN-STERNBERG CONVEXITY THEOREM Contents 1. The Atiyah-Guillemin-Sternberg Convexity Theorem 1 2. Proof of the Atiyah-Guillemin-Sternberg Convexity theorem 3 3. Morse theory
LECTURE 10: THE ATIYAH-GUILLEMIN-STERNBERG CONVEXITY THEOREM Contents 1. The Atiyah-Guillemin-Sternberg Convexity Theorem 1 2. Proof of the Atiyah-Guillemin-Sternberg Convexity theorem 3 3. Morse theory
On the Bellman equation for control problems with exit times and unbounded cost functionals 1
 On the Bellman equation for control problems with exit times and unbounded cost functionals 1 Michael Malisoff Department of Mathematics, Hill Center-Busch Campus Rutgers University, 11 Frelinghuysen Road
On the Bellman equation for control problems with exit times and unbounded cost functionals 1 Michael Malisoff Department of Mathematics, Hill Center-Busch Campus Rutgers University, 11 Frelinghuysen Road
MARKOV PARTITIONS FOR HYPERBOLIC SETS
 MARKOV PARTITIONS FOR HYPERBOLIC SETS TODD FISHER, HIMAL RATHNAKUMARA Abstract. We show that if f is a diffeomorphism of a manifold to itself, Λ is a mixing (or transitive) hyperbolic set, and V is a neighborhood
MARKOV PARTITIONS FOR HYPERBOLIC SETS TODD FISHER, HIMAL RATHNAKUMARA Abstract. We show that if f is a diffeomorphism of a manifold to itself, Λ is a mixing (or transitive) hyperbolic set, and V is a neighborhood
CHAPTER 7. Connectedness
 CHAPTER 7 Connectedness 7.1. Connected topological spaces Definition 7.1. A topological space (X, T X ) is said to be connected if there is no continuous surjection f : X {0, 1} where the two point set
CHAPTER 7 Connectedness 7.1. Connected topological spaces Definition 7.1. A topological space (X, T X ) is said to be connected if there is no continuous surjection f : X {0, 1} where the two point set
Smoothing causal functions.
 Smoothing causal functions. arxiv:1711.03883v2 [math.dg] 24 Mar 2018 Patrick Bernard 1, PSL Research University, École Normale Supérieure, NRS, DMA (UMR 8553) 45, rue d Ulm 75230 Paris edex 05, France
Smoothing causal functions. arxiv:1711.03883v2 [math.dg] 24 Mar 2018 Patrick Bernard 1, PSL Research University, École Normale Supérieure, NRS, DMA (UMR 8553) 45, rue d Ulm 75230 Paris edex 05, France
Threshold behavior and non-quasiconvergent solutions with localized initial data for bistable reaction-diffusion equations
 Threshold behavior and non-quasiconvergent solutions with localized initial data for bistable reaction-diffusion equations P. Poláčik School of Mathematics, University of Minnesota Minneapolis, MN 55455
Threshold behavior and non-quasiconvergent solutions with localized initial data for bistable reaction-diffusion equations P. Poláčik School of Mathematics, University of Minnesota Minneapolis, MN 55455
