(x k ) sequence in F, lim x k = x x F. If F : R n R is a function, level sets and sublevel sets of F are any sets of the form (respectively);
|
|
|
- Ronald Clarke
- 6 years ago
- Views:
Transcription
1 STABILITY OF EQUILIBRIA AND LIAPUNOV FUNCTIONS. By topological properties in general we mean qualitative geometric properties (of subsets of R n or of functions in R n ), that is, those that don t depend on measuring distance or angle. Examples: continuity of functions, convergence of sequences, compactness of sets (see below.) 1. Topological definitions. The open ball with center p and radius r > 0 in R n is the set: B r (p) = {x R n ; x p < r}. A set U R n is open if whenever p U the balls B r (p) are contained in U, for all sufficiently small r > 0. A set F R n is closed if it contains all its limit points: (x k ) sequence in F, lim x k = x x F. If F : R n R is a function, level sets and sublevel sets of F are any sets of the form (respectively); L c = {x; F (x) = c}; S c = {x; F (x) c}, where c R. If F is continuous, level sets and sublevel sets of F are closed. (Depending on the value of c, they may be empty!) A set K R n is compact if it is closed and bounded. (Bounded means it is contained in some ball B R (0), where R is sufficiently large. Compact sets K have an important property: any sequence of points in K has a convergent subsequence. A continuous function F : R n R is proper if either lim x F (x) = + or lim x F (x) =. The first statement is equivalent to: ( M > 0)( R > 0)( x)( x > R f(x) > M). For example, any polynomial function of the coordinates (x i ) in which they all appear with even degree, and positive coefficients, is a proper function. Say, in R 3 : F (x 1, x 2, x 3 ) = 2x x 4 2x x 8 2. Level sets and sublevel sets of continuous proper functions are compact. A continuous function F on R n is of class C 1 if all its first-order partial derivatives F x i are themselves continuous functions on R n. More generally, 1
2 we say F is of class C k if all its partial derivatives of total order up to k are continuous functions. The level sets L c of C 1 functions are C 1 (n 1)-dimensional surfaces (that is, have well-defined tangent planes of dimension n 1, varying continuously along the surface) without self-intersections, except at critical points x of L c (that is, F (x) = c, F (x) = 0). Recall from Calculus that at a regular point of L c (that is, a non-critical point) the normal direction is given by the gradient vector F. Combining all the above, we see that if F is C 1 and proper, those level sets of F which do not contain critical points are bounded C 1 surfaces (of dimension n 1) without self-intersections, but possibly consisting of more than one piece. The corresponding sublevel sets are compact subsets of R n, bounded by C 1 surfaces. 2. Definitions for vector fields. A vector field F : R n R n is of class C k if each if its component functions is. By the existence-uniqueness theorem, if F is a C 1 vector field, for each x R n there exists a unique solution x(t) = φ(t, x) to the initial-value problem x = F(x), x(0) = x, defined on a maximal interval: t I x = (α x, ω x ) (where α x or ω x may be infinite.) We have the semigroup property, which follows fom uniqueness [KP]: φ(t, (φ(s, x))) = φ(t + s, x) = φ(s, φ(t, x))), if t, s, s + t I x. The function φ(t, x) from D = {(t, x); x R n ; t I x } to R n is referred to as the flow of X, and the alternative notation φ t (x) = φ(t, x) is often used. In the following we re mostly interested in the case when ω x is infinite, or when I x = R. It follows from the E/U theorem that the first is guaranteed if the forward orbit is contained in a bounded set: O + (x) = {φ(t, x); t [0, ω x )}. The full orbit is: O(x) = {φ(t, x); t I x }. if we know the full orbit is contained in a bounded set, it follows that I x = R. The main interest is in the asymptotic behavior of solutions for large time: is it periodic? Does it converge to an equilibrium state? Does it exhibit oscilations for arbitrarily large time? Does it come arbitrarily close to different equilibrium states, for arbitrarily large times? These states approximated by the solution for large times are captured by the notion of ω-limit set. Suppose the solution is defined for all positive 2
3 times, so ω x = + Then we defined the ω-limit set of x as: ω(x) = {y R n ; (t k ) k 1 in R n ; t k + and φ(t k, x) y}. That is, ω(x) is the set of all limit points of the forward orbit O + (x). The α-limit set α(x) is denfined analogously, when α x = (let t k ). When non-empty, ω(x) and α(x) are closed in R n. For instance, if (x k ) is a sequence in ω(x) we may find for each k 1 sequences (t k n) n 1 tending to + with n, so that lim n φ(t n k, x) = x k. Then if x k y R n, considering the triangle inequality: φ(t k n, y) x φ(t k n, x) x k + x k y shows that if we take k large enough so that x k is close to y, and then n(k) large enough so that φ(t n(k), x) is close to x k, then for the sequence s k = t n(k) k we have φ(s k, x) is close to y and s k +, so y ω(x). The sets ω(x) or α(x) may be empty. One condition that guarantees ω(x) is: O + (x) is a bounded set. If K is compact and O + (x) K, then ω(x) is a non-empty subset of K. ω(x) has exactly one point x if and only if lim t + φ(t, x) = x. A set A R n is invariant under the flow of a vector field F if x A φ(t, x) A, t I x ; forward-invariant or backward-invariant if we take t [0, ω x ) or t (α x, 0]. ω limit sets are forward invariant: if y ω(x), by definition we may find a sequence t k + so that φ(t k, x) y. Given t > 0, the semigroup property gives: φ(t + t k, x) = φ t (φ(t k, x)) φ t (y), using the fact that φ t (x) depends continuously on x. Since t + t k +, this shows φ t (y) ω(x). (Analogously, α-limit sets are backwards invariant under the flow of F.) 3. Liapunov functions. Recall that a function E : R n R is a conserved quantity for the vector field F if, for every x R n, the function E(φ(t, x)) is constant in t (briefly: E is constant along solutions). By the chain rule, this happens exactly when: Ė(x) := E(x) F(x) = 0, x R n. When this happens, all orbits of F are contained in level sets of E. (Recall that these are (n 1)-dimensional surfaces, at points where E 0.) If 3
4 n = 2 the level sets of E are curves, so the orbits of F can be identified as arcs of level sets (often beginning or ending at a singular point of E.) Systems with conserved quantities are relatively rare, other than in conservative Classical Mechanics. But it is also very useful to find functions that decrease (or, at least, do not increase) along solutions. Definition. A function V : R n R is a Liapunov function for the vector field F in the open set U R n if V F 0 holds in U; a strict Liapunov function if we have V F < 0 in U. Geometrically, for a strict Liapunov function, at any boundary point of a sublevel set S c, the vector field F points into the sublevel set, since F makes an obtuse angle with the outward normal V. ( If the Liapunov function is not strict, F may be tangent to level sets at some points.) Thus V is non-increasing along orbits φ(t, x) as long as they are in U (or decreasing in the strict case.) The first use of Liapunov functions is in finding invariant sets: Proposition 1. Suppose V : R n R is a Liapunov function for the vector field F in the bounded open set U; let S c be a sublevel set of V. Assume the intersection S c U is closed in R n. Then S c U is forward-invariant under F. Proof. Let x S c U. Since V is non-increasing along solutions, V (x) c implies V (φ(x, t)) c, so φ(t, x) S c for t [0, ω x ). The problem is that the forward orbit of x might leave the open set U. Arguing by contradiction, suppose this happens, and let t 0 > 0 be the smallest t < ω x so that φ(t, x) U. Then there is a sequence t k t 0 so that x k = φ(t k, x) is in S c U. Thus x k converges to the point x = φ(t 0, x) R n. As a limit point of a sequence in S c U (a closed set by hypothesis) we must have x S c U, in contradiction with the way t 0 was chosen. This shows the forward orbit of x stays in U, for all t [0, ω x ). And since U is bounded, it follows that ω x = +, and φ(t, x) S c U t 0, proving the invariance. If V = 0 in all of R n, the proposition says simply that any bounded sublevel set of V is forward-invariant; and bounded is needed only to guarantee solutions are defined for all t 0. The next easiest case in which the hypothesis is satisfied occurs when the closed set S c (or its connected component intersecting U) is contained in the bounded open set U. The original use of Liapunov functions was to characterize stability of 4
5 equilibria. Recall x 0 is an isolated equilibrium for F if F(x 0 ) = 0 and there are no other equilibria in some ball B r (x 0 ) with center x 0. Definition. Let x 0 be an isolated equilibrium for the vector field F. A function V : R n R is a Liapunov function for x 0 if (i) V has a strict local minimum at x 0 ; (ii) V is a Liapunov function for F in the ball B r (x 0 ). V is a strict Liapunov function for x 0 if in (ii) we have that V is a strict Liapunov function for F in B r (x 0 ) \ {x 0 }. Liapunov s theorem. If x 0 is an isolated equilibrium for F and V is a Liapunov function (or strict Liapunov function) for x 0, then x 0 is stable (resp. asymptotically stable). Proof. For any r > 0 small enough, x 0 is the only equilibrium in B r (x 0 ), V is a Liapunov function in B r (x 0 ) and V (x) > V (x 0 ) there. Then we can find c > V (x 0 ) so that the component of the sublevel set for c containing x 0 (which we denote by S c ) is compact and contained in B r (x 0 ). We can then find a ball B s (x 0 ) so that: B s (x 0 ) S c B r (x 0 ). Let x B s (x 0 ). Then since V is a Liapunov function in B r (x 0 ) we have V (φ(t, x)) c for all t 0, so φ(t, x) S c, and in particular is in B r (x 0 ), for each t 0. This shows x 0 is stable. If V is a strict Liapunov function in B r (x 0 ) and x B s (x 0 ) is any point different from x 0 V (φ(t, x)) is strictly decreasing in t, hence has a limit L V (x 0 ). S c is compact and invariant; let x be a point in the ω-limit set ω(x), so φ(t k, x) x and V (φ(t k, x)) L = inf t 0 V (φ(t, x)) for some sequence t k, so V ( x) = L. If x x 0 we have V (φ(t, x)) < L for t > 0 small, while φ(t+t k, x) = φ(t, φ(t k, x)) is close to φ(t, x) for k large, hence is also smaller than L for k large, contradicting the fact that L is the inf. This shows ω(x) = {x 0 } for any x sufficiently close to x 0, so x 0 is asymptotically stable. Example: Gradient systems. Let V : R n R be a smooth function. The vector field F = V is the gradient system (or gradient flow ) associated to V. Then V is a Liapunov function for F in the whole space (U = R n ) and a strict Liapunov function on any open set U that has no critical points of V, since: V F = V
6 The critical points of V are the equilibria of F. If x 0 is a strict (isolated) local min for V, then V is a stirct Liapunov function on any open ball B r (x 0 ) not containing other critical points; and then Liapunov s theorem implies x 0 is asymptotically stable. It often happens that one can find a Liapunov function, but not a strict one, in a neighborhood of an isolated equilibrium; and still one would like to show that the equilibrium is asympotically stable. This situation is addressed by the next theorem. We use the notation V (x) = V (x) F(x), so V 0 in U, if V is a Liapunov function for F in U. Liapunov-La Salle invariance theorem. Let V : R n R be a Liapunov function for the vector field F on the bounded open set U. Suppose S c is a sublevel set of V, and the following hold: (i) S c U is closed in R n ; (ii) There is an isolated equilibrium x 0 S c U, and a ball B r (x 0 ) contained in S c U. (iii) Let Z = {x S c U; V (x) = 0}. If x Z and its forward orbit O + (x) is contained in Z, then x = x 0. Then x 0 is asymptotically stable, and for any x S c U, φ(t, x) x 0 as t +. Proof. From the proposition above, we know S c U is a compact forwardinvariant set. We first show that if x S c U, then V is constant in ω(x) (which is a non-empty, compact, forward-invariant subset of S c ). By contradiction, let x 1 x 2 be points in ω(x), with (say) V (x 1 ) < V (x 2 ). Then we may find sequences t k, s k tending to infinity to that V (φ(t k, x)) V (x 1 ) and V (φ(s k, x)) V (x 2 ). But then we may find indices k, k so that t k < s k and: V (x 2 ) ɛ < V (φ(s k ), x) V (φ(t k, x) < V (x 1 ) + ɛ, where the middle inequality follows from V nonincreasing along solutions. For ɛ small enough, this contradicts V (x 1 ) < V (x 2 ). This shows V is constant in ω(x). But ω(x) is non-empty, forward-invariant and contained in the compact set S c, so if x ω(x) the entire positive orbit O + ( x) is contained in ω(x). So V is constant along this orbit, which implies V 0 at each point of the forward orbit of x (which is contained in S c U). But then the hypothesis implies the forward orbit of x consists of the point x 0. This shows ω(x) = 6
7 {x 0 } for each x S c U, and since S c U contains a ball centered at x 0 this means x 0 is asymptotically stable. Remark: Note the difference between the strict Liapunov function case of Liapunov s theorem and the invariance theorem just proved. The conclusion is the same in both cases; but in the former the hypothesis is Z = {x 0 }, while the hypothesis of the second theorem is weaker. We only require: x Z and O + (x) Z x = x 0. (Also, in the invariance theorem we don t need to establish that {x 0 } is an strict local minimum of V.) Note also that it is part of the conclusion that the basin of attraction of {x 0 } (the set of points x R n whose forward orbit converges to x 0 ) contains the set S c U. The statement simplifies if V is a Liapunov function for F in all of R n : Corollary. Suppose V 0 in R n and x 0 is an isolated equilibrium. Let S c be a bounded sublevel set of V containing x 0 (and hence a compact forward-invariant set). With Z = {x S c V (x) = 0}, suppose the following holds: the only point of Z whose entire forward orbit is contained in Z is x 0. Then x 0 is asymptotically stable, and S c is contained in its basin of attraction. 7
1 Lyapunov theory of stability
 M.Kawski, APM 581 Diff Equns Intro to Lyapunov theory. November 15, 29 1 1 Lyapunov theory of stability Introduction. Lyapunov s second (or direct) method provides tools for studying (asymptotic) stability
M.Kawski, APM 581 Diff Equns Intro to Lyapunov theory. November 15, 29 1 1 Lyapunov theory of stability Introduction. Lyapunov s second (or direct) method provides tools for studying (asymptotic) stability
g 2 (x) (1/3)M 1 = (1/3)(2/3)M.
 COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
There is a more global concept that is related to this circle of ideas that we discuss somewhat informally. Namely, a region R R n with a (smooth)
 82 Introduction Liapunov Functions Besides the Liapunov spectral theorem, there is another basic method of proving stability that is a generalization of the energy method we have seen in the introductory
82 Introduction Liapunov Functions Besides the Liapunov spectral theorem, there is another basic method of proving stability that is a generalization of the energy method we have seen in the introductory
Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem
 56 Chapter 7 Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem Recall that C(X) is not a normed linear space when X is not compact. On the other hand we could use semi
56 Chapter 7 Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem Recall that C(X) is not a normed linear space when X is not compact. On the other hand we could use semi
Filters in Analysis and Topology
 Filters in Analysis and Topology David MacIver July 1, 2004 Abstract The study of filters is a very natural way to talk about convergence in an arbitrary topological space, and carries over nicely into
Filters in Analysis and Topology David MacIver July 1, 2004 Abstract The study of filters is a very natural way to talk about convergence in an arbitrary topological space, and carries over nicely into
MATH 31BH Homework 1 Solutions
 MATH 3BH Homework Solutions January 0, 04 Problem.5. (a) (x, y)-plane in R 3 is closed and not open. To see that this plane is not open, notice that any ball around the origin (0, 0, 0) will contain points
MATH 3BH Homework Solutions January 0, 04 Problem.5. (a) (x, y)-plane in R 3 is closed and not open. To see that this plane is not open, notice that any ball around the origin (0, 0, 0) will contain points
Nonlinear Dynamical Systems Eighth Class
 Nonlinear Dynamical Systems Eighth Class Alexandre Nolasco de Carvalho September 19, 2017 Now we exhibit a Morse decomposition for a dynamically gradient semigroup and use it to prove that a dynamically
Nonlinear Dynamical Systems Eighth Class Alexandre Nolasco de Carvalho September 19, 2017 Now we exhibit a Morse decomposition for a dynamically gradient semigroup and use it to prove that a dynamically
We are going to discuss what it means for a sequence to converge in three stages: First, we define what it means for a sequence to converge to zero
 Chapter Limits of Sequences Calculus Student: lim s n = 0 means the s n are getting closer and closer to zero but never gets there. Instructor: ARGHHHHH! Exercise. Think of a better response for the instructor.
Chapter Limits of Sequences Calculus Student: lim s n = 0 means the s n are getting closer and closer to zero but never gets there. Instructor: ARGHHHHH! Exercise. Think of a better response for the instructor.
Course 212: Academic Year Section 1: Metric Spaces
 Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
LECTURE 15: COMPLETENESS AND CONVEXITY
 LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
HYPERBOLIC SETS WITH NONEMPTY INTERIOR
 HYPERBOLIC SETS WITH NONEMPTY INTERIOR TODD FISHER, UNIVERSITY OF MARYLAND Abstract. In this paper we study hyperbolic sets with nonempty interior. We prove the folklore theorem that every transitive hyperbolic
HYPERBOLIC SETS WITH NONEMPTY INTERIOR TODD FISHER, UNIVERSITY OF MARYLAND Abstract. In this paper we study hyperbolic sets with nonempty interior. We prove the folklore theorem that every transitive hyperbolic
Math Advanced Calculus II
 Math 452 - Advanced Calculus II Manifolds and Lagrange Multipliers In this section, we will investigate the structure of critical points of differentiable functions. In practice, one often is trying to
Math 452 - Advanced Calculus II Manifolds and Lagrange Multipliers In this section, we will investigate the structure of critical points of differentiable functions. In practice, one often is trying to
Metric Spaces and Topology
 Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
P-adic Functions - Part 1
 P-adic Functions - Part 1 Nicolae Ciocan 22.11.2011 1 Locally constant functions Motivation: Another big difference between p-adic analysis and real analysis is the existence of nontrivial locally constant
P-adic Functions - Part 1 Nicolae Ciocan 22.11.2011 1 Locally constant functions Motivation: Another big difference between p-adic analysis and real analysis is the existence of nontrivial locally constant
Passivity-based Stabilization of Non-Compact Sets
 Passivity-based Stabilization of Non-Compact Sets Mohamed I. El-Hawwary and Manfredi Maggiore Abstract We investigate the stabilization of closed sets for passive nonlinear systems which are contained
Passivity-based Stabilization of Non-Compact Sets Mohamed I. El-Hawwary and Manfredi Maggiore Abstract We investigate the stabilization of closed sets for passive nonlinear systems which are contained
The Minimal Element Theorem
 The Minimal Element Theorem The CMC Dynamics Theorem deals with describing all of the periodic or repeated geometric behavior of a properly embedded CMC surface with bounded second fundamental form in
The Minimal Element Theorem The CMC Dynamics Theorem deals with describing all of the periodic or repeated geometric behavior of a properly embedded CMC surface with bounded second fundamental form in
Problem List MATH 5173 Spring, 2014
 Problem List MATH 5173 Spring, 2014 The notation p/n means the problem with number n on page p of Perko. 1. 5/3 [Due Wednesday, January 15] 2. 6/5 and describe the relationship of the phase portraits [Due
Problem List MATH 5173 Spring, 2014 The notation p/n means the problem with number n on page p of Perko. 1. 5/3 [Due Wednesday, January 15] 2. 6/5 and describe the relationship of the phase portraits [Due
Now I switch to nonlinear systems. In this chapter the main object of study will be
 Chapter 4 Stability 4.1 Autonomous systems Now I switch to nonlinear systems. In this chapter the main object of study will be ẋ = f(x), x(t) X R k, f : X R k, (4.1) where f is supposed to be locally Lipschitz
Chapter 4 Stability 4.1 Autonomous systems Now I switch to nonlinear systems. In this chapter the main object of study will be ẋ = f(x), x(t) X R k, f : X R k, (4.1) where f is supposed to be locally Lipschitz
B553 Lecture 1: Calculus Review
 B553 Lecture 1: Calculus Review Kris Hauser January 10, 2012 This course requires a familiarity with basic calculus, some multivariate calculus, linear algebra, and some basic notions of metric topology.
B553 Lecture 1: Calculus Review Kris Hauser January 10, 2012 This course requires a familiarity with basic calculus, some multivariate calculus, linear algebra, and some basic notions of metric topology.
Mathematische Annalen
 Math. Ann. 334, 457 464 (2006) Mathematische Annalen DOI: 10.1007/s00208-005-0743-2 The Julia Set of Hénon Maps John Erik Fornæss Received:6 July 2005 / Published online: 9 January 2006 Springer-Verlag
Math. Ann. 334, 457 464 (2006) Mathematische Annalen DOI: 10.1007/s00208-005-0743-2 The Julia Set of Hénon Maps John Erik Fornæss Received:6 July 2005 / Published online: 9 January 2006 Springer-Verlag
ADVANCED CALCULUS - MTH433 LECTURE 4 - FINITE AND INFINITE SETS
 ADVANCED CALCULUS - MTH433 LECTURE 4 - FINITE AND INFINITE SETS 1. Cardinal number of a set The cardinal number (or simply cardinal) of a set is a generalization of the concept of the number of elements
ADVANCED CALCULUS - MTH433 LECTURE 4 - FINITE AND INFINITE SETS 1. Cardinal number of a set The cardinal number (or simply cardinal) of a set is a generalization of the concept of the number of elements
Propagating terraces and the dynamics of front-like solutions of reaction-diffusion equations on R
 Propagating terraces and the dynamics of front-like solutions of reaction-diffusion equations on R P. Poláčik School of Mathematics, University of Minnesota Minneapolis, MN 55455 Abstract We consider semilinear
Propagating terraces and the dynamics of front-like solutions of reaction-diffusion equations on R P. Poláčik School of Mathematics, University of Minnesota Minneapolis, MN 55455 Abstract We consider semilinear
fy (X(g)) Y (f)x(g) gy (X(f)) Y (g)x(f)) = fx(y (g)) + gx(y (f)) fy (X(g)) gy (X(f))
 1. Basic algebra of vector fields Let V be a finite dimensional vector space over R. Recall that V = {L : V R} is defined to be the set of all linear maps to R. V is isomorphic to V, but there is no canonical
1. Basic algebra of vector fields Let V be a finite dimensional vector space over R. Recall that V = {L : V R} is defined to be the set of all linear maps to R. V is isomorphic to V, but there is no canonical
Introduction to Dynamical Systems
 Introduction to Dynamical Systems France-Kosovo Undergraduate Research School of Mathematics March 2017 This introduction to dynamical systems was a course given at the march 2017 edition of the France
Introduction to Dynamical Systems France-Kosovo Undergraduate Research School of Mathematics March 2017 This introduction to dynamical systems was a course given at the march 2017 edition of the France
An Algorithmic Approach to Chain Recurrence
 An Algorithmic Approach to Chain Recurrence W.D. Kalies, K. Mischaikow, and R.C.A.M. VanderVorst October 10, 2005 ABSTRACT. In this paper we give a new definition of the chain recurrent set of a continuous
An Algorithmic Approach to Chain Recurrence W.D. Kalies, K. Mischaikow, and R.C.A.M. VanderVorst October 10, 2005 ABSTRACT. In this paper we give a new definition of the chain recurrent set of a continuous
B5.6 Nonlinear Systems
 B5.6 Nonlinear Systems 5. Global Bifurcations, Homoclinic chaos, Melnikov s method Alain Goriely 2018 Mathematical Institute, University of Oxford Table of contents 1. Motivation 1.1 The problem 1.2 A
B5.6 Nonlinear Systems 5. Global Bifurcations, Homoclinic chaos, Melnikov s method Alain Goriely 2018 Mathematical Institute, University of Oxford Table of contents 1. Motivation 1.1 The problem 1.2 A
Numerical Sequences and Series
 Numerical Sequences and Series Written by Men-Gen Tsai email: b89902089@ntu.edu.tw. Prove that the convergence of {s n } implies convergence of { s n }. Is the converse true? Solution: Since {s n } is
Numerical Sequences and Series Written by Men-Gen Tsai email: b89902089@ntu.edu.tw. Prove that the convergence of {s n } implies convergence of { s n }. Is the converse true? Solution: Since {s n } is
Half of Final Exam Name: Practice Problems October 28, 2014
 Math 54. Treibergs Half of Final Exam Name: Practice Problems October 28, 24 Half of the final will be over material since the last midterm exam, such as the practice problems given here. The other half
Math 54. Treibergs Half of Final Exam Name: Practice Problems October 28, 24 Half of the final will be over material since the last midterm exam, such as the practice problems given here. The other half
Math 201 Topology I. Lecture notes of Prof. Hicham Gebran
 Math 201 Topology I Lecture notes of Prof. Hicham Gebran hicham.gebran@yahoo.com Lebanese University, Fanar, Fall 2015-2016 http://fs2.ul.edu.lb/math http://hichamgebran.wordpress.com 2 Introduction and
Math 201 Topology I Lecture notes of Prof. Hicham Gebran hicham.gebran@yahoo.com Lebanese University, Fanar, Fall 2015-2016 http://fs2.ul.edu.lb/math http://hichamgebran.wordpress.com 2 Introduction and
Convexity in R n. The following lemma will be needed in a while. Lemma 1 Let x E, u R n. If τ I(x, u), τ 0, define. f(x + τu) f(x). τ.
 Convexity in R n Let E be a convex subset of R n. A function f : E (, ] is convex iff f(tx + (1 t)y) (1 t)f(x) + tf(y) x, y E, t [0, 1]. A similar definition holds in any vector space. A topology is needed
Convexity in R n Let E be a convex subset of R n. A function f : E (, ] is convex iff f(tx + (1 t)y) (1 t)f(x) + tf(y) x, y E, t [0, 1]. A similar definition holds in any vector space. A topology is needed
MATH 23b, SPRING 2005 THEORETICAL LINEAR ALGEBRA AND MULTIVARIABLE CALCULUS Midterm (part 1) Solutions March 21, 2005
 MATH 23b, SPRING 2005 THEORETICAL LINEAR ALGEBRA AND MULTIVARIABLE CALCULUS Midterm (part 1) Solutions March 21, 2005 1. True or False (22 points, 2 each) T or F Every set in R n is either open or closed
MATH 23b, SPRING 2005 THEORETICAL LINEAR ALGEBRA AND MULTIVARIABLE CALCULUS Midterm (part 1) Solutions March 21, 2005 1. True or False (22 points, 2 each) T or F Every set in R n is either open or closed
Stability of Dynamical systems
 Stability of Dynamical systems Stability Isolated equilibria Classification of Isolated Equilibria Attractor and Repeller Almost linear systems Jacobian Matrix Stability Consider an autonomous system u
Stability of Dynamical systems Stability Isolated equilibria Classification of Isolated Equilibria Attractor and Repeller Almost linear systems Jacobian Matrix Stability Consider an autonomous system u
Geometry and topology of continuous best and near best approximations
 Journal of Approximation Theory 105: 252 262, Geometry and topology of continuous best and near best approximations Paul C. Kainen Dept. of Mathematics Georgetown University Washington, D.C. 20057 Věra
Journal of Approximation Theory 105: 252 262, Geometry and topology of continuous best and near best approximations Paul C. Kainen Dept. of Mathematics Georgetown University Washington, D.C. 20057 Věra
Optimality Conditions for Constrained Optimization
 72 CHAPTER 7 Optimality Conditions for Constrained Optimization 1. First Order Conditions In this section we consider first order optimality conditions for the constrained problem P : minimize f 0 (x)
72 CHAPTER 7 Optimality Conditions for Constrained Optimization 1. First Order Conditions In this section we consider first order optimality conditions for the constrained problem P : minimize f 0 (x)
INVERSE FUNCTION THEOREM and SURFACES IN R n
 INVERSE FUNCTION THEOREM and SURFACES IN R n Let f C k (U; R n ), with U R n open. Assume df(a) GL(R n ), where a U. The Inverse Function Theorem says there is an open neighborhood V U of a in R n so that
INVERSE FUNCTION THEOREM and SURFACES IN R n Let f C k (U; R n ), with U R n open. Assume df(a) GL(R n ), where a U. The Inverse Function Theorem says there is an open neighborhood V U of a in R n so that
3 Stability and Lyapunov Functions
 CDS140a Nonlinear Systems: Local Theory 02/01/2011 3 Stability and Lyapunov Functions 3.1 Lyapunov Stability Denition: An equilibrium point x 0 of (1) is stable if for all ɛ > 0, there exists a δ > 0 such
CDS140a Nonlinear Systems: Local Theory 02/01/2011 3 Stability and Lyapunov Functions 3.1 Lyapunov Stability Denition: An equilibrium point x 0 of (1) is stable if for all ɛ > 0, there exists a δ > 0 such
AN EXPLORATION OF THE METRIZABILITY OF TOPOLOGICAL SPACES
 AN EXPLORATION OF THE METRIZABILITY OF TOPOLOGICAL SPACES DUSTIN HEDMARK Abstract. A study of the conditions under which a topological space is metrizable, concluding with a proof of the Nagata Smirnov
AN EXPLORATION OF THE METRIZABILITY OF TOPOLOGICAL SPACES DUSTIN HEDMARK Abstract. A study of the conditions under which a topological space is metrizable, concluding with a proof of the Nagata Smirnov
THE INVERSE FUNCTION THEOREM
 THE INVERSE FUNCTION THEOREM W. PATRICK HOOPER The implicit function theorem is the following result: Theorem 1. Let f be a C 1 function from a neighborhood of a point a R n into R n. Suppose A = Df(a)
THE INVERSE FUNCTION THEOREM W. PATRICK HOOPER The implicit function theorem is the following result: Theorem 1. Let f be a C 1 function from a neighborhood of a point a R n into R n. Suppose A = Df(a)
2.31 Definition By an open cover of a set E in a metric space X we mean a collection {G α } of open subsets of X such that E α G α.
 Chapter 2. Basic Topology. 2.3 Compact Sets. 2.31 Definition By an open cover of a set E in a metric space X we mean a collection {G α } of open subsets of X such that E α G α. 2.32 Definition A subset
Chapter 2. Basic Topology. 2.3 Compact Sets. 2.31 Definition By an open cover of a set E in a metric space X we mean a collection {G α } of open subsets of X such that E α G α. 2.32 Definition A subset
ON THE REGULARITY OF SAMPLE PATHS OF SUB-ELLIPTIC DIFFUSIONS ON MANIFOLDS
 Bendikov, A. and Saloff-Coste, L. Osaka J. Math. 4 (5), 677 7 ON THE REGULARITY OF SAMPLE PATHS OF SUB-ELLIPTIC DIFFUSIONS ON MANIFOLDS ALEXANDER BENDIKOV and LAURENT SALOFF-COSTE (Received March 4, 4)
Bendikov, A. and Saloff-Coste, L. Osaka J. Math. 4 (5), 677 7 ON THE REGULARITY OF SAMPLE PATHS OF SUB-ELLIPTIC DIFFUSIONS ON MANIFOLDS ALEXANDER BENDIKOV and LAURENT SALOFF-COSTE (Received March 4, 4)
REAL VARIABLES: PROBLEM SET 1. = x limsup E k
 REAL VARIABLES: PROBLEM SET 1 BEN ELDER 1. Problem 1.1a First let s prove that limsup E k consists of those points which belong to infinitely many E k. From equation 1.1: limsup E k = E k For limsup E
REAL VARIABLES: PROBLEM SET 1 BEN ELDER 1. Problem 1.1a First let s prove that limsup E k consists of those points which belong to infinitely many E k. From equation 1.1: limsup E k = E k For limsup E
Contents: 1. Minimization. 2. The theorem of Lions-Stampacchia for variational inequalities. 3. Γ -Convergence. 4. Duality mapping.
 Minimization Contents: 1. Minimization. 2. The theorem of Lions-Stampacchia for variational inequalities. 3. Γ -Convergence. 4. Duality mapping. 1 Minimization A Topological Result. Let S be a topological
Minimization Contents: 1. Minimization. 2. The theorem of Lions-Stampacchia for variational inequalities. 3. Γ -Convergence. 4. Duality mapping. 1 Minimization A Topological Result. Let S be a topological
Chapter 2 Convex Analysis
 Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
Renormalization for Lorenz maps
 Renormalization for Lorenz maps Denis Gaidashev, Matematiska Institutionen, Uppsala Universitet Tieste, June 5, 2012 D. Gaidashev, Uppsala Universitet () Renormalization for Lorenz maps Tieste, June 5,
Renormalization for Lorenz maps Denis Gaidashev, Matematiska Institutionen, Uppsala Universitet Tieste, June 5, 2012 D. Gaidashev, Uppsala Universitet () Renormalization for Lorenz maps Tieste, June 5,
CHAPTER 7. Connectedness
 CHAPTER 7 Connectedness 7.1. Connected topological spaces Definition 7.1. A topological space (X, T X ) is said to be connected if there is no continuous surjection f : X {0, 1} where the two point set
CHAPTER 7 Connectedness 7.1. Connected topological spaces Definition 7.1. A topological space (X, T X ) is said to be connected if there is no continuous surjection f : X {0, 1} where the two point set
15 Real Analysis II Sequences and Limits , Math for Economists Fall 2004 Lecture Notes, 10/21/2004
 14.102, Math for Economists Fall 2004 Lecture Notes, 10/21/2004 These notes are primarily based on those written by Andrei Bremzen for 14.102 in 2002/3, and by Marek Pycia for the MIT Math Camp in 2003/4.
14.102, Math for Economists Fall 2004 Lecture Notes, 10/21/2004 These notes are primarily based on those written by Andrei Bremzen for 14.102 in 2002/3, and by Marek Pycia for the MIT Math Camp in 2003/4.
Commutative Banach algebras 79
 8. Commutative Banach algebras In this chapter, we analyze commutative Banach algebras in greater detail. So we always assume that xy = yx for all x, y A here. Definition 8.1. Let A be a (commutative)
8. Commutative Banach algebras In this chapter, we analyze commutative Banach algebras in greater detail. So we always assume that xy = yx for all x, y A here. Definition 8.1. Let A be a (commutative)
Solutions Final Exam May. 14, 2014
 Solutions Final Exam May. 14, 2014 1. Determine whether the following statements are true or false. Justify your answer (i.e., prove the claim, derive a contradiction or give a counter-example). (a) (10
Solutions Final Exam May. 14, 2014 1. Determine whether the following statements are true or false. Justify your answer (i.e., prove the claim, derive a contradiction or give a counter-example). (a) (10
1 Preliminaries on locally compact spaces and Radon measure
 1 Preliminaries on locally compact spaces and Radon measure Definition 1.1 A topological space is locally compact if every point has a compact neighborhood. The spaces we are concerned with in this presentation
1 Preliminaries on locally compact spaces and Radon measure Definition 1.1 A topological space is locally compact if every point has a compact neighborhood. The spaces we are concerned with in this presentation
Analysis Finite and Infinite Sets The Real Numbers The Cantor Set
 Analysis Finite and Infinite Sets Definition. An initial segment is {n N n n 0 }. Definition. A finite set can be put into one-to-one correspondence with an initial segment. The empty set is also considered
Analysis Finite and Infinite Sets Definition. An initial segment is {n N n n 0 }. Definition. A finite set can be put into one-to-one correspondence with an initial segment. The empty set is also considered
ORBITAL SHADOWING, INTERNAL CHAIN TRANSITIVITY
 ORBITAL SHADOWING, INTERNAL CHAIN TRANSITIVITY AND ω-limit SETS CHRIS GOOD AND JONATHAN MEDDAUGH Abstract. Let f : X X be a continuous map on a compact metric space, let ω f be the collection of ω-limit
ORBITAL SHADOWING, INTERNAL CHAIN TRANSITIVITY AND ω-limit SETS CHRIS GOOD AND JONATHAN MEDDAUGH Abstract. Let f : X X be a continuous map on a compact metric space, let ω f be the collection of ω-limit
NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY. (τ + arg z) + 1
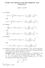 NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY JOHN M. ALONGI p.11 Replace ρ(t, z) = ρ(t, z) = p.11 Replace sin 2 z e τ ] 2 (τ + arg z) + 1 1 + z (e τ dτ. sin 2 (τ + arg z) + 1 z 2 z e τ ] 2 1 + z (e τ dτ.
NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY JOHN M. ALONGI p.11 Replace ρ(t, z) = ρ(t, z) = p.11 Replace sin 2 z e τ ] 2 (τ + arg z) + 1 1 + z (e τ dτ. sin 2 (τ + arg z) + 1 z 2 z e τ ] 2 1 + z (e τ dτ.
Dynamical Systems 2, MA 761
 Dynamical Systems 2, MA 761 Topological Dynamics This material is based upon work supported by the National Science Foundation under Grant No. 9970363 1 Periodic Points 1 The main objects studied in the
Dynamical Systems 2, MA 761 Topological Dynamics This material is based upon work supported by the National Science Foundation under Grant No. 9970363 1 Periodic Points 1 The main objects studied in the
Convergence Rate of Nonlinear Switched Systems
 Convergence Rate of Nonlinear Switched Systems Philippe JOUAN and Saïd NACIRI arxiv:1511.01737v1 [math.oc] 5 Nov 2015 January 23, 2018 Abstract This paper is concerned with the convergence rate of the
Convergence Rate of Nonlinear Switched Systems Philippe JOUAN and Saïd NACIRI arxiv:1511.01737v1 [math.oc] 5 Nov 2015 January 23, 2018 Abstract This paper is concerned with the convergence rate of the
4 Countability axioms
 4 COUNTABILITY AXIOMS 4 Countability axioms Definition 4.1. Let X be a topological space X is said to be first countable if for any x X, there is a countable basis for the neighborhoods of x. X is said
4 COUNTABILITY AXIOMS 4 Countability axioms Definition 4.1. Let X be a topological space X is said to be first countable if for any x X, there is a countable basis for the neighborhoods of x. X is said
Lebesgue Measure on R n
 CHAPTER 2 Lebesgue Measure on R n Our goal is to construct a notion of the volume, or Lebesgue measure, of rather general subsets of R n that reduces to the usual volume of elementary geometrical sets
CHAPTER 2 Lebesgue Measure on R n Our goal is to construct a notion of the volume, or Lebesgue measure, of rather general subsets of R n that reduces to the usual volume of elementary geometrical sets
Set, functions and Euclidean space. Seungjin Han
 Set, functions and Euclidean space Seungjin Han September, 2018 1 Some Basics LOGIC A is necessary for B : If B holds, then A holds. B A A B is the contraposition of B A. A is sufficient for B: If A holds,
Set, functions and Euclidean space Seungjin Han September, 2018 1 Some Basics LOGIC A is necessary for B : If B holds, then A holds. B A A B is the contraposition of B A. A is sufficient for B: If A holds,
A LITTLE REAL ANALYSIS AND TOPOLOGY
 A LITTLE REAL ANALYSIS AND TOPOLOGY 1. NOTATION Before we begin some notational definitions are useful. (1) Z = {, 3, 2, 1, 0, 1, 2, 3, }is the set of integers. (2) Q = { a b : aεz, bεz {0}} is the set
A LITTLE REAL ANALYSIS AND TOPOLOGY 1. NOTATION Before we begin some notational definitions are useful. (1) Z = {, 3, 2, 1, 0, 1, 2, 3, }is the set of integers. (2) Q = { a b : aεz, bεz {0}} is the set
n [ F (b j ) F (a j ) ], n j=1(a j, b j ] E (4.1)
![n [ F (b j ) F (a j ) ], n j=1(a j, b j ] E (4.1) n [ F (b j ) F (a j ) ], n j=1(a j, b j ] E (4.1)](/thumbs/81/82707553.jpg) 1.4. CONSTRUCTION OF LEBESGUE-STIELTJES MEASURES In this section we shall put to use the Carathéodory-Hahn theory, in order to construct measures with certain desirable properties first on the real line
1.4. CONSTRUCTION OF LEBESGUE-STIELTJES MEASURES In this section we shall put to use the Carathéodory-Hahn theory, in order to construct measures with certain desirable properties first on the real line
Dynamical Systems and Chaos Part I: Theoretical Techniques. Lecture 4: Discrete systems + Chaos. Ilya Potapov Mathematics Department, TUT Room TD325
 Dynamical Systems and Chaos Part I: Theoretical Techniques Lecture 4: Discrete systems + Chaos Ilya Potapov Mathematics Department, TUT Room TD325 Discrete maps x n+1 = f(x n ) Discrete time steps. x 0
Dynamical Systems and Chaos Part I: Theoretical Techniques Lecture 4: Discrete systems + Chaos Ilya Potapov Mathematics Department, TUT Room TD325 Discrete maps x n+1 = f(x n ) Discrete time steps. x 0
Fundamental Inequalities, Convergence and the Optional Stopping Theorem for Continuous-Time Martingales
 Fundamental Inequalities, Convergence and the Optional Stopping Theorem for Continuous-Time Martingales Prakash Balachandran Department of Mathematics Duke University April 2, 2008 1 Review of Discrete-Time
Fundamental Inequalities, Convergence and the Optional Stopping Theorem for Continuous-Time Martingales Prakash Balachandran Department of Mathematics Duke University April 2, 2008 1 Review of Discrete-Time
Lecture 4. Chapter 4: Lyapunov Stability. Eugenio Schuster. Mechanical Engineering and Mechanics Lehigh University.
 Lecture 4 Chapter 4: Lyapunov Stability Eugenio Schuster schuster@lehigh.edu Mechanical Engineering and Mechanics Lehigh University Lecture 4 p. 1/86 Autonomous Systems Consider the autonomous system ẋ
Lecture 4 Chapter 4: Lyapunov Stability Eugenio Schuster schuster@lehigh.edu Mechanical Engineering and Mechanics Lehigh University Lecture 4 p. 1/86 Autonomous Systems Consider the autonomous system ẋ
Synchronization, Chaos, and the Dynamics of Coupled Oscillators. Supplemental 1. Winter Zachary Adams Undergraduate in Mathematics and Biology
 Synchronization, Chaos, and the Dynamics of Coupled Oscillators Supplemental 1 Winter 2017 Zachary Adams Undergraduate in Mathematics and Biology Outline: The shift map is discussed, and a rigorous proof
Synchronization, Chaos, and the Dynamics of Coupled Oscillators Supplemental 1 Winter 2017 Zachary Adams Undergraduate in Mathematics and Biology Outline: The shift map is discussed, and a rigorous proof
COMPLETELY INVARIANT JULIA SETS OF POLYNOMIAL SEMIGROUPS
 Series Logo Volume 00, Number 00, Xxxx 19xx COMPLETELY INVARIANT JULIA SETS OF POLYNOMIAL SEMIGROUPS RICH STANKEWITZ Abstract. Let G be a semigroup of rational functions of degree at least two, under composition
Series Logo Volume 00, Number 00, Xxxx 19xx COMPLETELY INVARIANT JULIA SETS OF POLYNOMIAL SEMIGROUPS RICH STANKEWITZ Abstract. Let G be a semigroup of rational functions of degree at least two, under composition
Quick Tour of the Topology of R. Steven Hurder, Dave Marker, & John Wood 1
 Quick Tour of the Topology of R Steven Hurder, Dave Marker, & John Wood 1 1 Department of Mathematics, University of Illinois at Chicago April 17, 2003 Preface i Chapter 1. The Topology of R 1 1. Open
Quick Tour of the Topology of R Steven Hurder, Dave Marker, & John Wood 1 1 Department of Mathematics, University of Illinois at Chicago April 17, 2003 Preface i Chapter 1. The Topology of R 1 1. Open
An introduction to Birkhoff normal form
 An introduction to Birkhoff normal form Dario Bambusi Dipartimento di Matematica, Universitá di Milano via Saldini 50, 0133 Milano (Italy) 19.11.14 1 Introduction The aim of this note is to present an
An introduction to Birkhoff normal form Dario Bambusi Dipartimento di Matematica, Universitá di Milano via Saldini 50, 0133 Milano (Italy) 19.11.14 1 Introduction The aim of this note is to present an
MCE693/793: Analysis and Control of Nonlinear Systems
 MCE693/793: Analysis and Control of Nonlinear Systems Systems of Differential Equations Phase Plane Analysis Hanz Richter Mechanical Engineering Department Cleveland State University Systems of Nonlinear
MCE693/793: Analysis and Control of Nonlinear Systems Systems of Differential Equations Phase Plane Analysis Hanz Richter Mechanical Engineering Department Cleveland State University Systems of Nonlinear
Introduction to Topology
 Introduction to Topology Randall R. Holmes Auburn University Typeset by AMS-TEX Chapter 1. Metric Spaces 1. Definition and Examples. As the course progresses we will need to review some basic notions about
Introduction to Topology Randall R. Holmes Auburn University Typeset by AMS-TEX Chapter 1. Metric Spaces 1. Definition and Examples. As the course progresses we will need to review some basic notions about
Ergodic Theorems with Respect to Lebesgue
 Ergodic Theorems with Respect to Lebesgue ELEONORA CATSIGERAS Instituto de Matemática, Facultad de Ingeniería Universidad de la República Av. Herrera y Reissig 565, CP 200 Montevideo URUGUAY eleonora@fing.edu.uy
Ergodic Theorems with Respect to Lebesgue ELEONORA CATSIGERAS Instituto de Matemática, Facultad de Ingeniería Universidad de la República Av. Herrera y Reissig 565, CP 200 Montevideo URUGUAY eleonora@fing.edu.uy
In essence, Dynamical Systems is a science which studies differential equations. A differential equation here is the equation
 Lecture I In essence, Dynamical Systems is a science which studies differential equations. A differential equation here is the equation ẋ(t) = f(x(t), t) where f is a given function, and x(t) is an unknown
Lecture I In essence, Dynamical Systems is a science which studies differential equations. A differential equation here is the equation ẋ(t) = f(x(t), t) where f is a given function, and x(t) is an unknown
2. Metric Spaces. 2.1 Definitions etc.
 2. Metric Spaces 2.1 Definitions etc. The procedure in Section for regarding R as a topological space may be generalized to many other sets in which there is some kind of distance (formally, sets with
2. Metric Spaces 2.1 Definitions etc. The procedure in Section for regarding R as a topological space may be generalized to many other sets in which there is some kind of distance (formally, sets with
x 2 x n r n J(x + t(x x ))(x x )dt. For warming-up we start with methods for solving a single equation of one variable.
 Maria Cameron 1. Fixed point methods for solving nonlinear equations We address the problem of solving an equation of the form (1) r(x) = 0, where F (x) : R n R n is a vector-function. Eq. (1) can be written
Maria Cameron 1. Fixed point methods for solving nonlinear equations We address the problem of solving an equation of the form (1) r(x) = 0, where F (x) : R n R n is a vector-function. Eq. (1) can be written
Math 421, Homework #7 Solutions. We can then us the triangle inequality to find for k N that (x k + y k ) (L + M) = (x k L) + (y k M) x k L + y k M
 Math 421, Homework #7 Solutions (1) Let {x k } and {y k } be convergent sequences in R n, and assume that lim k x k = L and that lim k y k = M. Prove directly from definition 9.1 (i.e. don t use Theorem
Math 421, Homework #7 Solutions (1) Let {x k } and {y k } be convergent sequences in R n, and assume that lim k x k = L and that lim k y k = M. Prove directly from definition 9.1 (i.e. don t use Theorem
Math 541 Fall 2008 Connectivity Transition from Math 453/503 to Math 541 Ross E. Staffeldt-August 2008
 Math 541 Fall 2008 Connectivity Transition from Math 453/503 to Math 541 Ross E. Staffeldt-August 2008 Closed sets We have been operating at a fundamental level at which a topological space is a set together
Math 541 Fall 2008 Connectivity Transition from Math 453/503 to Math 541 Ross E. Staffeldt-August 2008 Closed sets We have been operating at a fundamental level at which a topological space is a set together
Optimization and Optimal Control in Banach Spaces
 Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
MASTERS EXAMINATION IN MATHEMATICS SOLUTIONS
 MASTERS EXAMINATION IN MATHEMATICS PURE MATHEMATICS OPTION SPRING 010 SOLUTIONS Algebra A1. Let F be a finite field. Prove that F [x] contains infinitely many prime ideals. Solution: The ring F [x] of
MASTERS EXAMINATION IN MATHEMATICS PURE MATHEMATICS OPTION SPRING 010 SOLUTIONS Algebra A1. Let F be a finite field. Prove that F [x] contains infinitely many prime ideals. Solution: The ring F [x] of
A Note on Some Properties of Local Random Attractors
 Northeast. Math. J. 24(2)(2008), 163 172 A Note on Some Properties of Local Random Attractors LIU Zhen-xin ( ) (School of Mathematics, Jilin University, Changchun, 130012) SU Meng-long ( ) (Mathematics
Northeast. Math. J. 24(2)(2008), 163 172 A Note on Some Properties of Local Random Attractors LIU Zhen-xin ( ) (School of Mathematics, Jilin University, Changchun, 130012) SU Meng-long ( ) (Mathematics
Competitive and Cooperative Differential Equations
 Chapter 3 Competitive and Cooperative Differential Equations 0. Introduction This chapter and the next one focus on ordinary differential equations in IR n. A natural partial ordering on IR n is generated
Chapter 3 Competitive and Cooperative Differential Equations 0. Introduction This chapter and the next one focus on ordinary differential equations in IR n. A natural partial ordering on IR n is generated
Real Analysis Notes. Thomas Goller
 Real Analysis Notes Thomas Goller September 4, 2011 Contents 1 Abstract Measure Spaces 2 1.1 Basic Definitions........................... 2 1.2 Measurable Functions........................ 2 1.3 Integration..............................
Real Analysis Notes Thomas Goller September 4, 2011 Contents 1 Abstract Measure Spaces 2 1.1 Basic Definitions........................... 2 1.2 Measurable Functions........................ 2 1.3 Integration..............................
LECTURE 8: DYNAMICAL SYSTEMS 7
 15-382 COLLECTIVE INTELLIGENCE S18 LECTURE 8: DYNAMICAL SYSTEMS 7 INSTRUCTOR: GIANNI A. DI CARO GEOMETRIES IN THE PHASE SPACE Damped pendulum One cp in the region between two separatrix Separatrix Basin
15-382 COLLECTIVE INTELLIGENCE S18 LECTURE 8: DYNAMICAL SYSTEMS 7 INSTRUCTOR: GIANNI A. DI CARO GEOMETRIES IN THE PHASE SPACE Damped pendulum One cp in the region between two separatrix Separatrix Basin
Lyapunov Stability Theory
 Lyapunov Stability Theory Peter Al Hokayem and Eduardo Gallestey March 16, 2015 1 Introduction In this lecture we consider the stability of equilibrium points of autonomous nonlinear systems, both in continuous
Lyapunov Stability Theory Peter Al Hokayem and Eduardo Gallestey March 16, 2015 1 Introduction In this lecture we consider the stability of equilibrium points of autonomous nonlinear systems, both in continuous
Contents Ordered Fields... 2 Ordered sets and fields... 2 Construction of the Reals 1: Dedekind Cuts... 2 Metric Spaces... 3
 Analysis Math Notes Study Guide Real Analysis Contents Ordered Fields 2 Ordered sets and fields 2 Construction of the Reals 1: Dedekind Cuts 2 Metric Spaces 3 Metric Spaces 3 Definitions 4 Separability
Analysis Math Notes Study Guide Real Analysis Contents Ordered Fields 2 Ordered sets and fields 2 Construction of the Reals 1: Dedekind Cuts 2 Metric Spaces 3 Metric Spaces 3 Definitions 4 Separability
Convex Analysis and Economic Theory Winter 2018
 Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory Winter 2018 Topic 7: Quasiconvex Functions I 7.1 Level sets of functions For an extended real-valued
Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory Winter 2018 Topic 7: Quasiconvex Functions I 7.1 Level sets of functions For an extended real-valued
MAT 570 REAL ANALYSIS LECTURE NOTES. Contents. 1. Sets Functions Countability Axiom of choice Equivalence relations 9
 MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University
 Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
Optimality Conditions for Nonsmooth Convex Optimization
 Optimality Conditions for Nonsmooth Convex Optimization Sangkyun Lee Oct 22, 2014 Let us consider a convex function f : R n R, where R is the extended real field, R := R {, + }, which is proper (f never
Optimality Conditions for Nonsmooth Convex Optimization Sangkyun Lee Oct 22, 2014 Let us consider a convex function f : R n R, where R is the extended real field, R := R {, + }, which is proper (f never
The Heine-Borel and Arzela-Ascoli Theorems
 The Heine-Borel and Arzela-Ascoli Theorems David Jekel October 29, 2016 This paper explains two important results about compactness, the Heine- Borel theorem and the Arzela-Ascoli theorem. We prove them
The Heine-Borel and Arzela-Ascoli Theorems David Jekel October 29, 2016 This paper explains two important results about compactness, the Heine- Borel theorem and the Arzela-Ascoli theorem. We prove them
April 13, We now extend the structure of the horseshoe to more general kinds of invariant. x (v) λ n v.
 April 3, 005 - Hyperbolic Sets We now extend the structure of the horseshoe to more general kinds of invariant sets. Let r, and let f D r (M) where M is a Riemannian manifold. A compact f invariant set
April 3, 005 - Hyperbolic Sets We now extend the structure of the horseshoe to more general kinds of invariant sets. Let r, and let f D r (M) where M is a Riemannian manifold. A compact f invariant set
Topology Homework Assignment 1 Solutions
 Topology Homework Assignment 1 Solutions 1. Prove that R n with the usual topology satisfies the axioms for a topological space. Let U denote the usual topology on R n. 1(a) R n U because if x R n, then
Topology Homework Assignment 1 Solutions 1. Prove that R n with the usual topology satisfies the axioms for a topological space. Let U denote the usual topology on R n. 1(a) R n U because if x R n, then
Real Analysis Math 131AH Rudin, Chapter #1. Dominique Abdi
 Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
One Dimensional Dynamical Systems
 16 CHAPTER 2 One Dimensional Dynamical Systems We begin by analyzing some dynamical systems with one-dimensional phase spaces, and in particular their bifurcations. All equations in this Chapter are scalar
16 CHAPTER 2 One Dimensional Dynamical Systems We begin by analyzing some dynamical systems with one-dimensional phase spaces, and in particular their bifurcations. All equations in this Chapter are scalar
Definitions & Theorems
 Definitions & Theorems Math 147, Fall 2009 December 19, 2010 Contents 1 Logic 2 1.1 Sets.................................................. 2 1.2 The Peano axioms..........................................
Definitions & Theorems Math 147, Fall 2009 December 19, 2010 Contents 1 Logic 2 1.1 Sets.................................................. 2 1.2 The Peano axioms..........................................
Discrete dynamics on the real line
 Chapter 2 Discrete dynamics on the real line We consider the discrete time dynamical system x n+1 = f(x n ) for a continuous map f : R R. Definitions The forward orbit of x 0 is: O + (x 0 ) = {x 0, f(x
Chapter 2 Discrete dynamics on the real line We consider the discrete time dynamical system x n+1 = f(x n ) for a continuous map f : R R. Definitions The forward orbit of x 0 is: O + (x 0 ) = {x 0, f(x
We will begin our study of topology from a set-theoretic point of view. As the subject
 p. 1 Math 490-01 Notes 5 Topology We will begin our study of topology from a set-theoretic point of view. As the subject expands, we will encounter various notions from analysis such as compactness, continuity,
p. 1 Math 490-01 Notes 5 Topology We will begin our study of topology from a set-theoretic point of view. As the subject expands, we will encounter various notions from analysis such as compactness, continuity,
MATH 722, COMPLEX ANALYSIS, SPRING 2009 PART 5
 MATH 722, COMPLEX ANALYSIS, SPRING 2009 PART 5.. The Arzela-Ascoli Theorem.. The Riemann mapping theorem Let X be a metric space, and let F be a family of continuous complex-valued functions on X. We have
MATH 722, COMPLEX ANALYSIS, SPRING 2009 PART 5.. The Arzela-Ascoli Theorem.. The Riemann mapping theorem Let X be a metric space, and let F be a family of continuous complex-valued functions on X. We have
The Inverse Function Theorem 1
 John Nachbar Washington University April 11, 2014 1 Overview. The Inverse Function Theorem 1 If a function f : R R is C 1 and if its derivative is strictly positive at some x R, then, by continuity of
John Nachbar Washington University April 11, 2014 1 Overview. The Inverse Function Theorem 1 If a function f : R R is C 1 and if its derivative is strictly positive at some x R, then, by continuity of
Euler Characteristic of Two-Dimensional Manifolds
 Euler Characteristic of Two-Dimensional Manifolds M. Hafiz Khusyairi August 2008 In this work we will discuss an important notion from topology, namely Euler Characteristic and we will discuss several
Euler Characteristic of Two-Dimensional Manifolds M. Hafiz Khusyairi August 2008 In this work we will discuss an important notion from topology, namely Euler Characteristic and we will discuss several
ON THE INVERSE FUNCTION THEOREM
 PACIFIC JOURNAL OF MATHEMATICS Vol. 64, No 1, 1976 ON THE INVERSE FUNCTION THEOREM F. H. CLARKE The classical inverse function theorem gives conditions under which a C r function admits (locally) a C Γ
PACIFIC JOURNAL OF MATHEMATICS Vol. 64, No 1, 1976 ON THE INVERSE FUNCTION THEOREM F. H. CLARKE The classical inverse function theorem gives conditions under which a C r function admits (locally) a C Γ
A LOCALIZATION PROPERTY AT THE BOUNDARY FOR MONGE-AMPERE EQUATION
 A LOCALIZATION PROPERTY AT THE BOUNDARY FOR MONGE-AMPERE EQUATION O. SAVIN. Introduction In this paper we study the geometry of the sections for solutions to the Monge- Ampere equation det D 2 u = f, u
A LOCALIZATION PROPERTY AT THE BOUNDARY FOR MONGE-AMPERE EQUATION O. SAVIN. Introduction In this paper we study the geometry of the sections for solutions to the Monge- Ampere equation det D 2 u = f, u
converges as well if x < 1. 1 x n x n 1 1 = 2 a nx n
 Solve the following 6 problems. 1. Prove that if series n=1 a nx n converges for all x such that x < 1, then the series n=1 a n xn 1 x converges as well if x < 1. n For x < 1, x n 0 as n, so there exists
Solve the following 6 problems. 1. Prove that if series n=1 a nx n converges for all x such that x < 1, then the series n=1 a n xn 1 x converges as well if x < 1. n For x < 1, x n 0 as n, so there exists
