ExpIntegralEi. Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation
|
|
|
- Kristin Cecily Freeman
- 5 years ago
- Views:
Transcription
1 ExpItegralEi Notatios Traditioal ame Expoetial itegral Ei Traditioal otatio Ei Mathematica StadardForm otatio ExpItegralEi Primary defiitio Ei k k 2 log log k Specific values Values at fixed poits Ei0 Values at ifiities Ei Ei Ei Π Ei Π Ei
2 2 Geeral characteristics Domai ad aalyticity Ei is a aalytical fuctio of which is defied over the whole complex -plae Ei Symmetries ad periodicities Mirror symmetry Ei Ei Periodicity No periodicity Poles ad essetial sigularities The fuctio Ei has a essetial sigularity at. At the same time, the poit is a brach poit ig Ei. Brach poits The fuctio Ei has two brach poits: 0,. At the same time, the poit is a essetial sigularity Ei 0, Ei, 0 log Ei, log Brach cuts The fuctio Ei is a sigle-valued fuctio o the -plae cut alog the iterval, 0 where it has discotiuities from both sides Ei, 0, lim Eix Ε Eix Π ; x 0 Ε lim Eix Ε Eix Π ; x 0 Ε0
3 3 Series represetatios Geeralied power series Expasios at geeric poit 0 For the fuctio itself arg Π Ei Ei 0 Π 2 log 0 arg 0 log 0 log 0 log log ; arg Π Ei Ei 0 Π 2 log 0 arg 0 log 0 log 0 log log O arg Π Ei Ei 0 Π arg 0 log 0 log 0 2 log 0 log 0 log 0 k 0 k k k, 0 0 k arg Π Ei Ei 0 Π arg 0 log 0 log 0 2 log k kj jk log 0 log k 0 j 0 k j arg Π Ei Ei 0 Π arg 0 log 0 log 0 2 log 0 log 0 log 0 0 k k j 0 j j 0 j k j 0 k arg Π Ei Ei 0 Π arg 0 log 0 log 0 2 log 0 log 0 log 0 k k k 0 0 2F 2, ; 2, 2 k; 0 0 k k k
4 arg Π Ei Ei 0 Π 2 log 0 log 0 log 0 arg 0 log 0 log 0 O 0 Expasios o brach cuts For the fuctio itself arg Π Ei Eix Π 2 Π arg x Π x x x x x 2 x 2 x 2 ; x x x arg Π Ei Eix Π 2 Π arg x Π x x x x x 2 x 2 x 2 O x 3 ; x x Ei Eix Π Π arg Π 2 Π arg x k x k k, x x k ; x x 0 k Ei Eix Π Π arg Π 2 Π arg x k kj x jk x x k ; x x 0 k j j Ei Eix Π Π arg Π 2 Π arg x k x k j 0 j j x j k j x k ; x x Ei Eix Π Π arg Π 2 Π arg x k x k k xk k 2F 2, ; 2, 2 k; x x k ; x x arg Π Ei Eix Π 2 Π arg x Π O x ; x x 0 Expasios at 0 For the fuctio itself Ei 2 log log Ei 2 log log ; O Ei 2 log log k k k
5 Ei log k k k Π arg Π 0 True Ei 2 F 2, ; 2, 2; 2 log log Ei 2 log log O ; Ei F ; F 2 log log k 2 Ei k 0 k 2 k 2 2 2F 2, 2; 3, 3; Summed form of the trucated series expasio k k k Ei j k 2 log log j Asymptotic series expasios Ei 2 log log log log 2 6 ; Ei 2F 0, ; ; 2 log log log log ; Ei 2 log log log log k 0 k ; k Ei k Π sgim ; k k Ei 2 log log log log O ; Ei Π Π arg 0 arg Π arg 0 ; True
6 Ei Π arg Π 2 Π Π arg Π 2 ; True Residue represetatios Ei 2 log log res s j 0 s 2 s s j s Ei log 2 log log res s s s s 0 res s j s s j s Other series represetatios L Eix x k x ; x 0 k 0 k Itegral represetatios O the real axis Of the direct fuctio t Ei t 0 t 2 log log t Eix t ; x x t x t Eix t ; x t Cotour itegral represetatios Ei 2 log Ei 2 log log log 2Π s s2 s 2 2Π Γ Γ s s 2 s s s 2 s s ; Γ 0 arg Π 2
7 Ei log 2 log Ei log 2 log log 2Π s2 s s s log Γ s 2 2Π Γ s s s ; 0 Γ arg Π 2 Cotiued fractio represetatios Ei Π sgim ; arg Π Ei Π sgim k k 2, 2 k ; arg Π Ei Π sgim ; arg Π Ei Π sgim k k 2, 2 k ; arg Π Differetial equatios Ordiary liear differetial equatios ad wroskias For the direct fuctio itself w 3 2 w w 0 ; w c Ei c 2 Ei c 3
8 W, Ei, Ei w 3 2 w w 0 ; w c Ei c 2 Shi c W, Ei, Shi w 3 2 w w 0 ; w c Ei c 2 Chi c W, Ei, Chi w 3 2 g g 3 g g w g 2 3 g 2 2 g g 2 g g3 g w 0 ; w c Eig c 2 Eig c W Eig, Eig, 2 g w 3 2 g 3 h g h g 2 4 h g g h g 2 3 g g w 6 h 2 3 g 2 6 h g h 2 g 2 h g 2 g g 3 h h g3 g w 6 h 3 4 g h 2 6 g h 2 6 h h 3 g 2 h 2 h g 2 g h h 3 g h 2 h 2 g h 2 h g 2 g h 3 g h h g 3 h g g 2 h h 3 h w 0 ; w c Eig h c 2 Eig h c 3 h W h Eig, h Eig, h 2 h3 g 3 g w 3 r 3 s 3 2 w a 2 r 2 2 r 3 s 2 r 2 r s 3 s w s a 2 r 2 2 r s 2 r s w 0 ; w c s Eia r c 2 s Eia r c 3 s W s Eia r, s Eia r, s 2 a r 3 3r3 s w 3 logr 3 logs w a 2 log 2 r r 2 3 log 2 s 2 logr logs w logs a 2 log 2 r r 2 log 2 s logr logs w 0 ; w c s Eia r c 2 s Eia r c 3 s
9 W s Eia r, s Eia r, s 2 a r s 3 log 3 r Trasformatios Trasformatios ad argumet simplificatios Argumet ivolvig basic arithmetic operatios Ei Ci Si log 2 log log Ei Ci Si log 2 log log Ei 2 Ei 2 log log log log 2 Shi Related trasformatios Eilog li Complex characteristics Real part ReEix y Chix logx 2 logx2 y 2 j y 2 j2 j 0 2 j 2 j 2 F 2 j ; x2, j 2; 2 4 x j y 2 j j 0 2 j 2 j F 2 j 2 ; 3 2, j 3 2 ; x ReEix y 2 logx2 y 2 k k x k y 2 x 2 k2 cos k ta y x ReEix y j y 2 j x k2 j 2 logx2 y 2 k 2 j k 2 j k 2 j 0 ReEix y 2 Ei x x y2 Ei x x y2 x 2 x 2
10 0 Imagiary part ImEix y 20 k y 2 k x 2 k 2 k 0 F 2 k ; 3 x2 20, k 2; 2 4 k y 2 k k 0 2 k 2 k F 2 k 2 ; 2, k 3 2 ; x2 4 2 ta x, y ta x, y y2 ImEix y k k x k x 2 k2 si k ta y x 2 ta x, y ta x, y j y 2 j x ImEix y k 2 j k 2 j 2 ta x, y ta x, y k j 0 k2 j ImEix y x y2 Ei x x y2 Ei x x y2 2 y x 2 x 2 x 2 Absolute value Eix y Ei x x y2 x 2 Ei x x y2 x 2 Argumet argeix y ta 2 Ei x x y2 x 2 Ei x x y2 x 2, x y2 Ei x x y2 Ei x x y2 2 y x 2 x 2 x 2 Cojugate value Eix y 2 Ei x x y2 Ei x x y2 x 2 x 2 x y2 Ei x x y2 Ei x x y2 2 y x 2 x 2 x 2 Sigum value
11 sgeix y y2 x Ei x x y2 Ei y2 x x Ei y2 x x Ei x x y2 y x 2 x 2 x 2 x 2 x 2 2 Ei x x y2 x 2 Ei y2 x 2 x x Differetiatio Low-order differetiatio Ei Ei 2 2 Symbolic differetiatio Ei k k Ei ; k k Ei 2 log log log, ; Ei Ei Boole 0, k k k k k 0 ; Ei Ei Boole 0,, ; Ei 2 F 2, ; 2, 2 ; ; Fractioal itegro-differetiatio Α Ei Α Α 2 F 2, ; 2, 2 Α; Α Α log Α Α 2 log log Itegratio
12 2 Idefiite itegratio Ivolvig oly oe direct fuctio Eib a b a Eib a ba a Eia Eia a a Eia Eia a a Ei Ei Ivolvig oe direct fuctio ad elemetary fuctios Ivolvig power fuctio Ivolvig power Liear argumet Α Eia Α Α, a a Α Eia Α Α Eia Α Α Α, a a Α Eia Α Ei Α Α Α, Α Ei Eia a2 Eia 2 a a 2 a Eia a 3 F 3,, ; 2, 2, 2; a log 2 Eia 2 0, a log 2 loga Eia a Eia a 2
13 3 Eib a a b Eia b a Eib a b Power argumets Α Eia r Α Α Α r, a r a r Α r Eia r Ivolvig expoetial fuctio Ivolvig exp Liear argumet b Eia b Eia Eia b b a Eia loga a Eia a Power argumets a r Eia r 2 r a r r r, a r log r a 0, 2 loga r loga r 2 G 2,2 2,3 a r r 0, 0, r Ivolvig expoetial fuctio ad a power fuctio Ivolvig exp ad power Liear argumets b Eia b b b k a b k k, a b Eia b Eia, b ; k a Eia a a k Eia, a log k k ;
14 b Eia b ab a b b b Eia a b Eia b b 2 a b b Eia b 3 b b b 2 Eia 2 Eia b a a b 2 b2 b ab b b 3 a b b Eia b 4 b b b b 6 Eia 6 a a b 3 b3 Eia b b ab b b 6 a 2 b 2 b b 5 a b 2 b b Α a Eia 2 Α Α, a 2 loga loga log a a Α Α G 2,2 2,3 a 0, Α 0, 0, Α a Eia a a k Eia, a log k k ; a Eia a a a Eia log a c Eib a a c 2 a c b c a ac ba a a c a c a b c Ei a c b a a a a c c b a c Eib a a Eia Eia 2 2 Power argumets Α a r Eia r Α 2 r a r Α r Α r, a r log r a 0, Α 2 loga r loga r 2 G 2,2 2,3 a r r 0, 0, Α r Ivolvig trigoometric fuctios Ivolvig si cosb Eia Eia b Eia b sib Eia 2 b
15 5 Ivolvig cos Eia b Eia b 2 Eia sib cosb Eia 2 b Ivolvig trigoometric fuctios ad a power fuctio Ivolvig si ad power b sib Eia 2 b b k b a k k, b a Eia b Eia, b k b k b a k k, a b Eia b Eia, b k ; sib Eia Eia b Eia b 2 Eia sib b cosb 2 b a a cosb b sib 2 b 2 a 2 b sib Eia a a 2 a 2 b 2 a 3 b 2 cosb b 2 a b 2 a 2 b 2 2 a a 2 2 b 2 sib b Eia b b 3 a 2 b 2 2 a 2 b 2 2 Eia b Eia b cosb 2 b sib sib Eia Eia b 6 b 4 b2 2 cosb 3 b sib 3 Eia b Eia b a 2 b 2 3 a2 b 2 3 b a a a 2 b b 2 a 2 b 2 a 2 5 b 2 b 2 2 a 3 a 4 8 b 2 a 2 9 b 4 cosb b 2 a 3 a 4 6 b 2 a 2 a 2 b 2 3 a 2 7 b 2 a b 4 b 2 a 2 b sib Ivolvig cos ad power
16 cosb Eia 2 b b k b a k k, b a b Eia b Eia, b k b k b a k k, a b Eia b Eia, b k ; cosb Eia Eia b Eia b 2 b a a sib b cosb 2 Eia cosb b sib 2 b 2 a 2 b cosb Eia a a 2 a 2 b 2 a 3 b 2 sib b 2 a b 2 a 2 b 2 2 a a 2 2 b 2 cosb b b 3 a 2 b 2 2 a 2 b 2 2 Eia b Eia b Eia 2 b cosb b sib cosb Eia b 4 a 2 b 2 3 b2 a 3 a 4 6 b 2 a 2 a 2 b 2 3 a 2 7 b 2 a b 4 b 2 a 2 b cosb 3 Eia b Eia b b a 2 b 2 3 a a a 2 b b 2 a 2 b 2 a 2 5 b 2 b 2 2 a 3 a 4 8 b 2 a 2 9 b 4 sib Eia 3 b cosb b b sib Ivolvig hyperbolic fuctios Ivolvig sih coshb Eia Eia b Eia b sihb Eia 2 b siha Eia a a Eia Ei2 a loga 2 a Ivolvig cosh Eia b Eia b 2 Eia sihb coshb Eia 2 b
17 Chi2 a loga 2 Eia siha Shi2 a cosha Eia 2 a Ivolvig hyperbolic fuctios ad a power fuctio Ivolvig sih ad power sihb Eia 2 b b k b a k k, b a Eia b Eia, b k b k a b k k, a b Eia b Eia, b k ; sihb Eia 2 a Eia, a, a 2 k k, 2 a a k Ei2 a log k k k ; sihb Eia Eia b Eia b 2 Eia b coshb sihb 2 b a b sihb a coshb 2 b 2 a 2 b sihb Eia a a 3 a 2 b 2 a 3 b 2 coshb b 2 a b 4 4 a b 2 a 2 b 2 2 a 3 sihb b Eia b b 3 a 2 b 2 2 a 2 b 2 2 Eia b Eia 2 b sihb b coshb sihb Eia 3 Eia b Eia b b 4 a b 3 a b 3 b2 a 2 3 b a a a 2 b b 2 a 4 6 b 2 a 2 5 b 4 b 2 2 a 3 a 4 8 b 2 a 2 9 b 4 coshb b 2 a 3 a 4 6 b 2 a 2 3 a 4 0 b 2 a 2 7 b 4 a b 4 b 2 a 2 b sihb Eia b b coshb 3 b sihb Ivolvig cosh ad power
18 coshb Eia 2 b b k b a k k, b a Eia b Eia, b k b k a b k k, a b Eia b Eia, b k ; coshb Eia 2 a Eia, a, a 2 k k, 2 a a k Ei2 a log k k k ; coshb Eia Eia b Eia b 2 Eia b sihb coshb 2 b a b coshb a sihb 2 b 2 b 2 a coshb Eia b 3 a 3 b 2 a a 2 a b 2 sihb b 2 a b 4 4 a b 2 a 2 b 2 2 a 3 coshb b Eia b a 2 b 2 2 a 2 b 2 2 Eia b Eia b sihb 2 b coshb coshb Eia Eia b b 4 b2 2 6 sihb 3 b coshb 3 Eia b Eia b a b 3 a b 3 a2 b 2 3 b 2 a 3 a 4 6 b 2 a 2 3 a 4 0 b 2 a 2 7 b 4 a b 4 b 2 a 2 b coshb b a a a 2 b b 2 a 4 6 b 2 a 2 5 b 4 b 2 2 a 3 a 4 8 b 2 a 2 9 b 4 sihb Ivolvig logarithm Ivolvig log logb Eia Eia a a logb a logb a Ivolvig logarithm ad a power fuctio
19 9 Ivolvig log ad power Α logb Eia Α 3 Α a Α 2 F 2 Α, Α; Α, Α ; a a Α Α Eia Α logb a Α Α log Α, a Α logb log Eia log Eia log Eia 4 a 2 Eia a2 2 2 a 2 log 2 2 a a 2 2 a log 9 a 3 Eia a3 3 3 a 3 log 3 6 a a 2 2 a 3 a a 2 log 7 6 a 4 Eia a4 4 4 a 4 log 4 24 a a 3 3 a a 4 a a a 6 log 38 Ivolvig fuctios of the direct fuctio Ivolvig elemetary fuctios of the direct fuctio Ivolvig powers of the direct fuctio Eia 2 a Eia 2 2 a Eia 2 Ei2 a a Ivolvig products of the direct fuctio Eia Eia a Eia Eia a Eia a a Eia Eib a b b a Eib a Eia b b Eib a b Eia b Ivolvig fuctios of the direct fuctio ad elemetary fuctios Ivolvig elemetary fuctios of the direct fuctio ad elemetary fuctios Ivolvig powers of the direct fuctio ad a power fuctio
20 Eia 2 2a Ei2 2 k k, 2 a a Eia, a Eia 2 ; k Eia 2 a2 2 Eia 2 2 a a Eia 2 a 2 Ei2 a Eia Eia 2 2 a 2 6 a 3 2 a3 Eia a 2 a 5 4 a a a 2 Eia 8 Ei2 a 4 a 4 a4 Eia a a a 8 2 a a a a 6 Eia 2 Ei2 a Ivolvig products of the direct fuctio ad a power fuctio Eia Eib a k a b k k, a b Eia b a a Eib, a a Eia k a b b b k a b k k, a b Eia b Eia, b k ; Eia Eia a a a Eia Eia Eia, a a k a k Eia, a log log k k k k ; Eia Eib 2 a 2 b 2 Eia b b b 2 2 Eib a 2 a b ab b 2 a a Eib a 2 b 2 Eia b Eia Eia 2 a 2 a a Eia a Eia a 2 Eia 2 a a 2 a log Eia Eib a b ab 2 a 2 b a b a b a 2 b 2 3 a 3 b 3 a b a b Eia b 3 3 Eib b b b 2 2 a 3 b 3 a a a 2 2 Eib 2 a 3 b 3 Eia b
21 Eia Eia 3 a 3 a 4 a a a a 2 Eia a Eia a a a 2 a 3 3 Eia Eia Eib Eia 4 a 4 b 4 b4 Eib 4 b 6 b b b 3 6 a 4 a b a b 2 ab b b 3 6 a 4 b b 2 b 5 9 a 3 b 2 b b 5 2 a 2 3 b 3 b 3 a 6 b 4 b 4 a a a a Eib 6 a 4 b 4 Eia b Eia Eia 4 a 4 a a a a 6 Eia a Eia a a a a 6 a 4 4 Eia 3 a a log Defiite itegratio Ivolvig the direct fuctio log t Eitt ; Re 0 Itegral trasforms Laplace trasforms log t Eit ; Re Operatios Limit operatio Π 0 arga Π Π argb Π Ima 0 Π argb Π 2 2 lim Eia b x x Π 0 arga Π argb Π Π arga 0 argb Π argb Π Ima 0 argb Π True Represetatios through more geeral fuctios Through hypergeometric fuctios
22 22 Ivolvig p F q Ei 2 F 2, ; 2, 2; 2 log log Ivolvig hypergeometric U Ei U,, log 2 log log Through Meijer G Classical cases for the direct fuctio itself Ei 2 log log G,2 2,3,, 0, Ei log 2 log log G 2,0,2 0, 0 Classical cases ivolvig exp Ei 2 log 2 log log G 2,,2 0 0, Ei 2 log log Π G 2, 2,3 0, 2 0, 0, Ei Π G 2, 2,3 0, 2 0, 0, 2 ;, 0 Classical cases for products of Ei Ei Ei Π 2 G 2,4 3, 2 4 0, 0, 0, 0, 2 ; Im 0 Through other fuctios Ei 0, 2 log log log Ei E 2 log log log
23 23 Represetatios through equivalet fuctios With related fuctios Ei Chi Shi 2 log log Ei Ci Si 2 log log log Ei li ; Π Im Π Theorems The real part of the Heiseberg-Euler Lagragia of quatum electrodyamics The real part of the Heiseberg Euler Lagragia of quatum electrodyamics L eff E, B ca be expressed as the followig series. ReL eff E, B c Α Π c 2coth Π k Η 2 Ξ Ci k Ξ cos k Ξ Si k Ξ si k Ξ coth Π k Ξ Η Ei k Ξ exp k Ξ Ei k Ξ exp k Ξ ; Ξ e Π c c 2 c 2 2 Η e Π c c 2 c 2 2 c 2 E2 B 2 c 2 E B, where E is the electric field, B is the magetic iductio ad Α is the fie structure costat. The Nambu-Goldstoe modes for weakly iteractig fermios i a magetic field The Nambu-Goldstoe modes for weakly iteractig fermios i a magetic field are described by m 2 VrΨr 0, where i 3+ dimesioal ladder quatum electrodyamics the potetial Vr takes the r 2 form Vr 2l 2 Ei r2, where l is the magetic legth. 2 2l History A. M. Legedre (8) O. Schlomilch (846) F. Ardt (847) J. W. L. Glaisher (870) itroduced the otatio Ei
24 24 Copyright This documet was dowloaded from fuctios.wolfram.com, a comprehesive olie compedium of formulas ivolvig the special fuctios of mathematics. For a key to the otatios used here, see Please cite this documet by referrig to the fuctios.wolfram.com page from which it was dowloaded, for example: To refer to a particular formula, cite fuctios.wolfram.com followed by the citatio umber. e.g.: This documet is curretly i a prelimiary form. If you have commets or suggestios, please commets@fuctios.wolfram.com , Wolfram Research, Ic.
Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation. Specialized values
 EulerPhi Notatios Traditioal ame Euler totiet fuctio Traditioal otatio Φ Mathematica StadardForm otatio EulerPhi Primary defiitio 3.06.02.000.0 Φ gcd,k, ; For oegative iteger, the Euler totiet fuctio Φ
EulerPhi Notatios Traditioal ame Euler totiet fuctio Traditioal otatio Φ Mathematica StadardForm otatio EulerPhi Primary defiitio 3.06.02.000.0 Φ gcd,k, ; For oegative iteger, the Euler totiet fuctio Φ
Introductions to HarmonicNumber2
 Itroductios to HarmoicNumber2 Itroductio to the differetiated gamma fuctios Geeral Almost simultaeously with the developmet of the mathematical theory of factorials, biomials, ad gamma fuctios i the 8th
Itroductios to HarmoicNumber2 Itroductio to the differetiated gamma fuctios Geeral Almost simultaeously with the developmet of the mathematical theory of factorials, biomials, ad gamma fuctios i the 8th
SphericalHarmonicY. Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation
 SphericalHaroicY Notatios Traditioal ae Spherical haroic Traditioal otatio Y, φ Matheatica StadardFor otatio SphericalHaroicY,,, φ Priary defiitio 05.0.0.000.0 Y, φ φ P cos ; 05.0.0.000.0 Y 0 k, φ k k
SphericalHaroicY Notatios Traditioal ae Spherical haroic Traditioal otatio Y, φ Matheatica StadardFor otatio SphericalHaroicY,,, φ Priary defiitio 05.0.0.000.0 Y, φ φ P cos ; 05.0.0.000.0 Y 0 k, φ k k
Introductions to PartitionsP
 Itroductios to PartitiosP Itroductio to partitios Geeral Iterest i partitios appeared i the 7th cetury whe G. W. Leibiz (669) ivestigated the umber of ways a give positive iteger ca be decomposed ito a
Itroductios to PartitiosP Itroductio to partitios Geeral Iterest i partitios appeared i the 7th cetury whe G. W. Leibiz (669) ivestigated the umber of ways a give positive iteger ca be decomposed ito a
Multinomial. Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation
 Multioial Notatios Traditioal ae Multioial coefficiet Traditioal otatio 1 2 ; 1, 2,, Matheatica StadardFor otatio Multioial 1, 2,, Priary defiitio 06.04.02.0001.01 1 2 ; 1, 2,, 06.04.02.0002.01 1 k k 1
Multioial Notatios Traditioal ae Multioial coefficiet Traditioal otatio 1 2 ; 1, 2,, Matheatica StadardFor otatio Multioial 1, 2,, Priary defiitio 06.04.02.0001.01 1 2 ; 1, 2,, 06.04.02.0002.01 1 k k 1
Binomial Notations Traditional name Traditional notation Mathematica StandardForm notation Primary definition
 Bioial Notatios Traditioal ae Bioial coefficiet Traditioal otatio Matheatica StadardFor otatio Bioial, Priary defiitio 06.03.0.0001.01 1 1 1 ; 0 For Ν, Κ egative itegers with, the bioial coefficiet Ν caot
Bioial Notatios Traditioal ae Bioial coefficiet Traditioal otatio Matheatica StadardFor otatio Bioial, Priary defiitio 06.03.0.0001.01 1 1 1 ; 0 For Ν, Κ egative itegers with, the bioial coefficiet Ν caot
The Gamma function. Marco Bonvini. October 9, dt e t t z 1. (1) Γ(z + 1) = z Γ(z) : (2) = e t t z. + z dt e t t z 1. = z Γ(z).
 The Gamma fuctio Marco Bovii October 9, 2 Gamma fuctio The Euler Gamma fuctio is defied as Γ() It is easy to show that Γ() satisfy the recursio relatio ideed, itegratig by parts, dt e t t. () Γ( + ) Γ()
The Gamma fuctio Marco Bovii October 9, 2 Gamma fuctio The Euler Gamma fuctio is defied as Γ() It is easy to show that Γ() satisfy the recursio relatio ideed, itegratig by parts, dt e t t. () Γ( + ) Γ()
1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y
![1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y 1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y](/thumbs/95/125864248.jpg) Questio (a) A square matrix A= A is called positive defiite if the quadratic form waw > 0 for every o-zero vector w [Note: Here (.) deotes the traspose of a matrix or a vector]. Let 0 A = 0 = show that:
Questio (a) A square matrix A= A is called positive defiite if the quadratic form waw > 0 for every o-zero vector w [Note: Here (.) deotes the traspose of a matrix or a vector]. Let 0 A = 0 = show that:
Introductions to LucasL
 Itroductios to LucasL Itroductio to the Fiboacci ad Lucas ubers The sequece ow ow as Fiboacci ubers (sequece 0,,,, 3,, 8, 3...) first appeared i the wor of a aciet Idia atheaticia, Pigala (40 or 00 BC).
Itroductios to LucasL Itroductio to the Fiboacci ad Lucas ubers The sequece ow ow as Fiboacci ubers (sequece 0,,,, 3,, 8, 3...) first appeared i the wor of a aciet Idia atheaticia, Pigala (40 or 00 BC).
Notes 12 Asymptotic Series
 ECE 6382 Fall 207 David R. Jackso otes 2 Asymptotic Series Asymptotic Series A asymptotic series (as ) is of the form a ( ) f as = 0 or f a + a a + + ( ) 2 0 2 ote the asymptotically equal to sig. The
ECE 6382 Fall 207 David R. Jackso otes 2 Asymptotic Series Asymptotic Series A asymptotic series (as ) is of the form a ( ) f as = 0 or f a + a a + + ( ) 2 0 2 ote the asymptotically equal to sig. The
( ) ( ) ( ) ( ) ( + ) ( )
 LSM Nov. 00 Cotet List Mathematics (AH). Algebra... kow ad use the otatio!, C r ad r.. kow the results = r r + + = r r r..3 kow Pascal's triagle. Pascal's triagle should be eteded up to = 7...4 kow ad
LSM Nov. 00 Cotet List Mathematics (AH). Algebra... kow ad use the otatio!, C r ad r.. kow the results = r r + + = r r r..3 kow Pascal's triagle. Pascal's triagle should be eteded up to = 7...4 kow ad
Introductions to ExpIntegralEi
 Introductions to ExpIntegralEi Introduction to the exponential integrals General The exponential-type integrals have a long history. After the early developments of differential calculus, mathematicians
Introductions to ExpIntegralEi Introduction to the exponential integrals General The exponential-type integrals have a long history. After the early developments of differential calculus, mathematicians
De Moivre s Theorem - ALL
 De Moivre s Theorem - ALL. Let x ad y be real umbers, ad be oe of the complex solutios of the equatio =. Evaluate: (a) + + ; (b) ( x + y)( x + y). [6]. (a) Sice is a complex umber which satisfies = 0,.
De Moivre s Theorem - ALL. Let x ad y be real umbers, ad be oe of the complex solutios of the equatio =. Evaluate: (a) + + ; (b) ( x + y)( x + y). [6]. (a) Sice is a complex umber which satisfies = 0,.
Notation List. For Cambridge International Mathematics Qualifications. For use from 2020
 Notatio List For Cambridge Iteratioal Mathematics Qualificatios For use from 2020 Notatio List for Cambridge Iteratioal Mathematics Qualificatios (For use from 2020) Mathematical otatio Eamiatios for CIE
Notatio List For Cambridge Iteratioal Mathematics Qualificatios For use from 2020 Notatio List for Cambridge Iteratioal Mathematics Qualificatios (For use from 2020) Mathematical otatio Eamiatios for CIE
The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j
![The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j](/thumbs/82/85448534.jpg) The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
EE / EEE SAMPLE STUDY MATERIAL. GATE, IES & PSUs Signal System. Electrical Engineering. Postal Correspondence Course
 Sigal-EE Postal Correspodece Course 1 SAMPLE STUDY MATERIAL Electrical Egieerig EE / EEE Postal Correspodece Course GATE, IES & PSUs Sigal System Sigal-EE Postal Correspodece Course CONTENTS 1. SIGNAL
Sigal-EE Postal Correspodece Course 1 SAMPLE STUDY MATERIAL Electrical Egieerig EE / EEE Postal Correspodece Course GATE, IES & PSUs Sigal System Sigal-EE Postal Correspodece Course CONTENTS 1. SIGNAL
Presentation of complex number in Cartesian and polar coordinate system
 a + bi, aεr, bεr i = z = a + bi a = Re(z), b = Im(z) give z = a + bi & w = c + di, a + bi = c + di a = c & b = d The complex cojugate of z = a + bi is z = a bi The sum of complex cojugates is real: z +
a + bi, aεr, bεr i = z = a + bi a = Re(z), b = Im(z) give z = a + bi & w = c + di, a + bi = c + di a = c & b = d The complex cojugate of z = a + bi is z = a bi The sum of complex cojugates is real: z +
Appendix: The Laplace Transform
 Appedix: The Laplace Trasform The Laplace trasform is a powerful method that ca be used to solve differetial equatio, ad other mathematical problems. Its stregth lies i the fact that it allows the trasformatio
Appedix: The Laplace Trasform The Laplace trasform is a powerful method that ca be used to solve differetial equatio, ad other mathematical problems. Its stregth lies i the fact that it allows the trasformatio
} is said to be a Cauchy sequence provided the following condition is true.
 Math 4200, Fial Exam Review I. Itroductio to Proofs 1. Prove the Pythagorea theorem. 2. Show that 43 is a irratioal umber. II. Itroductio to Logic 1. Costruct a truth table for the statemet ( p ad ~ r
Math 4200, Fial Exam Review I. Itroductio to Proofs 1. Prove the Pythagorea theorem. 2. Show that 43 is a irratioal umber. II. Itroductio to Logic 1. Costruct a truth table for the statemet ( p ad ~ r
C. Complex Numbers. x 6x + 2 = 0. This equation was known to have three real roots, given by simple combinations of the expressions
 C. Complex Numbers. Complex arithmetic. Most people thik that complex umbers arose from attempts to solve quadratic equatios, but actually it was i coectio with cubic equatios they first appeared. Everyoe
C. Complex Numbers. Complex arithmetic. Most people thik that complex umbers arose from attempts to solve quadratic equatios, but actually it was i coectio with cubic equatios they first appeared. Everyoe
APPM 4360/5360 Exam #2 Solutions Spring 2015
 APPM 436/536 Exam # Solutios Sprig 5 O the frot of your bluebook, write your ame ad make a gradig table. You re allowed oe sheet (letter-sized, frot ad back of otes. You are ot allowed to use textbooks,
APPM 436/536 Exam # Solutios Sprig 5 O the frot of your bluebook, write your ame ad make a gradig table. You re allowed oe sheet (letter-sized, frot ad back of otes. You are ot allowed to use textbooks,
x x x Using a second Taylor polynomial with remainder, find the best constant C so that for x 0,
 Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
j=1 dz Res(f, z j ) = 1 d k 1 dz k 1 (z c)k f(z) Res(f, c) = lim z c (k 1)! Res g, c = f(c) g (c)
 Problem. Compute the itegrals C r d for Z, where C r = ad r >. Recall that C r has the couter-clockwise orietatio. Solutio: We will use the idue Theorem to solve this oe. We could istead use other (perhaps
Problem. Compute the itegrals C r d for Z, where C r = ad r >. Recall that C r has the couter-clockwise orietatio. Solutio: We will use the idue Theorem to solve this oe. We could istead use other (perhaps
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
CHAPTER 1 SEQUENCES AND INFINITE SERIES
 CHAPTER SEQUENCES AND INFINITE SERIES SEQUENCES AND INFINITE SERIES (0 meetigs) Sequeces ad limit of a sequece Mootoic ad bouded sequece Ifiite series of costat terms Ifiite series of positive terms Alteratig
CHAPTER SEQUENCES AND INFINITE SERIES SEQUENCES AND INFINITE SERIES (0 meetigs) Sequeces ad limit of a sequece Mootoic ad bouded sequece Ifiite series of costat terms Ifiite series of positive terms Alteratig
Chapter 13: Complex Numbers
 Sectios 13.1 & 13.2 Comple umbers ad comple plae Comple cojugate Modulus of a comple umber 1. Comple umbers Comple umbers are of the form z = + iy,, y R, i 2 = 1. I the above defiitio, is the real part
Sectios 13.1 & 13.2 Comple umbers ad comple plae Comple cojugate Modulus of a comple umber 1. Comple umbers Comple umbers are of the form z = + iy,, y R, i 2 = 1. I the above defiitio, is the real part
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
Evaluation of Some Non-trivial Integrals from Finite Products and Sums
 Turkish Joural of Aalysis umber Theory 6 Vol. o. 6 7-76 Available olie at http://pubs.sciepub.com/tjat//6/5 Sciece Educatio Publishig DOI:.69/tjat--6-5 Evaluatio of Some o-trivial Itegrals from Fiite Products
Turkish Joural of Aalysis umber Theory 6 Vol. o. 6 7-76 Available olie at http://pubs.sciepub.com/tjat//6/5 Sciece Educatio Publishig DOI:.69/tjat--6-5 Evaluatio of Some o-trivial Itegrals from Fiite Products
CHAPTER 10 INFINITE SEQUENCES AND SERIES
 CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
NANYANG TECHNOLOGICAL UNIVERSITY SYLLABUS FOR ENTRANCE EXAMINATION FOR INTERNATIONAL STUDENTS A-LEVEL MATHEMATICS
 NANYANG TECHNOLOGICAL UNIVERSITY SYLLABUS FOR ENTRANCE EXAMINATION FOR INTERNATIONAL STUDENTS A-LEVEL MATHEMATICS STRUCTURE OF EXAMINATION PAPER 1. There will be oe -hour paper cosistig of 4 questios..
NANYANG TECHNOLOGICAL UNIVERSITY SYLLABUS FOR ENTRANCE EXAMINATION FOR INTERNATIONAL STUDENTS A-LEVEL MATHEMATICS STRUCTURE OF EXAMINATION PAPER 1. There will be oe -hour paper cosistig of 4 questios..
PAPER : IIT-JAM 2010
 MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
The natural exponential function
 The atural expoetial fuctio Attila Máté Brookly College of the City Uiversity of New York December, 205 Cotets The atural expoetial fuctio for real x. Beroulli s iequality.....................................2
The atural expoetial fuctio Attila Máté Brookly College of the City Uiversity of New York December, 205 Cotets The atural expoetial fuctio for real x. Beroulli s iequality.....................................2
of the Barnes function.
 O the Bares fuctio Victor Adamchik Caregie Mello Uiversity adamchik@cs.cmu.edu Abstract. The multiple Bares fuctio, defied as a geeraliatio of the Euler gamma fuctio, is used i may applicatios of pure
O the Bares fuctio Victor Adamchik Caregie Mello Uiversity adamchik@cs.cmu.edu Abstract. The multiple Bares fuctio, defied as a geeraliatio of the Euler gamma fuctio, is used i may applicatios of pure
Notes 8 Singularities
 ECE 6382 Fall 27 David R. Jackso Notes 8 Sigularities Notes are from D. R. Wilto, Dept. of ECE Sigularity A poit s is a sigularity of the fuctio f () if the fuctio is ot aalytic at s. (The fuctio does
ECE 6382 Fall 27 David R. Jackso Notes 8 Sigularities Notes are from D. R. Wilto, Dept. of ECE Sigularity A poit s is a sigularity of the fuctio f () if the fuctio is ot aalytic at s. (The fuctio does
) + 2. Mathematics 2 Outcome 1. Further Differentiation (8/9 pers) Cumulative total = 64 periods. Lesson, Outline, Approach etc.
 Further Differetiatio (8/9 pers Mathematics Outcome Go over the proofs of the derivatives o si ad cos. [use y = si => = siy etc.] * Ask studets to fid derivative of cos. * Ask why d d (si = (cos see graphs.
Further Differetiatio (8/9 pers Mathematics Outcome Go over the proofs of the derivatives o si ad cos. [use y = si => = siy etc.] * Ask studets to fid derivative of cos. * Ask why d d (si = (cos see graphs.
NANYANG TECHNOLOGICAL UNIVERSITY SYLLABUS FOR ENTRANCE EXAMINATION FOR INTERNATIONAL STUDENTS AO-LEVEL MATHEMATICS
 NANYANG TECHNOLOGICAL UNIVERSITY SYLLABUS FOR ENTRANCE EXAMINATION FOR INTERNATIONAL STUDENTS AO-LEVEL MATHEMATICS STRUCTURE OF EXAMINATION PAPER. There will be oe 2-hour paper cosistig of 4 questios.
NANYANG TECHNOLOGICAL UNIVERSITY SYLLABUS FOR ENTRANCE EXAMINATION FOR INTERNATIONAL STUDENTS AO-LEVEL MATHEMATICS STRUCTURE OF EXAMINATION PAPER. There will be oe 2-hour paper cosistig of 4 questios.
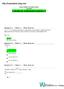 FINALTERM EXAMINATION Fall 9 Calculus & Aalytical Geometry-I Questio No: ( Mars: ) - Please choose oe Let f ( x) is a fuctio such that as x approaches a real umber a, either from left or right-had-side,
FINALTERM EXAMINATION Fall 9 Calculus & Aalytical Geometry-I Questio No: ( Mars: ) - Please choose oe Let f ( x) is a fuctio such that as x approaches a real umber a, either from left or right-had-side,
Fourier Series and their Applications
 Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
CALCULUS BASIC SUMMER REVIEW
 CALCULUS BASIC SUMMER REVIEW NAME rise y y y Slope of a o vertical lie: m ru Poit Slope Equatio: y y m( ) The slope is m ad a poit o your lie is, ). ( y Slope-Itercept Equatio: y m b slope= m y-itercept=
CALCULUS BASIC SUMMER REVIEW NAME rise y y y Slope of a o vertical lie: m ru Poit Slope Equatio: y y m( ) The slope is m ad a poit o your lie is, ). ( y Slope-Itercept Equatio: y m b slope= m y-itercept=
A) is empty. B) is a finite set. C) can be a countably infinite set. D) can be an uncountable set.
 M.A./M.Sc. (Mathematics) Etrace Examiatio 016-17 Max Time: hours Max Marks: 150 Istructios: There are 50 questios. Every questio has four choices of which exactly oe is correct. For correct aswer, 3 marks
M.A./M.Sc. (Mathematics) Etrace Examiatio 016-17 Max Time: hours Max Marks: 150 Istructios: There are 50 questios. Every questio has four choices of which exactly oe is correct. For correct aswer, 3 marks
The type of limit that is used to find TANGENTS and VELOCITIES gives rise to the central idea in DIFFERENTIAL CALCULUS, the DERIVATIVE.
 NOTES : LIMITS AND DERIVATIVES Name: Date: Period: Iitial: LESSON.1 THE TANGENT AND VELOCITY PROBLEMS Pre-Calculus Mathematics Limit Process Calculus The type of it that is used to fid TANGENTS ad VELOCITIES
NOTES : LIMITS AND DERIVATIVES Name: Date: Period: Iitial: LESSON.1 THE TANGENT AND VELOCITY PROBLEMS Pre-Calculus Mathematics Limit Process Calculus The type of it that is used to fid TANGENTS ad VELOCITIES
1. Complex numbers. Chapter 13: Complex Numbers. Modulus of a complex number. Complex conjugate. Complex numbers are of the form
 Comple umbers ad comple plae Comple cojugate Modulus of a comple umber Comple umbers Comple umbers are of the form Sectios 3 & 32 z = + i,, R, i 2 = I the above defiitio, is the real part of z ad is the
Comple umbers ad comple plae Comple cojugate Modulus of a comple umber Comple umbers Comple umbers are of the form Sectios 3 & 32 z = + i,, R, i 2 = I the above defiitio, is the real part of z ad is the
Chapter 4 : Laplace Transform
 4. Itroductio Laplace trasform is a alterative to solve the differetial equatio by the complex frequecy domai ( s = σ + jω), istead of the usual time domai. The DE ca be easily trasformed ito a algebraic
4. Itroductio Laplace trasform is a alterative to solve the differetial equatio by the complex frequecy domai ( s = σ + jω), istead of the usual time domai. The DE ca be easily trasformed ito a algebraic
Honors Calculus Homework 13 Solutions, due 12/8/5
 Hoors Calculus Homework Solutios, due /8/5 Questio Let a regio R i the plae be bouded by the curves y = 5 ad = 5y y. Sketch the regio R. The two curves meet where both equatios hold at oce, so where: y
Hoors Calculus Homework Solutios, due /8/5 Questio Let a regio R i the plae be bouded by the curves y = 5 ad = 5y y. Sketch the regio R. The two curves meet where both equatios hold at oce, so where: y
MATHEMATICS. 61. The differential equation representing the family of curves where c is a positive parameter, is of
 MATHEMATICS 6 The differetial equatio represetig the family of curves where c is a positive parameter, is of Order Order Degree (d) Degree (a,c) Give curve is y c ( c) Differetiate wrt, y c c y Hece differetial
MATHEMATICS 6 The differetial equatio represetig the family of curves where c is a positive parameter, is of Order Order Degree (d) Degree (a,c) Give curve is y c ( c) Differetiate wrt, y c c y Hece differetial
Chapter 7: The z-transform. Chih-Wei Liu
 Chapter 7: The -Trasform Chih-Wei Liu Outlie Itroductio The -Trasform Properties of the Regio of Covergece Properties of the -Trasform Iversio of the -Trasform The Trasfer Fuctio Causality ad Stability
Chapter 7: The -Trasform Chih-Wei Liu Outlie Itroductio The -Trasform Properties of the Regio of Covergece Properties of the -Trasform Iversio of the -Trasform The Trasfer Fuctio Causality ad Stability
Fall 2013 MTH431/531 Real analysis Section Notes
 Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
INTRODUCTORY MATHEMATICAL ANALYSIS
 INTRODUCTORY MATHEMATICAL ANALYSIS For Busiess, Ecoomics, ad the Life ad Social Scieces Chapter 4 Itegratio 0 Pearso Educatio, Ic. Chapter 4: Itegratio Chapter Objectives To defie the differetial. To defie
INTRODUCTORY MATHEMATICAL ANALYSIS For Busiess, Ecoomics, ad the Life ad Social Scieces Chapter 4 Itegratio 0 Pearso Educatio, Ic. Chapter 4: Itegratio Chapter Objectives To defie the differetial. To defie
Solutions for Math 411 Assignment #8 1
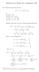 Solutios for Math Assigmet #8 A8. Fid the Lauret series of f() 3 2 + i (a) { < }; (b) { < < }; (c) { < 2 < 3}; (d) {0 < + < 2}. Solutio. We write f() as a sum of partial fractios: f() 3 2 + ( ) 2 ( + )
Solutios for Math Assigmet #8 A8. Fid the Lauret series of f() 3 2 + i (a) { < }; (b) { < < }; (c) { < 2 < 3}; (d) {0 < + < 2}. Solutio. We write f() as a sum of partial fractios: f() 3 2 + ( ) 2 ( + )
Name of the Student:
 SUBJECT NAME : Trasforms ad Partial Diff Eq SUBJECT CODE : MA MATERIAL NAME : Problem Material MATERIAL CODE : JM8AM6 REGULATION : R8 UPDATED ON : April-May 4 (Sca the above QR code for the direct dowload
SUBJECT NAME : Trasforms ad Partial Diff Eq SUBJECT CODE : MA MATERIAL NAME : Problem Material MATERIAL CODE : JM8AM6 REGULATION : R8 UPDATED ON : April-May 4 (Sca the above QR code for the direct dowload
MAS111 Convergence and Continuity
 MAS Covergece ad Cotiuity Key Objectives At the ed of the course, studets should kow the followig topics ad be able to apply the basic priciples ad theorems therei to solvig various problems cocerig covergece
MAS Covergece ad Cotiuity Key Objectives At the ed of the course, studets should kow the followig topics ad be able to apply the basic priciples ad theorems therei to solvig various problems cocerig covergece
SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0,
![SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0, SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0,](/thumbs/94/119566625.jpg) 4. Series Solutios of Differetial Equatios:Special Fuctios 4.. Illustrative examples.. 5. Obtai the geeral solutio of each of the followig differetial equatios i terms of Maclauri series: d y (a dx = xy,
4. Series Solutios of Differetial Equatios:Special Fuctios 4.. Illustrative examples.. 5. Obtai the geeral solutio of each of the followig differetial equatios i terms of Maclauri series: d y (a dx = xy,
Diploma Programme. Mathematics HL guide. First examinations 2014
 Diploma Programme First eamiatios 014 33 Topic 6 Core: Calculus The aim of this topic is to itroduce studets to the basic cocepts ad techiques of differetial ad itegral calculus ad their applicatio. 6.1
Diploma Programme First eamiatios 014 33 Topic 6 Core: Calculus The aim of this topic is to itroduce studets to the basic cocepts ad techiques of differetial ad itegral calculus ad their applicatio. 6.1
 COMPLEX NUMBERS AND DE MOIVRE'S THEOREM SYNOPSIS. Ay umber of the form x+iy where x, y R ad i = - is called a complex umber.. I the complex umber x+iy, x is called the real part ad y is called the imagiary
COMPLEX NUMBERS AND DE MOIVRE'S THEOREM SYNOPSIS. Ay umber of the form x+iy where x, y R ad i = - is called a complex umber.. I the complex umber x+iy, x is called the real part ad y is called the imagiary
A Class of Logarithmic Integrals. Victor Adamchik. Wolfram Research Inc. 100 Trade Center Dr. April 10, 1997
 A Class of Logarithmic Itegrals Victor Adamchik Wolfram Research Ic. Trade Ceter Dr. Champaig IL 68 USA April 997 Abstract. A class of deite itegrals ivolvig cyclotomic polyomials ad ested logarithms is
A Class of Logarithmic Itegrals Victor Adamchik Wolfram Research Ic. Trade Ceter Dr. Champaig IL 68 USA April 997 Abstract. A class of deite itegrals ivolvig cyclotomic polyomials ad ested logarithms is
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
arxiv: v1 [math.ca] 29 Jun 2018
![arxiv: v1 [math.ca] 29 Jun 2018 arxiv: v1 [math.ca] 29 Jun 2018](/thumbs/88/116557394.jpg) URAL MATHEMATICAL JOURNAL, Vol. 3, No., 207 arxiv:807.025v [math.ca] 29 Ju 208 EVALUATION OF SOME NON-ELEMENTARY INTEGRALS INVOLVING SINE, COSINE, EXPONENTIAL AND LOGARITHMIC INTEGRALS: PART II Victor
URAL MATHEMATICAL JOURNAL, Vol. 3, No., 207 arxiv:807.025v [math.ca] 29 Ju 208 EVALUATION OF SOME NON-ELEMENTARY INTEGRALS INVOLVING SINE, COSINE, EXPONENTIAL AND LOGARITHMIC INTEGRALS: PART II Victor
The Z-Transform. (t-t 0 ) Figure 1: Simplified graph of an impulse function. For an impulse, it can be shown that (1)
 The Z-Trasform Sampled Data The geeralied fuctio (t) (also kow as the impulse fuctio) is useful i the defiitio ad aalysis of sampled-data sigals. Figure below shows a simplified graph of a impulse. (t-t
The Z-Trasform Sampled Data The geeralied fuctio (t) (also kow as the impulse fuctio) is useful i the defiitio ad aalysis of sampled-data sigals. Figure below shows a simplified graph of a impulse. (t-t
HELM An outline EleQuant, Inc. 1
 HELM A outlie 1 Power Flow: Problem Statemet The equatios 1) The ukows 2) Y a V a a all all \ swig S sw = y zip) + I zip) + S = y zip) sw I zip) sw + Y sw,a V a a { all} = Re ) + j Im ) = e jθ ; all \
HELM A outlie 1 Power Flow: Problem Statemet The equatios 1) The ukows 2) Y a V a a all all \ swig S sw = y zip) + I zip) + S = y zip) sw I zip) sw + Y sw,a V a a { all} = Re ) + j Im ) = e jθ ; all \
Beyond simple iteration of a single function, or even a finite sequence of functions, results
 A Primer o the Elemetary Theory of Ifiite Compositios of Complex Fuctios Joh Gill Sprig 07 Abstract: Elemetary meas ot requirig the complex fuctios be holomorphic Theorem proofs are fairly simple ad are
A Primer o the Elemetary Theory of Ifiite Compositios of Complex Fuctios Joh Gill Sprig 07 Abstract: Elemetary meas ot requirig the complex fuctios be holomorphic Theorem proofs are fairly simple ad are
September 2012 C1 Note. C1 Notes (Edexcel) Copyright - For AS, A2 notes and IGCSE / GCSE worksheets 1
 September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
Lesson 10: Limits and Continuity
 www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
Informal Notes: Zeno Contours, Parametric Forms, & Integrals. John Gill March August S for a convex set S in the complex plane.
 Iformal Notes: Zeo Cotours Parametric Forms & Itegrals Joh Gill March August 3 Abstract: Elemetary classroom otes o Zeo cotours streamlies pathlies ad itegrals Defiitio: Zeo cotour[] Let gk ( z = z + ηk
Iformal Notes: Zeo Cotours Parametric Forms & Itegrals Joh Gill March August 3 Abstract: Elemetary classroom otes o Zeo cotours streamlies pathlies ad itegrals Defiitio: Zeo cotour[] Let gk ( z = z + ηk
Lecture 13. Graphical representation of the frequency response. Luca Ferrarini - Basic Automatic Control 1
 Lecture 3 Graphical represetatio of the frequecy respose Luca Ferrarii - Basic Automatic Cotrol Graphical represetatio of the frequecy respose Polar plot G Bode plot ( j), G Im 3 Re of the magitude G (
Lecture 3 Graphical represetatio of the frequecy respose Luca Ferrarii - Basic Automatic Cotrol Graphical represetatio of the frequecy respose Polar plot G Bode plot ( j), G Im 3 Re of the magitude G (
Chapter 1. Complex Numbers. Dr. Pulak Sahoo
 Chapter 1 Complex Numbers BY Dr. Pulak Sahoo Assistat Professor Departmet of Mathematics Uiversity Of Kalyai West Begal, Idia E-mail : sahoopulak1@gmail.com 1 Module-2: Stereographic Projectio 1 Euler
Chapter 1 Complex Numbers BY Dr. Pulak Sahoo Assistat Professor Departmet of Mathematics Uiversity Of Kalyai West Begal, Idia E-mail : sahoopulak1@gmail.com 1 Module-2: Stereographic Projectio 1 Euler
MATH 10550, EXAM 3 SOLUTIONS
 MATH 155, EXAM 3 SOLUTIONS 1. I fidig a approximate solutio to the equatio x 3 +x 4 = usig Newto s method with iitial approximatio x 1 = 1, what is x? Solutio. Recall that x +1 = x f(x ) f (x ). Hece,
MATH 155, EXAM 3 SOLUTIONS 1. I fidig a approximate solutio to the equatio x 3 +x 4 = usig Newto s method with iitial approximatio x 1 = 1, what is x? Solutio. Recall that x +1 = x f(x ) f (x ). Hece,
Complex Numbers in n Dimensions
 arxiv:math/00044v [math.cv] 8 Nov 000 Complex Numbers i Dimesios Silviu Olariu Istitute of Physics ad Nuclear Egieerig, Tadem Laboratory 76900 Magurele, P.O. Box MG-6, Bucharest, Romaia e-mail: olariu@ifi.ipe.ro
arxiv:math/00044v [math.cv] 8 Nov 000 Complex Numbers i Dimesios Silviu Olariu Istitute of Physics ad Nuclear Egieerig, Tadem Laboratory 76900 Magurele, P.O. Box MG-6, Bucharest, Romaia e-mail: olariu@ifi.ipe.ro
3 Gauss map and continued fractions
 ICTP, Trieste, July 08 Gauss map ad cotiued fractios I this lecture we will itroduce the Gauss map, which is very importat for its coectio with cotiued fractios i umber theory. The Gauss map G : [0, ]
ICTP, Trieste, July 08 Gauss map ad cotiued fractios I this lecture we will itroduce the Gauss map, which is very importat for its coectio with cotiued fractios i umber theory. The Gauss map G : [0, ]
Generalizing the DTFT. The z Transform. Complex Exponential Excitation. The Transfer Function. Systems Described by Difference Equations
 Geeraliig the DTFT The Trasform M. J. Roberts - All Rights Reserved. Edited by Dr. Robert Akl 1 The forward DTFT is defied by X e jω = x e jω i which = Ω is discrete-time radia frequecy, a real variable.
Geeraliig the DTFT The Trasform M. J. Roberts - All Rights Reserved. Edited by Dr. Robert Akl 1 The forward DTFT is defied by X e jω = x e jω i which = Ω is discrete-time radia frequecy, a real variable.
f t dt. Write the third-degree Taylor polynomial for G
 AP Calculus BC Homework - Chapter 8B Taylor, Maclauri, ad Power Series # Taylor & Maclauri Polyomials Critical Thikig Joural: (CTJ: 5 pts.) Discuss the followig questios i a paragraph: What does it mea
AP Calculus BC Homework - Chapter 8B Taylor, Maclauri, ad Power Series # Taylor & Maclauri Polyomials Critical Thikig Joural: (CTJ: 5 pts.) Discuss the followig questios i a paragraph: What does it mea
COMPUTING THE EULER S CONSTANT: A HISTORICAL OVERVIEW OF ALGORITHMS AND RESULTS
 COMPUTING THE EULER S CONSTANT: A HISTORICAL OVERVIEW OF ALGORITHMS AND RESULTS GONÇALO MORAIS Abstract. We preted to give a broad overview of the algorithms used to compute the Euler s costat. Four type
COMPUTING THE EULER S CONSTANT: A HISTORICAL OVERVIEW OF ALGORITHMS AND RESULTS GONÇALO MORAIS Abstract. We preted to give a broad overview of the algorithms used to compute the Euler s costat. Four type
Apply change-of-basis formula to rewrite x as a linear combination of eigenvectors v j.
 Eigevalue-Eigevector Istructor: Nam Su Wag eigemcd Ay vector i real Euclidea space of dimesio ca be uiquely epressed as a liear combiatio of liearly idepedet vectors (ie, basis) g j, j,,, α g α g α g α
Eigevalue-Eigevector Istructor: Nam Su Wag eigemcd Ay vector i real Euclidea space of dimesio ca be uiquely epressed as a liear combiatio of liearly idepedet vectors (ie, basis) g j, j,,, α g α g α g α
ENGI Series Page 6-01
 ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
PAijpam.eu ON DERIVATION OF RATIONAL SOLUTIONS OF BABBAGE S FUNCTIONAL EQUATION
 Iteratioal Joural of Pure ad Applied Mathematics Volume 94 No. 204, 9-20 ISSN: 3-8080 (prited versio); ISSN: 34-3395 (o-lie versio) url: http://www.ijpam.eu doi: http://dx.doi.org/0.2732/ijpam.v94i.2 PAijpam.eu
Iteratioal Joural of Pure ad Applied Mathematics Volume 94 No. 204, 9-20 ISSN: 3-8080 (prited versio); ISSN: 34-3395 (o-lie versio) url: http://www.ijpam.eu doi: http://dx.doi.org/0.2732/ijpam.v94i.2 PAijpam.eu
COMM 602: Digital Signal Processing
 COMM 60: Digital Sigal Processig Lecture 4 -Properties of LTIS Usig Z-Trasform -Iverse Z-Trasform Properties of LTIS Usig Z-Trasform Properties of LTIS Usig Z-Trasform -ve +ve Properties of LTIS Usig Z-Trasform
COMM 60: Digital Sigal Processig Lecture 4 -Properties of LTIS Usig Z-Trasform -Iverse Z-Trasform Properties of LTIS Usig Z-Trasform Properties of LTIS Usig Z-Trasform -ve +ve Properties of LTIS Usig Z-Trasform
COMPUTATION OF SOME WONDERFUL RESULTS INVOLVING CERTAIN POLYNOMIALS
 Iteratioal Research Joural of Egieerig ad Techology (IRJET) e-issn: 95-0056 Volume: 0 Issue: 0 Apr-05 www.irjet.et p-issn: 95-007 COMPUTATION OF SOME WONDERFUL RESULTS INVOLVING CERTAIN POLYNOMIALS Salahuddi,
Iteratioal Research Joural of Egieerig ad Techology (IRJET) e-issn: 95-0056 Volume: 0 Issue: 0 Apr-05 www.irjet.et p-issn: 95-007 COMPUTATION OF SOME WONDERFUL RESULTS INVOLVING CERTAIN POLYNOMIALS Salahuddi,
Created by T. Madas SERIES. Created by T. Madas
 SERIES SUMMATIONS BY STANDARD RESULTS Questio (**) Use stadard results o summatios to fid the value of 48 ( r )( 3r ). 36 FP-B, 66638 Questio (**+) Fid, i fully simplified factorized form, a expressio
SERIES SUMMATIONS BY STANDARD RESULTS Questio (**) Use stadard results o summatios to fid the value of 48 ( r )( 3r ). 36 FP-B, 66638 Questio (**+) Fid, i fully simplified factorized form, a expressio
PATH INTEGRAL for the HARMONIC OSCILLATOR
 PATH ITEGRAL for the HAROIC OSCILLATOR I class, I have showed how to use path itegral formalism to calculate the partitio fuctio of a quatum system. Formally, ] ZT = Tr e it Ĥ = ÛT, 0 = dx 0 Ux 0, T ;
PATH ITEGRAL for the HAROIC OSCILLATOR I class, I have showed how to use path itegral formalism to calculate the partitio fuctio of a quatum system. Formally, ] ZT = Tr e it Ĥ = ÛT, 0 = dx 0 Ux 0, T ;
MATH 1080: Calculus of One Variable II Fall 2017 Textbook: Single Variable Calculus: Early Transcendentals, 7e, by James Stewart.
 MATH 1080: Calculus of Oe Variable II Fall 2017 Textbook: Sigle Variable Calculus: Early Trascedetals, 7e, by James Stewart Uit 3 Skill Set Importat: Studets should expect test questios that require a
MATH 1080: Calculus of Oe Variable II Fall 2017 Textbook: Sigle Variable Calculus: Early Trascedetals, 7e, by James Stewart Uit 3 Skill Set Importat: Studets should expect test questios that require a
SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddharth Nagar, Narayanavanam Road QUESTION BANK (DESCRIPTIVE)
 QUESTION BANK 8 SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddharth Nagar, Narayaavaam Road 5758 QUESTION BANK (DESCRIPTIVE Subject with Code : (6HS6 Course & Brach: B.Tech AG Year & Sem: II-B.Tech& I-Sem
QUESTION BANK 8 SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddharth Nagar, Narayaavaam Road 5758 QUESTION BANK (DESCRIPTIVE Subject with Code : (6HS6 Course & Brach: B.Tech AG Year & Sem: II-B.Tech& I-Sem
1 6 = 1 6 = + Factorials and Euler s Gamma function
 Royal Holloway Uiversity of Lodo Departmet of Physics Factorials ad Euler s Gamma fuctio Itroductio The is a self-cotaied part of the course dealig, essetially, with the factorial fuctio ad its geeralizatio
Royal Holloway Uiversity of Lodo Departmet of Physics Factorials ad Euler s Gamma fuctio Itroductio The is a self-cotaied part of the course dealig, essetially, with the factorial fuctio ad its geeralizatio
Continuous Functions
 Cotiuous Fuctios Q What does it mea for a fuctio to be cotiuous at a poit? Aswer- I mathematics, we have a defiitio that cosists of three cocepts that are liked i a special way Cosider the followig defiitio
Cotiuous Fuctios Q What does it mea for a fuctio to be cotiuous at a poit? Aswer- I mathematics, we have a defiitio that cosists of three cocepts that are liked i a special way Cosider the followig defiitio
SOLUTIONS TO EXAM 3. Solution: Note that this defines two convergent geometric series with respective radii r 1 = 2/5 < 1 and r 2 = 1/5 < 1.
 SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
Matrix Operators and Functions Thereof
 Mathematics Notes Note 97 31 May 27 Matrix Operators a Fuctios Thereof Carl E. Baum Uiversity of New Mexico Departmet of Electrical a Computer Egieerig Albuquerque New Mexico 87131 Abstract This paper
Mathematics Notes Note 97 31 May 27 Matrix Operators a Fuctios Thereof Carl E. Baum Uiversity of New Mexico Departmet of Electrical a Computer Egieerig Albuquerque New Mexico 87131 Abstract This paper
PATH INTEGRAL for HARMONIC OSCILLATOR
 PATH ITEGRAL for HAROIC OSCILLATOR I class, I have showed how to use path itegral formalism to calculate the partitio fuctio of a quatum system. Formally, ] ZT = Tr e it Ĥ = ÛT, 0 = dx 0 Ux 0, T ; x 0,
PATH ITEGRAL for HAROIC OSCILLATOR I class, I have showed how to use path itegral formalism to calculate the partitio fuctio of a quatum system. Formally, ] ZT = Tr e it Ĥ = ÛT, 0 = dx 0 Ux 0, T ; x 0,
Chapter 10 Partial Differential Equations and Fourier Series
 Math-33 Chapter Partial Differetial Equatios November 6, 7 Chapter Partial Differetial Equatios ad Fourier Series Math-33 Chapter Partial Differetial Equatios November 6, 7. Boudary Value Problems for
Math-33 Chapter Partial Differetial Equatios November 6, 7 Chapter Partial Differetial Equatios ad Fourier Series Math-33 Chapter Partial Differetial Equatios November 6, 7. Boudary Value Problems for
AP Calculus Chapter 9: Infinite Series
 AP Calculus Chapter 9: Ifiite Series 9. Sequeces a, a 2, a 3, a 4, a 5,... Sequece: A fuctio whose domai is the set of positive itegers = 2 3 4 a = a a 2 a 3 a 4 terms of the sequece Begi with the patter
AP Calculus Chapter 9: Ifiite Series 9. Sequeces a, a 2, a 3, a 4, a 5,... Sequece: A fuctio whose domai is the set of positive itegers = 2 3 4 a = a a 2 a 3 a 4 terms of the sequece Begi with the patter
MATH2007* Partial Answers to Review Exercises Fall 2004
 MATH27* Partial Aswers to Review Eercises Fall 24 Evaluate each of the followig itegrals:. Let u cos. The du si ad Hece si ( cos 2 )(si ) (u 2 ) du. si u 2 cos 7 u 7 du Please fiish this. 2. We use itegratio
MATH27* Partial Aswers to Review Eercises Fall 24 Evaluate each of the followig itegrals:. Let u cos. The du si ad Hece si ( cos 2 )(si ) (u 2 ) du. si u 2 cos 7 u 7 du Please fiish this. 2. We use itegratio
wavelet collocation method for solving integro-differential equation.
 IOSR Joural of Egieerig (IOSRJEN) ISSN (e): 5-3, ISSN (p): 78-879 Vol. 5, Issue 3 (arch. 5), V3 PP -7 www.iosrje.org wavelet collocatio method for solvig itegro-differetial equatio. Asmaa Abdalelah Abdalrehma
IOSR Joural of Egieerig (IOSRJEN) ISSN (e): 5-3, ISSN (p): 78-879 Vol. 5, Issue 3 (arch. 5), V3 PP -7 www.iosrje.org wavelet collocatio method for solvig itegro-differetial equatio. Asmaa Abdalelah Abdalrehma
Quiz. Use either the RATIO or ROOT TEST to determine whether the series is convergent or not.
 Quiz. Use either the RATIO or ROOT TEST to determie whether the series is coverget or ot. e .6 POWER SERIES Defiitio. A power series i about is a series of the form c 0 c a c a... c a... a 0 c a where
Quiz. Use either the RATIO or ROOT TEST to determie whether the series is coverget or ot. e .6 POWER SERIES Defiitio. A power series i about is a series of the form c 0 c a c a... c a... a 0 c a where
f(w) w z =R z a 0 a n a nz n Liouville s theorem, we see that Q is constant, which implies that P is constant, which is a contradiction.
 Theorem 3.6.4. [Liouville s Theorem] Every bouded etire fuctio is costat. Proof. Let f be a etire fuctio. Suppose that there is M R such that M for ay z C. The for ay z C ad R > 0 f (z) f(w) 2πi (w z)
Theorem 3.6.4. [Liouville s Theorem] Every bouded etire fuctio is costat. Proof. Let f be a etire fuctio. Suppose that there is M R such that M for ay z C. The for ay z C ad R > 0 f (z) f(w) 2πi (w z)
Exact scattering and bound states solutions for novel hyperbolic potentials with inverse square singularity
 Exact scatterig ad boud states solutios for ovel hyperbolic potetials with iverse square sigularity A. D. Alhaidari Saudi Ceter for Theoretical Physics, P. O. Box 37, Jeddah 38, Saudi Arabia Abstract:
Exact scatterig ad boud states solutios for ovel hyperbolic potetials with iverse square sigularity A. D. Alhaidari Saudi Ceter for Theoretical Physics, P. O. Box 37, Jeddah 38, Saudi Arabia Abstract:
Indefinite Integral. Lecture 21 discussed antiderivatives. In this section, we introduce new notation and vocabulary. The notation f x dx
 67 Iefiite Itegral Lecture iscusse atierivatives. I this sectio, we itrouce ew otatio a vocabulary. The otatio f iicates the geeral form of the atierivative of f a is calle the iefiite itegral. From the
67 Iefiite Itegral Lecture iscusse atierivatives. I this sectio, we itrouce ew otatio a vocabulary. The otatio f iicates the geeral form of the atierivative of f a is calle the iefiite itegral. From the
MA 201-COMPLEX ANALYSIS
 MA 201-COMPLEX ANALYSIS Autum, 2009-10 Istructor: Devidas Pai Departmet of Mathematics Idia Istitute of Techology Gadhiagar Idia Name: Tutorial Batch: MA 201: Complex Aalysis (3-1-0-4) (Course cotets)
MA 201-COMPLEX ANALYSIS Autum, 2009-10 Istructor: Devidas Pai Departmet of Mathematics Idia Istitute of Techology Gadhiagar Idia Name: Tutorial Batch: MA 201: Complex Aalysis (3-1-0-4) (Course cotets)
Residue Integrals (4C)
 Residue Itegrals (4C) Iverse Laplace Trasform Copyright (c) 22 24 Youg W. Lim. Permissio is grated to copy, distribute ad/or modify this documet uder the terms of the GNU Free Documetatio Licese, Versio.2
Residue Itegrals (4C) Iverse Laplace Trasform Copyright (c) 22 24 Youg W. Lim. Permissio is grated to copy, distribute ad/or modify this documet uder the terms of the GNU Free Documetatio Licese, Versio.2
Course 4: Preparation for Calculus Unit 1: Families of Functions
 Course 4: Preparatio for Calculus Uit 1: Families of Fuctios Review ad exted properties of basic fuctio families ad their uses i mathematical modelig Develop strategies for fidig rules of fuctios whose
Course 4: Preparatio for Calculus Uit 1: Families of Fuctios Review ad exted properties of basic fuctio families ad their uses i mathematical modelig Develop strategies for fidig rules of fuctios whose
Definition of z-transform.
 - Trasforms Frequecy domai represetatios of discretetime sigals ad LTI discrete-time systems are made possible with the use of DTFT. However ot all discrete-time sigals e.g. uit step sequece are guarateed
- Trasforms Frequecy domai represetatios of discretetime sigals ad LTI discrete-time systems are made possible with the use of DTFT. However ot all discrete-time sigals e.g. uit step sequece are guarateed
IYGB. Special Extension Paper E. Time: 3 hours 30 minutes. Created by T. Madas. Created by T. Madas
 YGB Special Extesio Paper E Time: 3 hours 30 miutes Cadidates may NOT use ay calculator. formatio for Cadidates This practice paper follows the Advaced Level Mathematics Core ad the Advaced Level Further
YGB Special Extesio Paper E Time: 3 hours 30 miutes Cadidates may NOT use ay calculator. formatio for Cadidates This practice paper follows the Advaced Level Mathematics Core ad the Advaced Level Further
SHARP INEQUALITIES INVOLVING THE CONSTANT e AND THE SEQUENCE (1 + 1/n) n
 SHARP INEQUALITIES INVOLVING THE CONSTANT e AND THE SEQUENCE + / NECDET BATIR Abstract. Several ew ad sharp iequalities ivolvig the costat e ad the sequece + / are proved.. INTRODUCTION The costat e or
SHARP INEQUALITIES INVOLVING THE CONSTANT e AND THE SEQUENCE + / NECDET BATIR Abstract. Several ew ad sharp iequalities ivolvig the costat e ad the sequece + / are proved.. INTRODUCTION The costat e or
