SphericalHarmonicY. Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation
|
|
|
- Darleen Paul
- 5 years ago
- Views:
Transcription
1 SphericalHaroicY Notatios Traditioal ae Spherical haroic Traditioal otatio Y, φ Matheatica StadardFor otatio SphericalHaroicY,,, φ Priary defiitio Y, φ φ P cos ; Y 0 k, φ k k ; k Y, φ 0 ; Y, φ Y, φ ; The followig restrictios apply to all forulas of this fuctio Specific values Specialized values For fixed,, Y, 0 φ Y, φ
2 For fixed,, φ Y 0, φ 0 ; Y, φ 0 ; Y k, φ 0 ; 0 k Y od, φ φ Y od, φ φ For fixed,, φ Y 0, φ P cos Y, φ φ cos P cos P cos cos si Y, φ φ si Y, φ 0 Y, φ Y, φ φ si Y, φ 0 ; Y, φ 0 ; For fixed,, φ
3 φ cos Y si 0, φ Y, φ 3 φ cos cos si Y, φ 5 φ 3 cos 3 cos cos si Y 3, φ 7 φ 5 cos 3 5 cos 6 9 cos 4 cos si Y 4, φ 3 φ 05 cos 4 05 cos 3 45 cos 5 cos cos si Y 5, φ φ 945 cos cos cos cos cos cos si Y 6, φ 3 φ cos cos cos cos cos cos cos si Y 7, φ 5 φ cos cos cos cos cos cos cos cos si 8 8
4 Y 8, φ 7 φ cos cos cos cos cos cos cos cos cos si Y 9, φ 9 φ cos cos cos cos cos cos cos cos cos cos si Y 0, φ φ cos cos cos cos cos cos cos cos cos cos cos si Y, φ 4 φ cos si k k k k si k k Y, φ 0 ; Y, φ φ For fixed, φ si k k k cos cos k ; 0 k k k 0
5 Y 0 0, φ Y 0 k, φ k k ; k For fixed, φ Y 0 0, φ Y, φ φ 3 si Y 0, φ 3 cos Y, φ φ 3 si Y, φ 4 5 φ si Y, φ φ 5 cos si Y 0, φ cos Y, φ φ 5 cos si Y, φ 4 5 φ si
6 Y 3 3, φ 8 3 φ 35 si Y 3, φ 4 05 φ cos si Y 3, φ 6 φ 5 cos 3 si Y 0 3, φ 7 3 cos 5 cos Y 3, φ 6 φ 5 cos 3 si Y 3, φ 4 05 φ cos si Y 3 3, φ 8 3 φ 35 si Y 4 4, φ φ si Y 4 3, φ φ cos si Y 4, φ φ 7 cos si Y 4, φ φ cos 7 cos 3 si Y 0 4, φ 35 cos 4 30 cos 3 6
7 Y 4, φ φ cos 7 cos 3 si Y 4, φ φ 7 cos si Y 4 3, φ φ cos si Y 4 4, φ φ si Y 5 5, φ φ si Y 5 4, φ φ cos si Y 5 3, φ φ 9 cos si Y 5, φ 8 55 φ cos 3 cos si Y 0 5, φ 6 63 cos5 70 cos 3 5 cos Y 5, φ 6 65 φ cos 4 4 cos si Y 5, φ 8 55 φ cos 3 cos si
8 Y 5 3, φ φ 9 cos si Y 5 4, φ φ cos si Y 5 5, φ φ si 5 Geeral characteristics Doai ad aalyticity The fuctio Y, φ is defied over. For fixed,, the fuctio Y, φ is a polyoial i si of degree ultiplied o fuctio coa φy, φ si. Syetries ad periodicities Parity Y, φ φ Y, φ Y, φ Y, φ Y, φ φ Y, φ Y, φ Y, φ Y, φ Y, φ Mirror syetry Y, φ Y, φ ; φ Periodicity Y, φ is a periodic fuctio with respect to ad φ with periods ad respectively.
9 Y k, φ Y, φ ; k Y, φ k Y, φ ; k Phase shifts Y, φ Y, φ Y, φ Y, φ Y, φ Y, φ Poles ad essetial sigularities With respect to φ For fixed,,, the fuctio Y, φ has oly oe sigular poit at φ. It is a essetial sigular poit ig φ Y, φ, With respect to For fixed, φ, ;, the fuctio Y, φ does ot have poles ad essetial sigularities ig Y, φ ; For iteger, the fuctio Y, φ is polyoial ad has pole of order at cos ig Y, φ, ; Brach poits With respect to φ For fixed,,, the fuctio Y, φ does ot have brach poits φ Y, φ With respect to For fixed geeric, φ, ;, the fuctio Y, φ has the set of brach poits where: cos, cos ad cos. For fixed φ ad itegers, the fuctio Y, φ does ot have brach poits.
10 0 Brach cuts With respect to φ For fixed,,, the fuctio Y, φ does ot have brach cuts φ Y, φ With respect to For fixed geeric, φ, ;, the fuctio Y, φ is a sigle-valued fuctio o the -plae cut alog the itervals cos ad cos. For fixed φ ad itegers, the fuctio Y, φ is a polyoial ad does ot have brach cuts. Series represetatios Geeralized power series Expasios at si 0 Y, φ φ si si si ; si Y, φ φ si k j j kj j j k j si k ; si k 0 j Y, φ φ si F 0 ; ; si F, ; ; si Y, φ φ si O si ; si Y, φ φ si cos k k k k si k k 0
11 Y, φ φ ta si si k k si k k k 0 k Y, φ φ si k k si k k k 0 k Y, φ φ si k k si k k k 0 k Expasios at cos Y, φ φ csc si ta k k cos k 0 k k k Y, φ φ csc si cot k k cos k 0 k k k Y, φ φ si cos csc si k k cos k k k 0 k Y, φ φ csc sec csc si k k cos k k k 0 k Expasios at ta Y, φ sg φ cos csc si k k ta k k k k k 0 Expasios at cot 0
12 Y, φ sg φ si csc si k k cot kk k k k 0 Expasios at si Y, φ Y, φ k k k k Expasios at cos 0 k k si k k k Y, φ φ si csc si od k k k k cos k k Expasios at ta Y, φ φ cos csc si od k k k k ta k k Expasios at cot Y, φ φ si csc si k od k k k cot k k Expasios at 0 Y, φ φ O 8 ; 0 Y, φ φ O ; 0
13 3 Expasios at cos Y, φ φ cos si cos z cos cos ; cos cos 3 cos Y φ, φ cos cos k k si k 0 k k cos k Y φ, φ cos cos si F, ; ; cos Y φ, φ cos cos O si ; cos Cos φ Y, φ cos cos k k si k 0 k k cos k φ Y, φ 3 cos cos O si cos ; cos I Cartesia coordiates Y, φ x y z ijk, ij, x y j x y i z k ; i j k i j i 0 j 0 k 0 x cosφ si y siφ si z cos Itegral represetatios O the real axis
14 4 Of the direct fuctio Y, φ cos cost φ si t t Y, φ φ 4 csc P t t cos t ; 0 cos Y, φ φ 0 cos si cost cos tt Y, φ cos si cost φ t t Y, φ 3 φ si 0 cos si cost sit t ; Y, φ φ 4 0 t cos J t si t t ; cos 0 Ivolvig the direct fuctio Y, φ 0 J t si Multiple itegral represetatios Y, φ φ 4 csc J tt ; φ 0 si cos t 3 t P t t t t ; 0 Itegral represetatios of egative iteger order Y, φ r x y r z ; r x y z x r cosφ si y r siφ si z r cos 0
15 5 Y, φ φ si z ; z cos z Y, φ z φ si ; z cos z φ Y, φ cos cos cot si si z z ; z z cos Y, φ φ cos cos cot si si z z ; z z cos Y, φ 4 φ si P z z ; z cos Y, φ φ si z z ; z cos Y, φ φ si z z ; z cos Y, φ φ cos cot cot si z z ; z cos z Y, φ φ cos cot si ta z z ; z z cos Y, φ φ si P z ; z cos 0 z
16 6 Geeratig fuctios w cos w si w 4 Y, 0 ; 0 w w cos w si w 4 Y, 0 ; 0 w w cos w w w cos w si w 0 w Y, 0 ; Differetial equatios Ordiary liear differetial equatios ad wroskias For the direct fuctio itself With respect to si si Y, φ si Y, φ 0 With respect to φ Y, φ Y, φ 0 φ Partial differetial equatios φ Y, φ cot Y, φ φ Y, φ si si Y, φ Y, φ si φ Y, φ 0 Trasforatios
17 7 Trasforatios ad arguet siplificatios Arguet ivolvig basic arithetic operatios Y, φ Y, φ ; φ Y, φ φ Y, φ Y, φ Y, φ Y, φ φ Y, φ Y, φ Y, φ Y, φ Y, φ Products, sus, ad powers of the direct fuctio Products ivolvig the direct fuctio Clebsch-Gorda series for product of two spherical haroics Y, φ Y, φ k ax, k Y k, φ 0 0 k 0 k ; Clebsch-Gorda double series for product of three spherical haroics Y, φ Y, φ 3 Y 3, φ 3 4 k 3 k ax, k axk 3, 3 k Y k 3, φ 0 0 k 0 k k 3 k 0 k k 3 3 k 3 k 3 ; j j j j j,, 3 Clebsch-Gorda ultiple series for product of several spherical haroics
18 8 p j j Y j, φ p p j k 3 j k p p k ax,m k axk 3,M 3 k p axk p p,m p k p M p, φk j j 0 0 k j j k j 0 k j j M j j k j j k j M j ; Y kp p j j k p p k k k k k 0 M 0 0 M j k Idetities Recurrece idetities Cosecutive eighbors Y, φ 3 cos Y, φ 5 Y, φ Y, φ cos Y, φ 3 Y, φ ; Y, φ φ cot Y, φ φ Y, φ Y, φ 0 φ cot Y, φ φ Y, φ ; Fuctioal idetities Relatios betwee cotiguous fuctios Y, φ sec Y, φ 3 Y, φ Y, φ ta φ Y, φ φ Y, φ ; 0
19 9 Additioal relatios betwee cotiguous fuctios Below relatios are correct oly uder soe restrictios o the paraeters Y, φ csc φ 3 Y, φ Y, φ Y, φ csc φ Y, φ 3 Y, φ Y, φ φ csc cos Y, φ Y, φ ; Y, φ φ csc 3 Y, φ cos Y, φ Y, φ φ csc Y, φ cos Y, φ ; Y, φ φ csc cos Y, φ 3 Y, φ Relatios of special kid Y, 0 φ Y, φ Y, 0 Y, p ; p Coplex characteristics Cojugate value Y, φ Y, φ ; φ Differetiatio
20 0 Low-order differetiatio With respect to Y, φ cot Y, φ φ Y, φ Y, φ 4 φ csc cos P cos P cos Y, φ cot csc Y, φ φ cot Y, φ φ Y, φ Y, φ With respect to φ Y, φ Y, φ φ Y, φ φ Y, φ φ csc cos P cos si P cos Sybolic differetiatio With respect to φ p Y, φ p Y φ p, φ ; p Fractioal itegro-differetiatio With respect to φ Α Y, φ φ Α φ Α QΑ, 0, φ Y φ Α, φ Itegratio Idefiite itegratio
21 Ivolvig oly oe direct fuctio with respect to φ Y, φφ Y, φ Ivolvig oe direct fuctio ad eleetary fuctios with respect to φ Ivolvig power fuctio φ Α Y, φφ φ Α φ Α φ Α, φ Y, φ Ivolvig fuctios of the direct fuctio ad eleetary fuctios with respect to Ivolvig eleetary fuctios of the direct fuctio ad eleetary fuctios Ivolvig products of the direct fuctio ad trigooetric fuctios k k l si si Y k l, φ Y, φ l cos Y, φ Y k l, φ φ si k l k l k l k l Y, φ Y k l, φ Y, φ Y k l, φ Defiite itegratio Ivolvig the direct fuctio φ si Y, φ 0 ; φ si Y k, φ Y, φ csc Y, φ Y, φ ,k ; k 0 4, ; si cos p Y, φ 4 p φ ; p 0 p p
22 a b Y z cos z, φ Y cos z, φ z b Y cos b, φ Y cos b, φ Y cos b, φ Y cos b, φ a Y cos a, φ Y cos a, φ Y cos a, φ Y cos a, φ ; a b Multiple itegratio si Y, φ φ,0, si Y, φ Y, φ 3 Y 3, φφ si Y, φ Y, φ 3 Y 3, φφ ; si Y, φ Y, φ 3 Y 3, φφ ; Orthoorality relatios: si Y, φy, φφ,, ; si Y, φ Y, φφ,, ; si Y, φ Y, φφ,, ; 0 0 Suatio
23 3 Fiite suatio Ivolvig the direct fuctio Y, φ Y, φ P cos cos cosφ φ si si ; k φ k k, Y, φ ; φ Y, φ 0 ; φ Y, φ si ; φ Y, φ Y, φ cos ; φ Y, φ cos si cosφ ; φ p l w pl l p l l l l Y l, φ p si φ w cos w p C p p cos w w cos w ; 0 Ivolvig Clebsch-Gorda fuctios The iverse Clebsch-Gorda series: im, k axm, k M k L M Y k, φ Y Mk, φ L M L L M L 4 L 0 0 L 0 Y L M, φ ; Ifiite suatio
24 Y, φ w 0 φ w si φ 0 F ; ; w cos 0F ; ; w si ; p p si φ w cos p F Y, φ w p, p ; ; w si w cos ; 0 p φ w p p Y, φ w p p si φ w w cos w F p, p ; ; w F p, p ; ; w cos w ; 0 p p φ w L z Y, φ w si φ w cos w z w cos w z w si exp 0F ; ; ; 0 φ w w cos w 4 w cos w J w Y, φ w w si φ w cos ; 0 φ, J w Y, φ w w si φ cosw cos ; 0 φ , J w Y, φ w w si φ siw cos ; 0 φ
25 J w Y, φ Y, φ 0 k φ k k, w 4 3 J w si si w cos cos φ φ ; Multiple ifiite suatio Copleteess relatio: Y, φ Y, φ φ φ cos cos ; k φ k k, 0 Represetatios through ore geeral fuctios Through hypergeoetric fuctios Ivolvig F Y, φ cos φ F, ; ; si si Ivolvig F Y, φ cos φ F, ; ; si si ; Y, φ φ ta csc si F, ; ; si ; Y φ, φ cos cos si F, ; ; cos Y, φ sg φ si F, ; ; si
26 Y, φ sg φ si si F, ; ; csc ; Y, φ sg φ si F, ; ; cos Y, φ sg φ cos si F, ; ; sec ; Y, φ sg φ cos si F, ; ; ta Y, φ sg φ si si F, ; ; cot Through Meijer G Classical cases Y, φ 4 cos φ li si Ν G, si, si Ν Ν, Ν 0, ; Through other fuctios Ivolvig Legedre fuctios Y, φ Y, φ 4 φ P cos φ cos cos cos Ivolvig soe hypergeoetric-type fuctios Y, φ φ cos cot si ta P, cos
27 φ Y, φ csc si ta C cos Represetatios through equivalet fuctios With related fuctios Ivolvig Wiger-D fuctios Y, φ D 0, 0,, φ Y, φ Y, φ D 0, 0,, φ D,0 φ,, Y, φ D,0 φ,, 0 Zeros Whe Y, φ is ot idetically zero, it possesses a fiite uber of zeros i the iterval 0, all of which are odegeerate. For itegers ad with, the fuctio Y, φ has zeros i the iterval 0. If 0, there are also two ore zeros at 0,. All of these zeros are syetric about. Theores Eigefuctio to the agular part of the Laplace operator i spherical coordiates The fuctio Y, φ is a eigefuctio to the agular part L of the Laplace operator i spherical coordiates L si φ si si with eigevalue. Eigefuctio of the z-copoet of the quatu echaical agular oetu operator The fuctio Y, φ is a eigefuctio to the z-copoet of the quatu echaical agular oetu operator L z φ with eigevalue.
28 8 Eigefuctios of the curl operator i spherical coordiates The fuctio ur,, φ Λ r Ψr,, φ r Ψr,, φ with Ψr,, φ gry, φ ad gr Λ c J Λ r Λ r ur,, φ Λ ur,, φ. Multiple expasio theore Y Λ r are eigefuctios of the curl operator i spherical coordiates Λ r Ay fuctio f, φ that is square itegrable over 0, 0 φ ca be expaded i a series of spherical haroics Y, φ, with series coefficiets a, called the ultipole oets: f, φ 0 a, Y, φ ; a, 0 0 si Y, φ f, φφ. Expasio of two-poit distaces The power r r of the distace betwee two poits r ad r ca be expaded i the followig way (assuig r r ad Ω is the agle betwe r ad r ) (Sack 964): r r r l 0 l l r r l F l, ; l 3 ; r r P l cosω History A.M. Legedre (785); P.S. Laplace (785) gave the ae spherical haroic ; K.F. Gauss (88). Refereces L.C. Biedehar ad J.D. louck, Agular Moetu i Quatu Physics, Addiso-Wesley, Readig, 98. L.C. Biedehar ad J.D. louck, The Racah-Wiger Algebra i Quatu Theory, Addiso-Wesley, Readig, 98. E.W. Hobso, The Theory of Spherical ad Ellipsoidal Haroics, Cabridge Uiversity Press, Cabridge, 955. M.E. Rose, Eleetary Theory of Agular Moetu, Dover, New York, 995. D.A. Varshalovich, A.N. Moskalev ad V.K. Khersoskii, Quatu Theory of Agular Moetu, World Scietific, Sigapore, 988.
29 9 Copyright This docuet was dowloaded fro fuctios.wolfra.co, a coprehesive olie copediu of forulas ivolvig the special fuctios of atheatics. For a key to the otatios used here, see Please cite this docuet by referrig to the fuctios.wolfra.co page fro which it was dowloaded, for exaple: To refer to a particular forula, cite fuctios.wolfra.co followed by the citatio uber. e.g.: This docuet is curretly i a preliiary for. If you have coets or suggestios, please eail coets@fuctios.wolfra.co , Wolfra Research, Ic.
Multinomial. Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation
Multioial Notatios Traditioal ae Multioial coefficiet Traditioal otatio 1 2 ; 1, 2,, Matheatica StadardFor otatio Multioial 1, 2,, Priary defiitio 06.04.02.0001.01 1 2 ; 1, 2,, 06.04.02.0002.01 1 k k 1
Binomial Notations Traditional name Traditional notation Mathematica StandardForm notation Primary definition
Bioial Notatios Traditioal ae Bioial coefficiet Traditioal otatio Matheatica StadardFor otatio Bioial, Priary defiitio 06.03.0.0001.01 1 1 1 ; 0 For Ν, Κ egative itegers with, the bioial coefficiet Ν caot
Introductions to LucasL
Itroductios to LucasL Itroductio to the Fiboacci ad Lucas ubers The sequece ow ow as Fiboacci ubers (sequece 0,,,, 3,, 8, 3...) first appeared i the wor of a aciet Idia atheaticia, Pigala (40 or 00 BC).
ExpIntegralEi. Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation
ExpItegralEi Notatios Traditioal ame Expoetial itegral Ei Traditioal otatio Ei Mathematica StadardForm otatio ExpItegralEi Primary defiitio 06.35.02.000.0 Ei k k 2 log log k Specific values Values at fixed
Introductions to HarmonicNumber2
Itroductios to HarmoicNumber2 Itroductio to the differetiated gamma fuctios Geeral Almost simultaeously with the developmet of the mathematical theory of factorials, biomials, ad gamma fuctios i the 8th
Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation. Specialized values
EulerPhi Notatios Traditioal ame Euler totiet fuctio Traditioal otatio Φ Mathematica StadardForm otatio EulerPhi Primary defiitio 3.06.02.000.0 Φ gcd,k, ; For oegative iteger, the Euler totiet fuctio Φ
Introductions to PartitionsP
Itroductios to PartitiosP Itroductio to partitios Geeral Iterest i partitios appeared i the 7th cetury whe G. W. Leibiz (669) ivestigated the umber of ways a give positive iteger ca be decomposed ito a
x !1! + 1!2!
4 Euler-Maclauri Suatio Forula 4. Beroulli Nuber & Beroulli Polyoial 4.. Defiitio of Beroulli Nuber Beroulli ubers B (,,3,) are defied as coefficiets of the followig equatio. x e x - B x! 4.. Expreesio
Binomial transform of products
Jauary 02 207 Bioial trasfor of products Khristo N Boyadzhiev Departet of Matheatics ad Statistics Ohio Norther Uiversity Ada OH 4580 USA -boyadzhiev@ouedu Abstract Give the bioial trasfors { b } ad {
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
x+ 2 + c p () x c p () x is an arbitrary function. ( sin x ) dx p f() d d f() dx = x dx p cosx = cos x+ 2 d p () x + x-a r (1.
Super Derivative (No-iteger ties Derivative). Super Derivative ad Super Differetiatio Defitio.. p () obtaied by cotiuig aalytically the ide of the differetiatio operator of Higher Derivative of a fuctio
Ma/CS 6a Class 22: Power Series
Ma/CS 6a Class 22: Power Series By Ada Sheffer Power Series Mooial: ax i. Polyoial: a 0 + a 1 x + a 2 x 2 + + a x. Power series: A x = a 0 + a 1 x + a 2 x 2 + Also called foral power series, because we
Name Period ALGEBRA II Chapter 1B and 2A Notes Solving Inequalities and Absolute Value / Numbers and Functions
Nae Period ALGEBRA II Chapter B ad A Notes Solvig Iequalities ad Absolute Value / Nubers ad Fuctios SECTION.6 Itroductio to Solvig Equatios Objectives: Write ad solve a liear equatio i oe variable. Solve
Jacobi symbols. p 1. Note: The Jacobi symbol does not necessarily distinguish between quadratic residues and nonresidues. That is, we could have ( a
Jacobi sybols efiitio Let be a odd positive iteger If 1, the Jacobi sybol : Z C is the costat fuctio 1 1 If > 1, it has a decopositio ( as ) a product of (ot ecessarily distict) pries p 1 p r The Jacobi
18.S34 (FALL, 2007) GREATEST INTEGER PROBLEMS. n + n + 1 = 4n + 2.
18.S34 (FALL, 007) GREATEST INTEGER PROBLEMS Note: We use the otatio x for the greatest iteger x, eve if the origial source used the older otatio [x]. 1. (48P) If is a positive iteger, prove that + + 1
Notes 19 Bessel Functions
ECE 638 Fall 17 David R. Jackso Notes 19 Bessel Fuctios Notes are from D. R. Wilto, Dept. of ECE 1 Cylidrical Wave Fuctios Helmholtz equatio: ψ + k ψ = I cylidrical coordiates: ψ 1 ψ 1 ψ ψ ρ ρ ρ ρ φ z
(s)h(s) = K( s + 8 ) = 5 and one finite zero is located at z 1
ROOT LOCUS TECHNIQUE 93 should be desiged differetly to eet differet specificatios depedig o its area of applicatio. We have observed i Sectio 6.4 of Chapter 6, how the variatio of a sigle paraeter like
Automated Proofs for Some Stirling Number Identities
Autoated Proofs for Soe Stirlig Nuber Idetities Mauel Kauers ad Carste Scheider Research Istitute for Sybolic Coputatio Johaes Kepler Uiversity Altebergerstraße 69 A4040 Liz, Austria Subitted: Sep 1, 2007;
Bertrand s postulate Chapter 2
Bertrad s postulate Chapter We have see that the sequece of prie ubers, 3, 5, 7,... is ifiite. To see that the size of its gaps is ot bouded, let N := 3 5 p deote the product of all prie ubers that are
A New Type of q-szász-mirakjan Operators
Filoat 3:8 07, 567 568 https://doi.org/0.98/fil7867c Published by Faculty of Scieces ad Matheatics, Uiversity of Niš, Serbia Available at: http://www.pf.i.ac.rs/filoat A New Type of -Szász-Miraka Operators
Integrals of Functions of Several Variables
Itegrals of Fuctios of Several Variables We ofte resort to itegratios i order to deterie the exact value I of soe quatity which we are uable to evaluate by perforig a fiite uber of additio or ultiplicatio
1. Hydrogen Atom: 3p State
7633A QUANTUM MECHANICS I - solutio set - autum. Hydroge Atom: 3p State Let us assume that a hydroge atom is i a 3p state. Show that the radial part of its wave fuctio is r u 3(r) = 4 8 6 e r 3 r(6 r).
Bernoulli Polynomials Talks given at LSBU, October and November 2015 Tony Forbes
Beroulli Polyoials Tals give at LSBU, October ad Noveber 5 Toy Forbes Beroulli Polyoials The Beroulli polyoials B (x) are defied by B (x), Thus B (x) B (x) ad B (x) x, B (x) x x + 6, B (x) dx,. () B 3
Orthogonal Functions
Royal Holloway Uiversity of odo Departet of Physics Orthogoal Fuctios Motivatio Aalogy with vectors You are probably failiar with the cocept of orthogoality fro vectors; two vectors are orthogoal whe they
Sequences of Definite Integrals, Factorials and Double Factorials
47 6 Joural of Iteger Sequeces, Vol. 8 (5), Article 5.4.6 Sequeces of Defiite Itegrals, Factorials ad Double Factorials Thierry Daa-Picard Departmet of Applied Mathematics Jerusalem College of Techology
ECE Spring Prof. David R. Jackson ECE Dept. Notes 20
ECE 6341 Sprig 016 Prof. David R. Jackso ECE Dept. Notes 0 1 Spherical Wave Fuctios Cosider solvig ψ + k ψ = 0 i spherical coordiates z φ θ r y x Spherical Wave Fuctios (cot.) I spherical coordiates we
The Non-homogeneous Diffusion Equation
The No-hoogeeous Diffusio Equatio The o-hoogeeous diffusio equatio, with sources, has the geeral for, 2 r,t a 2 r,t Fr,t t a 2 is real ad The hoogeeous diffusio equatio, 2 r,t a 2 t r,t ca be solved by
Notes 8 Singularities
ECE 6382 Fall 27 David R. Jackso Notes 8 Sigularities Notes are from D. R. Wilto, Dept. of ECE Sigularity A poit s is a sigularity of the fuctio f () if the fuctio is ot aalytic at s. (The fuctio does
Bernoulli Number Identities via Euler-Maclaurin Summation
= Jacob eroulli 654-75 eroulli Nuber Idetities via Euler-Maclauri Suatio Hieu D. Nguye Math Dept Colloquiu Septeber 4, 8 Sus of Powers 3... 3... () 5,5 ()() 6 333,833,5 3...? ( ) 3... ( ) (Pythagoreas)
Orthogonal Function Solution of Differential Equations
Royal Holloway Uiversity of Loo Departet of Physics Orthogoal Fuctio Solutio of Differetial Equatios trouctio A give oriary ifferetial equatio will have solutios i ters of its ow fuctios Thus, for eaple,
The Gamma function. Marco Bonvini. October 9, dt e t t z 1. (1) Γ(z + 1) = z Γ(z) : (2) = e t t z. + z dt e t t z 1. = z Γ(z).
The Gamma fuctio Marco Bovii October 9, 2 Gamma fuctio The Euler Gamma fuctio is defied as Γ() It is easy to show that Γ() satisfy the recursio relatio ideed, itegratig by parts, dt e t t. () Γ( + ) Γ()
Double Derangement Permutations
Ope Joural of iscrete Matheatics, 206, 6, 99-04 Published Olie April 206 i SciRes http://wwwscirporg/joural/ojd http://dxdoiorg/04236/ojd2066200 ouble erageet Perutatios Pooya aeshad, Kayar Mirzavaziri
Application 10.5D Spherical Harmonic Waves
Applicatio 10.5D Spherical Haroic Waves I probles ivolvig regios that ejoy spherical syetry about the origi i space, it is appropriate to use spherical coordiates. The 3-diesioal Laplacia for a fuctio
Notation List. For Cambridge International Mathematics Qualifications. For use from 2020
Notatio List For Cambridge Iteratioal Mathematics Qualificatios For use from 2020 Notatio List for Cambridge Iteratioal Mathematics Qualificatios (For use from 2020) Mathematical otatio Eamiatios for CIE
f(w) w z =R z a 0 a n a nz n Liouville s theorem, we see that Q is constant, which implies that P is constant, which is a contradiction.
Theorem 3.6.4. [Liouville s Theorem] Every bouded etire fuctio is costat. Proof. Let f be a etire fuctio. Suppose that there is M R such that M for ay z C. The for ay z C ad R > 0 f (z) f(w) 2πi (w z)
NANYANG TECHNOLOGICAL UNIVERSITY SYLLABUS FOR ENTRANCE EXAMINATION FOR INTERNATIONAL STUDENTS AO-LEVEL MATHEMATICS
NANYANG TECHNOLOGICAL UNIVERSITY SYLLABUS FOR ENTRANCE EXAMINATION FOR INTERNATIONAL STUDENTS AO-LEVEL MATHEMATICS STRUCTURE OF EXAMINATION PAPER. There will be oe 2-hour paper cosistig of 4 questios.
) is a square matrix with the property that for any m n matrix A, the product AI equals A. The identity matrix has a ii
square atrix is oe that has the sae uber of rows as colus; that is, a atrix. he idetity atrix (deoted by I, I, or [] I ) is a square atrix with the property that for ay atrix, the product I equals. he
distinct distinct n k n k n! n n k k n 1 if k n, identical identical p j (k) p 0 if k > n n (k)
THE TWELVEFOLD WAY FOLLOWING GIAN-CARLO ROTA How ay ways ca we distribute objects to recipiets? Equivaletly, we wat to euerate equivalece classes of fuctios f : X Y where X = ad Y = The fuctios are subject
The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j
![The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j](/thumbs/82/85448534.jpg "The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j")
The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
Perturbation Theory, Zeeman Effect, Stark Effect
Chapter 8 Perturbatio Theory, Zeea Effect, Stark Effect Ufortuately, apart fro a few siple exaples, the Schrödiger equatio is geerally ot exactly solvable ad we therefore have to rely upo approxiative
1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y
![1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y](/thumbs/95/125864248.jpg "1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y")
Questio (a) A square matrix A= A is called positive defiite if the quadratic form waw > 0 for every o-zero vector w [Note: Here (.) deotes the traspose of a matrix or a vector]. Let 0 A = 0 = show that:
CALCULUS BASIC SUMMER REVIEW
CALCULUS BASIC SUMMER REVIEW NAME rise y y y Slope of a o vertical lie: m ru Poit Slope Equatio: y y m( ) The slope is m ad a poit o your lie is, ). ( y Slope-Itercept Equatio: y m b slope= m y-itercept=
Some results on the Apostol-Bernoulli and Apostol-Euler polynomials
Soe results o the Apostol-Beroulli ad Apostol-Euler polyoials Weipig Wag a, Cagzhi Jia a Tiaig Wag a, b a Departet of Applied Matheatics, Dalia Uiversity of Techology Dalia 116024, P. R. Chia b Departet
The Differential Transform Method for Solving Volterra s Population Model
AASCIT Couicatios Volue, Issue 6 Septeber, 15 olie ISSN: 375-383 The Differetial Trasfor Method for Solvig Volterra s Populatio Model Khatereh Tabatabaei Departet of Matheatics, Faculty of Sciece, Kafas
Higher Course Plan. Calculus and Relationships Expressions and Functions
Higher Course Pla Applicatios Calculus ad Relatioships Expressios ad Fuctios Topic 1: The Straight Lie Fid the gradiet of a lie Colliearity Kow the features of gradiets of: parallel lies perpedicular lies
( ) ( ) ( ) ( ) ( + ) ( )
LSM Nov. 00 Cotet List Mathematics (AH). Algebra... kow ad use the otatio!, C r ad r.. kow the results = r r + + = r r r..3 kow Pascal's triagle. Pascal's triagle should be eteded up to = 7...4 kow ad
Chapter 4 Postulates & General Principles of Quantum Mechanics
Chapter 4 Postulates & Geeral Priciples of Quatu Mechaics Backgroud: We have bee usig quite a few of these postulates already without realizig it. Now it is tie to forally itroduce the. State of a Syste
A Generalization of Ince s Equation
Joural of Applied Matheatics ad Physics 7-8 Published Olie Deceber i SciRes. http://www.scirp.org/oural/ap http://dx.doi.org/.36/ap..337 A Geeralizatio of Ice s Equatio Ridha Moussa Uiversity of Wiscosi
arxiv: v1 [math.ca] 17 Dec 2017
![arxiv: v1 [math.ca] 17 Dec 2017](/thumbs/88/116406083.jpg "arxiv: v1 [math.ca] 17 Dec 2017")
Fiite ad ifiite product trasforatios Marti Nicholso Several ifiite products are studied alog with their fiite couterparts. For certai values of the paraeters these ifiite products reduce to odular fors.
Apply change-of-basis formula to rewrite x as a linear combination of eigenvectors v j.
Eigevalue-Eigevector Istructor: Nam Su Wag eigemcd Ay vector i real Euclidea space of dimesio ca be uiquely epressed as a liear combiatio of liearly idepedet vectors (ie, basis) g j, j,,, α g α g α g α
j=1 dz Res(f, z j ) = 1 d k 1 dz k 1 (z c)k f(z) Res(f, c) = lim z c (k 1)! Res g, c = f(c) g (c)
Problem. Compute the itegrals C r d for Z, where C r = ad r >. Recall that C r has the couter-clockwise orietatio. Solutio: We will use the idue Theorem to solve this oe. We could istead use other (perhaps
Subject: Differential Equations & Mathematical Modeling-III
Power Series Solutios of Differetial Equatios about Sigular poits Subject: Differetial Equatios & Mathematical Modelig-III Lesso: Power series solutios of differetial equatios about Sigular poits Lesso
Transfer Function Analysis
Trasfer Fuctio Aalysis Free & Forced Resposes Trasfer Fuctio Syste Stability ME375 Trasfer Fuctios - Free & Forced Resposes Ex: Let s s look at a stable first order syste: τ y + y = Ku Take LT of the I/O
6 Integers Modulo n. integer k can be written as k = qn + r, with q,r, 0 r b. So any integer.
6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
Chapter 1. Complex Numbers. Dr. Pulak Sahoo
Chapter 1 Complex Numbers BY Dr. Pulak Sahoo Assistat Professor Departmet of Mathematics Uiversity Of Kalyai West Begal, Idia E-mail : sahoopulak1@gmail.com 1 Module-2: Stereographic Projectio 1 Euler
Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation. Specialized values
InverseJacobiCS Notations Traditional nae Inverse of the Jacobi elliptic function cs Traditional notation cs Matheatica StandardFor notation InverseJacobiCS, Priary definition 09.39.0.000.0 csw ; w cs
PARTIAL DIFFERENTIAL EQUATIONS SEPARATION OF VARIABLES
Diola Bagayoko (0 PARTAL DFFERENTAL EQUATONS SEPARATON OF ARABLES. troductio As discussed i previous lectures, partial differetial equatios arise whe the depedet variale, i.e., the fuctio, varies with
Appendix: The Laplace Transform
Appedix: The Laplace Trasform The Laplace trasform is a powerful method that ca be used to solve differetial equatio, ad other mathematical problems. Its stregth lies i the fact that it allows the trasformatio
Generating Functions and Their Applications
Geeratig Fuctios ad Their Applicatios Agustius Peter Sahaggau MIT Matheatics Departet Class of 2007 18.104 Ter Paper Fall 2006 Abstract. Geeratig fuctios have useful applicatios i ay fields of study. I
Subject: Differential Equations & Mathematical Modeling -III. Lesson: Power series solutions of Differential Equations. about ordinary points
Power series solutio of Differetial equatios about ordiary poits Subject: Differetial Equatios & Mathematical Modelig -III Lesso: Power series solutios of Differetial Equatios about ordiary poits Lesso
A Pair of Operator Summation Formulas and Their Applications
A Pair of Operator Suatio Forulas ad Their Applicatios Tia-Xiao He 1, Leetsch C. Hsu, ad Dogsheg Yi 3 1 Departet of Matheatics ad Coputer Sciece Illiois Wesleya Uiversity Blooigto, IL 6170-900, USA Departet
(1 x n ) 1, (1 + x n ). (1 + g n x n ) r n
COMBINATORIAL ANALYSIS OF INTEGER POWER PRODUCT EXPANSIONS HGINGOLD, WEST VIRGINIA UNIVERSITY, DEPARTMENT OF MATHEMATICS, MORGANTOWN WV 26506, USA, GINGOLD@MATHWVUEDU JOCELYN QUAINTANCE, UNIVERSITY OF
School of Mechanical Engineering Purdue University. ME375 Transfer Functions - 1
Trasfer Fuctio Aalysis Free & Forced Resposes Trasfer Fuctio Syste Stability ME375 Trasfer Fuctios - 1 Free & Forced Resposes Ex: Let s look at a stable first order syste: y y Ku Take LT of the I/O odel
GENERALIZED KERNEL AND MIXED INTEGRAL EQUATION OF FREDHOLM - VOLTERRA TYPE R. T. Matoog
GENERALIZED KERNEL AND MIXED INTEGRAL EQUATION OF FREDHOLM - VOLTERRA TYPE R. T. Matoog Assistat Professor. Deartet of Matheatics, Faculty of Alied Scieces,U Al-Qura Uiversity, Makkah, Saudi Arabia Abstract:
Randomly Generated Triangles whose Vertices are Vertices of a Regular Polygon
Radoly Geerated Triagles whose Vertices are Vertices of a Regular Polygo Aa Madras Drury Uiversity Shova KC Hope College Jauary, 6 Abstract We geerate triagles radoly by uiforly choosig a subset of three
} is said to be a Cauchy sequence provided the following condition is true.
Math 4200, Fial Exam Review I. Itroductio to Proofs 1. Prove the Pythagorea theorem. 2. Show that 43 is a irratioal umber. II. Itroductio to Logic 1. Costruct a truth table for the statemet ( p ad ~ r
PAPER : IIT-JAM 2010
MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
Acoustic Field inside a Rigid Cylinder with a Point Source
Acoustic Field iside a Rigid Cylider with a Poit Source 1 Itroductio The ai objectives of this Deo Model are to Deostrate the ability of Coustyx to odel a rigid cylider with a poit source usig Coustyx
2D DSP Basics: Systems Stability, 2D Sampling
- Digital Iage Processig ad Copressio D DSP Basics: Systes Stability D Saplig Stability ty Syste is stable if a bouded iput always results i a bouded output BIBO For LSI syste a sufficiet coditio for stability:
6. If si () + cos () =, the is equal to :. If < CHAPTER 10 INFINITE SEQUENCES AND SERIES
CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
AH Checklist (Unit 3) AH Checklist (Unit 3) Matrices
AH Checklist (Uit 3) AH Checklist (Uit 3) Matrices Skill Achieved? Kow that a matrix is a rectagular array of umbers (aka etries or elemets) i paretheses, each etry beig i a particular row ad colum Kow
Riemann Hypothesis Proof
Riea Hypothesis Proof H. Vic Dao 43 rd West Coast Nuber Theory Coferece, Dec 6-0, 009, Asiloar, CA. Revised 0/8/00. Riea Hypothesis Proof H. Vic Dao vic0@cocast.et March, 009 Revised Deceber, 009 Abstract
SPIN COHERENT STATES DEFINED IN THE BARUT-GIRARDELLO MANNER
THE PUBLIHING HOUE PROCEEDING OF THE ROMANIAN ACADEMY, eries A, OF THE ROMANIAN ACADEMY Volue 7, Nuber 4/6, pp. 38 335 PIN COHERENT TATE DEFINED IN THE BARUT-GIRARDELLO MANNER Duša POPOV Politehica Uiversity
Evaluation of Some Non-trivial Integrals from Finite Products and Sums
Turkish Joural of Aalysis umber Theory 6 Vol. o. 6 7-76 Available olie at http://pubs.sciepub.com/tjat//6/5 Sciece Educatio Publishig DOI:.69/tjat--6-5 Evaluatio of Some o-trivial Itegrals from Fiite Products
Chapter 7: The z-transform. Chih-Wei Liu
Chapter 7: The -Trasform Chih-Wei Liu Outlie Itroductio The -Trasform Properties of the Regio of Covergece Properties of the -Trasform Iversio of the -Trasform The Trasfer Fuctio Causality ad Stability
NANYANG TECHNOLOGICAL UNIVERSITY SYLLABUS FOR ENTRANCE EXAMINATION FOR INTERNATIONAL STUDENTS A-LEVEL MATHEMATICS
NANYANG TECHNOLOGICAL UNIVERSITY SYLLABUS FOR ENTRANCE EXAMINATION FOR INTERNATIONAL STUDENTS A-LEVEL MATHEMATICS STRUCTURE OF EXAMINATION PAPER 1. There will be oe -hour paper cosistig of 4 questios..
Ma 530 Introduction to Power Series
Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Primes of the form n 2 + 1
Itroductio Ladau s Probles are four robles i Nuber Theory cocerig rie ubers: Goldbach s Cojecture: This cojecture states that every ositive eve iteger greater tha ca be exressed as the su of two (ot ecessarily
Chapter 2. Periodic points of toral. automorphisms. 2.1 General introduction
Chapter 2 Periodic poits of toral automorphisms 2.1 Geeral itroductio The automorphisms of the two-dimesioal torus are rich mathematical objects possessig iterestig geometric, algebraic, topological ad
42 Dependence and Bases
42 Depedece ad Bases The spa s(a) of a subset A i vector space V is a subspace of V. This spa ay be the whole vector space V (we say the A spas V). I this paragraph we study subsets A of V which spa V
Bernoulli Numbers and a New Binomial Transform Identity
1 2 3 47 6 23 11 Joural of Iteger Sequece, Vol. 17 2014, Article 14.2.2 Beroulli Nuber ad a New Bioial Trafor Idetity H. W. Gould Departet of Matheatic Wet Virgiia Uiverity Morgatow, WV 26506 USA gould@ath.wvu.edu
Fourier Series and their Applications
Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
q-fibonacci polynomials and q-catalan numbers Johann Cigler [ ] (4) I don t know who has observed this well-known fact for the first time.
![q-fibonacci polynomials and q-catalan numbers Johann Cigler [ ] (4) I don t know who has observed this well-known fact for the first time.](/thumbs/79/80173725.jpg "q-fibonacci polynomials and q-catalan numbers Johann Cigler [ ] (4) I don t know who has observed this well-known fact for the first time.")
-Fiboacci polyoials ad -Catala ubers Joha Cigler The Fiboacci polyoials satisfy the recurrece F ( x s) = s x = () F ( x s) = xf ( x s) + sf ( x s) () with iitial values F ( x s ) = ad F( x s ) = These
Today in Physics 217: separation of variables IV
Today i Physics 27: separatio of variables IV Separatio i cylidrical coordiates Exaple of the split cylider (solutio sketched at right) More o orthogoality of trig fuctios ad Fourier s trick V = V V =
CHAPTER 1 SEQUENCES AND INFINITE SERIES
CHAPTER SEQUENCES AND INFINITE SERIES SEQUENCES AND INFINITE SERIES (0 meetigs) Sequeces ad limit of a sequece Mootoic ad bouded sequece Ifiite series of costat terms Ifiite series of positive terms Alteratig
6.4 Binomial Coefficients
64 Bioial Coefficiets Pascal s Forula Pascal s forula, aed after the seveteeth-cetury Frech atheaticia ad philosopher Blaise Pascal, is oe of the ost faous ad useful i cobiatorics (which is the foral ter
Mathematical Description of Discrete-Time Signals. 9/10/16 M. J. Roberts - All Rights Reserved 1
Mathematical Descriptio of Discrete-Time Sigals 9/10/16 M. J. Roberts - All Rights Reserved 1 Samplig ad Discrete Time Samplig is the acquisitio of the values of a cotiuous-time sigal at discrete poits
REGULARIZATION OF CERTAIN DIVERGENT SERIES OF POLYNOMIALS
REGULARIZATION OF CERTAIN DIVERGENT SERIES OF POLYNOMIALS LIVIU I. NICOLAESCU ABSTRACT. We ivestigate the geeralized covergece ad sums of series of the form P at P (x, where P R[x], a R,, ad T : R[x] R[x]
Annotations to Abramowitz & Stegun
Aotatios to Abraowitz & Stegu By Lias Vepstas 4 Jauary 4 corrected Dec 4, Dec The followig is a copediu of additios ad argi otes to the Hadbook of Matheatical Fuctios by Abraowitz
c z c z c z c z c c c c a a c A P( a ) a c a z c x z R j z z, z z z z I
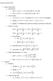. Quatu Spi States State Vectors c c i Ier Products: * * c c oralied. orthogoal c c c c c c * * i ii Probability that a particle i state ca be foud i state. c. States i S -basis y i i Geeral States. c
Discrete Orthogonal Moment Features Using Chebyshev Polynomials
Discrete Orthogoal Momet Features Usig Chebyshev Polyomials R. Mukuda, 1 S.H.Og ad P.A. Lee 3 1 Faculty of Iformatio Sciece ad Techology, Multimedia Uiversity 75450 Malacca, Malaysia. Istitute of Mathematical
Harmonic Interpolation, Bézier Curves and Trigonometric Interpolation
Haroic Iterpolatio, Bézier Curves ad Trigooetric Iterpolatio A Hardy ad W-H Steeb Iteratioal School for Scietific Coputig, Rad Afrikaas Uiversity, Aucklad Park 2006, South Africa Reprit requests to Prof
On p and q-horn s Matrix Function of Two Complex Variables
Alied Matheatics 437-44 doi:.436/a..3 Published Olie Deceber (htt://www.scirp.org/joural/a O ad -or s Matrix Fuctio of Two Colex Variables Abstract Aya Shehata Deartet of Matheatics Faculty of Sciece Assiut
HKDSE Exam Questions Distribution
HKDSE Eam Questios Distributio Sample Paper Practice Paper DSE 0 Topics A B A B A B. Biomial Theorem. Mathematical Iductio 0 3 3 3. More about Trigoometric Fuctios, 0, 3 0 3. Limits 6. Differetiatio 7
Math 4707 Spring 2018 (Darij Grinberg): midterm 2 page 1. Math 4707 Spring 2018 (Darij Grinberg): midterm 2 with solutions [preliminary version]
![Math 4707 Spring 2018 (Darij Grinberg): midterm 2 page 1. Math 4707 Spring 2018 (Darij Grinberg): midterm 2 with solutions [preliminary version]](/thumbs/85/91691469.jpg "Math 4707 Spring 2018 (Darij Grinberg): midterm 2 page 1. Math 4707 Spring 2018 (Darij Grinberg): midterm 2 with solutions [preliminary version]")
Math 4707 Sprig 08 Darij Griberg: idter page Math 4707 Sprig 08 Darij Griberg: idter with solutios [preliiary versio] Cotets 0.. Coutig first-eve tuples......................... 3 0.. Coutig legal paths
Chapter 8. Euler s Gamma function
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Lommel Polynomials. Dr. Klaus Braun taken from [GWa] source. , defined by ( [GWa] 9-6)
![Lommel Polynomials. Dr. Klaus Braun taken from [GWa] source. , defined by ( [GWa] 9-6)](/thumbs/75/72935537.jpg "Lommel Polynomials. Dr. Klaus Braun taken from [GWa] source. , defined by ( [GWa] 9-6)")
Loel Polyoials Dr Klaus Brau tae fro [GWa] source The Loel polyoials g (, efie by ( [GWa] 9-6 fulfill Puttig g / ( -! ( - g ( (,!( -!! ( ( g ( g (, g : g ( : h ( : g ( ( a relatio betwee the oifie Loel
Solution: APPM 1360 Final Spring 2013
APPM 36 Fial Sprig 3. For this proble let the regio R be the regio eclosed by the curve y l( ) ad the lies, y, ad y. (a) (6 pts) Fid the area of the regio R. (b) (6 pts) Suppose the regio R is revolved
A) is empty. B) is a finite set. C) can be a countably infinite set. D) can be an uncountable set.
M.A./M.Sc. (Mathematics) Etrace Examiatio 016-17 Max Time: hours Max Marks: 150 Istructios: There are 50 questios. Every questio has four choices of which exactly oe is correct. For correct aswer, 3 marks