Groups, partitions and representation functions
|
|
|
- Lesley Foster
- 5 years ago
- Views:
Transcription
1 Groups, partitions and representation functions Sándor Z. Kiss, Eszter Rozgonyi, Csaba Sándor bstract Let G be a finite (abelian) group. In this paper we determine all subsets G such that the number of solutions of g = x + y, x, y equals to the number of solutions of g = x + y, x, y G \. We discuss some related problems. 000 MS Mathematics subject classification number: 11B34. Key words and phrases: groups, representation functions. 1 Introduction Let X be a semigroup, written additively. Let 1,..., h be subsets of X and let x be an element of X. We define the ordered representation function R h (x) = #{(a 1,..., a h ) 1 h : a a h = x}. If i = for i = 1,..., h, then we write R (1),h (x) = #{(a 1,..., a h ) : a i : a a h = x}. Let X be an abelian semigroup, written additively. For X, let h denote the set of all h-tuples of. Two h-tuples (a 1,..., a h ) h and (a 1,..., a h ) h are equivalent if there Institute of Mathematics, Budapest University of Technology and Economics, MT-BME Lendület Future Internet Research Group, H-159 B.O. Box, Hungary; Computer and utomation Research Institute of the Hungarian cademy of Sciences, Budapest H-1111, Lágymányosi street 11; kisspest@cs.elte.hu; This author was supported by the OTK Grant No. K77476 and No. NK Institute of Mathematics, Budapest University of Technology and Economics, H-159 B.O. Box, Hungary, reszti@math.bme.hu, The work reported in the paper has been developed in the framework of the project "Talent care and cultivation in the scientific workshops of BME" project. This project is supported by the grant TÁMOP B-10/ This author was supported by the OTK Grant No. K Institute of Mathematics, Budapest University of Technology and Economics, H-159 B.O. Box, Hungary, csandor@math.bme.hu. This author was supported by the OTK Grant No. K
2 is a permutation α : {1,..., h} {1,..., h} such that a α(i) = a i for i = 1,..., h. Two other representation functions arise often and naturally in additive number theory. The unordered representation function,h (x) counts the number of equivalence classes of h-tuples (a 1,..., a h ) such that a a h = x. The unordered restricted representation function R (3),h (x) counts the number of equivalence classes of h-tuples (a 1,..., a h ) of pairwise distinct elements of such that a a h = x. lternative definitions for (x) and R(3) (x) are the following. Denote by D (x) = #{a : a, a + a = x} then and (x) = 1 R(1) (x) + 1 D (x) R (3) (x) = 1 R(1) (x) 1 D (x) Let N be the set of nonnegative integers. Let X = N. nswering a question of Sárközy, Lev [1] and independently Sándor [] characterized all subsets N such that (n) = N\ (n) or R(3) (n) = R(3) N\ (n) from a certain point on. The precise theorems are the following. Theorem (Lev, Sándor, 004). Let X = N. Let N be a positive integer. The equality (n) = R() N\ (n) holds for n N 1 if and only if [0, N 1] = N and m m, m + 1 m for m N. Theorem (Lev, Sándor, 004). Let X = N. Let N be a positive integer. The equality R (3) (n) = R(3) N\ (n) holds for n N 1 if and only if [0, N 1] = N and m m, m + 1 m for m N. Similar statement can not be formulated for the representation function R (1) (n) because R (1) (n) is odd if and only if n, therefore either R(1) (m) or R(1) N\ (m) is odd. nontrivial result is the following in this direction. Theorem 1. Let X = N. The equality R (1) +B (n) = R(1) N\+N\B (n) holds from a certain point on if and only if N \ ( B)) = B < The modular questions were solved by Chen and Yang [3]. Theorem (Chen, Yang, 01). Let X = Z m. The equality R (1) (n) = R(1) N\ (n) holds for all n Z m if and only if m is even and = m/.
3 Theorem (Chen, Yang, 01). Let X = Z m. For i {, 3}, the equality R (i) = R(i) Z (n) m\ holds for all n Z m if and only if m is even and t t + m/ for t = 0, 1,..., m/ 1. We extend the first theorem to arbitrary finite group G and the second theorem to finite abelian group. Theorem. Let X = G be a finite group. The equality R +B (g) = R G\+G\B (g) holds for all g G if and only if + B = G direct consequence is the following. Corollary 1. Let X = G be a finite group. The equality R (1) (g) = R(1) G\ (g) holds for all g G if and only if G is even and = G /. Theorem 3. Let X = G be a finite abelian group. For i {, 3}, the equality R (i) (g) = R (i) G\ (g) holds for all g G if and only if D (g) = D G\ (g) for every g G. Proof Proof of Theorem 1. Denote by S(x) the generating function of a subset S N, i.e. S(x) = x s. The generating function of R +B (n) is (x)b(x), while the generating s S function of R N\+N\B (n) is ( 1 (x))( 1 B(x)). Hence the condition R 1 x 1 x +B(n) = R N\+N\B (n) holds from a certain point on is equivalent to 1 (x)b(x) ( 1 x (x))( 1 B(x)) = p(x), 1 x where p(x) is a polynomial. This is equivalent to (x) + B(x) = 1 + p(x)(1 x). (1) 1 x Let (x) + B(x) = n=0 c nx n, where c n = 0, 1 or. The equation (1) holds if and only if c n = 1 except for finitely many integer n and the number of n for which c n = 0 is equal to the number of n for which c n =. This is equivalent to the condition N \ ( B)) = B <. Proof of Theorem. For a given S G denote by χ S its characteristic function, that is χ S (g) = 1 if g S and χ S (g) = 0 if g S for every g G. Then χ G\S = 1 χ S. 3
4 Obviously, for every g G we have R +B (g) R G\+G\B (g) = χ (c)χ B ( c + g) χ G\ (c)χ G\B ( c + g) = c G c G χ (c)χ B ( c+g) (c))(1 χ B ( c+g)) = c G c G(1 χ χ (c)+ χ B ( c+g) 1 = c G c G c G + B G. Hence if R +B (g) = R G\+G\B (g) for every g G then + B = G and if + B = G then R +B (g) = R G\+G\B (g) for every g G. Proof of Theorem 3. We only prove the case i =, because the proof of case i = 3 are very similar. Obviously, for every fixed g G we have = #{(a, y) : a, y G, a + y = g} = #{(a, y) : a, y, a + y = g} + #{(a, y) : a, y G \, a + y = g} = R + (g) + R +G\ (g) = (g) D (g) + R +G\ (g), thus Similarly, (g) = D (g) 1 R +G\(g). G \ = #{(x, b) : x G, b G \, x + b = g} = #{(x, b) : x G \, b G \, x + b = g} + #{(x, b) : x, b G \, x + b = g} = R G\+G\ (g) + R +G\ (g) = G\ (g) D G\(g) + R +G\ (g), thus G\ (g) = 1 G \ + 1 D G\(g) 1 R +G\(g). Hence for every g G we have (g) R() G\ (g) = D (g) ( 1 G \ + 1 D G\(g)) = 1 G + 1 (D (g) D G\ (g)). 4
5 Suppose that (g) = R() G\ (g) for every g G. Then we have ( ) + 1 = (g) = ( ) G \ + 1 G\ (g) =, therefore = G \, that is = G. Hence we get that D (g) = D G\ (g) for every g G. Finally, suppose that D (g) = D G\ (g) for every g G. Then we have = D (g) = D G\ (g) = G \, therefore = G, thus we get that (g) = R() G\ (g) for every g G, which completes the proof. References [1] Sándor, Csaba, Partitions of natural numbers and their representation functions. Integers 4 (004), 18, 5 pp. [] Lev, Vsevolod F., Reconstructing integer sets from their representation functions. Electron. J. Combin. 11 (004), no. 1, Research Paper 78, 6 pp. [3] Yang, Quan-Hui; Chen, Feng-Juan, Partitions of Z m with the same representation functions. ustralas. J. Combin. 53 (01),
Partitions of the set of nonnegative integers with the same representation functions
 Partitions of the set of nonnegative integers with the same representation functions Sándor Z. Kiss, Csaba Sándor arxiv:1606.0699v [math.nt] 10 Aug 016 Abstract For a set of nonnegative integers S let
Partitions of the set of nonnegative integers with the same representation functions Sándor Z. Kiss, Csaba Sándor arxiv:1606.0699v [math.nt] 10 Aug 016 Abstract For a set of nonnegative integers S let
Reconstructing integer sets from their representation functions
 Reconstructing integer sets from their representation functions Vsevolod F. Lev Department of Mathematics University of Haifa at Oranim Tivon 36006, Israel seva@math.haifa.ac.il Submitted: Oct 5, 2004;
Reconstructing integer sets from their representation functions Vsevolod F. Lev Department of Mathematics University of Haifa at Oranim Tivon 36006, Israel seva@math.haifa.ac.il Submitted: Oct 5, 2004;
#A45 INTEGERS 9 (2009), BALANCED SUBSET SUMS IN DENSE SETS OF INTEGERS. Gyula Károlyi 1. H 1117, Hungary
 #A45 INTEGERS 9 (2009, 591-603 BALANCED SUBSET SUMS IN DENSE SETS OF INTEGERS Gyula Károlyi 1 Institute of Mathematics, Eötvös University, Pázmány P. sétány 1/C, Budapest, H 1117, Hungary karolyi@cs.elte.hu
#A45 INTEGERS 9 (2009, 591-603 BALANCED SUBSET SUMS IN DENSE SETS OF INTEGERS Gyula Károlyi 1 Institute of Mathematics, Eötvös University, Pázmány P. sétány 1/C, Budapest, H 1117, Hungary karolyi@cs.elte.hu
MTHSC 3190 Section 2.9 Sets a first look
 MTHSC 3190 Section 2.9 Sets a first look Definition A set is a repetition free unordered collection of objects called elements. Definition A set is a repetition free unordered collection of objects called
MTHSC 3190 Section 2.9 Sets a first look Definition A set is a repetition free unordered collection of objects called elements. Definition A set is a repetition free unordered collection of objects called
CHARACTER EXPANSIVENESS IN FINITE GROUPS
 CHARACTER EXPANSIVENESS IN FINITE GROUPS Abstract. We say that a finite group G is conjugacy expansive if for any normal subset S and any conjugacy class C of G the normal set SC consists of at least as
CHARACTER EXPANSIVENESS IN FINITE GROUPS Abstract. We say that a finite group G is conjugacy expansive if for any normal subset S and any conjugacy class C of G the normal set SC consists of at least as
MATH 580, midterm exam SOLUTIONS
 MATH 580, midterm exam SOLUTIONS Solve the problems in the spaces provided on the question sheets. If you run out of room for an answer, continue on the back of the page or use the Extra space empty page
MATH 580, midterm exam SOLUTIONS Solve the problems in the spaces provided on the question sheets. If you run out of room for an answer, continue on the back of the page or use the Extra space empty page
Another Proof of Nathanson s Theorems
 1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 14 (2011), Article 11.8.4 Another Proof of Nathanson s Theorems Quan-Hui Yang School of Mathematical Sciences Nanjing Normal University Nanjing 210046
1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 14 (2011), Article 11.8.4 Another Proof of Nathanson s Theorems Quan-Hui Yang School of Mathematical Sciences Nanjing Normal University Nanjing 210046
Combinatorial Enumeration. Jason Z. Gao Carleton University, Ottawa, Canada
 Combinatorial Enumeration Jason Z. Gao Carleton University, Ottawa, Canada Counting Combinatorial Structures We are interested in counting combinatorial (discrete) structures of a given size. For example,
Combinatorial Enumeration Jason Z. Gao Carleton University, Ottawa, Canada Counting Combinatorial Structures We are interested in counting combinatorial (discrete) structures of a given size. For example,
ON MONOCHROMATIC LINEAR RECURRENCE SEQUENCES
 Volume 11, Number 2, Pages 58 62 ISSN 1715-0868 ON MONOCHROMATIC LINEAR RECURRENCE SEQUENCES Abstract. In this paper we prove some van der Waerden type theorems for linear recurrence sequences. Under the
Volume 11, Number 2, Pages 58 62 ISSN 1715-0868 ON MONOCHROMATIC LINEAR RECURRENCE SEQUENCES Abstract. In this paper we prove some van der Waerden type theorems for linear recurrence sequences. Under the
arxiv:math/ v2 [math.nt] 3 Dec 2003
![arxiv:math/ v2 [math.nt] 3 Dec 2003 arxiv:math/ v2 [math.nt] 3 Dec 2003](/thumbs/95/123663789.jpg) arxiv:math/0302091v2 [math.nt] 3 Dec 2003 Every function is the representation function of an additive basis for the integers Melvyn B. Nathanson Department of Mathematics Lehman College (CUNY) Bronx,
arxiv:math/0302091v2 [math.nt] 3 Dec 2003 Every function is the representation function of an additive basis for the integers Melvyn B. Nathanson Department of Mathematics Lehman College (CUNY) Bronx,
Definition: Let S and T be sets. A binary relation on SxT is any subset of SxT. A binary relation on S is any subset of SxS.
 4 Functions Before studying functions we will first quickly define a more general idea, namely the notion of a relation. A function turns out to be a special type of relation. Definition: Let S and T be
4 Functions Before studying functions we will first quickly define a more general idea, namely the notion of a relation. A function turns out to be a special type of relation. Definition: Let S and T be
arxiv: v2 [math.nt] 21 May 2016
![arxiv: v2 [math.nt] 21 May 2016 arxiv: v2 [math.nt] 21 May 2016](/thumbs/72/67332993.jpg) arxiv:165.156v2 [math.nt] 21 May 216 PROGRESSION-FREE SETS IN Z n 4 ARE EXPONENTIALLY SMALL ERNIE CROOT, VSEVOLOD F. LEV, AND PÉTER PÁL PACH Abstract. We show that for integer n 1, any subset A Z n 4 free
arxiv:165.156v2 [math.nt] 21 May 216 PROGRESSION-FREE SETS IN Z n 4 ARE EXPONENTIALLY SMALL ERNIE CROOT, VSEVOLOD F. LEV, AND PÉTER PÁL PACH Abstract. We show that for integer n 1, any subset A Z n 4 free
Mathematics for Cryptography
 Mathematics for Cryptography Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo Waterloo, Ontario, N2L 3G1, Canada March 15, 2016 1 Groups and Modular Arithmetic 1.1
Mathematics for Cryptography Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo Waterloo, Ontario, N2L 3G1, Canada March 15, 2016 1 Groups and Modular Arithmetic 1.1
Commentationes Mathematicae Universitatis Carolinae
 Commentationes Mathematicae Universitatis Carolinae Keresztély Corrádi; Sándor Szabó A Hajós type result on factoring finite abelian groups by subsets. II Commentationes Mathematicae Universitatis Carolinae,
Commentationes Mathematicae Universitatis Carolinae Keresztély Corrádi; Sándor Szabó A Hajós type result on factoring finite abelian groups by subsets. II Commentationes Mathematicae Universitatis Carolinae,
Invertible Matrices over Idempotent Semirings
 Chamchuri Journal of Mathematics Volume 1(2009) Number 2, 55 61 http://www.math.sc.chula.ac.th/cjm Invertible Matrices over Idempotent Semirings W. Mora, A. Wasanawichit and Y. Kemprasit Received 28 Sep
Chamchuri Journal of Mathematics Volume 1(2009) Number 2, 55 61 http://www.math.sc.chula.ac.th/cjm Invertible Matrices over Idempotent Semirings W. Mora, A. Wasanawichit and Y. Kemprasit Received 28 Sep
Today. Wrapup of Polynomials...and modular arithmetic. Coutability and Uncountability.
 Today. Wrapup of Polynomials...and modular arithmetic. Coutability and Uncountability. Reed-Solomon code. Problem: Communicate n packets m 1,...,m n on noisy channel that corrupts k packets. Reed-Solomon
Today. Wrapup of Polynomials...and modular arithmetic. Coutability and Uncountability. Reed-Solomon code. Problem: Communicate n packets m 1,...,m n on noisy channel that corrupts k packets. Reed-Solomon
What you learned in Math 28. Rosa C. Orellana
 What you learned in Math 28 Rosa C. Orellana Chapter 1 - Basic Counting Techniques Sum Principle If we have a partition of a finite set S, then the size of S is the sum of the sizes of the blocks of the
What you learned in Math 28 Rosa C. Orellana Chapter 1 - Basic Counting Techniques Sum Principle If we have a partition of a finite set S, then the size of S is the sum of the sizes of the blocks of the
A PROOF OF BURNSIDE S p a q b THEOREM
 A PROOF OF BURNSIDE S p a q b THEOREM OBOB Abstract. We prove that if p and q are prime, then any group of order p a q b is solvable. Throughout this note, denote by A the set of algebraic numbers. We
A PROOF OF BURNSIDE S p a q b THEOREM OBOB Abstract. We prove that if p and q are prime, then any group of order p a q b is solvable. Throughout this note, denote by A the set of algebraic numbers. We
arxiv: v1 [math.co] 26 Dec 2018
![arxiv: v1 [math.co] 26 Dec 2018 arxiv: v1 [math.co] 26 Dec 2018](/thumbs/93/111240580.jpg) ON MINIMAL COMPLEMENTS IN GROUPS ARINDAM BISWAS AND JYOTI PRAKASH SAHA arxiv:1812.10285v1 [math.co] 26 Dec 2018 Abstract. Let W,W G be nonempty subsets in an arbitrary group G. W is said to be a complement
ON MINIMAL COMPLEMENTS IN GROUPS ARINDAM BISWAS AND JYOTI PRAKASH SAHA arxiv:1812.10285v1 [math.co] 26 Dec 2018 Abstract. Let W,W G be nonempty subsets in an arbitrary group G. W is said to be a complement
Acta Acad. Paed. Agriensis, Sectio Mathematicae 28 (2001) 21 26
 Acta Acad. Paed. Agriensis, Sectio Mathematicae 8 (00) 6 APPROXIMATION BY QUOTIENTS OF TERMS OF SECOND ORDER LINEAR RECURSIVE SEQUENCES OF INTEGERS Sándor H.-Molnár (Budapest, Hungary) Abstract. In the
Acta Acad. Paed. Agriensis, Sectio Mathematicae 8 (00) 6 APPROXIMATION BY QUOTIENTS OF TERMS OF SECOND ORDER LINEAR RECURSIVE SEQUENCES OF INTEGERS Sándor H.-Molnár (Budapest, Hungary) Abstract. In the
Reachability-based matroid-restricted packing of arborescences
 Egerváry Research Group on Combinatorial Optimization Technical reports TR-2016-19. Published by the Egerváry Research Group, Pázmány P. sétány 1/C, H 1117, Budapest, Hungary. Web site: www.cs.elte.hu/egres.
Egerváry Research Group on Combinatorial Optimization Technical reports TR-2016-19. Published by the Egerváry Research Group, Pázmány P. sétány 1/C, H 1117, Budapest, Hungary. Web site: www.cs.elte.hu/egres.
On prime factors of subset sums
 On prime factors of subset sums by P. Erdös, A. Sárközy and C.L. Stewart * 1 Introduction For any set X let X denote its cardinality and for any integer n larger than one let ω(n) denote the number of
On prime factors of subset sums by P. Erdös, A. Sárközy and C.L. Stewart * 1 Introduction For any set X let X denote its cardinality and for any integer n larger than one let ω(n) denote the number of
COUNTING NUMERICAL SEMIGROUPS BY GENUS AND SOME CASES OF A QUESTION OF WILF
 COUNTING NUMERICAL SEMIGROUPS BY GENUS AND SOME CASES OF A QUESTION OF WILF NATHAN KAPLAN Abstract. The genus of a numerical semigroup is the size of its complement. In this paper we will prove some results
COUNTING NUMERICAL SEMIGROUPS BY GENUS AND SOME CASES OF A QUESTION OF WILF NATHAN KAPLAN Abstract. The genus of a numerical semigroup is the size of its complement. In this paper we will prove some results
Large Sets in Boolean and Non-Boolean Groups and Topology
 axioms Article Large Sets in Boolean and Non-Boolean Groups and Topology Ol ga V. Sipacheva ID Department of General Topology and Geometry, Lomonosov Moscow State University, Leninskie Gory 1, Moscow 119991,
axioms Article Large Sets in Boolean and Non-Boolean Groups and Topology Ol ga V. Sipacheva ID Department of General Topology and Geometry, Lomonosov Moscow State University, Leninskie Gory 1, Moscow 119991,
MODEL ANSWERS TO THE SEVENTH HOMEWORK. (b) We proved in homework six, question 2 (c) that. But we also proved homework six, question 2 (a) that
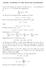 MODEL ANSWERS TO THE SEVENTH HOMEWORK 1. Let X be a finite set, and let A, B and A 1, A 2,..., A n be subsets of X. Let A c = X \ A denote the complement. (a) χ A (x) = A. x X (b) We proved in homework
MODEL ANSWERS TO THE SEVENTH HOMEWORK 1. Let X be a finite set, and let A, B and A 1, A 2,..., A n be subsets of X. Let A c = X \ A denote the complement. (a) χ A (x) = A. x X (b) We proved in homework
Downloaded 03/01/17 to Redistribution subject to SIAM license or copyright; see
 SIAM J. DISCRETE MATH. Vol. 31, No. 1, pp. 335 382 c 2017 Society for Industrial and Applied Mathematics PARTITION CONSTRAINED COVERING OF A SYMMETRIC CROSSING SUPERMODULAR FUNCTION BY A GRAPH ATTILA BERNÁTH,
SIAM J. DISCRETE MATH. Vol. 31, No. 1, pp. 335 382 c 2017 Society for Industrial and Applied Mathematics PARTITION CONSTRAINED COVERING OF A SYMMETRIC CROSSING SUPERMODULAR FUNCTION BY A GRAPH ATTILA BERNÁTH,
On reducible and primitive subsets of F p, II
 On reducible and primitive subsets of F p, II by Katalin Gyarmati Eötvös Loránd University Department of Algebra and Number Theory and MTA-ELTE Geometric and Algebraic Combinatorics Research Group H-1117
On reducible and primitive subsets of F p, II by Katalin Gyarmati Eötvös Loránd University Department of Algebra and Number Theory and MTA-ELTE Geometric and Algebraic Combinatorics Research Group H-1117
Reed-Solomon code. P(n + 2k)
 Reed-Solomon code. Problem: Communicate n packets m 1,...,m n on noisy channel that corrupts k packets. Reed-Solomon Code: 1. Make a polynomial, P(x) of degree n 1, that encodes message: coefficients,
Reed-Solomon code. Problem: Communicate n packets m 1,...,m n on noisy channel that corrupts k packets. Reed-Solomon Code: 1. Make a polynomial, P(x) of degree n 1, that encodes message: coefficients,
arxiv: v1 [math.nt] 11 Jun 2017
![arxiv: v1 [math.nt] 11 Jun 2017 arxiv: v1 [math.nt] 11 Jun 2017](/thumbs/93/111706441.jpg) Powerful numbers in (1 l +q l )( l +q l ) (n l +q l ) arxiv:1706.03350v1 [math.nt] 11 Jun 017 Quan-Hui Yang 1 Qing-Qing Zhao 1. School of Mathematics and Statistics, Nanjing University of Information Science
Powerful numbers in (1 l +q l )( l +q l ) (n l +q l ) arxiv:1706.03350v1 [math.nt] 11 Jun 017 Quan-Hui Yang 1 Qing-Qing Zhao 1. School of Mathematics and Statistics, Nanjing University of Information Science
0 Sets and Induction. Sets
 0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
CONSECUTIVE INTEGERS IN HIGH-MULTIPLICITY SUMSETS
 CONSECUTIVE INTEGERS IN HIGH-MULTIPLICITY SUMSETS VSEVOLOD F. LEV Abstract. Sharpening (a particular case of) a result of Szemerédi and Vu [4] and extending earlier results of Sárközy [3] and ourselves
CONSECUTIVE INTEGERS IN HIGH-MULTIPLICITY SUMSETS VSEVOLOD F. LEV Abstract. Sharpening (a particular case of) a result of Szemerédi and Vu [4] and extending earlier results of Sárközy [3] and ourselves
Maximal non-commuting subsets of groups
 Maximal non-commuting subsets of groups Umut Işık March 29, 2005 Abstract Given a finite group G, we consider the problem of finding the maximal size nc(g) of subsets of G that have the property that no
Maximal non-commuting subsets of groups Umut Işık March 29, 2005 Abstract Given a finite group G, we consider the problem of finding the maximal size nc(g) of subsets of G that have the property that no
On the indecomposability of polynomials
 On the indecomposability of polynomials Andrej Dujella, Ivica Gusić and Robert F. Tichy Abstract Applying a combinatorial lemma a new sufficient condition for the indecomposability of integer polynomials
On the indecomposability of polynomials Andrej Dujella, Ivica Gusić and Robert F. Tichy Abstract Applying a combinatorial lemma a new sufficient condition for the indecomposability of integer polynomials
Legendre s Equation. PHYS Southern Illinois University. October 18, 2016
 Legendre s Equation PHYS 500 - Southern Illinois University October 18, 2016 PHYS 500 - Southern Illinois University Legendre s Equation October 18, 2016 1 / 11 Legendre s Equation Recall We are trying
Legendre s Equation PHYS 500 - Southern Illinois University October 18, 2016 PHYS 500 - Southern Illinois University Legendre s Equation October 18, 2016 1 / 11 Legendre s Equation Recall We are trying
RESIDUAL SMALLNESS AND WEAK CENTRALITY
 RESIDUAL SMALLNESS AND WEAK CENTRALITY KEITH A. KEARNES AND EMIL W. KISS Abstract. We develop a method of creating skew congruences on subpowers of finite algebras using groups of twin polynomials, and
RESIDUAL SMALLNESS AND WEAK CENTRALITY KEITH A. KEARNES AND EMIL W. KISS Abstract. We develop a method of creating skew congruences on subpowers of finite algebras using groups of twin polynomials, and
May 6, Be sure to write your name on your bluebook. Use a separate page (or pages) for each problem. Show all of your work.
 Math 236H May 6, 2008 Be sure to write your name on your bluebook. Use a separate page (or pages) for each problem. Show all of your work. 1. (15 points) Prove that the symmetric group S 4 is generated
Math 236H May 6, 2008 Be sure to write your name on your bluebook. Use a separate page (or pages) for each problem. Show all of your work. 1. (15 points) Prove that the symmetric group S 4 is generated
The p n sequences of semigroup varieties generated by combinatorial 0-simple semigroups
 The p n sequences of semigroup varieties generated by combinatorial 0-simple semigroups Kamilla Kátai-Urbán and Csaba Szabó Abstract. We analyze the free spectra of semigroup varieties generated by finite
The p n sequences of semigroup varieties generated by combinatorial 0-simple semigroups Kamilla Kátai-Urbán and Csaba Szabó Abstract. We analyze the free spectra of semigroup varieties generated by finite
Powers of 2 with five distinct summands
 ACTA ARITHMETICA * (200*) Powers of 2 with five distinct summands by Vsevolod F. Lev (Haifa) 0. Summary. We show that every sufficiently large, finite set of positive integers of density larger than 1/3
ACTA ARITHMETICA * (200*) Powers of 2 with five distinct summands by Vsevolod F. Lev (Haifa) 0. Summary. We show that every sufficiently large, finite set of positive integers of density larger than 1/3
ABSOLUTELY FLAT IDEMPOTENTS
 ABSOLUTELY FLAT IDEMPOTENTS JONATHAN M GROVES, YONATAN HAREL, CHRISTOPHER J HILLAR, CHARLES R JOHNSON, AND PATRICK X RAULT Abstract A real n-by-n idempotent matrix A with all entries having the same absolute
ABSOLUTELY FLAT IDEMPOTENTS JONATHAN M GROVES, YONATAN HAREL, CHRISTOPHER J HILLAR, CHARLES R JOHNSON, AND PATRICK X RAULT Abstract A real n-by-n idempotent matrix A with all entries having the same absolute
Groups and Symmetries
 Groups and Symmetries Definition: Symmetry A symmetry of a shape is a rigid motion that takes vertices to vertices, edges to edges. Note: A rigid motion preserves angles and distances. Definition: Group
Groups and Symmetries Definition: Symmetry A symmetry of a shape is a rigid motion that takes vertices to vertices, edges to edges. Note: A rigid motion preserves angles and distances. Definition: Group
Discrete Mathematics, Spring 2004 Homework 4 Sample Solutions
 Discrete Mathematics, Spring 2004 Homework 4 Sample Solutions 4.2 #77. Let s n,k denote the number of ways to seat n persons at k round tables, with at least one person at each table. (The numbers s n,k
Discrete Mathematics, Spring 2004 Homework 4 Sample Solutions 4.2 #77. Let s n,k denote the number of ways to seat n persons at k round tables, with at least one person at each table. (The numbers s n,k
120A LECTURE OUTLINES
 120A LECTURE OUTLINES RUI WANG CONTENTS 1. Lecture 1. Introduction 1 2 1.1. An algebraic object to study 2 1.2. Group 2 1.3. Isomorphic binary operations 2 2. Lecture 2. Introduction 2 3 2.1. The multiplication
120A LECTURE OUTLINES RUI WANG CONTENTS 1. Lecture 1. Introduction 1 2 1.1. An algebraic object to study 2 1.2. Group 2 1.3. Isomorphic binary operations 2 2. Lecture 2. Introduction 2 3 2.1. The multiplication
ON GENERALIZED BALANCING SEQUENCES
 ON GENERALIZED BALANCING SEQUENCES ATTILA BÉRCZES, KÁLMÁN LIPTAI, AND ISTVÁN PINK Abstract. Let R i = R(A, B, R 0, R 1 ) be a second order linear recurrence sequence. In the present paper we prove that
ON GENERALIZED BALANCING SEQUENCES ATTILA BÉRCZES, KÁLMÁN LIPTAI, AND ISTVÁN PINK Abstract. Let R i = R(A, B, R 0, R 1 ) be a second order linear recurrence sequence. In the present paper we prove that
Chapter 5: Integer Compositions and Partitions and Set Partitions
 Chapter 5: Integer Compositions and Partitions and Set Partitions Prof. Tesler Math 184A Winter 2017 Prof. Tesler Ch. 5: Compositions and Partitions Math 184A / Winter 2017 1 / 32 5.1. Compositions A strict
Chapter 5: Integer Compositions and Partitions and Set Partitions Prof. Tesler Math 184A Winter 2017 Prof. Tesler Ch. 5: Compositions and Partitions Math 184A / Winter 2017 1 / 32 5.1. Compositions A strict
On the number of cycles in a graph with restricted cycle lengths
 On the number of cycles in a graph with restricted cycle lengths Dániel Gerbner, Balázs Keszegh, Cory Palmer, Balázs Patkós arxiv:1610.03476v1 [math.co] 11 Oct 2016 October 12, 2016 Abstract Let L be a
On the number of cycles in a graph with restricted cycle lengths Dániel Gerbner, Balázs Keszegh, Cory Palmer, Balázs Patkós arxiv:1610.03476v1 [math.co] 11 Oct 2016 October 12, 2016 Abstract Let L be a
Homework #2 Solutions Due: September 5, for all n N n 3 = n2 (n + 1) 2 4
 Do the following exercises from the text: Chapter (Section 3):, 1, 17(a)-(b), 3 Prove that 1 3 + 3 + + n 3 n (n + 1) for all n N Proof The proof is by induction on n For n N, let S(n) be the statement
Do the following exercises from the text: Chapter (Section 3):, 1, 17(a)-(b), 3 Prove that 1 3 + 3 + + n 3 n (n + 1) for all n N Proof The proof is by induction on n For n N, let S(n) be the statement
Permutations and Combinations
 Permutations and Combinations Permutations Definition: Let S be a set with n elements A permutation of S is an ordered list (arrangement) of its elements For r = 1,..., n an r-permutation of S is an ordered
Permutations and Combinations Permutations Definition: Let S be a set with n elements A permutation of S is an ordered list (arrangement) of its elements For r = 1,..., n an r-permutation of S is an ordered
Problems in Linear Algebra and Representation Theory
 Problems in Linear Algebra and Representation Theory (Most of these were provided by Victor Ginzburg) The problems appearing below have varying level of difficulty. They are not listed in any specific
Problems in Linear Algebra and Representation Theory (Most of these were provided by Victor Ginzburg) The problems appearing below have varying level of difficulty. They are not listed in any specific
Homework #5 Solutions
 Homework #5 Solutions p 83, #16. In order to find a chain a 1 a 2 a n of subgroups of Z 240 with n as large as possible, we start at the top with a n = 1 so that a n = Z 240. In general, given a i we will
Homework #5 Solutions p 83, #16. In order to find a chain a 1 a 2 a n of subgroups of Z 240 with n as large as possible, we start at the top with a n = 1 so that a n = Z 240. In general, given a i we will
Generating Permutations and Combinations
 Generating Permutations and Combinations March 0, 005 Generating Permutations We have learned that there are n! permutations of {,,, n} It is important in many instances to generate a list of such permutations
Generating Permutations and Combinations March 0, 005 Generating Permutations We have learned that there are n! permutations of {,,, n} It is important in many instances to generate a list of such permutations
A GUIDE FOR MORTALS TO TAME CONGRUENCE THEORY
 A GUIDE FOR MORTALS TO TAME CONGRUENCE THEORY Tame congruence theory is not an easy subject and it takes a considerable amount of effort to understand it. When I started this project, I believed that this
A GUIDE FOR MORTALS TO TAME CONGRUENCE THEORY Tame congruence theory is not an easy subject and it takes a considerable amount of effort to understand it. When I started this project, I believed that this
Chapter 5: Integer Compositions and Partitions and Set Partitions
 Chapter 5: Integer Compositions and Partitions and Set Partitions Prof. Tesler Math 184A Fall 2017 Prof. Tesler Ch. 5: Compositions and Partitions Math 184A / Fall 2017 1 / 46 5.1. Compositions A strict
Chapter 5: Integer Compositions and Partitions and Set Partitions Prof. Tesler Math 184A Fall 2017 Prof. Tesler Ch. 5: Compositions and Partitions Math 184A / Fall 2017 1 / 46 5.1. Compositions A strict
Incomplete Pairwise Comparison Matrices and Weighting Methods
 Incomplete Pairwise Comparison Matrices and Weighting Methods László Csató Lajos Rónyai arxiv:1507.00461v2 [math.oc] 27 Aug 2015 August 28, 2015 Abstract A special class of preferences, given by a directed
Incomplete Pairwise Comparison Matrices and Weighting Methods László Csató Lajos Rónyai arxiv:1507.00461v2 [math.oc] 27 Aug 2015 August 28, 2015 Abstract A special class of preferences, given by a directed
MA2501 Numerical Methods Spring 2015
 Norwegian University of Science and Technology Department of Mathematics MA5 Numerical Methods Spring 5 Solutions to exercise set 9 Find approximate values of the following integrals using the adaptive
Norwegian University of Science and Technology Department of Mathematics MA5 Numerical Methods Spring 5 Solutions to exercise set 9 Find approximate values of the following integrals using the adaptive
On zero-sum partitions and anti-magic trees
 Discrete Mathematics 09 (009) 010 014 Contents lists available at ScienceDirect Discrete Mathematics journal homepage: wwwelseviercom/locate/disc On zero-sum partitions and anti-magic trees Gil Kaplan,
Discrete Mathematics 09 (009) 010 014 Contents lists available at ScienceDirect Discrete Mathematics journal homepage: wwwelseviercom/locate/disc On zero-sum partitions and anti-magic trees Gil Kaplan,
COLLAPSING PERMUTATION GROUPS
 COLLAPSING PERMUTATION GROUPS KEITH A. KEARNES AND ÁGNES SZENDREI Abstract. It is shown in [3] that any nonregular quasiprimitive permutation group is collapsing. In this paper we describe a wider class
COLLAPSING PERMUTATION GROUPS KEITH A. KEARNES AND ÁGNES SZENDREI Abstract. It is shown in [3] that any nonregular quasiprimitive permutation group is collapsing. In this paper we describe a wider class
The power graph of a finite group, II
 The power graph of a finite group, II Peter J. Cameron School of Mathematical Sciences Queen Mary, University of London Mile End Road London E1 4NS, U.K. Abstract The directed power graph of a group G
The power graph of a finite group, II Peter J. Cameron School of Mathematical Sciences Queen Mary, University of London Mile End Road London E1 4NS, U.K. Abstract The directed power graph of a group G
Spanning, linear dependence, dimension
 Spanning, linear dependence, dimension In the crudest possible measure of these things, the real line R and the plane R have the same size (and so does 3-space, R 3 ) That is, there is a function between
Spanning, linear dependence, dimension In the crudest possible measure of these things, the real line R and the plane R have the same size (and so does 3-space, R 3 ) That is, there is a function between
Nilpotency and the number of word maps of a finite group
 Nilpotency and the number of word maps of a finite group arxiv:1704.08214v1 [math.gr] 26 Apr 2017 Alexander Bors September 20, 2018 Abstract For a finite group G and a non-negative integer d, denote by
Nilpotency and the number of word maps of a finite group arxiv:1704.08214v1 [math.gr] 26 Apr 2017 Alexander Bors September 20, 2018 Abstract For a finite group G and a non-negative integer d, denote by
Introduction to proofs. Niloufar Shafiei
 Introduction to proofs Niloufar Shafiei proofs Proofs are essential in mathematics and computer science. Some applications of proof methods Proving mathematical theorems Designing algorithms and proving
Introduction to proofs Niloufar Shafiei proofs Proofs are essential in mathematics and computer science. Some applications of proof methods Proving mathematical theorems Designing algorithms and proving
Inequalities for the First-Fit chromatic number
 Worcester Polytechnic Institute Digital WPI Computer Science Faculty Publications Department of Computer Science 9-007 Inequalities for the First-Fit chromatic number Zoltán Füredi Alfréd Rényi Institute,
Worcester Polytechnic Institute Digital WPI Computer Science Faculty Publications Department of Computer Science 9-007 Inequalities for the First-Fit chromatic number Zoltán Füredi Alfréd Rényi Institute,
Chapter 2 Formulas and Definitions:
 Chapter 2 Formulas and Definitions: (from 2.1) Definition of Polynomial Function: Let n be a nonnegative integer and let a n,a n 1,...,a 2,a 1,a 0 be real numbers with a n 0. The function given by f (x)
Chapter 2 Formulas and Definitions: (from 2.1) Definition of Polynomial Function: Let n be a nonnegative integer and let a n,a n 1,...,a 2,a 1,a 0 be real numbers with a n 0. The function given by f (x)
Homomorphisms of sparse graphs to small graphs
 LaBRI Université Bordeaux I France Graph Theory 2009 Fredericia, Denmark Thursday November 26 - Sunday November 29 Flow Let G be a directed graph, A be an abelian group. A-flow A-flow f of G is a mapping
LaBRI Université Bordeaux I France Graph Theory 2009 Fredericia, Denmark Thursday November 26 - Sunday November 29 Flow Let G be a directed graph, A be an abelian group. A-flow A-flow f of G is a mapping
Some thoughts concerning power sums
 Some thoughts concerning power sums Dedicated to the memory of Zoltán Szvetits (929 20 Gábor Nyul Institute of Mathematics, University of Debrecen H 00 Debrecen POBox 2, Hungary e mail: gnyul@scienceunidebhu
Some thoughts concerning power sums Dedicated to the memory of Zoltán Szvetits (929 20 Gábor Nyul Institute of Mathematics, University of Debrecen H 00 Debrecen POBox 2, Hungary e mail: gnyul@scienceunidebhu
SOME VARIANTS OF LAGRANGE S FOUR SQUARES THEOREM
 Acta Arith. 183(018), no. 4, 339 36. SOME VARIANTS OF LAGRANGE S FOUR SQUARES THEOREM YU-CHEN SUN AND ZHI-WEI SUN Abstract. Lagrange s four squares theorem is a classical theorem in number theory. Recently,
Acta Arith. 183(018), no. 4, 339 36. SOME VARIANTS OF LAGRANGE S FOUR SQUARES THEOREM YU-CHEN SUN AND ZHI-WEI SUN Abstract. Lagrange s four squares theorem is a classical theorem in number theory. Recently,
TOPOLOGICAL COMPLEXITY OF 2-TORSION LENS SPACES AND ku-(co)homology
 TOPOLOGICAL COMPLEXITY OF 2-TORSION LENS SPACES AND ku-(co)homology DONALD M. DAVIS Abstract. We use ku-cohomology to determine lower bounds for the topological complexity of mod-2 e lens spaces. In the
TOPOLOGICAL COMPLEXITY OF 2-TORSION LENS SPACES AND ku-(co)homology DONALD M. DAVIS Abstract. We use ku-cohomology to determine lower bounds for the topological complexity of mod-2 e lens spaces. In the
REPRESENTATION THEORY OF S n
 REPRESENTATION THEORY OF S n EVAN JENKINS Abstract. These are notes from three lectures given in MATH 26700, Introduction to Representation Theory of Finite Groups, at the University of Chicago in November
REPRESENTATION THEORY OF S n EVAN JENKINS Abstract. These are notes from three lectures given in MATH 26700, Introduction to Representation Theory of Finite Groups, at the University of Chicago in November
Notes for Math 290 using Introduction to Mathematical Proofs by Charles E. Roberts, Jr.
 Notes for Math 290 using Introduction to Mathematical Proofs by Charles E. Roberts, Jr. Chapter : Logic Topics:. Statements, Negation, and Compound Statements.2 Truth Tables and Logical Equivalences.3
Notes for Math 290 using Introduction to Mathematical Proofs by Charles E. Roberts, Jr. Chapter : Logic Topics:. Statements, Negation, and Compound Statements.2 Truth Tables and Logical Equivalences.3
arxiv: v1 [math.ra] 2 Mar 2008 Victor Bovdi, Tibor Rozgonyi 1
![arxiv: v1 [math.ra] 2 Mar 2008 Victor Bovdi, Tibor Rozgonyi 1 arxiv: v1 [math.ra] 2 Mar 2008 Victor Bovdi, Tibor Rozgonyi 1](/thumbs/89/97530889.jpg) ON THE UNITARY SUBGROUP OF MODULAR GROUP ALGEBRAS arxiv:0803.0118v1 [math.ra] 2 Mar 2008 Victor Bovdi, Tibor Rozgonyi 1 Abstract. It this note we investigate the structure of the group of σ-unitary units
ON THE UNITARY SUBGROUP OF MODULAR GROUP ALGEBRAS arxiv:0803.0118v1 [math.ra] 2 Mar 2008 Victor Bovdi, Tibor Rozgonyi 1 Abstract. It this note we investigate the structure of the group of σ-unitary units
ARITHMETIC PROGRESSIONS IN SPARSE SUMSETS. Dedicated to Ron Graham on the occasion of his 70 th birthday
 ARITHMETIC PROGRESSIONS IN SPARSE SUMSETS Dedicated to Ron Graham on the occasion of his 70 th birthday Ernie Croot 1 School of Mathematics, Georgia Institute of Technology, Atlanta, GA 30332 Imre Ruzsa
ARITHMETIC PROGRESSIONS IN SPARSE SUMSETS Dedicated to Ron Graham on the occasion of his 70 th birthday Ernie Croot 1 School of Mathematics, Georgia Institute of Technology, Atlanta, GA 30332 Imre Ruzsa
Acta Acad. Paed. Agriensis, Sectio Mathematicae 28 (2001) THE LIE AUGMENTATION TERMINALS OF GROUPS. Bertalan Király (Eger, Hungary)
 Acta Acad. Paed. Agriensis, Sectio Mathematicae 28 (2001) 93 97 THE LIE AUGMENTATION TERMINALS OF GROUPS Bertalan Király (Eger, Hungary) Abstract. In this paper we give necessary and sufficient conditions
Acta Acad. Paed. Agriensis, Sectio Mathematicae 28 (2001) 93 97 THE LIE AUGMENTATION TERMINALS OF GROUPS Bertalan Király (Eger, Hungary) Abstract. In this paper we give necessary and sufficient conditions
Topics in Algorithms. 1 Generation of Basic Combinatorial Objects. Exercises. 1.1 Generation of Subsets. 1. Consider the sum:
 Topics in Algorithms Exercises 1 Generation of Basic Combinatorial Objects 1.1 Generation of Subsets 1. Consider the sum: (ε 1,...,ε n) {0,1} n f(ε 1,..., ε n ) (a) Show that it may be calculated in O(n)
Topics in Algorithms Exercises 1 Generation of Basic Combinatorial Objects 1.1 Generation of Subsets 1. Consider the sum: (ε 1,...,ε n) {0,1} n f(ε 1,..., ε n ) (a) Show that it may be calculated in O(n)
Chapter 2 notes from powerpoints
 Chapter 2 notes from powerpoints Synthetic division and basic definitions Sections 1 and 2 Definition of a Polynomial Function: Let n be a nonnegative integer and let a n, a n-1,, a 2, a 1, a 0 be real
Chapter 2 notes from powerpoints Synthetic division and basic definitions Sections 1 and 2 Definition of a Polynomial Function: Let n be a nonnegative integer and let a n, a n-1,, a 2, a 1, a 0 be real
ON A PROBLEM OF PILLAI AND ITS GENERALIZATIONS
 ON A PROBLEM OF PILLAI AND ITS GENERALIZATIONS L. HAJDU 1 AND N. SARADHA Abstract. We study some generalizations of a problem of Pillai. We investigate the existence of an integer M such that for m M,
ON A PROBLEM OF PILLAI AND ITS GENERALIZATIONS L. HAJDU 1 AND N. SARADHA Abstract. We study some generalizations of a problem of Pillai. We investigate the existence of an integer M such that for m M,
MATH 131A: REAL ANALYSIS (BIG IDEAS)
 MATH 131A: REAL ANALYSIS (BIG IDEAS) Theorem 1 (The Triangle Inequality). For all x, y R we have x + y x + y. Proposition 2 (The Archimedean property). For each x R there exists an n N such that n > x.
MATH 131A: REAL ANALYSIS (BIG IDEAS) Theorem 1 (The Triangle Inequality). For all x, y R we have x + y x + y. Proposition 2 (The Archimedean property). For each x R there exists an n N such that n > x.
Procedure for Graphing Polynomial Functions
 Procedure for Graphing Polynomial Functions P(x) = a nx n + a n-1x n-1 + + a 1x + a 0 To graph P(x): As an example, we will examine the following polynomial function: P(x) = 2x 3 3x 2 23x + 12 1. Determine
Procedure for Graphing Polynomial Functions P(x) = a nx n + a n-1x n-1 + + a 1x + a 0 To graph P(x): As an example, we will examine the following polynomial function: P(x) = 2x 3 3x 2 23x + 12 1. Determine
Abelian Algebras and the Hamiltonian Property. Abstract. In this paper we show that a nite algebra A is Hamiltonian if the
 Abelian Algebras and the Hamiltonian Property Emil W. Kiss Matthew A. Valeriote y Abstract In this paper we show that a nite algebra A is Hamiltonian if the class HS(A A ) consists of Abelian algebras.
Abelian Algebras and the Hamiltonian Property Emil W. Kiss Matthew A. Valeriote y Abstract In this paper we show that a nite algebra A is Hamiltonian if the class HS(A A ) consists of Abelian algebras.
Permutation groups/1. 1 Automorphism groups, permutation groups, abstract
 Permutation groups Whatever you have to do with a structure-endowed entity Σ try to determine its group of automorphisms... You can expect to gain a deep insight into the constitution of Σ in this way.
Permutation groups Whatever you have to do with a structure-endowed entity Σ try to determine its group of automorphisms... You can expect to gain a deep insight into the constitution of Σ in this way.
Unions of Dominant Chains of Pairwise Disjoint, Completely Isolated Subsemigroups
 Palestine Journal of Mathematics Vol. 4 (Spec. 1) (2015), 490 495 Palestine Polytechnic University-PPU 2015 Unions of Dominant Chains of Pairwise Disjoint, Completely Isolated Subsemigroups Karen A. Linton
Palestine Journal of Mathematics Vol. 4 (Spec. 1) (2015), 490 495 Palestine Polytechnic University-PPU 2015 Unions of Dominant Chains of Pairwise Disjoint, Completely Isolated Subsemigroups Karen A. Linton
ORDERS OF ELEMENTS IN A GROUP
 ORDERS OF ELEMENTS IN A GROUP KEITH CONRAD 1. Introduction Let G be a group and g G. We say g has finite order if g n = e for some positive integer n. For example, 1 and i have finite order in C, since
ORDERS OF ELEMENTS IN A GROUP KEITH CONRAD 1. Introduction Let G be a group and g G. We say g has finite order if g n = e for some positive integer n. For example, 1 and i have finite order in C, since
Zero sum partition of Abelian groups into sets of the same order and its applications
 Zero sum partition of Abelian groups into sets of the same order and its applications Sylwia Cichacz Faculty of Applied Mathematics AGH University of Science and Technology Al. Mickiewicza 30, 30-059 Kraków,
Zero sum partition of Abelian groups into sets of the same order and its applications Sylwia Cichacz Faculty of Applied Mathematics AGH University of Science and Technology Al. Mickiewicza 30, 30-059 Kraków,
International Competition in Mathematics for Universtiy Students in Plovdiv, Bulgaria 1994
 International Competition in Mathematics for Universtiy Students in Plovdiv, Bulgaria 1994 1 PROBLEMS AND SOLUTIONS First day July 29, 1994 Problem 1. 13 points a Let A be a n n, n 2, symmetric, invertible
International Competition in Mathematics for Universtiy Students in Plovdiv, Bulgaria 1994 1 PROBLEMS AND SOLUTIONS First day July 29, 1994 Problem 1. 13 points a Let A be a n n, n 2, symmetric, invertible
Chapter 7 Polynomial Functions. Factoring Review. We will talk about 3 Types: ALWAYS FACTOR OUT FIRST! Ex 2: Factor x x + 64
 Chapter 7 Polynomial Functions Factoring Review We will talk about 3 Types: 1. 2. 3. ALWAYS FACTOR OUT FIRST! Ex 1: Factor x 2 + 5x + 6 Ex 2: Factor x 2 + 16x + 64 Ex 3: Factor 4x 2 + 6x 18 Ex 4: Factor
Chapter 7 Polynomial Functions Factoring Review We will talk about 3 Types: 1. 2. 3. ALWAYS FACTOR OUT FIRST! Ex 1: Factor x 2 + 5x + 6 Ex 2: Factor x 2 + 16x + 64 Ex 3: Factor 4x 2 + 6x 18 Ex 4: Factor
Week 4-5: Generating Permutations and Combinations
 Week 4-5: Generating Permutations and Combinations February 27, 2017 1 Generating Permutations We have learned that there are n! permutations of {1, 2,...,n}. It is important in many instances to generate
Week 4-5: Generating Permutations and Combinations February 27, 2017 1 Generating Permutations We have learned that there are n! permutations of {1, 2,...,n}. It is important in many instances to generate
Upper Bounds for Partitions into k-th Powers Elementary Methods
 Int. J. Contemp. Math. Sciences, Vol. 4, 2009, no. 9, 433-438 Upper Bounds for Partitions into -th Powers Elementary Methods Rafael Jaimczu División Matemática, Universidad Nacional de Luján Buenos Aires,
Int. J. Contemp. Math. Sciences, Vol. 4, 2009, no. 9, 433-438 Upper Bounds for Partitions into -th Powers Elementary Methods Rafael Jaimczu División Matemática, Universidad Nacional de Luján Buenos Aires,
THE INVERSE PROBLEM FOR REPRESENTATION FUNCTIONS FOR GENERAL LINEAR FORMS
 INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 8 (2008), #A16 THE INVERSE PROBLEM FOR REPRESENTATION FUNCTIONS FOR GENERAL LINEAR FORMS Peter Hegarty Department of Mathematics, Chalmers University
INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 8 (2008), #A16 THE INVERSE PROBLEM FOR REPRESENTATION FUNCTIONS FOR GENERAL LINEAR FORMS Peter Hegarty Department of Mathematics, Chalmers University
Selected exercises from Abstract Algebra by Dummit and Foote (3rd edition).
 Selected exercises from Abstract Algebra by Dummit and Foote (3rd edition). Bryan Félix Abril 12, 2017 Section 2.1 Exercise (6). Let G be an abelian group. Prove that T = {g G g < } is a subgroup of G.
Selected exercises from Abstract Algebra by Dummit and Foote (3rd edition). Bryan Félix Abril 12, 2017 Section 2.1 Exercise (6). Let G be an abelian group. Prove that T = {g G g < } is a subgroup of G.
Infinite rank of elliptic curves over Q ab and quadratic twists with positive rank
 Infinite rank of elliptic curves over Q ab and quadratic twists with positive rank Bo-Hae Im Chung-Ang University The 3rd East Asian Number Theory Conference National Taiwan University, Taipei January
Infinite rank of elliptic curves over Q ab and quadratic twists with positive rank Bo-Hae Im Chung-Ang University The 3rd East Asian Number Theory Conference National Taiwan University, Taipei January
Computation of the cycle index polynomial of a Permutation Group CS497-report
 Computation of the cycle index polynomial of a Permutation Group CS497-report Rohit Gurjar Y5383 Supervisor: Prof Piyush P. Kurur Dept. Of Computer Science and Engineering, IIT Kanpur November 3, 2008
Computation of the cycle index polynomial of a Permutation Group CS497-report Rohit Gurjar Y5383 Supervisor: Prof Piyush P. Kurur Dept. Of Computer Science and Engineering, IIT Kanpur November 3, 2008
Partition of Integers into Distinct Summands with Upper Bounds. Partition of Integers into Even Summands. An Example
 Partition of Integers into Even Summands We ask for the number of partitions of m Z + into positive even integers The desired number is the coefficient of x m in + x + x 4 + ) + x 4 + x 8 + ) + x 6 + x
Partition of Integers into Even Summands We ask for the number of partitions of m Z + into positive even integers The desired number is the coefficient of x m in + x + x 4 + ) + x 4 + x 8 + ) + x 6 + x
To Professor W. M. Schmidt on his 60th birthday
 ACTA ARITHMETICA LXVII.3 (1994) On the irreducibility of neighbouring polynomials by K. Győry (Debrecen) To Professor W. M. Schmidt on his 60th birthday 1. Introduction. Denote by P the length of a polynomial
ACTA ARITHMETICA LXVII.3 (1994) On the irreducibility of neighbouring polynomials by K. Győry (Debrecen) To Professor W. M. Schmidt on his 60th birthday 1. Introduction. Denote by P the length of a polynomial
Combining the cycle index and the Tutte polynomial?
 Combining the cycle index and the Tutte polynomial? Peter J. Cameron University of St Andrews Combinatorics Seminar University of Vienna 23 March 2017 Selections Students often meet the following table
Combining the cycle index and the Tutte polynomial? Peter J. Cameron University of St Andrews Combinatorics Seminar University of Vienna 23 March 2017 Selections Students often meet the following table
Finite groups determined by an inequality of the orders of their elements
 Publ. Math. Debrecen 80/3-4 (2012), 457 463 DOI: 10.5486/PMD.2012.5168 Finite groups determined by an inequality of the orders of their elements By MARIUS TĂRNĂUCEANU (Iaşi) Abstract. In this note we introduce
Publ. Math. Debrecen 80/3-4 (2012), 457 463 DOI: 10.5486/PMD.2012.5168 Finite groups determined by an inequality of the orders of their elements By MARIUS TĂRNĂUCEANU (Iaşi) Abstract. In this note we introduce
Coloring Vertices and Edges of a Path by Nonempty Subsets of a Set
 Coloring Vertices and Edges of a Path by Nonempty Subsets of a Set P.N. Balister E. Győri R.H. Schelp November 8, 28 Abstract A graph G is strongly set colorable if V (G) E(G) can be assigned distinct
Coloring Vertices and Edges of a Path by Nonempty Subsets of a Set P.N. Balister E. Győri R.H. Schelp November 8, 28 Abstract A graph G is strongly set colorable if V (G) E(G) can be assigned distinct
Defining the Integral
 Defining the Integral In these notes we provide a careful definition of the Lebesgue integral and we prove each of the three main convergence theorems. For the duration of these notes, let (, M, µ) be
Defining the Integral In these notes we provide a careful definition of the Lebesgue integral and we prove each of the three main convergence theorems. For the duration of these notes, let (, M, µ) be
Determining elements of minimal index in an infinite family of totally real bicyclic biquadratic number fields
 Determining elements of minimal index in an infinite family of totally real bicyclic biquadratic number fields István Gaál, University of Debrecen, Mathematical Institute H 4010 Debrecen Pf.12., Hungary
Determining elements of minimal index in an infinite family of totally real bicyclic biquadratic number fields István Gaál, University of Debrecen, Mathematical Institute H 4010 Debrecen Pf.12., Hungary
Transversal designs and induced decompositions of graphs
 arxiv:1501.03518v1 [math.co] 14 Jan 2015 Transversal designs and induced decompositions of graphs Csilla Bujtás 1 Zsolt Tuza 1,2 1 Department of Computer Science and Systems Technology University of Pannonia
arxiv:1501.03518v1 [math.co] 14 Jan 2015 Transversal designs and induced decompositions of graphs Csilla Bujtás 1 Zsolt Tuza 1,2 1 Department of Computer Science and Systems Technology University of Pannonia
EXTENDED LAGUERRE INEQUALITIES AND A CRITERION FOR REAL ZEROS
 EXTENDED LAGUERRE INEQUALITIES AND A CRITERION FOR REAL ZEROS DAVID A. CARDON Abstract. Let fz) = e bz2 f z) where b 0 and f z) is a real entire function of genus 0 or. We give a necessary and sufficient
EXTENDED LAGUERRE INEQUALITIES AND A CRITERION FOR REAL ZEROS DAVID A. CARDON Abstract. Let fz) = e bz2 f z) where b 0 and f z) is a real entire function of genus 0 or. We give a necessary and sufficient
Polynomial Functions
 Polynomial Functions Polynomials A Polynomial in one variable, x, is an expression of the form a n x 0 a 1 x n 1... a n 2 x 2 a n 1 x a n The coefficients represent complex numbers (real or imaginary),
Polynomial Functions Polynomials A Polynomial in one variable, x, is an expression of the form a n x 0 a 1 x n 1... a n 2 x 2 a n 1 x a n The coefficients represent complex numbers (real or imaginary),
The Symmetric Groups
 Chapter 7 The Symmetric Groups 7. Introduction In the investigation of finite groups the symmetric groups play an important role. Often we are able to achieve a better understanding of a group if we can
Chapter 7 The Symmetric Groups 7. Introduction In the investigation of finite groups the symmetric groups play an important role. Often we are able to achieve a better understanding of a group if we can
