SOME VARIANTS OF LAGRANGE S FOUR SQUARES THEOREM
|
|
|
- Annis Whitehead
- 5 years ago
- Views:
Transcription
1 Acta Arith. 183(018), no. 4, SOME VARIANTS OF LAGRANGE S FOUR SQUARES THEOREM YU-CHEN SUN AND ZHI-WEI SUN Abstract. Lagrange s four squares theorem is a classical theorem in number theory. Recently, Z.-W. Sun found that it can be further refined in various ways. In this paper we study some conjectures of Sun and obtain various refinements of Lagrange s theorem. We show that any nonnegative integer can be written as x + y + z + w (x, y, z, w Z) with x + y + z + w (or x + y + z + w, or x + y + 3z + w) a square (or a cube). Also, every n = 0, 1,,... can be represented by x +y +z +w (x, y, z, w Z) with x + y + 3z (or x + y + 3z) a square (or a cube), and each n = 0, 1,,... can be written as x + y + z + w (x, y, z, w Z) with (10w + x) + (1y + 36z) (or x y + 9y z + 9z x ) a square. We also provide an advance on the 1-3- conjecture of Sun. Our main results are proved by a new approach involving Euler s four-square identity. 1. Introduction In 1770 Lagrange showed that any n N = {0, 1,,...} can be written as the sum of four squares. This celebrated result is now known as Lagrange s four squares theorem. The classical proof of this theorem (cf. [, pp. -7] or [4]) depends heavily on Euler s four-square identity. It is known that (cf. [3]) only the following numbers have a unique representation as the sum of four unordered squares: 1, 3,, 7, 11, 1, 3, k+1 m (k N and m = 1, 3, 7). In 1834, Jacobi (cf. [1, p. 9] or [7, p. 83]) considered the fourth power of the theta function ϕ(q) = q n ( q < 1) n= and this led him to show that r 4 (n) = 8 d for all n Z + = {1,, 3,...}, d n & 4 d 010 Mathematics Subject Classification. Primary 11E; Secondary 11D8, 11E0, 11P0. Key words and phrases. Lagrange s four squares theorem, representations of integers, squares, cubes. 1
2 Y.-C. SUN AND Z.-W. SUN where r 4 (n) := {(w, x, y, z) Z 4 : w + x + y + z = n}. Recently, Sun [6] found that Lagrange s four squares theorem can be refined in various surprising ways. He [6] called a polynomial P (x, y, z, w) with integer coefficients suitable if any n N can be written as x + y + z + w with x, y, z, w N such that P (x, y, z, w) a square. He proved that x, x, x y, x y, x y + y z + z x, x y + 4y z + 4z x are all suitable, and conjectured that there are only finitely many linear suitable polynomials ax + by + cz + dw with a, b, c, d integers and gcd(a, b, c, d) squarefree (cf. the comments following [6, Definition 1.1], and [6, Conjectures 4.1, and 4.1]). Using the theory of ternary quadratic forms, he [6] showed that any n N can be written as x + y + z + w with x, y, z, w Z such that x + y + z (or x + y + z) is a square (or a cube). Our first theorem was originally conjectured by Sun [6, Conjecture 4.1 and Remark 4.10]. Theorem 1.1. (i) The polynomial x + 8yz is suitable, i.e., any n N can be written as x + y + z + w (x, y, z, w N) with x + 8yz a square. (ii) The polynomial x + y is suitable. Moreover, any n Z + can be written as x + y + z + w (x, y, z, w N) with x + y a positive square. Remark 1.1. In contrast with Theorem 1.1(ii), Sun [6, Theorem 1.1(iii)] proved that any n N can be written as x + y + z + w (x, y, z, w Z) with x + y a square (or a cube). Sun [6, Conjecture 4.1] also conjectured that x y is suitable, but we are unable to show this. Our following results deal with integer variables. Theorem 1.. (i) If P (x, y, z) is one of the polynomials x y, x y, x + y z and x + y z, then any n N can be written as x + y + z + w with x, y, z, w Z and P (x, y, z)(x + y + z) = 0. (ii) Let d {1,, 3} and m {, 3}. Then any n N can be written as x + y + z + w with x, y, z, w Z such that x + y + z = dt m for some t Z. Remark 1.. Sun [6, Remark 1.4, parts (iii) and (iv) of Conjecture 4.3] conjectured that the polynomials (x y)(x + y z), (x y)(x + y z), (x + y z)(x + y z), x y z, x + y z
3 are all suitable. SOME VARIANTS OF LAGRANGE S FOUR SQUARES THEOREM 3 Theorem 1.3. (i) For each m =, 3, any n N can be written as x + y + z + w with x, y, z, w Z such that x + y + z + w is an mth power. (ii) Let m, n Z + with n 8 (mod 3). If n can be written as x + y + z + w with x, y, z, w Z such that x + y + z + w is an m-th power, then we must have m 3. Remark 1.3. Sun [6, Conjecture 4.4(v)] conjectured that any positive integer can be written as w +x +y +z with w +x+y z a square, where w Z and x, y, z N with w x y z < x + y, and that any n N can be written as w + x + y + z with w + x + y z a nonnegative cube, where w, x, y, z are integers with x y z 0. Example 1.1. We illustrate Theorem 1.3(i) with m = by an example: 60 = ( ) with ( ) =. We establish the following general theorem via a new approach involving Euler s four-square identity. Theorem 1.4. Let a, b, c, d Z with a, b, c, d not all zero, and let λ {1, } and m {, 3}. Then any n N can be written as x + y + z + w with x, y, z, w Z/(a + b + c + d ) such that ax + by + cz + dw = λr m for some r N. With the help of Theorem 1.4, we obtain the following results. Theorem 1.. (i) Let λ {1, } and m {, 3}. Then any n N can be written as x + y + z + w (x, y, z, w Z) with x + y + 3z w {λr m : r N}. (ii) Any n N can be written as w + x + y + z with w, x, y, z Z for which w(x + y + 3z w) = 0 and hence w(x + y + 3z) is a square. (iii) For any n N, there are w, x, y, z Z with w + x + y + z = n for which (w + x)(w + x y 3z) = 0 and hence (10w + x) + (1y + 36z) is a square. Remark In contrast with Theorem 1.(i), Sun [6, Conjectures 4.4(iv) and 4.1(i)] conjectured that x + y + 3z w and x y + 3z w are both suitable. Concerning parts (ii) and (iii) of Theorem 1., Sun [6, Conjectures 4. and 4.8(i)] also conjectured that both w(x + y + 3z) and (10w + x) + (1y + 36z) are suitable.
4 4 Y.-C. SUN AND Z.-W. SUN Theorem 1.6. (i) Any n N can be written as w +x +y +z (w, x, y, z Z) with w(x + y + 3z) = 0 (or (x y)(x + y + 3z) = 0). Consequently, each n N can be written as w +x +y +z (w, x, y, z Z) with (x+y) +(4z) a square. (ii) Let λ {1, } and m {, 3}. Then any n N can be written as x + y + z + w (x, y, z, w Z) with x + y + 3z {λr m : r N}. Remark 1.. Sun [6, Conjecture 4.3(iv), Remark 1.4 and Conjecture 4.8(ii)] conjectured that x y + 3z and (x y)(x + y 3z) are suitable, and that any positive integer can be written as x + y + z + w with x, y, z, w N, y > z, and (x + y) + (4z) a square. We are also able to show Theorem 1.6(iii) with x, z N. Corollary 1.1. Let P (x, y, z) be one of the polynomials x y + 9y z + 9z x, x + 1yz, 9x 4yz, (x + 3y)z. Then any n Z + can be written as w + x + y + z (w Z \ {0} and x, y, z Z) with P (x, y, z) a square. Remark 1.6. Sun [6, Remark 1.4 and Conjecture 4.10(i)] conjectured that the polynomials x y +9y z +9z x, x +kyz (k = 1, 4, 3, 48, 84, 10, ) and 9x 4yz are all suitable. He also conjectured that any n Z + can be written as w + x + y + z with w, x, y N and z Z + such that (x + 3y)z is a square (cf. [6, Conjecture 4.(i)]). Theorem 1.7. (i) Each n N can be written as x +y +z +w (x, y, z, w Z) with w(x + y + z + w) = 0. (ii) Let λ {1, } and m {, 3}. Then any n N can be written as x + y + z + w (x, y, z, w Z) with x + y + z + w = λr m for some r N. (iii) Any n N can be written as x + y + z + w (x, y, z, w Z) with w(x + y + 3z) = 0. (iv) For each λ = 1,, 4 and m {, 3}, any n N can be written as x + y + z + w (x, y, z, w Z) with x + y + 3z {λr m : r N}. Remark 1.7. Sun [6, Conjectures 4.4(iv) and 1.(ii)] conjectured that both x+y z +w and x y z +w are suitable; in addition to Theorem 1.7(ii), we are also able to show that any n N can be written as x + y + z + w with x, y, w N and z Z such that x + y + z + w is a square. Theorem 1.7(iv) provides an advance on Sun s conjecture that both x + y 3z and x y + 3z are suitable (cf. [6, parts (iii) and (iv) of Conjecture 4.3]).
5 SOME VARIANTS OF LAGRANGE S FOUR SQUARES THEOREM Corollary 1.. Any n Z + can be written as x + y + z + w (x, y, z Z and w Z \ {0}) with x + 4yz a square. Also, each n Z + can be written as x +y +z +w (x, y, z Z and w Z\{0}) with 4x y +9y z +36z x a square. Theorem 1.8. Let λ {1, }, m {, 3} and n N. (i) We can write n as x + y + z + w with x, y, z, w Z such that x + 3y + z {λr m : r N}. (ii) We can write n as x + y + z + w with x, y, z, w Z/7 such that x + 3y + z {λr m : r N}. Remark 1.8. Theorem 1.8 provides a remarkable progress on the 1-3- conjecture of Sun (cf. [6, Conjecture 4.3(i)]) which asserts that x + 3y + z is suitable. Sun [6, Remark 4.3] also conjectured any n N can be written as x + y + z + w (x, y, z, w Z) with x + 3y + z a cube. We are going to show Theorems , and in Sections, 3 and 4 respectively. Throughout this paper, for a nonzero integer m and a prime power p a with p prime and a N, by p a m we mean p a m but p a+1 m.. Proofs of Theorems For any a, b, c Z + = {1,, 3,...}, we define E(a, b, c) := N \ {ax + by + cz : x, y, z Z}. We need the following well-known theorem. Gauss-Legendre Theorem ([, p. 3]). We have E(1, 1, 1) = {4 k (8l + 7) : k, l N}. (.1) Proof of Theorem 1.1. (i) If n E(1, 1, 1), then for some w, x, y N we have n = w + x + y + 0 with x + 8y 0 = x. Now suppose that n E(1, 1, 1). As E(1,, 3) E(1, 1, 1) = by [6, Lemma 3.], we can write n as w + v + 3z with w, v, z N. Let x = v z and y = v + z. Then and n = w + (v z) + (v + z) + z = w + x + y + z This proves Theorem 1.1(i). x + 8yz = v z + 8(v + z)z = (v + 3z).
6 6 Y.-C. SUN AND Z.-W. SUN (ii) Note that ( ) = For n = 1,,..., we can verify the desired result via a computer. Now fix n N with n > , and assume that any m = 0,..., n 1 can be written as x + y + z + w (x, y, z, w N) with x + y a positive square. If 16 n, then by the induction hypothesis there are x, y, z, w N such that x + y + z + w = n/16 and x + y is a positive square, hence n = (4x) + (4y) + (4z) + (4w) with 4x + (4y) = (x + y) a positive square. Below we suppose that 16 n. As n > , we have 4 n 4 n 10 and hence for each r = 0, 1 there is a positive integer j r such that 4 n (jr + r) < 4 n. We claim that n ((j r + r)) 4 E(1, 1, 1) for some r = 0, 1. Case 1. n. If n (10j 0 ) 4 7 (mod 8), then n (10j 1 + ) 4 6 (mod 8). So, n (10j 0 ) 4 or n (10j 1 + ) 4 does not belong to E(1, 1, 1). Case. 4 n. Write n = 4q with q odd. If q 1 (mod 4), then n (10j 0 ) 4 4 (mod 16) and hence n (10j 0 ) 4 E(1, 1, 1). If q 3 (mod 4), then n (10j 1 + ) 4 3 (mod 8) and hence n (10j 1 + ) 4 E(1, 1, 1). Case 3. n or 8 n. In this case, n (10j 0 ) 4 or 8 n (10j 0 ) 4, and hence n (10j 0 ) 4 E(1, 1, 1). By the claim, for some j {j 0, j 1 +1} we can write n (j) 4 = t +u + v with t, u, v N. As a square is congruent to one of 0, 1, 1 modulo, one of t, u, v must be divisible by. Without loss of generality, we assume that t and u v (mod ). (Note that u + v u (v) (mod ).) Set s = (j). Then n = s + t + u + v ( s ) ( t = + + ) u + v ( ) ( ) ( ) ( ) s + t s t u v u + v = with s + t + s t = s = (j).
7 SOME VARIANTS OF LAGRANGE S FOUR SQUARES THEOREM 7 As s n, we have t n s 4s and hence s t 0. This concludes our induction proof. Lemma.1. Suppose that n is the sum of three squares. Then we can write n = x + y + z + w (x, y, z, w Z) with x + y + z = 0. Proof. Clearly, n = u + v + w for some integers u, v, w (mod 3). (Note that if x (mod 3) then x (mod 3).) Obviously, two of u, v, w are congruent modulo 3. Without loss of generality, we suppose that u v (mod 3). Set Then y = u + v 3 and z = u + v. 3 n = u + v + w = (y z) + (z y) + w = (y z) + ( y) + z + w with (y z) + ( y) + z = 0. This ends the proof. Proof of Theorem 1.. (i) By [6, Lemma 3.], all the sets E(1, 1, ), E(1, 1, ), E(1,, 3), E(1,, 6) are subsets of N \ E(1, 1, 1). If n E(1, 1, ), then we can write n = x + y + z + w with x, y, z, w Z and x y = 0. If n E(1, 1, ), then we can write n = x + y + z + w with x, y, z, w Z and x y = 0. When n E(1,, 6), by [6, Lemma 3.3] we can write n = x + y + z + w with x, y, z, w N and x + y z = 0. If n E(1,, 3), then again by [6, Lemma 3.3] we can write n = x + y + z + w with x, y, z, w Z and x + y z = 0. Combining these with Lemma.1 we immediately finish the proof of Theorem 1.(i). (ii) For n = 0, 1,..., 4 m 1, we can verify the desired result in Theorem 1.(ii) directly. Now fix an integer n 4 m and assume the desired result for smaller values of n. Case 1. 4 m n. In this case, by the induction hypothesis, there are x, y, z, w Z with n/4 m = x + y + z + w such that x + y + z = dt m for some t Z. Hence n = ( m x) +( m y) +( m z) +( m w) with m x+( m y)+( m z) = m (x + y + z) = d(t) m. Case. 4 m n and n 4 k (8l + 7) for any k, l N.
8 8 Y.-C. SUN AND Z.-W. SUN In this case, by the Gauss-Legendre theorem and Lemma.1, we can write n as x + y + z + w (x, y, z, w Z) with x + y + z = 0 m. Case 3. n = 4 k (8l + 7) for some k, l N with k < m. We first consider the subcase d {1, }. We claim that {9n d, 9n d 4 m } {4 r (8q + 7) : q, r N}. In fact, for d = we have 8(9l + 7) + 3 if k = 0; 9n = 9 4 k (8l + 7) 4 = 4(8(9l + 7) + 6) if k = 1, 4(8(36l + 31) + 3) if k =. For d = 1, clearly 9n 1 = 9 4 k (8l + 7) 1 and when k = < m = 3 we have { 6 (mod 8) if k = 0, 3 (mod 8) if k = 1, 9n 4 3 = 9 4 (8l + 7) 4 3 = 4 (7l + 9) = 4 (8(9l + 7) + 3). Thus, by the Gauss-Legendre theorem, for some δ {1, m } there exist a, b, c Z such that 9n (dδ) = a + b + c. Clearly, we cannot have 3 abc since 9n (dδ) 0 (mod 3). Without loss of generality, we assume that c = 3w with w Z. As a + b (dδ) (mod 3), we must have 3 ab. We may simply suppose that a = 3u + dδ and b = 3v dδ with u, v Z. (Note that if x 1 (mod 3) then x (mod 3).) Since 1dδu 1dδv + 8(dδ) (3u + dδ) + (3v dδ) = a + b (dδ) (mod 9), we must have 3 dδ(u v) and hence u v (mod 3). Set y = u + v and z = u + v. 3 3 Then and hence 9n (dδ) =a + b + c = (3u + dδ) + (3v dδ) + 9w =(3(y z) + dδ) + (3(z y) dδ) + 9w =9(y z) + 9(z y) + 1dδ((y z) (z y)) + 8(dδ) + 9w n =(y z) + (z y) + 4dδ(y z) + w + (dδ) =(y z + dδ) + ( y) + z + w with (y z + dδ) + ( y) + z = dδ {dt m : t = 1, }.
9 SOME VARIANTS OF LAGRANGE S FOUR SQUARES THEOREM 9 Now we consider the subcase d = 3. For q = 0,..., 363, we can verify via a computer that 4 (8q + 7) can be written as x + y + z + w with x, y, z, w Z such that x + y + z = 3t 3 for some t Z; for example, 4 ( ) = = 8 + ( 148) with 8 + ( 148) + 16 = 3 3. From now on we assume that k < or l 364. When k {0, 1}, it is easy to see that n 3 m is congruent to 6 or 3 modulo 8. If m = 3 and k =, then n 6 m = 4 (8l + 7) = 4 (8(l 364) + 3). So, for some δ {3 m, 6 m } we have n δ {4 i (8j + 7) : i, j N}. By the Gauss-Legendre theorem, n δ = a + b + c for some a, b, c Z. Clearly, two of a, b, c, say a and b, are congruent modulo 3. Without loss of generality, we may assume that a b (mod 3). Let u = a δ and v = b + δ. Then u v (mod 3) since 3 δ. Set Then y = u + v 3 and z = u + v. 3 n δ = (u + δ) + (v δ) + c = (y z + δ) + (z y δ) + c. It follows that n = (y z + 3δ) + ( y) + z + c with (y z + 3δ) + ( y) + z = 3δ {3 t m : t = 3, 6} as desired. So far we have completed the proof of Theorem 1.. Proof of Theorem 1.3. (i) For n = 0, 1,..., 4 m 1, the desired result can be verified directly. Now let n 4 m be an integer and assume the desired result for smaller values of n. Case 1. 4 m n. By the induction hypothesis, we can write n 4 m = x + y + z + w with x, y, z, w Z such that x + y + z + w = s m for some s Z. Therefore, n = ( m x) + ( m y) + ( m z) + ( m w) with m x + m y + m z + m w = (s) m. Case. n but 4 m n.
10 10 Y.-C. SUN AND Z.-W. SUN If n 4 k (8l + 7) for all k, l N with k < m, then by the Gauss- Legendre theorem we can write n = u + v + w with u, v, w Z. Clearly, u + v + w n 0 (mod ). Let t = u + v + w, x = u + v + w, y = u v + w and z = u + v w. Then x + y = w, y + z = u, x + z = v, and x + y + z = t. Therefore, n =u + v + w = (y + z) + (x + z) + (x + y) =(x + y + z) + x + y + z = ( t) + x + y + z with ( t) + x + y + z = 0 m. When n = 4 k (8l+7) for some k, l N with k < m, we have k {1, } and hence n 4 m 1 4 a (8b + 7) for any a, b N. Thus, by the Gauss-Legendre theorem there are u, v, w Z such that n 4 m 1 = (u m 1 ) + (v m 1 ) + (w m 1 ). Set t = u + v + w, x = u + v + w, y = u v + w and z = u + v w. Then n =(u m 1 ) + (v m 1 ) + (w m 1 ) + 4 m 1 =(y + z m 1 ) + (x + z m 1 ) + (x + y m 1 ) + 4 m 1 =(x + y + z m ) + x + y + z = ( m t) + x + y + z with ( m t) + x + y + z = m. Case 3. n. As 4n 1 3 (mod 8), by the Gauss-Legendre theorem there are u, v, w Z such that 4n 1 = (u 1) +(v 1) +(w 1) = (u 1) +(v 1) +(w 1), where u = 1 u. When u + v + w is even, we set t = u + v + w, x = u + v + w, y = u v + w and deduce that Therefore 4n 1 =(u 1) + (v 1) + (w 1) and z = u + v w, =((y + z) 1) + ((x + z) 1) + ((x + y) 1) =4 ( (x + y + z 1) + x + y + z ) 1. n = (1 t) + x + y + z with (1 t) + x + y + z = 1 m.
11 SOME VARIANTS OF LAGRANGE S FOUR SQUARES THEOREM 11 Now assume that u + v + w is odd. Then u + v + w is even. Set t = u + v + w Then we get and hence, x = u + v + w, y = u v + w 4n 1 =(u 1) + (v 1) + (w 1) and z = u + v w, =((y + z) 1) + ((x + z) 1) + ((x + y) 1) n = (1 t ) + x + y + z with (1 t ) + x + y + z = 1 m. This concludes the proof of the first part of Theorem 1.3. (ii) Write n = 4(8l + 7) with l N. Suppose that n can be written as x + y + z + w with x, y, z, w Z such that x + y + z + w = t m for some t Z. Then n =(x + y + z t m ) + x + y + z =(x + y) + (y + z) + (z + x) t m ((x + y) + (y + z) + (z + x)) + t m and hence 4n t m = ((x + y) t m ) + ((y + z) t m ) + ((z + x) t m ) If m 4 and t = s with s Z, then 4n t m = 4 (8l + 7) (s) m = 4 (8(l m 7 s m ) + 7). If m 4 and t, then 4n t m = 4 (8l + 7) t m 1 7 (mod 8). So, in light of the Gauss-Legendre theorem, we must have m 3. The proof of Theorem 1.3 is now complete. 3. Proofs of Theorems and Corollary 1.1 Lemma 3.1. Let a, b, c, d be integers not all zero, and let x = as bt cu dv, a +b +c +d y = bs+at+du cv, a +b +c +d, a +b +c +d. a +b +c +d z = cs dt+au+bv w = ds+ct bu+av (3.1)
12 1 Y.-C. SUN AND Z.-W. SUN Then and ax + by + cz + dw = s, ay bx + cw dz = t, az bw cx + dy = u, aw + bz cy dx = v, (3.) (a + b + c + d )(x + y + z + w ) = s + t + u + v. (3.3) Proof. It is easy to verify (3.) directly. By (3.) and Euler s four-square identity, we immediately have (3.3). Proof of Theorem 1.4. Let n N. By [6, Theorem 1.1], we can write (a + b + c + d )n as (λr m ) + t + u + v with r, t, u, v N. Set s = λr m, and define x, y, z, w by (3.1). Then x, y, z, w Z/(a + b + c + d ). By Lemma 3.1, we have and x + y + z + w = s + t + u + v a + b + c + d = n ax + by + cz + dw = s = λr m. Lemma 3.. Suppose that 3n = s +t +u +v with n N and s, t, u, v Z. Define x = s t u, 3 y = s+t v, 3 (3.4) z = s+u+v, 3 w = t u+v Then we have 3. x + y + z + w = n and x + y + 3z w = s + u. Proof. Taking a = b = c = 1 and d = 0 in Lemma 3.1 we obtain that x + y + z + w = s + t + u + v = n. The equality x + y + 3z w = s + u follows from (3.4). Lemma 3.3. (Sun [6, Theorem 1.(iii)]) Let λ {1, } and m {, 3}. Then, any n N can be written as x + y + z + w with x, y, z, w Z such that x + y = λr m for some r N.
13 SOME VARIANTS OF LAGRANGE S FOUR SQUARES THEOREM 13 Proof of Theorem 1.. (i) By Lemma 3.3, we can write 3n in the form s + t + u + v with s, t, u, v Z and s + u = λr m for some r N. Since t + v (s + u ) = (s u) + (s + u) (mod 3), and a square is congruent to 0 or 1 modulo 3, without loss of generality we may assume that t s u (mod 3) and v s u (mod 3). Now define x, y, z, w as in (3.4). It is easy to see that x, y, z, w Z. In light of Lemma 3., x + y + z + w = n and x + y + 3z w = s + u = λr m. This proves Theorem 1.(i). (ii) If n E(1, 1, 1), then for some x, y, z Z we have n = 0 +x +y +z with 0(x + y + 3z 0) = 0 and 0(x + y + 3z) = 0. Now suppose that n E(1, 1, 1). By the Gauss-Legendre theorem, n = 4 k (8l + 7) for some k, l N. Since E(1, 1, ) = {4 i (8j + 3) : i, j N} by Dickson [, pp ], we have 3n = 4 k (8(3l + ) + ) E(1, 1, ). Hence there are s, t, u, v Z with u = s such that 3n = s + t + v = s + t + u + v. As t + v s (mod 3), we have 3 tv. Without loss of generality, we may assume that 3 t and v s (mod 3). Let x, y, z, w be given by (3.4). Clearly, x, y, z, w Z. In view of Lemma 3., we have x + y + z + w = n and x + y + 3z w = s + u = 0. Note that w(x + y + 3z) = w. This concludes our proof of Theorem 1.(ii). (iii) If n E(1, 1, ), then for some w, x, y, z Z we have n = w + x + y + z with x = w, thus (w + x)(w + x y 3z) = 0 and (10w + x) + (1y + 36z) = (1y + 36z). Now suppose that n E(1, 1, ). By Dickson [, pp ], E(1, 1, ) = {4 k (8l + 3) : k, l N}. So, n = 4 k (8l + 3) for some k, l N. As 3n = 4 k (8(3l + 1) + 1) E(1, 1, ), there are s, t, u, v Z with u = s such that 3n = s + t + v = s + t + u + v. As in the proof of Theorem 1.(i), without loss of generality we may assume that 3 t and v s (mod 3). Let x, y, z, w be given by (3.4). As in the proof of Theorem 1.(ii), we have x, y, z, w Z, x + y + z + w = n and x + y + 3z w = s + u = 0. Thus n = y + x + ( z) + w with and (y + x)(y + x w 3( z)) = 0 (10y + x) + (1w + 36( z)) = (y + x) + 1 (w 3z) = (13(y + x)). This proves Theorem 1.(iii).
14 14 Y.-C. SUN AND Z.-W. SUN Lemma 3.4. Suppose that 11n = s +t +u +v with n N and s, t, u, v Z. Define x = s+t 3u, 11 y = s t+3v, 11 (3.) z = 3s+u v, 11 w = 3t+u+v Then we have 11. x + y + z + w = n and x + y + 3z = s. Proof. Taking a = 1, b = 1, c = 3 and d = 0 in Lemma 3.1 we obtain that x + ( y) + z + w = s + t + u + v 1 + ( 1) = n. By (3.), we immediately see that x + y + 3z = s. Lemma 3.. Let m {, 3} and n N. (i) Suppose that 4 m n and n λ (q) m, where q is a positive odd integer. Then, for each λ = 1,, we can write n as (λr m ) + x + y + z with r {0, q, q} and x, y, z Z. (ii) Suppose that 4 m n and n λ q m, where q is a positive odd integer. Then n can be written as (4r m ) + x + y + z with r {0, q} and x, y, z Z. Proof. (i) Suppose that n is not the sum of three squares. By the Gauss- Legendre theorem, n = 4 k (8l + 7) for some k {0,..., m 1} and l N. Note that q m = 8v + 1 for some v N. Clearly, 8l + 7 λ (8v + 1) 3, 6 (mod 8) if k = 0, n λ q m 4(8l + 7) λ (8v + 1) 3 (mod 8) if k = λ = 1, = 4 k (8l 8v + 6) if k = 1 and λ =, 4(8(4l v + 3) + 3) if k = λ =. If λ = 1, k = and m = 3, then n λ (q) m = 4 (8l + 7) 6 (8v + 1) = 4 (8(l 4v) + 3). In view of the above and the Gauss-Legendre theorem, there exists r {0, q, q} such that n (λr m ) = x + y + z for some x, y, z Z. This proves Lemma 3.(i). (ii) Suppose that n is not the sum of three squares. By the Gauss- Legendre theorem, n = 4 k (8l + 7) for some k {1,..., m 1} and l N.
15 SOME VARIANTS OF LAGRANGE S FOUR SQUARES THEOREM 1 Note that q m = 8v + 1 for some v N. Clearly, { n 16q m 4(8l + 7) 16(8v + 1) = 4(8(l + 4v) + 3) if k = 1, = 4 (8l + 7) 16(8v + 1) = 4 (8(l v) + 6) if k =. In light of the above and the Gauss-Legendre theorem, there exists r {0, q} such that n (4r m ) = x + y + z for some x, y, z Z. This proves Lemma 3.(ii). Lemma 3.6. (see, e.g., Dickson [, pp ]) We have E(1, 1, ) = {4 k (16l + 14) : k, l N}. (3.6) Proof of Theorem 1.6. (i) If n E(1, 1, 1), then for some x, y, z Z we have n = 0 +x +y +z with 0(x+y+3z) = 0, and also (x+y) +(4 0) = (x+y) is a square. If n E(1, 1, ), then for some x, y, z, w Z with x = y we have n = x + y + z + w with (x y)(x + y + 3z) = 0, If n E(1, 1, 1), then by the Gauss-Legendre theorem, we have n = 4 k (8l + 7) for some k, l N, and hence 11n = 4 k (8(11l + 9) + ) E(1, 1, 1). If n E(1, 1, ), then by (3.6) n = 4 k (16l +14) for some k, l N, and hence 11n = 4 k (8(l + 19) + ) E(1, 1, 1) by the Gauss-Legendre theorem. Now suppose that 11n E(1, 1, 1). We can write 11n = s + t + u + v with s = 0 and t, u, v Z. Clearly, a square is congruent to one of 0, 1,, 3, modulo 11, and no sum of three distinct numbers among 0, 1,, 3, is divisible by 11. Thus two of t, u, v are congruent modulo 11. Without loss of generality, we may assume that u v (mod 11). As t u v (3u) (mod 11), without loss of generality we simply assume that t 3u (mod 11). Define x, y, z, w as in (3.). Then x, y, z, w Z. By Lemma 3.4, we have x +y +z +w = n and x+y +3z = s = 0. Therefore (x + y) + (4z) = ( 3z) + (4z) = (z). (ii) For n = 0, 1,..., λ m we can verify the desired result via a computer. Now fix an integer n λ m and assume that the desired result holds for smaller values of n. If 4 m n, then by the induction hypothesis we can write n/4 m = x + y + z + w (x, y, z, w Z) with x + y + 3z = λr m for some r N, hence n = ( m x) +( m y) +( m z) +( m w) with m x+ m y +3 m z = λ(r) m. Below we suppose that 4 m n. Applying Lemma 3.(i) with q = 11, we can write 11n as (λr m ) + t + u + v with r {0, 11, } and t, u, v Z.
16 16 Y.-C. SUN AND Z.-W. SUN As s := λr m 0 (mod 11), we have t + u + v = 11n s 0 (mod 11). Clearly, a square is congruent to one of 0, 1,, 3, 4, modulo 11, and no sum of three distinct numbers among 0, 1,, 3, 4, is divisible by 11. As t +u +v 0 (mod 11), two of t, u, v are congruent modulo 11. Without loss of generality, we may assume that u v (mod 11) and t 3u (mod 11). Define x, y, z, w Z by (3.). It is easy to see that x, y, z, w Z. By Lemma 3.4, x + y + z + w = n and x + y + 3z = s = λr m. This ends our proof of Theorem 1.6(ii). Combining the above, we have completed the proof of Theorem 1.6. Proof of Corollary 1.1. If n E(1, 1, 1), then there are w, x, y, z Z with w 0 and z = 0 such that n = w +x +y +z, hence x y +9y z +9z x = (xy), (x + 3y)z = 0, x + 1yz = x and 9x 4yz = (3x) are all squares. Now suppose that n E(1, 1, 1). By Theorem 1.6(i), n can be written as x +y +z +w with w(x+y 3z) = 0. Clearly, w 0 since n E(1, 1, 1). Thus x + y = 3z and hence x y + 9y z + 9z x =x y + (x + y )(3z) Note that and =x y + (x + xy + y xy)(x + xy + y + xy) =(x + xy + y ). x + 1yz = (3z y) + 1yz = (3z + y) 9z 4xy = (x + y) 4xy = (x y). Also, n = w + ( x) + z + y with ( x + 3z)y = y. This concludes our proof. 4. Proofs of Theorems and Corollary 1. Lemma 4.1. Suppose that 7n = s +t +u +v with n N and s, t, u, v Z. Define x = s t u v, 7 y = s+t+u v, 7 (4.1) z = s t+u+v, 7 w = s+t u+v Then we have 7. x + y + z + w = n and x + y + z + w = s.
17 SOME VARIANTS OF LAGRANGE S FOUR SQUARES THEOREM 17 Proof. Taking a = b = c = 1 and d = in Lemma 3.1 we obtain that x + y + z + w = s + t + u + v = n. By (4.1), we immediately see that x + y + z + w = s. Lemma 4.. Let x, y, z Z with x + y + z 0 (mod 7). Then y x (mod 7) or z x (mod 7). Proof. If 7 x, then y z (mod 7) and hence y z 0 x (mod 7) since 1 is a quadratic nonresidue modulo 7. In the case 7 x, there are c, d {0, 1,, 4} for which y cx (mod 7), z dx (mod 7) and c + d (mod 7), thus {c, d} = {1, 4} and hence x is congruent to y or z modulo 7. This ends the proof. Proof of Theorem 1.7. (i) If n E(1, 1, 1), then for some x, y, z, w Z with w = 0 we have n = x + y + z + w and w(x + y + z + w) = 0. Now assume that n E(1, 1, 1). By (.1), n = 4 k (8l+7) for some k, l N. As 7n = 4 k (8(7l + 6) + 1) E(1, 1, 1), we can write 7n = s + t + u + v with s = 0 and t, u, v Z. As t + u + v = 7n s 0 (mod 7), we have t (v) = 4v (mod 7) and u (3v) v (mod 7), or u (v) = 4v (mod 7) and t (3v) v (mod 7). Without any loss of generality, we simply assume that t v (mod 7) and u 3v (mod 7). Define x, y, z, w by (4.1). It is easy to see that x, y, z, w Z. In view of Lemma 4.1, x + y + z + w = n and x + y + z + w = s = 0. Thus w(x + y + z + w) = 0 as desired. (ii) We can easily verify the desired result for all n = 0,..., λ 14 m 1 via a computer. Now let n λ 14 m and assume the desired result for smaller values of n. If 4 m n, then by the induction hypothesis we have n 4 m = x +y +z +w with x, y, z, w Z and x+y+z+w {λr m : r N}, and hence n = ( m x) + ( m y) + ( m z) + ( m w) with m x + m y + m z + m w {λ(r) m : r N}. Now suppose that 4 m n. By Lemma 3. we can write 7n as (λr m ) +t + u + v with r {0, 7, 14} and t, u, v Z. Note that s = λr m 0 (mod 7). As in the proof of Theorem 1.7(i), without any loss of generality we may assume that t v (mod 7) and u 3v (mod 7). Define x, y, z, w by (4.1). Then x, y, z, w Z. By Lemma 4.1, x + y + z + w = n and x + y + z + w = s = λr m.
18 18 Y.-C. SUN AND Z.-W. SUN (iii) If n E(1, 1, 1), then for some x, y, z, w Z with w = 0 we have n = x + y + z + w and w(x + y + 3z) = 0. Now assume that n E(1, 1, 1). By (.1), n = 4 k (8l + 7) for some k, l N. As 7n = 4 k (8(7l + 6) + 1) E(1, 1, ) by (3.6), we can write 7n = s + t + u + v with s, t, u, v Z with s = t. As u + v = 7n s s (mod 7), without loss of generality we may assume that u s (mod 7) and v s (mod 7). Clearly, those x, y, z, w defined by (4.1) are integers, and x +y +z +w = n by Lemma 4.1. Note that w +x+3z = s t = 0. Hence n = w + x + z + y with y(w + x + 3z) = 0. (iv) For n = 0, 1,..., λ 14 m 1 1 we can verify the desired result via a computer. Now fix an integer n λ 14 m 1 and assume that the desired result holds for smaller values of n. If 4 m n, then by the induction hypothesis we can write n/4 m = x + y + z + w (x, y, z, w Z) with x + y + 3z = λr m for some r N, hence n = ( m x) +( m y) +( m z) +( m w) with m x+( m y)+3( m z) = λ(r) m. Below we suppose that 4 m n. Applying Lemma 3. with q = 7, we can write 14n = (λr m ) + a + b + c with r, a, b, c N. Clearly, two of a, b, c have the same parity. Without any loss of generality, we may assume that b c (mod ) and a λr m (mod ). Set s = a + λrm, t = a λrm, u = b + c, v = b c. Then s t = λr m 0 (mod 7). Note that 7n = (λrm ) + a + b + c = s + t + u + v. As t + u + v 0 (mod 7), by Lemma 4., one of u and v is congruent to t modulo 7, and another is congruent to (t) modulo 7. Without any loss of generality, we may assume that v t (mod 7) and u t (mod 7). Now we define x, y, z, w by (4.1). It is easy to see that x, y, z, w Z. By Lemma 4.1, x + y + z + w = n. Note that w + x + 3z = s t = λr m. In view of the above, we have completed the proof of Theorem 1.7. Proof of Corollary 1.. If n E(1, 1, 1), then there are w, x, y, z Z with w 0 and z = 0 such that w + x + y + z = n, hence x + 4yz = x and 4x y + 9y z + 36z x = (xy) are both squares. Now assume that n E(1, 1, 1). By Theorem 1.7(iii), n can be written as x +y +z +w (x, y, z, w Z) with w(x+y+3z) = 0. Since n E(1, 1, 1),
19 SOME VARIANTS OF LAGRANGE S FOUR SQUARES THEOREM 19 we have w 0 and x + y + 3z = 0. Thus x + y + ( z) + w = n with x + 4y( z) = (y + 3z) 4yz = (y 3z). Also, n = y + x + z + w with 4y x + 9x z + 36z y =4x y + (x + 4y )(3z) =(xy) + (x + 4y )(x + 4xy + 4y ) =(x + xy + 4y ). The proof of Corollary 1. is now complete. Proof of Theorem 1.8. (i) By Theorem 1.7(ii), there are s, t, u, v Z such that n = s + t + u + v and s + t + u + v = λr m for some r N. Note that a square is congruent to one of 0, 1, 1 modulo. As s + t + u + v 0 (mod ), one of s, t, u is congruent to v modulo. Without loss of generality, we assume that u v (v) (mod ) and hence u + v or u v is divisible by. Since (s) s t (mod ), if s t (mod ) then t s (mod ) and hence t 4s s (mod ). Without any loss of generality, we simply assume that s t (mod ) and hence t s (mod ). Define x = s t, y = s + t Then x, y, z, w are all integers and, z = u + v, w = u v. x + y + z + w = (s t) + (s + t) + (u + v) + (u v) = s + t + u + v = n. Note that x + 3y + z = (s t) + 3(s + t) + u + v = s + t + u + v = λr m. (ii) By Lemma 3.3, we can write 7n as s + t + u + v (s, t, u, v Z) with s + t = λr m for some r Z. Define x, y, z, w as in (4.1). Then 7x, 7y, 7z, 7w Z and x + y + z + w = n by Lemma 4.1. Note that x + 3y + w = s + t = λr m. The proof of Theorem 1.8 is now complete.
20 0 Y.-C. SUN AND Z.-W. SUN Acknowledgements. We would like to thank the referee for helpful comments. This research was supported by the National Natural Science Foundation of China (grant no ) and the NSFC-RFBR Cooperation and Exchange Program (grant ). References [1] B. C. Berndt, Number Theory in the Spirit of Ramanujan, Amer. Math. Soc., Providence, R.I., 006. [] L. E. Dickson, Modern Elementary Theory of Numbers, Univ. of Chicago Press, Chicago, [3] E. Grosswald, Representation of Integers as Sums of Squares, Springer, New York, 198. [4] C. J. Moreno and S. S. Wagstaff, Sums of Squares of Integers, Chapman & Hall/CRC, New York, 00. [] M. B. Nathanson, Additive Number Theory: The Classical Bases, Grad. Texts in Math., Vol. 164, Springer, New York, [6] Z.-W. Sun, Refining Lagrange s four-square theorem, J. Number Theory 17 (017), [7] K. S. Williams, Number Theory in the Spirit of Liouville, London Math. Soc. Student Texts, Vol. 76, Cambridge Univ. Press, Cambridge, 011. (Yu-Chen Sun) Department of Mathematics, Nanjing University, Nanjing 10093, People s Republic of China address: syc@smail.nju.edu.cn (Zhi-Wei Sun, corresponding author) Department of Mathematics, Nanjing University, Nanjing 10093, People s Republic of China address: zwsun@nju.edu.cn
Zhi-Wei Sun Department of Mathematics, Nanjing University Nanjing , People s Republic of China
 J. Number Theory 16(016), 190 11. A RESULT SIMILAR TO LAGRANGE S THEOREM Zhi-Wei Sun Department of Mathematics, Nanjing University Nanjing 10093, People s Republic of China zwsun@nju.edu.cn http://math.nju.edu.cn/
J. Number Theory 16(016), 190 11. A RESULT SIMILAR TO LAGRANGE S THEOREM Zhi-Wei Sun Department of Mathematics, Nanjing University Nanjing 10093, People s Republic of China zwsun@nju.edu.cn http://math.nju.edu.cn/
Colloq. Math. 145(2016), no. 1, ON SOME UNIVERSAL SUMS OF GENERALIZED POLYGONAL NUMBERS. 1. Introduction. x(x 1) (1.1) p m (x) = (m 2) + x.
 Colloq. Math. 145(016), no. 1, 149-155. ON SOME UNIVERSAL SUMS OF GENERALIZED POLYGONAL NUMBERS FAN GE AND ZHI-WEI SUN Abstract. For m = 3, 4,... those p m (x) = (m )x(x 1)/ + x with x Z are called generalized
Colloq. Math. 145(016), no. 1, 149-155. ON SOME UNIVERSAL SUMS OF GENERALIZED POLYGONAL NUMBERS FAN GE AND ZHI-WEI SUN Abstract. For m = 3, 4,... those p m (x) = (m )x(x 1)/ + x with x Z are called generalized
ON UNIVERSAL SUMS OF POLYGONAL NUMBERS
 Sci. China Math. 58(2015), no. 7, 1367 1396. ON UNIVERSAL SUMS OF POLYGONAL NUMBERS Zhi-Wei SUN Department of Mathematics, Nanjing University Nanjing 210093, People s Republic of China zwsun@nju.edu.cn
Sci. China Math. 58(2015), no. 7, 1367 1396. ON UNIVERSAL SUMS OF POLYGONAL NUMBERS Zhi-Wei SUN Department of Mathematics, Nanjing University Nanjing 210093, People s Republic of China zwsun@nju.edu.cn
The Conjecture and Related Topics
 Analytic Number Theory and Cryptography (Beijing, Nov. 18-20) and the 3rd Sichuan-Chongqing Number Theory Conf. (Dec. 10, 2016) Suzhou University (Jan. 11, 2017) The 1-3-5-Conjecture and Related Topics
Analytic Number Theory and Cryptography (Beijing, Nov. 18-20) and the 3rd Sichuan-Chongqing Number Theory Conf. (Dec. 10, 2016) Suzhou University (Jan. 11, 2017) The 1-3-5-Conjecture and Related Topics
Journal of Combinatorics and Number Theory 1(2009), no. 1, ON SUMS OF PRIMES AND TRIANGULAR NUMBERS. Zhi-Wei Sun
 Journal of Combinatorics and Number Theory 1(009), no. 1, 65 76. ON SUMS OF PRIMES AND TRIANGULAR NUMBERS Zhi-Wei Sun Department of Mathematics, Nanjing University Nanjing 10093, People s Republic of China
Journal of Combinatorics and Number Theory 1(009), no. 1, 65 76. ON SUMS OF PRIMES AND TRIANGULAR NUMBERS Zhi-Wei Sun Department of Mathematics, Nanjing University Nanjing 10093, People s Republic of China
Zhi-Wei Sun. Department of Mathematics Nanjing University Nanjing , P. R. China
 A talk given at National Cheng Kung Univ. (2007-06-28). SUMS OF SQUARES AND TRIANGULAR NUMBERS, AND RADO NUMBERS FOR LINEAR EQUATIONS Zhi-Wei Sun Department of Mathematics Nanjing University Nanjing 210093,
A talk given at National Cheng Kung Univ. (2007-06-28). SUMS OF SQUARES AND TRIANGULAR NUMBERS, AND RADO NUMBERS FOR LINEAR EQUATIONS Zhi-Wei Sun Department of Mathematics Nanjing University Nanjing 210093,
Polygonal Numbers, Primes and Ternary Quadratic Forms
 Polygonal Numbers, Primes and Ternary Quadratic Forms Zhi-Wei Sun Nanjing University Nanjing 210093, P. R. China zwsun@nju.edu.cn http://math.nju.edu.cn/ zwsun August 26, 2009 Modern number theory has
Polygonal Numbers, Primes and Ternary Quadratic Forms Zhi-Wei Sun Nanjing University Nanjing 210093, P. R. China zwsun@nju.edu.cn http://math.nju.edu.cn/ zwsun August 26, 2009 Modern number theory has
k 2r n k n n k) k 2r+1 k 2r (1.1)
 J. Number Theory 130(010, no. 1, 701 706. ON -ADIC ORDERS OF SOME BINOMIAL SUMS Hao Pan and Zhi-Wei Sun Abstract. We prove that for any nonnegative integers n and r the binomial sum ( n k r is divisible
J. Number Theory 130(010, no. 1, 701 706. ON -ADIC ORDERS OF SOME BINOMIAL SUMS Hao Pan and Zhi-Wei Sun Abstract. We prove that for any nonnegative integers n and r the binomial sum ( n k r is divisible
A talk given at the City Univ. of Hong Kong on April 14, ON HILBERT S TENTH PROBLEM AND RELATED TOPICS
 A talk given at the City Univ. of Hong Kong on April 14, 000. ON HILBERT S TENTH PROBLEM AND RELATED TOPICS Zhi-Wei Sun Department of Mathematics Nanjing University Nanjing 10093 People s Republic of China
A talk given at the City Univ. of Hong Kong on April 14, 000. ON HILBERT S TENTH PROBLEM AND RELATED TOPICS Zhi-Wei Sun Department of Mathematics Nanjing University Nanjing 10093 People s Republic of China
J. Combin. Theory Ser. A 116(2009), no. 8, A NEW EXTENSION OF THE ERDŐS-HEILBRONN CONJECTURE
 J. Combin. Theory Ser. A 116(2009), no. 8, 1374 1381. A NEW EXTENSION OF THE ERDŐS-HEILBRONN CONJECTURE Hao Pan and Zhi-Wei Sun Department of Mathematics, Naning University Naning 210093, People s Republic
J. Combin. Theory Ser. A 116(2009), no. 8, 1374 1381. A NEW EXTENSION OF THE ERDŐS-HEILBRONN CONJECTURE Hao Pan and Zhi-Wei Sun Department of Mathematics, Naning University Naning 210093, People s Republic
Ehrhart polynomial for lattice squares, cubes, and hypercubes
 Ehrhart polynomial for lattice squares, cubes, and hypercubes Eugen J. Ionascu UWG, REU, July 10th, 2015 math@ejionascu.ro, www.ejionascu.ro 1 Abstract We are investigating the problem of constructing
Ehrhart polynomial for lattice squares, cubes, and hypercubes Eugen J. Ionascu UWG, REU, July 10th, 2015 math@ejionascu.ro, www.ejionascu.ro 1 Abstract We are investigating the problem of constructing
Summary Slides for MATH 342 June 25, 2018
 Summary Slides for MATH 342 June 25, 2018 Summary slides based on Elementary Number Theory and its applications by Kenneth Rosen and The Theory of Numbers by Ivan Niven, Herbert Zuckerman, and Hugh Montgomery.
Summary Slides for MATH 342 June 25, 2018 Summary slides based on Elementary Number Theory and its applications by Kenneth Rosen and The Theory of Numbers by Ivan Niven, Herbert Zuckerman, and Hugh Montgomery.
A SHARP RESULT ON m-covers. Hao Pan and Zhi-Wei Sun
 Proc. Amer. Math. Soc. 35(2007), no., 355 3520. A SHARP RESULT ON m-covers Hao Pan and Zhi-Wei Sun Abstract. Let A = a s + Z k s= be a finite system of arithmetic sequences which forms an m-cover of Z
Proc. Amer. Math. Soc. 35(2007), no., 355 3520. A SHARP RESULT ON m-covers Hao Pan and Zhi-Wei Sun Abstract. Let A = a s + Z k s= be a finite system of arithmetic sequences which forms an m-cover of Z
Department of Mathematics, Nanjing University Nanjing , People s Republic of China
 Proc Amer Math Soc 1382010, no 1, 37 46 SOME CONGRUENCES FOR THE SECOND-ORDER CATALAN NUMBERS Li-Lu Zhao, Hao Pan Zhi-Wei Sun Department of Mathematics, Naning University Naning 210093, People s Republic
Proc Amer Math Soc 1382010, no 1, 37 46 SOME CONGRUENCES FOR THE SECOND-ORDER CATALAN NUMBERS Li-Lu Zhao, Hao Pan Zhi-Wei Sun Department of Mathematics, Naning University Naning 210093, People s Republic
The Riddle of Primes
 A talk given at Dalian Univ. of Technology (Nov. 16, 2012) and Nankai University (Dec. 1, 2012) The Riddle of Primes Zhi-Wei Sun Nanjing University Nanjing 210093, P. R. China zwsun@nju.edu.cn http://math.nju.edu.cn/
A talk given at Dalian Univ. of Technology (Nov. 16, 2012) and Nankai University (Dec. 1, 2012) The Riddle of Primes Zhi-Wei Sun Nanjing University Nanjing 210093, P. R. China zwsun@nju.edu.cn http://math.nju.edu.cn/
Necessary and Sufficient Conditions for the Central Norm to Equal 2 h in the Simple Continued Fraction Expansion of 2 h c for Any Odd Non-Square c > 1
 Necessary and Sufficient Conditions for the Central Norm to Equal 2 h in the Simple Continued Fraction Expansion of 2 h c for Any Odd Non-Square c > 1 R.A. Mollin Abstract We look at the simple continued
Necessary and Sufficient Conditions for the Central Norm to Equal 2 h in the Simple Continued Fraction Expansion of 2 h c for Any Odd Non-Square c > 1 R.A. Mollin Abstract We look at the simple continued
An Elementary Proof that any Natural Number can be Written as the Sum of Three Terms of the Sequence n2
 1 47 6 11 Journal of Integer Sequences, Vol. 17 (014), Article 14.7.6 An Elementary Proof that any Natural Number can be Written as the Sum of Three Terms of the Sequence n Bakir Farhi Department of Mathematics
1 47 6 11 Journal of Integer Sequences, Vol. 17 (014), Article 14.7.6 An Elementary Proof that any Natural Number can be Written as the Sum of Three Terms of the Sequence n Bakir Farhi Department of Mathematics
Advances in Applied Mathematics 48(2012), Constructing x 2 for primes p = ax 2 + by 2
 Advances in Applied Mathematics 4(01, 106-10 Constructing x for primes p ax + by Zhi-Hong Sun School of Mathematical Sciences, Huaiyin Normal University, Huaian, Jiangsu 3001, P.R. China E-mail: zhihongsun@yahoo.com
Advances in Applied Mathematics 4(01, 106-10 Constructing x for primes p ax + by Zhi-Hong Sun School of Mathematical Sciences, Huaiyin Normal University, Huaian, Jiangsu 3001, P.R. China E-mail: zhihongsun@yahoo.com
Strongly Nil -Clean Rings
 Strongly Nil -Clean Rings Abdullah HARMANCI Huanyin CHEN and A. Çiğdem ÖZCAN Abstract A -ring R is called strongly nil -clean if every element of R is the sum of a projection and a nilpotent element that
Strongly Nil -Clean Rings Abdullah HARMANCI Huanyin CHEN and A. Çiğdem ÖZCAN Abstract A -ring R is called strongly nil -clean if every element of R is the sum of a projection and a nilpotent element that
LESSON 6.2 POLYNOMIAL OPERATIONS I
 LESSON 6.2 POLYNOMIAL OPERATIONS I Overview In business, people use algebra everyday to find unknown quantities. For example, a manufacturer may use algebra to determine a product s selling price in order
LESSON 6.2 POLYNOMIAL OPERATIONS I Overview In business, people use algebra everyday to find unknown quantities. For example, a manufacturer may use algebra to determine a product s selling price in order
Introduction to Lucas Sequences
 A talk given at Liaoning Normal Univ. (Dec. 14, 017) Introduction to Lucas Sequences Zhi-Wei Sun Nanjing University Nanjing 10093, P. R. China zwsun@nju.edu.cn http://math.nju.edu.cn/ zwsun Dec. 14, 017
A talk given at Liaoning Normal Univ. (Dec. 14, 017) Introduction to Lucas Sequences Zhi-Wei Sun Nanjing University Nanjing 10093, P. R. China zwsun@nju.edu.cn http://math.nju.edu.cn/ zwsun Dec. 14, 017
S. Lie has thrown much new light on this operation. The assumption
 600 MATHEMATICS: A. E. ROSS PRoc. N. A. S. The operation of finding the limit of an infinite series has been one of the most fruitful operations of all mathematics. While this is not a group operation
600 MATHEMATICS: A. E. ROSS PRoc. N. A. S. The operation of finding the limit of an infinite series has been one of the most fruitful operations of all mathematics. While this is not a group operation
On the number of representations of n by ax 2 + by(y 1)/2, ax 2 + by(3y 1)/2 and ax(x 1)/2 + by(3y 1)/2
 ACTA ARITHMETICA 1471 011 On the number of representations of n by ax + byy 1/, ax + by3y 1/ and axx 1/ + by3y 1/ by Zhi-Hong Sun Huaian 1 Introduction For 3, 4,, the -gonal numbers are given by p n n
ACTA ARITHMETICA 1471 011 On the number of representations of n by ax + byy 1/, ax + by3y 1/ and axx 1/ + by3y 1/ by Zhi-Hong Sun Huaian 1 Introduction For 3, 4,, the -gonal numbers are given by p n n
CONGRUENCES RELATED TO THE RAMANUJAN/WATSON MOCK THETA FUNCTIONS ω(q) AND ν(q)
 CONGRUENCES RELATED TO THE RAMANUJAN/WATSON MOCK THETA FUNCTIONS ωq) AND νq) GEORGE E. ANDREWS, DONNY PASSARY, JAMES A. SELLERS, AND AE JA YEE Abstract. Recently, Andrews, Dixit, and Yee introduced partition
CONGRUENCES RELATED TO THE RAMANUJAN/WATSON MOCK THETA FUNCTIONS ωq) AND νq) GEORGE E. ANDREWS, DONNY PASSARY, JAMES A. SELLERS, AND AE JA YEE Abstract. Recently, Andrews, Dixit, and Yee introduced partition
Zhi-Wei Sun Department of Mathematics, Nanjing University Nanjing , People s Republic of China. Received 8 July 2005; accepted 2 February 2006
 Adv in Appl Math 382007, no 2, 267 274 A CONNECTION BETWEEN COVERS OF THE INTEGERS AND UNIT FRACTIONS Zhi-Wei Sun Department of Mathematics, Nanjing University Nanjing 20093, People s Republic of China
Adv in Appl Math 382007, no 2, 267 274 A CONNECTION BETWEEN COVERS OF THE INTEGERS AND UNIT FRACTIONS Zhi-Wei Sun Department of Mathematics, Nanjing University Nanjing 20093, People s Republic of China
CONGRUENCES RELATED TO THE RAMANUJAN/WATSON MOCK THETA FUNCTIONS ω(q) AND ν(q)
 CONGRUENCES RELATED TO THE RAMANUJAN/WATSON MOCK THETA FUNCTIONS ωq) AND νq) GEORGE E. ANDREWS, DONNY PASSARY, JAMES A. SELLERS, AND AE JA YEE Abstract. Recently, Andrews, Dixit and Yee introduced partition
CONGRUENCES RELATED TO THE RAMANUJAN/WATSON MOCK THETA FUNCTIONS ωq) AND νq) GEORGE E. ANDREWS, DONNY PASSARY, JAMES A. SELLERS, AND AE JA YEE Abstract. Recently, Andrews, Dixit and Yee introduced partition
HASSE-MINKOWSKI THEOREM
 HASSE-MINKOWSKI THEOREM KIM, SUNGJIN 1. Introduction In rough terms, a local-global principle is a statement that asserts that a certain property is true globally if and only if it is true everywhere locally.
HASSE-MINKOWSKI THEOREM KIM, SUNGJIN 1. Introduction In rough terms, a local-global principle is a statement that asserts that a certain property is true globally if and only if it is true everywhere locally.
#A22 INTEGERS 17 (2017) NEW CONGRUENCES FOR `-REGULAR OVERPARTITIONS
 #A22 INTEGERS 7 (207) NEW CONGRUENCES FOR `-REGULAR OVERPARTITIONS Shane Chern Department of Mathematics, Pennsylvania State University, University Park, Pennsylvania shanechern@psu.edu Received: 0/6/6,
#A22 INTEGERS 7 (207) NEW CONGRUENCES FOR `-REGULAR OVERPARTITIONS Shane Chern Department of Mathematics, Pennsylvania State University, University Park, Pennsylvania shanechern@psu.edu Received: 0/6/6,
arxiv:math/ v1 [math.nt] 9 Aug 2004
![arxiv:math/ v1 [math.nt] 9 Aug 2004 arxiv:math/ v1 [math.nt] 9 Aug 2004](/thumbs/75/71651629.jpg) arxiv:math/0408107v1 [math.nt] 9 Aug 2004 ELEMENTARY RESULTS ON THE BINARY QUADRATIC FORM a 2 + ab + b 2 UMESH P. NAIR Abstract. This paper examines with elementary proofs some interesting properties of
arxiv:math/0408107v1 [math.nt] 9 Aug 2004 ELEMENTARY RESULTS ON THE BINARY QUADRATIC FORM a 2 + ab + b 2 UMESH P. NAIR Abstract. This paper examines with elementary proofs some interesting properties of
arxiv: v5 [math.nt] 22 Aug 2013
![arxiv: v5 [math.nt] 22 Aug 2013 arxiv: v5 [math.nt] 22 Aug 2013](/thumbs/93/112250462.jpg) Prerint, arxiv:1308900 ON SOME DETERMINANTS WITH LEGENDRE SYMBOL ENTRIES arxiv:1308900v5 [mathnt] Aug 013 Zhi-Wei Sun Deartment of Mathematics, Nanjing University Nanjing 10093, Peole s Reublic of China
Prerint, arxiv:1308900 ON SOME DETERMINANTS WITH LEGENDRE SYMBOL ENTRIES arxiv:1308900v5 [mathnt] Aug 013 Zhi-Wei Sun Deartment of Mathematics, Nanjing University Nanjing 10093, Peole s Reublic of China
ELEMENTARY PROOFS OF PARITY RESULTS FOR 5-REGULAR PARTITIONS
 Bull Aust Math Soc 81 (2010), 58 63 doi:101017/s0004972709000525 ELEMENTARY PROOFS OF PARITY RESULTS FOR 5-REGULAR PARTITIONS MICHAEL D HIRSCHHORN and JAMES A SELLERS (Received 11 February 2009) Abstract
Bull Aust Math Soc 81 (2010), 58 63 doi:101017/s0004972709000525 ELEMENTARY PROOFS OF PARITY RESULTS FOR 5-REGULAR PARTITIONS MICHAEL D HIRSCHHORN and JAMES A SELLERS (Received 11 February 2009) Abstract
Bounds for the Representations of Integers by Positive Quadratic Forms
 22 MATHEMATICS MAGAZINE Bounds for the Representations of Integers by Positive Quadratic Forms KENNETH S. WILLIAMS Carleton University Ottawa, ON, Canada kennethwilliams@cunet.carleton.ca The fact that
22 MATHEMATICS MAGAZINE Bounds for the Representations of Integers by Positive Quadratic Forms KENNETH S. WILLIAMS Carleton University Ottawa, ON, Canada kennethwilliams@cunet.carleton.ca The fact that
Almost fifth powers in arithmetic progression
 Almost fifth powers in arithmetic progression L. Hajdu and T. Kovács University of Debrecen, Institute of Mathematics and the Number Theory Research Group of the Hungarian Academy of Sciences Debrecen,
Almost fifth powers in arithmetic progression L. Hajdu and T. Kovács University of Debrecen, Institute of Mathematics and the Number Theory Research Group of the Hungarian Academy of Sciences Debrecen,
CONGRUENCES CONCERNING LUCAS SEQUENCES ZHI-HONG SUN
 Int. J. Number Theory 004, no., 79-85. CONGRUENCES CONCERNING LUCAS SEQUENCES ZHI-HONG SUN School of Mathematical Sciences Huaiyin Normal University Huaian, Jiangsu 00, P.R. China zhihongsun@yahoo.com
Int. J. Number Theory 004, no., 79-85. CONGRUENCES CONCERNING LUCAS SEQUENCES ZHI-HONG SUN School of Mathematical Sciences Huaiyin Normal University Huaian, Jiangsu 00, P.R. China zhihongsun@yahoo.com
On a certain vector crank modulo 7
 On a certain vector crank modulo 7 Michael D Hirschhorn School of Mathematics and Statistics University of New South Wales Sydney, NSW, 2052, Australia mhirschhorn@unsweduau Pee Choon Toh Mathematics &
On a certain vector crank modulo 7 Michael D Hirschhorn School of Mathematics and Statistics University of New South Wales Sydney, NSW, 2052, Australia mhirschhorn@unsweduau Pee Choon Toh Mathematics &
x 9 or x > 10 Name: Class: Date: 1 How many natural numbers are between 1.5 and 4.5 on the number line?
 1 How many natural numbers are between 1.5 and 4.5 on the number line? 2 How many composite numbers are between 7 and 13 on the number line? 3 How many prime numbers are between 7 and 20 on the number
1 How many natural numbers are between 1.5 and 4.5 on the number line? 2 How many composite numbers are between 7 and 13 on the number line? 3 How many prime numbers are between 7 and 20 on the number
A Note on Indefinite Ternary Quadratic Forms Representing All Odd Integers. Key Words: Quadratic Forms, indefinite ternary quadratic.
 Bol. Soc. Paran. Mat. (3s.) v. 23 1-2 (2005): 85 92. c SPM ISNN-00378712 A Note on Indefinite Ternary Quadratic Forms Representing All Odd Integers Jean Bureau and Jorge Morales abstract: In this paper
Bol. Soc. Paran. Mat. (3s.) v. 23 1-2 (2005): 85 92. c SPM ISNN-00378712 A Note on Indefinite Ternary Quadratic Forms Representing All Odd Integers Jean Bureau and Jorge Morales abstract: In this paper
A Review Study on Presentation of Positive Integers as Sum of Squares
 A Review Study on Presentation of Positive Integers as Sum of Squares Ashwani Sikri Department of Mathematics, S. D. College Barnala-148101 ABSTRACT It can be easily seen that every positive integer is
A Review Study on Presentation of Positive Integers as Sum of Squares Ashwani Sikri Department of Mathematics, S. D. College Barnala-148101 ABSTRACT It can be easily seen that every positive integer is
CONSECUTIVE NUMBERS WITHTHESAMELEGENDRESYMBOL
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 130, Number 9, Pages 503 507 S 000-9939(0)06600-5 Article electronically ublished on Aril 17, 00 CONSECUTIVE NUMBERS WITHTHESAMELEGENDRESYMBOL ZHI-HONG
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 130, Number 9, Pages 503 507 S 000-9939(0)06600-5 Article electronically ublished on Aril 17, 00 CONSECUTIVE NUMBERS WITHTHESAMELEGENDRESYMBOL ZHI-HONG
Ramanujan-type congruences for overpartitions modulo 16. Nankai University, Tianjin , P. R. China
 Ramanujan-type congruences for overpartitions modulo 16 William Y.C. Chen 1,2, Qing-Hu Hou 2, Lisa H. Sun 1,2 and Li Zhang 1 1 Center for Combinatorics, LPMC-TJKLC Nankai University, Tianjin 300071, P.
Ramanujan-type congruences for overpartitions modulo 16 William Y.C. Chen 1,2, Qing-Hu Hou 2, Lisa H. Sun 1,2 and Li Zhang 1 1 Center for Combinatorics, LPMC-TJKLC Nankai University, Tianjin 300071, P.
Arithmetic properties of overcubic partition pairs
 Arithmetic properties of overcubic partition pairs Bernard L.S. Lin School of Sciences Jimei University Xiamen 3101, P.R. China linlsjmu@13.com Submitted: May 5, 014; Accepted: Aug 7, 014; Published: Sep
Arithmetic properties of overcubic partition pairs Bernard L.S. Lin School of Sciences Jimei University Xiamen 3101, P.R. China linlsjmu@13.com Submitted: May 5, 014; Accepted: Aug 7, 014; Published: Sep
The Diophantine equation x n = Dy 2 + 1
 ACTA ARITHMETICA 106.1 (2003) The Diophantine equation x n Dy 2 + 1 by J. H. E. Cohn (London) 1. Introduction. In [4] the complete set of positive integer solutions to the equation of the title is described
ACTA ARITHMETICA 106.1 (2003) The Diophantine equation x n Dy 2 + 1 by J. H. E. Cohn (London) 1. Introduction. In [4] the complete set of positive integer solutions to the equation of the title is described
Fermat numbers and integers of the form a k + a l + p α
 ACTA ARITHMETICA * (200*) Fermat numbers and integers of the form a k + a l + p α by Yong-Gao Chen (Nanjing), Rui Feng (Nanjing) and Nicolas Templier (Montpellier) 1. Introduction. In 1849, A. de Polignac
ACTA ARITHMETICA * (200*) Fermat numbers and integers of the form a k + a l + p α by Yong-Gao Chen (Nanjing), Rui Feng (Nanjing) and Nicolas Templier (Montpellier) 1. Introduction. In 1849, A. de Polignac
Strongly nil -clean rings
 J. Algebra Comb. Discrete Appl. 4(2) 155 164 Received: 12 June 2015 Accepted: 20 February 2016 Journal of Algebra Combinatorics Discrete Structures and Applications Strongly nil -clean rings Research Article
J. Algebra Comb. Discrete Appl. 4(2) 155 164 Received: 12 June 2015 Accepted: 20 February 2016 Journal of Algebra Combinatorics Discrete Structures and Applications Strongly nil -clean rings Research Article
A Four Integers Theorem and a Five Integers Theorem
 A Four Integers Theorem and a Five Integers Theorem Kenneth S. Williams Abstract. The recent exciting results by Bhargava, Conway, Hanke, Kaplansky, Rouse, and Schneeberger concerning the representabiltity
A Four Integers Theorem and a Five Integers Theorem Kenneth S. Williams Abstract. The recent exciting results by Bhargava, Conway, Hanke, Kaplansky, Rouse, and Schneeberger concerning the representabiltity
On the Representations of xy + yz + zx
 On the Representations of xy + yz + zx Jonathan Borwein and Kwok-Kwong Stephen Choi March 13, 2012 1 Introduction Recently, Crandall in [3] used Andrews identity for the cube of the Jacobian theta function
On the Representations of xy + yz + zx Jonathan Borwein and Kwok-Kwong Stephen Choi March 13, 2012 1 Introduction Recently, Crandall in [3] used Andrews identity for the cube of the Jacobian theta function
This theorem allows us to describe all integer solutions as follows:
 On the Diophantine equation a 3 + b 3 + c 3 + d 3 = 0 by RACHEL GAR-EL and LEONID VASERSTEIN (University Park, PA) Introduction. The equation a 3 + b 3 + c 3 + d 3 = 0 (1) has been studied by many mathematicians
On the Diophantine equation a 3 + b 3 + c 3 + d 3 = 0 by RACHEL GAR-EL and LEONID VASERSTEIN (University Park, PA) Introduction. The equation a 3 + b 3 + c 3 + d 3 = 0 (1) has been studied by many mathematicians
ARITHMETIC PROGRESSIONS IN CYCLES OF QUADRATIC POLYNOMIALS
 ARITHMETIC PROGRESSIONS IN CYCLES OF QUADRATIC POLYNOMIALS TIMO ERKAMA It is an open question whether n-cycles of complex quadratic polynomials can be contained in the field Q(i) of complex rational numbers
ARITHMETIC PROGRESSIONS IN CYCLES OF QUADRATIC POLYNOMIALS TIMO ERKAMA It is an open question whether n-cycles of complex quadratic polynomials can be contained in the field Q(i) of complex rational numbers
EXPLICIT CONGRUENCES FOR EULER POLYNOMIALS
 EXPLICIT CONGRUENCES FOR EULER POLYNOMIALS Zhi-Wei Sun Departent of Matheatics, Nanjing University Nanjing 10093, People s Republic of China zwsun@nju.edu.cn Abstract In this paper we establish soe explicit
EXPLICIT CONGRUENCES FOR EULER POLYNOMIALS Zhi-Wei Sun Departent of Matheatics, Nanjing University Nanjing 10093, People s Republic of China zwsun@nju.edu.cn Abstract In this paper we establish soe explicit
MATH 361: NUMBER THEORY FOURTH LECTURE
 MATH 361: NUMBER THEORY FOURTH LECTURE 1. Introduction Everybody knows that three hours after 10:00, the time is 1:00. That is, everybody is familiar with modular arithmetic, the usual arithmetic of the
MATH 361: NUMBER THEORY FOURTH LECTURE 1. Introduction Everybody knows that three hours after 10:00, the time is 1:00. That is, everybody is familiar with modular arithmetic, the usual arithmetic of the
Ternary Quadratic Forms and Eta Quotients
 Canad. Math. Bull. Vol. 58 (4), 015 pp. 858 868 http://dx.doi.org/10.4153/cmb-015-044-3 Canadian Mathematical Society 015 Ternary Quadratic Forms and Eta Quotients Kenneth S. Williams Abstract. Let η(z)
Canad. Math. Bull. Vol. 58 (4), 015 pp. 858 868 http://dx.doi.org/10.4153/cmb-015-044-3 Canadian Mathematical Society 015 Ternary Quadratic Forms and Eta Quotients Kenneth S. Williams Abstract. Let η(z)
On the power-free parts of consecutive integers
 ACTA ARITHMETICA XC4 (1999) On the power-free parts of consecutive integers by B M M de Weger (Krimpen aan den IJssel) and C E van de Woestijne (Leiden) 1 Introduction and main results Considering the
ACTA ARITHMETICA XC4 (1999) On the power-free parts of consecutive integers by B M M de Weger (Krimpen aan den IJssel) and C E van de Woestijne (Leiden) 1 Introduction and main results Considering the
LESSON 6.2 POLYNOMIAL OPERATIONS I
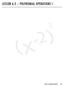 LESSON 6. POLYNOMIAL OPERATIONS I LESSON 6. POLYNOMIALS OPERATIONS I 63 OVERVIEW Here's what you'll learn in this lesson: Adding and Subtracting a. Definition of polynomial, term, and coefficient b. Evaluating
LESSON 6. POLYNOMIAL OPERATIONS I LESSON 6. POLYNOMIALS OPERATIONS I 63 OVERVIEW Here's what you'll learn in this lesson: Adding and Subtracting a. Definition of polynomial, term, and coefficient b. Evaluating
Acta Arith., 140(2009), no. 4, ON BIALOSTOCKI S CONJECTURE FOR ZERO-SUM SEQUENCES. 1. Introduction
 Acta Arith., 140(009), no. 4, 39 334. ON BIALOSTOCKI S CONJECTURE FOR ZERO-SUM SEQUENCES SONG GUO AND ZHI-WEI SUN* arxiv:081.174v3 [math.co] 16 Dec 009 Abstract. Let n be a positive even integer, and let
Acta Arith., 140(009), no. 4, 39 334. ON BIALOSTOCKI S CONJECTURE FOR ZERO-SUM SEQUENCES SONG GUO AND ZHI-WEI SUN* arxiv:081.174v3 [math.co] 16 Dec 009 Abstract. Let n be a positive even integer, and let
Predictive criteria for the representation of primes by binary quadratic forms
 ACTA ARITHMETICA LXX3 (1995) Predictive criteria for the representation of primes by binary quadratic forms by Joseph B Muskat (Ramat-Gan), Blair K Spearman (Kelowna, BC) and Kenneth S Williams (Ottawa,
ACTA ARITHMETICA LXX3 (1995) Predictive criteria for the representation of primes by binary quadratic forms by Joseph B Muskat (Ramat-Gan), Blair K Spearman (Kelowna, BC) and Kenneth S Williams (Ottawa,
CONGRUENCES MODULO 2 FOR CERTAIN PARTITION FUNCTIONS
 Bull. Aust. Math. Soc. 9 2016, 400 409 doi:10.1017/s000497271500167 CONGRUENCES MODULO 2 FOR CERTAIN PARTITION FUNCTIONS M. S. MAHADEVA NAIKA, B. HEMANTHKUMAR H. S. SUMANTH BHARADWAJ Received 9 August
Bull. Aust. Math. Soc. 9 2016, 400 409 doi:10.1017/s000497271500167 CONGRUENCES MODULO 2 FOR CERTAIN PARTITION FUNCTIONS M. S. MAHADEVA NAIKA, B. HEMANTHKUMAR H. S. SUMANTH BHARADWAJ Received 9 August
ON MONIC BINARY QUADRATIC FORMS
 ON MONIC BINARY QUADRATIC FORMS JEROME T. DIMABAYAO*, VADIM PONOMARENKO**, AND ORLAND JAMES Q. TIGAS*** Abstract. We consider the quadratic form x +mxy +ny, where m n is a prime number. Under the assumption
ON MONIC BINARY QUADRATIC FORMS JEROME T. DIMABAYAO*, VADIM PONOMARENKO**, AND ORLAND JAMES Q. TIGAS*** Abstract. We consider the quadratic form x +mxy +ny, where m n is a prime number. Under the assumption
Quadratic Diophantine Equations x 2 Dy 2 = c n
 Irish Math. Soc. Bulletin 58 2006, 55 68 55 Quadratic Diophantine Equations x 2 Dy 2 c n RICHARD A. MOLLIN Abstract. We consider the Diophantine equation x 2 Dy 2 c n for non-square positive integers D
Irish Math. Soc. Bulletin 58 2006, 55 68 55 Quadratic Diophantine Equations x 2 Dy 2 c n RICHARD A. MOLLIN Abstract. We consider the Diophantine equation x 2 Dy 2 c n for non-square positive integers D
(n = 0, 1, 2,... ). (2)
 Bull. Austral. Math. Soc. 84(2011), no. 1, 153 158. ON A CURIOUS PROPERTY OF BELL NUMBERS Zhi-Wei Sun and Don Zagier Abstract. In this paper we derive congruences expressing Bell numbers and derangement
Bull. Austral. Math. Soc. 84(2011), no. 1, 153 158. ON A CURIOUS PROPERTY OF BELL NUMBERS Zhi-Wei Sun and Don Zagier Abstract. In this paper we derive congruences expressing Bell numbers and derangement
REPRESENTATION OF A POSITIVE INTEGER BY A SUM OF LARGE FOUR SQUARES. Byeong Moon Kim. 1. Introduction
 Korean J. Math. 24 (2016), No. 1, pp. 71 79 http://dx.doi.org/10.11568/kjm.2016.24.1.71 REPRESENTATION OF A POSITIVE INTEGER BY A SUM OF LARGE FOUR SQUARES Byeong Moon Kim Abstract. In this paper, we determine
Korean J. Math. 24 (2016), No. 1, pp. 71 79 http://dx.doi.org/10.11568/kjm.2016.24.1.71 REPRESENTATION OF A POSITIVE INTEGER BY A SUM OF LARGE FOUR SQUARES Byeong Moon Kim Abstract. In this paper, we determine
(k, l)-universality OF TERNARY QUADRATIC FORMS ax 2 + by 2 + cz 2
 #A20 INTEGERS 18 (2018) (k, l)-universality OF TERNARY QUADRATIC FORMS ax 2 + by 2 + cz 2 Lerna Pehlivan Department of Mathematics and Statistics, Acadia University, Wolfville, Nova Scotia, Canada lerna.pehlivan@acadiau.ca
#A20 INTEGERS 18 (2018) (k, l)-universality OF TERNARY QUADRATIC FORMS ax 2 + by 2 + cz 2 Lerna Pehlivan Department of Mathematics and Statistics, Acadia University, Wolfville, Nova Scotia, Canada lerna.pehlivan@acadiau.ca
ON DIFFERENCES OF TWO SQUARES IN SOME QUADRATIC FIELDS
 ON DIFFERENCES OF TWO SQUARES IN SOME QUADRATIC FIELDS ANDREJ DUJELLA AND ZRINKA FRANUŠIĆ Abstract. It this paper, we study the problem of determining the elements in the rings of integers of quadratic
ON DIFFERENCES OF TWO SQUARES IN SOME QUADRATIC FIELDS ANDREJ DUJELLA AND ZRINKA FRANUŠIĆ Abstract. It this paper, we study the problem of determining the elements in the rings of integers of quadratic
Five regular or nearly-regular ternary quadratic forms
 ACTA ARITHMETICA LXXVII.4 (1996) Five regular nearly-regular ternary quadratic fms by William C. Jagy (Berkeley, Calif.) 1. Introduction. In a recent article [6], the positive definite ternary quadratic
ACTA ARITHMETICA LXXVII.4 (1996) Five regular nearly-regular ternary quadratic fms by William C. Jagy (Berkeley, Calif.) 1. Introduction. In a recent article [6], the positive definite ternary quadratic
Introduction to Arithmetic Geometry Fall 2013 Lecture #2 09/10/2013
 18.78 Introduction to Arithmetic Geometry Fall 013 Lecture # 09/10/013.1 Plane conics A conic is a plane projective curve of degree. Such a curve has the form C/k : ax + by + cz + dxy + exz + fyz with
18.78 Introduction to Arithmetic Geometry Fall 013 Lecture # 09/10/013.1 Plane conics A conic is a plane projective curve of degree. Such a curve has the form C/k : ax + by + cz + dxy + exz + fyz with
Some examples of two-dimensional regular rings
 Bull. Math. Soc. Sci. Math. Roumanie Tome 57(105) No. 3, 2014, 271 277 Some examples of two-dimensional regular rings by 1 Tiberiu Dumitrescu and 2 Cristodor Ionescu Abstract Let B be a ring and A = B[X,
Bull. Math. Soc. Sci. Math. Roumanie Tome 57(105) No. 3, 2014, 271 277 Some examples of two-dimensional regular rings by 1 Tiberiu Dumitrescu and 2 Cristodor Ionescu Abstract Let B be a ring and A = B[X,
Some new representation problems involving primes
 A talk given at Hong Kong Univ. (May 3, 2013) and 2013 ECNU q-series Workshop (Shanghai, July 30) Some new representation problems involving primes Zhi-Wei Sun Nanjing University Nanjing 210093, P. R.
A talk given at Hong Kong Univ. (May 3, 2013) and 2013 ECNU q-series Workshop (Shanghai, July 30) Some new representation problems involving primes Zhi-Wei Sun Nanjing University Nanjing 210093, P. R.
joint with Katherine Thompson July 29, 2015 The Wake Forest/Davidson Experience in Number Theory Research A Generalization of Mordell to Ternary
 to to joint with Katherine Thompson The Wake Forest/Davidson Experience in Number Theory Research July 29, 2015 cknowledgements to Thanks to UG and to the organizers. Special thanks to Dr. Jeremy Rouse,
to to joint with Katherine Thompson The Wake Forest/Davidson Experience in Number Theory Research July 29, 2015 cknowledgements to Thanks to UG and to the organizers. Special thanks to Dr. Jeremy Rouse,
Arithmetic Properties for Ramanujan s φ function
 Arithmetic Properties for Ramanujan s φ function Ernest X.W. Xia Jiangsu University ernestxwxia@163.com Nankai University Ernest X.W. Xia (Jiangsu University) Arithmetic Properties for Ramanujan s φ function
Arithmetic Properties for Ramanujan s φ function Ernest X.W. Xia Jiangsu University ernestxwxia@163.com Nankai University Ernest X.W. Xia (Jiangsu University) Arithmetic Properties for Ramanujan s φ function
D( 1)-QUADRUPLES AND PRODUCTS OF TWO PRIMES. Anitha Srinivasan Saint Louis University-Madrid campus, Spain
 GLASNIK MATEMATIČKI Vol. 50(70)(2015), 261 268 D( 1)-QUADRUPLES AND PRODUCTS OF TWO PRIMES Anitha Srinivasan Saint Louis University-Madrid campus, Spain Abstract. A D( 1)-quadruple is a set of positive
GLASNIK MATEMATIČKI Vol. 50(70)(2015), 261 268 D( 1)-QUADRUPLES AND PRODUCTS OF TWO PRIMES Anitha Srinivasan Saint Louis University-Madrid campus, Spain Abstract. A D( 1)-quadruple is a set of positive
Solving the general quadratic congruence. y 2 Δ (mod p),
 Quadratic Congruences Solving the general quadratic congruence ax 2 +bx + c 0 (mod p) for an odd prime p (with (a, p) = 1) is equivalent to solving the simpler congruence y 2 Δ (mod p), where Δ = b 2 4ac
Quadratic Congruences Solving the general quadratic congruence ax 2 +bx + c 0 (mod p) for an odd prime p (with (a, p) = 1) is equivalent to solving the simpler congruence y 2 Δ (mod p), where Δ = b 2 4ac
SOME CONGRUENCES FOR PARTITION FUNCTIONS RELATED TO MOCK THETA FUNCTIONS ω(q) AND ν(q) S.N. Fathima and Utpal Pore (Received October 13, 2017)
 NEW ZEALAND JOURNAL OF MATHEMATICS Volume 47 2017), 161-168 SOME CONGRUENCES FOR PARTITION FUNCTIONS RELATED TO MOCK THETA FUNCTIONS ωq) AND νq) S.N. Fathima and Utpal Pore Received October 1, 2017) Abstract.
NEW ZEALAND JOURNAL OF MATHEMATICS Volume 47 2017), 161-168 SOME CONGRUENCES FOR PARTITION FUNCTIONS RELATED TO MOCK THETA FUNCTIONS ωq) AND νq) S.N. Fathima and Utpal Pore Received October 1, 2017) Abstract.
A characterization of regular tetrahedra in Z3
 Columbus State University CSU epress Faculty Bibliography 2009 A characterization of regular tetrahedra in Z3 Eugen J. Ionascu Follow this and additional works at: http://csuepress.columbusstate.edu/bibliography_faculty
Columbus State University CSU epress Faculty Bibliography 2009 A characterization of regular tetrahedra in Z3 Eugen J. Ionascu Follow this and additional works at: http://csuepress.columbusstate.edu/bibliography_faculty
On integer solutions to x 2 dy 2 = 1, z 2 2dy 2 = 1
 ACTA ARITHMETICA LXXXII.1 (1997) On integer solutions to x 2 dy 2 = 1, z 2 2dy 2 = 1 by P. G. Walsh (Ottawa, Ont.) 1. Introduction. Let d denote a positive integer. In [7] Ono proves that if the number
ACTA ARITHMETICA LXXXII.1 (1997) On integer solutions to x 2 dy 2 = 1, z 2 2dy 2 = 1 by P. G. Walsh (Ottawa, Ont.) 1. Introduction. Let d denote a positive integer. In [7] Ono proves that if the number
New infinite families of congruences modulo 8 for partitions with even parts distinct
 New infinite families of congruences modulo for partitions with even parts distinct Ernest X.W. Xia Department of Mathematics Jiangsu University Zhenjiang, Jiangsu 212013, P. R. China ernestxwxia@13.com
New infinite families of congruences modulo for partitions with even parts distinct Ernest X.W. Xia Department of Mathematics Jiangsu University Zhenjiang, Jiangsu 212013, P. R. China ernestxwxia@13.com
Binary quadratic forms and sums of triangular numbers
 Binary quadratic forms and sums of triangular numbers Zhi-Hong Sun( ) Huaiyin Normal University http://www.hytc.edu.cn/xsjl/szh Notation: Z the set of integers, N the set of positive integers, [x] the
Binary quadratic forms and sums of triangular numbers Zhi-Hong Sun( ) Huaiyin Normal University http://www.hytc.edu.cn/xsjl/szh Notation: Z the set of integers, N the set of positive integers, [x] the
THUE S LEMMA AND IDONEAL QUADRATIC FORMS
 THUE S LEMMA AND IDONEAL QUADRATIC FORMS PETE L. CLARK Introduction Recently I learned about Thue s Lemma, an elementary result on congruences due to the Norwegian mathematician Axel Thue (1863-1922).
THUE S LEMMA AND IDONEAL QUADRATIC FORMS PETE L. CLARK Introduction Recently I learned about Thue s Lemma, an elementary result on congruences due to the Norwegian mathematician Axel Thue (1863-1922).
Integer Sequences Avoiding Prime Pairwise Sums
 1 3 47 6 3 11 Journal of Integer Sequences, Vol. 11 (008), Article 08.5.6 Integer Sequences Avoiding Prime Pairwise Sums Yong-Gao Chen 1 Department of Mathematics Nanjing Normal University Nanjing 10097
1 3 47 6 3 11 Journal of Integer Sequences, Vol. 11 (008), Article 08.5.6 Integer Sequences Avoiding Prime Pairwise Sums Yong-Gao Chen 1 Department of Mathematics Nanjing Normal University Nanjing 10097
1 i<j k (g ih j g j h i ) 0.
 CONSECUTIVE PRIMES IN TUPLES WILLIAM D. BANKS, TRISTAN FREIBERG, AND CAROLINE L. TURNAGE-BUTTERBAUGH Abstract. In a stunning new advance towards the Prime k-tuple Conjecture, Maynard and Tao have shown
CONSECUTIVE PRIMES IN TUPLES WILLIAM D. BANKS, TRISTAN FREIBERG, AND CAROLINE L. TURNAGE-BUTTERBAUGH Abstract. In a stunning new advance towards the Prime k-tuple Conjecture, Maynard and Tao have shown
DETERMINANT IDENTITIES FOR THETA FUNCTIONS
 DETERMINANT IDENTITIES FOR THETA FUNCTIONS SHAUN COOPER AND PEE CHOON TOH Abstract. Two proofs of a theta function identity of R. W. Gosper and R. Schroeppel are given. A cubic analogue is presented, and
DETERMINANT IDENTITIES FOR THETA FUNCTIONS SHAUN COOPER AND PEE CHOON TOH Abstract. Two proofs of a theta function identity of R. W. Gosper and R. Schroeppel are given. A cubic analogue is presented, and
Super congruences involving binomial coefficients and new series for famous constants
 Tal at the 5th Pacific Rim Conf. on Math. (Stanford Univ., 2010 Super congruences involving binomial coefficients and new series for famous constants Zhi-Wei Sun Nanjing University Nanjing 210093, P. R.
Tal at the 5th Pacific Rim Conf. on Math. (Stanford Univ., 2010 Super congruences involving binomial coefficients and new series for famous constants Zhi-Wei Sun Nanjing University Nanjing 210093, P. R.
Ramanujan-type congruences for broken 2-diamond partitions modulo 3
 Progress of Projects Supported by NSFC. ARTICLES. SCIENCE CHINA Mathematics doi: 10.1007/s11425-014-4846-7 Ramanujan-type congruences for broken 2-diamond partitions modulo 3 CHEN William Y.C. 1, FAN Anna
Progress of Projects Supported by NSFC. ARTICLES. SCIENCE CHINA Mathematics doi: 10.1007/s11425-014-4846-7 Ramanujan-type congruences for broken 2-diamond partitions modulo 3 CHEN William Y.C. 1, FAN Anna
On the prime divisors of elements of a D( 1) quadruple
 arxiv:1309.4347v1 [math.nt] 17 Sep 2013 On the prime divisors of elements of a D( 1) quadruple Anitha Srinivasan Abstract In [4] it was shown that if {1,b,c,d} is a D( 1) quadruple with b < c < d and b
arxiv:1309.4347v1 [math.nt] 17 Sep 2013 On the prime divisors of elements of a D( 1) quadruple Anitha Srinivasan Abstract In [4] it was shown that if {1,b,c,d} is a D( 1) quadruple with b < c < d and b
p-regular functions and congruences for Bernoulli and Euler numbers
 p-regular functions and congruences for Bernoulli and Euler numbers Zhi-Hong Sun( Huaiyin Normal University Huaian, Jiangsu 223001, PR China http://www.hytc.edu.cn/xsjl/szh Notation: Z the set of integers,
p-regular functions and congruences for Bernoulli and Euler numbers Zhi-Hong Sun( Huaiyin Normal University Huaian, Jiangsu 223001, PR China http://www.hytc.edu.cn/xsjl/szh Notation: Z the set of integers,
Homework #2 solutions Due: June 15, 2012
 All of the following exercises are based on the material in the handout on integers found on the class website. 1. Find d = gcd(475, 385) and express it as a linear combination of 475 and 385. That is
All of the following exercises are based on the material in the handout on integers found on the class website. 1. Find d = gcd(475, 385) and express it as a linear combination of 475 and 385. That is
Math 109 HW 9 Solutions
 Math 109 HW 9 Solutions Problems IV 18. Solve the linear diophantine equation 6m + 10n + 15p = 1 Solution: Let y = 10n + 15p. Since (10, 15) is 5, we must have that y = 5x for some integer x, and (as we
Math 109 HW 9 Solutions Problems IV 18. Solve the linear diophantine equation 6m + 10n + 15p = 1 Solution: Let y = 10n + 15p. Since (10, 15) is 5, we must have that y = 5x for some integer x, and (as we
Polynomials. In many problems, it is useful to write polynomials as products. For example, when solving equations: Example:
 Polynomials Monomials: 10, 5x, 3x 2, x 3, 4x 2 y 6, or 5xyz 2. A monomial is a product of quantities some of which are unknown. Polynomials: 10 + 5x 3x 2 + x 3, or 4x 2 y 6 + 5xyz 2. A polynomial is a
Polynomials Monomials: 10, 5x, 3x 2, x 3, 4x 2 y 6, or 5xyz 2. A monomial is a product of quantities some of which are unknown. Polynomials: 10 + 5x 3x 2 + x 3, or 4x 2 y 6 + 5xyz 2. A polynomial is a
0 Sets and Induction. Sets
 0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
Prime Numbers and Irrational Numbers
 Chapter 4 Prime Numbers and Irrational Numbers Abstract The question of the existence of prime numbers in intervals is treated using the approximation of cardinal of the primes π(x) given by Lagrange.
Chapter 4 Prime Numbers and Irrational Numbers Abstract The question of the existence of prime numbers in intervals is treated using the approximation of cardinal of the primes π(x) given by Lagrange.
ARITHMETIC PROGRESSIONS OF SQUARES, CUBES AND n-th POWERS
 ARITHMETIC PROGRESSIONS OF SQUARES, CUBES AND n-th POWERS L. HAJDU 1, SZ. TENGELY 2 Abstract. In this paper we continue the investigations about unlike powers in arithmetic progression. We provide sharp
ARITHMETIC PROGRESSIONS OF SQUARES, CUBES AND n-th POWERS L. HAJDU 1, SZ. TENGELY 2 Abstract. In this paper we continue the investigations about unlike powers in arithmetic progression. We provide sharp
2-UNIVERSAL POSITIVE DEFINITE INTEGRAL QUINARY QUADRATIC FORMS
 2-UNIVERSAL POSITIVE DEFINITE INTEGRAL QUINARY QUADRATIC FORMS Byeong Moon Kim, Myung-Hwan Kim and Byeong-Kweon Oh Dept. of Math., Kangnung Nat l Univ., Kangwondo 210-702, Korea (kbm@knusun.kangnung.ac.kr)
2-UNIVERSAL POSITIVE DEFINITE INTEGRAL QUINARY QUADRATIC FORMS Byeong Moon Kim, Myung-Hwan Kim and Byeong-Kweon Oh Dept. of Math., Kangnung Nat l Univ., Kangwondo 210-702, Korea (kbm@knusun.kangnung.ac.kr)
THE NUMBER OF DIOPHANTINE QUINTUPLES. Yasutsugu Fujita College of Industrial Technology, Nihon University, Japan
 GLASNIK MATEMATIČKI Vol. 45(65)(010), 15 9 THE NUMBER OF DIOPHANTINE QUINTUPLES Yasutsugu Fujita College of Industrial Technology, Nihon University, Japan Abstract. A set a 1,..., a m} of m distinct positive
GLASNIK MATEMATIČKI Vol. 45(65)(010), 15 9 THE NUMBER OF DIOPHANTINE QUINTUPLES Yasutsugu Fujita College of Industrial Technology, Nihon University, Japan Abstract. A set a 1,..., a m} of m distinct positive
THE PROBLEM OF DIOPHANTUS FOR INTEGERS OF Q( 3) Zrinka Franušić and Ivan Soldo
 RAD HAZU. MATEMATIČKE ZNANOSTI Vol. 8 = 59 (04): 5-5 THE PROBLEM OF DIOPHANTUS FOR INTEGERS OF Q( ) Zrinka Franušić and Ivan Soldo Abstract. We solve the problem of Diophantus for integers of the quadratic
RAD HAZU. MATEMATIČKE ZNANOSTI Vol. 8 = 59 (04): 5-5 THE PROBLEM OF DIOPHANTUS FOR INTEGERS OF Q( ) Zrinka Franušić and Ivan Soldo Abstract. We solve the problem of Diophantus for integers of the quadratic
PARITY OF THE PARTITION FUNCTION. (Communicated by Don Zagier)
 ELECTRONIC RESEARCH ANNOUNCEMENTS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 1, Issue 1, 1995 PARITY OF THE PARTITION FUNCTION KEN ONO (Communicated by Don Zagier) Abstract. Let p(n) denote the number
ELECTRONIC RESEARCH ANNOUNCEMENTS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 1, Issue 1, 1995 PARITY OF THE PARTITION FUNCTION KEN ONO (Communicated by Don Zagier) Abstract. Let p(n) denote the number
An Elementary and Simple Proof of Fermat s Last Theorem arxiv: v3 [math.gm] 13 Mar 2018
![An Elementary and Simple Proof of Fermat s Last Theorem arxiv: v3 [math.gm] 13 Mar 2018 An Elementary and Simple Proof of Fermat s Last Theorem arxiv: v3 [math.gm] 13 Mar 2018](/thumbs/77/74858104.jpg) An Elementary and Simple Proof of Fermat s Last Theorem arxiv:1412.1689v3 [math.gm] 13 Mar 2018 Mie Winler Faultät für Mathemati, Ruhr-Universität Bochum mie.winler@ruhr-uni-bochum.de www.miewinler.co.nf
An Elementary and Simple Proof of Fermat s Last Theorem arxiv:1412.1689v3 [math.gm] 13 Mar 2018 Mie Winler Faultät für Mathemati, Ruhr-Universität Bochum mie.winler@ruhr-uni-bochum.de www.miewinler.co.nf
On Arithmetic Properties of Bell Numbers, Delannoy Numbers and Schröder Numbers
 A tal given at the Institute of Mathematics, Academia Sinica (Taiwan (Taipei; July 6, 2011 On Arithmetic Properties of Bell Numbers, Delannoy Numbers and Schröder Numbers Zhi-Wei Sun Nanjing University
A tal given at the Institute of Mathematics, Academia Sinica (Taiwan (Taipei; July 6, 2011 On Arithmetic Properties of Bell Numbers, Delannoy Numbers and Schröder Numbers Zhi-Wei Sun Nanjing University
k, then n = p2α 1 1 pα k
 Powers of Integers An integer n is a perfect square if n = m for some integer m. Taking into account the prime factorization, if m = p α 1 1 pα k k, then n = pα 1 1 p α k k. That is, n is a perfect square
Powers of Integers An integer n is a perfect square if n = m for some integer m. Taking into account the prime factorization, if m = p α 1 1 pα k k, then n = pα 1 1 p α k k. That is, n is a perfect square
Notes on Primitive Roots Dan Klain
 Notes on Primitive Roots Dan Klain last updated March 22, 2013 Comments and corrections are welcome These supplementary notes summarize the presentation on primitive roots given in class, which differed
Notes on Primitive Roots Dan Klain last updated March 22, 2013 Comments and corrections are welcome These supplementary notes summarize the presentation on primitive roots given in class, which differed
LEGENDRE S THEOREM, LEGRANGE S DESCENT
 LEGENDRE S THEOREM, LEGRANGE S DESCENT SUPPLEMENT FOR MATH 370: NUMBER THEORY Abstract. Legendre gave simple necessary and sufficient conditions for the solvablility of the diophantine equation ax 2 +
LEGENDRE S THEOREM, LEGRANGE S DESCENT SUPPLEMENT FOR MATH 370: NUMBER THEORY Abstract. Legendre gave simple necessary and sufficient conditions for the solvablility of the diophantine equation ax 2 +
THE JACOBI SYMBOL AND A METHOD OF EISENSTEIN FOR CALCULATING IT
 THE JACOBI SYMBOL AND A METHOD OF EISENSTEIN FOR CALCULATING IT STEVEN H. WEINTRAUB ABSTRACT. We present an exposition of the asic properties of the Jacoi symol, with a method of calculating it due to
THE JACOBI SYMBOL AND A METHOD OF EISENSTEIN FOR CALCULATING IT STEVEN H. WEINTRAUB ABSTRACT. We present an exposition of the asic properties of the Jacoi symol, with a method of calculating it due to
