Internal Regret in On-line Portfolio Selection
|
|
|
- Robert Cole
- 5 years ago
- Views:
Transcription
1 Internal Regret in On-line Portfolio Selection Gilles Stoltz Département de Mathématiques et Applications, Ecole Normale Supérieure, Paris, France Gábor Lugosi Department of Economics, Pompeu Fabra University, Barcelona, Spain Abstract. This paper extends the game-theoretic notion of internal regret to the case of on-line potfolio selection problems. New sequential investment strategies are designed to minimize the cumulative internal regret for all possible market behaviors. Some of the introduced strategies, apart from achieving a small internal regret, achieve an accumulated wealth almost as large as that of the best constantly rebalanced portfolio. It is argued that the low-internal-regret property is related to stability and experiments on real stock exchange data demonstrate that the new strategies achieve better returns compared to some known algorithms. 1. Introduction The problem of sequential portfolio allocation is well-known to be closely related to the on-line prediction of individual sequences under expert advice, see, for example, Cover (1991), Cover and Ordentlich (1996), Helmbold, Schapire, Singer, and Warmuth (1998), Ordentlich and Cover (1998), Blum and Kalai (1999), Cesa-Bianchi and Lugosi (2000). In the on-line prediction problem the goal is to minimize the predictor s cumulative loss with respect to the best cumulative loss in a pool of experts. In a certain equivalent game-theoretic formulation of the problem, this is the same as minimizing the predictor s external regret, see Foster and Vohra (1999). External regret measures the difference between the predictor s cumulative loss and that of the best expert. However, another notion of regret, called internal regret in Foster and Vohra (1999) has also been in the focus of attention mostly in the theory of playing repeated games, see Foster and Vohra (1998; 1999), Fudenberg and Levine (1999), Hart and Mas- Colell (2000; 2001), Cesa-Bianchi and Lugosi (2003). Roughly speaking, An extended abstract appeared in the Proceedings of the 16th Annual Conference on Learning Theory and 7th Kernel Workshop, Springer, The work of the first author was supported by PAI Picasso grant 02543RM and by the French CNRS research network AS66 (SVM and kernel algorithms). The work of the second author was supported by DGI grant BMF c 2004 Kluwer Academic Publishers. Printed in the Netherlands. InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.1
2 2 a predictor has a small internal regret if for each pair of experts (i,j), the predictor does not regret of not having followed expert i each time it followed expert j. It is easy to see that requiring a small internal regret is a more difficult problem since a small internal regret in the prediction problem implies small external regret as well. A brief summary of the basic properties is given below. The goal in the sequential investment problem is to distribute one s capital in each trading period among a certain number of stocks such that the total achieved wealth is almost as large as the wealth of the largest in a certain class of investment strategies. This problem, known as the minimization of the worst-case logarithmic wealth ratio, is easily seen to be the generalization of an external regret minimization problem in the expert setting under the logarithmic loss function. The main purpose of this paper is to extend the notion of internal regret to the sequential investment problem, understand its relationship to the worst-case logarithmic wealth ratio, and design investment strategies minimizing this new notion of regret. The definition of internal regret given here has a natural interpretation and the investment strategies designed to minimize it have several desirable properties both in theory and in the experimental study described in the Appendix. The paper is organized as follows. In Sections 2 and 3 we briefly summarize the sequential prediction problem based on expert advice and describe the notions of internal and external regrets. In Section 4 the sequential portfolio selection problem is described, and basic properties of Cover s universal portfolio and the eg investment strategy are discussed. In Section 5 we introduce the notion of internal regret for sequential portfolio selection, and describe some basic properties. In Section 6 new investment strategies are presented aiming at the minimization of the internal regret. Finally, in Section 7 the notion of internal regret is generalized for an uncountable class of investment strategies and an algorithm inspired by Cover s universal portfolio is proposed which minimizes the new notion of internal regret. 2. Sequential prediction: external regret In the (randomized) sequential prediction problem the predictor, at each time instance t = 1,2,..., chooses a probability distribution P t = (P 1,t,...,P N,t ) over the set {1,2,...,N} of experts. After the choice is made, expert i suffers loss l i,t, and the predictor suffers loss N l t (P t ) = P i,t l i,t. i=1 InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.2
3 This loss may be interpreted as the expected loss if the predictor chooses an expert randomly, according to the distribution P t, and predicts as the selected expert s advice. The external regret of the predictor, after n rounds of play, is n n N n l t (P t ) min l i,t = max P j,t (l j,t l i,t ). i=1,...,n i=1,...,n j=1 If this external regret is o(n) uniformly over all possible values of the losses, then the corresponding predictor is said to suffer no external regret. This problem has been extensively studied since Hannan (1957) and Blackwell (1956). For example, it is well known (see, e.g., Cesa-Bianchi and Lugosi (1999)) that if the losses l i,t are all bounded between zero and B > 0, then the exponentially weighted average predictor defined, for t = 1,2,..., by exp( η t P i,t+1 = s=1 l i,s ) Nj=1 exp( η t s=1 l j,s ) has an external regret bounded by ln N η + n η 8 B2 = B (n/2)ln N, (1) with the (optimal) choice η = B 1 8ln N/n. The tuning parameter η can be set optimally only when the time length n is known in advance. However, we recall a simple modification of the exponentially weighted average algorithm, proposed by Auer, Cesa-Bianchi, and Gentile (2002), which does not need to know n in advance. A natural adaptive version of the optimal parameter η determined in the case of known time length is formed by defining the tuning parameter at round t by η t = B 1 8ln N/t. Now, the exponentially weighted average forecaster with time-varying tuning parameter predicts, at rounds t = 1,2,..., with P i,t+1 = exp ( η t+1 L i,t ) Nj=1 exp ( η t+1 L j,t ), 3 where L i,t = t s=1 l i,s. Denote the (expected) cumulative loss of the algorithm by L n = n l t (P t ). The following result is proved in Auer, Cesa-Bianchi, and Gentile (2002). Theorem 1. The exponentially weighted average forecaster with timevarying tuning parameter achieves, uniformly over all possible values InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.3
4 4 of the losses l i,t [0,B], n L n min L i,n B 2 i=1,...,n 2 lnn + ln N. 8 This result will be used in Section 6.1 to define an investment algorithm which does not need to know in advance the trading time length. A whole family of predictors with performance guarantees similar to those of the exponentially weighted forecaster may be defined, see, for example, Cesa-Bianchi and Lugosi (2003). Some of them do not require the knowledge of the time length, as is the case of the polynomial forecaster described below. Nevertheless, it is important to design a time-adaptive version of the exponentially weighted forecaster, for the latter is a popular method, usually achieving good results in practical situations (see also our experimental results in the Appendix). An important class of polynomial forecasters are those of the form P i,t+1 = ( ts=1 l s (P s ) l i,s ) p 1 + Nj=1 ( ts=1 l s (P s ) l j,s ) p 1 where p 1 and (x) + = max {x, 0} denotes the nonnegative part of the real number x. These forecasters satisfy the following bound, see Cesa-Bianchi and Lugosi (2003). Theorem 2. The polynomial forecaster with p 1 achieves, uniformly over all possible values of the losses l i,t [0,B], L n min L i,n B (p 1)nN 2/p. i=1,...,n Sequential prediction: internal regret 3.1. Definition of the internal regret The definition of external regret is based on the comparison to an external pool of strategies, the ones given by each expert. In the definition of the internal regret one is interested in modifications of the predictor s strategy obtained by replacing the action of the forecaster by expert j each time it chooses expert i. This is equivalent to selecting an expert according to the distribution P i j t obtained from P t by putting InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.4
5 probability mass 0 on i and P i,t +P j,t on j. This transformation is called the i j modified strategy. We require that none of these modified strategies is much better than the original strategy, that is, we seek strategies such that the difference between their (expected) cumulative loss and that of the best modified strategy is small. Thus, n n l t (P t ) min l t (P i j t ) i,j {1,...,N} should be as small as possible. This quantity is called the internal regret of the sequential predictor P t. The internal regret may be re-written as n max r (i,j),t i,j {1,...,N} where r (i,j),t = P i,t (l i,t l j,t ). Thus, r (i,j),t expresses the predictor s regret of having put the probability mass P i,t on the i-th expert instead of on the j-th one, and n n R (i,j),n = r (i,j),t = P i,t (l i,t l j,t ) is the corresponding cumulative regret. Similarly to the case of the external regret, if this quantity is uniformly o(n) over all possible values of the losses, then the corresponding predictor is said to exhibit no internal regret. Now clearly, the external regret of the predictor P t equals max j=1,...,n N R (i,j),n N i=1 5 max R (i,j),n (2) i,j {1,...,N} which shows that any algorithm with a small (i.e., sublinear in n) internal regret also has a small external regret. On the other hand, it is easy to see that a small external regret does not imply small internal regret. In fact, as it is shown in the next example, even the exponential weighted average algorithm defined above may have a linearly growing internal regret. Example 1. (Weighted average predictor has a large internal regret.) Consider the following example with three experts, A, B, and C. Let n be a large multiple of 3 and assume that time is divided in three equally long regimes, characterized by a constant loss for each expert. These losses are summarized in Table I. We claim that the regret R (B,C),n of InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.5
6 6 Table I. The losses for Example 1. Regimes l A,t l B,t l C,t 1 t n/ n/3 + 1 t 2n/ n/3 + 1 t n B versus C grows linearly with n, that is, where lim inf n 1 n n P B,t (l B,t l C,t ) = γ > 0, e ηl B,t P B,t = e ηl A,t + e ηl B,t + e ηl C,t denotes the weight assigned by the exponential weighted average predictor to expert B, where L i,t = t s=1 l(i,s) denotes the cumulative loss of expert i and η is chosen to minimize the external regret, that is, η = (1/5) (8ln 3)/n = 1/(K n) with K = 5/ 8ln 3. (Note that the same argument leads to a similar lower bound for η = γ/ n, where γ > 0 is any constant.) The intuition behind this example is that at the end of the second regime the predictor quickly switches from A to B, and the weight of expert C can never recover because of its disastrous behavior in the first two regimes. But since expert C behaves much better than B in the third regime, the weighted average predictor will regret of not having followed the advice of C each time it followed B. More precisely, we show that during the first two regimes, the number of times when P B,t is more than ε is of the order of n and that, in the third regime, P B,t is always more than a fixed constant (1/3, say). This is illustrated in Figure 1. In the first regime, a sufficient condition for P B,t ε is that e ηl B,t ε. This occurs whenever t t 0 = K ( ln ε) n. For the second regime, we lower bound the time instant t 1 when P B,t gets larger than ε. To this end, note that P B,t ε implies ( ) (1 ε)e ηl B,t ε e ηl A,t + e ηl C,t εe ηl A,t, which leads to t 1 2n 3 + K (ln ε 1 ε) n. Finally, in the third regime, we have at each time instant L B,t L A,t and L B,t L C,t, so that P B,t 1/3. Putting these three steps together, we obtain the following InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.6
7 weight of B First regime Second regime Third regime / t 0 t Figure 1. The evolution of the weight assigned to B in Example 1 for n = lower bound for the internal regret of B versus C: n P B,t (l B,t l C,t ) n ( ( 2n ε + K ln 1 ε ) ) n which is of the order n, for a sufficiently small ε > 0. ε 2, 3.2. A general way to design internal regret minimizing algorithms The example above shows that special algorithms need to be designed to guarantee a small internal regret. Indeed, such predictors exist, as was shown by Foster and Vohra (1998), see also Fudenberg and Levine (1999), Hart and Mas-Colell (2000; 2001). Here we briefly give a new insight on predictors studied in Cesa-Bianchi and Lugosi (2003) (see the remark at the end of this section), and based on Hart and Mas- Colell (2001), as well as a new, simple analysis of their performance guarantees. Consider the case of sequential prediction under expert advice, with N experts. At round t, the forecaster has already chosen the probability distributions P 1,...,P t 1. We define N(N 1) fictitious experts, indexed by pairs of integers i j, by their losses at time instants 1 s t 1, which equal l s (P i j s ). Define now a probability distribution t over the pairs i j by running one of the algorithms of Section 2 on this pool of fictitious experts, and choose P t such that the fixed point equality P t = (i,j):i j (i,j),t P i j t, (3) InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.7
8 8 holds. (We say that t induces P t.) The existence and the practical computation of such a P t is an application of Lemma 1 below. For instance, t = ( (i,j),t ) i j may be given by (i,j),t = ( exp η ) t 1 s=1 l s(p i j s ) (k,l):k l ( η exp ) t 1 s=1 l, s(p k l s ) tuned, as suggested by the theory, with η = 4B 1 ln N/n in case of known time horizon n. Indeed, this choice of η and the application of the bound (1) (with N(N 1) upper bounded by N 2 ) lead to n i j (i,j),t l t (P i j t ) min i j n l t (P i j t ) + B n ln N, that is, recalling the fixed point equality (3), the cumulative internal regret of the above strategy is bounded by max i j R (i,j),n B n ln N. Note that this improves the bound given in Corollary 8 of Cesa-Bianchi and Lugosi (2003), by a factor of two. The same analysis can be carried over for the polynomial forecasters or the time-adaptive version of the exponentially weighted forecaster, using Theorems 1 and 2, and is summarized in the following theorem. Theorem 3. The above exponentially weighted predictor achieves, uniformly over all possible values of the losses l i,t [0,B], max i j R (i,j),n B n lnn. With a time-adaptive tuning parameter the upper bound becomes ( max R (i,j),n B 2 ) ln N n lnn +. i j 2 Finally, with a polynomial predictor of order p 1, max R (i,j),n B (p 1)nN 4/p. i j Remark. The conversion trick illustrated above is a general trick which extends to any weighted average predictor, that is, to any predictor which, at each round, maintains one weight per expert. More InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.8
9 precisely, any weighted average predictor whose external regret is small may be converted into a strategy whose internal regret remains small. This will be illustrated for convex loss functions in Section 6.1 and for exp-concave ones in Section 7.1 and 7.2. Note also that in the case of randomized prediction under expert advice Blum and Mansour (2004) propose a different conversion trick, with about the same algorithmic complexity. Such tricks are valuable to extend results in an effortless way from the case of no external to no internal regret, like the time-adaptive exponentially weighted average predictor suited for the minimization of internal regret proposed by Theorem 3. It only remains to see the existence and the way to compute a fixed point of the equality (3). The following lemma proposes a more general result, needed for subsequent analysis in Section 7.1. The meaning of this result is that each probability distribution over the expert pairs induces naturally a probability distribution over the experts. Lemma 1. Let Q be a probability distributions over the N experts. For all probability distributions over the pairs of different experts i j and α [0,1], there exists a probability distribution P over the experts such that P = (1 α) i j (i,j) P i j + αq. 9 Moreover, P may be easily computed by a Gaussian elimination over a simple N N matrix. Proof. The equality P = (1 α) i j (i,j) P i j + αq means that for all m {1,...,N}, or equivalently, P m = (1 α) i j α (1 Q m ) + (1 α) j m (i,j) P i j m (m,j) N + αq m P m = i m P j, j=1 ((1 α) (i,m) + αq m ) P i, that is, P is an element of the kernel of the matrix A defined by InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.9
10 10 if i m, A m,i = w m,i, A m,m = j m, 1 j N w j,m, where, for i m, w m,i = (1 α) (i,m) + αq m. The elements of A have a modulus less than 1. An element of the kernel of A is a fixed point of the matrix S = A + I N, where I N is the N N identity matrix. But S is a column stochastic matrix (its columns are probability distributions), and thus admits a probability distribution P as a fixed point. Foster and Vohra (1999) suggest a Gaussian elimination method over A for the practical computation of P. Remark. Cesa-Bianchi and Lugosi (2003) show that, writing r t for the N(N 1)-vector with components r (i,j),t and R t = t s=1 r s, any predictor satisfying the so-called Blackwell condition Φ(R t 1 ) r t 0 (4) for all t 1, with Φ being either an exponential potential N Φ(u) = exp (ηu i ), i=1 with η possibly depending on t (when time-adaptive versions are considered) or a polynomial potential N Φ(u) = (u i ) p +, i=1 has the performance guarantees given by Theorem 3. But the choice (3) ensures that the Blackwell condition is satisfied with an equality, as Φ(R t 1 ) r t N = l i,t i=1 j=1,...,n, j i (i,j) Φ(R t 1 )P i,t j=1,...,n, j i (j,i) Φ(R t 1 )P j,t (see, e.g., Cesa-Bianchi and Lugosi (2003) for the details), which equals 0 as soon as (i,j) Φ(R t 1 )P i,t (j,i) Φ(R t 1 )P j,t = 0 j=1,...,n, j i j=1,...,n, j i InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.10
11 for all i = 1,...,N. The latter set of equations may be seen to be equivalent to (3), with the choice (i,j),t = (i,j) Φ(R t 1 ) k l (k,l)φ(r t 1 ), which was indeed the probability distribution proposed by the conversion trick introduced at the beginning of this section Sequential portfolio selection In this section we describe the problem of sequential portfolio selection, recall some previous results, and take a new look at the eg strategy of Helmbold, Schapire, Singer, and Warmuth (1998). A market vector x = (x 1,...,x N ) for N assets is a vector of nonnegative numbers representing price relatives for a given trading period. In other words, the quantity x i 0 denotes the ratio of closing to opening price of the i-th asset for that period. Hence, an initial wealth invested in the N assets according to fractions Q 1,...,Q N multiplies by a factor of N i=1 x i Q i at the end of period. The market behavior during n trading periods is represented by a sequence x n 1 = (x 1,...,x n ) of market vectors. x j,t, the j-th component of x t, denotes the factor by which the wealth invested in asset j increases in the t-th period. We denote the probability simplex in R N by X. An investment strategy Q for n trading periods consists in a sequence Q 1,...,Q n of vector-valued functions Q t : (R N + )t 1 X, where the i-th component Q i,t (x t 1 1 ) of the vector Q t (x t 1 1 ) denotes the fraction of the current wealth invested in the i-th asset at the beginning of the t-th period based on the past market behavior x t 1 1. We use ) S n (Q,x n 1) = ( n N x i,t Q i,t (x t 1 1 ) i=1 to denote the wealth factor of strategy Q after n trading periods. The simplest examples of investment strategies are the so called buy-and-hold strategies. A buy-and-hold strategy simply distributes its initial wealth among the N assets according to some distribution Q 1 X before the first trading period, and does not trade anymore, which amounts to investing, at day t and for 1 i N, as Q i,t (x t 1 1 ) = Q i,1 t 1 s=1 x i,s Nk=1 Q k,1 t 1 s=1 x k,s. InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.11
12 12 The wealth factor of such a strategy, after n periods, is simply N S n (Q,x n 1) = Q j,1 S n (j), j=1 where n S n (j) = x j,t is the accumulated wealth of stock j. Clearly, the wealth factor of any buy-and-hold strategy is at most as large as the gain max j=1,...,n S n (j) of the best stock over the investment period, and achieves this maximal wealth if Q 1 concentrates on the best stock. Another simple and important class of investment strategies is the class of constantly rebalanced portfolios. Such a strategy B is parametrized by a probability vector B = (B 1,...,B N ) X, and simply Q t (x t 1 1 ) = B regardless of t and the past market behavior x t 1 1. Thus, an investor following such a strategy rebalances, at every trading period, his current wealth according to the distribution B by investing a proportion B 1 of his wealth in the first stock, a proportion B 2 in the second stock, etc. The wealth factor achieved after n trading periods is ( n N ) S n (B,x n 1) = x i,t B i. i=1 Now given a class Q of investment strategies, we define the worst-case logarithmic wealth ratio of strategy P by W n (P, Q) = sup x n 1 sup Q Q ln S n(q,x n 1 ) S n (P,x n 1 ). The worst-case logarithmic wealth ratio is the analog of the external regret in the sequential portfolio selection problem. W n (P, Q) = o(n) means that the investment strategy P achieves the same exponent of growth as the best reference strategy in the class Q for all possible market behaviors. For example, it is immediate to see that if Q is the class of all buyand-hold strategies, then if P is chosen to be the buy-and-hold strategy based on the uniform distribution Q 1, then W n (P, Q) ln N. The class of constantly rebalanced portfolios is a significantly richer class and achieving a small worst-case logarithmic wealth ratio is a greater challenge. Cover s universal portfolio (1991) was the first example to achieve this goal. The universal portfolio strategy P is defined by P j,t (x t 1 1 ) = X B js t 1 (B,x t 1 1 )φ(b)db X S t 1(B,x t 1 1 )φ(b)db, j = 1,...,N,t = 1,...,n InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.12
13 where φ is a density function on X. In the simplest case φ is the uniform density over X. In that case, the worst-case logarithmic wealth ratio of P with respect to the class Q of all universal portfolios satisfies W n (P, Q) (N 1)ln(n + 1). If the universal portfolio is defined using the Dirichlet(1/2,,1/2) density φ, then the bound improves to W n (P, Q) N 1 2 ln n + ln Γ(1/2)N Γ(N/2) + N 1 ln 2 + o(1), 2 see Cover and Ordentlich (1996). The worst-case performance of the universal portfolio is basically unimprovable (see Ordentlich and Cover (1998)) but it has some practical disadvantages, including computational difficulties for not very small values of N. Helmbold, Schapire, Singer, and Warmuth (1998) suggest their eg strategy to overcome these difficulties. The eg strategy is defined by P i,t+1 = 13 P i,t exp (ηx i,t /P t x t ) Nj=1 P j,t exp (ηx j,t /P t x t ). (5) Helmbold, Schapire, Singer, and Warmuth (1998) prove that if the market values x i,t all fall between the positive constants m and M, then the worst-case logarithmic wealth ratio of the eg investment strategy is bounded by ln N η + nη 8 M 2 m 2 = M n m 2 ln N, where the equality holds for the choice η = (m/m) (8ln N)/n. Here we give a simple new proof of this result, mostly because the main idea is at the basis of other arguments that follow. Recall that the worst-case logarithmic wealth ratio is max max ln x n 1 B X n B x t n P t x t where in this case the first maximum is taken over market sequences satisfying the boundedness assumption. By using the elementary inequality ln(1 + u) u, we obtain ln n B x t n P t x t = n ( ln n N i=1 1 + (B P t) x t P t x t (B i P i,t )x i,t P t x t ) InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.13
14 14 = = n N N j=1 i=1 ( N n N B j j=1 i=1 P i,t B j x j,t P t x t P i,t ( xj,t P t x t N N P i,t x i,t B j P i=1 j=1 t x t x ) ) i,t. (6) P t x t Under the boundedness assumption 0 < m x i,t M, the quantities l i,t = M/m x i,t /(P t x t ) are within [0, M/m] and can therefore be interpreted as bounded loss functions. Thus, the minimization of the above upper bound on the worst-case logarithmic wealth ratio may be cast as a sequential prediction problem as described in Section 2. Observing that the eg investment algorithm is just the exponentially weighted average predictor for this prediction problem, and using the performance bound (1) we obtain the cited inequality of Helmbold, Schapire, Singer, and Warmuth (1998). Note that in (5), we could replace the fixed η by a time-adaptive η t = (m/m) (8ln N)/t. Applying Theorem 3 to the linear upper bound (6), we may prove that this still leads to a worst-case logarithmic wealth ratio less than something of the order of (M/m) n ln N. Remark. (Sub-optimality of the eg investment strategy.) Using the approach of bounding the worst-case logarithmic wealth ratio linearly as above is inevitably suboptimal. Indeed, the right-hand side of the linear upper bounding ( N n ( N ) ) N N ( n ) B j P i,t l i,t l j,t = B j P i,t (l i,t l j,t ) j=1 i=1 j=1 i=1 is maximized for a constantly rebalanced portfolio B lying in a corner of the simplex X, whereas the left-hand side is concave in B and therefore is possibly maximized in the interior of the simplex. Thus, no algorithm trying to minimize (in a worst-case sense) the linear upper bound on the external regret can be minimax optimal. However, as it is shown in Helmbold, Schapire, Singer, and Warmuth (1998), on real data good performance may be achieved. Note also that the bound obtained for the worst-case logarithmic wealth ratio of the eg strategy grows as n whereas that of Cover s universal portfolio has only a logarithmic growth. In Helmbold, Schapire, Singer, and Warmuth (1998) it is asked whether the suboptimal bound for the eg strategy is an artifact of the analysis or it is inherent in the InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.14
15 algorithm. The next simple example shows that no bound of a smaller order than n holds. Consider a market with two assets and market vectors x t = (1,1 ε), for all t. Then every wealth allocation P t satisfies 1 ε P t x t 1. Now, the best constantly rebalanced portfolio is clearly (1,0), and the worst-case logarithmic wealth ratio is simply In the case of the eg strategy, P 2,t = n 1 n ln 1 P 2,t ε P 2,t ε. ( exp η t 1 s=1 ( exp η t 1 (1 ε) s=1 1 P s x s ) + exp ( = exp ηε t 1 s=1 ( 1 + exp ηε t 1 s=1 ) 1 P s x s ) 1 P s x s P s x s ) exp ( η (ε/(1 ε)) (t 1)) 2 ( η ) t 1 (1 ε) s=1 P s x s Thus, the logarithmic wealth ratio of the eg algorithm is lower bounded by. 15 n exp ( η (ε/(1 ε)) (t 1)) ε 2 = ε 1 exp ( η (ε/(1 ε)) n) 2 1 exp ( η (ε/(1 ε))) = 1 n 2 8ln N + o( n). 5. Internal regret of investment strategies The aim of this section is to introduce the notion of internal regret to the sequential investment problem. In the latter, the loss function we consider is defined by l (Q,x) = lnq x for a portfolio Q and a market vector x. This is no longer a linear function of Q (as this was the case in Sections 2 and 3 for the expected loss of the predictor). Recall that in the framework of sequential prediction described in Section 2, the cumulative internal regret R (i,j),n for the pair of experts (i,j) may be interpreted as how much the predictor would have gained, had he replaced all values P i,t (t n) by zero and all values P j,t by P i,t +P j,t. Analogously, given an investment strategy P = (P 1,P 2,...), InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.15
16 16 we may define the internal regret of P with respect to the pair of assets (i,j) at day t (where 1 i,j N) by r (i,j),t = l (P t,x t ) l (P i j t,x t ) = ln Pi j t x t P t x t where the probability vector P i j t is defined such that its i-th component equals zero, its j-th component equals P j,t + P i,t, and all other components are equal to those of P t. r (i,j),t expresses the regret the investor using strategy P suffers after trading day t of not having invested all the capital he invested in stock i in stock j instead. The cumulative internal regret of P with respect to the pair (i,j) after n trading periods is simply R (i,j),n = n r (i,j),n. This notion of internal regret in on-line portfolio selection may be seen as a special case of the definition of internal regret for general loss functions proposed in Stoltz and Lugosi (2004), with the class of departure functions given by those functions that move all probability mass from a given component to another one. In Section 7.2, we study internal regret with respect to a much larger class, whose size is of the power of the continuum. It is a desirable property of an investment strategy that its cumulative internal regret grows sub-linearly for all possible pairs of assets, independently of the market outcomes. Indeed, otherwise the investor could exhibit a simple modification of his betting strategy which would have led to exponentially larger wealth. In this sense, the notion of internal regret is a measure of the efficiency of the strategy: the aim of the broker is not that the owner of the stocks gets rich, but that the owner cannot criticize easily the chosen strategy. Note that the worst-case logarithmic wealth ratio corresponds to the case when the owner compares his achieved wealths to those obtained by others who have different brokers. Based on this, we define the internal regret of the investment strategy P by R n = max 1 i,j N R (i,j),n and ask whether it is possible to guarantee that R n = o(n) for all possible market sequences. Thus, an investor using a strategy with a small internal regret is guaranteed that for any pair of stocks the total regret of not investing in one stock instead of the other becomes negligible. (Note that in Section 7.2 we introduce a richer class of possible departures from the original investment strategies.) InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.16
17 The next two examples show that it is not trivial to achieve a small internal regret. Indeed, the buy-and-hold and eg investment strategies have linearly increasing internal regret for some bounded market sequences. Example 2. (Buy-and-hold strategies may have large internal regret.) Consider a market with N = 3 assets which evolves according to the following repeated scheme: (1 ε,ε,ε), (ε,1 ε,1 ε), (1 ε,ε,ε), (ε,1 ε,1 ε),... where ε < 1 is a fixed positive number. The buy-and-hold strategy, which distributes its initial wealth uniformly among the assets invests, at odd t s, with ( 1 P t = 3, 1 3, 1 ( 2, so that P 3) 2 1 t = 3,0, 1, 3) and at even t s, with ( ) 1 ε P t = 1 + ε, ε 1 + ε, ε 1 + ε ( ) 1, so that P 2 1 t = 1 + ε,0, ε 1 + ε Straightforward calculation now shows that for an even n, the cumulative internal regret R (2,1),n of this strategy equals ( n (2 ε) 2 ) ln, 2 3(1 ε)(1 + ε) showing that even for bounded markets, the naive buy-and-hold strategy may incur a large internal regret. Later we will see a generalization of buy-and-hold with small internal regret. Example 3. (The eg strategy may have large internal regret.) The next example, showing that for some market sequence the eg algorithm of Helmbold, Schapire, Singer, and Warmuth (1998) has a linearly growing internal regret, is inspired by Example 1 above. Consider a market of three stocks A, B, and C. Divide the n trading periods into three different regimes of lengths n 1, n 2, and n 3. The wealth ratios (which are constant in each regime) are summarized in the Table II. We show that it is possible to set n 1,n 2, and n 3 in such a way that the cumulative internal regret R (B,C),n is lower bounded by a positive constant times n for n sufficiently large. The internal regret of B versus C can be lower bounded by using the inequality ln(1 + u) u: n ln QB C t Q t x t x t ( n Q B,t x C,t Qt B C x t x B,t Qt B C x t ), 17. InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.17
18 18 Table II. The market vectors for Example 3. Regimes x A,t x B,t x C,t 1 t T 1 = n T t T 2 = n 1 + n T t T 3 = n where the difference in the parenthesis is larger than 1 in the first regime, 3 in the second one and 0.05/2.05 in the third one. It suffices now to estimate Q B,t : where η = 4.1 Q B,t = e ηg B,t e ηg A,t + e ηg B,t + e ηg C,t, (7) 8ln 3 n ˆ= 1 C η n and G B,t = t s=1 x B,s Q s x s (and similarly for the two other stocks). We take n 1 = dn, where d > 0 will be determined later. In the first regime, a sufficient condition for Q B,t ε is that e ηg B,t/e ηg A,t ε, which can be ensured by G A,t G B,t = t 1 lnε, Q s x s η s=1 which is implied, since Q s x s 2, by t t 0 = 2C η ( ln ε) n. In the second regime, the Q B,t s increase. Let T 2 denote the first time instant t when Q B,t 1/2, and denote by n 2 = T 2 T 1 the length of this second regime. Now, it is easy to see that n 2 n 1 /4 and n 2 4n 1 + (2ln 2)C η n 5dn, for n sufficiently large. Moreover, the number of times that Q B,t is larger than ε in this regime is less than ( C η (ln 2 1 ε )) n. ε At the beginning of the third regime, we then have Q B,t 1/2, which means that G A,t G B,t and G C,t G B,t. The first inequality remains InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.18
19 true during the whole regime and we set n 3 such that the second one also remains true. This will imply that Q B,t 1/3 during the third regime. Now by the bounds on Q s x s in the different regimes, a sufficient condition on n 3 is 0.05n 3 n n 2 4, which, recalling the lower bound n 2 n 1 /4, is implied by n dn. It remains to set the value of d. We have to ensure that n 3 is not larger than 35dn/4 and that it is larger than γn, where γ is a universal constant denoting the fraction of time spent in the third regime. That is, we have to find d and γ such that { d + 5d + γ 1 d d d 1, where we used n 1 /n + n 2 /n + n 3 /n = 1 and the various bounds and constraints described above. γ = 1/7 and d = 1/7 are adequate choices. Summarizing, we have proved the following lower bound on the internal regret n x t 1 Q t x t 3 γ n ε(3(1 γ)) n + Ω ( ( ln ε) n ), ln QB C t and the proof that the eg strategy has a large internal regret is concluded by choosing ε > 0 small enough (for instance, ε = 1/5000) Investment strategies with small internal regret The investment algorithm introduced in the next section has the surprising property that, apart from a guaranteed sublinear internal regret, it also achieves a sublinear worst-case logarithmic wealth ratio not only with respect to the class of buy-and-hold strategies, but also with respect to the class of all constantly rebalanced portfolios A strategy with small internal and external regrets The investment strategy introduced in this section which we call b1exp is based on the same kind of linear upper bound on the internal regret as InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.19
20 20 the one that was used in our proof of the performance of the eg strategy in Section 4. This strategy may be seen as the algorithm that results from an application of the conversion trick explained in Section 3 to the eg strategy. However, this only proves the no-internal-regret property. Since the worst-case logarithmic wealth ratio is also minimized, we provide a detailed analysis below. The same argument as for the eg strategy may be used to upper bound the cumulative internal regret as R (i,j),n = n n ( ) ln P i j t x t ln (P t x t ) P i,t ( xj,t P t x t x i,t P t x t ). Introducing again x i,t l i,t =, P t x t we may use the internal-regret minimizing prediction algorithm of Section 3. For simplicity, we use exponential weighting. This definition, of course, requires the boundedness of the values of l i,t. This may be guaranteed by the same assumption as in the analysis of the eg investment strategy, that is, by assuming that the returns x i,t all fall in the interval [m,m] where m < M are positive constants. Then the internal regret of the algorithm b1exp may be bounded by the result of Theorem 3. An important additional property of the algorithm is that its worst-case logarithmic wealth ratio, with respect to the class of all constantly rebalanced portfolios, may be bounded similarly as that of the eg algorithm. These main properties are summarized in the following theorem. Theorem 4. Assume that m x i,t M for all 1 i N and 1 t n. Then the cumulative internal regret of the b1exp strategy P is bounded by R n ln N(N 1) η + nη 8 M 2 m 2 = M n lnn, m where we set η = 4(m/M) (ln N)/n. In addition, if Q denotes the class of all constantly rebalanced portfolios, then the worst-case logarithmic wealth ratio of P is bounded by W n (P, Q) N M m n ln N. InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.20
21 Proof. The bound for the internal regret R n follows from the linear upper bound described above and Theorem 3. To bound the worst-case logarithmic wealth ratio W n (P, Q), recall that by inequality (6), for any constantly rebalanced portfolio B, N N ( n ) W n (P, Q) B j P i,t (l i,t l j,t ) j=1 i=1 n ( xj,t N max P i,t x ) i,t 1 i,j N P t x t P t x t which is not larger than N times the upper bound obtained on the cumulative internal regret R n which completes the proof. 21 Remark. The computation of the investment strategy requires the inversion of an N N matrix at each trading period (see Lemma 1). This is quite feasible even for large markets in which N may be as large as about 100. Remark. Recalling Section 3 we observe that the b1exp strategy may be considered as an instance of the exponentially weighted average predictor, which uses the fictitious strategies P i j t as experts. Thus, instead of considering the single stocks, as eg, b1exp considers pairs of stocks and their relative behaviors. This may explain the greater stability observed on real data (see the Appendix). Remark. Just like in the case of the sequential prediction problem, exponential weighting may be replaced by others such as polynomial weighting. In that case the cumulative internal regret is bounded by M m n(p 1)N 2/p which is approximately optimized by the choice p = 4ln N. We call this investment strategy b1pol. Even though this strategy has comparable theoretical guarantees to those of b1exp, our experiments show a clear superiority of the use of exponential weighting. This and other practical issues are discussed in the Appendix. Remark. Similarly to eg, the strategy b1exp requires the knowledge of the time horizon n and the ratio M/m of the bounds assumed on the market. This first disadvantage may be avoided by either using the well-known doubling trick or considering a time-varying value of η and applying the second bound of Theorem 3. Both methods lead to internal regret and worst-case logarithmic wealth ratios bounded by quantities of the order of n. InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.21
22 Another strategy with small internal regret In this section we introduce a new algorithm, called b2pol. We use polynomial weighting and assume bounded market evolutions. The Blackwell condition (4) is sufficient to ensure the property of small internal regret. It may be written as (i,j),t r (i,j),t 0 (8) i j where ( R (i,j),t 1 ) p 1 (i,j),t = a b + ( ) p 1. R (a,b),t 1 Note that the (i,j),t s are nonnegative and sum up to one. The concavity of the logarithm and the definition of r (i,j),t lead to (i,j),t r (i,j),t = (i,j),t ln i j i j ln ( P i j i j (i,j),t P i j t + ) t x t ln (P t x t ) x t ln (P t x t ). It is now obvious that the Blackwell condition (4) is satisfied whenever P t = i j (i,j),t P i j t. Lemma 1 shows that such a portfolio P t indeed exists for all t. This defines a strategy which we call b2pol. The following theorem is an immediate consequence of Corollary 1 of Cesa-Bianchi and Lugosi (2003). Theorem 5. Assume that m x i,t M for all 1 i N and 1 t n. Then the cumulative internal regret of the b2pol strategy P is bounded by ( R n ln M ) n(p 1)N 2/p. m The above bound is approximately minimized for p = 4 ln N. Note also that it only differs from the bound on the cumulative internal regret of the b1pol strategy by a constant factor which is smaller here (ln(m/m) instead of M/m). InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.22
23 23 7. Generalizations 7.1. Generalized buy-and-hold strategy The gbh strategy performs buy-and-hold on the N(N 1) fictitious modified strategies, using the conversion trick explained in Section 3 (and, in the particular case of N = 2 assets, it reduces to the simple buy-and-hold strategy hence its name). The main property of this investment strategy is that its internal regret is bounded by a constant, as stated by the theorem below. More precisely, the gbh strategy is defined such that at each round t, we have the fixed point equality P t = i j W i j t 1 k l W k l t 1 P i j t, (9) where W t = t s=1 P s x s is the wealth achieved by the investment strategy we consider and W i j t = t s=1 P i j s x s is the fictitious wealth obtained by the i j modified version of it. The existence and the practical computation of such a portfolio P t are given by Lemma 1. Theorem 6. The gbh investment strategy incurs a cumulative internal regret R n ln N(N 1) for all n. Proof. The proof is done by a simple telescoping argument: n W n = P t x t = = n W i j t 1 Pi j t x t k l W t 1 k l i j i j W i j n N(N 1). The advantage of this algorithm is that its performance bounds do not depend on the market. Remark. Unlike in the sequential prediction problem described in Section 2, a small internal regret in the problem of sequential portfolio selection does not necessarily imply a small worst-case logarithmic wealth ratio, not even with respect to the class of all buy-and-hold strategies. This may be seen by considering the following numerical counterexample. Let the market be formed by three stocks and let it be cyclic such that at odd-indexed rounds the wealth ratios are respectively 1/2, 1, 2 and at even ones they equal 2, 1.1, 1/2. The accumulated InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.23
24 24 wealth of the best stock increases exponentially fast whereas the one of the gbh strategy is bounded. The reason is that the loss function l associated to this problem is no longer linear, and therefore, the argument of Equation (2) does not extend to it. However, there is a simple modification of the gbh strategy leading to internal regret less than 2ln N and external regret with respect to buy-and-hold strategies less than 2ln N. We call this modification the gbh2 algorithm. Instead of (9), the gbh2 strategy is such that P t = 1 k N S t 1(k)e k + i j W i j t 1 Pi j t 1 k N S t 1(k) + i j W i j t 1, (10) for every t, where e k denotes the portfolio that invests all its wealth in the k-th stock. Now a telescoping argument similar to that of the proof of Theorem 6 shows that the final wealth equals W n = 1 N 2 1 k N S n (k) + i j W i j n, thus ensuring that both regrets are less than the claimed upper bound 2ln N. Lemma 1 shows that (10) can be satisfied and how the portfolios P t are computed. The next section is an extension of gbh and gbh2 strategies to a continuum of fictitious experts A generalized universal portfolio Next we extend the notion of internal regret for investment strategies. Recall that the definition of internal regret R n considers the regret suffered by not moving one s capital from one stock to another. Moving the capital from one stock to another may be considered as a simple linear function from the probability simplex X to X. A more exigent definition is obtained by considering all linear functions g : X X. Clearly, any such function may be written as g(p t ) = AP t where A is a column-stochastic matrix. Denote the set of all column-stochastic matrices of order N by A and let the linear modifications AP t of the master strategy be denoted by P A t. The generalized internal regret is defined as max ln WA n A A W n InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.24
25 where W A n = n Ni=1 P A i,t x i,t. Linear modifications were already considered (in finite number) by Greenwald and Jafari (2003) in the case of sequential prediction. In that case, due to the linearity of the loss function l(p t ), it is not more difficult to have a low generalized internal regret than the usual internal regret. On the contrary here, due to the concavity of the logarithm, minimizing the generalized internal regret turns out to be a greater challenge. Since the algorithms b1exp and b1pol are based on a linear upper bounding of the internal regret, it is easy to see that their generalized internal regret is bounded by N times the bounds derived for the internal regret in Sections 6.1, leading to upper bounds both of the order of N n ln N. The main result of this section is that there exist investment strategies that achieve a much smaller generalized internal regret. The proof below is inspired by Theorem 6 and uses some techniques introduced by Blum and Kalai (1999). The investment strategy presented above may be seen as a modification of Cover s universal portfolio (1991) through a conversion trick to deal with generalized internal regret of the same flavor as the one explained in Section Theorem 7. There exists an investment strategy P such that max ln WA n N(N 1)ln(n + 1) + 1. A A W n Remark. The algorithm given in the proof has a computational complexity exponential in the number of stocks (at least in its straightforward implementation). However, it provides a theoretical bound which is likely to be of the best achievable order. The algorithm could also be easily modified, using the techniques of Section 7.1, to be competitive with respect to the best constantly rebalanced portfolio as well as to suffer a low generalized internal regret, with associated performance bounds for both of the order N 2 ln n. Proof. Denote a column-stochastic matrix A by [a 1,...,a N ], where the a j s are the columns of A. Let µ be the uniform measure over the simplex and let ν be the measure over A given by the product of N independent instances of µ: N ν(a) = µ(a j ). j=1 InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.25
26 26 If the investment strategy, at each time instant t, satisfied the equality P t = A A WA t 1 PA t dν(a) A A WA t 1 dν(a), (11) then the final wealth would be given by an average over all modified strategies, that is, W n = dν(a). (12) Wn A A A Fix a matrix A and consider the set χ α,a of column-stochastic matrices of the form (1 α)a + αz, z A. Similarly, denote by χ α,aj the set of probability vectors of the form (1 α)a j +αz j, z j X. It is easy to see that (with a slight abuse of notation) N χ α,a = χ α,aj. (13) j=1 Any element A of χ α,a may be seen to satisfy (component-wise) for all t and therefore P A t (1 α)p A t, W A n (1 α) n W A n. Finally, using equality (13), we have implying ν (χ α,a ) = N j=1 ) ( µ (χ α,aj = α N 1) N, A χ α,a W A n dν(a ) (1 α) n α N(N 1) W A n. Taking α = 1/(n + 1), recalling that (1 α) n α N(N 1) e 1 (n + 1) N(N 1), and combining this with 12, we obtain the theorem. Thus, it suffices to see that one may satisfy the set of linear equations (11). We denote an element A A by A = [A (i,j) ]. Writing only the equality for the ith components of both sides, ( ) Wt 1dν(A) A P i,t = A A A A W A t 1 ( N ) A (i,k) P k,t dν(a), k=1 InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.26
27 we see that P t has to be an element of the kernel of the matrix T defined by if i k, T i,k = w i,k, where T i,i = j i, 1 j N w j,i, w i,k = A A W A t 1A (i,k) dν(a). The same argument as in the proof of Lemma 1 shows that such a vector exists (and the computability of the latter depends on how easy it is to compute the elements of the matrix T). 27 Acknowledgements We thank Yoram Singer for sending us the NYSE data set used in the experiments. We also thank Dean Foster for his suggestions that lead us to the example showing that the exponential weighted average predictor has a large internal regret. We are grateful to the three anonymous reviewers for helpful comments. References P. Auer, N. Cesa-Bianchi, and C. Gentile. Adaptive and self-confident on-line learning algorithms. Journal of Computer and System Sciences, 64:48 75, D. Blackwell. An analog of the minimax theorem for vector payoffs. Pacific Journal of Mathematics, 6:1 8, A. Blum and A. Kalai. Universal portfolios with and without transaction costs. Machine Learning, 35: , A. Blum and Y. Mansour. From external to internal regret. Manuscript, A. Borodin, R. El-Yaniv, and V. Gogan. On the competitive theory and practice of portfolio selection (extended abstract). In Proc. of the 4th Latin American Symposium on Theoretical Informatics (LATIN 00), pages , Punta del Este, Uruguay, N. Cesa-Bianchi and G. Lugosi. On prediction of individual sequences. Annals of Statistics, 27: ,1999. N. Cesa-Bianchi and G. Lugosi. Minimax values and entropy bounds for portfolio selection problems. In Proceedings of the First World Congress of the Game Theory Society, N. Cesa-Bianchi and G. Lugosi. Potential-based algorithms in on-line prediction and game theory. Machine Learning, 51, T. Cover. An algorithm for maximizing expected log investment return. IEEE Transactions on Information Theory, 30: , InternalPortfolioDEF.tex; 19/11/2004; 9:55; p.27
Internal Regret in On-line Portfolio Selection
 Internal Regret in On-line Portfolio Selection Gilles Stoltz gilles.stoltz@ens.fr) Département de Mathématiques et Applications, Ecole Normale Supérieure, 75005 Paris, France Gábor Lugosi lugosi@upf.es)
Internal Regret in On-line Portfolio Selection Gilles Stoltz gilles.stoltz@ens.fr) Département de Mathématiques et Applications, Ecole Normale Supérieure, 75005 Paris, France Gábor Lugosi lugosi@upf.es)
Learning correlated equilibria in games with compact sets of strategies
 Learning correlated equilibria in games with compact sets of strategies Gilles Stoltz a,, Gábor Lugosi b a cnrs and Département de Mathématiques et Applications, Ecole Normale Supérieure, 45 rue d Ulm,
Learning correlated equilibria in games with compact sets of strategies Gilles Stoltz a,, Gábor Lugosi b a cnrs and Département de Mathématiques et Applications, Ecole Normale Supérieure, 45 rue d Ulm,
Applications of on-line prediction. in telecommunication problems
 Applications of on-line prediction in telecommunication problems Gábor Lugosi Pompeu Fabra University, Barcelona based on joint work with András György and Tamás Linder 1 Outline On-line prediction; Some
Applications of on-line prediction in telecommunication problems Gábor Lugosi Pompeu Fabra University, Barcelona based on joint work with András György and Tamás Linder 1 Outline On-line prediction; Some
Learning Methods for Online Prediction Problems. Peter Bartlett Statistics and EECS UC Berkeley
 Learning Methods for Online Prediction Problems Peter Bartlett Statistics and EECS UC Berkeley Course Synopsis A finite comparison class: A = {1,..., m}. Converting online to batch. Online convex optimization.
Learning Methods for Online Prediction Problems Peter Bartlett Statistics and EECS UC Berkeley Course Synopsis A finite comparison class: A = {1,..., m}. Converting online to batch. Online convex optimization.
Lecture 14: Approachability and regret minimization Ramesh Johari May 23, 2007
 MS&E 336 Lecture 4: Approachability and regret minimization Ramesh Johari May 23, 2007 In this lecture we use Blackwell s approachability theorem to formulate both external and internal regret minimizing
MS&E 336 Lecture 4: Approachability and regret minimization Ramesh Johari May 23, 2007 In this lecture we use Blackwell s approachability theorem to formulate both external and internal regret minimizing
A Second-order Bound with Excess Losses
 A Second-order Bound with Excess Losses Pierre Gaillard 12 Gilles Stoltz 2 Tim van Erven 3 1 EDF R&D, Clamart, France 2 GREGHEC: HEC Paris CNRS, Jouy-en-Josas, France 3 Leiden University, the Netherlands
A Second-order Bound with Excess Losses Pierre Gaillard 12 Gilles Stoltz 2 Tim van Erven 3 1 EDF R&D, Clamart, France 2 GREGHEC: HEC Paris CNRS, Jouy-en-Josas, France 3 Leiden University, the Netherlands
Efficient Algorithms for Universal Portfolios
 Efficient Algorithms for Universal Portfolios Adam Kalai CMU Department of Computer Science akalai@cs.cmu.edu Santosh Vempala y MIT Department of Mathematics and Laboratory for Computer Science vempala@math.mit.edu
Efficient Algorithms for Universal Portfolios Adam Kalai CMU Department of Computer Science akalai@cs.cmu.edu Santosh Vempala y MIT Department of Mathematics and Laboratory for Computer Science vempala@math.mit.edu
Sequential Investment, Universal Portfolio Algos and Log-loss
 1/37 Sequential Investment, Universal Portfolio Algos and Log-loss Chaitanya Ryali, ECE UCSD March 3, 2014 Table of contents 2/37 1 2 3 4 Definitions and Notations 3/37 A market vector x = {x 1,x 2,...,x
1/37 Sequential Investment, Universal Portfolio Algos and Log-loss Chaitanya Ryali, ECE UCSD March 3, 2014 Table of contents 2/37 1 2 3 4 Definitions and Notations 3/37 A market vector x = {x 1,x 2,...,x
Full-information Online Learning
 Introduction Expert Advice OCO LM A DA NANJING UNIVERSITY Full-information Lijun Zhang Nanjing University, China June 2, 2017 Outline Introduction Expert Advice OCO 1 Introduction Definitions Regret 2
Introduction Expert Advice OCO LM A DA NANJING UNIVERSITY Full-information Lijun Zhang Nanjing University, China June 2, 2017 Outline Introduction Expert Advice OCO 1 Introduction Definitions Regret 2
Learning, Games, and Networks
 Learning, Games, and Networks Abhishek Sinha Laboratory for Information and Decision Systems MIT ML Talk Series @CNRG December 12, 2016 1 / 44 Outline 1 Prediction With Experts Advice 2 Application to
Learning, Games, and Networks Abhishek Sinha Laboratory for Information and Decision Systems MIT ML Talk Series @CNRG December 12, 2016 1 / 44 Outline 1 Prediction With Experts Advice 2 Application to
Advanced Machine Learning
 Advanced Machine Learning Bandit Problems MEHRYAR MOHRI MOHRI@ COURANT INSTITUTE & GOOGLE RESEARCH. Multi-Armed Bandit Problem Problem: which arm of a K-slot machine should a gambler pull to maximize his
Advanced Machine Learning Bandit Problems MEHRYAR MOHRI MOHRI@ COURANT INSTITUTE & GOOGLE RESEARCH. Multi-Armed Bandit Problem Problem: which arm of a K-slot machine should a gambler pull to maximize his
Theory and Applications of A Repeated Game Playing Algorithm. Rob Schapire Princeton University [currently visiting Yahoo!
 Theory and Applications of A Repeated Game Playing Algorithm Rob Schapire Princeton University [currently visiting Yahoo! Research] Learning Is (Often) Just a Game some learning problems: learn from training
Theory and Applications of A Repeated Game Playing Algorithm Rob Schapire Princeton University [currently visiting Yahoo! Research] Learning Is (Often) Just a Game some learning problems: learn from training
The best expert versus the smartest algorithm
 Theoretical Computer Science 34 004 361 380 www.elsevier.com/locate/tcs The best expert versus the smartest algorithm Peter Chen a, Guoli Ding b; a Department of Computer Science, Louisiana State University,
Theoretical Computer Science 34 004 361 380 www.elsevier.com/locate/tcs The best expert versus the smartest algorithm Peter Chen a, Guoli Ding b; a Department of Computer Science, Louisiana State University,
0.1 Motivating example: weighted majority algorithm
 princeton univ. F 16 cos 521: Advanced Algorithm Design Lecture 8: Decision-making under total uncertainty: the multiplicative weight algorithm Lecturer: Sanjeev Arora Scribe: Sanjeev Arora (Today s notes
princeton univ. F 16 cos 521: Advanced Algorithm Design Lecture 8: Decision-making under total uncertainty: the multiplicative weight algorithm Lecturer: Sanjeev Arora Scribe: Sanjeev Arora (Today s notes
Advanced Machine Learning
 Advanced Machine Learning Learning and Games MEHRYAR MOHRI MOHRI@ COURANT INSTITUTE & GOOGLE RESEARCH. Outline Normal form games Nash equilibrium von Neumann s minimax theorem Correlated equilibrium Internal
Advanced Machine Learning Learning and Games MEHRYAR MOHRI MOHRI@ COURANT INSTITUTE & GOOGLE RESEARCH. Outline Normal form games Nash equilibrium von Neumann s minimax theorem Correlated equilibrium Internal
Lecture 8: Decision-making under total uncertainty: the multiplicative weight algorithm. Lecturer: Sanjeev Arora
 princeton univ. F 13 cos 521: Advanced Algorithm Design Lecture 8: Decision-making under total uncertainty: the multiplicative weight algorithm Lecturer: Sanjeev Arora Scribe: (Today s notes below are
princeton univ. F 13 cos 521: Advanced Algorithm Design Lecture 8: Decision-making under total uncertainty: the multiplicative weight algorithm Lecturer: Sanjeev Arora Scribe: (Today s notes below are
Strategies for Prediction Under Imperfect Monitoring
 MATHEMATICS OF OPERATIONS RESEARCH Vol. 33, No. 3, August 008, pp. 53 58 issn 0364-765X eissn 56-547 08 3303 053 informs doi 0.87/moor.080.03 008 INFORMS Strategies for Prediction Under Imperfect Monitoring
MATHEMATICS OF OPERATIONS RESEARCH Vol. 33, No. 3, August 008, pp. 53 58 issn 0364-765X eissn 56-547 08 3303 053 informs doi 0.87/moor.080.03 008 INFORMS Strategies for Prediction Under Imperfect Monitoring
The Multi-Arm Bandit Framework
 The Multi-Arm Bandit Framework A. LAZARIC (SequeL Team @INRIA-Lille) ENS Cachan - Master 2 MVA SequeL INRIA Lille MVA-RL Course In This Lecture A. LAZARIC Reinforcement Learning Algorithms Oct 29th, 2013-2/94
The Multi-Arm Bandit Framework A. LAZARIC (SequeL Team @INRIA-Lille) ENS Cachan - Master 2 MVA SequeL INRIA Lille MVA-RL Course In This Lecture A. LAZARIC Reinforcement Learning Algorithms Oct 29th, 2013-2/94
Adaptive Sampling Under Low Noise Conditions 1
 Manuscrit auteur, publié dans "41èmes Journées de Statistique, SFdS, Bordeaux (2009)" Adaptive Sampling Under Low Noise Conditions 1 Nicolò Cesa-Bianchi Dipartimento di Scienze dell Informazione Università
Manuscrit auteur, publié dans "41èmes Journées de Statistique, SFdS, Bordeaux (2009)" Adaptive Sampling Under Low Noise Conditions 1 Nicolò Cesa-Bianchi Dipartimento di Scienze dell Informazione Università
The No-Regret Framework for Online Learning
 The No-Regret Framework for Online Learning A Tutorial Introduction Nahum Shimkin Technion Israel Institute of Technology Haifa, Israel Stochastic Processes in Engineering IIT Mumbai, March 2013 N. Shimkin,
The No-Regret Framework for Online Learning A Tutorial Introduction Nahum Shimkin Technion Israel Institute of Technology Haifa, Israel Stochastic Processes in Engineering IIT Mumbai, March 2013 N. Shimkin,
Stat 260/CS Learning in Sequential Decision Problems. Peter Bartlett
 Stat 260/CS 294-102. Learning in Sequential Decision Problems. Peter Bartlett 1. Adversarial bandits Definition: sequential game. Lower bounds on regret from the stochastic case. Exp3: exponential weights
Stat 260/CS 294-102. Learning in Sequential Decision Problems. Peter Bartlett 1. Adversarial bandits Definition: sequential game. Lower bounds on regret from the stochastic case. Exp3: exponential weights
Gambling in a rigged casino: The adversarial multi-armed bandit problem
 Gambling in a rigged casino: The adversarial multi-armed bandit problem Peter Auer Institute for Theoretical Computer Science University of Technology Graz A-8010 Graz (Austria) pauer@igi.tu-graz.ac.at
Gambling in a rigged casino: The adversarial multi-armed bandit problem Peter Auer Institute for Theoretical Computer Science University of Technology Graz A-8010 Graz (Austria) pauer@igi.tu-graz.ac.at
Online Bounds for Bayesian Algorithms
 Online Bounds for Bayesian Algorithms Sham M. Kakade Computer and Information Science Department University of Pennsylvania Andrew Y. Ng Computer Science Department Stanford University Abstract We present
Online Bounds for Bayesian Algorithms Sham M. Kakade Computer and Information Science Department University of Pennsylvania Andrew Y. Ng Computer Science Department Stanford University Abstract We present
No-Regret Algorithms for Unconstrained Online Convex Optimization
 No-Regret Algorithms for Unconstrained Online Convex Optimization Matthew Streeter Duolingo, Inc. Pittsburgh, PA 153 matt@duolingo.com H. Brendan McMahan Google, Inc. Seattle, WA 98103 mcmahan@google.com
No-Regret Algorithms for Unconstrained Online Convex Optimization Matthew Streeter Duolingo, Inc. Pittsburgh, PA 153 matt@duolingo.com H. Brendan McMahan Google, Inc. Seattle, WA 98103 mcmahan@google.com
An adaptive algorithm for finite stochastic partial monitoring
 An adaptive algorithm for finite stochastic partial monitoring Gábor Bartók Navid Zolghadr Csaba Szepesvári Department of Computing Science, University of Alberta, AB, Canada, T6G E8 bartok@ualberta.ca
An adaptive algorithm for finite stochastic partial monitoring Gábor Bartók Navid Zolghadr Csaba Szepesvári Department of Computing Science, University of Alberta, AB, Canada, T6G E8 bartok@ualberta.ca
From Bandits to Experts: A Tale of Domination and Independence
 From Bandits to Experts: A Tale of Domination and Independence Nicolò Cesa-Bianchi Università degli Studi di Milano N. Cesa-Bianchi (UNIMI) Domination and Independence 1 / 1 From Bandits to Experts: A
From Bandits to Experts: A Tale of Domination and Independence Nicolò Cesa-Bianchi Università degli Studi di Milano N. Cesa-Bianchi (UNIMI) Domination and Independence 1 / 1 From Bandits to Experts: A
Game-Theoretic Learning:
 Game-Theoretic Learning: Regret Minimization vs. Utility Maximization Amy Greenwald with David Gondek, Amir Jafari, and Casey Marks Brown University University of Pennsylvania November 17, 2004 Background
Game-Theoretic Learning: Regret Minimization vs. Utility Maximization Amy Greenwald with David Gondek, Amir Jafari, and Casey Marks Brown University University of Pennsylvania November 17, 2004 Background
Advanced Topics in Machine Learning and Algorithmic Game Theory Fall semester, 2011/12
 Advanced Topics in Machine Learning and Algorithmic Game Theory Fall semester, 2011/12 Lecture 4: Multiarmed Bandit in the Adversarial Model Lecturer: Yishay Mansour Scribe: Shai Vardi 4.1 Lecture Overview
Advanced Topics in Machine Learning and Algorithmic Game Theory Fall semester, 2011/12 Lecture 4: Multiarmed Bandit in the Adversarial Model Lecturer: Yishay Mansour Scribe: Shai Vardi 4.1 Lecture Overview
Learning Methods for Online Prediction Problems. Peter Bartlett Statistics and EECS UC Berkeley
 Learning Methods for Online Prediction Problems Peter Bartlett Statistics and EECS UC Berkeley Online Learning Repeated game: Aim: minimize ˆL n = Decision method plays a t World reveals l t L n l t (a
Learning Methods for Online Prediction Problems Peter Bartlett Statistics and EECS UC Berkeley Online Learning Repeated game: Aim: minimize ˆL n = Decision method plays a t World reveals l t L n l t (a
Prediction and Playing Games
 Prediction and Playing Games Vineel Pratap vineel@eng.ucsd.edu February 20, 204 Chapter 7 : Prediction, Learning and Games - Cesa Binachi & Lugosi K-Person Normal Form Games Each player k (k =,..., K)
Prediction and Playing Games Vineel Pratap vineel@eng.ucsd.edu February 20, 204 Chapter 7 : Prediction, Learning and Games - Cesa Binachi & Lugosi K-Person Normal Form Games Each player k (k =,..., K)
Worst-Case Bounds for Gaussian Process Models
 Worst-Case Bounds for Gaussian Process Models Sham M. Kakade University of Pennsylvania Matthias W. Seeger UC Berkeley Abstract Dean P. Foster University of Pennsylvania We present a competitive analysis
Worst-Case Bounds for Gaussian Process Models Sham M. Kakade University of Pennsylvania Matthias W. Seeger UC Berkeley Abstract Dean P. Foster University of Pennsylvania We present a competitive analysis
Yevgeny Seldin. University of Copenhagen
 Yevgeny Seldin University of Copenhagen Classical (Batch) Machine Learning Collect Data Data Assumption The samples are independent identically distributed (i.i.d.) Machine Learning Prediction rule New
Yevgeny Seldin University of Copenhagen Classical (Batch) Machine Learning Collect Data Data Assumption The samples are independent identically distributed (i.i.d.) Machine Learning Prediction rule New
Adaptive Online Gradient Descent
 University of Pennsylvania ScholarlyCommons Statistics Papers Wharton Faculty Research 6-4-2007 Adaptive Online Gradient Descent Peter Bartlett Elad Hazan Alexander Rakhlin University of Pennsylvania Follow
University of Pennsylvania ScholarlyCommons Statistics Papers Wharton Faculty Research 6-4-2007 Adaptive Online Gradient Descent Peter Bartlett Elad Hazan Alexander Rakhlin University of Pennsylvania Follow
Blackwell s Approachability Theorem: A Generalization in a Special Case. Amy Greenwald, Amir Jafari and Casey Marks
 Blackwell s Approachability Theorem: A Generalization in a Special Case Amy Greenwald, Amir Jafari and Casey Marks Department of Computer Science Brown University Providence, Rhode Island 02912 CS-06-01
Blackwell s Approachability Theorem: A Generalization in a Special Case Amy Greenwald, Amir Jafari and Casey Marks Department of Computer Science Brown University Providence, Rhode Island 02912 CS-06-01
Online Aggregation of Unbounded Signed Losses Using Shifting Experts
 Proceedings of Machine Learning Research 60: 5, 207 Conformal and Probabilistic Prediction and Applications Online Aggregation of Unbounded Signed Losses Using Shifting Experts Vladimir V. V yugin Institute
Proceedings of Machine Learning Research 60: 5, 207 Conformal and Probabilistic Prediction and Applications Online Aggregation of Unbounded Signed Losses Using Shifting Experts Vladimir V. V yugin Institute
Minimax strategy for prediction with expert advice under stochastic assumptions
 Minimax strategy for prediction ith expert advice under stochastic assumptions Wojciech Kotłosi Poznań University of Technology, Poland otlosi@cs.put.poznan.pl Abstract We consider the setting of prediction
Minimax strategy for prediction ith expert advice under stochastic assumptions Wojciech Kotłosi Poznań University of Technology, Poland otlosi@cs.put.poznan.pl Abstract We consider the setting of prediction
Efficient Tracking of Large Classes of Experts
 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 11, NOVEMBER 2012 6709 Efficient Tracking of Large Classes of Experts András György, Member, IEEE, Tamás Linder, Senior Member, IEEE, and Gábor Lugosi
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 11, NOVEMBER 2012 6709 Efficient Tracking of Large Classes of Experts András György, Member, IEEE, Tamás Linder, Senior Member, IEEE, and Gábor Lugosi
The Online Approach to Machine Learning
 The Online Approach to Machine Learning Nicolò Cesa-Bianchi Università degli Studi di Milano N. Cesa-Bianchi (UNIMI) Online Approach to ML 1 / 53 Summary 1 My beautiful regret 2 A supposedly fun game I
The Online Approach to Machine Learning Nicolò Cesa-Bianchi Università degli Studi di Milano N. Cesa-Bianchi (UNIMI) Online Approach to ML 1 / 53 Summary 1 My beautiful regret 2 A supposedly fun game I
Meta Algorithms for Portfolio Selection. Technical Report
 Meta Algorithms for Portfolio Selection Technical Report Department of Computer Science and Engineering University of Minnesota 4-192 EECS Building 200 Union Street SE Minneapolis, MN 55455-0159 USA TR
Meta Algorithms for Portfolio Selection Technical Report Department of Computer Science and Engineering University of Minnesota 4-192 EECS Building 200 Union Street SE Minneapolis, MN 55455-0159 USA TR
Sequential prediction with coded side information under logarithmic loss
 under logarithmic loss Yanina Shkel Department of Electrical Engineering Princeton University Princeton, NJ 08544, USA Maxim Raginsky Department of Electrical and Computer Engineering Coordinated Science
under logarithmic loss Yanina Shkel Department of Electrical Engineering Princeton University Princeton, NJ 08544, USA Maxim Raginsky Department of Electrical and Computer Engineering Coordinated Science
Agnostic Online learnability
 Technical Report TTIC-TR-2008-2 October 2008 Agnostic Online learnability Shai Shalev-Shwartz Toyota Technological Institute Chicago shai@tti-c.org ABSTRACT We study a fundamental question. What classes
Technical Report TTIC-TR-2008-2 October 2008 Agnostic Online learnability Shai Shalev-Shwartz Toyota Technological Institute Chicago shai@tti-c.org ABSTRACT We study a fundamental question. What classes
Partial monitoring classification, regret bounds, and algorithms
 Partial monitoring classification, regret bounds, and algorithms Gábor Bartók Department of Computing Science University of Alberta Dávid Pál Department of Computing Science University of Alberta Csaba
Partial monitoring classification, regret bounds, and algorithms Gábor Bartók Department of Computing Science University of Alberta Dávid Pál Department of Computing Science University of Alberta Csaba
CS261: A Second Course in Algorithms Lecture #11: Online Learning and the Multiplicative Weights Algorithm
 CS61: A Second Course in Algorithms Lecture #11: Online Learning and the Multiplicative Weights Algorithm Tim Roughgarden February 9, 016 1 Online Algorithms This lecture begins the third module of the
CS61: A Second Course in Algorithms Lecture #11: Online Learning and the Multiplicative Weights Algorithm Tim Roughgarden February 9, 016 1 Online Algorithms This lecture begins the third module of the
Online Passive-Aggressive Algorithms
 Online Passive-Aggressive Algorithms Koby Crammer Ofer Dekel Shai Shalev-Shwartz Yoram Singer School of Computer Science & Engineering The Hebrew University, Jerusalem 91904, Israel {kobics,oferd,shais,singer}@cs.huji.ac.il
Online Passive-Aggressive Algorithms Koby Crammer Ofer Dekel Shai Shalev-Shwartz Yoram Singer School of Computer Science & Engineering The Hebrew University, Jerusalem 91904, Israel {kobics,oferd,shais,singer}@cs.huji.ac.il
Online Learning, Mistake Bounds, Perceptron Algorithm
 Online Learning, Mistake Bounds, Perceptron Algorithm 1 Online Learning So far the focus of the course has been on batch learning, where algorithms are presented with a sample of training data, from which
Online Learning, Mistake Bounds, Perceptron Algorithm 1 Online Learning So far the focus of the course has been on batch learning, where algorithms are presented with a sample of training data, from which
Perceptron Mistake Bounds
 Perceptron Mistake Bounds Mehryar Mohri, and Afshin Rostamizadeh Google Research Courant Institute of Mathematical Sciences Abstract. We present a brief survey of existing mistake bounds and introduce
Perceptron Mistake Bounds Mehryar Mohri, and Afshin Rostamizadeh Google Research Courant Institute of Mathematical Sciences Abstract. We present a brief survey of existing mistake bounds and introduce
The on-line shortest path problem under partial monitoring
 The on-line shortest path problem under partial monitoring András György Machine Learning Research Group Computer and Automation Research Institute Hungarian Academy of Sciences Kende u. 11-13, Budapest,
The on-line shortest path problem under partial monitoring András György Machine Learning Research Group Computer and Automation Research Institute Hungarian Academy of Sciences Kende u. 11-13, Budapest,
Lecture 16: Perceptron and Exponential Weights Algorithm
 EECS 598-005: Theoretical Foundations of Machine Learning Fall 2015 Lecture 16: Perceptron and Exponential Weights Algorithm Lecturer: Jacob Abernethy Scribes: Yue Wang, Editors: Weiqing Yu and Andrew
EECS 598-005: Theoretical Foundations of Machine Learning Fall 2015 Lecture 16: Perceptron and Exponential Weights Algorithm Lecturer: Jacob Abernethy Scribes: Yue Wang, Editors: Weiqing Yu and Andrew
Online Learning and Online Convex Optimization
 Online Learning and Online Convex Optimization Nicolò Cesa-Bianchi Università degli Studi di Milano N. Cesa-Bianchi (UNIMI) Online Learning 1 / 49 Summary 1 My beautiful regret 2 A supposedly fun game
Online Learning and Online Convex Optimization Nicolò Cesa-Bianchi Università degli Studi di Milano N. Cesa-Bianchi (UNIMI) Online Learning 1 / 49 Summary 1 My beautiful regret 2 A supposedly fun game
New bounds on the price of bandit feedback for mistake-bounded online multiclass learning
 Journal of Machine Learning Research 1 8, 2017 Algorithmic Learning Theory 2017 New bounds on the price of bandit feedback for mistake-bounded online multiclass learning Philip M. Long Google, 1600 Amphitheatre
Journal of Machine Learning Research 1 8, 2017 Algorithmic Learning Theory 2017 New bounds on the price of bandit feedback for mistake-bounded online multiclass learning Philip M. Long Google, 1600 Amphitheatre
Foundations of Machine Learning On-Line Learning. Mehryar Mohri Courant Institute and Google Research
 Foundations of Machine Learning On-Line Learning Mehryar Mohri Courant Institute and Google Research mohri@cims.nyu.edu Motivation PAC learning: distribution fixed over time (training and test). IID assumption.
Foundations of Machine Learning On-Line Learning Mehryar Mohri Courant Institute and Google Research mohri@cims.nyu.edu Motivation PAC learning: distribution fixed over time (training and test). IID assumption.
Regret Analysis of Stochastic and Nonstochastic Multi-armed Bandit Problems, Part I. Sébastien Bubeck Theory Group
 Regret Analysis of Stochastic and Nonstochastic Multi-armed Bandit Problems, Part I Sébastien Bubeck Theory Group i.i.d. multi-armed bandit, Robbins [1952] i.i.d. multi-armed bandit, Robbins [1952] Known
Regret Analysis of Stochastic and Nonstochastic Multi-armed Bandit Problems, Part I Sébastien Bubeck Theory Group i.i.d. multi-armed bandit, Robbins [1952] i.i.d. multi-armed bandit, Robbins [1952] Known
Bandit models: a tutorial
 Gdt COS, December 3rd, 2015 Multi-Armed Bandit model: general setting K arms: for a {1,..., K}, (X a,t ) t N is a stochastic process. (unknown distributions) Bandit game: a each round t, an agent chooses
Gdt COS, December 3rd, 2015 Multi-Armed Bandit model: general setting K arms: for a {1,..., K}, (X a,t ) t N is a stochastic process. (unknown distributions) Bandit game: a each round t, an agent chooses
Multi-armed bandit models: a tutorial
 Multi-armed bandit models: a tutorial CERMICS seminar, March 30th, 2016 Multi-Armed Bandit model: general setting K arms: for a {1,..., K}, (X a,t ) t N is a stochastic process. (unknown distributions)
Multi-armed bandit models: a tutorial CERMICS seminar, March 30th, 2016 Multi-Armed Bandit model: general setting K arms: for a {1,..., K}, (X a,t ) t N is a stochastic process. (unknown distributions)
Online Learning with Feedback Graphs
 Online Learning with Feedback Graphs Claudio Gentile INRIA and Google NY clagentile@gmailcom NYC March 6th, 2018 1 Content of this lecture Regret analysis of sequential prediction problems lying between
Online Learning with Feedback Graphs Claudio Gentile INRIA and Google NY clagentile@gmailcom NYC March 6th, 2018 1 Content of this lecture Regret analysis of sequential prediction problems lying between
Online Learning and Sequential Decision Making
 Online Learning and Sequential Decision Making Emilie Kaufmann CNRS & CRIStAL, Inria SequeL, emilie.kaufmann@univ-lille.fr Research School, ENS Lyon, Novembre 12-13th 2018 Emilie Kaufmann Online Learning
Online Learning and Sequential Decision Making Emilie Kaufmann CNRS & CRIStAL, Inria SequeL, emilie.kaufmann@univ-lille.fr Research School, ENS Lyon, Novembre 12-13th 2018 Emilie Kaufmann Online Learning
Lecture 4: Lower Bounds (ending); Thompson Sampling
 CMSC 858G: Bandits, Experts and Games 09/12/16 Lecture 4: Lower Bounds (ending); Thompson Sampling Instructor: Alex Slivkins Scribed by: Guowei Sun,Cheng Jie 1 Lower bounds on regret (ending) Recap from
CMSC 858G: Bandits, Experts and Games 09/12/16 Lecture 4: Lower Bounds (ending); Thompson Sampling Instructor: Alex Slivkins Scribed by: Guowei Sun,Cheng Jie 1 Lower bounds on regret (ending) Recap from
1 Markov decision processes
 2.997 Decision-Making in Large-Scale Systems February 4 MI, Spring 2004 Handout #1 Lecture Note 1 1 Markov decision processes In this class we will study discrete-time stochastic systems. We can describe
2.997 Decision-Making in Large-Scale Systems February 4 MI, Spring 2004 Handout #1 Lecture Note 1 1 Markov decision processes In this class we will study discrete-time stochastic systems. We can describe
Smooth Calibration, Leaky Forecasts, Finite Recall, and Nash Dynamics
 Smooth Calibration, Leaky Forecasts, Finite Recall, and Nash Dynamics Sergiu Hart August 2016 Smooth Calibration, Leaky Forecasts, Finite Recall, and Nash Dynamics Sergiu Hart Center for the Study of Rationality
Smooth Calibration, Leaky Forecasts, Finite Recall, and Nash Dynamics Sergiu Hart August 2016 Smooth Calibration, Leaky Forecasts, Finite Recall, and Nash Dynamics Sergiu Hart Center for the Study of Rationality
Online learning CMPUT 654. October 20, 2011
 Online learning CMPUT 654 Gábor Bartók Dávid Pál Csaba Szepesvári István Szita October 20, 2011 Contents 1 Shooting Game 4 1.1 Exercises...................................... 6 2 Weighted Majority Algorithm
Online learning CMPUT 654 Gábor Bartók Dávid Pál Csaba Szepesvári István Szita October 20, 2011 Contents 1 Shooting Game 4 1.1 Exercises...................................... 6 2 Weighted Majority Algorithm
Some Aspects of Universal Portfolio
 1 Some Aspects of Universal Portfolio Tomoyuki Ichiba (UC Santa Barbara) joint work with Marcel Brod (ETH Zurich) Conference on Stochastic Asymptotics & Applications Sixth Western Conference on Mathematical
1 Some Aspects of Universal Portfolio Tomoyuki Ichiba (UC Santa Barbara) joint work with Marcel Brod (ETH Zurich) Conference on Stochastic Asymptotics & Applications Sixth Western Conference on Mathematical
Adaptive Game Playing Using Multiplicative Weights
 Games and Economic Behavior 29, 79 03 (999 Article ID game.999.0738, available online at http://www.idealibrary.com on Adaptive Game Playing Using Multiplicative Weights Yoav Freund and Robert E. Schapire
Games and Economic Behavior 29, 79 03 (999 Article ID game.999.0738, available online at http://www.idealibrary.com on Adaptive Game Playing Using Multiplicative Weights Yoav Freund and Robert E. Schapire
Lecture 19: UCB Algorithm and Adversarial Bandit Problem. Announcements Review on stochastic multi-armed bandit problem
 Lecture 9: UCB Algorithm and Adversarial Bandit Problem EECS598: Prediction and Learning: It s Only a Game Fall 03 Lecture 9: UCB Algorithm and Adversarial Bandit Problem Prof. Jacob Abernethy Scribe:
Lecture 9: UCB Algorithm and Adversarial Bandit Problem EECS598: Prediction and Learning: It s Only a Game Fall 03 Lecture 9: UCB Algorithm and Adversarial Bandit Problem Prof. Jacob Abernethy Scribe:
EASINESS IN BANDITS. Gergely Neu. Pompeu Fabra University
 EASINESS IN BANDITS Gergely Neu Pompeu Fabra University EASINESS IN BANDITS Gergely Neu Pompeu Fabra University THE BANDIT PROBLEM Play for T rounds attempting to maximize rewards THE BANDIT PROBLEM Play
EASINESS IN BANDITS Gergely Neu Pompeu Fabra University EASINESS IN BANDITS Gergely Neu Pompeu Fabra University THE BANDIT PROBLEM Play for T rounds attempting to maximize rewards THE BANDIT PROBLEM Play
1 Overview. 2 Learning from Experts. 2.1 Defining a meaningful benchmark. AM 221: Advanced Optimization Spring 2016
 AM 1: Advanced Optimization Spring 016 Prof. Yaron Singer Lecture 11 March 3rd 1 Overview In this lecture we will introduce the notion of online convex optimization. This is an extremely useful framework
AM 1: Advanced Optimization Spring 016 Prof. Yaron Singer Lecture 11 March 3rd 1 Overview In this lecture we will introduce the notion of online convex optimization. This is an extremely useful framework
On Minimaxity of Follow the Leader Strategy in the Stochastic Setting
 On Minimaxity of Follow the Leader Strategy in the Stochastic Setting Wojciech Kot lowsi Poznań University of Technology, Poland wotlowsi@cs.put.poznan.pl Abstract. We consider the setting of prediction
On Minimaxity of Follow the Leader Strategy in the Stochastic Setting Wojciech Kot lowsi Poznań University of Technology, Poland wotlowsi@cs.put.poznan.pl Abstract. We consider the setting of prediction
Defensive forecasting for optimal prediction with expert advice
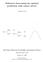 Defensive forecasting for optimal prediction with expert advice Vladimir Vovk $25 Peter Paul $0 $50 Peter $0 Paul $100 The Game-Theoretic Probability and Finance Project Working Paper #20 August 11, 2007
Defensive forecasting for optimal prediction with expert advice Vladimir Vovk $25 Peter Paul $0 $50 Peter $0 Paul $100 The Game-Theoretic Probability and Finance Project Working Paper #20 August 11, 2007
Minimax Policies for Combinatorial Prediction Games
 Minimax Policies for Combinatorial Prediction Games Jean-Yves Audibert Imagine, Univ. Paris Est, and Sierra, CNRS/ENS/INRIA, Paris, France audibert@imagine.enpc.fr Sébastien Bubeck Centre de Recerca Matemàtica
Minimax Policies for Combinatorial Prediction Games Jean-Yves Audibert Imagine, Univ. Paris Est, and Sierra, CNRS/ENS/INRIA, Paris, France audibert@imagine.enpc.fr Sébastien Bubeck Centre de Recerca Matemàtica
Online prediction with expert advise
 Online prediction with expert advise Jyrki Kivinen Australian National University http://axiom.anu.edu.au/~kivinen Contents 1. Online prediction: introductory example, basic setting 2. Classification with
Online prediction with expert advise Jyrki Kivinen Australian National University http://axiom.anu.edu.au/~kivinen Contents 1. Online prediction: introductory example, basic setting 2. Classification with
Worst-Case Analysis of the Perceptron and Exponentiated Update Algorithms
 Worst-Case Analysis of the Perceptron and Exponentiated Update Algorithms Tom Bylander Division of Computer Science The University of Texas at San Antonio San Antonio, Texas 7849 bylander@cs.utsa.edu April
Worst-Case Analysis of the Perceptron and Exponentiated Update Algorithms Tom Bylander Division of Computer Science The University of Texas at San Antonio San Antonio, Texas 7849 bylander@cs.utsa.edu April
Regret to the Best vs. Regret to the Average
 Regret to the Best vs. Regret to the Average Eyal Even-Dar 1, Michael Kearns 1, Yishay Mansour 2, Jennifer Wortman 1 1 Department of Computer and Information Science, University of Pennsylvania 2 School
Regret to the Best vs. Regret to the Average Eyal Even-Dar 1, Michael Kearns 1, Yishay Mansour 2, Jennifer Wortman 1 1 Department of Computer and Information Science, University of Pennsylvania 2 School
Learning to play partially-specified equilibrium
 Learning to play partially-specified equilibrium Ehud Lehrer and Eilon Solan August 29, 2007 August 29, 2007 First draft: June 2007 Abstract: In a partially-specified correlated equilibrium (PSCE ) the
Learning to play partially-specified equilibrium Ehud Lehrer and Eilon Solan August 29, 2007 August 29, 2007 First draft: June 2007 Abstract: In a partially-specified correlated equilibrium (PSCE ) the
arxiv: v1 [cs.lg] 8 Nov 2010
![arxiv: v1 [cs.lg] 8 Nov 2010 arxiv: v1 [cs.lg] 8 Nov 2010](/thumbs/87/97382970.jpg) Blackwell Approachability and Low-Regret Learning are Equivalent arxiv:0.936v [cs.lg] 8 Nov 200 Jacob Abernethy Computer Science Division University of California, Berkeley jake@cs.berkeley.edu Peter L.
Blackwell Approachability and Low-Regret Learning are Equivalent arxiv:0.936v [cs.lg] 8 Nov 200 Jacob Abernethy Computer Science Division University of California, Berkeley jake@cs.berkeley.edu Peter L.
Quitting games - An Example
 Quitting games - An Example E. Solan 1 and N. Vieille 2 January 22, 2001 Abstract Quitting games are n-player sequential games in which, at any stage, each player has the choice between continuing and
Quitting games - An Example E. Solan 1 and N. Vieille 2 January 22, 2001 Abstract Quitting games are n-player sequential games in which, at any stage, each player has the choice between continuing and
Existence of sparsely supported correlated equilibria
 Existence of sparsely supported correlated equilibria Fabrizio Germano fabrizio.germano@upf.edu Gábor Lugosi lugosi@upf.es Departament d Economia i Empresa Universitat Pompeu Fabra Ramon Trias Fargas 25-27
Existence of sparsely supported correlated equilibria Fabrizio Germano fabrizio.germano@upf.edu Gábor Lugosi lugosi@upf.es Departament d Economia i Empresa Universitat Pompeu Fabra Ramon Trias Fargas 25-27
The Game of Normal Numbers
 The Game of Normal Numbers Ehud Lehrer September 4, 2003 Abstract We introduce a two-player game where at each period one player, say, Player 2, chooses a distribution and the other player, Player 1, a
The Game of Normal Numbers Ehud Lehrer September 4, 2003 Abstract We introduce a two-player game where at each period one player, say, Player 2, chooses a distribution and the other player, Player 1, a
Handout 4: Some Applications of Linear Programming
 ENGG 5501: Foundations of Optimization 2018 19 First Term Handout 4: Some Applications of Linear Programming Instructor: Anthony Man Cho So October 15, 2018 1 Introduction The theory of LP has found many
ENGG 5501: Foundations of Optimization 2018 19 First Term Handout 4: Some Applications of Linear Programming Instructor: Anthony Man Cho So October 15, 2018 1 Introduction The theory of LP has found many
On-line Variance Minimization
 On-line Variance Minimization Manfred Warmuth Dima Kuzmin University of California - Santa Cruz 19th Annual Conference on Learning Theory M. Warmuth, D. Kuzmin (UCSC) On-line Variance Minimization COLT06
On-line Variance Minimization Manfred Warmuth Dima Kuzmin University of California - Santa Cruz 19th Annual Conference on Learning Theory M. Warmuth, D. Kuzmin (UCSC) On-line Variance Minimization COLT06
Introduction to Bandit Algorithms. Introduction to Bandit Algorithms
 Stochastic K-Arm Bandit Problem Formulation Consider K arms (actions) each correspond to an unknown distribution {ν k } K k=1 with values bounded in [0, 1]. At each time t, the agent pulls an arm I t {1,...,
Stochastic K-Arm Bandit Problem Formulation Consider K arms (actions) each correspond to an unknown distribution {ν k } K k=1 with values bounded in [0, 1]. At each time t, the agent pulls an arm I t {1,...,
Asymptotic Minimax Regret for Data Compression, Gambling, and Prediction
 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 46, NO. 2, MARCH 2000 431 Asymptotic Minimax Regret for Data Compression, Gambling, Prediction Qun Xie Andrew R. Barron, Member, IEEE Abstract For problems
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 46, NO. 2, MARCH 2000 431 Asymptotic Minimax Regret for Data Compression, Gambling, Prediction Qun Xie Andrew R. Barron, Member, IEEE Abstract For problems
Lecture 1: Entropy, convexity, and matrix scaling CSE 599S: Entropy optimality, Winter 2016 Instructor: James R. Lee Last updated: January 24, 2016
 Lecture 1: Entropy, convexity, and matrix scaling CSE 599S: Entropy optimality, Winter 2016 Instructor: James R. Lee Last updated: January 24, 2016 1 Entropy Since this course is about entropy maximization,
Lecture 1: Entropy, convexity, and matrix scaling CSE 599S: Entropy optimality, Winter 2016 Instructor: James R. Lee Last updated: January 24, 2016 1 Entropy Since this course is about entropy maximization,
Move from Perturbed scheme to exponential weighting average
 Move from Perturbed scheme to exponential weighting average Chunyang Xiao Abstract In an online decision problem, one makes decisions often with a pool of decisions sequence called experts but without
Move from Perturbed scheme to exponential weighting average Chunyang Xiao Abstract In an online decision problem, one makes decisions often with a pool of decisions sequence called experts but without
Explore no more: Improved high-probability regret bounds for non-stochastic bandits
 Explore no more: Improved high-probability regret bounds for non-stochastic bandits Gergely Neu SequeL team INRIA Lille Nord Europe gergely.neu@gmail.com Abstract This work addresses the problem of regret
Explore no more: Improved high-probability regret bounds for non-stochastic bandits Gergely Neu SequeL team INRIA Lille Nord Europe gergely.neu@gmail.com Abstract This work addresses the problem of regret
Distributed Optimization. Song Chong EE, KAIST
 Distributed Optimization Song Chong EE, KAIST songchong@kaist.edu Dynamic Programming for Path Planning A path-planning problem consists of a weighted directed graph with a set of n nodes N, directed links
Distributed Optimization Song Chong EE, KAIST songchong@kaist.edu Dynamic Programming for Path Planning A path-planning problem consists of a weighted directed graph with a set of n nodes N, directed links
Online Prediction: Bayes versus Experts
 Marcus Hutter - 1 - Online Prediction Bayes versus Experts Online Prediction: Bayes versus Experts Marcus Hutter Istituto Dalle Molle di Studi sull Intelligenza Artificiale IDSIA, Galleria 2, CH-6928 Manno-Lugano,
Marcus Hutter - 1 - Online Prediction Bayes versus Experts Online Prediction: Bayes versus Experts Marcus Hutter Istituto Dalle Molle di Studi sull Intelligenza Artificiale IDSIA, Galleria 2, CH-6928 Manno-Lugano,
Online Passive-Aggressive Algorithms
 Online Passive-Aggressive Algorithms Koby Crammer Ofer Dekel Shai Shalev-Shwartz Yoram Singer School of Computer Science & Engineering The Hebrew University, Jerusalem 91904, Israel {kobics,oferd,shais,singer}@cs.huji.ac.il
Online Passive-Aggressive Algorithms Koby Crammer Ofer Dekel Shai Shalev-Shwartz Yoram Singer School of Computer Science & Engineering The Hebrew University, Jerusalem 91904, Israel {kobics,oferd,shais,singer}@cs.huji.ac.il
Meta Optimization and its Application to Portfolio Selection
 Meta Optimization and its Application to Portfolio Selection Puja Das Dept of Computer Science & Engg Univ of Minnesota, win Cities pdas@cs.umn.edu Arindam Banerjee Dept of Computer Science & Engg Univ
Meta Optimization and its Application to Portfolio Selection Puja Das Dept of Computer Science & Engg Univ of Minnesota, win Cities pdas@cs.umn.edu Arindam Banerjee Dept of Computer Science & Engg Univ
No-regret algorithms for structured prediction problems
 No-regret algorithms for structured prediction problems Geoffrey J. Gordon December 21, 2005 CMU-CALD-05-112 School of Computer Science Carnegie-Mellon University Pittsburgh, PA 15213 Abstract No-regret
No-regret algorithms for structured prediction problems Geoffrey J. Gordon December 21, 2005 CMU-CALD-05-112 School of Computer Science Carnegie-Mellon University Pittsburgh, PA 15213 Abstract No-regret
Pure Exploration in Finitely Armed and Continuous Armed Bandits
 Pure Exploration in Finitely Armed and Continuous Armed Bandits Sébastien Bubeck INRIA Lille Nord Europe, SequeL project, 40 avenue Halley, 59650 Villeneuve d Ascq, France Rémi Munos INRIA Lille Nord Europe,
Pure Exploration in Finitely Armed and Continuous Armed Bandits Sébastien Bubeck INRIA Lille Nord Europe, SequeL project, 40 avenue Halley, 59650 Villeneuve d Ascq, France Rémi Munos INRIA Lille Nord Europe,
Mostly calibrated. Yossi Feinberg Nicolas S. Lambert
 Int J Game Theory (2015) 44:153 163 DOI 10.1007/s00182-014-0423-0 Mostly calibrated Yossi Feinberg Nicolas S. Lambert Accepted: 27 March 2014 / Published online: 16 April 2014 Springer-Verlag Berlin Heidelberg
Int J Game Theory (2015) 44:153 163 DOI 10.1007/s00182-014-0423-0 Mostly calibrated Yossi Feinberg Nicolas S. Lambert Accepted: 27 March 2014 / Published online: 16 April 2014 Springer-Verlag Berlin Heidelberg
Online Learning with Gaussian Payoffs and Side Observations
 Online Learning with Gaussian Payoffs and Side Observations Yifan Wu 1 András György 2 Csaba Szepesvári 1 1 Department of Computing Science University of Alberta 2 Department of Electrical and Electronic
Online Learning with Gaussian Payoffs and Side Observations Yifan Wu 1 András György 2 Csaba Szepesvári 1 1 Department of Computing Science University of Alberta 2 Department of Electrical and Electronic
Dirichlet s Theorem. Calvin Lin Zhiwei. August 18, 2007
 Dirichlet s Theorem Calvin Lin Zhiwei August 8, 2007 Abstract This paper provides a proof of Dirichlet s theorem, which states that when (m, a) =, there are infinitely many primes uch that p a (mod m).
Dirichlet s Theorem Calvin Lin Zhiwei August 8, 2007 Abstract This paper provides a proof of Dirichlet s theorem, which states that when (m, a) =, there are infinitely many primes uch that p a (mod m).
Games A game is a tuple = (I; (S i ;r i ) i2i) where ffl I is a set of players (i 2 I) ffl S i is a set of (pure) strategies (s i 2 S i ) Q ffl r i :
 On the Connection between No-Regret Learning, Fictitious Play, & Nash Equilibrium Amy Greenwald Brown University Gunes Ercal, David Gondek, Amir Jafari July, Games A game is a tuple = (I; (S i ;r i ) i2i)
On the Connection between No-Regret Learning, Fictitious Play, & Nash Equilibrium Amy Greenwald Brown University Gunes Ercal, David Gondek, Amir Jafari July, Games A game is a tuple = (I; (S i ;r i ) i2i)
Tutorial: PART 2. Online Convex Optimization, A Game- Theoretic Approach to Learning
 Tutorial: PART 2 Online Convex Optimization, A Game- Theoretic Approach to Learning Elad Hazan Princeton University Satyen Kale Yahoo Research Exploiting curvature: logarithmic regret Logarithmic regret
Tutorial: PART 2 Online Convex Optimization, A Game- Theoretic Approach to Learning Elad Hazan Princeton University Satyen Kale Yahoo Research Exploiting curvature: logarithmic regret Logarithmic regret
From External to Internal Regret
 From External to Internal Regret Avrim Blum School of Computer Science Carnegie Mellon University, Pittsburgh, PA 15213. Yishay Mansour School of Computer Science, Tel Aviv University, Tel Aviv, ISRAEL.
From External to Internal Regret Avrim Blum School of Computer Science Carnegie Mellon University, Pittsburgh, PA 15213. Yishay Mansour School of Computer Science, Tel Aviv University, Tel Aviv, ISRAEL.
1 The linear algebra of linear programs (March 15 and 22, 2015)
 1 The linear algebra of linear programs (March 15 and 22, 2015) Many optimization problems can be formulated as linear programs. The main features of a linear program are the following: Variables are real
1 The linear algebra of linear programs (March 15 and 22, 2015) Many optimization problems can be formulated as linear programs. The main features of a linear program are the following: Variables are real
Toward a Classification of Finite Partial-Monitoring Games
 Toward a Classification of Finite Partial-Monitoring Games Gábor Bartók ( *student* ), Dávid Pál, and Csaba Szepesvári Department of Computing Science, University of Alberta, Canada {bartok,dpal,szepesva}@cs.ualberta.ca
Toward a Classification of Finite Partial-Monitoring Games Gábor Bartók ( *student* ), Dávid Pál, and Csaba Szepesvári Department of Computing Science, University of Alberta, Canada {bartok,dpal,szepesva}@cs.ualberta.ca
Existence of sparsely supported correlated equilibria
 Existence of sparsely supported correlated equilibria Fabrizio Germano fabrizio.germano@upf.edu Gábor Lugosi lugosi@upf.es Departament d Economia i Empresa Universitat Pompeu Fabra Ramon Trias Fargas 25-27
Existence of sparsely supported correlated equilibria Fabrizio Germano fabrizio.germano@upf.edu Gábor Lugosi lugosi@upf.es Departament d Economia i Empresa Universitat Pompeu Fabra Ramon Trias Fargas 25-27
Statistical inference on Lévy processes
 Alberto Coca Cabrero University of Cambridge - CCA Supervisors: Dr. Richard Nickl and Professor L.C.G.Rogers Funded by Fundación Mutua Madrileña and EPSRC MASDOC/CCA student workshop 2013 26th March Outline
Alberto Coca Cabrero University of Cambridge - CCA Supervisors: Dr. Richard Nickl and Professor L.C.G.Rogers Funded by Fundación Mutua Madrileña and EPSRC MASDOC/CCA student workshop 2013 26th March Outline
Online Learning of Non-stationary Sequences
 Online Learning of Non-stationary Sequences Claire Monteleoni and Tommi Jaakkola MIT Computer Science and Artificial Intelligence Laboratory 200 Technology Square Cambridge, MA 02139 {cmontel,tommi}@ai.mit.edu
Online Learning of Non-stationary Sequences Claire Monteleoni and Tommi Jaakkola MIT Computer Science and Artificial Intelligence Laboratory 200 Technology Square Cambridge, MA 02139 {cmontel,tommi}@ai.mit.edu
