Probability, Statistics, and Reliability for Engineers and Scientists MULTIPLE RANDOM VARIABLES
|
|
|
- Edmund Hopkins
- 5 years ago
- Views:
Transcription
1 CHATER robability, Statistics, and Reliability or Engineers and Scientists MULTILE RANDOM VARIABLES Second Edition A. J. Clark School o Engineering Department o Civil and Environmental Engineering 6a robability and Statistics or Civil Engineers Department o Civil and Environmental Engineering University o Maryland, College ark CHAMAN HALL/CRC CHATER 6a. MULTILE RANDOM VARIABLES Slide No. Introduction In engineering, it is common to deal with two or more random variables simultaneously in solving problems. I the load applied to a structure is considered to be a random variable, then the structural response will also be a random variable.
2 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. Introduction The load and the response can be modeled separately as random variables; however, it is more prudent to model the uncertainty jointly. More inormation can be etracted rom the joint distributions. Thus, it is necessary to etend the discussion to multiple random variables. CHATER 6a. MULTILE RANDOM VARIABLES Slide No. Introduction In general, multiple random variables are encountered in the ollowing two orms:. Joint occurrences o multiple random variables that can be correlated or uncorrelated. Random variables that are known in terms o their unctional relationship with other basic random variables
3 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 4 Joint and Their robability Distributions The outcomes, E, E,, E n, that constitute a sample space S are mapped to an n-dimensional (n-d) space o real numbers. The unctions that establish such a transormation to the n-d space are called multiple random variables (or random vectors). CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 5 Joint and Their robability Distributions Multiple random variables are classiied into two types: Discrete random variables Continuous random variables A distinction is made between these two types because the computations o probabilities depend on their type.
4 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 6 robability or Discrete Random Vectors Joint robability Mass Function (JMF) The joint probability mass unction or a discrete multiple random variable or random vector = (,,.., n ) is given by ( ) = ( =, =,..., ) = Note that ( =, =,..., n = ) n n n CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 7 robability or Discrete Random Vectors Joint Cumulative Mass Function (JCMF) The joint cumulative mass unction or a discrete random variable or random vector = (,,.., n ) is given by F ( ) = (,,..., n n ) = (,,..., ) all n n (,,..., ) 4
5 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 8 robability or Discrete Random Vectors roperties o JCMF. F (all ) =. F (,,, i -,, n ) =, or any i =,,, n. F (,,, i -,, k -,, n ) =, or any values o i,, k 4. F (,,, i +,, n ) = F j ( j : j =,,, n and j i), called the marginal distribution o all the random variables ecept i 5. F (,,, i +,, k +,, n ) = F j ( j : j =,,, n and j i to k), called the marginal distribution o all the random variables ecept i to k 6. F (all + ) = 7. F () is a nonnegative and nondecreasing unction o CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 9 robability or Discrete Random Vectors roperties o JCMF The irst, second, and third properties deine the limiting behavior o F (); as one or more o the random variables approach -, F () approaches zero. The ourth and ith properties deine the possible marginal distributions as one or more o the random variables approaches +. The sith property is based on the probability aiom. The seventh property is based on the cumulative nature o F (). 5
6 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. robability or Two Discrete For simplicity, the presentation o the materials in the remaining part o this section is limited to two random variables. The presented concepts can be generalized to n random variables CHATER 6a. MULTILE RANDOM VARIABLES Slide No. robability or Two Discrete Conditional robability Mass Function where The conditional probability mass unction or two random variables and is given by (, ) ( ) = ( ) ( ) given that =. results in the probability o ( ) = marginal mass unction or = 6
7 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. robability or Two Discrete Conditional robability Mass Function where The conditional probability mass unction or two random variables and is given by (, ) ( ) = ( ) ( ) given that =. results in the probability o ( ) = marginal mass unction or = CHATER 6a. MULTILE RANDOM VARIABLES Slide No. robability or Two Discrete Marginal Distributions The marginal mass unction or that is not equal to zero is = ( ) ( ), all The marginal mass unction or that is not equal to zero is ( ) = ( ), all 7
8 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 4 robability or Two Discrete roperties I and are statistically independent (uncorrelated) random variables, then and, ( ) = ( ) ( ) = ( ) (, ) = ( ) ( ) The important relationship can be obtained : CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 5 robability or Two Discrete Eample: Two Discrete RV s The time to produce a typical engineering drawing, represented by a random variable, and its quality, represented by a random variable, are under consideration. Suppose can be 7, 8, 9, or hours. The quality o a drawing can be considered to be moderate, good, and ecellent, and can be considered to be,, and, respectively. Suppose that such drawing are evaluated and the inormation provided the net table is obtained. 8
9 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 6 robability or Two Discrete Eample (cont d): Two Discrete RV s CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 7 robability or Two Discrete Eample (cont d): Two Discrete RV s. Find the joint MF o and.. lot the marginal MF o and.. I only ecellent quality drawings are acceptable (i.e., = ), plot the conditional MF o. 9
10 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 8 robability or Two Discrete Eample (cont d): Two Discrete RV s. The joint MF, (, ) o and CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 9 robability or Two Discrete Eample (cont d): Two Discrete RV s =,. The marginal MF o ( ) ( ) all ( 7) = =. ( 8) = =. ( 9) = =. ( ) = =. 6
11 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. robability or Two Discrete ( ) Eample (cont d): Two Discrete RV s ( ) = ( ), Marginal MF o all CHATER 6a. MULTILE RANDOM VARIABLES Slide No. robability or Two Discrete Eample (cont d): Two Discrete RV s The marginal MF o ( ) ( ) =, all ( ) = = ( ) = = () = =. 47
12 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. robability or Two Discrete ( ) Eample (cont d): Two Discrete RV s Marginal MF o ( ) = ( ), all CHATER 6a. MULTILE RANDOM VARIABLES Slide No. robability or Two Discrete Eample (cont d): Two Discrete RV s. Conditional robability o ( ) = i ( 7 ) ( 8 ) ( 9 ) ( ) = (,) i ().5 = = = = = = ( ) = =. 47 (, ) ( )
13 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 4 robability or Two Discrete ( ) Eample (cont d): Two Discrete RV s ( ) (,) Conditional MF o Y = i = i () CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 5 robability or Continuous Random Vectors Joint robability Density Function (JDF) The joint probability density unction or a continuous multiple random variable or random vector = (,,.., n ) is used to deine Note that n l u ( ) =... ( ) l l l n + + ( < < + ) =... ( ) u + u u d d... d d d... d = n n
14 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 6 robability or Continuous Random Vectors Joint Cumulative Distribution Function (JCDF) The joint cumulative distribution unction o a continuous random variable is deined by F n ( ) = ( ) =... ( ) d d... d n CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 7 robability or Continuous Random Vectors roperties o JCDF. F (all ) =. F (,,, i -,, n ) =, or any i =,,, n. F (,,, i -,, k -,, n ) =, or any values o i,, k 4. F (,,, i +,, n ) = F j ( j : j =,,, n and j i), called the marginal distribution o all the random variables ecept i 5. F (,,, i +,, k +,, n ) = F j ( j : j =,,, n and j i to k), called the marginal distribution o all the random variables ecept i to k 6. F (all + ) = 7. F () is a nonnegative and nondecreasing unction o 4
15 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 8 robability or Continuous Random Vectors The joint density unction can be obtained rom the a given joint cumulative distribution unction as ollows: ( ) That is =... n n F ( ) (,,..., ) n F... n (,,..., )... n n CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 9 robability or Two Continuous For simplicity, the presentation o the materials in the remaining part o this section is limited to two random variables. The presented concepts can be generalized to n random variables 5
16 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. robability or Two Continuous Conditional robability Density Function The conditional probability density unction or two random variables and is given by (, ), ( ) = ( ), (, ) joint density unction o and. = ( ) = marginal density unction or that is not equal to zero. where CHATER 6a. MULTILE RANDOM VARIABLES Slide No. robability or Two Continuous Conditional robability Density Function The conditional probability density unction or two random variables and is given by (, ), ( ) = ( ), (, ) joint density unction o and. = ( ) = marginal density unction or that is not equal to zero. where 6
17 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. robability or Two Continuous Marginal Distributions The marginal density unction or that is not equal to zero is + =, ( ) ( ) d The marginal mass unction or that is not equal to zero is + =, ( ) ( ) d CHATER 6a. MULTILE RANDOM VARIABLES Slide No. robability or Two Continuous roperties I and are statistically independent (uncorrelated) random variables, then and ( ) = ( ) ( ) = ( ) (, ) = ( ) ( ) The important relationship can be obtained : 7
18 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 4 robability or Two Continuous Eample: Two Continuous RV s The joint density unctions o two random variables and Y can be epressed as c 4 y, Y (, y) = ( )( 9) or and y elsewhere (a) Determine the constant c. (b) Determine the marginal density unction or. (c) Determine the marginal density unction or Y. (d) Are and Y statistically independent? (e) Determine the probability o the ollowing event: F, Y (, ) CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 5 robability or Two Continuous Eample (cont d): Two Continuous RV s (a) c( 4)( y 9) ddy = or or or 6 y c 9y c = 96 6 c( y 9) 4 dy = c( y 9) =. dy =. 8
19 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 6 robability or Two Continuous Eample (cont d): Two Continuous RV s (a) c( 4)( y 9) ddy = or or or 6 y c 9y c = 96 6 c( y 9) 4 dy = c( y 9) =. dy =. CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 7 robability or Two Continuous Eample (cont d): Two Continuous RV s (b) ( ) = ( 4)( y 9) dy = ( 4) 96 6 (c) (d) Y ( ) y = ( 4)( y 9) d = ( y 9) 96 8 ( ) ( y) = ( 4) ( y 9) Y 6 8 = ( 4)( y 9) = ( ) Y ( y) 96 and Y are statistically independent random variables. 9
20 CHATER 6a. MULTILE RANDOM VARIABLES Slide No. 8 robability or Two Continuous Eample (cont d): Two Continuous RV s (e) F, Y = 96 (,) = ( 4) d ( y 9) dy. 6875
( x) f = where P and Q are polynomials.
 9.8 Graphing Rational Functions Lets begin with a deinition. Deinition: Rational Function A rational unction is a unction o the orm ( ) ( ) ( ) P where P and Q are polynomials. Q An eample o a simple rational
9.8 Graphing Rational Functions Lets begin with a deinition. Deinition: Rational Function A rational unction is a unction o the orm ( ) ( ) ( ) P where P and Q are polynomials. Q An eample o a simple rational
MODULE 6 LECTURE NOTES 1 REVIEW OF PROBABILITY THEORY. Most water resources decision problems face the risk of uncertainty mainly because of the
 MODULE 6 LECTURE NOTES REVIEW OF PROBABILITY THEORY INTRODUCTION Most water resources decision problems ace the risk o uncertainty mainly because o the randomness o the variables that inluence the perormance
MODULE 6 LECTURE NOTES REVIEW OF PROBABILITY THEORY INTRODUCTION Most water resources decision problems ace the risk o uncertainty mainly because o the randomness o the variables that inluence the perormance
ELEG 3143 Probability & Stochastic Process Ch. 4 Multiple Random Variables
 Department o Electrical Engineering University o Arkansas ELEG 3143 Probability & Stochastic Process Ch. 4 Multiple Random Variables Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Two discrete random variables
Department o Electrical Engineering University o Arkansas ELEG 3143 Probability & Stochastic Process Ch. 4 Multiple Random Variables Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Two discrete random variables
Stochastic Processes. Review of Elementary Probability Lecture I. Hamid R. Rabiee Ali Jalali
 Stochastic Processes Review o Elementary Probability bili Lecture I Hamid R. Rabiee Ali Jalali Outline History/Philosophy Random Variables Density/Distribution Functions Joint/Conditional Distributions
Stochastic Processes Review o Elementary Probability bili Lecture I Hamid R. Rabiee Ali Jalali Outline History/Philosophy Random Variables Density/Distribution Functions Joint/Conditional Distributions
Review of Elementary Probability Lecture I Hamid R. Rabiee
 Stochastic Processes Review o Elementar Probabilit Lecture I Hamid R. Rabiee Outline Histor/Philosoph Random Variables Densit/Distribution Functions Joint/Conditional Distributions Correlation Important
Stochastic Processes Review o Elementar Probabilit Lecture I Hamid R. Rabiee Outline Histor/Philosoph Random Variables Densit/Distribution Functions Joint/Conditional Distributions Correlation Important
Math Review and Lessons in Calculus
 Math Review and Lessons in Calculus Agenda Rules o Eponents Functions Inverses Limits Calculus Rules o Eponents 0 Zero Eponent Rule a * b ab Product Rule * 3 5 a / b a-b Quotient Rule 5 / 3 -a / a Negative
Math Review and Lessons in Calculus Agenda Rules o Eponents Functions Inverses Limits Calculus Rules o Eponents 0 Zero Eponent Rule a * b ab Product Rule * 3 5 a / b a-b Quotient Rule 5 / 3 -a / a Negative
10. Joint Moments and Joint Characteristic Functions
 10. Joint Moments and Joint Characteristic Functions Following section 6, in this section we shall introduce various parameters to compactly represent the inormation contained in the joint p.d. o two r.vs.
10. Joint Moments and Joint Characteristic Functions Following section 6, in this section we shall introduce various parameters to compactly represent the inormation contained in the joint p.d. o two r.vs.
3. Several Random Variables
 . Several Random Variables. Two Random Variables. Conditional Probabilit--Revisited. Statistical Independence.4 Correlation between Random Variables. Densit unction o the Sum o Two Random Variables. Probabilit
. Several Random Variables. Two Random Variables. Conditional Probabilit--Revisited. Statistical Independence.4 Correlation between Random Variables. Densit unction o the Sum o Two Random Variables. Probabilit
Mixed Signal IC Design Notes set 6: Mathematics of Electrical Noise
 ECE45C /8C notes, M. odwell, copyrighted 007 Mied Signal IC Design Notes set 6: Mathematics o Electrical Noise Mark odwell University o Caliornia, Santa Barbara rodwell@ece.ucsb.edu 805-893-344, 805-893-36
ECE45C /8C notes, M. odwell, copyrighted 007 Mied Signal IC Design Notes set 6: Mathematics o Electrical Noise Mark odwell University o Caliornia, Santa Barbara rodwell@ece.ucsb.edu 805-893-344, 805-893-36
Asymptote. 2 Problems 2 Methods
 Asymptote Problems Methods Problems Assume we have the ollowing transer unction which has a zero at =, a pole at = and a pole at =. We are going to look at two problems: problem is where >> and problem
Asymptote Problems Methods Problems Assume we have the ollowing transer unction which has a zero at =, a pole at = and a pole at =. We are going to look at two problems: problem is where >> and problem
CHAPTER 6c. NUMERICAL INTERPOLATION
 CHAPTER 6c. NUMERICAL INTERPOLATION A. J. Clark School o Egieerig Departmet o Civil ad Evirometal Egieerig y Dr. Irahim A. Assakka Sprig ENCE - Computatio Methods i Civil Egieerig II Departmet o Civil
CHAPTER 6c. NUMERICAL INTERPOLATION A. J. Clark School o Egieerig Departmet o Civil ad Evirometal Egieerig y Dr. Irahim A. Assakka Sprig ENCE - Computatio Methods i Civil Egieerig II Departmet o Civil
9.3 Graphing Functions by Plotting Points, The Domain and Range of Functions
 9. Graphing Functions by Plotting Points, The Domain and Range o Functions Now that we have a basic idea o what unctions are and how to deal with them, we would like to start talking about the graph o
9. Graphing Functions by Plotting Points, The Domain and Range o Functions Now that we have a basic idea o what unctions are and how to deal with them, we would like to start talking about the graph o
Differentiation. The main problem of differential calculus deals with finding the slope of the tangent line at a point on a curve.
 Dierentiation The main problem o dierential calculus deals with inding the slope o the tangent line at a point on a curve. deinition() : The slope o a curve at a point p is the slope, i it eists, o the
Dierentiation The main problem o dierential calculus deals with inding the slope o the tangent line at a point on a curve. deinition() : The slope o a curve at a point p is the slope, i it eists, o the
9.1 The Square Root Function
 Section 9.1 The Square Root Function 869 9.1 The Square Root Function In this section we turn our attention to the square root unction, the unction deined b the equation () =. (1) We begin the section
Section 9.1 The Square Root Function 869 9.1 The Square Root Function In this section we turn our attention to the square root unction, the unction deined b the equation () =. (1) We begin the section
Example: When describing where a function is increasing, decreasing or constant we use the x- axis values.
 Business Calculus Lecture Notes (also Calculus With Applications or Business Math II) Chapter 3 Applications o Derivatives 31 Increasing and Decreasing Functions Inormal Deinition: A unction is increasing
Business Calculus Lecture Notes (also Calculus With Applications or Business Math II) Chapter 3 Applications o Derivatives 31 Increasing and Decreasing Functions Inormal Deinition: A unction is increasing
ORF 245 Fundamentals of Statistics Joint Distributions
 ORF 245 Fundamentals of Statistics Joint Distributions Robert Vanderbei Fall 2015 Slides last edited on November 11, 2015 http://www.princeton.edu/ rvdb Introduction Joint Cumulative Distribution Function
ORF 245 Fundamentals of Statistics Joint Distributions Robert Vanderbei Fall 2015 Slides last edited on November 11, 2015 http://www.princeton.edu/ rvdb Introduction Joint Cumulative Distribution Function
CHAPTER 3a. INTRODUCTION TO NUMERICAL METHODS
 CHAPTER 3a. INTRODUCTION TO NUMERICAL METHODS A. J. Clark School of Engineering Department of Civil and Environmental Engineering by Dr. Ibrahim A. Assakkaf Spring 1 ENCE 3 - Computation in Civil Engineering
CHAPTER 3a. INTRODUCTION TO NUMERICAL METHODS A. J. Clark School of Engineering Department of Civil and Environmental Engineering by Dr. Ibrahim A. Assakkaf Spring 1 ENCE 3 - Computation in Civil Engineering
CHAPTER 6b. NUMERICAL INTERPOLATION
 CHAPTER 6. NUMERICAL INTERPOLATION A. J. Clrk School o Engineering Deprtment o Civil nd Environmentl Engineering y Dr. Irhim A. Asskk Spring ENCE - Computtion s in Civil Engineering II Deprtment o Civil
CHAPTER 6. NUMERICAL INTERPOLATION A. J. Clrk School o Engineering Deprtment o Civil nd Environmentl Engineering y Dr. Irhim A. Asskk Spring ENCE - Computtion s in Civil Engineering II Deprtment o Civil
RATIONAL FUNCTIONS. Finding Asymptotes..347 The Domain Finding Intercepts Graphing Rational Functions
 RATIONAL FUNCTIONS Finding Asymptotes..347 The Domain....350 Finding Intercepts.....35 Graphing Rational Functions... 35 345 Objectives The ollowing is a list o objectives or this section o the workbook.
RATIONAL FUNCTIONS Finding Asymptotes..347 The Domain....350 Finding Intercepts.....35 Graphing Rational Functions... 35 345 Objectives The ollowing is a list o objectives or this section o the workbook.
Analog Communication (10EC53)
 UNIT-1: RANDOM PROCESS: Random variables: Several random variables. Statistical averages: Function o Random variables, moments, Mean, Correlation and Covariance unction: Principles o autocorrelation unction,
UNIT-1: RANDOM PROCESS: Random variables: Several random variables. Statistical averages: Function o Random variables, moments, Mean, Correlation and Covariance unction: Principles o autocorrelation unction,
Syllabus Objective: 2.9 The student will sketch the graph of a polynomial, radical, or rational function.
 Precalculus Notes: Unit Polynomial Functions Syllabus Objective:.9 The student will sketch the graph o a polynomial, radical, or rational unction. Polynomial Function: a unction that can be written in
Precalculus Notes: Unit Polynomial Functions Syllabus Objective:.9 The student will sketch the graph o a polynomial, radical, or rational unction. Polynomial Function: a unction that can be written in
Joint ] X 5) P[ 6) P[ (, ) = y 2. x 1. , y. , ( x, y ) 2, (
![Joint ] X 5) P[ 6) P[ (, ) = y 2. x 1. , y. , ( x, y ) 2, ( Joint ] X 5) P[ 6) P[ (, ) = y 2. x 1. , y. , ( x, y ) 2, (](/thumbs/89/97775493.jpg) Two-dimensional Random Vectors Joint Cumulative Distrib bution Functio n F, (, ) P[ and ] Properties: ) F, (, ) = ) F, 3) F, F 4), (, ) = F 5) P[ < 6) P[ < (, ) is a non-decreasing unction (, ) = F ( ),,,
Two-dimensional Random Vectors Joint Cumulative Distrib bution Functio n F, (, ) P[ and ] Properties: ) F, (, ) = ) F, 3) F, F 4), (, ) = F 5) P[ < 6) P[ < (, ) is a non-decreasing unction (, ) = F ( ),,,
Probability, Statistics, and Reliability for Engineers and Scientists FUNDAMENTALS OF STATISTICAL ANALYSIS
 CHAPTER Probability, Statistics, and Reliability for Engineers and Scientists FUNDAMENTALS OF STATISTICAL ANALYSIS Second Edition A. J. Clark School of Engineering Department of Civil and Environmental
CHAPTER Probability, Statistics, and Reliability for Engineers and Scientists FUNDAMENTALS OF STATISTICAL ANALYSIS Second Edition A. J. Clark School of Engineering Department of Civil and Environmental
Engineering Decisions
 GSOE9 vicj@cse.unsw.edu.au www.cse.unsw.edu.au/~gs9 Outline Decision problem classes Decision problems can be classiied based on an agent s epistemic state: Decisions under certainty: the agent knows the
GSOE9 vicj@cse.unsw.edu.au www.cse.unsw.edu.au/~gs9 Outline Decision problem classes Decision problems can be classiied based on an agent s epistemic state: Decisions under certainty: the agent knows the
Ma 4121: Introduction to Lebesgue Integration Solutions to Homework Assignment 6
 Ma 4: Introduction to Lebesgue Integration Solutions to Homework Assignment 6 Pro. Wickerhauser Due Thursda, April 5th, 3 Please return our solutions to the instructor b the end o class on the due date.
Ma 4: Introduction to Lebesgue Integration Solutions to Homework Assignment 6 Pro. Wickerhauser Due Thursda, April 5th, 3 Please return our solutions to the instructor b the end o class on the due date.
Flip-Flop Functions KEY
 For each rational unction, list the zeros o the polynomials in the numerator and denominator. Then, using a calculator, sketch the graph in a window o [-5.75, 6] by [-5, 5], and provide an end behavior
For each rational unction, list the zeros o the polynomials in the numerator and denominator. Then, using a calculator, sketch the graph in a window o [-5.75, 6] by [-5, 5], and provide an end behavior
«Develop a better understanding on Partial fractions»
 «Develop a better understanding on Partial ractions» ackground inormation: The topic on Partial ractions or decomposing actions is irst introduced in O level dditional Mathematics with its applications
«Develop a better understanding on Partial ractions» ackground inormation: The topic on Partial ractions or decomposing actions is irst introduced in O level dditional Mathematics with its applications
Ex x xf xdx. Ex+ a = x+ a f x dx= xf x dx+ a f xdx= xˆ. E H x H x H x f x dx ˆ ( ) ( ) ( ) μ is actually the first moment of the random ( )
 Fall 03 Analysis o Eperimental Measurements B Eisenstein/rev S Errede The Epectation Value o a Random Variable: The epectation value E[ ] o a random variable is the mean value o, ie ˆ (aa μ ) For discrete
Fall 03 Analysis o Eperimental Measurements B Eisenstein/rev S Errede The Epectation Value o a Random Variable: The epectation value E[ ] o a random variable is the mean value o, ie ˆ (aa μ ) For discrete
Estimation of Parameters
 CHAPTER Probability, Statistics, and Reliability for Engineers and Scientists FUNDAMENTALS OF STATISTICAL ANALYSIS Second Edition A. J. Clark School of Engineering Department of Civil and Environmental
CHAPTER Probability, Statistics, and Reliability for Engineers and Scientists FUNDAMENTALS OF STATISTICAL ANALYSIS Second Edition A. J. Clark School of Engineering Department of Civil and Environmental
Lecture 8 Optimization
 4/9/015 Lecture 8 Optimization EE 4386/5301 Computational Methods in EE Spring 015 Optimization 1 Outline Introduction 1D Optimization Parabolic interpolation Golden section search Newton s method Multidimensional
4/9/015 Lecture 8 Optimization EE 4386/5301 Computational Methods in EE Spring 015 Optimization 1 Outline Introduction 1D Optimization Parabolic interpolation Golden section search Newton s method Multidimensional
Review: mostly probability and some statistics
 Review: mostly probability and some statistics C2 1 Content robability (should know already) Axioms and properties Conditional probability and independence Law of Total probability and Bayes theorem Random
Review: mostly probability and some statistics C2 1 Content robability (should know already) Axioms and properties Conditional probability and independence Law of Total probability and Bayes theorem Random
Analog Computing Technique
 Analog Computing Technique by obert Paz Chapter Programming Principles and Techniques. Analog Computers and Simulation An analog computer can be used to solve various types o problems. It solves them in
Analog Computing Technique by obert Paz Chapter Programming Principles and Techniques. Analog Computers and Simulation An analog computer can be used to solve various types o problems. It solves them in
Math-3 Lesson 1-4. Review: Cube, Cube Root, and Exponential Functions
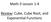 Math- Lesson -4 Review: Cube, Cube Root, and Eponential Functions Quiz - Graph (no calculator):. y. y ( ) 4. y What is a power? vocabulary Power: An epression ormed by repeated Multiplication o the same
Math- Lesson -4 Review: Cube, Cube Root, and Eponential Functions Quiz - Graph (no calculator):. y. y ( ) 4. y What is a power? vocabulary Power: An epression ormed by repeated Multiplication o the same
Chapter 4 Image Enhancement in the Frequency Domain
 Chapter 4 Image Enhancement in the Frequency Domain 3. Fourier transorm -D Let be a unction o real variable,the ourier transorm o is F { } F u ep jπu d j F { F u } F u ep[ jπ u ] du F u R u + ji u or F
Chapter 4 Image Enhancement in the Frequency Domain 3. Fourier transorm -D Let be a unction o real variable,the ourier transorm o is F { } F u ep jπu d j F { F u } F u ep[ jπ u ] du F u R u + ji u or F
Function Operations. I. Ever since basic math, you have been combining numbers by using addition, subtraction, multiplication, and division.
 Function Operations I. Ever since basic math, you have been combining numbers by using addition, subtraction, multiplication, and division. Add: 5 + Subtract: 7 Multiply: (9)(0) Divide: (5) () or 5 II.
Function Operations I. Ever since basic math, you have been combining numbers by using addition, subtraction, multiplication, and division. Add: 5 + Subtract: 7 Multiply: (9)(0) Divide: (5) () or 5 II.
OPTIMAL PLACEMENT AND UTILIZATION OF PHASOR MEASUREMENTS FOR STATE ESTIMATION
 OPTIMAL PLACEMENT AND UTILIZATION OF PHASOR MEASUREMENTS FOR STATE ESTIMATION Xu Bei, Yeo Jun Yoon and Ali Abur Teas A&M University College Station, Teas, U.S.A. abur@ee.tamu.edu Abstract This paper presents
OPTIMAL PLACEMENT AND UTILIZATION OF PHASOR MEASUREMENTS FOR STATE ESTIMATION Xu Bei, Yeo Jun Yoon and Ali Abur Teas A&M University College Station, Teas, U.S.A. abur@ee.tamu.edu Abstract This paper presents
References Ideal Nyquist Channel and Raised Cosine Spectrum Chapter 4.5, 4.11, S. Haykin, Communication Systems, Wiley.
 Baseand Data Transmission III Reerences Ideal yquist Channel and Raised Cosine Spectrum Chapter 4.5, 4., S. Haykin, Communication Systems, iley. Equalization Chapter 9., F. G. Stremler, Communication Systems,
Baseand Data Transmission III Reerences Ideal yquist Channel and Raised Cosine Spectrum Chapter 4.5, 4., S. Haykin, Communication Systems, iley. Equalization Chapter 9., F. G. Stremler, Communication Systems,
Comments on Problems. 3.1 This problem offers some practice in deriving utility functions from indifference curve specifications.
 CHAPTER 3 PREFERENCES AND UTILITY These problems provide some practice in eamining utilit unctions b looking at indierence curve maps and at a ew unctional orms. The primar ocus is on illustrating the
CHAPTER 3 PREFERENCES AND UTILITY These problems provide some practice in eamining utilit unctions b looking at indierence curve maps and at a ew unctional orms. The primar ocus is on illustrating the
1036: Probability & Statistics
 1036: Probabilit & Statistics Lecture 4 Mathematical pectation Prob. & Stat. Lecture04 - mathematical epectation cwliu@twins.ee.nctu.edu.tw 4-1 Mean o a Random Variable Let be a random variable with probabilit
1036: Probabilit & Statistics Lecture 4 Mathematical pectation Prob. & Stat. Lecture04 - mathematical epectation cwliu@twins.ee.nctu.edu.tw 4-1 Mean o a Random Variable Let be a random variable with probabilit
Chapter 6: Functions with severable variables and Partial Derivatives:
 Chapter 6: Functions with severable variables and Partial Derivatives: Functions o several variables: A unction involving more than one variable is called unction with severable variables. Eamples: y (,
Chapter 6: Functions with severable variables and Partial Derivatives: Functions o several variables: A unction involving more than one variable is called unction with severable variables. Eamples: y (,
Math 2412 Activity 1(Due by EOC Sep. 17)
 Math 4 Activity (Due by EOC Sep. 7) Determine whether each relation is a unction.(indicate why or why not.) Find the domain and range o each relation.. 4,5, 6,7, 8,8. 5,6, 5,7, 6,6, 6,7 Determine whether
Math 4 Activity (Due by EOC Sep. 7) Determine whether each relation is a unction.(indicate why or why not.) Find the domain and range o each relation.. 4,5, 6,7, 8,8. 5,6, 5,7, 6,6, 6,7 Determine whether
whose domain D is a set of n-tuples in is defined. The range of f is the set of all values f x1,..., x n
 Grade (MCV4UE) - AP Calculus Etended Page o A unction o n-variales is a real-valued unction... n whose domain D is a set o n-tuples... n in which... n is deined. The range o is the set o all values...
Grade (MCV4UE) - AP Calculus Etended Page o A unction o n-variales is a real-valued unction... n whose domain D is a set o n-tuples... n in which... n is deined. The range o is the set o all values...
Profit Maximization. Beattie, Taylor, and Watts Sections: 3.1b-c, 3.2c, , 5.2a-d
 Proit Maimization Beattie Talor and Watts Sections:.b-c.c 4.-4. 5.a-d Agenda Generalized Proit Maimization Proit Maimization ith One Inut and One Outut Proit Maimization ith To Inuts and One Outut Proit
Proit Maimization Beattie Talor and Watts Sections:.b-c.c 4.-4. 5.a-d Agenda Generalized Proit Maimization Proit Maimization ith One Inut and One Outut Proit Maimization ith To Inuts and One Outut Proit
Chapter 6 Reliability-based design and code developments
 Chapter 6 Reliability-based design and code developments 6. General Reliability technology has become a powerul tool or the design engineer and is widely employed in practice. Structural reliability analysis
Chapter 6 Reliability-based design and code developments 6. General Reliability technology has become a powerul tool or the design engineer and is widely employed in practice. Structural reliability analysis
Wind-Driven Circulation: Stommel s gyre & Sverdrup s balance
 Wind-Driven Circulation: Stommel s gyre & Sverdrup s balance We begin by returning to our system o equations or low o a layer o uniorm density on a rotating earth. du dv h + [ u( H + h)] + [ v( H t y d
Wind-Driven Circulation: Stommel s gyre & Sverdrup s balance We begin by returning to our system o equations or low o a layer o uniorm density on a rotating earth. du dv h + [ u( H + h)] + [ v( H t y d
Objectives. By the time the student is finished with this section of the workbook, he/she should be able
 FUNCTIONS Quadratic Functions......8 Absolute Value Functions.....48 Translations o Functions..57 Radical Functions...61 Eponential Functions...7 Logarithmic Functions......8 Cubic Functions......91 Piece-Wise
FUNCTIONS Quadratic Functions......8 Absolute Value Functions.....48 Translations o Functions..57 Radical Functions...61 Eponential Functions...7 Logarithmic Functions......8 Cubic Functions......91 Piece-Wise
8. THEOREM If the partial derivatives f x. and f y exist near (a, b) and are continuous at (a, b), then f is differentiable at (a, b).
 8. THEOREM I the partial derivatives and eist near (a b) and are continuous at (a b) then is dierentiable at (a b). For a dierentiable unction o two variables z= ( ) we deine the dierentials d and d to
8. THEOREM I the partial derivatives and eist near (a b) and are continuous at (a b) then is dierentiable at (a b). For a dierentiable unction o two variables z= ( ) we deine the dierentials d and d to
Numerical Methods - Lecture 2. Numerical Methods. Lecture 2. Analysis of errors in numerical methods
 Numerical Methods - Lecture 1 Numerical Methods Lecture. Analysis o errors in numerical methods Numerical Methods - Lecture Why represent numbers in loating point ormat? Eample 1. How a number 56.78 can
Numerical Methods - Lecture 1 Numerical Methods Lecture. Analysis o errors in numerical methods Numerical Methods - Lecture Why represent numbers in loating point ormat? Eample 1. How a number 56.78 can
Increasing and Decreasing Functions and the First Derivative Test. Increasing and Decreasing Functions. Video
 SECTION and Decreasing Functions and the First Derivative Test 79 Section and Decreasing Functions and the First Derivative Test Determine intervals on which a unction is increasing or decreasing Appl
SECTION and Decreasing Functions and the First Derivative Test 79 Section and Decreasing Functions and the First Derivative Test Determine intervals on which a unction is increasing or decreasing Appl
Short course A vademecum of statistical pattern recognition techniques with applications to image and video analysis. Agenda
 Short course A vademecum of statistical pattern recognition techniques with applications to image and video analysis Lecture Recalls of probability theory Massimo Piccardi University of Technology, Sydney,
Short course A vademecum of statistical pattern recognition techniques with applications to image and video analysis Lecture Recalls of probability theory Massimo Piccardi University of Technology, Sydney,
(One Dimension) Problem: for a function f(x), find x 0 such that f(x 0 ) = 0. f(x)
 Solving Nonlinear Equations & Optimization One Dimension Problem: or a unction, ind 0 such that 0 = 0. 0 One Root: The Bisection Method This one s guaranteed to converge at least to a singularity, i not
Solving Nonlinear Equations & Optimization One Dimension Problem: or a unction, ind 0 such that 0 = 0. 0 One Root: The Bisection Method This one s guaranteed to converge at least to a singularity, i not
Chapter 3 Single Random Variables and Probability Distributions (Part 1)
 Chapter 3 Single Random Variables and Probability Distributions (Part 1) Contents What is a Random Variable? Probability Distribution Functions Cumulative Distribution Function Probability Density Function
Chapter 3 Single Random Variables and Probability Distributions (Part 1) Contents What is a Random Variable? Probability Distribution Functions Cumulative Distribution Function Probability Density Function
Topic 4b. Open Methods for Root Finding
 Course Instructor Dr. Ramond C. Rump Oice: A 337 Phone: (915) 747 6958 E Mail: rcrump@utep.edu Topic 4b Open Methods or Root Finding EE 4386/5301 Computational Methods in EE Outline Open Methods or Root
Course Instructor Dr. Ramond C. Rump Oice: A 337 Phone: (915) 747 6958 E Mail: rcrump@utep.edu Topic 4b Open Methods or Root Finding EE 4386/5301 Computational Methods in EE Outline Open Methods or Root
A Fourier Transform Model in Excel #1
 A Fourier Transorm Model in Ecel # -This is a tutorial about the implementation o a Fourier transorm in Ecel. This irst part goes over adjustments in the general Fourier transorm ormula to be applicable
A Fourier Transorm Model in Ecel # -This is a tutorial about the implementation o a Fourier transorm in Ecel. This irst part goes over adjustments in the general Fourier transorm ormula to be applicable
Mathematical Notation Math Calculus & Analytic Geometry III
 Name : Mathematical Notation Math 221 - alculus & Analytic Geometry III Use Word or WordPerect to recreate the ollowing documents. Each article is worth 10 points and can e printed and given to the instructor
Name : Mathematical Notation Math 221 - alculus & Analytic Geometry III Use Word or WordPerect to recreate the ollowing documents. Each article is worth 10 points and can e printed and given to the instructor
1/100 Range: 1/10 1/ 2. 1) Constant: choose a value for the constant that can be graphed on the coordinate grid below.
 Name 1) Constant: choose a value or the constant that can be graphed on the coordinate grid below a y Toolkit Functions Lab Worksheet thru inverse trig ) Identity: y ) Reciprocal: 1 ( ) y / 1/ 1/1 1/ 1
Name 1) Constant: choose a value or the constant that can be graphed on the coordinate grid below a y Toolkit Functions Lab Worksheet thru inverse trig ) Identity: y ) Reciprocal: 1 ( ) y / 1/ 1/1 1/ 1
MHF 4U Unit 7: Combining Functions May 29, Review Solutions
 MHF 4U Unit 7: Combining Functions May 9, 008. Review Solutions Use the ollowing unctions to answer questions 5, ( ) g( ), h( ) sin, w {(, ), (3, ), (4, 7)}, r, and l ) log ( ) + (, ) Determine: a) + w
MHF 4U Unit 7: Combining Functions May 9, 008. Review Solutions Use the ollowing unctions to answer questions 5, ( ) g( ), h( ) sin, w {(, ), (3, ), (4, 7)}, r, and l ) log ( ) + (, ) Determine: a) + w
Bayesian Technique for Reducing Uncertainty in Fatigue Failure Model
 9IDM- Bayesian Technique or Reducing Uncertainty in Fatigue Failure Model Sriram Pattabhiraman and Nam H. Kim University o Florida, Gainesville, FL, 36 Copyright 8 SAE International ABSTRACT In this paper,
9IDM- Bayesian Technique or Reducing Uncertainty in Fatigue Failure Model Sriram Pattabhiraman and Nam H. Kim University o Florida, Gainesville, FL, 36 Copyright 8 SAE International ABSTRACT In this paper,
4.1 & 4.2 Student Notes Using the First and Second Derivatives. for all x in D, where D is the domain of f. The number f()
 4.1 & 4. Student Notes Using the First and Second Derivatives Deinition A unction has an absolute maimum (or global maimum) at c i ( c) ( ) or all in D, where D is the domain o. The number () c is called
4.1 & 4. Student Notes Using the First and Second Derivatives Deinition A unction has an absolute maimum (or global maimum) at c i ( c) ( ) or all in D, where D is the domain o. The number () c is called
Copyright 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley. Chapter 8 Section 6
 Copyright 008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Chapter 8 Section 6 8.6 Solving Equations with Radicals 1 3 4 Solve radical equations having square root radicals. Identify equations
Copyright 008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Chapter 8 Section 6 8.6 Solving Equations with Radicals 1 3 4 Solve radical equations having square root radicals. Identify equations
1. Definition: Order Statistics of a sample.
 AMS570 Order Statistics 1. Deinition: Order Statistics o a sample. Let X1, X2,, be a random sample rom a population with p.d.. (x). Then, 2. p.d.. s or W.L.O.G.(W thout Loss o Ge er l ty), let s ssu e
AMS570 Order Statistics 1. Deinition: Order Statistics o a sample. Let X1, X2,, be a random sample rom a population with p.d.. (x). Then, 2. p.d.. s or W.L.O.G.(W thout Loss o Ge er l ty), let s ssu e
MODULE - 2 LECTURE NOTES 3 LAGRANGE MULTIPLIERS AND KUHN-TUCKER CONDITIONS
 Water Resources Systems Plannin and Manaement: Introduction to Optimization: arane Multipliers MODUE - ECTURE NOTES 3 AGRANGE MUTIPIERS AND KUHN-TUCKER CONDITIONS INTRODUCTION In the previous lecture the
Water Resources Systems Plannin and Manaement: Introduction to Optimization: arane Multipliers MODUE - ECTURE NOTES 3 AGRANGE MUTIPIERS AND KUHN-TUCKER CONDITIONS INTRODUCTION In the previous lecture the
7. Two Random Variables
 7. Two Random Variables In man eeriments the observations are eressible not as a single quantit but as a amil o quantities. or eamle to record the height and weight o each erson in a communit or the number
7. Two Random Variables In man eeriments the observations are eressible not as a single quantit but as a amil o quantities. or eamle to record the height and weight o each erson in a communit or the number
Lecture Outline. Basics of Spatial Filtering Smoothing Spatial Filters. Sharpening Spatial Filters
 1 Lecture Outline Basics o Spatial Filtering Smoothing Spatial Filters Averaging ilters Order-Statistics ilters Sharpening Spatial Filters Laplacian ilters High-boost ilters Gradient Masks Combining Spatial
1 Lecture Outline Basics o Spatial Filtering Smoothing Spatial Filters Averaging ilters Order-Statistics ilters Sharpening Spatial Filters Laplacian ilters High-boost ilters Gradient Masks Combining Spatial
Quality control of risk measures: backtesting VAR models
 De la Pena Q 9/2/06 :57 pm Page 39 Journal o Risk (39 54 Volume 9/Number 2, Winter 2006/07 Quality control o risk measures: backtesting VAR models Victor H. de la Pena* Department o Statistics, Columbia
De la Pena Q 9/2/06 :57 pm Page 39 Journal o Risk (39 54 Volume 9/Number 2, Winter 2006/07 Quality control o risk measures: backtesting VAR models Victor H. de la Pena* Department o Statistics, Columbia
Other Continuous Probability Distributions
 CHAPTER Probability, Statistics, and Reliability for Engineers and Scientists Second Edition PROBABILITY DISTRIBUTION FOR CONTINUOUS RANDOM VARIABLES A. J. Clar School of Engineering Department of Civil
CHAPTER Probability, Statistics, and Reliability for Engineers and Scientists Second Edition PROBABILITY DISTRIBUTION FOR CONTINUOUS RANDOM VARIABLES A. J. Clar School of Engineering Department of Civil
Lecture 13: Applications of Fourier transforms (Recipes, Chapter 13)
 Lecture 13: Applications o Fourier transorms (Recipes, Chapter 13 There are many applications o FT, some o which involve the convolution theorem (Recipes 13.1: The convolution o h(t and r(t is deined by
Lecture 13: Applications o Fourier transorms (Recipes, Chapter 13 There are many applications o FT, some o which involve the convolution theorem (Recipes 13.1: The convolution o h(t and r(t is deined by
Roberto s Notes on Differential Calculus Chapter 8: Graphical analysis Section 1. Extreme points
 Roberto s Notes on Dierential Calculus Chapter 8: Graphical analysis Section 1 Extreme points What you need to know already: How to solve basic algebraic and trigonometric equations. All basic techniques
Roberto s Notes on Dierential Calculus Chapter 8: Graphical analysis Section 1 Extreme points What you need to know already: How to solve basic algebraic and trigonometric equations. All basic techniques
Integration of Basic Functions. Session 7 : 9/23 1
 Integration o Basic Fnctions Session 7 : 9/3 Antiderivation Integration Deinition: Taking the antiderivative, or integral, o some nction F(), reslts in the nction () i ()F() Pt simply: i yo take the integral
Integration o Basic Fnctions Session 7 : 9/3 Antiderivation Integration Deinition: Taking the antiderivative, or integral, o some nction F(), reslts in the nction () i ()F() Pt simply: i yo take the integral
Basic mathematics of economic models. 3. Maximization
 John Riley 1 January 16 Basic mathematics o economic models 3 Maimization 31 Single variable maimization 1 3 Multi variable maimization 6 33 Concave unctions 9 34 Maimization with non-negativity constraints
John Riley 1 January 16 Basic mathematics o economic models 3 Maimization 31 Single variable maimization 1 3 Multi variable maimization 6 33 Concave unctions 9 34 Maimization with non-negativity constraints
RELIABILITY OF BURIED PIPELINES WITH CORROSION DEFECTS UNDER VARYING BOUNDARY CONDITIONS
 REIABIITY OF BURIE PIPEIES WITH CORROSIO EFECTS UER VARYIG BOUARY COITIOS Ouk-Sub ee 1 and ong-hyeok Kim 1. School o Mechanical Engineering, InHa University #53, Yonghyun-ong, am-ku, Incheon, 40-751, Korea
REIABIITY OF BURIE PIPEIES WITH CORROSIO EFECTS UER VARYIG BOUARY COITIOS Ouk-Sub ee 1 and ong-hyeok Kim 1. School o Mechanical Engineering, InHa University #53, Yonghyun-ong, am-ku, Incheon, 40-751, Korea
A Function of Two Random Variables
 akultät Inormatik Institut ür Sstemarchitektur Proessur Rechnernete A unction o Two Random Variables Waltenegus Dargie Slides are based on the book: A. Papoulis and S.U. Pillai "Probabilit random variables
akultät Inormatik Institut ür Sstemarchitektur Proessur Rechnernete A unction o Two Random Variables Waltenegus Dargie Slides are based on the book: A. Papoulis and S.U. Pillai "Probabilit random variables
This is only a list of questions use a separate sheet to work out the problems. 1. (1.2 and 1.4) Use the given graph to answer each question.
 Mth Calculus Practice Eam Questions NOTE: These questions should not be taken as a complete list o possible problems. The are merel intended to be eamples o the diicult level o the regular eam questions.
Mth Calculus Practice Eam Questions NOTE: These questions should not be taken as a complete list o possible problems. The are merel intended to be eamples o the diicult level o the regular eam questions.
y2 = 0. Show that u = e2xsin(2y) satisfies Laplace's equation.
 Review 1 1) State the largest possible domain o deinition or the unction (, ) = 3 - ) Determine the largest set o points in the -plane on which (, ) = sin-1( - ) deines a continuous unction 3) Find the
Review 1 1) State the largest possible domain o deinition or the unction (, ) = 3 - ) Determine the largest set o points in the -plane on which (, ) = sin-1( - ) deines a continuous unction 3) Find the
Chapter 8: MULTIPLE CONTINUOUS RANDOM VARIABLES
 Charles Boncelet Probabilit Statistics and Random Signals" Oord Uniersit Press 06. ISBN: 978-0-9-0005-0 Chapter 8: MULTIPLE CONTINUOUS RANDOM VARIABLES Sections 8. Joint Densities and Distribution unctions
Charles Boncelet Probabilit Statistics and Random Signals" Oord Uniersit Press 06. ISBN: 978-0-9-0005-0 Chapter 8: MULTIPLE CONTINUOUS RANDOM VARIABLES Sections 8. Joint Densities and Distribution unctions
AP Calculus Notes: Unit 1 Limits & Continuity. Syllabus Objective: 1.1 The student will calculate limits using the basic limit theorems.
 Syllabus Objective:. The student will calculate its using the basic it theorems. LIMITS how the outputs o a unction behave as the inputs approach some value Finding a Limit Notation: The it as approaches
Syllabus Objective:. The student will calculate its using the basic it theorems. LIMITS how the outputs o a unction behave as the inputs approach some value Finding a Limit Notation: The it as approaches
Stochastic processes Lecture 1: Multiple Random Variables Ch. 5
 Stochastic processes Lecture : Multiple Random Variables Ch. 5 Dr. Ir. Richard C. Hendriks 26/04/8 Delft University of Technology Challenge the future Organization Plenary Lectures Book: R.D. Yates and
Stochastic processes Lecture : Multiple Random Variables Ch. 5 Dr. Ir. Richard C. Hendriks 26/04/8 Delft University of Technology Challenge the future Organization Plenary Lectures Book: R.D. Yates and
Extreme Values of Functions
 Extreme Values o Functions When we are using mathematics to model the physical world in which we live, we oten express observed physical quantities in terms o variables. Then, unctions are used to describe
Extreme Values o Functions When we are using mathematics to model the physical world in which we live, we oten express observed physical quantities in terms o variables. Then, unctions are used to describe
Curve Sketching. The process of curve sketching can be performed in the following steps:
 Curve Sketching So ar you have learned how to ind st and nd derivatives o unctions and use these derivatives to determine where a unction is:. Increasing/decreasing. Relative extrema 3. Concavity 4. Points
Curve Sketching So ar you have learned how to ind st and nd derivatives o unctions and use these derivatives to determine where a unction is:. Increasing/decreasing. Relative extrema 3. Concavity 4. Points
AP Calculus AB Summer Assignment
 AP Calculus AB Summer Assignment As Advanced placement students, our irst assignment or the 07-08 school ear is to come to class the ver irst da in top mathematical orm. Calculus is a world o change. While
AP Calculus AB Summer Assignment As Advanced placement students, our irst assignment or the 07-08 school ear is to come to class the ver irst da in top mathematical orm. Calculus is a world o change. While
Two-dimensional Random Vectors
 1 Two-dimensional Random Vectors Joint Cumulative Distribution Function (joint cd) [ ] F, ( x, ) P xand Properties: 1) F, (, ) = 1 ),, F (, ) = F ( x, ) = 0 3) F, ( x, ) is a non-decreasing unction 4)
1 Two-dimensional Random Vectors Joint Cumulative Distribution Function (joint cd) [ ] F, ( x, ) P xand Properties: 1) F, (, ) = 1 ),, F (, ) = F ( x, ) = 0 3) F, ( x, ) is a non-decreasing unction 4)
3.6 Conditional Distributions
 STAT 42 Lecture Notes 58 3.6 Conditional Distributions Definition 3.6.. Suppose that X and Y have a discrete joint distribution with joint p.f. f and let f 2 denote the marginal p.f. of Y. For each y such
STAT 42 Lecture Notes 58 3.6 Conditional Distributions Definition 3.6.. Suppose that X and Y have a discrete joint distribution with joint p.f. f and let f 2 denote the marginal p.f. of Y. For each y such
ESS011 Mathematical statistics and signal processing
 ESS011 Mathematical statistics and signal processing Lecture 9: Gaussian distribution, transformation formula for continuous random variables, and the joint distribution Tuomas A. Rajala Chalmers TU April
ESS011 Mathematical statistics and signal processing Lecture 9: Gaussian distribution, transformation formula for continuous random variables, and the joint distribution Tuomas A. Rajala Chalmers TU April
The achievable limits of operational modal analysis. * Siu-Kui Au 1)
 The achievable limits o operational modal analysis * Siu-Kui Au 1) 1) Center or Engineering Dynamics and Institute or Risk and Uncertainty, University o Liverpool, Liverpool L69 3GH, United Kingdom 1)
The achievable limits o operational modal analysis * Siu-Kui Au 1) 1) Center or Engineering Dynamics and Institute or Risk and Uncertainty, University o Liverpool, Liverpool L69 3GH, United Kingdom 1)
Mat 241 Homework Set 7key Due Professor David Schultz
 Mat 1 Homework Set 7ke Due Proessor David Schultz Directions: Show all algebraic steps neatl and concisel using proper mathematical smbolism. When graphs and technolog are to be implemented, do so appropriatel.
Mat 1 Homework Set 7ke Due Proessor David Schultz Directions: Show all algebraic steps neatl and concisel using proper mathematical smbolism. When graphs and technolog are to be implemented, do so appropriatel.
Spatial Vector Algebra
 A Short Course on The Easy Way to do Rigid Body Dynamics Roy Featherstone Dept. Inormation Engineering, RSISE The Australian National University Spatial vector algebra is a concise vector notation or describing
A Short Course on The Easy Way to do Rigid Body Dynamics Roy Featherstone Dept. Inormation Engineering, RSISE The Australian National University Spatial vector algebra is a concise vector notation or describing
Linear Equations in Linear Algebra
 1 Linear Equations in Linear Algebra 1.4 THE MATRIX EQUATION A = b MATRIX EQUATION A = b m n Definition: If A is an matri, with columns a 1, n, a n, and if is in, then the product of A and, denoted by
1 Linear Equations in Linear Algebra 1.4 THE MATRIX EQUATION A = b MATRIX EQUATION A = b m n Definition: If A is an matri, with columns a 1, n, a n, and if is in, then the product of A and, denoted by
Chapter 2. Basic concepts of probability. Summary. 2.1 Axiomatic foundation of probability theory
 Chapter Basic concepts o probability Demetris Koutsoyiannis Department o Water Resources and Environmental Engineering aculty o Civil Engineering, National Technical University o Athens, Greece Summary
Chapter Basic concepts o probability Demetris Koutsoyiannis Department o Water Resources and Environmental Engineering aculty o Civil Engineering, National Technical University o Athens, Greece Summary
. This is the Basic Chain Rule. x dt y dt z dt Chain Rule in this context.
 Math 18.0A Gradients, Chain Rule, Implicit Dierentiation, igher Order Derivatives These notes ocus on our things: (a) the application o gradients to ind normal vectors to curves suraces; (b) the generaliation
Math 18.0A Gradients, Chain Rule, Implicit Dierentiation, igher Order Derivatives These notes ocus on our things: (a) the application o gradients to ind normal vectors to curves suraces; (b) the generaliation
Chapter 2. Random Variable. Define single random variables in terms of their PDF and CDF, and calculate moments such as the mean and variance.
 Chapter 2 Random Variable CLO2 Define single random variables in terms of their PDF and CDF, and calculate moments such as the mean and variance. 1 1. Introduction In Chapter 1, we introduced the concept
Chapter 2 Random Variable CLO2 Define single random variables in terms of their PDF and CDF, and calculate moments such as the mean and variance. 1 1. Introduction In Chapter 1, we introduced the concept
Saturday X-tra X-Sheet: 8. Inverses and Functions
 Saturda X-tra X-Sheet: 8 Inverses and Functions Ke Concepts In this session we will ocus on summarising what ou need to know about: How to ind an inverse. How to sketch the inverse o a graph. How to restrict
Saturda X-tra X-Sheet: 8 Inverses and Functions Ke Concepts In this session we will ocus on summarising what ou need to know about: How to ind an inverse. How to sketch the inverse o a graph. How to restrict
Polynomials, Linear Factors, and Zeros. Factor theorem, multiple zero, multiplicity, relative maximum, relative minimum
 Polynomials, Linear Factors, and Zeros To analyze the actored orm o a polynomial. To write a polynomial unction rom its zeros. Describe the relationship among solutions, zeros, - intercept, and actors.
Polynomials, Linear Factors, and Zeros To analyze the actored orm o a polynomial. To write a polynomial unction rom its zeros. Describe the relationship among solutions, zeros, - intercept, and actors.
Functions. Essential Question What are some of the characteristics of the graph of a logarithmic function?
 5. Logarithms and Logarithmic Functions Essential Question What are some o the characteristics o the graph o a logarithmic unction? Ever eponential unction o the orm () = b, where b is a positive real
5. Logarithms and Logarithmic Functions Essential Question What are some o the characteristics o the graph o a logarithmic unction? Ever eponential unction o the orm () = b, where b is a positive real
Answer Key-Math 11- Optional Review Homework For Exam 2
 Answer Key-Math - Optional Review Homework For Eam 2. Compute the derivative or each o the ollowing unctions: Please do not simpliy your derivatives here. I simliied some, only in the case that you want
Answer Key-Math - Optional Review Homework For Eam 2. Compute the derivative or each o the ollowing unctions: Please do not simpliy your derivatives here. I simliied some, only in the case that you want
z-axis SUBMITTED BY: Ms. Harjeet Kaur Associate Professor Department of Mathematics PGGCG 11, Chandigarh y-axis x-axis
 z-ais - - SUBMITTED BY: - -ais - - - - - - -ais Ms. Harjeet Kaur Associate Proessor Department o Mathematics PGGCG Chandigarh CONTENTS: Function o two variables: Deinition Domain Geometrical illustration
z-ais - - SUBMITTED BY: - -ais - - - - - - -ais Ms. Harjeet Kaur Associate Proessor Department o Mathematics PGGCG Chandigarh CONTENTS: Function o two variables: Deinition Domain Geometrical illustration
Chapter 4 Imaging. Lecture 21. d (110) Chem 793, Fall 2011, L. Ma
 Chapter 4 Imaging Lecture 21 d (110) Imaging Imaging in the TEM Diraction Contrast in TEM Image HRTEM (High Resolution Transmission Electron Microscopy) Imaging or phase contrast imaging STEM imaging a
Chapter 4 Imaging Lecture 21 d (110) Imaging Imaging in the TEM Diraction Contrast in TEM Image HRTEM (High Resolution Transmission Electron Microscopy) Imaging or phase contrast imaging STEM imaging a
GENERALIZED ABSTRACT NONSENSE: CATEGORY THEORY AND ADJUNCTIONS
 GENERALIZED ABSTRACT NONSENSE: CATEGORY THEORY AND ADJUNCTIONS CHRIS HENDERSON Abstract. This paper will move through the basics o category theory, eventually deining natural transormations and adjunctions
GENERALIZED ABSTRACT NONSENSE: CATEGORY THEORY AND ADJUNCTIONS CHRIS HENDERSON Abstract. This paper will move through the basics o category theory, eventually deining natural transormations and adjunctions
Lecture 6 Random Variable. Compose of procedure & observation. From observation, we get outcomes
 ENM 07 Lecture 6 Random Variable Random Variable Eperiment (hysical Model) Compose of procedure & observation From observation we get outcomes From all outcomes we get a (mathematical) probability model
ENM 07 Lecture 6 Random Variable Random Variable Eperiment (hysical Model) Compose of procedure & observation From observation we get outcomes From all outcomes we get a (mathematical) probability model
Exponential, Logarithmic and Inverse Functions
 Chapter Review Sec.1 and. Eponential, Logarithmic and Inverse Functions I. Review o Inverrse I Functti ions A. Identiying One-to-One Functions is one-to-one i every element in the range corresponds to
Chapter Review Sec.1 and. Eponential, Logarithmic and Inverse Functions I. Review o Inverrse I Functti ions A. Identiying One-to-One Functions is one-to-one i every element in the range corresponds to
Section 1.2 Domain and Range
 Section 1. Domain and Range 1 Section 1. Domain and Range One o our main goals in mathematics is to model the real world with mathematical unctions. In doing so, it is important to keep in mind the limitations
Section 1. Domain and Range 1 Section 1. Domain and Range One o our main goals in mathematics is to model the real world with mathematical unctions. In doing so, it is important to keep in mind the limitations
