This Topic follows on from Calculus Topics C1 - C3 to give further rules and applications of differentiation.
|
|
|
- Tyrone Allison
- 5 years ago
- Views:
Transcription
1 CALCULUS C Topic Overview C FURTHER DIFFERENTIATION This Topic follows on from Calcls Topics C - C to give frther rles applications of differentiation. Yo shold be familiar with Logarithms (Algebra Topic A), Eponential Fnctions (Algebra Topic A) basic Trigonometric Fnctions (Trigonometr Topic T). LESSON PLAN Lesn No. LESSON TITLE Page Eamples SAQs C. The Eponential Fnction. C. C. The Natral Logarithm Fnction 4. C. C. Trigonometric Fnctions 5. C. 4 C.4 The Chain Rle.4 C.4 5 C.5 Instantaneos Rate of Change C.5 Appendi C. Soltions to the Self-Assessment Qestions Page
2 CALCULUS C Topic Overview SUMMARY TABLE OF STANDARD DERIVATIVES FUNCTION f() DERIVATIVE f'() Power n n n Constant (C) C 0 Eponential fnction e a a e a Natral logarithm ln(a) Trigonometic fnctions sin(a) a cos(a) cos(a) tan(a) a sin(a) a sec (a) where a is a constant. Page
3 C. The Derivative of the Eponential Fnction C. THE DERIVATIVE OF THE EXPONENTIAL FUNCTION The eponential fnction e a, where a is constant, is a fnction whose rate of change is proportional to its own magnitde. [Ref: Algebra Topic A Eponentials] The rle for differentiating the eponential fnction is a a f() e f '() a e where a is a constant. Note: The special case when a, f() e f '() e EXAMPLE. Differentiate: (i) e 4 (ii) e (iii) e e Soltion: (i) Appl the rle to f() e 4 f ' () 4e 4 (ii) Use the constant mltiple rle to differentiate f() g() where g() e [Ref: C.] f() e f '() ( e ) e (iii) Appling the sm of fnctions rle to f() e e f '() e ( )e e e SAQ C. Differentiate the following fnctions with respect to the variable: (a) e (b) e (c) e t e t Page
4 C. The Derivative of the Logarithmic Fnction C. THE DERIVATIVE OF THE NATURAL LOGARITHM FUNCTION The natral logarithm fnction (log e ), sall written as ln, is the inverse of the eponential fnction. The rle for differentiating the natral logarithm fnction is f() ln(a) f ' () where a is a constant a > 0 Note that the derivative of ln(a) does not involve a. EXAMPLE. Differentiate (i) ln (ii) ln (iii) 5ln Soltion: (i) f() ln f '() (ii) Using the constant mltiple rle to differentiate f() g() where g() ln [Ref: C.] f() ln f '() (iii) Using the constant mltiple rle to differentiate f() 5g() where g() ln f() 5ln f '() 5 5 SAQ C. Differentiate the following fnctions with respect to the variable: (a) ln (b) 4 ln(t) (c) ln Page 4
5 C. The Derivative of Trigonometric Fnctions C. THE DERIVATIVE OF TRIGONOMETRIC FUNCTIONS The rles for differentiating the basic trigonometric fnctions are f() sin(a) f() cos(a) f() tan(a) f ' () a cos(a) f ' () a sin(a) f ' () a sec (a) where a is a constant [Ref: Topic T. Trigonometric Ratios] sec() cos() EXAMPLE. Differentiate (i) sin t (ii) 5cos 4t (iii) sin πt cos πt Soltion: (i) f(t) sin t f '(t) cos t (ii) Using the constant mltiple rle to differentiate f(t) 5 g(t) where g(t) cos 4t f(t) 5 cos 4t f '(t) 5( 4sin 4t) 0sin 4t (iii) Appling the sm of fnctions rle to f(t) sin πt cos πt f '(t) (π cos πt) ( π sin πt) π cos πt π sin πt SAQ C. (a) Differentiate the following fnctions with respect to the variable: (i) sin (iii) tan t (ii) cos 5 (iv) 5(sin πt cos πt) (b) An alternating voltage is given b V 4 sin 00t where t is the time in seconds. Calclate the rate of change of voltage when t 0.0 seconds. Page 5
6 C.4 The Chain Rle C.4 THE CHAIN RULE for Differentiation This rle is sed to differentiate composite fnctions sch as, cos(5 ), which can be written as h(), where g(). sin e, The Chain Rle is: where is a fnction of is a fnction of. This process is al known as the "fnction of a fnction rle". EXAMPLE.4 Using the Chain Rle, differentiate the following with respect to the variable: (i) ( 4) (ii) (iii) cos(5 ) (iv) sin (v) (ln 4) (vi) e sin t Soltion: Method : Differentiation b sbstittion (i) If ( 4) we sbstitte 4, then. Hence, b differentiating with respect to, we obtain differentiating with respect to, we obtain. Now we can appl the formla for the Chain Rle to obtain. Then ( 4) 4, ( ) ( ) ( 4) Page
7 C.4 The Chain Rle Page ( ) Then, (ii) ) 5sin(5 )(5) sin ( sin 5 Then cos, 5 ) cos(5 (iii) cos sin ()(cos ) cos Then sin, (sin ) sin (iv) (ln4) ) ( Then ln4, (ln 4) (v) sin t sin t (cos t)e )(cos t) (e e cos t Then e, sin t e (vi)
8 C.4 The Chain Rle Method : Direct application of the Chain Rle Differentiate b starting from the otside fnction working inwards, alwas mltipling b the derivative of the inner fnction. This method is normall sed since it adapts easil to deal with a chain of or more fnctions of a fnction. (i) ( 4) ( 4) ( 4) ( 4) d () ( 4) (ii) ( ) ( d ) ( ) ( ) () (iii) cos(5 ) d sin(5 ) sin(5 )(5) 5sin(5 ) ( 5 ) (iv) sin (sin ) d (sin ) (sin )(cos ) sin cos ( sin ) (v) (ln 4) d (ln 4) (ln 4) (ln 4) ( ln4) (vi) sin t e ep(sin t) sin t d e sint e (cos t) ( sint) sint (cos t) e SAQ C.4 Using the Chain Rle, differentiate the following fnctions with respect to the variable: (a) ( ) 8 (b) (c) sin(t 4) (d) cos (e) ln (5 ) (f) e t Page 8
9 C.5 Instantaneos Rate of Change C.5 INSTANTANEOUS RATE OF CHANGE The real significance of the derivative of a fnction is that it provides a measre of the instantaneos rate of change of one variable with respect to another. Since speed is a familiar measre of a rate of change, we shall investigate the idea of average instantaneos rates of change with reference to speed. If an object travels at a stea speed, we can calclate the speed sing the formla: distance travelled Speed time taken If the speed is changing, this formla will onl give the average speed over a particlar interval. The following eample shows how the instantaneos speed can be calclated. EXAMPLE.5 An object moves awa from a point O in a straight line. Its distance, s metres, from O after t seconds is given b the formla s t Find (i) the average speed between t t (ii) the instantaneos speed when t Soltion: B definition: distance travelled change in distance from O δs Speed time taken change in time δt where δs represents a change in the vale of s similarl δt represents a change in the vale of t. (i) When t second, s () metre When t seconds, s () 4 metres Hence, the average speed between t t is δs 4 δt metres per second Page 9
10 C.5 Instantaneos Rate of Change (ii) The following table shows the distances of the object from O after varios times: Time (t) Distance (s) From the table we can see that the object is accelerating awa from O its speed is continall increasing. One wa of calclating the instantaneos speed when t, is to calclate average speed between t t h then allow h to approach zero. It is convenient to se fnctional notation write f(t) t instead of s t. The average speed between t t h is therefore given b δs δ(f(t)) δt δt f( h) f() ( h) ( h) () h h h h h h h h As h approaches 0, the average speed between t t h gets closer closer to, i.e. the instantaneos speed when t is metres per second. In general, the instantaneos speed after t seconds is given b the limiting δs vale of as δt tends to zero: δt δs f(t h) lim lim δt 0 δt h 0 h f(t) It follows that we can calclate the instantaneos speed when t in the above eample sing the derivative f'(t) directl: f(t) t gives f '(t) t (sing the rle for differentiating powers) Sbstitting t gives f '() Hence, the instantaneos speed when t is metres per second. Page 0
11 C.5 Instantaneos Rate of Change EXAMPLE. In testing for diabetes, it is necessar to determine how fast the bo metabolises glcose. One test involves ingesting a stard dose of glcose, waiting hor then monitoring the concentration of glcose remaining in the blood as time passes. Sppose the amont q mg of glcose remaining in cc of blood, t hors after the dose is administered is Find the glcose levels how fast the glcose was being metabolised: (i) when monitoring began at t (ii) 4 hors after the glcose was taken. Soltion: The rate of change in glcose levels is the derivative: (i) dq q 4.5 t.5 t When t, the glcose level was the metabolic rate was dq.5().5 mg per hor The negative sign means that the glcose level was decreasing b.5 mg per hor; a positive sign wold mean that the level was increasing. (ii) For hors after the dose was taken, ie. when t 4, the glcose level was: q(4) 4.5(4) the metabolic rate was: d 4.5 t d 4.5 t 4.5 t mg mg per hor q() 4.5() dq.5( mg per hor Note: After 4 hors there was less glcose in the blood the level was dropping more slowl. mg ) 4.5 mg Page
12 C.5 Instantaneos Rate of Change SAQ C.5 The temperatre s, in degrees Centigrade, in a corridor is given b s where is the distance, in metres, from a radiator at one end. (a) Find the average rate at which the temperatre changes with distance between the points represented b 0 5. (b) Calclate the instantaneos rate of change of temperatre with respect to distance at the point represented b 5. (c) Eplain wh or answers to (a) (b) are negative. Page
13 C. APPENDIX C. SOLUTIONS TO SELF-ASSESSMENT QUESTIONS SAQ C. Eponentials (a) f () e f '() e (b) f() e f'() e e (c) f(t) e t e t f '(t) e t e t SAQ C. Natral Logarithms (a) (b) (c) f() ln f(t) 4ln(t) f() ln f'() 4 f'(t) t f'(t) SAQ C. Trigonometric Fnctions (a) (i) f() sin f '() cos (ii) f() cos 5 f '() 0 sin 5 (iii) f(t) tan t f '(t) sec t (iv) f(t) 5(sin πt cos πt) 5sin πt 5cos πt f '(t) 0πcosπt 0sin πt 0π(cosπt sin πt) (b) f(t) 4 sin 00t f '(t) 400 cos 00t When t 0.0 seconds, f '(0.0) 400 cos(00 0.0) 400 cos(). volts per second SAQ C.4 The Chain Rle (a) then ( ), ( 8 )( ) or ( ) 8 8( ) ( ) () ( ) Page
14 C. APPENDIX Page 4 ( ) then, (b) cos sin sin ) )( ( sin then cos, (cos ) cos (d) 5 5 ) (5 5 then ln, 5 ) ln(5 (e) ( ) ) ) ( or ( 4) cos(t )() (cos cos then sin 4, t 4) sin(t (c) 4) cos(t 4)() cos(t 4) sin(t or cos sin sin ) )( (cos (cos ) cos or 5 5 ) (5 5 ) ln(5 or
15 C. APPENDIX (f) then t e t, (e )() e t e e or t e t (e )() t e SAQ C.5 Instantaneos Rate of Change (a) When When 400 s 0 0, 400 s 0 0 5, s Average rate at which the temperatre changes with distance between these two points is: Change in temperatre Change in distance (b) The instantaneos rate of change is given b the derivative s ( 400 ) 0 ds ( ) 0 ds When 5, ( 0) (c) The answers to (a) (b) above are both negative becase the temperatre s, is decreasing as the distance, from the radiator is increasing. If the graph of s against were to be drawn, then (at least for positive vales of ) the shape of the graph wold be a falling crve. Hence the gradient of the crve at an point wold be negative. Page 5
Differentiation of Exponential Functions
 Differentiation of Eponential Fnctions The net derivative rles that o will learn involve eponential fnctions. An eponential fnction is a fnction in the form of a constant raised to a variable power. The
Differentiation of Eponential Fnctions The net derivative rles that o will learn involve eponential fnctions. An eponential fnction is a fnction in the form of a constant raised to a variable power. The
Lecture 3Section 7.3 The Logarithm Function, Part II
 Lectre 3Section 7.3 The Logarithm Fnction, Part II Jiwen He Section 7.2: Highlights 2 Properties of the Log Fnction ln = t t, ln = 0, ln e =. (ln ) = > 0. ln(y) = ln + ln y, ln(/y) = ln ln y. ln ( r) =
Lectre 3Section 7.3 The Logarithm Fnction, Part II Jiwen He Section 7.2: Highlights 2 Properties of the Log Fnction ln = t t, ln = 0, ln e =. (ln ) = > 0. ln(y) = ln + ln y, ln(/y) = ln ln y. ln ( r) =
Section 7.4: Integration of Rational Functions by Partial Fractions
 Section 7.4: Integration of Rational Fnctions by Partial Fractions This is abot as complicated as it gets. The Method of Partial Fractions Ecept for a few very special cases, crrently we have no way to
Section 7.4: Integration of Rational Fnctions by Partial Fractions This is abot as complicated as it gets. The Method of Partial Fractions Ecept for a few very special cases, crrently we have no way to
m = Average Rate of Change (Secant Slope) Example:
 Average Rate o Change Secant Slope Deinition: The average change secant slope o a nction over a particlar interval [a, b] or [a, ]. Eample: What is the average rate o change o the nction over the interval
Average Rate o Change Secant Slope Deinition: The average change secant slope o a nction over a particlar interval [a, b] or [a, ]. Eample: What is the average rate o change o the nction over the interval
Math 263 Assignment #3 Solutions. 1. A function z = f(x, y) is called harmonic if it satisfies Laplace s equation:
 Math 263 Assignment #3 Soltions 1. A fnction z f(x, ) is called harmonic if it satisfies Laplace s eqation: 2 + 2 z 2 0 Determine whether or not the following are harmonic. (a) z x 2 + 2. We se the one-variable
Math 263 Assignment #3 Soltions 1. A fnction z f(x, ) is called harmonic if it satisfies Laplace s eqation: 2 + 2 z 2 0 Determine whether or not the following are harmonic. (a) z x 2 + 2. We se the one-variable
10.4 Solving Equations in Quadratic Form, Equations Reducible to Quadratics
 . Solving Eqations in Qadratic Form, Eqations Redcible to Qadratics Now that we can solve all qadratic eqations we want to solve eqations that are not eactl qadratic bt can either be made to look qadratic
. Solving Eqations in Qadratic Form, Eqations Redcible to Qadratics Now that we can solve all qadratic eqations we want to solve eqations that are not eactl qadratic bt can either be made to look qadratic
Logarithmic, Exponential and Other Transcendental Functions
 Logarithmic, Eponential an Other Transcenental Fnctions 5: The Natral Logarithmic Fnction: Differentiation The Definition First, yo mst know the real efinition of the natral logarithm: ln= t (where > 0)
Logarithmic, Eponential an Other Transcenental Fnctions 5: The Natral Logarithmic Fnction: Differentiation The Definition First, yo mst know the real efinition of the natral logarithm: ln= t (where > 0)
Integration of Basic Functions. Session 7 : 9/23 1
 Integration o Basic Fnctions Session 7 : 9/3 Antiderivation Integration Deinition: Taking the antiderivative, or integral, o some nction F(), reslts in the nction () i ()F() Pt simply: i yo take the integral
Integration o Basic Fnctions Session 7 : 9/3 Antiderivation Integration Deinition: Taking the antiderivative, or integral, o some nction F(), reslts in the nction () i ()F() Pt simply: i yo take the integral
ECON3120/4120 Mathematics 2, spring 2009
 University of Oslo Department of Economics Arne Strøm ECON3/4 Mathematics, spring 9 Problem soltions for Seminar 4, 6 Febrary 9 (For practical reasons some of the soltions may inclde problem parts that
University of Oslo Department of Economics Arne Strøm ECON3/4 Mathematics, spring 9 Problem soltions for Seminar 4, 6 Febrary 9 (For practical reasons some of the soltions may inclde problem parts that
Theorem (Change of Variables Theorem):
 Avance Higher Notes (Unit ) Prereqisites: Integrating (a + b) n, sin (a + b) an cos (a + b); erivatives of tan, sec, cosec, cot, e an ln ; sm/ifference rles; areas ner an between crves. Maths Applications:
Avance Higher Notes (Unit ) Prereqisites: Integrating (a + b) n, sin (a + b) an cos (a + b); erivatives of tan, sec, cosec, cot, e an ln ; sm/ifference rles; areas ner an between crves. Maths Applications:
EE2 Mathematics : Functions of Multiple Variables
 EE2 Mathematics : Fnctions of Mltiple Variables http://www2.imperial.ac.k/ nsjones These notes are not identical word-for-word with m lectres which will be gien on the blackboard. Some of these notes ma
EE2 Mathematics : Fnctions of Mltiple Variables http://www2.imperial.ac.k/ nsjones These notes are not identical word-for-word with m lectres which will be gien on the blackboard. Some of these notes ma
sin xdx = cos x + c We also run into antiderivatives for tan x, cot x, sec x and csc x in the section on Log integrals. They are: cos ax sec ax a
 Trig Integrals We already know antiderivatives for sin x, cos x, sec x tan x, csc x, sec x and csc x cot x. They are cos xdx = sin x sin xdx = cos x sec x tan xdx = sec x csc xdx = cot x sec xdx = tan
Trig Integrals We already know antiderivatives for sin x, cos x, sec x tan x, csc x, sec x and csc x cot x. They are cos xdx = sin x sin xdx = cos x sec x tan xdx = sec x csc xdx = cot x sec xdx = tan
PhysicsAndMathsTutor.com
 C Integration - By sbstittion PhysicsAndMathsTtor.com. Using the sbstittion cos +, or otherwise, show that e cos + sin d e(e ) (Total marks). (a) Using the sbstittion cos, or otherwise, find the eact vale
C Integration - By sbstittion PhysicsAndMathsTtor.com. Using the sbstittion cos +, or otherwise, show that e cos + sin d e(e ) (Total marks). (a) Using the sbstittion cos, or otherwise, find the eact vale
BLOOM S TAXONOMY. Following Bloom s Taxonomy to Assess Students
 BLOOM S TAXONOMY Topic Following Bloom s Taonomy to Assess Stdents Smmary A handot for stdents to eplain Bloom s taonomy that is sed for item writing and test constrction to test stdents to see if they
BLOOM S TAXONOMY Topic Following Bloom s Taonomy to Assess Stdents Smmary A handot for stdents to eplain Bloom s taonomy that is sed for item writing and test constrction to test stdents to see if they
STEP Support Programme. STEP III Hyperbolic Functions: Solutions
 STEP Spport Programme STEP III Hyperbolic Fnctions: Soltions Start by sing the sbstittion t cosh x. This gives: sinh x cosh a cosh x cosh a sinh x t sinh x dt t dt t + ln t ln t + ln cosh a ln ln cosh
STEP Spport Programme STEP III Hyperbolic Fnctions: Soltions Start by sing the sbstittion t cosh x. This gives: sinh x cosh a cosh x cosh a sinh x t sinh x dt t dt t + ln t ln t + ln cosh a ln ln cosh
CALCULUS APPLICATIONS OF DIFFERENTIATION LESSON PLAN. C3 Topic Overview
 CALCULUS C3 Topic Overview C3 APPLICATIONS OF DIFFERENTIATION Differentiation can be used to investigate the behaviour of a function, to find regions where the value of a function is increasing or decreasing
CALCULUS C3 Topic Overview C3 APPLICATIONS OF DIFFERENTIATION Differentiation can be used to investigate the behaviour of a function, to find regions where the value of a function is increasing or decreasing
FUNCTIONS OF ONE VARIABLE FUNCTION DEFINITIONS
 Page of 6 FUNCTIONS OF ONE VARIABLE FUNCTION DEFINITIONS 6. HYPERBOLIC FUNCTIONS These functions which are defined in terms of e will be seen later to be related to the trigonometic functions via comple
Page of 6 FUNCTIONS OF ONE VARIABLE FUNCTION DEFINITIONS 6. HYPERBOLIC FUNCTIONS These functions which are defined in terms of e will be seen later to be related to the trigonometic functions via comple
x f(x) x f(x) approaching 1 approaching 0.5 approaching 1 approaching 0.
 Engineering Mathematics 2 26 February 2014 Limits of functions Consier the function 1 f() = 1. The omain of this function is R + \ {1}. The function is not efine at 1. What happens when is close to 1?
Engineering Mathematics 2 26 February 2014 Limits of functions Consier the function 1 f() = 1. The omain of this function is R + \ {1}. The function is not efine at 1. What happens when is close to 1?
x f(x) x f(x) approaching 1 approaching 0.5 approaching 1 approaching 0.
 Engineering Mathematics 2 26 February 2014 Limits of functions Consier the function 1 f() = 1. The omain of this function is R + \ {1}. The function is not efine at 1. What happens when is close to 1?
Engineering Mathematics 2 26 February 2014 Limits of functions Consier the function 1 f() = 1. The omain of this function is R + \ {1}. The function is not efine at 1. What happens when is close to 1?
Methods for Advanced Mathematics (C3) FRIDAY 11 JANUARY 2008
 ADVANCED GCE 4753/ MATHEMATICS (MEI) Methods for Advanced Mathematics (C3) FRIDAY JANUARY 8 Additional materials: Answer Booklet (8 pages) Graph paper MEI Eamination Formlae and Tables (MF) Morning Time:
ADVANCED GCE 4753/ MATHEMATICS (MEI) Methods for Advanced Mathematics (C3) FRIDAY JANUARY 8 Additional materials: Answer Booklet (8 pages) Graph paper MEI Eamination Formlae and Tables (MF) Morning Time:
Math 116 First Midterm October 14, 2009
 Math 116 First Midterm October 14, 9 Name: EXAM SOLUTIONS Instrctor: Section: 1. Do not open this exam ntil yo are told to do so.. This exam has 1 pages inclding this cover. There are 9 problems. Note
Math 116 First Midterm October 14, 9 Name: EXAM SOLUTIONS Instrctor: Section: 1. Do not open this exam ntil yo are told to do so.. This exam has 1 pages inclding this cover. There are 9 problems. Note
Complex Variables. For ECON 397 Macroeconometrics Steve Cunningham
 Comple Variables For ECON 397 Macroeconometrics Steve Cnningham Open Disks or Neighborhoods Deinition. The set o all points which satis the ineqalit
Comple Variables For ECON 397 Macroeconometrics Steve Cnningham Open Disks or Neighborhoods Deinition. The set o all points which satis the ineqalit
sin u 5 opp } cos u 5 adj } hyp opposite csc u 5 hyp } sec u 5 hyp } opp Using Inverse Trigonometric Functions
 13 Big Idea 1 CHAPTER SUMMARY BIG IDEAS Using Trigonometric Fnctions Algebra classzone.com Electronic Fnction Library For Yor Notebook hypotense acent osite sine cosine tangent sin 5 hyp cos 5 hyp tan
13 Big Idea 1 CHAPTER SUMMARY BIG IDEAS Using Trigonometric Fnctions Algebra classzone.com Electronic Fnction Library For Yor Notebook hypotense acent osite sine cosine tangent sin 5 hyp cos 5 hyp tan
Slopes and Rates of Change
 Slopes and Rates of Change If a particle is moving in a straight line at a constant velocity, then the graph of the function of distance versus time is as follows s s = f(t) t s s t t = average velocity
Slopes and Rates of Change If a particle is moving in a straight line at a constant velocity, then the graph of the function of distance versus time is as follows s s = f(t) t s s t t = average velocity
UNIT 3: DERIVATIVES STUDY GUIDE
 Calculus I UNIT 3: Derivatives REVIEW Name: Date: UNIT 3: DERIVATIVES STUDY GUIDE Section 1: Section 2: Limit Definition (Derivative as the Slope of the Tangent Line) Calculating Rates of Change (Average
Calculus I UNIT 3: Derivatives REVIEW Name: Date: UNIT 3: DERIVATIVES STUDY GUIDE Section 1: Section 2: Limit Definition (Derivative as the Slope of the Tangent Line) Calculating Rates of Change (Average
 Obliqe Projection. A body is projected from a point with different angles of projections 0 0, 35 0, 45 0, 60 0 with the horizontal bt with same initial speed. Their respective horizontal ranges are R,
Obliqe Projection. A body is projected from a point with different angles of projections 0 0, 35 0, 45 0, 60 0 with the horizontal bt with same initial speed. Their respective horizontal ranges are R,
Roberto s Notes on Integral Calculus Chapter 3: Basics of differential equations Section 3. Separable ODE s
 Roberto s Notes on Integral Calculus Chapter 3: Basics of differential equations Section 3 Separable ODE s What ou need to know alread: What an ODE is and how to solve an eponential ODE. What ou can learn
Roberto s Notes on Integral Calculus Chapter 3: Basics of differential equations Section 3 Separable ODE s What ou need to know alread: What an ODE is and how to solve an eponential ODE. What ou can learn
3.4-Miscellaneous Equations
 .-Miscellaneos Eqations Factoring Higher Degree Polynomials: Many higher degree polynomials can be solved by factoring. Of particlar vale is the method of factoring by groping, however all types of factoring
.-Miscellaneos Eqations Factoring Higher Degree Polynomials: Many higher degree polynomials can be solved by factoring. Of particlar vale is the method of factoring by groping, however all types of factoring
On the Natural Logarithm Function and its Applications
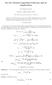 On the Natral Logarithm Fnction and its Applications By Edigles Gedes Febrary 4, 8 at March 7, 5 We love him, becase he rst loved s. - I John 4:9 Abstract. In present article, we create new integral representations
On the Natral Logarithm Fnction and its Applications By Edigles Gedes Febrary 4, 8 at March 7, 5 We love him, becase he rst loved s. - I John 4:9 Abstract. In present article, we create new integral representations
( )dt F. ( ) = y 2 sin y. ( ) = t 2 sint dt. ( ) = 1+ 2x. ( ) = 1+ 2t dt. ( ) = cos t 2. ( ) = cos x 2 ( ) ( ) = arctan 1 x 1 x 2 = 1 x 2 arctan 1 x
 Section. The Fndamental Theorem of Calcls Part Soltions. g y g y y ( ) t sint dt ( ) y sin y. g g ( ) + t dt ( ) +. F ( )dt ( ) cos t F ( )dt F ( ) cos t ( ) ( ) cos. h ( ) arctant dt ( ) arctan arctan
Section. The Fndamental Theorem of Calcls Part Soltions. g y g y y ( ) t sint dt ( ) y sin y. g g ( ) + t dt ( ) +. F ( )dt ( ) cos t F ( )dt F ( ) cos t ( ) ( ) cos. h ( ) arctant dt ( ) arctan arctan
Chapter 2 Difficulties associated with corners
 Chapter Difficlties associated with corners This chapter is aimed at resolving the problems revealed in Chapter, which are cased b corners and/or discontinos bondar conditions. The first section introdces
Chapter Difficlties associated with corners This chapter is aimed at resolving the problems revealed in Chapter, which are cased b corners and/or discontinos bondar conditions. The first section introdces
Solutions to Math 152 Review Problems for Exam 1
 Soltions to Math 5 Review Problems for Eam () If A() is the area of the rectangle formed when the solid is sliced at perpendiclar to the -ais, then A() = ( ), becase the height of the rectangle is and
Soltions to Math 5 Review Problems for Eam () If A() is the area of the rectangle formed when the solid is sliced at perpendiclar to the -ais, then A() = ( ), becase the height of the rectangle is and
Rules for Differentiation Finding the Derivative of a Product of Two Functions. What does this equation of f '(
 Rules for Differentiation Finding the Derivative of a Product of Two Functions Rewrite the function f( = ( )( + 1) as a cubic function. Then, find f '(. What does this equation of f '( represent, again?
Rules for Differentiation Finding the Derivative of a Product of Two Functions Rewrite the function f( = ( )( + 1) as a cubic function. Then, find f '(. What does this equation of f '( represent, again?
BIOSTATISTICAL METHODS
 BIOSTATISTICAL METHOS FOR TRANSLATIONAL & CLINICAL RESEARCH ROC Crve: IAGNOSTIC MEICINE iagnostic tests have been presented as alwas having dichotomos otcomes. In some cases, the reslt of the test ma be
BIOSTATISTICAL METHOS FOR TRANSLATIONAL & CLINICAL RESEARCH ROC Crve: IAGNOSTIC MEICINE iagnostic tests have been presented as alwas having dichotomos otcomes. In some cases, the reslt of the test ma be
Partial Differential Equations with Applications
 Universit of Leeds MATH 33 Partial Differential Eqations with Applications Eamples to spplement Chapter on First Order PDEs Eample (Simple linear eqation, k + = 0, (, 0) = ϕ(), k a constant.) The characteristic
Universit of Leeds MATH 33 Partial Differential Eqations with Applications Eamples to spplement Chapter on First Order PDEs Eample (Simple linear eqation, k + = 0, (, 0) = ϕ(), k a constant.) The characteristic
EXERCISES WAVE EQUATION. In Problems 1 and 2 solve the heat equation (1) subject to the given conditions. Assume a rod of length L.
 .4 WAVE EQUATION 445 EXERCISES.3 In Problems and solve the heat eqation () sbject to the given conditions. Assme a rod of length.. (, t), (, t) (, ),, > >. (, t), (, t) (, ) ( ) 3. Find the temperatre
.4 WAVE EQUATION 445 EXERCISES.3 In Problems and solve the heat eqation () sbject to the given conditions. Assme a rod of length.. (, t), (, t) (, ),, > >. (, t), (, t) (, ) ( ) 3. Find the temperatre
Higher Maths A1.3 Recurrence Relations - Revision
 Higher Maths A Recrrence Relations - Revision This revision pack covers the skills at Unit Assessment exam level or Recrrence Relations so yo can evalate yor learning o this otcome It is important that
Higher Maths A Recrrence Relations - Revision This revision pack covers the skills at Unit Assessment exam level or Recrrence Relations so yo can evalate yor learning o this otcome It is important that
MA261-A Calculus III 2006 Fall Homework 7 Solutions Due 10/20/2006 8:00AM
 MA26-A Calculus III 2006 Fall Homework 7 Solutions Due 0/20/2006 8:00AM 3 #4 Find the rst partial derivatives of the function f (; ) 5 + 3 3 2 + 3 4 f (; ) 5 4 + 9 2 2 + 3 4 f (; ) 6 3 + 2 3 3 #6 Find
MA26-A Calculus III 2006 Fall Homework 7 Solutions Due 0/20/2006 8:00AM 3 #4 Find the rst partial derivatives of the function f (; ) 5 + 3 3 2 + 3 4 f (; ) 5 4 + 9 2 2 + 3 4 f (; ) 6 3 + 2 3 3 #6 Find
4.2 Mean Value Theorem Calculus
 4. MEAN VALUE THEOREM The Mean Value Theorem is considered b some to be the most important theorem in all of calculus. It is used to prove man of the theorems in calculus that we use in this course as
4. MEAN VALUE THEOREM The Mean Value Theorem is considered b some to be the most important theorem in all of calculus. It is used to prove man of the theorems in calculus that we use in this course as
Mat 241 Homework Set 3 Due Professor David Schultz
 Mat 4 Homework Set De Professor David Schltz Directions: Show all algebraic steps neatly and concisely sing proper mathematical symbolism. When graphs and technology are to be implemented, do so appropriately.
Mat 4 Homework Set De Professor David Schltz Directions: Show all algebraic steps neatly and concisely sing proper mathematical symbolism. When graphs and technology are to be implemented, do so appropriately.
Math 144 Activity #10 Applications of Vectors
 144 p 1 Math 144 Actiity #10 Applications of Vectors In the last actiity, yo were introdced to ectors. In this actiity yo will look at some of the applications of ectors. Let the position ector = a, b
144 p 1 Math 144 Actiity #10 Applications of Vectors In the last actiity, yo were introdced to ectors. In this actiity yo will look at some of the applications of ectors. Let the position ector = a, b
MAT389 Fall 2016, Problem Set 6
 MAT389 Fall 016, Problem Set 6 Trigonometric and hperbolic fnctions 6.1 Show that e iz = cos z + i sin z for eer comple nmber z. Hint: start from the right-hand side and work or wa towards the left-hand
MAT389 Fall 016, Problem Set 6 Trigonometric and hperbolic fnctions 6.1 Show that e iz = cos z + i sin z for eer comple nmber z. Hint: start from the right-hand side and work or wa towards the left-hand
Solutions to O Level Add Math paper
 Solutions to O Level Add Math paper 4. Bab food is heated in a microwave to a temperature of C. It subsequentl cools in such a wa that its temperature, T C, t minutes after removal from the microwave,
Solutions to O Level Add Math paper 4. Bab food is heated in a microwave to a temperature of C. It subsequentl cools in such a wa that its temperature, T C, t minutes after removal from the microwave,
Uncertainties of measurement
 Uncertainties of measrement Laboratory tas A temperatre sensor is connected as a voltage divider according to the schematic diagram on Fig.. The temperatre sensor is a thermistor type B5764K [] with nominal
Uncertainties of measrement Laboratory tas A temperatre sensor is connected as a voltage divider according to the schematic diagram on Fig.. The temperatre sensor is a thermistor type B5764K [] with nominal
Math RE - Calculus I Exponential & Logarithmic Functions Page 1 of 9. y = f(x) = 2 x. y = f(x)
 Math 20-0-RE - Calculus I Eponential & Logarithmic Functions Page of 9 Eponential Function The general form of the eponential function equation is = f) = a where a is a real number called the base of the
Math 20-0-RE - Calculus I Eponential & Logarithmic Functions Page of 9 Eponential Function The general form of the eponential function equation is = f) = a where a is a real number called the base of the
Fundamental Theorem of Calculus
 Fundamental Theorem of Calculus MATH 6 Calculus I J. Robert Buchanan Department of Mathematics Summer 208 Remarks The Fundamental Theorem of Calculus (FTC) will make the evaluation of definite integrals
Fundamental Theorem of Calculus MATH 6 Calculus I J. Robert Buchanan Department of Mathematics Summer 208 Remarks The Fundamental Theorem of Calculus (FTC) will make the evaluation of definite integrals
10.2 Solving Quadratic Equations by Completing the Square
 . Solving Qadratic Eqations b Completing the Sqare Consider the eqation ( ) We can see clearl that the soltions are However, What if the eqation was given to s in standard form, that is 6 How wold we go
. Solving Qadratic Eqations b Completing the Sqare Consider the eqation ( ) We can see clearl that the soltions are However, What if the eqation was given to s in standard form, that is 6 How wold we go
Technical Note. ODiSI-B Sensor Strain Gage Factor Uncertainty
 Technical Note EN-FY160 Revision November 30, 016 ODiSI-B Sensor Strain Gage Factor Uncertainty Abstract Lna has pdated or strain sensor calibration tool to spport NIST-traceable measrements, to compte
Technical Note EN-FY160 Revision November 30, 016 ODiSI-B Sensor Strain Gage Factor Uncertainty Abstract Lna has pdated or strain sensor calibration tool to spport NIST-traceable measrements, to compte
Second-Order Wave Equation
 Second-Order Wave Eqation A. Salih Department of Aerospace Engineering Indian Institte of Space Science and Technology, Thirvananthapram 3 December 016 1 Introdction The classical wave eqation is a second-order
Second-Order Wave Eqation A. Salih Department of Aerospace Engineering Indian Institte of Space Science and Technology, Thirvananthapram 3 December 016 1 Introdction The classical wave eqation is a second-order
Chapter 3. Preferences and Utility
 Chapter 3 Preferences and Utilit Microeconomics stdies how individals make choices; different individals make different choices n important factor in making choices is individal s tastes or preferences
Chapter 3 Preferences and Utilit Microeconomics stdies how individals make choices; different individals make different choices n important factor in making choices is individal s tastes or preferences
CALCULUS EXPLORATION OF THE SECOND FUNDAMENTAL THEOREM OF CALCULUS. Second Fundamental Theorem of Calculus (Chain Rule Version): f t dt
 CALCULUS EXPLORATION OF THE SECOND FUNDAMENTAL THEOREM OF CALCULUS d d d d t dt 6 cos t dt Second Fundamental Theorem of Calculus: d f tdt d a d d 4 t dt d d a f t dt d d 6 cos t dt Second Fundamental
CALCULUS EXPLORATION OF THE SECOND FUNDAMENTAL THEOREM OF CALCULUS d d d d t dt 6 cos t dt Second Fundamental Theorem of Calculus: d f tdt d a d d 4 t dt d d a f t dt d d 6 cos t dt Second Fundamental
Chem 4501 Introduction to Thermodynamics, 3 Credits Kinetics, and Statistical Mechanics. Fall Semester Homework Problem Set Number 10 Solutions
 Chem 4501 Introdction to Thermodynamics, 3 Credits Kinetics, and Statistical Mechanics Fall Semester 2017 Homework Problem Set Nmber 10 Soltions 1. McQarrie and Simon, 10-4. Paraphrase: Apply Eler s theorem
Chem 4501 Introdction to Thermodynamics, 3 Credits Kinetics, and Statistical Mechanics Fall Semester 2017 Homework Problem Set Nmber 10 Soltions 1. McQarrie and Simon, 10-4. Paraphrase: Apply Eler s theorem
EXCITATION RATE COEFFICIENTS OF MOLYBDENUM ATOM AND IONS IN ASTROPHYSICAL PLASMA AS A FUNCTION OF ELECTRON TEMPERATURE
 EXCITATION RATE COEFFICIENTS OF MOLYBDENUM ATOM AND IONS IN ASTROPHYSICAL PLASMA AS A FUNCTION OF ELECTRON TEMPERATURE A.N. Jadhav Department of Electronics, Yeshwant Mahavidyalaya, Ned. Affiliated to
EXCITATION RATE COEFFICIENTS OF MOLYBDENUM ATOM AND IONS IN ASTROPHYSICAL PLASMA AS A FUNCTION OF ELECTRON TEMPERATURE A.N. Jadhav Department of Electronics, Yeshwant Mahavidyalaya, Ned. Affiliated to
Exact Equations. M(x,y) + N(x,y) y = 0, M(x,y) dx + N(x,y) dy = 0. M(x,y) + N(x,y) y = 0
 Eact Equations An eact equation is a first order differential equation that can be written in the form M(, + N(,, provided that there eists a function ψ(, such that = M (, and N(, = Note : Often the equation
Eact Equations An eact equation is a first order differential equation that can be written in the form M(, + N(,, provided that there eists a function ψ(, such that = M (, and N(, = Note : Often the equation
AMS 212B Perturbation Methods Lecture 05 Copyright by Hongyun Wang, UCSC
 AMS B Pertrbation Methods Lectre 5 Copright b Hongn Wang, UCSC Recap: we discssed bondar laer of ODE Oter epansion Inner epansion Matching: ) Prandtl s matching ) Matching b an intermediate variable (Skip
AMS B Pertrbation Methods Lectre 5 Copright b Hongn Wang, UCSC Recap: we discssed bondar laer of ODE Oter epansion Inner epansion Matching: ) Prandtl s matching ) Matching b an intermediate variable (Skip
Daily Lessons and Assessments for AP* Calculus AB, A Complete Course Page 584 Mark Sparks 2012
 The Second Fundamental Theorem of Calculus Functions Defined by Integrals Given the functions, f(t), below, use F( ) f ( t) dt to find F() and F () in terms of.. f(t) = 4t t. f(t) = cos t Given the functions,
The Second Fundamental Theorem of Calculus Functions Defined by Integrals Given the functions, f(t), below, use F( ) f ( t) dt to find F() and F () in terms of.. f(t) = 4t t. f(t) = cos t Given the functions,
Cosmic Microwave Background Radiation. Carl W. Akerlof April 7, 2013
 Cosmic Microwave Backgrond Radiation Carl W. Akerlof April 7, 013 Notes: Dry ice sblimation temperatre: Isopropyl alcohol freezing point: LNA operating voltage: 194.65 K 184.65 K 18.0 v he terrestrial
Cosmic Microwave Backgrond Radiation Carl W. Akerlof April 7, 013 Notes: Dry ice sblimation temperatre: Isopropyl alcohol freezing point: LNA operating voltage: 194.65 K 184.65 K 18.0 v he terrestrial
R S T. PreCalculus AB Final Exam SHOW YOUR WORK May 20, Name: 1. Find the area of this triangle. 2. Find the area of this trapezoid.
 1. Find the area of this triangle. 138 ft 6 18 ft. Find the area of this trapezoid. 10 ft 8 ft 57 11 ft 3. Find the area of this trapezoid. 10 ft 8 ft 59 1 ft [A] 88 ft [B] 176 ft [C] 75.3 ft [D] 8.9 ft.
1. Find the area of this triangle. 138 ft 6 18 ft. Find the area of this trapezoid. 10 ft 8 ft 57 11 ft 3. Find the area of this trapezoid. 10 ft 8 ft 59 1 ft [A] 88 ft [B] 176 ft [C] 75.3 ft [D] 8.9 ft.
METHODS OF DIFFERENTIATION. Contents. Theory Objective Question Subjective Question 10. NCERT Board Questions
 METHODS OF DIFFERENTIATION Contents Topic Page No. Theor 0 0 Objective Question 0 09 Subjective Question 0 NCERT Board Questions Answer Ke 4 Sllabus Derivative of a function, derivative of the sum, difference,
METHODS OF DIFFERENTIATION Contents Topic Page No. Theor 0 0 Objective Question 0 09 Subjective Question 0 NCERT Board Questions Answer Ke 4 Sllabus Derivative of a function, derivative of the sum, difference,
Differential calculus
 7.1 Kick off with CAS 7 7. Review of differentiation techniques Differential calculus 7.3 Applications of differentiation 7. Implicit and parametric differentiation 7.5 Second derivatives 7. Curve sketching
7.1 Kick off with CAS 7 7. Review of differentiation techniques Differential calculus 7.3 Applications of differentiation 7. Implicit and parametric differentiation 7.5 Second derivatives 7. Curve sketching
1 + x 2 d dx (sec 1 x) =
 Page This exam has: 8 multiple choice questions worth 4 points each. hand graded questions worth 4 points each. Important: No graphing calculators! Any non-graphing, non-differentiating, non-integrating
Page This exam has: 8 multiple choice questions worth 4 points each. hand graded questions worth 4 points each. Important: No graphing calculators! Any non-graphing, non-differentiating, non-integrating
Setting The K Value And Polarization Mode Of The Delta Undulator
 LCLS-TN-4- Setting The Vale And Polarization Mode Of The Delta Undlator Zachary Wolf, Heinz-Dieter Nhn SLAC September 4, 04 Abstract This note provides the details for setting the longitdinal positions
LCLS-TN-4- Setting The Vale And Polarization Mode Of The Delta Undlator Zachary Wolf, Heinz-Dieter Nhn SLAC September 4, 04 Abstract This note provides the details for setting the longitdinal positions
Vectors in Rn un. This definition of norm is an extension of the Pythagorean Theorem. Consider the vector u = (5, 8) in R 2
 MATH 307 Vectors in Rn Dr. Neal, WKU Matrices of dimension 1 n can be thoght of as coordinates, or ectors, in n- dimensional space R n. We can perform special calclations on these ectors. In particlar,
MATH 307 Vectors in Rn Dr. Neal, WKU Matrices of dimension 1 n can be thoght of as coordinates, or ectors, in n- dimensional space R n. We can perform special calclations on these ectors. In particlar,
Announcements. Topics: Homework: - sections 4.5 and * Read these sections and study solved examples in your textbook!
 Announcements Topics: - sections 4.5 and 5.1-5.5 * Read these sections and study solved examples in your textbook! Homework: - review lecture notes thoroughly - work on practice problems from the textbook
Announcements Topics: - sections 4.5 and 5.1-5.5 * Read these sections and study solved examples in your textbook! Homework: - review lecture notes thoroughly - work on practice problems from the textbook
Algebra/Pre-calc Review
 Algebra/Pre-calc Review The following pages contain various algebra and pre-calculus topics that are used in the stud of calculus. These pages were designed so that students can refresh their knowledge
Algebra/Pre-calc Review The following pages contain various algebra and pre-calculus topics that are used in the stud of calculus. These pages were designed so that students can refresh their knowledge
Lab Manual for Engrd 202, Virtual Torsion Experiment. Aluminum module
 Lab Manal for Engrd 202, Virtal Torsion Experiment Alminm modle Introdction In this modle, o will perform data redction and analsis for circlar cross section alminm samples. B plotting the torqe vs. twist
Lab Manal for Engrd 202, Virtal Torsion Experiment Alminm modle Introdction In this modle, o will perform data redction and analsis for circlar cross section alminm samples. B plotting the torqe vs. twist
The Cross Product of Two Vectors in Space DEFINITION. Cross Product. u * v = s ƒ u ƒƒv ƒ sin ud n
 12.4 The Cross Prodct 873 12.4 The Cross Prodct In stdying lines in the plane, when we needed to describe how a line was tilting, we sed the notions of slope and angle of inclination. In space, we want
12.4 The Cross Prodct 873 12.4 The Cross Prodct In stdying lines in the plane, when we needed to describe how a line was tilting, we sed the notions of slope and angle of inclination. In space, we want
Trigonometric. equations. Topic: Periodic functions and applications. Simple trigonometric. equations. Equations using radians Further trigonometric
 Trigonometric equations 6 sllabusref eferenceence Topic: Periodic functions and applications In this cha 6A 6B 6C 6D 6E chapter Simple trigonometric equations Equations using radians Further trigonometric
Trigonometric equations 6 sllabusref eferenceence Topic: Periodic functions and applications In this cha 6A 6B 6C 6D 6E chapter Simple trigonometric equations Equations using radians Further trigonometric
CALCULUS: Graphical,Numerical,Algebraic by Finney,Demana,Watts and Kennedy Chapter 3: Derivatives 3.3: Derivative of a function pg.
 CALCULUS: Graphical,Numerical,Algebraic b Finne,Demana,Watts and Kenned Chapter : Derivatives.: Derivative of a function pg. 116-16 What ou'll Learn About How to find the derivative of: Functions with
CALCULUS: Graphical,Numerical,Algebraic b Finne,Demana,Watts and Kenned Chapter : Derivatives.: Derivative of a function pg. 116-16 What ou'll Learn About How to find the derivative of: Functions with
VIBRATION MEASUREMENT UNCERTAINTY AND RELIABILITY DIAGNOSTICS RESULTS IN ROTATING SYSTEMS
 VIBRATIO MEASUREMET UCERTAITY AD RELIABILITY DIAGOSTICS RESULTS I ROTATIG SYSTEMS. Introdction M. Eidkevicite, V. Volkovas anas University of Technology, Lithania The rotating machinery technical state
VIBRATIO MEASUREMET UCERTAITY AD RELIABILITY DIAGOSTICS RESULTS I ROTATIG SYSTEMS. Introdction M. Eidkevicite, V. Volkovas anas University of Technology, Lithania The rotating machinery technical state
Exponential, Logarithmic &Trigonometric Derivatives
 1 U n i t 9 12CV Date: Name: Exponential, Logarithmic &Trigonometric Derivatives Tentative TEST date Big idea/learning Goals The world s population experiences exponential growth the rate of growth becomes
1 U n i t 9 12CV Date: Name: Exponential, Logarithmic &Trigonometric Derivatives Tentative TEST date Big idea/learning Goals The world s population experiences exponential growth the rate of growth becomes
CONTENTS. INTRODUCTION MEQ curriculum objectives for vectors (8% of year). page 2 What is a vector? What is a scalar? page 3, 4
 CONTENTS INTRODUCTION MEQ crriclm objectives for vectors (8% of year). page 2 What is a vector? What is a scalar? page 3, 4 VECTOR CONCEPTS FROM GEOMETRIC AND ALGEBRAIC PERSPECTIVES page 1 Representation
CONTENTS INTRODUCTION MEQ crriclm objectives for vectors (8% of year). page 2 What is a vector? What is a scalar? page 3, 4 VECTOR CONCEPTS FROM GEOMETRIC AND ALGEBRAIC PERSPECTIVES page 1 Representation
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES 3.6 Derivatives of Logarithmic Functions In this section, we: use implicit differentiation to find the derivatives of the logarithmic functions and, in particular,
3 DIFFERENTIATION RULES DIFFERENTIATION RULES 3.6 Derivatives of Logarithmic Functions In this section, we: use implicit differentiation to find the derivatives of the logarithmic functions and, in particular,
Module 5 Calculus. Module5 CALCULUS 5
 Module 5 Calculus Module5 CALCULUS 5 Table of Contents A Differentiation... 5. Derivatives... 5. Finding Derivatives from First Principles... 5. Gradient Functions... 5. Differentiability... 5.5 Derivatives
Module 5 Calculus Module5 CALCULUS 5 Table of Contents A Differentiation... 5. Derivatives... 5. Finding Derivatives from First Principles... 5. Gradient Functions... 5. Differentiability... 5.5 Derivatives
MATH Line integrals III Fall The fundamental theorem of line integrals. In general C
 MATH 255 Line integrals III Fall 216 In general 1. The fundamental theorem of line integrals v T ds depends on the curve between the starting point and the ending point. onsider two was to get from (1,
MATH 255 Line integrals III Fall 216 In general 1. The fundamental theorem of line integrals v T ds depends on the curve between the starting point and the ending point. onsider two was to get from (1,
Math RE - Calculus I Trigonometry Limits & Derivatives Page 1 of 8. x = 1 cos x. cos x 1 = lim
 Math 0-0-RE - Calculus I Trigonometry Limits & Derivatives Page of 8 Trigonometric Limits It has been shown in class that: lim 0 sin lim 0 sin lim 0 cos cos 0 lim 0 cos lim 0 + cos + To evaluate trigonometric
Math 0-0-RE - Calculus I Trigonometry Limits & Derivatives Page of 8 Trigonometric Limits It has been shown in class that: lim 0 sin lim 0 sin lim 0 cos cos 0 lim 0 cos lim 0 + cos + To evaluate trigonometric
5.5 U-substitution. Solution. Z
 CHAPTER 5. THE DEFINITE INTEGRAL 22 5.5 U-sbstittion Eample. (a) Fin the erivative of sin( 2 ). (b) Fin the anti-erivative cos( 2 ). Soltion. (a) We se the chain rle: sin(2 )=cos( 2 )( 2 ) 0 =cos( 2 )2
CHAPTER 5. THE DEFINITE INTEGRAL 22 5.5 U-sbstittion Eample. (a) Fin the erivative of sin( 2 ). (b) Fin the anti-erivative cos( 2 ). Soltion. (a) We se the chain rle: sin(2 )=cos( 2 )( 2 ) 0 =cos( 2 )2
Mathematics syllabus for Grade 11 and 12 For Bilingual Schools in the Sultanate of Oman
 03 04 Mathematics syllabus for Grade and For Bilingual Schools in the Sultanate of Oman Prepared By: A Stevens (Qurum Private School) M Katira (Qurum Private School) M Hawthorn (Al Sahwa Schools) In Conjunction
03 04 Mathematics syllabus for Grade and For Bilingual Schools in the Sultanate of Oman Prepared By: A Stevens (Qurum Private School) M Katira (Qurum Private School) M Hawthorn (Al Sahwa Schools) In Conjunction
Ground Rules. PC1221 Fundamentals of Physics I. Position and Displacement. Average Velocity. Lectures 7 and 8 Motion in Two Dimensions
 PC11 Fndamentals of Physics I Lectres 7 and 8 Motion in Two Dimensions A/Prof Tay Sen Chan 1 Grond Rles Switch off yor handphone and paer Switch off yor laptop compter and keep it No talkin while lectre
PC11 Fndamentals of Physics I Lectres 7 and 8 Motion in Two Dimensions A/Prof Tay Sen Chan 1 Grond Rles Switch off yor handphone and paer Switch off yor laptop compter and keep it No talkin while lectre
y sin n x dx cos x sin n 1 x n 1 y sin n 2 x cos 2 x dx y sin n xdx cos x sin n 1 x n 1 y sin n 2 x dx n 1 y sin n x dx
 SECTION 7. INTEGRATION BY PARTS 57 EXAPLE 6 Prove the reduction formula N Equation 7 is called a reduction formula because the eponent n has been reduced to n and n. 7 sin n n cos sinn n n sin n where
SECTION 7. INTEGRATION BY PARTS 57 EXAPLE 6 Prove the reduction formula N Equation 7 is called a reduction formula because the eponent n has been reduced to n and n. 7 sin n n cos sinn n n sin n where
Mathematics. Mathematics 2. hsn.uk.net. Higher HSN22000
 Higher Mathematics UNIT Mathematics HSN000 This document was produced speciall for the HSN.uk.net website, and we require that an copies or derivative works attribute the work to Higher Still Notes. For
Higher Mathematics UNIT Mathematics HSN000 This document was produced speciall for the HSN.uk.net website, and we require that an copies or derivative works attribute the work to Higher Still Notes. For
Student s Printed Name:
 MATH 1060 Test Answer Ke Spring 016 Calculus of One Variable I Version A Sections..9 Student s Printed Name: Instructor: CUID: Section: Instructions: You are not permitted to use a calculator on an portion
MATH 1060 Test Answer Ke Spring 016 Calculus of One Variable I Version A Sections..9 Student s Printed Name: Instructor: CUID: Section: Instructions: You are not permitted to use a calculator on an portion
Chapter 5 Review. 1. [No Calculator] Evaluate using the FTOC (the evaluation part) 2. [No Calculator] Evaluate using geometry
![Chapter 5 Review. 1. [No Calculator] Evaluate using the FTOC (the evaluation part) 2. [No Calculator] Evaluate using geometry Chapter 5 Review. 1. [No Calculator] Evaluate using the FTOC (the evaluation part) 2. [No Calculator] Evaluate using geometry](/thumbs/80/81403863.jpg) AP Calculus Chapter Review Name: Block:. [No Calculator] Evaluate using the FTOC (the evaluation part) a) 7 8 4 7 d b) 9 4 7 d. [No Calculator] Evaluate using geometry a) d c) 6 8 d. [No Calculator] Evaluate
AP Calculus Chapter Review Name: Block:. [No Calculator] Evaluate using the FTOC (the evaluation part) a) 7 8 4 7 d b) 9 4 7 d. [No Calculator] Evaluate using geometry a) d c) 6 8 d. [No Calculator] Evaluate
Evaluate Inverse Trigonometric Functions. 5p, }} 13p, }}
 13.4 a.1, a.3, 2A.4.C; P.3.A TEKS Evalate Inverse Trigonometri Fntions Before Yo fond vales of trigonometri fntions given angles. Now Yo will find angles given vales of trigonometri fntions. Wh? So o an
13.4 a.1, a.3, 2A.4.C; P.3.A TEKS Evalate Inverse Trigonometri Fntions Before Yo fond vales of trigonometri fntions given angles. Now Yo will find angles given vales of trigonometri fntions. Wh? So o an
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. B) = 2t + 1; D) = 2 - t;
 Eam Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Calculate the derivative of the function. Then find the value of the derivative as specified.
Eam Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Calculate the derivative of the function. Then find the value of the derivative as specified.
Definition 2.1 (The Derivative) (page 54) is a function. The derivative of a function f with respect to x, represented by. f ', is defined by
 Chapter DACS Lok 004/05 CHAPTER DIFFERENTIATION. THE GEOMETRICAL MEANING OF DIFFERENTIATION (page 54) Defiitio. (The Derivative) (page 54) Let f () is a fctio. The erivative of a fctio f with respect to,
Chapter DACS Lok 004/05 CHAPTER DIFFERENTIATION. THE GEOMETRICAL MEANING OF DIFFERENTIATION (page 54) Defiitio. (The Derivative) (page 54) Let f () is a fctio. The erivative of a fctio f with respect to,
MATH 175: Final Exam Review for Pre-calculus
 MATH 75: Final Eam Review for Pre-calculus In order to prepare for the final eam, you need too be able to work problems involving the following topics:. Can you graph rational functions by hand after algebraically
MATH 75: Final Eam Review for Pre-calculus In order to prepare for the final eam, you need too be able to work problems involving the following topics:. Can you graph rational functions by hand after algebraically
The Chain Rule. This is a generalization of the (general) power rule which we have already met in the form: then f (x) = r [g(x)] r 1 g (x).
![The Chain Rule. This is a generalization of the (general) power rule which we have already met in the form: then f (x) = r [g(x)] r 1 g (x). The Chain Rule. This is a generalization of the (general) power rule which we have already met in the form: then f (x) = r [g(x)] r 1 g (x).](/thumbs/78/77820746.jpg) The Chain Rule This is a generalization of the general) power rule which we have already met in the form: If f) = g)] r then f ) = r g)] r g ). Here, g) is any differentiable function and r is any real
The Chain Rule This is a generalization of the general) power rule which we have already met in the form: If f) = g)] r then f ) = r g)] r g ). Here, g) is any differentiable function and r is any real
DISTRIBUTED LEARNING
 DISTRIBUTED LEARNING RAVEN S WNCP GRADE 12 MATHEMATICS BC Pre Calculus Math 12 Alberta Mathematics 0 1 Saskatchewan Pre Calculus Math 0 Manitoba Pre Calculus Math 40S STUDENT GUIDE AND RESOURCE BOOK The
DISTRIBUTED LEARNING RAVEN S WNCP GRADE 12 MATHEMATICS BC Pre Calculus Math 12 Alberta Mathematics 0 1 Saskatchewan Pre Calculus Math 0 Manitoba Pre Calculus Math 40S STUDENT GUIDE AND RESOURCE BOOK The
Chapter 6. Inverse Circular Functions and Trigonometric Equations. Section 6.1 Inverse Circular Functions y = 0
 Chapter Inverse Circlar Fnctions and Trigonometric Eqations Section. Inverse Circlar Fnctions. onetoone. range. cos... = tan.. Sketch the reflection of the graph of f across the line =. 7. (a) [, ] é ù
Chapter Inverse Circlar Fnctions and Trigonometric Eqations Section. Inverse Circlar Fnctions. onetoone. range. cos... = tan.. Sketch the reflection of the graph of f across the line =. 7. (a) [, ] é ù
Geometric Image Manipulation. Lecture #4 Wednesday, January 24, 2018
 Geometric Image Maniplation Lectre 4 Wednesda, Janar 4, 08 Programming Assignment Image Maniplation: Contet To start with the obvios, an image is a D arra of piels Piel locations represent points on the
Geometric Image Maniplation Lectre 4 Wednesda, Janar 4, 08 Programming Assignment Image Maniplation: Contet To start with the obvios, an image is a D arra of piels Piel locations represent points on the
A Note on the Shifting Theorems for the Elzaki Transform
 Int. Jornal of Mh. Analysis, Vol. 8, 214, no. 1, 481-488 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/1.12988/ijma.214.4248 A Note on the Shifting Theorems for the Elzaki Transform Hwajoon Kim Kyngdong
Int. Jornal of Mh. Analysis, Vol. 8, 214, no. 1, 481-488 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/1.12988/ijma.214.4248 A Note on the Shifting Theorems for the Elzaki Transform Hwajoon Kim Kyngdong
2.5 CONTINUITY. a x. Notice that Definition l implicitly requires three things if f is continuous at a:
 SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
PhysicsAndMathsTutor.com
 Qestion Answer Marks (i) a = ½ B allow = ½ y y d y ( ). d ( ) 6 ( ) () dy * d y ( ) dy/d = 0 when = 0 ( ) = 0, = 0 or ¾ y = (¾) /½ = 7/, y = 0.95 (sf) [] B [9] y dy/d Gi Qotient (or prodct) rle consistent
Qestion Answer Marks (i) a = ½ B allow = ½ y y d y ( ). d ( ) 6 ( ) () dy * d y ( ) dy/d = 0 when = 0 ( ) = 0, = 0 or ¾ y = (¾) /½ = 7/, y = 0.95 (sf) [] B [9] y dy/d Gi Qotient (or prodct) rle consistent
Attn: Upcoming Functions Analytic Geometry students,
 Attn: Upcoming Functions Analtic Geometr students, All Functions Analtic Geometr students should complete this assignment prior to the first da of class. During the first week of school, time will be spent
Attn: Upcoming Functions Analtic Geometr students, All Functions Analtic Geometr students should complete this assignment prior to the first da of class. During the first week of school, time will be spent
Technical Calculus I Homework. Instructions
 Technical Calculus I Homework Instructions 1. Each assignment is to be done on one or more pieces of regular-sized notebook paper. 2. Your name and the assignment number should appear at the top of the
Technical Calculus I Homework Instructions 1. Each assignment is to be done on one or more pieces of regular-sized notebook paper. 2. Your name and the assignment number should appear at the top of the
u P(t) = P(x,y) r v t=0 4/4/2006 Motion ( F.Robilliard) 1
 y g j P(t) P(,y) r t0 i 4/4/006 Motion ( F.Robilliard) 1 Motion: We stdy in detail three cases of motion: 1. Motion in one dimension with constant acceleration niform linear motion.. Motion in two dimensions
y g j P(t) P(,y) r t0 i 4/4/006 Motion ( F.Robilliard) 1 Motion: We stdy in detail three cases of motion: 1. Motion in one dimension with constant acceleration niform linear motion.. Motion in two dimensions
3.3 Operations With Vectors, Linear Combinations
 Operations With Vectors, Linear Combinations Performance Criteria: (d) Mltiply ectors by scalars and add ectors, algebraically Find linear combinations of ectors algebraically (e) Illstrate the parallelogram
Operations With Vectors, Linear Combinations Performance Criteria: (d) Mltiply ectors by scalars and add ectors, algebraically Find linear combinations of ectors algebraically (e) Illstrate the parallelogram
4.9 Anti-derivatives. Definition. An anti-derivative of a function f is a function F such that F (x) = f (x) for all x.
 4.9 Anti-derivatives Anti-differentiation is exactly what it sounds like: the opposite of differentiation. That is, given a function f, can we find a function F whose derivative is f. Definition. An anti-derivative
4.9 Anti-derivatives Anti-differentiation is exactly what it sounds like: the opposite of differentiation. That is, given a function f, can we find a function F whose derivative is f. Definition. An anti-derivative
Primary dependent variable is fluid velocity vector V = V ( r ); where r is the position vector
 Chapter 4: Flids Kinematics 4. Velocit and Description Methods Primar dependent ariable is flid elocit ector V V ( r ); where r is the position ector If V is known then pressre and forces can be determined
Chapter 4: Flids Kinematics 4. Velocit and Description Methods Primar dependent ariable is flid elocit ector V V ( r ); where r is the position ector If V is known then pressre and forces can be determined
