Math 116 Practice for Exam 2
|
|
|
- Randell Daniel
- 5 years ago
- Views:
Transcription
1 Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem on which you are suck.. Do no separae he pages of he exam. If any pages do become separaed, wrie your name on hem and poin hem ou o your insrucor when you hand in he exam. 3. Please read he insrucions for each individual exercise carefully. One of he skills being esed on his exam is your abiliy o inerpre quesions, so insrucors will no answer quesions abou exam problems during he exam. 4. Show an appropriae amoun of work (including appropriae explanaion) for each exercise so ha he graders can see no only he answer bu also how you obained i. Include unis in your answers where appropriae. 5. You may use any calculaor excep a TI-9 (or oher calculaor wih a full alphanumeric keypad). However, you mus show work for any calculaion which we have learned how o do in his course. You are also allowed wo sides of a 3 5 noe card. 6. If you use graphs or ables o obain an answer, be cerain o include an explanaion and skech of he graph, and o wrie ou he enries of he able ha you use. 7. You mus use he mehods learned in his course o solve all problems. Semeser Exam Problem Name Poins Score Winer Winer 7 6 Venice Beach 3 Fall Fall 6 racking chip 4 Winer 6 3 O ghan 3 Toal 58 Recommended ime (based on poins): 58 minues
2 Winer, 7 Mah 6 Exam 3 Problem 4 Soluion
3 Mah 6 / Exam (March, 7) page 6 6. [3 poins] Anderson and Glen decide o ake a road rip saring from Venice Beach. They have no worries abou geing anywhere quickly, as hey enjoy each oher s company, so hey ake a very inefficien roue. Suppose ha Venice Beach is locaed a (,) and ha Anderson and Glen s posiion (x,y) (measured in miles) hours afer leaving Venice Beach is given by a pair of parameric equaions x = f(), y = g(). A graph of f() and a formula for g() are given below. Noe ha f() is linear on he inervals [,.5], [.5,.5], and [.5,3]. f() (mi) 3 g() = (hr) Noe: For each of he following, your final answer should no involve he leers f and g. a. [ poins] If heir roadrip las 3 hours, wha are he x and y coordinaes of heir final desinaion? Soluion: Noe ha a ime = 3, we have x = f(3) = and y = g(3) = 9. So he coordinaes of heir final desinaion are (, 9). b. [3 poins] A wha speed are hey raveling hours ino heir rip? Soluion: We have dx d = f dy () = and = d = g () = 5. = So heir speed a ime = is +5 = 5 miles per hour. c. [4 poins] Wrie, bu do no compue, an expression involving one or more inegrals ha gives he disance hey raveled, in miles, in he firs half hour of heir rip. Soluion: On he inerval (,.5), we see ha f() = 6, so on his inerval, we have f () = 6 and g () = The parameric arc lengh formula hen implies ha he disance hey ravelled from.5 = o =.5 is (6) +( 3 + 3) d miles. d. [4 poins] Wrie down a pair of parameric equaions using he parameer s for he line angen o heir pah a =.75 hours. Soluion: Noe ha df f(.75) =.5, d =, g(.75) = , and =.75 dg d =.85 =.75 There are many possible paramerizaions. There is no need o have his mach wih he parameer from earlier, so he answer below has he line passing hrough(.5, ) a s =. Answer: x(s) = s.5 and y(s) =.85s Winer, 7 Mah 6 Exam Problem 6 (Venice Beach) Soluion
4 Mah 6 / Final (December 9, 6) DO NOT WRITE YOUR NAME ON THIS PAGE page 8 8. [ poins] In his problem, we consider he parameric curve given by x = f() y = g() for all, where f and g are wice-differeniable funcions. Some values of f and g and heir derivaives are given in he ables below f() g() f () - 3 g () a. [poin] Inhespaceprovided, wrieaninegralhagiveshearclenghofheparameric curve from = o = 5. 5 (f ()) +(g ()) d Arc lengh = b. [3 poins] Use a midpoin sum wih as many subdivisions as possible o esimae your inegral from par a. Wrie ou all he erms in your sum, and do no simplify. Soluion: The midpoin sum is ( +( ) ). c. [3 poins] Find he Caresian equaion for he angen line o he parameric curve in he xy-plane a =. Soluion: In poin-slope form, he angen line is given by y 5 = (x+3). d. [poins] Considerheangenlinesoheparamericcurveahe-values =,,3,4,5. Are any of hese lines perpendicular o each oher? If so, lis any wo -values for which he angen lines are perpendicular. If no, wrie NO. Soluion: The angen lines corresponding o = and = 4 are perpendicular. e. [poins] Asrangesfromo5, hecorrespondingparofheparamericcurveinersecs he line y = x exacly once. Which inerval conains he -value for which he curve inersecs he line y = x? Circle your answer. You do no need o show any work. (,) (,3) (3,4) (4,5) Fall, 6 Mah 6 Exam 3 Problem 8 Soluion
5 Mah 6 / Miderm (November 4, 6) DO NOT WRITE YOUR NAME ON THIS PAGE page 9. [4 poins] Fearing ha she is losing auhoriy over her robo ward, Dr. Duran has insalled a racking chip in Seph s mainframe. The chip gives Seph s locaion separaely in x- and y-coordinaes, where he unis of he axes are miles, Dr. Duran s office corresponds o he origin (x,y) = (,), he posiive y-axis poins norh, and he posiive x-axis poins eas. On nigh, Dr. Duran noiced unusual levels of aciviy; hours afer midnigh, Seph began moving according o he parameric equaions x = f() y = g(), where f() and g() are ploed below for 5. f() g() (,.5) (4,.7) (,) (5,.7) a. [ poins] When was Seph farhes norh and souh on nigh? Wrie your answers in he blanks provided. You do no need o show your work. Soluion: Norh: 4 a.m. Souh: a.m. b. [3 poins] Wha was Seph s speed a = 4.9 on nigh? You may use he fac ha f (4.9) =. Include unis. Soluion: Her speed is ( ) +(.4) = 6.76 mi/hr. c. [ poins] Wha direcion was Seph moving a = on nigh? Circle only one answer. NORTH AND EAST EAST ONLY SOUTH AND EAST NORTH AND WEST WEST ONLY SOUTH AND WEST Fall, 6 Mah 6 Exam Problem (racking chip) Soluion
6 Mah 6 / Miderm (November 4, 6) DO NOT WRITE YOUR NAME ON THIS PAGE page (coninued). Recall ha on nigh, Seph s posiion was given by he parameric equaions x = f() y = g(), where f() and g() are ploed below for 5. As before, Dr. Duran s office is a he origin (x,y) = (,), he posiive y-axis poins norh, and he posiive x-axis poins eas. f() g() (,.5) (4,.7) (,) (5,.7) d. [3 poins] How far away was Seph from Dr. Duran s office a = on nigh? Soluion: Seph was +.5 = 3.5 mi away. On nigh, Seph s movemens were even sranger, following he parameric equaions x = f(s)ds y = g(s) ds. e. [ poins] Wha direcion was Seph moving a = on nigh? Circle only one answer. NORTH AND EAST EAST ONLY SOUTH AND EAST NORTH AND WEST WEST ONLY SOUTH AND WEST f. [ poins] Did Seph come o a sop beween midnigh and 5 a.m. on nigh? If so, a wha ime(s) did she come o a sop? Soluion: Yes; she came o a sop a 3 a.m. Fall, 6 Mah 6 Exam Problem (racking chip) Soluion
7 Mah 6 / Exam (March, 6) DO NOT WRITE YOUR NAME ON THIS PAGE page 6 3. [3 poins] O-guk s playful son, O-ghan, is running on he xy-plane. His posiion seconds afer he begins running is x = y = sin()+. Assume x and y are in meers. a. [3 poins] Does O-ghan pass hough he origin? Briefly jusify. Soluion: x = when = so when =. For his value of, y = sin()+. So he didn pass hrough he origin. b. [4 poins] How fas is O-ghan running a = 5? Give your answer in exac form (i.e. no decimal approximaions). Include unis. Soluion: ( 5 ) +(cos(5)) m s c. [6 poins] Find an equaion, in xy-coordinaes, of he angen line o his pah a =. Soluion: The slope of he angen line is given by m = dy/d dx/d = cos() = cos() The equaion of he angen line is y sin() = cos()(x ) or equivalenly y = cos()x+sin() Winer, 6 Mah 6 Exam Problem 3 (O ghan) Soluion
Math 116 Second Midterm March 21, 2016
 Mah 6 Second Miderm March, 06 UMID: EXAM SOLUTIONS Iniials: Insrucor: Secion:. Do no open his exam unil you are old o do so.. Do no wrie your name anywhere on his exam. 3. This exam has pages including
Mah 6 Second Miderm March, 06 UMID: EXAM SOLUTIONS Iniials: Insrucor: Secion:. Do no open his exam unil you are old o do so.. Do no wrie your name anywhere on his exam. 3. This exam has pages including
Math 115 Final Exam December 14, 2017
 On my honor, as a suden, I have neiher given nor received unauhorized aid on his academic work. Your Iniials Only: Iniials: Do no wrie in his area Mah 5 Final Exam December, 07 Your U-M ID # (no uniqname):
On my honor, as a suden, I have neiher given nor received unauhorized aid on his academic work. Your Iniials Only: Iniials: Do no wrie in his area Mah 5 Final Exam December, 07 Your U-M ID # (no uniqname):
Math 105 Second Midterm March 16, 2017
 Mah 105 Second Miderm March 16, 2017 UMID: Insrucor: Iniials: Secion: 1. Do no open his exam unil you are old o do so. 2. Do no wrie your name anywhere on his exam. 3. This exam has 9 pages including his
Mah 105 Second Miderm March 16, 2017 UMID: Insrucor: Iniials: Secion: 1. Do no open his exam unil you are old o do so. 2. Do no wrie your name anywhere on his exam. 3. This exam has 9 pages including his
!!"#"$%&#'()!"#&'(*%)+,&',-)./0)1-*23)
 "#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
"#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
AP CALCULUS AB 2003 SCORING GUIDELINES (Form B)
 SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
Math 111 Midterm I, Lecture A, version 1 -- Solutions January 30 th, 2007
 NAME: Suden ID #: QUIZ SECTION: Mah 111 Miderm I, Lecure A, version 1 -- Soluions January 30 h, 2007 Problem 1 4 Problem 2 6 Problem 3 20 Problem 4 20 Toal: 50 You are allowed o use a calculaor, a ruler,
NAME: Suden ID #: QUIZ SECTION: Mah 111 Miderm I, Lecure A, version 1 -- Soluions January 30 h, 2007 Problem 1 4 Problem 2 6 Problem 3 20 Problem 4 20 Toal: 50 You are allowed o use a calculaor, a ruler,
3, so θ = arccos
 Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
KINEMATICS IN ONE DIMENSION
 KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
AP Calculus BC Chapter 10 Part 1 AP Exam Problems
 AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
Parametrics and Vectors (BC Only)
 Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
15. Vector Valued Functions
 1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
Lecture 2-1 Kinematics in One Dimension Displacement, Velocity and Acceleration Everything in the world is moving. Nothing stays still.
 Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
AP Calculus BC 2004 Free-Response Questions Form B
 AP Calculus BC 200 Free-Response Quesions Form B The maerials included in hese files are inended for noncommercial use by AP eachers for course and exam preparaion; permission for any oher use mus be sough
AP Calculus BC 200 Free-Response Quesions Form B The maerials included in hese files are inended for noncommercial use by AP eachers for course and exam preparaion; permission for any oher use mus be sough
AP CALCULUS AB/CALCULUS BC 2016 SCORING GUIDELINES. Question 1. 1 : estimate = = 120 liters/hr
 AP CALCULUS AB/CALCULUS BC 16 SCORING GUIDELINES Quesion 1 (hours) R ( ) (liers / hour) 1 3 6 8 134 119 95 74 7 Waer is pumped ino a ank a a rae modeled by W( ) = e liers per hour for 8, where is measured
AP CALCULUS AB/CALCULUS BC 16 SCORING GUIDELINES Quesion 1 (hours) R ( ) (liers / hour) 1 3 6 8 134 119 95 74 7 Waer is pumped ino a ank a a rae modeled by W( ) = e liers per hour for 8, where is measured
10.1 EXERCISES. y 2 t 2. y 1 t y t 3. y e
 66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
ACCUMULATION. Section 7.5 Calculus AP/Dual, Revised /26/2018 7:27 PM 7.5A: Accumulation 1
 ACCUMULATION Secion 7.5 Calculus AP/Dual, Revised 2019 vie.dang@humbleisd.ne 12/26/2018 7:27 PM 7.5A: Accumulaion 1 APPLICATION PROBLEMS A. Undersand he quesion. I is ofen no necessary o as much compuaion
ACCUMULATION Secion 7.5 Calculus AP/Dual, Revised 2019 vie.dang@humbleisd.ne 12/26/2018 7:27 PM 7.5A: Accumulaion 1 APPLICATION PROBLEMS A. Undersand he quesion. I is ofen no necessary o as much compuaion
72 Calculus and Structures
 72 Calculus and Srucures CHAPTER 5 DISTANCE AND ACCUMULATED CHANGE Calculus and Srucures 73 Copyrigh Chaper 5 DISTANCE AND ACCUMULATED CHANGE 5. DISTANCE a. Consan velociy Le s ake anoher look a Mary s
72 Calculus and Srucures CHAPTER 5 DISTANCE AND ACCUMULATED CHANGE Calculus and Srucures 73 Copyrigh Chaper 5 DISTANCE AND ACCUMULATED CHANGE 5. DISTANCE a. Consan velociy Le s ake anoher look a Mary s
Chapter 7: Solving Trig Equations
 Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
dy dx = xey (a) y(0) = 2 (b) y(1) = 2.5 SOLUTION: See next page
 Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
Teaching parametric equations using graphing technology
 Teaching parameric equaions using graphing echnology The session will sar by looking a problems which help sudens o see ha parameric equaions are no here o make life difficul bu are imporan and give rise
Teaching parameric equaions using graphing echnology The session will sar by looking a problems which help sudens o see ha parameric equaions are no here o make life difficul bu are imporan and give rise
Math 23 Spring Differential Equations. Final Exam Due Date: Tuesday, June 6, 5pm
 Mah Spring 6 Differenial Equaions Final Exam Due Dae: Tuesday, June 6, 5pm Your name (please prin): Insrucions: This is an open book, open noes exam. You are free o use a calculaor or compuer o check your
Mah Spring 6 Differenial Equaions Final Exam Due Dae: Tuesday, June 6, 5pm Your name (please prin): Insrucions: This is an open book, open noes exam. You are free o use a calculaor or compuer o check your
PROBLEMS FOR MATH 162 If a problem is starred, all subproblems are due. If only subproblems are starred, only those are due. SLOPES OF TANGENT LINES
 PROBLEMS FOR MATH 6 If a problem is sarred, all subproblems are due. If onl subproblems are sarred, onl hose are due. 00. Shor answer quesions. SLOPES OF TANGENT LINES (a) A ball is hrown ino he air. Is
PROBLEMS FOR MATH 6 If a problem is sarred, all subproblems are due. If onl subproblems are sarred, onl hose are due. 00. Shor answer quesions. SLOPES OF TANGENT LINES (a) A ball is hrown ino he air. Is
4.5 Constant Acceleration
 4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
1998 Calculus AB Scoring Guidelines
 AB{ / BC{ 1999. The rae a which waer ows ou of a pipe, in gallons per hour, is given by a diereniable funcion R of ime. The able above shows he rae as measured every hours for a {hour period. (a) Use a
AB{ / BC{ 1999. The rae a which waer ows ou of a pipe, in gallons per hour, is given by a diereniable funcion R of ime. The able above shows he rae as measured every hours for a {hour period. (a) Use a
Answers to 1 Homework
 Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
The equation to any straight line can be expressed in the form:
 Sring Graphs Par 1 Answers 1 TI-Nspire Invesigaion Suden min Aims Deermine a series of equaions of sraigh lines o form a paern similar o ha formed by he cables on he Jerusalem Chords Bridge. Deermine he
Sring Graphs Par 1 Answers 1 TI-Nspire Invesigaion Suden min Aims Deermine a series of equaions of sraigh lines o form a paern similar o ha formed by he cables on he Jerusalem Chords Bridge. Deermine he
Displacement ( x) x x x
 Kinemaics Kinemaics is he branch of mechanics ha describes he moion of objecs wihou necessarily discussing wha causes he moion. 1-Dimensional Kinemaics (or 1- Dimensional moion) refers o moion in a sraigh
Kinemaics Kinemaics is he branch of mechanics ha describes he moion of objecs wihou necessarily discussing wha causes he moion. 1-Dimensional Kinemaics (or 1- Dimensional moion) refers o moion in a sraigh
Lesson 3.1 Recursive Sequences
 Lesson 3.1 Recursive Sequences 1) 1. Evaluae he epression 2(3 for each value of. a. 9 b. 2 c. 1 d. 1 2. Consider he sequence of figures made from riangles. Figure 1 Figure 2 Figure 3 Figure a. Complee
Lesson 3.1 Recursive Sequences 1) 1. Evaluae he epression 2(3 for each value of. a. 9 b. 2 c. 1 d. 1 2. Consider he sequence of figures made from riangles. Figure 1 Figure 2 Figure 3 Figure a. Complee
BEng (Hons) Telecommunications. Examinations for / Semester 2
 BEng (Hons) Telecommunicaions Cohor: BTEL/14/FT Examinaions for 2015-2016 / Semeser 2 MODULE: ELECTROMAGNETIC THEORY MODULE CODE: ASE2103 Duraion: 2 ½ Hours Insrucions o Candidaes: 1. Answer ALL 4 (FOUR)
BEng (Hons) Telecommunicaions Cohor: BTEL/14/FT Examinaions for 2015-2016 / Semeser 2 MODULE: ELECTROMAGNETIC THEORY MODULE CODE: ASE2103 Duraion: 2 ½ Hours Insrucions o Candidaes: 1. Answer ALL 4 (FOUR)
Math 333 Problem Set #2 Solution 14 February 2003
 Mah 333 Problem Se #2 Soluion 14 February 2003 A1. Solve he iniial value problem dy dx = x2 + e 3x ; 2y 4 y(0) = 1. Soluion: This is separable; we wrie 2y 4 dy = x 2 + e x dx and inegrae o ge The iniial
Mah 333 Problem Se #2 Soluion 14 February 2003 A1. Solve he iniial value problem dy dx = x2 + e 3x ; 2y 4 y(0) = 1. Soluion: This is separable; we wrie 2y 4 dy = x 2 + e x dx and inegrae o ge The iniial
Physics 20 Lesson 5 Graphical Analysis Acceleration
 Physics 2 Lesson 5 Graphical Analysis Acceleraion I. Insananeous Velociy From our previous work wih consan speed and consan velociy, we know ha he slope of a posiion-ime graph is equal o he velociy of
Physics 2 Lesson 5 Graphical Analysis Acceleraion I. Insananeous Velociy From our previous work wih consan speed and consan velociy, we know ha he slope of a posiion-ime graph is equal o he velociy of
x i v x t a dx dt t x
 Physics 3A: Basic Physics I Shoup - Miderm Useful Equaions A y A sin A A A y an A y A A = A i + A y j + A z k A * B = A B cos(θ) A B = A B sin(θ) A * B = A B + A y B y + A z B z A B = (A y B z A z B y
Physics 3A: Basic Physics I Shoup - Miderm Useful Equaions A y A sin A A A y an A y A A = A i + A y j + A z k A * B = A B cos(θ) A B = A B sin(θ) A * B = A B + A y B y + A z B z A B = (A y B z A z B y
2. What is the displacement of the bug between t = 0.00 s and t = 20.0 s? A) cm B) 39.9 cm C) cm D) 16.1 cm E) +16.
 1. For which one of he following siuaions will he pah lengh equal he magniude of he displacemen? A) A jogger is running around a circular pah. B) A ball is rolling down an inclined plane. C) A rain ravels
1. For which one of he following siuaions will he pah lengh equal he magniude of he displacemen? A) A jogger is running around a circular pah. B) A ball is rolling down an inclined plane. C) A rain ravels
AP CALCULUS BC 2016 SCORING GUIDELINES
 6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
SMT 2014 Calculus Test Solutions February 15, 2014 = 3 5 = 15.
 SMT Calculus Tes Soluions February 5,. Le f() = and le g() =. Compue f ()g (). Answer: 5 Soluion: We noe ha f () = and g () = 6. Then f ()g () =. Plugging in = we ge f ()g () = 6 = 3 5 = 5.. There is a
SMT Calculus Tes Soluions February 5,. Le f() = and le g() =. Compue f ()g (). Answer: 5 Soluion: We noe ha f () = and g () = 6. Then f ()g () =. Plugging in = we ge f ()g () = 6 = 3 5 = 5.. There is a
Math Week 14 April 16-20: sections first order systems of linear differential equations; 7.4 mass-spring systems.
 Mah 2250-004 Week 4 April 6-20 secions 7.-7.3 firs order sysems of linear differenial equaions; 7.4 mass-spring sysems. Mon Apr 6 7.-7.2 Sysems of differenial equaions (7.), and he vecor Calculus we need
Mah 2250-004 Week 4 April 6-20 secions 7.-7.3 firs order sysems of linear differenial equaions; 7.4 mass-spring sysems. Mon Apr 6 7.-7.2 Sysems of differenial equaions (7.), and he vecor Calculus we need
Ground Rules. PC1221 Fundamentals of Physics I. Kinematics. Position. Lectures 3 and 4 Motion in One Dimension. A/Prof Tay Seng Chuan
 Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
Math 334 Test 1 KEY Spring 2010 Section: 001. Instructor: Scott Glasgow Dates: May 10 and 11.
 1 Mah 334 Tes 1 KEY Spring 21 Secion: 1 Insrucor: Sco Glasgow Daes: Ma 1 and 11. Do NOT wrie on his problem saemen bookle, excep for our indicaion of following he honor code jus below. No credi will be
1 Mah 334 Tes 1 KEY Spring 21 Secion: 1 Insrucor: Sco Glasgow Daes: Ma 1 and 11. Do NOT wrie on his problem saemen bookle, excep for our indicaion of following he honor code jus below. No credi will be
AP Calculus BC - Parametric equations and vectors Chapter 9- AP Exam Problems solutions
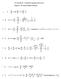 AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
AP CALCULUS AB 2017 SCORING GUIDELINES
 AP CALCULUS AB 17 SCORING GUIDELINES /CALCULUS BC 15 SCORING GUIDELINES Quesion (minues) v ( ) (meers per minue) 1 4 4 4 15 Johanna jogs along a sraigh pah. For 4, Johanna s velociy is given by a differeniable
AP CALCULUS AB 17 SCORING GUIDELINES /CALCULUS BC 15 SCORING GUIDELINES Quesion (minues) v ( ) (meers per minue) 1 4 4 4 15 Johanna jogs along a sraigh pah. For 4, Johanna s velociy is given by a differeniable
u(x) = e x 2 y + 2 ) Integrate and solve for x (1 + x)y + y = cos x Answer: Divide both sides by 1 + x and solve for y. y = x y + cos x
 . 1 Mah 211 Homework #3 February 2, 2001 2.4.3. y + (2/x)y = (cos x)/x 2 Answer: Compare y + (2/x) y = (cos x)/x 2 wih y = a(x)x + f(x)and noe ha a(x) = 2/x. Consequenly, an inegraing facor is found wih
. 1 Mah 211 Homework #3 February 2, 2001 2.4.3. y + (2/x)y = (cos x)/x 2 Answer: Compare y + (2/x) y = (cos x)/x 2 wih y = a(x)x + f(x)and noe ha a(x) = 2/x. Consequenly, an inegraing facor is found wih
23.2. Representing Periodic Functions by Fourier Series. Introduction. Prerequisites. Learning Outcomes
 Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
1.6. Slopes of Tangents and Instantaneous Rate of Change
 1.6 Slopes of Tangens and Insananeous Rae of Change When you hi or kick a ball, he heigh, h, in meres, of he ball can be modelled by he equaion h() 4.9 2 v c. In his equaion, is he ime, in seconds; c represens
1.6 Slopes of Tangens and Insananeous Rae of Change When you hi or kick a ball, he heigh, h, in meres, of he ball can be modelled by he equaion h() 4.9 2 v c. In his equaion, is he ime, in seconds; c represens
Solutions to Assignment 1
 MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
a. Show that these lines intersect by finding the point of intersection. b. Find an equation for the plane containing these lines.
 Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
Physics 3A: Basic Physics I Shoup Sample Midterm. Useful Equations. x f. x i v x. a x. x i. v xi v xf. 2a x f x i. y f. a r.
 Physics 3A: Basic Physics I Shoup Sample Miderm Useful Equaions A y Asin A A x A y an A y A x A = A x i + A y j + A z k A * B = A B cos(θ) A x B = A B sin(θ) A * B = A x B x + A y B y + A z B z A x B =
Physics 3A: Basic Physics I Shoup Sample Miderm Useful Equaions A y Asin A A x A y an A y A x A = A x i + A y j + A z k A * B = A B cos(θ) A x B = A B sin(θ) A * B = A x B x + A y B y + A z B z A x B =
1. Kinematics I: Position and Velocity
 1. Kinemaics I: Posiion and Velociy Inroducion The purpose of his eperimen is o undersand and describe moion. We describe he moion of an objec by specifying is posiion, velociy, and acceleraion. In his
1. Kinemaics I: Posiion and Velociy Inroducion The purpose of his eperimen is o undersand and describe moion. We describe he moion of an objec by specifying is posiion, velociy, and acceleraion. In his
HOMEWORK # 2: MATH 211, SPRING Note: This is the last solution set where I will describe the MATLAB I used to make my pictures.
 HOMEWORK # 2: MATH 2, SPRING 25 TJ HITCHMAN Noe: This is he las soluion se where I will describe he MATLAB I used o make my picures.. Exercises from he ex.. Chaper 2.. Problem 6. We are o show ha y() =
HOMEWORK # 2: MATH 2, SPRING 25 TJ HITCHMAN Noe: This is he las soluion se where I will describe he MATLAB I used o make my picures.. Exercises from he ex.. Chaper 2.. Problem 6. We are o show ha y() =
AP CALCULUS AB/CALCULUS BC 2016 SCORING GUIDELINES. Question 1
 AP CALCULUS AB/CALCULUS BC 6 SCORING GUIDELINES Quesion (hours) R ( ) (liers / hour) 6 4 9 95 74 7 Waer is pumped ino a ank a a rae modeled by W( ) = e liers per hour for, where is measured in hours. Waer
AP CALCULUS AB/CALCULUS BC 6 SCORING GUIDELINES Quesion (hours) R ( ) (liers / hour) 6 4 9 95 74 7 Waer is pumped ino a ank a a rae modeled by W( ) = e liers per hour for, where is measured in hours. Waer
MEI STRUCTURED MATHEMATICS 4758
 OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
Solution: b All the terms must have the dimension of acceleration. We see that, indeed, each term has the units of acceleration
 PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
Some Basic Information about M-S-D Systems
 Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Chapters 6 & 7: Trigonometric Functions of Angles and Real Numbers. Divide both Sides by 180
 Algebra Chapers & : Trigonomeric Funcions of Angles and Real Numbers Chapers & : Trigonomeric Funcions of Angles and Real Numbers - Angle Measures Radians: - a uni (rad o measure he size of an angle. rad
Algebra Chapers & : Trigonomeric Funcions of Angles and Real Numbers Chapers & : Trigonomeric Funcions of Angles and Real Numbers - Angle Measures Radians: - a uni (rad o measure he size of an angle. rad
Biol. 356 Lab 8. Mortality, Recruitment, and Migration Rates
 Biol. 356 Lab 8. Moraliy, Recruimen, and Migraion Raes (modified from Cox, 00, General Ecology Lab Manual, McGraw Hill) Las week we esimaed populaion size hrough several mehods. One assumpion of all hese
Biol. 356 Lab 8. Moraliy, Recruimen, and Migraion Raes (modified from Cox, 00, General Ecology Lab Manual, McGraw Hill) Las week we esimaed populaion size hrough several mehods. One assumpion of all hese
SPH3U: Projectiles. Recorder: Manager: Speaker:
 SPH3U: Projeciles Now i s ime o use our new skills o analyze he moion of a golf ball ha was ossed hrough he air. Le s find ou wha is special abou he moion of a projecile. Recorder: Manager: Speaker: 0
SPH3U: Projeciles Now i s ime o use our new skills o analyze he moion of a golf ball ha was ossed hrough he air. Le s find ou wha is special abou he moion of a projecile. Recorder: Manager: Speaker: 0
AP CALCULUS AB 2004 SCORING GUIDELINES (Form B)
 4 SCORING GUIDELINES (Form B) Quesion A es plane flies in a sraigh line wih (min) 5 1 15 5 5 4 posiive velociy v (), in miles per v ()(mpm) 7. 9. 9.5 7. 4.5.4.4 4. 7. minue a ime minues, where v is a differeniable
4 SCORING GUIDELINES (Form B) Quesion A es plane flies in a sraigh line wih (min) 5 1 15 5 5 4 posiive velociy v (), in miles per v ()(mpm) 7. 9. 9.5 7. 4.5.4.4 4. 7. minue a ime minues, where v is a differeniable
Applications of the Basic Equations Chapter 3. Paul A. Ullrich
 Applicaions of he Basic Equaions Chaper 3 Paul A. Ullrich paullrich@ucdavis.edu Par 1: Naural Coordinaes Naural Coordinaes Quesion: Why do we need anoher coordinae sysem? Our goal is o simplify he equaions
Applicaions of he Basic Equaions Chaper 3 Paul A. Ullrich paullrich@ucdavis.edu Par 1: Naural Coordinaes Naural Coordinaes Quesion: Why do we need anoher coordinae sysem? Our goal is o simplify he equaions
MEI Mechanics 1 General motion. Section 1: Using calculus
 Soluions o Exercise MEI Mechanics General moion Secion : Using calculus. s 4 v a 6 4 4 When =, v 4 a 6 4 6. (i) When = 0, s = -, so he iniial displacemen = - m. s v 4 When = 0, v = so he iniial velociy
Soluions o Exercise MEI Mechanics General moion Secion : Using calculus. s 4 v a 6 4 4 When =, v 4 a 6 4 6. (i) When = 0, s = -, so he iniial displacemen = - m. s v 4 When = 0, v = so he iniial velociy
Kinematics Vocabulary. Kinematics and One Dimensional Motion. Position. Coordinate System in One Dimension. Kinema means movement 8.
 Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Midterm Exam Review Questions Free Response Non Calculator
 Name: Dae: Block: Miderm Eam Review Quesions Free Response Non Calculaor Direcions: Solve each of he following problems. Choose he BEST answer choice from hose given. A calculaor may no be used. Do no
Name: Dae: Block: Miderm Eam Review Quesions Free Response Non Calculaor Direcions: Solve each of he following problems. Choose he BEST answer choice from hose given. A calculaor may no be used. Do no
UCLA: Math 3B Problem set 3 (solutions) Fall, 2018
 UCLA: Mah 3B Problem se 3 (soluions) Fall, 28 This problem se concenraes on pracice wih aniderivaives. You will ge los of pracice finding simple aniderivaives as well as finding aniderivaives graphically
UCLA: Mah 3B Problem se 3 (soluions) Fall, 28 This problem se concenraes on pracice wih aniderivaives. You will ge los of pracice finding simple aniderivaives as well as finding aniderivaives graphically
IB Physics Kinematics Worksheet
 IB Physics Kinemaics Workshee Wrie full soluions and noes for muliple choice answers. Do no use a calculaor for muliple choice answers. 1. Which of he following is a correc definiion of average acceleraion?
IB Physics Kinemaics Workshee Wrie full soluions and noes for muliple choice answers. Do no use a calculaor for muliple choice answers. 1. Which of he following is a correc definiion of average acceleraion?
23.5. Half-Range Series. Introduction. Prerequisites. Learning Outcomes
 Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
Logistic growth rate. Fencing a pen. Notes. Notes. Notes. Optimization: finding the biggest/smallest/highest/lowest, etc.
 Opimizaion: finding he bigges/smalles/highes/lowes, ec. Los of non-sandard problems! Logisic growh rae 7.1 Simple biological opimizaion problems Small populaions AND large populaions grow slowly N: densiy
Opimizaion: finding he bigges/smalles/highes/lowes, ec. Los of non-sandard problems! Logisic growh rae 7.1 Simple biological opimizaion problems Small populaions AND large populaions grow slowly N: densiy
Let us start with a two dimensional case. We consider a vector ( x,
 Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
Math 221: Mathematical Notation
 Mah 221: Mahemaical Noaion Purpose: One goal in any course is o properly use he language o ha subjec. These noaions summarize some o he major conceps and more diicul opics o he uni. Typing hem helps you
Mah 221: Mahemaical Noaion Purpose: One goal in any course is o properly use he language o ha subjec. These noaions summarize some o he major conceps and more diicul opics o he uni. Typing hem helps you
1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.
![1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx. 1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.](/thumbs/71/65799522.jpg) . Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
. Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
Testing What You Know Now
 Tesing Wha You Know Now To bes each you, I need o know wha you know now Today we ake a well-esablished quiz ha is designed o ell me his To encourage you o ake he survey seriously, i will coun as a clicker
Tesing Wha You Know Now To bes each you, I need o know wha you know now Today we ake a well-esablished quiz ha is designed o ell me his To encourage you o ake he survey seriously, i will coun as a clicker
Matlab and Python programming: how to get started
 Malab and Pyhon programming: how o ge sared Equipping readers he skills o wrie programs o explore complex sysems and discover ineresing paerns from big daa is one of he main goals of his book. In his chaper,
Malab and Pyhon programming: how o ge sared Equipping readers he skills o wrie programs o explore complex sysems and discover ineresing paerns from big daa is one of he main goals of his book. In his chaper,
2.1: What is physics? Ch02: Motion along a straight line. 2.2: Motion. 2.3: Position, Displacement, Distance
 Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
( ) a system of differential equations with continuous parametrization ( T = R + These look like, respectively:
 XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
MATH 4330/5330, Fourier Analysis Section 6, Proof of Fourier s Theorem for Pointwise Convergence
 MATH 433/533, Fourier Analysis Secion 6, Proof of Fourier s Theorem for Poinwise Convergence Firs, some commens abou inegraing periodic funcions. If g is a periodic funcion, g(x + ) g(x) for all real x,
MATH 433/533, Fourier Analysis Secion 6, Proof of Fourier s Theorem for Poinwise Convergence Firs, some commens abou inegraing periodic funcions. If g is a periodic funcion, g(x + ) g(x) for all real x,
15. Bicycle Wheel. Graph of height y (cm) above the axle against time t (s) over a 6-second interval. 15 bike wheel
 15. Biccle Wheel The graph We moun a biccle wheel so ha i is free o roae in a verical plane. In fac, wha works easil is o pu an exension on one of he axles, and ge a suden o sand on one side and hold he
15. Biccle Wheel The graph We moun a biccle wheel so ha i is free o roae in a verical plane. In fac, wha works easil is o pu an exension on one of he axles, and ge a suden o sand on one side and hold he
a 10.0 (m/s 2 ) 5.0 Name: Date: 1. The graph below describes the motion of a fly that starts out going right V(m/s)
 Name: Dae: Kinemaics Review (Honors. Physics) Complee he following on a separae shee of paper o be urned in on he day of he es. ALL WORK MUST BE SHOWN TO RECEIVE CREDIT. 1. The graph below describes he
Name: Dae: Kinemaics Review (Honors. Physics) Complee he following on a separae shee of paper o be urned in on he day of he es. ALL WORK MUST BE SHOWN TO RECEIVE CREDIT. 1. The graph below describes he
Exam 1 Solutions. 1 Question 1. February 10, Part (A) 1.2 Part (B) To find equilibrium solutions, set P (t) = C = dp
 Exam Soluions Februar 0, 05 Quesion. Par (A) To find equilibrium soluions, se P () = C = = 0. This implies: = P ( P ) P = P P P = P P = P ( + P ) = 0 The equilibrium soluion are hus P () = 0 and P () =..
Exam Soluions Februar 0, 05 Quesion. Par (A) To find equilibrium soluions, se P () = C = = 0. This implies: = P ( P ) P = P P P = P P = P ( + P ) = 0 The equilibrium soluion are hus P () = 0 and P () =..
The average rate of change between two points on a function is d t
 SM Dae: Secion: Objecive: The average rae of change beween wo poins on a funcion is d. For example, if he funcion ( ) represens he disance in miles ha a car has raveled afer hours, hen finding he slope
SM Dae: Secion: Objecive: The average rae of change beween wo poins on a funcion is d. For example, if he funcion ( ) represens he disance in miles ha a car has raveled afer hours, hen finding he slope
Homework sheet Exercises done during the lecture of March 12, 2014
 EXERCISE SESSION 2A FOR THE COURSE GÉOMÉTRIE EUCLIDIENNE, NON EUCLIDIENNE ET PROJECTIVE MATTEO TOMMASINI Homework shee 3-4 - Exercises done during he lecure of March 2, 204 Exercise 2 Is i rue ha he parameerized
EXERCISE SESSION 2A FOR THE COURSE GÉOMÉTRIE EUCLIDIENNE, NON EUCLIDIENNE ET PROJECTIVE MATTEO TOMMASINI Homework shee 3-4 - Exercises done during he lecure of March 2, 204 Exercise 2 Is i rue ha he parameerized
= ( ) ) or a system of differential equations with continuous parametrization (T = R
 XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
Math 36. Rumbos Spring Solutions to Assignment #6. 1. Suppose the growth of a population is governed by the differential equation.
 Mah 36. Rumbos Spring 1 1 Soluions o Assignmen #6 1. Suppose he growh of a populaion is governed by he differenial equaion where k is a posiive consan. d d = k (a Explain why his model predics ha he populaion
Mah 36. Rumbos Spring 1 1 Soluions o Assignmen #6 1. Suppose he growh of a populaion is governed by he differenial equaion where k is a posiive consan. d d = k (a Explain why his model predics ha he populaion
Chapter 15: Phenomena. Chapter 15 Chemical Kinetics. Reaction Rates. Reaction Rates R P. Reaction Rates. Rate Laws
 Chaper 5: Phenomena Phenomena: The reacion (aq) + B(aq) C(aq) was sudied a wo differen emperaures (98 K and 35 K). For each emperaure he reacion was sared by puing differen concenraions of he 3 species
Chaper 5: Phenomena Phenomena: The reacion (aq) + B(aq) C(aq) was sudied a wo differen emperaures (98 K and 35 K). For each emperaure he reacion was sared by puing differen concenraions of he 3 species
AP CALCULUS AB 2003 SCORING GUIDELINES (Form B)
 SCORING GUIDELINES (Form B) Quesion A ank conains 15 gallons of heaing oil a ime =. During he ime inerval 1 hours, heaing oil is pumped ino he ank a he rae 1 H ( ) = + ( 1 + ln( + 1) ) gallons per hour.
SCORING GUIDELINES (Form B) Quesion A ank conains 15 gallons of heaing oil a ime =. During he ime inerval 1 hours, heaing oil is pumped ino he ank a he rae 1 H ( ) = + ( 1 + ln( + 1) ) gallons per hour.
3.6 Derivatives as Rates of Change
 3.6 Derivaives as Raes of Change Problem 1 John is walking along a sraigh pah. His posiion a he ime >0 is given by s = f(). He sars a =0from his house (f(0) = 0) and he graph of f is given below. (a) Describe
3.6 Derivaives as Raes of Change Problem 1 John is walking along a sraigh pah. His posiion a he ime >0 is given by s = f(). He sars a =0from his house (f(0) = 0) and he graph of f is given below. (a) Describe
dt = C exp (3 ln t 4 ). t 4 W = C exp ( ln(4 t) 3) = C(4 t) 3.
 Mah Rahman Exam Review Soluions () Consider he IVP: ( 4)y 3y + 4y = ; y(3) = 0, y (3) =. (a) Please deermine he longes inerval for which he IVP is guaraneed o have a unique soluion. Soluion: The disconinuiies
Mah Rahman Exam Review Soluions () Consider he IVP: ( 4)y 3y + 4y = ; y(3) = 0, y (3) =. (a) Please deermine he longes inerval for which he IVP is guaraneed o have a unique soluion. Soluion: The disconinuiies
d = ½(v o + v f) t distance = ½ (initial velocity + final velocity) time
 BULLSEYE Lab Name: ANSWER KEY Dae: Pre-AP Physics Lab Projecile Moion Weigh = 1 DIRECTIONS: Follow he insrucions below, build he ramp, ake your measuremens, and use your measuremens o make he calculaions
BULLSEYE Lab Name: ANSWER KEY Dae: Pre-AP Physics Lab Projecile Moion Weigh = 1 DIRECTIONS: Follow he insrucions below, build he ramp, ake your measuremens, and use your measuremens o make he calculaions
WEEK-3 Recitation PHYS 131. of the projectile s velocity remains constant throughout the motion, since the acceleration a x
 WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
2.7. Some common engineering functions. Introduction. Prerequisites. Learning Outcomes
 Some common engineering funcions 2.7 Inroducion This secion provides a caalogue of some common funcions ofen used in Science and Engineering. These include polynomials, raional funcions, he modulus funcion
Some common engineering funcions 2.7 Inroducion This secion provides a caalogue of some common funcions ofen used in Science and Engineering. These include polynomials, raional funcions, he modulus funcion
Check in: 1 If m = 2(x + 1) and n = find y when. b y = 2m n 2
 7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
Mon Apr 9 EP 7.6 Convolutions and Laplace transforms. Announcements: Warm-up Exercise:
 Mah 225-4 Week 3 April 9-3 EP 7.6 - convoluions; 6.-6.2 - eigenvalues, eigenvecors and diagonalizabiliy; 7. - sysems of differenial equaions. Mon Apr 9 EP 7.6 Convoluions and Laplace ransforms. Announcemens:
Mah 225-4 Week 3 April 9-3 EP 7.6 - convoluions; 6.-6.2 - eigenvalues, eigenvecors and diagonalizabiliy; 7. - sysems of differenial equaions. Mon Apr 9 EP 7.6 Convoluions and Laplace ransforms. Announcemens:
Solutions from Chapter 9.1 and 9.2
 Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
Math 10C: Relations and Functions PRACTICE EXAM
 Mah C: Relaions and Funcions PRACTICE EXAM. Cailin rides her bike o school every day. The able of values shows her disance from home as ime passes. An equaion ha describes he daa is: ime (minues) disance
Mah C: Relaions and Funcions PRACTICE EXAM. Cailin rides her bike o school every day. The able of values shows her disance from home as ime passes. An equaion ha describes he daa is: ime (minues) disance
t is a basis for the solution space to this system, then the matrix having these solutions as columns, t x 1 t, x 2 t,... x n t x 2 t...
 Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
Fishing limits and the Logistic Equation. 1
 Fishing limis and he Logisic Equaion. 1 1. The Logisic Equaion. The logisic equaion is an equaion governing populaion growh for populaions in an environmen wih a limied amoun of resources (for insance,
Fishing limis and he Logisic Equaion. 1 1. The Logisic Equaion. The logisic equaion is an equaion governing populaion growh for populaions in an environmen wih a limied amoun of resources (for insance,
Variable acceleration, Mixed Exercise 11
 Variable acceleraion, Mixed Exercise 11 1 a v 1 P is a res when v 0. 0 1 b s 0 0 v d (1 ) 1 0 1 0 7. The disance ravelled by P is 7. m. 1 a v 6+ a d v 6 + When, a 6+ 0 The acceleraion of P when is 0 m
Variable acceleraion, Mixed Exercise 11 1 a v 1 P is a res when v 0. 0 1 b s 0 0 v d (1 ) 1 0 1 0 7. The disance ravelled by P is 7. m. 1 a v 6+ a d v 6 + When, a 6+ 0 The acceleraion of P when is 0 m
Physics 101 Fall 2006: Exam #1- PROBLEM #1
 Physics 101 Fall 2006: Exam #1- PROBLEM #1 1. Problem 1. (+20 ps) (a) (+10 ps) i. +5 ps graph for x of he rain vs. ime. The graph needs o be parabolic and concave upward. ii. +3 ps graph for x of he person
Physics 101 Fall 2006: Exam #1- PROBLEM #1 1. Problem 1. (+20 ps) (a) (+10 ps) i. +5 ps graph for x of he rain vs. ime. The graph needs o be parabolic and concave upward. ii. +3 ps graph for x of he person
Physics 218 Exam 1. with Solutions Fall 2010, Sections Part 1 (15) Part 2 (20) Part 3 (20) Part 4 (20) Bonus (5)
 Physics 18 Exam 1 wih Soluions Fall 1, Secions 51-54 Fill ou he informaion below bu o no open he exam unil insruce o o so! Name Signaure Suen ID E-mail Secion # ules of he exam: 1. You have he full class
Physics 18 Exam 1 wih Soluions Fall 1, Secions 51-54 Fill ou he informaion below bu o no open he exam unil insruce o o so! Name Signaure Suen ID E-mail Secion # ules of he exam: 1. You have he full class
Solutionbank Edexcel AS and A Level Modular Mathematics
 Page of 4 Soluionbank Edexcel AS and A Level Modular Mahemaics Exercise A, Quesion Quesion: Skech he graphs of (a) y = e x + (b) y = 4e x (c) y = e x 3 (d) y = 4 e x (e) y = 6 + 0e x (f) y = 00e x + 0
Page of 4 Soluionbank Edexcel AS and A Level Modular Mahemaics Exercise A, Quesion Quesion: Skech he graphs of (a) y = e x + (b) y = 4e x (c) y = e x 3 (d) y = 4 e x (e) y = 6 + 0e x (f) y = 00e x + 0
EXERCISES FOR SECTION 1.5
 1.5 Exisence and Uniqueness of Soluions 43 20. 1 v c 21. 1 v c 1 2 4 6 8 10 1 2 2 4 6 8 10 Graph of approximae soluion obained using Euler s mehod wih = 0.1. Graph of approximae soluion obained using Euler
1.5 Exisence and Uniqueness of Soluions 43 20. 1 v c 21. 1 v c 1 2 4 6 8 10 1 2 2 4 6 8 10 Graph of approximae soluion obained using Euler s mehod wih = 0.1. Graph of approximae soluion obained using Euler
Math 2214 Solution Test 1A Spring 2016
 Mah 14 Soluion Tes 1A Spring 016 sec Problem 1: Wha is he larges -inerval for which ( 4) = has a guaraneed + unique soluion for iniial value (-1) = 3 according o he Exisence Uniqueness Theorem? Soluion
Mah 14 Soluion Tes 1A Spring 016 sec Problem 1: Wha is he larges -inerval for which ( 4) = has a guaraneed + unique soluion for iniial value (-1) = 3 according o he Exisence Uniqueness Theorem? Soluion
Physics Notes - Ch. 2 Motion in One Dimension
 Physics Noes - Ch. Moion in One Dimension I. The naure o physical quaniies: scalars and ecors A. Scalar quaniy ha describes only magniude (how much), NOT including direcion; e. mass, emperaure, ime, olume,
Physics Noes - Ch. Moion in One Dimension I. The naure o physical quaniies: scalars and ecors A. Scalar quaniy ha describes only magniude (how much), NOT including direcion; e. mass, emperaure, ime, olume,
