Analytical models for fishery reference points
|
|
|
- Hector Parker
- 5 years ago
- Views:
Transcription
1 515 Analytical models for fishery reference points Jon T. Schnute and Laura J. Richards Abstract: Fishery reference points are widely applied in formulating harvest management policies. We supply precise mathematical definitions for several reference points in common use. We then derive analytical expressions for these quantities from age-structured population models. In particular, we explain how the maximum sustainable harvest rate and catch (h*, C*), two quantities of management importance, can replace the classical recruitment parameters (α, β) in the Beverton Holt and Ricker recruitment curves. We also demonstrate dependencies of various reference points on subsets of model parameters. Although our analysis is restricted to special cases, our models still have general utility. For example, simple calculations from analytical formulas enable checks on the output from more complex models and guide the choice of reference points for fishery management. Résumé : Certains paramètres de référence sont couramment employés pour la formulation des politiques d exploitation des pêches. Nous donnons une définition mathématique précise de divers paramètres de référence d usage courant et nous développons les formules d analyse correspondantes à partir de modèles de populations à structure par âges. Plus particulièrement, nous expliquons comment deux paramètres importants en gestion, soit le taux d exploitation maximal et les captures (h*, C*), peuvent remplacer les paramètres de recrutement classiques (α, β) dans les fonctions de recrutement de Beverton Holt et de Ricker. Nous montrons aussi le lien de dépendance qui existe entre divers paramètres de référence et des sous-ensembles de paramètres de modélisation. Bien que notre analyse ne porte que sur des cas spéciaux, nos modèles sont quand même d une utilité générale. Par exemple, de simples calculs, effectués avec les formules d analyse, permettent de vérifier les résultats de modèles plus complexes et guident le choix des paramètres de référence à retenir pour la gestion d une pêche. [Traduit par la Rédaction] Introduction Mathematical models have been used extensively to estimate fish population parameters from fishery data. These parameters typically govern the dynamics of recruitment, mortality, and growth. From a management perspective, the underlying population dynamics must be translated into decision rules, such as the biomass of fish that can safely be removed by the fishery. Thus, management focus shifts from biological parameters to quantities that more directly guide the decision process. Such quantities are commonly termed reference points. International agreements (e.g., United Nations 1995) now include specific recommendations on the use of precautionary reference points for fish stock conservation. Caddy and Mahon (1995), Caddy and McGarvey (1996), and Garcia (1994, 1996) discuss practical applications of this approach. Any reference point ultimately depends on the parameters that govern population dynamics. For example, the catch that can safely be removed must somehow depend on the population s recruitment patterns. In this paper, we give precise mathematical definitions for several proposed reference points, based on concepts of extinction, maximum sustainable yield, yield per recruit (Deriso 1982, 1987), and spawners per recruit (Shepherd 1982; Clark 1991, 1993; Mace 1994). We then derive analytical expressions for these quantities from Received April 2, Accepted June 11, J13940 J.T. Schnute 1 and L.J. Richards. Fisheries and Oceans Canada, Science Branch, Pacific Biological Station, 3190 Hammond Bay Road, Nanaimo, BC V9R 5K6, Canada. 1 Author to whom all correspondence should be addressed. schnutej@dfo-mpo.gc.ca Can. J. Fish. Aquat. Sci. 55: (1998) age-structured population models. Thus, at least for certain special cases, we express modern reference points in terms of classical biological parameters. Our formulas provide an intuitive and quantitative link between biology and fishery management. This paper consolidates a number of significant developments in the history of fishery assessment models. It includes yield per recruit analyses comparable with those originally proposed by Beverton and Holt (1957), as well as the recruitment models described by Schaefer (1954), Beverton and Holt (1957), Ricker (1958), Deriso (1980), and Schnute (1985). The age-structured models here contain some of the features discussed by Gulland (1965), Pope (1972), Fournier and Archibald (1982), and Deriso et al. (1985). We also derive moment equations similar to those found by Deriso (1980), Schnute (1985, 1987), and Fournier and Doonan (1987), as reviewed by Hilborn and Walters (1992, chap. 9). Following Deriso (1982, 1987), we use these moment equations to obtain analytic expressions for modern reference points. In particular, our analysis extends recent work by Schnute and Kronlund (1996), who showed that classical recruitment curves could be written explicitly in terms of management parameters. They considered only the case motivated by salmonid species, in which adults die after spawning. Here, we model agestructured populations that spawn multiple times, and our result includes that of Schnute and Kronlund (1996) as a special case. Analytical formulas for reference points in age-structured models require somewhat restrictive assumptions. We present two underlying models. The first deals only with population numbers, while the second describes stock biomass and fish growth. Because the second model contains the first as a special case, we could theoretically have confined our discussion
2 516 Table 1. Deterministic age-structured model for fish numbers, assuming knife-edged recruitment and maturity, with age at recruitment equal to age at maturity. Parameters (T1.1) F = (α, β, γ, δ) (T1.2) β >0;0<δ 1 (T1.3) α > δ Model 1: Age-structured population (T1.4) N 1t =αs t r (1 βγs t r ) 1/γ (T1.5) N at = (1 δ)(n a 1, t 1 C a 1, t 1 ); a 2 (T1.6) C at = h t N at (T1.7) (T1.8) (T1.9) (T1.10) S t = (N at C at ) Moments R t = N 1t P t = Nat C t = Cat Model 1A: Moment equations (T1.11) R t =αs t r (1 βγs t r ) 1/γ (T1.12) P t = R t + (1 δ)s t 1 (T1.13) (T1.14) C t = h t P t S t = P t C t entirely to the second. Unfortunately, the algebra and resulting formulas are much more complex in the general case, and we use the first model to develop intuition about the problem. Furthermore, by considering two models, we can investigate the role of key assumptions in the analytical results. To keep the paper compact and give the reader perspective on our analyses, we present most of our assumptions and results in tables. We distinguish equations in tables by using the prefix T. Thus, the symbols (2.3) and (T2.3) denote the third equation in section 2 and Table 2, respectively. We confine all mathematical proofs to Appendices A E. Section 1 defines our first model and presents corresponding moment equations and equilibrium conditions. Section 2 provides mathematical definitions for various reference points and expresses them analytically in terms of parameters for model 1. Section 3 extends these results to model 2. We discuss further implications of our analysis in section Age-structured model Our first model (model 1 in Table 1) consists of the four equations (T1.4) (T1.7). These represent an age-structured population that experiences recruitment, harvest, and survival. The matrix N at denotes the number of fish in age-class a at the start of year t. Similarly, C at indicates the number caught from ageclass a during year t. Fish are fully recruited into age-class 1, which corresponds to the actual age r. Thus, the spawning Can. J. Fish. Aquat. Sci. Vol. 55, 1998 stock S t r from year t rgives birth to recruits N 1t in year t. The first equation (T1.4) expresses this relationship with the recruitment function (1.1) f (S; α, β, γ) =αs(1 βγs) 1/γ. As discussed by Schnute (1985), (1.1) reduces to functions proposed by Beverton and Holt (1957), Ricker (1958), or Schaefer (1954) when γ is fixed at 1, 0, or 1, respectively. The parameters (α, β, γ) in (T1.4) have simple biological interpretations: α measures productivity at low stock sizes, β is a population scale parameter, and γ determines the overall shape of the recruitment curve. In particular, α and γ are dimensionless. The units of β relate to population measurements. For example, if S is measured in thousands of fish, then β has units 10 3 fish 1. For age-classes a 2, the second equation (T1.5) expresses the population N at as survivors from the population N a 1, t 1 in the preceding year. First, the catch C a 1, t 1 is removed; then the remaining population experiences a death rate δ, so that the fraction 1 δ survives. Fishery literature often uses a parameter M to quantify natural mortality. In this context, δ can be interpreted as (1.2) δ=1 e M. For small values of M, (1.2) implies the approximation δ M. The third equation (T1.6) relates the catch C at to the harvest rate h t in year t and the population N at. Thus, the fraction h t acts as a control variable in this model, related to the classical fishing mortality F t by (1.3) h t = 1 e F t. Again, h t F t for small F t. The final equation (T1.7) assumes that the stock S t available for future recruitment consists of all survivors from the fishery. Model 1 contains several simplifying assumptions. It represents a population with knife-edged selectivity by the fishery. New recruits at age r (age-class 1) enter the population at the start of each year t. Along with survivors from the previous year, these are equally vulnerable to the fishery, where the catch at age a is proportional to abundance at age a. After the fishery, the recruited population also comprises the spawning stock, and spawning occurs prior to natural mortality. Thus, the model assumes a regular annual cycle of recruitment, fishing, spawning, and natural mortality. In particular, fishing and natural mortality do not occur simultaneously. We make these assumptions to keep the model as simple as possible, although we could develop similar analyses starting from different assumptions about the population life cycle. Conceptually, model 1 specifies the process component of a state space model (Schnute 1994). The four equations recursively define the state variables N at, C at, and S t in terms of parameters (α, β, γ, δ) and controls h t. The controls must be fractions (1.4) 0 h t 1. Similarly, the parameters (T1.1) are subject to the constraints (T1.2). Also, the constraint (T1.3) is required to guarantee that the population can survive (Appendix D). For example, in the salmonid case contemplated by Ricker (1958), adults die when they spawn (δ =1). The condition α > 1 ensures that each adult produces at least one juvenile for the next generation. When
3 Schnute and Richards 517 some adults survive spawning (δ < 1), α can be less than 1, as long as the production rate dominates the death rate (α > δ). As shown in Appendix A, model 1 implies a corresponding model 1A (Table 1) for the four annual quantities S t, R t, P t, and C t, defined by (T1.7) (T1.10), respectively. The four equations (T1.11) (T1.14) give a sequential algorithm for computing the recruitment R t, population P t before fishing, catch C t, and spawning stock S t after the fishery. Both models 1 and 1A involve the four parameters (T1.1) and the harvest rate controls h t. Results that can be proved for model 1A automatically apply to model 1. Furthermore, model 1A has an obvious biological interpretation independent of its derivation from model 1. Thus, the simpler moment model 1A could also be considered a starting point for our analysis. If the harvest rate sequence h t is fixed at a constant value h, then both models 1 and 1A have equilibrium solutions that can be obtained by dropping the index t from the model equations. For example, model 1A then reduces to four simultaneous equations in the four constant states R, P, C, and S. Solving these equations (Appendix B) gives (T2.3) (T2.6) in Table 2. We simplify these results by introducing two new variables, the annual survival rate (1.5) σ t = (1 δ)(1 h t ), which is the product of survivals from natural and fishing mortality, and the recruit per spawner ratio (1.6) ρ t = R t /S t. For a given harvest rate h, equations in Table 2 can be applied sequentially to obtain analytical expressions for equilibrium values of all quantities in models 1 and 1A. These include the equilibrium rates (σ, ρ) obtained from (1.5) (1.6), the four states (R, P, C, S) in model 1A, and the age-structured population (N a ) in model Reference points The equilibrium results in Table 2 can be used to investigate how a population governed by model 1 or 1A responds to a long-term harvest rate h. For example, if (2.1) (α, β, γ, δ) = (1.42, 0.56, 1.0, 0.2), then Figs. 1A 1D represent P, C, C/R, and S/R, respectively, as functions of h. We choose δ=0.2 in (2.1) as typical for a marine species that is available to the fishery for years after recruitment. The parameter γ= 1 selects a Beverton Holt recruitment curve, and we explain below the significance of our choice for (α, β). Case 1 in Table 3 lists all parameters and other quantities associated with Fig. 1. From Fig. 1A, the population P declines with increasing harvest rate h, and extinction occurs when h = The total catch C in Fig. 1B increases to a maximum value 1 when h = 0.25 and then declines to zero at the extinction rate h = The parameters (α, β) in (2.1) have been chosen so that (h, C) = (0.25, 1.0) is the maximum point in Fig. 1B. The maximum C = 1 can be interpreted as one unit of population, which might be measured in thousands or millions of fish. Figure 1C portrays the yield per recruit (YPR) C/R as an increasing function of h, although the curve applies only to the range 0 h < 0.55 in which h is kept below the extinction level. Similarly, Fig. 1D shows that the number of spawners per Table 2. Equilibrium population states expressed as a function of constant harvest rate h, based on the model in Table 1 with ρ=r/s. (T2.1) σ(h) = (1 δ)(1 h) (T2.2) ρ(h)= 1 σ 1 h (T2.3) R(h) = ρ 1 ρ γ βγ α (T3.4) P(h) = R 1 σ (T2.5) (T2.6) (T2.7) C(h) = hp S(h) = (1 h)p N a (h) =σ a 1 R recruit (SPR) S/R declines steadily across the valid range of h. Because S/R is the reciprocal of the equilibrium value ρ from (1.6), it follows that ρ is an increasing function of h. The population trends illustrated in Fig. 1 apply generally to models 1 and 1A, given parameters (α, β, γ, δ) that meet the constraints (T1.2) (T1.3). Intuitively, the total population declines to an extinction level with increasing harvest rate (Fig. 1A). The catch, necessarily zero when h is zero or the extinction rate, follows a dome-shaped curve between these two points (Fig. 1B). The number caught per available recruit steadily increases as h increases (Fig. 1C). Similarly, a higher catch per recruit leaves fewer spawners per recruit (Fig. 1D). Based on these simple ideas, a variety of reference points have been proposed as measures for comparison with possible management actions. Table 4 presents mathematical definitions for common reference values of harvest rate h and catch C. For consistency with the framework being developed here, we use somewhat different notation from that in other literature. Equation (T4.1) defines h as the harvest rate that drives the population to extinction. For example, h = 0.55 in Fig. 1A (Table 3, case 1). The dagger symbol in this notation serves as a reminder of mortality and danger. We use an asterisk in (T4.2) to denote the harvest rate h* that gives the maximum catch C*, which is also termed the maximum sustainable yield (MSY). For example, (h*, C*) = (0.25,1.0) in Fig. 1B (Table 3, case 1). Similarly, the prime symbol in (T4.3) indicates the harvest rate h that maximizes the yield per recruit C/R. The corresponding catch C is defined by (T4.4). In both (T4.2) and (T4.3), the maximum must be taken across the range 0 h h because the equilibrium population P(h) = 0 for h h. Although h* <h (Fig. 1B), models 1 and 1A imply that h occurs at the upper limit h (Fig. 1C). Thus, for these models, h =h and C =0, and the maximum YPR has no interesting biological significance. Later in this paper, we show that the concepts in (T4.3) (T4.4) have greater relevance for biomass models that include fish growth. The remaining reference values (T4.5) (T4.8) in Table 4 are defined relative to an equilibrium population that experiences no harvest. The YPR curve in Fig. 1C has a slope that declines steadily as h increases from zero. Given a fraction x, the harvest rate h x in (T4.5) corresponds to the value h where the slope of this curve equals x times the slope at h = 0. Line segments in Fig. 1C illustrate this concept when x = 0.2. The reference point (h 0.2, C 0.2 ) = (0.31, 0.96) from (T4.5) (T4.6)
4 518 Can. J. Fish. Aquat. Sci. Vol. 55, 1998 Fig. 1. Equilibrium quantities P, C, C/R, and S/R from Table 2 expressed as functions of h with fixed parameters (C*, h*, δ, γ) = (1, 0.25, 0.2, 1), as in Table 3, case 1. Dotted lines correspond to (A) P(h*) and h*, (B) C* and h*, (C) h 0.2, and (D) (S/R) h and h Line segments in 0.35 Fig. 1C indicate slopes of the YPR relationship at h = 0 and h = h 0.2. Broken curves in Figs. 1C and 1D indicate values of h > h. corresponds to a harvest level somewhat higher than the MSY rate h* (Table 3, case 1). Similarly, the SPR curve in Fig. 1D declines steadily as h increases from zero. Given a fraction y, the harvest rate h y in (T4.7) corresponds to the value h at which the ratio S/R equals y times its value at h = 0. Figure 1D illustrates the choice y = 0.35, where the corresponding reference point (h 0.35, C 0.35 ) = (0.27, 1.00) from (T4.7) (T4.8) approximates the MSY point (h*, C*) (Table 3, case 1). The relationship h = 1 e F from (1.3) associates each harvest rate defined in Table 4 with a fishing mortality rate F. The corresponding F-value typically has a precedent in existing fishery literature. For example, the extinction rate h corresponds to F crash (ICES 1996; Cook et al. 1997). Similarly, h*, h, and h y are equivalent to F msy, F max, and F 100y% (Caddy and Mahon 1995). Our reference value h x, like F x in Deriso (1987), is computed from a ratio of slopes on the YPR curve. However, due to a technical difference (described below) in defining the slopes, h x and F x are not related by (1.3). For this reason, we use the reference value h 0.2 in Fig. 1C, rather than the common choice F 0.1 elsewhere. A close examination of definitions clarifies the relationship between h x and F z for different fractions x and z. We obtain h x by plotting YPR C/R in relation to h whereas F z comes from a plot of C/R versus F. Because h is a nonlinear function of F, these two graphs do not have proportional slopes. Define (2.2) h z = 1 e F z to be the harvest rate corresponding to the conventional reference value F z. Then (Appendix E) h x = h z if and only if either of the following two equivalent conditions hold: z (2.3) x =, z = x(1 h 1 h x ). z We show below that our reference value h x leads to simpler analytical results than h z, although (2.3) can be used to convert z to x and vice versa. The definitions in Table 4 apply to any fishery model for which the equilibrium catch C(h), recruitment R(h), and spawning stock S(h) can be expressed as functions of a constant harvest rate h. In general, these can be obtained numerically
5 Schnute and Richards 519 Table 3. Parameters and reference values for the Beverton Holt (γ= 1) and Ricker (γ=0) stock recruitment functions with C* = 1, two choices for (h*, δ), and additional parameters (, w, κ) = (1, 5, 0) for model 2. δ=0.2 δ=0.4 Model 1 Model 2 Model 1 Model 2 γ= 1 γ=0 γ= 1 γ=0 γ= 1 γ=0 γ= 1 γ=0 Case 1 a 2 3 b 4 c α β h* h h h h C* C C C a Case associated with Fig. 1. b Case associated with Fig. 2. c Case associated with Fig. 3. Table 4. Definitions of fishery reference values. Extinction (T4.1) P(h ) = 0 Maximum sustainable yield (MSY) (T4.2) (T4.3) (T4.4) C* = C(h*) = max C(h) 0 h h Yield per recruit (YPR) C(h ) R(h ) = max C(h) 0 h h R(h) C =C(h ) (T4.5) d(c/r) dh = x d(c/r) h=h x dh ; 0 x 1 h=0 (T4.6) C x = C(h x ) Spawners per recruit (SPR) (T4.7) (T4.8) (S/R) h=h y = y(s/r) h=0; 0 y 1 C y = C(h y ) from simulations. For example, with given parameters (T1.1) and constant harvest rate h, the dynamic equations (T1.4) (T1.7) of model 1 can be run sequentially until the moments (T1.7) (T1.10) reach equilibrium. Repeating this process for multiple values of h gives equilibrium functions that can be graphed to obtain the reference points illustrated in Fig. 1. In this paper, we avoid simulation by deriving analytical formulas for the reference points in Table 4. Table 5 relates h*, C*, h, h x, and h y to the parameters (α, β, γ, δ) in model 1. Although the MSY point (h*, C*) cannot be expressed analytically in terms of (α, β), equations (T5.2) (T5.3) give the opposite relationship: (2.4) (h*, C*) (α, β). For simplicity, these equations include the survival rate σ* in Table 5. Key equations for biological reference values derived from the equilibrium model in Table 2. (T5.1) (T5.2) (T5.3) β= σ* = (1 δ)(1 h*) α= 1 σ 1 + γh 1 h 1 σ (T5.1) associated with the MSY harvest h*. The example in Fig. 1 illustrates their application, where parameters (α, β) in (2.1) are computed by (T5.2) (T5.3) from the MSY point (h*, C*) = (0.25,1.0). More generally, this approach makes it possible to express the recruitment function (1.1) for model 1 directly in terms of (h*, C*). Schnute and Kronlund (1996) discuss the management implications of this function in the context of salmon populations, where adults die after spawning. When δ=1, our results (T5.2) (T5.3) reduce to theirs (Schnute and Kronlund 1996, equations (T3.3) (T3.4), p. 1283). Conversely, our analysis extends theirs to marine populations in which adults may survive to spawn multiple times. Reference values h, h, h x, and h y for model 1 can be computed from the simple analytic expressions (T5.4) (T5.6). The extinction rate h depends only on the productivity parameter α and the death rate δ. In particular, the condition (T1.3) guarantees that h > 0. Because h x and h y are derived from yield and spawners per recruit, these values depend only on δ and 1/γ h 2 (1 h )(1 σ +γh )C (T5.4) h = h = α δ 1 +α δ (T5.5) (T5.6) h x = δ x 1/2 1 x 1/2 1 δ ; δ α (1 +α δ)<x1/2 < 1 δ(1 y) h y = δ+(1 δ)y ; δ α < y < 1
6 520 Table 6. Explicit formulas for quantities associated with MSY, based on the equilibrium model in Table 2 when γ= 1 (Beverton Holt recruitment curve). (T6.1) ρ =(αδ) 1/2 (T6.2) h = (αδ)1/2 δ 1 +(αδ) 1/2 δ (T6.3) C = 1 β (α1/2 δ 1/2 ) 2 (T6.4) R = α1/2 β (α1/2 δ 1/2 ) (T6.5) P = 1 βδ 1/2 (α1/2 δ 1/2 )(1 +(αδ) 1/2 δ) (T6.6) S = 1 βδ 1/2 (α1/2 δ 1/2 ) the choice of fraction x or y, independent of the recruitment function (1.1). However, because the extinction rate depends on α, lower bounds for x and y also depend on α. The fractions x and y can always be adjusted to give equivalent reference points. For example, given x, h y = h x if (2.5) y = δ(1 h x). δ+(1 δ)h x The classical reference value h z in (2.2) can be expressed analytically for model 1 as (2.6) h z = δ 1 δ [δ 2 + 4z(1 δ)] 1/2 δ 2z(1 δ). 2z(1 δ) This result comes from a quadratic equation in h z (Appendix E). By contrast, a linear equation in h x gives the simpler expression (T5.5), which we prefer to (2.6). As stated earlier, the transformations (2.3) can be used to convert between x and z corresponding to equivalent reference values h x = h z. For the Beverton Holt recruitment curve (γ = 1) in model 1, simple analytic formulas can be obtained for all population variables associated with MSY (Table 6). Consistent with our earlier notation (h*, C*) for the MSY point, we denote other MSY state variables with an asterisk. In particular, the recruit to spawner ratio ρ* = R*/S* in this case is simply the geometric mean (T6.1) of the production rate α and death rate δ. Equations (T6.2) (T6.3) provide an inverse of the transformation (2.4) in (T5.2) (T5.3) when γ= 1. Thus, in the Beverton Holt context, h* and C* can be written explicitly in terms of (α, β, δ). The role of the dimensioned parameter β becomes clear in Table 6, where all population variables (C*, R*, P*, S*) are scaled to 1/β. 3. Weight-structured model Our second model (model 2 in Table 7) extends the first by including population weight structure. We assume that the weight w a of fish at age a conforms to the von Bertalanffy growth function (Ricker 1975, p. 221) (3.1) w a = w[1 e K(a a 0 ) ] with three parameters (w, K, a 0 ). This function can also be Table 7. Deterministic age-structured model that incorporates fish growth, where all population variables (3.3) have units of biomass. Parameters (T7.1) F = (α, β, γ, δ,, w, κ) (T7.2) β >0;0<δ 1; w ;0 κ<1 (T7.3) α (1 κ)(1 δ) δ+(1 κ)(1 δ) w >δ 1 Weights (T7.4) w a = w (w ) κ a 1 (T7.5) w a = (1 κ)w +κw a 1 written in the equivalent form (T7.4) with parameters (, w, κ), where is the weight of the first age-class from (3.1) and (3.2) κ=e K. Thus, the parameters (T7.1) for model 2 include the four parameters (T1.1) in model 1, plus the three growth parameters in (T7.4). Furthermore, (T7.4) implies the recursive relationship (T7.5), in which w a is an average of w and w a 1, weighted by 1 κ and κ, respectively. The four equations (T7.6) (T7.9) that define model 2 are identical to (T1.4) (T1.7) for model 1, except that the survival equation (T7.7) contains the weight adjustment factor w a /w a 1. w Model 2: Age-structured biomass (T7.6) N 1t =αs t r (1 βγs t r ) 1/γ (T7.7) (T7.8) (T7.9) (T7.10) (T7.11) (T7.12) N at = w a w a 1 (1 δ)(n a 1,t 1 C a 1,t 1 ) ; a 2 C at = h t N at S t = (N at C at ) Moments R t = N 1t (T7.13) W t = P t = Nat C t = Cat P t (N at /w a ) Model 2A: Moment equations (T7.14) R t =αs t r (1 βγs t r ) 1/γ (T7.15) (T7.16) (T7.17) (T7.18) P t = R t + (1 κ)w +κw t 1 W t 1 R t W t = P t +(1 δ) S 1 t 1 W t 1 C t = h t P t S t = P t C t Can. J. Fish. Aquat. Sci. Vol. 55, 1998 (1 δ)s t 1
7 Schnute and Richards 521 This factor accounts for biomass growth from age a 1 to age a. We redefine all population variables (3.3) N at, P t, R t, S t, C at, C t in model 2 to be measures of biomass, rather than numbers as in model 1. In particular, we use N at to denote biomass at age. Similarly, P t denotes total population biomass in place of the common notation B t (Hilborn and Walters 1992). We make this choice to avoid prolific notation, with replacement letters for each variable in (3.3). Three of the seven model parameters (T7.1) are dimensioned: β has units of inverse biomass, and and w have units of fish weight. Biomass and weight typically have different units. For example, individual fish and population biomass might be measured in kilograms and tonnes, respectively. Model parameters must conform to the obvious constraints (T7.2). In particular, because K > 0 in (3.1), κ in (3.2) must be a fraction. We allow the special case κ=0 (3.4) w a =, a = 1 w, a 2 which corresponds to the limit in (T7.4) as κ 0. In effect, fish reach the asymptotic weight w at age 2, so that only two weight-classes are present in the population. Incidentally, the case κ=1 is degenerate in (T7.4) because the free parameter w then cancels from the equation. Model 2 reduces to model 1 when (3.5) = w. In this case, (T7.4) implies constant weight w a = w ; consequently, w a /w a 1 = 1, and equations (T1.5) and (T7.7) become identical. The constraint (T7.3) for model 2 also reduces to the simpler constraint (T1.3) when = w. Intuitively, (T1.3) guarantees that a model 1 population can survive because recruitment exceeds losses from natural mortality. More generally (Appendix D), the constraint (T7.3) ensures that a model 2 population can survive because the combined effects of recruitment and growth exceed the loss of biomass through natural mortality. To construct moment equations for model 2, we define moments (T7.10) (T7.12) analogous to those for model 1. We also define the mean weight W t in (T7.13) as the ratio of total biomass P t to total population numbers. In particular, because N at denotes biomass, the total population at the start of year t is Σ a (N at /w a ). The assumptions and definitions (T7.6) (T7.13) of model 2 imply model 2A: five moment equations (T7.14) (T7.18) that recursively update the five population variables R t, P t, W t, C t, and S t (Appendix A). Intuitively, the survival equation (T7.15) comes partly from the growth relationship (T7.5). After 1 year, the mean size W t 1 grows to the new size (1 κ)w +κw t 1. The weight ratio in (T7.15) accounts for the growth of survivors (1 δ)s t 1 from year t 1. In the compact form listed in Table 7, model 2A is new to fisheries literature. It has the desirable property that the population mean weight W t responds naturally to the effects of recruitment R t and harvest rate h t. Logical connections between models 2 and 2A mirror those between models 1 and 1A. Results from model 2A automatically apply to model 2, and the simpler model 2A could be taken as a starting point for our analysis. Given a constant harvest rate h, equilibrium versions of the Table 8. Equilibrium population states expressed as a function of constant harvest rate h, based on the model in Table 7. (T8.1) σ(h) = (1 δ)(1 h) (T8.2) W(h)= (1 σ) +(1 κ)σw 1 κσ (T8.3) ρ(h) = 1 σ W 1 h (T8.4) R(h)= ρ 1 ρ γ βγ α (T8.5) P(h)= W R 1 σ (T8.6) (T8.7) (T8.8) C(h) = hp S(h) = (1 h)p N a (h)= w a σ a 1 R five equations in model 2A can be solved to obtain equilibrium functions W(h), R(h), P(h), C(h), and S(h) (Appendix B). Results of this analysis are summarized in Table 8, where we also include equilibrium versions of σ t and ρ t defined in (1.5) (1.6) and the age-structured biomass N at from model 2. In particular, the mean weight W(h) can be expressed as an average of and w, weighted in proportion to 1 σ and (1 κ)σ, respectively. Table 8 makes it easy to produce graphs for model 2 similar to those devised for model 1. For example, Fig. 2 corresponds to case 3 in Table 3. The parameters (h*, C*, γ, δ) = (0.25, 1.0, 1, 0.2) are identical to those used in Fig. 1 (Table 3, case 1); however, the choice (, w,, κ) = (1, 5, 0) corresponds to a growth relationship (3.4) in which fish older than age-class 1 have five times the weight of new recruits. At least two features distinguish Fig. 2 from Fig. 1. First, the extinction rate h = 0.61 is higher (Figs. 2A and 2B), due to the benefits of biomass growth. Second, the YPR curve (Fig. 2C) is dome shaped, with a maximum YPR achieved when h =0.38. A harvest rate higher than h reduces the proportion of large fish and, consequently, reduces the yield available from fish growth. Model 1, which does not consider growth, inherently lacks this feature (e.g., Fig. 1C). Equilibrium equations for model 2 can be used to derive analytic expressions for reference points, similar to those obtained for model 1 (Appendices C E). Table 9 illustrates some of the possibilities. Equations (T9.1) (T9.5) extend (T5.1) (T5.3) from model 1 to model 2, based on the MSY mean weight W* and another quantity Q* (discussed below). Thus, as in (2.4), α and β can be computed explicitly from the parameter vector (3.6) F* = (h*, C*, γ, δ,, w, κ) by the sequential algorithm (T9.1) (T9.5). In effect, (h*, C*) can replace (α, β) in the parameter vector (T7.1) for model 2. For example, these equations have been used to compute (α, β) for each case in Table 3 from specified MSY parameters (C* = 1; h* = 0.25 or 0.35). To avoid excessive complexity, the remaining reference points in Table 9 are obtained analytically only for the special
8 522 Can. J. Fish. Aquat. Sci. Vol. 55, 1998 Fig. 2. Equilibrium quantities P, C, C/R, and S/R from Table 8 expressed as functions of h with fixed parameters (C*, h*, δ, γ,, w, κ) = (1, 0.25, 0.2, 1, 1, 5, 0), as in Table 3, case 3. Dotted lines correspond to (A) P(h*) and h*, (B) C* and h*, (C) h 0.2, and (D) (S/R) h 0.35 Line segments in Fig. 2C indicate slopes of the YPR relationship at h = 0 and h = h 0.2. Broken curves in Figs. 2C and 2D indicate values of h > h. and h case κ=0 in (3.4). Furthermore, under the constant-weight condition (3.5), model 2 reduces to model 1, and the results in Table 9 simplify to those in Table 5. When (3.5) holds, W* = in (T9.2) and any quantity denoted Q in Table 9 becomes zero. From these facts, it is fairly easy to see by inspection that, given (3.5), expressions for α, β, h, h x, and h y in Table 9 reduce to their counterparts in Table 5. When κ=0, equations (T9.6) (T9.12) in Table 9 show the dependencies of various reference points on the remaining six parameters (α, β, γ, δ,, w ) from (T7.1). In particular, h depends only on (α, δ,, w ). Furthermore, as in Table 5, h, h x, and h y are independent of the recruitment parameters (α, β, γ). A modal YPR harvest rate h exists only if the condition w > /(1 δ) in (T9.8) holds. This condition can be given biological meaning in light of the growth function (3.4). The population consists of recruits with weight and survivors with weight w. The survivor weight must be large enough to compensate for biomass lost by the death of recruits. So far, our discussion of Table 3 has been confined to cases 1 and 3, used to construct Figs. 1 and 2. More generally, we examine two values δ, corresponding to relatively longlived (δ =0.2) and short-lived (δ =0.4) populations. We use values of h* close to δ, based on the concept that populations can sustain harvest rates near the natural mortality rate. Thus, (h*, δ) = (0.25, 0.2) in cases 1 4 and (h*, δ) = (0.35, 0.4) in cases 5 8. We also investigate Beverton Holt and Ricker recruitment functions, where the former has been used in both Figs. 1 and 2. For comparison, case 4 corresponds to a Ricker function with other parameters (3.6) the same as in case 3. Figure 3 illustrates equilibrium plots for case 4, which are similar to those in Fig. 2, except that the convexity of P(h) has changed. Reference values h 0.2 and h 0.35 for the examples in Table 3 are consistently more precautionary than h* for model 2 and less precautionary than h* for model 1. In particular, when δ=0.4, the value x = 0.2 in h x for model 1 (cases 5 and 6) violates the constraint in (T5.5). As discussed above, reference values h x and h y are independent of the recruitment parameters
9 Schnute and Richards 523 (α, β, γ). However, corresponding catch values C x and C y vary slightly with the choice of Beverton Holt or Ricker function. Furthermore, the extinction rate h is consistently lower for the Ricker function. 4. Discussion Models 1 and 2 provide a conceptual framework for modern stock assessment, including the analysis of fishery reference points. These models represent the basic processes of recruitment, fishing, natural mortality, and growth from which more realistic models can be developed. Although models 1 and 2 contain simplifying assumptions, we believe that they still have general utility. In particular, simple models serve to highlight important model features, such as dependencies of reference points on subsets of model parameters. For example, we have illustrated how reference values h x and h y in Tables 5 and 9 do not depend on the recruitment function, although admissible values x and y depend (through h ) on the productivity parameter α. Our appendices illustrate the derivation of analytical reference points from basic theoretical concepts. Thus, simple model assumptions lead to many interesting analytical results, such as the relationship (2.5) between h x and h y for a given x. Our proofs can be used to guide the exploration of other reference point definitions in the context of models similar to those discussed here. In addition, the logical framework here ties together a disparate literature on fisheries stock assessment. For simplicity, our models assume that natural mortality occurs after the fishery, in contrast with the typical Baranov assumption of concurrent fishing and natural mortality. As in (1.3), we express results in terms of harvest rates h, rather than fishing mortalities F. We distinguish reference values with mathematical accents to achieve compactness. Other less cryptic notation could be devised, such as h MSY = h*, h YPR, x = h x, and h SPR, y = h y. With appropriate choices of model parameters, our analytical results can be used to check the output from more realistic models. For example, although we have assumed knife-edged selectivity, age a = 1 could approximate the average age at recruitment for a population in which the fishery selectivity varies with age. Similarly, given the simplifying assumption κ=0 in (3.4) and Table 9, the weight parameter w could be selected to approximate the average population weight, exclusive of new recruits. The same approximation can be used for growth laws other than the von Bertalanffy relationship (T7.4). The classical YPR analysis of Beverton and Holt (1957) involves two control parameters: fishing mortality rate F and the first recruitment age r. We have considered models with only one control parameter, the harvest rate h = 1 e F. However, our models could easily be extended to include age r as a control in the classical sense. This could be achieved by including a death rate parameter in the recruitment equations (T1.4) and (T7.6) and by redefining as a function of r. Schnute and Kronlund (1996) argued that the transition (2.4) resulted in parameters (h*, C*) that had greater relevance to management policy and that possessed improved statistical properties relative to (α, β). However, they considered a simplified version of model 1 in which fish die after spawning. We have extended their analysis to multiple spawning Table 9. Key equations for biological reference points derived from the equilibrium model in Table 8. (T9.1) (T9.2) σ* = (1 δ)(1 h*) W = (1 σ ) +(1 κ)σ w 1 κσ (T9.3) Q = 1 1 σ W 1 κσ (T9.4) α= 1 σ 1 + γ(1 + Q )h W 1 h 1 σ (T9.5) β= (T9.6) Q = populations that experience von Bertalanffy growth. For these more general models, we have shown that the transition (2.4) can still be expressed analytically, so that (h*, C*, γ) canbe used as the set of recruitment parameters. One benefit of (2.4) is obvious from Table 3. With fixed values of (h*, C*, γ), the resulting values (α, β) are highly variable and difficult to interpret. In contrast, (h*, C*) represent reference points with clear biological meaning and widespread interest in fishery management. In the existing literature, some results have been obtained from stochastic differential equations for continuous processes (Beddington and May 1977; Thompson 1994). To achieve the analytical results here, we have confined our analysis to discrete deterministic process equations. These can be expanded into full state space models, which include stochastic error and observation equations (Schnute 1994; Schnute and Richards 1995; Richards et al. 1997). Thus, our analytical results might provide initial approximations to reference points and harvest strategies obtained from elaborate stochastic simulation models. One unique feature of model 2A is the mean weight moment equation (T7.16). This equation appears attractive for actual analyses because mean weights are commonly 1/γ (1 + Q )h 2 (1 h )[1 σ +γ(1 + Q )h ]C Special case k50 4α(1 δ) (1 +α δ) 2 w 1 (T9.7) h 1 = 1 +α δ (T9.8) h = δ 1 δ (T9.9) h x = δ 1 δ (T9.10) (T9.11) (T9.12) α δ+ w δ(w ) Q [1 +(1 + Q ) 1/2 ] 2 1/2 1 ; w > 1 1 δ 1/2 w δ(1 x)(w )+xw 1 ω= δ +(1 δ)w Q y = 4δ(w / 1)(1 δ)ωy [δ+(1 δ)ωy] 2 h y = 1 δ+(1 δ)ωy δ(1 ωy) + ωyq y [1 +(1 + Q y ) 1/2 ] 2
10 524 Can. J. Fish. Aquat. Sci. Vol. 55, 1998 Fig. 3. Equilibrium quantities P, C, C/R, and S/R from Table 8 expressed as functions of h with fixed parameters (C*, h*, δ, γ,, w, κ) = (1, 0.25, 0.2, 0, 1, 5, 0), as in Table 3, case 4. Dotted lines correspond to (A) P(h*) and h*, (B) C* and h*, (C) h 0.2, and (D) (S/R) h 0.35 Line segments in Fig. 3C indicate slopes of the YPR relationship at h = 0 and h =h 0.2. Broken curves in Figs. 3C and 3D indicate values of h > h. and h measured in fisheries data. Previous analyses (Deriso 1980; Schnute 1985) used second difference equations in P t rather than adding a weight moment (Hilborn and Walters 1992, p. 335). Although Schnute (1987) and Schnute et al. (1989) examined various weight-based moment measures, they did not include an explicit update equation analogous to (T7.16) for the mean weight W t. Here, we treat W t simply as another state variable in the model. Model 1A can similarly be extended to include an update equation analogous to (T7.16) for the mean age A t in year t, where (4.1) A t = anat /P t. It can be proved (Appendix A) from model 1 that (4.2) A t = 1 +(1 δ) S t 1 A P t 1. t To extend model 1A, insert (4.2) between equations (T1.12) and (T1.13). The resulting system sequentially updates the five variables R t, P t, A t, C t, and S t. This simple model could be used as a starting point for analysis of a fish stock with available age data. Our reference point definitions in Table 4 include only a few of the common approaches applied in fishery management. We have attempted to generalize our results with generic fractions x, y, and z, rather than specific choices, as in F 0.1. Furthermore, the fractions x, y, and z can be adjusted to match almost any reference point based on a constant harvest rate. Thus, our relationships provide a method for evaluating sensible choices. Other common reference points could also be defined and analyzed by our methods. However, some reference points such as F low, F med or F rep, and F high (Sissenwine and Shepherd 1987; Jakobsen 1992) are obtained from the observed ratio of recruits to spawners. These depend on estimates from observed data and so are not amenable to analytic expressions. The definitions in Table 4 are derived from equilibrium models. Much current fisheries research is directed to how fish
11 Schnute and Richards 525 populations respond to varying climatic conditions, including regime shifts (Beamish 1995). Clearly, future work should consider stochastic uncertainty associated with reference point definitions. For example, climatic-induced changes in weight at age could alter the growth parameters (, w, κ). In this case, reference points from Table 9 could take very different values under different climatic regimes. More generally, our analytical expressions provide a framework for exploring how stochasticity might affect reference point calculations. Thus, our methods can help guide the choice of reference points and link biology to fishery management. Acknowledgements We thank Grant Thompson and Carl Walters for helpful reviews. We dedicate this paper to David Cook on the occasion of his retirement as Editor of this journal. For more than a decade, our papers have benefited from his insights and guidance. References Beamish, R.J. (Editor) Climate change and northern fish populations. Can. Spec. Publ. Fish. Aquat. Sci. No Beddington, J.R., and May, R.M Harvesting natural populations in a randomly fluctuating environment. Science (Washington, D.C.), 197: Beverton, R.J.H., and Holt, S.J On the dynamics of exploited fish populations. Fish. Invest. Ser. 2 No. 19. Caddy, J.F., and Mahon, R Reference points for fisheries management. FAO Fish. Tech. Pap. No Caddy, J.F., and McGarvey, R Targets or limits for management of fisheries. N. Am. J. Fish. Manage. 16: Clark, W.G Groundfish exploitation rates based on life history parameters. Can. J. Fish. Aquat. Sci. 48: Clark, W.G The effect of recruitment variability on the choice of a target level of spawning biomass per recruit. Proceedings of the International Symposium on Management of Exploited Fish Populations. Alaska Sea Grant Rep pp Cook, R.M., Sinclair, A., and Stefánsson, G Potential collapse of North Sea cod stocks. Nature (Lond.), 385: Deriso, R.B Harvesting strategies and parameter estimation for an age-structured model. Can. J. Fish. Aquat. Sci. 37: Deriso, R.B Relationship of fishing mortality to natural mortality and growth at the level of maximum sustainable yield. Can. J. Fish. Aquat. Sci. 39: Deriso, R.B Optimal F 0.1 criteria and their relationship to maximum sustainable yield. Can. J. Fish. Aquat. Sci. 44(Suppl. 2): Deriso, R.B., Quinn, T.J., II, and Neal, P.R Catch age analysis with auxiliary information. Can. J. Fish. Aquat. Sci. 42: Fournier, D., and Archibald, C.P A general theory for analyzing catch at age data. Can. J. Fish. Aquat. Sci. 39: Fournier, D.A., and Doonan, I.J A length-based stock assessment method utilizing a generalized delay-difference model. Can. J. Fish. Aquat. Sci. 44: Garcia, S.M The precautionary principle: its implications in capture fisheries management. Ocean Coastal Manage. 22: Garcia, S.M Stock recruitment relationships and the precautionary approach to management of tropical shrimp fisheries. Mar. Freshwater Res. 47: Gulland, J.A Estimation of mortality rates. Annex to Arctic Fisheries Working Group Report. ICES C.M Doc. No. 3. Hilborn, R., and Walters, C.J Quantitative fisheries stock assessment: choice, dynamics, and uncertainty. Chapman and Hall, New York. ICES Report of the comprehensive fishery evaluation working group. ICES CM 1996/Asses:20. Jakobsen, T Biological reference points for North-East Arctic cod and haddock. ICES J. Mar. Sci. 49: Mace, P.M Relationships between common biological reference points used as thresholds and targets of fisheries management strategies. Can. J. Fish. Aquat. Sci. 51: Pope, J.G An investigation of the accuracy of virtual population analysis using cohort analysis. ICNAF Res. Bull. 9: Richards, L.J., Schnute, J.T., and Olsen, N Visualizing catch age analysis: a case study. Can. J. Fish. Aquat. Sci. 54: Ricker, W.E Handbook of computations for biological statistics of fish populations. Bull. Fish. Res. Board Can. No Ricker, W.E Computation and interpretation of biological statistics of fish populations. Bull. Fish. Res. Board Can. No Schaefer, M.B Some aspects of the dynamics of populations important to the management of the commercial marine fisheries. Inter-Am. Trop. Tuna Comm. Bull. 1: Schnute, J A general theory for the analysis of catch and effort data. Can. J. Fish. Aquat. Sci. 42: Schnute, J A general fishery model for a size-structured population. Can. J. Fish. Aquat. Sci. 44: Schnute, J.T A general framework for developing sequential fisheries models. Can. J. Fish. Aquat. Sci. 51: Schnute, J.T., and Kronlund, A.R A management oriented approach to stock recruitment analysis. Can. J. Fish. Aquat. Sci. 53: Schnute, J.T., and Richards, L.J The influence of error on population estimates from catch age analysis. Can. J. Fish. Aquat. Sci. 52: Schnute, J.T., Richards, L.J., and Cass, A.J Fish growth: investigations based on a size-structured model. Can. J. Fish. Aquat. Sci. 46: Shepherd, J.G A versatile new stock recruitment relationship for fisheries, and the construction of sustainable yield curves. J. Cons. Int. Explor. Mer, 40: Sissenwine, M.P., and Shepherd, J.G An alternative perspective on recruitment overfishing and biological reference points. Can. J. Fish. Aquat. Sci. 44: Thompson, G.G A general diffusion model of stock recruitment systems with stochastic mortality. ICES C.M. 1994/T:18. United Nations Agreement for the implementation of the provisions of the United Nations Convention on the Law of the Sea of 10 December 1982 relating to the conservation and management of straddling fish stocks and highly migratory fish stocks. U.N. Gen. Assembly Doc. A/CONF.164/37. Appendix A. Moment equations The paper s assumptions are contained in the age-structured models 1 and 2. From these, we derive moment equations (Appendix A), equilibrium conditions (Appendix B), and reference points for MSY (Appendix C), extinction (Appendix D), and YPR and SPR (Appendix E). We focus primarily on model 2 because results for model 1 usually follow as special cases from the additional assumption (3.5). We begin by proving the equations (T7.14) (T7.18) of model 2A from the assumptions (T7.6) (T7.9) and moment definitions (T7.10) (T7.13) of model 2. Equations (T7.14), (T7.17), and (T7.18) are straightforward consequences of (T7.6), (T7.8), and (T7.9), respectively, given the definitions (T7.10) (T7.12). The calculation
12 526 Can. J. Fish. Aquat. Sci. Vol. 55, 1998 (A.1) (A.2) (A.3) P t = N 1t + Na+1,t P t = R t + w a+1 (1 δ)(n w a,t 1 C a,t 1 ) a (1 κ)w +κw a P t = R t +(1 δ)(1 h t 1 ) N w a,t 1 a P t = R t +(1 δ)(1 h t 1 ) (1 κ)w P t 1 W t 1 +κp t 1 P t = R t + (1 κ)w +κw t 1 W t 1 (1 δ)s t 1 proves (T7.15). In this calculation, (A.1) uses (T7.4) and (T7.8), (A.2) incorporates the result Σ a (N at /w a ) = P t /W t from (T7.13), and (A.3) uses the equality (1 h t )P t = S t from (T7.8) (T7.9). Similarly, the calculation (A.4) (A.5) W t = P t N at w a W t = P t R t 1 = P R t t + +(1 δ)(1 h t 1 ) N a+1,t w a+1 N a,t 1 w a W t = P t R t +(1 δ)(1 h t 1 ) P t 1 W t 1 R t W t = P t +(1 δ) S 1 t 1 W t 1 proves (T7.16), where (A.4) and (A.5) depend on the definition (T7.13) of mean weight. This completes the proof of model 2A. Given the equality = w in (3.5), assumptions (T7.6) (T7.9) of model 2 become identical to (T1.4) (T1.7) in model 1. Furthermore, (T7.4) then implies that w a = w for every age a. Thus, from (T7.13), (A.6) W t = P t w 1 N at a = w. Substituting (A.6) into (T7.15) gives (T1.12). Because (3.5) and model 2 are equivalent to model 1, this completes the proof that model 1 implies model 1A. The additional moment equation (4.2) for model 1A follows from the calculation A t = 1 P t anat = 1 P R t + t (a + 1)Na+1,t A t = 1 P R t +(1 δ)(1 h t 1 ) t (a + 1)Na,t 1 W t = 1 [R P t +(1 δ)(1 h t 1 )(P t 1 A t 1 + P t 1 )] t W t = 1 P t [R t +(1 δ)s t 1 (1 + A t 1 )] W t = 1 +(1 δ) S t 1 A P t 1, t based on equations (4.1) and (T1.5) (T1.8). Appendix B. Equilibrium With a constant harvest rate h, equilibrium versions of (T7.14) (T7.18) give five equations in R, P, W, C, and S. We use these to prove the results in Table 8. Equations (T8.6) (T8.7) are immediate consequences of (T7.17) (T7.18). Define ρ=r/s, so that (T7.16) can be written as (B.1) 1 W = 1 P = ρs + w 1 ρ(1 h) + (1 δ)s W (1 δ)(1 h) W where S/P = 1 h from (T8.7). Solve (B.1) for ρ and apply the definition (T8.1) of σ to prove (T8.3). Next, divide the equilibrium version of (T7.15) by S to obtain (B.2) 1 1 h =ρ+(1 κ)w +κw (1 δ) W = W 1 σ 1 h + (1 κ)w +κw W, σ 1 h, based on the expressions (T8.1) and (T8.3) for σ and ρ, respectively. Solving (B.2) for W gives (T8.2). Similarly, divide the equilibrium version of (T7.14) by S to obtain (B.3) ρ=α(1 βγr/ρ) 1/γ, and solve (B.3) for R to prove (T8.4). Starting from (T8.7), the calculation (B.4) P = S 1 h = R ρ(1 h) = W 1 h R 1 σ1 h = W R 1 σ proves (T8.5), where (B.4) uses the result (T8.3). Finally, the equilibrium equation (T7.7), that is, (B.5) N a = w a (1 δ)(1 h)n w a 1 = w a σn a 1 w a 1, a 1 inductively implies (T8.8), starting from the condition N 1 = R. This completes the proof of all equations in Table 8. If = w, as in (3.5), then W = in (T8.2); consequently, equations (T2.2) (T2.6) in Table 2 follow from their counterparts (T8.3) (T8.7) in Table 8. Also, (3.5) implies that w a = in (T7.4); thus, (T8.8) proves (T2.7) in this case and completes the proof of Table 2. Appendix C. MSY We begin by proving (T9.4) (T9.5) in Table 9 from definitions (T9.1) (T9.3) and equilibrium results in Table 8. Functions of
Characteristics of Fish Populations
 Characteristics of Fish Populations Unexploited Populations Recruitment Mortality (natural) Growth Exploited Populations Recruitment and Yield Fishing and Natural Mortality Compensatory Growth Recruitment
Characteristics of Fish Populations Unexploited Populations Recruitment Mortality (natural) Growth Exploited Populations Recruitment and Yield Fishing and Natural Mortality Compensatory Growth Recruitment
population size at time t, then in continuous time this assumption translates into the equation for exponential growth dn dt = rn N(0)
 Appendix S1: Classic models of population dynamics in ecology and fisheries science Populations do not grow indefinitely. No concept is more fundamental to ecology and evolution. Malthus hypothesized that
Appendix S1: Classic models of population dynamics in ecology and fisheries science Populations do not grow indefinitely. No concept is more fundamental to ecology and evolution. Malthus hypothesized that
TOTAL EQUILIBRIUM YIELD
 TOTAL EQUILIBIUM YIELD ecall that the yield-per-recruit model enabled us to examine the problem of growth overfishing but, because we assumed that recruitment was constant, the model did not tell us whether
TOTAL EQUILIBIUM YIELD ecall that the yield-per-recruit model enabled us to examine the problem of growth overfishing but, because we assumed that recruitment was constant, the model did not tell us whether
Estimating reference fishing mortality rates. from noisy spawner-recruit data
 accepted: Canadian Journal of Fisheries and Aquatic Sciences Estimating reference fishing mortality rates from noisy spawner-recruit data A. Jamie F. Gibson 1,2 and Ransom A. Myers 1 1 Department of Biology,
accepted: Canadian Journal of Fisheries and Aquatic Sciences Estimating reference fishing mortality rates from noisy spawner-recruit data A. Jamie F. Gibson 1,2 and Ransom A. Myers 1 1 Department of Biology,
2 One-dimensional models in discrete time
 2 One-dimensional models in discrete time So far, we have assumed that demographic events happen continuously over time and can thus be written as rates. For many biological species with overlapping generations
2 One-dimensional models in discrete time So far, we have assumed that demographic events happen continuously over time and can thus be written as rates. For many biological species with overlapping generations
Fisheries, Population Dynamics, And Modelling p. 1 The Formulation Of Fish Population Dynamics p. 1 Equilibrium vs. Non-Equilibrium p.
 Fisheries, Population Dynamics, And Modelling p. 1 The Formulation Of Fish Population Dynamics p. 1 Equilibrium vs. Non-Equilibrium p. 4 Characteristics Of Mathematical Models p. 6 General Properties p.
Fisheries, Population Dynamics, And Modelling p. 1 The Formulation Of Fish Population Dynamics p. 1 Equilibrium vs. Non-Equilibrium p. 4 Characteristics Of Mathematical Models p. 6 General Properties p.
An Alternative SSASPM Stock Assessment of Gulf of Mexico Vermilion Snapper that Incorporates the Recent Decline in Shrimp Effort.
 An Alternative SSASPM Stock Assessment of Gulf of Mexico Vermilion Snapper that Incorporates the Recent Decline in Shrimp Effort. Brian Linton, Shannon L. Cass-Calay and Clay E. Porch NOAA Fisheries Southeast
An Alternative SSASPM Stock Assessment of Gulf of Mexico Vermilion Snapper that Incorporates the Recent Decline in Shrimp Effort. Brian Linton, Shannon L. Cass-Calay and Clay E. Porch NOAA Fisheries Southeast
Optimal Harvest in an Age Structured Model with Different Fishing Selectivity
 Environ Resource Econ (2012) 51:525 544 DOI 10.1007/s10640-011-9510-x Optimal Harvest in an Age Structured Model with Different Fishing Selectivity Anders Skonhoft Niels Vestergaard Martin Quaas Accepted:
Environ Resource Econ (2012) 51:525 544 DOI 10.1007/s10640-011-9510-x Optimal Harvest in an Age Structured Model with Different Fishing Selectivity Anders Skonhoft Niels Vestergaard Martin Quaas Accepted:
Progress report on development of a spatially explicit operating model for tropical tuna populations.
 IOTC-2018-WPTT20-27 Progress report on development of a spatially explicit operating model for tropical tuna populations. Prepared for Indian Ocean Tuna Commission September 2018 Prepared by: Simon Hoyle
IOTC-2018-WPTT20-27 Progress report on development of a spatially explicit operating model for tropical tuna populations. Prepared for Indian Ocean Tuna Commission September 2018 Prepared by: Simon Hoyle
Dab (Limanda limanda) in Subarea 4 and Division 3.a (North Sea, Skagerrak and Kattegat)
 ICES Advice on fishing opportunities, catch, and effort Greater North Sea Ecoregion Published 30 June 2017 DOI: 10.17895/ices.pub.3106 Dab (Limanda limanda) in Subarea 4 and Division 3.a (North Sea, Skagerrak
ICES Advice on fishing opportunities, catch, and effort Greater North Sea Ecoregion Published 30 June 2017 DOI: 10.17895/ices.pub.3106 Dab (Limanda limanda) in Subarea 4 and Division 3.a (North Sea, Skagerrak
Information to help interpret results from the data limited toolkit for Atlantic Blueline Tilefish north and south of Cape Hatteras.
 Information to help interpret results from the data limited toolkit for Atlantic Blueline Tilefish north and south of Cape Hatteras Rob Ahrens SEDAR50-RW01 Submitted: 4 August 2017 This information is
Information to help interpret results from the data limited toolkit for Atlantic Blueline Tilefish north and south of Cape Hatteras Rob Ahrens SEDAR50-RW01 Submitted: 4 August 2017 This information is
Tennessee State University, Murfreesboro, TN b Department of Mathematics, University of Tennessee and National Institute for
 This article was downloaded by: [Middle Tennessee State University] On: 7 April 25, At: :7 Publisher: Taylor & Francis Informa Ltd Registered in England and Wales Registered Number: 72954 Registered office:
This article was downloaded by: [Middle Tennessee State University] On: 7 April 25, At: :7 Publisher: Taylor & Francis Informa Ltd Registered in England and Wales Registered Number: 72954 Registered office:
PULSE-SEASONAL HARVESTING VIA NONLINEAR DELAY DIFFERENTIAL EQUATIONS AND APPLICATIONS IN FISHERY MANAGEMENT. Lev V. Idels
 PULSE-SEASONAL HARVESTING VIA NONLINEAR DELAY DIFFERENTIAL EQUATIONS AND APPLICATIONS IN FISHERY MANAGEMENT Lev V. Idels University-College Professor Mathematics Department Malaspina University-College
PULSE-SEASONAL HARVESTING VIA NONLINEAR DELAY DIFFERENTIAL EQUATIONS AND APPLICATIONS IN FISHERY MANAGEMENT Lev V. Idels University-College Professor Mathematics Department Malaspina University-College
ARCTIC FISHERIES: GOVERNANCE CHALLENGES AND OPPORTUNITIES
 Commentary ARCTIC FISHERIES: GOVERNANCE CHALLENGES AND OPPORTUNITIES FRANK MILLERD JULY 2011 Contact: fmillerd@wlu.ca Professor Emeritus, Department of Economics, Wilfrid Laurier University. Contact: fmillerd@wlu.ca.
Commentary ARCTIC FISHERIES: GOVERNANCE CHALLENGES AND OPPORTUNITIES FRANK MILLERD JULY 2011 Contact: fmillerd@wlu.ca Professor Emeritus, Department of Economics, Wilfrid Laurier University. Contact: fmillerd@wlu.ca.
Post-Graduation Plans stock assessment scientist (NOAA, hopefully)
 Update Report Period 3/1/2013-2/28/2014 Project E/I-20 - NMFS Population Dynamics Sea Grant Graduate Fellowship An evaluation of the stock assessment method for eastern Bering Sea snow crab incorporating
Update Report Period 3/1/2013-2/28/2014 Project E/I-20 - NMFS Population Dynamics Sea Grant Graduate Fellowship An evaluation of the stock assessment method for eastern Bering Sea snow crab incorporating
Canada s Policy for the Conservation of Wild Pacific Salmon: conservation planning for an uncertain future.
 Canada s Policy for the Conservation of Wild Pacific Salmon: conservation planning for an uncertain future. Brian Riddell and Blair Holtby, Dept. Fisheries & Oceans, Science Branch, Pacific Biological
Canada s Policy for the Conservation of Wild Pacific Salmon: conservation planning for an uncertain future. Brian Riddell and Blair Holtby, Dept. Fisheries & Oceans, Science Branch, Pacific Biological
Draft AFS Spatial Processes
 Effects of unequal capture probability on stock assessment abundance and mortality estimates: an example using the US Atlantic sea scallop fishery Journal: Manuscript ID cjfas-2016-0296.r2 Manuscript Type:
Effects of unequal capture probability on stock assessment abundance and mortality estimates: an example using the US Atlantic sea scallop fishery Journal: Manuscript ID cjfas-2016-0296.r2 Manuscript Type:
Adjoint-based parameter estimation for the spatially explicit model of large pelagics (with application to skipjack tuna).
 Inna Senina 1, John Sibert 1 and Patrick Lehodey 2 Adjoint-based parameter estimation for the spatially explicit model of large pelagics (with application to skipjack tuna). 1 Pelagic Fisheries Research
Inna Senina 1, John Sibert 1 and Patrick Lehodey 2 Adjoint-based parameter estimation for the spatially explicit model of large pelagics (with application to skipjack tuna). 1 Pelagic Fisheries Research
Ecological and Evolutionary Recovery of Exploited Fish Stocks
 ICES CM 2006/H:18 Ecological and Evolutionary Recovery of Exploited Fish Stocks Katja Enberg 1, Erin S. Dunlop 1, Mikko Heino 1,2,3 and Ulf Dieckmann 1 1 Evolution and Ecology Program, International Institute
ICES CM 2006/H:18 Ecological and Evolutionary Recovery of Exploited Fish Stocks Katja Enberg 1, Erin S. Dunlop 1, Mikko Heino 1,2,3 and Ulf Dieckmann 1 1 Evolution and Ecology Program, International Institute
2001 State of the Ocean: Chemical and Biological Oceanographic Conditions in the Newfoundland Region
 Stock Status Report G2-2 (2) 1 State of the Ocean: Chemical and Biological Oceanographic Conditions in the Background The Altantic Zone Monitoring Program (AZMP) was implemented in 1998 with the aim of
Stock Status Report G2-2 (2) 1 State of the Ocean: Chemical and Biological Oceanographic Conditions in the Background The Altantic Zone Monitoring Program (AZMP) was implemented in 1998 with the aim of
Optimal Harvesting for a Predator Prey Metapopulation
 Optimal Harvesting for a Predator Prey Metapopulation Asep K. Supriatna 1 and Hugh P. Possingham 2 1 Department of Applied Mathematics, University of Adelaide, SA 5005 Australia 2 Department of Environmental
Optimal Harvesting for a Predator Prey Metapopulation Asep K. Supriatna 1 and Hugh P. Possingham 2 1 Department of Applied Mathematics, University of Adelaide, SA 5005 Australia 2 Department of Environmental
Why Forecast Recruitment?
 Predictability of Future Recruitment by Parametric and Non-parametric models : Case study of G. of Alaska walleye pollock. Yong-Woo Lee 1* Bernard A. Megrey 1 S. Allen Macklin 2 National Oceanic and Atmospheric
Predictability of Future Recruitment by Parametric and Non-parametric models : Case study of G. of Alaska walleye pollock. Yong-Woo Lee 1* Bernard A. Megrey 1 S. Allen Macklin 2 National Oceanic and Atmospheric
A State-Space Model for Abundance Estimation from Bottom Trawl Data with Applications to Norwegian Winter Survey
 Dept. of Math. University of Oslo Statistical Research Report No 1 ISSN 0806 3842 September 2015 A State-Space Model for Abundance Estimation from Bottom Trawl Data with Applications to Norwegian Winter
Dept. of Math. University of Oslo Statistical Research Report No 1 ISSN 0806 3842 September 2015 A State-Space Model for Abundance Estimation from Bottom Trawl Data with Applications to Norwegian Winter
REVIEW OF AERIAL SURVEY ESTIMATES FOR RINGED SEALS (PHOCA HISPIDA) IN WESTERN HUDSON BAY
 Canadian Science Advisory Secretariat Science Advisory Report 2009/004 REVIEW OF AERIAL SURVEY ESTIMATES FOR RINGED SEALS (PHOCA HISPIDA) IN WESTERN HUDSON BAY J. Blair Dunn, DFO, Winnipeg, MB Context:
Canadian Science Advisory Secretariat Science Advisory Report 2009/004 REVIEW OF AERIAL SURVEY ESTIMATES FOR RINGED SEALS (PHOCA HISPIDA) IN WESTERN HUDSON BAY J. Blair Dunn, DFO, Winnipeg, MB Context:
Response of Cohort Analysis to Input Parameters. By D. Rivard and W. G. Doubleday. May 1979
 CAFSAC RESEARCH DOCUMENT 79/45 Response of Cohort Analysis to Input Parameters. By D. Rivard and W. G. Doubleday May 1979 Not to be cited without prior reference to the authors. CONTENTS Page Relative
CAFSAC RESEARCH DOCUMENT 79/45 Response of Cohort Analysis to Input Parameters. By D. Rivard and W. G. Doubleday May 1979 Not to be cited without prior reference to the authors. CONTENTS Page Relative
Exxon Valdez Oil Spill Restoration Project Annual Report
 Exxon Valdez Oil Spill Restoration Project Annual Report Ecology and Demographics of Pacific Sand Lance, Ammodytes hexapterus Pallas, in Lower Cook Inlet, Alaska Restoration Project 99306 Final Report
Exxon Valdez Oil Spill Restoration Project Annual Report Ecology and Demographics of Pacific Sand Lance, Ammodytes hexapterus Pallas, in Lower Cook Inlet, Alaska Restoration Project 99306 Final Report
A Stock-Recruitment Relationship Applicable to Pacific Bluefin Tuna and the Pacific Stock of Japanese Sardine
 American Journal of Climate Change, 2015, 4, 446-460 Published Online December 2015 in SciRes. http://www.scirp.org/journal/ajcc http://dx.doi.org/10.4236/ajcc.2015.45036 A Stock-Recruitment Relationship
American Journal of Climate Change, 2015, 4, 446-460 Published Online December 2015 in SciRes. http://www.scirp.org/journal/ajcc http://dx.doi.org/10.4236/ajcc.2015.45036 A Stock-Recruitment Relationship
2016 Marine Survival Forecast of Southern British Columbia Coho
 2016 Marine Survival Forecast of Southern British Columbia Coho 2016 MARINE SURVIVAL FORECAST OF SOUTHERN BRITISH COLUMBIA COHO Figure 1: Coho salmon at three life stages: freshwater rearing fry; ocean
2016 Marine Survival Forecast of Southern British Columbia Coho 2016 MARINE SURVIVAL FORECAST OF SOUTHERN BRITISH COLUMBIA COHO Figure 1: Coho salmon at three life stages: freshwater rearing fry; ocean
Optimal control of single species biological population
 Optimal control of single species biological population B. S. Goh Research Institute, Curtin University Sarawak Malaysia Biologists divide species into two groups. K-selected:- like humans, monkeys, whales,
Optimal control of single species biological population B. S. Goh Research Institute, Curtin University Sarawak Malaysia Biologists divide species into two groups. K-selected:- like humans, monkeys, whales,
Towards spatial life cycle modelling of eastern Channel sole
 Towards spatial life cycle modelling of eastern Channel sole B. Archambault, O. Le Pape, E. Rivot 27 mars 2014 Agrocampus Ouest 1 Spatialization of adults? So far (justified) focus on early stages Adult
Towards spatial life cycle modelling of eastern Channel sole B. Archambault, O. Le Pape, E. Rivot 27 mars 2014 Agrocampus Ouest 1 Spatialization of adults? So far (justified) focus on early stages Adult
Asynchronous and Synchronous Dispersals in Spatially Discrete Population Models
 SIAM J. APPLIED DYNAMICAL SYSTEMS Vol. 7, No. 2, pp. 284 310 c 2008 Society for Industrial and Applied Mathematics Asynchronous and Synchronous Dispersals in Spatially Discrete Population Models Abdul-Aziz
SIAM J. APPLIED DYNAMICAL SYSTEMS Vol. 7, No. 2, pp. 284 310 c 2008 Society for Industrial and Applied Mathematics Asynchronous and Synchronous Dispersals in Spatially Discrete Population Models Abdul-Aziz
Analysis of Environmental Data Conceptual Foundations: De te rm in istic Fu n c tio n s
 Analysis of Environmental Data Conceptual Foundations: De te rm in istic Fu n c tio n s 1. What is a deterministic (mathematical) function..................................... 2 2. Examples of deterministic
Analysis of Environmental Data Conceptual Foundations: De te rm in istic Fu n c tio n s 1. What is a deterministic (mathematical) function..................................... 2 2. Examples of deterministic
GROWTH IN LENGTH: a model for the growth of an individual
 GROWTH IN LENGTH: a model for the growth of an individual Consider the following differential equation: L' L What are the dimensions for parameters and? As was the case with the differential equation relating
GROWTH IN LENGTH: a model for the growth of an individual Consider the following differential equation: L' L What are the dimensions for parameters and? As was the case with the differential equation relating
Report for ICCAT-GBYP 04/2013
 Report for ICCAT-GBYP 4/213 Marie-Pierre Etienne 1, Tom Carruthers 2, and Murdoch McAllister 2 1 AgroParisTech 2 UBC January 15, 214 Contents 1 Introduction 2 2 Description of the main aspects of iscam
Report for ICCAT-GBYP 4/213 Marie-Pierre Etienne 1, Tom Carruthers 2, and Murdoch McAllister 2 1 AgroParisTech 2 UBC January 15, 214 Contents 1 Introduction 2 2 Description of the main aspects of iscam
World Oceans Day 2010 Our oceans: opportunities and challenges
 World Oceans Day 2010 Our oceans: opportunities and challenges Roundtable discussion on the United Nations Convention on the Law of the Sea fifteen years after its entry into force HOW EFFECTIVELY IS UNCLOS
World Oceans Day 2010 Our oceans: opportunities and challenges Roundtable discussion on the United Nations Convention on the Law of the Sea fifteen years after its entry into force HOW EFFECTIVELY IS UNCLOS
Use of Ocean Observations to Develop Forecasts in Support of Fisheries Management
 Use of Ocean Observations to Develop Forecasts in Support of Fisheries Management Phillip R. Mundy Alaska Fisheries Science Center Juneau, Alaska Danielle F. Evenson Alaska Department of Fish and Game
Use of Ocean Observations to Develop Forecasts in Support of Fisheries Management Phillip R. Mundy Alaska Fisheries Science Center Juneau, Alaska Danielle F. Evenson Alaska Department of Fish and Game
APPENDIX B SUMMARIES OF SUBJECT MATTER TOPICS WITH RELATED CALIFORNIA AND NCTM STANDARDS PART 1
 APPENDIX B SUMMARIES OF SUBJECT MATTER TOPICS WITH RELATED CALIFORNIA AND NCTM STANDARDS This appendix lists the summaries of the subject matter topics presented in Section 2 of the Statement. After each
APPENDIX B SUMMARIES OF SUBJECT MATTER TOPICS WITH RELATED CALIFORNIA AND NCTM STANDARDS This appendix lists the summaries of the subject matter topics presented in Section 2 of the Statement. After each
USE OF STATISTICAL BOOTSTRAPPING FOR SAMPLE SIZE DETERMINATION TO ESTIMATE LENGTH-FREQUENCY DISTRIBUTIONS FOR PACIFIC ALBACORE TUNA (THUNNUS ALALUNGA)
 FRI-UW-992 March 1999 USE OF STATISTICAL BOOTSTRAPPING FOR SAMPLE SIZE DETERMINATION TO ESTIMATE LENGTH-FREQUENCY DISTRIBUTIONS FOR PACIFIC ALBACORE TUNA (THUNNUS ALALUNGA) M. GOMEZ-BUCKLEY, L. CONQUEST,
FRI-UW-992 March 1999 USE OF STATISTICAL BOOTSTRAPPING FOR SAMPLE SIZE DETERMINATION TO ESTIMATE LENGTH-FREQUENCY DISTRIBUTIONS FOR PACIFIC ALBACORE TUNA (THUNNUS ALALUNGA) M. GOMEZ-BUCKLEY, L. CONQUEST,
Maryland Oyster Stock Assessment Update. December 18, 2017 St. Mary s City, MD
 Maryland Oyster Stock Assessment Update December 18, 2017 St. Mary s City, MD 1 What are the goals of a stock assessment? Stock assessments : 1. Estimate current fish stock status relative to relative
Maryland Oyster Stock Assessment Update December 18, 2017 St. Mary s City, MD 1 What are the goals of a stock assessment? Stock assessments : 1. Estimate current fish stock status relative to relative
MARITIMES RESEARCH VESSEL SURVEY TRENDS ON GEORGES BANK
 Canadian Science Advisory Secretariat Maritimes Region Science Response 23/5 MARITIMES RESEARCH VESSEL SURVEY TRENDS ON GEORGES BANK 5Zj 5Zg 5Zo 5Zh 5Zn 5Zm US CAN 65 Figure. Northwest Atlantic Fisheries
Canadian Science Advisory Secretariat Maritimes Region Science Response 23/5 MARITIMES RESEARCH VESSEL SURVEY TRENDS ON GEORGES BANK 5Zj 5Zg 5Zo 5Zh 5Zn 5Zm US CAN 65 Figure. Northwest Atlantic Fisheries
JMESTN Journal of Multidisciplinary Engineering Science and Technology (JMEST) ISSN: Vol. 2 Issue 4, April
 Population Dynamics of Harvesting Fishery and Predator Kinfe Hailemariam Hntsa School of Mathematical and Statistical Sciences, Hawassa University, P. O. Box 5, Hawassa, ETHIOPIA Email: kinfhail@gmail.com
Population Dynamics of Harvesting Fishery and Predator Kinfe Hailemariam Hntsa School of Mathematical and Statistical Sciences, Hawassa University, P. O. Box 5, Hawassa, ETHIOPIA Email: kinfhail@gmail.com
Characteristics of Fish Populations. Unexploited Populations. Exploited Populations. Recruitment - Birth Mortality (natural) Growth
 Characteristics of Fish Populations Unexploited Populations Recruitment - Birth Mortality (natural) Growth Exploited Populations Recruitment and Yield Fishing and Natural Mortality Compensatory Growth
Characteristics of Fish Populations Unexploited Populations Recruitment - Birth Mortality (natural) Growth Exploited Populations Recruitment and Yield Fishing and Natural Mortality Compensatory Growth
Final Anchovy TAC and Sardine TAB for 2011, Using OMP-08
 FIHERIE//WG-PEL/43 Final nchovy TC and ardine T for, Using OMP-08 Carryn L de Moor Correspondence email: carryn.demoor@uct.ac.za Following the recent recruit survey, the revised and final outh frican anchovy
FIHERIE//WG-PEL/43 Final nchovy TC and ardine T for, Using OMP-08 Carryn L de Moor Correspondence email: carryn.demoor@uct.ac.za Following the recent recruit survey, the revised and final outh frican anchovy
Spatial dynamics of small pelagic fish in the California Current system on the regime time-scale. Parallel processes in other species-ecosystems.
 PICES/GLOBEC Symposium Honolulu, Hawaii April 19-21, 2006 Spatial dynamics of small pelagic fish in the California Current system on the regime time-scale. Parallel processes in other species-ecosystems.
PICES/GLOBEC Symposium Honolulu, Hawaii April 19-21, 2006 Spatial dynamics of small pelagic fish in the California Current system on the regime time-scale. Parallel processes in other species-ecosystems.
SHIFT IN SIZE-AT-AGE OF THE STRAIT OF GEORGIA POPULATION OF PACIFIC HAKE (MERLUCCIUS PRODUCTUS)
 SHIFT IN SIZE-AT-AGE OF THE STRAIT OF GEORGIA POPULATION OF PACIFIC HAKE (MERLUCCIUS PRODUCTUS) JACQUELYNNE R. KING Pacific Biological Station Fisheries and Oceans Canada Nanaimo, British Columbia V9S
SHIFT IN SIZE-AT-AGE OF THE STRAIT OF GEORGIA POPULATION OF PACIFIC HAKE (MERLUCCIUS PRODUCTUS) JACQUELYNNE R. KING Pacific Biological Station Fisheries and Oceans Canada Nanaimo, British Columbia V9S
Stewardship of the Central Arctic Ocean: The Arctic 5 versus the international community
 Stewardship of the Central Arctic Ocean: The Arctic 5 versus the international community The Central Arctic Ocean Ilulissat Declaration 2008 By virtue of their sovereignty, sovereign rights and jurisdiction
Stewardship of the Central Arctic Ocean: The Arctic 5 versus the international community The Central Arctic Ocean Ilulissat Declaration 2008 By virtue of their sovereignty, sovereign rights and jurisdiction
SUPPLEMENTARY INFORMATION
 In the format provided by the authors and unedited. SUPPLEMENTARY INFORMATION VOLUME: 1 ARTICLE NUMBER: 188 Body size shifts and early warning signals precede the historic collapse of whale stocks Authors:
In the format provided by the authors and unedited. SUPPLEMENTARY INFORMATION VOLUME: 1 ARTICLE NUMBER: 188 Body size shifts and early warning signals precede the historic collapse of whale stocks Authors:
Lecture 4 The Centralized Economy: Extensions
 Lecture 4 The Centralized Economy: Extensions Leopold von Thadden University of Mainz and ECB (on leave) Advanced Macroeconomics, Winter Term 2013 1 / 36 I Motivation This Lecture considers some applications
Lecture 4 The Centralized Economy: Extensions Leopold von Thadden University of Mainz and ECB (on leave) Advanced Macroeconomics, Winter Term 2013 1 / 36 I Motivation This Lecture considers some applications
Population Dynamics of Gulf Blue Crabs. Caz Taylor & Erin Grey Department of Ecology & Evolutionary Biology Tulane University
 Population Dynamics of Gulf Blue Crabs Caz Taylor & Erin Grey Department of Ecology & Evolutionary Biology Tulane University Blue Crab Callinectes sapidus Economically important in the Atlantic and the
Population Dynamics of Gulf Blue Crabs Caz Taylor & Erin Grey Department of Ecology & Evolutionary Biology Tulane University Blue Crab Callinectes sapidus Economically important in the Atlantic and the
Poisson s ratio effect of slope stability calculations
 Poisson s ratio effect of slope stability calculations Murray Fredlund, & Robert Thode SoilVision Systems Ltd., Saskatoon, SK, Canada ABSTRACT This paper presents the results of a study on the effect of
Poisson s ratio effect of slope stability calculations Murray Fredlund, & Robert Thode SoilVision Systems Ltd., Saskatoon, SK, Canada ABSTRACT This paper presents the results of a study on the effect of
Global stability of periodic orbits of nonautonomous difference equations in population biology and the Cushing-Henson conjectures
 Global stability of periodic orbits of nonautonomous difference equations in population biology and the Cushing-Henson conjectures Saber Elaydi Department of Mathematics Trinity University San Antonio,
Global stability of periodic orbits of nonautonomous difference equations in population biology and the Cushing-Henson conjectures Saber Elaydi Department of Mathematics Trinity University San Antonio,
Assessing the impacts of endocrine disrupting compounds (EDCs) on fish population dynamics: a case study of smallmouth bass in Chesapeake Bay
 Assessing the impacts of endocrine disrupting compounds (EDCs) on fish population dynamics: a case study of smallmouth bass in Chesapeake Bay Yan Li 1, Tyler Wagner 2 1 Pennsylvania Cooperative Fish and
Assessing the impacts of endocrine disrupting compounds (EDCs) on fish population dynamics: a case study of smallmouth bass in Chesapeake Bay Yan Li 1, Tyler Wagner 2 1 Pennsylvania Cooperative Fish and
Behaviour of simple population models under ecological processes
 J. Biosci., Vol. 19, Number 2, June 1994, pp 247 254. Printed in India. Behaviour of simple population models under ecological processes SOMDATTA SINHA* and S PARTHASARATHY Centre for Cellular and Molecular
J. Biosci., Vol. 19, Number 2, June 1994, pp 247 254. Printed in India. Behaviour of simple population models under ecological processes SOMDATTA SINHA* and S PARTHASARATHY Centre for Cellular and Molecular
262 Stockhausen and Hermann Modeling Larval Dispersion of Rockfish
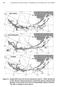 Stockhausen and Hermann Modeling Larval Dispersion of Rockfish 6 6 6 6 0 6 6 6 0 0 0 00 0 6 6 0 0 Figure. Sample IBM tracks for larvae released on April,. Numbered circles denote release locations; numbered
Stockhausen and Hermann Modeling Larval Dispersion of Rockfish 6 6 6 6 0 6 6 6 0 0 0 00 0 6 6 0 0 Figure. Sample IBM tracks for larvae released on April,. Numbered circles denote release locations; numbered
Chaos control in discrete population models (Harvesting and Dynamics)
 Ricker Clark Chaos control in discrete population s ( ) Departamento de Matemática Aplicada II Universidad de Vigo, Spain!!! "#$!%& "#! '("$)(*"'+(*,!-+(.$)$(-$! June 3, 2013 +(!/'..$)$(-$!$01*"'+(2! *(/!*33,'-*"'+(2!4'-/$*56%78!!!
Ricker Clark Chaos control in discrete population s ( ) Departamento de Matemática Aplicada II Universidad de Vigo, Spain!!! "#$!%& "#! '("$)(*"'+(*,!-+(.$)$(-$! June 3, 2013 +(!/'..$)$(-$!$01*"'+(2! *(/!*33,'-*"'+(2!4'-/$*56%78!!!
53 contributors for 35 individual reports in 2009 show 5% of figures today
 A Group Approach to Understanding Ecosystem Dynamics in the Northeast Pacific Ocean William Crawford and James Irvine, Fisheries and Oceans Canada (DFO) * * * 53 contributors for 35 individual reports
A Group Approach to Understanding Ecosystem Dynamics in the Northeast Pacific Ocean William Crawford and James Irvine, Fisheries and Oceans Canada (DFO) * * * 53 contributors for 35 individual reports
A Synthesis of Results from the Norwegian ESSAS (N-ESSAS) Project
 A Synthesis of Results from the Norwegian ESSAS (N-ESSAS) Project Ken Drinkwater Institute of Marine Research Bergen, Norway ken.drinkwater@imr.no ESSAS has several formally recognized national research
A Synthesis of Results from the Norwegian ESSAS (N-ESSAS) Project Ken Drinkwater Institute of Marine Research Bergen, Norway ken.drinkwater@imr.no ESSAS has several formally recognized national research
Dynamics of a migratory population under different fishing effort allocation schemes in time and space
 1186 Dynamics of a migratory population under different fishing effort allocation schemes in time and space Dominique Pelletier and Pierre Magal Abstract: Many exploited fish populations migrate or are
1186 Dynamics of a migratory population under different fishing effort allocation schemes in time and space Dominique Pelletier and Pierre Magal Abstract: Many exploited fish populations migrate or are
Two Concerns for Managers of Polar Bear Populations in the Near Future
 Two Concerns for Managers of Polar Bear Populations in the Near Future Presentation to the Polar Bear Range States Meeting 24-26 October, 2011 Ian Stirling, PhD, FRSC on behalf of the IUCN Polar Bear Specialist
Two Concerns for Managers of Polar Bear Populations in the Near Future Presentation to the Polar Bear Range States Meeting 24-26 October, 2011 Ian Stirling, PhD, FRSC on behalf of the IUCN Polar Bear Specialist
Age and growth. Assessing the status of fish stock for management: the collection and use of basic fisheries data and statistics
 C O M M O N W E A LT H SECREARIAT Age and growth Assessing the status of fish stock for management: the collection and use of basic fisheries data and statistics 27 November -8 December 2006, University
C O M M O N W E A LT H SECREARIAT Age and growth Assessing the status of fish stock for management: the collection and use of basic fisheries data and statistics 27 November -8 December 2006, University
POPULATION MODELS FOR MARINE RESERVE DESIGN: A RETROSPECTIVE AND PROSPECTIVE SYNTHESIS
 Ecological Applications, 13(1) Supplement, 2003, pp. S47 S64 2003 by the Ecological Society of America POPULATION MODELS FOR MARINE RESERVE DESIGN: A RETROSPECTIVE AND PROSPECTIVE SYNTHESIS LEAH R. GERBER,
Ecological Applications, 13(1) Supplement, 2003, pp. S47 S64 2003 by the Ecological Society of America POPULATION MODELS FOR MARINE RESERVE DESIGN: A RETROSPECTIVE AND PROSPECTIVE SYNTHESIS LEAH R. GERBER,
Rational Bézier Patch Differentiation using the Rational Forward Difference Operator
 Rational Bézier Patch Differentiation using the Rational Forward Difference Operator Xianming Chen, Richard F. Riesenfeld, Elaine Cohen School of Computing, University of Utah Abstract This paper introduces
Rational Bézier Patch Differentiation using the Rational Forward Difference Operator Xianming Chen, Richard F. Riesenfeld, Elaine Cohen School of Computing, University of Utah Abstract This paper introduces
3.5 Competition Models: Principle of Competitive Exclusion
 94 3. Models for Interacting Populations different dimensional parameter changes. For example, doubling the carrying capacity K is exactly equivalent to halving the predator response parameter D. The dimensionless
94 3. Models for Interacting Populations different dimensional parameter changes. For example, doubling the carrying capacity K is exactly equivalent to halving the predator response parameter D. The dimensionless
Impulsive Stabilization and Application to a Population Growth Model*
 Nonlinear Dynamics and Systems Theory, 2(2) (2002) 173 184 Impulsive Stabilization and Application to a Population Growth Model* Xinzhi Liu 1 and Xuemin Shen 2 1 Department of Applied Mathematics, University
Nonlinear Dynamics and Systems Theory, 2(2) (2002) 173 184 Impulsive Stabilization and Application to a Population Growth Model* Xinzhi Liu 1 and Xuemin Shen 2 1 Department of Applied Mathematics, University
Patterns of change in the size spectra of numbers and diversity of the North Sea fish assemblage, as reflected in surveys and models
 ICES Journal of Marine Science, 53: 1214 1225. 1996 Patterns of change in the size spectra of numbers and diversity of the North Sea fish assemblage, as reflected in surveys and models Jake Rice and Henrik
ICES Journal of Marine Science, 53: 1214 1225. 1996 Patterns of change in the size spectra of numbers and diversity of the North Sea fish assemblage, as reflected in surveys and models Jake Rice and Henrik
MULTIFAN-CL: a length-based, age-structured model for fisheries stock assessment, with application to South Pacific albacore, Thunnus alalunga
 1 MULTIFAN-CL: a length-based, age-structured model for fisheries stock assessment, with application to South Pacific albacore, Thunnus alalunga David A. Fournier, John Hampton, and John R. Sibert Abstract:
1 MULTIFAN-CL: a length-based, age-structured model for fisheries stock assessment, with application to South Pacific albacore, Thunnus alalunga David A. Fournier, John Hampton, and John R. Sibert Abstract:
CHAPTER 4 CRITICAL GROWTH SEASONS AND THE CRITICAL INFLOW PERIOD. The numbers of trawl and by bag seine samples collected by year over the study
 CHAPTER 4 CRITICAL GROWTH SEASONS AND THE CRITICAL INFLOW PERIOD The numbers of trawl and by bag seine samples collected by year over the study period are shown in table 4. Over the 18-year study period,
CHAPTER 4 CRITICAL GROWTH SEASONS AND THE CRITICAL INFLOW PERIOD The numbers of trawl and by bag seine samples collected by year over the study period are shown in table 4. Over the 18-year study period,
An initial investigation of the information content of sole catch-atlength distributions regarding recruitment trends
 An initial investigation of the information content of sole catch-atlength distributions regarding recruitment trends A. Ross-Gillespie and D.S. Butterworth 1 email: mlland028@myuct.ac.za Summary A simple
An initial investigation of the information content of sole catch-atlength distributions regarding recruitment trends A. Ross-Gillespie and D.S. Butterworth 1 email: mlland028@myuct.ac.za Summary A simple
Final Anchovy and Sardine TACs and TABs for 2016, Using OMP-14
 FIHERIE//JUL/WG-PEL/26 Final nchovy and ardine TCs and TBs for Using OMP-4 Carryn L de Moor Correspondence email: carryn.demoor@uct.ac.za Following the recent recruit survey the revised outh frican anchovy
FIHERIE//JUL/WG-PEL/26 Final nchovy and ardine TCs and TBs for Using OMP-4 Carryn L de Moor Correspondence email: carryn.demoor@uct.ac.za Following the recent recruit survey the revised outh frican anchovy
Environmental changes
 Environmental changes What are the fishery, environmental, and trophic effects in historical data? Can we use short-term predictions from multiple regression models? Two kind of predictions: What happens
Environmental changes What are the fishery, environmental, and trophic effects in historical data? Can we use short-term predictions from multiple regression models? Two kind of predictions: What happens
Features of Complex Adaptive Systems
 Features of Complex Adaptive Systems Rapid adaptation Codependent agents Emergent phenomena Tipping points Self-organized criticality Social dilemmas Stakeholder diversity Social Dilemmas Common Goods
Features of Complex Adaptive Systems Rapid adaptation Codependent agents Emergent phenomena Tipping points Self-organized criticality Social dilemmas Stakeholder diversity Social Dilemmas Common Goods
SARSIM Model Output for the Distribution of Sardine in Canadian, US and Mexican Waters. Richard Parrish October 13, 2015
 SARSIM Model Output for the Distribution of Sardine in Canadian, US and Mexican Waters. Richard Parrish October 13, 2015 Agenda Item H.1.c The information presented below was taken from a model that I
SARSIM Model Output for the Distribution of Sardine in Canadian, US and Mexican Waters. Richard Parrish October 13, 2015 Agenda Item H.1.c The information presented below was taken from a model that I
When Does it Take a Nixon to Go to China - Errata and Further Results
 When Does it Take a Nixon to Go to China - Errata and Further Results Alex Cukierman and Ehud Menirav September 19 2004 Abstract This note points out and corrects an algebraic error that occured in the
When Does it Take a Nixon to Go to China - Errata and Further Results Alex Cukierman and Ehud Menirav September 19 2004 Abstract This note points out and corrects an algebraic error that occured in the
3 rd Annual Fraser Sockeye Forecast Supplement
 3 rd Annual Fraser Sockeye Forecast Supplement Grant, Whitehouse, Tadey, Benner, Patterson, Hills, Selbie, Pon, Neville, Trudel, Perry, Lapointe, Huang Objective To improve our understanding of factors
3 rd Annual Fraser Sockeye Forecast Supplement Grant, Whitehouse, Tadey, Benner, Patterson, Hills, Selbie, Pon, Neville, Trudel, Perry, Lapointe, Huang Objective To improve our understanding of factors
Advice September 2012
 9.4.23 Advice September 2012 ECOREGION STOCK Widely distributed and migratory stocks European seabass in the Northeast Atlantic Advice for 2013 ICES advises on the basis of the approach to data-limited
9.4.23 Advice September 2012 ECOREGION STOCK Widely distributed and migratory stocks European seabass in the Northeast Atlantic Advice for 2013 ICES advises on the basis of the approach to data-limited
Solving Quadratic Equations Using Multiple Methods and Solving Systems of Linear and Quadratic Equations
 Algebra 1, Quarter 4, Unit 4.1 Solving Quadratic Equations Using Multiple Methods and Solving Systems of Linear and Quadratic Equations Overview Number of instructional days: 13 (1 day = 45 minutes) Content
Algebra 1, Quarter 4, Unit 4.1 Solving Quadratic Equations Using Multiple Methods and Solving Systems of Linear and Quadratic Equations Overview Number of instructional days: 13 (1 day = 45 minutes) Content
MANAGEMENT AND ANALYSIS OF BIOLOGICAL POPULATIONS
 ',' Developments in Agricultural and Managed-Forest Ecology, 8 MANAGEMENT AND ANALYSIS OF BIOLOGICAL POPULATIONS by BEAN-SAN GOH Department ofmathematics, University of Western Australia, Nedlands, W.A.
',' Developments in Agricultural and Managed-Forest Ecology, 8 MANAGEMENT AND ANALYSIS OF BIOLOGICAL POPULATIONS by BEAN-SAN GOH Department ofmathematics, University of Western Australia, Nedlands, W.A.
History and meaning of the word Ecology A. Definition 1. Oikos, ology - the study of the house - the place we live
 History and meaning of the word Ecology A. Definition 1. Oikos, ology - the study of the house - the place we live B. Etymology study of the origin and development of a word 1. Earliest - Haeckel (1869)
History and meaning of the word Ecology A. Definition 1. Oikos, ology - the study of the house - the place we live B. Etymology study of the origin and development of a word 1. Earliest - Haeckel (1869)
JABBA: Just Another Bayesian Biomass Assessment for Indian Ocean Blue shark
 JABBA: Just Another Bayesian Biomass Assessment for Indian Ocean Blue shark Henning Winker* and Felipe Carvalho IOTC-2017-WPEB13-31 *henning.winker@gmail.com felipe.carvalho@noaa.gov JABBA is a further
JABBA: Just Another Bayesian Biomass Assessment for Indian Ocean Blue shark Henning Winker* and Felipe Carvalho IOTC-2017-WPEB13-31 *henning.winker@gmail.com felipe.carvalho@noaa.gov JABBA is a further
Relationship between temperature and fluctuations in sandfish catch (Arctoscopus japonicus) in the coastal waters off Akita Prefecture
 ICES Journal of Marine Science, 54: 1 12. 1997 Relationship between temperature and fluctuations in sandfish catch (Arctoscopus japonicus) in the coastal waters off Akita Prefecture Kazumi Sakuramoto,
ICES Journal of Marine Science, 54: 1 12. 1997 Relationship between temperature and fluctuations in sandfish catch (Arctoscopus japonicus) in the coastal waters off Akita Prefecture Kazumi Sakuramoto,
Apprentissage automatique Méthodes à noyaux - motivation
 Apprentissage automatique Méthodes à noyaux - motivation MODÉLISATION NON-LINÉAIRE prédicteur non-linéaire On a vu plusieurs algorithmes qui produisent des modèles linéaires (régression ou classification)
Apprentissage automatique Méthodes à noyaux - motivation MODÉLISATION NON-LINÉAIRE prédicteur non-linéaire On a vu plusieurs algorithmes qui produisent des modèles linéaires (régression ou classification)
PRE-SEASON RUN SIZE FORECASTS FOR FRASER RIVER SOCKEYE (ONCORHYNCHUS NERKA) AND PINK (O. GORBUSCHA) SALMON IN 2017
 Canadian Science Advisory Secretariat Pacific Region Science Response 2017/016 PRE-SEASON RUN SIZE FORECASTS FOR FRASER RIVER SOCKEYE (ONCORHYNCHUS NERKA) AND PINK (O. GORBUSCHA) SALMON IN 2017 Context
Canadian Science Advisory Secretariat Pacific Region Science Response 2017/016 PRE-SEASON RUN SIZE FORECASTS FOR FRASER RIVER SOCKEYE (ONCORHYNCHUS NERKA) AND PINK (O. GORBUSCHA) SALMON IN 2017 Context
The Quantum-Classical Transition and Wave Packet Dispersion. C. L. Herzenberg
 The Quantum-Classical Transition and Wave Packet Dispersion C. L. Herzenberg Abstract Two recent studies have presented new information relevant to the transition from quantum behavior to classical behavior,
The Quantum-Classical Transition and Wave Packet Dispersion C. L. Herzenberg Abstract Two recent studies have presented new information relevant to the transition from quantum behavior to classical behavior,
Life history evolution
 Life history evolution Key concepts ˆ Cole s paradox ˆ Tradeoffs ad the evolution of iteroparity ˆ Bet hedging in random environments Life history theory The life history of a species consists of its life
Life history evolution Key concepts ˆ Cole s paradox ˆ Tradeoffs ad the evolution of iteroparity ˆ Bet hedging in random environments Life history theory The life history of a species consists of its life
Species specific geographical distribution patterns in a warm Barents Sea: haddock vs. cod
 Species specific geographical distribution patterns in a warm Barents Sea: haddock vs. cod Nordic Climate-Fish 2nd Conference: Latitudinal changes in marine resources, exploitation and society within the
Species specific geographical distribution patterns in a warm Barents Sea: haddock vs. cod Nordic Climate-Fish 2nd Conference: Latitudinal changes in marine resources, exploitation and society within the
Spanish Mackerel and Cobia Abundance Indices from SEAMAP Groundfish Surveys in the Northern Gulf of Mexico. AG Pollack and GW Ingram, Jr SEDAR28 DW03
 Spanish Mackerel and Cobia Abundance Indices from SEAMAP Groundfish Surveys in the Northern Gulf of Mexico AG Pollack and GW Ingram, Jr SEDAR28 DW03 Originally Submitted: 24 January 2012 Revised: 3 April
Spanish Mackerel and Cobia Abundance Indices from SEAMAP Groundfish Surveys in the Northern Gulf of Mexico AG Pollack and GW Ingram, Jr SEDAR28 DW03 Originally Submitted: 24 January 2012 Revised: 3 April
Bayesian state-space production models for the Indian Ocean bigeye tuna (Thunnus Obesus) and their predictive evaluation
 Received: 1 November 2016 Bayesian state-space production models for the Indian Ocean bigeye tuna (Thunnus Obesus) and their predictive evaluation Kento Otsuyama and Toshihide Kitakado * 1 Tokyo University
Received: 1 November 2016 Bayesian state-space production models for the Indian Ocean bigeye tuna (Thunnus Obesus) and their predictive evaluation Kento Otsuyama and Toshihide Kitakado * 1 Tokyo University
SCIENTIFIC COUNCIL MEETING JUNE Random Retrospective Pattern in Fish Stock Assessment. Antonio Vázquez Mónica Mandado
 NOT TO BE CITED WITHOUT PRIOR REFERENCE TO THE AUTHOR(S) Northwest Atlantic Fisheries Organization Serial No. N5794 NAFO SCR Doc. /36 SCIENTIFIC COUNCIL MEETING JUNE Random Retrospective Pattern in Fish
NOT TO BE CITED WITHOUT PRIOR REFERENCE TO THE AUTHOR(S) Northwest Atlantic Fisheries Organization Serial No. N5794 NAFO SCR Doc. /36 SCIENTIFIC COUNCIL MEETING JUNE Random Retrospective Pattern in Fish
Sequential Monte Carlo methods for filtering of unobservable components of multidimensional diffusion Markov processes
 Sequential Monte Carlo methods for filtering of unobservable components of multidimensional diffusion Markov processes Ellida M. Khazen * 13395 Coppermine Rd. Apartment 410 Herndon VA 20171 USA Abstract
Sequential Monte Carlo methods for filtering of unobservable components of multidimensional diffusion Markov processes Ellida M. Khazen * 13395 Coppermine Rd. Apartment 410 Herndon VA 20171 USA Abstract
Stock and recruitment in Baltic cod (Gadus morhua): a new, non-linear approach
 ICES Journal of Marine Science, 54: 427 443. 1997 Stock and recruitment in Baltic cod (Gadus morhua): a new, non-linear approach A. P. Solari, J. M. Martín-González, and C. Bas Solari, A. P., Martín-González,
ICES Journal of Marine Science, 54: 427 443. 1997 Stock and recruitment in Baltic cod (Gadus morhua): a new, non-linear approach A. P. Solari, J. M. Martín-González, and C. Bas Solari, A. P., Martín-González,
Dynamic Output Feedback Controller for a Harvested Fish Population System
 Dynamic Output Feedback Controller for a Harvested Fish Population System Achraf Ait Kaddour, El Houssine Elmazoudi, Noureddine Elalami Abstract This paper deals with the control of a continuous age structured
Dynamic Output Feedback Controller for a Harvested Fish Population System Achraf Ait Kaddour, El Houssine Elmazoudi, Noureddine Elalami Abstract This paper deals with the control of a continuous age structured
Basic Concepts. 1.0 renewable, nonrenewable, and environmental resources
 1 Basic Concepts 1.0 renewable, nonrenewable, and environmental resources Economics might be defined as the study of how society allocates scarce resources. The field of resource economics, would then
1 Basic Concepts 1.0 renewable, nonrenewable, and environmental resources Economics might be defined as the study of how society allocates scarce resources. The field of resource economics, would then
PREDICTIVE CONTROL OF NONLINEAR SYSTEMS. Received February 2008; accepted May 2008
 ICIC Express Letters ICIC International c 2008 ISSN 1881-803X Volume 2, Number 3, September 2008 pp. 239 244 PREDICTIVE CONTROL OF NONLINEAR SYSTEMS Martin Janík, Eva Miklovičová and Marián Mrosko Faculty
ICIC Express Letters ICIC International c 2008 ISSN 1881-803X Volume 2, Number 3, September 2008 pp. 239 244 PREDICTIVE CONTROL OF NONLINEAR SYSTEMS Martin Janík, Eva Miklovičová and Marián Mrosko Faculty
Figure 5: Bifurcation diagram for equation 4 as a function of K. n(t) << 1 then substituting into f(n) we get (using Taylor s theorem)
 Figure 5: Bifurcation diagram for equation 4 as a function of K n(t)
Figure 5: Bifurcation diagram for equation 4 as a function of K n(t)
Cover Page. The handle holds various files of this Leiden University dissertation
 Cover Page The handle http://hdl.handle.net/1887/39637 holds various files of this Leiden University dissertation Author: Smit, Laurens Title: Steady-state analysis of large scale systems : the successive
Cover Page The handle http://hdl.handle.net/1887/39637 holds various files of this Leiden University dissertation Author: Smit, Laurens Title: Steady-state analysis of large scale systems : the successive
RECOMMENDED STUDY PLAN 2018
 RECOMMENDED STUDY PLAN 2018 NAME DEGREE PROGRAM Master of Science STUDENT NUMBER MAJOR Trop Bio & Con-TSV (MSC-TBI) Level 5: Year 1 SP3 SP1 SP6/7 SP2 SP10/SP11 Major Core: BZ5215 Major Opt Skill Conservation
RECOMMENDED STUDY PLAN 2018 NAME DEGREE PROGRAM Master of Science STUDENT NUMBER MAJOR Trop Bio & Con-TSV (MSC-TBI) Level 5: Year 1 SP3 SP1 SP6/7 SP2 SP10/SP11 Major Core: BZ5215 Major Opt Skill Conservation
STABILITY ANALYSIS OF DAMPED SDOF SYSTEMS WITH TWO TIME DELAYS IN STATE FEEDBACK
 Journal of Sound and Vibration (1998) 214(2), 213 225 Article No. sv971499 STABILITY ANALYSIS OF DAMPED SDOF SYSTEMS WITH TWO TIME DELAYS IN STATE FEEDBACK H. Y. HU ANDZ. H. WANG Institute of Vibration
Journal of Sound and Vibration (1998) 214(2), 213 225 Article No. sv971499 STABILITY ANALYSIS OF DAMPED SDOF SYSTEMS WITH TWO TIME DELAYS IN STATE FEEDBACK H. Y. HU ANDZ. H. WANG Institute of Vibration
Taxes, compensations and renewable natural resources
 Taxes, compensations and renewable natural resources June 9, 2015 Abstract We start from a dynamic model of exploitation of renewable natural resources in which extinction is the expected outcome in the
Taxes, compensations and renewable natural resources June 9, 2015 Abstract We start from a dynamic model of exploitation of renewable natural resources in which extinction is the expected outcome in the
Ecological indicators: Software development
 Ecological indicators: Software development Sergei N. Rodionov Joint Institute for the Study of the Atmosphere and Ocean, University of Washington, Seattle, WA 98185, U.S.A. E-mail: sergei.rodionov@noaa.gov
Ecological indicators: Software development Sergei N. Rodionov Joint Institute for the Study of the Atmosphere and Ocean, University of Washington, Seattle, WA 98185, U.S.A. E-mail: sergei.rodionov@noaa.gov
September 16, 2004 The NEURON Book: Chapter 2
 Chapter 2 The ing perspective This and the following chapter deal with concepts that are not NEURON-specific but instead pertain equally well to any tools used for neural ing. Why? In order to achieve
Chapter 2 The ing perspective This and the following chapter deal with concepts that are not NEURON-specific but instead pertain equally well to any tools used for neural ing. Why? In order to achieve
