dq 1 (5) q 1 where the previously mentioned limit has been taken.
|
|
|
- Joseph Bishop
- 5 years ago
- Views:
Transcription
1 1 Vecto Calculus And Continuum Consevation Equations In Cuvilinea Othogonal Coodinates Robet Maska: Novembe 25, 2008 In ode to ewite the consevation equations(continuit, momentum, eneg) to some cuvilinea otogonal coodinate sstem(pola, spheical, elliptical etc.) it is a useful stateg to fist eview vecto analsis. A displacement vecto in some thee-dimensional otogonal metic coodinate sstem (q 1, q 2, q 3 ) can be witten b its base vectos b d = dq 1 ε 1 + dq 2 ε 2 + dq 3 ε 3 (1) whee ε coesponds to a base vecto. The base vectos do not necessail have unit magnitude and dimension length such as is the case in catesian coodinates. One can epand this in tems of unit vectos instead b letting ε i = h i e i whee h i is a scaling facto fo the base vecto, i.e. its length. The e i s ae mutuall othogonal and have unit magnitude. This gives fo the diffeential displacement d = dq 1 h 1 e 1 + dq 2 h 2 e 2 + dq 3 h 3 e 3 An eample of this is the displacement vecto in clindical pola coodinates (q 1, q 2, q 3 ) = (,, ), it can be witten as d = dˆ + dˆ + dˆ whee h 1, h 2, h 3 ae easil ecognied on inspection. It tanspies that these scaling factos does not necessail have unit magnitude and in fact could ca diffeent dimensions. In contast, a displacement vecto in catesian coodinates is witten d = dˆ + dŷ + dẑ whee all the h s have dimension and length of unit. The net diffeential displacement still caies the dimension length. Conside now a diffeential displacement in the space (q 1, q 2, q 3 ), its magnitude is d d = (ds) 2 = (h 1 dq 1 ) 2 + (h 2 dq 2 ) 2 + (h 3 dq 3 ) 2 (2) since the unit vectos ae mutuall othogonal. Gadient The component i of the gadient of a scala ψ is e i ψ = ψ s i = 1 h i ψ q i A genealiation gives the the gadient ψ = X i 1 ψ e i (3) h i q i Fo altenative deivations, see fo eample Afken&Webe[1]. Divegence The divegence of a vecto v is defined[1] H v dσ div v = R lim R (4) dτ 0 dτ Fo convenience, a ight-hand sstem has been chosen. A diffeential aea in the chosen space can be witten dσ = ds 2 ds 3 e 1 + ds 3 ds 1 e 2 + ds 1 ds 2 e 3 whee now, should it not be clea, ds i = h i dq i. In catesian coodinates fo instance, this would simpl educe to dσ = (dd)ˆ + (dd)ŷ + (dd)ẑ which is a slanted squae face. The above equation is a genealiation to cuved faces. This lets us evaluate the suface integal, the vecto poduct v dσ is integated temwise. Doing the v 1 dσ 1 tem fist one finds that the integal fo the two faces in the e 1 -diection is v 1 dσ 1 = v 1 ds 2 ds 3 + v 1 ds 2 ds 3 + (v 1ds 2 ds 3 ) dq 1 (5) whee the peviousl mentioned limit has been taken. ds 3 ds 1 e 2 e 3 ds 2 dσ 1 e 1 FIG. 1: Diffeential volume and sufaces. We will now eplain this, see FIG. 1 fo efeence. The fist tem is simpl the suface integal ove the face opposite the label dσ 1 in FIG. 1. The second tem comes fom a Talo epansion of the vecto component v 1 and the diffeential aea. This just means that the v 1 component changes b v 1 (q 1 + dq 1 ) = v 1 (q 1 ) + v 1 Similal the suface aea has changed b dσ 1 (q 1 + dq 1 ) = dσ 1 (q 1 ) + dσ 1 Fo notational easons we now denote v 1 (q 1 ) b v 1 and a simila fomalism fo dσ 1. Then the suface integal ove the second face is found b multiplication of v 1 (q 1 + dq 1 ) and dσ 1 (q 1 + dq 1 ) = v 1 dσ 1 + v 1 dσ 1 dq 1 + dσ 1 v 1 dq 1 + O(dq 2 1 ) = v 1 dσ 1 + (v 1dσ 1 ) which follows fom the poduct ule. Imposing the limit R dτ 0 leaves onl the fist ode tems and EQ. 5 is fulfilled. EQ. 5 now educes to v 1 dσ 1 = (v 1ds 2 ds 3 ) dq 1 = (v 1h 2 h 3 ) We have now integated ove two of the faces. The esult is of couse the same fo the othe fou faces, with a cclic pemutation of 123. In othe wods v 2 dσ 2 = (v 2ds 3 ds 1 ) dq 2 = (v 2h 3 h 1 ) v 3 dσ 3 = (v 3ds 1 ds 2 ) dq 3 = (v 3h 1 h 2 ) Addition of these thee integals gives the closed suface integal, as in EQ. 4. The diffeential volume is simpl ds 1 ds 2 ds 3 = Robet Maska: Novembe 25, 2008 Depatment Of Eneg And Pocess Engineeing Depatment Of Phsics
2 2 h 1 h 2 h 3. B collecting tems and imposing the limit we conclude that 1 (v1 h 2 h 3 ) div v = + (v 2h 3 h 1 ) + (v 3h 1 h 2 ) (6) h 1 h 2 h 3 q 3 As peviousl mentioned, in catesian coodinates the h i s ae equal to one. This allows us to wite the divegence as an inne poduct of and v. It is howeve common to adopt the notation v = div v even in cuvilinea coodinates. This is bad notation since it suggests that the divegence can be witten as an inne poduct which is not the case. Laplacian The Laplacian of a scala ψ(q 1, q 2, q 3 ) can be developed b taking the gadient of the divegence. That is, we choose the components of v as the vecto components of EQ. 3. This gives without dwelling on details div v = div gad ψ = 1 h2 h 3 ψ + h3 h 1 ψ h 1 h 2 h 3 h 1 h 2 + h1 h 2 ψ q 3 h 3 q 3 This is b definition the Laplacian and is sometimes witten 2 ψ. Some people seem to like confusing the Laplacian of a scala with the Laplacian of a vecto. A component of the Laplacian of a vecto is not the same as the Laplacian of the vecto component, as will be shown late. Cul The cul can be found using Stokes theoem S I (cul v) dσ = (7) v ds (8) One will meit fom doing this component-wise on an infinitesimal aea. Thus let the suface be made up of thee sufaces, each with q 1, q 3 o q 3 kept constant. (4) (q 2, q 3 ) e 2 ds 2 (q 3 ) (1) Suface q 1 = const (3) e (2) 3 ds 3 (q 2 + dq 2 ) FIG. 2: Temwise integation of EQ. 8 Conside fist the suface whee q 1 is constant. Following the loop in the figue counteclockwise fom the leftmost cone, the line integal is I v ds =v 2 ds 2 + v 3 ds 3 + (v 3ds 3 ) v 2 ds 2 + (v 2ds 2 ) = (h 3 v 3 ) dq 2 dq 3 v 3 ds 3 q 3 (h 2 v 2 ) dq 2 dq 3 q 3 This also follows b Talo epanding the vecto components. The fist integal along the line (1) is simpl = v 2 ds 2 Fo the second line integal (2), the infinitesimal length and the vecto component has changed accoding to a Talo seies v 3 (q 2 + dq 2 ) = v 3 (q 2 ) + v 3(q 2 ) dq 2 + O(dq 2 2 ) ds 3 (q 2 + dq 2 ) = ds 3 (q 2 ) + ds 3(q 2 ) dq 2 + O(dq 2 2 ) Using the same fomalism as ealie, v 3 (q 2 ) is denoted v 3 etc., combined with the poduct ule gives that the line integal (2) is = v 3 ds 3 + (v 3ds 3 ) dq 2 + O(dq 2 2) The emaining tems in EQ. 9 is found b identical agumentation on the two emaining line integals. Fo an infinitesimal aea, the left hand side of EQ. 8 can be witten (cul v) dσ = e 1 (cul v)ds 2 ds 3 S since the fist suface is oiented in the q 1 diection. Combining these esults with the limit of an infinitesimal aea gives [cul v] 1 = 1 (h 3 v 3 ) (h 2 v 2 ) h 2 h 3 q 3 since the highe-ode tems vanish in the limit. The emaining two components ae found in a simila wa, o b cclic pemutation of 123. Thus [cul v] 2 = 1 h 3 h 1 [cul v] 3 = 1 h 1 h 2 O in inde notation (h 1 v 1 ) (h 3 v 3 ) q 3 (h 2 v 2 ) (h 1 v 1 ) (9) [cul v] i = 1 h j h k ε ijk j (h k v k ) (10) whee ε ijk denotes the Levi-Civita pseudo-tenso. Occasionall, but ael, it is useful to wite this as a deteminant. It can then be witten e 1 h 1 e 2 h 2 e 3 h 3 1 cul v = h 1 h 2 h (11) 3 q 3 h 1 v 1 h 2 v 2 h 3 v 3 Net we will develop the divegence and cul in clindical and spheical pola coodinates. Vecto Calculus And Continuum Consevation Equations In Cuvilinea Othogonal Coodinates
3 3 θ FIG. 3: Clindical pola coodinates. FIG. 4: Spheical pola coodinates. Clindical Pola Coodinates In clindical pola coodinates (q 1, q 2, q 3 ) = (,, ) the elation between the clindical coodinates and the catesian is = cos ; = sin ; = A diffeential displacement can be witten which again gives One should now ecognie d = dˆ + dˆ + dˆ d d = (ds) 2 = (d) 2 + (d) 2 + (d) 2 h 1 = h = 1; h 2 = h = ; h 3 = h = 1 Going to EQ. 6 and EQ. 11, o EQ. 10, the divegence and cul is found b diect insetion to be div v = 1 (v ) v [cul v] = 1 v v [cul v] = v v [cul v] = 1 (v ) 1 v If one absolutel insists this can be witten in mati fom ˆ ˆ ˆ cul v = 1 v v v Spheical Pola Coodinates In spheical clindical coodinates (q 1, q 2, q 3 ) = (, θ, ) the elation to the catesian is = sin θ cos ; = sin θ sin ; = cos θ A diffeential displacement can be witten One should now ecognie d = dˆ + dθˆθ + d sin θ ˆ h 1 = h = 1; h 2 = h θ = ; h 3 = h = sin θ Going to EQ. 6 gives the divegence of a vecto v div v = 1 2 ( 2 v ) + 1 (v θ sin θ) + 1 sin θ θ sin θ Fom EQ. 10 the cul components can be found [cul v] = 1 (v sin θ) sin θ θ [cul v] θ = 1 sin θ [cul v] = 1 (v θ ) v 1 v θ (v) sin θ v θ This can be witten in mati fom following EQ. 11 ˆ ˆθ sin θ ˆ 1 cul v = 2 sin θ θ v v θ sin θv This is ael seen in pactice. The Consevation Equations In this tet we neglect the ewiting of the eneg equation and focus on the continuit equation and the incompessible Navie- Stokes equation. Fom hee on we adopt the notations cul v = v and div v = v. The full compessible equations ae in thei vecto fom given b[3] + div (v) = 0 (12) t and t + v v = 1 p + g + 1 τ ij (13) whee denotes the densit of the fluid and τ ij denotes the full viscous stess tenso including the second coefficient of viscosit. Including compessibilit into the Navie-Stokes equations makes fo a too cumbesome calculation. In the case of constant densit the final tem on the ight hand of EQ. 13 side educes to ν 2 v. We will stat b ewiting the Navie-Stokes equations[2]. Two vecto identities ae needed (v )v = v ( v) v 2 (14a) 2 v = ( v) ( v) (14b) Robet Maska: Novembe 25, 2008 Depatment Of Eneg And Pocess Engineeing Depatment Of Phsics
4 4 This can be found in an elementa book on calculus, and is in fact quite eas to show using the Levi-Civita tenso. This puts the Navie-Stokes equations on the fom v 1 t v ω+ 2 v 2 = 1 p+g+ν [ ( v) ω] (15) whee ω = v. The fluid velocit vecto is denoted b v and the components b v 1, v 2, v 3. The poblem with the vecto Laplacian is that we have 2 (ˆv + ˆv + ẑv ) = 2 (ˆv + ˆv ) + ẑ 2 v (16) Witing out the fist paanthesis on the ight hand side would equie seveal pages of equations. Convesel, the Laplacian in catesian coodinates is 2 (ˆv + ŷv + ẑv ) = ˆ 2 v + ŷ 2 v + ẑ 2 v This ma seem confusing at fist, but emembe that we ae not looking fo the Laplacian of a component v i, but looking fo component i of the Laplacian of v. Confusing these is a common mistake! Clindical Pola Coodinates In clindical pola coodinates, the gadient is given b EQ. 3, ω and ω ae given b EQ. 10 o EQ. 11. In ode not to confuse the densit with the adial coodinate, we denote the latte b. Stating with the tem ( v), these equations give afte some etensive ewiting [( v)] = 2 v v v v v [( v)] = 1 2 v v v v The tems ω ae(afte some ewiting) 1 2 [ ω] = v v [ ω] = v + v v 1 v v Notice that it is not necessa to calculate [( v) ω] because b EQ. 16 one finds that the vecto Laplacian [ 2 v] = 2 v. This is not tue fo the othe two components which is wh the need to be eplicitl calculated. In addition, the tem v ω is [v ω] = v [v ω] = v 1 (v) v v v v [v ω] = v v v v v 1 (v ) v 1 1 v v v v Thee is now onl one moe vecto tem which needs teatment, and that is the gadient of 1 2 v 2. B EQ. 3 this is 1 v 2 v 2 = v + v + v v 1 2 v 2 = v v + v + v v 1 2 v 2 v = v + v + v v We ae now in position to wite down the momentum equations b use of EQ. 15. Some viscous tems can be put into the Laplacian b EQ. 7, these tems ae put fist on the ight hand side of the equations above. Fo the adial component ˆ one finds v t + (v ) v v2 = 1 p + g + ν Similal the aimuthal component is vv + (v ) v t + 2 v 2 = 1 Finall, the vetical component is 2 v v p + g + ν 2 v v 2 v t + (v ) v = 1 p + g + ν 2 v whee the convective time-deivative is v = v + v + v It is eas to be led asta at this point since one might intuivel think that since [(v )v] = (v )v this also applies in cuvilinea coodinates. This, as in the case of the vecto Laplacian, is not tue. One should now have leaned the diffeence between the Laplacian of a vecto component and the component of a vecto Laplacian. To summaie [ 2 v] = 2 v v [ 2 v] = 2 v v v 2 [ 2 v] = 2 v The equation of continuit can be witten fom EQ. 4 t + 1 (v ) + 1 (v ) + (v ) The eneg equation is left out of this tet. Spheical Pola Coodinates The same tems ae needed, v ω, 1 2 v 2, ( v) and ω. We will howeve not go into the eplicit details on the calculation but cite the esult. B use of EQ. 3, 7, 10 and EQ. 14b one finds afte etensive use of the poduct ule and ewiting that the vecto Laplacian(the final tem in EQ. 15) is [ 2 v] = 2 v 2v 2 2 v θ 2 θ 2v θ 2 tan θ 2 2 sin θ [ 2 v] θ = 2 v θ [ 2 v] = 2 v v θ 2 sin 2 θ v θ v 2 sin 2 θ sin θ 2cos θ 2 sin 2 θ v + 2cos θ 2 sin 2 θ v θ Fo the left hand side of the Navie-Stokes equations one finds 1 v ω + 2 v 2 = (v )v v2 θ + v2 1 v ω + 2 v 2 = (v )v θ vv θ v 2 cot θ θ 1 v ω + 2 v 2 = (v )v vv + v θv cot θ Vecto Calculus And Continuum Consevation Equations In Cuvilinea Othogonal Coodinates
5 5 whee the convective tem is v = v + v θ θ + v sin θ To summaie, the incompessible Navie-Stokes equations ae (stating with the adial component) v t +(v )v v2 θ + v2 = 1 p 2 v 2v v θ θ The ˆθ component: 2v θ 2 tan θ 2 2 sin θ + g + ν v θ t +(v )v θ vv θ v cot θ = 1 p θ + g θ + ν ` 2 v θ v θ 2 sin 2 θ + 2 v 2 θ and finall the aimuthal component 2 cos θ 2 sin 2 θ t +(v )v vv + v θv cot θ + ν 2 v = 1 p sin θ + g v 2 sin 2 θ + 2 v 2 sin θ + 2cos θ 2 sin 2 θ v θ The equation of continuit can be witten fom EQ. 4 and is 1 t + ( 2 v ) (v θ sin θ) + 1 (v ) = 0 sin θ θ sin θ Fo constant densit, vanishes. The Navie-Stokes equations ae quite mess but ae sometimes useful. The eneg equation is best tansfomed b tansfoming each element in the viscous stess tenso. * Refeences [1] Geoge B. Afken and Hans J. Webe. Mathematical Methods Fo Phsicists. Academic Pess, 5th edition, [2] W.P. Gaebel. Advanced Fluid Mechanics. Academic Pess, 1st edition, [3] Hebet Oetel. Pandlt s Essentials of Fluid Mechanics, volume 158. Applied Mathematical Sciences, 2nd edition, Robet Maska: Novembe 25, 2008 Depatment Of Eneg And Pocess Engineeing Depatment Of Phsics
COORDINATE TRANSFORMATIONS - THE JACOBIAN DETERMINANT
 COORDINATE TRANSFORMATIONS - THE JACOBIAN DETERMINANT Link to: phsicspages home page. To leave a comment o epot an eo, please use the auilia blog. Refeence: d Inveno, Ra, Intoducing Einstein s Relativit
COORDINATE TRANSFORMATIONS - THE JACOBIAN DETERMINANT Link to: phsicspages home page. To leave a comment o epot an eo, please use the auilia blog. Refeence: d Inveno, Ra, Intoducing Einstein s Relativit
B da = 0. Q E da = ε. E da = E dv
 lectomagnetic Theo Pof Ruiz, UNC Asheville, doctophs on YouTube Chapte Notes The Maxwell quations in Diffeential Fom 1 The Maxwell quations in Diffeential Fom We will now tansfom the integal fom of the
lectomagnetic Theo Pof Ruiz, UNC Asheville, doctophs on YouTube Chapte Notes The Maxwell quations in Diffeential Fom 1 The Maxwell quations in Diffeential Fom We will now tansfom the integal fom of the
As is natural, our Aerospace Structures will be described in a Euclidean three-dimensional space R 3.
 Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
Stress, Cauchy s equation and the Navier-Stokes equations
 Chapte 3 Stess, Cauchy s equation and the Navie-Stokes equations 3. The concept of taction/stess Conside the volume of fluid shown in the left half of Fig. 3.. The volume of fluid is subjected to distibuted
Chapte 3 Stess, Cauchy s equation and the Navie-Stokes equations 3. The concept of taction/stess Conside the volume of fluid shown in the left half of Fig. 3.. The volume of fluid is subjected to distibuted
Vectors, Vector Calculus, and Coordinate Systems
 Apil 5, 997 A Quick Intoduction to Vectos, Vecto Calculus, and Coodinate Systems David A. Randall Depatment of Atmospheic Science Coloado State Univesity Fot Collins, Coloado 80523. Scalas and vectos Any
Apil 5, 997 A Quick Intoduction to Vectos, Vecto Calculus, and Coodinate Systems David A. Randall Depatment of Atmospheic Science Coloado State Univesity Fot Collins, Coloado 80523. Scalas and vectos Any
Appendix A. Appendices. A.1 ɛ ijk and cross products. Vector Operations: δ ij and ɛ ijk
 Appendix A Appendices A1 ɛ and coss poducts A11 Vecto Opeations: δ ij and ɛ These ae some notes on the use of the antisymmetic symbol ɛ fo expessing coss poducts This is an extemely poweful tool fo manipulating
Appendix A Appendices A1 ɛ and coss poducts A11 Vecto Opeations: δ ij and ɛ These ae some notes on the use of the antisymmetic symbol ɛ fo expessing coss poducts This is an extemely poweful tool fo manipulating
6 Vector Operators. 6.1 The Gradient Operator
 6 Vecto Opeatos 6. The Gadient Opeato In the B2 couse ou wee intoduced to the gadient opeato in Catesian coodinates. Fo an diffeentiable scala function f(x,, z), we can define a vecto function though (
6 Vecto Opeatos 6. The Gadient Opeato In the B2 couse ou wee intoduced to the gadient opeato in Catesian coodinates. Fo an diffeentiable scala function f(x,, z), we can define a vecto function though (
Review: Electrostatics and Magnetostatics
 Review: Electostatics and Magnetostatics In the static egime, electomagnetic quantities do not vay as a function of time. We have two main cases: ELECTROSTATICS The electic chages do not change postion
Review: Electostatics and Magnetostatics In the static egime, electomagnetic quantities do not vay as a function of time. We have two main cases: ELECTROSTATICS The electic chages do not change postion
THE NAVIER-STOKES EQUATION: The Queen of Fluid Dynamics. A proof simple, but complete.
 THE NAIER-TOKE EQUATION: The Queen of Fluid Dnamics. A poof simple, but complete. Leonado Rubino leonubino@ahoo.it eptembe 010 Rev. 00 Fo www.via.og Abstact: in this pape ou will find a simple demonstation
THE NAIER-TOKE EQUATION: The Queen of Fluid Dnamics. A poof simple, but complete. Leonado Rubino leonubino@ahoo.it eptembe 010 Rev. 00 Fo www.via.og Abstact: in this pape ou will find a simple demonstation
(read nabla or del) is defined by, k. (9.7.1*)
 9.7 Gadient of a scala field. Diectional deivative Some of the vecto fields in applications can be obtained fom scala fields. This is vey advantageous because scala fields can be handled moe easily. The
9.7 Gadient of a scala field. Diectional deivative Some of the vecto fields in applications can be obtained fom scala fields. This is vey advantageous because scala fields can be handled moe easily. The
J. N. R E DDY ENERGY PRINCIPLES AND VARIATIONAL METHODS APPLIED MECHANICS
 J. N. E DDY ENEGY PINCIPLES AND VAIATIONAL METHODS IN APPLIED MECHANICS T H I D E DI T IO N JN eddy - 1 MEEN 618: ENEGY AND VAIATIONAL METHODS A EVIEW OF VECTOS AND TENSOS ead: Chapte 2 CONTENTS Physical
J. N. E DDY ENEGY PINCIPLES AND VAIATIONAL METHODS IN APPLIED MECHANICS T H I D E DI T IO N JN eddy - 1 MEEN 618: ENEGY AND VAIATIONAL METHODS A EVIEW OF VECTOS AND TENSOS ead: Chapte 2 CONTENTS Physical
is the instantaneous position vector of any grid point or fluid
 Absolute inetial, elative inetial and non-inetial coodinates fo a moving but non-defoming contol volume Tao Xing, Pablo Caica, and Fed Sten bjective Deive and coelate the govening equations of motion in
Absolute inetial, elative inetial and non-inetial coodinates fo a moving but non-defoming contol volume Tao Xing, Pablo Caica, and Fed Sten bjective Deive and coelate the govening equations of motion in
Question 1: The dipole
 Septembe, 08 Conell Univesity, Depatment of Physics PHYS 337, Advance E&M, HW #, due: 9/5/08, :5 AM Question : The dipole Conside a system as discussed in class and shown in Fig.. in Heald & Maion.. Wite
Septembe, 08 Conell Univesity, Depatment of Physics PHYS 337, Advance E&M, HW #, due: 9/5/08, :5 AM Question : The dipole Conside a system as discussed in class and shown in Fig.. in Heald & Maion.. Wite
2. Electrostatics. Dr. Rakhesh Singh Kshetrimayum 8/11/ Electromagnetic Field Theory by R. S. Kshetrimayum
 2. Electostatics D. Rakhesh Singh Kshetimayum 1 2.1 Intoduction In this chapte, we will study how to find the electostatic fields fo vaious cases? fo symmetic known chage distibution fo un-symmetic known
2. Electostatics D. Rakhesh Singh Kshetimayum 1 2.1 Intoduction In this chapte, we will study how to find the electostatic fields fo vaious cases? fo symmetic known chage distibution fo un-symmetic known
Notation. 1 Vectors. 2 Spherical Coordinates The Problem
 Notation 1 Vectos As aleady noted, we neve wite vectos as pais o tiples of numbes; this notation is eseved fo coodinates, a quite diffeent concept. The symbols we use fo vectos have aows on them (to match
Notation 1 Vectos As aleady noted, we neve wite vectos as pais o tiples of numbes; this notation is eseved fo coodinates, a quite diffeent concept. The symbols we use fo vectos have aows on them (to match
3.3.1 Expanded forms of the Continuity Equation. θ (ρv θ)+ z (ρv z)=0. θ (ρv θ sin θ)+ 1
 Ke Equations 58 3.3 Ke Equations 3.3.1 Epanded foms of the Continuit Equation Rectangula coodinates: t (v (v z (v z0 Clindical coodinates: t 1 Spheical coodinates: (v 1 t 1 2 (2 v 1 θ (v θ z (v z0 θ (v
Ke Equations 58 3.3 Ke Equations 3.3.1 Epanded foms of the Continuit Equation Rectangula coodinates: t (v (v z (v z0 Clindical coodinates: t 1 Spheical coodinates: (v 1 t 1 2 (2 v 1 θ (v θ z (v z0 θ (v
MATH 300: Solutions for Problem Set 1
 Question.a: The de is MATH 300: Solutions fo Poblem Set 2u 4u 4u u 0: So a 2, b 2 and c 4. Hence b 2 ac 4 < 0. The de is ellitic. Question.b: The de is u 2u u u 0: So a, b and c. Hence b 2 ac 2. The de
Question.a: The de is MATH 300: Solutions fo Poblem Set 2u 4u 4u u 0: So a 2, b 2 and c 4. Hence b 2 ac 4 < 0. The de is ellitic. Question.b: The de is u 2u u u 0: So a, b and c. Hence b 2 ac 2. The de
AE301 Aerodynamics I UNIT B: Theory of Aerodynamics
 AE301 Aeodynamics I UNIT B: Theoy of Aeodynamics ROAD MAP... B-1: Mathematics fo Aeodynamics B-2: Flow Field Repesentations B-3: Potential Flow Analysis B-4: Applications of Potential Flow Analysis AE301
AE301 Aeodynamics I UNIT B: Theoy of Aeodynamics ROAD MAP... B-1: Mathematics fo Aeodynamics B-2: Flow Field Repesentations B-3: Potential Flow Analysis B-4: Applications of Potential Flow Analysis AE301
DonnishJournals
 DonnishJounals 041-1189 Donnish Jounal of Educational Reseach and Reviews. Vol 1(1) pp. 01-017 Novembe, 014. http:///dje Copyight 014 Donnish Jounals Oiginal Reseach Pape Vecto Analysis Using MAXIMA Savaş
DonnishJounals 041-1189 Donnish Jounal of Educational Reseach and Reviews. Vol 1(1) pp. 01-017 Novembe, 014. http:///dje Copyight 014 Donnish Jounals Oiginal Reseach Pape Vecto Analysis Using MAXIMA Savaş
ENGI 4430 Non-Cartesian Coordinates Page xi Fy j Fzk from Cartesian coordinates z to another orthonormal coordinate system u, v, ˆ i ˆ ˆi
 ENGI 44 Non-Catesian Coodinates Page 7-7. Conesions between Coodinate Systems In geneal, the conesion of a ecto F F xi Fy j Fzk fom Catesian coodinates x, y, z to anothe othonomal coodinate system u,,
ENGI 44 Non-Catesian Coodinates Page 7-7. Conesions between Coodinate Systems In geneal, the conesion of a ecto F F xi Fy j Fzk fom Catesian coodinates x, y, z to anothe othonomal coodinate system u,,
Physics 506 Winter 2006 Homework Assignment #9 Solutions
 Physics 506 Winte 2006 Homewok Assignment #9 Solutions Textbook poblems: Ch. 12: 12.2, 12.9, 12.13, 12.14 12.2 a) Show fom Hamilton s pinciple that Lagangians that diffe only by a total time deivative
Physics 506 Winte 2006 Homewok Assignment #9 Solutions Textbook poblems: Ch. 12: 12.2, 12.9, 12.13, 12.14 12.2 a) Show fom Hamilton s pinciple that Lagangians that diffe only by a total time deivative
Vectors Serway and Jewett Chapter 3
 Vectos Sewa and Jewett Chapte 3 Scalas and Vectos Vecto Components and Aithmetic Vectos in 3 Dimensions Unit vectos i, j, k Pactice Poblems: Chapte 3, poblems 9, 19, 31, 45, 55, 61 Phsical quantities ae
Vectos Sewa and Jewett Chapte 3 Scalas and Vectos Vecto Components and Aithmetic Vectos in 3 Dimensions Unit vectos i, j, k Pactice Poblems: Chapte 3, poblems 9, 19, 31, 45, 55, 61 Phsical quantities ae
An Exact Solution of Navier Stokes Equation
 An Exact Solution of Navie Stokes Equation A. Salih Depatment of Aeospace Engineeing Indian Institute of Space Science and Technology, Thiuvananthapuam, Keala, India. July 20 The pincipal difficulty in
An Exact Solution of Navie Stokes Equation A. Salih Depatment of Aeospace Engineeing Indian Institute of Space Science and Technology, Thiuvananthapuam, Keala, India. July 20 The pincipal difficulty in
This gives rise to the separable equation dr/r = 2 cot θ dθ which may be integrated to yield r(θ) = R sin 2 θ (3)
 Physics 506 Winte 2008 Homewok Assignment #10 Solutions Textbook poblems: Ch. 12: 12.10, 12.13, 12.16, 12.19 12.10 A chaged paticle finds itself instantaneously in the equatoial plane of the eath s magnetic
Physics 506 Winte 2008 Homewok Assignment #10 Solutions Textbook poblems: Ch. 12: 12.10, 12.13, 12.16, 12.19 12.10 A chaged paticle finds itself instantaneously in the equatoial plane of the eath s magnetic
Qualifying Examination Electricity and Magnetism Solutions January 12, 2006
 1 Qualifying Examination Electicity and Magnetism Solutions Januay 12, 2006 PROBLEM EA. a. Fist, we conside a unit length of cylinde to find the elationship between the total chage pe unit length λ and
1 Qualifying Examination Electicity and Magnetism Solutions Januay 12, 2006 PROBLEM EA. a. Fist, we conside a unit length of cylinde to find the elationship between the total chage pe unit length λ and
S7: Classical mechanics problem set 2
 J. Magoian MT 9, boowing fom J. J. Binney s 6 couse S7: Classical mechanics poblem set. Show that if the Hamiltonian is indepdent of a genealized co-odinate q, then the conjugate momentum p is a constant
J. Magoian MT 9, boowing fom J. J. Binney s 6 couse S7: Classical mechanics poblem set. Show that if the Hamiltonian is indepdent of a genealized co-odinate q, then the conjugate momentum p is a constant
PHYS 110B - HW #7 Spring 2004, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased
 PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
Homework # 3 Solution Key
 PHYSICS 631: Geneal Relativity Homewok # 3 Solution Key 1. You e on you hono not to do this one by hand. I ealize you can use a compute o simply look it up. Please don t. In a flat space, the metic in
PHYSICS 631: Geneal Relativity Homewok # 3 Solution Key 1. You e on you hono not to do this one by hand. I ealize you can use a compute o simply look it up. Please don t. In a flat space, the metic in
ANTENNAS. Vector and Scalar Potentials. Maxwell's Equations. D = εe. For a linear, homogeneous, isotropic medium µ and ε are contant.
 ANTNNAS Vecto and Scala Potentials Maxwell's quations jωb J + jωd D ρ B (M) (M) (M3) (M4) D ε B Fo a linea, homogeneous, isotopic medium and ε ae contant. Since B, thee exists a vecto A such that B A and
ANTNNAS Vecto and Scala Potentials Maxwell's quations jωb J + jωd D ρ B (M) (M) (M3) (M4) D ε B Fo a linea, homogeneous, isotopic medium and ε ae contant. Since B, thee exists a vecto A such that B A and
A New Approach to General Relativity
 Apeion, Vol. 14, No. 3, July 7 7 A New Appoach to Geneal Relativity Ali Rıza Şahin Gaziosmanpaşa, Istanbul Tukey E-mail: aizasahin@gmail.com Hee we pesent a new point of view fo geneal elativity and/o
Apeion, Vol. 14, No. 3, July 7 7 A New Appoach to Geneal Relativity Ali Rıza Şahin Gaziosmanpaşa, Istanbul Tukey E-mail: aizasahin@gmail.com Hee we pesent a new point of view fo geneal elativity and/o
PHZ 3113 Fall 2017 Homework #5, Due Friday, October 13
 PHZ 3113 Fall 2017 Homewok #5, Due Fiday, Octobe 13 1. Genealize the poduct ule (fg) = f g +f g to wite the divegence Ö (Ù Ú) of the coss poduct of the vecto fields Ù and Ú in tems of the cul of Ù and
PHZ 3113 Fall 2017 Homewok #5, Due Fiday, Octobe 13 1. Genealize the poduct ule (fg) = f g +f g to wite the divegence Ö (Ù Ú) of the coss poduct of the vecto fields Ù and Ú in tems of the cul of Ù and
Physics 235 Chapter 5. Chapter 5 Gravitation
 Chapte 5 Gavitation In this Chapte we will eview the popeties of the gavitational foce. The gavitational foce has been discussed in geat detail in you intoductoy physics couses, and we will pimaily focus
Chapte 5 Gavitation In this Chapte we will eview the popeties of the gavitational foce. The gavitational foce has been discussed in geat detail in you intoductoy physics couses, and we will pimaily focus
Math 124B February 02, 2012
 Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
Class #16 Monday, March 20, 2017
 D. Pogo Class #16 Monday, Mach 0, 017 D Non-Catesian Coodinate Systems A point in space can be specified by thee numbes:, y, and z. O, it can be specified by 3 diffeent numbes:,, and z, whee = cos, y =
D. Pogo Class #16 Monday, Mach 0, 017 D Non-Catesian Coodinate Systems A point in space can be specified by thee numbes:, y, and z. O, it can be specified by 3 diffeent numbes:,, and z, whee = cos, y =
Section 8.2 Polar Coordinates
 Section 8. Pola Coodinates 467 Section 8. Pola Coodinates The coodinate system we ae most familia with is called the Catesian coodinate system, a ectangula plane divided into fou quadants by the hoizontal
Section 8. Pola Coodinates 467 Section 8. Pola Coodinates The coodinate system we ae most familia with is called the Catesian coodinate system, a ectangula plane divided into fou quadants by the hoizontal
Vectors, Vector Calculus, and Coordinate Systems
 ! Revised Apil 11, 2017 1:48 PM! 1 Vectos, Vecto Calculus, and Coodinate Systems David Randall Physical laws and coodinate systems Fo the pesent discussion, we define a coodinate system as a tool fo descibing
! Revised Apil 11, 2017 1:48 PM! 1 Vectos, Vecto Calculus, and Coodinate Systems David Randall Physical laws and coodinate systems Fo the pesent discussion, we define a coodinate system as a tool fo descibing
THE LAPLACE EQUATION. The Laplace (or potential) equation is the equation. u = 0. = 2 x 2. x y 2 in R 2
 THE LAPLACE EQUATION The Laplace (o potential) equation is the equation whee is the Laplace opeato = 2 x 2 u = 0. in R = 2 x 2 + 2 y 2 in R 2 = 2 x 2 + 2 y 2 + 2 z 2 in R 3 The solutions u of the Laplace
THE LAPLACE EQUATION The Laplace (o potential) equation is the equation whee is the Laplace opeato = 2 x 2 u = 0. in R = 2 x 2 + 2 y 2 in R 2 = 2 x 2 + 2 y 2 + 2 z 2 in R 3 The solutions u of the Laplace
Transformation of the Navier-Stokes Equations in Curvilinear Coordinate Systems with Maple
 Global Jounal of Pue and Applied Mathematics. ISSN 0973-1768 Volume 12, Numbe 4 2016, pp. 3315 3325 Reseach India Publications http://www.ipublication.com/gjpam.htm Tansfomation of the Navie-Stokes Equations
Global Jounal of Pue and Applied Mathematics. ISSN 0973-1768 Volume 12, Numbe 4 2016, pp. 3315 3325 Reseach India Publications http://www.ipublication.com/gjpam.htm Tansfomation of the Navie-Stokes Equations
PROBLEM SET #1 SOLUTIONS by Robert A. DiStasio Jr.
 POBLM S # SOLUIONS by obet A. DiStasio J. Q. he Bon-Oppenheime appoximation is the standad way of appoximating the gound state of a molecula system. Wite down the conditions that detemine the tonic and
POBLM S # SOLUIONS by obet A. DiStasio J. Q. he Bon-Oppenheime appoximation is the standad way of appoximating the gound state of a molecula system. Wite down the conditions that detemine the tonic and
Math 2263 Solutions for Spring 2003 Final Exam
 Math 6 Solutions fo Sping Final Exam ) A staightfowad appoach to finding the tangent plane to a suface at a point ( x, y, z ) would be to expess the cuve as an explicit function z = f ( x, y ), calculate
Math 6 Solutions fo Sping Final Exam ) A staightfowad appoach to finding the tangent plane to a suface at a point ( x, y, z ) would be to expess the cuve as an explicit function z = f ( x, y ), calculate
EM Boundary Value Problems
 EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
Part V: Closed-form solutions to Loop Closure Equations
 Pat V: Closed-fom solutions to Loop Closue Equations This section will eview the closed-fom solutions techniques fo loop closue equations. The following thee cases will be consideed. ) Two unknown angles
Pat V: Closed-fom solutions to Loop Closue Equations This section will eview the closed-fom solutions techniques fo loop closue equations. The following thee cases will be consideed. ) Two unknown angles
π(x, y) = u x + v y = V (x cos + y sin ) κ(x, y) = u y v x = V (y cos x sin ) v u x y
 F17 Lectue Notes 1. Unifom flow, Souces, Sinks, Doublets Reading: Andeson 3.9 3.12 Unifom Flow Definition A unifom flow consists of a velocit field whee V φ = uî + vθˆ is a constant. In 2-D, this velocit
F17 Lectue Notes 1. Unifom flow, Souces, Sinks, Doublets Reading: Andeson 3.9 3.12 Unifom Flow Definition A unifom flow consists of a velocit field whee V φ = uî + vθˆ is a constant. In 2-D, this velocit
Much that has already been said about changes of variable relates to transformations between different coordinate systems.
 MULTIPLE INTEGRLS I P Calculus Cooinate Sstems Much that has alea been sai about changes of vaiable elates to tansfomations between iffeent cooinate sstems. The main cooinate sstems use in the solution
MULTIPLE INTEGRLS I P Calculus Cooinate Sstems Much that has alea been sai about changes of vaiable elates to tansfomations between iffeent cooinate sstems. The main cooinate sstems use in the solution
Physics 122, Fall October 2012
 hsics 1, Fall 1 3 Octobe 1 Toda in hsics 1: finding Foce between paallel cuents Eample calculations of fom the iot- Savat field law Ampèe s Law Eample calculations of fom Ampèe s law Unifom cuents in conductos?
hsics 1, Fall 1 3 Octobe 1 Toda in hsics 1: finding Foce between paallel cuents Eample calculations of fom the iot- Savat field law Ampèe s Law Eample calculations of fom Ampèe s law Unifom cuents in conductos?
Geometry of the homogeneous and isotropic spaces
 Geomety of the homogeneous and isotopic spaces H. Sonoda Septembe 2000; last evised Octobe 2009 Abstact We summaize the aspects of the geomety of the homogeneous and isotopic spaces which ae most elevant
Geomety of the homogeneous and isotopic spaces H. Sonoda Septembe 2000; last evised Octobe 2009 Abstact We summaize the aspects of the geomety of the homogeneous and isotopic spaces which ae most elevant
Physics 2B Chapter 22 Notes - Magnetic Field Spring 2018
 Physics B Chapte Notes - Magnetic Field Sping 018 Magnetic Field fom a Long Staight Cuent-Caying Wie In Chapte 11 we looked at Isaac Newton s Law of Gavitation, which established that a gavitational field
Physics B Chapte Notes - Magnetic Field Sping 018 Magnetic Field fom a Long Staight Cuent-Caying Wie In Chapte 11 we looked at Isaac Newton s Law of Gavitation, which established that a gavitational field
1 MathematicalPreliminaries
 1 MathematicalPeliminaies The enomous usefulness of mathematics in the natual sciences is something bodeing on the mysteious. Eugene Wigne (1960 1.1 Intoduction This chapte pesents a collection of mathematical
1 MathematicalPeliminaies The enomous usefulness of mathematics in the natual sciences is something bodeing on the mysteious. Eugene Wigne (1960 1.1 Intoduction This chapte pesents a collection of mathematical
Do not turn over until you are told to do so by the Invigilator.
 UNIVERSITY OF EAST ANGLIA School of Mathematics Main Seies UG Examination 2015 16 FLUID DYNAMICS WITH ADVANCED TOPICS MTH-MD59 Time allowed: 3 Hous Attempt QUESTIONS 1 and 2, and THREE othe questions.
UNIVERSITY OF EAST ANGLIA School of Mathematics Main Seies UG Examination 2015 16 FLUID DYNAMICS WITH ADVANCED TOPICS MTH-MD59 Time allowed: 3 Hous Attempt QUESTIONS 1 and 2, and THREE othe questions.
radians). Figure 2.1 Figure 2.2 (a) quadrant I angle (b) quadrant II angle is in standard position Terminal side Terminal side Terminal side
 . TRIGONOMETRIC FUNCTIONS OF GENERAL ANGLES In ode to etend the definitions of the si tigonometic functions to geneal angles, we shall make use of the following ideas: In a Catesian coodinate sstem, an
. TRIGONOMETRIC FUNCTIONS OF GENERAL ANGLES In ode to etend the definitions of the si tigonometic functions to geneal angles, we shall make use of the following ideas: In a Catesian coodinate sstem, an
ME 210 Applied Mathematics for Mechanical Engineers
 Tangent and Ac Length of a Cuve The tangent to a cuve C at a point A on it is defined as the limiting position of the staight line L though A and B, as B appoaches A along the cuve as illustated in the
Tangent and Ac Length of a Cuve The tangent to a cuve C at a point A on it is defined as the limiting position of the staight line L though A and B, as B appoaches A along the cuve as illustated in the
2 Governing Equations
 2 Govening Equations This chapte develops the govening equations of motion fo a homogeneous isotopic elastic solid, using the linea thee-dimensional theoy of elasticity in cylindical coodinates. At fist,
2 Govening Equations This chapte develops the govening equations of motion fo a homogeneous isotopic elastic solid, using the linea thee-dimensional theoy of elasticity in cylindical coodinates. At fist,
F Q E v B MAGNETOSTATICS. Creation of magnetic field B. Effect of B on a moving charge. On moving charges only. Stationary and moving charges
 MAGNETOSTATICS Ceation of magnetic field. Effect of on a moving chage. Take the second case: F Q v mag On moving chages only F QE v Stationay and moving chages dw F dl Analysis on F mag : mag mag Qv. vdt
MAGNETOSTATICS Ceation of magnetic field. Effect of on a moving chage. Take the second case: F Q v mag On moving chages only F QE v Stationay and moving chages dw F dl Analysis on F mag : mag mag Qv. vdt
Fluid flow in curved geometries: Mathematical Modeling and Applications
 Fluid flow in cuved geometies: Mathematical Modeling and Applications D. Muhammad Sajid Theoetical Plasma Physics Division PINSTECH, P.O. Niloe, PAEC, Islamabad Mach 01-06, 010 Islamabad, Paistan Pesentation
Fluid flow in cuved geometies: Mathematical Modeling and Applications D. Muhammad Sajid Theoetical Plasma Physics Division PINSTECH, P.O. Niloe, PAEC, Islamabad Mach 01-06, 010 Islamabad, Paistan Pesentation
Question Bank. Section A. is skew-hermitian matrix. is diagonalizable. (, ) , Evaluate (, ) 12 about = 1 and = Find, if
 Subject: Mathematics-I Question Bank Section A T T. Find the value of fo which the matix A = T T has ank one. T T i. Is the matix A = i is skew-hemitian matix. i. alculate the invese of the matix = 5 7
Subject: Mathematics-I Question Bank Section A T T. Find the value of fo which the matix A = T T has ank one. T T i. Is the matix A = i is skew-hemitian matix. i. alculate the invese of the matix = 5 7
Classical Mechanics Homework set 7, due Nov 8th: Solutions
 Classical Mechanics Homewok set 7, due Nov 8th: Solutions 1. Do deivation 8.. It has been asked what effect does a total deivative as a function of q i, t have on the Hamiltonian. Thus, lets us begin with
Classical Mechanics Homewok set 7, due Nov 8th: Solutions 1. Do deivation 8.. It has been asked what effect does a total deivative as a function of q i, t have on the Hamiltonian. Thus, lets us begin with
Vector Calculus Identities
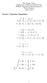 The Coope Union Depatment of Electical Engineeing ECE135 Engineeing Electomagnetics Vecto Analysis Mach 8, 2012 Vecto Calculus Identities A B B A A B C B C A C A B A B C B A C C A B fg f g + g f fg f G
The Coope Union Depatment of Electical Engineeing ECE135 Engineeing Electomagnetics Vecto Analysis Mach 8, 2012 Vecto Calculus Identities A B B A A B C B C A C A B A B C B A C C A B fg f g + g f fg f G
Final Review of AerE 243 Class
 Final Review of AeE 4 Class Content of Aeodynamics I I Chapte : Review of Multivaiable Calculus Chapte : Review of Vectos Chapte : Review of Fluid Mechanics Chapte 4: Consevation Equations Chapte 5: Simplifications
Final Review of AeE 4 Class Content of Aeodynamics I I Chapte : Review of Multivaiable Calculus Chapte : Review of Vectos Chapte : Review of Fluid Mechanics Chapte 4: Consevation Equations Chapte 5: Simplifications
B. Spherical Wave Propagation
 11/8/007 Spheical Wave Popagation notes 1/1 B. Spheical Wave Popagation Evey antenna launches a spheical wave, thus its powe density educes as a function of 1, whee is the distance fom the antenna. We
11/8/007 Spheical Wave Popagation notes 1/1 B. Spheical Wave Popagation Evey antenna launches a spheical wave, thus its powe density educes as a function of 1, whee is the distance fom the antenna. We
I. CONSTRUCTION OF THE GREEN S FUNCTION
 I. CONSTRUCTION OF THE GREEN S FUNCTION The Helmohltz equation in 4 dimensions is 4 + k G 4 x, x = δ 4 x x. In this equation, G is the Geen s function and 4 efes to the dimensionality. In the vey end,
I. CONSTRUCTION OF THE GREEN S FUNCTION The Helmohltz equation in 4 dimensions is 4 + k G 4 x, x = δ 4 x x. In this equation, G is the Geen s function and 4 efes to the dimensionality. In the vey end,
A Tutorial on Multiple Integrals (for Natural Sciences / Computer Sciences Tripos Part IA Maths)
 A Tutoial on Multiple Integals (fo Natual Sciences / Compute Sciences Tipos Pat IA Maths) Coections to D Ian Rud (http://people.ds.cam.ac.uk/ia/contact.html) please. This tutoial gives some bief eamples
A Tutoial on Multiple Integals (fo Natual Sciences / Compute Sciences Tipos Pat IA Maths) Coections to D Ian Rud (http://people.ds.cam.ac.uk/ia/contact.html) please. This tutoial gives some bief eamples
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II September 15, 2012 Prof. Alan Guth PROBLEM SET 2
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Depatment Physics 8.07: Electomagnetism II Septembe 5, 202 Pof. Alan Guth PROBLEM SET 2 DUE DATE: Monday, Septembe 24, 202. Eithe hand it in at the lectue,
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Depatment Physics 8.07: Electomagnetism II Septembe 5, 202 Pof. Alan Guth PROBLEM SET 2 DUE DATE: Monday, Septembe 24, 202. Eithe hand it in at the lectue,
Practice Integration Math 120 Calculus I Fall 2015
 Pactice Integation Math 0 Calculus I Fall 05 Hee s a list of pactice eecises. Thee s a hint fo each one as well as an answe with intemediate steps... ( + d. Hint. Answe. ( 8 t + t + This fist set of indefinite
Pactice Integation Math 0 Calculus I Fall 05 Hee s a list of pactice eecises. Thee s a hint fo each one as well as an answe with intemediate steps... ( + d. Hint. Answe. ( 8 t + t + This fist set of indefinite
2. Plane Elasticity Problems
 S0 Solid Mechanics Fall 009. Plane lasticity Poblems Main Refeence: Theoy of lasticity by S.P. Timoshenko and J.N. Goodie McGaw-Hill New Yok. Chaptes 3..1 The plane-stess poblem A thin sheet of an isotopic
S0 Solid Mechanics Fall 009. Plane lasticity Poblems Main Refeence: Theoy of lasticity by S.P. Timoshenko and J.N. Goodie McGaw-Hill New Yok. Chaptes 3..1 The plane-stess poblem A thin sheet of an isotopic
AST 121S: The origin and evolution of the Universe. Introduction to Mathematical Handout 1
 Please ead this fist... AST S: The oigin and evolution of the Univese Intoduction to Mathematical Handout This is an unusually long hand-out and one which uses in places mathematics that you may not be
Please ead this fist... AST S: The oigin and evolution of the Univese Intoduction to Mathematical Handout This is an unusually long hand-out and one which uses in places mathematics that you may not be
KEPLER S LAWS OF PLANETARY MOTION
 EPER S AWS OF PANETARY MOTION 1. Intoduction We ae now in a position to apply what we have leaned about the coss poduct and vecto valued functions to deive eple s aws of planetay motion. These laws wee
EPER S AWS OF PANETARY MOTION 1. Intoduction We ae now in a position to apply what we have leaned about the coss poduct and vecto valued functions to deive eple s aws of planetay motion. These laws wee
Practice Integration Math 120 Calculus I D Joyce, Fall 2013
 Pactice Integation Math 0 Calculus I D Joyce, Fall 0 This fist set of indefinite integals, that is, antideivatives, only depends on a few pinciples of integation, the fist being that integation is invese
Pactice Integation Math 0 Calculus I D Joyce, Fall 0 This fist set of indefinite integals, that is, antideivatives, only depends on a few pinciples of integation, the fist being that integation is invese
Analytic Evaluation of two-electron Atomic Integrals involving Extended Hylleraas-CI functions with STO basis
 Analytic Evaluation of two-electon Atomic Integals involving Extended Hylleaas-CI functions with STO basis B PADHY (Retd.) Faculty Membe Depatment of Physics, Khalikote (Autonomous) College, Behampu-760001,
Analytic Evaluation of two-electon Atomic Integals involving Extended Hylleaas-CI functions with STO basis B PADHY (Retd.) Faculty Membe Depatment of Physics, Khalikote (Autonomous) College, Behampu-760001,
Physics 121: Electricity & Magnetism Lecture 1
 Phsics 121: Electicit & Magnetism Lectue 1 Dale E. Ga Wenda Cao NJIT Phsics Depatment Intoduction to Clices 1. What ea ae ou?. Feshman. Sophomoe C. Junio D. Senio E. Othe Intoduction to Clices 2. How man
Phsics 121: Electicit & Magnetism Lectue 1 Dale E. Ga Wenda Cao NJIT Phsics Depatment Intoduction to Clices 1. What ea ae ou?. Feshman. Sophomoe C. Junio D. Senio E. Othe Intoduction to Clices 2. How man
IX INDUCTANCE AND MAGNETIC FIELDS
 IX INDUCTNCE ND MGNETIC FIELDS 9. Field in a solenoid vaying cuent in a conducto will poduce a vaying magnetic field. nd this vaying magnetic field then has the capability of inducing an EMF o voltage
IX INDUCTNCE ND MGNETIC FIELDS 9. Field in a solenoid vaying cuent in a conducto will poduce a vaying magnetic field. nd this vaying magnetic field then has the capability of inducing an EMF o voltage
7.2. Coulomb s Law. The Electric Force
 Coulomb s aw Recall that chaged objects attact some objects and epel othes at a distance, without making any contact with those objects Electic foce,, o the foce acting between two chaged objects, is somewhat
Coulomb s aw Recall that chaged objects attact some objects and epel othes at a distance, without making any contact with those objects Electic foce,, o the foce acting between two chaged objects, is somewhat
working pages for Paul Richards class notes; do not copy or circulate without permission from PGR 2004/11/3 10:50
 woking pages fo Paul Richads class notes; do not copy o ciculate without pemission fom PGR 2004/11/3 10:50 CHAPTER7 Solid angle, 3D integals, Gauss s Theoem, and a Delta Function We define the solid angle,
woking pages fo Paul Richads class notes; do not copy o ciculate without pemission fom PGR 2004/11/3 10:50 CHAPTER7 Solid angle, 3D integals, Gauss s Theoem, and a Delta Function We define the solid angle,
1 Spherical multipole moments
 Jackson notes 9 Spheical multipole moments Suppose we have a chage distibution ρ (x) wheeallofthechageiscontained within a spheical egion of adius R, as shown in the diagam. Then thee is no chage in the
Jackson notes 9 Spheical multipole moments Suppose we have a chage distibution ρ (x) wheeallofthechageiscontained within a spheical egion of adius R, as shown in the diagam. Then thee is no chage in the
Newton s Laws, Kepler s Laws, and Planetary Orbits
 Newton s Laws, Keple s Laws, and Planetay Obits PROBLEM SET 4 DUE TUESDAY AT START OF LECTURE 28 Septembe 2017 ASTRONOMY 111 FALL 2017 1 Newton s & Keple s laws and planetay obits Unifom cicula motion
Newton s Laws, Keple s Laws, and Planetay Obits PROBLEM SET 4 DUE TUESDAY AT START OF LECTURE 28 Septembe 2017 ASTRONOMY 111 FALL 2017 1 Newton s & Keple s laws and planetay obits Unifom cicula motion
Liquid gas interface under hydrostatic pressure
 Advances in Fluid Mechanics IX 5 Liquid gas inteface unde hydostatic pessue A. Gajewski Bialystok Univesity of Technology, Faculty of Civil Engineeing and Envionmental Engineeing, Depatment of Heat Engineeing,
Advances in Fluid Mechanics IX 5 Liquid gas inteface unde hydostatic pessue A. Gajewski Bialystok Univesity of Technology, Faculty of Civil Engineeing and Envionmental Engineeing, Depatment of Heat Engineeing,
Physics 121 Hour Exam #5 Solution
 Physics 2 Hou xam # Solution This exam consists of a five poblems on five pages. Point values ae given with each poblem. They add up to 99 points; you will get fee point to make a total of. In any given
Physics 2 Hou xam # Solution This exam consists of a five poblems on five pages. Point values ae given with each poblem. They add up to 99 points; you will get fee point to make a total of. In any given
Physics 111 Lecture 5 (Walker: 3.3-6) Vectors & Vector Math Motion Vectors Sept. 11, 2009
 Physics 111 Lectue 5 (Walke: 3.3-6) Vectos & Vecto Math Motion Vectos Sept. 11, 2009 Quiz Monday - Chap. 2 1 Resolving a vecto into x-component & y- component: Pola Coodinates Catesian Coodinates x y =
Physics 111 Lectue 5 (Walke: 3.3-6) Vectos & Vecto Math Motion Vectos Sept. 11, 2009 Quiz Monday - Chap. 2 1 Resolving a vecto into x-component & y- component: Pola Coodinates Catesian Coodinates x y =
Chapter Eight Notes N P U1C8S4-6
 Chapte Eight Notes N P UC8S-6 Name Peiod Section 8.: Tigonometic Identities An identit is, b definition, an equation that is alwas tue thoughout its domain. B tue thoughout its domain, that is to sa that
Chapte Eight Notes N P UC8S-6 Name Peiod Section 8.: Tigonometic Identities An identit is, b definition, an equation that is alwas tue thoughout its domain. B tue thoughout its domain, that is to sa that
Force of gravity and its potential function
 F. W. Phs0 E:\Ecel files\ch gavitational foce and potential.doc page of 6 0/0/005 8:9 PM Last pinted 0/0/005 8:9:00 PM Foce of gavit and its potential function (.) Let us calculate the potential function
F. W. Phs0 E:\Ecel files\ch gavitational foce and potential.doc page of 6 0/0/005 8:9 PM Last pinted 0/0/005 8:9:00 PM Foce of gavit and its potential function (.) Let us calculate the potential function
Green s Identities and Green s Functions
 LECTURE 7 Geen s Identities and Geen s Functions Let us ecall The ivegence Theoem in n-dimensions Theoem 7 Let F : R n R n be a vecto field ove R n that is of class C on some closed, connected, simply
LECTURE 7 Geen s Identities and Geen s Functions Let us ecall The ivegence Theoem in n-dimensions Theoem 7 Let F : R n R n be a vecto field ove R n that is of class C on some closed, connected, simply
Is there a magnification paradox in gravitational lensing?
 Is thee a magnification paadox in gavitational ing? Olaf Wucknitz wucknitz@asto.uni-bonn.de Astophysics semina/colloquium, Potsdam, 6 Novembe 7 Is thee a magnification paadox in gavitational ing? gavitational
Is thee a magnification paadox in gavitational ing? Olaf Wucknitz wucknitz@asto.uni-bonn.de Astophysics semina/colloquium, Potsdam, 6 Novembe 7 Is thee a magnification paadox in gavitational ing? gavitational
Scattering in Three Dimensions
 Scatteing in Thee Dimensions Scatteing expeiments ae an impotant souce of infomation about quantum systems, anging in enegy fom vey low enegy chemical eactions to the highest possible enegies at the LHC.
Scatteing in Thee Dimensions Scatteing expeiments ae an impotant souce of infomation about quantum systems, anging in enegy fom vey low enegy chemical eactions to the highest possible enegies at the LHC.
3 VECTOR CALCULUS I. 3.1 Divergence and curl of vector fields. 3.2 Important identities
 3 VECTOR CALCULU I 3.1 Divegence and cul of vecto fields Let = ( x, y, z ). eveal popeties of φ fo scala φ wee intoduced in section 1.2. The gadient opeato may also be applied to vecto fields. Let F =
3 VECTOR CALCULU I 3.1 Divegence and cul of vecto fields Let = ( x, y, z ). eveal popeties of φ fo scala φ wee intoduced in section 1.2. The gadient opeato may also be applied to vecto fields. Let F =
3. Electromagnetic Waves II
 Lectue 3 - Electomagnetic Waves II 9 3. Electomagnetic Waves II Last time, we discussed the following. 1. The popagation of an EM wave though a macoscopic media: We discussed how the wave inteacts with
Lectue 3 - Electomagnetic Waves II 9 3. Electomagnetic Waves II Last time, we discussed the following. 1. The popagation of an EM wave though a macoscopic media: We discussed how the wave inteacts with
Physics 161 Fall 2011 Extra Credit 2 Investigating Black Holes - Solutions The Following is Worth 50 Points!!!
 Physics 161 Fall 011 Exta Cedit Investigating Black Holes - olutions The Following is Woth 50 Points!!! This exta cedit assignment will investigate vaious popeties of black holes that we didn t have time
Physics 161 Fall 011 Exta Cedit Investigating Black Holes - olutions The Following is Woth 50 Points!!! This exta cedit assignment will investigate vaious popeties of black holes that we didn t have time
So, if we are finding the amount of work done over a non-conservative vector field F r, we do that long ur r b ur =
 3.4 Geen s Theoem Geoge Geen: self-taught English scientist, 793-84 So, if we ae finding the amount of wok done ove a non-consevative vecto field F, we do that long u b u 3. method Wok = F d F( () t )
3.4 Geen s Theoem Geoge Geen: self-taught English scientist, 793-84 So, if we ae finding the amount of wok done ove a non-consevative vecto field F, we do that long u b u 3. method Wok = F d F( () t )
Chapter 12: Kinematics of a Particle 12.8 CURVILINEAR MOTION: CYLINDRICAL COMPONENTS. u of the polar coordinate system are also shown in
 ME 01 DYNAMICS Chapte 1: Kinematics of a Paticle Chapte 1 Kinematics of a Paticle A. Bazone 1.8 CURVILINEAR MOTION: CYLINDRICAL COMPONENTS Pola Coodinates Pola coodinates ae paticlaly sitable fo solving
ME 01 DYNAMICS Chapte 1: Kinematics of a Paticle Chapte 1 Kinematics of a Paticle A. Bazone 1.8 CURVILINEAR MOTION: CYLINDRICAL COMPONENTS Pola Coodinates Pola coodinates ae paticlaly sitable fo solving
The Divergence Theorem
 13.8 The ivegence Theoem Back in 13.5 we ewote Geen s Theoem in vecto fom as C F n ds= div F x, y da ( ) whee C is the positively-oiented bounday cuve of the plane egion (in the xy-plane). Notice this
13.8 The ivegence Theoem Back in 13.5 we ewote Geen s Theoem in vecto fom as C F n ds= div F x, y da ( ) whee C is the positively-oiented bounday cuve of the plane egion (in the xy-plane). Notice this
But for simplicity, we ll define significant as the time it takes a star to lose all memory of its original trajectory, i.e.,
 Stella elaxation Time [Chandasekha 1960, Pinciples of Stella Dynamics, Chap II] [Ostike & Davidson 1968, Ap.J., 151, 679] Do stas eve collide? Ae inteactions between stas (as opposed to the geneal system
Stella elaxation Time [Chandasekha 1960, Pinciples of Stella Dynamics, Chap II] [Ostike & Davidson 1968, Ap.J., 151, 679] Do stas eve collide? Ae inteactions between stas (as opposed to the geneal system
Lecture 7: Angular Momentum, Hydrogen Atom
 Lectue 7: Angula Momentum, Hydogen Atom Vecto Quantization of Angula Momentum and Nomalization of 3D Rigid Roto wavefunctions Conside l, so L 2 2 2. Thus, we have L 2. Thee ae thee possibilities fo L z
Lectue 7: Angula Momentum, Hydogen Atom Vecto Quantization of Angula Momentum and Nomalization of 3D Rigid Roto wavefunctions Conside l, so L 2 2 2. Thus, we have L 2. Thee ae thee possibilities fo L z
Physics 122, Fall October 2012
 Today in Physics 1: electostatics eview David Blaine takes the pactical potion of his electostatics midtem (Gawke). 11 Octobe 01 Physics 1, Fall 01 1 Electostatics As you have pobably noticed, electostatics
Today in Physics 1: electostatics eview David Blaine takes the pactical potion of his electostatics midtem (Gawke). 11 Octobe 01 Physics 1, Fall 01 1 Electostatics As you have pobably noticed, electostatics
Notes follow and parts taken from sources in Bibliography
 PHYS 33 Notes follow and pats taken fom souces in Bibliogaph ectos The stud of electomagnetism equies the abilit to manipulate vecto quantities, since both electic and magnetic fields ae vecto fields.
PHYS 33 Notes follow and pats taken fom souces in Bibliogaph ectos The stud of electomagnetism equies the abilit to manipulate vecto quantities, since both electic and magnetic fields ae vecto fields.
Quantum theory of angular momentum
 Quantum theoy of angula momentum Igo Mazets igo.mazets+e141@tuwien.ac.at (Atominstitut TU Wien, Stadionallee 2, 1020 Wien Time: Fiday, 13:00 14:30 Place: Feihaus, Sem.R. DA gün 06B (exception date 18 Nov.:
Quantum theoy of angula momentum Igo Mazets igo.mazets+e141@tuwien.ac.at (Atominstitut TU Wien, Stadionallee 2, 1020 Wien Time: Fiday, 13:00 14:30 Place: Feihaus, Sem.R. DA gün 06B (exception date 18 Nov.:
transformation Earth V-curve (meridian) λ Conical projection. u,v curves on the datum surface projected as U,V curves on the projection surface
 . CONICAL PROJECTIONS In elementay texts on map pojections, the pojection sufaces ae often descibed as developable sufaces, such as the cylinde (cylindical pojections) and the cone (conical pojections),
. CONICAL PROJECTIONS In elementay texts on map pojections, the pojection sufaces ae often descibed as developable sufaces, such as the cylinde (cylindical pojections) and the cone (conical pojections),
d 2 x 0a d d =0. Relative to an arbitrary (accelerating frame) specified by x a = x a (x 0b ), the latter becomes: d 2 x a d 2 + a dx b dx c
 Chapte 6 Geneal Relativity 6.1 Towads the Einstein equations Thee ae seveal ways of motivating the Einstein equations. The most natual is pehaps though consideations involving the Equivalence Pinciple.
Chapte 6 Geneal Relativity 6.1 Towads the Einstein equations Thee ae seveal ways of motivating the Einstein equations. The most natual is pehaps though consideations involving the Equivalence Pinciple.
FI 2201 Electromagnetism
 FI Electomagnetim Aleande A. Ikanda, Ph.D. Phyic of Magnetim and Photonic Reeach Goup ecto Analyi CURILINEAR COORDINAES, DIRAC DELA FUNCION AND HEORY OF ECOR FIELDS Cuvilinea Coodinate Sytem Cateian coodinate:
FI Electomagnetim Aleande A. Ikanda, Ph.D. Phyic of Magnetim and Photonic Reeach Goup ecto Analyi CURILINEAR COORDINAES, DIRAC DELA FUNCION AND HEORY OF ECOR FIELDS Cuvilinea Coodinate Sytem Cateian coodinate:
ASTR415: Problem Set #6
 ASTR45: Poblem Set #6 Cuan D. Muhlbege Univesity of Mayland (Dated: May 7, 27) Using existing implementations of the leapfog and Runge-Kutta methods fo solving coupled odinay diffeential equations, seveal
ASTR45: Poblem Set #6 Cuan D. Muhlbege Univesity of Mayland (Dated: May 7, 27) Using existing implementations of the leapfog and Runge-Kutta methods fo solving coupled odinay diffeential equations, seveal
In many engineering and other applications, the. variable) will often depend on several other quantities (independent variables).
 II PARTIAL DIFFERENTIATION FUNCTIONS OF SEVERAL VARIABLES In man engineeing and othe applications, the behaviou o a cetain quantit dependent vaiable will oten depend on seveal othe quantities independent
II PARTIAL DIFFERENTIATION FUNCTIONS OF SEVERAL VARIABLES In man engineeing and othe applications, the behaviou o a cetain quantit dependent vaiable will oten depend on seveal othe quantities independent
Chapter 2: Basic Physics and Math Supplements
 Chapte 2: Basic Physics and Math Supplements Decembe 1, 215 1 Supplement 2.1: Centipetal Acceleation This supplement expands on a topic addessed on page 19 of the textbook. Ou task hee is to calculate
Chapte 2: Basic Physics and Math Supplements Decembe 1, 215 1 Supplement 2.1: Centipetal Acceleation This supplement expands on a topic addessed on page 19 of the textbook. Ou task hee is to calculate
MCV4U Final Exam Review. 1. Consider the function f (x) Find: f) lim. a) lim. c) lim. d) lim. 3. Consider the function: 4. Evaluate. lim. 5. Evaluate.
 MCVU Final Eam Review Answe (o Solution) Pactice Questions Conside the function f () defined b the following gaph Find a) f ( ) c) f ( ) f ( ) d) f ( ) Evaluate the following its a) ( ) c) sin d) π / π
MCVU Final Eam Review Answe (o Solution) Pactice Questions Conside the function f () defined b the following gaph Find a) f ( ) c) f ( ) f ( ) d) f ( ) Evaluate the following its a) ( ) c) sin d) π / π
