transformation Earth V-curve (meridian) λ Conical projection. u,v curves on the datum surface projected as U,V curves on the projection surface
|
|
|
- Hilda Willis
- 6 years ago
- Views:
Transcription
1 . CONICAL PROJECTIONS In elementay texts on map pojections, the pojection sufaces ae often descibed as developable sufaces, such as the cylinde (cylindical pojections) and the cone (conical pojections), o a plane (azimuthal pojections). These sufaces ae imagined as enveloping o touching the datum suface and by some means, usually geometic, the meidians, paallels and featues ae pojected onto these sufaces. In the case of the cone, a plane containing the axis of the cone cuts the cone on a line joining the base and the apex. If the cone is cut along this line (a geneato of the cone) it can be laid flat (developed). If the axis of the cone coincides with the axis of the Eath, the pojection is said to be nomal aspect, if the axis lies in the plane of the equato the pojection is known as tansvese and in any othe oientation it is known as oblique. [It is usual that the descipto "nomal" is implied in the name of a pojection, but fo diffeent oientations, the wods "tansvese" o "oblique" ae added to the name.] This simplified appoach is not adequate fo developing a geneal theoy of pojections (which as we can see is quite mathematical) but is useful fo descibing chaacteistics of cetain pojections. In the case of conical pojections, some chaacteistics ae a common featue: (i) Meidians ae equally spaced staight lines adiating fom a cental point O. (ii) Paallels, in geneal, ae unequally spaced concentic cicles having a cente at O. (iii) Meidians of longitude and paallels of latitude fom an othogonal netwok of lines. Pojection suface cone tansfomation Y θ P Datum suface Eath V-cuve (meidian) λ X U-cuve (paallel) Figue. Conical pojection. u,v cuves on the datum suface pojected as U,V cuves on the pojection suface Figue. shows a schematic diagam of a conical pojection demonstating the basic chaacteistics common to all conical pojections (nomal aspect). Conical pojections have a geneal cicula shape when the whole of the Eath is displayed; the U-cuves (paallels of latitude) ae concentic cicles and the V-cuves (meidians of longitude) ae equally spaced adial lines. In Figue., the cente fo the cicula U-cuves and the adial V-cuves is the 3, R.E. Deakin Map Pojection Theoy (3) 4
2 pole, but this is not always the case. In some conical pojections, the pole is shown as a line. The oigin of the X,Y Catesian coodinates is shown at the intesection of a cental V-cuve (a cental meidian λ ) and a selected U-cuve (a paallel of latitude ). A point P is shown on the pojection with pola coodinates, θ whee is a adial distance fom the cente of the pojection, the oigin of the pola coodinate system and θ is an angle measued positive anticlockwise, negative clockwise fom the cental meidian. All pojection equations fo conical pojections ae given in tems of pola coodinates... The Gaussian Fundamental Quantities of Conical Pojections Fo conical pojections, the pojection suface is a plane and the U,V cuvilinea coodinate system is an othogonal system of U and V-cuves that ae concentic cicula acs of adius and staight adial lines at angles θ fom a cental V- cuve. The functional elationships connecting the U,V coodinate system with the X,Y,Z Catesian coodinate system wee given peviously by equations (.) and ae estated hee in moe explicit fom 3 (, ) (, θ ) (, ) (, θ ) (, ) X = F U V = F Y = F U V = F Z = F U V = (.) Refeing to Figue., the X,Y Catesian coodinates ae elated to the, θ pola coodinates by the equations X = sinθ Y = cosθ (.) whee is the adius of the U-cuve (a paallel of latitude) passing though the X,Y coodinate oigin. The Gaussian Fundamental Quantities of the pojection suface ae given by equations (5.3) and ae estated hee ecognising that U-cuves ae cicula acs of adius and V-cuves ae adial lines at angles θ fom a cental meidian and Z = E F G X Y X Y = + = + U U X X Y Y X X Y Y = + = + U V U V X Y X Y = + = + V V (.3) X X The patial deivatives, etc can be obtained fom (.) 3, R.E. Deakin Map Pojection Theoy (3) 43
3 X Y = sinθ = cosθ X Y = cosθ = sinθ (.4) Substituting equations (.4) into (.3) gives X Y E = + = sin θ + cos θ = X X Y Y F = + = sinθcosθ sinθ cosθ = X Y G = + = cos θ + sin θ = (.5) Note that F =, which eflects the fact that the -cuves and θ -cuves (U and V-cuves that ae concentic cicles and adial lines) intesect at ight angles. Now, consideing the datum suface to be a sphee of adius R and the u,v cuves as paallels and meidians, λ, the Gaussian Fundamental Quantities E,F,G elating the functional elationships X = f Y = f ae (, λ) (, λ) (.6) E F G X Y = + X X Y Y = + λ λ X Y = + λ λ (.7) Expessions fo E,F,G can be obtained fom the Tansfomation Matix (6.7) in the following fom E E θ θ θ θ F = + F λ λ λ λ G G λ λ λ λ (.8) Noting that has eplaced U, θ has eplaced V, has eplaced u and λ has eplaced v. 3, R.E. Deakin Map Pojection Theoy (3) 44
4 Now fom equations (.5) we have E =, F = and Tansfomation Matix (.8) gives G =, and substituting into the E F G = + = + λ λ = + λ λ (.9) These expessions can be simplified if the following conditions fo nomal aspect Conical pojections ae enfoced (these conditions can be "undestood" by inspection of Figue.) (i) f ( ) = i.e., the adius of a paallel of latitude (a U-cuve) on the pojection is a function of the latitude only and (ii) θ = n ( λ λ ) i.e., the pola angle θ (the angle between a V-cuve and the cental meidian) is a linea function of λ only. n is a scala quantity known as the cone constant. These two conditions mean that =, =, = n λ λ (.) Substituting these diffeential elationships into (.9) gives the Gaussian Fundamental Quantities E,F,G fo nomal aspect Conical pojections E =, F =, G = λ (.) Using these diffeential elationships and paticula scale conditions we can deive CONFORMAL, EQUAL AREA and EQUIDISTANT Conical pojections. The scale conditions ae: Fo CONFORMAL Conical pojections: E G m = = e g J EQUAL AREA Conical pojections: j = E EQUIDISTANT Conical pojections: e = 3, R.E. Deakin Map Pojection Theoy (3) 45
5 In addition, since the datum suface is a sphee of adius R, the Gaussian Fundamental Quantities of the datum suface ae e= R f = g = R cos (.).. Confomal Conical Pojections Fo a Confomal Conical pojection the scale condition to be enfoced is E G m = = (.3) e g Altenatively, using the notation fo meidian and paallel scale factos we may wite the scale condition as h = k (.4) whee E h = = (.5) e R and G n k = = = g Rcos λ Rcos (.6) Note that in equation (.6) the cone constant n = (.7) λ is used, see equations (.) and the conditions fo nomal aspect Conical pojections. Enfocing the scale condition h = k gives the diffeential elationship n = R Rcos and eaanging gives d = d (.8) cos Note: The minus sign is intoduced to eflect the fact that the adius inceases as the latitude deceases. Integating (.8) gives 3, R.E. Deakin Map Pojection Theoy (3) 46
6 whee lnc = ( C C of logaithms, log ) d = d cos π ln + C = nln tan + + C 4 π ln = nln tan + + lnc 4 is the natual logaithm of the constants of integation. Using the laws p a M ploga M Taking antilogaithms of both sides gives = and log MN = log M + log N we may wite a a a π ln = ln tan + lnc 4 + = ln C tan + 4 = C tan + 4 (.9) and fom condition (ii) above ( ) θ = n λ λ (.) Equations (.9) and (.) ae the geneal equations fo Confomal Conic pojections, but the constants n and C must be detemined. To detemine the constants n (the cone constant) and C, geometic constaints elating to standad paallels ae employed, emembeing that a standad paallel is defined as a paallel of latitude along which the scale facto is constant and equal to unity. 3, R.E. Deakin Map Pojection Theoy (3) 47
7 Conside the case of a single standad paallel = tangent length N = meidian distance tansfomation S Eath cone standad paallel λ Figue. Schematic diagam of a Conical pojection with a single standad paallel having a adius. Setting the scale facto k in equation (.6) equal to unity along a standad paallel gives k n = R cos = That can be eaanged to give an equation fo the cone constant n as n R cos = (.) Inspection of equation (.) shows that if the adius of the standad paallel is fixed then the cone constant n can be detemined. Refeing to Figue., the two choices fo fixing ae: (a) (b) Make the adius of the standad paallel equal to the tangent length of the cone. = Rcot (.) Make the adius of the standad paallel equal to the meidian distance on the Eath fom the pole to the tangent point of the cone. = R π (.3) 3, R.E. Deakin Map Pojection Theoy (3) 48
8 ... Confomal Conic Pojection with a single standad paallel (adius = tangent length) Pojection equations: = C tan + 4 θ = n λ λ ( ) (.4) Rcos Rcos Cone constant: n = = = sin (.5) Rcot To detemine the constant C, conside the adius = C + = tan 4 tan R C = tan tan + 4 n R (.6) Figue.3 shows a Confomal Conic pojection of the nothen hemisphee. The pojection has a single standad paallel whose adius is equal to the tangent length of the cone. The gaticule inteval is 5, cental meidian λ = 3 and the X,Y coodinate oigin is at = 45. A point P is shown whose coodinates ae P = and λ P = 9. The pojection paametes, scale of the pojection and the X,Y coodinates of P can be computed in the following way. λ and = C tan + 4 θ = n λ λ ( ) R = 637 m R = = 637. m tan n = tan + = 4 n = sin =.777 C m 3, R.E. Deakin Map Pojection Theoy (3) 49
9 = 45 o Y X equato P λ 9 o = λ = 3 o Figue.3 Confomal Conic pojection, single standad paallel = 45 (adius of standad paallel = tangent length of cone). Gaticule inteval 5, cental meidian λ = 3, X,Y coodinate oigin at λ and = 45 The scale of the pojection can be obtained fom the geneal elationship ( ) ( ) distance on pojection map scale = = distance on Eath Eath Fom measuements on Figue.3, the length = 4.5 mm and fom the pevious calculations = 637 mm on the Eath. Note that this is eally the tangent length of a cone touching the Eath at latitude = 45. The scale of the pojection is then ( ) ( ) map 4.5 scale = = = o :55 million Eath , R.E. Deakin Map Pojection Theoy (3) 5
10 The Catesian equations fo Conical pojections (of the nothen hemisphee) ae The adius X = sinθ Y = cosθ of the paallel is given by (.4) and since the Catesian oigin is at the intesection of the cental meidian λ and the standad paallel then =. Fo the point P at = and λ = 9 and with C and n fo the pojection = C tan m 4 = θ = n ( λ λ ) = X = m = 5. mm Y = m = 5.6 mm 3, R.E. Deakin Map Pojection Theoy (3) 5
ME 210 Applied Mathematics for Mechanical Engineers
 Tangent and Ac Length of a Cuve The tangent to a cuve C at a point A on it is defined as the limiting position of the staight line L though A and B, as B appoaches A along the cuve as illustated in the
Tangent and Ac Length of a Cuve The tangent to a cuve C at a point A on it is defined as the limiting position of the staight line L though A and B, as B appoaches A along the cuve as illustated in the
Homework # 3 Solution Key
 PHYSICS 631: Geneal Relativity Homewok # 3 Solution Key 1. You e on you hono not to do this one by hand. I ealize you can use a compute o simply look it up. Please don t. In a flat space, the metic in
PHYSICS 631: Geneal Relativity Homewok # 3 Solution Key 1. You e on you hono not to do this one by hand. I ealize you can use a compute o simply look it up. Please don t. In a flat space, the metic in
Vectors, Vector Calculus, and Coordinate Systems
 Apil 5, 997 A Quick Intoduction to Vectos, Vecto Calculus, and Coodinate Systems David A. Randall Depatment of Atmospheic Science Coloado State Univesity Fot Collins, Coloado 80523. Scalas and vectos Any
Apil 5, 997 A Quick Intoduction to Vectos, Vecto Calculus, and Coodinate Systems David A. Randall Depatment of Atmospheic Science Coloado State Univesity Fot Collins, Coloado 80523. Scalas and vectos Any
Question Bank. Section A. is skew-hermitian matrix. is diagonalizable. (, ) , Evaluate (, ) 12 about = 1 and = Find, if
 Subject: Mathematics-I Question Bank Section A T T. Find the value of fo which the matix A = T T has ank one. T T i. Is the matix A = i is skew-hemitian matix. i. alculate the invese of the matix = 5 7
Subject: Mathematics-I Question Bank Section A T T. Find the value of fo which the matix A = T T has ank one. T T i. Is the matix A = i is skew-hemitian matix. i. alculate the invese of the matix = 5 7
ENGI 4430 Non-Cartesian Coordinates Page xi Fy j Fzk from Cartesian coordinates z to another orthonormal coordinate system u, v, ˆ i ˆ ˆi
 ENGI 44 Non-Catesian Coodinates Page 7-7. Conesions between Coodinate Systems In geneal, the conesion of a ecto F F xi Fy j Fzk fom Catesian coodinates x, y, z to anothe othonomal coodinate system u,,
ENGI 44 Non-Catesian Coodinates Page 7-7. Conesions between Coodinate Systems In geneal, the conesion of a ecto F F xi Fy j Fzk fom Catesian coodinates x, y, z to anothe othonomal coodinate system u,,
The geometric construction of Ewald sphere and Bragg condition:
 The geometic constuction of Ewald sphee and Bagg condition: The constuction of Ewald sphee must be done such that the Bagg condition is satisfied. This can be done as follows: i) Daw a wave vecto k in
The geometic constuction of Ewald sphee and Bagg condition: The constuction of Ewald sphee must be done such that the Bagg condition is satisfied. This can be done as follows: i) Daw a wave vecto k in
Lecture 8 - Gauss s Law
 Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
Math 209 Assignment 9 Solutions
 Math 9 Assignment 9 olutions 1. Evaluate 4y + 1 d whee is the fist octant pat of y x cut out by x + y + z 1. olution We need a paametic epesentation of the suface. (x, z). Now detemine the nomal vecto:
Math 9 Assignment 9 olutions 1. Evaluate 4y + 1 d whee is the fist octant pat of y x cut out by x + y + z 1. olution We need a paametic epesentation of the suface. (x, z). Now detemine the nomal vecto:
e.g: If A = i 2 j + k then find A. A = Ax 2 + Ay 2 + Az 2 = ( 2) = 6
 MOTION IN A PLANE 1. Scala Quantities Physical quantities that have only magnitude and no diection ae called scala quantities o scalas. e.g. Mass, time, speed etc. 2. Vecto Quantities Physical quantities
MOTION IN A PLANE 1. Scala Quantities Physical quantities that have only magnitude and no diection ae called scala quantities o scalas. e.g. Mass, time, speed etc. 2. Vecto Quantities Physical quantities
Phys 201A. Homework 5 Solutions
 Phys 201A Homewok 5 Solutions 3. In each of the thee cases, you can find the changes in the velocity vectos by adding the second vecto to the additive invese of the fist and dawing the esultant, and by
Phys 201A Homewok 5 Solutions 3. In each of the thee cases, you can find the changes in the velocity vectos by adding the second vecto to the additive invese of the fist and dawing the esultant, and by
Math 2263 Solutions for Spring 2003 Final Exam
 Math 6 Solutions fo Sping Final Exam ) A staightfowad appoach to finding the tangent plane to a suface at a point ( x, y, z ) would be to expess the cuve as an explicit function z = f ( x, y ), calculate
Math 6 Solutions fo Sping Final Exam ) A staightfowad appoach to finding the tangent plane to a suface at a point ( x, y, z ) would be to expess the cuve as an explicit function z = f ( x, y ), calculate
B. Spherical Wave Propagation
 11/8/007 Spheical Wave Popagation notes 1/1 B. Spheical Wave Popagation Evey antenna launches a spheical wave, thus its powe density educes as a function of 1, whee is the distance fom the antenna. We
11/8/007 Spheical Wave Popagation notes 1/1 B. Spheical Wave Popagation Evey antenna launches a spheical wave, thus its powe density educes as a function of 1, whee is the distance fom the antenna. We
2 Governing Equations
 2 Govening Equations This chapte develops the govening equations of motion fo a homogeneous isotopic elastic solid, using the linea thee-dimensional theoy of elasticity in cylindical coodinates. At fist,
2 Govening Equations This chapte develops the govening equations of motion fo a homogeneous isotopic elastic solid, using the linea thee-dimensional theoy of elasticity in cylindical coodinates. At fist,
7.2.1 Basic relations for Torsion of Circular Members
 Section 7. 7. osion In this section, the geomety to be consideed is that of a long slende cicula ba and the load is one which twists the ba. Such poblems ae impotant in the analysis of twisting components,
Section 7. 7. osion In this section, the geomety to be consideed is that of a long slende cicula ba and the load is one which twists the ba. Such poblems ae impotant in the analysis of twisting components,
THE LAPLACE EQUATION. The Laplace (or potential) equation is the equation. u = 0. = 2 x 2. x y 2 in R 2
 THE LAPLACE EQUATION The Laplace (o potential) equation is the equation whee is the Laplace opeato = 2 x 2 u = 0. in R = 2 x 2 + 2 y 2 in R 2 = 2 x 2 + 2 y 2 + 2 z 2 in R 3 The solutions u of the Laplace
THE LAPLACE EQUATION The Laplace (o potential) equation is the equation whee is the Laplace opeato = 2 x 2 u = 0. in R = 2 x 2 + 2 y 2 in R 2 = 2 x 2 + 2 y 2 + 2 z 2 in R 3 The solutions u of the Laplace
Geometry of the homogeneous and isotropic spaces
 Geomety of the homogeneous and isotopic spaces H. Sonoda Septembe 2000; last evised Octobe 2009 Abstact We summaize the aspects of the geomety of the homogeneous and isotopic spaces which ae most elevant
Geomety of the homogeneous and isotopic spaces H. Sonoda Septembe 2000; last evised Octobe 2009 Abstact We summaize the aspects of the geomety of the homogeneous and isotopic spaces which ae most elevant
Euclidean Figures and Solids without Incircles or Inspheres
 Foum Geometicoum Volume 16 (2016) 291 298. FOUM GEOM ISSN 1534-1178 Euclidean Figues and Solids without Incicles o Insphees Dimitis M. Chistodoulou bstact. ll classical convex plana Euclidean figues that
Foum Geometicoum Volume 16 (2016) 291 298. FOUM GEOM ISSN 1534-1178 Euclidean Figues and Solids without Incicles o Insphees Dimitis M. Chistodoulou bstact. ll classical convex plana Euclidean figues that
Lab #9: The Kinematics & Dynamics of. Circular Motion & Rotational Motion
 Reading Assignment: Lab #9: The Kinematics & Dynamics of Cicula Motion & Rotational Motion Chapte 6 Section 4 Chapte 11 Section 1 though Section 5 Intoduction: When discussing motion, it is impotant to
Reading Assignment: Lab #9: The Kinematics & Dynamics of Cicula Motion & Rotational Motion Chapte 6 Section 4 Chapte 11 Section 1 though Section 5 Intoduction: When discussing motion, it is impotant to
Rotational Motion. Lecture 6. Chapter 4. Physics I. Course website:
 Lectue 6 Chapte 4 Physics I Rotational Motion Couse website: http://faculty.uml.edu/andiy_danylov/teaching/physicsi Today we ae going to discuss: Chapte 4: Unifom Cicula Motion: Section 4.4 Nonunifom Cicula
Lectue 6 Chapte 4 Physics I Rotational Motion Couse website: http://faculty.uml.edu/andiy_danylov/teaching/physicsi Today we ae going to discuss: Chapte 4: Unifom Cicula Motion: Section 4.4 Nonunifom Cicula
Math 259 Winter Handout 6: In-class Review for the Cumulative Final Exam
 Math 259 Winte 2009 Handout 6: In-class Review fo the Cumulative Final Exam The topics coveed by the cumulative final exam include the following: Paametic cuves. Finding fomulas fo paametic cuves. Dawing
Math 259 Winte 2009 Handout 6: In-class Review fo the Cumulative Final Exam The topics coveed by the cumulative final exam include the following: Paametic cuves. Finding fomulas fo paametic cuves. Dawing
6 Vector Operators. 6.1 The Gradient Operator
 6 Vecto Opeatos 6. The Gadient Opeato In the B2 couse ou wee intoduced to the gadient opeato in Catesian coodinates. Fo an diffeentiable scala function f(x,, z), we can define a vecto function though (
6 Vecto Opeatos 6. The Gadient Opeato In the B2 couse ou wee intoduced to the gadient opeato in Catesian coodinates. Fo an diffeentiable scala function f(x,, z), we can define a vecto function though (
working pages for Paul Richards class notes; do not copy or circulate without permission from PGR 2004/11/3 10:50
 woking pages fo Paul Richads class notes; do not copy o ciculate without pemission fom PGR 2004/11/3 10:50 CHAPTER7 Solid angle, 3D integals, Gauss s Theoem, and a Delta Function We define the solid angle,
woking pages fo Paul Richads class notes; do not copy o ciculate without pemission fom PGR 2004/11/3 10:50 CHAPTER7 Solid angle, 3D integals, Gauss s Theoem, and a Delta Function We define the solid angle,
, the tangent line is an approximation of the curve (and easier to deal with than the curve).
 114 Tangent Planes and Linea Appoimations Back in-dimensions, what was the equation of the tangent line of f ( ) at point (, ) f ( )? (, ) ( )( ) = f Linea Appoimation (Tangent Line Appoimation) of f at
114 Tangent Planes and Linea Appoimations Back in-dimensions, what was the equation of the tangent line of f ( ) at point (, ) f ( )? (, ) ( )( ) = f Linea Appoimation (Tangent Line Appoimation) of f at
Graphs of Sine and Cosine Functions
 Gaphs of Sine and Cosine Functions In pevious sections, we defined the tigonometic o cicula functions in tems of the movement of a point aound the cicumfeence of a unit cicle, o the angle fomed by the
Gaphs of Sine and Cosine Functions In pevious sections, we defined the tigonometic o cicula functions in tems of the movement of a point aound the cicumfeence of a unit cicle, o the angle fomed by the
Chapter 2: Basic Physics and Math Supplements
 Chapte 2: Basic Physics and Math Supplements Decembe 1, 215 1 Supplement 2.1: Centipetal Acceleation This supplement expands on a topic addessed on page 19 of the textbook. Ou task hee is to calculate
Chapte 2: Basic Physics and Math Supplements Decembe 1, 215 1 Supplement 2.1: Centipetal Acceleation This supplement expands on a topic addessed on page 19 of the textbook. Ou task hee is to calculate
ESCI 342 Atmospheric Dynamics I Lesson 3 Fundamental Forces II
 Reading: Matin, Section. ROTATING REFERENCE FRAMES ESCI 34 Atmospheic Dnamics I Lesson 3 Fundamental Foces II A efeence fame in which an object with zeo net foce on it does not acceleate is known as an
Reading: Matin, Section. ROTATING REFERENCE FRAMES ESCI 34 Atmospheic Dnamics I Lesson 3 Fundamental Foces II A efeence fame in which an object with zeo net foce on it does not acceleate is known as an
OSCILLATIONS AND GRAVITATION
 1. SIMPLE HARMONIC MOTION Simple hamonic motion is any motion that is equivalent to a single component of unifom cicula motion. In this situation the velocity is always geatest in the middle of the motion,
1. SIMPLE HARMONIC MOTION Simple hamonic motion is any motion that is equivalent to a single component of unifom cicula motion. In this situation the velocity is always geatest in the middle of the motion,
Physics 506 Winter 2006 Homework Assignment #9 Solutions
 Physics 506 Winte 2006 Homewok Assignment #9 Solutions Textbook poblems: Ch. 12: 12.2, 12.9, 12.13, 12.14 12.2 a) Show fom Hamilton s pinciple that Lagangians that diffe only by a total time deivative
Physics 506 Winte 2006 Homewok Assignment #9 Solutions Textbook poblems: Ch. 12: 12.2, 12.9, 12.13, 12.14 12.2 a) Show fom Hamilton s pinciple that Lagangians that diffe only by a total time deivative
Chapter 10 Sample Exam
 Chapte Sample Exam Poblems maked with an asteisk (*) ae paticulaly challenging and should be given caeful consideation.. Conside the paametic cuve x (t) =e t, y (t) =e t, t (a) Compute the length of the
Chapte Sample Exam Poblems maked with an asteisk (*) ae paticulaly challenging and should be given caeful consideation.. Conside the paametic cuve x (t) =e t, y (t) =e t, t (a) Compute the length of the
EFFECTS OF FRINGING FIELDS ON SINGLE PARTICLE DYNAMICS. M. Bassetti and C. Biscari INFN-LNF, CP 13, Frascati (RM), Italy
 Fascati Physics Seies Vol. X (998), pp. 47-54 4 th Advanced ICFA Beam Dynamics Wokshop, Fascati, Oct. -5, 997 EFFECTS OF FRININ FIELDS ON SINLE PARTICLE DYNAMICS M. Bassetti and C. Biscai INFN-LNF, CP
Fascati Physics Seies Vol. X (998), pp. 47-54 4 th Advanced ICFA Beam Dynamics Wokshop, Fascati, Oct. -5, 997 EFFECTS OF FRININ FIELDS ON SINLE PARTICLE DYNAMICS M. Bassetti and C. Biscai INFN-LNF, CP
Math Notes on Kepler s first law 1. r(t) kp(t)
 Math 7 - Notes on Keple s fist law Planetay motion and Keple s Laws We conside the motion of a single planet about the sun; fo simplicity, we assign coodinates in R 3 so that the position of the sun is
Math 7 - Notes on Keple s fist law Planetay motion and Keple s Laws We conside the motion of a single planet about the sun; fo simplicity, we assign coodinates in R 3 so that the position of the sun is
Section 8.2 Polar Coordinates
 Section 8. Pola Coodinates 467 Section 8. Pola Coodinates The coodinate system we ae most familia with is called the Catesian coodinate system, a ectangula plane divided into fou quadants by the hoizontal
Section 8. Pola Coodinates 467 Section 8. Pola Coodinates The coodinate system we ae most familia with is called the Catesian coodinate system, a ectangula plane divided into fou quadants by the hoizontal
Chapter 13 Gravitation
 Chapte 13 Gavitation In this chapte we will exploe the following topics: -Newton s law of gavitation, which descibes the attactive foce between two point masses and its application to extended objects
Chapte 13 Gavitation In this chapte we will exploe the following topics: -Newton s law of gavitation, which descibes the attactive foce between two point masses and its application to extended objects
AH Mechanics Checklist (Unit 2) AH Mechanics Checklist (Unit 2) Circular Motion
 AH Mechanics Checklist (Unit ) AH Mechanics Checklist (Unit ) Cicula Motion No. kill Done 1 Know that cicula motion efes to motion in a cicle of constant adius Know that cicula motion is conveniently descibed
AH Mechanics Checklist (Unit ) AH Mechanics Checklist (Unit ) Cicula Motion No. kill Done 1 Know that cicula motion efes to motion in a cicle of constant adius Know that cicula motion is conveniently descibed
(read nabla or del) is defined by, k. (9.7.1*)
 9.7 Gadient of a scala field. Diectional deivative Some of the vecto fields in applications can be obtained fom scala fields. This is vey advantageous because scala fields can be handled moe easily. The
9.7 Gadient of a scala field. Diectional deivative Some of the vecto fields in applications can be obtained fom scala fields. This is vey advantageous because scala fields can be handled moe easily. The
Vectors, Vector Calculus, and Coordinate Systems
 ! Revised Apil 11, 2017 1:48 PM! 1 Vectos, Vecto Calculus, and Coodinate Systems David Randall Physical laws and coodinate systems Fo the pesent discussion, we define a coodinate system as a tool fo descibing
! Revised Apil 11, 2017 1:48 PM! 1 Vectos, Vecto Calculus, and Coodinate Systems David Randall Physical laws and coodinate systems Fo the pesent discussion, we define a coodinate system as a tool fo descibing
LINEAR PLATE BENDING
 LINEAR PLATE BENDING 1 Linea plate bending A plate is a body of which the mateial is located in a small egion aound a suface in the thee-dimensional space. A special suface is the mid-plane. Measued fom
LINEAR PLATE BENDING 1 Linea plate bending A plate is a body of which the mateial is located in a small egion aound a suface in the thee-dimensional space. A special suface is the mid-plane. Measued fom
Chapter 12. Kinetics of Particles: Newton s Second Law
 Chapte 1. Kinetics of Paticles: Newton s Second Law Intoduction Newton s Second Law of Motion Linea Momentum of a Paticle Systems of Units Equations of Motion Dynamic Equilibium Angula Momentum of a Paticle
Chapte 1. Kinetics of Paticles: Newton s Second Law Intoduction Newton s Second Law of Motion Linea Momentum of a Paticle Systems of Units Equations of Motion Dynamic Equilibium Angula Momentum of a Paticle
COUPLED MODELS OF ROLLING, SLIDING AND WHIRLING FRICTION
 ENOC 008 Saint Petesbug Russia June 30-July 4 008 COUPLED MODELS OF ROLLING SLIDING AND WHIRLING FRICTION Alexey Kieenkov Ins ti tu te fo P ob le ms in Me ch an ic s Ru ss ia n Ac ad em y of Sc ie nc es
ENOC 008 Saint Petesbug Russia June 30-July 4 008 COUPLED MODELS OF ROLLING SLIDING AND WHIRLING FRICTION Alexey Kieenkov Ins ti tu te fo P ob le ms in Me ch an ic s Ru ss ia n Ac ad em y of Sc ie nc es
PDF Created with deskpdf PDF Writer - Trial ::
 A APPENDIX D TRIGONOMETRY Licensed to: jsamuels@bmcc.cun.edu PDF Ceated with deskpdf PDF Wite - Tial :: http://www.docudesk.com D T i g o n o m e t FIGURE a A n g l e s Angles can be measued in degees
A APPENDIX D TRIGONOMETRY Licensed to: jsamuels@bmcc.cun.edu PDF Ceated with deskpdf PDF Wite - Tial :: http://www.docudesk.com D T i g o n o m e t FIGURE a A n g l e s Angles can be measued in degees
As is natural, our Aerospace Structures will be described in a Euclidean three-dimensional space R 3.
 Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
Coordinate Geometry. = k2 e 2. 1 e + x. 1 e. ke ) 2. We now write = a, and shift the origin to the point (a, 0). Referred to
 Coodinate Geomet Conic sections These ae pane cuves which can be descibed as the intesection of a cone with panes oiented in vaious diections. It can be demonstated that the ocus of a point which moves
Coodinate Geomet Conic sections These ae pane cuves which can be descibed as the intesection of a cone with panes oiented in vaious diections. It can be demonstated that the ocus of a point which moves
Chapter 2: Introduction to Implicit Equations
 Habeman MTH 11 Section V: Paametic and Implicit Equations Chapte : Intoduction to Implicit Equations When we descibe cuves on the coodinate plane with algebaic equations, we can define the elationship
Habeman MTH 11 Section V: Paametic and Implicit Equations Chapte : Intoduction to Implicit Equations When we descibe cuves on the coodinate plane with algebaic equations, we can define the elationship
Chapter 7-8 Rotational Motion
 Chapte 7-8 Rotational Motion What is a Rigid Body? Rotational Kinematics Angula Velocity ω and Acceleation α Unifom Rotational Motion: Kinematics Unifom Cicula Motion: Kinematics and Dynamics The Toque,
Chapte 7-8 Rotational Motion What is a Rigid Body? Rotational Kinematics Angula Velocity ω and Acceleation α Unifom Rotational Motion: Kinematics Unifom Cicula Motion: Kinematics and Dynamics The Toque,
AST 121S: The origin and evolution of the Universe. Introduction to Mathematical Handout 1
 Please ead this fist... AST S: The oigin and evolution of the Univese Intoduction to Mathematical Handout This is an unusually long hand-out and one which uses in places mathematics that you may not be
Please ead this fist... AST S: The oigin and evolution of the Univese Intoduction to Mathematical Handout This is an unusually long hand-out and one which uses in places mathematics that you may not be
PHYS 2135 Exam I February 13, 2018
 Exam Total /200 PHYS 2135 Exam I Febuay 13, 2018 Name: Recitation Section: Five multiple choice questions, 8 points each Choose the best o most nealy coect answe Fo questions 6-9, solutions must begin
Exam Total /200 PHYS 2135 Exam I Febuay 13, 2018 Name: Recitation Section: Five multiple choice questions, 8 points each Choose the best o most nealy coect answe Fo questions 6-9, solutions must begin
Vector d is a linear vector function of vector d when the following relationships hold:
 Appendix 4 Dyadic Analysis DEFINITION ecto d is a linea vecto function of vecto d when the following elationships hold: d x = a xxd x + a xy d y + a xz d z d y = a yxd x + a yy d y + a yz d z d z = a zxd
Appendix 4 Dyadic Analysis DEFINITION ecto d is a linea vecto function of vecto d when the following elationships hold: d x = a xxd x + a xy d y + a xz d z d y = a yxd x + a yy d y + a yz d z d z = a zxd
Circular Orbits. and g =
 using analyse planetay and satellite motion modelled as unifom cicula motion in a univesal gavitation field, a = v = 4π and g = T GM1 GM and F = 1M SATELLITES IN OBIT A satellite is any object that is
using analyse planetay and satellite motion modelled as unifom cicula motion in a univesal gavitation field, a = v = 4π and g = T GM1 GM and F = 1M SATELLITES IN OBIT A satellite is any object that is
B da = 0. Q E da = ε. E da = E dv
 lectomagnetic Theo Pof Ruiz, UNC Asheville, doctophs on YouTube Chapte Notes The Maxwell quations in Diffeential Fom 1 The Maxwell quations in Diffeential Fom We will now tansfom the integal fom of the
lectomagnetic Theo Pof Ruiz, UNC Asheville, doctophs on YouTube Chapte Notes The Maxwell quations in Diffeential Fom 1 The Maxwell quations in Diffeential Fom We will now tansfom the integal fom of the
Describing Circular motion
 Unifom Cicula Motion Descibing Cicula motion In ode to undestand cicula motion, we fist need to discuss how to subtact vectos. The easiest way to explain subtacting vectos is to descibe it as adding a
Unifom Cicula Motion Descibing Cicula motion In ode to undestand cicula motion, we fist need to discuss how to subtact vectos. The easiest way to explain subtacting vectos is to descibe it as adding a
m 2 r 1 = m 1 + m 2 M r 2 = m 1 = m 1m 2
 Celestial Mechanics - A.A. 2012-13 1 Calo Nipoti, Dipatimento di Fisica e Astonomia, Univesità di Bologna 26/3/2013 2. The gavitational two-body poblem 2.1 The educed mass [LL] Two-body poblem: two inteacting
Celestial Mechanics - A.A. 2012-13 1 Calo Nipoti, Dipatimento di Fisica e Astonomia, Univesità di Bologna 26/3/2013 2. The gavitational two-body poblem 2.1 The educed mass [LL] Two-body poblem: two inteacting
Math 451: Euclidean and Non-Euclidean Geometry MWF 3pm, Gasson 204 Homework 9 Solutions
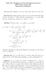 Math 451: Euclidean and Non-Euclidean Geomety MWF 3pm, Gasson 04 Homewok 9 Solutions Execises fom Chapte 3: 3.3, 3.8, 3.15, 3.19, 3.0, 5.11, 5.1, 5.13 Execise 3.3. Suppose that C and C ae two cicles with
Math 451: Euclidean and Non-Euclidean Geomety MWF 3pm, Gasson 04 Homewok 9 Solutions Execises fom Chapte 3: 3.3, 3.8, 3.15, 3.19, 3.0, 5.11, 5.1, 5.13 Execise 3.3. Suppose that C and C ae two cicles with
KEPLER S LAWS AND PLANETARY ORBITS
 KEPE S AWS AND PANETAY OBITS 1. Selected popeties of pola coodinates and ellipses Pola coodinates: I take a some what extended view of pola coodinates in that I allow fo a z diection (cylindical coodinates
KEPE S AWS AND PANETAY OBITS 1. Selected popeties of pola coodinates and ellipses Pola coodinates: I take a some what extended view of pola coodinates in that I allow fo a z diection (cylindical coodinates
CBN 98-1 Developable constant perimeter surfaces: Application to the end design of a tape-wound quadrupole saddle coil
 CBN 98-1 Developale constant peimete sufaces: Application to the end design of a tape-wound quadupole saddle coil G. Dugan Laoatoy of Nuclea Studies Conell Univesity Ithaca, NY 14853 1. Intoduction Constant
CBN 98-1 Developale constant peimete sufaces: Application to the end design of a tape-wound quadupole saddle coil G. Dugan Laoatoy of Nuclea Studies Conell Univesity Ithaca, NY 14853 1. Intoduction Constant
Physics 181. Assignment 4
 Physics 181 Assignment 4 Solutions 1. A sphee has within it a gavitational field given by g = g, whee g is constant and is the position vecto of the field point elative to the cente of the sphee. This
Physics 181 Assignment 4 Solutions 1. A sphee has within it a gavitational field given by g = g, whee g is constant and is the position vecto of the field point elative to the cente of the sphee. This
PHYS 110B - HW #7 Spring 2004, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased
 PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
 Page 1 of 6 Physics II Exam 1 155 points Name Discussion day/time Pat I. Questions 110. 8 points each. Multiple choice: Fo full cedit, cicle only the coect answe. Fo half cedit, cicle the coect answe and
Page 1 of 6 Physics II Exam 1 155 points Name Discussion day/time Pat I. Questions 110. 8 points each. Multiple choice: Fo full cedit, cicle only the coect answe. Fo half cedit, cicle the coect answe and
REVIEW Polar Coordinates and Equations
 REVIEW 9.1-9.4 Pola Coodinates and Equations You ae familia with plotting with a ectangula coodinate system. We ae going to look at a new coodinate system called the pola coodinate system. The cente of
REVIEW 9.1-9.4 Pola Coodinates and Equations You ae familia with plotting with a ectangula coodinate system. We ae going to look at a new coodinate system called the pola coodinate system. The cente of
Approach Parameters in Marine Navigation Graphical Interpretations
 http://www.tansnav.eu the Intenational Jounal on Maine Navigation and Safe of Sea anspotation olume 11 Numbe 3 Septembe 017 OI: 10.1716/1001.11.03.19 ppoach Paametes in Maine Navigation Gaphical Intepetations.S.
http://www.tansnav.eu the Intenational Jounal on Maine Navigation and Safe of Sea anspotation olume 11 Numbe 3 Septembe 017 OI: 10.1716/1001.11.03.19 ppoach Paametes in Maine Navigation Gaphical Intepetations.S.
Between any two masses, there exists a mutual attractive force.
 YEAR 12 PHYSICS: GRAVITATION PAST EXAM QUESTIONS Name: QUESTION 1 (1995 EXAM) (a) State Newton s Univesal Law of Gavitation in wods Between any two masses, thee exists a mutual attactive foce. This foce
YEAR 12 PHYSICS: GRAVITATION PAST EXAM QUESTIONS Name: QUESTION 1 (1995 EXAM) (a) State Newton s Univesal Law of Gavitation in wods Between any two masses, thee exists a mutual attactive foce. This foce
Green s Identities and Green s Functions
 LECTURE 7 Geen s Identities and Geen s Functions Let us ecall The ivegence Theoem in n-dimensions Theoem 7 Let F : R n R n be a vecto field ove R n that is of class C on some closed, connected, simply
LECTURE 7 Geen s Identities and Geen s Functions Let us ecall The ivegence Theoem in n-dimensions Theoem 7 Let F : R n R n be a vecto field ove R n that is of class C on some closed, connected, simply
From Gravitational Collapse to Black Holes
 Fom Gavitational Collapse to Black Holes T. Nguyen PHY 391 Independent Study Tem Pape Pof. S.G. Rajeev Univesity of Rocheste Decembe 0, 018 1 Intoduction The pupose of this independent study is to familiaize
Fom Gavitational Collapse to Black Holes T. Nguyen PHY 391 Independent Study Tem Pape Pof. S.G. Rajeev Univesity of Rocheste Decembe 0, 018 1 Intoduction The pupose of this independent study is to familiaize
(A) 2log( tan cot ) [ ], 2 MATHEMATICS. 1. Which of the following is correct?
![(A) 2log( tan cot ) [ ], 2 MATHEMATICS. 1. Which of the following is correct? (A) 2log( tan cot ) [ ], 2 MATHEMATICS. 1. Which of the following is correct?](/thumbs/76/73747145.jpg) MATHEMATICS. Which of the following is coect? A L.P.P always has unique solution Evey L.P.P has an optimal solution A L.P.P admits two optimal solutions If a L.P.P admits two optimal solutions then it
MATHEMATICS. Which of the following is coect? A L.P.P always has unique solution Evey L.P.P has an optimal solution A L.P.P admits two optimal solutions If a L.P.P admits two optimal solutions then it
Math 124B February 02, 2012
 Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
RECTIFYING THE CIRCUMFERENCE WITH GEOGEBRA
 ECTIFYING THE CICUMFEENCE WITH GEOGEBA A. Matín Dinnbie, G. Matín González and Anthony C.M. O 1 Intoducction The elation between the cicumfeence and the adius of a cicle is one of the most impotant concepts
ECTIFYING THE CICUMFEENCE WITH GEOGEBA A. Matín Dinnbie, G. Matín González and Anthony C.M. O 1 Intoducction The elation between the cicumfeence and the adius of a cicle is one of the most impotant concepts
Classical Mechanics Homework set 7, due Nov 8th: Solutions
 Classical Mechanics Homewok set 7, due Nov 8th: Solutions 1. Do deivation 8.. It has been asked what effect does a total deivative as a function of q i, t have on the Hamiltonian. Thus, lets us begin with
Classical Mechanics Homewok set 7, due Nov 8th: Solutions 1. Do deivation 8.. It has been asked what effect does a total deivative as a function of q i, t have on the Hamiltonian. Thus, lets us begin with
Right-handed screw dislocation in an isotropic solid
 Dislocation Mechanics Elastic Popeties of Isolated Dislocations Ou study of dislocations to this point has focused on thei geomety and thei ole in accommodating plastic defomation though thei motion. We
Dislocation Mechanics Elastic Popeties of Isolated Dislocations Ou study of dislocations to this point has focused on thei geomety and thei ole in accommodating plastic defomation though thei motion. We
Classical Wave Equations
 Classical Wave Equations Michael Fowle, Univesity of Viginia 5/16/07 Intoduction The aim of this section is to give a faily bief eview of waves in vaious shaped elastic media beginning with a taut sting,
Classical Wave Equations Michael Fowle, Univesity of Viginia 5/16/07 Intoduction The aim of this section is to give a faily bief eview of waves in vaious shaped elastic media beginning with a taut sting,
Review: Electrostatics and Magnetostatics
 Review: Electostatics and Magnetostatics In the static egime, electomagnetic quantities do not vay as a function of time. We have two main cases: ELECTROSTATICS The electic chages do not change postion
Review: Electostatics and Magnetostatics In the static egime, electomagnetic quantities do not vay as a function of time. We have two main cases: ELECTROSTATICS The electic chages do not change postion
PHYS 705: Classical Mechanics. Small Oscillations
 PHYS 705: Classical Mechanics Small Oscillations Fomulation of the Poblem Assumptions: V q - A consevative system with depending on position only - The tansfomation equation defining does not dep on time
PHYS 705: Classical Mechanics Small Oscillations Fomulation of the Poblem Assumptions: V q - A consevative system with depending on position only - The tansfomation equation defining does not dep on time
Physics 2A Chapter 10 - Moment of Inertia Fall 2018
 Physics Chapte 0 - oment of netia Fall 08 The moment of inetia of a otating object is a measue of its otational inetia in the same way that the mass of an object is a measue of its inetia fo linea motion.
Physics Chapte 0 - oment of netia Fall 08 The moment of inetia of a otating object is a measue of its otational inetia in the same way that the mass of an object is a measue of its inetia fo linea motion.
Galactic Contraction and the Collinearity Principle
 TECHNISCHE MECHANIK, Band 23, Heft 1, (2003), 21-28 Manuskipteingang: 12. August 2002 Galactic Contaction and the Collineaity Pinciple F.P.J. Rimott, FA. Salusti In a spial galaxy thee is not only a Keplefoce
TECHNISCHE MECHANIK, Band 23, Heft 1, (2003), 21-28 Manuskipteingang: 12. August 2002 Galactic Contaction and the Collineaity Pinciple F.P.J. Rimott, FA. Salusti In a spial galaxy thee is not only a Keplefoce
Black Body Radiation and Radiometric Parameters:
 Black Body Radiation and Radiometic Paametes: All mateials absob and emit adiation to some extent. A blackbody is an idealization of how mateials emit and absob adiation. It can be used as a efeence fo
Black Body Radiation and Radiometic Paametes: All mateials absob and emit adiation to some extent. A blackbody is an idealization of how mateials emit and absob adiation. It can be used as a efeence fo
Newton s Laws, Kepler s Laws, and Planetary Orbits
 Newton s Laws, Keple s Laws, and Planetay Obits PROBLEM SET 4 DUE TUESDAY AT START OF LECTURE 28 Septembe 2017 ASTRONOMY 111 FALL 2017 1 Newton s & Keple s laws and planetay obits Unifom cicula motion
Newton s Laws, Keple s Laws, and Planetay Obits PROBLEM SET 4 DUE TUESDAY AT START OF LECTURE 28 Septembe 2017 ASTRONOMY 111 FALL 2017 1 Newton s & Keple s laws and planetay obits Unifom cicula motion
Chapter 3 Optical Systems with Annular Pupils
 Chapte 3 Optical Systems with Annula Pupils 3 INTRODUCTION In this chapte, we discuss the imaging popeties of a system with an annula pupil in a manne simila to those fo a system with a cicula pupil The
Chapte 3 Optical Systems with Annula Pupils 3 INTRODUCTION In this chapte, we discuss the imaging popeties of a system with an annula pupil in a manne simila to those fo a system with a cicula pupil The
MATH 417 Homework 3 Instructor: D. Cabrera Due June 30. sin θ v x = v r cos θ v θ r. (b) Then use the Cauchy-Riemann equations in polar coordinates
 MATH 417 Homewok 3 Instucto: D. Cabea Due June 30 1. Let a function f(z) = u + iv be diffeentiable at z 0. (a) Use the Chain Rule and the fomulas x = cosθ and y = to show that u x = u cosθ u θ, v x = v
MATH 417 Homewok 3 Instucto: D. Cabea Due June 30 1. Let a function f(z) = u + iv be diffeentiable at z 0. (a) Use the Chain Rule and the fomulas x = cosθ and y = to show that u x = u cosθ u θ, v x = v
Kinematics in 2-D (II)
 Kinematics in 2-D (II) Unifom cicula motion Tangential and adial components of Relative velocity and acceleation a Seway and Jewett 4.4 to 4.6 Pactice Poblems: Chapte 4, Objective Questions 5, 11 Chapte
Kinematics in 2-D (II) Unifom cicula motion Tangential and adial components of Relative velocity and acceleation a Seway and Jewett 4.4 to 4.6 Pactice Poblems: Chapte 4, Objective Questions 5, 11 Chapte
KEPLER S LAWS OF PLANETARY MOTION
 EPER S AWS OF PANETARY MOTION 1. Intoduction We ae now in a position to apply what we have leaned about the coss poduct and vecto valued functions to deive eple s aws of planetay motion. These laws wee
EPER S AWS OF PANETARY MOTION 1. Intoduction We ae now in a position to apply what we have leaned about the coss poduct and vecto valued functions to deive eple s aws of planetay motion. These laws wee
Contact impedance of grounded and capacitive electrodes
 Abstact Contact impedance of gounded and capacitive electodes Andeas Hödt Institut fü Geophysik und extateestische Physik, TU Baunschweig The contact impedance of electodes detemines how much cuent can
Abstact Contact impedance of gounded and capacitive electodes Andeas Hödt Institut fü Geophysik und extateestische Physik, TU Baunschweig The contact impedance of electodes detemines how much cuent can
Qualifying Examination Electricity and Magnetism Solutions January 12, 2006
 1 Qualifying Examination Electicity and Magnetism Solutions Januay 12, 2006 PROBLEM EA. a. Fist, we conside a unit length of cylinde to find the elationship between the total chage pe unit length λ and
1 Qualifying Examination Electicity and Magnetism Solutions Januay 12, 2006 PROBLEM EA. a. Fist, we conside a unit length of cylinde to find the elationship between the total chage pe unit length λ and
Physics C Rotational Motion Name: ANSWER KEY_ AP Review Packet
 Linea and angula analogs Linea Rotation x position x displacement v velocity a T tangential acceleation Vectos in otational motion Use the ight hand ule to detemine diection of the vecto! Don t foget centipetal
Linea and angula analogs Linea Rotation x position x displacement v velocity a T tangential acceleation Vectos in otational motion Use the ight hand ule to detemine diection of the vecto! Don t foget centipetal
INTRODUCTION. 2. Vectors in Physics 1
 INTRODUCTION Vectos ae used in physics to extend the study of motion fom one dimension to two dimensions Vectos ae indispensable when a physical quantity has a diection associated with it As an example,
INTRODUCTION Vectos ae used in physics to extend the study of motion fom one dimension to two dimensions Vectos ae indispensable when a physical quantity has a diection associated with it As an example,
1.6. Trigonometric Functions. 48 Chapter 1: Preliminaries. Radian Measure
 48 Chapte : Peliminaies.6 Tigonometic Functions Cicle B' B θ C A Unit of cicle adius FIGURE.63 The adian measue of angle ACB is the length u of ac AB on the unit cicle centeed at C. The value of u can
48 Chapte : Peliminaies.6 Tigonometic Functions Cicle B' B θ C A Unit of cicle adius FIGURE.63 The adian measue of angle ACB is the length u of ac AB on the unit cicle centeed at C. The value of u can
radians). Figure 2.1 Figure 2.2 (a) quadrant I angle (b) quadrant II angle is in standard position Terminal side Terminal side Terminal side
 . TRIGONOMETRIC FUNCTIONS OF GENERAL ANGLES In ode to etend the definitions of the si tigonometic functions to geneal angles, we shall make use of the following ideas: In a Catesian coodinate sstem, an
. TRIGONOMETRIC FUNCTIONS OF GENERAL ANGLES In ode to etend the definitions of the si tigonometic functions to geneal angles, we shall make use of the following ideas: In a Catesian coodinate sstem, an
r cos, and y r sin with the origin of coordinate system located at
 Lectue 3-3 Kinematics of Rotation Duing ou peious lectues we hae consideed diffeent examples of motion in one and seeal dimensions. But in each case the moing object was consideed as a paticle-like object,
Lectue 3-3 Kinematics of Rotation Duing ou peious lectues we hae consideed diffeent examples of motion in one and seeal dimensions. But in each case the moing object was consideed as a paticle-like object,
Uniform Circular Motion
 Unifom Cicula Motion Intoduction Ealie we defined acceleation as being the change in velocity with time: a = v t Until now we have only talked about changes in the magnitude of the acceleation: the speeding
Unifom Cicula Motion Intoduction Ealie we defined acceleation as being the change in velocity with time: a = v t Until now we have only talked about changes in the magnitude of the acceleation: the speeding
rt () is constant. We know how to find the length of the radius vector by r( t) r( t) r( t)
 Cicula Motion Fom ancient times cicula tajectoies hae occupied a special place in ou model of the Uniese. Although these obits hae been eplaced by the moe geneal elliptical geomety, cicula motion is still
Cicula Motion Fom ancient times cicula tajectoies hae occupied a special place in ou model of the Uniese. Although these obits hae been eplaced by the moe geneal elliptical geomety, cicula motion is still
Trigonometry Standard Position and Radians
 MHF 4UI Unit 6 Day 1 Tigonomety Standad Position and Radians A. Standad Position of an Angle teminal am initial am Angle is in standad position when the initial am is the positive x-axis and the vetex
MHF 4UI Unit 6 Day 1 Tigonomety Standad Position and Radians A. Standad Position of an Angle teminal am initial am Angle is in standad position when the initial am is the positive x-axis and the vetex
Supplementary Figure 1. Circular parallel lamellae grain size as a function of annealing time at 250 C. Error bars represent the 2σ uncertainty in
 Supplementay Figue 1. Cicula paallel lamellae gain size as a function of annealing time at 50 C. Eo bas epesent the σ uncetainty in the measued adii based on image pixilation and analysis uncetainty contibutions
Supplementay Figue 1. Cicula paallel lamellae gain size as a function of annealing time at 50 C. Eo bas epesent the σ uncetainty in the measued adii based on image pixilation and analysis uncetainty contibutions
Appendix A. Appendices. A.1 ɛ ijk and cross products. Vector Operations: δ ij and ɛ ijk
 Appendix A Appendices A1 ɛ and coss poducts A11 Vecto Opeations: δ ij and ɛ These ae some notes on the use of the antisymmetic symbol ɛ fo expessing coss poducts This is an extemely poweful tool fo manipulating
Appendix A Appendices A1 ɛ and coss poducts A11 Vecto Opeations: δ ij and ɛ These ae some notes on the use of the antisymmetic symbol ɛ fo expessing coss poducts This is an extemely poweful tool fo manipulating
Fresnel Diffraction. monchromatic light source
 Fesnel Diffaction Equipment Helium-Neon lase (632.8 nm) on 2 axis tanslation stage, Concave lens (focal length 3.80 cm) mounted on slide holde, iis mounted on slide holde, m optical bench, micoscope slide
Fesnel Diffaction Equipment Helium-Neon lase (632.8 nm) on 2 axis tanslation stage, Concave lens (focal length 3.80 cm) mounted on slide holde, iis mounted on slide holde, m optical bench, micoscope slide
Much that has already been said about changes of variable relates to transformations between different coordinate systems.
 MULTIPLE INTEGRLS I P Calculus Cooinate Sstems Much that has alea been sai about changes of vaiable elates to tansfomations between iffeent cooinate sstems. The main cooinate sstems use in the solution
MULTIPLE INTEGRLS I P Calculus Cooinate Sstems Much that has alea been sai about changes of vaiable elates to tansfomations between iffeent cooinate sstems. The main cooinate sstems use in the solution
c n ψ n (r)e ient/ h (2) where E n = 1 mc 2 α 2 Z 2 ψ(r) = c n ψ n (r) = c n = ψn(r)ψ(r)d 3 x e 2r/a0 1 πa e 3r/a0 r 2 dr c 1 2 = 2 9 /3 6 = 0.
 Poblem {a} Fo t : Ψ(, t ψ(e iet/ h ( whee E mc α (α /7 ψ( e /a πa Hee we have used the gound state wavefunction fo Z. Fo t, Ψ(, t can be witten as a supeposition of Z hydogenic wavefunctions ψ n (: Ψ(,
Poblem {a} Fo t : Ψ(, t ψ(e iet/ h ( whee E mc α (α /7 ψ( e /a πa Hee we have used the gound state wavefunction fo Z. Fo t, Ψ(, t can be witten as a supeposition of Z hydogenic wavefunctions ψ n (: Ψ(,
Tutorial Exercises: Central Forces
 Tutoial Execises: Cental Foces. Tuning Points fo the Keple potential (a) Wite down the two fist integals fo cental motion in the Keple potential V () = µm/ using J fo the angula momentum and E fo the total
Tutoial Execises: Cental Foces. Tuning Points fo the Keple potential (a) Wite down the two fist integals fo cental motion in the Keple potential V () = µm/ using J fo the angula momentum and E fo the total
2 x 8 2 x 2 SKILLS Determine whether the given value is a solution of the. equation. (a) x 2 (b) x 4. (a) x 2 (b) x 4 (a) x 4 (b) x 8
 5 CHAPTER Fundamentals When solving equations that involve absolute values, we usually take cases. EXAMPLE An Absolute Value Equation Solve the equation 0 x 5 0 3. SOLUTION By the definition of absolute
5 CHAPTER Fundamentals When solving equations that involve absolute values, we usually take cases. EXAMPLE An Absolute Value Equation Solve the equation 0 x 5 0 3. SOLUTION By the definition of absolute
COORDINATE TRANSFORMATIONS - THE JACOBIAN DETERMINANT
 COORDINATE TRANSFORMATIONS - THE JACOBIAN DETERMINANT Link to: phsicspages home page. To leave a comment o epot an eo, please use the auilia blog. Refeence: d Inveno, Ra, Intoducing Einstein s Relativit
COORDINATE TRANSFORMATIONS - THE JACOBIAN DETERMINANT Link to: phsicspages home page. To leave a comment o epot an eo, please use the auilia blog. Refeence: d Inveno, Ra, Intoducing Einstein s Relativit
Scattering in Three Dimensions
 Scatteing in Thee Dimensions Scatteing expeiments ae an impotant souce of infomation about quantum systems, anging in enegy fom vey low enegy chemical eactions to the highest possible enegies at the LHC.
Scatteing in Thee Dimensions Scatteing expeiments ae an impotant souce of infomation about quantum systems, anging in enegy fom vey low enegy chemical eactions to the highest possible enegies at the LHC.
Related Rates - the Basics
 Related Rates - the Basics In this section we exploe the way we can use deivatives to find the velocity at which things ae changing ove time. Up to now we have been finding the deivative to compae the
Related Rates - the Basics In this section we exploe the way we can use deivatives to find the velocity at which things ae changing ove time. Up to now we have been finding the deivative to compae the
Physics 235 Chapter 5. Chapter 5 Gravitation
 Chapte 5 Gavitation In this Chapte we will eview the popeties of the gavitational foce. The gavitational foce has been discussed in geat detail in you intoductoy physics couses, and we will pimaily focus
Chapte 5 Gavitation In this Chapte we will eview the popeties of the gavitational foce. The gavitational foce has been discussed in geat detail in you intoductoy physics couses, and we will pimaily focus
The study of the motion of a body along a general curve. the unit vector normal to the curve. Clearly, these unit vectors change with time, u ˆ
 Section. Cuilinea Motion he study of the motion of a body along a geneal cue. We define u ˆ û the unit ecto at the body, tangential to the cue the unit ecto nomal to the cue Clealy, these unit ectos change
Section. Cuilinea Motion he study of the motion of a body along a geneal cue. We define u ˆ û the unit ecto at the body, tangential to the cue the unit ecto nomal to the cue Clealy, these unit ectos change
