f(x) = lim x 0 + x = lim f(x) =
|
|
|
- Barry Miller
- 5 years ago
- Views:
Transcription
1 Infinite Limits Having discussed in detail its as x ±, we would like to discuss in more detail its where f(x) ±. Once again we would like to emphasize that ± are not numbers, so if we write f(x) = we are not saying that the it exists. What we are actually saying is that the it does not exist, and it does not exist because the values of the function f(x) grow without bound as x x 0. Similarly, f(x) = means that the it as x x 0 of f(x) does not exist because the function values decrease without bound (become arbitrarily large in magnitude, and negative in sign). Throughout this discussion one-sided its will be particularly useful to us, because it is quite common that a function may approach from one side of a point, and from the other side of the point. Example Find and What can you conclude about x x 0 + x x 0 x? Solution When x 0 we are considering negative x values, which are becoming smaller and smaller, approaching 0. Since the magnitude of the denominator becomes very small, the magnitude of the fraction becomes very large, growing without bound. Since the x values are negative, it follows that x 0 x = x 0 When we look at x 0 + the values of x are becoming very small, but remain positive. Thus, x 0 + x = Since the one-sided its are different, we write that x 0 + does not exist. Note that x even if both f(x) = f(x) = x 0 x 0 + the it would still not exist, but we would write f(x) = x 0 to signify the it does not exist because as x 0 from both sides the values of f(x) grow without bound. Example 2 Find x 4 (x + 4) 4 Solution In analyzing this function, the first thing to notice is that we have a fourth power in the denominator, (x + 4) 4. Since (x + 4) is raised to an even power, the denominator is
2 always non-negative (it is 0 when x = 4 and positive otherwise). Since the numerator is always positive as well, it means that this function is always non-negative. As x 4 and x 4 + the denominator approaches 0, which means that the values of the fraction grow without bound (so the it does not exist). We write x 4 (x + 4) 4 = to signify the function values grow without bound as x 4 from both sides. Example 3 Find x 3 (x 3) 4 Solution The first thing for us to do is simplify this fraction as much as possible. If we factor from the numerator, we find that x 3 (x 3) = (x 3) 4 x 3 (x 3) = 4 x 3 (x 3) 3 Note that above we were able to cancel the factor of (x 3) because in looking at the it as x 3, we know that x 3, so the factor will never be 0 (we, of course, cannot divide by 0). In this case, unlike the previous one, we have an odd power in the denominator; that is, (x 3) is raised to the third power. Because of this, we will have (x 3) 3 < 0 when x < 3 and (x 3) 3 > 0 when x > 3 Since the sign of the denominator is different depending on what side x 3 from, we should look at the one-sided its rather than trying to calculuate a two-sided it directly (because they will have different signs, so unless they are both 0, the two-sided it will not exist). As x 3 the denominator is negative, so the entire fraction is positive (because there is a in the numerator). As x 3 + the denonominator is always positive, so the entire function is negative. In both cases the denominator approaches 0, so we find that x 3 (x 3) 4 = x 3 = and (x 3) 3 x 3 + (x 3) 4 = x 3 + (x 3) 3 = Since our function has no consistent behavior as x 3, all we can say is that the it does not exist. Having considered infinite its intuitively, let us introduce the formal definition.
3 Definition: Infinite Limits We write f(x) = if for every number B > 0 there exists a corresponding δ > 0 such that for all x with 0 < x x 0 < δ we have f(x) > B Similarly, we write f(x) = if for every number B < 0 there exists a corresponding δ > 0 such that for all x with 0 < x x 0 < δ we have f(x) < B Example 4 Prove that x = 2 Solution We will start as previously, but now consider B > 0, arbitrary. We need to find δ > 0 so that for all x with 0 < x 0 < δ we have /x 2 > B. Manipulating this relationship, we find that we require B > x2 which means that we need x < B x 0 Thus, we need to choose δ B For arbitrary x with x < δ we have f(x) > B; The conclusion follows. Just as we defined horizontal asymptotes by looking at functions with a finite it as x ±, we can define vertical asymptotes, which occur when f(x) ±. More precisely, the line x = a is a vertical asymptote of the graph of a function if either x a x a f(x) = ± or f(x) = ± + This means that if for any point a the magnitude of f(x) grows without bound (so f(x) ± ) as x a from either side, then x = a is a vertical asymptote of the graph of f(x). Example 5 Find the horizontal and vertical asymptotes of f(x) = x + 2 Solution Horizontal asymptotes correspond to constant values in the its as x and x, and x x + 2 = and x x + 2 = so the only horizontal asymptote is the line y =. To look for vertical asymptotes, we want to look at places where the denominator of the function approaches 0; in this case we need
4 to consider x 2. It is enough to begin with just a one-sided it, because we do not require a two-sided it to approach to classify a vertical line as an asymptote. Since x 2 + x + 2 = We conclude that x = 2 is a vertical asymptote. Since the denominator does not approach 0 in any other places, there are no other vertical asymptotes. For this function the horizontal and vertical asymptotes have a nice graphical interpretation. If we draw the lines corresponding to y = 2 and x =, we know the behavior as x ± and x 2 will be in some way represented by this asymptotes. In fact, our function looks exactly like /x, if we simply were to shift the x and y axes to be these two asymptotes. Example 6 Find the vertical asymptotes of f(x) = tan(x). Solution Since vertical asymptotes correspond to places where denominator approaches 0, we need to rewrite tan(x) = sin(x) cos(x) in order to progress in this problem. Since sin(x) is ± when cos(x) = 0, it follows that every time cos(x) has a zero, tan(x) will have a vertical asymptote. These occur every π radians, and more precisely, tan(x) has a vertical asymptote for x = π 2 + nπ Example 7 Find all asymptotes of f(x) = 3x 2 5 Solution In this case the denominator has zeroes at both x = /3 and x = 2. However, we cannot immediately conclude that x = /3 and x = 2 are vertical asymptotes, because if the numerator is also 0 in one of these places, we will have an indeterminate form of 0 0 (the only way we can be certain that we have found a vertical asymptote is by evaluating the appropriate it). If we look as x 2 we find that 3x 2 5 = (3x + )() = 3x + = 7 which is very far from a it which approaches. Thus, even though we seemed to have division by 0 in the denominator at x = 2, the numerator was also 0, so we had an undefined expression, of which we could not be certain if it would grow without bound (in this case it did not, but in others it might!). Looking at the other it which does not exist, because x /3 x /3 + 3x + 3x 2 5 = x /3 3x + = and x /3 3x + =
5 Nevertheless, we don t require the two-sided it approach ± for a vertical asymptote to existr; in conclusion, we have a vertical asymptote at x = /3 but not at x = 2. We also find that x ± f(x) = 0 so we have a horizontal asymptote of y = 0.
2 = = 0 Thus, the number which is largest in magnitude is equal to the number which is smallest in magnitude.
 Limits at Infinity Two additional topics of interest with its are its as x ± and its where f(x) ±. Before we can properly discuss the notion of infinite its, we will need to begin with a discussion on
Limits at Infinity Two additional topics of interest with its are its as x ± and its where f(x) ±. Before we can properly discuss the notion of infinite its, we will need to begin with a discussion on
Calculus 221 worksheet
 Calculus 221 worksheet Graphing A function has a global maximum at some a in its domain if f(x) f(a) for all other x in the domain of f. Global maxima are sometimes also called absolute maxima. A function
Calculus 221 worksheet Graphing A function has a global maximum at some a in its domain if f(x) f(a) for all other x in the domain of f. Global maxima are sometimes also called absolute maxima. A function
56 CHAPTER 3. POLYNOMIAL FUNCTIONS
 56 CHAPTER 3. POLYNOMIAL FUNCTIONS Chapter 4 Rational functions and inequalities 4.1 Rational functions Textbook section 4.7 4.1.1 Basic rational functions and asymptotes As a first step towards understanding
56 CHAPTER 3. POLYNOMIAL FUNCTIONS Chapter 4 Rational functions and inequalities 4.1 Rational functions Textbook section 4.7 4.1.1 Basic rational functions and asymptotes As a first step towards understanding
DuVal High School Summer Review Packet AP Calculus
 DuVal High School Summer Review Packet AP Calculus Welcome to AP Calculus AB. This packet contains background skills you need to know for your AP Calculus. My suggestion is, you read the information and
DuVal High School Summer Review Packet AP Calculus Welcome to AP Calculus AB. This packet contains background skills you need to know for your AP Calculus. My suggestion is, you read the information and
AP Calculus. Limits, Continuity, and Differentiability
 AP Calculus Limits, Continuity, and Differentiability Student Handout 016 017 EDITION Click on the following link or scan the QR code to complete the evaluation for the Study Session https://www.surveymonkey.com/r/s_sss
AP Calculus Limits, Continuity, and Differentiability Student Handout 016 017 EDITION Click on the following link or scan the QR code to complete the evaluation for the Study Session https://www.surveymonkey.com/r/s_sss
Step 1: Greatest Common Factor Step 2: Count the number of terms If there are: 2 Terms: Difference of 2 Perfect Squares ( + )( - )
 Review for Algebra 2 CC Radicals: r x p 1 r x p p r = x p r = x Imaginary Numbers: i = 1 Polynomials (to Solve) Try Factoring: i 2 = 1 Step 1: Greatest Common Factor Step 2: Count the number of terms If
Review for Algebra 2 CC Radicals: r x p 1 r x p p r = x p r = x Imaginary Numbers: i = 1 Polynomials (to Solve) Try Factoring: i 2 = 1 Step 1: Greatest Common Factor Step 2: Count the number of terms If
LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS
 LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS RECALL: VERTICAL ASYMPTOTES Remember that for a rational function, vertical asymptotes occur at values of x = a which have infinite its (either positive or
LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS RECALL: VERTICAL ASYMPTOTES Remember that for a rational function, vertical asymptotes occur at values of x = a which have infinite its (either positive or
The degree of a function is the highest exponent in the expression
 L1 1.1 Power Functions Lesson MHF4U Jensen Things to Remember About Functions A relation is a function if for every x-value there is only 1 corresponding y-value. The graph of a relation represents a function
L1 1.1 Power Functions Lesson MHF4U Jensen Things to Remember About Functions A relation is a function if for every x-value there is only 1 corresponding y-value. The graph of a relation represents a function
Review: Limits of Functions - 10/7/16
 Review: Limits of Functions - 10/7/16 1 Right and Left Hand Limits Definition 1.0.1 We write lim a f() = L to mean that the function f() approaches L as approaches a from the left. We call this the left
Review: Limits of Functions - 10/7/16 1 Right and Left Hand Limits Definition 1.0.1 We write lim a f() = L to mean that the function f() approaches L as approaches a from the left. We call this the left
6.1 Polynomial Functions
 6.1 Polynomial Functions Definition. A polynomial function is any function p(x) of the form p(x) = p n x n + p n 1 x n 1 + + p 2 x 2 + p 1 x + p 0 where all of the exponents are non-negative integers and
6.1 Polynomial Functions Definition. A polynomial function is any function p(x) of the form p(x) = p n x n + p n 1 x n 1 + + p 2 x 2 + p 1 x + p 0 where all of the exponents are non-negative integers and
Practice Test - Chapter 2
 Graph and analyze each function. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing. 1. f (x) = 0.25x 3 Evaluate the function for several
Graph and analyze each function. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing. 1. f (x) = 0.25x 3 Evaluate the function for several
MATH 1231 MATHEMATICS 1B CALCULUS. Section 5: - Power Series and Taylor Series.
 MATH 1231 MATHEMATICS 1B CALCULUS. Section 5: - Power Series and Taylor Series. The objective of this section is to become familiar with the theory and application of power series and Taylor series. By
MATH 1231 MATHEMATICS 1B CALCULUS. Section 5: - Power Series and Taylor Series. The objective of this section is to become familiar with the theory and application of power series and Taylor series. By
Hello Future Calculus Level One Student,
 Hello Future Calculus Level One Student, This assignment must be completed and handed in on the first day of class. This assignment will serve as the main review for a test on this material. The test will
Hello Future Calculus Level One Student, This assignment must be completed and handed in on the first day of class. This assignment will serve as the main review for a test on this material. The test will
Written Homework 7 Solutions
 Written Homework 7 Solutions Section 4.3 20. Find the local maxima and minima using the First and Second Derivative tests: Solution: First start by finding the first derivative. f (x) = x2 x 1 f (x) =
Written Homework 7 Solutions Section 4.3 20. Find the local maxima and minima using the First and Second Derivative tests: Solution: First start by finding the first derivative. f (x) = x2 x 1 f (x) =
O.K. But what if the chicken didn t have access to a teleporter.
 The intermediate value theorem, and performing algebra on its. This is a dual topic lecture. : The Intermediate value theorem First we should remember what it means to be a continuous function: A function
The intermediate value theorem, and performing algebra on its. This is a dual topic lecture. : The Intermediate value theorem First we should remember what it means to be a continuous function: A function
Limits, Continuity, and the Derivative
 Unit #2 : Limits, Continuity, and the Derivative Goals: Study and define continuity Review limits Introduce the derivative as the limit of a difference quotient Discuss the derivative as a rate of change
Unit #2 : Limits, Continuity, and the Derivative Goals: Study and define continuity Review limits Introduce the derivative as the limit of a difference quotient Discuss the derivative as a rate of change
SANDERSON HIGH SCHOOL AP CALCULUS AB/BC SUMMER REVIEW PACKET
 SANDERSON HIGH SCHOOL AP CALCULUS AB/BC SUMMER REVIEW PACKET 017-018 Name: 1. This packet is to be handed in on Monday August 8, 017.. All work must be shown on separate paper attached to the packet. 3.
SANDERSON HIGH SCHOOL AP CALCULUS AB/BC SUMMER REVIEW PACKET 017-018 Name: 1. This packet is to be handed in on Monday August 8, 017.. All work must be shown on separate paper attached to the packet. 3.
Rational Functions 4.5
 Math 4 Pre-Calculus Name Date Rational Function Rational Functions 4.5 g ( ) A function is a rational function if f ( ), where g ( ) and ( ) h ( ) h are polynomials. Vertical asymptotes occur at -values
Math 4 Pre-Calculus Name Date Rational Function Rational Functions 4.5 g ( ) A function is a rational function if f ( ), where g ( ) and ( ) h ( ) h are polynomials. Vertical asymptotes occur at -values
Graphs of Antiderivatives, Substitution Integrals
 Unit #10 : Graphs of Antiderivatives, Substitution Integrals Goals: Relationship between the graph of f(x) and its anti-derivative F (x) The guess-and-check method for anti-differentiation. The substitution
Unit #10 : Graphs of Antiderivatives, Substitution Integrals Goals: Relationship between the graph of f(x) and its anti-derivative F (x) The guess-and-check method for anti-differentiation. The substitution
This Week. Professor Christopher Hoffman Math 124
 This Week Sections 2.1-2.3,2.5,2.6 First homework due Tuesday night at 11:30 p.m. Average and instantaneous velocity worksheet Tuesday available at http://www.math.washington.edu/ m124/ (under week 2)
This Week Sections 2.1-2.3,2.5,2.6 First homework due Tuesday night at 11:30 p.m. Average and instantaneous velocity worksheet Tuesday available at http://www.math.washington.edu/ m124/ (under week 2)
Calculus I Practice Problems 8: Answers
 Calculus I Practice Problems : Answers. Let y x x. Find the intervals in which the function is increasing and decreasing, and where it is concave up and concave down. Sketch the graph. Answer. Differentiate
Calculus I Practice Problems : Answers. Let y x x. Find the intervals in which the function is increasing and decreasing, and where it is concave up and concave down. Sketch the graph. Answer. Differentiate
Finding Limits Analytically
 Finding Limits Analytically Most of this material is take from APEX Calculus under terms of a Creative Commons License In this handout, we explore analytic techniques to compute its. Suppose that f(x)
Finding Limits Analytically Most of this material is take from APEX Calculus under terms of a Creative Commons License In this handout, we explore analytic techniques to compute its. Suppose that f(x)
LIMITS AND DERIVATIVES
 2 LIMITS AND DERIVATIVES LIMITS AND DERIVATIVES 2.2 The Limit of a Function In this section, we will learn: About limits in general and about numerical and graphical methods for computing them. THE LIMIT
2 LIMITS AND DERIVATIVES LIMITS AND DERIVATIVES 2.2 The Limit of a Function In this section, we will learn: About limits in general and about numerical and graphical methods for computing them. THE LIMIT
The Relation between the Integral and the Derivative Graphs. Unit #10 : Graphs of Antiderivatives, Substitution Integrals
 Graphs of Antiderivatives - Unit #0 : Graphs of Antiderivatives, Substitution Integrals Goals: Relationship between the graph of f(x) and its anti-derivative F (x) The guess-and-check method for anti-differentiation.
Graphs of Antiderivatives - Unit #0 : Graphs of Antiderivatives, Substitution Integrals Goals: Relationship between the graph of f(x) and its anti-derivative F (x) The guess-and-check method for anti-differentiation.
Unit #10 : Graphs of Antiderivatives, Substitution Integrals
 Unit #10 : Graphs of Antiderivatives, Substitution Integrals Goals: Relationship between the graph of f(x) and its anti-derivative F(x) The guess-and-check method for anti-differentiation. The substitution
Unit #10 : Graphs of Antiderivatives, Substitution Integrals Goals: Relationship between the graph of f(x) and its anti-derivative F(x) The guess-and-check method for anti-differentiation. The substitution
Chapter 4: More Applications of Differentiation
 Chapter 4: More Applications of Differentiation Winter 2016 Department of Mathematics Hong Kong Baptist University 1 / 61 In the fall of 1972, President Nixon announced that, the rate of increase of inflation
Chapter 4: More Applications of Differentiation Winter 2016 Department of Mathematics Hong Kong Baptist University 1 / 61 In the fall of 1972, President Nixon announced that, the rate of increase of inflation
1.10 Continuity Brian E. Veitch
 1.10 Continuity Definition 1.5. A function is continuous at x = a if 1. f(a) exists 2. lim x a f(x) exists 3. lim x a f(x) = f(a) If any of these conditions fail, f is discontinuous. Note: From algebra
1.10 Continuity Definition 1.5. A function is continuous at x = a if 1. f(a) exists 2. lim x a f(x) exists 3. lim x a f(x) = f(a) If any of these conditions fail, f is discontinuous. Note: From algebra
2. If the values for f(x) can be made as close as we like to L by choosing arbitrarily large. lim
 Limits at Infinity and Horizontal Asymptotes As we prepare to practice graphing functions, we should consider one last piece of information about a function that will be helpful in drawing its graph the
Limits at Infinity and Horizontal Asymptotes As we prepare to practice graphing functions, we should consider one last piece of information about a function that will be helpful in drawing its graph the
Section 2.5. Evaluating Limits Algebraically
 Section 2.5 Evaluating Limits Algebraically (1) Determinate and Indeterminate Forms (2) Limit Calculation Techniques (A) Direct Substitution (B) Simplification (C) Conjugation (D) The Squeeze Theorem (3)
Section 2.5 Evaluating Limits Algebraically (1) Determinate and Indeterminate Forms (2) Limit Calculation Techniques (A) Direct Substitution (B) Simplification (C) Conjugation (D) The Squeeze Theorem (3)
MATH 1910 Limits Numerically and Graphically Introduction to Limits does not exist DNE DOES does not Finding Limits Numerically
 MATH 90 - Limits Numerically and Graphically Introduction to Limits The concept of a limit is our doorway to calculus. This lecture will explain what the limit of a function is and how we can find such
MATH 90 - Limits Numerically and Graphically Introduction to Limits The concept of a limit is our doorway to calculus. This lecture will explain what the limit of a function is and how we can find such
a x a y = a x+y a x a = y ax y (a x ) r = a rx and log a (xy) = log a (x) + log a (y) log a ( x y ) = log a(x) log a (y) log a (x r ) = r log a (x).
 You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
MATH 1130 Exam 1 Review Sheet
 MATH 1130 Exam 1 Review Sheet The Cartesian Coordinate Plane The Cartesian Coordinate Plane is a visual representation of the collection of all ordered pairs (x, y) where x and y are real numbers. This
MATH 1130 Exam 1 Review Sheet The Cartesian Coordinate Plane The Cartesian Coordinate Plane is a visual representation of the collection of all ordered pairs (x, y) where x and y are real numbers. This
Calculus I Exam 1 Review Fall 2016
 Problem 1: Decide whether the following statements are true or false: (a) If f, g are differentiable, then d d x (f g) = f g. (b) If a function is continuous, then it is differentiable. (c) If a function
Problem 1: Decide whether the following statements are true or false: (a) If f, g are differentiable, then d d x (f g) = f g. (b) If a function is continuous, then it is differentiable. (c) If a function
Chapter 4: More Applications of Differentiation
 Chapter 4: More Applications of Differentiation Autumn 2017 Department of Mathematics Hong Kong Baptist University 1 / 68 In the fall of 1972, President Nixon announced that, the rate of increase of inflation
Chapter 4: More Applications of Differentiation Autumn 2017 Department of Mathematics Hong Kong Baptist University 1 / 68 In the fall of 1972, President Nixon announced that, the rate of increase of inflation
Math 115 Spring 11 Written Homework 10 Solutions
 Math 5 Spring Written Homework 0 Solutions. For following its, state what indeterminate form the its are in and evaluate the its. (a) 3x 4x 4 x x 8 Solution: This is in indeterminate form 0. Algebraically,
Math 5 Spring Written Homework 0 Solutions. For following its, state what indeterminate form the its are in and evaluate the its. (a) 3x 4x 4 x x 8 Solution: This is in indeterminate form 0. Algebraically,
Section 11.1: Sequences
 Section 11.1: Sequences In this section, we shall study something of which is conceptually simple mathematically, but has far reaching results in so many different areas of mathematics - sequences. 1.
Section 11.1: Sequences In this section, we shall study something of which is conceptually simple mathematically, but has far reaching results in so many different areas of mathematics - sequences. 1.
Rational Functions. A rational function is a function that is a ratio of 2 polynomials (in reduced form), e.g.
 Rational Functions A rational function is a function that is a ratio of polynomials (in reduced form), e.g. f() = p( ) q( ) where p() and q() are polynomials The function is defined when the denominator
Rational Functions A rational function is a function that is a ratio of polynomials (in reduced form), e.g. f() = p( ) q( ) where p() and q() are polynomials The function is defined when the denominator
Summer 2017 Review For Students Entering AP Calculus AB/BC
 Summer 2017 Review For Students Entering AP Calculus AB/BC Holy Name High School AP Calculus Summer Homework 1 A.M.D.G. AP Calculus AB Summer Review Packet Holy Name High School Welcome to AP Calculus
Summer 2017 Review For Students Entering AP Calculus AB/BC Holy Name High School AP Calculus Summer Homework 1 A.M.D.G. AP Calculus AB Summer Review Packet Holy Name High School Welcome to AP Calculus
Unit #10 : Graphs of Antiderivatives; Substitution Integrals
 Unit #10 : Graphs of Antiderivatives; Substitution Integrals Goals: Relationship between the graph of f(x) and its anti-derivative F(x) The guess-and-check method for anti-differentiation. The substitution
Unit #10 : Graphs of Antiderivatives; Substitution Integrals Goals: Relationship between the graph of f(x) and its anti-derivative F(x) The guess-and-check method for anti-differentiation. The substitution
Advanced Mathematics Unit 2 Limits and Continuity
 Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Advanced Mathematics Unit 2 Limits and Continuity
 Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Infinite Limits. By Tuesday J. Johnson
 Infinite Limits By Tuesday J. Johnson Suggested Review Topics Algebra skills reviews suggested: Evaluating functions Graphing functions Working with inequalities Working with absolute values Trigonometric
Infinite Limits By Tuesday J. Johnson Suggested Review Topics Algebra skills reviews suggested: Evaluating functions Graphing functions Working with inequalities Working with absolute values Trigonometric
Section 2.6 Limits at infinity and infinite limits 2 Lectures. Dr. Abdulla Eid. College of Science. MATHS 101: Calculus I
 Section 2.6 Limits at infinity and infinite its 2 Lectures College of Science MATHS 0: Calculus I (University of Bahrain) Infinite Limits / 29 Finite its as ±. 2 Horizontal Asympotes. 3 Infinite its. 4
Section 2.6 Limits at infinity and infinite its 2 Lectures College of Science MATHS 0: Calculus I (University of Bahrain) Infinite Limits / 29 Finite its as ±. 2 Horizontal Asympotes. 3 Infinite its. 4
Math 180, Final Exam, Fall 2012 Problem 1 Solution
 Math 80, Final Exam, Fall 0 Problem Solution. Find the derivatives of the following functions: (a) ln(ln(x)) (b) x 6 + sin(x) e x (c) tan(x ) + cot(x ) (a) We evaluate the derivative using the Chain Rule.
Math 80, Final Exam, Fall 0 Problem Solution. Find the derivatives of the following functions: (a) ln(ln(x)) (b) x 6 + sin(x) e x (c) tan(x ) + cot(x ) (a) We evaluate the derivative using the Chain Rule.
APPLICATIONS OF DIFFERENTIATION
 4 APPLICATIONS OF DIFFERENTIATION APPLICATIONS OF DIFFERENTIATION The method we used to sketch curves in Section 4.5 was a culmination of much of our study of differential calculus. The graph was the final
4 APPLICATIONS OF DIFFERENTIATION APPLICATIONS OF DIFFERENTIATION The method we used to sketch curves in Section 4.5 was a culmination of much of our study of differential calculus. The graph was the final
MAT137 Calculus! Lecture 9
 MAT137 Calculus! Lecture 9 Today we will study: Limits at infinity. L Hôpital s Rule. Mean Value Theorem. (11.5,11.6, 4.1) PS3 is due this Friday June 16. Next class: Applications of the Mean Value Theorem.
MAT137 Calculus! Lecture 9 Today we will study: Limits at infinity. L Hôpital s Rule. Mean Value Theorem. (11.5,11.6, 4.1) PS3 is due this Friday June 16. Next class: Applications of the Mean Value Theorem.
MATH 151 Engineering Mathematics I
 MATH 151 Engineering Mathematics I Fall 2018, WEEK 3 JoungDong Kim Week 3 Section 2.3, 2.5, 2.6, Calculating Limits Using the Limit Laws, Continuity, Limits at Infinity; Horizontal Asymptotes. Section
MATH 151 Engineering Mathematics I Fall 2018, WEEK 3 JoungDong Kim Week 3 Section 2.3, 2.5, 2.6, Calculating Limits Using the Limit Laws, Continuity, Limits at Infinity; Horizontal Asymptotes. Section
Chapter 2. Limits and Continuity 2.6 Limits Involving Infinity; Asymptotes of Graphs
 2.6 Limits Involving Infinity; Asymptotes of Graphs Chapter 2. Limits and Continuity 2.6 Limits Involving Infinity; Asymptotes of Graphs Definition. Formal Definition of Limits at Infinity.. We say that
2.6 Limits Involving Infinity; Asymptotes of Graphs Chapter 2. Limits and Continuity 2.6 Limits Involving Infinity; Asymptotes of Graphs Definition. Formal Definition of Limits at Infinity.. We say that
Limits and Continuity
 Limits and Continuity MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After this lesson we will be able to: Determine the left-hand and right-hand limits
Limits and Continuity MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After this lesson we will be able to: Determine the left-hand and right-hand limits
Roots and Coefficients of a Quadratic Equation Summary
 Roots and Coefficients of a Quadratic Equation Summary For a quadratic equation with roots α and β: Sum of roots = α + β = and Product of roots = αβ = Symmetrical functions of α and β include: x = and
Roots and Coefficients of a Quadratic Equation Summary For a quadratic equation with roots α and β: Sum of roots = α + β = and Product of roots = αβ = Symmetrical functions of α and β include: x = and
Unit 6 Trigonometric Identities
 Unit 6 Trigonometric Identities Prove trigonometric identities Solve trigonometric equations Prove trigonometric identities, using: Reciprocal identities Quotient identities Pythagorean identities Sum
Unit 6 Trigonometric Identities Prove trigonometric identities Solve trigonometric equations Prove trigonometric identities, using: Reciprocal identities Quotient identities Pythagorean identities Sum
Revision notes for Pure 1(9709/12)
 Revision notes for Pure 1(9709/12) By WaqasSuleman A-Level Teacher Beaconhouse School System Contents 1. Sequence and Series 2. Functions & Quadratics 3. Binomial theorem 4. Coordinate Geometry 5. Trigonometry
Revision notes for Pure 1(9709/12) By WaqasSuleman A-Level Teacher Beaconhouse School System Contents 1. Sequence and Series 2. Functions & Quadratics 3. Binomial theorem 4. Coordinate Geometry 5. Trigonometry
MAT116 Final Review Session Chapter 3: Polynomial and Rational Functions
 MAT116 Final Review Session Chapter 3: Polynomial and Rational Functions Quadratic Function A quadratic function is defined by a quadratic or second-degree polynomial. Standard Form f x = ax 2 + bx + c,
MAT116 Final Review Session Chapter 3: Polynomial and Rational Functions Quadratic Function A quadratic function is defined by a quadratic or second-degree polynomial. Standard Form f x = ax 2 + bx + c,
University Calculus I. Worksheet # 8 Mar b. sin tan e. sin 2 sin 1 5. b. tan. c. sec sin 1 ( x )) cos 1 ( x )) f. csc. c.
 MATH 6 WINTER 06 University Calculus I Worksheet # 8 Mar. 06-0 The topic covered by this worksheet is: Derivative of Inverse Functions and the Inverse Trigonometric functions. SamplesolutionstoallproblemswillbeavailableonDL,
MATH 6 WINTER 06 University Calculus I Worksheet # 8 Mar. 06-0 The topic covered by this worksheet is: Derivative of Inverse Functions and the Inverse Trigonometric functions. SamplesolutionstoallproblemswillbeavailableonDL,
1.5 F15 O Brien. 1.5: Linear Equations and Inequalities
 1.5: Linear Equations and Inequalities I. Basic Terminology A. An equation is a statement that two expressions are equal. B. To solve an equation means to find all of the values of the variable that make
1.5: Linear Equations and Inequalities I. Basic Terminology A. An equation is a statement that two expressions are equal. B. To solve an equation means to find all of the values of the variable that make
Grade 11 or 12 Pre-Calculus
 Grade 11 or 12 Pre-Calculus Strands 1. Polynomial, Rational, and Radical Relationships 2. Trigonometric Functions 3. Modeling with Functions Strand 1: Polynomial, Rational, and Radical Relationships Standard
Grade 11 or 12 Pre-Calculus Strands 1. Polynomial, Rational, and Radical Relationships 2. Trigonometric Functions 3. Modeling with Functions Strand 1: Polynomial, Rational, and Radical Relationships Standard
MA1021 Calculus I B Term, Sign:
 MA1021 Calculus I B Term, 2014 Final Exam Print Name: Sign: Write up your solutions neatly and show all your work. 1. (28 pts) Compute each of the following derivatives: You do not have to simplify your
MA1021 Calculus I B Term, 2014 Final Exam Print Name: Sign: Write up your solutions neatly and show all your work. 1. (28 pts) Compute each of the following derivatives: You do not have to simplify your
2.4 The Precise Definition of a Limit
 2.4 The Precise Definition of a Limit Reminders/Remarks: x 4 < 3 means that the distance between x and 4 is less than 3. In other words, x lies strictly between 1 and 7. So, x a < δ means that the distance
2.4 The Precise Definition of a Limit Reminders/Remarks: x 4 < 3 means that the distance between x and 4 is less than 3. In other words, x lies strictly between 1 and 7. So, x a < δ means that the distance
AP Calculus Summer Packet
 AP Calculus Summer Packet Writing The Equation Of A Line Example: Find the equation of a line that passes through ( 1, 2) and (5, 7). ü Things to remember: Slope formula, point-slope form, slopeintercept
AP Calculus Summer Packet Writing The Equation Of A Line Example: Find the equation of a line that passes through ( 1, 2) and (5, 7). ü Things to remember: Slope formula, point-slope form, slopeintercept
AP Calculus AB Summer Math Packet
 Name Date Section AP Calculus AB Summer Math Packet This assignment is to be done at you leisure during the summer. It is meant to help you practice mathematical skills necessary to be successful in Calculus
Name Date Section AP Calculus AB Summer Math Packet This assignment is to be done at you leisure during the summer. It is meant to help you practice mathematical skills necessary to be successful in Calculus
Core Mathematics 2 Trigonometry
 Core Mathematics 2 Trigonometry Edited by: K V Kumaran Email: kvkumaran@gmail.com Core Mathematics 2 Trigonometry 2 1 Trigonometry Sine, cosine and tangent functions. Their graphs, symmetries and periodicity.
Core Mathematics 2 Trigonometry Edited by: K V Kumaran Email: kvkumaran@gmail.com Core Mathematics 2 Trigonometry 2 1 Trigonometry Sine, cosine and tangent functions. Their graphs, symmetries and periodicity.
Math 261 Calculus I. Test 1 Study Guide. Name. Decide whether the limit exists. If it exists, find its value. 1) lim x 1. f(x) 2) lim x -1/2 f(x)
 Math 261 Calculus I Test 1 Study Guide Name Decide whether the it exists. If it exists, find its value. 1) x 1 f(x) 2) x -1/2 f(x) Complete the table and use the result to find the indicated it. 3) If
Math 261 Calculus I Test 1 Study Guide Name Decide whether the it exists. If it exists, find its value. 1) x 1 f(x) 2) x -1/2 f(x) Complete the table and use the result to find the indicated it. 3) If
(x 3)(x + 5) = (x 3)(x 1) = x + 5. sin 2 x e ax bx 1 = 1 2. lim
 SMT Calculus Test Solutions February, x + x 5 Compute x x x + Answer: Solution: Note that x + x 5 x x + x )x + 5) = x )x ) = x + 5 x x + 5 Then x x = + 5 = Compute all real values of b such that, for fx)
SMT Calculus Test Solutions February, x + x 5 Compute x x x + Answer: Solution: Note that x + x 5 x x + x )x + 5) = x )x ) = x + 5 x x + 5 Then x x = + 5 = Compute all real values of b such that, for fx)
Albertson AP Calculus AB AP CALCULUS AB SUMMER PACKET DUE DATE: The beginning of class on the last class day of the first week of school.
 Albertson AP Calculus AB Name AP CALCULUS AB SUMMER PACKET 2015 DUE DATE: The beginning of class on the last class day of the first week of school. This assignment is to be done at you leisure during the
Albertson AP Calculus AB Name AP CALCULUS AB SUMMER PACKET 2015 DUE DATE: The beginning of class on the last class day of the first week of school. This assignment is to be done at you leisure during the
Topics from Algebra and Pre-Calculus. (Key contains solved problems)
 Topics from Algebra and Pre-Calculus (Key contains solved problems) Note: The purpose of this packet is to give you a review of basic skills. You are asked not to use the calculator, except on p. (8) and
Topics from Algebra and Pre-Calculus (Key contains solved problems) Note: The purpose of this packet is to give you a review of basic skills. You are asked not to use the calculator, except on p. (8) and
7.4 RECIPROCAL FUNCTIONS
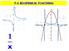 7.4 RECIPROCAL FUNCTIONS x VOCABULARY Word Know It Well Have Heard It or Seen It No Clue RECIPROCAL FUNCTION ASYMPTOTE VERTICAL ASYMPTOTE HORIZONTAL ASYMPTOTE RECIPROCAL a mathematical expression or function
7.4 RECIPROCAL FUNCTIONS x VOCABULARY Word Know It Well Have Heard It or Seen It No Clue RECIPROCAL FUNCTION ASYMPTOTE VERTICAL ASYMPTOTE HORIZONTAL ASYMPTOTE RECIPROCAL a mathematical expression or function
Name: AK-Nummer: Ergänzungsprüfung January 29, 2016
 INSTRUCTIONS: The test has a total of 32 pages including this title page and 9 questions which are marked out of 10 points; ensure that you do not omit a page by mistake. Please write your name and AK-Nummer
INSTRUCTIONS: The test has a total of 32 pages including this title page and 9 questions which are marked out of 10 points; ensure that you do not omit a page by mistake. Please write your name and AK-Nummer
October 27, 2018 MAT186 Week 3 Justin Ko. We use the following notation to describe the limiting behavior of functions.
 October 27, 208 MAT86 Week 3 Justin Ko Limits. Intuitive Definitions of Limits We use the following notation to describe the iting behavior of functions.. (Limit of a Function A it is written as f( = L
October 27, 208 MAT86 Week 3 Justin Ko Limits. Intuitive Definitions of Limits We use the following notation to describe the iting behavior of functions.. (Limit of a Function A it is written as f( = L
Calculus I. George Voutsadakis 1. LSSU Math 151. Lake Superior State University. 1 Mathematics and Computer Science
 Calculus I George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 151 George Voutsadakis (LSSU) Calculus I November 2014 1 / 67 Outline 1 Limits Limits, Rates
Calculus I George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 151 George Voutsadakis (LSSU) Calculus I November 2014 1 / 67 Outline 1 Limits Limits, Rates
A function is actually a simple concept; if it were not, history would have replaced it with a simpler one by now! Here is the definition:
 1.2 Functions and Their Properties A function is actually a simple concept; if it were not, history would have replaced it with a simpler one by now! Here is the definition: Definition: Function, Domain,
1.2 Functions and Their Properties A function is actually a simple concept; if it were not, history would have replaced it with a simpler one by now! Here is the definition: Definition: Function, Domain,
Pre-Calculus II: Trigonometry Exam 1 Preparation Solutions. Math&142 November 8, 2016
 Pre-Calculus II: Trigonometry Exam 1 Preparation Solutions Math&1 November 8, 016 1. Convert the angle in degrees to radian. Express the answer as a multiple of π. a 87 π rad 180 = 87π 180 rad b 16 π rad
Pre-Calculus II: Trigonometry Exam 1 Preparation Solutions Math&1 November 8, 016 1. Convert the angle in degrees to radian. Express the answer as a multiple of π. a 87 π rad 180 = 87π 180 rad b 16 π rad
The function graphed below is continuous everywhere. The function graphed below is NOT continuous everywhere, it is discontinuous at x 2 and
 Section 1.4 Continuity A function is a continuous at a point if its graph has no gaps, holes, breaks or jumps at that point. If a function is not continuous at a point, then we say it is discontinuous
Section 1.4 Continuity A function is a continuous at a point if its graph has no gaps, holes, breaks or jumps at that point. If a function is not continuous at a point, then we say it is discontinuous
Example 1a ~ Like # 1-39
 Example 1a ~ Like # 1-39 f(x) = A. The domain is {x x 2 1 0} = {x x 1} DOM: (, 1) ( 1, 1) (1, ) B. The x- and y-intercepts are both 0. C. Since f( x) = f(x), the function f is even. The curve is symmetric
Example 1a ~ Like # 1-39 f(x) = A. The domain is {x x 2 1 0} = {x x 1} DOM: (, 1) ( 1, 1) (1, ) B. The x- and y-intercepts are both 0. C. Since f( x) = f(x), the function f is even. The curve is symmetric
Practice Test - Chapter 2
 Graph and analyze each function. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing. 1. f (x) = 0.25x 3 Evaluate the function for several
Graph and analyze each function. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing. 1. f (x) = 0.25x 3 Evaluate the function for several
MTH4100 Calculus I. Lecture notes for Week 4. Thomas Calculus, Sections 2.4 to 2.6. Rainer Klages
 MTH4100 Calculus I Lecture notes for Week 4 Thomas Calculus, Sections 2.4 to 2.6 Rainer Klages School of Mathematical Sciences Queen Mary University of London Autumn 2009 One-sided its and its at infinity
MTH4100 Calculus I Lecture notes for Week 4 Thomas Calculus, Sections 2.4 to 2.6 Rainer Klages School of Mathematical Sciences Queen Mary University of London Autumn 2009 One-sided its and its at infinity
ter. on Can we get a still better result? Yes, by making the rectangles still smaller. As we make the rectangles smaller and smaller, the
 Area and Tangent Problem Calculus is motivated by two main problems. The first is the area problem. It is a well known result that the area of a rectangle with length l and width w is given by A = wl.
Area and Tangent Problem Calculus is motivated by two main problems. The first is the area problem. It is a well known result that the area of a rectangle with length l and width w is given by A = wl.
6.1 Inverse Functions. Outline
 6.1 Inverse Functions Tom Lewis Fall Semester 2018 Outline The inverse of a relation One-to-one functions Inverse functions Finding inverse functions The calculus of inverse functions Definition A relation
6.1 Inverse Functions Tom Lewis Fall Semester 2018 Outline The inverse of a relation One-to-one functions Inverse functions Finding inverse functions The calculus of inverse functions Definition A relation
SKILL BUILDER TEN. Graphs of Linear Equations with Two Variables. If x = 2 then y = = = 7 and (2, 7) is a solution.
 SKILL BUILDER TEN Graphs of Linear Equations with Two Variables A first degree equation is called a linear equation, since its graph is a straight line. In a linear equation, each term is a constant or
SKILL BUILDER TEN Graphs of Linear Equations with Two Variables A first degree equation is called a linear equation, since its graph is a straight line. In a linear equation, each term is a constant or
The Free Intuitive Calculus Course Integrals
 Intuitive-Calculus.com Presents The Free Intuitive Calculus Course Integrals Day 19: Trigonometric Integrals By Pablo Antuna 013 All Rights Reserved. The Intuitive Calculus Course - By Pablo Antuna Contents
Intuitive-Calculus.com Presents The Free Intuitive Calculus Course Integrals Day 19: Trigonometric Integrals By Pablo Antuna 013 All Rights Reserved. The Intuitive Calculus Course - By Pablo Antuna Contents
MTH30 Review Sheet. y = g(x) BRONX COMMUNITY COLLEGE of the City University of New York DEPARTMENT OF MATHEMATICS & COMPUTER SCIENCE
 BRONX COMMUNITY COLLEGE of the City University of New York DEPARTMENT OF MATHEMATICS & COMPUTER SCIENCE MTH0 Review Sheet. Given the functions f and g described by the graphs below: y = f(x) y = g(x) (a)
BRONX COMMUNITY COLLEGE of the City University of New York DEPARTMENT OF MATHEMATICS & COMPUTER SCIENCE MTH0 Review Sheet. Given the functions f and g described by the graphs below: y = f(x) y = g(x) (a)
Aim: How do we prepare for AP Problems on limits, continuity and differentiability? f (x)
 Name AP Calculus Date Supplemental Review 1 Aim: How do we prepare for AP Problems on limits, continuity and differentiability? Do Now: Use the graph of f(x) to evaluate each of the following: 1. lim x
Name AP Calculus Date Supplemental Review 1 Aim: How do we prepare for AP Problems on limits, continuity and differentiability? Do Now: Use the graph of f(x) to evaluate each of the following: 1. lim x
Chapter 1- Polynomial Functions
 Chapter 1- Polynomial Functions Lesson Package MHF4U Chapter 1 Outline Unit Goal: By the end of this unit, you will be able to identify and describe some key features of polynomial functions, and make
Chapter 1- Polynomial Functions Lesson Package MHF4U Chapter 1 Outline Unit Goal: By the end of this unit, you will be able to identify and describe some key features of polynomial functions, and make
function independent dependent domain range graph of the function The Vertical Line Test
 Functions A quantity y is a function of another quantity x if there is some rule (an algebraic equation, a graph, a table, or as an English description) by which a unique value is assigned to y by a corresponding
Functions A quantity y is a function of another quantity x if there is some rule (an algebraic equation, a graph, a table, or as an English description) by which a unique value is assigned to y by a corresponding
14 Increasing and decreasing functions
 14 Increasing and decreasing functions 14.1 Sketching derivatives READING Read Section 3.2 of Rogawski Reading Recall, f (a) is the gradient of the tangent line of f(x) at x = a. We can use this fact to
14 Increasing and decreasing functions 14.1 Sketching derivatives READING Read Section 3.2 of Rogawski Reading Recall, f (a) is the gradient of the tangent line of f(x) at x = a. We can use this fact to
MATH 250 TOPIC 11 LIMITS. A. Basic Idea of a Limit and Limit Laws. Answers to Exercises and Problems
 Math 5 T-Limits Page MATH 5 TOPIC LIMITS A. Basic Idea of a Limit and Limit Laws B. Limits of the form,, C. Limits as or as D. Summary for Evaluating Limits Answers to Eercises and Problems Math 5 T-Limits
Math 5 T-Limits Page MATH 5 TOPIC LIMITS A. Basic Idea of a Limit and Limit Laws B. Limits of the form,, C. Limits as or as D. Summary for Evaluating Limits Answers to Eercises and Problems Math 5 T-Limits
To get horizontal and slant asymptotes algebraically we need to know about end behaviour for rational functions.
 Concepts: Horizontal Asymptotes, Vertical Asymptotes, Slant (Oblique) Asymptotes, Transforming Reciprocal Function, Sketching Rational Functions, Solving Inequalities using Sign Charts. Rational Function
Concepts: Horizontal Asymptotes, Vertical Asymptotes, Slant (Oblique) Asymptotes, Transforming Reciprocal Function, Sketching Rational Functions, Solving Inequalities using Sign Charts. Rational Function
Announcements. Related Rates (last week), Linear approximations (today) l Hôpital s Rule (today) Newton s Method Curve sketching Optimization problems
 Announcements Assignment 4 is now posted. Midterm results should be available by the end of the week (assuming the scantron results are back in time). Today: Continuation of applications of derivatives:
Announcements Assignment 4 is now posted. Midterm results should be available by the end of the week (assuming the scantron results are back in time). Today: Continuation of applications of derivatives:
b n x n + b n 1 x n b 1 x + b 0
 Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
AP Calculus Summer Prep
 AP Calculus Summer Prep Topics from Algebra and Pre-Calculus (Solutions are on the Answer Key on the Last Pages) The purpose of this packet is to give you a review of basic skills. You are asked to have
AP Calculus Summer Prep Topics from Algebra and Pre-Calculus (Solutions are on the Answer Key on the Last Pages) The purpose of this packet is to give you a review of basic skills. You are asked to have
For a semi-circle with radius r, its circumfrence is πr, so the radian measure of a semi-circle (a straight line) is
 Radian Measure Given any circle with radius r, if θ is a central angle of the circle and s is the length of the arc sustained by θ, we define the radian measure of θ by: θ = s r For a semi-circle with
Radian Measure Given any circle with radius r, if θ is a central angle of the circle and s is the length of the arc sustained by θ, we define the radian measure of θ by: θ = s r For a semi-circle with
1.2 Supplement: Mathematical Models: A Catalog of Essential Functions
 Math 131 -copyright Angela Allen, Fall 2011 1 1.2 Supplement: Mathematical Models: A Catalog of Essential Functions Note: Some of these examples and figures come from your textbook Single Variable Calculus:
Math 131 -copyright Angela Allen, Fall 2011 1 1.2 Supplement: Mathematical Models: A Catalog of Essential Functions Note: Some of these examples and figures come from your textbook Single Variable Calculus:
Math 3 Variable Manipulation Part 3 Polynomials A
 Math 3 Variable Manipulation Part 3 Polynomials A 1 MATH 1 & 2 REVIEW: VOCABULARY Constant: A term that does not have a variable is called a constant. Example: the number 5 is a constant because it does
Math 3 Variable Manipulation Part 3 Polynomials A 1 MATH 1 & 2 REVIEW: VOCABULARY Constant: A term that does not have a variable is called a constant. Example: the number 5 is a constant because it does
2 Problem Set 2 Graphical Analysis
 2 PROBLEM SET 2 GRAPHICAL ANALYSIS 2 Problem Set 2 Graphical Analysis 1. Use graphical analysis to describe all orbits of the functions below. Also draw their phase portraits. (a) F(x) = 2x There is only
2 PROBLEM SET 2 GRAPHICAL ANALYSIS 2 Problem Set 2 Graphical Analysis 1. Use graphical analysis to describe all orbits of the functions below. Also draw their phase portraits. (a) F(x) = 2x There is only
Lecture 3 (Limits and Derivatives)
 Lecture 3 (Limits and Derivatives) Continuity In the previous lecture we saw that very often the limit of a function as is just. When this is the case we say that is continuous at a. Definition: A function
Lecture 3 (Limits and Derivatives) Continuity In the previous lecture we saw that very often the limit of a function as is just. When this is the case we say that is continuous at a. Definition: A function
Solving Polynomial and Rational Inequalities Algebraically. Approximating Solutions to Inequalities Graphically
 10 Inequalities Concepts: Equivalent Inequalities Solving Polynomial and Rational Inequalities Algebraically Approximating Solutions to Inequalities Graphically (Section 4.6) 10.1 Equivalent Inequalities
10 Inequalities Concepts: Equivalent Inequalities Solving Polynomial and Rational Inequalities Algebraically Approximating Solutions to Inequalities Graphically (Section 4.6) 10.1 Equivalent Inequalities
Five-Minute Check (over Lesson 8 3) CCSS Then/Now New Vocabulary Key Concept: Vertical and Horizontal Asymptotes Example 1: Graph with No Horizontal
 Five-Minute Check (over Lesson 8 3) CCSS Then/Now New Vocabulary Key Concept: Vertical and Horizontal Asymptotes Example 1: Graph with No Horizontal Asymptote Example 2: Real-World Example: Use Graphs
Five-Minute Check (over Lesson 8 3) CCSS Then/Now New Vocabulary Key Concept: Vertical and Horizontal Asymptotes Example 1: Graph with No Horizontal Asymptote Example 2: Real-World Example: Use Graphs
Geometry 21 Summer Work Packet Review and Study Guide
 Geometry Summer Work Packet Review and Study Guide This study guide is designed to accompany the Geometry Summer Work Packet. Its purpose is to offer a review of the ten specific concepts covered in the
Geometry Summer Work Packet Review and Study Guide This study guide is designed to accompany the Geometry Summer Work Packet. Its purpose is to offer a review of the ten specific concepts covered in the
Math 229 Mock Final Exam Solution
 Name: Math 229 Mock Final Exam Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and that it
Name: Math 229 Mock Final Exam Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and that it
Unit 6 Trigonometric Identities Prove trigonometric identities Solve trigonometric equations
 Unit 6 Trigonometric Identities Prove trigonometric identities Solve trigonometric equations Prove trigonometric identities, using: Reciprocal identities Quotient identities Pythagorean identities Sum
Unit 6 Trigonometric Identities Prove trigonometric identities Solve trigonometric equations Prove trigonometric identities, using: Reciprocal identities Quotient identities Pythagorean identities Sum
ACCUPLACER MATH 0311 OR MATH 0120
 The University of Teas at El Paso Tutoring and Learning Center ACCUPLACER MATH 0 OR MATH 00 http://www.academics.utep.edu/tlc MATH 0 OR MATH 00 Page Factoring Factoring Eercises 8 Factoring Answer to Eercises
The University of Teas at El Paso Tutoring and Learning Center ACCUPLACER MATH 0 OR MATH 00 http://www.academics.utep.edu/tlc MATH 0 OR MATH 00 Page Factoring Factoring Eercises 8 Factoring Answer to Eercises
