AP Calculus. Related Rates. Related Rates. Slide 1 / 101 Slide 2 / 101. Slide 4 / 101. Slide 3 / 101. Slide 4 (Answer) / 101.
|
|
|
- Allen Walsh
- 5 years ago
- Views:
Transcription
1 Slide 1 / 101 Slide 2 / 101 P alculus pplications of erivatives Slide 3 / 101 Slide 4 / 101 Table of ontents click on the topic to go to that section Related Rates Linear Motion Linear pproximation & ifferentials L'Hopital's Rule Horizontal Tangents Related Rates Return to Table of ontents Slide 4 () / 101 Slide 5 / 101 Related Rates Teacher Notes Related Rates is one of the topics which students struggle with more than any other. Take the necessary time on each question for students to comprehend and visualize the situation. Highly encourage them to draw pictures and work slowly but efficiently through the problem. Related Rates Return to Table of ontents Related Rates is the application of implicit differentiation (which we learned in the previous unit) to real life situations. In simplest terms, related rates are problems in which you need to figure out how fast one variable is changing when given the rate of change of another variable at a specific point in time. For example, if a spherical balloon is being filled with air at a rate of 20 ft 3 /min, how fast is the radius changing when the radius is 2 feet?
2 Slide 5 () / 101 Related Rates Students can usually comprehend Related Rates is the application the balloon of example, implicit differentiation understanding (which we learned in the previous that although unit) to the real air life is situations. being pumped in at a constant rate, the radius changes very quickly at first and then slows down as the balloon In simplest terms, related rates are problems in which you need gets larger. There is no need to to figure out how fast one solve variable this example is changing at this time, when it given is the rate of change of another just variable to give them at a specific an idea point of the in time. types of problems they will [This experience. object is a pull tab] For example, if a spherical balloon is being filled with air at a rate of 20 ft 3 /min, how fast is the radius changing when the radius is 2 feet? Teacher Notes Slide 6 / 101 Recall: Implicit ifferentiation efore we attempt a Related Rates example, let's practice a few implicit differentiation examples first. ifferentiate each equation with respect to time, t. Slide 6 () / 101 Recall: Implicit ifferentiation efore we attempt a Related Rates example, let's practice a few implicit differentiation examples first. ifferentiate each equation with respect to time, t. Slide 7 / 101 Helpful Steps for Solving Related Rates Problems 1) raw a picture. Label the picture with numbers if constant or variables if changing. 2) Identify which rate of change is given and which rate of change you are being asked to find. 3) Find a formula/equation that relates the variables whose rate of change you seek with one or more variables whose rate of change you know. 4) Implicitly differentiate with respect to time, t. 5) Plug in values you know. 6) Solve for rate of change you are being asked for. 7) the question. Try to write your answer in a sentence to eliminate confusion. Slide 7 () / 101 Helpful Steps for Solving mphasize to students: WRNING! Most mistakes are Related Rates made by Problems subsituting the given values too early. You must wait until 1) raw a picture. Label the picture with after numbers you differentiate! constant or variables if changing. *Note on Step 4: Occasionally, students may see a question where 2) Identify which rate of change is they given need and to differentiate which rate with of respect change you are being asked to find. to a different variable; however, most often it will be time. 3) Find a formula/equation that relates the variables whose rate of change you seek with one or more variables whose rate of change you know. Teacher Notes 4) Implicitly differentiate with respect to time, t. Slide 8 / 101 Step 3 Step 3 requires you to think of an equation to relate variables. Some questions on the P xam will provide the equation for you, but if not, think of: trigonometry similar triangles Pythagorean theorem common Geometry equations 5) Plug in values you know. 6) Solve for rate of change you are being asked for. 7) the question. Try to write your answer in a sentence to eliminate confusion.
3 Let's take a look back at this example... If a spherical balloon is being filled with air at a rate of 20 ft 3 /min, how fast is the radius changing when the radius is 2 feet? Slide 9 / 101 1) raw and label a picture. 2) Identify the rates of change you know and seek. 3) Find a formula/equation. 4) Implicitly differentiate with respect to time, t. 5) Plug in values you know. 6) Solve for rate of change you are being asked for. 7) the question. Let's take a look back at this example... If a spherical balloon r is being filled with air at a rate of 20 ft 3 Know: /min, how fast is the radius changing when the radius is 2 feet? 3. quation that relates volume of a sphere with radius of a sphere. 4. ifferentiate with respect to t. Slide 9 () / Picture 2. Identify Rates of hange 5. Substitute given values. Want: when r=2 1) raw and label a picture. 2) Identify the rates of change you know and seek. 3) Find a formula/equation. 4) Implicitly differentiate with respect to time, t. 5) Plug in values you know. 6) Solve for rate of change you are being asked for. 7) the question. 6. Solve for 7. the question. The radius is increasing at a rate of when the radius is 2 feet. Slide 10 / 101 Why is it important to write a sentence for an answer? In the last question we answered the following: The radius is increasing at a rate of when the radius is 2 feet. On the P xam, Related Rates questions are graded very critically. Graders will not award points without proper vocabulary usage (i.e. increasing or decreasing rate of change), appropriate units, and the actual correct answer. Take time when formulating your answer to make sure it makes logical sense and includes all needed information. Slide 11 / 101 Hands-On Related Rates Lab (OPTIONL) lick here to go to the lab titled "Related Rates" Slide 11 () / 101 students to observe the result. It helps Hands-On is Student does Related not watch Student Rates, Lab but just walks at whatever pace needed to (OPTIONL) keep the rope taut. Teacher Notes It may take several attempts for esired observation: Student is walking at a constant pace, Student begins at a slow rate, but then the rate increases as they approach the corner. lick URL here for Lab: to go to the lab titled "Related math/ap-calculus-ab/application-of- Rates" derivatives/hands-on-related-rates/ Slide 12 / 101 Hands-On Related Rates (OPTIONL) Items needed: 2 students 1 long rope/cord/string (at least 15 feet for best display) masking tape STP #1 Set up masking tape in a right angle classroom with enough room for each student to walk along the tape line.
4 Slide 12 () / 101 Hands-On Related Rates (OPTIONL) Items needed: 2 students 1 long rope/cord/string (at s least said before, 15 feet it may for take best several display) masking tape STP #1 Teacher Notes attempts for students to observe the result. It helps is Student does not watch Student, but just walks at whatever pace needed to keep the rope taught. Set up masking tape in a right angle classroom with enough room for each student to walk along the tape line. esired observation: Student is walking at a constant pace, Student begins at a slow rate, but then the rate increases as they approach the corner. Slide 13 / 101 Hands-On Related Rates (OPTIONL) STP #2 Student begins at the end of one piece of tape, and Student begins in the corner. ach student holds one end of the rope until it is taught. Slide 14 / 101 Hands-On Related Rates (OPTIONL) STP #3 It is imperative that student walks at a ONSTNT and slow pace forward while student simple walks at whatever pace needed to keep the rope taught. The class should watch Student 's rate of change over the course of his/her path. It may take several attempts to observe the result. Slide 15 / 101 balloon is rising straight up from a level ground and tracked by a range finder 500 feet from lift off point. t the moment the range finder's elevation reads the angle is increasing at a rate of 0.14 radians/ minute. How fast is the balloon rising at that moment? Slide 15 () / 101 Slide 16 / 101 bag is tied to the top of a 5m ladder resting against a vertical wall. Supposed the ladder begins sliding down the wall in such a way that the foot of the ladder is moving away from the wall at a constant rate of 2m/s. How fast is the bag descending at the instant the foot of the ladder is 4m from the wall?
5 Slide 16 () / 101 Slide 17 / 101 HLLNG! Water is pouring into an inverted conical tank at 2 cubic meters per minute. The tank is a right circular cone with height 16 meters and base radius of 4 meters. How fast is the water level rising when the water in the tank is 5 meters deep? Slide 17 () / 101 Slide 18 / person 6 feet tall is walking away from a streetlight 20 feet high at the rate of 7 ft/sec. t what rate is the length of the person's shadow increasing? The shadow is increasing at a rate of 3/7 ft/sec. The shadow is increasing at a rate of 7/3 ft/sec. The shadow is increasing at a rate of 14 ft/sec. The shadow is increasing at a rate of 3 ft/sec. The shadow is increasing at a rate of 7 ft/sec. Slide 18 () / 101 Slide 19 / Water leaking onto a floor forms a circular pool. The radius of the pool increases at a rate of 4 cm/min. How fast is the area of the pool increasing when the radius is 5 cm? The area of the circle is increasing at a rate of when the radius is 5cm. The area of the circle is increasing at a rate of when the radius is 5cm. The area of the circle is increasing at a rate of when the radius is 5cm. The area of the circle is increasing at a rate of when the radius is 5cm. The area of the circle is increasing at a rate of when the radius is 5cm. cm 2 /min cm 2 /min cm 2 /min cm 2 /min cm 2 /min
6 2 Slide 19 () / 101 Water leaking onto a floor r forms Know: a circular pool. The radius of the pool increases at a rate of 4 cm/min. How Want: when r = 5 fast is the area of the pool increasing when the radius is 3. Find an appropriate equation. 5 cm? 1. Picture 2. Identify Rates of hange 4. ifferentiate with respect to t. The area of 5. Substitute the circle given is values. increasing at a rate of cm 2 /min when the radius is 5cm. 6. Solve for The area of the circle is increasing at a rate of cm 2 /min 7. the question. when the radius is 5cm. The area of the hoice circle : The is area increasing of the circle at is increasing a rate at of a cm 2 /min rate of [This cm when the radius is 5cm. 2 /min object when is a the pull radius tab] is 5cm. The area of the circle is increasing at a rate of cm 2 /min when the radius is 5cm. The area of the circle is increasing at a rate of cm 2 /min when the radius is 5cm. Slide 20 / 101 Slide 20 () / 101 Slide 21 / trough of water is 8 meters long and its ends are in the shape of isosceles triangles whose width is 5 meters and height is 2 meters. If water is being pumped in at a constant rate of 6 m 3 /sec. t what rate is the height of the water changing when the water has a height of 120 cm? The height of the water is increasing at a rate of 0.3 m/sec when the water is 120cm high. The height of the water is increasing at a rate of 6 m/sec when the water is 120cm high. The height of the water is increasing at a rate of 0.25 m/sec when the water is 120cm high. The height of the water is increasing at a rate of 40 m/sec when the water is 120cm high. The height of the water is increasing at a rate of 20 m/sec when the water is 120cm high. Slide 21 () / trough of water is 8 meters long and its ends are in the shape of isosceles triangles whose width is 5 meters and 1. Picture 5 2. Identify Rates of hange height is 2 meters. 8 If water is being pumped in at a constant rate of 6 m 3 Know: /sec. t what rate is the height of the w water changing when the water Want: has a height when h=120cm of 120 cm? 2 h use 1.2m The height 3. of Find the an appropriate water is equation. increasing at a rate of 0.3 m/sec *use similar triangles to when the water is express 120cm w in terms high. of h The height 4. of ifferentiate the water with respect is increasing to t. at a rate of 6 m/sec when the water 5. Substitute is 120cm given values. high. The height 6. of Solve the for water is increasing at a rate of 0.25 m/sec when the water 7. is the 120cm question. high. The height of the hoice water : The is height increasing of the water is at rising a rate a rate of 40 m/sec of 0.25 m/s when [This object the water is a is pull 120cm tab] high. when the water is 120cm high. The height of the water is increasing at a rate of 20 m/sec when the water is 120cm high. Slide 22 / The sides of the rectangle pictured increase in such a way that and. t the instant where x=4 and y=3, what is the value of y z x
7 Slide 22 () / The sides of the rectangle pictured increase in such a way 1. Picture 2. Identify Rates of hange that and. t the instant where x=4 and y=3, z Know: y what is the value of x Want: when x=4 & y=3 y 7. the question. x z 3. Find an appropriate equation. 4. ifferentiate with respect to t. 5. Substitute given values. 6. Solve for hoice. 1 Slide 23 / If the base, b, of a triangle is increasing at a rate of 3 inches per minute while it's height, h, is decreasing at a rate of 3 inches per minute, which of the following must be true about the area,, of the triangle? is always increasing. is always decreasing. is decreasing only when b < h. is decreasing only when b > h. remains constant. Slide 23 () / If the base, b, of a triangle is increasing at a rate of 3 inches per minute 1. Picturewhile it's height, 2. Identify h, Rates is decreasing of hange at a rate of 3 inches per minute, which Know: of the following must be true about the area,, h of the triangle? b is always increasing. 3. Find an appropriate equation. is always decreasing. 4. ifferentiate with respect to t. is decreasing 5. Substitute given only values. when b < h. 6. Solve for is decreasing only when b > h. 7. the question. remains constant. Want: hoice : The [This area object is decreasing is a pull tab] only when b>h. Slide 24 / The minute hand of a certain clock is 4 in. long. Starting from the moment that the hand is pointing straight up, how fast is the area of the sector that is swept out by the hand increasing at any instant during the next revolution of the hand? Note: rea of a sector Slide 24 () / 101 Slide 25 / 101 Linear Motion Return to Table of ontents
8 Slide 26 / 101 Linear Motion nother useful application of derivatives is to describe the linear motion of an object in two dimensions, either left and right, or up and down. This is a concept where calculus is extremely applicable. We will revisit this topic again in the next unit involving graphing, and again in the unit about integrals! Slide 27 / 101 Position, Velocity & cceleration remarkable relationship exists among the position of an object, the velocity of an object and the acceleration of an object. First... let's review what each of these words mean. Position Velocity cceleration Slide 27 () / 101 Position, Velocity & cceleration Have students share thoughts and definitions remarkable relationship for exists each term. among e certain the to position listen for students of an object, the velocity of an object and referring the acceleration to velocity as speed. of an The object. next slide will clarify the difference. Teacher Notes Position - location of an object in regards to First... let's review what each its starting of these locationwords mean. Velocity - how fast N in what direction an Position object is moving cceleration - how fast N in what direction Velocity the velocity is changing cceleration [This object is a teacher notes pull tab] Slide 28 / 101 re Velocity and Speed the Same Thing? lthough you may hear velocity and speed interchanged often in common conversation, they are, in fact, 2 distinct quantities. Sometimes they are equivalent to each other, but this depends on the direction of the object. Velocity is a vector quantity meaning it has both magnitude and direction. For example, if the velocity of an object is -3 feet per second, then that object is moving backwards or to the left (direction) at a rate of 3 feet per second (magnitude). Slide 28 () / 101 re Velocity and Speed the Same Thing? lthough you may hear velocity and speed interchanged often in Note: The positive or common conversation, they are, in fact, negative 2 distinct direction quantities. is Sometimes they are equivalent to determined each other, by but the this object's depends on the direction of the object. initial position and what is Velocity is a vector quantity meaning determined it has both to magnitude be a and direction. positive/negative direction. For example, if the velocity of an object is -3 feet per second, then that object is moving backwards or to the left (direction) at a rate of 3 feet per second (magnitude). Teacher Notes Slide 29 / 101 istance vs. Position Similarly, there is a difference between distance and position. istance is how far something has traveled in total; distance is a quantity. Whereas position is the location of an object compared to a reference point; position is a distance with a direction.
9 Slide 30 / 101 Typical Notation for Linear Motion Problems is the notation for our position function is the notation for our velocity function Slide 31 / 101 onsider driving your car along the highway. The time it takes you to travel from mile marker 27 to mile marker 105 is an hour and a half. How fast were you driving? is the notation for our acceleration function Slide 31 () / 101 distance onsider driving your car along the highway. time The time it takes you to travel from mile marker 27 to mile marker 105 is an hour and a half. How fast were you driving? Important: This is the average velocity. It does not necessarily mean you were traveling 52mph the entire time. Slide 32 / 101 verage Velocity vs. Instantaneous Velocity We know that the average velocity can be found by dividing the distance traveled by the time; however, how can we find the instantaneous velocity (how fast you are traveling at a specific moment in time)? ecause we are interested in the instantaneous rate of change of a position, we are able to take the derivative of the position function and find the instantaneous velocity. Note: This requires a position function to be given. Slide 33 / 101 Slide 33 () / 101
10 Slide 34 / 101 race car is driven down a straight road such that after seconds it is feet from its origin. Slide 34 () / 101 d the instantaneous velocity seconds. race car is driven down a straight road such that after seconds it is feet from its origin. a) Find the instantaneous velocity after 8 seconds. a) Find the instantaneous velocity after 8 seconds. b) What is the car's acceleration? at is the car's acceleration? b) What is the car's acceleration? constant [This object acceleration is a pull tab] Slide 35 / 101 spring is pulled to 6 inches below its resting state and bounces up and down. Its position is modeled by. Slide 35 () / 101 spring is pulled to 6 inches below its resting state and bounces up and ty and acceleration at time t. down. Its position is modeled by. a) Find its velocity and acceleration at time t. a) Find its velocity and acceleration at time t. g's velocity and acceleration. b) Find the spring's velocity and acceleration after seconds. b) Find the spring's velocity and acceleration after seconds. s object is a pull tab] Slide 36 / 101 dynamite blast shoots a rock straight up into the air. Its height at any given time is feet after t seconds. a) How high does the rock travel? b) What is the velocity and speed of the rock when it is 256 feet above ground? c) What is the acceleration at any time, t? d) When does the rock hit the ground? Slide 36 () / 101 dynamite of this blast problem, shoots which is a more rock like questions straight seen up on into the P the air. Its xam. Work slowly and check for understanding frequently. height at any given time is feet after t seconds. *Students may struggle with comprehension and visualization a) How high does the rock travel? When the rock reaches its peak, the velocity will be equal to 0, then we can find the position at that time. a) How high does the rock travel? b) What is the velocity and speed of the rock when it is 256 feet above ground? b) What We first is must the find velocity at what time the and speed of the rock when it is 256 feet position is 256ft, and then find v(time). above ground? c) What is the acceleration at any time, t? cceleration is the 2nd derivative of position, and the 1st derivative of velocity. d) When does the rock hit the ground? c) What When the is rock the hits acceleration the ground its position at any time, t? will be equal to 0 feet. t t=0, that is it's starting position. d) When does the rock hit the ground?
11 Slide 37 / 101 One More Reminder! Slide 37 () / 101 One More Reminder! What is the difference between: verage Velocity Instantaneous Velocity What Sometimes is the difference when students between: begin practicing questions involving instantaneous velocity they forget how to calculate average velocity. Take a minute to reiterate the difference. verage Velocity Instantaneous Velocity In simple terms: Teacher Notes verage Velocity - slope formula with 2 points Instant. Velocity - derivative evaluated at 1 point. Slide 38 / 101 Slide 38 () / particle moves along the x-axis so that at any time t>0 seconds its velocity is given by m/s. What is the acceleration of the particle at time? 8 particle moves along the x-axis so that at any time t>0 seconds its velocity is given by m/s. What is the acceleration of the particle at time? Slide 39 / 101 Slide 39 () / 101
12 Slide 40 / 101 Slide 40 () / The position of a particle moving along a straight line at any time t is given by. What is the acceleration of the particle when t=4? 10 The position of a particle moving along a straight line at any time t is given by. What is the acceleration of the particle when t=4? Slide 41 / 101 Slide 41 () / mouse runs through a straight pipe such that his position at any time is inches. Find the average velocity during the first 5 seconds. 11 mouse runs through a straight pipe such that his position at any time is inches. Find the average velocity during the first 5 seconds. Slide 42 / n object moves along the x-axis so that at time t>0 its position is given by meters. Find the speed of the object at t=3 seconds. Slide 42 () / n object moves along the x-axis so that at time t>0 its position is given by meters. Find the speed of the object at t=3 seconds. *Note: question asks for speed, not velocity.
13 Slide 43 / 101 Slide 43 () / rock thrown vertically upward from the surface of the moon at a velocity of 24m/s reaches a height of meters in t seconds. Find the rock's acceleration as a function of time. 13 rock thrown vertically upward from the surface of the moon at a velocity of 24m/s reaches a height of meters in t seconds. Find the rock's acceleration as a function of time. Slide 44 / 101 Slide 44 () / rock thrown vertically upward from the surface of the moon at a velocity of 24m/s reaches a height of meters in t seconds. Find the rock's average velocity during the first 3 sec. 14 rock thrown vertically upward from the surface of the moon at a velocity of 24m/s reaches a height of meters in t seconds. Find the rock's average velocity during the first 3 sec. Slide 45 / 101 Slide 45 () / rock thrown vertically upward from the surface of the moon at a velocity of 24m/s reaches a height of meters in t seconds. Find the rock's instantaneous velocity at t=3 sec. 15 rock thrown vertically upward from the surface of the moon at a velocity of 24m/s reaches a height of meters in t seconds. Find the rock's instantaneous velocity at t=3 sec.
14 Slide 46 / 101 Slide 47 / 101 Linear pproximation Linear pproximation & ifferentials Return to Table of ontents In the last unit we explored what it meant for a differentiable function to be "locally linear". lso in the previous unit, we discussed how to find the equation of a tangent line to a function. In this section, we will expand on those ideas and how they become useful in a topic called Linear pproximation. Slide 48 / 101 Slide 49 / 101 Linear pproximation Observe the black tangent line to the function at x=9. If we write the equation of the tangent line at x=9, we can then use this line and substitute 8.9 into our equation to find an approximation for f(8.9). gain, it won't be exact, but will be much closer than just saying 3. Slide 50 / 101 Slide 50 () / 101
15 Slide 51 / 101 Slide 51 () / 101 Practice: Use linear approximation to approximate the value of f(8.9). Slide 52 / 101, ontinued Is our approximation greater than or less than the actual value of f(8.9)? Why or why not? Slide 52 () / 101, ontinued Is our approximation greater than or less than the actual value of f(8.9)? Why or why not? Often students have a misconception about why the approx. is high or low. Remind them that it depends on whether or not the tangent line lies above or below the curve at the point of interest, not simply whether one number is larger or smaller than the other. Teacher Notes [This object is a teacher notes pull tab] Slide 53 / 101 Slide 53 () / 101
16 Slide 54 / 101 Given, approximate. Slide 54 () / 101 Given, approximate. Slide 55 / Given pproximate Slide 55 () / Given pproximate Slide 56 / 101 Slide 56 () / For the previous question, is the approximation of greater than or less than the actual value? You may look at a graph of the function to decide. Recall Greater than Less than 17 For the previous question, is the approximation of greater than or less than the actual value? You may look at a graph of the function to decide. Recall Greater than Less than The approximation is greater than the actual value in this case, because at the point in consideration, the tangent line would lie above the curve, thus producing a high approximation. Note: Students haven't yet learned the concept of concavity, however you can mention it to them to foreshadow.
17 Slide 57 / 101 Slide 57 () / 101 Slide 58 / 101 Slide 58 () / 101 Slide 59 / Find the approximate value of using linear approximation. Slide 59 () / Find the approximate value Let of using linear approximation. Then
18 Slide 60 / 101 Slide 60 () / Given and approximate the value of Slide 61 / 101 Slide 61 () / 101 Slide 62 / 101 ifferentials So far we have been discussing and, but sometimes in calculus we are interested in only. We call this the differential. The process is fairly simple given we already know how to find. Slide 63 / 101 ifferentials Let's try an example: Find the differential. This is called differential form.
19 Slide 63 () / 101 Slide 64 / 101 ifferentials Let's try an example: Find the differential. Slide 64 () / 101 Slide 65 / 101 vs. Note the difference between and. If we calculate both, we can then compare the values to calculate the percentage change or approximation error. Slide 66 / 101 Slide 66 () / 101 The radius of a circle increases from 10 cm to 10.1 cm. Use to estimate the increase in the circle's rea,. ompare this estimate with the true change,, and find the approximation error.
20 23 Find the differential if Slide 67 / Find the differential if Slide 67 () / Find the differential if Slide 68 / Find the differential if Slide 68 () / 101 Slide 69 / 101 Slide 69 () / 101
21 Slide 70 / 101 Slide 70 () / Find and evaluate for the given values of and. 26 Find and evaluate for the given values of and. F F Slide 71 / 101 Slide 71 () / 101 Slide 72 / 101 Slide 72 () / 101
22 Slide 73 / 101 Slide 73 () / 101 Slide 74 / 101 Slide 75 / 101 L'Hopital's Rule L'Hopital's Rule One additional application of derivatives actually applies to solving limit questions! Return to Table of ontents Slide 76 / 101 Slide 77 / 101 L'Hopital's Rule (pronounced "Lho-pee-talls") Guillaume de L'Hopital was a french mathematicion from the 17th century. He is known most commonly for his work calculating limits involving indeterminate forms and. L'Hopital was the first to publish this notion, but gives credit to the ernoulli brothers for their work in this area. ool Fact! In the 17th and 18th centuries, the name was commonly spelled "L'Hospital", however, French spellings have been altered and the silent 's' has been dropped.
23 Slide 78 / 101 L'Hopital discovered an alternative way of dealing with these limits! L'HOPITL'S RUL Suppose you have one of the following cases: or Slide 78 () / 101 L'Hopital discovered an alternative way of dealing with these limits! Sometimes students will attempt to L'HOPITL'S use the quotient RUL rule on these problems. mphasize that the original question is asking for a limit, Suppose you have one of the following cases: and L'hopital's rule deals with the numerator and denominator as two distinct orfunctions and differentiates each separately. Teacher Notes Then, Then, Slide 79 / 101 L'Hopital's Rule What does this mean? You now have an alternative method for calculating these indeterminate limits. Why didn't you learn this method earlier? You didn't know how to find a derivative yet! Slide 80 / 101 Let's try L'Hopital's Rule on our previous example: Slide 80 () / 101 Let's try L'Hopital's Rule on our previous example: take derivative valuate the following limit: Slide 81 / 101 take derivative Our answers match!
24 Slide 81 () / 101 Slide 82 / 101 valuate the following limit: pplying L'Hopital's Rule... valuate the following limit: Note: L'Hopital's Rule can be applied more than one time, if needed. valuate the following limit: Slide 82 () / 101 pplying L'Hopital's Rule... Note: L'Hopital's Rule can be applied more than one time, if needed. still indeterminate! We can apply L'Hopital's Rule again! Slide 83 / 101 Important Fact to Remember: ONLY use L'Hopital's Rule on quotients that result in an indeterminate form upon substitution. Using the rule on other limits may, and often will, result in incorrect answers. Slide 84 / 101 Slide 84 () / valuate the following limit: 30 valuate the following limit:
25 Slide 85 / 101 Slide 85 () / valuate the following limit: 31 valuate the following limit: 32 valuate the following limit: Slide 86 / valuate the following limit: Slide 86 () / 101 iscuss with students why they cannot apply L'Hopital's Rule on this problem. Slide 87 / 101 Slide 87 () / valuate the following limit: 33 valuate the following limit: Rewrite as to apply L'Hopital's Rule. Hint: Sometimes it is helpful to rewrite before applying L'Hopital's Rule. Hint: Sometimes it is helpful to rewrite before applying L'Hopital's Rule.
26 Slide 88 / 101 Slide 88 () / valuate the following limit: 34 valuate the following limit: Students may recall the shortcut of using the highest power's coefficients, or may apply L'Hopital's rule twice. Slide 89 / 101 Slide 90 / 101 Horizontal Tangents Tangent Lines Recall what it means to be tangent to a function. We could draw an infinite amount of tangent lines below; however, looking at the ones given what observations can you make about the black tangent lines? Return to Table of ontents Slide 90 () / 101 Tangent Lines Recall what it means to be tangent llow to students a function. to We make could draw an infinite amount of tangent lines observations, below; however, and discuss looking with at the ones given what observations can you classmates. make about The the desired black tangent lines? observation is that they recognize the black tangent lines are the only ones that are horizontal, or have a slope of zero. Teacher Notes Slide 91 / 101 Horizontal Tangents o you think there is a way to find out where the horizontal tangents are occurring aside from just estimating?
27 Slide 91 () / 101 Horizontal Tangents It is critical to allow students time to think and o you think there discuss a way this to idea. find Some out where may not the come horizontal to the tangents are occurring aside from answer just estimating? on their own, so you may ask leading questions: What is another way to describe horizontal? > slope of zero What is another word for slope? > derivative Teacher Notes esired response, set the derivative = 0. Often students will confuse this idea with finding the derivative and evaluating at 0, rather than setting it equal to 0. e sure to clear up any confusion [This object between is a pull the tab] two ideas. Let's try an example... Slide 92 / 101 t what x-value(s) does the following function have a horizontal tangent line? Slide 92 () / 101 Slide 93 / 101 t what point(s) does the following function have a horizontal tangent line? ***Note the alternative wording. Pay attention on the P xam! Some questions will only ask for the x-value, but if you are asked at what point(s) the function has horizontal tangent lines, you need both the x- and y- coordinates. Slide 93 () / 101 t what point(s) does the following function have a horizontal tangent line? ***Note the alternative wording. Pay attention on the P xam! Some questions will only ask for the x-value, but if you are asked at what point(s) the function has horizontal tangent lines, you need both the x- and y- coordinates. Slide 94 / 101 t what x-value(s) does the following function have a horizontal tangent line?
28 Slide 94 () / 101 Slide 95 / 101 llow students to struggle with the meaning when they don't get a real solution for this t what x-value(s) does problem, the following and ask function them what have they a think horizontal that tangent line? means about this particular function. no real solutions... Therefore, no horizontal tangents It may also be helpful to have students check the graph of this function to visualize their answer. Slide 95 () / 101 Slide 96 / 101 Slide 96 () / 101 Slide 97 / t what point(s) does the following function have a horizontal tangent line?
29 Slide 97 () / 101 Slide 98 / t what point(s) does the following function have a horizontal tangent line? Slide 98 () / 101 Slide 99 / 101 Slide 99 () / 101 Slide 100 / t what point(s) does the following function have a horizontal tangent line?
30 Slide 100 () / 101 Slide 101 / t what point(s) does the following function have a horizontal tangent line? Slide 101 () / 101
AP Calculus. Slide 1 / 101. Slide 2 / 101. Slide 3 / 101. Applications of Derivatives. Table of Contents
 Slide 1 / 101 Slide 2 / 101 AP Calculus Applications of Derivatives 2015-11-03 www.njctl.org Table of Contents click on the topic to go to that section Slide 3 / 101 Related Rates Linear Motion Linear
Slide 1 / 101 Slide 2 / 101 AP Calculus Applications of Derivatives 2015-11-03 www.njctl.org Table of Contents click on the topic to go to that section Slide 3 / 101 Related Rates Linear Motion Linear
AP Calculus. Applications of Derivatives. Table of Contents
 AP Calculus 2015 11 03 www.njctl.org Table of Contents click on the topic to go to that section Related Rates Linear Motion Linear Approximation & Differentials L'Hopital's Rule Horizontal Tangents 1 Related
AP Calculus 2015 11 03 www.njctl.org Table of Contents click on the topic to go to that section Related Rates Linear Motion Linear Approximation & Differentials L'Hopital's Rule Horizontal Tangents 1 Related
AP Calculus AB Chapter 4 Packet Implicit Differentiation. 4.5: Implicit Functions
 4.5: Implicit Functions We can employ implicit differentiation when an equation that defines a function is so complicated that we cannot use an explicit rule to find the derivative. EXAMPLE 1: Find dy
4.5: Implicit Functions We can employ implicit differentiation when an equation that defines a function is so complicated that we cannot use an explicit rule to find the derivative. EXAMPLE 1: Find dy
Implicit Differentiation
 Week 6. Implicit Differentiation Let s say we want to differentiate the equation of a circle: y 2 + x 2 =9 Using the techniques we know so far, we need to write the equation as a function of one variable
Week 6. Implicit Differentiation Let s say we want to differentiate the equation of a circle: y 2 + x 2 =9 Using the techniques we know so far, we need to write the equation as a function of one variable
Guidelines for implicit differentiation
 Guidelines for implicit differentiation Given an equation with x s and y s scattered, to differentiate we use implicit differentiation. Some informal guidelines to differentiate an equation containing
Guidelines for implicit differentiation Given an equation with x s and y s scattered, to differentiate we use implicit differentiation. Some informal guidelines to differentiate an equation containing
4.1 & 4.2 Student Notes Using the First and Second Derivatives. for all x in D, where D is the domain of f. The number f()
 4.1 & 4. Student Notes Using the First and Second Derivatives Definition A function f has an absolute maximum (or global maximum) at c if f ( c) f ( x) for all x in D, where D is the domain of f. The number
4.1 & 4. Student Notes Using the First and Second Derivatives Definition A function f has an absolute maximum (or global maximum) at c if f ( c) f ( x) for all x in D, where D is the domain of f. The number
6.2 Related Rates Name: Notes
 Calculus Write your questions and thoughts here! 6.2 Related Rates Name: Notes Guidelines to solving related rate problems 1. Draw a picture. 2. Make a list of all known and unknown rates and quantities.
Calculus Write your questions and thoughts here! 6.2 Related Rates Name: Notes Guidelines to solving related rate problems 1. Draw a picture. 2. Make a list of all known and unknown rates and quantities.
Related Rates STEP 1 STEP 2:
 Related Rates You can use derivative analysis to determine how two related quantities also have rates of change which are related together. I ll lead off with this example. 3 Ex) A spherical ball is being
Related Rates You can use derivative analysis to determine how two related quantities also have rates of change which are related together. I ll lead off with this example. 3 Ex) A spherical ball is being
Related Rates. 2. List the relevant quantities in the problem and assign them appropriate variables. Then write down all the information given.
 Calculus 1 Lia Vas Related Rates The most important reason for a non-mathematics major to learn mathematics is to be able to apply it to problems from other disciplines or real life. In this section, we
Calculus 1 Lia Vas Related Rates The most important reason for a non-mathematics major to learn mathematics is to be able to apply it to problems from other disciplines or real life. In this section, we
with dt. with 2. If x = u, find an equation relating du dt
 MATH 2250 Royal Section 3.10: Related Rates EXPANDED VERSION In this section, we consider two (or more) dependent variables that depend on a third variable (the independent variable). Usually, the independent
MATH 2250 Royal Section 3.10: Related Rates EXPANDED VERSION In this section, we consider two (or more) dependent variables that depend on a third variable (the independent variable). Usually, the independent
4.6 Related Rates Notes RELATED RATES PROBLEMS --- IT S AS EASY AS 1 2-3!
 4.6 Related Rates Notes RELATED RATES PROBLEMS --- IT S AS EASY AS 1 2-3! 1) Draw a picture. Label all variables and constant values. Identify the given rate of change, the rate to be found, and when to
4.6 Related Rates Notes RELATED RATES PROBLEMS --- IT S AS EASY AS 1 2-3! 1) Draw a picture. Label all variables and constant values. Identify the given rate of change, the rate to be found, and when to
Section 4.1: Related Rates
 1 Section 4.1: Related Rates Practice HW from Stewart Textbook (not to hand in) p. 67 # 1-19 odd, 3, 5, 9 In a related rates problem, we want to compute the rate of change of one quantity in terms of the
1 Section 4.1: Related Rates Practice HW from Stewart Textbook (not to hand in) p. 67 # 1-19 odd, 3, 5, 9 In a related rates problem, we want to compute the rate of change of one quantity in terms of the
Chapter 8: Radical Functions
 Chapter 8: Radical Functions Chapter 8 Overview: Types and Traits of Radical Functions Vocabulary:. Radical (Irrational) Function an epression whose general equation contains a root of a variable and possibly
Chapter 8: Radical Functions Chapter 8 Overview: Types and Traits of Radical Functions Vocabulary:. Radical (Irrational) Function an epression whose general equation contains a root of a variable and possibly
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES If we are pumping air into a balloon, both the volume and the radius of the balloon are increasing and their rates of increase are related to each other. However,
3 DIFFERENTIATION RULES DIFFERENTIATION RULES If we are pumping air into a balloon, both the volume and the radius of the balloon are increasing and their rates of increase are related to each other. However,
4.1 Implicit Differentiation
 4.1 Implicit Differentiation Learning Objectives A student will be able to: Find the derivative of variety of functions by using the technique of implicit differentiation. Consider the equation We want
4.1 Implicit Differentiation Learning Objectives A student will be able to: Find the derivative of variety of functions by using the technique of implicit differentiation. Consider the equation We want
AP Calculus. Derivatives. Table of Contents
 P alculus erivatives 2015 11 03 www.njctl.org www.njctl.org Table of ontents Rate of hange Slope of a urve (Instantaneous RO) erivative Rules: Power, onstant, Sum/ifference Higher Order erivatives erivatives
P alculus erivatives 2015 11 03 www.njctl.org www.njctl.org Table of ontents Rate of hange Slope of a urve (Instantaneous RO) erivative Rules: Power, onstant, Sum/ifference Higher Order erivatives erivatives
Unit 5 ICM/AB Applications of the Derivative Fall Nov 10 Learn Velocity and Acceleration: HW p P ,103 p.
 Unit 5 ICM/AB Applications of the Derivative Fall 2016 Nov 4 Learn Optimization, New PS up on Optimization, HW pg. 216 3,5,17,19,21,23,25,27,29,33,39,41,49,50 a,b,54 Nov 7 Continue on HW from Nov 4 and
Unit 5 ICM/AB Applications of the Derivative Fall 2016 Nov 4 Learn Optimization, New PS up on Optimization, HW pg. 216 3,5,17,19,21,23,25,27,29,33,39,41,49,50 a,b,54 Nov 7 Continue on HW from Nov 4 and
Name Date Class. Logarithmic/Exponential Differentiation and Related Rates Review AP Calculus. Find dy. dx. 1. y 4 x. y 6. 3e x.
 Name Date Class Find dy d. Logarithmic/Eponential Differentiation and Related Rates Review AP Calculus 1. y 4. 1 y ln. y ln 1 4. y log9 1 5. e y 6. y log 7. y e 8. e y e 4 1 1 9. y e e 10. 1 y ln 1 e 11.
Name Date Class Find dy d. Logarithmic/Eponential Differentiation and Related Rates Review AP Calculus 1. y 4. 1 y ln. y ln 1 4. y log9 1 5. e y 6. y log 7. y e 8. e y e 4 1 1 9. y e e 10. 1 y ln 1 e 11.
1 The Derivative and Differrentiability
 1 The Derivative and Differrentiability 1.1 Derivatives and rate of change Exercise 1 Find the equation of the tangent line to f (x) = x 2 at the point (1, 1). Exercise 2 Suppose that a ball is dropped
1 The Derivative and Differrentiability 1.1 Derivatives and rate of change Exercise 1 Find the equation of the tangent line to f (x) = x 2 at the point (1, 1). Exercise 2 Suppose that a ball is dropped
APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS
 APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS PROBLEM SET #1 Related Rates ***Calculators Allowed*** 1. An oil tanker spills oil that spreads in a circular pattern whose radius increases at the rate of
APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS PROBLEM SET #1 Related Rates ***Calculators Allowed*** 1. An oil tanker spills oil that spreads in a circular pattern whose radius increases at the rate of
Days 3 & 4 Notes: Related Rates
 AP Calculus Unit 4 Applications of the Derivative Part 1 Days 3 & 4 Notes: Related Rates Implicitly differentiate the following formulas with respect to time. State what each rate in the differential equation
AP Calculus Unit 4 Applications of the Derivative Part 1 Days 3 & 4 Notes: Related Rates Implicitly differentiate the following formulas with respect to time. State what each rate in the differential equation
Calculus 437 Semester 1 Review Chapters 1, 2, and 3 January 2016
 Name: Class: Date: Calculus 437 Semester 1 Review Chapters 1, 2, and 3 January 2016 Short Answer 1. Decide whether the following problem can be solved using precalculus, or whether calculus is required.
Name: Class: Date: Calculus 437 Semester 1 Review Chapters 1, 2, and 3 January 2016 Short Answer 1. Decide whether the following problem can be solved using precalculus, or whether calculus is required.
Chapter 3.4 Practice Problems
 EXPECTED SKILLS: Chapter.4 Practice Problems Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible,
EXPECTED SKILLS: Chapter.4 Practice Problems Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible,
AP Calculus Related Rates Worksheet
 AP Calculus Related Rates Worksheet 1. A small balloon is released at a point 150 feet from an observer, who is on level ground. If the balloon goes straight up at a rate of 8 feet per second, how fast
AP Calculus Related Rates Worksheet 1. A small balloon is released at a point 150 feet from an observer, who is on level ground. If the balloon goes straight up at a rate of 8 feet per second, how fast
AP Calculus AB. Slide 1 / 175. Slide 2 / 175. Slide 3 / 175. Integration. Table of Contents
 Slide 1 / 175 Slide 2 / 175 AP Calculus AB Integration 2015-11-24 www.njctl.org Table of Contents click on the topic to go to that section Slide 3 / 175 Riemann Sums Trapezoid Approximation Area Under
Slide 1 / 175 Slide 2 / 175 AP Calculus AB Integration 2015-11-24 www.njctl.org Table of Contents click on the topic to go to that section Slide 3 / 175 Riemann Sums Trapezoid Approximation Area Under
Analyzing Functions. Implicit Functions and Implicit Differentiation
 Analyzing Functions Implicit Functions and Implicit Differentiation In mathematics, an implicit function is a generalization of the concept of a function in which the dependent variable, say, has not been
Analyzing Functions Implicit Functions and Implicit Differentiation In mathematics, an implicit function is a generalization of the concept of a function in which the dependent variable, say, has not been
Chapter 3.5: Related Rates
 Expected Skills: Chapter.5: Related Rates Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible, representing
Expected Skills: Chapter.5: Related Rates Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible, representing
Section 3.8 Related Rates
 Section 3.8 Related Rates Read and re-read the problem until you understand it. Draw and label a picture which gives the relevant information (if possible). Introduce notation. Assign a symbol to every
Section 3.8 Related Rates Read and re-read the problem until you understand it. Draw and label a picture which gives the relevant information (if possible). Introduce notation. Assign a symbol to every
( ) as a fraction. If both numerator and denominator are
 A. Limits and Horizontal Asymptotes What you are finding: You can be asked to find lim f x x a (H.A.) problem is asking you find lim f x x ( ) and lim f x x ( ). ( ) or lim f x x ± ( ). Typically, a horizontal
A. Limits and Horizontal Asymptotes What you are finding: You can be asked to find lim f x x a (H.A.) problem is asking you find lim f x x ( ) and lim f x x ( ). ( ) or lim f x x ± ( ). Typically, a horizontal
Final Exam Review / AP Calculus AB
 Chapter : Final Eam Review / AP Calculus AB Use the graph to find each limit. 1) lim f(), lim f(), and lim π - π + π f 5 4 1 y - - -1 - - -4-5 ) lim f(), - lim f(), and + lim f 8 6 4 y -4 - - -1-1 4 5-4
Chapter : Final Eam Review / AP Calculus AB Use the graph to find each limit. 1) lim f(), lim f(), and lim π - π + π f 5 4 1 y - - -1 - - -4-5 ) lim f(), - lim f(), and + lim f 8 6 4 y -4 - - -1-1 4 5-4
Implicit Differentiation
 Implicit Differentiation Much of our algebraic study of mathematics has dealt with functions. In pre-calculus, we talked about two different types of equations that relate x and y explicit and implicit.
Implicit Differentiation Much of our algebraic study of mathematics has dealt with functions. In pre-calculus, we talked about two different types of equations that relate x and y explicit and implicit.
Chapter 2 Derivatives
 Contents Chapter 2 Derivatives Motivation to Chapter 2 2 1 Derivatives and Rates of Change 3 1.1 VIDEO - Definitions................................................... 3 1.2 VIDEO - Examples and Applications
Contents Chapter 2 Derivatives Motivation to Chapter 2 2 1 Derivatives and Rates of Change 3 1.1 VIDEO - Definitions................................................... 3 1.2 VIDEO - Examples and Applications
College Calculus Final Review
 College Calculus Final Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Determine the following limit. (Hint: Use the graph to calculate the limit.)
College Calculus Final Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Determine the following limit. (Hint: Use the graph to calculate the limit.)
Solve for an unknown rate of change using related rates of change.
 Objectives: Solve for an unknown rate of change using related rates of change. 1. Draw a diagram. 2. Label your diagram, including units. If a quantity in the diagram is not changing, label it with a number.
Objectives: Solve for an unknown rate of change using related rates of change. 1. Draw a diagram. 2. Label your diagram, including units. If a quantity in the diagram is not changing, label it with a number.
To conduct the experiment, each person in your group should be given a role:
 Varying Motion NAME In this activity, your group of 3 will collect data based on one person s motion. From this data, you will create graphs comparing displacement, velocity, and acceleration to time.
Varying Motion NAME In this activity, your group of 3 will collect data based on one person s motion. From this data, you will create graphs comparing displacement, velocity, and acceleration to time.
DRAFT - Math 101 Lecture Note - Dr. Said Algarni
 3 Differentiation Rules 3.1 The Derivative of Polynomial and Exponential Functions In this section we learn how to differentiate constant functions, power functions, polynomials, and exponential functions.
3 Differentiation Rules 3.1 The Derivative of Polynomial and Exponential Functions In this section we learn how to differentiate constant functions, power functions, polynomials, and exponential functions.
Derivatives and Rates of Change
 Sec.1 Derivatives and Rates of Change A. Slope of Secant Functions rise Recall: Slope = m = = run Slope of the Secant Line to a Function: Examples: y y = y1. From this we are able to derive: x x x1 m y
Sec.1 Derivatives and Rates of Change A. Slope of Secant Functions rise Recall: Slope = m = = run Slope of the Secant Line to a Function: Examples: y y = y1. From this we are able to derive: x x x1 m y
p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems
 1 2 p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems Finding Related Rates We have used the chain rule to find dy/dx implicitly, but you can also use the
1 2 p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems Finding Related Rates We have used the chain rule to find dy/dx implicitly, but you can also use the
p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems
 p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems Finding Related Rates We have used the chain rule to find dy/dx implicitly, but you can also use the chain
p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems Finding Related Rates We have used the chain rule to find dy/dx implicitly, but you can also use the chain
UNIT 2 SIMPLE APPLICATION OF DIFFERENTIAL CALCULUS
 Calculus UNIT 2 SIMPLE APPLICATION OF DIFFERENTIAL CALCULUS Structure 2.0 Introduction 2.1 Objectives 2.2 Rate of Change of Quantities 2.3 Increasing and Decreasing Function 2.4 Maima and Minima of Functions
Calculus UNIT 2 SIMPLE APPLICATION OF DIFFERENTIAL CALCULUS Structure 2.0 Introduction 2.1 Objectives 2.2 Rate of Change of Quantities 2.3 Increasing and Decreasing Function 2.4 Maima and Minima of Functions
Math Exam 02 Review
 Math 10350 Exam 02 Review 1. A differentiable function g(t) is such that g(2) = 2, g (2) = 1, g (2) = 1/2. (a) If p(t) = g(t)e t2 find p (2) and p (2). (Ans: p (2) = 7e 4 ; p (2) = 28.5e 4 ) (b) If f(t)
Math 10350 Exam 02 Review 1. A differentiable function g(t) is such that g(2) = 2, g (2) = 1, g (2) = 1/2. (a) If p(t) = g(t)e t2 find p (2) and p (2). (Ans: p (2) = 7e 4 ; p (2) = 28.5e 4 ) (b) If f(t)
Compute the rate of change of one quantity in terms of the rate of change of another quantity.
 3.10 Related Rates Compute the rate of change of one quantity in terms of the rate of change of another quantity. Example 1: If x 2 y x + 4 = 0 and dx/dt = 3, find dy/dt when x = 1. Example 2: Air is being
3.10 Related Rates Compute the rate of change of one quantity in terms of the rate of change of another quantity. Example 1: If x 2 y x + 4 = 0 and dx/dt = 3, find dy/dt when x = 1. Example 2: Air is being
Unit #5 : Implicit Differentiation, Related Rates. Goals: Introduce implicit differentiation. Study problems involving related rates.
 Unit #5 : Implicit Differentiation, Related Rates Goals: Introduce implicit differentiation. Study problems involving related rates. Textbook reading for Unit #5 : Study Sections 3.7, 4.6 Unit 5 - Page
Unit #5 : Implicit Differentiation, Related Rates Goals: Introduce implicit differentiation. Study problems involving related rates. Textbook reading for Unit #5 : Study Sections 3.7, 4.6 Unit 5 - Page
dy dx dx dx as a BC Calculus 1 The Chain Rule is notation for a which says that we have the
 2.4 2.6 BC Calculus 1 The Chain Rule dy is notation for a which says that we have the for an expression set equal to (the dependent variable), where the variable is x. This is read dee why, dee or the
2.4 2.6 BC Calculus 1 The Chain Rule dy is notation for a which says that we have the for an expression set equal to (the dependent variable), where the variable is x. This is read dee why, dee or the
Math 1710 Final Review 1 1
 Math 7 Final Review. Use the ɛ δ definition of it to prove 3 (2 2 +)=4. 2. Use the ɛ δ definition of it to prove +7 2 + =3. 3. Use the ɛ-δ definition of it to prove (32 +5 ) = 3. 4. Prove that if f() =
Math 7 Final Review. Use the ɛ δ definition of it to prove 3 (2 2 +)=4. 2. Use the ɛ δ definition of it to prove +7 2 + =3. 3. Use the ɛ-δ definition of it to prove (32 +5 ) = 3. 4. Prove that if f() =
a right triangle), we see that x 200 or equivalently x = 200 tan θ. The rate at which the ray of light moves along the shore is
 Example 1: A revolving beacon in a lighthouse makes one revolution every 15 seconds. The beacon is 00 ft from the nearest point P on a straight shoreline. Find the rate at which a ray from the light moves
Example 1: A revolving beacon in a lighthouse makes one revolution every 15 seconds. The beacon is 00 ft from the nearest point P on a straight shoreline. Find the rate at which a ray from the light moves
AP Calculus AB. Integration. Table of Contents
 AP Calculus AB Integration 2015 11 24 www.njctl.org Table of Contents click on the topic to go to that section Riemann Sums Trapezoid Approximation Area Under a Curve (The Definite Integral) Antiderivatives
AP Calculus AB Integration 2015 11 24 www.njctl.org Table of Contents click on the topic to go to that section Riemann Sums Trapezoid Approximation Area Under a Curve (The Definite Integral) Antiderivatives
3.8 Exponential Growth and Decay
 3.8 Exponential Growth and Decay Suppose the rate of change of y with respect to t is proportional to y itself. So there is some constant k such that dy dt = ky The only solution to this equation is an
3.8 Exponential Growth and Decay Suppose the rate of change of y with respect to t is proportional to y itself. So there is some constant k such that dy dt = ky The only solution to this equation is an
Math 1131Q Section 10
 Math 1131Q Section 10 Section 3.9 and 3.10 Oct 19, 2010 Find the derivative of ln 3 5 e 2 ln 3 5 e 2 = ln 3 + ln 5/2 + ln e 2 = 3 ln + ( 5 ) ln + 2 2 (ln 3 5 e 2 ) = 3 + 5 2 + 2 Find the derivative of
Math 1131Q Section 10 Section 3.9 and 3.10 Oct 19, 2010 Find the derivative of ln 3 5 e 2 ln 3 5 e 2 = ln 3 + ln 5/2 + ln e 2 = 3 ln + ( 5 ) ln + 2 2 (ln 3 5 e 2 ) = 3 + 5 2 + 2 Find the derivative of
Chapter II.C Derivatives for Implicit Functions
 Chapter II.C Derivatives for Implicit Functions The first thing you may be asking after reading the title of this section is "What's an implicit function? " This is not unexpected since generally courses
Chapter II.C Derivatives for Implicit Functions The first thing you may be asking after reading the title of this section is "What's an implicit function? " This is not unexpected since generally courses
Section MWF 12 1pm SR 117
 Math 1431 Section 12485 MWF 12 1pm SR 117 Dr. Melahat Almus almus@math.uh.edu http://www.math.uh.edu/~almus COURSE WEBSITE: http://www.math.uh.edu/~almus/1431_sp16.html Visit my website regularly for announcements
Math 1431 Section 12485 MWF 12 1pm SR 117 Dr. Melahat Almus almus@math.uh.edu http://www.math.uh.edu/~almus COURSE WEBSITE: http://www.math.uh.edu/~almus/1431_sp16.html Visit my website regularly for announcements
(a) At what rate is the circumference of the circle changing when the radius is 10 inches? =2inches per minute and we want to find. c =2 r.
 3.11 Related Rates Problem 1 The radius of a circle is increasing at a rate of 2 inches per minute. (a) At what rate is the circumference of the circle changing when the radius is 10 inches? We know: dr
3.11 Related Rates Problem 1 The radius of a circle is increasing at a rate of 2 inches per minute. (a) At what rate is the circumference of the circle changing when the radius is 10 inches? We know: dr
AP Calculus BC Chapter 4 AP Exam Problems A) 4 B) 2 C) 1 D) 0 E) 2 A) 9 B) 12 C) 14 D) 21 E) 40
 Extreme Values in an Interval AP Calculus BC 1. The absolute maximum value of x = f ( x) x x 1 on the closed interval, 4 occurs at A) 4 B) C) 1 D) 0 E). The maximum acceleration attained on the interval
Extreme Values in an Interval AP Calculus BC 1. The absolute maximum value of x = f ( x) x x 1 on the closed interval, 4 occurs at A) 4 B) C) 1 D) 0 E). The maximum acceleration attained on the interval
Related Rates In each related rate problem there can be variations in the details. The problems, however, have the same general structure.
 Lab 6 Math 111 Spring 019 Related Rates In each related rate problem there can be variations in the details. The problems, however, have the same general structure. I. Relating Quantities: Independent
Lab 6 Math 111 Spring 019 Related Rates In each related rate problem there can be variations in the details. The problems, however, have the same general structure. I. Relating Quantities: Independent
Math 147 Exam II Practice Problems
 Math 147 Exam II Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Math 147 Exam II Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Math 2413 t2rsu14. Name: 06/06/ Find the derivative of the following function using the limiting process.
 Name: 06/06/014 Math 413 trsu14 1. Find the derivative of the following function using the limiting process. f( x) = 4x + 5x. Find the derivative of the following function using the limiting process. f(
Name: 06/06/014 Math 413 trsu14 1. Find the derivative of the following function using the limiting process. f( x) = 4x + 5x. Find the derivative of the following function using the limiting process. f(
Calculus I 5. Applications of differentiation
 2301107 Calculus I 5. Applications of differentiation Chapter 5:Applications of differentiation C05-2 Outline 5.1. Extreme values 5.2. Curvature and Inflection point 5.3. Curve sketching 5.4. Related rate
2301107 Calculus I 5. Applications of differentiation Chapter 5:Applications of differentiation C05-2 Outline 5.1. Extreme values 5.2. Curvature and Inflection point 5.3. Curve sketching 5.4. Related rate
PHYSICS Kinematics in One Dimension
 PHYSICS Kinematics in One Dimension August 13, 2012 www.njctl.org 1 Motion in One Dimension Return to Table of Contents 2 Distance We all know what the distance between two objects is... So what is it?
PHYSICS Kinematics in One Dimension August 13, 2012 www.njctl.org 1 Motion in One Dimension Return to Table of Contents 2 Distance We all know what the distance between two objects is... So what is it?
Name: Date: Period: Calculus Honors: 4-2 The Product Rule
 Name: Date: Period: Calculus Honors: 4- The Product Rule Warm Up: 1. Factor and simplify. 9 10 0 5 5 10 5 5. Find ' f if f How did you go about finding the derivative? Let s Eplore how to differentiate
Name: Date: Period: Calculus Honors: 4- The Product Rule Warm Up: 1. Factor and simplify. 9 10 0 5 5 10 5 5. Find ' f if f How did you go about finding the derivative? Let s Eplore how to differentiate
Chapter: Basic Physics-Motion
 Chapter: Basic Physics-Motion The Big Idea Speed represents how quickly an object is moving through space. Velocity is speed with a direction, making it a vector quantity. If an object s velocity changes
Chapter: Basic Physics-Motion The Big Idea Speed represents how quickly an object is moving through space. Velocity is speed with a direction, making it a vector quantity. If an object s velocity changes
Position, Velocity, Acceleration
 191 CHAPTER 7 Position, Velocity, Acceleration When we talk of acceleration we think of how quickly the velocity is changing. For example, when a stone is dropped its acceleration (due to gravity) is approximately
191 CHAPTER 7 Position, Velocity, Acceleration When we talk of acceleration we think of how quickly the velocity is changing. For example, when a stone is dropped its acceleration (due to gravity) is approximately
AP Calculus AB Semester 1 Practice Final
 Class: Date: AP Calculus AB Semester 1 Practice Final Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the limit (if it exists). lim x x + 4 x a. 6
Class: Date: AP Calculus AB Semester 1 Practice Final Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the limit (if it exists). lim x x + 4 x a. 6
Related Rates Problems. of h.
 Basic Related Rates Problems 1. If V is the volume of a cube and x the length of an edge. Express dv What is dv in terms of dx. when x is 5 and dx = 2? 2. If V is the volume of a sphere and r is the radius.
Basic Related Rates Problems 1. If V is the volume of a cube and x the length of an edge. Express dv What is dv in terms of dx. when x is 5 and dx = 2? 2. If V is the volume of a sphere and r is the radius.
AP Calculus. Derivatives.
 1 AP Calculus Derivatives 2015 11 03 www.njctl.org 2 Table of Contents Rate of Change Slope of a Curve (Instantaneous ROC) Derivative Rules: Power, Constant, Sum/Difference Higher Order Derivatives Derivatives
1 AP Calculus Derivatives 2015 11 03 www.njctl.org 2 Table of Contents Rate of Change Slope of a Curve (Instantaneous ROC) Derivative Rules: Power, Constant, Sum/Difference Higher Order Derivatives Derivatives
THE MOVING MAN: DISTANCE, DISPLACEMENT, SPEED & VELOCITY
 THE MOVING MAN: DISTANCE, DISPLACEMENT, SPEED & VELOCITY Background Remember graphs are not just an evil thing your teacher makes you create, they are a means of communication. Graphs are a way of communicating
THE MOVING MAN: DISTANCE, DISPLACEMENT, SPEED & VELOCITY Background Remember graphs are not just an evil thing your teacher makes you create, they are a means of communication. Graphs are a way of communicating
Math3A Exam #02 Solution Fall 2017
 Math3A Exam #02 Solution Fall 2017 1. Use the limit definition of the derivative to find f (x) given f ( x) x. 3 2. Use the local linear approximation for f x x at x0 8 to approximate 3 8.1 and write your
Math3A Exam #02 Solution Fall 2017 1. Use the limit definition of the derivative to find f (x) given f ( x) x. 3 2. Use the local linear approximation for f x x at x0 8 to approximate 3 8.1 and write your
5. Find the intercepts of the following equations. Also determine whether the equations are symmetric with respect to the y-axis or the origin.
 MATHEMATICS 1571 Final Examination Review Problems 1. For the function f defined by f(x) = 2x 2 5x find the following: a) f(a + b) b) f(2x) 2f(x) 2. Find the domain of g if a) g(x) = x 2 3x 4 b) g(x) =
MATHEMATICS 1571 Final Examination Review Problems 1. For the function f defined by f(x) = 2x 2 5x find the following: a) f(a + b) b) f(2x) 2f(x) 2. Find the domain of g if a) g(x) = x 2 3x 4 b) g(x) =
AP Physics 1 Kinematics 1D
 AP Physics 1 Kinematics 1D 1 Algebra Based Physics Kinematics in One Dimension 2015 08 25 www.njctl.org 2 Table of Contents: Kinematics Motion in One Dimension Position and Reference Frame Displacement
AP Physics 1 Kinematics 1D 1 Algebra Based Physics Kinematics in One Dimension 2015 08 25 www.njctl.org 2 Table of Contents: Kinematics Motion in One Dimension Position and Reference Frame Displacement
Algebra I. Slide 1 / 79. Slide 2 / 79. Slide 3 / 79. Equations. Table of Contents Click on a topic to go to that section
 Slide 1 / 79 Slide 2 / 79 lgebra I Equations 2015-08-21 www.njctl.org Table of ontents lick on a topic to go to that section. Slide 3 / 79 Equations with the Same Variable on oth Sides Solving Literal
Slide 1 / 79 Slide 2 / 79 lgebra I Equations 2015-08-21 www.njctl.org Table of ontents lick on a topic to go to that section. Slide 3 / 79 Equations with the Same Variable on oth Sides Solving Literal
Implicit Differentiation, Related Rates. Goals: Introduce implicit differentiation. Study problems involving related rates.
 Unit #5 : Implicit Differentiation, Related Rates Goals: Introduce implicit differentiation. Study problems involving related rates. Tangent Lines to Relations - Implicit Differentiation - 1 Implicit Differentiation
Unit #5 : Implicit Differentiation, Related Rates Goals: Introduce implicit differentiation. Study problems involving related rates. Tangent Lines to Relations - Implicit Differentiation - 1 Implicit Differentiation
The volume of a sphere and the radius of the same sphere are related by the formula:
 Related Rates Today is a day in which we explore the behavior of derivatives rather than trying to get new formulas for derivatives. Example Let s ask the following question: Suppose that you are filling
Related Rates Today is a day in which we explore the behavior of derivatives rather than trying to get new formulas for derivatives. Example Let s ask the following question: Suppose that you are filling
Math 2413 Final Exam Review 1. Evaluate, giving exact values when possible.
 Math 4 Final Eam Review. Evaluate, giving eact values when possible. sin cos cos sin y. Evaluate the epression. loglog 5 5ln e. Solve for. 4 6 e 4. Use the given graph of f to answer the following: y f
Math 4 Final Eam Review. Evaluate, giving eact values when possible. sin cos cos sin y. Evaluate the epression. loglog 5 5ln e. Solve for. 4 6 e 4. Use the given graph of f to answer the following: y f
PTF #AB 07 Average Rate of Change
 The average rate of change of f( ) over the interval following: 1. y dy d. f() b f() a b a PTF #AB 07 Average Rate of Change ab, can be written as any of the. Slope of the secant line through the points
The average rate of change of f( ) over the interval following: 1. y dy d. f() b f() a b a PTF #AB 07 Average Rate of Change ab, can be written as any of the. Slope of the secant line through the points
MATH1910Chapter2TestReview
 Class: Date: MATH1910Chapter2TestReview Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the slope m of the line tangent to the graph of the function
Class: Date: MATH1910Chapter2TestReview Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the slope m of the line tangent to the graph of the function
Chapter 27 AB Calculus Practice Test
 Chapter 7 AB Calculus Practice Test The Eam AP Calculus AB Eam SECTION I: Multiple-Choice Questions DO NOT OPEN THIS BOOKLET UNTIL YOU ARE TOLD TO DO SO. At a Glance Total Time 1 hour and 45 minutes Number
Chapter 7 AB Calculus Practice Test The Eam AP Calculus AB Eam SECTION I: Multiple-Choice Questions DO NOT OPEN THIS BOOKLET UNTIL YOU ARE TOLD TO DO SO. At a Glance Total Time 1 hour and 45 minutes Number
Applications of Derivatives
 Applications of Derivatives Big Ideas Connecting the graphs of f, f, f Differentiability Continuity Continuity Differentiability Critical values Mean Value Theorem for Derivatives: Hypothesis: If f is
Applications of Derivatives Big Ideas Connecting the graphs of f, f, f Differentiability Continuity Continuity Differentiability Critical values Mean Value Theorem for Derivatives: Hypothesis: If f is
WeBWorK demonstration assignment
 WeBWorK demonstration assignment The main purpose of this WeBWorK set is to familiarize yourself with WeBWorK. Here are some hints on how to use WeBWorK effectively: After first logging into WeBWorK change
WeBWorK demonstration assignment The main purpose of this WeBWorK set is to familiarize yourself with WeBWorK. Here are some hints on how to use WeBWorK effectively: After first logging into WeBWorK change
More Differentiation Page 1
 More Differentiation Page 1 Directions: Solve the following problems using the available space for scratchwork. Indicate your answers on the front page. Do not spend too much time on any one problem. Note:
More Differentiation Page 1 Directions: Solve the following problems using the available space for scratchwork. Indicate your answers on the front page. Do not spend too much time on any one problem. Note:
Math 121: Final Exam Review Sheet
 Exam Information Math 11: Final Exam Review Sheet The Final Exam will be given on Thursday, March 1 from 10:30 am 1:30 pm. The exam is cumulative and will cover chapters 1.1-1.3, 1.5, 1.6,.1-.6, 3.1-3.6,
Exam Information Math 11: Final Exam Review Sheet The Final Exam will be given on Thursday, March 1 from 10:30 am 1:30 pm. The exam is cumulative and will cover chapters 1.1-1.3, 1.5, 1.6,.1-.6, 3.1-3.6,
Math 2250, Spring 2017, Practice Sheet for Exam 2
 Math 2250, Spring 2017, Practice Sheet for Exam 2 (1) Find the derivative of the function f(x) = xx (x 2 4) 5 (x 1) 3 e xp x + e x (2) Solve for dy dx x 2 4y 2 =sin(xy) (3) Solve for dx dt given that e
Math 2250, Spring 2017, Practice Sheet for Exam 2 (1) Find the derivative of the function f(x) = xx (x 2 4) 5 (x 1) 3 e xp x + e x (2) Solve for dy dx x 2 4y 2 =sin(xy) (3) Solve for dx dt given that e
See animations and interactive applets of some of these at. Fall_2009/Math123/Notes
 MA123, Chapter 7 Word Problems (pp. 125-153) Chapter s Goal: In this chapter we study the two main types of word problems in Calculus. Optimization Problems. i.e., max - min problems Related Rates See
MA123, Chapter 7 Word Problems (pp. 125-153) Chapter s Goal: In this chapter we study the two main types of word problems in Calculus. Optimization Problems. i.e., max - min problems Related Rates See
4.5 Linearization Calculus 4.5 LINEARIZATION. Notecards from Section 4.5: Linearization; Differentials. Linearization
 4.5 Linearization Calculus 4.5 LINEARIZATION Notecards from Section 4.5: Linearization; Differentials Linearization The goal of linearization is to approximate a curve with a line. Why? Because it s easier
4.5 Linearization Calculus 4.5 LINEARIZATION Notecards from Section 4.5: Linearization; Differentials Linearization The goal of linearization is to approximate a curve with a line. Why? Because it s easier
As you already know by now, when you're finding derivatives, you're finding the slope.
 As you already know by now, when you're finding derivatives, you're finding the slope. Slope is a "rate of change" There are many other "rates of change" out there in the Real World. For example, a doctor
As you already know by now, when you're finding derivatives, you're finding the slope. Slope is a "rate of change" There are many other "rates of change" out there in the Real World. For example, a doctor
A = 1 2 ab da dt = 1 da. We can find how fast the area is growing at 3 seconds by plugging everything into that differentiated equation: da
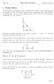 1 Related Rates In most related rates problems, we have an equation that relates a bunch of quantities that are changing over time. For example, suppose we have a right triangle whose base and height are
1 Related Rates In most related rates problems, we have an equation that relates a bunch of quantities that are changing over time. For example, suppose we have a right triangle whose base and height are
V = π 3 r2 h. dv dt = π [ r 2dh dt r2. dv 3 dt +2rhdr dt
 9 Related Rates Related rates is the phrase used to describe the situation when two or more related variables are changing with respect to time. The rate of change, as mentioned earlier, is another expression
9 Related Rates Related rates is the phrase used to describe the situation when two or more related variables are changing with respect to time. The rate of change, as mentioned earlier, is another expression
MATH 3A FINAL REVIEW
 MATH 3A FINAL REVIEW Guidelines to taking the nal exam You must show your work very clearly You will receive no credit if we do not understand what you are doing 2 You must cross out any incorrect work
MATH 3A FINAL REVIEW Guidelines to taking the nal exam You must show your work very clearly You will receive no credit if we do not understand what you are doing 2 You must cross out any incorrect work
Unit V Applications of Derivatives
 Unit V Applications of Derivatives Curve Sketching Inequalities (Not covered in 3205) Polynomial Rational Functions Related Rate Problems Optimization (Max/Min) Problems 1 Inequalities Linear Polynomial
Unit V Applications of Derivatives Curve Sketching Inequalities (Not covered in 3205) Polynomial Rational Functions Related Rate Problems Optimization (Max/Min) Problems 1 Inequalities Linear Polynomial
Unit V Applications of Derivatives
 Unit V Applications of Derivatives Curve Sketching Inequalities (Covered in 2200) Polynomial Rational Functions Related Rate Problems Optimization (Max/Min) Problems 1 Inequalities Linear Polynomial Rational
Unit V Applications of Derivatives Curve Sketching Inequalities (Covered in 2200) Polynomial Rational Functions Related Rate Problems Optimization (Max/Min) Problems 1 Inequalities Linear Polynomial Rational
AP Calculus BC Summer Assignment 2018
 AP Calculus BC Summer Assignment 018 Name: When you come back to school, I will epect you to have attempted every problem. These skills are all different tools that we will pull out of our toolbo at different
AP Calculus BC Summer Assignment 018 Name: When you come back to school, I will epect you to have attempted every problem. These skills are all different tools that we will pull out of our toolbo at different
RELATED RATE PROBLEMS
 MA123, Chapter 7a: Related Rates Word Problems (pp. 140-149, Gootman) Chapter Goals: In this Chapter we learn a general strategy on how to approach related rates problems, one of the main types of word
MA123, Chapter 7a: Related Rates Word Problems (pp. 140-149, Gootman) Chapter Goals: In this Chapter we learn a general strategy on how to approach related rates problems, one of the main types of word
Chapter 7: Practice/review problems The collection of problems listed below contains questions taken from previous MA123 exams.
 Word problems Chapter 7: Practice/review problems The collection of problems listed below contains questions taken from previous MA3 exams. Max-min problems []. A field has the shape of a rectangle with
Word problems Chapter 7: Practice/review problems The collection of problems listed below contains questions taken from previous MA3 exams. Max-min problems []. A field has the shape of a rectangle with
Review Sheet for Second Midterm Mathematics 1300, Calculus 1
 Review Sheet for Second Midterm Mathematics 300, Calculus. For what values of is the graph of y = 5 5 both increasing and concave up? >. 2. Where does the tangent line to y = 2 through (0, ) intersect
Review Sheet for Second Midterm Mathematics 300, Calculus. For what values of is the graph of y = 5 5 both increasing and concave up? >. 2. Where does the tangent line to y = 2 through (0, ) intersect
Motion, Velocity, Acceleration
 And thus, since God is the First Mover, simply, it is by His motion that everything seeks to be likened to God in its own way. Summa Theologica, IIa:Q109,A6 Introduction Objects in motion are moving at
And thus, since God is the First Mover, simply, it is by His motion that everything seeks to be likened to God in its own way. Summa Theologica, IIa:Q109,A6 Introduction Objects in motion are moving at
4.1 & 4.2 Student Notes Using the First and Second Derivatives. for all x in D, where D is the domain of f. The number f()
 4.1 & 4. Student Notes Using the First and Second Derivatives Deinition A unction has an absolute maimum (or global maimum) at c i ( c) ( ) or all in D, where D is the domain o. The number () c is called
4.1 & 4. Student Notes Using the First and Second Derivatives Deinition A unction has an absolute maimum (or global maimum) at c i ( c) ( ) or all in D, where D is the domain o. The number () c is called
MCV4U1 Worksheet 4.7. dh / dt if neither r nor h is constant?
 MCV4U1 Worksheet 4.7 This worksheet serves as an additional exercise to complement the lesson and the examples given. Worksheets may take more than one day to complete. If you are stuck, read again the
MCV4U1 Worksheet 4.7 This worksheet serves as an additional exercise to complement the lesson and the examples given. Worksheets may take more than one day to complete. If you are stuck, read again the
Chapter 9: Circular Motion
 Text: Chapter 9 Think and Explain: 1-5, 7-9, 11 Think and Solve: --- Chapter 9: Circular Motion NAME: Vocabulary: rotation, revolution, axis, centripetal, centrifugal, tangential speed, Hertz, rpm, rotational
Text: Chapter 9 Think and Explain: 1-5, 7-9, 11 Think and Solve: --- Chapter 9: Circular Motion NAME: Vocabulary: rotation, revolution, axis, centripetal, centrifugal, tangential speed, Hertz, rpm, rotational
Name: Date: Partners: LAB 2: ACCELERATED MOTION
 Name: Date: Partners: LAB 2: ACCELERATED MOTION OBJECTIVES After completing this lab you should be able to: Describe motion of an object from a velocitytime graph Draw the velocitytime graph of an object
Name: Date: Partners: LAB 2: ACCELERATED MOTION OBJECTIVES After completing this lab you should be able to: Describe motion of an object from a velocitytime graph Draw the velocitytime graph of an object
Solution: It could be discontinuous, or have a vertical tangent like y = x 1/3, or have a corner like y = x.
 1. Name three different reasons that a function can fail to be differentiable at a point. Give an example for each reason, and explain why your examples are valid. It could be discontinuous, or have a
1. Name three different reasons that a function can fail to be differentiable at a point. Give an example for each reason, and explain why your examples are valid. It could be discontinuous, or have a
2.6 Related Rates. The Derivative as a Rate of Change. = ft related rates 175
 2.6 related rates 175 2.6 Related Rates Throughout the next several tions we ll look at a variety of applications of derivatives. Probably no single application will be of interest or use to everyone,
2.6 related rates 175 2.6 Related Rates Throughout the next several tions we ll look at a variety of applications of derivatives. Probably no single application will be of interest or use to everyone,
Chapter 5: Limits and Derivatives
 Chapter 5: Limits and Derivatives Chapter 5 Overview: Introduction to Limits and Derivatives In a later chapter, maximum and minimum points of a curve will be found both by calculator and algebraically.
Chapter 5: Limits and Derivatives Chapter 5 Overview: Introduction to Limits and Derivatives In a later chapter, maximum and minimum points of a curve will be found both by calculator and algebraically.
