Related Rates. 2. List the relevant quantities in the problem and assign them appropriate variables. Then write down all the information given.
|
|
|
- Kelley Pitts
- 5 years ago
- Views:
Transcription
1 Calculus 1 Lia Vas Related Rates The most important reason for a non-mathematics major to learn mathematics is to be able to apply it to problems from other disciplines or real life. In this section, we focus on modeling real life scenarios using functions and then determining the rate of one quantity in terms of the rate of the other. Since the implicit differentiation formula relates the two rates, they are ofter referred to as the related rates. In modeling a problem and then solving it, following the steps below is often useful. 1. Read the problem carefully. Sketch a diagram if possible in order to visualize the relevant information. 2. List the relevant quantities in the problem and assign them appropriate variables. Then write down all the information given. 3. Write down the equation that relates all the variables. 4. Differentiate the equation using the implicit differentiation if necessary. 5. Solve for the unknown rate. Substitute the given information into the relation and determine the unknown rate. We illustrate this method with examples below. Example 1. Suppose a spherical balloon is inflated by 10 cubic centimeters per minute. Determine how fast the radius of the balloon increases at the time when the radius is 5 cm. Solution. Determine the relevant quantities. From the first sentence of the problem, conclude that the volume is increasing as time passes by so that the volume and time are two relevant quantities. We are also given the size of the radius at certain time so the third relevant quantity is the radius. Let us use V, r and t for the volume, radius and time respectively. Note that the volume and the radius depend on time so they are functions of time. Using this notation, note that the given information is that dv = 10 cm 3 /min and r = 5 cm. The problem is asking you to calculate. Relating the variables. Recall that the formula for the volume of a sphere is V = 4 3 πr3. Thus, this equation relates the quantities. Differentiate the equation. Keep in mind that you are differentiation with respect to time. d (V ) = d (4 3 πr3 ) dv = 4π 3 3r2 dv = 4πr2 1
2 This last equation relates the rates of V and r. Solve for the unknown rate. Substitute the given information dv and then solve for the unknown. dv = 4πr2 10 = 4π(5) 2 Example 2. A 20-foot ladder is leaning against the wall. If the base of the ladder is sliding away from the wall at the rate of 3 feet per second, find the rate at which the top of the ladder is sliding down when the top of the ladder is 8 feet from the ground. Solution. Determine the relevant quantities. The distance from the base of the ladder to the wall and the distance from the top of the ladder to the ground are the two relevant quantities. = 10 4π(25) = π = 1 10π = 10 cm 3 /min and r = 5 cm 0.32 cm per min. Let x denotes the first distance and y the second one. Note that as the ladder is sliding down x is increasing so that is positive and y is decreasing so that is negative. Using this notation, note that the given information is that = 3 ft/sec and y = 8 ft. The problem is asking you to calculate. Relating the variables. Since x and y are two sides of the right triangle with the 20-foot ladder as the hypotenuse, we have that x 2 + y 2 = Differentiate the equation with respect to time and solve for the unknown rate. d (x2 + y 2 ) = d (400) 2x + 2y = 0 = x y Find the missing value. Note that we have the values for and y = 8 but we are still missing the value of x. The x-value can be determined from the equation x 2 + y 2 = 400 using that y = 8. Thus x = 400 x 2 = 336 x = ± 336. Since we are looking for positive value, x Find the unknown rate. Substitute = 3 ft/sec, y = 8 ft and x = into the rate equation to get x = 18.33(3) = 6.87 ft/sec. Thus, the distance from the top of the ladder to the ground y 8 is decreasing by 6.87 feet per second. Example 3. A 6-feet-tall man walks at the rate of 5 feet per second towards a 24-feet-tall street lamp. Determine how fast is the tip of man s shadow moving along the ground. Solution. Determine the relevant quantities. Sketch a diagram of this scenario as on figure on the right. 2
3 Note that the rate of 5 feet per second given in the problem is referring to the rate of change of the distance of the person from the lamp. So, let us denote this by x. The problem is asking for the rate of change of the length of the shadow, so let us denote this length by y. Relate the variables. The diagram consists of two similar triangles, one with sides y and 6 and the other with sides x + y and 24. Thus y 6 = x + y 24 4y = x+y x = 3y or y = 1 3 x. Differentiate the equation and solve for the unknown rate. y = x = 1. Note that both 3 3 x and y are decreasing as time passes by so both rates are negative. Thus = 5 ft/sec and so = ft/sec. Thus, the shadow is decreasing in length by 1.67 feet per second. 3 Example 4. A conical tank of height 2 meters is full of water. The radius of the surface is 1 meter. If the water evaporates at the rate of 30 centimeters cubic per day, determine the rate at which the water level decreases when the water is 0.5 meters deep. Discuss if this rate is increasing or decreasing as the depth of the water becomes smaller. Solution. Determine and relate the relevant quantities. Sketch a diagram of this scenario as on figure on the right. The rate of 30 cubic centimeters per day refers to the rate of change of the volume of water. Let us denote the volume by V. The formula for the volume of the cone of height h with the radius of the base r is given by V = 1 3 r2 hπ. Since all three variables, V, r and h, are changing in time, we need to reduce the number of variables from three to two. So, we need to relate r and h. Relate the variables. Consider the two similar triangles on the diagram. Since r and h are the sides of one and 1 and 2 are sides of the other, we have that r h = 1 2 r = 1 2 h. Thus, we obtain the formula for the volume in terms of the height of the water alone. V = 1 3 ( ) 2 h hπ = h3 π. 3
4 Differentiate the equation and solve for the unknown rate. V = 1 12 h3 π dv = 1 dh 3h2 12 π = π dh h2 4 dh = 4 dv h 2 π. We are given that dv = 30 cm 3 /day (negative sign since the volume is decreasing) and h = 0.5 m. To have uniform units, convert either h to centimeters or dv to cubic meters. With h as 50 cm, we have that dh = 4( 30) cm per day. So, the radius is decreasing by cm per day π The formula dh = 4 dv also indicates that the rate increases when height is getting smaller. h 2 π Looking at the rate at which the sand is pouring down in an hourglass just before the sand completely poured out supports this conclusion. Practice problems. 1. Water leaking onto a floor creates a circular puddle with an area that increases at the rate of 3 square centimeters per minute. Determine how fast the radius of the puddle increases when the radius is 10 cm. 2. Assume that the number of bass in the pond is related to the level of polychlorinated biphenyls (PCBs, a group of industrial chemicals used in plasticizers, fire retardants and other materials) in the pond. The bass population is modeled by y = x where x represents the PCB level in parts per million (ppm) and y represents the number of bass in the pond. If the level of PCBs is increasing at the rate of 40 ppm per year, find the rate at which is the number of bass changing when there are 100 bass in the pond. 3. Two resistors with resistances R 1 and R 2 are connected in parallel into an electrical circuit. The total resistance R in ohms is computed by the formula 1 R = 1 R R 2. If R 1 and R 2 are increasing by 0.25 ohms per second, determine how fast is R changing when R 1 = 75 and R 2 = 100 ohms. 4
5 4. A conveyor belt is pouring sand down creating a conical pile whose diameter is twice as long as its height. If the belt is dumping sand at a rate of 40 cubic feet per minute, determine the rate at which the height is increasing when the pile is 7 feet high. 5. Water is leaking from a hole on the ceiling next to the wall. Sliding down the wall, the water is creating a semi-circular puddle on the floor next to the wall. The puddle is growing in surface area at a rate of 10 square inches per minute. Determine how rapidly the radius of the puddle is growing at the moment when the area of the puddle is 100 square inches. 6. One car is traveling east with speed of 60 miles per hour and the other car is traveling south with speed of 50 miles per hour. Both cars are headed towards the same spot. Determine the rate at which cars are approaching each other when the first car is 4 miles and the second car is 3 miles from the meeting spot. 7. A snowball is melting at the rate of 100 cubic centimeters per hour. Determine the rate at which the radius is decreasing at the time when radius is 5 centimeters. Solutions. 1. Determine the relevant quantities. From the first sentence of the problem, conclude that the area is increasing as time passes by so that the volume and time are two relevant quantities. We are also given the size of the radius at certain time so the third relevant quantity is the radius. Let us use A, r and t for the area, radius and time respectively. Note that the area and the radius depend on time. Using this notation, note that the given information is that da = 3 cm 2 /min and r = 10 cm. The problem is asking you to calculate. Relating the variables. Recall that the formula for the area of the circle with radius r is A = r 2 π. Thus, this equation relates the variables. Differentiate the equation and solve for the unknown rate. Keep in mind that you are differentiation with respect to time. d (A) = d (r2 π) da = 2πr da = 2πr. Plug the given information in the equation. Substitute the given information da = 3 cm 2 /min and r = 10 cm and solve for the unknown. Get = da = cm per minute. 2πr 2π(10) 5
6 2. Since the variables are alrea named, you can start by denoting the given information as = 40 ppm/ year, y = 100 bass and noting that the problem is asking for the unknown rate. The variables are also alrea related so you can differentiate the given equation and solve for the unknown rate. y = x = 2500(1 + x) 1 = 2500(1 + x) 2 = 2500 (1 + x) 2. Since this last formula involves x, you need to determine x given that y = 100. Use the equation relating x and y again. y = = 1 + x = 2500 = 25 x = 24. Compute the 1+x 1+x 100 unknown rate given this information as = frac 2500 (1 + x)2 = 2500(40) = 4000 = 160 bass per year (1 + 24) 2 25 Thus the number of bass is decreasing by 160 each year. 3. Since the variables are alrea named, you can start by denoting the given information as dr 1 = dr 2 = 0.25 ohms/sec, R 1 = and R 2 = ohms and noting that the problem is asking for the unknown rate dr. The variables are also alrea related so you can differentiate the given equation and solve for the unknown rate. R 1 = R1 1 + R2 1 2 dr R = dr 1 dr 2 R 2 1 R 2 dr ( ) = R2 R1 2 dr 1 + R2 2 dr 2. Since this equation involves R, you need to determine R given that R 1 = 75 and R 2 = R = R 1 R 2 R = R = R = Thus the unknown rate is dr = R ( ) ( ) 2 R 2 1 dr 1 + R 2 2 dr 2 = dr = ohms per second. 4. If we denote the volume of the pile by V, then dv = 40 ft 3 /min. The formula V = 1 3 r2 hπ computes the volume of the cone of height h with the radius of the base r. Since the diameter 2r is twice as long as its height h, we have that 2r = 2h r = h. Thus, V = 1 3 (h)2 hπ = 1 3 h3 π. Differentiate the equation and obtain V = 1 dh dh 3h2 π = h2 π dh 3 ft 3 /min and h = 7 ft, we have that dh = ft per min. 7 2 π = dv h 2 π. With dv = The formula for the area of a semi-circle of radius r is A = 1 2 r2 π. We are given that da = 10 square inches per minute and A = 100 square inches and the problem is asking for Differentiate the formula and solve for. A = 1 2 r2 π da = 1 2rπ = rπ. 2 rπ Since this last formula involves r, you need to determine r given that A = 100. A = 1 2 r2 π. = da 100 = 1 2 r2 π r 2 = 200 r ±7.98. We need the positive solution so r Thus π 0.40 inches per minute π 6. Try to work out the problem on your own. You should get the final answer of 1 5 (4( 60) + 3( 50)) = 78 miles/hour. Thus, the cars are approaching each other at the rate of 78 mph. 7. Try to work out the problem on your own. You should get the final answer of 0.32 cm per hour. Thus, the radius of the snowball is decreasing by 0.32 cm per hour. = 100 4π(5) 2 6
Days 3 & 4 Notes: Related Rates
 AP Calculus Unit 4 Applications of the Derivative Part 1 Days 3 & 4 Notes: Related Rates Implicitly differentiate the following formulas with respect to time. State what each rate in the differential equation
AP Calculus Unit 4 Applications of the Derivative Part 1 Days 3 & 4 Notes: Related Rates Implicitly differentiate the following formulas with respect to time. State what each rate in the differential equation
AP Calculus AB Chapter 4 Packet Implicit Differentiation. 4.5: Implicit Functions
 4.5: Implicit Functions We can employ implicit differentiation when an equation that defines a function is so complicated that we cannot use an explicit rule to find the derivative. EXAMPLE 1: Find dy
4.5: Implicit Functions We can employ implicit differentiation when an equation that defines a function is so complicated that we cannot use an explicit rule to find the derivative. EXAMPLE 1: Find dy
Chapter 3.4 Practice Problems
 EXPECTED SKILLS: Chapter.4 Practice Problems Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible,
EXPECTED SKILLS: Chapter.4 Practice Problems Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible,
Chapter 3.5: Related Rates
 Expected Skills: Chapter.5: Related Rates Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible, representing
Expected Skills: Chapter.5: Related Rates Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible, representing
AP Calculus Related Rates Worksheet
 AP Calculus Related Rates Worksheet 1. A small balloon is released at a point 150 feet from an observer, who is on level ground. If the balloon goes straight up at a rate of 8 feet per second, how fast
AP Calculus Related Rates Worksheet 1. A small balloon is released at a point 150 feet from an observer, who is on level ground. If the balloon goes straight up at a rate of 8 feet per second, how fast
Implicit Differentiation
 Week 6. Implicit Differentiation Let s say we want to differentiate the equation of a circle: y 2 + x 2 =9 Using the techniques we know so far, we need to write the equation as a function of one variable
Week 6. Implicit Differentiation Let s say we want to differentiate the equation of a circle: y 2 + x 2 =9 Using the techniques we know so far, we need to write the equation as a function of one variable
Chapter 8: Radical Functions
 Chapter 8: Radical Functions Chapter 8 Overview: Types and Traits of Radical Functions Vocabulary:. Radical (Irrational) Function an epression whose general equation contains a root of a variable and possibly
Chapter 8: Radical Functions Chapter 8 Overview: Types and Traits of Radical Functions Vocabulary:. Radical (Irrational) Function an epression whose general equation contains a root of a variable and possibly
4.6 Related Rates Notes RELATED RATES PROBLEMS --- IT S AS EASY AS 1 2-3!
 4.6 Related Rates Notes RELATED RATES PROBLEMS --- IT S AS EASY AS 1 2-3! 1) Draw a picture. Label all variables and constant values. Identify the given rate of change, the rate to be found, and when to
4.6 Related Rates Notes RELATED RATES PROBLEMS --- IT S AS EASY AS 1 2-3! 1) Draw a picture. Label all variables and constant values. Identify the given rate of change, the rate to be found, and when to
Math 131. Related Rates Larson Section 2.6
 Math 131. Related Rates Larson Section 2.6 There are many natural situations when there are related variables that are changing with respect to time. For example, a spherical balloon is being inflated
Math 131. Related Rates Larson Section 2.6 There are many natural situations when there are related variables that are changing with respect to time. For example, a spherical balloon is being inflated
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES If we are pumping air into a balloon, both the volume and the radius of the balloon are increasing and their rates of increase are related to each other. However,
3 DIFFERENTIATION RULES DIFFERENTIATION RULES If we are pumping air into a balloon, both the volume and the radius of the balloon are increasing and their rates of increase are related to each other. However,
Guidelines for implicit differentiation
 Guidelines for implicit differentiation Given an equation with x s and y s scattered, to differentiate we use implicit differentiation. Some informal guidelines to differentiate an equation containing
Guidelines for implicit differentiation Given an equation with x s and y s scattered, to differentiate we use implicit differentiation. Some informal guidelines to differentiate an equation containing
V = π 3 r2 h. dv dt = π [ r 2dh dt r2. dv 3 dt +2rhdr dt
 9 Related Rates Related rates is the phrase used to describe the situation when two or more related variables are changing with respect to time. The rate of change, as mentioned earlier, is another expression
9 Related Rates Related rates is the phrase used to describe the situation when two or more related variables are changing with respect to time. The rate of change, as mentioned earlier, is another expression
Related Rates Problems. of h.
 Basic Related Rates Problems 1. If V is the volume of a cube and x the length of an edge. Express dv What is dv in terms of dx. when x is 5 and dx = 2? 2. If V is the volume of a sphere and r is the radius.
Basic Related Rates Problems 1. If V is the volume of a cube and x the length of an edge. Express dv What is dv in terms of dx. when x is 5 and dx = 2? 2. If V is the volume of a sphere and r is the radius.
4.6 Related Rates 8 b o lk0uct5ai FSHopfitcwkadr9ee MLBL1Cv.0 h ca5lrlx 8rzi8gThzt Zs9 2rJejsqeprTvCeVdy.w Solve each related rate problem.
 -- g 52P0l33e 5Ktu3tlaY tswobfrtcwsawrkeq mlzlzcd.u 2 7AklGlf lrbiegkhjtbsa 9rlewsSeIr2vPeVdW.L 2 7Mza5dWeI gwbimtmhn bimnff0ieneistuet SCDallJcrulsuTsG.k Calculus 4.6 Related Rates 8 b230593 o lk0uct5ai
-- g 52P0l33e 5Ktu3tlaY tswobfrtcwsawrkeq mlzlzcd.u 2 7AklGlf lrbiegkhjtbsa 9rlewsSeIr2vPeVdW.L 2 7Mza5dWeI gwbimtmhn bimnff0ieneistuet SCDallJcrulsuTsG.k Calculus 4.6 Related Rates 8 b230593 o lk0uct5ai
Related Rates STEP 1 STEP 2:
 Related Rates You can use derivative analysis to determine how two related quantities also have rates of change which are related together. I ll lead off with this example. 3 Ex) A spherical ball is being
Related Rates You can use derivative analysis to determine how two related quantities also have rates of change which are related together. I ll lead off with this example. 3 Ex) A spherical ball is being
Solve for an unknown rate of change using related rates of change.
 Objectives: Solve for an unknown rate of change using related rates of change. 1. Draw a diagram. 2. Label your diagram, including units. If a quantity in the diagram is not changing, label it with a number.
Objectives: Solve for an unknown rate of change using related rates of change. 1. Draw a diagram. 2. Label your diagram, including units. If a quantity in the diagram is not changing, label it with a number.
Section MWF 12 1pm SR 117
 Math 1431 Section 12485 MWF 12 1pm SR 117 Dr. Melahat Almus almus@math.uh.edu http://www.math.uh.edu/~almus COURSE WEBSITE: http://www.math.uh.edu/~almus/1431_sp16.html Visit my website regularly for announcements
Math 1431 Section 12485 MWF 12 1pm SR 117 Dr. Melahat Almus almus@math.uh.edu http://www.math.uh.edu/~almus COURSE WEBSITE: http://www.math.uh.edu/~almus/1431_sp16.html Visit my website regularly for announcements
6.2 Related Rates Name: Notes
 Calculus Write your questions and thoughts here! 6.2 Related Rates Name: Notes Guidelines to solving related rate problems 1. Draw a picture. 2. Make a list of all known and unknown rates and quantities.
Calculus Write your questions and thoughts here! 6.2 Related Rates Name: Notes Guidelines to solving related rate problems 1. Draw a picture. 2. Make a list of all known and unknown rates and quantities.
Calculus 437 Semester 1 Review Chapters 1, 2, and 3 January 2016
 Name: Class: Date: Calculus 437 Semester 1 Review Chapters 1, 2, and 3 January 2016 Short Answer 1. Decide whether the following problem can be solved using precalculus, or whether calculus is required.
Name: Class: Date: Calculus 437 Semester 1 Review Chapters 1, 2, and 3 January 2016 Short Answer 1. Decide whether the following problem can be solved using precalculus, or whether calculus is required.
Implicit Differentiation
 Implicit Differentiation Much of our algebraic study of mathematics has dealt with functions. In pre-calculus, we talked about two different types of equations that relate x and y explicit and implicit.
Implicit Differentiation Much of our algebraic study of mathematics has dealt with functions. In pre-calculus, we talked about two different types of equations that relate x and y explicit and implicit.
Name Date Class. Logarithmic/Exponential Differentiation and Related Rates Review AP Calculus. Find dy. dx. 1. y 4 x. y 6. 3e x.
 Name Date Class Find dy d. Logarithmic/Eponential Differentiation and Related Rates Review AP Calculus 1. y 4. 1 y ln. y ln 1 4. y log9 1 5. e y 6. y log 7. y e 8. e y e 4 1 1 9. y e e 10. 1 y ln 1 e 11.
Name Date Class Find dy d. Logarithmic/Eponential Differentiation and Related Rates Review AP Calculus 1. y 4. 1 y ln. y ln 1 4. y log9 1 5. e y 6. y log 7. y e 8. e y e 4 1 1 9. y e e 10. 1 y ln 1 e 11.
4.1 Implicit Differentiation
 4.1 Implicit Differentiation Learning Objectives A student will be able to: Find the derivative of variety of functions by using the technique of implicit differentiation. Consider the equation We want
4.1 Implicit Differentiation Learning Objectives A student will be able to: Find the derivative of variety of functions by using the technique of implicit differentiation. Consider the equation We want
2.6 Related Rates. The Derivative as a Rate of Change. = ft related rates 175
 2.6 related rates 175 2.6 Related Rates Throughout the next several tions we ll look at a variety of applications of derivatives. Probably no single application will be of interest or use to everyone,
2.6 related rates 175 2.6 Related Rates Throughout the next several tions we ll look at a variety of applications of derivatives. Probably no single application will be of interest or use to everyone,
dy dx dx dx as a BC Calculus 1 The Chain Rule is notation for a which says that we have the
 2.4 2.6 BC Calculus 1 The Chain Rule dy is notation for a which says that we have the for an expression set equal to (the dependent variable), where the variable is x. This is read dee why, dee or the
2.4 2.6 BC Calculus 1 The Chain Rule dy is notation for a which says that we have the for an expression set equal to (the dependent variable), where the variable is x. This is read dee why, dee or the
Math 2413 t2rsu14. Name: 06/06/ Find the derivative of the following function using the limiting process.
 Name: 06/06/014 Math 413 trsu14 1. Find the derivative of the following function using the limiting process. f( x) = 4x + 5x. Find the derivative of the following function using the limiting process. f(
Name: 06/06/014 Math 413 trsu14 1. Find the derivative of the following function using the limiting process. f( x) = 4x + 5x. Find the derivative of the following function using the limiting process. f(
Review for the Final Exam
 Calculus Lia Vas. Integrals. Evaluate the following integrals. (a) ( x 4 x 2 ) dx (b) (2 3 x + x2 4 ) dx (c) (3x + 5) 6 dx (d) x 2 dx x 3 + (e) x 9x 2 dx (f) x dx x 2 (g) xe x2 + dx (h) 2 3x+ dx (i) x
Calculus Lia Vas. Integrals. Evaluate the following integrals. (a) ( x 4 x 2 ) dx (b) (2 3 x + x2 4 ) dx (c) (3x + 5) 6 dx (d) x 2 dx x 3 + (e) x 9x 2 dx (f) x dx x 2 (g) xe x2 + dx (h) 2 3x+ dx (i) x
AP Calculus. Applications of Derivatives. Table of Contents
 AP Calculus 2015 11 03 www.njctl.org Table of Contents click on the topic to go to that section Related Rates Linear Motion Linear Approximation & Differentials L'Hopital's Rule Horizontal Tangents 1 Related
AP Calculus 2015 11 03 www.njctl.org Table of Contents click on the topic to go to that section Related Rates Linear Motion Linear Approximation & Differentials L'Hopital's Rule Horizontal Tangents 1 Related
AP Calculus AB Chapter 2 Test Review #1
 AP Calculus AB Chapter Test Review # Open-Ended Practice Problems:. Nicole just loves drinking chocolate milk out of her special cone cup which has a radius of inches and a height of 8 inches. Nicole pours
AP Calculus AB Chapter Test Review # Open-Ended Practice Problems:. Nicole just loves drinking chocolate milk out of her special cone cup which has a radius of inches and a height of 8 inches. Nicole pours
MATH1910Chapter2TestReview
 Class: Date: MATH1910Chapter2TestReview Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the slope m of the line tangent to the graph of the function
Class: Date: MATH1910Chapter2TestReview Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the slope m of the line tangent to the graph of the function
Implicit Differentiation and Related Rates
 Math 3A Discussion Notes Week 5 October 7 and October 9, 05 Because of the mierm, we re a little behind lecture, but this week s topics will help prepare you for the quiz. Implicit Differentiation and
Math 3A Discussion Notes Week 5 October 7 and October 9, 05 Because of the mierm, we re a little behind lecture, but this week s topics will help prepare you for the quiz. Implicit Differentiation and
See animations and interactive applets of some of these at. Fall_2009/Math123/Notes
 MA123, Chapter 7 Word Problems (pp. 125-153) Chapter s Goal: In this chapter we study the two main types of word problems in Calculus. Optimization Problems. i.e., max - min problems Related Rates See
MA123, Chapter 7 Word Problems (pp. 125-153) Chapter s Goal: In this chapter we study the two main types of word problems in Calculus. Optimization Problems. i.e., max - min problems Related Rates See
AP Calculus. Slide 1 / 101. Slide 2 / 101. Slide 3 / 101. Applications of Derivatives. Table of Contents
 Slide 1 / 101 Slide 2 / 101 AP Calculus Applications of Derivatives 2015-11-03 www.njctl.org Table of Contents click on the topic to go to that section Slide 3 / 101 Related Rates Linear Motion Linear
Slide 1 / 101 Slide 2 / 101 AP Calculus Applications of Derivatives 2015-11-03 www.njctl.org Table of Contents click on the topic to go to that section Slide 3 / 101 Related Rates Linear Motion Linear
UNIT 2 SIMPLE APPLICATION OF DIFFERENTIAL CALCULUS
 Calculus UNIT 2 SIMPLE APPLICATION OF DIFFERENTIAL CALCULUS Structure 2.0 Introduction 2.1 Objectives 2.2 Rate of Change of Quantities 2.3 Increasing and Decreasing Function 2.4 Maima and Minima of Functions
Calculus UNIT 2 SIMPLE APPLICATION OF DIFFERENTIAL CALCULUS Structure 2.0 Introduction 2.1 Objectives 2.2 Rate of Change of Quantities 2.3 Increasing and Decreasing Function 2.4 Maima and Minima of Functions
Section 4.1: Related Rates
 1 Section 4.1: Related Rates Practice HW from Stewart Textbook (not to hand in) p. 67 # 1-19 odd, 3, 5, 9 In a related rates problem, we want to compute the rate of change of one quantity in terms of the
1 Section 4.1: Related Rates Practice HW from Stewart Textbook (not to hand in) p. 67 # 1-19 odd, 3, 5, 9 In a related rates problem, we want to compute the rate of change of one quantity in terms of the
MCV4U1 Worksheet 4.7. dh / dt if neither r nor h is constant?
 MCV4U1 Worksheet 4.7 This worksheet serves as an additional exercise to complement the lesson and the examples given. Worksheets may take more than one day to complete. If you are stuck, read again the
MCV4U1 Worksheet 4.7 This worksheet serves as an additional exercise to complement the lesson and the examples given. Worksheets may take more than one day to complete. If you are stuck, read again the
Section 3.8 Related Rates
 Section 3.8 Related Rates Read and re-read the problem until you understand it. Draw and label a picture which gives the relevant information (if possible). Introduce notation. Assign a symbol to every
Section 3.8 Related Rates Read and re-read the problem until you understand it. Draw and label a picture which gives the relevant information (if possible). Introduce notation. Assign a symbol to every
The volume of a sphere and the radius of the same sphere are related by the formula:
 Related Rates Today is a day in which we explore the behavior of derivatives rather than trying to get new formulas for derivatives. Example Let s ask the following question: Suppose that you are filling
Related Rates Today is a day in which we explore the behavior of derivatives rather than trying to get new formulas for derivatives. Example Let s ask the following question: Suppose that you are filling
AP Calculus AB Semester 1 Practice Final
 Class: Date: AP Calculus AB Semester 1 Practice Final Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the limit (if it exists). lim x x + 4 x a. 6
Class: Date: AP Calculus AB Semester 1 Practice Final Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the limit (if it exists). lim x x + 4 x a. 6
AP Calculus BC Chapter 4 AP Exam Problems A) 4 B) 2 C) 1 D) 0 E) 2 A) 9 B) 12 C) 14 D) 21 E) 40
 Extreme Values in an Interval AP Calculus BC 1. The absolute maximum value of x = f ( x) x x 1 on the closed interval, 4 occurs at A) 4 B) C) 1 D) 0 E). The maximum acceleration attained on the interval
Extreme Values in an Interval AP Calculus BC 1. The absolute maximum value of x = f ( x) x x 1 on the closed interval, 4 occurs at A) 4 B) C) 1 D) 0 E). The maximum acceleration attained on the interval
Mat 270 Final Exam Review Sheet Fall 2012 (Final on December 13th, 7:10 PM - 9:00 PM in PSH 153)
 Mat 70 Final Eam Review Sheet Fall 0 (Final on December th, 7:0 PM - 9:00 PM in PSH 5). Find the slope of the secant line to the graph of y f ( ) between the points f ( b) f ( a) ( a, f ( a)), and ( b,
Mat 70 Final Eam Review Sheet Fall 0 (Final on December th, 7:0 PM - 9:00 PM in PSH 5). Find the slope of the secant line to the graph of y f ( ) between the points f ( b) f ( a) ( a, f ( a)), and ( b,
1 The Derivative and Differrentiability
 1 The Derivative and Differrentiability 1.1 Derivatives and rate of change Exercise 1 Find the equation of the tangent line to f (x) = x 2 at the point (1, 1). Exercise 2 Suppose that a ball is dropped
1 The Derivative and Differrentiability 1.1 Derivatives and rate of change Exercise 1 Find the equation of the tangent line to f (x) = x 2 at the point (1, 1). Exercise 2 Suppose that a ball is dropped
Math 2250, Spring 2017, Practice Sheet for Exam 2
 Math 2250, Spring 2017, Practice Sheet for Exam 2 (1) Find the derivative of the function f(x) = xx (x 2 4) 5 (x 1) 3 e xp x + e x (2) Solve for dy dx x 2 4y 2 =sin(xy) (3) Solve for dx dt given that e
Math 2250, Spring 2017, Practice Sheet for Exam 2 (1) Find the derivative of the function f(x) = xx (x 2 4) 5 (x 1) 3 e xp x + e x (2) Solve for dy dx x 2 4y 2 =sin(xy) (3) Solve for dx dt given that e
MAC 2311 Review
 Name: Class: Date: MAC 2311 Review 2.6-2.9 Numeric Response 1. Calculate y. xy 4 +x 2 y =2x +3y 2. Calculate y. cos xy =x 6 y 3. The position function of a particle is given by s =t 3 10.5t 2 2t,t 0 When
Name: Class: Date: MAC 2311 Review 2.6-2.9 Numeric Response 1. Calculate y. xy 4 +x 2 y =2x +3y 2. Calculate y. cos xy =x 6 y 3. The position function of a particle is given by s =t 3 10.5t 2 2t,t 0 When
All work must be shown in this course for full credit. Unsupported answers may receive NO credit.
 AP Calculus.5 Worksheet All work must be shown in this course for full credit. Unsupported answers may receive NO credit. 1. Consider the function y = sin x. a) Find the equation of the tangent line when
AP Calculus.5 Worksheet All work must be shown in this course for full credit. Unsupported answers may receive NO credit. 1. Consider the function y = sin x. a) Find the equation of the tangent line when
Analyzing Functions. Implicit Functions and Implicit Differentiation
 Analyzing Functions Implicit Functions and Implicit Differentiation In mathematics, an implicit function is a generalization of the concept of a function in which the dependent variable, say, has not been
Analyzing Functions Implicit Functions and Implicit Differentiation In mathematics, an implicit function is a generalization of the concept of a function in which the dependent variable, say, has not been
4.1 & 4.2 Student Notes Using the First and Second Derivatives. for all x in D, where D is the domain of f. The number f()
 4.1 & 4. Student Notes Using the First and Second Derivatives Definition A function f has an absolute maximum (or global maximum) at c if f ( c) f ( x) for all x in D, where D is the domain of f. The number
4.1 & 4. Student Notes Using the First and Second Derivatives Definition A function f has an absolute maximum (or global maximum) at c if f ( c) f ( x) for all x in D, where D is the domain of f. The number
Lecture 9. Section 3.4 Derivative as a Rate of Change Section 3.8 Rates of Change per Unit Time. Jiwen He
 Review Section 3.4 Section 3.8 Lecture 9 Section 3.4 Derivative as a Rate of Change Section 3.8 Rates of Change per Unit Time Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu
Review Section 3.4 Section 3.8 Lecture 9 Section 3.4 Derivative as a Rate of Change Section 3.8 Rates of Change per Unit Time Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu
Related Rates. MATH 151 Calculus for Management. J. Robert Buchanan. Department of Mathematics. J. Robert Buchanan Related Rates
 Related Rates MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics 2014 Related Rates Problems Another common application of the derivative involved situations in which two or
Related Rates MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics 2014 Related Rates Problems Another common application of the derivative involved situations in which two or
APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS
 APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS PROBLEM SET #1 Related Rates ***Calculators Allowed*** 1. An oil tanker spills oil that spreads in a circular pattern whose radius increases at the rate of
APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS PROBLEM SET #1 Related Rates ***Calculators Allowed*** 1. An oil tanker spills oil that spreads in a circular pattern whose radius increases at the rate of
Derivatives and Rates of Change
 Sec.1 Derivatives and Rates of Change A. Slope of Secant Functions rise Recall: Slope = m = = run Slope of the Secant Line to a Function: Examples: y y = y1. From this we are able to derive: x x x1 m y
Sec.1 Derivatives and Rates of Change A. Slope of Secant Functions rise Recall: Slope = m = = run Slope of the Secant Line to a Function: Examples: y y = y1. From this we are able to derive: x x x1 m y
APPLICATIONS OF DERIVATIVES
 ALICATIONS OF DERIVATIVES 6 INTRODUCTION Derivatives have a wide range of applications in engineering, sciences, social sciences, economics and in many other disciplines In this chapter, we shall learn
ALICATIONS OF DERIVATIVES 6 INTRODUCTION Derivatives have a wide range of applications in engineering, sciences, social sciences, economics and in many other disciplines In this chapter, we shall learn
Related Rates In each related rate problem there can be variations in the details. The problems, however, have the same general structure.
 Lab 6 Math 111 Spring 019 Related Rates In each related rate problem there can be variations in the details. The problems, however, have the same general structure. I. Relating Quantities: Independent
Lab 6 Math 111 Spring 019 Related Rates In each related rate problem there can be variations in the details. The problems, however, have the same general structure. I. Relating Quantities: Independent
Final Exam Review / AP Calculus AB
 Chapter : Final Eam Review / AP Calculus AB Use the graph to find each limit. 1) lim f(), lim f(), and lim π - π + π f 5 4 1 y - - -1 - - -4-5 ) lim f(), - lim f(), and + lim f 8 6 4 y -4 - - -1-1 4 5-4
Chapter : Final Eam Review / AP Calculus AB Use the graph to find each limit. 1) lim f(), lim f(), and lim π - π + π f 5 4 1 y - - -1 - - -4-5 ) lim f(), - lim f(), and + lim f 8 6 4 y -4 - - -1-1 4 5-4
Math 241 Homework 6 Solutions
 Math 241 Homework 6 s Section 3.7 (Pages 161-163) Problem 2. Suppose that the radius r and surface area S = 4πr 2 of a sphere are differentiable functions of t. Write an equation that relates ds/ to /.
Math 241 Homework 6 s Section 3.7 (Pages 161-163) Problem 2. Suppose that the radius r and surface area S = 4πr 2 of a sphere are differentiable functions of t. Write an equation that relates ds/ to /.
Due: Wed Oct :30 AM MDT. Question Instructions Make sure you have easy access to all three of these documents.
 Related Rates II: Guided (10862409) Due: Wed Oct 4 2017 07:30 AM MDT Question 1 2 3 4 5 6 Instructions Make sure you have easy access to all three of these documents. Today's Notes and Learning Goals Tips
Related Rates II: Guided (10862409) Due: Wed Oct 4 2017 07:30 AM MDT Question 1 2 3 4 5 6 Instructions Make sure you have easy access to all three of these documents. Today's Notes and Learning Goals Tips
WW Prob Lib1 Math course-section, semester year
 Young-Seon Lee WW Prob Lib Math course-section, semester year WeBWorK assignment due /4/03 at :00 PM..( pt) Give the rational number whose decimal form is: 0 7333333 Answer:.( pt) Solve the following inequality:
Young-Seon Lee WW Prob Lib Math course-section, semester year WeBWorK assignment due /4/03 at :00 PM..( pt) Give the rational number whose decimal form is: 0 7333333 Answer:.( pt) Solve the following inequality:
with dt. with 2. If x = u, find an equation relating du dt
 MATH 2250 Royal Section 3.10: Related Rates EXPANDED VERSION In this section, we consider two (or more) dependent variables that depend on a third variable (the independent variable). Usually, the independent
MATH 2250 Royal Section 3.10: Related Rates EXPANDED VERSION In this section, we consider two (or more) dependent variables that depend on a third variable (the independent variable). Usually, the independent
RELATED RATE PROBLEMS
 MA123, Chapter 7a: Related Rates Word Problems (pp. 140-149, Gootman) Chapter Goals: In this Chapter we learn a general strategy on how to approach related rates problems, one of the main types of word
MA123, Chapter 7a: Related Rates Word Problems (pp. 140-149, Gootman) Chapter Goals: In this Chapter we learn a general strategy on how to approach related rates problems, one of the main types of word
The radius of a circle is increasing at a constant rate of the rate of increase in the area of the circle at the instant when the circumference is?
 Unit #11: Related Rates Topic: More Related Rates Problems Objective: SWBAT apply derivatives to real life applications. Warm Up #5: The radius of a circle is increasing at a constant rate of. What is
Unit #11: Related Rates Topic: More Related Rates Problems Objective: SWBAT apply derivatives to real life applications. Warm Up #5: The radius of a circle is increasing at a constant rate of. What is
p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems
 1 2 p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems Finding Related Rates We have used the chain rule to find dy/dx implicitly, but you can also use the
1 2 p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems Finding Related Rates We have used the chain rule to find dy/dx implicitly, but you can also use the
p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems
 p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems Finding Related Rates We have used the chain rule to find dy/dx implicitly, but you can also use the chain
p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems Finding Related Rates We have used the chain rule to find dy/dx implicitly, but you can also use the chain
(a) At what rate is the circumference of the circle changing when the radius is 10 inches? =2inches per minute and we want to find. c =2 r.
 3.11 Related Rates Problem 1 The radius of a circle is increasing at a rate of 2 inches per minute. (a) At what rate is the circumference of the circle changing when the radius is 10 inches? We know: dr
3.11 Related Rates Problem 1 The radius of a circle is increasing at a rate of 2 inches per minute. (a) At what rate is the circumference of the circle changing when the radius is 10 inches? We know: dr
CHAPTER 3: DERIVATIVES
 (Exercises for Section 3.1: Derivatives, Tangent Lines, and Rates of Change) E.3.1 CHAPTER 3: DERIVATIVES SECTION 3.1: DERIVATIVES, TANGENT LINES, and RATES OF CHANGE In these Exercises, use a version
(Exercises for Section 3.1: Derivatives, Tangent Lines, and Rates of Change) E.3.1 CHAPTER 3: DERIVATIVES SECTION 3.1: DERIVATIVES, TANGENT LINES, and RATES OF CHANGE In these Exercises, use a version
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. C) dc. D) dr dt = 2πdC dt
 MAC 3 Chapter Review Materials (Part III) Topics Include Related Rates, Differentials, and Linear Approximations MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers
MAC 3 Chapter Review Materials (Part III) Topics Include Related Rates, Differentials, and Linear Approximations MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers
Mth 201 Related Rates Practice Problems
 Mth 201 Related Rates Practice Problems 1. A spherical snowball is melting. Its radius is decreasing at 0.2 centimeters per hour when the radius is 15cm. How fast is the volume decreasing at this time?
Mth 201 Related Rates Practice Problems 1. A spherical snowball is melting. Its radius is decreasing at 0.2 centimeters per hour when the radius is 15cm. How fast is the volume decreasing at this time?
More Differentiation Page 1
 More Differentiation Page 1 Directions: Solve the following problems using the available space for scratchwork. Indicate your answers on the front page. Do not spend too much time on any one problem. Note:
More Differentiation Page 1 Directions: Solve the following problems using the available space for scratchwork. Indicate your answers on the front page. Do not spend too much time on any one problem. Note:
Applications of Derivatives
 Applications of Derivatives Big Ideas Connecting the graphs of f, f, f Differentiability Continuity Continuity Differentiability Critical values Mean Value Theorem for Derivatives: Hypothesis: If f is
Applications of Derivatives Big Ideas Connecting the graphs of f, f, f Differentiability Continuity Continuity Differentiability Critical values Mean Value Theorem for Derivatives: Hypothesis: If f is
College Calculus Final Review
 College Calculus Final Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Determine the following limit. (Hint: Use the graph to calculate the limit.)
College Calculus Final Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Determine the following limit. (Hint: Use the graph to calculate the limit.)
Review Questions, Exam 3
 Review Questions, Exam. A child is flying a kite. If the kite is 90 feet above the child s hand level and the wind is blowing it on a horizontal course at 5 feet per second, how fast is the child paying
Review Questions, Exam. A child is flying a kite. If the kite is 90 feet above the child s hand level and the wind is blowing it on a horizontal course at 5 feet per second, how fast is the child paying
Almost all of the questions involving Related Rates will require one of the following relationships to link together the various changing rates:
 Related Rates All quantities that we meet in every-day life change with time, this is especially true in scientific investigations. Related Rate problems are those in which an equation epresses some relationship
Related Rates All quantities that we meet in every-day life change with time, this is especially true in scientific investigations. Related Rate problems are those in which an equation epresses some relationship
Compute the rate of change of one quantity in terms of the rate of change of another quantity.
 3.10 Related Rates Compute the rate of change of one quantity in terms of the rate of change of another quantity. Example 1: If x 2 y x + 4 = 0 and dx/dt = 3, find dy/dt when x = 1. Example 2: Air is being
3.10 Related Rates Compute the rate of change of one quantity in terms of the rate of change of another quantity. Example 1: If x 2 y x + 4 = 0 and dx/dt = 3, find dy/dt when x = 1. Example 2: Air is being
3.8 Exponential Growth and Decay
 3.8 Exponential Growth and Decay Suppose the rate of change of y with respect to t is proportional to y itself. So there is some constant k such that dy dt = ky The only solution to this equation is an
3.8 Exponential Growth and Decay Suppose the rate of change of y with respect to t is proportional to y itself. So there is some constant k such that dy dt = ky The only solution to this equation is an
Stewart - Calculus 8e Chapter 2 Form A. 1. Differentiate. 2. Find the limit. 3. Differentiate.
 Stewart - Calculus 8e Chapter 2 Form A Multivariable Calculus 8th Edition Stewart TEST BANK Full clear download at: https://testbankreal.com/download/multivariable-calculus-8th-editionstewart-test-bank/
Stewart - Calculus 8e Chapter 2 Form A Multivariable Calculus 8th Edition Stewart TEST BANK Full clear download at: https://testbankreal.com/download/multivariable-calculus-8th-editionstewart-test-bank/
a right triangle), we see that x 200 or equivalently x = 200 tan θ. The rate at which the ray of light moves along the shore is
 Example 1: A revolving beacon in a lighthouse makes one revolution every 15 seconds. The beacon is 00 ft from the nearest point P on a straight shoreline. Find the rate at which a ray from the light moves
Example 1: A revolving beacon in a lighthouse makes one revolution every 15 seconds. The beacon is 00 ft from the nearest point P on a straight shoreline. Find the rate at which a ray from the light moves
4. Solve for x: 5. Use the FOIL pattern to multiply (4x 2)(x + 3). 6. Simplify using exponent rules: (6x 3 )(2x) 3
 SUMMER REVIEW FOR STUDENTS COMPLETING ALGEBRA I WEEK 1 1. Write the slope-intercept form of an equation of a. Write a definition of slope. 7 line with a slope of, and a y-intercept of 3. 11 3. You want
SUMMER REVIEW FOR STUDENTS COMPLETING ALGEBRA I WEEK 1 1. Write the slope-intercept form of an equation of a. Write a definition of slope. 7 line with a slope of, and a y-intercept of 3. 11 3. You want
Name Date Period. Multiple Choice
 Name Date Period Worksheet 3.8 Related Rates Show all work. Calculator permitted. Show all set-ups and analysis. Report all answers to 3 decimals and avoid intermediate rounding error. Multiple Choice
Name Date Period Worksheet 3.8 Related Rates Show all work. Calculator permitted. Show all set-ups and analysis. Report all answers to 3 decimals and avoid intermediate rounding error. Multiple Choice
CONNECTED RATE OF CHANGE PACK
 C4 CONNECTED RATE OF CHANGE PACK 1. A vase with a circular cross-section is shown in. Water is flowing into the vase. When the depth of the water is h cm, the volume of water V cm 3 is given by V = 4 πh(h
C4 CONNECTED RATE OF CHANGE PACK 1. A vase with a circular cross-section is shown in. Water is flowing into the vase. When the depth of the water is h cm, the volume of water V cm 3 is given by V = 4 πh(h
MA 137 Calculus 1 with Life Science Applications Related Rates (Section 4.4)
 . MA 137 Calculus 1 with Life Science Applications (Section 4.4). Alberto Corso alberto.corso@uky.edu Department of Mathematics University of Kentucky March 7, 2016 1/8 . An important application of implicit
. MA 137 Calculus 1 with Life Science Applications (Section 4.4). Alberto Corso alberto.corso@uky.edu Department of Mathematics University of Kentucky March 7, 2016 1/8 . An important application of implicit
Math 115 Practice for Exam 3
 Math 115 Practice for Exam 3 Generated March 16, 2017 Name: Instructor: Section Number: 1. This exam has 9 questions. Note that the problems are not of equal difficulty, so you may want to skip over and
Math 115 Practice for Exam 3 Generated March 16, 2017 Name: Instructor: Section Number: 1. This exam has 9 questions. Note that the problems are not of equal difficulty, so you may want to skip over and
Chapter 4 Overview: Derivatives as Rate of Change
 Chapter 4 Overview: Derivatives as Rate of Change Most of last year s derivative work (and the first two chapters) concentrated on tangent lines and extremes the geometric applications of the derivatives.
Chapter 4 Overview: Derivatives as Rate of Change Most of last year s derivative work (and the first two chapters) concentrated on tangent lines and extremes the geometric applications of the derivatives.
Solution: It could be discontinuous, or have a vertical tangent like y = x 1/3, or have a corner like y = x.
 1. Name three different reasons that a function can fail to be differentiable at a point. Give an example for each reason, and explain why your examples are valid. It could be discontinuous, or have a
1. Name three different reasons that a function can fail to be differentiable at a point. Give an example for each reason, and explain why your examples are valid. It could be discontinuous, or have a
Review Sheet for Second Midterm Mathematics 1300, Calculus 1
 Review Sheet for Second Midterm Mathematics 300, Calculus. For what values of is the graph of y = 5 5 both increasing and concave up? >. 2. Where does the tangent line to y = 2 through (0, ) intersect
Review Sheet for Second Midterm Mathematics 300, Calculus. For what values of is the graph of y = 5 5 both increasing and concave up? >. 2. Where does the tangent line to y = 2 through (0, ) intersect
A = 1 2 ab da dt = 1 da. We can find how fast the area is growing at 3 seconds by plugging everything into that differentiated equation: da
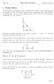 1 Related Rates In most related rates problems, we have an equation that relates a bunch of quantities that are changing over time. For example, suppose we have a right triangle whose base and height are
1 Related Rates In most related rates problems, we have an equation that relates a bunch of quantities that are changing over time. For example, suppose we have a right triangle whose base and height are
FINALS WEEK! MATH 34A TA: Jerry Luo Drop-in Session: TBA LAST UPDATED: 6:54PM, 12 December 2017
 FINALS WEEK! MATH 34A TA: Jerry Luo jerryluo8@math.ucsb.edu Drop-in Session: TBA LAST UPDATED: 6:54PM, 12 December 2017 On this worksheet are selected problems from homeworks 9 and 10 which were less done.
FINALS WEEK! MATH 34A TA: Jerry Luo jerryluo8@math.ucsb.edu Drop-in Session: TBA LAST UPDATED: 6:54PM, 12 December 2017 On this worksheet are selected problems from homeworks 9 and 10 which were less done.
Calculus I - Lecture 14 - Related Rates
 Calculus I - Lecture 14 - Related Rates Lecture Notes: http://www.math.ksu.edu/ gerald/math220d/ Course Syllabus: http://www.math.ksu.edu/math220/spring-2014/indexs14.html Gerald Hoehn (based on notes
Calculus I - Lecture 14 - Related Rates Lecture Notes: http://www.math.ksu.edu/ gerald/math220d/ Course Syllabus: http://www.math.ksu.edu/math220/spring-2014/indexs14.html Gerald Hoehn (based on notes
Implicit Differentiation and Related Rates
 Math 31A Discussion Session Week 5 Notes February 2 and 4, 2016 This week we re going to learn how to find tangent lines to curves which aren t necessarily graphs of functions, using an approach called
Math 31A Discussion Session Week 5 Notes February 2 and 4, 2016 This week we re going to learn how to find tangent lines to curves which aren t necessarily graphs of functions, using an approach called
AP Calculus. Related Rates. Related Rates. Slide 1 / 101 Slide 2 / 101. Slide 4 / 101. Slide 3 / 101. Slide 4 (Answer) / 101.
 Slide 1 / 101 Slide 2 / 101 P alculus pplications of erivatives 2015-11-03 www.njctl.org Slide 3 / 101 Slide 4 / 101 Table of ontents click on the topic to go to that section Related Rates Linear Motion
Slide 1 / 101 Slide 2 / 101 P alculus pplications of erivatives 2015-11-03 www.njctl.org Slide 3 / 101 Slide 4 / 101 Table of ontents click on the topic to go to that section Related Rates Linear Motion
Unit 5 ICM/AB Applications of the Derivative Fall Nov 10 Learn Velocity and Acceleration: HW p P ,103 p.
 Unit 5 ICM/AB Applications of the Derivative Fall 2016 Nov 4 Learn Optimization, New PS up on Optimization, HW pg. 216 3,5,17,19,21,23,25,27,29,33,39,41,49,50 a,b,54 Nov 7 Continue on HW from Nov 4 and
Unit 5 ICM/AB Applications of the Derivative Fall 2016 Nov 4 Learn Optimization, New PS up on Optimization, HW pg. 216 3,5,17,19,21,23,25,27,29,33,39,41,49,50 a,b,54 Nov 7 Continue on HW from Nov 4 and
Find the perimeter of the figure named and shown. Express the perimeter in the same unit of measure that appears on the given side or sides.
 Mth101 Chapter 8 HW Name Find the perimeter of the figure named and shown. Express the perimeter in the same unit of measure that appears on the given side or sides. 1) 1) Rectangle 6 in. 12 in. 12 in.
Mth101 Chapter 8 HW Name Find the perimeter of the figure named and shown. Express the perimeter in the same unit of measure that appears on the given side or sides. 1) 1) Rectangle 6 in. 12 in. 12 in.
MATH 135 Calculus 1 Solutions/Answers for Exam 3 Practice Problems November 18, 2016
 MATH 35 Calculus Solutions/Answers for Exam 3 Practice Problems November 8, 206 I. Find the indicated derivative(s) and simplify. (A) ( y = ln(x) x 7 4 ) x Solution: By the product rule and the derivative
MATH 35 Calculus Solutions/Answers for Exam 3 Practice Problems November 8, 206 I. Find the indicated derivative(s) and simplify. (A) ( y = ln(x) x 7 4 ) x Solution: By the product rule and the derivative
x f(x)
 1. Name three different reasons that a function can fail to be differential at a point. Give an example for each reason, and explain why your examples are valid. 2. Given the following table of values,
1. Name three different reasons that a function can fail to be differential at a point. Give an example for each reason, and explain why your examples are valid. 2. Given the following table of values,
x f(x)
 1. Name three different reasons that a function can fail to be differentiable at a point. Give an example for each reason, and explain why your examples are valid. 2. Given the following table of values,
1. Name three different reasons that a function can fail to be differentiable at a point. Give an example for each reason, and explain why your examples are valid. 2. Given the following table of values,
Math 147 Exam II Practice Problems
 Math 147 Exam II Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Math 147 Exam II Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Absolute Extrema and Constrained Optimization
 Calculus 1 Lia Vas Absolute Extrema and Constrained Optimization Recall that a function f (x) is said to have a relative maximum at x = c if f (c) f (x) for all values of x in some open interval containing
Calculus 1 Lia Vas Absolute Extrema and Constrained Optimization Recall that a function f (x) is said to have a relative maximum at x = c if f (c) f (x) for all values of x in some open interval containing
( ) as a fraction. If both numerator and denominator are
 A. Limits and Horizontal Asymptotes What you are finding: You can be asked to find lim f x x a (H.A.) problem is asking you find lim f x x ( ) and lim f x x ( ). ( ) or lim f x x ± ( ). Typically, a horizontal
A. Limits and Horizontal Asymptotes What you are finding: You can be asked to find lim f x x a (H.A.) problem is asking you find lim f x x ( ) and lim f x x ( ). ( ) or lim f x x ± ( ). Typically, a horizontal
Unit V Applications of Derivatives
 Unit V Applications of Derivatives Curve Sketching Inequalities (Not covered in 3205) Polynomial Rational Functions Related Rate Problems Optimization (Max/Min) Problems 1 Inequalities Linear Polynomial
Unit V Applications of Derivatives Curve Sketching Inequalities (Not covered in 3205) Polynomial Rational Functions Related Rate Problems Optimization (Max/Min) Problems 1 Inequalities Linear Polynomial
Unit V Applications of Derivatives
 Unit V Applications of Derivatives Curve Sketching Inequalities (Covered in 2200) Polynomial Rational Functions Related Rate Problems Optimization (Max/Min) Problems 1 Inequalities Linear Polynomial Rational
Unit V Applications of Derivatives Curve Sketching Inequalities (Covered in 2200) Polynomial Rational Functions Related Rate Problems Optimization (Max/Min) Problems 1 Inequalities Linear Polynomial Rational
Math3A Exam #02 Solution Fall 2017
 Math3A Exam #02 Solution Fall 2017 1. Use the limit definition of the derivative to find f (x) given f ( x) x. 3 2. Use the local linear approximation for f x x at x0 8 to approximate 3 8.1 and write your
Math3A Exam #02 Solution Fall 2017 1. Use the limit definition of the derivative to find f (x) given f ( x) x. 3 2. Use the local linear approximation for f x x at x0 8 to approximate 3 8.1 and write your
Math 103 Selected Homework Solutions, Section 3.9
 Math 103 Selected Homework Solutions, Section 3.9 9. Let s be the distance from the base of the light pole to the top of the man s shadow, and the distance from the light pole to the man. 15 s 6 s We know:
Math 103 Selected Homework Solutions, Section 3.9 9. Let s be the distance from the base of the light pole to the top of the man s shadow, and the distance from the light pole to the man. 15 s 6 s We know:
Mat 210 Business Calculus Final Exam Review Spring Final on April 28 in COOR HALL 199 at 7:30 AM
 f ( Mat Business Calculus Final Eam Review Spring Final on April 8 in COOR HALL 99 at 7: AM. A: Find the limit (if it eists) as indicated. Justify your answer. 8 a) lim (Ans: 6) b) lim (Ans: -) c) lim
f ( Mat Business Calculus Final Eam Review Spring Final on April 8 in COOR HALL 99 at 7: AM. A: Find the limit (if it eists) as indicated. Justify your answer. 8 a) lim (Ans: 6) b) lim (Ans: -) c) lim
