Perturbed Earth rotation. L. D. Akulenko, S. A. Kumakshev, and A. M. Shmatkov
|
|
|
- Jasmin Sherman
- 5 years ago
- Views:
Transcription
1 Perturbed Earth rotation L. D. Akulenko, S. A. Kumakshev, and A. M. Shmatkov 1 Introduction Numerous astrometric studies are based on the dynamic theory of the Earth s rotation with respect to the center of mass [1 5]. It is known from astronomical observations (since the second half of the 19th century and possibly much earlier) that the Earth s rotation axis varies through time in both Earth-fixed and inertial reference frames. This means that the poles and latitudes evolve noticeably within a year. Measurements indicate that this rather complex oscillatory process contains components with very diverse frequency and amplitude characteristics. For example, the small oscillations of the angular velocity vector in an Earth-fixed reference frame contain the main component with an amplitude of and a period of sidereal days [1 4]. The considerable difference between the Chandler period and the period predicted by the classical theory of rigid bodies (the Euler precession period of 305 days for the rigid figure of the Earth) required an explanation. An explanation was partially given on the basis of a model of deformable Earth in the studies of W. Thomson, S. Newcomb, H. Poincaré, H. Geoffreys, A. Love, F. A. Sludskii, M. S. Molodenskii, et al. [4]. Traditionally, this motion is referred to as the free nutation of the deformable Earth or the Chandler wobble of the pole (to be definite, of the North pole). There is also a noticeable component with an amplitude of and a pronounced period of one year (about sidereal days). The observed pole oscillations have a wobbling character. The trajectory of the pole on the Earth s surface is a winding and unwinding spiral with a period of about six years. Analyzing the pole trajectory and predicting its motion are of substantial interest in both scientific and applied aspects. The construction of a high-precision theoretical model of the deformable Earth s rotation, the identification of model parameters on the basis of IERS data, and a reliable prediction of the pole motion 1
2 are very important in inertial navigation problems [6] on time intervals sufficiently large for practical purposes and in a number of astrometric and geophysical problems [1 5]. Let us give some remarks concerning the statement of the problem. To describe the rotation of the deformable Earth and the polar motion, we use the mechanical model of a viscoelastic solid [7]. The Earth is represented as a two-layer planet consisting of an absolutely firm rigid core (a ball) and a viscoelastic mantle. Considering a more complicated model of the figure of the Earth is unjustified, since in this case one would not be able to determine the necessary physicalmechanical characteristics of the planet on the basis of measurements with the accuracy needed. The authors stick to the obvious postulate that the complexity of a model at all stages of its construction should be strictly adequate to the problem to be solved and the accuracy of observation data. From the viewpoint of theoretical mechanics, the analysis of oscillations of the Earth s pole is similar to the study of motions of the gyro axis under perturbing torques with viscoelastic strains taken into account in the quasistatic approximation. At the initial stage of the analysis of the polar motion under perturbing torques, we consider the three-dimensional version of the two-body problem [7, 8]. We assume that the center of mass of a deformable planet (Earth) and a point satellite (Moon) perform a known rotatory-progressive motion around a common center of mass (barycenter), which moves on an elliptic orbit around the Sun. In what follows, on the basis of an asymptotic analysis of the equations of motion in the osculating action-angle variables, we determine stable characteristics of the rotatory-progressive motion of the deformable Earth with respect to center of mass in the quasistatic approximation. First, we find the refined periods (frequencies) of the axial rotation and the Chandler wobble and make a comparison with the spectral analysis data [1 3]. Estimates of the free oscillation amplitudes of the angular velocity vector in the Earth-fixed reference frame are given, and we compare them with the observed values. Using the kinematic and dynamic Euler equations, we construct a mathematical model of the first approximation to the Chandler wobble. In conclusion, we 2
3 numerically determine the parameters of motion by the least squares method on the basis of daily IERS measurement data [2], construct the trajectory, and predict the polar motion, comparing the results with the IERS experimental data. 2 The first-approximation mathematical model of polar oscillations To construct a model of the rotation with respect to the center of mass, we represent the equations in the form of the classical Euler dynamic equations with variable inertia tensor J [1, 3 5, 7 9]: J ω + ω Jω = M, ω = (p, q, r) T, J = J + δj, J = const J = diag(a, B, C ), δj = δj(t), δj J (2.1) Here ω is the angular velocity vector in an Earth-fixed reference frame [4] approximately coinciding with the principal central axes of inertia J of the frozen Earth with regard to the equatorial bulge [1 5, 7]. The additional perturbing terms obtained by the differentiation of the deformable Earth s moment of momentum (see [8, 9]) are included in the perturbing torque M of rather involved structure. It is considered that small variations in the inertia tensor δj can contain various harmonic components caused by gravitational diurnal tides from the Sun and the Moon as well as possibly other components (annual, biannual, monthly, and semidiurnal). The main ingredients in the external perturbing torques M causing nutation oscillations are assumed to be gravitational. The possible presence of terms like Jω does not result in a refinement of the first-approximation model. Attempts to estimate these terms rigorously by taking into account geophysical factors are difficult and have not so far produced satisfactory results. The analysis of their effect in the existing literature is often completely speculative and scholastic, for it is not related to the actual determination of the torques (their amplitudes, direction, and frequency and phase characteristics). The Euler kinematic equations determining the orientation of the Earth-fixed 3
4 axes with respect to the orbital reference frame have the form [10] θ = p cos ϕ q sin ϕ ω 0 (ν) sin ψ, ν = ω 0 (ν) = ω (1 + e cos ν) 2 ψ = p sin ϕ + q cos ϕ sin θ ω 0 (ν) ctg θ cos ψ, e = ϕ = r (p sin ϕ + q cos ϕ) ctg θ + ω 0 (ν) cos ψ sin θ (2.2) Here ν(t) is the true anomaly, e is the eccentricity of the orbit, and ω is a constant determined by the gravitational and focal parameters. The analysis of system (2.1), (2.2) reveals that in the situation corresponding to the polar motion the terms proportional to ω 0 in Eqs. (2.2) prove to be much larger than p and q (approximately by a factor of 300) and are determining for θ and ϕ. This important property is not mentioned in scientific literature, and the abovemention terms were neglected without due justification (the orbital and rotatory motions were separated) [1 5]. Let us calculate the annual component of forced oscillations of the Earth s pole. The expressions for the components of the gravitational torque exerted by the Sun have the following structure [9]: M q = 3ω 2 [(A + δa (C + δc))γ r γ p + δj pq γ r γ q + +δj pr (γ 2 r γ 2 p) δj rq γ p γ q ], ω = ω (1 + e cos ν) 3/2 (2.3) γ p = sin θ sin ϕ, γ q = sin θ cos ϕ, γ r = cos θ To compute M p,r, one makes a cyclic permutation of the subscripts p, q, and r in (2.3). It follows from the analysis of (2.3) that the annual component of polar oscillations can be caused by the term containing the products γ p γ r and γ q γ r of direction cosines. To compute them, we integrate Eqs. (2.3) in the first approximation: r = r 0, ϕ rt + ϕ 0, ν ω t + ν 0, cos θ(ν) = a(θ 0, ψ 0 ) cos ν θ(0) = θ 0 = 66 33, 0.4 a 1, 0 ψ 0 2π (2.4) cos θ sin θ = b(θ 0, ψ 0 ) cos ν + d cos 3ν +..., 0.4 b 4 3π, d 1 The second and higher harmonics with respect to ν result in quantities smaller than the leading terms by a factor of and hence are not taken into account. 4
5 Next, B A is also substantially smaller than C A (approximately by a factor of 160). By estimating the terms for p and q in Eqs. (2.1), by taking into account the expressions (2.4), and by averaging with respect to the fast phase ϕ, we obtain a simplified analytical model of the form ṗ + N p q = æ q r 2 + 3bω 2 χ p cos ν, N p,q N = 2π/T 1 ( )ω q N q p = æ p r 2 3bω 2 χ q cos ν, p(0) = p 0, q(0) = q 0 (2.5) Here κ p and κ q are the mean values of δj pr /B and δj qr /A, which can be slow functions. The coefficients χ p and χ q are obtained by averaging the coefficients of cos ν in the Sun s gravitational torque components with respect to ϕ, and χ p = χ q. As was already indicated, they are due to diurnal tides. The effect of the Moon s gravitational torques on nutation oscillations is relatively small owing to a significant difference in frequencies, and these torques are not taken into account. The right-hand sides of Eqs. (2.5) explicitly contain a harmonic term with a period of one year, which explains the mechanism of the nutation oscillations observed in the IERS records. Although the sensitivity of the coefficients κ p,q is by five orders of magnitude higher than that of χ p,q, the explicit regular mechanism of annual force-torque action by internal (atmospheric, oceanic, and seasonal) geophysical factors with estimated amplitude M h 10 2 kg m 2 s 2 seems to be unfounded from the viewpoint of mechanics. The frequency analysis of the annual oscillations component also suggests that the geophysical interpretation is unsound [1]. The problem of constructing a gravitational-tidal oscillation mechanism with period sufficiently close to the Chandler period requires a separate investigation. 3 Numerical simulation results for the interpolation and prediction problems It is of interest to study the efficiency of the interpolation and prediction of the polar motion by the remarkably simple mathematical model 5
6 x(τ) = (ξ, f(τ)), ξ = (ξ 1,..., ξ 6 ) T, y(τ) = (η, f(τ)) η = (η 1,..., η 6 ) T (3.1) f(τ) = (1, τ, cos 2πΩτ, sin 2πΩτ, cos 2πτ, sin 2πτ) T, Ω = on the basis of known IERS daily data [2]. 0.3 x y Fig. 01. τ Figure 1 shows the theoretical curves x (τ) and y (τ) interpolating the daily measurements on the eight-year interval 0 τ 8 from 1988 to the end of 1995; open symbols indicate the measurement data. The standard deviations are 6
7 σ x = and σ y = 0.017, which shows that the model (3.1) corresponding to the optimal values ξ and η has satisfactory accuracy, where ξ = ( 0.041, , 0.034, 0.194, 0.023, 0.065) T (3.2) η = (0.300, 0.005, 0.193, 0.033, 0.060, 0.020) T The comparison of the coefficients ξ3 and η4 as well as ξ4 and η3, determining the Chandler components of the oscillations, and also ξ5 and η6 as well as ξ6 and η5 (with regard to the factor Ω = 0.845), corresponding to the annual component in (3.2), confirms the above-mentioned structural property of the model (3.1). x y τ Fig. 02. The IERS tries to provide forecasts of the polar motion for days ahead in the annual reports [2] and on the basis of current data (IERS, EOR Product Center, They 7
8 use their own model and technique, which result in a considerably imprecise and unstable forecast requiring weekly correction. The difference between forecasts can be comparable with the maximum deviation of the pole. Figure 2 shows the authors interpolation of observed polar motion on an eightyear interval of IERS daily observations ( ). The corresponding optimal values and standard deviations are ξ = (0.0407, , , , , ) T, σ x = η = (0.3282, , , , , ) T, σ y = Acknowledgments The research was supported by the Russian Foundation for Basic Research (grants Nos , , and ) and by Program NSh References 1. W. H. Munk and G. J. F. Macdonald, The Rotation of the Earth, Univ. Press, Cambridge, IERS Annual Reports, Central Bureau of IERS, Observatoire de Paris, 1990 July 1991 bis 2000 July H. Moritz and I. I. M uller, Earth Rotation: Theory and Observation, Ungar, New York, Yu. N. Avsyuk, Tidal Forces and Natural Processes [in Russian], Izd. OIFZ RAN, Moscow, N. S. Sidorenkov, Physics of Earth Rotation Instability [in Russian], Nauka, Moscow, A. Yu. Ishlinskii, Orientation, Gyros, and Inertial Navigation [in Russian], Nauka, Moscow,
9 7. L. D. Akulenko, S. A. Kumakshev, Yu. G. Markov, and L. V. Rykhlova, A Model for the Polar Motion of the Deformable Earth Adequate for Astrometric Data, Astronomy Reports, Vol. 46, No. 1, pp , L. D. Akulenko, S. A. Kumakshev, Yu. G. Markov, and L. V. Rykhlova, Forecasting the Polar Motions of the Deformable Earth, Astronomy Reports, Vol. 46, No. 10, pp , L. D. Akulenko, S. A. Kumakshev, and Yu. G. Markov, Motion of the Earth s Pole, Doklady Physics, Vol. 47, No. 1, pp , V. V. Beletskii, Satellite Motion Relative to the Center of Mass in a Gravitational Field [in Russian], Izd-vo MGU, Moscow, Yu. V. Linnik, The Least Squares Method and Basics of the Mathematical- Statistical Theory of Reduction of Observations [in Russian], Fizmatgiz, Moscow,
Astronomy 6570 Physics of the Planets. Precession: Free and Forced
 Astronomy 6570 Physics of the Planets Precession: Free and Forced Planetary Precession We have seen above how information concerning the distribution of density within a planet (in particular, the polar
Astronomy 6570 Physics of the Planets Precession: Free and Forced Planetary Precession We have seen above how information concerning the distribution of density within a planet (in particular, the polar
Physics 106a, Caltech 4 December, Lecture 18: Examples on Rigid Body Dynamics. Rotating rectangle. Heavy symmetric top
 Physics 106a, Caltech 4 December, 2018 Lecture 18: Examples on Rigid Body Dynamics I go through a number of examples illustrating the methods of solving rigid body dynamics. In most cases, the problem
Physics 106a, Caltech 4 December, 2018 Lecture 18: Examples on Rigid Body Dynamics I go through a number of examples illustrating the methods of solving rigid body dynamics. In most cases, the problem
expression that describes these corrections with the accuracy of the order of 4. frame usually connected with extragalactic objects.
 RUSSIAN JOURNAL OF EARTH SCIENCES, English Translation, VOL, NO, DECEMBER 998 Russian Edition: JULY 998 On the eects of the inertia ellipsoid triaxiality in the theory of nutation S. M. Molodensky Joint
RUSSIAN JOURNAL OF EARTH SCIENCES, English Translation, VOL, NO, DECEMBER 998 Russian Edition: JULY 998 On the eects of the inertia ellipsoid triaxiality in the theory of nutation S. M. Molodensky Joint
Torque and Rotation Lecture 7
 Torque and Rotation Lecture 7 ˆ In this lecture we finally move beyond a simple particle in our mechanical analysis of motion. ˆ Now we consider the so-called rigid body. Essentially, a particle with extension
Torque and Rotation Lecture 7 ˆ In this lecture we finally move beyond a simple particle in our mechanical analysis of motion. ˆ Now we consider the so-called rigid body. Essentially, a particle with extension
EART162: PLANETARY INTERIORS
 EART162: PLANETARY INTERIORS Francis Nimmo Last Week Applications of fluid dynamics to geophysical problems Navier-Stokes equation describes fluid flow: Convection requires solving the coupled equations
EART162: PLANETARY INTERIORS Francis Nimmo Last Week Applications of fluid dynamics to geophysical problems Navier-Stokes equation describes fluid flow: Convection requires solving the coupled equations
Revision of the physical backgrounds of Earth s rotation
 Revision of the physical backgrounds of Earth s rotation L. Völgyesi Budapest University of Technology and Economics, H-151 Budapest, Müegyetem rkp. 3. Hungary e-mail: lvolgyesi@epito.bme.hu bstract. Rotation
Revision of the physical backgrounds of Earth s rotation L. Völgyesi Budapest University of Technology and Economics, H-151 Budapest, Müegyetem rkp. 3. Hungary e-mail: lvolgyesi@epito.bme.hu bstract. Rotation
Physical Dynamics (SPA5304) Lecture Plan 2018
 Physical Dynamics (SPA5304) Lecture Plan 2018 The numbers on the left margin are approximate lecture numbers. Items in gray are not covered this year 1 Advanced Review of Newtonian Mechanics 1.1 One Particle
Physical Dynamics (SPA5304) Lecture Plan 2018 The numbers on the left margin are approximate lecture numbers. Items in gray are not covered this year 1 Advanced Review of Newtonian Mechanics 1.1 One Particle
Can we see evidence of post-glacial geoidal adjustment in the current slowing rate of rotation of the Earth?
 Can we see evidence of post-glacial geoidal adjustment in the current slowing rate of rotation of the Earth? BARRETO L., FORTIN M.-A., IREDALE A. In this simple analysis, we compare the historical record
Can we see evidence of post-glacial geoidal adjustment in the current slowing rate of rotation of the Earth? BARRETO L., FORTIN M.-A., IREDALE A. In this simple analysis, we compare the historical record
Classical Mechanics III (8.09) Fall 2014 Assignment 3
 Classical Mechanics III (8.09) Fall 2014 Assignment 3 Massachusetts Institute of Technology Physics Department Due September 29, 2014 September 22, 2014 6:00pm Announcements This week we continue our discussion
Classical Mechanics III (8.09) Fall 2014 Assignment 3 Massachusetts Institute of Technology Physics Department Due September 29, 2014 September 22, 2014 6:00pm Announcements This week we continue our discussion
Problem 1. Mathematics of rotations
 Problem 1. Mathematics of rotations (a) Show by algebraic means (i.e. no pictures) that the relationship between ω and is: φ, ψ, θ Feel free to use computer algebra. ω X = φ sin θ sin ψ + θ cos ψ (1) ω
Problem 1. Mathematics of rotations (a) Show by algebraic means (i.e. no pictures) that the relationship between ω and is: φ, ψ, θ Feel free to use computer algebra. ω X = φ sin θ sin ψ + θ cos ψ (1) ω
Angular Momentum L = I ω
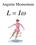 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Geometry of Earth Sun System
 12S56 Geometry of Earth Sun System Figure below shows the basic geometry Northern Hemisphere Winter ω equator Earth s Orbit Ecliptic ω ω SUN equator Northern Hemisphere Spring Northern Hemisphere Fall
12S56 Geometry of Earth Sun System Figure below shows the basic geometry Northern Hemisphere Winter ω equator Earth s Orbit Ecliptic ω ω SUN equator Northern Hemisphere Spring Northern Hemisphere Fall
Angular Momentum L = I ω
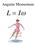 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Ay 1 Lecture 2. Starting the Exploration
 Ay 1 Lecture 2 Starting the Exploration 2.1 Distances and Scales Some Commonly Used Units Distance: Astronomical unit: the distance from the Earth to the Sun, 1 au = 1.496 10 13 cm ~ 1.5 10 13 cm Light
Ay 1 Lecture 2 Starting the Exploration 2.1 Distances and Scales Some Commonly Used Units Distance: Astronomical unit: the distance from the Earth to the Sun, 1 au = 1.496 10 13 cm ~ 1.5 10 13 cm Light
Modern Navigation. Thomas Herring
 12.215 Modern Navigation Thomas Herring Review of Monday s Class Spherical Trigonometry Review plane trigonometry Concepts in Spherical Trigonometry Distance measures Azimuths and bearings Basic formulas:
12.215 Modern Navigation Thomas Herring Review of Monday s Class Spherical Trigonometry Review plane trigonometry Concepts in Spherical Trigonometry Distance measures Azimuths and bearings Basic formulas:
Understanding Earth Rotation Part 2: Physical Foundations and Interpretation
 Understanding Earth Rotation Part 2: Physical Foundations and Interpretation Prof. Dr. Florian Seitz Technische Universität München (TUM) Deutsches Geodätisches Forschungsinstitut (DGFI) Munich, Germany
Understanding Earth Rotation Part 2: Physical Foundations and Interpretation Prof. Dr. Florian Seitz Technische Universität München (TUM) Deutsches Geodätisches Forschungsinstitut (DGFI) Munich, Germany
Laws of gyroscopes / cardanic gyroscope
 Principle If the axis of rotation of the force-free gyroscope is displaced slightly, a nutation is produced. The relationship between precession frequency or nutation frequency and gyrofrequency is examined
Principle If the axis of rotation of the force-free gyroscope is displaced slightly, a nutation is produced. The relationship between precession frequency or nutation frequency and gyrofrequency is examined
Analysis of Chandler wobble excitation, reconstructed from observations of the polar motion of the Earth
 Analysis of Chandler wobble excitation, reconstructed from observations of the polar motion of the Earth Leonid Zotov wolftempus@gmail.com Sternberg Astronomical Institute Lomonosov Moscow State University
Analysis of Chandler wobble excitation, reconstructed from observations of the polar motion of the Earth Leonid Zotov wolftempus@gmail.com Sternberg Astronomical Institute Lomonosov Moscow State University
Earth rotation and Earth gravity field from GRACE observations. Lucia Seoane, Christian Bizouard, Daniel Gambis
 Earth rotation and Earth gravity field from GRACE observations Lucia Seoane, Christian Bizouard, Daniel Gambis Observatoire de Paris SYRTE, 61 av. de l'observatoire, 7514 Paris Introduction Gravity field
Earth rotation and Earth gravity field from GRACE observations Lucia Seoane, Christian Bizouard, Daniel Gambis Observatoire de Paris SYRTE, 61 av. de l'observatoire, 7514 Paris Introduction Gravity field
LAWS OF GYROSCOPES / CARDANIC GYROSCOPE
 LAWS OF GYROSCOPES / CARDANC GYROSCOPE PRNCPLE f the axis of rotation of the force-free gyroscope is displaced slightly, a nutation is produced. The relationship between precession frequency or nutation
LAWS OF GYROSCOPES / CARDANC GYROSCOPE PRNCPLE f the axis of rotation of the force-free gyroscope is displaced slightly, a nutation is produced. The relationship between precession frequency or nutation
2. DYNAMICS OF CLIMATIC AND GEOPHYSICAL INDICES
 4 2. DYNAMICS OF CLIMATIC AND GEOPHYSICAL INDICES Regular and reliable climate observations with measurement and calculation of principal climatic indices were started only about 150 years ago, when organized
4 2. DYNAMICS OF CLIMATIC AND GEOPHYSICAL INDICES Regular and reliable climate observations with measurement and calculation of principal climatic indices were started only about 150 years ago, when organized
IAU 2006 NFA GLOSSARY
 IAU 2006 NFA GLOSSARY Prepared by the IAU Division I Working Group Nomenclature for Fundamental Astronomy'' (latest revision: 20 November 2007) Those definitions corresponding to the IAU 2000 resolutions
IAU 2006 NFA GLOSSARY Prepared by the IAU Division I Working Group Nomenclature for Fundamental Astronomy'' (latest revision: 20 November 2007) Those definitions corresponding to the IAU 2000 resolutions
Third Body Perturbation
 Third Body Perturbation p. 1/30 Third Body Perturbation Modeling the Space Environment Manuel Ruiz Delgado European Masters in Aeronautics and Space E.T.S.I. Aeronáuticos Universidad Politécnica de Madrid
Third Body Perturbation p. 1/30 Third Body Perturbation Modeling the Space Environment Manuel Ruiz Delgado European Masters in Aeronautics and Space E.T.S.I. Aeronáuticos Universidad Politécnica de Madrid
THE LUNAR LIBRATION: COMPARISONS BETWEEN VARIOUS MODELS- A MODEL FITTED TO LLR OBSERVATIONS
 THE LUNAR LIBRATION: COMPARISONS BETWEEN VARIOUS MODELS- A MODEL FITTED TO LLR OBSERVATIONS J. CHAPRONT, G. FRANCOU SYRTE - Observatoire de Paris - UMR 8630/CNRS 61, avenue de l Observatoire 75014 Paris
THE LUNAR LIBRATION: COMPARISONS BETWEEN VARIOUS MODELS- A MODEL FITTED TO LLR OBSERVATIONS J. CHAPRONT, G. FRANCOU SYRTE - Observatoire de Paris - UMR 8630/CNRS 61, avenue de l Observatoire 75014 Paris
On the definition and use of the ecliptic in modern astronomy
 On the definition and use of the ecliptic in modern astronomy Nicole Capitaine (1), Michael Soffel (2) (1) : Observatoire de Paris / SYRTE (2) : Lohrmann Observatory, Dresden Technical University Introduction
On the definition and use of the ecliptic in modern astronomy Nicole Capitaine (1), Michael Soffel (2) (1) : Observatoire de Paris / SYRTE (2) : Lohrmann Observatory, Dresden Technical University Introduction
Euler s Theorem: An arbitrary rotation may be expressed as the product of 3 successive rotations about 3 (in general) different axes.
 11.4 Euler s Angles So far we ve managed to make quite a lot of progress working just with the angular velocity ω a and we haven t needed to introduce an explicit parametrization of the configuration space
11.4 Euler s Angles So far we ve managed to make quite a lot of progress working just with the angular velocity ω a and we haven t needed to introduce an explicit parametrization of the configuration space
ATMOSPHERIC AND OCEANIC EXCITATION OF EARTH ROTATION
 ATMOSPHERIC AND OCEANIC EXCITATION OF EARTH ROTATION S. BÖHM, T. NILSSON, M. SCHINDELEGGER, H. SCHUH Institute of Geodesy and Geophysics, Advanced Geodesy Vienna University of Technology Gußhausstraße
ATMOSPHERIC AND OCEANIC EXCITATION OF EARTH ROTATION S. BÖHM, T. NILSSON, M. SCHINDELEGGER, H. SCHUH Institute of Geodesy and Geophysics, Advanced Geodesy Vienna University of Technology Gußhausstraße
27. Euler s Equations
 27 Euler s Equations Michael Fowler Introduction We ve just seen that by specifying the rotational direction and the angular phase of a rotating body using Euler s angles, we can write the Lagrangian in
27 Euler s Equations Michael Fowler Introduction We ve just seen that by specifying the rotational direction and the angular phase of a rotating body using Euler s angles, we can write the Lagrangian in
Principles of the Global Positioning System Lecture 18" Mathematical models in GPS" Mathematical models used in GPS"
 12.540 Principles of the Global Positioning System Lecture 18" Prof. Thomas Herring" Room 54-820A; 253-5941" tah@mit.edu" http://geoweb.mit.edu/~tah/12.540 " Mathematical models in GPS" Review assignment
12.540 Principles of the Global Positioning System Lecture 18" Prof. Thomas Herring" Room 54-820A; 253-5941" tah@mit.edu" http://geoweb.mit.edu/~tah/12.540 " Mathematical models in GPS" Review assignment
Dynamics of the Earth
 Time Dynamics of the Earth Historically, a day is a time interval between successive upper transits of a given celestial reference point. upper transit the passage of a body across the celestial meridian
Time Dynamics of the Earth Historically, a day is a time interval between successive upper transits of a given celestial reference point. upper transit the passage of a body across the celestial meridian
Lecture 2c: Satellite Orbits
 Lecture 2c: Satellite Orbits Outline 1. Newton s Laws of Mo3on 2. Newton s Law of Universal Gravita3on 3. Kepler s Laws 4. Pu>ng Newton and Kepler s Laws together and applying them to the Earth-satellite
Lecture 2c: Satellite Orbits Outline 1. Newton s Laws of Mo3on 2. Newton s Law of Universal Gravita3on 3. Kepler s Laws 4. Pu>ng Newton and Kepler s Laws together and applying them to the Earth-satellite
5.12 The Aerodynamic Assist Trajectories of Vehicles Propelled by Solar Radiation Pressure References...
 1 The Two-Body Problem... 1 1.1 Position of the Problem... 1 1.2 The Conic Sections and Their Geometrical Properties... 12 1.3 The Elliptic Orbits... 20 1.4 The Hyperbolic and Parabolic Trajectories...
1 The Two-Body Problem... 1 1.1 Position of the Problem... 1 1.2 The Conic Sections and Their Geometrical Properties... 12 1.3 The Elliptic Orbits... 20 1.4 The Hyperbolic and Parabolic Trajectories...
Physical Dynamics (PHY-304)
 Physical Dynamics (PHY-304) Gabriele Travaglini March 31, 2012 1 Review of Newtonian Mechanics 1.1 One particle Lectures 1-2. Frame, velocity, acceleration, number of degrees of freedom, generalised coordinates.
Physical Dynamics (PHY-304) Gabriele Travaglini March 31, 2012 1 Review of Newtonian Mechanics 1.1 One particle Lectures 1-2. Frame, velocity, acceleration, number of degrees of freedom, generalised coordinates.
AS3010: Introduction to Space Technology
 AS3010: Introduction to Space Technology L E C T U R E S 8-9 Part B, Lectures 8-9 23 March, 2017 C O N T E N T S In this lecture, we will look at factors that cause an orbit to change over time orbital
AS3010: Introduction to Space Technology L E C T U R E S 8-9 Part B, Lectures 8-9 23 March, 2017 C O N T E N T S In this lecture, we will look at factors that cause an orbit to change over time orbital
CALCULATION OF POSITION AND VELOCITY OF GLONASS SATELLITE BASED ON ANALYTICAL THEORY OF MOTION
 ARTIFICIAL SATELLITES, Vol. 50, No. 3 2015 DOI: 10.1515/arsa-2015-0008 CALCULATION OF POSITION AND VELOCITY OF GLONASS SATELLITE BASED ON ANALYTICAL THEORY OF MOTION W. Góral, B. Skorupa AGH University
ARTIFICIAL SATELLITES, Vol. 50, No. 3 2015 DOI: 10.1515/arsa-2015-0008 CALCULATION OF POSITION AND VELOCITY OF GLONASS SATELLITE BASED ON ANALYTICAL THEORY OF MOTION W. Góral, B. Skorupa AGH University
Space flying vehicles orbital motion control system synthesis: power invariants
 CHAOS 010, 3rd Chaotic Modeling and Simulation 1-4 June 010 Space flying vehicles orbital motion control system synthesis: power invariants Alexander A. Kolesnikov (PhD) Taganrog Institute of Technology
CHAOS 010, 3rd Chaotic Modeling and Simulation 1-4 June 010 Space flying vehicles orbital motion control system synthesis: power invariants Alexander A. Kolesnikov (PhD) Taganrog Institute of Technology
Tidal Effects on Earth s Surface
 Tidal Effects on Earth s Surface Tom Murphy February, 1 This treatment follows the conventions of F. D. Stacey s Physics of the Earth, and is largely an elaboration on this work. 1 Tidal Potential The
Tidal Effects on Earth s Surface Tom Murphy February, 1 This treatment follows the conventions of F. D. Stacey s Physics of the Earth, and is largely an elaboration on this work. 1 Tidal Potential The
The Pacemaker of the Chandler Wobble
 1 The Pacemaker of the Chandler Wobble Robert W. Grumbine, 1 Robert W. Grumbine, P.O.Box 1243, Greenbelt, MD, 20768, USA. (Robert.Grumbine@gmail.com) 1 Marine Modeling and Analysis Branch, Environmental
1 The Pacemaker of the Chandler Wobble Robert W. Grumbine, 1 Robert W. Grumbine, P.O.Box 1243, Greenbelt, MD, 20768, USA. (Robert.Grumbine@gmail.com) 1 Marine Modeling and Analysis Branch, Environmental
r( θ) = cos2 θ ω rotation rate θ g geographic latitude - - θ geocentric latitude - - Reference Earth Model - WGS84 (Copyright 2002, David T.
 1 Reference Earth Model - WGS84 (Copyright 22, David T. Sandwell) ω spheroid c θ θ g a parameter description formula value/unit GM e (WGS84) 3.9864418 x 1 14 m 3 s 2 M e mass of earth - 5.98 x 1 24 kg
1 Reference Earth Model - WGS84 (Copyright 22, David T. Sandwell) ω spheroid c θ θ g a parameter description formula value/unit GM e (WGS84) 3.9864418 x 1 14 m 3 s 2 M e mass of earth - 5.98 x 1 24 kg
Lecture 41: Highlights
 Lecture 41: Highlights The goal of this lecture is to remind you of some of the key points that we ve covered this semester Note that this is not the complete set of topics that may appear on the final
Lecture 41: Highlights The goal of this lecture is to remind you of some of the key points that we ve covered this semester Note that this is not the complete set of topics that may appear on the final
Ceres Rotation Solution under the Gravitational Torque of the Sun
 Ceres Rotation Solution under the Gravitational Torque of the Sun Martin Lara, Toshio Fukushima, Sebastián Ferrer (*) Real Observatorio de la Armada, San Fernando, Spain ( ) National Astronomical Observatory,
Ceres Rotation Solution under the Gravitational Torque of the Sun Martin Lara, Toshio Fukushima, Sebastián Ferrer (*) Real Observatorio de la Armada, San Fernando, Spain ( ) National Astronomical Observatory,
If the symmetry axes of a uniform symmetric body coincide with the coordinate axes, the products of inertia (Ixy etc.
 Prof. O. B. Wright, Autumn 007 Mechanics Lecture 9 More on rigid bodies, coupled vibrations Principal axes of the inertia tensor If the symmetry axes of a uniform symmetric body coincide with the coordinate
Prof. O. B. Wright, Autumn 007 Mechanics Lecture 9 More on rigid bodies, coupled vibrations Principal axes of the inertia tensor If the symmetry axes of a uniform symmetric body coincide with the coordinate
2 so that the (time-dependent) torque, as measured in space-xed coordinates, is ~N = ma2! 2 (^x cos!t +^y sin!t) 10 = a p 5 2 ^z ~ F 2 ~F 1 = a p 5^z
 1 PHYS 321 Homework Assignment #9 Due: Friday, 22 November 2002 (4 probs) 1. Problem 7-14, B&O p. 280. The situation is as shown above. We take the body-xed axes ^x 0 and ^y 0 to lie in the plane of the
1 PHYS 321 Homework Assignment #9 Due: Friday, 22 November 2002 (4 probs) 1. Problem 7-14, B&O p. 280. The situation is as shown above. We take the body-xed axes ^x 0 and ^y 0 to lie in the plane of the
Tides ( gravity waves ): this is what we see. (bay of Fundy, CAN)
 Tides ( gravity waves ): this is what we see (bay of Fundy, CAN) Which of the following are correct? A. Coastlines experience two high tides each day. B. Tides are 12 hours apart. C. High tide occurs simultaneously
Tides ( gravity waves ): this is what we see (bay of Fundy, CAN) Which of the following are correct? A. Coastlines experience two high tides each day. B. Tides are 12 hours apart. C. High tide occurs simultaneously
Dynamical properties of the Solar System. Second Kepler s Law. Dynamics of planetary orbits. ν: true anomaly
 First Kepler s Law The secondary body moves in an elliptical orbit, with the primary body at the focus Valid for bound orbits with E < 0 The conservation of the total energy E yields a constant semi-major
First Kepler s Law The secondary body moves in an elliptical orbit, with the primary body at the focus Valid for bound orbits with E < 0 The conservation of the total energy E yields a constant semi-major
The Cosmic Perspective Seventh Edition. Making Sense of the Universe: Understanding Motion, Energy, and Gravity. Chapter 4 Lecture
 Chapter 4 Lecture The Cosmic Perspective Seventh Edition Making Sense of the Universe: Understanding Motion, Energy, and Gravity 2014 Pearson Education, Inc. Making Sense of the Universe: Understanding
Chapter 4 Lecture The Cosmic Perspective Seventh Edition Making Sense of the Universe: Understanding Motion, Energy, and Gravity 2014 Pearson Education, Inc. Making Sense of the Universe: Understanding
MATHEMATICAL PHYSICS
 MATHEMATICAL PHYSICS Third Year SEMESTER 1 015 016 Classical Mechanics MP350 Prof. S. J. Hands, Prof. D. M. Heffernan, Dr. J.-I. Skullerud and Dr. M. Fremling Time allowed: 1 1 hours Answer two questions
MATHEMATICAL PHYSICS Third Year SEMESTER 1 015 016 Classical Mechanics MP350 Prof. S. J. Hands, Prof. D. M. Heffernan, Dr. J.-I. Skullerud and Dr. M. Fremling Time allowed: 1 1 hours Answer two questions
arxiv: v1 [nucl-th] 8 Sep 2011
![arxiv: v1 [nucl-th] 8 Sep 2011 arxiv: v1 [nucl-th] 8 Sep 2011](/thumbs/74/70056842.jpg) Tidal Waves a non-adiabatic microscopic description of the yrast states in near-spherical nuclei S. Frauendorf, Y. Gu, and J. Sun Department of Physics, University of Notre Dame, Notre Dame, IN 6556, USA
Tidal Waves a non-adiabatic microscopic description of the yrast states in near-spherical nuclei S. Frauendorf, Y. Gu, and J. Sun Department of Physics, University of Notre Dame, Notre Dame, IN 6556, USA
1 General Definitions and Numerical Standards
 This chapter provides general definitions for some topics and the values of numerical standards that are used in the document. Those are based on the most recent reports of the appropriate working groups
This chapter provides general definitions for some topics and the values of numerical standards that are used in the document. Those are based on the most recent reports of the appropriate working groups
On variation in spin rate of bodies in a variable gravity field. 1 Introduction. Yuriy A. Portnov. P.A.C.S.: Cc
 Annales de la Fondation Louis de Broglie, Volume 39, 2014 63 On variation in spin rate of bodies in a variable gravity field Yuriy A. Portnov Moscow State University of Printing Arts, Russia, 127550, Moscow,
Annales de la Fondation Louis de Broglie, Volume 39, 2014 63 On variation in spin rate of bodies in a variable gravity field Yuriy A. Portnov Moscow State University of Printing Arts, Russia, 127550, Moscow,
ANALYTICAL MODELING OF THE RIGID INTERNAL MOTIONS OF A THREE-LAYER CELESTIAL BODY THROUGH HAMILTON S PRINCIPLE
 ANALYTICAL MODELING OF THE RIGID INTERNAL MOTIONS OF A THREE-LAYER CELESTIAL BODY THROUGH HAMILTON S PRINCIPLE A. ESCAPA Department of Applied Mathematics, University of Alicante PO Box 99, E-03080 Alicante,
ANALYTICAL MODELING OF THE RIGID INTERNAL MOTIONS OF A THREE-LAYER CELESTIAL BODY THROUGH HAMILTON S PRINCIPLE A. ESCAPA Department of Applied Mathematics, University of Alicante PO Box 99, E-03080 Alicante,
arxiv:astro-ph/ v1 17 Jul 2003
 Astronomy & Astrophysics manuscript no. RB-letter September 25, 217 (DOI: will be inserted by hand later) Mercury s spin-orbit model and signature of its dynamical parameters arxiv:astro-ph/37328v1 17
Astronomy & Astrophysics manuscript no. RB-letter September 25, 217 (DOI: will be inserted by hand later) Mercury s spin-orbit model and signature of its dynamical parameters arxiv:astro-ph/37328v1 17
Introduction Fundamental definitions Motivation
 1 Introduction Fundamental definitions Motivation 1.1 Rotation and global shape of the Earth At a very elementary level, the Earth is considered to be an axially symmetric ellipsoid, rotating with uniform
1 Introduction Fundamental definitions Motivation 1.1 Rotation and global shape of the Earth At a very elementary level, the Earth is considered to be an axially symmetric ellipsoid, rotating with uniform
13. Rigid Body Dynamics II
 University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 13. Rigid Body Dynamics II Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 13. Rigid Body Dynamics II Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
Basics of Kepler and Newton. Orbits of the planets, moons,
 Basics of Kepler and Newton Orbits of the planets, moons, Kepler s Laws, as derived by Newton. Kepler s Laws Universal Law of Gravity Three Laws of Motion Deriving Kepler s Laws Recall: The Copernican
Basics of Kepler and Newton Orbits of the planets, moons, Kepler s Laws, as derived by Newton. Kepler s Laws Universal Law of Gravity Three Laws of Motion Deriving Kepler s Laws Recall: The Copernican
The Tides: Consider Moon s Gravity
 The Tides: Consider Moon s Gravity Pulls all points on Earth toward Moon s center of mass. near side of Earth is attracted more than far side because force of gravity decreases with increasing distance.
The Tides: Consider Moon s Gravity Pulls all points on Earth toward Moon s center of mass. near side of Earth is attracted more than far side because force of gravity decreases with increasing distance.
Prof. E. Calais Purdue University - EAS Department CIVL 3273
 Prof. E. Calais Purdue University - EAS Department CIVL 3273 ecalais@purdue.edu GPS Geodesy - Spring 2008 Geoid of Western Hemisphere. Image from University of Texas Center for Space Research and NASA.
Prof. E. Calais Purdue University - EAS Department CIVL 3273 ecalais@purdue.edu GPS Geodesy - Spring 2008 Geoid of Western Hemisphere. Image from University of Texas Center for Space Research and NASA.
Optimal Fault-Tolerant Configurations of Thrusters
 Optimal Fault-Tolerant Configurations of Thrusters By Yasuhiro YOSHIMURA ) and Hirohisa KOJIMA, ) ) Aerospace Engineering, Tokyo Metropolitan University, Hino, Japan (Received June st, 7) Fault tolerance
Optimal Fault-Tolerant Configurations of Thrusters By Yasuhiro YOSHIMURA ) and Hirohisa KOJIMA, ) ) Aerospace Engineering, Tokyo Metropolitan University, Hino, Japan (Received June st, 7) Fault tolerance
Physics 312, Winter 2007, Practice Final
 Physics 312, Winter 2007, Practice Final Time: Two hours Answer one of Question 1 or Question 2 plus one of Question 3 or Question 4 plus one of Question 5 or Question 6. Each question carries equal weight.
Physics 312, Winter 2007, Practice Final Time: Two hours Answer one of Question 1 or Question 2 plus one of Question 3 or Question 4 plus one of Question 5 or Question 6. Each question carries equal weight.
Which of the following are correct?
 The Tides: Consider Moon s Gravity Pulls all points on earth toward Moon s center of mass. near side of Earth is attracted more than far side because force of gravity decreases with increasing distance.
The Tides: Consider Moon s Gravity Pulls all points on earth toward Moon s center of mass. near side of Earth is attracted more than far side because force of gravity decreases with increasing distance.
8.012 Physics I: Classical Mechanics Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
8.012 Physics I: Classical Mechanics Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
Earth orientation parameters: excitation by atmosphere, oceans and geomagnetic jerks
 Earth orientation parameters: excitation by atmosphere, oceans and geomagnetic jerks Jan Vondrák and Cyril Ron, Astronomical Inst., Czech Academy of Sciences, Prague Contents: Introduction; Description
Earth orientation parameters: excitation by atmosphere, oceans and geomagnetic jerks Jan Vondrák and Cyril Ron, Astronomical Inst., Czech Academy of Sciences, Prague Contents: Introduction; Description
Rigid bodies - general theory
 Rigid bodies - general theory Kinetic Energy: based on FW-26 Consider a system on N particles with all their relative separations fixed: it has 3 translational and 3 rotational degrees of freedom. Motion
Rigid bodies - general theory Kinetic Energy: based on FW-26 Consider a system on N particles with all their relative separations fixed: it has 3 translational and 3 rotational degrees of freedom. Motion
Free polar motion of a triaxial and elastic body in Hamiltonian formalism: Application to the Earth and Mars
 A&A 43, 111 1113 (5) DOI: 1.151/4-6361:4131 c ESO 5 Astronomy & Astrophysics Free polar motion of a triaxial and elastic body in Hamiltonian formalism: Application to the Earth and Mars M. Folgueira 1,
A&A 43, 111 1113 (5) DOI: 1.151/4-6361:4131 c ESO 5 Astronomy & Astrophysics Free polar motion of a triaxial and elastic body in Hamiltonian formalism: Application to the Earth and Mars M. Folgueira 1,
Formation flying in elliptic orbits with the J 2 perturbation
 Research in Astron. Astrophys. 2012 Vol. 12 No. 11, 1563 1575 http://www.raa-journal.org http://www.iop.org/journals/raa Research in Astronomy and Astrophysics Formation flying in elliptic orbits with
Research in Astron. Astrophys. 2012 Vol. 12 No. 11, 1563 1575 http://www.raa-journal.org http://www.iop.org/journals/raa Research in Astronomy and Astrophysics Formation flying in elliptic orbits with
Chapter 4 The Equations of Motion
 Chapter 4 The Equations of Motion Flight Mechanics and Control AEM 4303 Bérénice Mettler University of Minnesota Feb. 20-27, 2013 (v. 2/26/13) Bérénice Mettler (University of Minnesota) Chapter 4 The Equations
Chapter 4 The Equations of Motion Flight Mechanics and Control AEM 4303 Bérénice Mettler University of Minnesota Feb. 20-27, 2013 (v. 2/26/13) Bérénice Mettler (University of Minnesota) Chapter 4 The Equations
Physics 106b/196b Problem Set 9 Due Jan 19, 2007
 Physics 06b/96b Problem Set 9 Due Jan 9, 2007 Version 3: January 8, 2007 This problem set focuses on dynamics in rotating coordinate systems (Section 5.2), with some additional early material on dynamics
Physics 06b/96b Problem Set 9 Due Jan 9, 2007 Version 3: January 8, 2007 This problem set focuses on dynamics in rotating coordinate systems (Section 5.2), with some additional early material on dynamics
TIDE PREDICTION FOR THE DOWNSTREAM BOUNDARY CONDITION OF THE CHAO- PHRAYA RIVER MODEL USING HARMONIC ANALYSIS
 TIDE PREDICTION FOR THE DOWNSTREAM BOUNDARY CONDITION OF THE CHAO- PHRAYA RIVER MODEL USING HARMONIC ANALYSIS Supatchaya Chuanpongpanich Dr-Ing. Phatcharasak Arlai Prof. Manfred Koch PAssoc. Prof. Keni
TIDE PREDICTION FOR THE DOWNSTREAM BOUNDARY CONDITION OF THE CHAO- PHRAYA RIVER MODEL USING HARMONIC ANALYSIS Supatchaya Chuanpongpanich Dr-Ing. Phatcharasak Arlai Prof. Manfred Koch PAssoc. Prof. Keni
Dynamics of the conservative and dissipative. spin orbit problem
 Dynamics of the conservative and dissipative spin orbit problem Alessandra Celletti Dipartimento di Matematica, Università di Roma Tor Vergata, Via della Ricerca Scientifica, I-0033 Roma (Italy), celletti@mat.uniroma2.it
Dynamics of the conservative and dissipative spin orbit problem Alessandra Celletti Dipartimento di Matematica, Università di Roma Tor Vergata, Via della Ricerca Scientifica, I-0033 Roma (Italy), celletti@mat.uniroma2.it
Autonomous Underwater Vehicles: Equations of Motion
 Autonomous Underwater Vehicles: Equations of Motion Monique Chyba - November 18, 2015 Departments of Mathematics, University of Hawai i at Mānoa Elective in Robotics 2015/2016 - Control of Unmanned Vehicles
Autonomous Underwater Vehicles: Equations of Motion Monique Chyba - November 18, 2015 Departments of Mathematics, University of Hawai i at Mānoa Elective in Robotics 2015/2016 - Control of Unmanned Vehicles
Principles of Global Positioning Systems Spring 2008
 MIT OpenCourseWare http://ocw.mit.edu 12.540 Principles of Global Positioning Systems Spring 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 12.540
MIT OpenCourseWare http://ocw.mit.edu 12.540 Principles of Global Positioning Systems Spring 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 12.540
Effects of zonal deformations and the Earth s rotation rate variations on precession-nutation
 A&A 428, 255 260 (2004) DOI: 10.1051/0004-6361:20035952 c ESO 2004 Astronomy & Astrophysics Effects of zonal deformations and the Earth s rotation rate variations on precession-nutation S. Lambert 1 and
A&A 428, 255 260 (2004) DOI: 10.1051/0004-6361:20035952 c ESO 2004 Astronomy & Astrophysics Effects of zonal deformations and the Earth s rotation rate variations on precession-nutation S. Lambert 1 and
Gravitorotational Dragging
 1 Gravitorotational Dragging Mohamed E. Hassani 1 Institute for Fundamental Research BP.197, CTR, GHARDAIA 478, ALGERIA Abstract: Previous work on the concept of gravitorotational acceleration field (GRAF)
1 Gravitorotational Dragging Mohamed E. Hassani 1 Institute for Fundamental Research BP.197, CTR, GHARDAIA 478, ALGERIA Abstract: Previous work on the concept of gravitorotational acceleration field (GRAF)
COMBINING GPS AND VLBI MEASUREMENTS OF CELESTIAL MOTION OF THE EARTH S SPIN AXIS AND UNIVERSAL TIME. Jan VONDRÁK* and Cyril RON
 Acta Geodyn. Geomater., Vol.2, No.3 (139), 87-94, 2005 COMBINING GPS AND VLBI MEASUREMENTS OF CELESTIAL MOTION OF THE EARTH S SPIN AXIS AND UNIVERSAL TIME Jan VONDRÁK* and Cyril RON Department of Galaxies
Acta Geodyn. Geomater., Vol.2, No.3 (139), 87-94, 2005 COMBINING GPS AND VLBI MEASUREMENTS OF CELESTIAL MOTION OF THE EARTH S SPIN AXIS AND UNIVERSAL TIME Jan VONDRÁK* and Cyril RON Department of Galaxies
ORBITS WRITTEN Q.E. (June 2012) Each of the five problems is valued at 20 points. (Total for exam: 100 points)
 ORBITS WRITTEN Q.E. (June 2012) Each of the five problems is valued at 20 points. (Total for exam: 100 points) PROBLEM 1 A) Summarize the content of the three Kepler s Laws. B) Derive any two of the Kepler
ORBITS WRITTEN Q.E. (June 2012) Each of the five problems is valued at 20 points. (Total for exam: 100 points) PROBLEM 1 A) Summarize the content of the three Kepler s Laws. B) Derive any two of the Kepler
Lecture 38: Equations of Rigid-Body Motion
 Lecture 38: Equations of Rigid-Body Motion It s going to be easiest to find the equations of motion for the object in the body frame i.e., the frame where the axes are principal axes In general, we can
Lecture 38: Equations of Rigid-Body Motion It s going to be easiest to find the equations of motion for the object in the body frame i.e., the frame where the axes are principal axes In general, we can
PHYS 705: Classical Mechanics. Euler s Equations
 1 PHYS 705: Classical Mechanics Euler s Equations 2 Euler s Equations (set up) We have seen how to describe the kinematic properties of a rigid body. Now, we would like to get equations of motion for it.
1 PHYS 705: Classical Mechanics Euler s Equations 2 Euler s Equations (set up) We have seen how to describe the kinematic properties of a rigid body. Now, we would like to get equations of motion for it.
arxiv: v1 [astro-ph.ep] 12 Dec 2016
![arxiv: v1 [astro-ph.ep] 12 Dec 2016 arxiv: v1 [astro-ph.ep] 12 Dec 2016](/thumbs/94/118262213.jpg) Astronomy & Astrophysics manuscript no. manuscript_arxiv c ESO 2018 December 20, 2018 Frequency-dependent tidal dissipation in a viscoelastic Saturnian core and expansion of Mimas semi-major axis arxiv:1612.03664v1
Astronomy & Astrophysics manuscript no. manuscript_arxiv c ESO 2018 December 20, 2018 Frequency-dependent tidal dissipation in a viscoelastic Saturnian core and expansion of Mimas semi-major axis arxiv:1612.03664v1
The final publication is available at Springer. DOI: / _6
 Originally published as: Seitz, F., H. Schuh: Earth Rotation. In: Sciences of Geodesy I: Advances and Future Directions, Xu, G. (Ed.), 185 227, Springer, Heidelberg, ISBN 978 3 642 11744, 21. The final
Originally published as: Seitz, F., H. Schuh: Earth Rotation. In: Sciences of Geodesy I: Advances and Future Directions, Xu, G. (Ed.), 185 227, Springer, Heidelberg, ISBN 978 3 642 11744, 21. The final
Love Numbers and Gravimetric Factor for Diurnal Tides. Piravonu M. Mathews
 Journal of the Geodetic Society of Japan Vol. 46, No. 4, (2001), pp. 231-236 Love Numbers and Gravimetric Factor for Diurnal Tides Piravonu M. Mathews Department of Theoretical Physics, University of Madras
Journal of the Geodetic Society of Japan Vol. 46, No. 4, (2001), pp. 231-236 Love Numbers and Gravimetric Factor for Diurnal Tides Piravonu M. Mathews Department of Theoretical Physics, University of Madras
Research Article Variation of the Equator due to a Highly Inclined and Eccentric Disturber
 Hindawi Publishing Corporation Mathematical Problems in Engineering Volume 009, Article ID 467865, 10 pages doi:10.1155/009/467865 Research Article Variation of the Equator due to a Highly Inclined and
Hindawi Publishing Corporation Mathematical Problems in Engineering Volume 009, Article ID 467865, 10 pages doi:10.1155/009/467865 Research Article Variation of the Equator due to a Highly Inclined and
Equation of orbital velocity: v 2 =GM(2/r 1/a) where: G is the gravitational constant (G=6.67x10 11 N/m 3 kg), M is the mass of the sun (or central
 Everything in Orbit Orbital Velocity Orbital velocity is the speed at which a planetary body moves in its orbit around another body. If orbits were circular, this velocity would be constant. However, from
Everything in Orbit Orbital Velocity Orbital velocity is the speed at which a planetary body moves in its orbit around another body. If orbits were circular, this velocity would be constant. However, from
Principles of the Global Positioning System Lecture 04"
 12.540 Principles of the Global Positioning System Lecture 04" Prof. Thomas Herring" Room 54-820A; 253-5941" tah@mit.edu" http://geoweb.mit.edu/~tah/12.540 " Review" So far we have looked at measuring
12.540 Principles of the Global Positioning System Lecture 04" Prof. Thomas Herring" Room 54-820A; 253-5941" tah@mit.edu" http://geoweb.mit.edu/~tah/12.540 " Review" So far we have looked at measuring
On Sun-Synchronous Orbits and Associated Constellations
 On Sun-Synchronous Orbits and Associated Constellations Daniele Mortari, Matthew P. Wilkins, and Christian Bruccoleri Department of Aerospace Engineering, Texas A&M University, College Station, TX 77843,
On Sun-Synchronous Orbits and Associated Constellations Daniele Mortari, Matthew P. Wilkins, and Christian Bruccoleri Department of Aerospace Engineering, Texas A&M University, College Station, TX 77843,
Introduction to Astronomy
 Introduction to Astronomy AST0111-3 (Astronomía) Semester 2014B Prof. Thomas H. Puzia Theme Our Sky 1. Celestial Sphere 2. Diurnal Movement 3. Annual Movement 4. Lunar Movement 5. The Seasons 6. Eclipses
Introduction to Astronomy AST0111-3 (Astronomía) Semester 2014B Prof. Thomas H. Puzia Theme Our Sky 1. Celestial Sphere 2. Diurnal Movement 3. Annual Movement 4. Lunar Movement 5. The Seasons 6. Eclipses
CHAPTER 6 SOLID EARTH TIDES
 CHAPTER 6 SOLID EARTH TIDES The solid Earth tide model is based on an abbreviated form of the Wahr model (Wahr, 98) using the Earth model 66A of Gilbert and Dziewonski (975). The Love numbers for the induced
CHAPTER 6 SOLID EARTH TIDES The solid Earth tide model is based on an abbreviated form of the Wahr model (Wahr, 98) using the Earth model 66A of Gilbert and Dziewonski (975). The Love numbers for the induced
Direct measurement of diurnal polar motion by ring laser gyroscopes
 JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 109,, doi:10.1029/2003jb002803, 2004 Direct measurement of diurnal polar motion by ring laser gyroscopes K. U. Schreiber, A. Velikoseltsev, and M. Rothacher Forschungseinrichtung
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 109,, doi:10.1029/2003jb002803, 2004 Direct measurement of diurnal polar motion by ring laser gyroscopes K. U. Schreiber, A. Velikoseltsev, and M. Rothacher Forschungseinrichtung
ROTATIONAL STABILITY OF A CHARGED DIELEC- TRIC RIGID BODY IN A UNIFORM MAGNETIC FIELD
 Progress In Electromagnetics Research Letters, Vol. 11, 103 11, 009 ROTATIONAL STABILITY OF A CHARGED DIELEC- TRIC RIGID BODY IN A UNIFORM MAGNETIC FIELD G.-Q. Zhou Department of Physics Wuhan University
Progress In Electromagnetics Research Letters, Vol. 11, 103 11, 009 ROTATIONAL STABILITY OF A CHARGED DIELEC- TRIC RIGID BODY IN A UNIFORM MAGNETIC FIELD G.-Q. Zhou Department of Physics Wuhan University
Transcendental cases in stability problem. Hamiltonian systems
 of Hamiltonian systems Boris S. Bardin Moscow Aviation Institute (Technical University) Faculty of Applied Mathematics and Physics Department of Theoretical Mechanics Hamiltonian Dynamics and Celestial
of Hamiltonian systems Boris S. Bardin Moscow Aviation Institute (Technical University) Faculty of Applied Mathematics and Physics Department of Theoretical Mechanics Hamiltonian Dynamics and Celestial
As a starting point of our derivation of the equations of motion for a rigid body, we employ d Alembert s principle:
 MEG6007: Advanced Dynamics -Principles and Computational Methods (Fall, 017) Lecture 10: Equations of Motion for a Rigid Body 10.1 D Alembert s Principle for A Free Rigid Body As a starting point of our
MEG6007: Advanced Dynamics -Principles and Computational Methods (Fall, 017) Lecture 10: Equations of Motion for a Rigid Body 10.1 D Alembert s Principle for A Free Rigid Body As a starting point of our
Satellite Communications
 Satellite Communications Lecture (3) Chapter 2.1 1 Gravitational Force Newton s 2nd Law: r r F = m a Newton s Law Of Universal Gravitation (assuming point masses or spheres): Putting these together: r
Satellite Communications Lecture (3) Chapter 2.1 1 Gravitational Force Newton s 2nd Law: r r F = m a Newton s Law Of Universal Gravitation (assuming point masses or spheres): Putting these together: r
Lecture 38: Equations of Rigid-Body Motion
 Lecture 38: Equations of Rigid-Body Motion It s going to be easiest to find the equations of motion for the object in the body frame i.e., the frame where the axes are principal axes In general, we can
Lecture 38: Equations of Rigid-Body Motion It s going to be easiest to find the equations of motion for the object in the body frame i.e., the frame where the axes are principal axes In general, we can
1/30. Rigid Body Rotations. Dave Frank
 . 1/3 Rigid Body Rotations Dave Frank A Point Particle and Fundamental Quantities z 2/3 m v ω r y x Angular Velocity v = dr dt = ω r Kinetic Energy K = 1 2 mv2 Momentum p = mv Rigid Bodies We treat a rigid
. 1/3 Rigid Body Rotations Dave Frank A Point Particle and Fundamental Quantities z 2/3 m v ω r y x Angular Velocity v = dr dt = ω r Kinetic Energy K = 1 2 mv2 Momentum p = mv Rigid Bodies We treat a rigid
ASTRONOMICAL REFERENCE SYSTEMS AND FRAMES, ASTROMETRIC TECHNIQUES AND CATALOGS
 1 ASTRONOMICAL REFERENCE SYSTEMS AND FRAMES, ASTROMETRIC TECHNIQUES AND CATALOGS Jan Vondrák, Astronomical Institute Prague P PART 1: Reference systems and frames used in astronomy:! Historical outline,
1 ASTRONOMICAL REFERENCE SYSTEMS AND FRAMES, ASTROMETRIC TECHNIQUES AND CATALOGS Jan Vondrák, Astronomical Institute Prague P PART 1: Reference systems and frames used in astronomy:! Historical outline,
Polhode Motion, Trapped Flux, and the GP-B Science Data Analysis. Alex Silbergleit, John Conklin
 Polhode Motion, Trapped Flux, and the GP-B Science Data Analysis Alex Silbergleit, John Conklin and the Polhode/Trapped Flux Mapping Task Team Outline 1. Gyro Polhode Motion, Trapped Flux, and GP-B Readout
Polhode Motion, Trapped Flux, and the GP-B Science Data Analysis Alex Silbergleit, John Conklin and the Polhode/Trapped Flux Mapping Task Team Outline 1. Gyro Polhode Motion, Trapped Flux, and GP-B Readout
Classical Mechanics. Luis Anchordoqui
 1 Rigid Body Motion Inertia Tensor Rotational Kinetic Energy Principal Axes of Rotation Steiner s Theorem Euler s Equations for a Rigid Body Eulerian Angles Review of Fundamental Equations 2 Rigid body
1 Rigid Body Motion Inertia Tensor Rotational Kinetic Energy Principal Axes of Rotation Steiner s Theorem Euler s Equations for a Rigid Body Eulerian Angles Review of Fundamental Equations 2 Rigid body
ESS314. Basics of Geophysical Fluid Dynamics by John Booker and Gerard Roe. Conservation Laws
 ESS314 Basics of Geophysical Fluid Dynamics by John Booker and Gerard Roe Conservation Laws The big differences between fluids and other forms of matter are that they are continuous and they deform internally
ESS314 Basics of Geophysical Fluid Dynamics by John Booker and Gerard Roe Conservation Laws The big differences between fluids and other forms of matter are that they are continuous and they deform internally
Tides: this is what we see
 Last time Wind generated waves and Tsunami These are wind and earthquake generated waves Today: Tides These are Gravity waves How are they generated What are their intersting complexities? Low tide (decrease
Last time Wind generated waves and Tsunami These are wind and earthquake generated waves Today: Tides These are Gravity waves How are they generated What are their intersting complexities? Low tide (decrease
UNITS AND MEASUREMENTS
 Chapter Two UNITS AND MEASUREMENTS MCQ I 2.1 The number of significant figures in 0.06900 is (a) 5 (b) 4 (c) 2 (d) 3 2.2 The sum of the numbers 436.32, 227.2 and 0.301 in appropriate significant figures
Chapter Two UNITS AND MEASUREMENTS MCQ I 2.1 The number of significant figures in 0.06900 is (a) 5 (b) 4 (c) 2 (d) 3 2.2 The sum of the numbers 436.32, 227.2 and 0.301 in appropriate significant figures
