Astronomy 6570 Physics of the Planets. Precession: Free and Forced
|
|
|
- Johnathan Walter Sharp
- 5 years ago
- Views:
Transcription
1 Astronomy 6570 Physics of the Planets Precession: Free and Forced
2 Planetary Precession We have seen above how information concerning the distribution of density within a planet (in particular, the polar moment of inertia factor, C/MR 2 ) can be derived from measurements of the oblateness and J 2 of a rotating planet. In some cases, notably the Earth and Mars and probably Saturn in the relatively near future, we can also obtain such information from studying the planet s spin-axis precession. Precession may take one (or both) of two forms free or Eulerian precession, and forced precession. Free precession ω! α C Let the principal moments of inertia of the planet (or satellite) be A B < C, and the corresponding body-fixed principal axes be denoted 1, 2, and 3. The angular momentum of the planet relative to its center of mass is H = I i ω!!! = Aω 1 ˆx 1 + Bω 2 ˆx 2 + Cω 3 ˆx 3 where I is the inertia tensor and ˆx! i are the principal axes. If there are no external torques onthe planet, then we have d! H dt =! H t +! ω! H = 0 ( ) =! I i! "ω +! ω! I i! ω Term due to rotating coordinate system
3 In terms of Cartesian components, A!ω 1 + ( C B)ω 2 ω 3 = 0 (1) B!ω 2 + ( A C)ω 3 ω 1 = 0 (2) C!ω 3 + ( B A)ω 1 ω 2 = 0 (3) These equations are know as Euler's equations. In the case of a planet flattened by rotation, so that A = B < C, they have a very simple solution: (3) C!ω 3 = 0 ω 3 = constant d (1) : A!! dt ω + C A 1 ( ) ω 3!ω 2 = 0 A!! ω 1 + ( C A) 2 ω 2 ω 3 1 A i.e.!! ω 1 + C A A ω 3 ω 1 = 0 2 = 0 from (2) Writing C A A ω = σ, the general solution is 3 ω 1 = β cos σ ( t t 0 ) A σβ ω 2 = + sin σ ( t t C A ω 0 ) 3 ( ) = β sin σ t t 0 i.e., the instantaneous angular velocity vector, ω, precesses around the C axis at a rate σ, with a constant " angular displacement, α, given by tan α = β ω (See diagram next slide)
4 Such a precessional motion (known as the "Chandler Wobble") is observed for the Earth, with a very small amplitude of α = 0 ʹʹ.2 = rad. (The corresponding linear displacement of ω from the C axis at the! Earth's poles is α R 6 meters.) The observed period, however, is 2π σ obs ~ 343 days, whereas the period predicted by the above solution is 2π A = σ obs C A i 2π # 306 days. ω 3 (see below) This discrepancy was unresolved for many years, but was eventually shown by Simon Newcomb to be due to non-rigidity of the Earth s mantle. This led to one of the earliest estimates of the Earth s elasticity by Lord Rayleigh*. (Exercise left to the student: describe the motion, relative to inertial space, of the Earth s C axis during a precessional cycle.) Footnote: Free precession is sometimes referred to as Eulerian nutation in mechanics books. This term is confusing, as the Earth also experiences an oscillatory component of its forced precession with an 18 year period which astronomers refer to as nutation. *More recent studies have suggested that the excitation of the Chandler wobble is due to variations in salinity and temperature of the ocean, as well as changes in ocean currents and atmospheric circulation. Other possible contributors include large earthquakes.
5 Observed variations in the Earth s Length of Day (LOD) and pole position (x, y) since Data from the Bureau of Time, Paris.
6 Forced Precession Because of the rotational flattening of a planet s figure, the sun and any large, non-equatorial satellites exert a torque on the planet which attempts to align the planet s spin axis with the normal to the orbit plane. The actual effect of such a torque is to force a precession of the spin axis about the orbit normal, as follows: ˆn = orbit normal!ω = spin vector i = inclination of orbit on planet's equator T = satellite/solar torque! H = C ω = spin angular momentum!! In time δt, the angular momentum changes by δ! H =! T δt. the angular momentum vector rotates about ˆn by an angle δφ = T δt H sini precession rate = dφ dt = = T Cω sin i T H sin i
7 To calculate T, we consider the reaction torque exerted by the planet on the satellite, averaged around one orbit: S = satellite/sun N = ascending node on Equator NP = φ SP = π 2 θ Orbit Equatorial plane (xy plane) C = planet's spin axis NS = u The planet's gravitational field is V G ( r,θ)! GM + GMR2 J r r 3 2 P 2 ( cosθ) which leads to an instantaneous torque on S of T = r ( m V G ), where m is the satellite mass = m V G ˆφ = 3 GMmR2 J θ r 3 2 sinθ cosθ ˆφ Since T varies in both amplitude and direction as the satellite moves around its orbit, we resolve T into cartesian componnets T x (towards N ) and T y, and average around one orbit: ˆφ = sinφ ˆx + cosφ ŷ T x = T 0 sinθ cosθ sinφ where T T y = T 0 sinθ cosθ cosφ 0 3GMmR2 J r 3 2 From spherical trigonometry we derive the relations cosθ = sinisinu tanφ = cosi tanu, while r is given by the equation of the orbit: ( ) ( ) 1+ ecos u ω r 1 =. a 1 e 2
8 We can simplify the algebra by assuming that (i) e! 0 (ii) i << π 2 so that we can set r! a, φ! u, sinθ! 1, and cosθ! isinu. We then have the approximate results: T x! T 0 i sin 2 u T y! T 0 i sinu cosu Upon averaging arounnd one orbit ( 0 u 2π ), T y cancels and we have T = 1 2 T 0 i ˆx = 3 R2 GMm 2 r 3 J 2 i ˆx A slightly more complicated analysis valid for all i yield T = 3 R2 GMm 4 a J sin 2i ˆx, 3 2 showing that T is zero for both i = 0 and i = π, and a maximum for i = π. 2 4 Returning to the precession rate formula, and noting that the torque exerted by the satellite on the planet is minus the above result, we have dφ GMmR 2 planet = 3 J 2 dt Cωa 3 2 cosi This expression can be further simplified by substituting ( J 2 = C A ) MR 2 and using Kepler's 3rd law: n 2 a 3 = G( M + m) : The factor dφ dt = 3 2 C A C m M + m is ~ m M m M + m n 2 ω cosi for satellite-induced precession, but ~1 for solar-induced precession.
9 Terrestrial forced precession Let us evaluate the solar and lunar contributions to the Earth s precession rate: Sun Moon m M + m 1.0 1/81.3 n 2 π /365 d 2 π /27.3 d ω 2 π /1 d 2 π /1 d m M + m i n2 ω 4.72 x x 10-5 = 15.1 x 10-5 d -1 So we see that the lunar term is dominant, and contributes ~ 69% of the total. The observed precession rate of the Earth s spin axis is dφ dt = 50 ʹʹ.4 yr 1 = d 1, corresponding to a period of 25,600 yrs., and the inclination of both the sun s and moon s orbits to the equator is i ~ 23.5, from which we may calculate the quantity for the Earth. C A C = = 1 305
10 Forced Precession & Nutation of the Earth s pole. Polaris Vega The 18.6 yr nutation is caused by the Moon s orbital precession. Source: Wikipedia.
11 This quantity may be combined with the measured value of To give the polar moment of inertia of the Earth: J 2 C A MR 2 = C MR 2 = Note that this direct determination of C/MR 2 is in good agreement with that inferred indirectly from the Earth s rotational flattening using the Darwin-Radau approximation. At present, no other planet but Mars has a measured forced precession rate (tracking of the 2 Viking landers on Mars was precise enough to do this), so we cannot generally apply this technique to determine accurate moments of inertia. In the future, however, such measurements may well be possible, at least Saturn.
12 Examples of spin precession periods. Object m ε T PRE Earth Sun ,600 yr. Earth Sun + Moon ,700 yr. Mars Sun ,000 yr. Jupiter Sun ,000 yr.* Saturn Sun ,800,000 yr.* Neptune Sun ,000,000 yr.* Moon Earth yr. Callisto Jupiter ~ yr. Titan Saturn ~ yr. Triton Neptune ~0. 65 yr. Iapetus Saturn ~9 29,000 yr? * Affected by solar torque on satellite orbits
13 Outer planet precession
14
15
16 The bars show limits on the precession rate of Saturn s ring plane, estimated at 0.5 /yr, or a period of ~2 Myr. Outer planet calculated precession periods and rates due to J 2 alone, and to the combined effects of J 2 and the principal equatorial satellites.
17 Digression: mutual precession We have discussed (a) the nodal precession rate of satellite orbits due to the planetary J 2, and (b) the precession of the planet s spin axis due to the satellite torque on the equatorial bulge. How are these 2 different view points to be reconciled, and what if anything, remains fixed in space? The answer, of course, is that (for an isolated planet and satellite system) only the total annular momentum vector remains inertially fixed; both the spin axis of the planet and the orbit normal precess about this vector. This is most easily shown using a vector notation for the torque, T, exerted by the planet on the satellite; T = T 0 sin i cosi ˆx = T 0 ŝ i ˆn ( ) ŝ ˆn where ŝ and ˆn are unit vectors parallel to the planet's spin axis and the satellite's orbit normal, resp., and T 0 = 3G ( C A )m. 2a 3 Writing the spin and orbital angular momenta as H = H ŝ and h = h ˆn we have the equations of motion:!h =!H ŝ + H ˆ!s = T = T 0 ŝ i ˆn!h =! h ˆn + h ˆ!n = T = T 0 ŝ i ˆn ( ) ŝ ˆn ( ) ŝ ˆn
18 Now ŝ and ˆn are unit vectors, so ˆ!s ŝ and ˆ!n ˆn, and the right-hand sides of both equations are ˆn and ŝ, so we must have!h = 0 and! h = 0. i.e., the magnitudes of H and h remain constant. Furthermore, the angle i between H and h is given by or so H hcosi = H i h cosi = ŝ i ˆn d ( cosi) = ˆ!s i ˆn + ŝ i ˆ!n = 0 dt since ˆ!s ~ ŝ ˆn ˆn and similarly for ˆ!n is ŝ. Thus the inclination remains constant also. Finally, we look at the orientation of the plane defined by H and h and whose normal is given by ŝ ˆn d dt ( ŝ ˆn ) = ˆ!s ˆn + ŝ ˆ!n ( ) ( ŝ ˆn ) ˆn ( H ŝ ŝ ˆn ) = T 0 ŝ ˆn ( ) {( ) ( h ˆn + Hŝ) } = T ŝ ˆn 0 ŝ ˆn Hh = T cosi 0 ŝ ˆn Hh ( ) H T h where H T is the (fixed) total angular momentum vector. Thus the vector ( ŝ ˆn ) precesses around H T at an angular rate dφ dt = T 0 H T Hh cosi.
19 We can readily verify that this general expression reduces to our previous results in the limiting cases h << H and H << h: (i) small satellite, h << H : H T! H, so dφ dt! T 0 h cosi Now so ( ) 1 2 m for e << 1, m << M h! GM a dφ dt satellite! G( C A)m cosi GM 2 m ( ) 1 2 a " as before, for e << 1. ( ) 1 2 J 2 R 2 cosi a 7 2 ( ) 2 cosi = 3 2 GM = 3 2 n J 2 (ii) large satellite, h >> H : R a H T ~ h, so dφ dt = T 0 H cosi dφ dt " as before. H = Cω planet! 3 2 = 3 2 G( C A)m cosi Cω a 3 GM m R 2 Cω a 3 J 2 cosi *Almost all satellites fall in case (i), except for Earth's moon which satisfies case (ii), and possibly Neptune's Triton, which may be an intermediate case. Case (ii) also applies to solar torques exerted on planetary spin vectors, and to planetary torques exerted on satellite spin vectors.
20 Summary of precession rate formulae Orbital precession:!"ω # n 0 3 "Ω # n 0 3!"ω # 1 4 n 0 J R 2 2 ( a ) 2 15 J R { 4 4 ( a ) 4 +$ } J R 2 2 ( a ) 2 9 J 2 15 J R { ( a ) 4 +$ } m ( s M ) α 2 (1) b 32 $ due to planet ( α ) α a a s ( ) "Ω #!" ω $ due to exterior satellite (1) Note : b 32!"ω # 1 n m s (1) 4 0 ( M )αb 32!"ω # 3 4 "Ω # 3 4 n 2 n ( a ) ( α ) α a s $ due to interior satellite ( 1 2sin 2 β ) n cosβ = planet's mean motion n $ due to the sun n 2 ( α ) # 3α + 45α α 5 8 ( ) $α << 1 β = obliquity ( ) 1 2 n 0 GM a 3 R { ( a ) 2 +$ } n # n J 2
21 Spin axis precession: Free precession: σ = C A C ω Forced precession, due to mass 'm' at distance 'a' Ω = 3 2 = ( ) GM C A C C A C C A C n 2 a 3 ω 1 cosβ ω cosβ m M n 2 ω " due to Sun cosi " due to Satellite Note typo in expression for dw/dt above: M à m.
Astronomy 6570: Physics of the Planets. Tidal Evolution
 Astronomy 6570: Physics of the Planets Tidal Evolution Tidal Interactions x = r sinθ z = r cosθ Accel'n of point P due to m = ( aẑ r cosθẑ r sinθ ˆx ) a = Gm! d 3 " Gm d 3 d! = Gm d 3 a z ( ) ẑ xˆx And
Astronomy 6570: Physics of the Planets Tidal Evolution Tidal Interactions x = r sinθ z = r cosθ Accel'n of point P due to m = ( aẑ r cosθẑ r sinθ ˆx ) a = Gm! d 3 " Gm d 3 d! = Gm d 3 a z ( ) ẑ xˆx And
Physics 106a, Caltech 4 December, Lecture 18: Examples on Rigid Body Dynamics. Rotating rectangle. Heavy symmetric top
 Physics 106a, Caltech 4 December, 2018 Lecture 18: Examples on Rigid Body Dynamics I go through a number of examples illustrating the methods of solving rigid body dynamics. In most cases, the problem
Physics 106a, Caltech 4 December, 2018 Lecture 18: Examples on Rigid Body Dynamics I go through a number of examples illustrating the methods of solving rigid body dynamics. In most cases, the problem
Revision of the physical backgrounds of Earth s rotation
 Revision of the physical backgrounds of Earth s rotation L. Völgyesi Budapest University of Technology and Economics, H-151 Budapest, Müegyetem rkp. 3. Hungary e-mail: lvolgyesi@epito.bme.hu bstract. Rotation
Revision of the physical backgrounds of Earth s rotation L. Völgyesi Budapest University of Technology and Economics, H-151 Budapest, Müegyetem rkp. 3. Hungary e-mail: lvolgyesi@epito.bme.hu bstract. Rotation
Astronomy 6570 Physics of the Planets
 Astronomy 6570 Physics of the Planets Planetary Rotation, Figures, and Gravity Fields Topics to be covered: 1. Rotational distortion & oblateness 2. Gravity field of an oblate planet 3. Free & forced planetary
Astronomy 6570 Physics of the Planets Planetary Rotation, Figures, and Gravity Fields Topics to be covered: 1. Rotational distortion & oblateness 2. Gravity field of an oblate planet 3. Free & forced planetary
Classical Mechanics. Luis Anchordoqui
 1 Rigid Body Motion Inertia Tensor Rotational Kinetic Energy Principal Axes of Rotation Steiner s Theorem Euler s Equations for a Rigid Body Eulerian Angles Review of Fundamental Equations 2 Rigid body
1 Rigid Body Motion Inertia Tensor Rotational Kinetic Energy Principal Axes of Rotation Steiner s Theorem Euler s Equations for a Rigid Body Eulerian Angles Review of Fundamental Equations 2 Rigid body
Information on internal structure from shape, gravity field and rotation
 Information on internal structure from shape, gravity field and rotation Seismological information is available only for the Earth and in limited amounts for the Moon. Various geodetic data put constraints
Information on internal structure from shape, gravity field and rotation Seismological information is available only for the Earth and in limited amounts for the Moon. Various geodetic data put constraints
AS3010: Introduction to Space Technology
 AS3010: Introduction to Space Technology L E C T U R E S 8-9 Part B, Lectures 8-9 23 March, 2017 C O N T E N T S In this lecture, we will look at factors that cause an orbit to change over time orbital
AS3010: Introduction to Space Technology L E C T U R E S 8-9 Part B, Lectures 8-9 23 March, 2017 C O N T E N T S In this lecture, we will look at factors that cause an orbit to change over time orbital
EART162: PLANETARY INTERIORS
 EART162: PLANETARY INTERIORS Francis Nimmo Last Week Applications of fluid dynamics to geophysical problems Navier-Stokes equation describes fluid flow: Convection requires solving the coupled equations
EART162: PLANETARY INTERIORS Francis Nimmo Last Week Applications of fluid dynamics to geophysical problems Navier-Stokes equation describes fluid flow: Convection requires solving the coupled equations
Physics 312, Winter 2007, Practice Final
 Physics 312, Winter 2007, Practice Final Time: Two hours Answer one of Question 1 or Question 2 plus one of Question 3 or Question 4 plus one of Question 5 or Question 6. Each question carries equal weight.
Physics 312, Winter 2007, Practice Final Time: Two hours Answer one of Question 1 or Question 2 plus one of Question 3 or Question 4 plus one of Question 5 or Question 6. Each question carries equal weight.
Rotation and Interior of Terrestrial Planets
 Rotation and Interior of Terrestrial Planets Veronique Dehant and Tim Van Hoolst Royal Observatory of Belgium introduction WHAT DO WE KNOW ABOUT THE MEAN ROTATION AND INTERIOR OF THE PLANETS? Orbit, rotation
Rotation and Interior of Terrestrial Planets Veronique Dehant and Tim Van Hoolst Royal Observatory of Belgium introduction WHAT DO WE KNOW ABOUT THE MEAN ROTATION AND INTERIOR OF THE PLANETS? Orbit, rotation
Research Article Variation of the Equator due to a Highly Inclined and Eccentric Disturber
 Hindawi Publishing Corporation Mathematical Problems in Engineering Volume 009, Article ID 467865, 10 pages doi:10.1155/009/467865 Research Article Variation of the Equator due to a Highly Inclined and
Hindawi Publishing Corporation Mathematical Problems in Engineering Volume 009, Article ID 467865, 10 pages doi:10.1155/009/467865 Research Article Variation of the Equator due to a Highly Inclined and
Lecture 2c: Satellite Orbits
 Lecture 2c: Satellite Orbits Outline 1. Newton s Laws of Mo3on 2. Newton s Law of Universal Gravita3on 3. Kepler s Laws 4. Pu>ng Newton and Kepler s Laws together and applying them to the Earth-satellite
Lecture 2c: Satellite Orbits Outline 1. Newton s Laws of Mo3on 2. Newton s Law of Universal Gravita3on 3. Kepler s Laws 4. Pu>ng Newton and Kepler s Laws together and applying them to the Earth-satellite
ANNEX 1. DEFINITION OF ORBITAL PARAMETERS AND IMPORTANT CONCEPTS OF CELESTIAL MECHANICS
 ANNEX 1. DEFINITION OF ORBITAL PARAMETERS AND IMPORTANT CONCEPTS OF CELESTIAL MECHANICS A1.1. Kepler s laws Johannes Kepler (1571-1630) discovered the laws of orbital motion, now called Kepler's laws.
ANNEX 1. DEFINITION OF ORBITAL PARAMETERS AND IMPORTANT CONCEPTS OF CELESTIAL MECHANICS A1.1. Kepler s laws Johannes Kepler (1571-1630) discovered the laws of orbital motion, now called Kepler's laws.
Dynamics of the Earth
 Time Dynamics of the Earth Historically, a day is a time interval between successive upper transits of a given celestial reference point. upper transit the passage of a body across the celestial meridian
Time Dynamics of the Earth Historically, a day is a time interval between successive upper transits of a given celestial reference point. upper transit the passage of a body across the celestial meridian
Torque and Rotation Lecture 7
 Torque and Rotation Lecture 7 ˆ In this lecture we finally move beyond a simple particle in our mechanical analysis of motion. ˆ Now we consider the so-called rigid body. Essentially, a particle with extension
Torque and Rotation Lecture 7 ˆ In this lecture we finally move beyond a simple particle in our mechanical analysis of motion. ˆ Now we consider the so-called rigid body. Essentially, a particle with extension
Perturbed Earth rotation. L. D. Akulenko, S. A. Kumakshev, and A. M. Shmatkov
 Perturbed Earth rotation L. D. Akulenko, S. A. Kumakshev, and A. M. Shmatkov 1 Introduction Numerous astrometric studies are based on the dynamic theory of the Earth s rotation with respect to the center
Perturbed Earth rotation L. D. Akulenko, S. A. Kumakshev, and A. M. Shmatkov 1 Introduction Numerous astrometric studies are based on the dynamic theory of the Earth s rotation with respect to the center
Solar vs. Lunar Tides
 1 2 3 4 Solar vs. Lunar Tides In the force equations M is the mass of the tide-causing object, r is the separation between the two objects. dr is the size of the object on which the tides are being raised.
1 2 3 4 Solar vs. Lunar Tides In the force equations M is the mass of the tide-causing object, r is the separation between the two objects. dr is the size of the object on which the tides are being raised.
2 so that the (time-dependent) torque, as measured in space-xed coordinates, is ~N = ma2! 2 (^x cos!t +^y sin!t) 10 = a p 5 2 ^z ~ F 2 ~F 1 = a p 5^z
 1 PHYS 321 Homework Assignment #9 Due: Friday, 22 November 2002 (4 probs) 1. Problem 7-14, B&O p. 280. The situation is as shown above. We take the body-xed axes ^x 0 and ^y 0 to lie in the plane of the
1 PHYS 321 Homework Assignment #9 Due: Friday, 22 November 2002 (4 probs) 1. Problem 7-14, B&O p. 280. The situation is as shown above. We take the body-xed axes ^x 0 and ^y 0 to lie in the plane of the
Planetary Interiors. Ulrich Christensen
 Planetary Interiors Ulrich Christensen Earth as a prototype planet Informations from shape, gravity and rotation Internal structure of terrestrial planets and icy moons The interior of gas planets Introduction
Planetary Interiors Ulrich Christensen Earth as a prototype planet Informations from shape, gravity and rotation Internal structure of terrestrial planets and icy moons The interior of gas planets Introduction
Physics 351, Spring 2015, Final Exam.
 Physics 351, Spring 2015, Final Exam. This closed-book exam has (only) 25% weight in your course grade. You can use one sheet of your own hand-written notes. Please show your work on these pages. The back
Physics 351, Spring 2015, Final Exam. This closed-book exam has (only) 25% weight in your course grade. You can use one sheet of your own hand-written notes. Please show your work on these pages. The back
Physical Dynamics (SPA5304) Lecture Plan 2018
 Physical Dynamics (SPA5304) Lecture Plan 2018 The numbers on the left margin are approximate lecture numbers. Items in gray are not covered this year 1 Advanced Review of Newtonian Mechanics 1.1 One Particle
Physical Dynamics (SPA5304) Lecture Plan 2018 The numbers on the left margin are approximate lecture numbers. Items in gray are not covered this year 1 Advanced Review of Newtonian Mechanics 1.1 One Particle
Chapter 5 - Part 1. Orbit Perturbations. D.Mortari - AERO-423
 Chapter 5 - Part 1 Orbit Perturbations D.Mortari - AERO-43 Orbital Elements Orbit normal i North Orbit plane Equatorial plane ϕ P O ω Ω i Vernal equinox Ascending node D. Mortari - AERO-43 Introduction
Chapter 5 - Part 1 Orbit Perturbations D.Mortari - AERO-43 Orbital Elements Orbit normal i North Orbit plane Equatorial plane ϕ P O ω Ω i Vernal equinox Ascending node D. Mortari - AERO-43 Introduction
is a revolution relative to a fixed celestial position. is the instant of transit of mean equinox relative to a fixed meridian position.
 PERIODICITY FORMULAS: Sidereal Orbit Tropical Year Eclipse Year Anomalistic Year Sidereal Lunar Orbit Lunar Mean Daily Sidereal Motion Lunar Synodical Period Centenial General Precession Longitude (365.25636042
PERIODICITY FORMULAS: Sidereal Orbit Tropical Year Eclipse Year Anomalistic Year Sidereal Lunar Orbit Lunar Mean Daily Sidereal Motion Lunar Synodical Period Centenial General Precession Longitude (365.25636042
An Introduction to Celestial Mechanics
 An Introduction to Celestial Mechanics This accessible text on classical celestial mechanics the principles governing the motions of bodies in the solar system provides a clear and concise treatment of
An Introduction to Celestial Mechanics This accessible text on classical celestial mechanics the principles governing the motions of bodies in the solar system provides a clear and concise treatment of
Lecture 16. Gravitation
 Lecture 16 Gravitation Today s Topics: The Gravitational Force Satellites in Circular Orbits Apparent Weightlessness lliptical Orbits and angular momentum Kepler s Laws of Orbital Motion Gravitational
Lecture 16 Gravitation Today s Topics: The Gravitational Force Satellites in Circular Orbits Apparent Weightlessness lliptical Orbits and angular momentum Kepler s Laws of Orbital Motion Gravitational
Introduction Fundamental definitions Motivation
 1 Introduction Fundamental definitions Motivation 1.1 Rotation and global shape of the Earth At a very elementary level, the Earth is considered to be an axially symmetric ellipsoid, rotating with uniform
1 Introduction Fundamental definitions Motivation 1.1 Rotation and global shape of the Earth At a very elementary level, the Earth is considered to be an axially symmetric ellipsoid, rotating with uniform
11 The Gravity Field and Gravitational Response to Rotation: Moments of Inertia
 11. The Gravity Field and Gravitational Response to Rotation: Moments of Inertia 113 11 The Gravity Field and Gravitational Response to Rotation: Moments of Inertia 11.1 The Gravity Field External to a
11. The Gravity Field and Gravitational Response to Rotation: Moments of Inertia 113 11 The Gravity Field and Gravitational Response to Rotation: Moments of Inertia 11.1 The Gravity Field External to a
AST111, Lecture 1b. Measurements of bodies in the solar system (overview continued) Orbital elements
 AST111, Lecture 1b Measurements of bodies in the solar system (overview continued) Orbital elements Planetary properties (continued): Measuring Mass The orbital period of a moon about a planet depends
AST111, Lecture 1b Measurements of bodies in the solar system (overview continued) Orbital elements Planetary properties (continued): Measuring Mass The orbital period of a moon about a planet depends
Third Body Perturbation
 Third Body Perturbation p. 1/30 Third Body Perturbation Modeling the Space Environment Manuel Ruiz Delgado European Masters in Aeronautics and Space E.T.S.I. Aeronáuticos Universidad Politécnica de Madrid
Third Body Perturbation p. 1/30 Third Body Perturbation Modeling the Space Environment Manuel Ruiz Delgado European Masters in Aeronautics and Space E.T.S.I. Aeronáuticos Universidad Politécnica de Madrid
Dynamical properties of the Solar System. Second Kepler s Law. Dynamics of planetary orbits. ν: true anomaly
 First Kepler s Law The secondary body moves in an elliptical orbit, with the primary body at the focus Valid for bound orbits with E < 0 The conservation of the total energy E yields a constant semi-major
First Kepler s Law The secondary body moves in an elliptical orbit, with the primary body at the focus Valid for bound orbits with E < 0 The conservation of the total energy E yields a constant semi-major
arxiv:astro-ph/ v1 17 Jul 2003
 Astronomy & Astrophysics manuscript no. RB-letter September 25, 217 (DOI: will be inserted by hand later) Mercury s spin-orbit model and signature of its dynamical parameters arxiv:astro-ph/37328v1 17
Astronomy & Astrophysics manuscript no. RB-letter September 25, 217 (DOI: will be inserted by hand later) Mercury s spin-orbit model and signature of its dynamical parameters arxiv:astro-ph/37328v1 17
Equation of orbital velocity: v 2 =GM(2/r 1/a) where: G is the gravitational constant (G=6.67x10 11 N/m 3 kg), M is the mass of the sun (or central
 Everything in Orbit Orbital Velocity Orbital velocity is the speed at which a planetary body moves in its orbit around another body. If orbits were circular, this velocity would be constant. However, from
Everything in Orbit Orbital Velocity Orbital velocity is the speed at which a planetary body moves in its orbit around another body. If orbits were circular, this velocity would be constant. However, from
arxiv: v1 [physics.geo-ph] 16 May 2012
![arxiv: v1 [physics.geo-ph] 16 May 2012 arxiv: v1 [physics.geo-ph] 16 May 2012](/thumbs/74/69620724.jpg) Obliquity of the Galilean satellites: The influence of a global internal liquid layer arxiv:125.3628v1 [physics.geo-ph] 16 May 212 Abstract Rose-Marie Baland a,b, Marie Yseboodt b, Tim Van Hoolst b a Université
Obliquity of the Galilean satellites: The influence of a global internal liquid layer arxiv:125.3628v1 [physics.geo-ph] 16 May 212 Abstract Rose-Marie Baland a,b, Marie Yseboodt b, Tim Van Hoolst b a Université
Physics 351 Monday, April 3, 2017
 Physics 351 Monday, April 3, 2017 This weekend you read Chapter 11 (coupled oscillators, normal modes, etc.), but it will take us another day or two to finish Chapter 10 in class: Euler angles; Lagrangian
Physics 351 Monday, April 3, 2017 This weekend you read Chapter 11 (coupled oscillators, normal modes, etc.), but it will take us another day or two to finish Chapter 10 in class: Euler angles; Lagrangian
Label next 2 pages in ISN Gas Giants. Make sure the following assignments are turned in:
 Do Now: Label next 2 pages in ISN Gas Giants Make sure the following assignments are turned in: A3K Article Analysis Small Group Test Corrections Form (if applicable) Astronomical Bodies in The Solar System
Do Now: Label next 2 pages in ISN Gas Giants Make sure the following assignments are turned in: A3K Article Analysis Small Group Test Corrections Form (if applicable) Astronomical Bodies in The Solar System
Determination of the rotation of Mercury from satellite gravimetry
 Mon. Not. R. Astron. Soc. 427, 468 482 (2012) doi:10.1111/j.1365-2966.2012.21919.x Determination of the rotation of Mercury from satellite gravimetry S. Cicalò and A. Milani Università degli Studi di Pisa,
Mon. Not. R. Astron. Soc. 427, 468 482 (2012) doi:10.1111/j.1365-2966.2012.21919.x Determination of the rotation of Mercury from satellite gravimetry S. Cicalò and A. Milani Università degli Studi di Pisa,
Supplementary Materials for
 www.sciencemag.org/content/345/622/1317/suppl/dc1 Supplementary Materials for Chaotic dynamics of stellar spin in binaries and the production of misaligned hot Jupiters Natalia I. Storch, Kassandra R.
www.sciencemag.org/content/345/622/1317/suppl/dc1 Supplementary Materials for Chaotic dynamics of stellar spin in binaries and the production of misaligned hot Jupiters Natalia I. Storch, Kassandra R.
Workshop on GNSS Data Application to Low Latitude Ionospheric Research May Fundamentals of Satellite Navigation
 2458-6 Workshop on GNSS Data Application to Low Latitude Ionospheric Research 6-17 May 2013 Fundamentals of Satellite Navigation HEGARTY Christopher The MITRE Corporation 202 Burlington Rd. / Rte 62 Bedford
2458-6 Workshop on GNSS Data Application to Low Latitude Ionospheric Research 6-17 May 2013 Fundamentals of Satellite Navigation HEGARTY Christopher The MITRE Corporation 202 Burlington Rd. / Rte 62 Bedford
Evolution of Mercury s obliquity
 Icarus 181 2006) 327 337 www.elsevier.com/locate/icarus Evolution of Mercury s obliquity Marie Yseboodt, Jean-Luc Margot Department of Astronomy, Cornell University, Ithaca, NY 14853, USA Received 24 June
Icarus 181 2006) 327 337 www.elsevier.com/locate/icarus Evolution of Mercury s obliquity Marie Yseboodt, Jean-Luc Margot Department of Astronomy, Cornell University, Ithaca, NY 14853, USA Received 24 June
Physical Dynamics (PHY-304)
 Physical Dynamics (PHY-304) Gabriele Travaglini March 31, 2012 1 Review of Newtonian Mechanics 1.1 One particle Lectures 1-2. Frame, velocity, acceleration, number of degrees of freedom, generalised coordinates.
Physical Dynamics (PHY-304) Gabriele Travaglini March 31, 2012 1 Review of Newtonian Mechanics 1.1 One particle Lectures 1-2. Frame, velocity, acceleration, number of degrees of freedom, generalised coordinates.
Continuum Polarization Induced by Tidal Distortion in Binary Stars
 Continuum Polarization Induced by Tidal Distortion in Binary Stars J. Patrick Harrington 1 1. On the Roche Potential of Close Binary Stars Let Ψ be the potential of a particle due to the gravitational
Continuum Polarization Induced by Tidal Distortion in Binary Stars J. Patrick Harrington 1 1. On the Roche Potential of Close Binary Stars Let Ψ be the potential of a particle due to the gravitational
Astronomy 241: Review Questions #2 Distributed: November 7, 2013
 Astronomy 241: Review Questions #2 Distributed: November 7, 2013 Review the questions below, and be prepared to discuss them in class. For each question, list (a) the general topic, and (b) the key laws
Astronomy 241: Review Questions #2 Distributed: November 7, 2013 Review the questions below, and be prepared to discuss them in class. For each question, list (a) the general topic, and (b) the key laws
Gravitation. Luis Anchordoqui
 Gravitation Kepler's law and Newton's Synthesis The nighttime sky with its myriad stars and shinning planets has always fascinated people on Earth. Towards the end of the XVI century the astronomer Tycho
Gravitation Kepler's law and Newton's Synthesis The nighttime sky with its myriad stars and shinning planets has always fascinated people on Earth. Towards the end of the XVI century the astronomer Tycho
APPENDIX B SUMMARY OF ORBITAL MECHANICS RELEVANT TO REMOTE SENSING
 APPENDIX B SUMMARY OF ORBITAL MECHANICS RELEVANT TO REMOTE SENSING Orbit selection and sensor characteristics are closely related to the strategy required to achieve the desired results. Different types
APPENDIX B SUMMARY OF ORBITAL MECHANICS RELEVANT TO REMOTE SENSING Orbit selection and sensor characteristics are closely related to the strategy required to achieve the desired results. Different types
Phys 214. Planets and Life
 Phys 214. Planets and Life Dr. Cristina Buzea Department of Physics Room 259 E-mail: cristi@physics.queensu.ca (Please use PHYS214 in e-mail subject) Lecture 28. Search for life on jovian moons. March
Phys 214. Planets and Life Dr. Cristina Buzea Department of Physics Room 259 E-mail: cristi@physics.queensu.ca (Please use PHYS214 in e-mail subject) Lecture 28. Search for life on jovian moons. March
PRECESSIONS IN RELATIVITY
 PRECESSIONS IN RELATIVITY COSTANTINO SIGISMONDI University of Rome La Sapienza Physics dept. and ICRA, Piazzale A. Moro 5 00185 Rome, Italy. e-mail: sigismondi@icra.it From Mercury s perihelion precession
PRECESSIONS IN RELATIVITY COSTANTINO SIGISMONDI University of Rome La Sapienza Physics dept. and ICRA, Piazzale A. Moro 5 00185 Rome, Italy. e-mail: sigismondi@icra.it From Mercury s perihelion precession
Patterns in the Solar System (Chapter 18)
 GEOLOGY 306 Laboratory Instructor: TERRY J. BOROUGHS NAME: Patterns in the Solar System (Chapter 18) For this assignment you will require: a calculator, colored pencils, a metric ruler, and meter stick.
GEOLOGY 306 Laboratory Instructor: TERRY J. BOROUGHS NAME: Patterns in the Solar System (Chapter 18) For this assignment you will require: a calculator, colored pencils, a metric ruler, and meter stick.
PHYSICS. Chapter 13 Lecture FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E RANDALL D. KNIGHT Pearson Education, Inc.
 PHYSICS FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E Chapter 13 Lecture RANDALL D. KNIGHT Chapter 13 Newton s Theory of Gravity IN THIS CHAPTER, you will learn to understand the motion of satellites
PHYSICS FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E Chapter 13 Lecture RANDALL D. KNIGHT Chapter 13 Newton s Theory of Gravity IN THIS CHAPTER, you will learn to understand the motion of satellites
11 Newton s Law of Universal Gravitation
 Physics 1A, Fall 2003 E. Abers 11 Newton s Law of Universal Gravitation 11.1 The Inverse Square Law 11.1.1 The Moon and Kepler s Third Law Things fall down, not in some other direction, because that s
Physics 1A, Fall 2003 E. Abers 11 Newton s Law of Universal Gravitation 11.1 The Inverse Square Law 11.1.1 The Moon and Kepler s Third Law Things fall down, not in some other direction, because that s
Rotational Motion and the Law of Gravity 1
 Rotational Motion and the Law of Gravity 1 Linear motion is described by position, velocity, and acceleration. Circular motion repeats itself in circles around the axis of rotation Ex. Planets in orbit,
Rotational Motion and the Law of Gravity 1 Linear motion is described by position, velocity, and acceleration. Circular motion repeats itself in circles around the axis of rotation Ex. Planets in orbit,
As a starting point of our derivation of the equations of motion for a rigid body, we employ d Alembert s principle:
 MEG6007: Advanced Dynamics -Principles and Computational Methods (Fall, 017) Lecture 10: Equations of Motion for a Rigid Body 10.1 D Alembert s Principle for A Free Rigid Body As a starting point of our
MEG6007: Advanced Dynamics -Principles and Computational Methods (Fall, 017) Lecture 10: Equations of Motion for a Rigid Body 10.1 D Alembert s Principle for A Free Rigid Body As a starting point of our
Gravitation. chapter 9
 chapter 9 Gravitation Circular orbits (Section 9.3) 1, 2, and 3 are simple exercises to supplement the quantitative calculations of Examples 4, 5, and 6 in Section 9.3. 1. Satellite near Earth s surface
chapter 9 Gravitation Circular orbits (Section 9.3) 1, 2, and 3 are simple exercises to supplement the quantitative calculations of Examples 4, 5, and 6 in Section 9.3. 1. Satellite near Earth s surface
Practice Test 3. Multiple Choice Identify the choice that best completes the statement or answers the question.
 Practice Test 3 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A wheel rotates about a fixed axis with an initial angular velocity of 20 rad/s. During
Practice Test 3 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A wheel rotates about a fixed axis with an initial angular velocity of 20 rad/s. During
AP Physics 1 Chapter 7 Circular Motion and Gravitation
 AP Physics 1 Chapter 7 Circular Motion and Gravitation Chapter 7: Circular Motion and Angular Measure Gravitation Angular Speed and Velocity Uniform Circular Motion and Centripetal Acceleration Angular
AP Physics 1 Chapter 7 Circular Motion and Gravitation Chapter 7: Circular Motion and Angular Measure Gravitation Angular Speed and Velocity Uniform Circular Motion and Centripetal Acceleration Angular
Lecture 23: Jupiter. Solar System. Jupiter s Orbit. The semi-major axis of Jupiter s orbit is a = 5.2 AU
 Lecture 23: Jupiter Solar System Jupiter s Orbit The semi-major axis of Jupiter s orbit is a = 5.2 AU Jupiter Sun a Kepler s third law relates the semi-major axis to the orbital period 1 Jupiter s Orbit
Lecture 23: Jupiter Solar System Jupiter s Orbit The semi-major axis of Jupiter s orbit is a = 5.2 AU Jupiter Sun a Kepler s third law relates the semi-major axis to the orbital period 1 Jupiter s Orbit
Earth-Moon System Fun with Gravity Sarazin. Sizes of Earth and Moon
 Earth-Moon System Fun with Gravity Sarazin Sizes of Earth and Moon Earth-Moon System Fun with Gravity Sarazin Sizes of Earth and Moon Precession: Gravity not parallel to rotation axis rotation axis gravity
Earth-Moon System Fun with Gravity Sarazin Sizes of Earth and Moon Earth-Moon System Fun with Gravity Sarazin Sizes of Earth and Moon Precession: Gravity not parallel to rotation axis rotation axis gravity
Angular Momentum L = I ω
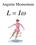 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
THE PLANE OF THE KUIPER BELT
 The Astronomical Journal, 127:2418 2423, 2004 April # 2004. The American Astronomical Society. All rights reserved. Printed in U.S.A. THE PLANE OF THE KUIPER BELT Michael E. Brown Division of Geological
The Astronomical Journal, 127:2418 2423, 2004 April # 2004. The American Astronomical Society. All rights reserved. Printed in U.S.A. THE PLANE OF THE KUIPER BELT Michael E. Brown Division of Geological
Calculation of the Gravitational Constant. Abstract. + α R 2 1. T 3 cos 12 β
 Calculation of the Gravitational Constant Abstract G 4 M ( π 5 α 2 ω + α R 2 tan θ R 2 2 ω 20T 5 cos 20 β π 3 α 2 ω 8 ω 2G4 T 3 cos 2 β G is the Gravitational constant and M is the mass of Earth. ω Angular
Calculation of the Gravitational Constant Abstract G 4 M ( π 5 α 2 ω + α R 2 tan θ R 2 2 ω 20T 5 cos 20 β π 3 α 2 ω 8 ω 2G4 T 3 cos 2 β G is the Gravitational constant and M is the mass of Earth. ω Angular
Lecture 13 REVIEW. Physics 106 Spring What should we know? What should we know? Newton s Laws
 Lecture 13 REVIEW Physics 106 Spring 2006 http://web.njit.edu/~sirenko/ What should we know? Vectors addition, subtraction, scalar and vector multiplication Trigonometric functions sinθ, cos θ, tan θ,
Lecture 13 REVIEW Physics 106 Spring 2006 http://web.njit.edu/~sirenko/ What should we know? Vectors addition, subtraction, scalar and vector multiplication Trigonometric functions sinθ, cos θ, tan θ,
13. Rigid Body Dynamics II
 University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 13. Rigid Body Dynamics II Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 13. Rigid Body Dynamics II Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
F 12. = G m m 1 2 F 21. = G m 1m 2 = F 12. Review: Newton s Law Of Universal Gravitation. Physics 201, Lecture 23. g As Function of Height
 Physics 01, Lecture Today s Topics n Universal Gravitation (Chapter 1 n Review: Newton s Law of Universal Gravitation n Properties of Gravitational Field (1.4 n Gravitational Potential Energy (1.5 n Escape
Physics 01, Lecture Today s Topics n Universal Gravitation (Chapter 1 n Review: Newton s Law of Universal Gravitation n Properties of Gravitational Field (1.4 n Gravitational Potential Energy (1.5 n Escape
Physics 201, Lecture 23
 Physics 201, Lecture 23 Today s Topics n Universal Gravitation (Chapter 13) n Review: Newton s Law of Universal Gravitation n Properties of Gravitational Field (13.4) n Gravitational Potential Energy (13.5)
Physics 201, Lecture 23 Today s Topics n Universal Gravitation (Chapter 13) n Review: Newton s Law of Universal Gravitation n Properties of Gravitational Field (13.4) n Gravitational Potential Energy (13.5)
Planetary Interiors. Earth s Interior Structure Hydrostatic Equilibrium Heating Constituent Relations Gravitational Fields Isostasy Magnetism
 Planetary Interiors Earth s Interior Structure Hydrostatic Equilibrium Heating Constituent Relations Gravitational Fields Isostasy Magnetism Isostasy Courtesy of U of Leeds Now apply this idea to topography
Planetary Interiors Earth s Interior Structure Hydrostatic Equilibrium Heating Constituent Relations Gravitational Fields Isostasy Magnetism Isostasy Courtesy of U of Leeds Now apply this idea to topography
Key-words: general relativity, Schwarzschild, Kerr, rotational transformation, time dilation, angle contraction.
 Rotational Transformation Between Schwarzschild Metric And Kerr Metric Ling Jun Wang Department of Physics, Geology and Astronomy University of Tennessee at Chattanooga Chattanooga, TN 37403 U.S.A. Abstract:
Rotational Transformation Between Schwarzschild Metric And Kerr Metric Ling Jun Wang Department of Physics, Geology and Astronomy University of Tennessee at Chattanooga Chattanooga, TN 37403 U.S.A. Abstract:
1 Summary of Chapter 2
 General Astronomy (9:61) Fall 01 Lecture 7 Notes, September 10, 01 1 Summary of Chapter There are a number of items from Chapter that you should be sure to understand. 1.1 Terminology A number of technical
General Astronomy (9:61) Fall 01 Lecture 7 Notes, September 10, 01 1 Summary of Chapter There are a number of items from Chapter that you should be sure to understand. 1.1 Terminology A number of technical
Yes, inner planets tend to be and outer planets tend to be.
 1. Planet Density Make some general comments about inner and outer planets density Inner Planets Density Outer Planets Density Is there a pattern or a trend in planet density? Yes, inner planets tend to
1. Planet Density Make some general comments about inner and outer planets density Inner Planets Density Outer Planets Density Is there a pattern or a trend in planet density? Yes, inner planets tend to
Angular Momentum L = I ω
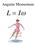 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
B ν (T) = 2hν3 c 3 1. e hν/kt 1. (4) For the solar radiation λ = 20µm photons are in the Rayleigh-Jean region, e hν/kt 1+hν/kT.
 Name: Astronomy 18 - Problem Set 8 1. Fundamental Planetary Science problem 14.4 a) Calculate the ratio of the light reflected by Earth at 0.5 µm to that emitted by the Sun at the same wavelength. The
Name: Astronomy 18 - Problem Set 8 1. Fundamental Planetary Science problem 14.4 a) Calculate the ratio of the light reflected by Earth at 0.5 µm to that emitted by the Sun at the same wavelength. The
8.012 Physics I: Classical Mechanics Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
r( θ) = cos2 θ ω rotation rate θ g geographic latitude - - θ geocentric latitude - - Reference Earth Model - WGS84 (Copyright 2002, David T.
 1 Reference Earth Model - WGS84 (Copyright 22, David T. Sandwell) ω spheroid c θ θ g a parameter description formula value/unit GM e (WGS84) 3.9864418 x 1 14 m 3 s 2 M e mass of earth - 5.98 x 1 24 kg
1 Reference Earth Model - WGS84 (Copyright 22, David T. Sandwell) ω spheroid c θ θ g a parameter description formula value/unit GM e (WGS84) 3.9864418 x 1 14 m 3 s 2 M e mass of earth - 5.98 x 1 24 kg
Today in Astronomy 111: rings, gaps and orbits
 Today in Astronomy 111: rings, gaps and orbits Gap sizes: the Hill radius Perturbations and resonances The variety of structures in planetary rings Spiral density waves Titan Bending waves Horseshoe and
Today in Astronomy 111: rings, gaps and orbits Gap sizes: the Hill radius Perturbations and resonances The variety of structures in planetary rings Spiral density waves Titan Bending waves Horseshoe and
TIDAL FORCES AND THE EXPANDING ORBIT OF MOON
 TIDAL FORCES AND THE EXPANDING ORBIT OF MOON CHRISTOPHER YANG DR. ROBIN REHAGEN FALL 206 LAS POSITAS COLLEGE PHYSICS 8A HONORS PROJECT 2 Table of Contents Project Abstract 4 Chapter : Integrating Gravitation
TIDAL FORCES AND THE EXPANDING ORBIT OF MOON CHRISTOPHER YANG DR. ROBIN REHAGEN FALL 206 LAS POSITAS COLLEGE PHYSICS 8A HONORS PROJECT 2 Table of Contents Project Abstract 4 Chapter : Integrating Gravitation
The Outer Planets (pages )
 The Outer Planets (pages 720 727) Gas Giants and Pluto (page 721) Key Concept: The first four outer planets Jupiter, Saturn, Uranus, and Neptune are much larger and more massive than Earth, and they do
The Outer Planets (pages 720 727) Gas Giants and Pluto (page 721) Key Concept: The first four outer planets Jupiter, Saturn, Uranus, and Neptune are much larger and more massive than Earth, and they do
Uranus & Neptune: The Ice Giants. Discovery of Uranus. Bode s Law. Discovery of Neptune
 Uranus & Neptune: The Ice Giants Discovery of Uranus Discovery of Uranus & Neptune Properties Density & Composition Internal Heat Source Magnetic fields Rings Uranus Rotational Axis by William Herschel
Uranus & Neptune: The Ice Giants Discovery of Uranus Discovery of Uranus & Neptune Properties Density & Composition Internal Heat Source Magnetic fields Rings Uranus Rotational Axis by William Herschel
Practice Test 3. Name: Date: ID: A. Multiple Choice Identify the choice that best completes the statement or answers the question.
 Name: Date: _ Practice Test 3 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A wheel rotates about a fixed axis with an initial angular velocity of 20
Name: Date: _ Practice Test 3 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A wheel rotates about a fixed axis with an initial angular velocity of 20
Chapter 11. Angular Momentum
 Chapter 11 Angular Momentum Angular Momentum Angular momentum plays a key role in rotational dynamics. There is a principle of conservation of angular momentum. In analogy to the principle of conservation
Chapter 11 Angular Momentum Angular Momentum Angular momentum plays a key role in rotational dynamics. There is a principle of conservation of angular momentum. In analogy to the principle of conservation
Moon Obs #1 Due! Moon visible: early morning through afternoon. 6 more due June 13 th. 15 total due June 25 th. Final Report Due June 28th
 Moon Obs #1 Due! Moon visible: early morning through afternoon 6 more due June 13 th 15 total due June 25 th Final Report Due June 28th Our Solar System Objectives Overview of what is in our solar system
Moon Obs #1 Due! Moon visible: early morning through afternoon 6 more due June 13 th 15 total due June 25 th Final Report Due June 28th Our Solar System Objectives Overview of what is in our solar system
The two-body Kepler problem
 The two-body Kepler problem set center of mass at the origin (X = 0) ignore all multipole moments (spherical bodies or point masses) define r := r 1 r 2,r:= r,m:= m 1 + m 2,µ:= m 1 m 2 /m reduces to effective
The two-body Kepler problem set center of mass at the origin (X = 0) ignore all multipole moments (spherical bodies or point masses) define r := r 1 r 2,r:= r,m:= m 1 + m 2,µ:= m 1 m 2 /m reduces to effective
Lecture Outlines. Chapter 6. Astronomy Today 7th Edition Chaisson/McMillan Pearson Education, Inc.
 Lecture Outlines Chapter 6 Astronomy Today 7th Edition Chaisson/McMillan Chapter 6 The Solar System Units of Chapter 6 6.1 An Inventory of the Solar System 6.2 Measuring the Planets 6.3 The Overall Layout
Lecture Outlines Chapter 6 Astronomy Today 7th Edition Chaisson/McMillan Chapter 6 The Solar System Units of Chapter 6 6.1 An Inventory of the Solar System 6.2 Measuring the Planets 6.3 The Overall Layout
PHY 5246: Theoretical Dynamics, Fall Assignment # 10, Solutions. (1.a) N = a. we see that a m ar a = 0 and so N = 0. ω 3 ω 2 = 0 ω 2 + I 1 I 3
 PHY 54: Theoretical Dynamics, Fall 015 Assignment # 10, Solutions 1 Graded Problems Problem 1 x 3 a ω First we calculate the moments of inertia: ( ) a I 1 = I = m 4 + b, 1 (1.a) I 3 = ma. b/ α The torque
PHY 54: Theoretical Dynamics, Fall 015 Assignment # 10, Solutions 1 Graded Problems Problem 1 x 3 a ω First we calculate the moments of inertia: ( ) a I 1 = I = m 4 + b, 1 (1.a) I 3 = ma. b/ α The torque
Planetary Atmospheres. Structure Composition Clouds Photochemistry Meteorology Atmospheric Escape
 Planetary Atmospheres Structure Composition Clouds Photochemistry Meteorology Atmospheric Escape Photochemistry We can characterize chemical reactions in the atmosphere in the following way: 1. Photolysis:
Planetary Atmospheres Structure Composition Clouds Photochemistry Meteorology Atmospheric Escape Photochemistry We can characterize chemical reactions in the atmosphere in the following way: 1. Photolysis:
Laws of gyroscopes / cardanic gyroscope
 Principle If the axis of rotation of the force-free gyroscope is displaced slightly, a nutation is produced. The relationship between precession frequency or nutation frequency and gyrofrequency is examined
Principle If the axis of rotation of the force-free gyroscope is displaced slightly, a nutation is produced. The relationship between precession frequency or nutation frequency and gyrofrequency is examined
arxiv: v2 [astro-ph.ep] 17 May 2017
![arxiv: v2 [astro-ph.ep] 17 May 2017 arxiv: v2 [astro-ph.ep] 17 May 2017](/thumbs/72/68061426.jpg) Signatures of the Martian rotation parameters in the Doppler and range observables Marie Yseboodt, Véronique Dehant, Marie-Julie Péters Royal Observatory of Belgium, Avenue circulaire 3, Brussels, Belgium,
Signatures of the Martian rotation parameters in the Doppler and range observables Marie Yseboodt, Véronique Dehant, Marie-Julie Péters Royal Observatory of Belgium, Avenue circulaire 3, Brussels, Belgium,
Lecture 3. Basic Physics of Astrophysics - Force and Energy.
 Lecture 3 Basic Physics of Astrophysics - Force and Energy http://apod.nasa.gov/apod/ Tue Wed Thur Thur ISB 165 Wed 5 Thur 4 Momentum (generally m F = Forces is the product of mass and velocity - a vector
Lecture 3 Basic Physics of Astrophysics - Force and Energy http://apod.nasa.gov/apod/ Tue Wed Thur Thur ISB 165 Wed 5 Thur 4 Momentum (generally m F = Forces is the product of mass and velocity - a vector
Physical Science 1 Chapter 16 INTRODUCTION. Astronomy is the study of the universe, which includes all matter, energy, space and time.
 INTRODUCTION Astronomy is the study of the universe, which includes all matter, energy, space and time. Although the universe is vast and almost beyond imagination, much is known about its make-up and
INTRODUCTION Astronomy is the study of the universe, which includes all matter, energy, space and time. Although the universe is vast and almost beyond imagination, much is known about its make-up and
Comparison between high precision precession models for the ecliptic and the equator
 A&A 421, 365 379 (2004) DOI: 10.1051/0004-6361:20035942 c ESO 2004 Astronomy & Astrophysics Comparison between high precision precession models for the ecliptic and the equator N. Capitaine 1,P.T.Wallace
A&A 421, 365 379 (2004) DOI: 10.1051/0004-6361:20035942 c ESO 2004 Astronomy & Astrophysics Comparison between high precision precession models for the ecliptic and the equator N. Capitaine 1,P.T.Wallace
Static Equilibrium, Gravitation, Periodic Motion
 This test covers static equilibrium, universal gravitation, and simple harmonic motion, with some problems requiring a knowledge of basic calculus. Part I. Multiple Choice 1. 60 A B 10 kg A mass of 10
This test covers static equilibrium, universal gravitation, and simple harmonic motion, with some problems requiring a knowledge of basic calculus. Part I. Multiple Choice 1. 60 A B 10 kg A mass of 10
Astronomy Test Review. 3 rd Grade
 Astronomy Test Review 3 rd Grade Match the vocabulary word to its definition. Outer Planets The path a planet takes around the sun. Inner Planets Orbit Sun The center of our solar system. Small, rocky
Astronomy Test Review 3 rd Grade Match the vocabulary word to its definition. Outer Planets The path a planet takes around the sun. Inner Planets Orbit Sun The center of our solar system. Small, rocky
F = ma. G mm r 2. S center
 In the early 17 th century, Kepler discovered the following three laws of planetary motion: 1. The planets orbit around the sun in an ellipse with the sun at one focus. 2. As the planets orbit around the
In the early 17 th century, Kepler discovered the following three laws of planetary motion: 1. The planets orbit around the sun in an ellipse with the sun at one focus. 2. As the planets orbit around the
AP PHYSICS 1 Learning Objectives Arranged Topically
 AP PHYSICS 1 Learning Objectives Arranged Topically with o Big Ideas o Enduring Understandings o Essential Knowledges o Learning Objectives o Science Practices o Correlation to Knight Textbook Chapters
AP PHYSICS 1 Learning Objectives Arranged Topically with o Big Ideas o Enduring Understandings o Essential Knowledges o Learning Objectives o Science Practices o Correlation to Knight Textbook Chapters
Chapter 13. Gravitation
 Chapter 13 Gravitation e = c/a A note about eccentricity For a circle c = 0 à e = 0 a Orbit Examples Mercury has the highest eccentricity of any planet (a) e Mercury = 0.21 Halley s comet has an orbit
Chapter 13 Gravitation e = c/a A note about eccentricity For a circle c = 0 à e = 0 a Orbit Examples Mercury has the highest eccentricity of any planet (a) e Mercury = 0.21 Halley s comet has an orbit
Observational Astronomy - Lecture 4 Orbits, Motions, Kepler s and Newton s Laws
 Observational Astronomy - Lecture 4 Orbits, Motions, Kepler s and Newton s Laws Craig Lage New York University - Department of Physics craig.lage@nyu.edu February 24, 2014 1 / 21 Tycho Brahe s Equatorial
Observational Astronomy - Lecture 4 Orbits, Motions, Kepler s and Newton s Laws Craig Lage New York University - Department of Physics craig.lage@nyu.edu February 24, 2014 1 / 21 Tycho Brahe s Equatorial
arxiv: v2 [astro-ph.ep] 28 Sep 2017
![arxiv: v2 [astro-ph.ep] 28 Sep 2017 arxiv: v2 [astro-ph.ep] 28 Sep 2017](/thumbs/88/115361465.jpg) Noname manuscript No. (will be inserted by the editor) Tilting Styx and Nix but not Uranus with a Spin-Precession-Mean-motion resonance Alice C. Quillen 1, Yuan-Yuan Chen 1,2, Benoît Noyelles 3, & Santiago
Noname manuscript No. (will be inserted by the editor) Tilting Styx and Nix but not Uranus with a Spin-Precession-Mean-motion resonance Alice C. Quillen 1, Yuan-Yuan Chen 1,2, Benoît Noyelles 3, & Santiago
Uniform Circular Motion
 Circular Motion Uniform Circular Motion Uniform Circular Motion Traveling with a constant speed in a circular path Even though the speed is constant, the acceleration is non-zero The acceleration responsible
Circular Motion Uniform Circular Motion Uniform Circular Motion Traveling with a constant speed in a circular path Even though the speed is constant, the acceleration is non-zero The acceleration responsible
Celestial Mechanics III. Time and reference frames Orbital elements Calculation of ephemerides Orbit determination
 Celestial Mechanics III Time and reference frames Orbital elements Calculation of ephemerides Orbit determination Orbital position versus time: The choice of units Gravitational constant: SI units ([m],[kg],[s])
Celestial Mechanics III Time and reference frames Orbital elements Calculation of ephemerides Orbit determination Orbital position versus time: The choice of units Gravitational constant: SI units ([m],[kg],[s])
Rotational Kinematics
 Rotational Kinematics Rotational Coordinates Ridged objects require six numbers to describe their position and orientation: 3 coordinates 3 axes of rotation Rotational Coordinates Use an angle θ to describe
Rotational Kinematics Rotational Coordinates Ridged objects require six numbers to describe their position and orientation: 3 coordinates 3 axes of rotation Rotational Coordinates Use an angle θ to describe
THE DETECTABILITY OF TRANSIT DEPTH VARIATIONS DUE TO EXOPLANETARY OBLATENESS AND SPIN PRECESSION
 ACCEPTED FOR PUBLICATION IN THE ASTROPHYSICAL JOURNAL Preprint typeset using LATEX style emulateapj v. 11/10/09 THE DETECTABILITY OF TRANSIT DEPTH VARIATIONS DUE TO EXOPLANETARY OBLATENESS AND SPIN PRECESSION
ACCEPTED FOR PUBLICATION IN THE ASTROPHYSICAL JOURNAL Preprint typeset using LATEX style emulateapj v. 11/10/09 THE DETECTABILITY OF TRANSIT DEPTH VARIATIONS DUE TO EXOPLANETARY OBLATENESS AND SPIN PRECESSION
Lecture 20 Angular Momentum Quantization (mostly) Chapter
 PHYS 172H: Modern Mechanics Fall 2012 Lecture 20 Angular Momentum Quantization (mostly) Chapter 11.8 11.11 EVENING EXAM III - 8:00-9:30 PM, TUE NOV 13, Room 112 r dl dt tot I R r =τ net θ Predicting Position
PHYS 172H: Modern Mechanics Fall 2012 Lecture 20 Angular Momentum Quantization (mostly) Chapter 11.8 11.11 EVENING EXAM III - 8:00-9:30 PM, TUE NOV 13, Room 112 r dl dt tot I R r =τ net θ Predicting Position
8.012 Physics I: Classical Mechanics Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
