LING 473: Day 3. START THE RECORDING Assignment 1 Review Probability. University of Washington Linguistics 473: Computational Linguistics Fundamentals
|
|
|
- Beverly Lee
- 5 years ago
- Views:
Transcription
1 LING 473: Day 3 START THE RECORDING Assignment 1 Review Probability 1
2 Probability textbook: Resources Available Charles Grinstead and J. Laurie Snell Introduction to Probability - online on course website Resources on course website Unicode, UTF-8, BOM Condor quick-start Resource Thread on GoPost 2
3 Announcement I will be out of town at a conference August 8 and August 10 Lectures will be recorded and uploaded I will be available electronically ( , GoPost) 3
4 Project 1 Due Thursday August 3 at 11:45pm Questions? Assignment 2 Due Tuesday August 8 at 4:30pm Pobability Harder than assignment 1, start early 4
5 1. Essays get full credit. 2. I saw that gas can explode Assignment 1 I saw (realized) that gas (in general) can explode I saw that (one) gas can explode I saw (realized) that (particular) gas can explode 5
6 Assignment 1 3. All possible six letter words (26 6 ) minus words with all consonants (21 6 ) minus words with all vowels (5 6 ) = 223,134,030 6
7 Assignment 1 4. Assuming that we consider identical characters to be indistinguishable in the output: ( 萄萄萄萄橙橙苹梨蕉 ) Repeated groups: 4, 2, 1, 1, 1 9! 4! 2! 1! 1! 1! = 7,560 7
8 Assignment 1 5a. How many pairwise comparisons are possible between documents on the same topic? = 60 5b. How many pairwise comparisons are possible between documents on different topics? = 111 8
9 Assignment 1 6. Extra Credit Write an expression that gives the number of unordered sets of k items that can be formed from a set of n distinct items while allowing repetition in the output set. Example: { a, b, c, d } choose 3 (unordered), but allowing repetition in the output: n = 4 k = 3 { a a a }, { a a b }, { a a c }, { a a d }, { a b b }, { a b c }, { a b d }, { a c c }, { a c d }, { a d d }, { b b b }, { b b c }, { b b d }, { b c c }, { b c d }, { b d d }, { c c c }, { c c d }, { c d d }, { d d d } 9
10 Assignment 1 Proof (hard version) Divide into groups and count them (remember: n = 4, k = 3): { a a a } { a a b } { a a c } { a a d } { a b b } { a b c } { a b d } { a c c } { a c d } { a d d } { b b b } { b b c } { b b d } { b c c } { b c d } { b d d } { c c c } { c c d } { c d d } { d d d } n! 4 2 $ + 4 = 10! 3 2 $ + 3 = 6! 2 2 # + 2 = 3! 1 2 $ + 1 = 1 i! "# k 1 ( + i+ = n + k 1 # ( = ## n k k (/ i 10
11 Proof (easy version) {a, b, c, d} multichoose 3 Assignment 1 Every time we choose, we should add back into the set a copy of whatever we just chose. E.g., if we choose a, we just add another a. If we choose b, we just add another b. We will do this k - 1 times. So we really have a set that looks like this: {a, b, c, d, X, X} Where each X is going to have a value equivalent to whatever the last chosen item was. So now we have a regular choose function. Our choose is: n + k 1 k The number of Xs 11
12 { a b c } Combinatorics Summary Permutation: how many different orderings? ( a b c ) ( a c b ) ( b a c ) ( b c a ) ( c a b ) ( c b a ) Combination: how many different subsets (i.e. of 2)? { a b } { a c } { b c } allowing repetition in the output { a a } { a b } { a c } { b b } { b c } { c c } Variations: how many different ordered subsets (i.e. of 2)? ( a b ) ( a c ) ( b a ) ( b c ) ( c a ) ( c b ) allowing repetition in the output ( a a ) ( a b ) ( a c ) ( b a ) ( b b ) ( b c ) ( c a ) ( c b ) ( c c ) n!! n k $ n + k 1 k n! (n k)! n k 12
13 Probability So far we ve considered counting and manipulating sets Probability talks about the event of selecting an item from a set. This is alternatively called a trial or an observation. We call the set the sample space and (arbitrarily) assign the whole set a probability mass of
14 Sample Space Ω is sometimes used to represent the sample space. Sample spaces can be continuous or discrete. Continuous: { the distance between planets } Discrete: { Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune } P(Ω) = 1.0. (all events are accounted for) 14
15 Outcomes By convention, events are often represented with an italic capital letter representing the single outcome of a lower-case letter. Ω = { a a b c } A is the event of selecting a from Ω B is the event of selecting b from Ω C is the event of selecting c from Ω A C is the complement of A (the event of not A) A + A C takes up the entire event space. E.g., P(A or A C ) = 1.0 An event can be any subset of Ω All individual outcomes are an event An event could be a combination of different outcomes: D is the event of choosing a or b An event could be multiple outcomes: Q is the event of choosing a followed by b 15
16 Rolling 2 dice The single occurrence of rolling a red die and a black die must have one of the following outcomes (red, black) Ω = { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6) } There are 6 6 = 36 outcomes; they are mutually exclusive and collectively exhaustive But there are many other events that we can talk about 16
17 A particular outcome A = { (3, 6) } Both dice are the same Some 2-dice Events E = { (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6) } The total is 5 F = { (1, 4), (2, 3), (3, 2), (4, 1) } The total is prime G = { (1, 1), (1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (4, 1), (4, 3), (5, 2), (5, 6), (6,1), (6, 5) } 17
18 Definition of Probability Let P be a function that satisfies the following: P(Ω) = 1 all possible outcomes are accounted for A Ω : 0 P(A) 1 probabilities are non-negative real numbers less than 1 { A, B } Ω, A B = * : P(A B) = P(A) + P(B) for any pair of events that are mutually exclusive, the union of their occurrence is the sum of their probabilities * denotes the empty set, { } 18
19 Definition of Probability For every trial, an event either occurs, or does not occur A Ω : P(A C ) = 1 - P(A) Each event A Ω can be thought of as partitioning the probability space 19
20 Mutual Exclusivity It is impossible for two mutually exclusive events to co-occur on the same trial For the 2 dice example, each of the 36 basic outcomes are mutually exclusive with each other, and the entire set is collectively exhaustive Therefore, one way of defining P is to assume that these outcomes are all equally likely: E = { (1, 6) } 1 P(E) = Ω = 1 36 =
21 Compositional Events Events which are not in the set of mutually-exclusive, collectively-exhaustive events can be composed from them Compositional events are handy for grouping together certain types of events that we might be interested in If the function P describes a valid probability space, then the definition of wellformed P allows us to calculate P for mutually exclusive compositional events P(A B) = P(A) + P(B) Every trial has an outcome, which may satisfy multiple events; this can be illustrated with Venn Diagrams 21
22 Both dice are the same 2 Dice Events E = { (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6) } P(E) = =.1667 The total is 5 F = { (1, 4), (2, 3), (3, 2), (4, 1) } P(F) = =.1111 The total is prime G = { (1, 1), (1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (4, 1), (4, 3), (5, 2), (5, 6), (6,1), (6, 5) } P(G) = =
23 Outcomes in Probability Space Ω (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) 23
24 Event Composition Ω E (2, 2) G (1, 2) (1, 6) (2, 1) F (3, 3) (4, 4) (1, 1) (2, 5) (3, 4) (4, 5) (5, 2) (5, 6) (6, 1) (1, 4) (2, 3) (3, 2) (4, 1) (5, 5) (6, 5) (6, 6) the other 16 outcomes are out here 24
25 Intersecting Events The previous slide shows that compositional events can be mutually exclusive E and F are mutually exclusive E F = E and G are not mutually exclusive E G = { (1, 1) } F and G are not mutually exclusive F G = { (1, 4), (2, 3), (3, 2), (4, 1) } = F 25
26 More on Adding Probabilities We have seen how to calculate probability of P(A or B) when A and B are mutually exclusive P(A U B) = P(A) + P(B), A B = If they are not, we can subtract the probability of the intersecting area P(A U B) = P(A) + P(B) P(A B) Probability of both dice being the same, or their total being prime in a single trial P(E U G) = P(E) + P(G) P(E G) = =
27 Joint Probability On the previous slide we knew that P(E G) =.0278 by noting that only 1 of the 36 mutually exclusive, collectively exhaustive outcomes is in the set intersection E G More generally though, how can we compute P(E G) from P(E) and P(G)? P(E G), or P(E and G), or P(EG) is the probability that two events both occur in the same trial This is called the joint probability For mutually exclusive events, the joint probability is obviously zero: { A, B } Ω, A B = : P(A B) = 0 27
28 Joint Probability Recall our example E = { (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6) } both dice are the same F = { (1, 4), (2, 3), (3, 2), (4, 1) } the total is 5 { A, B } Ω, A B = : P(A B) = 0 E F =, P(E F) = 0 The probability is zero, meaning it is not possible for both dice to be the same and for the total to be 5 on the same trial. 28
29 Perhaps it is the case that P(E G) = P(E) P(G) Let s try it Joint Probability No. This means that events E and G are not independent 29
30 Independent Events 2 events are mutually exclusive if they cannot both occur as the outcome of a single trial 2 events are independent if the occurrence of one does not affect the probability of the other occurring in the trial Does event A provide any information that would bias the outcome of event B? If so, A and B are not independent events; they are dependent Events E, F and G in the 2-dice example are not independent of each other ( {E, F}, {F, G} and {E, G} ) Even though E and F are mutually exclusive 30
31 Adding an independent event to our example Let s start with event F and try to think of an event that would be independent of F F = { (1, 4), (2, 3), (3, 2), (4, 1) } P(F) =.1111 the total is 5 It s not so easy to come up with an event that, in the same trial, will give us no information about F. Such an event must meet the following criteria: Since F does not partition Ω equally, a event that is independent of F must partition Ω equally, so as not to bias for or against F. For the same reason, the event must also partition F equally. Any ideas? 31
32 An event that is independent of F the red die shows an odd number H = { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6) } P(H) =.5 F = { (1, 4), (2, 3), (3, 2), (4, 1) } the total is 5 P(F) =.1111 H F = { (1, 4), (3, 2) } P(H F) =.0555 P(H) P(F)
33 Independent Events When two events are independent, the probability of both occurring in the same trial is P(A B) = P(A) P(B) Actually, the reverse of this is the definition of independence This is how we can test for independence of events we can compare the probability P(A B) obtained from counting to the product of P(A) and P(B). If they are equal, the events are independent 33
34 Conditional Probability But what if two events are not independent? How do we compute P(A B) from P(A) and P(B)? We must know how the events are related P(A B) is notation for the probability of event A, assuming that event B has co-occurred in the same trial This is called conditional probability the probability of A, given B Think of a constrained probability space which contains only those outcomes which satisfy event B or a pre-filter which selects only outcomes which satisfy B 34
35 Conditional Probability Because the reduced sample space is limited to events which satisfy B, we exclude from A any outcomes that do not satisfy B: P(A B) This lets us express the conditional probability in terms of the reduced sample space P(A B) = P(A B) P(B) If P(B) is 0, then P(A B) is undefined P(A B) = P(A B)P(B) 35
36 Marginal Probability Conditional probability introduces the idea that you might have information about part of a trial In the following equation, we are assuming that we can estimate or provide P(B) for an incomplete trial P(A B) = P(A B)P(B) P(B) here is called the marginal probability P(A B) = P(A B)P(B) joint probability = conditional probability marginal probability 36
37 Conditional probability and independence Note that conditional probability degrades gracefully in the case of independent events Assuming A and B are independent events: P(AB) = P(A) P(B) P(AB) = P(A B) P(B) P(A) P(B) = P(A B) P(B) P(A) = P(A B) If A and B are independent, then what you may know about one doesn t affect the probability of the other 37
38 P(A C ) = 1 P(A) P(A U B) = P(A) + P(B) P(A B) Summary of Event Probability If P(A B) = P(A) P(B), then A and B are called independent events Otherwise P(A B) = P(A B) P(B) = P(B A) P(A) Conditional probability P(A B) = P(A B) P(B) 38
39 Tuesday Next Week Random Variables, the Chain Rule, and Probability Distributions Thursday Project 1 due at 11:45 p.m. 39
Probability- describes the pattern of chance outcomes
 Chapter 6 Probability the study of randomness Probability- describes the pattern of chance outcomes Chance behavior is unpredictable in the short run, but has a regular and predictable pattern in the long
Chapter 6 Probability the study of randomness Probability- describes the pattern of chance outcomes Chance behavior is unpredictable in the short run, but has a regular and predictable pattern in the long
Probability Theory and Applications
 Probability Theory and Applications Videos of the topics covered in this manual are available at the following links: Lesson 4 Probability I http://faculty.citadel.edu/silver/ba205/online course/lesson
Probability Theory and Applications Videos of the topics covered in this manual are available at the following links: Lesson 4 Probability I http://faculty.citadel.edu/silver/ba205/online course/lesson
LECTURE 1. 1 Introduction. 1.1 Sample spaces and events
 LECTURE 1 1 Introduction The first part of our adventure is a highly selective review of probability theory, focusing especially on things that are most useful in statistics. 1.1 Sample spaces and events
LECTURE 1 1 Introduction The first part of our adventure is a highly selective review of probability theory, focusing especially on things that are most useful in statistics. 1.1 Sample spaces and events
CMPSCI 240: Reasoning about Uncertainty
 CMPSCI 240: Reasoning about Uncertainty Lecture 2: Sets and Events Andrew McGregor University of Massachusetts Last Compiled: January 27, 2017 Outline 1 Recap 2 Experiments and Events 3 Probabilistic Models
CMPSCI 240: Reasoning about Uncertainty Lecture 2: Sets and Events Andrew McGregor University of Massachusetts Last Compiled: January 27, 2017 Outline 1 Recap 2 Experiments and Events 3 Probabilistic Models
MATH 556: PROBABILITY PRIMER
 MATH 6: PROBABILITY PRIMER 1 DEFINITIONS, TERMINOLOGY, NOTATION 1.1 EVENTS AND THE SAMPLE SPACE Definition 1.1 An experiment is a one-off or repeatable process or procedure for which (a there is a well-defined
MATH 6: PROBABILITY PRIMER 1 DEFINITIONS, TERMINOLOGY, NOTATION 1.1 EVENTS AND THE SAMPLE SPACE Definition 1.1 An experiment is a one-off or repeatable process or procedure for which (a there is a well-defined
Probability Theory Review
 Cogsci 118A: Natural Computation I Lecture 2 (01/07/10) Lecturer: Angela Yu Probability Theory Review Scribe: Joseph Schilz Lecture Summary 1. Set theory: terms and operators In this section, we provide
Cogsci 118A: Natural Computation I Lecture 2 (01/07/10) Lecturer: Angela Yu Probability Theory Review Scribe: Joseph Schilz Lecture Summary 1. Set theory: terms and operators In this section, we provide
The enumeration of all possible outcomes of an experiment is called the sample space, denoted S. E.g.: S={head, tail}
 Random Experiment In random experiments, the result is unpredictable, unknown prior to its conduct, and can be one of several choices. Examples: The Experiment of tossing a coin (head, tail) The Experiment
Random Experiment In random experiments, the result is unpredictable, unknown prior to its conduct, and can be one of several choices. Examples: The Experiment of tossing a coin (head, tail) The Experiment
Review of Basic Probability
 Review of Basic Probability Erik G. Learned-Miller Department of Computer Science University of Massachusetts, Amherst Amherst, MA 01003 September 16, 2009 Abstract This document reviews basic discrete
Review of Basic Probability Erik G. Learned-Miller Department of Computer Science University of Massachusetts, Amherst Amherst, MA 01003 September 16, 2009 Abstract This document reviews basic discrete
7.1 What is it and why should we care?
 Chapter 7 Probability In this section, we go over some simple concepts from probability theory. We integrate these with ideas from formal language theory in the next chapter. 7.1 What is it and why should
Chapter 7 Probability In this section, we go over some simple concepts from probability theory. We integrate these with ideas from formal language theory in the next chapter. 7.1 What is it and why should
Axioms of Probability
 Sample Space (denoted by S) The set of all possible outcomes of a random experiment is called the Sample Space of the experiment, and is denoted by S. Example 1.10 If the experiment consists of tossing
Sample Space (denoted by S) The set of all possible outcomes of a random experiment is called the Sample Space of the experiment, and is denoted by S. Example 1.10 If the experiment consists of tossing
Statistical Inference
 Statistical Inference Lecture 1: Probability Theory MING GAO DASE @ ECNU (for course related communications) mgao@dase.ecnu.edu.cn Sep. 11, 2018 Outline Introduction Set Theory Basics of Probability Theory
Statistical Inference Lecture 1: Probability Theory MING GAO DASE @ ECNU (for course related communications) mgao@dase.ecnu.edu.cn Sep. 11, 2018 Outline Introduction Set Theory Basics of Probability Theory
Information Science 2
 Information Science 2 Probability Theory: An Overview Week 12 College of Information Science and Engineering Ritsumeikan University Agenda Terms and concepts from Week 11 Basic concepts of probability
Information Science 2 Probability Theory: An Overview Week 12 College of Information Science and Engineering Ritsumeikan University Agenda Terms and concepts from Week 11 Basic concepts of probability
Probability (Devore Chapter Two)
 Probability (Devore Chapter Two) 1016-345-01: Probability and Statistics for Engineers Fall 2012 Contents 0 Administrata 2 0.1 Outline....................................... 3 1 Axiomatic Probability 3
Probability (Devore Chapter Two) 1016-345-01: Probability and Statistics for Engineers Fall 2012 Contents 0 Administrata 2 0.1 Outline....................................... 3 1 Axiomatic Probability 3
Properties of Probability
 Econ 325 Notes on Probability 1 By Hiro Kasahara Properties of Probability In statistics, we consider random experiments, experiments for which the outcome is random, i.e., cannot be predicted with certainty.
Econ 325 Notes on Probability 1 By Hiro Kasahara Properties of Probability In statistics, we consider random experiments, experiments for which the outcome is random, i.e., cannot be predicted with certainty.
Venn Diagrams; Probability Laws. Notes. Set Operations and Relations. Venn Diagram 2.1. Venn Diagrams; Probability Laws. Notes
 Lecture 2 s; Text: A Course in Probability by Weiss 2.4 STAT 225 Introduction to Probability Models January 8, 2014 s; Whitney Huang Purdue University 2.1 Agenda s; 1 2 2.2 Intersection: the intersection
Lecture 2 s; Text: A Course in Probability by Weiss 2.4 STAT 225 Introduction to Probability Models January 8, 2014 s; Whitney Huang Purdue University 2.1 Agenda s; 1 2 2.2 Intersection: the intersection
(6, 1), (5, 2), (4, 3), (3, 4), (2, 5), (1, 6)
 Section 7.3: Compound Events Because we are using the framework of set theory to analyze probability, we can use unions, intersections and complements to break complex events into compositions of events
Section 7.3: Compound Events Because we are using the framework of set theory to analyze probability, we can use unions, intersections and complements to break complex events into compositions of events
Lecture 10: Probability distributions TUESDAY, FEBRUARY 19, 2019
 Lecture 10: Probability distributions DANIEL WELLER TUESDAY, FEBRUARY 19, 2019 Agenda What is probability? (again) Describing probabilities (distributions) Understanding probabilities (expectation) Partial
Lecture 10: Probability distributions DANIEL WELLER TUESDAY, FEBRUARY 19, 2019 Agenda What is probability? (again) Describing probabilities (distributions) Understanding probabilities (expectation) Partial
2. Probability. Chris Piech and Mehran Sahami. Oct 2017
 2. Probability Chris Piech and Mehran Sahami Oct 2017 1 Introduction It is that time in the quarter (it is still week one) when we get to talk about probability. Again we are going to build up from first
2. Probability Chris Piech and Mehran Sahami Oct 2017 1 Introduction It is that time in the quarter (it is still week one) when we get to talk about probability. Again we are going to build up from first
Dept. of Linguistics, Indiana University Fall 2015
 L645 Dept. of Linguistics, Indiana University Fall 2015 1 / 34 To start out the course, we need to know something about statistics and This is only an introduction; for a fuller understanding, you would
L645 Dept. of Linguistics, Indiana University Fall 2015 1 / 34 To start out the course, we need to know something about statistics and This is only an introduction; for a fuller understanding, you would
Executive Assessment. Executive Assessment Math Review. Section 1.0, Arithmetic, includes the following topics:
 Executive Assessment Math Review Although the following provides a review of some of the mathematical concepts of arithmetic and algebra, it is not intended to be a textbook. You should use this chapter
Executive Assessment Math Review Although the following provides a review of some of the mathematical concepts of arithmetic and algebra, it is not intended to be a textbook. You should use this chapter
Probability 1 (MATH 11300) lecture slides
 Probability 1 (MATH 11300) lecture slides Márton Balázs School of Mathematics University of Bristol Autumn, 2015 December 16, 2015 To know... http://www.maths.bris.ac.uk/ mb13434/prob1/ m.balazs@bristol.ac.uk
Probability 1 (MATH 11300) lecture slides Márton Balázs School of Mathematics University of Bristol Autumn, 2015 December 16, 2015 To know... http://www.maths.bris.ac.uk/ mb13434/prob1/ m.balazs@bristol.ac.uk
Math 3338: Probability (Fall 2006)
 Math 3338: Probability (Fall 2006) Jiwen He Section Number: 10853 http://math.uh.edu/ jiwenhe/math3338fall06.html Probability p.1/8 Chapter Two: Probability (I) Probability p.2/8 2.1 Sample Spaces and
Math 3338: Probability (Fall 2006) Jiwen He Section Number: 10853 http://math.uh.edu/ jiwenhe/math3338fall06.html Probability p.1/8 Chapter Two: Probability (I) Probability p.2/8 2.1 Sample Spaces and
Lecture Notes 1 Basic Probability. Elements of Probability. Conditional probability. Sequential Calculation of Probability
 Lecture Notes 1 Basic Probability Set Theory Elements of Probability Conditional probability Sequential Calculation of Probability Total Probability and Bayes Rule Independence Counting EE 178/278A: Basic
Lecture Notes 1 Basic Probability Set Theory Elements of Probability Conditional probability Sequential Calculation of Probability Total Probability and Bayes Rule Independence Counting EE 178/278A: Basic
Compound Events. The event E = E c (the complement of E) is the event consisting of those outcomes which are not in E.
 Compound Events Because we are using the framework of set theory to analyze probability, we can use unions, intersections and complements to break complex events into compositions of events for which it
Compound Events Because we are using the framework of set theory to analyze probability, we can use unions, intersections and complements to break complex events into compositions of events for which it
STA Module 4 Probability Concepts. Rev.F08 1
 STA 2023 Module 4 Probability Concepts Rev.F08 1 Learning Objectives Upon completing this module, you should be able to: 1. Compute probabilities for experiments having equally likely outcomes. 2. Interpret
STA 2023 Module 4 Probability Concepts Rev.F08 1 Learning Objectives Upon completing this module, you should be able to: 1. Compute probabilities for experiments having equally likely outcomes. 2. Interpret
Fundamentals of Probability CE 311S
 Fundamentals of Probability CE 311S OUTLINE Review Elementary set theory Probability fundamentals: outcomes, sample spaces, events Outline ELEMENTARY SET THEORY Basic probability concepts can be cast in
Fundamentals of Probability CE 311S OUTLINE Review Elementary set theory Probability fundamentals: outcomes, sample spaces, events Outline ELEMENTARY SET THEORY Basic probability concepts can be cast in
CIS 2033 Lecture 5, Fall
 CIS 2033 Lecture 5, Fall 2016 1 Instructor: David Dobor September 13, 2016 1 Supplemental reading from Dekking s textbook: Chapter2, 3. We mentioned at the beginning of this class that calculus was a prerequisite
CIS 2033 Lecture 5, Fall 2016 1 Instructor: David Dobor September 13, 2016 1 Supplemental reading from Dekking s textbook: Chapter2, 3. We mentioned at the beginning of this class that calculus was a prerequisite
the time it takes until a radioactive substance undergoes a decay
 1 Probabilities 1.1 Experiments with randomness Wewillusethetermexperimentinaverygeneralwaytorefertosomeprocess that produces a random outcome. Examples: (Ask class for some first) Here are some discrete
1 Probabilities 1.1 Experiments with randomness Wewillusethetermexperimentinaverygeneralwaytorefertosomeprocess that produces a random outcome. Examples: (Ask class for some first) Here are some discrete
The Practice of Statistics Third Edition
 The Practice of Statistics Third Edition Chapter 6: Probability and Simulation: The Study of Randomness Copyright 2008 by W. H. Freeman & Company Probability Rules True probability can only be found by
The Practice of Statistics Third Edition Chapter 6: Probability and Simulation: The Study of Randomness Copyright 2008 by W. H. Freeman & Company Probability Rules True probability can only be found by
Recitation 2: Probability
 Recitation 2: Probability Colin White, Kenny Marino January 23, 2018 Outline Facts about sets Definitions and facts about probability Random Variables and Joint Distributions Characteristics of distributions
Recitation 2: Probability Colin White, Kenny Marino January 23, 2018 Outline Facts about sets Definitions and facts about probability Random Variables and Joint Distributions Characteristics of distributions
Example: Suppose we toss a quarter and observe whether it falls heads or tails, recording the result as 1 for heads and 0 for tails.
 Example: Suppose we toss a quarter and observe whether it falls heads or tails, recording the result as 1 for heads and 0 for tails. (In Mathematical language, the result of our toss is a random variable,
Example: Suppose we toss a quarter and observe whether it falls heads or tails, recording the result as 1 for heads and 0 for tails. (In Mathematical language, the result of our toss is a random variable,
Econ 325: Introduction to Empirical Economics
 Econ 325: Introduction to Empirical Economics Lecture 2 Probability Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 3-1 3.1 Definition Random Experiment a process leading to an uncertain
Econ 325: Introduction to Empirical Economics Lecture 2 Probability Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 3-1 3.1 Definition Random Experiment a process leading to an uncertain
STT When trying to evaluate the likelihood of random events we are using following wording.
 Introduction to Chapter 2. Probability. When trying to evaluate the likelihood of random events we are using following wording. Provide your own corresponding examples. Subjective probability. An individual
Introduction to Chapter 2. Probability. When trying to evaluate the likelihood of random events we are using following wording. Provide your own corresponding examples. Subjective probability. An individual
1 Probability Theory. 1.1 Introduction
 1 Probability Theory Probability theory is used as a tool in statistics. It helps to evaluate the reliability of our conclusions about the population when we have only information about a sample. Probability
1 Probability Theory Probability theory is used as a tool in statistics. It helps to evaluate the reliability of our conclusions about the population when we have only information about a sample. Probability
Chapter 1 (Basic Probability)
 Chapter 1 (Basic Probability) What is probability? Consider the following experiments: 1. Count the number of arrival requests to a web server in a day. 2. Determine the execution time of a program. 3.
Chapter 1 (Basic Probability) What is probability? Consider the following experiments: 1. Count the number of arrival requests to a web server in a day. 2. Determine the execution time of a program. 3.
Statistical Theory 1
 Statistical Theory 1 Set Theory and Probability Paolo Bautista September 12, 2017 Set Theory We start by defining terms in Set Theory which will be used in the following sections. Definition 1 A set is
Statistical Theory 1 Set Theory and Probability Paolo Bautista September 12, 2017 Set Theory We start by defining terms in Set Theory which will be used in the following sections. Definition 1 A set is
Lecture notes for probability. Math 124
 Lecture notes for probability Math 124 What is probability? Probabilities are ratios, expressed as fractions, decimals, or percents, determined by considering results or outcomes of experiments whose result
Lecture notes for probability Math 124 What is probability? Probabilities are ratios, expressed as fractions, decimals, or percents, determined by considering results or outcomes of experiments whose result
Origins of Probability Theory
 1 16.584: INTRODUCTION Theory and Tools of Probability required to analyze and design systems subject to uncertain outcomes/unpredictability/randomness. Such systems more generally referred to as Experiments.
1 16.584: INTRODUCTION Theory and Tools of Probability required to analyze and design systems subject to uncertain outcomes/unpredictability/randomness. Such systems more generally referred to as Experiments.
INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR. NPTEL National Programme on Technology Enhanced Learning. Probability Methods in Civil Engineering
 INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR NPTEL National Programme on Technology Enhanced Learning Probability Methods in Civil Engineering Prof. Rajib Maity Department of Civil Engineering IIT Kharagpur
INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR NPTEL National Programme on Technology Enhanced Learning Probability Methods in Civil Engineering Prof. Rajib Maity Department of Civil Engineering IIT Kharagpur
HW MATH425/525 Lecture Notes 1
 HW MATH425/525 Lecture Notes 1 Definition 4.1 If an experiment can be repeated under the same condition, its outcome cannot be predicted with certainty, and the collection of its every possible outcome
HW MATH425/525 Lecture Notes 1 Definition 4.1 If an experiment can be repeated under the same condition, its outcome cannot be predicted with certainty, and the collection of its every possible outcome
CS626 Data Analysis and Simulation
 CS626 Data Analysis and Simulation Instructor: Peter Kemper R 104A, phone 221-3462, email:kemper@cs.wm.edu Today: Probability Primer Quick Reference: Sheldon Ross: Introduction to Probability Models 9th
CS626 Data Analysis and Simulation Instructor: Peter Kemper R 104A, phone 221-3462, email:kemper@cs.wm.edu Today: Probability Primer Quick Reference: Sheldon Ross: Introduction to Probability Models 9th
4 Lecture 4 Notes: Introduction to Probability. Probability Rules. Independence and Conditional Probability. Bayes Theorem. Risk and Odds Ratio
 4 Lecture 4 Notes: Introduction to Probability. Probability Rules. Independence and Conditional Probability. Bayes Theorem. Risk and Odds Ratio Wrong is right. Thelonious Monk 4.1 Three Definitions of
4 Lecture 4 Notes: Introduction to Probability. Probability Rules. Independence and Conditional Probability. Bayes Theorem. Risk and Odds Ratio Wrong is right. Thelonious Monk 4.1 Three Definitions of
Lecture 1. Chapter 1. (Part I) Material Covered in This Lecture: Chapter 1, Chapter 2 ( ). 1. What is Statistics?
 Lecture 1 (Part I) Material Covered in This Lecture: Chapter 1, Chapter 2 (2.1 --- 2.6). Chapter 1 1. What is Statistics? 2. Two definitions. (1). Population (2). Sample 3. The objective of statistics.
Lecture 1 (Part I) Material Covered in This Lecture: Chapter 1, Chapter 2 (2.1 --- 2.6). Chapter 1 1. What is Statistics? 2. Two definitions. (1). Population (2). Sample 3. The objective of statistics.
1. When applied to an affected person, the test comes up positive in 90% of cases, and negative in 10% (these are called false negatives ).
 CS 70 Discrete Mathematics for CS Spring 2006 Vazirani Lecture 8 Conditional Probability A pharmaceutical company is marketing a new test for a certain medical condition. According to clinical trials,
CS 70 Discrete Mathematics for CS Spring 2006 Vazirani Lecture 8 Conditional Probability A pharmaceutical company is marketing a new test for a certain medical condition. According to clinical trials,
Chapter 2.5 Random Variables and Probability The Modern View (cont.)
 Chapter 2.5 Random Variables and Probability The Modern View (cont.) I. Statistical Independence A crucially important idea in probability and statistics is the concept of statistical independence. Suppose
Chapter 2.5 Random Variables and Probability The Modern View (cont.) I. Statistical Independence A crucially important idea in probability and statistics is the concept of statistical independence. Suppose
CS4705. Probability Review and Naïve Bayes. Slides from Dragomir Radev
 CS4705 Probability Review and Naïve Bayes Slides from Dragomir Radev Classification using a Generative Approach Previously on NLP discriminative models P C D here is a line with all the social media posts
CS4705 Probability Review and Naïve Bayes Slides from Dragomir Radev Classification using a Generative Approach Previously on NLP discriminative models P C D here is a line with all the social media posts
Stat 225 Week 1, 8/20/12-8/24/12, Notes: Set Theory
 Stat 225 Week 1, 8/20/12-8/24/12, Notes: Set Theory The Fall 2012 Stat 225 T.A.s September 7, 2012 The material in this handout is intended to cover general set theory topics. Information includes (but
Stat 225 Week 1, 8/20/12-8/24/12, Notes: Set Theory The Fall 2012 Stat 225 T.A.s September 7, 2012 The material in this handout is intended to cover general set theory topics. Information includes (but
Discrete Mathematics and Probability Theory Spring 2016 Rao and Walrand Note 14
 CS 70 Discrete Mathematics and Probability Theory Spring 2016 Rao and Walrand Note 14 Introduction One of the key properties of coin flips is independence: if you flip a fair coin ten times and get ten
CS 70 Discrete Mathematics and Probability Theory Spring 2016 Rao and Walrand Note 14 Introduction One of the key properties of coin flips is independence: if you flip a fair coin ten times and get ten
STAT 302 Introduction to Probability Learning Outcomes. Textbook: A First Course in Probability by Sheldon Ross, 8 th ed.
 STAT 302 Introduction to Probability Learning Outcomes Textbook: A First Course in Probability by Sheldon Ross, 8 th ed. Chapter 1: Combinatorial Analysis Demonstrate the ability to solve combinatorial
STAT 302 Introduction to Probability Learning Outcomes Textbook: A First Course in Probability by Sheldon Ross, 8 th ed. Chapter 1: Combinatorial Analysis Demonstrate the ability to solve combinatorial
MATH 118 FINAL EXAM STUDY GUIDE
 MATH 118 FINAL EXAM STUDY GUIDE Recommendations: 1. Take the Final Practice Exam and take note of questions 2. Use this study guide as you take the tests and cross off what you know well 3. Take the Practice
MATH 118 FINAL EXAM STUDY GUIDE Recommendations: 1. Take the Final Practice Exam and take note of questions 2. Use this study guide as you take the tests and cross off what you know well 3. Take the Practice
Set/deck of playing cards. Spades Hearts Diamonds Clubs
 TC Mathematics S2 Coins Die dice Tale Head Set/deck of playing cards Spades Hearts Diamonds Clubs TC Mathematics S2 PROBABILITIES : intuitive? Experiment tossing a coin Event it s a head Probability 1/2
TC Mathematics S2 Coins Die dice Tale Head Set/deck of playing cards Spades Hearts Diamonds Clubs TC Mathematics S2 PROBABILITIES : intuitive? Experiment tossing a coin Event it s a head Probability 1/2
Independence. CS 109 Lecture 5 April 6th, 2016
 Independence CS 109 Lecture 5 April 6th, 2016 Today s Topics 2 Last time: Conditional Probability Bayes Theorem Today: Independence Conditional Independence Next time: Random Variables The Tragedy of Conditional
Independence CS 109 Lecture 5 April 6th, 2016 Today s Topics 2 Last time: Conditional Probability Bayes Theorem Today: Independence Conditional Independence Next time: Random Variables The Tragedy of Conditional
ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page α 2 θ 1 u 3. wear coat. θ 2 = warm u 2 = sweaty! θ 1 = cold u 3 = brrr!
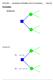 ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page 2-01 Probability Decision trees u 1 u 2 α 2 θ 1 u 3 θ 2 u 4 Example 2.01 θ 1 = cold u 1 = snug! α 1 wear coat θ 2 = warm u 2 = sweaty! θ
ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page 2-01 Probability Decision trees u 1 u 2 α 2 θ 1 u 3 θ 2 u 4 Example 2.01 θ 1 = cold u 1 = snug! α 1 wear coat θ 2 = warm u 2 = sweaty! θ
Lecture 3 - Axioms of Probability
 Lecture 3 - Axioms of Probability Sta102 / BME102 January 25, 2016 Colin Rundel Axioms of Probability What does it mean to say that: The probability of flipping a coin and getting heads is 1/2? 3 What
Lecture 3 - Axioms of Probability Sta102 / BME102 January 25, 2016 Colin Rundel Axioms of Probability What does it mean to say that: The probability of flipping a coin and getting heads is 1/2? 3 What
MATH MW Elementary Probability Course Notes Part I: Models and Counting
 MATH 2030 3.00MW Elementary Probability Course Notes Part I: Models and Counting Tom Salisbury salt@yorku.ca York University Winter 2010 Introduction [Jan 5] Probability: the mathematics used for Statistics
MATH 2030 3.00MW Elementary Probability Course Notes Part I: Models and Counting Tom Salisbury salt@yorku.ca York University Winter 2010 Introduction [Jan 5] Probability: the mathematics used for Statistics
Probability (Devore Chapter Two)
 Probability (Devore Chapter Two) 1016-345-01: Probability and Statistics for Engineers Spring 2013 Contents 0 Preliminaries 3 0.1 Motivation..................................... 3 0.2 Administrata...................................
Probability (Devore Chapter Two) 1016-345-01: Probability and Statistics for Engineers Spring 2013 Contents 0 Preliminaries 3 0.1 Motivation..................................... 3 0.2 Administrata...................................
 CHAPTER - 16 PROBABILITY Random Experiment : If an experiment has more than one possible out come and it is not possible to predict the outcome in advance then experiment is called random experiment. Sample
CHAPTER - 16 PROBABILITY Random Experiment : If an experiment has more than one possible out come and it is not possible to predict the outcome in advance then experiment is called random experiment. Sample
Probability Experiments, Trials, Outcomes, Sample Spaces Example 1 Example 2
 Probability Probability is the study of uncertain events or outcomes. Games of chance that involve rolling dice or dealing cards are one obvious area of application. However, probability models underlie
Probability Probability is the study of uncertain events or outcomes. Games of chance that involve rolling dice or dealing cards are one obvious area of application. However, probability models underlie
General Info. Grading
 Syllabus & Policies General Info Lecture 1: Introduction, Set Theory, and Boolean Algebra Classroom: Perkins 2-072 Time: Mon - Fri, 2:00-3:15 pm Wed, 3:30-4:30 pm Sta 111 Colin Rundel May 13, 2014 Professor:
Syllabus & Policies General Info Lecture 1: Introduction, Set Theory, and Boolean Algebra Classroom: Perkins 2-072 Time: Mon - Fri, 2:00-3:15 pm Wed, 3:30-4:30 pm Sta 111 Colin Rundel May 13, 2014 Professor:
Mean, Median and Mode. Lecture 3 - Axioms of Probability. Where do they come from? Graphically. We start with a set of 21 numbers, Sta102 / BME102
 Mean, Median and Mode Lecture 3 - Axioms of Probability Sta102 / BME102 Colin Rundel September 1, 2014 We start with a set of 21 numbers, ## [1] -2.2-1.6-1.0-0.5-0.4-0.3-0.2 0.1 0.1 0.2 0.4 ## [12] 0.4
Mean, Median and Mode Lecture 3 - Axioms of Probability Sta102 / BME102 Colin Rundel September 1, 2014 We start with a set of 21 numbers, ## [1] -2.2-1.6-1.0-0.5-0.4-0.3-0.2 0.1 0.1 0.2 0.4 ## [12] 0.4
The possible experimental outcomes: 1, 2, 3, 4, 5, 6 (Experimental outcomes are also known as sample points)
 Chapter 4 Introduction to Probability 1 4.1 Experiments, Counting Rules and Assigning Probabilities Example Rolling a dice you can get the values: S = {1, 2, 3, 4, 5, 6} S is called the sample space. Experiment:
Chapter 4 Introduction to Probability 1 4.1 Experiments, Counting Rules and Assigning Probabilities Example Rolling a dice you can get the values: S = {1, 2, 3, 4, 5, 6} S is called the sample space. Experiment:
Probability the chance that an uncertain event will occur (always between 0 and 1)
 Quantitative Methods 2013 1 Probability as a Numerical Measure of the Likelihood of Occurrence Probability the chance that an uncertain event will occur (always between 0 and 1) Increasing Likelihood of
Quantitative Methods 2013 1 Probability as a Numerical Measure of the Likelihood of Occurrence Probability the chance that an uncertain event will occur (always between 0 and 1) Increasing Likelihood of
CIVL Why are we studying probability and statistics? Learning Objectives. Basic Laws and Axioms of Probability
 CIVL 3103 Basic Laws and Axioms of Probability Why are we studying probability and statistics? How can we quantify risks of decisions based on samples from a population? How should samples be selected
CIVL 3103 Basic Laws and Axioms of Probability Why are we studying probability and statistics? How can we quantify risks of decisions based on samples from a population? How should samples be selected
Single Maths B: Introduction to Probability
 Single Maths B: Introduction to Probability Overview Lecturer Email Office Homework Webpage Dr Jonathan Cumming j.a.cumming@durham.ac.uk CM233 None! http://maths.dur.ac.uk/stats/people/jac/singleb/ 1 Introduction
Single Maths B: Introduction to Probability Overview Lecturer Email Office Homework Webpage Dr Jonathan Cumming j.a.cumming@durham.ac.uk CM233 None! http://maths.dur.ac.uk/stats/people/jac/singleb/ 1 Introduction
Chapter 4 - Introduction to Probability
 Chapter 4 - Introduction to Probability Probability is a numerical measure of the likelihood that an event will occur. Probability values are always assigned on a scale from 0 to 1. A probability near
Chapter 4 - Introduction to Probability Probability is a numerical measure of the likelihood that an event will occur. Probability values are always assigned on a scale from 0 to 1. A probability near
Lecture 11: Information theory THURSDAY, FEBRUARY 21, 2019
 Lecture 11: Information theory DANIEL WELLER THURSDAY, FEBRUARY 21, 2019 Agenda Information and probability Entropy and coding Mutual information and capacity Both images contain the same fraction of black
Lecture 11: Information theory DANIEL WELLER THURSDAY, FEBRUARY 21, 2019 Agenda Information and probability Entropy and coding Mutual information and capacity Both images contain the same fraction of black
Stats Probability Theory
 Stats 241.3 Probability Theory Instructor: Office: W.H.Laverty 235 McLean Hall Phone: 966-6096 Lectures: Evaluation: M T W Th F 1:30pm - 2:50pm Thorv 105 Lab: T W Th 3:00-3:50 Thorv 105 Assignments, Labs,
Stats 241.3 Probability Theory Instructor: Office: W.H.Laverty 235 McLean Hall Phone: 966-6096 Lectures: Evaluation: M T W Th F 1:30pm - 2:50pm Thorv 105 Lab: T W Th 3:00-3:50 Thorv 105 Assignments, Labs,
3.2 Probability Rules
 3.2 Probability Rules The idea of probability rests on the fact that chance behavior is predictable in the long run. In the last section, we used simulation to imitate chance behavior. Do we always need
3.2 Probability Rules The idea of probability rests on the fact that chance behavior is predictable in the long run. In the last section, we used simulation to imitate chance behavior. Do we always need
Sample Space: Specify all possible outcomes from an experiment. Event: Specify a particular outcome or combination of outcomes.
 Chapter 2 Introduction to Probability 2.1 Probability Model Probability concerns about the chance of observing certain outcome resulting from an experiment. However, since chance is an abstraction of something
Chapter 2 Introduction to Probability 2.1 Probability Model Probability concerns about the chance of observing certain outcome resulting from an experiment. However, since chance is an abstraction of something
BASICS OF PROBABILITY CHAPTER-1 CS6015-LINEAR ALGEBRA AND RANDOM PROCESSES
 BASICS OF PROBABILITY CHAPTER-1 CS6015-LINEAR ALGEBRA AND RANDOM PROCESSES COMMON TERMS RELATED TO PROBABILITY Probability is the measure of the likelihood that an event will occur Probability values are
BASICS OF PROBABILITY CHAPTER-1 CS6015-LINEAR ALGEBRA AND RANDOM PROCESSES COMMON TERMS RELATED TO PROBABILITY Probability is the measure of the likelihood that an event will occur Probability values are
lecture notes October 22, Probability Theory
 8.30 lecture notes October 22, 203 Probability Theory Lecturer: Michel Goemans These notes cover the basic definitions of discrete probability theory, and then present some results including Bayes rule,
8.30 lecture notes October 22, 203 Probability Theory Lecturer: Michel Goemans These notes cover the basic definitions of discrete probability theory, and then present some results including Bayes rule,
Lecture 10: Everything Else
 Math 94 Professor: Padraic Bartlett Lecture 10: Everything Else Week 10 UCSB 2015 This is the tenth week of the Mathematics Subject Test GRE prep course; here, we quickly review a handful of useful concepts
Math 94 Professor: Padraic Bartlett Lecture 10: Everything Else Week 10 UCSB 2015 This is the tenth week of the Mathematics Subject Test GRE prep course; here, we quickly review a handful of useful concepts
Discrete Random Variables
 Discrete Random Variables An Undergraduate Introduction to Financial Mathematics J. Robert Buchanan 2014 Introduction The markets can be thought of as a complex interaction of a large number of random
Discrete Random Variables An Undergraduate Introduction to Financial Mathematics J. Robert Buchanan 2014 Introduction The markets can be thought of as a complex interaction of a large number of random
Topic -2. Probability. Larson & Farber, Elementary Statistics: Picturing the World, 3e 1
 Topic -2 Probability Larson & Farber, Elementary Statistics: Picturing the World, 3e 1 Probability Experiments Experiment : An experiment is an act that can be repeated under given condition. Rolling a
Topic -2 Probability Larson & Farber, Elementary Statistics: Picturing the World, 3e 1 Probability Experiments Experiment : An experiment is an act that can be repeated under given condition. Rolling a
Lecture Lecture 5
 Lecture 4 --- Lecture 5 A. Basic Concepts (4.1-4.2) 1. Experiment: A process of observing a phenomenon that has variation in its outcome. Examples: (E1). Rolling a die, (E2). Drawing a card form a shuffled
Lecture 4 --- Lecture 5 A. Basic Concepts (4.1-4.2) 1. Experiment: A process of observing a phenomenon that has variation in its outcome. Examples: (E1). Rolling a die, (E2). Drawing a card form a shuffled
Name: (This only happens every four years or does it?)
 Name: (This only happens every four years or does it?) Calendars: Then and Now Name: 1. What is a leap year? What do you already know about leap years? 2. List at least three questions about leap years
Name: (This only happens every four years or does it?) Calendars: Then and Now Name: 1. What is a leap year? What do you already know about leap years? 2. List at least three questions about leap years
Basic Concepts of Probability
 Probability Probability theory is the branch of math that deals with random events Probability is used to describe how likely a particular outcome is in a random event the probability of obtaining heads
Probability Probability theory is the branch of math that deals with random events Probability is used to describe how likely a particular outcome is in a random event the probability of obtaining heads
Discrete Probability
 Discrete Probability Counting Permutations Combinations r- Combinations r- Combinations with repetition Allowed Pascal s Formula Binomial Theorem Conditional Probability Baye s Formula Independent Events
Discrete Probability Counting Permutations Combinations r- Combinations r- Combinations with repetition Allowed Pascal s Formula Binomial Theorem Conditional Probability Baye s Formula Independent Events
Statistics for Financial Engineering Session 2: Basic Set Theory March 19 th, 2006
 Statistics for Financial Engineering Session 2: Basic Set Theory March 19 th, 2006 Topics What is a set? Notations for sets Empty set Inclusion/containment and subsets Sample spaces and events Operations
Statistics for Financial Engineering Session 2: Basic Set Theory March 19 th, 2006 Topics What is a set? Notations for sets Empty set Inclusion/containment and subsets Sample spaces and events Operations
tossing a coin selecting a card from a deck measuring the commuting time on a particular morning
 2 Probability Experiment An experiment or random variable is any activity whose outcome is unknown or random upfront: tossing a coin selecting a card from a deck measuring the commuting time on a particular
2 Probability Experiment An experiment or random variable is any activity whose outcome is unknown or random upfront: tossing a coin selecting a card from a deck measuring the commuting time on a particular
Math 1313 Experiments, Events and Sample Spaces
 Math 1313 Experiments, Events and Sample Spaces At the end of this recording, you should be able to define and use the basic terminology used in defining experiments. Terminology The next main topic in
Math 1313 Experiments, Events and Sample Spaces At the end of this recording, you should be able to define and use the basic terminology used in defining experiments. Terminology The next main topic in
Come & Join Us at VUSTUDENTS.net
 Come & Join Us at VUSTUDENTS.net For Assignment Solution, GDB, Online Quizzes, Helping Study material, Past Solved Papers, Solved MCQs, Current Papers, E-Books & more. Go to http://www.vustudents.net and
Come & Join Us at VUSTUDENTS.net For Assignment Solution, GDB, Online Quizzes, Helping Study material, Past Solved Papers, Solved MCQs, Current Papers, E-Books & more. Go to http://www.vustudents.net and
Sampling Distributions
 Sampling Error As you may remember from the first lecture, samples provide incomplete information about the population In particular, a statistic (e.g., M, s) computed on any particular sample drawn from
Sampling Error As you may remember from the first lecture, samples provide incomplete information about the population In particular, a statistic (e.g., M, s) computed on any particular sample drawn from
Probability theory basics
 Probability theory basics Michael Franke Basics of probability theory: axiomatic definition, interpretation, joint distributions, marginalization, conditional probability & Bayes rule. Random variables:
Probability theory basics Michael Franke Basics of probability theory: axiomatic definition, interpretation, joint distributions, marginalization, conditional probability & Bayes rule. Random variables:
Random Signals and Systems. Chapter 1. Jitendra K Tugnait. Department of Electrical & Computer Engineering. James B Davis Professor.
 Random Signals and Systems Chapter 1 Jitendra K Tugnait James B Davis Professor Department of Electrical & Computer Engineering Auburn University 2 3 Descriptions of Probability Relative frequency approach»
Random Signals and Systems Chapter 1 Jitendra K Tugnait James B Davis Professor Department of Electrical & Computer Engineering Auburn University 2 3 Descriptions of Probability Relative frequency approach»
Lecture 3. Probability and elements of combinatorics
 Introduction to theory of probability and statistics Lecture 3. Probability and elements of combinatorics prof. dr hab.inż. Katarzyna Zakrzewska Katedra Elektroniki, AGH e-mail: zak@agh.edu.pl http://home.agh.edu.pl/~zak
Introduction to theory of probability and statistics Lecture 3. Probability and elements of combinatorics prof. dr hab.inż. Katarzyna Zakrzewska Katedra Elektroniki, AGH e-mail: zak@agh.edu.pl http://home.agh.edu.pl/~zak
STAT Chapter 3: Probability
 Basic Definitions STAT 515 --- Chapter 3: Probability Experiment: A process which leads to a single outcome (called a sample point) that cannot be predicted with certainty. Sample Space (of an experiment):
Basic Definitions STAT 515 --- Chapter 3: Probability Experiment: A process which leads to a single outcome (called a sample point) that cannot be predicted with certainty. Sample Space (of an experiment):
MATH2206 Prob Stat/20.Jan Weekly Review 1-2
 MATH2206 Prob Stat/20.Jan.2017 Weekly Review 1-2 This week I explained the idea behind the formula of the well-known statistic standard deviation so that it is clear now why it is a measure of dispersion
MATH2206 Prob Stat/20.Jan.2017 Weekly Review 1-2 This week I explained the idea behind the formula of the well-known statistic standard deviation so that it is clear now why it is a measure of dispersion
Conditional Probability and Bayes
 Conditional Probability and Bayes Chapter 2 Lecture 5 Yiren Ding Shanghai Qibao Dwight High School March 9, 2016 Yiren Ding Conditional Probability and Bayes 1 / 13 Outline 1 Independent Events Definition
Conditional Probability and Bayes Chapter 2 Lecture 5 Yiren Ding Shanghai Qibao Dwight High School March 9, 2016 Yiren Ding Conditional Probability and Bayes 1 / 13 Outline 1 Independent Events Definition
Recap. The study of randomness and uncertainty Chances, odds, likelihood, expected, probably, on average,... PROBABILITY INFERENTIAL STATISTICS
 Recap. Probability (section 1.1) The study of randomness and uncertainty Chances, odds, likelihood, expected, probably, on average,... PROBABILITY Population Sample INFERENTIAL STATISTICS Today. Formulation
Recap. Probability (section 1.1) The study of randomness and uncertainty Chances, odds, likelihood, expected, probably, on average,... PROBABILITY Population Sample INFERENTIAL STATISTICS Today. Formulation
EE 178 Lecture Notes 0 Course Introduction. About EE178. About Probability. Course Goals. Course Topics. Lecture Notes EE 178
 EE 178 Lecture Notes 0 Course Introduction About EE178 About Probability Course Goals Course Topics Lecture Notes EE 178: Course Introduction Page 0 1 EE 178 EE 178 provides an introduction to probabilistic
EE 178 Lecture Notes 0 Course Introduction About EE178 About Probability Course Goals Course Topics Lecture Notes EE 178: Course Introduction Page 0 1 EE 178 EE 178 provides an introduction to probabilistic
CSE 312, 2017 Winter, W.L.Ruzzo. 5. independence [ ]
![CSE 312, 2017 Winter, W.L.Ruzzo. 5. independence [ ] CSE 312, 2017 Winter, W.L.Ruzzo. 5. independence [ ]](/thumbs/95/123242418.jpg) CSE 312, 2017 Winter, W.L.Ruzzo 5. independence [ ] independence Defn: Two events E and F are independent if P(EF) = P(E) P(F) If P(F)>0, this is equivalent to: P(E F) = P(E) (proof below) Otherwise, they
CSE 312, 2017 Winter, W.L.Ruzzo 5. independence [ ] independence Defn: Two events E and F are independent if P(EF) = P(E) P(F) If P(F)>0, this is equivalent to: P(E F) = P(E) (proof below) Otherwise, they
Review Basic Probability Concept
 Economic Risk and Decision Analysis for Oil and Gas Industry CE81.9008 School of Engineering and Technology Asian Institute of Technology January Semester Presented by Dr. Thitisak Boonpramote Department
Economic Risk and Decision Analysis for Oil and Gas Industry CE81.9008 School of Engineering and Technology Asian Institute of Technology January Semester Presented by Dr. Thitisak Boonpramote Department
Discrete Probability. Mark Huiskes, LIACS Probability and Statistics, Mark Huiskes, LIACS, Lecture 2
 Discrete Probability Mark Huiskes, LIACS mark.huiskes@liacs.nl Probability: Basic Definitions In probability theory we consider experiments whose outcome depends on chance or are uncertain. How do we model
Discrete Probability Mark Huiskes, LIACS mark.huiskes@liacs.nl Probability: Basic Definitions In probability theory we consider experiments whose outcome depends on chance or are uncertain. How do we model
Mutually Exclusive Events
 172 CHAPTER 3 PROBABILITY TOPICS c. QS, 7D, 6D, KS Mutually Exclusive Events A and B are mutually exclusive events if they cannot occur at the same time. This means that A and B do not share any outcomes
172 CHAPTER 3 PROBABILITY TOPICS c. QS, 7D, 6D, KS Mutually Exclusive Events A and B are mutually exclusive events if they cannot occur at the same time. This means that A and B do not share any outcomes
Bayes Theorem. Jan Kracík. Department of Applied Mathematics FEECS, VŠB - TU Ostrava
 Jan Kracík Department of Applied Mathematics FEECS, VŠB - TU Ostrava Introduction Bayes theorem fundamental theorem in probability theory named after reverend Thomas Bayes (1701 1761) discovered in Bayes
Jan Kracík Department of Applied Mathematics FEECS, VŠB - TU Ostrava Introduction Bayes theorem fundamental theorem in probability theory named after reverend Thomas Bayes (1701 1761) discovered in Bayes
Week 2. Section Texas A& M University. Department of Mathematics Texas A& M University, College Station 22 January-24 January 2019
 Week 2 Section 1.2-1.4 Texas A& M University Department of Mathematics Texas A& M University, College Station 22 January-24 January 2019 Oğuz Gezmiş (TAMU) Topics in Contemporary Mathematics II Week2 1
Week 2 Section 1.2-1.4 Texas A& M University Department of Mathematics Texas A& M University, College Station 22 January-24 January 2019 Oğuz Gezmiş (TAMU) Topics in Contemporary Mathematics II Week2 1
Relative Risks (RR) and Odds Ratios (OR) 20
 BSTT523: Pagano & Gavreau, Chapter 6 1 Chapter 6: Probability slide: Definitions (6.1 in P&G) 2 Experiments; trials; probabilities Event operations 4 Intersection; Union; Complement Venn diagrams Conditional
BSTT523: Pagano & Gavreau, Chapter 6 1 Chapter 6: Probability slide: Definitions (6.1 in P&G) 2 Experiments; trials; probabilities Event operations 4 Intersection; Union; Complement Venn diagrams Conditional
Probability with Engineering Applications ECE 313 Section C Lecture 2. Lav R. Varshney 30 August 2017
 Probability with Engineering Applications ECE 313 Section C Lecture 2 Lav R. Varshney 30 August 2017 1 Logistics Text: ECE 313 course notes Hard copy sold through ECE Store Soft copy available on the course
Probability with Engineering Applications ECE 313 Section C Lecture 2 Lav R. Varshney 30 August 2017 1 Logistics Text: ECE 313 course notes Hard copy sold through ECE Store Soft copy available on the course
Chapter 2. Probability. Math 371. University of Hawai i at Mānoa. Summer 2011
 Chapter 2 Probability Math 371 University of Hawai i at Mānoa Summer 2011 W. DeMeo (williamdemeo@gmail.com) Chapter 2: Probability math.hawaii.edu/ williamdemeo 1 / 8 Outline 1 Chapter 2 Examples Definition
Chapter 2 Probability Math 371 University of Hawai i at Mānoa Summer 2011 W. DeMeo (williamdemeo@gmail.com) Chapter 2: Probability math.hawaii.edu/ williamdemeo 1 / 8 Outline 1 Chapter 2 Examples Definition
