NATIONAL OPEN UNIVERSITY OF NIGERIA SCHOOL OF SCIENCE AND TECHNOLOGY COURSE CODE: PHY 312 COURSE TITLE: MATHEMATICAL METHODS OF PHYSICS
|
|
|
- Marjorie Little
- 5 years ago
- Views:
Transcription
1 NATIONAL OPEN UNIVERSITY OF NIGERIA SCHOOL OF SCIENCE AND TECHNOLOGY COURSE CODE: PHY 3 COURSE TITLE: MATHEMATICAL METHODS OF PHYSICS
2 PHY3 COURSE GUIDE COURSE GUIDE PHY3 Couse Team Ouwaoyi K. Ogubamike Deveope/Wie - Wesey Uivesiy of Sciece & Techoogy, Odo D. S.O. Ajiboa Edio/Pogamme Leade - NOUN ii
3 PHY3 COURSE GUIDE NATIONAL OPEN UNIVERSITY OF NIGERIA Naioa Ope Uivesiy of Nigeia Headquaes 4/6 Ahmadu Beo Way Vicoia Isad Lagos Abuja Office 5, Da es Saaam See Off Amiu Kao Cesce Wuse II, Abuja e-mai: URL: Pubished By: Naioa Ope Uivesiy of Nigeia Fis Pied ISBN: A Righs Reseved iii
4 PHY3 COURSE GUIDE iv
5 PHY3 COURSE GUIDE CONTENTS PAGE Ioducio Wha You Wi Lea i This Couse... Couse Aim.. Couse Objecives... Wokig hough This Couse... Couse Maeias... Sudy Uis... Tebooks ad Refeeces... 3 Assessme... 3 Tuo-Maked Assigme Fia Eamiaios ad Gadig... 3 Peseaio Schedue... 4 Couse Makig Scheme... 4 How o Ge he Mos fom This Couse... 4 Faciiaos/Tuos ad Tuoias... 5 Summay v
6
7 Ioducio The couse Mahemaica Mehod of Physics - is mea o povide esseia mehods fo sovig mahemaica pobems. I scieific pobems, ofe imes we discove ha a faco depeds upo sevea ohe eaed facos. Fo isace, he aea of soid depeds o is egh ad beadh. Poeia eegy of a body depeds o gaviy, desiy ad heigh of he body ec. Moeove, he segh of a maeia depeds o empeaue, desiy, isoopy ad sofess ec. Wha You Wi Lea i This Couse This is a 3ui couse, i is gouped io fou 4 modues i.e. modue,, 3 ad 4. Modue has uis; modue aso has uis. Modue 3 has oy oe ui whie modue 4 has 3uis. I summay we have fou 4 modues ad 8 uis. The couse guide gives a bief summay of he oa coes coaied i he couse maeia. Fucios of sevea vaiabes seamie he eaioship bewee fucio ad vaiabes, he appicaio of acobia, dow o fucioa depedece ad idepedece. Aso discussed ae muipe, ie ad impope iegas. Couse Aim The ovea aim of his couse is o povide you wih he esseia mehods fo sovig mahemaica pobems i physics. Couse Objecives A he ed of his couse, you shoud be abe o: defie iea secod-ode paia diffeeia equaio i moe ha oe idepede vaiabe use he echique of sepaaio of vaiabes i sovig impoa secod ode iea paia diffeeia equaios i physics sove he eecises a he ed of his ui ideify whehe a give fucio is eve, odd o peiodic evauae he Fouie coefficies deive ad appy Fouie seies i foced vibaio pobems use Fouie Iega fo eaig vaious pobems ivovig peiodic fucio appy haf age epasio o souios of some pobems.
8 PHY3 Wokig hough This Couse This couse ivoves ha you woud be equied o sped o of ime o ead. The coe of his maeia is vey dese ad equie you spedig gea ime o sudy i. This accous fo he gea effo pu io is deveopme i he aemp o make i vey eadabe ad compehesibe. Neveheess, he effo equied of you is si emedous. I woud advice ha you avai yousef he oppouiy of aedig he uoia sessios whee you woud have he oppouiy of compaig kowedge wih you pees. Couse Maeias You wi be povided wih he foowig maeias: Couse guide Sudy uis I addiio, he couse comes wih a is of ecommeded ebooks, which hough ae o compusoy fo you o acquie o ideed ead, ae ecessay as suppemes o he couse maeia. Sudy Uis The foowig ae he sudy uis coaied i his couse. The uis ae aaged io fou ideifiabe bu eaed modues. Modue Ui Ui Modue Ui Ui Paia Diffeeia Equaios wih Appicaios i Physics Paia Diffeeia Equaios Fouie Seies Appicaio of Fouie o PDEs Legede poyomias ad Besse Fucios Legede Poyomias Besse Fucios ii
9 PHY3 Modue 3 Ui Ui Appicaio of Fouie o PDEs Hemie Poyomias ad Laguee Poyomias Hemie Poyomias Laguee Poyomias Tebook ad Refeeces The foowig ediios of hese books ae ecommeded fo fuhe eadig. Hidaba, F. B.d. Advaced Cacuus fo Appicaio. Muay, R. S.974. Schaums Ouie Seies o Theoy ad Pobem of Advaced Cacuus. Gea Biai: McGaw Hi Ic. Sepheo, G Mahemaica Mehods fo Sciece Sudes. Lodo: Logma, Goup Limied. Soud, K.A Egieeig Mahs 5h ed.. Pagaw. Vema, P.D.S Egieeig Mahemaics. New Dehi: Vikas Pubishig House PVT Ld. Assessme Thee ae wo compoes of assessme fo his couse. The Tuo- Maked Assigme TMA ad he ed of couse eamiaio. Tuo-Maked Assigme The TMA is he coiuous assessme compoe of you couse. I accous fo 3% of he oa scoe. You wi be give fou 4 TMAs o aswe. Thee of hese mus be asweed befoe you ae aowed o si fo he ed of couse eamiaio. The TMAs woud be give o you by you faciiao ad eued afe you have doe he assigme. Fia Eamiaios ad Gadig This eamiaio cocudes he assessme fo he couse. I cosiues 7% of he whoe couse. You wi be ifomed of he ime of he eamiaio. I may o may o coicide wih he Uivesiy Semese Eamiaio. iii
10 PHY3 Peseaio Schedue You couse maeias have impoa daes fo he eay ad imey compeio ad submissio of you TMAs ad aedig uoias. You shoud emembe ha you ae equied o submi a you assigmes by he sipuaed ime ad dae. You shoud guad agais faig behid i you wok. Couse Makig Scheme Assigme Assigmes -4 Ed of couse eamiaio Toa Maks Fou TMAs, bes hee maks of he fou cou a % each 3% of couse maks. 7% of ovea couse maks. % of couse maeias. A he ed of each ui, assigmes ae give o assis you o assess you udesadig of he opics ha have bee discussed. Couse Oveview Each sudy ui cosiss of hee hous wok. Each sudy ui icudes ioducio, specific objecives, diecios fo sudy, eadig maeias, cocusios, ad summay, Tuo -Maked Assigmes TMAs, efeeces / fuhe eadig. The uis diec you o wok o eecises eaed o he equied eadigs. I geea, hese eecises es you o he maeias you have jus coveed o equie you o appy i i some way ad heeby assis you o evauae you pogess ad o eifoce you compehesio of he maeia. Togehe wih TMAs, hese eecises wi hep you i achievig he saed eaig objecives of he idividua uis ad of he couse as a whoe. How o Ge he Mos Ou of This Couse Impici iees ad egua cuue of eadig ae of umos equiemes fo geig he bes ou of his couse. I is paamou ha you shoud a eas puchase oe of he ebooks ha ae ecommeded fo you. Moe impoay, aedig uoias sessios ad compeig you assigmes o ime wi ceaiy assis you o ge he bes ou of his couse. iv
11 PHY3 Faciiaos/Tuos ad Tuoias Thee ae 6 hous of uoias povided i suppo of his couse. You wi be oified of he daes, imes ad ocaios of hese uoias as we as he ame ad phoe umbe of you faciiao, as soo as you ae aocaed a uoia goup. You faciiao wi mak ad comme o you assigmes, keep a cose wach o you pogess ad ay difficuies you migh face ad povide assisace o you duig he couse. You ae epeced o mai you Tuo -Maked Assigme o you faciiao befoe he schedued dae a eas wo wokig days ae equied. They wi be maked by you uo ad eued o you as soo as possibe. Do o deay o coac you faciiao by eephoe o e-mai if you eed assisace. The foowig migh be cicumsaces i which you woud fid assisace ecessay. You woud have o coac you faciiao if: you do o udesad ay pa of he sudy o he assiged eadigs you have difficuy wih he sef-ess you have a quesio o pobem wih assigmes o wih he gadig of assigmes. You shoud edeavou o aed he uoias. This is he oy chace o have face o face coac wih you couse faciiao ad o ask quesios which ae asweed isay. You ca aise ay pobem ecoueed i he couse of you sudy. To gai much beefi fom couse uoias pepae a quesio is befoe aedig hem. You wi ea a o fom paicipaig acivey i discussios. Summay I is epeced ha, goig hough his couse, you have ea how o use Mehod of Sepaaio of Vaiabes o Sove Hea Coducio Equaio ad Wave Equaio especivey. The use of Fouie asfoms o sove some diffeeia Equaio, Bouday vaues pobems ec. You shoud aso have ea he use of Lapace asfomaio o sove some iiia ad Bouday vaue pobems, which ae difficu o hade i addiio o he appicaio of covouio heoy i sovig pobems. v
12 PHY3 Couse Code Couse Tie PHY3 Mahemaica Mehods of Physics I Couse Team Ouwaoyi K. Ogubamike Deveope/Wie - Wesey Uivesiy of Sciece & Techoogy, Odo D. S.O. Ajiboa Edio/Pogamme Leade - NOUN vi
13 PHY3 NATIONAL OPEN UNIVERSITY OF NIGERIA Naioa Ope Uivesiy of Nigeia Headquaes 4/6 Ahmadu Beo Way Vicoia Isad Lagos Abuja Office 5, Da es Saaam See Off Amiu Kao Cesce Wuse II, Abuja e-mai: URL: Pubished By: Naioa Ope Uivesiy of Nigeia Fis Pied ISBN: A Righs Reseved vii
14 PHY3 viii
15 PHY3 CONTENTS PAGE Modue Paia Diffeeia Equaios wih Appicaios i Physics... Ui Paia Diffeeia Equaios. Ui Fouie Seies.. 8 Modue Appicaio of Fouie o PDEs Legede Poyomias ad Besse Fucios Ui Legede Poyomias. 33 Ui Besse fucios Modue 3 Appicaio of Fouie o PDEs Hemie Poyomias ad Laguee Poyomias.. 64 Ui Hemie Poyomias Ui Laguee Poyomias. 8 i
16
17 PHY3 MODULE PARTIAL DIFFERENTIAL EQUATIONS WITH APPLICATIONS IN PHYSICS Ui Ui Paia Diffeeia Equaios Fouie Seies UNIT PARTIAL DIFFERENTIAL EQUATIONS CONTENTS. Ioducio. Objecives 3. Mai Coe 3. Defiiio 3. Liea Secod-Ode Paia Diffeeia Equaios 3.. Lapace s Equaio 3.. Wave Equaio 3..3 Hea Coducio Equaio 3..4 Poisso s Equaio 3.3 Mehod of Sepaaio of Vaiabes 3.3. Appicaio o Wave Equaio 3.3. Appicaio o Hea Coducio Equaio 3.4 Lapace Tasfom Souios of Bouday-Vaue Pobems 4. Cocusio 5. Summay 6. Tuo -Maked Assigme 7. Refeeces/Fuhe Readig. INTRODUCTION I his ui, we sha sudy some eemeay mehods of sovig paia diffeeia equaios which occu fequey i physics ad i egieeig. I geea, he souio of he paia diffeeia equaio peses a much moe difficu pobem ha he souio of odiay diffeeia equaios. We ae heefoe goig o imi ouseves o a few sovabe paia diffeeia equaios ha ae of physica iees.
18 PHY3. OBECTIVES A he ed of his ui, you shoud be abe o: defie iea secod-ode paia diffeeia equaio i moe ha oe idepede vaiabe use he echique of sepaaio of vaiabes i sovig impoa secod ode iea paia diffeeia equaios i physics sove he eecises a he ed of his ui. 3. MAIN CONTENT 3. Defiiio A equaio ivovig oe o moe paia deivaives of ukow fucios of wo o moe idepede vaiabes is caed a paia diffeeia equaio. The ode of a PDE is he highes ode paia deivaive o deivaives which appea i he equaio. Fo eampe, 3 U U U U z U e z y y z 3 is a hid ode PDE sice he highes ode em is give by 3 U 3 y A PDE is said o be iea if i is of he fis degee, i.e. o havig epoe geae ha i he depede vaiabe o is paia deivaives ad does o coai poduc of such ems i he equaio. Paia deivaives wih espec o a idepede vaiabe ae wie fo beviy as a subscip; hus U U ad U y U y The PDE U c U U yy U zz Whee c is a cosa is iea ad is of he secod ode whie eq. is a eampe of a oiea PDE.
19 PHY3 Eampe : Impoa iea paia diffeeia equaios of secod ode u c u c u u u u y u u f, y y u u u y z Oe dim esioa wave equaio Oe dimesioa hea equaio Two dimesioa Lapace equaio Two dim esioa poisso equaio Thee dimesioa Lapace equaio 3. Liea Secod-Ode Paia Diffeeia Equaios May impoa PDEs occuig i sciece ad egieeig ae secod ode iea PDEs. A geea fom of a secod ode iea PDE i wo idepede vaiabes ad y ca be epessed as u u u u u A B C D E Fu G y y y 3 whee A, B, C,G may be depede o vaiabes ad y. If G, he eq. 3 is caed homogeeous; ohewise i is said o be a ohomogeeous. The homogeeous fom of Eq. 3 esembes he equaio of a geea coic: a by cy d ey f We hus say ha eq. 3 is of eipic hypeboic paaboic ype B whe B B 4 AC 4 AC 4 AC < > 3
20 PHY3 Fo eampe, accodig o his cassificaio he wo-dimesioa Lapace equaio u u y is of eipic ype A C, B D E G, ad he equaio u u α α is a ea cosa y is of hypeboic ype. Simiay, he equaio u u α α is a ea cosa y is of paaboa ype. Some impoa iea secod-ode paia diffeeia equaios ha ae of physica iees ae ised beow. Eampe Eimiae A ad P fom he fucio Z Ae p si p Z Z Souio Le pae p si p ad p Ae p si p Z Z aso pae p cos p ad p Ae p si p Z Z p p i.e. p Ae si p p Ae si p Eampe 3 Sove he equaio u u u 7 6 y y Souio: Le u, y f y m g y m So ha m 7m 6 This impies ha m o 6 4 Hece u, y H y G y 6
21 PHY3 3.. Lapace s Equaio u 4 Whee is he Lapacia opeao. The y y fucio u may be he eecosaic poeia i a chage-fee egio o gaviaioa poeia i a egio coaiig o mae. 3.. Wave Equaio u u 5 v Whee u epeses he dispaceme associaed wih he wave ad v, he veociy of he wave Hea Coducio Equaio u α u 6 Whee u is he empeaue i a soid a ime. The cosa α is caed he diffusiviy ad is eaed o he hema coduciviy, he specific hea capaciy, ad he mass desiy of he objec Poisso s Equaio u ρ, y, z 7 Whee he fucio ρ, y, z is caed he souce desiy. Fo eampe, if u epeses he eecosaic poeia i a egio coaiig chages, he ρ is popoioa o he eecic chage desiy. Eampe 4 Lapace s equaio aises i amos a baches of aaysis. A simpe eampe ca be foud fom he moio of a icompessibe fuid. Is veociy v, y, z, ad he fuid desiy ρ, y, z, mus saisfy he equaio of coiuiy: ρ. ρv If ρ is cosa we he have v 5
22 PHY3 If fuhemoe, he moio is ioaioa, he veociy veco ca be epessed as he gadie of a scaa fucio V: v V ad he coiuiy becomes Lapace s equaio:. v. V, o V The scaa fucio V is caed he veociy poeia 3.3 Mehod of Sepaaio of Vaiabes The echique of sepaaio of vaiabes is widey used fo sovig may of he impoa secod ode iea PDEs. The basic appoach of his mehod i aempig o sove a diffeeia equaio say, wo idepede vaiabes ad y is o wie he depede vaiabe u, y as a poduc of fucios of he sepaae vaiabes u, X T. I may cases he paia diffeeia equaio educes o odiay equaios fo X ad T Appicaio o Wave Equaio Le us coside he vibaio of a easic sig goveed by he oedimesioa wave equaio u u c 8 whee u, y is he defecio of he sig. Sice he sig is fied a he eds ad, we have he wo bouday codiios u,, u, fo a 9 The fom of he moio of he sig wi deped o he iiia defecio defecio a ad o he iiia veociy veociy a. Deoig he iiia defecio by f ad he iiia veociy by g, he wo iiia codiios ae u, f u g This mehod epesses he souio of u, as he poduc of wo fucios wih hei vaiabes sepaaed, i.e. U, X T whee X ad T ae fucios of ad especivey. 6
23 PHY3 Subsiuig eq. i eq. 8, we obai o X T c X T X T X c T I ohe wods X X c T λ T 3 The oigia PDE is he sepaaed io wo ODEs, viz. ad X λ X 4 T λ c T 5 The bouday codiios give by eq. 9 impy ad X T X T Sice T is o ideicay zeo, he foowig codiios ae saisfied X ad X 6 Thus eq. 4 is o be soved subjec o codiios give by eq. 6. Thee ae 3 cases o be cosideed. Case λ > The souio o eq. 4 yieds X λ λ Ae Be 7 To saisfy he bouday codiio give by eq. 6, we mus have Ae λ Be λ Sice he deemia fomed by he coefficies of A ad B is o-zeo, he oy souio is A B. This yieds he ivia souio X. 7
24 PHY3 Case λ The souio o eq. 4 yieds X A B To saisfy he bouday codiio give by eq. 6, we mus have A ad A B impyig A, B Agai fo his case, a ivia souio is obaied Case 3 λ < Le λ k. The souio o eq. 4 yieds X Acos k Bsi k 8 To saisfy he bouday codiio give by eq. 6, we mus have A ad B si k To obai a souio whee B, we mus have k,,... Thus λ k 9 coespods o he ivia souio. The specific vaues of λ ae kow as he eigevaues of eq. 4 ad he coespodig souios, viz, si ae caed he eigefucios. Sice hee ae may possibe souios, each is subsciped by. Thus X B si,,3,... The souio o Eq. 5 wih λ give by Eq. 9 is T E cos c F si c,,3,... 8
25 PHY3 Whee E ad F ae abiay cosas. Thee ae hus may souios fo eq. 8 which is give by U, X T a cos c b si c si Whee a BE ad b BF. Sice eq. 8 is iea ad homogeeous, he geea souio is obaied as he iea supeposiio of a he souios give by eq., i.e. c c U, a cos b si si 3 Diffeeiaig wih espec o, we have c c c U, a si b cos si 4 The coefficies a ad b ae obaied by appyig he iiia codiios i eq.. Thus, U, f U, g a si b csi 5 6 I ode o deemie a ad b we use he ohogoaiy popeies of si i he age, i.e. m si si d δ m 7 Whee δ m is he Koecke dea fucio havig he popey m δ m 8 m Muipy eq. 5 by ad, we ge m si ad iegaig bewee he imis 9
26 PHY3 i.e. a m f si d m m a si si d a m 9 m f si d m Simiay muipyig eq. 6 by si ad iegaig bewee he imis ad, we ge m g si d m b csi si d i.e. b m b m m c m g si d mc 3 Wih am ad bm obaied fo m,..., eq. 3 is he souio o PDE give by eq. 8 subjec o he iiia codiios ad he bouday codiios Appicaio o Hea Coducio Equaio The oe-dimesioa hea fow i a od bouded by he paes ad a is of pacica iees. The souio appies o he case whee he y ad z dimesios eed o ifiiy. The empeaue disibuio is deemied by sovig he oe-dimesioa hea coducio equaio θ θ v 3 Whee θ epeses he empeaue ad k v 3 Cρ k, C ad ρ ae he hema coduciviy, specific hea ad desiy of he maeia especivey. We sha ea he case whee he bouday codiios ae give by θ, 33
27 PHY3 θ a, 34 The iiia empeaue disibuio is give by θ, f 35 Souio: Usig he mehod of sepaaio of vaiabes, he -depedece ad -depedece ae sepaaed ou as epessed by θ, X T 36 Subsiuig eq. 36 io eq. 3 yieds X d X d dt v T d α 37 We sha ow coside hee cases coespodig o diffee vaues of he cosaα. Case λ The sepaaed ODE fo X becomes i.e. d X d X A B 38 The bouday codiios epessed by eqs. 33 ad 34 ae especivey X ad X a 39 Sice T shoud o be ideicay zeo. Thus fo eq. 38 o saisfy he bouday codiios give by eq. 39, we mus have A, B. This gives he seady-sae souio whee empeaue i he od is eveywhee zeo. Case λ > Le α k. The ODE fo X becomes d X k X 4 d k k Theefoe X Ae Be Appyig he bouday codiios give i eq. 39, we ge
28 PHY3 A B ka Ae Be ka Agai we have A B Case 3 λ < Le α λ. The ODE fo X becomes d X d λ X 4 Thus X A cos λ Bsi λ The bouday codiios equie A Bsi λ a 4 i.e. λ a,, Sice hee ae muipe souios, each λ is desigaed by a subscip as λ. The souio of he ODE fo T is eadiy obaied as T λ Ce v 44 Thus he geea souio which is a supeposiio of a admissibe souio is give by λ v θ, De si 45 a To compee he souio iiia codiio D ep v si a a 46 D mus be deemied fom he emaiig i.e. f D si 47 a
29 PHY3 I ode o deemie D, we muipy eq. 47 by he imis ad a o obai m si ad iegae a a m f si d a a m a D a si si d Dm a a Thus D m a m f si d a a 48 Fo he specific case whee f θ cosa, he souio is give by 4θ θ, v si ep a a < < a 49 Fom eq. 49, i ca be deduced ha a ecagua puse of heigh θ fo < < a has he Fouie seies epasio give by 4θ si a Aso if f γ, he aγ v θ, si ep 5 a a If he ed boudaies ae maiai a diffee empeaue i.e. θ, θ θ a, θ 5 The case of he souio whee α, woud yied he seady-sae θ θ. The geea souio is give by a souio give by θ θ, φ, θ θ θ 5 a Whee φ, is he asie souio. 3
30 PHY3 The bouday codiios fo φ, ae obaied as foows: a : θ, θ φ, θ φ, a a: θ a, θ φ a, θ φ a, φ, is obaied ude case 3. SELF-ASSESSMENT EXERCISE. Sae he aue of each of he foowig equaios ha is, whehe eipic, paaboic o hypeboic a y y α b u u y 3 y y u a Show ha y, F 5 G 5 is a geea souio of b y y 4 5 Fid a paicua souio saisfyig he codiios y, y,, y, si, y,. 3. Sove he foowig PDEs u a 8y b u u 6e y y 3.4 Lapace Tasfom Souios of Bouday-Vaue Pobems Lapace ad Fouie asfoms ae usefu i sovig a vaiey of paia diffeeia equaios; he choice of he appopiae asfoms depeds o he ype of bouday codiios imposed o he pobem. Lapace asfoms ca be used i sovig bouday-vaue pobems of paia diffeeia equaio. 4
31 PHY3 Eampe 5 Sove he pobem u u 53 u, u3,, u, si 6si 4 54 Souio: Takig he Lapace asfom L of Eq. 53 wih espec o gives u u L L Now u L pl u u, ad u p L e u, d L[ u] Hee ad d idepede. Fo coveiece, e U U, p L u... ae iechageabe because ad ae p [, ] e u, d We he have U pu u, L fom which we obai, usig he give codiios 54, U pu 3si 4 5si. 55 The akig he Lapace asfom of he give codiios u, u3,, we have O L [ u, ], L[ u3, ] U, p, U 3, p. These ae he bouday codiios o U, p. Sovig eq. 55 subjec o hese codiios we fid U, p 5si p 6 3si 4 p 64 5
32 PHY3 The souio o eq. 55 ca ow be obaied by akig he ivese Lapace asfom u, L 6 64 [ U, p ] 5e si 36e si 4. SELF-ASSESSMENT EXERCISE. Diffeeiae bewee odiay diffeeia equaio ad paia diffeeia equaio.. Deive he PDE ha give ise o he fucio Z a y b y ab c 3. Use he mehod of sepaaio of vaiabe o fid he souio of he bouday vaue pobem y y y, > y, > y, si y, < 4. CONCLUSION I his ui, we have sudied he oio of a souio of paia diffeeia equaio. Aso some eemeay mehods of sovig iea paia diffeeia equaios which occu fequey i physics ad egieeig wee dea wih. 5. SUMMARY Hee i his ui you have ea abou secod ode paia diffeeia equaio. The cassica mehod of sepaaio of vaiabes was eesivey sudied aog wih he Lapace asfom souios of bouday-vaue pobems. 6. TUTOR- MARKED ASSIGNMENT. Fom he PDEs whose geea souios ae as foow: p a z Ae cos p y b z f. Sove he equaio u u 3 y y 6
33 PHY3 3. Fid he souio of he diffeeia equaio Whee y y α y, y, y, f y, g < < < L < L 4. Sove by Lapace asfoms he bouday-vaue pobem u u fo >, > k give ha u u a cosa o fo >, ad u fo >, 7. REFERENCES/ FURTHER READING Ewi, K. 99. Advaced Egieeig Mahemaics. oh Wiey & Sos, Ic. Pisky, M.A. 99.Paia Diffeeia Equaios ad Bouday-Vaue Pobems wih Appicaios. New Yok: McGaw-Hi. 7
34 PHY3 UNIT FOURIER SERIES CONTENTS. Ioducio. Objecives 3. Mai Coe 3. Peiodic Fucios 3. Eve ad Odd Fucios 3.3 Fouie Theoem 3.4 Evauaio of Fouie Coefficies 3.5 Appicaio of Fouie Seies i Foced Vibaios 3.6 Haf-Rage Epasios 3.7 Fouie Iega 3.8 Fouie Iegas of Eve ad Odd Fucios 4. Cocusio 5. Summay 6. Tuo-Maked Assigme 7. Refeeces/Fuhe Readig. INTRODUCTION I his ui, we sha discuss basic coceps, facs ad echiques i coecio wih Fouie seies. Iusaive eampes ad some impoa appicaios of Fouie seies o Paia diffeeia equaios wi be sudied. We wi aso sudy he cocep of peiodic fucios, eve ad odd fucios ad he codiios fo Fouie epasio.. OBECTIVES A he ed of his ui, you shoud abe o: ideify whehe a give fucio is eve, odd o peiodic evauae he Fouie coefficies deive ad appy Fouie seies i foced vibaio pobems use Fouie Iega fo eaig vaious pobems ivovig peiodic fucio appy haf age epasio o souios of some pobems. 8
35 PHY3 3. MAIN CONTENT 3. Peiodic Fucios A fucio f is said o be peiodic if i defied fo a ea ad if hee is some posiive umbe T such ha f T f This umbe T is he caed a peiod of f. Peiodic fucios occu vey fequey i may appicaio of mahemaics o vaious baches of sciece. May pheomea i aue such as popagaio of wae waves, igh waves, eecomageic waves, ec ae peiodic ad we eed peiodic fucios o descibe hem. Famiia eampes of peiodic fucios ae he sie ad cosie fucios. Eampe Fid he peiod of Ta. Souio: so ha Suppose T is is peiod f T Ta T Ta Ta T Ta usig igoomeic ideiy, we have TaT Ta TaTaT This impies ha TaT If ad oy if Ta Hece T Ta T 3. Eve ad Odd Fucios A fucio a, b is said o be a eve fucio if f f f defied o ieva [ ] 9
36 PHY3 I is odd ohewise, ha is f f 3 Eampe Le f si The f f i.e. si si Thus i is obvious ha sie fucio is aways a odd fucio whie cosie fucio is a eve fucio. 3.3 Fouie Theoem Accodig o he Fouie heoem, ay fiie, sige vaued peiodic fucio f which is eihe coiuous o possess oy a fiie umbe of discoiuiies of sope o magiude, ca be epeseed as he sum of he hamoic ems as f a a cos a cos... a cos b si b si... b si a a cos b si Evauaio of Fouie Coefficies Le us assume ha f is a peiodic fucio of peiod which ca be epeseed by a igoomeic seies f a a cos b si Give such a fucio f we wa o deemie he coefficies of a ad b i he coespodig seies i eq. 5. We fis deemie a. Iegaig o boh sides of eq. 4 fom o, we have f d a a cos b si d If em-by-em iegaio of he seies is aowed, he we obai f d a d a cosd b sid 5
37 PHY3 The fis em o he igh equas a. A ohe iegas o he igh ae zeo, as ca be eadiy see by pefomig he iegaio. Hece ou fis esu is a f d 6 We ow deemie a, a,... by a simia pocedue. We muipy Eq. 5 by cos m, whee m is ay fied posiive iege, ad he iegae fom o, f cosmd a a cos b si cosmd 7 Iegaig em-by-em, we see ha he igh-had side becomes a cosmd a cos cosmd b si cos md The fis iegaio is zeo. By appyig igoomeic ideiy, we obai cos cosmd si cosmd cos m d si m d cos m d si m d. Iegaio shows ha he fou ems o he igh ae zeo, ecep fo he as em i he fis ie which equas whe m. sice i eq. 7 his em is muipied by a m, he igh-had side i eq. 7 is equa o a, ad ou secod esu is m a m f cosmd m, We fiay deemie b... i eq.5 by si m b,, posiive iege, ad he iegae fom f si md o,... 8, whee m is ay fied we have a a cos b si si md 9 Iegaig em-by-em, we see ha he igh-had side becomes
38 PHY3 a si md a cossi md b si si md The fis iega is zeo. The e iega is of he ype cosideed befoe, ad we kow ha i is zeo fo a,,. Fo he iega we obai si simd cos m d cos m d The as em is zeo. The fis em o he igh is zeo whe m ad is whe m. Sice i eq. 9 his em is muipied byb m, he ighhad side i eq. 6 is equa o b, ad ou as esu is m b m f si md m,... Wiig i pace of m, we aogehe have he so-caed Eue fomuas a a f d b a f cos d,... c b f si d Eampe 3 Squae wave Fid he Fouie coefficies of he peiodic fucio k whe < < f ad f f k whe < < Fucios of his ype may occu as eea foces acig o mechaica sysems, eecomoive foces i eecic cicuis, ec Souio: Fom eq. a we obai a. This ca aso be see wihou iegaio sice he aea ude cuve of f bewee ad is zeo. Fom eq. b a f cos d kcos d k cos d
39 PHY3 si k si k Because si a, ad fo a,.simiay, fom Eq. c we obai b f si d ksi d k si d cos cos k k Sice cos α cosα ad cos, his yieds k k b [ cos cos cos cos] cos Now, cos, cos, cos3 ec, i geea fo odd, cos ad hus fo eve, fo odd, cos fo eve, Hece he Fouie coefficies b of ou fucio ae 4k 4k 4k b, b, b3, b4, b5 3 5 ad sice he a ae zeo, he coespodig Fouie seies is 4k si si3 si The paia sums ae 4k 4k S si, S si si 3, ec, 3 Fuhemoe, assumig ha f seig, we have is he sum of he seies ad o 4k f k
40 PHY3 SELF-ASSESSMENT EXERCISE. Defie he peiodic fucio. Give five eampes.. Fid he smaes posiive peiod T of he foowig fucios. a. si 3. Ae he foowig fucios odd, eve, o eihe odd o eve? a. e b. si 4. Fid he Fouie seies of he foowig fucios which ae assumed o have he a. peiod b. f 4 < < c. f si < < 3.5 Appicaio of Fouie Seies i Foced Vibaios We ow coside a impoa appicaio of Fouie seies i sovig a diffeeia equaio of he ype d d m Γ k F d d Fo eampe, he above equaio woud epese he foced vibaios of a damped osciao wih Γ epeseig he dampig cosa, F he eea foce ad m ad k epeseig he mass of he paice ad he foce cosa especivey. We wie eq. i he fom d d K ω G d d 3 Γ k F Whee K, ω ad G m m m. The souio of he homogeeous pa of eq. 3 ca be eadiy obaied ad is give by [ ω K θ ] K A e cos fo K A B e fo ω 4 > K > K ω 5 I ode o obai he souio of he ihomogeeous pa of eq. 3, we fis assume F o be a sie o cosie fucio; fo defiieess we assume 4
41 PHY3 G bsiω 6 The paicua souio of eq. 3 ca be wie i he fom C siω D cosω 7 The vaues of C ad D ca eadiy be obaied by subsiuig eq. 7 i eq. 3, ad compaig coefficies of siω ad cosω we obai D C ω ω ω ω ω ωk 4ω K ω 4ω K b b 8 Now, if G is o a sie o cosie fucio, a geea souio of eq. 3 is difficu o obai. Howeve, if we make a Fouie epasio of G he he geea souio of eq. 3 ca easiy be wie dow. As a specific eampe, we assume G α 9 The Fouie epasio of G ca eadiy be obaied as G b si ω Poceedig i a mae simia o ha descibed above we obaied he foowig souio fo he ihomogeeous pa of eq. 3 Whee D C [ C si D cosω] ω ω ω ω ω ωk 4 ω K ω ω b b 4 ω K hus, if G is a peiodic fucio wih peiod T he eq. wi be vaid fo a vaues of. 3.6 Haf-Rage Epasios I vaious physica ad egieeig pobems hee is a pacica eed fo appyig Fouie seies o fucios f which ae defied meey 5
42 PHY3 o some fiie ieva. The fucio f is defied o a ieva < < ad o his ieva we wa epese f by a Fouie seies. A haf-age Fouie seies fo a fucio f is a seies cosisig of he sie ad cosie ems oy. Such fucios ae defied o a ieva, ad we he obai a Fouie cosie seies which epeses a eve peiodic fucio f of peiod T so ha f a a cos < < 3 ad he coefficies ae a f d, a cos f d 4,... The we obai a Fouie sie seies which epeses a odd peiodic fucio f of peiod T so ha f 5 ad he coefficies ae b si < < b f si d, 6... The seies i eqs.3 ad 5 wih he coefficies i eqs.4 ad 6 ae caed haf-age epasios of he give fucio f Eampe 4 Fid he haf-age epasios of he fucio k f k whe whe < < < < 6
43 PHY3 Souio: Fom eq. 4 we obai a a k / k k d d / k / k cos d cos d / Now by iegaio by pa / / / cos d si si d si cos Simiay, cos d si cos cos / By iseig hese wo esus we obai Thus, a 6k u, 4k cos cos a 6k 6, 6k 6 a,... Ad a whe, 6,, 4,... Hece he fis haf-age epasio of f is k 6k 6 f cos cos... 6 This seies epeses he eve peiodic epasio of he fucio f. Simiay fom eq. 6 8k b si ad he ohe haf-age epasio of f is 8k 3 5 f si si si This seies epeses he odd peiodic eesio of f. 7
44 PHY3 Eampe 5 Fid a Fouie sie seies fo f o, 3. > Souio: Sice he fucio is odd, he a The b f si d 3 f si d si d si d Now by iegaio, we have 4 b cos cos 3 The seies hus becomes 4 f cos si 3 3 So ha f si si si Eampe 6 Fid he Fouie cosie seies fo f e o, Souio: Sice f is a odd fucio, he b e d e Aso b e cos d e cos Thus he seies becomes e e [ e ] cos 8
45 PHY3 SELF-ASSESSMENT EXERCISE. Fid he Fouie sie seies fo f e o,. Fid he Fouie seies fo f o < < cosisig of a sie seies oy b cosie seies oy 3.7 Fouie Iega Fouie seies ae powefu oos i eaig vaious pobems ivovig peiodic fucios. Whe he fudamea peiod is made ifiie, he imiig fom of he Fouie seies becomes a iega which is caed Fouie Iega Defiiio Le f saisfies he foowig codiios: f be defied ad sige vaued i he ieva [ L, L] i f is peiodic ad of peiod L ii f ad f ae piecewise coiuous iii f d is covege, he f ca be epessed as A α cosα B α α f si d 7 A α f cosαd 8 B α f siαd Fouie Iegas of Eve ad Odd Fucios. If I is of pacica iees o oe ha if a fucio is eve o odd ad ca be epeseed by a Fouie iega, ad he his epeseaio wi be simpe ha i he case of a abiay fucio. This foows immediaey fom ou pevious fomuas, as we sha ow see. If f is a eve fucio, he B α A α f cosαd 3 9
46 PHY3 ad eq. 7 educes o he simpe fom f A α cosαd f eve 3 Simiay, if f is odd, he A α i eq. 8, aso B α f siαd 3 ad f B α siαd f odd 33 These simpificaios ae quie simia o hose i he case of a Fouie seies discussed. Eampe 7 Fid he Fouie Iega of f Souio: A α f cosαd cosαd Usig iegaio by pas, we obai Aso So ha A α cosα siα α α α B α f siαd siαd α B cosα cosα α α α 3 α 3
47 PHY3 Fom eq. 7 f A α cosα B α siα d ad α f cosα siαd α α Hece α α f siα α d α 4. CONCLUSION I his ui, you have sudied he cocep of peiodic fucios, epeseaios of fucios by Fouie seies, ivovig sie ad cosie fucio ae give specia aeio. We aso use he seies epasio i he deemiaio of Fouie coefficies ad he haf-age epasios. 5. SUMMARY I his ui, you have sudied: Eve ad odd fucios Fouie Iega epeseaios ad Fouie seies epasio. Appicaio of Fouie Iega echique i he simpificaio of eve ad odd fucios. 6. TUTOR- MARKED ASSIGNMENT. Fid he smaes posiive peiod T of he foowig fucios a. i si b. ii cos k. Fid he Fouie seies fo 5 < < f whee f has peiod 3 < < 5 3. Fid he Fouie seies fo f fo < < 4. Fid he Fouie seies of fucio f whe < < ad f f α 3
48 PHY3 5. Epad he fucio T T f < < i a Fouie seies o show ha T f 4 cosω cosω cosω ake ω T 6. Repese he foowig fucios f by a Fouie cosie seies a f si < < b f e < < 7. Fid he Fouie iega epeseaio of he fucio whe <, f whe >. 7. REFERENCES/FURTHER READING Pui, S.P. 4. Tebook of Vibaios ad Waves. Macmia Idia Ld. Ghaak, A.K.; Goya, I.C. & Chua, S Mahemaica Physics. Macmia Idia Ld. Casaw, H.S. 95. Ioducio o he Fouie Seies ad Iega. New Yok: Dove Pubicaios. 3
49 PHY3 MODULE APPLICATION OF FOURIER TO PDES LEGENDRE POLYNOMIALS AND BESSEL FUNCTIONS Ui Ui Legede Poyomias Besse Fucios UNIT LEGENDRE POLYNOMIALS CONTENTS. Ioducio. Objecives 3. Mai Coe 3. Legede Equaio 3. The Poyomia Souio of he Legede s Equaio 3.3 The Geeaig Fucio 3.4 Rodigue s Fomua 3.5 Ohogoaiy of he Legede Poyomias 3.6 The Agua Momeum Pobem i Quaum Mechaics 3.7 Impoa Iegas Ivovig Legede Fucios 4. Cocusio 5. Summay 6. Tuo- Maked Assigme 7. Refeeces/Fuhe Readig. INTRODUCTION I his ui, you wi be ioduced o he poyomia souios of he Legede equaio, he geeaig fucio as we as he ohogoaiy of Legede poyomias. Aso we sha coside some impoa iegas ivovig Legede fucios which ae of cosideabe use i may aeas of physics.. OBECTIVES A he ed of his ui, you shoud be abe: deive he poyomia souio of he Legede equaio use he geeaig fucios o deive some impoa ideiies deemie he ohogoaiy of he Legede poyomias. 33
50 PHY3 3. MAIN CONTENT 3. Legede Equaio The equaio y y y whee is a cosa is kow as he Legede s diffeeia equaio. I his ui we wi discuss he souios of he above equaio i he domai < <. We wi show ha whe,,, 3,... oe of he souios of eq. becomes a poyomia. These poyomia souios ae kow as he Legede poyomias, which appea i may divese aeas of physics ad egieeig. 3. The Poyomia Souio of he Legede s Equaio If we compae eq. wih homogeeous, iea diffeeia equaios of he ype y U y V y we fid ha he coefficies U ad V 3 ae aayica a he oigi. Thus he poi is a odiay poi ad a seies souio of eq. usig Fobeius mehod shoud be possibe. Such ha whee Ad y CS CT 3 4 S... 4a! 4! T ! 5! b If.,,... boh eqs. 4a ad 4b ae ifiie seies ad covege oy if <. I may be eadiy see ha whe., 4,... 34
51 PHY3 The eve seies becomes a poyomia ad he odd seies emais a ifiie seies. Simiay fo, 3, 5,... he odd seies becomes a poyomia ad he eve seies emais a ifiie seies. Thus whe,,, 3,... oe of he souios becomes a poyomia. The Legede poyomia, o he Legede fucio of he fis kid is deoed by P ad is defied i ems of he emiaig seies as beow: Thus, S fo,, 4, 6,... S P 5 T fo, 3, 5, 7,... T P, P3 P5 8 P, P 3, , P , , Obviousy, P 7 Highe ode Legede poyomias ca easiy be obaied by usig he ecuece eaio P P P Sice fo eve vaues of he poyomias P coai oy eve powes of ad fo odd vaues of he poyomias coai oy odd powes of, we eadiy have P P ad obviousy 8 9 P 3.3 The Geeaig Fucio The geeaig fucio fo he Legede poyomias is give by G, P ;, < 35
52 PHY3 Le us assume ha G, K Whee K is a poyomia of degee. Puig i eq., we obai K Equaig he coefficies of fom boh sides, we have K 3... Now, if we ca show ha K saisfies eq., he K wi be ideica o P. Diffeeiaig G, wih espec o ad, we obai G G, 3 ad G G 4 Usig eqs., 3 ad 4, we have ad... K K 5 K K 6 Equaig he coefficie of o boh sides of eqs. 5 ad 6, we ge K K K 7 ad K K K 8 Repacig by i Eq. 8, we obai K K K 9 We e diffeeiae Eq. 7 wih espec o ad eimiae K wih hep of Eq. 8 o obai 36
53 PHY3 K K K If we muipy eq. 9 by ad subac i fom eq., we woud ge K K K Diffeeiaig he above equaio wih espec o, we have K K K K K Usig eqs. 9 ad, we obai K K K 3 which shows ha K is a souio of Legede equaio. I view of eqs. 7 ad ad he fac ha K is a poyomia i of degee, i foows ha K is ohig bu P. eq. 7 gives he ecuece eaio fo P P P P Rodigues Fomua Le φ 5 Diffeeiaig eq. 5, we ge o dφ d d φ dφ φ d d Diffeeiaig he above equaio imes wih espec o, we woud ge d φ dφ φ 6 d d whee d φ d φ [ ] 7 d d 37
54 PHY3 This shows ha φ is a souio of he Legede s equaio. Fuhe, i is obvious fom eq. 7 ha φ is a poyomia of degee i. Hece φ shoud be a cosa muipe of P, i.e. d [ ] CP d d [ ] [ ] d d d!!!!!!... 8! 9 I may be see ha a ems o he igh had side of eq. 9 coai a faco - ecep fo he as em. Hece d d! 3 Usig Eqs. 7, 8 ad 9, we obai C! 3 Theefoe d P 3! d This is kow as he Rodigues fomua fo he Legede poyomias. Fo eampe P d! d 3 Which is cosise wih eq Ohogoaiy of he Legede Poyomias Sice he Legede s diffeeia equaio is of he Sum-Liouvie fom i he ieva, wih P saisfyig he appopiae bouday codiios a ±. The Legede poyomias fom a ohogoa se of fucios i he ieva, i.e 38
55 PHY3 p pm d m 33 The Ohogoaiy of he Legede poyomias ca be poved as foows: P saisfies eq. which ca be wie i he Sum- Liouvie fom as d d Simiay d d dp P d 34 dp m m P m d m 35 Muipy eq. 34 by P m ad eq. 35 by P ad subacig eq. 35 fom eq. 34, we ge d d [ P P P P ] m m m m P P Iegaig he above equaio fom - o, we ge [ P ] Pm Pm P m m m P P d Because of he faco he ef had side of he above equaio vaishes; hece m P P d To deemie he vaue of he iega P m m d fo m we squae boh sides of eq. ad obai m Pm P 36 m Iegaig boh sides of he above equaio wih espec o fom - o ad usig eq. 33, we ge 39
56 PHY3 P d d Equaig he coefficies of have o boh sides of he above equaio, we P d,,, 3, Thus we may wie whee P Pm d δ δ m m if m if m Eampe We coside he fucio cos ad epad i i a seies i he domai < < up o he secod powe of : Now cos C C P cos P d Subsiuig fo P fom eq. 6 ad cayig ou bue foce iegaio, we eadiy ge Thus C ; C ; C 3 cos 4
57 PHY3 3.6 The Agua Momeum Pobem i Quaum Mechaics I eecosaics he poeia Φ saisfies he Lapace equaio Φ 38 We wish o sove he above equaio fo a pefecy coducig sphee of adius a, pace i a eecic fied which is i he absece of he sphee was of uifom magiude E aog z-diecio. We assume he oigi of ou coodiae sysem o be a he cee of he sphee. Because he sphee is a pefec coduco, he poeia o is suface wi be cosa which, wihou ay oss of geeaiy, may be assumed o be zeo. Thus, eq. 35 is said o be soved subjec o he bouday codiio Φ a 39 A a age disace fom he sphee he fied shoud emai uchaged ad hus E E zˆ Sice E Φ we have Φ E z C E cosθ C 4 Whee C is a cosa. Obviousy, we shoud use he spheica sysem of coodiaes so ha Φ Φ Φ siθ siθ θ θ Φ si θ φ 4 Fom he symmey of he pobem i is obvious ha Φ woud be idepede of he azimuha coodiae φ so ha eq. 4 simpifies o Φ Φ si θ siθ θ θ 4 Sepaaio of vaiabes wi yied Φ R Θ θ 4
58 PHY3 d R d dr d dθ siθ a cos a λ d Θsiθ dθ dθ 43 Chagig he idepede vaiabe fom θ o µ by he eaio µ cosθ I he agua equaio, we ge d Θ dθ µ µ λθ 44 dµ dµ I ode ha he souio of eq. 44 does o divege a µ ± θ ad, we mus have λ ;,,,... ad he Θ θ P cosθ 45 Thus he adia equaio ca be wie as d dr R d d o d R dr R 46 d d The above equaio is he Cauchy s diffeeia equaio ad is souio ca eadiy be wie as R A B Hece he compee souio of eq. 4 is give by Φ, θ B A P cosθ P cos θ [ A P θ A P cosθ A P cos...] o o cos θ Bo B Po cosθ P cosθ... Appyig he bouday codiio give by eq. 4, we ge Thus C, A E, A A3... A o B B Φ, θ C P cosθ E P cos θ 4
59 PHY3 B P cosθ... 3 Appyig he codiio a a [see eq. 39], we ge B C a Ea θ B Pcos a B B P cosθ P3 cosθ a a Sice he above equaio has o be saisfied fo a vaues of θ ad sice P cosθ fom a se of ohogoa fucios, he coefficies of P cosθ shoud be zeo givig Thus B B 3 ac, B Ea B3 B a a, θ C E cosθ 3 Φ 47 The poeia woud coespod o a chaged sphee ad, heefoe, fo a uchaged sphee we mus have C givig 3 a, θ E cosθ 48 Φ 3 This is he equied souio o he pobem. Oe ca easiy deemie he compoes of he eecic fied as: Φ a E E cosθ Φ a Eθ E siθ θ Φ E φ siθ φ Impoa Iegas Ivovig Legede Fucios We give beow some impoa iegas ivovig Legede fucios which ae of cosideabe use i may aeas of physics. [ θ ] cos dθ P
60 PHY3 P cos φ φ i φ θ dθ cos si cos 5 3 P d 5 m m! [ P ] d m m! 5 m! [ P ] d 53 m! SELF-ASSESSMENT EXERCISE. Show ha P P P. Usig he Rodigue s fomua show ha P 4. CONCLUSION The cocep of geeaig fucio fo he Legede poyomias aows us o eadiy deive some impoa ideiies. We have aso esabished i his ui, eaioship bewee Ohogoaiy of he Legede poyomias ad he geeaig fucio. 5. SUMMARY This ui deas wih Legede fucios ad is appicaios o physica pobems especiay i quaum mechaics. 6. TUTOR-MARKED ASSIGNMENT. Show ha P P P [ P P ]. Deemie he coefficies C C, C,, i he epasio, C3 si 3 C P < < 44
61 PHY3 3. Coside he fucio < f < Show ha f P P 4. Show ha he geeaig fucio [ ] P < < u u P u Hi: Sa fom he biomia epasio of v, se v u u, muipy he powes of u u ou, coec a he ems ivovig u, ad veify ha he sum of hese ems is P u. 7. REFERENCES/FURTHER READING Ghaak, A.K.; Goya, I.C. & Chua, S Mahemaica Physics. Macmia Idia Ld. Ewi, K. 99. Advaced Egieeig Mahemaics. oh Wiey & Sos, Ic. 45
62 PHY3 UNIT BESSEL FUNCTIONS CONTENTS. Ioducio. Objecives 3. Mai Coe 3. Besse Diffeeia Equaio 3. Seies Souio ad Besse Fucio of he Fis Kid 3.3 Recuece Reaios 3.4 The Geeaig Fucio 3.4. Deivaio of Recuece Reaio fom he Geeaig Fucio 3.5 Some Usefu Iegas 3.6 Spheica Besse fucios 3.7 Besse Fucio of he Secod Kid 3.8 Modified Besse fucios 4. Cocusio 5. Summay 6. Tuo-Maked Assigme 7. Refeeces/Fuhe Readig. INTRODUCTION I his ui we sha coside he seies souio as we as Besse fucios of he fis ad secod kids of ode. We wi aso be ioduced o some iegas which ae usefu i obaiig souios of some pobems.. OBECTIVES A he ed of his ui, you shoud be abe o: deive he souio of Besse fucio of he fis kid pove a eaioship bewee he ecuece eaio ad he geeaig fucios deive he souio of Besse fucio of he secod kid. 46
63 PHY3 3. MAIN CONTENT 3. Besse Diffeeia Equaio The equaio d y dy y d d Whee is a cosa kow as Besse s diffeeia equaio. Sice appeas i eq., we wi assume, wihou ay oss of geeaiy, ha is eihe zeo o a posiive umbe. The wo ieay idepede souios of eq. ae ad Whee is defied by he ifiie seies! Γ o 4.. Γ whee Γ epeses he gamma fucio. 3. Seies Souio ad Besse Fucio of he Fis Kid If we use eq. wih he homogeeous, iea diffeeia equaio of he ype y U y V y R 4 we fid he coefficies U ad V ae sigua a. Howeve, is a egua sigua poi of he diffeeia equaio ad a seies souio of eq. i ascedig powes of. Ideed, oe of he souios of eq. is give by 4 C ad whee C is a abiay cosa. This souio is aayic a fo ad coveges fo a fiie vaues of. If we choose C Γ 6 47
64 PHY3 he he eq. 5 is deoed by ad is kow as he Besse fucio of he fis kid of ode. Γ! Γ! Γ 4! Γ I paicua !! 3! Γ 3 5! Γ 5 9 Γ 7...! ! 5! si 9 I foows immediaey fom eqs. 7 ad 8 ha fo > ad If,,, 3,... he Eampe! Γ I his eampe we wi deemie he vaue of fom eq.. Thus Γ 3 Γ 3/ 7! Γ 5...! 4...! 4! cos Which is ieay idepede of [see eq. 9] ad i ca be 48 veified ha does i fac saisfy eq. fo ½. Thus
65 PHY3 ad / si / cos Usig he above wo equaios ad he ecuece eaio [see Eq. ] 3 We ca eadiy obai cosed fom epessio fo ± 3/, ± 5/, ± 7 /, ec. 3/ 3/ si cos cos si 3 3 si cos 5 / 5 / 3 cos 3 si Ne, we wi eamie eq. whe is a posiive iege. To be specific we assume 4; he he fis, secod, hid ad fouh ems i he seies give by eq. wi coai he ems,,, ad Γ 3 Γ Γ Γ especivey ad a hese ems ae zeo. I geea he fis ems of he seies woud vaish givig! Γ 8 If we pu k, we woud obai k k k k k! Γ k k k k! Γ k 9 49
66 PHY3 Thus fo,,, 3,..., does o epese he secod idepede souio of eq.. The secod idepede souio wi be discussed ae. 3.3 Recuece Reaios The foowig ae some vey usefu eaios ivovig : Thus Aso a b d d [ ] I ode o pove eq. a w.. o obai o o 3! Γ! Γ! Γ 4! Γ 5 Which poves eq. a. eq. 3 ca aso be wie as o /! Γ /! Γ /! Γ 6 5
67 PHY3 Which poves eq. b. Fom eq. 5 we eadiy obai d d [ ] 7 Fuhe, addig eqs. 5 ad 6 we ge 8 Usig eq. we may wie ec. The poof of eq. is simpe d [ ] d [Usig eq. b] 3 Now usig eq. a 33 Theefoe d Cosa 34 o d [Because ] 35 Equaio 3 gives us d 36 5
68 PHY3 Eampe I his eampe we wi evauae he iega 4 d i ems of ad. Sice d d p p [ ] p [see eq. ] we have p p p d p Thus 4 d [ ]d 3 d p [ ] pus, of couse, a cosa of iegaio. 3.4 The Geeaig Fucio Besse fucios ae ofe defied hough he geeaig fucio Gz, which is give by he foowig equaio z G z, ep 37 Fo evey fiie vaue of z, he fucio Gz, is a egua fucio of fo a ea o compe vaues of ecep a poi. Thus i ca be epaded i a Laue seies z ep z 38 I he above equaio, he coefficie of is defied as z ; we wi pesey show ha his defiiio is cosise wih seies give by eq. 3. Now, fo ay fiie vaue of z ad fo < < we may wie 5
69 PHY3 53! ep z z... 3!!! 3 3 z z z 39 ad! ep z z... 3!! 3 3 z z z 4 Thus he geeaig fucio ca be epessed as a seies of he fom z A z z G ep, 4 o... 3!!! 3 3 z z z z A... 3!!! 3 3 z z z 4 O he ohe had, he coefficie of wi be give by... 3!!! 6 4 z z z z A 43 Compaig he above equaio wih eq. 8, we fid z z A Simiay, he coefficie of o he igh had side of eq. 4 wi be give by...!!!! 4 z z z z A which whe compaed wih eq. 7 gives us z z A Povig z z ep I he above equaio, if we epace by -/y, we obai z y z y y y z ep
70 PHY3 Thus z z 3.4. Deivaio of he Recuece Reaios fom he Geeaig Fucio Diffeeiaig eq. 38 w.. z, we obai Thus z ep z z z z 44 Compaig he coefficies of, we obai z z z Simiay, if we diffeeiae eq. 38 w.. we wi obai z z z Compaig he coefficies of z z z [ ] z 3.5 Some Usefu Iegas Usig z cos[ siθ θ ] dθ Thus o, we ge / z θ dθ cos si 45 i siθ i siθ / α e e d e d dθ / si si dθ α i θ α i θ α / dθ α si θ α e 46 α e d 47 α 54
71 PHY3 whee i evauaig he iega o he igh had side of eq. 46, we have used he subsiuio y α coθ. By makigα, we ge d 48 Fom eq. 8, we have Thus Bu Thus Sice ad fo > > 49 [see eq. 35] [see eq. 48] Usig eq. 49, we have,,, 3,... 5 Repacig α by α iβ i eq. 47, we ge α iβ e d α iβ which i he imi of α becomes β i e d β 5 5 Fo β <, ad he igh had side is ea ad we have cos βd 53 β si β d Simiay, β >, he igh had side of Eq. 5 is imagiay ad we have cosβ d 55
72 PHY3 si βd 54 β 3.6 Spheica Besse Fucios We sa wih he Besse equaio eq. ] wih, i.e. d y dy y 55 d d whee,,,... The souios of eq. 55 ae ad If we make he asfomaio f y 56 we woud eadiy obai d df f 57 d d The above equaio epeses he spheica Besse equaio. Fom eqs. 55 ad 56 i eadiy foows ha he wo idepede souios of eq.57 ae ad The spheica Besse fucios ae defied hough he equaios ad j ad epese he wo idepede souios of eq. 57. Now, if we defie he fucio u f he eq. 57 akes he fom d u u d 6 56
73 PHY3 The above equaio aso appeas a may paces ad he geea souio is give by u c[ ] c[ ] 6 which aso be wie i he fom u A A 6 Fo, he souios of eq. 6 ae si ad cos Thus, fo he wo idepede souios of eq.57 ae si cos ad Ideed if we use he defiiios of j ad give eqs. 58 ad 59 especivey, we woud eadiy obai si j 63 cos 64 si cos j 65 cos si ec 66 Fuhe, if we muipy he ecuece eaio [Eq. ] by ad assume, we woud ge j 67 usig which we ca eadiy obai aayic epessio fo j, j3,... ec. Simiay, Besse Fucios of he Secod Kid: Y The Besse fucios of he secod kid, deoed by Y, ae souios of he Besse diffeeia equaio. They have a siguaiy a he oigi. Y is someimes aso caed he Neuma fucio. Fo oiege, i is eaed o by: 57
74 PHY3 58 µ µ si cos Y 69 o Y µ µ µ µ µ 7 We eed o show ow ha Y defied by eq.7 saisfies Eq. whee is eihe zeo o a iege. We kow ha µ µ µ µ 7 fo ay vaue of µ. Diffeeiaig he above equaio wih espec o µ, we ge d d d d µ µ µ µ µ µ µ µ µ 7 Simiay d d d d µ µ µ µ µ µ µ µ µ 73 Fom eqs. 7 ad 73, i is easy o show ha S S d d S d d µ µ µ µ [ ] µ µ µ 74 whee S µ µ µ µ µ 75 Thus Y is he secod souio of Besse s equaio fo a ea vaues of ad is kow as he Besse fucio of he secod kid of ode. The geea souio of eq. ca, heefoe, be wie as Y C C y 76 whee C ad C ae abiay cosas. The epessio fo Y fo...,,, ca be obaied by usig eqs. ad 7 ad is give beow
75 PHY3 Y / γ m / 4!! Whee ϕ s ; ϕ s ad γ Lim[ ϕ ]!! 4 [ ϕ ϕ ] 77 Eampe 3 I his eampe we wi sove he adia pa of he Schodige equaio d dr µ E ;,,, R 78 d d h i he egio < < a subjec o he foowig bouday codiios ha R a 79 ad R is fiie i he egio < < a. Equaio 78 ca be coveiey wie i he fom d dr ρ R ρ ρ dρ dρ ρ Whee ρ k ; k µ E / h / Thus he geea souio of he above equaio is give by R ρ Aj ρ B ρ 8 Bu ρ diveges a ρ, heefoe, we mus choose B. The bouday codiio Ra eads o he ascedea equaio j ka 8 Thus, fo, we have ka ;,, Which wi give aowed vaues of k. Simiay, fo, we ge a ka ka Modified Besse Fucios If we epace by i i eq., we obai y y y 84 59
76 PHY3 The wo souios of he above equaio wi obviousy be i ad i Y As hese fucios ae ea fo a vaues of, e us defie a ea fucio as I i i 85 o / 4 I 86!! This fucio wi be he souio of eq. 84 ad is kow as he Modified Besse fucio of he fis kid. Fo vey age vaues of e I ~ 87 The ohe souio kow as he Modified Besse fucio of he secod kid is defied as I I K 88 si Fo o-iege vaues of, I ad I ae ieay idepede ad as such K is a iea combiaio of hese fucios [compae wih eq. 69 which gives he defiiio of Y ]. Whe is a iege, i ca be show [see eq. 86] ha I I 89 ad heefoe K becomes ideemiae fo o a iege. As i he case of Y fo o a iege, we defie as I µ I µ K Lim 9 µ si µ o I µ I µ K 9 µ µ µ Fo vey age K ~ e 9 Fom eq. 88 i foows ha K K 93 K 6
77 PHY3 Which is ue fo a vaues of. ecuece eaios fo I ca be deived fom hose of ad Eq. 85. They ae I I I I I I 96 ad simiay K K K 97 K K K 98 K K K 99 Eampe 4 I his eampe we wi coside he souios of he equaio ; k ω / c [ k ] R,,... d R dr β d d < < a Whee > a ad < epeses he fee space wave umbe. The quaiy β epeses he popagaio cosa ad fo guided modes β akes discee vaues i he domai k < β < k Thus, i he egios fom < < a ad > a, eq. ca be wie i he d R dr U R d d a < < a. 3 ad d R dr W R d d a > a. 4 whee U a [ k β ] 5 ad W a [ β k ] 6 so ha V U W a k 7 is a cosa. The souios of Eq. 3 ae U ad Y U a a 8 6
78 PHY3 ad he ae souio has o be ejeced as i diveges a. Simiay, he souios of eq. 4 ae K W ad I W a a ad he secod souio has o be ejeced because i diveges as. Thus A U < < a U a ad R 9 A K W > a K W a whee he cosas have bee so chose ad R is coiuous a a. Coiuiy of dr/d a a gives us U U K WU U K U U which is he fudamea equaio deemiig he eigevaues β / k. SELF-ASSESSMENT EXERCISE. Usig.389,.5767, cacuae, 3, ad 4. Hi: Use Eq.. Show ha a a a d a a a 4. CONCLUSION I his ui, we have cosideed Besse fucio ad spheica Besse fucio. We have aso esabished i his ui, eaioship bewee he ecuece eaio ad he geeaig fucio. 5. SUMMARY This ui is o Besse fucios. I has a o of appicaio ha aises i umeous divese aeas of appied mahemaics. This ui wi be of sigifica impoace i he subseque couse i quaum mechaics. 6
79 PHY3 6. TUTOR- MARKED ASSIGNMENT. Usig.5767,.3583 cacuae 3, 4, ad 5. Hi: Use Eq.. Usig he iega m Γ Γ m d ; m >, > Γ m Pove ha m m m y y y dy Γ m 3. Hi: Use he epasio give by eq. ad iegae em by em. I pobem assume m, ad use eq. o deduce cos y dy y 4. Show ha he souio of he diffeeia equaio y ae b y is give by / y A B ξ ; ξ ae ; µ µ ξ µ b 7. REFERENCES/FURTHER READING Ewi, Keyszig 99. Advaced Egieeig Mahemaics. oh Wiey & Sos, Ic. Afke, G. 99. Mahemaica Mehods fo Physiciss. New Yok: Academic Pess 63
80 PHY3 MODULE 3 APPLICATION OF FOURIER TO PDES HERMITE POLYNOMIALS AND LAGUERRE POLYNOMIALS Ui Ui Hemie Poyomias Laguee Poyomias UNIT HERMITE POLYNOMIALS CONTENTS. Ioducio. Objecives 3. Mai Coe 3. Hemie Diffeeia Equaio 3. The Geeaig Fucio 3.3 Rodigues Fomua 3.4 Ohogoaiy of Hemie Poyomias 3.5 The Iega Repeseaio of he Hemie Poyomias 3.6 Fouie Tasfom of Hemie-Gauss Fucios 3.7 Some Impoa Fomuae Ivovig Hemie Poyomias 4. Cocusio 5. Summay 6. Tuo-Maked Assigme 7. Refeeces/Fuhe Readig. INTRODUCTION I his ui, we sha coside ceai bouday vaue pobems whose souios fom ohogoa se of fucios. I ca aso be see i his ui how he geeaig fucio ca eadiy be used o deive he Rodigues fomua.. OBECTIVES A he ed of his ui, you shoud be abe o: defie Hemie poyomias as he poyomia souios of he Hemie diffeeia equaio pove he Ohogoaiy of Hemie poyomias deive he Rodigues fomua which ca be used o obai epici epessios fo Hemie poyomias sove he eecises a he ed of his ui. 64
81 PHY3 3. MAIN CONTENT 3. Hemie Diffeeia Equaio The equaio y y λ y whee λ is a cosa is kow as he Hemie diffeeia equaio. Whe λ is a odd iege, i.e. whe λ ;,,,... Oe of he souios of eq. becomes a poyomia. These poyomia souios ae caed Hemie poyomias. Hemie poyomias appea i may divese aeas, he mos impoa beig he hamoic osciao pobem i quaum mechaics. Usig Fobeius mehod o sove eq., ad foowig he vaious seps, we have Sep: We subsiue he powe seies y C p 3 i eq. ad obai he ideiy C p p C p p [ C p p C p 3 λ ] Sep : Equaig o zeo he coefficies of vaious powes of, we obai i p o p 4a ii p p C 4b iii p 3 λ C C p p fo 4c Whe p, C becomes ideemiae; hece p wi yied boh he ieay idepede souios of eq.. Thus, we ge 3 λ C C fo which gives λ C C! 3 λ C 3 C,.. 3!. 5 65
Supplementary Information
 Supplemeay Ifomaio No-ivasive, asie deemiaio of he coe empeaue of a hea-geeaig solid body Dea Ahoy, Daipaya Saka, Aku Jai * Mechaical ad Aeospace Egieeig Depame Uivesiy of Texas a Aligo, Aligo, TX, USA.
Supplemeay Ifomaio No-ivasive, asie deemiaio of he coe empeaue of a hea-geeaig solid body Dea Ahoy, Daipaya Saka, Aku Jai * Mechaical ad Aeospace Egieeig Depame Uivesiy of Texas a Aligo, Aligo, TX, USA.
Comparing Different Estimators for Parameters of Kumaraswamy Distribution
 Compaig Diffee Esimaos fo Paamees of Kumaaswamy Disibuio ا.م.د نذير عباس ابراهيم الشمري جامعة النهرين/بغداد-العراق أ.م.د نشات جاسم محمد الجامعة التقنية الوسطى/بغداد- العراق Absac: This pape deals wih compaig
Compaig Diffee Esimaos fo Paamees of Kumaaswamy Disibuio ا.م.د نذير عباس ابراهيم الشمري جامعة النهرين/بغداد-العراق أ.م.د نشات جاسم محمد الجامعة التقنية الوسطى/بغداد- العراق Absac: This pape deals wih compaig
The Central Limit Theorems for Sums of Powers of Function of Independent Random Variables
 ScieceAsia 8 () : 55-6 The Ceal Limi Theoems fo Sums of Poes of Fucio of Idepede Radom Vaiables K Laipapo a ad K Neammaee b a Depame of Mahemaics Walailak Uivesiy Nakho Si Thammaa 86 Thailad b Depame of
ScieceAsia 8 () : 55-6 The Ceal Limi Theoems fo Sums of Poes of Fucio of Idepede Radom Vaiables K Laipapo a ad K Neammaee b a Depame of Mahemaics Walailak Uivesiy Nakho Si Thammaa 86 Thailad b Depame of
Spectrum of The Direct Sum of Operators. 1. Introduction
 Specu of The Diec Su of Opeaos by E.OTKUN ÇEVİK ad Z.I.ISMILOV Kaadeiz Techical Uivesiy, Faculy of Scieces, Depae of Maheaics 6080 Tabzo, TURKEY e-ail adess : zaeddi@yahoo.co bsac: I his wok, a coecio
Specu of The Diec Su of Opeaos by E.OTKUN ÇEVİK ad Z.I.ISMILOV Kaadeiz Techical Uivesiy, Faculy of Scieces, Depae of Maheaics 6080 Tabzo, TURKEY e-ail adess : zaeddi@yahoo.co bsac: I his wok, a coecio
Outline. Review Homework Problem. Review Homework Problem II. Review Dimensionless Problem. Review Convection Problem
 adial diffsio eqaio Febay 4 9 Diffsio Eqaios i ylidical oodiaes ay aeo Mechaical Egieeig 5B Seia i Egieeig Aalysis Febay 4, 9 Olie eview las class Gadie ad covecio boday codiio Diffsio eqaio i adial coodiaes
adial diffsio eqaio Febay 4 9 Diffsio Eqaios i ylidical oodiaes ay aeo Mechaical Egieeig 5B Seia i Egieeig Aalysis Febay 4, 9 Olie eview las class Gadie ad covecio boday codiio Diffsio eqaio i adial coodiaes
New Results on Oscillation of even Order Neutral Differential Equations with Deviating Arguments
 Advace i Pue Maheaic 9-53 doi: 36/ap3 Pubihed Oie May (hp://wwwscirpog/oua/ap) New Reu o Ociaio of eve Ode Neua Diffeeia Equaio wih Deviaig Ague Abac Liahog Li Fawei Meg Schoo of Maheaica Sye Sciece aiha
Advace i Pue Maheaic 9-53 doi: 36/ap3 Pubihed Oie May (hp://wwwscirpog/oua/ap) New Reu o Ociaio of eve Ode Neua Diffeeia Equaio wih Deviaig Ague Abac Liahog Li Fawei Meg Schoo of Maheaica Sye Sciece aiha
ECSE Partial fraction expansion (m<n) 3 types of poles Simple Real poles Real Equal poles
 ECSE- Lecue. Paial facio expasio (m
ECSE- Lecue. Paial facio expasio (m
Capítulo. of Particles: Energy and Momentum Methods
 Capíulo 5 Kieics of Paicles: Eegy ad Momeum Mehods Mecáica II Coes Ioducio Wok of a Foce Piciple of Wok & Eegy pplicaios of he Piciple of Wok & Eegy Powe ad Efficiecy Sample Poblem 3. Sample Poblem 3.
Capíulo 5 Kieics of Paicles: Eegy ad Momeum Mehods Mecáica II Coes Ioducio Wok of a Foce Piciple of Wok & Eegy pplicaios of he Piciple of Wok & Eegy Powe ad Efficiecy Sample Poblem 3. Sample Poblem 3.
On a Z-Transformation Approach to a Continuous-Time Markov Process with Nonfixed Transition Rates
 Ge. Mah. Noes, Vol. 24, No. 2, Ocobe 24, pp. 85-96 ISSN 229-784; Copyigh ICSRS Publicaio, 24 www.i-css.og Available fee olie a hp://www.gema.i O a Z-Tasfomaio Appoach o a Coiuous-Time Maov Pocess wih Nofixed
Ge. Mah. Noes, Vol. 24, No. 2, Ocobe 24, pp. 85-96 ISSN 229-784; Copyigh ICSRS Publicaio, 24 www.i-css.og Available fee olie a hp://www.gema.i O a Z-Tasfomaio Appoach o a Coiuous-Time Maov Pocess wih Nofixed
Comparison between Fourier and Corrected Fourier Series Methods
 Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
Redes de Computadores
 Redes de Compuadoes Deay Modes i Compue Newoks Maue P. Ricado Facudade de Egehaia da Uivesidade do Poo » Wha ae he commo muipexig saegies?» Wha is a Poisso pocess?» Wha is he Lie heoem?» Wha is a queue?»
Redes de Compuadoes Deay Modes i Compue Newoks Maue P. Ricado Facudade de Egehaia da Uivesidade do Poo » Wha ae he commo muipexig saegies?» Wha is a Poisso pocess?» Wha is he Lie heoem?» Wha is a queue?»
Relations on the Apostol Type (p, q)-frobenius-euler Polynomials and Generalizations of the Srivastava-Pintér Addition Theorems
 Tish Joal of Aalysis ad Nmbe Theoy 27 Vol 5 No 4 26-3 Available olie a hp://pbssciepbcom/ja/5/4/2 Sciece ad Edcaio Pblishig DOI:269/ja-5-4-2 Relaios o he Aposol Type (p -Fobeis-Ele Polyomials ad Geealizaios
Tish Joal of Aalysis ad Nmbe Theoy 27 Vol 5 No 4 26-3 Available olie a hp://pbssciepbcom/ja/5/4/2 Sciece ad Edcaio Pblishig DOI:269/ja-5-4-2 Relaios o he Aposol Type (p -Fobeis-Ele Polyomials ad Geealizaios
Physics of Elastic Magnetic Filaments
 Ieaioa Scieific Cooquium Modeig fo Maeia Pocessig iga, Jue 8-9, 6 Physics of Easic Mageic Fiames I. Javaiis Absac The mode of a easic mageic fiame is deveoped. Mode of easic mageic fiame aows ivesigaig
Ieaioa Scieific Cooquium Modeig fo Maeia Pocessig iga, Jue 8-9, 6 Physics of Easic Mageic Fiames I. Javaiis Absac The mode of a easic mageic fiame is deveoped. Mode of easic mageic fiame aows ivesigaig
Spectral Simulation of Turbulence. and Tracking of Small Particles
 Specra Siuaio of Turbuece ad Trackig of Sa Parices Hoogeeous Turbuece Saisica ie average properies RMS veociy fucuaios dissipaio rae are idepede of posiio. Hoogeeous urbuece ca be odeed wih radoy sirred
Specra Siuaio of Turbuece ad Trackig of Sa Parices Hoogeeous Turbuece Saisica ie average properies RMS veociy fucuaios dissipaio rae are idepede of posiio. Hoogeeous urbuece ca be odeed wih radoy sirred
Zhi-Wei Sun and Hao Pan (Nanjing)
 Aca Arih. 5(006, o., 39. IDENTITIES CONCERNING BERNOULLI AND EULER POLYNOMIALS Zhi-Wei Su ad Hao Pa (Najig Absrac. We esabish wo geera ideiies for Beroui ad Euer poyomias, which are of a ew ype ad have
Aca Arih. 5(006, o., 39. IDENTITIES CONCERNING BERNOULLI AND EULER POLYNOMIALS Zhi-Wei Su ad Hao Pa (Najig Absrac. We esabish wo geera ideiies for Beroui ad Euer poyomias, which are of a ew ype ad have
One of the common descriptions of curvilinear motion uses path variables, which are measurements made along the tangent t and normal n to the path of
 Oe of he commo descipios of cuilie moio uses ph ibles, which e mesuemes mde log he ge d oml o he ph of he picles. d e wo ohogol xes cosideed sepely fo eey is of moio. These coodies poide ul descipio fo
Oe of he commo descipios of cuilie moio uses ph ibles, which e mesuemes mde log he ge d oml o he ph of he picles. d e wo ohogol xes cosideed sepely fo eey is of moio. These coodies poide ul descipio fo
6.2 Improving Our 3-D Graphics Pipeline
 6.2. IMPROVING OUR 3-D GRAPHICS PIPELINE 8 6.2 Impovig Ou 3-D Gaphics Pipelie We iish ou basic 3D gaphics pipelie wih he implemeaio o pespecive. beoe we do his, we eview homogeeous coodiaes. 6.2. Homogeeous
6.2. IMPROVING OUR 3-D GRAPHICS PIPELINE 8 6.2 Impovig Ou 3-D Gaphics Pipelie We iish ou basic 3D gaphics pipelie wih he implemeaio o pespecive. beoe we do his, we eview homogeeous coodiaes. 6.2. Homogeeous
Available online at J. Math. Comput. Sci. 2 (2012), No. 4, ISSN:
 Available olie a h://scik.og J. Mah. Comu. Sci. 2 (22), No. 4, 83-835 ISSN: 927-537 UNBIASED ESTIMATION IN BURR DISTRIBUTION YASHBIR SINGH * Deame of Saisics, School of Mahemaics, Saisics ad Comuaioal
Available olie a h://scik.og J. Mah. Comu. Sci. 2 (22), No. 4, 83-835 ISSN: 927-537 UNBIASED ESTIMATION IN BURR DISTRIBUTION YASHBIR SINGH * Deame of Saisics, School of Mahemaics, Saisics ad Comuaioal
ODEs II, Supplement to Lectures 6 & 7: The Jordan Normal Form: Solving Autonomous, Homogeneous Linear Systems. April 2, 2003
 ODEs II, Suppleme o Lecures 6 & 7: The Jorda Normal Form: Solvig Auoomous, Homogeeous Liear Sysems April 2, 23 I his oe, we describe he Jorda ormal form of a marix ad use i o solve a geeral homogeeous
ODEs II, Suppleme o Lecures 6 & 7: The Jorda Normal Form: Solvig Auoomous, Homogeeous Liear Sysems April 2, 23 I his oe, we describe he Jorda ormal form of a marix ad use i o solve a geeral homogeeous
Degree of Approximation of Fourier Series
 Ieaioal Mahemaical Foum Vol. 9 4 o. 9 49-47 HIARI Ld www.m-hiai.com h://d.doi.og/.988/im.4.49 Degee o Aoimaio o Fouie Seies by N E Meas B. P. Padhy U.. Misa Maheda Misa 3 ad Saosh uma Naya 4 Deame o Mahemaics
Ieaioal Mahemaical Foum Vol. 9 4 o. 9 49-47 HIARI Ld www.m-hiai.com h://d.doi.og/.988/im.4.49 Degee o Aoimaio o Fouie Seies by N E Meas B. P. Padhy U.. Misa Maheda Misa 3 ad Saosh uma Naya 4 Deame o Mahemaics
On imploding cylindrical and spherical shock waves in a perfect gas
 J. Fluid Mech. (2006), vol. 560, pp. 103 122. c 2006 Cambidge Uivesiy Pess doi:10.1017/s0022112006000590 Pied i he Uied Kigdom 103 O implodig cylidical ad spheical shock waves i a pefec gas By N. F. PONCHAUT,
J. Fluid Mech. (2006), vol. 560, pp. 103 122. c 2006 Cambidge Uivesiy Pess doi:10.1017/s0022112006000590 Pied i he Uied Kigdom 103 O implodig cylidical ad spheical shock waves i a pefec gas By N. F. PONCHAUT,
On Interval Valued Generalized Difference Classes Defined by Orlicz Function
 Tuih oua of Aayi ad Numbe Theoy, 03, Vo., No., 48-53 Avaiabe oie a hp://pub.ciepub.com/ja///0 Sciece ad ducaio Pubihig DOI:0.69/ja---0 O Ieva Vaued Geeaized Diffeece Cae Defied by Oicz Fucio Ayha i, Bipa
Tuih oua of Aayi ad Numbe Theoy, 03, Vo., No., 48-53 Avaiabe oie a hp://pub.ciepub.com/ja///0 Sciece ad ducaio Pubihig DOI:0.69/ja---0 O Ieva Vaued Geeaized Diffeece Cae Defied by Oicz Fucio Ayha i, Bipa
Generalized Fibonacci-Type Sequence and its Properties
 Geelized Fibocci-Type Sequece d is Popeies Ompsh Sihwl shw Vys Devshi Tuoil Keshv Kuj Mdsu (MP Idi Resech Schol Fculy of Sciece Pcific Acdemy of Highe Educio d Resech Uivesiy Udipu (Rj Absc: The Fibocci
Geelized Fibocci-Type Sequece d is Popeies Ompsh Sihwl shw Vys Devshi Tuoil Keshv Kuj Mdsu (MP Idi Resech Schol Fculy of Sciece Pcific Acdemy of Highe Educio d Resech Uivesiy Udipu (Rj Absc: The Fibocci
S, we call the base curve and the director curve. The straight lines
 Developable Ruled Sufaces wih Daboux Fame i iowsi -Space Sezai KIZILTUĞ, Ali ÇAKAK ahemaics Depame, Faculy of As ad Sciece, Ezica Uivesiy, Ezica, Tuey ahemaics Depame, Faculy of Sciece, Aau Uivesiy, Ezuum,
Developable Ruled Sufaces wih Daboux Fame i iowsi -Space Sezai KIZILTUĞ, Ali ÇAKAK ahemaics Depame, Faculy of As ad Sciece, Ezica Uivesiy, Ezica, Tuey ahemaics Depame, Faculy of Sciece, Aau Uivesiy, Ezuum,
Ideal Amplifier/Attenuator. Memoryless. where k is some real constant. Integrator. System with memory
 Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
BINOMIAL THEOREM OBJECTIVE PROBLEMS in the expansion of ( 3 +kx ) are equal. Then k =
 wwwskshieduciocom BINOMIAL HEOREM OBJEIVE PROBLEMS he coefficies of, i e esio of k e equl he k /7 If e coefficie of, d ems i e i AP, e e vlue of is he coefficies i e,, 7 ems i e esio of e i AP he 7 7 em
wwwskshieduciocom BINOMIAL HEOREM OBJEIVE PROBLEMS he coefficies of, i e esio of k e equl he k /7 If e coefficie of, d ems i e i AP, e e vlue of is he coefficies i e,, 7 ems i e esio of e i AP he 7 7 em
Viewing in 3D. Viewing in 3D. Planar Geometric Projections. Taxonomy of Projections. How to specify which part of the 3D world is to be viewed?
 Viewig i 3D Viewig i 3D How o speci which pa o he 3D wo is o e viewe? 3D viewig voume How o asom 3D wo cooiaes o D ispa cooiae? Pojecios Cocepua viewig pipeie: Xom o ee coos 3D cippig Pojec Xom o viewpo
Viewig i 3D Viewig i 3D How o speci which pa o he 3D wo is o e viewe? 3D viewig voume How o asom 3D wo cooiaes o D ispa cooiae? Pojecios Cocepua viewig pipeie: Xom o ee coos 3D cippig Pojec Xom o viewpo
Extremal graph theory II: K t and K t,t
 Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mathematics
![F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mathematics F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mathematics](/thumbs/89/97771684.jpg) F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mahemaics Prelim Quesio Paper Soluio Q. Aemp ay FIVE of he followig : [0] Q.(a) Defie Eve ad odd fucios. [] As.: A fucio f() is said o be eve fucio if
F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mahemaics Prelim Quesio Paper Soluio Q. Aemp ay FIVE of he followig : [0] Q.(a) Defie Eve ad odd fucios. [] As.: A fucio f() is said o be eve fucio if
Calculus Limits. Limit of a function.. 1. One-Sided Limits...1. Infinite limits 2. Vertical Asymptotes...3. Calculating Limits Using the Limit Laws.
 Limi of a fucio.. Oe-Sided..... Ifiie limis Verical Asympoes... Calculaig Usig he Limi Laws.5 The Squeeze Theorem.6 The Precise Defiiio of a Limi......7 Coiuiy.8 Iermediae Value Theorem..9 Refereces..
Limi of a fucio.. Oe-Sided..... Ifiie limis Verical Asympoes... Calculaig Usig he Limi Laws.5 The Squeeze Theorem.6 The Precise Defiiio of a Limi......7 Coiuiy.8 Iermediae Value Theorem..9 Refereces..
A new generation of tools for trawls Dynamic numerical simulation
 A ew geeaio of oos fo aws Damic umeica simuaio Beoî INCENT IFREMER 8 ue F. Touec 5600 LORIENT Te : 33 (0) 97 87 38 04 emai : Beoi.ice@ifeme.f ABSTRACT IFREMER ad ECN have bee wokig ogehe fo amos e eas
A ew geeaio of oos fo aws Damic umeica simuaio Beoî INCENT IFREMER 8 ue F. Touec 5600 LORIENT Te : 33 (0) 97 87 38 04 emai : Beoi.ice@ifeme.f ABSTRACT IFREMER ad ECN have bee wokig ogehe fo amos e eas
( ) ( ) ( ) ( ) (b) (a) sin. (c) sin sin 0. 2 π = + (d) k l k l (e) if x = 3 is a solution of the equation x 5x+ 12=
 Eesio Mahemaics Soluios HSC Quesio Oe (a) d 6 si 4 6 si si (b) (c) 7 4 ( si ).si +. ( si ) si + 56 (d) k + l ky + ly P is, k l k l + + + 5 + 7, + + 5 9, ( 5,9) if is a soluio of he equaio 5+ Therefore
Eesio Mahemaics Soluios HSC Quesio Oe (a) d 6 si 4 6 si si (b) (c) 7 4 ( si ).si +. ( si ) si + 56 (d) k + l ky + ly P is, k l k l + + + 5 + 7, + + 5 9, ( 5,9) if is a soluio of he equaio 5+ Therefore
By the end of this section you will be able to prove the Chinese Remainder Theorem apply this theorem to solve simultaneous linear congruences
 Chapte : Theoy of Modula Aithmetic 8 Sectio D Chiese Remaide Theoem By the ed of this sectio you will be able to pove the Chiese Remaide Theoem apply this theoem to solve simultaeous liea cogueces The
Chapte : Theoy of Modula Aithmetic 8 Sectio D Chiese Remaide Theoem By the ed of this sectio you will be able to pove the Chiese Remaide Theoem apply this theoem to solve simultaeous liea cogueces The
BINOMIAL THEOREM An expression consisting of two terms, connected by + or sign is called a
 BINOMIAL THEOREM hapte 8 8. Oveview: 8.. A epessio cosistig of two tems, coected by + o sig is called a biomial epessio. Fo eample, + a, y,,7 4 5y, etc., ae all biomial epessios. 8.. Biomial theoem If
BINOMIAL THEOREM hapte 8 8. Oveview: 8.. A epessio cosistig of two tems, coected by + o sig is called a biomial epessio. Fo eample, + a, y,,7 4 5y, etc., ae all biomial epessios. 8.. Biomial theoem If
BINOMIAL THEOREM NCERT An expression consisting of two terms, connected by + or sign is called a
 8. Oveview: 8.. A epessio cosistig of two tems, coected by + o sig is called a biomial epessio. Fo eample, + a, y,,7 4, etc., ae all biomial 5y epessios. 8.. Biomial theoem BINOMIAL THEOREM If a ad b ae
8. Oveview: 8.. A epessio cosistig of two tems, coected by + o sig is called a biomial epessio. Fo eample, + a, y,,7 4, etc., ae all biomial 5y epessios. 8.. Biomial theoem BINOMIAL THEOREM If a ad b ae
The Nehari Manifold for a Class of Elliptic Equations of P-laplacian Type. S. Khademloo and H. Mohammadnia. afrouzi
 Wold Alied cieces Joal (8): 898-95 IN 88-495 IDOI Pblicaios = h x g x x = x N i W whee is a eal aamee is a boded domai wih smooh boday i R N 3 ad< < INTRODUCTION Whee s ha is s = I his ae we ove he exisece
Wold Alied cieces Joal (8): 898-95 IN 88-495 IDOI Pblicaios = h x g x x = x N i W whee is a eal aamee is a boded domai wih smooh boday i R N 3 ad< < INTRODUCTION Whee s ha is s = I his ae we ove he exisece
1. Solve by the method of undetermined coefficients and by the method of variation of parameters. (4)
 7 Differeial equaios Review Solve by he mehod of udeermied coefficies ad by he mehod of variaio of parameers (4) y y = si Soluio; we firs solve he homogeeous equaio (4) y y = 4 The correspodig characerisic
7 Differeial equaios Review Solve by he mehod of udeermied coefficies ad by he mehod of variaio of parameers (4) y y = si Soluio; we firs solve he homogeeous equaio (4) y y = 4 The correspodig characerisic
1 Notes on Little s Law (l = λw)
 Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
Moment Generating Function
 1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
Objectives. We will also get to know about the wavefunction and its use in developing the concept of the structure of atoms.
 Modue "Atomic physics and atomic stuctue" Lectue 7 Quantum Mechanica teatment of One-eecton atoms Page 1 Objectives In this ectue, we wi appy the Schodinge Equation to the simpe system Hydogen and compae
Modue "Atomic physics and atomic stuctue" Lectue 7 Quantum Mechanica teatment of One-eecton atoms Page 1 Objectives In this ectue, we wi appy the Schodinge Equation to the simpe system Hydogen and compae
EFFECT OF GRADIENTS IN INHOMOGENEOUS MEDIA ON PLANE WAVE REFLECTION COEFFICIENT RESONANCE
 EFFECT OF GRADIENTS IN INHOMOGENEOUS MEDIA ON PLANE WAVE REFLECTION COEFFICIENT RESONANCE PACS efeece: 43.3 Ma. Fokia Magaia; Fokia Vadimi Isiue of Appied Pysics Russia Academy of Scieces 46, Uyaov S.,
EFFECT OF GRADIENTS IN INHOMOGENEOUS MEDIA ON PLANE WAVE REFLECTION COEFFICIENT RESONANCE PACS efeece: 43.3 Ma. Fokia Magaia; Fokia Vadimi Isiue of Appied Pysics Russia Academy of Scieces 46, Uyaov S.,
Here are some solutions to the sample problems concerning series solution of differential equations with non-constant coefficients (Chapter 12).
 Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
K3 p K2 p Kp 0 p 2 p 3 p
 Mah 80-00 Mo Ar 0 Chaer 9 Fourier Series ad alicaios o differeial equaios (ad arial differeial equaios) 9.-9. Fourier series defiiio ad covergece. The idea of Fourier series is relaed o he liear algebra
Mah 80-00 Mo Ar 0 Chaer 9 Fourier Series ad alicaios o differeial equaios (ad arial differeial equaios) 9.-9. Fourier series defiiio ad covergece. The idea of Fourier series is relaed o he liear algebra
FIXED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE
 Mohia & Samaa, Vol. 1, No. II, December, 016, pp 34-49. ORIGINAL RESEARCH ARTICLE OPEN ACCESS FIED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE 1 Mohia S. *, Samaa T. K. 1 Deparme of Mahemaics, Sudhir Memorial
Mohia & Samaa, Vol. 1, No. II, December, 016, pp 34-49. ORIGINAL RESEARCH ARTICLE OPEN ACCESS FIED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE 1 Mohia S. *, Samaa T. K. 1 Deparme of Mahemaics, Sudhir Memorial
Other quantum algorithms
 Chapte 3 Othe uatum agoithms 3. Quick emide of Gove s agoithm We peset hee a uick emide of Gove s agoithm. Iput: a fuctio f : {0,}! {0,}. Goa: fid x such that f (x) =. Seach pobem We have a uatum access
Chapte 3 Othe uatum agoithms 3. Quick emide of Gove s agoithm We peset hee a uick emide of Gove s agoithm. Iput: a fuctio f : {0,}! {0,}. Goa: fid x such that f (x) =. Seach pobem We have a uatum access
Technical Report: Bessel Filter Analysis
 Sasa Mahmoodi 1 Techical Repot: Bessel Filte Aalysis 1 School of Electoics ad Compute Sciece, Buildig 1, Southampto Uivesity, Southampto, S17 1BJ, UK, Email: sm3@ecs.soto.ac.uk I this techical epot, we
Sasa Mahmoodi 1 Techical Repot: Bessel Filte Aalysis 1 School of Electoics ad Compute Sciece, Buildig 1, Southampto Uivesity, Southampto, S17 1BJ, UK, Email: sm3@ecs.soto.ac.uk I this techical epot, we
David Randall. ( )e ikx. k = u x,t. u( x,t)e ikx dx L. x L /2. Recall that the proof of (1) and (2) involves use of the orthogonality condition.
 ! Revised April 21, 2010 1:27 P! 1 Fourier Series David Radall Assume ha u( x,) is real ad iegrable If he domai is periodic, wih period L, we ca express u( x,) exacly by a Fourier series expasio: ( ) =
! Revised April 21, 2010 1:27 P! 1 Fourier Series David Radall Assume ha u( x,) is real ad iegrable If he domai is periodic, wih period L, we ca express u( x,) exacly by a Fourier series expasio: ( ) =
ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 9 Solutions [Theorems of Gauss and Stokes]
![ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 9 Solutions [Theorems of Gauss and Stokes] ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 9 Solutions [Theorems of Gauss and Stokes]](/thumbs/91/106162145.jpg) ENGI 44 Avance alculus fo Engineeing Faculy of Engineeing an Applie cience Poblem e 9 oluions [Theoems of Gauss an okes]. A fla aea A is boune by he iangle whose veices ae he poins P(,, ), Q(,, ) an R(,,
ENGI 44 Avance alculus fo Engineeing Faculy of Engineeing an Applie cience Poblem e 9 oluions [Theoems of Gauss an okes]. A fla aea A is boune by he iangle whose veices ae he poins P(,, ), Q(,, ) an R(,,
Cameras and World Geometry
 Caeas ad Wold Geoe How all is his woa? How high is he caea? Wha is he caea oaio w. wold? Which ball is close? Jaes Has Thigs o eebe Has Pihole caea odel ad caea (pojecio) ai Hoogeeous coodiaes allow pojecio
Caeas ad Wold Geoe How all is his woa? How high is he caea? Wha is he caea oaio w. wold? Which ball is close? Jaes Has Thigs o eebe Has Pihole caea odel ad caea (pojecio) ai Hoogeeous coodiaes allow pojecio
Quantum Mechanics Lecture Notes 10 April 2007 Meg Noah
 The -Patice syste: ˆ H V This is difficut to sove. y V 1 ˆ H V 1 1 1 1 ˆ = ad with 1 1 Hˆ Cete of Mass ˆ fo Patice i fee space He Reative Haitoia eative coodiate of the tota oetu Pˆ the tota oetu tota
The -Patice syste: ˆ H V This is difficut to sove. y V 1 ˆ H V 1 1 1 1 ˆ = ad with 1 1 Hˆ Cete of Mass ˆ fo Patice i fee space He Reative Haitoia eative coodiate of the tota oetu Pˆ the tota oetu tota
Sheffer sequences of polynomials and their applications
 Kim e a. Advaces i Differece Equaios 2013 2013:118 hp://www.advacesidiffereceequaios.com/coe/2013/1/118 R E V I E W Ope Access Sheffer sequeces of poyomias ad heir appicaios Dae Sa Kim 1 TaekyuKim 2* Seog-Hoo
Kim e a. Advaces i Differece Equaios 2013 2013:118 hp://www.advacesidiffereceequaios.com/coe/2013/1/118 R E V I E W Ope Access Sheffer sequeces of poyomias ad heir appicaios Dae Sa Kim 1 TaekyuKim 2* Seog-Hoo
GENERALIZED FRACTIONAL INTEGRAL OPERATORS AND THEIR MODIFIED VERSIONS
 GENERALIZED FRACTIONAL INTEGRAL OPERATORS AND THEIR MODIFIED VERSIONS HENDRA GUNAWAN Absac. Associaed o a fucio ρ :(, ) (, ), le T ρ be he opeao defied o a suiable fucio space by T ρ f(x) := f(y) dy, R
GENERALIZED FRACTIONAL INTEGRAL OPERATORS AND THEIR MODIFIED VERSIONS HENDRA GUNAWAN Absac. Associaed o a fucio ρ :(, ) (, ), le T ρ be he opeao defied o a suiable fucio space by T ρ f(x) := f(y) dy, R
7 Wave Equation in Higher Dimensions
 7 Wave Equaion in Highe Dimensions We now conside he iniial-value poblem fo he wave equaion in n dimensions, u c u x R n u(x, φ(x u (x, ψ(x whee u n i u x i x i. (7. 7. Mehod of Spheical Means Ref: Evans,
7 Wave Equaion in Highe Dimensions We now conside he iniial-value poblem fo he wave equaion in n dimensions, u c u x R n u(x, φ(x u (x, ψ(x whee u n i u x i x i. (7. 7. Mehod of Spheical Means Ref: Evans,
Integrality Gap for the Knapsack Problem
 Proof, beiefs, ad agorihms hrough he es of sum-of-squares 1 Iegraiy Gap for he Kapsack Probem Noe: These oes are si somewha rough. Suppose we have iems of ui size ad we wa o pack as may as possibe i a
Proof, beiefs, ad agorihms hrough he es of sum-of-squares 1 Iegraiy Gap for he Kapsack Probem Noe: These oes are si somewha rough. Suppose we have iems of ui size ad we wa o pack as may as possibe i a
The analysis of the method on the one variable function s limit Ke Wu
 Ieraioal Coferece o Advaces i Mechaical Egieerig ad Idusrial Iformaics (AMEII 5) The aalysis of he mehod o he oe variable fucio s i Ke Wu Deparme of Mahemaics ad Saisics Zaozhuag Uiversiy Zaozhuag 776
Ieraioal Coferece o Advaces i Mechaical Egieerig ad Idusrial Iformaics (AMEII 5) The aalysis of he mehod o he oe variable fucio s i Ke Wu Deparme of Mahemaics ad Saisics Zaozhuag Uiversiy Zaozhuag 776
19 Fourier Series and Practical Harmonic Analysis
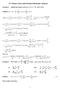 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
CHAPTER 4 FOURIER SERIES
 CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
Big O Notation for Time Complexity of Algorithms
 BRONX COMMUNITY COLLEGE of he Ciy Uiversiy of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI 33 Secio E01 Hadou 1 Fall 2014 Sepember 3, 2014 Big O Noaio for Time Complexiy of Algorihms Time
BRONX COMMUNITY COLLEGE of he Ciy Uiversiy of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI 33 Secio E01 Hadou 1 Fall 2014 Sepember 3, 2014 Big O Noaio for Time Complexiy of Algorihms Time
Mapping Radius of Regular Function and Center of Convex Region. Duan Wenxi
 d Iteatioal Cofeece o Electical Compute Egieeig ad Electoics (ICECEE 5 Mappig adius of egula Fuctio ad Cete of Covex egio Dua Wexi School of Applied Mathematics Beijig Nomal Uivesity Zhuhai Chia 363463@qqcom
d Iteatioal Cofeece o Electical Compute Egieeig ad Electoics (ICECEE 5 Mappig adius of egula Fuctio ad Cete of Covex egio Dua Wexi School of Applied Mathematics Beijig Nomal Uivesity Zhuhai Chia 363463@qqcom
Entanglement and its Manifestations in High Energy Physics
 EQua3 9 Beaix C. Hiesay Eagee ad is Maifesaios i High Eegy Physics by Beaix C. Hiesay Facuy of Physics Uivesiy of Viea Ausia Physics α Paice Physics β Quau Theoy expeiea pheoeoogica cocepua aheaica aspecs
EQua3 9 Beaix C. Hiesay Eagee ad is Maifesaios i High Eegy Physics by Beaix C. Hiesay Facuy of Physics Uivesiy of Viea Ausia Physics α Paice Physics β Quau Theoy expeiea pheoeoogica cocepua aheaica aspecs
MATH Midterm Solutions
 MATH 2113 - Midtem Solutios Febuay 18 1. A bag of mables cotais 4 which ae ed, 4 which ae blue ad 4 which ae gee. a How may mables must be chose fom the bag to guaatee that thee ae the same colou? We ca
MATH 2113 - Midtem Solutios Febuay 18 1. A bag of mables cotais 4 which ae ed, 4 which ae blue ad 4 which ae gee. a How may mables must be chose fom the bag to guaatee that thee ae the same colou? We ca
SUMMATION OF INFINITE SERIES REVISITED
 SUMMATION OF INFINITE SERIES REVISITED I several aricles over he las decade o his web page we have show how o sum cerai iiie series icludig he geomeric series. We wa here o eed his discussio o he geeral
SUMMATION OF INFINITE SERIES REVISITED I several aricles over he las decade o his web page we have show how o sum cerai iiie series icludig he geomeric series. We wa here o eed his discussio o he geeral
Sections 3.1 and 3.4 Exponential Functions (Growth and Decay)
 Secions 3.1 and 3.4 Eponenial Funcions (Gowh and Decay) Chape 3. Secions 1 and 4 Page 1 of 5 Wha Would You Rahe Have... $1million, o double you money evey day fo 31 days saing wih 1cen? Day Cens Day Cens
Secions 3.1 and 3.4 Eponenial Funcions (Gowh and Decay) Chape 3. Secions 1 and 4 Page 1 of 5 Wha Would You Rahe Have... $1million, o double you money evey day fo 31 days saing wih 1cen? Day Cens Day Cens
ABSOLUTE INDEXED SUMMABILITY FACTOR OF AN INFINITE SERIES USING QUASI-F-POWER INCREASING SEQUENCES
 Available olie a h://sciog Egieeig Maheaics Lees 2 (23) No 56-66 ISSN 249-9337 ABSLUE INDEED SUMMABILIY FACR F AN INFINIE SERIES USING QUASI-F-WER INCREASING SEQUENCES SKAIKRAY * RKJAI 2 UKMISRA 3 NCSAH
Available olie a h://sciog Egieeig Maheaics Lees 2 (23) No 56-66 ISSN 249-9337 ABSLUE INDEED SUMMABILIY FACR F AN INFINIE SERIES USING QUASI-F-WER INCREASING SEQUENCES SKAIKRAY * RKJAI 2 UKMISRA 3 NCSAH
MATH 507a ASSIGNMENT 4 SOLUTIONS FALL 2018 Prof. Alexander. g (x) dx = g(b) g(0) = g(b),
 MATH 57a ASSIGNMENT 4 SOLUTIONS FALL 28 Prof. Alexader (2.3.8)(a) Le g(x) = x/( + x) for x. The g (x) = /( + x) 2 is decreasig, so for a, b, g(a + b) g(a) = a+b a g (x) dx b so g(a + b) g(a) + g(b). Sice
MATH 57a ASSIGNMENT 4 SOLUTIONS FALL 28 Prof. Alexader (2.3.8)(a) Le g(x) = x/( + x) for x. The g (x) = /( + x) 2 is decreasig, so for a, b, g(a + b) g(a) = a+b a g (x) dx b so g(a + b) g(a) + g(b). Sice
Circular Motion. Radians. One revolution is equivalent to which is also equivalent to 2π radians. Therefore we can.
 1 Cicula Moion Radians One evoluion is equivalen o 360 0 which is also equivalen o 2π adians. Theefoe we can say ha 360 = 2π adians, 180 = π adians, 90 = π 2 adians. Hence 1 adian = 360 2π Convesions Rule
1 Cicula Moion Radians One evoluion is equivalen o 360 0 which is also equivalen o 2π adians. Theefoe we can say ha 360 = 2π adians, 180 = π adians, 90 = π 2 adians. Hence 1 adian = 360 2π Convesions Rule
BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS
 BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS Opimal ear Forecasig Alhough we have o meioed hem explicily so far i he course, here are geeral saisical priciples for derivig he bes liear forecas, ad
BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS Opimal ear Forecasig Alhough we have o meioed hem explicily so far i he course, here are geeral saisical priciples for derivig he bes liear forecas, ad
Existence and Smoothness of Solution of Navier-Stokes Equation on R 3
 Ieaioal Joual of Mode Noliea Theoy ad Applicaio, 5, 4, 7-6 Published Olie Jue 5 i SciRes. hp://www.scip.og/joual/ijma hp://dx.doi.og/.436/ijma.5.48 Exisece ad Smoohess of Soluio of Navie-Sokes Equaio o
Ieaioal Joual of Mode Noliea Theoy ad Applicaio, 5, 4, 7-6 Published Olie Jue 5 i SciRes. hp://www.scip.og/joual/ijma hp://dx.doi.og/.436/ijma.5.48 Exisece ad Smoohess of Soluio of Navie-Sokes Equaio o
12 th Mathematics Objective Test Solutions
 Maemaics Objecive Tes Soluios Differeiaio & H.O.D A oes idividual is saisfied wi imself as muc as oer are saisfied wi im. Name: Roll. No. Bac [Moda/Tuesda] Maimum Time: 90 Miues [Eac rig aswer carries
Maemaics Objecive Tes Soluios Differeiaio & H.O.D A oes idividual is saisfied wi imself as muc as oer are saisfied wi im. Name: Roll. No. Bac [Moda/Tuesda] Maimum Time: 90 Miues [Eac rig aswer carries
Lecture 15: Three-tank Mixing and Lead Poisoning
 Lecure 15: Three-ak Miig ad Lead Poisoig Eigevalues ad eigevecors will be used o fid he soluio of a sysem for ukow fucios ha saisfy differeial equaios The ukow fucios will be wrie as a 1 colum vecor [
Lecure 15: Three-ak Miig ad Lead Poisoig Eigevalues ad eigevecors will be used o fid he soluio of a sysem for ukow fucios ha saisfy differeial equaios The ukow fucios will be wrie as a 1 colum vecor [
In this section we will study periodic signals in terms of their frequency f t is said to be periodic if (4.1)
 Fourier Series Iroducio I his secio we will sudy periodic sigals i ers o heir requecy is said o be periodic i coe Reid ha a sigal ( ) ( ) ( ) () or every, where is a uber Fro his deiiio i ollows ha ( )
Fourier Series Iroducio I his secio we will sudy periodic sigals i ers o heir requecy is said o be periodic i coe Reid ha a sigal ( ) ( ) ( ) () or every, where is a uber Fro his deiiio i ollows ha ( )
A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY
 U.P.B. Sci. Bull., Series A, Vol. 78, Iss. 2, 206 ISSN 223-7027 A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY İbrahim Çaak I his paper we obai a Tauberia codiio i erms of he weighed classical
U.P.B. Sci. Bull., Series A, Vol. 78, Iss. 2, 206 ISSN 223-7027 A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY İbrahim Çaak I his paper we obai a Tauberia codiio i erms of he weighed classical
Energy Density / Energy Flux / Total Energy in 1D. Key Mathematics: density, flux, and the continuity equation.
 ecure Phys 375 Eergy Desiy / Eergy Flu / oal Eergy i D Overview ad Moivaio: Fro your sudy of waves i iroducory physics you should be aware ha waves ca raspor eergy fro oe place o aoher cosider he geeraio
ecure Phys 375 Eergy Desiy / Eergy Flu / oal Eergy i D Overview ad Moivaio: Fro your sudy of waves i iroducory physics you should be aware ha waves ca raspor eergy fro oe place o aoher cosider he geeraio
th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)
![th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x) th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)](/thumbs/80/81319353.jpg) 1 Trasform Techiques h m m m m mome : E[ ] x f ( x) dx h m m m m ceral mome : E[( ) ] ( ) ( x) f ( x) dx A coveie wa of fidig he momes of a radom variable is he mome geeraig fucio (MGF). Oher rasform echiques
1 Trasform Techiques h m m m m mome : E[ ] x f ( x) dx h m m m m ceral mome : E[( ) ] ( ) ( x) f ( x) dx A coveie wa of fidig he momes of a radom variable is he mome geeraig fucio (MGF). Oher rasform echiques
Conditional Convergence of Infinite Products
 Coditioal Covegece of Ifiite Poducts William F. Tech Ameica Mathematical Mothly 106 1999), 646-651 I this aticle we evisit the classical subject of ifiite poducts. Fo stadad defiitios ad theoems o this
Coditioal Covegece of Ifiite Poducts William F. Tech Ameica Mathematical Mothly 106 1999), 646-651 I this aticle we evisit the classical subject of ifiite poducts. Fo stadad defiitios ad theoems o this
λiv Av = 0 or ( λi Av ) = 0. In order for a vector v to be an eigenvector, it must be in the kernel of λi
 Liear lgebra Lecure #9 Noes This week s lecure focuses o wha migh be called he srucural aalysis of liear rasformaios Wha are he irisic properies of a liear rasformaio? re here ay fixed direcios? The discussio
Liear lgebra Lecure #9 Noes This week s lecure focuses o wha migh be called he srucural aalysis of liear rasformaios Wha are he irisic properies of a liear rasformaio? re here ay fixed direcios? The discussio
Jackson 3.3 Homework Problem Solution Dr. Christopher S. Baird University of Massachusetts Lowell
 Jackson 3.3 Homewok Pobem Soution D. Chistophe S. Baid Univesity of Massachusetts Lowe POBLEM: A thin, fat, conducting, cicua disc of adius is ocated in the x-y pane with its cente at the oigin, and is
Jackson 3.3 Homewok Pobem Soution D. Chistophe S. Baid Univesity of Massachusetts Lowe POBLEM: A thin, fat, conducting, cicua disc of adius is ocated in the x-y pane with its cente at the oigin, and is
Lecture 18: Kinetics of Phase Growth in a Two-component System: general kinetics analysis based on the dilute-solution approximation
 Lecue 8: Kineics of Phase Gowh in a Two-componen Sysem: geneal kineics analysis based on he dilue-soluion appoximaion Today s opics: In he las Lecues, we leaned hee diffeen ways o descibe he diffusion
Lecue 8: Kineics of Phase Gowh in a Two-componen Sysem: geneal kineics analysis based on he dilue-soluion appoximaion Today s opics: In he las Lecues, we leaned hee diffeen ways o descibe he diffusion
2012 GCE A Level H2 Maths Solution Paper Let x,
 GCE A Level H Maths Solutio Pape. Let, y ad z be the cost of a ticet fo ude yeas, betwee ad 5 yeas, ad ove 5 yeas categoies espectively. 9 + y + 4z =. 7 + 5y + z = 8. + 4y + 5z = 58.5 Fo ude, ticet costs
GCE A Level H Maths Solutio Pape. Let, y ad z be the cost of a ticet fo ude yeas, betwee ad 5 yeas, ad ove 5 yeas categoies espectively. 9 + y + 4z =. 7 + 5y + z = 8. + 4y + 5z = 58.5 Fo ude, ticet costs
Construction of mixed estimation for solving the first edge problem for the equation of non-isotropic diffusion
 ISSN: 350-038 Iteatioa Joua of AdvacedReseach i Sciece, Egieeig ad echoogy Vo. 5, Issue, Decembe 08 Costuctio of mixed estimatio fo sovig the fist edge pobem fo the equatio of o-isotopic diffusio okhi
ISSN: 350-038 Iteatioa Joua of AdvacedReseach i Sciece, Egieeig ad echoogy Vo. 5, Issue, Decembe 08 Costuctio of mixed estimatio fo sovig the fist edge pobem fo the equatio of o-isotopic diffusio okhi
The Combination of Several RCBDs
 Ausaia Joua of Basic ad Appied Scieces 5(4): 67-75 0 ISSN 99-878 The Comiaio of Sevea RCBDs Musofa Usma Pee Nuho 3 Faiz AM Efai ad 3 Jama I Daoud Depame of Mahemaics Facuy of Sciece Lampug Uivesiy Idoesia
Ausaia Joua of Basic ad Appied Scieces 5(4): 67-75 0 ISSN 99-878 The Comiaio of Sevea RCBDs Musofa Usma Pee Nuho 3 Faiz AM Efai ad 3 Jama I Daoud Depame of Mahemaics Facuy of Sciece Lampug Uivesiy Idoesia
2 f(x) dx = 1, 0. 2f(x 1) dx d) 1 4t t6 t. t 2 dt i)
 Mah PracTes Be sure o review Lab (ad all labs) There are los of good quesios o i a) Sae he Mea Value Theorem ad draw a graph ha illusraes b) Name a impora heorem where he Mea Value Theorem was used i he
Mah PracTes Be sure o review Lab (ad all labs) There are los of good quesios o i a) Sae he Mea Value Theorem ad draw a graph ha illusraes b) Name a impora heorem where he Mea Value Theorem was used i he
N! AND THE GAMMA FUNCTION
 N! AND THE GAMMA FUNCTION Cosider he produc of he firs posiive iegers- 3 4 5 6 (-) =! Oe calls his produc he facorial ad has ha produc of he firs five iegers equals 5!=0. Direcly relaed o he discree! fucio
N! AND THE GAMMA FUNCTION Cosider he produc of he firs posiive iegers- 3 4 5 6 (-) =! Oe calls his produc he facorial ad has ha produc of he firs five iegers equals 5!=0. Direcly relaed o he discree! fucio
STK4080/9080 Survival and event history analysis
 STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
Vector Spherical Harmonics and Spherical Waves
 DEPARTMENT OF PHYSICS INDIAN INSTITUTE OF TECHNOLOGY, MADRAS PH5020 Eectomagnetic Theoy Mach 2017 by Suesh Govinaajan, Depatment of Physics, IIT Maas Vecto Spheica Hamonics an Spheica Waves Let us sove
DEPARTMENT OF PHYSICS INDIAN INSTITUTE OF TECHNOLOGY, MADRAS PH5020 Eectomagnetic Theoy Mach 2017 by Suesh Govinaajan, Depatment of Physics, IIT Maas Vecto Spheica Hamonics an Spheica Waves Let us sove
The Non-Truncated Bulk Arrival Queue M x /M/1 with Reneging, Balking, State-Dependent and an Additional Server for Longer Queues
 Alied Maheaical Sciece Vol. 8 o. 5 747-75 The No-Tucaed Bul Aival Queue M x /M/ wih Reei Bali Sae-Deede ad a Addiioal Seve fo Loe Queue A. A. EL Shebiy aculy of Sciece Meofia Uiveiy Ey elhebiy@yahoo.co
Alied Maheaical Sciece Vol. 8 o. 5 747-75 The No-Tucaed Bul Aival Queue M x /M/ wih Reei Bali Sae-Deede ad a Addiioal Seve fo Loe Queue A. A. EL Shebiy aculy of Sciece Meofia Uiveiy Ey elhebiy@yahoo.co
Fuzzy Erlangian Queuing System with State Dependent Service Rate, Balking, Reneging and Retention of Reneged customers
 Iteatioa Joa of Basic & Aied Scieces IJBAS-IJENS Vo:4 No: 6 Fzzy Eagia Qeig System with State Deedet Sevice Rate Bakig Reegig ad Retetio of Reeged cstomes MS E Paomy Deatmet of Statistics Facty of Commece
Iteatioa Joa of Basic & Aied Scieces IJBAS-IJENS Vo:4 No: 6 Fzzy Eagia Qeig System with State Deedet Sevice Rate Bakig Reegig ad Retetio of Reeged cstomes MS E Paomy Deatmet of Statistics Facty of Commece
IMPACT VIBRATION ABSORBER OF PENDULUM TYPE
 7h Ieaioa DAAAM Baic Cofeece "INDUSTIAL ENGINEEING -4 Ai, Tai, Esoia IMPACT VIBATION ABSOBE OF PENDULUM TYPE Poukoshko, S.; Boyko A.; Kooova, O,; Sokoova, S. & Jevsigejev, V. Absac: I his wok he iac vibaio
7h Ieaioa DAAAM Baic Cofeece "INDUSTIAL ENGINEEING -4 Ai, Tai, Esoia IMPACT VIBATION ABSOBE OF PENDULUM TYPE Poukoshko, S.; Boyko A.; Kooova, O,; Sokoova, S. & Jevsigejev, V. Absac: I his wok he iac vibaio
Finite q-identities related to well-known theorems of Euler and Gauss. Johann Cigler
 Fiite -idetities elated to well-ow theoems of Eule ad Gauss Joha Cigle Faultät fü Mathemati Uivesität Wie A-9 Wie, Nodbegstaße 5 email: oha.cigle@uivie.ac.at Abstact We give geealizatios of a fiite vesio
Fiite -idetities elated to well-ow theoems of Eule ad Gauss Joha Cigle Faultät fü Mathemati Uivesität Wie A-9 Wie, Nodbegstaße 5 email: oha.cigle@uivie.ac.at Abstact We give geealizatios of a fiite vesio
ECON 3710/4710 Demography of developing countries STABLE AND STATIONARY POPULATIONS. Lecture note. Nico Keilman
 ECON 37/47 Demogaphy of deveoping counies STAE AND STATIONARY POPUATIONS ecue noe Nico Keiman Requied eading: Sabe and saionay modes Chape 9 in D Rowand Demogaphic Mehods and Conceps Ofod Univesiy Pess
ECON 37/47 Demogaphy of deveoping counies STAE AND STATIONARY POPUATIONS ecue noe Nico Keiman Requied eading: Sabe and saionay modes Chape 9 in D Rowand Demogaphic Mehods and Conceps Ofod Univesiy Pess
Topics in Fourier Analysis-I 1
 Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
MA 1201 Engineering Mathematics MO/2017 Tutorial Sheet No. 2
 BIRLA INSTITUTE OF TECHNOLOGY, MESRA, RANCHI DEPARTMENT OF MATHEMATICS MA Egieeig Matheatis MO/7 Tutoia Sheet No. Modue IV:. Defie Beta futio ad Gaa futio.. Pove that,,,. Pove that, d. Pove that. & whee
BIRLA INSTITUTE OF TECHNOLOGY, MESRA, RANCHI DEPARTMENT OF MATHEMATICS MA Egieeig Matheatis MO/7 Tutoia Sheet No. Modue IV:. Defie Beta futio ad Gaa futio.. Pove that,,,. Pove that, d. Pove that. & whee
Counting Functions and Subsets
 CHAPTER 1 Coutig Fuctios ad Subsets This chapte of the otes is based o Chapte 12 of PJE See PJE p144 Hee ad below, the efeeces to the PJEccles book ae give as PJE The goal of this shot chapte is to itoduce
CHAPTER 1 Coutig Fuctios ad Subsets This chapte of the otes is based o Chapte 12 of PJE See PJE p144 Hee ad below, the efeeces to the PJEccles book ae give as PJE The goal of this shot chapte is to itoduce
Multivector Functions
 I: J. Math. Aal. ad Appl., ol. 24, No. 3, c Academic Pess (968) 467 473. Multivecto Fuctios David Hestees I a pevious pape [], the fudametals of diffeetial ad itegal calculus o Euclidea -space wee expessed
I: J. Math. Aal. ad Appl., ol. 24, No. 3, c Academic Pess (968) 467 473. Multivecto Fuctios David Hestees I a pevious pape [], the fudametals of diffeetial ad itegal calculus o Euclidea -space wee expessed
ON POINTWISE APPROXIMATION OF FUNCTIONS BY SOME MATRIX MEANS OF FOURIER SERIES
 M aheaical I equaliies & A pplicaios Volue 19, Nube 1 (216), 287 296 doi:1.7153/ia-19-21 ON POINTWISE APPROXIMATION OF FUNCTIONS BY SOME MATRIX MEANS OF FOURIER SERIES W. ŁENSKI AND B. SZAL (Couicaed by
M aheaical I equaliies & A pplicaios Volue 19, Nube 1 (216), 287 296 doi:1.7153/ia-19-21 ON POINTWISE APPROXIMATION OF FUNCTIONS BY SOME MATRIX MEANS OF FOURIER SERIES W. ŁENSKI AND B. SZAL (Couicaed by
STRONG CONVERGENCE OF MODIFIED MANN ITERATIONS FOR LIPSCHITZ PSEUDOCONTRACTIONS
 Joura of Mahemaica Scieces: Advaces ad Appicaios Voume, Number, 009, Pages 47-59 STRONG CONVERGENCE OF MODIFIED MANN ITERATIONS FOR LIPSCHITZ PSEUDOCONTRACTIONS JING HAN ad YISHENG SONG Mahmaicas ad Sciece
Joura of Mahemaica Scieces: Advaces ad Appicaios Voume, Number, 009, Pages 47-59 STRONG CONVERGENCE OF MODIFIED MANN ITERATIONS FOR LIPSCHITZ PSEUDOCONTRACTIONS JING HAN ad YISHENG SONG Mahmaicas ad Sciece
12 Getting Started With Fourier Analysis
 Commuicaios Egieerig MSc - Prelimiary Readig Geig Sared Wih Fourier Aalysis Fourier aalysis is cocered wih he represeaio of sigals i erms of he sums of sie, cosie or complex oscillaio waveforms. We ll
Commuicaios Egieerig MSc - Prelimiary Readig Geig Sared Wih Fourier Aalysis Fourier aalysis is cocered wih he represeaio of sigals i erms of he sums of sie, cosie or complex oscillaio waveforms. We ll
10.3 Autocorrelation Function of Ergodic RP 10.4 Power Spectral Density of Ergodic RP 10.5 Normal RP (Gaussian RP)
 ENGG450 Probabiliy ad Saisics for Egieers Iroducio 3 Probabiliy 4 Probabiliy disribuios 5 Probabiliy Desiies Orgaizaio ad descripio of daa 6 Samplig disribuios 7 Ifereces cocerig a mea 8 Comparig wo reames
ENGG450 Probabiliy ad Saisics for Egieers Iroducio 3 Probabiliy 4 Probabiliy disribuios 5 Probabiliy Desiies Orgaizaio ad descripio of daa 6 Samplig disribuios 7 Ifereces cocerig a mea 8 Comparig wo reames
Consider the time-varying system, (14.1)
 Leue 4 // Oulie Moivaio Equivale Defiiios fo Lyapuov Sabiliy Uifomly Sabiliy ad Uifomly Asympoial Sabiliy 4 Covese Lyapuov Theoem 5 Ivaiae- lie Theoem 6 Summay Moivaio Taig poblem i ool, Suppose ha x (
Leue 4 // Oulie Moivaio Equivale Defiiios fo Lyapuov Sabiliy Uifomly Sabiliy ad Uifomly Asympoial Sabiliy 4 Covese Lyapuov Theoem 5 Ivaiae- lie Theoem 6 Summay Moivaio Taig poblem i ool, Suppose ha x (
= 5! 3! 2! = 5! 3! (5 3)!. In general, the number of different groups of r items out of n items (when the order is ignored) is given by n!
 0 Combiatoial Aalysis Copyight by Deiz Kalı 4 Combiatios Questio 4 What is the diffeece betwee the followig questio i How may 3-lette wods ca you wite usig the lettes A, B, C, D, E ii How may 3-elemet
0 Combiatoial Aalysis Copyight by Deiz Kalı 4 Combiatios Questio 4 What is the diffeece betwee the followig questio i How may 3-lette wods ca you wite usig the lettes A, B, C, D, E ii How may 3-elemet
