Masters Comprehensive Examination Department of Statistics, University of Florida
|
|
|
- Howard Lang
- 5 years ago
- Views:
Transcription
1 Masters Comprehensive Examination Department of Statistics, University of Florida May 10, 2002, 8:00am - 12:00 noon Instructions: 1. You have four hours to answer questions in this examination. 2. There are 10 problems of which you must answer Only your first 8 problems will be graded. 4. You must show your work to receive credit. 5. While the questions are equally weighted, some problems are more difficult than others. 6. Write only on one side of the paper, and start each question on a new page. 7. You are allowed to use a calculator. The following abbreviations are used throughout: ANOVA = analysis of variance iid = independent and identically distributed LRT = likelihood ratio test pdf = probability density function pmf = probability mass function MLE = maximum likelihood estimator MOM = method of moments UMP = uniformly most powerful UMVUE = uniformly minimum variance unbiased estimator ε i NID(0, σ 2 ) means that ε 1,..., ε n are iid N(0, σ 2 ). You may use the following facts/formulas without proof: Gamma Density: X Gamma(α, β) means X has pdf where α > 0 and β > 0. f(x; α, β) = 1 Γ(α) β α xα 1 e x/β I(x > 0) Distributional Result: If X Gamma(α x, β) and Y Gamma(α y, β) and X and Y are independent, then X/(X + Y ) Beta(α x, α y ). 1
2 1. Let X and Y be iid Exp(λ). (a) Find the joint distribution of V = X + Y and W = X. (b) Are V and W independent? (c) Express P (V + W < π) as a double integral. (You do not need to evaluate it.) (d) Find Cov(V, W ). (e) Show that, in general, for any two random variables S and T, E(S) = E [E(S T )], provided the expectations exist. (f) For our specific (V, W ), find E(W V ) and show that E [E(W V )] = E(W ). 2. Suppose that X 1,..., X n are iid Exp(θ) and that Y 1,..., Y m are iid Exp(µ). Assume further that X = (X 1,..., X n ) and Y = (Y 1,..., Y m ) are independent. (a) Find the MLE of θ. (b) Construct the LRT statistic for testing H 0 : θ = µ against H 1 : θ µ. (c) Show that the LRT statistic can be written in such a way that it involves the data only through the statistic n i=1 T = X i n i=1 X i + m i=1 Y. i (d) The general LRT theory tells us to reject H 0 when λ(x, y) < c. Give an equivalent rejection rule in terms of T. (e) Find the distribution of T under H 0. (f) Suppose that n = m = 1. Give the exact rejection region for the size 0.05 LRT of H 0 : θ = µ versus H 1 : θ µ. 3. Let X 1,..., X n be a random sample from a population with mean µ and (finite) variance σ 2. Let a 1,..., a n be constants. (a) Show that the estimator n i=1 a ix i is an unbiased estimator of µ if and only if n i=1 a i = 1. (b) Among all unbiased estimators of this form (called linear unbiased estimators) find the one with minimum variance and calculate the variance. Now let W 1,..., W k be unbiased estimators of a parameter θ with Var(W i ) = σ 2 i and Cov(W i, W j ) = 0 if i j. Assume that the σ 2 i s are all known and finite and, again, let a 1,..., a k be constants. (c) Show that, of all the unbiased estimators of θ having the form k i=1 a iw i, the one with the smallest variance is k i=1 W i σi φ(w 1,..., W k ) = 2 k, i=1 1 σi 2 and that Var [φ(w 1,..., W k )] = 1 k i=1 1 σ 2 i. 2
3 4. It is sometimes reasonable to think of the lifetime of a piece of equipment as a random variable following an Exp(λ) distribution where λ is unknown. Suppose n identical pieces of equipment are to be run until they fail and the (random) failure times are given by X 1,..., X n. Assume that these are a random sample from the Exp(λ) distribution. Consider the probability of early failure given by for some fixed x > 0. (a) Find the MLE of e(λ). e(λ) = P λ (X 1 < x) = 1 e x/λ (b) Find the best unbiased estimator (or UMVUE) of e(λ). (Your answer must be a closed form function of the data.) Hint: ( X P (X < x Y = y) = P Y < x ) Y = y. y 5. Suppose that X λ Poisson(λ) and that λ Gamma(α, β). (a) Show that the marginal mass function of X is given by for x {0, 1, 2,... }. P α,β (X = x) = (b) Find the marginal mean and variance of X. ( ) Γ(α + x) β x+α Γ(α) x! β α (1) β + 1 (c) Are there any (α, β) pairs for which X has a Geometric distribution? If yes, identify the success probability in terms of α and β. (d) Suppose that X 1,..., X n are iid from the pmf in (1). Find the MOM estimator of (α, β). (e) Why might one prefer the MLE of (α, β) over the MOM estimator derived in (d)? (f) Suppose that X 1, X 2 are iid from the following pmf P β (X = x) = ( ) Γ(2 + x) β x+2 Γ(2) x! β 2 β + 1 for x {0, 1, 2,... }. (This is, of course, the pmf in (1) with α known and equal to 2.) Find a UMP test of H 0 : β 1 against H 1 : β > 1 with level equal to
4 6. Two statistical analysts are given the same data for a single response variable Y, and a single independent variable. The independent variable has been labeled with levels 1,2,3,4. John treats the independent variable as interval scale, and assumes that the relationship between the dependent and independent variables is linear (he has no reason to believe the mean response is 0 when the independent variable is 0). Jane treats the independent variable as nominal scale (no distinct ordering among the levels), making no assumption about the relationship between the dependent and independent variables. Both John and Jane believe that error terms are independent and normally distributed with constant variance. (a) Write out John s statistical model. (b) Write out Jane s statistical model. (c) The following data were obtained. Give least squares estimates of all model parameters for John and Jane. (d) Give John s and Jane s Analyses of Variance. Trt (X) Responses (Y ) (e) State the null and alternative hypotheses for John and Jane to determine whether there is an association between treatment (X) and response (Y ). (f) Conduct your tests in part (e), each at α = Note, there is no need to adjust for simultaneous tests, as John and Jane are working independently. (g) Use the F -test for lack of fit to determine whether John s model is appropriate (H 0 ) or Jane s is (H A ), with α =
5 7. A plant foreman is interested in the effects of changes in labor (X 1 ) and capital (X 2 ) on the plant s output. She designs an experiment where she varies labor and capital, observing the output. She believes that output should increase linearly over these ranges of labor and capital, and that there is no interaction between these two factors. She fits the model: She obtains the following data: Y i = β 0 + β 1 X i1 + β 2 X i2 + ε i ε i NID(0, σ 2 ) (a) Give X X, X Y, and Y Y. i Y i X i1 X i (b) The least squares estimate (ˆβ), (X X) 1, and MS(Residual) are given below. Test whether the true effects of increasing labor by one unit and increasing capital by one unit are the same. Clearly state the null and alternative hypotheses, test statistic, and rejection region (based on α = 0.05 significance level). ˆβ = (X X) 1 = M S(Residual) = (c) Give the predicted value, residual, and their variances for the first observation; that is, find Ŷ1, e 1, s 2 (Ŷ1) and s 2 (e 1 ). 5
6 8. While lost in the woods, you find the following partial ANOVA table. The response being measured was the bird s height. The researcher has written 2-factor ANOVA (which is barely legible next to the sabre-tooth bite marks on the tattered output). The species that (s)he has analyzed are a random sample of species from this region. (a) How many birds were there in the sample? (b) How many species were there in the sample? Source df SS Species Gender Interaction 5 Error 25.0 Total (c) What was the number of replicates per species/gender combination? (d) Find MS(Species), MS(Gender), MS(Interaction) and MSE. (e) Find the test statistics for testing for interaction, species effects, and gender effects; that is, find F Interaction, F Species and F Gender. (f) Find the rejection regions for the tests in (e). 9. A shoe company executive is interested in comparing her company s (NIKE) top of the line shoe with those of her 2 biggest competitors (ADIDAS, REEBOK). The response she s interested in is the vertical leap (distance off the ground, in inches) for basketball players. Because she knows that there is a large amount of variation in players, she takes a sample of players, treats them as blocks, having each player wear each brand (in random order). She has no reason to believe the effects of the brands differ among the players. (a) Write out the statistical model for the randomized complete block design, very briefly defining all terms. (b) She obtains the following sample data. Give the Analysis of Variance. You may use the fact that n r i=1 j=1 (Y ij Y.. ) 2 = 660. Player Nike Adidas Reebok Pat Terry Kim Mel Chris (c) Test whether the true mean vertical leaps differ among the brands of shoes (use α = 0.05). Be sure to explicitly state the hypotheses, test statistic, rejection region and conclusion. (d) Give the decision rule based on Tukey s and Bonferroni s methods to determine whether the true means differ among all pairs of brands. That is, we should conclude µ i µ j if what? Be precise with your notation. 6
7 10. Consider a linear regression model with 2 independent variables and no intercept: Y i = β 1 X i1 + β 2 X i2 + ε i ε i NID(0, σ 2 ) (a) Derive the least squares estimates of β 1 and β 2 in terms of the actual data, (Y i, X i1, X i2 ). (Your answer to this question must be a closed form function of the data.) (b) Give s 2 { ˆβ 1 ˆβ 2 } in terms of the actual data, (Y i, X i1, X i2 ). (Again, your answer must be a closed form function of the data.) 7
First Year Examination Department of Statistics, University of Florida
 First Year Examination Department of Statistics, University of Florida August 19, 010, 8:00 am - 1:00 noon Instructions: 1. You have four hours to answer questions in this examination.. You must show your
First Year Examination Department of Statistics, University of Florida August 19, 010, 8:00 am - 1:00 noon Instructions: 1. You have four hours to answer questions in this examination.. You must show your
First Year Examination Department of Statistics, University of Florida
 First Year Examination Department of Statistics, University of Florida May 6, 2011, 8:00 am - 12:00 noon Instructions: 1. You have four hours to answer questions in this examination. 2. You must show your
First Year Examination Department of Statistics, University of Florida May 6, 2011, 8:00 am - 12:00 noon Instructions: 1. You have four hours to answer questions in this examination. 2. You must show your
First Year Examination Department of Statistics, University of Florida
 First Year Examination Department of Statistics, University of Florida August 20, 2009, 8:00 am - 2:00 noon Instructions:. You have four hours to answer questions in this examination. 2. You must show
First Year Examination Department of Statistics, University of Florida August 20, 2009, 8:00 am - 2:00 noon Instructions:. You have four hours to answer questions in this examination. 2. You must show
Masters Comprehensive Examination Department of Statistics, University of Florida
 Masters Comprehensive Examination Department of Statistics, University of Florida May 6, 003, 8:00 am - :00 noon Instructions: You have four hours to answer questions in this examination You must show
Masters Comprehensive Examination Department of Statistics, University of Florida May 6, 003, 8:00 am - :00 noon Instructions: You have four hours to answer questions in this examination You must show
STA 4322 Exam I Name: Introduction to Statistics Theory
 STA 4322 Exam I Name: Introduction to Statistics Theory Fall 2013 UF-ID: Instructions: There are 100 total points. You must show your work to receive credit. Read each part of each question carefully.
STA 4322 Exam I Name: Introduction to Statistics Theory Fall 2013 UF-ID: Instructions: There are 100 total points. You must show your work to receive credit. Read each part of each question carefully.
Statistics Masters Comprehensive Exam March 21, 2003
 Statistics Masters Comprehensive Exam March 21, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Masters Comprehensive Exam March 21, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Probability and Statistics qualifying exam, May 2015
 Probability and Statistics qualifying exam, May 2015 Name: Instructions: 1. The exam is divided into 3 sections: Linear Models, Mathematical Statistics and Probability. You must pass each section to pass
Probability and Statistics qualifying exam, May 2015 Name: Instructions: 1. The exam is divided into 3 sections: Linear Models, Mathematical Statistics and Probability. You must pass each section to pass
Ch 2: Simple Linear Regression
 Ch 2: Simple Linear Regression 1. Simple Linear Regression Model A simple regression model with a single regressor x is y = β 0 + β 1 x + ɛ, where we assume that the error ɛ is independent random component
Ch 2: Simple Linear Regression 1. Simple Linear Regression Model A simple regression model with a single regressor x is y = β 0 + β 1 x + ɛ, where we assume that the error ɛ is independent random component
Mathematics Qualifying Examination January 2015 STAT Mathematical Statistics
 Mathematics Qualifying Examination January 2015 STAT 52800 - Mathematical Statistics NOTE: Answer all questions completely and justify your derivations and steps. A calculator and statistical tables (normal,
Mathematics Qualifying Examination January 2015 STAT 52800 - Mathematical Statistics NOTE: Answer all questions completely and justify your derivations and steps. A calculator and statistical tables (normal,
Review. DS GA 1002 Statistical and Mathematical Models. Carlos Fernandez-Granda
 Review DS GA 1002 Statistical and Mathematical Models http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall16 Carlos Fernandez-Granda Probability and statistics Probability: Framework for dealing with
Review DS GA 1002 Statistical and Mathematical Models http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall16 Carlos Fernandez-Granda Probability and statistics Probability: Framework for dealing with
Problem 1 (20) Log-normal. f(x) Cauchy
 ORF 245. Rigollet Date: 11/21/2008 Problem 1 (20) f(x) f(x) 0.0 0.1 0.2 0.3 0.4 0.0 0.2 0.4 0.6 0.8 4 2 0 2 4 Normal (with mean -1) 4 2 0 2 4 Negative-exponential x x f(x) f(x) 0.0 0.1 0.2 0.3 0.4 0.5
ORF 245. Rigollet Date: 11/21/2008 Problem 1 (20) f(x) f(x) 0.0 0.1 0.2 0.3 0.4 0.0 0.2 0.4 0.6 0.8 4 2 0 2 4 Normal (with mean -1) 4 2 0 2 4 Negative-exponential x x f(x) f(x) 0.0 0.1 0.2 0.3 0.4 0.5
Master s Written Examination - Solution
 Master s Written Examination - Solution Spring 204 Problem Stat 40 Suppose X and X 2 have the joint pdf f X,X 2 (x, x 2 ) = 2e (x +x 2 ), 0 < x < x 2
Master s Written Examination - Solution Spring 204 Problem Stat 40 Suppose X and X 2 have the joint pdf f X,X 2 (x, x 2 ) = 2e (x +x 2 ), 0 < x < x 2
Mathematics Ph.D. Qualifying Examination Stat Probability, January 2018
 Mathematics Ph.D. Qualifying Examination Stat 52800 Probability, January 2018 NOTE: Answers all questions completely. Justify every step. Time allowed: 3 hours. 1. Let X 1,..., X n be a random sample from
Mathematics Ph.D. Qualifying Examination Stat 52800 Probability, January 2018 NOTE: Answers all questions completely. Justify every step. Time allowed: 3 hours. 1. Let X 1,..., X n be a random sample from
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003
 Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Master s Examination Solutions Option Statistics and Probability Fall 2011
 Master s Examination Solutions Option Statistics and Probability Fall 211 1. (STAT 41) Suppose that X, Y and Z are i.i.d. Uniform(,1). Let t > be a fixed constant. (i) Compute P ( X Y t). (ii) Compute
Master s Examination Solutions Option Statistics and Probability Fall 211 1. (STAT 41) Suppose that X, Y and Z are i.i.d. Uniform(,1). Let t > be a fixed constant. (i) Compute P ( X Y t). (ii) Compute
Stat 5102 Final Exam May 14, 2015
 Stat 5102 Final Exam May 14, 2015 Name Student ID The exam is closed book and closed notes. You may use three 8 1 11 2 sheets of paper with formulas, etc. You may also use the handouts on brand name distributions
Stat 5102 Final Exam May 14, 2015 Name Student ID The exam is closed book and closed notes. You may use three 8 1 11 2 sheets of paper with formulas, etc. You may also use the handouts on brand name distributions
STAT 525 Fall Final exam. Tuesday December 14, 2010
 STAT 525 Fall 2010 Final exam Tuesday December 14, 2010 Time: 2 hours Name (please print): Show all your work and calculations. Partial credit will be given for work that is partially correct. Points will
STAT 525 Fall 2010 Final exam Tuesday December 14, 2010 Time: 2 hours Name (please print): Show all your work and calculations. Partial credit will be given for work that is partially correct. Points will
Master s Written Examination
 Master s Written Examination Option: Statistics and Probability Spring 016 Full points may be obtained for correct answers to eight questions. Each numbered question which may have several parts is worth
Master s Written Examination Option: Statistics and Probability Spring 016 Full points may be obtained for correct answers to eight questions. Each numbered question which may have several parts is worth
Chapter 8: Hypothesis Testing Lecture 9: Likelihood ratio tests
 Chapter 8: Hypothesis Testing Lecture 9: Likelihood ratio tests Throughout this chapter we consider a sample X taken from a population indexed by θ Θ R k. Instead of estimating the unknown parameter, we
Chapter 8: Hypothesis Testing Lecture 9: Likelihood ratio tests Throughout this chapter we consider a sample X taken from a population indexed by θ Θ R k. Instead of estimating the unknown parameter, we
Final Exam. 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given.
 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
Spring 2012 Math 541A Exam 1. X i, S 2 = 1 n. n 1. X i I(X i < c), T n =
 Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Institute of Actuaries of India
 Institute of Actuaries of India Subject CT3 Probability & Mathematical Statistics May 2011 Examinations INDICATIVE SOLUTION Introduction The indicative solution has been written by the Examiners with the
Institute of Actuaries of India Subject CT3 Probability & Mathematical Statistics May 2011 Examinations INDICATIVE SOLUTION Introduction The indicative solution has been written by the Examiners with the
Central Limit Theorem ( 5.3)
 Central Limit Theorem ( 5.3) Let X 1, X 2,... be a sequence of independent random variables, each having n mean µ and variance σ 2. Then the distribution of the partial sum S n = X i i=1 becomes approximately
Central Limit Theorem ( 5.3) Let X 1, X 2,... be a sequence of independent random variables, each having n mean µ and variance σ 2. Then the distribution of the partial sum S n = X i i=1 becomes approximately
Problem Selected Scores
 Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
t x 1 e t dt, and simplify the answer when possible (for example, when r is a positive even number). In particular, confirm that EX 4 = 3.
 Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Inferences for Regression
 Inferences for Regression An Example: Body Fat and Waist Size Looking at the relationship between % body fat and waist size (in inches). Here is a scatterplot of our data set: Remembering Regression In
Inferences for Regression An Example: Body Fat and Waist Size Looking at the relationship between % body fat and waist size (in inches). Here is a scatterplot of our data set: Remembering Regression In
MATH 644: Regression Analysis Methods
 MATH 644: Regression Analysis Methods FINAL EXAM Fall, 2012 INSTRUCTIONS TO STUDENTS: 1. This test contains SIX questions. It comprises ELEVEN printed pages. 2. Answer ALL questions for a total of 100
MATH 644: Regression Analysis Methods FINAL EXAM Fall, 2012 INSTRUCTIONS TO STUDENTS: 1. This test contains SIX questions. It comprises ELEVEN printed pages. 2. Answer ALL questions for a total of 100
Comprehensive Examination Quantitative Methods Spring, 2018
 Comprehensive Examination Quantitative Methods Spring, 2018 Instruction: This exam consists of three parts. You are required to answer all the questions in all the parts. 1 Grading policy: 1. Each part
Comprehensive Examination Quantitative Methods Spring, 2018 Instruction: This exam consists of three parts. You are required to answer all the questions in all the parts. 1 Grading policy: 1. Each part
1 Introduction. P (n = 1 red ball drawn) =
 Introduction Exercises and outline solutions. Y has a pack of 4 cards (Ace and Queen of clubs, Ace and Queen of Hearts) from which he deals a random of selection 2 to player X. What is the probability
Introduction Exercises and outline solutions. Y has a pack of 4 cards (Ace and Queen of clubs, Ace and Queen of Hearts) from which he deals a random of selection 2 to player X. What is the probability
M2S2 Statistical Modelling
 UNIVERSITY OF LONDON BSc and MSci EXAMINATIONS (MATHEMATICS) May-June 2006 This paper is also taken for the relevant examination for the Associateship. M2S2 Statistical Modelling Date: Wednesday, 17th
UNIVERSITY OF LONDON BSc and MSci EXAMINATIONS (MATHEMATICS) May-June 2006 This paper is also taken for the relevant examination for the Associateship. M2S2 Statistical Modelling Date: Wednesday, 17th
Qualifying Exam in Probability and Statistics. https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf
 Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Statistics 135 Fall 2008 Final Exam
 Name: SID: Statistics 135 Fall 2008 Final Exam Show your work. The number of points each question is worth is shown at the beginning of the question. There are 10 problems. 1. [2] The normal equations
Name: SID: Statistics 135 Fall 2008 Final Exam Show your work. The number of points each question is worth is shown at the beginning of the question. There are 10 problems. 1. [2] The normal equations
A Note on UMPI F Tests
 A Note on UMPI F Tests Ronald Christensen Professor of Statistics Department of Mathematics and Statistics University of New Mexico May 22, 2015 Abstract We examine the transformations necessary for establishing
A Note on UMPI F Tests Ronald Christensen Professor of Statistics Department of Mathematics and Statistics University of New Mexico May 22, 2015 Abstract We examine the transformations necessary for establishing
Practice Final Exam. December 14, 2009
 Practice Final Exam December 14, 29 1 New Material 1.1 ANOVA 1. A purication process for a chemical involves passing it, in solution, through a resin on which impurities are adsorbed. A chemical engineer
Practice Final Exam December 14, 29 1 New Material 1.1 ANOVA 1. A purication process for a chemical involves passing it, in solution, through a resin on which impurities are adsorbed. A chemical engineer
(ii) Scan your answer sheets INTO ONE FILE only, and submit it in the drop-box.
 FINAL EXAM ** Two different ways to submit your answer sheet (i) Use MS-Word and place it in a drop-box. (ii) Scan your answer sheets INTO ONE FILE only, and submit it in the drop-box. Deadline: December
FINAL EXAM ** Two different ways to submit your answer sheet (i) Use MS-Word and place it in a drop-box. (ii) Scan your answer sheets INTO ONE FILE only, and submit it in the drop-box. Deadline: December
Lec 1: An Introduction to ANOVA
 Ying Li Stockholm University October 31, 2011 Three end-aisle displays Which is the best? Design of the Experiment Identify the stores of the similar size and type. The displays are randomly assigned to
Ying Li Stockholm University October 31, 2011 Three end-aisle displays Which is the best? Design of the Experiment Identify the stores of the similar size and type. The displays are randomly assigned to
Ch 3: Multiple Linear Regression
 Ch 3: Multiple Linear Regression 1. Multiple Linear Regression Model Multiple regression model has more than one regressor. For example, we have one response variable and two regressor variables: 1. delivery
Ch 3: Multiple Linear Regression 1. Multiple Linear Regression Model Multiple regression model has more than one regressor. For example, we have one response variable and two regressor variables: 1. delivery
Ph.D. Qualifying Exam Friday Saturday, January 3 4, 2014
 Ph.D. Qualifying Exam Friday Saturday, January 3 4, 2014 Put your solution to each problem on a separate sheet of paper. Problem 1. (5166) Assume that two random samples {x i } and {y i } are independently
Ph.D. Qualifying Exam Friday Saturday, January 3 4, 2014 Put your solution to each problem on a separate sheet of paper. Problem 1. (5166) Assume that two random samples {x i } and {y i } are independently
Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee
 Stochastic Processes Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee 1 Outline Methods of Mean Squared Error Bias and Unbiasedness Best Unbiased Estimators CR-Bound for variance
Stochastic Processes Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee 1 Outline Methods of Mean Squared Error Bias and Unbiasedness Best Unbiased Estimators CR-Bound for variance
Master s Written Examination
 Master s Written Examination Option: Statistics and Probability Spring 05 Full points may be obtained for correct answers to eight questions Each numbered question (which may have several parts) is worth
Master s Written Examination Option: Statistics and Probability Spring 05 Full points may be obtained for correct answers to eight questions Each numbered question (which may have several parts) is worth
Definition 3.1 A statistical hypothesis is a statement about the unknown values of the parameters of the population distribution.
 Hypothesis Testing Definition 3.1 A statistical hypothesis is a statement about the unknown values of the parameters of the population distribution. Suppose the family of population distributions is indexed
Hypothesis Testing Definition 3.1 A statistical hypothesis is a statement about the unknown values of the parameters of the population distribution. Suppose the family of population distributions is indexed
Lecture 6 Multiple Linear Regression, cont.
 Lecture 6 Multiple Linear Regression, cont. BIOST 515 January 22, 2004 BIOST 515, Lecture 6 Testing general linear hypotheses Suppose we are interested in testing linear combinations of the regression
Lecture 6 Multiple Linear Regression, cont. BIOST 515 January 22, 2004 BIOST 515, Lecture 6 Testing general linear hypotheses Suppose we are interested in testing linear combinations of the regression
FIRST YEAR EXAM Monday May 10, 2010; 9:00 12:00am
 FIRST YEAR EXAM Monday May 10, 2010; 9:00 12:00am NOTES: PLEASE READ CAREFULLY BEFORE BEGINNING EXAM! 1. Do not write solutions on the exam; please write your solutions on the paper provided. 2. Put the
FIRST YEAR EXAM Monday May 10, 2010; 9:00 12:00am NOTES: PLEASE READ CAREFULLY BEFORE BEGINNING EXAM! 1. Do not write solutions on the exam; please write your solutions on the paper provided. 2. Put the
STAT763: Applied Regression Analysis. Multiple linear regression. 4.4 Hypothesis testing
 STAT763: Applied Regression Analysis Multiple linear regression 4.4 Hypothesis testing Chunsheng Ma E-mail: cma@math.wichita.edu 4.4.1 Significance of regression Null hypothesis (Test whether all β j =
STAT763: Applied Regression Analysis Multiple linear regression 4.4 Hypothesis testing Chunsheng Ma E-mail: cma@math.wichita.edu 4.4.1 Significance of regression Null hypothesis (Test whether all β j =
Qualifying Exam in Probability and Statistics. https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf
 Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Linear Regression. In this problem sheet, we consider the problem of linear regression with p predictors and one intercept,
 Linear Regression In this problem sheet, we consider the problem of linear regression with p predictors and one intercept, y = Xβ + ɛ, where y t = (y 1,..., y n ) is the column vector of target values,
Linear Regression In this problem sheet, we consider the problem of linear regression with p predictors and one intercept, y = Xβ + ɛ, where y t = (y 1,..., y n ) is the column vector of target values,
Chapter 7. Hypothesis Testing
 Chapter 7. Hypothesis Testing Joonpyo Kim June 24, 2017 Joonpyo Kim Ch7 June 24, 2017 1 / 63 Basic Concepts of Testing Suppose that our interest centers on a random variable X which has density function
Chapter 7. Hypothesis Testing Joonpyo Kim June 24, 2017 Joonpyo Kim Ch7 June 24, 2017 1 / 63 Basic Concepts of Testing Suppose that our interest centers on a random variable X which has density function
Open book and notes. 120 minutes. Covers Chapters 8 through 14 of Montgomery and Runger (fourth edition).
 IE 330 Seat # Open book and notes 10 minutes Covers Chapters 8 through 14 of Montgomery and Runger (fourth edition) Cover page and eight pages of exam No calculator ( points) I have, or will, complete
IE 330 Seat # Open book and notes 10 minutes Covers Chapters 8 through 14 of Montgomery and Runger (fourth edition) Cover page and eight pages of exam No calculator ( points) I have, or will, complete
MS&E 226. In-Class Midterm Examination Solutions Small Data October 20, 2015
 MS&E 226 In-Class Midterm Examination Solutions Small Data October 20, 2015 PROBLEM 1. Alice uses ordinary least squares to fit a linear regression model on a dataset containing outcome data Y and covariates
MS&E 226 In-Class Midterm Examination Solutions Small Data October 20, 2015 PROBLEM 1. Alice uses ordinary least squares to fit a linear regression model on a dataset containing outcome data Y and covariates
Swarthmore Honors Exam 2012: Statistics
 Swarthmore Honors Exam 2012: Statistics 1 Swarthmore Honors Exam 2012: Statistics John W. Emerson, Yale University NAME: Instructions: This is a closed-book three-hour exam having six questions. You may
Swarthmore Honors Exam 2012: Statistics 1 Swarthmore Honors Exam 2012: Statistics John W. Emerson, Yale University NAME: Instructions: This is a closed-book three-hour exam having six questions. You may
STAT FINAL EXAM
 STAT101 2013 FINAL EXAM This exam is 2 hours long. It is closed book but you can use an A-4 size cheat sheet. There are 10 questions. Questions are not of equal weight. You may need a calculator for some
STAT101 2013 FINAL EXAM This exam is 2 hours long. It is closed book but you can use an A-4 size cheat sheet. There are 10 questions. Questions are not of equal weight. You may need a calculator for some
Biostatistics 533 Classical Theory of Linear Models Spring 2007 Final Exam. Please choose ONE of the following options.
 1 Biostatistics 533 Classical Theory of Linear Models Spring 2007 Final Exam Name: Problems do not have equal value and some problems will take more time than others. Spend your time wisely. You do not
1 Biostatistics 533 Classical Theory of Linear Models Spring 2007 Final Exam Name: Problems do not have equal value and some problems will take more time than others. Spend your time wisely. You do not
Weighted Least Squares
 Weighted Least Squares The standard linear model assumes that Var(ε i ) = σ 2 for i = 1,..., n. As we have seen, however, there are instances where Var(Y X = x i ) = Var(ε i ) = σ2 w i. Here w 1,..., w
Weighted Least Squares The standard linear model assumes that Var(ε i ) = σ 2 for i = 1,..., n. As we have seen, however, there are instances where Var(Y X = x i ) = Var(ε i ) = σ2 w i. Here w 1,..., w
Weighted Least Squares
 Weighted Least Squares The standard linear model assumes that Var(ε i ) = σ 2 for i = 1,..., n. As we have seen, however, there are instances where Var(Y X = x i ) = Var(ε i ) = σ2 w i. Here w 1,..., w
Weighted Least Squares The standard linear model assumes that Var(ε i ) = σ 2 for i = 1,..., n. As we have seen, however, there are instances where Var(Y X = x i ) = Var(ε i ) = σ2 w i. Here w 1,..., w
Multiple regression. CM226: Machine Learning for Bioinformatics. Fall Sriram Sankararaman Acknowledgments: Fei Sha, Ameet Talwalkar
 Multiple regression CM226: Machine Learning for Bioinformatics. Fall 2016 Sriram Sankararaman Acknowledgments: Fei Sha, Ameet Talwalkar Multiple regression 1 / 36 Previous two lectures Linear and logistic
Multiple regression CM226: Machine Learning for Bioinformatics. Fall 2016 Sriram Sankararaman Acknowledgments: Fei Sha, Ameet Talwalkar Multiple regression 1 / 36 Previous two lectures Linear and logistic
Problems. Suppose both models are fitted to the same data. Show that SS Res, A SS Res, B
 Simple Linear Regression 35 Problems 1 Consider a set of data (x i, y i ), i =1, 2,,n, and the following two regression models: y i = β 0 + β 1 x i + ε, (i =1, 2,,n), Model A y i = γ 0 + γ 1 x i + γ 2
Simple Linear Regression 35 Problems 1 Consider a set of data (x i, y i ), i =1, 2,,n, and the following two regression models: y i = β 0 + β 1 x i + ε, (i =1, 2,,n), Model A y i = γ 0 + γ 1 x i + γ 2
p y (1 p) 1 y, y = 0, 1 p Y (y p) = 0, otherwise.
 1. Suppose Y 1, Y 2,..., Y n is an iid sample from a Bernoulli(p) population distribution, where 0 < p < 1 is unknown. The population pmf is p y (1 p) 1 y, y = 0, 1 p Y (y p) = (a) Prove that Y is the
1. Suppose Y 1, Y 2,..., Y n is an iid sample from a Bernoulli(p) population distribution, where 0 < p < 1 is unknown. The population pmf is p y (1 p) 1 y, y = 0, 1 p Y (y p) = (a) Prove that Y is the
First Year Examination Department of Statistics, University of Florida
 Frst Year Examnaton Department of Statstcs, Unversty of Florda May 7, 010, 8:00 am - 1:00 noon Instructons: 1. You have four hours to answer questons n ths examnaton.. You must show your work to receve
Frst Year Examnaton Department of Statstcs, Unversty of Florda May 7, 010, 8:00 am - 1:00 noon Instructons: 1. You have four hours to answer questons n ths examnaton.. You must show your work to receve
Qualifying Exam in Probability and Statistics.
 Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
5. Let W follow a normal distribution with mean of μ and the variance of 1. Then, the pdf of W is
 Practice Final Exam Last Name:, First Name:. Please write LEGIBLY. Answer all questions on this exam in the space provided (you may use the back of any page if you need more space). Show all work but do
Practice Final Exam Last Name:, First Name:. Please write LEGIBLY. Answer all questions on this exam in the space provided (you may use the back of any page if you need more space). Show all work but do
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017
 Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
ISyE 6644 Fall 2014 Test 3 Solutions
 1 NAME ISyE 6644 Fall 14 Test 3 Solutions revised 8/4/18 You have 1 minutes for this test. You are allowed three cheat sheets. Circle all final answers. Good luck! 1. [4 points] Suppose that the joint
1 NAME ISyE 6644 Fall 14 Test 3 Solutions revised 8/4/18 You have 1 minutes for this test. You are allowed three cheat sheets. Circle all final answers. Good luck! 1. [4 points] Suppose that the joint
Statistics GIDP Ph.D. Qualifying Exam Theory Jan 11, 2016, 9:00am-1:00pm
 Statistics GIDP Ph.D. Qualifying Exam Theory Jan, 06, 9:00am-:00pm Instructions: Provide answers on the supplied pads of paper; write on only one side of each sheet. Complete exactly 5 of the 6 problems.
Statistics GIDP Ph.D. Qualifying Exam Theory Jan, 06, 9:00am-:00pm Instructions: Provide answers on the supplied pads of paper; write on only one side of each sheet. Complete exactly 5 of the 6 problems.
Direction: This test is worth 250 points and each problem worth points. DO ANY SIX
 Term Test 3 December 5, 2003 Name Math 52 Student Number Direction: This test is worth 250 points and each problem worth 4 points DO ANY SIX PROBLEMS You are required to complete this test within 50 minutes
Term Test 3 December 5, 2003 Name Math 52 Student Number Direction: This test is worth 250 points and each problem worth 4 points DO ANY SIX PROBLEMS You are required to complete this test within 50 minutes
Applied Statistics Comprehensive Exam
 Applied Statistics Comprehensive Exam August 2013 Ph.D Theory Exam This comprehensive exam consists of 10 questions pertaining to theoretical statistical topics. 1 This Ph.D level exam will run from 8:30
Applied Statistics Comprehensive Exam August 2013 Ph.D Theory Exam This comprehensive exam consists of 10 questions pertaining to theoretical statistical topics. 1 This Ph.D level exam will run from 8:30
1 General problem. 2 Terminalogy. Estimation. Estimate θ. (Pick a plausible distribution from family. ) Or estimate τ = τ(θ).
 Estimation February 3, 206 Debdeep Pati General problem Model: {P θ : θ Θ}. Observe X P θ, θ Θ unknown. Estimate θ. (Pick a plausible distribution from family. ) Or estimate τ = τ(θ). Examples: θ = (µ,
Estimation February 3, 206 Debdeep Pati General problem Model: {P θ : θ Θ}. Observe X P θ, θ Θ unknown. Estimate θ. (Pick a plausible distribution from family. ) Or estimate τ = τ(θ). Examples: θ = (µ,
14 Multiple Linear Regression
 B.Sc./Cert./M.Sc. Qualif. - Statistics: Theory and Practice 14 Multiple Linear Regression 14.1 The multiple linear regression model In simple linear regression, the response variable y is expressed in
B.Sc./Cert./M.Sc. Qualif. - Statistics: Theory and Practice 14 Multiple Linear Regression 14.1 The multiple linear regression model In simple linear regression, the response variable y is expressed in
Practice Problems Section Problems
 Practice Problems Section 4-4-3 4-4 4-5 4-6 4-7 4-8 4-10 Supplemental Problems 4-1 to 4-9 4-13, 14, 15, 17, 19, 0 4-3, 34, 36, 38 4-47, 49, 5, 54, 55 4-59, 60, 63 4-66, 68, 69, 70, 74 4-79, 81, 84 4-85,
Practice Problems Section 4-4-3 4-4 4-5 4-6 4-7 4-8 4-10 Supplemental Problems 4-1 to 4-9 4-13, 14, 15, 17, 19, 0 4-3, 34, 36, 38 4-47, 49, 5, 54, 55 4-59, 60, 63 4-66, 68, 69, 70, 74 4-79, 81, 84 4-85,
1. Point Estimators, Review
 AMS571 Prof. Wei Zhu 1. Point Estimators, Review Example 1. Let be a random sample from. Please find a good point estimator for Solutions. There are the typical estimators for and. Both are unbiased estimators.
AMS571 Prof. Wei Zhu 1. Point Estimators, Review Example 1. Let be a random sample from. Please find a good point estimator for Solutions. There are the typical estimators for and. Both are unbiased estimators.
Review. December 4 th, Review
 December 4 th, 2017 Att. Final exam: Course evaluation Friday, 12/14/2018, 10:30am 12:30pm Gore Hall 115 Overview Week 2 Week 4 Week 7 Week 10 Week 12 Chapter 6: Statistics and Sampling Distributions Chapter
December 4 th, 2017 Att. Final exam: Course evaluation Friday, 12/14/2018, 10:30am 12:30pm Gore Hall 115 Overview Week 2 Week 4 Week 7 Week 10 Week 12 Chapter 6: Statistics and Sampling Distributions Chapter
2017 Financial Mathematics Orientation - Statistics
 2017 Financial Mathematics Orientation - Statistics Written by Long Wang Edited by Joshua Agterberg August 21, 2018 Contents 1 Preliminaries 5 1.1 Samples and Population............................. 5
2017 Financial Mathematics Orientation - Statistics Written by Long Wang Edited by Joshua Agterberg August 21, 2018 Contents 1 Preliminaries 5 1.1 Samples and Population............................. 5
STAT 135 Lab 3 Asymptotic MLE and the Method of Moments
 STAT 135 Lab 3 Asymptotic MLE and the Method of Moments Rebecca Barter February 9, 2015 Maximum likelihood estimation (a reminder) Maximum likelihood estimation Suppose that we have a sample, X 1, X 2,...,
STAT 135 Lab 3 Asymptotic MLE and the Method of Moments Rebecca Barter February 9, 2015 Maximum likelihood estimation (a reminder) Maximum likelihood estimation Suppose that we have a sample, X 1, X 2,...,
STAT5044: Regression and Anova. Inyoung Kim
 STAT5044: Regression and Anova Inyoung Kim 2 / 47 Outline 1 Regression 2 Simple Linear regression 3 Basic concepts in regression 4 How to estimate unknown parameters 5 Properties of Least Squares Estimators:
STAT5044: Regression and Anova Inyoung Kim 2 / 47 Outline 1 Regression 2 Simple Linear regression 3 Basic concepts in regression 4 How to estimate unknown parameters 5 Properties of Least Squares Estimators:
ECE 302 Division 1 MWF 10:30-11:20 (Prof. Pollak) Final Exam Solutions, 5/3/2004. Please read the instructions carefully before proceeding.
 NAME: ECE 302 Division MWF 0:30-:20 (Prof. Pollak) Final Exam Solutions, 5/3/2004. Please read the instructions carefully before proceeding. If you are not in Prof. Pollak s section, you may not take this
NAME: ECE 302 Division MWF 0:30-:20 (Prof. Pollak) Final Exam Solutions, 5/3/2004. Please read the instructions carefully before proceeding. If you are not in Prof. Pollak s section, you may not take this
TA: Sheng Zhgang (Th 1:20) / 342 (W 1:20) / 343 (W 2:25) / 344 (W 12:05) Haoyang Fan (W 1:20) / 346 (Th 12:05) FINAL EXAM
 STAT 301, Fall 2011 Name Lec 4: Ismor Fischer Discussion Section: Please circle one! TA: Sheng Zhgang... 341 (Th 1:20) / 342 (W 1:20) / 343 (W 2:25) / 344 (W 12:05) Haoyang Fan... 345 (W 1:20) / 346 (Th
STAT 301, Fall 2011 Name Lec 4: Ismor Fischer Discussion Section: Please circle one! TA: Sheng Zhgang... 341 (Th 1:20) / 342 (W 1:20) / 343 (W 2:25) / 344 (W 12:05) Haoyang Fan... 345 (W 1:20) / 346 (Th
Correlation and Regression (Excel 2007)
 Correlation and Regression (Excel 2007) (See Also Scatterplots, Regression Lines, and Time Series Charts With Excel 2007 for instructions on making a scatterplot of the data and an alternate method of
Correlation and Regression (Excel 2007) (See Also Scatterplots, Regression Lines, and Time Series Charts With Excel 2007 for instructions on making a scatterplot of the data and an alternate method of
PhD Qualifying Examination Department of Statistics, University of Florida
 PhD Qualifying xamination Department of Statistics, University of Florida January 24, 2003, 8:00 am - 12:00 noon Instructions: 1 You have exactly four hours to answer questions in this examination 2 There
PhD Qualifying xamination Department of Statistics, University of Florida January 24, 2003, 8:00 am - 12:00 noon Instructions: 1 You have exactly four hours to answer questions in this examination 2 There
Part IB. Statistics. Year
 Part IB Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2004 2003 2002 2001 2018 42 Paper 1, Section I 7H X 1, X 2,..., X n form a random sample from a distribution whose probability
Part IB Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2004 2003 2002 2001 2018 42 Paper 1, Section I 7H X 1, X 2,..., X n form a random sample from a distribution whose probability
Simple Linear Regression
 Simple Linear Regression September 24, 2008 Reading HH 8, GIll 4 Simple Linear Regression p.1/20 Problem Data: Observe pairs (Y i,x i ),i = 1,...n Response or dependent variable Y Predictor or independent
Simple Linear Regression September 24, 2008 Reading HH 8, GIll 4 Simple Linear Regression p.1/20 Problem Data: Observe pairs (Y i,x i ),i = 1,...n Response or dependent variable Y Predictor or independent
IEOR165 Discussion Week 5
 IEOR165 Discussion Week 5 Sheng Liu University of California, Berkeley Feb 19, 2016 Outline 1 1st Homework 2 Revisit Maximum A Posterior 3 Regularization IEOR165 Discussion Sheng Liu 2 About 1st Homework
IEOR165 Discussion Week 5 Sheng Liu University of California, Berkeley Feb 19, 2016 Outline 1 1st Homework 2 Revisit Maximum A Posterior 3 Regularization IEOR165 Discussion Sheng Liu 2 About 1st Homework
Statistics STAT:5100 (22S:193), Fall Sample Final Exam B
 Statistics STAT:5 (22S:93), Fall 25 Sample Final Exam B Please write your answers in the exam books provided.. Let X, Y, and Y 2 be independent random variables with X N(µ X, σ 2 X ) and Y i N(µ Y, σ 2
Statistics STAT:5 (22S:93), Fall 25 Sample Final Exam B Please write your answers in the exam books provided.. Let X, Y, and Y 2 be independent random variables with X N(µ X, σ 2 X ) and Y i N(µ Y, σ 2
1. (Rao example 11.15) A study measures oxygen demand (y) (on a log scale) and five explanatory variables (see below). Data are available as
 ST 51, Summer, Dr. Jason A. Osborne Homework assignment # - Solutions 1. (Rao example 11.15) A study measures oxygen demand (y) (on a log scale) and five explanatory variables (see below). Data are available
ST 51, Summer, Dr. Jason A. Osborne Homework assignment # - Solutions 1. (Rao example 11.15) A study measures oxygen demand (y) (on a log scale) and five explanatory variables (see below). Data are available
Wooldridge, Introductory Econometrics, 4th ed. Appendix C: Fundamentals of mathematical statistics
 Wooldridge, Introductory Econometrics, 4th ed. Appendix C: Fundamentals of mathematical statistics A short review of the principles of mathematical statistics (or, what you should have learned in EC 151).
Wooldridge, Introductory Econometrics, 4th ed. Appendix C: Fundamentals of mathematical statistics A short review of the principles of mathematical statistics (or, what you should have learned in EC 151).
Part IB Statistics. Theorems with proof. Based on lectures by D. Spiegelhalter Notes taken by Dexter Chua. Lent 2015
 Part IB Statistics Theorems with proof Based on lectures by D. Spiegelhalter Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Part IB Statistics Theorems with proof Based on lectures by D. Spiegelhalter Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Two hours. To be supplied by the Examinations Office: Mathematical Formula Tables THE UNIVERSITY OF MANCHESTER. 21 June :45 11:45
 Two hours MATH20802 To be supplied by the Examinations Office: Mathematical Formula Tables THE UNIVERSITY OF MANCHESTER STATISTICAL METHODS 21 June 2010 9:45 11:45 Answer any FOUR of the questions. University-approved
Two hours MATH20802 To be supplied by the Examinations Office: Mathematical Formula Tables THE UNIVERSITY OF MANCHESTER STATISTICAL METHODS 21 June 2010 9:45 11:45 Answer any FOUR of the questions. University-approved
Linear models and their mathematical foundations: Simple linear regression
 Linear models and their mathematical foundations: Simple linear regression Steffen Unkel Department of Medical Statistics University Medical Center Göttingen, Germany Winter term 2018/19 1/21 Introduction
Linear models and their mathematical foundations: Simple linear regression Steffen Unkel Department of Medical Statistics University Medical Center Göttingen, Germany Winter term 2018/19 1/21 Introduction
The University of Hong Kong Department of Statistics and Actuarial Science STAT2802 Statistical Models Tutorial Solutions Solutions to Problems 71-80
 The University of Hong Kong Department of Statistics and Actuarial Science STAT2802 Statistical Models Tutorial Solutions Solutions to Problems 71-80 71. Decide in each case whether the hypothesis is simple
The University of Hong Kong Department of Statistics and Actuarial Science STAT2802 Statistical Models Tutorial Solutions Solutions to Problems 71-80 71. Decide in each case whether the hypothesis is simple
UNIVERSITY OF MASSACHUSETTS Department of Mathematics and Statistics Basic Exam - Applied Statistics Thursday, August 30, 2018
 UNIVERSITY OF MASSACHUSETTS Department of Mathematics and Statistics Basic Exam - Applied Statistics Thursday, August 30, 2018 Work all problems. 60 points are needed to pass at the Masters Level and 75
UNIVERSITY OF MASSACHUSETTS Department of Mathematics and Statistics Basic Exam - Applied Statistics Thursday, August 30, 2018 Work all problems. 60 points are needed to pass at the Masters Level and 75
A Very Brief Summary of Statistical Inference, and Examples
 A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2009 Prof. Gesine Reinert Our standard situation is that we have data x = x 1, x 2,..., x n, which we view as realisations of random
A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2009 Prof. Gesine Reinert Our standard situation is that we have data x = x 1, x 2,..., x n, which we view as realisations of random
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
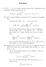 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
1. (Regular) Exponential Family
 1. (Regular) Exponential Family The density function of a regular exponential family is: [ ] Example. Poisson(θ) [ ] Example. Normal. (both unknown). ) [ ] [ ] [ ] [ ] 2. Theorem (Exponential family &
1. (Regular) Exponential Family The density function of a regular exponential family is: [ ] Example. Poisson(θ) [ ] Example. Normal. (both unknown). ) [ ] [ ] [ ] [ ] 2. Theorem (Exponential family &
MA 575 Linear Models: Cedric E. Ginestet, Boston University Midterm Review Week 7
 MA 575 Linear Models: Cedric E. Ginestet, Boston University Midterm Review Week 7 1 Random Vectors Let a 0 and y be n 1 vectors, and let A be an n n matrix. Here, a 0 and A are non-random, whereas y is
MA 575 Linear Models: Cedric E. Ginestet, Boston University Midterm Review Week 7 1 Random Vectors Let a 0 and y be n 1 vectors, and let A be an n n matrix. Here, a 0 and A are non-random, whereas y is
f (1 0.5)/n Z =
 Math 466/566 - Homework 4. We want to test a hypothesis involving a population proportion. The unknown population proportion is p. The null hypothesis is p = / and the alternative hypothesis is p > /.
Math 466/566 - Homework 4. We want to test a hypothesis involving a population proportion. The unknown population proportion is p. The null hypothesis is p = / and the alternative hypothesis is p > /.
Statement: With my signature I confirm that the solutions are the product of my own work. Name: Signature:.
 MATHEMATICAL STATISTICS Take-home final examination February 1 st -February 8 th, 019 Instructions You do not need to edit the solutions Just make sure the handwriting is legible The final solutions should
MATHEMATICAL STATISTICS Take-home final examination February 1 st -February 8 th, 019 Instructions You do not need to edit the solutions Just make sure the handwriting is legible The final solutions should
More about Single Factor Experiments
 More about Single Factor Experiments 1 2 3 0 / 23 1 2 3 1 / 23 Parameter estimation Effect Model (1): Y ij = µ + A i + ɛ ij, Ji A i = 0 Estimation: µ + A i = y i. ˆµ = y..  i = y i. y.. Effect Modell
More about Single Factor Experiments 1 2 3 0 / 23 1 2 3 1 / 23 Parameter estimation Effect Model (1): Y ij = µ + A i + ɛ ij, Ji A i = 0 Estimation: µ + A i = y i. ˆµ = y..  i = y i. y.. Effect Modell
UNIVERSITY OF MASSACHUSETTS. Department of Mathematics and Statistics. Basic Exam - Applied Statistics. Tuesday, January 17, 2017
 UNIVERSITY OF MASSACHUSETTS Department of Mathematics and Statistics Basic Exam - Applied Statistics Tuesday, January 17, 2017 Work all problems 60 points are needed to pass at the Masters Level and 75
UNIVERSITY OF MASSACHUSETTS Department of Mathematics and Statistics Basic Exam - Applied Statistics Tuesday, January 17, 2017 Work all problems 60 points are needed to pass at the Masters Level and 75
Lecture 15. Hypothesis testing in the linear model
 14. Lecture 15. Hypothesis testing in the linear model Lecture 15. Hypothesis testing in the linear model 1 (1 1) Preliminary lemma 15. Hypothesis testing in the linear model 15.1. Preliminary lemma Lemma
14. Lecture 15. Hypothesis testing in the linear model Lecture 15. Hypothesis testing in the linear model 1 (1 1) Preliminary lemma 15. Hypothesis testing in the linear model 15.1. Preliminary lemma Lemma
Hypothesis Test. The opposite of the null hypothesis, called an alternative hypothesis, becomes
 Neyman-Pearson paradigm. Suppose that a researcher is interested in whether the new drug works. The process of determining whether the outcome of the experiment points to yes or no is called hypothesis
Neyman-Pearson paradigm. Suppose that a researcher is interested in whether the new drug works. The process of determining whether the outcome of the experiment points to yes or no is called hypothesis
[y i α βx i ] 2 (2) Q = i=1
![[y i α βx i ] 2 (2) Q = i=1 [y i α βx i ] 2 (2) Q = i=1](/thumbs/75/72005858.jpg) Least squares fits This section has no probability in it. There are no random variables. We are given n points (x i, y i ) and want to find the equation of the line that best fits them. We take the equation
Least squares fits This section has no probability in it. There are no random variables. We are given n points (x i, y i ) and want to find the equation of the line that best fits them. We take the equation
Course: ESO-209 Home Work: 1 Instructor: Debasis Kundu
 Home Work: 1 1. Describe the sample space when a coin is tossed (a) once, (b) three times, (c) n times, (d) an infinite number of times. 2. A coin is tossed until for the first time the same result appear
Home Work: 1 1. Describe the sample space when a coin is tossed (a) once, (b) three times, (c) n times, (d) an infinite number of times. 2. A coin is tossed until for the first time the same result appear
