Spring 2012 Math 541A Exam 1. X i, S 2 = 1 n. n 1. X i I(X i < c), T n =
|
|
|
- Jordan Bond
- 5 years ago
- Views:
Transcription
1 Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically distributed normal with mean θ and variance θ 2, where θ > 0 is unknown. Let n X = X i, S 2 = 1 n n 1 (X i X) 2. Are X and S 2 independent? Prove your claim. (Hint: you can directly use the result in the first part of this problem. ) (c) Show that (X, S 2 ) is a sufficient statistic for θ, but it is not complete. 2. (a) Let X 1, X 2,, X n be exponentially distributed with density f(x) = λ exp( λx), x > 0. Let c > 0 be a constant and if X i < c, we observe X i, otherwise we observe c. S n = X i I(X i < c), T n = I(X i > c), where I(A) = 1 if event A occurs and I(A) = 0, otherwise. Write down the likelihood function of the observed values in terms of T n and S n. (b) Show the maximum likelihood estimator of λ is λ n = n T n S n + ct n.
2 Fall 2012 Math 541A Exam 1 1. (a) Let X 1,..., X n Poisson(λ) be an i.i.d. sample. Find the method of moments estimate ˆλ MOM and the maximum likelihood estimate ˆλ MLE of λ. (b) Is ˆλ MLE unbiased? Is it efficient? (c) Give an example of a distribution where the MOM estimate and the MLE are different. 2. (a) Prove that, for any (possibly correlated) collection of random variables X 1,..., X k, ( k ) Var X i k (b) Construct an example with k 2 where equality holds in (1). k Var(X i ). (1)
3 Spring 2013 Math 541A Exam 1 1. (a) Consider an independent identically distributed sequence X 1, X 2,, X n+1 taking values 0 or 1 with probability distribution P {X i = 1} = 1 P {X i = 0} = p. Uniformly choose M fragments F 1, F 2,, F M of length 2 starting in the interval [1, n], that is, F i = (X ji, X ji+1) for some 1 j i n. Let W = (1, 1). Let N W be the number of times the word W occurs among the M fragments. Calculate E(N W ). Calculate the probability P (F 1 = W, F 2 = W). Calculate Var(N W ). (Note: Due to time constraints, you can ignore the boundary effect.) 2. Let T and C be independent Geometric random variables with success probability of r and s, respectively. That is P [T = j] = r(1 r) j 1 ; j = 1, 2,, Let X = (min(t, C), I(T C)). indicator function. P [C = j] = s(1 s) j 1 ; j = 1, 2,, Denote X 1 = min(t, C), X 2 = I(T C), where I( ) is the (a) What is the joint distribution of X? (b) Calculate EX = (EX 1, EX 2 ) and the covariance matrix of X = (X 1, X 2 ). (c) Let T 1, T 2,, T n be a random sample from T, and C 1, C 2,, C n be a random sample from C. Define S 1 = S 2 = min(t i, C i ) I(T i C i ). What is the maximum likelihood estimate (ˆr, ŝ) of (r, s), in terms of S 1 and S 2?
4 Fall 2013 Math 541a Exam 1. For p (0, 1) unknown, let X 0, X 1,... be independent identically distributed random variables taking values in {0, 1} with distribution P (X i = 1) = 1 P (X i = 0) = p, and suppose that is observed. n 1 T n = I(X i = 1, X i+1 = 1). (1) i=0 (a) Calculate the mean and variance of T n. (b) Find a consistent method of moments p n = g n (T n ) estimator for the unknown p as a function g n of T n that may depend on n, and prove that your estimate is consistent for p. (c) Show that T n is not the sum of independent, identically distributed random variables. Nevertheless, determine the non-trivial limiting distribution of p n, after an appropriate centering and scaling, as if (1) was the sum of i.i.d. variables and has the same mean and variance as the one computed in part (a). (d) Explain why you would, or would not, expect p n to have the same limiting distribution as the one determined in part (c). 2. Let X 1, X 2,..., X n be independent identically distributed random variables with density given by f β (x) = xα 1 exp( x/β), for x > 0 β α Γ(α) where α > 0, and is known. Suppose it is desired to estimate β 3. (a) Find the Cramer-Rao lower bound for the variance of an unbiased estimator of β 3. (b) Find a complete and sufficient statistic for β. Then, compute its k th moment, where k is an positive integer. (c) If a UMVUE (uniform minimum variance unbiased estimator) exists, find its variance and compare it to the bound in part (a). 1
5 Spring 2014 Math 541a Exam 1. For known values x i,1, x i,2, i = 1,..., n let and Z i = β 1 x i,1 + ɛ i Y i = β 1 x i,1 + β 2 x i,2 + ɛ i i = 1,..., n, where ɛ i, i = 1, 2,..., n are independent normal random variables with mean 0 and variance 1. (a) Given the data Z = (Z 1,..., Z n ) compute the maximum likelihood estimate of β 1 and show that it achieves the Cramer-Rao lower bound. Throughout this part and the following, make explicit any non-degeneracy assumptions that may need to be made. (b) Based on Y = (Y 1,..., Y n ), compute the Cramer-Rao lower bound for the estimation of (β 1, β 2 ), and in particular compute a variance lower bound for the estimation of β 1 in the presence of the unknown β 2. (c) Compare the variance lower bound in (a), which is the same as the one for the model for Y i where β 2 is known to be equal to zero, to the one in (b), where β 2 is unknown, and show the latter one is always at least as large as the former. 2. Suppose we observe the pair (X, Y ) where X has a Poisson(λ) distribution and Y has a Bernoulli(λ/(1 + λ)) distribution, that is, P λ (X = j) = λj e λ, j = 0, 1, 2,... j! and P λ (Y = 1) = λ 1 + λ = 1 P λ(y = 0), with X and Y independent, and λ (0, ) unknown. (a) Find a one-dimensional sufficient statistic for λ based on (X, Y ). (b) Is there a UMVUE (uniform minimum variance unbiased estimator) of λ? If so, find it. (c) Is there a UMVUE of λ/(1 + λ)? If so, find it. 1
6 Fall 2014 Math 541a Exam 1. Let p, q be values in [0, 1] and α (0, 1]. Assume α and q known, and that p is an unknown parameter we would like to estimate. A coin is tossed n times, resulting in the sequence of zero one valued random variables X 1,..., X n. At each toss, independently of all other tosses, the coin has probability p of success with probability α, and probability q of success with probability 1 α. (a) Write out the probability function of the observed sequence, and compute the maximum likelihood estimate p of p, when p is considered a parameter over all of R. Verify that when α = 1 one recovers the standard estimator of the unknown probability. (b) Show p is unbiased, and calculate its variance. (c) Calculate the the information bound for p, and determine if it is achieved by p. (d) If one of the other parameters is unknown, can p still be estimated consistently? 2. Let X R n be distributed according the density or mass function p(x; θ) for θ Θ R d. (a) State the definition for T (X) to be sufficient for θ. (b) Prove that if the (discrete) mass functions p(x; θ) can be factored as h(x)g(t (x), θ) for some functions h and g, then T (X) is sufficient for θ. (c) Let X 1,..., X n be independent with the Cauchy distribution C(θ), θ R given by p(x; θ) = 1 π(1 + (x θ) 2 ). Prove that the unordered sample S = {X 1,..., X n } can be determined from any T (X) sufficient for θ.(hint: Produce a polynomial from which S can be determined). 1
7 Fall 2015 Math 541A Exam 1 1. Let (X 1, Y 1 ),..., (X n, Y n ) be a sample from the uniform distribution on a disc X 2 + Y 2 θ 2, where θ > 0 is unknown. That is, the probability density function of (X, Y ) is f (X,Y ) (x, y; θ) = 1 πθ 2 1 [0,θ]( x 2 + y 2 ) (a) Find a complete sufficient statistic of θ and its distribution. (b) Find the UMVU estimator of θ. (c) Find the maximum likelihood estimator of θ. 2. Let Y 1,..., Y n be independent with Y i N(αx i + β log x i, σ 2 ), where x 1,..., x n are given positive constants, not all equal, and α, β, σ are unknown parameters. (a) Prove that the MLE of β is where S ly = i (log x i )Y i, S x 2 = i β = S lys x 2 S lx S xy S x 2S l 2 Slx 2, (1) x 2 i, S l 2 = i (log x i ) 2, etc. (b) Find the distribution of β, including giving any parameter values for this distribution. Is β unbiased for β? Justify your answers. (c) Suppose now that you may choose the values of the x i, but each one must be either 1 or 10. How many of the n observations should you choose to make at x i = 1 in order to minimize the variance of the resulting β? You can assume that n is a fixed multiple of 11.
8 Fall 2016 Math 541A Exam 1 1. Let {P θ, θ Θ} be a family of probability distributions. A statistic V is called ancillary for θ if its distribution does not depend on θ. (a) Let X 1,..., X n have normal distribution N(µ, 1). Show that V = X 1 X is an ancillary statistic for µ. (b) Prove that if T is a complete sufficient statistic for the family {P θ, θ Θ}, then any ancillary statistic V is independent of T. (This is a theorem due to Basu). (Hint: show that for any (measurable) set A, and derive the conclusion). P θ (V A T = t) = P (V A T = t) = P (V A), 2. With θ > 0 unknown, let a sample consist of X 1,..., X n, independent observations with distribution F (y; θ) = 1 1 y θ, 0 < y < θ. (a) Prove that the maximum likelihood estimate of θ based on the sample is the maximum order statistic X (n) = max 1 i n X i. (b) Determine a sequence of positive numbers a n and a non-trivial distribution for a randon variable X such that a n (θ X (n) ) d X. (c) Compare the rate a n in part b) to the rate of a parametric estimation problem whose regularity would allow the application of the Cramer Rao bound. Comment.
9 Spring 2015 Math 541a Exam 1. For n 2 let X 1,, X n be independent samples from P θ, the uniform distribution U(θ, θ + 1), θ R. Let X (1) X (2) X (n) be the order statistics of the sample. (a) Show that (X (1), X (n) ) is a sufficient statistic for θ. (b) Is (X (1), X (n) ) complete? Prove your claim. (c) Find a n and b(θ) such that a n (b(θ) X (n) ) Z in distribution, where Z has an exponential distribution with density f(x) = e x, x > 0. (d) What is the maximum likelihood estimate of θ given the sample? 2. Let X and Y be independent random variables with X exponential(λ) and Y exponential(µ), where the exponential(ν) density is given by f(x; ν) = 1 ( ν exp x ). ν Let and Z = min{x, Y }, W = 1 if Z = X, and W = 0 otherwise. (a) Find the joint distribution of Z and W. (b) Prove that Z and W are independent. (c) Suppose that (X, Y ) are not observable. Instead, with n 2, we observe (Z 1, W 1 ),, (Z n, W n ), independent samples distributed as (Z, W ). Write down the likelihood function in terms of the sample averages (Z, W ), and find the maximum likelihood estimate ( µ n, λ n ) of (µ, λ). (d) Determining whether 1/ˆλ n is unbiased for 1/λ, and if not, construct an estimator that is. 1
10 Spring 2017 Math 541A Exam 1 1. Let X 1,..., X n be a random sample from the normal distribution N(µ, 1). Let u R be a given threshold value, and assume that we want to estimate the probability p = p(µ) = P µ (X 1 u). (a) Find an unbiased estimator of p. (b) Letting X = n 1 n X i denote the sample mean, show that the joint distribution of X and X 1 X is bivariate normal and find the parameters of this distribution. Use your answer to demonstrate that X and X 1 X are independent. (c) Use the estimator from part (1a), along with the Rao-Blackwell theorem and part (1b), to find the uniform minimal variance unbiased estimator (UMVUE) for p. 2. For all k = 0, 1,..., we have that x k e x4 /12 dx = 2 k 3 k ( ( 1) k + 1 ) ( ) k + 1 Γ. 4 (a) Determine c 1 such that p(x) = c 1 e x4 /12 is a density function. In the following we consider the location model (1) p(x; θ) = p(x θ), θ (, ) where p(x) is as in (1). Assume a sample X 1,..., X n of independent random variables with distribution p(x; θ) has been observed. (b) Prove that the maximizer of the likehood function is unique and can be found by setting the derivative of the log likelihood to zero. (c) Determine the maximum likelihood estimate θ of θ based on the sample in a form as explicit as you can in terms of the sample moments m k = 1 n Xi k. (d) Determine the information I X (θ) for θ in the sample X 1,..., X n, and the non-trivial limiting distribution of θ, when properly scaled and centered. You may assume regularity conditions hold without explicitly noting them.
11 Fall 2017 Math 541A Exam 1 1. For known α > 0 and unknown θ R, we observe the sequence X 1,..., X n of independent variables with distribution function 0 x θ F (x; θ) = (x θ) α x (θ, θ + 1] 1 x > θ + 1, and consider the estimator of θ given by a. Determine the distribution function of θ. θ = min{x 1,..., X n }. b. Determine a non-trivial distribution for a random variable Y and an increasing sequence a n of real numbers such that a n ( θ θ) d Y. c. What rates of (distributional) convergence to θ are possible for the estimator θ as α ranges over (0, )? 2. Let X 1,..., X n be i.i.d. with the N(θ, θ) distribution, for some θ > 0. (a) Find the MLE of θ. (b) Show that the MLE is a consistent estimator of θ. (c) Assume that n = 1. i. Show that T (X) = X is a sufficient statistic for θ. ii. Note that ˆθ(X) = X is an unbiased estimator of θ, but is not a function of T (X). Hence, it can be improved; apply the Rao-Blackwell theorem to find another estimator θ that is a function of T (X) and is unbiased for θ.
12 Spring 2018 Math 541A Exam 1 1. Let U 1,..., U n be iid with the uniform distribution U[β, β + 1] for β R and n 2, and let U (1) < < U (n) be the order statistics of the sample. a. Show that (U (1), U (n) ) is sufficient but not complete. b. Show that U n 1/2 is not a uniformly minimum variance estimator of β, where U n is the average of U 1,..., U n. 2. Fix n 2. (a) Let y (1)... y (n) be some ordered real numbers and define x k = i>k y (i) (n k)y (k) for k = 1,..., n, (1) where an empty sum denotes 0 by convention. Show that x k is a non-increasing sequence and x n = 0. (b) Let Y 1,..., Y n be independent with Y i N(θ i, σ 2 ) for unknown σ 2 > 0 and θ = (θ 1,..., θ n ) in the (n 1)-simplex θ θ n = 1 and θ i 0 for all i. (2) Based on the data Y 1 = y 1,..., Y n = y n : i. find the MLE θ of θ, subject to the constraints (2), by minimizing ( ) 1 (y i θ i ) 2 + λ θ i 1 2 i i (3) over θ i 0 and λ (Hint: Use part 2a, and consider the smallest k {1,..., n} such that x k < 1, and λ [y (k 1), y (k) ).) ii. find the MLE of σ 2. You can state your answer in terms of θ even if you don t solve part 2(b)i.
13 Fall 2018 Math 541A Exam 1 1. Let {P θ, θ Θ} be a family of probability distributions, and X P θ for some θ Θ. Let E be the set of all unbiased estimators of 0 with finite variances, and let T be an unbiased estimator of θ with Var(T ) <. (a) Assume that T is the uniformly minimum-variance unbiased estimator (UMVUE) of θ. Show that E θ [T (X)U(X)] = 0 for any U E and θ Θ. (b) Assume that E θ [T (X)U(X)] = 0 for any U E and θ Θ. Show that T is the UMVUE. (c) Assume now that the family of distributions is parametrized by k parameters θ 1,..., θ k, and that T j is the UMVUE of θ j, 1 j k. Use (a) and (b) to show that k j=1 α jt j is the UMVUE of k j=1 α jθ j for any α 1,..., α k. 2. Let X 1,..., X n be independent with distribution equal to that of X, a random variable with mean µ = E[X], variance σ 2, and finite sixth moment E[X 6 ] <. Define the skewness parameter τ = E[X µ]3 σ 3. Assume µ is known, and consider the estimation of τ by τ = m 3 σ 3 where m 3 = 1 n (X i µ) 3 and σ 3 = ( 1 n ) 3/2 (X i µ) 2. (a) Show that the parameter τ is invariant with respect to translation and positive scaling of X. (b) Determine, and justify, whether or not τ is UMVU when the X distribution is normal. (c) Assuming the X distribution is symmetric about its mean, find the mean and variance of (X i µ) 2 and (X i µ) 3, and their covariance. Apply the multivariate central limit theorem to yield the limiting distribution of the properly scaled and centered (bivariate) sum S n = 1 n ((X i µ) 2, (X i µ) 3 ). (d) Recall that when a sequence of vectors Y n in R d converges in distribution to Y 0, that is, n(yn EY n ) d Y 0, and g : R d R r is a nice function, the multivariate delta method yields that n(g(yn ) g(ey n )) d ġ T (E(Y 0 ))Y 0, where g = (g 1,..., g r ) and ġ is the matrix whose columns are the gradients of g 1,..., g r. That is, ġ = ( g 1,..., g r ). Use this result to derive a properly scaled limiting distribution for τ.
Problem Selected Scores
 Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003
 Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
1. (Regular) Exponential Family
 1. (Regular) Exponential Family The density function of a regular exponential family is: [ ] Example. Poisson(θ) [ ] Example. Normal. (both unknown). ) [ ] [ ] [ ] [ ] 2. Theorem (Exponential family &
1. (Regular) Exponential Family The density function of a regular exponential family is: [ ] Example. Poisson(θ) [ ] Example. Normal. (both unknown). ) [ ] [ ] [ ] [ ] 2. Theorem (Exponential family &
McGill University. Faculty of Science. Department of Mathematics and Statistics. Part A Examination. Statistics: Theory Paper
 McGill University Faculty of Science Department of Mathematics and Statistics Part A Examination Statistics: Theory Paper Date: 10th May 2015 Instructions Time: 1pm-5pm Answer only two questions from Section
McGill University Faculty of Science Department of Mathematics and Statistics Part A Examination Statistics: Theory Paper Date: 10th May 2015 Instructions Time: 1pm-5pm Answer only two questions from Section
Mathematical Statistics
 Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
Statistics Ph.D. Qualifying Exam: Part II November 3, 2001
 Statistics Ph.D. Qualifying Exam: Part II November 3, 2001 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Statistics Ph.D. Qualifying Exam: Part II November 3, 2001 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Mathematics Ph.D. Qualifying Examination Stat Probability, January 2018
 Mathematics Ph.D. Qualifying Examination Stat 52800 Probability, January 2018 NOTE: Answers all questions completely. Justify every step. Time allowed: 3 hours. 1. Let X 1,..., X n be a random sample from
Mathematics Ph.D. Qualifying Examination Stat 52800 Probability, January 2018 NOTE: Answers all questions completely. Justify every step. Time allowed: 3 hours. 1. Let X 1,..., X n be a random sample from
Mathematics Qualifying Examination January 2015 STAT Mathematical Statistics
 Mathematics Qualifying Examination January 2015 STAT 52800 - Mathematical Statistics NOTE: Answer all questions completely and justify your derivations and steps. A calculator and statistical tables (normal,
Mathematics Qualifying Examination January 2015 STAT 52800 - Mathematical Statistics NOTE: Answer all questions completely and justify your derivations and steps. A calculator and statistical tables (normal,
t x 1 e t dt, and simplify the answer when possible (for example, when r is a positive even number). In particular, confirm that EX 4 = 3.
 Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Statistics Ph.D. Qualifying Exam: Part II November 9, 2002
 Statistics Ph.D. Qualifying Exam: Part II November 9, 2002 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Statistics Ph.D. Qualifying Exam: Part II November 9, 2002 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Chapters 9. Properties of Point Estimators
 Chapters 9. Properties of Point Estimators Recap Target parameter, or population parameter θ. Population distribution f(x; θ). { probability function, discrete case f(x; θ) = density, continuous case The
Chapters 9. Properties of Point Estimators Recap Target parameter, or population parameter θ. Population distribution f(x; θ). { probability function, discrete case f(x; θ) = density, continuous case The
First Year Examination Department of Statistics, University of Florida
 First Year Examination Department of Statistics, University of Florida August 19, 010, 8:00 am - 1:00 noon Instructions: 1. You have four hours to answer questions in this examination.. You must show your
First Year Examination Department of Statistics, University of Florida August 19, 010, 8:00 am - 1:00 noon Instructions: 1. You have four hours to answer questions in this examination.. You must show your
ST5215: Advanced Statistical Theory
 Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
Probability and Statistics qualifying exam, May 2015
 Probability and Statistics qualifying exam, May 2015 Name: Instructions: 1. The exam is divided into 3 sections: Linear Models, Mathematical Statistics and Probability. You must pass each section to pass
Probability and Statistics qualifying exam, May 2015 Name: Instructions: 1. The exam is divided into 3 sections: Linear Models, Mathematical Statistics and Probability. You must pass each section to pass
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic
 Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
STAT 135 Lab 3 Asymptotic MLE and the Method of Moments
 STAT 135 Lab 3 Asymptotic MLE and the Method of Moments Rebecca Barter February 9, 2015 Maximum likelihood estimation (a reminder) Maximum likelihood estimation Suppose that we have a sample, X 1, X 2,...,
STAT 135 Lab 3 Asymptotic MLE and the Method of Moments Rebecca Barter February 9, 2015 Maximum likelihood estimation (a reminder) Maximum likelihood estimation Suppose that we have a sample, X 1, X 2,...,
Statistics GIDP Ph.D. Qualifying Exam Theory Jan 11, 2016, 9:00am-1:00pm
 Statistics GIDP Ph.D. Qualifying Exam Theory Jan, 06, 9:00am-:00pm Instructions: Provide answers on the supplied pads of paper; write on only one side of each sheet. Complete exactly 5 of the 6 problems.
Statistics GIDP Ph.D. Qualifying Exam Theory Jan, 06, 9:00am-:00pm Instructions: Provide answers on the supplied pads of paper; write on only one side of each sheet. Complete exactly 5 of the 6 problems.
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017
 Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Spring 2012 Math 541B Exam 1
 Spring 2012 Math 541B Exam 1 1. A sample of size n is drawn without replacement from an urn containing N balls, m of which are red and N m are black; the balls are otherwise indistinguishable. Let X denote
Spring 2012 Math 541B Exam 1 1. A sample of size n is drawn without replacement from an urn containing N balls, m of which are red and N m are black; the balls are otherwise indistinguishable. Let X denote
Two hours. Statistical Tables to be provided THE UNIVERSITY OF MANCHESTER. 14 January :45 11:45
 Two hours Statistical Tables to be provided THE UNIVERSITY OF MANCHESTER PROBABILITY 2 14 January 2015 09:45 11:45 Answer ALL four questions in Section A (40 marks in total) and TWO of the THREE questions
Two hours Statistical Tables to be provided THE UNIVERSITY OF MANCHESTER PROBABILITY 2 14 January 2015 09:45 11:45 Answer ALL four questions in Section A (40 marks in total) and TWO of the THREE questions
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Notes, March 4, 2013, R. Dudley Maximum likelihood estimation: actual or supposed
 18.466 Notes, March 4, 2013, R. Dudley Maximum likelihood estimation: actual or supposed 1. MLEs in exponential families Let f(x,θ) for x X and θ Θ be a likelihood function, that is, for present purposes,
18.466 Notes, March 4, 2013, R. Dudley Maximum likelihood estimation: actual or supposed 1. MLEs in exponential families Let f(x,θ) for x X and θ Θ be a likelihood function, that is, for present purposes,
Miscellaneous Errors in the Chapter 6 Solutions
 Miscellaneous Errors in the Chapter 6 Solutions 3.30(b In this problem, early printings of the second edition use the beta(a, b distribution, but later versions use the Poisson(λ distribution. If your
Miscellaneous Errors in the Chapter 6 Solutions 3.30(b In this problem, early printings of the second edition use the beta(a, b distribution, but later versions use the Poisson(λ distribution. If your
Qualifying Exam in Probability and Statistics. https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf
 Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Statistics STAT:5100 (22S:193), Fall Sample Final Exam B
 Statistics STAT:5 (22S:93), Fall 25 Sample Final Exam B Please write your answers in the exam books provided.. Let X, Y, and Y 2 be independent random variables with X N(µ X, σ 2 X ) and Y i N(µ Y, σ 2
Statistics STAT:5 (22S:93), Fall 25 Sample Final Exam B Please write your answers in the exam books provided.. Let X, Y, and Y 2 be independent random variables with X N(µ X, σ 2 X ) and Y i N(µ Y, σ 2
557: MATHEMATICAL STATISTICS II BIAS AND VARIANCE
 557: MATHEMATICAL STATISTICS II BIAS AND VARIANCE An estimator, T (X), of θ can be evaluated via its statistical properties. Typically, two aspects are considered: Expectation Variance either in terms
557: MATHEMATICAL STATISTICS II BIAS AND VARIANCE An estimator, T (X), of θ can be evaluated via its statistical properties. Typically, two aspects are considered: Expectation Variance either in terms
Conditional distributions (discrete case)
 Conditional distributions (discrete case) The basic idea behind conditional distributions is simple: Suppose (XY) is a jointly-distributed random vector with a discrete joint distribution. Then we can
Conditional distributions (discrete case) The basic idea behind conditional distributions is simple: Suppose (XY) is a jointly-distributed random vector with a discrete joint distribution. Then we can
Two hours. To be supplied by the Examinations Office: Mathematical Formula Tables THE UNIVERSITY OF MANCHESTER. 21 June :45 11:45
 Two hours MATH20802 To be supplied by the Examinations Office: Mathematical Formula Tables THE UNIVERSITY OF MANCHESTER STATISTICAL METHODS 21 June 2010 9:45 11:45 Answer any FOUR of the questions. University-approved
Two hours MATH20802 To be supplied by the Examinations Office: Mathematical Formula Tables THE UNIVERSITY OF MANCHESTER STATISTICAL METHODS 21 June 2010 9:45 11:45 Answer any FOUR of the questions. University-approved
f(x θ)dx with respect to θ. Assuming certain smoothness conditions concern differentiating under the integral the integral sign, we first obtain
 0.1. INTRODUCTION 1 0.1 Introduction R. A. Fisher, a pioneer in the development of mathematical statistics, introduced a measure of the amount of information contained in an observaton from f(x θ). Fisher
0.1. INTRODUCTION 1 0.1 Introduction R. A. Fisher, a pioneer in the development of mathematical statistics, introduced a measure of the amount of information contained in an observaton from f(x θ). Fisher
Evaluating the Performance of Estimators (Section 7.3)
 Evaluating the Performance of Estimators (Section 7.3) Example: Suppose we observe X 1,..., X n iid N(θ, σ 2 0 ), with σ2 0 known, and wish to estimate θ. Two possible estimators are: ˆθ = X sample mean
Evaluating the Performance of Estimators (Section 7.3) Example: Suppose we observe X 1,..., X n iid N(θ, σ 2 0 ), with σ2 0 known, and wish to estimate θ. Two possible estimators are: ˆθ = X sample mean
A Very Brief Summary of Statistical Inference, and Examples
 A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
Chapter 4. Chapter 4 sections
 Chapter 4 sections 4.1 Expectation 4.2 Properties of Expectations 4.3 Variance 4.4 Moments 4.5 The Mean and the Median 4.6 Covariance and Correlation 4.7 Conditional Expectation SKIP: 4.8 Utility Expectation
Chapter 4 sections 4.1 Expectation 4.2 Properties of Expectations 4.3 Variance 4.4 Moments 4.5 The Mean and the Median 4.6 Covariance and Correlation 4.7 Conditional Expectation SKIP: 4.8 Utility Expectation
Master s Written Examination
 Master s Written Examination Option: Statistics and Probability Spring 05 Full points may be obtained for correct answers to eight questions Each numbered question (which may have several parts) is worth
Master s Written Examination Option: Statistics and Probability Spring 05 Full points may be obtained for correct answers to eight questions Each numbered question (which may have several parts) is worth
Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee
 Stochastic Processes Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee 1 Outline Methods of Mean Squared Error Bias and Unbiasedness Best Unbiased Estimators CR-Bound for variance
Stochastic Processes Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee 1 Outline Methods of Mean Squared Error Bias and Unbiasedness Best Unbiased Estimators CR-Bound for variance
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
MATH c UNIVERSITY OF LEEDS Examination for the Module MATH2715 (January 2015) STATISTICAL METHODS. Time allowed: 2 hours
 MATH2750 This question paper consists of 8 printed pages, each of which is identified by the reference MATH275. All calculators must carry an approval sticker issued by the School of Mathematics. c UNIVERSITY
MATH2750 This question paper consists of 8 printed pages, each of which is identified by the reference MATH275. All calculators must carry an approval sticker issued by the School of Mathematics. c UNIVERSITY
Math 494: Mathematical Statistics
 Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
Principles of Statistics
 Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 81 Paper 4, Section II 28K Let g : R R be an unknown function, twice continuously differentiable with g (x) M for
Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 81 Paper 4, Section II 28K Let g : R R be an unknown function, twice continuously differentiable with g (x) M for
f (1 0.5)/n Z =
 Math 466/566 - Homework 4. We want to test a hypothesis involving a population proportion. The unknown population proportion is p. The null hypothesis is p = / and the alternative hypothesis is p > /.
Math 466/566 - Homework 4. We want to test a hypothesis involving a population proportion. The unknown population proportion is p. The null hypothesis is p = / and the alternative hypothesis is p > /.
STA 4322 Exam I Name: Introduction to Statistics Theory
 STA 4322 Exam I Name: Introduction to Statistics Theory Fall 2013 UF-ID: Instructions: There are 100 total points. You must show your work to receive credit. Read each part of each question carefully.
STA 4322 Exam I Name: Introduction to Statistics Theory Fall 2013 UF-ID: Instructions: There are 100 total points. You must show your work to receive credit. Read each part of each question carefully.
Final Exam. 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given.
 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
Statistics Ph.D. Qualifying Exam
 Department of Statistics Carnegie Mellon University May 7 2008 Statistics Ph.D. Qualifying Exam You are not expected to solve all five problems. Complete solutions to few problems will be preferred to
Department of Statistics Carnegie Mellon University May 7 2008 Statistics Ph.D. Qualifying Exam You are not expected to solve all five problems. Complete solutions to few problems will be preferred to
Course: ESO-209 Home Work: 1 Instructor: Debasis Kundu
 Home Work: 1 1. Describe the sample space when a coin is tossed (a) once, (b) three times, (c) n times, (d) an infinite number of times. 2. A coin is tossed until for the first time the same result appear
Home Work: 1 1. Describe the sample space when a coin is tossed (a) once, (b) three times, (c) n times, (d) an infinite number of times. 2. A coin is tossed until for the first time the same result appear
FIRST YEAR EXAM Monday May 10, 2010; 9:00 12:00am
 FIRST YEAR EXAM Monday May 10, 2010; 9:00 12:00am NOTES: PLEASE READ CAREFULLY BEFORE BEGINNING EXAM! 1. Do not write solutions on the exam; please write your solutions on the paper provided. 2. Put the
FIRST YEAR EXAM Monday May 10, 2010; 9:00 12:00am NOTES: PLEASE READ CAREFULLY BEFORE BEGINNING EXAM! 1. Do not write solutions on the exam; please write your solutions on the paper provided. 2. Put the
STAT 730 Chapter 4: Estimation
 STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
. Find E(V ) and var(v ).
 Math 6382/6383: Probability Models and Mathematical Statistics Sample Preliminary Exam Questions 1. A person tosses a fair coin until she obtains 2 heads in a row. She then tosses a fair die the same number
Math 6382/6383: Probability Models and Mathematical Statistics Sample Preliminary Exam Questions 1. A person tosses a fair coin until she obtains 2 heads in a row. She then tosses a fair die the same number
STAT 450: Final Examination Version 1. Richard Lockhart 16 December 2002
 Name: Last Name 1, First Name 1 Stdnt # StudentNumber1 STAT 450: Final Examination Version 1 Richard Lockhart 16 December 2002 Instructions: This is an open book exam. You may use notes, books and a calculator.
Name: Last Name 1, First Name 1 Stdnt # StudentNumber1 STAT 450: Final Examination Version 1 Richard Lockhart 16 December 2002 Instructions: This is an open book exam. You may use notes, books and a calculator.
Masters Comprehensive Examination Department of Statistics, University of Florida
 Masters Comprehensive Examination Department of Statistics, University of Florida May 6, 003, 8:00 am - :00 noon Instructions: You have four hours to answer questions in this examination You must show
Masters Comprehensive Examination Department of Statistics, University of Florida May 6, 003, 8:00 am - :00 noon Instructions: You have four hours to answer questions in this examination You must show
1 Probability Model. 1.1 Types of models to be discussed in the course
 Sufficiency January 18, 016 Debdeep Pati 1 Probability Model Model: A family of distributions P θ : θ Θ}. P θ (B) is the probability of the event B when the parameter takes the value θ. P θ is described
Sufficiency January 18, 016 Debdeep Pati 1 Probability Model Model: A family of distributions P θ : θ Θ}. P θ (B) is the probability of the event B when the parameter takes the value θ. P θ is described
Statistics Masters Comprehensive Exam March 21, 2003
 Statistics Masters Comprehensive Exam March 21, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Masters Comprehensive Exam March 21, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
First Year Examination Department of Statistics, University of Florida
 First Year Examination Department of Statistics, University of Florida August 20, 2009, 8:00 am - 2:00 noon Instructions:. You have four hours to answer questions in this examination. 2. You must show
First Year Examination Department of Statistics, University of Florida August 20, 2009, 8:00 am - 2:00 noon Instructions:. You have four hours to answer questions in this examination. 2. You must show
Final Examination. STA 215: Statistical Inference. Saturday, 2001 May 5, 9:00am 12:00 noon
 Final Examination Saturday, 2001 May 5, 9:00am 12:00 noon This is an open-book examination, but you may not share materials. A normal distribution table, a PMF/PDF handout, and a blank worksheet are attached
Final Examination Saturday, 2001 May 5, 9:00am 12:00 noon This is an open-book examination, but you may not share materials. A normal distribution table, a PMF/PDF handout, and a blank worksheet are attached
Ph.D. Qualifying Exam Monday Tuesday, January 4 5, 2016
 Ph.D. Qualifying Exam Monday Tuesday, January 4 5, 2016 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Find the maximum likelihood estimate of θ where θ is a parameter
Ph.D. Qualifying Exam Monday Tuesday, January 4 5, 2016 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Find the maximum likelihood estimate of θ where θ is a parameter
1 Introduction. P (n = 1 red ball drawn) =
 Introduction Exercises and outline solutions. Y has a pack of 4 cards (Ace and Queen of clubs, Ace and Queen of Hearts) from which he deals a random of selection 2 to player X. What is the probability
Introduction Exercises and outline solutions. Y has a pack of 4 cards (Ace and Queen of clubs, Ace and Queen of Hearts) from which he deals a random of selection 2 to player X. What is the probability
Practice Midterm 2 Partial Solutions
 8.440 Practice Midterm 2 Partial Solutions. (20 points) Let X and Y be independent Poisson random variables with parameter. Compute the following. (Give a correct formula involving sums does not need to
8.440 Practice Midterm 2 Partial Solutions. (20 points) Let X and Y be independent Poisson random variables with parameter. Compute the following. (Give a correct formula involving sums does not need to
EXAMINATIONS OF THE HONG KONG STATISTICAL SOCIETY GRADUATE DIPLOMA, Statistical Theory and Methods I. Time Allowed: Three Hours
 EXAMINATIONS OF THE HONG KONG STATISTICAL SOCIETY GRADUATE DIPLOMA, 008 Statistical Theory and Methods I Time Allowed: Three Hours Candidates should answer FIVE questions. All questions carry equal marks.
EXAMINATIONS OF THE HONG KONG STATISTICAL SOCIETY GRADUATE DIPLOMA, 008 Statistical Theory and Methods I Time Allowed: Three Hours Candidates should answer FIVE questions. All questions carry equal marks.
ECE 275B Homework # 1 Solutions Winter 2018
 ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
STA 2201/442 Assignment 2
 STA 2201/442 Assignment 2 1. This is about how to simulate from a continuous univariate distribution. Let the random variable X have a continuous distribution with density f X (x) and cumulative distribution
STA 2201/442 Assignment 2 1. This is about how to simulate from a continuous univariate distribution. Let the random variable X have a continuous distribution with density f X (x) and cumulative distribution
Estimation theory. Parametric estimation. Properties of estimators. Minimum variance estimator. Cramer-Rao bound. Maximum likelihood estimators
 Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
Lecture 1: August 28
 36-705: Intermediate Statistics Fall 2017 Lecturer: Siva Balakrishnan Lecture 1: August 28 Our broad goal for the first few lectures is to try to understand the behaviour of sums of independent random
36-705: Intermediate Statistics Fall 2017 Lecturer: Siva Balakrishnan Lecture 1: August 28 Our broad goal for the first few lectures is to try to understand the behaviour of sums of independent random
MAS223 Statistical Inference and Modelling Exercises
 MAS223 Statistical Inference and Modelling Exercises The exercises are grouped into sections, corresponding to chapters of the lecture notes Within each section exercises are divided into warm-up questions,
MAS223 Statistical Inference and Modelling Exercises The exercises are grouped into sections, corresponding to chapters of the lecture notes Within each section exercises are divided into warm-up questions,
1.1 Review of Probability Theory
 1.1 Review of Probability Theory Angela Peace Biomathemtics II MATH 5355 Spring 2017 Lecture notes follow: Allen, Linda JS. An introduction to stochastic processes with applications to biology. CRC Press,
1.1 Review of Probability Theory Angela Peace Biomathemtics II MATH 5355 Spring 2017 Lecture notes follow: Allen, Linda JS. An introduction to stochastic processes with applications to biology. CRC Press,
ECE 275B Homework # 1 Solutions Version Winter 2015
 ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
Qualifying Exam in Probability and Statistics. https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf
 Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Statistics & Data Sciences: First Year Prelim Exam May 2018
 Statistics & Data Sciences: First Year Prelim Exam May 2018 Instructions: 1. Do not turn this page until instructed to do so. 2. Start each new question on a new sheet of paper. 3. This is a closed book
Statistics & Data Sciences: First Year Prelim Exam May 2018 Instructions: 1. Do not turn this page until instructed to do so. 2. Start each new question on a new sheet of paper. 3. This is a closed book
Asymptotic Statistics-III. Changliang Zou
 Asymptotic Statistics-III Changliang Zou The multivariate central limit theorem Theorem (Multivariate CLT for iid case) Let X i be iid random p-vectors with mean µ and and covariance matrix Σ. Then n (
Asymptotic Statistics-III Changliang Zou The multivariate central limit theorem Theorem (Multivariate CLT for iid case) Let X i be iid random p-vectors with mean µ and and covariance matrix Σ. Then n (
M(t) = 1 t. (1 t), 6 M (0) = 20 P (95. X i 110) i=1
 Math 66/566 - Midterm Solutions NOTE: These solutions are for both the 66 and 566 exam. The problems are the same until questions and 5. 1. The moment generating function of a random variable X is M(t)
Math 66/566 - Midterm Solutions NOTE: These solutions are for both the 66 and 566 exam. The problems are the same until questions and 5. 1. The moment generating function of a random variable X is M(t)
More on Distribution Function
 More on Distribution Function The distribution of a random variable X can be determined directly from its cumulative distribution function F X. Theorem: Let X be any random variable, with cumulative distribution
More on Distribution Function The distribution of a random variable X can be determined directly from its cumulative distribution function F X. Theorem: Let X be any random variable, with cumulative distribution
ENEE 621 SPRING 2016 DETECTION AND ESTIMATION THEORY THE PARAMETER ESTIMATION PROBLEM
 c 2007-2016 by Armand M. Makowski 1 ENEE 621 SPRING 2016 DETECTION AND ESTIMATION THEORY THE PARAMETER ESTIMATION PROBLEM 1 The basic setting Throughout, p, q and k are positive integers. The setup With
c 2007-2016 by Armand M. Makowski 1 ENEE 621 SPRING 2016 DETECTION AND ESTIMATION THEORY THE PARAMETER ESTIMATION PROBLEM 1 The basic setting Throughout, p, q and k are positive integers. The setup With
Chapter 4 HOMEWORK ASSIGNMENTS. 4.1 Homework #1
 Chapter 4 HOMEWORK ASSIGNMENTS These homeworks may be modified as the semester progresses. It is your responsibility to keep up to date with the correctly assigned homeworks. There may be some errors in
Chapter 4 HOMEWORK ASSIGNMENTS These homeworks may be modified as the semester progresses. It is your responsibility to keep up to date with the correctly assigned homeworks. There may be some errors in
STA 260: Statistics and Probability II
 Al Nosedal. University of Toronto. Winter 2017 1 Properties of Point Estimators and Methods of Estimation 2 3 If you can t explain it simply, you don t understand it well enough Albert Einstein. Definition
Al Nosedal. University of Toronto. Winter 2017 1 Properties of Point Estimators and Methods of Estimation 2 3 If you can t explain it simply, you don t understand it well enough Albert Einstein. Definition
Statistics - Lecture One. Outline. Charlotte Wickham 1. Basic ideas about estimation
 Statistics - Lecture One Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Outline 1. Basic ideas about estimation 2. Method of Moments 3. Maximum Likelihood 4. Confidence
Statistics - Lecture One Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Outline 1. Basic ideas about estimation 2. Method of Moments 3. Maximum Likelihood 4. Confidence
6.041/6.431 Fall 2010 Quiz 2 Solutions
 6.04/6.43: Probabilistic Systems Analysis (Fall 200) 6.04/6.43 Fall 200 Quiz 2 Solutions Problem. (80 points) In this problem: (i) X is a (continuous) uniform random variable on [0, 4]. (ii) Y is an exponential
6.04/6.43: Probabilistic Systems Analysis (Fall 200) 6.04/6.43 Fall 200 Quiz 2 Solutions Problem. (80 points) In this problem: (i) X is a (continuous) uniform random variable on [0, 4]. (ii) Y is an exponential
Three hours. To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER.
 Three hours To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER EXTREME VALUES AND FINANCIAL RISK Examiner: Answer QUESTION 1, QUESTION
Three hours To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER EXTREME VALUES AND FINANCIAL RISK Examiner: Answer QUESTION 1, QUESTION
1 Complete Statistics
 Complete Statistics February 4, 2016 Debdeep Pati 1 Complete Statistics Suppose X P θ, θ Θ. Let (X (1),..., X (n) ) denote the order statistics. Definition 1. A statistic T = T (X) is complete if E θ g(t
Complete Statistics February 4, 2016 Debdeep Pati 1 Complete Statistics Suppose X P θ, θ Θ. Let (X (1),..., X (n) ) denote the order statistics. Definition 1. A statistic T = T (X) is complete if E θ g(t
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
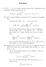 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Mathematical statistics
 October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
Statistics 3858 : Maximum Likelihood Estimators
 Statistics 3858 : Maximum Likelihood Estimators 1 Method of Maximum Likelihood In this method we construct the so called likelihood function, that is L(θ) = L(θ; X 1, X 2,..., X n ) = f n (X 1, X 2,...,
Statistics 3858 : Maximum Likelihood Estimators 1 Method of Maximum Likelihood In this method we construct the so called likelihood function, that is L(θ) = L(θ; X 1, X 2,..., X n ) = f n (X 1, X 2,...,
This exam is closed book and closed notes. (You will have access to a copy of the Table of Common Distributions given in the back of the text.
 TEST #3 STA 5326 December 4, 214 Name: Please read the following directions. DO NOT TURN THE PAGE UNTIL INSTRUCTED TO DO SO Directions This exam is closed book and closed notes. (You will have access to
TEST #3 STA 5326 December 4, 214 Name: Please read the following directions. DO NOT TURN THE PAGE UNTIL INSTRUCTED TO DO SO Directions This exam is closed book and closed notes. (You will have access to
IIT JAM : MATHEMATICAL STATISTICS (MS) 2013
 IIT JAM : MATHEMATICAL STATISTICS (MS 2013 Question Paper with Answer Keys Ctanujit Classes Of Mathematics, Statistics & Economics Visit our website for more: www.ctanujit.in IMPORTANT NOTE FOR CANDIDATES
IIT JAM : MATHEMATICAL STATISTICS (MS 2013 Question Paper with Answer Keys Ctanujit Classes Of Mathematics, Statistics & Economics Visit our website for more: www.ctanujit.in IMPORTANT NOTE FOR CANDIDATES
1 General problem. 2 Terminalogy. Estimation. Estimate θ. (Pick a plausible distribution from family. ) Or estimate τ = τ(θ).
 Estimation February 3, 206 Debdeep Pati General problem Model: {P θ : θ Θ}. Observe X P θ, θ Θ unknown. Estimate θ. (Pick a plausible distribution from family. ) Or estimate τ = τ(θ). Examples: θ = (µ,
Estimation February 3, 206 Debdeep Pati General problem Model: {P θ : θ Θ}. Observe X P θ, θ Θ unknown. Estimate θ. (Pick a plausible distribution from family. ) Or estimate τ = τ(θ). Examples: θ = (µ,
Theory of Statistics.
 Theory of Statistics. Homework V February 5, 00. MT 8.7.c When σ is known, ˆµ = X is an unbiased estimator for µ. If you can show that its variance attains the Cramer-Rao lower bound, then no other unbiased
Theory of Statistics. Homework V February 5, 00. MT 8.7.c When σ is known, ˆµ = X is an unbiased estimator for µ. If you can show that its variance attains the Cramer-Rao lower bound, then no other unbiased
Lecture 4: UMVUE and unbiased estimators of 0
 Lecture 4: UMVUE and unbiased estimators of Problems of approach 1. Approach 1 has the following two main shortcomings. Even if Theorem 7.3.9 or its extension is applicable, there is no guarantee that
Lecture 4: UMVUE and unbiased estimators of Problems of approach 1. Approach 1 has the following two main shortcomings. Even if Theorem 7.3.9 or its extension is applicable, there is no guarantee that
STAT 512 sp 2018 Summary Sheet
 STAT 5 sp 08 Summary Sheet Karl B. Gregory Spring 08. Transformations of a random variable Let X be a rv with support X and let g be a function mapping X to Y with inverse mapping g (A = {x X : g(x A}
STAT 5 sp 08 Summary Sheet Karl B. Gregory Spring 08. Transformations of a random variable Let X be a rv with support X and let g be a function mapping X to Y with inverse mapping g (A = {x X : g(x A}
Introduction to Estimation Methods for Time Series models Lecture 2
 Introduction to Estimation Methods for Time Series models Lecture 2 Fulvio Corsi SNS Pisa Fulvio Corsi Introduction to Estimation () Methods for Time Series models Lecture 2 SNS Pisa 1 / 21 Estimators:
Introduction to Estimation Methods for Time Series models Lecture 2 Fulvio Corsi SNS Pisa Fulvio Corsi Introduction to Estimation () Methods for Time Series models Lecture 2 SNS Pisa 1 / 21 Estimators:
18.440: Lecture 28 Lectures Review
 18.440: Lecture 28 Lectures 18-27 Review Scott Sheffield MIT Outline Outline It s the coins, stupid Much of what we have done in this course can be motivated by the i.i.d. sequence X i where each X i is
18.440: Lecture 28 Lectures 18-27 Review Scott Sheffield MIT Outline Outline It s the coins, stupid Much of what we have done in this course can be motivated by the i.i.d. sequence X i where each X i is
Masters Comprehensive Examination Department of Statistics, University of Florida
 Masters Comprehensive Examination Department of Statistics, University of Florida May 10, 2002, 8:00am - 12:00 noon Instructions: 1. You have four hours to answer questions in this examination. 2. There
Masters Comprehensive Examination Department of Statistics, University of Florida May 10, 2002, 8:00am - 12:00 noon Instructions: 1. You have four hours to answer questions in this examination. 2. There
BEST TESTS. Abstract. We will discuss the Neymann-Pearson theorem and certain best test where the power function is optimized.
 BEST TESTS Abstract. We will discuss the Neymann-Pearson theorem and certain best test where the power function is optimized. 1. Most powerful test Let {f θ } θ Θ be a family of pdfs. We will consider
BEST TESTS Abstract. We will discuss the Neymann-Pearson theorem and certain best test where the power function is optimized. 1. Most powerful test Let {f θ } θ Θ be a family of pdfs. We will consider
Practice Midterm 2 Partial Solutions
 8.440 Practice Midterm Partial Solutions. (0 points) Let and Y be independent Poisson random variables with parameter. Compute the following. (Give a correct formula involving sums does not need to be
8.440 Practice Midterm Partial Solutions. (0 points) Let and Y be independent Poisson random variables with parameter. Compute the following. (Give a correct formula involving sums does not need to be
System Identification, Lecture 4
 System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2012 F, FRI Uppsala University, Information Technology 30 Januari 2012 SI-2012 K. Pelckmans
System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2012 F, FRI Uppsala University, Information Technology 30 Januari 2012 SI-2012 K. Pelckmans
System Identification, Lecture 4
 System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2016 F, FRI Uppsala University, Information Technology 13 April 2016 SI-2016 K. Pelckmans
System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2016 F, FRI Uppsala University, Information Technology 13 April 2016 SI-2016 K. Pelckmans
This exam contains 6 questions. The questions are of equal weight. Print your name at the top of this page in the upper right hand corner.
 GROUND RULES: This exam contains 6 questions. The questions are of equal weight. Print your name at the top of this page in the upper right hand corner. This exam is closed book and closed notes. Show
GROUND RULES: This exam contains 6 questions. The questions are of equal weight. Print your name at the top of this page in the upper right hand corner. This exam is closed book and closed notes. Show
Chapter 4: Asymptotic Properties of the MLE (Part 2)
 Chapter 4: Asymptotic Properties of the MLE (Part 2) Daniel O. Scharfstein 09/24/13 1 / 1 Example Let {(R i, X i ) : i = 1,..., n} be an i.i.d. sample of n random vectors (R, X ). Here R is a response
Chapter 4: Asymptotic Properties of the MLE (Part 2) Daniel O. Scharfstein 09/24/13 1 / 1 Example Let {(R i, X i ) : i = 1,..., n} be an i.i.d. sample of n random vectors (R, X ). Here R is a response
Fall 2017 STAT 532 Homework Peter Hoff. 1. Let P be a probability measure on a collection of sets A.
 1. Let P be a probability measure on a collection of sets A. (a) For each n N, let H n be a set in A such that H n H n+1. Show that P (H n ) monotonically converges to P ( k=1 H k) as n. (b) For each n
1. Let P be a probability measure on a collection of sets A. (a) For each n N, let H n be a set in A such that H n H n+1. Show that P (H n ) monotonically converges to P ( k=1 H k) as n. (b) For each n
Week 9 The Central Limit Theorem and Estimation Concepts
 Week 9 and Estimation Concepts Week 9 and Estimation Concepts Week 9 Objectives 1 The Law of Large Numbers and the concept of consistency of averages are introduced. The condition of existence of the population
Week 9 and Estimation Concepts Week 9 and Estimation Concepts Week 9 Objectives 1 The Law of Large Numbers and the concept of consistency of averages are introduced. The condition of existence of the population
1 Probability and Random Variables
 1 Probability and Random Variables The models that you have seen thus far are deterministic models. For any time t, there is a unique solution X(t). On the other hand, stochastic models will result in
1 Probability and Random Variables The models that you have seen thus far are deterministic models. For any time t, there is a unique solution X(t). On the other hand, stochastic models will result in
Midterm Examination. STA 215: Statistical Inference. Due Wednesday, 2006 Mar 8, 1:15 pm
 Midterm Examination STA 215: Statistical Inference Due Wednesday, 2006 Mar 8, 1:15 pm This is an open-book take-home examination. You may work on it during any consecutive 24-hour period you like; please
Midterm Examination STA 215: Statistical Inference Due Wednesday, 2006 Mar 8, 1:15 pm This is an open-book take-home examination. You may work on it during any consecutive 24-hour period you like; please
A Very Brief Summary of Statistical Inference, and Examples
 A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2009 Prof. Gesine Reinert Our standard situation is that we have data x = x 1, x 2,..., x n, which we view as realisations of random
A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2009 Prof. Gesine Reinert Our standard situation is that we have data x = x 1, x 2,..., x n, which we view as realisations of random
Parameter Estimation
 Parameter Estimation Chapters 13-15 Stat 477 - Loss Models Chapters 13-15 (Stat 477) Parameter Estimation Brian Hartman - BYU 1 / 23 Methods for parameter estimation Methods for parameter estimation Methods
Parameter Estimation Chapters 13-15 Stat 477 - Loss Models Chapters 13-15 (Stat 477) Parameter Estimation Brian Hartman - BYU 1 / 23 Methods for parameter estimation Methods for parameter estimation Methods
Chapter 5 continued. Chapter 5 sections
 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
