Probability and Statistics qualifying exam, May 2015
|
|
|
- Louise Poole
- 6 years ago
- Views:
Transcription
1 Probability and Statistics qualifying exam, May 2015 Name: Instructions: 1. The exam is divided into 3 sections: Linear Models, Mathematical Statistics and Probability. You must pass each section to pass the exam. 2. M.S. students: in the Mathematical Statistics section, please choose a total of 4 questions (say, 4 from Group 1 plus 0 from Group 2; or 2 from Group 1 plus 2 from Group 2). Ph.D. students: do the 4 questions from Group M.S. students: in the Probability section, please choose a total of 4 questions (say, 4 from Group 1 plus 0 from Group 2; or 2 from Group 1 plus 2 from Group 2). Ph.D. students: do the 4 questions from Group remark: we consider a M.S. student to be someone whose goal is to get a M.S. degree in Statistics, irrespective of whether (s)he is also enrolled in the Ph.D. program. 5. Please justify all your answers. 6. Good luck!
2 Page 2 Linear Models 1. Consider data (X i, Y i ) R 2 related by Y i = β 0 + β 1 X i + ϵ i i = 1,..., n where β 0, β 1 R are constants, ϵ i N(0, σ 2 ) are iid, and σ 2 is some known constant. (a) Write the least squares estimate ˆβ of β = [β 0, β 1 ] in matrix form and identify its distribution. (b) Under what conditions are the estimates ˆβ 0, ˆβ 1 uncorrelated? (c) Suppose you have a new X 0 and believe that Y 0 = β 0 + β 1 X 0 + ϵ 0 where ϵ 0 N(0, σ 2 ) is independent of all other ϵ i. Find a 95% prediction interval for Y Consider a model Y = Xβ + ϵ where X = , β i = [ β0 β 1 ] and ϵ N(0, σ 2 I). (a) Demonstrate that this model s parameterization is identifiable. (b) Describe how you would test the hypothesis β 1 = 0 if σ 2 is a known constant. What is the rejection region for a size α test? (c) Describe an estimate of σ 2 and prove that it is (un)biased. 3. Let X R m n be some nonzero matrix and M the PPO onto C(X). (a) Prove that tr(m) = r(x). (b) Prove that 0 M ii 1. (c) Prove that if M has full rank, then M = I. 4. Let Y N(µ, Σ) where Y = [Y 1, Y 2, Y 3 ], µ = [0, 0, 0], Σ = σ 2 + ρ ρ 0 ρ σ 2 + ρ σ 2 = σ 2 I + ρee where ρ is not necessarily positive and e = [1, 1, 0]. (a) For a given σ 2 > 0, which restrictions on ρ ensure that Σ is positive definite?
3 Page 3 (b) Suppose that µ, σ 2 are known and you have observed Y = y. Find an equation for the MLE ˆρ of ρ. It may be helpful to note that det(a + uv ) = (1 + v A 1 u) det(a) (A + uv ) 1 = A 1 A 1 uv A 1 1+v A 1 u
4 Page 4 Mathematical Statistics Group 1 1. Consider a sample X 1,..., X n U[θ, θ + 1]. (a) Prove that T (X) = (X (1), X (n) ) is a minimal and sufficient statistic for θ. (b) Is the statistic T (X) complete? 2. Let X Bin(n, p), 0 < p < 1, and suppose that the prior distribution of p is Beta(α, β), i.e. where π(p) = Γ(α + β) Γ(α)Γ(β) pα 1 (1 p) β 1 1 (0,1) (p), α, β > 0, Γ(α) = (a) Find the posterior distribution of p, i.e., f(p x). 0 t α 1 e t dt. (b) Find the Bayes estimator of p under the squared loss function L(p, d) = (p d) Consider a sample X 1,..., X n f(x 1 θ), where the density f( θ) is given by Define the parameter g(θ) = θ 1. (a) Find the UMVU estimator of g(θ). f(x 1 θ) = θx θ (0,1) (x 1 ), θ > 1. (b) For a given n N, find a maximum likelihood estimator of g(θ). Describe its asymptotic distribution as n. 4. Consider the sample X 1,..., X n U[0, θ], θ > 0, and the composite hypotheses For a fixed α (0, 1), find the UMP test. H 0 : θ θ 0 vs H 1 : θ > θ 0. Group 2 1. Let X 1,..., X n N(µ, σ 2 ), where µ = σ > 0. (a) Show that ( n T (X) = X i, i=1 is minimal sufficient for this parametric family. (b) Is T (X) also complete? Please justify your answer. 2. Let X 1,..., X n N(θ, aθ 2 ), θ > 0, and a > 0 is known. (a) Find an explicit expression for an EL (efficient likelihood) estimator θ EL (X) of θ (this includes proving that θ EL (X) is, indeed, an EL estimator). n i=1 X 2 i )
5 Page 5 (b) Let g(θ) = log θ be a reparametrization. Show that g( θ EL (X)) is asymptotically unbiased for g(θ). 3. Suppose we have two independent samples X 1,..., X n λ 1, λ 2 > 0. (a) Find the GLR test for the hypotheses exp(λ 1 ), Y 1,..., Y m exp(λ 2 ), H 0 : λ 1 = λ 2 vs H 1 : λ 1 λ 2. (b) Show that the test in part (a) can be based on the statistic n i=1 T (X, Y) = X i n i=1 X i + m j=1 Y. j (c) Find the distribution of T (X, Y) when H 0 is true. 4. Let X 1,..., X n, n 2, be an sample from a Poi(λ), λ > 0, parametric family. (a) Prove that E(S 2 X) = X a.s. (b) Use part (a) to establish that S 2 is not UMVU for λ.
6 Page 6 Probability Group 1 1. For Borel sets A, B, define d(a, B) = P (A B), where A B = (A B)\(A B). Let {A n } n N, A be a collection of Borel sets. Prove that d(a n, A) 0 if and only if 1 An 1 A in the L 2 (P ) sense. 2. Suppose that {A n } n N are independent events such that P (A n ) < 1, n N. Prove that ( P n=1 A n ) = 1 P (A n i.o.) = Let X Cauchy(0, 1), i.e., f X (x) = 1 1 π 1 + x 2, x R. Find the density of the random variable Y = 1. 1+X 2 4. Prove the classical central limit theorem. In other words, let {X n } n N be an sequence such that EX 1 = µ and Var(X i ) = σ 2. Then, ( Xn µ ) d n N(0, 1), n, σ where X n = 1 n n i=1 X i. Group 2 1. Let {X n } n N be an sequence of non-degenerate random variables defined on a given probability space. Show that P (X n converges) = Let {X n } n N, X be random variables, and let {F n } n N, F be their respective distribution d functions. Assume that X n X, and that F is continuous. Prove that 3. Please answer the following questions. sup F n (x) F (x) 0, n. x R (a) Let X and Y be two a.c. random variables with joint density f X,Y (x, y). Show that a conditional density f X Y (x y) exists and establish its form. (b) Assume that P (W = c) = 1 for some c R, and let Z be some other random variable. Show that P (W = c Z = z) = 1, z R. 4. Let {X n } n N be an sequence on a given probability space such that P (X n = 0) = 1 2 = P (X n = 1), n N. Show that the random variable is well-defined and find its distribution. X := n=1 X n 2 n End of exam.
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003
 Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Ph.D. Qualifying Exam
 Department of Statistics Carnegie Mellon University May 7 2008 Statistics Ph.D. Qualifying Exam You are not expected to solve all five problems. Complete solutions to few problems will be preferred to
Department of Statistics Carnegie Mellon University May 7 2008 Statistics Ph.D. Qualifying Exam You are not expected to solve all five problems. Complete solutions to few problems will be preferred to
Qualifying Exam in Probability and Statistics. https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf
 Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Problem Selected Scores
 Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
McGill University. Faculty of Science. Department of Mathematics and Statistics. Part A Examination. Statistics: Theory Paper
 McGill University Faculty of Science Department of Mathematics and Statistics Part A Examination Statistics: Theory Paper Date: 10th May 2015 Instructions Time: 1pm-5pm Answer only two questions from Section
McGill University Faculty of Science Department of Mathematics and Statistics Part A Examination Statistics: Theory Paper Date: 10th May 2015 Instructions Time: 1pm-5pm Answer only two questions from Section
Statistics Ph.D. Qualifying Exam: Part II November 3, 2001
 Statistics Ph.D. Qualifying Exam: Part II November 3, 2001 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Statistics Ph.D. Qualifying Exam: Part II November 3, 2001 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Qualifying Exam in Probability and Statistics. https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf
 Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Statistics Ph.D. Qualifying Exam: Part II November 9, 2002
 Statistics Ph.D. Qualifying Exam: Part II November 9, 2002 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Statistics Ph.D. Qualifying Exam: Part II November 9, 2002 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Final Exam. 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given.
 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
Mathematics Ph.D. Qualifying Examination Stat Probability, January 2018
 Mathematics Ph.D. Qualifying Examination Stat 52800 Probability, January 2018 NOTE: Answers all questions completely. Justify every step. Time allowed: 3 hours. 1. Let X 1,..., X n be a random sample from
Mathematics Ph.D. Qualifying Examination Stat 52800 Probability, January 2018 NOTE: Answers all questions completely. Justify every step. Time allowed: 3 hours. 1. Let X 1,..., X n be a random sample from
Spring 2012 Math 541A Exam 1. X i, S 2 = 1 n. n 1. X i I(X i < c), T n =
 Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Spring 2012 Math 541B Exam 1
 Spring 2012 Math 541B Exam 1 1. A sample of size n is drawn without replacement from an urn containing N balls, m of which are red and N m are black; the balls are otherwise indistinguishable. Let X denote
Spring 2012 Math 541B Exam 1 1. A sample of size n is drawn without replacement from an urn containing N balls, m of which are red and N m are black; the balls are otherwise indistinguishable. Let X denote
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017
 Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Mathematics Qualifying Examination January 2015 STAT Mathematical Statistics
 Mathematics Qualifying Examination January 2015 STAT 52800 - Mathematical Statistics NOTE: Answer all questions completely and justify your derivations and steps. A calculator and statistical tables (normal,
Mathematics Qualifying Examination January 2015 STAT 52800 - Mathematical Statistics NOTE: Answer all questions completely and justify your derivations and steps. A calculator and statistical tables (normal,
Two hours. To be supplied by the Examinations Office: Mathematical Formula Tables THE UNIVERSITY OF MANCHESTER. 21 June :45 11:45
 Two hours MATH20802 To be supplied by the Examinations Office: Mathematical Formula Tables THE UNIVERSITY OF MANCHESTER STATISTICAL METHODS 21 June 2010 9:45 11:45 Answer any FOUR of the questions. University-approved
Two hours MATH20802 To be supplied by the Examinations Office: Mathematical Formula Tables THE UNIVERSITY OF MANCHESTER STATISTICAL METHODS 21 June 2010 9:45 11:45 Answer any FOUR of the questions. University-approved
Qualifying Exam in Probability and Statistics.
 Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Statistics GIDP Ph.D. Qualifying Exam Theory Jan 11, 2016, 9:00am-1:00pm
 Statistics GIDP Ph.D. Qualifying Exam Theory Jan, 06, 9:00am-:00pm Instructions: Provide answers on the supplied pads of paper; write on only one side of each sheet. Complete exactly 5 of the 6 problems.
Statistics GIDP Ph.D. Qualifying Exam Theory Jan, 06, 9:00am-:00pm Instructions: Provide answers on the supplied pads of paper; write on only one side of each sheet. Complete exactly 5 of the 6 problems.
Masters Comprehensive Examination Department of Statistics, University of Florida
 Masters Comprehensive Examination Department of Statistics, University of Florida May 10, 2002, 8:00am - 12:00 noon Instructions: 1. You have four hours to answer questions in this examination. 2. There
Masters Comprehensive Examination Department of Statistics, University of Florida May 10, 2002, 8:00am - 12:00 noon Instructions: 1. You have four hours to answer questions in this examination. 2. There
Statistics Masters Comprehensive Exam March 21, 2003
 Statistics Masters Comprehensive Exam March 21, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Masters Comprehensive Exam March 21, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
First Year Examination Department of Statistics, University of Florida
 First Year Examination Department of Statistics, University of Florida August 19, 010, 8:00 am - 1:00 noon Instructions: 1. You have four hours to answer questions in this examination.. You must show your
First Year Examination Department of Statistics, University of Florida August 19, 010, 8:00 am - 1:00 noon Instructions: 1. You have four hours to answer questions in this examination.. You must show your
Review and continuation from last week Properties of MLEs
 Review and continuation from last week Properties of MLEs As we have mentioned, MLEs have a nice intuitive property, and as we have seen, they have a certain equivariance property. We will see later that
Review and continuation from last week Properties of MLEs As we have mentioned, MLEs have a nice intuitive property, and as we have seen, they have a certain equivariance property. We will see later that
t x 1 e t dt, and simplify the answer when possible (for example, when r is a positive even number). In particular, confirm that EX 4 = 3.
 Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Math 494: Mathematical Statistics
 Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
MAS223 Statistical Inference and Modelling Exercises
 MAS223 Statistical Inference and Modelling Exercises The exercises are grouped into sections, corresponding to chapters of the lecture notes Within each section exercises are divided into warm-up questions,
MAS223 Statistical Inference and Modelling Exercises The exercises are grouped into sections, corresponding to chapters of the lecture notes Within each section exercises are divided into warm-up questions,
STAT 450: Final Examination Version 1. Richard Lockhart 16 December 2002
 Name: Last Name 1, First Name 1 Stdnt # StudentNumber1 STAT 450: Final Examination Version 1 Richard Lockhart 16 December 2002 Instructions: This is an open book exam. You may use notes, books and a calculator.
Name: Last Name 1, First Name 1 Stdnt # StudentNumber1 STAT 450: Final Examination Version 1 Richard Lockhart 16 December 2002 Instructions: This is an open book exam. You may use notes, books and a calculator.
Hypothesis Test. The opposite of the null hypothesis, called an alternative hypothesis, becomes
 Neyman-Pearson paradigm. Suppose that a researcher is interested in whether the new drug works. The process of determining whether the outcome of the experiment points to yes or no is called hypothesis
Neyman-Pearson paradigm. Suppose that a researcher is interested in whether the new drug works. The process of determining whether the outcome of the experiment points to yes or no is called hypothesis
Statistics 135 Fall 2008 Final Exam
 Name: SID: Statistics 135 Fall 2008 Final Exam Show your work. The number of points each question is worth is shown at the beginning of the question. There are 10 problems. 1. [2] The normal equations
Name: SID: Statistics 135 Fall 2008 Final Exam Show your work. The number of points each question is worth is shown at the beginning of the question. There are 10 problems. 1. [2] The normal equations
ECE 275B Homework # 1 Solutions Version Winter 2015
 ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
Information in Data. Sufficiency, Ancillarity, Minimality, and Completeness
 Information in Data Sufficiency, Ancillarity, Minimality, and Completeness Important properties of statistics that determine the usefulness of those statistics in statistical inference. These general properties
Information in Data Sufficiency, Ancillarity, Minimality, and Completeness Important properties of statistics that determine the usefulness of those statistics in statistical inference. These general properties
Ph.D. Qualifying Exam Friday Saturday, January 3 4, 2014
 Ph.D. Qualifying Exam Friday Saturday, January 3 4, 2014 Put your solution to each problem on a separate sheet of paper. Problem 1. (5166) Assume that two random samples {x i } and {y i } are independently
Ph.D. Qualifying Exam Friday Saturday, January 3 4, 2014 Put your solution to each problem on a separate sheet of paper. Problem 1. (5166) Assume that two random samples {x i } and {y i } are independently
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic
 Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
Comprehensive Examination Quantitative Methods Spring, 2018
 Comprehensive Examination Quantitative Methods Spring, 2018 Instruction: This exam consists of three parts. You are required to answer all the questions in all the parts. 1 Grading policy: 1. Each part
Comprehensive Examination Quantitative Methods Spring, 2018 Instruction: This exam consists of three parts. You are required to answer all the questions in all the parts. 1 Grading policy: 1. Each part
Statistics 135: Fall 2004 Final Exam
 Name: SID#: Statistics 135: Fall 2004 Final Exam There are 10 problems and the number of points for each is shown in parentheses. There is a normal table at the end. Show your work. 1. The designer of
Name: SID#: Statistics 135: Fall 2004 Final Exam There are 10 problems and the number of points for each is shown in parentheses. There is a normal table at the end. Show your work. 1. The designer of
Hypothesis testing: theory and methods
 Statistical Methods Warsaw School of Economics November 3, 2017 Statistical hypothesis is the name of any conjecture about unknown parameters of a population distribution. The hypothesis should be verifiable
Statistical Methods Warsaw School of Economics November 3, 2017 Statistical hypothesis is the name of any conjecture about unknown parameters of a population distribution. The hypothesis should be verifiable
1. Let A be a 2 2 nonzero real matrix. Which of the following is true?
 1. Let A be a 2 2 nonzero real matrix. Which of the following is true? (A) A has a nonzero eigenvalue. (B) A 2 has at least one positive entry. (C) trace (A 2 ) is positive. (D) All entries of A 2 cannot
1. Let A be a 2 2 nonzero real matrix. Which of the following is true? (A) A has a nonzero eigenvalue. (B) A 2 has at least one positive entry. (C) trace (A 2 ) is positive. (D) All entries of A 2 cannot
ECE 275B Homework # 1 Solutions Winter 2018
 ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
UNIVERSITY OF TORONTO SCARBOROUGH Department of Computer and Mathematical Sciences FINAL EXAMINATION, APRIL 2013
 UNIVERSITY OF TORONTO SCARBOROUGH Department of Computer and Mathematical Sciences FINAL EXAMINATION, APRIL 2013 STAB57H3 Introduction to Statistics Duration: 3 hours Last Name: First Name: Student number:
UNIVERSITY OF TORONTO SCARBOROUGH Department of Computer and Mathematical Sciences FINAL EXAMINATION, APRIL 2013 STAB57H3 Introduction to Statistics Duration: 3 hours Last Name: First Name: Student number:
Ph.D. Qualifying Exam Monday Tuesday, January 4 5, 2016
 Ph.D. Qualifying Exam Monday Tuesday, January 4 5, 2016 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Find the maximum likelihood estimate of θ where θ is a parameter
Ph.D. Qualifying Exam Monday Tuesday, January 4 5, 2016 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Find the maximum likelihood estimate of θ where θ is a parameter
parameter space Θ, depending only on X, such that Note: it is not θ that is random, but the set C(X).
 4. Interval estimation The goal for interval estimation is to specify the accurary of an estimate. A 1 α confidence set for a parameter θ is a set C(X) in the parameter space Θ, depending only on X, such
4. Interval estimation The goal for interval estimation is to specify the accurary of an estimate. A 1 α confidence set for a parameter θ is a set C(X) in the parameter space Θ, depending only on X, such
A Note on UMPI F Tests
 A Note on UMPI F Tests Ronald Christensen Professor of Statistics Department of Mathematics and Statistics University of New Mexico May 22, 2015 Abstract We examine the transformations necessary for establishing
A Note on UMPI F Tests Ronald Christensen Professor of Statistics Department of Mathematics and Statistics University of New Mexico May 22, 2015 Abstract We examine the transformations necessary for establishing
PhD Qualifying Examination Department of Statistics, University of Florida
 PhD Qualifying xamination Department of Statistics, University of Florida January 24, 2003, 8:00 am - 12:00 noon Instructions: 1 You have exactly four hours to answer questions in this examination 2 There
PhD Qualifying xamination Department of Statistics, University of Florida January 24, 2003, 8:00 am - 12:00 noon Instructions: 1 You have exactly four hours to answer questions in this examination 2 There
Lecture 32: Asymptotic confidence sets and likelihoods
 Lecture 32: Asymptotic confidence sets and likelihoods Asymptotic criterion In some problems, especially in nonparametric problems, it is difficult to find a reasonable confidence set with a given confidence
Lecture 32: Asymptotic confidence sets and likelihoods Asymptotic criterion In some problems, especially in nonparametric problems, it is difficult to find a reasonable confidence set with a given confidence
Chapter 4 HOMEWORK ASSIGNMENTS. 4.1 Homework #1
 Chapter 4 HOMEWORK ASSIGNMENTS These homeworks may be modified as the semester progresses. It is your responsibility to keep up to date with the correctly assigned homeworks. There may be some errors in
Chapter 4 HOMEWORK ASSIGNMENTS These homeworks may be modified as the semester progresses. It is your responsibility to keep up to date with the correctly assigned homeworks. There may be some errors in
1. Point Estimators, Review
 AMS571 Prof. Wei Zhu 1. Point Estimators, Review Example 1. Let be a random sample from. Please find a good point estimator for Solutions. There are the typical estimators for and. Both are unbiased estimators.
AMS571 Prof. Wei Zhu 1. Point Estimators, Review Example 1. Let be a random sample from. Please find a good point estimator for Solutions. There are the typical estimators for and. Both are unbiased estimators.
Final Examination. STA 215: Statistical Inference. Saturday, 2001 May 5, 9:00am 12:00 noon
 Final Examination Saturday, 2001 May 5, 9:00am 12:00 noon This is an open-book examination, but you may not share materials. A normal distribution table, a PMF/PDF handout, and a blank worksheet are attached
Final Examination Saturday, 2001 May 5, 9:00am 12:00 noon This is an open-book examination, but you may not share materials. A normal distribution table, a PMF/PDF handout, and a blank worksheet are attached
Lecture 26: Likelihood ratio tests
 Lecture 26: Likelihood ratio tests Likelihood ratio When both H 0 and H 1 are simple (i.e., Θ 0 = {θ 0 } and Θ 1 = {θ 1 }), Theorem 6.1 applies and a UMP test rejects H 0 when f θ1 (X) f θ0 (X) > c 0 for
Lecture 26: Likelihood ratio tests Likelihood ratio When both H 0 and H 1 are simple (i.e., Θ 0 = {θ 0 } and Θ 1 = {θ 1 }), Theorem 6.1 applies and a UMP test rejects H 0 when f θ1 (X) f θ0 (X) > c 0 for
MATH c UNIVERSITY OF LEEDS Examination for the Module MATH2715 (January 2015) STATISTICAL METHODS. Time allowed: 2 hours
 MATH2750 This question paper consists of 8 printed pages, each of which is identified by the reference MATH275. All calculators must carry an approval sticker issued by the School of Mathematics. c UNIVERSITY
MATH2750 This question paper consists of 8 printed pages, each of which is identified by the reference MATH275. All calculators must carry an approval sticker issued by the School of Mathematics. c UNIVERSITY
Master s Written Examination
 Master s Written Examination Option: Statistics and Probability Spring 016 Full points may be obtained for correct answers to eight questions. Each numbered question which may have several parts is worth
Master s Written Examination Option: Statistics and Probability Spring 016 Full points may be obtained for correct answers to eight questions. Each numbered question which may have several parts is worth
Master s Examination Solutions Option Statistics and Probability Fall 2011
 Master s Examination Solutions Option Statistics and Probability Fall 211 1. (STAT 41) Suppose that X, Y and Z are i.i.d. Uniform(,1). Let t > be a fixed constant. (i) Compute P ( X Y t). (ii) Compute
Master s Examination Solutions Option Statistics and Probability Fall 211 1. (STAT 41) Suppose that X, Y and Z are i.i.d. Uniform(,1). Let t > be a fixed constant. (i) Compute P ( X Y t). (ii) Compute
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
Asymptotic Statistics-III. Changliang Zou
 Asymptotic Statistics-III Changliang Zou The multivariate central limit theorem Theorem (Multivariate CLT for iid case) Let X i be iid random p-vectors with mean µ and and covariance matrix Σ. Then n (
Asymptotic Statistics-III Changliang Zou The multivariate central limit theorem Theorem (Multivariate CLT for iid case) Let X i be iid random p-vectors with mean µ and and covariance matrix Σ. Then n (
2017 Financial Mathematics Orientation - Statistics
 2017 Financial Mathematics Orientation - Statistics Written by Long Wang Edited by Joshua Agterberg August 21, 2018 Contents 1 Preliminaries 5 1.1 Samples and Population............................. 5
2017 Financial Mathematics Orientation - Statistics Written by Long Wang Edited by Joshua Agterberg August 21, 2018 Contents 1 Preliminaries 5 1.1 Samples and Population............................. 5
Test Code: STA/STB (Short Answer Type) 2013 Junior Research Fellowship for Research Course in Statistics
 Test Code: STA/STB (Short Answer Type) 2013 Junior Research Fellowship for Research Course in Statistics The candidates for the research course in Statistics will have to take two shortanswer type tests
Test Code: STA/STB (Short Answer Type) 2013 Junior Research Fellowship for Research Course in Statistics The candidates for the research course in Statistics will have to take two shortanswer type tests
ST5215: Advanced Statistical Theory
 Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
Statistics STAT:5100 (22S:193), Fall Sample Final Exam B
 Statistics STAT:5 (22S:93), Fall 25 Sample Final Exam B Please write your answers in the exam books provided.. Let X, Y, and Y 2 be independent random variables with X N(µ X, σ 2 X ) and Y i N(µ Y, σ 2
Statistics STAT:5 (22S:93), Fall 25 Sample Final Exam B Please write your answers in the exam books provided.. Let X, Y, and Y 2 be independent random variables with X N(µ X, σ 2 X ) and Y i N(µ Y, σ 2
(a) (3 points) Construct a 95% confidence interval for β 2 in Equation 1.
 Problem 1 (21 points) An economist runs the regression y i = β 0 + x 1i β 1 + x 2i β 2 + x 3i β 3 + ε i (1) The results are summarized in the following table: Equation 1. Variable Coefficient Std. Error
Problem 1 (21 points) An economist runs the regression y i = β 0 + x 1i β 1 + x 2i β 2 + x 3i β 3 + ε i (1) The results are summarized in the following table: Equation 1. Variable Coefficient Std. Error
Mathematical Statistics
 Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
Suggested solutions to written exam Jan 17, 2012
 LINKÖPINGS UNIVERSITET Institutionen för datavetenskap Statistik, ANd 73A36 THEORY OF STATISTICS, 6 CDTS Master s program in Statistics and Data Mining Fall semester Written exam Suggested solutions to
LINKÖPINGS UNIVERSITET Institutionen för datavetenskap Statistik, ANd 73A36 THEORY OF STATISTICS, 6 CDTS Master s program in Statistics and Data Mining Fall semester Written exam Suggested solutions to
Lecture 17: Likelihood ratio and asymptotic tests
 Lecture 17: Likelihood ratio and asymptotic tests Likelihood ratio When both H 0 and H 1 are simple (i.e., Θ 0 = {θ 0 } and Θ 1 = {θ 1 }), Theorem 6.1 applies and a UMP test rejects H 0 when f θ1 (X) f
Lecture 17: Likelihood ratio and asymptotic tests Likelihood ratio When both H 0 and H 1 are simple (i.e., Θ 0 = {θ 0 } and Θ 1 = {θ 1 }), Theorem 6.1 applies and a UMP test rejects H 0 when f θ1 (X) f
18.05 Final Exam. Good luck! Name. No calculators. Number of problems 16 concept questions, 16 problems, 21 pages
 Name No calculators. 18.05 Final Exam Number of problems 16 concept questions, 16 problems, 21 pages Extra paper If you need more space we will provide some blank paper. Indicate clearly that your solution
Name No calculators. 18.05 Final Exam Number of problems 16 concept questions, 16 problems, 21 pages Extra paper If you need more space we will provide some blank paper. Indicate clearly that your solution
18.05 Practice Final Exam
 No calculators. 18.05 Practice Final Exam Number of problems 16 concept questions, 16 problems. Simplifying expressions Unless asked to explicitly, you don t need to simplify complicated expressions. For
No calculators. 18.05 Practice Final Exam Number of problems 16 concept questions, 16 problems. Simplifying expressions Unless asked to explicitly, you don t need to simplify complicated expressions. For
Asymptotics. Hypothesis Testing UMP. Asymptotic Tests and p-values
 of the secod half Biostatistics 6 - Statistical Iferece Lecture 6 Fial Exam & Practice Problems for the Fial Hyu Mi Kag Apil 3rd, 3 Hyu Mi Kag Biostatistics 6 - Lecture 6 Apil 3rd, 3 / 3 Rao-Blackwell
of the secod half Biostatistics 6 - Statistical Iferece Lecture 6 Fial Exam & Practice Problems for the Fial Hyu Mi Kag Apil 3rd, 3 Hyu Mi Kag Biostatistics 6 - Lecture 6 Apil 3rd, 3 / 3 Rao-Blackwell
Applied Statistics Comprehensive Exam
 Applied Statistics Comprehensive Exam August 2013 Ph.D Theory Exam This comprehensive exam consists of 10 questions pertaining to theoretical statistical topics. 1 This Ph.D level exam will run from 8:30
Applied Statistics Comprehensive Exam August 2013 Ph.D Theory Exam This comprehensive exam consists of 10 questions pertaining to theoretical statistical topics. 1 This Ph.D level exam will run from 8:30
STAT 830 Bayesian Estimation
 STAT 830 Bayesian Estimation Richard Lockhart Simon Fraser University STAT 830 Fall 2011 Richard Lockhart (Simon Fraser University) STAT 830 Bayesian Estimation STAT 830 Fall 2011 1 / 23 Purposes of These
STAT 830 Bayesian Estimation Richard Lockhart Simon Fraser University STAT 830 Fall 2011 Richard Lockhart (Simon Fraser University) STAT 830 Bayesian Estimation STAT 830 Fall 2011 1 / 23 Purposes of These
Principles of Statistics
 Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 81 Paper 4, Section II 28K Let g : R R be an unknown function, twice continuously differentiable with g (x) M for
Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 81 Paper 4, Section II 28K Let g : R R be an unknown function, twice continuously differentiable with g (x) M for
STATISTICS SYLLABUS UNIT I
 STATISTICS SYLLABUS UNIT I (Probability Theory) Definition Classical and axiomatic approaches.laws of total and compound probability, conditional probability, Bayes Theorem. Random variable and its distribution
STATISTICS SYLLABUS UNIT I (Probability Theory) Definition Classical and axiomatic approaches.laws of total and compound probability, conditional probability, Bayes Theorem. Random variable and its distribution
Chapters 10. Hypothesis Testing
 Chapters 10. Hypothesis Testing Some examples of hypothesis testing 1. Toss a coin 100 times and get 62 heads. Is this coin a fair coin? 2. Is the new treatment more effective than the old one? 3. Quality
Chapters 10. Hypothesis Testing Some examples of hypothesis testing 1. Toss a coin 100 times and get 62 heads. Is this coin a fair coin? 2. Is the new treatment more effective than the old one? 3. Quality
ECON 4117/5111 Mathematical Economics
 Test 1 September 29, 2006 1. Use a truth table to show the following equivalence statement: (p q) (p q) 2. Consider the statement: A function f : X Y is continuous on X if for every open set V Y, the pre-image
Test 1 September 29, 2006 1. Use a truth table to show the following equivalence statement: (p q) (p q) 2. Consider the statement: A function f : X Y is continuous on X if for every open set V Y, the pre-image
IEOR165 Discussion Week 5
 IEOR165 Discussion Week 5 Sheng Liu University of California, Berkeley Feb 19, 2016 Outline 1 1st Homework 2 Revisit Maximum A Posterior 3 Regularization IEOR165 Discussion Sheng Liu 2 About 1st Homework
IEOR165 Discussion Week 5 Sheng Liu University of California, Berkeley Feb 19, 2016 Outline 1 1st Homework 2 Revisit Maximum A Posterior 3 Regularization IEOR165 Discussion Sheng Liu 2 About 1st Homework
Masters Comprehensive Examination Department of Statistics, University of Florida
 Masters Comprehensive Examination Department of Statistics, University of Florida May 6, 003, 8:00 am - :00 noon Instructions: You have four hours to answer questions in this examination You must show
Masters Comprehensive Examination Department of Statistics, University of Florida May 6, 003, 8:00 am - :00 noon Instructions: You have four hours to answer questions in this examination You must show
Estimation theory. Parametric estimation. Properties of estimators. Minimum variance estimator. Cramer-Rao bound. Maximum likelihood estimators
 Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
Math 494: Mathematical Statistics
 Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
Maximum Likelihood. F θ, θ Θ. X 1,..., X n. L(θ) = f(x i ; θ) l(θ) = ln L(θ) = i.i.d. i=1. n ln f(x i ; θ) Sometimes
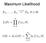 Maximum Likelihood X 1,..., X n i.i.d. F θ, θ Θ L(θ) = n i=1 f(x i ; θ) l(θ) = ln L(θ) = Sometimes n i=1 ln f(x i ; θ) Close your eyes and differentiate? Let X 1,..., X n be a random sample from a Gamma
Maximum Likelihood X 1,..., X n i.i.d. F θ, θ Θ L(θ) = n i=1 f(x i ; θ) l(θ) = ln L(θ) = Sometimes n i=1 ln f(x i ; θ) Close your eyes and differentiate? Let X 1,..., X n be a random sample from a Gamma
This exam contains 13 pages (including this cover page) and 10 questions. A Formulae sheet is provided with the exam.
 Probability and Statistics FS 2017 Session Exam 22.08.2017 Time Limit: 180 Minutes Name: Student ID: This exam contains 13 pages (including this cover page) and 10 questions. A Formulae sheet is provided
Probability and Statistics FS 2017 Session Exam 22.08.2017 Time Limit: 180 Minutes Name: Student ID: This exam contains 13 pages (including this cover page) and 10 questions. A Formulae sheet is provided
557: MATHEMATICAL STATISTICS II HYPOTHESIS TESTING: EXAMPLES
 557: MATHEMATICAL STATISTICS II HYPOTHESIS TESTING: EXAMPLES Example Suppose that X,..., X n N, ). To test H 0 : 0 H : the most powerful test at level α is based on the statistic λx) f π) X x ) n/ exp
557: MATHEMATICAL STATISTICS II HYPOTHESIS TESTING: EXAMPLES Example Suppose that X,..., X n N, ). To test H 0 : 0 H : the most powerful test at level α is based on the statistic λx) f π) X x ) n/ exp
WISE MA/PhD Programs Econometrics Instructor: Brett Graham Spring Semester, Academic Year Exam Version: A
 WISE MA/PhD Programs Econometrics Instructor: Brett Graham Spring Semester, 2016-17 Academic Year Exam Version: A INSTRUCTIONS TO STUDENTS 1 The time allowed for this examination paper is 2 hours. 2 This
WISE MA/PhD Programs Econometrics Instructor: Brett Graham Spring Semester, 2016-17 Academic Year Exam Version: A INSTRUCTIONS TO STUDENTS 1 The time allowed for this examination paper is 2 hours. 2 This
A Very Brief Summary of Bayesian Inference, and Examples
 A Very Brief Summary of Bayesian Inference, and Examples Trinity Term 009 Prof Gesine Reinert Our starting point are data x = x 1, x,, x n, which we view as realisations of random variables X 1, X,, X
A Very Brief Summary of Bayesian Inference, and Examples Trinity Term 009 Prof Gesine Reinert Our starting point are data x = x 1, x,, x n, which we view as realisations of random variables X 1, X,, X
Chapter 4: Asymptotic Properties of the MLE (Part 2)
 Chapter 4: Asymptotic Properties of the MLE (Part 2) Daniel O. Scharfstein 09/24/13 1 / 1 Example Let {(R i, X i ) : i = 1,..., n} be an i.i.d. sample of n random vectors (R, X ). Here R is a response
Chapter 4: Asymptotic Properties of the MLE (Part 2) Daniel O. Scharfstein 09/24/13 1 / 1 Example Let {(R i, X i ) : i = 1,..., n} be an i.i.d. sample of n random vectors (R, X ). Here R is a response
Statement: With my signature I confirm that the solutions are the product of my own work. Name: Signature:.
 MATHEMATICAL STATISTICS Homework assignment Instructions Please turn in the homework with this cover page. You do not need to edit the solutions. Just make sure the handwriting is legible. You may discuss
MATHEMATICAL STATISTICS Homework assignment Instructions Please turn in the homework with this cover page. You do not need to edit the solutions. Just make sure the handwriting is legible. You may discuss
simple if it completely specifies the density of x
 3. Hypothesis Testing Pure significance tests Data x = (x 1,..., x n ) from f(x, θ) Hypothesis H 0 : restricts f(x, θ) Are the data consistent with H 0? H 0 is called the null hypothesis simple if it completely
3. Hypothesis Testing Pure significance tests Data x = (x 1,..., x n ) from f(x, θ) Hypothesis H 0 : restricts f(x, θ) Are the data consistent with H 0? H 0 is called the null hypothesis simple if it completely
First Year Examination Department of Statistics, University of Florida
 First Year Examination Department of Statistics, University of Florida May 6, 2011, 8:00 am - 12:00 noon Instructions: 1. You have four hours to answer questions in this examination. 2. You must show your
First Year Examination Department of Statistics, University of Florida May 6, 2011, 8:00 am - 12:00 noon Instructions: 1. You have four hours to answer questions in this examination. 2. You must show your
40.530: Statistics. Professor Chen Zehua. Singapore University of Design and Technology
 Singapore University of Design and Technology Lecture 9: Hypothesis testing, uniformly most powerful tests. The Neyman-Pearson framework Let P be the family of distributions of concern. The Neyman-Pearson
Singapore University of Design and Technology Lecture 9: Hypothesis testing, uniformly most powerful tests. The Neyman-Pearson framework Let P be the family of distributions of concern. The Neyman-Pearson
Institute of Actuaries of India
 Institute of Actuaries of India Subject CT3 Probability & Mathematical Statistics May 2011 Examinations INDICATIVE SOLUTION Introduction The indicative solution has been written by the Examiners with the
Institute of Actuaries of India Subject CT3 Probability & Mathematical Statistics May 2011 Examinations INDICATIVE SOLUTION Introduction The indicative solution has been written by the Examiners with the
M(t) = 1 t. (1 t), 6 M (0) = 20 P (95. X i 110) i=1
 Math 66/566 - Midterm Solutions NOTE: These solutions are for both the 66 and 566 exam. The problems are the same until questions and 5. 1. The moment generating function of a random variable X is M(t)
Math 66/566 - Midterm Solutions NOTE: These solutions are for both the 66 and 566 exam. The problems are the same until questions and 5. 1. The moment generating function of a random variable X is M(t)
Chapters 10. Hypothesis Testing
 Chapters 10. Hypothesis Testing Some examples of hypothesis testing 1. Toss a coin 100 times and get 62 heads. Is this coin a fair coin? 2. Is the new treatment on blood pressure more effective than the
Chapters 10. Hypothesis Testing Some examples of hypothesis testing 1. Toss a coin 100 times and get 62 heads. Is this coin a fair coin? 2. Is the new treatment on blood pressure more effective than the
Chapter 5 continued. Chapter 5 sections
 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Statistics 351 Probability I Fall 2006 (200630) Final Exam Solutions. θ α β Γ(α)Γ(β) (uv)α 1 (v uv) β 1 exp v }
 Statistics 35 Probability I Fall 6 (63 Final Exam Solutions Instructor: Michael Kozdron (a Solving for X and Y gives X UV and Y V UV, so that the Jacobian of this transformation is x x u v J y y v u v
Statistics 35 Probability I Fall 6 (63 Final Exam Solutions Instructor: Michael Kozdron (a Solving for X and Y gives X UV and Y V UV, so that the Jacobian of this transformation is x x u v J y y v u v
Notes, March 4, 2013, R. Dudley Maximum likelihood estimation: actual or supposed
 18.466 Notes, March 4, 2013, R. Dudley Maximum likelihood estimation: actual or supposed 1. MLEs in exponential families Let f(x,θ) for x X and θ Θ be a likelihood function, that is, for present purposes,
18.466 Notes, March 4, 2013, R. Dudley Maximum likelihood estimation: actual or supposed 1. MLEs in exponential families Let f(x,θ) for x X and θ Θ be a likelihood function, that is, for present purposes,
Model Checking and Improvement
 Model Checking and Improvement Statistics 220 Spring 2005 Copyright c 2005 by Mark E. Irwin Model Checking All models are wrong but some models are useful George E. P. Box So far we have looked at a number
Model Checking and Improvement Statistics 220 Spring 2005 Copyright c 2005 by Mark E. Irwin Model Checking All models are wrong but some models are useful George E. P. Box So far we have looked at a number
Probability Theory and Statistics. Peter Jochumzen
 Probability Theory and Statistics Peter Jochumzen April 18, 2016 Contents 1 Probability Theory And Statistics 3 1.1 Experiment, Outcome and Event................................ 3 1.2 Probability............................................
Probability Theory and Statistics Peter Jochumzen April 18, 2016 Contents 1 Probability Theory And Statistics 3 1.1 Experiment, Outcome and Event................................ 3 1.2 Probability............................................
WISE MA/PhD Programs Econometrics Instructor: Brett Graham Spring Semester, Academic Year Exam Version: A
 WISE MA/PhD Programs Econometrics Instructor: Brett Graham Spring Semester, 2016-17 Academic Year Exam Version: A INSTRUCTIONS TO STUDENTS 1 The time allowed for this examination paper is 2 hours. 2 This
WISE MA/PhD Programs Econometrics Instructor: Brett Graham Spring Semester, 2016-17 Academic Year Exam Version: A INSTRUCTIONS TO STUDENTS 1 The time allowed for this examination paper is 2 hours. 2 This
Hypothesis Testing: The Generalized Likelihood Ratio Test
 Hypothesis Testing: The Generalized Likelihood Ratio Test Consider testing the hypotheses H 0 : θ Θ 0 H 1 : θ Θ \ Θ 0 Definition: The Generalized Likelihood Ratio (GLR Let L(θ be a likelihood for a random
Hypothesis Testing: The Generalized Likelihood Ratio Test Consider testing the hypotheses H 0 : θ Θ 0 H 1 : θ Θ \ Θ 0 Definition: The Generalized Likelihood Ratio (GLR Let L(θ be a likelihood for a random
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
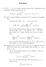 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Statistical Inference
 Statistical Inference Classical and Bayesian Methods Revision Class for Midterm Exam AMS-UCSC Th Feb 9, 2012 Winter 2012. Session 1 (Revision Class) AMS-132/206 Th Feb 9, 2012 1 / 23 Topics Topics We will
Statistical Inference Classical and Bayesian Methods Revision Class for Midterm Exam AMS-UCSC Th Feb 9, 2012 Winter 2012. Session 1 (Revision Class) AMS-132/206 Th Feb 9, 2012 1 / 23 Topics Topics We will
2014/2015 Smester II ST5224 Final Exam Solution
 014/015 Smester II ST54 Final Exam Solution 1 Suppose that (X 1,, X n ) is a random sample from a distribution with probability density function f(x; θ) = e (x θ) I [θ, ) (x) (i) Show that the family of
014/015 Smester II ST54 Final Exam Solution 1 Suppose that (X 1,, X n ) is a random sample from a distribution with probability density function f(x; θ) = e (x θ) I [θ, ) (x) (i) Show that the family of
Testing Hypothesis. Maura Mezzetti. Department of Economics and Finance Università Tor Vergata
 Maura Department of Economics and Finance Università Tor Vergata Hypothesis Testing Outline It is a mistake to confound strangeness with mystery Sherlock Holmes A Study in Scarlet Outline 1 The Power Function
Maura Department of Economics and Finance Università Tor Vergata Hypothesis Testing Outline It is a mistake to confound strangeness with mystery Sherlock Holmes A Study in Scarlet Outline 1 The Power Function
f(x θ)dx with respect to θ. Assuming certain smoothness conditions concern differentiating under the integral the integral sign, we first obtain
 0.1. INTRODUCTION 1 0.1 Introduction R. A. Fisher, a pioneer in the development of mathematical statistics, introduced a measure of the amount of information contained in an observaton from f(x θ). Fisher
0.1. INTRODUCTION 1 0.1 Introduction R. A. Fisher, a pioneer in the development of mathematical statistics, introduced a measure of the amount of information contained in an observaton from f(x θ). Fisher
Bayesian Regression (1/31/13)
 STA613/CBB540: Statistical methods in computational biology Bayesian Regression (1/31/13) Lecturer: Barbara Engelhardt Scribe: Amanda Lea 1 Bayesian Paradigm Bayesian methods ask: given that I have observed
STA613/CBB540: Statistical methods in computational biology Bayesian Regression (1/31/13) Lecturer: Barbara Engelhardt Scribe: Amanda Lea 1 Bayesian Paradigm Bayesian methods ask: given that I have observed
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
This exam is closed book and closed notes. (You will have access to a copy of the Table of Common Distributions given in the back of the text.
 TEST #3 STA 5326 December 4, 214 Name: Please read the following directions. DO NOT TURN THE PAGE UNTIL INSTRUCTED TO DO SO Directions This exam is closed book and closed notes. (You will have access to
TEST #3 STA 5326 December 4, 214 Name: Please read the following directions. DO NOT TURN THE PAGE UNTIL INSTRUCTED TO DO SO Directions This exam is closed book and closed notes. (You will have access to
