Mathematical Statistics
|
|
|
- Rosamund Lambert
- 6 years ago
- Views:
Transcription
1 Mathematical Statistics Chapter Three. Point Estimation
2 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution family, g(θ) the parameter to be estimated, and X = (X 1, X 2,, X n ) a sample from p(x; θ).
3 Definition Definition Suppose ĝ = ĝ(x) is an estimator for g(θ). Then E θ [ĝ g(θ)] 2 is called the mean squared error(mse)of ĝ.
4 Suppose both ĝ 1 and ĝ 2 are estimators for g(θ), and E θ [ĝ 1 g(θ)] 2 E θ [ĝ 2 g(θ)] 2, θ Θ. Then ĝ 2 is said to be no better than ĝ 1 in the terms of MSE.
5 Suppose both ĝ 1 and ĝ 2 are estimators for g(θ), and E θ [ĝ 1 g(θ)] 2 E θ [ĝ 2 g(θ)] 2, θ Θ. Then ĝ 2 is said to be no better than ĝ 1 in the terms of MSE. If the inequality holds for at least one θ Θ, then ĝ 1 is said to be better than ĝ 2.
6 Example Let X 1, X 2,, X n be a sample from a normal population N(µ, σ 2 ). Both Sn 2 = 1 n n 1 i=1 (X i X ) 2 and Sn 2 = 1 n n i=1 (X i X ) 2 are estimators for σ 2. Sn 2 is an unbiased estimator. Compute their MSE.
7 We know that (n 1)S n 2 /σ 2 χ 2 (n 1). By the definition of χ 2 (n), we know that if Y i are i.i.d. and N(0, 1),i = 1, 2,, n 1, then n 1 Yi 2 χ 2 (n 1). i=1
8 Let Y = AX, where A = (a ij ) is a n n orthogonal matrix and Y 1 = nx. Then we have (n 1)S n 2 = n i=2 Y 2 i.
9 Hence, Var{Sn 2 } =Var{ σ2 n 1 = σ4 n 1 Var(Y 2 1 ) = (n 1)Sn 2 } = σ 2 σ 4 (n 1) Var{ n 1 2 i=1 σ4 n 1 [EY 4 1 (EY 2 1 ) 2 ] = Y 2 i } 2σ4 n 1.
10 Hence, Var{Sn 2 } =Var{ σ2 n 1 = σ4 n 1 Var(Y 2 1 ) = (n 1)Sn 2 } = σ 2 The mean squared error of S n 2 is σ 4 (n 1) Var{ n 1 2 i=1 σ4 n 1 [EY 4 1 (EY 2 1 ) 2 ] = E{Sn 2 σ 2 } 2 = Var{Sn 2 } = 2σ4 n 1. Y 2 i } 2σ4 n 1.
11 For, Sn, 2 since Sn 2 = n 1S 2 n n, we have ESn 2 = n 1 n ES n 2 = n 1 n σ2.
12 The MSE of S 2 n is E{Sn 2 σ 2 } 2 =Var{Sn} 2 + (ESn 2 σ 2 ) 2 ( ) 2 n 1 = Var{S 2 n } + ( 1n ) 2 n σ2 ( ) 2 n 1 2σ 4 = n n 1 + σ4 n = 2n 1 σ 4. 2 n 2 E{S 2 n σ 2 } 2 < E{S n 2 σ 2 } 2. In terms of MSE, S 2 n is a better estimator for σ 2 than S n 2.
13 Existence Question: Does there exist such an estimator ĝ for g(θ) such that it is as good as or better than other estimators in terms of MSE? That is, is there a best estimator with the smallest MSE?
14 Existence Question: Does there exist such an estimator ĝ for g(θ) such that it is as good as or better than other estimators in terms of MSE? That is, is there a best estimator with the smallest MSE? The answer is NO.
15 In fact, if such a statistic ĝ for g(θ) does exist, then for any given θ 0, ĝ 2 g(θ 0 ) is also an estimator for g(θ). Hence the following should hold: E θ [ĝ g(θ)] 2 E θ [g(θ 0 ) g(θ)] 2, θ.
16 In particular, when θ = θ 0, we have E θ0 [ĝ g(θ 0 )] 2 = 0. Therefore, P θ0 {ĝ = g(θ 0 )} = 1. Since θ 0 is arbitrary, P θ [ĝ = g(θ)] = 1, θ that is ĝ = g(θ) a.s.
17 Best Unbiased Estimator As we noted, a comparison of estimators in terms of MSE may NOT yield a clear favorite. Indeed there is no one best MSE estimator. The reason there is no one best MSE estimator is that the class of all estimators is too large a class. One way to make the problem of finding a best estimator tractable is to limit the class of estimators. A popular way to restricting the class of estimator is to consider only unbiased estimators.
18 Let U g = {ĝ = ĝ(x) : E θ ĝ = g(θ), θ}. be the class of unbiased estimators for g(θ). The MSE of each statistic in U g is the variance of the statistic. When U g, we say that g(θ) is an redestimable parameter.
19 One example of estimable parameters is the population mean. However, not all parameters are estimable. Example Let X = (X 1, X 2,..., X n ) be a sample of size n from b(1, p), p unknown. g(p) = 1/p is not estimable.
20 In fact, for any statistic T (X), the expected value of T (X) E p [T (X)] = T (x)p i x i (1 p) n i x i, 0 < p < 1. x i =0,1;i=1,...,n The right-hand side is a degree n polynomial of p, which is bounded and it is impossible to equal to the unbounded function 1/p in the interval (0, 1). Therefore, unbiased estimators for g(p) = 1/p do NOT exist.
21 Constructing unbiased estimators for a parameter g(θ) is not an easy task. Unbiased estimators may be found among the existing estimators or by modifying the existing estimators. For instance, the unbiased estimator S 2 for σ 2 is the slight modification of the moment estimator Sn. 2
22 Example Let X 1,..., X n be a sample from a uniform distribution U(0, θ), θ > 0. Find an unbiased estimator for 1/θ.
23 Example Let X 1,..., X n be a sample from a uniform distribution U(0, θ), θ > 0. Find an unbiased estimator for 1/θ. Solution: Consider an estimator T (X (n) ), which is a function of the sufficient statistic X (n) = max 1 i n X i. Compute the expected value of T (X (n) ) is E θ [T (X (n) )] = θ 0 T (x) nx n 1 θ n dx.
24 In order for T (X (n) ) to be an unraised estimator for 1/θ, he following has to be true: 1 θ = θ 0 T (x) nx n 1 θ n dx, θ > 0.
25 That is, θ n 1 = θ 0 T (x)nx n 1 dx, θ > 0.
26 That is, θ n 1 = θ 0 T (x)nx n 1 dx, θ > 0. Differentiating both sides with respect to θ yields T (θ) = n 1 nθ. Hence T (x) = n 1 nx. When n 2, T (X (n) ) is an unbiased estimator for 1/θ.
27 When n = 1, T (X (n) ) 0, and E θ [T (X (n) )] 1/θ.
28 When n = 1, T (X (n) ) 0, and E θ [T (X (n) )] 1/θ. In this case, there is no unbiased estimator for 1/θ.
29 Suppose g(x) were an unbiased estimator for 1/θ. Then T (X (n) ) = E[g(X) X (n) ] is also an unbiased estimator for 1/θ (Why? Check it use the property of conditional expected value.) This once more implies that T (X (n) ) 0.
30 Definition Let F = {p(x; θ) : θ Θ} be a parametric distribution family, and X a sample from p(x; θ). Suppose g(θ) is an estimable parameter, and U g is the class of unbiased estimators for g(θ). If ĝ = ĝ (X) is an unbiased estimator such that, for all ĝ = ĝ(x) U g, Var θ {ĝ } Var θ {ĝ}, θ Θ, then ĝ is said to be a best unbiased estimator for g(θ), or a uniform minimum variance unbiased estimator (UMVUE) for g(θ).
31 It is not an easy job to find or verify UMVUE directly, but Rao-Blackwell Theorem provides an approach for finding UMVUE.
32 Theorem (Rao-Blackwell) Let T = T (X) be a sufficient statistic for the parameter θ Θ, and ϕ(x) an unbiased estimator for g(θ). Then ĝ(t ) = E{ϕ(X) T } is also an unbiased estimator for g(θ), and Var θ {ĝ(t )} Var{ϕ(X)}, θ Θ, the equality holds if and only if P θ {ϕ(x) = ĝ(t )} = 1, θ Θ.
33 The theorem tells us: Conditional expectation of an unbiased estimator on a sufficient statistic will improve the variance of an unbiased estimator;
34 The theorem tells us: Conditional expectation of an unbiased estimator on a sufficient statistic will improve the variance of an unbiased estimator; UMVUE must be a function of a sufficient statistic;
35 The theorem tells us: Conditional expectation of an unbiased estimator on a sufficient statistic will improve the variance of an unbiased estimator; UMVUE must be a function of a sufficient statistic; We need consider only statistics that are functions of sufficient statistic in our search for best unbiased estimators.
36 Proof: Since T is a sufficient statistic, then the conditional distribution of X given T is independent of θ. This further implies that the conditional expected value of ĝ(t ) = E{ϕ(X) T } is independent of θ, and hence it is a statistic. and E θ {ĝ(t )} = E θ [E{ϕ(X) T }] = E θ {ϕ(x)} = g(θ). Therefore, ĝ(t ) is an unbiased estimator for g(θ).
37 To prove the second part of Rao-Blackwell theorem, write ϕ = ϕ(x). Var θ {ϕ} =E θ {ϕ E θ (ϕ T ) + E θ (ϕ T ) E θ (ϕ)} 2 =E θ {ϕ E θ (ϕ T )} 2 + E θ {E θ (ϕ T ) E θ (ϕ)} 2 + 2E θ {[ ϕ Eθ (ϕ T ) ][ E θ (ϕ T ) E θ (ϕ) ]} =E θ {ϕ ĝ(t )} 2 + Var θ {ĝ(t )} + 2E θ {[ ϕ Eθ (ϕ T ) ][ E θ (ϕ T ) E θ (ϕ) ]}.
38 Notice that E θ {[ ϕ Eθ (ϕ T ) ][ E θ (ϕ T ) E θ (ϕ) ]} =E θ ( E θ { [ϕ Eθ (ϕ T ) ][ E θ (ϕ T ) E θ (ϕ) ] T }) =E θ ( E θ { [ϕ Eθ (ϕ T ) ] T } [E θ (ϕ T ) E θ (ϕ) ]) =E θ ([ Eθ (ϕ T ) E θ (ϕ T ) ] [E θ (ϕ T ) E θ (ϕ) ]) = 0.
39 We have Var θ {ϕ} =E θ {ϕ ĝ(t )} 2 + Var θ {ĝ(t )} Var θ {ĝ(t )}, θ Θ. The equality holds true if and only if E θ {ϕ ĝ(t )} 2 = 0. That is, P θ {ϕ = ĝ(t )} = 1.
40 Theorem Suppose T = T (X) is a sufficient statistic for the parameter θ Θ, ϕ(x) = (ϕ 1 (X),..., ϕ k (X)) is an unbiased estimator for R k -valued parameter g(θ). Then 1 ĝ(t ) = E{ϕ(X) T } is also an unbiased estimator for g(θ).
41 2 Let V(θ) = {Cov θ [ĝ i (T ), ĝ j (T )]} 1 i,j k, and U(θ) = {Cov θ [ϕ i (X), ϕ j (X)]} 1 i,j k be covariance matrices of ĝ(t ) and ϕ(x), respectively. Then U(θ) V(θ) is non-negative definite, θ Θ. And U(θ) V(θ) = O (zero matrix) if and only if P θ {ϕ(x) = ĝ(t )} = 1, θ Θ.
42 Example Let X 1, X 2,, X n be a sample from a Bernoulli distribution b(1, p). Discuss the unbiased estimator for p.
43 Example Let X 1, X 2,, X n be a sample from a Bernoulli distribution b(1, p). Discuss the unbiased estimator for p. We know that EX 1 = p. Hence X 1 is an unbiased estimator for p. Moreover, T = X X n is a sufficient statistic. Now we use conditional expectation to improve the unbiased estimator. E(X 1 T ) =E(X 2 T ) = = E(X n T ).
44 Thus, E(X 1 T ) = E(X 1 T ) + E(X 2 T ) + E(X n T ) n = E(X 1 + X 2 + X n T ) n E(T T ) = = T n n = X.
45 To see when an unbiased estimator is a best unbiased, we might ask how could we improve upon a given unbiased estimator?
46 To see when an unbiased estimator is a best unbiased, we might ask how could we improve upon a given unbiased estimator? Suppose that W satisfies E θ W = τ(θ), and we have another estimator U such that E θ U = 0 for all θ, that is, U is an unbiased estimator of 0. The estimator V a = W + au, where a is a constant, satisfies E θ V a = τ(θ) and hence is also an unbiased estimator of τ(θ).
47 Can V a be better than W? The variance of V a is VarV a = Var θ (W + au) = Var θ W + 2aCov θ (W, U) + a 2 Var θ U. Thus the relationship between W and the unbiased estimator of 0 is crucial in evaluating whether W is a best unbiased. This relationship, in fact, characterizes best unbiasedness.
48 Unbiased Estimator of Zero
49 Unbiased Estimator of Zero Theorem Theorem Suppose ĝ = ĝ(x) is an unbiased estimator for g(θ), and Var θ (ĝ) < for θ Θ. Let L = {l = l(x) : E θ (l(x)) = 0, θ Θ} be the set of all unbiased estimators of 0. If for l L, Cov θ (ĝ, l) = E θ (ĝ l) = 0, θ Θ, (3.4.2) then ĝ is the UMVUE for g(θ).
50 Example Let X 1, X 2,, X n be a sample from a Bernoulli distribution b(1, p). Show that X is the UMVUE for p.
51 Example Let X 1, X 2,, X n be a sample from a Bernoulli distribution b(1, p). Show that X is the UMVUE for p. Proof: Notice that E p (X ) = p and Var p (X ) = p(1 p)/n <. Applying Theorem 3.4.1, to prove that X is the UMVUE for p, we only need to show that X satisfies (3.4.2).
52 Now let l = l(x) be an unbiased estimator of 0. Then
53 Now let l = l(x) be an unbiased estimator of 0. Then 0 = E p (l) = l(x)p i x i (1 p) n i x i, 0 < p < 1. x i =0,1;i=1,...,n
54 Now let l = l(x) be an unbiased estimator of 0. Then 0 = E p (l) = x i =0,1;i=1,...,n l(x)p i x i (1 p) n i x i, 0 < p < 1. Let ϕ = p. Then we have 1 p 0 = l(x)ϕ i x i ϕ > 0 ( ). x i =0,1;i=1,...,n
55 Differentiating both sides of ( ) with respect to ϕ yields n 0 = l(x)( x i )ϕ i x i 1 x i =0,1;i=1,...,n i=1 ϕ > 0,
56 Differentiating both sides of ( ) with respect to ϕ yields n 0 = l(x)( x i )ϕ i x i 1 x i =0,1;i=1,...,n i=1 ϕ > 0, Thus, n 0 = l(x)( x i )ϕ i x i ϕ > 0. x i =0,1;i=1,...,n i=1 This implies that Cov p (X, l(x)) = E p (X l(x)) = 0, that is (3.4.2) holds. We conclude that X is the UMVUE for p.
57 Complete Sufficient Statistics Definition Let F = {p(x; θ) : θ Θ} be a parametric distribution family, T a statistic. If for any real-valued function ϕ(t), E θ ϕ(t ) = 0, θ Θ implies P θ {ϕ(t ) = 0} = 1, θ Θ. That is, the derived distribution family F T = {p T (t; θ) : θ Θ} of T is complete, then T is said to be a complete statistic.
58 Remark: A complete statistic means that among the functions of T, 0 is the only unbiased estimator for 0.
59 Rao-Blackwell Theorem shows: If T is sufficient, then an UMVUE for g(θ) can be derived from the functions of T. Completeness says: If T is also a sufficient statistic, only 0 is the unibiased estimator of 0, and hence it is uncorrelated to any statistic of the form ϕ(t ). Therefore, if T is sufficient and complete, then as long as ϕ(x) is unbiased, we have that E[ϕ(X) T ] is UMVUE.
60 Theorem Theorem ( Lehmann-Scheffe) Suppose S = S(X) is a complete sufficient statistic for θ. Then there is a unique UMVUE for the estimable parameter g(θ). If ϕ(x) is an unbiased estimator for g(θ), then E[ϕ(X) S]. is the unique UMVUE for g(θ).
61 The Lehmann-Scheffé Theorem represents a major achievement in mathematical statistics, tying together sufficiency, completeness, and uniqueness.
62 The theorem also provides two ways of finding UMVUE: 1. Method A. 1 Construct a sufficient and complete statistic S, 2 Find an unbiased estimator ϕ for the estimable parameter, 3 Compute the conditional expected value of E[ϕ S], and E[ϕ S] is UMVUE.
63 2. Method B. 1 First find a sufficient and complete statistic S, 2 Next find a function g(s) of S, such that g(s) is an unbiased estimator. 3 g(s) is the UMVUE.
64 For example: Let X = (X 1, X 2,, X n ) be a sample from a Bernoulli distribution family {B(1, p); 0 < p < 1}. We showed that T = n i=1 X i is a sufficient complete estimator for p. We want to derive an UMVUE for p 2.
65 Knowing that X 1 is an unbiased estimator for p, we have Then X is the UMVUE for p. E[X 1 T ] = T /n = X.
66 Knowing that X 1 is an unbiased estimator for p, we have Then X is the UMVUE for p. E[X 1 T ] = T /n = X.
67 Next we want to find UMVUE for p 2.
68 Next we want to find UMVUE for p 2. Since ET 2 = n i=1 EX 2 i + i j EX i EX j = ET + n(n 1)p 2, then solving for p 2 : Hence, is UMVUE for p 2. p 2 = E[T 2 T ] n(n 1). T 2 T n(n 1) = 1 n 1 [nx 2 X ]
69 Proof of The Lehmann-Scheffé Theorem: Uniqueness: Suppose both W = W (X) and Y = Y (X) are UMVUE for g(θ). Then E θ W = E θ Y = g(θ), Var θ (W ) = Var θ (Y ) θ.
70 Proof of The Lehmann-Scheffé Theorem: Uniqueness: Suppose both W = W (X) and Y = Y (X) are UMVUE for g(θ). Then E θ W = E θ Y = g(θ), Var θ (W ) = Var θ (Y ) θ. Notice that E θ (W Y ) 2 =Var θ (W Y ) =Var θ (W ) + Var θ (Y ) 2Cov θ (W, Y ) =2Var θ (W ) 2Cov θ (W, Y ).
71 If we can show that Cov θ (W, Y ) = Var θ (W ) = Var θ (Y ), then E θ (W Y ) 2 = 0, and this proves P θ (W = Y ) = 1, θ.
72 To show Cov θ (W, Y ) = Var θ (W ), we notice that Z = (W + Y )/2 is also an unbiased estimator for g(θ).
73 Since W is UMVUE, we deduce Var θ (W ) Var θ (Z) = 1 4 Var θ(w ) Var θ(y ) Cov θ(w, Y ) 1 4 Var θ(w ) Var θ(y ) [Var θ(w )] 1/2 [Var θ (Y )] 1/2 (Cauchy-Schwarz inequality) =Var θ (W ). Thus, Cov θ {W, Y } = Var θ {W } = Var θ {Y }.
74 Existence: Suppose ϕ = ϕ(x) is an unbiased estimator for an estimable parameter g(θ). We denote ĝ = ĝ(x) = E[ϕ S]. According to Rao-Blackwell Theorem, ĝ is also an unbiased estimator for g(θ).
75 Now we show that ĝ is UMVUE. Let f = f (X) be another arbitrary unbiased estimator for g(θ).
76 Now we show that ĝ is UMVUE. Let f = f (X) be another arbitrary unbiased estimator for g(θ). Rao-Blackwell implies that E[f S] is an unbiased estimator for g(θ) as well. Moreover, Var θ {E[f S]} Var θ {f }.
77 Since both ĝ and E[f S] are unbiased estimators for g(θ), E θ {ĝ E[f S]} = 0, θ.
78 Since both ĝ and E[f S] are unbiased estimators for g(θ), E θ {ĝ E[f S]} = 0, θ. Furthermore, S is complete, hence P θ {ĝ = E[f S]} = 1. Therefore, Var θ {ĝ} = Var θ {E[f S]} Var θ {f }. This shows that ĝ is UMVUE for g(θ).
79 Example Let X 1, X 2,, X n be a sample from a Poisson distribution with parameter λ, λ > 0. Derive the UMVUE for the probability P λ (k) = λk k! e λ.
80 Solution: The joint pmf for the sample X 1, X 2,, X n is P(X 1 = x 1, X 2 = x 2,, X n = x n ) =e λn λ x 1+x 2 + +x n 1 x 1!x 2! x n! I {x i = 0, 1, ; i = 1, 2,, n}. According the factorization theorem, T n = n i=1 X n is a sufficient statistic.
81 Now we prove that it is complete. Since T n P(nλ), if we have E λ f (T n ) = e nλ t=0 f (t) (nλ)t t! = 0, λ > 0,
82 then t=0 f (t) x t t! = 0, x > 0, which implies that the coefficient of x t has to be zero, that is, f (t) 1 t! = 0, t = 0, 1, 2,, Thus f (t) = 0, t = 0, 1, 2,, and P{f (T n ) = 0} = 1. Therefore, T n is complete.
83 It is trivial that the statistic 1, X 1 = k, ϕ k (X) = 0, X 1 k is an unbiased estimator for P λ (k).
84 E λ [ϕ k (X) T n = t] = P(X 1 = k T n = t) = P(X 1 = k, T n = t) P(T n = t) k! e λ [(n 1)λ]t k e (n 1)λ (t k)! λ k = (nλ) t t! e nλ = = P(X 1 = k)p(x X n = t k) P(T n = t) ( ) ( ) k ( t t k. k n n)
85 We conclude that P λ (k) = ( Tn k is the UMVUE for P λ (k). ) ( ) k ( ) Tn k. n n In particular, when k = 0, we have ( P λ (0) = 1 n) 1 Tn.
86 Example Let X 1, X 2,, X n be a sample from a uniform distribution U(0, θ), θ > 0. Find the UMVUE for θ, and compare the efficiency of UMVUE and moment estimator.
87 Example Let X 1, X 2,, X n be a sample from a uniform distribution U(0, θ), θ > 0. Find the UMVUE for θ, and compare the efficiency of UMVUE and moment estimator. Solution: First we need to find a sufficient and complete statistic. Knowing that T = X (n) is a sufficient statistic, we prove that it is also complete.
88 Example Let X 1, X 2,, X n be a sample from a uniform distribution U(0, θ), θ > 0. Find the UMVUE for θ, and compare the efficiency of UMVUE and moment estimator. Solution: First we need to find a sufficient and complete statistic. Knowing that T = X (n) is a sufficient statistic, we prove that it is also complete. The density function of X (n) is p(t; θ) = n θ n tn 1, 0 < t < θ.
89 If E θ ϕ(x (n) ) = then θ 0 θ 0 ϕ(t) n θ n tn 1 dt = 0, θ > 0, ϕ(t)t n 1 dt = 0, θ > 0. Taking derivative with respect to θ yields ϕ(θ)θ n 1 = 0, θ > 0, that is, ϕ(t) = 0, t > 0. Thus, P(ϕ(X (n) ) = 0) = 1 is complete.
90 Notice that EX (n) = θ 0 t n θ n tn 1 dt = n n + 1 θ. We see that θ = (1 + 1 n )X (n) is an unbiased estimator for θ. Since it is a function of a sufficient and complete statistic, it is the UMVUE for θ.
91 Next we compute the variance of θ:
92 Next we compute the variance of θ: EX 2 (n) = θ 0 t 2 n θ n tn 1 dt = n n + 2 θ2. Var( θ) = E θ 2 θ 2 = (1 + 1 n n )2 n + 2 θ2 θ 2 = θ 2 n(n + 2).
93 By EX = θ, θ = 2EX, we obtain the moment estimator for θ 2 and its variance θ 1 = 2X, Var( θ 1 ) = 4Var(X ) = 4 θ2 12n = θ2 3n.
94 By EX = θ, θ = 2EX, we obtain the moment estimator for θ 2 θ 1 = 2X, and its variance Var( θ 1 ) = 4Var(X ) = 4 θ2 12n = θ2 3n. It is obvious that UMVUE is better (or more effective) than the moment estimator.
95 Recall: Theorem Suppose the population distribution belongs to an exponential family. The joint pdf or pmf of a sample from this population is p(x; θ) = c (θ) exp { k j=1 Q j (θ)t j (x) } h (x), If the range of Q = (Q 1 (θ),, Q k (θ)) has non-empty interior, then T = (T1,..., Tk ) is a sufficient and complete statistic.
96 Example Let X 1, X 2,, X n be a sample from a normal population N(µ, σ 2 ). Find the UMVUE for µ and σ 2.
97 Solution: The joint density function of X = (X 1, X 2,, X n ) is { } 1 p(x; θ) = exp 1 (x (2πσ 2 ) n/2 2σ 2 i µ) 2 i } 1 = exp { nµ2 (2πσ 2 ) n/2 2σ {[ ] 2 [ ] [ µ ] [ exp x i + x 2 σ 2 i 1 ] } 2σ 2 i i
98 It is clear that the interior of the range of (µ/σ 2, 1/(2σ 2 )) is non-empty. Hence ( n i=1 X i, n i=1 X i 2 ) is sufficient and complete. Any one-to-one transformation of ( n i=1 X i, n i=1 X 2 i ) is still sufficient and complete. Furthermore, both X and S 2 are unbiased estimators for µ and σ 2, and X and S 2 are functions of ( n i=1 X i, n i=1 X i 2 ). Hence they are UMVUE for µσ 2.
99 Example Consider Gamma distribution gamma(α, λ), where α > 0 is known. Find the UMVUE for λ.
100 Solution: The joint density of a sample X = (X 1,..., X n ) from the Gamma distribution is p(x; λ) = λnα (Γ(α)) n n i=1 x α 1 i exp x i > 0, i = 1,, n; { λ } n x i, i=1
101 According to the properties of exponential family, when α is known, T = n i=1 X i is a sufficient and complete statistic for the distribution family.
102 According to the properties of exponential family, when α is known, T = n i=1 X i is a sufficient and complete statistic for the distribution family. Then by the additivity of Gamma distributions, we have T gamma(nα, λ), and E λ T = nα λ, that is, λ = nα E λ T.
103 [ ] 1 1 E λ = p(t; λ) = λnα T 0 t Γ(nα) λγ(nα 1) λ = = Γ(nα) nα 1. 0 t nα 1 1 e λt dt
104 [ ] 1 1 E λ = p(t; λ) = λnα T 0 t Γ(nα) λγ(nα 1) λ = = Γ(nα) nα 1. 0 t nα 1 1 e λt dt Thus, [ ] nα 1 E λ = λ. T
105 Applying Theorem 3.4.2, is the UMVUE for λ. λ = nα 1 n i=1 X i = nα 1 nx
106 Applying Theorem 3.4.2, is the UMVUE for λ. λ = nα 1 n i=1 X i = nα 1 nx When α = 1, (n 1)/(nX ) is the UMVUE for λ in the exponential distribution E(λ).
107 Alternative solution: We will find an unbiased estimator among the functions g(t ) of T.
108 Alternative solution: We will find an unbiased estimator among the functions g(t ) of T. Let g(t ) be an arbitrary function of T and E λ g(t ) = λnα Γ(nα) 0 g(t)t nα 1 e λt dt = λ, λ > 0,
109 Alternative solution: We will find an unbiased estimator among the functions g(t ) of T. Let g(t ) be an arbitrary function of T and that is, E λ g(t ) = 1 Γ(nα) λnα Γ(nα) 0 0 g(t)t nα 1 e λt dt = λ, λ > 0, g(t)t nα 1 e λt dt = λ nα+1, λ > 0.
110 Notice that 1 g(t)t nα 1 e λt dt Γ(nα) 0 1 = t (nα 1) 1 e λt dt Γ(nα 1) 0 = nα 1 t (nα 1) 1 e λt dt, λ > 0. Γ(nα) 0
111 Hence, 1 Γ(nα) 0 [ g(t) nα 1 ] t nα 1 e λt dt = 0, λ > 0. t The uniqueness of Laplace transformation yields We conclude is the UMVUE for λ. g(t) = nα 1. t λ = nα 1 n i=1 X i = nα 1 nx
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic
 Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
ST5215: Advanced Statistical Theory
 Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
557: MATHEMATICAL STATISTICS II BIAS AND VARIANCE
 557: MATHEMATICAL STATISTICS II BIAS AND VARIANCE An estimator, T (X), of θ can be evaluated via its statistical properties. Typically, two aspects are considered: Expectation Variance either in terms
557: MATHEMATICAL STATISTICS II BIAS AND VARIANCE An estimator, T (X), of θ can be evaluated via its statistical properties. Typically, two aspects are considered: Expectation Variance either in terms
Spring 2012 Math 541A Exam 1. X i, S 2 = 1 n. n 1. X i I(X i < c), T n =
 Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee
 Stochastic Processes Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee 1 Outline Methods of Mean Squared Error Bias and Unbiasedness Best Unbiased Estimators CR-Bound for variance
Stochastic Processes Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee 1 Outline Methods of Mean Squared Error Bias and Unbiasedness Best Unbiased Estimators CR-Bound for variance
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
February 26, 2017 COMPLETENESS AND THE LEHMANN-SCHEFFE THEOREM
 February 26, 2017 COMPLETENESS AND THE LEHMANN-SCHEFFE THEOREM Abstract. The Rao-Blacwell theorem told us how to improve an estimator. We will discuss conditions on when the Rao-Blacwellization of an estimator
February 26, 2017 COMPLETENESS AND THE LEHMANN-SCHEFFE THEOREM Abstract. The Rao-Blacwell theorem told us how to improve an estimator. We will discuss conditions on when the Rao-Blacwellization of an estimator
A General Overview of Parametric Estimation and Inference Techniques.
 A General Overview of Parametric Estimation and Inference Techniques. Moulinath Banerjee University of Michigan September 11, 2012 The object of statistical inference is to glean information about an underlying
A General Overview of Parametric Estimation and Inference Techniques. Moulinath Banerjee University of Michigan September 11, 2012 The object of statistical inference is to glean information about an underlying
Lecture 4: UMVUE and unbiased estimators of 0
 Lecture 4: UMVUE and unbiased estimators of Problems of approach 1. Approach 1 has the following two main shortcomings. Even if Theorem 7.3.9 or its extension is applicable, there is no guarantee that
Lecture 4: UMVUE and unbiased estimators of Problems of approach 1. Approach 1 has the following two main shortcomings. Even if Theorem 7.3.9 or its extension is applicable, there is no guarantee that
1. (Regular) Exponential Family
 1. (Regular) Exponential Family The density function of a regular exponential family is: [ ] Example. Poisson(θ) [ ] Example. Normal. (both unknown). ) [ ] [ ] [ ] [ ] 2. Theorem (Exponential family &
1. (Regular) Exponential Family The density function of a regular exponential family is: [ ] Example. Poisson(θ) [ ] Example. Normal. (both unknown). ) [ ] [ ] [ ] [ ] 2. Theorem (Exponential family &
Probability and Distributions
 Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
ECE 275B Homework # 1 Solutions Version Winter 2015
 ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
Last Lecture. Biostatistics Statistical Inference Lecture 14 Obtaining Best Unbiased Estimator. Related Theorems. Rao-Blackwell Theorem
 Last Lecture Biostatistics 62 - Statistical Inference Lecture 14 Obtaining Best Unbiased Estimator Hyun Min Kang February 28th, 213 For single-parameter exponential family, is Cramer-Rao bound always attainable?
Last Lecture Biostatistics 62 - Statistical Inference Lecture 14 Obtaining Best Unbiased Estimator Hyun Min Kang February 28th, 213 For single-parameter exponential family, is Cramer-Rao bound always attainable?
Estimation theory. Parametric estimation. Properties of estimators. Minimum variance estimator. Cramer-Rao bound. Maximum likelihood estimators
 Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
ECE 275B Homework # 1 Solutions Winter 2018
 ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
Proof In the CR proof. and
 Question Under what conditions will we be able to attain the Cramér-Rao bound and find a MVUE? Lecture 4 - Consequences of the Cramér-Rao Lower Bound. Searching for a MVUE. Rao-Blackwell Theorem, Lehmann-Scheffé
Question Under what conditions will we be able to attain the Cramér-Rao bound and find a MVUE? Lecture 4 - Consequences of the Cramér-Rao Lower Bound. Searching for a MVUE. Rao-Blackwell Theorem, Lehmann-Scheffé
Exercises and Answers to Chapter 1
 Exercises and Answers to Chapter The continuous type of random variable X has the following density function: a x, if < x < a, f (x), otherwise. Answer the following questions. () Find a. () Obtain mean
Exercises and Answers to Chapter The continuous type of random variable X has the following density function: a x, if < x < a, f (x), otherwise. Answer the following questions. () Find a. () Obtain mean
Evaluating the Performance of Estimators (Section 7.3)
 Evaluating the Performance of Estimators (Section 7.3) Example: Suppose we observe X 1,..., X n iid N(θ, σ 2 0 ), with σ2 0 known, and wish to estimate θ. Two possible estimators are: ˆθ = X sample mean
Evaluating the Performance of Estimators (Section 7.3) Example: Suppose we observe X 1,..., X n iid N(θ, σ 2 0 ), with σ2 0 known, and wish to estimate θ. Two possible estimators are: ˆθ = X sample mean
Summary. Ancillary Statistics What is an ancillary statistic for θ? .2 Can an ancillary statistic be a sufficient statistic?
 Biostatistics 62 - Statistical Inference Lecture 5 Hyun Min Kang 1 What is an ancillary statistic for θ? 2 Can an ancillary statistic be a sufficient statistic? 3 What are the location parameter and the
Biostatistics 62 - Statistical Inference Lecture 5 Hyun Min Kang 1 What is an ancillary statistic for θ? 2 Can an ancillary statistic be a sufficient statistic? 3 What are the location parameter and the
t x 1 e t dt, and simplify the answer when possible (for example, when r is a positive even number). In particular, confirm that EX 4 = 3.
 Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Limiting Distributions
 We introduce the mode of convergence for a sequence of random variables, and discuss the convergence in probability and in distribution. The concept of convergence leads us to the two fundamental results
We introduce the mode of convergence for a sequence of random variables, and discuss the convergence in probability and in distribution. The concept of convergence leads us to the two fundamental results
Chapter 5 continued. Chapter 5 sections
 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
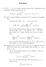 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Lecture 11. Multivariate Normal theory
 10. Lecture 11. Multivariate Normal theory Lecture 11. Multivariate Normal theory 1 (1 1) 11. Multivariate Normal theory 11.1. Properties of means and covariances of vectors Properties of means and covariances
10. Lecture 11. Multivariate Normal theory Lecture 11. Multivariate Normal theory 1 (1 1) 11. Multivariate Normal theory 11.1. Properties of means and covariances of vectors Properties of means and covariances
Stat 426 : Homework 1.
 Stat 426 : Homework 1. Moulinath Banerjee University of Michigan Announcement: The homework carries 120 points and contributes 10 points to the total grade. (1) A geometric random variable W takes values
Stat 426 : Homework 1. Moulinath Banerjee University of Michigan Announcement: The homework carries 120 points and contributes 10 points to the total grade. (1) A geometric random variable W takes values
Limiting Distributions
 Limiting Distributions We introduce the mode of convergence for a sequence of random variables, and discuss the convergence in probability and in distribution. The concept of convergence leads us to the
Limiting Distributions We introduce the mode of convergence for a sequence of random variables, and discuss the convergence in probability and in distribution. The concept of convergence leads us to the
Brief Review on Estimation Theory
 Brief Review on Estimation Theory K. Abed-Meraim ENST PARIS, Signal and Image Processing Dept. abed@tsi.enst.fr This presentation is essentially based on the course BASTA by E. Moulines Brief review on
Brief Review on Estimation Theory K. Abed-Meraim ENST PARIS, Signal and Image Processing Dept. abed@tsi.enst.fr This presentation is essentially based on the course BASTA by E. Moulines Brief review on
Continuous Random Variables
 1 / 24 Continuous Random Variables Saravanan Vijayakumaran sarva@ee.iitb.ac.in Department of Electrical Engineering Indian Institute of Technology Bombay February 27, 2013 2 / 24 Continuous Random Variables
1 / 24 Continuous Random Variables Saravanan Vijayakumaran sarva@ee.iitb.ac.in Department of Electrical Engineering Indian Institute of Technology Bombay February 27, 2013 2 / 24 Continuous Random Variables
ST5215: Advanced Statistical Theory
 Department of Statistics & Applied Probability Wednesday, October 5, 2011 Lecture 13: Basic elements and notions in decision theory Basic elements X : a sample from a population P P Decision: an action
Department of Statistics & Applied Probability Wednesday, October 5, 2011 Lecture 13: Basic elements and notions in decision theory Basic elements X : a sample from a population P P Decision: an action
MAS113 Introduction to Probability and Statistics
 MAS113 Introduction to Probability and Statistics School of Mathematics and Statistics, University of Sheffield 2018 19 Identically distributed Suppose we have n random variables X 1, X 2,..., X n. Identically
MAS113 Introduction to Probability and Statistics School of Mathematics and Statistics, University of Sheffield 2018 19 Identically distributed Suppose we have n random variables X 1, X 2,..., X n. Identically
Chapter 2: Fundamentals of Statistics Lecture 15: Models and statistics
 Chapter 2: Fundamentals of Statistics Lecture 15: Models and statistics Data from one or a series of random experiments are collected. Planning experiments and collecting data (not discussed here). Analysis:
Chapter 2: Fundamentals of Statistics Lecture 15: Models and statistics Data from one or a series of random experiments are collected. Planning experiments and collecting data (not discussed here). Analysis:
Sampling Distributions
 Sampling Distributions In statistics, a random sample is a collection of independent and identically distributed (iid) random variables, and a sampling distribution is the distribution of a function of
Sampling Distributions In statistics, a random sample is a collection of independent and identically distributed (iid) random variables, and a sampling distribution is the distribution of a function of
Qualifying Exam in Probability and Statistics. https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf
 Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Miscellaneous Errors in the Chapter 6 Solutions
 Miscellaneous Errors in the Chapter 6 Solutions 3.30(b In this problem, early printings of the second edition use the beta(a, b distribution, but later versions use the Poisson(λ distribution. If your
Miscellaneous Errors in the Chapter 6 Solutions 3.30(b In this problem, early printings of the second edition use the beta(a, b distribution, but later versions use the Poisson(λ distribution. If your
STT 441 Final Exam Fall 2013
 STT 441 Final Exam Fall 2013 (12:45-2:45pm, Thursday, Dec. 12, 2013) NAME: ID: 1. No textbooks or class notes are allowed in this exam. 2. Be sure to show all of your work to receive credit. Credits are
STT 441 Final Exam Fall 2013 (12:45-2:45pm, Thursday, Dec. 12, 2013) NAME: ID: 1. No textbooks or class notes are allowed in this exam. 2. Be sure to show all of your work to receive credit. Credits are
Chapter 3. Point Estimation. 3.1 Introduction
 Chapter 3 Point Estimation Let (Ω, A, P θ ), P θ P = {P θ θ Θ}be probability space, X 1, X 2,..., X n : (Ω, A) (IR k, B k ) random variables (X, B X ) sample space γ : Θ IR k measurable function, i.e.
Chapter 3 Point Estimation Let (Ω, A, P θ ), P θ P = {P θ θ Θ}be probability space, X 1, X 2,..., X n : (Ω, A) (IR k, B k ) random variables (X, B X ) sample space γ : Θ IR k measurable function, i.e.
Random Variables and Their Distributions
 Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
p y (1 p) 1 y, y = 0, 1 p Y (y p) = 0, otherwise.
 1. Suppose Y 1, Y 2,..., Y n is an iid sample from a Bernoulli(p) population distribution, where 0 < p < 1 is unknown. The population pmf is p y (1 p) 1 y, y = 0, 1 p Y (y p) = (a) Prove that Y is the
1. Suppose Y 1, Y 2,..., Y n is an iid sample from a Bernoulli(p) population distribution, where 0 < p < 1 is unknown. The population pmf is p y (1 p) 1 y, y = 0, 1 p Y (y p) = (a) Prove that Y is the
1 Probability Model. 1.1 Types of models to be discussed in the course
 Sufficiency January 18, 016 Debdeep Pati 1 Probability Model Model: A family of distributions P θ : θ Θ}. P θ (B) is the probability of the event B when the parameter takes the value θ. P θ is described
Sufficiency January 18, 016 Debdeep Pati 1 Probability Model Model: A family of distributions P θ : θ Θ}. P θ (B) is the probability of the event B when the parameter takes the value θ. P θ is described
18.440: Lecture 28 Lectures Review
 18.440: Lecture 28 Lectures 18-27 Review Scott Sheffield MIT Outline Outline It s the coins, stupid Much of what we have done in this course can be motivated by the i.i.d. sequence X i where each X i is
18.440: Lecture 28 Lectures 18-27 Review Scott Sheffield MIT Outline Outline It s the coins, stupid Much of what we have done in this course can be motivated by the i.i.d. sequence X i where each X i is
Expectation. DS GA 1002 Statistical and Mathematical Models. Carlos Fernandez-Granda
 Expectation DS GA 1002 Statistical and Mathematical Models http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall16 Carlos Fernandez-Granda Aim Describe random variables with a few numbers: mean, variance,
Expectation DS GA 1002 Statistical and Mathematical Models http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall16 Carlos Fernandez-Granda Aim Describe random variables with a few numbers: mean, variance,
MATH c UNIVERSITY OF LEEDS Examination for the Module MATH2715 (January 2015) STATISTICAL METHODS. Time allowed: 2 hours
 MATH2750 This question paper consists of 8 printed pages, each of which is identified by the reference MATH275. All calculators must carry an approval sticker issued by the School of Mathematics. c UNIVERSITY
MATH2750 This question paper consists of 8 printed pages, each of which is identified by the reference MATH275. All calculators must carry an approval sticker issued by the School of Mathematics. c UNIVERSITY
Probability Models. 4. What is the definition of the expectation of a discrete random variable?
 1 Probability Models The list of questions below is provided in order to help you to prepare for the test and exam. It reflects only the theoretical part of the course. You should expect the questions
1 Probability Models The list of questions below is provided in order to help you to prepare for the test and exam. It reflects only the theoretical part of the course. You should expect the questions
Sampling Distributions
 In statistics, a random sample is a collection of independent and identically distributed (iid) random variables, and a sampling distribution is the distribution of a function of random sample. For example,
In statistics, a random sample is a collection of independent and identically distributed (iid) random variables, and a sampling distribution is the distribution of a function of random sample. For example,
PCMI Introduction to Random Matrix Theory Handout # REVIEW OF PROBABILITY THEORY. Chapter 1 - Events and Their Probabilities
 PCMI 207 - Introduction to Random Matrix Theory Handout #2 06.27.207 REVIEW OF PROBABILITY THEORY Chapter - Events and Their Probabilities.. Events as Sets Definition (σ-field). A collection F of subsets
PCMI 207 - Introduction to Random Matrix Theory Handout #2 06.27.207 REVIEW OF PROBABILITY THEORY Chapter - Events and Their Probabilities.. Events as Sets Definition (σ-field). A collection F of subsets
APPM/MATH 4/5520 Solutions to Exam I Review Problems. f X 1,X 2. 2e x 1 x 2. = x 2
 APPM/MATH 4/5520 Solutions to Exam I Review Problems. (a) f X (x ) f X,X 2 (x,x 2 )dx 2 x 2e x x 2 dx 2 2e 2x x was below x 2, but when marginalizing out x 2, we ran it over all values from 0 to and so
APPM/MATH 4/5520 Solutions to Exam I Review Problems. (a) f X (x ) f X,X 2 (x,x 2 )dx 2 x 2e x x 2 dx 2 2e 2x x was below x 2, but when marginalizing out x 2, we ran it over all values from 0 to and so
Chapter 5. Chapter 5 sections
 1 / 43 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
1 / 43 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
STAT 512 sp 2018 Summary Sheet
 STAT 5 sp 08 Summary Sheet Karl B. Gregory Spring 08. Transformations of a random variable Let X be a rv with support X and let g be a function mapping X to Y with inverse mapping g (A = {x X : g(x A}
STAT 5 sp 08 Summary Sheet Karl B. Gregory Spring 08. Transformations of a random variable Let X be a rv with support X and let g be a function mapping X to Y with inverse mapping g (A = {x X : g(x A}
Moments. Raw moment: February 25, 2014 Normalized / Standardized moment:
 Moments Lecture 10: Central Limit Theorem and CDFs Sta230 / Mth 230 Colin Rundel Raw moment: Central moment: µ n = EX n ) µ n = E[X µ) 2 ] February 25, 2014 Normalized / Standardized moment: µ n σ n Sta230
Moments Lecture 10: Central Limit Theorem and CDFs Sta230 / Mth 230 Colin Rundel Raw moment: Central moment: µ n = EX n ) µ n = E[X µ) 2 ] February 25, 2014 Normalized / Standardized moment: µ n σ n Sta230
Foundations of Statistical Inference
 Foundations of Statistical Inference Jonathan Marchini Department of Statistics University of Oxford MT 2013 Jonathan Marchini (University of Oxford) BS2a MT 2013 1 / 27 Course arrangements Lectures M.2
Foundations of Statistical Inference Jonathan Marchini Department of Statistics University of Oxford MT 2013 Jonathan Marchini (University of Oxford) BS2a MT 2013 1 / 27 Course arrangements Lectures M.2
Math 362, Problem set 1
 Math 6, roblem set Due //. (4..8) Determine the mean variance of the mean X of a rom sample of size 9 from a distribution having pdf f(x) = 4x, < x
Math 6, roblem set Due //. (4..8) Determine the mean variance of the mean X of a rom sample of size 9 from a distribution having pdf f(x) = 4x, < x
LIST OF FORMULAS FOR STK1100 AND STK1110
 LIST OF FORMULAS FOR STK1100 AND STK1110 (Version of 11. November 2015) 1. Probability Let A, B, A 1, A 2,..., B 1, B 2,... be events, that is, subsets of a sample space Ω. a) Axioms: A probability function
LIST OF FORMULAS FOR STK1100 AND STK1110 (Version of 11. November 2015) 1. Probability Let A, B, A 1, A 2,..., B 1, B 2,... be events, that is, subsets of a sample space Ω. a) Axioms: A probability function
Section 9.1. Expected Values of Sums
 Section 9.1 Expected Values of Sums Theorem 9.1 For any set of random variables X 1,..., X n, the sum W n = X 1 + + X n has expected value E [W n ] = E [X 1 ] + E [X 2 ] + + E [X n ]. Proof: Theorem 9.1
Section 9.1 Expected Values of Sums Theorem 9.1 For any set of random variables X 1,..., X n, the sum W n = X 1 + + X n has expected value E [W n ] = E [X 1 ] + E [X 2 ] + + E [X n ]. Proof: Theorem 9.1
Statistics Ph.D. Qualifying Exam: Part II November 9, 2002
 Statistics Ph.D. Qualifying Exam: Part II November 9, 2002 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Statistics Ph.D. Qualifying Exam: Part II November 9, 2002 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Expectation. DS GA 1002 Probability and Statistics for Data Science. Carlos Fernandez-Granda
 Expectation DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Aim Describe random variables with a few numbers: mean,
Expectation DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Aim Describe random variables with a few numbers: mean,
Probability Background
 Probability Background Namrata Vaswani, Iowa State University August 24, 2015 Probability recap 1: EE 322 notes Quick test of concepts: Given random variables X 1, X 2,... X n. Compute the PDF of the second
Probability Background Namrata Vaswani, Iowa State University August 24, 2015 Probability recap 1: EE 322 notes Quick test of concepts: Given random variables X 1, X 2,... X n. Compute the PDF of the second
Properties of Random Variables
 Properties of Random Variables 1 Definitions A discrete random variable is defined by a probability distribution that lists each possible outcome and the probability of obtaining that outcome If the random
Properties of Random Variables 1 Definitions A discrete random variable is defined by a probability distribution that lists each possible outcome and the probability of obtaining that outcome If the random
Chapter 8.8.1: A factorization theorem
 LECTURE 14 Chapter 8.8.1: A factorization theorem The characterization of a sufficient statistic in terms of the conditional distribution of the data given the statistic can be difficult to work with.
LECTURE 14 Chapter 8.8.1: A factorization theorem The characterization of a sufficient statistic in terms of the conditional distribution of the data given the statistic can be difficult to work with.
Distributions of Functions of Random Variables. 5.1 Functions of One Random Variable
 Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
Advanced Signal Processing Introduction to Estimation Theory
 Advanced Signal Processing Introduction to Estimation Theory Danilo Mandic, room 813, ext: 46271 Department of Electrical and Electronic Engineering Imperial College London, UK d.mandic@imperial.ac.uk,
Advanced Signal Processing Introduction to Estimation Theory Danilo Mandic, room 813, ext: 46271 Department of Electrical and Electronic Engineering Imperial College London, UK d.mandic@imperial.ac.uk,
Brief Review of Probability
 Maura Department of Economics and Finance Università Tor Vergata Outline 1 Distribution Functions Quantiles and Modes of a Distribution 2 Example 3 Example 4 Distributions Outline Distribution Functions
Maura Department of Economics and Finance Università Tor Vergata Outline 1 Distribution Functions Quantiles and Modes of a Distribution 2 Example 3 Example 4 Distributions Outline Distribution Functions
STAT 730 Chapter 4: Estimation
 STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
Part IA Probability. Definitions. Based on lectures by R. Weber Notes taken by Dexter Chua. Lent 2015
 Part IA Probability Definitions Based on lectures by R. Weber Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
Part IA Probability Definitions Based on lectures by R. Weber Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
A Few Notes on Fisher Information (WIP)
 A Few Notes on Fisher Information (WIP) David Meyer dmm@{-4-5.net,uoregon.edu} Last update: April 30, 208 Definitions There are so many interesting things about Fisher Information and its theoretical properties
A Few Notes on Fisher Information (WIP) David Meyer dmm@{-4-5.net,uoregon.edu} Last update: April 30, 208 Definitions There are so many interesting things about Fisher Information and its theoretical properties
1 Review of Probability and Distributions
 Random variables. A numerically valued function X of an outcome ω from a sample space Ω X : Ω R : ω X(ω) is called a random variable (r.v.), and usually determined by an experiment. We conventionally denote
Random variables. A numerically valued function X of an outcome ω from a sample space Ω X : Ω R : ω X(ω) is called a random variable (r.v.), and usually determined by an experiment. We conventionally denote
ECE531 Lecture 8: Non-Random Parameter Estimation
 ECE531 Lecture 8: Non-Random Parameter Estimation D. Richard Brown III Worcester Polytechnic Institute 19-March-2009 Worcester Polytechnic Institute D. Richard Brown III 19-March-2009 1 / 25 Introduction
ECE531 Lecture 8: Non-Random Parameter Estimation D. Richard Brown III Worcester Polytechnic Institute 19-March-2009 Worcester Polytechnic Institute D. Richard Brown III 19-March-2009 1 / 25 Introduction
Week 9 The Central Limit Theorem and Estimation Concepts
 Week 9 and Estimation Concepts Week 9 and Estimation Concepts Week 9 Objectives 1 The Law of Large Numbers and the concept of consistency of averages are introduced. The condition of existence of the population
Week 9 and Estimation Concepts Week 9 and Estimation Concepts Week 9 Objectives 1 The Law of Large Numbers and the concept of consistency of averages are introduced. The condition of existence of the population
HT Introduction. P(X i = x i ) = e λ λ x i
 MODS STATISTICS Introduction. HT 2012 Simon Myers, Department of Statistics (and The Wellcome Trust Centre for Human Genetics) myers@stats.ox.ac.uk We will be concerned with the mathematical framework
MODS STATISTICS Introduction. HT 2012 Simon Myers, Department of Statistics (and The Wellcome Trust Centre for Human Genetics) myers@stats.ox.ac.uk We will be concerned with the mathematical framework
SUFFICIENT STATISTICS
 SUFFICIENT STATISTICS. Introduction Let X (X,..., X n ) be a random sample from f θ, where θ Θ is unknown. We are interested using X to estimate θ. In the simple case where X i Bern(p), we found that the
SUFFICIENT STATISTICS. Introduction Let X (X,..., X n ) be a random sample from f θ, where θ Θ is unknown. We are interested using X to estimate θ. In the simple case where X i Bern(p), we found that the
f(y θ) = g(t (y) θ)h(y)
 EXAM3, FINAL REVIEW (and a review for some of the QUAL problems): No notes will be allowed, but you may bring a calculator. Memorize the pmf or pdf f, E(Y ) and V(Y ) for the following RVs: 1) beta(δ,
EXAM3, FINAL REVIEW (and a review for some of the QUAL problems): No notes will be allowed, but you may bring a calculator. Memorize the pmf or pdf f, E(Y ) and V(Y ) for the following RVs: 1) beta(δ,
Stat 5101 Lecture Slides: Deck 7 Asymptotics, also called Large Sample Theory. Charles J. Geyer School of Statistics University of Minnesota
 Stat 5101 Lecture Slides: Deck 7 Asymptotics, also called Large Sample Theory Charles J. Geyer School of Statistics University of Minnesota 1 Asymptotic Approximation The last big subject in probability
Stat 5101 Lecture Slides: Deck 7 Asymptotics, also called Large Sample Theory Charles J. Geyer School of Statistics University of Minnesota 1 Asymptotic Approximation The last big subject in probability
STA 260: Statistics and Probability II
 Al Nosedal. University of Toronto. Winter 2017 1 Properties of Point Estimators and Methods of Estimation 2 3 If you can t explain it simply, you don t understand it well enough Albert Einstein. Definition
Al Nosedal. University of Toronto. Winter 2017 1 Properties of Point Estimators and Methods of Estimation 2 3 If you can t explain it simply, you don t understand it well enough Albert Einstein. Definition
3. Probability and Statistics
 FE661 - Statistical Methods for Financial Engineering 3. Probability and Statistics Jitkomut Songsiri definitions, probability measures conditional expectations correlation and covariance some important
FE661 - Statistical Methods for Financial Engineering 3. Probability and Statistics Jitkomut Songsiri definitions, probability measures conditional expectations correlation and covariance some important
1 Complete Statistics
 Complete Statistics February 4, 2016 Debdeep Pati 1 Complete Statistics Suppose X P θ, θ Θ. Let (X (1),..., X (n) ) denote the order statistics. Definition 1. A statistic T = T (X) is complete if E θ g(t
Complete Statistics February 4, 2016 Debdeep Pati 1 Complete Statistics Suppose X P θ, θ Θ. Let (X (1),..., X (n) ) denote the order statistics. Definition 1. A statistic T = T (X) is complete if E θ g(t
First Year Examination Department of Statistics, University of Florida
 First Year Examination Department of Statistics, University of Florida August 19, 010, 8:00 am - 1:00 noon Instructions: 1. You have four hours to answer questions in this examination.. You must show your
First Year Examination Department of Statistics, University of Florida August 19, 010, 8:00 am - 1:00 noon Instructions: 1. You have four hours to answer questions in this examination.. You must show your
ACM 116: Lectures 3 4
 1 ACM 116: Lectures 3 4 Joint distributions The multivariate normal distribution Conditional distributions Independent random variables Conditional distributions and Monte Carlo: Rejection sampling Variance
1 ACM 116: Lectures 3 4 Joint distributions The multivariate normal distribution Conditional distributions Independent random variables Conditional distributions and Monte Carlo: Rejection sampling Variance
6.041/6.431 Fall 2010 Quiz 2 Solutions
 6.04/6.43: Probabilistic Systems Analysis (Fall 200) 6.04/6.43 Fall 200 Quiz 2 Solutions Problem. (80 points) In this problem: (i) X is a (continuous) uniform random variable on [0, 4]. (ii) Y is an exponential
6.04/6.43: Probabilistic Systems Analysis (Fall 200) 6.04/6.43 Fall 200 Quiz 2 Solutions Problem. (80 points) In this problem: (i) X is a (continuous) uniform random variable on [0, 4]. (ii) Y is an exponential
Tom Salisbury
 MATH 2030 3.00MW Elementary Probability Course Notes Part V: Independence of Random Variables, Law of Large Numbers, Central Limit Theorem, Poisson distribution Geometric & Exponential distributions Tom
MATH 2030 3.00MW Elementary Probability Course Notes Part V: Independence of Random Variables, Law of Large Numbers, Central Limit Theorem, Poisson distribution Geometric & Exponential distributions Tom
Chapter 4. Chapter 4 sections
 Chapter 4 sections 4.1 Expectation 4.2 Properties of Expectations 4.3 Variance 4.4 Moments 4.5 The Mean and the Median 4.6 Covariance and Correlation 4.7 Conditional Expectation SKIP: 4.8 Utility Expectation
Chapter 4 sections 4.1 Expectation 4.2 Properties of Expectations 4.3 Variance 4.4 Moments 4.5 The Mean and the Median 4.6 Covariance and Correlation 4.7 Conditional Expectation SKIP: 4.8 Utility Expectation
System Identification, Lecture 4
 System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2012 F, FRI Uppsala University, Information Technology 30 Januari 2012 SI-2012 K. Pelckmans
System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2012 F, FRI Uppsala University, Information Technology 30 Januari 2012 SI-2012 K. Pelckmans
Formulas for probability theory and linear models SF2941
 Formulas for probability theory and linear models SF2941 These pages + Appendix 2 of Gut) are permitted as assistance at the exam. 11 maj 2008 Selected formulae of probability Bivariate probability Transforms
Formulas for probability theory and linear models SF2941 These pages + Appendix 2 of Gut) are permitted as assistance at the exam. 11 maj 2008 Selected formulae of probability Bivariate probability Transforms
System Identification, Lecture 4
 System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2016 F, FRI Uppsala University, Information Technology 13 April 2016 SI-2016 K. Pelckmans
System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2016 F, FRI Uppsala University, Information Technology 13 April 2016 SI-2016 K. Pelckmans
Problem Solving. Correlation and Covariance. Yi Lu. Problem Solving. Yi Lu ECE 313 2/51
 Yi Lu Correlation and Covariance Yi Lu ECE 313 2/51 Definition Let X and Y be random variables with finite second moments. the correlation: E[XY ] Yi Lu ECE 313 3/51 Definition Let X and Y be random variables
Yi Lu Correlation and Covariance Yi Lu ECE 313 2/51 Definition Let X and Y be random variables with finite second moments. the correlation: E[XY ] Yi Lu ECE 313 3/51 Definition Let X and Y be random variables
5 Operations on Multiple Random Variables
 EE360 Random Signal analysis Chapter 5: Operations on Multiple Random Variables 5 Operations on Multiple Random Variables Expected value of a function of r.v. s Two r.v. s: ḡ = E[g(X, Y )] = g(x, y)f X,Y
EE360 Random Signal analysis Chapter 5: Operations on Multiple Random Variables 5 Operations on Multiple Random Variables Expected value of a function of r.v. s Two r.v. s: ḡ = E[g(X, Y )] = g(x, y)f X,Y
18.440: Lecture 28 Lectures Review
 18.440: Lecture 28 Lectures 17-27 Review Scott Sheffield MIT 1 Outline Continuous random variables Problems motivated by coin tossing Random variable properties 2 Outline Continuous random variables Problems
18.440: Lecture 28 Lectures 17-27 Review Scott Sheffield MIT 1 Outline Continuous random variables Problems motivated by coin tossing Random variable properties 2 Outline Continuous random variables Problems
Part IA Probability. Theorems. Based on lectures by R. Weber Notes taken by Dexter Chua. Lent 2015
 Part IA Probability Theorems Based on lectures by R. Weber Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
Part IA Probability Theorems Based on lectures by R. Weber Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
Expectation of Random Variables
 1 / 19 Expectation of Random Variables Saravanan Vijayakumaran sarva@ee.iitb.ac.in Department of Electrical Engineering Indian Institute of Technology Bombay February 13, 2015 2 / 19 Expectation of Discrete
1 / 19 Expectation of Random Variables Saravanan Vijayakumaran sarva@ee.iitb.ac.in Department of Electrical Engineering Indian Institute of Technology Bombay February 13, 2015 2 / 19 Expectation of Discrete
March 10, 2017 THE EXPONENTIAL CLASS OF DISTRIBUTIONS
 March 10, 2017 THE EXPONENTIAL CLASS OF DISTRIBUTIONS Abstract. We will introduce a class of distributions that will contain many of the discrete and continuous we are familiar with. This class will help
March 10, 2017 THE EXPONENTIAL CLASS OF DISTRIBUTIONS Abstract. We will introduce a class of distributions that will contain many of the discrete and continuous we are familiar with. This class will help
Statistics STAT:5100 (22S:193), Fall Sample Final Exam B
 Statistics STAT:5 (22S:93), Fall 25 Sample Final Exam B Please write your answers in the exam books provided.. Let X, Y, and Y 2 be independent random variables with X N(µ X, σ 2 X ) and Y i N(µ Y, σ 2
Statistics STAT:5 (22S:93), Fall 25 Sample Final Exam B Please write your answers in the exam books provided.. Let X, Y, and Y 2 be independent random variables with X N(µ X, σ 2 X ) and Y i N(µ Y, σ 2
Part IB Statistics. Theorems with proof. Based on lectures by D. Spiegelhalter Notes taken by Dexter Chua. Lent 2015
 Part IB Statistics Theorems with proof Based on lectures by D. Spiegelhalter Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Part IB Statistics Theorems with proof Based on lectures by D. Spiegelhalter Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003
 Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Problem Selected Scores
 Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
1: PROBABILITY REVIEW
 1: PROBABILITY REVIEW Marek Rutkowski School of Mathematics and Statistics University of Sydney Semester 2, 2016 M. Rutkowski (USydney) Slides 1: Probability Review 1 / 56 Outline We will review the following
1: PROBABILITY REVIEW Marek Rutkowski School of Mathematics and Statistics University of Sydney Semester 2, 2016 M. Rutkowski (USydney) Slides 1: Probability Review 1 / 56 Outline We will review the following
Chapter 6: Random Processes 1
 Chapter 6: Random Processes 1 Yunghsiang S. Han Graduate Institute of Communication Engineering, National Taipei University Taiwan E-mail: yshan@mail.ntpu.edu.tw 1 Modified from the lecture notes by Prof.
Chapter 6: Random Processes 1 Yunghsiang S. Han Graduate Institute of Communication Engineering, National Taipei University Taiwan E-mail: yshan@mail.ntpu.edu.tw 1 Modified from the lecture notes by Prof.
Estimation and Detection
 stimation and Detection Lecture 2: Cramér-Rao Lower Bound Dr. ir. Richard C. Hendriks & Dr. Sundeep P. Chepuri 7//207 Remember: Introductory xample Given a process (DC in noise): x[n]=a + w[n], n=0,,n,
stimation and Detection Lecture 2: Cramér-Rao Lower Bound Dr. ir. Richard C. Hendriks & Dr. Sundeep P. Chepuri 7//207 Remember: Introductory xample Given a process (DC in noise): x[n]=a + w[n], n=0,,n,
Probability Theory and Statistics. Peter Jochumzen
 Probability Theory and Statistics Peter Jochumzen April 18, 2016 Contents 1 Probability Theory And Statistics 3 1.1 Experiment, Outcome and Event................................ 3 1.2 Probability............................................
Probability Theory and Statistics Peter Jochumzen April 18, 2016 Contents 1 Probability Theory And Statistics 3 1.1 Experiment, Outcome and Event................................ 3 1.2 Probability............................................
ENEE 621 SPRING 2016 DETECTION AND ESTIMATION THEORY THE PARAMETER ESTIMATION PROBLEM
 c 2007-2016 by Armand M. Makowski 1 ENEE 621 SPRING 2016 DETECTION AND ESTIMATION THEORY THE PARAMETER ESTIMATION PROBLEM 1 The basic setting Throughout, p, q and k are positive integers. The setup With
c 2007-2016 by Armand M. Makowski 1 ENEE 621 SPRING 2016 DETECTION AND ESTIMATION THEORY THE PARAMETER ESTIMATION PROBLEM 1 The basic setting Throughout, p, q and k are positive integers. The setup With
Two hours. Statistical Tables to be provided THE UNIVERSITY OF MANCHESTER. 14 January :45 11:45
 Two hours Statistical Tables to be provided THE UNIVERSITY OF MANCHESTER PROBABILITY 2 14 January 2015 09:45 11:45 Answer ALL four questions in Section A (40 marks in total) and TWO of the THREE questions
Two hours Statistical Tables to be provided THE UNIVERSITY OF MANCHESTER PROBABILITY 2 14 January 2015 09:45 11:45 Answer ALL four questions in Section A (40 marks in total) and TWO of the THREE questions
Qualifying Exam in Probability and Statistics. https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf
 Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
