Section 8.3. First Order Linear Differential Equations
|
|
|
- Claribel Rice
- 5 years ago
- Views:
Transcription
1 Section 8.3 First Order Linear Differential Equations We will now consider closed form solutions for another important class of differential equations. A differential equation ẋ = f(x, t with x( = x is called a linear equation if f(x, t = p(tx + q(t (8.3. for some functions p and q which depend only on t. We will assume that both p and q are continuous functions. Note that under certain circumstances, such as q(t = for all t, a linear equation is also separable. The solution of such equations is based on the following observation: If we let then P (t = p(sds, (8.3.2 xe P (t = xp(te P (t + ẋe P (t = e P (t (ẋ p(tx. (8.3.3 dt Now we want ẋ = p(tx + q(t, that is, ẋ p(tx = q(t, so we are looking for a function x such that xe P (t = q(te P (t. (8.3.4 dt Integrating (8.3.4 from to t (using u for our variable of integration, we have x(ue P (u du = q(ue P (u du. (8.3.5 du Now x(ue P (u du = x(ue P (u t du = x(te P (t x( e P ( = x(te P (t x (8.3.6 since P ( = and x( = x. Hence we want x(te P (t x = q(ue P (u du. (8.3.7
2 2 First Order Linear Differential Equations Section 8.3 Solving (8.3.7 fot x(t, we have x(t = e P (t ( q(ue P (u du + x. (8.3.8 Similar to our situation with separable equations, (8.3.8 provides a closed form solution to our equation only if the requisite integrals may be computed in closed form. If not, numerical techniques will be necessary. Linear equations If p and q are continuous, x satisfies the differential equation ẋ = p(tx + q(t (8.3.9 with x( = x, and then P (t = x(t = e P (t ( p(sds, (8.3. q(ue P (u du + x. (8.3. Example Consider the equation ẋ = x t + 4t with x( = 5. This is a linear equation with, in the notation used above, and Then P (t = p(t = t q(t = 4t. s ds = log(s t = log(t, where, in order for the integral to exist, we have restricted t to be positive. Thus, using (8.3., ( x = e log(t 4ue log(u du + 5 ( 4u = t u du + 5 ( = t 4du + 5 ( = t 4t t + 5 = t(4t 4 + 5t = 4t 2 + t.
3 Section 8.3 First Order Linear Differential Equations Figure 8.3. A solution of ẋ =.2( + e.t x Example The equation ẋ = p(tx with x( = x may be used as a model for growth or decay where the rate of growth or decay is not necessarily a constant. Such an equation may be solved by separating variables, but the solution also follows from (8.3.: Since q(t = for all t, we have x = x e p(sds. For example, if p(t = k for all t, where k is a constant, then we obtain the familiar solution x = x e kt. If p(t =.2( + e.t, as in an example in Section 8., then Hence p(sds =.2( + e.s ds =.2(s e.s =.2(t e.t.2( =.2t.2e.t +.2. x = x e.2t.2e.t The graph of x when x = 5 is shown in Figure You should compare this with the plot of an approximate solution in Figure Example A small reservoir holds, cubic feet of water. Water flows in at a rate of cubic feet per hour and out at the same rate. Suppose initially the water in the reservoir contains 5 grams of salt per cubic foot, but the water flowing in contains grams
4 4 First Order Linear Differential Equations Section Figure Graph of x =, 5, e.t of salt per cubic foot. Let x(t be the amount of salt in the reservoir after t hours. Note that salt is entering the reservoir at a rate of grams per hour. Assuming the water in the reservoir is well-mixed at all times, the concentration of salt in the reservoir at time t is x(t, grams per cubic foot, from which it follows that salt is leaving the reservoir at a rate of x(t, = x(t grams per hour. Thus the rate of change of salt in the reservoir is given by ẋ =.x. That is, x satisfies a linear differential equation with p(t =. and q(t =. Then P (t =.ds =.t, and so, using x( = (5(, = 5, grams, we have ( x = e.t e.u du + 5, In particular, note that = e.t(, e.u t + 5, = e.t (, e.t, + 5, =, 5, e.t. lim x(t = lim, 5, t t e.t =,, and we see that over time the concentration of salt in the reservoir will approach the concentration of salt in its intake water. The graph of x is shown in Figure
5 Section 8.3 First Order Linear Differential Equations 5 Problems. Solve each of the following linear differential equations. (a ẋ = 3x + 2t, x( = 2 (b ẋ = 2x t 2, x( = (c ẏ =.4y + 3, y( = 5 (d ẇ = w + e 2t, w( = 3 (e ẋ = 2x t + t2, x( = 4 (f ẏ = y + 2e t + t 2, y( = 2. In 99 the population of Botswana was.2 million. If x(t is the population of Botswana t years after 99, suppose x satisfies the differential equation ẋ = k(tx, where k(t represents the rate of growth of the population at time t. At the start of 99 the population of Botswana was growing at the rate of 2.9%, so k( =.29. (a Suppose the rate of growth of the population is decreasing toward.5% in such a way that k(t =.5( +.93e.4t. Solve for x. (b Compare your result in (a with the result for a constant rate of growth of k(t =.29 by plotting both solutions together. 3. Suppose the population of a certain country was 56 million in 2 and the natural rate of the growth of the population was 2% per year. Moreover, suppose k(t represents the net rate of growth of the population due to immigration and emigration t years after 2. (a Let y(t be the population of the country t years after 2. Explain why y should satisfy the differential equation with y( = 56. dy dt =.2y + k(t, (b Solve the equation if k(t =.4t. Plot your results. (c What does this model predict for the population of the country in the year 2? (d When will the population of the country reach million? (e Compare your results with the numerical results obtained for the same problem in Problem 9 of Section A 5 gallon tank is initially filled with water with a concentration of 4 grams of salt per gallon. Water flows into the tank at the rate of gallons per minute and is drawn off at the same rate. The concentration of salt in the intake water is 2 grams per gallon. Assume that the water in the tank is well-mixed at all times.
6 6 First Order Linear Differential Equations Section 8.3 (a Let x(t be the amount of salt in the tank at time t. Find a linear differential equation for x which models this situation. (b Solve the equation from (a and graph the solution. increases? What happens to x as t 5. Suppose a tank holds V liters of a liquid which contains a certain chemical at a concentration of k grams per liter. Liquid flows into the tank at rate of q liters per second and is drawn off at the same rate. The concentration of the chemical in the intake liquid is k grams per liter. (a If x(t is the amount of the chemical in the tank at time t, show that x satisfies the linear differential equation with x( = k V. ẋ = qk q V x (b Solve the equation in (a. What happens to x as t? 6. An equation of the form ẋ = p(tx + q(tx n (8.3.2 is called a Bernoulli equation. Note that the equation is linear if either n = or n =. (a Assume n and n. Show that the substitution w = x n in (8.3.2 results in the linear differential equation ẇ = ( np(tw + ( nq(t. (b Use the result of (a to solve the equation with x( =. ẋ = x t x2 (c Use the result of (a to solve the equation with x( =.5. =x( x 7. Note that (c of Problem 6 is a particular example of the logistic differential equation that we studied in Section 6.3 in our discussion of the inhibited population growth model. In general, we considered the logistic equation ẋ = α x(m x M with x( = x, where x(t is the size of the population at time t, α is the natural growth rate of the population, and M is the maximum size of the population that is
7 Section 8.3 First Order Linear Differential Equations 7 sustainable in the given environment. Write this equation in the form of a Bernoulli equation and use the result from (a of Problem 6 to show that x = M + βe αt where β = M x x.
A population is modeled by the differential equation
 Math 2, Winter 2016 Weekly Homework #8 Solutions 9.1.9. A population is modeled by the differential equation dt = 1.2 P 1 P ). 4200 a) For what values of P is the population increasing? P is increasing
Math 2, Winter 2016 Weekly Homework #8 Solutions 9.1.9. A population is modeled by the differential equation dt = 1.2 P 1 P ). 4200 a) For what values of P is the population increasing? P is increasing
(a) x cos 3x dx We apply integration by parts. Take u = x, so that dv = cos 3x dx, v = 1 sin 3x, du = dx. Thus
 Math 128 Midterm Examination 2 October 21, 28 Name 6 problems, 112 (oops) points. Instructions: Show all work partial credit will be given, and Answers without work are worth credit without points. You
Math 128 Midterm Examination 2 October 21, 28 Name 6 problems, 112 (oops) points. Instructions: Show all work partial credit will be given, and Answers without work are worth credit without points. You
( ) ( ). ( ) " d#. ( ) " cos (%) " d%
 Math 22 Fall 2008 Solutions to Homework #6 Problems from Pages 404-407 (Section 76) 6 We will use the technique of Separation of Variables to solve the differential equation: dy d" = ey # sin 2 (") y #
Math 22 Fall 2008 Solutions to Homework #6 Problems from Pages 404-407 (Section 76) 6 We will use the technique of Separation of Variables to solve the differential equation: dy d" = ey # sin 2 (") y #
Name: October 24, 2014 ID Number: Fall Midterm I. Number Total Points Points Obtained Total 40
 Math 307O: Introduction to Differential Equations Name: October 24, 204 ID Number: Fall 204 Midterm I Number Total Points Points Obtained 0 2 0 3 0 4 0 Total 40 Instructions.. Show all your work and box
Math 307O: Introduction to Differential Equations Name: October 24, 204 ID Number: Fall 204 Midterm I Number Total Points Points Obtained 0 2 0 3 0 4 0 Total 40 Instructions.. Show all your work and box
The Fundamental Theorem of Calculus: Suppose f continuous on [a, b]. 1.) If G(x) = x. f(t)dt = F (b) F (a) where F is any antiderivative
![The Fundamental Theorem of Calculus: Suppose f continuous on [a, b]. 1.) If G(x) = x. f(t)dt = F (b) F (a) where F is any antiderivative The Fundamental Theorem of Calculus: Suppose f continuous on [a, b]. 1.) If G(x) = x. f(t)dt = F (b) F (a) where F is any antiderivative](/thumbs/96/128959530.jpg) 1 Calulus pre-requisites you must know. Derivative = slope of tangent line = rate. Integral = area between curve and x-axis (where area can be negative). The Fundamental Theorem of Calculus: Suppose f
1 Calulus pre-requisites you must know. Derivative = slope of tangent line = rate. Integral = area between curve and x-axis (where area can be negative). The Fundamental Theorem of Calculus: Suppose f
Section 6.3. x m+1 x m = i n x m, (6.3.1)
 Difference Equations to Differential Equations Section 6.3 Models of Growth and Decay In this section we will look at several applications of the exponential and logarithm functions to problems involving
Difference Equations to Differential Equations Section 6.3 Models of Growth and Decay In this section we will look at several applications of the exponential and logarithm functions to problems involving
Chapters 8.1 & 8.2 Practice Problems
 EXPECTED SKILLS: Chapters 8.1 & 8. Practice Problems Be able to verify that a given function is a solution to a differential equation. Given a description in words of how some quantity changes in time
EXPECTED SKILLS: Chapters 8.1 & 8. Practice Problems Be able to verify that a given function is a solution to a differential equation. Given a description in words of how some quantity changes in time
Practice Questions From Calculus II. 0. State the following calculus rules (these are many of the key rules from Test 1 topics).
 Math 132. Practice Questions From Calculus II I. Topics Covered in Test I 0. State the following calculus rules (these are many of the key rules from Test 1 topics). (Trapezoidal Rule) b a f(x) dx (Fundamental
Math 132. Practice Questions From Calculus II I. Topics Covered in Test I 0. State the following calculus rules (these are many of the key rules from Test 1 topics). (Trapezoidal Rule) b a f(x) dx (Fundamental
Math 308 Exam I Practice Problems
 Math 308 Exam I Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture and all suggested homework problems..
Math 308 Exam I Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture and all suggested homework problems..
Briggs 6.1: Velocity and Net Change
 Briggs 6.: Velocity and Net Change Problem Consider an object moving along a line. The graph of the velocity, vt), of the object is shown in the figure below. In the figure above, graph the best you can)
Briggs 6.: Velocity and Net Change Problem Consider an object moving along a line. The graph of the velocity, vt), of the object is shown in the figure below. In the figure above, graph the best you can)
Math 308 Exam I Practice Problems
 Math 308 Exam I Practice Problems This review should not be used as your sole source of preparation for the exam. You should also re-work all examples given in lecture and all suggested homework problems..
Math 308 Exam I Practice Problems This review should not be used as your sole source of preparation for the exam. You should also re-work all examples given in lecture and all suggested homework problems..
Limited Growth (Logistic Equation)
 Chapter 2, Part 2 2.4. Applications Orthogonal trajectories Exponential Growth/Decay Newton s Law of Cooling/Heating Limited Growth (Logistic Equation) Miscellaneous Models 1 2.4.1. Orthogonal Trajectories
Chapter 2, Part 2 2.4. Applications Orthogonal trajectories Exponential Growth/Decay Newton s Law of Cooling/Heating Limited Growth (Logistic Equation) Miscellaneous Models 1 2.4.1. Orthogonal Trajectories
y0 = F (t0)+c implies C = y0 F (t0) Integral = area between curve and x-axis (where I.e., f(t)dt = F (b) F (a) wheref is any antiderivative 2.
 Calulus pre-requisites you must know. Derivative = slope of tangent line = rate. Integral = area between curve and x-axis (where area can be negative). The Fundamental Theorem of Calculus: Suppose f continuous
Calulus pre-requisites you must know. Derivative = slope of tangent line = rate. Integral = area between curve and x-axis (where area can be negative). The Fundamental Theorem of Calculus: Suppose f continuous
FINAL EXAM CALCULUS 2. Name PRACTICE EXAM SOLUTIONS
 FINAL EXAM CALCULUS MATH 00 FALL 08 Name PRACTICE EXAM SOLUTIONS Please answer all of the questions, and show your work. You must explain your answers to get credit. You will be graded on the clarity of
FINAL EXAM CALCULUS MATH 00 FALL 08 Name PRACTICE EXAM SOLUTIONS Please answer all of the questions, and show your work. You must explain your answers to get credit. You will be graded on the clarity of
Differential equations
 Differential equations Math 27 Spring 2008 In-term exam February 5th. Solutions This exam contains fourteen problems numbered through 4. Problems 3 are multiple choice problems, which each count 6% of
Differential equations Math 27 Spring 2008 In-term exam February 5th. Solutions This exam contains fourteen problems numbered through 4. Problems 3 are multiple choice problems, which each count 6% of
Exam 1 Review: Questions and Answers. Part I. Finding solutions of a given differential equation.
 Exam 1 Review: Questions and Answers Part I. Finding solutions of a given differential equation. 1. Find the real numbers r such that y = e x is a solution of y y 30y = 0. Answer: r = 6, 5 2. Find the
Exam 1 Review: Questions and Answers Part I. Finding solutions of a given differential equation. 1. Find the real numbers r such that y = e x is a solution of y y 30y = 0. Answer: r = 6, 5 2. Find the
MAT 311 Midterm #1 Show your work! 1. The existence and uniqueness theorem says that, given a point (x 0, y 0 ) the ODE. y = (1 x 2 y 2 ) 1/3
 MAT 3 Midterm # Show your work!. The existence and uniqueness theorem says that, given a point (x 0, y 0 ) the ODE y = ( x 2 y 2 ) /3 has a unique (local) solution with initial condition y(x 0 ) = y 0
MAT 3 Midterm # Show your work!. The existence and uniqueness theorem says that, given a point (x 0, y 0 ) the ODE y = ( x 2 y 2 ) /3 has a unique (local) solution with initial condition y(x 0 ) = y 0
1.5. Applications. Theorem The solution of the exponential decay equation with N(0) = N 0 is N(t) = N 0 e kt.
 6 Section Objective(s): The Radioactive Decay Equation Newton s Cooling Law Salt in a Water Tanks 151 Exponential Decay 15 Applications Definition 151 The exponential decay equation for N is N = k N, k
6 Section Objective(s): The Radioactive Decay Equation Newton s Cooling Law Salt in a Water Tanks 151 Exponential Decay 15 Applications Definition 151 The exponential decay equation for N is N = k N, k
MA 214 Calculus IV (Spring 2016) Section 2. Homework Assignment 2 Solutions
 MA 214 Calculus IV (Spring 2016) Section 2 Homework Assignment 2 Solutions 1 Boyce and DiPrima, p 60, Problem 2 Solution: Let M(t) be the mass (in grams) of salt in the tank after t minutes The initial-value
MA 214 Calculus IV (Spring 2016) Section 2 Homework Assignment 2 Solutions 1 Boyce and DiPrima, p 60, Problem 2 Solution: Let M(t) be the mass (in grams) of salt in the tank after t minutes The initial-value
Math 31S. Rumbos Fall Solutions to Exam 1
 Math 31S. Rumbos Fall 2011 1 Solutions to Exam 1 1. When people smoke, carbon monoxide is released into the air. Suppose that in a room of volume 60 m 3, air containing 5% carbon monoxide is introduced
Math 31S. Rumbos Fall 2011 1 Solutions to Exam 1 1. When people smoke, carbon monoxide is released into the air. Suppose that in a room of volume 60 m 3, air containing 5% carbon monoxide is introduced
Differential Equations Spring 2007 Assignments
 Differential Equations Spring 2007 Assignments Homework 1, due 1/10/7 Read the first two chapters of the book up to the end of section 2.4. Prepare for the first quiz on Friday 10th January (material up
Differential Equations Spring 2007 Assignments Homework 1, due 1/10/7 Read the first two chapters of the book up to the end of section 2.4. Prepare for the first quiz on Friday 10th January (material up
Exam 3. MA 114 Exam 3 Fall Multiple Choice Questions. 1. Find the average value of the function f (x) = 2 sin x sin 2x on 0 x π. C. 0 D. 4 E.
 Exam 3 Multiple Choice Questions 1. Find the average value of the function f (x) = sin x sin x on x π. A. π 5 π C. E. 5. Find the volume of the solid S whose base is the disk bounded by the circle x +
Exam 3 Multiple Choice Questions 1. Find the average value of the function f (x) = sin x sin x on x π. A. π 5 π C. E. 5. Find the volume of the solid S whose base is the disk bounded by the circle x +
Ordinary Differential Equations
 Ordinary Differential Equations Swaroop Nandan Bora swaroop@iitg.ernet.in Department of Mathematics Indian Institute of Technology Guwahati Guwahati-781039 A first-order differential equation is an equation
Ordinary Differential Equations Swaroop Nandan Bora swaroop@iitg.ernet.in Department of Mathematics Indian Institute of Technology Guwahati Guwahati-781039 A first-order differential equation is an equation
Unit #17 - Differential Equations Section 11.6
 Unit #7 - Differential Equations Section.6 Some material from Calculus, Single and MultiVariable by Hughes-Hallett, Gleason, McCallum et. al. Copyright 005 by John Wiley & Sons, Inc. This material is used
Unit #7 - Differential Equations Section.6 Some material from Calculus, Single and MultiVariable by Hughes-Hallett, Gleason, McCallum et. al. Copyright 005 by John Wiley & Sons, Inc. This material is used
MATH 307 Introduction to Differential Equations Autumn 2017 Midterm Exam Monday November
 MATH 307 Introduction to Differential Equations Autumn 2017 Midterm Exam Monday November 6 2017 Name: Student ID Number: I understand it is against the rules to cheat or engage in other academic misconduct
MATH 307 Introduction to Differential Equations Autumn 2017 Midterm Exam Monday November 6 2017 Name: Student ID Number: I understand it is against the rules to cheat or engage in other academic misconduct
Form A. 1. Which of the following is a second-order, linear, homogenous differential equation? 2
 Form A Math 4 Common Part of Final Exam December 6, 996 INSTRUCTIONS: Please enter your NAME, ID NUMBER, FORM designation, and INDEX NUMBER on your op scan sheet. The index number should be written in
Form A Math 4 Common Part of Final Exam December 6, 996 INSTRUCTIONS: Please enter your NAME, ID NUMBER, FORM designation, and INDEX NUMBER on your op scan sheet. The index number should be written in
Sample Questions, Exam 1 Math 244 Spring 2007
 Sample Questions, Exam Math 244 Spring 2007 Remember, on the exam you may use a calculator, but NOT one that can perform symbolic manipulation (remembering derivative and integral formulas are a part of
Sample Questions, Exam Math 244 Spring 2007 Remember, on the exam you may use a calculator, but NOT one that can perform symbolic manipulation (remembering derivative and integral formulas are a part of
University of Toronto Solutions to MAT187H1S TERM TEST of Thursday, March 20, 2008 Duration: 90 minutes
 University of Toronto Solutions to MAT187H1S TERM TEST of Thursday, March 2, 28 Duration: 9 minutes Only aids permitted: Casio 26, Sharp 52, or Texas Instrument 3 calculator. Instructions: Make sure this
University of Toronto Solutions to MAT187H1S TERM TEST of Thursday, March 2, 28 Duration: 9 minutes Only aids permitted: Casio 26, Sharp 52, or Texas Instrument 3 calculator. Instructions: Make sure this
+ 1 for x > 2 (B) (E) (B) 2. (C) 1 (D) 2 (E) Nonexistent
 dx = (A) 3 sin(3x ) + C 1. cos ( 3x) 1 (B) sin(3x ) + C 3 1 (C) sin(3x ) + C 3 (D) sin( 3x ) + C (E) 3 sin(3x ) + C 6 3 2x + 6x 2. lim 5 3 x 0 4x + 3x (A) 0 1 (B) 2 (C) 1 (D) 2 (E) Nonexistent is 2 x 3x
dx = (A) 3 sin(3x ) + C 1. cos ( 3x) 1 (B) sin(3x ) + C 3 1 (C) sin(3x ) + C 3 (D) sin( 3x ) + C (E) 3 sin(3x ) + C 6 3 2x + 6x 2. lim 5 3 x 0 4x + 3x (A) 0 1 (B) 2 (C) 1 (D) 2 (E) Nonexistent is 2 x 3x
APPLICATIONS OF INTEGRATION
 6 APPLICATIONS OF INTEGRATION APPLICATIONS OF INTEGRATION 6.5 Average Value of a Function In this section, we will learn about: Applying integration to find out the average value of a function. AVERAGE
6 APPLICATIONS OF INTEGRATION APPLICATIONS OF INTEGRATION 6.5 Average Value of a Function In this section, we will learn about: Applying integration to find out the average value of a function. AVERAGE
Math Assignment 2
 Math 2280 - Assignment 2 Dylan Zwick Spring 2014 Section 1.5-1, 15, 21, 29, 38, 42 Section 1.6-1, 3, 13, 16, 22, 26, 31, 36, 56 Section 2.1-1, 8, 11, 16, 29 Section 2.2-1, 10, 21, 23, 24 1 Section 1.5
Math 2280 - Assignment 2 Dylan Zwick Spring 2014 Section 1.5-1, 15, 21, 29, 38, 42 Section 1.6-1, 3, 13, 16, 22, 26, 31, 36, 56 Section 2.1-1, 8, 11, 16, 29 Section 2.2-1, 10, 21, 23, 24 1 Section 1.5
Goals: To develop skills needed to find the appropriate differential equations to use as mathematical models.
 Unit #16 : Differential Equations Goals: To develop skills needed to find the appropriate differential equations to use as mathematical models. Differential Equation Modelling - 1 Differential Equation
Unit #16 : Differential Equations Goals: To develop skills needed to find the appropriate differential equations to use as mathematical models. Differential Equation Modelling - 1 Differential Equation
( + ) 3. AP Calculus BC Chapter 6 AP Exam Problems. Antiderivatives. + + x + C. 2. If the second derivative of f is given by f ( x) = 2x cosx
 Chapter 6 AP Eam Problems Antiderivatives. ( ) + d = ( + ) + 5 + + 5 ( + ) 6 ( + ). If the second derivative of f is given by f ( ) = cos, which of the following could be f( )? + cos + cos + + cos + sin
Chapter 6 AP Eam Problems Antiderivatives. ( ) + d = ( + ) + 5 + + 5 ( + ) 6 ( + ). If the second derivative of f is given by f ( ) = cos, which of the following could be f( )? + cos + cos + + cos + sin
MATH 251 Examination I October 10, 2013 FORM A. Name: Student Number: Section:
 MATH 251 Examination I October 10, 2013 FORM A Name: Student Number: Section: This exam has 13 questions for a total of 100 points. Show all you your work! In order to obtain full credit for partial credit
MATH 251 Examination I October 10, 2013 FORM A Name: Student Number: Section: This exam has 13 questions for a total of 100 points. Show all you your work! In order to obtain full credit for partial credit
Exam 2 Solutions, Math March 17, ) = 1 2
 Eam Solutions, Math 56 March 7, 6. Use the trapezoidal rule with n = 3 to approimate (Note: The eact value of the integral is ln 5 +. (you do not need to verify this or use it in any way to complete this
Eam Solutions, Math 56 March 7, 6. Use the trapezoidal rule with n = 3 to approimate (Note: The eact value of the integral is ln 5 +. (you do not need to verify this or use it in any way to complete this
Tutorial 6 (week 6) Solutions
 THE UNIVERSITY OF SYDNEY PURE MATHEMATICS Linear Mathematics 9 Tutorial 6 week 6 s Suppose that A and P are defined as follows: A and P Define a sequence of numbers { u n n } by u, u, u and for all n,
THE UNIVERSITY OF SYDNEY PURE MATHEMATICS Linear Mathematics 9 Tutorial 6 week 6 s Suppose that A and P are defined as follows: A and P Define a sequence of numbers { u n n } by u, u, u and for all n,
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
 AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA CALCULUS AB SECTION I, Part A Time 55 minutes Number of questions 8 A CALCULATOR MAY NOT BE USED ON THIS PART OF THE EXAM. Directions: Solve each of the following problems,
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA CALCULUS AB SECTION I, Part A Time 55 minutes Number of questions 8 A CALCULATOR MAY NOT BE USED ON THIS PART OF THE EXAM. Directions: Solve each of the following problems,
Practice Exam 1 Solutions
 Practice Exam 1 Solutions 1a. Let S be the region bounded by y = x 3, y = 1, and x. Find the area of S. What is the volume of the solid obtained by rotating S about the line y = 1? Area A = Volume 1 1
Practice Exam 1 Solutions 1a. Let S be the region bounded by y = x 3, y = 1, and x. Find the area of S. What is the volume of the solid obtained by rotating S about the line y = 1? Area A = Volume 1 1
FINAL EXAM CALCULUS 2. Name PRACTICE EXAM
 FINAL EXAM CALCULUS 2 MATH 2300 FALL 208 Name PRACTICE EXAM Please answer all of the questions, and show your work. You must explain your answers to get credit. You will be graded on the clarity of your
FINAL EXAM CALCULUS 2 MATH 2300 FALL 208 Name PRACTICE EXAM Please answer all of the questions, and show your work. You must explain your answers to get credit. You will be graded on the clarity of your
(2) Let f(x) = a 2 x if x<2, 4 2x 2 ifx 2. (b) Find the lim f(x). (c) Find all values of a that make f continuous at 2. Justify your answer.
 (1) Let f(x) = x x 2 9. (a) Find the domain of f. (b) Write an equation for each vertical asymptote of the graph of f. (c) Write an equation for each horizontal asymptote of the graph of f. (d) Is f odd,
(1) Let f(x) = x x 2 9. (a) Find the domain of f. (b) Write an equation for each vertical asymptote of the graph of f. (c) Write an equation for each horizontal asymptote of the graph of f. (d) Is f odd,
Find the orthogonal trajectories for the family of curves. 9. The family of parabolas symmetric with respect to the x-axis and vertex at the origin.
 Exercises 2.4.1 Find the orthogonal trajectories for the family of curves. 1. y = Cx 3. 2. x = Cy 4. 3. y = Cx 2 + 2. 4. y 2 = 2(C x). 5. y = C cos x 6. y = Ce x 7. y = ln(cx) 8. (x + y) 2 = Cx 2 Find
Exercises 2.4.1 Find the orthogonal trajectories for the family of curves. 1. y = Cx 3. 2. x = Cy 4. 3. y = Cx 2 + 2. 4. y 2 = 2(C x). 5. y = C cos x 6. y = Ce x 7. y = ln(cx) 8. (x + y) 2 = Cx 2 Find
Section Exponential Functions
 121 Section 4.1 - Exponential Functions Exponential functions are extremely important in both economics and science. It allows us to discuss the growth of money in a money market account as well as the
121 Section 4.1 - Exponential Functions Exponential functions are extremely important in both economics and science. It allows us to discuss the growth of money in a money market account as well as the
(x! 4) (x! 4)10 + C + C. 2 e2x dx = 1 2 (1 + e 2x ) 3 2e 2x dx. # 8 '(4)(1 + e 2x ) 3 e 2x (2) = e 2x (1 + e 2x ) 3 & dx = 1
 33. x(x - 4) 9 Let u = x - 4, then du = and x = u + 4. x(x - 4) 9 = (u + 4)u 9 du = (u 0 + 4u 9 )du = u + 4u0 0 = (x! 4) + 2 5 (x! 4)0 (x " 4) + 2 5 (x " 4)0 ( '( = ()(x - 4)0 () + 2 5 (0)(x - 4)9 () =
33. x(x - 4) 9 Let u = x - 4, then du = and x = u + 4. x(x - 4) 9 = (u + 4)u 9 du = (u 0 + 4u 9 )du = u + 4u0 0 = (x! 4) + 2 5 (x! 4)0 (x " 4) + 2 5 (x " 4)0 ( '( = ()(x - 4)0 () + 2 5 (0)(x - 4)9 () =
Section 2.5 Mixing Problems. Key Terms: Tanks Mixing problems Input rate Output rate Volume rates Concentration
 Section 2.5 Mixing Problems Key Terms: Tanks Mixing problems Input rate Output rate Volume rates Concentration The problems we will discuss are called mixing problems. They employ tanks and other receptacles
Section 2.5 Mixing Problems Key Terms: Tanks Mixing problems Input rate Output rate Volume rates Concentration The problems we will discuss are called mixing problems. They employ tanks and other receptacles
2. Time-Domain Analysis of Continuous- Time Signals and Systems
 2. Time-Domain Analysis of Continuous- Time Signals and Systems 2.1. Continuous-Time Impulse Function (1.4.2) 2.2. Convolution Integral (2.2) 2.3. Continuous-Time Impulse Response (2.2) 2.4. Classification
2. Time-Domain Analysis of Continuous- Time Signals and Systems 2.1. Continuous-Time Impulse Function (1.4.2) 2.2. Convolution Integral (2.2) 2.3. Continuous-Time Impulse Response (2.2) 2.4. Classification
Will Murray s Differential Equations, IV. Applications, modeling, and word problems1
 Will Murray s Differential Equations, IV. Applications, modeling, and word problems1 IV. Applications, modeling, and word problems Lesson Overview Mixing: Smoke flows into the room; evenly mixed air flows
Will Murray s Differential Equations, IV. Applications, modeling, and word problems1 IV. Applications, modeling, and word problems Lesson Overview Mixing: Smoke flows into the room; evenly mixed air flows
On linear and non-linear equations.(sect. 2.4).
 On linear and non-linear equations.sect. 2.4). Review: Linear differential equations. Non-linear differential equations. Properties of solutions to non-linear ODE. The Bernoulli equation. Review: Linear
On linear and non-linear equations.sect. 2.4). Review: Linear differential equations. Non-linear differential equations. Properties of solutions to non-linear ODE. The Bernoulli equation. Review: Linear
CHAPTER 6 Differential Equations
 CHAPTER 6 Differential Equations Section 6. Slope Fields and Euler s Method.............. 55 Section 6. Differential Equations: Growth and Deca........ 557 Section 6. Separation of Variables and the Logistic
CHAPTER 6 Differential Equations Section 6. Slope Fields and Euler s Method.............. 55 Section 6. Differential Equations: Growth and Deca........ 557 Section 6. Separation of Variables and the Logistic
LECTURE 4-1 INTRODUCTION TO ORDINARY DIFFERENTIAL EQUATIONS
 130 LECTURE 4-1 INTRODUCTION TO ORDINARY DIFFERENTIAL EQUATIONS DIFFERENTIAL EQUATIONS: A differential equation (DE) is an equation involving an unknown function and one or more of its derivatives. A differential
130 LECTURE 4-1 INTRODUCTION TO ORDINARY DIFFERENTIAL EQUATIONS DIFFERENTIAL EQUATIONS: A differential equation (DE) is an equation involving an unknown function and one or more of its derivatives. A differential
Limits at Infinity. Use algebraic techniques to help with indeterminate forms of ± Use substitutions to evaluate limits of compositions of functions.
 SUGGESTED REFERENCE MATERIAL: Limits at Infinity As you work through the problems listed below, you should reference Chapter. of the recommended textbook (or the equivalent chapter in your alternative
SUGGESTED REFERENCE MATERIAL: Limits at Infinity As you work through the problems listed below, you should reference Chapter. of the recommended textbook (or the equivalent chapter in your alternative
MATH 162. FINAL EXAM ANSWERS December 17, 2006
 MATH 6 FINAL EXAM ANSWERS December 7, 6 Part A. ( points) Find the volume of the solid obtained by rotating about the y-axis the region under the curve y x, for / x. Using the shell method, the radius
MATH 6 FINAL EXAM ANSWERS December 7, 6 Part A. ( points) Find the volume of the solid obtained by rotating about the y-axis the region under the curve y x, for / x. Using the shell method, the radius
Topic 3 Notes Jeremy Orloff
 Topic 3 Notes Jeremy Orloff 3 Input-response models 3.1 Goals 1. Be able to use the language of systems and signals. 2. Be familiar with the physical examples in these notes. 3.2 Introduction In 18.03
Topic 3 Notes Jeremy Orloff 3 Input-response models 3.1 Goals 1. Be able to use the language of systems and signals. 2. Be familiar with the physical examples in these notes. 3.2 Introduction In 18.03
Chapter1. Ordinary Differential Equations
 Chapter1. Ordinary Differential Equations In the sciences and engineering, mathematical models are developed to aid in the understanding of physical phenomena. These models often yield an equation that
Chapter1. Ordinary Differential Equations In the sciences and engineering, mathematical models are developed to aid in the understanding of physical phenomena. These models often yield an equation that
University of Regina Department of Mathematics and Statistics Math 111 All Sections (Winter 2013) Final Exam April 25, 2013
 University of Regina Department of Mathematics and Statistics Math 111 All Sections (Winter 013) Final Exam April 5, 013 Name: Student Number: Please Check Off Your Instructor: Dr. R. McIntosh (001) Dr.
University of Regina Department of Mathematics and Statistics Math 111 All Sections (Winter 013) Final Exam April 5, 013 Name: Student Number: Please Check Off Your Instructor: Dr. R. McIntosh (001) Dr.
Practice Midterm 1 Solutions Written by Victoria Kala July 10, 2017
 Practice Midterm 1 Solutions Written by Victoria Kala July 10, 2017 1. Use the slope field plotter link in Gauchospace to check your solution. 2. (a) Not linear because of the y 2 sin x term (b) Not linear
Practice Midterm 1 Solutions Written by Victoria Kala July 10, 2017 1. Use the slope field plotter link in Gauchospace to check your solution. 2. (a) Not linear because of the y 2 sin x term (b) Not linear
Non-homogeneous equations (Sect. 3.6).
 Non-homogeneous equations (Sect. 3.6). We study: y + p(t) y + q(t) y = f (t). Method of variation of parameters. Using the method in an example. The proof of the variation of parameter method. Using the
Non-homogeneous equations (Sect. 3.6). We study: y + p(t) y + q(t) y = f (t). Method of variation of parameters. Using the method in an example. The proof of the variation of parameter method. Using the
UNIVERSITY OF HOUSTON HIGH SCHOOL MATHEMATICS CONTEST Spring 2018 Calculus Test
 UNIVERSITY OF HOUSTON HIGH SCHOOL MATHEMATICS CONTEST Spring 2018 Calculus Test NAME: SCHOOL: 1. Let f be some function for which you know only that if 0 < x < 1, then f(x) 5 < 0.1. Which of the following
UNIVERSITY OF HOUSTON HIGH SCHOOL MATHEMATICS CONTEST Spring 2018 Calculus Test NAME: SCHOOL: 1. Let f be some function for which you know only that if 0 < x < 1, then f(x) 5 < 0.1. Which of the following
Puxi High School Examinations Semester 1, AP Calculus (BC) Part 1. Wednesday, December 16 th, :45 pm 3:15 pm.
 Puxi High School Examinations Semester 1, 2009 2010 AP Calculus (BC) Part 1 Wednesday, December 16 th, 2009 12:45 pm 3:15 pm Time: 45 minutes Teacher: Mr. Surowski Testing Site: HS Gymnasium Student Name:
Puxi High School Examinations Semester 1, 2009 2010 AP Calculus (BC) Part 1 Wednesday, December 16 th, 2009 12:45 pm 3:15 pm Time: 45 minutes Teacher: Mr. Surowski Testing Site: HS Gymnasium Student Name:
Introduction to di erential equations
 Chapter 1 Introduction to di erential equations 1.1 What is this course about? A di erential equation is an equation where the unknown quantity is a function, and where the equation involves the derivative(s)
Chapter 1 Introduction to di erential equations 1.1 What is this course about? A di erential equation is an equation where the unknown quantity is a function, and where the equation involves the derivative(s)
Calculus I Sample Final exam
 Calculus I Sample Final exam Solutions [] Compute the following integrals: a) b) 4 x ln x) Substituting u = ln x, 4 x ln x) = ln 4 ln u du = u ln 4 ln = ln ln 4 Taking common denominator, using properties
Calculus I Sample Final exam Solutions [] Compute the following integrals: a) b) 4 x ln x) Substituting u = ln x, 4 x ln x) = ln 4 ln u du = u ln 4 ln = ln ln 4 Taking common denominator, using properties
Goals: To develop skills needed to find the appropriate differential equations to use as mathematical models.
 Unit #17 : Differential Equations Goals: To develop skills needed to find the appropriate differential equations to use as mathematical models. Reading: Sections 11.5-11.7. In workingwiththemodels insections11.5
Unit #17 : Differential Equations Goals: To develop skills needed to find the appropriate differential equations to use as mathematical models. Reading: Sections 11.5-11.7. In workingwiththemodels insections11.5
Practice Final Exam Solutions
 Important Notice: To prepare for the final exam, one should study the past exams and practice midterms (and homeworks, quizzes, and worksheets), not just this practice final. A topic not being on the practice
Important Notice: To prepare for the final exam, one should study the past exams and practice midterms (and homeworks, quizzes, and worksheets), not just this practice final. A topic not being on the practice
Homework 2 Solutions Math 307 Summer 17
 Homework 2 Solutions Math 307 Summer 17 July 8, 2017 Section 2.3 Problem 4. A tank with capacity of 500 gallons originally contains 200 gallons of water with 100 pounds of salt in solution. Water containing
Homework 2 Solutions Math 307 Summer 17 July 8, 2017 Section 2.3 Problem 4. A tank with capacity of 500 gallons originally contains 200 gallons of water with 100 pounds of salt in solution. Water containing
Exam 1 Review. Part I. Finding solutions of a given differential equation. 1. Find the real numbers r such that y = e rx is a solution of y y 30y = 0.
 Exam 1 Review Part I. Finding solutions of a given differential equation. 1. Find the real numbers r such that y = e rx is a solution of y y 30y = 0. 2. Find the real numbers r such that y = e rx is a
Exam 1 Review Part I. Finding solutions of a given differential equation. 1. Find the real numbers r such that y = e rx is a solution of y y 30y = 0. 2. Find the real numbers r such that y = e rx is a
SMA 208: Ordinary differential equations I
 SMA 208: Ordinary differential equations I Modeling with First Order differential equations Lecturer: Dr. Philip Ngare (Contacts: pngare@uonbi.ac.ke, Tue 12-2 PM) School of Mathematics, University of Nairobi
SMA 208: Ordinary differential equations I Modeling with First Order differential equations Lecturer: Dr. Philip Ngare (Contacts: pngare@uonbi.ac.ke, Tue 12-2 PM) School of Mathematics, University of Nairobi
Solution. Your sketch should show both x and y axes marked from 5 to 5 and circles of radius 1, 3, and 5 centered at the origin.
 Solutions of the Sample Problems for the First In-Class Exam Math 246, Fall 208, Professor David Levermore () (a) Sketch the graph that would be produced by the following Matlab command. fplot(@(t) 2/t,
Solutions of the Sample Problems for the First In-Class Exam Math 246, Fall 208, Professor David Levermore () (a) Sketch the graph that would be produced by the following Matlab command. fplot(@(t) 2/t,
Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: = 0 : homogeneous equation.
 Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: y y x y2 = 0 : homogeneous equation. x2 v = y dy, y = vx, and x v + x dv dx = v + v2. dx =
Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: y y x y2 = 0 : homogeneous equation. x2 v = y dy, y = vx, and x v + x dv dx = v + v2. dx =
Solutions of the Sample Problems for the First In-Class Exam Math 246, Fall 2017, Professor David Levermore
 Solutions of the Sample Problems for the First In-Class Exam Math 246, Fall 207, Professor David Levermore () (a) Give the integral being evaluated by the following Matlab command. int( x/(+xˆ4), x,0,inf)
Solutions of the Sample Problems for the First In-Class Exam Math 246, Fall 207, Professor David Levermore () (a) Give the integral being evaluated by the following Matlab command. int( x/(+xˆ4), x,0,inf)
FINAL REVIEW FALL 2017
 FINAL REVIEW FALL 7 Solutions to the following problems are found in the notes on my website. Lesson & : Integration by Substitution Ex. Evaluate 3x (x 3 + 6) 6 dx. Ex. Evaluate dt. + 4t Ex 3. Evaluate
FINAL REVIEW FALL 7 Solutions to the following problems are found in the notes on my website. Lesson & : Integration by Substitution Ex. Evaluate 3x (x 3 + 6) 6 dx. Ex. Evaluate dt. + 4t Ex 3. Evaluate
Modeling with differential equations
 Mathematical Modeling Lia Vas Modeling with differential equations When trying to predict the future value, one follows the following basic idea. Future value = present value + change. From this idea,
Mathematical Modeling Lia Vas Modeling with differential equations When trying to predict the future value, one follows the following basic idea. Future value = present value + change. From this idea,
Chapter 2 Notes, Kohler & Johnson 2e
 Contents 2 First Order Differential Equations 2 2.1 First Order Equations - Existence and Uniqueness Theorems......... 2 2.2 Linear First Order Differential Equations.................... 5 2.2.1 First
Contents 2 First Order Differential Equations 2 2.1 First Order Equations - Existence and Uniqueness Theorems......... 2 2.2 Linear First Order Differential Equations.................... 5 2.2.1 First
1. Find A and B so that f x Axe Bx. has a local minimum of 6 when. x 2.
 . Find A and B so that f Ae B has a local minimum of 6 when.. The graph below is the graph of f, the derivative of f; The domain of the derivative is 5 6. Note there is a cusp when =, a horizontal tangent
. Find A and B so that f Ae B has a local minimum of 6 when.. The graph below is the graph of f, the derivative of f; The domain of the derivative is 5 6. Note there is a cusp when =, a horizontal tangent
MATH 251 Examination I July 1, 2013 FORM A. Name: Student Number: Section:
 MATH 251 Examination I July 1, 2013 FORM A Name: Student Number: Section: This exam has 12 questions for a total of 100 points. Show all your work! In order to obtain full credit for partial credit problems,
MATH 251 Examination I July 1, 2013 FORM A Name: Student Number: Section: This exam has 12 questions for a total of 100 points. Show all your work! In order to obtain full credit for partial credit problems,
Solutions to Math 53 First Exam April 20, 2010
 Solutions to Math 53 First Exam April 0, 00. (5 points) Match the direction fields below with their differential equations. Also indicate which two equations do not have matches. No justification is necessary.
Solutions to Math 53 First Exam April 0, 00. (5 points) Match the direction fields below with their differential equations. Also indicate which two equations do not have matches. No justification is necessary.
Sections 2.7, 2.8 Rates of Change Part III Rates of Change in the Natural and Social Sciences
 Math 180 wwwtimetodarecom Sections 7, 8 Rates of Change Part III Rates of Change in the Natural and Social Sciences Physics s If s= f ( t) is the position function of a particle that is moving in a straight
Math 180 wwwtimetodarecom Sections 7, 8 Rates of Change Part III Rates of Change in the Natural and Social Sciences Physics s If s= f ( t) is the position function of a particle that is moving in a straight
First Order ODEs, Part II
 Craig J. Sutton craig.j.sutton@dartmouth.edu Department of Mathematics Dartmouth College Math 23 Differential Equations Winter 2013 Outline Existence & Uniqueness Theorems 1 Existence & Uniqueness Theorems
Craig J. Sutton craig.j.sutton@dartmouth.edu Department of Mathematics Dartmouth College Math 23 Differential Equations Winter 2013 Outline Existence & Uniqueness Theorems 1 Existence & Uniqueness Theorems
Problem Max. Possible Points Total
 MA 262 Exam 1 Fall 2011 Instructor: Raphael Hora Name: Max Possible Student ID#: 1234567890 1. No books or notes are allowed. 2. You CAN NOT USE calculators or any electronic devices. 3. Show all work
MA 262 Exam 1 Fall 2011 Instructor: Raphael Hora Name: Max Possible Student ID#: 1234567890 1. No books or notes are allowed. 2. You CAN NOT USE calculators or any electronic devices. 3. Show all work
Assignment: Practice Exam Big Losers
 Assignment: Practice Exam Big Losers AB Calculus - Hardtke Name Due Date: Tuesday, 4/30 Show all work and circle your answer. 1. A water tank contains 100 gallons of water at time t = 3 hours. Water is
Assignment: Practice Exam Big Losers AB Calculus - Hardtke Name Due Date: Tuesday, 4/30 Show all work and circle your answer. 1. A water tank contains 100 gallons of water at time t = 3 hours. Water is
Problem Set. Assignment #1. Math 3350, Spring Feb. 6, 2004 ANSWERS
 Problem Set Assignment #1 Math 3350, Spring 2004 Feb. 6, 2004 ANSWERS i Problem 1. [Section 1.4, Problem 4] A rocket is shot straight up. During the initial stages of flight is has acceleration 7t m /s
Problem Set Assignment #1 Math 3350, Spring 2004 Feb. 6, 2004 ANSWERS i Problem 1. [Section 1.4, Problem 4] A rocket is shot straight up. During the initial stages of flight is has acceleration 7t m /s
An object is launched straight upward so that its height, h, is a function of time, t, with
 WebAssign Lesson 13-3 Applications (Homework) Current Score : / 18 Due : Wednesday, April 30 2014 09:00 AM MDT Shari Dorsey Sp 14 Math 170, section 003, Spring 2014 Instructor: Shari Dorsey 1. /1 points
WebAssign Lesson 13-3 Applications (Homework) Current Score : / 18 Due : Wednesday, April 30 2014 09:00 AM MDT Shari Dorsey Sp 14 Math 170, section 003, Spring 2014 Instructor: Shari Dorsey 1. /1 points
SPS Mathematical Methods Lecture #7 - Applications of First-order Differential Equations
 1. Linear Models SPS 2281 - Mathematical Methods Lecture #7 - Applications of First-order Differential Equations (a) Growth and Decay (b) Half-life of Radioactive (c) Carbon Dating (d) Newton s Law of
1. Linear Models SPS 2281 - Mathematical Methods Lecture #7 - Applications of First-order Differential Equations (a) Growth and Decay (b) Half-life of Radioactive (c) Carbon Dating (d) Newton s Law of
Solution: APPM 1350 Final Exam Spring 2014
 APPM 135 Final Exam Spring 214 1. (a) (5 pts. each) Find the following derivatives, f (x), for the f given: (a) f(x) = x 2 sin 1 (x 2 ) (b) f(x) = 1 1 + x 2 (c) f(x) = x ln x (d) f(x) = x x d (b) (15 pts)
APPM 135 Final Exam Spring 214 1. (a) (5 pts. each) Find the following derivatives, f (x), for the f given: (a) f(x) = x 2 sin 1 (x 2 ) (b) f(x) = 1 1 + x 2 (c) f(x) = x ln x (d) f(x) = x x d (b) (15 pts)
Dynamical Systems. August 13, 2013
 Dynamical Systems Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 13, 2013 Dynamical Systems are systems, described by one or more equations, that evolve over time.
Dynamical Systems Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 13, 2013 Dynamical Systems are systems, described by one or more equations, that evolve over time.
Business and Life Calculus
 Business and Life Calculus George Voutsadakis Mathematics and Computer Science Lake Superior State University LSSU Math 2 George Voutsadakis (LSSU) Calculus For Business and Life Sciences Fall 203 / 55
Business and Life Calculus George Voutsadakis Mathematics and Computer Science Lake Superior State University LSSU Math 2 George Voutsadakis (LSSU) Calculus For Business and Life Sciences Fall 203 / 55
Math 116 Practice for Exam 3
 Math 116 Practice for Exam 3 Generated November 30, 2017 Name: SOLUTIONS Instructor: Section Number: 1. This exam has 6 questions. Note that the problems are not of equal difficulty, so you may want to
Math 116 Practice for Exam 3 Generated November 30, 2017 Name: SOLUTIONS Instructor: Section Number: 1. This exam has 6 questions. Note that the problems are not of equal difficulty, so you may want to
It is convenient to think that solutions of differential equations consist of a family of functions (just like indefinite integrals ).
 Section 1.1 Direction Fields Key Terms/Ideas: Mathematical model Geometric behavior of solutions without solving the model using calculus Graphical description using direction fields Equilibrium solution
Section 1.1 Direction Fields Key Terms/Ideas: Mathematical model Geometric behavior of solutions without solving the model using calculus Graphical description using direction fields Equilibrium solution
Virginia Tech Math 1226 : Past CTE problems
 Virginia Tech Math 16 : Past CTE problems 1. It requires 1 in-pounds of work to stretch a spring from its natural length of 1 in to a length of 1 in. How much additional work (in inch-pounds) is done in
Virginia Tech Math 16 : Past CTE problems 1. It requires 1 in-pounds of work to stretch a spring from its natural length of 1 in to a length of 1 in. How much additional work (in inch-pounds) is done in
DIFFERENTIAL EQUATIONS
 HANDOUT DIFFERENTIAL EQUATIONS For International Class Nikenasih Binatari NIP. 19841019 200812 2 005 Mathematics Educational Department Faculty of Mathematics and Natural Sciences State University of Yogyakarta
HANDOUT DIFFERENTIAL EQUATIONS For International Class Nikenasih Binatari NIP. 19841019 200812 2 005 Mathematics Educational Department Faculty of Mathematics and Natural Sciences State University of Yogyakarta
Calculus II - Fall 2013
 Calculus II - Fall Midterm Exam II, November, In the following problems you are required to show all your work and provide the necessary explanations everywhere to get full credit.. Find the area between
Calculus II - Fall Midterm Exam II, November, In the following problems you are required to show all your work and provide the necessary explanations everywhere to get full credit.. Find the area between
ANSWERS, Homework Problems, Fall 2014: Lectures Now You Try It, Supplemental problems in written homework, Even Answers. 24x + 72 (x 2 6x + 4) 4
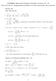 ANSWERS, Homework Problems, Fall 014: Lectures 19 35 Now You Try It, Supplemental problems in written homework, Even Answers Lecture 19 1. d [ 4 ] dx x 6x + 4) 3 = 4x + 7 x 6x + 4) 4. a) P 0) = 800 b)
ANSWERS, Homework Problems, Fall 014: Lectures 19 35 Now You Try It, Supplemental problems in written homework, Even Answers Lecture 19 1. d [ 4 ] dx x 6x + 4) 3 = 4x + 7 x 6x + 4) 4. a) P 0) = 800 b)
3. Identify and find the general solution of each of the following first order differential equations.
 Final Exam MATH 33, Sample Questions. Fall 6. y = Cx 3 3 is the general solution of a differential equation. Find the equation. Answer: y = 3y + 9 xy. y = C x + C is the general solution of a differential
Final Exam MATH 33, Sample Questions. Fall 6. y = Cx 3 3 is the general solution of a differential equation. Find the equation. Answer: y = 3y + 9 xy. y = C x + C is the general solution of a differential
CHAPTER 3 Graphs and Functions
 CHAPTER Graphs and Functions Section. The Rectangular Coordinate Sstem............ Section. Graphs of Equations..................... 7 Section. Slope and Graphs of Linear Equations........... 7 Section.
CHAPTER Graphs and Functions Section. The Rectangular Coordinate Sstem............ Section. Graphs of Equations..................... 7 Section. Slope and Graphs of Linear Equations........... 7 Section.
Unit #6 Basic Integration and Applications Homework Packet
 Unit #6 Basic Integration and Applications Homework Packet For problems, find the indefinite integrals below.. x 3 3. x 3x 3. x x 3x 4. 3 / x x 5. x 6. 3x x3 x 3 x w w 7. y 3 y dy 8. dw Daily Lessons and
Unit #6 Basic Integration and Applications Homework Packet For problems, find the indefinite integrals below.. x 3 3. x 3x 3. x x 3x 4. 3 / x x 5. x 6. 3x x3 x 3 x w w 7. y 3 y dy 8. dw Daily Lessons and
Find the orthogonal trajectories for the family of curves.
 Exercises, Section 2.4 Exercises 2.4.1 Find the orthogonal trajectories for the family of curves. 1. y = Cx 3. 2. x = Cy 4. 3. y = Cx 2 +2. 4. y 2 =2(C x). 5. y = C cos x 6. y = Ce x 7. y = ln(cx) 8. (x
Exercises, Section 2.4 Exercises 2.4.1 Find the orthogonal trajectories for the family of curves. 1. y = Cx 3. 2. x = Cy 4. 3. y = Cx 2 +2. 4. y 2 =2(C x). 5. y = C cos x 6. y = Ce x 7. y = ln(cx) 8. (x
8. Set up the integral to determine the force on the side of a fish tank that has a length of 4 ft and a heght of 2 ft if the tank is full.
 . Determine the volume of the solid formed by rotating the region bounded by y = 2 and y = 2 for 2 about the -ais. 2. Determine the volume of the solid formed by rotating the region bounded by the -ais
. Determine the volume of the solid formed by rotating the region bounded by y = 2 and y = 2 for 2 about the -ais. 2. Determine the volume of the solid formed by rotating the region bounded by the -ais
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES 3.8 Exponential Growth and Decay In this section, we will: Use differentiation to solve real-life problems involving exponentially growing quantities. EXPONENTIAL
3 DIFFERENTIATION RULES DIFFERENTIATION RULES 3.8 Exponential Growth and Decay In this section, we will: Use differentiation to solve real-life problems involving exponentially growing quantities. EXPONENTIAL
MAC 2233 Chapter 3 Practice for the Test
 Class: Date: MAC 33 Chapter 3 Practice for the Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. At which labeled point is the slope of the tangent
Class: Date: MAC 33 Chapter 3 Practice for the Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. At which labeled point is the slope of the tangent
x f(x)
 CALCULATOR SECTION. For y y 8 find d point (, ) on the curve. A. D. dy at the 7 E. 6. Suppose silver is being etracted from a.t mine at a rate given by A'( t) e, A(t) is measured in tons of silver and
CALCULATOR SECTION. For y y 8 find d point (, ) on the curve. A. D. dy at the 7 E. 6. Suppose silver is being etracted from a.t mine at a rate given by A'( t) e, A(t) is measured in tons of silver and
Chapter 6: Messy Integrals
 Chapter 6: Messy Integrals Review: Solve the following integrals x 4 sec x tan x 0 0 Find the average value of 3 1 x 3 3 Evaluate 4 3 3 ( x 1), then find the area of ( x 1) 4 Section 6.1: Slope Fields
Chapter 6: Messy Integrals Review: Solve the following integrals x 4 sec x tan x 0 0 Find the average value of 3 1 x 3 3 Evaluate 4 3 3 ( x 1), then find the area of ( x 1) 4 Section 6.1: Slope Fields
Solutions to the Review Questions
 Solutions to the Review Questions Short Answer/True or False. True or False, and explain: (a) If y = y + 2t, then 0 = y + 2t is an equilibrium solution. False: This is an isocline associated with a slope
Solutions to the Review Questions Short Answer/True or False. True or False, and explain: (a) If y = y + 2t, then 0 = y + 2t is an equilibrium solution. False: This is an isocline associated with a slope
