On the support of solutions of stochastic differential equations with path-dependent coefficients
|
|
|
- Abigail Briggs
- 5 years ago
- Views:
Transcription
1 On the uppot of olution of tochatic diffeential equation with path-dependent coefficient Rama Cont, Alexande Kalinin To cite thi veion: Rama Cont, Alexande Kalinin. On the uppot of olution of tochatic diffeential equation with path-dependent coefficient <hal v2> HAL Id: hal Submitted on 23 Jun 2018 HAL i a multi-diciplinay open acce achive fo the depoit and diemination of cientific eeach document, whethe they ae publihed o not. The document may come fom teaching and eeach intitution in Fance o aboad, o fom public o pivate eeach cente. L achive ouvete pluidiciplinaie HAL, et detinée au dépôt et à la diffuion de document cientifique de niveau echeche, publié ou non, émanant de établiement d eneignement et de echeche fançai ou étange, de laboatoie public ou pivé.
2 On the uppot of olution of tochatic diffeential equation with path-dependent coefficient Rama Cont Alexande Kalinin June 2018 Abtact Given a tochatic diffeential equation with path-dependent coefficient diven by a multidimenional Wiene poce, we how that the uppot of the law of the olution i given by the image of the Cameon-Matin pace unde the flow of the olution of a ytem of path-dependent odinay) diffeential equation. Ou eult extend the Stoock-Vaadhan uppot theoem fo diffuion pocee to the cae of SDE with path-dependent coefficient. The poof i baed on the Functional Ito calculu. MSC2010 claification: 60H10 ; 28C20 ; 34K50. Keywod: uppot theoem, tochatic diffeential equation, functional equation, emimatingale, Wiene pace, functional Ito calculu. Laboatoie de Pobabilité, Statitique et Modéliation, CNRS-Sobonne Univeité. Rama.Cont@math.cn.f Depatment of Mathematic, Impeial College, United Kingdom. a.kalinin@impeial.ac.uk. 1
3 Content 1 Oveview Suppot theoem fo tochatic diffeential equation Statement of main eult Peliminaie Non-anticipative functional calculu Mild olution to path-dependent ODE Stong olution fo path-dependent SDE Chaacteization of the uppot in Hölde topology Convegence in pobability in Hölde nom Hölde pace fo tochatic pocee A geneal Kolmogoov-Chentov etimate Convegence along a equence of patition Adapted linea intepolation of Bownian motion Auxiliay convegence eult Path-dependent ODE and SDE: poof Poof of Popoition Poof of Popoition Poof of main eult Decompoition into emainde tem Convegence of the fit two emainde Convegence of the thid emainde Poof of Theoem 8 and
4 1 Oveview 1.1 Suppot theoem fo tochatic diffeential equation A tochatic poce may be viewed a a andom vaiable taking value in a pace of path; the topological) uppot of thi andom vaiable then decibe the cloue of) the et of poible ample path and povide inight into the tuctue of ample path of the poce. The natue of the uppot ha been invetigated fo vaiou clae of tochatic pocee, with a focu on tochatic diffeential equation, unde diffeent function pace topologie. Fo diffuion pocee, the uppot unde the unifom nom wa fit decibed by Stoock and Vaadhan 20, 21], a eult known a the Stoock- Vaadhan uppot theoem. An extenion to unbounded coefficient wa given by Gyöngy 14]. The uppot of moe geneal Wiene functional and extenion to SDE in Hilbet pace ae dicued in Aida et al 2] and 1]. Thee eult wee extended to the Hölde topology by Ben Aou et al. 5] and, uing diffeent technique, by Millet and Sanz-Solé 16] ; Bally et al 4] ue imila method to deive a uppot theoem in Hölde nom fo paabolic SPDE. Suppot theoem in p-vaiation topology ae dicued by Ledoux et al 15] uing ough path technique. Suppot theoem in Hölde and p-vaiation topologie ae dicued in 13]. Pakkanen 18] give condition fo a tochatic integal ito have full uppot. In thi wok, we extend ome of thee eult to tochatic diffeential equation with path-dependent coefficient. Let Ω, F, F t ) t 0,T ], P ) be a filteed pobability pace on which thee i a tandad d-dimenional F t ) t 0,T ] - Bownian motion W. Conide the following tochatic diffeential equation dx t = bt, X t ) dt + σt, X t ) dw t fo t, T ], 1.1) whoe coefficient b :, T ] S R m and σ :, T ] S R m d ae nonanticipative i.e. bt, X), σt, X) depend on the path X t = Xt.) of the olution up to t. Unde Lipchitz condition on the coefficient b, σ, thi SDE ha a unique olution X 17,19] whoe ample path lie in ome Hölde pace C α 0, T ], R m ). Ou main eult i a deciption of the uppot of the olution in the Hölde topology: we how that the uppot of the law of the olution i given by the image of the Cameon-Matin pace H 1 unde the flow aociated with a ytem of functional diffeential equation. 3
5 1.2 Statement of main eult Let T > 0 and d, m N. To keep notation imple, we denote by the abolute value function, the Euclidean nom in R d and R m and the Fobeniu nom in R m d. Denote by S := C0, T ], R m ) 1.2) the pace of continuou R m -valued map on 0, T ] equipped with the upemum nom and by C α 0, T ], R m ) the pace of x S that ae α-höldecontinuou on, T ] fo α 0, 1], endowed with the delayed Hölde nom x α, := x + x) xt) up. 1.3),t,T ]: t t α We et C00, T ], R m ) := S and 0, := by convention. Then, unde the aumption tated below, 1.1) admit a unique tong olution whoe ample path lie in Hölde pace C α 0, T ], R m ) fo all α 0, 1/2). We denote H 1 0, T ], R m ) the pace of abolutely continuou function on, T ] whoe deivative ḣ i quae-integable with epect to the Lebegue meaue. We equip thi pace with the nom T 1/2 x H, := x + ẋ) d) ) Then H 1 0, T ], R m ) C 1/2 0, T ], R m ) and evey x H 1 0, T ], R m ) atifie x 1/2, x H,. Uing the concept of hoizontal and vetical diffeentiability fo nonanticipative functional 7, 12], we intoduce in Section 2.1 egulaity aumption on the coefficient σ C 1,2, T ) S, R m d ) and conide the map ρ :, T ) S R m given coodinatewie by d ρ k t, x) := x σ k,l t, x)σt, x)e l, 1.5) l=1 whee {e 1,..., e d } i the canonical bai of R d and x σ k,l :, T ) S R 1 m denote the vetical deivative 6,12] of the k, l)-coodinate function of σ fo any k {1,..., m} and l {1,..., d}. Note that ρ = x σ σ fo m = d = 1. In thi context, the uppot of the unique tong olution to 1.1) may be chaacteized by tudying the following path-dependent odinay diffeential equation diven by an element h H 1 0, T ], R d ): ẋ h t) = b 1/2)ρ)t, x t h) + σt, x t h) ḣt) fo t, T ]. 1.6) Ou main eult may be tated a follow: 4
6 Theoem 1 Suppot theoem fo path-dependent SDE). Let ˆx C0, T ], R m ) and σ C 1,2, T ) S, R m d ) with hoizontal ep. vetical) deivative denoted by t σ ep. x σ). Aume σ and x σ ae bounded and thee ae contant c, η, λ 0 and κ 0, 1) uch that bt, x) c1 + x κ ), bt, x) bt, y) λ x y, t σ k,l t, x) + xx σ k,l t, x) c1 + x η ), σ, y) σt, x) + x σ k,l, y) x σ k,l t, x) λ t 1/2 + y x t ) fo all, t, T ), x, y S, k {1,..., m} and l {1,..., d}. Then: i) Thee i a unique tong olution X to 1.1) atifying X = ˆx) fo all 0, ] a.. Futhe, E X 2p α,] < fo all p 1 and α 0, 1/2). ii) Fo any h H 1 0, T ], R d ) thee i a unique mild olution x h to 1.6) o that x h ) = ˆx) fo all 0, ] and we have x h H 1 0, T ], R m ). In addition, the map H 1 0, T ], R d ) H 1 0, T ], R m ), h x h i Lipchitz continuou on bounded et. iii) Fo each α 0, 1/2), the uppot of the image meaue P X 1 in the delayed Hölde pace C α 0, T ], R m ) i the cloue of the et of all mild olution x h to 1.6), whee h H 1 0, T ], R d ). That i, uppp X 1 ) = {x h h H 1 0, T ], R d )} in C α 0, T ], R m ). 1.7) Thi eult extend peviou eult 2,5,16,20] on the uppot of diffuion pocee to the cae of path-dependent coefficient. In the diffuion cae, we etieve the eult of 5, 16] unde weake aumption on σ. Ou poof adapt the appoach ued by Millet and Sanz-Solé 16] to the path-dependent cae, uing the tool of Functional Ito calculu 6, 12]. We contuct Hölde-continuou appoximation of the olution uing an adapted linea intepolation of Bownian motion and how that thi appoximation convege in pobability to the olution in Hölde nom. A key ingedient i the ue of functional etimate deived in 3] uing the Functional Ito calculu, combined with intepolation eo etimate in Hölde nom fo tochatic pocee. Outline. The emainde of the pape i devoted to the poof of Theoem Suppot Theoem. Section 2 dicue the vaiou building block of the poof. Section 2.1 ecall ome functional calculu concept fom 6] and etablihe eveal eult ueful in ou etting. Section 2.2 give condition fo exitence and uniquene of a mild) olution to the path-dependent ODE 1.6); Section 2.3 give condition fo the exitence of a unique tong olution 5
7 to 1.1); Section 2.4 dicue the intepolation method ued to chaacteize the uppot in Hölde topologie. Section 3 dicue Hölde pace fo tochatic pocee and the notion of convegence in pobability in Hölde nom in moe depth. Section 3.2 deive a vaiation on the Kolmogoov-Chentov theoem with an etimate fo the Hölde nom Lemma 12) and an impoved veion of a tatement fom 16] Popoition 14). Section 3.4 dicue adapted linea intepolation of Bownian motion, impoving ome eult fom 16]. Section 4 ue thee ingedient to pove the exitence and uniquene of mild olution to pathdependent ODE Sec. 4.1) and SDE Sec. 4.2). Finally, Section 5 combine thee ingedient to give a poof of the main eult. 2 Peliminaie We hall denote Id the d d identity matix; fo a matix A we denote by A it tanpoe. 2.1 Non-anticipative functional calculu Let D0, T ], R m ) denote the Banach pace of all R m -valued càdlàg map on 0, T ] equipped with the upemum nom and ecall the following notion fom 6, 8]. A functional F :, T ] D0, T ], R m ) R i non-anticipative if F t, x) = F t, x t ) fo all t, T ] and x D0, T ], R m ), whee x t i path x topped at time t: x t ) = x t) fo each 0, T ]. F i called boundedne-peeving if fo each n N thee i c n 0 uch that F t, x) c n fo evey t, T ] and x D0, T ], R m ) atifying x n. In othe wod, F i ought to be bounded on bounded et. We notice that the following peudometic on, T ] D0, T ], R m ) given by d t, x),, y)) := t 1/2 + x t y 2.1) i complete and if F i d -continuou, then it i non-anticipative. A obeved in 10], Lipchitz continuity with epect to d allow fo a Hölde moothne of degee 1/2 in the time vaiable. 6
8 Let u ecall the definition of the hoizontal and vetical deivative. A functional F :, T ) D0, T ], R m ) R i called hoizontally diffeentiable if fo each t, T ) and x D0, T ], R m ), the function 0, T t) R, h F t + h, x t ) i diffeentiable at 0. In thi cae, it deivative thee, will be denoted by t F t, x). We ay that F i vetically diffeentiable if fo all t, T ) and x D0, T ], R m ), the function R m R, h F t, x + h1t,t ]) i diffeentiable at 0. In thi cae, it deivative thee will be epeented by x F t, x). We call F patially vetically diffeentiable if fo all k {1,..., m}, t, T ) and x D0, T ], R m ), the function R R, h F t, x + hê k 1t,T ]) i diffeentiable at 0, whee {ê 1,..., ê m } i the canonical bai of R m. In thi cae, it deivative thee will be denoted by xi F t, x). By calculu, if F i vetically diffeentiable, then it i patially vetically diffeentiable and x F = x1 F,..., xm F ). F i twice vetically diffeentiable if it i vetically diffeentiable and the ame hold fo x F. In thi cae, we et xx F := x x F ) and xk x l F := xk xl F ) fo all k, l {1,..., m}. It follow fom Schwaz Lemma that if F i twice vetically diffeentiable and xx F i d -continuou, then xx F i ymmetic: xk x l F = xl x k F fo each k, l {1,..., m}. A functional G :, T ) D0, T ], R m ) R i aid to be of cla C 1,2 if it i once hoizontally and twice vetically diffeentiable uch that G itelf and the deivative t G, x G and xx G ae boundedne-peeving and d - continuou. By C 1,2, T ) S) 2.2) we denote the pace of functional F :, T ) S R m d that admit an extenion G :, T ) D0, T ], R m ) R of cla C 1,2, whee S i given by 1.2). Then it follow fom 6, Theoem 5.4.1] that t F := t G, x F := x G and xx F := xx G on, T ) S ae independent of the choice of the extenion G. Note that 2.2) allow u to ue the functional Itô fomula 9] in the poof of Popoition 34, which give one of the main agument to etablih 1.7). To conclude, we wite C, T ) S, R m d ) fo the linea pace of all map F :, T ) S R m d atifying F k,l C, T ) S) fo each k {1,..., m} and l {1,..., d}. 7
9 2.2 Mild olution to path-dependent ODE We how in thi ection a unique mild olution to the ODE 1.6), which belong to the delayed Cameon-Matin pace H 1 0, T ], R m ). To thi end, let u conide the geneal path-dependent odinay diffeential equation ẋt) = F t, x t ) fo t, T ], 2.3) whee F :, T ] S R m denote a non-anticipative poduct meauable map. Then fo each h H 1 0, T ], R d ) the choice F = b 1/2)ρ+σḣ, whee ρ i given by 1.5), yield the uppot chaacteizing ODE 1.6). A fo x S the map, T ] R m, t F t, x t ) may fail to be continuou, one may in geneal not expect to deive claical olution. So, we ecall the concept of a mild olution to 2.3), which i a path x S atifying T F, x ) d < and xt) = x) + F, x ) d fo all t, T ]. By definition, a mild olution x i abolutely continuou on, T ] and it become a claical olution if and only if the Boel meauable map, T ] R m, F, x ) i continuou. Let u intoduce the following egulaity condition, which ae atified unde the aumption of Theoem 1 fo the choice of F mentioned befoe. O.i) Thee exit a meauable function c F c F ) 2 d < and T F t, x) c F t) 1 + x + :, T ] 0, ) atifying T ẋ) d fo all t, T ) and x S that i abolutely continuou on, T ]. O.ii) Fo each n N thee i a meauable function λ F,n :, T ] 0, ) uch that T λ F,n) 2 d < and F t, x) F t, y) λ F,n t) x y H, fo all t, T ) and x, y H 1 0, T ], R m ) o that x H, y H, n. Unde the above gowth condition and Lipchitz moothne on bounded et, we obtain a unique mild olution that can be appoximated by a Picad iteation in the delayed Cameon-Matin nom H, given by 1.4). ) 8
10 Popoition 2. Let O.i) and O.ii) hold and ˆx C0, T ], R m ), then the ODE 2.3) admit a unique mild olution y F atifying y F ) = ˆx) fo all 0, ] and it hold that y F H 1 0, T ], R m ). Moeove, the equence x n ) n N0 in H 1 0, T ], R m ), ecuively defined via x 0 t) := ˆx t) and x n+1 t) := x 0 t) + t F, x n) d 2.4) fo all n N 0, convege in the delayed Cameon-Matin nom H, to y F. 2.3 Stong olution fo path-dependent SDE We tun to the deivation of a unique tong olution to 1.1), fo which a.e. path lie in C α 0, T ], R m ) fo any α 0, 1/2). We conide the tochatic diffeential equation with path-dependent coefficient dx t = Bt, X t ) dt + Σt, X t ) dw t fo t, T ], 2.5) whee B :, T ] S R m and Σ :, T ] S R m d ae two non-anticipative poduct meauable map. A tong olution to 2.5) i an F t ) t 0,T ] -adapted ight-continuou poce X : 0, T ] Ω R m with a.. continuou path atifying T B, X ) d + X t = X + T B, X ) d + Σ, X ) 2 d < Σ, X ) dw a.. and fo all t, T ] a.. Remak 3. The fact that we do not have to aume the uual condition i claified in Section 3.1 and iepective how B, y) and Σ, y) ae extended fo, T ] and any ight-continuou map y : 0, T ] R m that i not continuou, the above integal emain unchanged up to inditinguihability. We now tate the aumption on the coefficient, valid in the etting of Theoem 1 fo the choice B = b and Σ = σ. S.i) Thee ae a meauable function c B :, T ] 0, ) and a contant c Σ 0 uch that T c B) 2 d < and fo all t, x), T ) S, Bt, x) c B t)1 + x ) and Σt, x) c Σ 1 + x ). 9
11 S.ii) Thee ae α 0 0, 1/2), a meauable function λ B :, T ] 0, ) and a contant λ Σ 0 uch that T λ B) 2 d < and Bt, x) Bt, y) λ B t) x y α0,, Σt, x) Σt, y) λ Σ x y α0, fo all t, T ) and x, y C α 0 0, T ], R m ), whee α0, equal if α 0 = 0 and othewie i given by 1.3) when α i eplaced by α 0. Remak 4. If condition S.ii) hold, then it i alo tue if α 0 i eplaced by any α α 0, 1/2). Thu, it i tonget in the cae that α 0 = 0. Fo p 1 and α 0, 1] we let C α,p0, T ], R m ) denote the pace of all F t ) t 0,T ] -adapted ight-continuou pocee X : 0, T ] Ω R m atifying E X p α,] <, equipped with the intinic eminom C α,p0, T ], R m ) 0, ), X E X p α,]) 1/p, 2.6) which i complete, by Popoition 11. Moeove, if a equence n X) n N in thi linea pace convege with epect to the above eminom, then it alo convege in the delayed Hölde nom α, in pobability. Finally, we et C 0, T ], R m ) := p 1 C 0,p0, T ], R m ) and let C 1/2, 0, T ], R m ) denote the inteection of the pace C α,p0, T ], R m ) ove all p 1 and α 0, 1/2), which yield a completely peudometizable topological pace. Popoition 5. Aume S.i)-S.ii) and let ˆX C 0, T ], R m ). Then up to inditinguihability thee i a unique tong olution X to 2.5) uch that X = ˆX fo all 0, ] a.. we have that X C, 1/2 0, T ], R m ). Futhemoe, the equence n X) n N0 in 0, T ], R m ), ecuively given by 0 X t := ˆX t and C 1/2, n+1x t = 0 X t + t B, n X ) d + t Σ, n X ) dw 2.7) fo all n N 0, convege in the eminom 2.6) to X fo each p 2 and α 0, 1/2). In paticula, lim n P n X X α, ε) = 0 fo all ε > 0. Remak 6. Pathwie uniquene i hown in Lemma 30, equiing only the following Lipchitz condition on bounded et, which follow fom S.ii) in the tonget cae α 0 = 0: 10
12 S.iii) Fo each n N thee i a meauable function λ n :, T ] 0, ) atifying T λ n) 2 d < and Bt, x) Bt, y) + Σt, x) Σt, y) λ n t) x y fo all t, T ] and x, y S with x y n. 2.4 Chaacteization of the uppot in Hölde topology Section 2.2 and 2.3 povide the main agument to pove the fit two aetion of Theoem 1. Let u now decibe how we hall chaacteize the uppot 1.7). Fo n N let T n be a patition of, T ] that we wite in the fom T n = {t 0,n,..., t kn,n } fo ome k n N and t 0,n,..., t kn,n, T ] o that = t 0,n < < t kn,n = T and we denote it meh by T n = max i {0,...,kn 1}t i+1,n t i,n ). We aume that lim n T n = 0 and that the equence of patition i well-balanced in the ene of 11], that i, thee i c T 1 uch that T n c T inf i {0,...,k n 1} t i+1,n t i,n ) fo all n N. 2.8) Moeove, fo n N we define an F t ) t 0,T ] -adapted ight-continuou poce nw : 0, T ] Ω R d by etting n W t := W t fo t 0, t 1,n ), nw t := W ti 1,n + t t i,n ) W t i,n W ti 1,n t i+1,n t i,n 2.9) fo t t i,n, t i+1,n ) with i {1,..., k n 1} and n W T := W tkn 1,n. Then nw can be egaded a adapted linea intepolation of the d-dimenional F t ) t 0,T ] -Bownian motion W on, T ] and almot each of it path belong to H 1 0, T ], R d ). Thu, let u uppoe that the aumption and the fit two claim of Theoem 1 hold. To etablih uppp X 1 ) {x h h H 1 0, T ], R d )} in C α 0, T ], R m ) fo α 0, 1/2), we will jutify in Section 5.4 that it uffice to check that lim P x nw X α, ε) = 0 fo all ε > ) n By definition of a mild olution to 2.3), we ee fo each n N that x nw i a tong olution to the degeneate path-dependent SDE d n Y t = b 1/2)ρ)t, n Y t ) + σt, n Y t ) n Ẇ t ) dt fo t, T ] 11
13 with initial condition n Y = ˆx a.. Fo each h H 1 0, T ], R d ) and n N, we intoduce an a.. continuou local matingale h,n Z : 0, T ] Ω 0, ) by equiing that h,n Z = 1 a.. and h,nz t = exp ḣ) n Ẇ dw 1 ) t 2 ḣ) nẇ 2 d 2.11) fo all t, T ] a.. In fact, h,n Z i a matingale, a claified in Lemma 39. Hence, P h,n : F 0, 1] given by P h,n A) := E h,n Z T 1A] i a pobability meaue equivalent to P. By uing thi fact, we will how that the convee incluion in 1.7) follow once we have poven that lim P h,n X x h α, ε) = 0 fo all ε > ) n By Gianov theoem, the poce h,n W : 0, T ] Ω R d defined via h,nw t := W t t ḣ) n Ẇ d i a d-dimenional F t ) t 0,T ] -Bownian motion unde P h,n and X i a tong olution to the path-dependent SDE d n Y t = bt, n Y t ) + σt, n Y t )ḣt) nẇt) ) dt + σt, n Y t ) d h,n W t 2.13) fo t, T ] unde P h,n with initial condition n Y = ˆx a.. Hence, to pove 2.10) and 2.12) at the ame time, we conide the following geneal famewok. Namely, we let B :, T ] S R m and B H :, T ] S R m d be two non-anticipative poduct meauable map and B C 1,2, T ) S, R m d ). Then fo each n N we intoduce the path-dependent SDE d n Y t = Bt, n Y t ) + B H t, n Y t )ḣt) + Bt, ny t ) n Ẇ t ) dt + Σt, n Y t ) dw t fo t, T ], 2.14) whee Σ :, T ] S R m d i a non-anticipative poduct meauable map, a conideed in Section 2.3. In addition, we intoduce the path-dependent SDE dz t = B + R)t, Z t ) + B H t, Z t )ḣt)) dt + B + Σ)t, Z t ) dw t 2.15) fo t, T ], whee we equie the non-anticipative poduct meauable map R :, T ) S R m given coodinatewie by d R k, y) := x B k,l, y)1/2)b + Σ), y)e l. 2.16) l=1 12
14 In Theoem 8 below, we in paticula how that wheneve n Y and Z ae tong olution to 2.14) and 2.15), epectively, uch that n Y = Z = ˆx a.. fo each n N, then lim P ny Z α, ε) = 0 fo all ε > ) n Then the choice B = b 1/2)ρ, B H = 0, B = σ and Σ = 0 yield 2.10), ince R = 1/2)ρ in thi cae. Moeove, by chooing B = b, B H = σ, B = σ and Σ = σ intead, 2.12) follow. Since thee ae the two deied eult, we conide the following egulaity condition: C.i) B C 1,2, T ) S, R m d ) and thee ae c, η 0 and κ 0, 1) uch that fo all t, x), T ) S, Bt, x) + B H t, x) c1 + x κ ), m ) d 1/2 t Bt, x) + xx B k,l t, x) 2 c1 + x η ), k=1 l=1 m ) d 1/2 Bt, x) + x B k,l t, x) 2 + Σt, x) c. k=1 l=1 C.ii) B i Lipchitz continuou in x S, unifomly in t, T ), and B H, B, x B and Σ ae Lipchitz continuou with epect to d given by 2.1). C.iii) Thee i a meauable function b :, T ] R o that T and B, y) = Σ, y)b) fo all, y), T ) S. b) 2 d < Remak 7. Condition C.iii) allow u to pefom a change of meaue to get a unique tong olution to 2.14). Howeve, when deiving 2.17) in Section 5.1, 5.2 and 5.3 we meely aume that C.i) and C.ii) hold. Theoem 8. Let C.i)-C.iii) hold and h H 1 0, T ], R d ). Aume that ˆX C 0, T ], R m ) and n ˆX)n N i a equence in C 0, T ], R m ) atifying up E ˆX n 2p] < fo each p 1. n N Then the following thee aetion hold: i) Fo any n N thee i a unique tong olution n Y to 2.14) atifying ny = ˆX n a.. Moeove, up n N E n Y 2p α,] < fo all p 1 and α 0, 1/2). ii) Thee i a unique tong olution Z to 2.15) uch that Z = ˆX a.. and we have E Z 2p α,] < fo all p 1 and α 0, 1/2). 13
15 iii) Let α 0, 1/2) and lim n E ˆX n ˆX 2 ]/ T n 2α = 0, then it follow that lim E max ny tj,n Z tj,n 2] / T n 2α = ) n j {0,...,k n} In paticula, 2.17) hold, that i, n Y ) n N convege in the delayed Hölde nom α, in pobability to Z. 3 Convegence in pobability in Hölde nom 3.1 Hölde pace fo tochatic pocee Fo α 0, 1] let C α 0, T ], R m ) denote the linea pace of all R m -valued adapted ight-continuou pocee X atifying X C α 0, T ], R m ) a.., endowed with the peudometic C α 0, T ], R m ) C α 0, T ], R m ) 0, ), X, Y ) E X Y α, 1]. 3.1) We notice that a equence n X) n N in thi peudometic pace convege to ome X C α 0, T ], R m ) if and only if it convege to thi poce in the delayed Hölde nom α, in pobability. Put diffeently, n X X α, ) n N convege to zeo in pobability. Futhe, n X) n N i Cauchy if and only if it i Cauchy in the nom α, in pobability in the ene that lim up k n N: n k P n X k X α, ε) = 0 fo all ε > 0. Next, we et C 0, T ], R m ) := C 0 0, T ], R m ), which i the linea pace of all R m -valued adapted ight-continuou a.. continuou pocee. Depite the fact that we do not aume the uual condition, C 0, T ], R m ) i complete, which yield the following eult. Lemma 9. C α 0, T ], R m ) endowed with the metic 3.1) i complete. Poof. Let n X) n N be a Cauchy equence in C α 0, T ], R m ). By Lemma in 21], thee i X C 0, T ], R m ) to which n X) n N convege unifomly in pobability. Fo given ε, η > 0 thee i n 0 N uch that P up,t,t ]: t n X k X ) n X t k X t ) ε ) < η t α 2 2 fo all k, n N with k n n 0. We fix l N and et δ l := T )/l, then thee exit k l N uch that k l n 0 and P kl X X ε/4)δ α l ) < η/2. 14
16 Hence, P ) n X X ) n X t X t ) up > ε,t,t ]: t δ l t α < η fo all n N with n n 0. By the continuity of meaue, n X X α, ) n N convege in pobability to zeo. In paticula, X α, < a.. Fo p 1 we ecall that C,p0, α T ], R m ) denote the pace of all pocee X C α 0, T ], R m ) atifying E X p α,] <, endowed with the eminom 2.6). A equence n X) n N in thi pace i called p-fold unifomly integable if n X α, ) n N atifie thi popety in the uual ene. Lemma 10. Any equence n X) n N in C α,p0, T ], R m ) that i Cauchy with epect to the eminom 2.6) i p-fold unifomly integable. Poof. Let ε > 0, then thee i n 0 N o that E k X n X p α,] < ε/2 p fo all k, n N with k n n 0. A the andom vaiable Y := max n {1,...,n0 } n X α, i p-fold integable, we obtain that ]) up E n X p 1/p α, 1 A EY p 1A ]) 1/p + ε 1/p /2 n N fo all A F. Fit, by chooing A = Ω, thi give up n N E n X p α,] <. Secondly, by etting δ := ε/2 p, it follow that up n N E n X p α, 1 A] < ε fo all A F with EY p 1A] < δ. We conclude with the following convegence chaacteization. Popoition 11. A equence n X) n N in C,p0, α T ], R m ) convege in the eminom 2.6) if and only if it i p-fold unifomly integable and thee i X C α 0, T ], R m ) uch that lim P nx X α, ε) = 0 fo all ε > 0. n In the latte cae, we have E X p α,] < and lim n E n X X p α,] = 0. Moeove, C α,p0, T ], R m ) equipped with 2.6) i complete. Poof. By Lemma 9 and 10, it uffice to how the if-diection of the fit claim. To thi end, let ν n ) n N be a tictly inceaing equence in N uch that νn X X α, ) n N convege to zeo a.., then E X p α,] lim inf n E νn X p α, ] up E n X α,] p <, n N 15
17 by Fatou Lemma. Now let ε > 0, then thee exit δ > 0 and n 0 N uch that up n N E n X p α, 1 A] < ε/3) p fo each A F with P A) < δ and P n X X α, ε/3) < δ fo all n N with n n 0. Thu, E n X X p α, ]) 1/p E n X X p α, 1 { nx X α, ε/3} ]) 1/p + ε/3 < ε fo evey uch n N, ince imila eaoning a above give E X p α, 1 A] up n N E n X p α, 1 A] fo all A F. Thi complete the poof. 3.2 A geneal Kolmogoov-Chentov etimate In thi ection we eviit the poof of the Kolmogoov-Chentov Theoem to allow fo pocee that ae meely ight-continuou and to obtain a quantitative etimate of the Hölde nom. Let k α,q,p := 2 q+2p 2 q/2p) α 1) 2p 3.2) fo p 1/2, q > 0 and α 0, q/2p)) and note that lim α q/2p) k α,q,p =. Then we have the following eult. Popoition 12. Let H be a et of R m -valued ight-continuou pocee and, t, T ] be uch that < t. Aume that thee ae c 0 0, p 1/2 and q > 0 uch that up E U u U v 2p] c 0 u v 1+q 3.3) U H fo all u, v, t]. Then fo each α 0, q/2p)) it hold that up E U H up u,v,t]: u v ) 2p ] U u U v k u v α α,q,p c 0 t ) 1+q 2αp. Poof. Fo given n N 0 let D n be the n-th dyadic patition of, t], whoe point ae d i,n := + i2 n t ), whee i {0,..., 2 n }. We define n := {u, v) D n D n u v 2 n t )}, then it i eadily een that thee ae 2 n tuple u, v) n atifying u < v. Fo fixed U H we et V n := up u,v) n U u U v, then 3.3) give E ] Vn 2p E U u U v 2p] 2 nq c 0 t ) 1+q. 3.4) u,v) n: u<v 16
18 We now et D := n N 0 D n and let u, v D atify 0 < v u < 2 n t ) fo ome n N 0. Then fo each k N 0 thee ae unique i k, j k {1,..., 2 k } uch that d ik 1,k u < d ik,k, and d jk 1,k v < d jk,k fo v < t and d jk,k = t fo v = t, epectively. Since d ik,k) k N0 and d jk,k) k N0 ae two deceaing equence conveging to u and v, epectively, two telecoping um yield that U u U v = U din,n U djn,n + U U dik+1,k+1 d + ik U U,k djk+1,k+1 d. jk,k k=n k=n We note that eithe i n = j n o intead n 1, j n 2 and i n = j n 1, a 0 < v u < 2 n t ). In both cae, d in,n, d jn,n) n. Moeove, d ik,k, d ik+1,k+1), d jk,k, d jk+1,k+1) k+1 fo all k N 0, by contuction. So, U u U v V n + 2 V k+1 2 V k. 3.5) k=n k=n Next, pick u, v D uch that 0 < v u < t, then thee i a unique n N 0 uch that 2 n 1 t ) v u < 2 n t ). By 3.5), v u) α U u U v 2 1+α t ) α 2 αk V k becaue 2 αn 2 αk fo all k N 0 with k n. Clealy, u, v D atify v u = t if and only if u = and v = t. In thi cae, U U t /t ) α t ) α Z 0. Thu, we have hown that U u U v up u,v,t]: u v u v α 21+α t ) α k=n 2 αk V k, 3.6) k=0 a D i a countable dene et in, t] containing t and U i ight-continuou. Hence, 3.6), the tiangle inequality, monotone convegence and 3.4) yield that E up u,v,t]: u v ) 2p ]) 1 2p U u U v 2 1+α t ) α u v α k=0 2 1+α c 1 2p 0 t ) 1+q 2p α 2 αk E V 2p ]) 1 2p k k=0 2 α q 2p )k. The powe eie on the ight-hand ide convege abolutely to the invee of 1 2 α q/2p), ince α < q/2p). Fo thi eaon, the popoition follow. 17
19 3.3 Convegence along a equence of patition In thi ection, we tate a ufficient citeion fo a equence of pocee to convege in pobability in the delayed Hölde nom α, whee α 0, 1]. Fo thi pupoe, we equie the following etimate. Lemma 13. Let T be a patition of, T ] of the fom T = {t 0,..., t k } fo ome k N and t 0,..., t k, T ] uch that = t 0 < < t k = T. Then x) xt) up 2 max,t,t ]: t t α fo each map x :, T ] R m. up j {0,...,k 1} u,v t j,t j+1 ]: u v xt i ) xt j ) + max i,j {0,...,k}: i j t i t j α xu) xv) u v α Poof. Fit, aume that i, j {0,..., k 1} ae uch that i < j 1 and t i, t i+1 ), then x) xt j ) t α x) xt i+1) t i+1 α + xt i+1) xt j ) t i+1 t j α, becaue t > t i+1 t i+1 t j. Now uppoe that i, j {0,..., k 1} atify i < j, t i, t i+1 ) and t t j, t j+1 ). In thi cae, x) xt) t α x) xt i+1) t i+1 α + xt i+1) xt j ) t i+1 t j α + xt j) xt) t j t α, ince t > t i+1 t i+1 t j t j t. Now the aetion follow. Thi yield the befoe mentioned citeion. Popoition 14. Let n U) n N be a equence of R m -valued ight-continuou pocee and aume thee ae p, q > 0 o that fo each β 0, q/2p)) thee i c β 0 atifying P max up j {0,...,k n 1} u,v t j,n,t j+1,n ] ) n U u n U v λ c u v β β λ 2p 3.7) fo all n N and λ > 0. If n U ) n N and max j {0...,kn} n U tj,n / T n α ) n N convege in pobability to zeo, then o doe the equence n U α, ) n N fo all α 0, q/2p)). 18
20 Poof. Let n N and fix β α, q/2p)), then it follow that n U max up j {0,...,k n 1} t t j,n,t j+1,n ) n U t n U tj,n t t j,n β T n β + max j {0,...,k n 1} nu tj,n, ince n U t n U t n U tj,n / t t j,n β ) T n β + n U tj,n fo all j {0,..., k n 1} and t t j,n, t j+1,n ). Conequently, fom 3.7) we obtain that P n U ε ) c β 2/ε) 2p T n 2βp + P max nu tj,n ε/2 ) j {0,...,k n} fo all ε > 0, which diectly entail that n U ) n N convege in pobability to zeo. Next, fo fixed n N Lemma 13 give u that n U n U t up 2 max,t,t ]: t t α up j {0,...,k n 1} u,v t j,n,t j+1,n ]: u v n U ti,n n U tj,n + max i,j {0,...,k n}: i j t i,n t j,n. α n U u n U v u v α By uing the fact that u v β α T n β α and t i,n t j,n T n /c T fo all i, j {0,..., k n } with i j and u, v t j,n, t j+1,n ], we ee that P up,t,t ]: t ) n U n U t ε c t α β 4/ε) 2p T n β α)2p + P 2c α T max nu tj,n / T n α ε/2 j {0,...,k n} fo any ε > 0. A the tem on the ight-hand ide convege to zeo a n, the aetion i hown. Remak 15. If p 1/2 and thee i c 0 0 uch that E n U u n U v 2p ] c 0 u v 1+q fo all n N and u, v, T ], then Popoition 12 and Chebyhev inequality aue that condition 3.7) i atified. 3.4 Adapted linea intepolation of Bownian motion We tudy the equence n W ) n N of adapted linea intepolation of W given by 2.9) and fo which a.e. path lie in H 1 0, T ], R d ). To thi end, we intoduce the following notation. Fo given n N and t, T ), let i {0,..., k n 1} be uch that t t i,n, t i+1,n ), then we et t n := t i 1) 0,n, t n := t i,n and t n := t i+1,n. 3.8) ) 19
21 That i, t n i the pedeceo of t n with epect to T n, unle i = 0, and t n i the ucceo of t n. We alo et T n := t kn 1,n, T n := T and T n := T. In addition, we ue the following abbeviation: t i,n := t i,n t i 1,n ) and W ti,n := W ti,n W ti 1,n 3.9) fo each i {1,..., k n 1}. Afte thee pepaation, let u begin with a geneal integal epeentation. Lemma 16. Let n N and, t, T ] be uch that < t. Then each R m d -valued pogeively meauable quae-integable poce Y atifie Y un d n W u = t t i+1,n i,n t i 1,n Y un dw u a.., wheneve i {1,..., k n 1} i uch that, t t i,n, t i+1,n ], and Y un d n W u = t i+1,n + t i+1,n j 1,n t i,n i,n t i 1,n Y un dw u Y un dw u + t t j,n t j+1,n j,n t j 1,n Y un dw u a.., if i, j {1,..., k n 1} atify i < j, t i,n, t i+1,n ] and t t j,n, t j+1,n ]. In paticula, fo all j {1,..., k n } we have j,n Y un d n W u = j 1,n Y un dw u a.. Poof. A n W u = 0 fo each u, t 1,n ], the econd claim follow fom the fit, by chooing = t 1,n and t = t j,n fo j {1,..., k n }. To check the fit claim, uppoe initially that, t t i,n, t i+1,n ] fo ome i {1,..., k n 1}, then Y un d n W u = t t i+1,n Y ti 1,n W ti,n = t t i+1,n i,n t i 1,n Y un dw u a.. Now aume intead that thee ae i, j {1,..., k n 1} uch that i < j, t i,n, t i+1,n ] and t t j,n, t j+1,n ]. Then the a.. decompoition Y un d n W u = i+1,n Y un d n W u + j 1 h=i+1 h+1,n t h,n Y un d n W u + and the cae conideed above imply the aeted epeentation. t j,n Y un d n W u 20
22 Let u ecall that fo each p 1 thee i a contant w p > 0 depending only on p uch that fo evey R m d -valued pogeively meauable poce Y it hold that v 2p ] ) t p ] E up Y u dw u w p E Y u 2 du M) v,t] fo all, t, T ] with t. In fact, w p = 2 p p 3p /p 1/2) p and the dimenion m and d do not alte w p. We deive a coeponding eult fo the equence n W ) n N of adapted linea intepolation of W. Popoition 17. Fo each p 1 thee i a contant ŵ p > 0 uch that evey R m d -valued pogeively meauable poce Y atifie v 2p ] E up Y un d n W u ŵ p max E Y tj,n 2p] t ) p 3.10) j {0,...,k n}: t j,n n,t n ] v,t] fo each n N and, t, T ] with t. Poof. Fit, if t t 1,n, then v Y u n d n W u = 0 fo each v, t] a.. Fo < t 1,n and t t 1,n we have v Y un d n W u = v t 1,n Y un d n W u fo all v t 1,n, t] a.. Thu, let u ue Lemma 16 and aume that, t t i,n, t i+1,n ] fo ome i {1,..., k n 1}, then M) yield that v 2p ] t )2p E up Y un d n W u = t i+1,n ) E ti,n 2p ] Y 2p un dw u t i 1,n v,t] w p c p TE Y ti 1,n 2p] t ) p, whee c T i the contant appeaing in 2.8). Next, uppoe that thee ae i, j {1,..., k n 1} uch that i < j, t i,n, t i+1,n ] and t t j,n, t j+1,n ]. Then v max Y v,t] un d n W u t i+1,n i,n Y t i+1,n un dw u t i 1,n h,n + max Y h {i+1,...,j 1} un dw u + t t j,n tj,n Y un dw u a.. t j 1,n t i,n t j+1,n Thi i due to Lemma 16, which aet that the poce, t] Ω R m, v, ω) v Y u n ω) d n W u ω) i piecewie linea. Hence, we obtain that v 2p ] E up Y un d n W u ŵ p max E Y th,n 2p] t ) p h {i 1,...,j 1} v,t] fo ŵ p := 3 2p 1 w p c p T, which yield the claim. 21
23 Lemma 18. Fo each p, q 1 thee exit a contant ŵ p,q > 0 atifying ) t p ] E n Ẇ u q du ŵ p,q T n qp/2 t ) p 3.11) fo all, t, T ] with t and n N. Poof. Clealy, if t t 1,n, then nẇu q du = 0. Fo < t 1,n and t t 1,n we have n Ẇ u q du = n Ẇ u q du. t 1,n So, let now, t t i,n, t i+1,n ] fo ome i {1,..., k n 1} and Z be an R d -valued andom vecto uch that Z N 0, Id), then ) t p ] E n Ẇ u q du = E Z qp] t i,n ) qp/2 t i+1,n ) qp t )p c T n qp/2 t ) p, whee ŵ p,q := E Z qp ]c qp T and c T i the contant in 2.8). Next, let intead i, j {1,..., k n 1} be uch that i < j, t i,n, t i+1,n ] and t t j,n, t j+1,n ]. Then p ]) 1/p j ) E n Ẇ u du) q t th+1,n p ]) 1/p E n Ẇ u q du h=i t h,n ŵp,q 1/p T n q/2 t ), by what we have jut hown. Theefoe, the claim hold. 3.5 Auxiliay convegence eult Lemma 19. Let n U) n N be a equence of non-negative meauable pocee fo which thee ae p > 1 and c p > 0 uch that E n U 2p ] c p T n 2p fo each, T ) and n N. Then thee i c 1 > 0 atifying ) T 2 ] E nu n Ẇ d c 1 T n fo all n N. Poof. Let q > 1 be uch that 1/p+1/q = 1, then Lemma 18 give a contant ŵ q,2 > 0 that i independent of n uch that ) T q ] E n Ẇ 2 d ŵ q,2 T n q T ) q. 22
24 Thu, we define c 1,1 := ŵ 1/q q,2 T ) and c 1 := c 1/p p T )c 1,1, then it follow fom Cauchy-Schwaz and Hölde inequalitie that ) T 2 ] T p ]) 1/p E nu n Ẇ d E nu d) 2 c 1,1 T n 1 c 1 T n. Lemma 20. Let n N and fo evey ight-continuou map x : 0, T ] R m et L n x)t) := x t) fo all t 0, t 1,n ), L n x)t) := xt i 1,n ) + t t i,n ) xt i,n) xt i 1,n ) t i+1,n fo t t i,n, t i+1,n ) with i {1,..., k n 1} and L n x)t ) := xt kn 1,n). Then it hold that L n x) t x max j {1,...,kn 1}: t j,n t xt j,n ) and L n x) t x t 2 fo each t t 1,n, T ]. max up j {0,...,k n 1}: t j,n t t j,n,t j+1,n ] x t ) xt j 1) 0,n ) Poof. Fix t 1,n, t] and let i {1,..., k n 1} be o that t i,n, t i+1,n ], then L n x)) xt i 1,n ) xt i,n ), ince L n i linea on t i,n, t i+1,n ]. In addition, we immediately obtain that L n x)) x) x) xt i 1,n ) + xt i,n ) xt i 1,n ) and the aetion follow. 2 up v t i,n,t i+1,n ] x t v) xt i 1,n ) Lemma 21. Let n U) n N denote a equence of R m -valued ight-continuou pocee fo which thee ae c 0 0, p 1/2 and q > 0 uch that E n U n U t 2p] c 0 t 1+q fo all n N and, t, T ]. Then fo evey α 0, q/2p)), lim E n U L n n U) 2p] / T n 2αp = 0. n Poof. Fix β α, q/2p)). Fom Lemma 20 we obtain that n U L n n U) 2 1+β T n β 23 n U n U t up,t,t ]: t t β
25 fo evey n N. Conequently, Popoition 12 implie that the contant c β := 2 21+β)p k β,q,p c 0 T ) 1+q 2βp atifie E n U L n n U) 2p] c β T n 2βp fo all n N, whee k β,q,p i given by 3.2) when α i eplaced by β. Now the claim follow, ince α < β. Lemma 22. Let G :, T ] S R m be d -Lipchitz continuou, n U) n N be a equence in C 0, T ], R m ) and c 0 0 be uch that Gt, x) c x ) and E n U 2] + E n U n U t 2] / t c E n U 2]) fo all n N,, t, T ] with t and x S. Then thee i c 1 > 0 atifying fo each n N, ) tj,n E max G j {0,...,k n} n, n U n 2 ] n ) 1 d n c 1 T n 1 + E n U 2]). Poof. We aume that E n U 2 ] <, a othewie thee i nothing to how. By decompoing the integal, we can ewite that j,n G n, n U n ) n n d = j 1,n G n, n U n ) d fo each j {1,..., k n }. Thu, let λ 0 be a Lipchitz contant fo G, then tj 1,n 2 ] E max G n, n U n ) G n, n U n ) d j {1,...,k n} c 1,1 T n 1 + E n U 2]) with c 1,1 := 2λ 2 T ) c 0 ). In addition, we etimate that j,n 2 ] E max G j {1,...,k n} n, n U n ) d c t j 1,n 2,2 T n E n U 2]), whee c 2,2 := 2c c 0 ). So, the contant c 1 := 2c 1,1 + c 1,2 T )) yield the claim. Popoition 23. Let G :, T ] S R m d be d -Lipchitz continuou and n U) n N be a equence in C 0, T ], R m ). Suppoe thee ae c 0 0 and p > 1 uch that Gt, x) c x ) and ] E n U 2p] + E n U n U t 2p c t p 0 24
26 fo each n N,, t, T ] uch that t and x S. Then fo evey α 0, 1/2 1/2p)), lim T n 2α E n j,n max j {0,...,k n} 2 ] G n, n U n ) dn W W ) = 0. Poof. We fix n N and once again decompoe the integal to get that j,n G n, n U n ) dn W = j 1,n G n, n U n ) dw a.. fo all j {1,..., k n }. Let λ 0 denote a Lipchitz contant fo G, then E j 1,n max j {0,...,k n} G n, n U n ) G n, n U n ) dw 2 ] T 2w 1 λ 2 n n ) + E n U n n U ] n 2 d c 1 T n with c 1 := 2w 1 λ 2 T )1+c 1/p 0 ), whee w 1 i the contant atifying M) fo p = 1. Next, we let n M C 0, T ], R m ) be a quae-integable matingale atifying nm t = G n, n U n ) dw fo all t, T ] a.., then n M tj,n n M tj 1,n each j {1,..., k n }. Futhemoe, = j,n t j 1,n G n, n U n ) dw a.. fo E n M n M t 2p] 2 2p 1 w p c 2p 0 t ) p 1 + E n U 2p]) c 2 t ) p fo all, t, T ] with t, whee c 2 := 2 2p 1 w p c 2p c 0 ). Thu, let β α, 1/2 1/2p)), then it follow fom Popoition 12 that E up,t,t ]: t ) 2p ] n M n M t k t β β,p 1,p c 2 T ) 1 2β)p, ince p > 1, by aumption. Finally, we et c β := k β,p 1,p c 2 ) 1/p T ) 1 2β, then j,n 2 ] E max G j {1,...,k n} n, n U n ) dw c t j 1,n β T n 2β, by Hölde inequality, and the aetion follow. 25
27 4 Path-dependent ODE and SDE: poof In thi ection, we give the poof fo the exitence and uniquene of mild olution to path-dependent ODE in Section 2.2 and the exitence and uniquene of tong olution to path-dependent SDE in Section Poof of Popoition 2 We fit deive a global etimate fo any mild olution. Thi allow u to ue O.ii), the Lipchitz condition on bounded et, to deive exitence and uniquene eult. Lemma 24. Unde O.i), thee i c H > 0 depending only on T uch that any mild olution x to the ODE 2.3) atifie fo all t, T ], x t 2 H, c H e c t ) t H c F ) 2 d x 2 + c F ) 2 d. 4.1) Poof. By etimating x t + ẋ) d fo given t, T ], it follow eadily fom Gonwall inequality that x t + ) ẋ) d e 2 t t c F ) d x + 2 c F ) d. Moeove, fo c 1 := 2 2 T + 1) we have x t 2 H, 2 x 2 + c 1 c F ) x + ẋu) du) 2 d. 4.2) Thu, we et c H := 2e 2 c 1, then fom 2 c F ) d 1 + T ) c F ) 2 d we infe that x t + 2 ẋ) d) c H e c t ) t H c F ) 2 d x 2 + c F ) 2 d. The claim follow fom 4.2), the fundamental theoem of calculu fo Riemann- Stieltje integal and the tanitivity of abolutely continuou meaue. We now how uniquene of mild olution, which implie uniquene fo claical olution. 26
28 Lemma 25. Aume that O.i) and O.ii) hold, then any two mild olution x and y to the ODE 2.3) that atify x = y mut coincide. Poof. By Lemma 24, thee i n N uch that x H, y H, n. Thu, x t y t 2 H, 2T + 1) λ 2 F,n) x y 2 H, d fo all t, T ]. Gonwall inequality implie that x = y. Poof of Popoition 2. A the uniquene claim follow fom Lemma 25, we diectly tun to the exitence aetion. To thi end, let H be the et of all x H 1 0, T ], R m ) atifying x) = ˆx) fo evey 0, ] and the etimate 4.1), whee c H i choen lagely enough o that c H 2 4 T + 1) ) By Lemma 24, a map x S i a mild olution to the ODE 2.3) uch that x) = ˆx) fo all 0, ] if and only if x H and it i a fixed-point of the opeato Ψ : H H 1 0, T ], R m ) given by Ψy)t) := x 0 t) + t F, y ) d. We emak that condition 4.3) aue that Ψ map H into itelf. Indeed, thi follow by ineting 4.1) into the inequality Ψx) t 2 H, c H x c H c F ) x 2 H,) d, valid fo all x H and t, T ]. A x 0 H and x n = Ψx n 1 ) fo each n N, by definition 2.4), we now know that x n ) n N0 i a equence in H. Next, let u chooe l N atifying x H, l fo all x H and et c 1 := 2T + 1). Then we obtain that Ψx) t Ψy) t 2 H, c 1 λ F,l ) 2 x y 2 H, d fo each x, y H and t, T ], which in paticula how that Ψ mut be H, -Lipchitz continuou. Moeove, it follow inductively that x t n+1 x t n 2 H, δ2 ) t n c 1 λ F,l ) 2 d n! fo evey n N 0, whee we have et δ := Ψx 0 ) x 0 H,. Hence, the tiangle inequality give u that x n x k H, δ n 1 i=k ) 1/2 1 ) T i/2 c 1 λ F,l ) 2 d i! 27
29 fo all k, n N 0 with k < n. Now the atio tet yield that the eie i=0 1/i!) 1/2 x i/2 convege abolutely fo all x 0. Hence, we have hown that lim k up n N: n k x n x k H, = 0. A H i cloed with epect to the complete nom H,, thee exit a unique map y F H uch that lim n x n y F H, = 0. Lipchitz continuity of Ψ implie lim n x n+1 Ψy F ) H, = 0. Fo thi eaon, y F = Ψy F ) and the popoition i poven. 4.2 Poof of Popoition 5 Lemma 26. Let X be an R m -valued adapted ight-continuou poce and B R m be cloed, then τ := inf{t 0, T ] {X 0, t]} B } i a topping time atifying τ = inf{t 0, T ] X t B} on {X S}. Poof. Fit, we check that {τ t} = {{X 0, t]} B } fo fixed t 0, T ]. To thi end, it uffice to how that if t < T and ω Ω atifie τω) = t, then {X ω) 0, t]} B. In thi cae, fo each n N thee ae n 0, t + T t)/n) and y n B atifying y n X n ω) < 1/n. So, we chooe a tictly inceaing equence ν n ) n N in N uch that νn ) n N convege to ome 0, t], then it follow that X ω) = lim n X νn ω) B, which yield the intemediate claim. Next, we et B n := {x B x n} fo all n N and ue the notation ditx, C) = inf y C x y fo all x R m and C R m. Let t 0, T ] and D be a countable dene et in 0, t] containing t, then {τ t} = {inf ditx, B n ) = 0} = {ditx, B n ) < 1/k} F t, D n N n N k N D by the above epeentation of {τ t}. Finally, if ω Ω atifie Xω) S, then {X ω) 0, t]} i compact and in paticula cloed. Fo thi eaon, τω) < inf{t 0, T ] X t ω) B} would violate the definition of τω). Example 27. Let X C 0, T ], R m ) and n N, then the above lemma give a topping time τ n uch that τ n = inf{t 0, T ] X t n} a.. Thi enue that X t τn X n a.. fo all t, T ], ince we have that X t τn n a.. on { X n} and τ n = a.. on { X > n}. 28
30 In thi ection, wheneve p 1 and condition S.i) i atified, we et ) T p m p := c B ) 2 d + c 2p Σ w p, whee w p i the contant appeaing in M). Lemma 28. Unde S.i), fo each p > 2 and α 0, 1/2 1/p) thee i c α,p > 0 depending only on α, p and T uch that any tong olution X to 2.5) atifie fo all t, T ]. E X t 2p α,] cα,p e cα,pmpt ) E X 2p] + m p t ) ) 4.4) Poof. Aume that E X 2p ] < and let n N. Then Example 27 yield a topping time τ n uch that X τn X n a.. Fit, X t τn X t τn + B, X v τn ) d + up Σu, X u ) dw u a.. v,t] fo fixed t, T ]. Thu, fom Jenen and Cauchy-Schwaz inequality we obtain that E X t τn 2p] 3 2p 1 E X 2p] + 6 2p 1 m p t ) p E X τn 2p] d. Moeove, a imila computation how that E X τn u X τn v 2p ] 4 2p 1 m p v u) p E X τn 2p] d fo all u, v, t] with u < v. Theefoe, Popoition 12 yield that ) 2p ] Xu τn Xv τn E u v α up u,v,t]: u v k α,p 2,p 4 2p 1 m p t ) p 1 2αp 1 + E X τn 2p] d, whee the contant k α,p 2,p i given by 3.2) fo q = p 2. Thu, E ] X t τn 2 α, /cα,p E X 2p] + m p 1 + E X τn 2p] d fo c α,p := 12 2p k α,p 2,p )T + 1) p 1. By Gonwall inequality and Fatou lemma, E X t α,] 2p lim inf E X t τn α,] 2p cα,p e cα,pmpt ) E X 2p] +m p t ) ), n which i the claim. 29
31 Remak 29. If p 1 and α 0, 1/2) ae uch that α < 1/2 1/p fail, then, unde S.i), we till have that E X t 2p α,] E X t 2q α,]) p/q < fo any q > p uch that α < 1/2 1/q, by Hölde inequality. Lemma 30. Unde S.iii), pathwie uniquene hold fo 2.5). Poof. Let X and X be two weak olution to 2.5) defined on a common filteed pobability pace Ω, F, F t ) t 0,T ], P ) on which thee i a tandad d-dimenional F t ) t 0,T ] -Bownian motion W uch that X = X a.. We fix n N, then it follow fom Example 27 that thee i a topping time τ n uch that τ n = inf{t 0, T ] X t n o X t n} a.. Clealy, τn X t τn X t τn B, X ) B, X ) d v τn + up Σu, X u ) Σu, X u ) d W u v,t] fo given t, T ]. We et c 1 := T ) + w 1 ), whee w 1 i the contant in M) fo p = 1, then Ẽ X t τn X t τn 2] c 1 λ n ) 2 Ẽ X τn X τn 2] d. So, X τn τn = X a.., by Gonwall inequality. A τ n τ n+1 a.. fo all n N and up n N τ n = a.., we get that X t = lim n Xt τn = lim n n Xτ t = X t a.. fo all t, T ]. Right-continuity implie that X = X a.. Poof of Popoition 5. We define H be the et of all X C 0, T ], R m ) atifying X = ˆX fo all 0, ] a.. and the etimate 4.4) fo any p > 2 and α 0, 1/2 1/p), whee the contant c α,p i choen lagely enough o that c α,p 12 2p k α,p 2,p )T + 1) p ) By Lemma 28 and Remak 29, we have that H C, 1/2 0, T ], R m ) and a poce X C 0, T ], R m ) i a olution to 2.5) atifying X = ˆX fo all 0, ] a.. if and only if X H and it i a fixed point of the opeato Ψ : H C 0, T ], R m ) pecified by equiing that ΨY ) t = 0 X t + t B, Y ) d + t Σ, Y ) dw. fo all t 0, T ] a.. We te the fact that, due to Popoition 12 and condition 4.5), fo evey X H, p > 2 and α 0, 1/2 1/p) it follow that E ] ΨX) t 2p α, cα,p E 0 X 2p] + c α,p m p 1 + E X 2p] d 30 a..
32 fo all t, T ]. Thu, ΨH ) H follow fom plugging 4.4) into the above inequality. Since 0 X H and n X = Ψ n 1 X) a.. fo all n N, by 2.7), we have hown that n X) n N0 i a equence in H. Next, chooe p > 2 and α 0, 1/2) uch that α 0 α < 1/2 1/p, whee α 0 i the contant in the Lipchitz condition S.ii). Futhe, we et l p := T λ B) 2 d) p + λ 2p Σ w p, then E ΨX) t ΨY ) t 2p] 2 2p 1 l p t ) p 1 E X Y 2p α 0,] d fo all given X, Y H and t, T ]. Afte applying Popoition 12 and uing x α0, T + 1) α α 0 x α, fo all x C α 0, T ], R m ), we get E ΨX) t ΨY ) t 2p α, ] cα,p l p E X Y 2p α,] d with c α,p := 4 2p k α,p 2,p )T + 1) 2p 1. Hence, Gonwall inequality entail that thee i at mot a unique olution X to 2.5) atifying X = ˆX fo all 0, ] a.. We alo infe fom the above inequality that Ψ i Lipchitz continuou with epect to the eminom 2.6), whee p i eplaced by 2p. In addition, E ] n+1 X t n X t 2p δ 2p α, n! c α,pl p ) n t ) n fo each n N 0, by induction with δ := E Ψ 0 X) 0 X 2p α,]) 1/2p). Hence, the tiangle inequality give ]) E n X k X 2p 1 2p α, δ n 1 i=k ) 1 1 2p cα,p l p ) i i 2p T ) 2p i! fo each k, n N 0 with k < n. The atio tet implie that the eie i=0 1/i!) 1/2p) x i/2p) convege abolutely fo each x 0. So, lim up k n N: n k E n X k X 2p α,] = 0. Due to Popoition 11, becaue H i cloed with epect to the complete eminom 2.6), whee p i eplaced by 2p, thee exit a poce X H that i unique up to inditinguihability uch that lim E n X X α,] 2p = ) n 31
33 Lipchitz continuity of Ψ implie that lim n E n+1 X ΨX) 2p α,] = 0. Fo thi eaon, X = ΨX) a.. Finally, aume p 1 and α 0, 1/2) ae uch that α 0 α < 1/2 1/p fail. If α < α 0, then E ] n X X 2p α, T + 1) α 0 α)2p E ] n X X 2p α 0, fo all n N, which implie 4.6). Fo α 1/2 1/p we take q > p o that α < 1/2 1/q and ue that E n X X 2p α,] E n X X 2q α,]) p/q fo all n N. A thi alo give 4.6), the poof i complete. 5 Poof of main eult 5.1 Decompoition into emainde tem Popoition 31. Let C.i) hold, h H 1 0, T ], R d ) and B be d -Lipchitz continuou. Then fo each p 1 thee i c p > 0 uch that any n N and any tong olution n Y to 2.14) atify E n Y 2p] + E n Y n Y t 2p] / t p c p 1 + E n Y 2p]) 5.1) fo all, t, T ] with t. Poof. We let l N and ue Example 27 to define a topping time τ l,n uch that n Y τ l,n n Y l a.. Futhe, we etimate that τl,n n Y τ l,n n Y t τ l,n Bu, n Y u u ) + B H u, n Y )ḣu) du v τl,n + up Bu, v,t] n Y u ) n Ẇ u du v τl,n + up Σu, n Y u ) dw u a.. v,t] fo fixed, t, T ] with t. Thu, the tiangle inequality and the inequalitie of Cauchy-Schwaz and Jenen yield that E n Y τ l,n n Y t τ l,n 2p]) 1 2p + c p,1 t ) p E n Y u τ l,n 2κp] du E v τl,n up v,t] Bu, n Y u ) n Ẇ u du 32 ) 1 2p 2p ]) 1 2p, 5.2)
34 whee we have et c p,1 := 6c) 2p T ) p + T ḣu) 2 du) p + w p ) and w p i the contant appeaing in M). Since κ < 1, we can pick γ 1, κ 1 ), then Lemma 18 povide a contant c p,2 > 0 uch that 3.11) hold when q and p ae eplaced by 2 and p/1 γκ), epectively. Thi yield that ) t τl,n ) 2p ] E Bu, n Y u ) Bu n, n Y u n ) nẇu du ) t 2λ) 2p /2t ) p 1 u u n ) p du c 1 γκ p,2 T n p t ) p t ) t p ] + 2λ) 2p /2t ) p 1 E n Y u τ l,n n Y u n τ l,n 2p n Ẇ v 2 dv du c p,3 t ) p T n p E n Y u τ l,n n Y u n τ l,n 2p γκ ]) γκ du, by the inequalitie of Cauchy-Schwaz, Jenen and Hölde, whee λ 0 denote a Lipchitz contant fo B and c p,3 := 2 3p λ 2p T ) p c 1 γκ p,2. Note hee that the choice of c p,2 entail that E n Ẇ v 2 dv ) p 1 γκ ]) 1 γκ c 1 γκ p,2 T n p t ) p. Next, let c p,4 > 0 be a contant atifying 3.11) when q and p ae eplaced by 2 and p/γ 1)κ), epectively. Then Cauchy-Schwaz, Jenen and Hölde inequality imply that u τl,n E Bv, n Y v ) n Ẇ v dv u n 2c) 2p γκ 2 1 u u n ) p γκ 1 u ) 2p ] γκ u n 1 dv + 2c) 2p γκ 2 1 u u n ) p γκ 1 u u n E c p,5 T n p γκ ) 1 + E n Y u τ l,n 2p]) 1 γ ) γ 1 γ cp,4 T n p γκ u un ) p n Y v τ l,n 2p γ u γκ u n n Ẇ w 2 dw ) p γκ ] dv fo any given u, T ], whee we have et c p,5 := 4c) 2p)/γκ) c γ 1)/γ p,4, ince by the choice of c p,4 we can utilize that E u u n n Ẇ v 2 dv ) p ]) γ 1 γ 1)κ γ 33 γ 1 γ cp,4 T n p γκ u un ) p γκ.
Inference for A One Way Factorial Experiment. By Ed Stanek and Elaine Puleo
 Infeence fo A One Way Factoial Expeiment By Ed Stanek and Elaine Puleo. Intoduction We develop etimating equation fo Facto Level mean in a completely andomized one way factoial expeiment. Thi development
Infeence fo A One Way Factoial Expeiment By Ed Stanek and Elaine Puleo. Intoduction We develop etimating equation fo Facto Level mean in a completely andomized one way factoial expeiment. Thi development
On the quadratic support of strongly convex functions
 Int. J. Nonlinea Anal. Appl. 7 2016 No. 1, 15-20 ISSN: 2008-6822 electonic http://dx.doi.og/10.22075/ijnaa.2015.273 On the quadatic uppot of tongly convex function S. Abbazadeh a,b,, M. Ehaghi Godji a
Int. J. Nonlinea Anal. Appl. 7 2016 No. 1, 15-20 ISSN: 2008-6822 electonic http://dx.doi.og/10.22075/ijnaa.2015.273 On the quadatic uppot of tongly convex function S. Abbazadeh a,b,, M. Ehaghi Godji a
On Locally Convex Topological Vector Space Valued Null Function Space c 0 (S,T, Φ, ξ, u) Defined by Semi Norm and Orlicz Function
 Jounal of Intitute of Science and Technology, 204, 9(): 62-68, Intitute of Science and Technology, T.U. On Locally Convex Topological Vecto Space Valued Null Function Space c 0 (S,T, Φ, ξ, u) Defined by
Jounal of Intitute of Science and Technology, 204, 9(): 62-68, Intitute of Science and Technology, T.U. On Locally Convex Topological Vecto Space Valued Null Function Space c 0 (S,T, Φ, ξ, u) Defined by
Theorem 2: Proof: Note 1: Proof: Note 2:
 A New 3-Dimenional Polynomial Intepolation Method: An Algoithmic Appoach Amitava Chattejee* and Rupak Bhattachayya** A new 3-dimenional intepolation method i intoduced in thi pape. Coeponding to the method
A New 3-Dimenional Polynomial Intepolation Method: An Algoithmic Appoach Amitava Chattejee* and Rupak Bhattachayya** A new 3-dimenional intepolation method i intoduced in thi pape. Coeponding to the method
arxiv: v1 [math.cv] 7 Nov 2018
![arxiv: v1 [math.cv] 7 Nov 2018 arxiv: v1 [math.cv] 7 Nov 2018](/thumbs/90/101586781.jpg) INTERMEDIATE HANKEL OPERATORS ON THE FOCK SPACE OLIVIA CONSTANTIN axiv:181103137v1 [mathcv] 7 Nov 2018 Abtact We contuct a natual equence of middle Hankel opeato on the Fock pace, ie opeato which ae intemediate
INTERMEDIATE HANKEL OPERATORS ON THE FOCK SPACE OLIVIA CONSTANTIN axiv:181103137v1 [mathcv] 7 Nov 2018 Abtact We contuct a natual equence of middle Hankel opeato on the Fock pace, ie opeato which ae intemediate
Second Order Fuzzy S-Hausdorff Spaces
 Inten J Fuzzy Mathematical Achive Vol 1, 013, 41-48 ISSN: 30-34 (P), 30-350 (online) Publihed on 9 Febuay 013 wwweeachmathciog Intenational Jounal o Second Ode Fuzzy S-Haudo Space AKalaichelvi Depatment
Inten J Fuzzy Mathematical Achive Vol 1, 013, 41-48 ISSN: 30-34 (P), 30-350 (online) Publihed on 9 Febuay 013 wwweeachmathciog Intenational Jounal o Second Ode Fuzzy S-Haudo Space AKalaichelvi Depatment
Chapter 19 Webassign Help Problems
 Chapte 9 Webaign Help Poblem 4 5 6 7 8 9 0 Poblem 4: The pictue fo thi poblem i a bit mileading. They eally jut give you the pictue fo Pat b. So let fix that. Hee i the pictue fo Pat (a): Pat (a) imply
Chapte 9 Webaign Help Poblem 4 5 6 7 8 9 0 Poblem 4: The pictue fo thi poblem i a bit mileading. They eally jut give you the pictue fo Pat b. So let fix that. Hee i the pictue fo Pat (a): Pat (a) imply
Gravity. David Barwacz 7778 Thornapple Bayou SE, Grand Rapids, MI David Barwacz 12/03/2003
 avity David Bawacz 7778 Thonapple Bayou, and Rapid, MI 495 David Bawacz /3/3 http://membe.titon.net/daveb Uing the concept dicued in the peceding pape ( http://membe.titon.net/daveb ), I will now deive
avity David Bawacz 7778 Thonapple Bayou, and Rapid, MI 495 David Bawacz /3/3 http://membe.titon.net/daveb Uing the concept dicued in the peceding pape ( http://membe.titon.net/daveb ), I will now deive
SOME SOLVABILITY THEOREMS FOR NONLINEAR EQUATIONS
 Fixed Point Theoy, Volume 5, No. 1, 2004, 71-80 http://www.math.ubbcluj.o/ nodeacj/sfptcj.htm SOME SOLVABILITY THEOREMS FOR NONLINEAR EQUATIONS G. ISAC 1 AND C. AVRAMESCU 2 1 Depatment of Mathematics Royal
Fixed Point Theoy, Volume 5, No. 1, 2004, 71-80 http://www.math.ubbcluj.o/ nodeacj/sfptcj.htm SOME SOLVABILITY THEOREMS FOR NONLINEAR EQUATIONS G. ISAC 1 AND C. AVRAMESCU 2 1 Depatment of Mathematics Royal
Hyperbolic Partial Differential Equations
 Hyperbolic Partial Differential Equation Evolution equation aociated with irreverible phyical procee like diffuion heat conduction lead to parabolic partial differential equation. When the equation i a
Hyperbolic Partial Differential Equation Evolution equation aociated with irreverible phyical procee like diffuion heat conduction lead to parabolic partial differential equation. When the equation i a
Estimates on Invariant Tori near an Elliptic Equilibrium Point of a Hamiltonian System
 jounal of diffeential equation 131, 277303 (1996) aticle no. 0165 Etimate on Invaiant Toi nea an Elliptic Equilibium Point of a Hamiltonian Sytem Amadeu Delham* Depatament de Matema tica Aplicada I, Univeitat
jounal of diffeential equation 131, 277303 (1996) aticle no. 0165 Etimate on Invaiant Toi nea an Elliptic Equilibium Point of a Hamiltonian Sytem Amadeu Delham* Depatament de Matema tica Aplicada I, Univeitat
Determining the Best Linear Unbiased Predictor of PSU Means with the Data. included with the Random Variables. Ed Stanek
 Detemining te Bet Linea Unbiaed Pedicto of PSU ean wit te Data included wit te andom Vaiable Ed Stanek Intoduction We develop te equation fo te bet linea unbiaed pedicto of PSU mean in a two tage andom
Detemining te Bet Linea Unbiaed Pedicto of PSU ean wit te Data included wit te andom Vaiable Ed Stanek Intoduction We develop te equation fo te bet linea unbiaed pedicto of PSU mean in a two tage andom
Problem 1. Construct a filtered probability space on which a Brownian motion W and an adapted process X are defined and such that
 Stochatic Calculu Example heet 4 - Lent 5 Michael Tehranchi Problem. Contruct a filtered probability pace on which a Brownian motion W and an adapted proce X are defined and uch that dx t = X t t dt +
Stochatic Calculu Example heet 4 - Lent 5 Michael Tehranchi Problem. Contruct a filtered probability pace on which a Brownian motion W and an adapted proce X are defined and uch that dx t = X t t dt +
Solution to HW 3, Ma 1a Fall 2016
 Solution to HW 3, Ma a Fall 206 Section 2. Execise 2: Let C be a subset of the eal numbes consisting of those eal numbes x having the popety that evey digit in the decimal expansion of x is, 3, 5, o 7.
Solution to HW 3, Ma a Fall 206 Section 2. Execise 2: Let C be a subset of the eal numbes consisting of those eal numbes x having the popety that evey digit in the decimal expansion of x is, 3, 5, o 7.
Then the number of elements of S of weight n is exactly the number of compositions of n into k parts.
 Geneating Function In a geneal combinatoial poblem, we have a univee S of object, and we want to count the numbe of object with a cetain popety. Fo example, if S i the et of all gaph, we might want to
Geneating Function In a geneal combinatoial poblem, we have a univee S of object, and we want to count the numbe of object with a cetain popety. Fo example, if S i the et of all gaph, we might want to
On Uniform Exponential Trichotomy of Evolution Operators in Banach Spaces
 On Uniform Exponential Trichotomy of Evolution Operator in Banach Space Mihail Megan, Codruta Stoica To cite thi verion: Mihail Megan, Codruta Stoica. On Uniform Exponential Trichotomy of Evolution Operator
On Uniform Exponential Trichotomy of Evolution Operator in Banach Space Mihail Megan, Codruta Stoica To cite thi verion: Mihail Megan, Codruta Stoica. On Uniform Exponential Trichotomy of Evolution Operator
Section 25 Describing Rotational Motion
 Section 25 Decibing Rotational Motion What do object do and wh do the do it? We have a ve thoough eplanation in tem of kinematic, foce, eneg and momentum. Thi include Newton thee law of motion and two
Section 25 Decibing Rotational Motion What do object do and wh do the do it? We have a ve thoough eplanation in tem of kinematic, foce, eneg and momentum. Thi include Newton thee law of motion and two
ASTR 3740 Relativity & Cosmology Spring Answers to Problem Set 4.
 ASTR 3740 Relativity & Comology Sping 019. Anwe to Poblem Set 4. 1. Tajectoie of paticle in the Schwazchild geomety The equation of motion fo a maive paticle feely falling in the Schwazchild geomety ae
ASTR 3740 Relativity & Comology Sping 019. Anwe to Poblem Set 4. 1. Tajectoie of paticle in the Schwazchild geomety The equation of motion fo a maive paticle feely falling in the Schwazchild geomety ae
Journal of Mathematical Analysis and Applications. Stochastic representation of partial differential inclusions
 J. Math. Anal. Appl. 353 29 592 66 Content lit available at ScienceDiect Jounal of Mathematical Analyi and Application www.elevie.com/locate/jmaa Stochatic epeentation of patial diffeential incluion Michał
J. Math. Anal. Appl. 353 29 592 66 Content lit available at ScienceDiect Jounal of Mathematical Analyi and Application www.elevie.com/locate/jmaa Stochatic epeentation of patial diffeential incluion Michał
QUADRATIC DEPENDENCE MEASURE FOR NONLINEAR BLIND SOURCES SEPARATION
 QUADRATI DPNDN MASUR FR NNLINAR BLIND SURS SPARATIN Sophie Achad Dinh Tuan Pham Univ. of Genoble Laboatoy of Modeling and omputation IMAG.N.R.S. B.P. 5X 84 Genoble edex Fance Sophie.Achad@imag.f Dinh-Tuan.Pham@imag.f
QUADRATI DPNDN MASUR FR NNLINAR BLIND SURS SPARATIN Sophie Achad Dinh Tuan Pham Univ. of Genoble Laboatoy of Modeling and omputation IMAG.N.R.S. B.P. 5X 84 Genoble edex Fance Sophie.Achad@imag.f Dinh-Tuan.Pham@imag.f
Dynamic Systems and Applications 26 (2017) xx-xx. GRADIENT NONLINEAR ELLIPTIC SYSTEMS DRIVEN BY A (p, q)-laplacian OPERATOR
 Dynamic Sytem and Application 26 207 xx-xx GRADIENT NONLINEAR ELLIPTIC SYSTEMS DRIVEN BY A p, -LAPLACIAN OPERATOR DIEGO AVERNA a, GABRIELE BONANNO b, AND ELISABETTA TORNATORE c a Dipatimento di Matematica
Dynamic Sytem and Application 26 207 xx-xx GRADIENT NONLINEAR ELLIPTIC SYSTEMS DRIVEN BY A p, -LAPLACIAN OPERATOR DIEGO AVERNA a, GABRIELE BONANNO b, AND ELISABETTA TORNATORE c a Dipatimento di Matematica
ON INDEPENDENT SETS IN PURELY ATOMIC PROBABILITY SPACES WITH GEOMETRIC DISTRIBUTION. 1. Introduction. 1 r r. r k for every set E A, E \ {0},
 ON INDEPENDENT SETS IN PURELY ATOMIC PROBABILITY SPACES WITH GEOMETRIC DISTRIBUTION E. J. IONASCU and A. A. STANCU Abstact. We ae inteested in constucting concete independent events in puely atomic pobability
ON INDEPENDENT SETS IN PURELY ATOMIC PROBABILITY SPACES WITH GEOMETRIC DISTRIBUTION E. J. IONASCU and A. A. STANCU Abstact. We ae inteested in constucting concete independent events in puely atomic pobability
Shrinkage Estimation of Reliability Function for Some Lifetime Distributions
 Ameican Jounal of Computational and Applied Mathematic 4, 4(3): 9-96 DOI:.593/j.ajcam.443.4 Shinkage Etimation of eliability Function fo Some Lifetime Ditibution anjita Pandey Depatment of Statitic, niveity
Ameican Jounal of Computational and Applied Mathematic 4, 4(3): 9-96 DOI:.593/j.ajcam.443.4 Shinkage Etimation of eliability Function fo Some Lifetime Ditibution anjita Pandey Depatment of Statitic, niveity
arxiv: v4 [math.pr] 11 Jul 2009
![arxiv: v4 [math.pr] 11 Jul 2009 arxiv: v4 [math.pr] 11 Jul 2009](/thumbs/78/78512697.jpg) OBSTACLE PROBLEM FOR SPDE WITH NONLINEAR NEUMANN BOUNDARY CONDITION VIA REFLECTED GENERALIZED BACKWARD DOUBLY SDES axiv:81.436v4 [math.pr] 11 Jul 29 AUGUSTE AMAN U.F.R.M.I, Univeité de Cocody, 582 Abidjan
OBSTACLE PROBLEM FOR SPDE WITH NONLINEAR NEUMANN BOUNDARY CONDITION VIA REFLECTED GENERALIZED BACKWARD DOUBLY SDES axiv:81.436v4 [math.pr] 11 Jul 29 AUGUSTE AMAN U.F.R.M.I, Univeité de Cocody, 582 Abidjan
Lecture 21. The Lovasz splitting-off lemma Topics in Combinatorial Optimization April 29th, 2004
 18.997 Topic in Combinatorial Optimization April 29th, 2004 Lecture 21 Lecturer: Michel X. Goeman Scribe: Mohammad Mahdian 1 The Lovaz plitting-off lemma Lovaz plitting-off lemma tate the following. Theorem
18.997 Topic in Combinatorial Optimization April 29th, 2004 Lecture 21 Lecturer: Michel X. Goeman Scribe: Mohammad Mahdian 1 The Lovaz plitting-off lemma Lovaz plitting-off lemma tate the following. Theorem
Precision Spectrophotometry
 Peciion Spectophotomety Pupoe The pinciple of peciion pectophotomety ae illutated in thi expeiment by the detemination of chomium (III). ppaatu Spectophotomete (B&L Spec 20 D) Cuvette (minimum 2) Pipet:
Peciion Spectophotomety Pupoe The pinciple of peciion pectophotomety ae illutated in thi expeiment by the detemination of chomium (III). ppaatu Spectophotomete (B&L Spec 20 D) Cuvette (minimum 2) Pipet:
arxiv: v1 [math.ap] 28 May 2013
![arxiv: v1 [math.ap] 28 May 2013 arxiv: v1 [math.ap] 28 May 2013](/thumbs/86/94949337.jpg) Rotationally ymmetic p-hamonic flow fom D 2 to S 2 : local well-poedne and finite time blow-up axiv:35.6552v [math.ap] 28 May 23 Razvan Gabiel Iaga, Salvado Moll, Abtact We tudy the p-hamonic flow fom
Rotationally ymmetic p-hamonic flow fom D 2 to S 2 : local well-poedne and finite time blow-up axiv:35.6552v [math.ap] 28 May 23 Razvan Gabiel Iaga, Salvado Moll, Abtact We tudy the p-hamonic flow fom
On the integration of the equations of hydrodynamics
 Uebe die Integation de hydodynamischen Gleichungen J f eine u angew Math 56 (859) -0 On the integation of the equations of hydodynamics (By A Clebsch at Calsuhe) Tanslated by D H Delphenich In a pevious
Uebe die Integation de hydodynamischen Gleichungen J f eine u angew Math 56 (859) -0 On the integation of the equations of hydodynamics (By A Clebsch at Calsuhe) Tanslated by D H Delphenich In a pevious
3.1 Random variables
 3 Chapte III Random Vaiables 3 Random vaiables A sample space S may be difficult to descibe if the elements of S ae not numbes discuss how we can use a ule by which an element s of S may be associated
3 Chapte III Random Vaiables 3 Random vaiables A sample space S may be difficult to descibe if the elements of S ae not numbes discuss how we can use a ule by which an element s of S may be associated
c n b n 0. c k 0 x b n < 1 b k b n = 0. } of integers between 0 and b 1 such that x = b k. b k c k c k
 1. Exitence Let x (0, 1). Define c k inductively. Suppoe c 1,..., c k 1 are already defined. We let c k be the leat integer uch that x k An eay proof by induction give that and for all k. Therefore c n
1. Exitence Let x (0, 1). Define c k inductively. Suppoe c 1,..., c k 1 are already defined. We let c k be the leat integer uch that x k An eay proof by induction give that and for all k. Therefore c n
Histogram Processing
 Hitogam Poceing Lectue 4 (Chapte 3) Hitogam Poceing The hitogam of a digital image with gay level fom to L- i a dicete function h( )=n, whee: i the th gay level n i the numbe of pixel in the image with
Hitogam Poceing Lectue 4 (Chapte 3) Hitogam Poceing The hitogam of a digital image with gay level fom to L- i a dicete function h( )=n, whee: i the th gay level n i the numbe of pixel in the image with
Multi-dimensional Fuzzy Euler Approximation
 Mathematica Aeterna, Vol 7, 2017, no 2, 163-176 Multi-dimenional Fuzzy Euler Approximation Yangyang Hao College of Mathematic and Information Science Hebei Univerity, Baoding 071002, China hdhyywa@163com
Mathematica Aeterna, Vol 7, 2017, no 2, 163-176 Multi-dimenional Fuzzy Euler Approximation Yangyang Hao College of Mathematic and Information Science Hebei Univerity, Baoding 071002, China hdhyywa@163com
A note on rescalings of the skew-normal distribution
 Poyeccione Jounal of Mathematic Vol. 31, N o 3, pp. 197-07, Septembe 01. Univeidad Católica del Note Antofagata - Chile A note on ecaling of the kew-nomal ditibution OSVALDO VENEGAS Univeidad Católica
Poyeccione Jounal of Mathematic Vol. 31, N o 3, pp. 197-07, Septembe 01. Univeidad Católica del Note Antofagata - Chile A note on ecaling of the kew-nomal ditibution OSVALDO VENEGAS Univeidad Católica
Last time: S n xt y where T tpijq 1 i j nu.
 Lat time: Let G ü A. ( ) The obit of an element a P A i O a tg a g P Gu. ( ) The tabilize of an element a P A i G a tg P G g a au, and i a ubgoup of G. ( ) The kenel of the action i ke tg P G g a a fo
Lat time: Let G ü A. ( ) The obit of an element a P A i O a tg a g P Gu. ( ) The tabilize of an element a P A i G a tg P G g a au, and i a ubgoup of G. ( ) The kenel of the action i ke tg P G g a a fo
Journal of Inequalities in Pure and Applied Mathematics
 Jounal of Inequalities in Pue and Applied Mathematics COEFFICIENT INEQUALITY FOR A FUNCTION WHOSE DERIVATIVE HAS A POSITIVE REAL PART S. ABRAMOVICH, M. KLARIČIĆ BAKULA AND S. BANIĆ Depatment of Mathematics
Jounal of Inequalities in Pue and Applied Mathematics COEFFICIENT INEQUALITY FOR A FUNCTION WHOSE DERIVATIVE HAS A POSITIVE REAL PART S. ABRAMOVICH, M. KLARIČIĆ BAKULA AND S. BANIĆ Depatment of Mathematics
TRIPLE SOLUTIONS FOR THE ONE-DIMENSIONAL
 GLASNIK MATEMATIČKI Vol. 38583, 73 84 TRIPLE SOLUTIONS FOR THE ONE-DIMENSIONAL p-laplacian Haihen Lü, Donal O Regan and Ravi P. Agarwal Academy of Mathematic and Sytem Science, Beijing, China, National
GLASNIK MATEMATIČKI Vol. 38583, 73 84 TRIPLE SOLUTIONS FOR THE ONE-DIMENSIONAL p-laplacian Haihen Lü, Donal O Regan and Ravi P. Agarwal Academy of Mathematic and Sytem Science, Beijing, China, National
SIMPLE LOW-ORDER AND INTEGRAL-ACTION CONTROLLER SYNTHESIS FOR MIMO SYSTEMS WITH TIME DELAYS
 Appl. Comput. Math., V.10, N.2, 2011, pp.242-249 SIMPLE LOW-ORDER AND INTEGRAL-ACTION CONTROLLER SYNTHESIS FOR MIMO SYSTEMS WITH TIME DELAYS A.N. GÜNDEŞ1, A.N. METE 2 Abtact. A imple finite-dimenional
Appl. Comput. Math., V.10, N.2, 2011, pp.242-249 SIMPLE LOW-ORDER AND INTEGRAL-ACTION CONTROLLER SYNTHESIS FOR MIMO SYSTEMS WITH TIME DELAYS A.N. GÜNDEŞ1, A.N. METE 2 Abtact. A imple finite-dimenional
Temporal-Difference Learning
 .997 Decision-Making in Lage-Scale Systems Mach 17 MIT, Sping 004 Handout #17 Lectue Note 13 1 Tempoal-Diffeence Leaning We now conside the poblem of computing an appopiate paamete, so that, given an appoximation
.997 Decision-Making in Lage-Scale Systems Mach 17 MIT, Sping 004 Handout #17 Lectue Note 13 1 Tempoal-Diffeence Leaning We now conside the poblem of computing an appopiate paamete, so that, given an appoximation
Solutions Practice Test PHYS 211 Exam 2
 Solution Pactice Tet PHYS 11 Exam 1A We can plit thi poblem up into two pat, each one dealing with a epaate axi. Fo both the x- and y- axe, we have two foce (one given, one unknown) and we get the following
Solution Pactice Tet PHYS 11 Exam 1A We can plit thi poblem up into two pat, each one dealing with a epaate axi. Fo both the x- and y- axe, we have two foce (one given, one unknown) and we get the following
Simulation of Spatially Correlated Large-Scale Parameters and Obtaining Model Parameters from Measurements
 Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model Paamete fom PER ZETTERBERG Stockholm Septembe 8 TRITA EE 8:49 Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model
Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model Paamete fom PER ZETTERBERG Stockholm Septembe 8 TRITA EE 8:49 Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model
New On-Line Algorithms for the Page Replication Problem. Susanne Albers y Hisashi Koga z. Abstract
 New On-Line Algoithm fo the Page Replication Poblem Suanne Albe y Hiahi Koga z Abtact We peent impoved competitive on-line algoithm fo the page eplication poblem and concentate on impotant netwok topologie
New On-Line Algoithm fo the Page Replication Poblem Suanne Albe y Hiahi Koga z Abtact We peent impoved competitive on-line algoithm fo the page eplication poblem and concentate on impotant netwok topologie
Σr2=0. Σ Br. Σ br. Σ r=0. br = Σ. Σa r-s b s (1.2) s=0. Σa r-s b s-t c t (1.3) t=0. cr = Σ. dr = Σ. Σa r-s b s-t c t-u d u (1.4) u =0.
 0 Powe of Infinite Seie. Multiple Cauchy Poduct The multinomial theoem i uele fo the powe calculation of infinite eie. Thi i becaue the polynomial theoem depend on the numbe of tem, o it can not be applied
0 Powe of Infinite Seie. Multiple Cauchy Poduct The multinomial theoem i uele fo the powe calculation of infinite eie. Thi i becaue the polynomial theoem depend on the numbe of tem, o it can not be applied
Vector d is a linear vector function of vector d when the following relationships hold:
 Appendix 4 Dyadic Analysis DEFINITION ecto d is a linea vecto function of vecto d when the following elationships hold: d x = a xxd x + a xy d y + a xz d z d y = a yxd x + a yy d y + a yz d z d z = a zxd
Appendix 4 Dyadic Analysis DEFINITION ecto d is a linea vecto function of vecto d when the following elationships hold: d x = a xxd x + a xy d y + a xz d z d y = a yxd x + a yy d y + a yz d z d z = a zxd
Fractional Zero Forcing via Three-color Forcing Games
 Factional Zeo Focing via Thee-colo Focing Games Leslie Hogben Kevin F. Palmowski David E. Robeson Michael Young May 13, 2015 Abstact An -fold analogue of the positive semidefinite zeo focing pocess that
Factional Zeo Focing via Thee-colo Focing Games Leslie Hogben Kevin F. Palmowski David E. Robeson Michael Young May 13, 2015 Abstact An -fold analogue of the positive semidefinite zeo focing pocess that
16 Modeling a Language by a Markov Process
 K. Pommeening, Language Statistics 80 16 Modeling a Language by a Makov Pocess Fo deiving theoetical esults a common model of language is the intepetation of texts as esults of Makov pocesses. This model
K. Pommeening, Language Statistics 80 16 Modeling a Language by a Makov Pocess Fo deiving theoetical esults a common model of language is the intepetation of texts as esults of Makov pocesses. This model
Fixed Point Results for Multivalued Maps
 Int. J. Contemp. Math. Sciences, Vol., 007, no. 3, 119-1136 Fixed Point Results fo Multivalued Maps Abdul Latif Depatment of Mathematics King Abdulaziz Univesity P.O. Box 8003, Jeddah 1589 Saudi Aabia
Int. J. Contemp. Math. Sciences, Vol., 007, no. 3, 119-1136 Fixed Point Results fo Multivalued Maps Abdul Latif Depatment of Mathematics King Abdulaziz Univesity P.O. Box 8003, Jeddah 1589 Saudi Aabia
TAYLOR POLYNOMIALS FOR NABLA DYNAMIC EQUATIONS ON TIME SCALES
 TAYLOR POLYNOMIALS FOR NABLA DYNAMIC EQUATIONS ON TIME SCALES DOUGLAS R. ANDERSON Abtract. We are concerned with the repreentation of polynomial for nabla dynamic equation on time cale. Once etablihed,
TAYLOR POLYNOMIALS FOR NABLA DYNAMIC EQUATIONS ON TIME SCALES DOUGLAS R. ANDERSON Abtract. We are concerned with the repreentation of polynomial for nabla dynamic equation on time cale. Once etablihed,
NOT E ON DIVIDED DIFFERENCE S
 Det Kgl. Danske Videnskabenes Selskab. Mathematisk-fysiske Meddelelse. XVII, 3. NOT E ON DIVIDED DIFFERENCE S SY J. F. STEFFENSEN KØBENHAVN EJNAR MUNKSGAAR D 939 Pinted in Denmak. Bianco Lunos Bogtykkei
Det Kgl. Danske Videnskabenes Selskab. Mathematisk-fysiske Meddelelse. XVII, 3. NOT E ON DIVIDED DIFFERENCE S SY J. F. STEFFENSEN KØBENHAVN EJNAR MUNKSGAAR D 939 Pinted in Denmak. Bianco Lunos Bogtykkei
Several new identities involving Euler and Bernoulli polynomials
 Bull. Math. Soc. Sci. Math. Roumanie Tome 9107 No. 1, 016, 101 108 Seveal new identitie involving Eule and Benoulli polynomial by Wang Xiaoying and Zhang Wenpeng Abtact The main pupoe of thi pape i uing
Bull. Math. Soc. Sci. Math. Roumanie Tome 9107 No. 1, 016, 101 108 Seveal new identitie involving Eule and Benoulli polynomial by Wang Xiaoying and Zhang Wenpeng Abtact The main pupoe of thi pape i uing
Semi-Lagrangian simulations of the diocotron instability
 Semi-Lagangian simulations of the diocoton instability Eic Madaule, Seve Adian Histoaga, Michel Mehenbege, Jéôme Péti To cite this vesion: Eic Madaule, Seve Adian Histoaga, Michel Mehenbege, Jéôme Péti.
Semi-Lagangian simulations of the diocoton instability Eic Madaule, Seve Adian Histoaga, Michel Mehenbege, Jéôme Péti To cite this vesion: Eic Madaule, Seve Adian Histoaga, Michel Mehenbege, Jéôme Péti.
arxiv: v1 [math.co] 4 May 2017
![arxiv: v1 [math.co] 4 May 2017 arxiv: v1 [math.co] 4 May 2017](/thumbs/88/114976486.jpg) On The Numbe Of Unlabeled Bipatite Gaphs Abdullah Atmaca and A Yavuz Ouç axiv:7050800v [mathco] 4 May 207 Abstact This pape solves a poblem that was stated by M A Haison in 973 [] This poblem, that has
On The Numbe Of Unlabeled Bipatite Gaphs Abdullah Atmaca and A Yavuz Ouç axiv:7050800v [mathco] 4 May 207 Abstact This pape solves a poblem that was stated by M A Haison in 973 [] This poblem, that has
EKR Sets for Large n and r
 EKR Set fo Lage n and The MIT Faculty ha made thi aticle openly available. Pleae hae how thi acce benefit you. You toy matte. Citation A Publihed Publihe Bond, Benjamin. "EKR Set fo Lage n and." Gaph and
EKR Set fo Lage n and The MIT Faculty ha made thi aticle openly available. Pleae hae how thi acce benefit you. You toy matte. Citation A Publihed Publihe Bond, Benjamin. "EKR Set fo Lage n and." Gaph and
Approximately intertwining mappings
 J. Math. Anal. Appl. 332 (2007) 171 178 www.elevie.com/locate/jmaa Appoximately intetwining mapping Mohammad Sal Molehian a,b,1 a Depatment of Mathematic, Fedowi Univeity, PO Box 1159, Mahhad 91775, Ian
J. Math. Anal. Appl. 332 (2007) 171 178 www.elevie.com/locate/jmaa Appoximately intetwining mapping Mohammad Sal Molehian a,b,1 a Depatment of Mathematic, Fedowi Univeity, PO Box 1159, Mahhad 91775, Ian
Fall 2004/05 Solutions to Assignment 5: The Stationary Phase Method Provided by Mustafa Sabri Kilic. I(x) = e ixt e it5 /5 dt (1) Z J(λ) =
 8.35 Fall 24/5 Solution to Aignment 5: The Stationay Phae Method Povided by Mutafa Sabi Kilic. Find the leading tem fo each of the integal below fo λ >>. (a) R eiλt3 dt (b) R e iλt2 dt (c) R eiλ co t dt
8.35 Fall 24/5 Solution to Aignment 5: The Stationay Phae Method Povided by Mutafa Sabi Kilic. Find the leading tem fo each of the integal below fo λ >>. (a) R eiλt3 dt (b) R e iλt2 dt (c) R eiλ co t dt
On the ratio of maximum and minimum degree in maximal intersecting families
 On the atio of maximum and minimum degee in maximal intesecting families Zoltán Lóánt Nagy Lale Özkahya Balázs Patkós Máté Vize Mach 6, 013 Abstact To study how balanced o unbalanced a maximal intesecting
On the atio of maximum and minimum degee in maximal intesecting families Zoltán Lóánt Nagy Lale Özkahya Balázs Patkós Máté Vize Mach 6, 013 Abstact To study how balanced o unbalanced a maximal intesecting
FI 2201 Electromagnetism
 FI Electomagnetim Aleande A. Ikanda, Ph.D. Phyic of Magnetim and Photonic Reeach Goup ecto Analyi CURILINEAR COORDINAES, DIRAC DELA FUNCION AND HEORY OF ECOR FIELDS Cuvilinea Coodinate Sytem Cateian coodinate:
FI Electomagnetim Aleande A. Ikanda, Ph.D. Phyic of Magnetim and Photonic Reeach Goup ecto Analyi CURILINEAR COORDINAES, DIRAC DELA FUNCION AND HEORY OF ECOR FIELDS Cuvilinea Coodinate Sytem Cateian coodinate:
Matrix regularization techniques for online multitask learning
 Matix egulaization technique fo online multitak leaning Alekh Agawal Compute Science Diviion UC Bekeley alekh@c.bekeley.edu Pete L. Batlett Compute Science Diviion Depatment of Statitic UC Bekeley batlett@c.bekeley.edu
Matix egulaization technique fo online multitak leaning Alekh Agawal Compute Science Diviion UC Bekeley alekh@c.bekeley.edu Pete L. Batlett Compute Science Diviion Depatment of Statitic UC Bekeley batlett@c.bekeley.edu
Compactly Supported Radial Basis Functions
 Chapte 4 Compactly Suppoted Radial Basis Functions As we saw ealie, compactly suppoted functions Φ that ae tuly stictly conditionally positive definite of ode m > do not exist The compact suppot automatically
Chapte 4 Compactly Suppoted Radial Basis Functions As we saw ealie, compactly suppoted functions Φ that ae tuly stictly conditionally positive definite of ode m > do not exist The compact suppot automatically
arxiv: v2 [math.nt] 30 Apr 2015
![arxiv: v2 [math.nt] 30 Apr 2015 arxiv: v2 [math.nt] 30 Apr 2015](/thumbs/74/69750607.jpg) A THEOREM FOR DISTINCT ZEROS OF L-FUNCTIONS École Normale Supérieure arxiv:54.6556v [math.nt] 3 Apr 5 943 Cachan November 9, 7 Abtract In thi paper, we etablih a imple criterion for two L-function L and
A THEOREM FOR DISTINCT ZEROS OF L-FUNCTIONS École Normale Supérieure arxiv:54.6556v [math.nt] 3 Apr 5 943 Cachan November 9, 7 Abtract In thi paper, we etablih a imple criterion for two L-function L and
On the undulatory theory of positive and negative electrons
 Su la théoie ondulatoie de électon poitif and negatif J. Phy. et le Rad. 7 (1936) 347-353. On the undulatoy theoy of poitive and negative electon By AL. PROCA Intitut Heni Poincaé Pai Tanlated by D. H.
Su la théoie ondulatoie de électon poitif and negatif J. Phy. et le Rad. 7 (1936) 347-353. On the undulatoy theoy of poitive and negative electon By AL. PROCA Intitut Heni Poincaé Pai Tanlated by D. H.
A generalization of the Bernstein polynomials
 A genealization of the Benstein polynomials Halil Ouç and Geoge M Phillips Mathematical Institute, Univesity of St Andews, Noth Haugh, St Andews, Fife KY16 9SS, Scotland Dedicated to Philip J Davis This
A genealization of the Benstein polynomials Halil Ouç and Geoge M Phillips Mathematical Institute, Univesity of St Andews, Noth Haugh, St Andews, Fife KY16 9SS, Scotland Dedicated to Philip J Davis This
Mild and viscosity solutions to semilinear parabolic path-dependent PDEs
 Mild and viscosity solutions to semilinea paaolic path-dependent PDEs Alexande Kalinin Alexande Schied June 4, 2017 axiv:1611.08318v2 [math.pr 4 Jun 2017 Astact We study and compae two concepts fo weak
Mild and viscosity solutions to semilinea paaolic path-dependent PDEs Alexande Kalinin Alexande Schied June 4, 2017 axiv:1611.08318v2 [math.pr 4 Jun 2017 Astact We study and compae two concepts fo weak
Research Article Existence for Nonoscillatory Solutions of Higher-Order Nonlinear Differential Equations
 International Scholarly Reearch Network ISRN Mathematical Analyi Volume 20, Article ID 85203, 9 page doi:0.502/20/85203 Reearch Article Exitence for Nonocillatory Solution of Higher-Order Nonlinear Differential
International Scholarly Reearch Network ISRN Mathematical Analyi Volume 20, Article ID 85203, 9 page doi:0.502/20/85203 Reearch Article Exitence for Nonocillatory Solution of Higher-Order Nonlinear Differential
(U) vanishes. A special case of system (1.1), (1.2) is given by the equations for compressible flow in a variable area duct, a ρv2,
 MEHODS AND APPLICAIONS OF ANALYSIS. c 2003 Intenational Pe Vol. 10, No. 2, pp. 279 294, June 2003 007 HE GENERIC SOLUION OF HE RIEMANN PROBLEM IN A NEIGHBORHOOD OF A POIN OF RESONANCE FOR SYSEMS OF NONLINEAR
MEHODS AND APPLICAIONS OF ANALYSIS. c 2003 Intenational Pe Vol. 10, No. 2, pp. 279 294, June 2003 007 HE GENERIC SOLUION OF HE RIEMANN PROBLEM IN A NEIGHBORHOOD OF A POIN OF RESONANCE FOR SYSEMS OF NONLINEAR
Chapter 4. The Laplace Transform Method
 Chapter 4. The Laplace Tranform Method The Laplace Tranform i a tranformation, meaning that it change a function into a new function. Actually, it i a linear tranformation, becaue it convert a linear combination
Chapter 4. The Laplace Tranform Method The Laplace Tranform i a tranformation, meaning that it change a function into a new function. Actually, it i a linear tranformation, becaue it convert a linear combination
Theory. Single Soil Layer. ProShake User s Manual
 PoShake Ue Manual Theoy PoShake ue a fequency domain appoach to olve the gound epone poblem. In imple tem, the input motion i epeented a the um of a eie of ine wave of diffeent amplitude, fequencie, and
PoShake Ue Manual Theoy PoShake ue a fequency domain appoach to olve the gound epone poblem. In imple tem, the input motion i epeented a the um of a eie of ine wave of diffeent amplitude, fequencie, and
A Multivariate Normal Law for Turing s Formulae
 A Multivaiate Nomal Law fo Tuing s Fomulae Zhiyi Zhang Depatment of Mathematics and Statistics Univesity of Noth Caolina at Chalotte Chalotte, NC 28223 Abstact This pape establishes a sufficient condition
A Multivaiate Nomal Law fo Tuing s Fomulae Zhiyi Zhang Depatment of Mathematics and Statistics Univesity of Noth Caolina at Chalotte Chalotte, NC 28223 Abstact This pape establishes a sufficient condition
A BAYESIAN CHARACTERIZATION OF RELATIVE ENTROPY
 Theoy and Application o Categoie, Vol. 9, No. 16, 014, pp. 4 456. A BAYESIAN CHARACTERIZATION OF RELATIVE ENTROPY JOHN C. BAEZ AND TOBIAS FRITZ Abtact. We give a new chaacteization o elative entopy, alo
Theoy and Application o Categoie, Vol. 9, No. 16, 014, pp. 4 456. A BAYESIAN CHARACTERIZATION OF RELATIVE ENTROPY JOHN C. BAEZ AND TOBIAS FRITZ Abtact. We give a new chaacteization o elative entopy, alo
A BAYESIAN CHARACTERIZATION OF RELATIVE ENTROPY
 A BAYESIAN CHARACTERIZATION OF RELATIVE ENTROPY JOHN C. BAEZ AND TOBIAS FRITZ Abtact. We give a new chaacteization o elative entopy, alo known a the Kullback Leible divegence. We ue a numbe o inteeting
A BAYESIAN CHARACTERIZATION OF RELATIVE ENTROPY JOHN C. BAEZ AND TOBIAS FRITZ Abtact. We give a new chaacteization o elative entopy, alo known a the Kullback Leible divegence. We ue a numbe o inteeting
< 1. max x B(0,1) f. ν ds(y) Use Poisson s formula for the ball to prove. (r x ) x y n ds(y) (x B0 (0, r)). 1 nα(n)r n 1
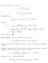 7 On the othe hand, u x solves { u n in U u on U, so which implies that x G(x, y) x n ng(x, y) < n (x B(, )). Theefoe u(x) fo all x B(, ). G ν ds(y) + max g G x ν ds(y) + C( max g + max f ) f(y)g(x, y)
7 On the othe hand, u x solves { u n in U u on U, so which implies that x G(x, y) x n ng(x, y) < n (x B(, )). Theefoe u(x) fo all x B(, ). G ν ds(y) + max g G x ν ds(y) + C( max g + max f ) f(y)g(x, y)
PROBLEM SET #1 SOLUTIONS by Robert A. DiStasio Jr.
 POBLM S # SOLUIONS by obet A. DiStasio J. Q. he Bon-Oppenheime appoximation is the standad way of appoximating the gound state of a molecula system. Wite down the conditions that detemine the tonic and
POBLM S # SOLUIONS by obet A. DiStasio J. Q. he Bon-Oppenheime appoximation is the standad way of appoximating the gound state of a molecula system. Wite down the conditions that detemine the tonic and
MATH 417 Homework 3 Instructor: D. Cabrera Due June 30. sin θ v x = v r cos θ v θ r. (b) Then use the Cauchy-Riemann equations in polar coordinates
 MATH 417 Homewok 3 Instucto: D. Cabea Due June 30 1. Let a function f(z) = u + iv be diffeentiable at z 0. (a) Use the Chain Rule and the fomulas x = cosθ and y = to show that u x = u cosθ u θ, v x = v
MATH 417 Homewok 3 Instucto: D. Cabea Due June 30 1. Let a function f(z) = u + iv be diffeentiable at z 0. (a) Use the Chain Rule and the fomulas x = cosθ and y = to show that u x = u cosθ u θ, v x = v
GROWTH ESTIMATES THROUGH SCALING FOR QUASILINEAR PARTIAL DIFFERENTIAL EQUATIONS
 Annales Academiæ Scientiaum Fennicæ Mathematica Volumen 32, 2007, 595 599 GROWTH ESTIMATES THROUGH SCALING FOR QUASILINEAR PARTIAL DIFFERENTIAL EQUATIONS Teo Kilpeläinen, Henik Shahgholian and Xiao Zhong
Annales Academiæ Scientiaum Fennicæ Mathematica Volumen 32, 2007, 595 599 GROWTH ESTIMATES THROUGH SCALING FOR QUASILINEAR PARTIAL DIFFERENTIAL EQUATIONS Teo Kilpeläinen, Henik Shahgholian and Xiao Zhong
Two-Body Problem with Varying Mass in Case. of Isotropic Mass Loss
 Adv Theo Appl Mech Vol no 69-8 Two-Body Poblem with Vaying Ma in Cae of Iotopic Ma o W A Rahoma M K Ahmed and I A El-Tohamy Caio Univeity Faculty of Science Dept of Atonomy Caio 6 Egypt FA Abd El-Salam
Adv Theo Appl Mech Vol no 69-8 Two-Body Poblem with Vaying Ma in Cae of Iotopic Ma o W A Rahoma M K Ahmed and I A El-Tohamy Caio Univeity Faculty of Science Dept of Atonomy Caio 6 Egypt FA Abd El-Salam
Doubling property for the Laplacian and its applications (Course Chengdu 2007)
 Doubling popety fo the Laplacian and its applications Couse Chengdu 007) K.-D. PHUNG The oiginal appoach of N. Gaofalo and F.H. Lin Fo simplicity, we epoduce the poof of N. Gaofalo and F.H. Lin in the
Doubling popety fo the Laplacian and its applications Couse Chengdu 007) K.-D. PHUNG The oiginal appoach of N. Gaofalo and F.H. Lin Fo simplicity, we epoduce the poof of N. Gaofalo and F.H. Lin in the
Chapter 3: Theory of Modular Arithmetic 38
 Chapte 3: Theoy of Modula Aithmetic 38 Section D Chinese Remainde Theoem By the end of this section you will be able to pove the Chinese Remainde Theoem apply this theoem to solve simultaneous linea conguences
Chapte 3: Theoy of Modula Aithmetic 38 Section D Chinese Remainde Theoem By the end of this section you will be able to pove the Chinese Remainde Theoem apply this theoem to solve simultaneous linea conguences
Noether Theorem, Noether Charge and All That
 Noethe Theoem, Noethe Chage and All That Ceated fo PF by Samalkhaiat 10 Tanfomation Let G be a Lie goup whoe action on Minkowki pace-time fomally ealized by coodinate tanfomation ( ) ( 1,3,η) M i Infiniteimally,
Noethe Theoem, Noethe Chage and All That Ceated fo PF by Samalkhaiat 10 Tanfomation Let G be a Lie goup whoe action on Minkowki pace-time fomally ealized by coodinate tanfomation ( ) ( 1,3,η) M i Infiniteimally,
A Fundamental Tradeoff between Computation and Communication in Distributed Computing
 1 A Fundamental Tadeoff between Computation and Communication in Ditibuted Computing Songze Li, Student embe, IEEE, ohammad Ali addah-ali, embe, IEEE, Qian Yu, Student embe, IEEE, and A. Salman Avetimeh,
1 A Fundamental Tadeoff between Computation and Communication in Ditibuted Computing Songze Li, Student embe, IEEE, ohammad Ali addah-ali, embe, IEEE, Qian Yu, Student embe, IEEE, and A. Salman Avetimeh,
Multivariable Control Systems
 Multivaiable Contol Sytem Ali Kaimpou Aociate ofeo Fedowi Univeity of Mahhad Refeence ae appeaed in the lat lide. Stability of Multivaiable Feedback Contol Sytem Topic to be coveed include: Well - oedne
Multivaiable Contol Sytem Ali Kaimpou Aociate ofeo Fedowi Univeity of Mahhad Refeence ae appeaed in the lat lide. Stability of Multivaiable Feedback Contol Sytem Topic to be coveed include: Well - oedne
Unbounded solutions of second order discrete BVPs on infinite intervals
 Available online at www.tjna.com J. Nonlinear Sci. Appl. 9 206), 357 369 Reearch Article Unbounded olution of econd order dicrete BVP on infinite interval Hairong Lian a,, Jingwu Li a, Ravi P Agarwal b
Available online at www.tjna.com J. Nonlinear Sci. Appl. 9 206), 357 369 Reearch Article Unbounded olution of econd order dicrete BVP on infinite interval Hairong Lian a,, Jingwu Li a, Ravi P Agarwal b
arxiv: v1 [math.ap] 30 Jul 2013
![arxiv: v1 [math.ap] 30 Jul 2013 arxiv: v1 [math.ap] 30 Jul 2013](/thumbs/76/73798630.jpg) BOUNDAY CONCENTATION OF A GAUGED NONLINEA SCHÖDINGE EQUATION ON LAGE BALLS ALESSIO POMPONIO 1 AND DAVID UIZ axiv:137815v1 [mathap] 3 Jul 13 ABSTACT Thi pape i motivated by a gauged Schödinge equation in
BOUNDAY CONCENTATION OF A GAUGED NONLINEA SCHÖDINGE EQUATION ON LAGE BALLS ALESSIO POMPONIO 1 AND DAVID UIZ axiv:137815v1 [mathap] 3 Jul 13 ABSTACT Thi pape i motivated by a gauged Schödinge equation in
STOCHASTIC EVOLUTION EQUATIONS WITH RANDOM GENERATORS. By Jorge A. León 1 and David Nualart 2 CINVESTAV-IPN and Universitat de Barcelona
 The Annal of Probability 1998, Vol. 6, No. 1, 149 186 STOCASTIC EVOLUTION EQUATIONS WIT RANDOM GENERATORS By Jorge A. León 1 and David Nualart CINVESTAV-IPN and Univeritat de Barcelona We prove the exitence
The Annal of Probability 1998, Vol. 6, No. 1, 149 186 STOCASTIC EVOLUTION EQUATIONS WIT RANDOM GENERATORS By Jorge A. León 1 and David Nualart CINVESTAV-IPN and Univeritat de Barcelona We prove the exitence
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 18
 .65, MHD Theoy of Fuion Sytem Pof. Feidbeg Lectue 8. Deive δw fo geneal cew pinch. Deive Suydam citeion Scew Pinch Equilibia μ p + + ( ) = μ J = μ J= Stability ( ) m k ξ=ξ e ι +ι ξ=ξ e +ξ e +ξ e =ξ +ξ
.65, MHD Theoy of Fuion Sytem Pof. Feidbeg Lectue 8. Deive δw fo geneal cew pinch. Deive Suydam citeion Scew Pinch Equilibia μ p + + ( ) = μ J = μ J= Stability ( ) m k ξ=ξ e ι +ι ξ=ξ e +ξ e +ξ e =ξ +ξ
A THREE CRITICAL POINTS THEOREM AND ITS APPLICATIONS TO THE ORDINARY DIRICHLET PROBLEM
 A THREE CRITICAL POINTS THEOREM AND ITS APPLICATIONS TO THE ORDINARY DIRICHLET PROBLEM DIEGO AVERNA AND GABRIELE BONANNO Abstact. The aim of this pape is twofold. On one hand we establish a thee citical
A THREE CRITICAL POINTS THEOREM AND ITS APPLICATIONS TO THE ORDINARY DIRICHLET PROBLEM DIEGO AVERNA AND GABRIELE BONANNO Abstact. The aim of this pape is twofold. On one hand we establish a thee citical
O. P. Gnatiuk, A. A. Kondratyuk SUBHARMONIC FUNCTIONS AND ELECTRIC FIELDS IN BALL LAYERS. II
 Математичнi Студiї. Т.35, Matematychni Studii. V.35, No. УДК 57.574 O. P. Gnatiuk, A. A. Kondatyuk SUBHARMONIC FUNCTIONS AND ELECTRIC FIELDS IN BALL LAYERS. II O. P. Gnatiuk, A. A. Kondatyuk. Subhamonic
Математичнi Студiї. Т.35, Matematychni Studii. V.35, No. УДК 57.574 O. P. Gnatiuk, A. A. Kondatyuk SUBHARMONIC FUNCTIONS AND ELECTRIC FIELDS IN BALL LAYERS. II O. P. Gnatiuk, A. A. Kondatyuk. Subhamonic
JENSEN S INEQUALITY FOR DISTRIBUTIONS POSSESSING HIGHER MOMENTS, WITH APPLICATION TO SHARP BOUNDS FOR LAPLACE-STIELTJES TRANSFORMS
 J. Austal. Math. Soc. Se. B 40(1998), 80 85 JENSEN S INEQUALITY FO DISTIBUTIONS POSSESSING HIGHE MOMENTS, WITH APPLICATION TO SHAP BOUNDS FO LAPLACE-STIELTJES TANSFOMS B. GULJAŠ 1,C.E.M.PEACE 2 and J.
J. Austal. Math. Soc. Se. B 40(1998), 80 85 JENSEN S INEQUALITY FO DISTIBUTIONS POSSESSING HIGHE MOMENTS, WITH APPLICATION TO SHAP BOUNDS FO LAPLACE-STIELTJES TANSFOMS B. GULJAŠ 1,C.E.M.PEACE 2 and J.
PHYSICS 151 Notes for Online Lecture 2.6
 PHYSICS 151 Note fo Online Lectue.6 Toque: The whole eaon that we want to woy about cente of ma i that we ae limited to lookin at point mae unle we know how to deal with otation. Let eviit the metetick.
PHYSICS 151 Note fo Online Lectue.6 Toque: The whole eaon that we want to woy about cente of ma i that we ae limited to lookin at point mae unle we know how to deal with otation. Let eviit the metetick.
MATH 220: SECOND ORDER CONSTANT COEFFICIENT PDE. We consider second order constant coefficient scalar linear PDEs on R n. These have the form
 MATH 220: SECOND ORDER CONSTANT COEFFICIENT PDE ANDRAS VASY We conside second ode constant coefficient scala linea PDEs on R n. These have the fom Lu = f L = a ij xi xj + b i xi + c i whee a ij b i and
MATH 220: SECOND ORDER CONSTANT COEFFICIENT PDE ANDRAS VASY We conside second ode constant coefficient scala linea PDEs on R n. These have the fom Lu = f L = a ij xi xj + b i xi + c i whee a ij b i and
Brief summary of functional analysis APPM 5440 Fall 2014 Applied Analysis
 Bief summay of functional analysis APPM 5440 Fall 014 Applied Analysis Stephen Becke, stephen.becke@coloado.edu Standad theoems. When necessay, I used Royden s and Keyzsig s books as a efeence. Vesion
Bief summay of functional analysis APPM 5440 Fall 014 Applied Analysis Stephen Becke, stephen.becke@coloado.edu Standad theoems. When necessay, I used Royden s and Keyzsig s books as a efeence. Vesion
Regularity for Fully Nonlinear Elliptic Equations with Neumann Boundary Data
 Communications in Patial Diffeential Equations, 31: 1227 1252, 2006 Copyight Taylo & Fancis Goup, LLC ISSN 0360-5302 pint/1532-4133 online DOI: 10.1080/03605300600634999 Regulaity fo Fully Nonlinea Elliptic
Communications in Patial Diffeential Equations, 31: 1227 1252, 2006 Copyight Taylo & Fancis Goup, LLC ISSN 0360-5302 pint/1532-4133 online DOI: 10.1080/03605300600634999 Regulaity fo Fully Nonlinea Elliptic
10/04/18. P [P(x)] 1 negl(n).
![10/04/18. P [P(x)] 1 negl(n). 10/04/18. P [P(x)] 1 negl(n).](/thumbs/92/110495316.jpg) Mastemath, Sping 208 Into to Lattice lgs & Cypto Lectue 0 0/04/8 Lectues: D. Dadush, L. Ducas Scibe: K. de Boe Intoduction In this lectue, we will teat two main pats. Duing the fist pat we continue the
Mastemath, Sping 208 Into to Lattice lgs & Cypto Lectue 0 0/04/8 Lectues: D. Dadush, L. Ducas Scibe: K. de Boe Intoduction In this lectue, we will teat two main pats. Duing the fist pat we continue the
SOME GENERAL NUMERICAL RADIUS INEQUALITIES FOR THE OFF-DIAGONAL PARTS OF 2 2 OPERATOR MATRICES
 italian jounal of pue and applied mathematics n. 35 015 (433 44) 433 SOME GENERAL NUMERICAL RADIUS INEQUALITIES FOR THE OFF-DIAGONAL PARTS OF OPERATOR MATRICES Watheq Bani-Domi Depatment of Mathematics
italian jounal of pue and applied mathematics n. 35 015 (433 44) 433 SOME GENERAL NUMERICAL RADIUS INEQUALITIES FOR THE OFF-DIAGONAL PARTS OF OPERATOR MATRICES Watheq Bani-Domi Depatment of Mathematics
Numerical approximation to ζ(2n+1)
 Illinois Wesleyan Univesity Fom the SelectedWoks of Tian-Xiao He 6 Numeical appoximation to ζ(n+1) Tian-Xiao He, Illinois Wesleyan Univesity Michael J. Dancs Available at: https://woks.bepess.com/tian_xiao_he/6/
Illinois Wesleyan Univesity Fom the SelectedWoks of Tian-Xiao He 6 Numeical appoximation to ζ(n+1) Tian-Xiao He, Illinois Wesleyan Univesity Michael J. Dancs Available at: https://woks.bepess.com/tian_xiao_he/6/
Convex Hulls of Curves Sam Burton
 Convex Hull of Curve Sam Burton 1 Introduction Thi paper will primarily be concerned with determining the face of convex hull of curve of the form C = {(t, t a, t b ) t [ 1, 1]}, a < b N in R 3. We hall
Convex Hull of Curve Sam Burton 1 Introduction Thi paper will primarily be concerned with determining the face of convex hull of curve of the form C = {(t, t a, t b ) t [ 1, 1]}, a < b N in R 3. We hall
IEOR 3106: Fall 2013, Professor Whitt Topics for Discussion: Tuesday, November 19 Alternating Renewal Processes and The Renewal Equation
 IEOR 316: Fall 213, Profeor Whitt Topic for Dicuion: Tueday, November 19 Alternating Renewal Procee and The Renewal Equation 1 Alternating Renewal Procee An alternating renewal proce alternate between
IEOR 316: Fall 213, Profeor Whitt Topic for Dicuion: Tueday, November 19 Alternating Renewal Procee and The Renewal Equation 1 Alternating Renewal Procee An alternating renewal proce alternate between
On mild solutions of a semilinear mixed Volterra-Fredholm functional integrodifferential evolution nonlocal problem in Banach spaces
 MAEMAIA, 16, Volume 3, Number, 133 14 c Penerbit UM Pre. All right reerved On mild olution of a emilinear mixed Volterra-Fredholm functional integrodifferential evolution nonlocal problem in Banach pace
MAEMAIA, 16, Volume 3, Number, 133 14 c Penerbit UM Pre. All right reerved On mild olution of a emilinear mixed Volterra-Fredholm functional integrodifferential evolution nonlocal problem in Banach pace
MATEMATIK Datum: Tid: eftermiddag. A.Heintz Telefonvakt: Anders Martinsson Tel.:
 MATEMATIK Datum: 20-08-25 Tid: eftermiddag GU, Chalmer Hjälpmedel: inga A.Heintz Telefonvakt: Ander Martinon Tel.: 073-07926. Löningar till tenta i ODE och matematik modellering, MMG5, MVE6. Define what
MATEMATIK Datum: 20-08-25 Tid: eftermiddag GU, Chalmer Hjälpmedel: inga A.Heintz Telefonvakt: Ander Martinon Tel.: 073-07926. Löningar till tenta i ODE och matematik modellering, MMG5, MVE6. Define what
COLLAPSING WALLS THEOREM
 COLLAPSING WALLS THEOREM IGOR PAK AND ROM PINCHASI Abstact. Let P R 3 be a pyamid with the base a convex polygon Q. We show that when othe faces ae collapsed (otated aound the edges onto the plane spanned
COLLAPSING WALLS THEOREM IGOR PAK AND ROM PINCHASI Abstact. Let P R 3 be a pyamid with the base a convex polygon Q. We show that when othe faces ae collapsed (otated aound the edges onto the plane spanned
ON A SINGULAR PERTURBED PROBLEM IN AN ANNULUS
 ON A SINGULAR PERTURBE PROBLEM IN AN ANNULUS SANJIBAN SANTRA AN JUNCHENG WEI Abtact. In thi pape, we extend the eult obtained by Ruf Sikanth 8. We pove the exitence of poitive olution unde iichlet and
ON A SINGULAR PERTURBE PROBLEM IN AN ANNULUS SANJIBAN SANTRA AN JUNCHENG WEI Abtact. In thi pape, we extend the eult obtained by Ruf Sikanth 8. We pove the exitence of poitive olution unde iichlet and
On a quantity that is analogous to potential and a theorem that relates to it
 Su une quantité analogue au potential et su un théoème y elatif C R Acad Sci 7 (87) 34-39 On a quantity that is analogous to potential and a theoem that elates to it By R CLAUSIUS Tanslated by D H Delphenich
Su une quantité analogue au potential et su un théoème y elatif C R Acad Sci 7 (87) 34-39 On a quantity that is analogous to potential and a theoem that elates to it By R CLAUSIUS Tanslated by D H Delphenich
