ME 391 Mechanical Engineering Analysis
|
|
|
- Noah Webster
- 5 years ago
- Views:
Transcription
1 Solve the following differential equations. ME 9 Mechanical Engineering Analysis Eam # Practice Problems Solutions. e u 5sin() with u(=)= We may rearrange this equation to e u 5sin() and note that it is not separable, there is no variable transformation, but since it is linear we can use the Integrating Factor Method. Hence we need to find F and G, so we may transform the equation to the form d F()u G() where e F ep ds ep Ei() where Ei is the Eponential Integral Function. Then sin() sin() G F ep Ei() Then our equation becomes d sin() ep Ei() u ep Ei() which is in separate and integrate form. Separating sin() dep Ei() u ep Ei() Integrating sin() ep Ei() u ep Ei() C Unfortunately, the integral over t does not eist in analytical form, so our final solution is sin() C u ep Ei() ep Ei() ep Ei()
2 ME 9 Mechanical Engineering Analysis u. 7u u with u(=0) = We can rearrange this equation to u u 7u which is clearly separable, so we may use the Separate and Integrate Method. Separating u u 7u Integrating u u 7u lnu 7/ C 6 Probably a good place to apply the initial condition ln() 7/ (0) C 6 ln/ C 6 Now solving for u u 7/ ep 6C 6C 7/ u ep Our final solution becomes u ep ln(/) 7/. ln() 8 with u(=) = 0 We can rearrange this equation to 8 ln() which is clearly separable, so we may use the Separate and Integrate Method. Separating 8 ln() Integrating 8 ln() ln u C
3 ME 9 Mechanical Engineering Analysis Applying the initial condition () ln() u( ) 0 () C Our final solution is ln u C C u. 9u with u(=) = The equation is clearly not separable. However, if we rearrange it by dividing through by u u 9 it should then be obvious that we can use the Variable Transformation Method, where = u/ Applying the transformation 9 We have shown d Substituting we have d 9 Rearranging d 8 which is in separable form. Now separating d 8 And integrating d ln(c) 8 tanh / ln(c) Solving for tanh ln(c) or u tanh ln(c) Applying the condition u( ) () tanh ln(c())
4 ME 9 Mechanical Engineering Analysis Solving for C tanh C ep (.75) / 5. cos()u sin()u / 9ln() with u(=) = This equation is not separable, there does not seem to be an appropriate variable transformation, and since it is nonlinear we cannot use an integrating factor. Let s check to see if it is eact. We have / / N(,u) cos()u and M(,u) sin()u 9ln() Then N / M sin()u and sin()u u So the equation is eact and we can use the Eact Equation Method. We start with f (u) g() N M to find f and g. Substituting for M and N / / f (u) g() cos()u sin()u 9ln() Integrating / / f (u) g() u cos() u cos() ln() f (u) g() ln() So that f (u) 0 g() ln() Substituting into M(,u) f (u) C / u Now rearranging cos() ln() 0 C / u cos() C ln() and solving for u C ln() u cos() Applying the initial condition / C () ln() u( ) cos(()) / C cos() /
5 ME 9 Mechanical Engineering Analysis Solving for C Finally C cos().7.7 ln() u cos() / u u 6. cos(u / ) with u(=) =0 The equation is clearly not separable. However, if we rearrange it by multiplying through by u u cos(u / ) it should then be obvious that we can use the Variable Transformation Method, where = u/. Applying the transformation cos( ) We have shown d Substituting we have d cos( ) Rearranging d cos( ) which is in separable form. Now separating d cos( ) And integrating d ln(c) cos( ) Unfortunately the integral is not analytic, so we must stop at this point. e dt e 7. 7cos() with T(=0) = 6 T T This equation is not separable, there does not seem to be an appropriate variable transformation, and since it is nonlinear we cannot use an integrating factor. Let s check to see if it is eact. We have e e N(,T) and M(,T) 7cos() T T 5
6 ME 9 Mechanical Engineering Analysis Then N e M e and T T T So the equation is eact and we can use the Eact Equation Method. We start with f (T) g() NdT M to find f and g. Substituting for M and N e e f (T) g() dt 7cos() T T Integrating e e f (T) g() 7sin() T T f(t) g() 7sin() So that f (T) 0 g() 7sin() Substituting into M(,T) f (T) C e 7sin() 0 C T Now rearranging and solving for T / e T C 7sin() Applying the initial condition (0) e T( 0) 6 C 7sin(0) Solving for C C 7 Finally 8. e T / 7 7sin() dy cos( ) / We can rearrange this equation to dy 8 e sin() cos() / e sin() 8 with y(=-) = 6
7 ME 9 Mechanical Engineering Analysis which is clearly separable, so we may use the Separate and Integrate Method. Separating 8 e sin() dy cos() Integrating 8 e sin() dy cos() 8 e sin() y C cos() Unfortunately the integral cannot be found analytically, so we have gone as far as we can go. 9. sin()u 5 with u(=) = 0 We may rearrange this equation to sin()u 5 and note that it is not separable, there is no variable transformation, but since it is linear we can use the Integrating Factor Method. Hence we need to find F and G, so we may transform the equation to the form d F()u G() where sin() ((sin()) ) F ep sin() where Ei is the Eponential Integral Function. Then sin() ((sin()) ) G F5 5 Then our equation becomes d sin() ((sin()) ) sin() ((sin()) ) u 5 which is in separate and integrate form. Separating sin() ((sin()) ) sin() ((sin()) ) d u 5 Integrating sin() ((sin()) ) sin() ((sin()) ) u 5 C sin() ((sin()) ) 5sin() 5 cos() 5 sin() u C 6 8 7
8 ME 9 Mechanical Engineering Analysis Solving for u 5sin() 0 cos() 0 sin() C u sin() ((sin()) ) sin() ((sin()) ) Applying the condition 5sin() 0 cos() 0 sin() C ( ) 0 sin() ((sin( )) ) sin() ((sin( )) C 0 0 ((0) ) 0 ((0) ) 5 C 0 Solving for C 5 C 8 Then our final solution becomes 5sin() 0 cos() 0 sin() 0 u sin() ((sin()) ) 0. ) u cos( u) 7t t with u(t=) = - Rearranging the equation cos(u) t 7t which is separable, so we can use the Separate and Integrate Method. Separating cos(u) t 7t Integrating cos(u) t 7t sin( u) 7 t t C Solving for u 9 u sin t t C Applying the initial condition 9 u(t ) sin () () Solving for C sin( 9) C Our final solution is 9 u sin t t sin( 9) 6 8 C
9 ME 9 Mechanical Engineering Analysis d u. 6u 0 with u(=) = and 0 0 We follow our step by step method. Step Equation is in the proper form. Step Substituting e m, m m 6 0 Step Solve for the roots of m. m m So that a - b < 0 Step Not Applicable Our solution becomes 0.5 u() e Acos Not Applicable 5.75 Bsin 5.75 Step 7 Applying our conditions to solve for and B 0.5 u( ) e Acos 5.75 Bsin 0.5 e A 5.75 sin 5.75 B cos e Acos 5.75 Bsin 5.75 at =0 0 B A Solving for A A 5.75B Substituting into our first condition e Bcos Bsin
10 ME 9 Mechanical Engineering Analysis Solving for B e B 5.75 cos So that our final solution is e u() 0.5() sin cos 5.75 cos 5.75 sin sin 5.75 d u. u 0 with u(=0) = and u(=) = 0 We follow our step by step method. Step Equation is in the proper form. Step Substituting e m, m m 0 Step Solve for the roots of m. m 6 6 m 6 6 So that a - b = 0 Step Not Applicable Not Applicable Our solution becomes u() (C C ) e Step 7 Applying our conditions to solve for C and C u( 0) C u( ) 0 ( C C = - So that our final solution is u() ( )e ) e 0
11 ME 9 Mechanical Engineering Analysis d u, 8 5u 0 with u(=0) = 0 and 0 We follow our step by step method. Step Equation is in the proper form. Step Substituting e m, m m.5 0 Step Solve for the roots of m. m m So that a - b > 0 Step () C ep C ep.5 u Not Applicable Not Applicable Step 7 Applying our conditions to solve for C and C u( 0) 0 C C 0.775C ep C ep C.5C 0 Substituting for C 0.775C.5C C = 0.08 C = So that our final solution is u() 0.08ep ep.5. Determine the position of the mass as a function of time for a spring-mass system with the following properties:
12 ME 9 Mechanical Engineering Analysis mass, M =.5 kg viscous damping, C =. kg/s spring molus, k = N/m forcing function, F(t) = 0 N dy initial conditions: y(t=0) = 0. m and 0 t0 We begin by writing our general for a mass-spring system ODE d y dy M C ky F(t) Setting F(t) = 0 and rearranging d y C dy k y 0 M M We recognize this equation as being in a form that we can apply the e m method where a = C/M =./.5 =.8 and b = k/m = /.5 = Then we can follow our step by step procere. Step Satisfied Step m + am + b = 0 Step.8 m (.8) () m (.8) (). 0.0 So that a b < 0 Step y(t) e.t Acos 0.0t Bsin0.0t Step 7 At t = 0 y(t 0) 0. A
13 ME 9 Mechanical Engineering Analysis dy e dy t0 B =.5.t t 0.0Asin0.0t 0.0Bcos0.0t.e. Acos 0.0t Bsin0.0t 0.0B.A So our final solution is.t y(t) e 0.cos 0.0t.5sin0.0t 5. Determine the position of the mass as a function of time for a spring-mass system with the following properties: mass, M = 0.75 kg viscous damping, C =. kg/s spring molus, k = N/m forcing function, F(t) = 0 N dy initial conditions: y(t=0) = 0 m and 0. m/s t0 We begin by writing our general for a mass-spring system ODE d y dy M C ky F(t) Setting F(t) = 0 and rearranging d y C dy k y 0 M M We recognize this equation as being in a form that we can apply the e m method where a = C/M =./0.75= 5.6 and b = k/m = /0.75 = Then we can follow our step by step procere. Step Satisfied Step m + am + b = 0 Step 5.6 m (5.6) () m (5.6) ().76 So that a b > 0 Step u() C e 0.8t.76t Ce
14 ME 9 Mechanical Engineering Analysis Step 7 At t = 0 y(t 0) 0 C C dy 0.8t 0.8Ce.76Ce dy C.76C t0 C = -C C.76C C = C = 0.05 So our final solution is 0.8t.76t u() 0.05e 0.05e.76t d u 6. 5u 5 with u(=0) = 0 and 0 0 This is a nd order, liner, constant coefficient, nonhomogeneous ODE. We know that the solution is composed of a homogenous part and a particular part or u() = u h + u p For the homogenous solution we will use the e m method and for the particular solution we use the method of undetermined coefficients. Beginning with the homogenous solution. Step Satisfied. Step m m 5 0 Step Solve for the roots of m. For a nd order equation, we will have m () (5) m () (5) Hence a b < 0 Step
15 ME 9 Mechanical Engineering Analysis Our homogenous solution becomes () e C cos C sin uh Step 7 Skip until we combine with the particular solution Now we apply the method of undetermined coefficients Step Since our forcing function is + 5, we assume a polynomial function for our particular solution of the form u p () = A + B + C Step Substituting into our differential equation A A B 5 A B C 5 Step Collecting like powers of terms : 5A = : 8A + 5B = 0 0 : A + B + 5C = 5 Step Solving for the undetermined coefficients A=0. B = -8A/5 = -0. C = (5-A -B)/5 =.76 Assemble out total solution u() e C cos C sin
16 ME 9 Mechanical Engineering Analysis Apply our conditions u( 0) 0 C.76 C.76 e C sin C cos e C cos C sin C C 0. 0 C = C + 0. = (-.76) + 0. = -.0 Then our final solution becomes u() e.76cos.0sin d u 7. 7 u 5cos() with u(=0) = 0 and u(=) = This is a nd order, liner, constant coefficient, nonhomogeneous ODE. We know that the solution is composed of a homogenous part and a particular part or u() = u h + u p For the homogenous solution we will use the e m method and for the particular solution we use the method of undetermined coefficients. Beginning with the homogenous solution. Step Satisfied. Step m 7m 0 Step Solve for the roots of m. For a nd order equation, we will have 7 m (7) () m (7) () 6.70 Hence a b > 0 Step Our homogenous solution becomes u () C e C e h 6
17 ME 9 Mechanical Engineering Analysis Step 7 Skip until we combine with the particular solution Now we apply the method of undetermined coefficients Step Since our forcing function is + 5cos(), we assume the following function for our particular solution u p () = A + B + Ccos() + Dsin() Step Substituting into our differential equation 6Ccos() 6Dsin() 7A Csin() Dcos() A B Ccos() Dsin() 5cos() Step Collecting like terms of : A = 0 : 7A + B = 0 cos(): -6C+8D+C = 5 sin(): -6D 8C + D = 0 Step Solving for the undetermined coefficients A = B = -.5 C = D = 0. Assemble out total solution 0.98 u() C e C e cos() + 0.sin() Apply our conditions u( 0) 0 C C u( ) Ce Ce cos() + 0.sin() from which we can solve for C and C. 7
18 ME 9 Mechanical Engineering Analysis 8. Determine the position of the mass as a function of time for a spring-mass system with the following properties: mass, M = 0.75 kg viscous damping, C =. kg/s spring molus, k = N/m forcing function, F(t) = 5e.t N dy initial conditions: y(t=0) =0. m and 0. m/s t0 We begin by writing our general for a mass-spring system ODE d y dy M C ky F(t) Setting F(t) and rearranging d y C dy k 5.t y e M M M where a = C/M =./0.75= 5.6 and b = k/m = /0.75 = and 5/M = 5/0.75 = This is a nd order, liner, constant coefficient, nonhomogeneous ODE. We know that the solution is composed of a homogenous part and a particular part or y(t) = y h + y p For the homogenous solution we will use the e m method and for the particular solution we use the method of undetermined coefficients. Beginning with the homogenous solution. Then we can follow our step by step procere. Step Satisfied Step m + am + b = 0 Step 5.6 m (5.6) () m (5.6) ().76 So that a b > 0 Step y (t) C e h 0.8t C e.76t 8
19 ME 9 Mechanical Engineering Analysis Step 7 Skip until we add the particular solution Now we apply the method of undetermined coefficients Step Since our forcing function is 6.67e.t, we assume the following function for our particular solution y p (t) = Ae.t Step Substituting into our differential equation.t.t.t (.) Ae 5.6(.)Ae Ae 6.667e Step Collecting like terms of.5a + 6.7A + A= Step Solving for the undetermined coefficients A = Assemble out total solution 0.8t y(t) C e C e.76t.t 0.578e Apply our conditions y(t 0) 0. C C dy 0.8t.76t 0.8C e.76ce 0.68 dy C.76C 0.68 t0 from which we can solve for C and C..t e.t 9
ME 391 Mechanical Engineering Analysis
 Fall 04 ME 39 Mechanical Engineering Analsis Eam # Soluions Direcions: Open noes (including course web posings). No books, compuers, or phones. An calculaor is fair game. Problem Deermine he posiion of
Fall 04 ME 39 Mechanical Engineering Analsis Eam # Soluions Direcions: Open noes (including course web posings). No books, compuers, or phones. An calculaor is fair game. Problem Deermine he posiion of
Math 266 Midterm Exam 2
 Math 266 Midterm Exam 2 March 2st 26 Name: Ground Rules. Calculator is NOT allowed. 2. Show your work for every problem unless otherwise stated (partial credits are available). 3. You may use one 4-by-6
Math 266 Midterm Exam 2 March 2st 26 Name: Ground Rules. Calculator is NOT allowed. 2. Show your work for every problem unless otherwise stated (partial credits are available). 3. You may use one 4-by-6
Forced Mechanical Vibrations
 Forced Mechanical Vibrations Today we use methods for solving nonhomogeneous second order linear differential equations to study the behavior of mechanical systems.. Forcing: Transient and Steady State
Forced Mechanical Vibrations Today we use methods for solving nonhomogeneous second order linear differential equations to study the behavior of mechanical systems.. Forcing: Transient and Steady State
Unit 3. Integration. 3A. Differentials, indefinite integration. y x. c) Method 1 (slow way) Substitute: u = 8 + 9x, du = 9dx.
 Unit 3. Integration 3A. Differentials, indefinite integration 3A- a) 7 6 d. (d(sin ) = because sin is a constant.) b) (/) / d c) ( 9 8)d d) (3e 3 sin + e 3 cos)d e) (/ )d + (/ y)dy = implies dy = / d /
Unit 3. Integration 3A. Differentials, indefinite integration 3A- a) 7 6 d. (d(sin ) = because sin is a constant.) b) (/) / d c) ( 9 8)d d) (3e 3 sin + e 3 cos)d e) (/ )d + (/ y)dy = implies dy = / d /
MATH 23 Exam 2 Review Solutions
 MATH 23 Exam 2 Review Solutions Problem 1. Use the method of reduction of order to find a second solution of the given differential equation x 2 y (x 0.1875)y = 0, x > 0, y 1 (x) = x 1/4 e 2 x Solution
MATH 23 Exam 2 Review Solutions Problem 1. Use the method of reduction of order to find a second solution of the given differential equation x 2 y (x 0.1875)y = 0, x > 0, y 1 (x) = x 1/4 e 2 x Solution
Ex. 1. Find the general solution for each of the following differential equations:
 MATH 261.007 Instr. K. Ciesielski Spring 2010 NAME (print): SAMPLE TEST # 2 Solve the following exercises. Show your work. (No credit will be given for an answer with no supporting work shown.) Ex. 1.
MATH 261.007 Instr. K. Ciesielski Spring 2010 NAME (print): SAMPLE TEST # 2 Solve the following exercises. Show your work. (No credit will be given for an answer with no supporting work shown.) Ex. 1.
HIGHER-ORDER LINEAR DIFFERENTIAL EQUATIONS
 CHAPTER 5 HIGHER-ORDER LINEAR DIFFERENTIAL EQUATIONS SECTION 5. INTRODUCTION: SECOND-ORDER LINEAR EQUATIONS In this section the central ideas of the theory of linear differential equations are introduced
CHAPTER 5 HIGHER-ORDER LINEAR DIFFERENTIAL EQUATIONS SECTION 5. INTRODUCTION: SECOND-ORDER LINEAR EQUATIONS In this section the central ideas of the theory of linear differential equations are introduced
First Order Linear Ordinary Differential Equations
 First Order Linear Ordinary Differential Equations The most general first order linear ODE is an equation of the form p t dy dt q t y t f t. 1 Herepqarecalledcoefficients f is referred to as the forcing
First Order Linear Ordinary Differential Equations The most general first order linear ODE is an equation of the form p t dy dt q t y t f t. 1 Herepqarecalledcoefficients f is referred to as the forcing
µ Differential Equations MAΘ National Convention 2017 For all questions, answer choice E) NOTA means that none of the above answers is correct.
 µ Differential Equations MAΘ National Convention 07 For all questions, answer choice E) NOTA means that none of the above answers is correct.. C) Since f (, ) = +, (0) = and h =. Use Euler s method, we
µ Differential Equations MAΘ National Convention 07 For all questions, answer choice E) NOTA means that none of the above answers is correct.. C) Since f (, ) = +, (0) = and h =. Use Euler s method, we
Homogeneous Equations with Constant Coefficients
 Homogeneous Equations with Constant Coefficients MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Spring 2018 General Second Order ODE Second order ODEs have the form
Homogeneous Equations with Constant Coefficients MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Spring 2018 General Second Order ODE Second order ODEs have the form
Basics Concepts and Ideas First Order Differential Equations. Dr. Omar R. Daoud
 Basics Concepts and Ideas First Order Differential Equations Dr. Omar R. Daoud Differential Equations Man Phsical laws and relations appear mathematicall in the form of Differentia Equations The are one
Basics Concepts and Ideas First Order Differential Equations Dr. Omar R. Daoud Differential Equations Man Phsical laws and relations appear mathematicall in the form of Differentia Equations The are one
Jim Lambers MAT 285 Spring Semester Practice Exam 2 Solution. y(t) = 5 2 e t 1 2 e 3t.
 . Solve the initial value problem which factors into Jim Lambers MAT 85 Spring Semester 06-7 Practice Exam Solution y + 4y + 3y = 0, y(0) =, y (0) =. λ + 4λ + 3 = 0, (λ + )(λ + 3) = 0. Therefore, the roots
. Solve the initial value problem which factors into Jim Lambers MAT 85 Spring Semester 06-7 Practice Exam Solution y + 4y + 3y = 0, y(0) =, y (0) =. λ + 4λ + 3 = 0, (λ + )(λ + 3) = 0. Therefore, the roots
Section 3.4. Second Order Nonhomogeneous. The corresponding homogeneous equation. is called the reduced equation of (N).
 Section 3.4. Second Order Nonhomogeneous Equations y + p(x)y + q(x)y = f(x) (N) The corresponding homogeneous equation y + p(x)y + q(x)y = 0 (H) is called the reduced equation of (N). 1 General Results
Section 3.4. Second Order Nonhomogeneous Equations y + p(x)y + q(x)y = f(x) (N) The corresponding homogeneous equation y + p(x)y + q(x)y = 0 (H) is called the reduced equation of (N). 1 General Results
Euler-Cauchy Using Undetermined Coefficients
 Euler-Cauchy Using Undetermined Coefficients Department of Mathematics California State University, Fresno doreendl@csufresno.edu Joint Mathematics Meetings January 14, 2010 Outline 1 2 3 Second Order
Euler-Cauchy Using Undetermined Coefficients Department of Mathematics California State University, Fresno doreendl@csufresno.edu Joint Mathematics Meetings January 14, 2010 Outline 1 2 3 Second Order
ENGI 3424 Mid Term Test Solutions Page 1 of 9
 ENGI 344 Mid Term Test 07 0 Solutions Page of 9. The displacement st of the free end of a mass spring sstem beond the equilibrium position is governed b the ordinar differential equation d s ds 3t 6 5s
ENGI 344 Mid Term Test 07 0 Solutions Page of 9. The displacement st of the free end of a mass spring sstem beond the equilibrium position is governed b the ordinar differential equation d s ds 3t 6 5s
Substituting this into the differential equation and solving for u, we have. + u2. du = 3x + c. ( )
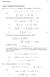 Worked Solutions 27 Chapter 6: Simplifying Through Substitution 6 a Let u = 3 + 3y + 2 Solving for y computing y we then see that 3y = u 3 2 y = u 3 2 3 = d [ u 3 2 3 = 3 Substituting this into the differential
Worked Solutions 27 Chapter 6: Simplifying Through Substitution 6 a Let u = 3 + 3y + 2 Solving for y computing y we then see that 3y = u 3 2 y = u 3 2 3 = d [ u 3 2 3 = 3 Substituting this into the differential
MATH 2250 Final Exam Solutions
 MATH 225 Final Exam Solutions Tuesday, April 29, 28, 6: 8:PM Write your name and ID number at the top of this page. Show all your work. You may refer to one double-sided sheet of notes during the exam
MATH 225 Final Exam Solutions Tuesday, April 29, 28, 6: 8:PM Write your name and ID number at the top of this page. Show all your work. You may refer to one double-sided sheet of notes during the exam
If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy. du du. If y = f (u) then y = f (u) u
 Section 3 4B The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then f (u) u The Chain Rule with the Power
Section 3 4B The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then f (u) u The Chain Rule with the Power
M343 Homework 6. Enrique Areyan May 31, 2013
 M343 Homework 6 Enrique Areyan May 31, 013 Section 3.5. + y + 5y = 3sin(t). The general solution is given by: y h : Characteristic equation: r + r + 5 = 0 r = 1 ± i. The solution in this case is: y h =
M343 Homework 6 Enrique Areyan May 31, 013 Section 3.5. + y + 5y = 3sin(t). The general solution is given by: y h : Characteristic equation: r + r + 5 = 0 r = 1 ± i. The solution in this case is: y h =
Nonhomogeneous Equations and Variation of Parameters
 Nonhomogeneous Equations Variation of Parameters June 17, 2016 1 Nonhomogeneous Equations 1.1 Review of First Order Equations If we look at a first order homogeneous constant coefficient ordinary differential
Nonhomogeneous Equations Variation of Parameters June 17, 2016 1 Nonhomogeneous Equations 1.1 Review of First Order Equations If we look at a first order homogeneous constant coefficient ordinary differential
Differential Equations Practice: 2nd Order Linear: Nonhomogeneous Equations: Undetermined Coefficients Page 1
 Differential Equations Practice: 2nd Order Linear: Nonhomogeneous Equations: Undetermined Coefficients Page 1 Questions Example (3.5.3) Find a general solution of the differential equation y 2y 3y = 3te
Differential Equations Practice: 2nd Order Linear: Nonhomogeneous Equations: Undetermined Coefficients Page 1 Questions Example (3.5.3) Find a general solution of the differential equation y 2y 3y = 3te
If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy. du du. If y = f (u) then y = f (u) u
 Section 3 4B Lecture The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then y = f (u) u The Chain Rule
Section 3 4B Lecture The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then y = f (u) u The Chain Rule
2 nd ORDER O.D.E.s SUBSTITUTIONS
 nd ORDER O.D.E.s SUBSTITUTIONS Question 1 (***+) d y y 8y + 16y = d d d, y 0, Find the general solution of the above differential equation by using the transformation equation t = y. Give the answer in
nd ORDER O.D.E.s SUBSTITUTIONS Question 1 (***+) d y y 8y + 16y = d d d, y 0, Find the general solution of the above differential equation by using the transformation equation t = y. Give the answer in
Edexcel Further Pure 2
 Edecel Further Pure Second order differential equations Section : Non-homogeneous second order differential equations Notes and Eamples These notes contain subsections on Finding particular integrals Finding
Edecel Further Pure Second order differential equations Section : Non-homogeneous second order differential equations Notes and Eamples These notes contain subsections on Finding particular integrals Finding
Second In-Class Exam Solutions Math 246, Professor David Levermore Thursday, 31 March 2011
 Second In-Class Exam Solutions Math 246, Professor David Levermore Thursday, 31 March 211 (1) [6] Give the interval of definition for the solution of the initial-value problem d 4 y dt 4 + 7 1 t 2 dy dt
Second In-Class Exam Solutions Math 246, Professor David Levermore Thursday, 31 March 211 (1) [6] Give the interval of definition for the solution of the initial-value problem d 4 y dt 4 + 7 1 t 2 dy dt
3.5 Undetermined Coefficients
 3.5. UNDETERMINED COEFFICIENTS 153 11. t 2 y + ty + 4y = 0, y(1) = 3, y (1) = 4 12. t 2 y 4ty + 6y = 0, y(0) = 1, y (0) = 1 3.5 Undetermined Coefficients In this section and the next we consider the nonhomogeneous
3.5. UNDETERMINED COEFFICIENTS 153 11. t 2 y + ty + 4y = 0, y(1) = 3, y (1) = 4 12. t 2 y 4ty + 6y = 0, y(0) = 1, y (0) = 1 3.5 Undetermined Coefficients In this section and the next we consider the nonhomogeneous
Math Assignment 5
 Math 2280 - Assignment 5 Dylan Zwick Fall 2013 Section 3.4-1, 5, 18, 21 Section 3.5-1, 11, 23, 28, 35, 47, 56 Section 3.6-1, 2, 9, 17, 24 1 Section 3.4 - Mechanical Vibrations 3.4.1 - Determine the period
Math 2280 - Assignment 5 Dylan Zwick Fall 2013 Section 3.4-1, 5, 18, 21 Section 3.5-1, 11, 23, 28, 35, 47, 56 Section 3.6-1, 2, 9, 17, 24 1 Section 3.4 - Mechanical Vibrations 3.4.1 - Determine the period
Section 3.4. Second Order Nonhomogeneous. The corresponding homogeneous equation. is called the reduced equation of (N).
 Section 3.4. Second Order Nonhomogeneous Equations y + p(x)y + q(x)y = f(x) (N) The corresponding homogeneous equation y + p(x)y + q(x)y = 0 (H) is called the reduced equation of (N). 1 General Results
Section 3.4. Second Order Nonhomogeneous Equations y + p(x)y + q(x)y = f(x) (N) The corresponding homogeneous equation y + p(x)y + q(x)y = 0 (H) is called the reduced equation of (N). 1 General Results
IV Higher Order Linear ODEs
 IV Higher Order Linear ODEs Boyce & DiPrima, Chapter 4 H.J.Eberl - MATH*2170 0 IV Higher Order Linear ODEs IV.1 General remarks Boyce & DiPrima, Section 4.1 H.J.Eberl - MATH*2170 1 Problem formulation
IV Higher Order Linear ODEs Boyce & DiPrima, Chapter 4 H.J.Eberl - MATH*2170 0 IV Higher Order Linear ODEs IV.1 General remarks Boyce & DiPrima, Section 4.1 H.J.Eberl - MATH*2170 1 Problem formulation
Systems of Ordinary Differential Equations
 Systems of Ordinary Differential Equations MATH 365 Ordinary Differential Equations J Robert Buchanan Department of Mathematics Fall 2018 Objectives Many physical problems involve a number of separate
Systems of Ordinary Differential Equations MATH 365 Ordinary Differential Equations J Robert Buchanan Department of Mathematics Fall 2018 Objectives Many physical problems involve a number of separate
MATH 251 Examination I October 5, 2017 FORM A. Name: Student Number: Section:
 MATH 251 Examination I October 5, 2017 FORM A Name: Student Number: Section: This exam has 13 questions for a total of 100 points. Show all your work! In order to obtain full credit for partial credit
MATH 251 Examination I October 5, 2017 FORM A Name: Student Number: Section: This exam has 13 questions for a total of 100 points. Show all your work! In order to obtain full credit for partial credit
Math 1B Final Exam, Solution. Prof. Mina Aganagic Lecture 2, Spring (6 points) Use substitution and integration by parts to find:
 Math B Final Eam, Solution Prof. Mina Aganagic Lecture 2, Spring 20 The eam is closed book, apart from a sheet of notes 8. Calculators are not allowed. It is your responsibility to write your answers clearly..
Math B Final Eam, Solution Prof. Mina Aganagic Lecture 2, Spring 20 The eam is closed book, apart from a sheet of notes 8. Calculators are not allowed. It is your responsibility to write your answers clearly..
Solutions to Homework 3
 Solutions to Homework 3 Section 3.4, Repeated Roots; Reduction of Order Q 1). Find the general solution to 2y + y = 0. Answer: The charactertic equation : r 2 2r + 1 = 0, solving it we get r = 1 as a repeated
Solutions to Homework 3 Section 3.4, Repeated Roots; Reduction of Order Q 1). Find the general solution to 2y + y = 0. Answer: The charactertic equation : r 2 2r + 1 = 0, solving it we get r = 1 as a repeated
6 Second Order Linear Differential Equations
 6 Second Order Linear Differential Equations A differential equation for an unknown function y = f(x) that depends on a variable x is any equation that ties together functions of x with y and its derivatives.
6 Second Order Linear Differential Equations A differential equation for an unknown function y = f(x) that depends on a variable x is any equation that ties together functions of x with y and its derivatives.
Differential Equations Practice: 2nd Order Linear: Nonhomogeneous Equations: Variation of Parameters Page 1
 Differential Equations Practice: 2nd Order Linear: Nonhomogeneous Equations: Variation of Parameters Page Questions Example (3.6.) Find a particular solution of the differential equation y 5y + 6y = 2e
Differential Equations Practice: 2nd Order Linear: Nonhomogeneous Equations: Variation of Parameters Page Questions Example (3.6.) Find a particular solution of the differential equation y 5y + 6y = 2e
Solutions to Math 53 Math 53 Practice Final
 Solutions to Math 5 Math 5 Practice Final 20 points Consider the initial value problem y t 4yt = te t with y 0 = and y0 = 0 a 8 points Find the Laplace transform of the solution of this IVP b 8 points
Solutions to Math 5 Math 5 Practice Final 20 points Consider the initial value problem y t 4yt = te t with y 0 = and y0 = 0 a 8 points Find the Laplace transform of the solution of this IVP b 8 points
Chapter 7: Trigonometric Equations and Identities
 Chapter 7: Trigonometric Equations and Identities In the last two chapters we have used basic definitions and relationships to simplify trigonometric expressions and equations. In this chapter we will
Chapter 7: Trigonometric Equations and Identities In the last two chapters we have used basic definitions and relationships to simplify trigonometric expressions and equations. In this chapter we will
ME 301 THEORY OFD MACHİNES I SOLVED PROBLEM SET 2
 ME 30 THEOY OFD MACHİNES I SOLVED POBLEM SET 2 POBLEM. For the given mechanisms, find the degree of freedom F. Show the link numbers on the figures. Number the links and label the joints on the figure.
ME 30 THEOY OFD MACHİNES I SOLVED POBLEM SET 2 POBLEM. For the given mechanisms, find the degree of freedom F. Show the link numbers on the figures. Number the links and label the joints on the figure.
Mathematical Models. MATH 365 Ordinary Differential Equations. J. Robert Buchanan. Spring Department of Mathematics
 Mathematical Models MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Spring 2018 Ordinary Differential Equations The topic of ordinary differential equations (ODEs)
Mathematical Models MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Spring 2018 Ordinary Differential Equations The topic of ordinary differential equations (ODEs)
Second-Order Linear ODEs
 Second-Order Linear ODEs A second order ODE is called linear if it can be written as y + p(t)y + q(t)y = r(t). (0.1) It is called homogeneous if r(t) = 0, and nonhomogeneous otherwise. We shall assume
Second-Order Linear ODEs A second order ODE is called linear if it can be written as y + p(t)y + q(t)y = r(t). (0.1) It is called homogeneous if r(t) = 0, and nonhomogeneous otherwise. We shall assume
Higher Order Linear Equations
 C H A P T E R 4 Higher Order Linear Equations 4.1 1. The differential equation is in standard form. Its coefficients, as well as the function g(t) = t, are continuous everywhere. Hence solutions are valid
C H A P T E R 4 Higher Order Linear Equations 4.1 1. The differential equation is in standard form. Its coefficients, as well as the function g(t) = t, are continuous everywhere. Hence solutions are valid
Mathematical Models. MATH 365 Ordinary Differential Equations. J. Robert Buchanan. Fall Department of Mathematics
 Mathematical Models MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Ordinary Differential Equations The topic of ordinary differential equations (ODEs) is
Mathematical Models MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Ordinary Differential Equations The topic of ordinary differential equations (ODEs) is
Ordinary Differential Equations
 Ordinary Differential Equations (MA102 Mathematics II) Shyamashree Upadhyay IIT Guwahati Shyamashree Upadhyay ( IIT Guwahati ) Ordinary Differential Equations 1 / 15 Method of Undetermined Coefficients
Ordinary Differential Equations (MA102 Mathematics II) Shyamashree Upadhyay IIT Guwahati Shyamashree Upadhyay ( IIT Guwahati ) Ordinary Differential Equations 1 / 15 Method of Undetermined Coefficients
ENGI Second Order Linear ODEs Page Second Order Linear Ordinary Differential Equations
 ENGI 344 - Second Order Linear ODEs age -01. Second Order Linear Ordinary Differential Equations The general second order linear ordinary differential equation is of the form d y dy x Q x y Rx dx dx Of
ENGI 344 - Second Order Linear ODEs age -01. Second Order Linear Ordinary Differential Equations The general second order linear ordinary differential equation is of the form d y dy x Q x y Rx dx dx Of
Math 20D Final Exam 8 December has eigenvalues 3, 3, 0 and find the eigenvectors associated with 3. ( 2) det
 Math D Final Exam 8 December 9. ( points) Show that the matrix 4 has eigenvalues 3, 3, and find the eigenvectors associated with 3. 4 λ det λ λ λ = (4 λ) det λ ( ) det + det λ = (4 λ)(( λ) 4) + ( λ + )
Math D Final Exam 8 December 9. ( points) Show that the matrix 4 has eigenvalues 3, 3, and find the eigenvectors associated with 3. 4 λ det λ λ λ = (4 λ) det λ ( ) det + det λ = (4 λ)(( λ) 4) + ( λ + )
MATH 251 Examination I February 23, 2017 FORM A. Name: Student Number: Section:
 MATH 251 Examination I February 23, 2017 FORM A Name: Student Number: Section: This exam has 12 questions for a total of 100 points. Show all you your work! In order to obtain full credit for partial credit
MATH 251 Examination I February 23, 2017 FORM A Name: Student Number: Section: This exam has 12 questions for a total of 100 points. Show all you your work! In order to obtain full credit for partial credit
Chapter 3: Second Order Equations
 Exam 2 Review This review sheet contains this cover page (a checklist of topics from Chapters 3). Following by all the review material posted pertaining to chapter 3 (all combined into one file). Chapter
Exam 2 Review This review sheet contains this cover page (a checklist of topics from Chapters 3). Following by all the review material posted pertaining to chapter 3 (all combined into one file). Chapter
Math 308 Exam II Practice Problems
 Math 38 Exam II Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture and all suggested homework problems..
Math 38 Exam II Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture and all suggested homework problems..
Nonhomogeneous Linear Differential Equations with Constant Coefficients - (3.4) Method of Undetermined Coefficients
 Nonhomogeneous Linear Differential Equations with Constant Coefficients - (3.4) Method of Undetermined Coefficients Consider an nth-order nonhomogeneous linear differential equation with constant coefficients:
Nonhomogeneous Linear Differential Equations with Constant Coefficients - (3.4) Method of Undetermined Coefficients Consider an nth-order nonhomogeneous linear differential equation with constant coefficients:
Lecture 17: Nonhomogeneous equations. 1 Undetermined coefficients method to find a particular
 Lecture 17: Nonhomogeneous equations 1 Undetermined coefficients method to find a particular solution The method of undetermined coefficients (sometimes referred to as the method of justicious guessing)
Lecture 17: Nonhomogeneous equations 1 Undetermined coefficients method to find a particular solution The method of undetermined coefficients (sometimes referred to as the method of justicious guessing)
Name: Solutions Final Exam
 Instructions. Answer each of the questions on your own paper. Put your name on each page of your paper. Be sure to show your work so that partial credit can be adequately assessed. Credit will not be given
Instructions. Answer each of the questions on your own paper. Put your name on each page of your paper. Be sure to show your work so that partial credit can be adequately assessed. Credit will not be given
1 Differential Equations
 Reading [Simon], Chapter 24, p. 633-657. 1 Differential Equations 1.1 Definition and Examples A differential equation is an equation involving an unknown function (say y = y(t)) and one or more of its
Reading [Simon], Chapter 24, p. 633-657. 1 Differential Equations 1.1 Definition and Examples A differential equation is an equation involving an unknown function (say y = y(t)) and one or more of its
A: Brief Review of Ordinary Differential Equations
 A: Brief Review of Ordinary Differential Equations Because of Principle # 1 mentioned in the Opening Remarks section, you should review your notes from your ordinary differential equations (odes) course
A: Brief Review of Ordinary Differential Equations Because of Principle # 1 mentioned in the Opening Remarks section, you should review your notes from your ordinary differential equations (odes) course
HIGHER-ORDER LINEAR ORDINARY DIFFERENTIAL EQUATIONS II: Nonhomogeneous Case and Vibrations
 HIGHER-ORDER LINEAR ORDINARY DIFFERENTIAL EQUATIONS II: Nonhomogeneous Case and Vibrations David Levermore Department of Mathematics University of Maryland 22 October 28 Because the presentation of this
HIGHER-ORDER LINEAR ORDINARY DIFFERENTIAL EQUATIONS II: Nonhomogeneous Case and Vibrations David Levermore Department of Mathematics University of Maryland 22 October 28 Because the presentation of this
FP2 Mark Schemes from old P4, P5, P6 and FP1, FP2, FP3 papers (back to June 2002)
 FP Mark Schemes from old P, P5, P6 and FP, FP, FP papers (back to June 00) Please note that the following pages contain mark schemes for questions from past papers. The standard of the mark schemes is
FP Mark Schemes from old P, P5, P6 and FP, FP, FP papers (back to June 00) Please note that the following pages contain mark schemes for questions from past papers. The standard of the mark schemes is
Brief Notes on Differential Equations
 Brief Notes on Differential Equations (A) Searable First-Order Differential Equations Solve the following differential equations b searation of variables: (a) (b) Solution ( 1 ) (a) The ODE becomes d and
Brief Notes on Differential Equations (A) Searable First-Order Differential Equations Solve the following differential equations b searation of variables: (a) (b) Solution ( 1 ) (a) The ODE becomes d and
Math 211. Substitute Lecture. November 20, 2000
 1 Math 211 Substitute Lecture November 20, 2000 2 Solutions to y + py + qy =0. Look for exponential solutions y(t) =e λt. Characteristic equation: λ 2 + pλ + q =0. Characteristic polynomial: λ 2 + pλ +
1 Math 211 Substitute Lecture November 20, 2000 2 Solutions to y + py + qy =0. Look for exponential solutions y(t) =e λt. Characteristic equation: λ 2 + pλ + q =0. Characteristic polynomial: λ 2 + pλ +
Solutions to Homework 1, Introduction to Differential Equations, 3450: , Dr. Montero, Spring y(x) = ce 2x + e x
 Solutions to Homewor 1, Introduction to Differential Equations, 3450:335-003, Dr. Montero, Spring 2009 problem 2. The problem says that the function yx = ce 2x + e x solves the ODE y + 2y = e x, and ass
Solutions to Homewor 1, Introduction to Differential Equations, 3450:335-003, Dr. Montero, Spring 2009 problem 2. The problem says that the function yx = ce 2x + e x solves the ODE y + 2y = e x, and ass
Particular Solutions
 Particular Solutions Our eamples so far in this section have involved some constant of integration, K. We now move on to see particular solutions, where we know some boundar conditions and we substitute
Particular Solutions Our eamples so far in this section have involved some constant of integration, K. We now move on to see particular solutions, where we know some boundar conditions and we substitute
INDEFINITE INTEGRAL5 DR.HEMA REDDY. Mathematics
 INDEFINITE INTEGRAL5 DR.HEMA REDDY METHODS OF INTEGRATION 1)Integration by substitution )Integration by partial fractions 3)Integration by parts Integrals of type a a d b p q b d c c d a cos bsin c a sin
INDEFINITE INTEGRAL5 DR.HEMA REDDY METHODS OF INTEGRATION 1)Integration by substitution )Integration by partial fractions 3)Integration by parts Integrals of type a a d b p q b d c c d a cos bsin c a sin
Math 2142 Homework 5 Part 1 Solutions
 Math 2142 Homework 5 Part 1 Solutions Problem 1. For the following homogeneous second order differential equations, give the general solution and the particular solution satisfying the given initial conditions.
Math 2142 Homework 5 Part 1 Solutions Problem 1. For the following homogeneous second order differential equations, give the general solution and the particular solution satisfying the given initial conditions.
FP2 Mark Schemes from old P4, P5, P6 and FP1, FP2, FP3 papers (back to June 2002)
 FP Mark Schemes from old P, P5, P6 and FP, FP, FP papers (back to June 00) Please note that the following pages contain mark schemes for questions from past papers. The standard of the mark schemes is
FP Mark Schemes from old P, P5, P6 and FP, FP, FP papers (back to June 00) Please note that the following pages contain mark schemes for questions from past papers. The standard of the mark schemes is
Solutions for homework 5
 1 Section 4.3 Solutions for homework 5 17. The following equation has repeated, real, characteristic roots. Find the general solution. y 4y + 4y = 0. The characteristic equation is λ 4λ + 4 = 0 which has
1 Section 4.3 Solutions for homework 5 17. The following equation has repeated, real, characteristic roots. Find the general solution. y 4y + 4y = 0. The characteristic equation is λ 4λ + 4 = 0 which has
US01CMTH02 UNIT-3. exists, then it is called the partial derivative of f with respect to y at (a, b) and is denoted by f. f(a, b + b) f(a, b) lim
 Study material of BSc(Semester - I US01CMTH02 (Partial Derivatives Prepared by Nilesh Y Patel Head,Mathematics Department,VPand RPTPScience College 1 Partial derivatives US01CMTH02 UNIT-3 The concept of
Study material of BSc(Semester - I US01CMTH02 (Partial Derivatives Prepared by Nilesh Y Patel Head,Mathematics Department,VPand RPTPScience College 1 Partial derivatives US01CMTH02 UNIT-3 The concept of
Laplace Transforms Chapter 3
 Laplace Transforms Important analytical method for solving linear ordinary differential equations. - Application to nonlinear ODEs? Must linearize first. Laplace transforms play a key role in important
Laplace Transforms Important analytical method for solving linear ordinary differential equations. - Application to nonlinear ODEs? Must linearize first. Laplace transforms play a key role in important
AMATH 351 Mar 15, 2013 FINAL REVIEW. Instructor: Jiri Najemnik
 AMATH 351 Mar 15, 013 FINAL REVIEW Instructor: Jiri Najemni ABOUT GRADES Scores I have so far will be posted on the website today sorted by the student number HW4 & Exam will be added early next wee Let
AMATH 351 Mar 15, 013 FINAL REVIEW Instructor: Jiri Najemni ABOUT GRADES Scores I have so far will be posted on the website today sorted by the student number HW4 & Exam will be added early next wee Let
Math Homework 3 Solutions. (1 y sin x) dx + (cos x) dy = 0. = sin x =
 2.6 #10: Determine if the equation is exact. If so, solve it. Math 315-01 Homework 3 Solutions (1 y sin x) dx + (cos x) dy = 0 Solution: Let P (x, y) = 1 y sin x and Q(x, y) = cos x. Note P = sin x = Q
2.6 #10: Determine if the equation is exact. If so, solve it. Math 315-01 Homework 3 Solutions (1 y sin x) dx + (cos x) dy = 0 Solution: Let P (x, y) = 1 y sin x and Q(x, y) = cos x. Note P = sin x = Q
Ordinary Differential Equations
 Ordinary Differential Equations for Engineers and Scientists Gregg Waterman Oregon Institute of Technology c 2017 Gregg Waterman This work is licensed under the Creative Commons Attribution 4.0 International
Ordinary Differential Equations for Engineers and Scientists Gregg Waterman Oregon Institute of Technology c 2017 Gregg Waterman This work is licensed under the Creative Commons Attribution 4.0 International
Candidates sitting FP2 may also require those formulae listed under Further Pure Mathematics FP1 and Core Mathematics C1 C4. e π.
 F Further IAL Pure PAPERS: Mathematics FP 04-6 AND SPECIMEN Candidates sitting FP may also require those formulae listed under Further Pure Mathematics FP and Core Mathematics C C4. Area of a sector A
F Further IAL Pure PAPERS: Mathematics FP 04-6 AND SPECIMEN Candidates sitting FP may also require those formulae listed under Further Pure Mathematics FP and Core Mathematics C C4. Area of a sector A
MATH 220 solution to homework 1
 MATH solution to homework Problem. Define z(s = u( + s, y + s, then z (s = u u ( + s, y + s + y ( + s, y + s = e y, z( y = u( y, = f( y, u(, y = z( = z( y + y If we prescribe the data u(, = f(, then z
MATH solution to homework Problem. Define z(s = u( + s, y + s, then z (s = u u ( + s, y + s + y ( + s, y + s = e y, z( y = u( y, = f( y, u(, y = z( = z( y + y If we prescribe the data u(, = f(, then z
ENGI 9420 Lecture Notes 1 - ODEs Page 1.01
 ENGI 940 Lecture Notes - ODEs Page.0. Ordinary Differential Equations An equation involving a function of one independent variable and the derivative(s) of that function is an ordinary differential equation
ENGI 940 Lecture Notes - ODEs Page.0. Ordinary Differential Equations An equation involving a function of one independent variable and the derivative(s) of that function is an ordinary differential equation
Math K (24564) - Homework Solutions 02
 Math 39100 K (24564) - Homework Solutions 02 Ethan Akin Office: NAC 6/287 Phone: 650-5136 Email: ethanakin@earthlink.net Spring, 2018 Contents Reduction of Order, B & D Chapter 3, p. 174 Constant Coefficient
Math 39100 K (24564) - Homework Solutions 02 Ethan Akin Office: NAC 6/287 Phone: 650-5136 Email: ethanakin@earthlink.net Spring, 2018 Contents Reduction of Order, B & D Chapter 3, p. 174 Constant Coefficient
MAE 82 Engineering Mathematics
 Class otes : First Order Differential Equation on Linear AE 8 Engineering athematics Universe on Linear umerical Linearization on Linear Special Cases Analtical o General Solution Linear Analtical General
Class otes : First Order Differential Equation on Linear AE 8 Engineering athematics Universe on Linear umerical Linearization on Linear Special Cases Analtical o General Solution Linear Analtical General
Linear Differential Equation (1st Order)
 Linear Differential Equation (1st Order) First Order Linear Differential Equation is an equation of the form y' Cp y = q For q = 0, this is a homogeneous equation and the solution is in the form of: y
Linear Differential Equation (1st Order) First Order Linear Differential Equation is an equation of the form y' Cp y = q For q = 0, this is a homogeneous equation and the solution is in the form of: y
Second order linear equations
 Second order linear equations Samy Tindel Purdue University Differential equations - MA 266 Taken from Elementary differential equations by Boyce and DiPrima Samy T. Second order equations Differential
Second order linear equations Samy Tindel Purdue University Differential equations - MA 266 Taken from Elementary differential equations by Boyce and DiPrima Samy T. Second order equations Differential
SOLVING DIFFERENTIAL EQUATIONS. Amir Asif. Department of Computer Science and Engineering York University, Toronto, ON M3J1P3
 SOLVING DIFFERENTIAL EQUATIONS Amir Asif Department of Computer Science and Engineering York University, Toronto, ON M3J1P3 ABSTRACT This article reviews a direct method for solving linear, constant-coefficient
SOLVING DIFFERENTIAL EQUATIONS Amir Asif Department of Computer Science and Engineering York University, Toronto, ON M3J1P3 ABSTRACT This article reviews a direct method for solving linear, constant-coefficient
MAE 105 Introduction to Mathematical Physics HOMEWORK 1. Due on Thursday October 1st 2015
 MAE 5 Introduction to Mathematical Physics HOMEWORK Due on Thursday October st 25 PROBEM : Evaluate the following integrals (where n =, 2, 3,... is an integer) and show all your steps: (a) x nπx We use
MAE 5 Introduction to Mathematical Physics HOMEWORK Due on Thursday October st 25 PROBEM : Evaluate the following integrals (where n =, 2, 3,... is an integer) and show all your steps: (a) x nπx We use
Homework Solutions:
 Homework Solutions: 1.1-1.3 Section 1.1: 1. Problems 1, 3, 5 In these problems, we want to compare and contrast the direction fields for the given (autonomous) differential equations of the form y = ay
Homework Solutions: 1.1-1.3 Section 1.1: 1. Problems 1, 3, 5 In these problems, we want to compare and contrast the direction fields for the given (autonomous) differential equations of the form y = ay
Ordinary Differential Equations
 II 12/01/2015 II Second order linear equations with constant coefficients are important in two physical processes, namely, Mechanical and Electrical oscillations. Actually from the Math point of view,
II 12/01/2015 II Second order linear equations with constant coefficients are important in two physical processes, namely, Mechanical and Electrical oscillations. Actually from the Math point of view,
Partial proof: y = ϕ 1 (t) is a solution to y + p(t)y = 0 implies. Thus y = cϕ 1 (t) is a solution to y + p(t)y = 0 since
 Existence and Uniqueness for LINEAR DEs. Homogeneous: y (n) + p 1 (t)y (n 1) +...p n 1 (t)y + p n (t)y = 0 Non-homogeneous: g(t) 0 y (n) + p 1 (t)y (n 1) +...p n 1 (t)y + p n (t)y = g(t) 1st order LINEAR
Existence and Uniqueness for LINEAR DEs. Homogeneous: y (n) + p 1 (t)y (n 1) +...p n 1 (t)y + p n (t)y = 0 Non-homogeneous: g(t) 0 y (n) + p 1 (t)y (n 1) +...p n 1 (t)y + p n (t)y = g(t) 1st order LINEAR
Differential and Difference LTI systems
 Signals and Systems Lecture: 6 Differential and Difference LTI systems Differential and difference linear time-invariant (LTI) systems constitute an extremely important class of systems in engineering.
Signals and Systems Lecture: 6 Differential and Difference LTI systems Differential and difference linear time-invariant (LTI) systems constitute an extremely important class of systems in engineering.
Form A. 1. Which of the following is a second-order, linear, homogenous differential equation? 2
 Form A Math 4 Common Part of Final Exam December 6, 996 INSTRUCTIONS: Please enter your NAME, ID NUMBER, FORM designation, and INDEX NUMBER on your op scan sheet. The index number should be written in
Form A Math 4 Common Part of Final Exam December 6, 996 INSTRUCTIONS: Please enter your NAME, ID NUMBER, FORM designation, and INDEX NUMBER on your op scan sheet. The index number should be written in
APPM 2360 Section Exam 3 Wednesday November 19, 7:00pm 8:30pm, 2014
 APPM 2360 Section Exam 3 Wednesday November 9, 7:00pm 8:30pm, 204 ON THE FRONT OF YOUR BLUEBOOK write: () your name, (2) your student ID number, (3) lecture section, (4) your instructor s name, and (5)
APPM 2360 Section Exam 3 Wednesday November 9, 7:00pm 8:30pm, 204 ON THE FRONT OF YOUR BLUEBOOK write: () your name, (2) your student ID number, (3) lecture section, (4) your instructor s name, and (5)
ODE Math 3331 (Summer 2014) June 16, 2014
 Page 1 of 12 Please go to the next page... Sample Midterm 1 ODE Math 3331 (Summer 2014) June 16, 2014 50 points 1. Find the solution of the following initial-value problem 1. Solution (S.O.V) dt = ty2,
Page 1 of 12 Please go to the next page... Sample Midterm 1 ODE Math 3331 (Summer 2014) June 16, 2014 50 points 1. Find the solution of the following initial-value problem 1. Solution (S.O.V) dt = ty2,
HOMEWORK # 3 SOLUTIONS
 HOMEWORK # 3 SOLUTIONS TJ HITCHMAN. Exercises from the text.. Chapter 2.4. Problem 32 We are to use variation of parameters to find the general solution to y + 2 x y = 8x. The associated homogeneous equation
HOMEWORK # 3 SOLUTIONS TJ HITCHMAN. Exercises from the text.. Chapter 2.4. Problem 32 We are to use variation of parameters to find the general solution to y + 2 x y = 8x. The associated homogeneous equation
Practice Midterm Solutions
 Practice Midterm Solutions Math 4B: Ordinary Differential Equations Winter 20 University of California, Santa Barbara TA: Victoria Kala DO NOT LOOK AT THESE SOLUTIONS UNTIL YOU HAVE ATTEMPTED EVERY PROBLEM
Practice Midterm Solutions Math 4B: Ordinary Differential Equations Winter 20 University of California, Santa Barbara TA: Victoria Kala DO NOT LOOK AT THESE SOLUTIONS UNTIL YOU HAVE ATTEMPTED EVERY PROBLEM
MATH 251 Examination I October 9, 2014 FORM A. Name: Student Number: Section:
 MATH 251 Examination I October 9, 2014 FORM A Name: Student Number: Section: This exam has 14 questions for a total of 100 points. Show all you your work! In order to obtain full credit for partial credit
MATH 251 Examination I October 9, 2014 FORM A Name: Student Number: Section: This exam has 14 questions for a total of 100 points. Show all you your work! In order to obtain full credit for partial credit
Advanced Eng. Mathematics
 Koya University Faculty of Engineering Petroleum Engineering Department Advanced Eng. Mathematics Lecture 6 Prepared by: Haval Hawez E-mail: haval.hawez@koyauniversity.org 1 Second Order Linear Ordinary
Koya University Faculty of Engineering Petroleum Engineering Department Advanced Eng. Mathematics Lecture 6 Prepared by: Haval Hawez E-mail: haval.hawez@koyauniversity.org 1 Second Order Linear Ordinary
dx n a 1(x) dy
 HIGHER ORDER DIFFERENTIAL EQUATIONS Theory of linear equations Initial-value and boundary-value problem nth-order initial value problem is Solve: a n (x) dn y dx n + a n 1(x) dn 1 y dx n 1 +... + a 1(x)
HIGHER ORDER DIFFERENTIAL EQUATIONS Theory of linear equations Initial-value and boundary-value problem nth-order initial value problem is Solve: a n (x) dn y dx n + a n 1(x) dn 1 y dx n 1 +... + a 1(x)
Math 4B Notes. Written by Victoria Kala SH 6432u Office Hours: T 12:45 1:45pm Last updated 7/24/2016
 Math 4B Notes Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: T 2:45 :45pm Last updated 7/24/206 Classification of Differential Equations The order of a differential equation is the
Math 4B Notes Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: T 2:45 :45pm Last updated 7/24/206 Classification of Differential Equations The order of a differential equation is the
Math 3313: Differential Equations Second-order ordinary differential equations
 Math 3313: Differential Equations Second-order ordinary differential equations Thomas W. Carr Department of Mathematics Southern Methodist University Dallas, TX Outline Mass-spring & Newton s 2nd law Properties
Math 3313: Differential Equations Second-order ordinary differential equations Thomas W. Carr Department of Mathematics Southern Methodist University Dallas, TX Outline Mass-spring & Newton s 2nd law Properties
A BRIEF INTRODUCTION INTO SOLVING DIFFERENTIAL EQUATIONS
 MATTHIAS GERDTS A BRIEF INTRODUCTION INTO SOLVING DIFFERENTIAL EQUATIONS Universität der Bundeswehr München Addresse des Autors: Matthias Gerdts Institut für Mathematik und Rechneranwendung Universität
MATTHIAS GERDTS A BRIEF INTRODUCTION INTO SOLVING DIFFERENTIAL EQUATIONS Universität der Bundeswehr München Addresse des Autors: Matthias Gerdts Institut für Mathematik und Rechneranwendung Universität
dy dy 2 dy d Y 2 dx dx Substituting these into the given differential equation d 2 Y dy 2Y = 2x + 3 ( ) ( 1 + 2b)= 3
 Solutions 14() 1 Coplete solutions to Eerise 14() 1. (a) Sine f()= 18 is a onstant so Y = C, differentiating this zero. Substituting for Y into Y = 18 C = 18, hene C = 9 The partiular integral Y = 9. (This
Solutions 14() 1 Coplete solutions to Eerise 14() 1. (a) Sine f()= 18 is a onstant so Y = C, differentiating this zero. Substituting for Y into Y = 18 C = 18, hene C = 9 The partiular integral Y = 9. (This
Lecture Notes in Mathematics. Arkansas Tech University Department of Mathematics
 Lecture Notes in Mathematics Arkansas Tech University Department of Mathematics Introductory Notes in Ordinary Differential Equations for Physical Sciences and Engineering Marcel B. Finan c All Rights
Lecture Notes in Mathematics Arkansas Tech University Department of Mathematics Introductory Notes in Ordinary Differential Equations for Physical Sciences and Engineering Marcel B. Finan c All Rights
Assignment # 8, Math 370, Fall 2018 SOLUTIONS:
 Assignment # 8, Math 370, Fall 018 SOLUTIONS: Problem 1: Solve the equations (a) y y = 3x + x 4, (i) y(0) = 1, y (0) = 1, y (0) = 1. Characteristic equation: α 3 α = 0 so α 1, = 0 and α 3 =. y c = C 1
Assignment # 8, Math 370, Fall 018 SOLUTIONS: Problem 1: Solve the equations (a) y y = 3x + x 4, (i) y(0) = 1, y (0) = 1, y (0) = 1. Characteristic equation: α 3 α = 0 so α 1, = 0 and α 3 =. y c = C 1
FLAP M6.1 Introducing differential equations COPYRIGHT 1998 THE OPEN UNIVERSITY S570 V1.1
 F1 (a) This equation is of first order and of first degree. It is a linear equation, since the dependent variable y and its derivative only appear raised to the first power, and there are no products of
F1 (a) This equation is of first order and of first degree. It is a linear equation, since the dependent variable y and its derivative only appear raised to the first power, and there are no products of
Ma 221 Final Exam Solutions 5/14/13
 Ma 221 Final Exam Solutions 5/14/13 1. Solve (a) (8 pts) Solution: The equation is separable. dy dx exy y 1 y0 0 y 1e y dy e x dx y 1e y dy e x dx ye y e y dy e x dx ye y e y e y e x c The last step comes
Ma 221 Final Exam Solutions 5/14/13 1. Solve (a) (8 pts) Solution: The equation is separable. dy dx exy y 1 y0 0 y 1e y dy e x dx y 1e y dy e x dx ye y e y dy e x dx ye y e y e y e x c The last step comes
The Method of Undetermined Coefficients.
 The Method of Undetermined Coefficients. James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University May 24, 2017 Outline 1 Annihilators 2 Finding The
The Method of Undetermined Coefficients. James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University May 24, 2017 Outline 1 Annihilators 2 Finding The
Section 2.4 Linear Equations
 Section 2.4 Linear Equations Key Terms: Linear equation Homogeneous linear equation Nonhomogeneous (inhomogeneous) linear equation Integrating factor General solution Variation of parameters A first-order
Section 2.4 Linear Equations Key Terms: Linear equation Homogeneous linear equation Nonhomogeneous (inhomogeneous) linear equation Integrating factor General solution Variation of parameters A first-order
2nd-Order Linear Equations
 4 2nd-Order Linear Equations 4.1 Linear Independence of Functions In linear algebra the notion of linear independence arises frequently in the context of vector spaces. If V is a vector space over the
4 2nd-Order Linear Equations 4.1 Linear Independence of Functions In linear algebra the notion of linear independence arises frequently in the context of vector spaces. If V is a vector space over the
