Approximation of the Fisher information and design in nonlinear mixed effects models
|
|
|
- Jared Roberts
- 5 years ago
- Views:
Transcription
1 of the Fisher information and design in nonlinear mixed effects models Tobias Mielke Optimum for Mixed Effects Non-Linear and Generalized Linear PODE
2 Outline 1 2 3
3 Mixed Effects Similar functions for different individuals Every individual has its own individual parameters Vectors of individual parameters are realizations of random vectors Mixed Effects
4 Mixed Effects Two-stage-model: 1. stage (intra-individual variation): Y ij = η(β i, x ij ) + ɛ ij, j = 1,..., m i, ɛ ij N(0, σ 2 ) 2. stage (inter-individual variation): β i = β + b i, i = 1,..., N, b i N p (0, σ 2 D) b i and ɛ ij are assumed to be independent. Variance parameters σ 2 and D assumed to be known. Aim: Estimation of β.
5 Individual observation vector: Y i = η(β i, ξ i ) + ɛ i, - m i - number of observations, - ξ i = (x i1,..., x imi ) - experimental settings, - η(β i, ξ i ) := (η(β i, x i1 ),..., η(β i, x imi )) T. matrix: F β := ( η(β i, ξ i ) βi T βi =β).
6 Optimal designs for estimating β cov( ˆβ)? For Y i with density f Yi (y i ) and l(β; y i ) := log(f Yi (y i )) : Maximization of the Fisher information M β = E( l(β; Y i) l(β; Y i ) β β T ). Often applied: Linearization.
7 For η nonlinear in β i : Linearization of the model (1): Y i = η(β i, ξ i ) + ɛ i η(β 0, ξ i ) + F β0 (β β 0 ) + F β0 (β i β) + ɛ i, with a guess β 0 of β (or β i ). Distribution assumptions yield: Y i N(η(β 0, ξ i ) + F β0 (β β 0 ), σ 2 V β0 ) with V β0 := I mi + F β0 DF T β 0 Linear mixed effects model.
8 For η nonlinear in β i : Linearization of the model (2): Y i = η(β i, ξ i ) + ɛ i η(β, ξ i ) + F β (β i β) + ɛ i with the true β. Distribution assumptions yield: Y i N(η(β, ξ i ), σ 2 V β ) with V β := I mi + F β DF T β Heteroscedastic nonlinear normal model.
9 Calculation of the Fisher information: Assumption: new model is true. Linear Mixed [Retout et. al (2001)]: M 1,β (ξ) = 1 σ 2 F β T 0 V 1 β 0 F β0 Nonlinear heteroscedastic [Retout et. al (2003)]: where S 0, with M 2,β (ξ) = 1 σ 2 F T β V 1 β F β S, S j,k = Tr [V 1 V β β V 1 V β β β ], j, k = 1,..., p. j β k
10 Example: Observations as Y i = exp(β i ) + ɛ i, β i N(β, d), ɛ i N(0, 1) yield M 1,β = exp(2β) 1 + d exp(2β) and M 2,β = exp(2β) 1 + d exp(2β) + 2d 2 exp(4β) (1 + d exp(2β)) 2.
11 Experiment settings ξ i for individuals: x ij X ξ i = ( x i1... x imi ) X m i. Alternative: Approximate individual designs - not here! Population design ζ: ( ) ξ1... ξ ζ = k, ω 1... ω k k ω j = 1, j=1 ω j : weight of indivdual design ξ j in the population. Population design ˆ= approximate design on X m
12 Individual information: M β (ξ i ) Population information: M β;pop (ζ) = k ω i M β (ξ i ) i=1 Population design ζ D-optimal if and only if: Efficiency: Tr M β;pop (ζ ) 1 M β (ξ) p, ξ X m δ(ζ) := ( ) 1 det(mβ;pop (ζ)) p. det(m β;pop (ζ ))
13 Example [Schmelter 2007]: Y i = η(β i, x i ) exp(ɛ i ), with ɛ i N(0, σ 2 ) η(β i, x i ) := β 1,i β 3,i β 1,i β 2,i [exp( β 2,i β 3,i x i ) exp( β 1,i x i )], β i,k = β k exp(b ik ) with b ik N(0, σ 2 d k ), k = 1, 2, 3,
14 Example: matters M 1,β -: ζ 1 = M 2,β -: ζ 2 = ( ) (0.10) (4.18) (24.00), δ(ζ ) = 0.66 ( ) (3.10) (5.18) (24.00), δ(ζ ) = 0.55
15 Remember: Y i = η(β i, ξ i ) + ɛ i, β i N(β, σ 2 D), ɛ i N(0, σ 2 I mi ) log-likelihood function: l(β; y i ) := log(f Yi (y i )), with f Yi (y i ) := 1 exp[ 1 R p c 1 2σ 2 l(β i, β; y i )]dβ i and l(β i, β; y i ) := (y i η(β i, ξ i )) T (y i η(β i, ξ i )) +(β i β) T D 1 (β i β). We search: M β = E( l(β; Y i) l(β; Y i ) β β T ).
16 Alternative representation: With E yi (β i ) := E(β i Y i = y i ): l(β; y i ) β = 1 σ 2 D 1 (E yi (β i ) β). For Var yi (β i ) = Var(β i Y i = y i ) follows: M β = 1 σ 2 D 1 Var(E Yi (β i ))D 1 1 σ 2 = 1 σ 2 D 1 1 σ 2 D 1 E(Var Yi (β i ))D 1 1 σ 2 of conditional moments.
17 Remark More general inter-individual model: Differentiable function g : R p 1 R p : β i = g(β) + b i, with β R p 1, b i N p (0, σ 2 D) With the (p p 1 )-Jacobi-matrix G(β) follows: M β = G(β) T 1 σ 2 D 1 Var(E Yi (β i ))D 1 1 σ 2 G(β) = G(β) T ( 1 σ 2 D 1 1 σ 2 D 1 E(Var Yi (β i ))D 1 1 σ 2 )G(β)T
18 of conditional moments: Quadrature rules Simulations dependence on experimental settings? computational intensive. Laplace approximation accuracy?
19 Laplace approximation: Problem in nonlinear mixed models: E(E Yi (β i )E Yi (β i ) T ) of E yi (β i ) given y i : E yi (β i ) = βi exp( l(β i,β;y i ) )dβ 2σ 2 i, with exp( l(β i,β;y i ) )dβ 2σ 2 i l(β i, β; y i ) := (y i η(β i, ξ i )) T (y i η(β i, ξ i )) +(β i β) T D 1 (β i β). Laplace approximation of both integrals. [Tierney and Kadane (1986)]
20 Laplace approximation: Idea: of f Yi (y i ) = where l(β i, β; y i ) is minimial. 1 i, β; y i ) exp( l(β c 1 2σ 2 )dβ i Second order Taylor expansion around β i with β i := argmin β i R p { l(β i, β; y i )} Linear part vanishes normal density. f Yi (y i ) 1 exp( l(β i, β; y i) c 2 (y i, β) 2σ 2 ). Dependence of β i on y i.
21 For approximating f βi Y i =y i = φ Y i β i (y i )φ βi (β i ) f Yi (y i ) Apply similar approximation to the numerator β i Yi =y i app. N(βi, σ2 M 1 βi ), with M β i := l(β i, β; y i ) β i βi T βi =βi. Problems: Dependence of β i Dependence of M 1 β i on y i on y i
22 Alternative: Just approximation of η(β i, ξ i ): η(β i, ξ i ) η( ˆβ i, ξ i ) + F ˆβi (β i ˆβ i ). in l(β i, β; y i ) with some ˆβ i R p. Same approximation to numerator yields β i Yi =y i app. N(µ(y i, ˆβ i, β), σ 2 M 1 ), with ˆβ i M ˆβ i := F Ṱ β i F ˆβ i + D 1 µ(y i, ˆβ i, β) := M 1 (F Ṱ (y ˆβ i β i η( ˆβ i, ξ i )) + F i ˆβi ˆβ i ) + D 1 β). Appropriate choice of ˆβ i?
23 For ˆβ i = β i minimizing l(β i, β; y i ): β i Yi =y i app. N(βi, σ2 M 1 ). Problem: Dependence on y i. For ˆβ i = β: β i β i Yi =y i app. N(β + M 1 β F β T (y i η(β, ξ i )), σ 2 M 1 β ). For ˆβ i = β i : β i Yi =y i app. N(µ(y i, β i, β), σ 2 M 1 β i ).
24 Fisher information approximations in ˆβ i = β: With V β := I mi + F β DFβ T : Conditional variance: M β = 1 σ 2 D 1 1 σ 2 D 1 E(Var Yi (β i ))D 1 1 σ 2 1 σ 2 F T β V 1 β F β =: M 1,β Conditional expectation: M β = 1 σ 2 D 1 Var(E Yi (β i ))D 1 1 σ 2 1 σ 4 F β T V 1 β Var(Y i)v 1 β F β =: M 3,β.
25 Fisher information approximation in ˆβ i = β i : With V βi := I mi + F βi DF T β i : Conditional variance: M 4,βi := 1 σ 2 F T β i V 1 β i F βi. consider here M 4,β := 1 σ 2 E(F T β i V 1 β i F βi ). Some other possible approximations: Nonlinear heteroscedastic normal model: Quasi-: M 2,β := 1 σ 2 F T β V 1 β F β S. M 5,β := F T β,ql Var(Y i) 1 F β,ql
26 Summary: With V βi := I mi + F βi DF T β i : M 1,β := 1 σ 2 F β T V 1 β F β M 2,β := 1 σ 2 F β T V 1 β F β S M 3,β := 1 σ 4 F T β V 1 β Var(Y i)v 1 M 4,β := 1 σ 2 E(F T β i V 1 β i F βi ) β F β M 5,β := F T β,ql Var(Y i) 1 F β,ql
27 : Log-Concentration: Y i = β 2i x i exp(β 1i β 2i ) + ɛ i, i = 1,..., N - ɛ i N(0, σ 2 ), ξ i = (x i ) [t min, t max ], - β i = (β 1i, β 2i ) T N(β, σ 2 D), - β = (β 1, β 2 ) T, D = diag(d 1, d 2 ).
28 - M 1,β : Red - M 2,β : Blue - M 3,β : Yellow - M 5,β : Green
29 matrices M 1,β (β) or M 5,β (β): For every pair of experimental settings x 1, x 2 [t min, t max ] with α(x 1, x 2 ) := σ 2 + cov(y (x 1 ), Y (x 2 )) = 0, the population design ζ 1 = ( (x1 ) ) (x 2 ) is D-optimal in the case of one allowed observation per individual.
30 How to see this: Equivalence theorem for D-optimality: ζ optimal g ζ (ξ) := Tr M β;pop (ζ ) 1 M β (ξ) p, ξ X m ( ) a b With general nonsingular M(ζ) = and ξ = x: b c ( ) c b g ζ (x) := F β (x) F b a β (ξ) T 2(ac b 2 )V β (x) 0 2 support points, weight: ω = 0.5. For ζ = ( (x1 ) ) (x 2 ) g ζ (x) = α(x 1,x 2 ) V (x 1 )V (x 2 ) (x x 2)(x x 1 ).
31 M 1,β -: ζ 1 = M 2,β -: ζ 2 = M 3,β -: ζ 3 = M 5,β -: ζ 5 = ( ) (1.13) (11.98), δ (ζ 1 ) = ( ) (0.96) ( 6.00), δ (ζ 2 ) = ( ) (1.70) (24.00), δ (ζ 3 ) = ( ) (0.93) (11.99), δ (ζ 5 ) =
32 Example: Observations as Y i = exp(β i ) + ɛ i, β i N(β, d), ɛ i N(0, 1) yield M 1,β = exp(2β) 1 + d exp(2β), M 2,β = M 3,β = M 5,β = exp(2β) 1 + d exp(2β) + 2d 2 exp(4β) (1 + d exp(2β)) 2, exp(2β)(exp(2β + d)(exp(d) 1) + 1) (1 + d exp(2β)) 2 and exp(2β + d) exp(2β + d)(exp(d) 1) + 1.
33 Y i = exp(β i ) + ɛ i ; β i N( 2, d = ρ 1 ρ ); ɛ i N(0, 1) Red: Simulated Fisher information; Blue: M 4,β M 1,β : solid, M 2,β : dashed, M 3,β : dot-dash, M 5,β : dotted
34 Y i = exp(β i ) + ɛ i ; β i N( 1, d = ρ 1 ρ ); ɛ i N(0, 1) Red: Simulated Fisher information; Blue: M 4,β M 1,β : solid, M 2,β : dashed, M 3,β : dot-dash, M 5,β : dotted
35 Y i = exp(β i ) + ɛ i ; β i N(0, d = ρ 1 ρ ); ɛ i N(0, 1) Red: Simulated Fisher information; Blue: M 4,β M 1,β : solid, M 2,β : dashed, M 3,β : dot-dash, M 5,β : dotted
36 Y i = exp(β i ) + ɛ i ; β i N(1, d = ρ 1 ρ ); ɛ i N(0, 1) Red: Simulated Fisher information; Blue: M 4,β M 1,β : solid, M 2,β : dashed, M 3,β : dot-dash, M 5,β : dotted
37 Y i = exp(β i ) + ɛ i ; β i N(2, d = ρ 1 ρ ); ɛ i N(0, 1) Red: Simulated Fisher information; Blue: M 4,β M 1,β : solid, M 2,β : dashed, M 3,β : dot-dash, M 5,β : dotted
38 Remember: Var(β i ) = E(Var Yi (β i )) + Var(E Yi (β i )) M β = 1 σ 2 D 1 Var(E Yi (β i ))D 1 1 σ 2 = 1 σ 2 D 1 1 σ 2 D 1 E(Var Yi (β i ))D 1 1 σ 2 Some explanation: d M β 0. d 0 Nonlinear regression M β 1 σ 2 F T β F β
39 Conclusions/Outlook Conclusions: - Motivation of model approximation - Different information different design - Big influence of inter-individual variance on the accuracy of approximations Outlook: - More insight needed on: - appropriateness of the approximations - approximation in β i or β i - Inclusion of variance parameters.
40 Thank you for your attention! Further informations needed (M 6,β,...)?
Machine Learning. Bayesian Regression & Classification. Marc Toussaint U Stuttgart
 Machine Learning Bayesian Regression & Classification learning as inference, Bayesian Kernel Ridge regression & Gaussian Processes, Bayesian Kernel Logistic Regression & GP classification, Bayesian Neural
Machine Learning Bayesian Regression & Classification learning as inference, Bayesian Kernel Ridge regression & Gaussian Processes, Bayesian Kernel Logistic Regression & GP classification, Bayesian Neural
STAT5044: Regression and Anova
 STAT5044: Regression and Anova Inyoung Kim 1 / 15 Outline 1 Fitting GLMs 2 / 15 Fitting GLMS We study how to find the maxlimum likelihood estimator ˆβ of GLM parameters The likelihood equaions are usually
STAT5044: Regression and Anova Inyoung Kim 1 / 15 Outline 1 Fitting GLMs 2 / 15 Fitting GLMS We study how to find the maxlimum likelihood estimator ˆβ of GLM parameters The likelihood equaions are usually
The consequences of misspecifying the random effects distribution when fitting generalized linear mixed models
 The consequences of misspecifying the random effects distribution when fitting generalized linear mixed models John M. Neuhaus Charles E. McCulloch Division of Biostatistics University of California, San
The consequences of misspecifying the random effects distribution when fitting generalized linear mixed models John M. Neuhaus Charles E. McCulloch Division of Biostatistics University of California, San
1/15. Over or under dispersion Problem
 1/15 Over or under dispersion Problem 2/15 Example 1: dogs and owners data set In the dogs and owners example, we had some concerns about the dependence among the measurements from each individual. Let
1/15 Over or under dispersion Problem 2/15 Example 1: dogs and owners data set In the dogs and owners example, we had some concerns about the dependence among the measurements from each individual. Let
Linear Methods for Prediction
 Chapter 5 Linear Methods for Prediction 5.1 Introduction We now revisit the classification problem and focus on linear methods. Since our prediction Ĝ(x) will always take values in the discrete set G we
Chapter 5 Linear Methods for Prediction 5.1 Introduction We now revisit the classification problem and focus on linear methods. Since our prediction Ĝ(x) will always take values in the discrete set G we
Modeling the scale parameter ϕ A note on modeling correlation of binary responses Using marginal odds ratios to model association for binary responses
 Outline Marginal model Examples of marginal model GEE1 Augmented GEE GEE1.5 GEE2 Modeling the scale parameter ϕ A note on modeling correlation of binary responses Using marginal odds ratios to model association
Outline Marginal model Examples of marginal model GEE1 Augmented GEE GEE1.5 GEE2 Modeling the scale parameter ϕ A note on modeling correlation of binary responses Using marginal odds ratios to model association
Chapter 1: Linear Regression with One Predictor Variable also known as: Simple Linear Regression Bivariate Linear Regression
 BSTT523: Kutner et al., Chapter 1 1 Chapter 1: Linear Regression with One Predictor Variable also known as: Simple Linear Regression Bivariate Linear Regression Introduction: Functional relation between
BSTT523: Kutner et al., Chapter 1 1 Chapter 1: Linear Regression with One Predictor Variable also known as: Simple Linear Regression Bivariate Linear Regression Introduction: Functional relation between
ML estimation: Random-intercepts logistic model. and z
 ML estimation: Random-intercepts logistic model log p ij 1 p = x ijβ + υ i with υ i N(0, συ) 2 ij Standardizing the random effect, θ i = υ i /σ υ, yields log p ij 1 p = x ij β + σ υθ i with θ i N(0, 1)
ML estimation: Random-intercepts logistic model log p ij 1 p = x ijβ + υ i with υ i N(0, συ) 2 ij Standardizing the random effect, θ i = υ i /σ υ, yields log p ij 1 p = x ij β + σ υθ i with θ i N(0, 1)
Lecture 13: Simple Linear Regression in Matrix Format. 1 Expectations and Variances with Vectors and Matrices
 Lecture 3: Simple Linear Regression in Matrix Format To move beyond simple regression we need to use matrix algebra We ll start by re-expressing simple linear regression in matrix form Linear algebra is
Lecture 3: Simple Linear Regression in Matrix Format To move beyond simple regression we need to use matrix algebra We ll start by re-expressing simple linear regression in matrix form Linear algebra is
Optimization. The value x is called a maximizer of f and is written argmax X f. g(λx + (1 λ)y) < λg(x) + (1 λ)g(y) 0 < λ < 1; x, y X.
 Optimization Background: Problem: given a function f(x) defined on X, find x such that f(x ) f(x) for all x X. The value x is called a maximizer of f and is written argmax X f. In general, argmax X f may
Optimization Background: Problem: given a function f(x) defined on X, find x such that f(x ) f(x) for all x X. The value x is called a maximizer of f and is written argmax X f. In general, argmax X f may
Lecture 6: Discrete Choice: Qualitative Response
 Lecture 6: Instructor: Department of Economics Stanford University 2011 Types of Discrete Choice Models Univariate Models Binary: Linear; Probit; Logit; Arctan, etc. Multinomial: Logit; Nested Logit; GEV;
Lecture 6: Instructor: Department of Economics Stanford University 2011 Types of Discrete Choice Models Univariate Models Binary: Linear; Probit; Logit; Arctan, etc. Multinomial: Logit; Nested Logit; GEV;
Regression Estimation - Least Squares and Maximum Likelihood. Dr. Frank Wood
 Regression Estimation - Least Squares and Maximum Likelihood Dr. Frank Wood Least Squares Max(min)imization Function to minimize w.r.t. β 0, β 1 Q = n (Y i (β 0 + β 1 X i )) 2 i=1 Minimize this by maximizing
Regression Estimation - Least Squares and Maximum Likelihood Dr. Frank Wood Least Squares Max(min)imization Function to minimize w.r.t. β 0, β 1 Q = n (Y i (β 0 + β 1 X i )) 2 i=1 Minimize this by maximizing
Modeling Real Estate Data using Quantile Regression
 Modeling Real Estate Data using Semiparametric Quantile Regression Department of Statistics University of Innsbruck September 9th, 2011 Overview 1 Application: 2 3 4 Hedonic regression data for house prices
Modeling Real Estate Data using Semiparametric Quantile Regression Department of Statistics University of Innsbruck September 9th, 2011 Overview 1 Application: 2 3 4 Hedonic regression data for house prices
Generalized linear models
 Generalized linear models Søren Højsgaard Department of Mathematical Sciences Aalborg University, Denmark October 29, 202 Contents Densities for generalized linear models. Mean and variance...............................
Generalized linear models Søren Højsgaard Department of Mathematical Sciences Aalborg University, Denmark October 29, 202 Contents Densities for generalized linear models. Mean and variance...............................
Previous lecture. Single variant association. Use genome-wide SNPs to account for confounding (population substructure)
 Previous lecture Single variant association Use genome-wide SNPs to account for confounding (population substructure) Estimation of effect size and winner s curse Meta-Analysis Today s outline P-value
Previous lecture Single variant association Use genome-wide SNPs to account for confounding (population substructure) Estimation of effect size and winner s curse Meta-Analysis Today s outline P-value
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017
 Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
A Resampling Method on Pivotal Estimating Functions
 A Resampling Method on Pivotal Estimating Functions Kun Nie Biostat 277,Winter 2004 March 17, 2004 Outline Introduction A General Resampling Method Examples - Quantile Regression -Rank Regression -Simulation
A Resampling Method on Pivotal Estimating Functions Kun Nie Biostat 277,Winter 2004 March 17, 2004 Outline Introduction A General Resampling Method Examples - Quantile Regression -Rank Regression -Simulation
1 One-way analysis of variance
 LIST OF FORMULAS (Version from 21. November 2014) STK2120 1 One-way analysis of variance Assume X ij = µ+α i +ɛ ij ; j = 1, 2,..., J i ; i = 1, 2,..., I ; where ɛ ij -s are independent and N(0, σ 2 ) distributed.
LIST OF FORMULAS (Version from 21. November 2014) STK2120 1 One-way analysis of variance Assume X ij = µ+α i +ɛ ij ; j = 1, 2,..., J i ; i = 1, 2,..., I ; where ɛ ij -s are independent and N(0, σ 2 ) distributed.
Using Estimating Equations for Spatially Correlated A
 Using Estimating Equations for Spatially Correlated Areal Data December 8, 2009 Introduction GEEs Spatial Estimating Equations Implementation Simulation Conclusion Typical Problem Assess the relationship
Using Estimating Equations for Spatially Correlated Areal Data December 8, 2009 Introduction GEEs Spatial Estimating Equations Implementation Simulation Conclusion Typical Problem Assess the relationship
The quantum mechanics approach to uncertainty modeling in structural dynamics
 p. 1/3 The quantum mechanics approach to uncertainty modeling in structural dynamics Andreas Kyprianou Department of Mechanical and Manufacturing Engineering, University of Cyprus Outline Introduction
p. 1/3 The quantum mechanics approach to uncertainty modeling in structural dynamics Andreas Kyprianou Department of Mechanical and Manufacturing Engineering, University of Cyprus Outline Introduction
Statistical Methods for Handling Incomplete Data Chapter 2: Likelihood-based approach
 Statistical Methods for Handling Incomplete Data Chapter 2: Likelihood-based approach Jae-Kwang Kim Department of Statistics, Iowa State University Outline 1 Introduction 2 Observed likelihood 3 Mean Score
Statistical Methods for Handling Incomplete Data Chapter 2: Likelihood-based approach Jae-Kwang Kim Department of Statistics, Iowa State University Outline 1 Introduction 2 Observed likelihood 3 Mean Score
The outline for Unit 3
 The outline for Unit 3 Unit 1. Introduction: The regression model. Unit 2. Estimation principles. Unit 3: Hypothesis testing principles. 3.1 Wald test. 3.2 Lagrange Multiplier. 3.3 Likelihood Ratio Test.
The outline for Unit 3 Unit 1. Introduction: The regression model. Unit 2. Estimation principles. Unit 3: Hypothesis testing principles. 3.1 Wald test. 3.2 Lagrange Multiplier. 3.3 Likelihood Ratio Test.
Regression diagnostics
 Regression diagnostics Kerby Shedden Department of Statistics, University of Michigan November 5, 018 1 / 6 Motivation When working with a linear model with design matrix X, the conventional linear model
Regression diagnostics Kerby Shedden Department of Statistics, University of Michigan November 5, 018 1 / 6 Motivation When working with a linear model with design matrix X, the conventional linear model
11. Regression and Least Squares
 11. Regression and Least Squares Prof. Tesler Math 186 Winter 2016 Prof. Tesler Ch. 11: Linear Regression Math 186 / Winter 2016 1 / 23 Regression Given n points ( 1, 1 ), ( 2, 2 ),..., we want to determine
11. Regression and Least Squares Prof. Tesler Math 186 Winter 2016 Prof. Tesler Ch. 11: Linear Regression Math 186 / Winter 2016 1 / 23 Regression Given n points ( 1, 1 ), ( 2, 2 ),..., we want to determine
Calibrating Environmental Engineering Models and Uncertainty Analysis
 Models and Cornell University Oct 14, 2008 Project Team Christine Shoemaker, co-pi, Professor of Civil and works in applied optimization, co-pi Nikolai Blizniouk, PhD student in Operations Research now
Models and Cornell University Oct 14, 2008 Project Team Christine Shoemaker, co-pi, Professor of Civil and works in applied optimization, co-pi Nikolai Blizniouk, PhD student in Operations Research now
Ph.D. Qualifying Exam Friday Saturday, January 3 4, 2014
 Ph.D. Qualifying Exam Friday Saturday, January 3 4, 2014 Put your solution to each problem on a separate sheet of paper. Problem 1. (5166) Assume that two random samples {x i } and {y i } are independently
Ph.D. Qualifying Exam Friday Saturday, January 3 4, 2014 Put your solution to each problem on a separate sheet of paper. Problem 1. (5166) Assume that two random samples {x i } and {y i } are independently
REGRESSION WITH SPATIALLY MISALIGNED DATA. Lisa Madsen Oregon State University David Ruppert Cornell University
 REGRESSION ITH SPATIALL MISALIGNED DATA Lisa Madsen Oregon State University David Ruppert Cornell University SPATIALL MISALIGNED DATA 10 X X X X X X X X 5 X X X X X 0 X 0 5 10 OUTLINE 1. Introduction 2.
REGRESSION ITH SPATIALL MISALIGNED DATA Lisa Madsen Oregon State University David Ruppert Cornell University SPATIALL MISALIGNED DATA 10 X X X X X X X X 5 X X X X X 0 X 0 5 10 OUTLINE 1. Introduction 2.
STAT 100C: Linear models
 STAT 100C: Linear models Arash A. Amini June 9, 2018 1 / 56 Table of Contents Multiple linear regression Linear model setup Estimation of β Geometric interpretation Estimation of σ 2 Hat matrix Gram matrix
STAT 100C: Linear models Arash A. Amini June 9, 2018 1 / 56 Table of Contents Multiple linear regression Linear model setup Estimation of β Geometric interpretation Estimation of σ 2 Hat matrix Gram matrix
Logistic regression. 11 Nov Logistic regression (EPFL) Applied Statistics 11 Nov / 20
 Logistic regression 11 Nov 2010 Logistic regression (EPFL) Applied Statistics 11 Nov 2010 1 / 20 Modeling overview Want to capture important features of the relationship between a (set of) variable(s)
Logistic regression 11 Nov 2010 Logistic regression (EPFL) Applied Statistics 11 Nov 2010 1 / 20 Modeling overview Want to capture important features of the relationship between a (set of) variable(s)
Linear Methods for Prediction
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
SVMs: Non-Separable Data, Convex Surrogate Loss, Multi-Class Classification, Kernels
 SVMs: Non-Separable Data, Convex Surrogate Loss, Multi-Class Classification, Kernels Karl Stratos June 21, 2018 1 / 33 Tangent: Some Loose Ends in Logistic Regression Polynomial feature expansion in logistic
SVMs: Non-Separable Data, Convex Surrogate Loss, Multi-Class Classification, Kernels Karl Stratos June 21, 2018 1 / 33 Tangent: Some Loose Ends in Logistic Regression Polynomial feature expansion in logistic
Lecture 34: Properties of the LSE
 Lecture 34: Properties of the LSE The following results explain why the LSE is popular. Gauss-Markov Theorem Assume a general linear model previously described: Y = Xβ + E with assumption A2, i.e., Var(E
Lecture 34: Properties of the LSE The following results explain why the LSE is popular. Gauss-Markov Theorem Assume a general linear model previously described: Y = Xβ + E with assumption A2, i.e., Var(E
Nonresponse weighting adjustment using estimated response probability
 Nonresponse weighting adjustment using estimated response probability Jae-kwang Kim Yonsei University, Seoul, Korea December 26, 2006 Introduction Nonresponse Unit nonresponse Item nonresponse Basic strategy
Nonresponse weighting adjustment using estimated response probability Jae-kwang Kim Yonsei University, Seoul, Korea December 26, 2006 Introduction Nonresponse Unit nonresponse Item nonresponse Basic strategy
MIT Spring 2015
 Regression Analysis MIT 18.472 Dr. Kempthorne Spring 2015 1 Outline Regression Analysis 1 Regression Analysis 2 Multiple Linear Regression: Setup Data Set n cases i = 1, 2,..., n 1 Response (dependent)
Regression Analysis MIT 18.472 Dr. Kempthorne Spring 2015 1 Outline Regression Analysis 1 Regression Analysis 2 Multiple Linear Regression: Setup Data Set n cases i = 1, 2,..., n 1 Response (dependent)
Estimation and Model Selection in Mixed Effects Models Part I. Adeline Samson 1
 Estimation and Model Selection in Mixed Effects Models Part I Adeline Samson 1 1 University Paris Descartes Summer school 2009 - Lipari, Italy These slides are based on Marc Lavielle s slides Outline 1
Estimation and Model Selection in Mixed Effects Models Part I Adeline Samson 1 1 University Paris Descartes Summer school 2009 - Lipari, Italy These slides are based on Marc Lavielle s slides Outline 1
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
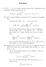 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Maximum Likelihood Estimation
 Maximum Likelihood Estimation Merlise Clyde STA721 Linear Models Duke University August 31, 2017 Outline Topics Likelihood Function Projections Maximum Likelihood Estimates Readings: Christensen Chapter
Maximum Likelihood Estimation Merlise Clyde STA721 Linear Models Duke University August 31, 2017 Outline Topics Likelihood Function Projections Maximum Likelihood Estimates Readings: Christensen Chapter
Linear models and their mathematical foundations: Simple linear regression
 Linear models and their mathematical foundations: Simple linear regression Steffen Unkel Department of Medical Statistics University Medical Center Göttingen, Germany Winter term 2018/19 1/21 Introduction
Linear models and their mathematical foundations: Simple linear regression Steffen Unkel Department of Medical Statistics University Medical Center Göttingen, Germany Winter term 2018/19 1/21 Introduction
Generalized Linear Models. Kurt Hornik
 Generalized Linear Models Kurt Hornik Motivation Assuming normality, the linear model y = Xβ + e has y = β + ε, ε N(0, σ 2 ) such that y N(μ, σ 2 ), E(y ) = μ = β. Various generalizations, including general
Generalized Linear Models Kurt Hornik Motivation Assuming normality, the linear model y = Xβ + e has y = β + ε, ε N(0, σ 2 ) such that y N(μ, σ 2 ), E(y ) = μ = β. Various generalizations, including general
Gauge Plots. Gauge Plots JAPANESE BEETLE DATA MAXIMUM LIKELIHOOD FOR SPATIALLY CORRELATED DISCRETE DATA JAPANESE BEETLE DATA
 JAPANESE BEETLE DATA 6 MAXIMUM LIKELIHOOD FOR SPATIALLY CORRELATED DISCRETE DATA Gauge Plots TuscaroraLisa Central Madsen Fairways, 996 January 9, 7 Grubs Adult Activity Grub Counts 6 8 Organic Matter
JAPANESE BEETLE DATA 6 MAXIMUM LIKELIHOOD FOR SPATIALLY CORRELATED DISCRETE DATA Gauge Plots TuscaroraLisa Central Madsen Fairways, 996 January 9, 7 Grubs Adult Activity Grub Counts 6 8 Organic Matter
Methods of Estimation
 Methods of Estimation MIT 18.655 Dr. Kempthorne Spring 2016 1 Outline Methods of Estimation I 1 Methods of Estimation I 2 X X, X P P = {P θ, θ Θ}. Problem: Finding a function θˆ(x ) which is close to θ.
Methods of Estimation MIT 18.655 Dr. Kempthorne Spring 2016 1 Outline Methods of Estimation I 1 Methods of Estimation I 2 X X, X P P = {P θ, θ Θ}. Problem: Finding a function θˆ(x ) which is close to θ.
Summer School in Statistics for Astronomers V June 1 - June 6, Regression. Mosuk Chow Statistics Department Penn State University.
 Summer School in Statistics for Astronomers V June 1 - June 6, 2009 Regression Mosuk Chow Statistics Department Penn State University. Adapted from notes prepared by RL Karandikar Mean and variance Recall
Summer School in Statistics for Astronomers V June 1 - June 6, 2009 Regression Mosuk Chow Statistics Department Penn State University. Adapted from notes prepared by RL Karandikar Mean and variance Recall
Parameter Estimation
 Parameter Estimation Consider a sample of observations on a random variable Y. his generates random variables: (y 1, y 2,, y ). A random sample is a sample (y 1, y 2,, y ) where the random variables y
Parameter Estimation Consider a sample of observations on a random variable Y. his generates random variables: (y 1, y 2,, y ). A random sample is a sample (y 1, y 2,, y ) where the random variables y
The regression model with one stochastic regressor (part II)
 The regression model with one stochastic regressor (part II) 3150/4150 Lecture 7 Ragnar Nymoen 6 Feb 2012 We will finish Lecture topic 4: The regression model with stochastic regressor We will first look
The regression model with one stochastic regressor (part II) 3150/4150 Lecture 7 Ragnar Nymoen 6 Feb 2012 We will finish Lecture topic 4: The regression model with stochastic regressor We will first look
STAT 420: Methods of Applied Statistics
 STAT 420: Methods of Applied Statistics Model Diagnostics Transformation Shiwei Lan, Ph.D. Course website: http://shiwei.stat.illinois.edu/lectures/stat420.html August 15, 2018 Department
STAT 420: Methods of Applied Statistics Model Diagnostics Transformation Shiwei Lan, Ph.D. Course website: http://shiwei.stat.illinois.edu/lectures/stat420.html August 15, 2018 Department
GLS and FGLS. Econ 671. Purdue University. Justin L. Tobias (Purdue) GLS and FGLS 1 / 22
 GLS and FGLS Econ 671 Purdue University Justin L. Tobias (Purdue) GLS and FGLS 1 / 22 In this lecture we continue to discuss properties associated with the GLS estimator. In addition we discuss the practical
GLS and FGLS Econ 671 Purdue University Justin L. Tobias (Purdue) GLS and FGLS 1 / 22 In this lecture we continue to discuss properties associated with the GLS estimator. In addition we discuss the practical
Paper Review: Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties by Jianqing Fan and Runze Li (2001)
 Paper Review: Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties by Jianqing Fan and Runze Li (2001) Presented by Yang Zhao March 5, 2010 1 / 36 Outlines 2 / 36 Motivation
Paper Review: Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties by Jianqing Fan and Runze Li (2001) Presented by Yang Zhao March 5, 2010 1 / 36 Outlines 2 / 36 Motivation
P n. This is called the law of large numbers but it comes in two forms: Strong and Weak.
 Large Sample Theory Large Sample Theory is a name given to the search for approximations to the behaviour of statistical procedures which are derived by computing limits as the sample size, n, tends to
Large Sample Theory Large Sample Theory is a name given to the search for approximations to the behaviour of statistical procedures which are derived by computing limits as the sample size, n, tends to
MAT2377. Rafa l Kulik. Version 2015/November/26. Rafa l Kulik
 MAT2377 Rafa l Kulik Version 2015/November/26 Rafa l Kulik Bivariate data and scatterplot Data: Hydrocarbon level (x) and Oxygen level (y): x: 0.99, 1.02, 1.15, 1.29, 1.46, 1.36, 0.87, 1.23, 1.55, 1.40,
MAT2377 Rafa l Kulik Version 2015/November/26 Rafa l Kulik Bivariate data and scatterplot Data: Hydrocarbon level (x) and Oxygen level (y): x: 0.99, 1.02, 1.15, 1.29, 1.46, 1.36, 0.87, 1.23, 1.55, 1.40,
REPEATED MEASURES. Copyright c 2012 (Iowa State University) Statistics / 29
 REPEATED MEASURES Copyright c 2012 (Iowa State University) Statistics 511 1 / 29 Repeated Measures Example In an exercise therapy study, subjects were assigned to one of three weightlifting programs i=1:
REPEATED MEASURES Copyright c 2012 (Iowa State University) Statistics 511 1 / 29 Repeated Measures Example In an exercise therapy study, subjects were assigned to one of three weightlifting programs i=1:
Fractional Imputation in Survey Sampling: A Comparative Review
 Fractional Imputation in Survey Sampling: A Comparative Review Shu Yang Jae-Kwang Kim Iowa State University Joint Statistical Meetings, August 2015 Outline Introduction Fractional imputation Features Numerical
Fractional Imputation in Survey Sampling: A Comparative Review Shu Yang Jae-Kwang Kim Iowa State University Joint Statistical Meetings, August 2015 Outline Introduction Fractional imputation Features Numerical
Model Specification Testing in Nonparametric and Semiparametric Time Series Econometrics. Jiti Gao
 Model Specification Testing in Nonparametric and Semiparametric Time Series Econometrics Jiti Gao Department of Statistics School of Mathematics and Statistics The University of Western Australia Crawley
Model Specification Testing in Nonparametric and Semiparametric Time Series Econometrics Jiti Gao Department of Statistics School of Mathematics and Statistics The University of Western Australia Crawley
Hypothesis Testing Based on the Maximum of Two Statistics from Weighted and Unweighted Estimating Equations
 Hypothesis Testing Based on the Maximum of Two Statistics from Weighted and Unweighted Estimating Equations Takeshi Emura and Hisayuki Tsukuma Abstract For testing the regression parameter in multivariate
Hypothesis Testing Based on the Maximum of Two Statistics from Weighted and Unweighted Estimating Equations Takeshi Emura and Hisayuki Tsukuma Abstract For testing the regression parameter in multivariate
3 Multiple Linear Regression
 3 Multiple Linear Regression 3.1 The Model Essentially, all models are wrong, but some are useful. Quote by George E.P. Box. Models are supposed to be exact descriptions of the population, but that is
3 Multiple Linear Regression 3.1 The Model Essentially, all models are wrong, but some are useful. Quote by George E.P. Box. Models are supposed to be exact descriptions of the population, but that is
Approximate Likelihoods
 Approximate Likelihoods Nancy Reid July 28, 2015 Why likelihood? makes probability modelling central l(θ; y) = log f (y; θ) emphasizes the inverse problem of reasoning y θ converts a prior probability
Approximate Likelihoods Nancy Reid July 28, 2015 Why likelihood? makes probability modelling central l(θ; y) = log f (y; θ) emphasizes the inverse problem of reasoning y θ converts a prior probability
DESIGN EVALUATION AND OPTIMISATION IN CROSSOVER PHARMACOKINETIC STUDIES ANALYSED BY NONLINEAR MIXED EFFECTS MODELS
 DESIGN EVALUATION AND OPTIMISATION IN CROSSOVER PHARMACOKINETIC STUDIES ANALYSED BY NONLINEAR MIXED EFFECTS MODELS Thu Thuy Nguyen, Caroline Bazzoli, France Mentré UMR 738 INSERM - University Paris Diderot,
DESIGN EVALUATION AND OPTIMISATION IN CROSSOVER PHARMACOKINETIC STUDIES ANALYSED BY NONLINEAR MIXED EFFECTS MODELS Thu Thuy Nguyen, Caroline Bazzoli, France Mentré UMR 738 INSERM - University Paris Diderot,
5.1 Model Specification and Data 5.2 Estimating the Parameters of the Multiple Regression Model 5.3 Sampling Properties of the Least Squares
 5.1 Model Specification and Data 5. Estimating the Parameters of the Multiple Regression Model 5.3 Sampling Properties of the Least Squares Estimator 5.4 Interval Estimation 5.5 Hypothesis Testing for
5.1 Model Specification and Data 5. Estimating the Parameters of the Multiple Regression Model 5.3 Sampling Properties of the Least Squares Estimator 5.4 Interval Estimation 5.5 Hypothesis Testing for
Outline of GLMs. Definitions
 Outline of GLMs Definitions This is a short outline of GLM details, adapted from the book Nonparametric Regression and Generalized Linear Models, by Green and Silverman. The responses Y i have density
Outline of GLMs Definitions This is a short outline of GLM details, adapted from the book Nonparametric Regression and Generalized Linear Models, by Green and Silverman. The responses Y i have density
STATS306B STATS306B. Discriminant Analysis. Jonathan Taylor Department of Statistics Stanford University. June 3, 2010
 STATS306B Discriminant Analysis Jonathan Taylor Department of Statistics Stanford University June 3, 2010 Spring 2010 Classification Given K classes in R p, represented as densities f i (x), 1 i K classify
STATS306B Discriminant Analysis Jonathan Taylor Department of Statistics Stanford University June 3, 2010 Spring 2010 Classification Given K classes in R p, represented as densities f i (x), 1 i K classify
Matrix Approach to Simple Linear Regression: An Overview
 Matrix Approach to Simple Linear Regression: An Overview Aspects of matrices that you should know: Definition of a matrix Addition/subtraction/multiplication of matrices Symmetric/diagonal/identity matrix
Matrix Approach to Simple Linear Regression: An Overview Aspects of matrices that you should know: Definition of a matrix Addition/subtraction/multiplication of matrices Symmetric/diagonal/identity matrix
Lecture 9: Quantile Methods 2
 Lecture 9: Quantile Methods 2 1. Equivariance. 2. GMM for Quantiles. 3. Endogenous Models 4. Empirical Examples 1 1. Equivariance to Monotone Transformations. Theorem (Equivariance of Quantiles under Monotone
Lecture 9: Quantile Methods 2 1. Equivariance. 2. GMM for Quantiles. 3. Endogenous Models 4. Empirical Examples 1 1. Equivariance to Monotone Transformations. Theorem (Equivariance of Quantiles under Monotone
. a m1 a mn. a 1 a 2 a = a n
 Biostat 140655, 2008: Matrix Algebra Review 1 Definition: An m n matrix, A m n, is a rectangular array of real numbers with m rows and n columns Element in the i th row and the j th column is denoted by
Biostat 140655, 2008: Matrix Algebra Review 1 Definition: An m n matrix, A m n, is a rectangular array of real numbers with m rows and n columns Element in the i th row and the j th column is denoted by
Analysis of Regression and Bayesian Predictive Uncertainty Measures
 Analysis of and Predictive Uncertainty Measures Dan Lu, Mary C. Hill, Ming Ye Florida State University, dl7f@fsu.edu, mye@fsu.edu, Tallahassee, FL, USA U.S. Geological Survey, mchill@usgs.gov, Boulder,
Analysis of and Predictive Uncertainty Measures Dan Lu, Mary C. Hill, Ming Ye Florida State University, dl7f@fsu.edu, mye@fsu.edu, Tallahassee, FL, USA U.S. Geological Survey, mchill@usgs.gov, Boulder,
Information in a Two-Stage Adaptive Optimal Design
 Information in a Two-Stage Adaptive Optimal Design Department of Statistics, University of Missouri Designed Experiments: Recent Advances in Methods and Applications DEMA 2011 Isaac Newton Institute for
Information in a Two-Stage Adaptive Optimal Design Department of Statistics, University of Missouri Designed Experiments: Recent Advances in Methods and Applications DEMA 2011 Isaac Newton Institute for
Applied Regression. Applied Regression. Chapter 2 Simple Linear Regression. Hongcheng Li. April, 6, 2013
 Applied Regression Chapter 2 Simple Linear Regression Hongcheng Li April, 6, 2013 Outline 1 Introduction of simple linear regression 2 Scatter plot 3 Simple linear regression model 4 Test of Hypothesis
Applied Regression Chapter 2 Simple Linear Regression Hongcheng Li April, 6, 2013 Outline 1 Introduction of simple linear regression 2 Scatter plot 3 Simple linear regression model 4 Test of Hypothesis
Stat 579: Generalized Linear Models and Extensions
 Stat 579: Generalized Linear Models and Extensions Linear Mixed Models for Longitudinal Data Yan Lu April, 2018, week 15 1 / 38 Data structure t1 t2 tn i 1st subject y 11 y 12 y 1n1 Experimental 2nd subject
Stat 579: Generalized Linear Models and Extensions Linear Mixed Models for Longitudinal Data Yan Lu April, 2018, week 15 1 / 38 Data structure t1 t2 tn i 1st subject y 11 y 12 y 1n1 Experimental 2nd subject
Generalized Method of Moments (GMM) Estimation
 Econometrics 2 Fall 2004 Generalized Method of Moments (GMM) Estimation Heino Bohn Nielsen of29 Outline of the Lecture () Introduction. (2) Moment conditions and methods of moments (MM) estimation. Ordinary
Econometrics 2 Fall 2004 Generalized Method of Moments (GMM) Estimation Heino Bohn Nielsen of29 Outline of the Lecture () Introduction. (2) Moment conditions and methods of moments (MM) estimation. Ordinary
Learning from Data: Regression
 November 3, 2005 http://www.anc.ed.ac.uk/ amos/lfd/ Classification or Regression? Classification: want to learn a discrete target variable. Regression: want to learn a continuous target variable. Linear
November 3, 2005 http://www.anc.ed.ac.uk/ amos/lfd/ Classification or Regression? Classification: want to learn a discrete target variable. Regression: want to learn a continuous target variable. Linear
X t = a t + r t, (7.1)
 Chapter 7 State Space Models 71 Introduction State Space models, developed over the past 10 20 years, are alternative models for time series They include both the ARIMA models of Chapters 3 6 and the Classical
Chapter 7 State Space Models 71 Introduction State Space models, developed over the past 10 20 years, are alternative models for time series They include both the ARIMA models of Chapters 3 6 and the Classical
Statistics 203: Introduction to Regression and Analysis of Variance Course review
 Statistics 203: Introduction to Regression and Analysis of Variance Course review Jonathan Taylor - p. 1/?? Today Review / overview of what we learned. - p. 2/?? General themes in regression models Specifying
Statistics 203: Introduction to Regression and Analysis of Variance Course review Jonathan Taylor - p. 1/?? Today Review / overview of what we learned. - p. 2/?? General themes in regression models Specifying
Linear Regression. In this problem sheet, we consider the problem of linear regression with p predictors and one intercept,
 Linear Regression In this problem sheet, we consider the problem of linear regression with p predictors and one intercept, y = Xβ + ɛ, where y t = (y 1,..., y n ) is the column vector of target values,
Linear Regression In this problem sheet, we consider the problem of linear regression with p predictors and one intercept, y = Xβ + ɛ, where y t = (y 1,..., y n ) is the column vector of target values,
Chapter 8: Estimation 1
 Chapter 8: Estimation 1 Jae-Kwang Kim Iowa State University Fall, 2014 Kim (ISU) Ch. 8: Estimation 1 Fall, 2014 1 / 33 Introduction 1 Introduction 2 Ratio estimation 3 Regression estimator Kim (ISU) Ch.
Chapter 8: Estimation 1 Jae-Kwang Kim Iowa State University Fall, 2014 Kim (ISU) Ch. 8: Estimation 1 Fall, 2014 1 / 33 Introduction 1 Introduction 2 Ratio estimation 3 Regression estimator Kim (ISU) Ch.
Lecture 13: Simple Linear Regression in Matrix Format
 See updates and corrections at http://www.stat.cmu.edu/~cshalizi/mreg/ Lecture 13: Simple Linear Regression in Matrix Format 36-401, Section B, Fall 2015 13 October 2015 Contents 1 Least Squares in Matrix
See updates and corrections at http://www.stat.cmu.edu/~cshalizi/mreg/ Lecture 13: Simple Linear Regression in Matrix Format 36-401, Section B, Fall 2015 13 October 2015 Contents 1 Least Squares in Matrix
Instrumental Variables and Two-Stage Least Squares
 Instrumental Variables and Two-Stage Least Squares Generalised Least Squares Professor Menelaos Karanasos December 2011 Generalised Least Squares: Assume that the postulated model is y = Xb + e, (1) where
Instrumental Variables and Two-Stage Least Squares Generalised Least Squares Professor Menelaos Karanasos December 2011 Generalised Least Squares: Assume that the postulated model is y = Xb + e, (1) where
GARCH Models Estimation and Inference
 GARCH Models Estimation and Inference Eduardo Rossi University of Pavia December 013 Rossi GARCH Financial Econometrics - 013 1 / 1 Likelihood function The procedure most often used in estimating θ 0 in
GARCH Models Estimation and Inference Eduardo Rossi University of Pavia December 013 Rossi GARCH Financial Econometrics - 013 1 / 1 Likelihood function The procedure most often used in estimating θ 0 in
Biostat Methods STAT 5820/6910 Handout #5a: Misc. Issues in Logistic Regression
 Biostat Methods STAT 5820/6910 Handout #5a: Misc. Issues in Logistic Regression Recall general χ 2 test setu: Y 0 1 Trt 0 a b Trt 1 c d I. Basic logistic regression Previously (Handout 4a): χ 2 test of
Biostat Methods STAT 5820/6910 Handout #5a: Misc. Issues in Logistic Regression Recall general χ 2 test setu: Y 0 1 Trt 0 a b Trt 1 c d I. Basic logistic regression Previously (Handout 4a): χ 2 test of
High-dimensional regression modeling
 High-dimensional regression modeling David Causeur Department of Statistics and Computer Science Agrocampus Ouest IRMAR CNRS UMR 6625 http://www.agrocampus-ouest.fr/math/causeur/ Course objectives Making
High-dimensional regression modeling David Causeur Department of Statistics and Computer Science Agrocampus Ouest IRMAR CNRS UMR 6625 http://www.agrocampus-ouest.fr/math/causeur/ Course objectives Making
From last time... The equations
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
Administration. Homework 1 on web page, due Feb 11 NSERC summer undergraduate award applications due Feb 5 Some helpful books
 STA 44/04 Jan 6, 00 / 5 Administration Homework on web page, due Feb NSERC summer undergraduate award applications due Feb 5 Some helpful books STA 44/04 Jan 6, 00... administration / 5 STA 44/04 Jan 6,
STA 44/04 Jan 6, 00 / 5 Administration Homework on web page, due Feb NSERC summer undergraduate award applications due Feb 5 Some helpful books STA 44/04 Jan 6, 00... administration / 5 STA 44/04 Jan 6,
Robust Testing and Variable Selection for High-Dimensional Time Series
 Robust Testing and Variable Selection for High-Dimensional Time Series Ruey S. Tsay Booth School of Business, University of Chicago May, 2017 Ruey S. Tsay HTS 1 / 36 Outline 1 Focus on high-dimensional
Robust Testing and Variable Selection for High-Dimensional Time Series Ruey S. Tsay Booth School of Business, University of Chicago May, 2017 Ruey S. Tsay HTS 1 / 36 Outline 1 Focus on high-dimensional
Math 423/533: The Main Theoretical Topics
 Math 423/533: The Main Theoretical Topics Notation sample size n, data index i number of predictors, p (p = 2 for simple linear regression) y i : response for individual i x i = (x i1,..., x ip ) (1 p)
Math 423/533: The Main Theoretical Topics Notation sample size n, data index i number of predictors, p (p = 2 for simple linear regression) y i : response for individual i x i = (x i1,..., x ip ) (1 p)
Covariance function estimation in Gaussian process regression
 Covariance function estimation in Gaussian process regression François Bachoc Department of Statistics and Operations Research, University of Vienna WU Research Seminar - May 2015 François Bachoc Gaussian
Covariance function estimation in Gaussian process regression François Bachoc Department of Statistics and Operations Research, University of Vienna WU Research Seminar - May 2015 François Bachoc Gaussian
For iid Y i the stronger conclusion holds; for our heuristics ignore differences between these notions.
 Large Sample Theory Study approximate behaviour of ˆθ by studying the function U. Notice U is sum of independent random variables. Theorem: If Y 1, Y 2,... are iid with mean µ then Yi n µ Called law of
Large Sample Theory Study approximate behaviour of ˆθ by studying the function U. Notice U is sum of independent random variables. Theorem: If Y 1, Y 2,... are iid with mean µ then Yi n µ Called law of
LIST OF FORMULAS FOR STK1100 AND STK1110
 LIST OF FORMULAS FOR STK1100 AND STK1110 (Version of 11. November 2015) 1. Probability Let A, B, A 1, A 2,..., B 1, B 2,... be events, that is, subsets of a sample space Ω. a) Axioms: A probability function
LIST OF FORMULAS FOR STK1100 AND STK1110 (Version of 11. November 2015) 1. Probability Let A, B, A 1, A 2,..., B 1, B 2,... be events, that is, subsets of a sample space Ω. a) Axioms: A probability function
Machine Learning. Regression Case Part 1. Linear Regression. Machine Learning: Regression Case.
 .. Cal Poly CSC 566 Advanced Data Mining Alexander Dekhtyar.. Machine Learning. Regression Case Part 1. Linear Regression Machine Learning: Regression Case. Dataset. Consider a collection of features X
.. Cal Poly CSC 566 Advanced Data Mining Alexander Dekhtyar.. Machine Learning. Regression Case Part 1. Linear Regression Machine Learning: Regression Case. Dataset. Consider a collection of features X
[y i α βx i ] 2 (2) Q = i=1
![[y i α βx i ] 2 (2) Q = i=1 [y i α βx i ] 2 (2) Q = i=1](/thumbs/75/72005858.jpg) Least squares fits This section has no probability in it. There are no random variables. We are given n points (x i, y i ) and want to find the equation of the line that best fits them. We take the equation
Least squares fits This section has no probability in it. There are no random variables. We are given n points (x i, y i ) and want to find the equation of the line that best fits them. We take the equation
Inference in non-linear time series
 Intro LS MLE Other Erik Lindström Centre for Mathematical Sciences Lund University LU/LTH & DTU Intro LS MLE Other General Properties Popular estimatiors Overview Introduction General Properties Estimators
Intro LS MLE Other Erik Lindström Centre for Mathematical Sciences Lund University LU/LTH & DTU Intro LS MLE Other General Properties Popular estimatiors Overview Introduction General Properties Estimators
Robust design in model-based analysis of longitudinal clinical data
 Robust design in model-based analysis of longitudinal clinical data Giulia Lestini, Sebastian Ueckert, France Mentré IAME UMR 1137, INSERM, University Paris Diderot, France PODE, June 0 016 Context Optimal
Robust design in model-based analysis of longitudinal clinical data Giulia Lestini, Sebastian Ueckert, France Mentré IAME UMR 1137, INSERM, University Paris Diderot, France PODE, June 0 016 Context Optimal
Day 4: Shrinkage Estimators
 Day 4: Shrinkage Estimators Kenneth Benoit Data Mining and Statistical Learning March 9, 2015 n versus p (aka k) Classical regression framework: n > p. Without this inequality, the OLS coefficients have
Day 4: Shrinkage Estimators Kenneth Benoit Data Mining and Statistical Learning March 9, 2015 n versus p (aka k) Classical regression framework: n > p. Without this inequality, the OLS coefficients have
Regression Shrinkage and Selection via the Lasso
 Regression Shrinkage and Selection via the Lasso ROBERT TIBSHIRANI, 1996 Presenter: Guiyun Feng April 27 () 1 / 20 Motivation Estimation in Linear Models: y = β T x + ɛ. data (x i, y i ), i = 1, 2,...,
Regression Shrinkage and Selection via the Lasso ROBERT TIBSHIRANI, 1996 Presenter: Guiyun Feng April 27 () 1 / 20 Motivation Estimation in Linear Models: y = β T x + ɛ. data (x i, y i ), i = 1, 2,...,
STAT 135 Lab 13 (Review) Linear Regression, Multivariate Random Variables, Prediction, Logistic Regression and the δ-method.
 STAT 135 Lab 13 (Review) Linear Regression, Multivariate Random Variables, Prediction, Logistic Regression and the δ-method. Rebecca Barter May 5, 2015 Linear Regression Review Linear Regression Review
STAT 135 Lab 13 (Review) Linear Regression, Multivariate Random Variables, Prediction, Logistic Regression and the δ-method. Rebecca Barter May 5, 2015 Linear Regression Review Linear Regression Review
Business Statistics. Tommaso Proietti. Linear Regression. DEF - Università di Roma 'Tor Vergata'
 Business Statistics Tommaso Proietti DEF - Università di Roma 'Tor Vergata' Linear Regression Specication Let Y be a univariate quantitative response variable. We model Y as follows: Y = f(x) + ε where
Business Statistics Tommaso Proietti DEF - Università di Roma 'Tor Vergata' Linear Regression Specication Let Y be a univariate quantitative response variable. We model Y as follows: Y = f(x) + ε where
Sparsity Regularization
 Sparsity Regularization Bangti Jin Course Inverse Problems & Imaging 1 / 41 Outline 1 Motivation: sparsity? 2 Mathematical preliminaries 3 l 1 solvers 2 / 41 problem setup finite-dimensional formulation
Sparsity Regularization Bangti Jin Course Inverse Problems & Imaging 1 / 41 Outline 1 Motivation: sparsity? 2 Mathematical preliminaries 3 l 1 solvers 2 / 41 problem setup finite-dimensional formulation
Nonconcave Penalized Likelihood with A Diverging Number of Parameters
 Nonconcave Penalized Likelihood with A Diverging Number of Parameters Jianqing Fan and Heng Peng Presenter: Jiale Xu March 12, 2010 Jianqing Fan and Heng Peng Presenter: JialeNonconcave Xu () Penalized
Nonconcave Penalized Likelihood with A Diverging Number of Parameters Jianqing Fan and Heng Peng Presenter: Jiale Xu March 12, 2010 Jianqing Fan and Heng Peng Presenter: JialeNonconcave Xu () Penalized
Classification. Chapter Introduction. 6.2 The Bayes classifier
 Chapter 6 Classification 6.1 Introduction Often encountered in applications is the situation where the response variable Y takes values in a finite set of labels. For example, the response Y could encode
Chapter 6 Classification 6.1 Introduction Often encountered in applications is the situation where the response variable Y takes values in a finite set of labels. For example, the response Y could encode
Topics in Probability and Statistics
 Topics in Probability and tatistics A Fundamental Construction uppose {, P } is a sample space (with probability P), and suppose X : R is a random variable. The distribution of X is the probability P X
Topics in Probability and tatistics A Fundamental Construction uppose {, P } is a sample space (with probability P), and suppose X : R is a random variable. The distribution of X is the probability P X
Computer Vision Group Prof. Daniel Cremers. 9. Gaussian Processes - Regression
 Group Prof. Daniel Cremers 9. Gaussian Processes - Regression Repetition: Regularized Regression Before, we solved for w using the pseudoinverse. But: we can kernelize this problem as well! First step:
Group Prof. Daniel Cremers 9. Gaussian Processes - Regression Repetition: Regularized Regression Before, we solved for w using the pseudoinverse. But: we can kernelize this problem as well! First step:
Is the cholesterol concentration in blood related to the body mass index (bmi)?
 Regression problems The fundamental (statistical) problems of regression are to decide if an explanatory variable affects the response variable and estimate the magnitude of the effect Major question:
Regression problems The fundamental (statistical) problems of regression are to decide if an explanatory variable affects the response variable and estimate the magnitude of the effect Major question:
2. Regression Review
 2. Regression Review 2.1 The Regression Model The general form of the regression model y t = f(x t, β) + ε t where x t = (x t1,, x tp ), β = (β 1,..., β m ). ε t is a random variable, Eε t = 0, Var(ε t
2. Regression Review 2.1 The Regression Model The general form of the regression model y t = f(x t, β) + ε t where x t = (x t1,, x tp ), β = (β 1,..., β m ). ε t is a random variable, Eε t = 0, Var(ε t
Unsupervised dimensionality reduction
 Unsupervised dimensionality reduction Guillaume Obozinski Ecole des Ponts - ParisTech SOCN course 2014 Guillaume Obozinski Unsupervised dimensionality reduction 1/30 Outline 1 PCA 2 Kernel PCA 3 Multidimensional
Unsupervised dimensionality reduction Guillaume Obozinski Ecole des Ponts - ParisTech SOCN course 2014 Guillaume Obozinski Unsupervised dimensionality reduction 1/30 Outline 1 PCA 2 Kernel PCA 3 Multidimensional
