MA6351 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS L T P C
|
|
|
- Edith Bradford
- 5 years ago
- Views:
Transcription
1 MA635 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS L T P C 3 4 OBJECTIVES: To itroduce Fourier series ysis which is cetr to my ppictios i egieerig prt from its use i sovig boudry vue probems? To cquit the studet with Fourier trsform techiques used i wide vriety of situtios. To itroduce the effective mthemtic toos for the soutios of prti differeti equtios tht mode sever physic processes d to deveop Z trsform techiques for discrete time Systems. UNIT I PARTIAL DIFFERENTIAL EQUATIONS 9+3 Formtio of prti differeti equtios Sigur itegrs -- Soutios of stdrd types of first order prti differeti equtios - Lgrge s ier equtio -- Lier prti differeti equtios of secod d higher order with costt coefficiets of both homogeeous d o-homogeeous types. UNIT II FOURIER SERIES 9+3 Dirichet s coditios Geer Fourier series Odd d eve fuctios Hf rge sie series Hf rge cosie series Compex form of Fourier series Prsev s idetity Hrmoic ysis. UNIT III APPLICATIONS OF PARTIAL DIFFERENTIAL 9+3 Cssifictio of PDE Method of seprtio of vribes - Soutios of oe dimesio wve equtio Oe dimesio equtio of het coductio Stedy stte soutio of two dimesio equtio of het coductio (excudig isuted edges). UNIT IV FOURIER TRANSFORMS 9+3 Sttemet of Fourier itegr theorem Fourier trsform pir Fourier sie d cosie trsforms Properties Trsforms of simpe fuctios Covoutio theorem Prsev s idetity. UNIT V Z - TRANSFORMS AND DIFFERENCE EQUATIONS 9+3 Z- trsforms - Eemetry properties Iverse Z - trsform (usig prti frctio d residues) Covoutio theorem - Formtio of differece equtios Soutio of differece equtios usig Z - trsform. TOTAL (L:45+T:5): 6 PERIODS. TEXT BOOKS:. Veerrj. T., "Trsforms d Prti Differeti Equtios", Tt McGrw Hi Eductio Pvt. Ltd., New Dehi, Secod reprit,.. Grew. B.S., "Higher Egieerig Mthemtics", 4d Editio, Kh Pubishers, Dehi,. 3. Nry.S., Micvchgom Piy.T.K d Rmih.G "Advced Mthemtics for Egieerig Studets" Vo. II & III, S.Viswth Pubishers Pvt. Ltd.998. REFERENCES:. Bi.N.P d Mish Goy, "A Textbook of Egieerig Mthemtics", 7th Editio, Lxmi Pubictios Pvt Ltd, 7.. Rm.B.V., "Higher Egieerig Mthemtics", Tt Mc Grw Hi Pubishig Compy Limited, NewDehi, Gy Jmes, "Advced Moder Egieerig Mthemtics", 3rd Editio, Perso Eductio, Erwi Kreysig, "Advced Egieerig Mthemtics", 8th Editio, Wiey Idi, Ry Wyie. C d Brrett.L.C, "Advced Egieerig Mthemtics" Tt Mc Grw Hi Eductio Pvt Ltd, Sixth Editio, New Dehi,. 6. Dtt.K.B., "Mthemtic Methods of Sciece d Egieerig", Cegge Lerig Idi Pvt Ltd, Dehi, 3.
2 CONTENTS S.NO TOPICS PAGE NO UNIT-I PARTIAL DIFFERENTIAL EQUATIONS. INTRODUCTION. FORMATION OF PARTIAL DIFFERNTIAL EQUATIONS.3 SOLUTIONS OF PARTIAL DIFFERENTIAL EQUATIONS 7.4 LAGRANGE S LINEAR EQUATIONS 3.5 PARTIAL DIFFERENTIAL EQUATIONS OF HIGHER ORDER WITH CONSTANT 9 CO-EFFECIENTS.6 NON-HOMOGENOUS LINEAR EQUATIONS 36 UNIT-II FOURIER SERIES. INTRODUCTION 4. PERIODIC FUNCTIONS 4.3 EVEN AND ODD FUNCTIONS 54.4 HALF RANGE SERIES 6.5 PARSEVAL S THEOREM 68.6 CHANGE OF INTERVAL 69.7 HARMONIC ANALYSIS 76.8 COMPLEX FORM OF FOURIER SERIES 8.9 SUMMARY 83 UNIT-III APPLICATIONS OF PARTIAL DIFFERENTILA EQUATIONS 3. INTRODUCTION SOLUTION OF WAVE EQUATION SOLUTION OF THE HEAT EQUATION SOLUTION OF LAPLACE EQUATIONS UNIT-IV FOURIER TRANSFORMS 4. INTRODUCTION INTEGRAL TRANSFORMS FOURIER INTEGRAL THEOREM FOURIER TRANSFORMS AND ITS PROPERTIES CONVOLUTION THEOREM AND PARSEVAL S THEOREM FOURIER SINE AND COSINE TRANSFORMS 54 UNIT-V Z-TRANSFORMS AND DIFFERENCE EQUATIONS 5. INTRODUCTION LINEAR DIFFERENCE EQUATIONS Z-TRANSFORMS AND ITS PROPERTIES INVERSE Z-TRANSFORMS CONVOLUTION THEOREM APPLICATIONS OF Z-TRANSFORMS TO DIFFERENCE EQUATIONS FORMATION OF DIFFERENCE EQUATIONS 99 BIBLIOGRAPHY
3 UNIT I PARTIAL DIFFERENTIAL EQUATIONS This uit covers topics tht expi the formtio of prti differeti equtios d the soutios of speci types of prti differeti equtios.. INTRODUCTION A prti differeti equtio is oe which ivoves oe or more prti derivtives. The order of the highest derivtive is ced the order of the equtio. A prti differeti equtio cotis more th oe idepedet vribe. But, here we sh cosider prti differeti equtios ivovig oe depedet vribe d oy two idepedet vribes x d y so tht = f(x,y). We sh deote = p, = q, = r, = s, = t. x y x xy y A prti differeti equtio is ier if it is of the first degree i the depedet vribe d its prti derivtives. If ech term of such equtio cotis either the depedet vribe or oe of its derivtives, the equtio is sid to be homogeeous, otherwise it is o homogeeous.. Formtio of Prti Differeti Equtios Prti differeti equtios c be obtied by the eimitio of rbitrry costts or by the eimitio of rbitrry fuctios. By the eimitio of rbitrry costts Let us cosider the fuctio ( x, y,,, b ) = () where & b re rbitrry costts Differetitig equtio () prtiy w.r.t x & y, we get x y + p = () + q = (3) Eimitig d b from equtios (), () d (3), we get prti differeti equtio of the first order of the form f (x,y,, p, q) =
4 Exmpe Eimite the rbitrry costts & b from = x + by + b Cosider = x + by + b () Differetitig () prtiy w.r.t x & y, we get x y = i.e, p= () = b i.e, q = b (3) Usig () & (3) i (), we get = px +qy+ pq which is the required prti differeti equtio. Exmpe Form the prti differeti equtio by eimitig the rbitrry costts d b from = ( x + ) ( y + b ) Give = ( x + ) ( y + b ) () Differetitig () prtiy w.r.t x & y, we get p = x (y + b ) q = y (x + ) Substitutig the vues of p d q i (), we get 4xy = pq which is the required prti differeti equtio.
5 Exmpe 3 Fid the prti differeti equtio of the fmiy of spheres of rdius oe whose cetre ie i the xy - pe. The equtio of the sphere is give by ( x ) + ( y- b) + = () Differetitig () prtiy w.r.t x & y, we get (x- ) + p = ( y-b ) + q = From these equtios we obti x- = -p () y -b = -q (3) Usig () d (3) i (), we get p + q + = or ( p + q + ) = Exmpe 4 Eimite the rbitrry costts, b & c from x y + + = d form the prti differeti equtio. b c The give equtio is x y + + = () b c
6 Differetitig () prtiy w.r.t x & y, we get x p + = c y q + = b c Therefore we get x p + = () c y q + = (3) b c Agi differetitig () prtiy w.r.t x, we set (/ ) + (/ c ) ( r + p ) = (4) Mutipyig ( 4) by x, we get x x r p x + + = c c From (), we hve p xr p x + + = c c c or -p + xr + p x = By the eimitio of rbitrry fuctios Let u d v be y two fuctios of x, y, d Φ(u, v ) =, where Φ is rbitrry fuctio. This retio c be expressed s u = f(v) ()
7 Differetitig () prtiy w.r.t x & y d eimitig the rbitrry fuctios from these retios, we get prti differeti equtio of the first order of the form f(x, y,, p, q ) =. Exmpe 5 Obti the prti differeti equtio by eimitig f from = ( x+y ) f ( x - y ) Let us ow cosider the equtio = (x+y ) f(x - y ) () Differetitig () prtiy w.r.t x & y, we get p = ( x + y ) f ' ( x - y ). x + f ( x - y ) q = ( x + y ) f ' ( x - y ). (-y) + f ( x - y ) These equtios c be writte s Hece, we get p - f ( x - y ) = ( x + y ) f '( x - y ). x () q - f ( x - y ) = ( x + y ) f '( x - y ).(-y) (3) p - f ( x - y ) q - f ( x - y ) = - x y i.e, py - yf( x - y ) = -qx +xf ( x - y ) i.e, py +qx = ( x+y ) f ( x - y ) Therefore, we hve by(), py +qx = Exmpe 6 Form the prti differeti equtio by eimitig the rbitrry fuctio f from = e y f (x + y) Cosider = e y f ( x +y ) ( ) Differetitig () prtiy w.r. t x & y, we get p = e y f ' (x + y) q = e y f '(x + y) + f(x + y). e y Hece, we hve q = p +
8 Exmpe 7 Form the PDE by eimitig f & Φ from = f (x +y ) + Φ ( x y) Cosider = f (x +y ) + Φ ( x y) () Differetitig () prtiy w.r.t x &y, we get p = f '(x +y ) + Φ' (x y) () q = f ' (x +y ). + Φ' (x y) ( -) (3) Differetitig () & (3) gi prtiy w.r.t x & y, we get r = f "( x+y) + Φ "( x y) t = f "( x+y). + Φ"( x y) (-) i.e, or t = { f"( x + y) + Φ"( x y)} t = r Exercises:. Form the prti differeti equtio by eimitig the rbitrry costts & b from the foowig equtios. (i) = x + by (ii) x + y + = b (iii) = x + by + + b (iv) x + by + c = (v) = x + b y + b. Fid the PDE of the fmiy of spheres of rdius hvig their cetres ie o the xy pe{hit: (x ) + (y b) + = } 3. Fid the PDE of spheres whose cetre ie o the (i) xis (ii) x-xis 4. Form the prti differeti equtios by eimitig the rbitrry fuctios i the foowig cses. (i) = f (x + y) (ii) = f (x y ) (iii) = f (x + y + ) (iv) (xy, x + y + ) =
9 (v) = x + y + f(xy) (vi) = xy + f (x + y ) (vii) = f xy (viii) F (xy +, x + y + ) = (ix) = f (x + iy) +f (x iy) (x) = f(x 3 + y) +g(x 3 y).3 SOLUTIONS OF A PARTIAL DIFFERENTIAL EQUATION A soutio or itegr of prti differeti equtio is retio coectig the depedet d the idepedet vribes which stisfies the give differeti equtio. A prti differeti equtio c resut both from eimitio of rbitrry costts d from eimitio of rbitrry fuctios s expied i sectio.. But, there is bsic differece i the two forms of soutios. A soutio cotiig s my rbitrry costts s there re idepedet vribes is ced compete itegr. Here, the prti differeti equtios coti oy two idepedet vribes so tht the compete itegr wi icude two costts.a soutio obtied by givig prticur vues to the rbitrry costts i compete itegr is ced prticur itegr. Sigur Itegr Let f (x,y,,p,q) = () be the prti differeti equtio whose compete itegr is (x,y,,,b) = () where d b re rbitrry costts. Differetitig () prtiy w.r.t. d b, we obti = (3) d = (4) b The eimit of d b from the equtios (), (3) d (4), whe it exists, is ced the sigur itegr of ().
10 Geer Itegr I the compete itegr (), put b = F(), we get (x,y,,, F() ) = (5) Differetitig (), prtiy w.r.t., we get F'() = (6) b The eimit of betwee (5) d (6), if it exists, is ced the geer itegr of (). SOLUTION OF STANDARD TYPES OF FIRST ORDER PARTIAL DIFFERENTIAL EQUATIONS. The first order prti differeti equtio c be writte s f(x,y,, p,q) =, where p = /x d q = / y. I this sectio, we sh sove some stdrd forms of equtios by speci methods. Stdrd I : f (p,q) =. i.e, equtios cotiig p d q oy. =. Suppose tht = x + by +c is soutio of the equtio f(p,q) =, where f (,b) Sovig this for b, we get b = F (). Hece the compete itegr is = x + F() y +c () Now, the sigur itegr is obtied by eimitig & c betwee = x + y F() + c = x + y F'() =. The st equtio beig bsurd, the sigur itegr does ot exist i this cse. To obti the geer itegr, et us tke c = ().
11 The, = x + F() y + () () Differetitig () prtiy w.r.t., we get = x + F'(). y + '() (3) Eimitig betwee () d (3), we get the geer itegr Exmpe 8 Sove pq = The give equtio is of the form f (p,q) = The soutio is = x + by +c, where b =. Sovig, b = The compete itegr is Z = x y + c () Differetitig () prtiy w.r.t c, we get =, which is bsurd. Hece, there is o sigur itegr. To fid the geer itegr, put c = () i (), we get Z = x y + () Differetitig prtiy w.r.t, we get = x y + () Eimitig betwee these equtios gives the geer itegr.
12 Exmpe 9 Sove pq + p +q = The give equtio is of the form f (p,q) =. The soutio is = x + by +c, where b + + b =. Sovig, we get b = Hece the compete Itegr is = x y+c () + Differetitig () prtiy w.r.t. c, we get =. The bove equtio beig bsurd, there is o sigur itegr for the give prti differeti equtio. To fid the geer itegr, put c = () i (), we hve = x y + () () + Differetitig () prtiy w.r.t, we get = x y + () (3) ( + ) Eimitig betwee () d (3) gives the geer itegr. Exmpe Sove p + q = pq The soutio of this equtio is = x + by + c, where + b = b. Sovig, we get + ( 4) b =
13 Hece the compete itegr is + 4 =x y + c () Differetitig () prtiy w.r.t c, we get =, which is bsurd. Therefore, there is o sigur itegr for the give equtio. To fid the geer Itegr, put C = (), we get + 4 = x y + () Differetitig prtiy w.r.t, we hve + 4 = x y + () The eimit of betwee these equtios gives the geer itegr Stdrd II : Equtios of the form f (x,p,q) =, f (y,p,q) = d f (,p,q) =. i.e, oe of the vribes x,y, occurs expicity. (i) Let us cosider the equtio f (x,p,q) =. Sice is fuctio of x d y, we hve d = dx dy x y or d = pdx + qdy Assume tht q =. The the give equtio tkes the form f (x, p, ) = Sovig, we get Therefore, p = (x,). d = (x,) dx + dy. Itegrtig, = (x,) dx + y + b which is compete Itegr.
14 (ii) Let us cosider the equtio f(y,p,q) =. Assume tht p =. The the equtio becomes f (y,, q) = Sovig, we get q = (y,). Therefore, d = dx + (y,) dy. Itegrtig, = x + (y,) dy + b, which is compete Itegr. (iii) Let us cosider the equtio f(, p, q) =. Assume tht q = p. The the equtio becomes f (, p, p) = Sovig, we get p = (,). Hece d = (,) dx + (, ) dy. d ie, = dx + dy. (,) Itegrtig, d = x + y + b, which is compete Itegr. (,) Exmpe Sove q = xp + p Give q = xp + p () This is of the form f (x,p,q) =. Put q = i (), we get = xp + p i.e, p + xp =. -x +(x + 4) Therefore, p =
15 x ± x + 4 Itegrtig, = dx + y + b x x x Thus, = ± (4 + x )+ si h y + b 4 4 Exmpe Sove q = yp This is of the form f (y,p,q) = The, put p =. Therfore, the give equtio becomes q = y. Sice d = pdx + qdy, we hve d = dx + y dy y Itegrtig, we get = x b Exmpe 3 Sove 9 (p + q ) = 4 This is of the form f (,p,q) = The, puttig q = p, the give equtio becomes 9 (p + p ) = 4 Therefore, p = ± ( + ) d q = ± ( + ) Sice d = pdx + qdy,
16 d = ± dx ± dy Mutipyig both sides by +, we get + d = dx dy, which o itegrtio gives, 3 3 (+ ) 3/ = x y + b. 3/ 3 3 or ( + ) 3/ = x + y + b. Stdrd III : f (x,p) = f (y,q). ie, equtios i which is bset d the vribes re seprbe. Let us ssume s trivi soutio tht f(x,p) = g(y,q) = (sy). Sovig for p d q, we get p = F(x,) d q = G(y,). But d = dx dy x y Hece d = pdx + qdy = F(x,) dx + G(y,) dy Therefore, = F(x,) dx + G(y,) dy + b, which is the compete itegr of the give equtio cotiig two costts d b. The sigur d geer itegrs re foud i the usu wy. Exmpe 4 Sove pq = xy The give equtio c be writte s p y = = (sy) x q
17 p Therefore, = impies p = x x y y d = impies q = q Sice d = pdx + qdy, we hve y d = xdx dy, which o itegrtio gives. x y = b Exmpe 5 Sove p + q = x + y The give equtio c be writte s p x = y q = (sy) p x = impies p = ( + x ) d y q = impies q = (y ) But d = pdx + qdy ie, d = + x dx + y dy Itegrtig, we get x x y y = ----x sih y cosh b Stdrd IV (Cirut s form) Equtio of the type = px + qy + f (p,q) () is kow s Cirut s form.
18 Differetitig () prtiy w.r.t x d y, we get p = d q = b. Therefore, the compete itegr is give by = x + by + f (,b). Exmpe 6 Sove = px + qy +pq The give equtio is i Cirut s form. Puttig p = d q = b, we hve = x + by + b () which is the compete itegr. To fid the sigur itegr, differetitig () prtiy w.r.t d b, we get = x + b = y + Therefore we hve, = -y d b= -x. Substitutig the vues of & b i (), we get = -xy xy + xy or + xy =, which is the sigur itegr. To get the geer itegr, put b = () i (). The = x + ()y + () () Differetitig () prtiy w.r.t, we hve = x + '() y + '() + () (3) Eimitig betwee () d (3), we get the geer itegr.
19 Exmpe 7 Fid the compete d sigur soutios of = px + qy + + p + q The compete itegr is give by = x + by b () To obti the sigur itegr, differetitig () prtiy w.r.t & b. The, = x b b = y b Therefore, x = () ( + + b ) b d y = (3) ( + + b ) Squrig () & (3) d ddig, we get + b x + y = b Now, x y = b i.e, + + b = x y Therefore, ( + + b ) = (4) x y Usig (4) i () & (3), we get
20 x = x y d y = b x y -x -y Hece, = d b = x y x y Substitutig the vues of & b i (), we get - x y = x y x y x y which o simpifictio gives = x y or x + y + =, which is the sigur itegr. Exercises Sove the foowig Equtios. pq = k. p + q = pq 3. p +q = x 4. p = y q 5. = p + q 6. p + q = x + y 7. p + q = 8. = px + qy - pq 9. { (px + qy)} = c + p + q. = px + qy + p q EQUATIONS REDUCIBLE TO THE STANDARD FORMS Sometimes, it is possibe to hve o ier prti differeti equtios of the first order which do ot beog to y of the four stdrd forms discussed erier. By chgig the vribes suitby, we wi reduce them ito y oe of the four stdrd forms. Type (i) : Equtios of the form F(x m p, y q) = (or) F (, x m p, y q) =. Cse(i) : If m d, the put x -m = X d y - = Y.
21 X Now, p = = = (-m) x -m x X x X Therefore, x m p = (-m) = ( m) P, where P = X X Simiry, y q = (-)Q, where Q = Y Hece, the give equtio tkes the form F(P,Q) = (or) F(,P,Q) =. Cse(ii) : If m = d =, the put og x = X d og y = Y. X Now, p = = = x X x X x Therefore, xp = = P. X Simiry, yq =Q. Exmpe 8 Sove x 4 p + y q = The give equtio c be expressed s (x p) + (y q) = Here m =, = Put X = x -m = x - d Y = y - = y -. We hve x m p = (-m) P d y q = (-)Q i.e, x p = -P d y q = -Q. Hece the give equtio becomes P Q = () This equtio is of the form f (,P,Q) =. Let us tke Q = P.
22 The equtio () reduces to P P = Hece, d Sice ( + 8) P = ( + 8) Q = d = PdX + QdY, we hve ( + 8) ( + 8) d = dx dy i.e, d ( + 8) = (dx + dy) Itegrtig, we get + 8 og = (X + Y) +b ( + 8) Therefore, og = b which is the compete soutio. x y Exmpe 9 Sove x p + y q = The give equtio c be writte s (xp) + (yq) = Here m =, =. Put X = og x d Y = og y.
23 The xp = P d yq = Q. Hece the give equtio becomes P + Q = () This equtio is of the form F(,P,Q) =. Therefore, et us ssume tht Q = P. Now, equtio () becomes, P + P = Hece P = (+ ) d Q = (+ ) Sice d = PdX + QdY, we hve d = dx dy. (+ ) (+ ) d i.e, (+ ) = dx + dy. Itegrtig, we get (+ ) og = X + Y + b. Therefore, (+ ) og = ogx + ogy + b, which is the compete soutio. Type (ii) : Equtios of the form F( k p, k q) = (or) F(x, k p) = G(y, k q). Cse (i) : If k -, put Z = k+, Z Z Now = = (k+) k = (k+) k p. x x x Z Therefore, k p = k+ x
24 Z Simiry, k q = k+ y Cse (ii) : If k = -, put Z = og. Z Z Now, = = p x x Z Simiry, = q. y Exmpe Sove 4 q p = The give equtio c so be writte s ( q) ( p) = Here k =. Puttig Z = k+ = 3, we get Z Z Z k p = d Z k q = k+ x k+ y Z Z i.e, Z p = d Z q = x 3 y Hece the give equtio reduces to i.e, Q 3P 9 =, Q P = 3 3 which is of the form F(P,Q) =. Hece its soutio is Z = x + by + c, where b 3 9 =. Sovig for b, b = ± (3 +9)
25 Hece the compete soutio is Z = x + (3 +9). y + c or 3 = x + (3 +9) y + c Exercises Sove the foowig equtios.. x p + y p =. (p +q ) = x + y 3. (p x + q ) = 4. x 4 p yq 3 = 5. p + x y q = x 6. x p + y q = 7. x /p + y /q = 8. (p q ) = 9. (p /x + q /y ) =. p x + q y =..4 Lgrge s Lier Equtio Equtios of the form Pp + Qq = R (), where P, Q d R re fuctios of x, y,, re kow s Lgrge s equtios d re ier i p d q.to sove this equtio, et us cosider the equtios u = d v = b, where, b re rbitrry costts d u, v re fuctios of x, y,. Sice u is costt, we hve du = (). But u s fuctio of x, y,, u u u du = dx + dy + d x y Comprig () d (3), we hve u u u dx + dy + d = (3) x y Simiry, v v v dx + dy + d = (4) x y
26 By cross-mutipictio, we hve dx dy d = = u v u v u v u v u v u v y y x x y x x y (or) dx dy d = = (5) P Q R Equtios (5) represet pir of simuteous equtios which re of the first order d of first degree.therefore, the two soutios of (5) re u = d v = b. Thus, ( u, v ) = is the required soutio of (). Note : To sove the Lgrge s equtio,we hve to form the subsidiry or uxiiry equtios dx dy d = = P Q R which c be soved either by the method of groupig or by the method of mutipiers. Exmpe Fid the geer soutio of px + qy =. Here, the subsidiry equtios re dx dy d = = x y Tkig the first two rtios, dx dy x = y Itegrtig, og x = og y + og c
27 or i.e, x = c y c = x / y From the st two rtios, dy d = y Itegrtig, og y = og + og c or i.e, y = c c = y / Hece the required geer soutio is Exmpe Φ( x/y, y/) =, where Φ is rbitrry Sove p t x + q t y = t The subsidiry equtios re dx dy d = = tx ty t Tkig the first two rtios, dx dy = tx ty ie, cotx dx = coty dy Itegrtig, og six = og siy + og c ie, six = c siy Therefore, c = six / siy Simiry, from the st two rtios, we get siy = c si i.e, c = siy / si Hece the geer soutio is
28 six siy Φ, =, where Φ is rbitrry. siy si Exmpe 3 Sove (y-) p + (-x) q = x-y Here the subsidiry equtios re dx dy d = = y- - x x y Usig mutipiers,,, dx + dy + d ech rtio = Therefore, dx + dy + d =. Itegrtig, x + y + = c () Agi usig mutipiers x, y d, ech rtio = xdx + ydy + d Therefore, xdx + ydy + d =. Itegrtig, x / + y / + / = costt or x + y + = c () Hece from () d (), the geer soutio is Φ ( x + y +, x + y + ) = Exmpe 4 Fid the geer soutio of (m - y) p + (x- )q = y - mx.
29 Here the subsidiry equtios re dx dy d = = m- y x - y - mx Usig the mutipiers x, y d, we get xdx + ydy + d ech frctio = ` xdx + ydy + d =, which o itegrtio gives x / + y / + / = costt or x + y + = c () Agi usig the mutipiers, m d, we hve dx + mdy + d ech frctio = ` dx + mdy + d =, which o itegrtio gives x + my + = c () Hece, the required geer soutio is Exmpe 5 Φ(x + y +, x + my + ) = Sove (x - y - ) p + xy q = x. The subsidiry equtios re dx dy d = = x -y - xy x Tkig the st two rtios, dx xy = d x
30 xy x ie, dy d = y Itegrtig, we get og y = og + og c or y = c i.e, c = y/ () Usig mutipiers x, y d, we get xdx + y dy + d xdx + y dy + d ech frctio = = x (x -y - )+xy +x x ( x + y + ) Comprig with the st rtio, we get xdx + y dy + d d = x ( x + y + ) x xdx + ydy + d d i.e, = x + y + Itegrtig, og ( x + y + ) = og + og c or x + y + = c x + y + i.e, c = () From () d (), the geer soutio is Φ(c, c ) =. x + y + i.e, Φ (y/), =
31 Exercises Sove the foowig equtios. px + qy =. py + qx = xy 3. xp yq = y x 4. y p + x q = y x 5. (x y) = px qy 6. ( x) p + (b y) q = c 7. (y p) /x + xq = y 8. (y + ) p xyq + x = 9. x p + y q = (x + y). p q = og (x+y). (x + y)p + (x y)q = x + y. (y )p (x + y)q = x +.5 PARTIAL DIFFERENTIAL EQUATIONS OF HIGHER ORDER WITH CONSTANT COEFFICIENTS. Homogeeous Lier Equtios with costt Coefficiets. A homogeeous ier prti differeti equtio of the th order is of the form c c c = F (x,y) () x x - y y where c, c, , c re costts d F is fuctio of x d y. It is homogeeous becuse its terms coti derivtives of the sme order. Equtio () c be expressed s (c D + c D - D ' c D ' ) = F (x,y) or f (D,D ' ) = F (x,y) (),
32 where, D d D '. x y As i the cse of ordiry ier equtios with costt coefficiets the compete soutio of () cosists of two prts, mey, the compemetry fuctio d the prticur itegr. The compemetry fuctio is the compete soutio of f (D,D ' ) = (3), which must coti rbitrry fuctios s the degree of the poyomi f(d,d ' ). The prticur itegr is the prticur soutio of equtio (). Fidig the compemetry fuctio Let us ow cosider the equtio f(d,d ' ) = F (x,y) The uxiiry equtio of (3) is obtied by repcig D by m d D ' by. i.e, c m + c m c = (4) Sovig equtio (4) for m, we get roots. Depedig upo the ture of the roots, the Compemetry fuctio is writte s give beow: Roots of the uxiiry Nture of the Compemetry fuctio(c.f) equtio roots m,m,m 3.,m distict roots f (y+m x)+f (y+m x) +.+f (y+m x). m = m = m, m 3,m 4,.,m two equ roots f (y+m x)+xf (y+m x) + f 3 (y+m 3 x) +.+ f (y+m x). m = m =.= m = m equ roots f (y+mx)+xf (y+mx) + x f 3 (y+mx) x - f (y+mx) Fidig the prticur Itegr Cosider the equtio f(d,d ' ) = F (x,y). Now, the P.I is give by F (x,y) f(d,d ' ) x +by Cse (i) : Whe F(x,y) = e P.I = e x+by f (D,D ' ) Repcig D by d D ' by b, we hve P.I = e x+by, where f (,b).
33 f (,b) Cse (ii) : Whe F(x,y) = si(x + by) (or) cos (x +by) P.I = si (x+by) or cos (x+by) f(d,dd ',D ' ) Repcig D = -, DD ' = -b d D ' = -b, we get P.I = si (x+by) or cos (x+by), where f(-, - b, -b ). f(-, - b, -b ) Cse (iii) : Whe F(x,y) = x m y, P.I = x m y f(d,d ' ) = [f (D, D ' )] - x m y Expd [f (D,D ' )] - i scedig powers of D or D ' d operte o x m y term by term. Cse (iv) : Whe F(x,y) is y fuctio of x d y. P.I = F (x,y). f (D,D ' ) Resove ito prti frctios cosiderig f (D,D ' ) s fuctio of D oe. f (D,D ' ) The operte ech prti frctio o F(x,y) i such wy tht F (x,y) = F(x,c-mx) dx, D md ' where c is repced by y+mx fter itegrtio Exmpe 6 Sove(D 3 3D D ' + 4D '3 ) = e x+y The uxiry equtio is m=m 3 3m + 4 =
34 The roots re m = -,, Therefore the C.F is f (y-x) + f (y+ x) + xf 3 (y+x). e x+y P.I.= (Repce D by d D ' by ) D 3 3D D ' +4D '3 e x+y = ()() + 4() 3 e x+y = Hece, the soutio is = C.F. + P.I e x+y ie, = f (y-x) + f (y+x) + x f 3 (y+x) Exmpe 7 Sove (D 4DD ' +4 D ' ) = cos (x y) The uxiiry equtio is m 4m + 4 = Sovig, we get m =,. Therefore the C.F is f (y+x) + xf (y+x). P.I = cos (x-y) D 4DD ' + 4D ' Repcig D by, DD ' by d D ' by 4, we hve P.I = cos (x-y) (-) 4 () + 4(-4) cos (x-y) =
35 Soutio is = f (y+x) + xf (y+x) Exmpe 8 Sove (D DD ' ) = x 3 y + e 5x The uxiiry equtio is m m =. Sovig, we get m =,. Hece the C.F is f (y) + f (y+x). x 3 y P.I = D DD ' = (x 3 y) D ' D D D ' = (x 3 y) D D D ' 4D ' = (x 3 y) D D D 4 = (x 3 y) D ' (x 3 y) D ' (x 3 y) D D D 4 = (x 3 y) (x 3 ) () D D D P.I = (x 3 y) (x 3 ) D D 3 x 5 y x 6 P.I =
36 e 5x P.I = (Repce D by 5 d D ' by ) D DD ' e 5x = x 5 y x 6 e 5x Soutio is Z = f (y) + f (y+x) Exmpe 9 Sove (D + DD ' 6 D ) = y cosx. The uxiiry equtio is m + m 6 =. Therefore, m = 3,. Hece the C.F is f (y-3x) + f (y + x). y cosx P.I = D + DD ' 6D ' y cosx = (D + 3D ' ) (D D ' ) = y cosx (D+3D ' ) (D D ' ) = (c x) cosx dx, where y = c x (D+3D ' ) = (c x) d (six) (D+3D ' ) = [(c x) (six) (-) ( - cosx)] (D+3D ' ) = [ y si x cos x)] (D+3D ' ) = [(c + 3x) six cosx] dx, where y = c + 3x
37 = (c + 3x) d( cosx) cosx dx = (c + 3x) ( cosx) (3) ( - six) six = y cosx + six Hece the compete soutio is = f (y 3x) + f (y + x) y cosx + six Exmpe 3 x +y Sove r 4s + 4t = e Give equtio is = e x + y x xy y i.e, (D 4DD ' + 4D ' ) = e x + y The uxiiry equtio is m 4m + 4 =. Therefore, m =, Hece the C.F is f (y + x) + x f (y + x). e x+y P.I. = D 4DD ' +4D ' Sice D 4DD ' +4D ' = for D = d D ' =, we hve to ppy the geer rue. e x+y P.I. = (D D ' ) (D D ' ) = e x+y (D D ' ) (D D ' ) = e x+c x dx, where y = c x. (D D ' )
38 = ec dx (D D ' ) = e c.x (D D ' ) = xe y+x D D ' = xe c-x + x dx, where y = c x. = xe c dx = e c. x / x e y+x = Hece the compete soutio is = f (y+x) + f (y+x) x e x+y.6 No Homogeeous Lier Equtios Let us cosider the prti differeti equtio f (D,D ' ) = F (x,y) () If f (D,D ' ) is ot homogeeous, the () is o homogeeous ier prti differeti equtio. Here so, the compete soutio = C.F + P.I. The methods for fidig the Prticur Itegrs re the sme s those for homogeeous ier equtios. But for fidig the C.F, we hve to fctorie f (D,D ' ) ito fctors of the form D md ' c. Cosider ow the equtio (D md ' c) = ().
39 This equtio c be expressed s p mq = c (3), which is i Lgrgi form. The subsidiry equtios re dx dy d = = (4) m c The soutios of (4) re y + mx = d = be cx. Tkig b = f (), we get = e cx f (y+mx) s the soutio of (). Note:. If (D-m D ' C ) (D m D ' -C ) (D m D ' -C ) = is the prti differeti equtio, the its compete soutio is = e c x f (y +m x) + e c x f (y+m x) e c x f (y+m x). I the cse of repeted fctors, the equtio (D-mD ' C) = hs compete soutio = e cx f (y +mx) + x e cx f (y+mx) x - e cx f (y+mx). Exmpe 3 Sove (D-D ' -) (D-D ' ) = e x y Here m =, m =, c =, c =. Therefore, the C.F is e x f (y+x) + e x f (y+x). e x-y P.I. = Put D =, D ' =. (D D ' ) (D-D ' ) e x-y = ( ( ) ) ( ( ) )
40 e x-y = e x-y Hece the soutio is = e x f (y+x) + e x f (y+x) Exmpe 3 Sove (D DD ' + D ' ) = cos (x + y) The give equtio c be rewritte s (D-D ' +) (D-) = cos (x + y) Here m =, m =, c = -, c =. Therefore, the C.F = e x f (y+x) + e x f (y) P.I = cos (x+y) [Put D =,DD ' = -,D ' = 4] (D DD ' + D ' ) = cos (x+y) ( ) + D ' = cos (x+y) D ' si (x+y) = Hece the soutio is = e -x f (y+x) e x f (y) Exmpe 33 Sove [(D + D ' ) (D + D ' 3)] = e x+y x +6y Here m =, m =, c =, c = 3. si(x+y)
41 Hece the C.F is = e x f (y x) + e 3x f (y x). e x+y P.I = [Put D =, D ' = ] (D+D ' ) (D + D ' 3) e x+y = (+ ) (+4 3) e x+y = P.I = (4 + 3x + 6y) (D+D ' ) (D + D ' 3) = (4 + 3x + 6y) D + D ' 3 [ (D+D ' )] D + D ' - = [ (D + D ' )] (4 +3x+6y) D + D ' = ----[ + (D + D ' )+ (D+D ' ) +...] (D+D ' ) +...] (4 + 3x +6y) 4 5 = D D ' (4 + 3x + 6y) 3 3 3
42 4 5 = x + 6y (3) (6) = x + y + 6 Hece the compete soutio is e x+y = e x f (y-x) + e 3x f (y x) x + y Exercises () Sove the foowig homogeeous Equtios = cos (x + y) x xy y = si x.cos y x xy 3. (D + 3DD ' + D ' ) = x + y 4. (D DD ' + D ' ) = xy + e x. coshy e y + e y e x+y + e x-y Hit: e x. coshy = e x = (D 3 7DD ' 6D ' 3 ) = si (x+y) + e x+y 6. (D + 4DD ' 5D ' ) = 3e x-y + si (x y) 7. (D DD ' 3D ' ) = xy + e 6x+y 8. (D 4D ' ) = cosx. cos3y 9. (D DD ' D ' ) = (y )e x
43 3x y. 4r + s + 9t = e (b) Sove the foowig o homogeeous equtios.. (DD ' + D ' 3D ' ) = 3 cos(3x y). (D + DD ' + D ' ) = e -x 3. r s + p = x + y 4. (D DD ' + D ' 3D + 3D ' + ) = (e 3x + e -y ) 5. (D D ' 3D + 3D ' ) = xy + 7.
44 UNIT II FOURIER SERIES. INTRODUCTION The cocept of Fourier series ws first itroduced by Jcques Fourier (768 83), Frech Physicist d Mthemtici. These series becme most importt too i Mthemtic physics d hd deep ifuece o the further deveopmet of mthemtics it sef.fourier series re series of cosies d sies d rise i represetig geer periodic fuctios tht occurs i my Sciece d Egieerig probems. Sice the periodic fuctios re ofte compicted, it is ecessry to express these i terms of the simpe periodic fuctios of sie d cosie. They py importt roe i sovig ordiry d prti differeti equtios.. PERIODIC FUNCTIONS A fuctio f (x) is ced periodic if it is defied for re x d if there is some positive umber p such tht f (x + p ) = f (x) for x. This umber p is ced period of f(x). If periodic fuctio f (x) hs smest period p (>), this is ofte ced the fudmet period of f(x). For exmpe, the fuctios cosx d six hve fudmet period. DIRICHLET CONDITIONS Ay fuctio f(x), defied i the iterv c x c +, c be deveoped s Fourier series of the form ( cosx + b six) provided the foowig = coditios re stisfied. f (x) is periodic, sige vued d fiite i [ c, c + ]. f (x) hs fiite umber of discotiuities i [ c, c + ]. f (x) hs t the most fiite umber of mxim d miim i [ c,c+ ]. These coditios re kow s Dirichet coditios. Whe these coditios re stisfied, the Fourier series coverges to f(x) t every poit of cotiuity. At poit of discotiuity x = c, the sum of the series is give by f(x) = (/) [ f (c-) + f (c+)],
45 where f (c-) is the imit o the eft d f (c+) is the imit o the right. EULER S FORMULAE The Fourier series for the fuctio f(x) i the iterv c < x < c + is give by f (x) = ( cosx + b six), where = C + = f (x) dx. C C + = f(x) cosx dx. C C + b = f (x) six dx. C These vues of,, b re kow s Euer s formue. The coefficiets,, b re so termed s Fourier coefficiets. Exmpe Expd f(x) = x s Fourier Series (Fs) i the iterv [ -π, π] Let f(x) = o [ cos x + b si x ] () π = Here o = f (x) dx π -π π = x dx π -π π = x π - π π π = - = π o =
46 π = --- f(x) cosx dx π -π π si x = x d π -π = (x) si x - () -cos x π π - π = cos π cos π π = π b = f(x) si x dx π -π π -cos x = x d π -π π -cosx -si x π = (x) - () - π = - πcos π πcosπ π = -π cosπ π b = (-) + [ cos π = (-) ] Substitutig the vues of o, & b i equtio (), we get f(x) = (-) + si x = x = six - six + si 3x - 3
47 Exmpe Expd f(x) = x s Fourier Series i the iterv ( - x ) d hece deduce tht = = = Let f(x) = + [ cosx + b six ] = Here = f(x) dx - = x dx - = x = o = 3 = f(x) cosx dx - = x cosx dx -
48 = x d six - = (x ) six (x)-cosx + () six 3 - = cos + cos = 4 (-) b = f(x) six dx - = x d -cosx - = (x ) cosx (x) -six + () cosx 3 - = - cos cos cos cos b = Substitutig the vues of, & b i equtio () we get f(x) = + 4 (-) cosx 6 = i.e, x = + 4 (-) cosx 3 = i.e, x = + 4 (-) cosx
49 3 = = + 4 -cosx + cosx cos3x x = - 4 cosx + cosx + cos3x () 3 3 Put x = i equtio () we get = i.e, + - = (3) 3 Put x = i equtio () we get = i.e, - = i.e, = (4) 3 6 Addig equtios (3) & (4) we get = i.e, = i.e, = Exmpe 3 Obti the Fourier Series of periodicity π for f(x) = e x i [-π, π] Let f(x) = ( cosx + b six) () =
50 π = f(x) dx π - π π = e x dx π - π π = [e x ] π - π = {e π e π } π = si hπ π π = f(x) cos x dx π - π π = e x cos x dx π - π π = e x [cosx + si x] π (+ ) -π = e π (-) e π (-) π + + = (-) ( e π - e π ) (+ ) π = ( -) si hπ π(+ ) π b = f(x) si x dx π - π π = e x si x dx π - π
51 π = e x (six cosx) π (+ ) -π = e π {-(-) } e - π {-(-) } π + + = (-) + ( e π - e π ) π(+ ) b = (-) + si hπ π(+ ) f(x) = si hπ + (-) sihπ cosx + (-)(-) sihπ six π = π(+ ) π(+ ) e x = si hπ + si hπ (-) π π = + (cos x si x) ie, e x = si hπ + (-) (cos x si x) π = + Exmpe 4 Let f (x) = x i (O, ) ( - x) i (, ) Fid the FS for f (x) d hece deduce tht = = (-) 8 Let f (x) = cosx + b si x () = Here = f(x) dx + f (x) dx o = x dx+ ( - x) dx o
52 x ( - x) = = = i.e, o = = x cos x dx + ( - x) cos x dx o si x si x = ---- x d ( - x) d si x -cos x si x cosx = ---- (x) () (-x) ( ) o cos cos cos = cos = = [( ) -] b = f(x) si x dx + f(x) si x dx o cos x cos x = ---- x d ( - x) d o cos x six cos x six = ---- (x) () (-x) ( )
53 o cos cos = = i.e, b =. f (x) = [ ( ) ] cos x = 4 cosx cos3x cos5x = () 3 5 Puttig x = i equtio(), we get 4 = i.e, = i.e, = = ( ) 8 Exmpe 5 Fid the Fourier series for f (x) = (x + x ) i (- < x < ) of percodicity d hece deduce tht (/ ) = /6. = Let f(x) = ( cosx + b six) = Here, = (x + x ) dx x x 3 =
54 3 3 = o = = f (x) cos x dx si x = (x + x ) d si x cosx six = (x + x ) (+x) () ( ) ( ) = (+ ) ( ) ( ) = b = f (x) si x dx cos x = (x + x ) d cosx six cosx = (x + x ) (+x) ()
55 ( ) ( ) ( ) ( ) = ( ) + b = ( ) ( ) + f(x) = cos x six 3 =. cosx cosx cos3x six = si x Here x = - d x = re the ed poits of the rge. The vue of FS t x = is the verge of the vues of f(x) t x = d x = -. f ( - ) + f () f(x) = = = Puttig x =, we get = i.e, =
56 Hece, = = 6 Exercises: Determie the Fourier expressios of the foowig fuctios i the give iterv.f(x) = ( - x), < x <.f(x) = i - < x < = i < x < 3.f(x) = x x i [-,] 4.f(x) = x(-x) i (,) 5.f(x) = sih x i [-, ] 6.f(x) = cosh x i [-, ] 7.f(x) = i < x < = i < x < 8.f(x) = -/4 whe - < x < = /4 whe < x < 9.f(x) = cosx, i - < x <, where is ot iteger.obti fourier series to represet e -x from x = - to x =. Hece derive the series for / sih.3 Eve d Odd fuctios A fuctio f(x) is sid to be eve if f (-x) = f (x). For exmpe x, cosx, x six, secx re eve fuctios. A fuctio f (x) is sid to be odd if f (-x) = - f (x). For exmpe, x 3, si x, x cos x,. re odd fuctios. () The Euer s formu for eve fuctio is f (x) = cosx = where o = ---- f(x) dx ; = f (x) cosx dx
57 () The Euer s formu for odd fuctio is f (x) = b si x = where b = f(x) si x dx Exmpe 6 Fid the Fourier Series for f (x) = x i ( -, ) Here, f(x) = x is odd fuctio. f(x) = b si x () = b = f (x) si x dx - cos x = x d cos x si x = (x) () cos = ( ) + b = ( ) + f (x)= si x = i.e, ( ) + x = si x = Exmpe 7
58 Expd f (x) = x i (-, ) s FS d hece deduce tht = Soutio Here f(x) = x is eve fuctio. o f (x) = cos x () = o = f(x) dx = x dx x = = = f (x) cos x dx si x = x d si x cos x = (x) () cos = = [( ) ] f (x)= [( ) ] cos x = 4 cos x cos3x cos5x
59 i.e, x = () 3 5 Puttig x = i equtio (), we get 4 = Hece, = Exmpe 8 x If f (x) = i ( -, ) x = i (, ) The fid the FS for f(x) d hece show tht (-) - = /8 = Here f (-x) i (-,) = f (x) i (,) f (-x) i (,) = f (x) i (-,) f(x) is eve fuctio o Let f (x) = cos x (). = x o = dx x = x =
60 x = cos x dx x si x = d x si x cosx = = [( ( ) ] 4 f (x)= [ ( ) ]cos x = 4 cos x cos3x cos5x = () 3 5 Put x = i equtio () we get or = = ( ) 8 Exmpe = ==> = Obti the FS expsio of f(x) = x six i (- < x<) d hece deduce tht =
61 Here f (x) = xsix is eve fuctio. o Let f (x) = cos x () = Now, o = xsi x dx = x d ( - cosx) = (x) (- cosx) () (- si x) = = f (x) cos x dx = x si x cosx dx = x [ si (+)x + si ( )x] dx cos (+)x cos ( ) x = x d cos (+)x cos ( ) x si (+)x si ( ) x = (x) () ( + ) ( ) cos (+) cos ( ) = [cos cos - si si] [cos cos - si si ]
62 = (+) ( ) + ( ) ( ) = ( ) = , Provided Whe = = x six cos x dx = x six dx - cosx = x d cos x -si x = (x) () Therefore, = -/ f (x)= cosx + cos x = ( -) = cosx cosx = - cosx cos3x cos4x ie, x six = cos x Puttig x = / i the bove equtio, we get
63 ----- = Hece, = Exercises: Determie Fourier expressios of the foowig fuctios i the give iterv: i. f(x) = / + x, - < x < / - x, < x < ii. f(x) = -x+ for + - < x < x+ for < x < iii. f(x) = six, - < x < iv. f(x) =x 3 i - < x < v. f(x) = xcosx, - < x < vi. f(x) = cosx, - < x < si si x si x 3si3x vii. Show tht for - < x <, si x = HALF RANGE SERIES It is ofte ecessry to obti Fourier expsio of fuctio for the rge (, ) which is hf the period of the Fourier series, the Fourier expsio of such fuctio cosists cosie or sie terms oy. (i) Hf Rge Cosie Series The Fourier cosie series for f(x) i the iterv (,) is give by f(x) = = cos x
64 where = f(x) dx d = f(x) cosx dx (ii) Hf Rge Sie Series The Fourier sie series for f(x) i the iterv (,) is give by f(x) = b six = where b = Exmpe f(x) six dx If c is the costt i ( < x < ) the show tht c = (4c / ) { six + (si3x /3) + si5x / 5) } Give f(x) = c i (,). Let f(x) = b six () = b = f(x) si x dx = c si x dx c - cosx = c -(-) = b = (c/) [ (-) ]
65 f(x) = (c / ) (-(-) ) six = Exmpe 4c si3x si5x i.e, c = --- six Fid the Fourier Hf Rge Sie Series d Cosie Series for f(x) = x i the iterv (,). Sie Series Let f(x) = b six () = Here b = f(x) sixdx = x d ( -cosx / ) - cosx - six = ---- (x) () (-) = (-) + b = f(x) = Cosie Series = ---- (-) + si x Let f(x) = cosx () = Here = f(x)dx
66 = xdx x = = = f(x) cosx dx = x d (six / ) six - cosx = ---- (x) () = (-) - f(x) = [ (-) - ] cosx = Exmpe 4 cosx cos3x cos5x => x = Fid the sie d cosie hf-rge series for the fuctio fuctio. f(x) = x, < x π/ = π-x, π/x< Sie series Let f (x) = b si x. =
67 π b = (/ ) f (x) si x dx =(/ ) / x si x dx + (-x) si x dx / / -cos x -cos x = (/ ) x.d + (-x) d / -cos x = (/ ) x -() -si x / cos x si x + (-x) - - -(-) - / -(/)cos (/) si (/) -(/)cos(/) si (/ ) = (/) + = (/) si(/) 4 = si (/) si(/) Therefore, f(x)= ( 4/ ) si x = si3x si5x ie, f (x)= ( 4/ ) six
68 Cosie series.let f(x) = ( o /) + cosx., where = o = (/) f(x) dx / =(/) x dx+ (-x) dx / 3 5 / =(/) (x /) + (x x /) = / / = (/) f(x) cosx dx =(/ ) / x cosx dx + (-x) cosx dx / / six six =(/ ) x d + (-x) d / six = (/ ) x -() -cosx / six cosx + (-x) -(-) - / ( /) si(/) cos (/) = (/) +
69 cosx ( /) si(/) cos (/) + + =(/) cos ( /) - {+(-) } cos ( /)- {+(-) } Therefore, f(x)= ( /4)+(/) cosx. = Exercises cos6x = ( /4)-(/) cosx Obti cosie d sie series for f(x) = x i the iterv < x <. Hece show tht / + /3 + /5 + = /8..Fid the hf rge cosie d sie series for f(x) = x i the rge < x < 3.Obti the hf-rge cosie series for the fuctio f(x) = xsix i (,).. 4.Obti cosie d sie series for f(x) = x (-x) i < x < 5.Fid the hf-rge cosie series for the fuctio 6.f(x) = (x) / 4, <x< (/) = (/4)(-x), / < x <. 7.Fid hf rge sie series d cosie series for f(x) = x i <x< (/) = i / < x <. 8.Fid hf rge sie series d cosie series for the fuctio f(x) == - x i the iterv < x <. 9.Fid the hf rge sie series of f(x) = x cosx i (,)
70 .Obti cosie series for f(x) = cos x, <x< (/) =, / < x <..5 Prsev s Theorem Root Me squre vue of the fuctio f(x) over iterv (, b) is defied s b [f(x)] dx [f (x)] r m s = b The use of r.m.s vue of periodic fuctio is frequety mde i the theory of mechic vibrtios d i eectric circuit theory. The r.m.s vue is so kow s the effective vue of the fuctio. Prsev s Theorem If f(x) defied i the iterv (c, c+π ), the the Prsev s Idetity is give by c+π [f (x)] c dx = (Rge) = ( π) o + ( + b ) 4 or o + ( + b ) 4 Exmpe 3 Obti the Fourier series for f(x) = x i π < x < π Hece show tht π = 9 π 4 (-) we hve o = 3, =, b =, for (Refer Exmpe ). By Prsev s Theorem, we hve π o
71 [ f(x)] dx = π + ½ ( + b ) = - π 4 π 4π 4 6(-) i.e, x 4 dx = π + / = - π 36 4 π π 4 i.e, x 5 = π + 8 = 5 -π 9 π 4 π 4 = + 8 = π 4 => = = Hece π = 9.6 CHANGE OF INTERVAL I most of the Egieerig ppictios, we require expsio of give fuctio over iterv other th. Suppose f(x) is fuctio defied i the iterv c< x < c+. The Fourier expsio for f(x) i the iterv c<x<c+ is give by x x f(x) = cos b si ---- = c+ where = f(x)dx c c+ = f(x) cos (x / ) dx & c c+ b = f(x) si (x / ) dx c
72 Eve d Odd Fuctio If f(x) is eve fuctio d is defied i the iterv ( c, c+ ), the x f(x) = cos ---- = where = f(x)dx = f(x) cos (x / ) dx If f(x) is odd fuctio d is defied i the iterv ( c, c+ ), the x f(x) = b si ---- = where b = f(x) si (x / ) dx Hf Rge Series Sie Series f(x) = b si ---- = x where b = f(x) si (x / ) dx Cosie series x f(x) = cos ---- =
73 where = f(x)dx = f(x) cos (x / ) dx Exmpe 4 Fid the Fourier series expsio for the fuctio f(x) = (c/)x i <x< = (c/)(- x) i <x< x x Let f (x) = cos b si = Now, = f(x)dx = (c/) x dx + (c/) ( - x) dx o = (c/) (x / ) + (c/) (x - x /) c = ---- = c = f(x) cos (x / ) dx x x = (c/)x cos dx + (c/)(- x) cos dx c si(x /) si(x /) = x d + (- x) d / /
74 x x si -cos c = ( x ) () x x si -cos + (- x) (-) c cos cos cos = + + c = { cos } c = { (-) } x b = f(x). si dx x x = (c/)x si dx + (c/)(- x) si dx c cos(x /) cos(x /) = x d - + (- x) d - / /
75 x x cos si c = (x) () x x cos si + (- x) (-) c cos cos = + =. c c { (-) } Therefore, f(x) = cos (x /) = Exmpe 5 Fid the Fourier series of periodicity 3 for f(x) = x x, i x 3. Here = 3. = 3 /. x x Let f (x) = cos b si = 3 3 where o = ( / 3) (x - x ) dx 3 = ( / 3) (x /) (x 3 /3) dx 3
76 =. 3 x = ( / 3) (x - x ) cos dx 3 3 si(x /3) = ( / 3) (x - x ) d (/3) si(x /3) cos(x /3) si(x/3) = ( / 3) (x - x ) ( -x) - + (-) - (/3) (4 /9) (8 3 3 /7) 3 = ( / 3) - ( 9 / ) ( 9 / ) = - 9 / 3 x b = ( / 3) (x - x ) si dx 3 3 cos(x /3) = ( / 3) (x - x ) d (/3) cos(x /3) si(x /3) cos(x/3) = ( / 3) (x - x ) ( -x) - (/3) (4 + (-) /9) (8 3 3 /7) 3 = ( / 3) ( 9 /) ( 7/ ) + ( 7/ ) x x Therefore, f (x) = - ( 9 / ) cos (3 / ) si = 3 3 Exercises = 3 /.Obti the Fourier series for f(x) = x i < x <..Fid the Fourier series to represet x i the iterv (-, ). 3.Fid Fourier series i (-, ), if f(x) =, - < x <
77 =, < x <. 4.Obti the Fourier series for f(x) = -x i < x < = i < x <. Hece deduce tht - (/3 ) +(/5) (/7) + = /4 & (/ ) + (/3 ) + (/5 ) + = ( /8) 5.If f(x) = x, < x < = (-x), < x <, Show tht i the iterv (,), cos x cos3x cos 5x f(x) = (/) (4/) Obti the Fourier series for f(x) = x i < x < = i < x < 7.Obti the Fourier series for f(x) = (cx / ) i < x < = (c/ ) ( - x ) i < x <. 8.Obti the Fourier series for f(x) = ( + x ), - < x <. = ( - x ), < x <. Deduce tht = ( ) 8 9.Obti hf-rge sie series for the fuctio f(x) = cx i < x < ( /) = c ( x) i (/) < x <.Express f(x) = x s hf rge sie series i < x <.Obti the hf-rge sie series for e x i < x <.
78 .Fid the hf rge cosie series for the fuctio f(x) = (x-) i the iterv < x <. Deduce tht = ( ) 8.7 Hrmoic Aysis The process of fidig the Fourier series for fuctio give by umeric vues is kow s hrmoic ysis. f(x) six & b = [me vues of f(x) six] = I (), the term ( cosx + b six) is ced the fudmet or first hrmoic, the term ( cosx + b six) is ced the secod hrmoic d so o. Exmpe 6 f (x) = ( cosx + b six), where = ie, f(x) = ( /) + ( cosx + b six) + ( cosx + b six) + ( 3 cos3x + b 3 si3x) () f(x) Here = [me vues of f(x)] = f(x) cosx = [me vues of f(x) cosx] = Compute the first three hrmoics of the Fourier series of f(x) give by the foowig tbe. x: π/3 π/3 π 4π/3 5π/3 π f(x): We excude the st poit x = π. Let f(x) = ( /) + ( cosx + b six) + ( cosx + b six) + To evute the coefficiets, we form the foowig tbe.
79 x f(x) cosx six cosx six cos3x si3x. π/ π/ π π/ π/ f(x) ( ) Now, = = = f(x) cosx = = f(x) cosx = = -. 6 f(x) cos3x 3 = =.33 6 f(x) six b = =.7 6 f(x) six b = = f(x) si3x b 3 = = 6 f(x) =.45.37cosx +.7 six.cosx.6 six +.33 cos3x+ Exmpe 7 Obti the first three coefficiets i the Fourier cosie series for y, where y is give i the foowig tbe: x: y: Tkig the iterv s 6 o, we hve : o 6 o o 8 o 4 o 3 o x: y: Fourier cosie series i the iterv (, π) is y = ( /) + cos + cos + 3 cos3 +.. To evute the coefficiets, we form the foowig tbe.
3.1 Laplace s Equation 3.2 The Method of Images 3.3 Separation of Variables
 Lecture Note #3B Chpter 3. Potetis 3. Lpce s Equtio 3. The Method of Imges 3.3 Seprtio of ribes 3.3. Crtesi Coordites 3.3. Spheric coordites 3.4 Mutipoe Expsio Boudry coditios re very importt to sove the
Lecture Note #3B Chpter 3. Potetis 3. Lpce s Equtio 3. The Method of Imges 3.3 Seprtio of ribes 3.3. Crtesi Coordites 3.3. Spheric coordites 3.4 Mutipoe Expsio Boudry coditios re very importt to sove the
INFINITE SERIES. ,... having infinite number of terms is called infinite sequence and its indicated sum, i.e., a 1
 Appedix A.. Itroductio As discussed i the Chpter 9 o Sequeces d Series, sequece,,...,,... hvig ifiite umber of terms is clled ifiite sequece d its idicted sum, i.e., + + +... + +... is clled ifite series
Appedix A.. Itroductio As discussed i the Chpter 9 o Sequeces d Series, sequece,,...,,... hvig ifiite umber of terms is clled ifiite sequece d its idicted sum, i.e., + + +... + +... is clled ifite series
MATH 174: Numerical Analysis. Lecturer: Jomar F. Rabajante 1 st Sem AY
 MATH 74: Numeric Aysis Lecturer: Jomr F. Rbjte st Sem AY - INTERPOLATION THEORY We wt to seect fuctio p from give css of fuctios i such wy tht the grph of y=p psses through fiite set of give dt poits odes.
MATH 74: Numeric Aysis Lecturer: Jomr F. Rbjte st Sem AY - INTERPOLATION THEORY We wt to seect fuctio p from give css of fuctios i such wy tht the grph of y=p psses through fiite set of give dt poits odes.
If a is any non zero real or imaginary number and m is the positive integer, then a...
 Idices d Surds.. Defiitio of Idices. If is o ero re or igir uer d is the positive iteger the...... ties. Here is ced the se d the ide power or epoet... Lws of Idices. 0 0 0. where d re rtio uers where
Idices d Surds.. Defiitio of Idices. If is o ero re or igir uer d is the positive iteger the...... ties. Here is ced the se d the ide power or epoet... Lws of Idices. 0 0 0. where d re rtio uers where
0 otherwise. sin( nx)sin( kx) 0 otherwise. cos( nx) sin( kx) dx 0 for all integers n, k.
 . Computtio of Fourier Series I this sectio, we compute the Fourier coefficiets, f ( x) cos( x) b si( x) d b, i the Fourier series To do this, we eed the followig result o the orthogolity of the trigoometric
. Computtio of Fourier Series I this sectio, we compute the Fourier coefficiets, f ( x) cos( x) b si( x) d b, i the Fourier series To do this, we eed the followig result o the orthogolity of the trigoometric
1. (25 points) Use the limit definition of the definite integral and the sum formulas to compute. [1 x + x2
 Mth 3, Clculus II Fil Exm Solutios. (5 poits) Use the limit defiitio of the defiite itegrl d the sum formuls to compute 3 x + x. Check your swer by usig the Fudmetl Theorem of Clculus. Solutio: The limit
Mth 3, Clculus II Fil Exm Solutios. (5 poits) Use the limit defiitio of the defiite itegrl d the sum formuls to compute 3 x + x. Check your swer by usig the Fudmetl Theorem of Clculus. Solutio: The limit
INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
 Mthemtics Revisio Guides Itegrtig Trig, Log d Ep Fuctios Pge of MK HOME TUITION Mthemtics Revisio Guides Level: AS / A Level AQA : C Edecel: C OCR: C OCR MEI: C INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
Mthemtics Revisio Guides Itegrtig Trig, Log d Ep Fuctios Pge of MK HOME TUITION Mthemtics Revisio Guides Level: AS / A Level AQA : C Edecel: C OCR: C OCR MEI: C INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK SUMMER EXAMINATION 2005 FIRST ENGINEERING
 OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK SUMMER EXAMINATION 2005 FIRST ENGINEERING MATHEMATICS MA008 Clculus d Lier
OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK SUMMER EXAMINATION 2005 FIRST ENGINEERING MATHEMATICS MA008 Clculus d Lier
We will begin by supplying the proof to (a).
 (The solutios of problem re mostly from Jeffrey Mudrock s HWs) Problem 1. There re three sttemet from Exmple 5.4 i the textbook for which we will supply proofs. The sttemets re the followig: () The spce
(The solutios of problem re mostly from Jeffrey Mudrock s HWs) Problem 1. There re three sttemet from Exmple 5.4 i the textbook for which we will supply proofs. The sttemets re the followig: () The spce
Strauss PDEs 2e: Section Exercise 4 Page 1 of 5. u tt = c 2 u xx ru t for 0 < x < l u = 0 at both ends u(x, 0) = φ(x) u t (x, 0) = ψ(x),
 Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
MAS221 Analysis, Semester 2 Exercises
 MAS22 Alysis, Semester 2 Exercises Srh Whitehouse (Exercises lbelled * my be more demdig.) Chpter Problems: Revisio Questio () Stte the defiitio of covergece of sequece of rel umbers, ( ), to limit. (b)
MAS22 Alysis, Semester 2 Exercises Srh Whitehouse (Exercises lbelled * my be more demdig.) Chpter Problems: Revisio Questio () Stte the defiitio of covergece of sequece of rel umbers, ( ), to limit. (b)
F x = 2x λy 2 z 3 = 0 (1) F y = 2y λ2xyz 3 = 0 (2) F z = 2z λ3xy 2 z 2 = 0 (3) F λ = (xy 2 z 3 2) = 0. (4) 2z 3xy 2 z 2. 2x y 2 z 3 = 2y 2xyz 3 = ) 2
 0 微甲 07- 班期中考解答和評分標準 5%) Fid the poits o the surfce xy z = tht re closest to the origi d lso the shortest distce betwee the surfce d the origi Solutio Cosider the Lgrge fuctio F x, y, z, λ) = x + y + z
0 微甲 07- 班期中考解答和評分標準 5%) Fid the poits o the surfce xy z = tht re closest to the origi d lso the shortest distce betwee the surfce d the origi Solutio Cosider the Lgrge fuctio F x, y, z, λ) = x + y + z
PROGRESSIONS AND SERIES
 PROGRESSIONS AND SERIES A sequece is lso clled progressio. We ow study three importt types of sequeces: () The Arithmetic Progressio, () The Geometric Progressio, () The Hrmoic Progressio. Arithmetic Progressio.
PROGRESSIONS AND SERIES A sequece is lso clled progressio. We ow study three importt types of sequeces: () The Arithmetic Progressio, () The Geometric Progressio, () The Hrmoic Progressio. Arithmetic Progressio.
Sequence and Series of Functions
 6 Sequece d Series of Fuctios 6. Sequece of Fuctios 6.. Poitwise Covergece d Uiform Covergece Let J be itervl i R. Defiitio 6. For ech N, suppose fuctio f : J R is give. The we sy tht sequece (f ) of fuctios
6 Sequece d Series of Fuctios 6. Sequece of Fuctios 6.. Poitwise Covergece d Uiform Covergece Let J be itervl i R. Defiitio 6. For ech N, suppose fuctio f : J R is give. The we sy tht sequece (f ) of fuctios
z-transform A generalization of the DTFT defined by
 The DTFT provides frequecy-domi represettio of discrete-time sigs d LTI discrete-time systems Becuse of the covergece coditio, i my cses, the DTFT of sequece my ot exist As resut, it is ot possie to mke
The DTFT provides frequecy-domi represettio of discrete-time sigs d LTI discrete-time systems Becuse of the covergece coditio, i my cses, the DTFT of sequece my ot exist As resut, it is ot possie to mke
Schrödinger Equation Via Laplace-Beltrami Operator
 IOSR Jourl of Mthemtics (IOSR-JM) e-issn: 78-578, p-issn: 39-765X. Volume 3, Issue 6 Ver. III (Nov. - Dec. 7), PP 9-95 www.iosrjourls.org Schrödiger Equtio Vi Lplce-Beltrmi Opertor Esi İ Eskitşçioğlu,
IOSR Jourl of Mthemtics (IOSR-JM) e-issn: 78-578, p-issn: 39-765X. Volume 3, Issue 6 Ver. III (Nov. - Dec. 7), PP 9-95 www.iosrjourls.org Schrödiger Equtio Vi Lplce-Beltrmi Opertor Esi İ Eskitşçioğlu,
radians A function f ( x ) is called periodic if it is defined for all real x and if there is some positive number P such that:
 Fourier Series. Graph of y Asix ad y Acos x Amplitude A ; period 36 radias. Harmoics y y six is the first harmoic y y six is the th harmoics 3. Periodic fuctio A fuctio f ( x ) is called periodic if it
Fourier Series. Graph of y Asix ad y Acos x Amplitude A ; period 36 radias. Harmoics y y six is the first harmoic y y six is the th harmoics 3. Periodic fuctio A fuctio f ( x ) is called periodic if it
POWER SERIES R. E. SHOWALTER
 POWER SERIES R. E. SHOWALTER. sequeces We deote by lim = tht the limit of the sequece { } is the umber. By this we me tht for y ε > 0 there is iteger N such tht < ε for ll itegers N. This mkes precise
POWER SERIES R. E. SHOWALTER. sequeces We deote by lim = tht the limit of the sequece { } is the umber. By this we me tht for y ε > 0 there is iteger N such tht < ε for ll itegers N. This mkes precise
FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES. To a 2π-periodic function f(x) we will associate a trigonometric series. a n cos(nx) + b n sin(nx),
 FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES To -periodic fuctio f() we will ssocite trigoometric series + cos() + b si(), or i terms of the epoetil e i, series of the form c e i. Z For most of the
FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES To -periodic fuctio f() we will ssocite trigoometric series + cos() + b si(), or i terms of the epoetil e i, series of the form c e i. Z For most of the
Fourier Series and their Applications
 Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Notes 17 Sturm-Liouville Theory
 ECE 638 Fll 017 Dvid R. Jckso Notes 17 Sturm-Liouville Theory Notes re from D. R. Wilto, Dept. of ECE 1 Secod-Order Lier Differetil Equtios (SOLDE) A SOLDE hs the form d y dy 0 1 p ( x) + p ( x) + p (
ECE 638 Fll 017 Dvid R. Jckso Notes 17 Sturm-Liouville Theory Notes re from D. R. Wilto, Dept. of ECE 1 Secod-Order Lier Differetil Equtios (SOLDE) A SOLDE hs the form d y dy 0 1 p ( x) + p ( x) + p (
( a n ) converges or diverges.
 Chpter Ifiite Series Pge of Sectio E Rtio Test Chpter : Ifiite Series By the ed of this sectio you will be ble to uderstd the proof of the rtio test test series for covergece by pplyig the rtio test pprecite
Chpter Ifiite Series Pge of Sectio E Rtio Test Chpter : Ifiite Series By the ed of this sectio you will be ble to uderstd the proof of the rtio test test series for covergece by pplyig the rtio test pprecite
: Transforms and Partial Differential Equations
 Trasforms ad Partial Differetial Equatios 018 SUBJECT NAME : Trasforms ad Partial Differetial Equatios SUBJECT CODE : MA 6351 MATERIAL NAME : Part A questios REGULATION : R013 WEBSITE : wwwharigaeshcom
Trasforms ad Partial Differetial Equatios 018 SUBJECT NAME : Trasforms ad Partial Differetial Equatios SUBJECT CODE : MA 6351 MATERIAL NAME : Part A questios REGULATION : R013 WEBSITE : wwwharigaeshcom
19 Fourier Series and Practical Harmonic Analysis
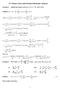 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
Taylor series expansion of nonlinear integrodifferential equations
 AMERCA JOURAL OF SCEFC AD DUSRAL RESEARCH 2, Sciece Huβ, http://www.scihu.org/ajsr SS: 253-649X doi:.525/jsir.2.2.3.376.38 yor series expsio of oier itegrodiffereti equtios Eke A.. d 2 Jckreece P. C. Deprtet
AMERCA JOURAL OF SCEFC AD DUSRAL RESEARCH 2, Sciece Huβ, http://www.scihu.org/ajsr SS: 253-649X doi:.525/jsir.2.2.3.376.38 yor series expsio of oier itegrodiffereti equtios Eke A.. d 2 Jckreece P. C. Deprtet
Math 124B January 24, 2012
 Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
Chapter 7 Infinite Series
 MA Ifiite Series Asst.Prof.Dr.Supree Liswdi Chpter 7 Ifiite Series Sectio 7. Sequece A sequece c be thought of s list of umbers writte i defiite order:,,...,,... 2 The umber is clled the first term, 2
MA Ifiite Series Asst.Prof.Dr.Supree Liswdi Chpter 7 Ifiite Series Sectio 7. Sequece A sequece c be thought of s list of umbers writte i defiite order:,,...,,... 2 The umber is clled the first term, 2
Name of the Student:
 SUBJECT NAME : Trasforms ad Partial Diff Eq SUBJECT CODE : MA MATERIAL NAME : Problem Material MATERIAL CODE : JM8AM6 REGULATION : R8 UPDATED ON : April-May 4 (Sca the above QR code for the direct dowload
SUBJECT NAME : Trasforms ad Partial Diff Eq SUBJECT CODE : MA MATERIAL NAME : Problem Material MATERIAL CODE : JM8AM6 REGULATION : R8 UPDATED ON : April-May 4 (Sca the above QR code for the direct dowload
ALGEBRA. Set of Equations. have no solution 1 b1. Dependent system has infinitely many solutions
 Qudrtic Equtios ALGEBRA Remider theorem: If f() is divided b( ), the remider is f(). Fctor theorem: If ( ) is fctor of f(), the f() = 0. Ivolutio d Evlutio ( + b) = + b + b ( b) = + b b ( + b) 3 = 3 +
Qudrtic Equtios ALGEBRA Remider theorem: If f() is divided b( ), the remider is f(). Fctor theorem: If ( ) is fctor of f(), the f() = 0. Ivolutio d Evlutio ( + b) = + b + b ( b) = + b b ( + b) 3 = 3 +
UNIVERSITY OF BRISTOL. Examination for the Degrees of B.Sc. and M.Sci. (Level C/4) ANALYSIS 1B, SOLUTIONS MATH (Paper Code MATH-10006)
 UNIVERSITY OF BRISTOL Exmitio for the Degrees of B.Sc. d M.Sci. (Level C/4) ANALYSIS B, SOLUTIONS MATH 6 (Pper Code MATH-6) My/Jue 25, hours 3 miutes This pper cotis two sectios, A d B. Plese use seprte
UNIVERSITY OF BRISTOL Exmitio for the Degrees of B.Sc. d M.Sci. (Level C/4) ANALYSIS B, SOLUTIONS MATH 6 (Pper Code MATH-6) My/Jue 25, hours 3 miutes This pper cotis two sectios, A d B. Plese use seprte
Review of the Riemann Integral
 Chpter 1 Review of the Riem Itegrl This chpter provides quick review of the bsic properties of the Riem itegrl. 1.0 Itegrls d Riem Sums Defiitio 1.0.1. Let [, b] be fiite, closed itervl. A prtitio P of
Chpter 1 Review of the Riem Itegrl This chpter provides quick review of the bsic properties of the Riem itegrl. 1.0 Itegrls d Riem Sums Defiitio 1.0.1. Let [, b] be fiite, closed itervl. A prtitio P of
Week 13 Notes: 1) Riemann Sum. Aim: Compute Area Under a Graph. Suppose we want to find out the area of a graph, like the one on the right:
 Week 1 Notes: 1) Riem Sum Aim: Compute Are Uder Grph Suppose we wt to fid out the re of grph, like the oe o the right: We wt to kow the re of the red re. Here re some wys to pproximte the re: We cut the
Week 1 Notes: 1) Riem Sum Aim: Compute Are Uder Grph Suppose we wt to fid out the re of grph, like the oe o the right: We wt to kow the re of the red re. Here re some wys to pproximte the re: We cut the
MAGIC058 & MATH64062: Partial Differential Equations 1
 MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
MA6351-TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS SUBJECT NOTES. Department of Mathematics FATIMA MICHAEL COLLEGE OF ENGINEERING & TECHNOLOGY
 MA635-TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS SUBJECT NOTES Deprtmet of Mthemtics FATIMA MICHAEL COLLEGE OF ENGINEERING & TECHNOLOGY MADURAI 65, Tmildu, Idi Bsic Formule DIFFERENTIATION &INTEGRATION
MA635-TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS SUBJECT NOTES Deprtmet of Mthemtics FATIMA MICHAEL COLLEGE OF ENGINEERING & TECHNOLOGY MADURAI 65, Tmildu, Idi Bsic Formule DIFFERENTIATION &INTEGRATION
SUTCLIFFE S NOTES: CALCULUS 2 SWOKOWSKI S CHAPTER 11
 UTCLIFFE NOTE: CALCULU WOKOWKI CHAPTER Ifiite eries Coverget or Diverget eries Cosider the sequece If we form the ifiite sum 0, 00, 000, 0 00 000, we hve wht is clled ifiite series We wt to fid the sum
UTCLIFFE NOTE: CALCULU WOKOWKI CHAPTER Ifiite eries Coverget or Diverget eries Cosider the sequece If we form the ifiite sum 0, 00, 000, 0 00 000, we hve wht is clled ifiite series We wt to fid the sum
FACULTY OF MATHEMATICAL STUDIES MATHEMATICS FOR PART I ENGINEERING. Lectures
 FACULTY OF MATHEMATICAL STUDIES MATHEMATICS FOR PART I ENGINEERING Lectures MODULE 0 FURTHER CALCULUS II. Sequeces d series. Rolle s theorem d me vlue theorems 3. Tlor s d Mcluri s theorems 4. L Hopitl
FACULTY OF MATHEMATICAL STUDIES MATHEMATICS FOR PART I ENGINEERING Lectures MODULE 0 FURTHER CALCULUS II. Sequeces d series. Rolle s theorem d me vlue theorems 3. Tlor s d Mcluri s theorems 4. L Hopitl
Linford 1. Kyle Linford. Math 211. Honors Project. Theorems to Analyze: Theorem 2.4 The Limit of a Function Involving a Radical (A4)
 Liford 1 Kyle Liford Mth 211 Hoors Project Theorems to Alyze: Theorem 2.4 The Limit of Fuctio Ivolvig Rdicl (A4) Theorem 2.8 The Squeeze Theorem (A5) Theorem 2.9 The Limit of Si(x)/x = 1 (p. 85) Theorem
Liford 1 Kyle Liford Mth 211 Hoors Project Theorems to Alyze: Theorem 2.4 The Limit of Fuctio Ivolvig Rdicl (A4) Theorem 2.8 The Squeeze Theorem (A5) Theorem 2.9 The Limit of Si(x)/x = 1 (p. 85) Theorem
In an algebraic expression of the form (1), like terms are terms with the same power of the variables (in this case
 Chpter : Algebr: A. Bckgroud lgebr: A. Like ters: I lgebric expressio of the for: () x b y c z x y o z d x... p x.. we cosider x, y, z to be vribles d, b, c, d,,, o,.. to be costts. I lgebric expressio
Chpter : Algebr: A. Bckgroud lgebr: A. Like ters: I lgebric expressio of the for: () x b y c z x y o z d x... p x.. we cosider x, y, z to be vribles d, b, c, d,,, o,.. to be costts. I lgebric expressio
Eigenfunction Expansion. For a given function on the internal a x b the eigenfunction expansion of f(x):
 Eigefuctio Epsio: For give fuctio o the iterl the eigefuctio epsio of f(): f ( ) cmm( ) m 1 Eigefuctio Epsio (Geerlized Fourier Series) To determie c s we multiply oth sides y Φ ()r() d itegrte: f ( )
Eigefuctio Epsio: For give fuctio o the iterl the eigefuctio epsio of f(): f ( ) cmm( ) m 1 Eigefuctio Epsio (Geerlized Fourier Series) To determie c s we multiply oth sides y Φ ()r() d itegrte: f ( )
[ 20 ] 1. Inequality exists only between two real numbers (not complex numbers). 2. If a be any real number then one and only one of there hold.
![[ 20 ] 1. Inequality exists only between two real numbers (not complex numbers). 2. If a be any real number then one and only one of there hold. [ 20 ] 1. Inequality exists only between two real numbers (not complex numbers). 2. If a be any real number then one and only one of there hold.](/thumbs/78/77732161.jpg) [ 0 ]. Iequlity eists oly betwee two rel umbers (ot comple umbers).. If be y rel umber the oe d oly oe of there hold.. If, b 0 the b 0, b 0.. (i) b if b 0 (ii) (iii) (iv) b if b b if either b or b b if
[ 0 ]. Iequlity eists oly betwee two rel umbers (ot comple umbers).. If be y rel umber the oe d oly oe of there hold.. If, b 0 the b 0, b 0.. (i) b if b 0 (ii) (iii) (iv) b if b b if either b or b b if
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Repeated Root and Common Root
 Repeted Root d Commo Root 1 (Method 1) Let α, β, γ e the roots of p(x) x + x + 0 (1) The α + β + γ 0, αβ + βγ + γα, αβγ - () (α - β) (α + β) - αβ (α + β) [ (βγ + γα)] + [(α + β) + γ (α + β)] +γ (α + β)
Repeted Root d Commo Root 1 (Method 1) Let α, β, γ e the roots of p(x) x + x + 0 (1) The α + β + γ 0, αβ + βγ + γα, αβγ - () (α - β) (α + β) - αβ (α + β) [ (βγ + γα)] + [(α + β) + γ (α + β)] +γ (α + β)
Unit 1. Extending the Number System. 2 Jordan School District
 Uit Etedig the Number System Jord School District Uit Cluster (N.RN. & N.RN.): Etedig Properties of Epoets Cluster : Etedig properties of epoets.. Defie rtiol epoets d eted the properties of iteger epoets
Uit Etedig the Number System Jord School District Uit Cluster (N.RN. & N.RN.): Etedig Properties of Epoets Cluster : Etedig properties of epoets.. Defie rtiol epoets d eted the properties of iteger epoets
BRAIN TEASURES INDEFINITE INTEGRATION+DEFINITE INTEGRATION EXERCISE I
 EXERCISE I t Q. d Q. 6 6 cos si Q. Q.6 d d Q. d Q. Itegrte cos t d by the substitutio z = + e d e Q.7 cos. l cos si d d Q. cos si si si si b cos Q.9 d Q. si b cos Q. si( ) si( ) d ( ) Q. d cot d d Q. (si
EXERCISE I t Q. d Q. 6 6 cos si Q. Q.6 d d Q. d Q. Itegrte cos t d by the substitutio z = + e d e Q.7 cos. l cos si d d Q. cos si si si si b cos Q.9 d Q. si b cos Q. si( ) si( ) d ( ) Q. d cot d d Q. (si
Review of Sections
 Review of Sectios.-.6 Mrch 24, 204 Abstrct This is the set of otes tht reviews the mi ides from Chpter coverig sequeces d series. The specific sectios tht we covered re s follows:.: Sequces..2: Series,
Review of Sectios.-.6 Mrch 24, 204 Abstrct This is the set of otes tht reviews the mi ides from Chpter coverig sequeces d series. The specific sectios tht we covered re s follows:.: Sequces..2: Series,
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Linear Programming. Preliminaries
 Lier Progrmmig Prelimiries Optimiztio ethods: 3L Objectives To itroduce lier progrmmig problems (LPP To discuss the stdrd d coicl form of LPP To discuss elemetry opertio for lier set of equtios Optimiztio
Lier Progrmmig Prelimiries Optimiztio ethods: 3L Objectives To itroduce lier progrmmig problems (LPP To discuss the stdrd d coicl form of LPP To discuss elemetry opertio for lier set of equtios Optimiztio
LEVEL I. ,... if it is known that a 1
 LEVEL I Fid the sum of first terms of the AP, if it is kow tht + 5 + 0 + 5 + 0 + = 5 The iterior gles of polygo re i rithmetic progressio The smllest gle is 0 d the commo differece is 5 Fid the umber of
LEVEL I Fid the sum of first terms of the AP, if it is kow tht + 5 + 0 + 5 + 0 + = 5 The iterior gles of polygo re i rithmetic progressio The smllest gle is 0 d the commo differece is 5 Fid the umber of
Topics in Fourier Analysis-I 1
 Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Lesson-2 PROGRESSIONS AND SERIES
 Lesso- PROGRESSIONS AND SERIES Arithmetic Progressio: A sequece of terms is sid to be i rithmetic progressio (A.P) whe the differece betwee y term d its preceedig term is fixed costt. This costt is clled
Lesso- PROGRESSIONS AND SERIES Arithmetic Progressio: A sequece of terms is sid to be i rithmetic progressio (A.P) whe the differece betwee y term d its preceedig term is fixed costt. This costt is clled
Infinite Series Sequences: terms nth term Listing Terms of a Sequence 2 n recursively defined n+1 Pattern Recognition for Sequences Ex:
 Ifiite Series Sequeces: A sequece i defied s fuctio whose domi is the set of positive itegers. Usully it s esier to deote sequece i subscript form rther th fuctio ottio.,, 3, re the terms of the sequece
Ifiite Series Sequeces: A sequece i defied s fuctio whose domi is the set of positive itegers. Usully it s esier to deote sequece i subscript form rther th fuctio ottio.,, 3, re the terms of the sequece
Fourier Series and Applications
 9/7/9 Fourier Series d Applictios Fuctios epsio is doe to uderstd the better i powers o etc. My iportt probles ivolvig prtil dieretil equtios c be solved provided give uctio c be epressed s iiite su o
9/7/9 Fourier Series d Applictios Fuctios epsio is doe to uderstd the better i powers o etc. My iportt probles ivolvig prtil dieretil equtios c be solved provided give uctio c be epressed s iiite su o
Chapter 5. The Riemann Integral. 5.1 The Riemann integral Partitions and lower and upper integrals. Note: 1.5 lectures
 Chpter 5 The Riem Itegrl 5.1 The Riem itegrl Note: 1.5 lectures We ow get to the fudmetl cocept of itegrtio. There is ofte cofusio mog studets of clculus betwee itegrl d tiderivtive. The itegrl is (iformlly)
Chpter 5 The Riem Itegrl 5.1 The Riem itegrl Note: 1.5 lectures We ow get to the fudmetl cocept of itegrtio. There is ofte cofusio mog studets of clculus betwee itegrl d tiderivtive. The itegrl is (iformlly)
Statistics for Financial Engineering Session 1: Linear Algebra Review March 18 th, 2006
 Sttistics for Ficil Egieerig Sessio : Lier Algebr Review rch 8 th, 6 Topics Itroductio to trices trix opertios Determits d Crmer s rule Eigevlues d Eigevectors Quiz The cotet of Sessio my be fmilir to
Sttistics for Ficil Egieerig Sessio : Lier Algebr Review rch 8 th, 6 Topics Itroductio to trices trix opertios Determits d Crmer s rule Eigevlues d Eigevectors Quiz The cotet of Sessio my be fmilir to
lecture 16: Introduction to Least Squares Approximation
 97 lecture 16: Itroductio to Lest Squres Approximtio.4 Lest squres pproximtio The miimx criterio is ituitive objective for pproximtig fuctio. However, i my cses it is more ppelig (for both computtio d
97 lecture 16: Itroductio to Lest Squres Approximtio.4 Lest squres pproximtio The miimx criterio is ituitive objective for pproximtig fuctio. However, i my cses it is more ppelig (for both computtio d
Solutions to Final Exam Review Problems
 . Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
. Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD
 Diol Bgoo () A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD I. Itroductio The first seprtio of vribles (see pplictios to Newto s equtios) is ver useful method
Diol Bgoo () A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD I. Itroductio The first seprtio of vribles (see pplictios to Newto s equtios) is ver useful method
Chapter System of Equations
 hpter 4.5 System of Equtios After redig th chpter, you should be ble to:. setup simulteous lier equtios i mtrix form d vice-vers,. uderstd the cocept of the iverse of mtrix, 3. kow the differece betwee
hpter 4.5 System of Equtios After redig th chpter, you should be ble to:. setup simulteous lier equtios i mtrix form d vice-vers,. uderstd the cocept of the iverse of mtrix, 3. kow the differece betwee
EVALUATING DEFINITE INTEGRALS
 Chpter 4 EVALUATING DEFINITE INTEGRALS If the defiite itegrl represets re betwee curve d the x-xis, d if you c fid the re by recogizig the shpe of the regio, the you c evlute the defiite itegrl. Those
Chpter 4 EVALUATING DEFINITE INTEGRALS If the defiite itegrl represets re betwee curve d the x-xis, d if you c fid the re by recogizig the shpe of the regio, the you c evlute the defiite itegrl. Those
sin m a d F m d F m h F dy a dy a D h m h m, D a D a c1cosh c3cos 0
 Q1. The free vibrtio of the plte is give by By ssumig h w w D t, si cos w W x y t B t Substitutig the deflectio ito the goverig equtio yields For the plte give, the mode shpe W hs the form h D W W W si
Q1. The free vibrtio of the plte is give by By ssumig h w w D t, si cos w W x y t B t Substitutig the deflectio ito the goverig equtio yields For the plte give, the mode shpe W hs the form h D W W W si
DETERMINANT. = 0. The expression a 1. is called a determinant of the second order, and is denoted by : y + c 1
 NOD6 (\Dt\04\Kot\J-Advced\SMP\Mths\Uit#0\NG\Prt-\0.Determits\0.Theory.p65. INTRODUCTION : If the equtios x + b 0, x + b 0 re stisfied by the sme vlue of x, the b b 0. The expressio b b is clled determit
NOD6 (\Dt\04\Kot\J-Advced\SMP\Mths\Uit#0\NG\Prt-\0.Determits\0.Theory.p65. INTRODUCTION : If the equtios x + b 0, x + b 0 re stisfied by the sme vlue of x, the b b 0. The expressio b b is clled determit
5.1 - Areas and Distances
 Mth 3B Midterm Review Writte by Victori Kl vtkl@mth.ucsb.edu SH 63u Office Hours: R 9:5 - :5m The midterm will cover the sectios for which you hve received homework d feedbck Sectios.9-6.5 i your book.
Mth 3B Midterm Review Writte by Victori Kl vtkl@mth.ucsb.edu SH 63u Office Hours: R 9:5 - :5m The midterm will cover the sectios for which you hve received homework d feedbck Sectios.9-6.5 i your book.
Solution of the exam in TMA4212 Monday 23rd May 2013 Time: 9:00 13:00
 Norwegi Uiversity of Sciece d Techology Deprtmet of Mthemticl Scieces Cotct durig the exm: Ele Celledoi, tlf. 735 93541 Pge 1 of 7 of the exm i TMA4212 Mody 23rd My 2013 Time: 9:00 13:00 Allowed ids: Approved
Norwegi Uiversity of Sciece d Techology Deprtmet of Mthemticl Scieces Cotct durig the exm: Ele Celledoi, tlf. 735 93541 Pge 1 of 7 of the exm i TMA4212 Mody 23rd My 2013 Time: 9:00 13:00 Allowed ids: Approved
SOLVING FUZZY LINEAR PROGRAMMING PROBLEM USING SUPPORT AND CORE OF FUZZY NUMBERS
 Itertio Jor of Scietific Reserch Egieerig & Techoogy (IJSRET ISSN 78 88 Vome 6 Isse 4 pri 7 44 SOLVING FUZZY LINER PROGRMMING PROBLEM USING SUPPORT ND CORE OF FUZZY NUMBERS Dr.S.Rmthigm K.Bmrg sst. Professor
Itertio Jor of Scietific Reserch Egieerig & Techoogy (IJSRET ISSN 78 88 Vome 6 Isse 4 pri 7 44 SOLVING FUZZY LINER PROGRMMING PROBLEM USING SUPPORT ND CORE OF FUZZY NUMBERS Dr.S.Rmthigm K.Bmrg sst. Professor
Math 3B Midterm Review
 Mth 3B Midterm Review Writte by Victori Kl vtkl@mth.ucsb.edu SH 643u Office Hours: R 11:00 m - 1:00 pm Lst updted /15/015 Here re some short otes o Sectios 7.1-7.8 i your ebook. The best idictio of wht
Mth 3B Midterm Review Writte by Victori Kl vtkl@mth.ucsb.edu SH 643u Office Hours: R 11:00 m - 1:00 pm Lst updted /15/015 Here re some short otes o Sectios 7.1-7.8 i your ebook. The best idictio of wht
Section 6.3: Geometric Sequences
 40 Chpter 6 Sectio 6.: Geometric Sequeces My jobs offer ul cost-of-livig icrese to keep slries cosistet with ifltio. Suppose, for exmple, recet college grdute fids positio s sles mger erig ul slry of $6,000.
40 Chpter 6 Sectio 6.: Geometric Sequeces My jobs offer ul cost-of-livig icrese to keep slries cosistet with ifltio. Suppose, for exmple, recet college grdute fids positio s sles mger erig ul slry of $6,000.
The Definite Riemann Integral
 These otes closely follow the presettio of the mteril give i Jmes Stewrt s textook Clculus, Cocepts d Cotexts (d editio). These otes re iteded primrily for i-clss presettio d should ot e regrded s sustitute
These otes closely follow the presettio of the mteril give i Jmes Stewrt s textook Clculus, Cocepts d Cotexts (d editio). These otes re iteded primrily for i-clss presettio d should ot e regrded s sustitute
ECEN 644 HOMEWORK #5 SOLUTION SET
 ECE 644 HOMEWORK #5 SOUTIO SET 7. x is a real valued sequece. The first five poits of its 8-poit DFT are: {0.5, 0.5 - j 0.308, 0, 0.5 - j 0.058, 0} To compute the 3 remaiig poits, we ca use the followig
ECE 644 HOMEWORK #5 SOUTIO SET 7. x is a real valued sequece. The first five poits of its 8-poit DFT are: {0.5, 0.5 - j 0.308, 0, 0.5 - j 0.058, 0} To compute the 3 remaiig poits, we ca use the followig
Numerical Methods in Fourier Series Applications
 Numerical Methods i Fourier Series Applicatios Recall that the basic relatios i usig the Trigoometric Fourier Series represetatio were give by f ( x) a o ( a x cos b x si ) () where the Fourier coefficiets
Numerical Methods i Fourier Series Applicatios Recall that the basic relatios i usig the Trigoometric Fourier Series represetatio were give by f ( x) a o ( a x cos b x si ) () where the Fourier coefficiets
2.1.1 Definition The Z-transform of a sequence x [n] is simply defined as (2.1) X re x k re x k r
![2.1.1 Definition The Z-transform of a sequence x [n] is simply defined as (2.1) X re x k re x k r 2.1.1 Definition The Z-transform of a sequence x [n] is simply defined as (2.1) X re x k re x k r](/thumbs/82/85448174.jpg) Z-Trsforms. INTRODUCTION TO Z-TRANSFORM The Z-trsform is coveiet d vluble tool for represetig, lyig d desigig discrete-time sigls d systems. It plys similr role i discrete-time systems to tht which Lplce
Z-Trsforms. INTRODUCTION TO Z-TRANSFORM The Z-trsform is coveiet d vluble tool for represetig, lyig d desigig discrete-time sigls d systems. It plys similr role i discrete-time systems to tht which Lplce
Content: Essential Calculus, Early Transcendentals, James Stewart, 2007 Chapter 1: Functions and Limits., in a set B.
 Review Sheet: Chpter Cotet: Essetil Clculus, Erly Trscedetls, Jmes Stewrt, 007 Chpter : Fuctios d Limits Cocepts, Defiitios, Lws, Theorems: A fuctio, f, is rule tht ssigs to ech elemet i set A ectly oe
Review Sheet: Chpter Cotet: Essetil Clculus, Erly Trscedetls, Jmes Stewrt, 007 Chpter : Fuctios d Limits Cocepts, Defiitios, Lws, Theorems: A fuctio, f, is rule tht ssigs to ech elemet i set A ectly oe
Linear Differential Equations of Higher Order Basic Theory: Initial-Value Problems d y d y dy
 Liear Differetial Equatios of Higher Order Basic Theory: Iitial-Value Problems d y d y dy Solve: a( ) + a ( )... a ( ) a0( ) y g( ) + + + = d d d ( ) Subject to: y( 0) = y0, y ( 0) = y,..., y ( 0) = y
Liear Differetial Equatios of Higher Order Basic Theory: Iitial-Value Problems d y d y dy Solve: a( ) + a ( )... a ( ) a0( ) y g( ) + + + = d d d ( ) Subject to: y( 0) = y0, y ( 0) = y,..., y ( 0) = y
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS. Assoc. Prof. Dr. Burak Kelleci. Spring 2018
 DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Assoc. Prof. Dr. Bur Kelleci Sprig 8 OUTLINE The Z-Trsform The Regio of covergece for the Z-trsform The Iverse Z-Trsform Geometric
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Assoc. Prof. Dr. Bur Kelleci Sprig 8 OUTLINE The Z-Trsform The Regio of covergece for the Z-trsform The Iverse Z-Trsform Geometric
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
f(bx) dx = f dx = dx l dx f(0) log b x a + l log b a 2ɛ log b a.
 Eercise 5 For y < A < B, we hve B A f fb B d = = A B A f d f d For y ɛ >, there re N > δ >, such tht d The for y < A < δ d B > N, we hve ba f d f A bb f d l By ba A A B A bb ba fb d f d = ba < m{, b}δ
Eercise 5 For y < A < B, we hve B A f fb B d = = A B A f d f d For y ɛ >, there re N > δ >, such tht d The for y < A < δ d B > N, we hve ba f d f A bb f d l By ba A A B A bb ba fb d f d = ba < m{, b}δ
1. The vibrating string problem revisited.
 Weeks 7 8: S eprtion of Vribes In the pst few weeks we hve expored the possibiity of soving first nd second order PDEs by trnsforming them into simper forms ( method of chrcteristics. Unfortuntey, this
Weeks 7 8: S eprtion of Vribes In the pst few weeks we hve expored the possibiity of soving first nd second order PDEs by trnsforming them into simper forms ( method of chrcteristics. Unfortuntey, this
y udv uv y v du 7.1 INTEGRATION BY PARTS
 7. INTEGRATION BY PARTS Ever differetitio rule hs correspodig itegrtio rule. For istce, the Substitutio Rule for itegrtio correspods to the Chi Rule for differetitio. The rule tht correspods to the Product
7. INTEGRATION BY PARTS Ever differetitio rule hs correspodig itegrtio rule. For istce, the Substitutio Rule for itegrtio correspods to the Chi Rule for differetitio. The rule tht correspods to the Product
 n. A Very Interesting Example + + = d. + x3. + 5x4. math 131 power series, part ii 7. One of the first power series we examined was. 2!
 mth power series, prt ii 7 A Very Iterestig Emple Oe of the first power series we emied ws! + +! + + +!! + I Emple 58 we used the rtio test to show tht the itervl of covergece ws (, ) Sice the series coverges
mth power series, prt ii 7 A Very Iterestig Emple Oe of the first power series we emied ws! + +! + + +!! + I Emple 58 we used the rtio test to show tht the itervl of covergece ws (, ) Sice the series coverges
Math 2414 Activity 17 (Due with Final Exam) Determine convergence or divergence of the following alternating series: a 3 5 2n 1 2n 1
 Mth 44 Activity 7 (Due with Fil Exm) Determie covergece or divergece of the followig ltertig series: l 4 5 6 4 7 8 4 {Hit: Loo t 4 } {Hit: } 5 {Hit: AST or just chec out the prtil sums} {Hit: AST or just
Mth 44 Activity 7 (Due with Fil Exm) Determie covergece or divergece of the followig ltertig series: l 4 5 6 4 7 8 4 {Hit: Loo t 4 } {Hit: } 5 {Hit: AST or just chec out the prtil sums} {Hit: AST or just
The Basic Properties of the Integral
 The Bsic Properties of the Itegrl Whe we compute the derivtive of complicted fuctio, like x + six, we usully use differetitio rules, like d [f(x)+g(x)] d f(x)+ d g(x), to reduce the computtio dx dx dx
The Bsic Properties of the Itegrl Whe we compute the derivtive of complicted fuctio, like x + six, we usully use differetitio rules, like d [f(x)+g(x)] d f(x)+ d g(x), to reduce the computtio dx dx dx
Double Sums of Binomial Coefficients
 Itertiol Mthemticl Forum, 3, 008, o. 3, 50-5 Double Sums of Biomil Coefficiets Athoy Sofo School of Computer Sciece d Mthemtics Victori Uiversity, PO Box 448 Melboure, VIC 800, Austrli thoy.sofo@vu.edu.u
Itertiol Mthemticl Forum, 3, 008, o. 3, 50-5 Double Sums of Biomil Coefficiets Athoy Sofo School of Computer Sciece d Mthemtics Victori Uiversity, PO Box 448 Melboure, VIC 800, Austrli thoy.sofo@vu.edu.u
Discrete Mathematics I Tutorial 12
 Discrete Mthemtics I Tutoril Refer to Chpter 4., 4., 4.4. For ech of these sequeces fid recurrece reltio stisfied by this sequece. (The swers re ot uique becuse there re ifiitely my differet recurrece
Discrete Mthemtics I Tutoril Refer to Chpter 4., 4., 4.4. For ech of these sequeces fid recurrece reltio stisfied by this sequece. (The swers re ot uique becuse there re ifiitely my differet recurrece
Numbers (Part I) -- Solutions
 Ley College -- For AMATYC SML Mth Competitio Cochig Sessios v.., [/7/00] sme s /6/009 versio, with presettio improvemets Numbers Prt I) -- Solutios. The equtio b c 008 hs solutio i which, b, c re distict
Ley College -- For AMATYC SML Mth Competitio Cochig Sessios v.., [/7/00] sme s /6/009 versio, with presettio improvemets Numbers Prt I) -- Solutios. The equtio b c 008 hs solutio i which, b, c re distict
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 2 Infinite Series Page 1 of 9
 Chpter Ifiite eries Pge of 9 Chpter : Ifiite eries ectio A Itroductio to Ifiite eries By the ed of this sectio you will be ble to uderstd wht is met by covergece d divergece of ifiite series recogise geometric
Chpter Ifiite eries Pge of 9 Chpter : Ifiite eries ectio A Itroductio to Ifiite eries By the ed of this sectio you will be ble to uderstd wht is met by covergece d divergece of ifiite series recogise geometric
Course 121, , Test III (JF Hilary Term)
 Course 2, 989 9, Test III (JF Hilry Term) Fridy 2d Februry 99, 3. 4.3pm Aswer y THREE questios. Let f: R R d g: R R be differetible fuctios o R. Stte the Product Rule d the Quotiet Rule for differetitig
Course 2, 989 9, Test III (JF Hilry Term) Fridy 2d Februry 99, 3. 4.3pm Aswer y THREE questios. Let f: R R d g: R R be differetible fuctios o R. Stte the Product Rule d the Quotiet Rule for differetitig
SM2H. Unit 2 Polynomials, Exponents, Radicals & Complex Numbers Notes. 3.1 Number Theory
 SMH Uit Polyomils, Epoets, Rdicls & Comple Numbers Notes.1 Number Theory .1 Addig, Subtrctig, d Multiplyig Polyomils Notes Moomil: A epressio tht is umber, vrible, or umbers d vribles multiplied together.
SMH Uit Polyomils, Epoets, Rdicls & Comple Numbers Notes.1 Number Theory .1 Addig, Subtrctig, d Multiplyig Polyomils Notes Moomil: A epressio tht is umber, vrible, or umbers d vribles multiplied together.
MA123, Chapter 9: Computing some integrals (pp )
 MA13, Chpter 9: Computig some itegrls (pp. 189-05) Dte: Chpter Gols: Uderstd how to use bsic summtio formuls to evlute more complex sums. Uderstd how to compute its of rtiol fuctios t ifiity. Uderstd how
MA13, Chpter 9: Computig some itegrls (pp. 189-05) Dte: Chpter Gols: Uderstd how to use bsic summtio formuls to evlute more complex sums. Uderstd how to compute its of rtiol fuctios t ifiity. Uderstd how
Indices and Logarithms
 the Further Mthemtics etwork www.fmetwork.org.uk V 7 SUMMARY SHEET AS Core Idices d Logrithms The mi ides re AQA Ed MEI OCR Surds C C C C Lws of idices C C C C Zero, egtive d frctiol idices C C C C Bsic
the Further Mthemtics etwork www.fmetwork.org.uk V 7 SUMMARY SHEET AS Core Idices d Logrithms The mi ides re AQA Ed MEI OCR Surds C C C C Lws of idices C C C C Zero, egtive d frctiol idices C C C C Bsic
*X203/701* X203/701. APPLIED MATHEMATICS ADVANCED HIGHER Numerical Analysis. Read carefully
 X0/70 NATIONAL QUALIFICATIONS 006 MONDAY, MAY.00 PM.00 PM APPLIED MATHEMATICS ADVANCED HIGHER Numerical Aalysis Read carefully. Calculators may be used i this paper.. Cadidates should aswer all questios.
X0/70 NATIONAL QUALIFICATIONS 006 MONDAY, MAY.00 PM.00 PM APPLIED MATHEMATICS ADVANCED HIGHER Numerical Aalysis Read carefully. Calculators may be used i this paper.. Cadidates should aswer all questios.
1.3 Convergence Theorems of Fourier Series. k k k k. N N k 1. With this in mind, we state (without proof) the convergence of Fourier series.
 .3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
.3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
 THEORY OF EQUATIONS SYNOPSIS. Polyomil Fuctio: If,, re rel d is positive iteger, the f)x) = + x + x +.. + x is clled polyomil fuctio.. Degree of the Polyomil: The highest power of x for which the coefficiet
THEORY OF EQUATIONS SYNOPSIS. Polyomil Fuctio: If,, re rel d is positive iteger, the f)x) = + x + x +.. + x is clled polyomil fuctio.. Degree of the Polyomil: The highest power of x for which the coefficiet
The Definite Integral
 The Defiite Itegrl A Riem sum R S (f) is pproximtio to the re uder fuctio f. The true re uder the fuctio is obtied by tkig the it of better d better pproximtios to the re uder f. Here is the forml defiitio,
The Defiite Itegrl A Riem sum R S (f) is pproximtio to the re uder fuctio f. The true re uder the fuctio is obtied by tkig the it of better d better pproximtios to the re uder f. Here is the forml defiitio,
Ma 4121: Introduction to Lebesgue Integration Solutions to Homework Assignment 5
 Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
BC Calculus Path to a Five Problems
 BC Clculus Pth to Five Problems # Topic Completed U -Substitutio Rule Itegrtio by Prts 3 Prtil Frctios 4 Improper Itegrls 5 Arc Legth 6 Euler s Method 7 Logistic Growth 8 Vectors & Prmetrics 9 Polr Grphig
BC Clculus Pth to Five Problems # Topic Completed U -Substitutio Rule Itegrtio by Prts 3 Prtil Frctios 4 Improper Itegrls 5 Arc Legth 6 Euler s Method 7 Logistic Growth 8 Vectors & Prmetrics 9 Polr Grphig
Definite Integral. The Left and Right Sums
 Clculus Li Vs Defiite Itegrl. The Left d Right Sums The defiite itegrl rises from the questio of fidig the re betwee give curve d x-xis o itervl. The re uder curve c be esily clculted if the curve is give
Clculus Li Vs Defiite Itegrl. The Left d Right Sums The defiite itegrl rises from the questio of fidig the re betwee give curve d x-xis o itervl. The re uder curve c be esily clculted if the curve is give
( ) dx ; f ( x ) is height and Δx is
 Mth : 6.3 Defiite Itegrls from Riem Sums We just sw tht the exct re ouded y cotiuous fuctio f d the x xis o the itervl x, ws give s A = lim A exct RAM, where is the umer of rectgles i the Rectgulr Approximtio
Mth : 6.3 Defiite Itegrls from Riem Sums We just sw tht the exct re ouded y cotiuous fuctio f d the x xis o the itervl x, ws give s A = lim A exct RAM, where is the umer of rectgles i the Rectgulr Approximtio
1 Approximating Integrals using Taylor Polynomials
 Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
Fast Fourier Transform 1) Legendre s Interpolation 2) Vandermonde Matrix 3) Roots of Unity 4) Polynomial Evaluation
 Algorithm Desig d Alsis Victor Admchi CS 5-45 Sprig 4 Lecture 3 J 7, 4 Cregie Mello Uiversit Outlie Fst Fourier Trsform ) Legedre s Iterpoltio ) Vdermode Mtri 3) Roots of Uit 4) Polomil Evlutio Guss (777
Algorithm Desig d Alsis Victor Admchi CS 5-45 Sprig 4 Lecture 3 J 7, 4 Cregie Mello Uiversit Outlie Fst Fourier Trsform ) Legedre s Iterpoltio ) Vdermode Mtri 3) Roots of Uit 4) Polomil Evlutio Guss (777
