Online Supplement for "Threshold Regression with Endogeneity" by Ping Yu and Peter C. B. Phillips
|
|
|
- Julius Kerry Johnston
- 5 years ago
- Views:
Transcription
1 Ole Sulemet fo "Tesold Regesso wt Edogeety" y Pg Yu ad Pete C. B. Plls. D cultes Alyg te DKE We tee ae o ote covaates esdes q, te DKE s a oula ocedue fo estmatg : Pote ad Yu () ovde some dscusso ad efeeces to te elated lteatue. I ts smle case, we ave te model y g(q) ( q) (q ) e wt E[ejq]. Te DKE s de ed as te extemum estmato DKE ag max () () wee () E[yjq ] E[yjq ] wt E[yjq ] P j w j()y j d j () ad E[yjq ] P j w j()y j ( d j ()) eg estmatos of E[yjq ] ad E[yjq ], ad d j () (q j ). I te de to of E[yjq. ], te wegt fucto w j () (q j ) (q l ), wee () l () s a escaled eel desty, ad s te adwdt. Due to te wegted aveage atue of eel smootes, () would e ea zeo f tee wee o jum at. Otewse, te d eece would e ea te magtude of te jum ( ) wc s assumed to e ozeo. Ts d eece esues tat te estmato DKE s cosstet. Pote ad Yu () ave ecetly sow tat DKE coveges at ate ad te asymtotc dstuto s elated to a comoud Posso ocess. Ts lmt teoy s exlaed y teetg as a mddle ouday ot of q (see Yu, ). Fo ouday ot estmato, t s wellow tat oly data a O egoood s fomatve, so te egoood te costucto of te DKE s tycally lage eoug to esue te -cosstecy of DKE. Gve DKE, te lteatue as also cosdeed te estmato of te jum magtude : But o estmato of s esetly avalale. We tee ae addtoal covaates, Delgado ad Hdalgo () suggested tat te DKE cotue to e used to estmate. I ts case, te ocedue ca e emloyed y xg some ot (say x o ) te suot of x ad ede g () as E[yjx o q ] E[yjxo q ], wee E[yjx o q ] s a estmato of te codtoal mea of y gve x x o ad q. Te ojectve fucto coveges to zeo we 6, ad to o (E[yjx o q ] E[yjx o q ]) we, so DKE s cosstet f o 6. Tee ae seveal d cultes alyg te DKE ts way. Fst, te selecto of x o ases d cultes, as sow te followg examle. Suose y (x q) (q > ) ", wee, te suots of x ad q ae ot [ ], ad edogeety taes te fom E ["jx q] x q. Fgue sows E[yjx q] ad E[yjx q ]. To detfy successfully we eed to select x o so tat o s lage, wc meas tat x o sould e o te ouday of x s suot. O te ote ad, we also eed f xjq (x o j ) to e lage so tat tee s su cet data to detfy. We te desty of f xjq (xj ) taes o a ell sae, as a tycal case, x o sould deally e te mddle of x s suot. Hece, te selecto of x o oses a dlemma ad a otetal tadeo tat s esetly uesolved fom ot teoy ad actcal esectves. Secod, cosstecy of DKE eques tat o 6, ut o ca e as sow te examle of Fgue. Delgado ad Hdalgo () aly te DKE to estmate, assumg tat x q ad 6 so tat o 6 does ot deed o te coce of x o. Moeove, te eel fucto uses data te egoood of q e cetly, so tat te covegece ate of DKE s qute slow, as dscussed fute Secto.. Futemoe, gve DKE, te duced estmato of uses oly data te egoood of (x o DKE ), so te covegece ate of DKE s also vey slow, esecally we te dmeso of x s lage. Oe mgt cosde eglectg te data of x, ad usg oly te data of q ad y to estmate. Ts wll geeate te DKE of Pote ad Yu (). Now, te jum sze E[x jq ] s a aveage of te jums at all x values, so may e zeo o small, wc esults det cato falue o wea det cato. Eve f E[x jq ] s lage, ts DKE mgt e less e cet ta te IDKE ecause te jum fomato at s ot fully exloed see footote 6 fo fute aalyss.
2 4 3 Fgue : E[yjx q] ad E[yjx q ] Wt Edogeety: Te Blue Les Reeset te Case Wtout Edogeety. D cultes Alyg Two Alteatve Estmatos It s ow (Secto 4.. of Pote ad Yu, ) tat te DKE s asymtotcally equvalet to te LSE ad te PLE we q s a sgle covaate. I wat follows, we de e te LSE ad te PLE we ote covaates ae eset ad dscuss te d cultes tat ase devg te asymtotc dstutos. De e te oaametc LSE of te geeal case as follows, wee f N LSE ag m jj6 y f cm f (x q )(q ) cm f (x q )(q > ) K j wt K j K x j (q j q ) s te eel estmato of f f(x q ), cm f (x q ) cm f (x q ) jj6 jj6 y j K x j (q j q q ) y j K x j (q j q q ) wt ( (u t) u (u t) ( u u t f t f t f t u t f t :
3 I te costucto of N LSE, we elmate te adom deomato as. We ext de e te PLE as wee P LE ag m g f (x q ) y f x (q ) f g f (x q ) () jj6 y j x j(q j ) K j : Ts desty-wegted ojectve fucto of te PLE was suggested L (996) wtout cosdeg te tesold e ects. I ot te LSE ad te PLE, s estmated y dg te est t etwee y ad a estmato of E[y jx q ] te d eece les tat d eet estmatos of E[y jx q ] ae used. Te ojectve fucto of te IDKE s sueo to tat of te LSE ad te PLE two esects. Fst, accodg to Yu (8, ), oly te fomato aoud te tesold ot s fomatve fo, so () te ojectve fucto of te IDKE s costucted usg oly data te egoood of. I cotast, te ojectve fuctos of te LSE ad te PLE use fomato ote aeas, ad te esultg ases eed to e adled caefully. Te ojectve fucto of te IDKE teefoe taes advatage of ts local costucto, weeas te gloal ojectve fuctos of te LSE ad te PLE ae ueced y te e ects of fomato tougout te dstuto. Secod, sce () te ojectve fucto of te IDKE s qj qj lea ad, t s easy to localze te egoood of, wc s ey to devg te covegece ate ad te asymtotc dstuto of. Howeve, te ojectve fuctos of te LSE ad PLE ae comlcated olea fuctos of, wc maes localzato extemely ad. I addto, te ojectve fucto of te IDKE does ot ely o te assumto tat (x q) x, weeas tat of te PLE does. 3. Poofs fo Teoem, 3, 5 ad Coollay Poof of Teoem. (998), we ave We st deve te fomula fo. Followg Aedx A. of Hecma et al. a (x ) (x ) (I d ) W W Y (I d ) H H W H H W Y (I d ) H W W Y (I d ) z jzj w A j (I d ) H M jj6 z jw j y j A 3
4 wee (x x q ) S. (x x q ) S (x x q ) S C. A (x x q ) S P (d )(d ) Y H dag I d I (d )(d ) H z j (x j x q j ) S H W dag K x (x x x ) (q ) K x (x x x ) (q ) dag w w ad a (x ) (x ) ae smlaly de ed wt y. y y W dag K x (x x x ) (q ) K x (x x x ) (q ). y C A elacg W. Next xq a (x ) a (x ) (x ) (x ), ad P (x ) (x ) (x ) xq P A : Te st ste devg te asymtotc dstuto of s to sow tat ca e elaced y. I ote wods, xq xq wee estmatos wt suesct deotes te ogal estmatos ut wt elaced y. Of couse, we eed oly sow A sce s just a lea comato xq xq xq xq xq xq A. Poosto 5 followg ts oof gves ts esult. A xq xq a (x ) a (x ) a (x ) a (x ) (x ) (x ) xq, a (x ) a (x ) a (x ) a (x ), (x ) (x ) (x ) (x ) 4
5 wee a (x ) (x ) s de ed y a (x ) m (x ) lm m(x ) ad y (x ) m (x ) lm (@m(x )@), wt a smla de to fo a (x ) (x ), ad a (x ) a (x ), : Note tat, ude ou sec cato, (x ) (x ) xq ad a (x ) a (x ) (x )( (x ) (x )) fo ay x. Also, (x ) (x ) (x ) We st deve te asymtotc dstuto (x ) (x ) xq Gve assumtos E, F, G, ad H, we ca aly te agumets Teoem 3 of Hecma et al. (998) to xq xq A 8 >< (I d ) >: M M e xq m M e A ad te cosde M m R R. 9, > > : wee M s te squae matx of sze P ( d )(d ) wt te l-t ow, t-t colum loc eg, fo l t, m (u x u q ) S(l) (u x u q ) S(t) K x (u x x ) (u q )f(x u x u q )du x du q s a P ( d )(d ) y vecto wt te t-t loc eg te tasose of (u x u q ) S(t) (u x u q ) S() m () (x ) K x (u x x ) (u q )f(x )du x du q ad m () (x) eg a ( d)( )(d ) vecto of te atal devatves of m(x q) at q, e jj6 z jw j e j wt z j ad w j eg z j ad w j ut avg elaced y, (I d ) R o () 5
6 ad te ojects wt suesct ae smlaly de ed. It tus out tat te tems assocated wt m wll cotute to te as ad te tems assocated wt e, wc s a U-statstc, wll cotute to te P vaace. Gve tat fq ( ), we eed oly cocetate o te umeato. Fst, aalyze te as. " E M (I d ) (I d ) M o B (I d ) m M m M m M m f(x jq )dx (q ) f(q )dq M o B E[g () (x ) q ]f q ( ) wee Mo ad B ae de ed te ma text, ad m () (x ) m () (x ) g () (x ) ude Assumto G. Note ee tat te eel K x s elaced y K ecause te data te egoood of te ouday of ca e eglected asymtotcally. Also, we ca calculate tat te vaace of ts tem s O o(), so t coveges oalty to ts exectato. Secod, aalyze te vaace. Tag te lt elemet A, we cosde xq xq # e l M e M e wc s a secod-ode U-statstc. Fom Lemma 8.4 of Newey ad McFadde (994), ts U-statstc s asymtotcally equvalet to P m (x j q j e j ) E e j m (x q e ), wee e l e l M z j w j e j M z j w j M z j w j e j x j q j e j M z j w j f(x q )dx dq We aly te Lauov cetal lmt teoem to deve te asymtotc dstuto. It s stadad to cec tat te Lauov codto s sats ed, so we cocetate o calculatg te asymtotc vaace as follows. " E e j "e E j "e E j R E e j 6 4 R e l T T T 3: e l M z j w j # e l M z j w j f(x q )dx dq # e l M z j w j f(x q )dx dq 3 M z j w j f(x q )dx dq 7 M z j w j f(x 5 q )dx dq e l # M z j w j f(x q )dx dq 6
7 We aalyze T, T ad T 3 tu. T E 4e j qj (u q ) e l M o " u x q # S 3 j K (u x ) du x du q 5 (x j ) (v q ) (u q ) e l M o (u x v q ) S K (ux ) du x du q f(x j )dx j dv q E (v q ) (x j )C l (v q) dv q jq j f q ( ): Smlaly, qj ad T 3 sce m (x q e ) T E (v q ) (x j )C l (v q ) dv q jq j f q ( ) qj. I summay, d N E (v q ) (x)c l (v q) (v q ) (x)c l (v q ) dv q q f q ( ) ad te asymtotc dstuto of xq xq follows as te teoem. We ext deve te asymtotc dstuto of. Gve tat O () ude Assumto H, te tem ca e eglected, ad as te same asymtotc dstuto as (x ) (x ) (x ) Fo te as, ote tat " E (x ) ( I d ) E (x ) ( I d ) (x ) ( I d ) M m M o B, (x ) (x ) M m Fo te vaace, te coesodg U-ojecto m (x q e ) s e j (x ) ( I d ) M z j w j M m # : M m f(x jq )dx (q ) f(q )dq M o B g () (x ) q f q ( ): M z j w j f(x q )dx dq : We ca oceed a smla faso to te aove devg te asymtotc vaace. Fo examle, te 7
8 coesodg fom to T s T E 4e j (q j ) (u q ) (x j ) ( I d ) M o (x j ) (v q ) (u q ) (x j ) ( I d ) M o E (v q ) (x j )C (x j v q ) dv q jq j f q ( ): " u x q # S 3 j K (u x ) du x du q 5 (u x v q ) S K (ux ) du x du q f(x j )dx j dv q Poosto 5: Ude te assumtos of Poof. We eed oly to sow (a (x ) a (x )) (x ) (x ) xq xq A : a (x ) a (x ) (x ) (x ) ad : (3) It s easy to see tat te st esult s mled y (a (x ) a (x )) a (x ) a (x ) ufomly x, (x ) (x ) (x ) (x ) ufomly x. Sce O ( ), falls to C C fo some ostve C wt ay lage oalty we s lage eoug. So we ca just ove tese esults y elacg y C C. Te coesodg a (x ) ad (x ) ae deoted as a C (x ) ad C (x ). Sce te esults fo a (x ) ad (x ) ae smlaly oved, we eed oly ove tat a C (x ) a (x ) ufomly x, (4) C (x ) (x ) ufomly x. Wtout loss of geealty, suose C >. Lemma 6 sows (3), ad Lemma 7 sows (4). Poof of Coollay. Te asymtotc dstuto of s moe volved sce t cludes vaatos fom two comoets as : 8
9 Fst ote tat N f q ( ) f q ( ) f q ( ) N f q ( ) fq ( ) f q ( ) f q ( ) N N N f q ( ) fq ( ) f q ( ) f q ( ) wee N ad N ae te umeatos of ad, ad f q ( ) P. Fom te eale aalyss te oof of Teoem, N N sats es N N e M o B M o B E[g () (x ) q ]f q ( ) e M e M e e j e M z j w j M z j w j f(x q )dx dq ad also j N E N fq ( ) E fq ( ) a (x ) a (x ) E a (x ) E : a (x ) It s ot ad to see tat tese two uece fuctos ae ucoelated, so te vaace of s te sum of te vaaces of tese two ats. Te vaace of te st at s deved te oof of Teoem. As to te secod at, ote tat " E a (x ) a (x ) # a (x ) a (x ) f(x q )dx dq (v q ) a (x ) a (x ) f(x )dx dv q (v q ) dv q E[ a (x ) a (x ) j ]f q ( ): 9
10 Smlaly, " E a (x ) a (x ) # " E # (v q ) dv q f q ( ) (v q ) dv q f q ( ) so te vaace of te secod at s aoxmately (v q ) dv q E[ a (x ) a (x ) j ]f q ( ) (v q ) dv q f q ( ) (v q ) dv q E[ a (x ) a (x ) j ] f q ( ): (v q ) dv q f q ( ) Fo te as of te secod at, ote tat E N f q ( ) (q ) a (x ) a (x ) f(x q )dx dq f q ( ) (v q ) a (x ) a (x ) f(x v q )dx dv q f q ( ) (v q ) a (x ) a (x ) (x ) (v q ) l dx dv q l l l (v q ) v q l dv q l l f (l) a (x ) a (x ) f (l) (x )dx wee f (l) (x ) s te lt ode atal devatve of f(x ) wt esect to evaluated at, ad E fq ( ) f q ( ) (q ) f(q )dq f q ( ) (v q ) f( v q )dv q f q ( ) (v q ) l l f (l) ( ) (v q ) l dv q l (v q ) v l q dv q f (l) ( l l ) wee f (l) ( ) s te lt ode devatve of f q () wt esect to evaluated at. I sum, te asymtotc dstuto of s as stated te teoem. Poof of Teoem 3. Fst deve te fomula fo e. x Fom (??), e x ( x ) ( x ) (q ) ( x ) (q ) (a (x ) a (x )) : By smla aalyss to te oof of Teoem, e x ca e elaced y wtout a ectg ts asymtotc dstuto. Also, a (x ) a (x ) ca e elaced y ts lea aoxmato wt o
11 asymtotc mact. I summay, e x q x ( x ) ( x ) (q ) e M m M m M ( x ) e M e wee M, m ad e ae de ed te oof of Teoem. By stadad metods, te deomato coveges oalty to M f q ( ), wee M s de ed te ma text, so we cocetate o te umeato. Fst, cosde te as tem. Fom te oof of Teoem, ( x ) e M m M m E ( x ) e M o B M o B g () (x ) q f q ( ): Next cosde te vaace. We eed to calculate te covaace etwee te lt ad tt elemet of te umeato, l t d. Tag te (l )t elemet of te umeato, l :d, we cosde x l e M e M e wc s a secod-ode U-statstc. Fom Lemma 8.4 of Newey ad McFadde (994), ts U-statstc s asymtotcally equvalet to P m l (x j q j e j ) E x l e j x l It s ot ad to sow tat m l (x q e )m t (x q e ) m l (x q e ), wee e e M z j w j e j M z j w j M z j w j e j x j q j e j M z j w j f(x q )dx dq : E x l x t (v q ) (x)c (v q) (v q ) (x)c (v q ) dv q q f q ( ): Te, alyg te Lauov cetal lmt teoem, te asymtotc dstuto of q ad exl xl, l d, follows as te teoem. We, e q O ( )O ( ) o (), so e ave te same asymtotc dstuto as. We 6, te covegece ate of e s. It s ovous tat q
12 q O ( )O ( ) o (). Also, q q q o () q q : q So e as te same asymtotc dstuto as q q. Poof of Teoem 5. Note tat GMM GMM G G G z (q ) z (q > ) (" x ( < q )) : By te cosstecy of ad Glveo-Catell, G G. Followg te oof of Teoem 3 of Cae ad Hase (4), we ca sow tat ude te momet estctos o x q, " ad z. We stll eed to sow tat z (q ) z (q x ( < q ) > P z x A ( < q ) ad z ( < q ) z ( < q ) " : Fo tese two esults, cosstecy of s ot eoug we eed ( ). But ts case, P z x P ( < q ) o z x o (), ad te secod esult olds smlaly. Gve tese two esults, stadad agumets yeld te asymtotc dstuto of te GMM estmato. 4. Poofs fo te Lemmas Lemma su Q () Q () : Poof. Notg tat Gve tat s comact we ave fom Lemma B. of Newey (994) tat su x su E () O (), x Q () () () E E [ q ()] O l d : E () () E [ ()] () O ql d
13 ufomly. By a Glveo-Catell teoem, su E () Note tat E E () Q (), te esult of teest follows. E E () : Lemma P l 4P T l o () ufomly v: Poof. We tae T 4 to llustate ad ave T 4 jj6 ( ) jj6 e j (q j ) K v j K j ( ) ( ) jj6 jj6 e j (q j ) K v j K j e j (q j ) Kx j e j ( q j ) qj v Kj x A ( ) qj jj6 P ( j ) A ufomly v, wee te secod to last equalty s fom te Lsctz cotuty of (). By te U-statstc ojecto, see, e.g., Lemma 8.4 of Newey ad McFadde (994), ( ) jj6 P ( j ) E [P ( j ) j j ] O P E ( j ) : j ( I ou case, E [P ( j ) j j ] e q j ) R j K x j f(x )dx O(e j ( q j )), ad E P ( j ) R (x d )f(x )dx O, so d E [P ( j ) j j ] e j ( q j ) A o () j j E P ( j ) O o(): d Lemma 3 P P (T 5 T 6 ) f (x ) () [( x ) e ] ( < q v )f(x ) f (x ) o (): 3
14 Poof. P T 5 f (x ) s a U-statstc ad we wte T 5 f (x ) jj6 e j ( < q j v )K j f (x ) E [P ( j ) j j ] O P E ( j ) j ( ) jj6 P ( j ) wee P ( j ) e j ( < q j v )K j f (x ) wt (x q e ), ad te last equalty s fom Lemma 8.4 of Newey ad McFadde (994). Te E [P ( j ) j j ] e j ( < q j v ) () d K x (x x j x ) f(x ) f (x )dx e j ( < q j v ) () K x (u x x j u x ) f(x j u x ) f (x j u x )du x e j ( < q j v ) ()f(x j ) f (x j ) ad so tat E P ( j ) O d d O d E [P ( j ) j j ] j E P ( j ) e ( < q v ) ()f(x ) f (x ) d d o(): Smlaly, T 6 f (x ) jj6 x j e j ( < q j v )K v j f (x ) [( x ) e ] ( < q v ) ()f(x ) f (x ) o (): Te esult follows y otg tat () (). Lemma 4 P 4 T l l P 4 T l o () ufomly v: l Poof. Tae T 4 as a examle. T 4 d O j d j e j (q j ) K v j K d e j (q j )K x xj j x o x o d e j ( q j )K x xj x o qj v x o A qj 4
15 ufomly v, wee te last equalty s fom te Lsctz cotuty of (). Sce E[T 4 ] O d o() T 4 o (). Lemma 5 T 5 T 6 T 5 T 6 d Do (v): Poof. Tae T 5 T 5 as a examle. We use te caactestc fucto to d ts wea lmt. De e T 5 P j T 5j P j t 5j (v < q j ) ad T 5 P j T 5j P j t 5j ( < q j v ), wee t 5j d e j K j, t 5j d e j K j, v < ad v >. Note tat Hece ex s T 5j ( v < q j ) ex s t 5j ex s T 5j ( < q j v ) ex s t 5j : E ex s T 5j s T 5j E ex s T5j E ex s T 5j E ( v < q j )E ex s t 5j qj E ( < q j v )E ex s t 5j qj R d R R o qj ex s v ej K(u x ) f(e j x o jq j )de j du x f(q j )dq j R d v R R o ex s qj e j K(u x ) f(e j x o jq j )de j du x f(q j )dq j v f q( ) R R ex s e j K(u x ) () f(e j x o jq j )de j du x v f q( ) R R ex s e j K(u x ) () f(e j x o jq j )de j du x v f q( ) R R d ex s e j K(u x ) () (K(u x)>) Vol(K(u f(e x)>) j x o jq j )de j du x v f q( ) R R d ex s e j K(u x ) () (K(u x)>) Vol(K(u f(e x)>) j x o jq j )de j du x v d f q ( )f xjq (x o j )E ex s e j K(U j ) () x j x o q j v d f q ( )f xjq (x o j )E ex s e j K(U j ) () x j x o q j v d f(x o )E ex s e j K(U j ) () xj x o q j v d f(x o )E ex s e j K(U j ) () xj x o q j wee Vol(K(u x ) > ) d s te volume of te aea of u x suc tat K(u x ) >, ad U j ad U j ae deedet of (e j x j q j) ad follow a ufom dstuto o te suot of K(). It follows tat 8 < E : Y E ex j T 5j s j T 5j j s T 5j s T 5j 93 A 5 ex v d f(x o )E ex s ek(u ) () x x o q v d f(x o )E ex s ek(u ) () x x o q : 5
16 Ts s te caactestc fucto of a comoud Posso ocess D 5 () evaluated at v 8 >< D 5 (v) >: N (jvj) P N (v) P ez, f v ez, f v > ad v, wee s a cadlag ocess wt D 5 (), ez e K(U ) (), ez e K(U ) (), ad e e U U, N () ad N () ae de ed Coollay. Geealzg ts agumet, we get te esult of teest. Lemma 6 P C P : Poof. C C C C ( q C ) O o () wee te equalty s fom te Lsctz cotuty of (). Lemma 7 Ufomly x, a C (x ) a (x ) C (x ) (x ) : Poof. Tae te st esult as a examle. We ave a C (x ) e e M C M e M e M a (x ) C e M C M C M C M M e M M C M M C M M M C C M M C wee M C ad C ae smlaly de ed as M ad ut wt elaced y C, ad te decomosto te last equalty s fom Lemma of Yu (). Sce M, M ad ae O (), we eed oly to sow tat M C M ufomly, C ufomly. 6
17 Tae te secod esult as a examle. C jj6 jj6 (x j x q j C ) S K x qj C (x j x x ) y j (x j x q j C ) S K x qj (x j x x ) y j : Tae te followg tem of C as a examle sce t s te adest to aalyze. jj6 jj6 jj6 jj6 q j C K x (x j x x ) qj C y j (q j ) K x qj (x j x x ) y j K x (x j x x ) C qj C y j K x (x j x x ) (q j ) ( q j C ) C y j : Fom Lemma B. of Newey (994), ot tems o te gt sde covege to te exectatos ufomly, ut t s easy to see tat tese exectatos ae O o(). Te esults of teest follow. Addtoal Refeeces L, Q., 996, O te Root-N-Cosstet Semaametc Estmato of Patally Lea Models, Ecoomcs Lettes, 5,
Professor Wei Zhu. 1. Sampling from the Normal Population
 AMS570 Pofesso We Zhu. Samplg fom the Nomal Populato *Example: We wsh to estmate the dstbuto of heghts of adult US male. It s beleved that the heght of adult US male follows a omal dstbuto N(, ) Def. Smple
AMS570 Pofesso We Zhu. Samplg fom the Nomal Populato *Example: We wsh to estmate the dstbuto of heghts of adult US male. It s beleved that the heght of adult US male follows a omal dstbuto N(, ) Def. Smple
L-MOMENTS EVALUATION FOR IDENTICALLY AND NONIDENTICALLY WEIBULL DISTRIBUTED RANDOM VARIABLES
 THE PUBLISHING HOUSE PROCEEDINGS OF THE ROMANIAN ACADEMY, Sees A, OF THE ROMANIAN ACADEMY Volume 8, Numbe 3/27,. - L-MOMENTS EVALUATION FOR IDENTICALLY AND NONIDENTICALLY WEIBULL DISTRIBUTED RANDOM VARIABLES
THE PUBLISHING HOUSE PROCEEDINGS OF THE ROMANIAN ACADEMY, Sees A, OF THE ROMANIAN ACADEMY Volume 8, Numbe 3/27,. - L-MOMENTS EVALUATION FOR IDENTICALLY AND NONIDENTICALLY WEIBULL DISTRIBUTED RANDOM VARIABLES
Threshold Regression with Endogeneity
 Tresold Regresso wt Edogeety Pg Yu Uversty of Aucklad Started: August 9 Frst Verso: Octoer Ts Verso: Arl 3 Astract Ts aer studes estmato ad sec cato testg tresold regresso wt edogeety. For estmato, tere
Tresold Regresso wt Edogeety Pg Yu Uversty of Aucklad Started: August 9 Frst Verso: Octoer Ts Verso: Arl 3 Astract Ts aer studes estmato ad sec cato testg tresold regresso wt edogeety. For estmato, tere
χ be any function of X and Y then
 We have show that whe we ae gve Y g(), the [ ] [ g() ] g() f () Y o all g ()() f d fo dscete case Ths ca be eteded to clude fuctos of ay ube of ado vaables. Fo eaple, suppose ad Y ae.v. wth jot desty fucto,
We have show that whe we ae gve Y g(), the [ ] [ g() ] g() f () Y o all g ()() f d fo dscete case Ths ca be eteded to clude fuctos of ay ube of ado vaables. Fo eaple, suppose ad Y ae.v. wth jot desty fucto,
are positive, and the pair A, B is controllable. The uncertainty in is introduced to model control failures.
 Lectue 4 8. MRAC Desg fo Affe--Cotol MIMO Systes I ths secto, we cosde MRAC desg fo a class of ult-ut-ult-outut (MIMO) olea systes, whose lat dyacs ae lealy aaetezed, the ucetates satsfy the so-called
Lectue 4 8. MRAC Desg fo Affe--Cotol MIMO Systes I ths secto, we cosde MRAC desg fo a class of ult-ut-ult-outut (MIMO) olea systes, whose lat dyacs ae lealy aaetezed, the ucetates satsfy the so-called
RECAPITULATION & CONDITIONAL PROBABILITY. Number of favourable events n E Total number of elementary events n S
 Fomulae Fo u Pobablty By OP Gupta [Ida Awad We, +91-9650 350 480] Impotat Tems, Deftos & Fomulae 01 Bascs Of Pobablty: Let S ad E be the sample space ad a evet a expemet espectvely Numbe of favouable evets
Fomulae Fo u Pobablty By OP Gupta [Ida Awad We, +91-9650 350 480] Impotat Tems, Deftos & Fomulae 01 Bascs Of Pobablty: Let S ad E be the sample space ad a evet a expemet espectvely Numbe of favouable evets
SUBSEQUENCE CHARACTERIZAT ION OF UNIFORM STATISTICAL CONVERGENCE OF DOUBLE SEQUENCE
 Reseach ad Coucatos atheatcs ad atheatcal ceces Vol 9 Issue 7 Pages 37-5 IN 39-6939 Publshed Ole o Novebe 9 7 7 Jyot cadec Pess htt//yotacadecessog UBEQUENCE CHRCTERIZT ION OF UNIFOR TTITIC CONVERGENCE
Reseach ad Coucatos atheatcs ad atheatcal ceces Vol 9 Issue 7 Pages 37-5 IN 39-6939 Publshed Ole o Novebe 9 7 7 Jyot cadec Pess htt//yotacadecessog UBEQUENCE CHRCTERIZT ION OF UNIFOR TTITIC CONVERGENCE
= y and Normed Linear Spaces
 304-50 LINER SYSTEMS Lectue 8: Solutos to = ad Nomed Lea Spaces 73 Fdg N To fd N, we eed to chaacteze all solutos to = 0 Recall that ow opeatos peseve N, so that = 0 = 0 We ca solve = 0 ecusvel backwads
304-50 LINER SYSTEMS Lectue 8: Solutos to = ad Nomed Lea Spaces 73 Fdg N To fd N, we eed to chaacteze all solutos to = 0 Recall that ow opeatos peseve N, so that = 0 = 0 We ca solve = 0 ecusvel backwads
Fairing of Parametric Quintic Splines
 ISSN 46-69 Eglad UK Joual of Ifomato ad omputg Scece Vol No 6 pp -8 Fag of Paametc Qutc Sples Yuau Wag Shagha Isttute of Spots Shagha 48 ha School of Mathematcal Scece Fuda Uvesty Shagha 4 ha { P t )}
ISSN 46-69 Eglad UK Joual of Ifomato ad omputg Scece Vol No 6 pp -8 Fag of Paametc Qutc Sples Yuau Wag Shagha Isttute of Spots Shagha 48 ha School of Mathematcal Scece Fuda Uvesty Shagha 4 ha { P t )}
( m is the length of columns of A ) spanned by the columns of A : . Select those columns of B that contain a pivot; say those are Bi
 Assgmet /MATH 47/Wte Due: Thusday Jauay The poblems to solve ae umbeed [] to [] below Fst some explaatoy otes Fdg a bass of the colum-space of a max ad povg that the colum ak (dmeso of the colum space)
Assgmet /MATH 47/Wte Due: Thusday Jauay The poblems to solve ae umbeed [] to [] below Fst some explaatoy otes Fdg a bass of the colum-space of a max ad povg that the colum ak (dmeso of the colum space)
Sandwich Theorems for Mcshane Integration
 It Joual of Math alyss, Vol 5, 20, o, 23-34 adwch Theoems fo Mcshae Itegato Ismet Temaj Pshta Uvesty Educato Faculty, Pshta, Kosovo temaj63@yahoocom go Tato Taa Polytechc Uvesty Mathematcs Egeeg Faculty,
It Joual of Math alyss, Vol 5, 20, o, 23-34 adwch Theoems fo Mcshae Itegato Ismet Temaj Pshta Uvesty Educato Faculty, Pshta, Kosovo temaj63@yahoocom go Tato Taa Polytechc Uvesty Mathematcs Egeeg Faculty,
Idea is to sample from a different distribution that picks points in important regions of the sample space. Want ( ) ( ) ( ) E f X = f x g x dx
 Importace Samplg Used for a umber of purposes: Varace reducto Allows for dffcult dstrbutos to be sampled from. Sestvty aalyss Reusg samples to reduce computatoal burde. Idea s to sample from a dfferet
Importace Samplg Used for a umber of purposes: Varace reducto Allows for dffcult dstrbutos to be sampled from. Sestvty aalyss Reusg samples to reduce computatoal burde. Idea s to sample from a dfferet
The Linear Probability Density Function of Continuous Random Variables in the Real Number Field and Its Existence Proof
 MATEC Web of Cofeeces ICIEA 06 600 (06) DOI: 0.05/mateccof/0668600 The ea Pobablty Desty Fucto of Cotuous Radom Vaables the Real Numbe Feld ad Its Estece Poof Yya Che ad Ye Collee of Softwae, Taj Uvesty,
MATEC Web of Cofeeces ICIEA 06 600 (06) DOI: 0.05/mateccof/0668600 The ea Pobablty Desty Fucto of Cotuous Radom Vaables the Real Numbe Feld ad Its Estece Poof Yya Che ad Ye Collee of Softwae, Taj Uvesty,
Lecture 10: Condensed matter systems
 Lectue 0: Codesed matte systems Itoducg matte ts codesed state.! Ams: " Idstgushable patcles ad the quatum atue of matte: # Cosequeces # Revew of deal gas etopy # Femos ad Bosos " Quatum statstcs. # Occupato
Lectue 0: Codesed matte systems Itoducg matte ts codesed state.! Ams: " Idstgushable patcles ad the quatum atue of matte: # Cosequeces # Revew of deal gas etopy # Femos ad Bosos " Quatum statstcs. # Occupato
Best Linear Unbiased Estimators of the Three Parameter Gamma Distribution using doubly Type-II censoring
 Best Lea Ubased Estmatos of the hee Paamete Gamma Dstbuto usg doubly ype-ii cesog Amal S. Hassa Salwa Abd El-Aty Abstact Recetly ode statstcs ad the momets have assumed cosdeable teest may applcatos volvg
Best Lea Ubased Estmatos of the hee Paamete Gamma Dstbuto usg doubly ype-ii cesog Amal S. Hassa Salwa Abd El-Aty Abstact Recetly ode statstcs ad the momets have assumed cosdeable teest may applcatos volvg
2.1.1 The Art of Estimation Examples of Estimators Properties of Estimators Deriving Estimators Interval Estimators
 . ploatoy Statstcs. Itoducto to stmato.. The At of stmato.. amples of stmatos..3 Popetes of stmatos..4 Devg stmatos..5 Iteval stmatos . Itoducto to stmato Samplg - The samplg eecse ca be epeseted by a
. ploatoy Statstcs. Itoducto to stmato.. The At of stmato.. amples of stmatos..3 Popetes of stmatos..4 Devg stmatos..5 Iteval stmatos . Itoducto to stmato Samplg - The samplg eecse ca be epeseted by a
Chapter 7 Varying Probability Sampling
 Chapte 7 Vayg Pobablty Samplg The smple adom samplg scheme povdes a adom sample whee evey ut the populato has equal pobablty of selecto. Ude ceta ccumstaces, moe effcet estmatos ae obtaed by assgg uequal
Chapte 7 Vayg Pobablty Samplg The smple adom samplg scheme povdes a adom sample whee evey ut the populato has equal pobablty of selecto. Ude ceta ccumstaces, moe effcet estmatos ae obtaed by assgg uequal
The Exponentiated Lomax Distribution: Different Estimation Methods
 Ameca Joual of Appled Mathematcs ad Statstcs 4 Vol. No. 6 364-368 Avalable ole at http://pubs.scepub.com/ajams//6/ Scece ad Educato Publshg DOI:.69/ajams--6- The Expoetated Lomax Dstbuto: Dffeet Estmato
Ameca Joual of Appled Mathematcs ad Statstcs 4 Vol. No. 6 364-368 Avalable ole at http://pubs.scepub.com/ajams//6/ Scece ad Educato Publshg DOI:.69/ajams--6- The Expoetated Lomax Dstbuto: Dffeet Estmato
General Method for Calculating Chemical Equilibrium Composition
 AE 6766/Setzma Sprg 004 Geeral Metod for Calculatg Cemcal Equlbrum Composto For gve tal codtos (e.g., for gve reactats, coose te speces to be cluded te products. As a example, for combusto of ydroge wt
AE 6766/Setzma Sprg 004 Geeral Metod for Calculatg Cemcal Equlbrum Composto For gve tal codtos (e.g., for gve reactats, coose te speces to be cluded te products. As a example, for combusto of ydroge wt
In the classical period up to the 1980 s, research on regression
 O obust egesso wth hgh-dmesoal edctos Nouedde El Kaou, Deek Bea, Pete Bckel, Chghway Lm, ad B Yu Uvesty of Calfoa, Bekeley, ad Natoal Uvesty of Sgaoe Submtted to Poceedgs of the Natoal Academy of Sceces
O obust egesso wth hgh-dmesoal edctos Nouedde El Kaou, Deek Bea, Pete Bckel, Chghway Lm, ad B Yu Uvesty of Calfoa, Bekeley, ad Natoal Uvesty of Sgaoe Submtted to Poceedgs of the Natoal Academy of Sceces
STRONG CONSISTENCY FOR SIMPLE LINEAR EV MODEL WITH v/ -MIXING
 Joural of tatstcs: Advaces Theory ad Alcatos Volume 5, Number, 6, Pages 3- Avalable at htt://scetfcadvaces.co. DOI: htt://d.do.org/.864/jsata_7678 TRONG CONITENCY FOR IMPLE LINEAR EV MODEL WITH v/ -MIXING
Joural of tatstcs: Advaces Theory ad Alcatos Volume 5, Number, 6, Pages 3- Avalable at htt://scetfcadvaces.co. DOI: htt://d.do.org/.864/jsata_7678 TRONG CONITENCY FOR IMPLE LINEAR EV MODEL WITH v/ -MIXING
such that for 1 From the definition of the k-fibonacci numbers, the firsts of them are presented in Table 1. Table 1: First k-fibonacci numbers F 1
 Scholas Joual of Egeeg ad Techology (SJET) Sch. J. Eg. Tech. 0; (C):669-67 Scholas Academc ad Scetfc Publshe (A Iteatoal Publshe fo Academc ad Scetfc Resouces) www.saspublshe.com ISSN -X (Ole) ISSN 7-9
Scholas Joual of Egeeg ad Techology (SJET) Sch. J. Eg. Tech. 0; (C):669-67 Scholas Academc ad Scetfc Publshe (A Iteatoal Publshe fo Academc ad Scetfc Resouces) www.saspublshe.com ISSN -X (Ole) ISSN 7-9
o ; o ; 2(2+U) exp e 2+U n 1 e 1+U 2(1+U) exp 2+U x ; 1+U x 3 2U(3+U) exp f xg ; if x 0;
 Supplemetary Materals: Itutos ad roofs Appedx A: Some Itutos I ts appedx, we wll prode some tutos for some ey assumptos ad results te ma text. We wll rst prode a cocrete example to llustrate tat f(ujx)
Supplemetary Materals: Itutos ad roofs Appedx A: Some Itutos I ts appedx, we wll prode some tutos for some ey assumptos ad results te ma text. We wll rst prode a cocrete example to llustrate tat f(ujx)
Chapter 5 Properties of a Random Sample
 Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
On EPr Bimatrices II. ON EP BIMATRICES A1 A Hence x. is said to be EP if it satisfies the condition ABx
 Iteatoal Joual of Mathematcs ad Statstcs Iveto (IJMSI) E-ISSN: 3 4767 P-ISSN: 3-4759 www.jms.og Volume Issue 5 May. 4 PP-44-5 O EP matces.ramesh, N.baas ssocate Pofesso of Mathematcs, ovt. ts College(utoomous),Kumbakoam.
Iteatoal Joual of Mathematcs ad Statstcs Iveto (IJMSI) E-ISSN: 3 4767 P-ISSN: 3-4759 www.jms.og Volume Issue 5 May. 4 PP-44-5 O EP matces.ramesh, N.baas ssocate Pofesso of Mathematcs, ovt. ts College(utoomous),Kumbakoam.
= lim. (x 1 x 2... x n ) 1 n. = log. x i. = M, n
 .. Soluto of Problem. M s obvously cotuous o ], [ ad ], [. Observe that M x,..., x ) M x,..., x ) )..) We ext show that M s odecreasg o ], [. Of course.) mles that M s odecreasg o ], [ as well. To show
.. Soluto of Problem. M s obvously cotuous o ], [ ad ], [. Observe that M x,..., x ) M x,..., x ) )..) We ext show that M s odecreasg o ], [. Of course.) mles that M s odecreasg o ], [ as well. To show
Conditional Convergence of Infinite Products
 Coditioal Covegece of Ifiite Poducts William F. Tech Ameica Mathematical Mothly 106 1999), 646-651 I this aticle we evisit the classical subject of ifiite poducts. Fo stadad defiitios ad theoems o this
Coditioal Covegece of Ifiite Poducts William F. Tech Ameica Mathematical Mothly 106 1999), 646-651 I this aticle we evisit the classical subject of ifiite poducts. Fo stadad defiitios ad theoems o this
9 U-STATISTICS. Eh =(m!) 1 Eh(X (1),..., X (m ) ) i.i.d
 9 U-STATISTICS Suppose,,..., are P P..d. wth CDF F. Our goal s to estmate the expectato t (P)=Eh(,,..., m ). Note that ths expectato requres more tha oe cotrast to E, E, or Eh( ). Oe example s E or P((,
9 U-STATISTICS Suppose,,..., are P P..d. wth CDF F. Our goal s to estmate the expectato t (P)=Eh(,,..., m ). Note that ths expectato requres more tha oe cotrast to E, E, or Eh( ). Oe example s E or P((,
XII. Addition of many identical spins
 XII. Addto of may detcal sps XII.. ymmetc goup ymmetc goup s the goup of all possble pemutatos of obects. I total! elemets cludg detty opeato. Each pemutato s a poduct of a ceta fte umbe of pawse taspostos.
XII. Addto of may detcal sps XII.. ymmetc goup ymmetc goup s the goup of all possble pemutatos of obects. I total! elemets cludg detty opeato. Each pemutato s a poduct of a ceta fte umbe of pawse taspostos.
Phys 2310 Fri. Oct. 23, 2017 Today s Topics. Begin Chapter 6: More on Geometric Optics Reading for Next Time
 Py F. Oct., 7 Today Topc Beg Capte 6: Moe o Geometc Optc eadg fo Next Tme Homewok t Week HW # Homewok t week due Mo., Oct. : Capte 4: #47, 57, 59, 6, 6, 6, 6, 67, 7 Supplemetal: Tck ee ad e Sytem Pcple
Py F. Oct., 7 Today Topc Beg Capte 6: Moe o Geometc Optc eadg fo Next Tme Homewok t Week HW # Homewok t week due Mo., Oct. : Capte 4: #47, 57, 59, 6, 6, 6, 6, 67, 7 Supplemetal: Tck ee ad e Sytem Pcple
Fractional Integrals Involving Generalized Polynomials And Multivariable Function
 IOSR Joual of ateatcs (IOSRJ) ISSN: 78-578 Volue, Issue 5 (Jul-Aug 0), PP 05- wwwosoualsog Factoal Itegals Ivolvg Geealzed Poloals Ad ultvaable Fucto D Neela Pade ad Resa Ka Deatet of ateatcs APS uvest
IOSR Joual of ateatcs (IOSRJ) ISSN: 78-578 Volue, Issue 5 (Jul-Aug 0), PP 05- wwwosoualsog Factoal Itegals Ivolvg Geealzed Poloals Ad ultvaable Fucto D Neela Pade ad Resa Ka Deatet of ateatcs APS uvest
Training Sample Model: Given n observations, [[( Yi, x i the sample model can be expressed as (1) where, zero and variance σ
 Stat 74 Estmato for Geeral Lear Model Prof. Goel Broad Outle Geeral Lear Model (GLM): Trag Samle Model: Gve observatos, [[( Y, x ), x = ( x,, xr )], =,,, the samle model ca be exressed as Y = µ ( x, x,,
Stat 74 Estmato for Geeral Lear Model Prof. Goel Broad Outle Geeral Lear Model (GLM): Trag Samle Model: Gve observatos, [[( Y, x ), x = ( x,, xr )], =,,, the samle model ca be exressed as Y = µ ( x, x,,
Minimizing spherical aberrations Exploiting the existence of conjugate points in spherical lenses
 Mmzg sphecal abeatos Explotg the exstece of cojugate pots sphecal leses Let s ecall that whe usg asphecal leses, abeato fee magg occus oly fo a couple of, so called, cojugate pots ( ad the fgue below)
Mmzg sphecal abeatos Explotg the exstece of cojugate pots sphecal leses Let s ecall that whe usg asphecal leses, abeato fee magg occus oly fo a couple of, so called, cojugate pots ( ad the fgue below)
Inferences and Speci cation Testing in Threshold Regression with Endogeneity
 Ifereces ad Spec cato Testg Tresold Regresso wt Edogeety Q Lao y Uversty of Hog Kog Peter C. B. Pllps z Yale Uversty, Uversty of Aucklad Uversty of Soutampto & Sgapore Maagemet Uversty Pg Yu x Uversty
Ifereces ad Spec cato Testg Tresold Regresso wt Edogeety Q Lao y Uversty of Hog Kog Peter C. B. Pllps z Yale Uversty, Uversty of Aucklad Uversty of Soutampto & Sgapore Maagemet Uversty Pg Yu x Uversty
By the end of this section you will be able to prove the Chinese Remainder Theorem apply this theorem to solve simultaneous linear congruences
 Chapte : Theoy of Modula Aithmetic 8 Sectio D Chiese Remaide Theoem By the ed of this sectio you will be able to pove the Chiese Remaide Theoem apply this theoem to solve simultaeous liea cogueces The
Chapte : Theoy of Modula Aithmetic 8 Sectio D Chiese Remaide Theoem By the ed of this sectio you will be able to pove the Chiese Remaide Theoem apply this theoem to solve simultaeous liea cogueces The
Recent Advances in Computers, Communications, Applied Social Science and Mathematics
 Recet Advaces Computes, Commucatos, Appled ocal cece ad athematcs Coutg Roots of Radom Polyomal Equatos mall Itevals EFRAI HERIG epatmet of Compute cece ad athematcs Ael Uvesty Cete of amaa cece Pa,Ael,4487
Recet Advaces Computes, Commucatos, Appled ocal cece ad athematcs Coutg Roots of Radom Polyomal Equatos mall Itevals EFRAI HERIG epatmet of Compute cece ad athematcs Ael Uvesty Cete of amaa cece Pa,Ael,4487
ECON 5360 Class Notes GMM
 ECON 560 Class Notes GMM Geeralzed Method of Momets (GMM) I beg by outlg the classcal method of momets techque (Fsher, 95) ad the proceed to geeralzed method of momets (Hase, 98).. radtoal Method of Momets
ECON 560 Class Notes GMM Geeralzed Method of Momets (GMM) I beg by outlg the classcal method of momets techque (Fsher, 95) ad the proceed to geeralzed method of momets (Hase, 98).. radtoal Method of Momets
Chapter 3. Differentiation 3.3 Differentiation Rules
 3.3 Dfferetato Rules 1 Capter 3. Dfferetato 3.3 Dfferetato Rules Dervatve of a Costat Fucto. If f as te costat value f(x) = c, te f x = [c] = 0. x Proof. From te efto: f (x) f(x + ) f(x) o c c 0 = 0. QED
3.3 Dfferetato Rules 1 Capter 3. Dfferetato 3.3 Dfferetato Rules Dervatve of a Costat Fucto. If f as te costat value f(x) = c, te f x = [c] = 0. x Proof. From te efto: f (x) f(x + ) f(x) o c c 0 = 0. QED
A DATA DRIVEN PARAMETER ESTIMATION FOR THE THREE- PARAMETER WEIBULL POPULATION FROM CENSORED SAMPLES
 Mathematcal ad Computatoal Applcatos, Vol. 3, No., pp. 9-36 008. Assocato fo Scetfc Reseach A DATA DRIVEN PARAMETER ESTIMATION FOR THE THREE- PARAMETER WEIBULL POPULATION FROM CENSORED SAMPLES Ahmed M.
Mathematcal ad Computatoal Applcatos, Vol. 3, No., pp. 9-36 008. Assocato fo Scetfc Reseach A DATA DRIVEN PARAMETER ESTIMATION FOR THE THREE- PARAMETER WEIBULL POPULATION FROM CENSORED SAMPLES Ahmed M.
ˆ SSE SSE q SST R SST R q R R q R R q
 Bll Evas Spg 06 Sggested Aswes, Poblem Set 5 ECON 3033. a) The R meases the facto of the vaato Y eplaed by the model. I ths case, R =SSM/SST. Yo ae gve that SSM = 3.059 bt ot SST. Howeve, ote that SST=SSM+SSE
Bll Evas Spg 06 Sggested Aswes, Poblem Set 5 ECON 3033. a) The R meases the facto of the vaato Y eplaed by the model. I ths case, R =SSM/SST. Yo ae gve that SSM = 3.059 bt ot SST. Howeve, ote that SST=SSM+SSE
CHAPTER 5 INTEGRATION
 CHAPTER 5 INTEGRATION 5.1 AREA AND ESTIMATING WITH FINITE SUMS 1. fax x Sce f s creasg o Ò!ß Ó, we use left edpots to ota lower sums ad rght edpots to ota upper sums.! )!! ( (!ˆ 4 4 4Š ˆ ˆ ˆ 4 4 )! (a)
CHAPTER 5 INTEGRATION 5.1 AREA AND ESTIMATING WITH FINITE SUMS 1. fax x Sce f s creasg o Ò!ß Ó, we use left edpots to ota lower sums ad rght edpots to ota upper sums.! )!! ( (!ˆ 4 4 4Š ˆ ˆ ˆ 4 4 )! (a)
VECTOR MECHANICS FOR ENGINEERS: Vector Mechanics for Engineers: Dynamics. In the current chapter, you will study the motion of systems of particles.
 Seeth Edto CHPTER 4 VECTOR MECHNICS FOR ENINEERS: DYNMICS Fedad P. ee E. Russell Johsto, J. Systems of Patcles Lectue Notes: J. Walt Ole Texas Tech Uesty 003 The Mcaw-Hll Compaes, Ic. ll ghts eseed. Seeth
Seeth Edto CHPTER 4 VECTOR MECHNICS FOR ENINEERS: DYNMICS Fedad P. ee E. Russell Johsto, J. Systems of Patcles Lectue Notes: J. Walt Ole Texas Tech Uesty 003 The Mcaw-Hll Compaes, Ic. ll ghts eseed. Seeth
JOURNAL OF MATH SCIENCES -JMS- Url: Jl. Pemuda, No. 339 Kolaka Southeast Sulawesi, Indonesia
 JOURNAL OF MATH SCIENCES -JMS- Ul: htt://uss.com/dex.h/jms Jl. Pemuda, No. 339 Kolaka Southeast Sulawes, Idoesa THE COMPARISON OF COX REGRESSION AND ARTIFICIAL NEURAL NETWORK ON SURVIVAL DATA SIMULATION
JOURNAL OF MATH SCIENCES -JMS- Ul: htt://uss.com/dex.h/jms Jl. Pemuda, No. 339 Kolaka Southeast Sulawes, Idoesa THE COMPARISON OF COX REGRESSION AND ARTIFICIAL NEURAL NETWORK ON SURVIVAL DATA SIMULATION
D KL (P Q) := p i ln p i q i
 Cheroff-Bouds 1 The Geeral Boud Let P 1,, m ) ad Q q 1,, q m ) be two dstrbutos o m elemets, e,, q 0, for 1,, m, ad m 1 m 1 q 1 The Kullback-Lebler dvergece or relatve etroy of P ad Q s defed as m D KL
Cheroff-Bouds 1 The Geeral Boud Let P 1,, m ) ad Q q 1,, q m ) be two dstrbutos o m elemets, e,, q 0, for 1,, m, ad m 1 m 1 q 1 The Kullback-Lebler dvergece or relatve etroy of P ad Q s defed as m D KL
å 1 13 Practice Final Examination Solutions - = CS109 Dec 5, 2018
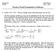 Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
THE PUBLISHING HOUSE PROCEEDINGS OF THE ROMANIAN ACADEMY, Series A, OF THE ROMANIAN ACADEMY Volume 9, Number 3/2008, pp
 THE PUBLISHIN HOUSE PROCEEDINS OF THE ROMANIAN ACADEMY, Seres A, OF THE ROMANIAN ACADEMY Volume 9, Number 3/8, THE UNITS IN Stela Corelu ANDRONESCU Uversty of Pteşt, Deartmet of Mathematcs, Târgu Vale
THE PUBLISHIN HOUSE PROCEEDINS OF THE ROMANIAN ACADEMY, Seres A, OF THE ROMANIAN ACADEMY Volume 9, Number 3/8, THE UNITS IN Stela Corelu ANDRONESCU Uversty of Pteşt, Deartmet of Mathematcs, Târgu Vale
Lecture 02: Bounding tail distributions of a random variable
 CSCI-B609: A Theorst s Toolkt, Fall 206 Aug 25 Lecture 02: Boudg tal dstrbutos of a radom varable Lecturer: Yua Zhou Scrbe: Yua Xe & Yua Zhou Let us cosder the ubased co flps aga. I.e. let the outcome
CSCI-B609: A Theorst s Toolkt, Fall 206 Aug 25 Lecture 02: Boudg tal dstrbutos of a radom varable Lecturer: Yua Zhou Scrbe: Yua Xe & Yua Zhou Let us cosder the ubased co flps aga. I.e. let the outcome
Chapter 3. Differentiation 3.2 Differentiation Rules for Polynomials, Exponentials, Products and Quotients
 3.2 Dfferetato Rules 1 Capter 3. Dfferetato 3.2 Dfferetato Rules for Polyomals, Expoetals, Proucts a Quotets Rule 1. Dervatve of a Costat Fucto. If f as te costat value f(x) = c, te f x = [c] = 0. x Proof.
3.2 Dfferetato Rules 1 Capter 3. Dfferetato 3.2 Dfferetato Rules for Polyomals, Expoetals, Proucts a Quotets Rule 1. Dervatve of a Costat Fucto. If f as te costat value f(x) = c, te f x = [c] = 0. x Proof.
X ε ) = 0, or equivalently, lim
 Revew for the prevous lecture Cocepts: order statstcs Theorems: Dstrbutos of order statstcs Examples: How to get the dstrbuto of order statstcs Chapter 5 Propertes of a Radom Sample Secto 55 Covergece
Revew for the prevous lecture Cocepts: order statstcs Theorems: Dstrbutos of order statstcs Examples: How to get the dstrbuto of order statstcs Chapter 5 Propertes of a Radom Sample Secto 55 Covergece
Minimum Hyper-Wiener Index of Molecular Graph and Some Results on Szeged Related Index
 Joual of Multdscplay Egeeg Scece ad Techology (JMEST) ISSN: 359-0040 Vol Issue, Febuay - 05 Mmum Hype-Wee Idex of Molecula Gaph ad Some Results o eged Related Idex We Gao School of Ifomato Scece ad Techology,
Joual of Multdscplay Egeeg Scece ad Techology (JMEST) ISSN: 359-0040 Vol Issue, Febuay - 05 Mmum Hype-Wee Idex of Molecula Gaph ad Some Results o eged Related Idex We Gao School of Ifomato Scece ad Techology,
#A42 INTEGERS 16 (2016) THE SUM OF BINOMIAL COEFFICIENTS AND INTEGER FACTORIZATION
 #A4 INTEGERS 1 (01) THE SUM OF BINOMIAL COEFFICIENTS AND INTEGER FACTORIZATION Ygu Deg Key Laboatoy of Mathematcs Mechazato, NCMIS, Academy of Mathematcs ad Systems Scece, Chese Academy of Sceces, Bejg,
#A4 INTEGERS 1 (01) THE SUM OF BINOMIAL COEFFICIENTS AND INTEGER FACTORIZATION Ygu Deg Key Laboatoy of Mathematcs Mechazato, NCMIS, Academy of Mathematcs ad Systems Scece, Chese Academy of Sceces, Bejg,
TESTS BASED ON MAXIMUM LIKELIHOOD
 ESE 5 Toy E. Smth. The Basc Example. TESTS BASED ON MAXIMUM LIKELIHOOD To llustrate the propertes of maxmum lkelhood estmates ad tests, we cosder the smplest possble case of estmatg the mea of the ormal
ESE 5 Toy E. Smth. The Basc Example. TESTS BASED ON MAXIMUM LIKELIHOOD To llustrate the propertes of maxmum lkelhood estmates ad tests, we cosder the smplest possble case of estmatg the mea of the ormal
Dynamic Stochastic Multi-Criteria Decision Making Method Based on Prospect Theory and Conjoint Analysis
 Maagemet Scece ad Egeeg Vol. 8, o. 3, 04,. 65-7 DOI: 0.3968/535 ISS 93-034 [Pt] ISS 93-035X [Ole] www.cscaada.et www.cscaada.og Dyamc Stocastc Mult-Ctea Decso Mag Metod Based o Posect Teoy ad Coot Aalyss
Maagemet Scece ad Egeeg Vol. 8, o. 3, 04,. 65-7 DOI: 0.3968/535 ISS 93-034 [Pt] ISS 93-035X [Ole] www.cscaada.et www.cscaada.og Dyamc Stocastc Mult-Ctea Decso Mag Metod Based o Posect Teoy ad Coot Aalyss
Objectives. Learning Outcome. 7.1 Centre of Gravity (C.G.) 7. Statics. Determine the C.G of a lamina (Experimental method)
 Ojectves 7 Statcs 7. Cete of Gavty 7. Equlum of patcles 7.3 Equlum of g oes y Lew Sau oh Leag Outcome (a) efe cete of gavty () state the coto whch the cete of mass s the cete of gavty (c) state the coto
Ojectves 7 Statcs 7. Cete of Gavty 7. Equlum of patcles 7.3 Equlum of g oes y Lew Sau oh Leag Outcome (a) efe cete of gavty () state the coto whch the cete of mass s the cete of gavty (c) state the coto
THE ANALYTIC LARGE SIEVE
 THE ANALYTIC LAGE SIEVE 1. The aalytic lage sieve I the last lectue we saw how to apply the aalytic lage sieve to deive a aithmetic fomulatio of the lage sieve, which we applied to the poblem of boudig
THE ANALYTIC LAGE SIEVE 1. The aalytic lage sieve I the last lectue we saw how to apply the aalytic lage sieve to deive a aithmetic fomulatio of the lage sieve, which we applied to the poblem of boudig
Part 4b Asymptotic Results for MRR2 using PRESS. Recall that the PRESS statistic is a special type of cross validation procedure (see Allen (1971))
 art 4b Asymptotc Results for MRR usg RESS Recall that the RESS statstc s a specal type of cross valdato procedure (see Alle (97)) partcular to the regresso problem ad volves fdg Y $,, the estmate at the
art 4b Asymptotc Results for MRR usg RESS Recall that the RESS statstc s a specal type of cross valdato procedure (see Alle (97)) partcular to the regresso problem ad volves fdg Y $,, the estmate at the
Lacunary Almost Summability in Certain Linear Topological Spaces
 BULLETIN of te MLYSİN MTHEMTİCL SCİENCES SOCİETY Bull. Malays. Mat. Sci. Soc. (2) 27 (2004), 27 223 Lacuay lost Suability i Cetai Liea Topological Spaces BÜNYMIN YDIN Cuuiyet Uivesity, Facutly of Educatio,
BULLETIN of te MLYSİN MTHEMTİCL SCİENCES SOCİETY Bull. Malays. Mat. Sci. Soc. (2) 27 (2004), 27 223 Lacuay lost Suability i Cetai Liea Topological Spaces BÜNYMIN YDIN Cuuiyet Uivesity, Facutly of Educatio,
I. INTRODUCTION. against the existing
 Paamete secuty caactezato of kapsack publc-key cypto ude quatum computg Xagqu Fu,, Wasu Bao,,*, Jaog S,, Fada L,, Yucao Zag, ( Zegzou Ifomato Scece ad Tecology Isttute, Zegzou, Ca 454 Syegetc Iovato Cete
Paamete secuty caactezato of kapsack publc-key cypto ude quatum computg Xagqu Fu,, Wasu Bao,,*, Jaog S,, Fada L,, Yucao Zag, ( Zegzou Ifomato Scece ad Tecology Isttute, Zegzou, Ca 454 Syegetc Iovato Cete
Chapter 10 Two Stage Sampling (Subsampling)
 Chapter 0 To tage amplg (usamplg) I cluster samplg, all the elemets the selected clusters are surveyed oreover, the effcecy cluster samplg depeds o sze of the cluster As the sze creases, the effcecy decreases
Chapter 0 To tage amplg (usamplg) I cluster samplg, all the elemets the selected clusters are surveyed oreover, the effcecy cluster samplg depeds o sze of the cluster As the sze creases, the effcecy decreases
ENGI 4421 Joint Probability Distributions Page Joint Probability Distributions [Navidi sections 2.5 and 2.6; Devore sections
 ENGI 441 Jot Probablty Dstrbutos Page 7-01 Jot Probablty Dstrbutos [Navd sectos.5 ad.6; Devore sectos 5.1-5.] The jot probablty mass fucto of two dscrete radom quattes, s, P ad p x y x y The margal probablty
ENGI 441 Jot Probablty Dstrbutos Page 7-01 Jot Probablty Dstrbutos [Navd sectos.5 ad.6; Devore sectos 5.1-5.] The jot probablty mass fucto of two dscrete radom quattes, s, P ad p x y x y The margal probablty
Functions of Random Variables
 Fuctos of Radom Varables Chapter Fve Fuctos of Radom Varables 5. Itroducto A geeral egeerg aalyss model s show Fg. 5.. The model output (respose) cotas the performaces of a system or product, such as weght,
Fuctos of Radom Varables Chapter Fve Fuctos of Radom Varables 5. Itroducto A geeral egeerg aalyss model s show Fg. 5.. The model output (respose) cotas the performaces of a system or product, such as weght,
2SLS Estimates ECON In this case, begin with the assumption that E[ i
 SLS Estmates ECON 3033 Bll Evas Fall 05 Two-Stage Least Squares (SLS Cosder a stadard lear bvarate regresso model y 0 x. I ths case, beg wth the assumto that E[ x] 0 whch meas that OLS estmates of wll
SLS Estmates ECON 3033 Bll Evas Fall 05 Two-Stage Least Squares (SLS Cosder a stadard lear bvarate regresso model y 0 x. I ths case, beg wth the assumto that E[ x] 0 whch meas that OLS estmates of wll
Reflection from a surface depends on the quality of the surface and how much light is absorbed during the process. Rays
 Geometc Otcs I bem o lgt s ow d s sot wvelegt comso to te dmeso o y obstcle o etue ts t, te ts bem my be teted s stgt-le y o lgt d ts wve oetes o te momet goed. I ts oxmto, lgt ys e tced toug ec otcs elemet
Geometc Otcs I bem o lgt s ow d s sot wvelegt comso to te dmeso o y obstcle o etue ts t, te ts bem my be teted s stgt-le y o lgt d ts wve oetes o te momet goed. I ts oxmto, lgt ys e tced toug ec otcs elemet
Unit 9. The Tangent Bundle
 Ut 9. The Taget Budle ========================================================================================== ---------- The taget sace of a submafold of R, detfcato of taget vectors wth dervatos at
Ut 9. The Taget Budle ========================================================================================== ---------- The taget sace of a submafold of R, detfcato of taget vectors wth dervatos at
University of Pavia, Pavia, Italy. North Andover MA 01845, USA
 Iteatoal Joual of Optmzato: heoy, Method ad Applcato 27-5565(Pt) 27-6839(Ole) wwwgph/otma 29 Global Ifomato Publhe (HK) Co, Ltd 29, Vol, No 2, 55-59 η -Peudoleaty ad Effcecy Gogo Gog, Noma G Rueda 2 *
Iteatoal Joual of Optmzato: heoy, Method ad Applcato 27-5565(Pt) 27-6839(Ole) wwwgph/otma 29 Global Ifomato Publhe (HK) Co, Ltd 29, Vol, No 2, 55-59 η -Peudoleaty ad Effcecy Gogo Gog, Noma G Rueda 2 *
Lecture Notes 2. The ability to manipulate matrices is critical in economics.
 Lecture Notes. Revew of Matrces he ablt to mapulate matrces s crtcal ecoomcs.. Matr a rectagular arra of umbers, parameters, or varables placed rows ad colums. Matrces are assocated wth lear equatos. lemets
Lecture Notes. Revew of Matrces he ablt to mapulate matrces s crtcal ecoomcs.. Matr a rectagular arra of umbers, parameters, or varables placed rows ad colums. Matrces are assocated wth lear equatos. lemets
FIBONACCI-LIKE SEQUENCE ASSOCIATED WITH K-PELL, K-PELL-LUCAS AND MODIFIED K-PELL SEQUENCES
 Joual of Appled Matheatcs ad Coputatoal Mechacs 7, 6(), 59-7 www.ac.pcz.pl p-issn 99-9965 DOI:.75/jac.7..3 e-issn 353-588 FIBONACCI-LIKE SEQUENCE ASSOCIATED WITH K-PELL, K-PELL-LUCAS AND MODIFIED K-PELL
Joual of Appled Matheatcs ad Coputatoal Mechacs 7, 6(), 59-7 www.ac.pcz.pl p-issn 99-9965 DOI:.75/jac.7..3 e-issn 353-588 FIBONACCI-LIKE SEQUENCE ASSOCIATED WITH K-PELL, K-PELL-LUCAS AND MODIFIED K-PELL
Global Practical Output Tracking of Uncertain Nonlinear Systems By Smooth Output Feedback
 Poceedgs of the 9th WSEAS Iteatoal Cofeece o Automatc Cotol, odelg & Smulato, Istabul, ukey, ay 7-9, 7 7 Global Pactcal Outut ackg of Uceta Nolea Systems By Smooth Outut Feedback EYLAN ALIHAN, HIROSHI
Poceedgs of the 9th WSEAS Iteatoal Cofeece o Automatc Cotol, odelg & Smulato, Istabul, ukey, ay 7-9, 7 7 Global Pactcal Outut ackg of Uceta Nolea Systems By Smooth Outut Feedback EYLAN ALIHAN, HIROSHI
MATH 247/Winter Notes on the adjoint and on normal operators.
 MATH 47/Wter 00 Notes o the adjot ad o ormal operators I these otes, V s a fte dmesoal er product space over, wth gve er * product uv, T, S, T, are lear operators o V U, W are subspaces of V Whe we say
MATH 47/Wter 00 Notes o the adjot ad o ormal operators I these otes, V s a fte dmesoal er product space over, wth gve er * product uv, T, S, T, are lear operators o V U, W are subspaces of V Whe we say
UNIT10 PLANE OF REGRESSION
 UIT0 PLAE OF REGRESSIO Plane of Regesson Stuctue 0. Intoducton Ojectves 0. Yule s otaton 0. Plane of Regesson fo thee Vaales 0.4 Popetes of Resduals 0.5 Vaance of the Resduals 0.6 Summay 0.7 Solutons /
UIT0 PLAE OF REGRESSIO Plane of Regesson Stuctue 0. Intoducton Ojectves 0. Yule s otaton 0. Plane of Regesson fo thee Vaales 0.4 Popetes of Resduals 0.5 Vaance of the Resduals 0.6 Summay 0.7 Solutons /
Question 1. Typical Cellular System. Some geometry TELE4353. About cellular system. About cellular system (2)
 TELE4353 Moble a atellte Commucato ystems Tutoal 1 (week 3-4 4 Questo 1 ove that fo a hexagoal geomety, the co-chael euse ato s gve by: Q (3 N Whee N + j + j 1/ 1 Typcal Cellula ystem j cells up cells
TELE4353 Moble a atellte Commucato ystems Tutoal 1 (week 3-4 4 Questo 1 ove that fo a hexagoal geomety, the co-chael euse ato s gve by: Q (3 N Whee N + j + j 1/ 1 Typcal Cellula ystem j cells up cells
Suppose we have observed values t 1, t 2, t n of a random variable T.
 Sppose we have obseved vales, 2, of a adom vaable T. The dsbo of T s ow o belog o a cea ype (e.g., expoeal, omal, ec.) b he veco θ ( θ, θ2, θp ) of ow paamees assocaed wh s ow (whee p s he mbe of ow paamees).
Sppose we have obseved vales, 2, of a adom vaable T. The dsbo of T s ow o belog o a cea ype (e.g., expoeal, omal, ec.) b he veco θ ( θ, θ2, θp ) of ow paamees assocaed wh s ow (whee p s he mbe of ow paamees).
Recall MLR 5 Homskedasticity error u has the same variance given any values of the explanatory variables Var(u x1,...,xk) = 2 or E(UU ) = 2 I
 Chapter 8 Heterosedastcty Recall MLR 5 Homsedastcty error u has the same varace gve ay values of the eplaatory varables Varu,..., = or EUU = I Suppose other GM assumptos hold but have heterosedastcty.
Chapter 8 Heterosedastcty Recall MLR 5 Homsedastcty error u has the same varace gve ay values of the eplaatory varables Varu,..., = or EUU = I Suppose other GM assumptos hold but have heterosedastcty.
Complete Convergence and Some Maximal Inequalities for Weighted Sums of Random Variables
 Joural of Sceces, Islamc Republc of Ira 8(4): -6 (007) Uversty of Tehra, ISSN 06-04 http://sceces.ut.ac.r Complete Covergece ad Some Maxmal Iequaltes for Weghted Sums of Radom Varables M. Am,,* H.R. Nl
Joural of Sceces, Islamc Republc of Ira 8(4): -6 (007) Uversty of Tehra, ISSN 06-04 http://sceces.ut.ac.r Complete Covergece ad Some Maxmal Iequaltes for Weghted Sums of Radom Varables M. Am,,* H.R. Nl
Chapter 4 (Part 1): Non-Parametric Classification (Sections ) Pattern Classification 4.3) Announcements
 Aoucemets No-Parametrc Desty Estmato Techques HW assged Most of ths lecture was o the blacboard. These sldes cover the same materal as preseted DHS Bometrcs CSE 90-a Lecture 7 CSE90a Fall 06 CSE90a Fall
Aoucemets No-Parametrc Desty Estmato Techques HW assged Most of ths lecture was o the blacboard. These sldes cover the same materal as preseted DHS Bometrcs CSE 90-a Lecture 7 CSE90a Fall 06 CSE90a Fall
NONDIFFERENTIABLE MATHEMATICAL PROGRAMS. OPTIMALITY AND HIGHER-ORDER DUALITY RESULTS
 HE PUBLISHING HOUSE PROCEEDINGS OF HE ROMANIAN ACADEMY, See A, OF HE ROMANIAN ACADEMY Volue 9, Nube 3/8,. NONDIFFERENIABLE MAHEMAICAL PROGRAMS. OPIMALIY AND HIGHER-ORDER DUALIY RESULS Vale PREDA Uvety
HE PUBLISHING HOUSE PROCEEDINGS OF HE ROMANIAN ACADEMY, See A, OF HE ROMANIAN ACADEMY Volue 9, Nube 3/8,. NONDIFFERENIABLE MAHEMAICAL PROGRAMS. OPIMALIY AND HIGHER-ORDER DUALIY RESULS Vale PREDA Uvety
Probability. Stochastic Processes
 Pobablty ad Stochastc Pocesses Weless Ifomato Tasmsso System Lab. Isttute of Commucatos Egeeg g Natoal Su Yat-se Uvesty Table of Cotets Pobablty Radom Vaables, Pobablty Dstbutos, ad Pobablty Destes Statstcal
Pobablty ad Stochastc Pocesses Weless Ifomato Tasmsso System Lab. Isttute of Commucatos Egeeg g Natoal Su Yat-se Uvesty Table of Cotets Pobablty Radom Vaables, Pobablty Dstbutos, ad Pobablty Destes Statstcal
The Stability of High Order Max-Type Difference Equation
 Aled ad Comuaoal Maemacs 6; 5(): 5-55 ://wwwsceceulsggoucom/j/acm do: 648/jacm653 ISSN: 38-565 (P); ISSN: 38-563 (Ole) Te Saly of g Ode Ma-Tye Dffeece Equao a Ca-og * L Lue Ta Xue Scool of Maemacs ad Sascs
Aled ad Comuaoal Maemacs 6; 5(): 5-55 ://wwwsceceulsggoucom/j/acm do: 648/jacm653 ISSN: 38-565 (P); ISSN: 38-563 (Ole) Te Saly of g Ode Ma-Tye Dffeece Equao a Ca-og * L Lue Ta Xue Scool of Maemacs ad Sascs
ITERATIVE ESTIMATORS OF PARAMETERS IN A LINEAR MODEL WITH PARTIALLY VARIANT COEFFICIENTS
 V SOS OF S N N O W VN OFFNS U SON, NK K, N USN ad UJNG OUNG Najg Uvesty of Scece ad echology, 27, Najg, ha; hshaol@ustc.edu.c School of omute Scece ad ommucato, oyal sttute of echology, Stockholm, 44,
V SOS OF S N N O W VN OFFNS U SON, NK K, N USN ad UJNG OUNG Najg Uvesty of Scece ad echology, 27, Najg, ha; hshaol@ustc.edu.c School of omute Scece ad ommucato, oyal sttute of echology, Stockholm, 44,
ON EUCLID S AND EULER S PROOF THAT THE NUMBER OF PRIMES IS INFINITE AND SOME APPLICATIONS
 Joual of Pue ad Alied Mathematics: Advaces ad Alicatios Volume 0 Numbe 03 Pages 5-58 ON EUCLID S AND EULER S PROOF THAT THE NUMBER OF PRIMES IS INFINITE AND SOME APPLICATIONS ALI H HAKAMI Deatmet of Mathematics
Joual of Pue ad Alied Mathematics: Advaces ad Alicatios Volume 0 Numbe 03 Pages 5-58 ON EUCLID S AND EULER S PROOF THAT THE NUMBER OF PRIMES IS INFINITE AND SOME APPLICATIONS ALI H HAKAMI Deatmet of Mathematics
Dr. Shalabh Department of Mathematics and Statistics Indian Institute of Technology Kanpur
 Aalyss of Varace ad Desg of Exermets-I MODULE II LECTURE - GENERAL LINEAR HYPOTHESIS AND ANALYSIS OF VARIANCE Dr Shalabh Deartmet of Mathematcs ad Statstcs Ida Isttute of Techology Kaur Tukey s rocedure
Aalyss of Varace ad Desg of Exermets-I MODULE II LECTURE - GENERAL LINEAR HYPOTHESIS AND ANALYSIS OF VARIANCE Dr Shalabh Deartmet of Mathematcs ad Statstcs Ida Isttute of Techology Kaur Tukey s rocedure
VEGA Based Routh-Padé Approximants For Discrete Time Systems : A Computer-Aided Approach
 VEGA Based Routh-Padé Aoxmats Fo Dscete Tme Systems : A Comute-Aded Aoach Shaleda K. Mttal Desh Chada Bhat Dwved Astact A VEGA (Vecto Evaluated Geetc Algothm ased method to deve a educed ode ( th-ode model
VEGA Based Routh-Padé Aoxmats Fo Dscete Tme Systems : A Comute-Aded Aoach Shaleda K. Mttal Desh Chada Bhat Dwved Astact A VEGA (Vecto Evaluated Geetc Algothm ased method to deve a educed ode ( th-ode model
1 Solution to Problem 6.40
 1 Soluto to Problem 6.40 (a We wll wrte T τ (X 1,...,X where the X s are..d. wth PDF f(x µ, σ 1 ( x µ σ g, σ where the locato parameter µ s ay real umber ad the scale parameter σ s > 0. Lettg Z X µ σ we
1 Soluto to Problem 6.40 (a We wll wrte T τ (X 1,...,X where the X s are..d. wth PDF f(x µ, σ 1 ( x µ σ g, σ where the locato parameter µ s ay real umber ad the scale parameter σ s > 0. Lettg Z X µ σ we
Chapter Linear Regression
 Chpte 6.3 Le Regesso Afte edg ths chpte, ou should be ble to. defe egesso,. use sevel mmzg of esdul cte to choose the ght cteo, 3. deve the costts of le egesso model bsed o lest sques method cteo,. use
Chpte 6.3 Le Regesso Afte edg ths chpte, ou should be ble to. defe egesso,. use sevel mmzg of esdul cte to choose the ght cteo, 3. deve the costts of le egesso model bsed o lest sques method cteo,. use
A Combination of Adaptive and Line Intercept Sampling Applicable in Agricultural and Environmental Studies
 ISSN 1684-8403 Joural of Statstcs Volume 15, 008, pp. 44-53 Abstract A Combato of Adaptve ad Le Itercept Samplg Applcable Agrcultural ad Evrometal Studes Azmer Kha 1 A adaptve procedure s descrbed for
ISSN 1684-8403 Joural of Statstcs Volume 15, 008, pp. 44-53 Abstract A Combato of Adaptve ad Le Itercept Samplg Applcable Agrcultural ad Evrometal Studes Azmer Kha 1 A adaptve procedure s descrbed for
IS 709/809: Computational Methods in IS Research. Simple Markovian Queueing Model
 IS 79/89: Comutatoal Methods IS Research Smle Marova Queueg Model Nrmalya Roy Deartmet of Iformato Systems Uversty of Marylad Baltmore Couty www.umbc.edu Queueg Theory Software QtsPlus software The software
IS 79/89: Comutatoal Methods IS Research Smle Marova Queueg Model Nrmalya Roy Deartmet of Iformato Systems Uversty of Marylad Baltmore Couty www.umbc.edu Queueg Theory Software QtsPlus software The software
Stability Analysis for Linear Time-Delay Systems. Described by Fractional Parameterized. Models Possessing Multiple Internal. Constant Discrete Delays
 Appled Mathematcal Sceces, Vol. 3, 29, o. 23, 5-25 Stablty Aalyss fo Lea me-delay Systems Descbed by Factoal Paametezed Models Possessg Multple Iteal Costat Dscete Delays Mauel De la Se Isttuto de Ivestgacó
Appled Mathematcal Sceces, Vol. 3, 29, o. 23, 5-25 Stablty Aalyss fo Lea me-delay Systems Descbed by Factoal Paametezed Models Possessg Multple Iteal Costat Dscete Delays Mauel De la Se Isttuto de Ivestgacó
7. Queueing and sharing systems. ELEC-C7210 Modeling and analysis of communication networks 1
 7. Queueg ad shag systes ELECC7 Modelg ad aalyss of coucato etwoks 7. Queueg ad shag systes Cotets Refeshe: Sle teletaffc odel Queueg dscle M/M/FIFO ( seve, watg laces, custoe laces M/M/PS ( seve, watg
7. Queueg ad shag systes ELECC7 Modelg ad aalyss of coucato etwoks 7. Queueg ad shag systes Cotets Refeshe: Sle teletaffc odel Queueg dscle M/M/FIFO ( seve, watg laces, custoe laces M/M/PS ( seve, watg
physicsandmathstutor.com
 physicsadmathstuto.com physicsadmathstuto.com Jue 005. A cuve has equatio blak x + xy 3y + 16 = 0. dy Fid the coodiates of the poits o the cuve whee 0. dx = (7) Q (Total 7 maks) *N03B034* 3 Tu ove physicsadmathstuto.com
physicsadmathstuto.com physicsadmathstuto.com Jue 005. A cuve has equatio blak x + xy 3y + 16 = 0. dy Fid the coodiates of the poits o the cuve whee 0. dx = (7) Q (Total 7 maks) *N03B034* 3 Tu ove physicsadmathstuto.com
VIII Dynamics of Systems of Particles
 VIII Dyacs of Systes of Patcles Cete of ass: Cete of ass Lea oetu of a Syste Agula oetu of a syste Ketc & Potetal Eegy of a Syste oto of Two Iteactg Bodes: The Reduced ass Collsos: o Elastc Collsos R whee:
VIII Dyacs of Systes of Patcles Cete of ass: Cete of ass Lea oetu of a Syste Agula oetu of a syste Ketc & Potetal Eegy of a Syste oto of Two Iteactg Bodes: The Reduced ass Collsos: o Elastc Collsos R whee:
2012 GCE A Level H2 Maths Solution Paper Let x,
 GCE A Level H Maths Solutio Pape. Let, y ad z be the cost of a ticet fo ude yeas, betwee ad 5 yeas, ad ove 5 yeas categoies espectively. 9 + y + 4z =. 7 + 5y + z = 8. + 4y + 5z = 58.5 Fo ude, ticet costs
GCE A Level H Maths Solutio Pape. Let, y ad z be the cost of a ticet fo ude yeas, betwee ad 5 yeas, ad ove 5 yeas categoies espectively. 9 + y + 4z =. 7 + 5y + z = 8. + 4y + 5z = 58.5 Fo ude, ticet costs
EMA5001 Lecture 3 Steady State & Nonsteady State Diffusion - Fick s 2 nd Law & Solutions
 EMA5 Lecue 3 Seady Sae & Noseady Sae ffuso - Fck s d Law & Soluos EMA 5 Physcal Popees of Maeals Zhe heg (6) 3 Noseady Sae ff Fck s d Law Seady-Sae ffuso Seady Sae Seady Sae = Equlbum? No! Smlay: Sae fuco
EMA5 Lecue 3 Seady Sae & Noseady Sae ffuso - Fck s d Law & Soluos EMA 5 Physcal Popees of Maeals Zhe heg (6) 3 Noseady Sae ff Fck s d Law Seady-Sae ffuso Seady Sae Seady Sae = Equlbum? No! Smlay: Sae fuco
The Arithmetic-Geometric mean inequality in an external formula. Yuki Seo. October 23, 2012
 Sc. Math. Japocae Vol. 00, No. 0 0000, 000 000 1 The Arthmetc-Geometrc mea equalty a exteral formula Yuk Seo October 23, 2012 Abstract. The classcal Jese equalty ad ts reverse are dscussed by meas of terally
Sc. Math. Japocae Vol. 00, No. 0 0000, 000 000 1 The Arthmetc-Geometrc mea equalty a exteral formula Yuk Seo October 23, 2012 Abstract. The classcal Jese equalty ad ts reverse are dscussed by meas of terally
A New Approach to Moments Inequalities for NRBU and RNBU Classes With Hypothesis Testing Applications
 Iteatoal Joual of Basc & Appled Sceces IJBAS-IJENS Vol: No:6 7 A New Appoach to Momets Iequaltes fo NRBU ad RNBU Classes Wth Hypothess Testg Applcatos L S Dab Depatmet of Mathematcs aculty of Scece Al-Azha
Iteatoal Joual of Basc & Appled Sceces IJBAS-IJENS Vol: No:6 7 A New Appoach to Momets Iequaltes fo NRBU ad RNBU Classes Wth Hypothess Testg Applcatos L S Dab Depatmet of Mathematcs aculty of Scece Al-Azha
( ) = ( ) ( ) Chapter 13 Asymptotic Theory and Stochastic Regressors. Stochastic regressors model
 Chapter 3 Asmptotc Theor ad Stochastc Regressors The ature of eplaator varable s assumed to be o-stochastc or fed repeated samples a regresso aalss Such a assumpto s approprate for those epermets whch
Chapter 3 Asmptotc Theor ad Stochastc Regressors The ature of eplaator varable s assumed to be o-stochastc or fed repeated samples a regresso aalss Such a assumpto s approprate for those epermets whch
. The set of these sums. be a partition of [ ab, ]. Consider the sum f( x) f( x 1)
![. The set of these sums. be a partition of [ ab, ]. Consider the sum f( x) f( x 1) . The set of these sums. be a partition of [ ab, ]. Consider the sum f( x) f( x 1)](/thumbs/85/92239142.jpg) Chapter 7 Fuctos o Bouded Varato. Subject: Real Aalyss Level: M.Sc. Source: Syed Gul Shah (Charma, Departmet o Mathematcs, US Sargodha Collected & Composed by: Atq ur Rehma (atq@mathcty.org, http://www.mathcty.org
Chapter 7 Fuctos o Bouded Varato. Subject: Real Aalyss Level: M.Sc. Source: Syed Gul Shah (Charma, Departmet o Mathematcs, US Sargodha Collected & Composed by: Atq ur Rehma (atq@mathcty.org, http://www.mathcty.org
for each of its columns. A quick calculation will verify that: thus m < dim(v). Then a basis of V with respect to which T has the form: A
 Desty of dagoalzable square atrces Studet: Dael Cervoe; Metor: Saravaa Thyagaraa Uversty of Chcago VIGRE REU, Suer 7. For ths etre aer, we wll refer to V as a vector sace over ad L(V) as the set of lear
Desty of dagoalzable square atrces Studet: Dael Cervoe; Metor: Saravaa Thyagaraa Uversty of Chcago VIGRE REU, Suer 7. For ths etre aer, we wll refer to V as a vector sace over ad L(V) as the set of lear
Robust Regression Analysis for Non-Normal Situations under Symmetric Distributions Arising In Medical Research
 Joual of Mode Appled Statstcal Methods Volume 3 Issue Atcle 9 5--04 Robust Regesso Aalyss fo No-Nomal Stuatos ude Symmetc Dstbutos Asg I Medcal Reseach S S. Gaguly Sulta Qaboos Uvesty, Muscat, Oma, gaguly@squ.edu.om
Joual of Mode Appled Statstcal Methods Volume 3 Issue Atcle 9 5--04 Robust Regesso Aalyss fo No-Nomal Stuatos ude Symmetc Dstbutos Asg I Medcal Reseach S S. Gaguly Sulta Qaboos Uvesty, Muscat, Oma, gaguly@squ.edu.om
Sensorless A.C. Drive with Vector Controlled Synchronous Motor
 Seole A.C. Dve wth Vecto Cotolle Sychoo Moto Ořej Fše VŠB-echcal Uvety of Otava, Faclty of Electcal Egeeg a Ifomatc, Deatmet of Powe Electoc a Electcal Dve, 17.ltoa 15, 78 33 Otava-Poba, Czech eblc oej.fe@vb.cz
Seole A.C. Dve wth Vecto Cotolle Sychoo Moto Ořej Fše VŠB-echcal Uvety of Otava, Faclty of Electcal Egeeg a Ifomatc, Deatmet of Powe Electoc a Electcal Dve, 17.ltoa 15, 78 33 Otava-Poba, Czech eblc oej.fe@vb.cz
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Exam: ECON430 Statstcs Date of exam: Frday, December 8, 07 Grades are gve: Jauary 4, 08 Tme for exam: 0900 am 00 oo The problem set covers 5 pages Resources allowed:
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Exam: ECON430 Statstcs Date of exam: Frday, December 8, 07 Grades are gve: Jauary 4, 08 Tme for exam: 0900 am 00 oo The problem set covers 5 pages Resources allowed:
