41. The ancient Babylonians (circa 1700 B.C.) approximated N by applying the formula. x n x n N x n. with respect to output
|
|
|
- Gerald Jonathan Hawkins
- 5 years ago
- Views:
Transcription
1 48 Chapter 2 Differentiation: Basic Concepts 4. The ancient Babylonians (circa 700 B.C.) approximated N by applying the formula x n 2 x n N x n for n, 2, 3,... (a) Show that this formula can be derived from the formula for Newton s method in Problem 38, then use it to estimate,265. Repeat the formula until two consecutive approximations agree to four decimal places. Use your calculator to check your result. (b) The spy wakes up one morning in Babylonia finds that his calculator has been stolen. Create a spy story problem based on using the ancient formula to compute a square root. 5 The Chain Rule 42. Sometimes Newton s method fails no matter what initial value x 0 is chosen (unless we are lucky enough to choose the root itself). Let f(x) 3 x choose x 0 arbitrarily (x 0 0). (a) Show that x n 2x n for n 0,, 2,... so that the successive guesses generated by Newton s method are x 0, 2x 0, 4x 0,... (b) Use your graphing utility to graph f(x) use an appropriate utility to draw the tangent lines to the graph of y f(x) at the points that correspond to x 0, 2x 0, 4x 0,... Why do these numbers fail to estimate a root of f(x) 0? In many practical situations, you find that the rate at which one quantity is changing can be expressed as the product of other rates. For example, suppose a car is traveling at 50 mph at a particular time when gasoline is being consumed at the rate of 0. gal/mile. Then, to find out how much gasoline is being used each hour, you would multiply the rates: (0. gal/mile)(50 miles/hour) 5 gal/hour Or, suppose the total manufacturing cost at a certain factory is a function of the number of units produced, which in turn is a function of the number of hours the factory has been operating. If C, q, t denote the cost, units produced, time, respectively, then dc (dollars per unit) dq rate of change of cost with respect to output dq dt rate of change of output with respect to time (units per hour) The product of these two rates is the rate of change of cost with respect to time; that is,
2 Chapter 2 Section 5 The Chain Rule 49 dc dt dc dq dq dt (dollars per hour) This formula is a special case of an important result in calculus called the chain rule. The Chain Rule Suppose y is a differentiable function of u, u is a differentiable function of x. Then y is a composite function of x du du That is, the derivative of y with respect to x is the derivative of y with respect to u times the derivative of u with respect to x. Note Notice that one way to remember the chain rule is to pretend that the derivatives are quotients to cancel du. That is, du du du du Here are two examples illustrating the use of the chain rule. Find if y u 3 3u 2 u x 2 2. Since EXAMPLE 5. it follows that du 3u2 6u Notice that this derivative is expressed in terms of the variables x u. Since you are thinking of y as a function of x, you may want to express in terms of x alone. To do this, substitute x 2 2 for u in the expression for simplify the answer as follows. du 2x du du (3u2 6u)(2x)
3 50 Chapter 2 Differentiation: Basic Concepts [3(x2 2) 2 6(x 2 2)](2x) 6x(x 2 2)[(x 2 2) 2] 6x(x 2 2)(x 2 ) 6x 3 (x 2 2) For practice, check this answer by first substituting u x 2 2 into the original expression for y then differentiating with respect to x. In the next example, you will see how to use the chain rule to calculate a derivative for a particular value of the independent variable. EXAMPLE 5.2 Find when x if y u u 3x 2. u Since (u )() u() du (u ) 2 (u ) 2 by the quotient rule it follows that du 6x du du 6x (u ) 2(6x) (u ) 2 The goal is to evaluate this derivative when x. One way to do this is to replace u by its algebraic formula, as in Example 5., then evaluate the resulting expression when x. However, it is easier to substitute numbers than algebraic expressions, so it is preferable to compute the numerical value of u first then substitute. In particular, when x, the original formula u 3x 2 gives u 3() 2 2. Now substitute x u 2 in the formula for to conclude that when x, 6() (2 ) In many practical problems, a quantity is given as a function of one variable, which, in turn, can be written as a function of a second variable, the goal is to find the rate of change of the original quantity with respect to the second variable. Such problems can be solved by means of the chain rule. Here is an example.
4 Chapter 2 Section 5 The Chain Rule 5 The cost of producing x units of a particular commodity is C(x) x 2 4x 53 3 dollars, the production level t hours into a particular production run is x(t) 0.2t t units. At what rate is cost changing with respect to time after 4 hours? so according to the chain rule, When t 4, the level of production is EXAMPLE 5.3 dc 2 3 x 4 dc dt 0.4t 0.03 dt dc dt 2 3 x 4 (0.4t 0.03) x(4) 0.2(4) (4) 3.32 units dc dt 2 3 (3.32 4) [0.4(4) 0.03] Thus, after 4 hours, cost is increasing at the rate of approximately $0.3 per hour. COMPOSITE FUNCTIONS Recall from Chapter, Section, that the composite function g[h(x)] is the function formed from functions g(u) h(x) by substituting h(x) for u in the formula for g(u). The chain rule is actually a rule for differentiating composite functions can be rewritten using functional notation as follows. The Chain Rule in Functional Notation If g(u) h(x) are differentiable functions, d g[h(x)] g[h(x)]h(x) To see that this is nothing more than a restatement of the previous version of the chain rule, suppose that y g[h(x)]. Then, y g(u) where u h(x)
5 52 Chapter 2 Differentiation: Basic Concepts, by the chain rule, The use of this form of the chain rule is illustrated in the next example. EXAMPLE 5.4 Differentiate the function f(x) x 2 3x 2. The form of the function is where the box du g(u)h(x) g[h(x)]h(x) du contains the expression x 2 3x 2. Then according to the chain rule, the derivative of the composite function f(x) is f(x) 2 ( )/2 ( ) f(x) ( ) /2 ( ) (x 2 3x 2) 2x 3 2 ( )/2 (2x 3) 2 (x2 3x 2) /2 (2x 3) 2x 3 2x 2 3x 2 THE GENERAL POWER RULE In Section 2, you learned the rule d (xn ) nx n for differentiating power functions. By combining this rule with the chain rule, you obtain the following rule for differentiating functions of the general form [h(x)] n. The General Power Rule For any real number n differentiable function h, d [h(x)]n n[h(x)] n d [h(x)]
6 Chapter 2 Section 5 The Chain Rule 53 To derive the general power rule, think of [h(x)] n as the composite function [h(x)] n g[h(x)] where g(u) u n Then, g(u) nun h(x) d [h(x)], by the chain rule, d [h(x)]n d g[h(x)] g[h(x)]h(x) d n[h(x)]n [h(x)] The use of the general power rule is illustrated in the following examples. EXAMPLE 5.5 Differentiate the function f(x) (2x 4 x) 3. One way to do this problem is to exp the function rewrite it as f(x) 8x 2 2x 9 6x 6 x 3 then differentiate this polynomial term by term to get f(x) 96x 08x 8 36x 5 3x 2 But see how much easier it is to use the general power rule. According to this rule, f(x) 3(2x 4 x) 2 d (2x4 x) 3(2x 4 x) 2 (8x 3 ) Not only is this method easier, but the answer even comes out in factored form! In the next example, the solution to Example 5.4 is written more compactly with the aid of the general power rule. EXAMPLE 5.6 Differentiate the function f(x) x 2 3x 2. Rewrite the function as f(x) (x 2 3x 2) /2 apply the general power rule:
7 54 Chapter 2 Differentiation: Basic Concepts f(x) 2 (x2 3x 2) /2 d (x2 3x 2) 2 (x2 3x 2) /2 (2x 3) 2x 3 2x 2 3x 2 EXAMPLE 5.7 Differentiate the function f(x). (2x 3) 5 Do not use the quotient rule! It s much easier to rewrite the function as apply the general power rule to get f(x) (2x 3) 5 f(x) 5(2x 3) 6 d (2x 3) 5(2x 3)6 (2) 0 (2x 3) 6 The chain rule is often used in combination with the other rules you learned in Sections 2 3. The next example involves the product rule. EXAMPLE 5.8 Differentiate the function f(x) (3x ) 4 (2x ) 5 simplify your answer. First apply the product rule to get f(x) (3x ) 4 d [(2x )5 ] (2x ) 5 d [(3x )4 ] Continue by applying the general power rule to each term: f(x) (3x ) 4 [5(2x ) 4 (2)] (2x ) 5 [4(3x ) 3 (3)] 0(3x ) 4 (2x ) 4 2(2x ) 5 (3x ) 3 Finally, simplify your answer by factoring:
8 Chapter 2 Section 5 The Chain Rule 55 f(x) 2(3x ) 3 (2x ) 4 [5(3x ) 6(2x )] 2(3x ) 3 (2x ) 4 [5x 5 2x 6] 2(3x ) 3 (2x ) 4 (27x ) EXAMPLE 5.9 Differentiate the function f(t) First rewrite the function as t t then apply the general power rule to get f(t) 2 t t /2 Now use the quotient rule to find that substitute the result into the equation for f(t): simplify your answer. f(t) t t /2 d dt t t d dt t (t )() (t )() t (t ) 2 2 (t ) 2 f(t) 2 t t /2 t t /2 2 2 (t ) 2 (t ) Note that f() is defined ( f() 0), but f() is not. EXAMPLE 5.0 An environmental stu of a certain suburban community suggests that the average daily level of carbon monoxide in the air will be c(p) 0.5p 2 7 parts per million when the population is p thous. It is estimated that t years from now, the population of the community will be p(t) 3. 0.t 2 thous. At what rate will the carbon monoxide level be changing with respect to time 3 years from now?
9 56 Chapter 2 Differentiation: Basic Concepts Explore! Store the function C(x).5x 2 7 in your graphing utility. Use the numeric differentiation feature of your utility, if you have one, to calculate C(3). The goal is to find when t 3. Since it follows from the chain rule that When t 3, so dc dt dc dp 2 (0.5p2 7) /2 [0.5(2p)] 2 p(0.5p2 7) /2 dc dc dp dt dp dt 2 p(0.5p2 7) /2 0.pt (0.2t) 0.5p 2 7 dc 0.(4)(3) dt 0.5(4) 2 7 dp 0.2t dt p(3) 3. 0.(3) part per million per year 25 5 P. R. O. B. L. E. M. S 2.5 In Problems through 0, use the chain rule to compute the derivative simplify your answer.. y u 2, u 3x 2 2. y 2u 2 u 5, u x 2 3. y u, u x 2 2x 3 4. y u 2 2u 3, u x 5. y, u x 2 6. y, u 3x 2 5 u 2 u 7. y, u x y u 2 u 2, u u x 9. y, u x 2 0. y u 2, u u x
10 Chapter 2 Section 5 The Chain Rule 57 In Problems through 6, use the chain rule to compute the derivative for the given value of x.. y 3u 4 4u 5, u x 3 2x 5; x 2 2. y u 5 3u 2 6u 5, u x 2 ; x 3. y u, u x 2 2x 6; x 3 4. y 3u 2 6u 2, u ; x x y, u 3 ; x u x y, u x 3 2x 5; x 0 u In Problems 7 through 36, differentiate the given function simplify your answer. 7. f(x) (2x ) 4 8. f(x) 5x f(x) (x 5 4x 3 7) f(t) (3t 4 7t 2 9) f(t) 22. f(x) 5t 2 6t 2 (6x 2 5x ) g(x) 24. f(s) 4x 2 5s f(x) 26. f(x) ( x 2 ) 4 3(5x 4 ) h(s) ( 3s) g(x) 3x 29. f(x) (x 2) 3 (2x ) f(x) 2(3x ) 4 (5x 3) 2 3x 3. G(x) 2x 32. f(y) y 2 2 y 3 (x ) 5 ( 2x) f(x) 34. F(x) ( x) 4 (3x ) 3 3y 5x f(y) 36. f(x) 4y 3 3 2x In Problems 37 through 40, find an equation of the line that is tangent to the graph of f for the given value of x. 37. f(x) (3x 2 ) 2 ; x 38. f(x) (x 2 3) 5 (2x ) 3 ; x 2
11 58 Chapter 2 Differentiation: Basic Concepts 39. f(x) ; x 40. f(x) x ; x 3 x 3 (2x ) 6 In Problems 4 through 46, find all values of x where the tangent line to y f(x) is horizontal. 4. f(x) (x 2 x) f(x) x 3 (2x 2 x 3) 2 x 2x f(x) 44. f(x) (3x 2) 2 ( 2x) f(x) x 2 4x f(x) (x ) 2 (2x 3) 3 In Problems differentiate the given function f(x) by two different methods, first by using the general power rule then by using the product rule. Show that the two answers are the same. 47. f(x) (3x 5) f(x) (7 4x) 2 ANNUAL EARNINGS 49. The gross annual earnings of a certain company are f(t) 0t 2 t 236 thous dollars t years after its formation in January 998. (a) At what rate will the gross annual earnings of the company be growing in January 2003? (b) At what percentage rate will the gross annual earnings be growing in January 2003? MANUFACTURING COST CONSUMER DEMAND CONSUMER DEMAND CONSUMER DEMAND 50. At a certain factory, the total cost of manufacturing q units during the daily production run is C(q) 0.2q 2 q 900 dollars. From experience it has been determined that approximately q(t) t 2 00t units are manufactured during the first t hours of a production run. Compute the rate at which the total manufacturing cost is changing with respect to time hour after production commences. 5. When electric blenders are sold for p dollars apiece, local consumers will buy 8,000 D(p) blenders a month. It is estimated that t months from now, the p price of the blenders will be p(t) 0.04t 3/2 5 dollars. Compute the rate at which the monthly dem for the blenders will be changing with respect to time 25 months from now. Will the dem be increasing or decreasing? 52. An importer of Brazilian coffee estimates that local consumers will buy 4,374 approximately D( p) pounds of the coffee per week when the price is p p 2 dollars per pound. It is also estimated that t weeks from now, the price of Brazilian coffee will be p(t) 0.02t 2 0.t 6 dollars per pound. At what rate will the weekly dem for the coffee be changing with respect to time 0 weeks from now? Will the dem be increasing or decreasing? 53. When a certain commodity is sold for p dollars per unit, consumers will buy 40,000 D( p) units per month. It is estimated that t months from now, the price p
12 Chapter 2 Section 5 The Chain Rule 59 AIR POLLUTION ANIMAL BEHAVIOR of the commodity will be p(t) 0.4t 3/2 6.8 dollars per unit. At what percentage rate will the monthly dem for the commodity be changing with respect to time 4 months from now? 54. It is estimated that t years from now, the population of a certain suburban community will be p(t) 20 thous. An environmental stu indicates that 6 t the average daily level of carbon monoxide in the air will be c( p) 0.5p 2 p 58 parts per million when the population is p thous. Find the rate at which the level of carbon monoxide will be changing with respect to time 2 years from now. 55. In a research paper,* V. A. Tucker K. Schmidt-Koenig demonstrated that a species of Australian parakeet (the Budgerigar) expends energy according to the formula E v [0.074(v 35)2 32] COMPOUND INTEREST BLOOD FLOW where v is the bird s velocity (in km/hr). Find a formula for the rate of change of E with respect to velocity v. 56. If $0,000 is invested at an annual rate r (expressed as a decimal) compounded weekly, the total amount (principal P interest) accumulated after 0 years is given by the formula A 0,000 r (a) Find the rate of change of A with respect to r. (b) Find the percentage rate of change of A with respect to r when r 0.05 (that is, 5%). 57. It has been determined that the flow of blood from an artery into a small capillary is given by the formula F kd 2 A C (cm 3 /sec) where D is the diameter of the capillary, A is the pressure in the artery, C is the pressure in the capillary, k is a positive constant. (a) By how much is the flow of blood F changing with respect to pressure C in the capillary if A D are kept constant? Does the flow increase or decrease with increasing C? (b) What is the percentage rate of change of flow F with respect to A if C D are kept constant? * V. A. Tucker K. Schmidt-Koenig, Flight Speeds of Birds in Relation to Energetics Wind Directions, The Auk, Vol. 88 (97), pages
13 60 Chapter 2 Differentiation: Basic Concepts LEARNING CURVES 58. When you first begin to stu a topic or practice a skill, you may not be very good at it, but in time, you will approach the limits of your ability. One model for describing this behavior involves the equation T all b where T is the time required for a particular person to learn the items on a list of L items a b are positive constants. dt (a) Find the derivative interpret it in terms of the learning model. dl (b) Read discuss in one paragraph an article on how learning curves can be used to stu worker productivity.* 59. Suppose L(x) is a function with the property that L(x). Use the chain rule x to find the derivatives of the following functions simplify your answers. (a) f(x) L(x 2 ) (b) f(x) (c) f(x) (d) f(x) L x L 2 3x L 2x x 60. Prove the general power rule for n 2 by using the product rule to compute if y [h(x)] Prove the general power rule for n 3 by using the product rule the result of Problem 60 to compute if y [h(x)] 3. [Hint: Begin by writing y as h(x)[h(x)] 2.] 62. Store the function f(x) 3 3.x in your graphing utility. Use the numeric differentiation feature of your utility to calculate f() f(3). Explore the graph of f(x). How many horizontal tangents does the graph have? 63. Store the function f(x) (2.7x 3 3x 5) 2/3 in your graphing utility. Use the numeric differentiation feature of the utility to calculate f(0) f(4.3). Explore the graph of f(x). How many horizontal tangents does it have? * You may wish to begin your research by consulting Philip E. Hicks, Industrial Engineering Management: A New Perspective, 2nd ed., Chapter 6, McGraw-Hill, Inc., New York, 994, pages
Chapter. Integration. 1. Antidifferentiation: The Indefinite Integral. 2. Integration by Substitution. 3. Introduction to Differential Equations
 Integration Chapter. Antidifferentiation: The Indefinite Integral 2. Integration by Substitution 3. Introduction to Differential Equations 4. Integration by Parts Chapter Summary and Review Problems Antidifferentiation:
Integration Chapter. Antidifferentiation: The Indefinite Integral 2. Integration by Substitution 3. Introduction to Differential Equations 4. Integration by Parts Chapter Summary and Review Problems Antidifferentiation:
Section 11.3 Rates of Change:
 Section 11.3 Rates of Change: 1. Consider the following table, which describes a driver making a 168-mile trip from Cleveland to Columbus, Ohio in 3 hours. t Time (in hours) 0 0.5 1 1.5 2 2.5 3 f(t) Distance
Section 11.3 Rates of Change: 1. Consider the following table, which describes a driver making a 168-mile trip from Cleveland to Columbus, Ohio in 3 hours. t Time (in hours) 0 0.5 1 1.5 2 2.5 3 f(t) Distance
Review for Final Review
 Topics Review for Final Review 1. Functions and equations and graphing: linear, absolute value, quadratic, polynomials, rational (first 1/3 of semester) 2. Simple Interest, compounded interest, and continuously
Topics Review for Final Review 1. Functions and equations and graphing: linear, absolute value, quadratic, polynomials, rational (first 1/3 of semester) 2. Simple Interest, compounded interest, and continuously
3.1 Derivative Formulas for Powers and Polynomials
 3.1 Derivative Formulas for Powers and Polynomials First, recall that a derivative is a function. We worked very hard in 2.2 to interpret the derivative of a function visually. We made the link, in Ex.
3.1 Derivative Formulas for Powers and Polynomials First, recall that a derivative is a function. We worked very hard in 2.2 to interpret the derivative of a function visually. We made the link, in Ex.
UNIT 2 DERIVATIVES 2.1 EXPONENTIAL AND LOGARITHMIC FUNCTION APPLICATIONS. Pre-Class:
 1830 UNIT 2 DERIVATIVES 2.1 EXPONENTIAL AND LOGARITHMIC FUNCTION APPLICATIONS Pre-Class: Take notes on the videos and readings (use the space below). Work and check problem #1 in the 2.1 NOTES section.
1830 UNIT 2 DERIVATIVES 2.1 EXPONENTIAL AND LOGARITHMIC FUNCTION APPLICATIONS Pre-Class: Take notes on the videos and readings (use the space below). Work and check problem #1 in the 2.1 NOTES section.
Final Exam Review. MATH Intuitive Calculus Fall 2013 Circle lab day: Mon / Fri. Name:. Show all your work.
 MATH 11012 Intuitive Calculus Fall 2013 Circle lab day: Mon / Fri Dr. Kracht Name:. 1. Consider the function f depicted below. Final Exam Review Show all your work. y 1 1 x (a) Find each of the following
MATH 11012 Intuitive Calculus Fall 2013 Circle lab day: Mon / Fri Dr. Kracht Name:. 1. Consider the function f depicted below. Final Exam Review Show all your work. y 1 1 x (a) Find each of the following
Lecture 7: Sections 2.3 and 2.4 Rational and Exponential Functions. Recall that a power function has the form f(x) = x r where r is a real number.
 L7-1 Lecture 7: Sections 2.3 and 2.4 Rational and Exponential Functions Recall that a power function has the form f(x) = x r where r is a real number. f(x) = x 1/2 f(x) = x 1/3 ex. Sketch the graph of
L7-1 Lecture 7: Sections 2.3 and 2.4 Rational and Exponential Functions Recall that a power function has the form f(x) = x r where r is a real number. f(x) = x 1/2 f(x) = x 1/3 ex. Sketch the graph of
Chapter 3 The Integral Business Calculus 197
 Chapter The Integral Business Calculus 97 Chapter Exercises. Let A(x) represent the area bounded by the graph and the horizontal axis and vertical lines at t=0 and t=x for the graph in Fig.. Evaluate A(x)
Chapter The Integral Business Calculus 97 Chapter Exercises. Let A(x) represent the area bounded by the graph and the horizontal axis and vertical lines at t=0 and t=x for the graph in Fig.. Evaluate A(x)
MAC 2233, Survey of Calculus, Exam 3 Review This exam covers lectures 21 29,
 MAC 2233, Survey of Calculus, Exam 3 Review This exam covers lectures 21 29, This review includes typical exam problems. It is not designed to be comprehensive, but to be representative of topics covered
MAC 2233, Survey of Calculus, Exam 3 Review This exam covers lectures 21 29, This review includes typical exam problems. It is not designed to be comprehensive, but to be representative of topics covered
2 Integration by Substitution
 86 Chapter 5 Integration 2 Integration by Substitution (a) Find a function P(x) that satisfies these conditions. Use the graphing utility of your calculator to graph this function. (b) Use trace and zoom
86 Chapter 5 Integration 2 Integration by Substitution (a) Find a function P(x) that satisfies these conditions. Use the graphing utility of your calculator to graph this function. (b) Use trace and zoom
Math 120 Final Exam Practice Problems, Form: A
 Math 120 Final Exam Practice Problems, Form: A Name: While every attempt was made to be complete in the types of problems given below, we make no guarantees about the completeness of the problems. Specifically,
Math 120 Final Exam Practice Problems, Form: A Name: While every attempt was made to be complete in the types of problems given below, we make no guarantees about the completeness of the problems. Specifically,
Chapter 4 Notes, Calculus I with Precalculus 3e Larson/Edwards
 4.1 The Derivative Recall: For the slope of a line we need two points (x 1,y 1 ) and (x 2,y 2 ). Then the slope is given by the formula: m = y x = y 2 y 1 x 2 x 1 On a curve we can find the slope of a
4.1 The Derivative Recall: For the slope of a line we need two points (x 1,y 1 ) and (x 2,y 2 ). Then the slope is given by the formula: m = y x = y 2 y 1 x 2 x 1 On a curve we can find the slope of a
Section 11.7 The Chain Rule
 Section.7 The Chain Rule Composition of Functions There is another way of combining two functions to obtain a new function. For example, suppose that y = fu) = u and u = gx) = x 2 +. Since y is a function
Section.7 The Chain Rule Composition of Functions There is another way of combining two functions to obtain a new function. For example, suppose that y = fu) = u and u = gx) = x 2 +. Since y is a function
Re: January 27, 2015 Math 080: Final Exam Review Page 1 of 6
 Re: January 7, 015 Math 080: Final Exam Review Page 1 of 6 Note: If you have difficulty with any of these problems, get help, then go back to the appropriate sections and work more problems! 1. Solve for
Re: January 7, 015 Math 080: Final Exam Review Page 1 of 6 Note: If you have difficulty with any of these problems, get help, then go back to the appropriate sections and work more problems! 1. Solve for
4.1 Exponential Functions. For Formula 1, the value of n is based on the frequency of compounding. Common frequencies include:
 Hartfield MATH 2040 Unit 4 Page 1 4.1 Exponential Functions Recall from algebra the formulas for Compound Interest: Formula 1 For Discretely Compounded Interest 1 A t P r n nt Formula 2 Continuously Compounded
Hartfield MATH 2040 Unit 4 Page 1 4.1 Exponential Functions Recall from algebra the formulas for Compound Interest: Formula 1 For Discretely Compounded Interest 1 A t P r n nt Formula 2 Continuously Compounded
MATH 162 R E V I E W F I N A L E X A M FALL 2016
 MATH 6 R E V I E W F I N A L E X A M FALL 06 BASICS Graphs. Be able to graph basic functions, such as polynomials (eg, f(x) = x 3 x, x + ax + b, x(x ) (x + ) 3, know about the effect of multiplicity of
MATH 6 R E V I E W F I N A L E X A M FALL 06 BASICS Graphs. Be able to graph basic functions, such as polynomials (eg, f(x) = x 3 x, x + ax + b, x(x ) (x + ) 3, know about the effect of multiplicity of
x C) y = - A) $20000; 14 years B) $28,000; 14 years C) $28,000; 28 years D) $30,000; 15 years
 Dr. Lee - Math 35 - Calculus for Business - Review of 3 - Show Complete Work for Each Problem MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find
Dr. Lee - Math 35 - Calculus for Business - Review of 3 - Show Complete Work for Each Problem MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find
Math 142 (Summer 2018) Business Calculus 5.8 Notes
 Math 142 (Summer 2018) Business Calculus 5.8 Notes Implicit Differentiation and Related Rates Why? We have learned how to take derivatives of functions, and we have seen many applications of this. However
Math 142 (Summer 2018) Business Calculus 5.8 Notes Implicit Differentiation and Related Rates Why? We have learned how to take derivatives of functions, and we have seen many applications of this. However
One-Variable Calculus
 POLI 270 - Mathematical and Statistical Foundations Department of Political Science University California, San Diego September 30, 2010 1 s,, 2 al Relationships Political Science, economics, sociology,
POLI 270 - Mathematical and Statistical Foundations Department of Political Science University California, San Diego September 30, 2010 1 s,, 2 al Relationships Political Science, economics, sociology,
2.3 Homework: The Product and Quotient Rules
 2.3 Homework: The Product and Quotient Rules 1. Find the derivatives of each of the following functions. Label the derivative you find with its name using proper notation. a) f(x) = (x 2 x)3 x b) h(y)
2.3 Homework: The Product and Quotient Rules 1. Find the derivatives of each of the following functions. Label the derivative you find with its name using proper notation. a) f(x) = (x 2 x)3 x b) h(y)
MAC 2233 Chapter 3 Practice for the Test
 Class: Date: MAC 33 Chapter 3 Practice for the Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. At which labeled point is the slope of the tangent
Class: Date: MAC 33 Chapter 3 Practice for the Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. At which labeled point is the slope of the tangent
Sec. 4.2 Logarithmic Functions
 Sec. 4.2 Logarithmic Functions The Logarithmic Function with Base a has domain all positive real numbers and is defined by Where and is the inverse function of So and Logarithms are inverses of Exponential
Sec. 4.2 Logarithmic Functions The Logarithmic Function with Base a has domain all positive real numbers and is defined by Where and is the inverse function of So and Logarithms are inverses of Exponential
Advanced Placement Calculus
 Advanced Placement Calculus Additional Definite Integral Topics Average Value of a Function Definite Integral as an Accumulator Average Value Problems 1-3: Use the property m(b a) integrals...without integrating!
Advanced Placement Calculus Additional Definite Integral Topics Average Value of a Function Definite Integral as an Accumulator Average Value Problems 1-3: Use the property m(b a) integrals...without integrating!
Final Exam Review Packet
 1 Exam 1 Material Sections A.1, A.2 and A.6 were review material. There will not be specific questions focused on this material but you should know how to: Simplify functions with exponents. Factor quadratics
1 Exam 1 Material Sections A.1, A.2 and A.6 were review material. There will not be specific questions focused on this material but you should know how to: Simplify functions with exponents. Factor quadratics
Final Exam Review Packet
 1 Exam 1 Material Sections A.1, A.2 and A.6 were review material. There will not be specific questions focused on this material but you should know how to: Simplify functions with exponents. Factor quadratics
1 Exam 1 Material Sections A.1, A.2 and A.6 were review material. There will not be specific questions focused on this material but you should know how to: Simplify functions with exponents. Factor quadratics
Final Exam Study Aid
 Math 112 Final Exam Study Aid 1 of 33 Final Exam Study Aid Note: This study aid is intended to help you review for the final exam. It covers the primary concepts in the course, with a large emphasis on
Math 112 Final Exam Study Aid 1 of 33 Final Exam Study Aid Note: This study aid is intended to help you review for the final exam. It covers the primary concepts in the course, with a large emphasis on
Chapter 2 Derivatives And Their Uses
 Chapter Derivatives And Their Uses 1. Complete the table and use it to predict the limit, if it eists. 6 f( ) 0. 1 lim f( )? 0.1 0.01 0.001 0.? 0.999 0.99 f ( ) 0.9 160.0 80.0 80.0 0. does not eist. Use
Chapter Derivatives And Their Uses 1. Complete the table and use it to predict the limit, if it eists. 6 f( ) 0. 1 lim f( )? 0.1 0.01 0.001 0.? 0.999 0.99 f ( ) 0.9 160.0 80.0 80.0 0. does not eist. Use
Midterm 1 Review Problems Business Calculus
 Midterm 1 Review Problems Business Calculus 1. (a) Show that the functions f and g are inverses of each other by showing that f g(x) = g f(x) given that (b) Sketch the functions and the line y = x f(x)
Midterm 1 Review Problems Business Calculus 1. (a) Show that the functions f and g are inverses of each other by showing that f g(x) = g f(x) given that (b) Sketch the functions and the line y = x f(x)
INTERNET MAT 117 Review Problems. (1) Let us consider the circle with equation. (b) Find the center and the radius of the circle given above.
 INTERNET MAT 117 Review Problems (1) Let us consider the circle with equation x 2 + y 2 + 2x + 3y + 3 4 = 0. (a) Find the standard form of the equation of the circle given above. (b) Find the center and
INTERNET MAT 117 Review Problems (1) Let us consider the circle with equation x 2 + y 2 + 2x + 3y + 3 4 = 0. (a) Find the standard form of the equation of the circle given above. (b) Find the center and
Rules of Differentiation
 Rules of Differentiation The process of finding the derivative of a function is called Differentiation. 1 In the previous chapter, the required derivative of a function is worked out by taking the limit
Rules of Differentiation The process of finding the derivative of a function is called Differentiation. 1 In the previous chapter, the required derivative of a function is worked out by taking the limit
Exponential and logarithm functions
 ucsc supplementary notes ams/econ 11a Exponential and logarithm functions c 2010 Yonatan Katznelson The material in this supplement is assumed to be mostly review material. If you have never studied exponential
ucsc supplementary notes ams/econ 11a Exponential and logarithm functions c 2010 Yonatan Katznelson The material in this supplement is assumed to be mostly review material. If you have never studied exponential
UNIVERSITY OF KWA-ZULU NATAL
 UNIVERSITY OF KWA-ZULU NATAL EXAMINATIONS: June 006 Solutions Subject, course and code: Mathematics 34 MATH34P Multiple Choice Answers. B. B 3. E 4. E 5. C 6. A 7. A 8. C 9. A 0. D. C. A 3. D 4. E 5. B
UNIVERSITY OF KWA-ZULU NATAL EXAMINATIONS: June 006 Solutions Subject, course and code: Mathematics 34 MATH34P Multiple Choice Answers. B. B 3. E 4. E 5. C 6. A 7. A 8. C 9. A 0. D. C. A 3. D 4. E 5. B
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 MAC 1105 Fall 2007 - Final Exam Dr. Schnackenberg If you do not agree with the given answers, answer "E" for "None of the above". MULTIPLE CHOICE. Choose the one alternative that best completes the statement
MAC 1105 Fall 2007 - Final Exam Dr. Schnackenberg If you do not agree with the given answers, answer "E" for "None of the above". MULTIPLE CHOICE. Choose the one alternative that best completes the statement
is all real numbers.
 Math 140 Spring 2017 Suggested Final Review Problems 1. Is each of the following statements true or false? Explain. (a) If f(x) = x 2, then f(x + h) = x 2 + h 2. (b) If g(x) = 3 x, then g(x) can never
Math 140 Spring 2017 Suggested Final Review Problems 1. Is each of the following statements true or false? Explain. (a) If f(x) = x 2, then f(x + h) = x 2 + h 2. (b) If g(x) = 3 x, then g(x) can never
Lecture 6: Sections 2.2 and 2.3 Polynomial Functions, Quadratic Models
 L6-1 Lecture 6: Sections 2.2 and 2.3 Polynomial Functions, Quadratic Models Polynomial Functions Def. A polynomial function of degree n is a function of the form f(x) = a n x n + a n 1 x n 1 +... + a 1
L6-1 Lecture 6: Sections 2.2 and 2.3 Polynomial Functions, Quadratic Models Polynomial Functions Def. A polynomial function of degree n is a function of the form f(x) = a n x n + a n 1 x n 1 +... + a 1
The Table of Integrals (pages of the text) and the Formula Page may be used. They will be attached to the nal exam.
 The Table of Integrals (pages 558-559 of the text) and the Formula Page may be used. They will be attached to the nal exam. 1. If f(x; y) =(xy +1) 2 p y 2 x 2,evaluatef( 2; 1). A. 1 B. 1 p 5 C. Not de
The Table of Integrals (pages 558-559 of the text) and the Formula Page may be used. They will be attached to the nal exam. 1. If f(x; y) =(xy +1) 2 p y 2 x 2,evaluatef( 2; 1). A. 1 B. 1 p 5 C. Not de
Contents CONTENTS 1. 1 Straight Lines and Linear Equations 1. 2 Systems of Equations 6. 3 Applications to Business Analysis 11.
 CONTENTS 1 Contents 1 Straight Lines and Linear Equations 1 2 Systems of Equations 6 3 Applications to Business Analysis 11 4 Functions 16 5 Quadratic Functions and Parabolas 21 6 More Simple Functions
CONTENTS 1 Contents 1 Straight Lines and Linear Equations 1 2 Systems of Equations 6 3 Applications to Business Analysis 11 4 Functions 16 5 Quadratic Functions and Parabolas 21 6 More Simple Functions
ANSWERS, Homework Problems, Fall 2014: Lectures Now You Try It, Supplemental problems in written homework, Even Answers. 24x + 72 (x 2 6x + 4) 4
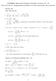 ANSWERS, Homework Problems, Fall 014: Lectures 19 35 Now You Try It, Supplemental problems in written homework, Even Answers Lecture 19 1. d [ 4 ] dx x 6x + 4) 3 = 4x + 7 x 6x + 4) 4. a) P 0) = 800 b)
ANSWERS, Homework Problems, Fall 014: Lectures 19 35 Now You Try It, Supplemental problems in written homework, Even Answers Lecture 19 1. d [ 4 ] dx x 6x + 4) 3 = 4x + 7 x 6x + 4) 4. a) P 0) = 800 b)
Chapter 2 Describing Change: Rates
 Chapter Describing Change: Rates Section.1 Change, Percentage Change, and Average Rates of Change 1. 3. $.30 $0.46 per day 5 days = The stock price rose an average of 46 cents per day during the 5-day
Chapter Describing Change: Rates Section.1 Change, Percentage Change, and Average Rates of Change 1. 3. $.30 $0.46 per day 5 days = The stock price rose an average of 46 cents per day during the 5-day
10 Exponential and Logarithmic Functions
 10 Exponential and Logarithmic Functions Concepts: Rules of Exponents Exponential Functions Power Functions vs. Exponential Functions The Definition of an Exponential Function Graphing Exponential Functions
10 Exponential and Logarithmic Functions Concepts: Rules of Exponents Exponential Functions Power Functions vs. Exponential Functions The Definition of an Exponential Function Graphing Exponential Functions
2. If the values for f(x) can be made as close as we like to L by choosing arbitrarily large. lim
 Limits at Infinity and Horizontal Asymptotes As we prepare to practice graphing functions, we should consider one last piece of information about a function that will be helpful in drawing its graph the
Limits at Infinity and Horizontal Asymptotes As we prepare to practice graphing functions, we should consider one last piece of information about a function that will be helpful in drawing its graph the
Lecture 2. Derivative. 1 / 26
 Lecture 2. Derivative. 1 / 26 Basic Concepts Suppose we wish to nd the rate at which a given function f (x) is changing with respect to x when x = c. The simplest idea is to nd the average rate of change
Lecture 2. Derivative. 1 / 26 Basic Concepts Suppose we wish to nd the rate at which a given function f (x) is changing with respect to x when x = c. The simplest idea is to nd the average rate of change
Math 116: Business Calculus Chapter 4 - Calculating Derivatives
 Math 116: Business Calculus Chapter 4 - Calculating Derivatives Instructor: Colin Clark Spring 2017 Exam 2 - Thursday March 9. 4.1 Techniques for Finding Derivatives. 4.2 Derivatives of Products and Quotients.
Math 116: Business Calculus Chapter 4 - Calculating Derivatives Instructor: Colin Clark Spring 2017 Exam 2 - Thursday March 9. 4.1 Techniques for Finding Derivatives. 4.2 Derivatives of Products and Quotients.
Brief Review. Chapter Linear Equations. 0.1 Example 1 Most people s favorite version of a linear equation is this: where
 Contents 0 Brief Review 2 0.1 Linear Equations........................... 2 0.2 Fractions............................... 8 0.3 Exponents............................... 9 0.4 Square roots..............................
Contents 0 Brief Review 2 0.1 Linear Equations........................... 2 0.2 Fractions............................... 8 0.3 Exponents............................... 9 0.4 Square roots..............................
Additional Applications of Definite Integration AVERAGE VALUE
 46 Chapter 6 Further Topics in Integration 3 INVENTORY STORAGE COSTS Additional Applications of Definite Integration AVERAGE VALUE OF A FUNCTION 44. A manufacturer receives N units of a certain raw material
46 Chapter 6 Further Topics in Integration 3 INVENTORY STORAGE COSTS Additional Applications of Definite Integration AVERAGE VALUE OF A FUNCTION 44. A manufacturer receives N units of a certain raw material
Notes for exponential functions The week of March 6. Math 140
 Notes for exponential functions The week of March 6 Math 140 Exponential functions: formulas An exponential function has the formula f (t) = ab t, where b is a positive constant; a is the initial value
Notes for exponential functions The week of March 6 Math 140 Exponential functions: formulas An exponential function has the formula f (t) = ab t, where b is a positive constant; a is the initial value
Business and Life Calculus
 Business and Life Calculus George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 112 George Voutsadakis (LSSU) Calculus For Business and Life Sciences Fall 2013
Business and Life Calculus George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 112 George Voutsadakis (LSSU) Calculus For Business and Life Sciences Fall 2013
Calculus I 5. Applications of differentiation
 2301107 Calculus I 5. Applications of differentiation Chapter 5:Applications of differentiation C05-2 Outline 5.1. Extreme values 5.2. Curvature and Inflection point 5.3. Curve sketching 5.4. Related rate
2301107 Calculus I 5. Applications of differentiation Chapter 5:Applications of differentiation C05-2 Outline 5.1. Extreme values 5.2. Curvature and Inflection point 5.3. Curve sketching 5.4. Related rate
MATH150-E01 Test #2 Summer 2016 Show all work. Name 1. Find an equation in slope-intercept form for the line through (4, 2) and (1, 3).
 1. Find an equation in slope-intercept form for the line through (4, 2) and (1, 3). 2. Let the supply and demand functions for sugar be given by p = S(q) = 1.4q 0.6 and p = D(q) = 2q + 3.2 where p is the
1. Find an equation in slope-intercept form for the line through (4, 2) and (1, 3). 2. Let the supply and demand functions for sugar be given by p = S(q) = 1.4q 0.6 and p = D(q) = 2q + 3.2 where p is the
Math 101 Final Exam Review Solutions. Eric Schmutz
 Math 101 Final Exam Review Solutions Eric Schmutz Problem 1. Write an equation of the line passing through (,7) and (-1,1). Let (x 1, y 1 ) = (, 7) and (x, y ) = ( 1, 1). The slope is m = y y 1 x x 1 =
Math 101 Final Exam Review Solutions Eric Schmutz Problem 1. Write an equation of the line passing through (,7) and (-1,1). Let (x 1, y 1 ) = (, 7) and (x, y ) = ( 1, 1). The slope is m = y y 1 x x 1 =
Exponential and Logarithmic Functions. 3. Pg #17-57 column; column and (need graph paper)
 Algebra 2/Trig Unit 6 Notes Packet Name: Period: # Exponential and Logarithmic Functions 1. Worksheet 2. Worksheet 3. Pg 483-484 #17-57 column; 61-73 column and 76-77 (need graph paper) 4. Pg 483-484 #20-60
Algebra 2/Trig Unit 6 Notes Packet Name: Period: # Exponential and Logarithmic Functions 1. Worksheet 2. Worksheet 3. Pg 483-484 #17-57 column; 61-73 column and 76-77 (need graph paper) 4. Pg 483-484 #20-60
MATH 122 FALL Final Exam Review Problems
 MATH 122 FALL 2013 Final Exam Review Problems Chapter 1 1. As a person hikes down from the top of a mountain, the variable t represents the time, in minutes, since the person left the top of the mountain,
MATH 122 FALL 2013 Final Exam Review Problems Chapter 1 1. As a person hikes down from the top of a mountain, the variable t represents the time, in minutes, since the person left the top of the mountain,
APPENDIX B: Strengthening the Concepts
 APPENDIX B: Strengthening the Concepts The Pythagorean Theorem B2 Section. Solving Exponential Equations Algebraically* B4 Section. Graphing Piecewise Functions B6 Section.2 Constructing Inverse Functions
APPENDIX B: Strengthening the Concepts The Pythagorean Theorem B2 Section. Solving Exponential Equations Algebraically* B4 Section. Graphing Piecewise Functions B6 Section.2 Constructing Inverse Functions
CHAPTER 2 Differentiation
 CHAPTER Differentiation Section. The Derivative and the Slope of a Graph............. 9 Section. Some Rules for Differentiation.................. 56 Section. Rates of Change: Velocit and Marginals.............
CHAPTER Differentiation Section. The Derivative and the Slope of a Graph............. 9 Section. Some Rules for Differentiation.................. 56 Section. Rates of Change: Velocit and Marginals.............
MA202 Calculus III Fall, 2009 Laboratory Exploration 2: Gradients, Directional Derivatives, Stationary Points
 MA0 Calculus III Fall, 009 Laboratory Exploration : Gradients, Directional Derivatives, Stationary Points Introduction: This lab deals with several topics from Chapter. Some of the problems should be done
MA0 Calculus III Fall, 009 Laboratory Exploration : Gradients, Directional Derivatives, Stationary Points Introduction: This lab deals with several topics from Chapter. Some of the problems should be done
GUIDED NOTES 6.1 EXPONENTIAL FUNCTIONS
 GUIDED NOTES 6.1 EXPONENTIAL FUNCTIONS LEARNING OBJECTIVES In this section, you will: Evaluate exponential functions. Find the equation of an exponential function. Use compound interest formulas. Evaluate
GUIDED NOTES 6.1 EXPONENTIAL FUNCTIONS LEARNING OBJECTIVES In this section, you will: Evaluate exponential functions. Find the equation of an exponential function. Use compound interest formulas. Evaluate
Study Guide - Part 2
 Math 116 Spring 2015 Study Guide - Part 2 1. Which of the following describes the derivative function f (x) of a quadratic function f(x)? (A) Cubic (B) Quadratic (C) Linear (D) Constant 2. Find the derivative
Math 116 Spring 2015 Study Guide - Part 2 1. Which of the following describes the derivative function f (x) of a quadratic function f(x)? (A) Cubic (B) Quadratic (C) Linear (D) Constant 2. Find the derivative
Chapter 2: Differentiation 1. Find the slope of the tangent line to the graph of the function below at the given point.
 Chapter : Differentiation 1. Find the slope of the tangent line to the graph of the function below at the given point. f( ) 10, (, ) 10 1 E) none of the above. Find the slope of the tangent line to the
Chapter : Differentiation 1. Find the slope of the tangent line to the graph of the function below at the given point. f( ) 10, (, ) 10 1 E) none of the above. Find the slope of the tangent line to the
Purdue University Study Guide for MA for students who plan to obtain credit in MA by examination.
 Purdue University Study Guide for MA 224 for students who plan to obtain credit in MA 224 by examination. Textbook: Applied Calculus For Business, Economics, and the Social and Life Sciences, Expanded
Purdue University Study Guide for MA 224 for students who plan to obtain credit in MA 224 by examination. Textbook: Applied Calculus For Business, Economics, and the Social and Life Sciences, Expanded
Chapter 4. Section Derivatives of Exponential and Logarithmic Functions
 Chapter 4 Section 4.2 - Derivatives of Exponential and Logarithmic Functions Objectives: The student will be able to calculate the derivative of e x and of lnx. The student will be able to compute the
Chapter 4 Section 4.2 - Derivatives of Exponential and Logarithmic Functions Objectives: The student will be able to calculate the derivative of e x and of lnx. The student will be able to compute the
Name: Practice A, Math Final Exam December 11, 2018
 Practice A, Math 10250 Final Exam December 11, 2018 Name: Instructor: Be sure that you have all 15 pages of the test. Calculators are allowed for this examination. The exam lasts for two hours. The Honor
Practice A, Math 10250 Final Exam December 11, 2018 Name: Instructor: Be sure that you have all 15 pages of the test. Calculators are allowed for this examination. The exam lasts for two hours. The Honor
3. If 4x = 0, the roots of the equation are (1) 25 and 25 (2) 25, only (3) 5 and 5 (4) 5, only 3
 ALGEBRA 1 Part I Answer all 24 questions in this part. Each correct answer will receive 2 credits. No partial credit will be allowed. For each statement or question, choose the word or expression that,
ALGEBRA 1 Part I Answer all 24 questions in this part. Each correct answer will receive 2 credits. No partial credit will be allowed. For each statement or question, choose the word or expression that,
A.P. Calculus BC First Semester Exam Calculators Allowed Two Hours Number of Questions 10
 A.P. Calculus BC First Semester Exam Calculators Allowed Two Hours Number of Questions 10 Each of the ten questions is worth 10 points. The problem whose solution you write counted again, so that the maximum
A.P. Calculus BC First Semester Exam Calculators Allowed Two Hours Number of Questions 10 Each of the ten questions is worth 10 points. The problem whose solution you write counted again, so that the maximum
1.1 Linear Equations and Inequalities
 1.1 Linear Equations and Inequalities Linear Equation in 1 Variable Any equation that can be written in the following form: ax + b = 0 a,b R, a 0 and x is a variable Any equation has a solution, sometimes
1.1 Linear Equations and Inequalities Linear Equation in 1 Variable Any equation that can be written in the following form: ax + b = 0 a,b R, a 0 and x is a variable Any equation has a solution, sometimes
Unit 8: Exponential & Logarithmic Functions
 Date Period Unit 8: Eponential & Logarithmic Functions DAY TOPIC ASSIGNMENT 1 8.1 Eponential Growth Pg 47 48 #1 15 odd; 6, 54, 55 8.1 Eponential Decay Pg 47 48 #16 all; 5 1 odd; 5, 7 4 all; 45 5 all 4
Date Period Unit 8: Eponential & Logarithmic Functions DAY TOPIC ASSIGNMENT 1 8.1 Eponential Growth Pg 47 48 #1 15 odd; 6, 54, 55 8.1 Eponential Decay Pg 47 48 #16 all; 5 1 odd; 5, 7 4 all; 45 5 all 4
Logarithmic and Exponential Equations and Inequalities College Costs
 Logarithmic and Exponential Equations and Inequalities ACTIVITY 2.6 SUGGESTED LEARNING STRATEGIES: Summarize/ Paraphrase/Retell, Create Representations Wesley is researching college costs. He is considering
Logarithmic and Exponential Equations and Inequalities ACTIVITY 2.6 SUGGESTED LEARNING STRATEGIES: Summarize/ Paraphrase/Retell, Create Representations Wesley is researching college costs. He is considering
Math Want to have fun with chapter 4? Find the derivative. 1) y = 5x2e3x. 2) y = 2xex - 2ex. 3) y = (x2-2x + 3) ex. 9ex 4) y = 2ex + 1
 Math 160 - Want to have fun with chapter 4? Name Find the derivative. 1) y = 52e3 2) y = 2e - 2e 3) y = (2-2 + 3) e 9e 4) y = 2e + 1 5) y = e - + 1 e e 6) y = 32 + 7 7) y = e3-1 5 Use calculus to find
Math 160 - Want to have fun with chapter 4? Name Find the derivative. 1) y = 52e3 2) y = 2e - 2e 3) y = (2-2 + 3) e 9e 4) y = 2e + 1 5) y = e - + 1 e e 6) y = 32 + 7 7) y = e3-1 5 Use calculus to find
2.2 THE DERIVATIVE 2.3 COMPUTATION OF DERIVATIVES: THE POWER RULE 2.4 THE PRODUCT AND QUOTIENT RULES 2.6 DERIVATIVES OF TRIGONOMETRIC FUNCTIONS
 Differentiation CHAPTER 2 2.1 TANGENT LINES AND VELOCITY 2.2 THE DERIVATIVE 2.3 COMPUTATION OF DERIVATIVES: THE POWER RULE 2.4 THE PRODUCT AND QUOTIENT RULES 25 2.5 THE CHAIN RULE 2.6 DERIVATIVES OF TRIGONOMETRIC
Differentiation CHAPTER 2 2.1 TANGENT LINES AND VELOCITY 2.2 THE DERIVATIVE 2.3 COMPUTATION OF DERIVATIVES: THE POWER RULE 2.4 THE PRODUCT AND QUOTIENT RULES 25 2.5 THE CHAIN RULE 2.6 DERIVATIVES OF TRIGONOMETRIC
3. Find the slope of the tangent line to the curve given by 3x y e x+y = 1 + ln x at (1, 1).
 1. Find the derivative of each of the following: (a) f(x) = 3 2x 1 (b) f(x) = log 4 (x 2 x) 2. Find the slope of the tangent line to f(x) = ln 2 ln x at x = e. 3. Find the slope of the tangent line to
1. Find the derivative of each of the following: (a) f(x) = 3 2x 1 (b) f(x) = log 4 (x 2 x) 2. Find the slope of the tangent line to f(x) = ln 2 ln x at x = e. 3. Find the slope of the tangent line to
Page Points Score Total: 100
 Math 1130 Spring 2019 Sample Midterm 3c 4/11/19 Name (Print): Username.#: Lecturer: Rec. Instructor: Rec. Time: This exam contains 10 pages (including this cover page) and 10 problems. Check to see if
Math 1130 Spring 2019 Sample Midterm 3c 4/11/19 Name (Print): Username.#: Lecturer: Rec. Instructor: Rec. Time: This exam contains 10 pages (including this cover page) and 10 problems. Check to see if
Math 142 Week-in-Review #4 (Sections , 4.1, and 4.2)
 Math 142 WIR, copyright Angie Allen, Fall 2018 1 Math 142 Week-in-Review #4 (Sections 3.1-3.3, 4.1, and 4.2) Note: This collection of questions is intended to be a brief overview of the exam material (with
Math 142 WIR, copyright Angie Allen, Fall 2018 1 Math 142 Week-in-Review #4 (Sections 3.1-3.3, 4.1, and 4.2) Note: This collection of questions is intended to be a brief overview of the exam material (with
Definition: If y = f(x), then. f(x + x) f(x) y = f (x) = lim. Rules and formulas: 1. If f(x) = C (a constant function), then f (x) = 0.
 Definition: If y = f(x), then Rules and formulas: y = f (x) = lim x 0 f(x + x) f(x). x 1. If f(x) = C (a constant function), then f (x) = 0. 2. If f(x) = x k (a power function), then f (x) = kx k 1. 3.
Definition: If y = f(x), then Rules and formulas: y = f (x) = lim x 0 f(x + x) f(x). x 1. If f(x) = C (a constant function), then f (x) = 0. 2. If f(x) = x k (a power function), then f (x) = kx k 1. 3.
Section 3.1 Extreme Values
 Math 132 Extreme Values Section 3.1 Section 3.1 Extreme Values Example 1: Given the following is the graph of f(x) Where is the maximum (x-value)? What is the maximum (y-value)? Where is the minimum (x-value)?
Math 132 Extreme Values Section 3.1 Section 3.1 Extreme Values Example 1: Given the following is the graph of f(x) Where is the maximum (x-value)? What is the maximum (y-value)? Where is the minimum (x-value)?
MATH 142 Business Mathematics II. Spring, 2015, WEEK 1. JoungDong Kim
 MATH 142 Business Mathematics II Spring, 2015, WEEK 1 JoungDong Kim Week 1: A8, 1.1, 1.2, 1.3 Chapter 1. Functions Section 1.1 and A.8 Definition. A function is a rule that assigns to each element x in
MATH 142 Business Mathematics II Spring, 2015, WEEK 1 JoungDong Kim Week 1: A8, 1.1, 1.2, 1.3 Chapter 1. Functions Section 1.1 and A.8 Definition. A function is a rule that assigns to each element x in
MATH 111: EXAM 03 BLAKE FARMAN UNIVERSITY OF SOUTH CAROLINA
 MATH 111: EXAM 03 BLAKE FARMAN UNIVERSITY OF SOUTH CAROLINA Answer the questions in the spaces provided on the question sheets and turn them in at the end of the class period Unless otherwise stated, all
MATH 111: EXAM 03 BLAKE FARMAN UNIVERSITY OF SOUTH CAROLINA Answer the questions in the spaces provided on the question sheets and turn them in at the end of the class period Unless otherwise stated, all
Functions. A function is a rule that gives exactly one output number to each input number.
 Functions A function is a rule that gives exactly one output number to each input number. Why it is important to us? The set of all input numbers to which the rule applies is called the domain of the function.
Functions A function is a rule that gives exactly one output number to each input number. Why it is important to us? The set of all input numbers to which the rule applies is called the domain of the function.
College Algebra. Word Problems
 College Algebra Word Problems Example 2 (Section P6) The table shows the numbers N (in millions) of subscribers to a cellular telecommunication service in the United States from 2001 through 2010, where
College Algebra Word Problems Example 2 (Section P6) The table shows the numbers N (in millions) of subscribers to a cellular telecommunication service in the United States from 2001 through 2010, where
INTERNET MAT 117. Solution for the Review Problems. (1) Let us consider the circle with equation. x 2 + 2x + y 2 + 3y = 3 4. (x + 1) 2 + (y + 3 2
 INTERNET MAT 117 Solution for the Review Problems (1) Let us consider the circle with equation x 2 + y 2 + 2x + 3y + 3 4 = 0. (a) Find the standard form of the equation of the circle given above. (i) Group
INTERNET MAT 117 Solution for the Review Problems (1) Let us consider the circle with equation x 2 + y 2 + 2x + 3y + 3 4 = 0. (a) Find the standard form of the equation of the circle given above. (i) Group
MATH 1710 College Algebra Final Exam Review
 MATH 1710 College Algebra Final Exam Review MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. 1) There were 480 people at a play.
MATH 1710 College Algebra Final Exam Review MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. 1) There were 480 people at a play.
Section 2.1 Limits: Approached Numerically and Graphically
 Section 2.1 Limits: Approached Numerically and Graphically Foundation Concepts: Limit Left-hand limit Right-hand limit 1 = 1 = tiny big Practice: 1. What can we say about lim,. f(x)? a) If lim, 3 4 f(x)=7
Section 2.1 Limits: Approached Numerically and Graphically Foundation Concepts: Limit Left-hand limit Right-hand limit 1 = 1 = tiny big Practice: 1. What can we say about lim,. f(x)? a) If lim, 3 4 f(x)=7
MAT 135. In Class Assignments
 MAT 15 In Class Assignments 1 Chapter 1 1. Simplify each expression: a) 5 b) (5 ) c) 4 d )0 6 4. a)factor 4,56 into the product of prime factors b) Reduce 4,56 5,148 to lowest terms.. Translate each statement
MAT 15 In Class Assignments 1 Chapter 1 1. Simplify each expression: a) 5 b) (5 ) c) 4 d )0 6 4. a)factor 4,56 into the product of prime factors b) Reduce 4,56 5,148 to lowest terms.. Translate each statement
Logarithms. Professor Richard Blecksmith Dept. of Mathematical Sciences Northern Illinois University
 Logarithms Professor Richard Blecksmith richard@math.niu.edu Dept. of Mathematical Sciences Northern Illinois University http://math.niu.edu/ richard/math211 1. Definition of Logarithm For a > 0, a 1,
Logarithms Professor Richard Blecksmith richard@math.niu.edu Dept. of Mathematical Sciences Northern Illinois University http://math.niu.edu/ richard/math211 1. Definition of Logarithm For a > 0, a 1,
Optimization and Newton s method
 Chapter 5 Optimization and Newton s method 5.1 Optimal Flying Speed According to R McNeil Alexander (1996, Optima for Animals, Princeton U Press), the power, P, required to propel a flying plane at constant
Chapter 5 Optimization and Newton s method 5.1 Optimal Flying Speed According to R McNeil Alexander (1996, Optima for Animals, Princeton U Press), the power, P, required to propel a flying plane at constant
Section Exponential Functions
 121 Section 4.1 - Exponential Functions Exponential functions are extremely important in both economics and science. It allows us to discuss the growth of money in a money market account as well as the
121 Section 4.1 - Exponential Functions Exponential functions are extremely important in both economics and science. It allows us to discuss the growth of money in a money market account as well as the
A.5. Solving Equations. Equations and Solutions of Equations. Linear Equations in One Variable. What you should learn. Why you should learn it
 A46 Appendi A Review of Fundamental Concepts of Algebra A.5 Solving Equations What you should learn Identify different types of equations. Solve linear equations in one variable and equations that lead
A46 Appendi A Review of Fundamental Concepts of Algebra A.5 Solving Equations What you should learn Identify different types of equations. Solve linear equations in one variable and equations that lead
f ', the first derivative of a differentiable function, f. Use the
 f, f ', and The graph given to the right is the graph of graph to answer the questions below. f '' Relationships and The Extreme Value Theorem 1. On the interval [0, 8], are there any values where f(x)
f, f ', and The graph given to the right is the graph of graph to answer the questions below. f '' Relationships and The Extreme Value Theorem 1. On the interval [0, 8], are there any values where f(x)
Differentiation. 1. What is a Derivative? CHAPTER 5
 CHAPTER 5 Differentiation Differentiation is a technique that enables us to find out how a function changes when its argument changes It is an essential tool in economics If you have done A-level maths,
CHAPTER 5 Differentiation Differentiation is a technique that enables us to find out how a function changes when its argument changes It is an essential tool in economics If you have done A-level maths,
Doug Clark The Learning Center 100 Student Success Center learningcenter.missouri.edu Overview
 Math 1400 Final Exam Review Saturday, December 9 in Ellis Auditorium 1:00 PM 3:00 PM, Saturday, December 9 Part 1: Derivatives and Applications of Derivatives 3:30 PM 5:30 PM, Saturday, December 9 Part
Math 1400 Final Exam Review Saturday, December 9 in Ellis Auditorium 1:00 PM 3:00 PM, Saturday, December 9 Part 1: Derivatives and Applications of Derivatives 3:30 PM 5:30 PM, Saturday, December 9 Part
3.4 The Fundamental Theorem of Algebra
 333371_0304.qxp 12/27/06 1:28 PM Page 291 3.4 The Fundamental Theorem of Algebra Section 3.4 The Fundamental Theorem of Algebra 291 The Fundamental Theorem of Algebra You know that an nth-degree polynomial
333371_0304.qxp 12/27/06 1:28 PM Page 291 3.4 The Fundamental Theorem of Algebra Section 3.4 The Fundamental Theorem of Algebra 291 The Fundamental Theorem of Algebra You know that an nth-degree polynomial
Looking Ahead to Chapter 4
 Looking Ahead to Chapter Focus In Chapter, you will learn about functions and function notation, and you will find the domain and range of a function. You will also learn about real numbers and their properties,
Looking Ahead to Chapter Focus In Chapter, you will learn about functions and function notation, and you will find the domain and range of a function. You will also learn about real numbers and their properties,
GUIDED NOTES 6.1 EXPONENTIAL FUNCTIONS
 GUIDED NOTES 6.1 EXPONENTIAL FUNCTIONS LEARNING OBJECTIVES In this section, you will: Evaluate exponential functions. Find the equation of an exponential function. Use compound interest formulas. Evaluate
GUIDED NOTES 6.1 EXPONENTIAL FUNCTIONS LEARNING OBJECTIVES In this section, you will: Evaluate exponential functions. Find the equation of an exponential function. Use compound interest formulas. Evaluate
Transformations of Functions and Exponential Functions January 24, / 35
 Exponential Functions January 24, 2017 Exponential Functions January 24, 2017 1 / 35 Review of Section 1.2 Reminder: Week-in-Review, Help Sessions, Oce Hours Mathematical Models Linear Regression Function
Exponential Functions January 24, 2017 Exponential Functions January 24, 2017 1 / 35 Review of Section 1.2 Reminder: Week-in-Review, Help Sessions, Oce Hours Mathematical Models Linear Regression Function
Sample Mathematics 106 Questions
 Sample Mathematics 106 Questions x 2 + 8x 65 (1) Calculate lim x 5. x 5 (2) Consider an object moving in a straight line for which the distance s (measured in feet) it s travelled from its starting point
Sample Mathematics 106 Questions x 2 + 8x 65 (1) Calculate lim x 5. x 5 (2) Consider an object moving in a straight line for which the distance s (measured in feet) it s travelled from its starting point
Every polynomial equation of degree 1 or greater has at least one root in the set of complex numbers.
 Sec 3.1 Polynomial Functions Fundamental Theorem of Algebra An important and famous German mathematician, Carl Friedrich Gauss, is credited with first proving the FUNDAMENTAL THEOREM OF ALGEBRA which states:
Sec 3.1 Polynomial Functions Fundamental Theorem of Algebra An important and famous German mathematician, Carl Friedrich Gauss, is credited with first proving the FUNDAMENTAL THEOREM OF ALGEBRA which states:
17 Exponential and Logarithmic Functions
 17 Exponential and Logarithmic Functions Concepts: Exponential Functions Power Functions vs. Exponential Functions The Definition of an Exponential Function Graphing Exponential Functions Exponential Growth
17 Exponential and Logarithmic Functions Concepts: Exponential Functions Power Functions vs. Exponential Functions The Definition of an Exponential Function Graphing Exponential Functions Exponential Growth
Chapter 2. Polynomial and Rational Functions. 2.6 Rational Functions and Their Graphs. Copyright 2014, 2010, 2007 Pearson Education, Inc.
 Chapter Polynomial and Rational Functions.6 Rational Functions and Their Graphs Copyright 014, 010, 007 Pearson Education, Inc. 1 Objectives: Find the domains of rational functions. Use arrow notation.
Chapter Polynomial and Rational Functions.6 Rational Functions and Their Graphs Copyright 014, 010, 007 Pearson Education, Inc. 1 Objectives: Find the domains of rational functions. Use arrow notation.
1. The dosage in milligrams D of a heartworm preventive for a dog who weighs X pounds is given by D x. Substitute 28 in place of x to get:
 1. The dosage in milligrams D of a heartworm preventive for a dog who weighs X pounds is given by D x 28 pounds. ( ) = 136 ( ). Find the proper dosage for a dog that weighs 25 x Substitute 28 in place
1. The dosage in milligrams D of a heartworm preventive for a dog who weighs X pounds is given by D x 28 pounds. ( ) = 136 ( ). Find the proper dosage for a dog that weighs 25 x Substitute 28 in place
CHAPTER FIVE. g(t) = t, h(n) = n, v(z) = z, w(c) = c, u(k) = ( 0.003)k,
 CHAPTER FIVE 5.1 SOLUTIONS 121 Solutions for Section 5.1 EXERCISES 1. Since the distance is decreasing, the rate of change is negative. The initial value of D is 1000 and it decreases by 50 each day, so
CHAPTER FIVE 5.1 SOLUTIONS 121 Solutions for Section 5.1 EXERCISES 1. Since the distance is decreasing, the rate of change is negative. The initial value of D is 1000 and it decreases by 50 each day, so
Mathematics for Economics ECON MA/MSSc in Economics-2017/2018. Dr. W. M. Semasinghe Senior Lecturer Department of Economics
 Mathematics for Economics ECON 53035 MA/MSSc in Economics-2017/2018 Dr. W. M. Semasinghe Senior Lecturer Department of Economics MATHEMATICS AND STATISTICS LERNING OUTCOMES: By the end of this course unit
Mathematics for Economics ECON 53035 MA/MSSc in Economics-2017/2018 Dr. W. M. Semasinghe Senior Lecturer Department of Economics MATHEMATICS AND STATISTICS LERNING OUTCOMES: By the end of this course unit
