Mathematics for Economics ECON MA/MSSc in Economics-2017/2018. Dr. W. M. Semasinghe Senior Lecturer Department of Economics
|
|
|
- Clare Kelly
- 5 years ago
- Views:
Transcription
1 Mathematics for Economics ECON MA/MSSc in Economics-2017/2018 Dr. W. M. Semasinghe Senior Lecturer Department of Economics
2 MATHEMATICS AND STATISTICS LERNING OUTCOMES: By the end of this course unit students will be able to demonstrate skills in mathematical and statistical methods that are highly useful in analyzing problems related to economic theory and practice and understand the uses of basic descriptive and inferential statistics in economic analysis. COURSE CONTENTS: This course unit consists of two parts: Part I: Mathematics - Functions and their applications in economics, Calculus and its applications in economics: Differentiation, Partial differentiation, Integration; Matrices; Maxima and Minima; Constrained Optimization with economic applications, Linear programming. Part II: Statistics - Probability and probability Theory; continuous and discrete variables, continuous and discrete variables distributions, Joint distributions; Moment generating functions; Hypothesis testing and confidence intervals.
3 Functions A function is a rule that gives exactly one output number to each input number. Why it is important to us?
4 If the value of variable y depends on the values of another variable say x, y is said to be a function of x and, denoted by, y = f (x) Where, y dependent variable or value of the function x independent variable or argument of the function f particular rule that applies
5 eg:- q = f(p) s = f(y d ) p = f(q) c = f (y d ) TC = f(q) TR = f(q) To denote a function the symbols F, G, g, h, and the Greek letters such as θ, φ, ψ, Φ, Ψ etc. are also used. If y and z depend on x, then y = f(x) and z = f(x) We can also write y = y(x) z = z(x)
6 The set of all input numbers to which the rule applies is called the domain of the function. The set of all output numbers is called the range.
7 y = 18x 3x 2 If the input (domain) x is any real number, then the output (range) y is also a real number, R. y = 2x + 3 x - 1 The output y is a real number if the input x is any real number other than 1. the domain is R {1}
8 Since, most variables in economic models are by their nature restricted to nonnegative real numbers, their domains are also restricted. eg. The total cost of a firm per day is a function of its daily output Q: C=150+7Q. The firm has a capacity limit of 100 units of output per day. What are the domain and rang of the cost function? Domain = Q 0 Q 100 Range = C 150 C 850
9 If a is any particular value of the function of x, the value of function f(x) for x = a is denoted by f(a). x y = f(x) = 7x + 1 f(a) = a/(7a + 1) f(4) = 4/ 29
10 Types of Functions Constant function: A function whose range consists of only one element. eg. y = 7 f(x) = 10 The value of the function does not change whatever the value of x.
11 In a coordinate plane, such a function will appears as a horizontal straight line. eg. In a national income model, the investment function which determined exogenously Y 0 I
12 Polynomial Functions The general form of a Polynomial Functions of Degree n f(x) = a 0 + a 1 x + a 2 x a n-1 x n-1 + a n x n n is a positive integer and a 0..a n are constants. a n 0 e.g. f(x) = 8x 6 + 3x 4 x 3 + 5x 2 + 2x + 3 (polynomial of degree 6) F(x) = x 8 + 2x 5 + 3x 4 + 7x 2 + 6x 5 (polynomial of degree 8)
13 Depending on the value of the integer n there are several subclasses of polynomial functions. when n = 0 y = a 0 Constant function n = 1 y = a 0 + a 1 x Linear function n = 2 y = a 0 + a 1 x + a 2 x 2 n = 3 y = a 0 + a 1 x + a 2 x 2 + a 3 x 3 (polynomial of degree 1) Quadratic function Cubic function
14 Rational Functions f(x) = g(x) h(x) g(x) and h(x) are polynomials of x and h(x) 0 f(x) is expressed as a ratio of two polynomial functions of variable x. (3x 2 + 5) f(x) = (2x 1)
15 Composite Function or Function of a Function If y = g(u) and u = f(x), y = g[f(x)] eg. 1. If y= u and u = 2x + 1 then, y= (2x+1) eg. 2. If y= x 3-3x + 5 and x = ½ t + 3 then, y =? y= (½ t+3) 3 3(½ t+3) +5
16 Non-algebraic Function The function such as y = e t y = b x which the independent variable appears in the exponent is called non-algebraic function. Logarithmic functions are also non- algebraic functions. y = log b x y = ln x
17 Functions of two or more independent variable z = f(x, y) z = ax + by z = a 0 + a 1 x + a 2 x 2 + b 1 y + b 2 y 2 y = a 1 x 1 + a 2 x 2 + a 3 x 3 +.a n x n V = AL α K β
18 Differentiation The process of finding the derivative (deferential coefficient) of a function is called differentiation. It stands for finding the rate of change of one variable, say y, with respect to the rate of change of another variable, say x. For a function y = f(x) the differential coefficient of y with respect to x is defined as dy dx f(x x) - f(x) xlim 0 xlim0 x y x
19 y = f(x) (1) Assume, when variable x is increased by x, variable y will be increased by y, y + Δy = f(x + Δx) (2) (2) - (1) Δy = f(x + Δx) f(x) (3) (3) Δx Δy Δx = f(x + Δx) f(x) Δx The limit of Δy/Δx when Δx lim differential coefficient of f(x) 0, is defined as the dy/dx is used to denote the limiting value Δy/Δx
20 eg. y = 3x.. (1) y + Δy = 3(x + Δx) (2) (2) (1) Δy = 3(x + Δx) 3x Δy = 3Δx (3) Δx Δy/Δx = 3 (3) lim Δy/Δx = 3 Δx 0
21 Rules of Differentiation When u, v and y are the functions of x and k is a constant, (1) Constant function rule y = f(x) = k dy dx d(k) = = f ' (x) = 0 dx (2) Linear function rule y = f(x) = kx + 2 dy/dx = k
22 (3) Power function rule y = f(x) = x n dy d(x n ) = = dx dx nx n-1 (4). Generalized power function rule y = kx n dy d(kx n ) = = knx n-1 dx dx
23 (5). Sum-difference rule y = [f(x) ± g(x)] dy d[f(x)] d[g(x)] = ± dx dx dx (6). Function of a function rule When y = [f(x)] n This type of a function is called function of a function. dy dx = n[f(x)] n-1 f '(x)
24 (7). Product rule y = [f(x).g(x)] dy d[g(x)] d[f(x)] = f(x) + g(x) dx dx dx f(x) = u and g(x) = v y = uv dy dv du = u + v dx dx dx
25 If u, v and w are functions of x, d (u,v,w) dw dv du = uv + uw + vw dx dx dx dx eg. y = x 2 (x 2 + 1) (x + 2)
26 (8). Quotient rule f(x) y = g(x) f(x) = u u y = v g(x) = v dy df(x) dg(x) = g(x) - f(x) dx dx dx [g(x)] 2 dy du dv = v - u dx dx dx v 2
27 When y = 1/f(x) dy dx f f ( x) ( x) 2 eg. y = 1/ (x 2 +1) dy dx 2x x 2 1 2
28 (9). Chain rule When y = f(u) and u = g(x) dy dx dy du =. du dx u Find dy/dx given y = and u u x 3 2 1
29 (10). Log-function rule When a variable is expressed as a function of logarithm of another variable, the function is referred to as a logarithmic function or log function. y = log b x y = log e x (= ln x) Which differ from each other only in regards to the base of logarithm. In calculus e takes as the base of logarithm. Logarithms on base e is called natural logarithm and denoted as log e or ln. eg. y = log e 2x or y = ln 2x
30 1. y = ln x dy d(ln x) 1 = = dx dx x 2. y = kln x dy d(ln x) 1 k = k = k = dx dx x x 3. If y = log e u and u = f(x) dy 1 du = dx u dx
31 (11). Exponential Function Rule Power (index) of the independent variable in a polynomial function is called exponent. eg. y = 2x 3 + 4x The functions which appears independent variable as the exponent is called Exponential function. eg. y = f(x) = b x (b>1) where, y and x are dependent and independent variables respectively and b is the base of the exponent. In calculus, an irrational number e (e = ) takes as the base of the exponent. eg. y = e x y = e 3x y = Ae rx
32 y = e x dy = e x dx eg. If y = e u and u = f(x) dy dx = e u du dx eg. y = e (3x + 2) dy = 3e (3x + 2) dx
33 Derivatives of Higher Order When derivative of a function is differentiable, it may have a derivative as well. If y = f(x), then dy/dx or f ' (x) is called 1 st derivative of the function. The derivative of dy/dx or f ' (x) is denoted by d 2 y/dx 2 or f '' (x) and is called the second derivative. If y = f(x) d (y) 1 st derivative: f '(x) = = dx dy dx d (dy/dx) d 2 y 2 nd derivative: f '' (x) = = dx dx 2
34 d (d 2 y/dx 2 ) d 3 y 3 rd derivative: f ''' (x) = = dx dx 3 d (d n-1 y/dx n-1 ) n th derivative: f n (x) = = dx Find d n y dx n i. y = x 4 + 3x 2 2x rd ii. y = x 1 2x 2 nd ii. y = 3x - 1 x rd
35 Partial differentiation So far we dealt with functions of a single independent variable x, which were generally expressed as y = f(x). However, there are many situations in which we must consider more than one independent variables. A function of two independent variables x and y can be expressed as z = f(x, y). Z is the dependent variable.
36 In general, if y is a function of n independent variables x 1, x 2, x n, it can be written as y = f(x 1, x 2,., x n ) Given a multivariable function y = f(x 1, x 2,., x n ), the partial derivative measures the rate of change of the dependent variable (y) with respect to change of one of the independent variables, while the other independent variables are held constant.
37 If z = f(x, y), the partial derivative of z with respect to x is obtained by treating y as a constant and applying ordinary rules of differentiation. The partial derivative of z with respect to x is symbolized by z/ x or f x. Similarly, the partial derivative of z with respect to y is symbolized by z/ y or f y.
38
39 eg. Find the partial derivatives (f x and f y ) of the following functions: i. f(x 1,x 2 ) = 3x 12 + x 1 x 2 + 4x 2 2 Find f x and f y ii. f(x, y) = (x 2 7y) (x 2) Find f x and f y iii. f(x,y) = (2x 3y)/(x + y) Find f x and f y iv. z = ln (x 2 + y 2 ) v. z = (x + y) e (x + y) vi. z = 3x 2 y + 4xy 2 + 6xy
40 Eg. 2. The indifference curve of a consumer is given as U = U(x 1, x 2 ) = (x 1 + 2) 2 (x 2 + 3) 2 Where, U is the total utility, x 1 and x 2 are the quantity consumed from the two goods X and Y. i. Derive the marginal utility functions of the two goods. ii. If consumer buys 3 items from each good, find the marginal utility of 1 st good. Eg. 3. Derive the marginal productivity functions of labor (MP L ) and capital (MP K ) from the production function V = AL α K β. Where, V is the output, L and K are labor and capital inputs respectively.
41 Partial Derivatives of Higher Order Higher partial derivatives are obtained in the same way as higher derivatives. For the function z = f(x, y), there are 4 second order partial derivatives: 2 z ( z/ x) i = = (f x ) x = f xx x 2 x 2 z ( z/ y) ii = = (f y ) y = f yy y 2 y
42 2 z ( z/ x) iii = = (f x ) y = f xy y x y 2 z ( z/ y) iv = = (f y ) x = f yx x y x Cross partial derivatives
43 Find all four partial derivatives of higher order z = 4x 6 3x 2 y 2 + 5y 4 z = x 2 e -y z = 7x ln(1 + y) z = (2x + 5y) (7x 3y) z = e4x 7y
44 Optimization Optimization is the choice of the best among the available alternatives. Optimization Maximization Profit Utility Growth rate Sales Output etc. Minimization Cost Risk etc.
45 y = f(x) This is called objective function, if the aim is to find the value of x which optimizes the value of dependent variable y. It may be a maximization or a minimization. x choice variable - decision variable - policy variable This indicates the value that it should take to maximize/minimize variable y'
46 Suppose a business firm seeks to maximize profit (π). Profit is maximized at the output (Q) which maximize the difference between total revenue (R) and total cost (C). Given state of technology and market demand, both R and C are functions of Q. There for π is also a function of Q. π = R(Q) C(Q) π indicates the goal of the firm i.e.what should optimize. Thus, itis the objective function of the optimization problem.q is the choicevariable.the aimis tofind the Q that maximize the π.
47 Determination of maxima and minima of a function A point on a graph that is higher than any other point in its vicinity is called a relative maximum. In other words, y = f(x) is said to have a relative maximum value at x = x 0 if f(x 0 ) is greater than immediately preceding or succeeding values of the function. Similarly, a point on a graph that is lower than any other point in its vicinity is called a relative minimum. In other words, y=f(x) is said to have a relative minimum value at x = x 0 if f(x 0 ) is smaller than immediately preceding or succeeding values of the function.
48 An extreme point (relative or local extremum) of a function is a point where the function is at a relative maximum or minimum. If the derivative of the function exists at an extreme point, the value of the derivative must be zero, and the tangent line, if exists, is horizontal. A point where the derivative equals zero or undefined is called a critical point. Since the derivative of a function at a relative extreme must be zero, a relative extreme can occur only at a critical point.
49 A point at which a curve crosses its tangent is called an inflection point. The sign of the first derivative can be positive or negative or can be zero for an inflection point. P 3 P 4 P 2 P 6 P 1 P 5 P 1, P 5 relative minimum P 3 relative maximum P 2, P 4, P 6 inflection points
50 Determination of maximum and minimum 1. First derivative test 2. Second derivative test First derivative test first derivative of the function is used to determine the extreme points. Necessary condition or first order condition If the first derivative of a function y = f(x) at point x = x 0 is zero i.e. f (x) = 0 then it is an extreme point. It may be a relative maximum or minimum or inflection point.
51 Sufficient condition or second order condition If the sign of the derivative f (x) changes from positive to negative from the left of the point x 0 to its right, x 0 is a relative maximum. Y 0 X 0 X If the sign of the derivative changes from negative to positive from the left of the point x 0 to its right, x 0 is a relative minimum ' f (x) Y 0 X 0 If f (x) has the same sign on both sides of point x 0, f(x) has neither maximum nor minimum value at x = x 0. It is an inflection point. X
52 Second Derivative Test Second derivative of the function is used to determine the extreme points. i Solve f (x) = 0 for the critical values. ii. For a critical value x = x 0 f(x) has a maximum value if f(x) has a minimum value if f ( x 0 ) f ( x 0 ) 0 0 However, the test fails if f ( x 0 ) 0 or becomes infinite?
53 i. If at x = x 0 f '(x 0 ) = 0, x 0 is a critical point. ii. If f ''(x 0 ) < 0, x 0 is a maximum point. Maximum dy/dx = f '(x) = d 2 y/dx 2 = f ''(x) < 0 iii. If f ''(x 0 ) > 0, x 0 is a minimum point. Minimum dy/dx = f ' (x) = 0 d 2 y/dx 2 = f ''(x) > 0 + +
54 If d 2 y/dx 2 = f ''(x) = 0? In a situation like this, (1) Examine how the sign of f (x) change when x substitutes values less than to higher than of x 0 i. If the sign changes + to at x = 0, the function has a maximum. ii. If the sign changes - to + at x = 0, the function has a minimum. iii. If the sign does not change the function has a inflection at x = 0
55 (2). Take successive higher order derivatives. Substitute x = x 0 to the first non-zero higher order derivative. If the value is odd, x = x 0 is an inflection point. If the value is even, x = x 0 is an extreme point. - If the even number is positive, the point is minimum - If the even number is negative, the point is maximum.
56 1. The total cost of producing a given commodity is TC = ¼ x x + 25 and the price of the commodity is P = 50 - ½ x. i. Find the level of output which yield the maximum profit i. Show that average cost is minimum at this output level. 2. Cost function of a perfectly competitive firm is TC = 1/3 q 3 5q q + 10 If price p = 6, find the profit maximizing output level.
57 Extreme Values of a Function of Two Choice Variables z = f(x, y) Condition Maximum Minimum First order or Sufficient f x =0, f y = 0 f x = 0, f y = 0 Second order or Necessary F xx, f yy < 0 and f xx f yy > 2 f xy f xx, f yy > 0 and f xx f yy > 2 f xy If f xx f yy < 2 f xy a saddle point
58 Economic applications Profit maximization Profit (Π) = Total Revenue (R) Total Cost (C) Π = R C R = f(q) and C = f(q) Π (q) = R(q) C(q) For profit maximization, the difference between R(q) and C(q) should be maximized. First order condition dπ/dq = Π' = 0
59 Π' (q) = R'(q) C'(q) = 0 iff R'(q) = C'(q) Thus, at the output level which yield maximum profit, R'(q) = C'(q) MR = MC This is the first order condition for profit maximization.
60 Second order condition d 2 Π/dq 2 = Π''(q) < 0 Π''(q) = R''(q) - C''(q) < 0 iff R''(q) < C''(q) Thus, to satisfy the second order condition R''(q) < C''(q). R''(q) = the rate of change of MR C''(q) the rate of change of MC At the output level which MC = MR, and R''(q) < C''(q) profit is maximized.
Functions. A function is a rule that gives exactly one output number to each input number.
 Functions A function is a rule that gives exactly one output number to each input number. Why it is important to us? The set of all input numbers to which the rule applies is called the domain of the function.
Functions A function is a rule that gives exactly one output number to each input number. Why it is important to us? The set of all input numbers to which the rule applies is called the domain of the function.
REVIEW OF MATHEMATICAL CONCEPTS
 REVIEW OF MATHEMATICAL CONCEPTS Variables, functions and slopes: A Variable is any entity that can take different values such as: price, output, revenue, cost, etc. In economics we try to 1. Identify the
REVIEW OF MATHEMATICAL CONCEPTS Variables, functions and slopes: A Variable is any entity that can take different values such as: price, output, revenue, cost, etc. In economics we try to 1. Identify the
Tvestlanka Karagyozova University of Connecticut
 September, 005 CALCULUS REVIEW Tvestlanka Karagyozova University of Connecticut. FUNCTIONS.. Definition: A function f is a rule that associates each value of one variable with one and only one value of
September, 005 CALCULUS REVIEW Tvestlanka Karagyozova University of Connecticut. FUNCTIONS.. Definition: A function f is a rule that associates each value of one variable with one and only one value of
Second Order Derivatives. Background to Topic 6 Maximisation and Minimisation
 Second Order Derivatives Course Manual Background to Topic 6 Maximisation and Minimisation Jacques (4 th Edition): Chapter 4.6 & 4.7 Y Y=a+bX a X Y= f (X) = a + bx First Derivative dy/dx = f = b constant
Second Order Derivatives Course Manual Background to Topic 6 Maximisation and Minimisation Jacques (4 th Edition): Chapter 4.6 & 4.7 Y Y=a+bX a X Y= f (X) = a + bx First Derivative dy/dx = f = b constant
STUDY MATERIALS. (The content of the study material is the same as that of Chapter I of Mathematics for Economic Analysis II of 2011 Admn.
 STUDY MATERIALS MATHEMATICAL TOOLS FOR ECONOMICS III (The content of the study material is the same as that of Chapter I of Mathematics for Economic Analysis II of 2011 Admn.) & MATHEMATICAL TOOLS FOR
STUDY MATERIALS MATHEMATICAL TOOLS FOR ECONOMICS III (The content of the study material is the same as that of Chapter I of Mathematics for Economic Analysis II of 2011 Admn.) & MATHEMATICAL TOOLS FOR
Economics 203: Intermediate Microeconomics. Calculus Review. A function f, is a rule assigning a value y for each value x.
 Economics 203: Intermediate Microeconomics Calculus Review Functions, Graphs and Coordinates Econ 203 Calculus Review p. 1 Functions: A function f, is a rule assigning a value y for each value x. The following
Economics 203: Intermediate Microeconomics Calculus Review Functions, Graphs and Coordinates Econ 203 Calculus Review p. 1 Functions: A function f, is a rule assigning a value y for each value x. The following
REVIEW OF MATHEMATICAL CONCEPTS
 REVIEW OF MATHEMATICAL CONCEPTS 1 Variables, functions and slopes A variable is any entity that can take different values such as: price, output, revenue, cost, etc. In economics we try to 1. Identify
REVIEW OF MATHEMATICAL CONCEPTS 1 Variables, functions and slopes A variable is any entity that can take different values such as: price, output, revenue, cost, etc. In economics we try to 1. Identify
1 Functions and Graphs
 1 Functions and Graphs 1.1 Functions Cartesian Coordinate System A Cartesian or rectangular coordinate system is formed by the intersection of a horizontal real number line, usually called the x axis,
1 Functions and Graphs 1.1 Functions Cartesian Coordinate System A Cartesian or rectangular coordinate system is formed by the intersection of a horizontal real number line, usually called the x axis,
Math 110 Final Exam General Review. Edward Yu
 Math 110 Final Exam General Review Edward Yu Da Game Plan Solving Limits Regular limits Indeterminate Form Approach Infinities One sided limits/discontinuity Derivatives Power Rule Product/Quotient Rule
Math 110 Final Exam General Review Edward Yu Da Game Plan Solving Limits Regular limits Indeterminate Form Approach Infinities One sided limits/discontinuity Derivatives Power Rule Product/Quotient Rule
ECON2285: Mathematical Economics
 ECON2285: Mathematical Economics Yulei Luo Economics, HKU September 17, 2018 Luo, Y. (Economics, HKU) ME September 17, 2018 1 / 46 Static Optimization and Extreme Values In this topic, we will study goal
ECON2285: Mathematical Economics Yulei Luo Economics, HKU September 17, 2018 Luo, Y. (Economics, HKU) ME September 17, 2018 1 / 46 Static Optimization and Extreme Values In this topic, we will study goal
EC5555 Economics Masters Refresher Course in Mathematics September 2013
 EC5555 Economics Masters Refresher Course in Mathematics September 013 Lecture 3 Differentiation Francesco Feri Rationale for Differentiation Much of economics is concerned with optimisation (maximise
EC5555 Economics Masters Refresher Course in Mathematics September 013 Lecture 3 Differentiation Francesco Feri Rationale for Differentiation Much of economics is concerned with optimisation (maximise
Math Review ECON 300: Spring 2014 Benjamin A. Jones MATH/CALCULUS REVIEW
 MATH/CALCULUS REVIEW SLOPE, INTERCEPT, and GRAPHS REVIEW (adapted from Paul s Online Math Notes) Let s start with some basic review material to make sure everybody is on the same page. The slope of a line
MATH/CALCULUS REVIEW SLOPE, INTERCEPT, and GRAPHS REVIEW (adapted from Paul s Online Math Notes) Let s start with some basic review material to make sure everybody is on the same page. The slope of a line
EC611--Managerial Economics
 EC611--Managerial Economics Optimization Techniques and New Management Tools Dr. Savvas C Savvides, European University Cyprus Models and Data Model a framework based on simplifying assumptions it helps
EC611--Managerial Economics Optimization Techniques and New Management Tools Dr. Savvas C Savvides, European University Cyprus Models and Data Model a framework based on simplifying assumptions it helps
Optimization Techniques
 Optimization Techniques Methods for maximizing or minimizing an objective function Examples Consumers maximize utility by purchasing an optimal combination of goods Firms maximize profit by producing and
Optimization Techniques Methods for maximizing or minimizing an objective function Examples Consumers maximize utility by purchasing an optimal combination of goods Firms maximize profit by producing and
Topic 6: Optimization I. Maximisation and Minimisation Jacques (4th Edition): Chapter 4.6 & 4.7
 Topic 6: Optimization I Maximisation and Minimisation Jacques (4th Edition): Chapter 4.6 & 4.7 1 For a straight line Y=a+bX Y= f (X) = a + bx First Derivative dy/dx = f = b constant slope b Second Derivative
Topic 6: Optimization I Maximisation and Minimisation Jacques (4th Edition): Chapter 4.6 & 4.7 1 For a straight line Y=a+bX Y= f (X) = a + bx First Derivative dy/dx = f = b constant slope b Second Derivative
DCDM BUSINESS SCHOOL FACULTY OF MANAGEMENT ECONOMIC TECHNIQUES 102 LECTURE 4 DIFFERENTIATION
 DCDM BUSINESS SCHOOL FACULTY OF MANAGEMENT ECONOMIC TECHNIUES 1 LECTURE 4 DIFFERENTIATION 1 Differentiation Managers are often concerned with the way that a variable changes over time Prices, for example,
DCDM BUSINESS SCHOOL FACULTY OF MANAGEMENT ECONOMIC TECHNIUES 1 LECTURE 4 DIFFERENTIATION 1 Differentiation Managers are often concerned with the way that a variable changes over time Prices, for example,
Definition: If y = f(x), then. f(x + x) f(x) y = f (x) = lim. Rules and formulas: 1. If f(x) = C (a constant function), then f (x) = 0.
 Definition: If y = f(x), then Rules and formulas: y = f (x) = lim x 0 f(x + x) f(x). x 1. If f(x) = C (a constant function), then f (x) = 0. 2. If f(x) = x k (a power function), then f (x) = kx k 1. 3.
Definition: If y = f(x), then Rules and formulas: y = f (x) = lim x 0 f(x + x) f(x). x 1. If f(x) = C (a constant function), then f (x) = 0. 2. If f(x) = x k (a power function), then f (x) = kx k 1. 3.
Final Exam Study Guide
 Final Exam Study Guide Final Exam Coverage: Sections 10.1-10.2, 10.4-10.5, 10.7, 11.2-11.4, 12.1-12.6, 13.1-13.2, 13.4-13.5, and 14.1 Sections/topics NOT on the exam: Sections 10.3 (Continuity, it definition
Final Exam Study Guide Final Exam Coverage: Sections 10.1-10.2, 10.4-10.5, 10.7, 11.2-11.4, 12.1-12.6, 13.1-13.2, 13.4-13.5, and 14.1 Sections/topics NOT on the exam: Sections 10.3 (Continuity, it definition
SCHOOL OF DISTANCE EDUCATION
 SCHOOL OF DISTANCE EDUCATION CCSS UG PROGRAMME MATHEMATICS (OPEN COURSE) (For students not having Mathematics as Core Course) MM5D03: MATHEMATICS FOR SOCIAL SCIENCES FIFTH SEMESTER STUDY NOTES Prepared
SCHOOL OF DISTANCE EDUCATION CCSS UG PROGRAMME MATHEMATICS (OPEN COURSE) (For students not having Mathematics as Core Course) MM5D03: MATHEMATICS FOR SOCIAL SCIENCES FIFTH SEMESTER STUDY NOTES Prepared
There are a number of related results that also go under the name of "chain rules." For example, if y=f(u) u=g(v), and v=h(x), dy = dx
 CHAIN RULE DIFFERENTIATION If y is a function of u ie y f(u) and u is a function of x ie u g(x) then y is related to x through the intermediate function u ie y f(g(x) ) y is differentiable with respect
CHAIN RULE DIFFERENTIATION If y is a function of u ie y f(u) and u is a function of x ie u g(x) then y is related to x through the intermediate function u ie y f(g(x) ) y is differentiable with respect
2. Which of the following is the ECONOMISTS inverse of the function y = 9/x 2 (i.e. find x as a function of y, x = f(y))
 Anwers for Review Quiz #1. Material Covered. Klein 1, 2; Schaums 1, 2 1. Solve the following system of equations for x, y and z: x + y = 2 2x + 2y + z = 5 7x + y + z = 9 Answers: x = 1, y = 1, z = 1. 2.
Anwers for Review Quiz #1. Material Covered. Klein 1, 2; Schaums 1, 2 1. Solve the following system of equations for x, y and z: x + y = 2 2x + 2y + z = 5 7x + y + z = 9 Answers: x = 1, y = 1, z = 1. 2.
Chapter 6: Sections 6.1, 6.2.1, Chapter 8: Section 8.1, 8.2 and 8.5. In Business world the study of change important
 Study Unit 5 : Calculus Chapter 6: Sections 6., 6.., 6.3. Chapter 8: Section 8., 8. and 8.5 In Business world the study of change important Example: change in the sales of a company; change in the value
Study Unit 5 : Calculus Chapter 6: Sections 6., 6.., 6.3. Chapter 8: Section 8., 8. and 8.5 In Business world the study of change important Example: change in the sales of a company; change in the value
Chapter 4 Differentiation
 Chapter 4 Differentiation 08 Section 4. The derivative of a function Practice Problems (a) (b) (c) 3 8 3 ( ) 4 3 5 4 ( ) 5 3 3 0 0 49 ( ) 50 Using a calculator, the values of the cube function, correct
Chapter 4 Differentiation 08 Section 4. The derivative of a function Practice Problems (a) (b) (c) 3 8 3 ( ) 4 3 5 4 ( ) 5 3 3 0 0 49 ( ) 50 Using a calculator, the values of the cube function, correct
September Math Course: First Order Derivative
 September Math Course: First Order Derivative Arina Nikandrova Functions Function y = f (x), where x is either be a scalar or a vector of several variables (x,..., x n ), can be thought of as a rule which
September Math Course: First Order Derivative Arina Nikandrova Functions Function y = f (x), where x is either be a scalar or a vector of several variables (x,..., x n ), can be thought of as a rule which
School of Business. Blank Page
 Maxima and Minima 9 This unit is designed to introduce the learners to the basic concepts associated with Optimization. The readers will learn about different types of functions that are closely related
Maxima and Minima 9 This unit is designed to introduce the learners to the basic concepts associated with Optimization. The readers will learn about different types of functions that are closely related
3.1 Derivative Formulas for Powers and Polynomials
 3.1 Derivative Formulas for Powers and Polynomials First, recall that a derivative is a function. We worked very hard in 2.2 to interpret the derivative of a function visually. We made the link, in Ex.
3.1 Derivative Formulas for Powers and Polynomials First, recall that a derivative is a function. We worked very hard in 2.2 to interpret the derivative of a function visually. We made the link, in Ex.
Contents CONTENTS 1. 1 Straight Lines and Linear Equations 1. 2 Systems of Equations 6. 3 Applications to Business Analysis 11.
 CONTENTS 1 Contents 1 Straight Lines and Linear Equations 1 2 Systems of Equations 6 3 Applications to Business Analysis 11 4 Functions 16 5 Quadratic Functions and Parabolas 21 6 More Simple Functions
CONTENTS 1 Contents 1 Straight Lines and Linear Equations 1 2 Systems of Equations 6 3 Applications to Business Analysis 11 4 Functions 16 5 Quadratic Functions and Parabolas 21 6 More Simple Functions
a x a y = a x+y a x a = y ax y (a x ) r = a rx and log a (xy) = log a (x) + log a (y) log a ( x y ) = log a(x) log a (y) log a (x r ) = r log a (x).
 You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
Differentiation. 1. What is a Derivative? CHAPTER 5
 CHAPTER 5 Differentiation Differentiation is a technique that enables us to find out how a function changes when its argument changes It is an essential tool in economics If you have done A-level maths,
CHAPTER 5 Differentiation Differentiation is a technique that enables us to find out how a function changes when its argument changes It is an essential tool in economics If you have done A-level maths,
Section 11.3 Rates of Change:
 Section 11.3 Rates of Change: 1. Consider the following table, which describes a driver making a 168-mile trip from Cleveland to Columbus, Ohio in 3 hours. t Time (in hours) 0 0.5 1 1.5 2 2.5 3 f(t) Distance
Section 11.3 Rates of Change: 1. Consider the following table, which describes a driver making a 168-mile trip from Cleveland to Columbus, Ohio in 3 hours. t Time (in hours) 0 0.5 1 1.5 2 2.5 3 f(t) Distance
Part I: Multiple Choice Questions (5 points each) d dx (x3 e 4x ) =
 Part I: Multiple Choice Questions (5 points each) 1. d dx (x3 e 4x ) = (a) 12x 2 e 4x (b) 3x 2 e 4x + 4x 4 e 4x 1 (c) x 3 e 4x + 12x 2 e 4x (d) 3x 2 e 4x + 4x 3 e 4x (e) 4x 3 e 4x 1 2. Suppose f(x) is
Part I: Multiple Choice Questions (5 points each) 1. d dx (x3 e 4x ) = (a) 12x 2 e 4x (b) 3x 2 e 4x + 4x 4 e 4x 1 (c) x 3 e 4x + 12x 2 e 4x (d) 3x 2 e 4x + 4x 3 e 4x (e) 4x 3 e 4x 1 2. Suppose f(x) is
1 Review of di erential calculus
 Review of di erential calculus This chapter presents the main elements of di erential calculus needed in probability theory. Often, students taking a course on probability theory have problems with concepts
Review of di erential calculus This chapter presents the main elements of di erential calculus needed in probability theory. Often, students taking a course on probability theory have problems with concepts
MATH 236 ELAC FALL 2017 CA 9 NAME: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 MATH 236 ELAC FALL 207 CA 9 NAME: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. ) 27 p 3 27 p 3 ) 2) If 9 t 3 4t 9-2t = 3, find t. 2) Solve the equation.
MATH 236 ELAC FALL 207 CA 9 NAME: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. ) 27 p 3 27 p 3 ) 2) If 9 t 3 4t 9-2t = 3, find t. 2) Solve the equation.
ERASMUS UNIVERSITY ROTTERDAM Information concerning the Entrance examination Mathematics level 2 for International Business Administration (IBA)
 ERASMUS UNIVERSITY ROTTERDAM Information concerning the Entrance examination Mathematics level 2 for International Business Administration (IBA) General information Availale time: 2.5 hours (150 minutes).
ERASMUS UNIVERSITY ROTTERDAM Information concerning the Entrance examination Mathematics level 2 for International Business Administration (IBA) General information Availale time: 2.5 hours (150 minutes).
FACULTY OF ARTS AND SCIENCE University of Toronto FINAL EXAMINATIONS, APRIL 2016 MAT 133Y1Y Calculus and Linear Algebra for Commerce
 FACULTY OF ARTS AND SCIENCE University of Toronto FINAL EXAMINATIONS, APRIL 206 MAT YY Calculus and Linear Algebra for Commerce Duration: Examiners: hours N. Hoell A. Igelfeld D. Reiss L. Shorser J. Tate
FACULTY OF ARTS AND SCIENCE University of Toronto FINAL EXAMINATIONS, APRIL 206 MAT YY Calculus and Linear Algebra for Commerce Duration: Examiners: hours N. Hoell A. Igelfeld D. Reiss L. Shorser J. Tate
Study Guide - Part 2
 Math 116 Spring 2015 Study Guide - Part 2 1. Which of the following describes the derivative function f (x) of a quadratic function f(x)? (A) Cubic (B) Quadratic (C) Linear (D) Constant 2. Find the derivative
Math 116 Spring 2015 Study Guide - Part 2 1. Which of the following describes the derivative function f (x) of a quadratic function f(x)? (A) Cubic (B) Quadratic (C) Linear (D) Constant 2. Find the derivative
CALCULUS. Berkant Ustaoğlu CRYPTOLOUNGE.NET
 CALCULUS Berkant Ustaoğlu CRYPTOLOUNGE.NET Secant 1 Definition Let f be defined over an interval I containing u. If x u and x I then f (x) f (u) Q = x u is the difference quotient. Also if h 0, such that
CALCULUS Berkant Ustaoğlu CRYPTOLOUNGE.NET Secant 1 Definition Let f be defined over an interval I containing u. If x u and x I then f (x) f (u) Q = x u is the difference quotient. Also if h 0, such that
Final Exam Review Packet
 1 Exam 1 Material Sections A.1, A.2 and A.6 were review material. There will not be specific questions focused on this material but you should know how to: Simplify functions with exponents. Factor quadratics
1 Exam 1 Material Sections A.1, A.2 and A.6 were review material. There will not be specific questions focused on this material but you should know how to: Simplify functions with exponents. Factor quadratics
Final Exam Review Packet
 1 Exam 1 Material Sections A.1, A.2 and A.6 were review material. There will not be specific questions focused on this material but you should know how to: Simplify functions with exponents. Factor quadratics
1 Exam 1 Material Sections A.1, A.2 and A.6 were review material. There will not be specific questions focused on this material but you should know how to: Simplify functions with exponents. Factor quadratics
Name Date Period. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 AB Fall Final Exam Review 200-20 Name Date Period MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. ) The position of a particle
AB Fall Final Exam Review 200-20 Name Date Period MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. ) The position of a particle
Math 116: Business Calculus Chapter 4 - Calculating Derivatives
 Math 116: Business Calculus Chapter 4 - Calculating Derivatives Instructor: Colin Clark Spring 2017 Exam 2 - Thursday March 9. 4.1 Techniques for Finding Derivatives. 4.2 Derivatives of Products and Quotients.
Math 116: Business Calculus Chapter 4 - Calculating Derivatives Instructor: Colin Clark Spring 2017 Exam 2 - Thursday March 9. 4.1 Techniques for Finding Derivatives. 4.2 Derivatives of Products and Quotients.
OR MSc Maths Revision Course
 OR MSc Maths Revision Course Tom Byrne School of Mathematics University of Edinburgh t.m.byrne@sms.ed.ac.uk 15 September 2017 General Information Today JCMB Lecture Theatre A, 09:30-12:30 Mathematics revision
OR MSc Maths Revision Course Tom Byrne School of Mathematics University of Edinburgh t.m.byrne@sms.ed.ac.uk 15 September 2017 General Information Today JCMB Lecture Theatre A, 09:30-12:30 Mathematics revision
ANSWERS, Homework Problems, Fall 2014: Lectures Now You Try It, Supplemental problems in written homework, Even Answers. 24x + 72 (x 2 6x + 4) 4
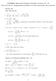 ANSWERS, Homework Problems, Fall 014: Lectures 19 35 Now You Try It, Supplemental problems in written homework, Even Answers Lecture 19 1. d [ 4 ] dx x 6x + 4) 3 = 4x + 7 x 6x + 4) 4. a) P 0) = 800 b)
ANSWERS, Homework Problems, Fall 014: Lectures 19 35 Now You Try It, Supplemental problems in written homework, Even Answers Lecture 19 1. d [ 4 ] dx x 6x + 4) 3 = 4x + 7 x 6x + 4) 4. a) P 0) = 800 b)
Calculus with business applications, Lehigh U, Lecture 01 notes Summer
 Calculus with business applications, Lehigh U, Lecture 01 notes Summer 2012 1 Functions 1. A company sells 100 widgets at a price of $20. Sales increase by 5 widgets for each $1 decrease in price. Write
Calculus with business applications, Lehigh U, Lecture 01 notes Summer 2012 1 Functions 1. A company sells 100 widgets at a price of $20. Sales increase by 5 widgets for each $1 decrease in price. Write
Essential Mathematics for Economics and Business, 4 th Edition CHAPTER 6 : WHAT IS THE DIFFERENTIATION.
 Essential Mathematics for Economics and Business, 4 th Edition CHAPTER 6 : WHAT IS THE DIFFERENTIATION. John Wiley and Sons 13 Slopes/rates of change Recall linear functions For linear functions slope
Essential Mathematics for Economics and Business, 4 th Edition CHAPTER 6 : WHAT IS THE DIFFERENTIATION. John Wiley and Sons 13 Slopes/rates of change Recall linear functions For linear functions slope
where u is the decision-maker s payoff function over her actions and S is the set of her feasible actions.
 Seminars on Mathematics for Economics and Finance Topic 3: Optimization - interior optima 1 Session: 11-12 Aug 2015 (Thu/Fri) 10:00am 1:00pm I. Optimization: introduction Decision-makers (e.g. consumers,
Seminars on Mathematics for Economics and Finance Topic 3: Optimization - interior optima 1 Session: 11-12 Aug 2015 (Thu/Fri) 10:00am 1:00pm I. Optimization: introduction Decision-makers (e.g. consumers,
Midterm Study Guide and Practice Problems
 Midterm Study Guide and Practice Problems Coverage of the midterm: Sections 10.1-10.7, 11.2-11.6 Sections or topics NOT on the midterm: Section 11.1 (The constant e and continuous compound interest, Section
Midterm Study Guide and Practice Problems Coverage of the midterm: Sections 10.1-10.7, 11.2-11.6 Sections or topics NOT on the midterm: Section 11.1 (The constant e and continuous compound interest, Section
Review for Final Review
 Topics Review for Final Review 1. Functions and equations and graphing: linear, absolute value, quadratic, polynomials, rational (first 1/3 of semester) 2. Simple Interest, compounded interest, and continuously
Topics Review for Final Review 1. Functions and equations and graphing: linear, absolute value, quadratic, polynomials, rational (first 1/3 of semester) 2. Simple Interest, compounded interest, and continuously
Math Refresher Course
 Math Refresher Course Columbia University Department of Political Science Fall 2007 Day 2 Prepared by Jessamyn Blau 6 Calculus CONT D 6.9 Antiderivatives and Integration Integration is the reverse of differentiation.
Math Refresher Course Columbia University Department of Political Science Fall 2007 Day 2 Prepared by Jessamyn Blau 6 Calculus CONT D 6.9 Antiderivatives and Integration Integration is the reverse of differentiation.
OBJECTIVE Find limits of functions, if they exist, using numerical or graphical methods.
 1.1 Limits: A Numerical and Graphical Approach OBJECTIVE Find limits of functions, if they exist, using numerical or graphical methods. 1.1 Limits: A Numerical and Graphical Approach DEFINITION: As x approaches
1.1 Limits: A Numerical and Graphical Approach OBJECTIVE Find limits of functions, if they exist, using numerical or graphical methods. 1.1 Limits: A Numerical and Graphical Approach DEFINITION: As x approaches
EconS 301. Math Review. Math Concepts
 EconS 301 Math Review Math Concepts Functions: Functions describe the relationship between input variables and outputs y f x where x is some input and y is some output. Example: x could number of Bananas
EconS 301 Math Review Math Concepts Functions: Functions describe the relationship between input variables and outputs y f x where x is some input and y is some output. Example: x could number of Bananas
ECON 186 Class Notes: Optimization Part 2
 ECON 186 Class Notes: Optimization Part 2 Jijian Fan Jijian Fan ECON 186 1 / 26 Hessians The Hessian matrix is a matrix of all partial derivatives of a function. Given the function f (x 1,x 2,...,x n ),
ECON 186 Class Notes: Optimization Part 2 Jijian Fan Jijian Fan ECON 186 1 / 26 Hessians The Hessian matrix is a matrix of all partial derivatives of a function. Given the function f (x 1,x 2,...,x n ),
Math for Economics 1 New York University FINAL EXAM, Fall 2013 VERSION A
 Math for Economics 1 New York University FINAL EXAM, Fall 2013 VERSION A Name: ID: Circle your instructor and lecture below: Jankowski-001 Jankowski-006 Ramakrishnan-013 Read all of the following information
Math for Economics 1 New York University FINAL EXAM, Fall 2013 VERSION A Name: ID: Circle your instructor and lecture below: Jankowski-001 Jankowski-006 Ramakrishnan-013 Read all of the following information
MAT1300 Final Review. Pieter Hofstra. December 4, 2009
 December 4, 2009 Sections from the book to study (8th Edition) Chapter 0: 0.1: Real line and Order 0.2: Absolute Value and Distance 0.3: Exponents and Radicals 0.4: Factoring Polynomials (you may omit
December 4, 2009 Sections from the book to study (8th Edition) Chapter 0: 0.1: Real line and Order 0.2: Absolute Value and Distance 0.3: Exponents and Radicals 0.4: Factoring Polynomials (you may omit
y = F (x) = x n + c dy/dx = F`(x) = f(x) = n x n-1 Given the derivative f(x), what is F(x)? (Integral, Anti-derivative or the Primitive function).
 Integration Course Manual Indefinite Integration 7.-7. Definite Integration 7.-7.4 Jacques ( rd Edition) Indefinite Integration 6. Definite Integration 6. y F (x) x n + c dy/dx F`(x) f(x) n x n- Given
Integration Course Manual Indefinite Integration 7.-7. Definite Integration 7.-7.4 Jacques ( rd Edition) Indefinite Integration 6. Definite Integration 6. y F (x) x n + c dy/dx F`(x) f(x) n x n- Given
ENGI Partial Differentiation Page y f x
 ENGI 3424 4 Partial Differentiation Page 4-01 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
ENGI 3424 4 Partial Differentiation Page 4-01 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
Math 180, Exam 2, Practice Fall 2009 Problem 1 Solution. f(x) = arcsin(2x + 1) = sin 1 (3x + 1), lnx
 Math 80, Exam, Practice Fall 009 Problem Solution. Differentiate the functions: (do not simplify) f(x) = x ln(x + ), f(x) = xe x f(x) = arcsin(x + ) = sin (3x + ), f(x) = e3x lnx Solution: For the first
Math 80, Exam, Practice Fall 009 Problem Solution. Differentiate the functions: (do not simplify) f(x) = x ln(x + ), f(x) = xe x f(x) = arcsin(x + ) = sin (3x + ), f(x) = e3x lnx Solution: For the first
Sect 2.4 Linear Functions
 36 Sect 2.4 Linear Functions Objective 1: Graphing Linear Functions Definition A linear function is a function in the form y = f(x) = mx + b where m and b are real numbers. If m 0, then the domain and
36 Sect 2.4 Linear Functions Objective 1: Graphing Linear Functions Definition A linear function is a function in the form y = f(x) = mx + b where m and b are real numbers. If m 0, then the domain and
4) Univariate and multivariate functions
 30C00300 Mathematical Methods for Economists (6 cr) 4) Univariate and multivariate functions Simon & Blume chapters: 13, 15 Slides originally by: Timo Kuosmanen Slides amended by: Anna Lukkarinen Lecture
30C00300 Mathematical Methods for Economists (6 cr) 4) Univariate and multivariate functions Simon & Blume chapters: 13, 15 Slides originally by: Timo Kuosmanen Slides amended by: Anna Lukkarinen Lecture
Higher Portfolio Quadratics and Polynomials
 Higher Portfolio Quadratics and Polynomials Higher 5. Quadratics and Polynomials Section A - Revision Section This section will help you revise previous learning which is required in this topic R1 I have
Higher Portfolio Quadratics and Polynomials Higher 5. Quadratics and Polynomials Section A - Revision Section This section will help you revise previous learning which is required in this topic R1 I have
3 Applications of partial differentiation
 Advanced Calculus Chapter 3 Applications of partial differentiation 37 3 Applications of partial differentiation 3.1 Stationary points Higher derivatives Let U R 2 and f : U R. The partial derivatives
Advanced Calculus Chapter 3 Applications of partial differentiation 37 3 Applications of partial differentiation 3.1 Stationary points Higher derivatives Let U R 2 and f : U R. The partial derivatives
Math 211 Business Calculus TEST 3. Question 1. Section 2.2. Second Derivative Test.
 Math 211 Business Calculus TEST 3 Question 1. Section 2.2. Second Derivative Test. p. 1/?? Math 211 Business Calculus TEST 3 Question 1. Section 2.2. Second Derivative Test. Question 2. Section 2.3. Graph
Math 211 Business Calculus TEST 3 Question 1. Section 2.2. Second Derivative Test. p. 1/?? Math 211 Business Calculus TEST 3 Question 1. Section 2.2. Second Derivative Test. Question 2. Section 2.3. Graph
EDEL 204 NUMERACY SKILLS FOR ENVIRONMENT AND DEVELOPMENT MODULE UNIVERSITY OF KWAZULU-NATAL PIETERMARITZBURG. January 2002
 EDEL 04 NUMERACY SKILLS FOR ENVIRONMENT AND DEVELOPMENT MODULE UNIVERSITY OF KWAZULU-NATAL PIETERMARITZBURG January 00 Compiled by: School of Statistics and Actuarial Science University of KwaZulu-Natal
EDEL 04 NUMERACY SKILLS FOR ENVIRONMENT AND DEVELOPMENT MODULE UNIVERSITY OF KWAZULU-NATAL PIETERMARITZBURG January 00 Compiled by: School of Statistics and Actuarial Science University of KwaZulu-Natal
Math 1120 Calculus Test 3
 March 27, 2002 Your name The first 7 problems count 5 points each Problems 8 through 11 are multiple choice and count 7 points each and the final ones counts as marked In the multiple choice section, circle
March 27, 2002 Your name The first 7 problems count 5 points each Problems 8 through 11 are multiple choice and count 7 points each and the final ones counts as marked In the multiple choice section, circle
MAT 122 Homework 7 Solutions
 MAT 1 Homework 7 Solutions Section 3.3, Problem 4 For the function w = (t + 1) 100, we take the inside function to be z = t + 1 and the outside function to be z 100. The derivative of the inside function
MAT 1 Homework 7 Solutions Section 3.3, Problem 4 For the function w = (t + 1) 100, we take the inside function to be z = t + 1 and the outside function to be z 100. The derivative of the inside function
Chapter 1. Functions, Graphs, and Limits
 Review for Final Exam Lecturer: Sangwook Kim Office : Science & Tech I, 226D math.gmu.eu/ skim22 Chapter 1. Functions, Graphs, an Limits A function is a rule that assigns to each objects in a set A exactly
Review for Final Exam Lecturer: Sangwook Kim Office : Science & Tech I, 226D math.gmu.eu/ skim22 Chapter 1. Functions, Graphs, an Limits A function is a rule that assigns to each objects in a set A exactly
Section 11.7 The Chain Rule
 Section.7 The Chain Rule Composition of Functions There is another way of combining two functions to obtain a new function. For example, suppose that y = fu) = u and u = gx) = x 2 +. Since y is a function
Section.7 The Chain Rule Composition of Functions There is another way of combining two functions to obtain a new function. For example, suppose that y = fu) = u and u = gx) = x 2 +. Since y is a function
6.1 Matrices. Definition: A Matrix A is a rectangular array of the form. A 11 A 12 A 1n A 21. A 2n. A m1 A m2 A mn A 22.
 61 Matrices Definition: A Matrix A is a rectangular array of the form A 11 A 12 A 1n A 21 A 22 A 2n A m1 A m2 A mn The size of A is m n, where m is the number of rows and n is the number of columns The
61 Matrices Definition: A Matrix A is a rectangular array of the form A 11 A 12 A 1n A 21 A 22 A 2n A m1 A m2 A mn The size of A is m n, where m is the number of rows and n is the number of columns The
Microeconomic theory focuses on a small number of concepts. The most fundamental concept is the notion of opportunity cost.
 Microeconomic theory focuses on a small number of concepts. The most fundamental concept is the notion of opportunity cost. Opportunity Cost (or "Wow, I coulda had a V8!") The underlying idea is derived
Microeconomic theory focuses on a small number of concepts. The most fundamental concept is the notion of opportunity cost. Opportunity Cost (or "Wow, I coulda had a V8!") The underlying idea is derived
SECTION 5.1: Polynomials
 1 SECTION 5.1: Polynomials Functions Definitions: Function, Independent Variable, Dependent Variable, Domain, and Range A function is a rule that assigns to each input value x exactly output value y =
1 SECTION 5.1: Polynomials Functions Definitions: Function, Independent Variable, Dependent Variable, Domain, and Range A function is a rule that assigns to each input value x exactly output value y =
Math Practice Final - solutions
 Math 151 - Practice Final - solutions 2 1-2 -1 0 1 2 3 Problem 1 Indicate the following from looking at the graph of f(x) above. All answers are small integers, ±, or DNE for does not exist. a) lim x 1
Math 151 - Practice Final - solutions 2 1-2 -1 0 1 2 3 Problem 1 Indicate the following from looking at the graph of f(x) above. All answers are small integers, ±, or DNE for does not exist. a) lim x 1
Exam A. Exam 3. (e) Two critical points; one is a local maximum, the other a local minimum.
 1.(6 pts) The function f(x) = x 3 2x 2 has: Exam A Exam 3 (a) Two critical points; one is a local minimum, the other is neither a local maximum nor a local minimum. (b) Two critical points; one is a local
1.(6 pts) The function f(x) = x 3 2x 2 has: Exam A Exam 3 (a) Two critical points; one is a local minimum, the other is neither a local maximum nor a local minimum. (b) Two critical points; one is a local
Lecture # 1 - Introduction
 Lecture # 1 - Introduction Mathematical vs. Nonmathematical Economics Mathematical Economics is an approach to economic analysis Purpose of any approach: derive a set of conclusions or theorems Di erences:
Lecture # 1 - Introduction Mathematical vs. Nonmathematical Economics Mathematical Economics is an approach to economic analysis Purpose of any approach: derive a set of conclusions or theorems Di erences:
Essential Maths 1. Macquarie University MAFC_Essential_Maths Page 1 of These notes were prepared by Anne Cooper and Catriona March.
 Essential Maths 1 The information in this document is the minimum assumed knowledge for students undertaking the Macquarie University Masters of Applied Finance, Graduate Diploma of Applied Finance, and
Essential Maths 1 The information in this document is the minimum assumed knowledge for students undertaking the Macquarie University Masters of Applied Finance, Graduate Diploma of Applied Finance, and
This chapter illustrates some of the basic features of Mathematica useful for finite mathematics and business calculus. Example
 The Mathematics Companion for Finite Mathematics and Business Calculus is a dictionary-like reference guide for learning and applying mathematical ideas, techniques, and formulas with the help of Mathematica,
The Mathematics Companion for Finite Mathematics and Business Calculus is a dictionary-like reference guide for learning and applying mathematical ideas, techniques, and formulas with the help of Mathematica,
1. Introduction. 2. Outlines
 1. Introduction Graphs are beneficial because they summarize and display information in a manner that is easy for most people to comprehend. Graphs are used in many academic disciplines, including math,
1. Introduction Graphs are beneficial because they summarize and display information in a manner that is easy for most people to comprehend. Graphs are used in many academic disciplines, including math,
2 Functions and Their
 CHAPTER Functions and Their Applications Chapter Outline Introduction The Concept of a Function Types of Functions Roots (Zeros) of a Function Some Useful Functions in Business and Economics Equilibrium
CHAPTER Functions and Their Applications Chapter Outline Introduction The Concept of a Function Types of Functions Roots (Zeros) of a Function Some Useful Functions in Business and Economics Equilibrium
LECTURE NOTES ON MICROECONOMICS
 LECTURE NOTES ON MICROECONOMICS ANALYZING MARKETS WITH BASIC CALCULUS William M. Boal Part : Mathematical tools Chapter : Introduction to multivariate calculus But those skilled in mathematical analysis
LECTURE NOTES ON MICROECONOMICS ANALYZING MARKETS WITH BASIC CALCULUS William M. Boal Part : Mathematical tools Chapter : Introduction to multivariate calculus But those skilled in mathematical analysis
STATE COUNCIL OF EDUCATIONAL RESEARCH AND TRAINING TNCF DRAFT SYLLABUS
 STATE COUNCIL OF EDUCATIONAL RESEARCH AND TRAINING TNCF 2017 - DRAFT SYLLABUS Subject :Business Maths Class : XI Unit 1 : TOPIC Matrices and Determinants CONTENT Determinants - Minors; Cofactors; Evaluation
STATE COUNCIL OF EDUCATIONAL RESEARCH AND TRAINING TNCF 2017 - DRAFT SYLLABUS Subject :Business Maths Class : XI Unit 1 : TOPIC Matrices and Determinants CONTENT Determinants - Minors; Cofactors; Evaluation
Partial derivatives, linear approximation and optimization
 ams 11b Study Guide 4 econ 11b Partial derivatives, linear approximation and optimization 1. Find the indicated partial derivatives of the functions below. a. z = 3x 2 + 4xy 5y 2 4x + 7y 2, z x = 6x +
ams 11b Study Guide 4 econ 11b Partial derivatives, linear approximation and optimization 1. Find the indicated partial derivatives of the functions below. a. z = 3x 2 + 4xy 5y 2 4x + 7y 2, z x = 6x +
5.1 - Polynomials. Ex: Let k(x) = x 2 +2x+1. Find (and completely simplify) the following: (a) k(1) (b) k( 2) (c) k(a)
 c Kathryn Bollinger, March 15, 2017 1 5.1 - Polynomials Def: A function is a rule (process) that assigns to each element in the domain (the set of independent variables, x) ONE AND ONLY ONE element in
c Kathryn Bollinger, March 15, 2017 1 5.1 - Polynomials Def: A function is a rule (process) that assigns to each element in the domain (the set of independent variables, x) ONE AND ONLY ONE element in
Purdue University Study Guide for MA for students who plan to obtain credit in MA by examination.
 Purdue University Study Guide for MA 224 for students who plan to obtain credit in MA 224 by examination. Textbook: Applied Calculus For Business, Economics, and the Social and Life Sciences, Expanded
Purdue University Study Guide for MA 224 for students who plan to obtain credit in MA 224 by examination. Textbook: Applied Calculus For Business, Economics, and the Social and Life Sciences, Expanded
Math 180, Final Exam, Fall 2007 Problem 1 Solution
 Problem Solution. Differentiate with respect to x. Write your answers showing the use of the appropriate techniques. Do not simplify. (a) x 27 x 2/3 (b) (x 2 2x + 2)e x (c) ln(x 2 + 4) (a) Use the Power
Problem Solution. Differentiate with respect to x. Write your answers showing the use of the appropriate techniques. Do not simplify. (a) x 27 x 2/3 (b) (x 2 2x + 2)e x (c) ln(x 2 + 4) (a) Use the Power
Calculus. Mathematics FRDIS. Mendel university in Brno
 Calculus Mathematics FRDIS Mendel university in Brno Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Calculus Mathematics FRDIS Mendel university in Brno Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Preliminaries Lectures. Dr. Abdulla Eid. Department of Mathematics MATHS 101: Calculus I
 Preliminaries 2 1 2 Lectures Department of Mathematics http://www.abdullaeid.net/maths101 MATHS 101: Calculus I (University of Bahrain) Prelim 1 / 35 Pre Calculus MATHS 101: Calculus MATHS 101 is all about
Preliminaries 2 1 2 Lectures Department of Mathematics http://www.abdullaeid.net/maths101 MATHS 101: Calculus I (University of Bahrain) Prelim 1 / 35 Pre Calculus MATHS 101: Calculus MATHS 101 is all about
Partial Differentiation
 CHAPTER 7 Partial Differentiation From the previous two chapters we know how to differentiate functions of one variable But many functions in economics depend on several variables: output depends on both
CHAPTER 7 Partial Differentiation From the previous two chapters we know how to differentiate functions of one variable But many functions in economics depend on several variables: output depends on both
Comparative Statics. Autumn 2018
 Comparative Statics Autumn 2018 What is comparative statics? Contents 1 What is comparative statics? 2 One variable functions Multiple variable functions Vector valued functions Differential and total
Comparative Statics Autumn 2018 What is comparative statics? Contents 1 What is comparative statics? 2 One variable functions Multiple variable functions Vector valued functions Differential and total
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES We have: Seen how to interpret derivatives as slopes and rates of change Seen how to estimate derivatives of functions given by tables of values Learned how
3 DIFFERENTIATION RULES DIFFERENTIATION RULES We have: Seen how to interpret derivatives as slopes and rates of change Seen how to estimate derivatives of functions given by tables of values Learned how
Lecture Notes for Chapter 9
 Lecture Notes for Chapter 9 Kevin Wainwright April 26, 2014 1 Optimization of One Variable 1.1 Critical Points A critical point occurs whenever the firest derivative of a function is equal to zero. ie.
Lecture Notes for Chapter 9 Kevin Wainwright April 26, 2014 1 Optimization of One Variable 1.1 Critical Points A critical point occurs whenever the firest derivative of a function is equal to zero. ie.
3.Applications of Differentiation
 3.Applications of Differentiation 3.1. Maximum and Minimum values Absolute Maximum and Absolute Minimum Values Absolute Maximum Values( Global maximum values ): Largest y-value for the given function Absolute
3.Applications of Differentiation 3.1. Maximum and Minimum values Absolute Maximum and Absolute Minimum Values Absolute Maximum Values( Global maximum values ): Largest y-value for the given function Absolute
Chapter 4. Section Derivatives of Exponential and Logarithmic Functions
 Chapter 4 Section 4.2 - Derivatives of Exponential and Logarithmic Functions Objectives: The student will be able to calculate the derivative of e x and of lnx. The student will be able to compute the
Chapter 4 Section 4.2 - Derivatives of Exponential and Logarithmic Functions Objectives: The student will be able to calculate the derivative of e x and of lnx. The student will be able to compute the
Sometimes the domains X and Z will be the same, so this might be written:
 II. MULTIVARIATE CALCULUS The first lecture covered functions where a single input goes in, and a single output comes out. Most economic applications aren t so simple. In most cases, a number of variables
II. MULTIVARIATE CALCULUS The first lecture covered functions where a single input goes in, and a single output comes out. Most economic applications aren t so simple. In most cases, a number of variables
Week 12: Optimisation and Course Review.
 Week 12: Optimisation and Course Review. MA161/MA1161: Semester 1 Calculus. Prof. Götz Pfeiffer School of Mathematics, Statistics and Applied Mathematics NUI Galway November 21-22, 2016 Assignments. Problem
Week 12: Optimisation and Course Review. MA161/MA1161: Semester 1 Calculus. Prof. Götz Pfeiffer School of Mathematics, Statistics and Applied Mathematics NUI Galway November 21-22, 2016 Assignments. Problem
Name Advanced Math Functions & Statistics. Non- Graphing Calculator Section A. B. C.
 1. Compare and contrast the following graphs. Non- Graphing Calculator Section A. B. C. 2. For R, S, and T as defined below, which of the following products is undefined? A. RT B. TR C. TS D. ST E. RS
1. Compare and contrast the following graphs. Non- Graphing Calculator Section A. B. C. 2. For R, S, and T as defined below, which of the following products is undefined? A. RT B. TR C. TS D. ST E. RS
Calculus Review Session. Brian Prest Duke University Nicholas School of the Environment August 18, 2017
 Calculus Review Session Brian Prest Duke University Nicholas School of the Environment August 18, 2017 Topics to be covered 1. Functions and Continuity 2. Solving Systems of Equations 3. Derivatives (one
Calculus Review Session Brian Prest Duke University Nicholas School of the Environment August 18, 2017 Topics to be covered 1. Functions and Continuity 2. Solving Systems of Equations 3. Derivatives (one
Lecture 2. Derivative. 1 / 26
 Lecture 2. Derivative. 1 / 26 Basic Concepts Suppose we wish to nd the rate at which a given function f (x) is changing with respect to x when x = c. The simplest idea is to nd the average rate of change
Lecture 2. Derivative. 1 / 26 Basic Concepts Suppose we wish to nd the rate at which a given function f (x) is changing with respect to x when x = c. The simplest idea is to nd the average rate of change
Limits at Infinity. Horizontal Asymptotes. Definition (Limits at Infinity) Horizontal Asymptotes
 Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
ANSWERS, Homework Problems, Spring 2014 Now You Try It, Supplemental problems in written homework, Even Answers R.6 8) 27, 30) 25
 ANSWERS, Homework Problems, Spring 2014, Supplemental problems in written homework, Even Answers Review Assignment: Precalculus Even Answers to Sections R1 R7 R.1 24) 4a 2 16ab + 16b 2 R.2 24) Prime 5x
ANSWERS, Homework Problems, Spring 2014, Supplemental problems in written homework, Even Answers Review Assignment: Precalculus Even Answers to Sections R1 R7 R.1 24) 4a 2 16ab + 16b 2 R.2 24) Prime 5x
3. Find the slope of the tangent line to the curve given by 3x y e x+y = 1 + ln x at (1, 1).
 1. Find the derivative of each of the following: (a) f(x) = 3 2x 1 (b) f(x) = log 4 (x 2 x) 2. Find the slope of the tangent line to f(x) = ln 2 ln x at x = e. 3. Find the slope of the tangent line to
1. Find the derivative of each of the following: (a) f(x) = 3 2x 1 (b) f(x) = log 4 (x 2 x) 2. Find the slope of the tangent line to f(x) = ln 2 ln x at x = e. 3. Find the slope of the tangent line to
