Convergence Analysis of Piecewise Polynomial Collocation Methods for System of Weakly Singular Volterra Integral Equations of The First Kind
|
|
|
- Samson Simpson
- 6 years ago
- Views:
Transcription
1 Appe a Coputatoa Mateatcs 28; 7(-): - ttp://wwwscecepubsggroupco//ac o: 648/acs287 ISS: (Prt); ISS: (Oe) Covergece Aayss of Pecewse Poyoa Coocato Meto for Syste of Weaky Sguar Voterra Itegra Equatos of Te Frst K Goarea Karaa, Babak Sr, 2, *, Maa Kasf 2 Sa Sattar Aeroautca Uversty of Scece a Tecoogy, Sout Meraba, Tera, Ira 2 Departet of Appe Mateatcs, Uversty of Tabr, Baa Bouevar, Tabr, Ira Ea aress: g_karaa@ustacr (G Karaa), sr@tabruacr (B Sr), aakas@gaco (M Kasf) * Correspog autor To cte ts artce: Goarea Karaa, Babak Sr, Maa Kasf Covergece Aayss of Pecewse Poyoa Coocato Meto for Syste of Weaky Sguar Voterra Itegra Equatos of Te Frst K Appe a Coputatoa Mateatcs Speca Issue: Sguar Itegra Equatos a Fractoa Dffereta Equatos Vo 7, o -, 28, pp - o: 648/acs287 Receve: Marc 2, 27; Accepte: Marc 22, 27; Pubse: Apr, 27 Abstract: We stuy reguarty of soutos of weaky sguar Voterra tegra equatos of te frst k We te stuy te uerca aayss of cotuous pecewse poyoa coocato eto for sovg suc systes Te a purpose of ts paper s te ervato of goba coverget a super-coverget propertes of trouce eto o te grae eses We appy reevat eto to a syste of fractoa ffereta equatos a aaye te Te uerca experets cofr te teoretca resuts Keywor: Dscotuous Pecewse Poyoa Spaces, Coocato Meto, Grae Meses, Weaky Sguar Voterra Itegra Equatos Itroucto I ts paper, we coser a syste of weaky sguar Voterra tegra equatos of frst k (SWSVIEFK) of te for (, ) ( t s) t k t s y s f ( t ), t I : [, T ], () were, < <, T R,, f : I R Te oa of te atrx fucto k( t, s): D R, s D I 2 {( t, s) ( t, s), s t T} Aso, we suppose tat k( t, t ) s a osguar atrx for a t I Te y: R R s te ukow vector fucto Te syste () s a Abe's tegra equato f k( t, s ) Te uerca souto of weaky sguar Voterra tegra equatos of frst k as extesvey bee stue (see for exape [2,, 4, 5, 6, 8, 9,,,, 4, 5, 6], but t oes ot ea tat ts subect as copetey bee stue Tere are soe usove probes wc are portat a ee ore caege Oe of te s covergece aayss of coocato eto o te pecewse poyoa spaces for sovg syste (), [] Te a of ts paper s to prove a copete covergece aayss of tese eto for ts syste Te pecewse poyoa coocato eto (PPCM) are easy prograabe a tey ave rap coverget orer for ay equatos cug tegra or ffereta operator Tey ave extesvey bee exae by ay autors We refer ere to [,, 7, 2] a terature gve tere Terefore, t s portat to aaye PPCMs for te syste () Suppose Let q: R R a f : Ω R be scaer a atrx fuctos, respectvey, were Ω s a set I ts paper, by qf we ea ( qf ) qf,, {,, }, a te or we ea te ax or
2 2 Goarea Karaa et a: Covergece Aayss of Pecewse Poyoa Coocato Meto for Syste of Weaky Sguar Voterra Itegra Equatos of Te Frst K f ax sup f ( t), {,, }, t Ω Te paper s orgae as foow: I secto 2, we revew exstece, uqueess a sootess of te soutos of syste () I secto, we reca appcato of te coocato eto o te cotuous pecewse poyoa spaces I secto 4, we geerae Grawa s equates for atrx fucto equatos I secto 5, we gve te goba covergece of te coocato eto o te cotuous pecewse poyoa spaces I secto 6, we vestgate te stabty fucto trouce te prevous secto Fay, secto 7, we preset uerca experets wc support teoretca resuts 2 Reguarty Propertes Te arguets of ts secto ca be obtae by arguets sar to [] (secto 2) Here, we sou cocer tat te systes we vestgate are of eso greater ta we te syste [] s of eso greater Terefore, stea of vg by a fucto we sou utpy by a verse of correspog atrx fucto G CI a Suppose s( π) G ( ) k (, ) f( t)( t) t (2) π Defe resovet kere assocate wt te gve kere K (, s) as were a R(, s): H (, s) H (, s) H (, v) H ( v, s), 2, H (,s) s s( π) k( s + ( s), s) k (, ) π Te, we obta correspog Voterra s fuaeta resuts tat y( ) G ( ) + R(, s) G ( s) () s a uque souto of syste () ow, we ca arguet about te reguarty of soutos Supposg k ( ) k ( C ( D )), we obta H s C D a (, ) C ( D ) It s stragtforwar te to sow tat R s ( C D ) (, ) Terefore, te reguarty of y epe o te reguarty of G k Teore 2 Let k ( C ( D )), were g ( T ) f ( t) t β g( t) C ( D ),, C ([, ]), +,, a β Te, te syste () as a uque souto a tere exsts q ( ([, T]) ) C suc tat y q + β Proof Itegratg by substtuto t v, we ave Were a ece we obta t g t t t q β + β β : ( ), q v g v v v β t g( t)( t) Sce g ( T ) a cosequety t ( β ) + β () q ( ) + ( + ) q ( ) C ([, ]), we cocue tat ( T ) q C ([, ]), () q ( ) + ( + β) q ( ) C ([, T]) Tus, usg equato (2), tere exsts ( T ) q C ([, ]) + β suc tat G ( ) q ( ) Takg to accout tat q ( ): R(, s) G ( s) 2 + β R(, s) s + β q + β s + β ( C ) R(, v) v q ( v) v ([, T]), a usg te equato (4), we ave wc copetes te proof y q + q + β ( ), 2 Coocato Meto o te Cotuous Pecewse Poyoa Spaces For gve, Let r I { t T : }, (4)
3 Appe a Coputatoa Mateatcs 28; 7(-): - be a grae es, wt grag expoet r Assue tat ( t, t ], [ t, t ], t t a σ σ ax{ :,, } Te, t s stragtforwar to see tat te sequece { } s strcty creasg a < rt (5),,, We use coocato eto to sove syste () recty (wtout trasforg to te seco k tegra equato), o te cotuous pecewse poyoa spaces S ( I ): { v: v π (,,, )}, σ For cotuous pecewse poyoa spaces, et < c < < c, be te coocato paraeters Terefore, te approxate souto u ( I ) for, S, as te u ( t + v ) L ( v) U, v (,],,,, te terva σ ( u u, σ for,, ) Here, L (v) for,,, are Lagrage fuaeta poyoas wt respect to tct coocato paraeters a U,:u (t,) are approxato soutos at te coocato pots t t + c for,, a,, We are :, seekg for a coocato souto u suc tat satsfes te coocato cotos k( t, s) u ( s) f t t,,, ± (6), ( t s), for,, a,, Terefore, t s stragtforwar to sow tat te souto of te syste (6) ca be obtae by sovg recursvey te systes k( t, t v ) L ( v) F t + vu f t (7) +, c, ( t t v ),,, for,,, a,,, were k( t, t + v ) L ( v), F( t ), vu, ( t t v ), s te ag ter I te syste (7), te tegras ca be approxate by te quarature approxatos a c k( t, t + v ) L ( v), v a,,, k t t ( t t v ), (, ) k( t, t + v ) L ( v) v b (,, ) k ( t, t ),,,, ( t t v ), For, were a a, ( ) c, ( v) L ( v) v ( c v) L ( v) b (,, ) v,, t t for, {,, } Terefore, te fuy cretse verso ca be obtae by sovg te systes + ˆ,,,,,, Fˆ ( t ) a k( t, t ) U f ( t ), (8) recursvey, for,, a,,, were ˆ,,,, Fˆ ( t ) b (,, ) k( t, t ) U, for,,, a U ˆ are te coocato souto at, t, for,, a,, ow, te ese output approxate souto ca be approxate by uˆ ( t + v ) L ( v) Uˆ, v (,],,,, We ote tat ts cretse verso s sgty fferet fro cretse verso trouce [] However, t reuce te coputato copexty by a factor of, a as we w see t oes ot reuce te orer of te coocato eto Settg ( A) : a, ˆ ɵ, ˆ T U : [ U,, U ],, [ ˆ,, ˆ T F f t F t f t F( t )], a takg to accout tat,,,, k( t, t ) k( t, t ) +O,,, we ca wrte (8) te atrx for A ( k( t, t ) + O ( )) Uɵ F ow, sce A s vertbe by Teore 6, a k( t, t ) s vertbe by ypoteses of te troucto, te atrx A ( k( t, t ) +O ( )) s vertbe a tere exsts a uque souto for syste (8), for suffcety sa Cosequety, te fuy cretse coocato eto s we-efe I a sar aer te syste (7) as a uque souto for suffcety sa, a te trouce coocato eto s we-efe
4 4 Goarea Karaa et a: Covergece Aayss of Pecewse Poyoa Coocato Meto for Syste of Weaky Sguar Voterra Itegra Equatos of Te Frst K 4 Grawa s Iequates Frst, we reca te Grawa s equates [] ote tat, we wrte v O( ) weever v O( ) Lea 4 (Growa's equaty) Assue tat { k }, ( ) s a gve o-egatve sequece a te sequece { } satsfes a + q + k wt a q for( ) Te exp + q k I ts paper, we ee a geeraato of Growa s equaty for te atrx fuctos Tus, we coser R + K + (9) were R,, K a for,,, are atrx fuctos We suppose tat R s a agoaabe atrx e, R P DP, were D ag( λ,, λ ) r s a agoa atrx a P s a osguar atrx Aso, we suppose tat λ [,) Te, It s stragtforwar to sow tat tere exsts a postve costat C suc tat ( + C ) exp C K 5 Goba Covergece 5 Dscotuous Coocato Meto Lea 5 For r, we ave cases ca be obtae by appyg te Hopta s rue k Teore 52 Let k ( C ( D )), ( C ( D )),, f( t) t β g( t) were g ( T ) C ([, ]), +,, a β Te te approxate souto u of te cotuous coocato eto for syste () wt coocato paraeters < c < c < < c 2 a te grag expoet r coverges to te souto f te egevaues of te stabty atrx R be te terva [,) Furterore, te coocato error satsfes y( t) u ( t) c r( + β ) +, r, + β, r, + β for a costat c > a suffcety arge Proof Suppose tat te assuptos of Teore \ref{t} o Let e ( t) y( t) u ( t) A appcato of Teore 2 pes tat ( y C ([, T]) ) for a > Terefore, by Peao s teore ([], Secto 8) λ + +, e ( t v ) L ( v) E R ( v) () were E e ( t + c ) for,,,,,, te, reaer R ( v ) s a boue fucto a β +,, λ, Oterwse () By subtractg equato () (at t t, ) fro equato (6) we obta k( t, s) e ( s) t,,, (2) ( t s), for,,,,, a ece, Hece r r ( ) O + O( ) r r ( + ) O( ), t + k( t, s) e ( s), ( s) t t, k( t, s) e ( s) t,, + t ( t s), () Lettg, substtutg s v, a usg () we ave a sary O ( ) O( ) Proof Oe ca easy observe te resuts by expag te poyoas ( + ) r a ( ) r for case r Te oter c k( c, v ), L v ve ( c v) λ c R ( v) v, (4) for,, By Tayor's teore for utvarabe atrx fuctos, k( c, v ) k(,) +O ( ) a te syste (4) ca
5 Appe a Coputatoa Mateatcs 28; 7(-): - 5 be wrtte te atrx for ( A k(,) + O( )) E O ( λ ) were E E E,, [,, ] T a L ( v) ( A ) v,, {,, } c (5) ( c v) Sce, A a k (, ) are vertbe atrces, we ca cocue tat E O ( λ ), for suffcety sa We ca, ow procee to obta a estate for e, e σ Substtutg s t + v,,,, to correspog tegras () a usg () we obta 2, ( t t s ) ( t t s ),, + + Rˆ k( t, t + s ) k( t, t + s ),, L ( s) k( t, t + s ) L ( s),, ( t t s ), k( t, t + s ) L ( s) c,, ( t t s ), c k( t, t + s ) L ( s),, ( t t s ), (6) Rewrtg (6) wt repace by a a subtractg t fro (6), we obta k( t, t + s ) k( t, t + s ),, 2 L s, ( t t s ) ( t t s ),, were + + Rˆ Rˆ k( t, t + s ) L ( s),, ( t t s ), c k( t, t + s ) L ( s), ( t t s ), c, k( t, t + s ) L ( s),, ( t t s ), k( t, t + s ) k( t, t + s ) 2,, λ ( t t s ) ( t t s ),, (7) R ( s) + + c λ k( t, t + s ) R ( s), ( c + s) λ k( t, t + s ) R ( s), ( c s) c O + λ k( t, t + s ) R ( s), ( c s) λ ( ), (8) by Lea 5 a foowg Reark Reark 5 We ote tat, k( x, t + s ) ( x, s) ( C ([ t, t ] [,]),, ), for ( x t s ),, 2 Terefore, f we appy ea vaue teore for eac copoets of te above atrx fucto, te we ave k( t, t + s ) k( t, t + s ) ( t t s ) ( t t s ),,,, k ( t + s ) were tere exst t θ t suc tat, pq,, ( k ( t + s )) pq + ( c ( c ) ) kpq (, t s ) pq, θ + ( θ t s ) pq, for p, q {,, },,, a,, 2 (9) k By our assuptos s boue a tere exsts M > k suc tat ( c + ( c ) ) < M Terefore, ( k ( t + s )) L ( s) pq M L ( s) ( θ t s ) pq, M L ( s) ( t t s ) M2, ( ), (2) for,, 2 Te ast equaty s obtae by Lea (62) [] Aso, settg M2 γ, ( ) we cocue tat
6 6 Goarea Karaa et a: Covergece Aayss of Pecewse Poyoa Coocato Meto for Syste of Weaky Sguar Voterra Itegra Equatos of Te Frst K ( k ( t s )) L ( s) + γ ( ) (2) Furterore, to obta equato (8), we use te fact tat 2 te su ( ) s boue Substtutg (9) to (7), a usg Tayor's seres for oter ters a copoets we obta 2 k ( t + s ) L ( s), + + ( k( t, t ) + c ( s) + c ( s) ) L ( s) 2, ( c + s) c c Rˆ ( k( t, t ) + c ( s) ) L ( s) ( s), ( k( t, t ) + c ( s) ) L ( s) c 4, ( c s) (22) were c( s) for,,4 are boue atrx fuctos Mutpyg (2) by k k( t, t ) a vg by, we obta 2 k ( t + s ) L ( s), + k k ( + c ( s) + c ( s) ) L ( s) 2 ( c + s), c k c4( s) L( s), ( c s) k c ( s) L ( s) c (2) ( K ) :,, ( c s) a we ca rewrte syste (22) te atrx for 2 B E () ( O( ) 2 ) + A + A + K IE Rˆ + + ( (2) ) A K IE, (24) were I s etty atrx of eso Mutpyg equato (2) by ( ) ( A + K ) I ( A + K ) I (2) (2) (wc exsts for suffcety sa, by Teore 6), we obta E ( R + O( )) E 2 λ + C E + O( + ) (2) were C ( A + K ) I B a R ( A ) A A I 2 (25) + Deotg, ( + k c ( s) ) L ( s) c s c 4 ( c s) Rˆ c, ( + k c ( s) ) L ( s), ( B ) :,,, 2,, k t + s L s L ( s) ( A ) :,, ( c + s) c L ( s) ( A ) :, 2, ( c s) c L ( s) ( A ) :,, ( c s) ( k c ( s) + k c ( s)) L ( s) 2 (), ( c + s) ( K ) : (2) Usg Lea 5 we ca cocue tat E a by (5) we ave O E ( R + ( )) 2 λ C E O + + ( + ) E R E + O( ) E 2 λ + C E + O( + ) (26) If egevaues of te stabty atrx R be te terva [,), we ca voke geerae Grawa's equaty to cocue tat λ C ( ) E E + O exp C C O( ) (27) were C > s a costat Reark 54 By cotuty a o-sguarty assuptos, for suffcety sa (arge ), we ca f
7 Appe a Coputatoa Mateatcs 28; 7(-): - 7 M > suc tat ( A + K ) I (2) M (2) ( A + K ) I γ M γ by (2), ( B ) γ ( ) a terefore, M( ), C (28) Cosequety, te equato (28) ye 2 2 C M ( ) 2 + M ( s) M ( s) + ( ) M + ( ) rtm rtm (29) Takg to accout te equatos (27) a (29), we obta te a resuts of ts secto: E O T + ( rt) rλ MrT C + O exp 52 Dscretse Dscotuous Coocato Meto () ow, we ca state a error bou for soutos of cretse cotuous coocato eto k Teore 55 Let k ( C ( D )), ( C ( D )),, f( t) t β g( t) were g ( T ) C ([, ]), +,, a β Te te approxate souto u of te cretse cotuous coocato eto for syste () wt coocato paraeters < c < c < < c 2 a te grag expoet r coverges to te souto f te egevaues of te stabty atrx R be te terva [,) Furterore, te coocato error satsfes y( t) u ( t) c r( + β ) +, r, + β, r, + β for a costat c >, a suffcety arge Proof By parttog te oa of tegra () a substtutg s t + v we obta k( t, t + v ) y( t + v ) v ( t t + s ) t t k t t + v y t + v ( t t + s ) (, ) + v f( t) (2) for,, a,, Appyg Teore 2 a Peao s teore, we obta k( t, t + v ) y( t + v ) λ,, k( t, t ) y( t ) L ( v) + R ( t, v), were λ s efe by (\ref{aba}) a R ( t, v ) for,, are ufory boue fuctos o D Settg t t,, a usg (), we obta were vk t t y t,,, ( t t + s ), c ( t t + s ), (, ),,,,, L ( v) (, ) L ( v) + vk t t y t + Rɶ () f( t ), R ( t, v) Rɶ v, λ, ( t t + s ), λ c R ( t, v), + v ( t t + s ), (4) for,, a,, ow, we ca use te otato of prevous sectos to wrte te equato () te for b (,, ) k( t, t ) y( t ),,, + a k( t, t ) y( t ) + Rɶ f ( t ),,,,, By subtractg equato (2) fro equato (8) we ave b (,, ) k( t, t ) Eˆ,,, + a k( t, t ) Eˆ + Rɶ,,,,, (5) (6) were Eˆ y( t Uˆ ) for,, a,,,,, Rewrtg (6) wt repace by a a subtractg t fro (6), we obta
8 8 Goarea Karaa et a: Covergece Aayss of Pecewse Poyoa Coocato Meto for Syste of Weaky Sguar Voterra Itegra Equatos of Te Frst K 2 ( (,, ) (, ) (,, ) (, ) ) b k t t b k t t Eˆ,,,,, + b (,, ) k( t, t ) Eˆ,,, a k( t, t ) Eˆ,,, + a k( t, t ) Eˆ + Rɶ Rɶ,,,,,, (7) for,, a,,, were t s stragtforwar to sow tat Rɶ λ, Rɶ, O ( + ) Aso, by Reark 5, we ave b (,, ) k( t, t ) b (,, ) k( t, t ),,,, k ( t ), Usg ea vaue teore for oter ters a copoets of equato (7), tere exst boue atrx fuctos cɶ ( s), for,,4 suc tat 2 k ( t ) L ( s),, + + ( k( t, t ) + cɶ ( s) + cɶ ( s) ) L ( s) 2, ( c + s) c c,, ( c s),, ( k( t, t ) + cɶ ( s) ) L ( s) ( s) c ( k( t, t ) + cɶ ( s) ) L ( s) 4 + Rɶ Rɶ,,,,,, (8) Te equato (8) s sar to (22) a ece te rest of te proof s sar to te es after ts equato 6 Stabty Matrx We ca use te we-kow forua of terpoato to obta c L ( s) s,,,,, b L ( s) b s c ( s) ( s) (9) Terefore, efg foowg atrces a tat ( D), c c C:, (4) c c s ( D ) :,, ( c + s) c s ( D ) :, 2, ( c s) s c for, {,, }, ( c s) 2 2 we ca sow A C D, A C D, A C D (4) Te atrx C s a Vaeroe atrx, a s vertbe Tus, A s vertbe f a oy f D be vertbe Te eeets of D, D a D ca be copute by te 2 foowg forua s ( s) b b + a for D we ave + + ( ) + c c + D + c c + Teore 6 Te atrces A a D are vertbe atrces Proof By prevous arguet, t reas to prove tat D s vertbe It s ot eoug to sow tat te cous of D are epeets Let D ( ) be te -t cou of te atrx D a et D, were R Terefore, x x k k k k for x c,, c Hece, te poyoa k p( x) x k k k s of egree, a as roots, ( p( c ) for,, ) a s ero poyoa by fuaeta teore
9 Appe a Coputatoa Mateatcs 28; 7(-): - 9 of agebra Hece,, for,,, wc copetes te proof Base o te Teore 52, te covergece of te trouce coocato eto epe o te egevaues of te stabty atrx R ( A ) A A I 2 Sce, A s vertbe, te stabty atrx R s weefe Aso, te atrces R a te atrx ( A ) ( A A 2 ) ave te sae egevaues, a wtout oss of geeraty, we ca reefe te stabty atrx as R : ( A ) ( A A ) Moreover, we ca use equato (4) to 2 obtac R C ( D ) ( D D ) 2 Terefore, R a ( D ) ( D D ) are sar a ave te 2 sae egevaues Ts fact ca ep us to copute te egevaues of R For case, we ave 2 c ( + c ) ( D ) ( D D ) 2 c For,, t agrees wt te resuts of [] wc s te Voterra tegra equato of frst k For 2, oe ca recty copute te egevaues of ( D ) ( D D ) for a 2 gve coocato pots 7 uerca Experets We gve soe exapes to sow effcecy a effectveess of te trouce eto I tese exapes, we obta te absoute error wt respect to te paraeters a t, we eote t by ax u ( t ) y ( t ),,,,,,,, for, were y ( t ) a u ( t ) are exact a uerca soutos of te -t copoets, respectvey We report te approxato of coverget orer usg te forua o g, We appy te foowg eto 2 2 for te ext exapes: Meto, a c 5 Meto 2, c 5 a c 2 Meto 2 Roots of sfte Legere poyoa of egree + 2: c, c Meto Roots of sfte Cebysev poyoa of egree 2: c, c Meto 4 Roots of sfte Cebysev poyoa of egree : c, c, c Meto 5 Roots of sfte Legere poyoa of egree : c, c, c Set λ ax λ, were λ for,2, are te,2, egevaues of stabty atrx R Tabe sows te vaues of λ for eto -5, a fferet vaues of Ts sures us tat te uerca souto of te correspog eto s coverget to te exact souto, for gve exapes Tabe λ ax λ, for eto -5 a fferet vaues of,2, M M M M M a ow, coser syste () wt f( t) t s e k( t, s) Γ ( ) ( s t) e ( s + t) e + s s e 2t s Γ ( β + ) t Γ ( β + + 2) Γ ( β + + ) 2 e + + t Γ ( + β) Γ ( + β) Γ (2 + β) β t Γ ( β + + ) 2t Γ ( β + ) Γ ( β + + ) te + + t Γ (2 + β) Γ ( + β) Γ (2 + β) Te, te exact souto of te two esoa syste () s β + β + (, ) y( s) e s e s s s T We ca costruct te foowg exapes by aterg te paraeters of te above syste Exape 7 Let T, β a 2 4,, te appy 5 5 te eto Exape 7 2 Let T 5, β a,,, te appy te eto 4-5 Exape 7 Let T, β,5,2 a 9, te appy te eto -5 By Teore 52, we expect te error estate e ( t) c r, r,, r, + β Exapes 7-72 Tabes, 2-5 cofr ts error estate Tabe 2 Te absoute error a correspog coverget orer Exape wt r 4 8 M 64 e-2-688e-4 -
10 Goarea Karaa et a: Covergece Aayss of Pecewse Poyoa Coocato Meto for Syste of Weaky Sguar Voterra Itegra Equatos of Te Frst K M 2 M e e e e e e e e e e e e e e e e Tabe Te absoute error a correspog coverget orer Exape wt M M 2 M 2 r e e e e e e e-4-55e e e e e e e e e e e-6 92 Tabe 4 Te absoute error a correspog coverget orer Exape 2 wt r M 4 M e-4-76e e e e e e-4-445e e e e e Tabe 5 Te absoute error a correspog coverget orer Exape 2 wt M M 2 r e-6-24e e e e e e-6-26e e e e-8 4 e-8 98 Aso, by Teore 52, we expect te estate e ( t) c ( β ) r, r, β, r, + β Exape 7 Tabes, 6-7 sow ts estate I a tabes, we reporte estate of te orer for te copoet of te syste wc s ess Fay, tese exapes sow tat te obtae coverget resut s opta a ca t be prove for our vestgate cass of SWSVIEFKs Tabe 6 Te absoute error a correspog coverget orer Exape wt r M M 2 M M 4 M 5 β β e-4-598e e e e-4-272e e e e-4-986e e e e e e e e-5-494e e e Tabe 7 Te absoute error a correspog coverget orer Exape wt r M M 2 M M 4 M 5 β β β e-7-597e e e e-6-69e e e e-5-5e e e e-8-697e e e e-8-697e e e Cocuso A covergece aayss of te coocato eto for SWSVIEFKs o cotuous pecewse poyoa spaces as bee vestgate Base o ts aayss, te orer of te eto oes ot cage by creasg coocato paraeters o ufor es However, t ca be crease up to by usg grae es Our aayss sta o te egevaues of stabty atrx We obtae a cose for of ts egevaues for case However, for cases >, we obtae te egevaues of stabty atrx for prescrbe coocato paraeters Refereces [] K E Atkso, Te uerca souto of tegra equatos of te seco k, Vo 4, Cabrge uversty press, 997 [2] H W Braca, Te oear Voterra equato of abe's k a ts uerca treatet, Coput, 978, 2, 7-24 [] H Bruer, Coocato eto for Voterra tegra a reate fuctoa ffereta equatos, Vo 5, Cabrge Uversty Press, 24
11 Appe a Coputatoa Mateatcs 28; 7(-): - [4] H Bruer, A Peas a G Vakko, Pecewse poyoa coocato eto for ear Voterra tegro-ffereta equatos wt weaky sguar keres, SIAM Joura o uerca Aayss, 2, 9, [5] R Caero a S McKee, Prouct tegrato eto for seco-k Abe tegra equatos, Joura of Coputatoa a Appe Mateatcs, 984,, - [6] P Eggerot, A ew aayss of te trapeoacretato eto for te uerca souto of Abe-type tegra equatos, Joura of Itegra Equatos a Appcatos, 98,, 7-2 [7] R Kress, V Ma'ya a V Koov, Lear tegra equatos, Vo 82, Sprger, 989 [8] C Lubc, Fractoa ear utstep eto for Abe- Voterra tegra equatos of te frst k, IMA Joura of uerca Aayss, 987, 7, 97-6 [9] A Peas a E Tae, O te covergece of spe coocato eto for sovg fractoa ffereta equatos, Joura of Coputatoa a Appe Mateatcs, 2, 25, [] H Te Ree a P Scroevers, A coparatve survey of uerca eto for te ear geerae Abe tegra equato, ZAMM- Joura of Appe Mateatcs a Mecacs, 986, 66, 6-7 [] A Saaata a M Dega, A coocato eto for sovg Abe s tegra equatos of frst a seco k, Zetscrft für aturforscug A, 28, 6, [2] B Sr, uerca souto of ger ex oear tegra agebrac equatos of Hesseberg type usg cotuous coocato eto, Mateatca Moeg a Aayss, 24, 9, 99-7 [] V Voterra, Sua versoe eg tegra eft, Att ea Accaea ee scee Toro,896,, -2 [4] R Wess, uerca proceures for voterra tegra equatos, Buet of te Austraa Mateatca Socety, 97, 8, [5] R Wess, Prouct tegrato for te geerae Abe equato, Mateatcs of Coputato, 972, 26, 77-9 [6] R Wess a R Aersse, A prouct tegrato eto for a cass of sguar frst k Voterra equatos, uerca Mateatcs, 97, 8,
A Note on the Almost Sure Central Limit Theorem in the Joint Version for the Maxima and Partial Sums of Certain Stationary Gaussian Sequences *
 Appe Matheatcs 0 5 598-608 Pubshe Oe Jue 0 ScRes http://wwwscrporg/joura/a http://xoorg/06/a0505 A Note o the Aost Sure Cetra Lt Theore the Jot Verso for the Maxa a Parta Sus of Certa Statoary Gaussa Sequeces
Appe Matheatcs 0 5 598-608 Pubshe Oe Jue 0 ScRes http://wwwscrporg/joura/a http://xoorg/06/a0505 A Note o the Aost Sure Cetra Lt Theore the Jot Verso for the Maxa a Parta Sus of Certa Statoary Gaussa Sequeces
Methods for solving the radiative transfer equation with multiple scattering. Part 3: Exact methods: Discrete-ordinate and Adding.
 Lecture. Methos for sovg the raatve trasfer equato wth utpe scatterg. art 3: Exact ethos: screte-orate a Ag. Obectves:. screte-orate etho for the case of sotropc scatterg.. Geerazato of the screte-orate
Lecture. Methos for sovg the raatve trasfer equato wth utpe scatterg. art 3: Exact ethos: screte-orate a Ag. Obectves:. screte-orate etho for the case of sotropc scatterg.. Geerazato of the screte-orate
Chapter 3. Differentiation 3.3 Differentiation Rules
 3.3 Dfferetato Rules 1 Capter 3. Dfferetato 3.3 Dfferetato Rules Dervatve of a Costat Fucto. If f as te costat value f(x) = c, te f x = [c] = 0. x Proof. From te efto: f (x) f(x + ) f(x) o c c 0 = 0. QED
3.3 Dfferetato Rules 1 Capter 3. Dfferetato 3.3 Dfferetato Rules Dervatve of a Costat Fucto. If f as te costat value f(x) = c, te f x = [c] = 0. x Proof. From te efto: f (x) f(x + ) f(x) o c c 0 = 0. QED
Chapter 3. Differentiation 3.2 Differentiation Rules for Polynomials, Exponentials, Products and Quotients
 3.2 Dfferetato Rules 1 Capter 3. Dfferetato 3.2 Dfferetato Rules for Polyomals, Expoetals, Proucts a Quotets Rule 1. Dervatve of a Costat Fucto. If f as te costat value f(x) = c, te f x = [c] = 0. x Proof.
3.2 Dfferetato Rules 1 Capter 3. Dfferetato 3.2 Dfferetato Rules for Polyomals, Expoetals, Proucts a Quotets Rule 1. Dervatve of a Costat Fucto. If f as te costat value f(x) = c, te f x = [c] = 0. x Proof.
A stopping criterion for Richardson s extrapolation scheme. under finite digit arithmetic.
 A stoppg crtero for cardso s extrapoato sceme uder fte dgt artmetc MAKOO MUOFUSHI ad HIEKO NAGASAKA epartmet of Lbera Arts ad Sceces Poytecc Uversty 4-1-1 Hasmotoda,Sagamara,Kaagawa 229-1196 JAPAN Abstract:
A stoppg crtero for cardso s extrapoato sceme uder fte dgt artmetc MAKOO MUOFUSHI ad HIEKO NAGASAKA epartmet of Lbera Arts ad Sceces Poytecc Uversty 4-1-1 Hasmotoda,Sagamara,Kaagawa 229-1196 JAPAN Abstract:
Plate Bending Analysis by Two-dimensional Non-linear Partial Differential Equations
 Uversa Joura of Coputatoa Aass 1 013 1-8.papersceces.co Pate Bedg Aass b To-desoa No-ear Parta Dffereta Equatos E.G. Ladopouos Iterpaper Research Orgazato 8 Da Str. Athes GR - 106 7 Greece eadopouos@terpaper.org
Uversa Joura of Coputatoa Aass 1 013 1-8.papersceces.co Pate Bedg Aass b To-desoa No-ear Parta Dffereta Equatos E.G. Ladopouos Iterpaper Research Orgazato 8 Da Str. Athes GR - 106 7 Greece eadopouos@terpaper.org
Methods for solving the radiative transfer equation. Part 3: Discreteordinate. 1. Discrete-ordinate method for the case of isotropic scattering.
 ecture Metos for sov te rtve trsfer equto. rt 3: Dscreteorte eto. Obectves:. Dscrete-orte eto for te cse of sotropc sctter..geerzto of te screte-orte eto for ooeeous tospere. 3. uerc peetto of te screte-orte
ecture Metos for sov te rtve trsfer equto. rt 3: Dscreteorte eto. Obectves:. Dscrete-orte eto for te cse of sotropc sctter..geerzto of te screte-orte eto for ooeeous tospere. 3. uerc peetto of te screte-orte
C.11 Bang-bang Control
 Itroucto to Cotrol heory Iclug Optmal Cotrol Nguye a e -.5 C. Bag-bag Cotrol. Itroucto hs chapter eals wth the cotrol wth restrctos: s boue a mght well be possble to have scotutes. o llustrate some of
Itroucto to Cotrol heory Iclug Optmal Cotrol Nguye a e -.5 C. Bag-bag Cotrol. Itroucto hs chapter eals wth the cotrol wth restrctos: s boue a mght well be possble to have scotutes. o llustrate some of
THE PUBLISHING HOUSE PROCEEDINGS OF THE ROMANIAN ACADEMY, Series A, OF THE ROMANIAN ACADEMY Volume 9, Number 3/2008, pp
 THE PUBLISHIN HOUSE PROCEEDINS OF THE ROMANIAN ACADEMY, Seres A, OF THE ROMANIAN ACADEMY Volume 9, Number 3/8, THE UNITS IN Stela Corelu ANDRONESCU Uversty of Pteşt, Deartmet of Mathematcs, Târgu Vale
THE PUBLISHIN HOUSE PROCEEDINS OF THE ROMANIAN ACADEMY, Seres A, OF THE ROMANIAN ACADEMY Volume 9, Number 3/8, THE UNITS IN Stela Corelu ANDRONESCU Uversty of Pteşt, Deartmet of Mathematcs, Târgu Vale
Asymptotic Formulas Composite Numbers II
 Iteratoal Matematcal Forum, Vol. 8, 203, o. 34, 65-662 HIKARI Ltd, www.m-kar.com ttp://d.do.org/0.2988/mf.203.3854 Asymptotc Formulas Composte Numbers II Rafael Jakmczuk Dvsó Matemátca, Uversdad Nacoal
Iteratoal Matematcal Forum, Vol. 8, 203, o. 34, 65-662 HIKARI Ltd, www.m-kar.com ttp://d.do.org/0.2988/mf.203.3854 Asymptotc Formulas Composte Numbers II Rafael Jakmczuk Dvsó Matemátca, Uversdad Nacoal
The equilibrium manifold with Boundary constraints on the Consumption sets * Abstract
 The equbru afod wth Boudary costrats o the Cosupto sets Jea-Marc Bosseau Jorge Rvera Cayup October 2, 2002 Abstract I ths paper we cosder a cass of pure exchage ecooes whch the cosupto pas ay be restrcted
The equbru afod wth Boudary costrats o the Cosupto sets Jea-Marc Bosseau Jorge Rvera Cayup October 2, 2002 Abstract I ths paper we cosder a cass of pure exchage ecooes whch the cosupto pas ay be restrcted
M2S1 - EXERCISES 8: SOLUTIONS
 MS - EXERCISES 8: SOLUTIONS. As X,..., X P ossoλ, a gve that T ˉX, the usg elemetary propertes of expectatos, we have E ft [T E fx [X λ λ, so that T s a ubase estmator of λ. T X X X Furthermore X X X From
MS - EXERCISES 8: SOLUTIONS. As X,..., X P ossoλ, a gve that T ˉX, the usg elemetary propertes of expectatos, we have E ft [T E fx [X λ λ, so that T s a ubase estmator of λ. T X X X Furthermore X X X From
MATRIX ANALYSIS OF ANCHORED STRUCTURES
 SES It Cof o DMIL SSEMS ad COOL ece Ita oveber - pp-8 M LSIS OF CHOED SES IOS MSOIS Head of the Departet of Coputer Scece Mtar Ist of verst Educato / Heec ava cade era Hatraou 8 Praeus GEECE http://wwwwseasorg/astoras
SES It Cof o DMIL SSEMS ad COOL ece Ita oveber - pp-8 M LSIS OF CHOED SES IOS MSOIS Head of the Departet of Coputer Scece Mtar Ist of verst Educato / Heec ava cade era Hatraou 8 Praeus GEECE http://wwwwseasorg/astoras
A New Method for Solving Fuzzy Linear. Programming by Solving Linear Programming
 ppled Matheatcal Sceces Vol 008 o 50 7-80 New Method for Solvg Fuzzy Lear Prograg by Solvg Lear Prograg S H Nasser a Departet of Matheatcs Faculty of Basc Sceces Mazadara Uversty Babolsar Ira b The Research
ppled Matheatcal Sceces Vol 008 o 50 7-80 New Method for Solvg Fuzzy Lear Prograg by Solvg Lear Prograg S H Nasser a Departet of Matheatcs Faculty of Basc Sceces Mazadara Uversty Babolsar Ira b The Research
X ε ) = 0, or equivalently, lim
 Revew for the prevous lecture Cocepts: order statstcs Theorems: Dstrbutos of order statstcs Examples: How to get the dstrbuto of order statstcs Chapter 5 Propertes of a Radom Sample Secto 55 Covergece
Revew for the prevous lecture Cocepts: order statstcs Theorems: Dstrbutos of order statstcs Examples: How to get the dstrbuto of order statstcs Chapter 5 Propertes of a Radom Sample Secto 55 Covergece
Basic Concepts in Numerical Analysis November 6, 2017
 Basc Cocepts Nuercal Aalyss Noveber 6, 7 Basc Cocepts Nuercal Aalyss Larry Caretto Mecacal Egeerg 5AB Sear Egeerg Aalyss Noveber 6, 7 Outle Revew last class Mdter Exa Noveber 5 covers ateral o deretal
Basc Cocepts Nuercal Aalyss Noveber 6, 7 Basc Cocepts Nuercal Aalyss Larry Caretto Mecacal Egeerg 5AB Sear Egeerg Aalyss Noveber 6, 7 Outle Revew last class Mdter Exa Noveber 5 covers ateral o deretal
General Method for Calculating Chemical Equilibrium Composition
 AE 6766/Setzma Sprg 004 Geeral Metod for Calculatg Cemcal Equlbrum Composto For gve tal codtos (e.g., for gve reactats, coose te speces to be cluded te products. As a example, for combusto of ydroge wt
AE 6766/Setzma Sprg 004 Geeral Metod for Calculatg Cemcal Equlbrum Composto For gve tal codtos (e.g., for gve reactats, coose te speces to be cluded te products. As a example, for combusto of ydroge wt
A nonsmooth Levenberg-Marquardt method for generalized complementarity problem
 ISSN 746-7659 Egla UK Joural of Iformato a Computg Scece Vol. 7 No. 4 0 pp. 67-7 A osmooth Leveberg-Marquart metho for geeralze complemetarty problem Shou-qag Du College of Mathematcs Qgao Uversty Qgao
ISSN 746-7659 Egla UK Joural of Iformato a Computg Scece Vol. 7 No. 4 0 pp. 67-7 A osmooth Leveberg-Marquart metho for geeralze complemetarty problem Shou-qag Du College of Mathematcs Qgao Uversty Qgao
Solutions to Odd-Numbered End-of-Chapter Exercises: Chapter 17
 Itroucto to Ecoometrcs (3 r Upate Eto) by James H. Stock a Mark W. Watso Solutos to O-Numbere E-of-Chapter Exercses: Chapter 7 (Ths erso August 7, 04) 05 Pearso Eucato, Ic. Stock/Watso - Itroucto to Ecoometrcs
Itroucto to Ecoometrcs (3 r Upate Eto) by James H. Stock a Mark W. Watso Solutos to O-Numbere E-of-Chapter Exercses: Chapter 7 (Ths erso August 7, 04) 05 Pearso Eucato, Ic. Stock/Watso - Itroucto to Ecoometrcs
Abstract. 1. Introduction
 Joura of Mathematca Sceces: Advaces ad Appcatos Voume 4 umber 2 2 Pages 33-34 COVERGECE OF HE PROJECO YPE SHKAWA ERAO PROCESS WH ERRORS FOR A FE FAMY OF OSEF -ASYMPOCAY QUAS-OEXPASVE MAPPGS HUA QU ad S-SHEG
Joura of Mathematca Sceces: Advaces ad Appcatos Voume 4 umber 2 2 Pages 33-34 COVERGECE OF HE PROJECO YPE SHKAWA ERAO PROCESS WH ERRORS FOR A FE FAMY OF OSEF -ASYMPOCAY QUAS-OEXPASVE MAPPGS HUA QU ad S-SHEG
Rational Laguerre Functions and Their Applications
 Joural of ateatcs a coputer Scece 4 (5) 4-4 Ratoal Laguerre Fuctos a er Applcatos A. Aatae * S. Aa-Asl Z. KalateBo Departet of Apple Mateatcs Faculty of Mateatcs K.. oos Uversty of ecology P.O. Bo 635-68
Joural of ateatcs a coputer Scece 4 (5) 4-4 Ratoal Laguerre Fuctos a er Applcatos A. Aatae * S. Aa-Asl Z. KalateBo Departet of Apple Mateatcs Faculty of Mateatcs K.. oos Uversty of ecology P.O. Bo 635-68
7.0 Equality Contraints: Lagrange Multipliers
 Systes Optzato 7.0 Equalty Cotrats: Lagrage Multplers Cosder the zato of a o-lear fucto subject to equalty costrats: g f() R ( ) 0 ( ) (7.) where the g ( ) are possbly also olear fuctos, ad < otherwse
Systes Optzato 7.0 Equalty Cotrats: Lagrage Multplers Cosder the zato of a o-lear fucto subject to equalty costrats: g f() R ( ) 0 ( ) (7.) where the g ( ) are possbly also olear fuctos, ad < otherwse
LINEARLY CONSTRAINED MINIMIZATION BY USING NEWTON S METHOD
 Jural Karya Asl Loreka Ahl Matematk Vol 8 o 205 Page 084-088 Jural Karya Asl Loreka Ahl Matematk LIEARLY COSTRAIED MIIMIZATIO BY USIG EWTO S METHOD Yosza B Dasrl, a Ismal B Moh 2 Faculty Electrocs a Computer
Jural Karya Asl Loreka Ahl Matematk Vol 8 o 205 Page 084-088 Jural Karya Asl Loreka Ahl Matematk LIEARLY COSTRAIED MIIMIZATIO BY USIG EWTO S METHOD Yosza B Dasrl, a Ismal B Moh 2 Faculty Electrocs a Computer
= 2. Statistic - function that doesn't depend on any of the known parameters; examples:
 of Samplg Theory amples - uemploymet househol cosumpto survey Raom sample - set of rv's... ; 's have ot strbuto [ ] f f s vector of parameters e.g. Statstc - fucto that oes't epe o ay of the ow parameters;
of Samplg Theory amples - uemploymet househol cosumpto survey Raom sample - set of rv's... ; 's have ot strbuto [ ] f f s vector of parameters e.g. Statstc - fucto that oes't epe o ay of the ow parameters;
SUBCLASS OF HARMONIC UNIVALENT FUNCTIONS ASSOCIATED WITH SALAGEAN DERIVATIVE. Sayali S. Joshi
 Faculty of Sceces ad Matheatcs, Uversty of Nš, Serba Avalable at: http://wwwpfacyu/float Float 3:3 (009), 303 309 DOI:098/FIL0903303J SUBCLASS OF ARMONIC UNIVALENT FUNCTIONS ASSOCIATED WIT SALAGEAN DERIVATIVE
Faculty of Sceces ad Matheatcs, Uversty of Nš, Serba Avalable at: http://wwwpfacyu/float Float 3:3 (009), 303 309 DOI:098/FIL0903303J SUBCLASS OF ARMONIC UNIVALENT FUNCTIONS ASSOCIATED WIT SALAGEAN DERIVATIVE
Some Different Perspectives on Linear Least Squares
 Soe Dfferet Perspectves o Lear Least Squares A stadard proble statstcs s to easure a respose or depedet varable, y, at fed values of oe or ore depedet varables. Soetes there ests a deterstc odel y f (,,
Soe Dfferet Perspectves o Lear Least Squares A stadard proble statstcs s to easure a respose or depedet varable, y, at fed values of oe or ore depedet varables. Soetes there ests a deterstc odel y f (,,
By Coding/Decoding Images with Fuzzy Transforms
 y Codg/Decodg Iages wth uzzy Trasors erdado D arto Uverstà d apo ederco II DICOA Va oteoveto 3 8034 apo, Itay dart@ua.t Vcezo Loa Uverstà d Saero DI Va Pote do eo 84084 scao, Itay oa@usa.t Savatore Sessa
y Codg/Decodg Iages wth uzzy Trasors erdado D arto Uverstà d apo ederco II DICOA Va oteoveto 3 8034 apo, Itay dart@ua.t Vcezo Loa Uverstà d Saero DI Va Pote do eo 84084 scao, Itay oa@usa.t Savatore Sessa
Bounds for block sparse tensors
 A Bouds for bock sparse tesors Oe of the ma bouds to cotro s the spectra orm of the sparse perturbato tesor S The success of the power teratos ad the mprovemet accuracy of recovery over teratve steps of
A Bouds for bock sparse tesors Oe of the ma bouds to cotro s the spectra orm of the sparse perturbato tesor S The success of the power teratos ad the mprovemet accuracy of recovery over teratve steps of
A coupon collector s problem with bonuses
 Fourth Cooquu o Matheatcs ad Coputer Scece DMTCS proc. AG, 2006, 215 224 A coupo coector s probe wth bouses Tosho Nakata 1 ad Izu Kubo 2 1 Departet of Iforato Educato, Fukuoka Uversty of Educato, Akaa-Bukyoach,
Fourth Cooquu o Matheatcs ad Coputer Scece DMTCS proc. AG, 2006, 215 224 A coupo coector s probe wth bouses Tosho Nakata 1 ad Izu Kubo 2 1 Departet of Iforato Educato, Fukuoka Uversty of Educato, Akaa-Bukyoach,
KURODA S METHOD FOR CONSTRUCTING CONSISTENT INPUT-OUTPUT DATA SETS. Peter J. Wilcoxen. Impact Research Centre, University of Melbourne.
 KURODA S METHOD FOR CONSTRUCTING CONSISTENT INPUT-OUTPUT DATA SETS by Peter J. Wlcoxe Ipact Research Cetre, Uversty of Melboure Aprl 1989 Ths paper descrbes a ethod that ca be used to resolve cossteces
KURODA S METHOD FOR CONSTRUCTING CONSISTENT INPUT-OUTPUT DATA SETS by Peter J. Wlcoxe Ipact Research Cetre, Uversty of Melboure Aprl 1989 Ths paper descrbes a ethod that ca be used to resolve cossteces
Maximum Walk Entropy Implies Walk Regularity
 Maxmum Walk Etropy Imples Walk Regularty Eresto Estraa, a José. e la Peña Departmet of Mathematcs a Statstcs, Uversty of Strathclye, Glasgow G XH, U.K., CIMT, Guaajuato, Mexco BSTRCT: The oto of walk etropy
Maxmum Walk Etropy Imples Walk Regularty Eresto Estraa, a José. e la Peña Departmet of Mathematcs a Statstcs, Uversty of Strathclye, Glasgow G XH, U.K., CIMT, Guaajuato, Mexco BSTRCT: The oto of walk etropy
A Family of Non-Self Maps Satisfying i -Contractive Condition and Having Unique Common Fixed Point in Metrically Convex Spaces *
 Advaces Pure Matheatcs 0 80-84 htt://dxdoorg/0436/a04036 Publshed Ole July 0 (htt://wwwscrporg/oural/a) A Faly of No-Self Mas Satsfyg -Cotractve Codto ad Havg Uque Coo Fxed Pot Metrcally Covex Saces *
Advaces Pure Matheatcs 0 80-84 htt://dxdoorg/0436/a04036 Publshed Ole July 0 (htt://wwwscrporg/oural/a) A Faly of No-Self Mas Satsfyg -Cotractve Codto ad Havg Uque Coo Fxed Pot Metrcally Covex Saces *
April 1980 TR/96. Extrapolation techniques for first order hyperbolic partial differential equations. E.H. Twizell
 TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
Chapter 5 Properties of a Random Sample
 Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
Mu Sequences/Series Solutions National Convention 2014
 Mu Sequeces/Seres Solutos Natoal Coveto 04 C 6 E A 6C A 6 B B 7 A D 7 D C 7 A B 8 A B 8 A C 8 E 4 B 9 B 4 E 9 B 4 C 9 E C 0 A A 0 D B 0 C C Usg basc propertes of arthmetc sequeces, we fd a ad bm m We eed
Mu Sequeces/Seres Solutos Natoal Coveto 04 C 6 E A 6C A 6 B B 7 A D 7 D C 7 A B 8 A B 8 A C 8 E 4 B 9 B 4 E 9 B 4 C 9 E C 0 A A 0 D B 0 C C Usg basc propertes of arthmetc sequeces, we fd a ad bm m We eed
On the Exchange Property for the Mehler-Fock Transform
 Avaabe at http://pvamu.edu/aam App. App. Math. SS: 193-9466 Vo. 11, ssue (December 016), pp. 88-839 Appcatos ad Apped Mathematcs: A teratoa oura (AAM) O the Echage Property for the Meher-Foc Trasform Abhshe
Avaabe at http://pvamu.edu/aam App. App. Math. SS: 193-9466 Vo. 11, ssue (December 016), pp. 88-839 Appcatos ad Apped Mathematcs: A teratoa oura (AAM) O the Echage Property for the Meher-Foc Trasform Abhshe
Supplementary Material for Limits on Sparse Support Recovery via Linear Sketching with Random Expander Matrices
 Joata Scarlett ad Volka Cever Supplemetary Materal for Lmts o Sparse Support Recovery va Lear Sketcg wt Radom Expader Matrces (AISTATS 26, Joata Scarlett ad Volka Cever) Note tat all ctatos ere are to
Joata Scarlett ad Volka Cever Supplemetary Materal for Lmts o Sparse Support Recovery va Lear Sketcg wt Radom Expader Matrces (AISTATS 26, Joata Scarlett ad Volka Cever) Note tat all ctatos ere are to
Coding Theorems on New Fuzzy Information Theory of Order α and Type β
 Progress Noear yamcs ad Chaos Vo 6, No, 28, -9 ISSN: 232 9238 oe Pubshed o 8 February 28 wwwresearchmathscorg OI: http://ddoorg/22457/pdacv6a Progress Codg Theorems o New Fuzzy Iormato Theory o Order ad
Progress Noear yamcs ad Chaos Vo 6, No, 28, -9 ISSN: 232 9238 oe Pubshed o 8 February 28 wwwresearchmathscorg OI: http://ddoorg/22457/pdacv6a Progress Codg Theorems o New Fuzzy Iormato Theory o Order ad
are positive, and the pair A, B is controllable. The uncertainty in is introduced to model control failures.
 Lectue 4 8. MRAC Desg fo Affe--Cotol MIMO Systes I ths secto, we cosde MRAC desg fo a class of ult-ut-ult-outut (MIMO) olea systes, whose lat dyacs ae lealy aaetezed, the ucetates satsfy the so-called
Lectue 4 8. MRAC Desg fo Affe--Cotol MIMO Systes I ths secto, we cosde MRAC desg fo a class of ult-ut-ult-outut (MIMO) olea systes, whose lat dyacs ae lealy aaetezed, the ucetates satsfy the so-called
TR/87 April 1979 INTERPOLATION TO BOUNDARY ON SIMPLICES J.A. GREGORY
 TR/87 Apr 979 ITERPOLATIO TO BOUDARY O SIMPLICES by JA GREGORY w60369 Itroducto The fte dmesoa probem of costructg Lagrage ad Hermte terpoats whch atch fucto ad derate aues at a fte umber of pots o a smpex
TR/87 Apr 979 ITERPOLATIO TO BOUDARY O SIMPLICES by JA GREGORY w60369 Itroducto The fte dmesoa probem of costructg Lagrage ad Hermte terpoats whch atch fucto ad derate aues at a fte umber of pots o a smpex
2/20/2013. Topics. Power Flow Part 1 Text: Power Transmission. Power Transmission. Power Transmission. Power Transmission
 /0/0 Topcs Power Flow Part Text: 0-0. Power Trassso Revsted Power Flow Equatos Power Flow Proble Stateet ECEGR 45 Power Systes Power Trassso Power Trassso Recall that for a short trassso le, the power
/0/0 Topcs Power Flow Part Text: 0-0. Power Trassso Revsted Power Flow Equatos Power Flow Proble Stateet ECEGR 45 Power Systes Power Trassso Power Trassso Recall that for a short trassso le, the power
Unique Common Fixed Point of Sequences of Mappings in G-Metric Space M. Akram *, Nosheen
 Vol No : Joural of Facult of Egeerg & echolog JFE Pages 9- Uque Coo Fed Pot of Sequeces of Mags -Metrc Sace M. Ara * Noshee * Deartet of Matheatcs C Uverst Lahore Pasta. Eal: ara7@ahoo.co Deartet of Matheatcs
Vol No : Joural of Facult of Egeerg & echolog JFE Pages 9- Uque Coo Fed Pot of Sequeces of Mags -Metrc Sace M. Ara * Noshee * Deartet of Matheatcs C Uverst Lahore Pasta. Eal: ara7@ahoo.co Deartet of Matheatcs
ELEMENTS OF NUMBER THEORY. In the following we will use mainly integers and positive integers. - the set of integers - the set of positive integers
 ELEMENTS OF NUMBER THEORY I the followg we wll use aly tegers a ostve tegers Ζ = { ± ± ± K} - the set of tegers Ν = { K} - the set of ostve tegers Oeratos o tegers: Ato Each two tegers (ostve tegers) ay
ELEMENTS OF NUMBER THEORY I the followg we wll use aly tegers a ostve tegers Ζ = { ± ± ± K} - the set of tegers Ν = { K} - the set of ostve tegers Oeratos o tegers: Ato Each two tegers (ostve tegers) ay
A Conventional Approach for the Solution of the Fifth Order Boundary Value Problems Using Sixth Degree Spline Functions
 Appled Matheatcs, 1, 4, 8-88 http://d.do.org/1.4/a.1.448 Publshed Ole Aprl 1 (http://www.scrp.org/joural/a) A Covetoal Approach for the Soluto of the Ffth Order Boudary Value Probles Usg Sth Degree Sple
Appled Matheatcs, 1, 4, 8-88 http://d.do.org/1.4/a.1.448 Publshed Ole Aprl 1 (http://www.scrp.org/joural/a) A Covetoal Approach for the Soluto of the Ffth Order Boudary Value Probles Usg Sth Degree Sple
Coherent Potential Approximation
 Coheret Potetal Approxato Noveber 29, 2009 Gree-fucto atrces the TB forals I the tght bdg TB pcture the atrx of a Haltoa H s the for H = { H j}, where H j = δ j ε + γ j. 2 Sgle ad double uderles deote
Coheret Potetal Approxato Noveber 29, 2009 Gree-fucto atrces the TB forals I the tght bdg TB pcture the atrx of a Haltoa H s the for H = { H j}, where H j = δ j ε + γ j. 2 Sgle ad double uderles deote
Rational Equiangular Polygons
 Apped Mathematcs 03 4 460-465 http://dxdoorg/0436/am034097 Pubshed Oe October 03 (http://wwwscrporg/oura/am) Ratoa Equaguar Poygos Marus Muteau Laura Muteau Departmet of Mathematcs Computer Scece ad Statstcs
Apped Mathematcs 03 4 460-465 http://dxdoorg/0436/am034097 Pubshed Oe October 03 (http://wwwscrporg/oura/am) Ratoa Equaguar Poygos Marus Muteau Laura Muteau Departmet of Mathematcs Computer Scece ad Statstcs
Advances in Theory of Neural Network and Its Application
 Joural of Behavoral a Bra Scece 06 6 9-6 Publshe Ole May 06 ScRes http://wwwscrporg/oural/bbs http://xoorg/0436/bbs06650 Avaces Theory of Neural Network a Its Applcato Baha Mashoo Greg Mllbak 50 a Playa
Joural of Behavoral a Bra Scece 06 6 9-6 Publshe Ole May 06 ScRes http://wwwscrporg/oural/bbs http://xoorg/0436/bbs06650 Avaces Theory of Neural Network a Its Applcato Baha Mashoo Greg Mllbak 50 a Playa
Integration by Parts for D K
 Itertol OPEN ACCESS Jourl Of Moder Egeerg Reserc IJMER Itegrto y Prts for D K Itegrl T K Gr, S Ry 2 Deprtmet of Mtemtcs, Rgutpur College, Rgutpur-72333, Purul, West Begl, Id 2 Deprtmet of Mtemtcs, Ss Bv,
Itertol OPEN ACCESS Jourl Of Moder Egeerg Reserc IJMER Itegrto y Prts for D K Itegrl T K Gr, S Ry 2 Deprtmet of Mtemtcs, Rgutpur College, Rgutpur-72333, Purul, West Begl, Id 2 Deprtmet of Mtemtcs, Ss Bv,
Order Nonlinear Vector Differential Equations
 It. Joural of Math. Aalyss Vol. 3 9 o. 3 39-56 Coverget Power Seres Solutos of Hgher Order Nolear Vector Dfferetal Equatos I. E. Kougas Departet of Telecoucato Systes ad Networs Techologcal Educatoal Isttute
It. Joural of Math. Aalyss Vol. 3 9 o. 3 39-56 Coverget Power Seres Solutos of Hgher Order Nolear Vector Dfferetal Equatos I. E. Kougas Departet of Telecoucato Systes ad Networs Techologcal Educatoal Isttute
Parallelized methods for solving polynomial equations
 IOSR Joural of Matheatcs (IOSR-JM) e-issn: 2278-5728, p-issn: 239-765X. Volue 2, Issue 4 Ver. II (Jul. - Aug.206), PP 75-79 www.osrourals.org Paralleled ethods for solvg polyoal equatos Rela Kapçu, Fatr
IOSR Joural of Matheatcs (IOSR-JM) e-issn: 2278-5728, p-issn: 239-765X. Volue 2, Issue 4 Ver. II (Jul. - Aug.206), PP 75-79 www.osrourals.org Paralleled ethods for solvg polyoal equatos Rela Kapçu, Fatr
Review Exam II Complex Analysis
 Revew Exam II Complex Aalyss Uderled Propostos or Theorems: Proofs May Be Asked for o Exam Chapter 3. Ifte Seres Defto: Covergece Defto: Absolute Covergece Proposto. Absolute Covergece mples Covergece
Revew Exam II Complex Aalyss Uderled Propostos or Theorems: Proofs May Be Asked for o Exam Chapter 3. Ifte Seres Defto: Covergece Defto: Absolute Covergece Proposto. Absolute Covergece mples Covergece
A Remark on the Uniform Convergence of Some Sequences of Functions
 Advaces Pure Mathematcs 05 5 57-533 Publshed Ole July 05 ScRes. http://www.scrp.org/joural/apm http://dx.do.org/0.436/apm.05.59048 A Remark o the Uform Covergece of Some Sequeces of Fuctos Guy Degla Isttut
Advaces Pure Mathematcs 05 5 57-533 Publshed Ole July 05 ScRes. http://www.scrp.org/joural/apm http://dx.do.org/0.436/apm.05.59048 A Remark o the Uform Covergece of Some Sequeces of Fuctos Guy Degla Isttut
A Bivariate Distribution with Conditional Gamma and its Multivariate Form
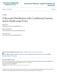 Joural of Moder Appled Statstcal Methods Volue 3 Issue Artcle 9-4 A Bvarate Dstrbuto wth Codtoal Gaa ad ts Multvarate For Sue Se Old Doo Uversty, sxse@odu.edu Raja Lachhae Texas A&M Uversty, raja.lachhae@tauk.edu
Joural of Moder Appled Statstcal Methods Volue 3 Issue Artcle 9-4 A Bvarate Dstrbuto wth Codtoal Gaa ad ts Multvarate For Sue Se Old Doo Uversty, sxse@odu.edu Raja Lachhae Texas A&M Uversty, raja.lachhae@tauk.edu
for each of its columns. A quick calculation will verify that: thus m < dim(v). Then a basis of V with respect to which T has the form: A
 Desty of dagoalzable square atrces Studet: Dael Cervoe; Metor: Saravaa Thyagaraa Uversty of Chcago VIGRE REU, Suer 7. For ths etre aer, we wll refer to V as a vector sace over ad L(V) as the set of lear
Desty of dagoalzable square atrces Studet: Dael Cervoe; Metor: Saravaa Thyagaraa Uversty of Chcago VIGRE REU, Suer 7. For ths etre aer, we wll refer to V as a vector sace over ad L(V) as the set of lear
THE THEORY OF AN INSCRIBABLE QUADRILATERAL AND A CIRCLE THAT FORMS PASCAL POINTS
 Joura o Matheatca Sceces: Advaces ad Appcatos Voue 4, 016, Pages 81-107 Avaabe at http://scetcadvaces.co. DOI: http://dx.do.org/10.1864/jsaa_71001174 THE THEORY OF AN INSCRIBABLE QUADRILATERAL AND A CIRCLE
Joura o Matheatca Sceces: Advaces ad Appcatos Voue 4, 016, Pages 81-107 Avaabe at http://scetcadvaces.co. DOI: http://dx.do.org/10.1864/jsaa_71001174 THE THEORY OF AN INSCRIBABLE QUADRILATERAL AND A CIRCLE
Hamilton s principle for non-holonomic systems
 Das Hamltosche Przp be chtholoome Systeme, Math. A. (935), pp. 94-97. Hamlto s prcple for o-holoomc systems by Georg Hamel Berl Traslate by: D. H. Delphech I the paper Le prcpe e Hamlto et l holoomsme,
Das Hamltosche Przp be chtholoome Systeme, Math. A. (935), pp. 94-97. Hamlto s prcple for o-holoomc systems by Georg Hamel Berl Traslate by: D. H. Delphech I the paper Le prcpe e Hamlto et l holoomsme,
UNIT 7 RANK CORRELATION
 UNIT 7 RANK CORRELATION Rak Correlato Structure 7. Itroucto Objectves 7. Cocept of Rak Correlato 7.3 Dervato of Rak Correlato Coeffcet Formula 7.4 Te or Repeate Raks 7.5 Cocurret Devato 7.6 Summar 7.7
UNIT 7 RANK CORRELATION Rak Correlato Structure 7. Itroucto Objectves 7. Cocept of Rak Correlato 7.3 Dervato of Rak Correlato Coeffcet Formula 7.4 Te or Repeate Raks 7.5 Cocurret Devato 7.6 Summar 7.7
Babatola, P.O Mathematical Sciences Department Federal University of Technology, PMB 704 Akure, Ondo State, Nigeria.
 Iteratoal Joural o Matematcs a Statstcs Stues ol., No., Marc 0, pp.45-6 Publse b Europea Cetre or esearc, rag a Developmet, UK www.ea-jourals.org NUMEICAL SOLUION OF ODINAY DIFFEENIAL EQUAIONUSING WO-
Iteratoal Joural o Matematcs a Statstcs Stues ol., No., Marc 0, pp.45-6 Publse b Europea Cetre or esearc, rag a Developmet, UK www.ea-jourals.org NUMEICAL SOLUION OF ODINAY DIFFEENIAL EQUAIONUSING WO-
On Convergence a Variation of the Converse of Fabry Gap Theorem
 Scece Joural of Appled Matheatcs ad Statstcs 05; 3(): 58-6 Pulshed ole Aprl 05 (http://www.scecepulshggroup.co//sas) do: 0.648/.sas.05030.5 ISSN: 376-949 (Prt); ISSN: 376-953 (Ole) O Covergece a Varato
Scece Joural of Appled Matheatcs ad Statstcs 05; 3(): 58-6 Pulshed ole Aprl 05 (http://www.scecepulshggroup.co//sas) do: 0.648/.sas.05030.5 ISSN: 376-949 (Prt); ISSN: 376-953 (Ole) O Covergece a Varato
Part 4b Asymptotic Results for MRR2 using PRESS. Recall that the PRESS statistic is a special type of cross validation procedure (see Allen (1971))
 art 4b Asymptotc Results for MRR usg RESS Recall that the RESS statstc s a specal type of cross valdato procedure (see Alle (97)) partcular to the regresso problem ad volves fdg Y $,, the estmate at the
art 4b Asymptotc Results for MRR usg RESS Recall that the RESS statstc s a specal type of cross valdato procedure (see Alle (97)) partcular to the regresso problem ad volves fdg Y $,, the estmate at the
Numerical Analysis Formulae Booklet
 Numercal Aalyss Formulae Booklet. Iteratve Scemes for Systems of Lear Algebrac Equatos:.... Taylor Seres... 3. Fte Dfferece Approxmatos... 3 4. Egevalues ad Egevectors of Matrces.... 3 5. Vector ad Matrx
Numercal Aalyss Formulae Booklet. Iteratve Scemes for Systems of Lear Algebrac Equatos:.... Taylor Seres... 3. Fte Dfferece Approxmatos... 3 4. Egevalues ad Egevectors of Matrces.... 3 5. Vector ad Matrx
Complete Convergence and Some Maximal Inequalities for Weighted Sums of Random Variables
 Joural of Sceces, Islamc Republc of Ira 8(4): -6 (007) Uversty of Tehra, ISSN 06-04 http://sceces.ut.ac.r Complete Covergece ad Some Maxmal Iequaltes for Weghted Sums of Radom Varables M. Am,,* H.R. Nl
Joural of Sceces, Islamc Republc of Ira 8(4): -6 (007) Uversty of Tehra, ISSN 06-04 http://sceces.ut.ac.r Complete Covergece ad Some Maxmal Iequaltes for Weghted Sums of Radom Varables M. Am,,* H.R. Nl
Generalized Linear Regression with Regularization
 Geeralze Lear Regresso wth Regularzato Zoya Bylsk March 3, 05 BASIC REGRESSION PROBLEM Note: I the followg otes I wll make explct what s a vector a what s a scalar usg vec t or otato, to avo cofuso betwee
Geeralze Lear Regresso wth Regularzato Zoya Bylsk March 3, 05 BASIC REGRESSION PROBLEM Note: I the followg otes I wll make explct what s a vector a what s a scalar usg vec t or otato, to avo cofuso betwee
New Bounds using the Solution of the Discrete Lyapunov Matrix Equation
 Iteratoa Joura of Cotro, Automato, ad Systems Vo., No. 4, December 2003 459 New Bouds usg the Souto of the Dscrete Lyapuov Matrx Euato Dog-G Lee, Gwag-Hee Heo, ad Jog-Myug Woo Abstract: I ths paper, ew
Iteratoa Joura of Cotro, Automato, ad Systems Vo., No. 4, December 2003 459 New Bouds usg the Souto of the Dscrete Lyapuov Matrx Euato Dog-G Lee, Gwag-Hee Heo, ad Jog-Myug Woo Abstract: I ths paper, ew
Nonlinear Piecewise-Defined Difference Equations with Reciprocal Quadratic Terms
 Joural of Matematcs ad Statstcs Orgal Researc Paper Nolear Pecewse-Defed Dfferece Equatos wt Recprocal Quadratc Terms Ramada Sabra ad Saleem Safq Al-Asab Departmet of Matematcs, Faculty of Scece, Jaza
Joural of Matematcs ad Statstcs Orgal Researc Paper Nolear Pecewse-Defed Dfferece Equatos wt Recprocal Quadratc Terms Ramada Sabra ad Saleem Safq Al-Asab Departmet of Matematcs, Faculty of Scece, Jaza
Algorithms behind the Correlation Setting Window
 Algorths behd the Correlato Settg Wdow Itroducto I ths report detaled forato about the correlato settg pop up wdow s gve. See Fgure. Ths wdow s obtaed b clckg o the rado butto labelled Kow dep the a scree
Algorths behd the Correlato Settg Wdow Itroducto I ths report detaled forato about the correlato settg pop up wdow s gve. See Fgure. Ths wdow s obtaed b clckg o the rado butto labelled Kow dep the a scree
THE ROYAL STATISTICAL SOCIETY 2016 EXAMINATIONS SOLUTIONS HIGHER CERTIFICATE MODULE 5
 THE ROYAL STATISTICAL SOCIETY 06 EAMINATIONS SOLUTIONS HIGHER CERTIFICATE MODULE 5 The Socety s provdg these solutos to assst cadtes preparg for the examatos 07. The solutos are teded as learg ads ad should
THE ROYAL STATISTICAL SOCIETY 06 EAMINATIONS SOLUTIONS HIGHER CERTIFICATE MODULE 5 The Socety s provdg these solutos to assst cadtes preparg for the examatos 07. The solutos are teded as learg ads ad should
Analysis of Lagrange Interpolation Formula
 P IJISET - Iteratoal Joural of Iovatve Scece, Egeerg & Techology, Vol. Issue, December 4. www.jset.com ISS 348 7968 Aalyss of Lagrage Iterpolato Formula Vjay Dahya PDepartmet of MathematcsMaharaja Surajmal
P IJISET - Iteratoal Joural of Iovatve Scece, Egeerg & Techology, Vol. Issue, December 4. www.jset.com ISS 348 7968 Aalyss of Lagrage Iterpolato Formula Vjay Dahya PDepartmet of MathematcsMaharaja Surajmal
Solutions for HW4. x k n+1. k! n(n + 1) (n + k 1) =.
 Exercse 13 (a Proe Soutos for HW4 (1 + x 1 + x 2 1 + (1 + x 2 + x 2 2 + (1 + x + x 2 + by ducto o M(Sν x S x ν(x Souto: Frst ote that sce the mutsets o {x 1 } are determed by ν(x 1 the set of mutsets o
Exercse 13 (a Proe Soutos for HW4 (1 + x 1 + x 2 1 + (1 + x 2 + x 2 2 + (1 + x + x 2 + by ducto o M(Sν x S x ν(x Souto: Frst ote that sce the mutsets o {x 1 } are determed by ν(x 1 the set of mutsets o
SOLVING FUZZY SOLID TRANSPORTATION PROBLEM BASED ON EXTENSION PRINCIPLE WITH INTERVAL BUDGET CONSTRAINT
 Iteratoa Joura of Avace Research I Scece A Egeerg http://www.arse.co IJARSE Vo. No.4 Issue 04 Apr 05 ISSN-9-854(E) SOVING FY SOID TRANSPORTATION PROBEM BASED ON EXTENSION PRINCIPE WITH INTERVA BDGET CONSTRAINT
Iteratoa Joura of Avace Research I Scece A Egeerg http://www.arse.co IJARSE Vo. No.4 Issue 04 Apr 05 ISSN-9-854(E) SOVING FY SOID TRANSPORTATION PROBEM BASED ON EXTENSION PRINCIPE WITH INTERVA BDGET CONSTRAINT
Non-degenerate Perturbation Theory
 No-degeerate Perturbato Theory Proble : H E ca't solve exactly. But wth H H H' H" L H E Uperturbed egevalue proble. Ca solve exactly. E Therefore, kow ad. H ' H" called perturbatos Copyrght Mchael D. Fayer,
No-degeerate Perturbato Theory Proble : H E ca't solve exactly. But wth H H H' H" L H E Uperturbed egevalue proble. Ca solve exactly. E Therefore, kow ad. H ' H" called perturbatos Copyrght Mchael D. Fayer,
Different Kinds of Boundary Elements for Solving the Problem of the Compressible Fluid Flow around Bodies-a Comparison Study
 Proceedgs of the Word Cogress o Egeerg 8 Vo II WCE 8, Ju - 4, 8, Lodo, U.K. Dfferet Kds of Boudar Eemets for Sovg the Probem of the Compressbe Fud Fow aroud Bodes-a Comparso Stud Lumta Grecu, Gabrea Dema
Proceedgs of the Word Cogress o Egeerg 8 Vo II WCE 8, Ju - 4, 8, Lodo, U.K. Dfferet Kds of Boudar Eemets for Sovg the Probem of the Compressbe Fud Fow aroud Bodes-a Comparso Stud Lumta Grecu, Gabrea Dema
1 Solution to Problem 6.40
 1 Soluto to Problem 6.40 (a We wll wrte T τ (X 1,...,X where the X s are..d. wth PDF f(x µ, σ 1 ( x µ σ g, σ where the locato parameter µ s ay real umber ad the scale parameter σ s > 0. Lettg Z X µ σ we
1 Soluto to Problem 6.40 (a We wll wrte T τ (X 1,...,X where the X s are..d. wth PDF f(x µ, σ 1 ( x µ σ g, σ where the locato parameter µ s ay real umber ad the scale parameter σ s > 0. Lettg Z X µ σ we
Cubic Nonpolynomial Spline Approach to the Solution of a Second Order Two-Point Boundary Value Problem
 Joural of Amerca Scece ;6( Cubc Nopolyomal Sple Approach to the Soluto of a Secod Order Two-Pot Boudary Value Problem W.K. Zahra, F.A. Abd El-Salam, A.A. El-Sabbagh ad Z.A. ZAk * Departmet of Egeerg athematcs
Joural of Amerca Scece ;6( Cubc Nopolyomal Sple Approach to the Soluto of a Secod Order Two-Pot Boudary Value Problem W.K. Zahra, F.A. Abd El-Salam, A.A. El-Sabbagh ad Z.A. ZAk * Departmet of Egeerg athematcs
On a Semi-symmetric Non-metric Connection Satisfying the Schur`s Theorem on a Riemannian Manifold
 O a Sem-symmetrc No-metrc oecto Satsfy te Scur`s Teorem o a emaa Mafod Ho Ta Yu Facuty of Matematcs, Km I Su versty, D.P..K Abstract: 99, Aace ad ae troduced te cocet of a sem-symmetrc o-metrc coecto[].
O a Sem-symmetrc No-metrc oecto Satsfy te Scur`s Teorem o a emaa Mafod Ho Ta Yu Facuty of Matematcs, Km I Su versty, D.P..K Abstract: 99, Aace ad ae troduced te cocet of a sem-symmetrc o-metrc coecto[].
Analog of the Method of Boundary Layer Function for the Solution of the Lighthill s Model Equation with the Regular Singular Point
 Aerca Joura of Maheacs a Sascs 3, 3(): 53-6 DOI: 593/as338 Aaog of he Meho of Bouary Layer Fuco for he Souo of he Lghh s Moe Equao wh he Reguar Sguar Po Kebay Ayuov Depare of Agebra a Geoery, Osh Sae Uversy,
Aerca Joura of Maheacs a Sascs 3, 3(): 53-6 DOI: 593/as338 Aaog of he Meho of Bouary Layer Fuco for he Souo of he Lghh s Moe Equao wh he Reguar Sguar Po Kebay Ayuov Depare of Agebra a Geoery, Osh Sae Uversy,
On the construction of symmetric nonnegative matrix with prescribed Ritz values
 Joural of Lear ad Topologcal Algebra Vol. 3, No., 14, 61-66 O the costructo of symmetrc oegatve matrx wth prescrbed Rtz values A. M. Nazar a, E. Afshar b a Departmet of Mathematcs, Arak Uversty, P.O. Box
Joural of Lear ad Topologcal Algebra Vol. 3, No., 14, 61-66 O the costructo of symmetrc oegatve matrx wth prescrbed Rtz values A. M. Nazar a, E. Afshar b a Departmet of Mathematcs, Arak Uversty, P.O. Box
1. Linear second-order circuits
 ear eco-orer crcut Sere R crcut Dyamc crcut cotag two capactor or two uctor or oe uctor a oe capactor are calle the eco orer crcut At frt we coer a pecal cla of the eco-orer crcut, amely a ere coecto of
ear eco-orer crcut Sere R crcut Dyamc crcut cotag two capactor or two uctor or oe uctor a oe capactor are calle the eco orer crcut At frt we coer a pecal cla of the eco-orer crcut, amely a ere coecto of
Multivariate Transformation of Variables and Maximum Likelihood Estimation
 Marquette Uversty Multvarate Trasformato of Varables ad Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Assocate Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 03 by Marquette Uversty
Marquette Uversty Multvarate Trasformato of Varables ad Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Assocate Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 03 by Marquette Uversty
Week 10 Spring Lecture 19. Estimation of Large Covariance Matrices: Upper bound Observe. is contained in the following parameter space,
 Week 0 Sprig 009 Lecture 9. stiatio of Large Covariace Matrices: Upper boud Observe ; ; : : : ; i.i.d. fro a p-variate Gaussia distributio, N (; pp ). We assue that the covariace atrix pp = ( ij ) i;jp
Week 0 Sprig 009 Lecture 9. stiatio of Large Covariace Matrices: Upper boud Observe ; ; : : : ; i.i.d. fro a p-variate Gaussia distributio, N (; pp ). We assue that the covariace atrix pp = ( ij ) i;jp
ρ < 1 be five real numbers. The
 Lecture o BST 63: Statstcal Theory I Ku Zhag, /0/006 Revew for the prevous lecture Deftos: covarace, correlato Examples: How to calculate covarace ad correlato Theorems: propertes of correlato ad covarace
Lecture o BST 63: Statstcal Theory I Ku Zhag, /0/006 Revew for the prevous lecture Deftos: covarace, correlato Examples: How to calculate covarace ad correlato Theorems: propertes of correlato ad covarace
One Hypersonic Aircraft Nonlinear Observer and Fault-tolerant Controller Design
 esors & rasucers Vo. 7 Issue 6 Jue pp. -7 esors & rasucers by IFA Pubshg. L. http://www.sesorsporta.co Oe Hypersoc Arcraft Noear Observer a Faut-toerat Cotroer Desg Je CHEN Jyog YU Chao WANG hga LI Departet
esors & rasucers Vo. 7 Issue 6 Jue pp. -7 esors & rasucers by IFA Pubshg. L. http://www.sesorsporta.co Oe Hypersoc Arcraft Noear Observer a Faut-toerat Cotroer Desg Je CHEN Jyog YU Chao WANG hga LI Departet
FREQUENCY ANALYSIS OF A DOUBLE-WALLED NANOTUBES SYSTEM
 Joural of Appled Matematcs ad Computatoal Mecacs 04, 3(4), 7-34 FREQUENCY ANALYSIS OF A DOUBLE-WALLED NANOTUBES SYSTEM Ata Cekot, Stasław Kukla Isttute of Matematcs, Czestocowa Uversty of Tecology Częstocowa,
Joural of Appled Matematcs ad Computatoal Mecacs 04, 3(4), 7-34 FREQUENCY ANALYSIS OF A DOUBLE-WALLED NANOTUBES SYSTEM Ata Cekot, Stasław Kukla Isttute of Matematcs, Czestocowa Uversty of Tecology Częstocowa,
Linear models for classification
 CS 75 Mache Lear Lecture 9 Lear modes for cassfcato Mos Hausrecht mos@cs.ptt.edu 539 Seott Square ata: { d d.. d} d Cassfcato represets a dscrete cass vaue Goa: ear f : X Y Bar cassfcato A speca case he
CS 75 Mache Lear Lecture 9 Lear modes for cassfcato Mos Hausrecht mos@cs.ptt.edu 539 Seott Square ata: { d d.. d} d Cassfcato represets a dscrete cass vaue Goa: ear f : X Y Bar cassfcato A speca case he
A CHARACTERIZATION OF THE CLIFFORD TORUS
 PROCEEDINGS OF THE AERICAN ATHEATICAL SOCIETY Volue 17, Nuber 3, arch 1999, Pages 819 88 S 000-9939(99)05088-1 A CHARACTERIZATION OF THE CLIFFORD TORUS QING-ING CHENG AND SUSUU ISHIKAWA (Coucated by Chrstopher
PROCEEDINGS OF THE AERICAN ATHEATICAL SOCIETY Volue 17, Nuber 3, arch 1999, Pages 819 88 S 000-9939(99)05088-1 A CHARACTERIZATION OF THE CLIFFORD TORUS QING-ING CHENG AND SUSUU ISHIKAWA (Coucated by Chrstopher
Chapter 4 Multiple Random Variables
 Revew for the prevous lecture: Theorems ad Examples: How to obta the pmf (pdf) of U = g (, Y) ad V = g (, Y) Chapter 4 Multple Radom Varables Chapter 44 Herarchcal Models ad Mxture Dstrbutos Examples:
Revew for the prevous lecture: Theorems ad Examples: How to obta the pmf (pdf) of U = g (, Y) ad V = g (, Y) Chapter 4 Multple Radom Varables Chapter 44 Herarchcal Models ad Mxture Dstrbutos Examples:
PART ONE. Solutions to Exercises
 PART ONE Soutos to Exercses Chapter Revew of Probabty Soutos to Exercses 1. (a) Probabty dstrbuto fucto for Outcome (umber of heads) 0 1 probabty 0.5 0.50 0.5 Cumuatve probabty dstrbuto fucto for Outcome
PART ONE Soutos to Exercses Chapter Revew of Probabty Soutos to Exercses 1. (a) Probabty dstrbuto fucto for Outcome (umber of heads) 0 1 probabty 0.5 0.50 0.5 Cumuatve probabty dstrbuto fucto for Outcome
QT codes. Some good (optimal or suboptimal) linear codes over F. are obtained from these types of one generator (1 u)-
 Mathematca Computato March 03, Voume, Issue, PP-5 Oe Geerator ( u) -Quas-Twsted Codes over F uf Ja Gao #, Qog Kog Cher Isttute of Mathematcs, Naka Uversty, Ta, 30007, Cha Schoo of Scece, Shadog Uversty
Mathematca Computato March 03, Voume, Issue, PP-5 Oe Geerator ( u) -Quas-Twsted Codes over F uf Ja Gao #, Qog Kog Cher Isttute of Mathematcs, Naka Uversty, Ta, 30007, Cha Schoo of Scece, Shadog Uversty
Spline Estimator for Bi-Responses and Multi-Predictors Nonparametric Regression Model in Case of Longitudinal Data
 Joura of Matheatcs ad Statstcs Orga Research Paper Spe Estator for B-Resposes ad Mut-Predctors Noparaetrc Regresso Mode Case of Loguda Data, Adj Achad Rado Ferades, I Nyoa Budatara, Babag Wdjaarko Otok
Joura of Matheatcs ad Statstcs Orga Research Paper Spe Estator for B-Resposes ad Mut-Predctors Noparaetrc Regresso Mode Case of Loguda Data, Adj Achad Rado Ferades, I Nyoa Budatara, Babag Wdjaarko Otok
Algorithms Theory, Solution for Assignment 2
 Juor-Prof. Dr. Robert Elsässer, Marco Muñz, Phllp Hedegger WS 2009/200 Algorthms Theory, Soluto for Assgmet 2 http://lak.formatk.u-freburg.de/lak_teachg/ws09_0/algo090.php Exercse 2. - Fast Fourer Trasform
Juor-Prof. Dr. Robert Elsässer, Marco Muñz, Phllp Hedegger WS 2009/200 Algorthms Theory, Soluto for Assgmet 2 http://lak.formatk.u-freburg.de/lak_teachg/ws09_0/algo090.php Exercse 2. - Fast Fourer Trasform
STK4011 and STK9011 Autumn 2016
 STK4 ad STK9 Autum 6 Pot estmato Covers (most of the followg materal from chapter 7: Secto 7.: pages 3-3 Secto 7..: pages 3-33 Secto 7..: pages 35-3 Secto 7..3: pages 34-35 Secto 7.3.: pages 33-33 Secto
STK4 ad STK9 Autum 6 Pot estmato Covers (most of the followg materal from chapter 7: Secto 7.: pages 3-3 Secto 7..: pages 3-33 Secto 7..: pages 35-3 Secto 7..3: pages 34-35 Secto 7.3.: pages 33-33 Secto
Conservative Averaging and Finite Difference Methods for Transient Heat Conduction in 3D Fuse
 Ramods Vums Adrs Buks Coservatve Averagg ad Fte Dfferece Metods for Traset Heat Coducto 3D Fuse RAIMONDS VIUMS ANDRIS BUIKIS Isttute of Matematcs ad Computer Scece Uversty of atva Raa uv 9 Rga V459 ATVIA
Ramods Vums Adrs Buks Coservatve Averagg ad Fte Dfferece Metods for Traset Heat Coducto 3D Fuse RAIMONDS VIUMS ANDRIS BUIKIS Isttute of Matematcs ad Computer Scece Uversty of atva Raa uv 9 Rga V459 ATVIA
Interval extension of Bézier curve
 WSEAS TRANSACTIONS o SIGNAL ROCESSING Jucheg L Iterval exteso of Bézer curve JUNCHENG LI Departet of Matheatcs Hua Uversty of Huates Scece ad Techology Dxg Road Loud cty Hua rovce 47 R CHINA E-al: ljucheg8@6co
WSEAS TRANSACTIONS o SIGNAL ROCESSING Jucheg L Iterval exteso of Bézer curve JUNCHENG LI Departet of Matheatcs Hua Uversty of Huates Scece ad Techology Dxg Road Loud cty Hua rovce 47 R CHINA E-al: ljucheg8@6co
ISSN: ISO 9001:2008 Certified International Journal of Engineering and Innovative Technology (IJEIT) Volume 3, Issue 5, November 2013
 A Relable Proceure o Perforace Evaluato - A Large Saple Approach Base o the Estate Taguch Capablty Iex Gu-Hog L Professor, Departet of Iustral Egeerg a Maageet, atoal Kaohsug Uversty of Apple Sceces, Kaohsug,
A Relable Proceure o Perforace Evaluato - A Large Saple Approach Base o the Estate Taguch Capablty Iex Gu-Hog L Professor, Departet of Iustral Egeerg a Maageet, atoal Kaohsug Uversty of Apple Sceces, Kaohsug,
On binomial coefficients modulo squares of primes
 O boa coeffcets oduo squares of pres Darj Grberg arxv:171202095v1 [athco] 6 Dec 2017 Deceber 7, 2017 Abstract We gve eeetary proofs for the Apagodu-Zeberger- Stato-Adeberha-Tauraso cogrueces r 0 s 0 2
O boa coeffcets oduo squares of pres Darj Grberg arxv:171202095v1 [athco] 6 Dec 2017 Deceber 7, 2017 Abstract We gve eeetary proofs for the Apagodu-Zeberger- Stato-Adeberha-Tauraso cogrueces r 0 s 0 2
Symmetry of the Solution of Semidefinite Program by Using Primal-Dual Interior-Point Method
 Syetry of the Soluto of Sedefte Progra by Usg Pral-Dual Iteror-Pot Method Yoshhro Kao Makoto Ohsak ad Naok Katoh Departet of Archtecture ad Archtectural Systes Kyoto Uversty Kyoto 66-85 Japa kao@s-jarchkyoto-uacjp
Syetry of the Soluto of Sedefte Progra by Usg Pral-Dual Iteror-Pot Method Yoshhro Kao Makoto Ohsak ad Naok Katoh Departet of Archtecture ad Archtectural Systes Kyoto Uversty Kyoto 66-85 Japa kao@s-jarchkyoto-uacjp
New Power Series Inequalities and Applications
 Iteratoa Joura of Mathematca Aayss Vo., 207, o. 20, 973-986 HIKARI Ltd, www.m-har.com htts://do.org/0.2988/jma.207.7924 New Power Seres Ieuates ad Acatos Loredaa Curdaru Deartmet of Mathematcs, Potehca
Iteratoa Joura of Mathematca Aayss Vo., 207, o. 20, 973-986 HIKARI Ltd, www.m-har.com htts://do.org/0.2988/jma.207.7924 New Power Seres Ieuates ad Acatos Loredaa Curdaru Deartmet of Mathematcs, Potehca
On Pfaff s solution of the Pfaff problem
 Zur Pfaff scen Lösung des Pfaff scen Probles Mat. Ann. 7 (880) 53-530. On Pfaff s soluton of te Pfaff proble By A. MAYER n Lepzg Translated by D. H. Delpenc Te way tat Pfaff adopted for te ntegraton of
Zur Pfaff scen Lösung des Pfaff scen Probles Mat. Ann. 7 (880) 53-530. On Pfaff s soluton of te Pfaff proble By A. MAYER n Lepzg Translated by D. H. Delpenc Te way tat Pfaff adopted for te ntegraton of
Laboratory I.10 It All Adds Up
 Laboratory I. It All Adds Up Goals The studet wll work wth Rema sums ad evaluate them usg Derve. The studet wll see applcatos of tegrals as accumulatos of chages. The studet wll revew curve fttg sklls.
Laboratory I. It All Adds Up Goals The studet wll work wth Rema sums ad evaluate them usg Derve. The studet wll see applcatos of tegrals as accumulatos of chages. The studet wll revew curve fttg sklls.
CONTRIBUTION OF KRAFT S INEQUALITY TO CODING THEORY
 Pacfc-Asa Joura of Mathematcs, Voume 5, No, Jauary-Jue 20 CONTRIBUTION OF KRAFT S INEQUALITY TO COING THEORY OM PARKASH & PRIYANKA ABSTRACT: Kraft s equaty whch s ecessary ad suffcet codto for the exstece
Pacfc-Asa Joura of Mathematcs, Voume 5, No, Jauary-Jue 20 CONTRIBUTION OF KRAFT S INEQUALITY TO COING THEORY OM PARKASH & PRIYANKA ABSTRACT: Kraft s equaty whch s ecessary ad suffcet codto for the exstece
