arxiv: v4 [math.ap] 14 Apr 2016
|
|
|
- Susanna Willis
- 6 years ago
- Views:
Transcription
1 SOME OBSEVATIONS ON THE GEEN FUNCTION FO THE BALL IN THE FACTIONAL LAPLACE FAMEWOK arxiv:5.6468v4 [math.ap] 4 Apr 6 CLAUDIA BUCU Claudia Bucur Dipartimento di Matematica Federigo Enriques Università degli Studi di Milano Via Cesare Saldini, 5, I-33, Milano, Italy Abstract. We consider a fractional Laplace equation and we give a selfcontained elementary exposition of the representation formula for the Green function on the ball. In this exposition, only elementary calculus techniques will be used, in particular, no probabilistic methods or computer assisted algebraic manipulations are needed. The main result in itself is not new (see for instance [, 9]), however we believe that the exposition is original and easy to follow, hence we hope that this paper will be accessible to a wide audience of young researchers and graduate students that want to approach the subject, and even to professors that would like to present a complete proof in a PhD or Master Degree course. Contents. Introduction. Preliminaries 8.. The s-mean value property 8.. The fundamental solution.3. The Poisson kernel 3. The Green function for the ball Formula of the Green function for the ball epresentation formula for the fractional Poisson equation Computation of the normalization constants 3 Appendix A. Appendix 34 A.. The Gamma, Beta and hypergeometric functions 34 A.. Point inversion transformations 36 A.3. Some useful integral identities 37 Acknowledgments 44 eferences Mathematics Subject Classification. Primary: 35C5, 35S5. Secondary: 35S3, 3B. Key words and phrases. Fractional Laplacian, Green function, Poisson Kernel, Fundamental solution, Mean value property.
2 CLAUDIA BUCU. Introduction The Green function for the ball in a fractional Laplace framework naturally arises in the study of the representation formulas for the fractional Laplace equations. In particular, in analogy to the classical case of the Laplacian, given an equation with a known forcing term on the ball and vanishing Dirichlet data outside the ball, the representation formula for the solution is precisely the convolution of the Green function with the forcing term. As in the classical case, the Green function is introduced in terms of the Poisson kernel. For this, we will provide both the representation formulas for the problems # p q s u in B r, (.) u g in and (.) # p q s u g in B r, u in in terms of the fractional Poisson kernel and respectively the Green function. Moreover, we will prove an explicit formula for the Green function on the ball. Here follow some notations and a few preliminary notions on the fractional Laplace operator and on the four kernels that play particular roles in our study: the s-mean kernel, the fundamental solution, the Poisson kernel and the Green function. We briefly introduce the Schwartz space (refer to [] for details) as the functional space " * Sp n q : f P C 8 p n q β P N n, sup x β D α fpxq ă `8. xp n In other words, the Schwartz space consists of smooth functions whose derivatives (including the function itself) decay at infinity faster than any power of x; we say, for short, that Schwartz functions are rapidly decreasing. Endowed with the family of seminorms (.3) rfs α,n Sp n q sup xp n p ` x q N ÿ α ďn D α fpxq, the Schwartz space is a locally convex topological space. We denote by S p n q the space of tempered distributions, the topological dual of Sp n q. We set the following notations for the Fourier and the inverse Fourier transform (see for instance, [8] for details) pfpξq Ffpξq : n fpxqe πix ξ dx respectively qfpxq F fpxq fpξqe πix ξ dξ. n Here the original space variable is denoted by x P n and the frequency variable by ξ P n. We recall that the Fourier and the inverse transform are well defined for
3 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 3 f P L p n q, whereas fpxq F`F fqpxq F `Ffqpxq almost everywhere if both f and f p P L p n q, and pointwise if f is also continuous. Also for all f, g P L p n q fpξqgpξq p dξ fpξqpgpξq dξ. n n The pointwise product is taken into the convolution product and vice versa, namely for all f, g P L p n q Fpf gq Fpfq Fpgq. On the Schwartz space, the Fourier transform gives a continuous bijection between Sp n q and Sp n q. We say that f p is the Fourier transform of f in a distributional sense, for f that satisfies ş fpxq n ` x dx ă 8 for some p P N if, for any ϕ P Sp n q we p have that (.4) fpxqϕpxq p dx fpxq pϕpxq dx. n n We remark that the integral notation is used in a formal manner whenever the arguments are not integrable. Let s P p, q be fixed. We introduce the fractional Laplacian for u belonging to the Schwartz space. Definition.. The fractional Laplacian of u P Sp n q is defined as p q s upxq upyq upxq : Cpn, sqp.v. dy x y n`s (.5) n upxq upyq Cpn, sq lim dy, εñ n zb εpxq x y n`s where Cpn, sq is a constant depending only on n and s. Here, P.V. is a commonly used abbreviation for in the principal value sense (as defined by the latter equation). The dimensional constant Cpn, sq is given in [4], formula 3., as : ˆ (.6) Cpn, sq : n cospη q η n`s dη, where η is, up to rotations, the first coordinate of η P n. emark.. The definition (.5) is well posed for smooth functions belonging to a weighted L space, that we define as follows. For s P p, q! L sp n q : u P L locp n upxq ) q s.t. ` x n`s dx ă 8, endowed naturally with the norm }u} L s p n q : n n upxq dx. ` x n`s Let ε be positive, sufficiently small. Then indeed, for u P L sp n q and C,s`ε (or C,s`ε for s ě {) in a neighborhood of x P n, the fractional Laplacian is well defined in x as in (.5). See for the proof Proposition..4 in [], where an approximation with Schwartz functions is performed. We often use this type of regularity to obtain pointwise solutions to the posed equations. We will always write C s`ε to denote both C,s`ε for s ă { and C,s`ε for s ě {.
4 4 CLAUDIA BUCU In definition (.5), the singular integral can be substituted with a weighted second order differential quotient by performing the changes of variables ỹ x ` y and ỹ x y and summing up. In this way, the singularity at the origin can be removed, as we observe in the following lemma (see for the proof Section 3. in [3]). Lemma.3. Let p q s be the fractional Laplace operator defined by (.5). Then for any smooth u (.7) p q s Cpn, sq upxq upx ` yq upx yq upxq y n`s dy. n For u P Sp n q the fractional Laplace operator can also be expressed by means of the Fourier transform, according to the following lemma (see Proposition 3.3 in [4] for the proof). Lemma.4. Let p q s be the fractional Laplace operator defined by (.5). Then for any u P Sp n q (.8) p q s upxq F `π ξ spupξq. We refer usually to pointwise solutions, nevertheless distributional solution will also be employed. Following the approach in [] (see Definition..3), we introduce a suitable functional space where distributional solutions can be defined. Let! ) S s p n q : f P C 8 p n q P N n, sup ` ` x n`s D α fpxq ă `8. xp n The linear space S s p n q endowed with the family of seminorms rfs α S sp n q : sup xp n ` ` x n`s D α fpxq is a locally convex topological space. We denote with S sp n q the topological dual of S s p n q. We notice that if ϕ P Sp n q then p q s ϕ P S s p n q, which makes this framework appropriate for the distributional formulation. In order to prove this, we observe that for any x P n zb the bound (.9) p q s ϕpxq ď c n,s x n s follows from the upcoming computation and the fact that ϕ P Sp n q p q s ϕpxq ď B x ˇ ˇϕpxq ϕpx yq ϕpx ` yqˇˇ y n`s dy ` ď c n,s x n sˆ n zb x ˇ ˇϕpxq ϕpx ` yqˇˇ y n`s sup p ` z q n` D ϕpzq ` sup p ` z q n ϕpzq ` }ϕ} L p n q zp n zp n Moreover, we observe that, up to constants, B xi p q s ϕpxq B xi F ξ s pϕpξq pxq F iξ i ξ s pϕpξq pxq F ξ s Bxi zϕpξq pxq p q s B xi ϕpxq. Hence, by iterating the presented argument, one proves that p q s ϕ P S s p n q, which assures our claim. Then we have the following definition. dy.
5 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 5 Definition.5. Let f P S p n q, we say that u P S sp n q is a distributional solution of p q s u f in n if (.) ă u, p q s ϕ ą s fpxqϕpxq dx n for any ϕ P Sp n q, where ă, ą s denotes the duality pairing of S sp n q and S s p n q and the latter (formal) integral notation designates the pairing Sp n q and S p n q. We also use the integral notation for the pairing ă, ą s in a purely formal manner whenever the arguments are not integrable. We notice that the inclusion L sp n q Ă S sp n q holds, in particular for any u P L sp n q and ψ P S s p n q we have (.) ˇ ă u, ψ ą s ˇˇˇ ď upxq ψpxq dx ď n ď rψs S sp n q }u} L s pn q. n upxq ` x n`s p ` x n`s q ψpxq dx We introduce now the four functions A r, Φ, P r and G, namely the s-mean kernel, the fundamental solution, the Poisson kernel and the Green function. The reader can see Section. in [7] for the theory in the classical case. Definition.6. Let r ą be fixed. The function A r is defined by $ & r s cpn, sq (.) A r pyq : p y % r q s y n y P, y P B r, where cpn, sq is a constant depending only on n and s. Definition.7. For any x P n ztu the function Φ is defined by $ & apn, sq x n`s if n s, (.3) Φpxq : % a, log x if n s, where apn, sq is a constant depending only on n and s. Definition.8. Let r ą be fixed. For any x P B r and any y P, the Poisson kernel P r is defined by s (.4) P r py, xq : cpn, sq r x y r x y n. The Poisson kernel is used to build a function which is known outside the ball and s-harmonic in B r. Indeed, it is used to give the representation formula for problem (.), as stated in the following theorem. Theorem.. Let r ą, g P L sp n q X Cp n q and let $ & P r py, xqgpyq dy if x P B r, (.5) u g pxq : % n zb r gpxq if x P.
6 6 CLAUDIA BUCU Then u g is the unique pointwise continuous solution of the problem (.) # p q s u in B r, u g in. Definition.9. Let r ą be fixed. For any x, z P B r and x z, the function G is defined by (.6) Gpx, zq : Φpx zq Φpz yqp r py, xq dy. From this definition, a formula that is more suitable for applications can be deduced. Indeed, one of the main goals is to prove this simpler, explicit formula for the Green function on the ball, by means of elementary calculus techniques. At this purpose, Theorem 3. establishes a symmetrical expression for G. Theorem 3.. Let r ą be fixed and let G be the function defined in (.6). Then if n s (.7) Gpx, zq κpn, sq z x s n rpx,zq where (.8) r px, zq pr x qpr z q r x z t s pt ` q n dt, and κpn, sq is a constant depending only on n and s. For n s, the following holds (.9) Gpx, zq κ, log ˆr xz ` apr x qpr z q r z x This result is not new (see [, 9]), however, the proof we provide uses only calculus techniques, therefore we hope it will be accessible to a wide audience. It makes elementary use of special functions like the Euler-Gamma function, the Beta and the hypergeometric function, that are introduced in the Appendix (see the book [] for details). Moreover, the point inversion transformations and some basic calculus facts, that are also outlined in the Appendix, are used in the course of this proof. The main property of the Green function is stated in the upcoming Theorem 3.. The function G is used to build the solution of an equation with a given forcing term in a ball and vanishing Dirichlet data outside the ball, by convolution with the forcing term. While this convolution property in itself may be easily guessed from the superposition effect induced by the linear character of the equation, the main property that we point out is that the convolution kernel is explicitly given by the function G. Theorem 3.. Let r ą, h P C s`ε pb r q X CpB r q and let $ & hpyqgpx, yq dy if x P B r, upxq : B % r if x P..
7 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 7 Then u is the unique pointwise continuous solution of the problem (.) # p q s u h in B r, u in. The proof is classical, and makes use of the properties and representation formulas involving the two functions Φ and P r. We are also interested in the values of the normalization constants that appear in the definitions of the s-mean kernel (and the Poisson kernel) and of the fundamental solution. We will deal separately with the two cases n s and n s. We have the following definition: Definition.. The constant apn, sq introduced in definition (.3) is apn, sq : Γp n (.) sq for n s, s π n Γpsq a, (.) : for n s. π The constant cpn, sq introduced in definition (.) is (.) cpn, sq : Γp n q sin πs π n `. These constants are used for normalization purposes, and we explicitly clarify how their values arise. However, these values are only needed to compute the constant κpn, sq introduced in Theorem 3., and have no role for the rest of our discussion. The value of κpn, sq is given in terms of the Euler-Gamma function as: Theorem 3.3. The constant κpn, sq introduced in identity (.7) is Γp n κpn, sq q for n s, s π n Γ psq κ, for n s. π One interesting thing that we want to point out here is related to the two constants Cpn, sq and cpn, sq. The constant Cpn, sq is given in [4] in the definition of the fractional Laplacian, and we defined it here in (.6). The constant cpn, sq is introduced in [] in the definition of the s-mean kernel and the Poisson-kernel, and is here given in (.). These two constants are used for different normalization purposes. We observe that they have similar asymptotic properties, however they are not equal. In the following proposition we explicitly compute the value of Cpn, sq defined in (.6). Theorem 3.5. The constant Cpn, sq introduced in (.6) is given by (.3) Cpn, sq s sγ ` n ` s π n Γp sq. This paper is structured as follows: in the Preliminaries (Section ) we introduce some kernels related to the fractional Laplacian. In Subsection. we define the s-mean value property by means of the s-mean kernel and prove that if a function is s-harmonic, then it has the s-mean value property. Subsection. deals with the study of the function Φ as the fundamental solution of the fractional Laplacian. The fractional Poisson kernel is introduced in Subsection.3, and the representation
8 8 CLAUDIA BUCU formula for equation (.) is obtained. Section 3 focuses on the Green function, presenting two main theorems: Theorem 3. gives a more basic formula of the function G for the ball and is treated in Subsection 3.; Theorem 3., that illustrates how the solution to equation (.) is built by means of the function G, is dealt with in Subsection 3.. The computation of the normalization constants introduced along this notes is done in Subsection 3.3. The Appendix A introduces three special functions (Gamma, Beta and hypergeometric), the point inversion transformations and some calculus identities that we use throughout this paper.. Preliminaries In this section, we deal with the s-mean kernel, the fundamental solution and the Poisson kernel. Let s P p, q... The s-mean value property. In this subsection, we define the s-mean value property of the function u, namely, an average property defined by convolution of u with the s-mean kernel. Definition. (s-mean value property). Let x P n. We say that u belonging to L sp n q and continuous in a neighborhood of x has the s-mean value property at x if, for any r ą arbitrarily small, (.) upxq A r upxq. We say that u has the s-mean value property in Ω Ď n if for any r ą arbitrarily small, identity (.) is satisfied at any point x P Ω. The kernel A r defined in (.) is used to state the s-mean value property, which makes it reasonable to say that A r plays the role of the s-mean kernel. The main result that we state here is that if a function has the s-mean value property, then it is s-harmonic (i.e u satisfies the classical relation p q s u ). Theorem.. Let u P L sp n q be C s`ε in a neighborhood of x P n. If u has the s-mean value property at x, then u is s-harmonic at x. Proof. The function u has the s-mean value property for any r ą arbitrarily small, namely upxq A r upxq A r pyqupx yq dy. Using identity (A.9) we obtain that upxq A r pyqupx yq dy cpn, sqr s thus, since r ą (.) upxq upx yq p y r q s dy. y n upxq upx yq p y r q s y n dy, Hence, in order to obtain p q s upxq we prove that upxq upx yq upxq upx yq (.3) lim rñ y n`s dy lim rñ p y r q s y n dy.
9 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 9 Let ą r?. We write the integral in (.) as upxq upx yq p y r q s y n dy (.4) n zb In I pr, q we see that upxq upx yq p y r q s y n dy ` I pr, q ` I pr, q. upxq upx yq p y r q s y n B zb r y y r ă and obtain that upxq upx yq p y r q s y n dy upxq upx yq ď s y n`s P L p n zb, dyq, as u P L sp n q. We can use the dominated convergence theorem, send r Ñ and conclude that upxq upx yq (.5) lim I pr, q rñ y n`s dy. n zb Now, for r ă y ă and u P C s`ε (for s ă {) in a neighborhood of x we have the bound ˇ ˇupxq upx yqˇˇ ď c y s`ε, while for s ě { and u P C,s`ε we use that upxq upx yq y upxq ˇ y` upx tyq upxq dtˇ y upxq p y r q s y n and y upxq y s`n ď y ď cps, εq y s`ε. B zb r ˇ ˇ upx tyq upxqˇ dt Notice that are even functions, hence they vanish when integrated on the symmetrical domain B zb r. Therefore, by setting upxq upx yq (.6) Jpr, q : I pr, q y s`n dy we have that Jpr, q B zb r upxq upx yq y upxq p y r q s y n upxq upx yq y upxq y s`n dy and by passing to polar coordinates and afterwards making the change of variables ρ rt we get Jpr, q ď cps, εq p y r q s y n y n s dy cpn, s, εq y s`ε B zb r ε ˆ ρ r ă cpn, s, εqr ε r t ε ˆ ρ s pρ r q s dρ ts pt q s dt
10 CLAUDIA BUCU since t{pt ` q ą. Now for t P p,? q we have that? ε ˆ? ts t pt q s dt ď cpsq ˆpt q s t s dt cpsq. On the other hand, for t ě? and we have that r lim rñ t? t ε ˆ ts s s ď? t s pt q s dt ď Thus by sending r Ñ we obtain that and therefore in (.6) 8? t ε s dt t 8 ď cpsq? t ε dt cps, εq. lim Jpr, q rñ lim I upxq upx yq pr, q lim rñ rñ B zb r y s`n dy. Using this and (.5) and passing to the limit in (.4), claim (.3) follows and hence the conclusion that p q s upxq... The fundamental solution. We claim that the function Φ plays the role of the fundamental solution of the fractional Laplacian, namely the fractional Laplacian of Φ is equal in the distributional sense to the Dirac Delta function evaluated at zero. The following theorem provides the motivation for this claim. Theorem.3. In the distributional sense (given by definition (.)) p q s Φ δ. The computation of the Fourier transform of the fundamental solution is required in order to prove Theorem.3. Proposition.4. a) For n ą s, let f P L p n q X Cp n q with q f P S s p n q, b) for n ď s, let f P L pq X Cpq X C `p 8, q Y p, `8q with q f P S s pq such that (.7) fpxq ď c x s fpxq ď c x for x P for x ą f pxq ď c x s for ă x ď Then f pxq ď c x for x ą. Φpxqfpxq q dx n pπ x q s fpxq dx. n
11 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN Proof. We notice that the conditions (.7) on f assure that the integrals are well defined. Indeed, since Φ P L sp n q Ă Ssp n q the left hand side is finite thanks to (.). The right hand side is also finite since, for n ą s, fpxq x s dx ď c n sup fpxq ρ n s dρ ` fpxq x s dx n xpb n zb ď c n sup fpxq ` }f} L p n q xpb and for n ď s we have that fpxq x s dx ď fpxq x s dx ` c zb ď }f} L pq ` c. B dx a) For n ą s we prove that (.8) apn, sq x n`s fpxq q dx pπ x q s fpxq dx. n n We use the Fourier transform of the Gaussian distribution as the starting point of the proof. For any δ ą we have that Fpe πδ x q δ n e π x δ. In particular for any f P L p n q and f q P S s p n q (which is a subspace of L p n q), by Parseval identity we obtain n n fpxq q dx δ e π x δ fpxq dx. n e πδ x We multiply both sides by δ n s, integrate in δ from to 8. We use the notations 8 I δ n s e πδ x fpxq q dx dδ n and I 8 x δ s e π δ fpxq dx dδ, n having I I. We perform in I the change of variable α δ x and obtain that 8 I x n`s fpxq q α n s e πα dα dx. n We set (.9) c : 8 α n s e πα dα, which is a finite quantity since n s ą. On the other hand in I we change the variable α x {δ and obtain that 8 I α s e πα dα dx. We then set n x s fpxq (.) c : 8 α s e πα dα,
12 CLAUDIA BUCU which is finite since s ą. As I I it yields that c x n`s fpxq q dx pπ x q s c pπq s fpxq dx. n n We take (.) apn, sq c c pπq s and the claim (.8) follows. This concludes the proof for n ą s. b) For n ă s (hence n and s ą {), let ą be as large as we wish (we will make go to 8 in sequel). Then x s fpxq q dx x qfpxq ` fp xq q dx B x s fpξq cospπξxq dξ dx fpξq x s cospπξxq dx dξ. We use the change of variables x πx (but still write x as the variable of integration for simplicity) and let π. Then x s cospπξxq dx pπq s x s cospξxq dx. We have that x B s fpxq q s dx π s fpξq x s cospξxq dx Integrating by parts and changing variables ξ x t we obtain that Therefore x s s sinpξxq cospξxq dx x ξ ˇ (.) x B s fpxq q s dx We claim that π s s sinpξ q ξ s s ps q π s ps q dξ. s sinpξxq x dx ξ ξ ps q ξ s t s sin t dt. sinpξ q fpξq dξ ξ ξ fpξq ξ sˆ (.3) lim s sinpξ q fpξq dξ. Ñ8 ξ t s sin t dt dξ.
13 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 3 We integrate by parts and obtain that 8 sinpξ q ˇ fpξq dξ ξ ˇ ď fpξq cospξ q ξ ˇ ` By (.7), for ξ large we have that 8 8 cospξ q f pξq ξ ` ˆ 8 f pξq cospξ ξ q cospξ ď c q ξ, hence lim For ξ small we have that f pξq ξ ď c ξ s fpξq, hence lim ξñ ξ dξ. fpξq ξñ8 ξ cospξ cospξ q q fpξq ξ cospξ q.. Furthermore, by changing variables t ξ (and noticing that the constants may change value from line to line) we have that 8 and 8 Hence f pξq ξ cospξ q dξ ď c f pξq cospξ ξ q dξ ď c ď c s ξ s cospξ q dξ ` c 8 t s cos t dt ` c ξ s cospξ q dξ ` c 8 ď c s t s cos t dt ` c ˇˇˇ ˇ 8 sinpξ q fpξq ξ and in the same way we obtain sinpξ q ˇ fpξq dξ ξ ˇ ˇ 8 8 dξ ˇ ď c, sinpξ q fp ξq ξ ξ 3 cospξ q dξ 8 dξ t 3 cos t dt ď c ξ cospξ q dξ 8 dξ ˇ ď c. t cos t dt ď c. Therefore lim s sinpξ q fpξq dξ Ñ8 ξ and we have proved the claim (.3). Now we claim that (and this holds also for n s) (.4) lim Ñ8 fpξq ξ s ξ t s sin t dt dξ cospπsqγps q fpξq ξ s dξ. In order to prove this, we estimate the difference 8 ξ ˇ t s sin t dt t s sin t dt ˇ ď 8 ˇ t s sin t dt ˇ ξ 8 8 ď t s cos t ˇ ` ps q t s 3 cos t dt ď cp ξ q s. ξ ξ
14 4 CLAUDIA BUCU We then have that 8 ˇ fpξq ξ s t s sin t dt ď c s Hence we obtain ξ fpξq ξ s lim Ñ8 ď c s ˆ ξ fpξq ξ dξ c ξ s dξ ` c 8 t s sin t dt dξ t s sin t dt dξ ˇ ξ 3 dξ s c. fpξq ξ s ˆ 8 t s sin t dt dξ and the claim (.4) follows from the identity (A.36) in the Appendix. By sending to infinity in (.) we finally obtain that x s q s fpxq dx π s ps q cospπsqγps q ξ s fpξq dξ (.5) cospπsqγpsq pπ ξ q s fpξq dξ. Therefore taking ap, sq p cospπsqγpsqq we obtain that ap, sq x s fpxq q dx pπ x q s fpxq dx, hence the result for n ă s. Now, for n s we have that log x fpxq q dx B fpξq log x cospπξxq dx dξ. We change variables x πx (but still write x as the variable of integration for simplicity) and let π. Then we have that log x cospπξxq dx π We integrate by parts and obtain that log x cospξxq dx log We thus have that log x fpxq q dx B π log We claim that (.6) lim log Ñ8 log x logpπq cospξxq dx π log x cospξxq dx logpπq π sinpξ q ξ ξ sin t dt. ξ t sinpξ q. ξ sinpξ q fpξq dξ ξ fpξq ξ sin t dt dξ. ξ π t sinpξ q fpξq dξ. ξ
15 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 5 Indeed we have that { sinpξ q ˇ fpξq dξ ξ ˇ ď { Moreover integrating by parts we have that 8 sinpξ q ˇ fpξq dξ ξ ˇ ď fpξq cospξ q ξ ˇ { We have that for ξ large 8 ` { fpξq ξ ξ dξ ď c 8 { { ` 8 { f pξq cospξ ξ q dξ f pξq cospξ q ď c cospξ ξ q ξ hence f pξq cospξ lim q. ξñ8 ξ On the other hand by using the change of variables t ξ 8 { Moreover 8 { Hence f pξq ξ cospξ q dξ ď c { c f pξq cospξ ξ q dξ ď c c { lim log Ñ8 cospξ q ξ cos t t cospξ q ξ cos t t 8 dξ ` c 8 dt ` c 8 dt ` c dξ ` c 8. ξ dξ c. f pξq ξ cospξ q dξ cospξ q ξ 3 dξ t 3 cos t dt ď c log ` c. 8 sinpξ q fpξq dξ ξ and since the same bounds hold for ş 8 Also, the proof of the claim (.4) assures us that lim Ñ8 8 fpξq ξ ˆ ξ sin t t dt dξ fpξq sinpξ q ξ π 8 8 cospξ q ξ dξ t cos t dt ď c log ` c. dξ, the claim (.6) follows. fpξq ξ ˆ 8 fpξq ξ dξ. sin t t dt dξ It follows that log x fpxq q dx ξ fpξq dξ, hence (.7) log x fpxq π q dx pπ ξ q fpξq dξ and the result holds for n s. This concludes the proof of the Proposition.
16 6 CLAUDIA BUCU emark.5. It is now clear that we have chosen apn, sq in Definition. in order to normalize the Fourier transform of the fundamental solution. Indeed, for n ą s, we perform the change of variable πα t in (.9) and by (A.) we obtain that c π s n 8 t n s e t dt π s n Γˆn s Also in (.) we change the variable πα t and get that Therefore 8 c π s t s e t dt π s Γpsq. c πs n Γp n sq, hence by (.) apn, sq Γp n sq c Γpsq s π n Γpsq. The value ap, sq is computed in (.5). We point out that we can rewrite this value using (A.6) and (A.4), as follows ap, sq Γp{ sq cospπsqγpsq s? πγpsq. Moreover, we observe that identity (.7) says that ˆ a, π. By applying this latter Proposition.4, we prove Theorem.3. Proof of Theorem.3. For any f P Sp n q we have that F ξ s fpξq p P S s p n q (according to definition (.8) and to (.9)). Notice that ξ s fpξq p P L p n qxcp n q, since x s fpxq p dx ď rfs p,n` Sp n q n x s n dx ` sup fpxq p ď cpfq, n zb xpb where we use the seminorm defined in (.3). Moreover, for n ď s we have that. ξ s p fpξq ď } p f} L 8 pq ξ s c ξ s for ξ P, ξ s p fpξq ď r p fpξqs,3 Spq ξ s 3 ď c ξ Also for ξ ď ˇ d s ` ξ fpξq ˇˇˇ p ď s ξ s fpξq dξ p ` ξ sˇˇˇ d fpξq dξ p ˇ ď ξ s ˆs} f} p L8 pq ` d fpξq p dξ for ξ ą. L8 pq and for ξ ą ˇ d s ` ξ fpξq ˇˇˇ p ď s ξ s fpξq dξ p ` ξ sˇˇˇ d fpξq dξ p ˇ c ξ s ď sr p fs, Spq ξ s 3 ` ξ s 3 r p fs,3 Spq ď c ξ,
17 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 7 which proves that f satisfies (.7). From Proposition.4 it follows that ă Φ, p q s f ą s ΦpxqF pπ ξ q fpξq s p pxq dx n pπ ξ q s pπ ξ q s fpξq p dξ fpξq p dξ fpq. n n Therefore in the distributional sense p q s Φ δ. We have the following Lemma. Lemma.6. Let f P C c p n q, then f Φ P L sp n q. Proof. To prove that f Φ P L sp n q, we suppose that supp f Ď B and we compute ˆ f Φpxq Φpx yq dx fpyq dx dy ` x n`s n B ` x n`s ˆ n Φpx yq ď }f} L8 p n q dx dy. ` x n`s We set (.8) c n,s, : B ˆ n B n Φpx yq dx dy ` x n`s and prove it is a finite quantity. We take for simplicity and remark that the constants in the next computations may change value from line to line. For n ą s we have that ˆ ˆ Φpx yq n x y s n dx dy apn, sq dx dy. B ` x n`s n B ` x n`s For x small we have that ˆ x y B B s n ˆ dx dy ď x y s n dx dy ` x n`s B B ˆ ` y ď c n t s dt dy B c n,s p ` tq s t n dt c n,s. For x large, we use that x y ě x y and ` x n`s ą x n`s, thus ˆ x y B nzb s n ˆ dx dy ď p x y q s n x n s dx dy ` x n`s B n zb n ˆ 8 c n t pρ tq s n ρ n s ρ n dρ dt 8 ď c n pρ q s n dρ c n,s.
18 8 CLAUDIA BUCU Hence for n ą s the quantity c n,s, in (.8) is finite. Meanwhile, for n ă s for x small the same bound as for n ą s holds. For x large, we have that ˆ x y B zb s ˆ dx dy ď p x ` y q s x s dx dy ` x `s B zb ˆ 8 c pρ ` tq s ρ s dρ dt c s. In the case n s from the triangle inequality we have that ˆ log x y B ` x dx dy ď c logpt ` q dt c and B B ˆ log x y zb ` x dx dy ď 8 logpt ` qt dt c. Hence c n,s, in (.8) is finite and we have that f Φpxqpxq (.9) ` x n`s dx ď c n,s,}f} L 8 p n q. n It follows that f Φ P L sp n q, as stated. Before continuing with the main result of this section, we introduce the following lemma, that will be the main ingredient in the proof of the upcoming Theorem.8. Lemma.7. Let f P C 8 c p n q, let ϕ be an arbitrary function such that we have qϕ P S s p n q and the following hold: a) for n ą s, ϕ P L p n q X Cp n q, b) for n ď s, ϕ P L pq X Cpq X C `p 8, q Y p, 8q q and Then (.) ϕpxq ď c x s ϕpxq ď c x for x P for x ą ϕ pxq ď c x s for ă x ď ϕ pxq ď c x for x ą. f Φpxq qϕpxq dx pπ x q s fpxqϕpxq q dx. n n Proof. In order to prove identity (.) we notice that by the Fubini-Tonelli theorem we have that ˆ f Φpxq qϕpxqdx Φpyqfpx yq dy qϕpxq dx n n n ˆ Φpyq fpx yq qϕpxq dx dy. n n We denote f qϕpyq : fpx yq qϕpxq dx fpxq qϕpx ` yq dx n n
19 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 9 and write (.) f Φpxq qϕpxqdx Φpyqf qϕpyq dy. n n The operation is well defined for f P C 8 c p n q and qϕ P S s p n q, furthermore it is easy to see that Fpf qϕqpxq q fpxqϕpxq. We notice at first that since ϕ and qϕ are continuous, Fp qϕq ϕ on n. We define (.) ψpxq : Fpf qϕqpxq q fpxqϕpxq and we write (.) as (.3) f Φpxq qϕpxqdx n Φpyqψpyq q dy. n To apply Proposition.4, we have to check that ψ verifies (.7). Since ψpxq dx fpxq ϕpxq q dx ď } f} q L8 p n q}ϕ} L p n q, n n we have that ψ P L p n q. Also, ψ P Cp n q as a product of continuous functions. We claim that f qϕ P S s p n q. Indeed, suppose supp f Ď B for ą. We remark that in the next computations the constants may change from line to line. Then for x ď we have that p ` x n`s q f qϕpxq ď c n,s, fpy xq qϕpyq dy For x ą we have that B pxq ď c n,s, }f} L8 pb q} qϕ} L8 pb 3 q. x n`s f qϕpxq ď }f} L 8 pb qr qϕs S sp n q x n`s B x ` y n s dy and we remark that y ď x { (otherwise y supp f). Then we use the bound x ` y ě x y ě x { and we have that x n`s f qϕpxq ď }f} 8 r qϕs S sp n q x n`s B x n s dy c n,s,. We can iterate the same method to prove that p ` x n`s q D α f qϕpxq is bounded since D α f qϕpxq f D α qϕpxq and D α qϕ P S s p n q. For n ď s we have that ψpxq ď q fpxq ϕpxq ď } q f} L8 pqc x s for x ď, c ψpxq ď fpxq ϕpxq q ď } f} q L8 pq x for x ą. Moreover, for x ą ψ pxq ď fpxq ϕ q pxq ` ˇ d fpxqϕpxq dx q ˇ ď } f} q c L8 pq x ` ˇ fpξqpiξqe ixξ ˇ dξˇ ϕpxq ď } f} q c L 8 pq x ` }ξfpξq} L pq x ď C x c
20 CLAUDIA BUCU and for x ď, since f P Cc 8 pq ψ pxq ď fpxq ϕ q pxq ` ˇ d fpxq dx q ˇ ˇ ϕpxq ď } q f} L8 pqc x s ` c x s }ξfpξq} L8 pq x C x s. Hence ψ satisfies (.7). Taking into account (.3) and applying Proposition.4 we have that f Φpxq qϕpxq dx n Φpxqψpxq q dx n ψpxq dx, n and from (.) we conclude that f Φpxq qϕpxq dx pπ x q s fpxqϕpxq q dx. n n The function Φ gives the representation formula for equation p q s u f both in the distributional sense and pointwise. Theorem.8. Let f P Cc s`ε p n q and let u be defined as upxq : Φ f pxq. Then u P L sp n q and in the distributional sense p q s u f. Moreover, u P C s`ε p n q and pointwise in n p q s upxq fpxq. Proof. From Lemma.6, we have that u P L sp n q. We prove at first the statement for f P Cc 8 p n q. We notice that for ϕ P Sp n q, the function F ppπ ξq s pϕpξqq P S s p n q and pπ ξq s pϕpξq satisfies the hypothesis of Lemma.7. Hence, by (.) ă upxq, p q s ϕ ą s f ΦpxqF pπ ξ q s pϕpξq pxq dx n fpξq q pϕpξq dξ fpxqϕpxq dx. n n The last equality follows since q f P L p n q, which is assured by the infinite differentiability of f. We conclude that u is the distributional solution of p q s u f. We consider now f P Cc s`ε p n q. We take a sequence of functions pf k q k P Cc 8 p n q such that }f k f} L 8 p n q ÝÑ and we consider u k Φ f k. Then we kñ8 have that for any ϕ P Sp n q ă u k, p q s ϕ ą s f k pxqϕpxq dx. n By definition of f k lim kñ`8 f k pxqϕpxq dx n fpxqϕpxq dx, n
21 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN moreover, using (.) and (.9) we have that ă u k u, p q s ϕ ą s ď rp q s ϕs S sp n q }u k u} L s p n q ď c n,s, rp q s ϕs S sp n q }f k f} L 8 p n q ÝÑ kñ8. We thus obtain that for any ϕ P Sp n q ă u, p q s ϕ ą s fpxqϕpxq dx. n Hence in the distributional sense p q s u f on n for any f P Cc s`ε p n q. To obtain the pointwise solution, we notice that thanks to Theorem 9.3 in [3] we have that u P C s`ε p n q. This, together with the fact that u P L sp n q implies that the fractional Laplacian of u is well defined, according to emark.. Moreover, from the continuity of the mapping n Q x ÞÑ p q s upxq, according to Proposition..7 from [], we have that ş p q s upxqϕpxq dx is well defined. For any ϕ P C 8 n c p n q we have that upxqp q s ϕpxq dx n fpxqϕpxq dx. n Thanks to Fubini-Tonelli s Theorem and changing variables we obtain that for any ϕ P Cc 8 p n q fpxqϕpxq dx n upxqp q s ϕpxq dx n p q s upxqϕpxq dx. n Since both f and p q s u are continuous, we conclude that pointwise in n p q s upxq fpxq. As a corollary, we have a representation formula for a C 8 c p n q function. Corollary.9. For any f P C 8 c p n q there exists a function ϕ P C 8 p n q such that and ϕpxq Op x n s q as x Ñ 8. Proof. For f P C 8 c p n q, we define ϕ as fpxq ϕ Φpxq, ϕpxq : p q s fpxq. The bound established in (.9) assures the asymptotic behavior of ϕ, while it is not hard to see that ϕ P C 8 p n q. Then by using Theorem.8 we have that pointwise in n ϕ Φpxq p q s f Φpxq fpxq..3. The Poisson kernel. We claim that P r plays the role of the fractional Poisson kernel. Indeed, the function P r arises in the construction of the solution to Dirichlet problem with vanishing Laplacian inside the ball and a known forcing term outside the ball, as stated in the next Theorem.. Theorem.. Let r ą, g P L sp n q X Cp n q and let $ & P r py, xqgpyq dy if x P B r, (.4) u g pxq : % n zb r gpxq if x P.
22 CLAUDIA BUCU Then u g is the unique pointwise continuous solution of the problem (.) # p q s u in B r, u g in. Proof of Theorem.. We see at first that u g P L sp n q. Take ą r and x P B r, then by using (A.), the inequality x y ą y r and for y ą the bound (.5) we have that u g pxq ď ą y ąr ď cpn, sq y n`s p y r q s x y n ď n`s P r py, xq gpyq dy ` P r py, xq gpyq dy y ą sup gpyq ` n`s cpn, sqpr x q s ypb zb r ď cpn, sq sup gpyq ` n`s cpn, sqr s ypb zb r y ą y ą gpyq dy. y n`s gpyq dy y n`s Since g P L sp n q, the last integral is bounded, and so u g is bounded in B r. It follows that u g P L sp n q, as stated. Moreover, the local C 8 regularity of u g in B r follows from the regularity of the Poisson kernel. Let us fix x P B r and prove that u g has the s-mean value property in x. If this holds, indeed, Theorem. implies that p q s upxq, and given the arbitrary choice of x, the same is true in the whole B r. We claim that for any ρ such that ă ρ ă r x we have (.6) A ρ u g pxq u g pxq. Let at first g be in Cc 8 p n q. By Corollary.9, there exists a function ϕ P C 8 p n q such that gpyq Φpz yqϕpzq dz n and at infinity ϕpzq Op z n s q. For r ą fixed, we write g as (.7) gpyq Φpt yqϕptq dt ` Φpz yqϕpzq dz. B r Using identity (A.33) we have that ˆ Φpz yqϕpzq dz P r pt, zqφpy tq dt ϕpzq dz B r B r ˆ Φpy tq P r pt, zqϕpzq dz dt. B r Therefore, in (.7) it follows that (.8) gpyq Φpy tqψptq dt,
23 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 3 where ψptq ϕptq ` şb r P r pt, zqϕpzq dz. In particular, using (.4) and (.8) we have that ˆ u g pxq P r py, xq Φpy tqψptq dt dy y ąr t ąr ˆ ψptq P r py, xqφpy tq dy dt ψptqφpx tq dt t ąr y ąr thanks to (A.33). Furthermore, we compute ˆ A ρ u g pxq A ρ pyq y ąρ t ąr t ąr ψptqφpx y tq dt t ąr ˆ ψptq A ρ pyqφpx y tq dy y ąρ dy dt. Having chosen ρ ď r x we have that x t ě t x ě ρ and from (A.3) we obtain A ρ u g pxq ψptqφpx tq dt. t ąr Consequently A ρ u g pxq u g pxq, thus for g P C 8 c p n q the claim (.6) is proved. We now prove the claim (.6) for any forcing term g P L sp n q X Cp n q. In particular, let η k P Cc 8 p n q be such that η k pxq P r, s, η k in B k and η k in B k`. Then g k : η k g P Cc 8 p n q and we have that g k ÝÑ g pointwise in n, in kñ8 norm L sp n q and uniformly on compact sets. So, for any k ě the function u gk pxq has the s-mean value property in x. Precisely, for any ρ ą small independent of k, (.9) `Aρ u gk pxq ugk pxq. We claim that (.3) lim kñ8 u gk pxq u g pxq and that for any ρ ą small (.3) lim kñ8 `Aρ u gk pxq Aρ u g pxq. Let ε be any arbitrarily small quantity. For k large and ą r, we take advantage of (.5) and obtain that for x P B r u gk pxq u g pxq ď g k pyq gpyq P r py, xq dy ď n`s cpn, sqpr x q s g k pyq gpyq n zb y n`s dy ` sup g k pyq gpyq P r py, xq dy ypb zb r B zb r g k pyq gpyq ď cpn, s, rq n zb y n`s dy ` sup g k pyq gpyq ď ε ypb zb r by the convergence in L sp n q norm, the uniform convergence on compact sets of g k to g and integrability in of the Poisson kernel (by identity (A.)). Hence,
24 4 CLAUDIA BUCU claim (.3) is proved. In order to prove claim (.3), we notice that for any ρ ą small we have that A ρ u gk pxq A ρ u g pxq ď A ρ pyq u gk px yq u g px yq dy (.3) ď y ąρ y ąρ x y ěr ` z ąr I ` I. A ρ pyq g k px yq gpx yq dy g k pzq gpzq y ąρ x y ăr A ρ pyqp r pz, x yqdy dz Let ą ρ. Thanks to the bound (.5) for y ą, the convergence in L sp n q norm, the uniform convergence on compact sets of g k to g and the integrability in n zb ρ of the s-mean kernel (by identity (A.9)) we have that for k large I cpn, sqr s g k px yq gpx yq y ąρ p y ρ q s y n dy x y ěr ď n`s g k px yq gpx yq cpn, s, rq dy y ą y n`s ` sup g k px yq gpx yq ypb zb ρ ą y ąρ A ρ pyq dy ď ε. Once more, for ą r and z ą we use the bound (.5) and we have that I g k pzq gpzq A ρ pyqp r pz, x yqdy dz z ą ` ą z ąr y ąρ x y ăr g k pzq gpzq y ąρ x y ăr A ρ pyqp r pz, x yq dy dz ď cpn, sq A ρ pyqpr x y q s g k pzq gpzq y ąρ z ą p z r q s dz dy z x`y n x y ăr ` sup g k pzq gpzq A ρ pyq P r pz, x yq dz dy y ąρ zpb zb r ą z ąr x y ăr g k pzq gpzq ď cpn, s, rq z ą z n`s dz ` sup g k pzq gpzq zpb zb r since by identity (A.9) and (A.) A ρ pyq y ąρ x y ăr ą z ąr P r pz, y xq dz dy ď. Therefore again by the convergence in L sp n q norm, the uniform convergence on compact sets of g k we have that I ď ε. In (.3) it follows that thus the desired result (.3). lim `Aρ u gk pxq Aρ u g pxq, kñ8
25 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 5 By (.9), (.3) and (.3) we have that A ρ u g pxq lim kñ8 A ρ u gk pxq lim kñ8 u gk pxq u g pxq, thus u g has the s-mean value property at x. This concludes the proof of the claim (.6). We now prove the continuity of u g. Of course, u g is continuous in B r and in. We need to check the continuity at the boundary of B r. Let y P BB r and ε ą arbitrarily small to be fixed, δ ε ą be such that, if y P B δε py q then gpyq gpy q ă ε. We fix µ arbitrarily small such that ă µ ă δε, ą r, and x P B r X B µ py q. Notice that r x pr ` x qpr x q ă r y x ă rµ. From (A.) we have that (.33) u g pxq gpy q ď ˇˇgpyq gpy qˇˇp r py, xq dy. For r ă y ă and y y ě δ ε we have that x y ě δ ε µ ą δε. Meanwhile, for y ą we use the bound (.5). We have that gpyq gpy q P r py, xq dy y ąr y y ěδ ε ď cpn, s, qµ sˆn δ n ε gpyq ` gpy q ą y ąr p y r q s y y ěδ ε dy ` n`s ď cpn, s, qµ sˆn δε n cpr,, s, gq ` n`s }g} L s p n q ` cpg, s, q Cpn, s,, r, g, δ ε qµ s. From this and the fact that gpyq gpy q P r py, xq dy ď ε y ąr y y ăδ ε y ą gpyq ` gpy q y n`s P r py, xq dy ε dy by (A.) and the continuity of g, we can pass to the limit in (.33). Sending first µ Ñ and afterwards ε Ñ we obtain that lim xñy `ug pxq gpy q, thus the continuity of u g. The uniqueness of the solution follows from the Maximum Principle. Indeed, if one takes u and u two different continuous solutions of the Dirichlet problem, then u u u is a continuous solution to the problem p q s upxq, in B r upxq, in. By Theorem in [3], the solution u is constant, hence null since it is continuous in n and vanishing outside of B r. This concludes the proof of the Theorem.
26 6 CLAUDIA BUCU 3. The Green function for the ball The purpose of this section is to prove Theorems 3. and 3.. Theorem 3. introduces a formula for the Green function on the ball, that is more suitable for applications. In Theorem 3. the solution to the Dirichlet problem with vanishing data outside the ball and a given term inside the ball is built in terms of the Green function. We also compute the normalization constants needed in the formula of the Green function on the ball. 3.. Formula of the Green function for the ball. This subsection focuses on the proof of Theorem 3., that we recall here. Theorem 3.. Let r ą be fixed and let G be the function defined in (.6). Then if n s rpx,zq Gpx, zq κpn, sq z x s n t s dt, pt ` q n where (3.) r px, zq pr x qpr z q r x z and κpn, sq is a constant depending only on n and s. For n s, the following holds (3.) Gpx, zq κ, ˆr xz ` apr log x qpr z q. r z x We consider the three cases n ą s, n ă s and n s separately. Proof of Theorem 3. for n ą s. Let x, z P B r be fixed. We insert the explicit formula (.3) into definition (.6) and obtain that (3.3) Gpx, zq apn, sq` z x s n Apx, zq, where Apx, zq : y ąr P r py, xq dy. y z n s Inserting also definition (.4) we have that pr x q s Apx, zq cpn, sq y z n s p y r q s y x n dy. y ąr We use the point inversion transformation that is detailed in the Appendix. Let x P and y P B r be the inversion of x, respectively y with center at z, defined by the relation (A.7). With this transformation, using formulas (A.8a), (A.8b) and (A.8c) we obtain that Apx, zq cpn, sq z x s n p x r q s pr y q s x y n dy. B r We continue the proof for n ą 3. However, the results hold for n ď 3 and can be proved with similar computations. We use hyperspherical coordinates with ρ ą and θ, θ,..., θ n 3 P r, πs, θ n P r, πs (see (A.3) in the Appendix and observations therein). Without loss of generality and up to rotations, we assume
27 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 7 that x x e n, so we have the identity x y ρ ` x x ρ cos θ (see Figure in the Appendix for clarity). With this change of coordinates, we obtain Apx, zq cpn, sq z x s n p x r q s π r n 3 ź k π sin k θ dθ ρ n ˆ π sin n θ pr ρ q s dθ dρ. pρ ` x x ρ cos θqn{ Let τ : x ρ (notice that τ ą ). We have that π sin n θ π sin n θ dθ pρ ` x x ρ cos θqn{ ρ n dθ. pτ ` τ cos θqn{ Thanks to identity (A.34) we obtain that π sin n θ dθ pρ ` x x ρ cos θqn{ ρ n τ n pτ sin n α dα q π x n p x ρ sin n α dα. q Then, using identity (A.35) and inserting the explicit value of cpn, sq given by (.), we arrive at (3.4) where Apx, zq sinpπsq ` x z x s n r s π x n sinpπsq ` x z x s n r s π x n Jpx q r r Jpx q, ρ n pr ρ q s p x ρ q dρ. Now we define the constant (3.5) kpn, sq : ˆ τ n s p τ q s dτ π ρ n pr ρ q s p x ρ q dρ (we compute its explicit value in Subsection 3.3). Then we have that r ρ n ˆ Jpx q kpn, sq pr ρ q s p x ρ τ n s p τ q s dτ dρ. q We perform the change of variables t τρ and apply the Fubini-Tonelli s theorem to obtain that r ˆ ρ ρ Jpx q kpn, sq pr ρ q s p x ρ t n s pρ t q s dt dρ q n s ˆ r r ρpρ t q s kpn, sq t pr ρ q s p x ρ q dρ dt. t
28 8 CLAUDIA BUCU We change variables ρ t τ and r τ t ρ to obtain where Jpx q kpn, sq kpn, sq kpn, sq r r r n s ˆ r t t t n s ˆ r t t n s Iptq dt, Iptq r t τ s pr τ t q s p x τ t q dτ pr t ρq s ρ s p x ` ρ r q dρ dt pr t ρq s ρ s p x ` ρ r q dρ. Using Proposition A. for α r t and β x r we have that Iptq π p x t q s sinpπsq p x r q s. dt Hence in Jpx q, with the changes of variables x t τ and then τ t we have that π r Jpx q kpn, sq sinpπsq p x r q s t n s p x t q s dt. π x n kpn, sq sinpπsq p x r q s π x n kpn, sq sinpπsq p x r q s 8 x r 8 x r r pτ q s dτ τ n ts dt. pt ` qn{ Using formula (A.8a) and definition (3.) we have the equalities x r r pr x qpr z q r x z Therefore inserting Jpx q into (3.4) it follows that Apx, zq kpn, sq z x s n 8 By inserting this into (3.3) we obtain that r px,zq Gpx, zq apn, sq z x s nˆ kpn, sq 8 r px, zq. t s dt. pt ` qn{ r px,zq t s dt. pt ` qn{ Now we change the variable t {τ in definition (3.5) and obtain that (3.6) kpn, sq It follows that We set 8 t s pt ` q n dt. Gpx, zq apn, sqkpn, sq z x s n rpx,zq (3.7) κpn, sq : apn, sqkpn, sq t s pt ` q n dt.
29 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 9 and conclude that Gpx, zq κpn, sq z x s n rpx,zq Hence the desired result in the case n ą s. t s pt ` q n Proof of Theorem 3. for n ă s. We consider without loss of generality r (by rescaling, the statement of the theorem is verified in the more general case). By (.3) and definition (.6) we have that (3.8) Gpx, zq ap, sq` z x s Apx, zq, where Apx, zq : Using definition (.4) we have that Apx, zq cp, sq zp,q zp,q P py, xq dy. z y s dt. p x q s y z s py q s y x dy. We proceed exactly as in the case n ą s performing the point inversion transformation and we arrive at Apx, zq cp, sq z x s where x ą. By symmetry we have that px q s p y q s x y dy, (3.9) Apx, zq cp, sq z x s px q s x Jpx q, with Jpx q p y q s px y q dy. We change the variable y t and obtain that Jpx q t { p tq s t x x dt. By the integral representation (A.4) of the hypergeometric function, it follows that Γp ˆ qγp sq Jpx q x Γp 3 sq F,, 3 s,. x We use the linear transformation (A.5d) (notice that `{x ă ) and obtain that (3.) ˆ F,, 3 s, Γp 3 sqγp sq ˆ x Γp, x sqγp sqf, s `, x s ˆx Γp 3 ` sqγpsq ˆ x x ΓpqΓp q F s, s, s,. x The first hypergeometric function obtained in the sum (3.) is transformed according to (A.5c) as ˆ F, x, s `, ˆ x F, s, s `, x. x
30 3 CLAUDIA BUCU For s ` ą s ą and x ă the convergence conditions are fulfilled for the integral representation (A.4) of the hypergeometric function. Therefore we may write ˆ F, x, s `, Γps ` q x x Γpsq t s ` ` px qt { dt. On the other hand, for the second hypergeometric function obtained in identity (3.), we use transformations (A.5b) and (A.5c) and arrive at ˆ x F s, s, s, ˆ x s x F s,, s, x x x s x F ˆ,, s, x x We use the Gauss expansion (A.) with a, b x, c s and w (we notice that ą c a b ą for s ą { and w ă, thus the series is convergent). Since a, all the terms of the series vanish, except for k. Hence we obtain that and therefore Consequently Jpx q x ˆ F, x, s, x ˆ x F s, s, s, x s x. x ˆΓp qγp sqγps ` q Γp sqγpsq. t s ΓpsqΓp sq dt `. ` ` px qt { px q s We recall that cp, sq `ΓpsqΓp sq and we define the constant (3.) kp, sq : cp, sq Γp qγp sqγps ` q Γp sqγpsq. We insert Jpx q into (3.9) and have that Apx, zq kp, sq z x s px q s t s ` ` px qt { dt ` z x s. With the change of variables px qt τ we obtain that x Apx, zq kp, sq z x s t s pt ` q dt ` z x s. Inserting this into (3.8) and noticing that x r px, zq it follows that We call Gpx, zq ap, sqkp, sq z x s rpx,zq (3.) κp, sq ap, sqkp, sq and conclude the proof of Theorem 3. for n ă s. t s pt ` q dt.
31 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 3 Proof of Theorem 3. for n s. Without loss of generality, we assume r. We insert the explicit formulas (.3) and (.4) into definition (.6). Moreover, we use the explicit values of the constant a, from (.) and c, from (.). We obtain that (3.3) Gpx, zq d x log x z ` π π log y z dy y x y. Let Apx, zq : y ě y ě d x log y z dy y x y. We perform the change of variables v yx y x. Since v ě, we have that v ď. We set w : xz z x and observe that w ě. It follows that ˆ v w dv Apx, zq log ` log z x? v x. v v ď We use identity (A.3) and since w ě and x ď we obtain that Apx, zq π log w { ` pw q ` π log x z Inserting this into (3.3) we obtain that π logp zx ` ap x qp z qq. Gpx, zq π log ˆ zx ` a p x qp z q x z This completes the proof of Theorem 3. for n s. 3.. epresentation formula for the fractional Poisson equation. This subsection is dedicated to the proof of Theorem 3., which we recall here. Theorem 3.. Let r ą, h P C s`ε pb r q X CpB r q and let $ & hpyqgpx, yq dy if x P B r, upxq : B % r if x P. Then u is the unique pointwise continuous solution of the problem (.) # p q s u h in B r, u in. Proof of Theorem 3.. We identify h with its Cc s`ε p n q extension, namely we consider h P Cc s`ε p n q with B r Ă supp h such that h h on B r. Then, by definition (.6) we have that in B r upxq hpzqgpx, zq dz B r ˆ hpzqφpz xqdz hpzq Φpy zqp r py, xqdy dz B r B r n zb r h Φpxq P r py, xq`h Φ pyq dy..
32 3 CLAUDIA BUCU Let gpxq : h Φpxq for any x P n. As we have seen in Theorem.8, g P L sp n q X Cp n q. Let for any x P n upxq v pxq v pxq, where v pxq gpxq in n and $ & P r py, xqgpyq dy if x P B r, v pxq % n zb r gpxq if x P. Then for x P B r, thanks to Theorems.8 and. p q s upxq hpxq hpxq, hence u is solution (.). Also, Theorem.8 and Theorem. assure the continuity of u in n. The uniqueness of the solution follows from the simple application of the Maximum Principle for the fractional Laplacian (see Theorem in [3]) Computation of the normalization constants. This subsection is dedicated to the computation of the constant κpn, sq in Theorem 3.. We first compute the constant kpn, sq given in (3.5) for n ą s. We claim that (3.4) kpn, sq Γp n q Γp n sqγpsq. Indeed, using definition (3.5) and taking the change of variable τ t we have that kpn, sq τ n s p τ q s dt t n s p tq s dt. We use identities (A.9) and (A.) to obtain that t n s p tq s dt Γp n sqγpsq Γp n q, which is exactly the result. We now prove Theorem 3.3, namely we compute the constant κpn, sq encountered in the formula of the Green function G. Theorem 3.3. The constant κpn, sq introduced in identity (.7) is Γp n κpn, sq q s π n Γ psq κ, π for n s, for n s. Proof of Theorem 3.3. For n ą s, we insert the values of apn, sq from (.) and of kpn, sq from (3.4) into (3.7) and we obtain that κpn, sq apn, sqkpn, sq Γp n q s π n Γ psq.
33 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 33 For n ă s, we recall definitions (3.), (3.) and (.), we use identities (A.5), (A.7) and (A.3) relative to the Gamma function and obtain that κp, sq ap, sqkp, sq p sqγp sq s Γpsq Γp sqγpsq s Γ psq. On the other hand, we recall that κ, π, as we have seen in the proof of Theorem 3. for n s. This concludes the proof of Theorem 3.3. We make now a remark on the constants Cpn, sq defined by (.6) and cpn, sq defined in (.). These two constants are both used in various works in the definition of the fractional Laplacian, but as we have seen in the course of this paper, they arise for different normalization purposes. The constant Cpn, sq as defined by [4] is consistent with the Fourier expression of the fractional Laplacian, meanwhile cpn, sq as introduced in [] is used to normalize the Poisson kernel (and the s-mean kernel), and is consistent with the constants used for the fundamental solution and the Green function. We first introduce the direct computation of the fractional Laplacian of a particular function. Namely: Lemma 3.4. Let upxq p x q s`. Then in B p q s upxq Cpn, sq ω n Bps, sq, where B is the Beta function defined in (A.8). The more general case (more precisely, for the function upxq p x q p` for any p ą ) was proved in [6, 5]. With small modifications with respect to the general case, the proof of Lemma 3.4 can be also found in Section 3.6 in [3]. Theorem 3.5. The constant Cpn, sq introduced in (.6) is given by (3.5) Cpn, sq s sγ ` n ` s π n Γp sq. Proof of Theorem 3.5. By Lemma 3.4 we have that in B p q s upxq Cpn, sq ω n Bp s, sq. We use Theorem 3. and for n s, we obtain that upxq Cpn, sq ω n Bp s, sqgpx, yqdy B Cpn, sq ω ˆ rpx,yq n Bp s, sqκpn, sq x y s n t s B pt ` q n dt dy. We compute the latter identity in zero and have that (3.6) Cpn, sq ω ˆ y n Bp s, sqκpn, sq y s n y B t s pt ` q n dt dy.
34 34 CLAUDIA BUCU We compute the double integral, by using Fubini-Tonelli s theorem B y s n ˆ y y t s pt ` q n s ˆ ρ ρ dt dy ω n ρ t s dt dρ pt ` q n 8 t s ˆ? t` ω n ρ s dρ dt pt ` q n ω 8 n t s s pt ` q n `s dt ω ˆ n s B s, n. By inserting this, the value of κpn, sq from Theorem 3.3 and the measure of the pn q-dimensional unit sphere ω n pπ n{ q{γpn{q into (3.6) and using (A.) we obtain that Cpn, sq s sγp n ` sq π n Γp sq. For n s we have that p q s upxq C p, {q π. Thanks to Theorem 3. ˆ upxq C, π Gpx, yq dy. Using formula (3.) and computing u at zero, we obtain that ˆ C, log ` a y dy πc y ˆ, Hence C p, {q {π and this concludes the proof of the Theorem. Appendix A. Appendix A.. The Gamma, Beta and hypergeometric functions. We recall here a few notions on the special functions Gamma, Beta and hypergeometric (see [], Chapters 6 and 5 for details). Gamma function. The Gamma function is defined for x ą as (see [], Chapter 6): (A.) Γpxq : 8 t x e t dt. The Gamma function has an unique continuation to the whole except at the negative integers, by means of Euler s infinite product. We have that Γpq Γpq and Γp{q? π. We also recall the next useful identities: (A.) (A.3) (A.4) (A.5) (A.6) (A.7). Γpn ` q n! for any n P N, Γpx ` q xγpxq for any x ą,? Γp{ ` xq π x for any x ą, Γpxq Γpxq ΓpsqΓp sq π sinpπsq for s P p, q, π Γp{ sqγp{ ` sq cospπsq for s P p, q, Γp sq p sqγp sq for s P p, q.
35 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 35 Beta function. The Beta function can be represented as an integral (see [], Section 6.), namely for x, y ą (A.8) Bpx, yq and equivalently (A.9) Bpx, yq 8 t x dt p ` tqx`y t x p tq y dt. Furthermore, in relation to the Gamma function we have the identity (A.) Bpx, yq ΓpxqΓpyq Γpx ` yq. Hypergeometric functions. There are several representations for the hypergeometric function (see [], Chapter 5). We recall the ones useful for our own purposes. () Gauss series (A.) F pa, b, c, wq 8ÿ k paq k pbq k pcq k w k k!, where pqq k is the Pochhammer symbol defined by: # for k, (A.) pqq k qpq ` q pq ` k q for k ą. The interval of convergence of the series is w ď. The Gauss series, on its interval of convergence, diverges when c a b ď, is absolutely convergent when c a b ą and is conditionally convergent when w ă and ă c a b ď. Also, the series is not defined when c is a negative integer m, provided a or b is a positive integer n and n ă m. Some useful elementary computations are (A.3a) (A.3b) () Integral representation (A.4) F pa, b, c, wq : F pa, b, b, wq p wq a. F a, ` a, w, p ` wq a ` p wq a. Γpcq ΓpbqΓpc bq t b p tq c b p wtq a dt. The integral is convergent (thus F is defined) when c ą b ą and w ă. (3) Linear transformation formulas
36 36 CLAUDIA BUCU From the integral representation (A.4), the following transformations can be deduced. (A.5a) F pa, b, c, wq p wq c a b F pc a, c b, c, wq, p wq a w (A.5b) F a, c b, c,, w (A.5c) p wq b F b, c a, c,, (A.5d) w w ΓpcqΓpc a bq F pa, b, a ` b c `, wq Γpc aqγpc bq c a b ΓpcqΓpa ` b cq ` p wq when ă w ă. ΓpaqΓpbq F pc a, c b, c a b `, wq, A.. Point inversion transformations. The purpose of this appendix is to recall some basic geometric features of the point inversion, related to the so-called Kelvin transformation. Let r ą to be fixed. Definition A.. Let x P B r be a fixed point. The inversion with center x is a point transformation that maps an arbitrary point y P n ztx u to the point K x pyq such that the points y, x, K x pyq lie on one line, x separates y and K x pyq and (A.6) K x pyq : x r x `y x. y x This is a bijective map from n ztx u onto itself. Of course, K x`kx pxq x. When this does not generate any confusion, we will use the notation y : K x pyq and x : K x pxq to denote the inversion of y and x respectively, with center at x. emark A.. It is not hard to see, from definition (A.6), that (A.7) y x y x r x. Proposition A.3. Let x P B r be a fixed point, and x and y be the inversion of x P n ztx u respectively y P n ztx u with center at x. Then: a) points on the sphere BB r are mapped into points on the same sphere, b) points outside the sphere BB r are mapped into points inside the sphere, (A.8a) y x c) pr x qpr y q y r, (A.8b) dy dy d) y x n y x n, (A.8c) e) y x pr x y x q y x x x.
37 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 37 The Kelvin point inversion transformation is well known (see, for instance, the Appendix in []) and elementary geometrical considerations can be used to prove this lemma. We give here a sketch of the proof. Sketch of the proof. A simple way to prove claims a) to c) is to consider the first triangle in Figure. Figure. Inversion of x, y with center at x We denote b : OY y, b : OY y, α : X Y y x and β : X Y y x. Let OH be the perpendicular from O onto Y Y. We apply the Pythagorean Theorem in the three triangles OY H, OHX, OHY, add the equation (A.7) and by solving the system, one gets that b βr ` αr βb. α From this, claims a) to c) follow after elementary computations. In order to prove d), without loss of generality, one can consider the point inversion of radius one with center at zero y y{ y and take its derivative. Since the point inversion transformation is invariant under rotation, we can assume that y y e and the desired result plainly follows. To prove e), see the Appendix in [], or consider the second triangle in Figure. We denote a : X X x x, b : X Y y x, α : XY x y and β : X Y x y. Let Y H and Y H be perpendiculars from Y, respectively Y onto the segment XX. By applying the Pythagorean Theorem in the four triangles X Y H, XY H, X Y H, X Y H, adding relation (A.7) and using that Y H is parallel to Y H, one gets after solving the system that β pr x qα, ab which is the desired result. A.3. Some useful integral identities. We present here a few detailed computations related to the functions Φ, A r and P r and some other useful integral identities.
38 38 CLAUDIA BUCU Lemma A.4. For any r ą (A.9) A r pyq dy. Proof. Using (.) and passing to polar coordinates we have that r A r pyq dy cpn, sq nzbr s p y r q s y n dy cpn, sqω n 8 r r s ρpρ r q s dρ, where ω n π n{ {Γpn{q is the measure of the pn q-dimensional unit sphere. We change the variable z pρ{rq and have that cpn, sq 8 (A.) A r pyq dy ω n pz ` qz s dz. We apply identities (A.8) and (A.) and use identity (A.5) to obtain that (A.) 8 dz Γp sqγpsq π pz ` qzs sin πs. Using the definition (.) of cpn, sq it follows that ş A r pyq dy, as desired. Lemma A.5. For any r ą and any x P B r (A.) P r py, xq dy. Proof. From the definition (.4) of P r we have that r x P r py, xq dy cpn, sq y r s x y n dy. We make the proof for n ą 3. However, the results hold for n ď 3. We change variables using the hyperspherical coordinates with radius ρ ą and angles θ, θ,..., θ n 3 P r, πs, θ n P r, πs y ρ sin θ sin θ... sin θ n 3 sin θ n (A.3) y ρ sin θ sin θ... sin θ n 3 cos θ n y 3 ρ sin θ sin θ... cos θ n 3... y n ρ cos θ. The Jacobian of the transformation is given by ρ n sin n θ sin n 3 θ... sin θ n 3. We only remark that for n 3 the usual spherical coordinates can be used y ρ sin θ sin θ, y ρ sin θ cos θ and y 3 ρ cos θ, while for n and n similar computations can be performed. Without loss of generality and up to rotations, we assume that x x e n to obtain the identity x y ρ ` x x ρ cos θ (see Figure for clarity). With
39 GEEN FUNCTION FO THE FACTIONAL LAPLACIAN 39 this change of coordinates, we obtain P r py, xq dy cpn, sqpr x q s π n 3 ź k π sin k θ dθ 8 π r ρ n sin n θ dθ dρ pρ r q s pρ ` x ρ x cos θq n{. We do the substitution r r{ x and ρ ρ{ x but still use r and ρ for simplicity Figure. and we remark that now ρ ą and r ą. We obtain that (A.4) P r py, xq dy cpn, sqpr q s π Let n 3 ź k We claim that, for ρ ą π ipρq : (A.5) ipρq 8 sin k θ dθ r π ρ n ˆ π pρ r q s sin n θ dθ. pρ ρ cos θ ` qn{ ρ n pρ q π sin n θ dθ. To prove this, we use the following change of coordinates sin θ (A.6) a ρ ρ cos θ ` sin α ρ. We have that (A.7) dθ cos α a dα. ρ sin α sin n θ dθ dρ. pρ ` ρ cos θq n{
Singular integral operators and the Riesz transform
 Singular integral operators and the Riesz transform Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto November 17, 017 1 Calderón-Zygmund kernels Let ω n 1 be the measure
Singular integral operators and the Riesz transform Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto November 17, 017 1 Calderón-Zygmund kernels Let ω n 1 be the measure
Tempered Distributions
 Tempered Distributions Lionel Fiske and Cairn Overturf May 9, 26 In the classical study of partial differential equations one requires a solution to be differentiable. While intuitively this requirement
Tempered Distributions Lionel Fiske and Cairn Overturf May 9, 26 In the classical study of partial differential equations one requires a solution to be differentiable. While intuitively this requirement
arxiv: v1 [math.ca] 4 Apr 2017
![arxiv: v1 [math.ca] 4 Apr 2017 arxiv: v1 [math.ca] 4 Apr 2017](/thumbs/88/115044967.jpg) ON LOCALIZATION OF SCHRÖDINGER MEANS PER SJÖLIN Abstract. Localization properties for Schrödinger means are studied in dimension higher than one. arxiv:704.00927v [math.ca] 4 Apr 207. Introduction Let
ON LOCALIZATION OF SCHRÖDINGER MEANS PER SJÖLIN Abstract. Localization properties for Schrödinger means are studied in dimension higher than one. arxiv:704.00927v [math.ca] 4 Apr 207. Introduction Let
We denote the space of distributions on Ω by D ( Ω) 2.
 Sep. 1 0, 008 Distributions Distributions are generalized functions. Some familiarity with the theory of distributions helps understanding of various function spaces which play important roles in the study
Sep. 1 0, 008 Distributions Distributions are generalized functions. Some familiarity with the theory of distributions helps understanding of various function spaces which play important roles in the study
REAL ANALYSIS II TAKE HOME EXAM. T. Tao s Lecture Notes Set 5
 REAL ANALYSIS II TAKE HOME EXAM CİHAN BAHRAN T. Tao s Lecture Notes Set 5 1. Suppose that te 1, e 2, e 3,... u is a countable orthonormal system in a complex Hilbert space H, and c 1, c 2,... is a sequence
REAL ANALYSIS II TAKE HOME EXAM CİHAN BAHRAN T. Tao s Lecture Notes Set 5 1. Suppose that te 1, e 2, e 3,... u is a countable orthonormal system in a complex Hilbert space H, and c 1, c 2,... is a sequence
LECTURE 16: UNITARY REPRESENTATIONS LECTURE BY SHEELA DEVADAS STANFORD NUMBER THEORY LEARNING SEMINAR FEBRUARY 14, 2018 NOTES BY DAN DORE
 LECTURE 16: UNITARY REPRESENTATIONS LECTURE BY SHEELA DEVADAS STANFORD NUMBER THEORY LEARNING SEMINAR FEBRUARY 14, 2018 NOTES BY DAN DORE Let F be a local field with valuation ring O F, and G F the group
LECTURE 16: UNITARY REPRESENTATIONS LECTURE BY SHEELA DEVADAS STANFORD NUMBER THEORY LEARNING SEMINAR FEBRUARY 14, 2018 NOTES BY DAN DORE Let F be a local field with valuation ring O F, and G F the group
A Bowl of Kernels. By Nuriye Atasever, Cesar Alvarado, and Patrick Doherty. December 03, 2013
 December 03, 203 Introduction When we studied Fourier series we improved convergence by convolving with the Fejer and Poisson kernels on T. The analogous Fejer and Poisson kernels on the real line help
December 03, 203 Introduction When we studied Fourier series we improved convergence by convolving with the Fejer and Poisson kernels on T. The analogous Fejer and Poisson kernels on the real line help
# 1 χ ramified χ unramified
 LECTURE 14: LOCAL UNCTIONAL EQUATION LECTURE BY ASI ZAMAN STANORD NUMBER THEORY LEARNING SEMINAR JANUARY 31, 018 NOTES BY DAN DORE AND ASI ZAMAN Let be a local field. We fix ψ P p, ψ 1, such that ψ p d
LECTURE 14: LOCAL UNCTIONAL EQUATION LECTURE BY ASI ZAMAN STANORD NUMBER THEORY LEARNING SEMINAR JANUARY 31, 018 NOTES BY DAN DORE AND ASI ZAMAN Let be a local field. We fix ψ P p, ψ 1, such that ψ p d
MATH 360 Final Exam Thursday, December 14, a n 2. a n 1 1
 MATH 36 Final Exam Thursday, December 4, 27 Name. The sequence ta n u is defined by a and a n (a) Prove that lim a n exists by showing that ta n u is bounded and monotonic and invoking an appropriate result.
MATH 36 Final Exam Thursday, December 4, 27 Name. The sequence ta n u is defined by a and a n (a) Prove that lim a n exists by showing that ta n u is bounded and monotonic and invoking an appropriate result.
Chapter One. The Calderón-Zygmund Theory I: Ellipticity
 Chapter One The Calderón-Zygmund Theory I: Ellipticity Our story begins with a classical situation: convolution with homogeneous, Calderón- Zygmund ( kernels on R n. Let S n 1 R n denote the unit sphere
Chapter One The Calderón-Zygmund Theory I: Ellipticity Our story begins with a classical situation: convolution with homogeneous, Calderón- Zygmund ( kernels on R n. Let S n 1 R n denote the unit sphere
NOTES ON SOME EXERCISES OF LECTURE 5, MODULE 2
 NOTES ON SOME EXERCISES OF LECTURE 5, MODULE 2 MARCO VITTURI Contents 1. Solution to exercise 5-2 1 2. Solution to exercise 5-3 2 3. Solution to exercise 5-7 4 4. Solution to exercise 5-8 6 5. Solution
NOTES ON SOME EXERCISES OF LECTURE 5, MODULE 2 MARCO VITTURI Contents 1. Solution to exercise 5-2 1 2. Solution to exercise 5-3 2 3. Solution to exercise 5-7 4 4. Solution to exercise 5-8 6 5. Solution
Ground States are generically a periodic orbit
 Gonzalo Contreras CIMAT Guanajuato, Mexico Ergodic Optimization and related topics USP, Sao Paulo December 11, 2013 Expanding map X compact metric space. T : X Ñ X an expanding map i.e. T P C 0, Dd P Z`,
Gonzalo Contreras CIMAT Guanajuato, Mexico Ergodic Optimization and related topics USP, Sao Paulo December 11, 2013 Expanding map X compact metric space. T : X Ñ X an expanding map i.e. T P C 0, Dd P Z`,
NONLINEAR EVOLUTION EQUATIONS SHORT NOTES WEEK #1
 NONLNEA EVOLUTON EQUATONS SHOT NOTES WEEK #. Free Schrödinger Equation Let Bx 2 `...`Bx 2 n denote the Laplacian on d with d ě. The initial-value problem for the free Schrödinger equation (in d space dimensions)
NONLNEA EVOLUTON EQUATONS SHOT NOTES WEEK #. Free Schrödinger Equation Let Bx 2 `...`Bx 2 n denote the Laplacian on d with d ě. The initial-value problem for the free Schrödinger equation (in d space dimensions)
Topics in Harmonic Analysis Lecture 6: Pseudodifferential calculus and almost orthogonality
 Topics in Harmonic Analysis Lecture 6: Pseudodifferential calculus and almost orthogonality Po-Lam Yung The Chinese University of Hong Kong Introduction While multiplier operators are very useful in studying
Topics in Harmonic Analysis Lecture 6: Pseudodifferential calculus and almost orthogonality Po-Lam Yung The Chinese University of Hong Kong Introduction While multiplier operators are very useful in studying
Approximation of Weighted Local Mean Operators
 Approximation of Weighted Local ean Operators Jianzhong Wang Department of athematics and Statistics Sam Houston State University Huntsville, TX 7734 Abstract Recently, weighted local mean operators are
Approximation of Weighted Local ean Operators Jianzhong Wang Department of athematics and Statistics Sam Houston State University Huntsville, TX 7734 Abstract Recently, weighted local mean operators are
Fourier Transform & Sobolev Spaces
 Fourier Transform & Sobolev Spaces Michael Reiter, Arthur Schuster Summer Term 2008 Abstract We introduce the concept of weak derivative that allows us to define new interesting Hilbert spaces the Sobolev
Fourier Transform & Sobolev Spaces Michael Reiter, Arthur Schuster Summer Term 2008 Abstract We introduce the concept of weak derivative that allows us to define new interesting Hilbert spaces the Sobolev
Mariusz Jurkiewicz, Bogdan Przeradzki EXISTENCE OF SOLUTIONS FOR HIGHER ORDER BVP WITH PARAMETERS VIA CRITICAL POINT THEORY
 DEMONSTRATIO MATHEMATICA Vol. XLVIII No 1 215 Mariusz Jurkiewicz, Bogdan Przeradzki EXISTENCE OF SOLUTIONS FOR HIGHER ORDER BVP WITH PARAMETERS VIA CRITICAL POINT THEORY Communicated by E. Zadrzyńska Abstract.
DEMONSTRATIO MATHEMATICA Vol. XLVIII No 1 215 Mariusz Jurkiewicz, Bogdan Przeradzki EXISTENCE OF SOLUTIONS FOR HIGHER ORDER BVP WITH PARAMETERS VIA CRITICAL POINT THEORY Communicated by E. Zadrzyńska Abstract.
arxiv: v2 [math.ca] 13 May 2015
![arxiv: v2 [math.ca] 13 May 2015 arxiv: v2 [math.ca] 13 May 2015](/thumbs/88/114667751.jpg) ON THE CLOSURE OF TRANSLATION-DILATION INVARIANT LINEAR SPACES OF POLYNOMIALS arxiv:1505.02370v2 [math.ca] 13 May 2015 J. M. ALMIRA AND L. SZÉKELYHIDI Abstract. Assume that a linear space of real polynomials
ON THE CLOSURE OF TRANSLATION-DILATION INVARIANT LINEAR SPACES OF POLYNOMIALS arxiv:1505.02370v2 [math.ca] 13 May 2015 J. M. ALMIRA AND L. SZÉKELYHIDI Abstract. Assume that a linear space of real polynomials
Finite-dimensional spaces. C n is the space of n-tuples x = (x 1,..., x n ) of complex numbers. It is a Hilbert space with the inner product
 Chapter 4 Hilbert Spaces 4.1 Inner Product Spaces Inner Product Space. A complex vector space E is called an inner product space (or a pre-hilbert space, or a unitary space) if there is a mapping (, )
Chapter 4 Hilbert Spaces 4.1 Inner Product Spaces Inner Product Space. A complex vector space E is called an inner product space (or a pre-hilbert space, or a unitary space) if there is a mapping (, )
Topics in Harmonic Analysis Lecture 1: The Fourier transform
 Topics in Harmonic Analysis Lecture 1: The Fourier transform Po-Lam Yung The Chinese University of Hong Kong Outline Fourier series on T: L 2 theory Convolutions The Dirichlet and Fejer kernels Pointwise
Topics in Harmonic Analysis Lecture 1: The Fourier transform Po-Lam Yung The Chinese University of Hong Kong Outline Fourier series on T: L 2 theory Convolutions The Dirichlet and Fejer kernels Pointwise
Fourier transform of tempered distributions
 Fourier transform of tempered distributions 1 Test functions and distributions As we have seen before, many functions are not classical in the sense that they cannot be evaluated at any point. For eample,
Fourier transform of tempered distributions 1 Test functions and distributions As we have seen before, many functions are not classical in the sense that they cannot be evaluated at any point. For eample,
Fourier transforms. Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x L or L x L) as Fourier series: a n cos L
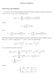 ourier transforms Motivation and definition Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x or x ) as ourier series: fpxq a 0 8 nπx a n cos n b n sin nπx where
ourier transforms Motivation and definition Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x or x ) as ourier series: fpxq a 0 8 nπx a n cos n b n sin nπx where
NOTES WEEK 14 DAY 2 SCOT ADAMS
 NOTES WEEK 14 DAY 2 SCOT ADAMS For this lecture, we fix the following: Let n P N, let W : R n, let : 2 P N pr n q and let I : id R n : R n Ñ R n be the identity map, defined by Ipxq x. For any h : W W,
NOTES WEEK 14 DAY 2 SCOT ADAMS For this lecture, we fix the following: Let n P N, let W : R n, let : 2 P N pr n q and let I : id R n : R n Ñ R n be the identity map, defined by Ipxq x. For any h : W W,
Riemann integral and volume are generalized to unbounded functions and sets. is an admissible set, and its volume is a Riemann integral, 1l E,
 Tel Aviv University, 26 Analysis-III 9 9 Improper integral 9a Introduction....................... 9 9b Positive integrands................... 9c Special functions gamma and beta......... 4 9d Change of
Tel Aviv University, 26 Analysis-III 9 9 Improper integral 9a Introduction....................... 9 9b Positive integrands................... 9c Special functions gamma and beta......... 4 9d Change of
Homework for MATH 4604 (Advanced Calculus II) Spring 2017
 Homework for MATH 4604 (Advanced Calculus II) Spring 2017 Homework 14: Due on Tuesday 2 May 55. Let m, n P N, A P R mˆn and v P R n. Show: L A pvq 2 ď A 2 v 2. 56. Let n P N and let A P R nˆn. Let I n
Homework for MATH 4604 (Advanced Calculus II) Spring 2017 Homework 14: Due on Tuesday 2 May 55. Let m, n P N, A P R mˆn and v P R n. Show: L A pvq 2 ď A 2 v 2. 56. Let n P N and let A P R nˆn. Let I n
Lecture 15: Quadratic approximation and the second variation formula
 Lecture 15: Quadratic approximation and the second variation formula Symmetric ilinear forms and inner products (15.1) The associated self-adjoint operator. Let V e a finite dimensional real vector space
Lecture 15: Quadratic approximation and the second variation formula Symmetric ilinear forms and inner products (15.1) The associated self-adjoint operator. Let V e a finite dimensional real vector space
1 Continuity Classes C m (Ω)
 0.1 Norms 0.1 Norms A norm on a linear space X is a function : X R with the properties: Positive Definite: x 0 x X (nonnegative) x = 0 x = 0 (strictly positive) λx = λ x x X, λ C(homogeneous) x + y x +
0.1 Norms 0.1 Norms A norm on a linear space X is a function : X R with the properties: Positive Definite: x 0 x X (nonnegative) x = 0 x = 0 (strictly positive) λx = λ x x X, λ C(homogeneous) x + y x +
DS-GA 1002: PREREQUISITES REVIEW SOLUTIONS VLADIMIR KOBZAR
 DS-GA 2: PEEQUISIES EVIEW SOLUIONS VLADIMI KOBZA he following is a selection of questions (drawn from Mr. Bernstein s notes) for reviewing the prerequisites for DS-GA 2. Questions from Ch, 8, 9 and 2 of
DS-GA 2: PEEQUISIES EVIEW SOLUIONS VLADIMI KOBZA he following is a selection of questions (drawn from Mr. Bernstein s notes) for reviewing the prerequisites for DS-GA 2. Questions from Ch, 8, 9 and 2 of
A review: The Laplacian and the d Alembertian. j=1
 Chapter One A review: The Laplacian and the d Alembertian 1.1 THE LAPLACIAN One of the main goals of this course is to understand well the solution of wave equation both in Euclidean space and on manifolds
Chapter One A review: The Laplacian and the d Alembertian 1.1 THE LAPLACIAN One of the main goals of this course is to understand well the solution of wave equation both in Euclidean space and on manifolds
2 A Model, Harmonic Map, Problem
 ELLIPTIC SYSTEMS JOHN E. HUTCHINSON Department of Mathematics School of Mathematical Sciences, A.N.U. 1 Introduction Elliptic equations model the behaviour of scalar quantities u, such as temperature or
ELLIPTIC SYSTEMS JOHN E. HUTCHINSON Department of Mathematics School of Mathematical Sciences, A.N.U. 1 Introduction Elliptic equations model the behaviour of scalar quantities u, such as temperature or
The Dirichlet s P rinciple. In this lecture we discuss an alternative formulation of the Dirichlet problem for the Laplace equation:
 Oct. 1 The Dirichlet s P rinciple In this lecture we discuss an alternative formulation of the Dirichlet problem for the Laplace equation: 1. Dirichlet s Principle. u = in, u = g on. ( 1 ) If we multiply
Oct. 1 The Dirichlet s P rinciple In this lecture we discuss an alternative formulation of the Dirichlet problem for the Laplace equation: 1. Dirichlet s Principle. u = in, u = g on. ( 1 ) If we multiply
S chauder Theory. x 2. = log( x 1 + x 2 ) + 1 ( x 1 + x 2 ) 2. ( 5) x 1 + x 2 x 1 + x 2. 2 = 2 x 1. x 1 x 2. 1 x 1.
 Sep. 1 9 Intuitively, the solution u to the Poisson equation S chauder Theory u = f 1 should have better regularity than the right hand side f. In particular one expects u to be twice more differentiable
Sep. 1 9 Intuitively, the solution u to the Poisson equation S chauder Theory u = f 1 should have better regularity than the right hand side f. In particular one expects u to be twice more differentiable
Mathematical Finance
 ETH Zürich, HS 2017 Prof. Josef Teichmann Matti Kiiski Mathematical Finance Solution sheet 14 Solution 14.1 Denote by Z pz t q tpr0,t s the density process process of Q with respect to P. (a) The second
ETH Zürich, HS 2017 Prof. Josef Teichmann Matti Kiiski Mathematical Finance Solution sheet 14 Solution 14.1 Denote by Z pz t q tpr0,t s the density process process of Q with respect to P. (a) The second
SCHWARTZ SPACES ASSOCIATED WITH SOME NON-DIFFERENTIAL CONVOLUTION OPERATORS ON HOMOGENEOUS GROUPS
 C O L L O Q U I U M M A T H E M A T I C U M VOL. LXIII 1992 FASC. 2 SCHWARTZ SPACES ASSOCIATED WITH SOME NON-DIFFERENTIAL CONVOLUTION OPERATORS ON HOMOGENEOUS GROUPS BY JACEK D Z I U B A Ń S K I (WROC
C O L L O Q U I U M M A T H E M A T I C U M VOL. LXIII 1992 FASC. 2 SCHWARTZ SPACES ASSOCIATED WITH SOME NON-DIFFERENTIAL CONVOLUTION OPERATORS ON HOMOGENEOUS GROUPS BY JACEK D Z I U B A Ń S K I (WROC
CHAPTER 6 bis. Distributions
 CHAPTER 6 bis Distributions The Dirac function has proved extremely useful and convenient to physicists, even though many a mathematician was truly horrified when the Dirac function was described to him:
CHAPTER 6 bis Distributions The Dirac function has proved extremely useful and convenient to physicists, even though many a mathematician was truly horrified when the Dirac function was described to him:
17 The functional equation
 18.785 Number theory I Fall 16 Lecture #17 11/8/16 17 The functional equation In the previous lecture we proved that the iemann zeta function ζ(s) has an Euler product and an analytic continuation to the
18.785 Number theory I Fall 16 Lecture #17 11/8/16 17 The functional equation In the previous lecture we proved that the iemann zeta function ζ(s) has an Euler product and an analytic continuation to the
i=1 β i,i.e. = β 1 x β x β 1 1 xβ d
 66 2. Every family of seminorms on a vector space containing a norm induces ahausdorff locally convex topology. 3. Given an open subset Ω of R d with the euclidean topology, the space C(Ω) of real valued
66 2. Every family of seminorms on a vector space containing a norm induces ahausdorff locally convex topology. 3. Given an open subset Ω of R d with the euclidean topology, the space C(Ω) of real valued
MATH 426, TOPOLOGY. p 1.
 MATH 426, TOPOLOGY THE p-norms In this document we assume an extended real line, where is an element greater than all real numbers; the interval notation [1, ] will be used to mean [1, ) { }. 1. THE p
MATH 426, TOPOLOGY THE p-norms In this document we assume an extended real line, where is an element greater than all real numbers; the interval notation [1, ] will be used to mean [1, ) { }. 1. THE p
Tools from Lebesgue integration
 Tools from Lebesgue integration E.P. van den Ban Fall 2005 Introduction In these notes we describe some of the basic tools from the theory of Lebesgue integration. Definitions and results will be given
Tools from Lebesgue integration E.P. van den Ban Fall 2005 Introduction In these notes we describe some of the basic tools from the theory of Lebesgue integration. Definitions and results will be given
Entropy and Ergodic Theory Notes 22: The Kolmogorov Sinai entropy of a measure-preserving system
 Entropy and Ergodic Theory Notes 22: The Kolmogorov Sinai entropy of a measure-preserving system 1 Joinings and channels 1.1 Joinings Definition 1. If px, µ, T q and py, ν, Sq are MPSs, then a joining
Entropy and Ergodic Theory Notes 22: The Kolmogorov Sinai entropy of a measure-preserving system 1 Joinings and channels 1.1 Joinings Definition 1. If px, µ, T q and py, ν, Sq are MPSs, then a joining
ADVANCE TOPICS IN ANALYSIS - REAL. 8 September September 2011
 ADVANCE TOPICS IN ANALYSIS - REAL NOTES COMPILED BY KATO LA Introductions 8 September 011 15 September 011 Nested Interval Theorem: If A 1 ra 1, b 1 s, A ra, b s,, A n ra n, b n s, and A 1 Ě A Ě Ě A n
ADVANCE TOPICS IN ANALYSIS - REAL NOTES COMPILED BY KATO LA Introductions 8 September 011 15 September 011 Nested Interval Theorem: If A 1 ra 1, b 1 s, A ra, b s,, A n ra n, b n s, and A 1 Ě A Ě Ě A n
Laplace s Equation. Chapter Mean Value Formulas
 Chapter 1 Laplace s Equation Let be an open set in R n. A function u C 2 () is called harmonic in if it satisfies Laplace s equation n (1.1) u := D ii u = 0 in. i=1 A function u C 2 () is called subharmonic
Chapter 1 Laplace s Equation Let be an open set in R n. A function u C 2 () is called harmonic in if it satisfies Laplace s equation n (1.1) u := D ii u = 0 in. i=1 A function u C 2 () is called subharmonic
APPROXIMATE HOMOMORPHISMS BETWEEN THE BOOLEAN CUBE AND GROUPS OF PRIME ORDER
 APPROXIMATE HOMOMORPHISMS BETWEEN THE BOOLEAN CUBE AND GROUPS OF PRIME ORDER TOM SANDERS The purpose of this note is to highlight a question raised by Shachar Lovett [Lov], and to offer some motivation
APPROXIMATE HOMOMORPHISMS BETWEEN THE BOOLEAN CUBE AND GROUPS OF PRIME ORDER TOM SANDERS The purpose of this note is to highlight a question raised by Shachar Lovett [Lov], and to offer some motivation
Integration and Fourier Theory. Lecture 14
 Integration and Fourier Theory Lecture 4 Morten Grud Rasmussen March 5, 03 Trigonometric Series Denote the unit circle in the complex plane by T tx P C x u ( T for torus ). Note that R Q t ÞÑ e it P T
Integration and Fourier Theory Lecture 4 Morten Grud Rasmussen March 5, 03 Trigonometric Series Denote the unit circle in the complex plane by T tx P C x u ( T for torus ). Note that R Q t ÞÑ e it P T
The Calderon-Vaillancourt Theorem
 The Calderon-Vaillancourt Theorem What follows is a completely self contained proof of the Calderon-Vaillancourt Theorem on the L 2 boundedness of pseudo-differential operators. 1 The result Definition
The Calderon-Vaillancourt Theorem What follows is a completely self contained proof of the Calderon-Vaillancourt Theorem on the L 2 boundedness of pseudo-differential operators. 1 The result Definition
A COUNTEREXAMPLE TO AN ENDPOINT BILINEAR STRICHARTZ INEQUALITY TERENCE TAO. t L x (R R2 ) f L 2 x (R2 )
 Electronic Journal of Differential Equations, Vol. 2006(2006), No. 5, pp. 6. ISSN: 072-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) A COUNTEREXAMPLE
Electronic Journal of Differential Equations, Vol. 2006(2006), No. 5, pp. 6. ISSN: 072-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) A COUNTEREXAMPLE
1.5 Approximate Identities
 38 1 The Fourier Transform on L 1 (R) which are dense subspaces of L p (R). On these domains, P : D P L p (R) and M : D M L p (R). Show, however, that P and M are unbounded even when restricted to these
38 1 The Fourier Transform on L 1 (R) which are dense subspaces of L p (R). On these domains, P : D P L p (R) and M : D M L p (R). Show, however, that P and M are unbounded even when restricted to these
Fourier transform, assorted stuff...
 Fourier transform, assorted stuff... M. Carlsson October 9, 2013 1 An example from control theory To get an idea of where real applications are, lets begin with an example from control theory. Example
Fourier transform, assorted stuff... M. Carlsson October 9, 2013 1 An example from control theory To get an idea of where real applications are, lets begin with an example from control theory. Example
be the set of complex valued 2π-periodic functions f on R such that
 . Fourier series. Definition.. Given a real number P, we say a complex valued function f on R is P -periodic if f(x + P ) f(x) for all x R. We let be the set of complex valued -periodic functions f on
. Fourier series. Definition.. Given a real number P, we say a complex valued function f on R is P -periodic if f(x + P ) f(x) for all x R. We let be the set of complex valued -periodic functions f on
Lectures on. Sobolev Spaces. S. Kesavan The Institute of Mathematical Sciences, Chennai.
 Lectures on Sobolev Spaces S. Kesavan The Institute of Mathematical Sciences, Chennai. e-mail: kesh@imsc.res.in 2 1 Distributions In this section we will, very briefly, recall concepts from the theory
Lectures on Sobolev Spaces S. Kesavan The Institute of Mathematical Sciences, Chennai. e-mail: kesh@imsc.res.in 2 1 Distributions In this section we will, very briefly, recall concepts from the theory
1 Fourier Integrals on L 2 (R) and L 1 (R).
 18.103 Fall 2013 1 Fourier Integrals on L 2 () and L 1 (). The first part of these notes cover 3.5 of AG, without proofs. When we get to things not covered in the book, we will start giving proofs. The
18.103 Fall 2013 1 Fourier Integrals on L 2 () and L 1 (). The first part of these notes cover 3.5 of AG, without proofs. When we get to things not covered in the book, we will start giving proofs. The
1 Math 241A-B Homework Problem List for F2015 and W2016
 1 Math 241A-B Homework Problem List for F2015 W2016 1.1 Homework 1. Due Wednesday, October 7, 2015 Notation 1.1 Let U be any set, g be a positive function on U, Y be a normed space. For any f : U Y let
1 Math 241A-B Homework Problem List for F2015 W2016 1.1 Homework 1. Due Wednesday, October 7, 2015 Notation 1.1 Let U be any set, g be a positive function on U, Y be a normed space. For any f : U Y let
ON THE REGULARITY OF ONE PARAMETER TRANSFORMATION GROUPS IN BARRELED LOCALLY CONVEX TOPOLOGICAL VECTOR SPACES
 Communications on Stochastic Analysis Vol. 9, No. 3 (2015) 413-418 Serials Publications www.serialspublications.com ON THE REGULARITY OF ONE PARAMETER TRANSFORMATION GROUPS IN BARRELED LOCALLY CONVEX TOPOLOGICAL
Communications on Stochastic Analysis Vol. 9, No. 3 (2015) 413-418 Serials Publications www.serialspublications.com ON THE REGULARITY OF ONE PARAMETER TRANSFORMATION GROUPS IN BARRELED LOCALLY CONVEX TOPOLOGICAL
Average theorem, Restriction theorem and Strichartz estimates
 Average theorem, Restriction theorem and trichartz estimates 2 August 27 Abstract We provide the details of the proof of the average theorem and the restriction theorem. Emphasis has been placed on the
Average theorem, Restriction theorem and trichartz estimates 2 August 27 Abstract We provide the details of the proof of the average theorem and the restriction theorem. Emphasis has been placed on the
EXISTENCE RESULTS FOR QUASILINEAR HEMIVARIATIONAL INEQUALITIES AT RESONANCE. Leszek Gasiński
 DISCRETE AND CONTINUOUS Website: www.aimsciences.org DYNAMICAL SYSTEMS SUPPLEMENT 2007 pp. 409 418 EXISTENCE RESULTS FOR QUASILINEAR HEMIVARIATIONAL INEQUALITIES AT RESONANCE Leszek Gasiński Jagiellonian
DISCRETE AND CONTINUOUS Website: www.aimsciences.org DYNAMICAL SYSTEMS SUPPLEMENT 2007 pp. 409 418 EXISTENCE RESULTS FOR QUASILINEAR HEMIVARIATIONAL INEQUALITIES AT RESONANCE Leszek Gasiński Jagiellonian
ANALYSIS QUALIFYING EXAM FALL 2017: SOLUTIONS. 1 cos(nx) lim. n 2 x 2. g n (x) = 1 cos(nx) n 2 x 2. x 2.
 ANALYSIS QUALIFYING EXAM FALL 27: SOLUTIONS Problem. Determine, with justification, the it cos(nx) n 2 x 2 dx. Solution. For an integer n >, define g n : (, ) R by Also define g : (, ) R by g(x) = g n
ANALYSIS QUALIFYING EXAM FALL 27: SOLUTIONS Problem. Determine, with justification, the it cos(nx) n 2 x 2 dx. Solution. For an integer n >, define g n : (, ) R by Also define g : (, ) R by g(x) = g n
ALMOST AUTOMORPHIC GENERALIZED FUNCTIONS
 Novi Sad J. Math. Vol. 45 No. 1 2015 207-214 ALMOST AUTOMOPHIC GENEALIZED FUNCTIONS Chikh Bouzar 1 Mohammed Taha Khalladi 2 and Fatima Zohra Tchouar 3 Abstract. The paper deals with a new algebra of generalized
Novi Sad J. Math. Vol. 45 No. 1 2015 207-214 ALMOST AUTOMOPHIC GENEALIZED FUNCTIONS Chikh Bouzar 1 Mohammed Taha Khalladi 2 and Fatima Zohra Tchouar 3 Abstract. The paper deals with a new algebra of generalized
q-de Rham cohomology via Λ-rings
 q-de Rham cohomology via Λ-rings J.P.Pridham arxiv:1608.07142 1 / 21 q-analogues (Gauss) rns q : qn 1 q 1 1 q... qn 1 rns q! : rns q... r2s q r1s q, ¹ n 1 i 0 n 1 ¹ i 0 p1 p1 n k q : rns q! rn ksq!rksq!
q-de Rham cohomology via Λ-rings J.P.Pridham arxiv:1608.07142 1 / 21 q-analogues (Gauss) rns q : qn 1 q 1 1 q... qn 1 rns q! : rns q... r2s q r1s q, ¹ n 1 i 0 n 1 ¹ i 0 p1 p1 n k q : rns q! rn ksq!rksq!
Quadratic reciprocity (after Weil) 1. Standard set-up and Poisson summation
 (September 17, 010) Quadratic reciprocity (after Weil) Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ I show that over global fields (characteristic not ) the quadratic norm residue
(September 17, 010) Quadratic reciprocity (after Weil) Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ I show that over global fields (characteristic not ) the quadratic norm residue
Asymptotic Analysis 1: Limits and Asymptotic Equality
 Asymptotic Analysis 1: Limits and Asymptotic Equality Andreas Klappenecker and Hyunyoung Lee Texas A&M University 1 / 15 Motivation In asymptotic analysis, our goal is to compare a function f pnq with
Asymptotic Analysis 1: Limits and Asymptotic Equality Andreas Klappenecker and Hyunyoung Lee Texas A&M University 1 / 15 Motivation In asymptotic analysis, our goal is to compare a function f pnq with
An introduction to Birkhoff normal form
 An introduction to Birkhoff normal form Dario Bambusi Dipartimento di Matematica, Universitá di Milano via Saldini 50, 0133 Milano (Italy) 19.11.14 1 Introduction The aim of this note is to present an
An introduction to Birkhoff normal form Dario Bambusi Dipartimento di Matematica, Universitá di Milano via Saldini 50, 0133 Milano (Italy) 19.11.14 1 Introduction The aim of this note is to present an
Folland: Real Analysis, Chapter 8 Sébastien Picard
 Folland: Real Analysis, Chapter 8 Sébastien Picard Problem 8.3 Let η(t) = e /t for t >, η(t) = for t. a. For k N and t >, η (k) (t) = P k (/t)e /t where P k is a polynomial of degree 2k. b. η (k) () exists
Folland: Real Analysis, Chapter 8 Sébastien Picard Problem 8.3 Let η(t) = e /t for t >, η(t) = for t. a. For k N and t >, η (k) (t) = P k (/t)e /t where P k is a polynomial of degree 2k. b. η (k) () exists
DS-GA 3001: PROBLEM SESSION 2 SOLUTIONS VLADIMIR KOBZAR
 DS-GA 3: PROBLEM SESSION SOLUTIONS VLADIMIR KOBZAR Note: In this discussion we allude to the fact the dimension of a vector space is given by the number of basis vectors. We will shortly establish this
DS-GA 3: PROBLEM SESSION SOLUTIONS VLADIMIR KOBZAR Note: In this discussion we allude to the fact the dimension of a vector space is given by the number of basis vectors. We will shortly establish this
Topological properties
 CHAPTER 4 Topological properties 1. Connectedness Definitions and examples Basic properties Connected components Connected versus path connected, again 2. Compactness Definition and first examples Topological
CHAPTER 4 Topological properties 1. Connectedness Definitions and examples Basic properties Connected components Connected versus path connected, again 2. Compactness Definition and first examples Topological
SOLUTIONS TO HOMEWORK ASSIGNMENT 4
 SOLUTIONS TO HOMEWOK ASSIGNMENT 4 Exercise. A criterion for the image under the Hilbert transform to belong to L Let φ S be given. Show that Hφ L if and only if φx dx = 0. Solution: Suppose first that
SOLUTIONS TO HOMEWOK ASSIGNMENT 4 Exercise. A criterion for the image under the Hilbert transform to belong to L Let φ S be given. Show that Hφ L if and only if φx dx = 0. Solution: Suppose first that
Quadratic reciprocity (after Weil) 1. Standard set-up and Poisson summation
 (December 19, 010 Quadratic reciprocity (after Weil Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ I show that over global fields k (characteristic not the quadratic norm residue symbol
(December 19, 010 Quadratic reciprocity (after Weil Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ I show that over global fields k (characteristic not the quadratic norm residue symbol
S. K. Mohanta, Srikanta Mohanta SOME FIXED POINT RESULTS FOR MAPPINGS IN G-METRIC SPACES
 DEMONSTRATIO MATHEMATICA Vol. XLVII No 1 2014 S. K. Mohanta Srikanta Mohanta SOME FIXED POINT RESULTS FOR MAPPINGS IN G-METRIC SPACES Abstract. We prove a common fixed point theorem for a pair of self
DEMONSTRATIO MATHEMATICA Vol. XLVII No 1 2014 S. K. Mohanta Srikanta Mohanta SOME FIXED POINT RESULTS FOR MAPPINGS IN G-METRIC SPACES Abstract. We prove a common fixed point theorem for a pair of self
u xx + u yy = 0. (5.1)
 Chapter 5 Laplace Equation The following equation is called Laplace equation in two independent variables x, y: The non-homogeneous problem u xx + u yy =. (5.1) u xx + u yy = F, (5.) where F is a function
Chapter 5 Laplace Equation The following equation is called Laplace equation in two independent variables x, y: The non-homogeneous problem u xx + u yy =. (5.1) u xx + u yy = F, (5.) where F is a function
A NOTE ON FAITHFUL TRACES ON A VON NEUMANN ALGEBRA
 A NOTE ON FAITHFUL TRACES ON A VON NEUMANN ALGEBRA F. BAGARELLO, C. TRAPANI, AND S. TRIOLO Abstract. In this short note we give some techniques for constructing, starting from a sufficient family F of
A NOTE ON FAITHFUL TRACES ON A VON NEUMANN ALGEBRA F. BAGARELLO, C. TRAPANI, AND S. TRIOLO Abstract. In this short note we give some techniques for constructing, starting from a sufficient family F of
An introduction to Mathematical Theory of Control
 An introduction to Mathematical Theory of Control Vasile Staicu University of Aveiro UNICA, May 2018 Vasile Staicu (University of Aveiro) An introduction to Mathematical Theory of Control UNICA, May 2018
An introduction to Mathematical Theory of Control Vasile Staicu University of Aveiro UNICA, May 2018 Vasile Staicu (University of Aveiro) An introduction to Mathematical Theory of Control UNICA, May 2018
NOTES WEEK 13 DAY 2 SCOT ADAMS
 NOTES WEEK 13 DAY 2 SCOT ADAMS Recall: Let px, dq be a metric space. Then, for all S Ď X, we have p S is sequentially compact q ñ p S is closed and bounded q. DEFINITION 0.1. Let px, dq be a metric space.
NOTES WEEK 13 DAY 2 SCOT ADAMS Recall: Let px, dq be a metric space. Then, for all S Ď X, we have p S is sequentially compact q ñ p S is closed and bounded q. DEFINITION 0.1. Let px, dq be a metric space.
Sobolev Spaces. Chapter 10
 Chapter 1 Sobolev Spaces We now define spaces H 1,p (R n ), known as Sobolev spaces. For u to belong to H 1,p (R n ), we require that u L p (R n ) and that u have weak derivatives of first order in L p
Chapter 1 Sobolev Spaces We now define spaces H 1,p (R n ), known as Sobolev spaces. For u to belong to H 1,p (R n ), we require that u L p (R n ) and that u have weak derivatives of first order in L p
Introduction to Differential Equations
 Introduction to Differential Equations J. M. Veal, Ph. D. version 13.08.30 Contents 1 Introduction to Differential Equations 2 1.1 Definitions and Terminology.................... 2 1.2 Initial-Value Problems.......................
Introduction to Differential Equations J. M. Veal, Ph. D. version 13.08.30 Contents 1 Introduction to Differential Equations 2 1.1 Definitions and Terminology.................... 2 1.2 Initial-Value Problems.......................
Approximation in the Zygmund Class
 Approximation in the Zygmund Class Odí Soler i Gibert Joint work with Artur Nicolau Universitat Autònoma de Barcelona New Developments in Complex Analysis and Function Theory, 02 July 2018 Approximation
Approximation in the Zygmund Class Odí Soler i Gibert Joint work with Artur Nicolau Universitat Autònoma de Barcelona New Developments in Complex Analysis and Function Theory, 02 July 2018 Approximation
Wiener Measure and Brownian Motion
 Chapter 16 Wiener Measure and Brownian Motion Diffusion of particles is a product of their apparently random motion. The density u(t, x) of diffusing particles satisfies the diffusion equation (16.1) u
Chapter 16 Wiener Measure and Brownian Motion Diffusion of particles is a product of their apparently random motion. The density u(t, x) of diffusing particles satisfies the diffusion equation (16.1) u
Entropy and Ergodic Theory Lecture 27: Sinai s factor theorem
 Entropy and Ergodic Theory Lecture 27: Sinai s factor theorem What is special about Bernoulli shifts? Our main result in Lecture 26 is weak containment with retention of entropy. If ra Z, µs and rb Z,
Entropy and Ergodic Theory Lecture 27: Sinai s factor theorem What is special about Bernoulli shifts? Our main result in Lecture 26 is weak containment with retention of entropy. If ra Z, µs and rb Z,
Almost Conservation Laws for KdV and Cubic NLS. UROP Final Paper, Summer 2018
 Almost Conservation Laws for KdV and Cubic NLS UROP Final Paper, Summer 2018 Zixuan Xu Mentor: Ricardo Grande Izquierdo Project suggested by: Gigliola Staffilani Abstract In this paper, we explore the
Almost Conservation Laws for KdV and Cubic NLS UROP Final Paper, Summer 2018 Zixuan Xu Mentor: Ricardo Grande Izquierdo Project suggested by: Gigliola Staffilani Abstract In this paper, we explore the
Variational inequality formulation of chance-constrained games
 Variational inequality formulation of chance-constrained games Joint work with Vikas Singh from IIT Delhi Université Paris Sud XI Computational Management Science Conference Bergamo, Italy May, 2017 Outline
Variational inequality formulation of chance-constrained games Joint work with Vikas Singh from IIT Delhi Université Paris Sud XI Computational Management Science Conference Bergamo, Italy May, 2017 Outline
Erdinç Dündar, Celal Çakan
 DEMONSTRATIO MATHEMATICA Vol. XLVII No 3 2014 Erdinç Dündar, Celal Çakan ROUGH I-CONVERGENCE Abstract. In this work, using the concept of I-convergence and using the concept of rough convergence, we introduced
DEMONSTRATIO MATHEMATICA Vol. XLVII No 3 2014 Erdinç Dündar, Celal Çakan ROUGH I-CONVERGENCE Abstract. In this work, using the concept of I-convergence and using the concept of rough convergence, we introduced
Sobolev spaces. May 18
 Sobolev spaces May 18 2015 1 Weak derivatives The purpose of these notes is to give a very basic introduction to Sobolev spaces. More extensive treatments can e.g. be found in the classical references
Sobolev spaces May 18 2015 1 Weak derivatives The purpose of these notes is to give a very basic introduction to Sobolev spaces. More extensive treatments can e.g. be found in the classical references
Introduction to Partial Differential Equations
 niversität Tübingen Fachbereich Mathematik Introduction to Partial Differential Equations Based on a course given by Prof. Dr. Marcello Porta Written by Dr. Giovanni Antinucci 27-28 2 Introduction These
niversität Tübingen Fachbereich Mathematik Introduction to Partial Differential Equations Based on a course given by Prof. Dr. Marcello Porta Written by Dr. Giovanni Antinucci 27-28 2 Introduction These
Here we used the multiindex notation:
 Mathematics Department Stanford University Math 51H Distributions Distributions first arose in solving partial differential equations by duality arguments; a later related benefit was that one could always
Mathematics Department Stanford University Math 51H Distributions Distributions first arose in solving partial differential equations by duality arguments; a later related benefit was that one could always
SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS. Massimo Grosi Filomena Pacella S. L. Yadava. 1. Introduction
 Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 21, 2003, 211 226 SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS Massimo Grosi Filomena Pacella S.
Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 21, 2003, 211 226 SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS Massimo Grosi Filomena Pacella S.
FOURIER TRANSFORMS. 1. Fourier series 1.1. The trigonometric system. The sequence of functions
 FOURIER TRANSFORMS. Fourier series.. The trigonometric system. The sequence of functions, cos x, sin x,..., cos nx, sin nx,... is called the trigonometric system. These functions have period π. The trigonometric
FOURIER TRANSFORMS. Fourier series.. The trigonometric system. The sequence of functions, cos x, sin x,..., cos nx, sin nx,... is called the trigonometric system. These functions have period π. The trigonometric
Interpolation Theory and Applications to the Boundedness of Operators in Analysis
 Master Thesis Master Advanced Mathematics Interpolation Theory and Applications to the Boundedness of Operators in Analysis Author: Jordi Lendínez Capdevila Supervisor: Department: Dr F Javier Soria de
Master Thesis Master Advanced Mathematics Interpolation Theory and Applications to the Boundedness of Operators in Analysis Author: Jordi Lendínez Capdevila Supervisor: Department: Dr F Javier Soria de
Notes on Distributions
 Notes on Distributions Functional Analysis 1 Locally Convex Spaces Definition 1. A vector space (over R or C) is said to be a topological vector space (TVS) if it is a Hausdorff topological space and the
Notes on Distributions Functional Analysis 1 Locally Convex Spaces Definition 1. A vector space (over R or C) is said to be a topological vector space (TVS) if it is a Hausdorff topological space and the
8 Singular Integral Operators and L p -Regularity Theory
 8 Singular Integral Operators and L p -Regularity Theory 8. Motivation See hand-written notes! 8.2 Mikhlin Multiplier Theorem Recall that the Fourier transformation F and the inverse Fourier transformation
8 Singular Integral Operators and L p -Regularity Theory 8. Motivation See hand-written notes! 8.2 Mikhlin Multiplier Theorem Recall that the Fourier transformation F and the inverse Fourier transformation
TOOLS FROM HARMONIC ANALYSIS
 TOOLS FROM HARMONIC ANALYSIS BRADLY STADIE Abstract. The Fourier transform can be thought of as a map that decomposes a function into oscillatory functions. In this paper, we will apply this decomposition
TOOLS FROM HARMONIC ANALYSIS BRADLY STADIE Abstract. The Fourier transform can be thought of as a map that decomposes a function into oscillatory functions. In this paper, we will apply this decomposition
Existence of weak adiabatic limit in almost all models of perturbative QFT
 Existence of weak adiabatic limit in almost all models of perturbative QFT Paweł Duch Jagiellonian University, Cracow, Poland LQP 40 Foundations and Constructive Aspects of Quantum Field Theory, 23.06.2017
Existence of weak adiabatic limit in almost all models of perturbative QFT Paweł Duch Jagiellonian University, Cracow, Poland LQP 40 Foundations and Constructive Aspects of Quantum Field Theory, 23.06.2017
Partial Differential Equations
 Part II Partial Differential Equations Year 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2015 Paper 4, Section II 29E Partial Differential Equations 72 (a) Show that the Cauchy problem for u(x,
Part II Partial Differential Equations Year 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2015 Paper 4, Section II 29E Partial Differential Equations 72 (a) Show that the Cauchy problem for u(x,
C*-algebras - a case study
 - a case study Definition Suppose that H is a Hilbert space. A C -algebra is an operator-norm closed -subalgebra of BpHq. are closed under ultraproducts and subalgebras so they should be captured by continous
- a case study Definition Suppose that H is a Hilbert space. A C -algebra is an operator-norm closed -subalgebra of BpHq. are closed under ultraproducts and subalgebras so they should be captured by continous
FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES
 FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES JAIRO BOCHI Abstract. This is a revised version of some notes written ą 0 years ago. I thank Anthony Quas for pointing to a gap in the previous
FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES JAIRO BOCHI Abstract. This is a revised version of some notes written ą 0 years ago. I thank Anthony Quas for pointing to a gap in the previous
MATH 205C: STATIONARY PHASE LEMMA
 MATH 205C: STATIONARY PHASE LEMMA For ω, consider an integral of the form I(ω) = e iωf(x) u(x) dx, where u Cc (R n ) complex valued, with support in a compact set K, and f C (R n ) real valued. Thus, I(ω)
MATH 205C: STATIONARY PHASE LEMMA For ω, consider an integral of the form I(ω) = e iωf(x) u(x) dx, where u Cc (R n ) complex valued, with support in a compact set K, and f C (R n ) real valued. Thus, I(ω)
LARGE DEVIATIONS OF TYPICAL LINEAR FUNCTIONALS ON A CONVEX BODY WITH UNCONDITIONAL BASIS. S. G. Bobkov and F. L. Nazarov. September 25, 2011
 LARGE DEVIATIONS OF TYPICAL LINEAR FUNCTIONALS ON A CONVEX BODY WITH UNCONDITIONAL BASIS S. G. Bobkov and F. L. Nazarov September 25, 20 Abstract We study large deviations of linear functionals on an isotropic
LARGE DEVIATIONS OF TYPICAL LINEAR FUNCTIONALS ON A CONVEX BODY WITH UNCONDITIONAL BASIS S. G. Bobkov and F. L. Nazarov September 25, 20 Abstract We study large deviations of linear functionals on an isotropic
Bochner s Theorem on the Fourier Transform on R
 Bochner s heorem on the Fourier ransform on Yitao Lei October 203 Introduction ypically, the Fourier transformation sends suitable functions on to functions on. his can be defined on the space L ) + L
Bochner s heorem on the Fourier ransform on Yitao Lei October 203 Introduction ypically, the Fourier transformation sends suitable functions on to functions on. his can be defined on the space L ) + L
3. Fourier decomposition of functions
 22 C. MOUHOT 3.1. The Fourier transform. 3. Fourier decomposition of functions Definition 3.1 (Fourier Transform on L 1 (R d )). Given f 2 L 1 (R d ) define its Fourier transform F(f)( ) := R d e 2i x
22 C. MOUHOT 3.1. The Fourier transform. 3. Fourier decomposition of functions Definition 3.1 (Fourier Transform on L 1 (R d )). Given f 2 L 1 (R d ) define its Fourier transform F(f)( ) := R d e 2i x
NOTES WEEK 15 DAY 1 SCOT ADAMS
 NOTES WEEK 15 DAY 1 SCOT ADAMS We fix some notation for the entire class today: Let n P N, W : R n, : 2 P N pw q, W : LpW, W q, I : id W P W, z : 0 W 0 n. Note that W LpR n, R n q. Recall, for all T P
NOTES WEEK 15 DAY 1 SCOT ADAMS We fix some notation for the entire class today: Let n P N, W : R n, : 2 P N pw q, W : LpW, W q, I : id W P W, z : 0 W 0 n. Note that W LpR n, R n q. Recall, for all T P
THE LOCAL THEORY OF ELLIPTIC OPERATORS AND THE HODGE THEOREM
 THE LOCAL THEORY OF ELLIPTIC OPERATORS AND THE HODGE THEOREM BEN LOWE Abstract. In this paper, we develop the local theory of elliptic operators with a mind to proving the Hodge Decomposition Theorem.
THE LOCAL THEORY OF ELLIPTIC OPERATORS AND THE HODGE THEOREM BEN LOWE Abstract. In this paper, we develop the local theory of elliptic operators with a mind to proving the Hodge Decomposition Theorem.
Dangerous and Illegal Operations in Calculus Do we avoid differentiating discontinuous functions because it s impossible, unwise, or simply out of
 Dangerous and Illegal Operations in Calculus Do we avoid differentiating discontinuous functions because it s impossible, unwise, or simply out of ignorance and fear? Despite the risks, many natural phenomena
Dangerous and Illegal Operations in Calculus Do we avoid differentiating discontinuous functions because it s impossible, unwise, or simply out of ignorance and fear? Despite the risks, many natural phenomena
An Introduction to Complex Analysis and Geometry John P. D Angelo, Pure and Applied Undergraduate Texts Volume 12, American Mathematical Society, 2010
 An Introduction to Complex Analysis and Geometry John P. D Angelo, Pure and Applied Undergraduate Texts Volume 12, American Mathematical Society, 2010 John P. D Angelo, Univ. of Illinois, Urbana IL 61801.
An Introduction to Complex Analysis and Geometry John P. D Angelo, Pure and Applied Undergraduate Texts Volume 12, American Mathematical Society, 2010 John P. D Angelo, Univ. of Illinois, Urbana IL 61801.
