Interpolation Theory and Applications to the Boundedness of Operators in Analysis
|
|
|
- Chester Robertson
- 5 years ago
- Views:
Transcription
1 Master Thesis Master Advanced Mathematics Interpolation Theory and Applications to the Boundedness of Operators in Analysis Author: Jordi Lendínez Capdevila Supervisor: Department: Dr F Javier Soria de Diego Matemàtiques i Informàtica Barcelona, June 6, 26
2
3 Contents Acknowledgments iii Introduction Basic Notions and Preliminary Results 3 Complex Analysis 3 Poisson Kernel in the Strip 5 2 Functional Analysis 6 2 Completeness 6 22 Weak Topologies 7 23 Bochner Integral 24 Fréchet Spaces and the Big Theorems 2 3 Harmonic Analysis 4 3 The Weak-L p Spaces 4 32 Lebesgue Differentiation Theorem 2 33 Fourier Transform Schwarz Class 23 4 Distribution Theory 28 4 Tempered Distributions 29 2 Classical Methods 3 2 Riesz-Thorin Theorem 3 22 The Marcinkiewicz Theorem An Application of Marcinkiewicz Theorem 38 3 Real Interpolation 4 3 Real Interpolation Methods 4 3 K-method 4 i
4 ii CONTENTS 32 J-Method The Equivalence Theorem Some Properties of pa, A q θ,p 6 34 The Reiteration Theorem Duality Theorem 74 4 Complex Interpolation 77 4 Definition of Methods 77 4 Functional C θ 8 42 Functional C θ Some properties of C θ The Equivalence Theorem The Reiteration Theorem 92 5 Interpolation Spaces 95 5 Lorentz Spaces 95 5 Definition Interpolation Hardy Spaces 52 Definition 522 Interpolation 2 6 Boundedness of Operators 7 6 Fourier Multipliers 7 62 Hilbert Transform Bibliography 9
5 Acknowledgments To begin I want to thank to my supervisor F Javier Soria for his support and all the help brought during this course and during the production of this final project Without his help this work could not emerge Also, for all the hours that he spent on revising the different versions of this work, helping in my English, L A TEX, and mathematical problems Finally, I want to thank to my master s colleagues and friends for their unconditional support during all this year, for the greatest moments that we live together, for still here in the bad moments, for made this course to be more tolerable and for made me a better person because without all these moments the life could have been harder iii
6
7 Introduction The objective of this work is to introduce some results and applications of Interpolation Theory (as a reference we use the books [4] and [3]) The interpolation theory was aimed in the two classical theorems: The Riesz-Thorin Interpolation Theorem that motivates the complex interpolation and was proved by Riesz in 927 but only for the lower-triangle case, and the general case by Thorin in 938; and the Marcinkiewicz Interpolation Theorem that motivates the real interpolation and was proved by Marcinkiewicz in 939 In the first chapter, we will introduce some tools in complex, functional and harmonic analysis that will be useful in the following chapters to state and prove theorems In the second chapter, we will give the statements and proofs of the two classical theorems and see several applications of the Marcinkiewicz theorem for the Fourier Transform for L p spaces and L p pωq with p P r, 2s and ωpθq θ np2 pq being a weight on R n In the third chapter, we will introduce the real interpolation methods, in particular, we will study the K and J functionals and the interpolation spaces generated by this functionals, giving the definitions and some properties of those methods and those spaces Also we will see that the spaces generated by the K functionals are the same than the spaces generated by the J functional Finally, we will see the Reiteration Theorem which tells us that interpolate two interpolation spaces is the same that interpolate the original spaces In the fourth chapter, we will introduce the complex interpolation methods, in particular, we will study the C θ and C θ functionals and the interpolation spaces generated by these functionals, giving the definitions and some properties of those methods and spaces Also we will see that in this case, the spaces generated by the C θ functionals are not the same than the spaces generated by the C θ functional, but there are some inclusions between them Finally, we will see the Reiteration Theorem which tells us that interpolate two interpolation spaces is the same that interpolate the original spaces In the fifth chapter, we will see some applications of those methods in some functional spaces For example, we will interpolate L p spaces and see that we obtain the Lorentz spaces, also we will interpolate the Hardy spaces In the last chapter, we will apply those methods to the boundedness of operators between some Banach spaces For example, we will use them in the case of the Fourier Multipliers and the Hilbert Transform
8
9 Chapter Basic Notions and Preliminary Results In this chapter we will introduce a few results of Complex Analysis, Functional Analysis and Harmonic Analysis which will be useful in the next chapters Complex Analysis In this section we introduce some tools in order to prove the Riesz-Thorin Interpolation Theorem 2, in particular, we will need the Hadamard Three Line Theorem and the Phragmén-Lindelöf Principle Also, we will define what is a conformal mapping, the Poisson kernel and give an expression for the Poisson kernel in the strip tz P C : ď Rz ď u The aim of the Phragmén-Lindelöf Principle is to generalize on the horizontal strip of the complex plane, the maximum modulus principle, which does not apply to unbounded regions Theorem (Phragmén-Lindelöf Principle) Let f be a holomorphic function on the horizontal strip " z : π 2 ď Ipzq ď π * 2 If cosh CRpzq fpzq À e for some constant ď C ă and fpzq ď on the edges of the strip Then, fpzq ď in the interior of the strip Proof This proof reduces to the maximum modulus principle Fix D such that C ă D ă and fix ε ą The function ε cosh Dz F ε pzq fpzq{e is bounded by on the edges of the strip, and in the interior goes to uniformly in y as x Ñ 8 Then, on a rectangle " R Tε z : π 2 ď Ipzq ď π * 2, T ε ď x ď T ε 3
10 4 CHAPTER BASIC NOTIONS AND PRELIMINARY RESULTS the function F ε is bounded by on the edges Then, the maximum modulus principle implies that F ε is bounded by in the whole rectangle That is, for each z fixed in the strip, fpz q ď exppε cosh DRpz qq We can let ε Ñ `, giving fpz q ď Now, we can prove the Hadamard Three Line Theorem which says that if we have an holomorphic function inside a strip of the form tz ` iz 2 : a ď z ď bu in the complex plane, and this function is continuous on the whole strip then the logarithm of Mpz q sup z2 fpz ` iz 2 q is a convex function in the interval ra, bs Theorem 2 (Hadamard Three Line Theorem) Let f pzq be a bounded function of z z ` iz 2 defined on the strip tz ` iz 2 : a ď z ď bu holomorphic in the interior and continuous on the whole strip If we define Mpz q sup fpz ` iz 2 q y then logpmpz qq is a convex function in ra, bs That is, if z ta ` p tqb with t P r, s then Mpz q ď Mpaq t Mpbq t Proof We can assume that the interval ra, bs is r, s, this assumption only change some constants in the proof and reduces the notation Then, by hypothesis we have that fpyiq ď Mpq and fp ` yiq ď Mpq Let ε be positive and λ be a real number Define F ε pzq : exppεz 2 ` λzqfpzq Where z z ` z 2 i P C with z P r, s Notice that we have F ε pzq : exppεpz 2 z 2 2q ` λz q exppipεp2z z 2 q ` λz 2 qqfpzq Since z, fpzq and exppipεp2z z 2 q ` λz 2 qq are bounded we have that We also have that and that F ε pzq Ñ as z 2 Ñ 8 F ε piz 2 q e z2 2 ε e iλz 2 fpiz 2 q ď fpz 2 iq ď Mpq, F ε p ` iz 2 q exppεp z 2 2q ` λq exppipε2z 2 ` λyqq fpz 2 iq ď exppεp z 2 2q ` λq fp ` z 2 iq ď e ε`λ fp ` z 2 iq ď e ε`λ Mpq Now using Theorem with Rpzq εpz 2 z2 2 q ` λz, we obtain F ε pzq ď maxpmpq, e ε`λ Mpqq
11 COMPLEX ANALYSIS 5 Hence, F ε pz ` z 2 iq ď expp εpz 2 z2qq 2 maxpmpqe zλ, e ε`λp zq Mpqq This holds for any z Now, taking ε Ñ we obtain that F pzq ď maxpmpqe zλ, e λp zq Mpqq The right hand side is as small as possible when Mpqe zλ e λp zq Mpq So, we get F pz ` z 2 iq ď Mpq z Mpq z () Taking z ta ` p tqb t with t P r, s we can write () as F pz ` z 2 iq ď Mpq t Mpq t as we want Poisson Kernel in the Strip In this section we will give some notions that will be useful in the Section 43 and in the Section 52 We will begin by defining conformal maps Definition 3 Let Ω be a domain in C and f P HolpCq We say that f is a conformal mapping if f pzq for all z P Ω Recall that if z x ` iy then f pzq Bf Bz pzq 2 ˆBf Bx ibf pzq By Now we are going to give some expressions of the Poisson kernel in the unit disk and in the strip S First we will see an expression for the unit disk, this will be used in the Section 52 Definition 4 Let D be the unit disk in the complex plane, and let ă r ď We define a Poisson kernel in D as P r pz, e it q r2 z 2 re it z 2 Then, we define the Poisson integral of a function f in the unit disk as 2π fpe iθ qp r pz, e it qdθ 2π Now, we are going to see two expressions of the Poisson kernel in the strip S Definition 5 Let s ` it P S We define a Poisson kernel in S as P ps ` it, τq e πpτ tq sin πs sin 2 πs ` pcos πs e πpτ tq q 2
12 6 CHAPTER BASIC NOTIONS AND PRELIMINARY RESULTS Definition 6 Let s ` it P S We define a Poisson kernel in S as P ps ` it, τq e πpτ tq sin πs sin 2 πs ` pcos πs ` e πpτ tq q 2 Those expressions will we used in the Section 43, and some properties of those expressions will be seen in the mentioned section Also, it can be proved that the Poisson kernel in the unit disk and those expressions are equivalent under some conformal mapping from D to S (see [, Chapter 4, Theorem 48]) 2 Functional Analysis In this section we will introduce the most useful topics in functional analysis, in particular, we will see how integrate functions with values in Banach spaces Also, we will see the Completeness Theorem in Banach spaces 2 Completeness When we study if a normed space is complete it will be useful to work with series instead of sequences The following theorem tells us that in normed spaces the convergence of Cauchy sequences is equivalent to proving that all absolutely convergent series are convergent Theorem 2 (Completeness) Let E be a normed space Then the following are equivalent: E is a Banach space 2 all absolutely convergent series are convergent Proof p2q ñ pq Let px n q n Ă E be a Cauchy sequence such that If ε ñ Dn : }x m x n } ă if m, n ě n, If ε 2 k ñ Dn : }x m x n } ă 2 k if m, n ě n k Take # y y k + x n ñ }y k } ď 2 k x nk x nk Then, ř k y k is absolutely convergent, so ř k y k is convergent By definition it is equivalent to say that Nÿ k is convergent in E Therefore, px n q n has a partial which is convergent But, as we can do it for all the partials of px n q n we have that px n q n is convergent y k N
13 2 FUNCTIONAL ANALYSIS 7 pq ñ p2q Let ř 8 j x j be an absolutely convergent series, and assume that m ą n Define nÿ S n x j Then, mÿ }S m S n } x j ď j n j mÿ }x j } Ñ, as m, n Ò 8 j n So, ps n q n is a Cauchy sequence which implies that ps n q n is convergent to S ř 8 j x j Consequently, ř 8 j x j is a convergent series 22 Weak Topologies In this section we will introduce what the weak topologies for a normed space X and its dual X Also, we will see the Banach-Alaoglu Theorem which deals with weak compactness of the unit ball in X We will begin by defining the dual space of a normed space and a seminorm, since the weak topology is defined in terms of the dual space and seminorms Definition 22 Let X be a normed space in the field F, we define its dual space, X, as the set of ω satisfying that ω : X Ñ F such that ω is linear and continuous We define the norm in X as }ω} X sup ωpxq }x} X Usually we will denote ωpxq as xω, xy which means the action of ω over x Definition 23 Let V be a vector space in the field F, then a function σ : V Ñ F is called a seminorm if satisfies σpxq ě for all x P V, 2 σpx ` yq ď σpxq ` σpyq for all x, y P V, 3 σpλxq λ σpxq for all x P V and for all λ P F Notice that can happens that σpxq and x Now we are going to define the weak and the weak topologies Definition 24 Let X be a normed space and X its dual, we call the weak topology in X to the topology induced by the family of seminorms of the form where x P X and ω P X σ ω pxq xω, xy
14 8 CHAPTER BASIC NOTIONS AND PRELIMINARY RESULTS Definition 25 Let X be a normed space and X its dual, let px n q n Ă X and x P X We say that x n converges in the weak topology (or converges weakly) if We denote this convergence as x n w Ñ x Remark 26 ωpx n q Ñ P X (i) In the literature the weak convergence can be found as x n á x (ii) A subset B of X is called weakly closed if B is closed with the weak topology The same happens with the notions of weakly compact, weakly open and weak closure Definition 27 Let X be a normed space, ϕ P X and let pϕ n q n Ă X be a sequence in X Then, we say that ϕ n converges to ϕ in the weak topology if lim ϕ npxq P X nò8 We will write this as ϕ n w Ñ ϕ Also we need to define what is a reflexive Banach space Definition 28 Let X be a Banach space and X its dual We say that X is reflexive if X is isomorphic and isometric to the dual of X, this is the bidual of X This means that there exists an isomorphism ϕ from X to px q X 2 such that for all x P X we have that }x} X }ϕpxq} X 2 Finally, we are going to prove the Banach-Alaoglu Theorem, but in order to do this we need the Tychonov Theorem Theorem 29 (Tychonov s Theorem) Let tx α : U α u be a family of compact spaces Then ś α X α endowed with the product topology is compact The proof can be found in [5, Chapter, section 8] Theorem 2 (Banach-Alaoglu Theorem) Let X be a normed space and X its dual Then, the unit ball of X is weak compact Proof Let X be a normed space and X its dual and let B tt P X : }T } ď u If T P B, then T pxq P r }x}, }x}s for all x P X Consider the cartesian product P ź xpxr }x}, }x}s A point in P is a function f : X Ñ R such that fpxq P r }x}, }x}s, and P is the collection of all such functions The set B is a subset of P and inherits the product topology of P On the other hand, since B Ă X we have that B also inherits the weak topology of X Then we have to prove the following things:
15 2 FUNCTIONAL ANALYSIS 9 (i) These two topologies coincide on B (ii) B is closed in its relative product topology Let us prove (i), every weak open neighborhood of a point T P X contains an open set of the form O tt P X : T px j q T px j q ă δ for some δ ą, and for finite x j, j,, nu Likewise, every neighborhood of T P P open in the product topology of P contains an open set of the form V tf P P : fpx j q T px j q ă δ for some δ ą, and for finite x j, j,, nu These open sets form a base for the corresponding topologies Since B P X X, we have that O X B V X B These intersections form a base for the corresponding relative topologies inherited by B Therefore, the weak topology and the product topology coincide in B In order to prove (ii), let f be in the closure of B in the relative product topology Fix x, y P X and α, β P R and consider the three points For ε ą, the sets a x, x 2 y, x 3 αx ` βy V ε tf P P : fpx j q f px j q ă ε for j, 2, 3u are open neighborhoods of f Since they intersect B, there exists T P B such that f pxq T pxq ă ε, f pyq T pyq ă ε and since T is lineal, f pαx ` βyq αt pxq βt pyq ă ε Using this three inequalities we have that f pαx ` βyq αf pxq βf pyq ă p ` α ` β qε So, we have that f is linear and as it holds for any ε ą, we have that f P B Since the intervals r }x}, }x}s are compact in the euclidean topology, by the Tychonov s Theorem 29 we have that P is compact in the product topology But since by (ii) B is closed in P with this topology, we have that B is compact with the product topology Now by (i) the product topology and the weak topology coincide in B, therefore B is compact with the weak topology Corollary 2 If X is a reflexive Banach space, then if we apply the Banach-Alaoglu Theorem 2 we will have that the unit ball of X is weak compact
16 CHAPTER BASIC NOTIONS AND PRELIMINARY RESULTS 23 Bochner Integral In this section we give a vision on vector calculus In fact, we will define the Bochner integral and give a generalization of the Riemann-Stieltjes integral for functions with values in Banach spaces Since the J-method 32 is defined in terms of the Bochner integral, we need to see how to integrate a function that takes values in a Banach space We are going to follow the book [2, Chapter V, Section 5] The aim of the Bochner integral is to extend the Lebesgue integral to functions that take values in a Banach space The way to define this integral is the usual, we start integrating a simple function, and later we take the limit of integrals of simple functions So, let us start defining the integral for simple functions Definition 22 Let xpsq be a simple function defined on a measure space ps, F, µq with values in a Banach space X That is, # x i, s P B i P F xpsq, s P Sz Y i B i where B i X B j H for all i j P t,, nu and µpb i q ă 8 for all i P t,, nu Then, we define the integral as nÿ xpsqµpdsq : x i µpb i q S The following definition will be useful to prove that this integral is well defined Definition 23 Let xpsq be a function defined on a measure space ps, F, µq with values in a Banach space X xpsq is said to be a strongly F -measurable if there exists a sequence of simple functions convergent to xpsq µ-ae (ie except in sets of measure ) on S Definition 24 A function xpsq defined on a measure space ps, F, µq with values in a Banach space X is said to be Bochner integrable, if there exists a sequence of simple functions tx n psqu which is s-convergent (convergent in S) to xpsq µ ae in such a way that lim nò8 S i }xpsq x n psq}µpdsq (2) For any set B P F, the Bochner integral of xpsq over B is defined as xpsqµpdsq S lim χ B psqx n psqµpdsq (3) nò8 B where χ B psq is the characteristic function of the set B ie χ B psq if s P B; 2 χ B psq if s P SzB Lemma 25 The Bochner integral is well-defined S
17 2 FUNCTIONAL ANALYSIS Proof We have to see that (3) exists and that this value does not depend on tx n psqu First note that (2) makes sense because xpsq is strongly F-measurable From the inequality x n psqµpdsq x k psqµpdsq x n psq x k psqµpdsq B B X B X ď }x n psq x k psq} X µpdsq B ď }x n psq x k psq} X µpdsq S ď }x n psq xpsq} X µpdsq S ` }xpsq x k psq} X µpdsq, and this tends to Since X is a Banach space we have that S lim C B psqx n psqµpdsq nò8 S exists Now, we will see the independence of tx n psqu Let tx n u and ty n u be two sequences such that but satisfying that Then, taking pz n q such that S lim nò8 S lim nò8 z n psq x n psq Ñ xpsq y n psq Ñ xpsq S S S C B psqx n psqµpdsq a C B psqy n psqµpdsq b # x n psq, y n psq, S if n is odd if n is even, we have that pz n q converges to xpsq, and S lim C B psqz n psqµpdsq nò8 has to be convergent Therefore a b and this implies that this integral does not depend on the sequence The following proposition will be useful in the proof of Proposition 32 Proposition 26 Let T be a bounded linear operator on a Banach space X into a Banach space Y If xpsq takes values in X and is a Bochner integrable function, then T xpsq takes values in Y and, also, is Bochner integrable Moreover, ˆ T xpsqµpdsq T xpsqµpdsq B B
18 2 CHAPTER BASIC NOTIONS AND PRELIMINARY RESULTS Proof Let a sequence of simple functions ty n psqu satisfying and }y n psq} X ď }xpsq} X p ` n q S lim nò8 y n psq xpsq µ ae Then, by linearity and continuity of T, we have that ˆ T y n psqµpdsq T y n psqµpdsq Also, by the continuity of T, B }T y n psq} X ď }T } XÑY }y n psq} X ď }T } XÑY }xpsq} X p ` n q B And S lim nò8 T y n psq T xpsq µ ae Hence T xpsq is Bochner integrable and T xpsqµpdsq S lim T y n psqµpdsq S lim B nò8 B ˆ T xpsqµpdsq B nò8 T ˆ B y n psqµpdsq As happens when we integrate functions with values in R or in C, we can extend the Bochner integral in the way that instead of integrate with respect to µpdsq we integrate with respect to other function which takes values in a Banach space, defining the vector-valued Stieltjes Integral This generalization will be useful when we prove the Theorem 4 24 Fréchet Spaces and the Big Theorems In this section we will define the Fréchet Spaces and we will see some of the most important theorems in the functional analysis In the following lemma we will define what is a Fréchet norm Lemma 27 Given an increasing sequence of seminorms as in Definition 23, p pxq ď p 2 pxq ď ď p n pxq ď p n` pxq, such that p k pxq for all k implies x, then is a Fréchet norm, that is }x} nÿ k p k pxq 2 k p ` p k pxqq
19 2 FUNCTIONAL ANALYSIS 3 (a) }x ` y} ď }x} ` }y}, (b) } x} }x}, (c) }x} ñ x Proof Since p k are seminorms we have that p k p xq p k pxq for all k, then (b) is satisfied Also, we have that p k pxq ě, then the only way that }x} is that p k pxq for all k but, by hypothesis, this implies that x Therefore, (c) holds In order to prove (a) we will use that ϕptq t t ` is an increasing function with respect to t, and that p k are seminorms, then we have that p k px ` yq ` p k px ` yq ď p kpxq ` p k pyq ` p k pxq ` p k pyq ď p kpxq ` p k pxq ` pkpyq ` p k pyq This implies (a) Now we are going to define the Fréchet spaces Definition 28 A Fréchet space is a topological vector space endowed with a Fréchet norm so that it is complete The first theorem that we will see is the Baire s Theorem, this theorem deals with the union of open and dense sets, and will be useful for the proof of the Open Mapping Theorem Theorem 29 (Baire s Theorem) If pg n q n is a sequence of open and dense sets in a complete metric space, E, then Ť n G n is also dense Proof Let G be an open set, we want to prove that G X px n G n q H Since G is dense we have that there exists a ball Bpx, r q with r ă and x P G X G such that ClpBpx, r qq Ă GXG Then, since G 2 is dense we have that there exists a ball BpX 2, r 2 q with r 2 ă {2 and x 2 P Bpx, r q X G 2 such that ClpBpx 2, r 2 qq Ă Bpx, r q X G 2 Now, iterating this we obtain that for all n ClpBpx n, r n qq Ă Bpx n, r n q X G n, with r n ă {n Now, if p, q ě n then the distance between x p and x q is less than or equal to 2{n Therefore the sequence px p q p Ă E is a Cauchy sequence, so there exists x lim p x p On the other hand, by construction we have that x k P ClpBpx n, r n qq for all k ě n this implies that x P ClpBpx n, r n qq Ă G n for all n Hence, x P X n G n But, in particular, x P ClpBpx n, r n qq so x P G X px n G n q Corollary 22 If pf n q n is a countable collection of closed sets in a complete metric space such that the interior of F n is the empty set, F n H for all n, then Ť n F n H The next theorem is the Open Mapping Theorem and is, maybe, one of the most useful theorems in functional analysis
20 4 CHAPTER BASIC NOTIONS AND PRELIMINARY RESULTS Theorem 22 (Open Mapping Theorem) Let E and F be two Fréchet spaces If T : E Ñ F is a linear continuous operator so that T peq F then T is open, ie for all G open set in E T pgq is open in F If T is also injective, then T is also continuous The proof of this theorem can be found in [9, Theorem 2 and Corollary 22] Theorem 222 (Closed Graph Theorem) Let E and F be two Fréchet spaces Then a linear map T : E Ñ F is continuous if and only if GraphpT q tpx, T xq : x P Eu is closed in E ˆ F Proof Assume that T is continuous, and take a sequence px n, T x n q convergent to px, yq we want to see that y T x, but since T is continuous we have that if x n Ñ x then T x n Ñ T x Therefore y T x because px n, T x n q Ñ px, yq implies that x n Ñ x and that T x n Ñ y In order to see the other implication, since GraphpT q is closed then it is a Fréchet space Let us consider the mappings π : GraphpT q Ñ E, π 2 : GraphpT q Ñ F Since π is linear, continuous and exhaustive we have that by the Open Mapping Theorem 22 π is continuous So is continuous T x pπ 2 π qpxq 3 Harmonic Analysis In this section we will study the results in harmonic analysis that will be of interest for our work 3 The Weak-L p Spaces In this section we will define the weak-l p spaces, but in order to define these spaces first we need to introduce the distribution function and the non-increasing rearrangement of f, this topic will be important for give the statement and the proof of the Marcinkiewicz Interpolation Theorem and the next chapters So, let us define the distribution function of f Definition 3 Let px, µq be a measure space, and let f P MpXq, where MpXq is the space of measurable functions Fix t ą and consider the level set f t tx P X : fpxq ą tu Then, we define the distribution function of f as λ f ptq µpf t q
21 3 HARMONIC ANALYSIS 5 Now, we are going to see some properties of the distribution function Remarks 32 (i) λ f P r, 8s (ii) If s ă t and x P f t, then fpxq ą t ą s, in other words, f t Ă f s Hence, λ f psq ě λ f ptq Therefore, λ f is a decreasing function (iii) Let α P C, E P σpxq, and take f αχ E P MpXq Then, λ f ptq µpeqχ r, α s ptq (iv) Let f, f 2 P MpXq Then, λ f`f 2 pt ` t 2 q ď λ f pt q ` λ f2 pt 2 q In fact, this follows because tx P X : f pxq ` f 2 pxq ą t ` t 2 u Ă tx : f pxq ą t u Y tx : f 2 pxq ą t 2 u (v) If ă f ď f 2, then λ f ptq ď λ f2 ptq So, the distribution function is a increasing function as a function of f The next remark is important in order to the proof of Proposition 37 Remark 33 Let px, µq be a measure space, and let f P MpXq Then, λ f is rightcontinuous Proof Recall f t tx P X : fpxq ą tu, and fix t ą The sets f t are increasing as t decrease, and f t ď 8ď f t f t` n tąt Hence, we can apply the Monotone Convergence Theorem, (MCT), ˆ lim λ f t ` lim µ f n n n t` n 8ď MCT µ µpf t q λ f pt q n n f t` n The following proposition gives us a characterization of the L p norm of f in the space px, µq Proposition 34 For any ă p ă 8, the following equality holds 8 f p dµ p t p λ f ptqdt X Proof Assume that µ is smooth enough in order to be able to apply Fubini 8 8 t p λ f ptqdt t p dµdt Fubini X tx : fpxq ątu fpxq t p dtdµ X p tp fpxq dµ fpxq p dµ p X
22 6 CHAPTER BASIC NOTIONS AND PRELIMINARY RESULTS The following definition that we need is the non-increasing rearrangement of f (or decreasing rearrangement of f) Definition 35 We define the non-increasing rearrangement of f as f ptq infts ą : λ f psq ď tu The non-increasing rearrangement of f is also known as the right-inverse of the distribution function of f Now let us see some properties of f ptq Remarks 36 (i) If λ f is a bijection then f λ f (ii) If t ą t 2, then f pt 2 q ě f pt q, since λ f psq ď t 2 ă t, where s is the infimum of ts ą : λ f psq ď t 2 u (iii) Let α P C, E P σpxq, and take f αχ E P MpXq Then, f ptq α χ p,µpeqq ptq (iv) Let f, f 2 P MpXq Then, pf ` f 2 q pt ` t 2 q ď f pt q ` f 2 pt 2q f We can characterize the L p pxq norm of f using the non-increasing rearrangement of Proposition 37 Let ă p ă 8 and f P MpXq Then, 8 }f} p p f p pf ptqq p dt X Before we prove this result we introduce what means that two functions are equimeasurable Definition 38 We say that f and f 2 are equimeasurable if λ f λ f2 Remark 39 By Proposition 34 that f and f 2 are equimeasurable implies that }f } p }f 2 } ă p ă 8 Proof of Proposition 37: We have to see that λ f λ f Because, if this happens then by Proposition 34 we obtain X f p p 8 So, let us see that λ f λ f t p λ f ptqdt p 8 t p λ f ptqdt 8 pf ptqq p dt As f is measurable we can take a sequence of a nonnegative simple functions pf n q n such that f n Ò f Then, if we are able to prove that for each n λ fn ptq λ f n ptq,
23 3 HARMONIC ANALYSIS 7 using the monotone convergence theorem we will have that λ f ptq lim n λ fn ptq lim n λ f n ptq λ f ptq Then, we verify that λ fn ptq λ f n ptq for each n Fix n, then f n pxq rÿ a j χ Ej pxq j Where E j are disjoint measurable sets in X Call m j jÿ µpe i q, if j ě i m Now, we can observe that f ptq if t ě m r, f ptq a r if m r ą t ě m r, and so on Then, f nptq rÿ a j χ rmj,m j qptq j Note that, the coefficients of f n and f n are the same a j So, if f n pxq ă s implies that f nptq ă s And, as by definition of m j, the measure of E j is the measure of m j m j we have that λ fn ptq λ f ptq n Definition 3 Let T n : B Ñ MpXq be a sequence of lineal operators We define the maximal operator T fpxq sup T n fpxq npn Remark 3 T is sublinear, this means that T satisfies (i) T pf ` gqpxq ď T fpxq ` T gpxq (sub-additive), (ii) T pαfqpxq α T fpxq (homogeneous) The following definition is the main estimates in the Marcinkiewicz Interpolation Theorem Definition 32 Given ď p ď 8, we define the weak-type (p,8) space as follows L p,8 is also called weak-l p space L p,8 tf P MpR n q : }f} p,8 sup tλ {p f ptq ă 8u tą Remarks 33 (i) L p,8 is a linear space and } } p,8 is a quasi-norm, ie (a) }f} p,8 ě and }f} p,8 ô f, (b) }αf} p,8 α }f} p,8, (c) }f ` g} p,8 ď C p p}f} p,8 ` }g} p,8 q with C p ą
24 8 CHAPTER BASIC NOTIONS AND PRELIMINARY RESULTS Moreover, pl p,8, } } p,8 q is a quasi-banach space (ii) If p ą, then L p,8 is a Banach space (iii) L p Ł L p,8, this inclusion is the Chebyshev s inequality Let us see an example of function that belongs in L p,8 but not in L p Example 34 Let f α pxq x α with α ą Then, it is clear that f α R L p Now, compute the distribution function of f α λ fα ptq ˇˇtx P R n : x α ˇ ą tuˇˇ ˇtx P R n : x ą t α uˇˇˇ Cn t n α Then, putting this in }f α } p,8 }f α } p,8 sup t t n αp ă 8 ô n tą αp ô α n p Therefore, x n{p belongs in L p,8 but not in L p Now we will define what is a weak type pp, pq operator and see a simpler example of a weak type p, q operator Definition 35 Let ď p ă 8 We say that T is a weak type pp, pq operator, if If T : L p Ñ L p,8 T : L p Ñ L p We say that T is a strong type pp, pq operator Now let us give a simpler example of a weak type p, q operator Definition 36 Let f P L loc pr`q We define the Hardy operator as Sfptq t t fpsqds Before proving that is a weak-type p, q we need the Minkowski s integral inequalities Theorem 37 (Minkowski s integral inequalities) Let F : X ˆ Y Ñ R`, ď p ď 8 Then, ˆ ˆ p ˆ p F px, yqdx dy ď F px, yq p p dy dx Y Proof If p the theorem holds by Fubini X If p 8, in this case we have to change the integrals by the essential supremum and since sup sup α i,j sup sup α i,j, j i i j if we can take α i,j F px, yq, sup i sup xpx and sup j sup ypy, then we have the equality X Y
25 3 HARMONIC ANALYSIS 9 If ă p ă 8, then via Hölder s inequality we have that ˇ ˇş fgˇˇ }f} p sup gpl }g} p p Now, if we define then }f} p sup }g} p ď ˇ Y fpyq : X fpyqgpyqdy ˇ F px, yqdx sup }g} p ď ˇ Y X F px, yqdxgpyqdy ˇ Applying Fubini we have ˆ }f} p ď sup F px, yq gpyq dydx Hölder ď sup }g} p F px, yq p dy dx }g} p ď X Y }g} p ď X Y And now, since we are taking }g} p ď we can take out the supremum and we are done }f} p ď ˆ ˆ sup }g} p F px, yq p dy dx F px, yq p dy dx }g} p ď X Y X Y Once we have proved the Minkowski s integral inequality, we are able to prove the Hardy s inequality that says that the Hardy operator is a strong type pp, pq operator if p ą and a weak type operator if p Theorem 38 (Hardy s inequalities) If ă p ď 8 then S : L p Ñ L p Moreover, S : L Ñ L,8 Proof If p 8, then Sfptq ď t If ă p ă 8, then Sfptq t t t fpsq ds ď t fpsqds t t }f} 8 ds }f} 8 tfptrqdr fptrqdr Thus, ˆ 8 }Sfptq} p ˇ fprtqdr ˇ p p dt
26 2 CHAPTER BASIC NOTIONS AND PRELIMINARY RESULTS Applying the Minkowski s integral inequality, we get }Sfptq} p ď ˆ 8 dr }f} p f p p prtqdt dr r p ˆ 8 r p p }f} p p }f} p f p psq ds p dr r So, we have proved that S is a strong type pp, pq operator if ă p ď 8 Now, let us see it is a weak type p, q operator For this purpose we first check that exists f P L such that Sf R L Let f χ p,q, then So, Sfptq R L Sfptq t t χ p,q psqds #, ă t ă t, t ě Now take f P L and we want to see that Sf belongs in L,8 So, we have to compute the λ Sf " λ Sf ptq ˇ s ą : s ˇ s fprqdr ˇ *ˇˇˇˇ ą t ď }f} t ñ sup t }f} t }f} Therefore, }Sf},8 ď }f} Then S is a weak type p, q operator 32 Lebesgue Differentiation Theorem In this section we will prove the Lebesgue differentiation theorem that is an analogous version of the Fundamental Calculus Theorem, and it will be useful when we want to prove that the Fourier multipliers, M 2, are the functions of L 8 pr n q In order to prove the Lebesgue differentiation theorem we need to define the Hardy- Littlewood maximal function Definition 39 Let f P L loc prn q, we define the Hardy-Littlewood maximal function of f as Mfpxq : sup f pyq dy rą Bpx, rq Bpx,rq where Bpx, rq is the ball of radius r and center x Remark 32 The Hardy-Littlewood maximal function of f satisfies the following properties: (a) Let f P L loc prn q, then Mfpxq ě and there exists x P R n such that Mfpxq if and only if f ae x (b) f, g P L loc prn q, then Mpf ` gqpxq ď Mfpxq ` Mgpxq and Mpαgqpxq α Mgpxq for all α P R n
27 3 HARMONIC ANALYSIS 2 (c) If f P L 8 pr n q then for all x P R n we have that Mfpxq ď }f} 8 So, we have that }Mf} 8 ď }f} 8 and that }M} (d) If f P L pr n qztu then Mf R L pr n q }Mf} 8 sup fpl 8 pr n q }f} 8 The following theorem shows that the Hardy-Littlewood maximal function, is a continuous operator from L pr n q to L,8 pr n q, the proof of this theorem can be found in [3, Chapter 3, pg 9] Theorem 32 (Hardy-Littlewood Theorem) Let M be the Hardy-Littlewood maximal function, then M : L pr n q Ñ L,8 pr n q Theorem 322 (Lebesgue Differentiation Theorem) If f P L loc prn q then lim fpyqdy fpxq ae x P R n ró Bpx, rq Bpx,rq where Bpx, rq is the ball of radius r and center x Proof Let Q j be cubes in R n such that Q j are disjoint and R n Ť j Q j Then, it suffices to prove the result for fχ Qj P L pr n q Observe that if g P CpR q X L pr n q then, by the Fundamental Calculus Theorem, we have that lim gpyqdy P R n (4) ró Bpx, rq Bpx,rq Assume that f P L pr n q, we only need to prove that for a given j P N the set # + A j : x P R n : lim sup fpyqdy fpxq rñ ˇ Bpx, rq ˇ ą j Bpx,rq has measure Take ε ą and g P CpR q X L pr n q such that }g f} ă ε Define h f g and put f h ` g, by (4) we can rewrite A j as # + A j : x P R n : lim sup hpyqdy hpxq rñ ˇ Bpx, rq ˇ ą j Bpx,rq But, by the inclusion ta ` b ą tu Ă ta ą t{2u Y tb ą t{2u we have that " A j ď ˇ x P R n : Mhpxq ą " 2j *ˇˇˇˇ ` ˇ x P R n : hpxq ą 2j *ˇˇˇˇ Now, using the Hardy-Littlewood Theorem 32 and the Chebyshev theorem we have that " A j ď ˇ x P R n : Mhpxq ą " 2j *ˇˇˇˇ ` ˇ x P R n : hpxq ą 2j *ˇˇˇˇ ď K2jε ` 2jε 2jεpK ` q, where K is the constant such that }Mh},8 ď K}h} Moreover, since 2jpK ` q is fixed and independent of ε we have that A j ď 2jεpK ` q Ñ, as ε Ñ
28 22 CHAPTER BASIC NOTIONS AND PRELIMINARY RESULTS 33 Fourier Transform In this section we will introduce the Fourier Transform and some of its properties for functions of L pr n q and L 2 pr n q Let us begin by defining the Fourier Transform for functions in L pr n q Definition 323 For all f P L pr n q we define its Fourier Transform as ˆfpξq with ξ P R n R n fpxqe ix ξ dx Proposition 324 The Fourier transform is a continuous map from L pr n q to L 8 pr n q Proof Let f P L pr n q, then we have that sup ˆfpξq ď sup fpxq e ix ξ dx sup ξpr n ξpr n R n ξpr n R n fpxq dx sup ξpr n }f} }f} Theorem 325 (Hat Theorem) If f, g P L pr n q, then ˆfpξqgpξqdξ R n fpxqĝpxqdx R n Proof The proof of this theorem follows by applying Fubini s Theorem to the definition of F In fact, by definition of ˆf we have that ˆ ˆfpξqgpξqdξ R n R n fpxqe ix ξ dx R n gpξqdξ Now, since f, g P L we can apply Fubini and we obtain that ˆ ˆ fpxqe ix ξ dx gpξqdξ fpxq R n R n R n R n gpξqe ix ξ dξ dx fpxqĝpxqdx R n Now, we will define the convolution of two functions Definition 326 Let f, g P L and Ω R n, then we define the convolution of f and g as pf gqpxq gpx yqfpyqdy Λ f pτ x gq, R n where gpzq gp zq and τ x gpyq gpy xq Remark 327 If f, g P L pr n q, then (a) pτ y x fqpξq ˆfpξqe ix ξ, where τ x fpyq fpy xq (b) pe ix y fpyqqˆpξq τ x ˆfpξq (c) pf z gqpξq ˆfpξqĝpξq (d) If λ ą and hpxq fpx{λq then ĥpξq λn ˆfpλξq
29 3 HARMONIC ANALYSIS Schwarz Class In this section we will introduce the class of Schwarz functions and we will see some properties of this class, in particular, we will apply the Fourier Transform to this class and use some of these results to prove some properties of F in L Let P be a polynomial of n variables of the form P pξq ÿ α C α ξ α ξαn n Let D α i α D α, ie D α nź ˆ B ibx j j αj Then, P pdq ř α C αd α and P p Dq ř α C αp q α D α This definition of P pdq will be the main definition in the chapter of PDE s Now we are going to define the space S Definition 328 A function f P C 8 pr n q belongs in the space S n p Sq if for all N P N we have that P N pfq sup p ` x 2 q N D α fpxq ă 8 xpr n α ďn Remark 329 (a) If f P S and Q is any polynomial then D α fpxq À P R n (b) ps, tp n u n q is a Fréchet space Theorem 33 (a) If P is a polynomial and g P S then the following mappings are linear and continuous S Ñ S f ÞÑ P f f ÞÑ gf f ÞÑ D α f (b) If f P S then pp pdqfqˆ P ˆf and pp fqˆ P p Dq ˆf (c) The mapping F : S Ñ S is linear and continuous Proof We will begin by prove (a) First P f P C 8, and for all N P N by Leibniz Formula we have that sup p ` x 2 q N D α pp fqpxq ď CP N`M pfq ď 8 xpr n α ďn
30 24 CHAPTER BASIC NOTIONS AND PRELIMINARY RESULTS where M degpp q To see that gf P S we have to use the same argument Now since S is a Fréchet space the continuity follows from the Closed Graph Theorem 222 In fact and f n Ñ f in S ñ f n pxq Ñ fpxq@x, gf n Ñ h in S ñ gpxqf n pxq Ñ hpxq@x That f ÞÑ D α f is continuous follows since S is Fréchet and f P C 8 Now we are going to prove (b), but we can reduce to prove for P pxq x by symmetry and iteration First we will see that S Ă L Let g P S then gpxq dx p ` x 2 q N gpxq R n R n p ` x 2 q N dx ď P Npgq R n p ` x 2 q N dx But this type of integrals are finite if and only if 2N ą n So taking N big enough we have that R n gpxq dx ă 8 So, since S Ă L we have that pp pdqfqˆpξq P pdqfpxqe ix ξ dx R n i R n df dx pxqe ix ξ dx Now using Fubini and taking x px 2,, x n q, we obtain that df pxqe ix ξ dx ˆ df pxqe ix ξ dx i R n dx i R n R dx Now integrating by parts ˆ df pxqe ix ξ dx i dx R n R e i x ξd x R n ξ i e i x ξd x ˆ df ξ pxqe ix ξ dx R dx df pxqe ix ξ dx ξ ˆfpξq dx R n P pξq ˆfpξq e i x ξd x Therefore, we have that pp pdqfqˆ P ˆf Now we will see that pp fqˆ P p Dq ˆf Let t pt,, t n q and t pt ` ε,, t n q Then But, ˆfpt q ˆfptq e ixε x fpxq e ix t dx iε R n iεx lim εñ ˆfpt q ˆfptq iε i In the other hand, since x fpxq P L pr n q and e ix ε iεx d dx ˆfptq
31 3 HARMONIC ANALYSIS 25 is bounded, we can apply the Dominated Convergence Theorem, and we arrive at the fact that there exists d ˆf dx and Then i xp f i It remains to see (c), let f P S and define d ˆfptq pp fqˆ dx d ˆfptq P p Dqf dx gpxq p q α x α fpxq P S then ĝpξq D α ˆfpξq Therefore, P pξqĝ pp pdqgqˆpξq P L 8, then ˆf P S The linearity of F follows from definition and the continuity follows from the Closed Graph Theorem 222 using that if f i Ñ f in S then f i Ñ f in L and therefore ˆf i pξq Ñ fpξq for all ξ Remark 33 The function φpxq expp x 2 {2q P S and φ ˆφ Now, we are going to see two Inversion Theorems, the first version deals with functions in S and the second deals with functions in L Theorem 332 (Inversion Theorem) (a) If g P S then gpxq ĝpξqe ix ξ dξ R n (b) The Fourier Transform F is an injective and continuous mapping from S to S, it has period 4 and its inverse F : S Ñ S is continuous Proof We will begin by proving (a), let φpxq expp x 2 {2q and g P S, then by the Hat Theorem 325 R n g ˆ t ˆφptqdt λ n ĝpλtqφptqdt ĝptqφ λ R n R n ˆ t dt λ Using again the Dominated Convergence Theorem, the Remark 33 and letting λ Ñ 8 we obtain that gpq gpq ˆφ φpq ĝpxqdx ĝpxqdx R n R n So, we have (a) proved for x Now consider x, then gpxq pτ x gqpq pτ x gqˆpyqdy R n ĝpyqe ix y dy R n
32 26 CHAPTER BASIC NOTIONS AND PRELIMINARY RESULTS Now we are going to see (b), but by (a) by know that F is one-to-one, also we proved the continuity in last Theorem, so if we see that F 2 g gp gp xqq then we will have that F 4 g g and that F F 3 which is continuous But we have that gp xq pτ x gqpq pτ x gqˆpyqdy R n ĝpyqe ix y dy F 2 gpxq R n Corollary 333 If f, g P S then we have (a) f g P S Ź (b) pf gqpξq ˆfpξqĝpξq Proof We will begin by proving (a), since f, g P S we have that ˆf, ĝ P S, this implies that ˆfĝ pf gqˆp S Therefore, f g P S The proof of (b) is the same that for L pr n q The following theorem deals with functions in L pr n q Theorem 334 (Inversion Theorem) If f and ˆf are in L pr n q, then fpxq ˆfpξqe iξx dξ ae x R n Proof Let and g P S Then f pxq f pxqĝpxqdx R n R n R n ˆ ˆfptqe ixt dt R n ˆfptqe ixt dt ĝpxqdx Using Fubini and the Hat Theorem 325 we arrive at R n ˆ R n Since F : S Ñ S we can write ĝ as g Then ˆ ˆfptqe ixt dt ĝpxqdx ĝpxqdxe ixt ˆf ptqdt R n R n gptq ˆfptqdt fptqĝptqdt R n R n R n pf P S Then, by density f ptq fptq aet Theorem 335 (Plancherel s Theorem) If f P L pr n q X L 2 pr n q, then }f} 2 } ˆf} 2
33 3 HARMONIC ANALYSIS 27 Proof Let f P L pr n q X L 2 pr n q, then we have that }f} 2 2 fpxq 2 dx p f fqpq, R n where fpxq fp xq and f is the conjugate of f Since f, f P L pr n q, by the Remark 327, we have that g f f is continuous and is in L pr n q Moreover ĝpξq ˆ fpξq ˆ fpξq ˆfpξq ˆfpξq ˆfpξq 2 Now, we can apply the inversion Theorem 334 and obtain that gpxq ˆfpξq 2 e ix ξ dξ ae x R n In particular, for x, we have that }f} 2 2 gpq ˆfpξq 2 dξ } ˆf} 2 2 R n Then, we have that }f} 2 } ˆf} 2 Proposition 336 The space L pr n q X L 2 pr n q is dense in L 2 pr n q Proof Let f P L 2 pr n q and let f T pxq fpxqχ Bp,T q pxq, we are going to see that f T P L pr n q X L 2 pr n q Since }f T } 2 ď }f} 2 we have that f T P L 2 pr n q, also since f P L 2 pr n q we have that f P L loc prn q so f T P L pr n q Therefore f T P L pr n q X L 2 pr n q Notice that lim f T pxq fpxq aex P R n T Ò8 Even more, since f T pxq fpxq ď fpxq we can dominate f T pxq fpxq 2 by fpxq 2 Then we can apply the Dominated Convergence Theorem to lim T Ò8 f T pxq fpxq 2 dx R n lim f T pxq fpxq 2 dx R n T Ò8 With this we can conclude that L pr n q X L 2 pr n q is dense in L 2 pr n q Remark 337 Let f P L 2 pr n q since, by Proposition 336 L pr n q X L 2 pr n q is dense in L 2 pr n q, we have that if pf j q j Ă L X L 2 so that f L 2 lim f j, then by Plancherel s Theorem 335, we have that }f j f i } 2 } ˆf j ˆf i } 2 ñ DL 2 lim ˆf j Hence, we can define the Fourier Transform in L 2 pr n q as such that f j Ñ f in L 2 pr n q F pfqpξq L 2 lim ˆf j, Remark 338 (a) The Fourier Transform in L 2 pr n q is well defined (b) If f P L pr n q X L 2 pr n q, then F pfq ˆf
34 28 CHAPTER BASIC NOTIONS AND PRELIMINARY RESULTS (c) If f P L 2 pr n q and f r fχ Brpq P L pr n q X L 2 pr n q, then f r Ñ f For n ą it still unknown if in L 2 ñ F f L 2 lim ˆfr L 2 lim fpxqe ixξ dx rò8 rò8 B rpq F fpξq lim RÒ8 fpxqe ix ξ dx ae x B R pq As a consequence of Plancherel s Theorem 335 and Remark 337 we have the following theorem Theorem 339 (Parseval s Theorem) If f P L 2 pr n q then }Fpfq} 2 }f} 2 Proof By Remark 337 the Fourier transform extends in a uniquely way in L 2 pr n q Moreover we have that, if g i P L pr n q X L 2 pr n q satisfying that L 2 lim iò8 g i pxq fpxq, then, by Plancherel s Theorem 335, we have that }Fpfq} 2 } lim iò8 ĝ i } 2 lim iò8 }g i } 2 }f} 2 4 Distribution Theory In this section we are going to define what is a distribution and a tempered distribution, also we will see that if f P L loc prn q then we can construct a distribution that acts by integration Let Ω be an open set in R n and for each compact set K Ă Ω (K P KpΩq), consider the subspace D K tf P C 8 pωq : supppfq Ă Ku with the topology induced by C 8 pωq Recall that pc 8 pωq, tp Kj,ju j q is a Fréchet space (see Section 24), where K j Ă P Kj,jpfq sup D α fpxq α ďj xpk j K j` Ă Ă Ω, Ť K j Ω and Since D K is closed in C 8 pωq, we have that D K is also a Fréchet space Observe that in this subspace the topology is also given by the following family of seminorms: }f} N : sup D α fpxq α ďn xpω Now we are going to define the test functions space
35 4 DISTRIBUTION THEORY 29 Definition 4 The test space is DpΩq Ť KPKpΩq D K, that is the set of all C 8 pωq functions with compact support in Ω In general, DpΩq is not a Fréchet space Definition 42 Let ϕ, pϕ j q j Ă DpΩq we say that ϕ j Ñ ϕ if and only if there exist K P KpΩq and j P N such ě j we have that ϕ j P D K and ϕ j Ñ ϕ in D K Now we can define what is a distribution Definition 43 A distribution, Λ, is a linear and continuous functional over DpΩq such that Λ P D pωq and Λ : DpΩq Ñ K in the following P KpΩq there exist N P N and C ą such that Λpϕq ď C}ϕ} P D K And we will say that pλ j q j Ă D pωq converges to Λ P D pωq if and only if Remark 44 The map Λ j pϕq Ñ P D K L loc pωq Ñ D pωq f Ñ Λ f where is injective but not exhaustive Λ f pϕq fpxqϕpxqdx R n 4 Tempered Distributions The aim of the tempered distributions is that if ϕ P D and ˆϕ is its Fourier Transform then we never have that ˆϕ P D So, in general, we cannot apply the Fourier Transform to distributions Definition 45 A tempered distribution u is an element of the dual space S Remark 46 Let u P S as D ãñ S we have that u D is a distribution Theorem 47 If P is a polynomial, g P S and u P S then D α u, P u and gu are also tempered distributions The proof of this theorem can be found in [9, Theorem 73] Definition 48 If u P S we define ûpϕq : up ˆϕq where ϕ P S
36 3 CHAPTER BASIC NOTIONS AND PRELIMINARY RESULTS Now we are going to see that this definition is consistent when f P L pr n q and u P S is of the form u f pφq fpxqφpxqdx R n Let ϕ P S, then by definition we have that û f pϕq u f p ˆϕq fpxq ˆϕpxqdx R n Using the Hat Theorem 325 we arrive at û f pϕq u f p ˆϕq fpxq ˆϕpxqdx R n ϕpxq ˆfpxqdx u ˆf pϕq R n Remark 49 The map F : S Ñ S is continuous, bijective, has period 4 and its inverse is also continuous The proof of this result can be found in [9, Theorem 75] Example 4 ˆ δ and ˆδ Let ϕ P SpRq, by the Definition 48 we have that ˆpϕq p ˆϕq ˆϕpxqdx ˆϕpxqe ix dx And, by the Inversion Theorem 332 we obtain that ˆpϕq ˆϕpxqe ix dx ϕpq δ pϕq R R Therefore, ˆ δ in the sense of distributions Now, again by the Definition 48 we have that ˆδ pϕq δ p ˆϕq ˆϕpq ϕpxqdx pϕq R n Hence, ˆδ in the sense of distributions R
37 Chapter 2 Classical Methods in the Interpolation Theory In this chapter we study the classical methods in the interpolation theory, these are the Riesz-Thorin Theorem and the Marcinkiewicz Theorem These results provided the impetus for the study of the interpolation theory, the proof of the first theorem gives the idea behind the complex interpolation method, meanwhile the proof of the second theorem provides the construction of the real interpolation method 2 Riesz-Thorin Theorem The first theorem that we will prove is the Riesz-Thorin Theorem For this theorem we assume that the scalars are complex numbers Theorem 2 (Riesz-Thorin interpolation Theorem) Let pu, µq and pv, νq be two measurable spaces Assume that p p, q q, and that is bounded with norm M, and that is also bounded with norm M Then is bounded with norm provided that ă θ ă and T : L p puq Ñ L q pv q T : L p puq Ñ L q pv q T : L p puq Ñ L q pv q p θ ` θ, p p M ď M θ M θ q θ ` θ (2) q q Notice that the points p{p, {qq described in (2) can be geometrically interpreted as the points in the line with end points p p, q q and p p, q q 3
38 32 CHAPTER 2 CLASSICAL METHODS p p, q ( p, q ) ( p, q ) ( p, q ) q Figure 2: Geometric interpretation of (2) Proof Let p θ ` θ, p p V q θ ` θ q q And let q q Then, by Hölder s inequality, * M sup "ˇˇˇˇ T fpyqgpyqdν ˇ : }f} p }g} q Since p ă 8, q ă 8 we can assume that f P L p and g P L q are bounded with compact supports For ď Rpzq ď, we put ppzq z ` z, p p q pzq z q ` z q, and ϕpzq ϕpx, zq fpxq p ppzq fpxq fpxq, x P U, ψpzq ψpy, zq gpyq q gpyq q pzq gpyq, y P V Now, we will see that ϕpzq P L p j puq }ϕ} p p ϕpx, zq p j dµ U U U fpxq p jp{ppzq fpxq p j fpxq p dµ j fpxq pjp{ppzq dµ ď fpxq Rppjp{ppzqq dµ U
39 2 RIESZ-THORIN THEOREM 33 Since, ď Rpzq ď, we have that p j {Rpppzqq ď Then, we obtain U ϕpx, zq p j dµ ď ď U U fpxq Rpp jp{ppzqq dµ fpxq p dµ ď }f} p p And the same argument can be used to see that ψpzq P L q jpv q Since ϕpzq P L p j puq, then T ϕ P L q j pv q with j, Also, we can check that ϕ pzq P L p j puq, ψ pzq P L q jpv q and thus also that pt ϕq pzq P L qj pv q if p ă Rpzq ă q This implies the existence of F pzq T ϕpyqψpyqdν, ď Rpzq ď V Even more, we have that F is an analytic function on the open strip ă Rpzq ă, and bounded and continuous on the closed strip ď Rpzq ď Also, by definition of ϕ and ψ we have that }ϕpitq} p } f p{p } p }f} p{p p, }ϕp ` itq} p } f p{p } p }f} p{p p, and the same for ψ }ψpitq} q }ψp ` itq} q Therefore, we obtain F pitq Hölder ď }T ϕpitq} p }ψpitq} q ď M, F p ` itq Hölder ď }T ϕp ` itq} p }ψp ` itq} q ď M Moreover, since ppθq p and q pθq q, we have and so, ϕpθq f, ψpθq g, F pθq V T fpyqgpyqdν Using now Theorem 2 we obtain ˇ T fpyqgpyqdν ˇ ď M θ M θ, V or what is the same (taking supremum in the both sides and using that M θ M θ is constant) M ď M θ M θ
40 34 CHAPTER 2 CLASSICAL METHODS 22 The Marcinkiewicz Theorem In this section we give the statement and the proof of the Marcinkiewicz Interpolation Theorem As we said before this theorem contains the main ideas used in the real interpolation method We are going to use some results seen in Section 3 Also, it is important to note that from now the functions f can take values in R and in C as a difference with the Riesz-Thorin Theorem 2 where the values had to be complex Another important difference between these two theorems is that now, in the hypothesis, we replace the strong spaces (L p ) for the weak spaces who are largest spaces Therefore, this theorem can be used where Theorem 2 fails So, let us give the statement of the Marcinkiewicz Interpolation Theorem Theorem 22 (The Marcinkiewicz Interpolation Theorem) Let pu, µq and pv, νq be two measurable spaces Assume that p p, q q, and that is bounded with norm M, and that is also bounded with norm M Let p θ ` θ, p p and assume that T : L p puq Ñ L q,8 pv q T : L p puq Ñ L q,8 pv q q θ ` θ, q q p ď q (22) Then, with norm M satisfying T : L p puq Ñ L q pv q M ď C θ pm q θ pm q θ Before we start with the proof we pay attention with the statement Notice that we have one hypothesis more than in the Theorem 2 that is the restriction (22) Moreover, notice that in this theorem M satisfies M ď C θ pm q θ pm q θ while M ď pm q θ pm q θ this is because if the scalars are real then we can only prove the convexity inequality M ď C θ pm q θ pm q θ Now, let us prove the theorem but only for q p and p q The general case can be found in [3, Theorem 46, p2]
REAL ANALYSIS II TAKE HOME EXAM. T. Tao s Lecture Notes Set 5
 REAL ANALYSIS II TAKE HOME EXAM CİHAN BAHRAN T. Tao s Lecture Notes Set 5 1. Suppose that te 1, e 2, e 3,... u is a countable orthonormal system in a complex Hilbert space H, and c 1, c 2,... is a sequence
REAL ANALYSIS II TAKE HOME EXAM CİHAN BAHRAN T. Tao s Lecture Notes Set 5 1. Suppose that te 1, e 2, e 3,... u is a countable orthonormal system in a complex Hilbert space H, and c 1, c 2,... is a sequence
Singular integral operators and the Riesz transform
 Singular integral operators and the Riesz transform Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto November 17, 017 1 Calderón-Zygmund kernels Let ω n 1 be the measure
Singular integral operators and the Riesz transform Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto November 17, 017 1 Calderón-Zygmund kernels Let ω n 1 be the measure
NOTES ON SOME EXERCISES OF LECTURE 5, MODULE 2
 NOTES ON SOME EXERCISES OF LECTURE 5, MODULE 2 MARCO VITTURI Contents 1. Solution to exercise 5-2 1 2. Solution to exercise 5-3 2 3. Solution to exercise 5-7 4 4. Solution to exercise 5-8 6 5. Solution
NOTES ON SOME EXERCISES OF LECTURE 5, MODULE 2 MARCO VITTURI Contents 1. Solution to exercise 5-2 1 2. Solution to exercise 5-3 2 3. Solution to exercise 5-7 4 4. Solution to exercise 5-8 6 5. Solution
Functional Analysis. Martin Brokate. 1 Normed Spaces 2. 2 Hilbert Spaces The Principle of Uniform Boundedness 32
 Functional Analysis Martin Brokate Contents 1 Normed Spaces 2 2 Hilbert Spaces 2 3 The Principle of Uniform Boundedness 32 4 Extension, Reflexivity, Separation 37 5 Compact subsets of C and L p 46 6 Weak
Functional Analysis Martin Brokate Contents 1 Normed Spaces 2 2 Hilbert Spaces 2 3 The Principle of Uniform Boundedness 32 4 Extension, Reflexivity, Separation 37 5 Compact subsets of C and L p 46 6 Weak
DS-GA 1002: PREREQUISITES REVIEW SOLUTIONS VLADIMIR KOBZAR
 DS-GA 2: PEEQUISIES EVIEW SOLUIONS VLADIMI KOBZA he following is a selection of questions (drawn from Mr. Bernstein s notes) for reviewing the prerequisites for DS-GA 2. Questions from Ch, 8, 9 and 2 of
DS-GA 2: PEEQUISIES EVIEW SOLUIONS VLADIMI KOBZA he following is a selection of questions (drawn from Mr. Bernstein s notes) for reviewing the prerequisites for DS-GA 2. Questions from Ch, 8, 9 and 2 of
Tempered Distributions
 Tempered Distributions Lionel Fiske and Cairn Overturf May 9, 26 In the classical study of partial differential equations one requires a solution to be differentiable. While intuitively this requirement
Tempered Distributions Lionel Fiske and Cairn Overturf May 9, 26 In the classical study of partial differential equations one requires a solution to be differentiable. While intuitively this requirement
JUHA KINNUNEN. Harmonic Analysis
 JUHA KINNUNEN Harmonic Analysis Department of Mathematics and Systems Analysis, Aalto University 27 Contents Calderón-Zygmund decomposition. Dyadic subcubes of a cube.........................2 Dyadic cubes
JUHA KINNUNEN Harmonic Analysis Department of Mathematics and Systems Analysis, Aalto University 27 Contents Calderón-Zygmund decomposition. Dyadic subcubes of a cube.........................2 Dyadic cubes
Functional Analysis I
 Functional Analysis I Course Notes by Stefan Richter Transcribed and Annotated by Gregory Zitelli Polar Decomposition Definition. An operator W B(H) is called a partial isometry if W x = X for all x (ker
Functional Analysis I Course Notes by Stefan Richter Transcribed and Annotated by Gregory Zitelli Polar Decomposition Definition. An operator W B(H) is called a partial isometry if W x = X for all x (ker
NONLINEAR EVOLUTION EQUATIONS SHORT NOTES WEEK #1
 NONLNEA EVOLUTON EQUATONS SHOT NOTES WEEK #. Free Schrödinger Equation Let Bx 2 `...`Bx 2 n denote the Laplacian on d with d ě. The initial-value problem for the free Schrödinger equation (in d space dimensions)
NONLNEA EVOLUTON EQUATONS SHOT NOTES WEEK #. Free Schrödinger Equation Let Bx 2 `...`Bx 2 n denote the Laplacian on d with d ě. The initial-value problem for the free Schrödinger equation (in d space dimensions)
arxiv: v1 [math.ca] 4 Apr 2017
![arxiv: v1 [math.ca] 4 Apr 2017 arxiv: v1 [math.ca] 4 Apr 2017](/thumbs/88/115044967.jpg) ON LOCALIZATION OF SCHRÖDINGER MEANS PER SJÖLIN Abstract. Localization properties for Schrödinger means are studied in dimension higher than one. arxiv:704.00927v [math.ca] 4 Apr 207. Introduction Let
ON LOCALIZATION OF SCHRÖDINGER MEANS PER SJÖLIN Abstract. Localization properties for Schrödinger means are studied in dimension higher than one. arxiv:704.00927v [math.ca] 4 Apr 207. Introduction Let
Chapter 2 Metric Spaces
 Chapter 2 Metric Spaces The purpose of this chapter is to present a summary of some basic properties of metric and topological spaces that play an important role in the main body of the book. 2.1 Metrics
Chapter 2 Metric Spaces The purpose of this chapter is to present a summary of some basic properties of metric and topological spaces that play an important role in the main body of the book. 2.1 Metrics
Integration and Fourier Theory. Lecture 14
 Integration and Fourier Theory Lecture 4 Morten Grud Rasmussen March 5, 03 Trigonometric Series Denote the unit circle in the complex plane by T tx P C x u ( T for torus ). Note that R Q t ÞÑ e it P T
Integration and Fourier Theory Lecture 4 Morten Grud Rasmussen March 5, 03 Trigonometric Series Denote the unit circle in the complex plane by T tx P C x u ( T for torus ). Note that R Q t ÞÑ e it P T
B. Appendix B. Topological vector spaces
 B.1 B. Appendix B. Topological vector spaces B.1. Fréchet spaces. In this appendix we go through the definition of Fréchet spaces and their inductive limits, such as they are used for definitions of function
B.1 B. Appendix B. Topological vector spaces B.1. Fréchet spaces. In this appendix we go through the definition of Fréchet spaces and their inductive limits, such as they are used for definitions of function
PROBLEMS. (b) (Polarization Identity) Show that in any inner product space
 1 Professor Carl Cowen Math 54600 Fall 09 PROBLEMS 1. (Geometry in Inner Product Spaces) (a) (Parallelogram Law) Show that in any inner product space x + y 2 + x y 2 = 2( x 2 + y 2 ). (b) (Polarization
1 Professor Carl Cowen Math 54600 Fall 09 PROBLEMS 1. (Geometry in Inner Product Spaces) (a) (Parallelogram Law) Show that in any inner product space x + y 2 + x y 2 = 2( x 2 + y 2 ). (b) (Polarization
ADVANCE TOPICS IN ANALYSIS - REAL. 8 September September 2011
 ADVANCE TOPICS IN ANALYSIS - REAL NOTES COMPILED BY KATO LA Introductions 8 September 011 15 September 011 Nested Interval Theorem: If A 1 ra 1, b 1 s, A ra, b s,, A n ra n, b n s, and A 1 Ě A Ě Ě A n
ADVANCE TOPICS IN ANALYSIS - REAL NOTES COMPILED BY KATO LA Introductions 8 September 011 15 September 011 Nested Interval Theorem: If A 1 ra 1, b 1 s, A ra, b s,, A n ra n, b n s, and A 1 Ě A Ě Ě A n
Ground States are generically a periodic orbit
 Gonzalo Contreras CIMAT Guanajuato, Mexico Ergodic Optimization and related topics USP, Sao Paulo December 11, 2013 Expanding map X compact metric space. T : X Ñ X an expanding map i.e. T P C 0, Dd P Z`,
Gonzalo Contreras CIMAT Guanajuato, Mexico Ergodic Optimization and related topics USP, Sao Paulo December 11, 2013 Expanding map X compact metric space. T : X Ñ X an expanding map i.e. T P C 0, Dd P Z`,
MATH6081A Homework 8. In addition, when 1 < p 2 the above inequality can be refined using Lorentz spaces: f
 MATH68A Homework 8. Prove the Hausdorff-Young inequality, namely f f L L p p for all f L p (R n and all p 2. In addition, when < p 2 the above inequality can be refined using Lorentz spaces: f L p,p f
MATH68A Homework 8. Prove the Hausdorff-Young inequality, namely f f L L p p for all f L p (R n and all p 2. In addition, when < p 2 the above inequality can be refined using Lorentz spaces: f L p,p f
arxiv: v4 [math.ap] 14 Apr 2016
![arxiv: v4 [math.ap] 14 Apr 2016 arxiv: v4 [math.ap] 14 Apr 2016](/thumbs/76/73571665.jpg) SOME OBSEVATIONS ON THE GEEN FUNCTION FO THE BALL IN THE FACTIONAL LAPLACE FAMEWOK arxiv:5.6468v4 [math.ap] 4 Apr 6 CLAUDIA BUCU Claudia Bucur Dipartimento di Matematica Federigo Enriques Università degli
SOME OBSEVATIONS ON THE GEEN FUNCTION FO THE BALL IN THE FACTIONAL LAPLACE FAMEWOK arxiv:5.6468v4 [math.ap] 4 Apr 6 CLAUDIA BUCU Claudia Bucur Dipartimento di Matematica Federigo Enriques Università degli
Lebesgue Integration on R n
 Lebesgue Integration on R n The treatment here is based loosely on that of Jones, Lebesgue Integration on Euclidean Space We give an overview from the perspective of a user of the theory Riemann integration
Lebesgue Integration on R n The treatment here is based loosely on that of Jones, Lebesgue Integration on Euclidean Space We give an overview from the perspective of a user of the theory Riemann integration
Functional Analysis. Franck Sueur Metric spaces Definitions Completeness Compactness Separability...
 Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
Chapter One. The Calderón-Zygmund Theory I: Ellipticity
 Chapter One The Calderón-Zygmund Theory I: Ellipticity Our story begins with a classical situation: convolution with homogeneous, Calderón- Zygmund ( kernels on R n. Let S n 1 R n denote the unit sphere
Chapter One The Calderón-Zygmund Theory I: Ellipticity Our story begins with a classical situation: convolution with homogeneous, Calderón- Zygmund ( kernels on R n. Let S n 1 R n denote the unit sphere
THEOREMS, ETC., FOR MATH 515
 THEOREMS, ETC., FOR MATH 515 Proposition 1 (=comment on page 17). If A is an algebra, then any finite union or finite intersection of sets in A is also in A. Proposition 2 (=Proposition 1.1). For every
THEOREMS, ETC., FOR MATH 515 Proposition 1 (=comment on page 17). If A is an algebra, then any finite union or finite intersection of sets in A is also in A. Proposition 2 (=Proposition 1.1). For every
MATH 360 Final Exam Thursday, December 14, a n 2. a n 1 1
 MATH 36 Final Exam Thursday, December 4, 27 Name. The sequence ta n u is defined by a and a n (a) Prove that lim a n exists by showing that ta n u is bounded and monotonic and invoking an appropriate result.
MATH 36 Final Exam Thursday, December 4, 27 Name. The sequence ta n u is defined by a and a n (a) Prove that lim a n exists by showing that ta n u is bounded and monotonic and invoking an appropriate result.
CHAPTER VIII HILBERT SPACES
 CHAPTER VIII HILBERT SPACES DEFINITION Let X and Y be two complex vector spaces. A map T : X Y is called a conjugate-linear transformation if it is a reallinear transformation from X into Y, and if T (λx)
CHAPTER VIII HILBERT SPACES DEFINITION Let X and Y be two complex vector spaces. A map T : X Y is called a conjugate-linear transformation if it is a reallinear transformation from X into Y, and if T (λx)
Mathematische Methoden der Unsicherheitsquantifizierung
 Mathematische Methoden der Unsicherheitsquantifizierung Oliver Ernst Professur Numerische Mathematik Sommersemester 2014 Contents 1 Introduction 1.1 What is Uncertainty Quantification? 1.2 A Case Study:
Mathematische Methoden der Unsicherheitsquantifizierung Oliver Ernst Professur Numerische Mathematik Sommersemester 2014 Contents 1 Introduction 1.1 What is Uncertainty Quantification? 1.2 A Case Study:
Real Analysis Notes. Thomas Goller
 Real Analysis Notes Thomas Goller September 4, 2011 Contents 1 Abstract Measure Spaces 2 1.1 Basic Definitions........................... 2 1.2 Measurable Functions........................ 2 1.3 Integration..............................
Real Analysis Notes Thomas Goller September 4, 2011 Contents 1 Abstract Measure Spaces 2 1.1 Basic Definitions........................... 2 1.2 Measurable Functions........................ 2 1.3 Integration..............................
MAT 570 REAL ANALYSIS LECTURE NOTES. Contents. 1. Sets Functions Countability Axiom of choice Equivalence relations 9
 MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
ANALYSIS QUALIFYING EXAM FALL 2017: SOLUTIONS. 1 cos(nx) lim. n 2 x 2. g n (x) = 1 cos(nx) n 2 x 2. x 2.
 ANALYSIS QUALIFYING EXAM FALL 27: SOLUTIONS Problem. Determine, with justification, the it cos(nx) n 2 x 2 dx. Solution. For an integer n >, define g n : (, ) R by Also define g : (, ) R by g(x) = g n
ANALYSIS QUALIFYING EXAM FALL 27: SOLUTIONS Problem. Determine, with justification, the it cos(nx) n 2 x 2 dx. Solution. For an integer n >, define g n : (, ) R by Also define g : (, ) R by g(x) = g n
Mariusz Jurkiewicz, Bogdan Przeradzki EXISTENCE OF SOLUTIONS FOR HIGHER ORDER BVP WITH PARAMETERS VIA CRITICAL POINT THEORY
 DEMONSTRATIO MATHEMATICA Vol. XLVIII No 1 215 Mariusz Jurkiewicz, Bogdan Przeradzki EXISTENCE OF SOLUTIONS FOR HIGHER ORDER BVP WITH PARAMETERS VIA CRITICAL POINT THEORY Communicated by E. Zadrzyńska Abstract.
DEMONSTRATIO MATHEMATICA Vol. XLVIII No 1 215 Mariusz Jurkiewicz, Bogdan Przeradzki EXISTENCE OF SOLUTIONS FOR HIGHER ORDER BVP WITH PARAMETERS VIA CRITICAL POINT THEORY Communicated by E. Zadrzyńska Abstract.
Banach Spaces II: Elementary Banach Space Theory
 BS II c Gabriel Nagy Banach Spaces II: Elementary Banach Space Theory Notes from the Functional Analysis Course (Fall 07 - Spring 08) In this section we introduce Banach spaces and examine some of their
BS II c Gabriel Nagy Banach Spaces II: Elementary Banach Space Theory Notes from the Functional Analysis Course (Fall 07 - Spring 08) In this section we introduce Banach spaces and examine some of their
2) Let X be a compact space. Prove that the space C(X) of continuous real-valued functions is a complete metric space.
 University of Bergen General Functional Analysis Problems with solutions 6 ) Prove that is unique in any normed space. Solution of ) Let us suppose that there are 2 zeros and 2. Then = + 2 = 2 + = 2. 2)
University of Bergen General Functional Analysis Problems with solutions 6 ) Prove that is unique in any normed space. Solution of ) Let us suppose that there are 2 zeros and 2. Then = + 2 = 2 + = 2. 2)
An introduction to some aspects of functional analysis
 An introduction to some aspects of functional analysis Stephen Semmes Rice University Abstract These informal notes deal with some very basic objects in functional analysis, including norms and seminorms
An introduction to some aspects of functional analysis Stephen Semmes Rice University Abstract These informal notes deal with some very basic objects in functional analysis, including norms and seminorms
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University
 Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
Introduction to Real Analysis Alternative Chapter 1
 Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
Lecture Notes in Functional Analysis
 Lecture Notes in Functional Analysis Please report any mistakes, misprints or comments to aulikowska@mimuw.edu.pl LECTURE 1 Banach spaces 1.1. Introducton to Banach Spaces Definition 1.1. Let X be a K
Lecture Notes in Functional Analysis Please report any mistakes, misprints or comments to aulikowska@mimuw.edu.pl LECTURE 1 Banach spaces 1.1. Introducton to Banach Spaces Definition 1.1. Let X be a K
Seminorms and locally convex spaces
 (April 23, 2014) Seminorms and locally convex spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/fun/notes 2012-13/07b seminorms.pdf]
(April 23, 2014) Seminorms and locally convex spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/fun/notes 2012-13/07b seminorms.pdf]
A Bowl of Kernels. By Nuriye Atasever, Cesar Alvarado, and Patrick Doherty. December 03, 2013
 December 03, 203 Introduction When we studied Fourier series we improved convergence by convolving with the Fejer and Poisson kernels on T. The analogous Fejer and Poisson kernels on the real line help
December 03, 203 Introduction When we studied Fourier series we improved convergence by convolving with the Fejer and Poisson kernels on T. The analogous Fejer and Poisson kernels on the real line help
Analytic families of multilinear operators
 Analytic families of multilinear operators Mieczysław Mastyło Adam Mickiewicz University in Poznań Nonlinar Functional Analysis Valencia 17-20 October 2017 Based on a joint work with Loukas Grafakos M.
Analytic families of multilinear operators Mieczysław Mastyło Adam Mickiewicz University in Poznań Nonlinar Functional Analysis Valencia 17-20 October 2017 Based on a joint work with Loukas Grafakos M.
The weak topology of locally convex spaces and the weak-* topology of their duals
 The weak topology of locally convex spaces and the weak-* topology of their duals Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto April 3, 2014 1 Introduction These notes
The weak topology of locally convex spaces and the weak-* topology of their duals Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto April 3, 2014 1 Introduction These notes
Analysis Comprehensive Exam Questions Fall F(x) = 1 x. f(t)dt. t 1 2. tf 2 (t)dt. and g(t, x) = 2 t. 2 t
 Analysis Comprehensive Exam Questions Fall 2. Let f L 2 (, ) be given. (a) Prove that ( x 2 f(t) dt) 2 x x t f(t) 2 dt. (b) Given part (a), prove that F L 2 (, ) 2 f L 2 (, ), where F(x) = x (a) Using
Analysis Comprehensive Exam Questions Fall 2. Let f L 2 (, ) be given. (a) Prove that ( x 2 f(t) dt) 2 x x t f(t) 2 dt. (b) Given part (a), prove that F L 2 (, ) 2 f L 2 (, ), where F(x) = x (a) Using
Approximation of Weighted Local Mean Operators
 Approximation of Weighted Local ean Operators Jianzhong Wang Department of athematics and Statistics Sam Houston State University Huntsville, TX 7734 Abstract Recently, weighted local mean operators are
Approximation of Weighted Local ean Operators Jianzhong Wang Department of athematics and Statistics Sam Houston State University Huntsville, TX 7734 Abstract Recently, weighted local mean operators are
Reminder Notes for the Course on Distribution Theory
 Reminder Notes for the Course on Distribution Theory T. C. Dorlas Dublin Institute for Advanced Studies School of Theoretical Physics 10 Burlington Road, Dublin 4, Ireland. Email: dorlas@stp.dias.ie March
Reminder Notes for the Course on Distribution Theory T. C. Dorlas Dublin Institute for Advanced Studies School of Theoretical Physics 10 Burlington Road, Dublin 4, Ireland. Email: dorlas@stp.dias.ie March
Finite-dimensional spaces. C n is the space of n-tuples x = (x 1,..., x n ) of complex numbers. It is a Hilbert space with the inner product
 Chapter 4 Hilbert Spaces 4.1 Inner Product Spaces Inner Product Space. A complex vector space E is called an inner product space (or a pre-hilbert space, or a unitary space) if there is a mapping (, )
Chapter 4 Hilbert Spaces 4.1 Inner Product Spaces Inner Product Space. A complex vector space E is called an inner product space (or a pre-hilbert space, or a unitary space) if there is a mapping (, )
Spectral Theory, with an Introduction to Operator Means. William L. Green
 Spectral Theory, with an Introduction to Operator Means William L. Green January 30, 2008 Contents Introduction............................... 1 Hilbert Space.............................. 4 Linear Maps
Spectral Theory, with an Introduction to Operator Means William L. Green January 30, 2008 Contents Introduction............................... 1 Hilbert Space.............................. 4 Linear Maps
MATHS 730 FC Lecture Notes March 5, Introduction
 1 INTRODUCTION MATHS 730 FC Lecture Notes March 5, 2014 1 Introduction Definition. If A, B are sets and there exists a bijection A B, they have the same cardinality, which we write as A, #A. If there exists
1 INTRODUCTION MATHS 730 FC Lecture Notes March 5, 2014 1 Introduction Definition. If A, B are sets and there exists a bijection A B, they have the same cardinality, which we write as A, #A. If there exists
1/12/05: sec 3.1 and my article: How good is the Lebesgue measure?, Math. Intelligencer 11(2) (1989),
 Real Analysis 2, Math 651, Spring 2005 April 26, 2005 1 Real Analysis 2, Math 651, Spring 2005 Krzysztof Chris Ciesielski 1/12/05: sec 3.1 and my article: How good is the Lebesgue measure?, Math. Intelligencer
Real Analysis 2, Math 651, Spring 2005 April 26, 2005 1 Real Analysis 2, Math 651, Spring 2005 Krzysztof Chris Ciesielski 1/12/05: sec 3.1 and my article: How good is the Lebesgue measure?, Math. Intelligencer
Mathematics for Economists
 Mathematics for Economists Victor Filipe Sao Paulo School of Economics FGV Metric Spaces: Basic Definitions Victor Filipe (EESP/FGV) Mathematics for Economists Jan.-Feb. 2017 1 / 34 Definitions and Examples
Mathematics for Economists Victor Filipe Sao Paulo School of Economics FGV Metric Spaces: Basic Definitions Victor Filipe (EESP/FGV) Mathematics for Economists Jan.-Feb. 2017 1 / 34 Definitions and Examples
Entropy and Ergodic Theory Notes 22: The Kolmogorov Sinai entropy of a measure-preserving system
 Entropy and Ergodic Theory Notes 22: The Kolmogorov Sinai entropy of a measure-preserving system 1 Joinings and channels 1.1 Joinings Definition 1. If px, µ, T q and py, ν, Sq are MPSs, then a joining
Entropy and Ergodic Theory Notes 22: The Kolmogorov Sinai entropy of a measure-preserving system 1 Joinings and channels 1.1 Joinings Definition 1. If px, µ, T q and py, ν, Sq are MPSs, then a joining
Problem Set 2: Solutions Math 201A: Fall 2016
 Problem Set 2: s Math 201A: Fall 2016 Problem 1. (a) Prove that a closed subset of a complete metric space is complete. (b) Prove that a closed subset of a compact metric space is compact. (c) Prove that
Problem Set 2: s Math 201A: Fall 2016 Problem 1. (a) Prove that a closed subset of a complete metric space is complete. (b) Prove that a closed subset of a compact metric space is compact. (c) Prove that
2 (Bonus). Let A X consist of points (x, y) such that either x or y is a rational number. Is A measurable? What is its Lebesgue measure?
 MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due 9/5). Prove that every countable set A is measurable and µ(a) = 0. 2 (Bonus). Let A consist of points (x, y) such that either x or y is
MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due 9/5). Prove that every countable set A is measurable and µ(a) = 0. 2 (Bonus). Let A consist of points (x, y) such that either x or y is
MAA6617 COURSE NOTES SPRING 2014
 MAA6617 COURSE NOTES SPRING 2014 19. Normed vector spaces Let X be a vector space over a field K (in this course we always have either K = R or K = C). Definition 19.1. A norm on X is a function : X K
MAA6617 COURSE NOTES SPRING 2014 19. Normed vector spaces Let X be a vector space over a field K (in this course we always have either K = R or K = C). Definition 19.1. A norm on X is a function : X K
On the existence of non-oscillatory phase functions for second order ordinary differential equations in the high-frequency regime
 We observe that solutions of a large class of highly oscillatory second order linear ordinary differential equations can be approximated using nonoscillatory phase functions. In addition, we describe numerical
We observe that solutions of a large class of highly oscillatory second order linear ordinary differential equations can be approximated using nonoscillatory phase functions. In addition, we describe numerical
NOTES WEEK 15 DAY 1 SCOT ADAMS
 NOTES WEEK 15 DAY 1 SCOT ADAMS We fix some notation for the entire class today: Let n P N, W : R n, : 2 P N pw q, W : LpW, W q, I : id W P W, z : 0 W 0 n. Note that W LpR n, R n q. Recall, for all T P
NOTES WEEK 15 DAY 1 SCOT ADAMS We fix some notation for the entire class today: Let n P N, W : R n, : 2 P N pw q, W : LpW, W q, I : id W P W, z : 0 W 0 n. Note that W LpR n, R n q. Recall, for all T P
FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES
 FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES JAIRO BOCHI Abstract. This is a revised version of some notes written ą 0 years ago. I thank Anthony Quas for pointing to a gap in the previous
FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES JAIRO BOCHI Abstract. This is a revised version of some notes written ą 0 years ago. I thank Anthony Quas for pointing to a gap in the previous
Singular Integrals. 1 Calderon-Zygmund decomposition
 Singular Integrals Analysis III Calderon-Zygmund decomposition Let f be an integrable function f dx 0, f = g + b with g Cα almost everywhere, with b
Singular Integrals Analysis III Calderon-Zygmund decomposition Let f be an integrable function f dx 0, f = g + b with g Cα almost everywhere, with b
Fourier Transform & Sobolev Spaces
 Fourier Transform & Sobolev Spaces Michael Reiter, Arthur Schuster Summer Term 2008 Abstract We introduce the concept of weak derivative that allows us to define new interesting Hilbert spaces the Sobolev
Fourier Transform & Sobolev Spaces Michael Reiter, Arthur Schuster Summer Term 2008 Abstract We introduce the concept of weak derivative that allows us to define new interesting Hilbert spaces the Sobolev
HARMONIC ANALYSIS. Date:
 HARMONIC ANALYSIS Contents. Introduction 2. Hardy-Littlewood maximal function 3. Approximation by convolution 4. Muckenhaupt weights 4.. Calderón-Zygmund decomposition 5. Fourier transform 6. BMO (bounded
HARMONIC ANALYSIS Contents. Introduction 2. Hardy-Littlewood maximal function 3. Approximation by convolution 4. Muckenhaupt weights 4.. Calderón-Zygmund decomposition 5. Fourier transform 6. BMO (bounded
MATH MEASURE THEORY AND FOURIER ANALYSIS. Contents
 MATH 3969 - MEASURE THEORY AND FOURIER ANALYSIS ANDREW TULLOCH Contents 1. Measure Theory 2 1.1. Properties of Measures 3 1.2. Constructing σ-algebras and measures 3 1.3. Properties of the Lebesgue measure
MATH 3969 - MEASURE THEORY AND FOURIER ANALYSIS ANDREW TULLOCH Contents 1. Measure Theory 2 1.1. Properties of Measures 3 1.2. Constructing σ-algebras and measures 3 1.3. Properties of the Lebesgue measure
3 (Due ). Let A X consist of points (x, y) such that either x or y is a rational number. Is A measurable? What is its Lebesgue measure?
 MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due ). Show that the open disk x 2 + y 2 < 1 is a countable union of planar elementary sets. Show that the closed disk x 2 + y 2 1 is a countable
MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due ). Show that the open disk x 2 + y 2 < 1 is a countable union of planar elementary sets. Show that the closed disk x 2 + y 2 1 is a countable
MAT 578 FUNCTIONAL ANALYSIS EXERCISES
 MAT 578 FUNCTIONAL ANALYSIS EXERCISES JOHN QUIGG Exercise 1. Prove that if A is bounded in a topological vector space, then for every neighborhood V of 0 there exists c > 0 such that tv A for all t > c.
MAT 578 FUNCTIONAL ANALYSIS EXERCISES JOHN QUIGG Exercise 1. Prove that if A is bounded in a topological vector space, then for every neighborhood V of 0 there exists c > 0 such that tv A for all t > c.
LECTURE 16: UNITARY REPRESENTATIONS LECTURE BY SHEELA DEVADAS STANFORD NUMBER THEORY LEARNING SEMINAR FEBRUARY 14, 2018 NOTES BY DAN DORE
 LECTURE 16: UNITARY REPRESENTATIONS LECTURE BY SHEELA DEVADAS STANFORD NUMBER THEORY LEARNING SEMINAR FEBRUARY 14, 2018 NOTES BY DAN DORE Let F be a local field with valuation ring O F, and G F the group
LECTURE 16: UNITARY REPRESENTATIONS LECTURE BY SHEELA DEVADAS STANFORD NUMBER THEORY LEARNING SEMINAR FEBRUARY 14, 2018 NOTES BY DAN DORE Let F be a local field with valuation ring O F, and G F the group
Fourier transform, assorted stuff...
 Fourier transform, assorted stuff... M. Carlsson October 9, 2013 1 An example from control theory To get an idea of where real applications are, lets begin with an example from control theory. Example
Fourier transform, assorted stuff... M. Carlsson October 9, 2013 1 An example from control theory To get an idea of where real applications are, lets begin with an example from control theory. Example
Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem
 56 Chapter 7 Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem Recall that C(X) is not a normed linear space when X is not compact. On the other hand we could use semi
56 Chapter 7 Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem Recall that C(X) is not a normed linear space when X is not compact. On the other hand we could use semi
Hilbert spaces. 1. Cauchy-Schwarz-Bunyakowsky inequality
 (October 29, 2016) Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/fun/notes 2016-17/03 hsp.pdf] Hilbert spaces are
(October 29, 2016) Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/fun/notes 2016-17/03 hsp.pdf] Hilbert spaces are
On Borel maps, calibrated σ-ideals and homogeneity
 On Borel maps, calibrated σ-ideals and homogeneity Institute of Mathematics University of Warsaw Ideals and exceptional sets in Polish spaces, Lausanne, 4-8 June 2018 The results come from a joint paper
On Borel maps, calibrated σ-ideals and homogeneity Institute of Mathematics University of Warsaw Ideals and exceptional sets in Polish spaces, Lausanne, 4-8 June 2018 The results come from a joint paper
Sobolev Spaces. Chapter Hölder spaces
 Chapter 2 Sobolev Spaces Sobolev spaces turn out often to be the proper setting in which to apply ideas of functional analysis to get information concerning partial differential equations. Here, we collect
Chapter 2 Sobolev Spaces Sobolev spaces turn out often to be the proper setting in which to apply ideas of functional analysis to get information concerning partial differential equations. Here, we collect
FUNCTIONAL ANALYSIS LECTURE NOTES: WEAK AND WEAK* CONVERGENCE
 FUNCTIONAL ANALYSIS LECTURE NOTES: WEAK AND WEAK* CONVERGENCE CHRISTOPHER HEIL 1. Weak and Weak* Convergence of Vectors Definition 1.1. Let X be a normed linear space, and let x n, x X. a. We say that
FUNCTIONAL ANALYSIS LECTURE NOTES: WEAK AND WEAK* CONVERGENCE CHRISTOPHER HEIL 1. Weak and Weak* Convergence of Vectors Definition 1.1. Let X be a normed linear space, and let x n, x X. a. We say that
MTH 503: Functional Analysis
 MTH 53: Functional Analysis Semester 1, 215-216 Dr. Prahlad Vaidyanathan Contents I. Normed Linear Spaces 4 1. Review of Linear Algebra........................... 4 2. Definition and Examples...........................
MTH 53: Functional Analysis Semester 1, 215-216 Dr. Prahlad Vaidyanathan Contents I. Normed Linear Spaces 4 1. Review of Linear Algebra........................... 4 2. Definition and Examples...........................
Some Background Material
 Chapter 1 Some Background Material In the first chapter, we present a quick review of elementary - but important - material as a way of dipping our toes in the water. This chapter also introduces important
Chapter 1 Some Background Material In the first chapter, we present a quick review of elementary - but important - material as a way of dipping our toes in the water. This chapter also introduces important
Heat Kernel and Analysis on Manifolds Excerpt with Exercises. Alexander Grigor yan
 Heat Kernel and Analysis on Manifolds Excerpt with Exercises Alexander Grigor yan Department of Mathematics, University of Bielefeld, 33501 Bielefeld, Germany 2000 Mathematics Subject Classification. Primary
Heat Kernel and Analysis on Manifolds Excerpt with Exercises Alexander Grigor yan Department of Mathematics, University of Bielefeld, 33501 Bielefeld, Germany 2000 Mathematics Subject Classification. Primary
Topological properties
 CHAPTER 4 Topological properties 1. Connectedness Definitions and examples Basic properties Connected components Connected versus path connected, again 2. Compactness Definition and first examples Topological
CHAPTER 4 Topological properties 1. Connectedness Definitions and examples Basic properties Connected components Connected versus path connected, again 2. Compactness Definition and first examples Topological
Topological vectorspaces
 (July 25, 2011) Topological vectorspaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ Natural non-fréchet spaces Topological vector spaces Quotients and linear maps More topological
(July 25, 2011) Topological vectorspaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ Natural non-fréchet spaces Topological vector spaces Quotients and linear maps More topological
Functional Analysis
 The Hahn Banach Theorem : Functional Analysis 1-9-06 Extensions of Linear Forms and Separation of Convex Sets Let E be a vector space over R and F E be a subspace. A function f : F R is linear if f(αx
The Hahn Banach Theorem : Functional Analysis 1-9-06 Extensions of Linear Forms and Separation of Convex Sets Let E be a vector space over R and F E be a subspace. A function f : F R is linear if f(αx
Harmonic Analysis Homework 5
 Harmonic Analysis Homework 5 Bruno Poggi Department of Mathematics, University of Minnesota November 4, 6 Notation Throughout, B, r is the ball of radius r with center in the understood metric space usually
Harmonic Analysis Homework 5 Bruno Poggi Department of Mathematics, University of Minnesota November 4, 6 Notation Throughout, B, r is the ball of radius r with center in the understood metric space usually
Mathematical Finance
 ETH Zürich, HS 2017 Prof. Josef Teichmann Matti Kiiski Mathematical Finance Solution sheet 14 Solution 14.1 Denote by Z pz t q tpr0,t s the density process process of Q with respect to P. (a) The second
ETH Zürich, HS 2017 Prof. Josef Teichmann Matti Kiiski Mathematical Finance Solution sheet 14 Solution 14.1 Denote by Z pz t q tpr0,t s the density process process of Q with respect to P. (a) The second
Topology. Xiaolong Han. Department of Mathematics, California State University, Northridge, CA 91330, USA address:
 Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
Topology, Math 581, Fall 2017 last updated: November 24, Topology 1, Math 581, Fall 2017: Notes and homework Krzysztof Chris Ciesielski
 Topology, Math 581, Fall 2017 last updated: November 24, 2017 1 Topology 1, Math 581, Fall 2017: Notes and homework Krzysztof Chris Ciesielski Class of August 17: Course and syllabus overview. Topology
Topology, Math 581, Fall 2017 last updated: November 24, 2017 1 Topology 1, Math 581, Fall 2017: Notes and homework Krzysztof Chris Ciesielski Class of August 17: Course and syllabus overview. Topology
Notes on Distributions
 Notes on Distributions Functional Analysis 1 Locally Convex Spaces Definition 1. A vector space (over R or C) is said to be a topological vector space (TVS) if it is a Hausdorff topological space and the
Notes on Distributions Functional Analysis 1 Locally Convex Spaces Definition 1. A vector space (over R or C) is said to be a topological vector space (TVS) if it is a Hausdorff topological space and the
16 1 Basic Facts from Functional Analysis and Banach Lattices
 16 1 Basic Facts from Functional Analysis and Banach Lattices 1.2.3 Banach Steinhaus Theorem Another fundamental theorem of functional analysis is the Banach Steinhaus theorem, or the Uniform Boundedness
16 1 Basic Facts from Functional Analysis and Banach Lattices 1.2.3 Banach Steinhaus Theorem Another fundamental theorem of functional analysis is the Banach Steinhaus theorem, or the Uniform Boundedness
4 Hilbert spaces. The proof of the Hilbert basis theorem is not mathematics, it is theology. Camille Jordan
 The proof of the Hilbert basis theorem is not mathematics, it is theology. Camille Jordan Wir müssen wissen, wir werden wissen. David Hilbert We now continue to study a special class of Banach spaces,
The proof of the Hilbert basis theorem is not mathematics, it is theology. Camille Jordan Wir müssen wissen, wir werden wissen. David Hilbert We now continue to study a special class of Banach spaces,
Tools from Lebesgue integration
 Tools from Lebesgue integration E.P. van den Ban Fall 2005 Introduction In these notes we describe some of the basic tools from the theory of Lebesgue integration. Definitions and results will be given
Tools from Lebesgue integration E.P. van den Ban Fall 2005 Introduction In these notes we describe some of the basic tools from the theory of Lebesgue integration. Definitions and results will be given
CONTENTS. 4 Hausdorff Measure Introduction The Cantor Set Rectifiable Curves Cantor Set-Like Objects...
 Contents 1 Functional Analysis 1 1.1 Hilbert Spaces................................... 1 1.1.1 Spectral Theorem............................. 4 1.2 Normed Vector Spaces.............................. 7 1.2.1
Contents 1 Functional Analysis 1 1.1 Hilbert Spaces................................... 1 1.1.1 Spectral Theorem............................. 4 1.2 Normed Vector Spaces.............................. 7 1.2.1
Fourier transforms. Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x L or L x L) as Fourier series: a n cos L
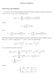 ourier transforms Motivation and definition Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x or x ) as ourier series: fpxq a 0 8 nπx a n cos n b n sin nπx where
ourier transforms Motivation and definition Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x or x ) as ourier series: fpxq a 0 8 nπx a n cos n b n sin nπx where
Contents: 1. Minimization. 2. The theorem of Lions-Stampacchia for variational inequalities. 3. Γ -Convergence. 4. Duality mapping.
 Minimization Contents: 1. Minimization. 2. The theorem of Lions-Stampacchia for variational inequalities. 3. Γ -Convergence. 4. Duality mapping. 1 Minimization A Topological Result. Let S be a topological
Minimization Contents: 1. Minimization. 2. The theorem of Lions-Stampacchia for variational inequalities. 3. Γ -Convergence. 4. Duality mapping. 1 Minimization A Topological Result. Let S be a topological
A SHORT INTRODUCTION TO BANACH LATTICES AND
 CHAPTER A SHORT INTRODUCTION TO BANACH LATTICES AND POSITIVE OPERATORS In tis capter we give a brief introduction to Banac lattices and positive operators. Most results of tis capter can be found, e.g.,
CHAPTER A SHORT INTRODUCTION TO BANACH LATTICES AND POSITIVE OPERATORS In tis capter we give a brief introduction to Banac lattices and positive operators. Most results of tis capter can be found, e.g.,
We denote the space of distributions on Ω by D ( Ω) 2.
 Sep. 1 0, 008 Distributions Distributions are generalized functions. Some familiarity with the theory of distributions helps understanding of various function spaces which play important roles in the study
Sep. 1 0, 008 Distributions Distributions are generalized functions. Some familiarity with the theory of distributions helps understanding of various function spaces which play important roles in the study
Functional Analysis Winter 2018/2019
 Functional Analysis Winter 2018/2019 Peer Christian Kunstmann Karlsruher Institut für Technologie (KIT) Institut für Analysis Englerstr. 2, 76131 Karlsruhe e-mail: peer.kunstmann@kit.edu These lecture
Functional Analysis Winter 2018/2019 Peer Christian Kunstmann Karlsruher Institut für Technologie (KIT) Institut für Analysis Englerstr. 2, 76131 Karlsruhe e-mail: peer.kunstmann@kit.edu These lecture
Hardy-Littlewood maximal operator in weighted Lorentz spaces
 Hardy-Littlewood maximal operator in weighted Lorentz spaces Elona Agora IAM-CONICET Based on joint works with: J. Antezana, M. J. Carro and J. Soria Function Spaces, Differential Operators and Nonlinear
Hardy-Littlewood maximal operator in weighted Lorentz spaces Elona Agora IAM-CONICET Based on joint works with: J. Antezana, M. J. Carro and J. Soria Function Spaces, Differential Operators and Nonlinear
JUHA KINNUNEN. Real Analysis
 JUH KINNUNEN Real nalysis Department of Mathematics and Systems nalysis, alto University Updated 3 pril 206 Contents L p spaces. L p functions..................................2 L p norm....................................
JUH KINNUNEN Real nalysis Department of Mathematics and Systems nalysis, alto University Updated 3 pril 206 Contents L p spaces. L p functions..................................2 L p norm....................................
Chapter 3: Baire category and open mapping theorems
 MA3421 2016 17 Chapter 3: Baire category and open mapping theorems A number of the major results rely on completeness via the Baire category theorem. 3.1 The Baire category theorem 3.1.1 Definition. A
MA3421 2016 17 Chapter 3: Baire category and open mapping theorems A number of the major results rely on completeness via the Baire category theorem. 3.1 The Baire category theorem 3.1.1 Definition. A
DS-GA 3001: PROBLEM SESSION 2 SOLUTIONS VLADIMIR KOBZAR
 DS-GA 3: PROBLEM SESSION SOLUTIONS VLADIMIR KOBZAR Note: In this discussion we allude to the fact the dimension of a vector space is given by the number of basis vectors. We will shortly establish this
DS-GA 3: PROBLEM SESSION SOLUTIONS VLADIMIR KOBZAR Note: In this discussion we allude to the fact the dimension of a vector space is given by the number of basis vectors. We will shortly establish this
Part II Probability and Measure
 Part II Probability and Measure Theorems Based on lectures by J. Miller Notes taken by Dexter Chua Michaelmas 2016 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Part II Probability and Measure Theorems Based on lectures by J. Miller Notes taken by Dexter Chua Michaelmas 2016 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
MATH 426, TOPOLOGY. p 1.
 MATH 426, TOPOLOGY THE p-norms In this document we assume an extended real line, where is an element greater than all real numbers; the interval notation [1, ] will be used to mean [1, ) { }. 1. THE p
MATH 426, TOPOLOGY THE p-norms In this document we assume an extended real line, where is an element greater than all real numbers; the interval notation [1, ] will be used to mean [1, ) { }. 1. THE p
Real Analysis Math 131AH Rudin, Chapter #1. Dominique Abdi
 Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
Measure, Integration & Real Analysis
 v Measure, Integration & Real Analysis preliminary edition 10 August 2018 Sheldon Axler Dedicated to Paul Halmos, Don Sarason, and Allen Shields, the three mathematicians who most helped me become a mathematician.
v Measure, Integration & Real Analysis preliminary edition 10 August 2018 Sheldon Axler Dedicated to Paul Halmos, Don Sarason, and Allen Shields, the three mathematicians who most helped me become a mathematician.
Recall that if X is a compact metric space, C(X), the space of continuous (real-valued) functions on X, is a Banach space with the norm
 Chapter 13 Radon Measures Recall that if X is a compact metric space, C(X), the space of continuous (real-valued) functions on X, is a Banach space with the norm (13.1) f = sup x X f(x). We want to identify
Chapter 13 Radon Measures Recall that if X is a compact metric space, C(X), the space of continuous (real-valued) functions on X, is a Banach space with the norm (13.1) f = sup x X f(x). We want to identify
Probability and Measure
 Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 84 Paper 4, Section II 26J Let (X, A) be a measurable space. Let T : X X be a measurable map, and µ a probability
Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 84 Paper 4, Section II 26J Let (X, A) be a measurable space. Let T : X X be a measurable map, and µ a probability
Lecture 4 Lebesgue spaces and inequalities
 Lecture 4: Lebesgue spaces and inequalities 1 of 10 Course: Theory of Probability I Term: Fall 2013 Instructor: Gordan Zitkovic Lecture 4 Lebesgue spaces and inequalities Lebesgue spaces We have seen how
Lecture 4: Lebesgue spaces and inequalities 1 of 10 Course: Theory of Probability I Term: Fall 2013 Instructor: Gordan Zitkovic Lecture 4 Lebesgue spaces and inequalities Lebesgue spaces We have seen how
CHAPTER V DUAL SPACES
 CHAPTER V DUAL SPACES DEFINITION Let (X, T ) be a (real) locally convex topological vector space. By the dual space X, or (X, T ), of X we mean the set of all continuous linear functionals on X. By the
CHAPTER V DUAL SPACES DEFINITION Let (X, T ) be a (real) locally convex topological vector space. By the dual space X, or (X, T ), of X we mean the set of all continuous linear functionals on X. By the
MATH 722, COMPLEX ANALYSIS, SPRING 2009 PART 5
 MATH 722, COMPLEX ANALYSIS, SPRING 2009 PART 5.. The Arzela-Ascoli Theorem.. The Riemann mapping theorem Let X be a metric space, and let F be a family of continuous complex-valued functions on X. We have
MATH 722, COMPLEX ANALYSIS, SPRING 2009 PART 5.. The Arzela-Ascoli Theorem.. The Riemann mapping theorem Let X be a metric space, and let F be a family of continuous complex-valued functions on X. We have
