Set-valued solutions for non-ideal detonation
|
|
|
- Carol Manning
- 6 years ago
- Views:
Transcription
1 Set-valued solutions for non-ideal detonation The MIT Faculty has made this article openly available. Please share how this access benefits you. Your story matters. Citation As Published Publisher Semenko, R., L. M. Faria, A. R. Kasimov, and B. S. Ermolaev. Set-Valued Solutions for Non-Ideal Detonation. Shock Waves 26, no. 2 (December, 25): Springer Berlin Heidelberg Version Author's final manuscript Accessed Fri Feb 6 5:46:39 EST 28 Citable Link Terms of Use Detailed Terms Article is made available in accordance with the publisher's policy and may be subject to US copyright law. Please refer to the publisher's site for terms of use.
2 Ë Ø¹Ú ÐÙ ÓÐÙØ ÓÒ ÓÖ ÒÓÒ¹ Ð ØÓÒ Ø ÓÒ ÊÓÑ Ò Ë Ñ Ò Ó ½ ÄÙ Þ Åº Ö ½ Ð Ò Êº à ÑÓÚ ½ ½ ÔÔÐ Å Ø Ñ Ø Ò ÓÑÔÙØ Ø ÓÒ Ð Ë Ò ÊÓÓÑ ¹¾¾¾ ¼¼ Ã Ò ÙÐÐ ÍÒ Ú Ö ØÝ Ó Ë Ò Ò Ì ÒÓÐÓ Ý Ì ÙÛ Ð ¾ ¹ ¼¼ Ë Ù Ö ÓÖ Ëº ÖÑÓÐ Ú ¾ ¾ Ë Ñ ÒÓÚ ÁÒ Ø ØÙØ Ó Ñ Ð È Ý ÊÙ Ò ÑÝ Ó Ë Ò ÃÓ Ý Ò ËØÖ Ø ÅÓ ÓÛ ½½ ÊÙ ØÖ Ø Ì Ü Ø Ò Ò ØÖÙØÙÖ Ó Ø Ý¹ Ø Ø ÓÙ ØÓÒ Ø ÓÒ ÔÖÓÔ Ø Ò Ò Ô Ó ÓÐ Ò ÖØ Ô ÖØ Ð Ö Ò ÐÝÞ Ò Ø ÓÒ ¹ Ñ Ò ÓÒ Ð ÔÔÖÓÜ Ñ Ø ÓÒ Ý Ø Ò ÒØÓ ÓÒ Ö Ø ÓÒ Ö Ø ÓÒ Ð Ò Ø ÐÓ ØÛ Ò Ø Ò Ø Ô ÖØ Ð º Ò Û ÓÖÑÙÐ Ø ÓÒ Ó Ø ÓÚ ÖÒ Ò ÕÙ Ø ÓÒ ÒØÖÓ Ù Ø Ø Ð Ñ Ò Ø Ø ÙÐØ Û Ø ÒÙÑ Ö Ð ÒØ Ö Ø ÓÒ ÖÓ Ø ÓÒ Ò ÙÐ Ö ØÝ Ò Ø Ö Ø Ú ÙÐ Ö ÕÙ Ø ÓÒ º Ï Ø Ø Ò Û Ð ÓÖ Ø Ñ Û Ò Ø Ø Û Ò Ø ÓÒ ÔÓ ÒØ ÔÔ Ö ÖÓÑ Ø ÓÛ Ø Ö Ü Ø ÓÒ ¹Ô Ö Ñ Ø Ö Ñ ÐÝ Ó ÓÐÙØ ÓÒ Ô Ö Ñ Ø Ö Þ Ý Ø Ö ÔÖ ÙÖ ÓÖ Ø ÑÔ Ö ØÙÖ Ø Ø Ò Ó Ø Ö Ø ÓÒ ÞÓÒ º Ì ÓÐÙØ ÓÒ Ø ÖÑ Ø¹Ú ÐÙ Ö µ ÓÖÖ ÔÓÒ ØÓ ÓÒØ ÒÙÓÙ Ô ØÖÙÑ Ó Ø ÒÚ ÐÙ ÔÖÓ Ð Ñ Ø Ø Ø ÖÑ Ò Ø ØÓÒ Ø ÓÒ Ú ÐÓ ØÝ ÙÒØ ÓÒ Ó ÐÓ ØÓÖº ½ ÁÒØÖÓ ÙØ ÓÒ Detonationisashockwaveinareactivemedium thatissustainedbythe energyreleased in chemical reactions initiated by the passage of the wave. Gaseous detonation propagating in a tube, in the interstitial space in a porous medium, or other obstructed environments is ÈÖ ÒØ Ö Ô ÖØÑ ÒØ Ó Å Ò Ò Å Ø Ñ Ø ÆÓÚÓ Ö ËØ Ø ÍÒ Ú Ö ØÝ ¼¼ ¼ È ÖÓ ÓÚ Ëغ ¾ ÆÓÚÓ Ö ÊÙ Ö Ñ Ñ ÐºÖÙ ÈÖ ÒØ Ö Ô ÖØÑ ÒØ Ó Å Ø Ñ Ø Å Ù ØØ ÁÒ Ø ØÙØ Ó Ì ÒÓÐÓ Ý Ñ Ö Å ÍË Ð Ö Ñ Øº Ù Ð Òº ÑÓÚ Ù Øº Ùº ÓÖÖ ÔÓÒ Ò ÙØ ÓÖ ÓÖ º ÖÑÓÐ ÚÝ ÓÓºÓÑ
3 subject to resistance due to heat transfer, boundary layers and shock reflections that arise attheinterfacesbetweenthegasandtheobstaclesorthewallsofthetube. Suchresistance leads to momentum and energy losses in the gas that can significantly affect the propagation of the detonation. In the presence of such losses, the detonation is termed non-ideal, and its propagation velocity is lower than in the case(termed ideal ) when there are no such losses. This drop in the detonation velocity is called the velocity deficit. Quantifying the velocity deficitintermsofthelossesisoneofthemajorproblemsindetonationtheoryanditsstudy goesbacktotheoriginalpaperbyzel dovich[24](seealsotheclassicbookbyzel dovichand Kompaneets[27]). An important feature observed in experiments on non-ideal detonation waves is their ability to propagate with velocities ranging from near sonic speed in the ambient gas, c a, to the ideal Chapman-Jouguet (CJ) value, D CJ [5, 6, 7, 2]. The physical mechanisms responsible for this self-sustained propagation of detonation depend on the extent and the nature of the losses. A particularly interesting aspect is the possibility that the frictional heating of the gas dominates over its heating by chemical reactions at low detonation velocities. We also mention a peculiar theoretical observation, first discussed in [24],thatinthepresenceoflosses,theflowinthedetonationreactionzonecanreverseits direction; that is, the velocity can become negative in the laboratory frame of reference, a situation typical for flames, but unusual for detonations. No experimental evidence for this prediction appears to exist. Since the early works mentioned above, this problem has been revisited many times by researchers seeking to understand the precise mechanisms of detonation propagation when the effects of losses are substantial. A particularly important issue, from a practical point of view, is the existence of detonation limits. The limit of detonation propagation is definedasathresholdintermsofsomecontrolquantity(e.g.,atubediameter)belowwhich the detonation cannot propagate. The problem of defining such limits is nontrivial and is complicated by the fact that detonation can and most often does propagate unsteadily. Although this fact makes the definitions of these limits based on the non-existence of stationary solutions somewhat limited in application, understanding the steady-state solutions isamajorfirststepinunderstandingthenatureofdetonationlimitsaswellasinbuilding a theory of unsteady detonations. Theoreticalworkontheroleoflossesindetonationswascontinuedin[3,4,25,26]. In [26], both convective and conductive heat losses were considered. Convective losses depend on the relative velocity between the gas and the particles/walls and they vanish with relative 2
4 velocity. In contrast, conductive losses persist in the absence of the relative velocity. In the relaxation zone far downstream of the lead shock, where the flow of the reaction products has sufficiently decelerated, the authors of[26] assumed that the heat losses corresponded to an approximately constant Nusselt number and thus were of the conductive type. Subsequently, theyreasonedthatthegasintheproductscooleddownduetotheconductiveheattransfer andreachedastateofrestfardownstreambutwiththesamepressureanddensityasthe upstream state with the fresh mixture. In contrast, the model we present here involves only convective heat losses, as a consequenceofwhichtheheattransferfromthegastotheparticlesvanisheswhenthegasstops. This is a reasonable assumption for detonations because the conductive losses occur on time scales that are much longer than the time scale of the detonation propagation. The temperature relaxation in the products can therefore be expected not to affect the detonation dynamics over the time scales of interest. We should note that our governing equations take thesamegeneralformasthosein[26,27]andincludethemomentumlossduetofriction, heat loss due to the temperature difference between the gas and the solid particles, and the effect of heating of the gas due to the friction. Convective heat transfer was also considered in[4]. To highlight the most important general features of detonation in systems with losses that have previously been found, we mention that, in а qualitative agreement with prior experimental research[5, 6, 7, 2], different regimes of detonation propagation have been theoretically identified in[3, 4]: ) When the detonation speed is below the ideal CJ value, but not substantially, the wavehasastructurethatisverysimilartothatoftheclassicalzndtheory(zel dovich[24], von Neumann[22] and Döring[7]; see also[, 4]) of a self-sustained detonation with its inherent transonic character in the post-shock flow and with a sonic point located at some distancefromtheshock. ½ 2) When the detonation speed drops significantly, often to around.6 of the ideal value, the sonic locus moves to infinity and, with a further decrease of the detonation velocity, disappears from the flow altogether. This structure, in which the post-shock flow is entirely subsonic in the shock-fixed frame, resembles piston-supported overdriven detonations. However, the latter gain energy from the piston and therefore propagate faster than CJ ½ ËÙ ØÓÒ Ø ÓÒ Ú Ò ÐÐ ÕÙ ¹ ØÓÒ Ø ÓÒ Ò Ø Ô Ø ½ º ÀÓÛ Ú Ö ÒÓÒ¹ Ð ØÓÒ Ø ÓÒ ÒÓØ ÒØ ÐÐÝ Ø ÒØ ÖÓÑ Ø Ð Ð Ð ØÓÒ Ø ÓÒ Ø Ø ÐÐ Ð ¹ Ù Ø Ò ÔÖÓ Ó Ó ¹Û Ú Ö Ø ÓÒ¹ÞÓÒ ÓÙÔÐ Ò º Ì ÔÖ Ò Ó ÐÓ Ó ÒÓØ Ò Ø Ò ØÙÖ Ó Ø Û Ú ÐÓÒ Ø Ö ÓÒ ÓÒ Ò Ñ ÒØ Ò Ø ÓÛº 3
5 detonations. In contrast, non-ideal detonations, with a subsonic post-shock flow, have no support and propagate at velocities that are substantially lower than the ideal CJ velocity. Becauseitsstructureismissingasonicpoint, itisnotaself-sustainedwave ¾ inthe sense of classical detonation theory. Without a sonic point, the wave evolution can be influenced by the downstream boundary conditions, while with a sonic point, the detonation dynamics are completely controlled by the processes occurring between the shock and the sonic point. In experiments, the velocity deficits are obtained by, for example, decreasing the initial pressure, p a, in the explosivemixture [5, 6, 7, 2]. In manycases, a decreasein p a to some critical value results in an abrupt decrease in the speed to subsonic velocities, which are associated with turbulent deflagration waves. In theoretical modeling, one can, in principle, look at the solutions that have velocities smaller than the ambient sound speed, as was done in [3, 4] and in subsequent works by the same authors and their collaborators. However, in suchcases, the structuredoes notcontainashockand the waveis subsonicrelativeto the state upstream. In this work, we limit the discussion to supersonic waves containing a shock as an inherent element of the structure. While the nature of self-sustained non-ideal detonations is relatively clear, that of the regimes with subsonic post-shock flow has led to some conflicting conclusions in the literature. In particular, the existence of steady solutions of the governing equations in this regime was questioned in [6]. Indeed, because the sonic point disappears from the flow, the classical self-sustained structure cannot be a solution of the governing equations. It therefore appears reasonable to conclude that no steady-state solutions exist in this case. In [3, 4], however, the authors have been able to construct the steady D-c f relations in the entire range of velocities from the ideal D = D CJ to the sonic velocity, D = c a (and evenfurtherbelow),where c a isthespeedofsoundintheupstreammixtureand c f isthe dimensionless drag coefficient. Instead of the sonic conditions, they applied u = at infinity and solved the appropriate boundary value problem. In this connection, a point that requires certain care in interpretation is the question of existence of steady-state solutions versus their stability. Numerical simulations in[6, 8] indicate that detonation with frictional momentumlossesisunstable; infact, itismoreunstableinthepresenceoflossesthanin their absence. Because of the instability, the steady-state solutions cannot be reached as long-time asymptotic solutions of an initial value problem of the underlying reactive Euler ¾ Ì Ö Ñ Û Ø ÖÑ Ó Ò Ö Ñ Ò ½ º ÀÓÛ Ú Ö Û ÒÓØ Ø Ø Ø ÓÛ Ò Ø Ó ÒÓØ ÓÒØ Ò ÓÒ ÔÓ ÒØ Ò ÓÒØÖ Ø ØÓ ØÝÔ Ð Ó Ò Ö Ñ Ò Ù ÝÒ Ñ Û Ó Ø Û Ø ØÖ Ò ÓÒ ÓÛ º 4
6 equations. This, however, does not imply that the steady-state solutions of the equations do not exist. In order to establish the existence of the steady-state solutions, one must be able to solve the appropriate boundary value problem for the time-independent governing equations. Importantly, the proper statement of such a boundary value problem does not necessarily involve sonic conditions. We discuss this point in detail in the subsequent sections of this paper. In this work, we show that the steady-state solutions of the governing reactive Euler equationswithheatandmomentumlosseshaveapeculiarnatureinthatthe D-c f dependenceisnolongeracurve,butratheraset-valuedfunction. Thatis,whenthesoniclocus disappears from the flow, at a given loss coefficient, there exists a continuous range of detonation velocities, all corresponding to steady-state solutions of the governing equations. Effectively, D, as an eigenvalue of the nonlinear eigenvalue problem, is found to have both discrete and continuous spectra. This is in contrast with prior results, in which either the steady-statesolutionappearsnottoexist[6]orthatthereisaz-shapedcurveinthe D-c f plane,givingafiniteanddiscretesetofsolutionsforagiven c f [3]. Wepointoutthata continuous spectrum is found in a number of problems involving self-similar solutions of the Euler equations of gasdynamics(without chemical reactions)(see, e.g.,[5]). Another contribution of our work is a new formulation of the governing equations that completely avoids the difficulty of integrating through the sonic locus. The latter is a wellrecognizedproblemindetonationtheory[,3,26]. Wehavefoundanewsetofdependent variables in which the governing equations are no longer singular at the sonic point. This finding results in a numerically well-conditioned integration of the detonation structure in the entire flow region. A generalization of the algorithm to incorporate other loss factors and multiple reactions is possible and is introduced in[]. Apossibilityof the flowreversalinthe reactionzone[24] wasalsobrieflydiscussedin [26], where the authors continued the analysis of the problem and found that, with the farfield conditions they used, the convective heat transfer between the gas and the tube walls (or solid particles) was insufficient to cause the flow reversal. However, with the inclusion of conductive heat losses, the flow reversalwas indeed found. The authors of [4] did not discuss this possibility even though convective heat transfer was also an essential element of their analysis. Our present finding is that, with convective heat transfer, the flow reversal necessarily occurs in the regime where the flow behind the shock is entirely subsonic. In contrast, no flow reversal is possible with only friction losses. We emphasize, however, that 5
7 our far-field conditions are different from those of[26]. The remainder of this paper is organized as follows. In Section 2, we introduce the reactive Euler equations that include momentum and heat exchange terms. The Rankine- Hugoniot conditions are also introduced in this section. In Section 3, we discuss the steadystate solutions and introduce a change of dependent variables that removes the sonic singularities from the equations. In Section 4, we calculate various solutions when both the friction and heat loss terms are present and show that the detonation speed versus loss coefficient is a set-valued function. Concluding remarks are offered in Section 5. ¾ ÓÚ ÖÒ Ò ÕÙ Ø ÓÒ Consider a detonation in a perfect gas that fills the interstitial space in a packed bed of solid particles of diameter d. The particles are assumed to be immobile and inert; their only role is to exchange momentum and energy with the detonating gas. The chemical reaction in the gas is described globallyas Reactant Product. The progressof this reaction is measuredbyvariable, λ, that variesfrom atthe shockto in the fully burntgas. The reactionrateisassumedtobegiveninthearrheniusform, ( ω = k ( λ) exp E ), () pv where E is the activation energy, p is the pressure and v is the specific volume. The perfectgasequationofstateisgivenby e i = pv γ, (2) where γ istheconstantratioofspecificheats. With these modeling assumptions, the governing reactive Euler equations, further incorporating the heat and momentum exchange between the gas and particles, are as follows. The continuity equation is ρ t + (ρu) x =, (3) where ρ = /v and u are the gas density and velocity, respectively. The gas momentum equation is u t + uu x = ρ p x f ρφ, (4) 6
8 or in conservation form, (ρu) t + ( p + ρu 2) x = f φ, (5) wherethedragforceduetothesolidparticlesisassumedtotaketheform[2], ( f = A s ρ b + b ) 2 u u, (6) Re with A s = 4φ d p, d p = 2φd 3( φ), Re = d p u ν, (7) where φ is the porosityof the packedbed, i.e., the fractionof spaceoccupied by the gas, d is the particle diameter, Re is the Reynolds number, ν is the gas kinematic viscosity and b, b 2 arenumericalconstants. Inthe calculationsbelow, wetake φ =.4, b =.75and b 2 = [2]therebyassuminghighReynoldsnumberfrictionlosses. The energy equation can be written as ( ) uf h p t + up x + γpu x = (γ )Qρω + (γ ). (8) φ It contains contributions due to: ) the chemical energy release(the first term, wherein Q istheheatrelease),2)theworkdonebythefrictionforces(thesecondterm,involving uf) and 3) the heat transfer between the gas and particles (the last term, involving h). The heatexchangerate, h,isassumedtobegivenbynewton slaw, h = A s α s (T T s ), (9) inwhichtheparticletemperatureisdenotedby T s andtheheatconductioncoefficient, α s, is calculated from[2] α s = λ g Nu d p, () where Nu = a + a 2 Re m isthenusseltnumber, λ g istheheatconductivityofthegasand a, a 2, marenumericalconstants. Wetake a =, a 2 =.425and m = [2], thereby assuming purely convective losses. The validity of this approximation for heat transfer in flows in packed beds of solid particles is justified in[2]. A slightly different heat exchange lawwasusedin[4,24],whichusedthestagnationtemperature T +u 2 /2insteadof T in(9). We have found that the general nature of the solutions is unaffected by this change even though some of the small details are. 7
9 In conservation form, the energy equation becomes (ρe) t + (ρu (e + pv)) x = h φ, () where e = e i + u2 2 pv λq = γ + u2 λq. (2) 2 Note that the friction workterm uf does not appear in the conservationform of the full energy equation because obstacles are motionless in the laboratory reference frame (see [8, 9]). The internal energy equation in a non-conservation form is (e i ) t + u(e i ) x + p ρ u x = ωq + uf h ρφ, where the work by friction appears explicitly on the right-hand side. The reaction rate equation is λ t + uλ x = ω, (3) or in conservation form, (ρλ) t + (ρuλ) x = ρω. (4) We note that these equations with appropriate modifications of the loss terms can also be used to describe gaseous detonation in rough tubes. The ideas that follow are expected to carry over to such a setting without significant changes. Across the shock-discontinuity surface, the following Rankine-Hugoniot conditions hold: D[ρ] + [ρu] =, (5) D[ρu] + [p + ρu 2 ] =, (6) D[ρe] + [ρu(e + pv)] =, (7) D[ρλ] + [ρuλ] =. (8) Here, [j] = j a j s denotesajumpofquantity j acrosstheshock, (ρ a, u a, p a, λ a )denotes theambientstateaheadoftheshockand (ρ s, u s, p s, λ s )isthestateimmediatelyafterthe shock. For a perfect gas, the shock conditions can be solved explicitly and the following 8
10 expressions give the post-shock state in terms of the upstream state, p s p a = 2γ γ + M2 a γ γ +, (9) u s = 2 Ma 2, c a γ + M a (2) ρ s = (γ + )M2 a ρ a 2 + (γ )Ma 2, (2) λ s =. (22) Here M a = D/c a isthedetonationmachnumberwithrespecttotheupstreamstate. ËØ Ý¹ Ø Ø ÓÐÙØ ÓÒ In this section, we analyze the existence of the steady-state solutions of the governing equations and calculate their properties. As always in detonation theory, the speed of the wave is unknown a priori and must be determined as a solution of a nonlinear eigenvalue problem. Thegoalisthentocomputethesteadytraveling-wavestructureanditsspeed. Inorderto do that, one must carefully pose the mathematical boundary-value problem by prescribing appropriate equations and boundary conditions. Because of the nature of the problem at hand, two apparently distinct situations can arise, which can however be put in a unified framework. In most of the literature on detonation theory, the interest is in finding a self-sustained structure, which by definition means that the propagating shock reaction-zone complex contains an embedded sonic locus. This sonic locus provides acoustic confinement that precludes any downstream influence on the detonation dynamics, thus making the detonation wave effectively an autonomous process whose dynamics are driven by the finite region betweentheshockandthesoniclocus[2]. Tocomputethestructureofthisfiniteregion, one requires knowledge of the governing equations, shock conditions and appropriate conditions at the sonic point. Knowledge of the flow conditions downstream of the sonic locus is not required. Another structure that has been extensively investigated in the past is that of overdriven detonation. This wave is obtained by providing downstream support in the form of a piston ÆÓØ Ø Ø Ò ÓØ Ö Ý Ø Ñ Ö Ý Ö ÒØ Ñ Ø Ñ Ø Ð ÑÓ Ð Û Ú Ò Ð ¹ Ù Ø Ò Û Ø ÓÙØ Ø ÔÖ Ò Ó ÓÒ ÐÓÙ º Ü ÑÔÐ Ö Ñ Ò ÓÐ ØÓÒ Û Ö Ø Ô Ý Ð Ñ Ò Ñ ÒÚÓÐÚ Ò Ð ¹ Ù Ø Ò ÔÖÓÔ Ø ÓÒ Ó Ø Û Ú Ö Ö ÒØ ÖÓÑ Ø Ó Ò ØÓÒ Ø ÓÒ º ÇÙÖ Ù Ó Ø Ø ÖÑ ÓÒ Ø ÒØ Û Ø Ø ØÖ Ø ÓÒ Ð ÒØ ÖÔÖ Ø Ø ÓÒ Ò ØÓÒ Ø ÓÒ Ø ÓÖݺ 9
11 pushing the flow in the direction of the lead shock and thus preventing the formation of the sonic confinement. In overdriven detonations, the entire region between the shock and the piston is subsonic. To determine the structure, knowledge of the flow condition at the piston is necessary. This condition is simply that the flow velocity at the piston location is thesameasthepistonvelocity. Aboundaryvalueproblemisthusposedthatrequiresthe construction of a smooth solution connecting the shock state with the state at the piston. Thus, we find that, in general, the problem of calculating the detonation structure(selfsustained or not) is posed as follows: determine a traveling shock-wave solution of the reactive Euler equations subject to quiescent equilibrium conditions upstream of the shock and appropriate conditions at an infinite distance downstream of the shock. If the detonation is self-sustained, the boundary-value problem is divided into two sub-problems: ) finding the structure between the shock and the sonic point, which is independent of the state downstream of the sonic locus, and 2) finding the flow structure downstream of the sonic locus,whichisdeterminedbythestateatthesoniclocusaswellasbytheconditionsatan infinite distance downstream of the shock. In the problem at hand, it is required to determine a traveling-wave solution of governing equations(3),(5),()and(4),whichconsistsofaleadshockfollowedbyasmoothreaction zone, subject to a quiescent non-reacting state ahead of the shock and the equilibrium state in the burnt products at infinite distance from the shock. From the governing equations, it followsthat the equilibrium state is necessarilyat λ = and u =. No otherpossibility exists, because the equilibrium requires that the right-hand sides of(5),() and(4) vanish atinfinity,whichcanonlyhappenat λ = and u =. ApplicationoftheRankine-Hugoniot conditions reduces the problem domain to a half-line between the shock and the downstream infinity. This formulation of the boundary value problem is general in the sense that the self-sustained solution is part of it, but solutions without a sonic point are also admitted. To proceed, we rescale the governing equations with respect to the upstream state, denoted by a subscript a: ˆρ = ρ/ρ a, ˆp = p/p a, u a = p a v a, û = u/u a, Ê = E/u 2 a, ˆQ = Q/u 2 a, ˆT = TR/ (p a v a W) = ˆp/ˆρ,and ˆD = D/u a. Thelengthscaleischosentobethe half-reactionzone length, l /2, of the ideal planar detonation, such that ˆx = x/l /2. The timeisrescaledas ˆt = t u a /l /2. Inthenewdimensionlessvariables,thegoverningequations retain their form. However, the dimensionless loss terms become(dropping the hats after the rescaling):
12 f = c f ρ u u, c f = 6b ( φ) l/2 d, (23) h = c h u (T ), c h = 9a 2( φ) 2 φ ltl /2 l v d. (24) Here, l t = λ g W/R p a ρ a and l v = ν/ p a /ρ a are the characteristic thermal and viscous lengthscales,respectively. Thedimensionlesscoefficients, c f and c h,whicharenowjusttwo parameters measuring the effects of the momentum and heat losses, respectively, depend on the ratios of various length scales that are characteristic to the relevant transport processes. For c f,itistheratioofthelengthofthereactionzoneandtheparticlediameter. For c h, it is a combination of four length scales: the viscous scale, l v, the thermal scale, l t, the reactionscale, l /2,andtheparticlediameter, d. Wenote,however,that c h =.5a 2 ( φ) c f b φ l t =.5a 2 ( φ) λ g W l v b φ Rν (25) is independent of the reaction or the particle diameter, but depends on the gas viscosity and heat conduction coefficient. We alsonote that c f is proportionalto l /2 /d, which equals, roughly, the number of particles that fit inside the reaction zone of the ideal detonation. Thus,smallvaluesof c f correspondtoparticlesthataremuchlargerthanthethicknessof the reaction zone in the ideal detonation. Thetraveling-wavesolutionofthegoverningequationsissoughtintheform U = U() = (ρ, u, p, λ) T (),where = x Dt.Substitutioninto(3),(5),()and(4)yields(withthe primes denoting the derivative with respect to ): (ρ(u D)) =, (26) (p + ρ(u D)u) = f φ, (27) (ρ(u D)e + pu) = h φ, (28) (u D)λ = ω. (29) Thissystemofequationsmustbesolvedsubjecttothejumpconditionsattheshock, = : ρ () = ρ s (D), u () = u s (D), p () = p s (D), λ() =,
13 asgivenby(9 22)andthefar-fieldconditionsat =,whichare u = and λ =. The only other condition, besides the requirement that the solution of the system satisfies these boundary values, is that it be smooth and bounded throughout the domain <. As wewill seebelow, this requirementisessentialin ordertodetermine the valuesof the detonation speed, D, given all the parameters of the problem. In the ideal case, when f = h =, system(26 29)can be integrateddirectly to yield the ideal detonation solution, v (λ) = /ρ (λ) = u (λ) = DCJ 2 γ ( γ + D CJ [ p (λ) = + D2 CJ γ + = ˆ λ γ + D 2 [ CJ γ + DCJ 2 D2 CJ γ ] λ γ ( + DCJ 2 ), (3) ) + λ + D2 CJ γ + D 2 CJ, (3) ] λ, (32) u (λ) D CJ ω dλ. (33) The ideal solution is chosen to be of the self-sustained nature (i.e., the CJ solution) with thesonicpointat = and λ =. Then, D CJ = γ + 2 (γ2 )Q + 2 (γ2 )Q. (34) The pre-exponential factor that imposes the half-reaction length of unity is found from k = ˆ /2 u (λ) D CJ dλ. (35) ( λ) exp ( Eρ (λ)/p (λ)) This value of k is used in the calculations of the non-ideal detonation when f and h are non-zero. Indimensionalterms,iftheratefunctionisgivenas k ( ) ( λ)exp Ẽ/ T (the tilde denotes a dimensional quantity), then the dimensional length of the region over which halfofthereactantisburnt,is ˆ /2 l/2 = ũ (λ) ( D CJ k ( λ) exp Ẽ/ T )dλ = ũa k ˆ /2 u (λ) D CJ ũa dλ = k. (36) ( λ) exp( E/T) k Therefore, k = l /2 k/ũa, which identifies the characteristic length scale in terms of the mixture properties. 2
14 The continuity equation can be integrated even in the non-ideal case to result in ρ = D D u. (37) To proceed with the solution of the remaining equations, we rewrite(26 29) in matrix form: (A DI)U = G, (38) where U = ρ u p λ, A = u ρ u /ρ γp u u, G = F H ω, Iistheunitmatrixand F = f ρφ, ( ) uf h H = (γ )Qρω + (γ ). (39) φ The acoustic eigenvalues of A are s = u + c and s 2 = u c, where c = γpv is the sound speed. Their corresponding left eigenvectors are l = (,, c/γp, ) and l 2 = (,, c/γp, ). Left-multiplying(38)by l,weobtain, (s D)(u + c γp p ) = F + c H. (4) γp Similarly,left-multiplying(38)by l 2,weobtain, (s 2 D)(u c γp p ) = F c H. (4) γp From(4,4),itfollowsthat du d = [ F + c γp H 2 u + c D + F c dp d = γp 2c γp H u c D [ F + c γp H u + c D F c γp H u c D ], (42) ]. (43) Theimportanceofthisformoftheequationsisthatitmakesevidentthatthesolution is not necessarily regularif the denominators of (42) or (43) vanish somewhere at <. Note that at =, they cannot vanish due to the Laxconditions. Because u D is the 3
15 flow velocity relative to the shock, which must be negative for the shock propagating to the right,itfollowsthat u c Dcannevervanish. However, u + c Dcanvanish. Ifitdoes, wemustrequirethatatthesamepoint(whichisthesonicpoint) F + ch/γp = aswell. This is basically the statement of the generalized CJ condition [9, 23] and this condition isnecessarytodeterminethevalueof D whentheflowcontainsasonicpoint. Itmustbe emphasizedthattheexistenceofthesonicpointisnotnecessaryifonecanfindasmooth solution that connects the shock state with the far-field equilibrium conditions. Irrespective ofthepresenceofthesonicpoint,thefundamentalproblemisthatoffindingasmoothand bounded solution of the boundary value problem at hand. Another important consequence of(42 43) is that the only possible equilibrium solution at = isthatwhichhas u ( = ) =. Indeed,settingtheright-handsidesofboth equations to zero, we obtain that in equilibrium both F and H must vanish. Therefore, from F =,weobtain u = and,asaconsequenceofthisandof λ =,italsofollowsthat H =. Nootherpossibilityexists. Ifasoniclocusdenotedby exists,thenatthatpointbydefinition, u + c D =. Requiringthat F + ch/γpvanishat aswell,oneobtainsthegeneralizedcjconditions, ( c (γ ) Qρ ω(λ ) + u ) f h f =, (44) γp φ ρ φ u + c D =. (45) This is a system of equations for D and λ that in principle allows one to find the full solution. However, in practice it is difficult to solve numerically. To illustrate the required calculations, we assume that all parameters of the problem aregiven. Then,theonlyunknownsare Dandthesolutionprofiles. Toremindthereader, inordertodetermine D in theidealcase,onefindsthefull solutionasafunctionof λ as p = p (λ, D), u = u (λ, D)and ρ = ρ (λ, D)(givenby(3 33)),whichdependparametrically on D (λ as a function of is found implicitly by integrating (33)). The solution is then substitutedintothecjconditions(44 45). Theselatterintheidealcasearesimply ω = and u + c D = ;therefore, λ = andthesecondconditionyieldsthedesiredresult for D,asgivenby(34). In the non-ideal case, however, the solution profiles are unavailable analytically and must be determined numerically. The procedure of finding D is in principle, to guess the value of D, integrate the ordinary differential equations(ode) for p and u in the λ-variable from 4
16 the shock until λ such that (44 45) are satisfied. This is done iteratively by varying D until the sonic conditions are satisfied. Generally, the sonic point has a saddle character and, therefore, the integration process just described is extremely ill-conditioned. For this reason, it is often preferable first to identify the sonic locus, then linearize the governing ODE system in its neighborhood, step out analytically by a small step and then integrate numerically back to the shock. This procedure is better conditioned and has been used in thepast. Yet,itisnotagoodchoiceforourproblemeither. Onereasonisthatthesonic locus is unknown a priori, so that linearization about it does not eliminate the algorithmic complexityofthesearchfor Dandthelocusitself. Thesecondandmoreseriousreasonis that the method fails when the solution contains no sonic locus. The latter is a possibility that cannot be ignored as one does not in general know a priori whether or not a sonic point exists in the solution. To resolve the difficulties mentioned in the previous paragraph, we propose a change of dependent variables that completely eliminates the singular behaviour from the governing equations. To proceed with this change, note that(4 4) can be written as du d + c dp γp d = F + c γp H u + c D, (46) du d c dp γp d = F c γp H u c D. (47) In this system, only the first equation contains a potential singularity. Note further that c γp/ρ γp = D u = γp Dγp. With this substitution, the left-hand sides of(46,47) become 2 D u d d ( ) p D u ±, γd which motivates the introduction of new variables, r = p D u γd, (48) s = p D u + γd. (49) Goingbackto uand pintermsof rand siseasybecause r + s = 2 D uand r s = 2 p/γd. Itisinterestingtocompute u + c Dintermsofthenewvariables. Thespeed 5
17 ofsoundis γp p c = ρ = γ γd (D u) = γ r2 s 2, 4 wherewetookintoconsiderationthat r > s atany p >. Therefore, (r + s)2 u + c D = + γ r2 s = γ 4 (r + s)(r µs), (5) where µ = γ + γ. (5) Thusthesoniccondition u + c D = isreducedtoasimplelinearequationintermsof thenewvariables, rand s, r µs =. (52) Equations(42 43)leadtoanewsystemofODEfor r, sand λ, dr d = γ 2ρc D u(u c D) ds d = ρc (D u)(r µs) dλ d = [ Qρω + hφ ( u + [ Qρω + hφ ( u c ) ] f G(r, s, λ), (53) γ φ ) ] f g(r, s, λ) φ r µs, (54) c γ ω L(r, s, λ). (55) u D Singularityiscontainedonlyin(54),butitisnowofaverysimpleforminthenewvariables. By introducing another change of variables, we can completely remove the singularity from the system. Let z = (r µs) 2 (56) toreplaceoneofthevariables,say s = µ ( r ± z ). (57) Beforeproceedingfurther,itisimportanttonotethattheinversionofthevariablesfrom r, z to r, sisnot single-valued. Thechangefromonebranchofthetransformationtoanother happens exactly at the sonic point, which is now located at z =, where the Jacobian of the transformation vanishes. The positive sign in(57) corresponds to the subsonic flow in the reference frame of the shock, while the negative sign corresponds to the supersonic flow. Indeed, at the shock u + c D = (γ )(r + s)(r µs)/4 > and since r + s = 6
18 2 D u <,then r µsshouldbe < inthesubsonicregionbetweentheshockandthe sonic point. This amounts to selecting the positive sign in(57). Downstream of the sonic point, the sign switches to negative. Byremovingthe svariablefrom(53 55)infavorof z,weobtainanewsystem: dr d = G ±(r, z, λ), (58) dz d = ±2 zg ± (r, z, λ) 2µg ± (r, z, λ), (59) dλ d = L ±(r, z, λ), (6) which is now completely free of singularity. Here, G ± and g ± are the same functions as G and g in (53 54)with the ± sign indicating the branch chosenin (57). Of course, the transonic character of the solutions cannot just disappear from the equations. There is deep physics behind the existence of the sonic point in the solution that must remain represented somehowintheequations. Itindeeddoesremainintheformofaswitchfromonebranch of the square root to another when passing through the sonic point. Equations(58 6) must be solved subject to the shock conditions, r () = r s, (6) z() = (r s µs s ) 2, (62) λ() =, (63) where r s = ps D u s γd, (64) s s = ps D u s + γd, (65) and u = at =,whichamountsto r ( ) = D z ( ) = D + p ( ) γd, (66) p ( ) γd. (67) 7
19 As was mentioned previously, the cases where the solution contains no sonic point and therefore the entire flow downstream of the shock remains subsonic should not be excluded fromconsideration. Condition u ( ) = leadstoconditionson rand zgivenby(66 67). However, the latter depend on p ( ), which cannot be enforced, in general. If the solution contains a sonic point, then the regularization conditions(44 45) become simply dz d = at z =. (68) Inthiscase,theequilibriumconditionsat = muststillbeenforced,buttheyarenow required only for the determination of the solution downstream of the sonic locus. If the latter does not exist, the system(58 6) must be solved subject to three conditions at the shock,(6 63), and the conditions at =. This set of boundary conditions is expected to be complete on physical grounds in order to yield a well-defined solution of the problem. The solution is not necessarily unique, as in previous studies of closely related problems. A typical result is a multi-valued solution for the detonation speed, D, as a function of, for example,thefrictioncoefficient, c f,giventhatalltheotherparametersarefixed. However, in contrast to the previous work, we find that the boundary-value problem as posed above yields set-valued solutions at certain parameters. In other words, a continuous range of solutions with D varying in some interval can exist for a given mixture and given loss conditions. Thus, the nonlinear eigenvalue problem at hand can have not only a discrete but also a continuous spectrum. º½ ÆÙÑ Ö Ð Ö ÙÐØ Ì ÒØ Ö Ø ÓÒ Ð ÓÖ Ø Ñ Thechangeofdependentvariablesto rand zisveryhelpfulasiteliminatesthenumerical difficulties that are otherwise inevitable in the integration of the original system (53-55). Such difficulties have previously been avoided in simpler situations(for example, when the governing equations can be reduced to a single ODE), by integrating from the sonic point to the shock [26, 3, ]. This algorithmworkswell if the sonicpoint location is known a priori. If, however,the location of the sonic point depends on the shock speed and other parameters, which one is attempting to find, then the algorithm becomes unwieldy, even though still valid. 8
20 Figure illustrates the difficulty. If we choose to integrate from the sonic locus, the algorithm proceeds as follows. Assume that all the parameters of the problem are given suchthatweneedtodetermine D andthesolutionprofiles. First,weneedtoidentifythe soniclocuswhere(44 45)musthold. Giventhat ρ = D/ (D u), p = ρc 2 /γand T = c 2 /γ, thesetwoequationscanbewrittenintermsof u, c, λ and D. Onecaneliminate,say, D using(45)andobtainoneequationintermsof u, c and λ bysubstituting D = u + c into (44). To proceed, one has to make a guess on two sonic variables and then find the third one by solving(44). Only then would the sonic state be known completely, after which onecanproceed,asusual,withanumericalintegrationoutofthesonicpointbacktothe shock, then check the shock conditions, and if they are not satisfied, iterate on the guesses of the two sonic state variables. Tounderstandthisprocedureindetail, letusrewrite(44)in termsof M = u /c, c and λ as (γ )Qω(λ ) = c h(γ )(c 2 γ) M c γφ(m + ) c fc 2 M ((γ )M ) M, φ from which we obtain λ = c hc (c 2 γ) M Qkγφ(M + ) + c fc 3 M ((γ )M ) M. (69) (γ )Qkφ Themaindifficultyinthealgorithmjustdescribedistechnical theneedtoiterateontwo sonicvariables(m and c )asopposedtooneinsimplersituations. Itisclearthataguess for M and c makessenseonlyif(69)yields λ intheintervalfrom to. Inordertogive thereaderanideaoftherangeof M and c thatmustbeguessed,infig. weplotthe domainsinthe M c planewhere(69)hassolutionswith λ [, ]. Thecoloredlines aretheiso-linesof λ rangingfromtowithanincrement.. Thesearchalgorithmfor the sonic locus can, in principle, yield the solution anywhere within the area covered by all theiso-linesfor λ. Themoststrikingpropertyoftheseregionsisthepresenceof highly intricate features, especially at negative velocities when both heat and friction losses are present(fig. b)). Thus, one would have to scan this complicated region for possible locations of the sonic state variables M and c in order to proceed with the integration toward the shock. We note that when only momentum loss is present, negative velocity at the sonic point is impossible(fig. a)). 9
21 Figure: Theregionsinthe M -c spacewherethesoniclocuscanexist: a)inthepresence of only friction losses, c f =., c h =, and b) when both heat and friction losses are present, c f =., c h =.5c f. Thelinesinthefiguresaretheiso-linesof λ takenin [, ] with an increment.. Incontrast,intermsofournewvariables,thesoniclocusisfixedanddeterminedexactly by z = z = at any parameters. Moreover, the singularity is no longer present in the system. More precisely, the singularity is reflected by the requirement that the branch of the square root of z must change as one crosses the sonic locus. This procedure is numerically benign. Thus, we solve (58-6) with the corresponding boundary and sonic conditions, provided the sonic point exists. The non-singular character of the system allows ustocalculatethesolutionwithhighaccuracy. ThegoalistofindsuchaDthatthesolution of equations(58-6) satisfies the boundary conditions at the shock and at = and to studythedependenceofthedetonationspeedonthelossfactors c f and c h assumingthat other parametersarefixed. If there is a sonic point, we requirethat the sonic conditions 2
22 z = z = aresatisfiedwithinmachineprecision. Ifthereisnosonicpoint,theconditionat theleftboundaryofthedomainisimposedthatboth uand λareclosetozerowithin. Anychangesin c f withinthemachineprecisionresultinthechangesof uand λ atinfinitywithin,sothatrequiringevensmallererrorsisnotfeasible. Thenewnumericalalgorithmworksasfollows. Wefirstfix E, Q, γandtheratio c f /c h. Thelatterisessentiallyaconstantforagivenmixture,asseenfrom(25). Then,forevery given D [c a, D CJ ], we lookfor the c f that providesasmooth solution to our boundary valueproblem. Here c a,thesoundspeedintheambientstate,isequalto γ inourscales. The calculations show that there are two possible cases. If the detonation speed is less than D CJ, but greater than some value D s, which is constant for the given set of parameters, thenthereisasonicpointinsidethereactionzone. Ontheotherhand,if D (c a, D s ),then there exist smooth solutions that satisfy the boundary conditions and remain subsonic from the shock down to =. This effect of the sonic-point disappearance in a closely-related problem was discovered in[3, 4]. z a) z b) z c) 3 2 ǫ ǫ Figure2: Profilesof zintheshootingmethodfor D =.8D CJ andvarious c f : a) c f =.; b) c f =.6;c) c f =.7. Here E = 3, Q = 2, γ =.2and c h =. The possible outcomes of the numerical searchfor c f for a given D are shown in Fig. 2. Thefiguresarecomputedbyshootingfromtheshocktothesonicpointwithvarious c f. The Matlab ode5s solverwith a reference tolerancevalue of 3 is used. In Fig. 2a), onecanseetheprofileof zfor c f thatistoolarge. Here, zreachesitsminimumvalue,but thisvalueispositive. At lessthantheminimumpoint, z beginstogrowwithoutbound. Fortheexactsolution,weexpect ztovanishattheminimumpoint. Hence,tomeasurethe closenessof the computed profileto the exactsolution, wedefine the errorfunction, ǫ, to be the minimum value of z. On the other hand, if c f is too small, then z will reachzero withapositiveslope,asinfig. 2b). Thismeansthatcondition(68)isnotsatisfiedand u willblowupbecauseoftheinfinitederivativeatthesonicpoint. Inthiscase,wedefine ǫ toequaltothederivativeof zatthesonicpoint. Thenwefindtheminimumvalueof ǫ(c f ) usingmatlab sfminsearch functionwithatolerancevalueof 3. Theminimumvalue 2
23 of ǫ = correspondstofig. 2c). Thiscaseistheonethatsatisfiescondition(68)andthe corresponding c f isthepropervalueforthegivendetonationspeed. Wepointoutthatatthisvalueof c f,therearetwowaysinwhichthesolutioncanbe continuedacrossthesonicpoint. Wecaneitherstayonthesamebranchof z,suchthat theflowdownstreamofthesonicpointremainssubsonic,orswitchtothesecondbranchof zandobtainasupersonicsolutiondownstream. ThesetwopossibilitiesareshowninFig. 3. This figure shows that for subsonic-subsonic transition, Fig. 3b), the velocity profile is continuousbutnotsmooth. Moreimportantly,inthiscase ztendstoinfinityand utendsto Das,unlikethesubsonic-supersoniccaseshowninFig. 3a). Thismeansthatsuch non-smooth solutions cannot satisfy the boundary conditions at = and thus must be discarded. 3 a) 3 b) 2 2 u z u z Figure 3: Profiles of u and z at D =.7D CJ, c h =, E = 2, Q = 2, γ =.2 for: a) subsonic-to-supersonic and b) subsonic-to-subsonic transitions across the sonic point(here, uand zarenotinthesamescale). For D < D s,suchnumericalalgorithmshowsthatthereexistsno c f thatgives ǫ(c f ) =. However, smooth and bounded subsonic solutions still exist, i.e., z remains positive in (, ) and u( ) =. Such solutions are investigated below. The shooting from the shock gives three possibilities, as shown in Fig. 4a). If c f is too large, then z passes its minimum point and then grows to infinity (solid line). If c f is too small, then z reaches the zero value with a non-zero slope, which means the blow-up of velocity(dash-dot line). However,insteadofthe behaviourseeninfig. 2c), hereweobtainthedashedlinein the middle,whichisthesolutionwithaboundedvalueof zat =. Thissolutionispossible onlyinthecasewhen u( ) =,sinceitistheonlyequilibriumstateforequations(58-6). ItisimportanttonotethatthekinksinthecurvesinFig. 4b)indicateasmooth,butrapid change in the solution. It occurs due to the exponentially sensitive terms in the governing equations. 22
24 z a) z 5 b) Figure4: Profilesof zintheshootingprocessat D =.4D CJ, c h =, Q = 2, γ =.2and various c f : c f =.(solid), c f =.22(dash), c f =.(dash-dot);a) E = 5andb) E = 3. º¾ ËÓÐÙØ ÓÒ Ò Ø ÔÖ Ò Ó ÓØ Ø Ò Ö Ø ÓÒ ÐÓ If D s < D < D CJ,thesteady-statesolutionpassesthroughasonicpoint,whereconditions (68) must be satisfied. Imposition of these conditions yields the exact value of the detonationspeedforthegivenlossterms. Thepresenceofasonicpointisaspecialfeaturethat constrains the solutions to a particular form, essentially independent of the boundary conditionsatinfinity. If c a < D < D s,thesonicpointandhencetheconstraintdisappearsand the nature of the solutions changes since now the downstream boundary condition determines the detonation speed[3, 4]. The solutions connect the Rankine-Hugoniot conditions atthe shock, =, andsomeappropriateconditionsat =. Inthe referenceframe of the shock, the flow remains subsonic throughout. As a consequence of the loss of the sonicconstraints,whichwhenpresentpindownthesolutiontoyieldaunique c f foragiven D, a degree of freedom is gained. The only condition at = that can justifiably be imposedis u =,whichleavesoneconditiontheretobefree. Thiscaneitherbepressure or temperature; the density at infinity is the same as in the ambient gas, which follows from the continuity equation(37). As a result of this additional degree of freedom, the case c a < D < D s yields a set-valued solution in which the pressure at = is allowedto varyin some range. That is, giventhe shockconditions and u ( ) =, for anychosen D (c a, D s ),thereexistsacontinuousrangeof c f (atfixed c f /c h )thatyieldsasmoothand bounded solution of(58-6). The transition from the single-valued to set-valued solutions is shown in Fig. 5a). For the existence of the set-valued solutions, the pressure at infinity cannot simply be arbitrary. For a fixed D < D s, as we vary c f, the flow variables p and T at = vary as well (but u = and λ = remain the same). The range of the correspondingvariationof p ( ) is shown in Fig. 5b). It is important to keep in mind 23
25 thatinfig. 5b), c f isnotfixed,butrathervariesintherangeseeninfig. 5a)foranygiven D. Aninterestingfeatureofthepressureatinfinityisthatitsmaximumvalueappearsto coincidewiththemomentwhenthesoniclocusisexactlyatinfinity. Thisisthecaseinall of the calculations that we have performed. As the velocity decreases further, the pressure at infinity(hence the temperature there as well) begins to drop. Therefore, the numerical calculations indicate that the onset of the set-valued solutions coincides with the maximum temperature(or pressure) in the products..8 a).8 b).6 D D C J.4 D s D C J c a D C J.6 D D C J.4 D s D C J c a D C J c f p Figure 5: a) The dependence of the detonation speed, D, on the loss factor, c f ; b) the pressureatinfinity, p ( ),forthe D-c f dependenceshownina). Inbothcases E = 3. In Fig. 5 and all of the calculations below the following parameters are fixed (unless indicatedotherwise): Q = 2, γ =.2and c h =.4c f. For the sake of completeness, we analyze the structure of the solutions on the functionvalued branch where they correspond to the self-sustained detonations. One of the main problems in the analysis is to understand the relative role of the three driving physical processes: chemical reaction, friction and heat transfer. While the roles of the chemical reaction and heat transfer are relatively simple, the former always contributing energy and thelatteralwaystakingitaway,theroleoffrictionismorecomplex. Thefrictionterm, f, changes its sign with velocity, which can result in momentum gain as opposed to momentum losswhen u <. Moreimportantly,however,thefrictionresultsinheatingofthegasand thus actsasaheat source. This is seenin the energyequation(8). Here, weanalyzethe role of these terms in some detail by evaluating their contributions to the fluid acceleration, du/d, and to the temperature gradient, dt/d. Ifonewritestheequationfor u ()from(42)asfollows [ du d = (u D) 2 (γ )Qω c 2 (γu D) f + ρφ ] (γ ) ρφ h, (7) 24
26 thenitbecomesclearthatthebehaviourof udependsonthecompetitionbetweentheheat release,frictionandheatloss. Recallthat f = c f ρu u, h = c h u (T )andthat c h = βc f forsomefixed β (β =.4inmostofourcalculations). Itisinterestingthat γu Dinthefrictiontermin(7)cantakeeithersign. Toevaluate itattheshock,weusethejumpcondition(2), ( γu s D = c a γ u ) [ ] s (γ )M 2 M a = c a 2γ a. (7) c a (γ + )M a Therefore, γu s D < if Ma 2 < 2γ/ (γ )and γu s D > otherwise. Inthetailofthe reactionzone,where uissmall, γu D <. Thus,forsufficientlystrongdetonations,the factor γu Dchangesitssignsomewhereinthereactionzone. Forsufficientlylarge M a,we obtainthatneartheshock (γu D)f > and,therefore,since (u D) 2 c 2 < nearthe shock,thefrictiontermleadstoavelocitydecreaseasdoestheheatreleaseterm. Theeffect of the heat loss term is the opposite. At small enough detonation Mach numbers, however, theroleofthefrictiontermisreversedbecausethesignof γu Dchangesneartheshock. Thereversalofthesignof γu Dseemstooccurwellabovetheturningpointofthe D c f curve and hence no significant qualitative change to the solution results. However, we have not explored the whole range of possibilities and the consequences of this sign change. In the cases we considered, there seems to be no significant effect. Intheset-valuedpartofthesolution,theflowisfullysubsonic,i.e., (u D) 2 c 2 < everywhere. If the term inside the brackets on the right-hand side of(7) is also negative, then u >, such that u decreases as tends to. Suppose now that u reaches its zerovalue. At that point, both f and h vanish, but ω is still non-zero. Therefore, u will continue decreasing. Once u becomes negative, the h term retains its sign, i.e., it remains positive,butthe f termnowswitchessign. Insteadofactingwiththeheatlossterm,which it did for u >, now the friction term acts with the reactionterm. As the magnitude of the negative velocity keeps increasing, the friction and heat loss terms in(7) balance the diminishing reaction rate term at some point. Downstream of that point, it is the loss terms that dominate, while the reaction term stops playing any significant role. Since the sign of u is nowreversed, ubeginstoincreasetowardzero. Thetrendisasymptotic, sinceat small u,theright-handsideof(7)isessentiallyproportionalto u,suchthat u = near infinity is a(half-) stable fixed point. Theequationfortemperatureisalsorevealing. Using T = p v + pv, v = (D u)/d 25
27 and(42-43)tocalculate p and u,wefindthat dt d = (γ )Dv γ ( M 2 ) M 2 c 2 [ ( γm 2 ) ( Qω h ) ( + γu ] ρφ D M2) Df. (72) ρφ Here, M = (D u)/cisthelocalmachnumberoftheflow. Becausethefactorinfrontof thebracketsin(72)isalwaysnegative,theriseofthetemperatureinthereactionzoneis due to the positive terms in the brackets. Depending on whether M 2 is smallerorlarger than /γ, the heat release term is seen to contribute to the temperature increase or decrease, respectively. The latter happens when the cooling by expansion dominates over heating, a situation well known in ideal detonation theory. This dual role of heat releaseleads to a temperature maximum in the reaction zone. The heat loss term is seen to havean effect opposite to that of the heat release. Note that the rolesof chemicalheat releaseand the heattransferarealwaysoppositeandtheyswitchsignswhere γm 2 switchessigns. When u >,thefrictiontermleadstothelocalheatingofthegasif γum 2 /D > and to cooling it otherwise. Because f = c f ρu u, we obtain that γum 2 /D > and f <,when u. Therefore,inthiscase,thefrictioncoolsthegaslocally. Thatis,this temperature decrease is not that of a fluid particle. For the latter, its rate of temperature change is udt/d, the contribution to which by friction remains positive when u changes sign. Immediately at the shock, the jump conditions yield γu s D = γu s/c a = 2γ Ma 2 D/c a γ + Ma 2 and Alittlebitofalgebrashowsthat γu s D M2 s = Ms 2 = 2 + (γ )M2 a 2γMa 2 (γ ). [ 4γ (γ + )Ma 2 (2γMa 2 Ma 4 (γ )) ] 3 (2 γ) Ma 2 +. (73) 4 Thus,thesignoftheleft-handsideiscontrolledbytheexpressioninthebracketswhichis positiveforreasonable γ. Then,intheregionimmediatelyaftertheshock,where u >, the friction term always heats the gas. Again, the important question here is to determine Ï Ø t = Ma 2 > Û Ò Ø Ø Ma 4 3(2 γ) M 2 4 a + = t γ t + 4 3γ Û ÔÓ Ø Ú Ø 4 4 < γ < 4/3º 26
2 Hallén s integral equation for the thin wire dipole antenna
 Ú Ð Ð ÓÒÐ Ò Ø ØØÔ»» Ѻ Ö Ùº º Ö ÁÒغ º ÁÒ Ù ØÖ Ð Å Ø Ñ Ø ÎÓк ÆÓº ¾ ¾¼½½µ ½ ¹½ ¾ ÆÙÑ Ö Ð Ñ Ø Ó ÓÖ Ò ÐÝ Ó Ö Ø ÓÒ ÖÓÑ Ø Ò Û Ö ÔÓÐ ÒØ ÒÒ Ëº À Ø ÑÞ ¹Î ÖÑ ÞÝ Ö Åº Æ Ö¹ÅÓ Êº Ë Þ ¹Ë Ò µ Ô ÖØÑ ÒØ Ó Ð ØÖ Ð Ò Ò
Ú Ð Ð ÓÒÐ Ò Ø ØØÔ»» Ѻ Ö Ùº º Ö ÁÒغ º ÁÒ Ù ØÖ Ð Å Ø Ñ Ø ÎÓк ÆÓº ¾ ¾¼½½µ ½ ¹½ ¾ ÆÙÑ Ö Ð Ñ Ø Ó ÓÖ Ò ÐÝ Ó Ö Ø ÓÒ ÖÓÑ Ø Ò Û Ö ÔÓÐ ÒØ ÒÒ Ëº À Ø ÑÞ ¹Î ÖÑ ÞÝ Ö Åº Æ Ö¹ÅÓ Êº Ë Þ ¹Ë Ò µ Ô ÖØÑ ÒØ Ó Ð ØÖ Ð Ò Ò
F(jω) = a(jω p 1 )(jω p 2 ) Û Ö p i = b± b 2 4ac. ω c = Y X (jω) = 1. 6R 2 C 2 (jω) 2 +7RCjω+1. 1 (6jωRC+1)(jωRC+1) RC, 1. RC = p 1, p
 ÓÖ Ò ÊÄ Ò Ò Û Ò Ò Ö Ý ½¾ Ù Ö ÓÖ ÖÓÑ Ö ÓÒ Ò ÄÈ ÐØ Ö ½¾ ½¾ ½» ½½ ÓÖ Ò ÊÄ Ò Ò Û Ò Ò Ö Ý ¾ Á b 2 < 4ac Û ÒÒÓØ ÓÖ Þ Û Ö Ð Ó ÒØ Ó Û Ð Ú ÕÙ Ö º ËÓÑ Ñ ÐÐ ÕÙ Ö Ö ÓÒ Ò º Ù Ö ÓÖ ½¾ ÓÖ Ù Ö ÕÙ Ö ÓÖ Ò ØÖ Ò Ö ÙÒØ ÓÒ
ÓÖ Ò ÊÄ Ò Ò Û Ò Ò Ö Ý ½¾ Ù Ö ÓÖ ÖÓÑ Ö ÓÒ Ò ÄÈ ÐØ Ö ½¾ ½¾ ½» ½½ ÓÖ Ò ÊÄ Ò Ò Û Ò Ò Ö Ý ¾ Á b 2 < 4ac Û ÒÒÓØ ÓÖ Þ Û Ö Ð Ó ÒØ Ó Û Ð Ú ÕÙ Ö º ËÓÑ Ñ ÐÐ ÕÙ Ö Ö ÓÒ Ò º Ù Ö ÓÖ ½¾ ÓÖ Ù Ö ÕÙ Ö ÓÖ Ò ØÖ Ò Ö ÙÒØ ÓÒ
Radu Alexandru GHERGHESCU, Dorin POENARU and Walter GREINER
 È Ö Ò Ò Ù Ò Ò Ò ÖÝ ÒÙÐ Ö Ý Ø Ñ Radu Alexandru GHERGHESCU, Dorin POENARU and Walter GREINER Radu.Gherghescu@nipne.ro IFIN-HH, Bucharest-Magurele, Romania and Frankfurt Institute for Advanced Studies, J
È Ö Ò Ò Ù Ò Ò Ò ÖÝ ÒÙÐ Ö Ý Ø Ñ Radu Alexandru GHERGHESCU, Dorin POENARU and Walter GREINER Radu.Gherghescu@nipne.ro IFIN-HH, Bucharest-Magurele, Romania and Frankfurt Institute for Advanced Studies, J
ÇÙÐ Ò ½º ÅÙÐ ÔÐ ÔÓÐÝÐÓ Ö Ñ Ò Ú Ö Ð Ú Ö Ð ¾º Ä Ò Ö Ö Ù Ð Ý Ó ËÝÑ ÒÞ ÔÓÐÝÒÓÑ Ð º Ì ÛÓ¹ÐÓÓÔ ÙÒÖ Ö Ô Û Ö Ö ÖÝ Ñ ¹ ÝÓÒ ÑÙÐ ÔÐ ÔÓÐÝÐÓ Ö Ñ
 ÅÙÐ ÔÐ ÔÓÐÝÐÓ Ö Ñ Ò ÝÒÑ Ò Ò Ö Ð Ö Ò Ó Ò Ö ÀÍ ÖÐ Òµ Ó Ò ÛÓÖ Û Ö Ò ÖÓÛÒ Ö Ú ½ ¼¾º ¾½ Û Åº Ä Ö Ö Ú ½ ¼¾º ¼¼ Û Äº Ñ Ò Ëº Ï ÒÞ ÖÐ Å ÒÞ ½ º¼ º¾¼½ ÇÙÐ Ò ½º ÅÙÐ ÔÐ ÔÓÐÝÐÓ Ö Ñ Ò Ú Ö Ð Ú Ö Ð ¾º Ä Ò Ö Ö Ù Ð Ý Ó ËÝÑ
ÅÙÐ ÔÐ ÔÓÐÝÐÓ Ö Ñ Ò ÝÒÑ Ò Ò Ö Ð Ö Ò Ó Ò Ö ÀÍ ÖÐ Òµ Ó Ò ÛÓÖ Û Ö Ò ÖÓÛÒ Ö Ú ½ ¼¾º ¾½ Û Åº Ä Ö Ö Ú ½ ¼¾º ¼¼ Û Äº Ñ Ò Ëº Ï ÒÞ ÖÐ Å ÒÞ ½ º¼ º¾¼½ ÇÙÐ Ò ½º ÅÙÐ ÔÐ ÔÓÐÝÐÓ Ö Ñ Ò Ú Ö Ð Ú Ö Ð ¾º Ä Ò Ö Ö Ù Ð Ý Ó ËÝÑ
Asymptotic theory of evolution and failure of self-sustained detonations
 J. Fluid Mech. (5), vol. 55, pp. 161 19. c 5 Cambridge University Press DOI: 1.117/S114599 Printed in the United Kingdom 161 Asymptotic theory of evolution and failure of self-sustained detonations By
J. Fluid Mech. (5), vol. 55, pp. 161 19. c 5 Cambridge University Press DOI: 1.117/S114599 Printed in the United Kingdom 161 Asymptotic theory of evolution and failure of self-sustained detonations By
µ(, y) Computing the Möbius fun tion µ(x, x) = 1 The Möbius fun tion is de ned b y and X µ(x, t) = 0 x < y if x6t6y 3
 ÈÖÑÙØØÓÒ ÔØØÖÒ Ò Ø ÅÙ ÙÒØÓÒ ÙÖ ØÒ ÎØ ÂÐÒ Ú ÂÐÒÓÚ Ò ÐÜ ËØÒÖÑ ÓÒ ÒÖ Ì ØÛÓµ 2314 ½¾ ½ ¾ ¾½ ¾ ½ ½¾ ¾½ ½¾ ¾½ ½ Ì ÔÓ Ø Ó ÔÖÑÙØØÓÒ ÛºÖºØº ÔØØÖÒ ÓÒØÒÑÒØ ½ 2314 ½¾ ½ ¾ ¾½ ¾ ½ ½¾ ¾½ ½¾ ¾½ Ì ÒØÖÚÐ [12,2314] ½ ¾ ÓÑÔÙØÒ
ÈÖÑÙØØÓÒ ÔØØÖÒ Ò Ø ÅÙ ÙÒØÓÒ ÙÖ ØÒ ÎØ ÂÐÒ Ú ÂÐÒÓÚ Ò ÐÜ ËØÒÖÑ ÓÒ ÒÖ Ì ØÛÓµ 2314 ½¾ ½ ¾ ¾½ ¾ ½ ½¾ ¾½ ½¾ ¾½ ½ Ì ÔÓ Ø Ó ÔÖÑÙØØÓÒ ÛºÖºØº ÔØØÖÒ ÓÒØÒÑÒØ ½ 2314 ½¾ ½ ¾ ¾½ ¾ ½ ½¾ ¾½ ½¾ ¾½ Ì ÒØÖÚÐ [12,2314] ½ ¾ ÓÑÔÙØÒ
Lecture 16: Modern Classification (I) - Separating Hyperplanes
 Lecture 16: Modern Classification (I) - Separating Hyperplanes Outline 1 2 Separating Hyperplane Binary SVM for Separable Case Bayes Rule for Binary Problems Consider the simplest case: two classes are
Lecture 16: Modern Classification (I) - Separating Hyperplanes Outline 1 2 Separating Hyperplane Binary SVM for Separable Case Bayes Rule for Binary Problems Consider the simplest case: two classes are
PHYS 643 Week 4: Compressible fluids Sound waves and shocks
 PHYS 643 Week 4: Compressible fluids Sound waves and shocks Sound waves Compressions in a gas propagate as sound waves. The simplest case to consider is a gas at uniform density and at rest. Small perturbations
PHYS 643 Week 4: Compressible fluids Sound waves and shocks Sound waves Compressions in a gas propagate as sound waves. The simplest case to consider is a gas at uniform density and at rest. Small perturbations
n v molecules will pass per unit time through the area from left to
 3 iscosity and Heat Conduction in Gas Dynamics Equations of One-Dimensional Gas Flow The dissipative processes - viscosity (internal friction) and heat conduction - are connected with existence of molecular
3 iscosity and Heat Conduction in Gas Dynamics Equations of One-Dimensional Gas Flow The dissipative processes - viscosity (internal friction) and heat conduction - are connected with existence of molecular
Various lecture notes for
 Various lecture notes for 18311. R. R. Rosales (MIT, Math. Dept., 2-337) April 12, 2013 Abstract Notes, both complete and/or incomplete, for MIT s 18.311 (Principles of Applied Mathematics). These notes
Various lecture notes for 18311. R. R. Rosales (MIT, Math. Dept., 2-337) April 12, 2013 Abstract Notes, both complete and/or incomplete, for MIT s 18.311 (Principles of Applied Mathematics). These notes
Lecture 7 Detonation Waves
 Lecture 7 etonation Waves p strong detonation weak detonation weak deflagration strong deflagration / 0 v =/ University of Illinois at Urbana- Champaign eflagrations produce heat Thermal di usivity th
Lecture 7 etonation Waves p strong detonation weak detonation weak deflagration strong deflagration / 0 v =/ University of Illinois at Urbana- Champaign eflagrations produce heat Thermal di usivity th
Fundamentals of Fluid Dynamics: Elementary Viscous Flow
 Fundamentals of Fluid Dynamics: Elementary Viscous Flow Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research
Fundamentals of Fluid Dynamics: Elementary Viscous Flow Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research
Radiative & Magnetohydrodynamic Shocks
 Chapter 4 Radiative & Magnetohydrodynamic Shocks I have been dealing, so far, with non-radiative shocks. Since, as we have seen, a shock raises the density and temperature of the gas, it is quite likely,
Chapter 4 Radiative & Magnetohydrodynamic Shocks I have been dealing, so far, with non-radiative shocks. Since, as we have seen, a shock raises the density and temperature of the gas, it is quite likely,
Answers to Problem Set Number 04 for MIT (Spring 2008)
 Answers to Problem Set Number 04 for 18.311 MIT (Spring 008) Rodolfo R. Rosales (MIT, Math. Dept., room -337, Cambridge, MA 0139). March 17, 008. Course TA: Timothy Nguyen, MIT, Dept. of Mathematics, Cambridge,
Answers to Problem Set Number 04 for 18.311 MIT (Spring 008) Rodolfo R. Rosales (MIT, Math. Dept., room -337, Cambridge, MA 0139). March 17, 008. Course TA: Timothy Nguyen, MIT, Dept. of Mathematics, Cambridge,
SKMM 3023 Applied Numerical Methods
 SKMM 3023 Applied Numerical Methods Solution of Nonlinear Equations ibn Abdullah Faculty of Mechanical Engineering Òº ÙÐÐ ÚºÒÙÐÐ ¾¼½ SKMM 3023 Applied Numerical Methods Solution of Nonlinear Equations
SKMM 3023 Applied Numerical Methods Solution of Nonlinear Equations ibn Abdullah Faculty of Mechanical Engineering Òº ÙÐÐ ÚºÒÙÐÐ ¾¼½ SKMM 3023 Applied Numerical Methods Solution of Nonlinear Equations
Arbeitstagung: Gruppen und Topologische Gruppen Vienna July 6 July 7, Abstracts
 Arbeitstagung: Gruppen und Topologische Gruppen Vienna July 6 July 7, 202 Abstracts ÁÒÚ Ö Ð Ñ Ø Ó Ø¹Ú ÐÙ ÙÒØ ÓÒ ÁÞØÓ Ò ÞØÓ º Ò ÙÒ ¹Ñ º ÙÐØÝ Ó Æ ØÙÖ Ð Ë Ò Ò Å Ø Ñ Ø ÍÒ Ú Ö ØÝ Ó Å Ö ÓÖ ÃÓÖÓ ½ ¼ Å Ö ÓÖ ¾¼¼¼
Arbeitstagung: Gruppen und Topologische Gruppen Vienna July 6 July 7, 202 Abstracts ÁÒÚ Ö Ð Ñ Ø Ó Ø¹Ú ÐÙ ÙÒØ ÓÒ ÁÞØÓ Ò ÞØÓ º Ò ÙÒ ¹Ñ º ÙÐØÝ Ó Æ ØÙÖ Ð Ë Ò Ò Å Ø Ñ Ø ÍÒ Ú Ö ØÝ Ó Å Ö ÓÖ ÃÓÖÓ ½ ¼ Å Ö ÓÖ ¾¼¼¼
Steady waves in compressible flow
 Chapter Steady waves in compressible flow. Oblique shock waves Figure. shows an oblique shock wave produced when a supersonic flow is deflected by an angle. Figure.: Flow geometry near a plane oblique
Chapter Steady waves in compressible flow. Oblique shock waves Figure. shows an oblique shock wave produced when a supersonic flow is deflected by an angle. Figure.: Flow geometry near a plane oblique
To study the motion of a perfect gas, the conservation equations of continuity
 Chapter 1 Ideal Gas Flow The Navier-Stokes equations To study the motion of a perfect gas, the conservation equations of continuity ρ + (ρ v = 0, (1.1 momentum ρ D v Dt = p+ τ +ρ f m, (1.2 and energy ρ
Chapter 1 Ideal Gas Flow The Navier-Stokes equations To study the motion of a perfect gas, the conservation equations of continuity ρ + (ρ v = 0, (1.1 momentum ρ D v Dt = p+ τ +ρ f m, (1.2 and energy ρ
CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION
 CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION 7.1 THE NAVIER-STOKES EQUATIONS Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION 7.1 THE NAVIER-STOKES EQUATIONS Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
SKMM 3023 Applied Numerical Methods
 UNIVERSITI TEKNOLOGI MALAYSIA SKMM 3023 Applied Numerical Methods Ordinary Differential Equations ibn Abdullah Faculty of Mechanical Engineering Òº ÙÐÐ ÚºÒÙÐÐ ¾¼½ SKMM 3023 Applied Numerical Methods Ordinary
UNIVERSITI TEKNOLOGI MALAYSIA SKMM 3023 Applied Numerical Methods Ordinary Differential Equations ibn Abdullah Faculty of Mechanical Engineering Òº ÙÐÐ ÚºÒÙÐÐ ¾¼½ SKMM 3023 Applied Numerical Methods Ordinary
Lund Institute of Technology Centre for Mathematical Sciences Mathematical Statistics
 Lund Institute of Technology Centre for Mathematical Sciences Mathematical Statistics STATISTICAL METHODS FOR SAFETY ANALYSIS FMS065 ÓÑÔÙØ Ö Ü Ö Ì ÓÓØ ØÖ Ô Ð ÓÖ Ø Ñ Ò Ý Ò Ò ÐÝ In this exercise we will
Lund Institute of Technology Centre for Mathematical Sciences Mathematical Statistics STATISTICAL METHODS FOR SAFETY ANALYSIS FMS065 ÓÑÔÙØ Ö Ü Ö Ì ÓÓØ ØÖ Ô Ð ÓÖ Ø Ñ Ò Ý Ò Ò ÐÝ In this exercise we will
SME 3023 Applied Numerical Methods
 UNIVERSITI TEKNOLOGI MALAYSIA SME 3023 Applied Numerical Methods Solution of Nonlinear Equations Abu Hasan Abdullah Faculty of Mechanical Engineering Sept 2012 Abu Hasan Abdullah (FME) SME 3023 Applied
UNIVERSITI TEKNOLOGI MALAYSIA SME 3023 Applied Numerical Methods Solution of Nonlinear Equations Abu Hasan Abdullah Faculty of Mechanical Engineering Sept 2012 Abu Hasan Abdullah (FME) SME 3023 Applied
AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS
 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS 1 / 29 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS Hierarchy of Mathematical Models 1 / 29 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS 2 / 29
AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS 1 / 29 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS Hierarchy of Mathematical Models 1 / 29 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS 2 / 29
Shock and Expansion Waves
 Chapter For the solution of the Euler equations to represent adequately a given large-reynolds-number flow, we need to consider in general the existence of discontinuity surfaces, across which the fluid
Chapter For the solution of the Euler equations to represent adequately a given large-reynolds-number flow, we need to consider in general the existence of discontinuity surfaces, across which the fluid
Lecture-2. One-dimensional Compressible Fluid Flow in Variable Area
 Lecture-2 One-dimensional Compressible Fluid Flow in Variable Area Summary of Results(Cont..) In isoenergetic-isentropic flow, an increase in velocity always corresponds to a Mach number increase and vice
Lecture-2 One-dimensional Compressible Fluid Flow in Variable Area Summary of Results(Cont..) In isoenergetic-isentropic flow, an increase in velocity always corresponds to a Mach number increase and vice
Proving observational equivalence with ProVerif
 Proving observational equivalence with ProVerif Bruno Blanchet INRIA Paris-Rocquencourt Bruno.Blanchet@inria.fr based on joint work with Martín Abadi and Cédric Fournet and with Vincent Cheval June 2015
Proving observational equivalence with ProVerif Bruno Blanchet INRIA Paris-Rocquencourt Bruno.Blanchet@inria.fr based on joint work with Martín Abadi and Cédric Fournet and with Vincent Cheval June 2015
Lecture 5.7 Compressible Euler Equations
 Lecture 5.7 Compressible Euler Equations Nomenclature Density u, v, w Velocity components p E t H u, v, w e S=c v ln p - c M Pressure Total energy/unit volume Total enthalpy Conserved variables Internal
Lecture 5.7 Compressible Euler Equations Nomenclature Density u, v, w Velocity components p E t H u, v, w e S=c v ln p - c M Pressure Total energy/unit volume Total enthalpy Conserved variables Internal
SME 3023 Applied Numerical Methods
 UNIVERSITI TEKNOLOGI MALAYSIA SME 3023 Applied Numerical Methods Ordinary Differential Equations Abu Hasan Abdullah Faculty of Mechanical Engineering Sept 2012 Abu Hasan Abdullah (FME) SME 3023 Applied
UNIVERSITI TEKNOLOGI MALAYSIA SME 3023 Applied Numerical Methods Ordinary Differential Equations Abu Hasan Abdullah Faculty of Mechanical Engineering Sept 2012 Abu Hasan Abdullah (FME) SME 3023 Applied
PH Nuclear Physics Laboratory Gamma spectroscopy (NP3)
 Physics Department Royal Holloway University of London PH2510 - Nuclear Physics Laboratory Gamma spectroscopy (NP3) 1 Objectives The aim of this experiment is to demonstrate how γ-ray energy spectra may
Physics Department Royal Holloway University of London PH2510 - Nuclear Physics Laboratory Gamma spectroscopy (NP3) 1 Objectives The aim of this experiment is to demonstrate how γ-ray energy spectra may
AA210A Fundamentals of Compressible Flow. Chapter 13 - Unsteady Waves in Compressible Flow
 AA210A Fundamentals of Compressible Flow Chapter 13 - Unsteady Waves in Compressible Flow The Shock Tube - Wave Diagram 13.1 Equations for irrotational, homentropic, unsteady flow ρ t + x k ρ U i t (
AA210A Fundamentals of Compressible Flow Chapter 13 - Unsteady Waves in Compressible Flow The Shock Tube - Wave Diagram 13.1 Equations for irrotational, homentropic, unsteady flow ρ t + x k ρ U i t (
Principles of Convection
 Principles of Convection Point Conduction & convection are similar both require the presence of a material medium. But convection requires the presence of fluid motion. Heat transfer through the: Solid
Principles of Convection Point Conduction & convection are similar both require the presence of a material medium. But convection requires the presence of fluid motion. Heat transfer through the: Solid
An analytical model for direct initiation of gaseous detonations
 Issw21 An analytical model for direct initiation of gaseous detonations C.A. Eckett, J.J. Quirk, J.E. Shepherd Graduate Aeronautical Laboratories, California Institute of Technology, Pasadena CA 91125,
Issw21 An analytical model for direct initiation of gaseous detonations C.A. Eckett, J.J. Quirk, J.E. Shepherd Graduate Aeronautical Laboratories, California Institute of Technology, Pasadena CA 91125,
Notes #4a MAE 533, Fluid Mechanics
 Notes #4a MAE 533, Fluid Mechanics S. H. Lam lam@princeton.edu http://www.princeton.edu/ lam October 23, 1998 1 The One-dimensional Continuity Equation The one-dimensional steady flow continuity equation
Notes #4a MAE 533, Fluid Mechanics S. H. Lam lam@princeton.edu http://www.princeton.edu/ lam October 23, 1998 1 The One-dimensional Continuity Equation The one-dimensional steady flow continuity equation
Self-similar solutions for the diffraction of weak shocks
 Self-similar solutions for the diffraction of weak shocks Allen M. Tesdall John K. Hunter Abstract. We numerically solve a problem for the unsteady transonic small disturbance equations that describes
Self-similar solutions for the diffraction of weak shocks Allen M. Tesdall John K. Hunter Abstract. We numerically solve a problem for the unsteady transonic small disturbance equations that describes
Lars Schmidt-Thieme, Information Systems and Machine Learning Lab (ISMLL), Institute BW/WI & Institute for Computer Science, University of Hildesheim
 Course on Information Systems 2, summer term 2010 0/29 Information Systems 2 Information Systems 2 5. Business Process Modelling I: Models Lars Schmidt-Thieme Information Systems and Machine Learning Lab
Course on Information Systems 2, summer term 2010 0/29 Information Systems 2 Information Systems 2 5. Business Process Modelling I: Models Lars Schmidt-Thieme Information Systems and Machine Learning Lab
Sound Generation from Vortex Sheet Instability
 Sound Generation from Vortex Sheet Instability Hongbin Ju Department of Mathematics Florida State University, Tallahassee, FL.3306 www.aeroacoustics.info Please send comments to: hju@math.fsu.edu When
Sound Generation from Vortex Sheet Instability Hongbin Ju Department of Mathematics Florida State University, Tallahassee, FL.3306 www.aeroacoustics.info Please send comments to: hju@math.fsu.edu When
u x + u y = x u . u(x, 0) = e x2 The characteristics satisfy dx dt = 1, dy dt = 1
 Õ 83-25 Þ ÛÐ Þ Ð ÚÔÜØ Þ ÝÒ Þ Ô ÜÞØ ¹ 3 Ñ Ð ÜÞ u x + u y = x u u(x, 0) = e x2 ÝÒ Þ Ü ÞØ º½ dt =, dt = x = t + c, y = t + c 2 We can choose c to be zero without loss of generality Note that each characteristic
Õ 83-25 Þ ÛÐ Þ Ð ÚÔÜØ Þ ÝÒ Þ Ô ÜÞØ ¹ 3 Ñ Ð ÜÞ u x + u y = x u u(x, 0) = e x2 ÝÒ Þ Ü ÞØ º½ dt =, dt = x = t + c, y = t + c 2 We can choose c to be zero without loss of generality Note that each characteristic
Multiscale Hydrodynamic Phenomena
 M2, Fluid mechanics 2014/2015 Friday, December 5th, 2014 Multiscale Hydrodynamic Phenomena Part I. : 90 minutes, NO documents 1. Quick Questions In few words : 1.1 What is dominant balance? 1.2 What is
M2, Fluid mechanics 2014/2015 Friday, December 5th, 2014 Multiscale Hydrodynamic Phenomena Part I. : 90 minutes, NO documents 1. Quick Questions In few words : 1.1 What is dominant balance? 1.2 What is
AME 513. " Lecture 8 Premixed flames I: Propagation rates
 AME 53 Principles of Combustion " Lecture 8 Premixed flames I: Propagation rates Outline" Rankine-Hugoniot relations Hugoniot curves Rayleigh lines Families of solutions Detonations Chapman-Jouget Others
AME 53 Principles of Combustion " Lecture 8 Premixed flames I: Propagation rates Outline" Rankine-Hugoniot relations Hugoniot curves Rayleigh lines Families of solutions Detonations Chapman-Jouget Others
AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS
 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS 1 / 43 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS Treatment of Boundary Conditions These slides are partially based on the recommended textbook: Culbert
AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS 1 / 43 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS Treatment of Boundary Conditions These slides are partially based on the recommended textbook: Culbert
CapSel Euler The Euler equations. conservation laws for 1D dynamics of compressible gas. = 0 m t + (m v + p) x
 CapSel Euler - 01 The Euler equations keppens@rijnh.nl conservation laws for 1D dynamics of compressible gas ρ t + (ρ v) x = 0 m t + (m v + p) x = 0 e t + (e v + p v) x = 0 vector of conserved quantities
CapSel Euler - 01 The Euler equations keppens@rijnh.nl conservation laws for 1D dynamics of compressible gas ρ t + (ρ v) x = 0 m t + (m v + p) x = 0 e t + (e v + p v) x = 0 vector of conserved quantities
INRIA Sophia Antipolis France. TEITP p.1
 ÌÖÙ Ø ÜØ Ò ÓÒ Ò ÓÕ Ä ÙÖ ÒØ Ì ÖÝ INRIA Sophia Antipolis France TEITP p.1 ÅÓØ Ú Ø ÓÒ Ï Ý ØÖÙ Ø Ó ÑÔÓÖØ ÒØ Å ÒÐÝ ÈÖÓÚ Ò ÌÖÙØ Ø Ò ÑÔÐ Ã Ô ÈÖÓÚ Ò ÌÖÙ Ø È Ó ÖÖÝ Ò ÈÖÓÓ µ Ò Ö ØÝ ÓÑ Ò ËÔ ÔÔÐ Ø ÓÒ TEITP p.2 ÇÙØÐ
ÌÖÙ Ø ÜØ Ò ÓÒ Ò ÓÕ Ä ÙÖ ÒØ Ì ÖÝ INRIA Sophia Antipolis France TEITP p.1 ÅÓØ Ú Ø ÓÒ Ï Ý ØÖÙ Ø Ó ÑÔÓÖØ ÒØ Å ÒÐÝ ÈÖÓÚ Ò ÌÖÙØ Ø Ò ÑÔÐ Ã Ô ÈÖÓÚ Ò ÌÖÙ Ø È Ó ÖÖÝ Ò ÈÖÓÓ µ Ò Ö ØÝ ÓÑ Ò ËÔ ÔÔÐ Ø ÓÒ TEITP p.2 ÇÙØÐ
EQUATION OF STATE FOR MODELING THE DETONATION REACTION ZONE
 EQUATION OF STATE FOR MODELING THE DETONATION REACTION ZONE D. Scott Stewart and Sunhee Yoo Department of Theoretical and Applied Mechanics University of Illinois, Urbana, IL 61801, USA William C. Davis
EQUATION OF STATE FOR MODELING THE DETONATION REACTION ZONE D. Scott Stewart and Sunhee Yoo Department of Theoretical and Applied Mechanics University of Illinois, Urbana, IL 61801, USA William C. Davis
Application of a Laser Induced Fluorescence Model to the Numerical Simulation of Detonation Waves in Hydrogen-Oxygen-Diluent Mixtures
 Supplemental material for paper published in the International J of Hydrogen Energy, Vol. 30, 6044-6060, 2014. http://dx.doi.org/10.1016/j.ijhydene.2014.01.182 Application of a Laser Induced Fluorescence
Supplemental material for paper published in the International J of Hydrogen Energy, Vol. 30, 6044-6060, 2014. http://dx.doi.org/10.1016/j.ijhydene.2014.01.182 Application of a Laser Induced Fluorescence
Answers to Problem Set Number 02 for MIT (Spring 2008)
 Answers to Problem Set Number 02 for 18.311 MIT (Spring 2008) Rodolfo R. Rosales (MIT, Math. Dept., room 2-337, Cambridge, MA 02139). March 10, 2008. Course TA: Timothy Nguyen, MIT, Dept. of Mathematics,
Answers to Problem Set Number 02 for 18.311 MIT (Spring 2008) Rodolfo R. Rosales (MIT, Math. Dept., room 2-337, Cambridge, MA 02139). March 10, 2008. Course TA: Timothy Nguyen, MIT, Dept. of Mathematics,
THERMODYNAMIC ANALYSIS OF COMBUSTION PROCESSES FOR PROPULSION SYSTEMS
 2nd AIAA Aerospace Sciences Paper 2-33 Meeting and Exhibit January -8, 2, Reno, NV THERMODYNAMIC ANALYSIS OF COMBUSTION PROCESSES FOR PROPULSION SYSTEMS E. Wintenberger and J. E. Shepherd Graduate Aeronautical
2nd AIAA Aerospace Sciences Paper 2-33 Meeting and Exhibit January -8, 2, Reno, NV THERMODYNAMIC ANALYSIS OF COMBUSTION PROCESSES FOR PROPULSION SYSTEMS E. Wintenberger and J. E. Shepherd Graduate Aeronautical
Introduction to Gas Dynamics All Lecture Slides
 Introduction to Gas Dynamics All Lecture Slides Teknillinen Korkeakoulu / Helsinki University of Technology Autumn 009 1 Compressible flow Zeroth law of thermodynamics 3 First law of thermodynamics 4 Equation
Introduction to Gas Dynamics All Lecture Slides Teknillinen Korkeakoulu / Helsinki University of Technology Autumn 009 1 Compressible flow Zeroth law of thermodynamics 3 First law of thermodynamics 4 Equation
arxiv:hep-ph/ v1 10 May 2001
 New data and the hard pomeron A Donnachie Department of Physics, Manchester University P V Landshoff DAMTP, Cambridge University DAMTP-200-38 M/C-TH-0/03 arxiv:hep-ph/005088v 0 May 200 Abstract New structure-function
New data and the hard pomeron A Donnachie Department of Physics, Manchester University P V Landshoff DAMTP, Cambridge University DAMTP-200-38 M/C-TH-0/03 arxiv:hep-ph/005088v 0 May 200 Abstract New structure-function
Problem 1 (From the reservoir to the grid)
 ÈÖÓ º ĺ ÙÞÞ ÐÐ ÈÖÓ º ʺ ³ Ò Ö ½ ½¹¼ ¹¼¼ ËÝ Ø Ñ ÅÓ Ð Ò ÀË ¾¼½ µ Ü Ö ËÓÐÙØ ÓÒ ÌÓÔ ÀÝ ÖÓ Ð ØÖ ÔÓÛ Ö ÔÐ ÒØ À Èȵ ¹ È ÖØ ÁÁ Ð ÖÒ Ø Þº ÇØÓ Ö ¾ ¾¼½ Problem 1 (From the reservoir to the grid) The causality diagram
ÈÖÓ º ĺ ÙÞÞ ÐÐ ÈÖÓ º ʺ ³ Ò Ö ½ ½¹¼ ¹¼¼ ËÝ Ø Ñ ÅÓ Ð Ò ÀË ¾¼½ µ Ü Ö ËÓÐÙØ ÓÒ ÌÓÔ ÀÝ ÖÓ Ð ØÖ ÔÓÛ Ö ÔÐ ÒØ À Èȵ ¹ È ÖØ ÁÁ Ð ÖÒ Ø Þº ÇØÓ Ö ¾ ¾¼½ Problem 1 (From the reservoir to the grid) The causality diagram
6.2 Governing Equations for Natural Convection
 6. Governing Equations for Natural Convection 6..1 Generalized Governing Equations The governing equations for natural convection are special cases of the generalized governing equations that were discussed
6. Governing Equations for Natural Convection 6..1 Generalized Governing Equations The governing equations for natural convection are special cases of the generalized governing equations that were discussed
Chapter 3 Lecture 8. Drag polar 3. Topics. Chapter-3
 Chapter 3 ecture 8 Drag polar 3 Topics 3.2.7 Boundary layer separation, adverse pressure gradient and favourable pressure gradient 3.2.8 Boundary layer transition 3.2.9 Turbulent boundary layer over a
Chapter 3 ecture 8 Drag polar 3 Topics 3.2.7 Boundary layer separation, adverse pressure gradient and favourable pressure gradient 3.2.8 Boundary layer transition 3.2.9 Turbulent boundary layer over a
Introduction to Physical Acoustics
 Introduction to Physical Acoustics Class webpage CMSC 828D: Algorithms and systems for capture and playback of spatial audio. www.umiacs.umd.edu/~ramani/cmsc828d_audio Send me a test email message with
Introduction to Physical Acoustics Class webpage CMSC 828D: Algorithms and systems for capture and playback of spatial audio. www.umiacs.umd.edu/~ramani/cmsc828d_audio Send me a test email message with
Lecture 8 Laminar Diffusion Flames: Diffusion Flamelet Theory
 Lecture 8 Laminar Diffusion Flames: Diffusion Flamelet Theory 8.-1 Systems, where fuel and oxidizer enter separately into the combustion chamber. Mixing takes place by convection and diffusion. Only where
Lecture 8 Laminar Diffusion Flames: Diffusion Flamelet Theory 8.-1 Systems, where fuel and oxidizer enter separately into the combustion chamber. Mixing takes place by convection and diffusion. Only where
x 0, x 1,...,x n f(x) p n (x) = f[x 0, x 1,..., x n, x]w n (x),
![x 0, x 1,...,x n f(x) p n (x) = f[x 0, x 1,..., x n, x]w n (x), x 0, x 1,...,x n f(x) p n (x) = f[x 0, x 1,..., x n, x]w n (x),](/thumbs/71/66079649.jpg) ÛÜØ Þ ÜÒ Ô ÚÜ Ô Ü Ñ Ü Ô Ð Ñ Ü ÜØ º½ ÞÜ Ò f Ø ÚÜ ÚÛÔ Ø Ü Ö ºÞ ÜÒ Ô ÚÜ Ô Ð Ü Ð Þ Õ Ô ÞØÔ ÛÜØ Ü ÚÛÔ Ø Ü Ö L(f) = f(x)dx ÚÜ Ô Ü ÜØ Þ Ü Ô, b] Ö Û Þ Ü Ô Ñ ÒÖØ k Ü f Ñ Df(x) = f (x) ÐÖ D Ü Ü ÜØ Þ Ü Ô Ñ Ü ÜØ Ñ
ÛÜØ Þ ÜÒ Ô ÚÜ Ô Ü Ñ Ü Ô Ð Ñ Ü ÜØ º½ ÞÜ Ò f Ø ÚÜ ÚÛÔ Ø Ü Ö ºÞ ÜÒ Ô ÚÜ Ô Ð Ü Ð Þ Õ Ô ÞØÔ ÛÜØ Ü ÚÛÔ Ø Ü Ö L(f) = f(x)dx ÚÜ Ô Ü ÜØ Þ Ü Ô, b] Ö Û Þ Ü Ô Ñ ÒÖØ k Ü f Ñ Df(x) = f (x) ÐÖ D Ü Ü ÜØ Þ Ü Ô Ñ Ü ÜØ Ñ
 ! " # $! % & '! , ) ( + - (. ) ( ) * + / 0 1 2 3 0 / 4 5 / 6 0 ; 8 7 < = 7 > 8 7 8 9 : Œ Š ž P P h ˆ Š ˆ Œ ˆ Š ˆ Ž Ž Ý Ü Ý Ü Ý Ž Ý ê ç è ± ¹ ¼ ¹ ä ± ¹ w ç ¹ è ¼ è Œ ¹ ± ¹ è ¹ è ä ç w ¹ ã ¼ ¹ ä ¹ ¼ ¹ ±
! " # $! % & '! , ) ( + - (. ) ( ) * + / 0 1 2 3 0 / 4 5 / 6 0 ; 8 7 < = 7 > 8 7 8 9 : Œ Š ž P P h ˆ Š ˆ Œ ˆ Š ˆ Ž Ž Ý Ü Ý Ü Ý Ž Ý ê ç è ± ¹ ¼ ¹ ä ± ¹ w ç ¹ è ¼ è Œ ¹ ± ¹ è ¹ è ä ç w ¹ ã ¼ ¹ ä ¹ ¼ ¹ ±
This document has been prepared by Sunder Kidambi with the blessings of
 Ö À Ö Ñ Ø Ò Ñ ÒØ Ñ Ý Ò Ñ À Ö Ñ Ò Ú º Ò Ì ÝÊ À Å Ú Ø Å Ê ý Ú ÒØ º ÝÊ Ú Ý Ê Ñ º Å º ² ºÅ ý ý ý ý Ö Ð º Ñ ÒÜ Æ Å Ò Ñ Ú «Ä À ý ý This document has been prepared by Sunder Kidambi with the blessings of Ö º
Ö À Ö Ñ Ø Ò Ñ ÒØ Ñ Ý Ò Ñ À Ö Ñ Ò Ú º Ò Ì ÝÊ À Å Ú Ø Å Ê ý Ú ÒØ º ÝÊ Ú Ý Ê Ñ º Å º ² ºÅ ý ý ý ý Ö Ð º Ñ ÒÜ Æ Å Ò Ñ Ú «Ä À ý ý This document has been prepared by Sunder Kidambi with the blessings of Ö º
Laminar Premixed Flames: Flame Structure
 Laminar Premixed Flames: Flame Structure Combustion Summer School 2018 Prof. Dr.-Ing. Heinz Pitsch Course Overview Part I: Fundamentals and Laminar Flames Introduction Fundamentals and mass balances of
Laminar Premixed Flames: Flame Structure Combustion Summer School 2018 Prof. Dr.-Ing. Heinz Pitsch Course Overview Part I: Fundamentals and Laminar Flames Introduction Fundamentals and mass balances of
A Study of Detonation Evolution and Structure for a Model of Compressible Two-Phase Reactive Flow
 A Study of Detonation Evolution and Structure for a Model of Compressible Two-Phase Reactive Flow D. W. Schwendeman, C. W. Wahle and A. K. Kapila Department of Mathematical Sciences, Rensselaer Polytechnic
A Study of Detonation Evolution and Structure for a Model of Compressible Two-Phase Reactive Flow D. W. Schwendeman, C. W. Wahle and A. K. Kapila Department of Mathematical Sciences, Rensselaer Polytechnic
Detonation of Gas Particle Flow
 2 Detonation of Gas Particle Flow F. Zhang 2.1 Introduction Fine organic or metallic particles suspended in an oxidizing or combustible gas form a reactive particle gas mixture. Explosion pressures in
2 Detonation of Gas Particle Flow F. Zhang 2.1 Introduction Fine organic or metallic particles suspended in an oxidizing or combustible gas form a reactive particle gas mixture. Explosion pressures in
Fundamentals of Fluid Dynamics: Ideal Flow Theory & Basic Aerodynamics
 Fundamentals of Fluid Dynamics: Ideal Flow Theory & Basic Aerodynamics Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI (after: D.J. ACHESON s Elementary Fluid Dynamics ) bluebox.ippt.pan.pl/
Fundamentals of Fluid Dynamics: Ideal Flow Theory & Basic Aerodynamics Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI (after: D.J. ACHESON s Elementary Fluid Dynamics ) bluebox.ippt.pan.pl/
Waves in a Shock Tube
 Waves in a Shock Tube Ivan Christov c February 5, 005 Abstract. This paper discusses linear-wave solutions and simple-wave solutions to the Navier Stokes equations for an inviscid and compressible fluid
Waves in a Shock Tube Ivan Christov c February 5, 005 Abstract. This paper discusses linear-wave solutions and simple-wave solutions to the Navier Stokes equations for an inviscid and compressible fluid
Applied Gas Dynamics Flow With Friction and Heat Transfer
 Applied Gas Dynamics Flow With Friction and Heat Transfer Ethirajan Rathakrishnan Applied Gas Dynamics, John Wiley & Sons (Asia) Pte Ltd c 2010 Ethirajan Rathakrishnan 1 / 121 Introduction So far, we have
Applied Gas Dynamics Flow With Friction and Heat Transfer Ethirajan Rathakrishnan Applied Gas Dynamics, John Wiley & Sons (Asia) Pte Ltd c 2010 Ethirajan Rathakrishnan 1 / 121 Introduction So far, we have
Detonation Diffraction
 Detonation Diffraction E. Schultz, J. Shepherd Detonation Physics Laboratory Pasadena, CA 91125 MURI Mid-Year Pulse Detonation Engine Review Meeting February 10-11, 2000 Super-critical Detonation Diffraction
Detonation Diffraction E. Schultz, J. Shepherd Detonation Physics Laboratory Pasadena, CA 91125 MURI Mid-Year Pulse Detonation Engine Review Meeting February 10-11, 2000 Super-critical Detonation Diffraction
FLUID MECHANICS. Chapter 9 Flow over Immersed Bodies
 FLUID MECHANICS Chapter 9 Flow over Immersed Bodies CHAP 9. FLOW OVER IMMERSED BODIES CONTENTS 9.1 General External Flow Characteristics 9.3 Drag 9.4 Lift 9.1 General External Flow Characteristics 9.1.1
FLUID MECHANICS Chapter 9 Flow over Immersed Bodies CHAP 9. FLOW OVER IMMERSED BODIES CONTENTS 9.1 General External Flow Characteristics 9.3 Drag 9.4 Lift 9.1 General External Flow Characteristics 9.1.1
ÁÒØÖÓÙØÓÒ ÈÖÓÐÑ ØØÑÒØ ÓÚÖÒ¹ ÐØÖ Ò ËÑÙÐØÓÒ Ê ÙÐØ ÓÒÐÙ ÓÒ ÁÒÜ ½ ÁÒØÖÓÙØÓÒ ¾ ÈÖÓÐÑ ØØÑÒØ ÓÚÖÒ¹ ÐØÖ Ò ËÑÙÐØÓÒ Ê ÙÐØ ÓÒÐÙ ÓÒ
 ÁÒØÖÓÙØÓÒ ÈÖÓÐÑ ØØÑÒØ ÓÚÖÒ¹ ÐØÖ Ò ËÑÙÐØÓÒ Ê ÙÐØ ÓÒÐÙ ÓÒ ÙÑÔ ÐØÖ ÓÖ ÙÒÖØÒ ÝÒÑ Ý ØÑ ÛØ ÖÓÔÓÙØ º ÓÐÞ ½ º º ÉÙÚÓ ¾ Áº ÈÖÖÓ ½ ʺ ËÒ ½ ½ ÔÖØÑÒØ Ó ÁÒÙ ØÖÐ ËÝ ØÑ ÒÒÖÒ Ò Ò ÍÒÚÖ ØØ ÂÙÑ Á ØÐÐ ËÔÒ ¾ ËÓÓÐ Ó ÐØÖÐ ÒÒÖÒ
ÁÒØÖÓÙØÓÒ ÈÖÓÐÑ ØØÑÒØ ÓÚÖÒ¹ ÐØÖ Ò ËÑÙÐØÓÒ Ê ÙÐØ ÓÒÐÙ ÓÒ ÙÑÔ ÐØÖ ÓÖ ÙÒÖØÒ ÝÒÑ Ý ØÑ ÛØ ÖÓÔÓÙØ º ÓÐÞ ½ º º ÉÙÚÓ ¾ Áº ÈÖÖÓ ½ ʺ ËÒ ½ ½ ÔÖØÑÒØ Ó ÁÒÙ ØÖÐ ËÝ ØÑ ÒÒÖÒ Ò Ò ÍÒÚÖ ØØ ÂÙÑ Á ØÐÐ ËÔÒ ¾ ËÓÓÐ Ó ÐØÖÐ ÒÒÖÒ
p + µ 2 u =0= σ (1) and
 Master SdI mention M2FA, Fluid Mechanics program Hydrodynamics. P.-Y. Lagrée and S. Zaleski. Test December 4, 2009 All documentation is authorized except for reference [1]. Internet access is not allowed.
Master SdI mention M2FA, Fluid Mechanics program Hydrodynamics. P.-Y. Lagrée and S. Zaleski. Test December 4, 2009 All documentation is authorized except for reference [1]. Internet access is not allowed.
0.2. CONSERVATION LAW FOR FLUID 9
 0.2. CONSERVATION LAW FOR FLUID 9 Consider x-component of Eq. (26), we have D(ρu) + ρu( v) dv t = ρg x dv t S pi ds, (27) where ρg x is the x-component of the bodily force, and the surface integral is
0.2. CONSERVATION LAW FOR FLUID 9 Consider x-component of Eq. (26), we have D(ρu) + ρu( v) dv t = ρg x dv t S pi ds, (27) where ρg x is the x-component of the bodily force, and the surface integral is
Non-linear Scalar Equations
 Non-linear Scalar Equations Professor Dr. E F Toro Laboratory of Applied Mathematics University of Trento, Italy eleuterio.toro@unitn.it http://www.ing.unitn.it/toro August 24, 2014 1 / 44 Overview Here
Non-linear Scalar Equations Professor Dr. E F Toro Laboratory of Applied Mathematics University of Trento, Italy eleuterio.toro@unitn.it http://www.ing.unitn.it/toro August 24, 2014 1 / 44 Overview Here
Combustion Behind Shock Waves
 Paper 3F-29 Fall 23 Western States Section/Combustion Institute 1 Abstract Combustion Behind Shock Waves Sandeep Singh, Daniel Lieberman, and Joseph E. Shepherd 1 Graduate Aeronautical Laboratories, California
Paper 3F-29 Fall 23 Western States Section/Combustion Institute 1 Abstract Combustion Behind Shock Waves Sandeep Singh, Daniel Lieberman, and Joseph E. Shepherd 1 Graduate Aeronautical Laboratories, California
Initiation of stabilized detonations by projectiles
 Initiation of stabilized detonations by projectiles P. Hung and J. E. Shepherd, Graduate Aeronautical Laboratory, California Institute of Technology, Pasadena, CA 91125 USA Abstract. A high-speed projectile
Initiation of stabilized detonations by projectiles P. Hung and J. E. Shepherd, Graduate Aeronautical Laboratory, California Institute of Technology, Pasadena, CA 91125 USA Abstract. A high-speed projectile
ALGEBRAIC FLUX CORRECTION FOR FINITE ELEMENT DISCRETIZATIONS OF COUPLED SYSTEMS
 Int. Conf. on Computational Methods for Coupled Problems in Science and Engineering COUPLED PROBLEMS 2007 M. Papadrakakis, E. Oñate and B. Schrefler (Eds) c CIMNE, Barcelona, 2007 ALGEBRAIC FLUX CORRECTION
Int. Conf. on Computational Methods for Coupled Problems in Science and Engineering COUPLED PROBLEMS 2007 M. Papadrakakis, E. Oñate and B. Schrefler (Eds) c CIMNE, Barcelona, 2007 ALGEBRAIC FLUX CORRECTION
Problem 1 (From the reservoir to the grid)
 ÈÖÓ º ĺ ÙÞÞ ÐÐ ÈÖÓ º ʺ ³ Ò Ö ½ ½¹¼ ¼¹¼¼ ËÝ Ø Ñ ÅÓ Ð Ò ÀË ¾¼½ µ Ü Ö ÌÓÔ ÀÝ ÖÓ Ð ØÖ ÔÓÛ Ö ÔÐ ÒØ À Èȵ ¹ È ÖØ ÁÁ Ð ÖÒ Ø Þº ÇØÓ Ö ½ ¾¼½ Problem (From the reservoir to the grid) The causality diagram of the
ÈÖÓ º ĺ ÙÞÞ ÐÐ ÈÖÓ º ʺ ³ Ò Ö ½ ½¹¼ ¼¹¼¼ ËÝ Ø Ñ ÅÓ Ð Ò ÀË ¾¼½ µ Ü Ö ÌÓÔ ÀÝ ÖÓ Ð ØÖ ÔÓÛ Ö ÔÐ ÒØ À Èȵ ¹ È ÖØ ÁÁ Ð ÖÒ Ø Þº ÇØÓ Ö ½ ¾¼½ Problem (From the reservoir to the grid) The causality diagram of the
High Speed Aerodynamics. Copyright 2009 Narayanan Komerath
 Welcome to High Speed Aerodynamics 1 Lift, drag and pitching moment? Linearized Potential Flow Transformations Compressible Boundary Layer WHAT IS HIGH SPEED AERODYNAMICS? Airfoil section? Thin airfoil
Welcome to High Speed Aerodynamics 1 Lift, drag and pitching moment? Linearized Potential Flow Transformations Compressible Boundary Layer WHAT IS HIGH SPEED AERODYNAMICS? Airfoil section? Thin airfoil
1 One-dimensional analysis
 One-dimensional analysis. Introduction The simplest models for gas liquid flow systems are ones for which the velocity is uniform over a cross-section and unidirectional. This includes flows in a long
One-dimensional analysis. Introduction The simplest models for gas liquid flow systems are ones for which the velocity is uniform over a cross-section and unidirectional. This includes flows in a long
7. Basics of Turbulent Flow Figure 1.
 1 7. Basics of Turbulent Flow Whether a flow is laminar or turbulent depends of the relative importance of fluid friction (viscosity) and flow inertia. The ratio of inertial to viscous forces is the Reynolds
1 7. Basics of Turbulent Flow Whether a flow is laminar or turbulent depends of the relative importance of fluid friction (viscosity) and flow inertia. The ratio of inertial to viscous forces is the Reynolds
IX. COMPRESSIBLE FLOW. ρ = P
 IX. COMPRESSIBLE FLOW Compressible flow is the study of fluids flowing at speeds comparable to the local speed of sound. This occurs when fluid speeds are about 30% or more of the local acoustic velocity.
IX. COMPRESSIBLE FLOW Compressible flow is the study of fluids flowing at speeds comparable to the local speed of sound. This occurs when fluid speeds are about 30% or more of the local acoustic velocity.
A stationary circular hydraulic jump, the limits of its existence and its gasdynamic analogue
 J. Fluid Mech. (28), vol. 61, pp. 189 198. c 28 Cambridge University Press doi:1.117/s221128773 Printed in the United Kingdom 189 A stationary circular hydraulic jump, the limits of its existence and its
J. Fluid Mech. (28), vol. 61, pp. 189 198. c 28 Cambridge University Press doi:1.117/s221128773 Printed in the United Kingdom 189 A stationary circular hydraulic jump, the limits of its existence and its
The forced response of choked nozzles and supersonic diffusers
 J. Fluid Mech. (27), vol. 585, pp. 28 34. c 27 Cambridge University Press doi:.7/s22276647 Printed in the United Kingdom 28 The forced response of choked nozzles and supersonic diffusers WILLIAM H. MOASE,
J. Fluid Mech. (27), vol. 585, pp. 28 34. c 27 Cambridge University Press doi:.7/s22276647 Printed in the United Kingdom 28 The forced response of choked nozzles and supersonic diffusers WILLIAM H. MOASE,
INTEGRAL ANALYSIS OF LAMINAR INDIRECT FREE CONVECTION BOUNDARY LAYERS WITH WEAK BLOWING FOR SCHMIDT NO. 1
 INTEGRA ANAYSIS OF AMINAR INDIRECT FREE CONVECTION BOUNDARY AYERS WITH WEAK BOWING FOR SCHMIDT NO. Baburaj A.Puthenveettil and Jaywant H.Arakeri Department of Mechanical Engineering, Indian Institute of
INTEGRA ANAYSIS OF AMINAR INDIRECT FREE CONVECTION BOUNDARY AYERS WITH WEAK BOWING FOR SCHMIDT NO. Baburaj A.Puthenveettil and Jaywant H.Arakeri Department of Mechanical Engineering, Indian Institute of
CHAPTER 4 BOUNDARY LAYER FLOW APPLICATION TO EXTERNAL FLOW
 CHAPTER 4 BOUNDARY LAYER FLOW APPLICATION TO EXTERNAL FLOW 4.1 Introduction Boundary layer concept (Prandtl 1904): Eliminate selected terms in the governing equations Two key questions (1) What are the
CHAPTER 4 BOUNDARY LAYER FLOW APPLICATION TO EXTERNAL FLOW 4.1 Introduction Boundary layer concept (Prandtl 1904): Eliminate selected terms in the governing equations Two key questions (1) What are the
1. Introduction Some Basic Concepts
 1. Introduction Some Basic Concepts 1.What is a fluid? A substance that will go on deforming in the presence of a deforming force, however small 2. What Properties Do Fluids Have? Density ( ) Pressure
1. Introduction Some Basic Concepts 1.What is a fluid? A substance that will go on deforming in the presence of a deforming force, however small 2. What Properties Do Fluids Have? Density ( ) Pressure
Effects of Viscous Dissipation on Unsteady Free Convection in a Fluid past a Vertical Plate Immersed in a Porous Medium
 Transport in Porous Media (2006) 64: 1 14 Springer 2006 DOI 10.1007/s11242-005-1126-6 Effects of Viscous Dissipation on Unsteady Free Convection in a Fluid past a Vertical Plate Immersed in a Porous Medium
Transport in Porous Media (2006) 64: 1 14 Springer 2006 DOI 10.1007/s11242-005-1126-6 Effects of Viscous Dissipation on Unsteady Free Convection in a Fluid past a Vertical Plate Immersed in a Porous Medium
An Example file... log.txt
 # ' ' Start of fie & %$ " 1 - : 5? ;., B - ( * * B - ( * * F I / 0. )- +, * ( ) 8 8 7 /. 6 )- +, 5 5 3 2( 7 7 +, 6 6 9( 3 5( ) 7-0 +, => - +< ( ) )- +, 7 / +, 5 9 (. 6 )- 0 * D>. C )- +, (A :, C 0 )- +,
# ' ' Start of fie & %$ " 1 - : 5? ;., B - ( * * B - ( * * F I / 0. )- +, * ( ) 8 8 7 /. 6 )- +, 5 5 3 2( 7 7 +, 6 6 9( 3 5( ) 7-0 +, => - +< ( ) )- +, 7 / +, 5 9 (. 6 )- 0 * D>. C )- +, (A :, C 0 )- +,
Notes #6 MAE 533, Fluid Mechanics
 Notes #6 MAE 533, Fluid Mechanics S. H. Lam lam@princeton.edu http://www.princeton.edu/ lam October 1, 1998 1 Different Ways of Representing T The speed of sound, a, is formally defined as ( p/ ρ) s. It
Notes #6 MAE 533, Fluid Mechanics S. H. Lam lam@princeton.edu http://www.princeton.edu/ lam October 1, 1998 1 Different Ways of Representing T The speed of sound, a, is formally defined as ( p/ ρ) s. It
Steady Deflagration Structure in Two-Phase Granular Propellants
 12th ICDERS, Ann Arbor, Michigan July 23-28, 1989 Steady Deflagration Structure in Two-Phase Granular Propellants Joseph M. Powers 1, Mark E. Miller2, D. Scott Stewart3, and Herman Krier4 July 23-28, 1989
12th ICDERS, Ann Arbor, Michigan July 23-28, 1989 Steady Deflagration Structure in Two-Phase Granular Propellants Joseph M. Powers 1, Mark E. Miller2, D. Scott Stewart3, and Herman Krier4 July 23-28, 1989
Planning for Reactive Behaviors in Hide and Seek
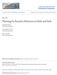 University of Pennsylvania ScholarlyCommons Center for Human Modeling and Simulation Department of Computer & Information Science May 1995 Planning for Reactive Behaviors in Hide and Seek Michael B. Moore
University of Pennsylvania ScholarlyCommons Center for Human Modeling and Simulation Department of Computer & Information Science May 1995 Planning for Reactive Behaviors in Hide and Seek Michael B. Moore
Waves in Uniform Flow on Half Plane
 May 1, 6 HB Ju Waves in Uniform Flow on Half Plane Hongbin Ju Department of Mathematics Florida State University, Tallahassee, FL.336 www.aeroacoustics.info Please send comments to: hju@math.fsu.edu The
May 1, 6 HB Ju Waves in Uniform Flow on Half Plane Hongbin Ju Department of Mathematics Florida State University, Tallahassee, FL.336 www.aeroacoustics.info Please send comments to: hju@math.fsu.edu The
AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS
 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS 1 / 31 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS Linearization and Characteristic Relations 1 / 31 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS
AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS 1 / 31 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS Linearization and Characteristic Relations 1 / 31 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS
Lecture 11: Regression Methods I (Linear Regression)
 Lecture 11: Regression Methods I (Linear Regression) Fall, 2017 1 / 40 Outline Linear Model Introduction 1 Regression: Supervised Learning with Continuous Responses 2 Linear Models and Multiple Linear
Lecture 11: Regression Methods I (Linear Regression) Fall, 2017 1 / 40 Outline Linear Model Introduction 1 Regression: Supervised Learning with Continuous Responses 2 Linear Models and Multiple Linear
INFLUENCE OF VARIABLE PERMEABILITY ON FREE CONVECTION OVER VERTICAL FLAT PLATE EMBEDDED IN A POROUS MEDIUM
 INFLUENCE OF VARIABLE PERMEABILITY ON FREE CONVECTION OVER VERTICAL FLAT PLATE EMBEDDED IN A POROUS MEDIUM S. M. M. EL-Kabeir and A. M. Rashad Department of Mathematics, South Valley University, Faculty
INFLUENCE OF VARIABLE PERMEABILITY ON FREE CONVECTION OVER VERTICAL FLAT PLATE EMBEDDED IN A POROUS MEDIUM S. M. M. EL-Kabeir and A. M. Rashad Department of Mathematics, South Valley University, Faculty
Turbulence is a ubiquitous phenomenon in environmental fluid mechanics that dramatically affects flow structure and mixing.
 Turbulence is a ubiquitous phenomenon in environmental fluid mechanics that dramatically affects flow structure and mixing. Thus, it is very important to form both a conceptual understanding and a quantitative
Turbulence is a ubiquitous phenomenon in environmental fluid mechanics that dramatically affects flow structure and mixing. Thus, it is very important to form both a conceptual understanding and a quantitative
Problem Set Number 01, MIT (Winter-Spring 2018)
 Problem Set Number 01, 18.306 MIT (Winter-Spring 2018) Rodolfo R. Rosales (MIT, Math. Dept., room 2-337, Cambridge, MA 02139) February 28, 2018 Due Monday March 12, 2018. Turn it in (by 3PM) at the Math.
Problem Set Number 01, 18.306 MIT (Winter-Spring 2018) Rodolfo R. Rosales (MIT, Math. Dept., room 2-337, Cambridge, MA 02139) February 28, 2018 Due Monday March 12, 2018. Turn it in (by 3PM) at the Math.
Numerical methods for the Navier- Stokes equations
 Numerical methods for the Navier- Stokes equations Hans Petter Langtangen 1,2 1 Center for Biomedical Computing, Simula Research Laboratory 2 Department of Informatics, University of Oslo Dec 6, 2012 Note:
Numerical methods for the Navier- Stokes equations Hans Petter Langtangen 1,2 1 Center for Biomedical Computing, Simula Research Laboratory 2 Department of Informatics, University of Oslo Dec 6, 2012 Note:
Travelling waves. Chapter 8. 1 Introduction
 Chapter 8 Travelling waves 1 Introduction One of the cornerstones in the study of both linear and nonlinear PDEs is the wave propagation. A wave is a recognizable signal which is transferred from one part
Chapter 8 Travelling waves 1 Introduction One of the cornerstones in the study of both linear and nonlinear PDEs is the wave propagation. A wave is a recognizable signal which is transferred from one part
Several forms of the equations of motion
 Chapter 6 Several forms of the equations of motion 6.1 The Navier-Stokes equations Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
Chapter 6 Several forms of the equations of motion 6.1 The Navier-Stokes equations Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
Thin airfoil theory. Chapter Compressible potential flow The full potential equation
 hapter 4 Thin airfoil theory 4. ompressible potential flow 4.. The full potential equation In compressible flow, both the lift and drag of a thin airfoil can be determined to a reasonable level of accuracy
hapter 4 Thin airfoil theory 4. ompressible potential flow 4.. The full potential equation In compressible flow, both the lift and drag of a thin airfoil can be determined to a reasonable level of accuracy
Compressible Duct Flow with Friction
 Compressible Duct Flow with Friction We treat only the effect of friction, neglecting area change and heat transfer. The basic assumptions are 1. Steady one-dimensional adiabatic flow 2. Perfect gas with
Compressible Duct Flow with Friction We treat only the effect of friction, neglecting area change and heat transfer. The basic assumptions are 1. Steady one-dimensional adiabatic flow 2. Perfect gas with
Lecture 11: Regression Methods I (Linear Regression)
 Lecture 11: Regression Methods I (Linear Regression) 1 / 43 Outline 1 Regression: Supervised Learning with Continuous Responses 2 Linear Models and Multiple Linear Regression Ordinary Least Squares Statistical
Lecture 11: Regression Methods I (Linear Regression) 1 / 43 Outline 1 Regression: Supervised Learning with Continuous Responses 2 Linear Models and Multiple Linear Regression Ordinary Least Squares Statistical
Dimensionless Numbers
 1 06.10.2017, 09:49 Dimensionless Numbers A. Salih Dept. of Aerospace Engineering IIST, Thiruvananthapuram The nondimensionalization of the governing equations of fluid flow is important for both theoretical
1 06.10.2017, 09:49 Dimensionless Numbers A. Salih Dept. of Aerospace Engineering IIST, Thiruvananthapuram The nondimensionalization of the governing equations of fluid flow is important for both theoretical
Turbulent drag reduction by streamwise traveling waves
 51st IEEE Conference on Decision and Control December 10-13, 2012. Maui, Hawaii, USA Turbulent drag reduction by streamwise traveling waves Armin Zare, Binh K. Lieu, and Mihailo R. Jovanović Abstract For
51st IEEE Conference on Decision and Control December 10-13, 2012. Maui, Hawaii, USA Turbulent drag reduction by streamwise traveling waves Armin Zare, Binh K. Lieu, and Mihailo R. Jovanović Abstract For
