Multivariable Calculus : Change of Variables in Multiple Integrals
|
|
|
- Debra Francine Jackson
- 6 years ago
- Views:
Transcription
1 Multivariable Calculus : Change of Variables in Multiple Integrals Monday, November 24 and Tuesday, November 25, 2008
2 Introduction Consider integrating some function, such as f( x, y) = 4x+ 8 y, over the parallelogram in the xyplane with vertices ( 1,3, ) ( 1, 3, ) ( 3, 1, ) and ( 1,5. ) This would require several separate integrals because of the shape of the domain. In this lesson, we explore a less complicated way to integrate over strangely-shaped regions.
3 Exercise 1 Find equations in terms of x and y for the lines that comprise the boundary of the region of integration.
4 Exercise 1 Find equations in terms of x and y for the lines that comprise the boundary of the region of integration. The line from ( 1,3) to (1, 3) is y= 3. x The line from (1, 3) to (3, 1) is y= x 4. The line from (3, 1) to (1,5) is y= 3x+ 8. The line from (1,5) to ( 1,3) is y= x+ 4. (A) (B) (C) (D)
5 Exercise 2 x= 1( u+ v) Use the substitutions 4 to find y = 1( v 3u) 4 equations in terms of u and v for the lines that comprise the boundary of the region of integration.
6 Exercise 2 x= 1( u+ v) Use the substitutions 4 to find y = 1( v 3u) 4 equations in terms of u and v for the lines that comprise the boundary of the region of integration. (A): v=0 (B): u=4 (C): v=8 (D): u= 4
7 The Jacobian Determinant (2D) For a transformation T 2 from ² to ²that takes (x,y) to (u,v) whose inverse is given by x= x( uv, ) and y= y( uv, ), we define the Jacobian determinant as ( xy, ) x u x v = ( uv, ) y u y v
8 The Jacobian Determinant (3D) For a transformation T 3 from ³ to ³that takes (x,y,z) to (u,v,w) whose inverse is given by x= x( uvw,, ), y= y( uvw,, ), and z= z( uvw,, ), the Jacobian is x u x v x w ( xyz,,) = y u y v y w ( uvw,, ) z u z v z w
9 With T 2 given by Exercise 3 1( ) x= 4 u+ v y= ( v 3u) 1 4, determinant for the transformation. find the Jacobian
10 With T 2 given by Exercise 3 1( ) x= 4 u+ v y= ( v 3u) 1 4, determinant for the transformation. find the Jacobian x u x v = y u y v = ( )( ) ( )( ) = = 14
11 Application To integrate a new function f( uv, ) given by making the substitutions from a transformation T 2 with a nonzero Jacobian into the original f( x, y), we evaluate ( ) ( xy, f uv, ) da ( uv, ) R uv over the new region found by transforming the boundaries of the xy-region of integration to that in the uv-plane.
12 Informal Justification This is a higher-dimensional analogue of the technique of integration by u-substitution. Consider substituting u= u( x) to evaluate an b integral f ( x ) dx : we find a fu ( ), rewrite the limits du using the transformation, and since du= dx dx, we du substitute for dx. We have effectively divided du dx by the size of the transformation : if we had u= 2 x, we would find du= 2 dx; since du is twice dx, we divide by two in the integral that involves fu ( ).
13 Informal Justification The size of a transformation of several variables is given by the Jacobian determinant, a concept which will be explored further in the semester of linear algebra.
14 Informal Justification For a simple example, consider the transformation u= 2x which doubles each coordinate, thus multiplying the area of the unit da by four. We thus v= 2y must divide by four to undo this. The transformation is equivalent to x= u 2, and the Jacobian is y= v So when we multiply by that, we divide by four to undo the area increase, as we would expect.
15 Exercise 4 1( ) Substitute x= 4 u+ v into the integrand 1( ) y= 4 v 3u f( x, y) = 4x+ 8y to find f( uv, ). Then evaluate the new integral, including the term of the Jacobian determinant, to find described originally. R xy f x, y da ( ) with R xy as
16 Exercise 4 Make the given substitution, then evaluate the new integral, including the term of the Jacobian determinant, to find described originally. f x, y da ( ) with R xy as The integrand becomes 5u+ 3 v, and we have already found the limits and the Jacobian. Therefore the integral is which evaluates to 192. R xy ( ) 5u+ 3v 1 4dvdu
17 Exercise 5 Use a substitution to evaluate xyda; R xy is the square with vertices (0,0), (1,1), (2,0), and (1, 1). R xy
18 Exercise 5 Use a substitution to evaluate xyda; R xy is the square with vertices (0,0), (1,1), (2,0), and (1, 1). Calling the vertices of the boundary A, B, C, and D, respectively, the lines that enclose the boundary are AB: y= x BC: y= 2 x CD: y= x 2 AD: y= x R xy
19 Exercise 5 Use a substitution to evaluate xyda; R xy is the square with vertices (0,0), (1,1), (2,0), and (1, 1). This suggests that we might wish to use the substitution u= y x 1 1, which gives x= 2u+ 2v. 1 1 v=+ y x y= 2u+ 2v The domain then becomes u [ 2,0 ] and v [ 0,2 ]. Substituting into R f( x, y) = xy gives f( uv, ) = u² + v². 4 xy
20 Exercise 5 Use a substitution to evaluate xyda; R xy is the square with vertices (0,0), (1,1), (2,0), and (1, 1). The Jacobian is ( xy, ) = = 1, so the ( uv, ) integral is evaluates to u² + v² 4 12 R xy dvdu which
21 Exercise 5 Use a substitution to evaluate xyda; R xy is the square with vertices (0,0), (1,1), (2,0), and (1, 1). We might have anticipated this because f( x, y) = xy is an odd function of y, and the region described is symmetric about the x-axis. R xy
22 Exercise 6 Use the transformation x= rcosθ to show that the y= rsinθ Jacobian determinant for the transformation from Cartesian to polar coordinates is r.
23 Exercise 6 Use the transformation x= rcosθ to show that the y= rsinθ Jacobian determinant for the transformation from Cartesian to polar coordinates is r. The Jacobian is ( xy, ) x r x θ = ( r, θ) y r y θ cosθ r sinθ = = r( cos² θ+ sin² θ) = r. sinθ r cosθ
24 Exercise 7 x= ρsinϕcosθ Use the transformation y = ρsinϕsinθ to show z = ρcosϕ that the Jacobian for the transformation from Cartesian to spherical coordinates is ρ²sin ϕ.
25 Exercise 7 Use the given transformation to show that the Jacobian for the transformation from Cartesian to spherical coordinates is ρ²sin ϕ. x ρ x θ x ϕ The Jacobian is ( xyz,,) = y ρ y θ y ϕ ( ρθϕ,, ) z ρ z θ z ϕ sinϕcosθ ρsinϕsinθ ρcosϕcosθ = sinϕsinθ ρsinϕcosθ ρcosϕsinθ cosϕ 0 ρsinϕ
26 Exercise 7 Use the given transformation to show that the Jacobian for the transformation from Cartesian to spherical coordinates is ρ²sin ϕ. which is easiest to evaluate by taking minors across the bottom row: cos ϕ( ρ²sinϕcosϕsin² θ ρ²sinϕcosϕcos² θ) ρsinϕ( ρsin² ϕcos² θ+ ρsin² ϕsin² θ) = ρ²sinϕcos² ϕ() 1 ρ²sin³ ϕ= ρ²sin ϕ, of which we take the absolute value to get ρ²sin ϕ.
27 Exercise 8 Use the transformation of the general ellipsoid x= au y = bv to find the volume z = cw x² + y² + z² = 1. a² b² c²
28 Exercise 8 Use the given transformation to find the volume of the general ellipsoid x² a² + y² b² + z² c² = 1. a 0 0 The Jacobian is ( xyz,,) = 0 b 0 = abc. The ( uvw,, ) 0 0 c ellipsoid s equation transforms to u² + v² + z² = 1, which is a sphere in uvw-space with radius 1 and volume 4π 3. We multiply that by the Jacobian to give the ellipsoid s volume V= 4 π abc. 3
29 Exercise 9 A transformation from the uv-plane to the xy-plane 3 2 is given by u= x+ y. v= x+ 4y (a) Find the Jacobian for this transformation.
30 Exercise 9 A transformation from the uv-plane to the xy-plane 3 2 is given by u= x+ y. v= x+ 4y (a) Find the Jacobian for this transformation. Since 2 1 x= 5u 5v, 1 3 y= 10u+ 10v the Jacobian is =1 10.
31 Exercise 9 With the previously given transformation, (b) Find the image of the triangular region in the first quadrant of the xy-plane bounded by the coordinate axes and the line x+= y 1.
32 Exercise 9 With the previously given transformation, (b) Find the image of the triangular region in the first quadrant of the xy-plane bounded by the coordinate axes and the line x+= y 1. The region is bounded by the lines v= u 3, v= 2 u, and and v= 10 3 u.
33 Exercise 9 With the previously given transformation, (c) evaluate R xy 3x + 14xy+ 8y da ( 2 2) where R xy is the region in the xy-plane bounded by the lines y= x+ 1, y= x+ 3, y= x, and y= x
34 Exercise 9 With the previously given transformation, (c) evaluate the given integral over the given region. The boundaries transform to, respectively, u=2, u= 6, v= 0, and v= 4, and making the substitutions into f x, y = 3 x² + 14xy+ 8 y² gives fuv (, ) = uv, so ( ) the integral is uv 1 dvdu=
35
Math 2433 Notes Week Triple Integrals. Integration over an arbitrary solid: Applications: 1. Volume of hypersolid = f ( x, y, z ) dxdydz
 Math 2433 Notes Week 11 15.6 Triple Integrals Integration over an arbitrary solid: Applications: 1. Volume of hypersolid = f ( x, y, z ) dxdydz S 2. Volume of S = dxdydz S Reduction to a repeated integral
Math 2433 Notes Week 11 15.6 Triple Integrals Integration over an arbitrary solid: Applications: 1. Volume of hypersolid = f ( x, y, z ) dxdydz S 2. Volume of S = dxdydz S Reduction to a repeated integral
Use partial integration with respect to y to compute the inner integral (treating x as a constant.)
 Math 54 ~ Multiple Integration 4. Iterated Integrals and Area in the Plane Iterated Integrals f ( x, y) dydx = f ( x, y) dy dx b g ( x) b g ( x) a g ( x) a g ( x) Use partial integration with respect to
Math 54 ~ Multiple Integration 4. Iterated Integrals and Area in the Plane Iterated Integrals f ( x, y) dydx = f ( x, y) dy dx b g ( x) b g ( x) a g ( x) a g ( x) Use partial integration with respect to
42. Change of Variables: The Jacobian
 . Change of Variables: The Jacobian It is common to change the variable(s) of integration, the main goal being to rewrite a complicated integrand into a simpler equivalent form. However, in doing so, the
. Change of Variables: The Jacobian It is common to change the variable(s) of integration, the main goal being to rewrite a complicated integrand into a simpler equivalent form. However, in doing so, the
Distance Formula in 3-D Given any two points P 1 (x 1, y 1, z 1 ) and P 2 (x 2, y 2, z 2 ) the distance between them is ( ) ( ) ( )
 Vectors and the Geometry of Space Vector Space The 3-D coordinate system (rectangular coordinates ) is the intersection of three perpendicular (orthogonal) lines called coordinate axis: x, y, and z. Their
Vectors and the Geometry of Space Vector Space The 3-D coordinate system (rectangular coordinates ) is the intersection of three perpendicular (orthogonal) lines called coordinate axis: x, y, and z. Their
4.4 Change of Variable in Integrals: The Jacobian
 4.4. CHANGE OF VAIABLE IN INTEGALS: THE JACOBIAN 4 4.4 Change of Variable in Integrals: The Jacobian In this section, we generalize to multiple integrals the substitution technique used with definite integrals.
4.4. CHANGE OF VAIABLE IN INTEGALS: THE JACOBIAN 4 4.4 Change of Variable in Integrals: The Jacobian In this section, we generalize to multiple integrals the substitution technique used with definite integrals.
Vector Calculus. Dr. D. Sukumar
 Vector Calculus Dr. D. Sukumar Space co-ordinates Change of variable Cartesian co-ordinates < x < Cartesian co-ordinates < x < < y < Cartesian co-ordinates < x < < y < < z < Cylindrical Cylindrical Cylindrical
Vector Calculus Dr. D. Sukumar Space co-ordinates Change of variable Cartesian co-ordinates < x < Cartesian co-ordinates < x < < y < Cartesian co-ordinates < x < < y < < z < Cylindrical Cylindrical Cylindrical
McGill University April Calculus 3. Tuesday April 29, 2014 Solutions
 McGill University April 4 Faculty of Science Final Examination Calculus 3 Math Tuesday April 9, 4 Solutions Problem (6 points) Let r(t) = (t, cos t, sin t). i. Find the velocity r (t) and the acceleration
McGill University April 4 Faculty of Science Final Examination Calculus 3 Math Tuesday April 9, 4 Solutions Problem (6 points) Let r(t) = (t, cos t, sin t). i. Find the velocity r (t) and the acceleration
Substitutions in Multiple Integrals
 Substitutions in Multiple Integrals P. Sam Johnson April 10, 2017 P. Sam Johnson (NIT Karnataka) Substitutions in Multiple Integrals April 10, 2017 1 / 23 Overview In the lecture, we discuss how to evaluate
Substitutions in Multiple Integrals P. Sam Johnson April 10, 2017 P. Sam Johnson (NIT Karnataka) Substitutions in Multiple Integrals April 10, 2017 1 / 23 Overview In the lecture, we discuss how to evaluate
Calculus III - Problem Solving Drill 18: Double Integrals in Polar Coordinates and Applications of Double Integrals
 Calculus III - Problem Solving Drill 8: Double Integrals in Polar Coordinates and Applications of Double Integrals Question No. of 0 Instructions: () ead the problem and answer choices carefully (2) Work
Calculus III - Problem Solving Drill 8: Double Integrals in Polar Coordinates and Applications of Double Integrals Question No. of 0 Instructions: () ead the problem and answer choices carefully (2) Work
(2,4,5).. ...
 12 Three Dimensions ½¾º½ Ì ÓÓÖ Ò Ø ËÝ Ø Ñ So far wehave been investigatingfunctions ofthe form y = f(x), withone independent and one dependent variable Such functions can be represented in two dimensions,
12 Three Dimensions ½¾º½ Ì ÓÓÖ Ò Ø ËÝ Ø Ñ So far wehave been investigatingfunctions ofthe form y = f(x), withone independent and one dependent variable Such functions can be represented in two dimensions,
MULTIVARIABLE INTEGRATION
 MULTIVARIABLE INTEGRATION (SPHERICAL POLAR COORDINATES) Question 1 a) Determine with the aid of a diagram an expression for the volume element in r, θ, ϕ. spherical polar coordinates, ( ) [You may not
MULTIVARIABLE INTEGRATION (SPHERICAL POLAR COORDINATES) Question 1 a) Determine with the aid of a diagram an expression for the volume element in r, θ, ϕ. spherical polar coordinates, ( ) [You may not
Chapter 5 Trigonometric Functions of Angles
 Chapter 5 Trigonometric Functions of Angles Section 3 Points on Circles Using Sine and Cosine Signs Signs I Signs (+, +) I Signs II (+, +) I Signs II (, +) (+, +) I Signs II (, +) (+, +) I III Signs II
Chapter 5 Trigonometric Functions of Angles Section 3 Points on Circles Using Sine and Cosine Signs Signs I Signs (+, +) I Signs II (+, +) I Signs II (, +) (+, +) I Signs II (, +) (+, +) I III Signs II
Multivariable Calculus Lecture #11 Notes
 Multivariable alculus Lecture #11 Notes In this lecture, we ll discuss changing coordinates more generally in multiple integrals. We ll also discuss the idea of integration along a curve and the application
Multivariable alculus Lecture #11 Notes In this lecture, we ll discuss changing coordinates more generally in multiple integrals. We ll also discuss the idea of integration along a curve and the application
Note: Each problem is worth 14 points except numbers 5 and 6 which are 15 points. = 3 2
 Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
COMPLETE Chapter 15 Multiple Integrals. Section 15.1 Double Integrals Over Rectangles. Section 15.2 Iterated Integrals
 Mat 7 Calculus III Updated on /3/7 Dr. Firoz COMPLT Chapter 5 Multiple Integrals Section 5. Double Integrals Over ectangles amples:. valuate the iterated integral a) (5 ) da, {(, ), } and b) (4 ) da, [,]
Mat 7 Calculus III Updated on /3/7 Dr. Firoz COMPLT Chapter 5 Multiple Integrals Section 5. Double Integrals Over ectangles amples:. valuate the iterated integral a) (5 ) da, {(, ), } and b) (4 ) da, [,]
Dimensions = xyz dv. xyz dv as an iterated integral in rectangular coordinates.
 Math Show Your Work! Page of 8. () A rectangular box is to hold 6 cubic meters. The material used for the top and bottom of the box is twice as expensive per square meter than the material used for the
Math Show Your Work! Page of 8. () A rectangular box is to hold 6 cubic meters. The material used for the top and bottom of the box is twice as expensive per square meter than the material used for the
Multiple Choice. Compute the Jacobian, (u, v), of the coordinate transformation x = u2 v 4, y = uv. (a) 2u 2 + 4v 4 (b) xu yv (c) 3u 2 + 7v 6
 .(5pts) y = uv. ompute the Jacobian, Multiple hoice (x, y) (u, v), of the coordinate transformation x = u v 4, (a) u + 4v 4 (b) xu yv (c) u + 7v 6 (d) u (e) u v uv 4 Solution. u v 4v u = u + 4v 4..(5pts)
.(5pts) y = uv. ompute the Jacobian, Multiple hoice (x, y) (u, v), of the coordinate transformation x = u v 4, (a) u + 4v 4 (b) xu yv (c) u + 7v 6 (d) u (e) u v uv 4 Solution. u v 4v u = u + 4v 4..(5pts)
Integrals in cylindrical, spherical coordinates (Sect. 15.7)
 Integrals in clindrical, spherical coordinates (Sect. 15.7 Integration in spherical coordinates. Review: Clindrical coordinates. Spherical coordinates in space. Triple integral in spherical coordinates.
Integrals in clindrical, spherical coordinates (Sect. 15.7 Integration in spherical coordinates. Review: Clindrical coordinates. Spherical coordinates in space. Triple integral in spherical coordinates.
Introduction to Vector Calculus
 Introduction to Vector Calculus Phillip Zenor Department of Mathematics Auburn University Edward E. Slaminka Department of Mathematics Auburn University Donald Thaxton Department of Physics Auburn University
Introduction to Vector Calculus Phillip Zenor Department of Mathematics Auburn University Edward E. Slaminka Department of Mathematics Auburn University Donald Thaxton Department of Physics Auburn University
51. General Surface Integrals
 51. General urface Integrals The area of a surface in defined parametrically by r(u, v) = x(u, v), y(u, v), z(u, v) over a region of integration in the input-variable plane is given by d = r u r v da.
51. General urface Integrals The area of a surface in defined parametrically by r(u, v) = x(u, v), y(u, v), z(u, v) over a region of integration in the input-variable plane is given by d = r u r v da.
MATH 12 CLASS 23 NOTES, NOV Contents 1. Change of variables: the Jacobian 1
 MATH 12 CLASS 23 NOTES, NOV 11 211 Contents 1. Change of variables: the Jacobian 1 1. Change of variables: the Jacobian So far, we have seen three examples of situations where we change variables to help
MATH 12 CLASS 23 NOTES, NOV 11 211 Contents 1. Change of variables: the Jacobian 1 1. Change of variables: the Jacobian So far, we have seen three examples of situations where we change variables to help
The Probability Lifesaver: Change of Variable Theorem. Steven J. Miller
 The Probability Lifesaver: Change of Variable Theorem Steven J. Miller January, 206 Contents Change of Variable Formula 3. Statement 3.2 Sketch of Proof 5.3 Special Cases 9 2 Greetings again! In this supplemental
The Probability Lifesaver: Change of Variable Theorem Steven J. Miller January, 206 Contents Change of Variable Formula 3. Statement 3.2 Sketch of Proof 5.3 Special Cases 9 2 Greetings again! In this supplemental
Section A brief on transformations
 Section 127 A brief on transformations consider the transformation another name for it: change of variable x = rcosθ The determinant y = rsinθ r y r is called the Jacobian determinant of x,y with respect
Section 127 A brief on transformations consider the transformation another name for it: change of variable x = rcosθ The determinant y = rsinθ r y r is called the Jacobian determinant of x,y with respect
Math 3435 Homework Set 11 Solutions 10 Points. x= 1,, is in the disk of radius 1 centered at origin
 Math 45 Homework et olutions Points. ( pts) The integral is, x + z y d = x + + z da 8 6 6 where is = x + z 8 x + z = 4 o, is the disk of radius centered on the origin. onverting to polar coordinates then
Math 45 Homework et olutions Points. ( pts) The integral is, x + z y d = x + + z da 8 6 6 where is = x + z 8 x + z = 4 o, is the disk of radius centered on the origin. onverting to polar coordinates then
18.02 Multivariable Calculus Fall 2007
 MIT OpenCourseWare http://ocw.mit.edu 18.02 Multivariable Calculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 3. Double Integrals 3A. Double
MIT OpenCourseWare http://ocw.mit.edu 18.02 Multivariable Calculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 3. Double Integrals 3A. Double
Notes on multivariable calculus
 Notes on multivariable calculus Jonathan Wise February 2, 2010 1 Review of trigonometry Trigonometry is essentially the study of the relationship between polar coordinates and Cartesian coordinates in
Notes on multivariable calculus Jonathan Wise February 2, 2010 1 Review of trigonometry Trigonometry is essentially the study of the relationship between polar coordinates and Cartesian coordinates in
SINGLE MATHEMATICS B : Vectors Summary Notes
 Preprint typeset in JHEP style - HYPER VERSION SINGLE MATHEMATICS B : Vectors Summary Notes Ruth Gregory Abstract: These notes sum up all you need to know about the mathematics of vectors at this stage.
Preprint typeset in JHEP style - HYPER VERSION SINGLE MATHEMATICS B : Vectors Summary Notes Ruth Gregory Abstract: These notes sum up all you need to know about the mathematics of vectors at this stage.
The Change-of-Variables Formula for Double Integrals
 The Change-of-Variables Formula for Double Integrals Minh-Tam Trinh In this document, I suggest ideas about how to solve some of the exercises in ection 15.9 of tewart, Multivariable Calculus, 8th Ed.
The Change-of-Variables Formula for Double Integrals Minh-Tam Trinh In this document, I suggest ideas about how to solve some of the exercises in ection 15.9 of tewart, Multivariable Calculus, 8th Ed.
11.1 Three-Dimensional Coordinate System
 11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
Math Vector Calculus II
 Math 255 - Vector Calculus II Review Notes Vectors We assume the reader is familiar with all the basic concepts regarding vectors and vector arithmetic, such as addition/subtraction of vectors in R n,
Math 255 - Vector Calculus II Review Notes Vectors We assume the reader is familiar with all the basic concepts regarding vectors and vector arithmetic, such as addition/subtraction of vectors in R n,
1 4 (1 cos(4θ))dθ = θ 4 sin(4θ)
 M48M Final Exam Solutions, December 9, 5 ) A polar curve Let C be the portion of the cloverleaf curve r = sin(θ) that lies in the first quadrant a) Draw a rough sketch of C This looks like one quarter
M48M Final Exam Solutions, December 9, 5 ) A polar curve Let C be the portion of the cloverleaf curve r = sin(θ) that lies in the first quadrant a) Draw a rough sketch of C This looks like one quarter
Practice Final Solutions
 Practice Final Solutions Math 1, Fall 17 Problem 1. Find a parameterization for the given curve, including bounds on the parameter t. Part a) The ellipse in R whose major axis has endpoints, ) and 6, )
Practice Final Solutions Math 1, Fall 17 Problem 1. Find a parameterization for the given curve, including bounds on the parameter t. Part a) The ellipse in R whose major axis has endpoints, ) and 6, )
Instructions: No books. No notes. Non-graphing calculators only. You are encouraged, although not required, to show your work.
 Exam 3 Math 850-007 Fall 04 Odenthal Name: Instructions: No books. No notes. Non-graphing calculators only. You are encouraged, although not required, to show your work.. Evaluate the iterated integral
Exam 3 Math 850-007 Fall 04 Odenthal Name: Instructions: No books. No notes. Non-graphing calculators only. You are encouraged, although not required, to show your work.. Evaluate the iterated integral
Archive of Calculus IV Questions Noel Brady Department of Mathematics University of Oklahoma
 Archive of Calculus IV Questions Noel Brady Department of Mathematics University of Oklahoma This is an archive of past Calculus IV exam questions. You should first attempt the questions without looking
Archive of Calculus IV Questions Noel Brady Department of Mathematics University of Oklahoma This is an archive of past Calculus IV exam questions. You should first attempt the questions without looking
Math 1272 Solutions for Fall 2005 Final Exam
 Math 7 Solutions for Fall 5 Final Exam ) This fraction appears in Problem 5 of the undated-? exam; a solution can be found in that solution set. (E) ) This integral appears in Problem 6 of the Fall 4 exam;
Math 7 Solutions for Fall 5 Final Exam ) This fraction appears in Problem 5 of the undated-? exam; a solution can be found in that solution set. (E) ) This integral appears in Problem 6 of the Fall 4 exam;
p. 1/ Section 1.4: Cylindrical and Spherical Coordinates
 p. 1/ Section 1.4: Cylindrical and Spherical Coordinates p. / Cylindrical Coordinate (r,θ,w) where θ is measured counterclockwise as viewed from the positive w-axis. p. / Cylindrical Coordinate (r,θ,w)
p. 1/ Section 1.4: Cylindrical and Spherical Coordinates p. / Cylindrical Coordinate (r,θ,w) where θ is measured counterclockwise as viewed from the positive w-axis. p. / Cylindrical Coordinate (r,θ,w)
Figure 25:Differentials of surface.
 2.5. Change of variables and Jacobians In the previous example we saw that, once we have identified the type of coordinates which is best to use for solving a particular problem, the next step is to do
2.5. Change of variables and Jacobians In the previous example we saw that, once we have identified the type of coordinates which is best to use for solving a particular problem, the next step is to do
Tribhuvan University Institute of Science and Technology 2065
 1CSc. MTH 104-2065 Tribhuvan University Institute of Science and Technology 2065 Bachelor Level/First Year/ First Semester/ Science Full Marks: 80 Computer Science and Information Technology (MTH. 104)
1CSc. MTH 104-2065 Tribhuvan University Institute of Science and Technology 2065 Bachelor Level/First Year/ First Semester/ Science Full Marks: 80 Computer Science and Information Technology (MTH. 104)
MAT 211 Final Exam. Fall Jennings.
 MAT 211 Final Exam. Fall 218. Jennings. Useful formulas polar coordinates spherical coordinates: SHOW YOUR WORK! x = rcos(θ) y = rsin(θ) da = r dr dθ x = ρcos(θ)cos(φ) y = ρsin(θ)cos(φ) z = ρsin(φ) dv
MAT 211 Final Exam. Fall 218. Jennings. Useful formulas polar coordinates spherical coordinates: SHOW YOUR WORK! x = rcos(θ) y = rsin(θ) da = r dr dθ x = ρcos(θ)cos(φ) y = ρsin(θ)cos(φ) z = ρsin(φ) dv
Solutions to Homework 11
 Solutions to Homework 11 Read the statement of Proposition 5.4 of Chapter 3, Section 5. Write a summary of the proof. Comment on the following details: Does the proof work if g is piecewise C 1? Or did
Solutions to Homework 11 Read the statement of Proposition 5.4 of Chapter 3, Section 5. Write a summary of the proof. Comment on the following details: Does the proof work if g is piecewise C 1? Or did
Answer sheet: Final exam for Math 2339, Dec 10, 2010
 Answer sheet: Final exam for Math 9, ec, Problem. Let the surface be z f(x,y) ln(y + cos(πxy) + e ). (a) Find the gradient vector of f f(x,y) y + cos(πxy) + e πy sin(πxy), y πx sin(πxy) (b) Evaluate f(,
Answer sheet: Final exam for Math 9, ec, Problem. Let the surface be z f(x,y) ln(y + cos(πxy) + e ). (a) Find the gradient vector of f f(x,y) y + cos(πxy) + e πy sin(πxy), y πx sin(πxy) (b) Evaluate f(,
Double Integrals. Advanced Calculus. Lecture 2 Dr. Lahcen Laayouni. Department of Mathematics and Statistics McGill University.
 Lecture Department of Mathematics and Statistics McGill University January 9, 7 Polar coordinates Change of variables formula Polar coordinates In polar coordinates, we have x = r cosθ, r = x + y y = r
Lecture Department of Mathematics and Statistics McGill University January 9, 7 Polar coordinates Change of variables formula Polar coordinates In polar coordinates, we have x = r cosθ, r = x + y y = r
Student name: Student ID: Math 265 (Butler) Midterm III, 10 November 2011
 Student name: Student ID: Math 265 (Butler) Midterm III, November 2 This test is closed book and closed notes. No calculator is allowed for this test. For full credit show all of your work (legibly!).
Student name: Student ID: Math 265 (Butler) Midterm III, November 2 This test is closed book and closed notes. No calculator is allowed for this test. For full credit show all of your work (legibly!).
Math 340 Final Exam December 16, 2006
 Math 34 Final Exam December 6, 6. () Suppose A 3 4. a) Find the row-reduced echelon form of A. 3 4 so the row reduced echelon form is b) What is rank(a)? 3 4 4 The rank is two since there are two pivots.
Math 34 Final Exam December 6, 6. () Suppose A 3 4. a) Find the row-reduced echelon form of A. 3 4 so the row reduced echelon form is b) What is rank(a)? 3 4 4 The rank is two since there are two pivots.
Vector Calculus Æ Z 4 { 9
 Vector Calculus 2008ôÆ 9 4ß ii 1 Much of the material presented here and some figures are copied from Vector Calculus of J. Marsden and A. Tromba for teaching purpose only. Please do not distribute This
Vector Calculus 2008ôÆ 9 4ß ii 1 Much of the material presented here and some figures are copied from Vector Calculus of J. Marsden and A. Tromba for teaching purpose only. Please do not distribute This
MULTIVARIABLE INTEGRATION
 MULTIVARIABLE INTEGRATION (PLANE & CYLINDRICAL POLAR COORDINATES) PLANE POLAR COORDINATES Question 1 The finite region on the x-y plane satisfies 1 x + y 4, y 0. Find, in terms of π, the value of I. I
MULTIVARIABLE INTEGRATION (PLANE & CYLINDRICAL POLAR COORDINATES) PLANE POLAR COORDINATES Question 1 The finite region on the x-y plane satisfies 1 x + y 4, y 0. Find, in terms of π, the value of I. I
Vectors in the Plane
 Vectors in the Plane MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Vectors vs. Scalars scalar quantity having only a magnitude (e.g. temperature, volume, length, area) and
Vectors in the Plane MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Vectors vs. Scalars scalar quantity having only a magnitude (e.g. temperature, volume, length, area) and
MATH 52 FINAL EXAM SOLUTIONS
 MAH 5 FINAL EXAM OLUION. (a) ketch the region R of integration in the following double integral. x xe y5 dy dx R = {(x, y) x, x y }. (b) Express the region R as an x-simple region. R = {(x, y) y, x y }
MAH 5 FINAL EXAM OLUION. (a) ketch the region R of integration in the following double integral. x xe y5 dy dx R = {(x, y) x, x y }. (b) Express the region R as an x-simple region. R = {(x, y) y, x y }
Contents. MATH 32B-2 (18W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables. 1 Multiple Integrals 3. 2 Vector Fields 9
 MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
Math Exam IV - Fall 2011
 Math 233 - Exam IV - Fall 2011 December 15, 2011 - Renato Feres NAME: STUDENT ID NUMBER: General instructions: This exam has 16 questions, each worth the same amount. Check that no pages are missing and
Math 233 - Exam IV - Fall 2011 December 15, 2011 - Renato Feres NAME: STUDENT ID NUMBER: General instructions: This exam has 16 questions, each worth the same amount. Check that no pages are missing and
Complex Numbers Class Work. Complex Numbers Homework. Pre-Calc Polar & Complex #s ~1~ NJCTL.org. Simplify using i b 4 3.
 Complex Numbers Class Work Simplify using i. 1. 16 2. 36b 4 3. 8a 2 4. 32x 6 y 7 5. 16 25 6. 8 10 7. 3i 4i 5i 8. 2i 4i 6i 8i 9. i 9 10. i 22 11. i 75 Complex Numbers Homework Simplify using i. 12. 81 13.
Complex Numbers Class Work Simplify using i. 1. 16 2. 36b 4 3. 8a 2 4. 32x 6 y 7 5. 16 25 6. 8 10 7. 3i 4i 5i 8. 2i 4i 6i 8i 9. i 9 10. i 22 11. i 75 Complex Numbers Homework Simplify using i. 12. 81 13.
Solution. This is a routine application of the chain rule.
 EXAM 2 SOLUTIONS 1. If z = e r cos θ, r = st, θ = s 2 + t 2, find the partial derivatives dz ds chain rule. Write your answers entirely in terms of s and t. dz and dt using the Solution. This is a routine
EXAM 2 SOLUTIONS 1. If z = e r cos θ, r = st, θ = s 2 + t 2, find the partial derivatives dz ds chain rule. Write your answers entirely in terms of s and t. dz and dt using the Solution. This is a routine
7a3 2. (c) πa 3 (d) πa 3 (e) πa3
 1.(6pts) Find the integral x, y, z d S where H is the part of the upper hemisphere of H x 2 + y 2 + z 2 = a 2 above the plane z = a and the normal points up. ( 2 π ) Useful Facts: cos = 1 and ds = ±a sin
1.(6pts) Find the integral x, y, z d S where H is the part of the upper hemisphere of H x 2 + y 2 + z 2 = a 2 above the plane z = a and the normal points up. ( 2 π ) Useful Facts: cos = 1 and ds = ±a sin
Without fully opening the exam, check that you have pages 1 through 12.
 MTH 34 Solutions to Exam November 9, 8 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through.
MTH 34 Solutions to Exam November 9, 8 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through.
f(p i )Area(T i ) F ( r(u, w) ) (r u r w ) da
 MAH 55 Flux integrals Fall 16 1. Review 1.1. Surface integrals. Let be a surface in R. Let f : R be a function defined on. efine f ds = f(p i Area( i lim mesh(p as a limit of Riemann sums over sampled-partitions.
MAH 55 Flux integrals Fall 16 1. Review 1.1. Surface integrals. Let be a surface in R. Let f : R be a function defined on. efine f ds = f(p i Area( i lim mesh(p as a limit of Riemann sums over sampled-partitions.
If the pull is downward (Fig. 1), we want C to point into the page. If the pull is upward (Fig. 2), we want C to point out of the page.
 11.5 Cross Product Contemporary Calculus 1 11.5 CROSS PRODUCT This section is the final one about the arithmetic of vectors, and it introduces a second type of vector vector multiplication called the cross
11.5 Cross Product Contemporary Calculus 1 11.5 CROSS PRODUCT This section is the final one about the arithmetic of vectors, and it introduces a second type of vector vector multiplication called the cross
Name: SOLUTIONS Date: 11/9/2017. M20550 Calculus III Tutorial Worksheet 8
 Name: SOLUTIONS Date: /9/7 M55 alculus III Tutorial Worksheet 8. ompute R da where R is the region bounded by x + xy + y 8 using the change of variables given by x u + v and y v. Solution: We know R is
Name: SOLUTIONS Date: /9/7 M55 alculus III Tutorial Worksheet 8. ompute R da where R is the region bounded by x + xy + y 8 using the change of variables given by x u + v and y v. Solution: We know R is
MATH 200 WEEK 10 - WEDNESDAY THE JACOBIAN & CHANGE OF VARIABLES
 WEEK - WEDNESDAY THE JACOBIAN & CHANGE OF VARIABLES GOALS Be able to convert integrals in rectangular coordinates to integrals in alternate coordinate systems DEFINITION Transformation: A transformation,
WEEK - WEDNESDAY THE JACOBIAN & CHANGE OF VARIABLES GOALS Be able to convert integrals in rectangular coordinates to integrals in alternate coordinate systems DEFINITION Transformation: A transformation,
1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is
 1. The value of the double integral (a) 15 26 (b) 15 8 (c) 75 (d) 105 26 5 4 0 1 1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is 2. What is the value of the double integral interchange the order
1. The value of the double integral (a) 15 26 (b) 15 8 (c) 75 (d) 105 26 5 4 0 1 1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is 2. What is the value of the double integral interchange the order
1 Integration in many variables.
 MA2 athaye Notes on Integration. Integration in many variables.. Basic efinition. The integration in one variable was developed along these lines:. I f(x) dx, where I is any interval on the real line was
MA2 athaye Notes on Integration. Integration in many variables.. Basic efinition. The integration in one variable was developed along these lines:. I f(x) dx, where I is any interval on the real line was
Figure 21:The polar and Cartesian coordinate systems.
 Figure 21:The polar and Cartesian coordinate systems. Coordinate systems in R There are three standard coordinate systems which are used to describe points in -dimensional space. These coordinate systems
Figure 21:The polar and Cartesian coordinate systems. Coordinate systems in R There are three standard coordinate systems which are used to describe points in -dimensional space. These coordinate systems
MATHS 267 Answers to Stokes Practice Dr. Jones
 MATH 267 Answers to tokes Practice Dr. Jones 1. Calculate the flux F d where is the hemisphere x2 + y 2 + z 2 1, z > and F (xz + e y2, yz, z 2 + 1). Note: the surface is open (doesn t include any of the
MATH 267 Answers to tokes Practice Dr. Jones 1. Calculate the flux F d where is the hemisphere x2 + y 2 + z 2 1, z > and F (xz + e y2, yz, z 2 + 1). Note: the surface is open (doesn t include any of the
QMUL, School of Physics and Astronomy Date: 18/01/2019
 QMUL, School of Physics and stronomy Date: 8//9 PHY Mathematical Techniques Solutions for Exercise Class Script : Coordinate Systems and Double Integrals. Calculate the integral: where the region is defined
QMUL, School of Physics and stronomy Date: 8//9 PHY Mathematical Techniques Solutions for Exercise Class Script : Coordinate Systems and Double Integrals. Calculate the integral: where the region is defined
Solutions for the Practice Final - Math 23B, 2016
 olutions for the Practice Final - Math B, 6 a. True. The area of a surface is given by the expression d, and since we have a parametrization φ x, y x, y, f x, y with φ, this expands as d T x T y da xy
olutions for the Practice Final - Math B, 6 a. True. The area of a surface is given by the expression d, and since we have a parametrization φ x, y x, y, f x, y with φ, this expands as d T x T y da xy
Solution Midterm 2, Math 53, Summer (a) (10 points) Let f(x, y, z) be a differentiable function of three variables and define
 Solution Midterm, Math 5, Summer. (a) ( points) Let f(,, z) be a differentiable function of three variables and define F (s, t) = f(st, s + t, s t). Calculate the partial derivatives F s and F t in terms
Solution Midterm, Math 5, Summer. (a) ( points) Let f(,, z) be a differentiable function of three variables and define F (s, t) = f(st, s + t, s t). Calculate the partial derivatives F s and F t in terms
SOLUTIONS TO THE FINAL EXAM. December 14, 2010, 9:00am-12:00 (3 hours)
 SOLUTIONS TO THE 18.02 FINAL EXAM BJORN POONEN December 14, 2010, 9:00am-12:00 (3 hours) 1) For each of (a)-(e) below: If the statement is true, write TRUE. If the statement is false, write FALSE. (Please
SOLUTIONS TO THE 18.02 FINAL EXAM BJORN POONEN December 14, 2010, 9:00am-12:00 (3 hours) 1) For each of (a)-(e) below: If the statement is true, write TRUE. If the statement is false, write FALSE. (Please
5. Triple Integrals. 5A. Triple integrals in rectangular and cylindrical coordinates. 2 + y + z x=0. y Outer: 1
 5. Triple Integrals 5A. Triple integrals in rectangular and clindrical coordinates ] 5A- a) (x + + )dxdd Inner: x + x( + ) + + x ] ] Middle: + + + ( ) + Outer: + 6 x ] x b) x ddxd Inner: x x 3 4 ] ] +
5. Triple Integrals 5A. Triple integrals in rectangular and clindrical coordinates ] 5A- a) (x + + )dxdd Inner: x + x( + ) + + x ] ] Middle: + + + ( ) + Outer: + 6 x ] x b) x ddxd Inner: x x 3 4 ] ] +
FOCUS ON THEORY. We now consider a general change of variable, where x; y coordinates are related to s; t coordinates by the differentiable functions
 FOCUS ON HEOY 753 CHANGE OF VAIABLES IN A MULIPLE INEGAL In the previous sections, we used polar, clindrical, and spherical coordinates to simplif iterated integrals. In this section, we discuss more general
FOCUS ON HEOY 753 CHANGE OF VAIABLES IN A MULIPLE INEGAL In the previous sections, we used polar, clindrical, and spherical coordinates to simplif iterated integrals. In this section, we discuss more general
Brief Review of Vector Algebra
 APPENDIX Brief Review of Vector Algebra A.0 Introduction Vector algebra is used extensively in computational mechanics. The student must thus understand the concepts associated with this subject. The current
APPENDIX Brief Review of Vector Algebra A.0 Introduction Vector algebra is used extensively in computational mechanics. The student must thus understand the concepts associated with this subject. The current
1 Matrices and matrix algebra
 1 Matrices and matrix algebra 1.1 Examples of matrices A matrix is a rectangular array of numbers and/or variables. For instance 4 2 0 3 1 A = 5 1.2 0.7 x 3 π 3 4 6 27 is a matrix with 3 rows and 5 columns
1 Matrices and matrix algebra 1.1 Examples of matrices A matrix is a rectangular array of numbers and/or variables. For instance 4 2 0 3 1 A = 5 1.2 0.7 x 3 π 3 4 6 27 is a matrix with 3 rows and 5 columns
Volume in n Dimensions
 Volume in n Dimensions MA 305 Kurt Bryan Introduction You ve seen that if we have two vectors v and w in two dimensions then the area spanned by these vectors can be computed as v w = v 1 w 2 v 2 w 1 (where
Volume in n Dimensions MA 305 Kurt Bryan Introduction You ve seen that if we have two vectors v and w in two dimensions then the area spanned by these vectors can be computed as v w = v 1 w 2 v 2 w 1 (where
The choice of origin, axes, and length is completely arbitrary.
 Polar Coordinates There are many ways to mark points in the plane or in 3-dim space for purposes of navigation. In the familiar rectangular coordinate system, a point is chosen as the origin and a perpendicular
Polar Coordinates There are many ways to mark points in the plane or in 3-dim space for purposes of navigation. In the familiar rectangular coordinate system, a point is chosen as the origin and a perpendicular
Math 261 Solutions To Sample Exam 2 Problems
 Solutions to Sample Eam Problems Math 6 Math 6 Solutions To Sample Eam Problems. Given to the right is the graph of a portion of four curves:,, and + 4. Note that these curves divide the plane into separate
Solutions to Sample Eam Problems Math 6 Math 6 Solutions To Sample Eam Problems. Given to the right is the graph of a portion of four curves:,, and + 4. Note that these curves divide the plane into separate
Rotation of Axes. By: OpenStaxCollege
 Rotation of Axes By: OpenStaxCollege As we have seen, conic sections are formed when a plane intersects two right circular cones aligned tip to tip and extending infinitely far in opposite directions,
Rotation of Axes By: OpenStaxCollege As we have seen, conic sections are formed when a plane intersects two right circular cones aligned tip to tip and extending infinitely far in opposite directions,
MATH2321, Calculus III for Science and Engineering, Fall Name (Printed) Print your name, the date, and then sign the exam on the line
 MATH2321, Calculus III for Science and Engineering, Fall 218 1 Exam 2 Name (Printed) Date Signature Instructions STOP. above. Print your name, the date, and then sign the exam on the line This exam consists
MATH2321, Calculus III for Science and Engineering, Fall 218 1 Exam 2 Name (Printed) Date Signature Instructions STOP. above. Print your name, the date, and then sign the exam on the line This exam consists
Practice problems **********************************************************
 Practice problems I will not test spherical and cylindrical coordinates explicitly but these two coordinates can be used in the problems when you evaluate triple integrals. 1. Set up the integral without
Practice problems I will not test spherical and cylindrical coordinates explicitly but these two coordinates can be used in the problems when you evaluate triple integrals. 1. Set up the integral without
Solutions to Sample Questions for Final Exam
 olutions to ample Questions for Final Exam Find the points on the surface xy z 3 that are closest to the origin. We use the method of Lagrange Multipliers, with f(x, y, z) x + y + z for the square of the
olutions to ample Questions for Final Exam Find the points on the surface xy z 3 that are closest to the origin. We use the method of Lagrange Multipliers, with f(x, y, z) x + y + z for the square of the
CURRENT MATERIAL: Vector Calculus.
 Math 275, section 002 (Ultman) Fall 2011 FINAL EXAM REVIEW The final exam will be held on Wednesday 14 December from 10:30am 12:30pm in our regular classroom. You will be allowed both sides of an 8.5 11
Math 275, section 002 (Ultman) Fall 2011 FINAL EXAM REVIEW The final exam will be held on Wednesday 14 December from 10:30am 12:30pm in our regular classroom. You will be allowed both sides of an 8.5 11
Solutions to the Final Exam, Math 53, Summer 2012
 olutions to the Final Exam, Math 5, ummer. (a) ( points) Let be the boundary of the region enclosedby the parabola y = x and the line y = with counterclockwise orientation. alculate (y + e x )dx + xdy.
olutions to the Final Exam, Math 5, ummer. (a) ( points) Let be the boundary of the region enclosedby the parabola y = x and the line y = with counterclockwise orientation. alculate (y + e x )dx + xdy.
A Quantum Mechanical Model for the Vibration and Rotation of Molecules. Rigid Rotor
 A Quantum Mechanical Model for the Vibration and Rotation of Molecules Harmonic Oscillator Rigid Rotor Degrees of Freedom Translation: quantum mechanical model is particle in box or free particle. A molecule
A Quantum Mechanical Model for the Vibration and Rotation of Molecules Harmonic Oscillator Rigid Rotor Degrees of Freedom Translation: quantum mechanical model is particle in box or free particle. A molecule
(1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3
 Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
1. (16 points) Write but do not evaluate the following integrals:
 MATH xam # Solutions. (6 points) Write but do not evaluate the following integrals: (a) (6 points) A clindrical integral to calculate the volume of the solid which lies in the first octant (where x,, and
MATH xam # Solutions. (6 points) Write but do not evaluate the following integrals: (a) (6 points) A clindrical integral to calculate the volume of the solid which lies in the first octant (where x,, and
Change of Variables In Multiple Integrals
 Change of Variables In Multiple Integrals When we convert a double integral from rectangular to polar coordinates, recall the changes that must be made to, and da. = (, r θ = rcosθ θ = (, r θ = rsinθ da
Change of Variables In Multiple Integrals When we convert a double integral from rectangular to polar coordinates, recall the changes that must be made to, and da. = (, r θ = rcosθ θ = (, r θ = rsinθ da
1 Differential Operators in Curvilinear Coordinates
 1 Differential Operators in Curvilinear Coordinates worked out and written by Timo Fleig February/March 2012 Revision 1, Feb. 15, 201 Revision 2, Sep. 1, 2015 Université Paul Sabatier using LaTeX and git
1 Differential Operators in Curvilinear Coordinates worked out and written by Timo Fleig February/March 2012 Revision 1, Feb. 15, 201 Revision 2, Sep. 1, 2015 Université Paul Sabatier using LaTeX and git
1. (a) (5 points) Find the unit tangent and unit normal vectors T and N to the curve. r (t) = 3 cos t, 0, 3 sin t, r ( 3π
 1. a) 5 points) Find the unit tangent and unit normal vectors T and N to the curve at the point P 3, 3π, r t) 3 cos t, 4t, 3 sin t 3 ). b) 5 points) Find curvature of the curve at the point P. olution:
1. a) 5 points) Find the unit tangent and unit normal vectors T and N to the curve at the point P 3, 3π, r t) 3 cos t, 4t, 3 sin t 3 ). b) 5 points) Find curvature of the curve at the point P. olution:
Fundamentals of Applied Electromagnetics. Chapter 2 - Vector Analysis
 Fundamentals of pplied Electromagnetics Chapter - Vector nalsis Chapter Objectives Operations of vector algebra Dot product of two vectors Differential functions in vector calculus Divergence of a vector
Fundamentals of pplied Electromagnetics Chapter - Vector nalsis Chapter Objectives Operations of vector algebra Dot product of two vectors Differential functions in vector calculus Divergence of a vector
ENGI Multiple Integration Page 8-01
 ENGI 345 8. Multiple Integration Page 8-01 8. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple integration include
ENGI 345 8. Multiple Integration Page 8-01 8. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple integration include
Mathematical Structures for Computer Graphics Steven J. Janke John Wiley & Sons, 2015 ISBN: Exercise Answers
 Mathematical Structures for Computer Graphics Steven J. Janke John Wiley & Sons, 2015 ISBN: 978-1-118-71219-1 Updated /17/15 Exercise Answers Chapter 1 1. Four right-handed systems: ( i, j, k), ( i, j,
Mathematical Structures for Computer Graphics Steven J. Janke John Wiley & Sons, 2015 ISBN: 978-1-118-71219-1 Updated /17/15 Exercise Answers Chapter 1 1. Four right-handed systems: ( i, j, k), ( i, j,
Jim Lambers MAT 280 Fall Semester Practice Final Exam Solution
 Jim Lambers MAT 8 Fall emester 6-7 Practice Final Exam olution. Use Lagrange multipliers to find the point on the circle x + 4 closest to the point (, 5). olution We have f(x, ) (x ) + ( 5), the square
Jim Lambers MAT 8 Fall emester 6-7 Practice Final Exam olution. Use Lagrange multipliers to find the point on the circle x + 4 closest to the point (, 5). olution We have f(x, ) (x ) + ( 5), the square
Arnie Pizer Rochester Problem Library Fall 2005 WeBWorK assignment VMultIntegrals1Double due 04/03/2008 at 02:00am EST.
 WeBWorK assignment VMultIntegralsouble due 04/03/2008 at 02:00am ST.. ( pt) rochesterlibrary/setvmultintegralsouble/ur vc 8.pg Consider the solid that lies above the square = [0,2] [0,2] and below the
WeBWorK assignment VMultIntegralsouble due 04/03/2008 at 02:00am ST.. ( pt) rochesterlibrary/setvmultintegralsouble/ur vc 8.pg Consider the solid that lies above the square = [0,2] [0,2] and below the
Solutions to old Exam 3 problems
 Solutions to old Exam 3 problems Hi students! I am putting this version of my review for the Final exam review here on the web site, place and time to be announced. Enjoy!! Best, Bill Meeks PS. There are
Solutions to old Exam 3 problems Hi students! I am putting this version of my review for the Final exam review here on the web site, place and time to be announced. Enjoy!! Best, Bill Meeks PS. There are
Math 53 Homework 7 Solutions
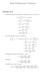 Math 5 Homework 7 Solutions Section 5.. To find the mass of the lamina, we integrate ρ(x, y over the box: m a b a a + x + y dy y + x y + y yb y b + bx + b bx + bx + b x ab + a b + ab a b + ab + ab. We
Math 5 Homework 7 Solutions Section 5.. To find the mass of the lamina, we integrate ρ(x, y over the box: m a b a a + x + y dy y + x y + y yb y b + bx + b bx + bx + b x ab + a b + ab a b + ab + ab. We
EXERCISES ON DETERMINANTS, EIGENVALUES AND EIGENVECTORS. 1. Determinants
 EXERCISES ON DETERMINANTS, EIGENVALUES AND EIGENVECTORS. Determinants Ex... Let A = 0 4 4 2 0 and B = 0 3 0. (a) Compute 0 0 0 0 A. (b) Compute det(2a 2 B), det(4a + B), det(2(a 3 B 2 )). 0 t Ex..2. For
EXERCISES ON DETERMINANTS, EIGENVALUES AND EIGENVECTORS. Determinants Ex... Let A = 0 4 4 2 0 and B = 0 3 0. (a) Compute 0 0 0 0 A. (b) Compute det(2a 2 B), det(4a + B), det(2(a 3 B 2 )). 0 t Ex..2. For
Introduction and Vectors Lecture 1
 1 Introduction Introduction and Vectors Lecture 1 This is a course on classical Electromagnetism. It is the foundation for more advanced courses in modern physics. All physics of the modern era, from quantum
1 Introduction Introduction and Vectors Lecture 1 This is a course on classical Electromagnetism. It is the foundation for more advanced courses in modern physics. All physics of the modern era, from quantum
36. Double Integration over Non-Rectangular Regions of Type II
 36. Double Integration over Non-Rectangular Regions of Type II When establishing the bounds of a double integral, visualize an arrow initially in the positive x direction or the positive y direction. A
36. Double Integration over Non-Rectangular Regions of Type II When establishing the bounds of a double integral, visualize an arrow initially in the positive x direction or the positive y direction. A
Solutions to the Calculus and Linear Algebra problems on the Comprehensive Examination of January 28, 2011
 Solutions to the Calculus and Linear Algebra problems on the Comprehensive Examination of January 8, Solutions to Problems 5 are omitted since they involve topics no longer covered on the Comprehensive
Solutions to the Calculus and Linear Algebra problems on the Comprehensive Examination of January 8, Solutions to Problems 5 are omitted since they involve topics no longer covered on the Comprehensive
Peter Alfeld Math , Fall 2005
 WeBWorK assignment due 9/2/05 at :59 PM..( pt) Consider the parametric equation x = 2(cosθ + θsinθ) y = 2(sinθ θcosθ) What is the length of the curve for θ = 0 to θ = 7 6 π? 2.( pt) Let a = (-2 4 2) and
WeBWorK assignment due 9/2/05 at :59 PM..( pt) Consider the parametric equation x = 2(cosθ + θsinθ) y = 2(sinθ θcosθ) What is the length of the curve for θ = 0 to θ = 7 6 π? 2.( pt) Let a = (-2 4 2) and
a (x,y,z) dvs. a (u,v,w)
 1. Overview In Unit 3 we discussed the role of the Jacobian determinant in evaluating double integrals involving a change of variables. technique generalizes very nicely to triple integrals. In fact, except
1. Overview In Unit 3 we discussed the role of the Jacobian determinant in evaluating double integrals involving a change of variables. technique generalizes very nicely to triple integrals. In fact, except
********************************************************** 1. Evaluate the double or iterated integrals:
 Practice problems 1. (a). Let f = 3x 2 + 4y 2 + z 2 and g = 2x + 3y + z = 1. Use Lagrange multiplier to find the extrema of f on g = 1. Is this a max or a min? No max, but there is min. Hence, among the
Practice problems 1. (a). Let f = 3x 2 + 4y 2 + z 2 and g = 2x + 3y + z = 1. Use Lagrange multiplier to find the extrema of f on g = 1. Is this a max or a min? No max, but there is min. Hence, among the
Matrices and Vectors
 Matrices and Vectors James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 11, 2013 Outline 1 Matrices and Vectors 2 Vector Details 3 Matrix
Matrices and Vectors James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 11, 2013 Outline 1 Matrices and Vectors 2 Vector Details 3 Matrix
