SAMPLE. Rates of Change
|
|
|
- Arnold Singleton
- 6 years ago
- Views:
Transcription
1 Objectives C H A P T E R 18 Rates of Change To recognise relationships between variables. To calculate average rates of change. To estimate gradients of curves. To estimate instantaneous rates of change. To estimate and calculate rates of change of algebraic functions. To appl the estimation and calculation of rates of change to solving problems. When the relationship between two variables has been considered in chapters 2 6 and chapters 15 and 16, the idea that one variable, for eample, is a function of another variable, such as, has been used and developed. The variable is often considered to be the independent variable and the dependent variable. The value of depends on the value of and is found b appling the rule connecting the two variables for the given value of. So, the rule that connects and enables the value of to be determined for a given value of. For eample, for the rule = , if = 3, then = 5. Furthermore, such relationships have been represented graphicall, and ke features such as ais intercepts, turning points and asmptotes have been considered. Analsis of the graphical representation can also be used to see how that relationship is changing. How the relationship is changing is of critical importance in establishing how accuratel a given rule models the relationship between the variables in question. As changes in values of are considered, the question of how the corresponding values of are changing arises. If increases, for eample, does also increase, or does it decrease or remain unaltered? And, if it does change, does it do so consistentl, quickl, slowl, indefinitel etc.? A connection can be made between the manner and the rate at which a function is changing and the slope or gradient of the graph representing the function. 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard 52
2 Chapter 18 Rates of Change Recognising relationships Polnomial, eponential, logarithmic and circular functions have been considered in previous chapters, and it has been shown that man real-life situations ma be modelled b these functions. In this first section several real situations concerning two particular variables are considered, and in particular the form of the relationships between the variables through graphs. The algebraic relationship is not established. Eample 1 a b c d Water is being poured steadil into each of these vessels. Draw a graph that shows the relationship between the height of the water (h) and the volume (V ) that has been poured in. Solution a h c h Eample 2 The graph shows the displacement, D metres, of a particle from a fied point O,overaperiod of 2 minutes. Describe the motion of the particle. V V b d h h 1 5 O D(m) 3 7 V V t (min) 2 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
3 54 Essential Mathematical Methods 1&2CAS Solution The object is initiall5mfrom O. Ittravels awa from O for 3 minutes at a constant speed of 5 m/min. It then remains stationar at a distance of 1 m from O for 3 4 minutes before returning to O at a speed which is graduall decreasing so that it comes to rest at O at time t = 2 minutes. B eamining the graph representing a function, it can be determined whether the rate of change is positive, negative or, in fact, neither. If the graph of against for a function with rule = f (), for a given domain, shows an increase in as increases, it can be said that the rate of change of with respect to is positive for that domain. It is also said that the function is increasing for that domain. The slope of the curve is positive. If the graph of against for a function with rule = f (), for a given domain, shows a decrease in as increases, it can be said that the rate of change of with respect to is negative for that domain. It is also said that the function is decreasing for that domain. The slope of the curve is negative. If remains the same value as changes, the corresponding graph is a horizontal line and the rate of change of with respect to is said to be zero. All of this is consistent with the gradient (rate of change) of a linear function, which was discussed in Chapter 2. Eample 3 For the graph shown below for [ 5, 2], describe, using interval notation, the set of values of for which: a the value of is increasing as is increasing b the rate of change of with respect to is positive. ( 3, 2) Solution a The value of is increasing for [ 5, 3) (, 2]. b The rate of change of with respect to is positive over the intervals [ 5, 3) (, 2]. 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
4 Chapter 18 Rates of Change 55 Eercise 18A For questions 1 4 there ma not be a single correct answer. Your written eplanations are an important part of the eercise. 1 The manager of a theatre wishes to know what effect changing the price of admission will have on the profit he makes. a b Which one of the following graphs would show the effect of change. Eplain our choice, including comments on scales and aes and what the point of intersection of the aes represents. A B C profit profit D profit price charged for admission price E profit price price F profit profit 2 Sketch a graph to show how the height of a person might var with age. 3 A motorist starts a journe at the point marked A on a countr road, drives 2 km along the route shown, and stops at a point marked B. Heisable todrive at 1 km/h but must slow down at corners. a b Eplain briefl how the car s speed varies along the route. Sketch a graph showing how the A 1 km car s speed varies along the route..25 km.25 km (Label the vertical ais Car s speed, and the horizontal ais Distance from A.) price price.3 km 4 An athlete is a competitor in a 1 m race. Below are a selection of graphs which could show the relationship between the speed of the runner and the distance covered. a b Eplain the meaning of each graph in words. Which graph is the most realistic for a winning athlete?.2 km B 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
5 56 Essential Mathematical Methods 1&2CAS Eample 1 A speed distance covered D speed distance covered B speed distance covered E speed distance covered C F speed speed distance covered distance covered If ou do not think an of these graphs are realistic draw our own version and eplain it full. 5 A sprinter covers 1 metres at a constant speed of 1 m/s. Sketch: a the distance time graph b the speed time graph 6 Water is being poured steadil into these vessels. a b c d Draw a graph that shows the relationship between the height of the water and the volume that has been poured in. 7 For the vessel shown, sketch a reasonable curve for the volume, V,ofwater in the vessel as a function of the height, h,ofthe water in the vessel. 8 The graph relating the distance a car travels distance to the time taken is a straight line as shown. (km) The graph shows that the car is: A speeding up B slowing down time (hours) C travelling uphill D travelling at a constant speed E stationar 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
6 Eample 3 Chapter 18 Rates of Change 57 9 Which one of these graphs best represents the rate of cost of living slowing down? A cost of B cost of living living C cost of living time time time 1 For the graph shown below for [ 7, 3], use interval notation to describe the set of values of for which: a the value of is increasing as is increasing b the rate of change of with respect to is positive D cost of living 11 For the graph shown below for [ 5, 2], describe, using interval notation, the set of values of for which: a the value of is decreasing as is increasing b the rate of change of with respect 6 to is negative Constant rates of change An function that is linear will have a constant rate of change. That rate of change is simpl the gradient of the graph and, given appropriate information, the rate can be calculated from the graph of the function or simpl read from the rule of the function if it is stated. Eample 4 A car travels from Copahunga to Charlegum, a distance of 15 km, in 2 hours (12 minutes). If the car travels at a constant speed, draw a distance time graph and calculate the speed. time 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
7 58 Essential Mathematical Methods 1&2CAS Solution We denote the function b D. (km) The graph of the function X is shown. 15 The rule of the function 125 = D(t) ma be written: 1 D(t) = t = 5 75 B 4 t 5 Note that XY YO = BA AO = 5 25 A Y 4 O The gradient of the graph gives the speed in kilometres per minute. Therefore, the speed of this car is 5 ( 5 ). 4 kilometres per minute 4 km/min This speed ma be epressed in kilometres per hour (km/h). Speed (km/h) = 5 6 = 75 4 Eample 5 t (min) Three cars are driven over a 2-kilometre straight track. The are all to go from point A to point B. Each car travels with constant speed. It is not a race as: the speed of car Y is twice that of car X, and the speed of car Z is half that of car X. Illustrate this situation with a distance time graph. Assume that car X travels at 1 km/min. Solution distance (metres) 2 1 Car Y Car X Car Z time (seconds) Note: The gradient of the graph for car X is 2 12 = The gradient of the graph for car Y is 2 6 = The gradient of the graph for car Z is 2 24 = Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
8 Chapter 18 Rates of Change 59 Eample 4 An object whose motion can be described b a linear distance time graph is travelling at a constant speed equal to the gradient of the linear graph. There are man other eamples, as well as constant speed motion, in which a real-life situation is usefull modelled b a straight line graph in such a wa that the gradient of the graph is meaningful. In all these situations the gradient of the straight line graph represents a rate. Eamples include: i Petrol consumption of a car A straight line graph has been used as a model, and its gradient represents the rate of consumption of petrol, which is measured in km per litre. Such a model makes fairl large assumptions. kilometres What are these? litres ii The echange rate for currencies The gradient of the graph gives the echange rate of dollars to en. Yen 3 2 Eercise 18B $ 1 A car travels from Bomba to Pune, a distance of 2 km, at a constant speed. The journe takes 15 minutes. Draw a distance time graph and calculate the speed. 2 The echange rate for the Australian dollar in terms of the American dollar is A$1 = US$.75. US$ 6 Draw a straight line graph 5 that illustrates this relationship. The aes 4 should be as shown A$ 3 Find the speed for each of the following (assume constant speed): a Distance travelled 12 km, time taken 2 hours b Distance travelled 6 m, time taken 2 seconds c Distance travelled 8 m, time taken 2 minutes d Distance travelled 2 km, time taken 5 hours 4 minutes e Distance travelled 6542 m, time taken 5 minutes 2 seconds 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
9 51 Essential Mathematical Methods 1&2CAS 4 Find the rate of flow from the following taps in litres/min: a A tap which fills a 4 litre drum in 5 minutes b A tap which fills a 6 litre tank in 12 minutes c A tap which takes 17 minutes to fill a 2 litre tank d A tap which takes 17 minutes 2 seconds to fill a 18 litre tank 5 Water comes out of a tap at the rate of 15 litres/min. a Cop and complete this table showing the amount which has come out at time t: b Time in minutes t Amount in litres A Draw a graph from the table. 6 Aworker is paid $2 for 13 hours work. What is their rate of pa per hour? 7 An aircraft travelling at a constant speed took 24 seconds to travel 5 metres. What was the speed of the plane in metres per second? 8 A spherical balloon is blown up so that its volume is increasing b 8 cm 3 ever second. Sketch a graph to show how the volume of the sphere changes with time Non-constant rate of change and average rate of change Constant speed is not the onl form of motion for an object. Man moving objects do not travel with constant speed. For eample, the speedometer of a car being driven in cit traffic rarel stas still for long. Similarl not all functions are linear so not all functions have constant rates of change. For a function that is nonlinear the rate of change of the function varies and ma in fact be different for ever different point on the graph representing the function. Before eploring was of finding the gradient at ever different point on the graph, the average gradient of a function or the average rate of change of a function over a specified interval will be considered. Again a displacement time graph will be used to illustrate this idea. The straight line graph through D shows a constant speed of 6 km/h. B comparison, the graph through points A, B and C shows a motorist travelling at varing speeds. The motorist accelerates to reach 6 km/h at A before slowing for the lights at B,where there is a ten-second standstill. There is then another short burst of speed before another standstill at C. 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
10 Chapter 18 Rates of Change 511 d (m) A D constant speed 6 km/h B cit journe O t (s) Although we do not know the actual speed of the car at an particular time other than when it is stationar, we can work out the average speed of the car travelling in the cit over the full 6 seconds. distance travelled The average speed is given b = 3,which gives an average speed of time taken 6 5 metres per second. The average speed is the gradient of the line OC. The average ma also be calculated for an given time interval. For eample, for the time interval t = 15 to t = 3, the average speed is given b the gradient of the line joining points A and B. This is 1 15 = 62 metres per second. 3 total distance travelled In general, average speed =,sothe average speed of an object for total time taken a t b is given b the gradient of the chord PQ d (secant PQ,which is the line passing through points P and Q). Q P a b t In general, for an function with rule = f (), the average rate of change of with respect to over the interval [a, b]isthe gradient of the line joining (a, f (a)) to (b, f (b)), (b, f(b)) f (b) f (a) i.e. average rate of change =. b a (a, f(a)) = f() C a b 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
11 512 Essential Mathematical Methods 1&2CAS Foreample, the average rate of change of with respect to over the interval [1, 3] for the function with the graph shown is given b the gradient of PQ: Eample 6 gradient = = 4 The distance travelled (metres) against time distance (seconds) graph for the motion of an object is shown. Find the average speed of the object in m/s over the interval from t = 2tot = 12. Solution total distance travelled Average speed = total time taken 3 12 = 12 2 = 18 1 = 1.8 m/s Eample 7 A(2, 12) P(1, 1) Q(3, 9) time B(12, 3) Find the average rate of change of the function with rule f () = aschanges from 1to5. Solution change in Average rate of change = change in f (1) = (1) 2 2(1) + 5 = 4 f (5) = (5) 2 2(5) + 5 = 2 Average rate of change = = 4 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
12 Chapter 18 Rates of Change 513 Eample 7 Eample 8 Find the average rate of change of the function depicted in the graph below for the interval [ 2, 5] Solution Average rate of change for the interval [ 2, 4] = ( 2) = 16 7 Eample 9 A( 2, 4) B(5, 2) The air temperature T ( C) at a weather station on a particular da is modelled b the equation 6 T =,where t is the time after 6. pm. t 2 + 2t + 3 a Find the temperature at 6. pm. b Find the temperature at midnight. c Find the average rate of change of the air temperature from 6. pm till midnight. Solution a At 6. pm t = 6 Hence T = () 2 + 2() + 3 = 2 C b At midnight, t = 6 6 Hence T = (6) 2 + 2(6) + 3 = 7.69 C (correct to 2 decimal places) c Average rate of change of temperature = = 2.5 C/hour 6 Eercise 18C 1 For each of the following functions, find the average rate of change over the stated interval: a f () = 2 + 5, [, 3] b f () = , [ 1, 2] 2 c f () = ( 3) + 4, [4, 7] d f () = 5, [, 4] 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
13 514 Essential Mathematical Methods 1&2CAS Eample 8 Eample 9 2 Find the average rate of change of with respect to from point A to point B for each of the following graphs. a b c 4 A ( 5, 3) A(, 3) 5 B (2, 5) 5 B(3, 15) d A( 1.5, 14) 1 B(2, 5) A( a, b) B(2a, 5b) 3 The displacement, S m, of an object t seconds after it starts to move is given b the function S(t) = t 3 + t 2 2t, t >. Find the average rate of change of displacement (speed) of the object: a in the first 2 seconds b in the net 2 seconds 4 A person invests $2 dollars, which will increase in value b 7% per ear for the net 3ears. a Calculate the value of the investment after 3 ears. b Calculate the average rate of change in the value of the investment over that time. 5 The depth, d cm, of water in a bath tub t minutes after the tap is turned on is modelled b the function d(t) = 3 + 5, t >. (t + 6) Find the average rate of change of the depth of the water in the tub over the first 1 minutes after the tap is turned on. 6 In the graph the average speed from t = tot = 3is A 2 m/s B 1 m/s distance (m) C 2 3 m/s D 11 2 m/s time (s) 7 Two cars start together and travel with constant speed over a1kilometre straight track. Car 1 has speed 6 km/h; car 2 travels at 3 of this speed. 4 Illustrate this situation with distance time graphs for both cars on the one set of aes. 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
14 Chapter 18 Rates of Change Finding the gradient of a curve at a given point In the previous section the average rate of change of a function over a stated interval has been considered. It has also been established that, in general (ecept for linear functions), the rate of change of a function is different at each different point on the graph of the function. If we are to full analse how a function is behaving we need to be able to establish the rate of change of the function at ever given point. Defining tangent Foracircle a tangent is a line which intersects the circle at one and onl one point. There are other curves for which tangenc can be defined in this wa, e.g. an ellipse. However, for some ver simple curves, the tangent cannot be described b the definition we use to describe tangents to circles. Consider, for eample, a parabola. The tangent at P intersects the graph onl at (, ). But the line parallel to the -ais through P also has this propert. We ma tr to get around this problem b indicating that the tangent line must onl touch the curve, but does not cross it. For man curves, however, this is not true. The tangent to this curve at the point (, ) is the -ais and it certainl crosses the curve. P(, ) = 3 To define tangent adequatel for all curves demands mathematics which we will meet in the following chapters. For the present we state that the tangent at a point P of a curve is a line through P which has a gradient that is the same as the gradient of the curve at P. The rate of change at a given point can be determined b finding the gradient of the tangent at that point. We refer to this rate of change at a specific point as the instantaneous rate of change. Q 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
15 516 Essential Mathematical Methods 1&2CAS If = f (), then the instantaneous rate of change of with respect to at the point (a, f (a)) is the gradient of the tangent line to the graph of = f () atthe point (a, f (a)). tangent line = f() (a, f(a)) Initiall, the instantaneous rate of change at a given point will be estimated b drawing the tangent at the specified point and finding the gradient of this tangent. An attempt to draw a tangent b hand is unlikel to be ver accurate, so this technique will provide us with an approimation onl. Eample 1 This graph represents the temperature T ( C) T ( C) 6 of a kettle at time t (min) after taking it 5 (1, 5) from the heat and putting it outside. a What does the gradient represent? 4 b Find the average rate of change of temperature between t = 2 and t = (2, 3) c Draw the tangent at P and hence find an approimate value for the 1 P (4, 1) (6, 6) rate of change at t = t (min) Solution a The gradient represents the rate of increase of temperature with respect to time. b Average rate of change = = 24 4 = 6 C per minute c T ( C) 6 gradient of the tangent at P = (1, 5) = (2, 3) 2 P (4, 1) 1 (6, 6) t (min) 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
16 Chapter 18 Rates of Change 517 Another technique that ma be used to find an approimation for the instantaneous rate of change is to use the gradient of a chord from the point in question, P, toanother point on the curve, Q, that is ver close to P.Sothe gradient of the chord PQ gives us an approimation to the gradient of the tangent at P,which is of course equal to the gradient of the curve at P. We can consider chords PQ 1, PQ 2,...,PQ n,... As the point Q n is chosen closer to P it can be seen that the gradient of the the chord PQ n is closer to the gradient of the tangent at P. The Q gradient of the curve at P is the gradient of the 1 Q tangent at P. 2 Q 3 Q n P Eample 11 Area The graph represents the area covered (cm2) b aspreading plant. Area is measured 8 in square cm and time in weeks. 6 a Find the gradient of the chord PQ. Q(7, 6) b Q 4 Q'(3, 33) has coordinates (3, 33). Find the gradient of PQ and hence 2 P(2, 3) give an approimate value of the gradient of the graph at P Time (weeks) Solution 6 3 a Gradient of chord PQ = 7 2 = 3 5 = 6 i.e. the average rate of increase of area for the plant from t = 2tot = 7is6cm 2 per week b Gradient of PQ = 1 = 3 gradient at P is approimatel 3 i.e. the rate of change of area with respect to time is approimatel 3 cm 2 per week when t = Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
17 518 Essential Mathematical Methods 1&2CAS Eample 12 Estimate the gradient of the curve = 3 + 1atthe point (2, 9). Solution Consider the points P(2, 9) and Q(2.1, (2.1) 3 + 1). The gradient of PQ = (2.1) = An even better approimation ma be made b choosing P(2, 9) and Q(2.1, (2.1) 3 + 1). Eample 13 B considering the chord joining the points where = 3 and = 3.1 estimate, without accurate drawing, the gradient of the curve = 2 at = 3. Repeat for = 3.1 and = 3.1. Solution When = 3, = 8. When = 3.1, = (correct to 4 decimal places). The gradient of the line joining (3, 8) to (3.1, ) = An estimate of the gradient of = 2 at = 3is When = 3.1, = and the gradient = (Note the true gradient (to 4 decimal places) is ). The above method of approimating the rate of change at a single point ma be modified slightl. The gradient of = at the point (, 1) will be investigated. The graph of = isshown R 2. R S First find the gradient of RS where R = (.75, ), S = (.25,.578). Gradient of RS = (values of R and S were found to 4 decimal places). Consider a new chord R 1 S where R 1 = (.25, ) and S = (.25,.578). Gradient of R 1 S = When using a calculator, zoom in on the region of the graph in the vicinit of =, and it can be seen that this section of the graph appears increasingl linear. B assuming this section is in fact linear and finding the gradient of this section of the curve, an approimation to the gradient of the curve at = can be found. 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
18 Chapter 18 Rates of Change 519 Eample 1 Consider a chord AB where A = (.1, ) and B = (.1,.85). A particular section of the graph around (, 1) can be plotted. A From this section of graph it can 1.2 be seen that the gradient of the section of the curve being considered.4 1. is 2, and the final approimation can B be made that the gradient of the curve = is 2atthe point with coordinates (, 1) This method ma be used without even sketching the graph. Eercise 18D 1 The graph shown below is the weight time graph for the growth of a bab bo measured at 2-monthl intervals for the first 18 months of his life. B drawing a tangent at the appropriate points: a estimate the average rate of growth of the bab over these 18 months b estimate the rate of growth of the bab at 6 months c estimate the rate of growth of the bab at 15 months. weight (kg) time (months) 2 Abuilding is heated b gas. The volume time graph for a 27-second period is shown: volume (m 3 ) P time (s) a Place a rule along the tangent at P and hence find the rate of use of gas at time t = 12. b Find the rate of use at t = 16. c Find the rate of use at t = Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
19 52 Essential Mathematical Methods 1&2CAS 3 Cardiac output is an important factor in athletic endurance. The graph shows a stress-test graph of cardiac output (measured in litres/min of blood) versus workload (measured in kg m/min). a Estimate the average rate of change cardiac output of cardiac output with respect (litres/min) to workload as the workload increases from to 12 kg m/min b Estimate the instantaneous 1 rate of change of cardiac 5 output with respect to workload at the point where the workload is 45 kg m/min workload (kg m/min) 4 The graph of a person s height h (cm) versus h t (ears) from some time after birth (cm) to age 2 is shown. 2 a When is the growth rate greatest? 15 b Estimate the growth rate after 5 ears t (ears) 5 Temperature (T C) varies with time (t hours) over a 24-hour period, as illustrated in the graph. a Estimate the maimum temperature and the time at which this occurs. T ( C) 25 b The temperature rise between 1. and 14. is approimatel linear. Estimate the rate at which the temperature is increasing in this period c Estimate the instantaneous rate of change of temperature at t = t (hours) 6 B considering the chord joining the points at which = 1.2 and = 1.4, estimate without accurate drawing the gradient of the curve = 1 at = 1.3. Eample 12 7 Draw the graph of = 16 2, 4 4. Use an appropriate technique to find an estimate for the gradient of the curve at the points: a = b = 2 c = 3 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
20 Chapter 18 Rates of Change It is known that the straight line = 4 4touches the curve = 2 at the point (2, 4). Sketch the graphs of both of these functions on the one set of aes. Find the gradient of = 2 at (2, 4). 9 Water is being collected in a water tank. The volume, V cubic metres, of water in the tank after time t minutes is given b V = 3t 2 + 4t + 2. a Find the average rate of change of volume between times t = 1 and t = 3. b Find an estimate for the rate of change of volume at t = 1. 1 A population of bacteria is growing. The population, P million, after time t minutes is given b P = 3 2 t. a Find the average rate of change of population between times t = 2 and t = 4. b Find an estimate for the rate of change of population at t = Water is flowing out of a water tank. The volume, V cubic metres, of water in the tank after t minutes is given b V = t, t 12. a Find the average rate of change of volume between times t = and t = 5. b Find an estimate for the rate of change of volume when t = 6. c Find an estimate for the rate of change of volume when t = B considering the chord joining the points where = 1.2 and = 1.3 estimate the gradient of the curve = at = Use the technique of eamples 12 and 13 to estimate the gradients of each of the following at the stated point: a = , (1, 3) b = , (1, 5) c = , (2, 8) d = , (3, 26) 14 The volume, V,ofacube with edge length is given b V = 3. a Find the average rate at which the volume of the cube changes with respect to as increases from = 2to = 4. b Find the instantaneous rate at which V changes with respect to when = Let = a Find the average rate at which changes with respect to over the interval [1, 4]. b Find the instantaneous rate at which changes with respect to when = Let = sin : a Find the average rate at which changes with respect to over each of the following intervals: [ i, ] [ ii, ] iii [,.5] iv [,.1] 2 4 b Estimate the instantaneous rate of change of with respect to when =. 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
21 522 Essential Mathematical Methods 1&2CAS 17 Let = 1 : a Find the average rate at which changes with respect to over each of the following intervals: i [, 1] ii [,.5] iii [,.1] iv [,.1] b Estimate the instantaneous rate of change of with respect to when = Displacement, velocit and acceleration One of the ke applications of rates of change is in the stud of the motion of a particle. In this section onl motion in a straight line is considered. The displacement of a particle is a specification of its position. Consider motion on a straight line with reference point O. = 8.96 O = 6.25 We sa that displacement to the right of O is positive and to the left negative. A particle is moving along the straight line, let metres denote its displacement relative to O. At time t =, = (time is measured in seconds) At time t = 5, = 6.25 At time t = 8, = At t = the particle starts from rest and moves to the right. At t = 5 the particle stops and moves back in the opposite direction. Its displacement time graph is shown below. Note that from t = until t = 7.1 the displacement is positive; i.e. the 1 position of the particle is to the right of O. Fortgreater than 7.1 the particle 5 is to the left of O;ithasnegative displacement Velocit is the rate of change of displacement with respect to time. change in displacement The average velocit = time elapsed Foreample, for the time interval t 5 average velocit = 6.25 = 1.25 metres per second (m/s) 5 t 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
22 Chapter 18 Rates of Change 523 displacement (m) 6 velocit (m/s) 4 2 velocit displacement time (s) For the time interval 5 t average velocit = 3 = 5.7 metres per second (m/s) For < t < 5 the velocit is positive. For t > 5 the velocit is negative. The negative velocit indicates that the particle is travelling from right to left. The relationship between displacement and velocit is illustrated in the preceding graph. The vertical ais is in both metres per second for velocit and metres for displacement. Note that when t = 5 the velocit is. Acceleration is the rate of change of velocit with respect to time. We show both the velocit time and the acceleration time graphs on the one set of aes. The units of acceleration are metres per second per second and we abbreviate this to m/s 2. Note that the acceleration is for t 2.98 and this occurs when the velocit changes from increasing to decreasing. The instantaneous velocit of the particle at time t is given b the gradient of the displacement time graph for the point corresponding to time t. acceleration (m/s 2 ) 2 velocit 1 (m/s) 1 velocit acceleration Eample time (s) A particle is moving in a straight line. It was initiall at rest at a point O. Itmoves to the right of O with a constant velocit and reaches a point A, 15metres from O, after 5 seconds. It then returns to O. The return trip takes 1 seconds. It stops at O. On the one set of aes draw the displacement time graph and the velocit time graph for the motion. 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
23 524 Essential Mathematical Methods 1&2CAS Solution Note: The gradient of the velocit (m/s) 15 displacement time graph for displacement (m) 1 < t < 5is3. The gradient for 5 < t < 15 is 1.5. The gradient of the 5 3 displacement time graph 1.5 determines the velocit time graph. Eample 15 The graph shown is the displacement time graph that corresponds to the ccle trip of a bo who lives at the edge of a long straight road. The road runs north south and north displacement (km) 2 is chosen to be the positive direction. a Describe his trip. b Draw the corresponding velocit time graph. 1 Solution a The bo heads north for 2 hours. His velocit for this period is 2 = 1 km/h. 2 He turns and rides south for 2 hours. 1 2 His velocit for this period is = 15 km/h. 2 He turns and rides north until he reaches home. His velocit for this period is ( 1) = 1 km/h. 1 b velocit (km/h) time (hours) displacement time velocit time time (s) time (hours) 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
24 Chapter 18 Rates of Change 525 Eample 16 The displacement of a particle moving in a straight line is given b the function S(t) = t 3 6t 2, t. The graph of S against t is shown. The corresponding velocit time graph is also shown. The function describing the velocit is V(t) = 3t 2 12t. S S(t) = t 3 6t t V a Find the average velocit of the particle for the intervals: i [3.5, 4.5] ii [3.9, 4.1] iii [3.99, 4.1] b From part a what is the instantaneous velocit when t = 4? c i Forwhat values of t is the velocit positive? ii Forwhat values of t is the velocit negative? V(t) = 3t 2 12t Solution S(4.5) S(3.5) a i Average velocit = = = ii Average velocit = S(4.1) S(3.9) = = iii Average velocit = S(4.1) S(3.99) =.2 =.1 b The results of part a give the instantaneous velocit as zero when t = 4 and this is consistent with the result suggested b both graphs. c i From the displacement time graph it can be seen that the velocit is positive for t > 4. ii From the displacement time graph it can be seen that the velocit is negative for t < 4. Eercise 18E 1 Let s(t) = 6t 2t 3 be the displacement function of a particle moving in a straight line, where t is in seconds and s is in metres. a Find the average velocit for the time interval [, 1]. b Find the average velocit for the time interval [.8, 1]. t 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
25 526 Essential Mathematical Methods 1&2CAS Eample 15 c Find an estimate for the instantaneous velocit for t = 1. d State the values of t for which the displacement, s, ispositive. e State the values of t for which the velocit is positive. 2 The following is the displacement s time graph for a train travelling (kilometres) on a straight track. Displacement is 8 measured from the door of the station 6 master s office at Jimbara station. a What was the train s velocit over each of the following time intervals: i [, 2] ii [2, 5] iii [5, 8] t (hours) b Describe the train journe. c Draw a velocit time graph for the train s motion for the interval [, 8]. 3 The motion of a particle moving in a straight line is described b the following information: For the time period (, 2), velocit = 3. For the time period (2, 5), velocit = 3. For the time period (5, 7), velocit = 4. Draw the displacement time graph for the interval [, 7]. 4 Match each displacement time graph shown with its velocit time graph. a s t b s A v t B v t t c C s v t t 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
26 Chapter 18 Rates of Change 527 Eample 16 5 The graphs of four displacement time graphs are shown. In each case determine the sign of the velocit and whether the particle is speeding up or slowing down. a s b s c s 6 The distance time graph for a 4-metre runner is shown. Eplain what is happening between: a O and A b A and B c B and C t t d s t t distance 4 O A B 6 C time (t) 7 The table shows the distance, d metres, of a ball from its starting position t seconds after being thrown into the air. t d Use scales 2 cm = 1 second and 1 cm = 5mand draw the graph of d against t. From our graph find: a when the ball returns to the starting point b the average velocit of the ball from t = 1tot = 2 c the average velocit of the ball from t = 1tot = 1.5 d an estimate of the velocit of the ball when t = 1 e an estimate of the velocit of the ball when t = 4 f an estimate of the velocit of the ball when t = Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
27 528 Essential Mathematical Methods 1&2CAS 8 A particle moves along a horizontal straight line. It starts from rest at a point O. The graph is the displacement time graph for this motion. a At what time is the velocit zero? b Forwhich values of t is the velocit positive? c If to the right of O is taken as positive displacement, how far does the particle go to the right? d How long does it take to return to O? (m) 6 e Estimate the velocit of the particle at t = A stone is thrown verticall upwards from the edge of a platform which is 1 m above the ground. The displacement time displacement (m) 15 1 graph for the motion of the stone is shown. 5 The motion of the stone is in a straight line and the reference point for displacement is taken as a point at ground level, directl below where the stone was thrown t (s) a From the graph estimate the velocit with which the stone is thrown. b What is the maimum height reached b the stone? c At what time does the stone reach its maimum height? d At what time does the stone hit the ground? e From the graph estimate the speed at which the stone hits the ground. 1 A particle is moving in a horizontal straight line. Displacement is measured from a point O. The particle starts at a point 2 m to the left of O. The displacement time graph for the motion of the particle is as shown. (m) a At which times is the particle at O? b Forwhich values of t is the particle moving to the right? c Forwhich values of t is the particle stationar? t (s) t (s) 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
28 Chapter 18 Rates of Change 529 Chapter summar Where a real-life situation is modelled b a straight line graph, the gradient represents a rate of change of one quantit with respect to a second. total distance travelled Average speed = total time taken If = f (), then the average rate of change of with respect to over the interval [a, b]isthe gradient of the secant line joining (a, f (a)) to (b, f (b)). If = f (), then the instantaneous rate of change of with respect to at the point (a, f (a)) is the gradient of the tangent line to the graph of = f () atthe point (a, f (a)). Multiple-choice questions = f() (a, f(a)) a secant line (b, f(b)) b tangent line (a, f(a)) = f() 1 Abushwalker walks 12 km in 2 hours, stops for 45 minutes and then walks a further 8 km in another 1.25 hours. The average walking speed of the bushwalker over the entire walk is A 1 km/h B 9 km/h C 5 km/h D 4 km/h E 7.2 km/h 2 Postal workers sort 12 letters during the normal da shift of 8 hours and, with a reduced workforce during the 2 hours overtime shift, the sort a further 25 letters. The average rate of letter sorting per hour is A 1375 letters per hour B 145 letters per hour C 13 letters per hour D 14 letters per hour E 15 letters per hour Questions 3 to 5 refer to the following information: The graph shows the movement of avehicle over a period of time. It represents the distance(s) from a fied point at agiven time (t). s A B C D E Review O t 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
29 53 Essential Mathematical Methods 1&2CAS Review 3 The line segment OA represents a stage of the movement during which the vehicle is A speeding up B slowing down C travelling north D travelling at a constant speed E stationar 4 The line segment AB represents a stage of the movement during which the vehicle is A speeding up B slowing down C travelling east D travelling at a constant speed greater than zero E stationar 5 The section(s) of the graph which represent(s) the vehicle when it is stationar is/are A at O B at A and C C between C and D D between A and B and D and E E at no time 6 The average rate of change of the function = 3 2 over the interval [, 2] is A 9 B 4.5 C 12 D 6 E 5 7 The population of trout in a trout pond is growing. If the population P, after t weeks is given b P = t, the average rate of growth of the population during the 5 th week is closest to A 16 trout per week B 15 trout per week C 1.5 trout per week D 4 trout per week E trout per week 8 Given f () = , the average rate of change of f () with respect to for the interval [ 2, 2] is A B 22 C 11 D 22 E 11 Questions 9 to 1 refer to the following information: A particle moves along a horizontal line. displacement The graph of the particle s displacement (m) relative to the origin over time is shown. (2, ) (, 4) (8, 8) 9 The particle has a velocit of zero at A 8sand 13 s B 2s C s D 8sand7s E 4s 1 The time interval(s) during which the particle has a negative velocit are A 8 < t < 13 B < t < 2 and 8 < t < 13 C < t < 2 D 7 < t < 8 E (, ) (13, 7) time (s) 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
30 Chapter 18 Rates of Change 531 Short-answer questions (technolog-free) 1 A liquid is poured at a constant rate into each of the containers shown below. For each container, draw a graph to show how the depth of the water varies with time. a b c d e f 2 a A car travels from New Delhi to Agra, a distance of 2 km, in 3 hours. If the car travels at a constant speed, draw a distance time graph and calculate this constant speed. For the distance time graph, use minutes as the unit of time. b A girl walks at a constant speed of 1.5 m/s for 2 seconds. Draw a distance time graph to illustrate this. c A car travels along a road for 6 1 hours. The trip can be described in three sections. 2 Section A Car travels at a constant speed of 4 km/h for 1 hour. Section B Section C Car travels at a constant speed of 8 km/h for hours. Car travels at a constant speed of 9 km/h for 2 hours. Draw a distance time graph which illustrates this motion. 3 The surface area s cm 2 of a cube is given b the epression s = 6 2,where cm is the length of each edge of the cube. Find the average rate at which the surface area changes with respect to,as increases from = 2to = 4. 4 Let = 3.Find the average rate at which changes with respect to over each of the following intervals: a [, 1] b [1, 3] 5 Let s(t) = 4t 6t 3 be the displacement function of a particle moving in a straight line, where t is in seconds and s is in metres. a Find the average velocit for the time interval [, 1]. b Find the average velocit for the time interval [.9, 1]. c Estimate the instantaneous velocit for t = 1. Review 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
31 532 Essential Mathematical Methods 1&2CAS Review Etended-response questions 1 The resistance of a copper wire is measured at various temperatures with the following results: Temperature ( C) Resistance (ohms) a Plot the data to see whether the resistance rises approimatel linearl with temperature. b If it does, find the rate of increase in ohms per C. 2 A rock is allowed to fall from the top of a high cliff. It falls metres in t seconds, where = 4.9t 2. a Find the average speed of the rock between: i t = and t = 2 ii t = 2 and t = 4 b i How far has the rock fallen between t = 4 h and t = 4? ii What is the average speed between t = 4 h and t = 4? iii If it hits the bottom when t = 4, find the speed of impact b using the result of ii and taking h =.2,.1,.5,.1,.1. 3 The graph shows the speed s (in metres per second) of a car travelling along a straight highwa at time t seconds measured from the time it crosses an intersection. s (m/s) t (s) a Use the graph to show how ou find: i the average rate at which the car s speed is increasing between times t = 3 and t = 5 ii an estimate of the rate at which the car s speed is increasing when t = 3. b Sketch a graph showing the rate of increase of speed against time for t = tot = Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
32 Chapter 18 Rates of Change The table shows the girth (w cm) of a watermelon, n das after being fed with a fertiliser. n (das) w (cm) a Use a scale of 2 cm for 1 da and 2 cm for 1 cm of girth to draw the graph illustrating the information. b Find the gradient of the chord joining the points where n = 3 and n = 7 and interpret the result. c From the same graph estimate the gradient of the curve at n = 4. 5 Avending machine in a bus terminus contains cans of soft drinks. On a tpical da: the machine starts 1 4 full no drinks are sold between 1. am and 6. am the machine is filled at 2. pm. Sketch a graph to show how the number of cans in the machine ma var from 6. am to 12 midnight. 6 a P(a, a 2 ) and Q(b, b 2 ) are two points on the curve with equation = 2. Find the gradient of the line joining the points. (Answer in terms of a and b.) b Use this result to find the gradient of the line for points with a = 1 and b = 2. c Use this result to find the gradient of the line if a = 2 and b = The figure shows part of the curve with equation = 4 and P is the point at which = 2. a A 1 and A 2 are points on the curve whose -coordinates are 1.5 and 2.5 respectivel. Use our calculator to find their 4 4 = -coordinates and hence the gradient of A 1 A 2. 2 P b Repeat for B 1 and B 2 whose -coordinates are 1.9 and 2.1 respectivel c Repeat for C 1 and C 2 whose -coordinates are 1.99 and 2.1 respectivel. d Repeat for D 1 and D 2 whose -coordinates are and 2.1 respectivel. e What do the results of parts a d suggest for the value of the gradient at = 2? 8 Use the method of Question 7 to find the gradient of = (2 1) 3 at = 1. Review 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
33 534 Essential Mathematical Methods 1&2CAS Review 9 The following graphs compare the weights of two people over weight (kg) the first 18 ears of their lives. 8 Clive a What was the average rate 6 of change of weight with respect to time for Andrea 4 Andrea between the ages of and 18? 2 b What was the average rate of change of weight with respect to time for Clive between the age (ears) ages of and 18? c During which periods did Andrea weigh more than Clive? d During which periods of time was Clive growing more rapidl than Andrea? 1 The graph below shows an eponential model for Acubaland s population growth. In eponential growth the rate of increase of the population at an time is proportional to the size of the population at that time. a b c d population Population is in billions where 1 billion = ear From the graph find the population of Acubaland in: i 196 ii 2 Calculate the average annual rate of population increase (in billions per ear) over the ears from 196 to 2. From the graph estimate the rate of population increase in: i 196 ii 2 How man ears do ou epect that it will take to double the 22 population? Eplain our reasoning. 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
34 Chapter 18 Rates of Change a Draw the graph of = 1 and find the gradient of the chord joining the points: i = 2.5 and = 2.8 ii = 2.6 and = 2.8 iii = 2.7 and = 2.8 iv = 2.75 and = 2.8 b Comment on our result and investigate further. 12 a Use the result that a 3 b 3 = (a b)(a 2 + ab + b 2 )tofind an epression for the gradient of the line joining points P(a, a 3 ) and Q(b, b 3 )onthe curve with equation = 3. b Find the gradient of the line for a = 1, b = 2. c Find the gradient of the line for a = 2, and b = 2.1. d Forour epression for the gradient in terms of a and b (in part a) let a = b and write our new epression in simplest terms. Interpret this result. 13 The rough sketch graph below shows what happens when three swimmers compete in a 1-metre race. (The vertical ais shows distance travelled b a swimmer.) a Who wins the race? distance b Who is in front at the 5 m mark? (metres) c What is the approimate distance separating first and third place when 1 the winner finishes? 5 A B C d What is the approimate time difference between first and third place? e What is the average speed of each swimmer? time f Describe the race as if ou were a commentator. (seconds) 14 In the following, f ()isthe rule for a well-behaved function f. a If for = f () the average rate of change of with respect to is m, inthe interval [a, b], then for the same interval find the rate of change of with respect to, where: i = f () + c ii = cf () iii = f () b Give similar statements for the instantaneous rates of change. Review 28 Evans, Lipson, Wallace TI-Nspire & Casio ClassPad material prepared in collaboration with Jan Honnens & David Hibbard
SAMPLE. Revision. Revision of Chapters 1 7. The implied (largest possible) domain for the function with the rule y = is: 2 x. 1 a
 C H P T R 8 of Chapters 7 8. Multiple-choice questions The domain of the function whose graph is shown is: 3, ] B, 3] C [, 3] D [, 3), 3) 3 3 Which of the following sets of ordered pairs does not represent
C H P T R 8 of Chapters 7 8. Multiple-choice questions The domain of the function whose graph is shown is: 3, ] B, 3] C [, 3] D [, 3), 3) 3 3 Which of the following sets of ordered pairs does not represent
SAMPLE. A Gallery of Graphs. To recognise the rules of a number of common algebraic relationships: y = x 1,
 Objectives C H A P T E R 5 A Galler of Graphs To recognise the rules of a number of common algebraic relationships: =, =, = / and + =. To be able to sketch the graphs and simple transformations of these
Objectives C H A P T E R 5 A Galler of Graphs To recognise the rules of a number of common algebraic relationships: =, =, = / and + =. To be able to sketch the graphs and simple transformations of these
5A Exponential functions
 Chapter 5 5 Eponential and logarithmic functions bjectives To graph eponential and logarithmic functions and transformations of these functions. To introduce Euler s number e. To revise the inde and logarithm
Chapter 5 5 Eponential and logarithmic functions bjectives To graph eponential and logarithmic functions and transformations of these functions. To introduce Euler s number e. To revise the inde and logarithm
UNCORRECTED PAGE PROOFS
 12 Introduction to differential calculus 12.1 Kick off with CAS 12.2 Rates of change 12.3 Gradients of secants 12.4 The derivative function 12.5 Differentiation of polnomials b rule 12.6 Review 12.1 Kick
12 Introduction to differential calculus 12.1 Kick off with CAS 12.2 Rates of change 12.3 Gradients of secants 12.4 The derivative function 12.5 Differentiation of polnomials b rule 12.6 Review 12.1 Kick
UNCORRECTED SAMPLE PAGES. 3Quadratics. Chapter 3. Objectives
 Chapter 3 3Quadratics Objectives To recognise and sketch the graphs of quadratic polnomials. To find the ke features of the graph of a quadratic polnomial: ais intercepts, turning point and ais of smmetr.
Chapter 3 3Quadratics Objectives To recognise and sketch the graphs of quadratic polnomials. To find the ke features of the graph of a quadratic polnomial: ais intercepts, turning point and ais of smmetr.
Learning Outcomes and Assessment Standards
 Lesson 5 CALCULUS (8) Rate of change Learning Outcomes and Assessment Standards Learning Outcome : Functions and Algebra Assessment standard 1..7(e) Solve practical problems involving optimisation and
Lesson 5 CALCULUS (8) Rate of change Learning Outcomes and Assessment Standards Learning Outcome : Functions and Algebra Assessment standard 1..7(e) Solve practical problems involving optimisation and
c) domain {x R, x 3}, range {y R}
 Answers Chapter 1 Functions 1.1 Functions, Domain, and Range 1. a) Yes, no vertical line will pass through more than one point. b) No, an vertical line between = 6 and = 6 will pass through two points..
Answers Chapter 1 Functions 1.1 Functions, Domain, and Range 1. a) Yes, no vertical line will pass through more than one point. b) No, an vertical line between = 6 and = 6 will pass through two points..
2 MOTION ALONG A STRAIGHT LINE
 MOTION ALONG A STRAIGHT LINE Download full Solution manual for Universit phsics with modern phsics 14t http://testbankcollection.com/download/solution-manual-for-universit-phsics-withmodern-phsics-14th.1.
MOTION ALONG A STRAIGHT LINE Download full Solution manual for Universit phsics with modern phsics 14t http://testbankcollection.com/download/solution-manual-for-universit-phsics-withmodern-phsics-14th.1.
SAMPLE. Exponential and logarithmic functions
 Objectives C H A P T E R 5 Eponential and logarithmic functions To graph eponential and logarithmic functions. To graph transformations of the graphs of eponential and logarithmic functions. To introduce
Objectives C H A P T E R 5 Eponential and logarithmic functions To graph eponential and logarithmic functions. To graph transformations of the graphs of eponential and logarithmic functions. To introduce
1.5. Analyzing Graphs of Functions. The Graph of a Function. What you should learn. Why you should learn it. 54 Chapter 1 Functions and Their Graphs
 0_005.qd /7/05 8: AM Page 5 5 Chapter Functions and Their Graphs.5 Analzing Graphs of Functions What ou should learn Use the Vertical Line Test for functions. Find the zeros of functions. Determine intervals
0_005.qd /7/05 8: AM Page 5 5 Chapter Functions and Their Graphs.5 Analzing Graphs of Functions What ou should learn Use the Vertical Line Test for functions. Find the zeros of functions. Determine intervals
8.4. If we let x denote the number of gallons pumped, then the price y in dollars can $ $1.70 $ $1.70 $ $1.70 $ $1.
 8.4 An Introduction to Functions: Linear Functions, Applications, and Models We often describe one quantit in terms of another; for eample, the growth of a plant is related to the amount of light it receives,
8.4 An Introduction to Functions: Linear Functions, Applications, and Models We often describe one quantit in terms of another; for eample, the growth of a plant is related to the amount of light it receives,
Section A Plotting Straight Line Graphs Grade D / C
 Name: Teacher Assessment Section A Plotting Straight Line Grade D / C. The diagram shows the points P (0, 4) and Q (5, 2). Q O Find the coordinates of the mid-point of the line segment PQ. P Answer (...,...
Name: Teacher Assessment Section A Plotting Straight Line Grade D / C. The diagram shows the points P (0, 4) and Q (5, 2). Q O Find the coordinates of the mid-point of the line segment PQ. P Answer (...,...
6.4 graphs OF logarithmic FUnCTIOnS
 SECTION 6. graphs of logarithmic functions 9 9 learning ObjeCTIveS In this section, ou will: Identif the domain of a logarithmic function. Graph logarithmic functions. 6. graphs OF logarithmic FUnCTIOnS
SECTION 6. graphs of logarithmic functions 9 9 learning ObjeCTIveS In this section, ou will: Identif the domain of a logarithmic function. Graph logarithmic functions. 6. graphs OF logarithmic FUnCTIOnS
y = f(x + 4) a) Example: A repeating X by using two linear equations y = ±x. b) Example: y = f(x - 3). The translation is
 Answers Chapter Function Transformations. Horizontal and Vertical Translations, pages to. a h, k h, k - c h -, k d h 7, k - e h -, k. a A (-,, B (-,, C (-,, D (,, E (, A (-, -, B (-,, C (,, D (, -, E (,
Answers Chapter Function Transformations. Horizontal and Vertical Translations, pages to. a h, k h, k - c h -, k d h 7, k - e h -, k. a A (-,, B (-,, C (-,, D (,, E (, A (-, -, B (-,, C (,, D (, -, E (,
STRAND: GRAPHS Unit 1 Straight Lines
 CMM Subject Support Strand: GRAPHS Unit Straight Lines: Text STRAND: GRAPHS Unit Straight Lines TEXT Contents Section. Gradient. Gradients of Perpendicular Lines. Applications of Graphs. The Equation of
CMM Subject Support Strand: GRAPHS Unit Straight Lines: Text STRAND: GRAPHS Unit Straight Lines TEXT Contents Section. Gradient. Gradients of Perpendicular Lines. Applications of Graphs. The Equation of
Derivatives 2: The Derivative at a Point
 Derivatives 2: The Derivative at a Point 69 Derivatives 2: The Derivative at a Point Model 1: Review of Velocit In the previous activit we eplored position functions (distance versus time) and learned
Derivatives 2: The Derivative at a Point 69 Derivatives 2: The Derivative at a Point Model 1: Review of Velocit In the previous activit we eplored position functions (distance versus time) and learned
SAMPLE. Inequalities and linear programming. 9.1 Linear inequalities in one variable
 C H A P T E R 9 Inequalities and linear programming What is a linear inequalit? How do we solve linear inequalities? What is linear programming and how is it used? In Chapter 3, Linear graphs and models,
C H A P T E R 9 Inequalities and linear programming What is a linear inequalit? How do we solve linear inequalities? What is linear programming and how is it used? In Chapter 3, Linear graphs and models,
Differentiation Techniques
 C H A P T E R Differentiation Techniques Objectives To differentiate functions having negative integer powers. To understand and use the chain rule. To differentiate rational powers. To find second derivatives
C H A P T E R Differentiation Techniques Objectives To differentiate functions having negative integer powers. To understand and use the chain rule. To differentiate rational powers. To find second derivatives
Methods of Integration
 U96-b)! Use the substitution u = - to evaluate U95-b)! 4 Methods of Integration d. Evaluate 9 d using the substitution u = + 9. UNIT MATHEMATICS (HSC) METHODS OF INTEGRATION CSSA «8» U94-b)! Use the substitution
U96-b)! Use the substitution u = - to evaluate U95-b)! 4 Methods of Integration d. Evaluate 9 d using the substitution u = + 9. UNIT MATHEMATICS (HSC) METHODS OF INTEGRATION CSSA «8» U94-b)! Use the substitution
A11.1 Areas under curves
 Applications 11.1 Areas under curves A11.1 Areas under curves Before ou start You should be able to: calculate the value of given the value of in algebraic equations of curves calculate the area of a trapezium.
Applications 11.1 Areas under curves A11.1 Areas under curves Before ou start You should be able to: calculate the value of given the value of in algebraic equations of curves calculate the area of a trapezium.
Problems to practice for FINAL. 1. Below is the graph of a function ( ) At which of the marked values ( and ) is: (a) ( ) greatest = (b) ( ) least
 Problems to practice for FINAL. Below is the graph of a function () At which of the marked values ( and ) is: (a) () greatest = (b) () least = (c) () the greatest = (d) () the least = (e) () = = (f) ()
Problems to practice for FINAL. Below is the graph of a function () At which of the marked values ( and ) is: (a) () greatest = (b) () least = (c) () the greatest = (d) () the least = (e) () = = (f) ()
Functions. Introduction CHAPTER OUTLINE
 Functions,00 P,000 00 0 970 97 980 98 990 99 000 00 00 Figure Standard and Poor s Inde with dividends reinvested (credit "bull": modification of work b Praitno Hadinata; credit "graph": modification of
Functions,00 P,000 00 0 970 97 980 98 990 99 000 00 00 Figure Standard and Poor s Inde with dividends reinvested (credit "bull": modification of work b Praitno Hadinata; credit "graph": modification of
One of the most common applications of Calculus involves determining maximum or minimum values.
 8 LESSON 5- MAX/MIN APPLICATIONS (OPTIMIZATION) One of the most common applications of Calculus involves determining maimum or minimum values. Procedure:. Choose variables and/or draw a labeled figure..
8 LESSON 5- MAX/MIN APPLICATIONS (OPTIMIZATION) One of the most common applications of Calculus involves determining maimum or minimum values. Procedure:. Choose variables and/or draw a labeled figure..
Applications of differential calculus
 Chapter 22 Applications of differential calculus Sllabus reference: 7.4, 7.5 Contents: A B C Properties of curves Rates of change Optimisation 648 APPLICATIONS OF DIFFERENTIAL CALCULUS (Chapter 22) OPENING
Chapter 22 Applications of differential calculus Sllabus reference: 7.4, 7.5 Contents: A B C Properties of curves Rates of change Optimisation 648 APPLICATIONS OF DIFFERENTIAL CALCULUS (Chapter 22) OPENING
P.4 Lines in the Plane
 28 CHAPTER P Prerequisites P.4 Lines in the Plane What ou ll learn about Slope of a Line Point-Slope Form Equation of a Line Slope-Intercept Form Equation of a Line Graphing Linear Equations in Two Variables
28 CHAPTER P Prerequisites P.4 Lines in the Plane What ou ll learn about Slope of a Line Point-Slope Form Equation of a Line Slope-Intercept Form Equation of a Line Graphing Linear Equations in Two Variables
Applications of Differentiation of Polynomials
 C H A P T E R 20 Applications of Differentiation of Polynomials Objectives To be able to find the equation of the tangent and the normal at a given point of a polynomial curve. To use the derivative of
C H A P T E R 20 Applications of Differentiation of Polynomials Objectives To be able to find the equation of the tangent and the normal at a given point of a polynomial curve. To use the derivative of
Motion Along a Straight Line
 PHYS 101 Previous Exam Problems CHAPTER Motion Along a Straight Line Position & displacement Average & instantaneous velocity Average & instantaneous acceleration Constant acceleration Free fall Graphical
PHYS 101 Previous Exam Problems CHAPTER Motion Along a Straight Line Position & displacement Average & instantaneous velocity Average & instantaneous acceleration Constant acceleration Free fall Graphical
LESSON #12 - FORMS OF A LINE COMMON CORE ALGEBRA II
 LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
MATH 1710 College Algebra Final Exam Review
 MATH 7 College Algebra Final Eam Review MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. ) There were 80 people at a pla. The admission price was $
MATH 7 College Algebra Final Eam Review MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. ) There were 80 people at a pla. The admission price was $
Unit 3: Relations and Functions
 Unit 3: Relations and Functions 5-1: Binar Relations Binar Relation: - a set ordered pairs (coordinates) that include two variables (elements). (, ) = horizontal = vertical Domain: - all the -values (first
Unit 3: Relations and Functions 5-1: Binar Relations Binar Relation: - a set ordered pairs (coordinates) that include two variables (elements). (, ) = horizontal = vertical Domain: - all the -values (first
LESSON #11 - FORMS OF A LINE COMMON CORE ALGEBRA II
 LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
Exponential and Logarithmic Functions
 Eponential and Logarithmic Functions 6 Figure Electron micrograph of E. Coli bacteria (credit: Mattosaurus, Wikimedia Commons) CHAPTER OUTLINE 6. Eponential Functions 6. Logarithmic Properties 6. Graphs
Eponential and Logarithmic Functions 6 Figure Electron micrograph of E. Coli bacteria (credit: Mattosaurus, Wikimedia Commons) CHAPTER OUTLINE 6. Eponential Functions 6. Logarithmic Properties 6. Graphs
Unit 10 - Graphing Quadratic Functions
 Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
Functions. Introduction
 Functions,00 P,000 00 0 970 97 980 98 990 99 000 00 00 Figure Standard and Poor s Inde with dividends reinvested (credit "bull": modification of work b Praitno Hadinata; credit "graph": modification of
Functions,00 P,000 00 0 970 97 980 98 990 99 000 00 00 Figure Standard and Poor s Inde with dividends reinvested (credit "bull": modification of work b Praitno Hadinata; credit "graph": modification of
Higher. Differentiation 28
 Higher Mathematics UNIT OUTCOME Differentiation Contents Differentiation 8 Introduction to Differentiation 8 Finding the Derivative 9 Differentiating with Respect to Other Variables 4 Rates of Change 4
Higher Mathematics UNIT OUTCOME Differentiation Contents Differentiation 8 Introduction to Differentiation 8 Finding the Derivative 9 Differentiating with Respect to Other Variables 4 Rates of Change 4
2.5 CONTINUITY. a x. Notice that Definition l implicitly requires three things if f is continuous at a:
 SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
Lesson 4.1 Interpreting Graphs
 Lesson 4.1 Interpreting Graphs 1. Describe the pattern of the graph of each of the following situations as the graphs are read from left to right as increasing, decreasing, increasing and then decreasing,
Lesson 4.1 Interpreting Graphs 1. Describe the pattern of the graph of each of the following situations as the graphs are read from left to right as increasing, decreasing, increasing and then decreasing,
Mathematical models. Prior learning topics. 492 Topic 6 Mathematical models
 6 Mathematical models Suppose ou are given a problem it ma be a practical question that a friend asks ou, or an issue that ou have noticed ourself to which ou want to find a solution; it ma even be a mathematical
6 Mathematical models Suppose ou are given a problem it ma be a practical question that a friend asks ou, or an issue that ou have noticed ourself to which ou want to find a solution; it ma even be a mathematical
(2) Find the domain of f (x) = 2x3 5 x 2 + x 6
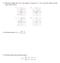 CHAPTER FUNCTIONS AND MODELS () Determine whether the curve is the graph of a function of. If it is state the domain and the range of the function. 5 8 Determine whether the curve is the graph of a function
CHAPTER FUNCTIONS AND MODELS () Determine whether the curve is the graph of a function of. If it is state the domain and the range of the function. 5 8 Determine whether the curve is the graph of a function
Speed (km/h) How can you determine the inverse of a function?
 .7 Inverse of a Function Engineers have been able to determine the relationship between the speed of a car and its stopping distance. A tpical function describing this relationship is D.v, where D is the
.7 Inverse of a Function Engineers have been able to determine the relationship between the speed of a car and its stopping distance. A tpical function describing this relationship is D.v, where D is the
Introducing Instantaneous Rate of Change
 Introducing Instantaneous Rate of Change The diagram shows a door with an automatic closer. At time t = 0 seconds someone pushes the door. It swings open, slows down, stops, starts closing, then closes
Introducing Instantaneous Rate of Change The diagram shows a door with an automatic closer. At time t = 0 seconds someone pushes the door. It swings open, slows down, stops, starts closing, then closes
3.2 LOGARITHMIC FUNCTIONS AND THEIR GRAPHS
 Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
CHAPTER 2 Polynomial and Rational Functions
 CHAPTER Polnomial and Rational Functions Section. Quadratic Functions..................... 9 Section. Polnomial Functions of Higher Degree.......... Section. Real Zeros of Polnomial Functions............
CHAPTER Polnomial and Rational Functions Section. Quadratic Functions..................... 9 Section. Polnomial Functions of Higher Degree.......... Section. Real Zeros of Polnomial Functions............
Pre-Calculus Module 4
 Pre-Calculus Module 4 4 th Nine Weeks Table of Contents Precalculus Module 4 Unit 9 Rational Functions Rational Functions with Removable Discontinuities (1 5) End Behavior of Rational Functions (6) Rational
Pre-Calculus Module 4 4 th Nine Weeks Table of Contents Precalculus Module 4 Unit 9 Rational Functions Rational Functions with Removable Discontinuities (1 5) End Behavior of Rational Functions (6) Rational
Introduction Direct Variation Rates of Change Scatter Plots. Introduction. EXAMPLE 1 A Mathematical Model
 APPENDIX B Mathematical Modeling B1 Appendi B Mathematical Modeling B.1 Modeling Data with Linear Functions Introduction Direct Variation Rates of Change Scatter Plots Introduction The primar objective
APPENDIX B Mathematical Modeling B1 Appendi B Mathematical Modeling B.1 Modeling Data with Linear Functions Introduction Direct Variation Rates of Change Scatter Plots Introduction The primar objective
Cubic and quartic functions
 3 Cubic and quartic functions 3A Epanding 3B Long division of polnomials 3C Polnomial values 3D The remainder and factor theorems 3E Factorising polnomials 3F Sum and difference of two cubes 3G Solving
3 Cubic and quartic functions 3A Epanding 3B Long division of polnomials 3C Polnomial values 3D The remainder and factor theorems 3E Factorising polnomials 3F Sum and difference of two cubes 3G Solving
BRAIN WORKS Direct Proportion
 BRAIN WORKS 16. California, the third largest state in the United States, has an east-west dimension of 480 km. (a) A map of California, drawn with a scale of 1 : 1,500,000, fits eactl from north to south
BRAIN WORKS 16. California, the third largest state in the United States, has an east-west dimension of 480 km. (a) A map of California, drawn with a scale of 1 : 1,500,000, fits eactl from north to south
Answer Explanations. The SAT Subject Tests. Mathematics Level 1 & 2 TO PRACTICE QUESTIONS FROM THE SAT SUBJECT TESTS STUDENT GUIDE
 The SAT Subject Tests Answer Eplanations TO PRACTICE QUESTIONS FROM THE SAT SUBJECT TESTS STUDENT GUIDE Mathematics Level & Visit sat.org/stpractice to get more practice and stud tips for the Subject Test
The SAT Subject Tests Answer Eplanations TO PRACTICE QUESTIONS FROM THE SAT SUBJECT TESTS STUDENT GUIDE Mathematics Level & Visit sat.org/stpractice to get more practice and stud tips for the Subject Test
Practice Problem List II
 Math 46 Practice Problem List II -------------------------------------------------------------------------------------------------------------------- Section 4.: 3, 3, 5, 9, 3, 9, 34, 39, 43, 53, 6-7 odd
Math 46 Practice Problem List II -------------------------------------------------------------------------------------------------------------------- Section 4.: 3, 3, 5, 9, 3, 9, 34, 39, 43, 53, 6-7 odd
Quick Review 4.1 (For help, go to Sections 1.2, 2.1, 3.5, and 3.6.)
 Section 4. Etreme Values of Functions 93 EXPLORATION Finding Etreme Values Let f,.. Determine graphicall the etreme values of f and where the occur. Find f at these values of.. Graph f and f or NDER f,,
Section 4. Etreme Values of Functions 93 EXPLORATION Finding Etreme Values Let f,.. Determine graphicall the etreme values of f and where the occur. Find f at these values of.. Graph f and f or NDER f,,
UNCORRECTED. To recognise the rules of a number of common algebraic relations: y = x 1 y 2 = x
 5A galler of graphs Objectives To recognise the rules of a number of common algebraic relations: = = = (rectangular hperbola) + = (circle). To be able to sketch the graphs of these relations. To be able
5A galler of graphs Objectives To recognise the rules of a number of common algebraic relations: = = = (rectangular hperbola) + = (circle). To be able to sketch the graphs of these relations. To be able
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
Differentiation and applications
 FS O PA G E PR O U N C O R R EC TE D Differentiation and applications. Kick off with CAS. Limits, continuit and differentiabilit. Derivatives of power functions.4 C oordinate geometr applications of differentiation.5
FS O PA G E PR O U N C O R R EC TE D Differentiation and applications. Kick off with CAS. Limits, continuit and differentiabilit. Derivatives of power functions.4 C oordinate geometr applications of differentiation.5
LESSON #24 - POWER FUNCTIONS COMMON CORE ALGEBRA II
 1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
7-1. Exploring Exponential Models. Vocabulary. Review. Vocabulary Builder. Use Your Vocabulary. 1. Cross out the expressions that are NOT powers.
 7-1 Eploring Eponential Models Vocabular Review 1. Cross out the epressions that are NOT powers. 16 6a 1 7. Circle the eponents in the epressions below. 5 6 5a z Vocabular Builder eponential deca (noun)
7-1 Eploring Eponential Models Vocabular Review 1. Cross out the epressions that are NOT powers. 16 6a 1 7. Circle the eponents in the epressions below. 5 6 5a z Vocabular Builder eponential deca (noun)
5.6 RATIOnAl FUnCTIOnS. Using Arrow notation. learning ObjeCTIveS
 CHAPTER PolNomiAl ANd rational functions learning ObjeCTIveS In this section, ou will: Use arrow notation. Solve applied problems involving rational functions. Find the domains of rational functions. Identif
CHAPTER PolNomiAl ANd rational functions learning ObjeCTIveS In this section, ou will: Use arrow notation. Solve applied problems involving rational functions. Find the domains of rational functions. Identif
Data transformation. Core: Data analysis. Chapter 5
 Chapter 5 5 Core: Data analsis Data transformation ISBN 978--7-56757-3 Jones et al. 6 66 Core Chapter 5 Data transformation 5A Introduction You first encountered data transformation in Chapter where ou
Chapter 5 5 Core: Data analsis Data transformation ISBN 978--7-56757-3 Jones et al. 6 66 Core Chapter 5 Data transformation 5A Introduction You first encountered data transformation in Chapter where ou
Differential Calculus I - - : Fundamentals
 Differential Calculus I - - : Fundamentals Assessment statements 6. Informal ideas of limits and convergence. Limit notation. Definition of derivative from first principles f9() 5 lim f ( h) f () h ( h
Differential Calculus I - - : Fundamentals Assessment statements 6. Informal ideas of limits and convergence. Limit notation. Definition of derivative from first principles f9() 5 lim f ( h) f () h ( h
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
8Revision of Chapters 1 7
 8 of hapters 7 8 Technolog-free questions State the maimal domain and range of each of the following: a f = + f = b c f = d h = e f = 5 + Find the inverse of the function with the rule f = + and sketch
8 of hapters 7 8 Technolog-free questions State the maimal domain and range of each of the following: a f = + f = b c f = d h = e f = 5 + Find the inverse of the function with the rule f = + and sketch
Derivatives of Multivariable Functions
 Chapter 0 Derivatives of Multivariable Functions 0. Limits Motivating Questions In this section, we strive to understand the ideas generated b the following important questions: What do we mean b the limit
Chapter 0 Derivatives of Multivariable Functions 0. Limits Motivating Questions In this section, we strive to understand the ideas generated b the following important questions: What do we mean b the limit
Homework Assignments Math /02 Spring 2015
 Homework Assignments Math 1-01/0 Spring 015 Assignment 1 Due date : Frida, Januar Section 5.1, Page 159: #1-, 10, 11, 1; Section 5., Page 16: Find the slope and -intercept, and then plot the line in problems:
Homework Assignments Math 1-01/0 Spring 015 Assignment 1 Due date : Frida, Januar Section 5.1, Page 159: #1-, 10, 11, 1; Section 5., Page 16: Find the slope and -intercept, and then plot the line in problems:
Graphs and polynomials
 1 1A The inomial theorem 1B Polnomials 1C Division of polnomials 1D Linear graphs 1E Quadratic graphs 1F Cuic graphs 1G Quartic graphs Graphs and polnomials AreAS of STud Graphs of polnomial functions
1 1A The inomial theorem 1B Polnomials 1C Division of polnomials 1D Linear graphs 1E Quadratic graphs 1F Cuic graphs 1G Quartic graphs Graphs and polnomials AreAS of STud Graphs of polnomial functions
New Functions from Old Functions
 .3 New Functions rom Old Functions In this section we start with the basic unctions we discussed in Section. and obtain new unctions b shiting, stretching, and relecting their graphs. We also show how
.3 New Functions rom Old Functions In this section we start with the basic unctions we discussed in Section. and obtain new unctions b shiting, stretching, and relecting their graphs. We also show how
3.2 Introduction to Functions
 8 CHAPTER Graphs and Functions Write each statement as an equation in two variables. Then graph each equation. 97. The -value is more than three times the -value. 98. The -value is - decreased b twice
8 CHAPTER Graphs and Functions Write each statement as an equation in two variables. Then graph each equation. 97. The -value is more than three times the -value. 98. The -value is - decreased b twice
ANIL TUTORIALS. Motion IMPORTANT NOTES ANIL TUTORIALS,SECTOR-5,DEVENDRA NAGAR,HOUSE NO-D/156,RAIPUR,C.G,PH
 Motion 1. Rest : When a body does not change its position with respect to time and its surroundings, the body is said to be at rest. 2. Motion : When a body continuously changes its position with respect
Motion 1. Rest : When a body does not change its position with respect to time and its surroundings, the body is said to be at rest. 2. Motion : When a body continuously changes its position with respect
13.1. For further details concerning the physics involved and animations of the trajectories of the particles, see the following websites:
 8 CHAPTER VECTOR FUNCTIONS N Some computer algebra sstems provide us with a clearer picture of a space curve b enclosing it in a tube. Such a plot enables us to see whether one part of a curve passes in
8 CHAPTER VECTOR FUNCTIONS N Some computer algebra sstems provide us with a clearer picture of a space curve b enclosing it in a tube. Such a plot enables us to see whether one part of a curve passes in
Logarithms. Bacteria like Staph aureus are very common.
 UNIT 10 Eponentials and Logarithms Bacteria like Staph aureus are ver common. Copright 009, K1 Inc. All rights reserved. This material ma not be reproduced in whole or in part, including illustrations,
UNIT 10 Eponentials and Logarithms Bacteria like Staph aureus are ver common. Copright 009, K1 Inc. All rights reserved. This material ma not be reproduced in whole or in part, including illustrations,
(x a) (a, b, c) P. (z c) E (y b)
 ( a). FUNCTIONS OF TWO VARIABLES 67 G (,, ) ( c) (a, b, c) P E ( b) Figure.: The diagonal PGgives the distance between the points (,, ) and (a, b, c) F Using Pthagoras theorem twice gives (PG) =(PF) +(FG)
( a). FUNCTIONS OF TWO VARIABLES 67 G (,, ) ( c) (a, b, c) P E ( b) Figure.: The diagonal PGgives the distance between the points (,, ) and (a, b, c) F Using Pthagoras theorem twice gives (PG) =(PF) +(FG)
Active Maths 2 Old Syllabus Strand 5
 Junior certificate HIGHER LEVEL Active Maths Old Sllabus Strand 5 πr m = - - πr Oliver Murph Contents. Functions.... Functions and Graphs...5.3 Graphs...7.4 Linear Graphs...7.5 Quadratic Graphs...9.6 Real-Life
Junior certificate HIGHER LEVEL Active Maths Old Sllabus Strand 5 πr m = - - πr Oliver Murph Contents. Functions.... Functions and Graphs...5.3 Graphs...7.4 Linear Graphs...7.5 Quadratic Graphs...9.6 Real-Life
Solutions to O Level Add Math paper
 Solutions to O Level Add Math paper 4. Bab food is heated in a microwave to a temperature of C. It subsequentl cools in such a wa that its temperature, T C, t minutes after removal from the microwave,
Solutions to O Level Add Math paper 4. Bab food is heated in a microwave to a temperature of C. It subsequentl cools in such a wa that its temperature, T C, t minutes after removal from the microwave,
Physics 30S Unit 2 Motion Graphs. Mrs. Kornelsen Teulon Collegiate Institute
 Physics 30S Unit 2 Motion Graphs Mrs. Kornelsen Teulon Collegiate Institute 1 Grade 11 Physics Graphing Properties Property d-t Graph v-t Graph a-t Graph Not Moving Does Not Apply Constant Velocity Change
Physics 30S Unit 2 Motion Graphs Mrs. Kornelsen Teulon Collegiate Institute 1 Grade 11 Physics Graphing Properties Property d-t Graph v-t Graph a-t Graph Not Moving Does Not Apply Constant Velocity Change
8 Differential Calculus 1 Introduction
 8 Differential Calculus Introduction The ideas that are the basis for calculus have been with us for a ver long time. Between 5 BC and 5 BC, Greek mathematicians were working on problems that would find
8 Differential Calculus Introduction The ideas that are the basis for calculus have been with us for a ver long time. Between 5 BC and 5 BC, Greek mathematicians were working on problems that would find
CHAPTER 3 Polynomial Functions
 CHAPTER Polnomial Functions Section. Quadratic Functions and Models............. 7 Section. Polnomial Functions of Higher Degree......... 7 Section. Polnomial and Snthetic Division............ Section.
CHAPTER Polnomial Functions Section. Quadratic Functions and Models............. 7 Section. Polnomial Functions of Higher Degree......... 7 Section. Polnomial and Snthetic Division............ Section.
SAMPLE. Exponential Functions and Logarithms
 Objectives C H A P T E R 5 Eponential Functions and Logarithms To define and understand eponential functions. To sketch graphs of the various tpes of eponential functions. To understand the rules for manipulating
Objectives C H A P T E R 5 Eponential Functions and Logarithms To define and understand eponential functions. To sketch graphs of the various tpes of eponential functions. To understand the rules for manipulating
Summary EXPLANATION AND EXAMPLES CHECKING BASIC CONCEPTS FOR SECTION 2.5. ƒ 2x - 1 ƒ 5. CHAPTER 2 Summary 157
 6360_ch0pp076-68.qd 0/6/08 4:3 PM Page 57 CHAPTER Summar 57 CHECKING BASIC CONCEPTS FOR SECTION.5. Rewrite 4 b using an absolute value.. Graph = ƒ 3 - ƒ b hand. 3. (a) Solve the equation ƒ - ƒ = 5. (b)
6360_ch0pp076-68.qd 0/6/08 4:3 PM Page 57 CHAPTER Summar 57 CHECKING BASIC CONCEPTS FOR SECTION.5. Rewrite 4 b using an absolute value.. Graph = ƒ 3 - ƒ b hand. 3. (a) Solve the equation ƒ - ƒ = 5. (b)
2.1 The Rectangular Coordinate System
 . The Rectangular Coordinate Sstem In this section ou will learn to: plot points in a rectangular coordinate sstem understand basic functions of the graphing calculator graph equations b generating a table
. The Rectangular Coordinate Sstem In this section ou will learn to: plot points in a rectangular coordinate sstem understand basic functions of the graphing calculator graph equations b generating a table
NCC Precalculus Partnership Program Final Examination, 2004
 NCC Precalculus Partnership Program Final Eamination, 2004 Part I: Answer onl 20 of the 25 questions below. Each question is worth 2 points. Place our answers on the answer sheet provided. Write the word
NCC Precalculus Partnership Program Final Eamination, 2004 Part I: Answer onl 20 of the 25 questions below. Each question is worth 2 points. Place our answers on the answer sheet provided. Write the word
Power Functions. A polynomial expression is an expression of the form a n. x n 2... a 3. ,..., a n. , a 1. A polynomial function has the form f(x) a n
 1.1 Power Functions A rock that is tossed into the water of a calm lake creates ripples that move outward in a circular pattern. The area, A, spanned b the ripples can be modelled b the function A(r) πr,
1.1 Power Functions A rock that is tossed into the water of a calm lake creates ripples that move outward in a circular pattern. The area, A, spanned b the ripples can be modelled b the function A(r) πr,
= x. Algebra II Notes Quadratic Functions Unit Graphing Quadratic Functions. Math Background
 Algebra II Notes Quadratic Functions Unit 3.1 3. Graphing Quadratic Functions Math Background Previousl, ou Identified and graphed linear functions Applied transformations to parent functions Graphed quadratic
Algebra II Notes Quadratic Functions Unit 3.1 3. Graphing Quadratic Functions Math Background Previousl, ou Identified and graphed linear functions Applied transformations to parent functions Graphed quadratic
In which row is the size of the vector equal to the size of the scalar?
 1 Each row contains a vector and a scalar. In which row is the size of the vector equal to the size of the scalar? vector displacement of a car velocity of a car velocity of a car weight of a car scalar
1 Each row contains a vector and a scalar. In which row is the size of the vector equal to the size of the scalar? vector displacement of a car velocity of a car velocity of a car weight of a car scalar
For use after the chapter Graphing Linear Equations and Functions 3 D. 7. 4y 2 3x 5 4; (0, 1) x-intercept: 6 y-intercept: 3.
 Chapter Test A Write the coordinates of the point.. A. B. D. C. A. D C B.... Tell whether the ordered pair is a solution of the equation.. ; (, ) 7.. ; (, ). 7. ; (, ). Draw the line that has the given
Chapter Test A Write the coordinates of the point.. A. B. D. C. A. D C B.... Tell whether the ordered pair is a solution of the equation.. ; (, ) 7.. ; (, ). 7. ; (, ). Draw the line that has the given
Exponential, Logistic, and Logarithmic Functions
 CHAPTER 3 Eponential, Logistic, and Logarithmic Functions 3.1 Eponential and Logistic Functions 3.2 Eponential and Logistic Modeling 3.3 Logarithmic Functions and Their Graphs 3.4 Properties of Logarithmic
CHAPTER 3 Eponential, Logistic, and Logarithmic Functions 3.1 Eponential and Logistic Functions 3.2 Eponential and Logistic Modeling 3.3 Logarithmic Functions and Their Graphs 3.4 Properties of Logarithmic
Review Sheet for Second Midterm Mathematics 1300, Calculus 1
 Review Sheet for Second Midterm Mathematics 300, Calculus. For what values of is the graph of y = 5 5 both increasing and concave up? >. 2. Where does the tangent line to y = 2 through (0, ) intersect
Review Sheet for Second Midterm Mathematics 300, Calculus. For what values of is the graph of y = 5 5 both increasing and concave up? >. 2. Where does the tangent line to y = 2 through (0, ) intersect
y=5 y=1+x 2 AP Calculus Chapter 5 Testbank Part I. Multiple-Choice Questions
 AP Calculus Chapter 5 Testbank Part I. Multiple-Choice Questions. Which of the following integrals correctly corresponds to the area of the shaded region in the figure to the right? (A) (B) (C) (D) (E)
AP Calculus Chapter 5 Testbank Part I. Multiple-Choice Questions. Which of the following integrals correctly corresponds to the area of the shaded region in the figure to the right? (A) (B) (C) (D) (E)
3.2. Properties of Graphs of Quadratic Relations. LEARN ABOUT the Math. Reasoning from a table of values and a graph of a quadratic model
 3. Properties of Graphs of Quadratic Relations YOU WILL NEED grid paper ruler graphing calculator GOAL Describe the ke features of the graphs of quadratic relations, and use the graphs to solve problems.
3. Properties of Graphs of Quadratic Relations YOU WILL NEED grid paper ruler graphing calculator GOAL Describe the ke features of the graphs of quadratic relations, and use the graphs to solve problems.
Chapter Nine Chapter Nine
 Chapter Nine Chapter Nine 6 CHAPTER NINE ConcepTests for Section 9.. Table 9. shows values of f(, ). Does f appear to be an increasing or decreasing function of? Of? Table 9. 0 0 0 7 7 68 60 0 80 77 73
Chapter Nine Chapter Nine 6 CHAPTER NINE ConcepTests for Section 9.. Table 9. shows values of f(, ). Does f appear to be an increasing or decreasing function of? Of? Table 9. 0 0 0 7 7 68 60 0 80 77 73
Section 4.1 Increasing and Decreasing Functions
 Section.1 Increasing and Decreasing Functions The graph of the quadratic function f 1 is a parabola. If we imagine a particle moving along this parabola from left to right, we can see that, while the -coordinates
Section.1 Increasing and Decreasing Functions The graph of the quadratic function f 1 is a parabola. If we imagine a particle moving along this parabola from left to right, we can see that, while the -coordinates
Review of Essential Skills and Knowledge
 Review of Essential Skills and Knowledge R Eponent Laws...50 R Epanding and Simplifing Polnomial Epressions...5 R 3 Factoring Polnomial Epressions...5 R Working with Rational Epressions...55 R 5 Slope
Review of Essential Skills and Knowledge R Eponent Laws...50 R Epanding and Simplifing Polnomial Epressions...5 R 3 Factoring Polnomial Epressions...5 R Working with Rational Epressions...55 R 5 Slope
1. For each of the following, state the domain and range and whether the given relation defines a function. b)
 Eam Review Unit 0:. For each of the following, state the domain and range and whether the given relation defines a function. (,),(,),(,),(5,) a) { }. For each of the following, sketch the relation and
Eam Review Unit 0:. For each of the following, state the domain and range and whether the given relation defines a function. (,),(,),(,),(5,) a) { }. For each of the following, sketch the relation and
1.1 Motion and Motion Graphs
 Figure 1 A highway is a good example of the physics of motion in action. kinematics the study of motion without considering the forces that produce the motion dynamics the study of the causes of motion
Figure 1 A highway is a good example of the physics of motion in action. kinematics the study of motion without considering the forces that produce the motion dynamics the study of the causes of motion
Chapter 8 Notes SN AA U2C8
 Chapter 8 Notes SN AA U2C8 Name Period Section 8-: Eploring Eponential Models Section 8-2: Properties of Eponential Functions In Chapter 7, we used properties of eponents to determine roots and some of
Chapter 8 Notes SN AA U2C8 Name Period Section 8-: Eploring Eponential Models Section 8-2: Properties of Eponential Functions In Chapter 7, we used properties of eponents to determine roots and some of
and y f ( x ). given the graph of y f ( x ).
 FUNCTIONS AND RELATIONS CHAPTER OBJECTIVES:. Concept of function f : f ( ) : domain, range; image (value). Odd and even functions Composite functions f g; Identit function. One-to-one and man-to-one functions.
FUNCTIONS AND RELATIONS CHAPTER OBJECTIVES:. Concept of function f : f ( ) : domain, range; image (value). Odd and even functions Composite functions f g; Identit function. One-to-one and man-to-one functions.
y=5 y=1+x 2 AP Calculus Chapter 5 Testbank Part I. Multiple-Choice Questions
 AP Calculus Chapter 5 Testbank Part I. Multiple-Choice Questions. Which of the following integrals correctly corresponds to the area of the shaded region in the figure to the right? (A) (B) (C) (D) (E)
AP Calculus Chapter 5 Testbank Part I. Multiple-Choice Questions. Which of the following integrals correctly corresponds to the area of the shaded region in the figure to the right? (A) (B) (C) (D) (E)
PART A: Answer in the space provided. Each correct answer is worth one mark each.
 PART A: Answer in the space provided. Each correct answer is worth one mark each. 1. Find the slope of the tangent to the curve at the point (,6). =. If the tangent line to the curve k( ) = is horizontal,
PART A: Answer in the space provided. Each correct answer is worth one mark each. 1. Find the slope of the tangent to the curve at the point (,6). =. If the tangent line to the curve k( ) = is horizontal,
Pre-Calculus First Semester Review
 NON CALCULATOR Pre-Calculus First Semester Review Unit 1: 1 37 Unit : 1 18, 38 49 Unit 3: 19,, 5 6 [1.] Find the domain. Epress the answer in interval notation. 1. f( ) log ( 5) = +. 3 f( ) = 7 + 4 [1.]
NON CALCULATOR Pre-Calculus First Semester Review Unit 1: 1 37 Unit : 1 18, 38 49 Unit 3: 19,, 5 6 [1.] Find the domain. Epress the answer in interval notation. 1. f( ) log ( 5) = +. 3 f( ) = 7 + 4 [1.]
Reteaching -1. Relating Graphs to Events
 - Relating Graphs to Events The graph at the right shows the outside temperature during 6 hours of one da. You can see how the temperature changed throughout the da. The temperature rose F from A.M. to
- Relating Graphs to Events The graph at the right shows the outside temperature during 6 hours of one da. You can see how the temperature changed throughout the da. The temperature rose F from A.M. to
Study Guide and Intervention
 6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
Bridge-Thickness Experiment. Student 2
 Applications 1. Below are some results from the bridge-thickness eperiment. Bridge-Thickness Eperiment Thickness (laers) Breaking Weight (pennies) 15 5 5 a. Plot the (thickness, breaking weight) data.
Applications 1. Below are some results from the bridge-thickness eperiment. Bridge-Thickness Eperiment Thickness (laers) Breaking Weight (pennies) 15 5 5 a. Plot the (thickness, breaking weight) data.
v t t t t a t v t d dt t t t t t 23.61
 SECTION 4. MAXIMUM AND MINIMUM VALUES 285 The values of f at the endpoints are f 0 0 and f 2 2 6.28 Comparing these four numbers and using the Closed Interval Method, we see that the absolute minimum value
SECTION 4. MAXIMUM AND MINIMUM VALUES 285 The values of f at the endpoints are f 0 0 and f 2 2 6.28 Comparing these four numbers and using the Closed Interval Method, we see that the absolute minimum value
