Lecture Notes for Topics in Calculus Math 176
|
|
|
- Ira Cunningham
- 5 years ago
- Views:
Transcription
1 Lecture Notes for Topics in Calculus Math 176 Oscar Levin Fall 2011
2 Math 176 Lecture Notes August 22, Functions and Change 1.1 What is a Function? So what is a function anyway? Let s play a game: you say a number, and I will respond with a number. (my number will be one more than twice yours). What am I doing? Write a lits of inputs and outputs. Can we figure out a formula? This is a function. There are inputs (the domain) and outputs (the range). The key thing is, for a given input, there is one and only one possible output. Other examples of functions: the daily high temperature. A person s bear number. But not a person s phone number (why not?). It is okay if two different inputs have the same output. But not the other way around. How to represent a function: There are four ways: 1. With a table - we did this when we were collecting data. What does the uniqueness of the output mean here? 2. With a formula - we found one for the function above. What do the variables mean. What about y = f(x) notation? 3. With a graph - Let s graph the function we used above. The inputs will be numbers on the horizontal axis, the outputs numbers on the vertical axis. Put a dot where the input has a corresponding output. What pictures count (vertical line test). 4. In words - how would you describe the function in our example? Function notation - Instead of y = 2x + 1, we will often give the function a name, f. We write: y = f(x). So f(x) = 2x + 1. The advantage is we can no write things like f(3). What is that? Ex: The remaining principal of my mortgage P is a function of the number of payments I have made. So P = g(t), where t is the number of payments I have made. What does g(3) = 175 mean? What are the units here? What is the meaning of g(10)? Intercepts - the intercepts of a function are the inputs or outputs for which the other is zero. So where the graph crosses one of the axis. What would the intercepts be for the mortgage example above? What do they mean? Increasing/Decreasing. If you look at a graph, some might be increasing, other s decreasing. We always read from left to right. We say that the function f is increasing if the values of f(x) increase as x increases. 2
3 Math 176 Lecture Notes August 22, 2011 What would the definition of f is decreasing be? The values of f(x) decrease as x increases. Is the mortgage function above an increasing or decreasing function? 3
4 Math 176 Lecture Notes August 24, Linear Functions You may remember that the equation of a line is y = mx + b. We now think of y as a function of x, and get linear functions. Ex. Suppose a certain college charges $2750 if you take 5 credits, and $3950 if you take 9 credits. How much would 15 credits cost? Let s first find a function f(x) which gives the cost of taking x credits. What do the slope and vertical intercepts represent? This example was given in words. But of course we could start with any of the four ways to represent a function. A table: Find the equation that fits the data: line. x f(x) Then graph the What if we start with a graph of a line. We can do a random example. If we start with an equation, we should be able to draw a graph, create a table, or describe the situation (with some context provided). Ex. Suppose the trash company charges C(x) = x, where x is the number of extra bins you dispose of per period. Graph, and interpret the slope and intercepts. The thing to remember here is that to find a linear function, we need to know the slope and vertical intercept, or the slope and one point, or two points. If we have two points (x 1, f(x 1 )) and (x 2, f(x 2 )), we can find the slope by: m =. That is, rise over run. f(x 2 ) f(x 1 ) x 2 x 1 Once you have the slope, you can use the vertical asymptote b to get f(x) = b + mx or use the y y 1 = m(x x 1 ) and then solve for y. Ex. You rent out a empty retail space for $300 a week to teach Zumba. You charge $20 per person. Express your income as a function of the number of clients. How many people do you need to teach to break even? Not all functions are linear! How do you tell the difference? For example, which of the following functions could be linear? x f(x) The first and third are, the second is not. x f(x) x f(x)
5 Math 176 Lecture Notes August 26, 2011 Note on the quiz: Don t forget, f(1000) = 3500 is read f of 1000 is You cannot separate the f and the On the graph, remember a graph is giving you a LOT of points - it shows how one variable changes when the other one does. 1.3 Average Rate of Change Understanding change is crucial to recognizing trends. Sometimes it is possible to find the exact rate of change in a function. But for more chaotic functions, we can still calculate the rate of change on average. Ex: The table below shows the closing stock price of MSFT during the first week of August, Find the average rate of change in price over the week. Date: Price: (Average rate of change: change in price over change in time: = 0.292) This example shows how to calculate avg. rate of change when presented with data. We could also start with on of the other 3 ways to represent a function. Ex: Suppose your number of sales S in a particular month is a function of the amount a you spend on advertising. You find that S = f(a) = a. What is the average rate of change in sales with respect to dollars spent on ads between a = 0 and a = 10? What are the units? Perhaps it is surprising that the answer to the above question is just 3, the slope. But look at how you compute average rate of change! It s the change in y over the change in x. The difference is - slope can only be computed for functions which are linear. We can compute the average rate of change for any function. Graphically: Start with a graph representing population with respect to time. Find the average rate of change from t = 2 to t = 5. This is like a slope, but the slope of what? The secant line! A special case: Suppose you drive from Denver to Greeley. You pass the Loveland exit (240) at 3:00pm, and take the Greeley exit (257) at 3:15. What was the average rate of change in your distance with respect to time. In other words, what was your average velocity? (17/.25 = 68) What do graphs with positive avg rate of change look like? What if the avg rate of change is increasing? Discuss concave up/concave down. 5
6 Math 176 Lecture Notes August 29, Applications to Economics Cost, Revenue and Profit Cost function, Revenue function. They are functions of q, the production level. What is the profit function? How do you determine the break-even point? Profit is zero, so revenue and cost are equal. What does this look like on a graph? Fixed cost and marginal cost. The marginal cost is the cost to produce the next item. We can also consider marginal revenue and marginal profit. If you have a linear cost function, what do the fixed cost and marginal cost represent graphically? Ex: You start a business making friendship bracelets. You have $100 in startup costs, and materials cost $3 for each bracelet. You sell the bracelets for $10 each. Find the cost, revenue and profit functions. Find the marginal cost, revenue and profit. How many bracelets do you need to sell to make a profit? Budget Constraint Suppose you budget $30 per week to be spent on coffee and tacos. Each cup of coffee costs $3 and each taco costs $2. Create an equation for the budget constraint. Graph. What are the intercepts, and what do they represent? Supply and Demand What do demand curves and supply curves look like? On the graph, the horizontal axis measures q (quantity) and the vertical axis p (price). Note this is an odd carryover from olden days. Should the demand curve be increasing or decreasing? What about supply. The equilibrium point is the point (q, p ) (the equilibrium quantity and price) for which supply and demand are equal. On the graph, the two curves cross at this point. We assume the market natural settles on this point. Say the supply curve passes through the point q = 20, p = 5. What does this mean? What if the demand curve passes through the point q = 20, p = 7? What will happen? Ex: Suppose the demand curve is give by q = 150 3p and the supply is given by q = 4p 60. Find the equilibrium quantity and price. Then what if the government charged the company a tax of $7 per item sold. What is the new equilibrium. Note that this will change the supply equation to q = 4(p 7) 70, since the company is making $7 less for each item. (The new equilibrium price is $34.) 6
7 Math 176 Lecture Notes August 31, Exponential Functions Earlier we saw how to represent a function when the y-values were increasing by a constant amount as x-increased. Now we consider functions whose y-values increase at a constant percentage rate. Ex: You start a mosquito breading business with 500 bugs. Find a formula for the number of mosquitoes after t weeks if the population increases at a rate of 40 mosquitoes per week. Then find a formula if the population increases by 5% per week. In general, we say P (t) is an exponential function of t with base a if it has the form P = P 0 a t P 0 is the initial quantity (t = 0). If we let a = 1+r, then r is the decimal representation of the percent rate of change. If a > 1 (so r is positive), then the function represents exponential growth. If a < 1, so r < 0, we have exponential decay. Ex: After taking a particular drug, the amount remaining in the body decays at a rate of 20% per hour. If you take 500mg at noon, how much of the drug is in your body at 5pm? (P = ) What does a graph of exponential growth look like? Note that it is increasing and concave up. The graph of exponential decay is decreasing (obviously) put also concave up. If you know a function is exponential, you can find an equation from two data points. Ex: Suppose your bracelet sales are increasing exponentially. Your initial sales figures were 20 bracelets. Ten sales later, you are up to 50. What is the percentage rate of growth per sale? ( 10 5/2 = 1.096) How do you recognize exponential functions? With linear functions, we looked for constant rate of change. For exponential, we seek constant percentage (relative) rate of change. Ex: Which of the following tables could represent linear functions? Which are exponential? x x x f(x) f(x) f(x)
8 Math 176 Lecture Notes September 2, The Natural Logarithm Our goal: solve equations like 100 = t. In other words, how long will it take for $3 to increase to $100 at a 10% interest rate? We need a way to rescue the t from the exponent. Enter ln x. The function ln x tells us what power of e (the number) is needed to get x. So ln x = c means e c = x. For example, since e , what is ln 20.09? Note that ln x is only defined for positive values of x, since e c is always positive. To use ln to solve equations, we need to know 5 properties of logarithms: 1. ln(ab) = ln A + ln B 2. ln ( A B ) = ln A ln B 3. ln(a p ) = p ln(a) 4. ln(e x ) = x (obvious?) 5. e ln x = x Note: ln 1 = 0 and ln e = 1 Ex: Now let s see how this works. We solve 100 = t. First get the 1.1 t by itself: = 1.1 t Take ln of both sides (not multiplication!). We get ln(33.33) = ln(1.1 t ). Use property 3: ln = t ln 1.1 Use a calculator: = t Now solve for t We get t = Let s try some others. Solve for t: 16 = 2 t. What about 20 = e 4t. Continuous growth In calculating interest, the formula P = P 0 a t is for interest compounded annually (or whatever the units of t are). If you want the interest to be compounded continuously, you use the formula P = P 0 e kt. k is the rate. We can use ln to convert between these. Ex: Convert the function P = t to the form P = P 0 e kt. (k = 0.049) Ex: Convert the function P = 120e.2t to the form P = P 0 a t. (a = 0.82) Note that the rate for continuous growth is smaller than the rate for annual growth, although they produce the same values. Compounding continuously works! The rate for continuous decay (20%) is larger than the rate for annual decay (18%). 8
9 Math 176 Lecture Notes September 7, Exponential growth and decay Today we will wrap up our discussion of exponential functions with a few applications. Half-life and Doubling time The half-life of a decaying substance is the time it takes for only half of the substance to remain. Similarly, the doubling time is the time it takes for a growing quantity to double. Ex: What is the doubling time for a savings account with 4% interest, compounded continuously? Note that it does not matter what the starting amount is. We get t = ln(2)/ Heard of the Rule of 70? For small interest rates r, the doubling time is close to 70/r. Note 70/4 = You try one: If a substance decays at a continuous rate of 25%, what is the half-life? Ex: We can go the other way: if a savings account promises to double your money in seven years, what interest rate are they offering? (9.9%) Ex: Suppose the half life of a material is 6 years. If you have 80 grams of the substance today, how much will you have in 30 years? Present and Future Value Ex: Would you rather get $50,000 today, or $18,000 after each of the next three years? Ignore taxes and assume 4% interest rate, compounded continuously. Compare present values. Compare future values. The future value of the $50,000 is $56,374. The future value of the 3 payments are = $ The present value is $50,000 for the first option. To calculate the present value of the first payment, we ask what we would need to deposit today to get $18,000 after one year. Note that if F V = P V e.04 then P V = F V/e.04 So the first has a present value of , the second s PV is and the third s is All together: $
10 Math 176 Lecture Notes September 9, New Functions from Old Today we learn how to combine and modify functions. We start with... Composite functions Ex: Suppose the cost to produce q items is given by C(q) = 5q Now suppose the number of items produced is a function of time: q(t) = 10e.2t. Can we write a function which tells us our cost at any time t? This is an example of composite functions. If you plug-in one function into another, you get a composite function. Ex: Let f(x) = x and g(x) = e 4x. Find f(g(x)). Find g(f(x)). Find f(f(f(x))). What is f(g(0))? Ex: Find f(g(0)), g(f(0)), f(f(0)), and g(g(1)) using the table below. What is f(0)g(0)? x f(x) g(x) Ex: Find function f(x) and g(x) so that the f(g(x)) = e 3x2. Then f(g(x)) = 3(e x +2) 4. Stretches and flips and shifts Other things we can do with functions: multiply by a constant, add or subtract a constant. We can do this to the whole function, or just to the input. What is the relationship between f(x) and 3f(x)? What about 3f(x), f(x)/3, and f(3x)? all of these stretch or squish the function, or flip it over. We can also shift the function by adding or subtracting. If we want to shift the function up and down we need to add or subtract from the y-values. Thus we shift up with f(x) + k and down with f(x) k. Ex: Shift f(x) = x 2 up three units. What does f(x) = 4 x 2 look like? To shift left or right, we need to add or subtract from the x-value. So f(x k) shifts to the right, and f(x + k) to the left. Ex: What is the equation for a standard parabola with vertex at the point (3, 5), opening upward? Draw a function, and then another copy somewhere else. How do you get from one to the other? 10
11 Math 176 Lecture Notes September 12, Proportionality and Power Functions Proportionality The idea: if two quantities are proportional, as one grows, then so does the other. To be more precise, if y is proportional to x, then y = kx where k is the constant of proportionality. If x decreases as y increases, then we say y is inversely proportional to x, and have y = k/x for constant k. Ex: The amount my dog is overweight is proportional to the number of treats I give him. So W = kt. Now suppose that if I give him 10 treats, he is 2 lbs overweight. Can we find k? Yes. Note that our definition of proportionality is a little more rigorous that average usage. It would be wrong to say that grade point average is proportional to the number of hours studied. What about the relationship between area of a circle and its radius? In this case, the area is proportional to the square of the radius. Ex: In physics, the force due to gravity between two objects is inversely proportional to the square of the distance between the objects. What does this equation look like? Power Functions A power function is any function of the form Q(x) = k x p. That is, Q(x) is proportional to some power (p) of x. Often power functions wear disguises. Write these in the form k x p : 4/x 2, 3 x/2, 5(3x 4 ) 2, 3x 2 4x 5, etc. Graphs of power functions? End behavior? Polynomials A polynomial is the sum of power functions. For example, x 2 + 4x 2. Yes, 2 is a power function (what is p?). We will see quadratic functions (polynomials of degree 2) quite a bit. For example... Ex: Suppose the demand for a particular product is linear and such that the company will sell 20 items at a price of $100, and 30 items at a price of $80. Find a function for demand, and then use that to find the revenue function (R = pq - we have q(p) so substitute). Then use the graph to find the quantity that maximizes profit. (p = 70). 11
12 Math 176 Lecture Notes September 14, Rate of Change: The derivative 2.1 Instantaneous Rate of Change Velocity: What is speed? What does it mean to say that after 2 minutes, my car was going 34 mph? We start with an example to illustrate the relationship between average and instantaneous velocity. A bike travels along a straight line. Every second, the total distance traveled is recored: time (s) distance (ft) How fast was the bike traveling? On average? When t = 2? To get a better estimate: t d From this data we can find the average velocity over various time intervals: time interval [2,3] [2, 2.5] [2,2.4] [2, 2.3] [2,2.2] [2, 2.1] avg velocity What is the instantaneous velocity at t = 2? In other words, let d = f(t). Average velocity on the interval [2, t] is: What happens as t 2. f(t) f(2) t 2 Rate of Change We can do the same thing to compute instantaneous rate of change. Ex: Suppose your rabbit population is given by P = 20e.2t. Approximate the instantaneous rate of change at the start of the 3rd year. We take (P (3.01) P (3))/(3.01 3). This is approx What are the units? Meaning? Compare with the growth rate of 20%. Let s give this a name: The derivative of f at a, written f (a) is defined to be the instantaneous rate of change of f at the point a. What does this process look like graphically? Note that we are computing slopes. But slopes of what? Draw a curvy graph and represent the average rate of change and derivative graphically. The derivate at a is the slope of the line tangent to f at that point. We will usually just say that f (a) is the slope of f at a. Ex: Draw the graph of a function f. What can we deduce about f (a) for various points a. 12
13 Math 176 Lecture Notes September 16, The Derivative Function We should all now know how to approximate f (a) for a given function f at a given point a. Now we see what happens if we let a vary. Ex: Let s investigate f (a) for different values of a when f(x) = x 2 + 3x. In groups, approximate f (a) - write the results up on the board. What does this data suggest. Could we give a rule that tells us what f (a) is in terms of a? This is an example of the derivative function. It is a function which tells you the slope of a curve at any point. That is, you give it an x value, it spits out the slope of f at that point. In other words, f (x) is a function which gives the (instantaneous) rate of change of f at any x. Although we will not learn how to find a formula for f (x) for a couple of weeks, we can still approximate it, especially graphically. Ex: Draw a function f made out of line segments. From this, draw a graph of the derivative. Ex: Repeat with a smooth curvy graph. Ex: Repeat with an exponential graph. Knowing information about the derivative is helpful! What if the f is positive on an interval? Then f must be increasing. If f is negative, then f is decreasing. If f = 0, then f is constant. 13
14 Math 176 Lecture Notes September 19, Interpretations of the Derivative Introduce Leibniz notation: f (x) = dy dx y x. When evaluating the derivative at a point, we write f (2) or dy dx x=2 This notation helps us to interpret the derivative in real world terms. Ex: Let C = f(q) be the cost of producing q items. Interpret the statements f(100) = 500 and f (100) = 2. Ex: Suppose P (t) gives the population of a town in thousands t years after Interpret the statements f(5) = 200 and f (5) = 6. Then approximate the number of people living in the town in Ex: If f(t) gives the number of barrels of oil spilled per day in the gulf t days after the oil rig failed, what do f(100) = 2700 and f (100) = 300 mean? Approximate f(101). Note that we are using the derivative f (a) to approximate values of f near x = a. What are we really doing here? The Local Linear Approximation of a function f(x) for values near x = a is f(x) f(a) + f (a)( x) where x = x a. This works because y f (x) x. Ex: Last time we guessed that if f(x) = x 2 + 3x, then f (x) = 2x + 3. Use this to approximate f(4.1). Relative rate of change So far, we have considered the rate of change as the number increase per unit. What if we want the percentage increase? The relative rate of change of y = f(t) at t = a is defined to be f (a)/f(a). Ex: Suppose the profit from selling a x items is given by P (x). If P (100) = 50 and P (100) = 2, find the relative rate of change and give its meaning. Ex: If the population of rabbits is given by P (t) = t, what is P (5)? Note that P (5)/P (5) should be But P (5) = So P (5) = =
15 Math 176 Lecture Notes September 21, The Second Derivative Recall when we discussed the shape of graphs, we talked about increasing/decreasing. But also about concavity. Draw a graph which is increasing and concave up. Draw a graph which is increasing and concave down. What can we say about the derivative of these two functions? Since the functions are increasing, the derivatives must be positive. However, when f is concave up, the derivative is increasing itself. So its derivative must be positive. Visa versa for when f is concave down. The derivative of the derivative... this is called the second derivative of f. We write the second derivative as f (x) or d2 y dx 2 which is really d dx ( dy dx ) To reiterate: if f > 0 on an interval, then f is concave up (and f is increasing) If f < 0 on an interval, then f is decreasing, so f is concave down. Ex: Draw a graph and mark some points. Say whether f, f and f are positive, negative or zero at those points. What does the second derivative mean? If f gives the distance traveled, then f gives the velocity. f gives the rate at which the velocity is changing - i.e., the acceleration. A note about linear approximation: If f is concave up, then the tangent line is below the graph. So a linear approximation is an underestimate. Ex: Suppose f(50) = 100 and f (50) = 4 and f (50) > 0. Approximate f(51). Is it an over or under estimate? Say what all these mean if f(t) gives the number of website hits t days after launch. 15
16 Math 176 Lecture Notes September 23, Marginal Cost and Revenue We have already encountered marginal cost and revenue when we discussed linear functions. They were the slope of the lines. The marginal cost (revenue) is the cost to produce (revenue generated by) the next item. In other words, it is the rate at which the cost (revenue) is changing. In other words, marginal cost MC is the derivative of cost C. Similarly MR = R. Ex: Suppose C(100) = 4000, C (100) = 50, R(100) = 5000 and R (100) = 75. What do all these mean in practical terms? What is the profit for producing 100 items. Approximately, what is the profit of producing 101 items? Should you increase or decrease production? The above example is one of marginal analysis - use the marginal cost/revenue to analyze whether production should be increased. Ex: Graphically: graph a wavy cost function and linear revenue function. (The cost function starts concave down, then concave up.) Where is the break even point? For which intervals are you losing money or making money? At a point just right of the break even point, what does the marginal analysis say to do? 16
17 Math 176 Lecture Notes September 30, Shortcuts to Differentiation 3.1 Powers and Polynomials From the graphs: What is the derivative of a constant function f(x) = c? What is the derivative of a linear function f(x) = mx + b? Now what about power functions? The rule: if f(x) = x n, then f (x) = nx n 1. This works for any real number n. Ex: Find the derivatives of: f(x) = x 5, f(x) = x, f(x) = x 3.2, f(x) = 1 x Exponential and Logarithmic Functions What is the derivative of 3 x? Note we can not use the power rule. Recall when we graphed exponential functions and their derivatives, the derivative graphs was basically the same. In fact, if f(x) = e x, then f (x) = e x. This works only for the base e. If f(x) = a x, then f (x) = ln(a) a x. Ex: Find f : f(x) = 3 x. f(x) = e 2x. For this second one, we can write e 2x as (e 2 ) x. Then f = ln(e 2 )(e 2 ) x = 2e 2x This suggests the rule: If f(x) = e kx, then f (x) = ke kx. For example? For logs: If f(x) = ln(x), then f (x) = 1 x. Combining functions If you multiply a function by a constant, what happens to the derivative? The rule: (c f(x)) = c f (x). If you add two functions, what happens to the derivative? The rule: (f(x) + g(x)) = f (x) + g (x). Ex: Find f : f(x) = 4x 5 3e x + 7. f(x) = 5 x + x 5 ln(x) Ex: Some harder ones: Find f : f(x) = x2 +x 3 x 4. Ex: Find the equation of the line tangent to y = x 3 + x + 1 at the point (2,11). Ex: If C(q) = q q + 10, find the marginal cost for the production level 5. 17
18 Math 176 Lecture Notes October 3, The Chain Rule Today we learn how to find the derivative of composite functions. Ex: Suppose the cost of producing rabbit skins is given by C(q) = 3q 2 + 5q Additionally, the number of rabbit skins available to produce is a function of time: q(t) = 30e.2t. Find the rate in dollars per month at which your cost is changing at the start of the 6th month. (q(6) 100 and q (6) 20 C (100) = 605, = Hopefully it is clear that multiplying is the correct thing to do above. This leads us to believe the Chain Rule: [f(g(x)] = f (g(x)) g (x) Or if y = f(z) and z = g(x): dy dx = dy dz dz dx The trick is to find which function is f and which is g. Ex: Find the derivatives of the following functions. 1. f(x) = (x 2 + 1) 5 2. f(x) = (e x + ln(x)) 3. f(x) = e x2 +x 4. f(x) = ln(4x 3 ) 5. f(x) = 3 e x +x f(x) = e 3 ln(x) 7. f(x) = 50(e x2 + (e x ) 2 ) 8 18
19 Math 176 Lecture Notes October 5, The Product and Quotient Rules Today we learn how to find the derivative of functions which are formed by taking a product or quotient of two simpler functions. The product rule: (f g) = f g + f g The quotient rule: ( f g ) = f g f g g 2 Work a bunch of examples. 19
20 Math 176 Lecture Notes October 10, Using the Derivative 4.1 Local Maxima and Minima A function has a local maximum at the point x = p if f(p) is greater than or equal to all values of f near p. Local minimum is defined similarly. We have already noticed that if f has a local maximum or minimum at a point p, then f (p) = 0. We call points p for which f (p) = 0 (or f (p) does not exist) critical points. corresponding y-values (f(p)) are called critical values. The Since the only points at which a function can have a max/min are critical points (or endpoints) the first step in finding max and min points is to locate the critical points. Once you find a critical point, how do you know if it is a max, a min, or neither (how is it possible that it is neither?). You use either the first or second derivative tests: First derivative test: Suppose p is a critical point of f then, reading left to right: 1. If f changes from increasing to decreasing at p, then f has a local max at p. 2. If f changes from decreasing to increasing at p, then f has a local min at p. Second derivative test: Suppose p is a critical point of f. 1. If f is concave up at p, then f has a local min at p. 2. If f is concave down at p, then f has a local max at p. Why are these called the first and second derivative tests? Increasing/decreasing is determined by the first derivative! The second derivative tells us whether f is concave up or down. Ex: Find local max/min for f(x) = 3x 4 4x 3 36x First us the first derivative test (sign chart). Then check your work using the second derivative test. Ex: Find local max/min: f(x) = x 4 4x 3. Ex: Give the graph of f and use it to find the local maximum of f. Ex: Below is a table which gives the values of f (not of the original function f). Find the critical points and classify them as max/mins. x f (x)
21 Math 176 Lecture Notes October 12, Inflection Points An inflection points is a x-value p at which f changes concavity. Draw a picture - label the inflection points. Ex: Find the inflection points of f(x) = 3x 4 4x 3 36x To do this, note that we are looking for points at which the graph goes from concave down to concave up. So where the second derivative changes from positive to negative. What does an inflection point signify? Draw a graph for cost - increasing, first concave up, then concave down. The inflection point is the value at which costs are increasing the fastest. Note that an inflection point of f is a critical point of f. If fact, the inflection points of f are the local min/max points of the derivative f. Ex: Draw a graph of f. Find the location of the local max/mins of f, as well as the inflection points of f. Ex: Find the local max/min and inflection points of f(x) = xe x. 21
22 Math 176 Lecture Notes October 14, Global Maxima and Minima A graph can have many local max/min points. If we look for the largest and smallest of all these, we get the global max/min. Where can a global max or min occur. Draw some pictures. Note that some functions do not have global maxima and/or minima. However, if we look at the function on a closed interval, these points must exist. In fact, a continuous function on a closed interval achieves its maximum or minimum value at either a critical point or one of the endpoints. This suggests a method for finding global maxima and minima: find the critical points and end points. Then test each to see which is largest and smallest. Ex: Find the absolute max/min of: 1. f(x) = x 3 3x on the interval 1/2 x f(x) = x 3 6x 2 + 9x + 2 on [ 1, 4]. 22
23 Math 176 Lecture Notes October 17, Profit, Cost, and Revenue We have already seen that to maximize profit, you should equate marginal cost and marginal revenue. That is, the largest gap between revenue and cost occurs when the slopes of the cost and revenue function are equal. Illustrate this on a graph. Of course, profit is simply revenue minus cost. So we can also use our calculus techniques to maximize this profit function. To find the (global) maximum of the profit function, first find the critical points - points at which the derivative is zero. Also consider end points (0 and your maximum production level). Ex: Suppose R(q) = 200q and C(q) = q 2. Find the production level that maximizes profit. What is the maximum profit? (P (50) = 4500). Ex: Your friendship bracelets cost $4 each to make, after a start-up cost of $50. You sell them for $10 a piece. You can make up to 100 before your fingers give out. What production level maximizes profit? Maximizing Revenue Sometimes cost is not relevant - for example, 100% of costs are fixed. In this case, you want to simply maximize revenue. Of course price can depend on quantity, so we might have to do some work to find the revenue function to maximize. Ex: If you charge $10 for admission to your haunted corn maze, you will attract 300 people per night. For ever increase of $2 in ticket prices, you will loose 30 customers. What ticket price maximizes revenue? (R(p) = 15p p so p = 15 will maximize revenue.) 23
24 Math 176 Lecture Notes October 19, Average Cost Given a cost function C(q), we can compute the average cost a(q) by C(q)/q. What are the units of a(q)? Note that although it is $ per item, the same as marginal cost, average cost is not the same as marginal cost. Ex: The cost of producing q items is C(q) = q + q 2. What is the average cost of producing 50 items? (a(50) = 63) What happens to the average cost if we increase production? This depends on the shape of the cost function. What if C = q? As production increases, average costs decrease. We would like to minimize average cost. We know how to minimize a function. Ex: For the example above, what production level minimizes average cost? (q = 20). What is the average cost at that point? What is the marginal cost at that point? Notice, at the point where average cost is minimized, the average cost is actually equal to the marginal cost. Does this make sense? Yes. Suppose at a product level of 100 units, the average cost is $5 per unit. What happens to the average cost if marginal cost is (a) $1 or (b) $10? Picture this on a graph - draw a wavy cost function. The average cost is the slope of the line from the origin to the point. The marginal cost is the slope of the tangent line at that point. Where on the graph is average cost minimized? Note that at such a point, the tangent line goes through the origin. Ex: Make up a random cost function and find marginal cost, average cost, and the minimal average cost. 24
25 Math 176 Lecture Notes October 21, Elasticity of Demand The idea: we would like a number which informs us about the relationship between change in price and change in demand. For example, if we increase the price by $5, how does that decrease demand? Say by 20 units. But to compare these, we should really view them in the context of the current price and current demand. (Maybe 20 units is a very small percentage of the current demand.) So we really want to compare the percent change in price with the percent change in demand. That is, how does p/p compare to q/q? To make this into one number, we take the ratio and call it the elasticity of demand: E q/q p/p = p q q p We can find it exactly with a derivative: E = p q dq dp. Ex: Return to our haunted corn maze problem: If you charge $10 for admission you will attract 300 people per night. For ever increase of $2 in ticket prices, you will loose 30 customers. What is E? Ex: If you have a demand function, say q = 500 3p 2, you can find the elasticity of demand exactly. Do so. What does elasticity tell you about revenue? If E < 1 then the percent change in price is larger than the percent change in demand. That is, an increase in price will result in a relatively smaller decrease in demand. So you will make up for lost customers with higher prices. On the other hand, if E > 1, demand changes more than price. So a small increase in price will result in a larger decrease in demand, so increasing price is a bad idea. Note that this can tell us whether to increase or decrease prices to maximize revenue. E can vary depending on the product, and within the product as price changes. What are some product with low elasticity? With high? Will elasticity increase or decrease as price increases? Ex: Make up an example demand function and use it to maximize revenue. 25
26 Math 176 Lecture Notes October 31, Accumulated Change: The Definite Integral 5.1 Distance and Accumulated Change How can we approximate total distance traveled from velocity? Distance = velocity * time. Ex: The velocity of a car is given in the table below. How far did the car travel? t (sec) (LHS: 1135, RHS: 1215) v (ft/sec) Now, what is happening graphically? Sketch a velocity curve and draw RHS and LHS boxes. So the distance we found is also the area under the curve. What we have is just an approximation: there is area over the curve we shouldn t count and area below the curve we should count but are not. To get a better approximation, we should use more, thus skinnier, boxes. Whenever we do this process, what are we calculating? The area under the curve (if f is positive). The total distance traveled (if f is velocity). The total change (if f is the rate of change). Ex: You pancakes are selling like hot-cakes: you sell 25 per day the first week, 20 per day the second week, and 30 per day the third week. How many have you sold total? 26
27 Math 176 Lecture Notes October 31, The Definite Integral Now let s try to do this same process for any function, say f(t) from t = a to t = b. First divide the interval [a, b] up into n sub-intervals for some n. The larger the n, the better our approximation will be. The width of each sub-interval will be t = (b a)/n. To find the height of each box, we need to know how far up to go - we go to the function on either the left or right side of the box. So we evaluate f(t i ). To find the total, we add up all of the f(t i ) t s - the areas of the boxes. We give a name for the thing we are trying to approximate with this process: the definite integral of f(t) from a to b: b a f(t) dt New terms: Integral sign, limits of integration (lower limit, upper limit), integrand, Ex: Evaluate integrals by approximation: t 2 t + 1 dt using a left hand sum. 1 dt using n = 5, and a right hand sum. t You should be able to approximate these integrals with a left- or right-hand sum. However, you should also know that you can get a very good approximation with your calculator. Do an example. 27
28 Math 176 Lecture Notes November 2, The Definite Integral as Area First, review the integral stuff from 5.1 and 5.2. Do an example from a table, and one from a function. To find the integral when just given a graph of a function, what do you do? If f is positive, you can just calculate the area under the curve (and above the x-axis). What if f is negative? Ex: Approximate 2 2 x2 4 dx. We can use the interpretation of integration as area to find integrals exactly. Ex: Find Ex: Find 5 2 π π x 3 dx sin(x) dx (from the graph - just give the graph, not the notation). We can use this to find the area between two curves. Say g(x) f(x) on the interval we care about. To find the area between g and f, we could take the area under f and subtract the area under g. This is b a f(x) g(x) dx. Ex: Find the area between x 2 and x. (between 0 and 1). So 1 0 x x 2 dx =.33 28
29 Math 176 Lecture Notes November 4, Interpretations of Integrals What are the units of b f(x) dx? Of course it depends on the units of f(x) and x. a Suppose f(x) give the number of sales per day where x is in days. What if f(x) was the rate of population growth in people per year, where x is years. What if f(x) gives the marginal cost of producing x items? For all of these, remember that b f(x) dx is really just a sum of f(x) x. So the units a of b f(x) dx are the units of f(x) times the units of x. a In fact, if f(t) is the rate of change of a quantity, then b f(t) dt is the total change in a the quantity between t = a and t = b. Ex: If the rate at which oil leaks out of a tanker in gallons per hour is given by f(t) = 5e t2, find an expression for the total amount of oil that has leaked out in the first 4 hours. Ex: Draw two graphs on the same axis representing dropout rates for two high schools. On peaks earlier and higher than the other. Which high school had a larger maximum dropout rate? Which high school had more dropouts over the 10 year period? Ex: Suppose your marginal cost is given by MC = 3q What is the total change in cost between the production levels q = 0 and q = 50? First, write an integral for this. Now let s think about another way to solve it: if we knew the cost function, we could plug in 50, plug in 0, and find the difference. Any ideas what the cost function is? Remember, we took the derivative of it to get MC. 29
30 Math 176 Lecture Notes November 7, Fundamental Theorem of Calculus Last time we saw that b a f (x) dx gave the total change in f between x = a and x = b. Note that f (x) is the rate of change in the quantity f(x). In other words, we have: Theorem (The Fundamental Theorem of Calculus). If F (t) is continuous for a t b, then b a F (t) dt = F (b) F (a). That is, the definite integral of the derivative of a function gives the total change in the function. Why is the theorem so fundamental? It relates the two main concepts in calculus - derivatives and integrals. Ex: Suppose the rate of population growth is given by P (t) = 100e.5t, where t is in years after Find an expression for the total change in population between 2000 and Will this tell us what the population is in 2010? Only if we know what the population was in 2000 as well. Last time we did a similar example with marginal cost. To review, what do we get when we integrate the marginal cost function? b a C (q) dq give the change in cost between production levels q = a and q = b. What then is b 0 C (q) dq? The change in cost between producing no items and producing b items. In other words, the variable cost of producing b items. Thus the total cost of producing b items is the fixed cost (C(0)) plus the variable cost. So C(b) = C(0) + b 0 C (q) dq. Ex: A graphical example: Draw a line graph for f. Assume f(0) = 1. Find the other values of f(x) (like problem 13 on homework). 30
31 Math 176 Lecture Notes November 9, Antiderivatives 7.1 Constructing antiderivatives analytically We saw in chapter 5 that we can evaluate the integral of f (x) exactly if we know what f(x) is. Today we learn how to find f(x) from f (x). We say that f(x) is an antiderivative of f (x). An because there could be more than one. In fact, we could add any constant to f(x) to get another antiderivative. Some notation: to denote the antiderivative of f(x) we write f(x) dx. We say this is the indefinite integral of f(x) with respect to x. Note that this is different from b f(x) dx, which is the definite integral. Definite a integrals give numbers, indefinite integrals give (classes of) functions. We can come up with rules for antiderivatives based on the rules for derivatives: x n dx = 1 n+1 xn+1 + C (The +C denotes that we can add any constant). k dx = kx + C for any constant k. 1 dx = ln x + C. We take x since ln(x) is not defined for negative values of x. x e x dx = e x + C e kx dx = 1 k ekx + C How can we combine antiderivatives? Like derivatives, if we integrate the sum or difference of functions, we can do each part separately. Similarly for multiplying by a constant. However, we cannot take the antiderivative of productions, quotients or compositions (easily). Do LOTS of examples. 7.3 Using the FTC to find Definite Integrals Recall, b a F (x) dx = F (b) F (a) - this is the Fundamental Theorem of Calculus. Now that we can find F (x) from F (x) (we can find antiderivatives), we can compute definite integrals exactly. Ex: Find 5 2 2x dx. Then 3 0 x2 dx and 4 0 ex dx and a bunch more. 31
32 Math 176 Lecture Notes November 14, Using the Definite Integral 6.1 Average Value We will see how to use integral to find the average value of a function. Let s start by remembering how we found the average value of a rate of change function: velocity. Remember, if I give you a distance function f(t), you can find the average velocity between t = a and t = b by f(b) f(a) b a. 1 This is, of course, the same as (f(b) f(a). b a familiar - we ve seen it in the fundamental theorem of calculus. But wait: that f(b) f(a) looks Since f(b) f(a) = b f 1 (t) dt, we get that the average velocity is a course, f (t) is the velocity function. b a b a f (t) dt. Of In other words, one way to find the average value of a function, is to integrate it and then divide by the length of the interval: Average value of f between a and b = 1 b a b a f(x) dx Ex: Find the average value of the function f(x) = x between x = 0 and x = 3. Graph the function and locate the average value graphically. Graphically, we see that the average value of f is the area under f divided by the length of the interval. That is, the average value is the height of a rectangle which has the same area as f. Ex: Graph a function and use the graph to approximate the average value. Do one approximately and then one exactly (line graph). 6.2 Consumer and Producer Surplus From economics, the consumer surplus measures the consumers gain from trade. It is the total amount gained by consumers by buying the item at the current price rather than the price they would have been willing to pay. The producer surplus measures the suppliers gain from trade. It is the total amount gained by producers by selling at the current price, rather than the price they would have been willing to accept. The current price could be set by price controls or is simply the equilibrium price. 32
33 Math 176 Lecture Notes November 14, 2011 Draw supply and demand curves (demand is decreasing, supply increasing). Mark the equilibrium price. Notice that while some consumers bought the product at precisely the price they were willing to pay, some would have been willing to pay more. Similarly, some suppliers would have produced the item for less than the current price. Surplus measures by how much. Draw in some rectangles. At the far left, the rectangle represents the amount of money consumers would have payed if they payed their maximum agreeable price. As the rectangles move to the right, they grow shorter: those consumers would have had less expenditures. Thus the area under the demand curve (up to the equilibrium point) is the total expenditures consumers are willing to pay for the product. However, the actually expenditures are given by the rectangle with height p. The consumer surplus is the extra area. We should be able to analyze the supplier surplus in the same way. between the line at p and the supply curve. It is the area Draw graphs with supplier and consumer surplus shaded (2 graphs). Make up an example with linear supply and demand curves and calculate the exact suppliers and consumer surpluses. Wage and price controls What happens if an outside force sets price higher or lower than the equilibrium? If the price is set higher or lower than the equilibrium, then fewer items will be sold (because either the consumer or the supplier will not buy or sell as many items). Draw on a graph the new surpluses. Note that over all, there is a loss in combined surplus. 33
34 Math 176 Lecture Notes November 16, Present and Future Value Earlier this semester we learned how to compute future value and present value given a few individual payments. Now we investigate how to find these values if the payments come in at a near constant rate. Say you get $10000 per year at the end of each year, for 3 years. Given a continuously compounded annual interest rate of 6%, we can find the present value by P V = 10000e.06(1) e.06(2) e.06(3) = What if our payments came in more frequently? What if we received a payment every day? We would then need to add up amounts - way to much work. Luckily, we have a tool: integrals are very good at adding up lots of little bits quickly. In fact, integrals are the only way we can add up these payments if we assume they are arriving continuously. So say we have an income stream of $10000 per year, with the same interest rate (6%). Then the present value is P V = e.06t dt. We can find this value exactly: P V = 10000/.06e /.06e.06 0 = Does it make sense that this number is higher than the present value we had before? In general, if S(t) is a function which gives your income stream at any time t with t running between 0 and M, with continuously compounded interest at rate r, then present value is given by: P V = M 0 S(t)e rt dt To find future value, we can take the present value and project that M years to the future: F V = P V e rm Ex: Find the future value of your income over 5 years with a continuous constant income stream of $5000 per year earning interest at 4%. (First find the present value.) 34
Final Exam Review Packet
 1 Exam 1 Material Sections A.1, A.2 and A.6 were review material. There will not be specific questions focused on this material but you should know how to: Simplify functions with exponents. Factor quadratics
1 Exam 1 Material Sections A.1, A.2 and A.6 were review material. There will not be specific questions focused on this material but you should know how to: Simplify functions with exponents. Factor quadratics
Final Exam Review Packet
 1 Exam 1 Material Sections A.1, A.2 and A.6 were review material. There will not be specific questions focused on this material but you should know how to: Simplify functions with exponents. Factor quadratics
1 Exam 1 Material Sections A.1, A.2 and A.6 were review material. There will not be specific questions focused on this material but you should know how to: Simplify functions with exponents. Factor quadratics
Final Exam Study Guide
 Final Exam Study Guide Final Exam Coverage: Sections 10.1-10.2, 10.4-10.5, 10.7, 11.2-11.4, 12.1-12.6, 13.1-13.2, 13.4-13.5, and 14.1 Sections/topics NOT on the exam: Sections 10.3 (Continuity, it definition
Final Exam Study Guide Final Exam Coverage: Sections 10.1-10.2, 10.4-10.5, 10.7, 11.2-11.4, 12.1-12.6, 13.1-13.2, 13.4-13.5, and 14.1 Sections/topics NOT on the exam: Sections 10.3 (Continuity, it definition
Math 112 Group Activity: The Vertical Speed of a Shell
 Name: Section: Math 112 Group Activity: The Vertical Speed of a Shell A shell is fired straight up by a mortar. The graph below shows its altitude as a function of time. 400 300 altitude (in feet) 200
Name: Section: Math 112 Group Activity: The Vertical Speed of a Shell A shell is fired straight up by a mortar. The graph below shows its altitude as a function of time. 400 300 altitude (in feet) 200
Section 11.3 Rates of Change:
 Section 11.3 Rates of Change: 1. Consider the following table, which describes a driver making a 168-mile trip from Cleveland to Columbus, Ohio in 3 hours. t Time (in hours) 0 0.5 1 1.5 2 2.5 3 f(t) Distance
Section 11.3 Rates of Change: 1. Consider the following table, which describes a driver making a 168-mile trip from Cleveland to Columbus, Ohio in 3 hours. t Time (in hours) 0 0.5 1 1.5 2 2.5 3 f(t) Distance
0 Review: Lines, Fractions, Exponents Lines Fractions Rules of exponents... 4
 Contents 0 Review: Lines, Fractions, Exponents 3 0.1 Lines................................... 3 0.2 Fractions................................ 3 0.3 Rules of exponents........................... 4 1 Functions
Contents 0 Review: Lines, Fractions, Exponents 3 0.1 Lines................................... 3 0.2 Fractions................................ 3 0.3 Rules of exponents........................... 4 1 Functions
Final Exam Review. MATH Intuitive Calculus Fall 2013 Circle lab day: Mon / Fri. Name:. Show all your work.
 MATH 11012 Intuitive Calculus Fall 2013 Circle lab day: Mon / Fri Dr. Kracht Name:. 1. Consider the function f depicted below. Final Exam Review Show all your work. y 1 1 x (a) Find each of the following
MATH 11012 Intuitive Calculus Fall 2013 Circle lab day: Mon / Fri Dr. Kracht Name:. 1. Consider the function f depicted below. Final Exam Review Show all your work. y 1 1 x (a) Find each of the following
0 Review: Lines, Fractions, Exponents Lines Fractions Rules of exponents... 4
 Contents 0 Review: Lines, Fractions, Exponents 2 0.1 Lines................................... 2 0.2 Fractions................................ 3 0.3 Rules of exponents........................... 4 1 Functions
Contents 0 Review: Lines, Fractions, Exponents 2 0.1 Lines................................... 2 0.2 Fractions................................ 3 0.3 Rules of exponents........................... 4 1 Functions
3.1 Derivative Formulas for Powers and Polynomials
 3.1 Derivative Formulas for Powers and Polynomials First, recall that a derivative is a function. We worked very hard in 2.2 to interpret the derivative of a function visually. We made the link, in Ex.
3.1 Derivative Formulas for Powers and Polynomials First, recall that a derivative is a function. We worked very hard in 2.2 to interpret the derivative of a function visually. We made the link, in Ex.
Brief Review. Chapter Linear Equations. 0.1 Example 1 Most people s favorite version of a linear equation is this: where
 Contents 0 Brief Review 2 0.1 Linear Equations........................... 2 0.2 Fractions............................... 8 0.3 Exponents............................... 9 0.4 Square roots..............................
Contents 0 Brief Review 2 0.1 Linear Equations........................... 2 0.2 Fractions............................... 8 0.3 Exponents............................... 9 0.4 Square roots..............................
MAC 2233, Survey of Calculus, Exam 3 Review This exam covers lectures 21 29,
 MAC 2233, Survey of Calculus, Exam 3 Review This exam covers lectures 21 29, This review includes typical exam problems. It is not designed to be comprehensive, but to be representative of topics covered
MAC 2233, Survey of Calculus, Exam 3 Review This exam covers lectures 21 29, This review includes typical exam problems. It is not designed to be comprehensive, but to be representative of topics covered
1 Functions And Change
 1 Functions And Change 1.1 What Is a Function? * Function A function is a rule that takes certain numbers as inputs and assigns to each a definite output number. The set of all input numbers is called
1 Functions And Change 1.1 What Is a Function? * Function A function is a rule that takes certain numbers as inputs and assigns to each a definite output number. The set of all input numbers is called
Doug Clark The Learning Center 100 Student Success Center learningcenter.missouri.edu Overview
 Math 1400 Final Exam Review Saturday, December 9 in Ellis Auditorium 1:00 PM 3:00 PM, Saturday, December 9 Part 1: Derivatives and Applications of Derivatives 3:30 PM 5:30 PM, Saturday, December 9 Part
Math 1400 Final Exam Review Saturday, December 9 in Ellis Auditorium 1:00 PM 3:00 PM, Saturday, December 9 Part 1: Derivatives and Applications of Derivatives 3:30 PM 5:30 PM, Saturday, December 9 Part
Math Want to have fun with chapter 4? Find the derivative. 1) y = 5x2e3x. 2) y = 2xex - 2ex. 3) y = (x2-2x + 3) ex. 9ex 4) y = 2ex + 1
 Math 160 - Want to have fun with chapter 4? Name Find the derivative. 1) y = 52e3 2) y = 2e - 2e 3) y = (2-2 + 3) e 9e 4) y = 2e + 1 5) y = e - + 1 e e 6) y = 32 + 7 7) y = e3-1 5 Use calculus to find
Math 160 - Want to have fun with chapter 4? Name Find the derivative. 1) y = 52e3 2) y = 2e - 2e 3) y = (2-2 + 3) e 9e 4) y = 2e + 1 5) y = e - + 1 e e 6) y = 32 + 7 7) y = e3-1 5 Use calculus to find
ANSWERS, Homework Problems, Spring 2014 Now You Try It, Supplemental problems in written homework, Even Answers R.6 8) 27, 30) 25
 ANSWERS, Homework Problems, Spring 2014, Supplemental problems in written homework, Even Answers Review Assignment: Precalculus Even Answers to Sections R1 R7 R.1 24) 4a 2 16ab + 16b 2 R.2 24) Prime 5x
ANSWERS, Homework Problems, Spring 2014, Supplemental problems in written homework, Even Answers Review Assignment: Precalculus Even Answers to Sections R1 R7 R.1 24) 4a 2 16ab + 16b 2 R.2 24) Prime 5x
CLASS NOTES: BUSINESS CALCULUS
 CLASS NOTES: BUSINESS CALCULUS These notes can be thought of as the logical skeleton of my lectures, although they will generally contain a fuller exposition of concepts but fewer examples than my lectures.
CLASS NOTES: BUSINESS CALCULUS These notes can be thought of as the logical skeleton of my lectures, although they will generally contain a fuller exposition of concepts but fewer examples than my lectures.
3. Find the slope of the tangent line to the curve given by 3x y e x+y = 1 + ln x at (1, 1).
 1. Find the derivative of each of the following: (a) f(x) = 3 2x 1 (b) f(x) = log 4 (x 2 x) 2. Find the slope of the tangent line to f(x) = ln 2 ln x at x = e. 3. Find the slope of the tangent line to
1. Find the derivative of each of the following: (a) f(x) = 3 2x 1 (b) f(x) = log 4 (x 2 x) 2. Find the slope of the tangent line to f(x) = ln 2 ln x at x = e. 3. Find the slope of the tangent line to
UNIT 2 DERIVATIVES 2.1 EXPONENTIAL AND LOGARITHMIC FUNCTION APPLICATIONS. Pre-Class:
 1830 UNIT 2 DERIVATIVES 2.1 EXPONENTIAL AND LOGARITHMIC FUNCTION APPLICATIONS Pre-Class: Take notes on the videos and readings (use the space below). Work and check problem #1 in the 2.1 NOTES section.
1830 UNIT 2 DERIVATIVES 2.1 EXPONENTIAL AND LOGARITHMIC FUNCTION APPLICATIONS Pre-Class: Take notes on the videos and readings (use the space below). Work and check problem #1 in the 2.1 NOTES section.
1 Functions, Graphs and Limits
 1 Functions, Graphs and Limits 1.1 The Cartesian Plane In this course we will be dealing a lot with the Cartesian plane (also called the xy-plane), so this section should serve as a review of it and its
1 Functions, Graphs and Limits 1.1 The Cartesian Plane In this course we will be dealing a lot with the Cartesian plane (also called the xy-plane), so this section should serve as a review of it and its
Final Exam Review Exercise Set A, Math 1551, Fall 2017
 Final Exam Review Exercise Set A, Math 1551, Fall 2017 This review set gives a list of topics that we explored throughout this course, as well as a few practice problems at the end of the document. A complete
Final Exam Review Exercise Set A, Math 1551, Fall 2017 This review set gives a list of topics that we explored throughout this course, as well as a few practice problems at the end of the document. A complete
Review Assignment II
 MATH 11012 Intuitive Calculus KSU Name:. Review Assignment II 1. Let C(x) be the cost, in dollars, of manufacturing x widgets. Fill in the table with a mathematical expression and appropriate units corresponding
MATH 11012 Intuitive Calculus KSU Name:. Review Assignment II 1. Let C(x) be the cost, in dollars, of manufacturing x widgets. Fill in the table with a mathematical expression and appropriate units corresponding
GLOSSARY. Accumulation function A function of the form a
 GLOSSARY Absolute maximum The output value of the highest point on a graph over a given input interval or over all possible input values. An absolute maximum point either is a local maximum point or occurs
GLOSSARY Absolute maximum The output value of the highest point on a graph over a given input interval or over all possible input values. An absolute maximum point either is a local maximum point or occurs
MATH 1101 Exam 1 Review. Spring 2018
 MATH 1101 Exam 1 Review Spring 2018 Topics Covered Section 2.1 Functions in the Real World Section 2.2 Describing the Behavior of Functions Section 2.3 Representing Functions Symbolically Section 2.4 Mathematical
MATH 1101 Exam 1 Review Spring 2018 Topics Covered Section 2.1 Functions in the Real World Section 2.2 Describing the Behavior of Functions Section 2.3 Representing Functions Symbolically Section 2.4 Mathematical
Chapter 3 The Integral Business Calculus 197
 Chapter The Integral Business Calculus 97 Chapter Exercises. Let A(x) represent the area bounded by the graph and the horizontal axis and vertical lines at t=0 and t=x for the graph in Fig.. Evaluate A(x)
Chapter The Integral Business Calculus 97 Chapter Exercises. Let A(x) represent the area bounded by the graph and the horizontal axis and vertical lines at t=0 and t=x for the graph in Fig.. Evaluate A(x)
Calculus with business applications, Lehigh U, Lecture 01 notes Summer
 Calculus with business applications, Lehigh U, Lecture 01 notes Summer 2012 1 Functions 1. A company sells 100 widgets at a price of $20. Sales increase by 5 widgets for each $1 decrease in price. Write
Calculus with business applications, Lehigh U, Lecture 01 notes Summer 2012 1 Functions 1. A company sells 100 widgets at a price of $20. Sales increase by 5 widgets for each $1 decrease in price. Write
(MATH 1203, 1204, 1204R)
 College Algebra (MATH 1203, 1204, 1204R) Departmental Review Problems For all questions that ask for an approximate answer, round to two decimal places (unless otherwise specified). The most closely related
College Algebra (MATH 1203, 1204, 1204R) Departmental Review Problems For all questions that ask for an approximate answer, round to two decimal places (unless otherwise specified). The most closely related
Spring 2003, MTH Practice for Exam 3 4.2, 4.3, 4.4, 4.7, 4.8, 5.1, 5.2, 5.3, 5.4, 5.5, 6.1
 Spring 23, MTH 3 - Practice for Exam 3 4.2, 4.3, 4.4, 4.7, 4.8, 5., 5.2, 5.3, 5.4, 5.5, 6.. An object travels with a velocity function given by the following table. Assume the velocity is increasing. t(hr)..5..5
Spring 23, MTH 3 - Practice for Exam 3 4.2, 4.3, 4.4, 4.7, 4.8, 5., 5.2, 5.3, 5.4, 5.5, 6.. An object travels with a velocity function given by the following table. Assume the velocity is increasing. t(hr)..5..5
MATH 122 FALL Final Exam Review Problems
 MATH 122 FALL 2013 Final Exam Review Problems Chapter 1 1. As a person hikes down from the top of a mountain, the variable t represents the time, in minutes, since the person left the top of the mountain,
MATH 122 FALL 2013 Final Exam Review Problems Chapter 1 1. As a person hikes down from the top of a mountain, the variable t represents the time, in minutes, since the person left the top of the mountain,
Unit IV Derivatives 20 Hours Finish by Christmas
 Unit IV Derivatives 20 Hours Finish by Christmas Calculus There two main streams of Calculus: Differentiation Integration Differentiation is used to find the rate of change of variables relative to one
Unit IV Derivatives 20 Hours Finish by Christmas Calculus There two main streams of Calculus: Differentiation Integration Differentiation is used to find the rate of change of variables relative to one
Unit IV Derivatives 20 Hours Finish by Christmas
 Unit IV Derivatives 20 Hours Finish by Christmas Calculus There two main streams of Calculus: Differentiation Integration Differentiation is used to find the rate of change of variables relative to one
Unit IV Derivatives 20 Hours Finish by Christmas Calculus There two main streams of Calculus: Differentiation Integration Differentiation is used to find the rate of change of variables relative to one
MATH 236 ELAC FALL 2017 CA 9 NAME: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 MATH 236 ELAC FALL 207 CA 9 NAME: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. ) 27 p 3 27 p 3 ) 2) If 9 t 3 4t 9-2t = 3, find t. 2) Solve the equation.
MATH 236 ELAC FALL 207 CA 9 NAME: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. ) 27 p 3 27 p 3 ) 2) If 9 t 3 4t 9-2t = 3, find t. 2) Solve the equation.
MATH 1325 Business Calculus Guided Notes
 MATH 135 Business Calculus Guided Notes LSC North Harris By Isabella Fisher Section.1 Functions and Theirs Graphs A is a rule that assigns to each element in one and only one element in. Set A Set B Set
MATH 135 Business Calculus Guided Notes LSC North Harris By Isabella Fisher Section.1 Functions and Theirs Graphs A is a rule that assigns to each element in one and only one element in. Set A Set B Set
Unit #4 : Interpreting Derivatives, Local Linearity, Marginal Rates
 Unit #4 : Interpreting Derivatives, Local Linearity, Marginal Rates Goals: Develop natural language interpretations of the derivative Create and use linearization/tangent line formulae Describe marginal
Unit #4 : Interpreting Derivatives, Local Linearity, Marginal Rates Goals: Develop natural language interpretations of the derivative Create and use linearization/tangent line formulae Describe marginal
Sample Mathematics 106 Questions
 Sample Mathematics 106 Questions x 2 + 8x 65 (1) Calculate lim x 5. x 5 (2) Consider an object moving in a straight line for which the distance s (measured in feet) it s travelled from its starting point
Sample Mathematics 106 Questions x 2 + 8x 65 (1) Calculate lim x 5. x 5 (2) Consider an object moving in a straight line for which the distance s (measured in feet) it s travelled from its starting point
Math 1501 Calc I Fall 2013 Lesson 9 - Lesson 20
 Math 1501 Calc I Fall 2013 Lesson 9 - Lesson 20 Instructor: Sal Barone School of Mathematics Georgia Tech August 19 - August 6, 2013 (updated October 4, 2013) L9: DIFFERENTIATION RULES Covered sections:
Math 1501 Calc I Fall 2013 Lesson 9 - Lesson 20 Instructor: Sal Barone School of Mathematics Georgia Tech August 19 - August 6, 2013 (updated October 4, 2013) L9: DIFFERENTIATION RULES Covered sections:
Midterm Study Guide and Practice Problems
 Midterm Study Guide and Practice Problems Coverage of the midterm: Sections 10.1-10.7, 11.2-11.6 Sections or topics NOT on the midterm: Section 11.1 (The constant e and continuous compound interest, Section
Midterm Study Guide and Practice Problems Coverage of the midterm: Sections 10.1-10.7, 11.2-11.6 Sections or topics NOT on the midterm: Section 11.1 (The constant e and continuous compound interest, Section
3. Go over old quizzes (there are blank copies on my website try timing yourself!)
 final exam review General Information The time and location of the final exam are as follows: Date: Tuesday, June 12th Time: 10:15am-12:15pm Location: Straub 254 The exam will be cumulative; that is, it
final exam review General Information The time and location of the final exam are as follows: Date: Tuesday, June 12th Time: 10:15am-12:15pm Location: Straub 254 The exam will be cumulative; that is, it
MA 151, Applied Calculus, Fall 2017, Final Exam Preview Identify each of the graphs below as one of the following functions:
 MA 5, Applie Calculus, Fall 207, Final Exam Preview Basic Functions. Ientify each of the graphs below as one of the following functions: x 3 4x 2 + x x 2 e x x 3 ln(x) (/2) x 2 x 4 + 4x 2 + 0 5x + 0 5x
MA 5, Applie Calculus, Fall 207, Final Exam Preview Basic Functions. Ientify each of the graphs below as one of the following functions: x 3 4x 2 + x x 2 e x x 3 ln(x) (/2) x 2 x 4 + 4x 2 + 0 5x + 0 5x
Purdue University Study Guide for MA Credit Exam
 Purdue University Study Guide for MA 16010 Credit Exam Students who pass the credit exam will gain credit in MA16010. The credit exam is a two-hour long exam with multiple choice questions. No books or
Purdue University Study Guide for MA 16010 Credit Exam Students who pass the credit exam will gain credit in MA16010. The credit exam is a two-hour long exam with multiple choice questions. No books or
Differentiation. 1. What is a Derivative? CHAPTER 5
 CHAPTER 5 Differentiation Differentiation is a technique that enables us to find out how a function changes when its argument changes It is an essential tool in economics If you have done A-level maths,
CHAPTER 5 Differentiation Differentiation is a technique that enables us to find out how a function changes when its argument changes It is an essential tool in economics If you have done A-level maths,
Calculus AB Topics Limits Continuity, Asymptotes
 Calculus AB Topics Limits Continuity, Asymptotes Consider f x 2x 1 x 3 1 x 3 x 3 Is there a vertical asymptote at x = 3? Do not give a Precalculus answer on a Calculus exam. Consider f x 2x 1 x 3 1 x 3
Calculus AB Topics Limits Continuity, Asymptotes Consider f x 2x 1 x 3 1 x 3 x 3 Is there a vertical asymptote at x = 3? Do not give a Precalculus answer on a Calculus exam. Consider f x 2x 1 x 3 1 x 3
Calculus Review Session. Brian Prest Duke University Nicholas School of the Environment August 18, 2017
 Calculus Review Session Brian Prest Duke University Nicholas School of the Environment August 18, 2017 Topics to be covered 1. Functions and Continuity 2. Solving Systems of Equations 3. Derivatives (one
Calculus Review Session Brian Prest Duke University Nicholas School of the Environment August 18, 2017 Topics to be covered 1. Functions and Continuity 2. Solving Systems of Equations 3. Derivatives (one
Math 101 Final Exam Review Solutions. Eric Schmutz
 Math 101 Final Exam Review Solutions Eric Schmutz Problem 1. Write an equation of the line passing through (,7) and (-1,1). Let (x 1, y 1 ) = (, 7) and (x, y ) = ( 1, 1). The slope is m = y y 1 x x 1 =
Math 101 Final Exam Review Solutions Eric Schmutz Problem 1. Write an equation of the line passing through (,7) and (-1,1). Let (x 1, y 1 ) = (, 7) and (x, y ) = ( 1, 1). The slope is m = y y 1 x x 1 =
MATH 115 SECOND MIDTERM EXAM
 MATH 115 SECOND MIDTERM EXAM November 22, 2005 NAME: SOLUTION KEY INSTRUCTOR: SECTION NO: 1. Do not open this exam until you are told to begin. 2. This exam has 10 pages including this cover. There are
MATH 115 SECOND MIDTERM EXAM November 22, 2005 NAME: SOLUTION KEY INSTRUCTOR: SECTION NO: 1. Do not open this exam until you are told to begin. 2. This exam has 10 pages including this cover. There are
Section K MATH 211 Homework Due Friday, 8/30/96 Professor J. Beachy Average: 15.1 / 20. ), and f(a + 1).
 Section K MATH 211 Homework Due Friday, 8/30/96 Professor J. Beachy Average: 15.1 / 20 # 18, page 18: If f(x) = x2 x 2 1, find f( 1 2 ), f( 1 2 ), and f(a + 1). # 22, page 18: When a solution of acetylcholine
Section K MATH 211 Homework Due Friday, 8/30/96 Professor J. Beachy Average: 15.1 / 20 # 18, page 18: If f(x) = x2 x 2 1, find f( 1 2 ), f( 1 2 ), and f(a + 1). # 22, page 18: When a solution of acetylcholine
1.4 Techniques of Integration
 .4 Techniques of Integration Recall the following strategy for evaluating definite integrals, which arose from the Fundamental Theorem of Calculus (see Section.3). To calculate b a f(x) dx. Find a function
.4 Techniques of Integration Recall the following strategy for evaluating definite integrals, which arose from the Fundamental Theorem of Calculus (see Section.3). To calculate b a f(x) dx. Find a function
Chapter 5. Increasing and Decreasing functions Theorem 1: For the interval (a,b) f (x) f(x) Graph of f + Increases Rises - Decreases Falls
 Chapter 5 Section 5.1 First Derivative and Graphs Objectives: The student will be able to identify increasing and decreasing functions and local extrema The student will be able to apply the first derivative
Chapter 5 Section 5.1 First Derivative and Graphs Objectives: The student will be able to identify increasing and decreasing functions and local extrema The student will be able to apply the first derivative
MATH 1113 Exam 1 Review
 MATH 1113 Exam 1 Review Topics Covered Section 1.1: Rectangular Coordinate System Section 1.3: Functions and Relations Section 1.4: Linear Equations in Two Variables and Linear Functions Section 1.5: Applications
MATH 1113 Exam 1 Review Topics Covered Section 1.1: Rectangular Coordinate System Section 1.3: Functions and Relations Section 1.4: Linear Equations in Two Variables and Linear Functions Section 1.5: Applications
Calculus I Review Solutions
 Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
Math 120 Final Exam Practice Problems, Form: A
 Math 120 Final Exam Practice Problems, Form: A Name: While every attempt was made to be complete in the types of problems given below, we make no guarantees about the completeness of the problems. Specifically,
Math 120 Final Exam Practice Problems, Form: A Name: While every attempt was made to be complete in the types of problems given below, we make no guarantees about the completeness of the problems. Specifically,
Math 180, Lowman, Summer 2008, Old Exam Problems 1 Limit Problems
 Math 180, Lowman, Summer 2008, Old Exam Problems 1 Limit Problems 1. Find the limit of f(x) = (sin x) x x 3 as x 0. 2. Use L Hopital s Rule to calculate lim x 2 x 3 2x 2 x+2 x 2 4. 3. Given the function
Math 180, Lowman, Summer 2008, Old Exam Problems 1 Limit Problems 1. Find the limit of f(x) = (sin x) x x 3 as x 0. 2. Use L Hopital s Rule to calculate lim x 2 x 3 2x 2 x+2 x 2 4. 3. Given the function
a x a y = a x+y a x a = y ax y (a x ) r = a rx and log a (xy) = log a (x) + log a (y) log a ( x y ) = log a(x) log a (y) log a (x r ) = r log a (x).
 You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
North Carolina State University
 North Carolina State University MA 141 Course Text Calculus I by Brenda Burns-Williams and Elizabeth Dempster August 7, 2014 Section1 Functions Introduction In this section, we will define the mathematical
North Carolina State University MA 141 Course Text Calculus I by Brenda Burns-Williams and Elizabeth Dempster August 7, 2014 Section1 Functions Introduction In this section, we will define the mathematical
Business and Life Calculus
 Business and Life Calculus George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 112 George Voutsadakis (LSSU) Calculus For Business and Life Sciences Fall 2013
Business and Life Calculus George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 112 George Voutsadakis (LSSU) Calculus For Business and Life Sciences Fall 2013
Fall 2009 Math 113 Final Exam Solutions. f(x) = 1 + ex 1 e x?
 . What are the domain and range of the function Fall 9 Math 3 Final Exam Solutions f(x) = + ex e x? Answer: The function is well-defined everywhere except when the denominator is zero, which happens when
. What are the domain and range of the function Fall 9 Math 3 Final Exam Solutions f(x) = + ex e x? Answer: The function is well-defined everywhere except when the denominator is zero, which happens when
The questions listed below are drawn from midterm and final exams from the last few years at OSU. As the text book and structure of the class have
 The questions listed below are drawn from midterm and final eams from the last few years at OSU. As the tet book and structure of the class have recently changed, it made more sense to list the questions
The questions listed below are drawn from midterm and final eams from the last few years at OSU. As the tet book and structure of the class have recently changed, it made more sense to list the questions
Chapter 0. Brief Review. 0.1 Linear Equations
 Contents 0 Brief Review 2 0.1 Linear Equations........................... 2 0.2 Fractions............................... 12 0.3 Exponents............................... 14 0.4 Square roots..............................
Contents 0 Brief Review 2 0.1 Linear Equations........................... 2 0.2 Fractions............................... 12 0.3 Exponents............................... 14 0.4 Square roots..............................
MA 181 Lecture Chapter 7 College Algebra and Calculus by Larson/Hodgkins Limits and Derivatives
 7.5) Rates of Change: Velocity and Marginals MA 181 Lecture Chapter 7 College Algebra and Calculus by Larson/Hodgkins Limits and Derivatives Previously we learned two primary applications of derivatives.
7.5) Rates of Change: Velocity and Marginals MA 181 Lecture Chapter 7 College Algebra and Calculus by Larson/Hodgkins Limits and Derivatives Previously we learned two primary applications of derivatives.
Math 110 Final Exam General Review. Edward Yu
 Math 110 Final Exam General Review Edward Yu Da Game Plan Solving Limits Regular limits Indeterminate Form Approach Infinities One sided limits/discontinuity Derivatives Power Rule Product/Quotient Rule
Math 110 Final Exam General Review Edward Yu Da Game Plan Solving Limits Regular limits Indeterminate Form Approach Infinities One sided limits/discontinuity Derivatives Power Rule Product/Quotient Rule
Math 142 Week-in-Review #11 (Final Exam Review: All previous sections as well as sections 6.6 and 6.7)
 Math 142 Week-in-Review #11 (Final Exam Review: All previous sections as well as sections 6.6 and 6.7) Note: This review is intended to highlight the topics covered on the Final Exam (with emphasis on
Math 142 Week-in-Review #11 (Final Exam Review: All previous sections as well as sections 6.6 and 6.7) Note: This review is intended to highlight the topics covered on the Final Exam (with emphasis on
Unit #1 - Transformation of Functions, Exponentials and Logarithms
 Unit #1 - Transformation of Functions, Exponentials and Logarithms Some problems and solutions selected or adapted from Hughes-Hallett Calculus. Note: This unit, being review of pre-calculus has substantially
Unit #1 - Transformation of Functions, Exponentials and Logarithms Some problems and solutions selected or adapted from Hughes-Hallett Calculus. Note: This unit, being review of pre-calculus has substantially
ANSWERS, Homework Problems, Fall 2014: Lectures Now You Try It, Supplemental problems in written homework, Even Answers. 24x + 72 (x 2 6x + 4) 4
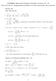 ANSWERS, Homework Problems, Fall 014: Lectures 19 35 Now You Try It, Supplemental problems in written homework, Even Answers Lecture 19 1. d [ 4 ] dx x 6x + 4) 3 = 4x + 7 x 6x + 4) 4. a) P 0) = 800 b)
ANSWERS, Homework Problems, Fall 014: Lectures 19 35 Now You Try It, Supplemental problems in written homework, Even Answers Lecture 19 1. d [ 4 ] dx x 6x + 4) 3 = 4x + 7 x 6x + 4) 4. a) P 0) = 800 b)
Math Practice Final - solutions
 Math 151 - Practice Final - solutions 2 1-2 -1 0 1 2 3 Problem 1 Indicate the following from looking at the graph of f(x) above. All answers are small integers, ±, or DNE for does not exist. a) lim x 1
Math 151 - Practice Final - solutions 2 1-2 -1 0 1 2 3 Problem 1 Indicate the following from looking at the graph of f(x) above. All answers are small integers, ±, or DNE for does not exist. a) lim x 1
1 Cost, Revenue and Profit
 MATH 104 - SECTION 101 FIN AL REVIEW 1 Cost, Revenue and Profit C(x), R(x), and P(x); marginal cost MC(x), marginal revenue MR(x), and marginal profit M P(x). 1. Profit is the difference between cost and
MATH 104 - SECTION 101 FIN AL REVIEW 1 Cost, Revenue and Profit C(x), R(x), and P(x); marginal cost MC(x), marginal revenue MR(x), and marginal profit M P(x). 1. Profit is the difference between cost and
Free Response Questions Compiled by Kaye Autrey for face-to-face student instruction in the AP Calculus classroom
 Free Response Questions 1969-010 Compiled by Kaye Autrey for face-to-face student instruction in the AP Calculus classroom 1 AP Calculus Free-Response Questions 1969 AB 1 Consider the following functions
Free Response Questions 1969-010 Compiled by Kaye Autrey for face-to-face student instruction in the AP Calculus classroom 1 AP Calculus Free-Response Questions 1969 AB 1 Consider the following functions
Course Outline. Linear Equations Linear Inequalities (1.6)
 Course Outline Functions/Graphing Solving Equations Applications Definitions of function, graph, domain, range, x- and y- intercepts, vertical line test(.-.) Linear functions (.-.5) -Parallel and perpendicular
Course Outline Functions/Graphing Solving Equations Applications Definitions of function, graph, domain, range, x- and y- intercepts, vertical line test(.-.) Linear functions (.-.5) -Parallel and perpendicular
ALGEBRA II: A. Survey of Functions. Jeff Shriner
 ALGEBRA II: A Survey of Functions Jeff Shriner J S Created for University of Colorado PCDP, Summer 2014 1 C O N T E N T S 0 0.1: pre-requisite review 5 0 0.2: functions 7 0 0.3: inverse functions 11 0
ALGEBRA II: A Survey of Functions Jeff Shriner J S Created for University of Colorado PCDP, Summer 2014 1 C O N T E N T S 0 0.1: pre-requisite review 5 0 0.2: functions 7 0 0.3: inverse functions 11 0
Review for Final Review
 Topics Review for Final Review 1. Functions and equations and graphing: linear, absolute value, quadratic, polynomials, rational (first 1/3 of semester) 2. Simple Interest, compounded interest, and continuously
Topics Review for Final Review 1. Functions and equations and graphing: linear, absolute value, quadratic, polynomials, rational (first 1/3 of semester) 2. Simple Interest, compounded interest, and continuously
Chapter 4 Differentiation
 Chapter 4 Differentiation 08 Section 4. The derivative of a function Practice Problems (a) (b) (c) 3 8 3 ( ) 4 3 5 4 ( ) 5 3 3 0 0 49 ( ) 50 Using a calculator, the values of the cube function, correct
Chapter 4 Differentiation 08 Section 4. The derivative of a function Practice Problems (a) (b) (c) 3 8 3 ( ) 4 3 5 4 ( ) 5 3 3 0 0 49 ( ) 50 Using a calculator, the values of the cube function, correct
is all real numbers.
 Math 140 Spring 2017 Suggested Final Review Problems 1. Is each of the following statements true or false? Explain. (a) If f(x) = x 2, then f(x + h) = x 2 + h 2. (b) If g(x) = 3 x, then g(x) can never
Math 140 Spring 2017 Suggested Final Review Problems 1. Is each of the following statements true or false? Explain. (a) If f(x) = x 2, then f(x + h) = x 2 + h 2. (b) If g(x) = 3 x, then g(x) can never
Practice Questions for Math 131 Exam # 1
 Practice Questions for Math 131 Exam # 1 1) A company produces a product for which the variable cost per unit is $3.50 and fixed cost 1) is $20,000 per year. Next year, the company wants the total cost
Practice Questions for Math 131 Exam # 1 1) A company produces a product for which the variable cost per unit is $3.50 and fixed cost 1) is $20,000 per year. Next year, the company wants the total cost
Ex 1: Identify the open intervals for which each function is increasing or decreasing.
 MATH 2040 Notes: Unit 4 Page 1 5.1/5.2 Increasing and Decreasing Functions Part a Relative Extrema Ex 1: Identify the open intervals for which each In algebra we defined increasing and decreasing behavior
MATH 2040 Notes: Unit 4 Page 1 5.1/5.2 Increasing and Decreasing Functions Part a Relative Extrema Ex 1: Identify the open intervals for which each In algebra we defined increasing and decreasing behavior
Business Calculus
 Business Calculus 978-1-63545-025-5 To learn more about all our offerings Visit Knewtonalta.com Source Author(s) (Text or Video) Title(s) Link (where applicable) OpenStax Senior Contributing Authors: Gilbert
Business Calculus 978-1-63545-025-5 To learn more about all our offerings Visit Knewtonalta.com Source Author(s) (Text or Video) Title(s) Link (where applicable) OpenStax Senior Contributing Authors: Gilbert
Applied Calculus I Practice Final Exam Solution Notes
 AMS 5 (Fall, 2009). Solve for x: 0 3 2x = 3 (.2) x Taking the natural log of both sides, we get Applied Calculus I Practice Final Exam Solution Notes Joe Mitchell ln 0 + 2xln 3 = ln 3 + xln.2 x(2ln 3 ln.2)
AMS 5 (Fall, 2009). Solve for x: 0 3 2x = 3 (.2) x Taking the natural log of both sides, we get Applied Calculus I Practice Final Exam Solution Notes Joe Mitchell ln 0 + 2xln 3 = ln 3 + xln.2 x(2ln 3 ln.2)
Study Guide - Part 2
 Math 116 Spring 2015 Study Guide - Part 2 1. Which of the following describes the derivative function f (x) of a quadratic function f(x)? (A) Cubic (B) Quadratic (C) Linear (D) Constant 2. Find the derivative
Math 116 Spring 2015 Study Guide - Part 2 1. Which of the following describes the derivative function f (x) of a quadratic function f(x)? (A) Cubic (B) Quadratic (C) Linear (D) Constant 2. Find the derivative
MATH 142 Business Mathematics II. Spring, 2015, WEEK 1. JoungDong Kim
 MATH 142 Business Mathematics II Spring, 2015, WEEK 1 JoungDong Kim Week 1: A8, 1.1, 1.2, 1.3 Chapter 1. Functions Section 1.1 and A.8 Definition. A function is a rule that assigns to each element x in
MATH 142 Business Mathematics II Spring, 2015, WEEK 1 JoungDong Kim Week 1: A8, 1.1, 1.2, 1.3 Chapter 1. Functions Section 1.1 and A.8 Definition. A function is a rule that assigns to each element x in
Foothill High School. AP Calculus BC. Note Templates Semester 1, Student Name.
 Foothill High School AP Calculus BC Note Templates Semester 1, 2011-2012 Student Name Teacher: Burt Dixon bdixon@pleasanton.k12.ca.us 2.1 Limits Chap1-2 Page 1 Chap1-2 Page 2 Chap1-2 Page 3 Chap1-2 Page
Foothill High School AP Calculus BC Note Templates Semester 1, 2011-2012 Student Name Teacher: Burt Dixon bdixon@pleasanton.k12.ca.us 2.1 Limits Chap1-2 Page 1 Chap1-2 Page 2 Chap1-2 Page 3 Chap1-2 Page
Calculus I 5. Applications of differentiation
 2301107 Calculus I 5. Applications of differentiation Chapter 5:Applications of differentiation C05-2 Outline 5.1. Extreme values 5.2. Curvature and Inflection point 5.3. Curve sketching 5.4. Related rate
2301107 Calculus I 5. Applications of differentiation Chapter 5:Applications of differentiation C05-2 Outline 5.1. Extreme values 5.2. Curvature and Inflection point 5.3. Curve sketching 5.4. Related rate
Section 4.2 Logarithmic Functions & Applications
 34 Section 4.2 Logarithmic Functions & Applications Recall that exponential functions are one-to-one since every horizontal line passes through at most one point on the graph of y = b x. So, an exponential
34 Section 4.2 Logarithmic Functions & Applications Recall that exponential functions are one-to-one since every horizontal line passes through at most one point on the graph of y = b x. So, an exponential
June If you want, you may scan your assignment and convert it to a.pdf file and it to me.
 Summer Assignment Pre-Calculus Honors June 2016 Dear Student: This assignment is a mandatory part of the Pre-Calculus Honors course. Students who do not complete the assignment will be placed in the regular
Summer Assignment Pre-Calculus Honors June 2016 Dear Student: This assignment is a mandatory part of the Pre-Calculus Honors course. Students who do not complete the assignment will be placed in the regular
2.1 The Tangent and Velocity Problems
 2.1 The Tangent and Velocity Problems Tangents What is a tangent? Tangent lines and Secant lines Estimating slopes from discrete data: Example: 1. A tank holds 1000 gallons of water, which drains from
2.1 The Tangent and Velocity Problems Tangents What is a tangent? Tangent lines and Secant lines Estimating slopes from discrete data: Example: 1. A tank holds 1000 gallons of water, which drains from
Solutions Manual for Precalculus An Investigation of Functions
 Solutions Manual for Precalculus An Investigation of Functions David Lippman, Melonie Rasmussen nd Edition Solutions created at The Evergreen State College and Shoreline Community College Last edited 9/6/17
Solutions Manual for Precalculus An Investigation of Functions David Lippman, Melonie Rasmussen nd Edition Solutions created at The Evergreen State College and Shoreline Community College Last edited 9/6/17
MAT1300 Final Review. Pieter Hofstra. December 4, 2009
 December 4, 2009 Sections from the book to study (8th Edition) Chapter 0: 0.1: Real line and Order 0.2: Absolute Value and Distance 0.3: Exponents and Radicals 0.4: Factoring Polynomials (you may omit
December 4, 2009 Sections from the book to study (8th Edition) Chapter 0: 0.1: Real line and Order 0.2: Absolute Value and Distance 0.3: Exponents and Radicals 0.4: Factoring Polynomials (you may omit
Daily Update. Dondi Ellis. January 27, 2015
 Daily Update Dondi Ellis January 27, 2015 CLASS 1: Introduction and Section 1.1 REMINDERS: Assignment: Read sections 1.1 and 1.2, and Student Guide (online). Buy a TI-84 or other graphing calculator satisfying
Daily Update Dondi Ellis January 27, 2015 CLASS 1: Introduction and Section 1.1 REMINDERS: Assignment: Read sections 1.1 and 1.2, and Student Guide (online). Buy a TI-84 or other graphing calculator satisfying
AP Calculus Free-Response Questions 1969-present AB
 AP Calculus Free-Response Questions 1969-present AB 1969 1. Consider the following functions defined for all x: f 1 (x) = x, f (x) = xcos x, f 3 (x) = 3e x, f 4 (x) = x - x. Answer the following questions
AP Calculus Free-Response Questions 1969-present AB 1969 1. Consider the following functions defined for all x: f 1 (x) = x, f (x) = xcos x, f 3 (x) = 3e x, f 4 (x) = x - x. Answer the following questions
The plot shows the graph of the function f (x). Determine the quantities.
 MATH 211 SAMPLE EXAM 1 SOLUTIONS 6 4 2-2 2 4-2 1. The plot shows the graph of the function f (x). Determine the quantities. lim f (x) (a) x 3 + Solution: Look at the graph. Let x approach 3 from the right.
MATH 211 SAMPLE EXAM 1 SOLUTIONS 6 4 2-2 2 4-2 1. The plot shows the graph of the function f (x). Determine the quantities. lim f (x) (a) x 3 + Solution: Look at the graph. Let x approach 3 from the right.
Solutions to Second Midterm(pineapple)
 Math 125 Solutions to Second Midterm(pineapple) 1. Compute each of the derivatives below as indicated. 4 points (a) f(x) = 3x 8 5x 4 + 4x e 3. Solution: f (x) = 24x 7 20x + 4. Don t forget that e 3 is
Math 125 Solutions to Second Midterm(pineapple) 1. Compute each of the derivatives below as indicated. 4 points (a) f(x) = 3x 8 5x 4 + 4x e 3. Solution: f (x) = 24x 7 20x + 4. Don t forget that e 3 is
See animations and interactive applets of some of these at. Fall_2009/Math123/Notes
 MA123, Chapter 7 Word Problems (pp. 125-153) Chapter s Goal: In this chapter we study the two main types of word problems in Calculus. Optimization Problems. i.e., max - min problems Related Rates See
MA123, Chapter 7 Word Problems (pp. 125-153) Chapter s Goal: In this chapter we study the two main types of word problems in Calculus. Optimization Problems. i.e., max - min problems Related Rates See
Math Final Exam Review. 1. The following equation gives the rate at which the angle between two objects is changing during a game:
 Math 131 Spring 2008 c Sherry Scarborough and Heather Ramsey Page 1 Math 131 - Final Exam Review 1. The following equation gives the rate at which the angle between two objects is changing during a game:
Math 131 Spring 2008 c Sherry Scarborough and Heather Ramsey Page 1 Math 131 - Final Exam Review 1. The following equation gives the rate at which the angle between two objects is changing during a game:
4x 2-5x+3. 7x-1 HOMEWORK 1-1
 HOMEWORK 1-1 As it is always the case that correct answers without sufficient mathematical justification may not receive full credit, make sure that you show all your work. Please circle, draw a box around,
HOMEWORK 1-1 As it is always the case that correct answers without sufficient mathematical justification may not receive full credit, make sure that you show all your work. Please circle, draw a box around,
V. Graph Sketching and Max-Min Problems
 V. Graph Sketching and Max-Min Problems The signs of the first and second derivatives of a function tell us something about the shape of its graph. In this chapter we learn how to find that information.
V. Graph Sketching and Max-Min Problems The signs of the first and second derivatives of a function tell us something about the shape of its graph. In this chapter we learn how to find that information.
Midterm 1 Review Problems Business Calculus
 Midterm 1 Review Problems Business Calculus 1. (a) Show that the functions f and g are inverses of each other by showing that f g(x) = g f(x) given that (b) Sketch the functions and the line y = x f(x)
Midterm 1 Review Problems Business Calculus 1. (a) Show that the functions f and g are inverses of each other by showing that f g(x) = g f(x) given that (b) Sketch the functions and the line y = x f(x)
1 Functions and Graphs
 1 Functions and Graphs 1.1 Functions Cartesian Coordinate System A Cartesian or rectangular coordinate system is formed by the intersection of a horizontal real number line, usually called the x axis,
1 Functions and Graphs 1.1 Functions Cartesian Coordinate System A Cartesian or rectangular coordinate system is formed by the intersection of a horizontal real number line, usually called the x axis,
Section 3.1 Extreme Values
 Math 132 Extreme Values Section 3.1 Section 3.1 Extreme Values Example 1: Given the following is the graph of f(x) Where is the maximum (x-value)? What is the maximum (y-value)? Where is the minimum (x-value)?
Math 132 Extreme Values Section 3.1 Section 3.1 Extreme Values Example 1: Given the following is the graph of f(x) Where is the maximum (x-value)? What is the maximum (y-value)? Where is the minimum (x-value)?
Contents CONTENTS 1. 1 Straight Lines and Linear Equations 1. 2 Systems of Equations 6. 3 Applications to Business Analysis 11.
 CONTENTS 1 Contents 1 Straight Lines and Linear Equations 1 2 Systems of Equations 6 3 Applications to Business Analysis 11 4 Functions 16 5 Quadratic Functions and Parabolas 21 6 More Simple Functions
CONTENTS 1 Contents 1 Straight Lines and Linear Equations 1 2 Systems of Equations 6 3 Applications to Business Analysis 11 4 Functions 16 5 Quadratic Functions and Parabolas 21 6 More Simple Functions
The First Derivative Test
 The First Derivative Test We have already looked at this test in the last section even though we did not put a name to the process we were using. We use a y number line to test the sign of the first derivative
The First Derivative Test We have already looked at this test in the last section even though we did not put a name to the process we were using. We use a y number line to test the sign of the first derivative
AP CALCULUS BC SUMMER PREVIEW
 AP CALCULUS BC SUMMER PREVIEW Name: Your summer homework assignment is to write complete solutions for all of the problems listed in this packet. It is important that you have mastered the concepts covered
AP CALCULUS BC SUMMER PREVIEW Name: Your summer homework assignment is to write complete solutions for all of the problems listed in this packet. It is important that you have mastered the concepts covered
2. (12 points) Find an equation for the line tangent to the graph of f(x) =
 November 23, 2010 Name The total number of points available is 153 Throughout this test, show your work Throughout this test, you are expected to use calculus to solve problems Graphing calculator solutions
November 23, 2010 Name The total number of points available is 153 Throughout this test, show your work Throughout this test, you are expected to use calculus to solve problems Graphing calculator solutions
Chapter 6 Overview: Applications of Derivatives
 Chapter 6 Overview: Applications of Derivatives There are two main contets for derivatives: graphing and motion. In this chapter, we will consider the graphical applications of the derivative. Much of
Chapter 6 Overview: Applications of Derivatives There are two main contets for derivatives: graphing and motion. In this chapter, we will consider the graphical applications of the derivative. Much of
