Suggested solutions for the exam in SF2863 Systems Engineering. December 19,
|
|
|
- Irene Hardy
- 5 years ago
- Views:
Transcription
1 Suggested solutions for the exam in SF863 Systems Engineering. December 19, Examiner: Per Enqvist, phone: We can think of the support center as a Jackson network. The reception is a M M queue with arrival intensity λ R and service intensity µ R = 16 per server. Frasse s service is a M M 1 queue with arrival intensity λ F and service intensity µ F = 10 per server. The reception is a M M 1 queue with arrival intensity λ H and service intensity µ R = 16 per server. (a) Let λ 0 = 16 be the arrival intensity from the outside and λ R be the intensity in to the reception. The traffic balance equations are λ 0 + 1/4λ F + 1/λ H = λ R, λ F = 1/3λ R and λ H = 1/λ R which yields, λ R = 4, λ F = 8 and λ H = 1. We can now check that the low traffic requirements are satisfied, i.e., that λ R = 4 < µ A = 3, λ F = 8 < µ F = 10, and λ H = 1 < µ H = 16. The probability that a random customer gets the problem solved is equal to the ratio of callers from the outside divided by callers being helped = (6 + 6)/16 = 3/4. (b) Let V R, V F and V H be the average time it takes from a call arrives to one of the service stations until it leaves it, i.e., V R = L R /λ R = ρ R /(1 ρ R )/λ R = 4/7/4 = 1/7, V F = L F /λ F = ρ F /(1 ρ F )/λ F = 4/8 = 1/, and V H = L H /λ H = ρ H /(1 ρ H )/λ H = 3/1 = 1/4. Letting W R be the average time from a call arrives to station R until it exits the system, W F be the average time from a call arrives to station F until it exits the system, and W H be the average time from the call arrives to station H until it exits the system, then W R = V R + 1/3W F + 1/W H W F = V F + 1/4W R W H = V H + 1/W R and W R = 73/11.. (a) Introduce the state, s l = how many dollars Frasse has day l. We know that s 0 = 1000, and s l {0, 500, 1000, 1500, 000}, where all states are not reachable at all times. The state 0 is absorbing. Let x l be the strategy of Frasse day l, and let it be 1 if he plays fair and 0 if he counts cards. Define the value function Vl (s) to be the maximal expected winning of Frasse if he starts day l with s dollars and use the optimal playing strategy. 1
2 Page of 5 Solutions Exam SF863 The DynP equation becomes Vl (s) = max {E V l (s, x)} = x=0,1 = max { 0.6Vl+1 } (s + 500) + 0.4Vl+1 (s 500), 0.7Vl+1 (s + 500) + 0.1Vl+1 (s 500), The boundary condition is that V (s) = s. (b) Use the recursion. First V (s) = s. Then V for x 1 = 1, V 1 (1500) = max {0.6V (500) = max {0.6V x 1 = 0, V 1 (0) = 0 (000) + 0.4V (1000), 0.7V (000) + 0.1V (1000)} = (1000) + 0.4V (0), 0.7V (1000) + 0.1V (0)} = 700 for Then V0 (1000) = max {0.6V 1 (1500) + 0.4V 1 (500), 0.7V 1 (1500) + 0.1V 1 (500)} = 140 for x 1 = 0, 1. The first day the strategy of Frasse does not matter, both are optimal. The second day he should play fair if he won the first day and he should count cards if he lost the first day, and if got thrown out the first day he can do nothing. 3. (a) Let f be equal to p, and g = n H + n L + n C be the total number of boxes. (Maximizing p is equivalent to minimizing f) Then both f and g are clearly separable, so we can just check the properties of f k and g k for k = 1,, 3. Note that f k (x) = p k n p H (n) p L (n) p C (n) so it is decreasing and g k (x) = 1 so it is increasing. Note that f k (x) = p k n p H (n) p L (n) p C (n) and g k (x) = 0 they are both integer convex for the given numbers. (b) When we apply the marginal allocation algorithm we want to compare the quotients f k (x)/ g k (x) and find the largest elements when k = 1,, 3 and n = 1, 1,,.
3 SF863 Solutions Exam Page 3 of 5 n f H (n) f L (n) f C (n) The largest element is 7, so n (1) = (0, 0, 1) is the optimal allocation for sum of n is 1 and f(n (1) ) = 7, g(n (1) ) = 1. The largest element is 5 (in two places), so n () = (1, 0, 1) is an optimal allocation for sum of n is and f(n () ) = 1, g(n () ) =. The largest element is 5, so n (3) = (1, 0, ) is the optimal allocation forsum of n is 3 and f(n (3) ) = 17, g(n (3) ) = 3 The largest element is 3 (in three places), so n (4) = (1, 1, ) is an optimal allocation for sum of n is 4 and f(n (4) ) = 0, g(n (4) ) = 4 The largest element is 3 (in two places), so n (5) = (, 1, ) is an optimal allocation for sum of n is 5 and f(n (5) ) = 3, g(n (5) ) = 5 The largest element is 3, so n (6) = (, 1, 3) is the optimal allocation for sum of n is 6 and f(n (6) ) = 6, g(n (6) ) = 6 The largest element is (in two places), so n (7) = (3, 1, 3) is an optimal allocation for sum of n is 7 and f(n (7) ) = 8, g(n (7) ) = 7 The largest element is, so n (8) = (3,, 3) is the optimal allocation for sum of n is 8 and f(n (8) ) = 30, g(n (8) ) = 8 4. (a) We need to keep track of the mood of Heathcliff, define the state s k = { 1 if Heathcliffs mood is up at beginning of day k 0 if Heathcliffs mood is down at beginning of day k Define the decisions 1 if Frasse does nothing day k x k = if Frasse buys a medal day k 3 if Frasse takes Heathcliff out on day (evening) k In the costs we include the revenue with negative sign. Then the costs of making decision x k = 1 is C 11 = 60 if s k = 1 and C 01 = 30 if s k = 0, the cost of making decision x k = is C 1 = 55 if s k = 1 and C 0 = 5 if s k = 0, and the cost of making decision x k = 3 is C 13 = 30 if s k = 1 and C 03 = 0 if s k = 0. Starting policy: Always make decision x k = 1. Use the policy iteration algorithm. Let v 0 = 0, then the value determination equations g + v 1 = v v 0 g + v 0 = v v 0
4 Page 4 of 5 Solutions Exam SF863 (b) Let gives g = 50, v 1 = 50. To find out if it is optimal we do one step of the policy iteration. For i = 1 (Heathcliff is up) min {C 1k + (p 11 (k)v 1 + p 10 (k)v 0 )} = k=1,,3 = min{c 11 +(p 11 (1)v 1 +p 10 (1)v 0 ), C 1 +(p 11 ()v 1 +p 10 ()v 0 ), C 13 +(p 11 (3)v 1 +p 10 (3)v 0 ), } = min{ 60 + (0.8v v 0 ), 55 + (0.9v 1 + 0v 0 ), 30 + (v 1 ), } = 100 = g+v 1 for k = 1.(and k = ) }{{}}{{}}{{} For i = 0 (Heathcliff is down) min {C 0k + (p 00 (k)v 0 + p 01 (k)v 1 )} = k=1,,3 = min{c 01 +(p 01 (1)v 1 +p 00 (1)v 0 ), C 0 +(p 01 ()v 1 +p 00 ()v 0 ), C 03 +(p 01 ()v 1 +p 00 ()v 0 ), } = min{ 30 + (0.4v v 0 ), 5 + (0.6v v 0 ), 0 + (v 1 ), } = 55 for k =. }{{}}{{}}{{} So the policy R 1 = [ 1], to buy a medal if Heathcliff is down and do nothing when he is up is better than R 0 = [1 1], i.e. to always do nothing. Let v 0 = 0, then solve the value determination equations again for the new policy g + v 1 = v v 0 g + v 0 = v v 0 gives g = 51.5, v 1 = The expected revenue increases by 1.5 dollars per day. Then y = [ y 01 y 0 y 03 y 11 y 1 y 13 ] T c = [ C 01 C 0 C 03 C 11 C 1 ] T [ C 13 = ] T 30, A = 1 p 00 (1) 1 p 00 () 1 p 00 (3) p 10 (1) p 10 () p 10 (3) = p 01 (1) p 01 () p 01 (3) 1 p 11 (1) 1 p 11 () 1 p 11 (3) = and b = [1 0 0] T. Then solving the LP gives y = [ 0 1/ /4 0 ] T then π 0 = y 01 + y 0 + y 03 = 1/4 and π 0 = y 01 + y 0 + y 03 = 3/4. Finally D ik = y ik /π i, so D 01 = 0, D 0 = 1, D 03 = 0, D 11 = 0, D 1 = 1, D 13 = 0, determines the optimal deterministic policy which is to always buy Heathcliff an employee of the day medal.
5 SF863 Solutions Exam Page 5 of 5 5. This can be solved using the newsboy problem formulation. Let p =, h = 8 and c = 5. Then the optimal target price satisfies p c p+h = 7 10 = F (S ). F is the cumulative distribution function of the stock prize, which is assumed to be uniform on the interval (0,1000), i.e. F (t) = t/1000 on the interval. F (700) = 0.7 and therefore S = 700. The optimal expected profit is given by 1000 t C(700) = dt t dt =
Advanced Computer Networks Lecture 3. Models of Queuing
 Advanced Computer Networks Lecture 3. Models of Queuing Husheng Li Min Kao Department of Electrical Engineering and Computer Science University of Tennessee, Knoxville Spring, 2016 1/13 Terminology of
Advanced Computer Networks Lecture 3. Models of Queuing Husheng Li Min Kao Department of Electrical Engineering and Computer Science University of Tennessee, Knoxville Spring, 2016 1/13 Terminology of
Suggested solutions for the exam in SF2863 Systems Engineering. June 12,
 Suggested solutons for the exam n SF2863 Systems Engneerng. June 12, 2012 14.00 19.00 Examner: Per Enqvst, phone: 790 62 98 1. We can thnk of the farm as a Jackson network. The strawberry feld s modelled
Suggested solutons for the exam n SF2863 Systems Engneerng. June 12, 2012 14.00 19.00 Examner: Per Enqvst, phone: 790 62 98 1. We can thnk of the farm as a Jackson network. The strawberry feld s modelled
Homework 1 - SOLUTION
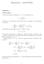 Homework - SOLUTION Problem M/M/ Queue ) Use the fact above to express π k, k > 0, as a function of π 0. π k = ( ) k λ π 0 µ 2) Using λ < µ and the fact that all π k s sum to, compute π 0 (as a function
Homework - SOLUTION Problem M/M/ Queue ) Use the fact above to express π k, k > 0, as a function of π 0. π k = ( ) k λ π 0 µ 2) Using λ < µ and the fact that all π k s sum to, compute π 0 (as a function
Buzen s algorithm. Cyclic network Extension of Jackson networks
 Outline Buzen s algorithm Mean value analysis for Jackson networks Cyclic network Extension of Jackson networks BCMP network 1 Marginal Distributions based on Buzen s algorithm With Buzen s algorithm,
Outline Buzen s algorithm Mean value analysis for Jackson networks Cyclic network Extension of Jackson networks BCMP network 1 Marginal Distributions based on Buzen s algorithm With Buzen s algorithm,
Queueing Theory (Part 4)
 Queueing Theory (Part 4) Nonexponential Queueing Systems and Economic Analysis Queueing Theory-1 Queueing Models with Nonexponential Distributions M/G/1 Model Poisson input process, general service time
Queueing Theory (Part 4) Nonexponential Queueing Systems and Economic Analysis Queueing Theory-1 Queueing Models with Nonexponential Distributions M/G/1 Model Poisson input process, general service time
Readings: Finish Section 5.2
 LECTURE 19 Readings: Finish Section 5.2 Lecture outline Markov Processes I Checkout counter example. Markov process: definition. -step transition probabilities. Classification of states. Example: Checkout
LECTURE 19 Readings: Finish Section 5.2 Lecture outline Markov Processes I Checkout counter example. Markov process: definition. -step transition probabilities. Classification of states. Example: Checkout
Answers to selected exercises
 Answers to selected exercises A First Course in Stochastic Models, Henk C. Tijms 1.1 ( ) 1.2 (a) Let waiting time if passengers already arrived,. Then,, (b) { (c) Long-run fraction for is (d) Let waiting
Answers to selected exercises A First Course in Stochastic Models, Henk C. Tijms 1.1 ( ) 1.2 (a) Let waiting time if passengers already arrived,. Then,, (b) { (c) Long-run fraction for is (d) Let waiting
Queueing Theory I Summary! Little s Law! Queueing System Notation! Stationary Analysis of Elementary Queueing Systems " M/M/1 " M/M/m " M/M/1/K "
 Queueing Theory I Summary Little s Law Queueing System Notation Stationary Analysis of Elementary Queueing Systems " M/M/1 " M/M/m " M/M/1/K " Little s Law a(t): the process that counts the number of arrivals
Queueing Theory I Summary Little s Law Queueing System Notation Stationary Analysis of Elementary Queueing Systems " M/M/1 " M/M/m " M/M/1/K " Little s Law a(t): the process that counts the number of arrivals
Discrete Event and Process Oriented Simulation (2)
 B. Maddah ENMG 622 Simulation 11/04/08 Discrete Event and Process Oriented Simulation (2) Discrete event hand simulation of an (s, S) periodic review inventory system Consider a retailer who sells a commodity
B. Maddah ENMG 622 Simulation 11/04/08 Discrete Event and Process Oriented Simulation (2) Discrete event hand simulation of an (s, S) periodic review inventory system Consider a retailer who sells a commodity
Control of Fork-Join Networks in Heavy-Traffic
 in Heavy-Traffic Asaf Zviran Based on MSc work under the guidance of Rami Atar (Technion) and Avishai Mandelbaum (Technion) Industrial Engineering and Management Technion June 2010 Introduction Network
in Heavy-Traffic Asaf Zviran Based on MSc work under the guidance of Rami Atar (Technion) and Avishai Mandelbaum (Technion) Industrial Engineering and Management Technion June 2010 Introduction Network
NANYANG TECHNOLOGICAL UNIVERSITY SEMESTER I EXAMINATION MH4702/MAS446/MTH437 Probabilistic Methods in OR
 NANYANG TECHNOLOGICAL UNIVERSITY SEMESTER I EXAMINATION 2013-201 MH702/MAS6/MTH37 Probabilistic Methods in OR December 2013 TIME ALLOWED: 2 HOURS INSTRUCTIONS TO CANDIDATES 1. This examination paper contains
NANYANG TECHNOLOGICAL UNIVERSITY SEMESTER I EXAMINATION 2013-201 MH702/MAS6/MTH37 Probabilistic Methods in OR December 2013 TIME ALLOWED: 2 HOURS INSTRUCTIONS TO CANDIDATES 1. This examination paper contains
IOE 202: lectures 11 and 12 outline
 IOE 202: lectures 11 and 12 outline Announcements Last time... Queueing models intro Performance characteristics of a queueing system Steady state analysis of an M/M/1 queueing system Other queueing systems,
IOE 202: lectures 11 and 12 outline Announcements Last time... Queueing models intro Performance characteristics of a queueing system Steady state analysis of an M/M/1 queueing system Other queueing systems,
An M/M/1/N Queuing system with Encouraged Arrivals
 Global Journal of Pure and Applied Mathematics. ISS 0973-1768 Volume 13, umber 7 (2017), pp. 3443-3453 Research India Publications http://www.ripublication.com An M/M/1/ Queuing system with Encouraged
Global Journal of Pure and Applied Mathematics. ISS 0973-1768 Volume 13, umber 7 (2017), pp. 3443-3453 Research India Publications http://www.ripublication.com An M/M/1/ Queuing system with Encouraged
NUMERICAL ANALYSIS PROBLEMS
 NUMERICAL ANALYSIS PROBLEMS JAMES KEESLING The problems that follow illustrate the methods covered in class. They are typical of the types of problems that will be on the tests.. Solving Equations Problem.
NUMERICAL ANALYSIS PROBLEMS JAMES KEESLING The problems that follow illustrate the methods covered in class. They are typical of the types of problems that will be on the tests.. Solving Equations Problem.
Handout 1: Introduction to Dynamic Programming. 1 Dynamic Programming: Introduction and Examples
 SEEM 3470: Dynamic Optimization and Applications 2013 14 Second Term Handout 1: Introduction to Dynamic Programming Instructor: Shiqian Ma January 6, 2014 Suggested Reading: Sections 1.1 1.5 of Chapter
SEEM 3470: Dynamic Optimization and Applications 2013 14 Second Term Handout 1: Introduction to Dynamic Programming Instructor: Shiqian Ma January 6, 2014 Suggested Reading: Sections 1.1 1.5 of Chapter
A PARAMETRIC DECOMPOSITION BASED APPROACH FOR MULTI-CLASS CLOSED QUEUING NETWORKS WITH SYNCHRONIZATION STATIONS
 A PARAMETRIC DECOMPOSITION BASED APPROACH FOR MULTI-CLASS CLOSED QUEUING NETWORKS WITH SYNCHRONIZATION STATIONS Kumar Satyam and Ananth Krishnamurthy Department of Decision Sciences and Engineering Systems,
A PARAMETRIC DECOMPOSITION BASED APPROACH FOR MULTI-CLASS CLOSED QUEUING NETWORKS WITH SYNCHRONIZATION STATIONS Kumar Satyam and Ananth Krishnamurthy Department of Decision Sciences and Engineering Systems,
Queuing Networks: Burke s Theorem, Kleinrock s Approximation, and Jackson s Theorem. Wade Trappe
 Queuing Networks: Burke s Theorem, Kleinrock s Approximation, and Jackson s Theorem Wade Trappe Lecture Overview Network of Queues Introduction Queues in Tandem roduct Form Solutions Burke s Theorem What
Queuing Networks: Burke s Theorem, Kleinrock s Approximation, and Jackson s Theorem Wade Trappe Lecture Overview Network of Queues Introduction Queues in Tandem roduct Form Solutions Burke s Theorem What
15 Closed production networks
 5 Closed production networks In the previous chapter we developed and analyzed stochastic models for production networks with a free inflow of jobs. In this chapter we will study production networks for
5 Closed production networks In the previous chapter we developed and analyzed stochastic models for production networks with a free inflow of jobs. In this chapter we will study production networks for
21 Markov Decision Processes
 2 Markov Decision Processes Chapter 6 introduced Markov chains and their analysis. Most of the chapter was devoted to discrete time Markov chains, i.e., Markov chains that are observed only at discrete
2 Markov Decision Processes Chapter 6 introduced Markov chains and their analysis. Most of the chapter was devoted to discrete time Markov chains, i.e., Markov chains that are observed only at discrete
STAT/MA 416 Answers Homework 4 September 27, 2007 Solutions by Mark Daniel Ward PROBLEMS
 STAT/MA 416 Answers Homework 4 September 27, 2007 Solutions by Mark Daniel Ward PROBLEMS 2. We ust examine the 36 possible products of two dice. We see that 1/36 for i = 1, 9, 16, 25, 36 2/36 for i = 2,
STAT/MA 416 Answers Homework 4 September 27, 2007 Solutions by Mark Daniel Ward PROBLEMS 2. We ust examine the 36 possible products of two dice. We see that 1/36 for i = 1, 9, 16, 25, 36 2/36 for i = 2,
Queueing Theory II. Summary. ! M/M/1 Output process. ! Networks of Queue! Method of Stages. ! General Distributions
 Queueing Theory II Summary! M/M/1 Output process! Networks of Queue! Method of Stages " Erlang Distribution " Hyperexponential Distribution! General Distributions " Embedded Markov Chains M/M/1 Output
Queueing Theory II Summary! M/M/1 Output process! Networks of Queue! Method of Stages " Erlang Distribution " Hyperexponential Distribution! General Distributions " Embedded Markov Chains M/M/1 Output
15 Closed production networks
 5 Closed production networks In the previous chapter we developed and analyzed stochastic models for production networks with a free inflow of jobs. In this chapter we will study production networks for
5 Closed production networks In the previous chapter we developed and analyzed stochastic models for production networks with a free inflow of jobs. In this chapter we will study production networks for
OPTIMALITY OF RANDOMIZED TRUNK RESERVATION FOR A PROBLEM WITH MULTIPLE CONSTRAINTS
 OPTIMALITY OF RANDOMIZED TRUNK RESERVATION FOR A PROBLEM WITH MULTIPLE CONSTRAINTS Xiaofei Fan-Orzechowski Department of Applied Mathematics and Statistics State University of New York at Stony Brook Stony
OPTIMALITY OF RANDOMIZED TRUNK RESERVATION FOR A PROBLEM WITH MULTIPLE CONSTRAINTS Xiaofei Fan-Orzechowski Department of Applied Mathematics and Statistics State University of New York at Stony Brook Stony
Introduction to Markov Chains, Queuing Theory, and Network Performance
 Introduction to Markov Chains, Queuing Theory, and Network Performance Marceau Coupechoux Telecom ParisTech, departement Informatique et Réseaux marceau.coupechoux@telecom-paristech.fr IT.2403 Modélisation
Introduction to Markov Chains, Queuing Theory, and Network Performance Marceau Coupechoux Telecom ParisTech, departement Informatique et Réseaux marceau.coupechoux@telecom-paristech.fr IT.2403 Modélisation
1.225 Transportation Flow Systems Quiz (December 17, 2001; Duration: 3 hours)
 1.225 Transportation Flow Systems Quiz (December 17, 2001; Duration: 3 hours) Student Name: Alias: Instructions: 1. This exam is open-book 2. No cooperation is permitted 3. Please write down your name
1.225 Transportation Flow Systems Quiz (December 17, 2001; Duration: 3 hours) Student Name: Alias: Instructions: 1. This exam is open-book 2. No cooperation is permitted 3. Please write down your name
Quality of Real-Time Streaming in Wireless Cellular Networks : Stochastic Modeling and Analysis
 Quality of Real-Time Streaming in Wireless Cellular Networs : Stochastic Modeling and Analysis B. Blaszczyszyn, M. Jovanovic and M. K. Karray Based on paper [1] WiOpt/WiVid Mai 16th, 2014 Outline Introduction
Quality of Real-Time Streaming in Wireless Cellular Networs : Stochastic Modeling and Analysis B. Blaszczyszyn, M. Jovanovic and M. K. Karray Based on paper [1] WiOpt/WiVid Mai 16th, 2014 Outline Introduction
IE 5112 Final Exam 2010
 IE 5112 Final Exam 2010 1. There are six cities in Kilroy County. The county must decide where to build fire stations. The county wants to build as few fire stations as possible while ensuring that there
IE 5112 Final Exam 2010 1. There are six cities in Kilroy County. The county must decide where to build fire stations. The county wants to build as few fire stations as possible while ensuring that there
MULTIPLE CHOICE QUESTIONS DECISION SCIENCE
 MULTIPLE CHOICE QUESTIONS DECISION SCIENCE 1. Decision Science approach is a. Multi-disciplinary b. Scientific c. Intuitive 2. For analyzing a problem, decision-makers should study a. Its qualitative aspects
MULTIPLE CHOICE QUESTIONS DECISION SCIENCE 1. Decision Science approach is a. Multi-disciplinary b. Scientific c. Intuitive 2. For analyzing a problem, decision-makers should study a. Its qualitative aspects
Discrete Random Variables
 Chapter 5 Discrete Random Variables Suppose that an experiment and a sample space are given. A random variable is a real-valued function of the outcome of the experiment. In other words, the random variable
Chapter 5 Discrete Random Variables Suppose that an experiment and a sample space are given. A random variable is a real-valued function of the outcome of the experiment. In other words, the random variable
Sandwich shop : a queuing net work with finite disposable resources queue and infinite resources queue
 Sandwich shop : a queuing net work with finite disposable resources queue and infinite resources queue Final project for ISYE 680: Queuing systems and Applications Hongtan Sun May 5, 05 Introduction As
Sandwich shop : a queuing net work with finite disposable resources queue and infinite resources queue Final project for ISYE 680: Queuing systems and Applications Hongtan Sun May 5, 05 Introduction As
Chapter 3: Markov Processes First hitting times
 Chapter 3: Markov Processes First hitting times L. Breuer University of Kent, UK November 3, 2010 Example: M/M/c/c queue Arrivals: Poisson process with rate λ > 0 Example: M/M/c/c queue Arrivals: Poisson
Chapter 3: Markov Processes First hitting times L. Breuer University of Kent, UK November 3, 2010 Example: M/M/c/c queue Arrivals: Poisson process with rate λ > 0 Example: M/M/c/c queue Arrivals: Poisson
Linear Model Predictive Control for Queueing Networks in Manufacturing and Road Traffic
 Linear Model Predictive Control for ueueing Networks in Manufacturing and Road Traffic Yoni Nazarathy Swinburne University of Technology, Melbourne. Joint work with: Erjen Lefeber (manufacturing), Hai
Linear Model Predictive Control for ueueing Networks in Manufacturing and Road Traffic Yoni Nazarathy Swinburne University of Technology, Melbourne. Joint work with: Erjen Lefeber (manufacturing), Hai
56:171 Operations Research Final Exam December 12, 1994
 56:171 Operations Research Final Exam December 12, 1994 Write your name on the first page, and initial the other pages. The response "NOTA " = "None of the above" Answer both parts A & B, and five sections
56:171 Operations Research Final Exam December 12, 1994 Write your name on the first page, and initial the other pages. The response "NOTA " = "None of the above" Answer both parts A & B, and five sections
Dual Interpretations and Duality Applications (continued)
 Dual Interpretations and Duality Applications (continued) Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/ yyye (LY, Chapters
Dual Interpretations and Duality Applications (continued) Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/ yyye (LY, Chapters
Graphing Equations Chapter Test
 1. Which line on the graph has a slope of 2/3? Graphing Equations Chapter Test A. Line A B. Line B C. Line C D. Line D 2. Which equation is represented on the graph? A. y = 4x 6 B. y = -4x 6 C. y = 4x
1. Which line on the graph has a slope of 2/3? Graphing Equations Chapter Test A. Line A B. Line B C. Line C D. Line D 2. Which equation is represented on the graph? A. y = 4x 6 B. y = -4x 6 C. y = 4x
Non-Linear Optimization
 Non-Linear Optimization Distinguishing Features Common Examples EOQ Balancing Risks Minimizing Risk 15.057 Spring 03 Vande Vate 1 Hierarchy of Models Network Flows Linear Programs Mixed Integer Linear
Non-Linear Optimization Distinguishing Features Common Examples EOQ Balancing Risks Minimizing Risk 15.057 Spring 03 Vande Vate 1 Hierarchy of Models Network Flows Linear Programs Mixed Integer Linear
Math 115 Second Midterm Exam
 Math 115 Second Midterm Exam November 14, 006 Name: Instructor: SOLUTIONS Section Number: 1. Do not open this exam until you are told to begin.. This exam has 8 pages including this cover. There are 7
Math 115 Second Midterm Exam November 14, 006 Name: Instructor: SOLUTIONS Section Number: 1. Do not open this exam until you are told to begin.. This exam has 8 pages including this cover. There are 7
Waiting time characteristics in cyclic queues
 Waiting time characteristics in cyclic queues Sanne R. Smits, Ivo Adan and Ton G. de Kok April 16, 2003 Abstract In this paper we study a single-server queue with FIFO service and cyclic interarrival and
Waiting time characteristics in cyclic queues Sanne R. Smits, Ivo Adan and Ton G. de Kok April 16, 2003 Abstract In this paper we study a single-server queue with FIFO service and cyclic interarrival and
Math 115 Second Midterm Exam
 Math 115 Second Midterm Exam November 14, 2006 Name: Instructor: Section Number: 1. Do not open this exam until you are told to begin. 2. This exam has 8 pages including this cover. There are 7 questions.
Math 115 Second Midterm Exam November 14, 2006 Name: Instructor: Section Number: 1. Do not open this exam until you are told to begin. 2. This exam has 8 pages including this cover. There are 7 questions.
2905 Queueing Theory and Simulation PART IV: SIMULATION
 2905 Queueing Theory and Simulation PART IV: SIMULATION 22 Random Numbers A fundamental step in a simulation study is the generation of random numbers, where a random number represents the value of a random
2905 Queueing Theory and Simulation PART IV: SIMULATION 22 Random Numbers A fundamental step in a simulation study is the generation of random numbers, where a random number represents the value of a random
Improved Algorithms for Machine Allocation in Manufacturing Systems
 Improved Algorithms for Machine Allocation in Manufacturing Systems Hans Frenk Martine Labbé Mario van Vliet Shuzhong Zhang October, 1992 Econometric Institute, Erasmus University Rotterdam, the Netherlands.
Improved Algorithms for Machine Allocation in Manufacturing Systems Hans Frenk Martine Labbé Mario van Vliet Shuzhong Zhang October, 1992 Econometric Institute, Erasmus University Rotterdam, the Netherlands.
Economics th April 2011
 Economics 401 8th April 2011 Instructions: Answer 7 of the following 9 questions. All questions are of equal weight. Indicate clearly on the first page which questions you want marked. 1. Answer both parts.
Economics 401 8th April 2011 Instructions: Answer 7 of the following 9 questions. All questions are of equal weight. Indicate clearly on the first page which questions you want marked. 1. Answer both parts.
THIELE CENTRE. The M/M/1 queue with inventory, lost sale and general lead times. Mohammad Saffari, Søren Asmussen and Rasoul Haji
 THIELE CENTRE for applied mathematics in natural science The M/M/1 queue with inventory, lost sale and general lead times Mohammad Saffari, Søren Asmussen and Rasoul Haji Research Report No. 11 September
THIELE CENTRE for applied mathematics in natural science The M/M/1 queue with inventory, lost sale and general lead times Mohammad Saffari, Søren Asmussen and Rasoul Haji Research Report No. 11 September
Discrete Event Systems Exam
 Computer Engineering and Networks Laboratory TEC, NSG, DISCO HS 2016 Prof. L. Thiele, Prof. L. Vanbever, Prof. R. Wattenhofer Discrete Event Systems Exam Friday, 3 rd February 2017, 14:00 16:00. Do not
Computer Engineering and Networks Laboratory TEC, NSG, DISCO HS 2016 Prof. L. Thiele, Prof. L. Vanbever, Prof. R. Wattenhofer Discrete Event Systems Exam Friday, 3 rd February 2017, 14:00 16:00. Do not
QUEUING MODELS AND MARKOV PROCESSES
 QUEUING MODELS AND MARKOV ROCESSES Queues form when customer demand for a service cannot be met immediately. They occur because of fluctuations in demand levels so that models of queuing are intrinsically
QUEUING MODELS AND MARKOV ROCESSES Queues form when customer demand for a service cannot be met immediately. They occur because of fluctuations in demand levels so that models of queuing are intrinsically
Tutorial: Optimal Control of Queueing Networks
 Department of Mathematics Tutorial: Optimal Control of Queueing Networks Mike Veatch Presented at INFORMS Austin November 7, 2010 1 Overview Network models MDP formulations: features, efficient formulations
Department of Mathematics Tutorial: Optimal Control of Queueing Networks Mike Veatch Presented at INFORMS Austin November 7, 2010 1 Overview Network models MDP formulations: features, efficient formulations
Course 16:198:520: Introduction To Artificial Intelligence Lecture 13. Decision Making. Abdeslam Boularias. Wednesday, December 7, 2016
 Course 16:198:520: Introduction To Artificial Intelligence Lecture 13 Decision Making Abdeslam Boularias Wednesday, December 7, 2016 1 / 45 Overview We consider probabilistic temporal models where the
Course 16:198:520: Introduction To Artificial Intelligence Lecture 13 Decision Making Abdeslam Boularias Wednesday, December 7, 2016 1 / 45 Overview We consider probabilistic temporal models where the
Stability and Rare Events in Stochastic Models Sergey Foss Heriot-Watt University, Edinburgh and Institute of Mathematics, Novosibirsk
 Stability and Rare Events in Stochastic Models Sergey Foss Heriot-Watt University, Edinburgh and Institute of Mathematics, Novosibirsk ANSAPW University of Queensland 8-11 July, 2013 1 Outline (I) Fluid
Stability and Rare Events in Stochastic Models Sergey Foss Heriot-Watt University, Edinburgh and Institute of Mathematics, Novosibirsk ANSAPW University of Queensland 8-11 July, 2013 1 Outline (I) Fluid
Some notes on Markov Decision Theory
 Some notes on Markov Decision Theory Nikolaos Laoutaris laoutaris@di.uoa.gr January, 2004 1 Markov Decision Theory[1, 2, 3, 4] provides a methodology for the analysis of probabilistic sequential decision
Some notes on Markov Decision Theory Nikolaos Laoutaris laoutaris@di.uoa.gr January, 2004 1 Markov Decision Theory[1, 2, 3, 4] provides a methodology for the analysis of probabilistic sequential decision
A Multi-Item Inventory Control Model for Perishable Items with Two Shelves
 The Eighth International Symposium on Operations Research and Its Applications (ISORA 9) Zhangjiajie, China, September 2 22, 29 Copyright 29 ORSC & APORC, pp. 36 314 A Multi-Item Inventory Control Model
The Eighth International Symposium on Operations Research and Its Applications (ISORA 9) Zhangjiajie, China, September 2 22, 29 Copyright 29 ORSC & APORC, pp. 36 314 A Multi-Item Inventory Control Model
Management of demand-driven production systems
 Management of demand-driven production systems Mike Chen, Richard Dubrawski, and Sean Meyn November 4, 22 Abstract Control-synthesis techniques are developed for demand-driven production systems. The resulting
Management of demand-driven production systems Mike Chen, Richard Dubrawski, and Sean Meyn November 4, 22 Abstract Control-synthesis techniques are developed for demand-driven production systems. The resulting
Name of the Student:
 SUBJECT NAME : Probability & Queueing Theory SUBJECT CODE : MA 6453 MATERIAL NAME : Part A questions REGULATION : R2013 UPDATED ON : November 2017 (Upto N/D 2017 QP) (Scan the above QR code for the direct
SUBJECT NAME : Probability & Queueing Theory SUBJECT CODE : MA 6453 MATERIAL NAME : Part A questions REGULATION : R2013 UPDATED ON : November 2017 (Upto N/D 2017 QP) (Scan the above QR code for the direct
DRAFT Formulation and Analysis of Linear Programs
 DRAFT Formulation and Analysis of Linear Programs Benjamin Van Roy and Kahn Mason c Benjamin Van Roy and Kahn Mason September 26, 2005 1 2 Contents 1 Introduction 7 1.1 Linear Algebra..........................
DRAFT Formulation and Analysis of Linear Programs Benjamin Van Roy and Kahn Mason c Benjamin Van Roy and Kahn Mason September 26, 2005 1 2 Contents 1 Introduction 7 1.1 Linear Algebra..........................
SOME HISTORY OF STOCHASTIC PROGRAMMING
 SOME HISTORY OF STOCHASTIC PROGRAMMING Early 1950 s: in applications of Linear Programming unknown values of coefficients: demands, technological coefficients, yields, etc. QUOTATION Dantzig, Interfaces
SOME HISTORY OF STOCHASTIC PROGRAMMING Early 1950 s: in applications of Linear Programming unknown values of coefficients: demands, technological coefficients, yields, etc. QUOTATION Dantzig, Interfaces
OPTIMAL CONTROL OF A FLEXIBLE SERVER
 Adv. Appl. Prob. 36, 139 170 (2004) Printed in Northern Ireland Applied Probability Trust 2004 OPTIMAL CONTROL OF A FLEXIBLE SERVER HYUN-SOO AHN, University of California, Berkeley IZAK DUENYAS, University
Adv. Appl. Prob. 36, 139 170 (2004) Printed in Northern Ireland Applied Probability Trust 2004 OPTIMAL CONTROL OF A FLEXIBLE SERVER HYUN-SOO AHN, University of California, Berkeley IZAK DUENYAS, University
Optimeringslära för F (SF1811) / Optimization (SF1841)
 Optimeringslära för F (SF1811) / Optimization (SF1841) 1. Information about the course 2. Examples of optimization problems 3. Introduction to linear programming Introduction - Per Enqvist 1 Linear programming
Optimeringslära för F (SF1811) / Optimization (SF1841) 1. Information about the course 2. Examples of optimization problems 3. Introduction to linear programming Introduction - Per Enqvist 1 Linear programming
Chapter 16 focused on decision making in the face of uncertainty about one future
 9 C H A P T E R Markov Chains Chapter 6 focused on decision making in the face of uncertainty about one future event (learning the true state of nature). However, some decisions need to take into account
9 C H A P T E R Markov Chains Chapter 6 focused on decision making in the face of uncertainty about one future event (learning the true state of nature). However, some decisions need to take into account
Time Reversibility and Burke s Theorem
 Queuing Analysis: Time Reversibility and Burke s Theorem Hongwei Zhang http://www.cs.wayne.edu/~hzhang Acknowledgement: this lecture is partially based on the slides of Dr. Yannis A. Korilis. Outline Time-Reversal
Queuing Analysis: Time Reversibility and Burke s Theorem Hongwei Zhang http://www.cs.wayne.edu/~hzhang Acknowledgement: this lecture is partially based on the slides of Dr. Yannis A. Korilis. Outline Time-Reversal
A Mechanism for Pricing Service Guarantees
 A Mechanism for Pricing Service Guarantees Bruce Hajek Department of Electrical and Computer Engineering and the Coordinated Science Laboratory University of Illinois at Urbana-Champaign Sichao Yang Qualcomm
A Mechanism for Pricing Service Guarantees Bruce Hajek Department of Electrical and Computer Engineering and the Coordinated Science Laboratory University of Illinois at Urbana-Champaign Sichao Yang Qualcomm
On the static assignment to parallel servers
 On the static assignment to parallel servers Ger Koole Vrije Universiteit Faculty of Mathematics and Computer Science De Boelelaan 1081a, 1081 HV Amsterdam The Netherlands Email: koole@cs.vu.nl, Url: www.cs.vu.nl/
On the static assignment to parallel servers Ger Koole Vrije Universiteit Faculty of Mathematics and Computer Science De Boelelaan 1081a, 1081 HV Amsterdam The Netherlands Email: koole@cs.vu.nl, Url: www.cs.vu.nl/
Stochastic Optimization
 Chapter 27 Page 1 Stochastic Optimization Operations research has been particularly successful in two areas of decision analysis: (i) optimization of problems involving many variables when the outcome
Chapter 27 Page 1 Stochastic Optimization Operations research has been particularly successful in two areas of decision analysis: (i) optimization of problems involving many variables when the outcome
1 Markov decision processes
 2.997 Decision-Making in Large-Scale Systems February 4 MI, Spring 2004 Handout #1 Lecture Note 1 1 Markov decision processes In this class we will study discrete-time stochastic systems. We can describe
2.997 Decision-Making in Large-Scale Systems February 4 MI, Spring 2004 Handout #1 Lecture Note 1 1 Markov decision processes In this class we will study discrete-time stochastic systems. We can describe
A tandem queue under an economical viewpoint
 A tandem queue under an economical viewpoint B. D Auria 1 Universidad Carlos III de Madrid, Spain joint work with S. Kanta The Basque Center for Applied Mathematics, Bilbao, Spain B. D Auria (Univ. Carlos
A tandem queue under an economical viewpoint B. D Auria 1 Universidad Carlos III de Madrid, Spain joint work with S. Kanta The Basque Center for Applied Mathematics, Bilbao, Spain B. D Auria (Univ. Carlos
CSE548, AMS542: Analysis of Algorithms, Fall 2017 Date: October 11. In-Class Midterm. ( 7:05 PM 8:20 PM : 75 Minutes )
 CSE548, AMS542: Analysis of Algorithms, Fall 2017 Date: October 11 In-Class Midterm ( 7:05 PM 8:20 PM : 75 Minutes ) This exam will account for either 15% or 30% of your overall grade depending on your
CSE548, AMS542: Analysis of Algorithms, Fall 2017 Date: October 11 In-Class Midterm ( 7:05 PM 8:20 PM : 75 Minutes ) This exam will account for either 15% or 30% of your overall grade depending on your
Part A. Ch (a) Thus, order quantity is 39-12=27. (b) Now b=5. Thus, order quantity is 29-12=17
 Homework2Solution Part A. Ch 2 12 (a) b = 65 40 = 25 from normal distribution table Thus, order quantity is 39-12=27 (b) Now b=5 from normal distribution table Thus, order quantity is 29-12=17 It is interesting
Homework2Solution Part A. Ch 2 12 (a) b = 65 40 = 25 from normal distribution table Thus, order quantity is 39-12=27 (b) Now b=5 from normal distribution table Thus, order quantity is 29-12=17 It is interesting
1 Answer Key for exam2162sp07 vl
 Ma 162 College Algebra Second Exam vl 9 1 Answer Key for exam2162sp07 vl 1. [ x =, 2, y =, 3, z =, 1, w =, 3, Mary, [63.5, 2, 1]] 2. ABC: 1 L1 L2 1CDE:L1 11 L2 3. P =1.8 x +1.8 y +1.5 z 0 x,0 y 9 x +10y
Ma 162 College Algebra Second Exam vl 9 1 Answer Key for exam2162sp07 vl 1. [ x =, 2, y =, 3, z =, 1, w =, 3, Mary, [63.5, 2, 1]] 2. ABC: 1 L1 L2 1CDE:L1 11 L2 3. P =1.8 x +1.8 y +1.5 z 0 x,0 y 9 x +10y
57:022 Principles of Design II Final Exam Solutions - Spring 1997
 57:022 Principles of Design II Final Exam Solutions - Spring 1997 Part: I II III IV V VI Total Possible Pts: 52 10 12 16 13 12 115 PART ONE Indicate "+" if True and "o" if False: + a. If a component's
57:022 Principles of Design II Final Exam Solutions - Spring 1997 Part: I II III IV V VI Total Possible Pts: 52 10 12 16 13 12 115 PART ONE Indicate "+" if True and "o" if False: + a. If a component's
Notes on induction proofs and recursive definitions
 Notes on induction proofs and recursive definitions James Aspnes December 13, 2010 1 Simple induction Most of the proof techniques we ve talked about so far are only really useful for proving a property
Notes on induction proofs and recursive definitions James Aspnes December 13, 2010 1 Simple induction Most of the proof techniques we ve talked about so far are only really useful for proving a property
The problems that follow illustrate the methods covered in class. They are typical of the types of problems that will be on the tests.
 NUMERICAL ANALYSIS PRACTICE PROBLEMS JAMES KEESLING The problems that follow illustrate the methods covered in class. They are typical of the types of problems that will be on the tests.. Solving Equations
NUMERICAL ANALYSIS PRACTICE PROBLEMS JAMES KEESLING The problems that follow illustrate the methods covered in class. They are typical of the types of problems that will be on the tests.. Solving Equations
Queueing Review. Christos Alexopoulos and Dave Goldsman 10/6/16. (mostly from BCNN) Georgia Institute of Technology, Atlanta, GA, USA
 1 / 24 Queueing Review (mostly from BCNN) Christos Alexopoulos and Dave Goldsman Georgia Institute of Technology, Atlanta, GA, USA 10/6/16 2 / 24 Outline 1 Introduction 2 Queueing Notation 3 Transient
1 / 24 Queueing Review (mostly from BCNN) Christos Alexopoulos and Dave Goldsman Georgia Institute of Technology, Atlanta, GA, USA 10/6/16 2 / 24 Outline 1 Introduction 2 Queueing Notation 3 Transient
Advanced linear programming
 Advanced linear programming http://www.staff.science.uu.nl/~akker103/alp/ Chapter 10: Integer linear programming models Marjan van den Akker 1 Intro. Marjan van den Akker Master Mathematics TU/e PhD Mathematics
Advanced linear programming http://www.staff.science.uu.nl/~akker103/alp/ Chapter 10: Integer linear programming models Marjan van den Akker 1 Intro. Marjan van den Akker Master Mathematics TU/e PhD Mathematics
Probability Exercises. Problem 1.
 Probability Exercises. Ma 162 Spring 2010 Ma 162 Spring 2010 April 21, 2010 Problem 1. ˆ Conditional Probability: It is known that a student who does his online homework on a regular basis has a chance
Probability Exercises. Ma 162 Spring 2010 Ma 162 Spring 2010 April 21, 2010 Problem 1. ˆ Conditional Probability: It is known that a student who does his online homework on a regular basis has a chance
Data analysis and stochastic modeling
 Data analysis and stochastic modeling Lecture 7 An introduction to queueing theory Guillaume Gravier guillaume.gravier@irisa.fr with a lot of help from Paul Jensen s course http://www.me.utexas.edu/ jensen/ormm/instruction/powerpoint/or_models_09/14_queuing.ppt
Data analysis and stochastic modeling Lecture 7 An introduction to queueing theory Guillaume Gravier guillaume.gravier@irisa.fr with a lot of help from Paul Jensen s course http://www.me.utexas.edu/ jensen/ormm/instruction/powerpoint/or_models_09/14_queuing.ppt
Lecture 9: Deterministic Fluid Models and Many-Server Heavy-Traffic Limits. IEOR 4615: Service Engineering Professor Whitt February 19, 2015
 Lecture 9: Deterministic Fluid Models and Many-Server Heavy-Traffic Limits IEOR 4615: Service Engineering Professor Whitt February 19, 2015 Outline Deterministic Fluid Models Directly From Data: Cumulative
Lecture 9: Deterministic Fluid Models and Many-Server Heavy-Traffic Limits IEOR 4615: Service Engineering Professor Whitt February 19, 2015 Outline Deterministic Fluid Models Directly From Data: Cumulative
1 Bewley Economies with Aggregate Uncertainty
 1 Bewley Economies with Aggregate Uncertainty Sofarwehaveassumedawayaggregatefluctuations (i.e., business cycles) in our description of the incomplete-markets economies with uninsurable idiosyncratic risk
1 Bewley Economies with Aggregate Uncertainty Sofarwehaveassumedawayaggregatefluctuations (i.e., business cycles) in our description of the incomplete-markets economies with uninsurable idiosyncratic risk
3. (1.2.13, 19, 31) Find the given limit. If necessary, state that the limit does not exist.
 Departmental Review for Survey of Calculus Revised Fall 2013 Directions: All work should be shown and all answers should be exact and simplified (unless stated otherwise) to receive full credit on the
Departmental Review for Survey of Calculus Revised Fall 2013 Directions: All work should be shown and all answers should be exact and simplified (unless stated otherwise) to receive full credit on the
Probabilistic Model Checking Michaelmas Term Dr. Dave Parker. Department of Computer Science University of Oxford
 Probabilistic Model Checking Michaelmas Term 20 Dr. Dave Parker Department of Computer Science University of Oxford Overview PCTL for MDPs syntax, semantics, examples PCTL model checking next, bounded
Probabilistic Model Checking Michaelmas Term 20 Dr. Dave Parker Department of Computer Science University of Oxford Overview PCTL for MDPs syntax, semantics, examples PCTL model checking next, bounded
Queueing Theory. VK Room: M Last updated: October 17, 2013.
 Queueing Theory VK Room: M1.30 knightva@cf.ac.uk www.vincent-knight.com Last updated: October 17, 2013. 1 / 63 Overview Description of Queueing Processes The Single Server Markovian Queue Multi Server
Queueing Theory VK Room: M1.30 knightva@cf.ac.uk www.vincent-knight.com Last updated: October 17, 2013. 1 / 63 Overview Description of Queueing Processes The Single Server Markovian Queue Multi Server
MATH 445/545 Homework 1: Due February 11th, 2016
 MATH 445/545 Homework 1: Due February 11th, 2016 Answer the following questions Please type your solutions and include the questions and all graphics if needed with the solution 1 A business executive
MATH 445/545 Homework 1: Due February 11th, 2016 Answer the following questions Please type your solutions and include the questions and all graphics if needed with the solution 1 A business executive
MS-E2140. Lecture 1. (course book chapters )
 Linear Programming MS-E2140 Motivations and background Lecture 1 (course book chapters 1.1-1.4) Linear programming problems and examples Problem manipulations and standard form problems Graphical representation
Linear Programming MS-E2140 Motivations and background Lecture 1 (course book chapters 1.1-1.4) Linear programming problems and examples Problem manipulations and standard form problems Graphical representation
Queueing Networks and Insensitivity
 Lukáš Adam 29. 10. 2012 1 / 40 Table of contents 1 Jackson networks 2 Insensitivity in Erlang s Loss System 3 Quasi-Reversibility and Single-Node Symmetric Queues 4 Quasi-Reversibility in Networks 5 The
Lukáš Adam 29. 10. 2012 1 / 40 Table of contents 1 Jackson networks 2 Insensitivity in Erlang s Loss System 3 Quasi-Reversibility and Single-Node Symmetric Queues 4 Quasi-Reversibility in Networks 5 The
SECTION 5.1: Polynomials
 1 SECTION 5.1: Polynomials Functions Definitions: Function, Independent Variable, Dependent Variable, Domain, and Range A function is a rule that assigns to each input value x exactly output value y =
1 SECTION 5.1: Polynomials Functions Definitions: Function, Independent Variable, Dependent Variable, Domain, and Range A function is a rule that assigns to each input value x exactly output value y =
1.4 Linear Functions of Several Variables
 .4 Linear Functions of Several Variables Question : What is a linear function of several independent variables? Question : What do the coefficients of the variables tell us? Question : How do you find
.4 Linear Functions of Several Variables Question : What is a linear function of several independent variables? Question : What do the coefficients of the variables tell us? Question : How do you find
Chapter 10. Queuing Systems. D (Queuing Theory) Queuing theory is the branch of operations research concerned with waiting lines.
 Chapter 10 Queuing Systems D. 10. 1. (Queuing Theory) Queuing theory is the branch of operations research concerned with waiting lines. D. 10.. (Queuing System) A ueuing system consists of 1. a user source.
Chapter 10 Queuing Systems D. 10. 1. (Queuing Theory) Queuing theory is the branch of operations research concerned with waiting lines. D. 10.. (Queuing System) A ueuing system consists of 1. a user source.
Dynamic Service Placement in Geographically Distributed Clouds
 Dynamic Service Placement in Geographically Distributed Clouds Qi Zhang 1 Quanyan Zhu 2 M. Faten Zhani 1 Raouf Boutaba 1 1 School of Computer Science University of Waterloo 2 Department of Electrical and
Dynamic Service Placement in Geographically Distributed Clouds Qi Zhang 1 Quanyan Zhu 2 M. Faten Zhani 1 Raouf Boutaba 1 1 School of Computer Science University of Waterloo 2 Department of Electrical and
32. Use a graphing utility to find the equation of the line of best fit. Write the equation of the line rounded to two decimal places, if necessary.
 Pre-Calculus A Final Review Part 2 Calculator Name 31. The price p and the quantity x sold of a certain product obey the demand equation: p = x + 80 where r = xp. What is the revenue to the nearest dollar
Pre-Calculus A Final Review Part 2 Calculator Name 31. The price p and the quantity x sold of a certain product obey the demand equation: p = x + 80 where r = xp. What is the revenue to the nearest dollar
IS 709/809: Computational Methods in IS Research Fall Exam Review
 IS 709/809: Computational Methods in IS Research Fall 2017 Exam Review Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Exam When: Tuesday (11/28) 7:10pm
IS 709/809: Computational Methods in IS Research Fall 2017 Exam Review Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Exam When: Tuesday (11/28) 7:10pm
The use of relative priorities in optimizing the performance of a queueing system
 The use of relative priorities in optimizing the performance of a queueing system Refael Hassin Justo Puerto 2 Francisco R. Fernández 3 November 5, 2007 Abstract Relative priorities in an n-class queueing
The use of relative priorities in optimizing the performance of a queueing system Refael Hassin Justo Puerto 2 Francisco R. Fernández 3 November 5, 2007 Abstract Relative priorities in an n-class queueing
Departure time choice equilibrium problem with partial implementation of congestion pricing
 Departure time choice equilibrium problem with partial implementation of congestion pricing Tokyo Institute of Technology Postdoctoral researcher Katsuya Sakai 1 Contents 1. Introduction 2. Method/Tool
Departure time choice equilibrium problem with partial implementation of congestion pricing Tokyo Institute of Technology Postdoctoral researcher Katsuya Sakai 1 Contents 1. Introduction 2. Method/Tool
Asymptotically Optimal Inventory Control For Assemble-to-Order Systems
 Asymptotically Optimal Inventory Control For Assemble-to-Order Systems Marty Reiman Columbia Univerisity joint work with Mustafa Dogru, Haohua Wan, and Qiong Wang May 16, 2018 Outline The Assemble-to-Order
Asymptotically Optimal Inventory Control For Assemble-to-Order Systems Marty Reiman Columbia Univerisity joint work with Mustafa Dogru, Haohua Wan, and Qiong Wang May 16, 2018 Outline The Assemble-to-Order
Chapter 5. Continuous-Time Markov Chains. Prof. Shun-Ren Yang Department of Computer Science, National Tsing Hua University, Taiwan
 Chapter 5. Continuous-Time Markov Chains Prof. Shun-Ren Yang Department of Computer Science, National Tsing Hua University, Taiwan Continuous-Time Markov Chains Consider a continuous-time stochastic process
Chapter 5. Continuous-Time Markov Chains Prof. Shun-Ren Yang Department of Computer Science, National Tsing Hua University, Taiwan Continuous-Time Markov Chains Consider a continuous-time stochastic process
Minimizing response times and queue lengths in systems of parallel queues
 Minimizing response times and queue lengths in systems of parallel queues Ger Koole Department of Mathematics and Computer Science, Vrije Universiteit, De Boelelaan 1081a, 1081 HV Amsterdam, The Netherlands
Minimizing response times and queue lengths in systems of parallel queues Ger Koole Department of Mathematics and Computer Science, Vrije Universiteit, De Boelelaan 1081a, 1081 HV Amsterdam, The Netherlands
Math Practice Final - solutions
 Math 151 - Practice Final - solutions 2 1-2 -1 0 1 2 3 Problem 1 Indicate the following from looking at the graph of f(x) above. All answers are small integers, ±, or DNE for does not exist. a) lim x 1
Math 151 - Practice Final - solutions 2 1-2 -1 0 1 2 3 Problem 1 Indicate the following from looking at the graph of f(x) above. All answers are small integers, ±, or DNE for does not exist. a) lim x 1
Relations and Functions
 Lesson 5.1 Objectives Identify the domain and range of a relation. Write a rule for a sequence of numbers. Determine if a relation is a function. Relations and Functions You can estimate the distance of
Lesson 5.1 Objectives Identify the domain and range of a relation. Write a rule for a sequence of numbers. Determine if a relation is a function. Relations and Functions You can estimate the distance of
THE ON NETWORK FLOW EQUATIONS AND SPLITTG FORMULAS TRODUCTION FOR SOJOURN TIMES IN QUEUEING NETWORKS 1 NO FLOW EQUATIONS
 Applied Mathematics and Stochastic Analysis 4, Number 2, Summer 1991, III-I16 ON NETWORK FLOW EQUATIONS AND SPLITTG FORMULAS FOR SOJOURN TIMES IN QUEUEING NETWORKS 1 HANS DADUNA Institut flit Mathematische
Applied Mathematics and Stochastic Analysis 4, Number 2, Summer 1991, III-I16 ON NETWORK FLOW EQUATIONS AND SPLITTG FORMULAS FOR SOJOURN TIMES IN QUEUEING NETWORKS 1 HANS DADUNA Institut flit Mathematische
reversed chain is ergodic and has the same equilibrium probabilities (check that π j =
 Lecture 10 Networks of queues In this lecture we shall finally get around to consider what happens when queues are part of networks (which, after all, is the topic of the course). Firstly we shall need
Lecture 10 Networks of queues In this lecture we shall finally get around to consider what happens when queues are part of networks (which, after all, is the topic of the course). Firstly we shall need
Exam 1 - Math Solutions
 Exam 1 - Math 3200 - Solutions Spring 2013 1. Without actually expanding, find the coefficient of x y 2 z 3 in the expansion of (2x y z) 6. (A) 120 (B) 60 (C) 30 (D) 20 (E) 10 (F) 10 (G) 20 (H) 30 (I)
Exam 1 - Math 3200 - Solutions Spring 2013 1. Without actually expanding, find the coefficient of x y 2 z 3 in the expansion of (2x y z) 6. (A) 120 (B) 60 (C) 30 (D) 20 (E) 10 (F) 10 (G) 20 (H) 30 (I)
Optimal and Heuristic Resource Allocation Policies in Serial Production Systems
 Clemson University TigerPrints All Theses Theses 12-2008 Optimal and Heuristic Resource Allocation Policies in Serial Production Systems Ramesh Arumugam Clemson University, rarumug@clemson.edu Follow this
Clemson University TigerPrints All Theses Theses 12-2008 Optimal and Heuristic Resource Allocation Policies in Serial Production Systems Ramesh Arumugam Clemson University, rarumug@clemson.edu Follow this
STOCHASTIC MODELS FOR RELIABILITY, AVAILABILITY, AND MAINTAINABILITY
 STOCHASTIC MODELS FOR RELIABILITY, AVAILABILITY, AND MAINTAINABILITY Ph.D. Assistant Professor Industrial and Systems Engineering Auburn University RAM IX Summit November 2 nd 2016 Outline Introduction
STOCHASTIC MODELS FOR RELIABILITY, AVAILABILITY, AND MAINTAINABILITY Ph.D. Assistant Professor Industrial and Systems Engineering Auburn University RAM IX Summit November 2 nd 2016 Outline Introduction
Computations - Show all your work. (30 pts)
 Math 1012 Final Name: Computations - Show all your work. (30 pts) 1. Fractions. a. 1 7 + 1 5 b. 12 5 5 9 c. 6 8 2 16 d. 1 6 + 2 5 + 3 4 2.a Powers of ten. i. 10 3 10 2 ii. 10 2 10 6 iii. 10 0 iv. (10 5
Math 1012 Final Name: Computations - Show all your work. (30 pts) 1. Fractions. a. 1 7 + 1 5 b. 12 5 5 9 c. 6 8 2 16 d. 1 6 + 2 5 + 3 4 2.a Powers of ten. i. 10 3 10 2 ii. 10 2 10 6 iii. 10 0 iv. (10 5
