Discrete Event and Process Oriented Simulation (2)
|
|
|
- Sybil Dennis
- 6 years ago
- Views:
Transcription
1 B. Maddah ENMG 622 Simulation 11/04/08 Discrete Event and Process Oriented Simulation (2) Discrete event hand simulation of an (s, S) periodic review inventory system Consider a retailer who sells a commodity having a random weekly demand D. At the beginning every week, the retailer reviews the inventory level of the commodity, and computes the inventory position. The inventory position is defined as the inventory on-hand plus on-order minus backlogged demand. If the inventory position is less or equal than the reorder point s, an order is placed to raise the inventory to the order-up-to level S. An order has a fixed cost of K dollars and a variable cost of c $/unit. Note that since all demand is going to be met, we will ignore the variable ordering cost. An order has a lead time of L weeks, and is assumed to be delivered at the beginning of the week. Demand is assumed to occur at the end of the week. If demand in a week exceeds the on-hand inventory at the beginning of the week, then excess demand is backlogged. 1
2 When an order arrives (at the beginning of a week), it is immediately used to meet backlogged demand (if any). Backlogged demand at the beginning of a week has a penalty cost of p $/unit/week. On-hand inventory at the beginning of a week incurs a holding cost of h $/unit/week. In a discrete-event simulation of this system, the events are 1. Start of the simulation. 2. Arrival of an order at the beginning of a week. 3. Placing an order at the beginning of a week 4. Demand for the product at the end of a week. 5. End of the simulation after n weeks. Inventory Level S s Net Inventory L L Time Inventory Position 2
3 In the following, we will do a simple hand simulation in tabular form assuming that random demands have been generated for the n weeks. The objective of the simulation is determining the optimal (s, S) policy that minimizes weekly cost. Let o I t = the net inventory (inventory on hand or amount backordered), at the beginning of week t ; o D t = Demand at the end of week t ; o O t = Amount ordered at the beginning of week t. Then, It+ 1 = It + Ot L Dt, t = 2,3, K We will set I 1 = S, assuming that the system starts fully stocked. Note that I t may be < 0, in the event of a backlog. For example, Suppose S = 69, s = 45, demand is Poisson (λ = 18), h = 1, p = 9, K = 32, L = 2 periods and n = 15. First, we generate demand for 15 weeks based on the Poisson distribution (see below). Let H t, P t, and OC t be the holding, penalty, and ordering cost incurred in a week, and let IP t be the inventory position at the beginning of week t. 3
4 Then, the hand simulation is as follows. S s L K h p Week, t I t IP t D t O t H t P t OC t Σ Mean weekly cost $41.3 Arena (process oriented) simulation of serial and parallel processing (Section 3.5 KSS). Applications arrive to a loan application office according to a Poisson process with rate λ = 1/1.25 applications/hour. The processing of each application requires four steps: Credit check, preparing covenant, pricing, and fund disbursement. 4
5 The office has four employees (Alfie, Betty, Chuck and Doris, if you care). Each employee can handle any of the four loan processing steps in an exponentially distributed time with mean 1 hour. The main question here is how to assign employees to tasks. Should employees be allocated in series with each employee handling one step of the loan processing? λ = 0.8 μ = 1, C S 2 = 1 μ = 1, C S 2 = 1 μ = 1, C S 2 = 1 μ = 1, C S 2 = 1 Or, should all employees work together in parallel with an employee handling an application from A to Z? μ = 1/4, C S 2 = 1/4 λ = 0.8 5
6 Parallel system seems to be better because (i) employees will have less idle times; and (ii) service time variability is less (as measured by C 2 S, the coefficient of variation). Series system could have some advantage such as improving the efficiency of dedicated employees due to learning. But learning is not considered here. The simulation of both systems in Arena for 16,000 hours to confirm these claims. The total waiting time in queue (delay) is hours in the series system and 2.12 hours in the parallel system, indicating that the parallel system is much more efficient. Validation of the series vs. parallel problem If you still don t believe that parallel is better in this case, we ll do an analytical validation/verification of the simulation results. The mean delay in the series system is computed from an exact analytical expression by utilizing the following fact. Fact 1. The departure process from an M/M/c queue with arrival rate λ is a Poisson process with rate λ. Each station of the series system can be seen as a M/M/1. 6
7 The mean delay in the series is therefore, 1/ W (series) = q 4 Wq( M / M /1) = ρ hrs. μ λ = 1 1/1.25 = 0.2 = The mean delay in the parallel (M/GI/4) system is computed approximately using the following facts. Fact 2. The sum of k independent exponential random variables with mean 1/μ is an Erlang random variable with mean k/μ and variance k/μ 2. Fact 3. The mean delay in an M/M/c queue is c a Wq ( M / M / c) = 2 p0, c!( cμ) (1 ρ) where a = λ/μ and c 1 n c a a p0 = P{0 customers in system} = +. n= 0 n! c!(1 ρ) Fact 4 (QNA approximation). (i) The mean delay in a GI/GI/c queue can be approximated by 2 2 CA + C S Wq( GI / GI / c) Wq( M / M / c), 2 where C 2 A and C 2 S are the coefficients of variation of interarrival and service times, and W q (M/M/c) is the mean delay in an M/M/c with the same mean inter-arrival and service times. 1 7
8 2 (ii) The approximation in (i) is valid for small values of C A and C 2 S. (For M/M/c, C 2 A = C 2 S = 1. Values in the ball park of 1 are ok.) In the case of our parallel system, C 2 A = 1, and C 2 S = 1/4 (by Fact 2), and the QNA approximation is likely to be valid. Then, the mean delay in the system can be approximated by 1+ 1/4 Wq(parallel) Wq( M / M / 4), 2 where, with λ = 0.8, μ = 1/4, a = λ/μ = 3.2 and ρ = a/c = 0.8, by Fact 3, c Wq ( M / M / c) = 2 + 4[4(1/ 4)](1 0.8) n= 0 n! 4!(1 0.8) = 2.98 hrs. Then, W q (parallel) = 1.86 hrs. 8
Queuing Analysis. Chapter Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall
 Queuing Analysis Chapter 13 13-1 Chapter Topics Elements of Waiting Line Analysis The Single-Server Waiting Line System Undefined and Constant Service Times Finite Queue Length Finite Calling Problem The
Queuing Analysis Chapter 13 13-1 Chapter Topics Elements of Waiting Line Analysis The Single-Server Waiting Line System Undefined and Constant Service Times Finite Queue Length Finite Calling Problem The
ISyE 2030 Practice Test 2
 1 NAME ISyE 2030 Practice Test 2 Summer 2005 This test is open notes, open books. You have exactly 75 minutes. 1. Short-Answer Questions (a) TRUE or FALSE? If arrivals occur according to a Poisson process
1 NAME ISyE 2030 Practice Test 2 Summer 2005 This test is open notes, open books. You have exactly 75 minutes. 1. Short-Answer Questions (a) TRUE or FALSE? If arrivals occur according to a Poisson process
Queueing Review. Christos Alexopoulos and Dave Goldsman 10/6/16. (mostly from BCNN) Georgia Institute of Technology, Atlanta, GA, USA
 1 / 24 Queueing Review (mostly from BCNN) Christos Alexopoulos and Dave Goldsman Georgia Institute of Technology, Atlanta, GA, USA 10/6/16 2 / 24 Outline 1 Introduction 2 Queueing Notation 3 Transient
1 / 24 Queueing Review (mostly from BCNN) Christos Alexopoulos and Dave Goldsman Georgia Institute of Technology, Atlanta, GA, USA 10/6/16 2 / 24 Outline 1 Introduction 2 Queueing Notation 3 Transient
Advanced Computer Networks Lecture 3. Models of Queuing
 Advanced Computer Networks Lecture 3. Models of Queuing Husheng Li Min Kao Department of Electrical Engineering and Computer Science University of Tennessee, Knoxville Spring, 2016 1/13 Terminology of
Advanced Computer Networks Lecture 3. Models of Queuing Husheng Li Min Kao Department of Electrical Engineering and Computer Science University of Tennessee, Knoxville Spring, 2016 1/13 Terminology of
Chapter 6 Queueing Models. Banks, Carson, Nelson & Nicol Discrete-Event System Simulation
 Chapter 6 Queueing Models Banks, Carson, Nelson & Nicol Discrete-Event System Simulation Purpose Simulation is often used in the analysis of queueing models. A simple but typical queueing model: Queueing
Chapter 6 Queueing Models Banks, Carson, Nelson & Nicol Discrete-Event System Simulation Purpose Simulation is often used in the analysis of queueing models. A simple but typical queueing model: Queueing
Generation of Discrete Random variables
 Simulation Simulation is the imitation of the operation of a realworld process or system over time. The act of simulating something first requires that a model be developed; this model represents the key
Simulation Simulation is the imitation of the operation of a realworld process or system over time. The act of simulating something first requires that a model be developed; this model represents the key
Homework 1 - SOLUTION
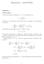 Homework - SOLUTION Problem M/M/ Queue ) Use the fact above to express π k, k > 0, as a function of π 0. π k = ( ) k λ π 0 µ 2) Using λ < µ and the fact that all π k s sum to, compute π 0 (as a function
Homework - SOLUTION Problem M/M/ Queue ) Use the fact above to express π k, k > 0, as a function of π 0. π k = ( ) k λ π 0 µ 2) Using λ < µ and the fact that all π k s sum to, compute π 0 (as a function
Slides 9: Queuing Models
 Slides 9: Queuing Models Purpose Simulation is often used in the analysis of queuing models. A simple but typical queuing model is: Queuing models provide the analyst with a powerful tool for designing
Slides 9: Queuing Models Purpose Simulation is often used in the analysis of queuing models. A simple but typical queuing model is: Queuing models provide the analyst with a powerful tool for designing
Queueing Review. Christos Alexopoulos and Dave Goldsman 10/25/17. (mostly from BCNN) Georgia Institute of Technology, Atlanta, GA, USA
 1 / 26 Queueing Review (mostly from BCNN) Christos Alexopoulos and Dave Goldsman Georgia Institute of Technology, Atlanta, GA, USA 10/25/17 2 / 26 Outline 1 Introduction 2 Queueing Notation 3 Transient
1 / 26 Queueing Review (mostly from BCNN) Christos Alexopoulos and Dave Goldsman Georgia Institute of Technology, Atlanta, GA, USA 10/25/17 2 / 26 Outline 1 Introduction 2 Queueing Notation 3 Transient
5/15/18. Operations Research: An Introduction Hamdy A. Taha. Copyright 2011, 2007 by Pearson Education, Inc. All rights reserved.
 The objective of queuing analysis is to offer a reasonably satisfactory service to waiting customers. Unlike the other tools of OR, queuing theory is not an optimization technique. Rather, it determines
The objective of queuing analysis is to offer a reasonably satisfactory service to waiting customers. Unlike the other tools of OR, queuing theory is not an optimization technique. Rather, it determines
Queueing Theory I Summary! Little s Law! Queueing System Notation! Stationary Analysis of Elementary Queueing Systems " M/M/1 " M/M/m " M/M/1/K "
 Queueing Theory I Summary Little s Law Queueing System Notation Stationary Analysis of Elementary Queueing Systems " M/M/1 " M/M/m " M/M/1/K " Little s Law a(t): the process that counts the number of arrivals
Queueing Theory I Summary Little s Law Queueing System Notation Stationary Analysis of Elementary Queueing Systems " M/M/1 " M/M/m " M/M/1/K " Little s Law a(t): the process that counts the number of arrivals
Performance Evaluation of Queuing Systems
 Performance Evaluation of Queuing Systems Introduction to Queuing Systems System Performance Measures & Little s Law Equilibrium Solution of Birth-Death Processes Analysis of Single-Station Queuing Systems
Performance Evaluation of Queuing Systems Introduction to Queuing Systems System Performance Measures & Little s Law Equilibrium Solution of Birth-Death Processes Analysis of Single-Station Queuing Systems
Basic Queueing Theory
 After The Race The Boston Marathon is a local institution with over a century of history and tradition. The race is run on Patriot s Day, starting on the Hopkinton green and ending at the Prudential Center
After The Race The Boston Marathon is a local institution with over a century of history and tradition. The race is run on Patriot s Day, starting on the Hopkinton green and ending at the Prudential Center
PBW 654 Applied Statistics - I Urban Operations Research
 PBW 654 Applied Statistics - I Urban Operations Research Lecture 2.I Queuing Systems An Introduction Operations Research Models Deterministic Models Linear Programming Integer Programming Network Optimization
PBW 654 Applied Statistics - I Urban Operations Research Lecture 2.I Queuing Systems An Introduction Operations Research Models Deterministic Models Linear Programming Integer Programming Network Optimization
NATCOR: Stochastic Modelling
 NATCOR: Stochastic Modelling Queueing Theory II Chris Kirkbride Management Science 2017 Overview of Today s Sessions I Introduction to Queueing Modelling II Multiclass Queueing Models III Queueing Control
NATCOR: Stochastic Modelling Queueing Theory II Chris Kirkbride Management Science 2017 Overview of Today s Sessions I Introduction to Queueing Modelling II Multiclass Queueing Models III Queueing Control
Queueing systems. Renato Lo Cigno. Simulation and Performance Evaluation Queueing systems - Renato Lo Cigno 1
 Queueing systems Renato Lo Cigno Simulation and Performance Evaluation 2014-15 Queueing systems - Renato Lo Cigno 1 Queues A Birth-Death process is well modeled by a queue Indeed queues can be used to
Queueing systems Renato Lo Cigno Simulation and Performance Evaluation 2014-15 Queueing systems - Renato Lo Cigno 1 Queues A Birth-Death process is well modeled by a queue Indeed queues can be used to
Introduction to Queueing Theory with Applications to Air Transportation Systems
 Introduction to Queueing Theory with Applications to Air Transportation Systems John Shortle George Mason University February 28, 2018 Outline Why stochastic models matter M/M/1 queue Little s law Priority
Introduction to Queueing Theory with Applications to Air Transportation Systems John Shortle George Mason University February 28, 2018 Outline Why stochastic models matter M/M/1 queue Little s law Priority
Queuing Theory. Using the Math. Management Science
 Queuing Theory Using the Math 1 Markov Processes (Chains) A process consisting of a countable sequence of stages, that can be judged at each stage to fall into future states independent of how the process
Queuing Theory Using the Math 1 Markov Processes (Chains) A process consisting of a countable sequence of stages, that can be judged at each stage to fall into future states independent of how the process
MSA 640 Homework #2 Due September 17, points total / 20 points per question Show all work leading to your answers
 Name MSA 640 Homework #2 Due September 17, 2010 100 points total / 20 points per question Show all work leading to your answers 1. The annual demand for a particular type of valve is 3,500 units. The cost
Name MSA 640 Homework #2 Due September 17, 2010 100 points total / 20 points per question Show all work leading to your answers 1. The annual demand for a particular type of valve is 3,500 units. The cost
Answers to selected exercises
 Answers to selected exercises A First Course in Stochastic Models, Henk C. Tijms 1.1 ( ) 1.2 (a) Let waiting time if passengers already arrived,. Then,, (b) { (c) Long-run fraction for is (d) Let waiting
Answers to selected exercises A First Course in Stochastic Models, Henk C. Tijms 1.1 ( ) 1.2 (a) Let waiting time if passengers already arrived,. Then,, (b) { (c) Long-run fraction for is (d) Let waiting
λ, µ, ρ, A n, W n, L(t), L, L Q, w, w Q etc. These
 Queuing theory models systems with servers and clients (presumably waiting in queues). Notation: there are many standard symbols like λ, µ, ρ, A n, W n, L(t), L, L Q, w, w Q etc. These represent the actual
Queuing theory models systems with servers and clients (presumably waiting in queues). Notation: there are many standard symbols like λ, µ, ρ, A n, W n, L(t), L, L Q, w, w Q etc. These represent the actual
Classification of Queuing Models
 Classification of Queuing Models Generally Queuing models may be completely specified in the following symbol form:(a/b/c):(d/e)where a = Probability law for the arrival(or inter arrival)time, b = Probability
Classification of Queuing Models Generally Queuing models may be completely specified in the following symbol form:(a/b/c):(d/e)where a = Probability law for the arrival(or inter arrival)time, b = Probability
B. Maddah ENMG 622 ENMG /27/07
 B. Maddah ENMG 622 ENMG 5 3/27/7 Queueig Theory () What is a queueig system? A queueig system cosists of servers (resources) that provide service to customers (etities). A Customer requestig service will
B. Maddah ENMG 622 ENMG 5 3/27/7 Queueig Theory () What is a queueig system? A queueig system cosists of servers (resources) that provide service to customers (etities). A Customer requestig service will
Non Markovian Queues (contd.)
 MODULE 7: RENEWAL PROCESSES 29 Lecture 5 Non Markovian Queues (contd) For the case where the service time is constant, V ar(b) = 0, then the P-K formula for M/D/ queue reduces to L s = ρ + ρ 2 2( ρ) where
MODULE 7: RENEWAL PROCESSES 29 Lecture 5 Non Markovian Queues (contd) For the case where the service time is constant, V ar(b) = 0, then the P-K formula for M/D/ queue reduces to L s = ρ + ρ 2 2( ρ) where
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science 6.262 Discrete Stochastic Processes Midterm Quiz April 6, 2010 There are 5 questions, each with several parts.
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science 6.262 Discrete Stochastic Processes Midterm Quiz April 6, 2010 There are 5 questions, each with several parts.
Queueing Systems: Lecture 3. Amedeo R. Odoni October 18, Announcements
 Queueing Systems: Lecture 3 Amedeo R. Odoni October 18, 006 Announcements PS #3 due tomorrow by 3 PM Office hours Odoni: Wed, 10/18, :30-4:30; next week: Tue, 10/4 Quiz #1: October 5, open book, in class;
Queueing Systems: Lecture 3 Amedeo R. Odoni October 18, 006 Announcements PS #3 due tomorrow by 3 PM Office hours Odoni: Wed, 10/18, :30-4:30; next week: Tue, 10/4 Quiz #1: October 5, open book, in class;
Outline. Finite source queue M/M/c//K Queues with impatience (balking, reneging, jockeying, retrial) Transient behavior Advanced Queue.
 Outline Finite source queue M/M/c//K Queues with impatience (balking, reneging, jockeying, retrial) Transient behavior Advanced Queue Batch queue Bulk input queue M [X] /M/1 Bulk service queue M/M [Y]
Outline Finite source queue M/M/c//K Queues with impatience (balking, reneging, jockeying, retrial) Transient behavior Advanced Queue Batch queue Bulk input queue M [X] /M/1 Bulk service queue M/M [Y]
Review of Queuing Models
 Review of Queuing Models Recitation, Apr. 1st Guillaume Roels 15.763J Manufacturing System and Supply Chain Design http://michael.toren.net/slides/ipqueue/slide001.html 2005 Guillaume Roels Outline Overview,
Review of Queuing Models Recitation, Apr. 1st Guillaume Roels 15.763J Manufacturing System and Supply Chain Design http://michael.toren.net/slides/ipqueue/slide001.html 2005 Guillaume Roels Outline Overview,
Hand Simulations. Christos Alexopoulos and Dave Goldsman 9/2/14. Georgia Institute of Technology, Atlanta, GA, USA 1 / 26
 1 / 26 Hand Simulations Christos Alexopoulos and Dave Goldsman Georgia Institute of Technology, Atlanta, GA, USA 9/2/14 2 / 26 Outline 1 Monte Carlo Integration 2 Making Some π 3 Single-Server Queue 4
1 / 26 Hand Simulations Christos Alexopoulos and Dave Goldsman Georgia Institute of Technology, Atlanta, GA, USA 9/2/14 2 / 26 Outline 1 Monte Carlo Integration 2 Making Some π 3 Single-Server Queue 4
7.1 INTRODUCTION. In this era of extreme competition, each subsystem in different
 7.1 INTRODUCTION In this era of extreme competition, each subsystem in different echelons of integrated model thrives to improve their operations, reduce costs and increase profitability. Currently, the
7.1 INTRODUCTION In this era of extreme competition, each subsystem in different echelons of integrated model thrives to improve their operations, reduce costs and increase profitability. Currently, the
Queues and Queueing Networks
 Queues and Queueing Networks Sanjay K. Bose Dept. of EEE, IITG Copyright 2015, Sanjay K. Bose 1 Introduction to Queueing Models and Queueing Analysis Copyright 2015, Sanjay K. Bose 2 Model of a Queue Arrivals
Queues and Queueing Networks Sanjay K. Bose Dept. of EEE, IITG Copyright 2015, Sanjay K. Bose 1 Introduction to Queueing Models and Queueing Analysis Copyright 2015, Sanjay K. Bose 2 Model of a Queue Arrivals
BIRTH DEATH PROCESSES AND QUEUEING SYSTEMS
 BIRTH DEATH PROCESSES AND QUEUEING SYSTEMS Andrea Bobbio Anno Accademico 999-2000 Queueing Systems 2 Notation for Queueing Systems /λ mean time between arrivals S = /µ ρ = λ/µ N mean service time traffic
BIRTH DEATH PROCESSES AND QUEUEING SYSTEMS Andrea Bobbio Anno Accademico 999-2000 Queueing Systems 2 Notation for Queueing Systems /λ mean time between arrivals S = /µ ρ = λ/µ N mean service time traffic
Queueing Theory (Part 4)
 Queueing Theory (Part 4) Nonexponential Queueing Systems and Economic Analysis Queueing Theory-1 Queueing Models with Nonexponential Distributions M/G/1 Model Poisson input process, general service time
Queueing Theory (Part 4) Nonexponential Queueing Systems and Economic Analysis Queueing Theory-1 Queueing Models with Nonexponential Distributions M/G/1 Model Poisson input process, general service time
Queuing Theory. 3. Birth-Death Process. Law of Motion Flow balance equations Steady-state probabilities: , if
 1 Queuing Theory 3. Birth-Death Process Law of Motion Flow balance equations Steady-state probabilities: c j = λ 0λ 1...λ j 1 µ 1 µ 2...µ j π 0 = 1 1+ j=1 c j, if j=1 c j is finite. π j = c j π 0 Example
1 Queuing Theory 3. Birth-Death Process Law of Motion Flow balance equations Steady-state probabilities: c j = λ 0λ 1...λ j 1 µ 1 µ 2...µ j π 0 = 1 1+ j=1 c j, if j=1 c j is finite. π j = c j π 0 Example
Quiz Queue II. III. ( ) ( ) =1.3333
 Quiz Queue UMJ, a mail-order company, receives calls to place orders at an average of 7.5 minutes intervals. UMJ hires one operator and can handle each call in about every 5 minutes on average. The inter-arrival
Quiz Queue UMJ, a mail-order company, receives calls to place orders at an average of 7.5 minutes intervals. UMJ hires one operator and can handle each call in about every 5 minutes on average. The inter-arrival
Introduction to queuing theory
 Introduction to queuing theory Queu(e)ing theory Queu(e)ing theory is the branch of mathematics devoted to how objects (packets in a network, people in a bank, processes in a CPU etc etc) join and leave
Introduction to queuing theory Queu(e)ing theory Queu(e)ing theory is the branch of mathematics devoted to how objects (packets in a network, people in a bank, processes in a CPU etc etc) join and leave
Waiting time characteristics in cyclic queues
 Waiting time characteristics in cyclic queues Sanne R. Smits, Ivo Adan and Ton G. de Kok April 16, 2003 Abstract In this paper we study a single-server queue with FIFO service and cyclic interarrival and
Waiting time characteristics in cyclic queues Sanne R. Smits, Ivo Adan and Ton G. de Kok April 16, 2003 Abstract In this paper we study a single-server queue with FIFO service and cyclic interarrival and
EE 368. Weeks 3 (Notes)
 EE 368 Weeks 3 (Notes) 1 State of a Queuing System State: Set of parameters that describe the condition of the system at a point in time. Why do we need it? Average size of Queue Average waiting time How
EE 368 Weeks 3 (Notes) 1 State of a Queuing System State: Set of parameters that describe the condition of the system at a point in time. Why do we need it? Average size of Queue Average waiting time How
Suggested solutions for the exam in SF2863 Systems Engineering. December 19,
 Suggested solutions for the exam in SF863 Systems Engineering. December 19, 011 14.00 19.00 Examiner: Per Enqvist, phone: 790 6 98 1. We can think of the support center as a Jackson network. The reception
Suggested solutions for the exam in SF863 Systems Engineering. December 19, 011 14.00 19.00 Examiner: Per Enqvist, phone: 790 6 98 1. We can think of the support center as a Jackson network. The reception
YORK UNIVERSITY FACULTY OF ARTS DEPARTMENT OF MATHEMATICS AND STATISTICS MATH , YEAR APPLIED OPTIMIZATION (TEST #4 ) (SOLUTIONS)
 YORK UNIVERSITY FACULTY OF ARTS DEPARTMENT OF MATHEMATICS AND STATISTICS Instructor : Dr. Igor Poliakov MATH 4570 6.0, YEAR 2006-07 APPLIED OPTIMIZATION (TEST #4 ) (SOLUTIONS) March 29, 2007 Name (print)
YORK UNIVERSITY FACULTY OF ARTS DEPARTMENT OF MATHEMATICS AND STATISTICS Instructor : Dr. Igor Poliakov MATH 4570 6.0, YEAR 2006-07 APPLIED OPTIMIZATION (TEST #4 ) (SOLUTIONS) March 29, 2007 Name (print)
Probability and Stochastic Processes Homework Chapter 12 Solutions
 Probability and Stochastic Processes Homework Chapter 1 Solutions Problem Solutions : Yates and Goodman, 1.1.1 1.1.4 1.3. 1.4.3 1.5.3 1.5.6 1.6.1 1.9.1 1.9.4 1.10.1 1.10.6 1.11.1 1.11.3 1.11.5 and 1.11.9
Probability and Stochastic Processes Homework Chapter 1 Solutions Problem Solutions : Yates and Goodman, 1.1.1 1.1.4 1.3. 1.4.3 1.5.3 1.5.6 1.6.1 1.9.1 1.9.4 1.10.1 1.10.6 1.11.1 1.11.3 1.11.5 and 1.11.9
10.2 For the system in 10.1, find the following statistics for population 1 and 2. For populations 2, find: Lq, Ls, L, Wq, Ws, W, Wq 0 and SL.
 Bibliography Asmussen, S. (2003). Applied probability and queues (2nd ed). New York: Springer. Baccelli, F., & Bremaud, P. (2003). Elements of queueing theory: Palm martingale calculus and stochastic recurrences
Bibliography Asmussen, S. (2003). Applied probability and queues (2nd ed). New York: Springer. Baccelli, F., & Bremaud, P. (2003). Elements of queueing theory: Palm martingale calculus and stochastic recurrences
CDA5530: Performance Models of Computers and Networks. Chapter 4: Elementary Queuing Theory
 CDA5530: Performance Models of Computers and Networks Chapter 4: Elementary Queuing Theory Definition Queuing system: a buffer (waiting room), service facility (one or more servers) a scheduling policy
CDA5530: Performance Models of Computers and Networks Chapter 4: Elementary Queuing Theory Definition Queuing system: a buffer (waiting room), service facility (one or more servers) a scheduling policy
Queuing Theory. The present section focuses on the standard vocabulary of Waiting Line Models.
 Queuing Theory Introduction Waiting lines are the most frequently encountered problems in everyday life. For example, queue at a cafeteria, library, bank, etc. Common to all of these cases are the arrivals
Queuing Theory Introduction Waiting lines are the most frequently encountered problems in everyday life. For example, queue at a cafeteria, library, bank, etc. Common to all of these cases are the arrivals
Single-part-type, multiple stage systems
 MIT 2.853/2.854 Introduction to Manufacturing Systems Single-part-type, multiple stage systems Stanley B. Gershwin Laboratory for Manufacturing and Productivity Massachusetts Institute of Technology Single-stage,
MIT 2.853/2.854 Introduction to Manufacturing Systems Single-part-type, multiple stage systems Stanley B. Gershwin Laboratory for Manufacturing and Productivity Massachusetts Institute of Technology Single-stage,
Course Outline Introduction to Transportation Highway Users and their Performance Geometric Design Pavement Design
 Course Outline Introduction to Transportation Highway Users and their Performance Geometric Design Pavement Design Speed Studies - Project Traffic Queuing Intersections Level of Service in Highways and
Course Outline Introduction to Transportation Highway Users and their Performance Geometric Design Pavement Design Speed Studies - Project Traffic Queuing Intersections Level of Service in Highways and
Multi Heterogeneous Queueing Server System. General Exam Oral Examination Fall 2012 prepared by Husnu Saner Narman
 Multi Heterogeneous Queueing Server System General Exam Oral Examination Fall 2012 prepared by Husnu Saner Narman Content Motivation Contribution Multi Heterogeneous System First Model Analysis of First
Multi Heterogeneous Queueing Server System General Exam Oral Examination Fall 2012 prepared by Husnu Saner Narman Content Motivation Contribution Multi Heterogeneous System First Model Analysis of First
Exercises Stochastic Performance Modelling. Hamilton Institute, Summer 2010
 Exercises Stochastic Performance Modelling Hamilton Institute, Summer Instruction Exercise Let X be a non-negative random variable with E[X ]
Exercises Stochastic Performance Modelling Hamilton Institute, Summer Instruction Exercise Let X be a non-negative random variable with E[X ]
NANYANG TECHNOLOGICAL UNIVERSITY SEMESTER I EXAMINATION MH4702/MAS446/MTH437 Probabilistic Methods in OR
 NANYANG TECHNOLOGICAL UNIVERSITY SEMESTER I EXAMINATION 2013-201 MH702/MAS6/MTH37 Probabilistic Methods in OR December 2013 TIME ALLOWED: 2 HOURS INSTRUCTIONS TO CANDIDATES 1. This examination paper contains
NANYANG TECHNOLOGICAL UNIVERSITY SEMESTER I EXAMINATION 2013-201 MH702/MAS6/MTH37 Probabilistic Methods in OR December 2013 TIME ALLOWED: 2 HOURS INSTRUCTIONS TO CANDIDATES 1. This examination paper contains
Expected Time Delay in Multi-Item Inventory Systems with Correlated Demands
 Expected Time Delay in Multi-Item Inventory Systems with Correlated Demands Rachel Q. Zhang Department of Industrial and Operations Engineering, University of Michigan, Ann Arbor, Michigan 48109 Received
Expected Time Delay in Multi-Item Inventory Systems with Correlated Demands Rachel Q. Zhang Department of Industrial and Operations Engineering, University of Michigan, Ann Arbor, Michigan 48109 Received
1.225 Transportation Flow Systems Quiz (December 17, 2001; Duration: 3 hours)
 1.225 Transportation Flow Systems Quiz (December 17, 2001; Duration: 3 hours) Student Name: Alias: Instructions: 1. This exam is open-book 2. No cooperation is permitted 3. Please write down your name
1.225 Transportation Flow Systems Quiz (December 17, 2001; Duration: 3 hours) Student Name: Alias: Instructions: 1. This exam is open-book 2. No cooperation is permitted 3. Please write down your name
Chapter 5: Special Types of Queuing Models
 Chapter 5: Special Types of Queuing Models Some General Queueing Models Discouraged Arrivals Impatient Arrivals Bulk Service and Bulk Arrivals OR37-Dr.Khalid Al-Nowibet 1 5.1 General Queueing Models 1.
Chapter 5: Special Types of Queuing Models Some General Queueing Models Discouraged Arrivals Impatient Arrivals Bulk Service and Bulk Arrivals OR37-Dr.Khalid Al-Nowibet 1 5.1 General Queueing Models 1.
Scientiae Mathematicae Japonicae Online, Vol. 5, (2001), POSSIBILITY THAT THE CUSTOMERS GIVE UP PURCHASING THE MERCHANDISE
 Scientiae Mathematicae Japonicae Online, Vol. 5, (00), 7 79 7 A DUOPOLISTIC INVENTORY PROBLEM INCLUDING THE POSSIBILITY THAT THE CUSTOMERS GIVE UP PURCHASING THE MERCHANDISE HITOSHI HOHJO and YOSHINOBU
Scientiae Mathematicae Japonicae Online, Vol. 5, (00), 7 79 7 A DUOPOLISTIC INVENTORY PROBLEM INCLUDING THE POSSIBILITY THAT THE CUSTOMERS GIVE UP PURCHASING THE MERCHANDISE HITOSHI HOHJO and YOSHINOBU
Zero-Inventory Conditions For a Two-Part-Type Make-to-Stock Production System
 Zero-Inventory Conditions For a Two-Part-Type Make-to-Stock Production System MichaelH.Veatch Francis de Véricourt October 9, 2002 Abstract We consider the dynamic scheduling of a two-part-type make-tostock
Zero-Inventory Conditions For a Two-Part-Type Make-to-Stock Production System MichaelH.Veatch Francis de Véricourt October 9, 2002 Abstract We consider the dynamic scheduling of a two-part-type make-tostock
Improving Supply Chain Performance: Real-Time Demand Information and Flexible Deliveries
 Improving Supply Chain Performance: Real-Time Demand Information and Flexible Deliveries Kevin H. Shang Sean X. Zhou Geert-Jan van Houtum The Fuqua School of Business, Duke University, Durham, North Carolina
Improving Supply Chain Performance: Real-Time Demand Information and Flexible Deliveries Kevin H. Shang Sean X. Zhou Geert-Jan van Houtum The Fuqua School of Business, Duke University, Durham, North Carolina
2. Assumptions and Notation
 Volume 8 o. 08, 77-735 ISS: 34-3395 (on-line version) url: http://acadpubl.eu/hub ijpam.eu A IVETORY MODEL FOR DETERIORATIG ITEMS WITHI FIITE PLAIG HORIZO UDER THE EFFECT OF PERMISSIBLE DELAY AD PRESERVATIO
Volume 8 o. 08, 77-735 ISS: 34-3395 (on-line version) url: http://acadpubl.eu/hub ijpam.eu A IVETORY MODEL FOR DETERIORATIG ITEMS WITHI FIITE PLAIG HORIZO UDER THE EFFECT OF PERMISSIBLE DELAY AD PRESERVATIO
Networking = Plumbing. Queueing Analysis: I. Last Lecture. Lecture Outline. Jeremiah Deng. 29 July 2013
 Networking = Plumbing TELE302 Lecture 7 Queueing Analysis: I Jeremiah Deng University of Otago 29 July 2013 Jeremiah Deng (University of Otago) TELE302 Lecture 7 29 July 2013 1 / 33 Lecture Outline Jeremiah
Networking = Plumbing TELE302 Lecture 7 Queueing Analysis: I Jeremiah Deng University of Otago 29 July 2013 Jeremiah Deng (University of Otago) TELE302 Lecture 7 29 July 2013 1 / 33 Lecture Outline Jeremiah
Chapter 8 Queuing Theory Roanna Gee. W = average number of time a customer spends in the system.
 8. Preliminaries L, L Q, W, W Q L = average number of customers in the system. L Q = average number of customers waiting in queue. W = average number of time a customer spends in the system. W Q = average
8. Preliminaries L, L Q, W, W Q L = average number of customers in the system. L Q = average number of customers waiting in queue. W = average number of time a customer spends in the system. W Q = average
A A Multi-Echelon Inventory Model for a Reparable Item with one-for. for- one Replenishment
 A A Multi-Echelon Inventory Model for a Reparable Item with one-for for- one Replenishment Steve Graves, 1985 Management Science, 31(10) Presented by Hongmin Li This summary presentation is based on: Graves,
A A Multi-Echelon Inventory Model for a Reparable Item with one-for for- one Replenishment Steve Graves, 1985 Management Science, 31(10) Presented by Hongmin Li This summary presentation is based on: Graves,
Systems Simulation Chapter 6: Queuing Models
 Systems Simulation Chapter 6: Queuing Models Fatih Cavdur fatihcavdur@uludag.edu.tr April 2, 2014 Introduction Introduction Simulation is often used in the analysis of queuing models. A simple but typical
Systems Simulation Chapter 6: Queuing Models Fatih Cavdur fatihcavdur@uludag.edu.tr April 2, 2014 Introduction Introduction Simulation is often used in the analysis of queuing models. A simple but typical
M/M/1 Queueing systems with inventory
 Queueing Syst 2006 54:55 78 DOI 101007/s11134-006-8710-5 M/M/1 Queueing systems with inventory Maike Schwarz Cornelia Sauer Hans Daduna Rafal Kulik Ryszard Szekli Received: 11 August 2004 / Revised: 6
Queueing Syst 2006 54:55 78 DOI 101007/s11134-006-8710-5 M/M/1 Queueing systems with inventory Maike Schwarz Cornelia Sauer Hans Daduna Rafal Kulik Ryszard Szekli Received: 11 August 2004 / Revised: 6
Since D has an exponential distribution, E[D] = 0.09 years. Since {A(t) : t 0} is a Poisson process with rate λ = 10, 000, A(0.
![Since D has an exponential distribution, E[D] = 0.09 years. Since {A(t) : t 0} is a Poisson process with rate λ = 10, 000, A(0. Since D has an exponential distribution, E[D] = 0.09 years. Since {A(t) : t 0} is a Poisson process with rate λ = 10, 000, A(0.](/thumbs/95/124116804.jpg) IEOR 46: Introduction to Operations Research: Stochastic Models Chapters 5-6 in Ross, Thursday, April, 4:5-5:35pm SOLUTIONS to Second Midterm Exam, Spring 9, Open Book: but only the Ross textbook, the
IEOR 46: Introduction to Operations Research: Stochastic Models Chapters 5-6 in Ross, Thursday, April, 4:5-5:35pm SOLUTIONS to Second Midterm Exam, Spring 9, Open Book: but only the Ross textbook, the
Optimal Control of a Production-Inventory System with both Backorders and Lost Sales
 Optimal Control of a Production-Inventory System with both Backorders and Lost Sales Saif Benjaafar Mohsen ElHafsi Tingliang Huang 3 Industrial & Systems Engineering, Department of Mechanical Engineering,
Optimal Control of a Production-Inventory System with both Backorders and Lost Sales Saif Benjaafar Mohsen ElHafsi Tingliang Huang 3 Industrial & Systems Engineering, Department of Mechanical Engineering,
All models are wrong / inaccurate, but some are useful. George Box (Wikipedia). wkc/course/part2.pdf
 PART II (3) Continuous Time Markov Chains : Theory and Examples -Pure Birth Process with Constant Rates -Pure Death Process -More on Birth-and-Death Process -Statistical Equilibrium (4) Introduction to
PART II (3) Continuous Time Markov Chains : Theory and Examples -Pure Birth Process with Constant Rates -Pure Death Process -More on Birth-and-Death Process -Statistical Equilibrium (4) Introduction to
Queuing Theory. Richard Lockhart. Simon Fraser University. STAT 870 Summer 2011
 Queuing Theory Richard Lockhart Simon Fraser University STAT 870 Summer 2011 Richard Lockhart (Simon Fraser University) Queuing Theory STAT 870 Summer 2011 1 / 15 Purposes of Today s Lecture Describe general
Queuing Theory Richard Lockhart Simon Fraser University STAT 870 Summer 2011 Richard Lockhart (Simon Fraser University) Queuing Theory STAT 870 Summer 2011 1 / 15 Purposes of Today s Lecture Describe general
Stochastic Models of Manufacturing Systems
 Stochastic Models of Manufacturing Systems Ivo Adan Systems 2/49 Continuous systems State changes continuously in time (e.g., in chemical applications) Discrete systems State is observed at fixed regular
Stochastic Models of Manufacturing Systems Ivo Adan Systems 2/49 Continuous systems State changes continuously in time (e.g., in chemical applications) Discrete systems State is observed at fixed regular
Dr. Maddah ENMG 617 EM Statistics 10/15/12. Nonparametric Statistics (2) (Goodness of fit tests)
 Dr. Maddah ENMG 617 EM Statistics 10/15/12 Nonparametric Statistics (2) (Goodness of fit tests) Introduction Probability models used in decision making (Operations Research) and other fields require fitting
Dr. Maddah ENMG 617 EM Statistics 10/15/12 Nonparametric Statistics (2) (Goodness of fit tests) Introduction Probability models used in decision making (Operations Research) and other fields require fitting
Solutions to COMP9334 Week 8 Sample Problems
 Solutions to COMP9334 Week 8 Sample Problems Problem 1: Customers arrive at a grocery store s checkout counter according to a Poisson process with rate 1 per minute. Each customer carries a number of items
Solutions to COMP9334 Week 8 Sample Problems Problem 1: Customers arrive at a grocery store s checkout counter according to a Poisson process with rate 1 per minute. Each customer carries a number of items
Link Models for Circuit Switching
 Link Models for Circuit Switching The basis of traffic engineering for telecommunication networks is the Erlang loss function. It basically allows us to determine the amount of telephone traffic that can
Link Models for Circuit Switching The basis of traffic engineering for telecommunication networks is the Erlang loss function. It basically allows us to determine the amount of telephone traffic that can
Chapter 16 focused on decision making in the face of uncertainty about one future
 9 C H A P T E R Markov Chains Chapter 6 focused on decision making in the face of uncertainty about one future event (learning the true state of nature). However, some decisions need to take into account
9 C H A P T E R Markov Chains Chapter 6 focused on decision making in the face of uncertainty about one future event (learning the true state of nature). However, some decisions need to take into account
Queueing Theory II. Summary. ! M/M/1 Output process. ! Networks of Queue! Method of Stages. ! General Distributions
 Queueing Theory II Summary! M/M/1 Output process! Networks of Queue! Method of Stages " Erlang Distribution " Hyperexponential Distribution! General Distributions " Embedded Markov Chains M/M/1 Output
Queueing Theory II Summary! M/M/1 Output process! Networks of Queue! Method of Stages " Erlang Distribution " Hyperexponential Distribution! General Distributions " Embedded Markov Chains M/M/1 Output
Stochastic Optimization
 Chapter 27 Page 1 Stochastic Optimization Operations research has been particularly successful in two areas of decision analysis: (i) optimization of problems involving many variables when the outcome
Chapter 27 Page 1 Stochastic Optimization Operations research has been particularly successful in two areas of decision analysis: (i) optimization of problems involving many variables when the outcome
QUEUING SYSTEM. Yetunde Folajimi, PhD
 QUEUING SYSTEM Yetunde Folajimi, PhD Part 2 Queuing Models Queueing models are constructed so that queue lengths and waiting times can be predicted They help us to understand and quantify the effect of
QUEUING SYSTEM Yetunde Folajimi, PhD Part 2 Queuing Models Queueing models are constructed so that queue lengths and waiting times can be predicted They help us to understand and quantify the effect of
Perishable Inventory System at Service Facilities with Multiple Server Vacations and Impatient Customers
 J. Stat. Appl. Pro. Lett. 3, o. 3, 63-73 (2014) 63 Journal of Statistics Applications & Probability Letters An International Journal http://dx.doi.org/10.12785/jsapl/010303 Perishable Inventory System
J. Stat. Appl. Pro. Lett. 3, o. 3, 63-73 (2014) 63 Journal of Statistics Applications & Probability Letters An International Journal http://dx.doi.org/10.12785/jsapl/010303 Perishable Inventory System
Queuing Theory. Queuing Theory. Fatih Cavdur April 27, 2015
 Queuing Theory Fatih Cavdur fatihcavdur@uludag.edu.tr April 27, 2015 Introduction Introduction Simulation is often used in the analysis of queuing models. A simple but typical model is the single-server
Queuing Theory Fatih Cavdur fatihcavdur@uludag.edu.tr April 27, 2015 Introduction Introduction Simulation is often used in the analysis of queuing models. A simple but typical model is the single-server
P (L d k = n). P (L(t) = n),
 4 M/G/1 queue In the M/G/1 queue customers arrive according to a Poisson process with rate λ and they are treated in order of arrival The service times are independent and identically distributed with
4 M/G/1 queue In the M/G/1 queue customers arrive according to a Poisson process with rate λ and they are treated in order of arrival The service times are independent and identically distributed with
4.7 Finite Population Source Model
 Characteristics 1. Arrival Process R independent Source All sources are identical Interarrival time is exponential with rate for each source No arrivals if all sources are in the system. OR372-Dr.Khalid
Characteristics 1. Arrival Process R independent Source All sources are identical Interarrival time is exponential with rate for each source No arrivals if all sources are in the system. OR372-Dr.Khalid
QUEUING MODELS AND MARKOV PROCESSES
 QUEUING MODELS AND MARKOV ROCESSES Queues form when customer demand for a service cannot be met immediately. They occur because of fluctuations in demand levels so that models of queuing are intrinsically
QUEUING MODELS AND MARKOV ROCESSES Queues form when customer demand for a service cannot be met immediately. They occur because of fluctuations in demand levels so that models of queuing are intrinsically
Chapter 11 Output Analysis for a Single Model. Banks, Carson, Nelson & Nicol Discrete-Event System Simulation
 Chapter 11 Output Analysis for a Single Model Banks, Carson, Nelson & Nicol Discrete-Event System Simulation Purpose Objective: Estimate system performance via simulation If q is the system performance,
Chapter 11 Output Analysis for a Single Model Banks, Carson, Nelson & Nicol Discrete-Event System Simulation Purpose Objective: Estimate system performance via simulation If q is the system performance,
Lecture Notes of Communication Network I y: part 5. Lijun Qian. Rutgers The State University of New Jersey. 94 Brett Road. Piscataway, NJ
 Lecture Notes of Communication Network I y: part 5 Lijun Qian Department of Electrical Engineering Rutgers The State University of New Jersey 94 Brett Road Piscataway, NJ 08854-8058 October 6, 1998 Abstract
Lecture Notes of Communication Network I y: part 5 Lijun Qian Department of Electrical Engineering Rutgers The State University of New Jersey 94 Brett Road Piscataway, NJ 08854-8058 October 6, 1998 Abstract
Class 11 Non-Parametric Models of a Service System; GI/GI/1, GI/GI/n: Exact & Approximate Analysis.
 Service Engineering Class 11 Non-Parametric Models of a Service System; GI/GI/1, GI/GI/n: Exact & Approximate Analysis. G/G/1 Queue: Virtual Waiting Time (Unfinished Work). GI/GI/1: Lindley s Equations
Service Engineering Class 11 Non-Parametric Models of a Service System; GI/GI/1, GI/GI/n: Exact & Approximate Analysis. G/G/1 Queue: Virtual Waiting Time (Unfinished Work). GI/GI/1: Lindley s Equations
Link Models for Packet Switching
 Link Models for Packet Switching To begin our study of the performance of communications networks, we will study a model of a single link in a message switched network. The important feature of this model
Link Models for Packet Switching To begin our study of the performance of communications networks, we will study a model of a single link in a message switched network. The important feature of this model
LUNG CHEUNG GOVERNMENT SECONDARY SCHOOL Mock Examination 2006 / 2007 Mathematics and Statistics
 S.7 LUNG CHEUNG GOVERNMENT SECONDARY SCHOOL Mock Examination 006 / 007 Mathematics and Statistics Maximum Mark: 100 Date: 1 007 Time: 8 30 11 30 1. This paper consists of Section A and Section B.. Answer
S.7 LUNG CHEUNG GOVERNMENT SECONDARY SCHOOL Mock Examination 006 / 007 Mathematics and Statistics Maximum Mark: 100 Date: 1 007 Time: 8 30 11 30 1. This paper consists of Section A and Section B.. Answer
Computer Networks More general queuing systems
 Computer Networks More general queuing systems Saad Mneimneh Computer Science Hunter College of CUNY New York M/G/ Introduction We now consider a queuing system where the customer service times have a
Computer Networks More general queuing systems Saad Mneimneh Computer Science Hunter College of CUNY New York M/G/ Introduction We now consider a queuing system where the customer service times have a
Queueing Theory. VK Room: M Last updated: October 17, 2013.
 Queueing Theory VK Room: M1.30 knightva@cf.ac.uk www.vincent-knight.com Last updated: October 17, 2013. 1 / 63 Overview Description of Queueing Processes The Single Server Markovian Queue Multi Server
Queueing Theory VK Room: M1.30 knightva@cf.ac.uk www.vincent-knight.com Last updated: October 17, 2013. 1 / 63 Overview Description of Queueing Processes The Single Server Markovian Queue Multi Server
Waiting Line Models: Queuing Theory Basics. Metodos Cuantitativos M. En C. Eduardo Bustos Farias 1
 Waiting Line Models: Queuing Theory Basics Cuantitativos M. En C. Eduardo Bustos Farias 1 Agenda Queuing system structure Performance measures Components of queuing systems Arrival process Service process
Waiting Line Models: Queuing Theory Basics Cuantitativos M. En C. Eduardo Bustos Farias 1 Agenda Queuing system structure Performance measures Components of queuing systems Arrival process Service process
Coordinated Replenishments at a Single Stocking Point
 Chapter 11 Coordinated Replenishments at a Single Stocking Point 11.1 Advantages and Disadvantages of Coordination Advantages of Coordination 1. Savings on unit purchase costs.. Savings on unit transportation
Chapter 11 Coordinated Replenishments at a Single Stocking Point 11.1 Advantages and Disadvantages of Coordination Advantages of Coordination 1. Savings on unit purchase costs.. Savings on unit transportation
Test 2 VERSION A STAT 3090 Fall 2017
 Multiple Choice: (Questions 1 20) Answer the following questions on the scantron provided using a #2 pencil. Bubble the response that best answers the question. Each multiple choice correct response is
Multiple Choice: (Questions 1 20) Answer the following questions on the scantron provided using a #2 pencil. Bubble the response that best answers the question. Each multiple choice correct response is
I, A BRIEF REVIEW ON INFINITE QUEUE MODEL M.
 A BRIEF REVIEW ON INFINITE QUEUE MODEL M. Vasuki*, A. Dinesh Kumar** & G. Vijayaprabha** * Assistant Professor, Department of Mathematics, Srinivasan College of Arts and Science, Perambalur, Tamilnadu
A BRIEF REVIEW ON INFINITE QUEUE MODEL M. Vasuki*, A. Dinesh Kumar** & G. Vijayaprabha** * Assistant Professor, Department of Mathematics, Srinivasan College of Arts and Science, Perambalur, Tamilnadu
ECE 3511: Communications Networks Theory and Analysis. Fall Quarter Instructor: Prof. A. Bruce McDonald. Lecture Topic
 ECE 3511: Communications Networks Theory and Analysis Fall Quarter 2002 Instructor: Prof. A. Bruce McDonald Lecture Topic Introductory Analysis of M/G/1 Queueing Systems Module Number One Steady-State
ECE 3511: Communications Networks Theory and Analysis Fall Quarter 2002 Instructor: Prof. A. Bruce McDonald Lecture Topic Introductory Analysis of M/G/1 Queueing Systems Module Number One Steady-State
f X (x) = λe λx, , x 0, k 0, λ > 0 Γ (k) f X (u)f X (z u)du
 11 COLLECTED PROBLEMS Do the following problems for coursework 1. Problems 11.4 and 11.5 constitute one exercise leading you through the basic ruin arguments. 2. Problems 11.1 through to 11.13 but excluding
11 COLLECTED PROBLEMS Do the following problems for coursework 1. Problems 11.4 and 11.5 constitute one exercise leading you through the basic ruin arguments. 2. Problems 11.1 through to 11.13 but excluding
B. Maddah INDE 504 Discrete-Event Simulation. Output Analysis (1)
 B. Maddah INDE 504 Discrete-Event Simulation Output Analysis (1) Introduction The basic, most serious disadvantage of simulation is that we don t get exact answers. Two different runs of the same model
B. Maddah INDE 504 Discrete-Event Simulation Output Analysis (1) Introduction The basic, most serious disadvantage of simulation is that we don t get exact answers. Two different runs of the same model
IE 5112 Final Exam 2010
 IE 5112 Final Exam 2010 1. There are six cities in Kilroy County. The county must decide where to build fire stations. The county wants to build as few fire stations as possible while ensuring that there
IE 5112 Final Exam 2010 1. There are six cities in Kilroy County. The county must decide where to build fire stations. The county wants to build as few fire stations as possible while ensuring that there
Bulk input queue M [X] /M/1 Bulk service queue M/M [Y] /1 Erlangian queue M/E k /1
![Bulk input queue M [X] /M/1 Bulk service queue M/M [Y] /1 Erlangian queue M/E k /1 Bulk input queue M [X] /M/1 Bulk service queue M/M [Y] /1 Erlangian queue M/E k /1](/thumbs/80/81986225.jpg) Advanced Markovian queues Bulk input queue M [X] /M/ Bulk service queue M/M [Y] / Erlangian queue M/E k / Bulk input queue M [X] /M/ Batch arrival, Poisson process, arrival rate λ number of customers in
Advanced Markovian queues Bulk input queue M [X] /M/ Bulk service queue M/M [Y] / Erlangian queue M/E k / Bulk input queue M [X] /M/ Batch arrival, Poisson process, arrival rate λ number of customers in
Queuing Networks: Burke s Theorem, Kleinrock s Approximation, and Jackson s Theorem. Wade Trappe
 Queuing Networks: Burke s Theorem, Kleinrock s Approximation, and Jackson s Theorem Wade Trappe Lecture Overview Network of Queues Introduction Queues in Tandem roduct Form Solutions Burke s Theorem What
Queuing Networks: Burke s Theorem, Kleinrock s Approximation, and Jackson s Theorem Wade Trappe Lecture Overview Network of Queues Introduction Queues in Tandem roduct Form Solutions Burke s Theorem What
Stochastic inventory system with two types of services
 Int. J. Adv. Appl. Math. and Mech. 2() (204) 20-27 ISSN: 2347-2529 Available online at www.ijaamm.com International Journal of Advances in Applied Mathematics and Mechanics Stochastic inventory system
Int. J. Adv. Appl. Math. and Mech. 2() (204) 20-27 ISSN: 2347-2529 Available online at www.ijaamm.com International Journal of Advances in Applied Mathematics and Mechanics Stochastic inventory system
0utline. 1. Tools from Operations Research. 2. Applications
 0utline 1. Tools from Operations Research Little s Law (average values) Unreliable Machine(s) (operation dependent) Buffers (zero buffers & infinite buffers) M/M/1 Queue (effects of variation) 2. Applications
0utline 1. Tools from Operations Research Little s Law (average values) Unreliable Machine(s) (operation dependent) Buffers (zero buffers & infinite buffers) M/M/1 Queue (effects of variation) 2. Applications
Online Appendices: Inventory Control in a Spare Parts Distribution System with Emergency Stocks and Pipeline Information
 Online Appendices: Inventory Control in a Spare Parts Distribution System with Emergency Stocks and Pipeline Information Christian Howard christian.howard@vti.se VTI - The Swedish National Road and Transport
Online Appendices: Inventory Control in a Spare Parts Distribution System with Emergency Stocks and Pipeline Information Christian Howard christian.howard@vti.se VTI - The Swedish National Road and Transport
Appendix: Simple Methods for Shift Scheduling in Multi-Skill Call Centers
 Appendix: Simple Methods for Shift Scheduling in Multi-Skill Call Centers Sandjai Bhulai, Ger Koole & Auke Pot Vrije Universiteit, De Boelelaan 1081a, 1081 HV Amsterdam, The Netherlands Supplementary Material
Appendix: Simple Methods for Shift Scheduling in Multi-Skill Call Centers Sandjai Bhulai, Ger Koole & Auke Pot Vrije Universiteit, De Boelelaan 1081a, 1081 HV Amsterdam, The Netherlands Supplementary Material
ADMISSION CONTROL IN THE PRESENCE OF PRIORITIES: A SAMPLE PATH APPROACH
 Chapter 1 ADMISSION CONTROL IN THE PRESENCE OF PRIORITIES: A SAMPLE PATH APPROACH Feng Chen Department of Statistics and Operations Research University of North Carolina at Chapel Hill chenf@email.unc.edu
Chapter 1 ADMISSION CONTROL IN THE PRESENCE OF PRIORITIES: A SAMPLE PATH APPROACH Feng Chen Department of Statistics and Operations Research University of North Carolina at Chapel Hill chenf@email.unc.edu
