Andrei D. Polyanin, Alexander V. Manzhirov. Andrei D. Polyanin, Alexander V. Manzhirov Published online on: 27 Nov 2006
|
|
|
- Sibyl Gardner
- 5 years ago
- Views:
Transcription
1 This rtile ws downloded y: On: 08 Nov 08 ess detils: susription numer Pulisher: Press Inform Ltd egistered in Englnd nd Wles egistered Numer: egistered offie: 5 Howik Ple, London SWP WG, UK Hndook of Mthemtis for Engineers nd Sientists ndrei D. Polynin, lexnder V. Mnzhirov Elementry Geometry Pulition detils ndrei D. Polynin, lexnder V. Mnzhirov Pulished online on: 7 Nov 006 How to ite :- ndrei D. Polynin, lexnder V. Mnzhirov. 7 Nov 006, Elementry Geometry from: Hndook of Mthemtis for Engineers nd Sientists Press essed on: 08 Nov 08 PLESE SOLL DOWN FO DOUMENT Full terms nd onditions of use: This Doument PDF my e used for reserh, tehing nd privte study purposes. ny sustntil or systemti reprodutions, re-distriution, re-selling, lon or su-liensing, systemti supply or distriution in ny form to nyone is expressly foridden. The pulisher does not give ny wrrnty express or implied or mke ny representtion tht the ontents will e omplete or urte or up to dte. The pulisher shll not e lile for n loss, tions, lims, proeedings, demnd or osts or dmges whtsoever or howsoever used rising diretly or indiretly in onnetion with or rising out of the use of this mteril.
2 Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 hpter 3 Elementry Geometry 3.. Plne Geometry 3... Tringles Plne tringle nd its properties..plne tringle, orsimplytringle, isplnefigure ounded y three stright line segments (sides) onneting three nonolliner points (verties) (Fig. 3.). The smller ngle etween the two rys issuing from vertex nd pssing through the other two verties is lled n (interior) ngle of the tringle. The ngle djent to n interior ngle is lled n externl ngle of the tringle. n externl ngle is equl to the sum of the two interior ngles to whih it is not djent. β () γ α () Figure 3.. Plnetringle(). Midline of tringle (). tringle is uniquely determined y ny of the following sets of its prts:. Two ngles nd their inluded side.. Two sides nd their inluded ngle. 3. Three sides. Depending on the ngles, tringle is sid to e:. ute if ll three ngles re ute.. ight (or right-ngled) if one of the ngles is right. 3. Otuse if one of the ngles is otuse. Depending on the reltion etween the side lengths, tringle is sid to e:. egulr (or equilterl) if ll sides hve the sme length.. Isoseles if two of the sides re of equl length. 3. Slene if ll sides hve different lengths.. ongruene tests for tringles:. If two sides of tringle nd their inluded ngle re ongruent to the orresponding prts of nother tringle, then the tringles re ongruent.. If two ngles of tringle nd their inluded side re ongruent to the orresponding prts of nother tringle, then the tringles re ongruent. 007 y Tylor & Frnis Group, LL 43
3 44 ELEMENTY GEOMETY Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 3. If three sides of tringle re ongruent to the orresponding sides of nother tringle, then the tringles re ongruent. 3. Tringles re sid to e similr if their orresponding ngles re equl nd their orresponding sides re proportionl. Similrity tests for tringles:. If ll three pirs of orresponding sides in pir of tringles re in proportion, then the tringles re similr.. If two pirs of orresponding ngles in pir of tringles re ongruent, then the tringles re similr. 3. If two pirs of orresponding sides in pir of tringles re in proportion nd the inluded ngles re ongruent, then the tringles re similr. The res of similr tringles re proportionl to the squres of the orresponding liner prts (suh s sides, ltitudes, digonls, et.). 4. The line onneting the midpoints of two sides of tringle is lled midline of the tringle. The midline is prllel to nd hlf s long s the third side (Fig. 3.). Let,, nd e the lengths of the sides of tringle; let α, β, ndγ e the respetive opposite ngles (Fig. 3.); let nd r e the irumrdius nd the inrdius, respetively; nd let p = ( + + ) e the semiperimeter. Tle 3. represents the si properties nd reltions hrterizing tringles. TLE 3. si properties nd reltions hrterizing plne tringles No. The nme of property Properties nd reltions Tringle inequlity Sum of ngles of tringle 3 Lw of sines The length of ny side of tringle does not exeed the sum of lengths of the other two sides sin α = α + β + γ = 80 sin β = sin γ = 4 Lw of osines = + os γ 5 Lw of tngents + = tn [ ( (α + β)] tn [ ot γ) tn [ (α β)] 6 Theorem on projetions (lw of osines) = os β + os α 7 Trigonometri ngle formuls sin γ = (p )(p ) 8 Lw of tngents tn γ = 9 Mollweide s formuls 007 y Tylor & Frnis Group, LL, os γ p(p ) =, tn γ (p )(p ) =, sinγ = p(p )(p )(p ) p(p ) + sin α os α = = os[ (α β)] sin ( = sin[ sin β os β [ os (α β)] = γ) os [, (α + β)] [ (α β)] sin (α β)] = γ) sin [ (α + β)] os (
4 3.. PLNE GEOMETY 45 Tle 3. permits one to find the sides nd ngles of n ritrry tringle if three ppropritely hosen sides nd/or ngles re given. From the reltions given in Tles 3. nd 3., one n derive ll missing reltions y yli permuttions of the sides,, nd nd the ngles α, β,ndγ. Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 No. Three prts speified Three sides,, Two sides, nd the inluded ngle γ 3 side nd the two ngles α, β djent to it 4 Two sides, nd the ngle α opposite one of them TLE 3. Solution of plne tringles Formuls for the remining prts First method. One of the ngles is determined y the lw of osines, os α = +. Then either the lw of sines or the lw of osines is pplied. Seond method. One of the ngles is determined y trigonometri ngle formuls. Further proeed in similr wy. emrk. The sum of lengths of ny two sides must e greter thn the length of the third side. First method. The side is determined y the lw of osines, = + os γ. The ngle α is determined y either the lw of osines or the lw of sines. The ngle β is determined from the sum of ngles in tringle, β = 80 α γ. Seond method. α + β is found from the sum of ngles in tringle, α + β = 80 γ; α β is found from the lw of tngents, tn α β = + ot γ. Then α nd β n e found. The third side is determined y either the lw of osines or the lw of sines. The third ngle γ is found from the sum of ngles in tringle, γ = 80 α β. Sides nd re determined y the lw of sines. The seond ngle is determined y the lw of sines, sin β = sin α. The third ngle is γ = 80 α β. The third side is determined y the lw of sines, = sin γ sin α. emrk. Five ses re possile:. > ; i.e., the ngle is opposite the greter side. Then α > β, β < 90 (the lrger ngle is opposite the lrger side), nd the tringle is determined uniquely.. = ; i.e., the tringle is isoseles nd is determined uniquely. 3. < nd sin α <. Then there re two solutions, β + β = < nd sin α =. Then the solution is unique, β = < nd sin α >. Then there re no solutions Medins, ngle isetors, nd ltitudes of tringle. stright line through vertex of tringle nd the midpoint of the opposite side is lled medin of the tringle (Fig. 3.). The three medins of tringle interset in single point lying stritly inside the tringle, whih is lled the entroid or enter of grvity of the tringle. This point uts the medins in the rtio : (ounting from the orresponding verties). 007 y Tylor & Frnis Group, LL
5 46 ELEMENTY GEOMETY () () () Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 m Figure 3.. Medins (), ngle isetors (), nd ltitudes () oftringle. The length of the medin m to the side opposite the ngle α is equl to m = ( + ) = h h h + + os γ. (3...) n ngle isetor of tringle is line segment etween vertex nd point of the opposite side nd dividing the ngle t tht vertex into two equl prts (Fig. 3.). The three ngle isetors interset in single point lying stritly inside the tringle. This point is equidistnt from ll sides nd is lled the inenter (the enter of the inirle of the tringle). onerning the rdius r of the inirle, see Prgrph The ngle isetor through vertex uts the opposite side in rtio proportionl to the djent sides of the tringle. The length of the ngle isetor l drwn to the side is given y the formuls l = [( + ) = ] 4p(p ) =, l = os( α) + = + + ( sin β sin γ os [ sin = p β) sin ( γ), (β γ)] sin β +sinγ (3...) where nd re the segments of the side ut y isetor l nd djent to the sides nd, respetively, nd is the irumrdius (see Prgrph 3..-3). n ltitude of tringle is stright line pssing through vertex nd perpendiulr to the stright line ontining the opposite side (Fig. 3.). The three ltitudes of tringle interset in single point, lled the orthoenter of the tringle. The length of the ltitude h to the side is given y the formuls h = sin γ = sin β =, h = (p )os α os β os γ = (p )sin α sin β os γ. (3...3) The lengths of the ltitude, the ngle isetor, nd the medin through the sme vertex stisfy the inequlity h l m.ifh = l = m, then the tringle is isoseles; moreover, the first equlity implies the seond, nd vie vers irumirle, inirle, nd exirles. stright line pssing through the midpoint of segment nd perpendiulr to it is lled the perpendiulr isetor of the segment. The irle pssing through the verties of tringle is lled the irumirle of the tringle. The enter O of the irumirle, lled the irumenter, is the point where the perpendiulr isetors of the sides of the tringle 007 y Tylor & Frnis Group, LL
6 3.. PLNE GEOMETY 47 () Simpson line () () Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 O O Q Euler line Figure 3.3. The irumirle of tringle. The irumenter (), the Simpson line (), nd the Euler line (). meet (Fig. 3.3). The feet of the perpendiulrs drwn from point Q on the irumirle to the three sides of the tringle lie on the sme stright line lled the Simpson line of Q with respet to the tringle (Fig. 3.3). The irumenter, the orthoenter, nd the entroid lie on single line, lled the Euler line (Fig. 3.3). The irle tngent to the three sides of tringle nd lying inside the tringle is lled the inirle of the tringle. The enter O of the inirle (the inenter) is the point where the ngle isetors meet (Fig. 3.4). The stright lines onneting the verties of tringle with the points t whih the inirle is tngent to the respetive opposite sides interset in single point G lled the Gergonne point (Fig. 3.4). () O O Figure 3.4. The inirle of tringle (). The inenter nd the Gergonne point (). The irle tngent to one side of tringle nd to the extensions of the other two sides is lled n exirle of the tringle. Eh tringle hs three exirles. The enter of n exirle (n exenter) is the point of onurreny of two externl ngle isetors nd n interior ngle isetor. The stright lines onneting the verties of tringle with the points t whih the respetive opposite sides re tngent to the exirles interset in single point N, lled the Ngel point (Fig. 3.5). The inrdius r, the irumrdius, nd the exrdii ρ, ρ,ndρ stisfy the reltions (p )(p )(p ) r = = p tn α p tn β tn γ sin α = sin β = sin γ = 4S = = 4 sin α sin β sin γ =(p )tn γ = S p, (3...4) () p 4 os ( α) os ( = β) os (, (3...5) γ) r = + +. (3...6) ρ ρ ρ 007 y Tylor & Frnis Group, LL G O
7 48 ELEMENTY GEOMETY Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 O N Figure 3.5. Exirles of tringle. The Ngel point. The distne d etween the irumenter nd the inenter nd the distne d etween the irumenter nd the exenter re given y the expressions re of tringle. The re S of tringle is given y the formuls d = r, (3...7) d = + ρ. (3...8) S = h = sin γ = rp, S = p(p )(p )(p ) (Heron s formul), S = 4 = sin α sin β sin γ, sin α sin β S = sin γ sin α sin β = sin(α + β) Theorems out points nd lines relted to tringle. O (3...9) EV S THEOEM. Let points,,nd lie on the sides,, nd, respetively, of tringle (Fig. 3.6). The stright lines,,nd re onurrent or prllel if nd only if =. (3...0) STEWT S THEOEM. If stright line through vertex of tringle divides the opposite side into segments of lengths m nd n (Fig. 3.7), then 007 y Tylor & Frnis Group, LL (m + n)(p + mn) = m + n. (3...)
8 3.. PLNE GEOMETY 49 p Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 Figure 3.6. ev s theorem. m Figure 3.7. Stewrt s theorem. MENELUS S THEOEM. If stright line intersets sides,,nd of tringle (Fig. 3.8) or their extensions t points,,nd, respetively, then Figure 3.8. Menelus s theorem. =. (3...) Figure 3.9. Morley s theorem. Stright lines dividing the interior ngles of tringle into three equl prts re lled ngle trisetors. MOLEY S THEOEM. The three points of intersetion of djent ngle trisetors of tringle form n equilterl tringle (Fig. 3.9). In tringle, the midpoints of the three sides, the feet of the three ltitudes, nd the midpoints of the segments of the ltitudes etween the orthoenter nd the verties ll lie on single irle, the nine-point irle (Fig. 3.0). O Euler line Figure 3.0. Nine-point irle. FEUEH S THEOEM. The nine-point irle is tngent to the inirle nd the three exirles. The points of tngeny re lled the Feuerh points. The enter of the nine-point irle lies on the Euler line (see Prgrph 3..-3). 007 y Tylor & Frnis Group, LL n
9 50 ELEMENTY GEOMETY Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h ight (right-ngled) tringles. β h α m n с Figure 3.. right tringle. right tringle is tringle with right ngle. The side opposite the right ngle is lled the hypotenuse, nd the other two sides re lled the legs (Fig. 3.). The hypotenuse, the legs nd, nd the ngles α nd β opposite the legs stisfy the following reltions: α + β = 90 ; One lso hs sin α =osβ =, sinβ =osα =, tn α =otβ =, tnβ =otα =. (3...3) + = (PYTHGOEN THEOEM), (3...4) h = mn, = m, = n, (3...5) where h is the length of the ltitude drwn to the hypotenuse; moreover, the ltitude uts the hypotenuse into segments of lengths m nd n. In right tringle, the length of the medin m drwn from the vertex of the right ngle oinides with the irumrdius nd is equl to hlf the length of the hypotenuse, m = =. The inrdius is given y the formul r = ( + ). The re of the right tringle is S = h = (see lso Prgrphs 3..- to 3..-4) Isoseles nd equilterl tringles..nisoseles tringle is tringle with two equl sides. These sides re lled the legs, nd the third side is lled the se (Fig. 3.). 007 y Tylor & Frnis Group, LL α () () α Figure 3.. n isoseles tringle (). n equilterl tringle ().
10 3.. PLNE GEOMETY 5 Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 Properties of isoseles tringles:. In n isoseles tringle, the ngles djent to the se re equl.. In n isoseles tringle, the medin drwn to the se is the ngle isetor nd the ltitude. 3. In n isoseles tringle, the sum of distnes from point of the se to the legs is onstnt. riteri for tringle to e isoseles:. If two ngles in tringle re equl, then the tringle is isoseles.. If medin in tringle is lso n ltitude, then the tringle is isoseles. 3. If isetor in tringle is lso n ltitude, then the tringle is isoseles..nequilterl (or regulr) tringle is tringle with ll three sides equl (Fig. 3.). ll ngles of n equilterl tringle re equl to 60. In n equilterl tringle, the irumrdius nd the inrdius r stisfy the reltion = r. For n equilterl tringle with side length, the irumrdius nd the inrdius re given y the formuls = 3 3 nd r = 3 6, nd the re is equl to S = Polygons Polygons. si informtion. polygon is plne figure ounded y losed roken line, i.e., line otined if one tkes n distint points suh tht no three suessive points re olliner nd drws stright line segment etween eh of these points nd its suessor s well s etween the lst point nd the first point (Fig. 3.3). The segments forming polygon re lled the sides (or edges), nd the points themselves re lled the verties of the polygon. Two sides shring vertex, s well s two suessive verties (the endpoints of the sme edge), re sid to e djent. polygon n e self-interseting, ut the points of self-intersetion should not e verties (Fig. 3.3). polygon is sid to e plne if its verties re oplnr. polygon is sid to e simple if its nondjent sides do not hve ommon interior or endpoints. polygon is sid to e onvex if it lies on one side of ny stright line pssing through two neighoring verties (Fig. 3.3). In wht follows, we onsider only plne simple onvex polygons. () () Figure 3.3. Polygons. Nonself-interseting (), self-interseting (), nd onvex () polygon. n (interior) ngle of onvex polygon is the ngle etween two sides meeting in vertex. n ngle djent to n interior ngle is lled n externl ngle of the onvex polygon. onvex polygon is sid to e insried in irle if ll of its verties lie on the irle. polygon is sid to e irumsried out irle if ll of its sides re tngent to the irle. For onvex polygon with n sides, the sum of interior ngles is equl to 80 (n ), nd the sum of externl ngles is equl to y Tylor & Frnis Group, LL ()
11 5 ELEMENTY GEOMETY One n find the re of n ritrry polygon y dividing it into tringles Properties of qudrilterls. Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3. The digonls of onvex qudrilterl meet.. The sum of interior ngles of onvex qudrilterl is equl to 360 (Fig. 3.4 nd ). 3. The lengths of the sides,,, ndd, the digonls d nd d, nd the segment m onneting the midpoints of the digonls stisfy the reltion d = d + d + 4m. 4. onvex qudrilterl is irumsried if nd only if + = + d. 5. onvex qudrilterl is insried if nd only if α + γ = β + δ. 6. The reltion + d = d d holds for insried qudrilterls (PTOLEMY S THEOEM). φ m res of qudrilterls. The re of onvex qudrilterl is equl to S = d d sin ϕ = d () () d d β α Figure 3.4. Qudrilterls. p(p )(p )(p )(p d) d os where ϕ is the ngle etween the digonls d nd d nd p = ( d). The re of n insried qudrilterl is The re of irumsried qudrilterl is γ d δ β + δ, (3...) S = p(p )(p )(p )(p d). (3...) S = d sin If qudrilterl is simultneously insried nd irumsried, then si qudrilterls. β + δ. (3...3) S = d. (3...4).prllelogrm is qudrilterl suh tht oth pirs of opposite sides re prllel (Fig. 3.5). 007 y Tylor & Frnis Group, LL
12 3.. PLNE GEOMETY 53 () () Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 h d d d Figure 3.5. prllelogrm () nd rhomus (). ttriutes of prllelogrms ( qudrilterl is prllelogrm if):. oth pirs of opposite sides hve equl length.. oth pirs of opposite ngles re equl. 3. Two opposite sides re prllel nd hve equl length. 4. The digonls meet nd iset eh other. Properties of prllelogrms:. The digonls meet nd iset eh other.. Opposite sides hve equl length, nd opposite ngles re equl. 3. The digonls nd the sides stisfy the reltion d + d = ( + ). 4. The re of prllelogrm is S = h,wherehis the ltitude (see lso Prgrph 3..-3)..rhomus is prllelogrm in whih ll sides re of equl length (Fig. 3.5). Properties of rhomi:. The digonls re perpendiulr.. The digonls re ngle isetors. 3. The re of rhomus is S = h = sin α = d d. 3.retngle is prllelogrm in whih ll ngles re right ngles (Fig. 3.6). () Properties of retngles:. The digonls hve equl lengths.. The re of retngle is S =. d α () Figure 3.6. retngle () nd squre (). 4.squre is retngle in whih ll sides hve equl lengths (Fig. 3.6). squre is lso speil se of rhomus (ll ngles re right ngles). 007 y Tylor & Frnis Group, LL d d d
13 54 ELEMENTY GEOMETY Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 Properties of squres:. ll ngles re right ngles.. The digonls re equl to d =. 3. The digonls meet t right ngle nd re ngle isetors. 4. The re of squre is equl to S = = d. 5.trpezoid is qudrilterl in whih two sides re prllel nd the other two sides re nonprllel (Fig. 3.7). The prllel sides nd re lled the ses of the trpezoid, nd the other two sides re lled the legs. Innisoseles trpezoid, the legs re of equl length. The line segment onneting the midpoints of the legs is lled the medin of the trpezoid. The length of the medin is equl to hlf the sum of the lengths of the ses, m = ( + ). h m Figure 3.7. trpezoid. The perpendiulr distne etween the ses is lled the ltitude of trpezoid. Properties of trpezoids:. trpezoid is irumsried if nd only if + = + d.. trpezoid is insried if nd only if it is isoseles. 3. The re of trpezoid is S = ( + )h = mh = d d sin ϕ, whereϕ is the ngle etween the digonls d nd d. 4. The segment onneting the midpoints of the digonls is prllel to the ses nd hs the length ( ). Exmple. onsider n pplition of plne geometry to mesuring distnes in geodesy. Suppose tht the ngles α, β, γ,ndδ etween stright line nd the diretions to points D nd re known t points nd (Fig. 3.8). Suppose lso tht the distne = (or = D) is known nd the tsk is to find the distne = D (or = ). () () D α β D ψ φ σ x z O φ β σ δ γ α γ Figure 3.8. pplitions of plne geometry in geodesy. Let us find the ngles ϕ nd ψ. Sine σ is the ngle t the vertex O in oth tringles O nd DO, it follows tht α + γ = ϕ + ψ. Let ε = (ϕ + ψ). We twie pply the lw of sines (Tle 3.) nd find the hlf-differene of the desired ngles. The min formuls red 007 y Tylor & Frnis Group, LL D = sin γ sin(π α β γ) = sin γ sin(α + β + γ), d y ψ = sin α sin(α + γ + δ),
14 3.. PLNE GEOMETY 55 Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 D = sin β sin γ, These reltions imply tht nd hene = = sin δ sin ϕ. sin β sin γ sin ψ sin(α + β + γ) = sin ϕ sin ψ sin δ sin α sin ϕ sin(α + γ + δ) = sin δ sin α sin(α + β + γ) sin β sin γ sin(α + γ + δ) =otη, where η is n uxiliry ngle. y dding nd sutrting, we otin sin ϕ sinψ sin ϕ +sinψ = ot η [ ot η +, os (ϕ + ψ)] sin [ ( (ϕ ψ)] sin [ (ϕ + ψ)] os [ ot = π) ot η 4 (ϕ ψ)] ot η +ot ( π), 4 tn ϕ ψ =tn ϕ + ψ ( π ) ot 4 + η =tn α + γ ( π ) ot 4 + η. (3...5) From this we find ε = (ϕ ψ) nd, sustituting ϕ = ε + ε nd ψ = ε ε into (3...5), otin the desired distne. Exmple. Suppose tht the mutul position of three points,, nd is determined y the segments = nd =, nd the ngle = γ. Suppose tht the following ngles hve een mesured t some point D: D = α nd D = β. In the generl se, one n find the position of point D with respet to,, nd, i.e., uniquely determine the segments x, y, ndz (Fig. 3.8). For this to e possile, it is neessry tht D does not lie on the irumirle of the tringle. Wehve y the lw of sines (Tle 3.), we otin whih implies tht ϕ + ψ = π (α + β + γ) = ε. (3...6) sin ϕ = z sin α, sinψ = z sin β, (3...7) sin ϕ sin ψ = sin α sin β =otη, (3...8) where η is n uxiliry ngle. We find the ngles ϕ nd ψ from (3...6) nd (3...8), sustitute them into (3...7) to determine z,ndfinlly pply the lw of sines to otin x nd y egulr polygons. onvex polygon is sid to e regulr if ll of its sides hve the sme length nd ll of its interior ngles re equl. onvex n-gon is regulr if nd only if it is tken to itself y the rottion y n ngle of π/n out some point O. The point O is lled the enter of the regulr polygon. The ngle etween two rys issuing from the enter nd pssing through two neighoring verties is lled the entrl ngle (Fig. 3.9). 007 y Tylor & Frnis Group, LL r α Figure 3.9. regulr polygon. γ β
15 56 ELEMENTY GEOMETY Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 Properties of regulr polygons:. The enter is equidistnt from ll verties s well s from ll sides of regulr polygon.. regulr polygon is simultneously insried nd irumsried; the enters of the irumirle nd the inirle oinide with the enter of the polygon itself. 3. In regulr polygon, the entrl ngle is α = 360 /n, the externl ngle is β = 360 /n, nd the interior ngle is γ = 80 β. 4. The irumrdius, the inrdius r, nd the side length of regulr polygon stisfy the reltions = r = sin α = r tn α. (3...9) 5. The re S of regulr n-gon is given y the formul S = rn = nr tn α = n sin α = 4 n ot α. (3...0) Tle 3.3 presents severl useful formuls for regulr polygons. TLE 3.3 egulr polygons ( is the side length) No. Nme Inrdius r irumrdius re S egulr polygon tn π sin π n n rn Tringle Squre 4 Pentgon Hexgon Otgon + + ( + ) 7 Ennegon Dodegon irle Some definitions nd formuls ( + 3) The irle of rdius entered t O is the set of ll points of the plne t fixed distne from fixed point O (Fig. 3.0). plne figure ounded y irle is lled disk. segment onneting two points on irle is lled hord. hord pssing through the enter of irle is lled dimeter of the irle (Fig. 3.0). The dimeter length is d =. stright line tht meets irle t single point is lled tngent, ndthe ommon point is lled the point of tngeny (Fig. 3.0). n ngle formed y two rdii is lled entrl ngle. n ngle formed y two hords with ommon endpoint is lled n insried ngle. 007 y Tylor & Frnis Group, LL
16 3.. PLNE GEOMETY 57 () () () Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 O O Figure 3.0. irle(). dimeter () nd tngent ()ofirle. Properties of irles nd disks:. The irumferene is L = π = πd = πs.. The re of disk is S = π = 4 πd = 4 Ld. 3. The dimeter of irle is longest hord. 4. The dimeter pssing through the midpoint of the hord is perpendiulr to the hord. 5. The rdius drwn to the point of tngeny is perpendiulr to the tngent. 6. n insried ngle is hlf the entrl ngle sutended y the sme hord, α = O (Fig. 3.). 7. The ngle etween hord nd the tngent to the irle t n endpoint of the hord is β = O (Fig. 3.). 8. The ngle etween two hords is γ = ( + ED) (Fig. 3.). 9. The ngle etween two sents is α = ( DE ) (Fig. 3.). E α β D () O α β O () () d F β α D E d O O () Figure 3.. Properties of irles nd disks. 0. The ngle etween sent nd the tngent to the irle t n endpoint of the sent is 007 y Tylor & Frnis Group, LL γ O E D α
17 58 ELEMENTY GEOMETY Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 β = ( FE F) (Fig. 3.).. The ngle etween two tngents is α = ( D E) (Fig. 3.d).. If two hords meet, then D = E = m (Fig. 3.). 3. For sents, D = E = m (Fig. 3.). 4. For tngent nd sent, F F = D (Fig. 3.) Segment nd setor. plnefigure ounded y two rdii nd one of the sutending rs is lled (irulr) setor. plnefigure ounded y n r nd the orresponding hord is lled segment (Fig. 3.). If is the rdius of the irle, l is the r length, is the hord length, α is the entrl ngle (in degrees), nd h is the height of the segment, then the following formuls hold: = h h = sin α, ( h = 4 = os α ) = tn α 4, (3..3.) l = πα α. 360 The re of irulr setor is given y the formul S = l = π α α, (3..3.) nd the re of segment not equl to hlf-disk is given y the expression S = π α 360 S Δ, (3..3.3) where S Δ is the re of the tringle with verties t the enter of the disk nd t the endpoints of the rdii ounding the orresponding setor. One tkes the minus sign for α < 80 nd the plus sign for α > 80. The r length nd the re of segment n e found y the pproximte formuls l 8, l 3 + 6h 3, h(6 + 8) S, 5 where is the hord of the hlf-segment (see Fig. 3.) nnulus. (3..3.4) n nnulus is plne figure ounded y two onentri irles of distint rdii (Fig. 3.). Let e the outer rdius of n nnulus (the rdius of the outer ounding irle), nd let r 007 y Tylor & Frnis Group, LL
18 3.. SOLID GEOMETY 59 Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 () α h l Figure 3.. segment() nd n nnulus (). e the inner rdius (the rdius of the inner ounding irle). Then the re of the nnulus is given y the formul S = π( r )= π 4 (D d )= πρδ, (3..3.5) where D = nd d = r re the outer nd inner dimeters, ρ = ( + r) is the midrdius, nd δ = r is the width of the nnulus. The re of the prt of the nnulus ontined in setor of entrl ngle ϕ, givenin degrees (see Fig. 3.), is given y the formul S = πϕ 360 ( r )= πϕ 440 (D d )= πϕ ρδ. (3..3.6) Solid Geometry 3... Stright Lines, Plnes, nd ngles in Spe Mutul rrngement of stright lines nd plnes.. Two distint stright lines lying in single plne either hve extly one point of intersetion or do not meet t ll. In the ltter se, they re sid to e prllel. If two stright lines do not lie in single plne, then they re lled skew lines. The ngle etween skew lines is determined s the ngle etween lines prllel to them nd lying in single plne (Fig. 3.3). The distne etween skew lines is the length of the stright line segment tht meets oth lines nd is perpendiulr to them. () () Figure 3.3. The ngle etween skew lines ().Thengleetweenlinendplne().. Two distint plnes either interset in stright line or do not hve ommon points. In the ltter se, they re sid to e prllel. oiniding plnes re lso ssumed to e prllel. If two plnes re perpendiulr to single stright line or eh of them ontins pir of interseting stright lines prllel to the orresponding lines in the other pir, then the plnes re prllel. 007 y Tylor & Frnis Group, LL φ () α r
19 60 ELEMENTY GEOMETY Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 3. stright line either entirely lies in the plne, meets the plne t single point, or hs no ommon points with the plne. In the lst se, the line is sid to e prllel to the plne. The ngle etween stright line nd plne is equl to the ngle etween the line nd its projetion onto the plne (Fig. 3.3). If stright line is perpendiulr to two interseting stright lines on plne, then it is perpendiulr to eh line on the plne, i.e., perpendiulr to the plne Polyhedrl ngles..dihedrl ngle is figure in spe formed y two hlf-plnes issuing from single stright line s well s the prt of spe ounded y these hlf-plnes. The hlf-plnes re lled the fes of the dihedrl ngle, nd their ommon stright line is lled the edge. dihedrl ngle is mesured y its liner ngle (Fig. 3.4), i.e., y the ngle etween the perpendiulrs rised to the edge DE of the dihedrl ngle in oth plnes (fes) tthe sme point. () () E D Figure 3.4. dihedrl() nd trihedrl () ngle.. prt of spe ounded y n infinite tringulr pyrmid is lled trihedrl ngle (Fig. 3.4). The fes of this pyrmid re lled the fes of the trihedrl ngle, nd the vertex of the pyrmid is lled the vertex of trihedrl ngle. The rys in whih the fes interset re lled the edges of trihedrl ngle. The edges form fe ngles, nd the fes form the dihedrl ngles of the trihedrl ngle. s rule, one onsiders trihedrl ngles with dihedrl ngles less thn π (or 80 ), i.e., onvex trihedrl ngles. Eh fe ngle of onvex trihedrl ngle is less thn the sum of the other two fe ngles nd greter thn their differene. Two trihedrl ngles re equl if one of the following onditions is stisfied:. Two fe ngles, together with the inluded dihedrl ngle, of the first trihedrl ngle re equl to the respetive prts (rrnged in the sme order) of the seond trihedrl ngle.. Two dihedrl ngles, together with the inluded fe ngle, of the first trihedrl ngle re equl to the respetive prts (rrnged in the sme order) of the seond trihedrl ngle. 3. The three fe ngles of the first trihedrl ngle re equl to the respetive fe ngles (rrnged in the sme order) of the seond trihedrl ngle. 4. The three dihedrl ngles of the first trihedrl ngle re equl to the respetive dihedrl ngles (rrnged in the sme order) of the seond trihedrl ngle. 3.polyhedrl ngle ODE (Fig. 3.5) is formed y severl plnes (fes)hving single ommon point (the vertex) nd suessively interseting long stright lines O, 007 y Tylor & Frnis Group, LL
20 E 3.. SOLID GEOMETY 6 () () O Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 D Figure 3.5. polyhedrl () nd solid () ngle. O,..., OE (the edges). Two edges elonging to the sme fe form fe ngle of the polyhedrl ngle, nd two neighoring fes form dihedrl ngle. Polyhedrl ngles re equl (ongruent) if one n e trnsformed into the other y trnsltions nd rottions. For polyhedrl ngles to e ongruent, the orresponding prts (fe nd dihedrl ngles) must e equl. However, if the orresponding equl prts re rrnged in reverse order, then the polyhedrl ngles nnot e trnsformed into eh other y trnsltions nd rottions. In this se, they re sid to e symmetri. onvex polyhedrl ngle lies entirely on one side of eh of its fes. The sum O + O + + EO of fe ngles (Fig. 3.5) of ny onvex polyhedrl ngle is less tht π (or 360 ). 4.solid ngle is prt of spe ounded y stright lines issuing from single point (vertex) to ll points of some losed urve (Fig. 3.5). Trihedrl nd polyhedrl ngles re speil ses of solid ngles. solid ngle is mesured y the re ut y the solid ngle on the sphere of unit rdius entered t the vertex. Solid ngles re mesured in sterdins. The entire sphere forms solid ngle of 4π sterdins Polyhedr Generl onepts. polyhedron is solid ounded y plnes. In other words, polyhedron is set of finitely mny plne polygons stisfying the following onditions:. Eh side of eh polygon is simultneously side of unique other polygon, whih is sid to e djent to the first polygon (vi this side).. From eh of the polygons forming polyhedron, one n reh ny other polygon y suessively pssing to djent polygons. These polygons re lled the fes, their sides re lled the edges, nd their verties re lled the verties of polyhedron. polyhedron is sid to e onvex if it lies entirely on one side of the plne of ny of its fes; if polyhedron is onvex, then so re its fes. EULE S THEOEM. If the numer of verties in onvex polyhedron is e, the numer of edges is f, nd the numer of fes is g, thene + f g = Prism. Prllelepiped..prism is polyhedron in whih two fes re n-gons (the se fes of the prism) nd the remining n fes (joining fes) re prllelogrms. The se fes of prism re 007 y Tylor & Frnis Group, LL
21 6 ELEMENTY GEOMETY () () Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 Figure 3.6. prism() nd trunted prism (). equl (ongruent) nd lie in prllel plnes (Fig. 3.6). right prism is prism in whih the joining fes re perpendiulr to the se fes. right prism is sid to e regulr if its se fe is regulr polygon. If l is the joining edge length, S is the re of the se fe, H is the ltitude of the prism, P se is the perimeter of perpendiulr setion, nd S se is the re of the perpendiulr setion, then the re of the lterl surfe S lt nd the volume V of the prism n e determined y the formuls S lt = P se l (3...) V = SH = S se l. The portion of prism ut y plne nonprllel to the se fe is lled trunted prism (Fig. 3.6). The volume of trunted prism is V = LP, (3...) where L is the length of the segment onneting the enters of the se fes nd P is the re of the setion of the prism y plne perpendiulr to this segment.. prism whose ses re prllelogrms is lled prllelepiped. ll four digonls in prllelepiped interset t single point nd iset eh other (Fig. 3.7). prllelepiped is sid to e retngulr if it is right prism nd its se fes re retngles. In retngulr prllelepiped, ll digonls re equl (Fig. 3.7). () () Figure 3.7. prllelepiped () nd retngulr prllelepiped (). If,, nd re the lengths of the edges of retngulr prllelepiped, then the digonl d n e determined y the formul d = + +. The volume of retngulr prllelepiped is given y the formul V =, nd the lterl surfe re is S lt = PH, where P is the perimeter of the se fe. 3. retngulr prllelepiped ll of whose edges re equl ( = = ) is lled ue. The digonl of ue is given y the formul d = 3. The volume of the ue is V = 3, nd the lterl surfe re is S lt = y Tylor & Frnis Group, LL d
22 3.. SOLID GEOMETY 63 Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h Pyrmid, oelisk, nd wedge..pyrmid is polyhedron in whih one fe (the se of the pyrmid) is n ritrry polygon nd the other (lterl) fes re tringles with ommon vertex, lled the pex of the pyrmid (Fig. 3.8). The se of n n-sided pyrmid is n n-gon. The perpendiulr through the pex to the se of pyrmid is lled the ltitude of the pyrmid. () () D H Figure 3.8. pyrmid(). The ttitude DO, the plne DE, nd the side in tringulr pyrmid (). The volume of pyrmid is given y the formul O E V = SH, (3...3) 3 where S is the re of the se nd H is the ltitude of the pyrmid. The pex of pyrmid is projeted onto the irumenter of the se if one of the following onditions is stisfied:. The lengths of ll lterl edges re equl.. ll lterl edges mke equl ngles with the se plne. The pex of pyrmid is projeted onto the inenter of the se if one of the following onditions is stisfied: 3. ll lterl fes hve equl pothems. 4. The ngles etween ll lterl fes nd the se re the sme. If DO is the ltitude of the pyrmid D nd D, then the plne DE is perpendiulr to (Fig. 3.8). If the pyrmid is ut y plne (Fig. 3.9) prllel to the se, then S = S = = SO O O, ( ) S DEF SO (3...4) =, S D E F SO where SO is the ltitude of the pyrmid, i.e., the segment of the perpendiulr through the vertex to the se. The ltitude of tringulr pyrmid psses through the orthoenter of the se if nd only if ll pirs of opposite edges of the pyrmid re perpendiulr. The volume of tringulr pyrmid (Fig. 3.9), where D =, D =, D =, = p, = q, nd = r, is given y the formul 0 r q V = r 0 p 88 q p 0, (3...5) y Tylor & Frnis Group, LL
23 64 ELEMENTY GEOMETY Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 () () S D F E F O D E r O D q Figure 3.9. The pyrmid ut y plne nd the originl pyrmid (). tringulr pyrmid (). where the right-hnd side ontins determinnt. pyrmid is sid to e regulr if its se is regulr n-gon nd the ltitude psses through the enter of the se. The ltitude (issuing from the pex) of lterl fe is lled the pothem of regulr pyrmid. For regulr pyrmid, the lterl surfe re is where P is the perimeter of the se nd l is the pothem. S lt = Pl, (3...6). If pyrmid is ut y plne prllel to the se, then it splits into two prts, pyrmid similr to the originl pyrmid nd the frustum (Fig. 3.30). The volume of the frustum is V = 3 h(s + S + S S )= 3 hs [ + p ] +, (3...7) where S nd S re the res of the ses, nd re two respetive sides of the ses, nd h is the ltitude (the perpendiulr distne etween the ses). S () () () S h h Figure frustum of pyrmid (), n oelisk (), nd wedge (). For regulr frustum, the lterl surfe re is S lt = (P + P )l, (3...8) where P nd P re the perimeters of the ses nd l is the ltitude of the lterl fe. 007 y Tylor & Frnis Group, LL h
24 3.. SOLID GEOMETY hexhedron whose ses re retngles lying in prllel plnes nd whose lterl fes form equl ngles with the se, ut do not meet t single point, is lled n oelisk (Fig. 3.30). If, nd, re the sides of the ses nd h is the ltitude, then the volume of the hexhedron is Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 V = h 6 [( + ) +( + ) ]. (3...9) 4. penthedron whose se is retngle nd whose lterl fes re isoseles tringles nd isoseles trpezoids is lled wedge (Fig. 3.30). The volume of the wedge is egulr polyhedr. V = h 6 ( + ). (3...0) polyhedron is sid to e regulr if ll of its fes re equl regulr polygons nd ll polyhedrl ngles re equl to eh other. There exist five regulr polyhedr (Fig. 3.3), whose properties re given in Tle 3.4. Tetrhedron ue Othedron Dodehedron Figure 3.3. Five regulr polyhedr Solids Formed y evolution of Lines ylinder. Ioshedron ylindril surfe is surfe in spe swept y stright line (the genertor) moving prllel to given diretion long some urve (the diretrix) (Fig. 3.3).. solid ounded y losed ylindril surfe nd two plnes is lled ylinder; the plnes re lled the ses of the ylinder (Fig. 3.3). If P is the perimeter of the se, P se is the perimeter of the setion perpendiulr to the genertor, S se is the re of this setion, S s is the re of the se, nd l is the length of 007 y Tylor & Frnis Group, LL
25 66 ELEMENTY GEOMETY TLE 3.4 egulr polyhedr ( is the edge length) No. Nme Numer of fes nd its shpe Numer of verties Numer of edges Totl surfe re Volume Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 Tetrhedron 4 tringles ue 6 squres Othedron 8 tringles Dodehedron pentgons Ioshedron 0 tringles () () H Figure 3.3. ylindril surfe (). ylinder (). l ( ) 5 3 (3 + 5) the genertor, then the lterl surfe re S lt nd the volume V of the ylinder re given y the formuls S lt = PH = P se l, (3..3.) V = S s H = S se l. In right ylinder, the ses re perpendiulr to the genertor. In prtiulr, if the ses re disks, then one speks of right irulr ylinder. The volume, the lterl surfe re, nd the totl surfe re of right irulr ylinder re given y the formuls V = π H, S lt = πh, S = π( + H), where is the rdius of the se. right irulr ylinder is lso lled round ylinder, orsimplyylinder. (3..3.). The prt of ylinder ut y plne nonprllel to the se is lled trunted ylinder (Fig. 3.33). The volume, the lterl surfe re, nd the totl surfe re of trunted ylinder 007 y Tylor & Frnis Group, LL
26 3.. SOLID GEOMETY 67 () () () r Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 H re given y the formuls H φ Figure trunted ylinder (), hoof (), nd ylindril tue (). V = π H + H, S lt = π(h + H ), [ ( ) ] H S = π H + H + + H +, where H nd H re the mximl nd miniml genertors. h H (3..3.3) 3.segment of round ylinder ( hoof ) is portion of the ylinder ut y plne tht is nonprllel to the se nd intersets it. If is the rdius of the ylindril segment, h is the height of the hoof, nd is its width (for the other nottion, see Fig. 3.33), then the volume V nd the lterl surfe re S lt of the hoof n e determined y the formuls V = h [ (3 )+3 ( )α ] ( ) = h3 sin α sin3 α α os α, 3 3 S lt = π [( )α + ], where α = ϕ is mesured in rdins. (3..3.4) 4. solid ounded y two losed ylindril surfes nd two plnes is lled ylindril tue; the plnes re lled the ses of the tue. The volume of round ylindril tue (Fig. 3.33) is V = πh( r )=πhδ( r) =πhδ(r + δ) = πhδρ, (3..3.5) where nd r re the outer nd inner rdii, δ = r is the thikness, ρ = ( + r) isthe midrdius, nd H is the height of the pipe onil surfe. one. Frustum of one. onil surfe is the union of stright lines (genertors) pssing through fixed point (the pex) in spe nd ny point of some spe urve (the diretrix) (Fig. 3.34). 007 y Tylor & Frnis Group, LL
27 68 ELEMENTY GEOMETY () () () () d Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 H H Figure onil surfe (). one (), right irulr one (), nd frustum of one (d).. solid ounded y onil surfe with losed diretrix nd plne is lled one; the plne is the se of the one (Fig. 3.34). The volume of n ritrry one is given y the formul l h V = 3 HS s, (3..3.6) where H is the ltitude of the one nd S s is the re of the se. right irulr one (Fig. 3.34) hs disk s the se, nd its vertex is projeted onto the enter of the disk. If l is the length of the genertor nd is the rdius of the se, then the volume, the lterl surfe re, nd the totl surfe re of the right irulr one re given y the formuls V = 3 π H, S lt = πl = π + H, S = π( + l). r l (3..3.7). If one is ut y plne prllel to the se, then we otin frustum of one (Fig. 3.34d). The length l of the genertor, the volume V, the lterl surfe re S lt,nd the totl surfe re S of the frustum of right irulr one re given y the formuls l = h +( r), V = πh 3 ( + r + r), S lt = πl( + r), S = π[l( + r)+ + r ], where r is the rdius of the upper se nd h is the ltitude of the frustum of one Sphere. Spheril prts. Torus. (3..3.8).Thesphere of rdius entered t O is the set of points in spe t the distne from the point O (Fig. 3.35). solid ounded y sphere is lled ll. ny setion of the sphere y plne is irle. The setion of the sphere y plne pssing through its enter is lled gret irle of rdius. There exists extly one gret irle pssing through two ritrry points on the sphere tht re not ntipodl (i.e., re not the opposite endpoints of dimeter). The smller r of this gret irle is the shortest distne on the sphere etween these points. onerning the geometry of the sphere, see Setion 3.3. The 007 y Tylor & Frnis Group, LL
28 3.. SOLID GEOMETY 69 Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 surfe re S of the sphere nd the volume V of the ll ounded y the sphere re given y the formuls S = 4π = πd = 3 36πV, V = 4π3 3 where D = is the dimeter of the sphere. = πd3 6 = 6 S 3 () () () h π, (3..3.9) Figure sphere (), spheril p (), nd spheril setor ().. portion of ll ut from it y plne is lled spheril p (Fig. 3.35). The width, the re S lt of the urved surfe, the totl surfe re S, nd the volume V of spheril p n e found from the formuls = h( h), S lt = πh = π( + h ), S = S lt + π = π(h + )=π(h + ), V = πh 6 (3 + h )= πh (3 h), 3 where nd h re the rdius nd the height of the spheril p. h (3..3.0) 3. portion of ll ounded y the urved surfe of spheril p nd the onil surfe whose se is the se of the p nd whose vertex is the enter of the ll is lled spheril setor (Fig. 3.35). The totl surfe re S nd the volume V of spheril setor re given y the formuls S = π(h + ), V = 3 π h, where is the width, h is the height, nd is the rdius of the setor. (3..3.) 4. portion of ll ontined etween two prllel plne sents is lled spheril segment (Fig. 3.36). The urved surfe of spheril segment is lled spheril zone, nd the plne irulr surfes re the ses of spheril segment. The rdius of the ll, the rdii nd of the ses, nd the height h of spheril segment stisfy the reltion 007 y Tylor & Frnis Group, LL ( = h ) +. (3..3.) h
29 70 ELEMENTY GEOMETY The urved surfe re S lt, the totl surfe re S, nd the volume V of spheril segment re given y the formuls Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 S lt = πh, S = S lt + π( + )=π(h + + ), V = πh 6 ( h ). () () () h h r (3..3.3) Figure spheril segment () nd spheril segment without the trunted one insried in it (). torus (). If V is the volume of the trunted one insried in spheril segment (Fig. 3.36) nd l is the length of its genertor, then V V = πhl 6. (3..3.4) 4.torus is surfe generted y revolving irle out n xis oplnr with the irle ut not interseting it. If the diretrix is irle (Fig. 3.36), the rdius of the diretrix is not less thn the rdius r of the generting irle ( r), nd the enter of the genertor moves long the diretrix, then the surfe re nd the volume of the torus re given y the formuls S = 4π r = π Dd, V = π r = π Dd (3..3.5), 4 where D = nd d = r re the dimeters of the genertor nd the diretrix Spheril Trigonometry Spheril Geometry Gret irle. gret irle is setion of sphere y plne pssing through the enter. Properties of gret irles:. The rdius of gret irle is equl to the rdius of the sphere.. There is only one gret irle through two ritrry points tht re not the opposite endpoints of dimeter. The smller r of the gret irle through two given points is lled geodesi, ndthe length of this r is the shortest distne on the sphere etween the two points. The gret irles on the sphere ply role similr to the role of stright lines on the plne. 007 y Tylor & Frnis Group, LL
30 3.3. SPHEIL TIGONOMETY 7 Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 ny two points on the sphere determine penil of plnes. The intersetion of eh plne in the penil with the sphere is irle. If two points re not the opposite endpoints of dimeter, then the plne pssing through the enter of the sphere determines the lrgest irle in the penil, whih is gret irle. The other irles re lled smll irles; the intersetion with the sphere of the plne perpendiulr to the plne ontining the gret irle is the smllest irle Mesurement of rs nd ngles on sphere. Spheril ingles. The distnes on the sphere re mesured long gret irle rs. The gret irle r length etween points nd is given y the reltion = α, (3.3..) where is the rdius of the sphere nd α is the orresponding entrl ngle (in rdins). If only the unit sphere (the rdius = ) is onsidered, then eh gret irle r n e hrterized y the orresponding entrl ngle (in rdins). The ngle etween two interseting gret irle rs is mesured y the liner ngle etween the tngents to the gret irles t the point of intersetion or, whih is the sme, y the dihedrl ngle etween the plnes of the gret irles. Two interseting gret irles on the sphere form four spheril ingles. The re of spheril ingle with the ngle α is given y the formul Spheril Tringles si notions nd properties. S = α. (3.3..) figure formed y three gret irle rs pirwise onneting three ritrry points on the sphere is lled spheril tringle (Fig. 3.37). The verties of spheril tringle re the points of intersetion of three rys issuing from the enter of the sphere with the sphere. The ngles less thn π etween the rys re lled the sides,,nd of spheril tringle. Suh spheril tringles re lled Euler tringles. To eh side of tringle there orresponds gret irle r on the sphere. The ngles α, β, ndγ opposite the sides,, nd of spheril tringle re the ngles etween the gret irle rs orresponding to the sides of the tringle, or, equivlently, the ngles etween the plnes determined y these rys. 007 y Tylor & Frnis Group, LL () α γ β Figure spheril tringle. γ α () β
31 7 ELEMENTY GEOMETY Downloded y: t: 9:5 08 Nov 08; For: , hpter3, 0.0/ h3 y nlogy with the irumirle of plne tringle, there is irumsried one of revolution tht ontins the three stright lines determining the tringle; the xis of this one is the intersetion of the plnes perpendiulr to the sides t their midpoints. There lso exists n insried one of revolution tht is tngent to the three plnes orresponding to the spheril tringle; the xis of this one is the intersetion of the ngle isetor plnes. The irumrdius nd the inrdius r re defined s the ngles equl to hlf the ngles t the verties of the first nd the seond one, respetively. If is the rdius of the sphere, then the re S of the spheril tringle is given y the formul S = ε, (3.3..) where ε is the spheril exess defined s ε = α + β + γ π (3.3..) nd mesured in rdins. spheril tringle is uniquely determined (up to symmetry trnsformtion) y:. Three sides.. Three ngles. 3. Two sides nd their inluded ngle. 4. Two ngles nd their inluded side. Let α, β,ndγ e the ngles nd,,ndthe sides opposite these ngles in spheril tringle (Fig. 3.37). Tle 3.5 presents the si properties nd reltions hrterizing spheril tringles (with the nottion p = + + nd P = α + β + γ π). From the reltions given in Tle 3.5, one n derive ll missing reltions y ylilly permuting the sides,,nd nd the ngles α, β, ndγ. LEGENDE S THEOEM. The re of spheril tringle with smll sides (i.e., with sides tht re smll ompred with the rdius of the sphere) is pproximtely equl to the re of plne tringle with the sme sides; the differene etween eh ngle of the plne tringle nd the orresponding ngle of the spheril tringle is pproximtely equl to one-third of the spheril exess. The lw of sines, the lw of osines, nd the hlf-ngle theorem in spheril trigonometry for smll sides eome the orresponding theorems of the liner (plne) trigonometry. Tle 3.6 llows one to find the sides nd ngles of n ritrry spheril tringle if three ppropritely hosen sides nd/or ngles re given etngulr spheril tringle. spheril tringle is sid to e retngulr if t lest one of its ngles, for exmple, γ, is equl to π (Fig. 3.38); the opposite side is lled the hypotenuse. 007 y Tylor & Frnis Group, LL π α () β π () π α β Figure retngulr spheril tringle (). The Neper rules ().
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
m m m m m m m m P m P m ( ) m m P( ) ( ). The o-ordinte of the point P( ) dividing the line segment joining the two points ( ) nd ( ) eternll in the r
 CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
Mathematics 10 Page 1 of 5 Properties of Triangle s and Quadrilaterals. Isosceles Triangle. - 2 sides and 2 corresponding.
 Mthemtis 10 Pge 1 of 5 Properties of s Pthgoren Theorem 2 2 2 used to find the length of sides of right tringle Tpe of s nd Some s Theorems ngles s Slene Isoseles Equilterl ute - ll ngles re less thn 90
Mthemtis 10 Pge 1 of 5 Properties of s Pthgoren Theorem 2 2 2 used to find the length of sides of right tringle Tpe of s nd Some s Theorems ngles s Slene Isoseles Equilterl ute - ll ngles re less thn 90
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Geometry of the Circle - Chords and Angles. Geometry of the Circle. Chord and Angles. Curriculum Ready ACMMG: 272.
 Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
PYTHAGORAS THEOREM,TRIGONOMETRY,BEARINGS AND THREE DIMENSIONAL PROBLEMS
 PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
THREE DIMENSIONAL GEOMETRY
 MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
3 Angle Geometry. 3.1 Measuring Angles. 1. Using a protractor, measure the marked angles.
 3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
 Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
2.1 ANGLES AND THEIR MEASURE. y I
 .1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
.1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
Two Triads of Congruent Circles from Reflections
 Forum Geometriorum Volume 8 (2008) 7 12. FRUM GEM SSN 1534-1178 Two Trids of ongruent irles from Refletions Qung Tun ui strt. Given tringle, we onstrut two trids of ongruent irles through the verties,
Forum Geometriorum Volume 8 (2008) 7 12. FRUM GEM SSN 1534-1178 Two Trids of ongruent irles from Refletions Qung Tun ui strt. Given tringle, we onstrut two trids of ongruent irles through the verties,
PROPERTIES OF TRIANGLES
 PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
Similar Right Triangles
 Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
MATHEMATICS AND STATISTICS 1.6
 MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
m A 1 1 A ! and AC 6
 REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
Trigonometry and Constructive Geometry
 Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
4. Statements Reasons
 Chpter 9 Answers Prentie-Hll In. Alterntive Ativity 9-. Chek students work.. Opposite sides re prllel. 3. Opposite sides re ongruent. 4. Opposite ngles re ongruent. 5. Digonls iset eh other. 6. Students
Chpter 9 Answers Prentie-Hll In. Alterntive Ativity 9-. Chek students work.. Opposite sides re prllel. 3. Opposite sides re ongruent. 4. Opposite ngles re ongruent. 5. Digonls iset eh other. 6. Students
VECTOR ALGEBRA. Syllabus :
 MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
Exercise sheet 6: Solutions
 Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
H (2a, a) (u 2a) 2 (E) Show that u v 4a. Explain why this implies that u v 4a, with equality if and only u a if u v 2a.
 Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
Identifying and Classifying 2-D Shapes
 Ientifying n Clssifying -D Shpes Wht is your sign? The shpe n olour of trffi signs let motorists know importnt informtion suh s: when to stop onstrution res. Some si shpes use in trffi signs re illustrte
Ientifying n Clssifying -D Shpes Wht is your sign? The shpe n olour of trffi signs let motorists know importnt informtion suh s: when to stop onstrution res. Some si shpes use in trffi signs re illustrte
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
Perimeter, area and volume
 6 Perimeter, re nd volume Syllus topi M. Perimeter, re nd volume This topi will develop your skills to ompetently solve prolems involving perimeter, re, volume nd pity. Outomes Clulte the re of irles nd
6 Perimeter, re nd volume Syllus topi M. Perimeter, re nd volume This topi will develop your skills to ompetently solve prolems involving perimeter, re, volume nd pity. Outomes Clulte the re of irles nd
Lesson-5 PROPERTIES AND SOLUTIONS OF TRIANGLES
 Leon-5 PROPERTIES ND SOLUTIONS OF TRINGLES Reltion etween the ide nd trigonometri rtio of the ngle of tringle In ny tringle, the ide, oppoite to the ngle, i denoted y ; the ide nd, oppoite to the ngle
Leon-5 PROPERTIES ND SOLUTIONS OF TRINGLES Reltion etween the ide nd trigonometri rtio of the ngle of tringle In ny tringle, the ide, oppoite to the ngle, i denoted y ; the ide nd, oppoite to the ngle
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
( ) { } [ ] { } [ ) { } ( ] { }
![( ) { } [ ] { } [ ) { } ( ] { } ( ) { } [ ] { } [ ) { } ( ] { }](/thumbs/96/129291861.jpg) Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Perimeter and Area. Mathletics Instant Workbooks. Copyright
 Perimeter nd Are Student Book - Series J- L B Mthletis Instnt Workooks Copyright Student Book - Series J Contents Topis Topi - Plne shpes Topi 2 - Perimeter of regulr shpes Topi 3 - Perimeter of irregulr
Perimeter nd Are Student Book - Series J- L B Mthletis Instnt Workooks Copyright Student Book - Series J Contents Topis Topi - Plne shpes Topi 2 - Perimeter of regulr shpes Topi 3 - Perimeter of irregulr
Something found at a salad bar
 Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
THE KENNESAW STATE UNIVERSITY HIGH SCHOOL MATHEMATICS COMPETITION PART I MULTIPLE CHOICE NO CALCULATORS 90 MINUTES
 THE 08 09 KENNESW STTE UNIVERSITY HIGH SHOOL MTHEMTIS OMPETITION PRT I MULTIPLE HOIE For ech of the following questions, crefully blcken the pproprite box on the nswer sheet with # pencil. o not fold,
THE 08 09 KENNESW STTE UNIVERSITY HIGH SHOOL MTHEMTIS OMPETITION PRT I MULTIPLE HOIE For ech of the following questions, crefully blcken the pproprite box on the nswer sheet with # pencil. o not fold,
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Individual Group. Individual Events I1 If 4 a = 25 b 1 1. = 10, find the value of.
 Answers: (000-0 HKMO Het Events) Creted y: Mr. Frnis Hung Lst udted: July 0 00-0 33 3 7 7 5 Individul 6 7 7 3.5 75 9 9 0 36 00-0 Grou 60 36 3 0 5 6 7 7 0 9 3 0 Individul Events I If = 5 = 0, find the vlue
Answers: (000-0 HKMO Het Events) Creted y: Mr. Frnis Hung Lst udted: July 0 00-0 33 3 7 7 5 Individul 6 7 7 3.5 75 9 9 0 36 00-0 Grou 60 36 3 0 5 6 7 7 0 9 3 0 Individul Events I If = 5 = 0, find the vlue
GEOMETRICAL PROPERTIES OF ANGLES AND CIRCLES, ANGLES PROPERTIES OF TRIANGLES, QUADRILATERALS AND POLYGONS:
 GEOMETRICL PROPERTIES OF NGLES ND CIRCLES, NGLES PROPERTIES OF TRINGLES, QUDRILTERLS ND POLYGONS: 1.1 TYPES OF NGLES: CUTE NGLE RIGHT NGLE OTUSE NGLE STRIGHT NGLE REFLEX NGLE 40 0 4 0 90 0 156 0 180 0
GEOMETRICL PROPERTIES OF NGLES ND CIRCLES, NGLES PROPERTIES OF TRINGLES, QUDRILTERLS ND POLYGONS: 1.1 TYPES OF NGLES: CUTE NGLE RIGHT NGLE OTUSE NGLE STRIGHT NGLE REFLEX NGLE 40 0 4 0 90 0 156 0 180 0
Chapter 12. Lesson Geometry Worked-Out Solution Key. Prerequisite Skills (p. 790) A 5 } perimeter Guided Practice (pp.
 Chpter 1 Prerequisite Skills (p. 790) 1. The re of regulr polygon is given by the formul A 5 1 p P, where is the pothem nd P is the perimeter.. Two polygons re similr if their corresponding ngles re congruent
Chpter 1 Prerequisite Skills (p. 790) 1. The re of regulr polygon is given by the formul A 5 1 p P, where is the pothem nd P is the perimeter.. Two polygons re similr if their corresponding ngles re congruent
Non Right Angled Triangles
 Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
15 - TRIGONOMETRY Page 1 ( Answers at the end of all questions )
 - TRIGONOMETRY Pge P ( ) In tringle PQR, R =. If tn b c = 0, 0, then Q nd tn re the roots of the eqution = b c c = b b = c b = c [ AIEEE 00 ] ( ) In tringle ABC, let C =. If r is the inrdius nd R is the
- TRIGONOMETRY Pge P ( ) In tringle PQR, R =. If tn b c = 0, 0, then Q nd tn re the roots of the eqution = b c c = b b = c b = c [ AIEEE 00 ] ( ) In tringle ABC, let C =. If r is the inrdius nd R is the
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
MCH T 111 Handout Triangle Review Page 1 of 3
 Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
= x x 2 = 25 2
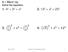 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
Triangles The following examples explore aspects of triangles:
 Tringles The following exmples explore spects of tringles: xmple 1: ltitude of right ngled tringle + xmple : tringle ltitude of the symmetricl ltitude of n isosceles x x - 4 +x xmple 3: ltitude of the
Tringles The following exmples explore spects of tringles: xmple 1: ltitude of right ngled tringle + xmple : tringle ltitude of the symmetricl ltitude of n isosceles x x - 4 +x xmple 3: ltitude of the
Lesson 5.1 Polygon Sum Conjecture
 Lesson 5.1 olgon Sum onjeture me eriod te In erises 1 nd 2, find eh lettered ngle mesure. 1.,,, 2.,,, d, e d, e, f d e e d 97 f 26 85 44 3. ne eterior ngle of regulr polgon mesures 10. Wht is the mesure
Lesson 5.1 olgon Sum onjeture me eriod te In erises 1 nd 2, find eh lettered ngle mesure. 1.,,, 2.,,, d, e d, e, f d e e d 97 f 26 85 44 3. ne eterior ngle of regulr polgon mesures 10. Wht is the mesure
Ellipses. The second type of conic is called an ellipse.
 Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
1.3 SCALARS AND VECTORS
 Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Math Lesson 4-5 The Law of Cosines
 Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Coimisiún na Scrúduithe Stáit State Examinations Commission
 M 30 Coimisiún n Scrúduithe Stáit Stte Exmintions Commission LEAVING CERTIFICATE EXAMINATION, 005 MATHEMATICS HIGHER LEVEL PAPER ( 300 mrks ) MONDAY, 3 JUNE MORNING, 9:30 to :00 Attempt FIVE questions
M 30 Coimisiún n Scrúduithe Stáit Stte Exmintions Commission LEAVING CERTIFICATE EXAMINATION, 005 MATHEMATICS HIGHER LEVEL PAPER ( 300 mrks ) MONDAY, 3 JUNE MORNING, 9:30 to :00 Attempt FIVE questions
Figure 1. The left-handed and right-handed trefoils
 The Knot Group A knot is n emedding of the irle into R 3 (or S 3 ), k : S 1 R 3. We shll ssume our knots re tme, mening the emedding n e extended to solid torus, K : S 1 D 2 R 3. The imge is lled tuulr
The Knot Group A knot is n emedding of the irle into R 3 (or S 3 ), k : S 1 R 3. We shll ssume our knots re tme, mening the emedding n e extended to solid torus, K : S 1 D 2 R 3. The imge is lled tuulr
Lesson 4.1 Triangle Sum Conjecture
 Lesson 4.1 ringle um onjeture me eriod te n erises 1 9, determine the ngle mesures. 1. p, q 2., 3., 31 82 p 98 q 28 53 17 79 23 50 4. r, s, 5., 6. t t s r 100 85 100 30 4 7 31 7. s 8. m 9. m s 76 35 m
Lesson 4.1 ringle um onjeture me eriod te n erises 1 9, determine the ngle mesures. 1. p, q 2., 3., 31 82 p 98 q 28 53 17 79 23 50 4. r, s, 5., 6. t t s r 100 85 100 30 4 7 31 7. s 8. m 9. m s 76 35 m
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
A Formulary for Mathematics
 A Formulry for Mthemtis A olletion of the Formuls, Fts nd Figures often needed in mthemtis These re some of the pges of the first rough drft of ooklet whih hs now een pulished It is in hndier A5 size,
A Formulry for Mthemtis A olletion of the Formuls, Fts nd Figures often needed in mthemtis These re some of the pges of the first rough drft of ooklet whih hs now een pulished It is in hndier A5 size,
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
GEOMETRY OF THE CIRCLE TANGENTS & SECANTS
 Geometry Of The ircle Tngents & Secnts GEOMETRY OF THE IRLE TNGENTS & SENTS www.mthletics.com.u Tngents TNGENTS nd N Secnts SENTS Tngents nd secnts re lines tht strt outside circle. Tngent touches the
Geometry Of The ircle Tngents & Secnts GEOMETRY OF THE IRLE TNGENTS & SENTS www.mthletics.com.u Tngents TNGENTS nd N Secnts SENTS Tngents nd secnts re lines tht strt outside circle. Tngent touches the
8.3 THE HYPERBOLA OBJECTIVES
 8.3 THE HYPERBOLA OBJECTIVES 1. Define Hperol. Find the Stndrd Form of the Eqution of Hperol 3. Find the Trnsverse Ais 4. Find the Eentriit of Hperol 5. Find the Asmptotes of Hperol 6. Grph Hperol HPERBOLAS
8.3 THE HYPERBOLA OBJECTIVES 1. Define Hperol. Find the Stndrd Form of the Eqution of Hperol 3. Find the Trnsverse Ais 4. Find the Eentriit of Hperol 5. Find the Asmptotes of Hperol 6. Grph Hperol HPERBOLAS
8Similarity UNCORRECTED PAGE PROOFS. 8.1 Kick off with CAS 8.2 Similar objects 8.3 Linear scale factors. 8.4 Area and volume scale factors 8.
 8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8. re nd volume scle fctors 8. Review U N O R R E TE D P G E PR O O FS 8.1 Kick off with S Plese refer to the Resources t in the Prelims
8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8. re nd volume scle fctors 8. Review U N O R R E TE D P G E PR O O FS 8.1 Kick off with S Plese refer to the Resources t in the Prelims
Part I: Study the theorem statement.
 Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
are coplanar. ˆ ˆ ˆ and iˆ
 SML QUSTION Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor ii The question pper onsists of 6 questions divided into three Setions, B nd C iii Question No
SML QUSTION Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor ii The question pper onsists of 6 questions divided into three Setions, B nd C iii Question No
3.1 Review of Sine, Cosine and Tangent for Right Angles
 Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
Basic Angle Rules 5. A Short Hand Geometric Reasons. B Two Reasons. 1 Write in full the meaning of these short hand geometric reasons.
 si ngle Rules 5 6 Short Hnd Geometri Resons 1 Write in full the mening of these short hnd geometri resons. Short Hnd Reson Full Mening ) se s isos Δ re =. ) orr s // lines re =. ) sum s t pt = 360. d)
si ngle Rules 5 6 Short Hnd Geometri Resons 1 Write in full the mening of these short hnd geometri resons. Short Hnd Reson Full Mening ) se s isos Δ re =. ) orr s // lines re =. ) sum s t pt = 360. d)
Inspiration and formalism
 Inspirtion n formlism Answers Skills hek P(, ) Q(, ) PQ + ( ) PQ A(, ) (, ) grient ( ) + Eerise A opposite sies of regulr hegon re equl n prllel A ED i FC n ED ii AD, DA, E, E n FC No, sies of pentgon
Inspirtion n formlism Answers Skills hek P(, ) Q(, ) PQ + ( ) PQ A(, ) (, ) grient ( ) + Eerise A opposite sies of regulr hegon re equl n prllel A ED i FC n ED ii AD, DA, E, E n FC No, sies of pentgon
UNIT 31 Angles and Symmetry: Data Sheets
 UNIT 31 Angles nd Symmetry Dt Sheets Dt Sheets 31.1 Line nd Rottionl Symmetry 31.2 Angle Properties 31.3 Angles in Tringles 31.4 Angles nd Prllel Lines: Results 31.5 Angles nd Prllel Lines: Exmple 31.6
UNIT 31 Angles nd Symmetry Dt Sheets Dt Sheets 31.1 Line nd Rottionl Symmetry 31.2 Angle Properties 31.3 Angles in Tringles 31.4 Angles nd Prllel Lines: Results 31.5 Angles nd Prllel Lines: Exmple 31.6
SEMI-EXCIRCLE OF QUADRILATERAL
 JP Journl of Mthemtil Sienes Volume 5, Issue &, 05, Pges - 05 Ishn Pulishing House This pper is ville online t http://wwwiphsiom SEMI-EXCIRCLE OF QUADRILATERAL MASHADI, SRI GEMAWATI, HASRIATI AND HESY
JP Journl of Mthemtil Sienes Volume 5, Issue &, 05, Pges - 05 Ishn Pulishing House This pper is ville online t http://wwwiphsiom SEMI-EXCIRCLE OF QUADRILATERAL MASHADI, SRI GEMAWATI, HASRIATI AND HESY
The Ellipse. is larger than the other.
 The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
, where P is called the tail and Q is called the nose of the vector.
 6 VECTORS 1 INTRODUCTION TO VECTOR ALGEBRA 11 Slrs nd Vetors Slr: A slr is quntity tht hs only mgnitude ut no diretion Slr quntity is expressed s single numer, followed y pproprite unit, eg length, re,
6 VECTORS 1 INTRODUCTION TO VECTOR ALGEBRA 11 Slrs nd Vetors Slr: A slr is quntity tht hs only mgnitude ut no diretion Slr quntity is expressed s single numer, followed y pproprite unit, eg length, re,
Mathematics. Area under Curve.
 Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
Vectors. Chapter14. Syllabus reference: 4.1, 4.2, 4.5 Contents:
 hpter Vetors Syllus referene:.,.,.5 ontents: D E F G H I J K Vetors nd slrs Geometri opertions with vetors Vetors in the plne The mgnitude of vetor Opertions with plne vetors The vetor etween two points
hpter Vetors Syllus referene:.,.,.5 ontents: D E F G H I J K Vetors nd slrs Geometri opertions with vetors Vetors in the plne The mgnitude of vetor Opertions with plne vetors The vetor etween two points
Bravais lattices and crystal systems
 3 Brvis ltties nd rystl systems 3. Introdution The definitions of the motif, the repeting unit of pttern, nd the lttie, n rry of points in spe in whih eh point hs n identil environment, hold in three dimensions
3 Brvis ltties nd rystl systems 3. Introdution The definitions of the motif, the repeting unit of pttern, nd the lttie, n rry of points in spe in whih eh point hs n identil environment, hold in three dimensions
8 Measurement. How is measurement used in your home? 8E Area of a circle 8B Circumference of a circle. 8A Length and perimeter
 8A Length nd perimeter 8E Are of irle 8B Cirumferene of irle 8F Surfe re 8C Are of retngles nd tringles 8G Volume of prisms 8D Are of other qudrilterls 8H Are nd volume onversions SA M PL E Mesurement
8A Length nd perimeter 8E Are of irle 8B Cirumferene of irle 8F Surfe re 8C Are of retngles nd tringles 8G Volume of prisms 8D Are of other qudrilterls 8H Are nd volume onversions SA M PL E Mesurement
ONLINE PAGE PROOFS. Trigonometry Kick off with CAS 12.2 Trigonometry 12.3 Pythagorean triads
 12 12.1 Kik off with S 12.2 Trigonometry 12.3 Pythgoren trids Trigonometry 12.4 Three-dimensionl Pythgors theorem 12.5 Trigonometri rtios 12.6 The sine rule 12.7 miguous se of the sine rule 12.8 The osine
12 12.1 Kik off with S 12.2 Trigonometry 12.3 Pythgoren trids Trigonometry 12.4 Three-dimensionl Pythgors theorem 12.5 Trigonometri rtios 12.6 The sine rule 12.7 miguous se of the sine rule 12.8 The osine
Linear Algebra Introduction
 Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Pythagoras theorem and surds
 HPTER Mesurement nd Geometry Pythgors theorem nd surds In IE-EM Mthemtis Yer 8, you lernt out the remrkle reltionship etween the lengths of the sides of right-ngled tringle. This result is known s Pythgors
HPTER Mesurement nd Geometry Pythgors theorem nd surds In IE-EM Mthemtis Yer 8, you lernt out the remrkle reltionship etween the lengths of the sides of right-ngled tringle. This result is known s Pythgors
Log1 Contest Round 3 Theta Individual. 4 points each 1 What is the sum of the first 5 Fibonacci numbers if the first two are 1, 1?
 008 009 Log1 Contest Round Thet Individul Nme: points ech 1 Wht is the sum of the first Fiboncci numbers if the first two re 1, 1? If two crds re drwn from stndrd crd deck, wht is the probbility of drwing
008 009 Log1 Contest Round Thet Individul Nme: points ech 1 Wht is the sum of the first Fiboncci numbers if the first two re 1, 1? If two crds re drwn from stndrd crd deck, wht is the probbility of drwing
4.3 The Sine Law and the Cosine Law
 4.3 Te Sine Lw nd te osine Lw Te ee Tower is te tllest prt of nd s rliment uildings. ronze mst, wi flies te ndin flg, stnds on top of te ee Tower. From point 25 m from te foot of te tower, te ngle of elevtion
4.3 Te Sine Lw nd te osine Lw Te ee Tower is te tllest prt of nd s rliment uildings. ronze mst, wi flies te ndin flg, stnds on top of te ee Tower. From point 25 m from te foot of te tower, te ngle of elevtion
Trigonometry. Trigonometry. labelling conventions. Evaluation of areas of non-right-angled triangles using the formulas A = 1 ab sin (C )
 8 8 Pythgors theorem 8 Pythgoren trids 8 Three-dimensionl Pythgors theorem 8D Trigonometri rtios 8E The sine rule 8F miguous se of the sine rule 8G The osine rule 8H Speil tringles 8I re of tringles res
8 8 Pythgors theorem 8 Pythgoren trids 8 Three-dimensionl Pythgors theorem 8D Trigonometri rtios 8E The sine rule 8F miguous se of the sine rule 8G The osine rule 8H Speil tringles 8I re of tringles res
Applications of Definite Integral
 Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Calculus Cheat Sheet. Integrals Definitions. where F( x ) is an anti-derivative of f ( x ). Fundamental Theorem of Calculus. dx = f x dx g x dx
 Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
No. Diagram Given Condition Conclusion Abbreviation a and b are adjacent angles on a straight a b 180. a, b and c are angles at a point
 Pge 46 REVITION USE IN EUTIVE GEOMETR. Properties of Plne Geometry No. igrm Given ondition onlusion revition nd re djent 1 ngles on stright 180 dj. s on st. line line 2, nd re ngles t point 360 s t pt.
Pge 46 REVITION USE IN EUTIVE GEOMETR. Properties of Plne Geometry No. igrm Given ondition onlusion revition nd re djent 1 ngles on stright 180 dj. s on st. line line 2, nd re ngles t point 360 s t pt.
Section 2.1 Special Right Triangles
 Se..1 Speil Rigt Tringles 49 Te --90 Tringle Setion.1 Speil Rigt Tringles Te --90 tringle (or just 0-60-90) is so nme euse of its ngle mesures. Te lengts of te sies, toug, ve very speifi pttern to tem
Se..1 Speil Rigt Tringles 49 Te --90 Tringle Setion.1 Speil Rigt Tringles Te --90 tringle (or just 0-60-90) is so nme euse of its ngle mesures. Te lengts of te sies, toug, ve very speifi pttern to tem
8 THREE PHASE A.C. CIRCUITS
 8 THREE PHSE.. IRUITS The signls in hpter 7 were sinusoidl lternting voltges nd urrents of the so-lled single se type. n emf of suh type n e esily generted y rotting single loop of ondutor (or single winding),
8 THREE PHSE.. IRUITS The signls in hpter 7 were sinusoidl lternting voltges nd urrents of the so-lled single se type. n emf of suh type n e esily generted y rotting single loop of ondutor (or single winding),
Geometry AP Book 8, Part 2: Unit 3
 Geometry ook 8, rt 2: Unit 3 IMRTNT NTE: For mny questions in this unit, there re multiple correct nswers, e.g. line segment cn e written s, RST is the sme s TSR, etc. Where pproprite, techers should e
Geometry ook 8, rt 2: Unit 3 IMRTNT NTE: For mny questions in this unit, there re multiple correct nswers, e.g. line segment cn e written s, RST is the sme s TSR, etc. Where pproprite, techers should e
for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx
![for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx](/thumbs/74/70408252.jpg) Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
8Similarity ONLINE PAGE PROOFS. 8.1 Kick off with CAS 8.2 Similar objects 8.3 Linear scale factors. 8.4 Area and volume scale factors 8.
 8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8.4 re nd volume scle fctors 8. Review Plese refer to the Resources t in the Prelims section of your eookplus for comprehensive step-y-step
8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8.4 re nd volume scle fctors 8. Review Plese refer to the Resources t in the Prelims section of your eookplus for comprehensive step-y-step
HOMEWORK FOR CLASS XII ( )
 HOMEWORK FOR CLASS XII 8-9 Show tht the reltion R on the set Z of ll integers defined R,, Z,, is, divisile,, is n equivlene reltion on Z Let f: R R e defined if f if Is f one-one nd onto if If f, g : R
HOMEWORK FOR CLASS XII 8-9 Show tht the reltion R on the set Z of ll integers defined R,, Z,, is, divisile,, is n equivlene reltion on Z Let f: R R e defined if f if Is f one-one nd onto if If f, g : R
MEP Practice Book ES3. 1. Calculate the size of the angles marked with a letter in each diagram. None to scale
 ME rctice ook ES3 3 ngle Geometr 3.3 ngle Geometr 1. lculte the size of the ngles mrked with letter in ech digrm. None to scle () 70 () 20 54 65 25 c 36 (d) (e) (f) 56 62 d e 60 40 70 70 f 30 g (g) (h)
ME rctice ook ES3 3 ngle Geometr 3.3 ngle Geometr 1. lculte the size of the ngles mrked with letter in ech digrm. None to scle () 70 () 20 54 65 25 c 36 (d) (e) (f) 56 62 d e 60 40 70 70 f 30 g (g) (h)
2. VECTORS AND MATRICES IN 3 DIMENSIONS
 2 VECTORS AND MATRICES IN 3 DIMENSIONS 21 Extending the Theory of 2-dimensionl Vectors x A point in 3-dimensionl spce cn e represented y column vector of the form y z z-xis y-xis z x y x-xis Most of the
2 VECTORS AND MATRICES IN 3 DIMENSIONS 21 Extending the Theory of 2-dimensionl Vectors x A point in 3-dimensionl spce cn e represented y column vector of the form y z z-xis y-xis z x y x-xis Most of the
Pythagoras Theorem. Pythagoras Theorem. Curriculum Ready ACMMG: 222, 245.
 Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
13.3 CLASSICAL STRAIGHTEDGE AND COMPASS CONSTRUCTIONS
 33 CLASSICAL STRAIGHTEDGE AND COMPASS CONSTRUCTIONS As simple ppliction of the results we hve obtined on lgebric extensions, nd in prticulr on the multiplictivity of extension degrees, we cn nswer (in
33 CLASSICAL STRAIGHTEDGE AND COMPASS CONSTRUCTIONS As simple ppliction of the results we hve obtined on lgebric extensions, nd in prticulr on the multiplictivity of extension degrees, we cn nswer (in
