Solutions of Two Japanese Ellipse Problems
|
|
|
- Ambrose Sullivan
- 5 years ago
- Views:
Transcription
1 Forum Geometricorum Volume ) FORUM GEOM ISSN Solutions of Two Japanese Ellipse Prolems J. Marshall Unger Astract. Two premodern Japanese theorems involving an ellipse and tangent circles are stated as prolems in [1] and 6.2.4). Neither can e proven easily y elementary means. But a proof of the second prolem follows from another Japanese proposition, for which I give an original proof. It is ased on the first part of an elegant proof of a generalization of the first theorem, which I present in edited form. 1. Introduction Among the many theorems involving ellipses stated as prolems in [1], two and 6.2.4) stand out as particularly challenging. The first theorem Figure 1) concerns two intersecting tangents to an ellipse and the circles that touch oth tangents and the ellipse. If the diameters of the two that touch the ellipse externally are d 1, d 4, and those of the two that touch it internally are d 2, d 3, then d 1 : d 2 = d 3 : d 4. d 42 d 22 d 32 d 12 Figure 1 The second theorem states that, in Figure 2, v = R r) Rr+u 2 ur+r) 2, Rr where u, v are the semi-major and semi-minor axes of the ellipse and R, r are the radii of the two circles touching the ellipse and the sides of the square that are touched y it. Pulication Date: March 29, Communicating Editor: Paul Yiu.
2 86 J. M. Unger Figure 2 The first theorem is attriuted to S. Iwata [3], ut to Kosan Iwata ) in [1]. 1 Iwata does not give the solution, which he found in the spring of 1866, saying it took up 52 pages. Readers are told to drop y the journal office if they want to see the whole thing! Papers y H. Terao 1885), J. Mizuhara n.d.), and T. Hayashi 1895) that prove and generalize Iwata s theorem were presented in English y Y. Mikami in [3]. In his paper, Terao Hisashi ), a founder of modern astronomy in Japan, proves the following theorem, of which Iwata s is a special case: Theorem Terao). Given two intersecting tangents to an ellipse or hyperola, consider the ellipses or hyperolas, homothetic to one another, that touch the tangents and the first conic. If the major axes of the two that touch the first conic externally are a 1, a 4 and those of the two that touch it internally are a 2, a 3, then a 1 : a 2 = a 3 : a 4. So too for the minor axes: 1 : 2 = 3 : 4. Terao s proof deserves wider recognition, so I have edited Mikami s version and present it in section 2. In section 3, I use the key proposition in Terao s proof to prove a well-known ut difficult Japanese theorem not presented in [1]. This proposition makes it easy to prove the second theorem, as shown in section Terao s theorem [1], 6.4.7) Take the tangents in Figure 1 to e axes of a not necessarily orthogonal) coordinate system with origin O. A conic touching oth axes at distances a, > 0 from 1 Iwata s article, signed appeared in 1: ) cited in [1]), followed y a commentary y Fukugawa Riken paraphrased in [3]). Iwata s personal name was Senpei ; K ōsan loves to calculate ) was his pen-name. N.B. the author of [2], Iwata Shik ō, is a mid-20th-century mathematician.
3 Solutions of two Japanese ellipse prolems 87 O along the x,y axes, respectively, has the equation Q k 2 x a + y 1 ) 2 4xy = 0 for some k > 0. Expanding Q, k 2 a 2x2 + 2k2 2a) xy+ k2 a 2y2 2k2 2k2 x a y +k2 = 0, so, as a general conic of the form Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0, its discriminant is B 2 4AC = 4k2 2a) 2 a 2 2 4k4 a 2 2 = 16a k2 ). a We readily see that the discriminant, which is negative for an ellipse and positive for a hyperola, has the same sign as a k 2. Let P k 2 x a + y ) 2 1 4xy = 0 e a second conic touching the same axes. A line through the points where Q and P intersect is Q P k 2 x a + y ) 2 1 k 2 x a + y ) 2 1 = 0. Since the right side of this equation can e factored into linear terms, it represents a degenerate conic consisting of two intersecting lines, viz. the two common chords lue in the Figures 3 6) of Q and P. Their equations are x k a + y ) 1 = ±k x a + y ) 1. i.e., one chord is and the other is ) ) k a + k k a x+ + k y = k +k ) ) k a k k a x+ k y = k k. Figure 3 Figure 4 Now suppose we fix a,, k and vary a,, k until the endpoints of one chord or the other coincide and the chord ecomes a common tangent of Q and P.
4 88 J. M. Unger Figure 5 Figure 6 Starting with the first common chord and assuming that k a + k a 0, we use the chord s equation to get y and sustitute it into Q, which ecomes a quadratic in x. Its two roots are equal if and only if the chord touches Q at a single point, so we set the discriminant to zero and solve. The result is E k 2 k 2 1 a 1 a ) 1 1 ) k+k ) 2 = 0. If k + k = 0 and k a + k a 0, we use one chord s equation to get x and sustitute it into Q to get a quadratic in y, ut the result is the same. Similarly, starting with the second chord, if k k = 0 and k a k a 0, we get I k 2 k 2 1 a 1 a ) 1 1 ) k k ) 2 = 0. As we are taking Q as fixed, we can say that P elongs to genus E or genus I depending on which chord we start with. If k + k = 0 and k a + k a = 0, then there is no conic in genus E that touches Q, and if k k = 0 and k a k a = 0, there is no conic in genus I that touches Q. This occurs when Q and P are homothetic. Now two ellipses or two hyperolas resp. an ellipse and a hyperola) that touch oth axes and each other make contact externally if and only if their centers lie on opposite sides resp. same side) of the common tangent. Contact that is not external is internal. We now prove that the contact of Q and P is always external for P in genus E. Suppose that the common tangent of Q and P is the line tx,y) = 0. If the centers of Q and P are g,h) and g,h ), then tg,h) 0 and tg,h ) 0 ecause the centers certainly do not lie on the tangent. The signs of tg,h) and tg,h ) are the same if and only if g,h) and g,h ) lie in the same half-plane. The sign of tg,h) tg,h ) is therefore positive when they do. Because the conicqis symmetrical, the lines Q Q x = 0 and y = 0 intersect at its center, so we solve the equations k2 x a a + y 1) 2y = 0 and k2 x a + y 1) 2x = 0 simultaneously to find its coordinates. For Q, this yields g = k 2 a 2k 2 a), h = k 2 2k 2 a).
5 Solutions of two Japanese ellipse prolems 89 Likewise, for P, g = k 2 a 2k 2 a ), h = k 2 2k 2 a ). If we start with the first common chord, then Q elongs to genus E and ) ) k tx,y) = a + k k a x+ + k k +k ). Therefore, tg,h) = Correspondingly, Thus we have k 2 k 2 a + k 2 k a 2k 2 a) a + ) k +k ) k 2 k ) a + 2k 2 a) a + = k +k )a k 2 k2 k a k a a 2 a + )) = a k 2 k k a a a 2 a + = k +k )a k 2 k k 2 a tg,h ) = a k 2 a kk 2 a k k 2 a) tg,h) = k2 k 2 a a kk 2 a ) a tg,h ) = k2 k 2 a )) k+k ) ). 1 1 )) ) a 2 a + k+k ). 1 1 a 2 a a 2 a + )) k k+k ), )) kk +k ). But E may e rewritten k 2 k a a 2 a + )) k k+k )+ k2 k 2 a 1 1 )) a 2 a + kk+k ) = 0. Therefore, k k 2 a) a tg,h) + kk2 a ) a tg,h ) = 0, and tg, h) tg,h ) = k k 2 a) a a kk 2 a ). Since a,, k, a,, k are all positive, the sign of tg,h) tg,h ) depends entirely on the signs of k 2 a and k 2 a. As remarked aove, these are positive for an ellipse and negative for a hyperola. The sign of tg,h) tg,h ) is therefore negative when Q and P are oth ellipses or oth hyperolas, and positive when one is an ellipse and other a hyperola. Hence the centers lie on opposite sides in the former case, on the same side in the latter, and the contact is always external for P in genus E. One can prove that the contact is always internal for P in genus I in the same fashion y repeating the steps descried aove starting with the equation of the second common chord instead of the first.
6 90 J. M. Unger Now if we select a memer of Q with the equation x P 0 k0 2 + y ) 2 1 4xy = 0, a 0 0 then for every conic homothetic top 0, there exists a constant λ such thata = λa 0, = λ 0, and k = λk 0. That is, x P k0 2 + y ) 2 λ 4xy = 0, a 0 0 for some λ > 0. The equations of the major and minor axes of the conics represented y P are linear and homogeneous ecause their axes are parallel to the corresponding axes ofp 0. If, for example, the major axism 0 isfk 0,a 0, 0,θ), where θ is the angle etween the coordinate axes, and major axism isfk,a,,θ), then fλk 0,λa 0,λ 0,θ) = λfk 0,a 0, 0,θ), or M = λm 0. Similarly, for the minor axis m,m = λm 0. For the same reason, the tangency conditions E and I can e conflated into λ k 2 k0 2 a 1 ) λ a 0 1 ) λk 0 ±k) 2 = 0, 0 where it is understood that we select the plus sign to get the equation of E and minus sign to get the equation fori. As a quadratic inλ, this conflated equation is ) k k a 1 λ 2 kk ) ) k a 0 a 0 ±2 λ+k = 0, a 0 0 solving which gives us two values of λ for E and another two for I. The products of oth pairs of roots are equal ecause the leading coefficients and constant terms in oth equations are the same. Writing the products asλ 1 λ 4 = λ 2 λ 3, we have λ 1 λ 2 = λ 3 λ 4, and, since, for instance, m 1 λ 1 = m 2 λ 2 = m 3 λ 3 = m 4 λ 4 = m 0, the same proportions apply to the respective axes of the conics that touchqand its two tangents. This proves Terao s theorem, of which Iwata s is clearly the special case of ellipses in Q and circles in P. 3. The intermediate result Proposition 98 in the well-known work Sanpō jojutsu concerns an ellipse with major and minor axes p, q inscried in a rectangle of sides m, n, and a circle of diameter d touching the ellipse externally and two adjacent sides of the rectangle internally. It states that mn+ m 2 n 2 p 2 q 2 2 m+n+ mn ) m 2 n 2 p 2 q 2 d+d 2 = 0. A long and difficult algeraic proof of this, ascried to Ajima Naonou ), is recounted algeraically in [4]. The same proof is interpreted using trigonometry in [6]. According to [4], a simpler proof using matrices appears in [2],
7 Solutions of two Japanese ellipse prolems 91 0,) m = 2g v = q/2 r = d/2 g,h) u = p/2 n = 2h O a,0) Figure 7 ut I have not seen it. The following proof of my own using matrices, inspired y Terao s proof of Iwata s theorem, may e similar to the one in [2]. First, we restate the proposition with modern conventions and a little more care: Proposition. Given an ellipse with semimajor and semiminor axes u, v inscried in a rectangle, designate one of its vertices as the origin and take the adjacent sides as the positive x, y axes of a coordinate system. There are two circles that touch the ellipse externally and oth these axes. If the center of the ellipse isg,h), then the radii of these circles are the solutions of gh+ g 2 h 2 u 2 v 2 2 Following Terao, let g +h+ gh g 2 h 2 u 2 v 2 ) ρ+ρ 2 = 0. Q k 2 x a + y 1 ) 2 4xy = 0 define the ellipse. In homogeneous coordinates, Q corresponds to the symmetric matrix A = 1 1 a 2 a 2 k 1 2 k a 2 1 a 1 1 a 1 1 That is, x y 1) A x y 1) T = 0. Writing M for the determinant of M and A 33 for the minor of A with its third row and third column omitted, we know that, for a non-degenerate conic, A 0; for an ellipse, A 33 > 0 A 33 is the discriminant); and for the ellipse to e real, TrA 33 ) A < 0. The first and third conditions always hold for positive a,, k; the second is equivalent tok 2 > a. In addition, if λ and µ are the eigenvalues of A 33, then the reduced equation of the ellipse is λx 2 +µy 2 + A Q A 33 = 0,.
8 92 J. M. Unger or, in canonic form, A 33 λ A Q x2 A 33 µ A Q y2 = 1. This is the equation of the congruent ellipse centered on the origin with major axis on the line y = 0. From it, we readily see that u 2 = A Q A 33 λ and v2 = A Q A 33 µ. Since in general λµ = A 33, this means that u 2 v 2 = A Q 2 A If now P k 2 x a + y 1 ) 2 4xy = 0 is a conic that touches the axes at distances a, from O, we know thanks to Terao) that P is externally tangent to Q if and only if k 2 k 2 1 a 1 a ) 1 1 ) k +k ) 2 = 0. If k 2 > a and a = = ρ, P should e the circle of radius ρ centered at ρ,ρ), and indeed P can e rearranged asx ρ) 2 +y ρ) 2 = ρ 2 provided that k = ρ ) 2. The external tangency condition thus ecomes2k 2 1 a ρ) ρ k+ρ 2) 2, or, as a quadratic inρ, 2k+ k 2 k 2 2 a + k2 ) ρ+2 k 2 a a ) ρ 2 = 0. To each of it roots, R > r, one of a pair of parallel tangents to the ellipse corresponds. The x- and y-intercepts of each tangent, together with O, are the vertices of a right triangle. The incircle of the smaller triangle is the circle with centerr, r) and radius r, and the excircle on the hypotenuse is the one with center R, R) and radiusr. Each circle touches the ellipse at the same point it touches their common tangent. Thus the last equation is a sufficient and necessary condition for constructing the circle in the prolem figure exactly for a given ellipse and rectangle. From its form, we immediately see that Rr = k2 a. But, as we know, 2k 2 a) g = k2 a 2k 2 a), h = k2. Hence, Rr = g = ah. We can therefore sustitute 2k 2 a) Rr for a, into either the equation for g or the equation for h. Whichever we h, Rr g choose, the result is k = Rr 2 2gh Rr. We can therefore rewrite Q and the external tangency condition exclusively in terms of g, h, R,r. The matrix for this new form of Q is A = h2 Rr gh hrr Rr gh g 2 grr hrr grr R 2 r 2 and the external tangency condition ecomes Rr 2g +h+ 2gh Rr)ρ+ρ 2 = 0.
9 Solutions of two Japanese ellipse prolems 93 Note that A = R 2 r 2 2gh Rr) 2 and A 33 = Rr2gh Rr). Hence, from u 2 v 2 = A 2 A 33, 3 u 2 v 2 = Rr2gh Rr), g 2 h 2 u 2 v 2 = gh Rr) 2, g 2 h 2 u 2 v 2 = ±gh Rr). Selecting the negative sign on the right, we see at once that the external tangency condition is equivalent to gh+ g 2 h 2 u 2 v 2 2 g +h+ gh ) g 2 h 2 u 2 v 2 ρ+ρ 2 = Shiraishi s formula [1, 6.2.4] We now turn to our the second theorem. The formula v = R r) Rr+u 2 ur+r) 2 Rr appears in [5] with example data R = 36, 2r = 2, 2u = 16, v = 9) ut no proof. But let us return tou 2 v 2 = Rr2gh Rr) in the foregoing proof. This time, we solve for gh, otaining gh = R2 r 2 +u 2 v 2. 2Rr Since g 2 + h 2 = u 2 +v 2 the director circle theorem for ellipses), we have g + h) 2 = 2gh + u 2 + v 2. We can therefore rewrite gh and g + h in the tangency condition Rr 2g +h+ 2gh Rr)ρ+ρ 2 = 0 in terms of u, v, R,r,ρ. Having done so, if we sustitute r for ρ, we get R r 2 +Rr 2r 2 r 2 +u 2 v 2 R Rr + 2 r 2 +u 2 v 2 Rr Rr Sustituting instead R for ρ, we get +u 2 +v 2 ) = 0. ) R R 2 +Rr 2R 2 r 2 +u 2 v 2 R Rr+ 2 r 2 +u 2 v 2 +u Rr Rr 2 +v 2 = 0. Solving either of these for v yields v = 1 Rr 3 2R 2 r 2 +rr 3 +2R 2 +r 2 )u 2 2R 2 r 2 )u Rr+u 2. 2 Rr As the long radicand here factors to R r) 2, Rr +u ur+r)) 2 we see that one can deduce Shiraishi s formula from the theorem in Sanpō jojutsu proven in section 3. Most likely, that was how Shiraishi arrived at it.
10 94 J. M. Unger 5. Concluding remark Given just R and r in Figure 2, an infinite numer of ellipses touch the coordinate axes and oth circles. One more condition, such as the length of u, must e given to identify a particular ellipse. The ellipse always touches the extouch point of the hypotenuse of the larger right triangle defined in section 3, ut it need not touch its legs at their extouch points. If it does, it is the Mandart inellipse of the triangle, and one can prove that the distance etween the parallel tangents is then exactly 2r. Shiraishi s example is not a Mandart inellipse, ut the theorem is too nice not to mention. References [1] H. Fukagawa and D. Pedoe, Japanese Temple Geometry Prolems, Winnipeg: Charles Baage Research Centre, [2] S. Iwata, Kikagaku daijiten Great encyclopedia of geometry), 6 vols, T ōky ō, [3] Y. Mikami compiled and edited), Mathematical Papers from the Far East, Ahandlungen zur Geschichte der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen, 28 Leipzig: B. G. Teuner, 1910). [4] N. Nakamura, Wasan no zukei k ōshikiwasan formulae with diagrams), n.p.: 2008). [5] N. Shiraishi, Shamei Sanpu, [6] T. Yoneyama, Sokuen-jutsu 6: An-shi ik ō sokuen-kai ni-j ō dai-ni, Ellipse Methods VI. Two posthumous solutions of Ajima, No. 2), T ōky ō University Bulletin: Natural Sciences 55) T ōky ō: March 2011). J. Marshall Unger: Emeritus Professor, Department of East Asian Languages & Literatures, The Ohio State University, Columus, Ohio , USA address: unger.26@osu.edu
Integer Sequences and Circle Chains Inside a Circular Segment
 Forum Geometricorum Volume 18 018) 47 55. FORUM GEOM ISSN 1534-1178 Integer Sequences and Circle Chains Inside a Circular Segment Giovanni Lucca Astract. We derive the conditions for inscriing, inside
Forum Geometricorum Volume 18 018) 47 55. FORUM GEOM ISSN 1534-1178 Integer Sequences and Circle Chains Inside a Circular Segment Giovanni Lucca Astract. We derive the conditions for inscriing, inside
An Unsolved Problem in the Yamaguchi s Travell Diary
 Sangaku Journal of Mathematics (SJM) c SJM ISSN 2534-9562 Volume 2 (2018), pp. 43-53 Received 5 September 2018. Published on-line 10 September 2018 web: http://www.sangaku-journal.eu/ c The Author(s) This
Sangaku Journal of Mathematics (SJM) c SJM ISSN 2534-9562 Volume 2 (2018), pp. 43-53 Received 5 September 2018. Published on-line 10 September 2018 web: http://www.sangaku-journal.eu/ c The Author(s) This
QUADRATIC EQUATIONS EXPECTED BACKGROUND KNOWLEDGE
 6 QUADRATIC EQUATIONS In this lesson, you will study aout quadratic equations. You will learn to identify quadratic equations from a collection of given equations and write them in standard form. You will
6 QUADRATIC EQUATIONS In this lesson, you will study aout quadratic equations. You will learn to identify quadratic equations from a collection of given equations and write them in standard form. You will
3.5 Solving Quadratic Equations by the
 www.ck1.org Chapter 3. Quadratic Equations and Quadratic Functions 3.5 Solving Quadratic Equations y the Quadratic Formula Learning ojectives Solve quadratic equations using the quadratic formula. Identify
www.ck1.org Chapter 3. Quadratic Equations and Quadratic Functions 3.5 Solving Quadratic Equations y the Quadratic Formula Learning ojectives Solve quadratic equations using the quadratic formula. Identify
The Arbelos and Nine-Point Circles
 Forum Geometricorum Volume 7 (2007) 115 120. FORU GEO ISSN 1534-1178 The rbelos and Nine-Point Circles uang Tuan ui bstract. We construct some new rchimedean circles in an arbelos in connection with the
Forum Geometricorum Volume 7 (2007) 115 120. FORU GEO ISSN 1534-1178 The rbelos and Nine-Point Circles uang Tuan ui bstract. We construct some new rchimedean circles in an arbelos in connection with the
Forum Geometricorum Volume 13 (2013) 1 6. FORUM GEOM ISSN Soddyian Triangles. Frank M. Jackson
 Forum Geometricorum Volume 3 (203) 6. FORUM GEOM ISSN 534-78 Soddyian Triangles Frank M. Jackson bstract. Soddyian triangle is a triangle whose outer Soddy circle has degenerated into a straight line.
Forum Geometricorum Volume 3 (203) 6. FORUM GEOM ISSN 534-78 Soddyian Triangles Frank M. Jackson bstract. Soddyian triangle is a triangle whose outer Soddy circle has degenerated into a straight line.
A Ladder Ellipse Problem
 Forum Geometricorum Volume 16 (2016) 63 67. FORUM GEOM ISSN 1534-1178 A Ladder Ellipse Problem Alan Horwitz Abstract. We consider a problem similar to the well-known ladder box problem, but where the box
Forum Geometricorum Volume 16 (2016) 63 67. FORUM GEOM ISSN 1534-1178 A Ladder Ellipse Problem Alan Horwitz Abstract. We consider a problem similar to the well-known ladder box problem, but where the box
Heptagonal Triangles and Their Companions
 Forum Geometricorum Volume 9 (009) 15 148. FRUM GEM ISSN 1534-1178 Heptagonal Triangles and Their ompanions Paul Yiu bstract. heptagonal triangle is a non-isosceles triangle formed by three vertices of
Forum Geometricorum Volume 9 (009) 15 148. FRUM GEM ISSN 1534-1178 Heptagonal Triangles and Their ompanions Paul Yiu bstract. heptagonal triangle is a non-isosceles triangle formed by three vertices of
Rational Steiner Porism
 Forum Geometricorum Volume 0. FORUM GEOM ISSN -8 Rational Steiner Porism Paul Yiu Abstract. We establish formulas relating the radii of neighboring circles in a Steiner chain, a chain of mutually tangent
Forum Geometricorum Volume 0. FORUM GEOM ISSN -8 Rational Steiner Porism Paul Yiu Abstract. We establish formulas relating the radii of neighboring circles in a Steiner chain, a chain of mutually tangent
SM2H Unit 6 Circle Notes
 Name: Period: SM2H Unit 6 Circle Notes 6.1 Circle Vocabulary, Arc and Angle Measures Circle: All points in a plane that are the same distance from a given point, called the center of the circle. Chord:
Name: Period: SM2H Unit 6 Circle Notes 6.1 Circle Vocabulary, Arc and Angle Measures Circle: All points in a plane that are the same distance from a given point, called the center of the circle. Chord:
Distance and Midpoint Formula 7.1
 Distance and Midpoint Formula 7.1 Distance Formula d ( x - x ) ( y - y ) 1 1 Example 1 Find the distance between the points (4, 4) and (-6, -). Example Find the value of a to make the distance = 10 units
Distance and Midpoint Formula 7.1 Distance Formula d ( x - x ) ( y - y ) 1 1 Example 1 Find the distance between the points (4, 4) and (-6, -). Example Find the value of a to make the distance = 10 units
Circle Chains Inside a Circular Segment
 Forum eometricorum Volume 9 (009) 73 79. FRUM EM ISSN 534-78 ircle hains Inside a ircular Segment iovanni Lucca bstract. We consider a generic circles chain that can be drawn inside a circular segment
Forum eometricorum Volume 9 (009) 73 79. FRUM EM ISSN 534-78 ircle hains Inside a ircular Segment iovanni Lucca bstract. We consider a generic circles chain that can be drawn inside a circular segment
Introduction to conic sections. Author: Eduard Ortega
 Introduction to conic sections Author: Eduard Ortega 1 Introduction A conic is a two-dimensional figure created by the intersection of a plane and a right circular cone. All conics can be written in terms
Introduction to conic sections Author: Eduard Ortega 1 Introduction A conic is a two-dimensional figure created by the intersection of a plane and a right circular cone. All conics can be written in terms
The circumcircle and the incircle
 hapter 4 The circumcircle and the incircle 4.1 The Euler line 4.1.1 nferior and superior triangles G F E G D The inferior triangle of is the triangle DEF whose vertices are the midpoints of the sides,,.
hapter 4 The circumcircle and the incircle 4.1 The Euler line 4.1.1 nferior and superior triangles G F E G D The inferior triangle of is the triangle DEF whose vertices are the midpoints of the sides,,.
Conic Sections: THE ELLIPSE
 Conic Sections: THE ELLIPSE An ellipse is the set of all points,such that the sum of the distance between, and two distinct points is a constant. These two distinct points are called the foci (plural of
Conic Sections: THE ELLIPSE An ellipse is the set of all points,such that the sum of the distance between, and two distinct points is a constant. These two distinct points are called the foci (plural of
Construction of Ajima Circles via Centers of Similitude
 Forum Geometricorum Volume 15 (2015) 203 209. FORU GEO SS 1534-1178 onstruction of jima ircles via enters of Similitude ikolaos Dergiades bstract. We use the notion of the centers of similitude of two
Forum Geometricorum Volume 15 (2015) 203 209. FORU GEO SS 1534-1178 onstruction of jima ircles via enters of Similitude ikolaos Dergiades bstract. We use the notion of the centers of similitude of two
The Apollonius Circle and Related Triangle Centers
 Forum Geometricorum Qolume 3 (2003) 187 195. FORUM GEOM ISSN 1534-1178 The Apollonius Circle and Related Triangle Centers Milorad R. Stevanović Abstract. We give a simple construction of the Apollonius
Forum Geometricorum Qolume 3 (2003) 187 195. FORUM GEOM ISSN 1534-1178 The Apollonius Circle and Related Triangle Centers Milorad R. Stevanović Abstract. We give a simple construction of the Apollonius
Rotation of Axes. By: OpenStaxCollege
 Rotation of Axes By: OpenStaxCollege As we have seen, conic sections are formed when a plane intersects two right circular cones aligned tip to tip and extending infinitely far in opposite directions,
Rotation of Axes By: OpenStaxCollege As we have seen, conic sections are formed when a plane intersects two right circular cones aligned tip to tip and extending infinitely far in opposite directions,
The Apollonius Circle as a Tucker Circle
 Forum Geometricorum Volume 2 (2002) 175 182 FORUM GEOM ISSN 1534-1178 The Apollonius Circle as a Tucker Circle Darij Grinberg and Paul Yiu Abstract We give a simple construction of the circular hull of
Forum Geometricorum Volume 2 (2002) 175 182 FORUM GEOM ISSN 1534-1178 The Apollonius Circle as a Tucker Circle Darij Grinberg and Paul Yiu Abstract We give a simple construction of the circular hull of
by Abhijit Kumar Jha
 SET I. If the locus of the point of intersection of perpendicular tangents to the ellipse x a circle with centre at (0, 0), then the radius of the circle would e a + a /a ( a ). There are exactl two points
SET I. If the locus of the point of intersection of perpendicular tangents to the ellipse x a circle with centre at (0, 0), then the radius of the circle would e a + a /a ( a ). There are exactl two points
Conics and their duals
 9 Conics and their duals You always admire what you really don t understand. Blaise Pascal So far we dealt almost exclusively with situations in which only points and lines were involved. Geometry would
9 Conics and their duals You always admire what you really don t understand. Blaise Pascal So far we dealt almost exclusively with situations in which only points and lines were involved. Geometry would
Simple Proofs of Feuerbach s Theorem and Emelyanov s Theorem
 Forum Geometricorum Volume 18 (2018) 353 359. FORUM GEOM ISSN 1534-1178 Simple Proofs of Feuerbach s Theorem and Emelyanov s Theorem Nikolaos Dergiades and Tran Quang Hung Abstract. We give simple proofs
Forum Geometricorum Volume 18 (2018) 353 359. FORUM GEOM ISSN 1534-1178 Simple Proofs of Feuerbach s Theorem and Emelyanov s Theorem Nikolaos Dergiades and Tran Quang Hung Abstract. We give simple proofs
1 2 2 Circulant Matrices
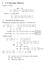 Circulant Matrices General matrix a c d Ax x ax + cx x x + dx General circulant matrix a x ax + x a x x + ax. Evaluating the Eigenvalues Find eigenvalues and eigenvectors of general circulant matrix: a
Circulant Matrices General matrix a c d Ax x ax + cx x x + dx General circulant matrix a x ax + x a x x + ax. Evaluating the Eigenvalues Find eigenvalues and eigenvectors of general circulant matrix: a
MATH10000 Mathematical Workshop Project 2 Part 1 Conic Sections
 MATH10000 Mathematical Workshop Project 2 Part 1 Conic Sections The aim of this project is to introduce you to an area of geometry known as the theory of conic sections, which is one of the most famous
MATH10000 Mathematical Workshop Project 2 Part 1 Conic Sections The aim of this project is to introduce you to an area of geometry known as the theory of conic sections, which is one of the most famous
SYSTEM OF CIRCLES OBJECTIVES (a) Touch each other internally (b) Touch each other externally
 SYSTEM OF CIRCLES OBJECTIVES. A circle passes through (0, 0) and (, 0) and touches the circle x + y = 9, then the centre of circle is (a) (c) 3,, (b) (d) 3,, ±. The equation of the circle having its centre
SYSTEM OF CIRCLES OBJECTIVES. A circle passes through (0, 0) and (, 0) and touches the circle x + y = 9, then the centre of circle is (a) (c) 3,, (b) (d) 3,, ±. The equation of the circle having its centre
Circles. Example 2: Write an equation for a circle if the enpoints of a diameter are at ( 4,5) and (6, 3).
 Conics Unit Ch. 8 Circles Equations of Circles The equation of a circle with center ( hk, ) and radius r units is ( x h) ( y k) r. Example 1: Write an equation of circle with center (8, 3) and radius 6.
Conics Unit Ch. 8 Circles Equations of Circles The equation of a circle with center ( hk, ) and radius r units is ( x h) ( y k) r. Example 1: Write an equation of circle with center (8, 3) and radius 6.
SKILL BUILDER TEN. Graphs of Linear Equations with Two Variables. If x = 2 then y = = = 7 and (2, 7) is a solution.
 SKILL BUILDER TEN Graphs of Linear Equations with Two Variables A first degree equation is called a linear equation, since its graph is a straight line. In a linear equation, each term is a constant or
SKILL BUILDER TEN Graphs of Linear Equations with Two Variables A first degree equation is called a linear equation, since its graph is a straight line. In a linear equation, each term is a constant or
Conic Sections and Polar Graphing Lab Part 1 - Circles
 MAC 1114 Name Conic Sections and Polar Graphing Lab Part 1 - Circles 1. What is the standard equation for a circle with center at the origin and a radius of k? 3. Consider the circle x + y = 9. a. What
MAC 1114 Name Conic Sections and Polar Graphing Lab Part 1 - Circles 1. What is the standard equation for a circle with center at the origin and a radius of k? 3. Consider the circle x + y = 9. a. What
Complex Numbers in Geometry
 Complex Numers in Geometry Seastian Jeon Decemer 3, 206 The Complex Plane. Definitions I assume familiarity with most, if not all, of the following definitions. Some knowledge of linear algera is also
Complex Numers in Geometry Seastian Jeon Decemer 3, 206 The Complex Plane. Definitions I assume familiarity with most, if not all, of the following definitions. Some knowledge of linear algera is also
January 21, 2018 Math 9. Geometry. The method of coordinates (continued). Ellipse. Hyperbola. Parabola.
 January 21, 2018 Math 9 Ellipse Geometry The method of coordinates (continued) Ellipse Hyperbola Parabola Definition An ellipse is a locus of points, such that the sum of the distances from point on the
January 21, 2018 Math 9 Ellipse Geometry The method of coordinates (continued) Ellipse Hyperbola Parabola Definition An ellipse is a locus of points, such that the sum of the distances from point on the
Theorem 1.2 (Converse of Pythagoras theorem). If the lengths of the sides of ABC satisfy a 2 + b 2 = c 2, then the triangle has a right angle at C.
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
Sample Solutions from the Student Solution Manual
 1 Sample Solutions from the Student Solution Manual 1213 If all the entries are, then the matrix is certainly not invertile; if you multiply the matrix y anything, you get the matrix, not the identity
1 Sample Solutions from the Student Solution Manual 1213 If all the entries are, then the matrix is certainly not invertile; if you multiply the matrix y anything, you get the matrix, not the identity
New Jersey Center for Teaching and Learning. Progressive Mathematics Initiative
 Slide 1 / 150 New Jersey Center for Teaching and Learning Progressive Mathematics Initiative This material is made freely available at www.njctl.org and is intended for the non-commercial use of students
Slide 1 / 150 New Jersey Center for Teaching and Learning Progressive Mathematics Initiative This material is made freely available at www.njctl.org and is intended for the non-commercial use of students
Module 9: Further Numbers and Equations. Numbers and Indices. The aim of this lesson is to enable you to: work with rational and irrational numbers
 Module 9: Further Numers and Equations Lesson Aims The aim of this lesson is to enale you to: wor with rational and irrational numers wor with surds to rationalise the denominator when calculating interest,
Module 9: Further Numers and Equations Lesson Aims The aim of this lesson is to enale you to: wor with rational and irrational numers wor with surds to rationalise the denominator when calculating interest,
Fundamentals of Engineering (FE) Exam Mathematics Review
 Fundamentals of Engineering (FE) Exam Mathematics Review Dr. Garey Fox Professor and Buchanan Endowed Chair Biosystems and Agricultural Engineering October 16, 2014 Reference Material from FE Review Instructor
Fundamentals of Engineering (FE) Exam Mathematics Review Dr. Garey Fox Professor and Buchanan Endowed Chair Biosystems and Agricultural Engineering October 16, 2014 Reference Material from FE Review Instructor
Chapter-wise questions
 hapter-wise questions ircles 1. In the given figure, is circumscribing a circle. ind the length of. 3 15cm 5 2. In the given figure, is the center and. ind the radius of the circle if = 18 cm and = 3cm
hapter-wise questions ircles 1. In the given figure, is circumscribing a circle. ind the length of. 3 15cm 5 2. In the given figure, is the center and. ind the radius of the circle if = 18 cm and = 3cm
Midcircles and the Arbelos
 Forum Geometricorum Volume 7 (2007) 53 65. FORUM GEOM ISSN 1534-1178 Midcircles and the rbelos Eric Danneels and Floor van Lamoen bstract. We begin with a study of inversions mapping one given circle into
Forum Geometricorum Volume 7 (2007) 53 65. FORUM GEOM ISSN 1534-1178 Midcircles and the rbelos Eric Danneels and Floor van Lamoen bstract. We begin with a study of inversions mapping one given circle into
TS EAMCET 2016 SYLLABUS ENGINEERING STREAM
 TS EAMCET 2016 SYLLABUS ENGINEERING STREAM Subject: MATHEMATICS 1) ALGEBRA : a) Functions: Types of functions Definitions - Inverse functions and Theorems - Domain, Range, Inverse of real valued functions.
TS EAMCET 2016 SYLLABUS ENGINEERING STREAM Subject: MATHEMATICS 1) ALGEBRA : a) Functions: Types of functions Definitions - Inverse functions and Theorems - Domain, Range, Inverse of real valued functions.
On the Generalized Gergonne Point and Beyond
 Forum Geometricorum Volume 8 (2008) 151 155. FORUM GEOM SSN 1534-1178 On the Generalized Gergonne Point and Beyond Miklós Hoffmann and Sonja Gorjanc Abstract. n this paper we further extend the generalization
Forum Geometricorum Volume 8 (2008) 151 155. FORUM GEOM SSN 1534-1178 On the Generalized Gergonne Point and Beyond Miklós Hoffmann and Sonja Gorjanc Abstract. n this paper we further extend the generalization
The following document was developed by Learning Materials Production, OTEN, DET.
 NOTE CAREFULLY The following document was developed y Learning Materials Production, OTEN, DET. This material does not contain any 3 rd party copyright items. Consequently, you may use this material in
NOTE CAREFULLY The following document was developed y Learning Materials Production, OTEN, DET. This material does not contain any 3 rd party copyright items. Consequently, you may use this material in
Isotomic Inscribed Triangles and Their Residuals
 Forum Geometricorum Volume 3 (2003) 125 134. FORUM GEOM ISSN 1534-1178 Isotomic Inscribed Triangles and Their Residuals Mario Dalcín bstract. We prove some interesting results on inscribed triangles which
Forum Geometricorum Volume 3 (2003) 125 134. FORUM GEOM ISSN 1534-1178 Isotomic Inscribed Triangles and Their Residuals Mario Dalcín bstract. We prove some interesting results on inscribed triangles which
Math 216 Second Midterm 28 March, 2013
 Math 26 Second Midterm 28 March, 23 This sample exam is provided to serve as one component of your studying for this exam in this course. Please note that it is not guaranteed to cover the material that
Math 26 Second Midterm 28 March, 23 This sample exam is provided to serve as one component of your studying for this exam in this course. Please note that it is not guaranteed to cover the material that
MATHEMATICS. IMPORTANT FORMULAE AND CONCEPTS for. Summative Assessment -II. Revision CLASS X Prepared by
 MATHEMATICS IMPORTANT FORMULAE AND CONCEPTS for Summative Assessment -II Revision CLASS X 06 7 Prepared by M. S. KUMARSWAMY, TGT(MATHS) M. Sc. Gold Medallist (Elect.), B. Ed. Kendriya Vidyalaya GaCHiBOWli
MATHEMATICS IMPORTANT FORMULAE AND CONCEPTS for Summative Assessment -II Revision CLASS X 06 7 Prepared by M. S. KUMARSWAMY, TGT(MATHS) M. Sc. Gold Medallist (Elect.), B. Ed. Kendriya Vidyalaya GaCHiBOWli
Information About Ellipses
 Information About Ellipses David Eberly, Geometric Tools, Redmond WA 9805 https://www.geometrictools.com/ This work is licensed under the Creative Commons Attribution 4.0 International License. To view
Information About Ellipses David Eberly, Geometric Tools, Redmond WA 9805 https://www.geometrictools.com/ This work is licensed under the Creative Commons Attribution 4.0 International License. To view
Linear Algebra. Chapter 8: Eigenvalues: Further Applications and Computations Section 8.2. Applications to Geometry Proofs of Theorems.
 Linear Algebra Chapter 8: Eigenvalues: Further Applications and Computations Section 8.2. Applications to Geometry Proofs of Theorems May 1, 2018 () Linear Algebra May 1, 2018 1 / 8 Table of contents 1
Linear Algebra Chapter 8: Eigenvalues: Further Applications and Computations Section 8.2. Applications to Geometry Proofs of Theorems May 1, 2018 () Linear Algebra May 1, 2018 1 / 8 Table of contents 1
Gergonne Meets Sangaku
 Forum Geometricorum Volume 17 (2017) 143 148. FORUM GEOM ISSN 1534-1178 Gergonne Meets Sangaku Paris Pamfilos bstract. In this article we discuss the relation of some hyperbolas, naturally associated with
Forum Geometricorum Volume 17 (2017) 143 148. FORUM GEOM ISSN 1534-1178 Gergonne Meets Sangaku Paris Pamfilos bstract. In this article we discuss the relation of some hyperbolas, naturally associated with
9.1 Circles and Parabolas. Copyright Cengage Learning. All rights reserved.
 9.1 Circles and Parabolas Copyright Cengage Learning. All rights reserved. What You Should Learn Recognize a conic as the intersection of a plane and a double-napped cone. Write equations of circles in
9.1 Circles and Parabolas Copyright Cengage Learning. All rights reserved. What You Should Learn Recognize a conic as the intersection of a plane and a double-napped cone. Write equations of circles in
Constructing a Triangle from Two Vertices and the Symmedian Point
 Forum Geometricorum Volume 18 (2018) 129 1. FORUM GEOM ISSN 154-1178 Constructing a Triangle from Two Vertices and the Symmedian Point Michel Bataille Abstract. Given three noncollinear points A, B, K,
Forum Geometricorum Volume 18 (2018) 129 1. FORUM GEOM ISSN 154-1178 Constructing a Triangle from Two Vertices and the Symmedian Point Michel Bataille Abstract. Given three noncollinear points A, B, K,
Trans Web Educational Services Pvt. Ltd B 147,1st Floor, Sec-6, NOIDA, UP
 Solved Examples Example 1: Find the equation of the circle circumscribing the triangle formed by the lines x + y = 6, 2x + y = 4, x + 2y = 5. Method 1. Consider the equation (x + y 6) (2x + y 4) + λ 1
Solved Examples Example 1: Find the equation of the circle circumscribing the triangle formed by the lines x + y = 6, 2x + y = 4, x + 2y = 5. Method 1. Consider the equation (x + y 6) (2x + y 4) + λ 1
The Cauchy-Schwarz inequality
 The Cauchy-Schwarz inequality Finbarr Holland, f.holland@ucc.ie April, 008 1 Introduction The inequality known as the Cauchy-Schwarz inequality, CS for short, is probably the most useful of all inequalities,
The Cauchy-Schwarz inequality Finbarr Holland, f.holland@ucc.ie April, 008 1 Introduction The inequality known as the Cauchy-Schwarz inequality, CS for short, is probably the most useful of all inequalities,
Contents. 1 Vectors, Lines and Planes 1. 2 Gaussian Elimination Matrices Vector Spaces and Subspaces 124
 Matrices Math 220 Copyright 2016 Pinaki Das This document is freely redistributable under the terms of the GNU Free Documentation License For more information, visit http://wwwgnuorg/copyleft/fdlhtml Contents
Matrices Math 220 Copyright 2016 Pinaki Das This document is freely redistributable under the terms of the GNU Free Documentation License For more information, visit http://wwwgnuorg/copyleft/fdlhtml Contents
Traditional Mathematics in the Aomori Prefecture
 International Mathematical Forum, Vol. 9, 014, no. 33, 1639-1645 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.1988/imf.014.49158 Traditional Mathematics in the Aomori Prefecture Noriaki Nagase Department
International Mathematical Forum, Vol. 9, 014, no. 33, 1639-1645 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.1988/imf.014.49158 Traditional Mathematics in the Aomori Prefecture Noriaki Nagase Department
x = x y and y = x + y.
 8. Conic sections We can use Legendre s theorem, (7.1), to characterise all rational solutions of the general quadratic equation in two variables ax 2 + bxy + cy 2 + dx + ey + ef 0, where a, b, c, d, e
8. Conic sections We can use Legendre s theorem, (7.1), to characterise all rational solutions of the general quadratic equation in two variables ax 2 + bxy + cy 2 + dx + ey + ef 0, where a, b, c, d, e
2014 Summer Review for Students Entering Algebra 2. TI-84 Plus Graphing Calculator is required for this course.
 1. Solving Linear Equations 2. Solving Linear Systems of Equations 3. Multiplying Polynomials and Solving Quadratics 4. Writing the Equation of a Line 5. Laws of Exponents and Scientific Notation 6. Solving
1. Solving Linear Equations 2. Solving Linear Systems of Equations 3. Multiplying Polynomials and Solving Quadratics 4. Writing the Equation of a Line 5. Laws of Exponents and Scientific Notation 6. Solving
Distances Among the Feuerbach Points
 Forum Geometricorum Volume 16 016) 373 379 FORUM GEOM ISSN 153-1178 Distances mong the Feuerbach Points Sándor Nagydobai Kiss bstract We find simple formulas for the distances from the Feuerbach points
Forum Geometricorum Volume 16 016) 373 379 FORUM GEOM ISSN 153-1178 Distances mong the Feuerbach Points Sándor Nagydobai Kiss bstract We find simple formulas for the distances from the Feuerbach points
Geometry. Class Examples (July 8) Paul Yiu. Department of Mathematics Florida Atlantic University. Summer 2014
 Geometry lass Examples (July 8) Paul Yiu Department of Mathematics Florida tlantic University c b a Summer 2014 1 The incircle The internal angle bisectors of a triangle are concurrent at the incenter
Geometry lass Examples (July 8) Paul Yiu Department of Mathematics Florida tlantic University c b a Summer 2014 1 The incircle The internal angle bisectors of a triangle are concurrent at the incenter
Arithmetic progressions of rectangles on a conic
 Notes on Number Theory and Discrete Mathematics ISSN 1310 5132 Vol. 20, 2014, No. 4, 53 57 Arithmetic progressions of rectangles on a conic Ajai Choudhry 13/4 A Clay Square, Lucknow 226001, India e-mail:
Notes on Number Theory and Discrete Mathematics ISSN 1310 5132 Vol. 20, 2014, No. 4, 53 57 Arithmetic progressions of rectangles on a conic Ajai Choudhry 13/4 A Clay Square, Lucknow 226001, India e-mail:
Radii of Circles in Apollonius Problem
 Forum Geometricorum Volume 7 (207 359 372. FORUM GEOM ISSN 534-78 Radii of ircles in pollonius Problem Milorad R. Stevanović, Predrag. Petrović, and Marina M. Stevanović bstract. The paper presents the
Forum Geometricorum Volume 7 (207 359 372. FORUM GEOM ISSN 534-78 Radii of ircles in pollonius Problem Milorad R. Stevanović, Predrag. Petrović, and Marina M. Stevanović bstract. The paper presents the
Standardized Test Practice
 Standardized Test Practice. A store uses a matrix to show their inventory of jeans by waist size (in inches) and style of leg. What is a 3? A a. straight boot cut flared tapered 3 3 3 3 3 3 7 3 3 9 b.
Standardized Test Practice. A store uses a matrix to show their inventory of jeans by waist size (in inches) and style of leg. What is a 3? A a. straight boot cut flared tapered 3 3 3 3 3 3 7 3 3 9 b.
58. The Triangle Inequality for vectors is. dot product.] 59. The Parallelogram Law states that
![58. The Triangle Inequality for vectors is. dot product.] 59. The Parallelogram Law states that 58. The Triangle Inequality for vectors is. dot product.] 59. The Parallelogram Law states that](/thumbs/86/94310732.jpg) 786 CAPTER 12 VECTORS AND TE GEOETRY OF SPACE 0, 0, 1, and 1, 1, 1 as shown in the figure. Then the centroid is. ( 1 2, 1 2, 1 2 ) ] x z C 54. If c a a, where a,, and c are all nonzero vectors, show that
786 CAPTER 12 VECTORS AND TE GEOETRY OF SPACE 0, 0, 1, and 1, 1, 1 as shown in the figure. Then the centroid is. ( 1 2, 1 2, 1 2 ) ] x z C 54. If c a a, where a,, and c are all nonzero vectors, show that
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 2 NOVEMBER 2016
 SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY NOVEMBER 06 Mark Scheme: Each part of Question is worth 4 marks which are awarded solely for the correct answer.
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY NOVEMBER 06 Mark Scheme: Each part of Question is worth 4 marks which are awarded solely for the correct answer.
The Love for the Three Conics
 Forum Geometricorum Volume 18 (2018) 419 430. FORUM GEOM ISSN 1534-1178 The Love for the Three Conics Stefan Liebscher and Dierck-E. Liebscher Abstract. Neville s theorem of the three focus-sharing conics
Forum Geometricorum Volume 18 (2018) 419 430. FORUM GEOM ISSN 1534-1178 The Love for the Three Conics Stefan Liebscher and Dierck-E. Liebscher Abstract. Neville s theorem of the three focus-sharing conics
QUESTION BANK ON. CONIC SECTION (Parabola, Ellipse & Hyperbola)
 QUESTION BANK ON CONIC SECTION (Parabola, Ellipse & Hyperbola) Question bank on Parabola, Ellipse & Hyperbola Select the correct alternative : (Only one is correct) Q. Two mutually perpendicular tangents
QUESTION BANK ON CONIC SECTION (Parabola, Ellipse & Hyperbola) Question bank on Parabola, Ellipse & Hyperbola Select the correct alternative : (Only one is correct) Q. Two mutually perpendicular tangents
Q1. If (1, 2) lies on the circle. x 2 + y 2 + 2gx + 2fy + c = 0. which is concentric with the circle x 2 + y 2 +4x + 2y 5 = 0 then c =
 Q1. If (1, 2) lies on the circle x 2 + y 2 + 2gx + 2fy + c = 0 which is concentric with the circle x 2 + y 2 +4x + 2y 5 = 0 then c = a) 11 b) -13 c) 24 d) 100 Solution: Any circle concentric with x 2 +
Q1. If (1, 2) lies on the circle x 2 + y 2 + 2gx + 2fy + c = 0 which is concentric with the circle x 2 + y 2 +4x + 2y 5 = 0 then c = a) 11 b) -13 c) 24 d) 100 Solution: Any circle concentric with x 2 +
GAT-UGTP-2018 Page 1 of 5
 SECTION A: MATHEMATICS UNIT 1 SETS, RELATIONS AND FUNCTIONS: Sets and their representation, Union, Intersection and compliment of sets, and their algebraic properties, power set, Relation, Types of relation,
SECTION A: MATHEMATICS UNIT 1 SETS, RELATIONS AND FUNCTIONS: Sets and their representation, Union, Intersection and compliment of sets, and their algebraic properties, power set, Relation, Types of relation,
Newbattle Community High School Higher Mathematics. Key Facts Q&A
 Key Facts Q&A Ways of using this booklet: 1) Write the questions on cards with the answers on the back and test yourself. ) Work with a friend who is also doing to take turns reading a random question
Key Facts Q&A Ways of using this booklet: 1) Write the questions on cards with the answers on the back and test yourself. ) Work with a friend who is also doing to take turns reading a random question
45. The Parallelogram Law states that. product of a and b is the vector a b a 2 b 3 a 3 b 2, a 3 b 1 a 1 b 3, a 1 b 2 a 2 b 1. a c. a 1. b 1.
 SECTION 10.4 THE CROSS PRODUCT 537 42. Suppose that all sides of a quadrilateral are equal in length and opposite sides are parallel. Use vector methods to show that the diagonals are perpendicular. 43.
SECTION 10.4 THE CROSS PRODUCT 537 42. Suppose that all sides of a quadrilateral are equal in length and opposite sides are parallel. Use vector methods to show that the diagonals are perpendicular. 43.
(D) (A) Q.3 To which of the following circles, the line y x + 3 = 0 is normal at the point ? 2 (A) 2
 CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
UNIT 6. BELL WORK: Draw 3 different sized circles, 1 must be at LEAST 15cm across! Cut out each circle. The Circle
 UNIT 6 BELL WORK: Draw 3 different sized circles, 1 must be at LEAST 15cm across! Cut out each circle The Circle 1 Questions How are perimeter and area related? How are the areas of polygons and circles
UNIT 6 BELL WORK: Draw 3 different sized circles, 1 must be at LEAST 15cm across! Cut out each circle The Circle 1 Questions How are perimeter and area related? How are the areas of polygons and circles
The 3rd Olympiad of Metropolises
 The 3rd Olympiad of Metropolises Day 1. Solutions Problem 1. Solve the system of equations in real numbers: (x 1)(y 1)(z 1) xyz 1, Answer: x 1, y 1, z 1. (x )(y )(z ) xyz. (Vladimir Bragin) Solution 1.
The 3rd Olympiad of Metropolises Day 1. Solutions Problem 1. Solve the system of equations in real numbers: (x 1)(y 1)(z 1) xyz 1, Answer: x 1, y 1, z 1. (x )(y )(z ) xyz. (Vladimir Bragin) Solution 1.
Introduction to Number Theory
 Introduction to Number Theory Paul Yiu Department of Mathematics Florida Atlantic University Spring 017 March 7, 017 Contents 10 Pythagorean and Heron triangles 57 10.1 Construction of Pythagorean triangles....................
Introduction to Number Theory Paul Yiu Department of Mathematics Florida Atlantic University Spring 017 March 7, 017 Contents 10 Pythagorean and Heron triangles 57 10.1 Construction of Pythagorean triangles....................
On the Circumcenters of Cevasix Configurations
 Forum Geometricorum Volume 3 (2003) 57 63. FORUM GEOM ISSN 1534-1178 On the ircumcenters of evasix onfigurations lexei Myakishev and Peter Y. Woo bstract. We strengthen Floor van Lamoen s theorem that
Forum Geometricorum Volume 3 (2003) 57 63. FORUM GEOM ISSN 1534-1178 On the ircumcenters of evasix onfigurations lexei Myakishev and Peter Y. Woo bstract. We strengthen Floor van Lamoen s theorem that
Generalized Archimedean Arbelos Twins
 Forum Geometricorum Volume 4 (204) 409 48 FORUM GEOM ISSN 534-78 Generalized rchimedean rbelos Twins Nikolaos Dergiades bstract We generalize the well known rchimedean arbelos twins by extending the notion
Forum Geometricorum Volume 4 (204) 409 48 FORUM GEOM ISSN 534-78 Generalized rchimedean rbelos Twins Nikolaos Dergiades bstract We generalize the well known rchimedean arbelos twins by extending the notion
8. Diagonalization.
 8. Diagonalization 8.1. Matrix Representations of Linear Transformations Matrix of A Linear Operator with Respect to A Basis We know that every linear transformation T: R n R m has an associated standard
8. Diagonalization 8.1. Matrix Representations of Linear Transformations Matrix of A Linear Operator with Respect to A Basis We know that every linear transformation T: R n R m has an associated standard
At first numbers were used only for counting, and 1, 2, 3,... were all that was needed. These are called positive integers.
 1 Numers One thread in the history of mathematics has een the extension of what is meant y a numer. This has led to the invention of new symols and techniques of calculation. When you have completed this
1 Numers One thread in the history of mathematics has een the extension of what is meant y a numer. This has led to the invention of new symols and techniques of calculation. When you have completed this
Affine Transformations
 Solutions to hapter Problems 435 Then, using α + β + γ = 360, we obtain: ( ) x a = (/2) bc sin α a + ac sin β b + ab sin γ c a ( ) = (/2) bc sin α a 2 + (ac sin β)(ab cos γ ) + (ab sin γ )(ac cos β) =
Solutions to hapter Problems 435 Then, using α + β + γ = 360, we obtain: ( ) x a = (/2) bc sin α a + ac sin β b + ab sin γ c a ( ) = (/2) bc sin α a 2 + (ac sin β)(ab cos γ ) + (ab sin γ )(ac cos β) =
Projects in Geometry for High School Students
 Projects in Geometry for High School Students Goal: Our goal in more detail will be expressed on the next page. Our journey will force us to understand plane and three-dimensional geometry. We will take
Projects in Geometry for High School Students Goal: Our goal in more detail will be expressed on the next page. Our journey will force us to understand plane and three-dimensional geometry. We will take
Recognise the Equation of a Circle. Solve Problems about Circles Centred at O. Co-Ordinate Geometry of the Circle - Outcomes
 1 Co-Ordinate Geometry of the Circle - Outcomes Recognise the equation of a circle. Solve problems about circles centred at the origin. Solve problems about circles not centred at the origin. Determine
1 Co-Ordinate Geometry of the Circle - Outcomes Recognise the equation of a circle. Solve problems about circles centred at the origin. Solve problems about circles not centred at the origin. Determine
ARCHIMEDEAN CIRCLES PASSING THROUGH A SPECIAL POINT
 INTERNATIONAL JOURNAL OF GEOMETRY Vol. 4 (2015), No. 1, 5-10 ARCHIMEDEAN CIRCLES PASSING THROUGH A SPECIAL POINT HIROSHI OKUMURA Abstract. We consider infinitely many Archimedean circles of the arbelos
INTERNATIONAL JOURNAL OF GEOMETRY Vol. 4 (2015), No. 1, 5-10 ARCHIMEDEAN CIRCLES PASSING THROUGH A SPECIAL POINT HIROSHI OKUMURA Abstract. We consider infinitely many Archimedean circles of the arbelos
Symmetry: The Quarterly of the International Society for the Interdisciplinary Study of Symmetry (ISIS-Symmetry) Volume 8, Number 1, 1997
 Symmetry: The Quarterly of the International Society for the Interdisciplinary Study of Symmetry (ISIS-Symmetry) Volume 8, Number 1, 1997 Symmetry: Culture and Science Vol 8, No.I, 4-23, 1997 SYMMETRY."
Symmetry: The Quarterly of the International Society for the Interdisciplinary Study of Symmetry (ISIS-Symmetry) Volume 8, Number 1, 1997 Symmetry: Culture and Science Vol 8, No.I, 4-23, 1997 SYMMETRY."
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg ( )
 Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2009-03-26) Logic Rule 0 No unstated assumptions may be used in a proof.
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2009-03-26) Logic Rule 0 No unstated assumptions may be used in a proof.
Senior Math Circles February 18, 2009 Conics III
 University of Waterloo Faculty of Mathematics Senior Math Circles February 18, 2009 Conics III Centre for Education in Mathematics and Computing Eccentricity of Conics Fix a point F called the focus, a
University of Waterloo Faculty of Mathematics Senior Math Circles February 18, 2009 Conics III Centre for Education in Mathematics and Computing Eccentricity of Conics Fix a point F called the focus, a
The Kiepert Pencil of Kiepert Hyperbolas
 Forum Geometricorum Volume 1 (2001) 125 132. FORUM GEOM ISSN 1534-1178 The Kiepert Pencil of Kiepert Hyperbolas Floor van Lamoen and Paul Yiu bstract. We study Kiepert triangles K(φ) and their iterations
Forum Geometricorum Volume 1 (2001) 125 132. FORUM GEOM ISSN 1534-1178 The Kiepert Pencil of Kiepert Hyperbolas Floor van Lamoen and Paul Yiu bstract. We study Kiepert triangles K(φ) and their iterations
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 2 NOVEMBER 2011
 SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY NOVEMBER 011 Mark Scheme: Each part of Question 1 is worth four marks which are awarded solely for the correct
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY NOVEMBER 011 Mark Scheme: Each part of Question 1 is worth four marks which are awarded solely for the correct
Circle Chains Inscribed in Symmetrical Lunes and Integer Sequences
 Forum Geometricorum Volume 17 (017) 1 9. FORUM GEOM ISSN 1534-1178 Circle Chains Inscribed in Symmetrical Lunes and Integer Sequences Giovanni Lucca Abstract. We derive the conditions for inscribing, inside
Forum Geometricorum Volume 17 (017) 1 9. FORUM GEOM ISSN 1534-1178 Circle Chains Inscribed in Symmetrical Lunes and Integer Sequences Giovanni Lucca Abstract. We derive the conditions for inscribing, inside
A Note on the Barycentric Square Roots of Kiepert Perspectors
 Forum Geometricorum Volume 6 (2006) 263 268. FORUM GEOM ISSN 1534-1178 Note on the arycentric Square Roots of Kiepert erspectors Khoa Lu Nguyen bstract. Let be an interior point of a given triangle. We
Forum Geometricorum Volume 6 (2006) 263 268. FORUM GEOM ISSN 1534-1178 Note on the arycentric Square Roots of Kiepert erspectors Khoa Lu Nguyen bstract. Let be an interior point of a given triangle. We
C=2πr C=πd. Chapter 10 Circles Circles and Circumference. Circumference: the distance around the circle
 10.1 Circles and Circumference Chapter 10 Circles Circle the locus or set of all points in a plane that are A equidistant from a given point, called the center When naming a circle you always name it by
10.1 Circles and Circumference Chapter 10 Circles Circle the locus or set of all points in a plane that are A equidistant from a given point, called the center When naming a circle you always name it by
ax 2 + bx + c = 0 where
 Chapter P Prerequisites Section P.1 Real Numbers Real numbers The set of numbers formed by joining the set of rational numbers and the set of irrational numbers. Real number line A line used to graphically
Chapter P Prerequisites Section P.1 Real Numbers Real numbers The set of numbers formed by joining the set of rational numbers and the set of irrational numbers. Real number line A line used to graphically
Australian Intermediate Mathematics Olympiad 2016
 Australian Intermediate Mathematics Olympiad 06 Questions. Find the smallest positive integer x such that x = 5y, where y is a positive integer. [ marks]. A 3-digit number in base 7 is also a 3-digit number
Australian Intermediate Mathematics Olympiad 06 Questions. Find the smallest positive integer x such that x = 5y, where y is a positive integer. [ marks]. A 3-digit number in base 7 is also a 3-digit number
MAT1035 Analytic Geometry
 MAT1035 Analytic Geometry Lecture Notes R.A. Sabri Kaan Gürbüzer Dokuz Eylül University 2016 2 Contents 1 Review of Trigonometry 5 2 Polar Coordinates 7 3 Vectors in R n 9 3.1 Located Vectors..............................................
MAT1035 Analytic Geometry Lecture Notes R.A. Sabri Kaan Gürbüzer Dokuz Eylül University 2016 2 Contents 1 Review of Trigonometry 5 2 Polar Coordinates 7 3 Vectors in R n 9 3.1 Located Vectors..............................................
Dynamical Systems Solutions to Exercises
 Dynamical Systems Part 5-6 Dr G Bowtell Dynamical Systems Solutions to Exercises. Figure : Phase diagrams for i, ii and iii respectively. Only fixed point is at the origin since the equations are linear
Dynamical Systems Part 5-6 Dr G Bowtell Dynamical Systems Solutions to Exercises. Figure : Phase diagrams for i, ii and iii respectively. Only fixed point is at the origin since the equations are linear
Number Plane Graphs and Coordinate Geometry
 Numer Plane Graphs and Coordinate Geometr Now this is m kind of paraola! Chapter Contents :0 The paraola PS, PS, PS Investigation: The graphs of paraolas :0 Paraolas of the form = a + + c PS Fun Spot:
Numer Plane Graphs and Coordinate Geometr Now this is m kind of paraola! Chapter Contents :0 The paraola PS, PS, PS Investigation: The graphs of paraolas :0 Paraolas of the form = a + + c PS Fun Spot:
DISCRIMINANT EXAM QUESTIONS
 DISCRIMINANT EXAM QUESTIONS Question 1 (**) Show by using the discriminant that the graph of the curve with equation y = x 4x + 10, does not cross the x axis. proof Question (**) Show that the quadratic
DISCRIMINANT EXAM QUESTIONS Question 1 (**) Show by using the discriminant that the graph of the curve with equation y = x 4x + 10, does not cross the x axis. proof Question (**) Show that the quadratic
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca Euclid Contest. Wednesday, April 15, 2015
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 015 Euclid Contest Wednesday, April 15, 015 (in North America and South America) Thursday, April 16, 015 (outside of North America
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 015 Euclid Contest Wednesday, April 15, 015 (in North America and South America) Thursday, April 16, 015 (outside of North America
2005 Euclid Contest. Solutions
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 2005 Euclid Contest Tuesday, April 19, 2005 Solutions c
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 2005 Euclid Contest Tuesday, April 19, 2005 Solutions c
Worked solutions. 1 Algebra and functions 1: Manipulating algebraic expressions. Prior knowledge 1 page 2. Exercise 1.2A page 8. Exercise 1.
 WORKED SOLUTIONS Worked solutions Algera and functions : Manipulating algeraic epressions Prior knowledge page a (a + ) a + c( d) c cd c e ( f g + eh) e f e g + e h d i( + j) + 7(k j) i + ij + 7k j e l(l
WORKED SOLUTIONS Worked solutions Algera and functions : Manipulating algeraic epressions Prior knowledge page a (a + ) a + c( d) c cd c e ( f g + eh) e f e g + e h d i( + j) + 7(k j) i + ij + 7k j e l(l
SYSTEM OF CIRCLES If d is the distance between the centers of two intersecting circles with radii r 1, r 2 and θ is the
 SYSTEM OF CIRCLES Theorem: If d is the distance between the centers of two intersecting circles with radii r 1, r 2 and θ is the 2 2 2 d r1 r2 angle between the circles then cos θ =. 2r r 1 2 Proof: Let
SYSTEM OF CIRCLES Theorem: If d is the distance between the centers of two intersecting circles with radii r 1, r 2 and θ is the 2 2 2 d r1 r2 angle between the circles then cos θ =. 2r r 1 2 Proof: Let
On Emelyanov s Circle Theorem
 Journal for Geometry and Graphics Volume 9 005, No., 55 67. On Emelyanov s ircle Theorem Paul Yiu Department of Mathematical Sciences, Florida Atlantic University Boca Raton, Florida, 3343, USA email:
Journal for Geometry and Graphics Volume 9 005, No., 55 67. On Emelyanov s ircle Theorem Paul Yiu Department of Mathematical Sciences, Florida Atlantic University Boca Raton, Florida, 3343, USA email:
Arcs and Inscribed Angles of Circles
 Arcs and Inscribed Angles of Circles Inscribed angles have: Vertex on the circle Sides are chords (Chords AB and BC) Angle ABC is inscribed in the circle AC is the intercepted arc because it is created
Arcs and Inscribed Angles of Circles Inscribed angles have: Vertex on the circle Sides are chords (Chords AB and BC) Angle ABC is inscribed in the circle AC is the intercepted arc because it is created
9 Mixed Exercise. vector equation is. 4 a
 9 Mixed Exercise a AB r i j k j k c OA AB 7 i j 7 k A7,, and B,,8 8 AB 6 A vector equation is 7 r x 7 y z (i j k) j k a x y z a a 7, Pearson Education Ltd 7. Copying permitted for purchasing institution
9 Mixed Exercise a AB r i j k j k c OA AB 7 i j 7 k A7,, and B,,8 8 AB 6 A vector equation is 7 r x 7 y z (i j k) j k a x y z a a 7, Pearson Education Ltd 7. Copying permitted for purchasing institution
