41st International Mathematical Olympiad
|
|
|
- Evelyn Barrie Ford
- 6 years ago
- Views:
Transcription
1 41st International Mathematical Olympiad Taejon, Korea July 13 25, 2001 Problems Problem 1 A B is tangent to the circles C A M N and N M B D. M lies between C and D on the line C D, and C D is parallel to A B. The chords N A and C M meet at P; the chords N B and M D meet at Q. The rays C A and D B meet at E. Prove that P E = Q E Problem 2 A, B, C are positive reals with product 1. Prove that A 1 1 B B 1 1 C C 1 1 A 1. Problem 3 k is a positive real. N is an integer greater than 1. N points are placed on a line, not all coincident. A move is carried out as follows. Pick any two points A and B which are not coincident. Suppose that A lies to the right of B. Replace B by another point B to the right of A such that A B = k B A. For what values of k can we move the points arbitrarily far to the right by repeated moves? Problem cards are numbered 1 to 100 (each card different) and placed in 3 boxes (at least one card in each box). How many ways can this be done so that if two boxes are selected and a card is taken from each, then the knowledge of their sum alone is always sufficient to identify the third box? Problem 5 Can we find N divisible by just 2000 different primes, so that N divides 2 N 1? [N may be divisible by a prime power.] Problem 6 A 1 A 2 A 3 is an acute-angled triangle. The foot of the altitude from A i is K i and the incircle touches the side opposite A i at L i. The line K 1 K 2 is reflected in the line L 1 L 2. Similarly, the line K 2 K 3 is reflected in L 2 L 3 and K 3 K 1 is reflected in L 3 L 1. Show that the three new lines form a triangle with vertices on the incircle.
2 2 IMO 2000 Competition Problems Problems with s Problem 1 A B is tangent to the circles C A M N and N M B D. M lies between C and D on the line C D, and C D is parallel to A B. The chords N A and C M meet at P; the chords N B and M D meet at Q. The rays C A and D B meet at E. Prove that P E = Q E Angle E B A angle B D M because C D is parallel to A B angle A B M (because A B is tangent at B). So A B bisects E B M. Similarly, B A bisects angle E A M. Hence E is the reflection of M in A B. So E M is perpendicular to A B and hence to C D. So it suffices to show that M P M Q. Let the ray N M meet A B at X. X A is a tangent so X A 2 X M.X N. Similarly, X B is a tangent, so X B 2 X M.X N. Hence X A X B. But A B and P Q are parallel, so M P M Q. Problem 2 A, B, C are positive reals with product 1. Prove that A 1 1 B B 1 1 C C 1 1 A 1. An elegant solution due to Robin Chapman is as follows: B 1 1 C B 1 1 B 1 B C B 1 A 1 B. Hence, A 1 1 B B 1 1 C B A B 2 B A 2. So the square of the product of all three B A 2 C B 2 A C 2 1. Actually, that is not quite true. The last sentence would not follow if we had some negative left hand sides, because then we could not multiply the inequalities. But it is easy to deal separately with the case where A 1 1 B, B 1 1 C, C 1 1 A are not all positive. If one of the three terms is negative, then the other two must be positive. For example, if A 1 1 B 0, then A 1, so C 1 1 A 0, and B 1, so B 1 1 C 0. But if one term is negative and two are positive, then their product is negative and hence less than 1. Few people would manage this under exam conditions, but there are plenty of longer and easier to find solutions! Problem 3 k is a positive real. N is an integer greater than 1. N points are placed on a line, not all coincident. A move is carried out as follows. Pick any two points A and B which are not coincident. Suppose that A lies to the right of B. Replace B by another point B to the right of A such that A B = k B A. For what values of k can we move the points arbitrarily far to the right by repeated moves? Answer: k 1 n 1. An elegant solution by Gerhard Woeginger is as follows: Suppose k 1 n 1, so that k 0 1 k n 1 0. Let X be the sum of the distances of the points from the rightmost point. If a move does not change the rightmost point, then it reduces X. If it moves the rightmost point a distance z to the right, then it reduces X by at least z k n 1 z k 0 z. X cannot be reduced below nil. So the total distance moved by the rightmost point is at most X 0 k 0, where X 0 is the initial value of X.
3 IMO 2000 Competition Problems 3 Conversely, suppose k 1 n 1, so that k 1 n 1 1 k 0. We always move the leftmost point. This has the effect of moving the rightmost point z 0 and increasing X by n 1 z z k k 1 z 0. So X is never decreased. But z k X n 1 k X 0 n 1 0. So we can move the rightmost point arbitarily far to the right (and hence all the points, since another n 1 moves will move the other points to the right of the rightmost point). Problem cards are numbered 1 to 100 (each card different) and placed in 3 boxes (at least one card in each box). How many ways can this be done so that if two boxes are selected and a card is taken from each, then the knowledge of their sum alone is always sufficient to identify the third box? Answer: 12. Place 1, 2, 3 in different boxes (6 possibilities) and then place n in the same box as its residue mod 3. Or place 1 and 100 in different boxes and 2 99 in the third box (6 possibilities). An elegant solution communicated (in outline) by both Mohd Suhaimi Ramly and Fokko J van de Bult is as follows: Let H n be the corresponding result that for cards numbered 1 to n the only solutions are by residue mod 3, or 1 and n in separate boxes and 2 to n 1 in the third box. It is easy to check that they are solutions. H n is the assertion that there are no others. H 3 is obviously true (although the two cases coincide). We now use induction on n. So suppose that the result is true for n and consider the case n 1. Suppose n 1 is alone in its box. If 1 is not also alone, then let N be the sum of the largest cards in each of the boxes not containing n 1. Since n 2 N n n 1 2 n 1, we can achieve the same sum N as from a different pair of boxes as n 1 N n 1. Contradiction. So 1 must be alone and we have one of the solutions envisaged in H n 1. If n 1 is not alone, then if we remove it, we must have a solution for n. But that solution cannot be the n, 1, 2 to n 1 solution. For we can easily check that none of the three boxes will then accomodate n 1. So it must be the mod 3 solution. We can easily check that in this case n 1 must go in the box with matching residue, which makes the n 1 solution the other solution envisaged by H n 1. That completes the induction. My much more plodding solution (which I was quite pleased with until I saw the more elegant solution above) follows. It took about half-an-hour and shows the kind of kludge one is likely to come up with under time pressure in an exam! With a suitable labeling of the boxes as A, B, C, there are 4 cases to consider: Case 1: A contains 1; B contains 2; C contains 3 Case 2: A contains 1, 2 Case 3: A contains 1, 3; B contains 2 Case 4: A contains 1; B contains 2, 3. We show that Cases 1 and 4 each yield just one possible arrangement and Cases 2 and 3 none. In Case 1, it is an easy induction that n must be placed in the same box as its residue (in other words numbers with residue 1 mod 3 go into A, numbers with residue 2 go into B, and numbers with residue 0 go into C ). For n 1 n 2 n n 1. Hence n 1 must go in the same box as n 2 (if they were in different boxes, then we would have two pairs from different pairs of boxes with the same sum). It is also clear that this is a possible arrangement. Given the sum of two numbers from different boxes, take its residue mod 3. A residue of 0 indicates that the third (unused) box was C, a residue of 1 indicates that the third box was A, and a residue of 2 indicates that the third box was B. Note that this unique arrangement gives 6 ways for the question, because there are 6 ways of arranging 1, 2 and 3 in the given boxes.
4 4 IMO 2000 Competition Problems In Case 2, let n be the smallest number not in box A. Suppose it is in box B. Let m be the smallest number in the third box, C. m 1 cannot be in C. If it is in A, then m n 1 m 1 n. Contradiction (m is in C, n 1 is in A, so that pair identifies B as the third box, but m 1 is in A and n is in B, identifying C). So m 1 must be in B. But m 1 2 m 1. Contradiction. So Case 2 is not possible. In Case 3, let n be the smallest number in box C, so n 1 must be in A or B. If n 1 is in A, then n 1 2 n 2. Contradiction (a sum of numbers in A and B equals a sum from C and A). If n 1 is in B, then n 1 3 n 2. Contradiction (a sum from B and A equals a sum from C and B). So Case 3 is not possible. In Case 4, let n be the smallest number in box C. n 1 cannot be in A, or n n (pair from A, B with same sum as pair from B, C), so n 1 must be in B. Now n 1 cannot be in A (or n n), or in B or C (or 1 n 1 2 n). So n 1 cannot exist and hence n 100. It is now an easy induction that all of 4, 5, 98 must be in B. For given that m is in B, if m 1 were in A, we would have 100 m 99 m 1. But this arrangement (1 in A, 2 99 in B, 100 in C) is certainly possible: sums identify C as the third box, sum 101 identifies B as the third box, and sums identify A as the third box. Finally, as in Case 1, this unique arrangement corresponds to 6 ways of arranging the cards in the given boxes. Problem 5 Can we find N divisible by just 2000 different primes, so that N divides 2 N 1? [N may be divisible by a prime power.] Answer: yes. Note that for b odd we have 2 a b 1 2 a 1 2 a b 1 2 a b 2 1, and so 2 a 1 is a factor of 2 a b 1. It is sufficient therefore to find m such that (1) m has only a few distinct prime factors, (2) 2 m 1 has a large number of distinct prime factors, (3) m divides 2 m 1. For then we can take k, a product of enough distinct primes dividing 2 m 1 (but not m), so that k m has exactly 2000 factors. Then k m still divides 2 m 1 and hence 2 k m 1. The simplest case is where m has only one distinct prime factor p, in other words it is a power of p. But if p is a prime, then p divides 2 p 2, so the only p for which p divides 2 p 1 is 3. So the questions are whether a h 2 m 1 is (1) divisible by m 3 h and (2) has a large number of distinct prime factors. a h 1 a h 2 2 m 2 m 1, where m 3 h. But 2 m a h 1, so a h 1 a h a h 2 3 a h 3. Now a 1 9, so an easy induction shows that 3 h 1 divides a h, which answers (1) affirmatively. Also, since a h is a factor of a h 1, any prime dividing a h also divides a h 1. Put a h 3 h 1 b h. Then b h 1 b h 3 2 h 1 b h 2 3 h 2 b h 1. Now 3 2 h 1 b h 2 3 h 2 b h 1 1, so it must have some prime factor p 1. But p be 3 or divide b h (since 3 2 h 1 b h 2 3 h 2 b h 1 is a multiple of 3 b h plus 1), so b h 1 has at least one prime factor p 3 which does not divide b h. So b h 1 has at least h distinct prime factors greater than 3, which answers (2) affirmatively. But that is all we need. We can take m in the first paragraph above to be : (1) m has only one distinct prime factor, (2) 2 m b 2000 has at least 1999 distinct prime factors other than 3, (3) m divides 2 m 1. Take k to be a product of 1999 distinct prime factors dividing b Then N k m is the required number with exactly 2000 distinct prime factors which divides 2 N 1. Problem 6 A 1 A 2 A 3 is an acute-angled triangle. The foot of the altitude from A i is K i and the incircle touches the side opposite A i at L i. The line K 1 K 2 is reflected in the line L 1 L 2. Similarly, the line K 2 K 3 is reflected in L 2 L 3 and K 3 K 1 is reflected in L 3 L 1. Show that the three new lines form a triangle with vertices on the incircle.
5 IMO 2000 Competition Problems 5 Let O be the centre of the incircle. Let the line parallel to A 1 A 2 through L 2 meet the line A 2 O at X. We will show that X is the reflection of K 2 in L 2 L 3. Let A 1 A 3 meet the line A 2 O at B 2. Now A 2 K 2 is perpendicular to K 2 B 2 and O L 2 is perpendicular to L 2 B 2, so A 2 K 2 B 2 and O L 2 B 2 are similar. Hence K 2 L 2 L 2 B 2 A 2 O O B 2. But O A 3 is the angle bisector in the triangle A 2 A 3 B 2, so A 2 O O B 2 A 2 A 3 B 2 A 3. Take B 2 on the line A 2 O such that L 2 B 2 L 2 B 2 (B 2 is distinct from B 2 unless L 2 B 2 is perpendicular to the line). Then angle L 2 B 2 X angle A 3 B 2 A 2. Also, since L 2 X is parallel to A 2 A 1, angle L 2 X B 2 angle A 3 A 2 B 2. So the triangles L 2 X B 2 and A 3 A 2 B 2 are similar. Hence A 2 A 3 B 2 A 3 X L 2 B 2 L 2 X L 2 B 2 L 2 (since B 2 L 2 B 2 L 2 ). Thus we have shown that K 2 L 2 L 2 B 2 X L 2 B 2 L 2 and hence that K 2 L 2 X L 2. L 2 X is parallel to A 2 A 1 so angle A 2 A 1 A 3 angle A 1 L 2 X angle L 2 X K 2 angle L 2 K 2 X 2 angle L 2 X K 2 (isosceles). So angle L 2 X K angle A 2 A 1 A 3 angle A 2 A 1 O. L 2 X and A 2 A 1 are parallel, so K 2 X and O A 1 are parallel. But O A 1 is perpendicular to L 2 L 3, so K 2 X is also perpendicular to L 2 L 3 and hence X is the reflection of K 2 in L 2 L 3. Now the angle K 3 K 2 A 1 angle A 1 A 2 A 3, because it is 90 angle K 3 K 2 A 2 90 angle K 3 A 3 A 2 A 2 A 3 K 2 K 3 is cyclic with A 2 A 3 a diameter angle A 1 A 2 A 3. So the reflection of K 2 K 3 in L 2 L 3 is a line through X making an angle A 1 A 2 A 3 with L 2 X, in other words, it is the line through X parallel to A 2 A 3. Let M i be the reflection of L i in A i O. The angle M 2 X L 2 2 angle O X L 2 2 angle A 1 A 2 O since A 1 A 2 is parallel to L 2 X angle A 1 A 2 A 3, which is the angle between L 2 X and A 2 A 3. So M 2 X is parallel to A 2 A 3, in other words, M 2 lies on the reflection of K 2 K 3 in L 2 L 3. If follows similarly that M 3 lies on the reflection. Similarly, the line M 1 M 3 is the reflection of K 1 K 3 in L 1 L 3, and the line M 1 M 2 is the reflection of K 1 K 2 in L 1 L 2 and hence the triangle formed by the intersections of the three reflections is just M 1 M 2 M 3.
41st International Mathematical Olympiad
 41st International Mathematical Olympiad Taejon, Korea, July 2000 1 Two circles Γ 1 and Γ 2 intersect at M and N Let l be the common tangent to Γ 1 and Γ 2 so that M is closer to l than N is Let l touch
41st International Mathematical Olympiad Taejon, Korea, July 2000 1 Two circles Γ 1 and Γ 2 intersect at M and N Let l be the common tangent to Γ 1 and Γ 2 so that M is closer to l than N is Let l touch
IMO Training Camp Mock Olympiad #2 Solutions
 IMO Training Camp Mock Olympiad #2 Solutions July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the
IMO Training Camp Mock Olympiad #2 Solutions July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the
Chapter-wise questions
 hapter-wise questions ircles 1. In the given figure, is circumscribing a circle. ind the length of. 3 15cm 5 2. In the given figure, is the center and. ind the radius of the circle if = 18 cm and = 3cm
hapter-wise questions ircles 1. In the given figure, is circumscribing a circle. ind the length of. 3 15cm 5 2. In the given figure, is the center and. ind the radius of the circle if = 18 cm and = 3cm
International Mathematical Olympiad. Preliminary Selection Contest 2011 Hong Kong. Outline of Solutions
 International Mathematical Olympiad Preliminary Selection Contest Hong Kong Outline of Solutions Answers:.. 76... 6. 7.. 6.. 6. 6.... 6. 7.. 76. 6. 7 Solutions:. Such fractions include. They can be grouped
International Mathematical Olympiad Preliminary Selection Contest Hong Kong Outline of Solutions Answers:.. 76... 6. 7.. 6.. 6. 6.... 6. 7.. 76. 6. 7 Solutions:. Such fractions include. They can be grouped
IMO from 1959 to Collected from :
 IMO from 1959 to 2003 Collected from : http://www.kalva.demon.co.uk/imo.html 44th IMO 2003 1 A1. S is the set {1, 2, 3,..., 1000000}. Show that for any subset A of S with 101 elements we can find 100 distinct
IMO from 1959 to 2003 Collected from : http://www.kalva.demon.co.uk/imo.html 44th IMO 2003 1 A1. S is the set {1, 2, 3,..., 1000000}. Show that for any subset A of S with 101 elements we can find 100 distinct
11 th Philippine Mathematical Olympiad Questions, Answers, and Hints
 view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
Australian Intermediate Mathematics Olympiad 2016
 Australian Intermediate Mathematics Olympiad 06 Questions. Find the smallest positive integer x such that x = 5y, where y is a positive integer. [ marks]. A 3-digit number in base 7 is also a 3-digit number
Australian Intermediate Mathematics Olympiad 06 Questions. Find the smallest positive integer x such that x = 5y, where y is a positive integer. [ marks]. A 3-digit number in base 7 is also a 3-digit number
40th International Mathematical Olympiad
 40th International Mathematical Olympiad Bucharest, Romania, July 999 Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points
40th International Mathematical Olympiad Bucharest, Romania, July 999 Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points
Baltic Way 2003 Riga, November 2, 2003
 altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
9th Bay Area Mathematical Olympiad
 9th Bay rea Mathematical Olympiad February 27, 2007 Problems with Solutions 1 15-inch-long stick has four marks on it, dividing it into five segments of length 1,2,3,4, and 5 inches (although not neccessarily
9th Bay rea Mathematical Olympiad February 27, 2007 Problems with Solutions 1 15-inch-long stick has four marks on it, dividing it into five segments of length 1,2,3,4, and 5 inches (although not neccessarily
IMO Training Camp Mock Olympiad #2
 IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
Unofficial Solutions
 Canadian Open Mathematics Challenge 2016 Unofficial Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2016/practice.html
Canadian Open Mathematics Challenge 2016 Unofficial Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2016/practice.html
Math. Model Exam (1) Mid-year. Fifth primary. Question 1: Question 2: Answer the following: a = (to the nearest )
 Model Exam (1) Question 1: Answer the following: a- 65.3814 + 63.4027 = (to the nearest ) b- 53.27 2.1 = (to the nearest tenth) c- (3.425 + 1.07) 2.8 = (to the nearest hundredth) d- 9.568 9 = (to the nearest
Model Exam (1) Question 1: Answer the following: a- 65.3814 + 63.4027 = (to the nearest ) b- 53.27 2.1 = (to the nearest tenth) c- (3.425 + 1.07) 2.8 = (to the nearest hundredth) d- 9.568 9 = (to the nearest
1 2n. i=1. 2m+1 i = m, while. 2m + 1 = 1. is the best possible for any odd n.
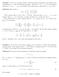 Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
2013 Sharygin Geometry Olympiad
 Sharygin Geometry Olympiad 2013 First Round 1 Let ABC be an isosceles triangle with AB = BC. Point E lies on the side AB, and ED is the perpendicular from E to BC. It is known that AE = DE. Find DAC. 2
Sharygin Geometry Olympiad 2013 First Round 1 Let ABC be an isosceles triangle with AB = BC. Point E lies on the side AB, and ED is the perpendicular from E to BC. It is known that AE = DE. Find DAC. 2
Baltic Way 2008 Gdańsk, November 8, 2008
 Baltic Way 008 Gdańsk, November 8, 008 Problems and solutions Problem 1. Determine all polynomials p(x) with real coefficients such that p((x + 1) ) = (p(x) + 1) and p(0) = 0. Answer: p(x) = x. Solution:
Baltic Way 008 Gdańsk, November 8, 008 Problems and solutions Problem 1. Determine all polynomials p(x) with real coefficients such that p((x + 1) ) = (p(x) + 1) and p(0) = 0. Answer: p(x) = x. Solution:
Australian Intermediate Mathematics Olympiad 2016
 A u s t r a l i a n M at h e m at i c a l O ly m p i a d C o m m i t t e e a d e p a r t m e n t o f t h e a u s t r a l i a n m at h e m at i c s t r u s t Australian Intermediate Mathematics Olympiad
A u s t r a l i a n M at h e m at i c a l O ly m p i a d C o m m i t t e e a d e p a r t m e n t o f t h e a u s t r a l i a n m at h e m at i c s t r u s t Australian Intermediate Mathematics Olympiad
27 th Annual ARML Scrimmage
 27 th Annual ARML Scrimmage Featuring: Howard County ARML Team (host) Baltimore County ARML Team ARML Team Alumni Citizens By Raymond Cheong May 23, 2012 Reservoir HS Individual Round (10 min. per pair
27 th Annual ARML Scrimmage Featuring: Howard County ARML Team (host) Baltimore County ARML Team ARML Team Alumni Citizens By Raymond Cheong May 23, 2012 Reservoir HS Individual Round (10 min. per pair
INTERNATIONAL MATHEMATICAL OLYMPIADS. Hojoo Lee, Version 1.0. Contents 1. Problems 1 2. Answers and Hints References
 INTERNATIONAL MATHEMATICAL OLYMPIADS 1990 2002 Hojoo Lee, Version 1.0 Contents 1. Problems 1 2. Answers and Hints 15 3. References 16 1. Problems 021 Let n be a positive integer. Let T be the set of points
INTERNATIONAL MATHEMATICAL OLYMPIADS 1990 2002 Hojoo Lee, Version 1.0 Contents 1. Problems 1 2. Answers and Hints 15 3. References 16 1. Problems 021 Let n be a positive integer. Let T be the set of points
5 Find an equation of the circle in which AB is a diameter in each case. a A (1, 2) B (3, 2) b A ( 7, 2) B (1, 8) c A (1, 1) B (4, 0)
 C2 CRDINATE GEMETRY Worksheet A 1 Write down an equation of the circle with the given centre and radius in each case. a centre (0, 0) radius 5 b centre (1, 3) radius 2 c centre (4, 6) radius 1 1 d centre
C2 CRDINATE GEMETRY Worksheet A 1 Write down an equation of the circle with the given centre and radius in each case. a centre (0, 0) radius 5 b centre (1, 3) radius 2 c centre (4, 6) radius 1 1 d centre
1 Hanoi Open Mathematical Competition 2017
 1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
Plane geometry Circles: Problems with some Solutions
 The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
Sums of Squares. Bianca Homberg and Minna Liu
 Sums of Squares Bianca Homberg and Minna Liu June 24, 2010 Abstract For our exploration topic, we researched the sums of squares. Certain properties of numbers that can be written as the sum of two squares
Sums of Squares Bianca Homberg and Minna Liu June 24, 2010 Abstract For our exploration topic, we researched the sums of squares. Certain properties of numbers that can be written as the sum of two squares
Hanoi Open Mathematical Competition 2017
 Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
Edexcel New GCE A Level Maths workbook Circle.
 Edexcel New GCE A Level Maths workbook Circle. Edited by: K V Kumaran kumarmaths.weebly.com 1 Finding the Midpoint of a Line To work out the midpoint of line we need to find the halfway point Midpoint
Edexcel New GCE A Level Maths workbook Circle. Edited by: K V Kumaran kumarmaths.weebly.com 1 Finding the Midpoint of a Line To work out the midpoint of line we need to find the halfway point Midpoint
Objective Mathematics
 . In BC, if angles, B, C are in geometric seq- uence with common ratio, then is : b c a (a) (c) 0 (d) 6. If the angles of a triangle are in the ratio 4 : :, then the ratio of the longest side to the perimeter
. In BC, if angles, B, C are in geometric seq- uence with common ratio, then is : b c a (a) (c) 0 (d) 6. If the angles of a triangle are in the ratio 4 : :, then the ratio of the longest side to the perimeter
Pythagoras Theorem and Its Applications
 Lecture 10 Pythagoras Theorem and Its pplications Theorem I (Pythagoras Theorem) or a right-angled triangle with two legs a, b and hypotenuse c, the sum of squares of legs is equal to the square of its
Lecture 10 Pythagoras Theorem and Its pplications Theorem I (Pythagoras Theorem) or a right-angled triangle with two legs a, b and hypotenuse c, the sum of squares of legs is equal to the square of its
2010 Shortlist JBMO - Problems
 Chapter 1 2010 Shortlist JBMO - Problems 1.1 Algebra A1 The real numbers a, b, c, d satisfy simultaneously the equations abc d = 1, bcd a = 2, cda b = 3, dab c = 6. Prove that a + b + c + d 0. A2 Determine
Chapter 1 2010 Shortlist JBMO - Problems 1.1 Algebra A1 The real numbers a, b, c, d satisfy simultaneously the equations abc d = 1, bcd a = 2, cda b = 3, dab c = 6. Prove that a + b + c + d 0. A2 Determine
36th United States of America Mathematical Olympiad
 36th United States of America Mathematical Olympiad 1. Let n be a positive integer. Define a sequence by setting a 1 = n and, for each k > 1, letting a k be the unique integer in the range 0 a k k 1 for
36th United States of America Mathematical Olympiad 1. Let n be a positive integer. Define a sequence by setting a 1 = n and, for each k > 1, letting a k be the unique integer in the range 0 a k k 1 for
37th United States of America Mathematical Olympiad
 37th United States of America Mathematical Olympiad 1. Prove that for each positive integer n, there are pairwise relatively prime integers k 0, k 1,..., k n, all strictly greater than 1, such that k 0
37th United States of America Mathematical Olympiad 1. Prove that for each positive integer n, there are pairwise relatively prime integers k 0, k 1,..., k n, all strictly greater than 1, such that k 0
1. Suppose that a, b, c and d are four different integers. Explain why. (a b)(a c)(a d)(b c)(b d)(c d) a 2 + ab b = 2018.
 New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
6.2: Isosceles Triangles
 6.2: Isosceles Triangles Dec 5 4:34 PM 1 Define an Isosceles Triangle. A triangle that has (at least) two sides of equal length. Dec 5 4:34 PM 2 Draw an Isosceles Triangle. Label all parts and mark the
6.2: Isosceles Triangles Dec 5 4:34 PM 1 Define an Isosceles Triangle. A triangle that has (at least) two sides of equal length. Dec 5 4:34 PM 2 Draw an Isosceles Triangle. Label all parts and mark the
Olimpiada Matemática de Centroamérica y el Caribe
 Olimpiada Matemática de Centroamérica y el Caribe 1st Centromerican 1999 Problem A1 A, B, C, D, E each has a unique piece of news. They make a series of phone calls to each other. In each call, the caller
Olimpiada Matemática de Centroamérica y el Caribe 1st Centromerican 1999 Problem A1 A, B, C, D, E each has a unique piece of news. They make a series of phone calls to each other. In each call, the caller
The sum x 1 + x 2 + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E): None of the above. How many pairs of positive integers (x, y) are there, those satisfy
 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
Math 46 Final Exam Review Packet
 Math 46 Final Exam Review Packet Question 1. Perform the indicated operation. Simplify if possible. 7 x x 2 2x + 3 2 x Question 2. The sum of a number and its square is 72. Find the number. Question 3.
Math 46 Final Exam Review Packet Question 1. Perform the indicated operation. Simplify if possible. 7 x x 2 2x + 3 2 x Question 2. The sum of a number and its square is 72. Find the number. Question 3.
Unit 4-Review. Part 1- Triangle Theorems and Rules
 Unit 4-Review - Triangle Theorems and Rules Name of Theorem or relationship In words/ Symbols Diagrams/ Hints/ Techniques 1. Side angle relationship 2. Triangle inequality Theorem 3. Pythagorean Theorem
Unit 4-Review - Triangle Theorems and Rules Name of Theorem or relationship In words/ Symbols Diagrams/ Hints/ Techniques 1. Side angle relationship 2. Triangle inequality Theorem 3. Pythagorean Theorem
Downloaded from
 MODEL TEST PAPER SUMMATIVE ASSESSMENT-I SOLVED Time : 3 hrs. Maximum Marks: 80 General Instructions. Section-A consists of 8 parts carrying 1 mark each Section-B Q2 to Q11 carry 2 marks each Section-C
MODEL TEST PAPER SUMMATIVE ASSESSMENT-I SOLVED Time : 3 hrs. Maximum Marks: 80 General Instructions. Section-A consists of 8 parts carrying 1 mark each Section-B Q2 to Q11 carry 2 marks each Section-C
45-th Moldova Mathematical Olympiad 2001
 45-th Moldova Mathematical Olympiad 200 Final Round Chişinǎu, March 2 Grade 7. Prove that y 3 2x+ x 3 2y x 2 + y 2 for any numbers x,y [, 2 3 ]. When does equality occur? 2. Let S(n) denote the sum of
45-th Moldova Mathematical Olympiad 200 Final Round Chişinǎu, March 2 Grade 7. Prove that y 3 2x+ x 3 2y x 2 + y 2 for any numbers x,y [, 2 3 ]. When does equality occur? 2. Let S(n) denote the sum of
UNC Charlotte 2005 Comprehensive March 7, 2005
 March 7, 2005 1. The numbers x and y satisfy 2 x = 15 and 15 y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D Solution: C. Note that (2 x ) y = 15 y = 32 so 2 xy = 2 5 and
March 7, 2005 1. The numbers x and y satisfy 2 x = 15 and 15 y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D Solution: C. Note that (2 x ) y = 15 y = 32 so 2 xy = 2 5 and
2007 Fermat Contest (Grade 11)
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 007 Fermat Contest (Grade 11) Tuesday, February 0, 007 Solutions
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 007 Fermat Contest (Grade 11) Tuesday, February 0, 007 Solutions
1966 IMO Shortlist. IMO Shortlist 1966
 IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
SEQUENCES, MATHEMATICAL INDUCTION, AND RECURSION
 CHAPTER 5 SEQUENCES, MATHEMATICAL INDUCTION, AND RECURSION Copyright Cengage Learning. All rights reserved. SECTION 5.4 Strong Mathematical Induction and the Well-Ordering Principle for the Integers Copyright
CHAPTER 5 SEQUENCES, MATHEMATICAL INDUCTION, AND RECURSION Copyright Cengage Learning. All rights reserved. SECTION 5.4 Strong Mathematical Induction and the Well-Ordering Principle for the Integers Copyright
OLYMON. Produced by the Canadian Mathematical Society and the Department of Mathematics of the University of Toronto. Issue 10:3.
 OLYMON Produced by the Canadian Mathematical Society and the Department of Mathematics of the University of Toronto. Please send your solutions to Rosu Mihai 54 Judith Crescent Brampton, ON L6S 3J4 Issue
OLYMON Produced by the Canadian Mathematical Society and the Department of Mathematics of the University of Toronto. Please send your solutions to Rosu Mihai 54 Judith Crescent Brampton, ON L6S 3J4 Issue
Chapter 3. The angle bisectors. 3.1 The angle bisector theorem
 hapter 3 The angle bisectors 3.1 The angle bisector theorem Theorem 3.1 (ngle bisector theorem). The bisectors of an angle of a triangle divide its opposite side in the ratio of the remaining sides. If
hapter 3 The angle bisectors 3.1 The angle bisector theorem Theorem 3.1 (ngle bisector theorem). The bisectors of an angle of a triangle divide its opposite side in the ratio of the remaining sides. If
For math conventions used on the GRE, refer to this link:
 GRE Review ISU Student Success Center Quantitative Workshop One Quantitative Section: Overview Your test will include either two or three 35-minute quantitative sections. There will be 20 questions in
GRE Review ISU Student Success Center Quantitative Workshop One Quantitative Section: Overview Your test will include either two or three 35-minute quantitative sections. There will be 20 questions in
Solution: By direct calculation, or observe that = = ( ) 2222 = =
 1 Fillins 1. Find the last 4 digits of 3333 6666. Solution: 7778. By direct calculation, or observe that 3333 6666 = 9999 2222 = (10000 1) 2222 = 22220000 2222 = 22217778. 2. How many ways are there to
1 Fillins 1. Find the last 4 digits of 3333 6666. Solution: 7778. By direct calculation, or observe that 3333 6666 = 9999 2222 = (10000 1) 2222 = 22220000 2222 = 22217778. 2. How many ways are there to
chapter 1 vector geometry solutions V Consider the parallelogram shown alongside. Which of the following statements are true?
 chapter vector geometry solutions V. Exercise A. For the shape shown, find a single vector which is equal to a)!!! " AB + BC AC b)! AD!!! " + DB AB c)! AC + CD AD d)! BC + CD!!! " + DA BA e) CD!!! " "
chapter vector geometry solutions V. Exercise A. For the shape shown, find a single vector which is equal to a)!!! " AB + BC AC b)! AD!!! " + DB AB c)! AC + CD AD d)! BC + CD!!! " + DA BA e) CD!!! " "
3. A square has 4 sides, so S = 4. A pentagon has 5 vertices, so P = 5. Hence, S + P = 9. = = 5 3.
 JHMMC 01 Grade Solutions October 1, 01 1. By counting, there are 7 words in this question.. (, 1, ) = 1 + 1 + = 9 + 1 + =.. A square has sides, so S =. A pentagon has vertices, so P =. Hence, S + P = 9..
JHMMC 01 Grade Solutions October 1, 01 1. By counting, there are 7 words in this question.. (, 1, ) = 1 + 1 + = 9 + 1 + =.. A square has sides, so S =. A pentagon has vertices, so P =. Hence, S + P = 9..
2017 OHMIO Individual Competition
 2017 OHMIO Individual Competition 1. On a winter hike with friends (all of whom were wearing either a scarlet or gray hat), I saw twice as many scarlet hats as gray. That s silly, said a friend. I see
2017 OHMIO Individual Competition 1. On a winter hike with friends (all of whom were wearing either a scarlet or gray hat), I saw twice as many scarlet hats as gray. That s silly, said a friend. I see
Problems and Solutions
 46 th Canadian Mathematical Olympiad Wednesday, April 2, 204 Problems and Solutions. Let a, a 2,..., a n be positive real numbers whose product is. Show that the sum a a 2 + + a ( + a )( + a 2 ) + a 3
46 th Canadian Mathematical Olympiad Wednesday, April 2, 204 Problems and Solutions. Let a, a 2,..., a n be positive real numbers whose product is. Show that the sum a a 2 + + a ( + a )( + a 2 ) + a 3
XX Asian Pacific Mathematics Olympiad
 XX Asian Pacific Mathematics Olympiad March, 008 Problem 1. Let ABC be a triangle with A < 60. Let X and Y be the points on the sides AB and AC, respectively, such that CA + AX = CB + BX and BA + AY =
XX Asian Pacific Mathematics Olympiad March, 008 Problem 1. Let ABC be a triangle with A < 60. Let X and Y be the points on the sides AB and AC, respectively, such that CA + AX = CB + BX and BA + AY =
USA Mathematical Talent Search Round 3 Solutions Year 20 Academic Year
 1/3/20. Let S be the set of all 10-digit numbers (which by definition may not begin with 0) in which each digit 0 through 9 appears exactly once. For example, the number 3,820,956,714 is in S. A number
1/3/20. Let S be the set of all 10-digit numbers (which by definition may not begin with 0) in which each digit 0 through 9 appears exactly once. For example, the number 3,820,956,714 is in S. A number
Solutions to Problems for Math. H90 Issued 27 Aug. 2007
 Problem 1: Given is an ellipse E neither a circle nor degenerate (i.e. a straight line segment). Let be the largest of the areas of triangles inscribed in E. How many inscribed triangles have maximal area?
Problem 1: Given is an ellipse E neither a circle nor degenerate (i.e. a straight line segment). Let be the largest of the areas of triangles inscribed in E. How many inscribed triangles have maximal area?
USA Mathematics Talent Search
 16 3 1 (a) Since x and y are 3-digit integers, we begin by noting that the condition 6(x y) = (y x) is equivalent to 6(1, 000x + y) = 1, 000y + x = 5, 999x = 994y, which (after factoring out a 7 by long
16 3 1 (a) Since x and y are 3-digit integers, we begin by noting that the condition 6(x y) = (y x) is equivalent to 6(1, 000x + y) = 1, 000y + x = 5, 999x = 994y, which (after factoring out a 7 by long
CANADIAN MATHEMATICAL OLYMPIAD 2010 PROBLEMS AND SOLUTIONS
 CANADIAN MATHEMATICAL OLYMPIAD 2010 PROBLEMS AND SOLUTIONS (1) For a positive integer n, an n-staircase is a figure consisting of unit squares, with one square in the first row, two squares in the second
CANADIAN MATHEMATICAL OLYMPIAD 2010 PROBLEMS AND SOLUTIONS (1) For a positive integer n, an n-staircase is a figure consisting of unit squares, with one square in the first row, two squares in the second
Singapore Mathematical Society
 Singapore Mathematical Society Interschool Mathematical Competition 1990 Part A Saturday, 23 June 1990 100Q-1100 Attempt as many questions as you can. No calculators are allowed. Circle your answers on
Singapore Mathematical Society Interschool Mathematical Competition 1990 Part A Saturday, 23 June 1990 100Q-1100 Attempt as many questions as you can. No calculators are allowed. Circle your answers on
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca Cayley Contest. (Grade 10) Tuesday, February 27, 2018
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 018 Cayley Contest (Grade 10) Tuesday, February 7, 018 (in North America and South America) Wednesday, February 8, 018 (outside of
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 018 Cayley Contest (Grade 10) Tuesday, February 7, 018 (in North America and South America) Wednesday, February 8, 018 (outside of
CBSE X Mathematics 2012 Solution (SET 1) Section B
 CBSE X Mathematics 01 Solution (SET 1) Section B Q11. Find the value(s) of k so that the quadratic equation x kx + k = 0 has equal roots. Given equation is x kx k 0 For the given equation to have equal
CBSE X Mathematics 01 Solution (SET 1) Section B Q11. Find the value(s) of k so that the quadratic equation x kx + k = 0 has equal roots. Given equation is x kx k 0 For the given equation to have equal
Gordon solutions. n=1 1. p n
 Gordon solutions 1. A positive integer is called a palindrome if its base-10 expansion is unchanged when it is reversed. For example, 121 and 7447 are palindromes. Show that if we denote by p n the nth
Gordon solutions 1. A positive integer is called a palindrome if its base-10 expansion is unchanged when it is reversed. For example, 121 and 7447 are palindromes. Show that if we denote by p n the nth
XIV GEOMETRICAL OLYMPIAD IN HONOUR OF I.F.SHARYGIN The correspondence round. Solutions
 XIV GEOMETRIL OLYMPI IN HONOUR OF I.F.SHRYGIN The correspondence round. Solutions 1. (L.Shteingarts, grade 8) Three circles lie inside a square. Each of them touches externally two remaining circles. lso
XIV GEOMETRIL OLYMPI IN HONOUR OF I.F.SHRYGIN The correspondence round. Solutions 1. (L.Shteingarts, grade 8) Three circles lie inside a square. Each of them touches externally two remaining circles. lso
Chapter 7 Quadratic Equations
 Chapter 7 Quadratic Equations We have worked with trinomials of the form ax 2 + bx + c. Now we are going to work with equations of this form ax 2 + bx + c = 0 quadratic equations. When we write a quadratic
Chapter 7 Quadratic Equations We have worked with trinomials of the form ax 2 + bx + c. Now we are going to work with equations of this form ax 2 + bx + c = 0 quadratic equations. When we write a quadratic
SOUTH AFRICAN TERTIARY MATHEMATICS OLYMPIAD
 SOUTH AFRICAN TERTIARY MATHEMATICS OLYMPIAD. Determine the following value: 7 August 6 Solutions π + π. Solution: Since π
SOUTH AFRICAN TERTIARY MATHEMATICS OLYMPIAD. Determine the following value: 7 August 6 Solutions π + π. Solution: Since π
a 2 + b 2 = (p 2 q 2 ) 2 + 4p 2 q 2 = (p 2 + q 2 ) 2 = c 2,
 5.3. Pythagorean triples Definition. A Pythagorean triple is a set (a, b, c) of three integers such that (in order) a 2 + b 2 c 2. We may as well suppose that all of a, b, c are non-zero, and positive.
5.3. Pythagorean triples Definition. A Pythagorean triple is a set (a, b, c) of three integers such that (in order) a 2 + b 2 c 2. We may as well suppose that all of a, b, c are non-zero, and positive.
Unit 8. ANALYTIC GEOMETRY.
 Unit 8. ANALYTIC GEOMETRY. 1. VECTORS IN THE PLANE A vector is a line segment running from point A (tail) to point B (head). 1.1 DIRECTION OF A VECTOR The direction of a vector is the direction of the
Unit 8. ANALYTIC GEOMETRY. 1. VECTORS IN THE PLANE A vector is a line segment running from point A (tail) to point B (head). 1.1 DIRECTION OF A VECTOR The direction of a vector is the direction of the
Solutions and scoring for 1st Midterm Exam Geometry 515 Fall Oct 2 Mon 4:00-5:20 pm
 Solutions and scoring for 1st Midterm Exam Geometry 515 Fall 2017 Oct 2 Mon 4:00-5:20 pm 1. On the line AB you have the point O between the points A and B (i.e. rays OA and OB form a straight angle AOB).
Solutions and scoring for 1st Midterm Exam Geometry 515 Fall 2017 Oct 2 Mon 4:00-5:20 pm 1. On the line AB you have the point O between the points A and B (i.e. rays OA and OB form a straight angle AOB).
NEW YORK CITY INTERSCHOLASTIC MATHEMATICS LEAGUE Senior A Division CONTEST NUMBER 1
 Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
Circles in Neutral Geometry
 Everything we do in this set of notes is Neutral. Definitions: 10.1 - Circles in Neutral Geometry circle is the set of points in a plane which lie at a positive, fixed distance r from some fixed point.
Everything we do in this set of notes is Neutral. Definitions: 10.1 - Circles in Neutral Geometry circle is the set of points in a plane which lie at a positive, fixed distance r from some fixed point.
All variables a, b, n, etc are integers unless otherwise stated. Each part of a problem is worth 5 points.
 Math 152, Problem Set 2 solutions (2018-01-24) All variables a, b, n, etc are integers unless otherwise stated. Each part of a problem is worth 5 points. 1. Let us look at the following equation: x 5 1
Math 152, Problem Set 2 solutions (2018-01-24) All variables a, b, n, etc are integers unless otherwise stated. Each part of a problem is worth 5 points. 1. Let us look at the following equation: x 5 1
SOLUTIONS FOR IMO 2005 PROBLEMS
 SOLUTIONS FOR IMO 005 PROBLEMS AMIR JAFARI AND KASRA RAFI Problem. Six points are chosen on the sides of an equilateral triangle AB: A, A on B; B, B on A;, on AB. These points are the vertices of a convex
SOLUTIONS FOR IMO 005 PROBLEMS AMIR JAFARI AND KASRA RAFI Problem. Six points are chosen on the sides of an equilateral triangle AB: A, A on B; B, B on A;, on AB. These points are the vertices of a convex
Q.1 If a, b, c are distinct positive real in H.P., then the value of the expression, (A) 1 (B) 2 (C) 3 (D) 4. (A) 2 (B) 5/2 (C) 3 (D) none of these
 Q. If a, b, c are distinct positive real in H.P., then the value of the expression, b a b c + is equal to b a b c () (C) (D) 4 Q. In a triangle BC, (b + c) = a bc where is the circumradius of the triangle.
Q. If a, b, c are distinct positive real in H.P., then the value of the expression, b a b c + is equal to b a b c () (C) (D) 4 Q. In a triangle BC, (b + c) = a bc where is the circumradius of the triangle.
XIII GEOMETRICAL OLYMPIAD IN HONOUR OF I.F.SHARYGIN The correspondence round. Solutions
 XIII GEOMETRIL OLYMPID IN HONOUR OF I.F.SHRYGIN The correspondence round. Solutions 1. (.Zaslavsky) (8) Mark on a cellular paper four nodes forming a convex quadrilateral with the sidelengths equal to
XIII GEOMETRIL OLYMPID IN HONOUR OF I.F.SHRYGIN The correspondence round. Solutions 1. (.Zaslavsky) (8) Mark on a cellular paper four nodes forming a convex quadrilateral with the sidelengths equal to
2013 IMO Shortlist. a b c d 1
 IMO Shortlist 2013 Algebra A1 A2 Letnbeapositiveintegerandleta 1,...,a n 1 bearbitraryrealnumbers. Define the sequences u 0,...,u n and v 0,...,v n inductively by u 0 = u 1 = v 0 = v 1 = 1, and u k+1 =
IMO Shortlist 2013 Algebra A1 A2 Letnbeapositiveintegerandleta 1,...,a n 1 bearbitraryrealnumbers. Define the sequences u 0,...,u n and v 0,...,v n inductively by u 0 = u 1 = v 0 = v 1 = 1, and u k+1 =
1998 IMO Shortlist BM BN BA BC AB BC CD DE EF BC CA AE EF FD
 IMO Shortlist 1998 Geometry 1 A convex quadrilateral ABCD has perpendicular diagonals. The perpendicular bisectors of the sides AB and CD meet at a unique point P inside ABCD. the quadrilateral ABCD is
IMO Shortlist 1998 Geometry 1 A convex quadrilateral ABCD has perpendicular diagonals. The perpendicular bisectors of the sides AB and CD meet at a unique point P inside ABCD. the quadrilateral ABCD is
PRIMES Math Problem Set
 PRIMES Math Problem Set PRIMES 017 Due December 1, 01 Dear PRIMES applicant: This is the PRIMES 017 Math Problem Set. Please send us your solutions as part of your PRIMES application by December 1, 01.
PRIMES Math Problem Set PRIMES 017 Due December 1, 01 Dear PRIMES applicant: This is the PRIMES 017 Math Problem Set. Please send us your solutions as part of your PRIMES application by December 1, 01.
Solutions to Practice Final
 s to Practice Final 1. (a) What is φ(0 100 ) where φ is Euler s φ-function? (b) Find an integer x such that 140x 1 (mod 01). Hint: gcd(140, 01) = 7. (a) φ(0 100 ) = φ(4 100 5 100 ) = φ( 00 5 100 ) = (
s to Practice Final 1. (a) What is φ(0 100 ) where φ is Euler s φ-function? (b) Find an integer x such that 140x 1 (mod 01). Hint: gcd(140, 01) = 7. (a) φ(0 100 ) = φ(4 100 5 100 ) = φ( 00 5 100 ) = (
Mathematics. Single Correct Questions
 Mathematics Single Correct Questions +4 1.00 1. If and then 2. The number of solutions of, in the interval is : 3. If then equals : 4. A plane bisects the line segment joining the points and at right angles.
Mathematics Single Correct Questions +4 1.00 1. If and then 2. The number of solutions of, in the interval is : 3. If then equals : 4. A plane bisects the line segment joining the points and at right angles.
International Mathematics TOURNAMENT OF TOWNS. Senior A-Level Paper Fall 2012.
 5 International Mathematics TOURNAMENT OF TOWNS Senior A-Level Paper Fall 2012. 1. Given an infinite sequence of numbers a 1,a 2,a 3,... For each positive integer k there exists a positive integer t =
5 International Mathematics TOURNAMENT OF TOWNS Senior A-Level Paper Fall 2012. 1. Given an infinite sequence of numbers a 1,a 2,a 3,... For each positive integer k there exists a positive integer t =
Chapter (Circle) * Circle - circle is locus of such points which are at equidistant from a fixed point in
 Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
34 th United States of America Mathematical Olympiad
 34 th United States of America Mathematical Olympiad 1. Determine all composite positive integers n for which it is possible to arrange all divisors of n that are greater than 1 in a circle so that no
34 th United States of America Mathematical Olympiad 1. Determine all composite positive integers n for which it is possible to arrange all divisors of n that are greater than 1 in a circle so that no
CHAPTER 1 REAL NUMBERS KEY POINTS
 CHAPTER 1 REAL NUMBERS 1. Euclid s division lemma : KEY POINTS For given positive integers a and b there exist unique whole numbers q and r satisfying the relation a = bq + r, 0 r < b. 2. Euclid s division
CHAPTER 1 REAL NUMBERS 1. Euclid s division lemma : KEY POINTS For given positive integers a and b there exist unique whole numbers q and r satisfying the relation a = bq + r, 0 r < b. 2. Euclid s division
2008 Euclid Contest. Solutions. Canadian Mathematics Competition. Tuesday, April 15, c 2008 Centre for Education in Mathematics and Computing
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 008 Euclid Contest Tuesday, April 5, 008 Solutions c 008
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 008 Euclid Contest Tuesday, April 5, 008 Solutions c 008
MA094 Part 2 - Beginning Algebra Summary
 MA094 Part - Beginning Algebra Summary Page of 8/8/0 Big Picture Algebra is Solving Equations with Variables* Variable Variables Linear Equations x 0 MA090 Solution: Point 0 Linear Inequalities x < 0 page
MA094 Part - Beginning Algebra Summary Page of 8/8/0 Big Picture Algebra is Solving Equations with Variables* Variable Variables Linear Equations x 0 MA090 Solution: Point 0 Linear Inequalities x < 0 page
International Mathematical Olympiad. Preliminary Selection Contest 2017 Hong Kong. Outline of Solutions 5. 3*
 International Mathematical Olympiad Preliminary Selection Contest Hong Kong Outline of Solutions Answers: 06 0000 * 6 97 7 6 8 7007 9 6 0 6 8 77 66 7 7 0 6 7 7 6 8 9 8 0 0 8 *See the remar after the solution
International Mathematical Olympiad Preliminary Selection Contest Hong Kong Outline of Solutions Answers: 06 0000 * 6 97 7 6 8 7007 9 6 0 6 8 77 66 7 7 0 6 7 7 6 8 9 8 0 0 8 *See the remar after the solution
Solutions and Marking Schemes
 THIRTY FIRST IRISH MATHEMATICAL OLYMPIAD 1. Proposed by Bernd Kreussler. Saturday, 1 May 018 First Paper Solutions and Marking Schemes Mary and Pat play the following number game. Mary picks an initial
THIRTY FIRST IRISH MATHEMATICAL OLYMPIAD 1. Proposed by Bernd Kreussler. Saturday, 1 May 018 First Paper Solutions and Marking Schemes Mary and Pat play the following number game. Mary picks an initial
Part 2 - Beginning Algebra Summary
 Part - Beginning Algebra Summary Page 1 of 4 1/1/01 1. Numbers... 1.1. Number Lines... 1.. Interval Notation.... Inequalities... 4.1. Linear with 1 Variable... 4. Linear Equations... 5.1. The Cartesian
Part - Beginning Algebra Summary Page 1 of 4 1/1/01 1. Numbers... 1.1. Number Lines... 1.. Interval Notation.... Inequalities... 4.1. Linear with 1 Variable... 4. Linear Equations... 5.1. The Cartesian
Georgia Tech HSMC 2010
 Georgia Tech HSMC 2010 Varsity Multiple Choice February 27 th, 2010 1. A cube of SPAM defined by S = {(x, y, z) 0 x, y, z 1} is cut along the planes x = y, y = z, z = x. How many pieces are there? (No
Georgia Tech HSMC 2010 Varsity Multiple Choice February 27 th, 2010 1. A cube of SPAM defined by S = {(x, y, z) 0 x, y, z 1} is cut along the planes x = y, y = z, z = x. How many pieces are there? (No
Olympiad Combinatorics. Pranav A. Sriram
 Olympiad Combinatorics Pranav A. Sriram August 2014 Chapter 4: Existence 1 Copyright notices All USAMO and USA Team Selection Test problems in this chapter are copyrighted by the Mathematical Association
Olympiad Combinatorics Pranav A. Sriram August 2014 Chapter 4: Existence 1 Copyright notices All USAMO and USA Team Selection Test problems in this chapter are copyrighted by the Mathematical Association
Mathematics Extension 1
 Name: St George Girls High School Trial Higher School Certificate Examination 2014 Mathematics Extension 1 General Instructions Reading time 5 minutes Working time 2 hours Write using blue or black pen.
Name: St George Girls High School Trial Higher School Certificate Examination 2014 Mathematics Extension 1 General Instructions Reading time 5 minutes Working time 2 hours Write using blue or black pen.
Solutions to Exercises in Chapter 1
 Solutions to Exercises in hapter 1 1.6.1 heck that the formula 1 a c b d works for rectangles but not for 4 parallelograms. b a c a d d b c FIGURE S1.1: Exercise 1.6.1. rectangle and a parallelogram For
Solutions to Exercises in hapter 1 1.6.1 heck that the formula 1 a c b d works for rectangles but not for 4 parallelograms. b a c a d d b c FIGURE S1.1: Exercise 1.6.1. rectangle and a parallelogram For
D - E - F - G (1967 Jr.) Given that then find the number of real solutions ( ) of this equation.
 D - E - F - G - 18 1. (1975 Jr.) Given and. Two circles, with centres and, touch each other and also the sides of the rectangle at and. If the radius of the smaller circle is 2, then find the radius of
D - E - F - G - 18 1. (1975 Jr.) Given and. Two circles, with centres and, touch each other and also the sides of the rectangle at and. If the radius of the smaller circle is 2, then find the radius of
This class will demonstrate the use of bijections to solve certain combinatorial problems simply and effectively.
 . Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
. Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
2 BAMO 2015 Problems and Solutions February 26, 2015
 17TH AY AREA MATHEMATIAL OLYMPIAD PROLEMS AND SOLUTIONS A: There are 7 boxes arranged in a row and numbered 1 through 7. You have a stack of 2015 cards, which you place one by one in the boxes. The first
17TH AY AREA MATHEMATIAL OLYMPIAD PROLEMS AND SOLUTIONS A: There are 7 boxes arranged in a row and numbered 1 through 7. You have a stack of 2015 cards, which you place one by one in the boxes. The first
International Mathematics TOURNAMENT OF THE TOWNS
 International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2011 1 Pete has marked at least 3 points in the plane such that all distances between them are different A pair of marked points
International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2011 1 Pete has marked at least 3 points in the plane such that all distances between them are different A pair of marked points
(q 1)p q. = 1 (p 1)(q 1).
 altic Way 001 Hamburg, November 4, 001 Problems 1. set of 8 problems was prepared for an examination. Each student was given 3 of them. No two students received more than one common problem. What is the
altic Way 001 Hamburg, November 4, 001 Problems 1. set of 8 problems was prepared for an examination. Each student was given 3 of them. No two students received more than one common problem. What is the
International Mathematics TOURNAMENT OF THE TOWNS: SOLUTIONS
 International Mathematics TOURNAMENT OF THE TOWNS: SOLUTIONS Juniors (Grades up to 10) A-Level Paper Spring 2003. 1 Answer: Yes. Example. Consider quadratic equation x 2 + 5x + 6 = 0. It could be transformed
International Mathematics TOURNAMENT OF THE TOWNS: SOLUTIONS Juniors (Grades up to 10) A-Level Paper Spring 2003. 1 Answer: Yes. Example. Consider quadratic equation x 2 + 5x + 6 = 0. It could be transformed
XII Geometrical Olympiad in honour of I.F.Sharygin Final round. Solutions. First day. 8 grade
 XII Geometrical Olympiad in honour of I.F.Sharygin Final round. Solutions. First day. 8 grade Ratmino, 2016, July 31 1. (Yu.linkov) n altitude H of triangle bisects a median M. Prove that the medians of
XII Geometrical Olympiad in honour of I.F.Sharygin Final round. Solutions. First day. 8 grade Ratmino, 2016, July 31 1. (Yu.linkov) n altitude H of triangle bisects a median M. Prove that the medians of
Singapore International Mathematical Olympiad 2008 Senior Team Training. Take Home Test Solutions. 15x 2 7y 2 = 9 y 2 0 (mod 3) x 0 (mod 3).
 Singapore International Mathematical Olympiad 2008 Senior Team Training Take Home Test Solutions. Show that the equation 5x 2 7y 2 = 9 has no solution in integers. If the equation has a solution in integer,
Singapore International Mathematical Olympiad 2008 Senior Team Training Take Home Test Solutions. Show that the equation 5x 2 7y 2 = 9 has no solution in integers. If the equation has a solution in integer,
2005 Euclid Contest. Solutions
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 2005 Euclid Contest Tuesday, April 19, 2005 Solutions c
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 2005 Euclid Contest Tuesday, April 19, 2005 Solutions c
Written test, 25 problems / 90 minutes
 Sponsored by: UGA Math Department and UGA Math Club Written test, 5 problems / 90 minutes October, 06 WITH SOLUTIONS Problem. Let a represent a digit from to 9. Which a gives a! aa + a = 06? Here aa indicates
Sponsored by: UGA Math Department and UGA Math Club Written test, 5 problems / 90 minutes October, 06 WITH SOLUTIONS Problem. Let a represent a digit from to 9. Which a gives a! aa + a = 06? Here aa indicates
Trigonometrical identities and inequalities
 Trigonometrical identities and inequalities Finbarr Holland January 1, 010 1 A review of the trigonometrical functions These are sin, cos, & tan. These are discussed in the Maynooth Olympiad Manual, which
Trigonometrical identities and inequalities Finbarr Holland January 1, 010 1 A review of the trigonometrical functions These are sin, cos, & tan. These are discussed in the Maynooth Olympiad Manual, which
