Unofficial Solutions
|
|
|
- Ethelbert Fowler
- 5 years ago
- Views:
Transcription
1 Canadian Open Mathematics Challenge 2016 Unofficial Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit These solutions are unofficial. If you notice an error or a lack of clarity in the solutions, please us at comc2016@cms.math.ca The COMC has 3 sections: A. Short answer questions worth 4 marks each. A correct answer receives full marks. Partial marks may be awarded for work shown if a correct answer is not provided. B. Short answer questions worth 6 marks each. A correct answer receives full marks. Partial marks may be awarded for work shown if a correct answer is not provided. C. Multi-part full solution questions worth 10 marks each. Solutions must be complete and clearly presented to receive full marks. c 2016 Canadian Mathematical Society Page 1
2 Unofficial Solutions COMC 2016 Section A 4 marks each 1. Pat has ten tests to write in the school year. He can obtain a maximum score of 100 on each test. The average score of Pat s first eight tests is 80 and the average score of all of Pat s tests is N. What is the maximum possible value of N? Solution: Pat s average will be highest if he scores as high as possible on his last two tests and the highest he can score on each test is 100. His total score for the ten tests will be = 840 and his average will be 840/10 = A square is inscribed in a circle, as shown in the figure. If the area of the circle is 16π cm 2 and the area of the square is S cm 2, what is the value of S? Solution: The area of a circle with radius r is πr 2. Since this circle has area 16π, we have r 2 = 16, and r = 4. So the circle has radius 4 and diameter 8. Let t be the side length of the square. By the Pythagorean Theorem, t 2 + t 2 = 8 2 so t 2 = 32, which is the area of the square. Page 2 c 2016 Canadian Mathematical Society
3 COMC Unofficial Solutions 3. Determine the pair of real numbers x, y which satisfy the system of equations: 1 x + 1 y = 1 2 x + 3 y = 4 Solution 1: Let a = 1 x and b = 1 y. We can rewrite our equations as: a + b = 1 2a + 3b = 4 Subtracting twice the first equation from the second equation gives b = 2. Substituting this into one of the equations gives a = 1. These give x = 1 and y = 1 2. Solution 2: Taking 3 times the first equation and subtracting the second equation gives 1 x = 1, so x = 1. Substituting this into the first equation gives y = 1 which yields y = 1 2. Thus (x, y) = ( 1, 1 2 ). 4. Three males and two females write their names on sheets of paper, and randomly arrange them in order, from left to right. What is the probability that all of the female names appear to the right of all the male names? Solution 1: We need the first (leftmost) three names to be males and the last two names to be females. The probability that the fifth name is female is 2 5. Given that the fifth name is female, the probability that the fourth name is also female is 1 4. The probability that both are female is therefore = Solution 2: We need the first (leftmost) three names to be males and the last two names to be females. There are ( 5 2) = 10 choices for which two names are the female names, so the probability the last two names are females is c 2016 Canadian Mathematical Society Page 3
4 Unofficial Solutions COMC 2016 Section B 6 marks each 1. If the cubic equation x 3 10x 2 + P x 30 = 0 has three positive integer roots, determine the value of P. Solution 1: If the equation has roots x 1, x 2, x 3, then x 1 +x 2 +x 3 = 10, x 1 x 2 +x 2 x 3 +x 3 x 1 = P and x 1 x 2 x 3 = 30. Suppose x 1 = 1 is a root. Then x 2 + x 3 = 9 and x 2 x 3 = 30. For any pair of integers which multiply to 30, their sum is at least 11, so this is not possible, and 1 is not a root. The only other possibility is that the roots are 2, 3, 5, which gives P = = 31. Solution 2: The roots of the equation are integers and have a product of 30. The possible sets of roots are (1, 1, 30), (1, 2, 15), (1, 3, 10), (1, 5, 6), (2, 3, 5). Of these, only (2, 3, 5) sums to 10, so it must be our set of roots. To find P, we substitute x = 2 into the equation to get P 30 = 0, which yields P = The squares of a 6 6 square grid are each labeled with a point value. As shown in the diagram below, the point value of the square in row i and column j is i j. A path in the grid is a sequence of squares, such that consecutive squares share an edge and no square occurs twice in the sequence. The score of a path is the sum of the point values of all squares in the path. Determine the highest possible score of a path that begins with the bottom left corner of the grid and ends with the top right corner. Solution: Let us colour the squares of the grid with a checkerboard pattern of black and white, starting with black in the bottom left-hand corner. A path in the grid will alternate between black and white squares, beginning and ending on black. Thus, any path cannot contain all 18 white squares. The path in the figure below contains all squares except for the white square with the lowest point value (2), so it will have the highest possible score. The sum of the point values for all the squares is ( )( ) = 441, and the score of the path is 439. Page 4 c 2016 Canadian Mathematical Society
5 COMC Unofficial Solutions 3. A hexagon ABCDEF has AB = 18cm, BC = 8cm, CD = 10cm, DE = 15cm, EF = 20cm, F A = 1cm, F AB = 90, CDE = 90 and BC is parallel to EF. Determine the area of this hexagon, in cm 2. Solution: First, we determine the length of BF and CE. By the Pythagorean theorem, BF = AB 2 + AF 2 = = 325cm and CE = CD 2 + DE 2 = = 325cm. Furthermore, note that BF = CE. Since BC is parallel to CF and BF = CE, BCEF is an isosceles trapezoid with CE = BF. The hexagon comprises of two right-angled triangles F AB and CDE and the isosceles trapezoid BCEF. The area of F AB is F A AB/2 = 1 18/2 = 9cm 2 and the area of CDE is CD DE/2 = 10 15/2 = 75cm 2. Now, we determine the area of the isosceles trapezoid BCEF. Note that BC is parallel to EF and BC < EF and BF = CE. Drop the perpendicular from B, C to side EF, touching EF at X, Y, respectively. Then XY = BC = 8cm, F X + XY + Y E = EF = 20cm and F X = Y E, since BCEF is an isosceles trapezoid. Since F X + Y E = 20 XY = 20 8 = 12cm, F X = Y E = 6cm. Therefore, by the Pythagorean Theorem, BX = BF 2 F X 2 = = 289 = 17cm. Therefore, the height of the trapezoid BCEF is 17cm. Hence, the area of the trapezoid is (BC + EF ) BX/2 = (8 + 20) 17/2 = = 238cm 2. Summing all three pieces, the area of the hexagon is = 322cm 2. c 2016 Canadian Mathematical Society Page 5
6 Unofficial Solutions COMC Let n be a positive integer. Given a real number x, let x be the greatest integer less than or equal to x. For example, 2.4 = 2, 3 = 3 and π = 3. Define a sequence a 1, a 2, a 3,... where a 1 = n and am 1 a m =, 3 for all integers m 2. The sequence stops when it reaches zero. The number n is said to be lucky if 0 is the only number in the sequence that is divisible by 3. For example, 7 is lucky, since a 1 = 7, a 2 = 2, a 3 = 0, and none of 7, 2 are divisible by 3. But 10 is not lucky, since a 1 = 10, a 2 = 3, a 3 = 1, a 4 = 0, and a 2 = 3 is divisible by 3. Determine the number of lucky positive integers less than or equal to Solution: Note that m/3 is simply chopping off the right-most digit of the base 3 representation of m. Hence, what the sequence is doing is that given an integer n, we repeatedly chop the right-most digit of the base 3 representation of n, until no digits remain. A base 3 representation is divisible by 3 if and only if the right most digit is zero. Then n is lucky if and only if none of the digits of the base 3 representation of n is zero. We convert the integer n to base 3. We first find the base 3 representation of Note that 1000/3 = /3, 333 = /3, 111 = /3, 37/3 = /3, 12/3 = 4 + 0/3, 4/3 = 1 + 1/3 and 1/3 = 0 + 1/3. Therefore, the base 3 representation of 1000 is We need to find the number of base 3 representations, whose digits does not contain zero, less than or equal to this number. Note that the largest lucky number less than or equal to is is Lucky numbers less than or equal to 1000 are those whose base 3 representation consists of only digits 1 and 2, and has at most 6 digits. There are 2 k such numbers whose base 3 representation has k digits. Therefore, the total number of lucky numbers is = 126. Page 6 c 2016 Canadian Mathematical Society
7 COMC Unofficial Solutions Section C 10 marks each 1. A sequence of three numbers a, b, c form an arithmetic sequence if the difference between successive terms in the sequence is the same. That is, when b a = c b. (a) The sequence 2, b, 8 forms an arithmetic sequence. Determine b. (b) Given a sequence a, b, c, let d 1 be the non-negative number to increase or decrease b by so that, without changing a or c, the result is an arithmetic sequence. Let d 2 be the positive number to increase or decrease c by so that, without changing a or b, the result is an arithmetic sequence. For example, if the three-term sequence is 3, 10, 13, then we need to decrease 10 to 8 to make the arithmetic sequence 3, 8, 13. We decreased b by 2, so d 1 = 2. If we change the third term, we need to increase 13 to 17 to make the arithmetic sequence 3, 10, 17. We increased 13 by 4, so d 2 = 4. Suppose the original three term sequence is 1, 13, 17. Determine d 1 and d 2. (c) Define d 1, d 2 as in part (b). For all three-term sequences, prove that 2d 1 = d 2. (a) Solution 1: We require that b a = c b, so b 2 = 8 b and b = 5. Solution 2: b must be in the middle of a and c, so b = (8 + 2)/2 = 5. Solution 3: 2, 5, 8 forms an arithmetic sequence, so b = 5. (b) Solution 1: b a = c b, and a = 1, c = 17. Substituting into the equation and solving gives b = 9. Since we have 13, as our middle term, the difference must be d 1 = 13 9 = 4. Similarly, if we have a = 1, b = 13, solving gives c = 25. The difference must be d 2 = = 8. Solution 2: The second number must be 9 to form an arithmetic sequence, so d 1 = 13 9 = 4. Similarly, the third number must be 25 to form an arithmetic sequence, so d 2 = = 8. (c) Solution 1: We can rewrite the relation for an arithmetic sequence as 2b = a+c. Suppose we have a sequence (not necessarily arithmetic) a, b, c, then we can write 2(b±d 1 ) = a+c, and we can also write 2b = a + (c ± d 2 ). Subtracting one equation from the other we are left with 2d 1 = ±d 2 and since both d 1 and d 2 are positive 2d 1 = d 2. Solution 2: We first determine d 1. Let b be the number we replace b with to form an c 2016 Canadian Mathematical Society Page 7
8 Unofficial Solutions COMC 2016 arithmetic sequence. Then b a = c b. Therefore, b = (a + c)/2. Hence, we changed b by (a + c)/2 b. Hence, d 1 = (a + c)/2 b = (a + c 2b)/2, where denotes absolute value. (The contestant shouldn t need to use absolute value. Any explanation that we take the positive version of the number would suffice.) We next determine d 2. Let c be the number to replace c by to make the sequence arithmetic. Then c b = b a. Therefore, c = 2b a. Hence, we change c by c c = 2b a c. Therefore, d 2 = 2b a c = 2 (2b a c)/2 = 2 (a+c 2b)/2 = 2d 1, as desired. Solution 3: Place the points A(1, a), B(2, b), C(3, c) on the coordinate plane. Let b be the number so that a, b, c is an arithmetic sequence and c the number so that a, b, c is an arithmetic sequence. Let B = (2, b ) and C = (3, c ). Then A, B, C lie on a straight line and A, B, C lie on a straight line. Furthermore, B is the midpoint of AC and B is the midpoint of AC. Note that d 1 is the distance between B and B and d 2 is the distance between C and C. Consider triangle ACC. Since BB, CC are both vertical, they are parallel. Therefore, ABB and AC C are similar, with ratio 1 : 2. Therefore, CC is twice the length of BB, yielding d 2 = 2d 1. Page 8 c 2016 Canadian Mathematical Society
9 COMC Unofficial Solutions 2. Alice and Bob play a game, taking turns, playing on a row of n seats. On a player s turn, he or she places a coin on any seat provided there is no coin on that seat or on an adjacent seat. Alice moves first. The player who does not have a valid move loses the game. (a) Show that Alice has a winning strategy when n = 5. (b) Show that Alice has a winning strategy when n = 6. (c) Show that Bob has a winning strategy when n = 8. (a) Solution: On her first turn, Alice places a coin on seat 3. Bob can now only place coins on seats 1 or 5. Whichever seat Bob places a coin on, Alice can then place a coin on the other seat. After this, Bob is unable to play and so loses the game. (b) Solution: On her first turn, Alice places the coin on seat 3. Bob can now only place coins on seats 1, 5, or 6. If Bob places the coin on 1, Alice places a coin on 5, and Bob is unable to play on 6, and so loses. If Bob places the coin in 5 or 6, then the other can no longer have a coin placed on it. Alice places a coin on 1, and then Bob has no place to play, and so he loses. (c) Solution: If Alice places her first coin on seat 1 or seat 8, there are now 6 consecutive seats that could have coins places on them. This is equivalent to part (b), except Bob goes first, so he will win this game. Similarly, if Alice places her first coin on seat 2 or 7, there are now 5 consecutive seats that could have coins placed on them, and this is equivalent to (a), except Bob goes first. If Alice places her first coin in seat 3 or 6, Bob places his first coin in the other. Now, only seats 1 and 8 can have a coin played in them, and whichever one Alice plays on, Bob will play on the other, winning the game. If Alice places her coin in seat 4, Bob places his coin in 6. This leaves 1, 2, and 8 as places that a coin may be placed. As in part (b), we see that exactly two more turns will occur, meaning Bob wins. If Alice places first coin in 5, Bob plays symmetrically to the aforementioned case. c 2016 Canadian Mathematical Society Page 9
10 Unofficial Solutions COMC Let A = (0, a), O = (0, 0), C = (c, 0), B = (c, b), where a, b, c are positive integers. Let P = (p, 0) be the point on line segment OC that minimizes the distance AP +P B, over all choices of P. Let X = AP + P B. (a) Show that this minimum distance is X = c 2 + (a + b) 2 (b) If c = 12, find all pairs (a, b) for which a, b, p, and X are positive integers. (c) If a, b, p, X are all positive integers, prove that there exists an integer n 3 that divides both a and b. (a) Solution: Reflect the point B in the horizontal x-axis to get the point B. Then P B = P B. By the triangle inequality, P A + P B AB. The line AB will pass through the segment OC, so taking P along AB is where P A + P B will attain its minimum. By the Pythagorean Theorem, the length of AB is X = c 2 + (a + b) 2. (b) Solution: Observe that at the minimum point attained in (a), P OA and P CB are similar triangles. Let a + b = n. We have X 2 = n 2, or (X n)(x + n) = 144. Since X and n are both integers, we have X n and X + n are the same parity. Since their product is a multiple of 2, each must also be a multiple of 2. We can factor 144 in the following ways, where both factors are even: (72, 2), (36, 4), (18, 8), (12, 12), (24, 6). These yield (X, n) pairs of (37, 35), (20, 16), (13, 5), (12, 0), (15, 9). We can immediately eliminate (12, 0), as n must be positive. Notice that by similar triangles, p/12 = a/n, so p = 12a/n. If n = 5, 35, there is no value of a for which b will also be positive. When n = 9, we have (a, b) = (3, 6), (6, 3) and when n = 16, we have (a, b) = (4, 12), (8, 8), (12, 4). (c) Solution: Let q = c b. By similar triangles, p = ac/(a + b) and q = bc/(a + b). Let k be the smallest integer such that kc is divisible by a + b. Then since p and q are integers, k must divide a and b. If k = 1, then c = m(a + b) for some integer m, and X = 1 + m 2 (a + b). This is only an integer when m = 0, which it cannot be, since then c = 0. This k > 1. If k = 2, then 2c = m(a + b) for some integer m, and X = ( a+b 2 ) 4 + m 2. Again, this is only an integer when m = 0, so k > 2, as required. Page 10 c 2016 Canadian Mathematical Society
11 COMC Unofficial Solutions 4. Two lines intersect at a point Q at an angle θ, where 0 < θ < 180. A frog is originally at a point other than Q on the angle bisector of this angle. The frog alternately jumps over these two lines, where a jump over a line results in the frog landing at a point which is the reflection across the line of the frog s jumping point. The frog stops when it lands on one of the two lines. (a) Suppose θ = 90. Show that the frog never stops. (b) Suppose θ = 72. Show that the frog eventually stops. (c) Determine the number of integer values of θ, with 0 < θ < 180, for which the frog never stops. (a) Solution: Suppose we orient the lines so that l 1 is the x-axis and l 2 is the y-axis. Again, suppose that the frog jumps over l 1 first. If the frog begins at a point (r, r), where r > 0. Then the subsequent points of the frog are (r, r), ( r, r), ( r, r), (r, r) and back to (r, r). The frog then repeats these four locations indefinitely. Hence, the frog never stops. (b) Solution: Let l 1, l 2 be the two lines, and let l be the angle bisector of the 72 angle. The frog is originally on a point F on l, not on point O. By symmetry, we can assume that the frog is jumping over l 1. Note that the lines l and l 1 intersect at 36. Let F be the point of reflection of F across l 1. Then OF and l 1 intersect at 36. Consequently, OF and l 2 intersect at 108. Note that the external (obtuse) angle formed by l 1 and l 2 is equal to = 108. Hence, on the frog s next jump, the frog will land on l 1 and the frog stops. (c) Solution: We will show that the frog stops if and only if θ is a multiple of 8. From this, we see that there are 179/8 = 22 multiples of 8 from 1 to 179 (inclusively). Therefore, there are = 157 integer values of θ for which the frog never stops. Let O be the origin on the coordinate plane, with l 1 coincide with the x-axis, and l 2 is placed so that it forms the angle θ with the positive x-axis of l 1. The first key observation is that the frog is always the same distance from O after it jumps. This is because the two lines intersect at O, and reflection across these two lines preserve the distance of the frog to O, since distances are preserved on reflection. Hence, we can measure the size of the directed angle, in the counter-clockwise direction, formed by the ray starting at O toward the positive x-axis (i.e. of l 1 ) to the ray OF, where F is the location of the frog. We will use the size of this angle to measure where the frog is. Since a full circle is 360, angles that are equal modulo 360, are equal. 1 1 Yes, this is polar coordinates. But I m trying not to use this terminology in the solution. c 2016 Canadian Mathematical Society Page 11
12 Unofficial Solutions COMC 2016 There are four locations on which the frog can land on the line, particular at angles 0, θ, 180 and θ. If the frog is forced to land in one of these four positions, then the frog will stop. Given a location α, let f(α) be the location of the frog after jumping across l 1 and g(α) be the location of the frog after jumping across l 2. We first determine explicit formulae for f(α) and g(α). f(α) is simply a reflection about the x-axis. Therefore, f(α) = α, where again we consider these values modulo 360. g(α) is a reflection about the line l 2, which passes through the location θ. To determine g(α), we rotate the line clockwise by θ, perform the reflection, and re-rotate the line counterclockwise by θ. Rotating the line clockwise by θ changes α to α θ. Reflecting across the x-axis yields θ α. Then rotating back counterclockwise by θ yields 2θ α. Therefore, g(α) = 2θ α. Let α 1, α 2, α 3, be the sequence of locations of the frog after each jump, where α 1 is the frog s original location, which is θ/2. Without loss of generality, suppose the frog jumps across l 1 first. Then α 2 = f(α 1 ) = α 1 = θ/2. Furthermore, α 3 = g(α 2 ) = g(f(α 1 )) and α 4 = f(α 3 ) = f(g(α 2 )). Generally, α n+2 = g(f(α n )) for all odd n and α n+2 = f(g(α n )) for all even n. Note that f(g(α)) = f(2θ α) = α 2θ and g(f(α)) = g( α) = 2θ + α. Therefore, α 1 = θ 2, α 3 = 2θ + θ 2.α 5 = 4θ + θ/2. In general, α 2k+1 = 2kθ + θ/2 for all non-negative integers k. In the even case, α 2 = θ 2.α 4 = 2θ θ/2, α 6 = 4θ θ/2. In general, α 2k+2 = 2kθ θ/2 for all non-negative integers k. Now, the frog will stop if there exists a non-negative integer k where either 2kθ + θ/2 or 2kθ θ/2 is equal to any one of 0, θ, 180, θ, modulo 360. This is equivalent to 2kθ + θ/2 or 2kθ θ/2 is equal to any one of 0 or θ modulo 180. Note that 2kθ + θ/2 0 (mod 180) if and only if (4k + 1)θ 0 (mod 360). Since 4k + 1 is odd and 360 is divisible by 8, θ must be divisible by 8 for there to be a solution. Conversely, if θ is divisible by 8, then setting k = 11 yields a value of 45k on the left side, which is indeed divisible by 360. Note that 2kθ + θ/2 θ (mod 180) if and only if (4k 1)θ 0 (mod 360). Since 4k 1 is odd and 360 is divisible by 8, θ must be divisible by 8 for there to be a solution. Conversely, if θ is divisible by 8, then setting k = 34 yields a value of 135k = 3 45k on the left hand side, and 45k would be divisible by 360. Note that 2kθ θ/2 0 (mod 180) if and only if (4k + 1)θ 0 (mod 360). This is the same situation as in the first case. Note that 2kθ θ/2 θ (mod 180) if and only if (4k + 3)θ 0 (mod 360). Since 4k + 3 is odd and 360 is divisible by 8, θ must be divisible by 8 for there to be a solution. Conversely, if θ is divisible by 8, then setting k = 33 yields a value of (4k +3)θ = 135k = 3 45k on the left side, which is divisible by 360. Hence, in all cases, there exists a non-negative integer k such that one of α 2k+1, α 2k+2 lies on l 1, l 2, which only occurs if and only if θ is divisible by 8. This completes the problem. Page 12 c 2016 Canadian Mathematical Society
Hanoi Open Mathematical Competition 2017
 Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
2009 Math Olympics Level II Solutions
 Saginaw Valley State University 009 Math Olympics Level II Solutions 1. f (x) is a degree three monic polynomial (leading coefficient is 1) such that f (0) 3, f (1) 5 and f () 11. What is f (5)? (a) 7
Saginaw Valley State University 009 Math Olympics Level II Solutions 1. f (x) is a degree three monic polynomial (leading coefficient is 1) such that f (0) 3, f (1) 5 and f () 11. What is f (5)? (a) 7
Sun Life Financial Canadian Open Mathematics Challenge Section A 4 marks each. Official Solutions
 Sun Life Financial Canadian Open Mathematics Challenge 2015 Official Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2015/practice.html
Sun Life Financial Canadian Open Mathematics Challenge 2015 Official Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2015/practice.html
11 th Philippine Mathematical Olympiad Questions, Answers, and Hints
 view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
2008 Euclid Contest. Solutions. Canadian Mathematics Competition. Tuesday, April 15, c 2008 Centre for Education in Mathematics and Computing
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 008 Euclid Contest Tuesday, April 5, 008 Solutions c 008
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 008 Euclid Contest Tuesday, April 5, 008 Solutions c 008
Georgia Tech High School Math Competition
 Georgia Tech High School Math Competition Multiple Choice Test February 28, 2015 Each correct answer is worth one point; there is no deduction for incorrect answers. Make sure to enter your ID number on
Georgia Tech High School Math Competition Multiple Choice Test February 28, 2015 Each correct answer is worth one point; there is no deduction for incorrect answers. Make sure to enter your ID number on
2007 Fermat Contest (Grade 11)
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 007 Fermat Contest (Grade 11) Tuesday, February 0, 007 Solutions
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 007 Fermat Contest (Grade 11) Tuesday, February 0, 007 Solutions
The sum x 1 + x 2 + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E): None of the above. How many pairs of positive integers (x, y) are there, those satisfy
 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST,
 BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 014 Solutions Junior Preliminary 1. Rearrange the sum as (014 + 01 + 010 + + ) (013 + 011 + 009 + + 1) = (014 013) + (01 011) + + ( 1) = 1 + 1 + +
BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 014 Solutions Junior Preliminary 1. Rearrange the sum as (014 + 01 + 010 + + ) (013 + 011 + 009 + + 1) = (014 013) + (01 011) + + ( 1) = 1 + 1 + +
1 Hanoi Open Mathematical Competition 2017
 1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
2015 Canadian Team Mathematics Contest
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 205 Canadian Team Mathematics Contest April 205 Solutions 205 University of Waterloo 205 CTMC Solutions Page 2 Individual Problems.
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 205 Canadian Team Mathematics Contest April 205 Solutions 205 University of Waterloo 205 CTMC Solutions Page 2 Individual Problems.
State Math Contest Senior Exam SOLUTIONS
 State Math Contest Senior Exam SOLUTIONS 1. The following pictures show two views of a non standard die (however the numbers 1-6 are represented on the die). How many dots are on the bottom face of figure?
State Math Contest Senior Exam SOLUTIONS 1. The following pictures show two views of a non standard die (however the numbers 1-6 are represented on the die). How many dots are on the bottom face of figure?
2018 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST
 08 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST. A right triangle has hypotenuse 9 and one leg. What is the length of the other leg?. Don is /3 of the way through his run. After running another / mile, he
08 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST. A right triangle has hypotenuse 9 and one leg. What is the length of the other leg?. Don is /3 of the way through his run. After running another / mile, he
3. A square has 4 sides, so S = 4. A pentagon has 5 vertices, so P = 5. Hence, S + P = 9. = = 5 3.
 JHMMC 01 Grade Solutions October 1, 01 1. By counting, there are 7 words in this question.. (, 1, ) = 1 + 1 + = 9 + 1 + =.. A square has sides, so S =. A pentagon has vertices, so P =. Hence, S + P = 9..
JHMMC 01 Grade Solutions October 1, 01 1. By counting, there are 7 words in this question.. (, 1, ) = 1 + 1 + = 9 + 1 + =.. A square has sides, so S =. A pentagon has vertices, so P =. Hence, S + P = 9..
nx + 1 = (n + 1)x 13(n + 1) and nx = (n + 1)x + 27(n + 1).
 1. (Answer: 630) 001 AIME SOLUTIONS Let a represent the tens digit and b the units digit of an integer with the required property. Then 10a + b must be divisible by both a and b. It follows that b must
1. (Answer: 630) 001 AIME SOLUTIONS Let a represent the tens digit and b the units digit of an integer with the required property. Then 10a + b must be divisible by both a and b. It follows that b must
2005 Euclid Contest. Solutions
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 2005 Euclid Contest Tuesday, April 19, 2005 Solutions c
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 2005 Euclid Contest Tuesday, April 19, 2005 Solutions c
Math Wrangle Practice Problems
 Math Wrangle Practice Problems American Mathematics Competitions November 19, 2010 1. Find the sum of all positive two-digit integers that are divisible by each of their digits. 2. A finite set S of distinct
Math Wrangle Practice Problems American Mathematics Competitions November 19, 2010 1. Find the sum of all positive two-digit integers that are divisible by each of their digits. 2. A finite set S of distinct
= 126 possible 5-tuples.
 19th Philippine Mathematical Olympiad 1 January, 017 JUDGES COPY EASY 15 seconds, points 1. If g (x) = x x 5 Answer: 14 Solution: Note that x x and f ( g ( x)) = x, find f (). x 6 = = x = 1. Hence f ()
19th Philippine Mathematical Olympiad 1 January, 017 JUDGES COPY EASY 15 seconds, points 1. If g (x) = x x 5 Answer: 14 Solution: Note that x x and f ( g ( x)) = x, find f (). x 6 = = x = 1. Hence f ()
Solutions th AMC 10 B 2
 Solutions 2004 5 th AMC 10 B 2 1. (C) There are 22 12 + 1 = 11 reserved rows. Because there are 33 seats in each row, there are (33)(11) = 363 reserved seats. 2. (B) There are 10 two-digit numbers with
Solutions 2004 5 th AMC 10 B 2 1. (C) There are 22 12 + 1 = 11 reserved rows. Because there are 33 seats in each row, there are (33)(11) = 363 reserved seats. 2. (B) There are 10 two-digit numbers with
1. The sides of a triangle are in the ratio 3 : 5 : 9. Which of the following words best describes the triangle?
 UNIVERSITY OF NORTH CAROLINA CHARLOTTE 999 HIGH SCHOOL MATHEMATICS CONTEST March 8, 999 The sides of a triangle are in the ratio : 5 : 9 Which of the following words best describes the triangle? (A) obtuse
UNIVERSITY OF NORTH CAROLINA CHARLOTTE 999 HIGH SCHOOL MATHEMATICS CONTEST March 8, 999 The sides of a triangle are in the ratio : 5 : 9 Which of the following words best describes the triangle? (A) obtuse
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca Cayley Contest. (Grade 10) Thursday, February 20, 2014
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 2014 Cayley Contest (Grade 10) Thursday, February 20, 2014 (in North America and South America) Friday, February 21, 2014 (outside
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 2014 Cayley Contest (Grade 10) Thursday, February 20, 2014 (in North America and South America) Friday, February 21, 2014 (outside
HSMC 2017 Free Response
 HSMC 207 Free Response. What are the first three digits of the least common multiple of 234 and 360? Solution: 468. Note that 234 = 2 3 2 3, and 360 = 2 3 3 2 5. Thus, lcm =2 3 3 2 5 3 = 0 36 3 = 4680.
HSMC 207 Free Response. What are the first three digits of the least common multiple of 234 and 360? Solution: 468. Note that 234 = 2 3 2 3, and 360 = 2 3 3 2 5. Thus, lcm =2 3 3 2 5 3 = 0 36 3 = 4680.
2016 Canadian Team Mathematics Contest
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 016 Canadian Team Mathematics Contest April 016 Solutions 016 University of Waterloo 016 CTMC Solutions Page Individual Problems
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 016 Canadian Team Mathematics Contest April 016 Solutions 016 University of Waterloo 016 CTMC Solutions Page Individual Problems
SMT 2011 General Test and Solutions February 19, F (x) + F = 1 + x. 2 = 3. Now take x = 2 2 F ( 1) = F ( 1) = 3 2 F (2)
 SMT 0 General Test and Solutions February 9, 0 Let F () be a real-valued function defined for all real 0, such that ( ) F () + F = + Find F () Answer: Setting =, we find that F () + F ( ) = Now take =,
SMT 0 General Test and Solutions February 9, 0 Let F () be a real-valued function defined for all real 0, such that ( ) F () + F = + Find F () Answer: Setting =, we find that F () + F ( ) = Now take =,
Solution: By direct calculation, or observe that = = ( ) 2222 = =
 1 Fillins 1. Find the last 4 digits of 3333 6666. Solution: 7778. By direct calculation, or observe that 3333 6666 = 9999 2222 = (10000 1) 2222 = 22220000 2222 = 22217778. 2. How many ways are there to
1 Fillins 1. Find the last 4 digits of 3333 6666. Solution: 7778. By direct calculation, or observe that 3333 6666 = 9999 2222 = (10000 1) 2222 = 22220000 2222 = 22217778. 2. How many ways are there to
HIGH SCHOOL - SOLUTIONS = n = 2315
 PURPLE COMET! MATH MEET April 018 HIGH SCHOOL - SOLUTIONS Copyright c Titu Andreescu and Jonathan Kane Problem 1 Find the positive integer n such that 1 3 + 5 6 7 8 + 9 10 11 1 = n 100. Answer: 315 1 3
PURPLE COMET! MATH MEET April 018 HIGH SCHOOL - SOLUTIONS Copyright c Titu Andreescu and Jonathan Kane Problem 1 Find the positive integer n such that 1 3 + 5 6 7 8 + 9 10 11 1 = n 100. Answer: 315 1 3
2009 Euclid Contest. Solutions
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 009 Euclid Contest Tuesday, April 7, 009 Solutions c 009
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 009 Euclid Contest Tuesday, April 7, 009 Solutions c 009
USA Mathematical Talent Search Round 2 Solutions Year 20 Academic Year
 //0. Sarah and Joe play a standard 3-by-3 game of tic-tac-toe. Sarah goes first and plays X, and Joe goes second and plays O. They alternate turns placing their letter in an empty space, and the first
//0. Sarah and Joe play a standard 3-by-3 game of tic-tac-toe. Sarah goes first and plays X, and Joe goes second and plays O. They alternate turns placing their letter in an empty space, and the first
BC Exam Solutions Texas A&M High School Math Contest October 24, p(1) = b + 2 = 3 = b = 5.
 C Exam Solutions Texas &M High School Math Contest October 4, 01 ll answers must be simplified, and If units are involved, be sure to include them. 1. p(x) = x + ax + bx + c has three roots, λ i, with
C Exam Solutions Texas &M High School Math Contest October 4, 01 ll answers must be simplified, and If units are involved, be sure to include them. 1. p(x) = x + ax + bx + c has three roots, λ i, with
Math Contest, Fall 2017 BC EXAM , z =
 Math Contest, Fall 017 BC EXAM 1. List x, y, z in order from smallest to largest fraction: x = 111110 111111, y = 1 3, z = 333331 333334 Consider 1 x = 1 111111, 1 y = thus 1 x > 1 z > 1 y, and so x
Math Contest, Fall 017 BC EXAM 1. List x, y, z in order from smallest to largest fraction: x = 111110 111111, y = 1 3, z = 333331 333334 Consider 1 x = 1 111111, 1 y = thus 1 x > 1 z > 1 y, and so x
SOUTH AFRICAN TERTIARY MATHEMATICS OLYMPIAD
 SOUTH AFRICAN TERTIARY MATHEMATICS OLYMPIAD. Determine the following value: 7 August 6 Solutions π + π. Solution: Since π
SOUTH AFRICAN TERTIARY MATHEMATICS OLYMPIAD. Determine the following value: 7 August 6 Solutions π + π. Solution: Since π
Instructions. Do not open your test until instructed to do so!
 st Annual King s College Math Competition King s College welcomes you to this year s mathematics competition and to our campus. We wish you success in this competition and in your future studies. Instructions
st Annual King s College Math Competition King s College welcomes you to this year s mathematics competition and to our campus. We wish you success in this competition and in your future studies. Instructions
OLYMON. Produced by the Canadian Mathematical Society and the Department of Mathematics of the University of Toronto. Issue 10:3.
 OLYMON Produced by the Canadian Mathematical Society and the Department of Mathematics of the University of Toronto. Please send your solutions to Rosu Mihai 54 Judith Crescent Brampton, ON L6S 3J4 Issue
OLYMON Produced by the Canadian Mathematical Society and the Department of Mathematics of the University of Toronto. Please send your solutions to Rosu Mihai 54 Judith Crescent Brampton, ON L6S 3J4 Issue
CHMMC 2015 Individual Round Problems
 CHMMC 05 Individual Round Problems November, 05 Problem 0.. The following number is the product of the divisors of n. What is n? 6 3 3 Solution.. In general, the product of the divisors of n is n # of
CHMMC 05 Individual Round Problems November, 05 Problem 0.. The following number is the product of the divisors of n. What is n? 6 3 3 Solution.. In general, the product of the divisors of n is n # of
UNC Charlotte 2005 Comprehensive March 7, 2005
 March 7, 2005 1. The numbers x and y satisfy 2 x = 15 and 15 y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D Solution: C. Note that (2 x ) y = 15 y = 32 so 2 xy = 2 5 and
March 7, 2005 1. The numbers x and y satisfy 2 x = 15 and 15 y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D Solution: C. Note that (2 x ) y = 15 y = 32 so 2 xy = 2 5 and
Non-standard MMC problems
 Non-standard MMC problems Carl Joshua Quines 1 Algebra 1. (15S/9B/E6) A quadratic function f(x) satisfies f(0) = 30 and f(2) = 0. Determine all the zeros of f(x). [2 and 15] 2. (15S/IVB/E6) What is the
Non-standard MMC problems Carl Joshua Quines 1 Algebra 1. (15S/9B/E6) A quadratic function f(x) satisfies f(0) = 30 and f(2) = 0. Determine all the zeros of f(x). [2 and 15] 2. (15S/IVB/E6) What is the
Joe Holbrook Memorial Math Competition
 Joe Holbrook Memorial Math Competition 8th Grade Solutions October 9th, 06. + (0 ( 6( 0 6 ))) = + (0 ( 6( 0 ))) = + (0 ( 6)) = 6 =. 80 (n ). By the formula that says the interior angle of a regular n-sided
Joe Holbrook Memorial Math Competition 8th Grade Solutions October 9th, 06. + (0 ( 6( 0 6 ))) = + (0 ( 6( 0 ))) = + (0 ( 6)) = 6 =. 80 (n ). By the formula that says the interior angle of a regular n-sided
1 2n. i=1. 2m+1 i = m, while. 2m + 1 = 1. is the best possible for any odd n.
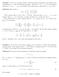 Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
High School Math Contest
 High School Math Contest University of South Carolina February th, 017 Problem 1. If (x y) = 11 and (x + y) = 169, what is xy? (a) 11 (b) 1 (c) 1 (d) (e) 8 Solution: Note that xy = (x + y) (x y) = 169
High School Math Contest University of South Carolina February th, 017 Problem 1. If (x y) = 11 and (x + y) = 169, what is xy? (a) 11 (b) 1 (c) 1 (d) (e) 8 Solution: Note that xy = (x + y) (x y) = 169
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 31 OCTOBER 2018
 SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY OCTOBER 8 Mark Scheme: Each part of Question is worth marks which are awarded solely for the correct answer. Each
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY OCTOBER 8 Mark Scheme: Each part of Question is worth marks which are awarded solely for the correct answer. Each
Olimpiada Matemática de Centroamérica y el Caribe
 Olimpiada Matemática de Centroamérica y el Caribe 1st Centromerican 1999 Problem A1 A, B, C, D, E each has a unique piece of news. They make a series of phone calls to each other. In each call, the caller
Olimpiada Matemática de Centroamérica y el Caribe 1st Centromerican 1999 Problem A1 A, B, C, D, E each has a unique piece of news. They make a series of phone calls to each other. In each call, the caller
Canadian Open Mathematics Challenge
 The Canadian Mathematical Society in collaboration with The CENTRE for EDUCATION in MATHEMATICS and COMPUTING presents the Canadian Open Mathematics Challenge Wednesday, November, 006 Supported by: Solutions
The Canadian Mathematical Society in collaboration with The CENTRE for EDUCATION in MATHEMATICS and COMPUTING presents the Canadian Open Mathematics Challenge Wednesday, November, 006 Supported by: Solutions
number. However, unlike , three of the digits of N are 3, 4 and 5, and N is a multiple of 6.
 C1. The positive integer N has six digits in increasing order. For example, 124 689 is such a number. However, unlike 124 689, three of the digits of N are 3, 4 and 5, and N is a multiple of 6. How many
C1. The positive integer N has six digits in increasing order. For example, 124 689 is such a number. However, unlike 124 689, three of the digits of N are 3, 4 and 5, and N is a multiple of 6. How many
T-2 In the equation A B C + D E F = G H I, each letter denotes a distinct non-zero digit. Compute the greatest possible value of G H I.
 2016 ARML Local Problems and Solutions Team Round Solutions T-1 All the shelves in a library are the same length. When filled, two shelves side-by-side can hold exactly 12 algebra books and 10 geometry
2016 ARML Local Problems and Solutions Team Round Solutions T-1 All the shelves in a library are the same length. When filled, two shelves side-by-side can hold exactly 12 algebra books and 10 geometry
2016 State Mathematics Contest Geometry Test
 2016 State Mathematics Contest Geometry Test In each of the following, choose the BEST answer and record your choice on the answer sheet provided. To ensure correct scoring, be sure to make all erasures
2016 State Mathematics Contest Geometry Test In each of the following, choose the BEST answer and record your choice on the answer sheet provided. To ensure correct scoring, be sure to make all erasures
BmMT 2017 Individual Round Solutions November 19, 2017
 1. It s currently 6:00 on a 12 hour clock. What time will be shown on the clock 100 hours from now? Express your answer in the form hh : mm. Answer: 10:00 Solution: We note that adding any multiple of
1. It s currently 6:00 on a 12 hour clock. What time will be shown on the clock 100 hours from now? Express your answer in the form hh : mm. Answer: 10:00 Solution: We note that adding any multiple of
2018 Best Student Exam Solutions Texas A&M High School Students Contest October 20, 2018
 08 Best Student Exam Solutions Texas A&M High School Students Contest October 0, 08. You purchase a stock and later sell it for $44 per share. When you do, you notice that the percent increase was the
08 Best Student Exam Solutions Texas A&M High School Students Contest October 0, 08. You purchase a stock and later sell it for $44 per share. When you do, you notice that the percent increase was the
Syllabus. + + x + n 1 n. + x + 2
 1. Special Functions This class will cover problems involving algebraic functions other than polynomials, such as square roots, the floor function, and logarithms. Example Problem: Let n be a positive
1. Special Functions This class will cover problems involving algebraic functions other than polynomials, such as square roots, the floor function, and logarithms. Example Problem: Let n be a positive
Math Wrangle Practice Problems
 Math Wrangle Practice Problems American Mathematics Competitions December 22, 2011 ((3!)!)! 1. Given that, = k. n!, where k and n are positive integers and n 3. is as large as possible, find k + n. 2.
Math Wrangle Practice Problems American Mathematics Competitions December 22, 2011 ((3!)!)! 1. Given that, = k. n!, where k and n are positive integers and n 3. is as large as possible, find k + n. 2.
14 th Annual Harvard-MIT Mathematics Tournament Saturday 12 February 2011
 14 th Annual Harvard-MIT Mathematics Tournament Saturday 1 February 011 1. Let a, b, and c be positive real numbers. etermine the largest total number of real roots that the following three polynomials
14 th Annual Harvard-MIT Mathematics Tournament Saturday 1 February 011 1. Let a, b, and c be positive real numbers. etermine the largest total number of real roots that the following three polynomials
2017 Canadian Team Mathematics Contest
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 017 Canadian Team Mathematics Contest April 017 Solutions 017 University of Waterloo 017 CTMC Solutions Page Individual Problems
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 017 Canadian Team Mathematics Contest April 017 Solutions 017 University of Waterloo 017 CTMC Solutions Page Individual Problems
PURPLE COMET MATH MEET April 2012 MIDDLE SCHOOL - SOLUTIONS
 PURPLE COMET MATH MEET April 2012 MIDDLE SCHOOL - SOLUTIONS Copyright c Titu Andreescu and Jonathan Kane Problem 1 Evaluate 5 4 4 3 3 2 2 1 1 0. Answer: 549 The expression equals 625 64 9 2 1 = 549. Problem
PURPLE COMET MATH MEET April 2012 MIDDLE SCHOOL - SOLUTIONS Copyright c Titu Andreescu and Jonathan Kane Problem 1 Evaluate 5 4 4 3 3 2 2 1 1 0. Answer: 549 The expression equals 625 64 9 2 1 = 549. Problem
MATH CIRCLE Session # 2, 9/29/2018
 MATH CIRCLE Session # 2, 9/29/2018 SOLUTIONS 1. The n-queens Problem. You do NOT need to know how to play chess to work this problem! This is a classical problem; to look it up today on the internet would
MATH CIRCLE Session # 2, 9/29/2018 SOLUTIONS 1. The n-queens Problem. You do NOT need to know how to play chess to work this problem! This is a classical problem; to look it up today on the internet would
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 2 NOVEMBER 2011
 SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY NOVEMBER 011 Mark Scheme: Each part of Question 1 is worth four marks which are awarded solely for the correct
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY NOVEMBER 011 Mark Scheme: Each part of Question 1 is worth four marks which are awarded solely for the correct
2016 AMC 12/AHSME. 3 The remainder can be defined for all real numbers x and y with y 0 by. x rem(x,y) = x y y
 AMC 12/AHSME 2016 A 1 What is the value of 11! 10!? 9! (A) 99 (B) 100 (C) 110 (D) 121 (E) 132 2 For what value of x does 10 x 100 2x = 1000 5? (A) 1 (B) 2 (C) 3 (D) 4 (E) 5 3 The remainder can be defined
AMC 12/AHSME 2016 A 1 What is the value of 11! 10!? 9! (A) 99 (B) 100 (C) 110 (D) 121 (E) 132 2 For what value of x does 10 x 100 2x = 1000 5? (A) 1 (B) 2 (C) 3 (D) 4 (E) 5 3 The remainder can be defined
BRITISH COLUMBIA COLLEGES High School Mathematics Contest 2003 Solutions
 BRITISH COLUMBIA COLLEGES High School Mathematics Contest 3 Solutions Junior Preliminary. Solve the equation x = Simplify the complex fraction by multiplying numerator and denominator by x. x = = x = (x
BRITISH COLUMBIA COLLEGES High School Mathematics Contest 3 Solutions Junior Preliminary. Solve the equation x = Simplify the complex fraction by multiplying numerator and denominator by x. x = = x = (x
1999 Solutions Fermat Contest (Grade 11)
 Canadian Mathematics Competition n activity of The Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 999 s Fermat Contest (Grade ) for the wards 999 Waterloo
Canadian Mathematics Competition n activity of The Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 999 s Fermat Contest (Grade ) for the wards 999 Waterloo
Math is Cool Masters
 Sponsored by: GENIE Industries 7 th Grade November 19, 2005 Individual Contest Express all answers as reduced fractions unless stated otherwise. Leave answers in terms of π where applicable. Do not round
Sponsored by: GENIE Industries 7 th Grade November 19, 2005 Individual Contest Express all answers as reduced fractions unless stated otherwise. Leave answers in terms of π where applicable. Do not round
State Math Contest (Junior)
 Name: Student ID: State Math Contest (Junior) Instructions: Do not turn this page until your proctor tells you. Enter your name, grade, and school information following the instructions given by your proctor.
Name: Student ID: State Math Contest (Junior) Instructions: Do not turn this page until your proctor tells you. Enter your name, grade, and school information following the instructions given by your proctor.
Baltic Way 2003 Riga, November 2, 2003
 altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
Math 46 Final Exam Review Packet
 Math 46 Final Exam Review Packet Question 1. Perform the indicated operation. Simplify if possible. 7 x x 2 2x + 3 2 x Question 2. The sum of a number and its square is 72. Find the number. Question 3.
Math 46 Final Exam Review Packet Question 1. Perform the indicated operation. Simplify if possible. 7 x x 2 2x + 3 2 x Question 2. The sum of a number and its square is 72. Find the number. Question 3.
1998 IMO Shortlist BM BN BA BC AB BC CD DE EF BC CA AE EF FD
 IMO Shortlist 1998 Geometry 1 A convex quadrilateral ABCD has perpendicular diagonals. The perpendicular bisectors of the sides AB and CD meet at a unique point P inside ABCD. the quadrilateral ABCD is
IMO Shortlist 1998 Geometry 1 A convex quadrilateral ABCD has perpendicular diagonals. The perpendicular bisectors of the sides AB and CD meet at a unique point P inside ABCD. the quadrilateral ABCD is
Solutions th AMC 12 A (E) Since $20 is 2000 cents, she pays (0.0145)(2000) = 29 cents per hour in local taxes.
 Solutions 2004 55 th AMC 12 A 2 1. (E) Since $20 is 2000 cents, she pays (0.0145)(2000) = 29 cents per hour in local taxes. 2. (C) The 8 unanswered problems are worth (2.5)(8) = 20 points, so Charlyn must
Solutions 2004 55 th AMC 12 A 2 1. (E) Since $20 is 2000 cents, she pays (0.0145)(2000) = 29 cents per hour in local taxes. 2. (C) The 8 unanswered problems are worth (2.5)(8) = 20 points, so Charlyn must
Question 1 (3 points) Find the midpoint of the line segment connecting the pair of points (3, -10) and (3, 6).
 Geometry Semester Final Exam Practice Select the best answer Question (3 points) Find the midpoint of the line segment connecting the pair of points (3, -0) and (3, 6). A) (3, -) C) (3, -) B) (3, 4.5)
Geometry Semester Final Exam Practice Select the best answer Question (3 points) Find the midpoint of the line segment connecting the pair of points (3, -0) and (3, 6). A) (3, -) C) (3, -) B) (3, 4.5)
USA Mathematics Talent Search
 16 3 1 (a) Since x and y are 3-digit integers, we begin by noting that the condition 6(x y) = (y x) is equivalent to 6(1, 000x + y) = 1, 000y + x = 5, 999x = 994y, which (after factoring out a 7 by long
16 3 1 (a) Since x and y are 3-digit integers, we begin by noting that the condition 6(x y) = (y x) is equivalent to 6(1, 000x + y) = 1, 000y + x = 5, 999x = 994y, which (after factoring out a 7 by long
USA Mathematical Talent Search Round 3 Solutions Year 20 Academic Year
 1/3/20. Let S be the set of all 10-digit numbers (which by definition may not begin with 0) in which each digit 0 through 9 appears exactly once. For example, the number 3,820,956,714 is in S. A number
1/3/20. Let S be the set of all 10-digit numbers (which by definition may not begin with 0) in which each digit 0 through 9 appears exactly once. For example, the number 3,820,956,714 is in S. A number
Written test, 25 problems / 90 minutes
 Sponsored by: UGA Math Department and UGA Math Club Written test, 5 problems / 90 minutes October, 06 WITH SOLUTIONS Problem. Let a represent a digit from to 9. Which a gives a! aa + a = 06? Here aa indicates
Sponsored by: UGA Math Department and UGA Math Club Written test, 5 problems / 90 minutes October, 06 WITH SOLUTIONS Problem. Let a represent a digit from to 9. Which a gives a! aa + a = 06? Here aa indicates
If something is repeated, look for what stays unchanged!
 LESSON 5: INVARIANTS Invariants are very useful in problems concerning algorithms involving steps that are repeated again and again (games, transformations). While these steps are repeated, the system
LESSON 5: INVARIANTS Invariants are very useful in problems concerning algorithms involving steps that are repeated again and again (games, transformations). While these steps are repeated, the system
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca Euclid Contest. Tuesday, April 12, 2016
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 016 Euclid Contest Tuesday, April 1, 016 (in North America and South America) Wednesday, April 13, 016 (outside of North America
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 016 Euclid Contest Tuesday, April 1, 016 (in North America and South America) Wednesday, April 13, 016 (outside of North America
41st International Mathematical Olympiad
 41st International Mathematical Olympiad Taejon, Korea, July 2000 1 Two circles Γ 1 and Γ 2 intersect at M and N Let l be the common tangent to Γ 1 and Γ 2 so that M is closer to l than N is Let l touch
41st International Mathematical Olympiad Taejon, Korea, July 2000 1 Two circles Γ 1 and Γ 2 intersect at M and N Let l be the common tangent to Γ 1 and Γ 2 so that M is closer to l than N is Let l touch
Problems and Solutions
 46 th Canadian Mathematical Olympiad Wednesday, April 2, 204 Problems and Solutions. Let a, a 2,..., a n be positive real numbers whose product is. Show that the sum a a 2 + + a ( + a )( + a 2 ) + a 3
46 th Canadian Mathematical Olympiad Wednesday, April 2, 204 Problems and Solutions. Let a, a 2,..., a n be positive real numbers whose product is. Show that the sum a a 2 + + a ( + a )( + a 2 ) + a 3
10! = ?
 AwesomeMath Team Contest 013 Solutions Problem 1. Define the value of a letter as its position in the alphabet. For example, C is the third letter, so its value is 3. The value of a word is the sum of
AwesomeMath Team Contest 013 Solutions Problem 1. Define the value of a letter as its position in the alphabet. For example, C is the third letter, so its value is 3. The value of a word is the sum of
Due to the detail of some problems, print the contests using a normal or high quality setting.
 General Contest Guidelines: Keep the contests secure. Discussion about contest questions is not permitted prior to giving the contest. Due to the detail of some problems, print the contests using a normal
General Contest Guidelines: Keep the contests secure. Discussion about contest questions is not permitted prior to giving the contest. Due to the detail of some problems, print the contests using a normal
Write your Name, Registration Number, Test Centre, Test Code and the Number of this booklet in the appropriate places on the answersheet.
 2009 Booklet No. Test Code : SIA Forenoon Questions : 30 Time : 2 hours Write your Name, Registration Number, Test Centre, Test Code and the Number of this booklet in the appropriate places on the answersheet.
2009 Booklet No. Test Code : SIA Forenoon Questions : 30 Time : 2 hours Write your Name, Registration Number, Test Centre, Test Code and the Number of this booklet in the appropriate places on the answersheet.
SMT China 2014 Team Test Solutions August 23, 2014
 . Compute the remainder when 2 30 is divided by 000. Answer: 824 Solution: Note that 2 30 024 3 24 3 mod 000). We will now consider 24 3 mod 8) and 24 3 mod 25). Note that 24 3 is divisible by 8, but 24
. Compute the remainder when 2 30 is divided by 000. Answer: 824 Solution: Note that 2 30 024 3 24 3 mod 000). We will now consider 24 3 mod 8) and 24 3 mod 25). Note that 24 3 is divisible by 8, but 24
The Sun Life Financial Canadian Open Mathematics Challenge Wednesday, November 2, 2011
 The Sun Life Financial Canadian Open Mathematics Challenge Wednesday, November 2, 2011 Please print TEST SUPERVISOR NAME: Signature: STUDENT NAME: First: Last: Student Signature: GENDER: Male Female E
The Sun Life Financial Canadian Open Mathematics Challenge Wednesday, November 2, 2011 Please print TEST SUPERVISOR NAME: Signature: STUDENT NAME: First: Last: Student Signature: GENDER: Male Female E
Organization Team Team ID#
 1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
chapter 1 vector geometry solutions V Consider the parallelogram shown alongside. Which of the following statements are true?
 chapter vector geometry solutions V. Exercise A. For the shape shown, find a single vector which is equal to a)!!! " AB + BC AC b)! AD!!! " + DB AB c)! AC + CD AD d)! BC + CD!!! " + DA BA e) CD!!! " "
chapter vector geometry solutions V. Exercise A. For the shape shown, find a single vector which is equal to a)!!! " AB + BC AC b)! AD!!! " + DB AB c)! AC + CD AD d)! BC + CD!!! " + DA BA e) CD!!! " "
2008 Cayley Contest. Solutions
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 008 Cayley Contest (Grade 10) Tuesday, February 19, 008
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 008 Cayley Contest (Grade 10) Tuesday, February 19, 008
The Second Annual West Windsor-Plainsboro Mathematics Tournament
 The Second Annual West Windsor-Plainsboro Mathematics Tournament Saturday October 9th, 0 Grade 8 Test RULES The test consists of 0 multiple choice problems and 0 short answer problems to be done in 0 minutes.
The Second Annual West Windsor-Plainsboro Mathematics Tournament Saturday October 9th, 0 Grade 8 Test RULES The test consists of 0 multiple choice problems and 0 short answer problems to be done in 0 minutes.
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca Cayley Contest. (Grade 10) Tuesday, February 27, 2018
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 018 Cayley Contest (Grade 10) Tuesday, February 7, 018 (in North America and South America) Wednesday, February 8, 018 (outside of
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 018 Cayley Contest (Grade 10) Tuesday, February 7, 018 (in North America and South America) Wednesday, February 8, 018 (outside of
2018 Canadian Team Mathematics Contest
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 08 Canadian Team Mathematics Contest April 08 Solutions 08 University of Waterloo 08 CTMC Solutions Page Individual Problems. Since
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 08 Canadian Team Mathematics Contest April 08 Solutions 08 University of Waterloo 08 CTMC Solutions Page Individual Problems. Since
Some practice questions for CIMC.
 1. Determine the value of {2008 Cayley #2} Some practice questions for CIMC. 25 16 25 16. 25 16 25 16 = 9 5 4 = 3 1 = 3 2. In the diagram, P T and QS are straight lines intersecting at R such that QP =
1. Determine the value of {2008 Cayley #2} Some practice questions for CIMC. 25 16 25 16. 25 16 25 16 = 9 5 4 = 3 1 = 3 2. In the diagram, P T and QS are straight lines intersecting at R such that QP =
2016 King s College Math Competition. Instructions
 06 King s College Math Competition King s College welcomes you to this year s mathematics competition and to our campus. We wish you success in this competition and in your future studies. Instructions
06 King s College Math Competition King s College welcomes you to this year s mathematics competition and to our campus. We wish you success in this competition and in your future studies. Instructions
The Alberta High School Mathematics Competition Solution to Part I, 2014.
 The Alberta High School Mathematics Competition Solution to Part I, 2014. Question 1. When the repeating decimal 0.6 is divided by the repeating decimal 0.3, the quotient is (a) 0.2 (b) 2 (c) 0.5 (d) 0.5
The Alberta High School Mathematics Competition Solution to Part I, 2014. Question 1. When the repeating decimal 0.6 is divided by the repeating decimal 0.3, the quotient is (a) 0.2 (b) 2 (c) 0.5 (d) 0.5
HMMT November 2017 November 11, 2017
 HMMT November 017 November 11, 017 Theme Round 1. Two ordered pairs (a, b) and (c, d), where a, b, c, d are real numbers, form a basis of the coordinate plane if ad bc. Determine the number of ordered
HMMT November 017 November 11, 017 Theme Round 1. Two ordered pairs (a, b) and (c, d), where a, b, c, d are real numbers, form a basis of the coordinate plane if ad bc. Determine the number of ordered
1966 IMO Shortlist. IMO Shortlist 1966
 IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
The problems in this booklet are organized into strands. A problem often appears in multiple strands. The problems are suitable for most students in
 The problems in this booklet are organized into strands. A problem often appears in multiple strands. The problems are suitable for most students in Grade 11 or higher. Problem E What s Your Angle? A
The problems in this booklet are organized into strands. A problem often appears in multiple strands. The problems are suitable for most students in Grade 11 or higher. Problem E What s Your Angle? A
NORTHWESTERN UNIVERSITY Thrusday, Oct 6th, 2011 ANSWERS FALL 2011 NU PUTNAM SELECTION TEST
 Problem A1. Let a 1, a 2,..., a n be n not necessarily distinct integers. exist a subset of these numbers whose sum is divisible by n. Prove that there - Answer: Consider the numbers s 1 = a 1, s 2 = a
Problem A1. Let a 1, a 2,..., a n be n not necessarily distinct integers. exist a subset of these numbers whose sum is divisible by n. Prove that there - Answer: Consider the numbers s 1 = a 1, s 2 = a
Australian Intermediate Mathematics Olympiad 2016
 A u s t r a l i a n M at h e m at i c a l O ly m p i a d C o m m i t t e e a d e p a r t m e n t o f t h e a u s t r a l i a n m at h e m at i c s t r u s t Australian Intermediate Mathematics Olympiad
A u s t r a l i a n M at h e m at i c a l O ly m p i a d C o m m i t t e e a d e p a r t m e n t o f t h e a u s t r a l i a n m at h e m at i c s t r u s t Australian Intermediate Mathematics Olympiad
HMMT November 2013 Saturday 9 November 2013
 . [5] Evaluate + 5 + 8 + + 0. 75 There are 0 HMMT November 0 Saturday 9 November 0 Guts Round = 4 terms with average +0, so their sum is 7 0 = 75.. [5] Two fair six-sided dice are rolled. What is the probability
. [5] Evaluate + 5 + 8 + + 0. 75 There are 0 HMMT November 0 Saturday 9 November 0 Guts Round = 4 terms with average +0, so their sum is 7 0 = 75.. [5] Two fair six-sided dice are rolled. What is the probability
BRITISH COLUMBIA COLLEGES High School Mathematics Contest 2004 Solutions
 BRITISH COLUMBI COLLEGES High School Mathematics Contest 004 Solutions Junior Preliminary 1. Let U, H, and F denote, respectively, the set of 004 students, the subset of those wearing Hip jeans, and the
BRITISH COLUMBI COLLEGES High School Mathematics Contest 004 Solutions Junior Preliminary 1. Let U, H, and F denote, respectively, the set of 004 students, the subset of those wearing Hip jeans, and the
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca Cayley Contest. (Grade 10) Tuesday, February 28, 2017
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 2017 Cayley Contest (Grade 10) Tuesday, February 28, 2017 (in North America and South America) Wednesday, March 1, 2017 (outside
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 2017 Cayley Contest (Grade 10) Tuesday, February 28, 2017 (in North America and South America) Wednesday, March 1, 2017 (outside
2010 Fermat Contest (Grade 11)
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 010 Fermat Contest (Grade 11) Thursday, February 5, 010
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 010 Fermat Contest (Grade 11) Thursday, February 5, 010
Organization Team Team ID#
 1. [5] A positive integer is called primer if it has a prime number of distinct prime factors. Find the smallest primer number. 2. [5] Pascal has a triangle. In the nth row, there are n + 1 numbers a n,0,
1. [5] A positive integer is called primer if it has a prime number of distinct prime factors. Find the smallest primer number. 2. [5] Pascal has a triangle. In the nth row, there are n + 1 numbers a n,0,
MATHEMATICS TEST 60 Minutes 60 Questions
 MATHEMATICS TEST 60 Minutes 60 Questions DIRECTIONS: Solve each problem, choose the correct answer, and then fill in the corresponding oval on your answer document. Do not linger over problems that take
MATHEMATICS TEST 60 Minutes 60 Questions DIRECTIONS: Solve each problem, choose the correct answer, and then fill in the corresponding oval on your answer document. Do not linger over problems that take
2017 AMC 12A 10A Problems
 AMC 12/AHSME 2017 2017 AMC 12/AHSME 2017 AMC 12A 10A Problems A 1 Pablo buys popsicles for his friends. The store sells single popsicles for $1 each, 3-popsicle boxes for $2, and 5-popsicle boxes for $3.
AMC 12/AHSME 2017 2017 AMC 12/AHSME 2017 AMC 12A 10A Problems A 1 Pablo buys popsicles for his friends. The store sells single popsicles for $1 each, 3-popsicle boxes for $2, and 5-popsicle boxes for $3.
2016 Pascal Contest (Grade 9)
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 06 Pascal Contest (Grade 9) Wednesday, February, 06 (in North America and South America) Thursday, February, 06 (outside of North
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 06 Pascal Contest (Grade 9) Wednesday, February, 06 (in North America and South America) Thursday, February, 06 (outside of North
2005 Pascal Contest (Grade 9)
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 005 Pascal Contest (Grade 9) Wednesday, February 3, 005
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 005 Pascal Contest (Grade 9) Wednesday, February 3, 005
Glossary. Glossary 981. Hawkes Learning Systems. All rights reserved.
 A Glossary Absolute value The distance a number is from 0 on a number line Acute angle An angle whose measure is between 0 and 90 Addends The numbers being added in an addition problem Addition principle
A Glossary Absolute value The distance a number is from 0 on a number line Acute angle An angle whose measure is between 0 and 90 Addends The numbers being added in an addition problem Addition principle
