Squaring the Circle. A Case Study in the History of Mathematics
|
|
|
- Bryan Reynolds
- 6 years ago
- Views:
Transcription
1 Squaring the Circle A Case Study in the History of Mathematics
2 The Problem Using only a compass and straightedge, construct for any given circle, a square with the same area as the circle. The general problem of constructing a square with the same area as a given figure is known as the Quadrature of that figure. So, we seek a quadrature of the circle.
3 The Answer It has been known since 1822 that the quadrature of a circle with straightedge and compass is impossible. Notes: First of all we are not saying that a square of equal area does not exist. If the circle has area A, then a square with side A clearly has the same area. Secondly, we are not saying that a quadrature of a circle is impossible, since it is possible, but not under the restriction of using only a straightedge and compass.
4 Precursors It has been written, in many places, that the quadrature problem appears in one of the earliest extant mathematical sources, the Rhind Papyrus (~ 1650 B.C.). This is not really an accurate statement. If one means by the quadrature of the circle simply a quadrature by any means, then one is just asking for the determination of the area of a circle. This problem does appear in the Rhind Papyrus, but I consider it as just a precursor to the construction problem we are examining.
5 The Rhind Papyrus The papyrus was found in Thebes (Luxor) in the ruins of a small building near the Ramesseum. 1 It was purchased in 1858 in Egypt by the Scottish Egyptologist A. Henry Rhind and acquired by the British Museum after his death. The papyrus, written in hieratic, the cursive form of hieroglyphics, is a single roll which was originally about 5.4 meters long by 32 cms wide (~18 feet by 13 inches).
6 The Rhind Papyrus However, when the British Museum acquired it, it was shorter and in two pieces, missing the central portion. About 4 years after Rhind made his purchase, the American Egyptologist Edwin Smith bought, in Egypt, what he thought was a medical papyrus. This was given to the New York Historical Society in 1932, where it was discovered that beneath a fraudulent covering lay the missing piece of the Rhind Paprus. The Society then gave the scroll to the British Museum. 2
7 The Ahmes (Rhind) Papyrus The Rhind Papyrus has been dated to about 1650 B.C. and there is only one older mathematical papyrus, the Moscow Papyrus dated 1850 B.C. The papyrus was written by an Egyptian scribe A'h-mosè, commonly called Ahmes by modern writers. It appears to be a copy of an older work. Accurate reckoning of entering into things, knowledge of existing things all, mysteries, secrets all. Now was copied book this in year 33, month four of the inundation season, [under the majesty] of the king of [Upper and] Lower Egypt, 'A-user-Rê' [15th Dynasty reign of the Hyksos Pharaoh, Apepi I], endowed with life, in likeness to writings of old made in the time of the king of Upper [and Lower] Egypt, Ne-ma'et-Rê' [Amenemhet III ( B.C.)]. Lo the scribe A'h-mosè writes copy this. 3
8 The Ahmes (Rhind) Papyrus The scroll consists of 87 problems (with solutions) and is a rich primary source of ancient Egyptian mathematics, describing the Egyptian methods of multiplying and dividing, the Egyptian use of unit fractions, their employment of false position, and many applications of mathematics to practical problems.
9 The Ahmes (Rhind) Papyrus Our concern is with problem 50 which reads: A circular field has diameter 9 khet. What is its area? (A khet is a length measurement of about 50 meters.) Photo of Problem 50
10 The Ahmes (Rhind) Papyrus This problem (and solution) as well as all the other problems is phrased in terms of specific numbers. Does this mean that the problems are meant to be illustrative of general methods, or are all problems with different parameters considered different? Examination of other problems indicates that a definite algorithm was being used since the same technique is applied to different parameters.
11 Ahmes Papyrus: Problem 50 Ahmes' solution is: Take away thou 1/9 of it, namely 1; the remainder is 8. Make thou the multiplication 8 times 8; becomes it 64; the amount of it, this is, in area 64 setat. If we take this solution as a general formula, then in modern notation we obtain the formula for the area A of a circle of diameter d as: A = d d 2 9 = d 2. From this we deduce (since A = π d 2 /4) that the ancient Egyptians implicitly used the value π = 256/81 = (4/3) 4 =
12 Ahmes Papyrus: Problem 48
13 Ahmes Papyrus: Problem 48 Problem 48 is the only problem in the papyrus which does not have a statement. It consists only of a diagram and a calculation of 8 2 and 9 2. Chace's interpretation is This problem compares the areas of a circle of radius[sic] 9 and the circumscribing square. Gillings 4 challenges this interpretation, pointing out how well the circles of problems 50 and 41 are drawn. Prob. 48 Prob. 50 Prob. 41
14 Ahmes Papyrus: Problem 48 Gillings' interpretation of this problem is that Ahmes is providing the justification of the rule for finding the area of a circle. He proceeds to show how the rule could be obtained by examining the areas of an octagon (which would be close to the area of a circle) and the square which circumscribes it. In his discussion he makes the tongue in cheek comment that Ahmes should be considered the first circle squarer! 5 Others have seemingly missed the point that Gillings was joking, and have in all seriousness claimed this honor for Ahmes.
15 Earliest Greek Study To talk about the quadrature problem with straightedge and compass, one must turn to the ancient Greeks; for these were the tools of the Greek geometers. The first Greek known to be connected to the problem is Anaxagoras (c. 499 c. 427 B.C.). Although his chief work was in philosophy, where his prime postulate was reason rules the world, he was interested in mathematics and wrote on the quadrature of the circle and perspective. Plutarch (c.46 - c.120) reports that he did this mathematical work while he was in jail (for being a Persian sympathizer) 6. Only fragments of his work are extant, and it is unclear what his contribution actually is.
16 Lunes of Hippocrates Hippocrates of Chios (c. 440 B.C.) was a contemporary of Anaxagoras and was described by Aristotle as being skilled in geometry but otherwise stupid and weak 7. [Not to be confused with Hippocrates of Cos who also lived around this time on an island not far from the island of Chios and is considered to be the father of medicine ; originator of the Hippocratic Oath.] Hippocrates of Chios is mentioned by ancient writers as the first to arrange the propositions of geometry in a scientific fashion and as having published the secrets of Pythagoras in the field of geometry. Proclus (c. 460) credits him with the method of reduction... reducing a problem to a simpler one, solving the simpler problem and then reversing the process.
17 Lunes of Hippocrates Hippocrates enters our story because he provided the first example of a quadrature of a curvilinear figure (one whose sides are not line segments). He worked with certain lunes (crescents) formed by two circular arcs. This work is also historically important, since it is the first known proof. We don't have Hippocrates' original words, rather Simplicius' summary (530 A.D.) of Eudemus' account (335 B.C.) in his now lost History of Geometry, of Hippocrates' proof (440 B.C.) 8.
18 Lunes of Hippocrates Hippocrates' proof uses three preliminary results: 1. The Pythagorean Theorem (a 2 + b 2 = c 2 ) 2. An angle subtended by a semicircle is a right angle. 3. The ratio of the areas of two circles is the same as the ratio of the squares of their diameters. (Euclid XII.2) The first two of these were well known to geometers of Hippocrates' time. Eudemos (again via Simplicus) credits Hippocrates with the third result, but Archimedes (c. 225 B.C.) implies that the result is due to Eudoxus (408 c. 355 B.C.) 9. This puts the credit for the proof in doubt and current thinking is that Hippocrates probably didn't have a rigorous proof.
19 Euclid XII 2 Before we examine Hippocrates' lunes, let's consider this result on the areas of circles. We examine the result as given in Euclid's (c. 300 B.C.) masterpiece, The Elements. It is clear that this work is, at least in part, a compilation of earlier Greek work. The second proposition in book XII (out of 13) is: Circles are to one another as the squares on the diameters. Notice how the proposition is phrased in geometrical terms not the squares of the diameters an algebraic operation, but the squares on the diameters referring to the geometric square with side equal to a diameter. The ancient Greeks had only a rudimentary algebraic notation and relied almost exclusively on geometric ideas in their writing and thinking.
20 Euclid XII 2 Today we would state the result as: The ratio of the areas of two circles equals the ratio of the squares of their diameters. This phrasing underlines the more algebraic way in which we view such problems. One needs to be careful in studying ancient mathematics not to dismiss the difficulties that were overcome by the ancients because they appear simple to us. This simplicity is a result of a viewpoint that took thousands of years to develop. Euclid's proof is an example of the method of exhaustion, a technique used several times in Euclid and according to Archimedes, perfected by the mathematician Eudoxus. Simply put, the idea is to exhaust the area of a given circle by inscribing in it polygons of increasingly many sides. This is combined with a double reductio ad absurdum, that is, he proves A = B by showing that A < B and B < A both lead to contradictions.
21 Quadrature of Hippocrate's Lunes Given an isosceles right triangle, the area of the lunes determined by the semicircle on the hypotenuse and the semicircles on the sides of the triangle is equal to the area of the triangle. The theorem remains true for any right triangle, but Hippocrates does not seem to be aware of this.
22 Lunes of Hippocrates Consider a regular hexagon inscribed in a circle whose side is ½ of the diameter of the circle. The figure above can be thought of in two ways: circle + 6 lunes = hexagon + 6 semicircles. Since the diameter of the red semicircles is ½ the diameter of the blue circle, circle = 4 circles = 8 semicircles. So, we get 1 circle = 2 semicircles = hexagon 6 lunes. So if we can square these lunes, we can square a circle but these are not Hippocrates' lunes!
23 A Literary Aside Arguments such as this may have engendered a hope that with enough work a quadrature of the circle could be accomplished. The desire to find such a quadrature must have been well known to the general Greek populace, and not just the small set of mathematicians, for we find it referenced in one of Aristophanes famous comedies. Not only is the problem known, but in order to achieve the comic effect, it must have been known as a fruitless endeavor.
24 Aristophanes In the Birds, performed in 414 BC, a new city has to be founded from scratch. The main character, Peisthetaerus, is visited by various people who offer their services. 11 Enter METON: I come amongst you... PEISTHETAERUS: Some new misery this! Come to do what? What's your scheme's form and outline? What's your design? What buskin's on your foot? METON: I come to land-survey this Air of yours, and mete it out by acres. PEISTHETAERUS: Heaven and earth! Whoever are you? METON: Whoever am I? I'm Meton, known throughout Hellas and Colonnus. PEISTHETAERUS: Aye, and what are these?
25 Aristophanes METON: They're rods for Air-surveying. I'll just explain. The Air's, in outline, like one vast extinguisher; so then, observe, applying here my flexible rod, and fixing my compass there, - you understand? PEISTHETAERUS: I don't. METON: With the straight rod I measure out, that so the circle may be squared; and in the centre a market-place; and streets be leading to it straight to the very centre; just as from a star, though circular, straight rays flash out in all directions. PEISTHETAERUS: Why, the man's a Thales!
26 π It is lost in the mists of pre-history who first realized that the ratio of the circumference of a circle to its diameter is a constant. All the ancient civilizations knew this fact. Today we call this ratio π and express this relationship by saying that for any circle, the circumference C and the diameter d satisfy: C = πd. The use of the symbol π for this ratio is of relatively recent origin; the Greeks did not use the symbol. π was first used by the English mathematicians Oughtred (1647), Isaac Barrow (1664) and David Gregory (1697) to represent the circumference of a circle. The first use of π to represent the ratio of circumference to diameter was the English writer William Jones (1706). However, it did not come into common use until Euler adopted the symbol in
27 Archimedes Euclid XII.2 says that the ratio of the area of any circle to the square of its diameter is also a constant, but does not determine the value of this constant. It was Archimedes ( B.C.) who determined the constant in his remarkable treatise Measurement of a Circle. There are only three propositions in this short work (or at least, that is all of that work that has come down to us) and the second proposition is out of place indicating that what we have is probably not the original version. 2 We shall look at the first and third proposition.
28 Archimedes A few preliminary ideas: The area of a regular polygon is easily determined if you know that the area of a triangle = ½bh (b the length of a side, h the length of the altitude drawn to that side). In a regular polygon of n sides (all sides equal, all angles equal), draw the lines from the center to each of the vertices creating n congruent triangles. apothem The area is thus n times the area of one of the triangles = n(½sa) where s is the length of a side and a the length of an apothem (line drawn from center perpendicular to a side). Since ns is the perimeter (Q) of the polygon we get : A = ½aQ.
29 Archimedes Consider a regular polygon inscribed in a circle. Let K be the difference in the areas (area of circle area of polygon). If you now double the number of sides of the polygon, the area you have added to the original polygon is more than ½K. By repeating the procedure, you can make the area difference as small as you like, or in other words, for any positive number K, you can find a regular polygon (with enough sides) inscribed in a circle so that the area difference is less than K. This is Eudoxus' method of exhaustion. It also works for circumscribed polygons.
30 Archimedes Archimedes has proved that for any circle, A = ½rC, and since we know that C = πd, we get A = ½r(πd) = ½r(π2r) = πr 2 our familiar high school formula. Even though Archimedes showed the equivalence of a circle with a rectilinear figure, easily converted to a square, this is not a solution of the quadrature problem. The proof is indirect, it does not give a means for constructing the triangle with straightedge and compass. Before looking at Proposition 3, let's consider one of several methods known to the Greeks of using curves to perform a quadrature of the circle however, the curves used in this way can not themselves be constructed with straightedge and compass!
31 Archimedes In proposition 3 Archimedes turns his attention to the circumference of a circle. Again using inscribed and circumscribed regular polygons, their perimeters provide upper and lower bounds for the circumference of the circle. This gives him a means of calculating bounds for the number π. Proposition 3: The ratio of the circumference of any circle to its diameter is less than 3 1/7 (22/7) but greater than 3 10/71 (223/71). ( < π < ) What is remarkable about this result is not the underlying idea, but rather the skill of Archimedes in carrying out the computations. He started with inscribed and circumscribed hexagons, then doubled the size, and again, and again and yet again, ending with 96-sided polygons. At each step he calculates the perimeters. This involves approximating radicals which is where he shows his genius.
32 The Computation of π Early Phase There has always been an interest in the precise value of π. As we have seen, the ancient Egyptians used π = Other ancient civilizations were not as precise, generally using π = 3. This can be seen in Babylonian clay tablets and in the Bible (I Kings: 7:23) Then He made the molten sea (circular), ten cubits from brim to brim, while a line of 30 cubits measured it around. After Archimedes improvements were made by taking larger and larger polygons (except for the Romans not very concerned with precision, they dropped back to the value 3 1/8) 6.
33 The Computation of π Early Phase 7 ca. 150 A.D. - The first improvement over Archimedes values was given by Claudius Ptolemy of Alexandria in the Almagest, the most famous Greek work on astronomy. Ptolemy gives a value of π = 377/120 = ca. 480 The early Chinese worker in mechanics, Tsu Ch'ung-chih, gave the approximation π = 355/113 = correct to 6 decimal places. ca. 530 The early Hindu mathematician Āryabhata gave π = 62,832/20,000 = as an approximation. It is not known how this was obtained, but it could have been calculated as the perimeter of a regular inscribed polygon of 384 sides.
34 The Computation of π Early Phase ca The later Hindu mathematician Bhāskara gave several approximations. He gave 3927/1250 as an accurate value, 22/7 as an inaccurate value, and 10 for ordinary work Al-Kashi, astronomer royal to Ulugh Beg of Samarkand, computed π to sixteen decimal places using perimeters The eminent French mathematician François Viète found π correct to nine decimal places using polygons having 393,216 sides Adriaen van Roomen, more commonly known as Adrianus Romanus, of the Netherlands, found π correct to 15 places using polygons having 2 30 sides.
35 The Computation of π Early Phase 1610 Ludolph van Ceulen of the Netherlands computed π to 35 decimal places using polygons having 2 62 sides. He spent a large part of his life on this task, and his achievement was considered so extraordinary that his widow had the number engraved on his tombstone (now lost). To this day, the number is sometimes referred to as the Ludophine number The Dutch physicist Willebrord Snell, best known for his discovery of the law of refraction, devised a trigonometric improvement of the classical method so that from each pair of bounds given by the classical method he was able to obtain considerably closer bounds. By his method, he was able to get van Ceulen's 35 places using a polygon with only 2 30 sides.
36 The Computation of π Early Phase 1630 Grienberger, using Snell's refinement, computed π to 39 decimal places. This was the last major attempt to compute π by the method of Archimedes.
AMA1D01C Egypt and Mesopotamia
 Hong Kong Polytechnic University 2017 Outline Cultures we will cover: Ancient Egypt Ancient Mesopotamia (Babylon) Ancient Greece Ancient India Medieval Islamic World Europe since Renaissance References
Hong Kong Polytechnic University 2017 Outline Cultures we will cover: Ancient Egypt Ancient Mesopotamia (Babylon) Ancient Greece Ancient India Medieval Islamic World Europe since Renaissance References
Greece In 700 BC, Greece consisted of a collection of independent city-states covering a large area including modern day Greece, Turkey, and a multitu
 Chapter 3 Greeks Greece In 700 BC, Greece consisted of a collection of independent city-states covering a large area including modern day Greece, Turkey, and a multitude of Mediterranean islands. The Greeks
Chapter 3 Greeks Greece In 700 BC, Greece consisted of a collection of independent city-states covering a large area including modern day Greece, Turkey, and a multitude of Mediterranean islands. The Greeks
π is a mathematical constant that symbolizes the ratio of a circle s circumference to its
 Ziya Chen Math 4388 Shanyu Ji Origin of π π is a mathematical constant that symbolizes the ratio of a circle s circumference to its diameter, which is approximately 3.14159265 We have been using this symbol
Ziya Chen Math 4388 Shanyu Ji Origin of π π is a mathematical constant that symbolizes the ratio of a circle s circumference to its diameter, which is approximately 3.14159265 We have been using this symbol
Study Guide for Exam 1
 Study Guide for Exam 1 Math 330: History of Mathematics October 2, 2006. 1 Introduction What follows is a list of topics that might be on the exam. Of course, the test will only contain only a selection
Study Guide for Exam 1 Math 330: History of Mathematics October 2, 2006. 1 Introduction What follows is a list of topics that might be on the exam. Of course, the test will only contain only a selection
Euclidean Geometry. The Elements of Mathematics
 Euclidean Geometry The Elements of Mathematics Euclid, We Hardly Knew Ye Born around 300 BCE in Alexandria, Egypt We really know almost nothing else about his personal life Taught students in mathematics
Euclidean Geometry The Elements of Mathematics Euclid, We Hardly Knew Ye Born around 300 BCE in Alexandria, Egypt We really know almost nothing else about his personal life Taught students in mathematics
Grade 8 Chapter 7: Rational and Irrational Numbers
 Grade 8 Chapter 7: Rational and Irrational Numbers In this chapter we first review the real line model for numbers, as discussed in Chapter 2 of seventh grade, by recalling how the integers and then the
Grade 8 Chapter 7: Rational and Irrational Numbers In this chapter we first review the real line model for numbers, as discussed in Chapter 2 of seventh grade, by recalling how the integers and then the
Grade 6 Math Circles. Ancient Mathematics
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 Introduction Grade 6 Math Circles October 17/18, 2017 Ancient Mathematics Centre for Education in Mathematics and Computing Have you ever wondered where
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Introduction Grade 6 Math Circles October 17/18, 2017 Ancient Mathematics Centre for Education in Mathematics and Computing Have you ever wondered where
MEI Conference Squaring the Circle and Other Shapes
 MEI Conference 2017 Squaring the Circle and Other Shapes Kevin Lord kevin.lord@mei.org.uk Can you prove that the area of the square and the rectangle are equal? Use the triangle HPN to show that area of
MEI Conference 2017 Squaring the Circle and Other Shapes Kevin Lord kevin.lord@mei.org.uk Can you prove that the area of the square and the rectangle are equal? Use the triangle HPN to show that area of
THE GEOMETRY OF THALES
 THE GEOMETRY OF THALES BY PERCY J. HARDING. In this paper there will, of course, be found no new facts ; but merely a review of well-known historical statements and an attempt to connect them. It has often
THE GEOMETRY OF THALES BY PERCY J. HARDING. In this paper there will, of course, be found no new facts ; but merely a review of well-known historical statements and an attempt to connect them. It has often
Credited with formulating the method of exhaustion for approximating a circle by polygons
 MATH 300 History of Mathematics Figures in Greek Mathematics Sixth Century BCE Thales of Miletus May have formulated earliest theorems in geometry (e.g., ASA) Predicted an eclipse in 585 BCE Pythagoras
MATH 300 History of Mathematics Figures in Greek Mathematics Sixth Century BCE Thales of Miletus May have formulated earliest theorems in geometry (e.g., ASA) Predicted an eclipse in 585 BCE Pythagoras
Chapter 1: Euclid s Elements. Ancient Geometry. MthEd/Math 362 Summer /19/2009. Chapter 1 Slides Handout 1. Or,
 MthEd/Math 362 6/19/2009 Chapter 1: Or, It s All His Fault 1 Ancient Geometry Early civilizations such as those in Egypt, Mesopotamia, and India were concerned mainly with the utility of mathematics in
MthEd/Math 362 6/19/2009 Chapter 1: Or, It s All His Fault 1 Ancient Geometry Early civilizations such as those in Egypt, Mesopotamia, and India were concerned mainly with the utility of mathematics in
MATHEMATICS AND ITS HISTORY. Jimmie Lawson
 MATHEMATICS AND ITS HISTORY Jimmie Lawson Spring, 2005 Chapter 1 Mathematics of Ancient Egypt 1.1 History Egyptian mathematics dates back at least almost 4000 years ago. The main sources about mathematics
MATHEMATICS AND ITS HISTORY Jimmie Lawson Spring, 2005 Chapter 1 Mathematics of Ancient Egypt 1.1 History Egyptian mathematics dates back at least almost 4000 years ago. The main sources about mathematics
Greece. Chapter 5: Euclid of Alexandria
 Greece Chapter 5: Euclid of Alexandria The Library at Alexandria What do we know about it? Well, a little history Alexander the Great In about 352 BC, the Macedonian King Philip II began to unify the numerous
Greece Chapter 5: Euclid of Alexandria The Library at Alexandria What do we know about it? Well, a little history Alexander the Great In about 352 BC, the Macedonian King Philip II began to unify the numerous
Lecture 6. Three Famous Geometric Construction Problems
 Lecture 6. Three Famous Geometric Construction Problems The first Athenian school: the Sophist School After the final defeat of the Persians at Mycale in 479 B.C., Athens became a major city and commercial
Lecture 6. Three Famous Geometric Construction Problems The first Athenian school: the Sophist School After the final defeat of the Persians at Mycale in 479 B.C., Athens became a major city and commercial
Foundations of Basic Geometry
 GENERAL I ARTICLE Foundations of Basic Geometry Jasbir S Chahal Jasbir S Chahal is Professor of Mathematics at Brigham Young University, Provo, Utah, USA. His research interest is in number theory. The
GENERAL I ARTICLE Foundations of Basic Geometry Jasbir S Chahal Jasbir S Chahal is Professor of Mathematics at Brigham Young University, Provo, Utah, USA. His research interest is in number theory. The
Chapter 1 Primitive Man
 Chapter 1 Primitive Man Oh, So Mysterious Egyptian Mathematics! Lewinter and Widulski The Saga of Mathematics 1 Hunter/gatherers Counted Simple Notches on wolf bone Groups of pebbles and stones Development
Chapter 1 Primitive Man Oh, So Mysterious Egyptian Mathematics! Lewinter and Widulski The Saga of Mathematics 1 Hunter/gatherers Counted Simple Notches on wolf bone Groups of pebbles and stones Development
Geometry and axiomatic Method
 Chapter 1 Geometry and axiomatic Method 1.1 Origin of Geometry The word geometry has its roots in the Greek word geometrein, which means earth measuring. Before the time of recorded history, geometry originated
Chapter 1 Geometry and axiomatic Method 1.1 Origin of Geometry The word geometry has its roots in the Greek word geometrein, which means earth measuring. Before the time of recorded history, geometry originated
Math Number 842 Professor R. Roybal MATH History of Mathematics 24th October, Project 1 - Proofs
 Math Number 842 Professor R. Roybal MATH 331 - History of Mathematics 24th October, 2017 Project 1 - Proofs Mathematical proofs are an important concept that was integral to the development of modern mathematics.
Math Number 842 Professor R. Roybal MATH 331 - History of Mathematics 24th October, 2017 Project 1 - Proofs Mathematical proofs are an important concept that was integral to the development of modern mathematics.
Chapte Chapt r 1: Euclid s Elements Elemen Or, It s All His Fau Fa l u t Summer 2009 MthEd/Math 362 Chapter 1 1
 Chapter 1: Euclid s Elements Or, It s All His Fault Summer 2009 MthEd/Math 362 Chapter 1 1 Ancient Geometry Early civilizations such as those in Egypt, Mesopotamia, and India were concerned mainly with
Chapter 1: Euclid s Elements Or, It s All His Fault Summer 2009 MthEd/Math 362 Chapter 1 1 Ancient Geometry Early civilizations such as those in Egypt, Mesopotamia, and India were concerned mainly with
Mathematics in Ancient Egypt. Amber Hedgpeth. June 8, 2017
 Mathematics in Ancient Egypt Amber Hedgpeth June 8, 2017 The culture of ancient Egypt is rich and fascinating, with its pharaohs, pyramids, and life around the Nile River. With a rich history of massive
Mathematics in Ancient Egypt Amber Hedgpeth June 8, 2017 The culture of ancient Egypt is rich and fascinating, with its pharaohs, pyramids, and life around the Nile River. With a rich history of massive
Study Guide for Exam 2
 Study Guide for Exam 2 Math 330: History of Mathematics November 7, 2005. 1 Introduction What follows is a list of topics that might be on the exam. Of course, the test will only contain a selection of
Study Guide for Exam 2 Math 330: History of Mathematics November 7, 2005. 1 Introduction What follows is a list of topics that might be on the exam. Of course, the test will only contain a selection of
Chapter 7 Sect. 2. A pythagorean triple is a set of three nonzero whole numbers a, b, and c, that satisfy the equation a 2 + b 2 = c 2.
 Chapter 7 Sect. 2 The well-known right triangle relationship called the Pythagorean Theorem is named for Pythagoras, a Greek mathematician who lived in the sixth century b.c. We now know that the Babylonians,
Chapter 7 Sect. 2 The well-known right triangle relationship called the Pythagorean Theorem is named for Pythagoras, a Greek mathematician who lived in the sixth century b.c. We now know that the Babylonians,
Egyptian Mathematics
 Egyptian Mathematics Dr. Carmen Bruni David R. Cheriton School of Computer Science University of Waterloo November 1st, 2017 Three Part Series Egyptian Mathematics Diophantus and Alexandria Tartaglia,
Egyptian Mathematics Dr. Carmen Bruni David R. Cheriton School of Computer Science University of Waterloo November 1st, 2017 Three Part Series Egyptian Mathematics Diophantus and Alexandria Tartaglia,
Squaring the Circle. A Classical Problem
 Squaring the Circle A Classical Problem The Rules Find a square which has the same area as a circle Limited to using only a ruler and compass Only a finite amount of steps may be used Image from OneMomsBattle.com,
Squaring the Circle A Classical Problem The Rules Find a square which has the same area as a circle Limited to using only a ruler and compass Only a finite amount of steps may be used Image from OneMomsBattle.com,
Solving Polynomial Equations
 Solving Polynomial Equations Introduction We will spend the next few lectures looking at the history of the solutions of polynomial equations. We will organize this examination by the degree of the equations,
Solving Polynomial Equations Introduction We will spend the next few lectures looking at the history of the solutions of polynomial equations. We will organize this examination by the degree of the equations,
History of π. Andrew Dolbee. November 7, 2012
 History of Andrew Dolbee November 7, 01 The search for the ratio between a circle's circumference and its diameter, known as PI(), has been a very long one; appearing in some of the oldest mathematical
History of Andrew Dolbee November 7, 01 The search for the ratio between a circle's circumference and its diameter, known as PI(), has been a very long one; appearing in some of the oldest mathematical
What is proof? Lesson 1
 What is proof? Lesson The topic for this Math Explorer Club is mathematical proof. In this post we will go over what was covered in the first session. The word proof is a normal English word that you might
What is proof? Lesson The topic for this Math Explorer Club is mathematical proof. In this post we will go over what was covered in the first session. The word proof is a normal English word that you might
History of the Pythagorean Theorem
 History of the Pythagorean Theorem Laura Swenson, (LSwenson) Joy Sheng, (JSheng) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of
History of the Pythagorean Theorem Laura Swenson, (LSwenson) Joy Sheng, (JSheng) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of
Introduction to Trigonometry: Grade 9
 Introduction to Trigonometry: Grade 9 Andy Soper October 6, 2013 This document was constructed and type-set using P C T E X (a dielect of L A T E X) 1 1 Before you start 1.1 About these notes. These notes
Introduction to Trigonometry: Grade 9 Andy Soper October 6, 2013 This document was constructed and type-set using P C T E X (a dielect of L A T E X) 1 1 Before you start 1.1 About these notes. These notes
CHAPTER 1 NUMBER SYSTEMS. 1.1 Introduction
 N UMBER S YSTEMS NUMBER SYSTEMS CHAPTER. Introduction In your earlier classes, you have learnt about the number line and how to represent various types of numbers on it (see Fig..). Fig.. : The number
N UMBER S YSTEMS NUMBER SYSTEMS CHAPTER. Introduction In your earlier classes, you have learnt about the number line and how to represent various types of numbers on it (see Fig..). Fig.. : The number
Euclid s Elements Part II
 Euclid s Elements Part II The discovery of incommensurable magnitudes steered the ancient Greeks away from the study of number and towards the development of geometry. s a result, geometry was pushed in
Euclid s Elements Part II The discovery of incommensurable magnitudes steered the ancient Greeks away from the study of number and towards the development of geometry. s a result, geometry was pushed in
Exhaustion: From Eudoxus to Archimedes
 Exhaustion: From Eudoxus to Archimedes Franz Lemmermeyer April 22, 2005 Abstract Disclaimer: Eventually, I plan to polish this and use my own diagrams; so far, most of it is lifted from the web. Exhaustion
Exhaustion: From Eudoxus to Archimedes Franz Lemmermeyer April 22, 2005 Abstract Disclaimer: Eventually, I plan to polish this and use my own diagrams; so far, most of it is lifted from the web. Exhaustion
Exploring the Rhind Papyrus
 Exploring the Rhind Papyrus Dana Hartnett and Lauren Koepfle, Miami University In this article, we introduce the ancient Rhind papyrus. The Rhind papyrus serves as the foundation of mathematics today as
Exploring the Rhind Papyrus Dana Hartnett and Lauren Koepfle, Miami University In this article, we introduce the ancient Rhind papyrus. The Rhind papyrus serves as the foundation of mathematics today as
CHAPTER 5 INTRODUCTION TO EUCLID S GEOMETRY. 5.1 Introduction
 78 MATHEMATICS INTRODUCTION TO EUCLID S GEOMETRY CHAPTER 5 5.1 Introduction The word geometry comes form the Greek words geo, meaning the earth, and metrein, meaning to measure. Geometry appears to have
78 MATHEMATICS INTRODUCTION TO EUCLID S GEOMETRY CHAPTER 5 5.1 Introduction The word geometry comes form the Greek words geo, meaning the earth, and metrein, meaning to measure. Geometry appears to have
Classwork 8.1. Perform the indicated operation and simplify each as much as possible. 1) 24 2) ) 54w y 11) wy 6) 5 9.
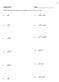 - 7 - Classwork 8.1 Name Perform the indicated operation and simplify each as much as possible. 1) 4 7) 16+ 5 49 ) 5 4 8) 11 6 81 ) 5 4x 9) 9 x + 49x 4) 75w 10) 6 5 54w y 5) 80wy 11) 15 6 6) 5 9 1) 15x
- 7 - Classwork 8.1 Name Perform the indicated operation and simplify each as much as possible. 1) 4 7) 16+ 5 49 ) 5 4 8) 11 6 81 ) 5 4x 9) 9 x + 49x 4) 75w 10) 6 5 54w y 5) 80wy 11) 15 6 6) 5 9 1) 15x
Eratosthenes method of measuring the Earth
 Eratosthenes method of measuring the Earth Credit for the first determination of the size of the Earth goes to the Greek polymath Eratosthenes, who lived from around 276 BC to 195 BC. Born in the Greek
Eratosthenes method of measuring the Earth Credit for the first determination of the size of the Earth goes to the Greek polymath Eratosthenes, who lived from around 276 BC to 195 BC. Born in the Greek
Final Exam Extra Credit Opportunity
 Final Exam Extra Credit Opportunity For extra credit, counted toward your final exam grade, you can write a 3-5 page paper on (i) Chapter II, Conceptions in Antiquity, (ii) Chapter V, Newton and Leibniz,
Final Exam Extra Credit Opportunity For extra credit, counted toward your final exam grade, you can write a 3-5 page paper on (i) Chapter II, Conceptions in Antiquity, (ii) Chapter V, Newton and Leibniz,
Grade 6 Math Circles November 1 st /2 nd. Egyptian Mathematics
 Faculty of Mathematics Waterloo, Ontario N2L 3G Centre for Education in Mathematics and Computing Grade 6 Math Circles November st /2 nd Egyptian Mathematics Ancient Egypt One of the greatest achievements
Faculty of Mathematics Waterloo, Ontario N2L 3G Centre for Education in Mathematics and Computing Grade 6 Math Circles November st /2 nd Egyptian Mathematics Ancient Egypt One of the greatest achievements
ANCIENT EGYPTIAN MATHEMATICS
 ANCIENT EGYPTIAN MATHEMATICS Searching for the Origins of Math Nida Haider University of Houston-MATH 4388 ANCEINT EGYPTAIN MATHEMATICS Searching for the Origins of Math In the study of mathematics, the
ANCIENT EGYPTIAN MATHEMATICS Searching for the Origins of Math Nida Haider University of Houston-MATH 4388 ANCEINT EGYPTAIN MATHEMATICS Searching for the Origins of Math In the study of mathematics, the
Upon Whose Shoulders We Stand: A History of Astronomy Up to 200 A.D. Dick Mallot 3/17/2005
 Upon Whose Shoulders We Stand: A History of Astronomy Up to 200 A.D. Dick Mallot 3/17/2005 Who were these ancient astronomers? Where did real astronomy begin? What did we know about astronomy 2000+ years
Upon Whose Shoulders We Stand: A History of Astronomy Up to 200 A.D. Dick Mallot 3/17/2005 Who were these ancient astronomers? Where did real astronomy begin? What did we know about astronomy 2000+ years
A Brief History of Pi
 Mathπath 2017 Mt. Holyoke College Proof School July 1, 2017 We re Catching Up! But first, this update on the score: We re Catching Up! But first, this update on the score: We re Catching Up! But first,
Mathπath 2017 Mt. Holyoke College Proof School July 1, 2017 We re Catching Up! But first, this update on the score: We re Catching Up! But first, this update on the score: We re Catching Up! But first,
221 MATH REFRESHER session 3 SAT2015_P06.indd 221 4/23/14 11:39 AM
 Math Refresher Session 3 1 Area, Perimeter, and Volume Problems Area, Perimeter, and Volume 301. Formula Problems. Here, you are given certain data about one or more geometric figures, and you are asked
Math Refresher Session 3 1 Area, Perimeter, and Volume Problems Area, Perimeter, and Volume 301. Formula Problems. Here, you are given certain data about one or more geometric figures, and you are asked
I named this section Egypt and Babylon because the surviving documents from Egypt are older. But I m going to discuss Babylon first so sue me.
 I. Ancient Times All the major ancient civilizations developed around river valleys. By 000 BC, there were civilizations thriving around the Nile (Egypt), the Tigris and Euphrates (Babylon), the Ganges
I. Ancient Times All the major ancient civilizations developed around river valleys. By 000 BC, there were civilizations thriving around the Nile (Egypt), the Tigris and Euphrates (Babylon), the Ganges
Pythagoras, Euclid, Archimedes and a new Trigonometry
 Pythagoras, Euclid, rchimedes and a new Trigonometry N J Wildberger School of Mathematics UNSW Sydney 05 ustralia webpages: http://web.maths.unsw.edu/~norman/ October 13, 006 bstract Pythagoras theorem,
Pythagoras, Euclid, rchimedes and a new Trigonometry N J Wildberger School of Mathematics UNSW Sydney 05 ustralia webpages: http://web.maths.unsw.edu/~norman/ October 13, 006 bstract Pythagoras theorem,
How can you find decimal approximations of square roots that are not rational? ACTIVITY: Approximating Square Roots
 . Approximating Square Roots How can you find decimal approximations of square roots that are not rational? ACTIVITY: Approximating Square Roots Work with a partner. Archimedes was a Greek mathematician,
. Approximating Square Roots How can you find decimal approximations of square roots that are not rational? ACTIVITY: Approximating Square Roots Work with a partner. Archimedes was a Greek mathematician,
PROJECTS. Project work in mathematics may be performed individually by a
 PROJECTS Project work in mathematics may be performed individually by a student or jointly by a group of students. These projects may be in the form of construction such as curve sketching or drawing of
PROJECTS Project work in mathematics may be performed individually by a student or jointly by a group of students. These projects may be in the form of construction such as curve sketching or drawing of
1 01:00:47:07 01:00:48:20 CHAPIN: Measurement is the process 2 01:00:48:22 01:00:52:25 of quantifying properties of objects, and to do that, 3
 1 01:00:47:07 01:00:48:20 CHAPIN: Measurement is the process 2 01:00:48:22 01:00:52:25 of quantifying properties of objects, and to do that, 3 01:00:52:27 01:00:56:21 we have set procedures that enable
1 01:00:47:07 01:00:48:20 CHAPIN: Measurement is the process 2 01:00:48:22 01:00:52:25 of quantifying properties of objects, and to do that, 3 01:00:52:27 01:00:56:21 we have set procedures that enable
Lecture 1: Axioms and Models
 Lecture 1: Axioms and Models 1.1 Geometry Although the study of geometry dates back at least to the early Babylonian and Egyptian societies, our modern systematic approach to the subject originates in
Lecture 1: Axioms and Models 1.1 Geometry Although the study of geometry dates back at least to the early Babylonian and Egyptian societies, our modern systematic approach to the subject originates in
EGYPTIAN MATHEMATICS
 EGYPTIAN MATHEMATICS TIMELINE Archaic Period (3100-2650 BC) Old Kingdom (2650-2134 BC) Large pyramids built; rich and productive period 1 st Intermediate Period (2200-2050) BC Chaotic Middle Kingdom (2050-1640
EGYPTIAN MATHEMATICS TIMELINE Archaic Period (3100-2650 BC) Old Kingdom (2650-2134 BC) Large pyramids built; rich and productive period 1 st Intermediate Period (2200-2050) BC Chaotic Middle Kingdom (2050-1640
7 th Grade Algebra & Geometry Main Lesson Lesson Plan Outline
 Day #1 7 th Grade Algebra & Geometry Main Lesson Lesson Plan Outline Ask students: "What do you think algebra is?" The essence of algebra is: It is the universal language of mathematics. Everywhere in
Day #1 7 th Grade Algebra & Geometry Main Lesson Lesson Plan Outline Ask students: "What do you think algebra is?" The essence of algebra is: It is the universal language of mathematics. Everywhere in
Lecture 8. Eudoxus and the Avoidance of a Fundamental Conflict
 Lecture 8. Eudoxus and the Avoidance of a Fundamental Conflict Eudoxus of Cnidus Eudoxus, 480 BC - 355 BC, was a Greek philosopher, mathematician and astronomer who contributed to Euclid s Elements. His
Lecture 8. Eudoxus and the Avoidance of a Fundamental Conflict Eudoxus of Cnidus Eudoxus, 480 BC - 355 BC, was a Greek philosopher, mathematician and astronomer who contributed to Euclid s Elements. His
MthEd/Math 300 Williams Fall 2011 Midterm Exam 2
 Name: MthEd/Math 300 Williams Fall 2011 Midterm Exam 2 Closed Book / Closed Note. Answer all problems. You may use a calculator for numerical computations. Section 1: For each event listed in the first
Name: MthEd/Math 300 Williams Fall 2011 Midterm Exam 2 Closed Book / Closed Note. Answer all problems. You may use a calculator for numerical computations. Section 1: For each event listed in the first
Astronomical Distances
 Astronomical Distances 13 April 2012 Astronomical Distances 13 April 2012 1/27 Last Time We ve been discussing methods to measure lengths and objects such as mountains, trees, and rivers. Astronomical
Astronomical Distances 13 April 2012 Astronomical Distances 13 April 2012 1/27 Last Time We ve been discussing methods to measure lengths and objects such as mountains, trees, and rivers. Astronomical
Math 1230, Notes 2. Aug. 28, Math 1230, Notes 2 Aug. 28, / 17
 Math 1230, Notes 2 Aug. 28, 2014 Math 1230, Notes 2 Aug. 28, 2014 1 / 17 This fills in some material between pages 10 and 11 of notes 1. We first discuss the relation between geometry and the quadratic
Math 1230, Notes 2 Aug. 28, 2014 Math 1230, Notes 2 Aug. 28, 2014 1 / 17 This fills in some material between pages 10 and 11 of notes 1. We first discuss the relation between geometry and the quadratic
Peter G. Brown. 1 π = 4
 Parabola Volume 34, Issue (998) ASLICE OF THE PI Peter G. Brown. Ifyouweretoaskavarietyofpeoplewhatπ was,youwouldprobablygetavarietyof different answers. The Bible gives π as 3, or at least implies this
Parabola Volume 34, Issue (998) ASLICE OF THE PI Peter G. Brown. Ifyouweretoaskavarietyofpeoplewhatπ was,youwouldprobablygetavarietyof different answers. The Bible gives π as 3, or at least implies this
Senior Math. Binary numbers are based on the powers of 2: 2 0 = 1, 2 1 = 2, 2 2 = 4, 2 3 = 8, 2 4 = 16, Binary numbers use only two digits: 0 and 1
 Academic Coaches Conference Senior Math Senior Math Fertile Crescent I. Numeration Systems 12% A. Binary (base 2) and Sexagesimal (base 60) Systems B. Convert to and from base 10 C. Add and subtract in
Academic Coaches Conference Senior Math Senior Math Fertile Crescent I. Numeration Systems 12% A. Binary (base 2) and Sexagesimal (base 60) Systems B. Convert to and from base 10 C. Add and subtract in
MA 341 Topics in Geometry
 MA 341 Topics in Geometry Dr. David Royster david.royster@uky.edu Patterson Office Tower 759 Spotted on the back of a t-shirt worn by LAPD Bomb Squad: If you see me running, try to keep up! 24-Aug-2011
MA 341 Topics in Geometry Dr. David Royster david.royster@uky.edu Patterson Office Tower 759 Spotted on the back of a t-shirt worn by LAPD Bomb Squad: If you see me running, try to keep up! 24-Aug-2011
In today s world, people with basic calculus knowledge take the subject for granted. As
 Ziya Chen Math 4388 Shanyu Ji Calculus In today s world, people with basic calculus knowledge take the subject for granted. As long as they plug in numbers into the right formula and do the calculation
Ziya Chen Math 4388 Shanyu Ji Calculus In today s world, people with basic calculus knowledge take the subject for granted. As long as they plug in numbers into the right formula and do the calculation
Chapter 12: Ruler and compass constructions
 Chapter 12: Ruler and compass constructions Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4120, Spring 2014 M. Macauley (Clemson) Chapter
Chapter 12: Ruler and compass constructions Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4120, Spring 2014 M. Macauley (Clemson) Chapter
DISCOVERING GEOMETRY Over 6000 years ago, geometry consisted primarily of practical rules for measuring land and for
 Name Period GEOMETRY Chapter One BASICS OF GEOMETRY Geometry, like much of mathematics and science, developed when people began recognizing and describing patterns. In this course, you will study many
Name Period GEOMETRY Chapter One BASICS OF GEOMETRY Geometry, like much of mathematics and science, developed when people began recognizing and describing patterns. In this course, you will study many
Anticipations of Calculus - Archimedes
 Anticipations of Calculus - Archimedes Let ABC be a segment of a parabola bounded by the straight line AC and the parabola ABC, and let D be the middle point of AC. Draw the straight line DBE parallel
Anticipations of Calculus - Archimedes Let ABC be a segment of a parabola bounded by the straight line AC and the parabola ABC, and let D be the middle point of AC. Draw the straight line DBE parallel
Euclidean Geometry Proofs
 Euclidean Geometry Proofs History Thales (600 BC) First to turn geometry into a logical discipline. Described as the first Greek philosopher and the father of geometry as a deductive study. Relied on rational
Euclidean Geometry Proofs History Thales (600 BC) First to turn geometry into a logical discipline. Described as the first Greek philosopher and the father of geometry as a deductive study. Relied on rational
PREFACE. Synergy for Success in Mathematics 9 is designed for Grade 9 students. The textbook
 Synergy for Success in Mathematics 9 is designed for Grade 9 students. The textbook contains all the required learning competencies and is supplemented with some additional topics for enrichment. Lessons
Synergy for Success in Mathematics 9 is designed for Grade 9 students. The textbook contains all the required learning competencies and is supplemented with some additional topics for enrichment. Lessons
Astronomical Distances. Astronomical Distances 1/30
 Astronomical Distances Astronomical Distances 1/30 Last Time We ve been discussing methods to measure lengths and objects such as mountains, trees, and rivers. Today we ll look at some more difficult problems.
Astronomical Distances Astronomical Distances 1/30 Last Time We ve been discussing methods to measure lengths and objects such as mountains, trees, and rivers. Today we ll look at some more difficult problems.
35 Chapter CHAPTER 4: Mathematical Proof
 35 Chapter 4 35 CHAPTER 4: Mathematical Proof Faith is different from proof; the one is human, the other is a gift of God. Justus ex fide vivit. It is this faith that God Himself puts into the heart. 21
35 Chapter 4 35 CHAPTER 4: Mathematical Proof Faith is different from proof; the one is human, the other is a gift of God. Justus ex fide vivit. It is this faith that God Himself puts into the heart. 21
How the Greeks Used Geometry to Understand the Stars
 previous index next How the Greeks Used Geometry to Understand the Stars Michael Fowler, University of Virginia 9/16/2008 Crystal Spheres: Plato, Eudoxus, Aristotle Plato, with his belief that the world
previous index next How the Greeks Used Geometry to Understand the Stars Michael Fowler, University of Virginia 9/16/2008 Crystal Spheres: Plato, Eudoxus, Aristotle Plato, with his belief that the world
Jennifer Duong Daniel Szara October 9, 2009
 Jennifer Duong Daniel Szara October 9, 2009 By around 2000 BC, Geometry was developed further by the Babylonians who conquered the Sumerians. By around 2000 BC, Rational and Irrational numbers were used
Jennifer Duong Daniel Szara October 9, 2009 By around 2000 BC, Geometry was developed further by the Babylonians who conquered the Sumerians. By around 2000 BC, Rational and Irrational numbers were used
CHAPTER (multiply by 10) 2 10 (double first line) 4 20 (double third line) 8 40 (double fourth line) (halve first line)
 CHAPTER 1 1. The answers are given in the answer section of the text. For the Egyptian hieroglyphics, 375 is three hundreds, seven tens and five ones, while 4856 is four thousands, eight hundreds, five
CHAPTER 1 1. The answers are given in the answer section of the text. For the Egyptian hieroglyphics, 375 is three hundreds, seven tens and five ones, while 4856 is four thousands, eight hundreds, five
5.3 Multiplying Decimals
 370 CHAPTER 5. DECIMALS 5.3 Multiplying Decimals Multiplying decimal numbers involves two steps: (1) multiplying the numbers as whole numbers, ignoring the decimal point, and (2) placing the decimal point
370 CHAPTER 5. DECIMALS 5.3 Multiplying Decimals Multiplying decimal numbers involves two steps: (1) multiplying the numbers as whole numbers, ignoring the decimal point, and (2) placing the decimal point
Area. HS PUMP. Spring 2009 CSUN Math. NSF Grant Measuring Aera A Candel
 Area 1. What is the area of the state of California? of Nevada? of Missouri? April 28, 2009 1 Computing areas of planar figures, or comparing them, has been one of the first mathematical problems. Pythagoras
Area 1. What is the area of the state of California? of Nevada? of Missouri? April 28, 2009 1 Computing areas of planar figures, or comparing them, has been one of the first mathematical problems. Pythagoras
Traces and Ancient Egypt
 August 26, 2018 Table of contents 1 2 Concepts and Relationships Early Number Bases Spacial Relationships Outline 1 2 Concepts and Relationships Early Number Bases Spacial Relationships Concepts and Relationships
August 26, 2018 Table of contents 1 2 Concepts and Relationships Early Number Bases Spacial Relationships Outline 1 2 Concepts and Relationships Early Number Bases Spacial Relationships Concepts and Relationships
Integrated Math II. IM2.1.2 Interpret given situations as functions in graphs, formulas, and words.
 Standard 1: Algebra and Functions Students graph linear inequalities in two variables and quadratics. They model data with linear equations. IM2.1.1 Graph a linear inequality in two variables. IM2.1.2
Standard 1: Algebra and Functions Students graph linear inequalities in two variables and quadratics. They model data with linear equations. IM2.1.1 Graph a linear inequality in two variables. IM2.1.2
Name Period Date. GEO2.2: Area of Circles Derive the area formula for circles. Solve application problems that involve areas of circles.
 Name Period Date GEOMETRY AND MEASUREMENT Student Pages for Packet 2: Circles GEO2.1 Circumference Use multiple representations to explore the relationship between the diameter and the circumference of
Name Period Date GEOMETRY AND MEASUREMENT Student Pages for Packet 2: Circles GEO2.1 Circumference Use multiple representations to explore the relationship between the diameter and the circumference of
Extending The Natural Numbers. Whole Numbers. Integer Number Set. History of Zero
 Whole Numbers Are the whole numbers with the property of addition a group? Extending The Natural Numbers Natural or Counting Numbers {1,2,3 } Extend to Whole Numbers { 0,1,2,3 } to get an additive identity.
Whole Numbers Are the whole numbers with the property of addition a group? Extending The Natural Numbers Natural or Counting Numbers {1,2,3 } Extend to Whole Numbers { 0,1,2,3 } to get an additive identity.
Archimedes Quadrature of the Parabola
 Archimedes and the Quadrature of the Parabola MATH 110 Topics in Mathematics Mathematics Through Time November 1, 2013 Outline Introduction 1 Introduction 2 3 Who was Archimedes? Lived ca. 287-212 BCE,
Archimedes and the Quadrature of the Parabola MATH 110 Topics in Mathematics Mathematics Through Time November 1, 2013 Outline Introduction 1 Introduction 2 3 Who was Archimedes? Lived ca. 287-212 BCE,
Geometry I (CM122A, 5CCM122B, 4CCM122A)
 Geometry I (CM122A, 5CCM122B, 4CCM122A) Lecturer: Giuseppe Tinaglia Office: S5.31 Office Hours: Wed 1-3 or by appointment. E-mail: giuseppe.tinaglia@kcl.ac.uk Course webpage: http://www.mth.kcl.ac.uk/
Geometry I (CM122A, 5CCM122B, 4CCM122A) Lecturer: Giuseppe Tinaglia Office: S5.31 Office Hours: Wed 1-3 or by appointment. E-mail: giuseppe.tinaglia@kcl.ac.uk Course webpage: http://www.mth.kcl.ac.uk/
Infinity and Infinite Series
 Infinity and Infinite Series Numbers rule the Universe Pythagoras (-580-500 BC) God is a geometer Plato (-427-347 BC) God created everything by numbers Isaac Newton (1642-1727) The Great Architect of
Infinity and Infinite Series Numbers rule the Universe Pythagoras (-580-500 BC) God is a geometer Plato (-427-347 BC) God created everything by numbers Isaac Newton (1642-1727) The Great Architect of
Hence, the sequence of triangular numbers is given by., the. n th square number, is the sum of the first. S n
 Appendix A: The Principle of Mathematical Induction We now present an important deductive method widely used in mathematics: the principle of mathematical induction. First, we provide some historical context
Appendix A: The Principle of Mathematical Induction We now present an important deductive method widely used in mathematics: the principle of mathematical induction. First, we provide some historical context
I.31 Now given a circular field, the circumference is 30 bu and the diameter 10 bu. Question: What is the area? Answer:
 Chapter 9 Areas of circular regions 9.1 Problems I31 38 1 I.31 Now given a circular field, the circumference is 30 bu and the diameter 10 bu. I.3 Given another circular field, the circumference is 181
Chapter 9 Areas of circular regions 9.1 Problems I31 38 1 I.31 Now given a circular field, the circumference is 30 bu and the diameter 10 bu. I.3 Given another circular field, the circumference is 181
The Computation of π by Archimedes. Bill McKeeman Dartmouth College
 The Computation of π by Archimedes Bill McKeeman Dartmouth College 2012.02.15 Abstract It is famously known that Archimedes approximated π by computing the perimeters of manysided regular polygons, one
The Computation of π by Archimedes Bill McKeeman Dartmouth College 2012.02.15 Abstract It is famously known that Archimedes approximated π by computing the perimeters of manysided regular polygons, one
Numbers and Counting. Number. Numbers and Agriculture. The fundamental abstraction.
 Numbers and Counting Number The fundamental abstraction. There is archaeological evidence of counters and counting systems in some of the earliest of human cultures. In early civilizations, counting and
Numbers and Counting Number The fundamental abstraction. There is archaeological evidence of counters and counting systems in some of the earliest of human cultures. In early civilizations, counting and
1. For any integer a, a 0, 1 a and a a. 4. If a b and b c then a c. 5. If a b and b a then a = ±b.
 4. Euclidean Number Theory Books VII, VIII and IX of the Elements were on Number Theory. Two major results are: Proposition 14 which says that every integer greater or equal 2 can be factored as a product
4. Euclidean Number Theory Books VII, VIII and IX of the Elements were on Number Theory. Two major results are: Proposition 14 which says that every integer greater or equal 2 can be factored as a product
Chapter 0. Introduction. An Overview of the Course
 Chapter 0 Introduction An Overview of the Course In the first part of these notes we consider the problem of calculating the areas of various plane figures. The technique we use for finding the area of
Chapter 0 Introduction An Overview of the Course In the first part of these notes we consider the problem of calculating the areas of various plane figures. The technique we use for finding the area of
The area of a geometric figure is a measure of how big a region is enclosed inside the figure.
 59 CH 7 GEOMETRY Introduction G eo: Greek for earth, and metros: Greek for measure. These roots are the origin of the word geometry, which literally means earth measurement. The study of geometry has gone
59 CH 7 GEOMETRY Introduction G eo: Greek for earth, and metros: Greek for measure. These roots are the origin of the word geometry, which literally means earth measurement. The study of geometry has gone
Geometry Pre-Unit 1 Intro: Area, Perimeter, Pythagorean Theorem, Square Roots, & Quadratics. P-1 Square Roots and SRF
 Geometry Pre-Unit 1 Intro: Area, Perimeter, Pythagorean Theorem, Square Roots, & Quadratics P-1 Square Roots and SRF Square number the product of a number multiplied by itself. 1 * 1 = 1 1 is a square
Geometry Pre-Unit 1 Intro: Area, Perimeter, Pythagorean Theorem, Square Roots, & Quadratics P-1 Square Roots and SRF Square number the product of a number multiplied by itself. 1 * 1 = 1 1 is a square
Basic Ideas in Greek Mathematics
 previous index next Basic Ideas in Greek Mathematics Michael Fowler UVa Physics Department Closing in on the Square Root of 2 In our earlier discussion of the irrationality of the square root of 2, we
previous index next Basic Ideas in Greek Mathematics Michael Fowler UVa Physics Department Closing in on the Square Root of 2 In our earlier discussion of the irrationality of the square root of 2, we
Math Round. Any figure shown may not be drawn to scale.
 Indiana Academic Super Bowl Math Round 2019 Coaches Practice A Program of the Indiana Association of School Principals Students: Throughout this round we will be pronouncing mathematic symbols and concepts
Indiana Academic Super Bowl Math Round 2019 Coaches Practice A Program of the Indiana Association of School Principals Students: Throughout this round we will be pronouncing mathematic symbols and concepts
The Mathematics of Renaissance Europe
 The Mathematics of Renaissance Europe The 15 th and 16 th centuries in Europe are often referred to as the Renaissance. The word renaissance means rebirth and describes the renewed interest in intellectual
The Mathematics of Renaissance Europe The 15 th and 16 th centuries in Europe are often referred to as the Renaissance. The word renaissance means rebirth and describes the renewed interest in intellectual
MSM 707 Number Systems for Middle School Teachers Semester Project
 MSM 707 Number Systems for Middle School Teachers Semester Project During the course of the semester, we will discuss some important concepts of Number Theory. The following projects are designed to give
MSM 707 Number Systems for Middle School Teachers Semester Project During the course of the semester, we will discuss some important concepts of Number Theory. The following projects are designed to give
A π day celebration! Everyone s favorite geometric constant!
 A π day celebration! Everyone s favorite geometric constant! Math Circle March 10, 2019 The circumference of a circle is another word for its perimeter. A circle s circumference is proportional to its
A π day celebration! Everyone s favorite geometric constant! Math Circle March 10, 2019 The circumference of a circle is another word for its perimeter. A circle s circumference is proportional to its
Activity Sheet 1: Constructions
 Name ctivity Sheet 1: Constructions Date 1. Constructing a line segment congruent to a given line segment: Given a line segment B, B a. Use a straightedge to draw a line, choose a point on the line, and
Name ctivity Sheet 1: Constructions Date 1. Constructing a line segment congruent to a given line segment: Given a line segment B, B a. Use a straightedge to draw a line, choose a point on the line, and
From Hipparchus to a Helix Ruler
 From Hipparchus to a Helix Ruler Jerold Mathews This paper gives a brief history of the chord function { a precursor of the sine function { from the mathematics/astronomy of Hipparchus and Ptolemy to the
From Hipparchus to a Helix Ruler Jerold Mathews This paper gives a brief history of the chord function { a precursor of the sine function { from the mathematics/astronomy of Hipparchus and Ptolemy to the
Astronomy 311: Historical Astronomy
 Astronomy 311: Historical Astronomy Greek scientific thought started with a school of Philosphers in Ionia in the sixth century BC. The most prominent was Thales. Examples of this early thought was that
Astronomy 311: Historical Astronomy Greek scientific thought started with a school of Philosphers in Ionia in the sixth century BC. The most prominent was Thales. Examples of this early thought was that
Reserve your right to think, for even to think wrongly is better than not to think at all. To teach superstitions as truth is a most m terrible
 Reserve your right to think, for even to think wrongly is better than not to think at all. To teach superstitions as truth is a most m terrible thing. - Hypatia Bit of Administration. Reading Bless, Chapters
Reserve your right to think, for even to think wrongly is better than not to think at all. To teach superstitions as truth is a most m terrible thing. - Hypatia Bit of Administration. Reading Bless, Chapters
Homework 1 from Lecture 1 to Lecture 10
 Homework from Lecture to Lecture 0 June, 207 Lecture. Ancient Egyptians calculated product essentially by using additive. For example, to find 9 7, they considered multiple doublings of 7: Since 9 = +
Homework from Lecture to Lecture 0 June, 207 Lecture. Ancient Egyptians calculated product essentially by using additive. For example, to find 9 7, they considered multiple doublings of 7: Since 9 = +
History of Mathematics
 History of Mathematics A Course for High Schools (Session #132) Chuck Garner, Ph.D. Department of Mathematics Rockdale Magnet School for Science and Technology Georgia Math Conference at Rock Eagle, October
History of Mathematics A Course for High Schools (Session #132) Chuck Garner, Ph.D. Department of Mathematics Rockdale Magnet School for Science and Technology Georgia Math Conference at Rock Eagle, October
PHASE 9 Ali PERFECT ALI-PI.
 PHASE 9 PERFECT ALI-PI Pi as a Fraction pi is written and expressed as definite fraction and ratio of two numbers: pi = 19 /6 = 3.16666666. pi = 3 + 1/6 Any rational number which cannot be expressed as
PHASE 9 PERFECT ALI-PI Pi as a Fraction pi is written and expressed as definite fraction and ratio of two numbers: pi = 19 /6 = 3.16666666. pi = 3 + 1/6 Any rational number which cannot be expressed as
Measuring Distant Objects
 Measuring Distant Objects 17 March 2014 Measuring Distant Objects 17 March 2014 1/30 How can you measure the length of an object? Ideally, you use a ruler, a tape measure, or some other measuring device.
Measuring Distant Objects 17 March 2014 Measuring Distant Objects 17 March 2014 1/30 How can you measure the length of an object? Ideally, you use a ruler, a tape measure, or some other measuring device.
October 16, Geometry, the Common Core, and Proof. John T. Baldwin, Andreas Mueller. The motivating problem. Euclidean Axioms and Diagrams
 October 16, 2012 Outline 1 2 3 4 5 Agenda 1 G-C0-1 Context. 2 Activity: Divide a line into n pieces -with string; via construction 3 Reflection activity (geometry/ proof/definition/ common core) 4 mini-lecture
October 16, 2012 Outline 1 2 3 4 5 Agenda 1 G-C0-1 Context. 2 Activity: Divide a line into n pieces -with string; via construction 3 Reflection activity (geometry/ proof/definition/ common core) 4 mini-lecture
Number Systems. There are 10 kinds of people those that understand binary, those that don t, and those that expected this joke to be in base 2
 Number Systems There are 10 kinds of people those that understand binary, those that don t, and those that expected this joke to be in base 2 A Closer Look at the Numbers We Use What is the difference
Number Systems There are 10 kinds of people those that understand binary, those that don t, and those that expected this joke to be in base 2 A Closer Look at the Numbers We Use What is the difference
