arxiv: v2 [math.co] 30 Oct 2018
|
|
|
- Branden Ray
- 5 years ago
- Views:
Transcription
1 THE SET SPLITTABILITY PROBLEM arxiv:6.0542v2 [math.co] 30 Oct 208 PETER BERNSTEIN, CASHOUS BORTNER, SAMUEL COSKEY, SHUNI LI, AND CONNOR SIMPSON ABSTRACT. Th st splittability prblm is th fllwing: givn a finit cllctin f finit sts, ds thr xits a singl st that slcts half th lmnts frm ach st in th cllctin? (If a st has dd siz, w allw th flr r ciling.) It is natural t study th st splittability prblm in th cntxt f cmbinatrial discrpancy thry and its applicatins, sinc a cllctin is splittabl if and nly if it has discrpancy. W intrduc a variant f th splittability prblm calld th p-splittability prblm, in which n sks t slct th fractin p frm ach st instad f half. W shw that th p- splittability prblm is NP-cmplt. W thn invstigat svral critria fr p-splittability, giving a cmplt charactrizatin f p-splittability fr thr r fwr sts. In th cas f rdinary st splittability (p = 2 ) w xtnd th charactrizatin t fur r fwr sts. Finally w shw that whn thr ar sufficintly many lmnts, unsplittability is asympttically much mr rar than splittability.. INTRODUCTION Lt B = {B,..., B n } b a cllctin f finit sts and lt 0 p. W say th cllctin B is p-splittabl if thr xists a st S (calld a p-splittr) such that fr all i n, w hav that S B i = p B i, th narst intgr t p B i. Of curs, th narst intgr p B i is nt wll-dfind whn p B i is a half-intgr, and in this cas w adpt th cnvntin that S B i may b ithr th flr r th ciling. Whn p = 2, w will smtims simply say thatb is splittabl and that S is a splittr. It is natural t study splittability and its gnralizatins in th cntxt f cmbinatrial discrpancy thry. Givn a cllctin B as abv, th discrpancy f B is disc(b) = min S max i n B i S B i \ S. Intuitivly, th discrpancy masurs t what xtnt it is pssibl t simultanusly and vnly split ach st in th cllctin. In fact disc(b) if and nly if B is (p = 2 ) splittabl. 200 Mathmatics Subjct Classificatin. 05D05, 05C5, K38, 68Q7.
2 THE SET SPLITTABILITY PROBLEM 2 Uppr bunds fr th discrpancy hav bn studid in rcnt dcads. In 98 Bck and Fiala shwd that if vry lmnt f B is cntaind in at mst t f th sts inb, thn disc(b) 2t 2 [BF8]. Incrmntal imprvmnts t this bund can b fund in wrks such as [BH97, Hl99, Buk3]. In 985, Spncr gav an uppr bund fr th discrpancy f an arbitrary cllctin: disc(b) K n whr K is an abslut cnstant and n is th numbr f sts [Sp85]. Th uppr bund f O( n) is asympttically tight fr gnral cllctins. Of curs th discrpancy f any givn cllctin may b much smallr than this bund, and sinc last discrpancy is usually bst, it is natural t study th discrpancy cas. St splittability can als b viwd as a cmbinatrial vrsin f th utcm f th ham sandwich thrm: givn Lbsgu masurabl substs B,..., B n R n thr xists a hyprplan H such that fr all i n xactly half th masur f B i lis t ach sid f H. If Lbsgu masur is rplacd by a discntinuus masur, thn sm f th mass f B i may li n H itslf. In this cas th cnclusin must b mdifid t say that that at mst half th masur f B i lis t ach sid f H [EH]. Thus a ham sandwich hyprplan ds nt prcisly slv th splittability prblm, nr ds st splittability hlp t find a gmtric hyprplan. Nvrthlss th tw prblms ar clsly rlatd. A third way t think f st splittability is as a vry strng frm f hyprgraph 2- clrability. Rcall that a hyprgraph with hyprdgs B,..., B n is 2-clrabl if thr xists a{rd, blu}-clring f its vrtics such that n hyprdg is mnchrmatic. With p-splittability w ask nt simply that bth clrs ar rprsntd in ach hyprdg, but that th clr rd always appars a prscribd prcntag f th tim. In th nxt sctin w xplr th cmputatinal cmplxity f p-splittability. In th cas p = 2 it is knwn that th qustin f dciding whthr a givn cllctin is splittabl is NP-cmplt. This fllws frm th fact that it is NP-hard t distinguish cllctins f discrpancy 0 frm cllctins f discrpancy Ω( n) [CNN]. Th significanc f this rsult is that whil thr ar algrithms t find witnsss t Spncr s thrm [Ban0, LM2], in gnral vn if a cllctin has discrpancy ( n) n cannt hp t fficintly find a witnss fr this. In anthr rlatd rsult, th prblm f dciding whthr a givn hyprgraph is 2-clrabl is NP-cmplt [Lv73]. W will stablish th crrspnding hardnss rsults in th cas f p-splittability fr arbitrary p. That is, w shw that fr any 0 < p <, th p-splittability prblm is NP-cmplt. Th fact that th p-splittability dcisin prblm is hard mans w cannt hp t find a gnral and usful charactrizatin f p-splittability. Hwvr it is pssibl t d s fr
3 THE SET SPLITTABILITY PROBLEM 3 small cllctins and fr thr spcial cllctins f sts. Fr an xampl invlving (vry) small cllctins, w will shw that a cllctin B f at mst tw sts is p-splittabl fr any p. Fr an xampl invlving spcial cllctins, supps that B = {B,..., B n } is a cllctin f n sts such that vry lmnt x lis in xactly n sts fb. In this cas w will shw thatb is p-splittabl if and nly if th sum p B + + p B n is divisibl by n. Th calculatins usd in ths tw rsults vntually lad us t a cmplt algbraic charactrizatin f p-splittability fr cllctins B f at mst thr sts. If n spcializs t th imprtant cas p = 2, sm things bcm simplr and nw charactrizatins bcm tractabl. Fr xampl, if B is a cllctin f thr sts thn B is 2-unsplittabl if and nly if ach Vnn rgin f multiplicity 2 is dd, and all thr Vnn rgins ar mpty. (This rsult was prviusly bsrvd in [CCSS6].) With th hlp f a suprcmputr, w wr als abl t prvid a cmplt charactrizatin f th 2-unsplittabl cllctins f fur sts in trms f th sizs f its Vnn rgins. Th prf f th rsult rsts n an xhaustiv sarch fr unsplittabl cnfiguratins with a small numbr f lmnts, tgthr with a rductin lmma which implis that if B is unsplittabl thn it rmains unsplittabl aftr rducing th numbr f lmnts f ach Vnn rgin mdul 2. Ths Vnn-styl charactrizatins f th 2-unsplittabl cnfiguratins asily imply that unsplittability is xtrmly rar fr cllctins f thr and fur sts. Althugh ur mthd f finding unsplittabl cnfiguratins bcms intractabl fr cllctins f fiv r mr sts, this rarity phnmnn rmains tru. Spcifically w shw that if n and k grws sufficintly fast rlativ t n, thn th prbability that a cllctin with n sts and k lmnts is splittabl cnvrgs t. In particular if n is fixd and k is larg nugh thn mst cllctins with n sts and k lmnts ar splittabl. Th rst f this papr is rganizd as fllws. In Sctin 2 w prv that th prblm f dciding whthr a givn cllctin is p-splittabl is NP-cmplt. In Sctin 3, w giv critria fr dciding whthr sm spcial cllctins ar p-splittabl, and prvid a cmplt charactrizatin f p-splittability fr cllctins f at mst thr sts. In Sctin 4, w giv furthr splittability critria fr th spcial cas p = 2 and us thm t giv a cmplt charactrizatin f 2-splittability fr cllctins f at mst fur sts. Finally w shw that fr cllctins with sufficintly many lmnts, splittability is by far mr cmmn than unsplittability. Acknwldgmnt. This articl rprsnts a prtin f th rsarch carrid ut during th 206 math REU prgram at Bis Stat Univrsity. Th prgram was supprtd by NSF grant #DMS and by Bis Stat Univrsity.
4 THE SET SPLITTABILITY PROBLEM 4 2. THE COMPLEXITY OF p-splittability In this sctin w stablish that th p-splittability prblm is hard. Bfr prcding, lt us clarify hw w rgard th p-splittability prblm frmally as a dcisin prblm, which w dnt p-split. IfB = {B,..., B n } is a finit cllctin f substs f{,..., m} thn th incidnc matrix fb is th n m matrix M whs(i, j) ntry is whnvr j B i, and 0 thrwis. An instanc f p-split cnsists f an incidnc matrix M f a cllctin B. Th matrix M lis in p-split if and nly if thr xists a binary vctr y such that (My) i = p B i. Indd, such a vctr y is th indicatr functin f a st S that is a p-splittr fb. In this sctin w will mak significant us f th ntatins: M i fr th ith rw f M; fr a vctr f s f lngth dtrmind by cntxt, and; M i fr th numbr f s in th ith rw f M. It is imprtant t nt that th valus f th right-hand sids p B i frm th prvius paragraph can b dtrmind just frm th matrix M bcaus w hav p B i = pm i. Thrm 2.. Fr any 0 < p <, th prblm p-split f dtrmining whthr a cllctin is p-splittabl is NP-cmplt. Nt that p-split lis in NP bcaus givn an instanc M f p-split and a charactristic vctr y f an stnsibl splittr, n can asily dcid in plynmial tim whthr(my) i is qual t pm i fr ach i. T stablish that p-split is NP-cmplt, w will xhibit a plynmial-tim rductin frm th dcisin prblm ZOE (which is vry similar t zr-n intgr prgramming [Kar72]) t p-split. Hr ZOE stands fr zr n quatins, and is frmalizd as fllws. An instanc f ZOE cnsists f a binary matrix A. Th matrix A lis in ZOE if and nly if thr xists a binary vctr x such that Ax =. It is knwn that ZOE is NP-cmplt [DPV06]. In th dfinitin f ZOE, w can clarly assum withut lss f gnrality that th matrix A has n zr rws. W can als assum that at last n rw f A has at last tw s. Indd, if A has just n in ach rw thn Ax = is trivial t slv. Nw in rdr t stablish Thrm 2., w will dscrib a mapping frm binary matrics A t incidnc matrics M, with th prprty that A lis in ZOE if and nly if M lis in p-split. In rdr t guarant this, th matrix M that w cnstruct will hav th spcial prprtis: (a) A is an uppr-lft submatrix f M; (b) any slutin x t Ax = xtnds t a slutin y t(my) i = pm i ; and
5 THE SET SPLITTABILITY PROBLEM 5 (c) any slutin y t(my) i = pm i rstricts t a slutin x t Ax =. Having dscribd ur gnral apprach, w nw prcd with th dtails. 2.. Spcificatin f th cnstructin. Lt A b a givn a r a c binary matrix, and assum that A i > 0 fr all i and that at last n A i >. Additinally lt p 2 b givn. W will nw cnstruct a blck matrix M f th frm: M := [ A B C 0 D E Bfr w dscrib th blcks B, C, D, and E, lt us lt s := max i A i and lt T b indics f th s clumns fllwing th clumns f A. Nxt lt q = p p and lt F b th indics f th max{ qs s+, q + } many clumns t th right f th clumns indxd by T. Nw B is an a r T matrix whs ith rw cntains A i many s, fllwd by all 0 s. And C is an a r F matrix whs ith rw cntains qa i A i + many s, fllwd by all 0 s. Th blcks D and E ach cnsist f sublcks. Fr i T, lt D i b th ( F q ) T matrix whs ith clumn cnsists f s, and all thr clumns cnsist f 0 s. And lt E 0 dnt a ( F ) F matrix whs rws cnsist f th indicatr functins f th substs f q {,..., F } f siz q. Thn w lt D = D. D T, and E = ]. E 0. Hr thr ar T many cpis f E 0 in E. It is asy t s that th dimnsins f th matrix M ar plynmial in th dimnsins f th matrix A. (Rcall hr that p is a fixd paramtr f th cnstructin.) Hnc th cnstructin is a plynmial-tim mapping Exampl f th cnstructin. Bfr prving that th cnstructin satisfis ur rquirmnts, lt us giv an xampl. Supps that p = 3 and w ar givn th ZOE systm [ ] [ ] 0 0 Ax = x =. 0 Thn w hav A = 2, A 2 = 3, s = max i A i = 3, and q = p p = 2. Thus T cnsists f th s = 2 clumns{5, 6}, and F cnsists f th qs s+ = 4 clumns {7, 8, 9, 0}. E 0
6 THE SET SPLITTABILITY PROBLEM 6 Th blck B is thus a 2 2 matrix with A = many s in th first rw and A 2 = 2 many s in th scnd rw. Th blck C is a 2 4 matrix with qa A + = 3 many s in th first rw and qa 2 A 2 + = 4 many s in th scnd rw. Nxt, th blcks D and D 2 ar ach ( F q ) T which cms t 6 2. Blck D is a clumn f s fllwd by a clumn f 0 s, and blck D 2 is a clumn f 0 s fllwd by a clumn f s. Finally, th blck E 0 is ( F q ) F which cms t 6 4. Th 6 rws f E 0 crrspnd t th 6 substs f {,..., F } = {,..., 4} f siz q = 2. Th full matrix is displayd in Figur My = y = FIGURE. Th cnstructd matrix M, and th crrspnding quatin f a splittability dcisin prblm. Having givn th xampl cnstructin, w brifly prviw hw th prf will play ut in this cas. Th matrix M givs ris t th cllctin {B,..., B 4 } f substs f {, 2,..., 0}, whr th charactristic vctr f B i is th ith rw f M. Th cllctin is splittabl if and nly if th linar systm(my) i = pm i has a binary slutin. In ur xampl th valus n th right-hand sid ar pm = 2, pm 2 = 3, and pm i = fr i > 2. Nt that if Ax =, thn x xtnds t a slutin f (My) i = pm i by stting th variabls f T t b and th variabls f F t b 0. Cnvrsly, if My = p B i thn carfully inspcting th D and E blcks f M, th variabls f T ar frcd t b and th variabls f F ar frcd t b 0. Sinc th rws f th blck B hav n fwr than
7 THE SET SPLITTABILITY PROBLEM 7 th rws f A (and th crrspnding right-hand sid), such a y rstricts t a slutin t Ax = Prf f th main thrm. W nw stablish that th cnstructin dscribd abv is indd a rductin frm ZOE t p-split. W will assum thrughut that 0 < p 2, sinc it is clar that a cllctin is p-splittabl if and nly if it is p splittabl. T bgin, w prsnt a simpl runding calculatin that will b usd blw. Lmma 2.2. Lt 0 < p 2 Prf. Lt ε = qm qm. Thn and q = p p as bfr. Thn fr any m N w hav p(m+ qm ) = m. p(m+ qm ) = p(m+qm+ε) = pm+m( p)+ pε = m+ pε = m+ pε Sinc ε < and p 2, w hav pε < 2, which givs that th last quantity quals m as dsird. Nxt w stablish th valus f th right-hand sids f th systm(my) i = pm i that w hav cnstructd. Lmma 2.3. Lt 0 < p 2, lt A b a r a c, and lt M b cnstructd as abv. Thn pm i = A i fr all i a r, and pm i = fr all i > a r. Prf. First cnsidr i a r. Thn pm i = p(a i + B i +C i ) = p (A i +(A i )+ ( qa i A i + )) = p(a i + qa i ) By Lmma 2.2, th lattr quantity is simply A i, as claimd. Nxt cnsidr i > a r. Hr w hav pm i = p(d i + E i ) = p(+ q ). Again using Lmma 2.2, th lattr quantity is, as dsird.
8 THE SET SPLITTABILITY PROBLEM 8 T cmmnc with th prf prpr, w first shw that if Ax = has a slutin, thn (My) i = pm i has a slutin. Givn a slutin x t Ax =, w xtnd x t a vctr y by appnding T many s fllwd by F many 0 s. Thn fr i a r w hav M i y = A i x+ B i +C i 0 = +(A i ) = A i By Lmma 2.3, A i = pm i. On th thr hand fr i > a r, w hav M i y = 0x+ D i +E0 = D i = Again by Lmma 2.3, this is qual t pm i, as dsird. Fr th cnvrs, w shw that if (My) i = pm i has a slutin thn Ax = has a slutin. W mak a sris f claims abut th structur f y that will nabl us t crat frm it a slutin x t Ax =. Claim 2.4. Eithr thr is an indx j T such that y j = r thr is an indx k F such that y k =, but nt bth. Prf f claim. Supps twards a cntradictin that j T, k F and y j = y k =. Rcalling th dfinitins f D and E, w can find a rw indx i > a r such that M i has a in its jth and kth clumns. It fllws that M i y 2, which cntradicts th calculatin frm Lmma 2.3 that M i y = pm i =. Claim 2.5. If 0 < p < 2, thn fr all indics i T, y i = and fr all indics j F, y j = 0. Prf f claim. Supps twards a cntradictin that thr is a j F such y j =. By th prvius claim, fr all i T w hav y i = 0. If thr is just n such j F with y j =, thn by cnstructin f E 0 w can find a rwl > a r such that th jth ntry f M l is 0. This implis that M l y = 0 cntradicting that M l y = pm l =. On th thr hand if thr ar tw distinct j, j F with y j = y j =, thn sinc p < 2 implis q >, w can find a rw l > a r such that th jth and j th ntry f M l is. This implis that M l y 2 again cntradicting that M l y =. Thus w hav shwn that y j = 0 fr all j F. It fllws frm th cnstructin f D that y i = fr all i T. T cntinu th prf, lt us assum first that p < 2. Thn fr all i T w hav y i = and fr all j F w hav y j = 0. Ltting x dnt th rstrictin f y t its first a c ntris, fr any i a r w hav(my) i = Ax+(A i ). By Lmma 2.3 w als knw that (My) i = A i. It fllws that Ax =. Nxt cnsidr th cas whn p = 2. Thn q = s bth D and E hav xactly n pr rw. It fllws that w ithr hav
9 I. y i = fr all i T and y j = 0 fr all j F, r II. y i = 0 fr all i T and y j = fr all j F. THE SET SPLITTABILITY PROBLEM 9 If I hlds, w can d as w did whn p < 2, s w ar dn. Othrwis, if II hlds, lt y = y. Thn M i y = M i ( y) = M i M i p. W knw that A i has th ppsit parity f A i = B i, and that C i = whn p = 2. Thrfr, M i is vn, s M i M i p = M i p, maning that M i y = b. Thus, y als crrspnds t a valid splittr f B, and sinc y i = fr all i T w must als hav that its first a c ntris pick ut xactly n pr rw f A by th argumnt usd fr whn p < 2. Thrfr, taking x t b rstrictin f y t its first a c ntris, w find that Ax = nc again. This cncluds th prf that th cnstructin f M is a rductin frm ZOE t p-split. 3. p-splittability CRITERIA AND CHARACTERIZATIONS Th rsult f th prvius sctin implis that it is nt asy t find a gnral charactrizatin f p-splittability. Nvrthlss, in this sctin w prvid svral p-splittability critria fr spcial typs f cllctins. Furthrmr w cmpltly charactriz p-splittability fr cllctins f at mst thr sts. Bfr w bgin ur study, it is ncssary t intrduc th fllwing ntatin. Fr a cllctinb = {B,..., B n } and an lmnt x, th multiplicity f x is th numbr m x f sts B i such that x B i. Givn a subsqunc f th sts B i,..., B ik w can frm a Vnn rgin R f B cnsisting f th lmnts x that li in B i,..., B ik and in n thr B j. If R cnsists f lmnts f multiplicity k, w will als say that R has multiplicity k. In th fllwing rsult, w will say that a squnc {t i } is a targt squnc fr B if 0 t i B i fr all i. Th targt squnc t i is achivabl if thr is a st S such that S B i = t i fr all i. Lmma 3. (Parity Lmma). Lt B b a cllctin and assum that fr vry x B th multiplicity m x is divisibl by m. If th targt squnc {t i } is achivabl, thn t i is divisibl by m. Prf. Lt S b a st witnssing that{t i } is achivabl. Thn t i = S B i = m x i n i n x S By hypthsis, m x is divisibl by m fr all x, s th right-hand sid is als divisibl by m.
10 THE SET SPLITTABILITY PROBLEM 0 Sinc B is p-splittabl if and nly if th targt squnc t i = p B i is achivabl, th cntrapsitiv f Lmma 3. prvids a usful cnditin fr shwing that crtain cllctins ar nt p-splittabl. Whil th cnvrs f Lmma 3. is fals in gnral, w d hav th fllwing partial cnvrs. Lmma 3.2. Lt B = {B,..., B n } b a cllctin such that fr all x B, m x = n. If p B i is divisibl by n, thn B is p-splittabl. Prf. Lt b i = B B i b th siz f th (uniqu) Vnn rgin f multiplicity n which is nt cntaind in B i. Ltting t i = p B i b th targt squnc, w wish t find valus b i such that 0 b i b i and j =i bj = t i. Th lattr systm f quatins is squar and invrtibl, s an lmntary calculatin givs th uniqu slutin: ( ) () bi = (n 2)t i + n t j. j =i Nt that b i is always an intgr, bcaus th abv xprssin is qual t ( t n j ) (n )t i + t j = t i + n j j and t j is divisibl by n by hypthsis. Hnc it rmains nly t stablish that 0 b i b i. Fr this, nt that t i = p B i = j =i pb j = ǫ i + j =i pb j whr ǫ i 2. Substituting this xprssin in fr vry t i in Equatin (), w nt that pb i ccurs n tims in th parnthss whil all thr pb j ccur n 2 tims ngativly and n 2 tims psitivly. Thus, th pb j cancl, laving us just with pb i and rrr trms as fllws: ( ) (2) bi = pb i + (n 2)ǫ i + n ǫ j. j =i Thr ar 2n 3 many ǫ trms in th parnthss, s w can cnclud that b i = pb i + E whr E <. Sinc 0 pb i b i and all f 0, b i, b i ar intgrs, it fllws that 0 b i b i t. Rmark 3.3. It is ncssary t amnd th statmnt f th prvius rsult if any f th p B i ar half-intgrs. In this cas th prprty p B i is divisibl by n shuld b rplacd by it is pssibl t slct th valus f p B i in such a way that p B i is divisibl by n. Svral f th rsults blw will hav similar amndmnts, as w will nt brifly ach tim.
11 THE SET SPLITTABILITY PROBLEM B a b a 2 B 2 a a b 2 B 3 B 2 b 2 B 3 a 3 b c FIGURE 2. At lft: sizs f th Vnn rgins f a tw lmnt cllctin {B, B 2 }. At right: sizs f th Vnn rgins f a thr lmnt cllctin {B, B 2, B 3 }. W ar nw rady t bgin ur classificatin f p-splittability fr cllctins f siz 3. W bgin with th simpl cas f just tw sts, bcaus it hlps mtivat sm f th stps fr th thr st cas blw. Thrm 3.4. Evry cllctin f tw sts is p-splittabl fr vry 0 p. Prf. LtB = {B, B 2 } b a givn tw-st cllctin. Rplacing p with p if ncssary, w can supps that p 2. W fix th fllwing ntatin fr th sizs f th rgins fb: a = B B2 c, a 2 = B c B 2, and b = B B 2 (s Figur 2). Nxt lt t = p(a + b) and t 2 = p(a 2 + b) dnt th targt cardinalitis fr S B and S B 2 fr a p-splittr S. T shw B is p-splittabl it suffics t find intgrs ā i, b such that: (i) 0 ā i a i ; (ii) 0 b b, and; (iii) ā i + b = t i. Fr this w lt b = pb and ā i = t i b s that (ii) and (iii) ar clarly satisfid. Of curs th dfinitins f bth t i and b may b ambiguus; in such cass w nd nly mak sur that if a i = 0 thn w chs ā i = 0 t. T s that (i) is satisfid, writ ε = b pb fr th runding rrr in cmputing b and ǫ i = t i p(a i + b) fr th runding rrr in cmputing t i. Thn th quatins asily imply that w hav ā i = pa i +(ǫ i ε). Sinc ǫ i 2 and ε 2 w knw that ǫ i ε. Assuming a i > 0 th abv quatin givs < ā i < a i +, and sinc ā i and a i ar intgrs, (i) is satisfid. On th thr hand if a i = 0 thn ā i = 0 t and (i) is clarly satisfid. T stat ur rsults fr thr sts, w xtnd th ntatin frm th prvius prf. Fr a thr-st cllctinb = {B, B 2, B 3 } w lt a i dnt th numbr f multiplicity lmnts f B i, lt b i dnt th numbr f multiplicity 2 lmnts nt in B i, and lt c dnt th
12 THE SET SPLITTABILITY PROBLEM 2 numbr f multiplicity 3 lmnts (s Figur 2). As in th prvius prf w lt t i = p B i b th targts and ǫ i = t i p B i b th runding rrr. Finally w st th valus ρ i = ǫ i + j =i ǫ j. Lmma 3.5. Assum that p 2, and lt B = {B, B 2, B 3 } b givn. Als assum thr ar n multiplicity lmnts, that is, all a i = 0. Thn B is nt p-splittabl if and nly if t i is dd and n f th cnditins hlds: (a) c = 0; r (b) pc < 2 and sm pb i + 2 (pc +ρ i) < 0. Prf. Rcall that B is p-splittabl if and nly if n can find valus b i and c such that 0 b i b, 0 c c, and c+ j =i bi = t i. Assuming n has chsn th valu f c, th quatins hav th uniqu slutin: ( ) (3) bi = t i + 2 t j c. j =i At this pint w can bsrv that in rdr t achiv intgr valus f b i, n must chs th valu c t hav th sam parity as t j. Nxt w substitut t j = pc+ p k =j b k + ǫ j t rwrit th abv quatin as (4) bi = pb i + 2 (pc c+ρ i). Nw assum that t i is dd and that ithr (a) r (b) hlds. W hav alrady shwn in Lmma 3. that if cnditin (a) hlds thn B is unsplittabl. Nxt assum that (b) hlds. Sinc t i is dd, w cannt chs c t b f vn parity and in particular cannt chs c = 0. Cnditin (b) tgthr with Equatin (4) clarly implis that any psitiv valu f c rsults in b i < 0. ThusB is nc again unsplittabl. Fr th cnvrs w will nd t shw that if ithr t i is vn r bth (a) and (b) ar fals, thn B is splittabl. First w claim that th chic c = pc always nsurs that 0 b i b i. T s this nt first that this chic nsurs pc c 2. Mrvr w can always assum ρ i < 3 2, sinc thrwis all ǫ j = 2 and w wuld b abl t chang th runding f th targts t i (vn whil prsrving th parity f t i ). Thus Equatin (4) implis that b i = pb i + E whr E <, and w can thrfr argu as in th prf f Lmma 3. t cmplt th claim. Of curs w cannt ncssarily chs c = pc, sinc this may nt hav th sam parity as t j. Thus w als claim that n f th tw chics c := pc r c + := pc + rsults in 0 b i b i. Indd th tw chics rsult in valus f pc c and
13 THE SET SPLITTABILITY PROBLEM 3 pc c + that diffr by 2 and hav abslut valu 3 2. Manwhil th ρ i li in sm intrval f lngth 2 which is cntaind in ( 3 2, 3 2 ). It is an asy xrcis t cnclud that ithr all pc c + ρ i < 2 r all pc c + + ρ i < 2. Thus n f tw chics c = c r c + givs valus b i = pb i + E whr E <, and w ar again dn as in th prvius claim. Nw assum that t i is vn. Thn if pc is vn w hav alrady argud c = pc lads t a slutin. And if pc is dd thn w always hav 0 pc ± c (hr w ar using p 2 ). Thus n f th chics c = pc ± lads t a slutin as wll. Finally assum bth (a) and (b) ar fals. Sinc (a) is fals and p 2 w hav that pc + c. On th thr hand sinc (b) is fals w ithr hav (i) pc 2, r ls (ii) pc < 2 and all pb i + 2 (pc +ρ i) 0. In cas (i) w hav 0 pc ± c, which w hav prviusly shwn implis B is splittabl. In cas (ii) w hav pc + = and mrvr that th chic c = lads t a valid slutin fr all b i. This cncluds th prf. In th lmma, if any f th p B i is a half-intgr, thn B is splittabl. Indd, in this cas w can slct th st targt t i t mak t i vn. W als rcrd hr that if cas (b) f th lmma hlds, thn thr is in fact a uniqu i such that 2pb i + pc +ρ i < 0, and mrvr w must hav that ρ i <, that ǫ i > 0, and that th thr tw ǫ j < 0. In th nxt rsult w cnsidr th cas whn a cllctin B f thr sts has lmnts f multiplicity. Lmma 3.6. Assum that p 2, and lt B = {B, B 2, B 3 } b a givn cllctin with a i, b i, c as in Figur 2. Thn prvidd at last n f th a i is sufficintly larg, B is p-splittabl. Prf. First lt B (0) b th cllctin btaind frm B by rmving all lmnts f multiplicity. Fr th rst f th prf, lt b i, c, t i, ρ i b as in th prvius lmma, fr th cllctin B (0). Supps first thatb (0) is p-splittabl. Thn B is splittabl t; in fact w claim that any splittabl cllctin rmains splittabl aftr adding lmnts f multiplicity. T s this, it suffics t shw it whn w add just n lmnt a f multiplicity t sm st B i. Nw if adding a raiss th valu f t i by, thn w includ a in th splittr; thrwis w wuld xclud a frm th splittr. Nxt supps that B (0) is p-unsplittabl. Thn by Equatin (3) w can split th cllctin B (0) by stting c = 0 and b ) i = 2 ( t i + j =i t j. Hwvr ths chics f b i will b half-intgrs, and nd nt satisfy 0 b i b i.
14 THE SET SPLITTABILITY PROBLEM 4 W claim that fr all i w hav 2 b i b i + 2, and that thr is at mst n i such that b i = 2 r b i = b i + 2. Th first part f th claim fllws dirctly frm Equatin (4), tgthr with c = 0 and pc < 2. Fr th scnd part f th claim, th nly plausibl cntrary cas is n whr tw f th b i hav ppsit rrr, say b 2 = 2 and b 3 = b W nw shw this implis that b 3 = 0. Indd, Equatin (4) fr b 2 says 2 = pb (pc+ρ 2) and this implis ρ 2 <. Sinc all ρ i li within an intrval f lngth 2, it fllws that ρ 3 <. Thn Equatin (4) fr b 3 says b = pb (pc+ρ i). Nw p 2, pc < 2, and ρ 3 < all tgthr imply b 3 = 0. Using b 3 = 0, w btain in particular that t 3 t 2. On th thr hand Equatin (3) fr b 2 says = t t 2 + t 3, and this implis t 2 > t 3. This is a cntradictin, and cmplts th prf f th claim. Nw w can finish th prf as fllws. Lt B () b th cllctin btaind frm B by rmving just th lmnts f B 2 and B 3 f multiplicity. That is, B () is btaind by zring ut a 2 and a 3. W will shw that if a is sufficintly larg, thnb () is splittabl. Fr this, w will us th ntatin t () fr th targt valu f B as it wuld b dfind frb () (r quivalntly frb). Thus in particular t () t. In th nxt paragraph w will nly hav nd f small valus f a, s that w nd nly cnsidr th cass t () = t and t () = t +. Our abv claim implis that at last n f th tw tripls { b 2, b 2 + 2, b } r { b + 2, b 2 2, b 3 2 } lis within th dsird bunds[0, b ],[0, b 2 ],[0, b 3 ]. In th first cas if a is larg nugh that t () = t + thn th tripl is a valid splitting. In th scnd cas if a = and t () = t thn th tripl xtnds t a valid splitting by slcting th singl lmnt f a. And if a 2 and t () = t + thn th tripl xtnds t a valid splitting by slcting tw lmnts frm a. Thus w hav shwn in ach cas that thr xists a valu f a that rsults inb () bing splittabl. By ur claim frm th scnd paragraph, any largr valu f a will als rsult in B () bing splittabl. Again using th claim frm th scnd paragraph, this always implis B is splittabl. Th abv lmma may sm natural, sinc intuitivly th prsnc f lmnts f multiplicity maks it asir t find a splittr. Hwvr th analgus rsult is fals fr cllctins f fur r mr sts. Indd an unsplittabl cllctin f Typ 0 f Appndix A may hav a Vnn rgin f multiplicity f arbitrary siz.
15 THE SET SPLITTABILITY PROBLEM 5 W claim that th argumnt f th prvius lmma is ptimal. That is, in th cas whn B (0) is unsplittabl, B will b splittabl if and nly at last n f th a i as at last as larg as w ndd in ur prf. W mit th cas-by-cas justificatin f this fact. Thus th rsults f this sctin prvid a simpl prcdur t dcid whthr a givn cnfiguratin B is p-splittabl. First n can rplac p with p if ncssary t assum that p 2. Nxt givn B n can btain B(0) as in Lmma 3.6, and us Lmma 3.5 t dcid whthr B (0) is splittabl. If it is, thn B is splittabl, and if nt, thn n can us th dtails f th prf f Lmma 3.6 t dtrmin whthr any a i is larg nugh t mak B is splittabl SPLITTABILITY CRITERIA AND CHARACTERIZATIONS In th prvius sctin, w xamind p-splittability critria fr arbitrary p. In this sctin w spcializ t th imprtant cas p = 2. Aftr prviding anthr vry gnral lmma, w us it t giv a cmplt charactrizatin f splittability fr cllctins f at mst fur sts. Thrughut this sctin, th trm splittability will always rfr t 2 - splittability. Th fllwing rsult, whil quit simpl, is usful fr cnvrting ur undrstanding f cllctins with fw lmnts int mr gnral thrms. Lmma 4. (Rductin Lmma). LtB b a givn cllctin, and lt B b a cllctin btaind frm B by adding an vn numbr f lmnts t any f its Vnn rgins. Thn if B is splittabl, s is B. Prf. If S is a splittr fr B, thn w can cnstruct a splittr S fr B as fllws. Bgin by putting all th lmnts f S int S. Thn fr ach Vnn rgin R fb and crrspnding Vnn rgin R f B, put half f th lmnts f R \ R int S. It is asy t s that S is a splittr frb. Bfr stating ur charactrizatin f splittability fr cnfiguratins with fur sts, w rviw th knwn charactrizatin f splittability fr cnfiguratins with thr r fwr sts. Prpsitin 4.2. Any cllctin f n r tw sts is splittabl. unsplittabl if and nly if bth: A cllctin f thr sts is (a) vry Vnn rgin f multiplicity 2 cntains an dd numbr f lmnts; and (b) all thr Vnn rgins ar mpty.
16 THE SET SPLITTABILITY PROBLEM 6 Th prpsitin can asily b xtractd frm th rsults f th prvius sctin. It is als pssibl t giv a simpl and dirct prf, as was dn in [CCSS6]. Thrm 4.3. Any family f fur sts is unsplittabl if and nly if it falls int n f th lvn typs dscribd in Appndix A. Prf. First w claim that ach f th typs dscribd in Appndix A is unsplittabl. Th cllctins f Typ 0 ar by dfinitin ths which hav sm thr-st subcllctin that is unsplittabl. It is tdius but straightfrward t chck that all f Typs 0 ar unsplittabl; as an xampl w prvid th prf that Typ is unsplittabl in Prpsitin A.. In rdr t prv that all familis nt matching Typs 0 0 ar in fact splittabl, nt first that w hav usd a suprcmputr t tst splittability fr vry cllctin f fur sts with all Vnn rgins f siz 3. Th cd and its utput ar availabl in [REU6]. Nw supps that B is a cllctin f fur sts which is nt f any f Typs 0 0. W wish t shw that B is splittabl. Lt B (2) b a cllctin btaind frm B mptying ach Vnn rgin R that is vn in B, and laving just lmnt in ach Vnn rgin R that is dd in B. In thr wrds,b (2) is btaind by taking ach Vnn rgin mdul 2. If B (2) is als nt f any f th lvn typs, thn sinc its rgins all hav siz 3 ur sftwar has chckd that B (2) is splittabl. By th Rductin lmma (Lmma 4.), B is als splittabl, and w ar dn in this cas. On th thr hand, supps that B (2) is f n f th lvn typs, say typ T. Thn sinc B is nt f typ T, thr must xist a Vnn rgin R, labld 0 (mpty) r r 0/, such that th siz f R in B (2) is strictly lss than th siz f R in B. Nw lt B b th cnfiguratin btaind frm B (2) by adding 2 lmnts t R. Thus B is nt amng th Typs 0 0. And sinc th rgins f B still hav siz 3, ur sftwar has chckd that B is splittabl. It again fllws frm Lmma 4. that B is splittabl, which cncluds th prf. Lking at th unsplittabl typs f cllctins f fur sts in Appndix A, n might surmis that unsplittabl cnfiguratins shuld hav many Vnn rgins with fw r zr lmnts. W nxt prvid a rsult which says that if a cllctin has sufficintly many Vnn rgins which ar sufficintly larg, thn it must b splittabl. Thrm 4.4. Lt D b an intgr bund n th discrpancy f cllctins f n sts. Supps that B is a cllctin f n sts such that ach Vnn rgin f multiplicity cntains at last D lmnts. Thn B is splittabl. Prf. Lt B = {B,..., B n } b such a cllctin, and lt R i dnt th Vnn rgin f multiplicity cntaind in B i. Thn in B, ach rgin R i has at last D lmnts, s
17 THE SET SPLITTABILITY PROBLEM 7 w may lt B (0) = {B (0),..., B(0) n } b th cllctin btaind frm B by dlting D lmnts frm ach f th Vnn rgins R i. Sinc disc(b (0) ) D, w can find a st S (0) such that fr all i w hav D B (0) i S (0) B (0) i \ S (0) D Nw fr ach i w rstr th D dltd lmnts f th Vnn rgin R i. As w d s, w build a st S by bginning with S (0), and thn placing sm f th D rstrd lmnts int S and th rst int S c. It is asy t d s in such a way that B i S B i \ S and as a rsult S splitsb. Of curs in th abv rsult, D can b takn t b th ciling f Spncr s bund K n discussd in th intrductin. 4.. Th prvalnc f splittability. In this subsctin w addrss svral qustins abut hw cmmnly splittabl and unsplittabl cllctins ccur. Our rsults fr small cllctins f sts indicat that unsplittability is vry rar. It is natural t ask whthr this rmains tru fr cllctins with a largr numbr f sts. W first cnsidr th prvalnc f splittability whn th numbr f lmnts is fixd and th numbr f sts is larg. In th fllwing rsult, w lt f(n, k) dnt th fractin f all n-st cllctins n k lmnts which ar splittabl. Prpsitin 4.5. Supps that k 3. Thn f(n, k) 0 as n. Intuitivly, th prpsitin hlds bcaus thr xists a thr-st cnfiguratin with thr lmnts that is unsplittabl, namly B 0 = {{, 2},{, 3},{2, 3}}. As th numbr f sts in th cllctin incrass, th prbability that its rstrictin t th pints, 2, 3 cntains th cllctin B 0 bcms highly likly. On th thr hand, if w fix th numbr n f sts and lt k thn th argumnt f th nxt rsult implis that f(n, k) cnvrgs t. In fact, th sam hlds vn if w lt n, k with k grwing fast nugh with rspct t n. Thrm 4.6. Supps that k = k(n) lis in ω(2 n n), that is, k grws asympttically strictly fastr than 2 n n. Thn f(n, k) as n. Prf. Lt D = K n whr K is th cnstant f Thrm 4.4. Our stratgy is t shw that if k is as larg as in ur hypthsis, thn it is unlikly that any f th multiplicity
18 THE SET SPLITTABILITY PROBLEM 8 rgins will cntain fwr than D lmnts. Thus by Thrm 4.4 it is likly that a givn cnfiguratin will b splittabl. Fr this nt that if a singl lmnt is randmly assignd t ach f n sts, thn th prbability that th lmnt will li in any givn Vnn rgin is q = 2. Nxt assign k n lmnts randmly and indpndntly t th sts, and lt th randm variabl X dnt th numbr lmnts f a fixd Vnn rgin f multiplicity. By th basic prprtis f th binmial distributin, th xpctd valu f X is µ = kq = k 2 and th standard dviatin n f X is σ = kq( q) = k 2 ( n 2 ). n W nw wish t bund frm abv Pr[X < D]. Ltting t = µ K n σ, w hav that Pr[X < D] Pr[ X µ tσ]. Chbychv s inquality nw givs Pr[X < D] t 2 Substituting th xprssins fr t, µ, σ and simplifying w btain Pr[X < D] k 2 ( n 2 ) n ( k 2 K n) 2 n 2 n k 2K n Our hypthsis abut th grwth f k implis that th lattr quantity is (/n). Finally th prbability that any f th n rgins f multiplicity has fwr than D lmnts is bundd by n Pr[X < D] and is thus (), r in thr wrds, cnvrgs t 0. APPENDIX A. UNSPLITTABLE CONFIGURATIONS OF FOUR SETS Hr w prvid a catalgu f th unsplittabl cnfiguratins f fur r fwr sts. Our catalgu cnsists f labld fur-st Vnn diagrams, shwn as fur-lbd harts with ach lb rprsnting n st. Th diagram blw shws fur f th diagrams; n with ach f th fur sts shadd. Figur 3 illustrats xampls f ach typ f unsplittabl cnfiguratin f fur sts. In th diagrams w us th fllwing abbrviatins: th symbl dnts an dd numbr f lmnts, dnts an vn numbr f lmnts, dnts n lmnt, 0/ dnts zr
19 THE SET SPLITTABILITY PROBLEM 9 r n lmnt, x dnts any numbr f lmnts, and a blank dnts zr lmnts. Nt that tw sparat instancs f a symbl d nt ncssarily dnt th sam quantity. 0/ Typ Typ 2 Typ 3 Typ 4 0 Typ 5 Typ 6 Typ 7 Typ 8 0/ 0/ b c c 2 a a 2 b 2 x Typ 9 Typ 0 Typ 0 FIGURE 3. Unsplittabl 4-st cnfiguratins Sm additinal rmarks abut th typs ar in rdr. First, ach f th typs has analgus instancs in which th sts B,..., B 4 ar prmutd. In Typ 0, w additinally rquir that a + a 2, b + b 2, and c + c 2 all t b dd numbrs. This typ cvrs th cass whn sm subcllctin f thr f th sts is unsplittabl. In th instanc dpictd, th first thr sts frm an unsplittabl cnfiguratin. Thr is sm vrlap btwn Typ 0 and dgnrat instancs f thr typs. W nw brifly addrss th claim, ndd fr Thrm 4.3, that cnfiguratins lying in any f th lvn typs ar indd unsplittabl. Th unsplittability f Typ 0 is handld in Prp 4.2. Th unsplittability f Typs 4 and 5 fllws frm Lmma 3.. Th unsplittability f th rmaining typs all bil dwn t lmntary linar algbra, and as an xampl lt us vrify Typ is unsplittabl. Prpsitin A.. If B is a cllctin f Typ, thn B is unsplittabl.
20 THE SET SPLITTABILITY PROBLEM 20 Prf. Lt i dnt th numbr f lmnts f j =i B j Bi c, s that i is an dd numbr. Lt t i = 2 (+ j =i i ) b th targt quantity fr S B i. Thn finding a splittr S fr B is quivalnt t slving th intgr systm: a t a 2 a 3 t 2 = t 3 a 4 t 4 b subjct t th cnstraints that 0 a i i, and 0 b. Slving this systm fr a in trms f th right-hand sids and b, w btain th quatin: a = 3 (t + t 2 + t 3 2t 4 b) = ( = ( b) ) b If b = 0 thn this implis a = 6 (3 + ). This is a cntradictin sinc dd implis that (md 6). On th thr hand if b = thn a = 2, which is clarly a cntradictin frm dd. REFERENCES [Ban0] N. Bansal. Cnstructiv algrithms fr discrpancy minimizatin. In Prcdings f th 200 IEEE 5st Annual Sympsium n Fundatins f Cmputr Scinc, FOCS 0, pags 3 0. IEEE Cmputr Scity, 200. [BF8] Józsf Bck and Tibr Fiala. Intgr-making thrms. Discrt Appl. Math., 3(): 8, 98. [BH97] Db Bdnarchak and Martin Hlm. A nt n th bck-fiala thrm. Cmbinatrica, 7():47 49, 997. [Buk3] B. Bukh. An imprvmnt f th bck-fiala thrm. ArXiv -prints, Jun 203. [CCSS6] D. Cndn, S. Csky, L. Srafin, and C. Stckdal. On gnralizatins f sparating and splitting familis. Elctrnic Jurnal f Cmbinatrics, 23(3):#P3.36, 206. [CNN] Mss Charikar, Alantha Nwman, and Alksandar Niklv. Tight hardnss rsults fr minimizing discrpancy. In Prcdings f th Twnty-Scnd Annual ACM-SIAM Sympsium n Discrt Algrithms, pags SIAM, Philadlphia, PA, 20. [DPV06] S. Dasgupta, C. Papadimitrius, and U. Vazirani. Algrithms. McGraw Hill, [EH] Jhn Eltn and Thdr Hill. Ham sandwich with may: A strngr cnclusin t th classical ham sandwich thrm [math.mg]. [Hl99] Martin Hlm. On th bck-fiala thrm. Discrt Mathmatics, 207():73 87, 999.
21 THE SET SPLITTABILITY PROBLEM 2 [Kar72] Richard M. Karp. Rducibility amng cmbinatrial prblms. In Cmplxity f cmputr cmputatins (Prc. Symps., IBM Thmas J. Watsn Rs. Cntr, Yrktwn Hights, N.Y., 972), pags Plnum, Nw Yrk, 972. [LM2] Shachar Lvtt and Raghu Mka. Cnstructiv discrpancy minimizatin by walking n th dgs. CRR, abs/ , 202. [Lv73] L. Lvász. Cvrings and clring f hyprgraphs. In Prcdings f th Furth Suthastrn Cnfrnc n Cmbinatrics, Graph Thry, and Cmputing (Flrida Atlantic Univ., Bca Ratn, Fla., 973), pags 3 2. Utilitas Math., Winnipg, Man., 973. [REU6] 206 REU. Split chckr public rpsitry, [Sp85] J. Spncr. Six standard dviatins suffic. Transactins f th AMS, 289(2): , 985. PETER BERNSTEIN, TUFTS UNIVERSITY, MEDFORD, MA addrss: ptr.brnstin@tufts.du CASHOUS BORTNER, UNIVERSITY OF NEBRASKA, LINCOLN, NE addrss: cashus.brtnr@huskrs.unl.du SAMUEL COSKEY, BOISE STATE UNIVERSITY, BOISE, ID addrss: scsky@gmail.cm SHUNI LI, MACALESTER COLLEGE, SAINT PAUL, MN addrss: sli@macalstr.du CONNOR SIMPSON, CORNELL UNIVERSITY, ITHACA, NY addrss: cgs93@crnll.du
Topic 5: Discrete-Time Fourier Transform (DTFT)
 ELEC36: Signals And Systms Tpic 5: Discrt-Tim Furir Transfrm (DTFT) Dr. Aishy Amr Cncrdia Univrsity Elctrical and Cmputr Enginring DT Furir Transfrm Ovrviw f Furir mthds DT Furir Transfrm f Pridic Signals
ELEC36: Signals And Systms Tpic 5: Discrt-Tim Furir Transfrm (DTFT) Dr. Aishy Amr Cncrdia Univrsity Elctrical and Cmputr Enginring DT Furir Transfrm Ovrviw f Furir mthds DT Furir Transfrm f Pridic Signals
Lecture 26: Quadrature (90º) Hybrid.
 Whits, EE 48/58 Lctur 26 Pag f Lctur 26: Quadratur (9º) Hybrid. Back in Lctur 23, w bgan ur discussin f dividrs and cuplrs by cnsidring imprtant gnral prprtis f thrand fur-prt ntwrks. This was fllwd by
Whits, EE 48/58 Lctur 26 Pag f Lctur 26: Quadratur (9º) Hybrid. Back in Lctur 23, w bgan ur discussin f dividrs and cuplrs by cnsidring imprtant gnral prprtis f thrand fur-prt ntwrks. This was fllwd by
Lecture 27: The 180º Hybrid.
 Whits, EE 48/58 Lctur 7 Pag f 0 Lctur 7: Th 80º Hybrid. Th scnd rciprcal dirctinal cuplr w will discuss is th 80º hybrid. As th nam implis, th utputs frm such a dvic can b 80º ut f phas. Thr ar tw primary
Whits, EE 48/58 Lctur 7 Pag f 0 Lctur 7: Th 80º Hybrid. Th scnd rciprcal dirctinal cuplr w will discuss is th 80º hybrid. As th nam implis, th utputs frm such a dvic can b 80º ut f phas. Thr ar tw primary
cycle that does not cross any edges (including its own), then it has at least
 W prov th following thorm: Thorm If a K n is drawn in th plan in such a way that it has a hamiltonian cycl that dos not cross any dgs (including its own, thn it has at last n ( 4 48 π + O(n crossings Th
W prov th following thorm: Thorm If a K n is drawn in th plan in such a way that it has a hamiltonian cycl that dos not cross any dgs (including its own, thn it has at last n ( 4 48 π + O(n crossings Th
Chapter 33 Gauss s Law
 Chaptr 33 Gauss s Law 33 Gauss s Law Whn askd t find th lctric flux thrugh a clsd surfac du t a spcifid nn-trivial charg distributin, flks all t ftn try th immnsly cmplicatd apprach f finding th lctric
Chaptr 33 Gauss s Law 33 Gauss s Law Whn askd t find th lctric flux thrugh a clsd surfac du t a spcifid nn-trivial charg distributin, flks all t ftn try th immnsly cmplicatd apprach f finding th lctric
Modern Physics. Unit 5: Schrödinger s Equation and the Hydrogen Atom Lecture 5.6: Energy Eigenvalues of Schrödinger s Equation for the Hydrogen Atom
 Mdrn Physics Unit 5: Schrödingr s Equatin and th Hydrgn Atm Lctur 5.6: Enrgy Eignvalus f Schrödingr s Equatin fr th Hydrgn Atm Rn Rifnbrgr Prfssr f Physics Purdu Univrsity 1 Th allwd nrgis E cm frm th
Mdrn Physics Unit 5: Schrödingr s Equatin and th Hydrgn Atm Lctur 5.6: Enrgy Eignvalus f Schrödingr s Equatin fr th Hydrgn Atm Rn Rifnbrgr Prfssr f Physics Purdu Univrsity 1 Th allwd nrgis E cm frm th
LECTURE 5 Guassian Wave Packet
 LECTURE 5 Guassian Wav Pact 1.5 Eampl f a guassian shap fr dscribing a wav pact Elctrn Pact ψ Guassian Assumptin Apprimatin ψ As w hav sn in QM th wav functin is ftn rprsntd as a Furir transfrm r sris.
LECTURE 5 Guassian Wav Pact 1.5 Eampl f a guassian shap fr dscribing a wav pact Elctrn Pact ψ Guassian Assumptin Apprimatin ψ As w hav sn in QM th wav functin is ftn rprsntd as a Furir transfrm r sris.
120~~60 o D 12~0 1500~30O, 15~30 150~30. ..,u 270,,,, ~"~"-4-~qno 240 2~o 300 v 240 ~70O 300
 1 Find th plar crdinats that d nt dscrib th pint in th givn graph. (-2, 30 ) C (2,30 ) B (-2,210 ) D (-2,-150 ) Find th quatin rprsntd in th givn graph. F 0=3 H 0=2~ G r=3 J r=2 0 :.1 2 3 ~ 300 2"~ 2,
1 Find th plar crdinats that d nt dscrib th pint in th givn graph. (-2, 30 ) C (2,30 ) B (-2,210 ) D (-2,-150 ) Find th quatin rprsntd in th givn graph. F 0=3 H 0=2~ G r=3 J r=2 0 :.1 2 3 ~ 300 2"~ 2,
Even/Odd Mode Analysis of the Wilkinson Divider
 //9 Wilkinn Dividr Evn and Odd Md Analyi.dc / Evn/Odd Md Analyi f th Wilkinn Dividr Cnidr a matchd Wilkinn pwr dividr, with a urc at prt : Prt Prt Prt T implify thi chmatic, w rmv th grund plan, which
//9 Wilkinn Dividr Evn and Odd Md Analyi.dc / Evn/Odd Md Analyi f th Wilkinn Dividr Cnidr a matchd Wilkinn pwr dividr, with a urc at prt : Prt Prt Prt T implify thi chmatic, w rmv th grund plan, which
Another Explanation of the Cosmological Redshift. April 6, 2010.
 Anthr Explanatin f th Csmlgical Rdshift April 6, 010. Jsé Francisc García Juliá C/ Dr. Marc Mrncian, 65, 5. 4605 Valncia (Spain) E-mail: js.garcia@dival.s h lss f nrgy f th phtn with th tim by missin f
Anthr Explanatin f th Csmlgical Rdshift April 6, 010. Jsé Francisc García Juliá C/ Dr. Marc Mrncian, 65, 5. 4605 Valncia (Spain) E-mail: js.garcia@dival.s h lss f nrgy f th phtn with th tim by missin f
BINOMIAL COEFFICIENTS INVOLVING INFINITE POWERS OF PRIMES
 BINOMIAL COEFFICIENTS INVOLVING INFINITE POWERS OF PRIMES DONALD M. DAVIS Abstract. If p is a prim (implicit in notation and n a positiv intgr, lt ν(n dnot th xponnt of p in n, and U(n n/p ν(n, th unit
BINOMIAL COEFFICIENTS INVOLVING INFINITE POWERS OF PRIMES DONALD M. DAVIS Abstract. If p is a prim (implicit in notation and n a positiv intgr, lt ν(n dnot th xponnt of p in n, and U(n n/p ν(n, th unit
Homework #3. 1 x. dx. It therefore follows that a sum of the
 Danil Cannon CS 62 / Luan March 5, 2009 Homwork # 1. Th natural logarithm is dfind by ln n = n 1 dx. It thrfor follows that a sum of th 1 x sam addnd ovr th sam intrval should b both asymptotically uppr-
Danil Cannon CS 62 / Luan March 5, 2009 Homwork # 1. Th natural logarithm is dfind by ln n = n 1 dx. It thrfor follows that a sum of th 1 x sam addnd ovr th sam intrval should b both asymptotically uppr-
Section 6.1. Question: 2. Let H be a subgroup of a group G. Then H operates on G by left multiplication. Describe the orbits for this operation.
 MAT 444 H Barclo Spring 004 Homwork 6 Solutions Sction 6 Lt H b a subgroup of a group G Thn H oprats on G by lft multiplication Dscrib th orbits for this opration Th orbits of G ar th right costs of H
MAT 444 H Barclo Spring 004 Homwork 6 Solutions Sction 6 Lt H b a subgroup of a group G Thn H oprats on G by lft multiplication Dscrib th orbits for this opration Th orbits of G ar th right costs of H
INCOMPLETE KLOOSTERMAN SUMS AND MULTIPLICATIVE INVERSES IN SHORT INTERVALS. xy 1 (mod p), (x, y) I (j)
 INCOMPLETE KLOOSTERMAN SUMS AND MULTIPLICATIVE INVERSES IN SHORT INTERVALS T D BROWNING AND A HAYNES Abstract W invstigat th solubility of th congrunc xy (mod ), whr is a rim and x, y ar rstrictd to li
INCOMPLETE KLOOSTERMAN SUMS AND MULTIPLICATIVE INVERSES IN SHORT INTERVALS T D BROWNING AND A HAYNES Abstract W invstigat th solubility of th congrunc xy (mod ), whr is a rim and x, y ar rstrictd to li
ECE602 Exam 1 April 5, You must show ALL of your work for full credit.
 ECE62 Exam April 5, 27 Nam: Solution Scor: / This xam is closd-book. You must show ALL of your work for full crdit. Plas rad th qustions carfully. Plas chck your answrs carfully. Calculators may NOT b
ECE62 Exam April 5, 27 Nam: Solution Scor: / This xam is closd-book. You must show ALL of your work for full crdit. Plas rad th qustions carfully. Plas chck your answrs carfully. Calculators may NOT b
BINOMIAL COEFFICIENTS INVOLVING INFINITE POWERS OF PRIMES. 1. Statement of results
 BINOMIAL COEFFICIENTS INVOLVING INFINITE POWERS OF PRIMES DONALD M. DAVIS Abstract. If p is a prim and n a positiv intgr, lt ν p (n dnot th xponnt of p in n, and u p (n n/p νp(n th unit part of n. If α
BINOMIAL COEFFICIENTS INVOLVING INFINITE POWERS OF PRIMES DONALD M. DAVIS Abstract. If p is a prim and n a positiv intgr, lt ν p (n dnot th xponnt of p in n, and u p (n n/p νp(n th unit part of n. If α
Introduction to Arithmetic Geometry Fall 2013 Lecture #20 11/14/2013
 18.782 Introduction to Arithmtic Gomtry Fall 2013 Lctur #20 11/14/2013 20.1 Dgr thorm for morphisms of curvs Lt us rstat th thorm givn at th nd of th last lctur, which w will now prov. Thorm 20.1. Lt φ:
18.782 Introduction to Arithmtic Gomtry Fall 2013 Lctur #20 11/14/2013 20.1 Dgr thorm for morphisms of curvs Lt us rstat th thorm givn at th nd of th last lctur, which w will now prov. Thorm 20.1. Lt φ:
Revision: August 21, E Main Suite D Pullman, WA (509) Voice and Fax
 2.7.1: Sinusidal signals, cmplx xpnntials, and phasrs Rvisin: ugust 21, 2010 215 E Main Suit D ullman, W 99163 (509 334 6306 ic and Fax Ovrviw In this mdul, w will rviw prprtis f sinusidal functins and
2.7.1: Sinusidal signals, cmplx xpnntials, and phasrs Rvisin: ugust 21, 2010 215 E Main Suit D ullman, W 99163 (509 334 6306 ic and Fax Ovrviw In this mdul, w will rviw prprtis f sinusidal functins and
CPSC 665 : An Algorithmist s Toolkit Lecture 4 : 21 Jan Linear Programming
 CPSC 665 : An Algorithmist s Toolkit Lctur 4 : 21 Jan 2015 Lcturr: Sushant Sachdva Linar Programming Scrib: Rasmus Kyng 1. Introduction An optimization problm rquirs us to find th minimum or maximum) of
CPSC 665 : An Algorithmist s Toolkit Lctur 4 : 21 Jan 2015 Lcturr: Sushant Sachdva Linar Programming Scrib: Rasmus Kyng 1. Introduction An optimization problm rquirs us to find th minimum or maximum) of
Problem Set 6 Solutions
 6.04/18.06J Mathmatics for Computr Scinc March 15, 005 Srini Dvadas and Eric Lhman Problm St 6 Solutions Du: Monday, March 8 at 9 PM in Room 3-044 Problm 1. Sammy th Shark is a financial srvic providr
6.04/18.06J Mathmatics for Computr Scinc March 15, 005 Srini Dvadas and Eric Lhman Problm St 6 Solutions Du: Monday, March 8 at 9 PM in Room 3-044 Problm 1. Sammy th Shark is a financial srvic providr
COUNTING TAMELY RAMIFIED EXTENSIONS OF LOCAL FIELDS UP TO ISOMORPHISM
 COUNTING TAMELY RAMIFIED EXTENSIONS OF LOCAL FIELDS UP TO ISOMORPHISM Jim Brown Dpartmnt of Mathmatical Scincs, Clmson Univrsity, Clmson, SC 9634, USA jimlb@g.clmson.du Robrt Cass Dpartmnt of Mathmatics,
COUNTING TAMELY RAMIFIED EXTENSIONS OF LOCAL FIELDS UP TO ISOMORPHISM Jim Brown Dpartmnt of Mathmatical Scincs, Clmson Univrsity, Clmson, SC 9634, USA jimlb@g.clmson.du Robrt Cass Dpartmnt of Mathmatics,
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Construction of asymmetric orthogonal arrays of strength three via a replacement method
 isid/ms/26/2 Fbruary, 26 http://www.isid.ac.in/ statmath/indx.php?modul=prprint Construction of asymmtric orthogonal arrays of strngth thr via a rplacmnt mthod Tian-fang Zhang, Qiaoling Dng and Alok Dy
isid/ms/26/2 Fbruary, 26 http://www.isid.ac.in/ statmath/indx.php?modul=prprint Construction of asymmtric orthogonal arrays of strngth thr via a rplacmnt mthod Tian-fang Zhang, Qiaoling Dng and Alok Dy
5 Curl-free fields and electrostatic potential
 5 Curl-fr filds and lctrstatic tntial Mathmaticall, w can gnrat a curl-fr vctr fild E(,, ) as E = ( V, V, V ), b taking th gradint f an scalar functin V (r) =V (,, ). Th gradint f V (,, ) is dfind t b
5 Curl-fr filds and lctrstatic tntial Mathmaticall, w can gnrat a curl-fr vctr fild E(,, ) as E = ( V, V, V ), b taking th gradint f an scalar functin V (r) =V (,, ). Th gradint f V (,, ) is dfind t b
Square of Hamilton cycle in a random graph
 Squar of Hamilton cycl in a random graph Andrzj Dudk Alan Friz Jun 28, 2016 Abstract W show that p = n is a sharp thrshold for th random graph G n,p to contain th squar of a Hamilton cycl. This improvs
Squar of Hamilton cycl in a random graph Andrzj Dudk Alan Friz Jun 28, 2016 Abstract W show that p = n is a sharp thrshold for th random graph G n,p to contain th squar of a Hamilton cycl. This improvs
ELEC 372 LECTURE NOTES, WEEK 11 Dr. Amir G. Aghdam Concordia University
 ELEC 37 LECTURE NOTES, WEE Dr Amir Aghdam Cncrdia Univrity Part f th nt ar adaptd frm th matrial in th fllwing rfrnc: Mdrn Cntrl Sytm by Richard C Drf and Rbrt H Bihp, Prntic Hall Fdback Cntrl f Dynamic
ELEC 37 LECTURE NOTES, WEE Dr Amir Aghdam Cncrdia Univrity Part f th nt ar adaptd frm th matrial in th fllwing rfrnc: Mdrn Cntrl Sytm by Richard C Drf and Rbrt H Bihp, Prntic Hall Fdback Cntrl f Dynamic
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
Some remarks on Kurepa s left factorial
 Som rmarks on Kurpa s lft factorial arxiv:math/0410477v1 [math.nt] 21 Oct 2004 Brnd C. Kllnr Abstract W stablish a connction btwn th subfactorial function S(n) and th lft factorial function of Kurpa K(n).
Som rmarks on Kurpa s lft factorial arxiv:math/0410477v1 [math.nt] 21 Oct 2004 Brnd C. Kllnr Abstract W stablish a connction btwn th subfactorial function S(n) and th lft factorial function of Kurpa K(n).
Week 3: Connected Subgraphs
 Wk 3: Connctd Subgraphs Sptmbr 19, 2016 1 Connctd Graphs Path, Distanc: A path from a vrtx x to a vrtx y in a graph G is rfrrd to an xy-path. Lt X, Y V (G). An (X, Y )-path is an xy-path with x X and y
Wk 3: Connctd Subgraphs Sptmbr 19, 2016 1 Connctd Graphs Path, Distanc: A path from a vrtx x to a vrtx y in a graph G is rfrrd to an xy-path. Lt X, Y V (G). An (X, Y )-path is an xy-path with x X and y
Cryptographically Strong de Bruijn Sequences with Large Periods
 Cryptgraphically Strng d Bruijn Squncs with Larg Prids Kalikinkar Mandal, and Guang Gng Dpartmnt f Elctrical and Cmputr Enginring Univrsity f Watrl Watrl, Ontari, N2L 3G1, CANADA {kmandal, ggng}@uwatrl.ca
Cryptgraphically Strng d Bruijn Squncs with Larg Prids Kalikinkar Mandal, and Guang Gng Dpartmnt f Elctrical and Cmputr Enginring Univrsity f Watrl Watrl, Ontari, N2L 3G1, CANADA {kmandal, ggng}@uwatrl.ca
Einstein Equations for Tetrad Fields
 Apiron, Vol 13, No, Octobr 006 6 Einstin Equations for Ttrad Filds Ali Rıza ŞAHİN, R T L Istanbul (Turky) Evry mtric tnsor can b xprssd by th innr product of ttrad filds W prov that Einstin quations for
Apiron, Vol 13, No, Octobr 006 6 Einstin Equations for Ttrad Filds Ali Rıza ŞAHİN, R T L Istanbul (Turky) Evry mtric tnsor can b xprssd by th innr product of ttrad filds W prov that Einstin quations for
SCHUR S THEOREM REU SUMMER 2005
 SCHUR S THEOREM REU SUMMER 2005 1. Combinatorial aroach Prhas th first rsult in th subjct blongs to I. Schur and dats back to 1916. On of his motivation was to study th local vrsion of th famous quation
SCHUR S THEOREM REU SUMMER 2005 1. Combinatorial aroach Prhas th first rsult in th subjct blongs to I. Schur and dats back to 1916. On of his motivation was to study th local vrsion of th famous quation
1 Minimum Cut Problem
 CS 6 Lctur 6 Min Cut and argr s Algorithm Scribs: Png Hui How (05), Virginia Dat: May 4, 06 Minimum Cut Problm Today, w introduc th minimum cut problm. This problm has many motivations, on of which coms
CS 6 Lctur 6 Min Cut and argr s Algorithm Scribs: Png Hui How (05), Virginia Dat: May 4, 06 Minimum Cut Problm Today, w introduc th minimum cut problm. This problm has many motivations, on of which coms
NEW APPLICATIONS OF THE ABEL-LIOUVILLE FORMULA
 NE APPLICATIONS OF THE ABEL-LIOUVILLE FORMULA Mirca I CÎRNU Ph Dp o Mathmatics III Faculty o Applid Scincs Univrsity Polithnica o Bucharst Cirnumirca @yahoocom Abstract In a rcnt papr [] 5 th indinit intgrals
NE APPLICATIONS OF THE ABEL-LIOUVILLE FORMULA Mirca I CÎRNU Ph Dp o Mathmatics III Faculty o Applid Scincs Univrsity Polithnica o Bucharst Cirnumirca @yahoocom Abstract In a rcnt papr [] 5 th indinit intgrals
Roadmap. XML Indexing. DataGuide example. DataGuides. Strong DataGuides. Multiple DataGuides for same data. CPS Topics in Database Systems
 Roadmap XML Indxing CPS 296.1 Topics in Databas Systms Indx fabric Coopr t al. A Fast Indx for Smistructurd Data. VLDB, 2001 DataGuid Goldman and Widom. DataGuids: Enabling Qury Formulation and Optimization
Roadmap XML Indxing CPS 296.1 Topics in Databas Systms Indx fabric Coopr t al. A Fast Indx for Smistructurd Data. VLDB, 2001 DataGuid Goldman and Widom. DataGuids: Enabling Qury Formulation and Optimization
Addition of angular momentum
 Addition of angular momntum April, 07 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat
Addition of angular momntum April, 07 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat
CS 361 Meeting 12 10/3/18
 CS 36 Mting 2 /3/8 Announcmnts. Homwork 4 is du Friday. If Friday is Mountain Day, homwork should b turnd in at my offic or th dpartmnt offic bfor 4. 2. Homwork 5 will b availabl ovr th wknd. 3. Our midtrm
CS 36 Mting 2 /3/8 Announcmnts. Homwork 4 is du Friday. If Friday is Mountain Day, homwork should b turnd in at my offic or th dpartmnt offic bfor 4. 2. Homwork 5 will b availabl ovr th wknd. 3. Our midtrm
Cramér-Rao Inequality: Let f(x; θ) be a probability density function with continuous parameter
 WHEN THE CRAMÉR-RAO INEQUALITY PROVIDES NO INFORMATION STEVEN J. MILLER Abstract. W invstigat a on-paramtr family of probability dnsitis (rlatd to th Parto distribution, which dscribs many natural phnomna)
WHEN THE CRAMÉR-RAO INEQUALITY PROVIDES NO INFORMATION STEVEN J. MILLER Abstract. W invstigat a on-paramtr family of probability dnsitis (rlatd to th Parto distribution, which dscribs many natural phnomna)
6. Negative Feedback in Single- Transistor Circuits
 Lctur 8: Intrductin t lctrnic analg circuit 36--366 6. Ngativ Fdback in Singl- Tranitr ircuit ugn Paprn, 2008 Our aim i t tudy t ffct f ngativ fdback n t mall-ignal gain and t mall-ignal input and utput
Lctur 8: Intrductin t lctrnic analg circuit 36--366 6. Ngativ Fdback in Singl- Tranitr ircuit ugn Paprn, 2008 Our aim i t tudy t ffct f ngativ fdback n t mall-ignal gain and t mall-ignal input and utput
A Propagating Wave Packet Group Velocity Dispersion
 Lctur 8 Phys 375 A Propagating Wav Packt Group Vlocity Disprsion Ovrviw and Motivation: In th last lctur w lookd at a localizd solution t) to th 1D fr-particl Schrödingr quation (SE) that corrsponds to
Lctur 8 Phys 375 A Propagating Wav Packt Group Vlocity Disprsion Ovrviw and Motivation: In th last lctur w lookd at a localizd solution t) to th 1D fr-particl Schrödingr quation (SE) that corrsponds to
On the irreducibility of some polynomials in two variables
 ACTA ARITHMETICA LXXXII.3 (1997) On th irrducibility of som polynomials in two variabls by B. Brindza and Á. Pintér (Dbrcn) To th mmory of Paul Erdős Lt f(x) and g(y ) b polynomials with intgral cofficints
ACTA ARITHMETICA LXXXII.3 (1997) On th irrducibility of som polynomials in two variabls by B. Brindza and Á. Pintér (Dbrcn) To th mmory of Paul Erdős Lt f(x) and g(y ) b polynomials with intgral cofficints
Lecture 2a. Crystal Growth (cont d) ECE723
 Lctur 2a rystal Grwth (cnt d) 1 Distributin f Dpants As a crystal is pulld frm th mlt, th dping cncntratin incrpratd int th crystal (slid) is usually diffrnt frm th dping cncntratin f th mlt (liquid) at
Lctur 2a rystal Grwth (cnt d) 1 Distributin f Dpants As a crystal is pulld frm th mlt, th dping cncntratin incrpratd int th crystal (slid) is usually diffrnt frm th dping cncntratin f th mlt (liquid) at
Chapter 2 Linear Waveshaping: High-pass Circuits
 Puls and Digital Circuits nkata Ra K., Rama Sudha K. and Manmadha Ra G. Chaptr 2 Linar Wavshaping: High-pass Circuits. A ramp shwn in Fig.2p. is applid t a high-pass circuit. Draw t scal th utput wavfrm
Puls and Digital Circuits nkata Ra K., Rama Sudha K. and Manmadha Ra G. Chaptr 2 Linar Wavshaping: High-pass Circuits. A ramp shwn in Fig.2p. is applid t a high-pass circuit. Draw t scal th utput wavfrm
That is, we start with a general matrix: And end with a simpler matrix:
 DIAGON ALIZATION OF THE STR ESS TEN SOR INTRO DUCTIO N By th us of Cauchy s thorm w ar abl to rduc th numbr of strss componnts in th strss tnsor to only nin valus. An additional simplification of th strss
DIAGON ALIZATION OF THE STR ESS TEN SOR INTRO DUCTIO N By th us of Cauchy s thorm w ar abl to rduc th numbr of strss componnts in th strss tnsor to only nin valus. An additional simplification of th strss
Limiting value of higher Mahler measure
 Limiting valu of highr Mahlr masur Arunabha Biswas a, Chris Monico a, a Dpartmnt of Mathmatics & Statistics, Txas Tch Univrsity, Lubbock, TX 7949, USA Abstract W considr th k-highr Mahlr masur m k P )
Limiting valu of highr Mahlr masur Arunabha Biswas a, Chris Monico a, a Dpartmnt of Mathmatics & Statistics, Txas Tch Univrsity, Lubbock, TX 7949, USA Abstract W considr th k-highr Mahlr masur m k P )
Fourier Transforms and the Wave Equation. Key Mathematics: More Fourier transform theory, especially as applied to solving the wave equation.
 Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
Revisiting the Socrates Example
 Sectin 1.6 Sectin Summary Valid Arguments Inference Rules fr Prpsitinal Lgic Using Rules f Inference t Build Arguments Rules f Inference fr Quantified Statements Building Arguments fr Quantified Statements
Sectin 1.6 Sectin Summary Valid Arguments Inference Rules fr Prpsitinal Lgic Using Rules f Inference t Build Arguments Rules f Inference fr Quantified Statements Building Arguments fr Quantified Statements
N J of oscillators in the three lowest quantum
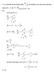 . a) Calculat th fractinal numbr f scillatrs in th thr lwst quantum stats (j,,,) fr fr and Sl: ( ) ( ) ( ) ( ) ( ).6.98. fr usth sam apprach fr fr j fr frm q. b) .) a) Fr a systm f lcalizd distinguishabl
. a) Calculat th fractinal numbr f scillatrs in th thr lwst quantum stats (j,,,) fr fr and Sl: ( ) ( ) ( ) ( ) ( ).6.98. fr usth sam apprach fr fr j fr frm q. b) .) a) Fr a systm f lcalizd distinguishabl
First derivative analysis
 Robrto s Nots on Dirntial Calculus Chaptr 8: Graphical analysis Sction First drivativ analysis What you nd to know alrady: How to us drivativs to idntiy th critical valus o a unction and its trm points
Robrto s Nots on Dirntial Calculus Chaptr 8: Graphical analysis Sction First drivativ analysis What you nd to know alrady: How to us drivativs to idntiy th critical valus o a unction and its trm points
Separating principles below Ramsey s Theorem for Pairs
 Sparating principls blow Ramsy s Thorm for Pairs Manul Lrman, Rd Solomon, Hnry Towsnr Fbruary 4, 2013 1 Introduction In rcnt yars, thr has bn a substantial amount of work in rvrs mathmatics concrning natural
Sparating principls blow Ramsy s Thorm for Pairs Manul Lrman, Rd Solomon, Hnry Towsnr Fbruary 4, 2013 1 Introduction In rcnt yars, thr has bn a substantial amount of work in rvrs mathmatics concrning natural
EEO 401 Digital Signal Processing Prof. Mark Fowler
 EEO 401 Digital Signal Procssing Prof. Mark Fowlr Dtails of th ot St #19 Rading Assignmnt: Sct. 7.1.2, 7.1.3, & 7.2 of Proakis & Manolakis Dfinition of th So Givn signal data points x[n] for n = 0,, -1
EEO 401 Digital Signal Procssing Prof. Mark Fowlr Dtails of th ot St #19 Rading Assignmnt: Sct. 7.1.2, 7.1.3, & 7.2 of Proakis & Manolakis Dfinition of th So Givn signal data points x[n] for n = 0,, -1
1 Isoparametric Concept
 UNIVERSITY OF CALIFORNIA BERKELEY Dpartmnt of Civil Enginring Spring 06 Structural Enginring, Mchanics and Matrials Profssor: S. Govindj Nots on D isoparamtric lmnts Isoparamtric Concpt Th isoparamtric
UNIVERSITY OF CALIFORNIA BERKELEY Dpartmnt of Civil Enginring Spring 06 Structural Enginring, Mchanics and Matrials Profssor: S. Govindj Nots on D isoparamtric lmnts Isoparamtric Concpt Th isoparamtric
A Unified Theory of rf Plasma Heating. J.e. Sprott. July 1968
 A Unifid Thry f rf Plasma Hating by J.. Sprtt July 968 PLP 3 Plasma Studis Univrsity f iscnsin INTRODUCfION In this papr, th majr rsults f PLP's 86 and 07 will b drivd in a mr cncis and rigrus way, and
A Unifid Thry f rf Plasma Hating by J.. Sprtt July 968 PLP 3 Plasma Studis Univrsity f iscnsin INTRODUCfION In this papr, th majr rsults f PLP's 86 and 07 will b drivd in a mr cncis and rigrus way, and
(Upside-Down o Direct Rotation) β - Numbers
 Amrican Journal of Mathmatics and Statistics 014, 4(): 58-64 DOI: 10593/jajms0140400 (Upsid-Down o Dirct Rotation) β - Numbrs Ammar Sddiq Mahmood 1, Shukriyah Sabir Ali,* 1 Dpartmnt of Mathmatics, Collg
Amrican Journal of Mathmatics and Statistics 014, 4(): 58-64 DOI: 10593/jajms0140400 (Upsid-Down o Dirct Rotation) β - Numbrs Ammar Sddiq Mahmood 1, Shukriyah Sabir Ali,* 1 Dpartmnt of Mathmatics, Collg
SOME PARAMETERS ON EQUITABLE COLORING OF PRISM AND CIRCULANT GRAPH.
 SOME PARAMETERS ON EQUITABLE COLORING OF PRISM AND CIRCULANT GRAPH. K VASUDEVAN, K. SWATHY AND K. MANIKANDAN 1 Dpartmnt of Mathmatics, Prsidncy Collg, Chnnai-05, India. E-Mail:vasu k dvan@yahoo.com. 2,
SOME PARAMETERS ON EQUITABLE COLORING OF PRISM AND CIRCULANT GRAPH. K VASUDEVAN, K. SWATHY AND K. MANIKANDAN 1 Dpartmnt of Mathmatics, Prsidncy Collg, Chnnai-05, India. E-Mail:vasu k dvan@yahoo.com. 2,
Recall that by Theorems 10.3 and 10.4 together provide us the estimate o(n2 ), S(q) q 9, q=1
 Chaptr 11 Th singular sris Rcall that by Thorms 10 and 104 togthr provid us th stimat 9 4 n 2 111 Rn = SnΓ 2 + on2, whr th singular sris Sn was dfind in Chaptr 10 as Sn = q=1 Sq q 9, with Sq = 1 a q gcda,q=1
Chaptr 11 Th singular sris Rcall that by Thorms 10 and 104 togthr provid us th stimat 9 4 n 2 111 Rn = SnΓ 2 + on2, whr th singular sris Sn was dfind in Chaptr 10 as Sn = q=1 Sq q 9, with Sq = 1 a q gcda,q=1
Function Spaces. a x 3. (Letting x = 1 =)) a(0) + b + c (1) = 0. Row reducing the matrix. b 1. e 4 3. e 9. >: (x = 1 =)) a(0) + b + c (1) = 0
 unction Spacs Prrquisit: Sction 4.7, Coordinatization n this sction, w apply th tchniqus of Chaptr 4 to vctor spacs whos lmnts ar functions. Th vctor spacs P n and P ar familiar xampls of such spacs. Othr
unction Spacs Prrquisit: Sction 4.7, Coordinatization n this sction, w apply th tchniqus of Chaptr 4 to vctor spacs whos lmnts ar functions. Th vctor spacs P n and P ar familiar xampls of such spacs. Othr
22/ Breakdown of the Born-Oppenheimer approximation. Selection rules for rotational-vibrational transitions. P, R branches.
 Subjct Chmistry Papr No and Titl Modul No and Titl Modul Tag 8/ Physical Spctroscopy / Brakdown of th Born-Oppnhimr approximation. Slction ruls for rotational-vibrational transitions. P, R branchs. CHE_P8_M
Subjct Chmistry Papr No and Titl Modul No and Titl Modul Tag 8/ Physical Spctroscopy / Brakdown of th Born-Oppnhimr approximation. Slction ruls for rotational-vibrational transitions. P, R branchs. CHE_P8_M
The Language of SOCIAL MEDIA. Christine Dugan
 Th Languag f SOCIAL MEDIA Christin Dugan Tabl f Cntnts Gt th Wrd Out...4 A Nw Kind f Languag...6 Scial Mdia Talk...12 Cnncting with Othrs...28 Changing th Dictinary...36 Glssary...42 Indx...44 Chck It
Th Languag f SOCIAL MEDIA Christin Dugan Tabl f Cntnts Gt th Wrd Out...4 A Nw Kind f Languag...6 Scial Mdia Talk...12 Cnncting with Othrs...28 Changing th Dictinary...36 Glssary...42 Indx...44 Chck It
LINEAR DELAY DIFFERENTIAL EQUATION WITH A POSITIVE AND A NEGATIVE TERM
 Elctronic Journal of Diffrntial Equations, Vol. 2003(2003), No. 92, pp. 1 6. ISSN: 1072-6691. URL: http://jd.math.swt.du or http://jd.math.unt.du ftp jd.math.swt.du (login: ftp) LINEAR DELAY DIFFERENTIAL
Elctronic Journal of Diffrntial Equations, Vol. 2003(2003), No. 92, pp. 1 6. ISSN: 1072-6691. URL: http://jd.math.swt.du or http://jd.math.unt.du ftp jd.math.swt.du (login: ftp) LINEAR DELAY DIFFERENTIAL
Division of Mechanics Lund University MULTIBODY DYNAMICS. Examination Name (write in block letters):.
 Division of Mchanics Lund Univrsity MULTIBODY DYNMICS Examination 7033 Nam (writ in block lttrs):. Id.-numbr: Writtn xamination with fiv tasks. Plas chck that all tasks ar includd. clan copy of th solutions
Division of Mchanics Lund Univrsity MULTIBODY DYNMICS Examination 7033 Nam (writ in block lttrs):. Id.-numbr: Writtn xamination with fiv tasks. Plas chck that all tasks ar includd. clan copy of th solutions
Derangements and Applications
 2 3 47 6 23 Journal of Intgr Squncs, Vol. 6 (2003), Articl 03..2 Drangmnts and Applications Mhdi Hassani Dpartmnt of Mathmatics Institut for Advancd Studis in Basic Scincs Zanjan, Iran mhassani@iasbs.ac.ir
2 3 47 6 23 Journal of Intgr Squncs, Vol. 6 (2003), Articl 03..2 Drangmnts and Applications Mhdi Hassani Dpartmnt of Mathmatics Institut for Advancd Studis in Basic Scincs Zanjan, Iran mhassani@iasbs.ac.ir
Search sequence databases 3 10/25/2016
 Sarch squnc databass 3 10/25/2016 Etrm valu distribution Ø Suppos X is a random variabl with probability dnsity function p(, w sampl a larg numbr S of indpndnt valus of X from this distribution for an
Sarch squnc databass 3 10/25/2016 Etrm valu distribution Ø Suppos X is a random variabl with probability dnsity function p(, w sampl a larg numbr S of indpndnt valus of X from this distribution for an
Advanced Use of Pointers. CS2023 Winter 2004
 Advancd Us f Pintrs CS2023 Wintr 2004 Outcms: Advancd us f Pintrs C fr Java Prgrammrs, Chaptr 8, sctin 8.11, 8.15 Othr txtbks n C n rsrv Aftr th cnclusin f this sctin yu shuld b abl t Allcat and dallcat
Advancd Us f Pintrs CS2023 Wintr 2004 Outcms: Advancd us f Pintrs C fr Java Prgrammrs, Chaptr 8, sctin 8.11, 8.15 Othr txtbks n C n rsrv Aftr th cnclusin f this sctin yu shuld b abl t Allcat and dallcat
The Equitable Dominating Graph
 Intrnational Journal of Enginring Rsarch and Tchnology. ISSN 0974-3154 Volum 8, Numbr 1 (015), pp. 35-4 Intrnational Rsarch Publication Hous http://www.irphous.com Th Equitabl Dominating Graph P.N. Vinay
Intrnational Journal of Enginring Rsarch and Tchnology. ISSN 0974-3154 Volum 8, Numbr 1 (015), pp. 35-4 Intrnational Rsarch Publication Hous http://www.irphous.com Th Equitabl Dominating Graph P.N. Vinay
Triangular fully packed loop configurations of excess 2
 FPSAC 25, Dajn, Suth Kra DMTCS prc. FPSAC 5, 25, 985 996 Triangular fully packd lp cnfiguratins f xcss 2 Sabin Bil Univrsität Win, Fakultät für Mathmatik, Oskar-Mrgnstrn-Platz, 9 Win, Austria Abstract.
FPSAC 25, Dajn, Suth Kra DMTCS prc. FPSAC 5, 25, 985 996 Triangular fully packd lp cnfiguratins f xcss 2 Sabin Bil Univrsität Win, Fakultät für Mathmatik, Oskar-Mrgnstrn-Platz, 9 Win, Austria Abstract.
Addition of angular momentum
 Addition of angular momntum April, 0 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat th
Addition of angular momntum April, 0 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat th
Higher order derivatives
 Robrto s Nots on Diffrntial Calculus Chaptr 4: Basic diffrntiation ruls Sction 7 Highr ordr drivativs What you nd to know alrady: Basic diffrntiation ruls. What you can larn hr: How to rpat th procss of
Robrto s Nots on Diffrntial Calculus Chaptr 4: Basic diffrntiation ruls Sction 7 Highr ordr drivativs What you nd to know alrady: Basic diffrntiation ruls. What you can larn hr: How to rpat th procss of
On spanning trees and cycles of multicolored point sets with few intersections
 On spanning trs and cycls of multicolord point sts with fw intrsctions M. Kano, C. Mrino, and J. Urrutia April, 00 Abstract Lt P 1,..., P k b a collction of disjoint point sts in R in gnral position. W
On spanning trs and cycls of multicolord point sts with fw intrsctions M. Kano, C. Mrino, and J. Urrutia April, 00 Abstract Lt P 1,..., P k b a collction of disjoint point sts in R in gnral position. W
. This is made to keep the kinetic energy at outlet a minimum.
 Runnr Francis Turbin Th shap th blads a Francis runnr is cmplx. Th xact shap dpnds n its spciic spd. It is bvius rm th quatin spciic spd (Eq.5.8) that highr spciic spd mans lwr had. This rquirs that th
Runnr Francis Turbin Th shap th blads a Francis runnr is cmplx. Th xact shap dpnds n its spciic spd. It is bvius rm th quatin spciic spd (Eq.5.8) that highr spciic spd mans lwr had. This rquirs that th
Equidistribution and Weyl s criterion
 Euidistribution and Wyl s critrion by Brad Hannigan-Daly W introduc th ida of a sunc of numbrs bing uidistributd (mod ), and w stat and prov a thorm of Hrmann Wyl which charactrizs such suncs. W also discuss
Euidistribution and Wyl s critrion by Brad Hannigan-Daly W introduc th ida of a sunc of numbrs bing uidistributd (mod ), and w stat and prov a thorm of Hrmann Wyl which charactrizs such suncs. W also discuss
EE 119 Homework 6 Solution
 EE 9 Hmwrk 6 Slutin Prr: J Bkr TA: Xi Lu Slutin: (a) Th angular magniicatin a tlcp i m / th cal lngth th bjctiv ln i m 4 45 80cm (b) Th clar aprtur th xit pupil i 35 mm Th ditanc btwn th bjctiv ln and
EE 9 Hmwrk 6 Slutin Prr: J Bkr TA: Xi Lu Slutin: (a) Th angular magniicatin a tlcp i m / th cal lngth th bjctiv ln i m 4 45 80cm (b) Th clar aprtur th xit pupil i 35 mm Th ditanc btwn th bjctiv ln and
A Brief and Elementary Note on Redshift. May 26, 2010.
 A Brif and Elmntary Nt n Rdshift May 26, 2010. Jsé Francisc García Juliá C/ Dr. Marc Mrncian, 65, 5. 46025 Valncia (Spain) E-mail: js.garcia@dival.s Abstract A rasnabl xplanatin f bth rdshifts: csmlgical
A Brif and Elmntary Nt n Rdshift May 26, 2010. Jsé Francisc García Juliá C/ Dr. Marc Mrncian, 65, 5. 46025 Valncia (Spain) E-mail: js.garcia@dival.s Abstract A rasnabl xplanatin f bth rdshifts: csmlgical
u x v x dx u x v x v x u x dx d u x v x u x v x dx u x v x dx Integration by Parts Formula
 7. Intgration by Parts Each drivativ formula givs ris to a corrsponding intgral formula, as w v sn many tims. Th drivativ product rul yilds a vry usful intgration tchniqu calld intgration by parts. Starting
7. Intgration by Parts Each drivativ formula givs ris to a corrsponding intgral formula, as w v sn many tims. Th drivativ product rul yilds a vry usful intgration tchniqu calld intgration by parts. Starting
section 1 Influencing Change Toolkit How to: Influence People
 Influncing Chang Tlkit Hw t: Influnc Ppl Influncing ppl mans having an ffct n thm, changing r mdifying thir viw. In rdr t influnc chang, w nd t influnc th ppl wh ar in a psitin t mak that chang happn.
Influncing Chang Tlkit Hw t: Influnc Ppl Influncing ppl mans having an ffct n thm, changing r mdifying thir viw. In rdr t influnc chang, w nd t influnc th ppl wh ar in a psitin t mak that chang happn.
Quasi-Classical States of the Simple Harmonic Oscillator
 Quasi-Classical Stats of th Simpl Harmonic Oscillator (Draft Vrsion) Introduction: Why Look for Eignstats of th Annihilation Oprator? Excpt for th ground stat, th corrspondnc btwn th quantum nrgy ignstats
Quasi-Classical Stats of th Simpl Harmonic Oscillator (Draft Vrsion) Introduction: Why Look for Eignstats of th Annihilation Oprator? Excpt for th ground stat, th corrspondnc btwn th quantum nrgy ignstats
Effect of sampling on frequency domain analysis
 LIGO-T666--R Ec sampling n rquncy dmain analysis David P. Nrwd W rviw h wll-knwn cs digial sampling n h rquncy dmain analysis an analg signal, wih mphasis n h cs upn ur masurmns. This discussin llws h
LIGO-T666--R Ec sampling n rquncy dmain analysis David P. Nrwd W rviw h wll-knwn cs digial sampling n h rquncy dmain analysis an analg signal, wih mphasis n h cs upn ur masurmns. This discussin llws h
The van der Waals interaction 1 D. E. Soper 2 University of Oregon 20 April 2012
 Th van dr Waals intraction D. E. Sopr 2 Univrsity of Orgon 20 pril 202 Th van dr Waals intraction is discussd in Chaptr 5 of J. J. Sakurai, Modrn Quantum Mchanics. Hr I tak a look at it in a littl mor
Th van dr Waals intraction D. E. Sopr 2 Univrsity of Orgon 20 pril 202 Th van dr Waals intraction is discussd in Chaptr 5 of J. J. Sakurai, Modrn Quantum Mchanics. Hr I tak a look at it in a littl mor
GEOMETRICAL PHENOMENA IN THE PHYSICS OF SUBATOMIC PARTICLES. Eduard N. Klenov* Rostov-on-Don, Russia
 GEOMETRICAL PHENOMENA IN THE PHYSICS OF SUBATOMIC PARTICLES Eduard N. Klnov* Rostov-on-Don, Russia Th articl considrs phnomnal gomtry figurs bing th carrirs of valu spctra for th pairs of th rmaining additiv
GEOMETRICAL PHENOMENA IN THE PHYSICS OF SUBATOMIC PARTICLES Eduard N. Klnov* Rostov-on-Don, Russia Th articl considrs phnomnal gomtry figurs bing th carrirs of valu spctra for th pairs of th rmaining additiv
Unit 2 Part 2 Particles, Bonding and Structure Interatomic and Intermolecular Bonding UNIT 2 PARTICLES, BONDING AND STRUCTURE
 Unit 2 Part 2 Particls, nding and Structur Intratmic and Intrmlcular nding UNIT 2 PARTICLES, NDING AND STRUCTURE PART 2 INTERATMIC AND INTERMLECULAR NDING Cntnts 1. Inic nding 2. Cvalnt nding 3. Mtallic
Unit 2 Part 2 Particls, nding and Structur Intratmic and Intrmlcular nding UNIT 2 PARTICLES, NDING AND STRUCTURE PART 2 INTERATMIC AND INTERMLECULAR NDING Cntnts 1. Inic nding 2. Cvalnt nding 3. Mtallic
Sundials and Linear Algebra
 Sundials and Linar Algbra M. Scot Swan July 2, 25 Most txts on crating sundials ar dirctd towards thos who ar solly intrstd in making and using sundials and usually assums minimal mathmatical background.
Sundials and Linar Algbra M. Scot Swan July 2, 25 Most txts on crating sundials ar dirctd towards thos who ar solly intrstd in making and using sundials and usually assums minimal mathmatical background.
Thus, because if either [G : H] or [H : K] is infinite, then [G : K] is infinite, then [G : K] = [G : H][H : K] for all infinite cases.
![Thus, because if either [G : H] or [H : K] is infinite, then [G : K] is infinite, then [G : K] = [G : H][H : K] for all infinite cases. Thus, because if either [G : H] or [H : K] is infinite, then [G : K] is infinite, then [G : K] = [G : H][H : K] for all infinite cases.](/thumbs/74/70009716.jpg) Homwork 5 M 373K Solutions Mark Lindbrg and Travis Schdlr 1. Prov that th ring Z/mZ (for m 0) is a fild if and only if m is prim. ( ) Proof by Contrapositiv: Hr, thr ar thr cass for m not prim. m 0: Whn
Homwork 5 M 373K Solutions Mark Lindbrg and Travis Schdlr 1. Prov that th ring Z/mZ (for m 0) is a fild if and only if m is prim. ( ) Proof by Contrapositiv: Hr, thr ar thr cass for m not prim. m 0: Whn
MAGNETIC MONOPOLE THEORY
 AGNETIC ONOPOLE THEORY S HUSSAINSHA Rsarch schlar f ECE, G.Pullaiah Cllg f Enginring and Tchnlgy, Kurnl, Andhra Pradsh, India Eail: ssshaik80@gail.c Cll: +91 9000390153 Abstract: Th principal bjctiv f
AGNETIC ONOPOLE THEORY S HUSSAINSHA Rsarch schlar f ECE, G.Pullaiah Cllg f Enginring and Tchnlgy, Kurnl, Andhra Pradsh, India Eail: ssshaik80@gail.c Cll: +91 9000390153 Abstract: Th principal bjctiv f
u r du = ur+1 r + 1 du = ln u + C u sin u du = cos u + C cos u du = sin u + C sec u tan u du = sec u + C e u du = e u + C
 Tchniqus of Intgration c Donald Kridr and Dwight Lahr In this sction w ar going to introduc th first approachs to valuating an indfinit intgral whos intgrand dos not hav an immdiat antidrivativ. W bgin
Tchniqus of Intgration c Donald Kridr and Dwight Lahr In this sction w ar going to introduc th first approachs to valuating an indfinit intgral whos intgrand dos not hav an immdiat antidrivativ. W bgin
Basic Polyhedral theory
 Basic Polyhdral thory Th st P = { A b} is calld a polyhdron. Lmma 1. Eithr th systm A = b, b 0, 0 has a solution or thr is a vctorπ such that π A 0, πb < 0 Thr cass, if solution in top row dos not ist
Basic Polyhdral thory Th st P = { A b} is calld a polyhdron. Lmma 1. Eithr th systm A = b, b 0, 0 has a solution or thr is a vctorπ such that π A 0, πb < 0 Thr cass, if solution in top row dos not ist
A Simple Set of Test Matrices for Eigenvalue Programs*
 Simple Set f Test Matrices fr Eigenvalue Prgrams* By C. W. Gear** bstract. Sets f simple matrices f rder N are given, tgether with all f their eigenvalues and right eigenvectrs, and simple rules fr generating
Simple Set f Test Matrices fr Eigenvalue Prgrams* By C. W. Gear** bstract. Sets f simple matrices f rder N are given, tgether with all f their eigenvalues and right eigenvectrs, and simple rules fr generating
COMPUTER GENERATED HOLOGRAMS Optical Sciences 627 W.J. Dallas (Monday, April 04, 2005, 8:35 AM) PART I: CHAPTER TWO COMB MATH.
 C:\Dallas\0_Courss\03A_OpSci_67\0 Cgh_Book\0_athmaticalPrliminaris\0_0 Combath.doc of 8 COPUTER GENERATED HOLOGRAS Optical Scincs 67 W.J. Dallas (onday, April 04, 005, 8:35 A) PART I: CHAPTER TWO COB ATH
C:\Dallas\0_Courss\03A_OpSci_67\0 Cgh_Book\0_athmaticalPrliminaris\0_0 Combath.doc of 8 COPUTER GENERATED HOLOGRAS Optical Scincs 67 W.J. Dallas (onday, April 04, 005, 8:35 A) PART I: CHAPTER TWO COB ATH
Elements of Statistical Thermodynamics
 24 Elmnts of Statistical Thrmodynamics Statistical thrmodynamics is a branch of knowldg that has its own postulats and tchniqus. W do not attmpt to giv hr vn an introduction to th fild. In this chaptr,
24 Elmnts of Statistical Thrmodynamics Statistical thrmodynamics is a branch of knowldg that has its own postulats and tchniqus. W do not attmpt to giv hr vn an introduction to th fild. In this chaptr,
Alpha and beta decay equation practice
 Alpha and bta dcay quation practic Introduction Alpha and bta particls may b rprsntd in quations in svral diffrnt ways. Diffrnt xam boards hav thir own prfrnc. For xampl: Alpha Bta α β alpha bta Dspit
Alpha and bta dcay quation practic Introduction Alpha and bta particls may b rprsntd in quations in svral diffrnt ways. Diffrnt xam boards hav thir own prfrnc. For xampl: Alpha Bta α β alpha bta Dspit
Chapter 10. The singular integral Introducing S(n) and J(n)
 Chaptr Th singular intgral Our aim in this chaptr is to rplac th functions S (n) and J (n) by mor convnint xprssions; ths will b calld th singular sris S(n) and th singular intgral J(n). This will b don
Chaptr Th singular intgral Our aim in this chaptr is to rplac th functions S (n) and J (n) by mor convnint xprssions; ths will b calld th singular sris S(n) and th singular intgral J(n). This will b don
Brief Introduction to Statistical Mechanics
 Brif Introduction to Statistical Mchanics. Purpos: Ths nots ar intndd to provid a vry quick introduction to Statistical Mchanics. Th fild is of cours far mor vast than could b containd in ths fw pags.
Brif Introduction to Statistical Mchanics. Purpos: Ths nots ar intndd to provid a vry quick introduction to Statistical Mchanics. Th fild is of cours far mor vast than could b containd in ths fw pags.
The second condition says that a node α of the tree has exactly n children if the arity of its label is n.
 CS 6110 S14 Hanout 2 Proof of Conflunc 27 January 2014 In this supplmntary lctur w prov that th λ-calculus is conflunt. This is rsult is u to lonzo Church (1903 1995) an J. arkly Rossr (1907 1989) an is
CS 6110 S14 Hanout 2 Proof of Conflunc 27 January 2014 In this supplmntary lctur w prov that th λ-calculus is conflunt. This is rsult is u to lonzo Church (1903 1995) an J. arkly Rossr (1907 1989) an is
Abstract Interpretation: concrete and abstract semantics
 Abstract Intrprtation: concrt and abstract smantics Concrt smantics W considr a vry tiny languag that manags arithmtic oprations on intgrs valus. Th (concrt) smantics of th languags cab b dfind by th funzcion
Abstract Intrprtation: concrt and abstract smantics Concrt smantics W considr a vry tiny languag that manags arithmtic oprations on intgrs valus. Th (concrt) smantics of th languags cab b dfind by th funzcion
Chapter Summary. Mathematical Induction Strong Induction Recursive Definitions Structural Induction Recursive Algorithms
 Chapter 5 1 Chapter Summary Mathematical Inductin Strng Inductin Recursive Definitins Structural Inductin Recursive Algrithms Sectin 5.1 3 Sectin Summary Mathematical Inductin Examples f Prf by Mathematical
Chapter 5 1 Chapter Summary Mathematical Inductin Strng Inductin Recursive Definitins Structural Inductin Recursive Algrithms Sectin 5.1 3 Sectin Summary Mathematical Inductin Examples f Prf by Mathematical
2.3 Matrix Formulation
 23 Matrix Formulation 43 A mor complicatd xampl ariss for a nonlinar systm of diffrntial quations Considr th following xampl Exampl 23 x y + x( x 2 y 2 y x + y( x 2 y 2 (233 Transforming to polar coordinats,
23 Matrix Formulation 43 A mor complicatd xampl ariss for a nonlinar systm of diffrntial quations Considr th following xampl Exampl 23 x y + x( x 2 y 2 y x + y( x 2 y 2 (233 Transforming to polar coordinats,
EXST Regression Techniques Page 1
 EXST704 - Rgrssion Tchniqus Pag 1 Masurmnt rrors in X W hav assumd that all variation is in Y. Masurmnt rror in this variabl will not ffct th rsults, as long as thy ar uncorrlatd and unbiasd, sinc thy
EXST704 - Rgrssion Tchniqus Pag 1 Masurmnt rrors in X W hav assumd that all variation is in Y. Masurmnt rror in this variabl will not ffct th rsults, as long as thy ar uncorrlatd and unbiasd, sinc thy
CS 477/677 Analysis of Algorithms Fall 2007 Dr. George Bebis Course Project Due Date: 11/29/2007
 CS 477/677 Analysis f Algrithms Fall 2007 Dr. Gerge Bebis Curse Prject Due Date: 11/29/2007 Part1: Cmparisn f Srting Algrithms (70% f the prject grade) The bjective f the first part f the assignment is
CS 477/677 Analysis f Algrithms Fall 2007 Dr. Gerge Bebis Curse Prject Due Date: 11/29/2007 Part1: Cmparisn f Srting Algrithms (70% f the prject grade) The bjective f the first part f the assignment is
Admissibility Conditions and Asymptotic Behavior of Strongly Regular Graphs
 Admissibility Cnditins and Asympttic Behavir f Strngly Regular Graphs VASCO MOÇO MANO Department f Mathematics University f Prt Oprt PORTUGAL vascmcman@gmailcm LUÍS ANTÓNIO DE ALMEIDA VIEIRA Department
Admissibility Cnditins and Asympttic Behavir f Strngly Regular Graphs VASCO MOÇO MANO Department f Mathematics University f Prt Oprt PORTUGAL vascmcman@gmailcm LUÍS ANTÓNIO DE ALMEIDA VIEIRA Department
, which yields. where z1. and z2
 The Gaussian r Nrmal PDF, Page 1 The Gaussian r Nrmal Prbability Density Functin Authr: Jhn M Cimbala, Penn State University Latest revisin: 11 September 13 The Gaussian r Nrmal Prbability Density Functin
The Gaussian r Nrmal PDF, Page 1 The Gaussian r Nrmal Prbability Density Functin Authr: Jhn M Cimbala, Penn State University Latest revisin: 11 September 13 The Gaussian r Nrmal Prbability Density Functin
Cosmology. Outline. Relativity and Astrophysics Lecture 17 Terry Herter. Redshift (again) The Expanding Universe Applying Hubble s Law
 Csmlgy Csmlgy Rlativity and Astrphysics ctur 17 Trry Hrtr Outlin Rdshit (again) Th Expanding Univrs Applying Hubbl s aw Distanc rm Rdshit Csmlgical Principl Olbrs Paradx A90-17 Csmlgy A90-17 1 Csmlgy Rdshit
Csmlgy Csmlgy Rlativity and Astrphysics ctur 17 Trry Hrtr Outlin Rdshit (again) Th Expanding Univrs Applying Hubbl s aw Distanc rm Rdshit Csmlgical Principl Olbrs Paradx A90-17 Csmlgy A90-17 1 Csmlgy Rdshit
